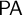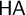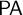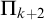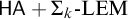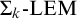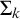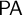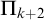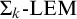1 Introduction
It is well-known that classical first-order arithmetic
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() $\Pi _2$
-conservative over intuitionistic first-order arithmetic
$\Pi _2$
-conservative over intuitionistic first-order arithmetic
![]() $\mathsf {HA}$
. There are several approaches to prove this fundamental fact. One simple and well-known approach is to apply the negative (or double negation) translation followed by the Friedman A-translation [Reference Troelstra and van Dalen4]. Another possible approach is to apply a generalized negative translation developed systematically by Ishihara [Reference Troelstra and van Dalen9, Reference Troelstra and van Dalen10]. In fact, the latter is a combination of Gentzen’s negative translation and the Friedman A-translation (cf. [Reference Troelstra and van Dalen10, Section 4]). In [Reference Troelstra and van Dalen7, Theorem 6.14], the authors showed a conservation result which generalizes the aforementioned conservation result on
$\mathsf {HA}$
. There are several approaches to prove this fundamental fact. One simple and well-known approach is to apply the negative (or double negation) translation followed by the Friedman A-translation [Reference Troelstra and van Dalen4]. Another possible approach is to apply a generalized negative translation developed systematically by Ishihara [Reference Troelstra and van Dalen9, Reference Troelstra and van Dalen10]. In fact, the latter is a combination of Gentzen’s negative translation and the Friedman A-translation (cf. [Reference Troelstra and van Dalen10, Section 4]). In [Reference Troelstra and van Dalen7, Theorem 6.14], the authors showed a conservation result which generalizes the aforementioned conservation result on
![]() $\mathsf {PA}$
and
$\mathsf {PA}$
and
![]() $\mathsf {HA}$
in the context of semi-classical arithmetic (which lies between classical and intuitionistic arithmetic). In fact, the following is an immediate corollary of [Reference Troelstra and van Dalen7, Theorem 6.14]:
$\mathsf {HA}$
in the context of semi-classical arithmetic (which lies between classical and intuitionistic arithmetic). In fact, the following is an immediate corollary of [Reference Troelstra and van Dalen7, Theorem 6.14]:
Proposition 1.1.
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() $\Pi _{k+2}$
-conservative over
$\Pi _{k+2}$
-conservative over
![]() $\mathsf {HA} +{\Sigma _{k}}\text {-}\mathrm {LEM}$
where
$\mathsf {HA} +{\Sigma _{k}}\text {-}\mathrm {LEM}$
where
![]() ${\Sigma _{k}}\text {-}\mathrm {LEM}$
is the axiom scheme of the law-of-excluded-middle restricted to formulas in
${\Sigma _{k}}\text {-}\mathrm {LEM}$
is the axiom scheme of the law-of-excluded-middle restricted to formulas in
![]() $\Sigma _k$
.Footnote
1
$\Sigma _k$
.Footnote
1
The proof of [Reference Troelstra and van Dalen7, Theorem 6.14] in that paper is similar to the former approach in the sense of using the Friedman A-translation. However, the proof has somewhat intricate structure in dealing with the Friedman A-translation of the inner part of Kuroda’s negative translation. In Section 3, by extending the latter approach from [Reference Troelstra and van Dalen9, Reference Troelstra and van Dalen10] in the context of semi-classical arithmetic, we provide a much more structured proof of [Reference Troelstra and van Dalen7, Theorem 6.14]. As an advantage of the structured proof, we obtain an extended conservation result for much larger classes of formulas (see Theorem 3.17 and Remark 3.18).
In Section 4, we relate the classes used in Section 3 (which are based on the classes introduced in [Reference Troelstra and van Dalen9]) to the classes
![]() $\mathrm {U}_k$
and
$\mathrm {U}_k$
and
![]() $\mathrm {E}_k$
introduced in Akama et al. [Reference Akama, Berardi, Hayashi and Kohlenbach1] for studying the hierarchy of the constructively-meaningful fragments of classical axioms (including the law-of-excluded-middle and the double-negation-elimination). The classes
$\mathrm {E}_k$
introduced in Akama et al. [Reference Akama, Berardi, Hayashi and Kohlenbach1] for studying the hierarchy of the constructively-meaningful fragments of classical axioms (including the law-of-excluded-middle and the double-negation-elimination). The classes
![]() $\mathrm {E}_k$
and
$\mathrm {E}_k$
and
![]() $\mathrm {U}_k$
correspond to classical
$\mathrm {U}_k$
correspond to classical
![]() $\Sigma _k$
and
$\Sigma _k$
and
![]() $\Pi _k$
respectively in the sense that every formula in
$\Pi _k$
respectively in the sense that every formula in
![]() $\mathrm {E}_k$
(resp.
$\mathrm {E}_k$
(resp.
![]() $\mathrm {U}_k$
) is equivalent over
$\mathrm {U}_k$
) is equivalent over
![]() $\mathsf {PA}$
to some formula in
$\mathsf {PA}$
to some formula in
![]() $\Sigma _k$
(resp.
$\Sigma _k$
(resp.
![]() $\Pi _k$
) and vice versa. This investigation reveals that our extended conservation theorem for
$\Pi _k$
) and vice versa. This investigation reveals that our extended conservation theorem for
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
is applicable to all formulas in
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
is applicable to all formulas in
![]() $\mathrm {E}_{k+1}$
(see Corollary 4.3).
$\mathrm {E}_{k+1}$
(see Corollary 4.3).
In Sections 5–7, we investigate the entire structure of conservation theorems in the arithmetical hierarchy of classical principles which was systematically studied first in Akama et al. [Reference Akama, Berardi, Hayashi and Kohlenbach1] and further extended by the authors recently in [Reference Troelstra and van Dalen6]. The first motivation of this investigation comes from the observation that for any semi-classical arithmetic
![]() ${T}$
such that
${T}$
such that
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() $\Pi _{k+2}$
-conservative over
$\Pi _{k+2}$
-conservative over
![]() ${T}$
, T proves
${T}$
, T proves
![]() ${\Sigma _{k}}\text {-}\mathrm {LEM}$
(cf. Lemma 5.5). This means that Proposition 1.1 is optimal in the sense that one cannot replace
${\Sigma _{k}}\text {-}\mathrm {LEM}$
(cf. Lemma 5.5). This means that Proposition 1.1 is optimal in the sense that one cannot replace
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
by any semi-classical arithmetic which does not prove
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
by any semi-classical arithmetic which does not prove
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
. Another motivating fact is that for any semi-classical arithmetic
${\Sigma _k}\text {-}\mathrm {LEM}$
. Another motivating fact is that for any semi-classical arithmetic
![]() ${T}$
,
${T}$
,
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() $\Pi _{2}$
-conservative over
$\Pi _{2}$
-conservative over
![]() ${T}$
if and only if
${T}$
if and only if
![]() ${T}$
is closed under Markov’s rule for primitive recursive predicate (cf. [Reference Troelstra and van Dalen14, Section 3.5.1]). Thus the
${T}$
is closed under Markov’s rule for primitive recursive predicate (cf. [Reference Troelstra and van Dalen14, Section 3.5.1]). Thus the
![]() $\Pi _{2}$
-conservativity is also characterized by the
$\Pi _{2}$
-conservativity is also characterized by the
![]() $\Sigma _1$
-fragment of the double-negation-elimination rule. Then it is natural to ask whether this can be relativized in the context of semi-classical arithmetic. Motivated by these facts, in Sections 5 and 6, we study the conservation theorems for the well-studied classes (including
$\Sigma _1$
-fragment of the double-negation-elimination rule. Then it is natural to ask whether this can be relativized in the context of semi-classical arithmetic. Motivated by these facts, in Sections 5 and 6, we study the conservation theorems for the well-studied classes (including
![]() $\Pi _k$
,
$\Pi _k$
,
![]() $\Sigma _k$
, the classes in [Reference Akama, Berardi, Hayashi and Kohlenbach1] and their closed variants) and characterize them by fragments of classical axioms or rules. The conservativity for a class of formulas is equivalent to that restricted only to sentences if the class is closed under taking a universal closure. Then the strength of the conservativity e.g.,
$\Sigma _k$
, the classes in [Reference Akama, Berardi, Hayashi and Kohlenbach1] and their closed variants) and characterize them by fragments of classical axioms or rules. The conservativity for a class of formulas is equivalent to that restricted only to sentences if the class is closed under taking a universal closure. Then the strength of the conservativity e.g.,
![]() $\Pi _k$
does not vary even if we restrict them only to sentences. On the other hand, since
$\Pi _k$
does not vary even if we restrict them only to sentences. On the other hand, since
![]() $\Sigma _{k}$
etc. are not closed under taking a universal closure, this is not the case for such classes. We investigate the conservation theorems for classes of formulas in Section 5 and those for sentences in Section 6. Through a lot of delicate arguments in semi-classical arithmetic, we reveal the detailed structure consisting of the conservation theorems and some fragments of logical principles, which are summarized in Section 7. This exhaustive investigation shed light on the close connection between the notion of conservativity and classical axioms and rules in semi-classical arithmetic. For the purpose of future use, we present our characterization results in a generalized form with adding a set X of sentences into the theories in question.
$\Sigma _{k}$
etc. are not closed under taking a universal closure, this is not the case for such classes. We investigate the conservation theorems for classes of formulas in Section 5 and those for sentences in Section 6. Through a lot of delicate arguments in semi-classical arithmetic, we reveal the detailed structure consisting of the conservation theorems and some fragments of logical principles, which are summarized in Section 7. This exhaustive investigation shed light on the close connection between the notion of conservativity and classical axioms and rules in semi-classical arithmetic. For the purpose of future use, we present our characterization results in a generalized form with adding a set X of sentences into the theories in question.
In the end of this paper, as an appendix, we show the relativized soundness theorem of the Friedman A-translation for
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
. By this relativized soundness theorem, one may obtain a simple proof of Proposition 1.1 just by imitating the aforementioned Friedman’s approach.
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
. By this relativized soundness theorem, one may obtain a simple proof of Proposition 1.1 just by imitating the aforementioned Friedman’s approach.
2 Framework
We work with a standard formulation of intuitionistic arithmetic
![]() $\mathsf {HA}$
described e.g., in [Reference Troelstra and van Dalen13, Section 1.3], which has function symbols for all primitive recursive functions. Our language contains all the logical constants
$\mathsf {HA}$
described e.g., in [Reference Troelstra and van Dalen13, Section 1.3], which has function symbols for all primitive recursive functions. Our language contains all the logical constants
![]() $\forall , \exists , \to , \land , \lor $
and
$\forall , \exists , \to , \land , \lor $
and
![]() $ \perp $
. In our proofs, when we use some principle (including induction hypothesis [I.H.]) which is not available in
$ \perp $
. In our proofs, when we use some principle (including induction hypothesis [I.H.]) which is not available in
![]() $\mathsf {HA}$
, it will be exhibited explicitly. As regards basic reasoning over intuitionistic first-order logic, we refer the reader to [Reference Troelstra and van Dalen3, Section 6.2].
$\mathsf {HA}$
, it will be exhibited explicitly. As regards basic reasoning over intuitionistic first-order logic, we refer the reader to [Reference Troelstra and van Dalen3, Section 6.2].
Throughout this paper, let k be a natural number (possibly
![]() $0$
). The classes
$0$
). The classes
![]() $\Sigma _k$
and
$\Sigma _k$
and
![]() $\Pi _k$
of
$\Pi _k$
of
![]() $\mathsf {HA}$
-formulas are defined as follows:
$\mathsf {HA}$
-formulas are defined as follows:
-
• Let
 $\Sigma _0 $
and
$\Sigma _0 $
and
 $ \Pi _0$
be the set of all quantifier-free formulas;
$ \Pi _0$
be the set of all quantifier-free formulas; -
•
 $\Sigma _{k+1} : = \{\exists x_1, \dots , x_n \, \varphi \mid \varphi \in \Pi _k\}$
;
$\Sigma _{k+1} : = \{\exists x_1, \dots , x_n \, \varphi \mid \varphi \in \Pi _k\}$
; -
•
 $\Pi _{k+1} : = \{\forall x_1, \dots , x_n\, \varphi \mid \varphi \in \Sigma _k\}$
.
$\Pi _{k+1} : = \{\forall x_1, \dots , x_n\, \varphi \mid \varphi \in \Sigma _k\}$
.
Let
![]() $\mathrm { FV} \left ({\varphi }\right )$
denote the set of all free variables in
$\mathrm { FV} \left ({\varphi }\right )$
denote the set of all free variables in
![]() $\varphi $
. Note that every formula
$\varphi $
. Note that every formula
![]() $\varphi $
in
$\varphi $
in
![]() $\Sigma _{k+1}$
(resp.
$\Sigma _{k+1}$
(resp.
![]() $\Pi _{k+1}$
) is equivalent over
$\Pi _{k+1}$
) is equivalent over
![]() $\mathsf {HA}$
to some formula
$\mathsf {HA}$
to some formula
![]() $\psi $
in
$\psi $
in
![]() $\Sigma _{k+1}$
(resp.
$\Sigma _{k+1}$
(resp.
![]() $\Pi _{k+1}$
) such that
$\Pi _{k+1}$
) such that
![]() $\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\psi }\right )$
and
$\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\psi }\right )$
and
![]() $\psi $
is of the form
$\psi $
is of the form
![]() $\exists x \psi '$
(resp.
$\exists x \psi '$
(resp.
![]() $\forall x \psi '$
) where
$\forall x \psi '$
) where
![]() $\psi '$
is
$\psi '$
is
![]() $\Pi _k$
(resp.
$\Pi _k$
(resp.
![]() $\Sigma _k$
). For convenience, we assume that
$\Sigma _k$
). For convenience, we assume that
![]() $\Sigma _m$
and
$\Sigma _m$
and
![]() $\Pi _m$
denote the empty set for negative integers m.
$\Pi _m$
denote the empty set for negative integers m.
The classical variant
![]() $\mathsf {PA}$
of
$\mathsf {PA}$
of
![]() $\mathsf {HA}$
is defined as
$\mathsf {HA}$
is defined as
![]() $\mathsf {HA} + {\textrm {LEM}}$
or
$\mathsf {HA} + {\textrm {LEM}}$
or
![]() $\mathsf {HA} + {\textrm {DNE}}$
, where
$\mathsf {HA} + {\textrm {DNE}}$
, where
![]() ${\textrm {LEM}}$
is the axiom scheme of the law-of-excluded-middle
${\textrm {LEM}}$
is the axiom scheme of the law-of-excluded-middle
![]() ${\varphi \lor \neg \varphi }$
and
${\varphi \lor \neg \varphi }$
and
![]() ${\textrm {DNE}}$
is that of the double-negation-elimination
${\textrm {DNE}}$
is that of the double-negation-elimination
![]() ${\neg \neg \varphi \to \varphi }$
. Recall that
${\neg \neg \varphi \to \varphi }$
. Recall that
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
and
${\Sigma _k}\text {-}\mathrm {LEM}$
and
![]() ${\Sigma _k}\text {-}\mathrm {DNE}$
are
${\Sigma _k}\text {-}\mathrm {DNE}$
are
![]() ${\textrm {LEM}}$
and
${\textrm {LEM}}$
and
![]() ${\textrm {DNE}}$
restricted to formulas in
${\textrm {DNE}}$
restricted to formulas in
![]() $\Sigma _k$
(possibly containing free variables) respectively. Similarly,
$\Sigma _k$
(possibly containing free variables) respectively. Similarly,
![]() ${\Pi _k}\text {-}\mathrm {LEM}$
and
${\Pi _k}\text {-}\mathrm {LEM}$
and
![]() ${\Pi _k}\text {-}\mathrm {DNE}$
are defined for
${\Pi _k}\text {-}\mathrm {DNE}$
are defined for
![]() $\Pi _k$
. We call a theory
$\Pi _k$
. We call a theory
![]() ${T}$
such that
${T}$
such that
![]() $\mathsf {HA} \subseteq {T} \subseteq \mathsf {PA}$
semi-classical arithmetic.
$\mathsf {HA} \subseteq {T} \subseteq \mathsf {PA}$
semi-classical arithmetic.
Unless otherwise stated, the inclusion between classes of
![]() $\mathsf {HA}$
-formulas is to be understood modulo equivalences over
$\mathsf {HA}$
-formulas is to be understood modulo equivalences over
![]() $\mathsf {HA}$
. That is, for classes
$\mathsf {HA}$
. That is, for classes
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma '$
of
$\Gamma '$
of
![]() $\mathsf {HA}$
-formulas,
$\mathsf {HA}$
-formulas,
![]() $\Gamma \subseteq \Gamma '$
denotes that for all
$\Gamma \subseteq \Gamma '$
denotes that for all
![]() $\varphi \in \Gamma $
, there exists
$\varphi \in \Gamma $
, there exists
![]() $\varphi '\in \Gamma '$
such that
$\varphi '\in \Gamma '$
such that
![]() $\mathrm {FV} \left ({\varphi }\right )=\mathrm {FV} \left ({\varphi '}\right )$
and
$\mathrm {FV} \left ({\varphi }\right )=\mathrm {FV} \left ({\varphi '}\right )$
and
![]() $\mathsf {HA} \vdash \varphi '\leftrightarrow \varphi $
, and
$\mathsf {HA} \vdash \varphi '\leftrightarrow \varphi $
, and
![]() $\Gamma = \Gamma '$
denotes
$\Gamma = \Gamma '$
denotes
![]() $\Gamma \subseteq \Gamma '$
and
$\Gamma \subseteq \Gamma '$
and
![]() $\Gamma ' \subseteq \Gamma $
. In this sense, one may think of
$\Gamma ' \subseteq \Gamma $
. In this sense, one may think of
![]() $\Sigma _k$
and
$\Sigma _k$
and
![]() $\Pi _k$
as sub-classes of
$\Pi _k$
as sub-classes of
![]() $\Sigma _{k'}$
and
$\Sigma _{k'}$
and
![]() $\Pi _{k'}$
for all
$\Pi _{k'}$
for all
![]() $k'>k$
(see [Reference Troelstra and van Dalen7, Remark 2.5]).
$k'>k$
(see [Reference Troelstra and van Dalen7, Remark 2.5]).
3 A relativization of Ishihara’s conservation result in semi-classical arithmetic
In this section, we simulate Ishihara’s proof of [Reference Troelstra and van Dalen9, Theorem 10] in the specific context of semi-classical arithmetic studied in [Reference Akama, Berardi, Hayashi and Kohlenbach1, Reference Troelstra and van Dalen7] with some additional arguments. We first recall the translation studied in [Reference Troelstra and van Dalen9]. In the context of the translation, without otherwise stated, we work in the language with an additional predicate symbol
![]() of arity
of arity
![]() $0$
, which behaves as “place holder” (see [Reference Troelstra and van Dalen9, Reference Troelstra and van Dalen10] for more information). Let
$0$
, which behaves as “place holder” (see [Reference Troelstra and van Dalen9, Reference Troelstra and van Dalen10] for more information). Let
![]() denote
denote
![]() $\mathsf {HA}$
in that language. On the other hand,
$\mathsf {HA}$
in that language. On the other hand,
![]() denotes
denotes
![]() augmented with
augmented with
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
for “
${\Sigma _k}\text {-}\mathrm {LEM}$
for “
![]() $\mathsf {HA}$
”-formulas.
$\mathsf {HA}$
”-formulas.
Definition 3.1 (cf. [Reference Troelstra and van Dalen9, Definition 3]).
Let
![]() denote
denote
![]() . For each formula
. For each formula
![]() $\varphi $
, its
$\varphi $
, its
![]() -translation
-translation
![]() is defined inductively by the following clauses:
is defined inductively by the following clauses:
-
• For P prime such that
 $P \not \equiv \, \perp $
,
$P \not \equiv \, \perp $
,
 ;
; -
•
 ;
; -
•
 for
for
 $\circ \in \{ \land , \to \}$
;
$\circ \in \{ \land , \to \}$
; -
•
 ;
; -
•
 ;
; -
•
 .
.
It is straightforward to see
![]() .
.
Proposition 3.2 (cf. [Reference Troelstra and van Dalen9, Proposition 4] and [Reference Troelstra and van Dalen10, Section 4]).
-
1. For any
 $\mathsf {HA}$
-formula
$\mathsf {HA}$
-formula
 $\varphi $
,
$\varphi $
,

-
2. For any
 $\mathsf {HA}$
-formula
$\mathsf {HA}$
-formula
 $\varphi $
and any set X of
$\varphi $
and any set X of
 $\mathsf {HA}$
-sentences, if
$\mathsf {HA}$
-sentences, if
 $\mathsf {PA} +X \vdash \varphi $
, then
$\mathsf {PA} +X \vdash \varphi $
, then
 , where
, where
 .
.
Proof The proofs are routine: One can show (1) by induction on the structure of formulas, and (2) by induction on the length of the proof of
![]() $\varphi $
in
$\varphi $
in
![]() $\mathsf {PA} +X$
.
$\mathsf {PA} +X$
.
Corollary 3.3. For any
![]() $\mathsf {HA}$
-formulas
$\mathsf {HA}$
-formulas
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
, if
$\varphi _2$
, if
![]() $\mathsf {PA} \vdash \varphi _1 \leftrightarrow \varphi _2$
, then
$\mathsf {PA} \vdash \varphi _1 \leftrightarrow \varphi _2$
, then
![]() .
.
Proof If
![]() $\mathsf {PA} $
proves
$\mathsf {PA} $
proves
![]() $\varphi _1 \leftrightarrow \varphi _2$
, by Proposition 3.2.(2), we have that
$\varphi _1 \leftrightarrow \varphi _2$
, by Proposition 3.2.(2), we have that
![]() proves
proves
![]() , which is in fact
, which is in fact
![]() .
.
Lemma 3.4. For a quantifier-free formula
![]() ${\varphi }_{\mathrm {qf}}$
of
${\varphi }_{\mathrm {qf}}$
of
![]() $\mathsf {HA}$
,
$\mathsf {HA}$
,
![]() proves
proves
![]() .
.
Proof By induction on the structure of quantifier-free formulas of
![]() $\mathsf {HA}$
.
$\mathsf {HA}$
.
The case of
![]() $ \perp $
: Since
$ \perp $
: Since
![]() , we have trivially
, we have trivially
![]() .
.
The case of that
![]() ${\varphi }_{\mathrm {qf}}$
is a prime formula but
${\varphi }_{\mathrm {qf}}$
is a prime formula but
![]() $\perp $
: It is trivial that
$\perp $
: It is trivial that
![]() proves
proves
![]() . On the other hand, since
. On the other hand, since
![]() proves
proves
![]() ${\varphi }_{\mathrm {qf}} \lor \neg {\varphi }_{\mathrm {qf}}$
and
${\varphi }_{\mathrm {qf}} \lor \neg {\varphi }_{\mathrm {qf}}$
and
![]() , we also have that
, we also have that
![]() proves
proves
![]() .
.
The case of
![]() ${\varphi }_{\mathrm {qf}}\equiv \varphi _1 \land \varphi _2$
: We have that
${\varphi }_{\mathrm {qf}}\equiv \varphi _1 \land \varphi _2$
: We have that
proves
The case of
![]() ${\varphi }_{\mathrm {qf}}\equiv \varphi _1 \lor \varphi _2$
: Since
${\varphi }_{\mathrm {qf}}\equiv \varphi _1 \lor \varphi _2$
: Since
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
are decidable in
$\varphi _2$
are decidable in
![]() $\mathsf {HA}$
(note that they are quantifier-free), we have that
$\mathsf {HA}$
(note that they are quantifier-free), we have that
proves
![]() $(\varphi _1 \lor \varphi _2) \lor (\neg \varphi _1 \land \neg \varphi _2)$
. In the latter case of the disjunction, we have
$(\varphi _1 \lor \varphi _2) \lor (\neg \varphi _1 \land \neg \varphi _2)$
. In the latter case of the disjunction, we have
. Thus
proves
On the other hand,
also proves
Thus
proves
The case of
![]() ${\varphi }_{\mathrm {qf}}\equiv \varphi _1 \to \varphi _2$
: Assume
${\varphi }_{\mathrm {qf}}\equiv \varphi _1 \to \varphi _2$
: Assume
. Then we have
Since
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
are decidable in
$\varphi _2$
are decidable in
![]() $\mathsf {HA}$
(note that they are quantifier-free), we have that
$\mathsf {HA}$
(note that they are quantifier-free), we have that
proves
![]() $(\varphi _2 \lor \neg \varphi _1) \lor (\varphi _1 \land \neg \varphi _2)$
. In the former case, we have
$(\varphi _2 \lor \neg \varphi _1) \lor (\varphi _1 \land \neg \varphi _2)$
. In the former case, we have
![]() $\varphi _1 \to \varphi _2$
. In the latter case, by (1), we have
$\varphi _1 \to \varphi _2$
. In the latter case, by (1), we have
. Thus
proves
On the other hand,
also proves
Thus
proves
The following lemma is the key for our generalized conservation result:
Lemma 3.5. For a formula
![]() $\varphi $
of
$\varphi $
of
![]() $\mathsf {HA}$
, the following hold:
$\mathsf {HA}$
, the following hold:
-
1. If
 $\varphi \in \Pi _{k}$
,
$\varphi \in \Pi _{k}$
,

-
2. If
 $\varphi \in \Sigma _{k}$
,
$\varphi \in \Sigma _{k}$
,

Note that
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
is an axiom scheme in the language of
${\Sigma _k}\text {-}\mathrm {LEM}$
is an axiom scheme in the language of
![]() $\mathsf {HA}$
(which does not contain $).
$\mathsf {HA}$
(which does not contain $).
Proof By simultaneous induction on k. The base case is by Lemma 3.4. Assume items 1 and 2 for k to show those for
![]() $k+1$
. First, for the first item, let
$k+1$
. First, for the first item, let
![]() $\varphi :\equiv \forall x \varphi _1$
where
$\varphi :\equiv \forall x \varphi _1$
where
![]() $\varphi _1 \in \Sigma _k$
. By the induction hypothesis, we have
$\varphi _1 \in \Sigma _k$
. By the induction hypothesis, we have
. Note that
proves
. In the following, we show the converse
inside
. Since
![]() $\neg \varphi _1$
has some equivalent formula in
$\neg \varphi _1$
has some equivalent formula in
![]() $\Pi _k$
in the presence of
$\Pi _k$
in the presence of
![]() ${\Sigma _{k-1}}\text {-}\mathrm {DNE}$
(cf. Remark 5.3), by
${\Sigma _{k-1}}\text {-}\mathrm {DNE}$
(cf. Remark 5.3), by
![]() ${\Sigma _{k+1}}\text {-}\mathrm {LEM}$
, we have now
${\Sigma _{k+1}}\text {-}\mathrm {LEM}$
, we have now
![]() $\exists x \neg \varphi _1 \lor \neg \exists x \neg \varphi _1$
. In the former case, we have $ by using our assumption
$\exists x \neg \varphi _1 \lor \neg \exists x \neg \varphi _1$
. In the former case, we have $ by using our assumption
. In the latter case, we have
![]() $\forall x \varphi _1$
since
$\forall x \varphi _1$
since
![]() $\neg \exists x \neg \varphi _1 \leftrightarrow \forall x \neg \neg \varphi _1$
and
$\neg \exists x \neg \varphi _1 \leftrightarrow \forall x \neg \neg \varphi _1$
and
![]() ${\Sigma _{k+1}}\text {-}\mathrm {LEM}$
implies
${\Sigma _{k+1}}\text {-}\mathrm {LEM}$
implies
![]() ${\Sigma _{k+1}}\text {-}\mathrm {DNE}$
. Thus
${\Sigma _{k+1}}\text {-}\mathrm {DNE}$
. Thus
proves
. Then we have that
proves
Next, for the second item, let
![]() $\varphi :\equiv \exists x \varphi _1$
where
$\varphi :\equiv \exists x \varphi _1$
where
![]() $\varphi _1 \in \Pi _k$
. Note that
$\varphi _1 \in \Pi _k$
. Note that
![]() is
is
![]() . By the induction hypothesis, we have
. By the induction hypothesis, we have
![]() proves
proves
![]() , and hence,
, and hence,
![]() . Then it is trivial that
. Then it is trivial that
![]() proves
proves
![]() . In the following, we show the converse direction inside
. In the following, we show the converse direction inside
![]() . By
. By
![]() ${\Sigma _{k+1}}\text {-}\mathrm {LEM}$
, we have now
${\Sigma _{k+1}}\text {-}\mathrm {LEM}$
, we have now
![]() $ \exists x \varphi _1 \lor \neg \exists x \varphi _1 $
. Then it suffices to show
$ \exists x \varphi _1 \lor \neg \exists x \varphi _1 $
. Then it suffices to show
![]() , which is trivial since
, which is trivial since
![]() .
.
Corollary 3.6. For a formula
![]() $\varphi $
of
$\varphi $
of
![]() $\mathsf {HA}$
, if
$\mathsf {HA}$
, if
![]() $\varphi \equiv \exists x \varphi _1 $
with
$\varphi \equiv \exists x \varphi _1 $
with
![]() $\varphi _1 \in \Pi _{k}$
, then
$\varphi _1 \in \Pi _{k}$
, then
![]()
In the context of intuitionistic/semi-classical arithmetic, a formula does not have an equivalent formula of the prenex normal form (namely, formula in
![]() $\Sigma _k$
or
$\Sigma _k$
or
![]() $\Pi _k$
) while it does in classical arithmetic. Because of this fact, the conservation theorem only for prenex formulas is not applicable in many practical cases. On the other hand, Akama et al. [Reference Akama, Berardi, Hayashi and Kohlenbach1] introduced the classes
$\Pi _k$
) while it does in classical arithmetic. Because of this fact, the conservation theorem only for prenex formulas is not applicable in many practical cases. On the other hand, Akama et al. [Reference Akama, Berardi, Hayashi and Kohlenbach1] introduced the classes
![]() $\mathrm {U}_k $
and
$\mathrm {U}_k $
and
![]() $\mathrm {E}_k$
of formulas which correspond to classical
$\mathrm {E}_k$
of formulas which correspond to classical
![]() $\Pi _k$
and
$\Pi _k$
and
![]() $\Sigma _k$
respectively in the sense that every formula in
$\Sigma _k$
respectively in the sense that every formula in
![]() $\mathrm {U}_k$
(resp.
$\mathrm {U}_k$
(resp.
![]() $\mathrm {E}_k$
) is equivalent over
$\mathrm {E}_k$
) is equivalent over
![]() $\mathsf {PA}$
to some formula in
$\mathsf {PA}$
to some formula in
![]() $\Pi _k$
(resp.
$\Pi _k$
(resp.
![]() $\Sigma _k$
) and vice versa. In addition, the authors introduced in [Reference Troelstra and van Dalen7] the classes
$\Sigma _k$
) and vice versa. In addition, the authors introduced in [Reference Troelstra and van Dalen7] the classes
![]() $\mathrm {U}_k^+ $
and
$\mathrm {U}_k^+ $
and
![]() $\mathrm {E}_k^+$
, which are cumulative versions of
$\mathrm {E}_k^+$
, which are cumulative versions of
![]() $\mathrm {U}_k $
and
$\mathrm {U}_k $
and
![]() $\mathrm {E}_k$
. For obtaining the conservation results for the classes as large as possible, we introduce classes
$\mathrm {E}_k$
. For obtaining the conservation results for the classes as large as possible, we introduce classes
![]() $\mathcal {R}_k$
and
$\mathcal {R}_k$
and
![]() $\mathcal {J}_k$
(see Definition 3.11), which relativize
$\mathcal {J}_k$
(see Definition 3.11), which relativize
![]() $\mathcal {R}$
and
$\mathcal {R}$
and
![]() $\mathcal {J}$
in [Reference Troelstra and van Dalen9] respectively with regard to the formulas of degree
$\mathcal {J}$
in [Reference Troelstra and van Dalen9] respectively with regard to the formulas of degree
![]() $\leq k$
in the sense of [Reference Akama, Berardi, Hayashi and Kohlenbach1, Reference Troelstra and van Dalen7].
$\leq k$
in the sense of [Reference Akama, Berardi, Hayashi and Kohlenbach1, Reference Troelstra and van Dalen7].
To make the definitions absolutely clear, we recall some notions in [Reference Akama, Berardi, Hayashi and Kohlenbach1, Reference Troelstra and van Dalen7]: An alternation path is a finite sequence of
![]() $+$
and
$+$
and
![]() $-$
in which
$-$
in which
![]() $+$
and
$+$
and
![]() $-$
appear alternatively. For an alternation path s, let
$-$
appear alternatively. For an alternation path s, let
![]() $i(s)$
denote the first symbol of s if
$i(s)$
denote the first symbol of s if
![]() $s \not \equiv {\langle \, \rangle } $
(empty sequence);
$s \not \equiv {\langle \, \rangle } $
(empty sequence);
![]() $ \times $
if
$ \times $
if
![]() $s \equiv {\langle \, \rangle } $
. Let
$s \equiv {\langle \, \rangle } $
. Let
![]() $s^{\perp }$
denote the alternation path which is obtained by switching
$s^{\perp }$
denote the alternation path which is obtained by switching
![]() $+$
and
$+$
and
![]() $-$
in s, and let
$-$
in s, and let
![]() $l(s) $
denote the length of s. For a formula
$l(s) $
denote the length of s. For a formula
![]() $\varphi $
, the set of alternation paths
$\varphi $
, the set of alternation paths
![]() $\mathit {Alt}(\varphi )$
of
$\mathit {Alt}(\varphi )$
of
![]() $\varphi $
is defined as follows:
$\varphi $
is defined as follows:
-
• If
 $\varphi $
is prime, then
$\varphi $
is prime, then
 $\mathit {Alt}(\varphi ) := \{ {\langle \, \rangle } \}$
;
$\mathit {Alt}(\varphi ) := \{ {\langle \, \rangle } \}$
; -
• Otherwise,
 $\mathit {Alt}(\varphi )$
is defined inductively by the following clauses:
$\mathit {Alt}(\varphi )$
is defined inductively by the following clauses:-
– If
 $\varphi \equiv \varphi _1 \land \varphi _2$
or
$\varphi \equiv \varphi _1 \land \varphi _2$
or
 $\varphi \equiv \varphi _1 \lor \varphi _2$
, then
$\varphi \equiv \varphi _1 \lor \varphi _2$
, then
 $\mathit {Alt}(\varphi ) := \mathit {Alt}(\varphi _1) \cup \mathit {Alt}(\varphi _2)$
;
$\mathit {Alt}(\varphi ) := \mathit {Alt}(\varphi _1) \cup \mathit {Alt}(\varphi _2)$
; -
– If
 $\varphi \equiv \varphi _1 \to \varphi _2$
, then
$\varphi \equiv \varphi _1 \to \varphi _2$
, then
 $\mathit {Alt}(\varphi ) := \{ s^{\perp } \mid s \in \mathit {Alt}(\varphi _1)\} \cup \mathit {Alt}(\varphi _2)$
;
$\mathit {Alt}(\varphi ) := \{ s^{\perp } \mid s \in \mathit {Alt}(\varphi _1)\} \cup \mathit {Alt}(\varphi _2)$
; -
– If
 $\varphi \equiv \forall x \varphi _1 $
, then
$\varphi \equiv \forall x \varphi _1 $
, then
 $\mathit {Alt}(\varphi ) :=\{s \mid s\in \mathit {Alt}(\varphi _1) \text { and } i(s)\equiv {-}\} \cup \{-s \mid s\in \mathit {Alt}(\varphi _1) \text { and } i(s)\not \equiv {-} \} $
;
$\mathit {Alt}(\varphi ) :=\{s \mid s\in \mathit {Alt}(\varphi _1) \text { and } i(s)\equiv {-}\} \cup \{-s \mid s\in \mathit {Alt}(\varphi _1) \text { and } i(s)\not \equiv {-} \} $
; -
– If
 $\varphi \equiv \exists x \varphi _1 $
, then
$\varphi \equiv \exists x \varphi _1 $
, then
 $\mathit {Alt}(\varphi ) :=\{s \mid s\in \mathit {Alt}(\varphi _1) \text { and } i(s)\equiv + \} \cup \{+s \mid s\in \mathit {Alt}(\varphi _1) \text { and } i(s)\not \equiv + \} $
.
$\mathit {Alt}(\varphi ) :=\{s \mid s\in \mathit {Alt}(\varphi _1) \text { and } i(s)\equiv + \} \cup \{+s \mid s\in \mathit {Alt}(\varphi _1) \text { and } i(s)\not \equiv + \} $
.
-
In addition, for a formula
![]() $\varphi $
, the degree
$\varphi $
, the degree
![]() $\mathit {deg}(\varphi )$
of
$\mathit {deg}(\varphi )$
of
![]() $\varphi $
is defined as
$\varphi $
is defined as
Definition 3.7 (cf. [Reference Akama, Berardi, Hayashi and Kohlenbach1, Definition 2.4] and [Reference Troelstra and van Dalen7, Definition 2.11]).
The classes
![]() $\mathrm {F}_k, \mathrm {U}_k, \mathrm {E}_k $
,
$\mathrm {F}_k, \mathrm {U}_k, \mathrm {E}_k $
,
![]() $\mathrm {F}_k^+$
,
$\mathrm {F}_k^+$
,
![]() $\mathrm {U}_k^+ $
and
$\mathrm {U}_k^+ $
and
![]() $ \mathrm {E}_k^+ $
of
$ \mathrm {E}_k^+ $
of
![]() $\mathsf {HA}$
-formulas are defined as follows:
$\mathsf {HA}$
-formulas are defined as follows:
-
•
 $\mathrm {F}_k := \{ \varphi \mid \mathit {deg}(\varphi )=k \} ;\,\, \mathrm {F}_k^+ := \{ \varphi \mid \mathit {deg}(\varphi )\leq k \} ;$
$\mathrm {F}_k := \{ \varphi \mid \mathit {deg}(\varphi )=k \} ;\,\, \mathrm {F}_k^+ := \{ \varphi \mid \mathit {deg}(\varphi )\leq k \} ;$
-
•
 $\mathrm {U}_0:=\mathrm {E}_0:=\mathrm {F}_0 \, (=\Sigma _0 =\Pi _0)$
;
$\mathrm {U}_0:=\mathrm {E}_0:=\mathrm {F}_0 \, (=\Sigma _0 =\Pi _0)$
; -
•
 $\mathrm {U}_{k+1} := \{ \varphi \in \mathrm {F}_{k+1} \mid i(s) \equiv {-} \text { for all }s\in \mathit {Alt}(\varphi ) \text { such that }l(s) =k+1 \}$
;
$\mathrm {U}_{k+1} := \{ \varphi \in \mathrm {F}_{k+1} \mid i(s) \equiv {-} \text { for all }s\in \mathit {Alt}(\varphi ) \text { such that }l(s) =k+1 \}$
; -
•
 $\mathrm {E}_{k+1} := \{ \varphi \in \mathrm {F}_{k+1} \mid i(s) \equiv + \text { for all }s\in \mathit {Alt}(\varphi ) \text { such that }l(s) =k+1 \}$
;
$\mathrm {E}_{k+1} := \{ \varphi \in \mathrm {F}_{k+1} \mid i(s) \equiv + \text { for all }s\in \mathit {Alt}(\varphi ) \text { such that }l(s) =k+1 \}$
; -
•
 $\displaystyle \mathrm {U}_k^+ := \mathrm {U}_k \cup \bigcup _{i<k} \mathrm {F}_i;\, \, \mathrm {E}_k^+ := \mathrm {E}_k \cup \bigcup _{i<k} \mathrm {F}_i. $
$\displaystyle \mathrm {U}_k^+ := \mathrm {U}_k \cup \bigcup _{i<k} \mathrm {F}_i;\, \, \mathrm {E}_k^+ := \mathrm {E}_k \cup \bigcup _{i<k} \mathrm {F}_i. $
Remark 3.8. As shown in [Reference Troelstra and van Dalen7, Proposition 4.6], for any
![]() $\varphi \in \mathrm {U}_k^+$
and
$\varphi \in \mathrm {U}_k^+$
and
![]() $\psi \in \mathrm {E}_k^+$
, there exist
$\psi \in \mathrm {E}_k^+$
, there exist
![]() $\varphi '\in \mathrm {U}_k$
and
$\varphi '\in \mathrm {U}_k$
and
![]() $\psi ' \in \mathrm {E}_k$
such that
$\psi ' \in \mathrm {E}_k$
such that
![]() $\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi '}\right )$
,
$\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi '}\right )$
,
![]() $\mathrm { FV} \left ({\psi }\right )=\mathrm { FV} \left ({\psi '}\right )$
,
$\mathrm { FV} \left ({\psi }\right )=\mathrm { FV} \left ({\psi '}\right )$
,
![]() $\mathsf {HA} \vdash \varphi \leftrightarrow \varphi '$
and
$\mathsf {HA} \vdash \varphi \leftrightarrow \varphi '$
and
![]() $\mathsf {HA} \vdash \psi \leftrightarrow \psi '$
. Then it also follows that for any
$\mathsf {HA} \vdash \psi \leftrightarrow \psi '$
. Then it also follows that for any
![]() $\varphi \in \mathrm {F}_k^+$
, there exists
$\varphi \in \mathrm {F}_k^+$
, there exists
![]() $\varphi '\in \mathrm {F}_k$
such that
$\varphi '\in \mathrm {F}_k$
such that
![]() $\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi '}\right )$
and
$\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi '}\right )$
and
![]() $\mathsf {HA} \vdash \varphi \leftrightarrow \varphi '$
. Thus one may identify
$\mathsf {HA} \vdash \varphi \leftrightarrow \varphi '$
. Thus one may identify
![]() $\mathrm {E}_k^+, \mathrm {U}_k^+$
and
$\mathrm {E}_k^+, \mathrm {U}_k^+$
and
![]() $\mathrm {F}_k^+$
with
$\mathrm {F}_k^+$
with
![]() $\mathrm {E}_k, \mathrm {U}_k$
and
$\mathrm {E}_k, \mathrm {U}_k$
and
![]() $\mathrm {F}_k$
respectively over
$\mathrm {F}_k$
respectively over
![]() $\mathsf {HA}$
without loss of generality.
$\mathsf {HA}$
without loss of generality.
Then the authors showed the following prenex normal form theorem:
Theorem 3.9 (cf. [Reference Troelstra and van Dalen7, Theorem 5.3] which corrects [Reference Akama, Berardi, Hayashi and Kohlenbach1, Theorem 2.7]).
For a
![]() $\mathsf {HA}$
-formula
$\mathsf {HA}$
-formula
![]() $\varphi $
, the following hold:
$\varphi $
, the following hold:
-
1. If
 $\varphi \in \mathrm {E}_k^+$
, then there exists
$\varphi \in \mathrm {E}_k^+$
, then there exists
 $\varphi ' \in \Sigma _k$
such that
$\varphi ' \in \Sigma _k$
such that
 $\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi '}\right )$
and
$\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi '}\right )$
and  $$ \begin{align*}\mathsf{HA} + {\Sigma_k}\text{-}\mathrm{DNE} +{\mathrm{U}_k}\text{-}\mathrm{DNS} \vdash \varphi \leftrightarrow \varphi'; \end{align*} $$
$$ \begin{align*}\mathsf{HA} + {\Sigma_k}\text{-}\mathrm{DNE} +{\mathrm{U}_k}\text{-}\mathrm{DNS} \vdash \varphi \leftrightarrow \varphi'; \end{align*} $$
-
2. If
 $\varphi \in \mathrm {U}_k^+$
, then there exists
$\varphi \in \mathrm {U}_k^+$
, then there exists
 $\varphi ' \in \Pi _k$
such that
$\varphi ' \in \Pi _k$
such that
 $\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi '}\right )$
and
$\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi '}\right )$
and  $$ \begin{align*}\mathsf{HA} + {(\Pi_k\lor \Pi_k)}\text{-}\mathrm{DNE} \vdash \varphi \leftrightarrow \varphi'; \end{align*} $$
$$ \begin{align*}\mathsf{HA} + {(\Pi_k\lor \Pi_k)}\text{-}\mathrm{DNE} \vdash \varphi \leftrightarrow \varphi'; \end{align*} $$
where
![]() ${\mathrm {U}_k}\text {-}\mathrm {DNS}$
is the axiom scheme of the double-negation-shift restricted to formulas in
${\mathrm {U}_k}\text {-}\mathrm {DNS}$
is the axiom scheme of the double-negation-shift restricted to formulas in
![]() $\mathrm {U}_k$
and
$\mathrm {U}_k$
and
![]() ${(\Pi _k\lor \Pi _k)}\text {-}\mathrm {DNE}$
is
${(\Pi _k\lor \Pi _k)}\text {-}\mathrm {DNE}$
is
![]() ${\textrm {DNE}}$
restricted to formulas of the form
${\textrm {DNE}}$
restricted to formulas of the form
![]() $\varphi \lor \psi $
with
$\varphi \lor \psi $
with
![]() $\varphi , \psi \in \Pi _k$
.
$\varphi , \psi \in \Pi _k$
.
Remark 3.10.
![]() $\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM}$
proves
$\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM}$
proves
![]() ${\Sigma _k}\text {-}\mathrm {DNE}$
,
${\Sigma _k}\text {-}\mathrm {DNE}$
,
![]() ${\mathrm {U}_k}\text {-}\mathrm {DNS}$
and
${\mathrm {U}_k}\text {-}\mathrm {DNS}$
and
![]() ${(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}$
. Then the prenex normal form theorems for
${(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}$
. Then the prenex normal form theorems for
![]() $\mathrm {E}_k^+$
and
$\mathrm {E}_k^+$
and
![]() $\mathrm {U}_k^+$
are available in
$\mathrm {U}_k^+$
are available in
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
.
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
.
Definition 3.11 (cf. [Reference Troelstra and van Dalen9, Definition 6]).
Define
![]() $\mathcal {R}_0:=\mathcal {J}_0:=\Sigma _0 \, (=\Pi _0)$
. In addition, we define simultaneously classes
$\mathcal {R}_0:=\mathcal {J}_0:=\Sigma _0 \, (=\Pi _0)$
. In addition, we define simultaneously classes
![]() $\mathcal {R}_{k+1}$
and
$\mathcal {R}_{k+1}$
and
![]() $\mathcal {J}_{k+1}$
as follows: Let F range over formulas in
$\mathcal {J}_{k+1}$
as follows: Let F range over formulas in
![]() $\mathrm {F}_k^+$
, R and
$\mathrm {F}_k^+$
, R and
![]() $R'$
over those in
$R'$
over those in
![]() $\mathcal {R}_{k+1}$
, and J and
$\mathcal {R}_{k+1}$
, and J and
![]() $J'$
over those in
$J'$
over those in
![]() $\mathcal {J}_{k+1}$
respectively. Then
$\mathcal {J}_{k+1}$
respectively. Then
![]() $\mathcal {R}_{k+1}$
and
$\mathcal {R}_{k+1}$
and
![]() $\mathcal {J}_{k+1}$
are inductively generated by the clauses
$\mathcal {J}_{k+1}$
are inductively generated by the clauses
-
1.
 $F, R\land R', R \lor R', \forall x R, J \to R\in \mathcal {R}_{k+1}$
;
$F, R\land R', R \lor R', \forall x R, J \to R\in \mathcal {R}_{k+1}$
; -
2.
 $F, J\land J', J \lor J', \exists x J, R \to J\in \mathcal {J}_{k+1}$
.
$F, J\land J', J \lor J', \exists x J, R \to J\in \mathcal {J}_{k+1}$
.
Lemma 3.12 (A relativized version of [Reference Troelstra and van Dalen9, Proposition 7(2, 3)]).
For a
![]() $\mathsf {HA}$
-formula
$\mathsf {HA}$
-formula
![]() $\varphi $
, the following hold:
$\varphi $
, the following hold:
-
1. If
 $\varphi \in \mathcal {R}_{k+1}$
, then
$\varphi \in \mathcal {R}_{k+1}$
, then
 proves
proves

-
2. If
 $\varphi \in \mathcal {J}_{k+1}$
, then
$\varphi \in \mathcal {J}_{k+1}$
, then
 proves
proves
 .
.
Proof We show items 1 and 2 simultaneously by induction on the structure of formulas.
Let
![]() $\varphi $
be prime. Since
$\varphi $
be prime. Since
![]() $\varphi $
is in
$\varphi $
is in
![]() $\mathrm {F}_0$
, we have
$\mathrm {F}_0$
, we have
![]() $\varphi \in \mathcal {R}_{k+1} \cap \mathcal {J}_{k+1}$
. Since
$\varphi \in \mathcal {R}_{k+1} \cap \mathcal {J}_{k+1}$
. Since
![]() $\mathsf {HA} \vdash \varphi \lor \neg \varphi $
, we have
$\mathsf {HA} \vdash \varphi \lor \neg \varphi $
, we have
![]() . Then we have item 1 by Lemma 3.4. Item 2 is trivial.
. Then we have item 1 by Lemma 3.4. Item 2 is trivial.
The induction step is the same as that for [Reference Troelstra and van Dalen9, Proposition 7] in addition with the cases of
![]() $\varphi :\equiv \forall x \varphi _1 \in \mathcal {J}_{k+1}$
and
$\varphi :\equiv \forall x \varphi _1 \in \mathcal {J}_{k+1}$
and
![]() $\varphi :\equiv \exists x \varphi _1 \in \mathcal {R}_{k+1}$
:
$\varphi :\equiv \exists x \varphi _1 \in \mathcal {R}_{k+1}$
:
If
![]() $\varphi :\equiv \forall x \varphi _1 \in \mathcal {J}_{k+1}$
, then we have
$\varphi :\equiv \forall x \varphi _1 \in \mathcal {J}_{k+1}$
, then we have
![]() $\varphi \in \mathrm {F}_k^+$
, and hence,
$\varphi \in \mathrm {F}_k^+$
, and hence,
![]() $\varphi \in \mathrm {U}_k^+$
. By Remark 3.10, one may assume
$\varphi \in \mathrm {U}_k^+$
. By Remark 3.10, one may assume
![]() $\varphi \in \Pi _k$
. By Lemma 3.5.(1), we have
$\varphi \in \Pi _k$
. By Lemma 3.5.(1), we have
![]() . Since
. Since
![]() implies
implies
![]() , we have
, we have
![]() .
.
If
![]() $\varphi :\equiv \exists x \varphi _1 \in \mathcal {R}_{k+1}$
, then we have
$\varphi :\equiv \exists x \varphi _1 \in \mathcal {R}_{k+1}$
, then we have
![]() $\varphi \in \mathrm {F}_k^+$
, and hence,
$\varphi \in \mathrm {F}_k^+$
, and hence,
![]() $\varphi \in \mathrm {E}_k^+$
(and
$\varphi \in \mathrm {E}_k^+$
(and
![]() $k>0$
). By Remark 3.10, one may assume
$k>0$
). By Remark 3.10, one may assume
![]() $ \varphi _1\in \Pi _{k-1}$
. Reason in
$ \varphi _1\in \Pi _{k-1}$
. Reason in
![]() . Now we have
. Now we have
![]() $\exists x \varphi _1 \lor \neg \exists x \varphi _1$
. In the latter case, we have
$\exists x \varphi _1 \lor \neg \exists x \varphi _1$
. In the latter case, we have
![]() in the presence of
in the presence of
![]() . Thus we have
. Thus we have
![]() . By Corollary 3.6, we have that
. By Corollary 3.6, we have that
![]() implies
implies
![]() , and hence,
, and hence,
![]() .
.
Definition 3.13 (cf. [Reference Troelstra and van Dalen9, Definition 6]).
Define
![]() $\mathcal {Q}_0:=\Sigma _0\, (=\Pi _0)$
. In addition, we define a class
$\mathcal {Q}_0:=\Sigma _0\, (=\Pi _0)$
. In addition, we define a class
![]() $\mathcal {Q}_{k+1}$
as follows. Let P range over prime formulas, Q and
$\mathcal {Q}_{k+1}$
as follows. Let P range over prime formulas, Q and
![]() $Q'$
over formulas in
$Q'$
over formulas in
![]() $\mathcal {Q}_{k+1}$
, and J over those in
$\mathcal {Q}_{k+1}$
, and J over those in
![]() $\mathcal {J}_{k+1}$
. Then
$\mathcal {J}_{k+1}$
. Then
![]() $\mathcal {Q}_{k+1}$
is inductively generated by the clause
$\mathcal {Q}_{k+1}$
is inductively generated by the clause
Lemma 3.14 (A relativized version of [Reference Troelstra and van Dalen9, Proposition 7(1)]).
For a
![]() $\mathsf {HA}$
-formula
$\mathsf {HA}$
-formula
![]() $\varphi $
, if
$\varphi $
, if
![]() $\varphi \in \mathcal {Q}_{k+1}$
, then
$\varphi \in \mathcal {Q}_{k+1}$
, then
![]() .
.
Proof By induction on the structure of formulas, we show that for any
![]() $\mathsf {HA}$
-formula
$\mathsf {HA}$
-formula
![]() $\varphi $
, if
$\varphi $
, if
![]() $\varphi \in \mathcal {Q}_{k+1}$
, then
$\varphi \in \mathcal {Q}_{k+1}$
, then
![]() .
.
If
![]() $\varphi $
is prime, then we have
$\varphi $
is prime, then we have
![]() trivially by the definition of
trivially by the definition of
![]() . If
. If
![]() $\varphi :\equiv \varphi _1 \land \varphi _2$
,
$\varphi :\equiv \varphi _1 \land \varphi _2$
,
![]() $\varphi :\equiv \varphi _1 \lor \varphi _2$
,
$\varphi :\equiv \varphi _1 \lor \varphi _2$
,
![]() $\varphi :\equiv \forall x \varphi _1$
or
$\varphi :\equiv \forall x \varphi _1$
or
![]() $\varphi :\equiv \exists x \varphi _1$
, we have
$\varphi :\equiv \exists x \varphi _1$
, we have
![]() in a straightforward way by using the induction hypothesis (as for [Reference Troelstra and van Dalen9, Proposition 7(1)]).
in a straightforward way by using the induction hypothesis (as for [Reference Troelstra and van Dalen9, Proposition 7(1)]).
Assume
![]() $\varphi :\equiv \varphi _1 \to \varphi _2\in \mathcal {Q}_{k+1}$
. Then we have
$\varphi :\equiv \varphi _1 \to \varphi _2\in \mathcal {Q}_{k+1}$
. Then we have
![]() $\varphi _1 \in \mathcal {J}_{k+1}$
and
$\varphi _1 \in \mathcal {J}_{k+1}$
and
![]() $\varphi _2 \in \mathcal {Q}_{k+1}$
. By the induction hypothesis, we have
$\varphi _2 \in \mathcal {Q}_{k+1}$
. By the induction hypothesis, we have
. On the other hand, by Lemma 3.12.(2), we have
. Since
by Proposition 3.2.(1), we have that
proves

Now we define a class
![]() $\mathcal {V}_k$
of
$\mathcal {V}_k$
of
![]() $\mathsf {HA}$
-formulas by using the class
$\mathsf {HA}$
-formulas by using the class
![]() $\mathcal {J}_k$
in Definitions 3.11.
$\mathcal {J}_k$
in Definitions 3.11.
Definition 3.15. Let J range over formulas in
![]() $\mathcal {J}_k$
, V and
$\mathcal {J}_k$
, V and
![]() $V'$
over those in
$V'$
over those in
![]() $\mathcal {V}_{k}$
. Then
$\mathcal {V}_{k}$
. Then
![]() $\mathcal {V}_{k}$
is inductively generated by the clause
$\mathcal {V}_{k}$
is inductively generated by the clause
For our conservation result, we use the following fact on substitution.
Lemma 3.16 (cf. [Reference Troelstra and van Dalen3, Theorem 6.2.4] and [Reference Troelstra and van Dalen7, Lemma 6.10]).
Let X be a set of
![]() $\mathsf {HA}$
-sentences and
$\mathsf {HA}$
-sentences and
![]() $\varphi $
be a
$\varphi $
be a
![]() -formula. If
-formula. If
![]() , then
, then
![]() for any
for any
![]() $\mathsf {HA}$
-formula
$\mathsf {HA}$
-formula
![]() $\psi $
such that the free variables of
$\psi $
such that the free variables of
![]() $\psi $
are not bounded in
$\psi $
are not bounded in
![]() $\varphi $
, where
$\varphi $
, where
![]() is the
is the
![]() $\mathsf {HA}$
-formula obtained from
$\mathsf {HA}$
-formula obtained from
![]() $\varphi $
by replacing all the occurrences of
$\varphi $
by replacing all the occurrences of
![]() in
in
![]() $\varphi $
with
$\varphi $
with
![]() $\psi $
.
$\psi $
.
Theorem 3.17. For any
![]() $\mathsf {HA}$
-formulas
$\mathsf {HA}$
-formulas
![]() $\varphi \in \mathcal {V}_{k+1}$
and
$\varphi \in \mathcal {V}_{k+1}$
and
![]() $\psi \in \mathcal {Q}_{k+1}$
, if
$\psi \in \mathcal {Q}_{k+1}$
, if
![]() $ \mathsf {PA} \vdash \psi \to \varphi $
, then
$ \mathsf {PA} \vdash \psi \to \varphi $
, then
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi $
.
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi $
.
Proof Since one can freely replace the bounded variables, it suffices to show that for any
![]() $\mathsf {HA}$
-formulas
$\mathsf {HA}$
-formulas
![]() $\varphi \in \mathcal {V}_{k+1}$
and
$\varphi \in \mathcal {V}_{k+1}$
and
![]() $\psi \in \mathcal {Q}_{k+1}$
such that the free variables of
$\psi \in \mathcal {Q}_{k+1}$
such that the free variables of
![]() $\varphi $
are not bounded in
$\varphi $
are not bounded in
![]() $\psi $
, if
$\psi $
, if
![]() $ \mathsf {PA} \vdash \psi \to \varphi $
, then
$ \mathsf {PA} \vdash \psi \to \varphi $
, then
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi $
. We show this assertion by induction on the structure of formulas in
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi $
. We show this assertion by induction on the structure of formulas in
![]() $\mathcal {V}_{k+1}$
.
$\mathcal {V}_{k+1}$
.
Case of
![]() $\varphi \in \mathcal {J}_{k+1}$
: Fix
$\varphi \in \mathcal {J}_{k+1}$
: Fix
![]() $\psi \in \mathcal {Q}_{k+1}$
such that the free variables of
$\psi \in \mathcal {Q}_{k+1}$
such that the free variables of
![]() $\varphi $
are not bounded in
$\varphi $
are not bounded in
![]() $\psi $
. Suppose
$\psi $
. Suppose
![]() $\mathsf {PA} \vdash \psi \to \varphi $
. Then, by Proposition 3.2.(2), we have
$\mathsf {PA} \vdash \psi \to \varphi $
. Then, by Proposition 3.2.(2), we have
![]() . By Lemma 3.14 and Lemma 3.12.(2), we have
. By Lemma 3.14 and Lemma 3.12.(2), we have
![]() . By Lemma 3.16, we have that
. By Lemma 3.16, we have that
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
![]() $\psi \to ((\varphi \to \varphi ) \to \varphi )$
, equivalently,
$\psi \to ((\varphi \to \varphi ) \to \varphi )$
, equivalently,
![]() $\psi \to \varphi $
.
$\psi \to \varphi $
.
Case of
![]() $\varphi :\equiv \varphi _1 \land \varphi _2 \in \mathcal {V}_{k+1}$
: Then
$\varphi :\equiv \varphi _1 \land \varphi _2 \in \mathcal {V}_{k+1}$
: Then
![]() $\varphi _1 , \varphi _2 \in \mathcal {V}_{k+1}$
. Fix
$\varphi _1 , \varphi _2 \in \mathcal {V}_{k+1}$
. Fix
![]() $\psi \in \mathcal {Q}_{k+1}$
such that the free variables of
$\psi \in \mathcal {Q}_{k+1}$
such that the free variables of
![]() $\varphi _1 \land \varphi _2$
are not bounded in
$\varphi _1 \land \varphi _2$
are not bounded in
![]() $\psi $
. Suppose
$\psi $
. Suppose
![]() $\mathsf {PA} \vdash \psi \to \varphi _1 \land \varphi _2$
. Then
$\mathsf {PA} \vdash \psi \to \varphi _1 \land \varphi _2$
. Then
![]() $\mathsf {PA} \vdash \psi \to \varphi _1 $
and
$\mathsf {PA} \vdash \psi \to \varphi _1 $
and
![]() $\mathsf {PA} \vdash \psi \to \varphi _2$
. By the induction hypothesis, we have
$\mathsf {PA} \vdash \psi \to \varphi _2$
. By the induction hypothesis, we have
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi _1 $
and
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi _1 $
and
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi _2 $
, and hence,
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi _2 $
, and hence,
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi _1 \land \varphi _2 $
.
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi _1 \land \varphi _2 $
.
Case of
![]() $\varphi : \equiv \forall x \varphi _1 \in \mathcal {V}_{k+1}$
: Then
$\varphi : \equiv \forall x \varphi _1 \in \mathcal {V}_{k+1}$
: Then
![]() $ \varphi _1 \in \mathcal {V}_{k+1}$
. Fix
$ \varphi _1 \in \mathcal {V}_{k+1}$
. Fix
![]() $\psi \in \mathcal {Q}_{k+1}$
such that the free variables of
$\psi \in \mathcal {Q}_{k+1}$
such that the free variables of
![]() $\forall x \varphi _1$
are not bounded in
$\forall x \varphi _1$
are not bounded in
![]() $\psi $
. In addition, assume that x does not appear in
$\psi $
. In addition, assume that x does not appear in
![]() $\psi $
without loss of generality. Suppose
$\psi $
without loss of generality. Suppose
![]() $\mathsf {PA} \vdash \psi \to \forall x \varphi _1$
. Then
$\mathsf {PA} \vdash \psi \to \forall x \varphi _1$
. Then
![]() $\mathsf {PA} \vdash \psi \to \varphi _1$
. By the induction hypothesis, we have that
$\mathsf {PA} \vdash \psi \to \varphi _1$
. By the induction hypothesis, we have that
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
![]() $\psi \to \varphi _1$
. Since
$\psi \to \varphi _1$
. Since
![]() $x \notin \mathrm { FV} \left ({\psi }\right )$
, we have
$x \notin \mathrm { FV} \left ({\psi }\right )$
, we have
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \forall x \varphi _1$
.
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \forall x \varphi _1$
.
Remark 3.18. Since
![]() $\Pi _{k+2} $
is a sub-class of
$\Pi _{k+2} $
is a sub-class of
![]() $\mathcal {V}_{k+1}$
and
$\mathcal {V}_{k+1}$
and
![]() $\mathcal {Q}_{k+1}$
contains all prenex formulas, we have [Reference Troelstra and van Dalen7, Theorem 6.14] (and a-fortiori Proposition 1.1) as a corollary of Theorem 3.17.
$\mathcal {Q}_{k+1}$
contains all prenex formulas, we have [Reference Troelstra and van Dalen7, Theorem 6.14] (and a-fortiori Proposition 1.1) as a corollary of Theorem 3.17.
Corollary 3.19. Let X be a set of
![]() $\mathsf {HA}$
-sentences in
$\mathsf {HA}$
-sentences in
![]() $\mathcal {Q}_{k+1}$
. For any
$\mathcal {Q}_{k+1}$
. For any
![]() $\mathsf {HA}$
-formulas
$\mathsf {HA}$
-formulas
![]() $\varphi \in \mathcal {V}_{k+1}$
and
$\varphi \in \mathcal {V}_{k+1}$
and
![]() $\psi \in \mathcal {Q}_{k+1}$
, if
$\psi \in \mathcal {Q}_{k+1}$
, if
![]() $ \mathsf {PA} + X \vdash \psi \to \varphi $
, then
$ \mathsf {PA} + X \vdash \psi \to \varphi $
, then
![]() $\mathsf {HA} +X +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi $
.
$\mathsf {HA} +X +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi $
.
Proof Assume
![]() $\mathsf {PA} +X \vdash \psi \to \varphi $
. Then there exists a finite number of sentences
$\mathsf {PA} +X \vdash \psi \to \varphi $
. Then there exists a finite number of sentences
![]() $\psi _0, \dots , \psi _m \in X $
such that
$\psi _0, \dots , \psi _m \in X $
such that
![]() $\mathsf {PA} + \psi _0+ \dots + \psi _m \vdash \psi \to \varphi $
. Since
$\mathsf {PA} + \psi _0+ \dots + \psi _m \vdash \psi \to \varphi $
. Since
![]() $\mathsf {PA}$
satisfies the deduction theorem, we have
$\mathsf {PA}$
satisfies the deduction theorem, we have
![]() $\mathsf {PA} \vdash \psi _0 \land \dots \land \psi _m \land \psi \to \varphi $
. Since
$\mathsf {PA} \vdash \psi _0 \land \dots \land \psi _m \land \psi \to \varphi $
. Since
![]() $\psi _0 \land \dots \land \psi _m \land \psi \in \mathcal {Q}_{k+1}$
, by Theorem 3.17, we have
$\psi _0 \land \dots \land \psi _m \land \psi \in \mathcal {Q}_{k+1}$
, by Theorem 3.17, we have
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi _0 \land \dots \land \psi _m \land \psi \to \varphi $
, and hence,
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi _0 \land \dots \land \psi _m \land \psi \to \varphi $
, and hence,
![]() $\mathsf {HA} + X +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi $
.
$\mathsf {HA} + X +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \psi \to \varphi $
.
4 The relation of the classes
 $\mathcal {R}_k$
and
$\mathcal {R}_k$
and
 $\mathcal {J}_k$
with the existing classes
$\mathcal {J}_k$
with the existing classes
 $\mathrm {U}_k$
and
$\mathrm {U}_k$
and
 $\mathrm {E}_k$
$\mathrm {E}_k$
In the following, we show that our classes
![]() $\mathcal {R}_k$
and
$\mathcal {R}_k$
and
![]() $\mathcal {J}_k$
in Definition 3.11 are in fact equivalent over
$\mathcal {J}_k$
in Definition 3.11 are in fact equivalent over
![]() $\mathsf {HA}$
to
$\mathsf {HA}$
to
![]() $\mathrm {U}_k $
and
$\mathrm {U}_k $
and
![]() $\mathrm {E}_k$
(see Definition 3.7) respectively.
$\mathrm {E}_k$
(see Definition 3.7) respectively.
Proposition 4.1.
![]() $\mathrm {U}_k^+=\mathcal {R}_k$
and
$\mathrm {U}_k^+=\mathcal {R}_k$
and
![]() $\mathrm {E}_k^+ = \mathcal {J}_k$
.
$\mathrm {E}_k^+ = \mathcal {J}_k$
.
Proof By induction on k. The base case is trivial. For the induction step, assume
![]() $\mathrm {U}_k^+=\mathcal {R}_k$
and
$\mathrm {U}_k^+=\mathcal {R}_k$
and
![]() $\mathrm {E}_k^+ = \mathcal {J}_k$
. We show
$\mathrm {E}_k^+ = \mathcal {J}_k$
. We show
-
1.
 $\varphi \in \mathrm {U}_{k+1}^+$
if and only if
$\varphi \in \mathrm {U}_{k+1}^+$
if and only if
 $\varphi \in \mathcal {R}_{k+1}$
,
$\varphi \in \mathcal {R}_{k+1}$
, -
2.
 $\varphi \in \mathrm {E}_{k+1}^+$
if and only if
$\varphi \in \mathrm {E}_{k+1}^+$
if and only if
 $\varphi \in \mathcal {J}_{k+1}$
,
$\varphi \in \mathcal {J}_{k+1}$
,
simultaneously by induction on the structure of formulas. If
![]() $\varphi $
is prime, since
$\varphi $
is prime, since
![]() $\varphi \in \mathrm {F}_0$
, we are done. Assume that items 1 and 2 hold for
$\varphi \in \mathrm {F}_0$
, we are done. Assume that items 1 and 2 hold for
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
. Using [Reference Troelstra and van Dalen7, Lemma 4.5(1)], we have
$\varphi _2$
. Using [Reference Troelstra and van Dalen7, Lemma 4.5(1)], we have
In the same manner, we also have
![]() $\varphi _1 \land \varphi _2 \in \mathrm {E}_{k+1}^+ \Leftrightarrow \varphi _1 \land \varphi _2\in \mathcal {J}_{k+1}$
,
$\varphi _1 \land \varphi _2 \in \mathrm {E}_{k+1}^+ \Leftrightarrow \varphi _1 \land \varphi _2\in \mathcal {J}_{k+1}$
,
![]() $\varphi _1 \lor \varphi _2 \in \mathrm {U}_{k+1}^+ \Leftrightarrow \varphi _1 \lor \varphi _2\in \mathcal {R}_{k+1}$
,
$\varphi _1 \lor \varphi _2 \in \mathrm {U}_{k+1}^+ \Leftrightarrow \varphi _1 \lor \varphi _2\in \mathcal {R}_{k+1}$
,
![]() $\varphi _1 \lor \varphi _2 \in \mathrm {E}_{k+1}^+ \Leftrightarrow \varphi _1 \lor \varphi _2\in \mathcal {J}_{k+1}$
. For
$\varphi _1 \lor \varphi _2 \in \mathrm {E}_{k+1}^+ \Leftrightarrow \varphi _1 \lor \varphi _2\in \mathcal {J}_{k+1}$
. For
![]() $\varphi _1 \to \varphi _2$
, using [Reference Troelstra and van Dalen7, Lemma 4.5(3)] we have
$\varphi _1 \to \varphi _2$
, using [Reference Troelstra and van Dalen7, Lemma 4.5(3)] we have
 $$ \begin{align*}\begin{array}{cl} & \varphi_1 \to \varphi_2 \in \mathrm{U}_{k+1}^+ \\[2pt] \Longleftrightarrow & \varphi_1 \in \mathrm{E}_{k+1}^+ \text{ and } \varphi_2 \in \mathrm{U}_{k+1}^+\\[2pt] \underset{\text{I.H.}}{\Longleftrightarrow} & \varphi_1 \in J_{k+1} \text{ and } \varphi_2 \in \mathcal{R}_{k+1} \\ \Longleftrightarrow & \varphi_1 \to \varphi_2 \in \mathcal{R}_{k+1}. \end{array} \end{align*} $$
$$ \begin{align*}\begin{array}{cl} & \varphi_1 \to \varphi_2 \in \mathrm{U}_{k+1}^+ \\[2pt] \Longleftrightarrow & \varphi_1 \in \mathrm{E}_{k+1}^+ \text{ and } \varphi_2 \in \mathrm{U}_{k+1}^+\\[2pt] \underset{\text{I.H.}}{\Longleftrightarrow} & \varphi_1 \in J_{k+1} \text{ and } \varphi_2 \in \mathcal{R}_{k+1} \\ \Longleftrightarrow & \varphi_1 \to \varphi_2 \in \mathcal{R}_{k+1}. \end{array} \end{align*} $$
In the same manner, we also have
![]() $\varphi _1 \to \varphi _2 \in \mathrm {E}_{k+1}^+ \Leftrightarrow \varphi _1 \to \varphi _2\in \mathcal {J}_{k+1}$
. For
$\varphi _1 \to \varphi _2 \in \mathrm {E}_{k+1}^+ \Leftrightarrow \varphi _1 \to \varphi _2\in \mathcal {J}_{k+1}$
. For
![]() $\forall x \varphi _1$
, using [Reference Troelstra and van Dalen7, Lemma 4.5(4,6)], we have
$\forall x \varphi _1$
, using [Reference Troelstra and van Dalen7, Lemma 4.5(4,6)], we have
and
In the same manner, we also have
![]() $\exists x \varphi _1 \in \mathrm {U}_{k+1}^+ \Leftrightarrow \exists x \varphi _1 \in \mathcal {R}_{k+1}$
and
$\exists x \varphi _1 \in \mathrm {U}_{k+1}^+ \Leftrightarrow \exists x \varphi _1 \in \mathcal {R}_{k+1}$
and
![]() $\exists x \varphi _1 \in \mathrm {E}_{k+1}^+ \Leftrightarrow \exists x \varphi _1 \in \mathcal {J}_{k+1}$
.
$\exists x \varphi _1 \in \mathrm {E}_{k+1}^+ \Leftrightarrow \exists x \varphi _1 \in \mathcal {J}_{k+1}$
.
Corollary 4.2.
![]() $\mathrm {U}_k=\mathcal {R}_k$
and
$\mathrm {U}_k=\mathcal {R}_k$
and
![]() $\mathrm {E}_k = \mathcal {J}_k$
.
$\mathrm {E}_k = \mathcal {J}_k$
.
Corollary 4.3. For a set X of
![]() $\mathsf{HA}$
-sentences in
$\mathsf{HA}$
-sentences in
![]() $\mathcal {Q}_{k+1}$
,
$\mathcal {Q}_{k+1}$
,
![]() $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
![]() $\mathrm {E}_{k+1}$
-conservative over
$\mathrm {E}_{k+1}$
-conservative over
![]() $\mathsf {HA} +X + {\Sigma _k}\text {-}\mathrm {LEM}$
.
$\mathsf {HA} +X + {\Sigma _k}\text {-}\mathrm {LEM}$
.
Proof Immediate from Corollaries 3.19 and 4.2 since
![]() $\mathcal {J}_{k+1}\subseteq \mathcal {V}_{k+1}$
.
$\mathcal {J}_{k+1}\subseteq \mathcal {V}_{k+1}$
.
Remark 4.4. Corollary 4.3 deals with the conservativity of the class of formulas in
![]() $\mathrm {E}_{k+1}$
, which seems to be strictly stronger than that for sentences in
$\mathrm {E}_{k+1}$
, which seems to be strictly stronger than that for sentences in
![]() $\mathrm {E}_{k+1}$
(cf. Section 6.1).
$\mathrm {E}_{k+1}$
(cf. Section 6.1).
Remark 4.5. Similar to Definition 3.11, define the classes
![]() $\mathcal {R}^{\prime }_k$
and
$\mathcal {R}^{\prime }_k$
and
![]() $\mathcal {J}^{\prime }_k$
as follows. Define
$\mathcal {J}^{\prime }_k$
as follows. Define
![]() $\mathcal {R}^{\prime }_0:=\mathcal {J}^{\prime }_0:=\Sigma _0 \, (=\Pi _0)$
and
$\mathcal {R}^{\prime }_0:=\mathcal {J}^{\prime }_0:=\Sigma _0 \, (=\Pi _0)$
and
![]() $\mathcal {R}^{\prime }_{k+1}$
and
$\mathcal {R}^{\prime }_{k+1}$
and
![]() $\mathcal {J}^{\prime }_{k+1}$
simultaneously as follows: Let E range over formulas in
$\mathcal {J}^{\prime }_{k+1}$
simultaneously as follows: Let E range over formulas in
![]() $\mathrm {E}_k^+$
, U over those in
$\mathrm {E}_k^+$
, U over those in
![]() $\mathrm {U}_k^+$
, R and
$\mathrm {U}_k^+$
, R and
![]() $R'$
over those in
$R'$
over those in
![]() $\mathcal {R}^{\prime }_{k+1}$
, and J and
$\mathcal {R}^{\prime }_{k+1}$
, and J and
![]() $J'$
over those in
$J'$
over those in
![]() $\mathcal {J}^{\prime }_{k+1}$
respectively. Then
$\mathcal {J}^{\prime }_{k+1}$
respectively. Then
![]() $\mathcal {R}^{\prime }_{k+1}$
and
$\mathcal {R}^{\prime }_{k+1}$
and
![]() $\mathcal {J}^{\prime }_{k+1}$
are inductively generated by the clauses
$\mathcal {J}^{\prime }_{k+1}$
are inductively generated by the clauses
-
1.
 $E, R\land R', R \lor R', \forall x R, J \to R\in \mathcal {R}^{\prime }_{k+1}$
;
$E, R\land R', R \lor R', \forall x R, J \to R\in \mathcal {R}^{\prime }_{k+1}$
; -
2.
 $U, J\land J', J \lor J', \exists x J, R \to J\in \mathcal {J}^{\prime }_{k+1}$
.
$U, J\land J', J \lor J', \exists x J, R \to J\in \mathcal {J}^{\prime }_{k+1}$
.
Then the proof of Proposition 4.1 shows that
![]() $\mathrm {U}_k^+=\mathcal {R}^{\prime }_k$
and
$\mathrm {U}_k^+=\mathcal {R}^{\prime }_k$
and
![]() $\mathrm {E}_k^+ = \mathcal {J}^{\prime }_k$
. Hence
$\mathrm {E}_k^+ = \mathcal {J}^{\prime }_k$
. Hence
![]() $\mathcal {R}_k=\mathcal {R}^{\prime }_k$
and
$\mathcal {R}_k=\mathcal {R}^{\prime }_k$
and
![]() $\mathcal {J}_k = \mathcal {J}^{\prime }_k$
.
$\mathcal {J}_k = \mathcal {J}^{\prime }_k$
.
Remark 4.6. Define
![]() $\mathcal {R}_{k+1}"$
and
$\mathcal {R}_{k+1}"$
and
![]() $\mathcal {J}_{k+1}"$
as for
$\mathcal {J}_{k+1}"$
as for
![]() $\mathcal {R}_{k+1}'$
and
$\mathcal {R}_{k+1}'$
and
![]() $\mathcal {J}_{k+1}'$
in Remark 4.5 with replacing
$\mathcal {J}_{k+1}'$
in Remark 4.5 with replacing
![]() $\mathrm {E}_k^+$
and
$\mathrm {E}_k^+$
and
![]() $\mathrm {U}_k^+$
by
$\mathrm {U}_k^+$
by
![]() $\Sigma _k$
and
$\Sigma _k$
and
![]() $\Pi _k$
. Then, as in the proof of Proposition 4.1 with using the prenex normal form theorems in
$\Pi _k$
. Then, as in the proof of Proposition 4.1 with using the prenex normal form theorems in
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
(cf. Remark 3.10), one can show
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
(cf. Remark 3.10), one can show
![]() $\mathrm {U}_{k+1}^+=\mathcal {R}^{\prime \prime }_{k+1}$
and
$\mathrm {U}_{k+1}^+=\mathcal {R}^{\prime \prime }_{k+1}$
and
![]() $\mathrm {E}_{k+1}^+ = \mathcal {J}^{\prime \prime }_{k+1}$
over
$\mathrm {E}_{k+1}^+ = \mathcal {J}^{\prime \prime }_{k+1}$
over
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
.
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
.
As described in Definition 3.7, the classes
![]() $\mathrm {E}_k$
and
$\mathrm {E}_k$
and
![]() $\mathrm {U}_k$
are originally defined by using the notion of alternation path. On the other hand, Remark 4.6 reveals that one can define these classes (via Remark 3.8) inductively without using the notion of alternation path. A technical advantage of this usual way of defining classes is that one can prove properties of these classes by induction on the structure of formulas in those classes.
$\mathrm {U}_k$
are originally defined by using the notion of alternation path. On the other hand, Remark 4.6 reveals that one can define these classes (via Remark 3.8) inductively without using the notion of alternation path. A technical advantage of this usual way of defining classes is that one can prove properties of these classes by induction on the structure of formulas in those classes.
5 Conservation theorems for the classes of formulas
In this section, we explore the notion that
![]() $\mathsf {PA} $
is
$\mathsf {PA} $
is
![]() $\Gamma $
-conservative over
$\Gamma $
-conservative over
![]() ${T}$
for semi-classical arithmetic
${T}$
for semi-classical arithmetic
![]() ${T}$
and a class
${T}$
and a class
![]() $\Gamma $
of formulas (especially,
$\Gamma $
of formulas (especially,
![]() $\Pi _k, \Sigma _k, \mathrm {U}_k, \mathrm {E}_k, \mathrm {F}_k$
etc.).
$\Pi _k, \Sigma _k, \mathrm {U}_k, \mathrm {E}_k, \mathrm {F}_k$
etc.).
Definition 5.1. For classes of
![]() $\mathsf {HA}$
-formulas
$\mathsf {HA}$
-formulas
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma '$
,
$\Gamma '$
,
![]() $\Gamma \lor \Gamma '$
is the class of formulas of form
$\Gamma \lor \Gamma '$
is the class of formulas of form
![]() $\varphi \lor \psi $
where
$\varphi \lor \psi $
where
![]() $\varphi \in \Gamma $
and
$\varphi \in \Gamma $
and
![]() $\psi \in \Gamma '$
.
$\psi \in \Gamma '$
.
We recall the notion of duals for prenex formulas from [Reference Akama, Berardi, Hayashi and Kohlenbach1, Reference Troelstra and van Dalen6].
Definition 5.2 (cf. [Reference Troelstra and van Dalen6, Definition 3.2]).
For any formula
![]() $\varphi $
in prenex normal form, we define the dual
$\varphi $
in prenex normal form, we define the dual
![]() $\varphi ^{\perp }$
of
$\varphi ^{\perp }$
of
![]() $\varphi $
inductively as follows:
$\varphi $
inductively as follows:
-
1.
 $\varphi ^{\perp } : \equiv \neg \varphi $
if
$\varphi ^{\perp } : \equiv \neg \varphi $
if
 $\varphi $
is quantifier-free;
$\varphi $
is quantifier-free; -
2.
 $(\forall x \varphi )^{\perp } : \equiv \exists x (\varphi )^{\perp }$
;
$(\forall x \varphi )^{\perp } : \equiv \exists x (\varphi )^{\perp }$
; -
3.
 $(\exists x \varphi )^{\perp } : \equiv \forall x (\varphi )^{\perp }$
.
$(\exists x \varphi )^{\perp } : \equiv \forall x (\varphi )^{\perp }$
.
Remark 5.3. For
![]() $\varphi $
in
$\varphi $
in
![]() $\Sigma _k$
(resp.
$\Sigma _k$
(resp.
![]() $\Pi _k$
),
$\Pi _k$
),
![]() $\varphi ^{\perp }$
is in
$\varphi ^{\perp }$
is in
![]() $\Pi _k$
(resp.
$\Pi _k$
(resp.
![]() $\Sigma _k$
),
$\Sigma _k$
),
![]() $\mathrm { FV} \left ({\varphi ^{\perp }}\right )=\mathrm { FV} \left ({\varphi }\right )$
and
$\mathrm { FV} \left ({\varphi ^{\perp }}\right )=\mathrm { FV} \left ({\varphi }\right )$
and
![]() $\left ( \varphi ^{\perp } \right )^{\perp }$
is equivalent to
$\left ( \varphi ^{\perp } \right )^{\perp }$
is equivalent to
![]() $\varphi $
over
$\varphi $
over
![]() $\mathsf {HA}$
. For each prenex formula
$\mathsf {HA}$
. For each prenex formula
![]() $\varphi $
,
$\varphi $
,
![]() $\varphi ^{\perp }$
implies
$\varphi ^{\perp }$
implies
![]() $\neg \varphi $
intuitionistically. On the other hand, the converse direction for formulas in
$\neg \varphi $
intuitionistically. On the other hand, the converse direction for formulas in
![]() $\Sigma _k$
(resp.
$\Sigma _k$
(resp.
![]() $\Pi _k$
) is equivalent to
$\Pi _k$
) is equivalent to
![]() ${\Sigma _{k-1}}\text {-}\mathrm {DNE}$
(resp.
${\Sigma _{k-1}}\text {-}\mathrm {DNE}$
(resp.
![]() ${\Sigma _{k}}\text {-}\mathrm {DNE}$
). Then it follows that for
${\Sigma _{k}}\text {-}\mathrm {DNE}$
). Then it follows that for
![]() $\varphi \in \Sigma _k$
there exists
$\varphi \in \Sigma _k$
there exists
![]() $\varphi '\in \Pi _k$
such that
$\varphi '\in \Pi _k$
such that
![]() $\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\varphi }\right )$
and
$\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\varphi }\right )$
and
![]() $\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {DNE} \vdash \varphi ' \leftrightarrow \neg \varphi $
(cf. [Reference Troelstra and van Dalen7, Lemma 4.8(2)]). In addition,
$\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {DNE} \vdash \varphi ' \leftrightarrow \neg \varphi $
(cf. [Reference Troelstra and van Dalen7, Lemma 4.8(2)]). In addition,
![]() $\neg \varphi ^{\perp }$
implies
$\neg \varphi ^{\perp }$
implies
![]() $\neg \neg \varphi $
in the presence of
$\neg \neg \varphi $
in the presence of
![]() ${\Sigma _{k-1}}\text {-}\mathrm {DNE}$
for the both cases of
${\Sigma _{k-1}}\text {-}\mathrm {DNE}$
for the both cases of
![]() $\varphi \in \Sigma _k$
and
$\varphi \in \Sigma _k$
and
![]() $\varphi \in \Pi _k$
. Note also that
$\varphi \in \Pi _k$
. Note also that
![]() $\mathsf {PA}$
proves
$\mathsf {PA}$
proves
![]() $\varphi \lor \varphi ^{\perp }$
for each prenex formula
$\varphi \lor \varphi ^{\perp }$
for each prenex formula
![]() $\varphi $
. We refer the reader to [Reference Troelstra and van Dalen6, Section 3] for more information about the dual principles for prenex formulas in semi-classical arithmetic.
$\varphi $
. We refer the reader to [Reference Troelstra and van Dalen6, Section 3] for more information about the dual principles for prenex formulas in semi-classical arithmetic.
5.1 Conservation theorems for
 $\Pi _{k}, \Sigma _k, \mathrm {E}_k$
and
$\Pi _{k}, \Sigma _k, \mathrm {E}_k$
and
 $\mathrm {F}_k$
$\mathrm {F}_k$
Definition 5.4. Let
![]() ${T}$
be a theory in the language of
${T}$
be a theory in the language of
![]() $\mathsf {HA}$
and
$\mathsf {HA}$
and
![]() $\Gamma $
be a class of
$\Gamma $
be a class of
![]() $\mathsf {HA}$
-formulas.
$\mathsf {HA}$
-formulas.
-
•
 ${T}$
is closed under
${T}$
is closed under
 ${\Gamma }\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
if
${\Gamma }\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
if
 ${T} \vdash \neg \neg \varphi $
implies
${T} \vdash \neg \neg \varphi $
implies
 ${T} \vdash \varphi $
for all
${T} \vdash \varphi $
for all
 $\varphi \in \Gamma $
.
$\varphi \in \Gamma $
. -
•
 ${T}$
is closed under
${T}$
is closed under
 ${\Gamma }\text {-}\mathrm {CD}\text {-}\mathrm {R}$
if
${\Gamma }\text {-}\mathrm {CD}\text {-}\mathrm {R}$
if
 ${T} \vdash \forall x (\varphi \lor \psi ) $
implies
${T} \vdash \forall x (\varphi \lor \psi ) $
implies
 ${T} \vdash \varphi \lor \forall x \psi $
for all
${T} \vdash \varphi \lor \forall x \psi $
for all
 $\varphi ,\psi \in \Gamma $
such that
$\varphi ,\psi \in \Gamma $
such that
 $x \notin \mathrm { FV} \left ({\varphi }\right )$
.
$x \notin \mathrm { FV} \left ({\varphi }\right )$
. -
•
 ${T}$
is closed under
${T}$
is closed under
 ${\Gamma }\text {-}\mathrm {DML}\text {-}\mathrm {R}$
(resp.
${\Gamma }\text {-}\mathrm {DML}\text {-}\mathrm {R}$
(resp.
 ${\Gamma }\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
) if
${\Gamma }\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
) if
 ${T} \vdash \neg (\varphi \land \psi ) $
implies
${T} \vdash \neg (\varphi \land \psi ) $
implies
 ${T} \vdash \neg \varphi \lor \neg \psi $
(resp.
${T} \vdash \neg \varphi \lor \neg \psi $
(resp.
 ${T} \vdash \varphi ^{\perp } \lor \psi ^{\perp }$
) for all
${T} \vdash \varphi ^{\perp } \lor \psi ^{\perp }$
) for all
 $\varphi , \psi \in \Gamma $
.
$\varphi , \psi \in \Gamma $
.
Note that
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
in the above may contain free variables.
$\psi $
in the above may contain free variables.
As mentioned in [Reference Troelstra and van Dalen14, Section 3.5.1],
![]() ${\Sigma _1}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
is known as Markov’s rule (for primitive recursive predicates). The fact that
${\Sigma _1}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
is known as Markov’s rule (for primitive recursive predicates). The fact that
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() $\Sigma _1$
-conservative (equivalently,
$\Sigma _1$
-conservative (equivalently,
![]() $\Pi _2$
-conservative) over
$\Pi _2$
-conservative) over
![]() $\mathsf {HA}$
implies that
$\mathsf {HA}$
implies that
![]() $\mathsf {HA}$
is closed under Markov’s rule (
$\mathsf {HA}$
is closed under Markov’s rule (
![]() ${\Sigma _1}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
), and vice versa. The generalization
${\Sigma _1}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
), and vice versa. The generalization
![]() ${\Sigma _k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
of Markov’s rule is already mentioned in [Reference Troelstra and van Dalen8, Section 4.4]. It is easy to see that for semi-classical arithmetic
${\Sigma _k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
of Markov’s rule is already mentioned in [Reference Troelstra and van Dalen8, Section 4.4]. It is easy to see that for semi-classical arithmetic
![]() ${T}$
, if
${T}$
, if
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() $\Sigma _k$
-conservative over
$\Sigma _k$
-conservative over
![]() ${T}$
, then
${T}$
, then
![]() ${T}$
is closed under
${T}$
is closed under
![]() ${\Sigma _k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
. Then it is natural to ask about the converse. As we show in Theorem 5.9, this is also the case (note that the case for
${\Sigma _k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
. Then it is natural to ask about the converse. As we show in Theorem 5.9, this is also the case (note that the case for
![]() $k=2$
is essentially shown in the proof of [Reference Troelstra and van Dalen12, Proposition 3.3]).
$k=2$
is essentially shown in the proof of [Reference Troelstra and van Dalen12, Proposition 3.3]).
The following are our “reversal” results.
Lemma 5.5. Let
![]() ${T} $
be a theory containing
${T} $
be a theory containing
![]() $\mathsf {HA}$
. If
$\mathsf {HA}$
. If
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() $\left (\Sigma _k\lor \Pi _k\right )$
-conservative over
$\left (\Sigma _k\lor \Pi _k\right )$
-conservative over
![]() ${T}$
, then
${T}$
, then
![]() $T \vdash {\Sigma _{k}}\text {-}\mathrm {LEM}$
.
$T \vdash {\Sigma _{k}}\text {-}\mathrm {LEM}$
.
Proof Fix
![]() $\xi \in \Sigma _{k}$
. Let
$\xi \in \Sigma _{k}$
. Let
![]() $\xi ^{\perp }\in \Pi _{k}$
be the dual of
$\xi ^{\perp }\in \Pi _{k}$
be the dual of
![]() $\xi $
. Since
$\xi $
. Since
![]() $\mathsf {PA} \vdash \xi \lor \xi ^{\perp }$
, by our assumption, we have
$\mathsf {PA} \vdash \xi \lor \xi ^{\perp }$
, by our assumption, we have
![]() ${T} \vdash \xi \lor \xi ^{\perp }$
, and hence,
${T} \vdash \xi \lor \xi ^{\perp }$
, and hence,
![]() ${T} \vdash \xi \lor \neg \xi $
.
${T} \vdash \xi \lor \neg \xi $
.
Lemma 5.6. Let
![]() ${T}$
be a theory containing
${T}$
be a theory containing
![]() $\mathsf {HA}$
. If
$\mathsf {HA}$
. If
![]() ${T}$
is closed under
${T}$
is closed under
![]() ${\Sigma _{k+1}}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
, then T proves
${\Sigma _{k+1}}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
, then T proves
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
.
${\Sigma _k}\text {-}\mathrm {LEM}$
.
Proof We show that for all
![]() $m\leq k$
,
$m\leq k$
,
![]() ${T}$
proves
${T}$
proves
![]() ${\Sigma _m}\text {-}\mathrm {LEM}$
, by induction on m. Since
${\Sigma _m}\text {-}\mathrm {LEM}$
, by induction on m. Since
![]() ${T}$
contains
${T}$
contains
![]() $\mathsf {HA}$
, the base case is trivial. Assume
$\mathsf {HA}$
, the base case is trivial. Assume
![]() $m+1\leq k$
and
$m+1\leq k$
and
![]() ${T} \vdash {\Sigma _m}\text {-}\mathrm {LEM}$
. Let
${T} \vdash {\Sigma _m}\text {-}\mathrm {LEM}$
. Let
![]() $\varphi \in \Sigma _{m+1}$
. Since
$\varphi \in \Sigma _{m+1}$
. Since
![]() $\mathsf {HA} \vdash \neg \neg (\varphi \lor \neg \varphi )$
, by Remark 5.3 and the fact that
$\mathsf {HA} \vdash \neg \neg (\varphi \lor \neg \varphi )$
, by Remark 5.3 and the fact that
![]() ${\Sigma _m}\text {-}\mathrm {LEM}$
implies
${\Sigma _m}\text {-}\mathrm {LEM}$
implies
![]() ${\Sigma _m}\text {-}\mathrm {DNE}$
, we have
${\Sigma _m}\text {-}\mathrm {DNE}$
, we have
![]() ${T} \vdash \neg \neg (\varphi \lor \varphi ^{\perp })$
where
${T} \vdash \neg \neg (\varphi \lor \varphi ^{\perp })$
where
![]() $\varphi ^{\perp } \in \Pi _{m+1}$
. Since
$\varphi ^{\perp } \in \Pi _{m+1}$
. Since
![]() $\varphi \lor \varphi ^{\perp }$
is equivalent over
$\varphi \lor \varphi ^{\perp }$
is equivalent over
![]() $\mathsf {HA}$
to some formula in
$\mathsf {HA}$
to some formula in
![]() $\Sigma _{m+2}$
(cf. [Reference Troelstra and van Dalen7, Lemma 4.4]), by
$\Sigma _{m+2}$
(cf. [Reference Troelstra and van Dalen7, Lemma 4.4]), by
![]() ${\Sigma _{k+1}}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
, we have
${\Sigma _{k+1}}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
, we have
![]() ${T} \vdash \varphi \lor \varphi ^{\perp }$
, and hence,
${T} \vdash \varphi \lor \varphi ^{\perp }$
, and hence,
![]() $\varphi \lor \neg \varphi $
. Thus we have shown
$\varphi \lor \neg \varphi $
. Thus we have shown
![]() ${T} \vdash {\Sigma _{m+1}}\text {-}\mathrm {LEM}$
.
${T} \vdash {\Sigma _{m+1}}\text {-}\mathrm {LEM}$
.
Lemma 5.7. Let
![]() ${T}$
be a theory containing
${T}$
be a theory containing
![]() $\mathsf {HA}$
. If
$\mathsf {HA}$
. If
![]() ${T}$
is closed under
${T}$
is closed under
![]() ${\Sigma _{k}}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
, then T proves
${\Sigma _{k}}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
, then T proves
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
.
${\Sigma _k}\text {-}\mathrm {LEM}$
.
Proof We show that for all
![]() $m\leq k$
,
$m\leq k$
,
![]() ${T}$
proves
${T}$
proves
![]() ${\Sigma _m}\text {-}\mathrm {LEM}$
, by induction on m. Since
${\Sigma _m}\text {-}\mathrm {LEM}$
, by induction on m. Since
![]() ${T}$
contains
${T}$
contains
![]() $\mathsf {HA}$
, the base case is trivial. Assume
$\mathsf {HA}$
, the base case is trivial. Assume
![]() $m+1\leq k$
and
$m+1\leq k$
and
![]() ${T} \vdash {\Sigma _m}\text {-}\mathrm {LEM}$
. Let
${T} \vdash {\Sigma _m}\text {-}\mathrm {LEM}$
. Let
![]() $\varphi :\equiv \exists x \varphi _1$
where
$\varphi :\equiv \exists x \varphi _1$
where
![]() $\varphi _1\in \Pi _m$
. Since
$\varphi _1\in \Pi _m$
. Since
![]() ${T}$
proves
${T}$
proves
![]() ${\Pi _m}\text {-}\mathrm {LEM}$
and
${\Pi _m}\text {-}\mathrm {LEM}$
and
![]() ${\Sigma _m}\text {-}\mathrm {DNE}$
, we have
${\Sigma _m}\text {-}\mathrm {DNE}$
, we have
![]() ${T} \vdash \varphi _1 \lor \neg \varphi _1$
, and hence,
${T} \vdash \varphi _1 \lor \neg \varphi _1$
, and hence,
![]() ${T}\vdash \varphi _1 \lor \varphi _1^{\perp }$
(cf. Remark 5.3). Then
${T}\vdash \varphi _1 \lor \varphi _1^{\perp }$
(cf. Remark 5.3). Then
![]() ${T} \vdash \forall x(\exists x \varphi _1 \lor \varphi _1^{\perp })$
follows. Since
${T} \vdash \forall x(\exists x \varphi _1 \lor \varphi _1^{\perp })$
follows. Since
![]() $\exists x \varphi _1 ,\varphi _1^{\perp } \in \Sigma _{m+1}$
, by
$\exists x \varphi _1 ,\varphi _1^{\perp } \in \Sigma _{m+1}$
, by
![]() ${\Sigma _{k}}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
, we have
${\Sigma _{k}}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
, we have
![]() ${T} \vdash \exists x \varphi _1 \lor \forall x \varphi _1^{\perp }$
, and hence,
${T} \vdash \exists x \varphi _1 \lor \forall x \varphi _1^{\perp }$
, and hence,
![]() ${T} \vdash \exists x \varphi _1 \lor \neg \exists x \varphi _1$
. Thus we have shown
${T} \vdash \exists x \varphi _1 \lor \neg \exists x \varphi _1$
. Thus we have shown
![]() ${T} \vdash {\Sigma _{m+1}}\text {-}\mathrm {LEM}$
.
${T} \vdash {\Sigma _{m+1}}\text {-}\mathrm {LEM}$
.
Lemma 5.8. Let
![]() ${T}$
be a theory containing
${T}$
be a theory containing
![]() $\mathsf {HA}$
. Then
$\mathsf {HA}$
. Then
![]() ${T}$
is closed under
${T}$
is closed under
![]() ${\Pi _{k}}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
if and only if
${\Pi _{k}}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
if and only if
![]() ${T}$
is closed under
${T}$
is closed under
![]() ${\Sigma _{k}}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
.
${\Sigma _{k}}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
.
Proof We first show the “only if” direction. Assume that
![]() ${T}$
is closed under
${T}$
is closed under
![]() ${\Pi _{k}}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
and
${\Pi _{k}}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
and
![]() ${T} \vdash \neg \neg \varphi $
where
${T} \vdash \neg \neg \varphi $
where
![]() $\varphi \in \Sigma _k$
. Since
$\varphi \in \Sigma _k$
. Since
![]() $\neg \neg \varphi $
is equivalent over
$\neg \neg \varphi $
is equivalent over
![]() $\mathsf {HA}$
to
$\mathsf {HA}$
to
![]() $\neg (\neg \varphi \land \neg \varphi )$
, by Remark 5.3, we have
$\neg (\neg \varphi \land \neg \varphi )$
, by Remark 5.3, we have
Since
![]() $\varphi ^{\perp } \in \Pi _k$
, by
$\varphi ^{\perp } \in \Pi _k$
, by
![]() ${\Pi _{k}}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
, we have
${\Pi _{k}}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
, we have
![]() ${T} \vdash \left (\varphi ^{\perp }\right )^{\perp } \lor \left ( \varphi ^{\perp } \right )^{\perp }$
, and hence,
${T} \vdash \left (\varphi ^{\perp }\right )^{\perp } \lor \left ( \varphi ^{\perp } \right )^{\perp }$
, and hence,
![]() ${T} \vdash \varphi $
(cf. Remark 5.3).
${T} \vdash \varphi $
(cf. Remark 5.3).
For the converse direction, assume that
![]() ${T}$
is closed under
${T}$
is closed under
![]() ${\Sigma _{k}}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
and
${\Sigma _{k}}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
and
![]() ${T} \vdash \neg (\varphi \land \psi )$
where
${T} \vdash \neg (\varphi \land \psi )$
where
![]() $\varphi , \psi \in \Pi _k$
. Since
$\varphi , \psi \in \Pi _k$
. Since
![]() $\neg (\varphi \land \psi )$
is intuitionistically equivalent to
$\neg (\varphi \land \psi )$
is intuitionistically equivalent to
![]() $\neg (\neg \neg \varphi \land \neg \neg \psi )$
, by Lemma 5.6 and Remark 5.3 (note that
$\neg (\neg \neg \varphi \land \neg \neg \psi )$
, by Lemma 5.6 and Remark 5.3 (note that
![]() ${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
implies
${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
implies
![]() ${\Sigma _{k-1}}\text {-}\mathrm {DNE}$
), we have
${\Sigma _{k-1}}\text {-}\mathrm {DNE}$
), we have
![]() ${T} \vdash \neg \left (\neg \varphi ^{\perp } \land \neg \psi ^{\perp } \right )$
where
${T} \vdash \neg \left (\neg \varphi ^{\perp } \land \neg \psi ^{\perp } \right )$
where
![]() $\varphi ^{\perp } , \psi ^{\perp } \in \Sigma _k$
. Then
$\varphi ^{\perp } , \psi ^{\perp } \in \Sigma _k$
. Then
![]() ${T} \vdash \neg \neg \left (\varphi ^{\perp } \lor \psi ^{\perp } \right )$
follows. By
${T} \vdash \neg \neg \left (\varphi ^{\perp } \lor \psi ^{\perp } \right )$
follows. By
![]() ${\Sigma _{k}}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
, we have
${\Sigma _{k}}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
, we have
![]() ${T} \vdash \varphi ^{\perp } \lor \psi ^{\perp }$
.
${T} \vdash \varphi ^{\perp } \lor \psi ^{\perp }$
.
Theorem 5.9. Let
![]() ${T}$
be semi-classical arithmetic and X be a set of
${T}$
be semi-classical arithmetic and X be a set of
![]() $\mathsf {HA}$
-sentences in
$\mathsf {HA}$
-sentences in
![]() $\mathcal {Q}_{k+1}$
. The following are pairwise equivalent:
$\mathcal {Q}_{k+1}$
. The following are pairwise equivalent:
-
1.
 $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
 $\mathcal {V}_{k+1}$
-conservative over
$\mathcal {V}_{k+1}$
-conservative over
 ${T} +X ;$
${T} +X ;$
-
2.
 $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
 $\Pi _{k+2}$
-conservative over
$\Pi _{k+2}$
-conservative over
 ${T}+X ;$
${T}+X ;$
-
3.
 $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
 $\Sigma _{k+1}$
-conservative over
$\Sigma _{k+1}$
-conservative over
 ${T}+X ;$
${T}+X ;$
-
4.
 ${T}+X$
is closed under
${T}+X$
is closed under
 ${\Sigma _{k+1}}\text {-}\mathrm {DNE}\text {-}\mathrm {R};$
${\Sigma _{k+1}}\text {-}\mathrm {DNE}\text {-}\mathrm {R};$
-
5.
 ${T}+X$
is closed under
${T}+X$
is closed under
 ${\Pi _{k+1}}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R};$
${\Pi _{k+1}}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R};$
-
6.
 $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
 $\mathrm {E}_{k+1}$
-conservative over
$\mathrm {E}_{k+1}$
-conservative over
 ${T}+X ;$
${T}+X ;$
-
7.
 $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
 $\mathrm {F}_{k}$
-conservative over
$\mathrm {F}_{k}$
-conservative over
 ${T}+X ;$
${T}+X ;$
-
8.
 $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
 $\left (\Sigma _k\lor \Pi _k\right )$
-conservative over
$\left (\Sigma _k\lor \Pi _k\right )$
-conservative over
 ${T}+X ;$
${T}+X ;$
-
9.
 ${T} +X \vdash {\Sigma _k}\text {-}\mathrm {LEM};$
${T} +X \vdash {\Sigma _k}\text {-}\mathrm {LEM};$
-
10.
 ${T} +X \vdash {\Sigma _k}\text {-}\mathrm {CD};$
${T} +X \vdash {\Sigma _k}\text {-}\mathrm {CD};$
-
11.
 ${T} +X $
is closed under
${T} +X $
is closed under
 ${\Sigma _k}\text {-}\mathrm {CD}\text {-}\mathrm {R};$
${\Sigma _k}\text {-}\mathrm {CD}\text {-}\mathrm {R};$
where
![]() ${\Sigma _k}\text {-}\mathrm {CD}$
is the scheme
${\Sigma _k}\text {-}\mathrm {CD}$
is the scheme
![]() $\forall x (\varphi \lor \psi ) \to \varphi \lor \forall x \psi $
with
$\forall x (\varphi \lor \psi ) \to \varphi \lor \forall x \psi $
with
![]() $\varphi ,\psi \in \Sigma _k$
such that
$\varphi ,\psi \in \Sigma _k$
such that
![]() $x \notin \mathrm { FV} \left ({\varphi }\right )$
(cf. [Reference Troelstra and van Dalen6, Section 7]).
$x \notin \mathrm { FV} \left ({\varphi }\right )$
(cf. [Reference Troelstra and van Dalen6, Section 7]).
Proof The implications (1)
![]() $\to $
(6)
$\to $
(6)
![]() $\to $
(7)
$\to $
(7)
![]() $\to $
(8), (1)
$\to $
(8), (1)
![]() $\to $
(2)
$\to $
(2)
![]() $\to $
(3)
$\to $
(3)
![]() $\to $
(4) and (9)
$\to $
(4) and (9)
![]() $\to $
(10)
$\to $
(10)
![]() $\to $
(11) are trivial (cf. Corollary 4.3 and Remark 3.18). The implications (8)
$\to $
(11) are trivial (cf. Corollary 4.3 and Remark 3.18). The implications (8)
![]() $\to $
(9), (4)
$\to $
(9), (4)
![]() $\to $
(9), (11)
$\to $
(9), (11)
![]() $\to $
(9) and (9)
$\to $
(9) and (9)
![]() $\to $
(1) are by Lemmata 5.5, 5.6, 5.7 and Corollary 3.19 respectively. The equivalence (4)
$\to $
(1) are by Lemmata 5.5, 5.6, 5.7 and Corollary 3.19 respectively. The equivalence (4)
![]() $\leftrightarrow $
(5) is by Lemma 5.8.
$\leftrightarrow $
(5) is by Lemma 5.8.
5.2 Conservation theorem for
 $\mathrm {U}_k$
$\mathrm {U}_k$
In contrast to the fact that
![]() $\mathrm {E}_{k+1}$
-conservativity and
$\mathrm {E}_{k+1}$
-conservativity and
![]() $\mathrm {F}_{k}$
-conservativity are characterized by
$\mathrm {F}_{k}$
-conservativity are characterized by
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
(see Theorem 5.9),
${\Sigma _k}\text {-}\mathrm {LEM}$
(see Theorem 5.9),
![]() $\mathrm {U}_{k+1}$
-conservativity requires more than
$\mathrm {U}_{k+1}$
-conservativity requires more than
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
:
${\Sigma _k}\text {-}\mathrm {LEM}$
:
Proposition 5.10.
![]() $\mathsf {PA} $
is not
$\mathsf {PA} $
is not
![]() $(\Pi _1\lor \Pi _1)$
-conservative over
$(\Pi _1\lor \Pi _1)$
-conservative over
![]() $\mathsf {HA}$
.
$\mathsf {HA}$
.
Proof We use the same argument as in [Reference Troelstra and van Dalen7, Section 3]. Suppose that
![]() $\mathsf {PA} $
is conservative over
$\mathsf {PA} $
is conservative over
![]() $\mathsf {HA}$
for all formulas
$\mathsf {HA}$
for all formulas
![]() $\varphi \lor \psi $
with
$\varphi \lor \psi $
with
![]() $\varphi , \psi \in \Pi _1$
. Let
$\varphi , \psi \in \Pi _1$
. Let
![]() $\Phi (x)$
be the following formula:
$\Phi (x)$
be the following formula:
where
![]() ${\textrm {T}}$
and
${\textrm {T}}$
and
![]() ${\textrm {U}}$
are the standard primitive recursive predicate and function from the Kleene normal form theorem. Since
${\textrm {U}}$
are the standard primitive recursive predicate and function from the Kleene normal form theorem. Since
is provable in
![]() $\mathsf {HA}$
, we have
$\mathsf {HA}$
, we have
![]() $\mathsf {PA} \vdash \Phi (x)$
. Then, by our assumption, we have
$\mathsf {PA} \vdash \Phi (x)$
. Then, by our assumption, we have
![]() $\mathsf {HA} \vdash \Phi (x)$
, and hence,
$\mathsf {HA} \vdash \Phi (x)$
, and hence,
![]() $\mathsf {HA} \vdash \forall x \Phi (x)$
. On the other hand, as shown in the proof of [Reference Troelstra and van Dalen7, Proposition 3.1],
$\mathsf {HA} \vdash \forall x \Phi (x)$
. On the other hand, as shown in the proof of [Reference Troelstra and van Dalen7, Proposition 3.1],
![]() $\neg \forall x \Phi (x) $
is provable in
$\neg \forall x \Phi (x) $
is provable in
![]() $\mathsf {HA} + {\textrm {CT}}_0$
where
$\mathsf {HA} + {\textrm {CT}}_0$
where
![]() ${\textrm {CT}}_0$
is the arithmetical form of Church’s thesis from [Reference Troelstra and van Dalen13, Section 3.2.14]. Then we have
${\textrm {CT}}_0$
is the arithmetical form of Church’s thesis from [Reference Troelstra and van Dalen13, Section 3.2.14]. Then we have
![]() $\mathsf {HA} + {\textrm {CT}}_0 \vdash \perp $
, which is a contradiction by [Reference Troelstra and van Dalen13, Section 3.2.22].
$\mathsf {HA} + {\textrm {CT}}_0 \vdash \perp $
, which is a contradiction by [Reference Troelstra and van Dalen13, Section 3.2.22].
Let
![]() ${T}$
be semi-classical arithmetic. By Theorems 3.9.(2) and 5.9, if
${T}$
be semi-classical arithmetic. By Theorems 3.9.(2) and 5.9, if
![]() ${T}$
proves
${T}$
proves
![]() ${(\Pi _{k+1} \lor \Pi _{k+1})}\text {-}\mathrm {DNE}$
, then
${(\Pi _{k+1} \lor \Pi _{k+1})}\text {-}\mathrm {DNE}$
, then
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() $\mathrm {U}_{k+1}$
-conservative (and hence, a-fortiori
$\mathrm {U}_{k+1}$
-conservative (and hence, a-fortiori
![]() $(\Pi _{k+1} \lor \Pi _{k+1})$
-conservative) over
$(\Pi _{k+1} \lor \Pi _{k+1})$
-conservative) over
![]() ${T}$
. On the other hand, if
${T}$
. On the other hand, if
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() $(\Pi _{k+1} \lor \Pi _{k+1})$
-conservative over
$(\Pi _{k+1} \lor \Pi _{k+1})$
-conservative over
![]() ${T}$
, then
${T}$
, then
![]() ${T}$
proves
${T}$
proves
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
by Lemma 5.5 and the fact that both of
${\Sigma _k}\text {-}\mathrm {LEM}$
by Lemma 5.5 and the fact that both of
![]() $\Sigma _k$
and
$\Sigma _k$
and
![]() $\Pi _k$
can be seen as sub-classes of
$\Pi _k$
can be seen as sub-classes of
![]() $\Pi _{k+1}$
. Thus
$\Pi _{k+1}$
. Thus
![]() ${(\Pi _{k+1} \lor \Pi _{k+1})}\text {-}\mathrm {DNE}$
implies the
${(\Pi _{k+1} \lor \Pi _{k+1})}\text {-}\mathrm {DNE}$
implies the
![]() $\mathrm {U}_{k+1}$
-conservativity, which implies the
$\mathrm {U}_{k+1}$
-conservativity, which implies the
![]() $(\Pi _{k+1} \lor \Pi _{k+1})$
-conservativity, which implies
$(\Pi _{k+1} \lor \Pi _{k+1})$
-conservativity, which implies
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
and not vice versa. For further studying the relation of the
${\Sigma _k}\text {-}\mathrm {LEM}$
and not vice versa. For further studying the relation of the
![]() $\mathrm {U}_{k+1}$
/
$\mathrm {U}_{k+1}$
/
![]() $(\Pi _{k+1} \lor \Pi _{k+1})$
-conservativity and semi-classical arithmetic, we introduce some extended classes of
$(\Pi _{k+1} \lor \Pi _{k+1})$
-conservativity and semi-classical arithmetic, we introduce some extended classes of
![]() $\Pi _k$
and
$\Pi _k$
and
![]() $\Sigma _k$
.
$\Sigma _k$
.
Definition 5.11.
-
•
 $\bigvee \Pi _k$
denotes the class consisting of disjunctions of formulas in
$\bigvee \Pi _k$
denotes the class consisting of disjunctions of formulas in
 $\Pi _k$
.
$\Pi _k$
. -
• A class
 $\mathrm {E}\Pi _k$
is defined by the following clauses:
$\mathrm {E}\Pi _k$
is defined by the following clauses:-
–
 $\varphi \in \Pi _k$
;
$\varphi \in \Pi _k$
; -
– If
 $\varphi , \psi \in \mathrm {E}\Pi _k$
, then
$\varphi , \psi \in \mathrm {E}\Pi _k$
, then
 $\varphi \lor \psi \in \mathrm {E}\Pi _k$
;
$\varphi \lor \psi \in \mathrm {E}\Pi _k$
; -
– If
 $\varphi \in \mathrm {E}\Pi _k$
, then
$\varphi \in \mathrm {E}\Pi _k$
, then
 $\forall x \varphi \in \mathrm {E}\Pi _k$
.
$\forall x \varphi \in \mathrm {E}\Pi _k$
.
-
-
•
 $\mathrm {E}\Sigma _{k+1}$
denotes the class consisting of formulas of the form
$\mathrm {E}\Sigma _{k+1}$
denotes the class consisting of formulas of the form
 $\exists x_1, \dots , x_n \varphi $
where
$\exists x_1, \dots , x_n \varphi $
where
 $\varphi \in \mathrm {E}\Pi _k$
.
$\varphi \in \mathrm {E}\Pi _k$
.
Remark 5.12.
![]() $\Pi _k \subseteq \Pi _k \lor \Pi _k \subseteq \bigvee \Pi _k \subseteq \mathrm {E}\Pi _k \subseteq \mathrm {E}\Sigma _{k+1}$
.
$\Pi _k \subseteq \Pi _k \lor \Pi _k \subseteq \bigvee \Pi _k \subseteq \mathrm {E}\Pi _k \subseteq \mathrm {E}\Sigma _{k+1}$
.
Lemma 5.13. For any
![]() $\mathsf {HA}$
-formulas
$\mathsf {HA}$
-formulas
![]() $\varphi , \psi \in \mathrm {E}\Pi _k$
, there exists
$\varphi , \psi \in \mathrm {E}\Pi _k$
, there exists
![]() $\xi \in \mathrm {E}\Pi _k$
such that
$\xi \in \mathrm {E}\Pi _k$
such that
![]() $\mathrm { FV} \left ({\xi }\right )=\mathrm { FV} \left ({\varphi \land \psi }\right )$
and
$\mathrm { FV} \left ({\xi }\right )=\mathrm { FV} \left ({\varphi \land \psi }\right )$
and
![]() $\mathsf {HA} \vdash \xi \leftrightarrow \varphi \land \psi $
.
$\mathsf {HA} \vdash \xi \leftrightarrow \varphi \land \psi $
.
Proof By induction on the sum of the complexity of
![]() $\varphi $
and
$\varphi $
and
![]() $ \psi $
.
$ \psi $
.
If both of
![]() $\varphi $
and
$\varphi $
and
![]() $ \psi $
are in
$ \psi $
are in
![]() $\Pi _k$
, then we are done by [Reference Troelstra and van Dalen7, Lemma 4.3(2)].
$\Pi _k$
, then we are done by [Reference Troelstra and van Dalen7, Lemma 4.3(2)].
Suppose
![]() $\psi :\equiv \psi _1\lor \psi _2$
where
$\psi :\equiv \psi _1\lor \psi _2$
where
![]() $\psi _1, \psi _2 \in \mathrm {E}\Pi _k$
. By the induction hypothesis, there exist
$\psi _1, \psi _2 \in \mathrm {E}\Pi _k$
. By the induction hypothesis, there exist
![]() $\xi _1, \xi _2\in \mathrm {E}\Pi _k$
such that
$\xi _1, \xi _2\in \mathrm {E}\Pi _k$
such that
![]() $\mathrm { FV} \left ({\xi _1}\right )=\mathrm { FV} \left ({\varphi \land \psi _1}\right )$
,
$\mathrm { FV} \left ({\xi _1}\right )=\mathrm { FV} \left ({\varphi \land \psi _1}\right )$
,
![]() $\mathrm { FV} \left ({\xi _2}\right )=\mathrm { FV} \left ({\varphi \land \psi _2}\right )$
,
$\mathrm { FV} \left ({\xi _2}\right )=\mathrm { FV} \left ({\varphi \land \psi _2}\right )$
,
![]() $\mathsf {HA} \vdash \xi _1 \leftrightarrow \varphi \land \psi _1$
and
$\mathsf {HA} \vdash \xi _1 \leftrightarrow \varphi \land \psi _1$
and
![]() $\mathsf {HA} \vdash \xi _2 \leftrightarrow \varphi \land \psi _2$
. Then we have that
$\mathsf {HA} \vdash \xi _2 \leftrightarrow \varphi \land \psi _2$
. Then we have that
and that
![]() $\mathsf {HA}$
proves
$\mathsf {HA}$
proves
Thus one can take
![]() $\xi _1 \lor \xi _2 \in \mathrm {E}\Pi _k$
as a witness.
$\xi _1 \lor \xi _2 \in \mathrm {E}\Pi _k$
as a witness.
Suppose
![]() $\psi :\equiv \forall x \psi _1$
where
$\psi :\equiv \forall x \psi _1$
where
![]() $\psi _1 \in \mathrm {E}\Pi _k$
. Without loss of generality, assume
$\psi _1 \in \mathrm {E}\Pi _k$
. Without loss of generality, assume
![]() $x\notin \mathrm { FV} \left ({\varphi }\right )$
. By the induction hypothesis, there exists
$x\notin \mathrm { FV} \left ({\varphi }\right )$
. By the induction hypothesis, there exists
![]() $\xi _1\in \mathrm {E}\Pi _k$
such that
$\xi _1\in \mathrm {E}\Pi _k$
such that
![]() $\mathrm { FV} \left ({\xi _1}\right )=\mathrm { FV} \left ({\varphi \land \psi _1}\right )$
and
$\mathrm { FV} \left ({\xi _1}\right )=\mathrm { FV} \left ({\varphi \land \psi _1}\right )$
and
![]() $\mathsf {HA} \vdash \xi _1 \leftrightarrow \varphi \land \psi _1$
. Then we have
$\mathsf {HA} \vdash \xi _1 \leftrightarrow \varphi \land \psi _1$
. Then we have
and that
![]() $\mathsf {HA}$
proves
$\mathsf {HA}$
proves
Thus one can take
![]() $\forall x \xi _1 \in \mathrm {E}\Pi _k$
as a witness.
$\forall x \xi _1 \in \mathrm {E}\Pi _k$
as a witness.
In what follows, we use [Reference Troelstra and van Dalen7, Lemma 4.5] many times implicitly.
Lemma 5.14. For a
![]() $\mathsf {HA}$
-formula
$\mathsf {HA}$
-formula
![]() $\varphi $
, the following hold:
$\varphi $
, the following hold:
-
1. If
 $\varphi \in \mathrm {U}_{k+1}^+$
, then there exists
$\varphi \in \mathrm {U}_{k+1}^+$
, then there exists
 $\varphi '\in \mathrm {E}\Pi _{k+1}$
such that
$\varphi '\in \mathrm {E}\Pi _{k+1}$
such that
 $\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
$\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
 $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ' \to \varphi $
and
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ' \to \varphi $
and
 $\mathsf {PA} \vdash \varphi \to \varphi ' ;$
$\mathsf {PA} \vdash \varphi \to \varphi ' ;$
-
2. If
 $\varphi \in \mathrm {E}_{k+1}^+$
, then there exists
$\varphi \in \mathrm {E}_{k+1}^+$
, then there exists
 $\varphi '\in \mathrm {E}\Pi _{k+1}$
such that
$\varphi '\in \mathrm {E}\Pi _{k+1}$
such that
 $\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
$\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
 $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ' \to \neg \varphi $
and
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ' \to \neg \varphi $
and
 $\mathsf {PA} \vdash \neg \varphi \to \varphi '$
.
$\mathsf {PA} \vdash \neg \varphi \to \varphi '$
.
Proof We show items
![]() $1$
and
$1$
and
![]() $2$
by simultaneous induction on the structure of formulas. We suppress the arguments on free variables when they are clear from the context.
$2$
by simultaneous induction on the structure of formulas. We suppress the arguments on free variables when they are clear from the context.
If
![]() $\varphi $
is prime, then items
$\varphi $
is prime, then items
![]() $1$
and
$1$
and
![]() $2$
are trivial since
$2$
are trivial since
![]() $\varphi $
is decidable in
$\varphi $
is decidable in
![]() $\mathsf {HA}$
. For the induction step, assume items
$\mathsf {HA}$
. For the induction step, assume items
![]() $1$
and
$1$
and
![]() $2$
hold for
$2$
hold for
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
.
$\varphi _2$
.
Case of
![]() $\varphi :\equiv \varphi _1 \lor \varphi _2$
: For item
$\varphi :\equiv \varphi _1 \lor \varphi _2$
: For item
![]() $1$
, suppose
$1$
, suppose
![]() $\varphi _1 \lor \varphi _2 \in \mathrm {U}_{k+1}^+$
. Then
$\varphi _1 \lor \varphi _2 \in \mathrm {U}_{k+1}^+$
. Then
![]() $\varphi _1 , \varphi _2 \in \mathrm {U}_{k+1}^+$
. By using the induction hypothesis, there exist
$\varphi _1 , \varphi _2 \in \mathrm {U}_{k+1}^+$
. By using the induction hypothesis, there exist
![]() $\varphi _1', \varphi _2'\in \mathrm {E}\Pi _{k+1}$
such that
$\varphi _1', \varphi _2'\in \mathrm {E}\Pi _{k+1}$
such that
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} $
proves
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} $
proves
![]() $\varphi _1' \to \varphi _1$
and
$\varphi _1' \to \varphi _1$
and
![]() $\varphi _2' \to \varphi _2$
and
$\varphi _2' \to \varphi _2$
and
![]() $\mathsf {PA} $
proves
$\mathsf {PA} $
proves
![]() $\varphi _1 \to \varphi _1'$
and
$\varphi _1 \to \varphi _1'$
and
![]() $\varphi _2 \to \varphi _2'$
. Now
$\varphi _2 \to \varphi _2'$
. Now
![]() $\varphi _1' \lor \varphi _2' \in \mathrm {E}\Pi _{k+1}$
and
$\varphi _1' \lor \varphi _2' \in \mathrm {E}\Pi _{k+1}$
and
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
On the other hand,
![]() $\mathsf {PA}$
proves the converse. For item
$\mathsf {PA}$
proves the converse. For item
![]() $2$
, suppose
$2$
, suppose
![]() $\varphi _1 \lor \varphi _2\in \mathrm {E}_{k+1}^+$
. Then
$\varphi _1 \lor \varphi _2\in \mathrm {E}_{k+1}^+$
. Then
![]() $\varphi _1 , \varphi _2 \in \mathrm {E}_{k+1}^+$
. By the induction hypothesis, there exist
$\varphi _1 , \varphi _2 \in \mathrm {E}_{k+1}^+$
. By the induction hypothesis, there exist
![]() $\varphi _1', \varphi _2'\in \mathrm {E}\Pi _{k+1}$
such that
$\varphi _1', \varphi _2'\in \mathrm {E}\Pi _{k+1}$
such that
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} $
proves
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} $
proves
![]() $\varphi _1' \to \neg \varphi _1$
and
$\varphi _1' \to \neg \varphi _1$
and
![]() $\varphi _2' \to \neg \varphi _2$
and
$\varphi _2' \to \neg \varphi _2$
and
![]() $\mathsf {PA} $
proves
$\mathsf {PA} $
proves
![]() $\neg \varphi _1 \to \varphi _1'$
and
$\neg \varphi _1 \to \varphi _1'$
and
![]() $\neg \varphi _2 \to \varphi _2'$
. By Lemma 5.13, there exists
$\neg \varphi _2 \to \varphi _2'$
. By Lemma 5.13, there exists
![]() $\varphi '\in \mathrm {E}\Pi _{k+1}$
such that
$\varphi '\in \mathrm {E}\Pi _{k+1}$
such that
![]() $\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\varphi _1' \land \varphi _2'}\right )$
and
$\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\varphi _1' \land \varphi _2'}\right )$
and
![]() $\mathsf {HA} \vdash \varphi ' \leftrightarrow \varphi _1' \land \varphi _2'$
. Then we have that
$\mathsf {HA} \vdash \varphi ' \leftrightarrow \varphi _1' \land \varphi _2'$
. Then we have that
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} $
proves
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} $
proves
and also
![]() $\mathsf {PA} $
proves the converse.
$\mathsf {PA} $
proves the converse.
Case of
![]() $\varphi :\equiv \varphi _1 \land \varphi _2$
: For item
$\varphi :\equiv \varphi _1 \land \varphi _2$
: For item
![]() $1$
, suppose
$1$
, suppose
![]() $\varphi _1 \land \varphi _2 \in \mathrm {U}_{k+1}^+$
. Then
$\varphi _1 \land \varphi _2 \in \mathrm {U}_{k+1}^+$
. Then
![]() $\varphi _1 , \varphi _2 \in \mathrm {U}_{k+1}^+$
. By using the induction hypothesis and Lemma 5.13, one can take a witness for
$\varphi _1 , \varphi _2 \in \mathrm {U}_{k+1}^+$
. By using the induction hypothesis and Lemma 5.13, one can take a witness for
![]() $\varphi _1 \land \varphi _2$
in a straightforward way. Item
$\varphi _1 \land \varphi _2$
in a straightforward way. Item
![]() $2$
follows from the induction hypothesis as in the case of
$2$
follows from the induction hypothesis as in the case of
![]() $\varphi :\equiv \varphi _1 \lor \varphi _2$
:
$\varphi :\equiv \varphi _1 \lor \varphi _2$
:
![]() $\varphi _1' \lor \varphi _2' \in \mathrm {E}\Pi _{k+1}$
is the witness since
$\varphi _1' \lor \varphi _2' \in \mathrm {E}\Pi _{k+1}$
is the witness since
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
and
![]() $\mathsf {PA}$
proves the converse.
$\mathsf {PA}$
proves the converse.
Case of
![]() $\varphi :\equiv \varphi _1 \to \varphi _2$
: For item
$\varphi :\equiv \varphi _1 \to \varphi _2$
: For item
![]() $1$
, suppose
$1$
, suppose
![]() $\varphi _1 \to \varphi _2 \in \mathrm {U}_{k+1}^+$
. Then
$\varphi _1 \to \varphi _2 \in \mathrm {U}_{k+1}^+$
. Then
![]() $\varphi _1 \in \mathrm {E}_{k+1}^+$
and
$\varphi _1 \in \mathrm {E}_{k+1}^+$
and
![]() $\varphi _2 \in \mathrm {U}_{k+1}^+$
. By the induction hypothesis, there exist
$\varphi _2 \in \mathrm {U}_{k+1}^+$
. By the induction hypothesis, there exist
![]() $\varphi _1', \varphi _2'\in \mathrm {E}\Pi _{k+1}$
such that
$\varphi _1', \varphi _2'\in \mathrm {E}\Pi _{k+1}$
such that
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} $
proves
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} $
proves
![]() $\varphi _1' \to \neg \varphi _1$
and
$\varphi _1' \to \neg \varphi _1$
and
![]() $\varphi _2' \to \varphi _2$
and
$\varphi _2' \to \varphi _2$
and
![]() $\mathsf {PA} $
proves
$\mathsf {PA} $
proves
![]() $\neg \varphi _1 \to \varphi _1'$
and
$\neg \varphi _1 \to \varphi _1'$
and
![]() $ \varphi _2 \to \varphi _2'$
. Now
$ \varphi _2 \to \varphi _2'$
. Now
![]() $\varphi _1' \lor \varphi _2' \in \mathrm {E}\Pi _{k+1}$
and
$\varphi _1' \lor \varphi _2' \in \mathrm {E}\Pi _{k+1}$
and
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
On the other hand,
![]() $\mathsf {PA}$
proves the converse. For item
$\mathsf {PA}$
proves the converse. For item
![]() $2$
, suppose
$2$
, suppose
![]() $\varphi _1 \to \varphi _2 \in \mathrm {E}_{k+1}^+$
. Then
$\varphi _1 \to \varphi _2 \in \mathrm {E}_{k+1}^+$
. Then
![]() $\varphi _1 \in \mathrm {U}_{k+1}^+$
and
$\varphi _1 \in \mathrm {U}_{k+1}^+$
and
![]() $\varphi _2 \in \mathrm {E}_{k+1}^+$
. By the induction hypothesis, there exist
$\varphi _2 \in \mathrm {E}_{k+1}^+$
. By the induction hypothesis, there exist
![]() $\varphi _1', \varphi _2'\in \mathrm {E}\Pi _{k+1}$
such that
$\varphi _1', \varphi _2'\in \mathrm {E}\Pi _{k+1}$
such that
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} $
proves
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} $
proves
![]() $\varphi _1' \to \varphi _1$
and
$\varphi _1' \to \varphi _1$
and
![]() $\varphi _2' \to \neg \varphi _2$
and
$\varphi _2' \to \neg \varphi _2$
and
![]() $\mathsf {PA} $
proves
$\mathsf {PA} $
proves
![]() $\varphi _1 \to \varphi _1'$
and
$\varphi _1 \to \varphi _1'$
and
![]() $ \neg \varphi _2 \to \varphi _2'$
. By Lemma 5.13, there exists
$ \neg \varphi _2 \to \varphi _2'$
. By Lemma 5.13, there exists
![]() $\varphi '\in \mathrm {E}\Pi _{k+1}$
such that
$\varphi '\in \mathrm {E}\Pi _{k+1}$
such that
![]() $\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\varphi _1' \land \varphi _2'}\right )$
and
$\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\varphi _1' \land \varphi _2'}\right )$
and
![]() $\mathsf {HA} \vdash \varphi ' \leftrightarrow \varphi _1' \land \varphi _2'$
. Then we have that
$\mathsf {HA} \vdash \varphi ' \leftrightarrow \varphi _1' \land \varphi _2'$
. Then we have that
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
and also that
![]() $\mathsf {PA}$
proves the converse.
$\mathsf {PA}$
proves the converse.
Case of
![]() $\varphi :\equiv \exists x \varphi _1$
: For item
$\varphi :\equiv \exists x \varphi _1$
: For item
![]() $1$
, suppose
$1$
, suppose
![]() $\exists x \varphi _1 \in \mathrm {U}_{k+1}^+$
. Then
$\exists x \varphi _1 \in \mathrm {U}_{k+1}^+$
. Then
![]() $\exists x \varphi _1 \in \mathrm {E}_{k}^+$
. By Remark 3.10, there exists
$\exists x \varphi _1 \in \mathrm {E}_{k}^+$
. By Remark 3.10, there exists
![]() $\varphi '\in \Sigma _k$
such that
$\varphi '\in \Sigma _k$
such that
![]() $\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\varphi }\right )$
and
$\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\varphi }\right )$
and
![]() $\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ' \leftrightarrow \varphi $
. Since
$\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ' \leftrightarrow \varphi $
. Since
![]() $\Sigma _k$
can be seen as a subclass of
$\Sigma _k$
can be seen as a subclass of
![]() $\Pi _{k+1}$
, we are done. For item
$\Pi _{k+1}$
, we are done. For item
![]() $2$
, suppose
$2$
, suppose
![]() $\exists x \varphi _1 \in \mathrm {E}_{k+1}^+$
. Then
$\exists x \varphi _1 \in \mathrm {E}_{k+1}^+$
. Then
![]() $\varphi _1 \in \mathrm {E}_{k+1}^+$
. By the induction hypothesis, there exists
$\varphi _1 \in \mathrm {E}_{k+1}^+$
. By the induction hypothesis, there exists
![]() $\varphi _1' \in \mathrm {E}\Pi _{k+1}$
such that
$\varphi _1' \in \mathrm {E}\Pi _{k+1}$
such that
![]() $\mathrm { FV} \left ({\varphi _1'}\right )=\mathrm { FV} \left ({\varphi _1}\right ) $
,
$\mathrm { FV} \left ({\varphi _1'}\right )=\mathrm { FV} \left ({\varphi _1}\right ) $
,
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi _1' \to \neg \varphi _1$
and
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi _1' \to \neg \varphi _1$
and
![]() $\mathsf {PA} \vdash \neg \varphi _1 \to \varphi _1'$
. Now
$\mathsf {PA} \vdash \neg \varphi _1 \to \varphi _1'$
. Now
![]() $\forall x \varphi _1'\in \mathrm {E}\Pi _{k+1}$
and
$\forall x \varphi _1'\in \mathrm {E}\Pi _{k+1}$
and
![]() $\mathrm { FV} \left ({\forall x\varphi _1'}\right )=\mathrm { FV} \left ({\exists x \varphi _1}\right )$
. Then we have that
$\mathrm { FV} \left ({\forall x\varphi _1'}\right )=\mathrm { FV} \left ({\exists x \varphi _1}\right )$
. Then we have that
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM}$
proves
and also that
![]() $\mathsf {PA}$
proves the converse.
$\mathsf {PA}$
proves the converse.
Case of
![]() $\varphi :\equiv \forall x \varphi _1$
: For item
$\varphi :\equiv \forall x \varphi _1$
: For item
![]() $1$
, suppose
$1$
, suppose
![]() $\forall x \varphi _1 \in \mathrm {U}_{k+1}^+$
. Then
$\forall x \varphi _1 \in \mathrm {U}_{k+1}^+$
. Then
![]() $ \varphi _1 \in \mathrm {U}_{k+1}^+$
. By the induction hypothesis, there exists
$ \varphi _1 \in \mathrm {U}_{k+1}^+$
. By the induction hypothesis, there exists
![]() $\varphi _1' \in \mathrm {E}\Pi _{k+1}$
such that
$\varphi _1' \in \mathrm {E}\Pi _{k+1}$
such that
![]() $\mathrm { FV} \left ({\varphi _1'}\right )=\mathrm { FV} \left ({\varphi _1}\right ) $
,
$\mathrm { FV} \left ({\varphi _1'}\right )=\mathrm { FV} \left ({\varphi _1}\right ) $
,
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi _1' \to \varphi _1$
and
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi _1' \to \varphi _1$
and
![]() $\mathsf {PA} \vdash \varphi _1 \to \varphi _1'$
. It is straightforward to see that
$\mathsf {PA} \vdash \varphi _1 \to \varphi _1'$
. It is straightforward to see that
![]() $\forall x \varphi _1'\in \mathrm {E}\Pi _{k+1}$
is a witness for
$\forall x \varphi _1'\in \mathrm {E}\Pi _{k+1}$
is a witness for
![]() $\forall x \varphi _1 \in \mathrm {U}_{k+1}^+$
. For item
$\forall x \varphi _1 \in \mathrm {U}_{k+1}^+$
. For item
![]() $2$
, suppose
$2$
, suppose
![]() $\forall x \varphi _1 \in \mathrm {E}_{k+1}^+$
. Then
$\forall x \varphi _1 \in \mathrm {E}_{k+1}^+$
. Then
![]() $\forall x \varphi _1 \in \mathrm {U}_{k}^+$
. By Remark 3.10, there exists
$\forall x \varphi _1 \in \mathrm {U}_{k}^+$
. By Remark 3.10, there exists
![]() $\varphi '\in \Pi _k$
such that
$\varphi '\in \Pi _k$
such that
![]() $\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\varphi }\right )$
and
$\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\varphi }\right )$
and
![]() $\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ' \leftrightarrow \varphi $
. Since
$\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ' \leftrightarrow \varphi $
. Since
![]() $\neg \varphi '$
is equivalent to some
$\neg \varphi '$
is equivalent to some
![]() $\varphi " \in \Sigma _k$
in the presence of
$\varphi " \in \Sigma _k$
in the presence of
![]() ${\Sigma _k}\text {-}\mathrm {DNE}$
(cf. Remark 5.3), we are done.
${\Sigma _k}\text {-}\mathrm {DNE}$
(cf. Remark 5.3), we are done.
Lemma 5.15. Let
![]() ${T}$
be a theory containing
${T}$
be a theory containing
![]() $\mathsf {HA}$
and X be a set of
$\mathsf {HA}$
and X be a set of
![]() $\mathsf {HA}$
-sentences. If
$\mathsf {HA}$
-sentences. If
![]() $\mathsf {PA} + X$
is
$\mathsf {PA} + X$
is
![]() $\mathrm {E}\Pi _{k+1}$
-conservative over
$\mathrm {E}\Pi _{k+1}$
-conservative over
![]() ${T} +X $
, then so is
${T} +X $
, then so is
![]() $\mathrm {U}_{k+1}$
-conservative.
$\mathrm {U}_{k+1}$
-conservative.
Proof Let
![]() $\varphi \in \mathrm {U}_{k+1}$
. Suppose
$\varphi \in \mathrm {U}_{k+1}$
. Suppose
![]() $\mathsf {PA} + X \vdash \varphi $
. By Lemma 5.14, there exists
$\mathsf {PA} + X \vdash \varphi $
. By Lemma 5.14, there exists
![]() $\varphi '\in \mathrm {E}\Pi _{k+1}$
such that
$\varphi '\in \mathrm {E}\Pi _{k+1}$
such that
![]() $\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
$\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ' \to \varphi $
and
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ' \to \varphi $
and
![]() $\mathsf {PA} \vdash \varphi \to \varphi '$
. Then
$\mathsf {PA} \vdash \varphi \to \varphi '$
. Then
![]() $\mathsf {PA} + X \vdash \varphi '$
. By our assumption, we have
$\mathsf {PA} + X \vdash \varphi '$
. By our assumption, we have
![]() ${T} + X \vdash \varphi '$
. As in the proof of Lemma 5.5, one can show
${T} + X \vdash \varphi '$
. As in the proof of Lemma 5.5, one can show
![]() ${T} + X \vdash {\Sigma _k}\text {-}\mathrm {LEM}$
by using the
${T} + X \vdash {\Sigma _k}\text {-}\mathrm {LEM}$
by using the
![]() $\mathrm {E}\Pi _{k+1}$
-conservativity. Then
$\mathrm {E}\Pi _{k+1}$
-conservativity. Then
![]() ${T} + X \vdash \varphi $
follows.
${T} + X \vdash \varphi $
follows.
Theorem 5.16. Let
![]() ${T}$
be semi-classical arithmetic and X be a set of
${T}$
be semi-classical arithmetic and X be a set of
![]() $\mathsf {HA}$
-sentences in
$\mathsf {HA}$
-sentences in
![]() $\mathcal {Q}_{k+1}$
. Then the following are pairwise equivalent:
$\mathcal {Q}_{k+1}$
. Then the following are pairwise equivalent:
-
1.
 $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
 $\mathrm {U}_{k+1}$
-conservative over
$\mathrm {U}_{k+1}$
-conservative over
 ${T} +X ;$
${T} +X ;$
-
2.
 $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
 $\mathrm {E}\Pi _{k+1}$
-conservative over
$\mathrm {E}\Pi _{k+1}$
-conservative over
 ${T} +X ;$
${T} +X ;$
-
3.
 ${T} +X$
is closed under
${T} +X$
is closed under
 ${\mathrm {E}\Pi _{k+1}}\text {-}\mathrm {DNE}\text {-}\mathrm {R} ;$
${\mathrm {E}\Pi _{k+1}}\text {-}\mathrm {DNE}\text {-}\mathrm {R} ;$
-
4.
 ${T} +X$
is closed under
${T} +X$
is closed under
 ${\mathrm {E}\Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R} ;$
${\mathrm {E}\Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R} ;$
-
5.
 ${T} +X$
is closed under
${T} +X$
is closed under
 ${\mathrm {U}_{k+1}}\text {-}\mathrm {DNE}\text {-}\mathrm {R} ;$
${\mathrm {U}_{k+1}}\text {-}\mathrm {DNE}\text {-}\mathrm {R} ;$
-
6.
 ${T} +X$
is closed under
${T} +X$
is closed under
 ${\mathrm {U}_{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R} $
.
${\mathrm {U}_{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R} $
.
Proof Since
![]() $\mathrm {E}\Pi _{k+1} \subseteq \mathrm {U}_{k+1}$
, the equivalence between (1) and (2) follows immediately from Lemma 5.15.
$\mathrm {E}\Pi _{k+1} \subseteq \mathrm {U}_{k+1}$
, the equivalence between (1) and (2) follows immediately from Lemma 5.15.
(2
![]() $\to $
3): Let
$\to $
3): Let
![]() $\varphi \in \mathrm {E}\Pi _{k+1}$
and assume
$\varphi \in \mathrm {E}\Pi _{k+1}$
and assume
![]() ${T} + X \vdash \neg \neg \varphi $
. Since
${T} + X \vdash \neg \neg \varphi $
. Since
![]() ${T} + X \subseteq \mathsf {PA} + X$
, we have
${T} + X \subseteq \mathsf {PA} + X$
, we have
![]() $\mathsf {PA} + X \vdash \varphi $
. By (2), we have
$\mathsf {PA} + X \vdash \varphi $
. By (2), we have
![]() ${T} + X \vdash \varphi $
.
${T} + X \vdash \varphi $
.
(3
![]() $\to $
4): Let
$\to $
4): Let
![]() $\varphi , \psi (x)\in \mathrm {E}\Pi _{k+1}$
and
$\varphi , \psi (x)\in \mathrm {E}\Pi _{k+1}$
and
![]() $x \notin \mathrm { FV} \left ({\varphi }\right )$
. Assume
$x \notin \mathrm { FV} \left ({\varphi }\right )$
. Assume
![]() ${T} +X \vdash \forall x (\varphi \lor \psi (x))$
. Since
${T} +X \vdash \forall x (\varphi \lor \psi (x))$
. Since
![]() $\mathsf {HA}$
proves
$\mathsf {HA}$
proves
![]() $\neg \neg (\varphi \lor \neg \varphi )$
and
$\neg \neg (\varphi \lor \neg \varphi )$
and
![]() $(\varphi \lor \neg \varphi )\land \forall x (\varphi \lor \psi (x)) \to \varphi \lor \forall x \psi (x)$
, we have
$(\varphi \lor \neg \varphi )\land \forall x (\varphi \lor \psi (x)) \to \varphi \lor \forall x \psi (x)$
, we have
![]() ${T} +X \vdash \neg \neg (\varphi \lor \forall x \psi (x))$
. Since
${T} +X \vdash \neg \neg (\varphi \lor \forall x \psi (x))$
. Since
![]() $\varphi \lor \forall x \psi (x) \in \mathrm {E}\Pi _{k+1}$
, by
$\varphi \lor \forall x \psi (x) \in \mathrm {E}\Pi _{k+1}$
, by
![]() ${\mathrm {E}\Pi _{k+1}}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
, we have
${\mathrm {E}\Pi _{k+1}}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
, we have
![]() ${T} +X \vdash \varphi \lor \forall x \psi (x)$
.
${T} +X \vdash \varphi \lor \forall x \psi (x)$
.
(4
![]() $\to $
2): Assume that
$\to $
2): Assume that
![]() ${T} +X$
is closed under
${T} +X$
is closed under
![]() ${\mathrm {E}\Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R} $
. By Lemma 5.7, we have
${\mathrm {E}\Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R} $
. By Lemma 5.7, we have
![]() ${T}+X \vdash {\Sigma _k}\text {-}\mathrm {LEM}$
. We show that
${T}+X \vdash {\Sigma _k}\text {-}\mathrm {LEM}$
. We show that
![]() $\mathsf {PA} + X \vdash \varphi _1 \lor \dots \lor \varphi _n$
implies
$\mathsf {PA} + X \vdash \varphi _1 \lor \dots \lor \varphi _n$
implies
![]() ${T} + X \vdash \varphi _1 \lor \dots \lor \varphi _n$
for any
${T} + X \vdash \varphi _1 \lor \dots \lor \varphi _n$
for any
![]() $\varphi _1, \dots , \varphi _n \in \mathrm {E}\Pi _{k+1}$
by induction on the sum of the complexity of
$\varphi _1, \dots , \varphi _n \in \mathrm {E}\Pi _{k+1}$
by induction on the sum of the complexity of
![]() $\varphi _1, \dots , \varphi _n \in \mathrm {E}\Pi _{k+1}$
.
$\varphi _1, \dots , \varphi _n \in \mathrm {E}\Pi _{k+1}$
.
First, suppose that all of
![]() $\varphi _1, \dots , \varphi _n$
are in
$\varphi _1, \dots , \varphi _n$
are in
![]() $\Pi _{k+1}$
. Let
$\Pi _{k+1}$
. Let
![]() $\varphi _i:\equiv \forall x_i \varphi _{i}'$
with
$\varphi _i:\equiv \forall x_i \varphi _{i}'$
with
![]() $\varphi _i'\in \Sigma _k$
for each
$\varphi _i'\in \Sigma _k$
for each
![]() $i\in \{ 1,\dots , n\}$
. Assume
$i\in \{ 1,\dots , n\}$
. Assume
![]() $\mathsf {PA} +X \vdash \varphi _1 \lor \dots \lor \varphi _n$
. Then
$\mathsf {PA} +X \vdash \varphi _1 \lor \dots \lor \varphi _n$
. Then
![]() $\mathsf {PA} +X \vdash \varphi _1' \lor \dots \lor \varphi _n'$
. Since
$\mathsf {PA} +X \vdash \varphi _1' \lor \dots \lor \varphi _n'$
. Since
![]() ${T} +X \vdash {\Sigma _k}\text {-}\mathrm {LEM}$
and
${T} +X \vdash {\Sigma _k}\text {-}\mathrm {LEM}$
and
![]() $X\subseteq \mathcal {Q}_{k+1}$
, by Corollary 4.3, we have
$X\subseteq \mathcal {Q}_{k+1}$
, by Corollary 4.3, we have
![]() ${T} +X \vdash \varphi _1' \lor \dots \lor \varphi _n'$
. Then
${T} +X \vdash \varphi _1' \lor \dots \lor \varphi _n'$
. Then
![]() ${T} +X \vdash \forall x_1 (\varphi _1' \lor \dots \lor \varphi _n')$
follows. By
${T} +X \vdash \forall x_1 (\varphi _1' \lor \dots \lor \varphi _n')$
follows. By
![]() ${\mathrm {E}\Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
, we have
${\mathrm {E}\Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
, we have
![]() ${T} +X \vdash \forall x_1 \varphi _1' \lor \varphi _2' \lor \dots \lor \varphi _n'$
. Iterating this procedure for more
${T} +X \vdash \forall x_1 \varphi _1' \lor \varphi _2' \lor \dots \lor \varphi _n'$
. Iterating this procedure for more
![]() $n-1$
times, we have
$n-1$
times, we have
![]() ${T} +X \vdash \forall x_1 \varphi _1' \lor \dots \lor \forall x_n \varphi _n'$
.
${T} +X \vdash \forall x_1 \varphi _1' \lor \dots \lor \forall x_n \varphi _n'$
.
Secondly, suppose
![]() $\varphi _1, \dots , \varphi _n \in \mathrm {E}\Pi _{k+1}$
and
$\varphi _1, \dots , \varphi _n \in \mathrm {E}\Pi _{k+1}$
and
![]() $\varphi _n:\equiv \varphi _n' \lor \varphi _n"$
with
$\varphi _n:\equiv \varphi _n' \lor \varphi _n"$
with
![]() $\varphi _n', \varphi _n"\in \mathrm {E}\Pi _{k+1}$
. Without loss of generality, let
$\varphi _n', \varphi _n"\in \mathrm {E}\Pi _{k+1}$
. Without loss of generality, let
![]() $n>1$
. Assume
$n>1$
. Assume
![]() $\mathsf {PA} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n$
, equivalently,
$\mathsf {PA} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n$
, equivalently,
![]() $\mathsf {PA} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n' \lor \varphi _n"$
. By the induction hypothesis, we have
$\mathsf {PA} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n' \lor \varphi _n"$
. By the induction hypothesis, we have
![]() ${T} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n' \lor \varphi _n"$
, equivalently,
${T} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n' \lor \varphi _n"$
, equivalently,
![]() ${T} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n$
.
${T} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n$
.
Finally, suppose
![]() $\varphi _1, \dots , \varphi _n \in \mathrm {E}\Pi _{k+1}$
and
$\varphi _1, \dots , \varphi _n \in \mathrm {E}\Pi _{k+1}$
and
![]() $\varphi _n: \equiv \forall x_n \varphi _n'$
with
$\varphi _n: \equiv \forall x_n \varphi _n'$
with
![]() $\varphi _n' \in \mathrm {E}\Pi _{k+1}$
. Without loss of generality, let
$\varphi _n' \in \mathrm {E}\Pi _{k+1}$
. Without loss of generality, let
![]() $n>1$
. Assume
$n>1$
. Assume
![]() $\mathsf {PA} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n$
. Then
$\mathsf {PA} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n$
. Then
![]() $\mathsf {PA} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n'$
follows. By the induction hypothesis, we have
$\mathsf {PA} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n'$
follows. By the induction hypothesis, we have
![]() ${T} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n'$
, and hence,
${T} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n'$
, and hence,
![]() ${T} +X \vdash \forall x_n( \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n')$
. By
${T} +X \vdash \forall x_n( \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n')$
. By
![]() ${\mathrm {E}\Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
, we have
${\mathrm {E}\Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
, we have
![]() ${T} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n$
.
${T} +X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n$
.
The implications (1
![]() $\to $
5) and (5
$\to $
5) and (5
![]() $\to $
6) are shown as for (2
$\to $
6) are shown as for (2
![]() $\to $
3) and (3
$\to $
3) and (3
![]() $\to $
4) respectively. In addition, (6
$\to $
4) respectively. In addition, (6
![]() $\to $
4) is trivial.
$\to $
4) is trivial.
Next, we characterize the
![]() $(\Pi _{k+1}\lor \Pi _{k+1})$
-conservativity by several rules.
$(\Pi _{k+1}\lor \Pi _{k+1})$
-conservativity by several rules.
Lemma 5.17. Let
![]() ${T}$
be a theory containing
${T}$
be a theory containing
![]() $\mathsf {HA}$
. If
$\mathsf {HA}$
. If
![]() ${T}$
is closed under
${T}$
is closed under
![]() ${(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
, then so is
${(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
, then so is
![]() ${\Pi _{k}}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
.
${\Pi _{k}}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
.
Lemma 5.18. Let
![]() ${T}$
be a theory containing
${T}$
be a theory containing
![]() $\mathsf {HA}$
. Then
$\mathsf {HA}$
. Then
![]() ${T}$
is closed under
${T}$
is closed under
![]() ${\Sigma _{k}}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
if and only if
${\Sigma _{k}}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
if and only if
![]() ${T}$
is closed under
${T}$
is closed under
![]() ${\left (\Pi _{k} \lor \Pi _{k}\right )}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
.
${\left (\Pi _{k} \lor \Pi _{k}\right )}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
.
Proof One can show the “only if” direction as in the proof of that in Lemma 5.8. For the converse direction, again by the corresponding proof in Lemma 5.8, it suffices to show that if
![]() ${T}$
is closed under
${T}$
is closed under
![]() ${\left (\Pi _{k} \lor \Pi _{k}\right )}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
, then
${\left (\Pi _{k} \lor \Pi _{k}\right )}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
, then
![]() $T $
proves
$T $
proves
![]() ${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
. The latter is the case by Lemmata 5.17 and 5.7.
${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
. The latter is the case by Lemmata 5.17 and 5.7.
Theorem 5.19. Let
![]() ${T}$
be semi-classical arithmetic and X be a set of
${T}$
be semi-classical arithmetic and X be a set of
![]() $\mathsf {HA}$
-sentences in
$\mathsf {HA}$
-sentences in
![]() $\mathcal {Q}_{k+1}$
. Then the following are pairwise equivalent:
$\mathcal {Q}_{k+1}$
. Then the following are pairwise equivalent:
-
1.
 $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
 $\left (\Pi _{k+1} \lor \Pi _{k+1} \right )$
-conservative over
$\left (\Pi _{k+1} \lor \Pi _{k+1} \right )$
-conservative over
 ${T} +X\kern-1pt;$
${T} +X\kern-1pt;$
-
2.
 ${T} +X$
is closed under
${T} +X$
is closed under
 ${ (\Pi _{k+1} \lor \Pi _{k+1})}\text {-}\mathrm {DNE}\text {-}\mathrm {R} ;$
${ (\Pi _{k+1} \lor \Pi _{k+1})}\text {-}\mathrm {DNE}\text {-}\mathrm {R} ;$
-
3.
 ${T} +X$
is closed under
${T} +X$
is closed under
 ${ \Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R} ;$
${ \Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R} ;$
-
4.
 ${T} +X$
is closed under
${T} +X$
is closed under
 ${ \Sigma _{k+1}}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R} ;$
${ \Sigma _{k+1}}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R} ;$
-
5.
 ${T} +X$
is closed under
${T} +X$
is closed under
 ${ \Sigma _{k+1}}\text {-}\mathrm {DML}\text {-}\mathrm {R}$
and
${ \Sigma _{k+1}}\text {-}\mathrm {DML}\text {-}\mathrm {R}$
and
 $T+X$
proves
$T+X$
proves
 ${\Sigma _{k}}\text {-}\mathrm {DNE}$
.
${\Sigma _{k}}\text {-}\mathrm {DNE}$
.
Proof One can show (1
![]() $\to $
2) as in the proof of (2
$\to $
2) as in the proof of (2
![]() $\to $
3) of Theorem 5.16. The implication (2
$\to $
3) of Theorem 5.16. The implication (2
![]() $\to $
3) is by Lemma 5.17.
$\to $
3) is by Lemma 5.17.
We show (3
![]() $\to $
1). Assume that
$\to $
1). Assume that
![]() ${T} +X$
is closed under
${T} +X$
is closed under
![]() ${ \Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R} $
. By Lemma 5.7, we have
${ \Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R} $
. By Lemma 5.7, we have
![]() ${T} + X \vdash {\Sigma _k}\text {-}\mathrm {LEM}$
. Let
${T} + X \vdash {\Sigma _k}\text {-}\mathrm {LEM}$
. Let
![]() $\varphi _1:\equiv \forall x_1 \psi _1$
and
$\varphi _1:\equiv \forall x_1 \psi _1$
and
![]() $\varphi _2: \equiv \forall x_2 \psi _2$
with
$\varphi _2: \equiv \forall x_2 \psi _2$
with
![]() $\psi _1, \psi _2 \in \Sigma _{k}$
. Suppose
$\psi _1, \psi _2 \in \Sigma _{k}$
. Suppose
![]() $\mathsf {PA} + X \vdash \forall x_1\psi _1 \lor \forall x_2\psi _2$
. Then
$\mathsf {PA} + X \vdash \forall x_1\psi _1 \lor \forall x_2\psi _2$
. Then
![]() $\mathsf {PA} + X \vdash \neg \left ( \exists x_1 \psi _1^{\perp } \land \exists x_2 \psi _2^{\perp } \right )$
. Since
$\mathsf {PA} + X \vdash \neg \left ( \exists x_1 \psi _1^{\perp } \land \exists x_2 \psi _2^{\perp } \right )$
. Since
![]() $\exists x_1 \psi _1^{\perp } \land \exists _2 \psi _2^{\perp }$
is equivalent to a formula in
$\exists x_1 \psi _1^{\perp } \land \exists _2 \psi _2^{\perp }$
is equivalent to a formula in
![]() $\Sigma _{k+1}$
(cf. [Reference Troelstra and van Dalen7, Lemma 4.3(2)]), by Remark 5.3, there exists
$\Sigma _{k+1}$
(cf. [Reference Troelstra and van Dalen7, Lemma 4.3(2)]), by Remark 5.3, there exists
![]() $\xi \in \Pi _{k+1}$
such that
$\xi \in \Pi _{k+1}$
such that
![]() $\mathrm { FV} \left ({\xi }\right ) =\mathrm { FV} \left ({\forall x_1 \psi _1 \lor \forall x \psi _2}\right )$
and
$\mathrm { FV} \left ({\xi }\right ) =\mathrm { FV} \left ({\forall x_1 \psi _1 \lor \forall x \psi _2}\right )$
and
![]() $\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {DNE} \vdash \xi \leftrightarrow \neg \left ( \exists x_1 \psi _1^{\perp } \land \exists x_2 \psi _2^{\perp } \right )$
. Then we have
$\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {DNE} \vdash \xi \leftrightarrow \neg \left ( \exists x_1 \psi _1^{\perp } \land \exists x_2 \psi _2^{\perp } \right )$
. Then we have
![]() $\mathsf {PA} + X \vdash \xi $
. Since
$\mathsf {PA} + X \vdash \xi $
. Since
![]() $X\subseteq \mathcal {Q}_{k+1}$
, by Corollary 3.19, we have
$X\subseteq \mathcal {Q}_{k+1}$
, by Corollary 3.19, we have
![]() $\mathsf {HA} + X + {\Sigma _{k}}\text {-}\mathrm {LEM} \vdash \xi $
. Since
$\mathsf {HA} + X + {\Sigma _{k}}\text {-}\mathrm {LEM} \vdash \xi $
. Since
![]() ${\Sigma _k}\text {-}\mathrm {DNE}$
is derivable from
${\Sigma _k}\text {-}\mathrm {DNE}$
is derivable from
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
, we have that
${\Sigma _k}\text {-}\mathrm {LEM}$
, we have that
![]() $T + X $
proves
$T + X $
proves
![]() $\neg \left ( \exists x_1 \psi _1^{\perp } \land \exists x_2 \psi _2^{\perp } \right )$
, equivalently,
$\neg \left ( \exists x_1 \psi _1^{\perp } \land \exists x_2 \psi _2^{\perp } \right )$
, equivalently,
![]() $\forall x_1, x_2 \neg \left ( \psi _1^{\perp } \land \psi _2^{\perp } \right )$
. Since
$\forall x_1, x_2 \neg \left ( \psi _1^{\perp } \land \psi _2^{\perp } \right )$
. Since
![]() ${T} + X \vdash {\Sigma _k}\text {-}\mathrm {DNE}$
, again by Remark 5.3, we have that
${T} + X \vdash {\Sigma _k}\text {-}\mathrm {DNE}$
, again by Remark 5.3, we have that
![]() $T + X $
proves
$T + X $
proves
![]() $\forall x_1, x_2 \neg \left ( \neg \psi _1\land \neg \psi _2 \right )$
, equivalently,
$\forall x_1, x_2 \neg \left ( \neg \psi _1\land \neg \psi _2 \right )$
, equivalently,
![]() $ \forall x_1, x_2 \neg \neg (\psi _1 \lor \psi _2)$
. Since
$ \forall x_1, x_2 \neg \neg (\psi _1 \lor \psi _2)$
. Since
![]() $\psi _1 \lor \psi _2$
is equivalent to a formula in
$\psi _1 \lor \psi _2$
is equivalent to a formula in
![]() $\Sigma _k$
(cf. [Reference Troelstra and van Dalen7, Lemma 4.4]),
$\Sigma _k$
(cf. [Reference Troelstra and van Dalen7, Lemma 4.4]),
![]() ${T} + X \vdash \forall x_1, x_2 (\psi _1 \lor \psi _2)$
follows. By using
${T} + X \vdash \forall x_1, x_2 (\psi _1 \lor \psi _2)$
follows. By using
![]() ${\Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
twice, we have
${\Pi _{k+1}}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
twice, we have
![]() ${T} +X \vdash \forall x_1\psi _1 \lor \forall x_2\psi _2$
.
${T} +X \vdash \forall x_1\psi _1 \lor \forall x_2\psi _2$
.
The equivalence (2
![]() $\leftrightarrow $
4) is by Lemma 5.18. The implication (5
$\leftrightarrow $
4) is by Lemma 5.18. The implication (5
![]() $\to $
4) is by the fact that for
$\to $
4) is by the fact that for
![]() $\varphi \in \Sigma _{k+1}$
,
$\varphi \in \Sigma _{k+1}$
,
![]() $\varphi ^{\perp }$
is derived from
$\varphi ^{\perp }$
is derived from
![]() $\neg \varphi $
in the presence of
$\neg \varphi $
in the presence of
![]() ${\Sigma _k}\text {-}\mathrm {DNE}$
(cf. Remark 5.3). The implication (3
${\Sigma _k}\text {-}\mathrm {DNE}$
(cf. Remark 5.3). The implication (3
![]() $\, \& \,$
4
$\, \& \,$
4
![]() $\to $
5) is by Lemma 5.7 (note that
$\to $
5) is by Lemma 5.7 (note that
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
implies
${\Sigma _k}\text {-}\mathrm {LEM}$
implies
![]() ${\Sigma _k}\text {-}\mathrm {DNE}$
).
${\Sigma _k}\text {-}\mathrm {DNE}$
).
Remark 5.20. From the perspective of Remark 5.12, it is natural to ask the status of the
![]() $\bigvee \Pi _{k+1}$
-conservativity. As in the proof of Theorem 5.19, one can show the following equivalence:
$\bigvee \Pi _{k+1}$
-conservativity. As in the proof of Theorem 5.19, one can show the following equivalence:
-
1.
 $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
 $\bigvee \Pi _{k+1}$
-conservative over
$\bigvee \Pi _{k+1}$
-conservative over
 ${T} +X\kern-1pt;$
${T} +X\kern-1pt;$
-
2. For any
 $\varphi _1 , \dots , \varphi _n\in \Pi _{k+1}$
, if
$\varphi _1 , \dots , \varphi _n\in \Pi _{k+1}$
, if
 ${T} + X \vdash \neg \neg (\varphi _1 \lor \dots \lor \varphi _n)$
, then
${T} + X \vdash \neg \neg (\varphi _1 \lor \dots \lor \varphi _n)$
, then
 ${T} + X \vdash \varphi _1 \lor \dots \lor \varphi _n;$
${T} + X \vdash \varphi _1 \lor \dots \lor \varphi _n;$
-
3. For any
 $\varphi _1 , \dots , \varphi _n\in \Pi _{k+1}$
such that
$\varphi _1 , \dots , \varphi _n\in \Pi _{k+1}$
such that
 $x \notin \mathrm { FV} \left ({\varphi _1 \lor \dots \lor \varphi _{n-1}}\right )$
, if
$x \notin \mathrm { FV} \left ({\varphi _1 \lor \dots \lor \varphi _{n-1}}\right )$
, if
 ${T} + X \vdash \forall x (\varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n)$
, then
${T} + X \vdash \forall x (\varphi _1 \lor \dots \lor \varphi _{n-1} \lor \varphi _n)$
, then
 ${T} + X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \forall x \varphi _n;$
${T} + X \vdash \varphi _1 \lor \dots \lor \varphi _{n-1} \lor \forall x \varphi _n;$
-
4. For any
 $\varphi _1 , \dots , \varphi _n\in \Sigma _{k+1}$
, if
$\varphi _1 , \dots , \varphi _n\in \Sigma _{k+1}$
, if
 ${T} + X \vdash \neg (\varphi _1 \land \dots \land \varphi _n)$
, then
${T} + X \vdash \neg (\varphi _1 \land \dots \land \varphi _n)$
, then
 ${T} + X \vdash \varphi _1^{\perp } \lor \dots \lor \varphi _n^{\perp } ;$
${T} + X \vdash \varphi _1^{\perp } \lor \dots \lor \varphi _n^{\perp } ;$
-
5.
 ${T} +X$
proves
${T} +X$
proves
 ${\Sigma _k}\text {-}\mathrm {DNE}$
and for any
${\Sigma _k}\text {-}\mathrm {DNE}$
and for any
 $\varphi _1 , \dots , \varphi _n\in \Sigma _{k+1}$
, if
$\varphi _1 , \dots , \varphi _n\in \Sigma _{k+1}$
, if
 ${T} + X \vdash \neg (\varphi _1 \land \dots \land \varphi _n)$
, then
${T} + X \vdash \neg (\varphi _1 \land \dots \land \varphi _n)$
, then
 ${T} + X \vdash \neg \varphi _1 \lor \dots \lor \neg \varphi _n;$
${T} + X \vdash \neg \varphi _1 \lor \dots \lor \neg \varphi _n;$
where
![]() $X\subseteq \mathcal {Q}_{k+1}$
. This characterization suggests that the
$X\subseteq \mathcal {Q}_{k+1}$
. This characterization suggests that the
![]() $\bigvee \Pi _{k+1}$
-conservativity lies strictly between the
$\bigvee \Pi _{k+1}$
-conservativity lies strictly between the
![]() $\mathrm {U}_{k+1}$
-conservativity and the
$\mathrm {U}_{k+1}$
-conservativity and the
![]() $\left (\Pi _{k+1}\lor \Pi _{k+1}\right )$
-conservativity, but we do not have the proof of the strictness.
$\left (\Pi _{k+1}\lor \Pi _{k+1}\right )$
-conservativity, but we do not have the proof of the strictness.
Remark 5.21. From the comparison between [Reference Troelstra and van Dalen6, Corollary 7.6] and the equivalences in Theorem 5.19, it is natural to ask whether the (contrapositive) collection rule restricted to formulas in
![]() $\Pi _{k+1}$
is also equivalent to the items in Theorem 5.19. This question is still open.
$\Pi _{k+1}$
is also equivalent to the items in Theorem 5.19. This question is still open.
6 Conservation theorems for the classes of sentences
In the study of fragments of
![]() $\mathsf {PA}$
, the conservativity for classes of sentences has been studied extensively e.g., in [Reference Troelstra and van Dalen11, Section 2]. The following proposition states that the conservativity for a class of formulas is equivalent to that restricted only to sentences if the class is closed under taking a universal closure:
$\mathsf {PA}$
, the conservativity for classes of sentences has been studied extensively e.g., in [Reference Troelstra and van Dalen11, Section 2]. The following proposition states that the conservativity for a class of formulas is equivalent to that restricted only to sentences if the class is closed under taking a universal closure:
Proposition 6.1. Let
![]() $\Gamma $
be a class of
$\Gamma $
be a class of
![]() $\mathsf {HA}$
-formulas such that
$\mathsf {HA}$
-formulas such that
![]() $\Gamma $
is closed under taking a universal closure. For any theories
$\Gamma $
is closed under taking a universal closure. For any theories
![]() ${T}$
and
${T}$
and
![]() ${T}'$
containing
${T}'$
containing
![]() $\mathsf {HA}$
in the language of
$\mathsf {HA}$
in the language of
![]() $\mathsf {HA}$
, if
$\mathsf {HA}$
, if
![]() ${T}' $
is conservative over
${T}' $
is conservative over
![]() ${T}$
for any sentences in
${T}$
for any sentences in
![]() $\Gamma $
, then
$\Gamma $
, then
![]() ${T}' $
is
${T}' $
is
![]() $\Gamma $
-conservative over
$\Gamma $
-conservative over
![]() ${T}$
.
${T}$
.
Proof Let
![]() $\varphi \in \Gamma $
. Assume
$\varphi \in \Gamma $
. Assume
![]() ${T}' \vdash \varphi $
. Then we have
${T}' \vdash \varphi $
. Then we have
![]() ${T}' \vdash \widetilde {\varphi }$
where
${T}' \vdash \widetilde {\varphi }$
where
![]() $\widetilde {\varphi }$
is the universal closure of
$\widetilde {\varphi }$
is the universal closure of
![]() $\varphi $
. Since
$\varphi $
. Since
![]() $\widetilde {\varphi }$
is a sentence in
$\widetilde {\varphi }$
is a sentence in
![]() $\Gamma $
, by our assumption, we have
$\Gamma $
, by our assumption, we have
![]() ${T} \vdash \widetilde {\varphi }$
, and hence,
${T} \vdash \widetilde {\varphi }$
, and hence,
![]() ${T} \vdash \varphi $
.
${T} \vdash \varphi $
.
Therefore, for classes as
![]() $\Pi _{k}, \mathrm {U}_{k}, \mathrm {E}\Pi _{k}$
etc., the strength of the conservativity does not vary even if we restrict them only to sentences. On the other hand, since
$\Pi _{k}, \mathrm {U}_{k}, \mathrm {E}\Pi _{k}$
etc., the strength of the conservativity does not vary even if we restrict them only to sentences. On the other hand, since
![]() $\Sigma _{k}, \mathrm {E}_{k}, \mathrm {F}_{k}$
etc. are not closed under taking a universal closure, this is not the case for such classes. In what follows, we explore the relation on the notion that
$\Sigma _{k}, \mathrm {E}_{k}, \mathrm {F}_{k}$
etc. are not closed under taking a universal closure, this is not the case for such classes. In what follows, we explore the relation on the notion that
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() $\Gamma $
-conservative over
$\Gamma $
-conservative over
![]() ${T}$
for semi-classical arithmetic
${T}$
for semi-classical arithmetic
![]() ${T}$
and the class
${T}$
and the class
![]() $\Gamma $
of sentences.
$\Gamma $
of sentences.
Definition 6.2. For a class
![]() $\Gamma $
of
$\Gamma $
of
![]() $\mathsf {HA}$
-formulas,
$\mathsf {HA}$
-formulas,
![]() denotes the class of
denotes the class of
![]() $\mathsf {HA}$
-sentences in
$\mathsf {HA}$
-sentences in
![]() $\Gamma $
.
$\Gamma $
.
6.1 Conservation theorems for
 $\Sigma _k$
sentences and
$\Sigma _k$
sentences and
 $\mathrm {E}_k$
sentences
$\mathrm {E}_k$
sentences
For the
![]() -conservativity, we have the following:
-conservativity, we have the following:
Proposition 6.3. Let
![]() ${T}$
be semi-classical arithmetic containing
${T}$
be semi-classical arithmetic containing
![]() ${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
, and X be a set of
${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
, and X be a set of
![]() $\mathsf {HA}$
-sentences in
$\mathsf {HA}$
-sentences in
![]() $\mathcal {Q}_{k}$
. Then
$\mathcal {Q}_{k}$
. Then
![]() $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
![]() -conservative over
-conservative over
![]() ${T}+X $
if and only if
${T}+X $
if and only if
![]() ${T}+X$
is closed under
${T}+X$
is closed under
![]() .
.
Proof We first show the “only if” direction. Let
![]() . Assume
. Assume
![]() ${T} +X \vdash \neg \neg \varphi $
. Then
${T} +X \vdash \neg \neg \varphi $
. Then
![]() $\mathsf {PA} + X \vdash \varphi $
. Since
$\mathsf {PA} + X \vdash \varphi $
. Since
![]() $\mathsf {PA} +X$
is now
$\mathsf {PA} +X$
is now
![]() -conservative over
-conservative over
![]() ${T}+X$
, we have
${T}+X$
, we have
![]() ${T} + X \vdash \varphi $
.
${T} + X \vdash \varphi $
.
In the following, we show the converse direction. Without loss of generality, assume
![]() $k>0$
. Let
$k>0$
. Let
![]() with
with
![]() $\psi $
in
$\psi $
in
![]() $\Sigma _{k-1}$
. Assume
$\Sigma _{k-1}$
. Assume
![]() $\mathsf {PA} +X \vdash \exists x \forall y \psi $
. By Proposition 3.2.(2), we have
$\mathsf {PA} +X \vdash \exists x \forall y \psi $
. By Proposition 3.2.(2), we have
![]() , and hence,
, and hence,
![]() by Lemma 3.14. Using Lemma 3.5.(2), we have
by Lemma 3.14. Using Lemma 3.5.(2), we have
![]() . By substituting $ with
. By substituting $ with
![]() $\perp $
(cf. Lemma 3.16), we have
$\perp $
(cf. Lemma 3.16), we have
![]() $\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM} + X \vdash \neg \neg \exists x \forall y \psi $
. Since
$\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM} + X \vdash \neg \neg \exists x \forall y \psi $
. Since
![]() ${T}$
is semi-classical arithmetic containing
${T}$
is semi-classical arithmetic containing
![]() ${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
, we have
${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
, we have
![]() ${T} +X \vdash \neg \neg \exists x \forall y \psi $
. By
${T} +X \vdash \neg \neg \exists x \forall y \psi $
. By
![]() ,
,
![]() ${T} +X \vdash \exists x \forall y \psi $
follows.
${T} +X \vdash \exists x \forall y \psi $
follows.
Proposition 6.3 is a counterpart of the equivalence between (3) and (4) in Theorem 5.9 for the case of sentences. In what follows, we deal with the
![]() -conservativity. In particular, we show that the
-conservativity. In particular, we show that the
![]() -conservativity can be reduced to
-conservativity can be reduced to
![]() -conservativity.
-conservativity.
Lemma 6.4. For
![]() $\mathsf {HA}$
-formulas
$\mathsf {HA}$
-formulas
![]() $\varphi _1, \varphi _2\in \mathrm {E}\Sigma _{k+1}$
, there exist
$\varphi _1, \varphi _2\in \mathrm {E}\Sigma _{k+1}$
, there exist
![]() $\psi , \xi \in \mathrm {E}\Sigma _{k+1}$
such that
$\psi , \xi \in \mathrm {E}\Sigma _{k+1}$
such that
![]() $\mathrm { FV} \left ({\psi }\right ) =\mathrm { FV} \left ({\varphi _1 \land \varphi _2}\right ) = \mathrm { FV} \left ({\varphi _1 \lor \varphi _2}\right ) = \mathrm { FV} \left ({\xi }\right )$
and
$\mathrm { FV} \left ({\psi }\right ) =\mathrm { FV} \left ({\varphi _1 \land \varphi _2}\right ) = \mathrm { FV} \left ({\varphi _1 \lor \varphi _2}\right ) = \mathrm { FV} \left ({\xi }\right )$
and
![]() $\mathsf {HA}$
proves
$\mathsf {HA}$
proves
![]() $\psi \leftrightarrow \varphi _1 \land \varphi _2$
and
$\psi \leftrightarrow \varphi _1 \land \varphi _2$
and
![]() $\xi \leftrightarrow \varphi _1 \lor \varphi _2$
.
$\xi \leftrightarrow \varphi _1 \lor \varphi _2$
.
Proof Let
![]() $\varphi _1:\equiv \exists x_1, \dots , x_n \varphi _1'$
and
$\varphi _1:\equiv \exists x_1, \dots , x_n \varphi _1'$
and
![]() $\varphi _2:\equiv \exists y_1, \dots , y_m \varphi _2'$
with
$\varphi _2:\equiv \exists y_1, \dots , y_m \varphi _2'$
with
![]() $\varphi _1', \varphi _2' \in \mathrm {E}\Pi _{k}$
. Without loss of generality, assume
$\varphi _1', \varphi _2' \in \mathrm {E}\Pi _{k}$
. Without loss of generality, assume
![]() $x_1, \dots , x_n \notin \mathrm { FV} \left ({\varphi _2'}\right ) $
and
$x_1, \dots , x_n \notin \mathrm { FV} \left ({\varphi _2'}\right ) $
and
![]() $y_1, \dots , y_m \notin \mathrm { FV} \left ({\varphi _1'}\right )$
.
$y_1, \dots , y_m \notin \mathrm { FV} \left ({\varphi _1'}\right )$
.
By Lemma 5.13, there exists
![]() $\psi ' \in \mathrm {E}\Pi _{k}$
such that
$\psi ' \in \mathrm {E}\Pi _{k}$
such that
![]() $\mathrm { FV} \left ({\psi '}\right )=\mathrm { FV} \left ({\varphi _1' \land \varphi _2'}\right )$
and
$\mathrm { FV} \left ({\psi '}\right )=\mathrm { FV} \left ({\varphi _1' \land \varphi _2'}\right )$
and
![]() $\mathsf {HA} \vdash \psi ' \leftrightarrow \varphi _1' \land \varphi _2'$
. Put
$\mathsf {HA} \vdash \psi ' \leftrightarrow \varphi _1' \land \varphi _2'$
. Put
![]() $\psi :\equiv \exists x_1, \dots , x_n, y_1, \dots , y_m \, \psi '$
, which is in
$\psi :\equiv \exists x_1, \dots , x_n, y_1, \dots , y_m \, \psi '$
, which is in
![]() $ \mathrm {E}\Sigma _{k+1}$
. Then it is trivial that
$ \mathrm {E}\Sigma _{k+1}$
. Then it is trivial that
![]() $\mathrm { FV} \left ({\psi }\right ) = \mathrm { FV} \left ({\varphi _1 \land \varphi _2}\right )$
and
$\mathrm { FV} \left ({\psi }\right ) = \mathrm { FV} \left ({\varphi _1 \land \varphi _2}\right )$
and
![]() $\mathsf {HA} \vdash \psi \leftrightarrow \varphi _1 \land \varphi _2$
.
$\mathsf {HA} \vdash \psi \leftrightarrow \varphi _1 \land \varphi _2$
.
Put
![]() $\xi :\equiv \exists x_1, \dots , x_n, y_1, \dots , y_m \left (\varphi _1' \lor \varphi _2'\right )$
, which is in
$\xi :\equiv \exists x_1, \dots , x_n, y_1, \dots , y_m \left (\varphi _1' \lor \varphi _2'\right )$
, which is in
![]() $ \mathrm {E}\Sigma _{k+1}$
. Since
$ \mathrm {E}\Sigma _{k+1}$
. Since
![]() $\xi $
is equivalent to
$\xi $
is equivalent to
![]() $\exists x_1, \dots , x_n \varphi _1' \lor \exists y_1, \dots , y_m \varphi _2'$
over
$\exists x_1, \dots , x_n \varphi _1' \lor \exists y_1, \dots , y_m \varphi _2'$
over
![]() $\mathsf {HA}$
, we have that
$\mathsf {HA}$
, we have that
![]() $\mathrm { FV} \left ({\xi }\right ) = \mathrm { FV} \left ({\varphi _1 \lor \varphi _2}\right )$
and
$\mathrm { FV} \left ({\xi }\right ) = \mathrm { FV} \left ({\varphi _1 \lor \varphi _2}\right )$
and
![]() $\mathsf {HA} \vdash \xi \leftrightarrow \varphi _1 \lor \varphi _2$
.
$\mathsf {HA} \vdash \xi \leftrightarrow \varphi _1 \lor \varphi _2$
.
Lemma 6.5. For a
![]() $\mathsf {HA}$
-formula
$\mathsf {HA}$
-formula
![]() $\varphi $
, the following hold:
$\varphi $
, the following hold:
-
1. If
 $\varphi \in \mathrm {U}_{k+1}^+$
, then there exists
$\varphi \in \mathrm {U}_{k+1}^+$
, then there exists
 $\varphi '\in \mathrm {E}\Sigma _{k+1}$
such that
$\varphi '\in \mathrm {E}\Sigma _{k+1}$
such that
 $\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
$\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
 $\mathsf {HA}+{\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \varphi ' \to \neg \varphi $
and
$\mathsf {HA}+{\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \varphi ' \to \neg \varphi $
and
 $\mathsf {PA} \vdash \neg \varphi \to \varphi '$
.
$\mathsf {PA} \vdash \neg \varphi \to \varphi '$
. -
2. If
 $\varphi \in \mathrm {E}_{k+1}^+$
, then there exists
$\varphi \in \mathrm {E}_{k+1}^+$
, then there exists
 $\varphi '\in \mathrm {E}\Sigma _{k+1}$
such that
$\varphi '\in \mathrm {E}\Sigma _{k+1}$
such that
 $\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
$\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
 $\mathsf {HA}+{\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \varphi ' \to \varphi $
and
$\mathsf {HA}+{\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \varphi ' \to \varphi $
and
 $\mathsf {PA} \vdash \varphi \to \varphi '$
.
$\mathsf {PA} \vdash \varphi \to \varphi '$
.
Proof Note that
![]() $\mathrm {U}_{k+1}^+ = \mathcal {R}_{k+1}'$
and
$\mathrm {U}_{k+1}^+ = \mathcal {R}_{k+1}'$
and
![]() $\mathrm {E}_{k+1}^+ =\mathcal {J}_{k+1}'$
where
$\mathrm {E}_{k+1}^+ =\mathcal {J}_{k+1}'$
where
![]() $\mathcal {R}_{k+1}'$
and
$\mathcal {R}_{k+1}'$
and
![]() $\mathcal {J}_{k+1}'$
are the classes defined in Remark 4.5. Then it suffices to show items
$\mathcal {J}_{k+1}'$
are the classes defined in Remark 4.5. Then it suffices to show items
![]() $1$
and
$1$
and
![]() $2$
where
$2$
where
![]() $\mathrm {U}_{k+1}^+$
and
$\mathrm {U}_{k+1}^+$
and
![]() $\mathrm {E}_{k+1}^+$
are replaced by
$\mathrm {E}_{k+1}^+$
are replaced by
![]() $\mathcal {R}_{k+1}'$
and
$\mathcal {R}_{k+1}'$
and
![]() $\mathcal {J}_{k+1}'$
respectively. In the following, we show the assertions by induction on the constructions of
$\mathcal {J}_{k+1}'$
respectively. In the following, we show the assertions by induction on the constructions of
![]() $\mathcal {R}_{k+1}'$
and
$\mathcal {R}_{k+1}'$
and
![]() $\mathcal {J}_{k+1}'$
.
$\mathcal {J}_{k+1}'$
.
For
![]() $\varphi \in \mathrm {E}_k^+ \subseteq \mathcal {R}^{\prime }_{k+1}$
, by Lemma 5.14, there exists
$\varphi \in \mathrm {E}_k^+ \subseteq \mathcal {R}^{\prime }_{k+1}$
, by Lemma 5.14, there exists
![]() $\varphi '\in \mathrm {E}\Pi _k (\subseteq \mathrm {E}\Sigma _{k+1})$
such that
$\varphi '\in \mathrm {E}\Pi _k (\subseteq \mathrm {E}\Sigma _{k+1})$
such that
![]() $\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \varphi ' \to \neg \varphi $
and
$\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \varphi ' \to \neg \varphi $
and
![]() $\mathsf {PA} \vdash \neg \varphi \to \varphi '$
. For
$\mathsf {PA} \vdash \neg \varphi \to \varphi '$
. For
![]() $\varphi \in \mathrm {U}_k^+ \subseteq \mathcal {J}^{\prime }_{k+1}$
, by Lemma 5.14, there exists
$\varphi \in \mathrm {U}_k^+ \subseteq \mathcal {J}^{\prime }_{k+1}$
, by Lemma 5.14, there exists
![]() $\varphi '\in \mathrm {E}\Pi _k (\subseteq \mathrm {E}\Sigma _{k+1})$
such that
$\varphi '\in \mathrm {E}\Pi _k (\subseteq \mathrm {E}\Sigma _{k+1})$
such that
![]() $\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \varphi ' \to \varphi $
and
$\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \varphi ' \to \varphi $
and
![]() $\mathsf {PA} \vdash \varphi \to \varphi '$
. For the induction step, let
$\mathsf {PA} \vdash \varphi \to \varphi '$
. For the induction step, let
![]() $\varphi _1, \varphi _2\in \mathcal {R}_{k+1}'$
and
$\varphi _1, \varphi _2\in \mathcal {R}_{k+1}'$
and
![]() $\psi _1, \psi _2\in \mathcal {J}_{k+1}'$
and
$\psi _1, \psi _2\in \mathcal {J}_{k+1}'$
and
![]() $\varphi _1', \varphi _2',\psi _1',\psi _2' \in \mathrm {E}\Sigma _{k+1}$
satisfy
$\varphi _1', \varphi _2',\psi _1',\psi _2' \in \mathrm {E}\Sigma _{k+1}$
satisfy
![]() $\mathrm { FV} \left ({\varphi _1}\right )=\mathrm { FV} \left ({\varphi _1'}\right )$
,
$\mathrm { FV} \left ({\varphi _1}\right )=\mathrm { FV} \left ({\varphi _1'}\right )$
,
![]() $\mathrm { FV} \left ({\varphi _2}\right )=\mathrm { FV} \left ({\varphi _2'}\right )$
,
$\mathrm { FV} \left ({\varphi _2}\right )=\mathrm { FV} \left ({\varphi _2'}\right )$
,
![]() $\mathrm { FV} \left ({\psi _1}\right )=\mathrm { FV} \left ({\psi _1'}\right )$
,
$\mathrm { FV} \left ({\psi _1}\right )=\mathrm { FV} \left ({\psi _1'}\right )$
,
![]() $\mathrm { FV} \left ({\psi _2}\right )=\mathrm { FV} \left ({\psi _2'}\right )$
and that
$\mathrm { FV} \left ({\psi _2}\right )=\mathrm { FV} \left ({\psi _2'}\right )$
and that
![]() $\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {LEM} $
proves
$\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {LEM} $
proves
![]() $ \varphi _1' \to \neg \varphi _1$
,
$ \varphi _1' \to \neg \varphi _1$
,
![]() $ \varphi _2' \to \neg \varphi _2$
,
$ \varphi _2' \to \neg \varphi _2$
,
![]() $ \psi _1' \to \psi _1$
,
$ \psi _1' \to \psi _1$
,
![]() $ \psi _2' \to \psi _2$
and
$ \psi _2' \to \psi _2$
and
![]() $\mathsf {PA}$
proves
$\mathsf {PA}$
proves
![]() $\neg \varphi _1 \to \varphi _1'$
,
$\neg \varphi _1 \to \varphi _1'$
,
![]() $\neg \varphi _2 \to \varphi _2'$
,
$\neg \varphi _2 \to \varphi _2'$
,
![]() $\psi _1 \to \psi _1'$
,
$\psi _1 \to \psi _1'$
,
![]() $\psi _2 \to \psi _2'$
. By Lemma 6.4, for any conjunction and disjunction of
$\psi _2 \to \psi _2'$
. By Lemma 6.4, for any conjunction and disjunction of
![]() $\varphi _1', \varphi _2',\psi _1',\psi _2' \in \mathrm {E}\Sigma _{k+1}$
, there exists an equivalent (over
$\varphi _1', \varphi _2',\psi _1',\psi _2' \in \mathrm {E}\Sigma _{k+1}$
, there exists an equivalent (over
![]() $\mathsf {HA}$
)
$\mathsf {HA}$
)
![]() $\xi \in \mathrm {E}\Sigma _{k+1}$
which preserves the free variables. For
$\xi \in \mathrm {E}\Sigma _{k+1}$
which preserves the free variables. For
![]() $\varphi :\equiv \varphi _1 \lor \varphi _2 \in \mathcal {R}_{k+1}'$
, take
$\varphi :\equiv \varphi _1 \lor \varphi _2 \in \mathcal {R}_{k+1}'$
, take
![]() $\varphi '\in \mathrm {E}\Sigma _{k+1}$
as an equivalent of
$\varphi '\in \mathrm {E}\Sigma _{k+1}$
as an equivalent of
![]() $\varphi _1' \land \varphi _2'$
. For
$\varphi _1' \land \varphi _2'$
. For
![]() $\varphi :\equiv \psi _1 \lor \psi _2 \in \mathcal {J}_{k+1}'$
, take
$\varphi :\equiv \psi _1 \lor \psi _2 \in \mathcal {J}_{k+1}'$
, take
![]() $\varphi ' \in \mathrm {E}\Sigma _{k+1}$
as an equivalent of
$\varphi ' \in \mathrm {E}\Sigma _{k+1}$
as an equivalent of
![]() $\psi _1' \lor \psi _2'$
. For
$\psi _1' \lor \psi _2'$
. For
![]() $\varphi :\equiv \varphi _1 \land \varphi _2 \in \mathcal {R}_{k+1}'$
, take
$\varphi :\equiv \varphi _1 \land \varphi _2 \in \mathcal {R}_{k+1}'$
, take
![]() $\varphi ' \in \mathrm {E}\Sigma _{k+1}$
as an equivalent of
$\varphi ' \in \mathrm {E}\Sigma _{k+1}$
as an equivalent of
![]() $ \varphi _1' \lor \varphi _2'$
. For
$ \varphi _1' \lor \varphi _2'$
. For
![]() $\varphi :\equiv \psi _1 \land \psi _2 \in \mathcal {J}_{k+1}'$
, take
$\varphi :\equiv \psi _1 \land \psi _2 \in \mathcal {J}_{k+1}'$
, take
![]() $\varphi '\in \mathrm {E}\Sigma _{k+1}$
as an equivalent of
$\varphi '\in \mathrm {E}\Sigma _{k+1}$
as an equivalent of
![]() $\psi _1' \land \psi _2'$
. For
$\psi _1' \land \psi _2'$
. For
![]() $\varphi :\equiv \psi _1 \to \varphi _2 \in \mathcal {R}_{k+1}'$
, take
$\varphi :\equiv \psi _1 \to \varphi _2 \in \mathcal {R}_{k+1}'$
, take
![]() $\varphi '\in \mathrm {E}\Sigma _{k+1}$
as an equivalent of
$\varphi '\in \mathrm {E}\Sigma _{k+1}$
as an equivalent of
![]() $\psi _1' \land \varphi _2'$
. For
$\psi _1' \land \varphi _2'$
. For
![]() $\varphi :\equiv \varphi _1 \to \psi _2 \in \mathcal {J}_{k+1}'$
, take
$\varphi :\equiv \varphi _1 \to \psi _2 \in \mathcal {J}_{k+1}'$
, take
![]() $\varphi '\in \mathrm {E}\Sigma _{k+1}$
as an equivalent of
$\varphi '\in \mathrm {E}\Sigma _{k+1}$
as an equivalent of
![]() $\varphi _1' \lor \psi _2'$
. For
$\varphi _1' \lor \psi _2'$
. For
![]() $\varphi :\equiv \forall x \varphi _1 \in \mathcal {R}_{k+1}'$
, take
$\varphi :\equiv \forall x \varphi _1 \in \mathcal {R}_{k+1}'$
, take
![]() $\varphi ':\equiv \exists x \varphi _1'\in \mathrm {E}\Sigma _{k+1}$
. For
$\varphi ':\equiv \exists x \varphi _1'\in \mathrm {E}\Sigma _{k+1}$
. For
![]() $\varphi :\equiv \exists x \psi _1 \in \mathcal {J}_{k+1}'$
, take
$\varphi :\equiv \exists x \psi _1 \in \mathcal {J}_{k+1}'$
, take
![]() $\varphi ' :\equiv \exists x \psi _1' \in \mathrm {E}\Sigma _{k+1}$
. We leave the routine verification for the reader.
$\varphi ' :\equiv \exists x \psi _1' \in \mathrm {E}\Sigma _{k+1}$
. We leave the routine verification for the reader.
Corollary 6.6. For a
![]() $\mathsf {HA}$
-formula
$\mathsf {HA}$
-formula
![]() $\varphi $
, the following hold:
$\varphi $
, the following hold:
-
1. If
 $\varphi \in \mathrm {U}_{k+1}^+$
, then there exists
$\varphi \in \mathrm {U}_{k+1}^+$
, then there exists
 $\varphi '\in \Sigma _{k+1}$
such that
$\varphi '\in \Sigma _{k+1}$
such that
 $\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
$\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
 $\mathsf {HA}+{(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE} \vdash \varphi ' \to \neg \varphi $
and
$\mathsf {HA}+{(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE} \vdash \varphi ' \to \neg \varphi $
and
 $\mathsf {PA} \vdash \neg \varphi \to \varphi '$
.
$\mathsf {PA} \vdash \neg \varphi \to \varphi '$
. -
2. If
 $\varphi \in \mathrm {E}_{k+1}^+$
, then there exists
$\varphi \in \mathrm {E}_{k+1}^+$
, then there exists
 $\varphi '\in \Sigma _{k+1}$
such that
$\varphi '\in \Sigma _{k+1}$
such that
 $\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
$\mathrm { FV} \left ({\varphi }\right ) = \mathrm { FV} \left ({\varphi '}\right )$
,
 $\mathsf {HA}+{(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE} \vdash \varphi ' \to \varphi $
and
$\mathsf {HA}+{(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE} \vdash \varphi ' \to \varphi $
and
 $\mathsf {PA} \vdash \varphi \to \varphi '$
.
$\mathsf {PA} \vdash \varphi \to \varphi '$
.
Proof Since
![]() $\varphi '\in \mathrm {E}\Sigma _{k+1}$
is of the form
$\varphi '\in \mathrm {E}\Sigma _{k+1}$
is of the form
![]() $\exists x \varphi _1'$
where
$\exists x \varphi _1'$
where
![]() $\varphi _1'\in \mathrm {E}\Pi _k \subseteq \mathrm {U}_k^+$
, by Theorem 3.9.(2), there exists
$\varphi _1'\in \mathrm {E}\Pi _k \subseteq \mathrm {U}_k^+$
, by Theorem 3.9.(2), there exists
![]() $\psi \in \Sigma _{k+1}$
such that
$\psi \in \Sigma _{k+1}$
such that
![]() $\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\psi }\right )$
and
$\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\psi }\right )$
and
![]() $\mathsf {HA} + {(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE} \vdash \varphi ' \leftrightarrow \psi $
. Since
$\mathsf {HA} + {(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE} \vdash \varphi ' \leftrightarrow \psi $
. Since
![]() $\mathsf {HA} + {(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}$
proves
$\mathsf {HA} + {(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}$
proves
![]() ${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
, our corollary follows from Lemma 6.5.
${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
, our corollary follows from Lemma 6.5.
Theorem 6.7. Let
![]() ${T}$
be semi-classical arithmetic and X be a set of
${T}$
be semi-classical arithmetic and X be a set of
![]() $\mathsf {HA}$
-sentences. Then
$\mathsf {HA}$
-sentences. Then
![]() $\mathsf {PA} + X$
is
$\mathsf {PA} + X$
is
![]() -conservative over
-conservative over
![]() ${T} + X$
if and only if
${T} + X$
if and only if
![]() $\mathsf {PA} + X$
is
$\mathsf {PA} + X$
is
![]() -conservative over
-conservative over
![]() ${T} + X$
.
${T} + X$
.
Proof The “only if” direction is trivial since
![]() . We show the converse direction. Let
. We show the converse direction. Let
![]() . Assume
. Assume
![]() $\mathsf {PA} + X \vdash \varphi $
. By Lemma 6.5, there exists
$\mathsf {PA} + X \vdash \varphi $
. By Lemma 6.5, there exists
![]() such that
such that
![]() $\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \varphi ' \to \varphi $
and
$\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \varphi ' \to \varphi $
and
![]() $\mathsf {PA} \vdash \varphi \to \varphi '$
. Then
$\mathsf {PA} \vdash \varphi \to \varphi '$
. Then
![]() $\mathsf {PA} + X \vdash \varphi '$
. By our assumption, we have
$\mathsf {PA} + X \vdash \varphi '$
. By our assumption, we have
![]() ${T} + X \vdash \varphi '$
. On the other hand, as in the proof of Lemma 5.5, one can show
${T} + X \vdash \varphi '$
. On the other hand, as in the proof of Lemma 5.5, one can show
![]() ${T} +X \vdash {\Sigma _{k-1}}\text {-}\mathrm {LEM}$
(note that
${T} +X \vdash {\Sigma _{k-1}}\text {-}\mathrm {LEM}$
(note that
![]() can be seen as a sub-class of
can be seen as a sub-class of
![]() and the
and the
![]() -conservativity implies the
-conservativity implies the
![]() $\mathrm {E}\Pi _{k}$
-conservativity by Proposition 6.1). Then we have
$\mathrm {E}\Pi _{k}$
-conservativity by Proposition 6.1). Then we have
![]() ${T}+X \vdash \varphi $
.
${T}+X \vdash \varphi $
.
6.2 Conservation theorem for
 $\mathrm {F}_k$
sentences
$\mathrm {F}_k$
sentences
Next, we characterize the
![]() -conservativity. To investigate the class
-conservativity. To investigate the class
![]() $\mathrm {F}_{k}$
, it is convenient to consider the following class:
$\mathrm {F}_{k}$
, it is convenient to consider the following class:
Definition 6.8. Let
![]() $\mathrm {B}_k^+$
be the class of formulas which are constructed from formulas in
$\mathrm {B}_k^+$
be the class of formulas which are constructed from formulas in
![]() $\mathrm {E}_k^+ \cup \mathrm {U}_k^+$
by using logical connectives
$\mathrm {E}_k^+ \cup \mathrm {U}_k^+$
by using logical connectives
![]() $\land , \lor $
and
$\land , \lor $
and
![]() $\to $
. Let
$\to $
. Let
![]() ${\mathrm {B}_k^+}\text {-}\mathrm {LEM}$
be
${\mathrm {B}_k^+}\text {-}\mathrm {LEM}$
be
![]() ${\textrm {LEM}}$
restricted to formulas in
${\textrm {LEM}}$
restricted to formulas in
![]() $\mathrm {B}_k^+$
.
$\mathrm {B}_k^+$
.
Proposition 6.9.
![]() $\mathsf {HA} \vdash {\Sigma _k}\text {-}\mathrm {LEM} \leftrightarrow {\mathrm {B}_k^+}\text {-}\mathrm {LEM}$
.
$\mathsf {HA} \vdash {\Sigma _k}\text {-}\mathrm {LEM} \leftrightarrow {\mathrm {B}_k^+}\text {-}\mathrm {LEM}$
.
Proof First,
![]() $\mathsf {HA} + {\mathrm {B}_k^+}\text {-}\mathrm {LEM} \vdash {\Sigma _k}\text {-}\mathrm {LEM} $
is trivial since
$\mathsf {HA} + {\mathrm {B}_k^+}\text {-}\mathrm {LEM} \vdash {\Sigma _k}\text {-}\mathrm {LEM} $
is trivial since
![]() $\Sigma _k \subseteq \mathrm {E}_k^+$
. We show the converse direction. By Remark 3.10, inside
$\Sigma _k \subseteq \mathrm {E}_k^+$
. We show the converse direction. By Remark 3.10, inside
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
, one may assume that
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
, one may assume that
![]() $\varphi \in \mathrm {B}_k^+$
is constructed from formulas in
$\varphi \in \mathrm {B}_k^+$
is constructed from formulas in
![]() $\Sigma _k \cup \Pi _k$
by using logical connectives
$\Sigma _k \cup \Pi _k$
by using logical connectives
![]() $\land , \lor $
and
$\land , \lor $
and
![]() $\to $
. Then we have
$\to $
. Then we have
![]() $\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM} \vdash {\mathrm {B}_k^+}\text {-}\mathrm {LEM}$
in a straightforward way.
$\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM} \vdash {\mathrm {B}_k^+}\text {-}\mathrm {LEM}$
in a straightforward way.
Proposition 6.10.
![]() $\mathrm {B}_k^+ = \mathrm {F}_k$
.
$\mathrm {B}_k^+ = \mathrm {F}_k$
.
Proof Since
![]() $\mathrm {F}_k^+ = \mathrm {F}_k$
(cf. Remark 3.8), it suffices to show
$\mathrm {F}_k^+ = \mathrm {F}_k$
(cf. Remark 3.8), it suffices to show
![]() $\mathrm {B}_k^+ = \mathrm {F}_k^+$
.
$\mathrm {B}_k^+ = \mathrm {F}_k^+$
.
First,
![]() $\mathrm {B}_k^+ \subseteq \mathrm {F}_k^+$
is trivial since
$\mathrm {B}_k^+ \subseteq \mathrm {F}_k^+$
is trivial since
![]() $\mathrm {E}_k^+ \subseteq \mathrm {F}_k^+$
,
$\mathrm {E}_k^+ \subseteq \mathrm {F}_k^+$
,
![]() $\mathrm {U}_k^+ \subseteq \mathrm {F}_k^+$
and the fact that
$\mathrm {U}_k^+ \subseteq \mathrm {F}_k^+$
and the fact that
![]() $\mathrm {F}_k^+$
is closed under
$\mathrm {F}_k^+$
is closed under
![]() $\land , \lor $
and
$\land , \lor $
and
![]() $\to $
.
$\to $
.
We show that
![]() $\varphi \in \mathrm {F}_k^+$
implies
$\varphi \in \mathrm {F}_k^+$
implies
![]() $\varphi \in \mathrm {B}_k^+$
for all
$\varphi \in \mathrm {B}_k^+$
for all
![]() $\mathsf {HA}$
-formulas
$\mathsf {HA}$
-formulas
![]() $\varphi $
by induction on the structure of formulas. If
$\varphi $
by induction on the structure of formulas. If
![]() $\varphi $
is prime, since
$\varphi $
is prime, since
![]() $\varphi \in \mathrm {B}_k^+$
, then we are done. For the induction step, assume that it holds for
$\varphi \in \mathrm {B}_k^+$
, then we are done. For the induction step, assume that it holds for
![]() $\varphi _1$
and
$\varphi _1$
and
![]() $\varphi _2$
. If
$\varphi _2$
. If
![]() $\varphi _1 \land \varphi _2 \in \mathrm {F}_k^+$
, then
$\varphi _1 \land \varphi _2 \in \mathrm {F}_k^+$
, then
![]() $\varphi _1, \varphi _2 \in \mathrm {F}_k^+$
follows. By the induction hypothesis, we have
$\varphi _1, \varphi _2 \in \mathrm {F}_k^+$
follows. By the induction hypothesis, we have
![]() $\varphi _1, \varphi _2 \in \mathrm {B}_k^+$
, and hence,
$\varphi _1, \varphi _2 \in \mathrm {B}_k^+$
, and hence,
![]() $\varphi _1 \land \varphi _2 \in \mathrm {B}_k^+$
. The cases of
$\varphi _1 \land \varphi _2 \in \mathrm {B}_k^+$
. The cases of
![]() $\varphi _1 \lor \varphi _2$
and
$\varphi _1 \lor \varphi _2$
and
![]() $\varphi _1 \to \varphi _2 $
are similar. If
$\varphi _1 \to \varphi _2 $
are similar. If
![]() $\forall x \varphi _1\in \mathrm {F}_k^+$
, by the definition, we have
$\forall x \varphi _1\in \mathrm {F}_k^+$
, by the definition, we have
![]() $\forall x \varphi _1 \in \mathrm {U}_k^+$
, and hence,
$\forall x \varphi _1 \in \mathrm {U}_k^+$
, and hence,
![]() $\forall x \varphi _1 \in \mathrm {B}_k^+$
. The case of
$\forall x \varphi _1 \in \mathrm {B}_k^+$
. The case of
![]() $\exists x \varphi _1\in \mathrm {F}_k^+$
is similar.
$\exists x \varphi _1\in \mathrm {F}_k^+$
is similar.
Corollary 6.11 (cf. [Reference Akama, Berardi, Hayashi and Kohlenbach1, Corollary 2.8(i)]).
![]() $\mathsf {HA} \vdash {\Sigma _k}\text {-}\mathrm {LEM} \leftrightarrow {\mathrm {F}_k}\text {-}\mathrm {LEM}$
.
$\mathsf {HA} \vdash {\Sigma _k}\text {-}\mathrm {LEM} \leftrightarrow {\mathrm {F}_k}\text {-}\mathrm {LEM}$
.
Remark 6.12. By using Proposition 6.10 and Theorem 3.9, one can show the following: If
![]() $\varphi \in \mathrm {F}_k$
, then
$\varphi \in \mathrm {F}_k$
, then
![]() . This is an extension of Lemma 3.5.
. This is an extension of Lemma 3.5.
Lemma 6.13. For all
![]() $\varphi \in \mathrm {B}_k^+$
, there exist
$\varphi \in \mathrm {B}_k^+$
, there exist
![]() $\varphi '$
and
$\varphi '$
and
![]() $\varphi "$
which are constructed from formulas in
$\varphi "$
which are constructed from formulas in
![]() $\mathrm {E}\Pi _k \bigcup \Sigma _k$
by using
$\mathrm {E}\Pi _k \bigcup \Sigma _k$
by using
![]() $\land $
and
$\land $
and
![]() $\lor $
only, and satisfy
$\lor $
only, and satisfy
![]() $\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\varphi "}\right )=\mathrm { FV} \left ({\varphi }\right )$
,
$\mathrm { FV} \left ({\varphi '}\right )=\mathrm { FV} \left ({\varphi "}\right )=\mathrm { FV} \left ({\varphi }\right )$
,
![]() $\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {LEM}$
proves
$\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {LEM}$
proves
![]() $\varphi ' \to \varphi $
and
$\varphi ' \to \varphi $
and
![]() $\varphi " \to \neg \varphi $
, and
$\varphi " \to \neg \varphi $
, and
![]() $\mathsf {PA}$
proves
$\mathsf {PA}$
proves
![]() $\varphi \to \varphi '$
and
$\varphi \to \varphi '$
and
![]() $\neg \varphi \to \varphi "$
.
$\neg \varphi \to \varphi "$
.
Proof By induction on the construction of
![]() $\mathrm {B}_k^+$
.
$\mathrm {B}_k^+$
.
For the base case, first assume
![]() $\varphi \in \mathrm {U}_{k}^+$
. By Lemma 5.14, there exists
$\varphi \in \mathrm {U}_{k}^+$
. By Lemma 5.14, there exists
![]() $\varphi '\in \mathrm {E}\Pi _k$
such that
$\varphi '\in \mathrm {E}\Pi _k$
such that
![]() $\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi '}\right )$
,
$\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi '}\right )$
,
![]() $\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM}\vdash \varphi ' \to \varphi $
and
$\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM}\vdash \varphi ' \to \varphi $
and
![]() $\mathsf {PA} \vdash \varphi \to \varphi '$
. By Corollary 6.6, there exists
$\mathsf {PA} \vdash \varphi \to \varphi '$
. By Corollary 6.6, there exists
![]() $\varphi "\in \Sigma _k$
such that
$\varphi "\in \Sigma _k$
such that
![]() $\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi "}\right )$
,
$\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi "}\right )$
,
![]() $\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM}\vdash \varphi " \to \neg \varphi $
(cf. Remark 3.10) and
$\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM}\vdash \varphi " \to \neg \varphi $
(cf. Remark 3.10) and
![]() $\mathsf {PA} \vdash \neg \varphi \to \varphi "$
. Next assume
$\mathsf {PA} \vdash \neg \varphi \to \varphi "$
. Next assume
![]() $\varphi \in \mathrm {E}_{k}^+$
. By Corollary 6.6, there exists
$\varphi \in \mathrm {E}_{k}^+$
. By Corollary 6.6, there exists
![]() $\varphi '\in \Sigma _k$
such that
$\varphi '\in \Sigma _k$
such that
![]() $\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi '}\right )$
,
$\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi '}\right )$
,
![]() $\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM}\vdash \varphi ' \to \varphi $
and
$\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM}\vdash \varphi ' \to \varphi $
and
![]() $\mathsf {PA} \vdash \varphi \to \varphi '$
. By Lemma 5.14, there exists
$\mathsf {PA} \vdash \varphi \to \varphi '$
. By Lemma 5.14, there exists
![]() $\varphi "\in \mathrm {E}\Pi _k$
such that
$\varphi "\in \mathrm {E}\Pi _k$
such that
![]() $\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi "}\right )$
,
$\mathrm { FV} \left ({\varphi }\right )=\mathrm { FV} \left ({\varphi "}\right )$
,
![]() $\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM}\vdash \varphi " \to \neg \varphi $
and
$\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM}\vdash \varphi " \to \neg \varphi $
and
![]() $\mathsf {PA} \vdash \neg \varphi \to \varphi "$
.
$\mathsf {PA} \vdash \neg \varphi \to \varphi "$
.
For the induction step, let
![]() $\varphi _1, \varphi _2\in \mathrm {B}_k^+$
and
$\varphi _1, \varphi _2\in \mathrm {B}_k^+$
and
![]() $\varphi _1', \varphi _1", \varphi _2', \varphi _2"$
constructed from formulas in
$\varphi _1', \varphi _1", \varphi _2', \varphi _2"$
constructed from formulas in
![]() $\mathrm {E}\Pi _k \bigcup \Sigma _k$
by using
$\mathrm {E}\Pi _k \bigcup \Sigma _k$
by using
![]() $\land $
and
$\land $
and
![]() $\lor $
only satisfy the following:
$\lor $
only satisfy the following:
![]() $\mathrm { FV} \left ({\varphi _1'}\right )=\mathrm { FV} \left ({\varphi _1"}\right )=\mathrm { FV} \left ({\varphi _1}\right )$
,
$\mathrm { FV} \left ({\varphi _1'}\right )=\mathrm { FV} \left ({\varphi _1"}\right )=\mathrm { FV} \left ({\varphi _1}\right )$
,
![]() $\mathrm { FV} \left ({\varphi _2'}\right )=\mathrm { FV} \left ({\varphi _2"}\right )=\mathrm { FV} \left ({\varphi _2}\right )$
,
$\mathrm { FV} \left ({\varphi _2'}\right )=\mathrm { FV} \left ({\varphi _2"}\right )=\mathrm { FV} \left ({\varphi _2}\right )$
,
![]() $\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {LEM}$
proves
$\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {LEM}$
proves
![]() $\varphi _1' \to \varphi _1$
,
$\varphi _1' \to \varphi _1$
,
![]() $\varphi _2' \to \varphi _2$
,
$\varphi _2' \to \varphi _2$
,
![]() $\varphi _1" \to \neg \varphi _1$
,
$\varphi _1" \to \neg \varphi _1$
,
![]() $\varphi _2" \to \neg \varphi _2$
and
$\varphi _2" \to \neg \varphi _2$
and
![]() $\mathsf {PA}$
proves
$\mathsf {PA}$
proves
![]() $\varphi _1 \to \varphi _1'$
,
$\varphi _1 \to \varphi _1'$
,
![]() $\varphi _2 \to \varphi _2'$
,
$\varphi _2 \to \varphi _2'$
,
![]() $\neg \varphi _1 \to \varphi _1"$
,
$\neg \varphi _1 \to \varphi _1"$
,
![]() $\neg \varphi _2 \to \varphi _2"$
. For
$\neg \varphi _2 \to \varphi _2"$
. For
![]() $\varphi :\equiv \varphi _1 \land \varphi _2$
, take
$\varphi :\equiv \varphi _1 \land \varphi _2$
, take
![]() $\varphi ':\equiv \varphi _1'\land \varphi _2'$
and
$\varphi ':\equiv \varphi _1'\land \varphi _2'$
and
![]() $\varphi ":\equiv \varphi _1" \lor \varphi _2" $
. For
$\varphi ":\equiv \varphi _1" \lor \varphi _2" $
. For
![]() $\varphi :\equiv \varphi _1 \lor \varphi _2$
, take
$\varphi :\equiv \varphi _1 \lor \varphi _2$
, take
![]() $\varphi ':\equiv \varphi _1'\lor \varphi _2'$
and
$\varphi ':\equiv \varphi _1'\lor \varphi _2'$
and
![]() $\varphi ":\equiv \varphi _1" \land \varphi _2" $
. For
$\varphi ":\equiv \varphi _1" \land \varphi _2" $
. For
![]() $\varphi :\equiv \varphi _1 \to \varphi _2$
, take
$\varphi :\equiv \varphi _1 \to \varphi _2$
, take
![]() $\varphi ':\equiv \varphi _1" \lor \varphi _2'$
and
$\varphi ':\equiv \varphi _1" \lor \varphi _2'$
and
![]() $\varphi ":\equiv \varphi _1' \land \varphi _2" $
. We leave the routine verification for the reader.
$\varphi ":\equiv \varphi _1' \land \varphi _2" $
. We leave the routine verification for the reader.
Theorem 6.14. Let
![]() ${T}$
be semi-classical arithmetic and X be a set of
${T}$
be semi-classical arithmetic and X be a set of
![]() $\mathsf {HA}$
-sentences. Then
$\mathsf {HA}$
-sentences. Then
![]() $\mathsf {PA} + X$
is
$\mathsf {PA} + X$
is
![]() -conservative over
-conservative over
![]() ${T} + X$
if and only if
${T} + X$
if and only if
![]() $\mathsf {PA} + X$
is
$\mathsf {PA} + X$
is
![]() -conservative over
-conservative over
![]() ${T} + X$
.
${T} + X$
.
Proof The “only if” direction is trivial since
![]() . We show the converse direction. Let
. We show the converse direction. Let
![]() . Assume
. Assume
![]() $\mathsf {PA} + X \vdash \varphi $
. By Lemma 6.13 and Proposition 6.10, there exist
$\mathsf {PA} + X \vdash \varphi $
. By Lemma 6.13 and Proposition 6.10, there exist
![]() $\varphi '$
which is constructed from formulas in
$\varphi '$
which is constructed from formulas in
![]() by using
by using
![]() $\land $
and
$\land $
and
![]() $\lor $
only, and satisfy
$\lor $
only, and satisfy
![]() $\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {LEM}\vdash \varphi ' \to \varphi $
and
$\mathsf {HA} +{\Sigma _{k-1}}\text {-}\mathrm {LEM}\vdash \varphi ' \to \varphi $
and
![]() $\mathsf {PA}\vdash \varphi \to \varphi '$
. Without loss of generality, one may assume that
$\mathsf {PA}\vdash \varphi \to \varphi '$
. Without loss of generality, one may assume that
![]() $\varphi '$
is of conjunctive normal form such that each conjunct is a disjunction of sentences in
$\varphi '$
is of conjunctive normal form such that each conjunct is a disjunction of sentences in
![]() . Since disjunction of sentences in
. Since disjunction of sentences in
![]() is equivalent to a sentence in
is equivalent to a sentence in
![]() over
over
![]() $\mathsf {HA}$
and
$\mathsf {HA}$
and
![]() is closed under
is closed under
![]() $\lor $
, each conjunct can be assumed to be of the form
$\lor $
, each conjunct can be assumed to be of the form
![]() $\psi \lor \xi $
where
$\psi \lor \xi $
where
![]() and
and
![]() . Let
. Let
![]() $\varphi ':\equiv \bigwedge _{1\leq i\leq n} \left ( \psi _i \lor \xi _i \right )$
where
$\varphi ':\equiv \bigwedge _{1\leq i\leq n} \left ( \psi _i \lor \xi _i \right )$
where
![]() and
and
![]() . Since
. Since
![]() $\mathsf {PA} + X \vdash \varphi '$
, by the
$\mathsf {PA} + X \vdash \varphi '$
, by the
![]() -conservativity, we have that
-conservativity, we have that
![]() ${T} + X$
proves
${T} + X$
proves
![]() $ \psi _i \lor \xi _i$
for each i. Then we have
$ \psi _i \lor \xi _i$
for each i. Then we have
![]() ${T} + X \vdash \varphi '$
. Since
${T} + X \vdash \varphi '$
. Since
![]() $\mathsf {PA} + X$
is now
$\mathsf {PA} + X$
is now
![]() $\mathrm {E}\Pi _{k}$
-conservative over
$\mathrm {E}\Pi _{k}$
-conservative over
![]() ${T} + X$
(cf. Proposition 6.1), as in the proof of Lemma 5.5, we have
${T} + X$
(cf. Proposition 6.1), as in the proof of Lemma 5.5, we have
![]() ${T} + X \vdash {\Sigma _{k-1}}\text {-}\mathrm {LEM}$
. Then
${T} + X \vdash {\Sigma _{k-1}}\text {-}\mathrm {LEM}$
. Then
![]() ${T} + X \vdash \varphi $
follows.
${T} + X \vdash \varphi $
follows.
In what follows, by further investigating the
![]() -conservativity in Theorem 6.14, we give a characterization of the
-conservativity in Theorem 6.14, we give a characterization of the
![]() -conservativity by axiom schemata.
-conservativity by axiom schemata.
Definition 6.15. Let
![]() $\Gamma $
be a class of
$\Gamma $
be a class of
![]() $\mathsf {HA}$
-formulas. We introduce the following axiom schemata:
$\mathsf {HA}$
-formulas. We introduce the following axiom schemata:
-
•

-
•

where
![]() $\varphi \in \Gamma $
and
$\varphi \in \Gamma $
and
![]() $\widetilde {\neg \neg \varphi }$
and
$\widetilde {\neg \neg \varphi }$
and
![]() $\widetilde {\varphi }$
are universal closures of
$\widetilde {\varphi }$
are universal closures of
![]() $\neg \neg \varphi $
and
$\neg \neg \varphi $
and
![]() $\varphi $
respectively.
$\varphi $
respectively.
Proposition 6.16. Let
![]() $\Gamma $
be a class of
$\Gamma $
be a class of
![]() $\mathsf {HA}$
-formulas such that
$\mathsf {HA}$
-formulas such that
![]() $\Gamma $
is closed under taking a universal closure. Then
$\Gamma $
is closed under taking a universal closure. Then
![]() is equivalent to
is equivalent to
![]() over
over
![]() $\mathsf {HA}$
.
$\mathsf {HA}$
.
Proof It is trivial that
![]() implies
implies
![]() and also
and also
![]() . We show
. We show
![]() . Let
. Let
![]() $\varphi \in \Gamma $
. By
$\varphi \in \Gamma $
. By
![]() ,
,
![]() $\widetilde {\neg \neg \varphi }$
implies
$\widetilde {\neg \neg \varphi }$
implies
![]() $\neg \neg \widetilde {\varphi }$
. Since
$\neg \neg \widetilde {\varphi }$
. Since
![]() $\widetilde {\varphi }$
is now in
$\widetilde {\varphi }$
is now in
![]() $\Gamma $
, by
$\Gamma $
, by
![]() ,
,
![]() $\neg \neg \widetilde {\varphi }$
implies
$\neg \neg \widetilde {\varphi }$
implies
![]() $\widetilde {\varphi }$
. Thus we have
$\widetilde {\varphi }$
. Thus we have
![]()
Lemma 6.17. Let
![]() ${T}$
be a theory containing
${T}$
be a theory containing
![]() $\mathsf {HA}$
and satisfying the deduction theorem, and X be a set of
$\mathsf {HA}$
and satisfying the deduction theorem, and X be a set of
![]() $\mathsf {HA}$
-sentences in
$\mathsf {HA}$
-sentences in
![]() $\mathcal {Q}_k$
. If
$\mathcal {Q}_k$
. If
![]() ${T} + X $
proves
${T} + X $
proves
![]() and
and
![]() ${T} +X$
is closed under
${T} +X$
is closed under
![]() ${\mathrm {E}\Pi _k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
with assumptions of sentences in
${\mathrm {E}\Pi _k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
with assumptions of sentences in
![]() $\Pi _k:$
$\Pi _k:$
![]() ${T} +X \vdash \psi \to \neg \neg \varphi $
implies
${T} +X \vdash \psi \to \neg \neg \varphi $
implies
![]() ${T} +X \vdash \psi \to \varphi $
for all
${T} +X \vdash \psi \to \varphi $
for all
![]() and
and
![]() $\varphi \in \mathrm {E}\Pi _k$
, then
$\varphi \in \mathrm {E}\Pi _k$
, then
![]() $\mathsf {PA}+X$
is
$\mathsf {PA}+X$
is
![]() -conservative over
-conservative over
![]() ${T} + X$
.
${T} + X$
.
Proof Let
![]() and
and
![]() . Assume
. Assume
![]() $\mathsf {PA} + X \vdash \varphi \lor \psi $
. Since
$\mathsf {PA} + X \vdash \varphi \lor \psi $
. Since
![]() ${T}$
satisfies the deduction theorem and
${T}$
satisfies the deduction theorem and
![]() , by our second assumption, we have that
, by our second assumption, we have that
![]() ${T} + X + \varphi ^{\perp }$
is closed under
${T} + X + \varphi ^{\perp }$
is closed under
![]() ${\mathrm {E}\Pi _k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
. Since
${\mathrm {E}\Pi _k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
. Since
![]() $\varphi ^{\perp } \in \mathcal {Q}_k$
, by Theorem 5.16, we have that
$\varphi ^{\perp } \in \mathcal {Q}_k$
, by Theorem 5.16, we have that
![]() $\mathsf {PA} +X+\varphi ^{\perp }$
is
$\mathsf {PA} +X+\varphi ^{\perp }$
is
![]() $\mathrm {E}\Pi _k$
-conservative over
$\mathrm {E}\Pi _k$
-conservative over
![]() ${T} + X + \varphi ^{\perp }$
. Since
${T} + X + \varphi ^{\perp }$
. Since
![]() $\mathsf {PA} + X + \varphi ^{\perp } \vdash \psi $
, we have
$\mathsf {PA} + X + \varphi ^{\perp } \vdash \psi $
, we have
![]() ${T} + X + \varphi ^{\perp } \vdash \psi $
, and hence,
${T} + X + \varphi ^{\perp } \vdash \psi $
, and hence,
by the deduction theorem. In addition, by our second assumption and Theorem 5.16, we have that
![]() ${T} + X$
is closed under
${T} + X$
is closed under
![]() ${\mathrm {E}\Pi _k}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
, and hence,
${\mathrm {E}\Pi _k}\text {-}\mathrm {CD}\text {-}\mathrm {R}$
, and hence,
![]() ${T}+ X \vdash {\Sigma _{k-1}}\text {-}\mathrm {LEM}$
by Lemma 5.7. Then, by Remark 5.3, we have
${T}+ X \vdash {\Sigma _{k-1}}\text {-}\mathrm {LEM}$
by Lemma 5.7. Then, by Remark 5.3, we have
![]() ${T}+X \vdash \neg \varphi \to \varphi ^{\perp }$
, and hence,
${T}+X \vdash \neg \varphi \to \varphi ^{\perp }$
, and hence,
![]() ${T} + X \vdash \neg \varphi \to \psi $
by (3). On the other hand, by our first assumption, we have
${T} + X \vdash \neg \varphi \to \psi $
by (3). On the other hand, by our first assumption, we have
![]() $ {T}+X \vdash \varphi \lor \neg \varphi $
. Then
$ {T}+X \vdash \varphi \lor \neg \varphi $
. Then
![]() ${T}+X \vdash \varphi \lor \psi $
follows.
${T}+X \vdash \varphi \lor \psi $
follows.
Theorem 6.18. Let
![]() ${T}$
be semi-classical arithmetic satisfying the deduction theorem and X be a set of
${T}$
be semi-classical arithmetic satisfying the deduction theorem and X be a set of
![]() $\mathsf {HA}$
-sentences in
$\mathsf {HA}$
-sentences in
![]() $\mathcal {Q}_{k}$
. Then the following are pairwise equivalent:
$\mathcal {Q}_{k}$
. Then the following are pairwise equivalent:
-
1.
 $\mathsf {PA} + X$
is
$\mathsf {PA} + X$
is
 -conservative over
-conservative over
 ${T} + X;$
${T} + X;$
-
2.
 ${T} + X $
proves
${T} + X $
proves
 and
and

-
3.
 ${T} + X $
proves
${T} + X $
proves
 and
and

-
4.
 ${T} + X $
proves
${T} + X $
proves
 and
and
 .
.
Proof (1
![]() $\to $
2): Let
$\to $
2): Let
![]() . Then
. Then
![]() . Since
. Since
![]() $\mathsf {PA} \vdash \varphi \lor \neg \varphi $
, we have
$\mathsf {PA} \vdash \varphi \lor \neg \varphi $
, we have
![]() ${T} + X \vdash \varphi \lor \neg \varphi $
by (1). Let
${T} + X \vdash \varphi \lor \neg \varphi $
by (1). Let
![]() $\psi \in \mathrm {U}_k$
. Then
$\psi \in \mathrm {U}_k$
. Then
![]() . Since
. Since
![]() $\mathsf {PA} \vdash \widetilde {\neg \neg \psi }\to \neg \neg \widetilde {\psi }$
, we have
$\mathsf {PA} \vdash \widetilde {\neg \neg \psi }\to \neg \neg \widetilde {\psi }$
, we have
![]() ${T} + X \vdash \widetilde {\neg \neg \psi }\to \neg \neg \widetilde {\psi }$
by (1).
${T} + X \vdash \widetilde {\neg \neg \psi }\to \neg \neg \widetilde {\psi }$
by (1).
(2
![]() $\to $
3): It suffices to show
$\to $
3): It suffices to show
![]() by using
by using
![]() and
and
![]() . Since
. Since
![]() and
and
![]() implies
implies
![]() , by Proposition 6.16, we are done.
, by Proposition 6.16, we are done.
(4
![]() $\to $
1): By Theorem 6.14 and Lemma 6.17, it suffices for (1) to show that
$\to $
1): By Theorem 6.14 and Lemma 6.17, it suffices for (1) to show that
![]() ${T} +X$
is closed under
${T} +X$
is closed under
![]() ${\mathrm {E}\Pi _k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
with assumptions of
${\mathrm {E}\Pi _k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
with assumptions of
![]() $\Pi _k$
sentences. Let
$\Pi _k$
sentences. Let
![]() and
and
![]() $\varphi \in \mathrm {E}\Pi _k$
. Assume
$\varphi \in \mathrm {E}\Pi _k$
. Assume
![]() ${T} +X \vdash \psi \to \neg \neg \varphi $
. Then
${T} +X \vdash \psi \to \neg \neg \varphi $
. Then
![]() ${T} + X + \psi \vdash \widetilde {\neg \neg \varphi }$
. Since
${T} + X + \psi \vdash \widetilde {\neg \neg \varphi }$
. Since
![]() ${T} + X$
proves
${T} + X$
proves
![]() now, we have
now, we have
![]() ${T} + X + \psi \vdash \widetilde {\varphi }$
, and hence,
${T} + X + \psi \vdash \widetilde {\varphi }$
, and hence,
![]() ${T} + X + \psi \vdash \varphi $
. Since
${T} + X + \psi \vdash \varphi $
. Since
![]() ${T}$
satisfies the deduction theorem,
${T}$
satisfies the deduction theorem,
![]() ${T} + X \vdash \psi \to \varphi $
follows.
${T} + X \vdash \psi \to \varphi $
follows.
Remark 6.19.
![]() in Theorem 6.18.(2) is equivalent over
in Theorem 6.18.(2) is equivalent over
![]() $\mathsf {HA}$
to the closed fragment of
$\mathsf {HA}$
to the closed fragment of
![]() ${\mathrm {U}_k}\text {-}\mathrm {DNS}$
:
${\mathrm {U}_k}\text {-}\mathrm {DNS}$
:
where
![]() $\varphi \in \mathrm {U}_k$
such that
$\varphi \in \mathrm {U}_k$
such that
![]() $\mathrm { FV} \left ({\varphi }\right )=\{x\}$
.
$\mathrm { FV} \left ({\varphi }\right )=\{x\}$
.
In the following, we show that
![]() and
and
![]() in Theorem 6.18.(2) are independent over
in Theorem 6.18.(2) are independent over
![]() $\mathsf {HA}$
.
$\mathsf {HA}$
.
Proposition 6.20.
![]() for any class
for any class
![]() $\Gamma $
of
$\Gamma $
of
![]() $\mathsf {HA}$
-formulas.
$\mathsf {HA}$
-formulas.
Proof Suppose
![]() . As in the proof of Proposition 5.10, let
. As in the proof of Proposition 5.10, let
![]() $\phi (x) \in \Pi _1 \lor \Pi _1$
be formula (2). Since
$\phi (x) \in \Pi _1 \lor \Pi _1$
be formula (2). Since
![]() $\mathsf {HA} \vdash \forall x \neg \neg \phi (x)$
, we have
$\mathsf {HA} \vdash \forall x \neg \neg \phi (x)$
, we have
![]() . Since the double negation of each instance of
. Since the double negation of each instance of
![]() is provable in
is provable in
![]() $\mathsf {HA}$
, by (the proof of) [Reference Troelstra and van Dalen7, Lemma 4.1], we have
$\mathsf {HA}$
, by (the proof of) [Reference Troelstra and van Dalen7, Lemma 4.1], we have
![]() $\mathsf {HA} \vdash \neg \neg \forall x \phi (x)$
. This is a contradiction as shown in the proof of Proposition 5.10.
$\mathsf {HA} \vdash \neg \neg \forall x \phi (x)$
. This is a contradiction as shown in the proof of Proposition 5.10.
Proposition 6.21.
![]() where
where
![]() $\mathrm {DNS}$
is the axiom scheme of the double-negation-shift
$\mathrm {DNS}$
is the axiom scheme of the double-negation-shift
![]() $\forall x (\forall y \neg \neg \varphi (x,y)\to \neg \neg \forall y \varphi (x, y)) $
.
$\forall x (\forall y \neg \neg \varphi (x,y)\to \neg \neg \forall y \varphi (x, y)) $
.
Proof Let
![]() $\varphi $
be a sentence in
$\varphi $
be a sentence in
![]() $\Pi _1$
such that
$\Pi _1$
such that
![]() $\mathsf {PA}\nvdash \varphi $
and
$\mathsf {PA}\nvdash \varphi $
and
![]() $\mathsf {PA} \nvdash \neg \varphi $
(e.g., the Gödel sentence for Gödel’s first incompleteness theorem). Since each instance of
$\mathsf {PA} \nvdash \neg \varphi $
(e.g., the Gödel sentence for Gödel’s first incompleteness theorem). Since each instance of
![]() $\mathrm {DNS}$
is intuitionistically equivalent to a negated sentence (cf. [Reference Troelstra and van Dalen7, Remark 2.8]), by [Reference Troelstra and van Dalen13, Theorem 3.1.4 and Lemma 3.1.6], we have that
$\mathrm {DNS}$
is intuitionistically equivalent to a negated sentence (cf. [Reference Troelstra and van Dalen7, Remark 2.8]), by [Reference Troelstra and van Dalen13, Theorem 3.1.4 and Lemma 3.1.6], we have that
![]() $\mathsf {HA} + \mathrm {DNS}$
has the disjunction property. Suppose
$\mathsf {HA} + \mathrm {DNS}$
has the disjunction property. Suppose
![]() $\mathsf {HA} + \mathrm {DNS} \vdash \varphi ^{\perp } \lor \neg \varphi ^{\perp }$
(where
$\mathsf {HA} + \mathrm {DNS} \vdash \varphi ^{\perp } \lor \neg \varphi ^{\perp }$
(where
![]() ). Then, by the disjunction property, we have
). Then, by the disjunction property, we have
![]() $\mathsf {HA} + \mathrm {DNS} \vdash \varphi ^{\perp }$
or
$\mathsf {HA} + \mathrm {DNS} \vdash \varphi ^{\perp }$
or
![]() $\mathsf {HA} + \mathrm {DNS} \vdash \neg \varphi ^{\perp }$
, and hence,
$\mathsf {HA} + \mathrm {DNS} \vdash \neg \varphi ^{\perp }$
, and hence,
![]() $\mathsf {PA} \vdash \neg \varphi $
or
$\mathsf {PA} \vdash \neg \varphi $
or
![]() $\mathsf {PA} \vdash \varphi $
. This is a contradiction.
$\mathsf {PA} \vdash \varphi $
. This is a contradiction.
Remark 6.22. By using the disjunction property of
![]() $\mathsf {HA}+\mathrm {DNS}$
as in the proof of Proposition 6.21, one can extend Proposition 5.10 to that
$\mathsf {HA}+\mathrm {DNS}$
as in the proof of Proposition 6.21, one can extend Proposition 5.10 to that
![]() $\mathsf {PA}$
is not
$\mathsf {PA}$
is not
![]() $\left ( \Pi _1 \lor \Pi _1\right )$
-conservative over
$\left ( \Pi _1 \lor \Pi _1\right )$
-conservative over
![]() $\mathsf {HA} +\mathrm {DNS}$
: Suppose that
$\mathsf {HA} +\mathrm {DNS}$
: Suppose that
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() $\left ( \Pi _1 \lor \Pi _1\right )$
-conservative over
$\left ( \Pi _1 \lor \Pi _1\right )$
-conservative over
![]() $\mathsf {HA} +\mathrm {DNS}$
. Then, by (the proof of) Theorem 5.19,
$\mathsf {HA} +\mathrm {DNS}$
. Then, by (the proof of) Theorem 5.19,
![]() $\mathsf {HA} +\mathrm {DNS}$
is closed under
$\mathsf {HA} +\mathrm {DNS}$
is closed under
![]() ${\Sigma _1}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
. Let
${\Sigma _1}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
. Let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
be sentences in
$\psi $
be sentences in
![]() $\Sigma _1$
such that
$\Sigma _1$
such that
![]() $\mathsf {HA}$
proves
$\mathsf {HA}$
proves
and
where
![]() $\mathrm {Pf}\left ({z} , \left\ulcorner {\xi } \right\urcorner \right )$
denotes a proof predicate asserting that z is a code of the proof
$\mathrm {Pf}\left ({z} , \left\ulcorner {\xi } \right\urcorner \right )$
denotes a proof predicate asserting that z is a code of the proof
![]() $\xi $
in
$\xi $
in
![]() $ \mathsf {HA} +\mathrm {DNS}$
(cf. [Reference Boolos2, Chapter 2]). Since
$ \mathsf {HA} +\mathrm {DNS}$
(cf. [Reference Boolos2, Chapter 2]). Since
![]() $\mathsf {HA} \vdash \neg (\varphi \land \psi )$
, by using
$\mathsf {HA} \vdash \neg (\varphi \land \psi )$
, by using
![]() ${\Sigma _1}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
, we have
${\Sigma _1}\text {-}\mathrm {DML^{\perp }}\text {-}\mathrm {R}$
, we have
![]() $\mathsf {HA} +\mathrm {DNS} \vdash \varphi ^{\perp } \lor \psi ^{\perp } $
. Since
$\mathsf {HA} +\mathrm {DNS} \vdash \varphi ^{\perp } \lor \psi ^{\perp } $
. Since
![]() $\mathsf {HA} +\mathrm {DNS}$
has the disjunction property, we have that
$\mathsf {HA} +\mathrm {DNS}$
has the disjunction property, we have that
![]() $\mathsf {HA} +\mathrm {DNS} \vdash \varphi ^{\perp }$
or
$\mathsf {HA} +\mathrm {DNS} \vdash \varphi ^{\perp }$
or
![]() $\mathsf {HA} +\mathrm {DNS} \vdash \psi ^{\perp }$
. However, in both cases, we have a contradiction by our choice of
$\mathsf {HA} +\mathrm {DNS} \vdash \psi ^{\perp }$
. However, in both cases, we have a contradiction by our choice of
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
.
$\psi $
.
Next, we show that
![]() ,
,
![]() in Theorem 6.18 and the rule in Lemma 6.17 are pairwise equivalent.
in Theorem 6.18 and the rule in Lemma 6.17 are pairwise equivalent.
Proposition 6.23. Let
![]() ${T}$
be semi-classical arithmetic satisfying the deduction theorem and X be a set of
${T}$
be semi-classical arithmetic satisfying the deduction theorem and X be a set of
![]() $\mathsf {HA}$
-sentences in
$\mathsf {HA}$
-sentences in
![]() $\mathcal {Q}_{k}$
. Then the following are pairwise equivalent:
$\mathcal {Q}_{k}$
. Then the following are pairwise equivalent:
-
1.

-
2.

-
3.
 ${T}+X$
is closed under
${T}+X$
is closed under
 ${\mathrm {E}\Pi _k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
with assumptions of sentences in
${\mathrm {E}\Pi _k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
with assumptions of sentences in
 $\Pi _k;$
$\Pi _k;$
-
4. For any
 ,
,
 $\mathsf {PA} +X+\psi $
is
$\mathsf {PA} +X+\psi $
is
 $\mathrm {U}_k$
-conservative over
$\mathrm {U}_k$
-conservative over
 ${T} +X+\psi ;$
${T} +X+\psi ;$
-
5.
 ${T}+X$
is closed under
${T}+X$
is closed under
 ${\mathrm {U}_k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
with assumptions of sentences in
${\mathrm {U}_k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
with assumptions of sentences in
 $\mathrm {U}_k;$
$\mathrm {U}_k;$
-
6.
 ${T}+X$
is closed under
${T}+X$
is closed under
 ${\mathrm {U}_k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
with assumptions of any sentences.
${\mathrm {U}_k}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
with assumptions of any sentences.
Proof The implications (1
![]() $\to $
2) and (6
$\to $
2) and (6
![]() $\to $
5) are trivial.
$\to $
5) are trivial.
(2
![]() $\to $
3): By the proof of (4
$\to $
3): By the proof of (4
![]() $\to $
1) in Theorem 6.18.
$\to $
1) in Theorem 6.18.
(3
![]() $\to $
4): Fix
$\to $
4): Fix
![]() . Let
. Let
![]() $\varphi \in \mathrm {U}_k$
. Assume
$\varphi \in \mathrm {U}_k$
. Assume
![]() $\mathsf {PA} + X +\psi \vdash \varphi $
. Since
$\mathsf {PA} + X +\psi \vdash \varphi $
. Since
![]() $X \cup \{\psi \} \subseteq \mathcal {Q}_{k}$
, by Theorem 5.16, we have
$X \cup \{\psi \} \subseteq \mathcal {Q}_{k}$
, by Theorem 5.16, we have
![]() ${T} + X +\psi \vdash \varphi $
.
${T} + X +\psi \vdash \varphi $
.
(4
![]() $\to $
5): Assume
$\to $
5): Assume
![]() ${T} +X \vdash \psi \to \neg \neg \varphi $
where
${T} +X \vdash \psi \to \neg \neg \varphi $
where
![]() and
and
![]() $\varphi \in \mathrm {U}_k$
. By Corollary 6.6.(1), there exists
$\varphi \in \mathrm {U}_k$
. By Corollary 6.6.(1), there exists
![]() such that
such that
![]() $\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \psi ' \to \neg \psi $
(cf. Remark 3.10) and
$\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \psi ' \to \neg \psi $
(cf. Remark 3.10) and
![]() $\mathsf {PA} \vdash \neg \psi \to \psi '$
. Let
$\mathsf {PA} \vdash \neg \psi \to \psi '$
. Let
![]() $\psi ":\equiv \left ( \psi ' \right )^{\perp }$
. By Remark 5.3, we have
$\psi ":\equiv \left ( \psi ' \right )^{\perp }$
. By Remark 5.3, we have
![]() ,
,
![]() $\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \neg \neg \psi \to \psi "$
and
$\mathsf {HA} + {\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \neg \neg \psi \to \psi "$
and
![]() $\mathsf {PA} \vdash \psi " \to \psi $
. Then we have now
$\mathsf {PA} \vdash \psi " \to \psi $
. Then we have now
![]() $\mathsf {PA} + X + \psi " \vdash \varphi $
. By our assumption,
$\mathsf {PA} + X + \psi " \vdash \varphi $
. By our assumption,
![]() ${T} + X + \psi " \vdash \varphi $
follows. Since T satisfies the deduction theorem, we have
${T} + X + \psi " \vdash \varphi $
follows. Since T satisfies the deduction theorem, we have
![]() ${T} + X \vdash \psi " \to \varphi $
. On the other hand, by (the proof of) Lemma 5.5 and our assumption, we have
${T} + X \vdash \psi " \to \varphi $
. On the other hand, by (the proof of) Lemma 5.5 and our assumption, we have
![]() ${T}+ X \vdash {\Sigma _{k-1}}\text {-}\mathrm {LEM}$
. Then
${T}+ X \vdash {\Sigma _{k-1}}\text {-}\mathrm {LEM}$
. Then
![]() ${T}+ X \vdash \psi \to \varphi $
follows.
${T}+ X \vdash \psi \to \varphi $
follows.
(5
![]() $\to $
1): Let
$\to $
1): Let
![]() $\varphi \in \mathrm {U}_k$
. Note that
$\varphi \in \mathrm {U}_k$
. Note that
![]() . Since
. Since
![]() ${T}+X+ \widetilde {\neg \neg \varphi } \vdash \neg \neg \varphi $
, by the deduction theorem, we have
${T}+X+ \widetilde {\neg \neg \varphi } \vdash \neg \neg \varphi $
, by the deduction theorem, we have
![]() $ {T}+X \vdash \widetilde {\neg \neg \varphi } \to \neg \neg \varphi $
. By our assumption, we have
$ {T}+X \vdash \widetilde {\neg \neg \varphi } \to \neg \neg \varphi $
. By our assumption, we have
![]() $ {T}+X \vdash \widetilde {\neg \neg \varphi } \to \varphi $
, and hence,
$ {T}+X \vdash \widetilde {\neg \neg \varphi } \to \varphi $
, and hence,
![]() $ {T}+X \vdash \widetilde {\neg \neg \varphi } \to \widetilde {\varphi }$
.
$ {T}+X \vdash \widetilde {\neg \neg \varphi } \to \widetilde {\varphi }$
.
(1
![]() $\to $
6): Assume
$\to $
6): Assume
![]() ${T} +X \vdash \psi \to \neg \neg \varphi $
where
${T} +X \vdash \psi \to \neg \neg \varphi $
where
![]() $\psi $
is a sentence and
$\psi $
is a sentence and
![]() $\varphi \in \mathrm {U}_k$
. Then we have
$\varphi \in \mathrm {U}_k$
. Then we have
![]() ${T}+X +\psi \vdash \widetilde {\neg \neg \varphi }$
. By our assumption, we have
${T}+X +\psi \vdash \widetilde {\neg \neg \varphi }$
. By our assumption, we have
![]() ${T}+X +\psi \vdash \widetilde {\varphi }$
, and hence,
${T}+X +\psi \vdash \widetilde {\varphi }$
, and hence,
![]() ${T}+X +\psi \vdash \varphi $
. Since T satisfies the deduction theorem,
${T}+X +\psi \vdash \varphi $
. Since T satisfies the deduction theorem,
![]() ${T}+X \vdash \psi \to \varphi $
follows.
${T}+X \vdash \psi \to \varphi $
follows.
Corollary 6.24. Let X be a set of
![]() $\mathsf {HA}$
-sentences in
$\mathsf {HA}$
-sentences in
![]() $\mathcal {Q}_k$
. Then
$\mathcal {Q}_k$
. Then
![]() $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
![]() $\mathrm {U}_k$
-conservative over
$\mathrm {U}_k$
-conservative over
![]() .
.
7 Interrelations between conservation theorems and logical principles
The
![]() -conservativity implies both of
-conservativity implies both of
![]() -conservativity and
-conservativity and
![]() -conservativity. In what follows, we investigate the relation among them.
-conservativity. In what follows, we investigate the relation among them.
Proposition 7.1. Let
![]() ${T}$
be semi-classical arithmetic and X be a set of
${T}$
be semi-classical arithmetic and X be a set of
![]() $\mathsf {HA}$
-sentences. If
$\mathsf {HA}$
-sentences. If
![]() $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
![]() -conservative over
-conservative over
![]() ${T}+X$
and
${T}+X$
and
![]() ${T}+X$
proves
${T}+X$
proves
![]() ${(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}$
, then
${(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}$
, then
![]() $\mathsf {PA} +X$
is
$\mathsf {PA} +X$
is
![]() -conservative over
-conservative over
![]() ${T}+X$
.
${T}+X$
.
Proof By Theorem 6.7, it suffices to show
![]() -conservativity instead of the
-conservativity instead of the
![]() -conservativity. Let
-conservativity. Let
![]() with
with
![]() $\psi \in \mathrm {E}\Pi _k$
. Assume
$\psi \in \mathrm {E}\Pi _k$
. Assume
![]() $\mathsf {PA} + X\vdash \varphi $
. By Theorem 3.9.(2), there exists
$\mathsf {PA} + X\vdash \varphi $
. By Theorem 3.9.(2), there exists
![]() $\psi ' \in \Pi _k$
such that
$\psi ' \in \Pi _k$
such that
![]() $\mathrm { FV} \left ({\psi }\right )=\mathrm { FV} \left ({\psi '}\right )$
and
$\mathrm { FV} \left ({\psi }\right )=\mathrm { FV} \left ({\psi '}\right )$
and
![]() $\mathsf {HA} + {(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE} \vdash \psi '\leftrightarrow \psi $
. Now we have
$\mathsf {HA} + {(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE} \vdash \psi '\leftrightarrow \psi $
. Now we have
![]() $\mathsf {PA} + X \vdash \exists x_1,\dots , x_n\, \psi '$
. Since
$\mathsf {PA} + X \vdash \exists x_1,\dots , x_n\, \psi '$
. Since
![]() , by our first assumption, we have that
, by our first assumption, we have that
![]() ${T} +X \vdash \exists x_1,\dots , x_n\, \psi '$
. By our second assumption,
${T} +X \vdash \exists x_1,\dots , x_n\, \psi '$
. By our second assumption,
![]() ${T}+ X \vdash \varphi $
follows.
${T}+ X \vdash \varphi $
follows.
Proposition 7.2. Let
![]() ${T}$
be a theory containing
${T}$
be a theory containing
![]() $\mathsf {HA}$
. If
$\mathsf {HA}$
. If
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() -conservative over
-conservative over
![]() ${T}$
, then
${T}$
, then
![]() ${T}$
proves
${T}$
proves
![]() and also
and also
![]() ${\Sigma _{k-2}}\text {-}\mathrm {LEM}$
.
${\Sigma _{k-2}}\text {-}\mathrm {LEM}$
.
Proof Assume that
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() -conservative over
-conservative over
![]() ${T}$
. Then
${T}$
. Then
![]() $\mathsf {PA}$
is
$\mathsf {PA}$
is
![]() $\Pi _k$
-conservative over
$\Pi _k$
-conservative over
![]() ${T}$
(cf. Proposition 6.1), and hence,
${T}$
(cf. Proposition 6.1), and hence,
![]() ${T}$
proves
${T}$
proves
![]() ${\Sigma _{k-2}}\text {-}\mathrm {LEM}$
by (the proof of) Theorem 5.9. Let
${\Sigma _{k-2}}\text {-}\mathrm {LEM}$
by (the proof of) Theorem 5.9. Let
![]() . Then
. Then
![]() . Since
. Since
![]() and
and
![]() can be seen as sub-classes of
can be seen as sub-classes of
![]() and
and
![]() is closed under
is closed under
![]() $\lor $
(in the sense of [Reference Troelstra and van Dalen7, Lemma 4.4]), one may assume
$\lor $
(in the sense of [Reference Troelstra and van Dalen7, Lemma 4.4]), one may assume
![]() . Since
. Since
![]() $\mathsf {PA} \vdash \varphi \lor \varphi ^{\perp } $
, by our assumption, we have
$\mathsf {PA} \vdash \varphi \lor \varphi ^{\perp } $
, by our assumption, we have
![]() ${T} \vdash \varphi \lor \varphi ^{\perp }$
, and hence,
${T} \vdash \varphi \lor \varphi ^{\perp }$
, and hence,
![]() ${T} \vdash \varphi \lor \neg \varphi $
.
${T} \vdash \varphi \lor \neg \varphi $
.
Corollary 7.3. Let
![]() ${T}$
be semi-classical arithmetic satisfying the deduction theorem and X be a set of
${T}$
be semi-classical arithmetic satisfying the deduction theorem and X be a set of
![]() $\mathsf {HA}$
-sentences in
$\mathsf {HA}$
-sentences in
![]() $\mathcal {Q}_{k}$
. If
$\mathcal {Q}_{k}$
. If
![]() $\mathsf {PA} +X $
is
$\mathsf {PA} +X $
is
![]() -conservative over
-conservative over
![]() ${T}+X$
and
${T}+X$
and
![]() ${T}$
proves
${T}$
proves
![]() , then
, then
![]() $\mathsf {PA}+X$
is
$\mathsf {PA}+X$
is
![]() -conservative over
-conservative over
![]() ${T}+X$
.
${T}+X$
.
Remark 7.4. By using Theorem 3.9.(2), one can show that
![]() ${(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}$
implies
${(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}$
implies
![]() in a straightforward way. On the other hand,
in a straightforward way. On the other hand,
![]() implies the
implies the
![]() $\mathrm {U}_k$
-conservativity by Corollary 6.24. In contrast,
$\mathrm {U}_k$
-conservativity by Corollary 6.24. In contrast,
![]() ${(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}$
does not imply
${(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}$
does not imply
![]() -conservativity since the latter is characterized by
-conservativity since the latter is characterized by
![]() (cf. Theorem 6.18) and
(cf. Theorem 6.18) and
![]() ${(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}$
does not imply
${(\Pi _k \lor \Pi _k)}\text {-}\mathrm {DNE}$
does not imply
![]() (see [Reference Troelstra and van Dalen5]).
(see [Reference Troelstra and van Dalen5]).
Remark 7.5. It is straightforward to see that if a theory
![]() ${T}$
containing
${T}$
containing
![]() $\mathsf {HA}$
proves
$\mathsf {HA}$
proves
![]() , then
, then
![]() ${T}$
is closed under
${T}$
is closed under
![]() ${(\Pi _k\lor \Pi _k)}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
. Thus
${(\Pi _k\lor \Pi _k)}\text {-}\mathrm {DNE}\text {-}\mathrm {R}$
. Thus
![]() implies the
implies the
![]() $(\Pi _k\lor \Pi _k)$
-conservativity (cf. Theorem 5.19). On the other hand,
$(\Pi _k\lor \Pi _k)$
-conservativity (cf. Theorem 5.19). On the other hand,
![]() is a fragment of
is a fragment of
![]() .
.
Proposition 7.6. Let X be a set of
![]() $\mathsf {HA}$
-sentences in
$\mathsf {HA}$
-sentences in
![]() $\mathcal {Q}_k$
. Then
$\mathcal {Q}_k$
. Then
![]() $\mathsf {PA}+X$
is
$\mathsf {PA}+X$
is
![]() -conservative over
-conservative over
![]() .
.
Proof Since
![]() contains
contains
![]() ${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
and is closed under
${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
and is closed under
![]() , by Proposition 6.3, we are done.
, by Proposition 6.3, we are done.
Remark 7.7. Propositions 7.6 and 7.2 reveal that the
![]() -conservativity lies between
-conservativity lies between
![]() and
and
![]() . This seems to be another view of the status of the
. This seems to be another view of the status of the
![]() -conservativity.
-conservativity.
Our results on the relation between conservation theorems and logical principles are summarized in Figure 1 where
![]() $\Gamma $
-CONS denotes the
$\Gamma $
-CONS denotes the
![]() $\Gamma $
-conservativity for class
$\Gamma $
-conservativity for class
![]() $\Gamma $
of
$\Gamma $
of
![]() $\mathsf {HA}$
-formulas. Figure 1 reveals that the logical principle
$\mathsf {HA}$
-formulas. Figure 1 reveals that the logical principle
![]() , which has been first studied in the current paper (cf. Definition 6.15), is closely related to the conservation theorems. For the comprehensive information on the arithmetical hierarchy of logical principles including
, which has been first studied in the current paper (cf. Definition 6.15), is closely related to the conservation theorems. For the comprehensive information on the arithmetical hierarchy of logical principles including
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
and
${\Sigma _k}\text {-}\mathrm {LEM}$
and
![]() ${(\Pi _{k} \lor \Pi _{k})}\text {-}\mathrm {DNE}$
, we refer the reader to [Reference Troelstra and van Dalen6]. For the underivability, we know only that
${(\Pi _{k} \lor \Pi _{k})}\text {-}\mathrm {DNE}$
, we refer the reader to [Reference Troelstra and van Dalen6]. For the underivability, we know only that
![]() ${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
does not imply
${\Sigma _{k-1}}\text {-}\mathrm {LEM}$
does not imply
![]() $(\Pi _k \lor \Pi _k)$
-CONS (cf. Proposition 5.10) and that
$(\Pi _k \lor \Pi _k)$
-CONS (cf. Proposition 5.10) and that
![]() ${(\Pi _k\lor \Pi _k)}\text {-}\mathrm {DNE}$
does not imply
${(\Pi _k\lor \Pi _k)}\text {-}\mathrm {DNE}$
does not imply
![]() -CONS (cf. Remark 7.4). In addition, for
-CONS (cf. Remark 7.4). In addition, for
![]() , we have characterized
, we have characterized
![]() $\Gamma $
-CONS by some fragment of the double-negation-elimination rule
$\Gamma $
-CONS by some fragment of the double-negation-elimination rule
![]() ${\textrm{DNE}\text{-}\textrm{R}}$
. On the other hand, we have not achieved that for
${\textrm{DNE}\text{-}\textrm{R}}$
. On the other hand, we have not achieved that for
![]() and
and
![]() .
.

Figure 1 Conservation theorems in the arithmetical hierarchy of logical principles.
8 Appendix: A relativized soundness theorem of the Friedman A-translation for
 $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
We provide a detailed proof of a relativized soundness theorem of the Friedman A-translation [Reference Troelstra and van Dalen4] for
![]() $\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
(see Theorem 8.3). In fact, this result was suggested already in [Reference Troelstra and van Dalen8, Section 4.4] and the detailed proof for
$\mathsf {HA}+{\Sigma _k}\text {-}\mathrm {LEM}$
(see Theorem 8.3). In fact, this result was suggested already in [Reference Troelstra and van Dalen8, Section 4.4] and the detailed proof for
![]() $k=1$
can be found in [Reference Troelstra and van Dalen12, Lemma 3.1]. The authors, however, couldn’t find the proof for arbitrary natural number k anywhere, which is the reason why we present the detailed proof here. For the relativized soundness theorem, we use a variant of Lemma 3.5 with respect to the Friedman A-translation.
$k=1$
can be found in [Reference Troelstra and van Dalen12, Lemma 3.1]. The authors, however, couldn’t find the proof for arbitrary natural number k anywhere, which is the reason why we present the detailed proof here. For the relativized soundness theorem, we use a variant of Lemma 3.5 with respect to the Friedman A-translation.
We first recall the definition of the Friedman A-translation. In this section, we use symbol
![]() $*$
for place holder instead of $ in the previous sections.
$*$
for place holder instead of $ in the previous sections.
Definition 8.1 (A-translation [Reference Troelstra and van Dalen4]).
For a
![]() $\mathsf {HA}$
-formula
$\mathsf {HA}$
-formula
![]() $\varphi $
, we define
$\varphi $
, we define
![]() $\varphi ^{*} $
as a formula obtained from
$\varphi ^{*} $
as a formula obtained from
![]() $\varphi $
by replacing all the prime formulas
$\varphi $
by replacing all the prime formulas
![]() $\varphi _{\textrm {p}}$
in
$\varphi _{\textrm {p}}$
in
![]() $\varphi $
with
$\varphi $
with
![]() $\varphi _{\textrm {p}} \lor {*} $
(of course,
$\varphi _{\textrm {p}} \lor {*} $
(of course,
![]() $\varphi ^{*} $
is officially defined by induction on the logical structure of
$\varphi ^{*} $
is officially defined by induction on the logical structure of
![]() $\varphi $
). In particular,
$\varphi $
). In particular,
![]() $\perp ^{*} :\equiv \left (\perp \lor \, {*} \right )$
, which is equivalent to
$\perp ^{*} :\equiv \left (\perp \lor \, {*} \right )$
, which is equivalent to
![]() ${*} $
over
${*} $
over
![]() $\mathsf {HA}^{*} $
(
$\mathsf {HA}^{*} $
(
![]() $\mathsf {HA}$
in the language with a place holder
$\mathsf {HA}$
in the language with a place holder
![]() $*$
). In what follows,
$*$
). In what follows,
![]() $\neg _{*}\, \varphi $
denotes
$\neg _{*}\, \varphi $
denotes
![]() $\varphi \to {*} $
. Note that
$\varphi \to {*} $
. Note that
![]() $\mathrm { FV} \left ({\varphi }\right ) =\mathrm { FV} \left ({\varphi ^{*}}\right )$
for all
$\mathrm { FV} \left ({\varphi }\right ) =\mathrm { FV} \left ({\varphi ^{*}}\right )$
for all
![]() $\mathsf {HA}$
-formulas
$\mathsf {HA}$
-formulas
![]() $\varphi $
.
$\varphi $
.
The following is a variant of Lemma 3.5 with respect to the Friedman A-translation.
Lemma 8.2. For a formula
![]() $\varphi $
of
$\varphi $
of
![]() $\mathsf {HA}$
, the following hold:
$\mathsf {HA}$
, the following hold:
-
1. If
 $\varphi \in \Pi _{k}$
,
$\varphi \in \Pi _{k}$
,
 $\mathsf {HA}^{*} + {\Sigma _{k}}\text {-}\mathrm {LEM} \vdash \varphi ^{*} \leftrightarrow \varphi \lor {*} ;$
$\mathsf {HA}^{*} + {\Sigma _{k}}\text {-}\mathrm {LEM} \vdash \varphi ^{*} \leftrightarrow \varphi \lor {*} ;$
-
2. If
 $\varphi \in \Sigma _{k}$
,
$\varphi \in \Sigma _{k}$
,
 $\mathsf {HA}^{*} + {\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \varphi ^{*} \leftrightarrow \varphi \lor {*}.$
$\mathsf {HA}^{*} + {\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \varphi ^{*} \leftrightarrow \varphi \lor {*}.$
Proof By simultaneous induction on k. The base case is verified by a routine inspection. Assume items 1 and 2 for k to show those for
![]() $k+1$
. The first item for
$k+1$
. The first item for
![]() $k+1$
is shown by using the second item for k as in the proof of Lemma 3.5. For the second item, let
$k+1$
is shown by using the second item for k as in the proof of Lemma 3.5. For the second item, let
![]() $\varphi :\equiv \exists x \varphi _1$
where
$\varphi :\equiv \exists x \varphi _1$
where
![]() $\varphi _1 \in \Pi _k$
. Then we have that
$\varphi _1 \in \Pi _k$
. Then we have that
![]() $\mathsf {HA} + {\Sigma _{k}}\text {-}\mathrm {LEM}$
proves
$\mathsf {HA} + {\Sigma _{k}}\text {-}\mathrm {LEM}$
proves
Theorem 8.3. If
![]() $\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi $
, then
$\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi $
, then
![]() $\mathsf {HA}^{*} + {\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ^{*}$
.
$\mathsf {HA}^{*} + {\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ^{*}$
.
Proof By induction on the length of the proof of
![]() $\varphi $
in
$\varphi $
in
![]() $\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM}$
. By (the proof of) [Reference Troelstra and van Dalen4, Lemma 2], it suffices to show
$\mathsf {HA} + {\Sigma _k}\text {-}\mathrm {LEM}$
. By (the proof of) [Reference Troelstra and van Dalen4, Lemma 2], it suffices to show
![]() $\mathsf {HA}^{*} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ^{*}$
for each instance
$\mathsf {HA}^{*} +{\Sigma _k}\text {-}\mathrm {LEM} \vdash \varphi ^{*}$
for each instance
![]() $\varphi $
of
$\varphi $
of
![]() ${\Sigma _k}\text {-}\mathrm {LEM}$
. Fix
${\Sigma _k}\text {-}\mathrm {LEM}$
. Fix
![]() $\varphi : \equiv \exists x \varphi _1 \lor \neg \exists x \varphi _1$
with
$\varphi : \equiv \exists x \varphi _1 \lor \neg \exists x \varphi _1$
with
![]() $\varphi _1 \in \Pi _{k-1}$
. By Lemma 8.2.(1),
$\varphi _1 \in \Pi _{k-1}$
. By Lemma 8.2.(1),
![]() $\mathsf {HA}^{*} + {\Sigma _{k-1}}\text {-}\mathrm {LEM}$
proves
$\mathsf {HA}^{*} + {\Sigma _{k-1}}\text {-}\mathrm {LEM}$
proves
 $$ \begin{align*}\begin{array}{ccl} \varphi^{*} &\longleftrightarrow & \exists x \left( {\varphi_1}^{*}\right) \lor \neg_{*} \exists x \left( {\varphi_1}^{*} \right) \\ &\underset{{\Sigma_{k-1}}\text{-}\mathrm{LEM}}{\longleftrightarrow} & \exists x \left( \varphi_1 \lor * \right) \lor \neg_{*} \exists x \left( \varphi_1\lor * \right)\\ & \longleftrightarrow & \exists x \left( \varphi_1 \lor * \right) \lor \neg_{*} \exists x \varphi_1, \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{ccl} \varphi^{*} &\longleftrightarrow & \exists x \left( {\varphi_1}^{*}\right) \lor \neg_{*} \exists x \left( {\varphi_1}^{*} \right) \\ &\underset{{\Sigma_{k-1}}\text{-}\mathrm{LEM}}{\longleftrightarrow} & \exists x \left( \varphi_1 \lor * \right) \lor \neg_{*} \exists x \left( \varphi_1\lor * \right)\\ & \longleftrightarrow & \exists x \left( \varphi_1 \lor * \right) \lor \neg_{*} \exists x \varphi_1, \end{array}\end{align*} $$
which is derived from
![]() $\exists x \varphi _1 \lor \neg \exists x \varphi _1$
over
$\exists x \varphi _1 \lor \neg \exists x \varphi _1$
over
![]() $\mathsf {HA}^{*}$
. Thus
$\mathsf {HA}^{*}$
. Thus
![]() $\mathsf {HA}^{*} +{\Sigma _k}\text {-}\mathrm {LEM} $
proves
$\mathsf {HA}^{*} +{\Sigma _k}\text {-}\mathrm {LEM} $
proves
![]() $\varphi ^{*}$
.
$\varphi ^{*}$
.
By the relativized soundness theorem of the Friedman A-translation combined with the usual negative translation, one can show Proposition 1.1 as follows:
Proof Sketch of Proposition 1.1 Assume
![]() $\mathsf {PA} \vdash \forall x \exists y \varphi $
where
$\mathsf {PA} \vdash \forall x \exists y \varphi $
where
![]() $\varphi \in \Pi _{k}$
. By using Kuroda’s negative translation (cf. [Reference Troelstra and van Dalen7, Proposition 6.4]), we have
$\varphi \in \Pi _{k}$
. By using Kuroda’s negative translation (cf. [Reference Troelstra and van Dalen7, Proposition 6.4]), we have
![]() $\mathsf {HA} \vdash \forall x \neg \neg \exists y \varphi _N$
where
$\mathsf {HA} \vdash \forall x \neg \neg \exists y \varphi _N$
where
![]() $\varphi _N$
is defined as in [Reference Troelstra and van Dalen7, Definition 6.1]. Since
$\varphi _N$
is defined as in [Reference Troelstra and van Dalen7, Definition 6.1]. Since
![]() $\mathsf {HA}+{\Sigma _{k-1}}\text {-}\mathrm {LEM} $
proves
$\mathsf {HA}+{\Sigma _{k-1}}\text {-}\mathrm {LEM} $
proves
![]() ${\Sigma _{k-1}}\text {-}\mathrm {DNE}$
, we have
${\Sigma _{k-1}}\text {-}\mathrm {DNE}$
, we have
![]() $\mathsf {HA}+{\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \neg \neg \exists y \varphi $
(cf. [Reference Troelstra and van Dalen7, Lemma 6.5(2)]). By Theorem 8.3, we have
$\mathsf {HA}+{\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \neg \neg \exists y \varphi $
(cf. [Reference Troelstra and van Dalen7, Lemma 6.5(2)]). By Theorem 8.3, we have
![]() $\mathsf {HA}^{*}+{\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \neg _{*} \neg _{*} \exists y \varphi ^{*}$
, and hence,
$\mathsf {HA}^{*}+{\Sigma _{k-1}}\text {-}\mathrm {LEM} \vdash \neg _{*} \neg _{*} \exists y \varphi ^{*}$
, and hence,
![]() $\mathsf {HA}^{*}+{\Sigma _k}\text {-}\mathrm {LEM} \vdash \neg _{*} \neg _{*} \exists y \varphi $
by Lemma 8.2.(1). By substituting
$\mathsf {HA}^{*}+{\Sigma _k}\text {-}\mathrm {LEM} \vdash \neg _{*} \neg _{*} \exists y \varphi $
by Lemma 8.2.(1). By substituting
![]() $*$
with
$*$
with
![]() $\exists y \varphi $
(cf. Lemma 3.16), we have that
$\exists y \varphi $
(cf. Lemma 3.16), we have that
![]() $\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} $
proves
$\mathsf {HA} +{\Sigma _k}\text {-}\mathrm {LEM} $
proves
![]() $ \exists y \varphi $
, and hence,
$ \exists y \varphi $
, and hence,
![]() $\forall x \exists y \varphi $
.
$\forall x \exists y \varphi $
.
The proof of [Reference Troelstra and van Dalen14, Theorem 3.5.5] (due to Visser) shows that any theory
![]() ${T}$
which contains
${T}$
which contains
![]() $\mathsf {HA}$
and is sound for the Friedman A-translation is closed under the independence-of-premise rule:
$\mathsf {HA}$
and is sound for the Friedman A-translation is closed under the independence-of-premise rule:
where
![]() $x\notin \mathrm { FV} \left ({\neg \varphi }\right )$
. Then, by using Theorem 8.3, we also have the following:
$x\notin \mathrm { FV} \left ({\neg \varphi }\right )$
. Then, by using Theorem 8.3, we also have the following:
Theorem 8.4.
![]() $\mathsf {HA} + {\Sigma _{k}}\text {-}\mathrm {LEM}$
is closed under the independence-of-premise rule.
$\mathsf {HA} + {\Sigma _{k}}\text {-}\mathrm {LEM}$
is closed under the independence-of-premise rule.
Acknowledgements
The first author was supported by JSPS KAKENHI Grant Numbers JP19J01239 and JP20K14354, and the second author by JP19K14586.