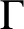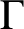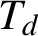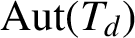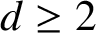1 Introduction
Let G be a compactly generated, totally disconnected, locally compact (cgtdlc) group. A locally finite, connected graph
![]() $\Gamma $
on which G acts vertex-transitively with compact, open vertex stabilizers is called a Cayley–Abels graph for G. Cayley–Abels graphs were introduced by Abels [Reference Abels1] in the context of Specker compactifications of locally compact groups. A totally disconnected, locally compact group has a Cayley–Abels graph if and only if it is compactly generated. The relation between G and a Cayley–Abels graph
$\Gamma $
on which G acts vertex-transitively with compact, open vertex stabilizers is called a Cayley–Abels graph for G. Cayley–Abels graphs were introduced by Abels [Reference Abels1] in the context of Specker compactifications of locally compact groups. A totally disconnected, locally compact group has a Cayley–Abels graph if and only if it is compactly generated. The relation between G and a Cayley–Abels graph
![]() $\Gamma $
is in many ways similar to the relation between a finitely generated group and its Cayley graph with respect to a finite generating set; see [Reference Krön and Möller19]. In this work we are interested in the minimal degree
$\Gamma $
is in many ways similar to the relation between a finitely generated group and its Cayley graph with respect to a finite generating set; see [Reference Krön and Möller19]. In this work we are interested in the minimal degree
![]() $\mathrm{md}(G)$
of a Cayley–Abels graph for G. The following general questions seem natural starting points for an investigation of this invariant.
$\mathrm{md}(G)$
of a Cayley–Abels graph for G. The following general questions seem natural starting points for an investigation of this invariant.
-
(1) What does the minimal degree tell us about the group?
-
(2) How does the minimal degree relate to other properties of the group?
-
(3) What is the minimal degree for some interesting groups?
We tackle all of these questions to some extent.
If
![]() $\mathrm{md}(G)=0, 1, 2$
we can characterize G: the first two parts of the following theorem are obvious facts, the third is a part of Theorem 4.1.
$\mathrm{md}(G)=0, 1, 2$
we can characterize G: the first two parts of the following theorem are obvious facts, the third is a part of Theorem 4.1.
Theorem A. Let G be a cgtdlc group. Then
![]() $\mathrm{md}(G)$
is:
$\mathrm{md}(G)$
is:
-
(1) equal to
 $0$
if and only if G is compact;
$0$
if and only if G is compact; -
(2) never equal to
 $1$
;
$1$
; -
(3) equal to
 $2$
if and only if G has a compact, open, normal subgroup K such that
$2$
if and only if G has a compact, open, normal subgroup K such that
 $G/K$
is isomorphic to
$G/K$
is isomorphic to
 $\mathbb {Z}$
or the infinite dihedral group
$\mathbb {Z}$
or the infinite dihedral group
 $D_{\infty }$
.
$D_{\infty }$
.
The characterization in the third part resembles the characterization of finitely generated groups with two ends. In a companion paper to this work [Reference Árnadóttir, Lederle and Möller3], vertex-transitive group actions on cubic graphs with infinite vertex stabilizers are studied. These results have consequences for groups with minimal degree
![]() $3$
; for example, if G is a cgtdlc group with minimal degree 3 and does not have a compact, open, normal subgroup then G is not uniscalar (that is, there exists an element in G that does not normalize a compact, open subgroup of G).
$3$
; for example, if G is a cgtdlc group with minimal degree 3 and does not have a compact, open, normal subgroup then G is not uniscalar (that is, there exists an element in G that does not normalize a compact, open subgroup of G).
In Section 3 we elaborate on groups having a compact, open, normal subgroup. We prove that this property can be detected from a minimal-degree Cayley–Abels graph.
Theorem B (Corollary 3.10)
Let G be a cgtdlc group. If G has a compact, open, normal subgroup, then G acts on some minimal-degree Cayley–Abels graph with a compact, open, normal kernel.
Our investigation of the second question starts with a study of the modular function and its relationship to the action of a group on a Cayley–Abels graph; see Section 5.1. Many of the results in Section 5.1 are contained in the first author’s master’s thesis [Reference Árnadóttir2]. We present a method to ‘read’ the values of the modular function off the graph and generalize a theorem by Praeger to higher dimensions. Furthermore, we get a bound on the minimal degree based on the modular function of which the following is a special case.
Theorem C (Theorem 5.4)
Let G be a noncompact, cgtdlc group. Assume the image of the modular function is generated by
![]() $p/q$
, where p and q are coprime, positive integers. Then
$p/q$
, where p and q are coprime, positive integers. Then
![]() $\mathrm{md}(G) \geq p+q$
.
$\mathrm{md}(G) \geq p+q$
.
Then we turn to the relationship of the minimal degree with the local structure of the group (that is, the structure of compact, open subgroups); see Section 6. We introduce a new local invariant, the local simple content, that is inspired by the local prime content introduced by Glöckner [Reference Glöckner12]. It is the set of all (isomorphism classes of) finite, simple groups that appear as composition factors of every compact, open subgroup. To treat this concept, a Jordan–Hölder theorem for profinite groups is needed (Theorem 6.2).
Theorem D (Theorem 6.6)
Let G be a cgtdlc group. Assume that G does not have any compact, normal subgroup. Then the local simple content of G is finite. Moreover,
![]() $\mathrm{md}(G)$
is strictly bigger than the smallest n such that every element of the local simple content is a subquotient of the symmetric group
$\mathrm{md}(G)$
is strictly bigger than the smallest n such that every element of the local simple content is a subquotient of the symmetric group
![]() $S_{n}$
.
$S_{n}$
.
This is a refinement of a theorem about the local prime content by Caprace et al. from [Reference Caprace, Reid and Willis8]. We relate their result to the values of the scale function. If p is the largest prime that occurs as a factor in any value of the scale function then
![]() $\mathrm{md}(G)\geq p+1$
(see Corollary 6.15); this holds, in particular, for nonuniscalar p-adic Lie groups (Corollary 6.16).
$\mathrm{md}(G)\geq p+1$
(see Corollary 6.15); this holds, in particular, for nonuniscalar p-adic Lie groups (Corollary 6.16).
The archetypal totally disconnected, locally compact groups are the automorphism groups of regular trees. Theorems E and F are simple applications of Theorems D and C, except for the result in part (1) of Theorem E in the case of
![]() $\mathrm{Aut}(T_{5})$
. A special argument for
$\mathrm{Aut}(T_{5})$
. A special argument for
![]() $\mathrm{Aut}(T_{5})$
is necessary because the alternating group
$\mathrm{Aut}(T_{5})$
is necessary because the alternating group
![]() $A_{4}$
is not simple. Proving that
$A_{4}$
is not simple. Proving that
![]() $\mathrm{md}(\mathrm{Aut}(T_{5}))=5$
is surprisingly tricky and is done in Section 7.
$\mathrm{md}(\mathrm{Aut}(T_{5}))=5$
is surprisingly tricky and is done in Section 7.
Theorem E (Corollaries 6.7, 5.5, Example 5.6, Theorem 7.1)
Let
![]() $T_{d}$
be a regular tree of degree
$T_{d}$
be a regular tree of degree
![]() $d \geq 2$
. Let
$d \geq 2$
. Let
![]() $\omega $
be an end of
$\omega $
be an end of
![]() $T_{d}$
.
$T_{d}$
.
-
(1) The tree
 $T_{d}$
is a minimal-degree Cayley–Abels graph for the automorphism group
$T_{d}$
is a minimal-degree Cayley–Abels graph for the automorphism group
 $\mathrm{Aut}(T_{d})$
and the end stabilizer
$\mathrm{Aut}(T_{d})$
and the end stabilizer
 $\mathrm{Aut}(T_{d})_{\omega }$
. In particular,
$\mathrm{Aut}(T_{d})_{\omega }$
. In particular,
 $\mathrm{md}(\mathrm{Aut}(T_{d}))=d$
.
$\mathrm{md}(\mathrm{Aut}(T_{d}))=d$
. -
(2) Let
 $\mathrm{Aut}^{+}(T_{d})$
be the index-
$\mathrm{Aut}^{+}(T_{d})$
be the index-
 $2$
subgroup of
$2$
subgroup of
 $\mathrm{Aut}(T_{d})$
. Then
$\mathrm{Aut}(T_{d})$
. Then
 $\mathrm{md}(\mathrm{Aut}^{+}(T_{d})) \leq 2d+2$
and
$\mathrm{md}(\mathrm{Aut}^{+}(T_{d})) \leq 2d+2$
and
 $\mathrm{md}(\mathrm{Aut}^{+}(T_{d})_{\omega }) = (d-1)^{2}+1$
.
$\mathrm{md}(\mathrm{Aut}^{+}(T_{d})_{\omega }) = (d-1)^{2}+1$
.
More generally, for biregular trees we prove the following result.
Theorem F (Example 5.6, Corollary 5.5)
Let
![]() $T_{d,d^{\prime }}$
be a biregular tree of degrees
$T_{d,d^{\prime }}$
be a biregular tree of degrees
![]() $d> d^{\prime } \geq 2$
. Let
$d> d^{\prime } \geq 2$
. Let
![]() $\omega $
be an end of
$\omega $
be an end of
![]() $T_{d,d^{\prime }}$
. Then the automorphism group
$T_{d,d^{\prime }}$
. Then the automorphism group
![]() $\mathrm{Aut}(T_{d,d^{\prime }})$
satisfies
$\mathrm{Aut}(T_{d,d^{\prime }})$
satisfies
![]() $\mathrm{md}(\mathrm{Aut}(T_{d,d^{\prime }})) \leq d+d^{\prime }+2$
and the end stabilizer
$\mathrm{md}(\mathrm{Aut}(T_{d,d^{\prime }})) \leq d+d^{\prime }+2$
and the end stabilizer
![]() $\mathrm{Aut}(T_{d,d^{\prime }})_{\omega }$
satisfies
$\mathrm{Aut}(T_{d,d^{\prime }})_{\omega }$
satisfies
![]() $\mathrm{md}(\mathrm{Aut}(T_{d,d^{\prime }})_{\omega })=(d-1)(d^{\prime }-1)+1$
.
$\mathrm{md}(\mathrm{Aut}(T_{d,d^{\prime }})_{\omega })=(d-1)(d^{\prime }-1)+1$
.
The authors conjecture that
![]() $\mathrm{md}(\mathrm{Aut}(T_{d,d^{\prime }}))=d+d^{\prime }+2$
.
$\mathrm{md}(\mathrm{Aut}(T_{d,d^{\prime }}))=d+d^{\prime }+2$
.
2 Notation and preliminaries
2.1 Graphs
An (undirected) graph
![]() $\Gamma $
is defined as a pair
$\Gamma $
is defined as a pair
![]() $(\mathrm V\Gamma , \mathrm E\Gamma )$
, where
$(\mathrm V\Gamma , \mathrm E\Gamma )$
, where
![]() $\mathrm V\Gamma $
is the set of vertices and
$\mathrm V\Gamma $
is the set of vertices and
![]() $\mathrm E\Gamma $
is a set of two-element subsets of
$\mathrm E\Gamma $
is a set of two-element subsets of
![]() $\mathrm V\Gamma $
, whose elements we call the edges of
$\mathrm V\Gamma $
, whose elements we call the edges of
![]() $\Gamma $
. Our graphs thus have neither loops nor multiple edges. The set of arcs of
$\Gamma $
. Our graphs thus have neither loops nor multiple edges. The set of arcs of
![]() $\Gamma $
, denoted by
$\Gamma $
, denoted by
![]() $\mathrm A\Gamma $
, is the set of all ordered pairs
$\mathrm A\Gamma $
, is the set of all ordered pairs
![]() $(\alpha , \beta )$
such that
$(\alpha , \beta )$
such that
![]() $\{\alpha , \beta \}\in \mathrm E\Gamma $
. Two vertices
$\{\alpha , \beta \}\in \mathrm E\Gamma $
. Two vertices
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are called adjacent, or neighbours, if
$\beta $
are called adjacent, or neighbours, if
![]() $\{\alpha , \beta \}$
is an edge. The set of neighbours of a vertex
$\{\alpha , \beta \}$
is an edge. The set of neighbours of a vertex
![]() $\alpha $
is denoted by
$\alpha $
is denoted by
![]() $\Gamma (\alpha )$
and the degree of
$\Gamma (\alpha )$
and the degree of
![]() $\alpha $
is the cardinality of
$\alpha $
is the cardinality of
![]() $\Gamma (\alpha )$
. A graph is regular if all vertices have the same degree d, and then we say that d is the degree of the graph. A graph is locally finite if every vertex has finite degree.
$\Gamma (\alpha )$
. A graph is regular if all vertices have the same degree d, and then we say that d is the degree of the graph. A graph is locally finite if every vertex has finite degree.
We also consider digraphs (directed graphs). A digraph consists of a vertex set
![]() $\mathrm V\Gamma $
and a subset
$\mathrm V\Gamma $
and a subset
![]() $\mathrm A\Gamma \subseteq \mathrm V\Gamma \times \mathrm V\Gamma $
that does not intersect the diagonal. Elements of
$\mathrm A\Gamma \subseteq \mathrm V\Gamma \times \mathrm V\Gamma $
that does not intersect the diagonal. Elements of
![]() $\mathrm V\Gamma $
are called vertices and elements of
$\mathrm V\Gamma $
are called vertices and elements of
![]() $\mathrm A\Gamma $
are called arcs. The underlying undirected graph of a digraph
$\mathrm A\Gamma $
are called arcs. The underlying undirected graph of a digraph
![]() $\Gamma $
has the same vertex set as
$\Gamma $
has the same vertex set as
![]() $\Gamma $
and the set of edges is the set of all pairs
$\Gamma $
and the set of edges is the set of all pairs
![]() $\{\alpha , \beta \}$
where
$\{\alpha , \beta \}$
where
![]() $(\alpha , \beta )$
or
$(\alpha , \beta )$
or
![]() $(\,\beta , \alpha )$
is an arc in
$(\,\beta , \alpha )$
is an arc in
![]() $\Gamma $
. If
$\Gamma $
. If
![]() $\alpha \in \mathrm V\Gamma $
in a digraph
$\alpha \in \mathrm V\Gamma $
in a digraph
![]() $\Gamma $
we define the set of in-neighbours as
$\Gamma $
we define the set of in-neighbours as
![]() $\in(\alpha)=\{\beta\in{\mathrm V}\Gamma\mid (\beta,\alpha)\in{\mathrm A}\Gamma\}$
and the set of out-neighbours as
$\in(\alpha)=\{\beta\in{\mathrm V}\Gamma\mid (\beta,\alpha)\in{\mathrm A}\Gamma\}$
and the set of out-neighbours as
![]() $\mathrm{out}(\alpha)=\{\beta\in{\mathrm V}\Gamma\mid (\alpha,\beta)\in{\mathrm A}\Gamma\}$
. The cardinality of
$\mathrm{out}(\alpha)=\{\beta\in{\mathrm V}\Gamma\mid (\alpha,\beta)\in{\mathrm A}\Gamma\}$
. The cardinality of
![]() $\mathrm{in}(\alpha )$
is the in-degree of
$\mathrm{in}(\alpha )$
is the in-degree of
![]() $\alpha $
and the cardinality of
$\alpha $
and the cardinality of
![]() $\mathrm{out}(\alpha )$
is the out-degree of
$\mathrm{out}(\alpha )$
is the out-degree of
![]() $\alpha $
. A digraph is regular if any two vertices have the same in-degree and also the same out-degree.
$\alpha $
. A digraph is regular if any two vertices have the same in-degree and also the same out-degree.
For an integer
![]() $s \geq 0$
an s-arc in
$s \geq 0$
an s-arc in
![]() $\Gamma $
(here
$\Gamma $
(here
![]() $\Gamma $
can be an undirected graph or a digraph) is an
$\Gamma $
can be an undirected graph or a digraph) is an
![]() $(s+1)$
-tuple
$(s+1)$
-tuple
![]() $(\alpha _{0},\ldots ,\alpha _{s})$
of vertices such that for every
$(\alpha _{0},\ldots ,\alpha _{s})$
of vertices such that for every
![]() $0 \leq i \leq s-1$
the ordered pair
$0 \leq i \leq s-1$
the ordered pair
![]() $(\alpha _{i},\alpha _{i+1})$
is an arc in
$(\alpha _{i},\alpha _{i+1})$
is an arc in
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $\alpha _{i-1} \neq \alpha _{i+1}$
for all
$\alpha _{i-1} \neq \alpha _{i+1}$
for all
![]() $1 \leq i \leq s-1$
. Infinite arcs come in three different shapes. There are one-way infinite arcs
$1 \leq i \leq s-1$
. Infinite arcs come in three different shapes. There are one-way infinite arcs
![]() $(\alpha _{0}, \alpha _{1}, \ldots )$
and
$(\alpha _{0}, \alpha _{1}, \ldots )$
and
![]() $(\ldots , \alpha _{-1}, \alpha _{0})$
, and there are two-way infinite arcs
$(\ldots , \alpha _{-1}, \alpha _{0})$
, and there are two-way infinite arcs
![]() $(\ldots , \alpha _{-1}, \alpha _{0}, \alpha _{1}, \ldots )$
. In all cases we insist that
$(\ldots , \alpha _{-1}, \alpha _{0}, \alpha _{1}, \ldots )$
. In all cases we insist that
![]() $(\alpha _{i},\alpha _{i+1})$
is an arc in
$(\alpha _{i},\alpha _{i+1})$
is an arc in
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $\alpha _{i-1} \neq \alpha _{i+1}$
for all i.
$\alpha _{i-1} \neq \alpha _{i+1}$
for all i.
A graph
![]() $\Gamma $
is said to be connected if for every pair of vertices
$\Gamma $
is said to be connected if for every pair of vertices
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
in
$\beta $
in
![]() $\Gamma $
there exists an s-arc
$\Gamma $
there exists an s-arc
![]() $(\alpha _{0},\ldots ,\alpha _{s})$
with
$(\alpha _{0},\ldots ,\alpha _{s})$
with
![]() $\alpha = \alpha _{0}$
and
$\alpha = \alpha _{0}$
and
![]() $\beta = \alpha _{s}$
. The smallest possible s is the distance between
$\beta = \alpha _{s}$
. The smallest possible s is the distance between
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
and is denoted by
$\beta $
and is denoted by
![]() $d_{\Gamma }(\alpha , \beta )$
. A digraph is said to be connected if the underlying undirected graph is connected.
$d_{\Gamma }(\alpha , \beta )$
. A digraph is said to be connected if the underlying undirected graph is connected.
2.2 Group actions
Let
![]() $\mathrm {Sym}(\Omega )$
denote the group of all permutations of the set
$\mathrm {Sym}(\Omega )$
denote the group of all permutations of the set
![]() $\Omega $
. By a permutation group on
$\Omega $
. By a permutation group on
![]() $\Omega $
we mean a subgroup of
$\Omega $
we mean a subgroup of
![]() $\mathrm {Sym}(\Omega )$
. An action of a group G on a set
$\mathrm {Sym}(\Omega )$
. An action of a group G on a set
![]() $\Omega $
is defined as a homomorphism
$\Omega $
is defined as a homomorphism
![]() $\pi : G\to \mathrm {Sym}(\Omega )$
. We write our group action on the right so that if
$\pi : G\to \mathrm {Sym}(\Omega )$
. We write our group action on the right so that if
![]() $\alpha \in \Omega $
and
$\alpha \in \Omega $
and
![]() $g\in G$
then
$g\in G$
then
![]() $\alpha g$
denotes the image of
$\alpha g$
denotes the image of
![]() $\alpha $
under the permutation
$\alpha $
under the permutation
![]() $\pi (g)$
. The kernel of the action (that is, the kernel of the homomorphism
$\pi (g)$
. The kernel of the action (that is, the kernel of the homomorphism
![]() $\pi $
) is equal to the set
$\pi $
) is equal to the set
![]() $K=\{g\in G\mid \alpha g=\alpha , \mathrm{\ for\ all\ }\alpha \in \Omega \}$
. If
$K=\{g\in G\mid \alpha g=\alpha , \mathrm{\ for\ all\ }\alpha \in \Omega \}$
. If
![]() $K=\{1\}$
, we say that the action is faithful. Set
$K=\{1\}$
, we say that the action is faithful. Set
![]() $G^{\Omega }=G/K$
. The homomorphism
$G^{\Omega }=G/K$
. The homomorphism
![]() $\pi $
induces an injective homomorphism
$\pi $
induces an injective homomorphism
![]() $G^{\Omega }\to \mathrm {Sym}(\Omega )$
giving an action of
$G^{\Omega }\to \mathrm {Sym}(\Omega )$
giving an action of
![]() $G^{\Omega }$
on
$G^{\Omega }$
on
![]() $\Omega $
. This action is clearly faithful and thus we can think of
$\Omega $
. This action is clearly faithful and thus we can think of
![]() $G^{\Omega }$
as a permutation group on
$G^{\Omega }$
as a permutation group on
![]() $\Omega $
. We call
$\Omega $
. We call
![]() $G^{\Omega }$
the permutation group on
$G^{\Omega }$
the permutation group on
![]() $\Omega $
induced by the action of G. If the action
$\Omega $
induced by the action of G. If the action
![]() $\pi $
is faithful, then
$\pi $
is faithful, then
![]() $G^{\Omega }=G$
and we can think of G itself as a permutation group.
$G^{\Omega }=G$
and we can think of G itself as a permutation group.
The stabilizer in G of
![]() $\alpha \in \Omega $
is the subgroup
$\alpha \in \Omega $
is the subgroup
![]() $G_{\alpha }=\{g\in G\mid \alpha g=\alpha \}$
. For a set
$G_{\alpha }=\{g\in G\mid \alpha g=\alpha \}$
. For a set
![]() $A\subseteq \Omega $
the pointwise stabilizer of A is defined as the subgroup
$A\subseteq \Omega $
the pointwise stabilizer of A is defined as the subgroup
and the setwise stabilizer is defined as the subgroup
![]() ${G_{\{A\}}=\{g\in G\mid A g=A\}}$
.
${G_{\{A\}}=\{g\in G\mid A g=A\}}$
.
The orbit of a point
![]() $\alpha \in \Omega $
under G is the set
$\alpha \in \Omega $
under G is the set
![]() $\alpha G=\{\alpha g\mid g \in G\}$
, and for
$\alpha G=\{\alpha g\mid g \in G\}$
, and for
![]() $S\subseteq G$
we define the S-orbit of
$S\subseteq G$
we define the S-orbit of
![]() $\alpha $
as the set
$\alpha $
as the set
![]() $\alpha S=\{\alpha g\mid g \in S\}$
. The orbits of
$\alpha S=\{\alpha g\mid g \in S\}$
. The orbits of
![]() $G_{\alpha }$
are called suborbits of G. An action is said to be transitive if for any two points
$G_{\alpha }$
are called suborbits of G. An action is said to be transitive if for any two points
![]() $\alpha , \beta \in \Omega $
there is an element
$\alpha , \beta \in \Omega $
there is an element
![]() $g\in G$
such that
$g\in G$
such that
![]() $\alpha g=\beta $
, that is, every orbit under G is all of
$\alpha g=\beta $
, that is, every orbit under G is all of
![]() $\Omega $
. A permutation group G on a set
$\Omega $
. A permutation group G on a set
![]() $\Omega $
is called free (or semiregular) if
$\Omega $
is called free (or semiregular) if
![]() $G_{\alpha }=\{1\}$
for all points
$G_{\alpha }=\{1\}$
for all points
![]() $\alpha \in \Omega $
and regular if it is free and transitive.
$\alpha \in \Omega $
and regular if it is free and transitive.
Let
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Delta $
be graphs (or digraphs). A graph morphism (or a digraph morphism)
$\Delta $
be graphs (or digraphs). A graph morphism (or a digraph morphism)
![]() $\varphi : \Gamma \to \Delta $
is a map
$\varphi : \Gamma \to \Delta $
is a map
![]() $\varphi \colon \mathrm V\Gamma \to \mathrm V\Delta $
such that if
$\varphi \colon \mathrm V\Gamma \to \mathrm V\Delta $
such that if
![]() $(\alpha , \beta ) \in \mathrm A\Gamma $
then
$(\alpha , \beta ) \in \mathrm A\Gamma $
then
![]() $(\varphi (\alpha ),\varphi (\,\beta )) \in \mathrm A\Delta $
. If a graph morphism
$(\varphi (\alpha ),\varphi (\,\beta )) \in \mathrm A\Delta $
. If a graph morphism
![]() $\varphi :\Gamma \to \Gamma $
is bijective and
$\varphi :\Gamma \to \Gamma $
is bijective and
![]() $\varphi $
induces a bijective map
$\varphi $
induces a bijective map
![]() $\mathrm A\Gamma \to \mathrm A\Gamma $
, then
$\mathrm A\Gamma \to \mathrm A\Gamma $
, then
![]() $\varphi $
is an automorphism of
$\varphi $
is an automorphism of
![]() $\Gamma $
. The set of all automorphisms of
$\Gamma $
. The set of all automorphisms of
![]() $\Gamma $
is a group, the automorphism group of
$\Gamma $
is a group, the automorphism group of
![]() $\Gamma $
, denoted by
$\Gamma $
, denoted by
![]() $\mathrm {Aut}(\Gamma )$
. We think of
$\mathrm {Aut}(\Gamma )$
. We think of
![]() $\mathrm{Aut}(\Gamma )$
as a permutation group on
$\mathrm{Aut}(\Gamma )$
as a permutation group on
![]() $\mathrm V\Gamma $
, and the action on the vertex set induces actions on the set of edges and the set of arcs. When we say that ‘a group G acts on a graph
$\mathrm V\Gamma $
, and the action on the vertex set induces actions on the set of edges and the set of arcs. When we say that ‘a group G acts on a graph
![]() $\Gamma $
’ we always mean an action by automorphisms. Such an action is described by a homomorphism
$\Gamma $
’ we always mean an action by automorphisms. Such an action is described by a homomorphism
![]() $G\to \mathrm{Aut}(\Gamma )$
. The permutation group on the vertex set induced by G is denoted by
$G\to \mathrm{Aut}(\Gamma )$
. The permutation group on the vertex set induced by G is denoted by
![]() $G^{\Gamma }$
.
$G^{\Gamma }$
.
A graph or a digraph
![]() $\Gamma $
is vertex-transitive if the automorphism group acts transitively on the vertex set. We say that
$\Gamma $
is vertex-transitive if the automorphism group acts transitively on the vertex set. We say that
![]() $\Gamma $
is edge-transitive (arc-transitive, s-arc-transitive) if the automorphism group acts transitively on the edge set (the arc set, the set of s-arcs). When the automorphism group is s-arc-transitive for all s, then
$\Gamma $
is edge-transitive (arc-transitive, s-arc-transitive) if the automorphism group acts transitively on the edge set (the arc set, the set of s-arcs). When the automorphism group is s-arc-transitive for all s, then
![]() $\Gamma $
is said to be highly arc-transitive.
$\Gamma $
is said to be highly arc-transitive.
Consider now a group G that acts vertex-transitively on a graph
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $\alpha \in \mathrm V\Gamma $
. The stabilizer
$\alpha \in \mathrm V\Gamma $
. The stabilizer
![]() $G_{\alpha }$
clearly leaves the set
$G_{\alpha }$
clearly leaves the set
![]() $\Gamma (\alpha )$
invariant and thus induces an action on it. The kernel of this action is
$\Gamma (\alpha )$
invariant and thus induces an action on it. The kernel of this action is
![]() $G_{(\Gamma (\alpha ))} \cap G_{\alpha }$
and the quotient
$G_{(\Gamma (\alpha ))} \cap G_{\alpha }$
and the quotient
 $G_{\alpha }^{\Gamma (\alpha )}=G_{\alpha } / (G_{(\Gamma (\alpha ))} \cap G_{\alpha })$
embeds as a subgroup into
$G_{\alpha }^{\Gamma (\alpha )}=G_{\alpha } / (G_{(\Gamma (\alpha ))} \cap G_{\alpha })$
embeds as a subgroup into
![]() $\mathrm {Sym}(\Gamma (\alpha ))$
. Now let
$\mathrm {Sym}(\Gamma (\alpha ))$
. Now let
![]() $\alpha ^{\prime }$
be another vertex of
$\alpha ^{\prime }$
be another vertex of
![]() $\Gamma $
. By assumption there exists
$\Gamma $
. By assumption there exists
![]() $g \in G$
with
$g \in G$
with
![]() $\alpha g = \alpha ^{\prime }$
, and
$\alpha g = \alpha ^{\prime }$
, and
![]() $G_{\alpha ^{\prime }}=g^{-1} G_{\alpha } g$
acts on
$G_{\alpha ^{\prime }}=g^{-1} G_{\alpha } g$
acts on
![]() $\Gamma (\alpha ^{\prime })$
. The actions of
$\Gamma (\alpha ^{\prime })$
. The actions of
![]() $G_{\alpha }$
on
$G_{\alpha }$
on
![]() $\Gamma (\alpha )$
and
$\Gamma (\alpha )$
and
![]() $G_{\alpha ^{\prime }}$
on
$G_{\alpha ^{\prime }}$
on
![]() $\Gamma (\alpha ^{\prime })=\Gamma (\alpha )g$
are conjugate via g and hence isomorphic. Thus, the following definition is independent of the choice of
$\Gamma (\alpha ^{\prime })=\Gamma (\alpha )g$
are conjugate via g and hence isomorphic. Thus, the following definition is independent of the choice of
![]() $\alpha $
.
$\alpha $
.
Definition 2.1. Let
![]() $\Gamma $
be a graph of degree d on which a group G acts vertex-transitively. Let
$\Gamma $
be a graph of degree d on which a group G acts vertex-transitively. Let
![]() $\alpha \in \mathrm V\Gamma $
. The local action of G on
$\alpha \in \mathrm V\Gamma $
. The local action of G on
![]() $\Gamma $
is the conjugacy class of the group
$\Gamma $
is the conjugacy class of the group
![]() $G_{\alpha }/(G_{(\Gamma (\alpha ))} \cap G_{\alpha })$
, seen as a subgroup of the symmetric group
$G_{\alpha }/(G_{(\Gamma (\alpha ))} \cap G_{\alpha })$
, seen as a subgroup of the symmetric group
![]() $S_{d}$
.
$S_{d}$
.
Given a group G acting on a set
![]() $\Omega $
, we say that an equivalence relation on
$\Omega $
, we say that an equivalence relation on
![]() $\Omega $
is a G-congruence if
$\Omega $
is a G-congruence if
![]() $\alpha g$
is equivalent to
$\alpha g$
is equivalent to
![]() $\beta g$
if and only if
$\beta g$
if and only if
![]() $\alpha $
is equivalent to
$\alpha $
is equivalent to
![]() $\beta $
. The orbits of a normal subgroup
$\beta $
. The orbits of a normal subgroup
![]() $N\trianglelefteq G$
form the equivalence classes of a G-congruence.
$N\trianglelefteq G$
form the equivalence classes of a G-congruence.
When
![]() $\sim $
denotes an equivalence relation on the vertex set of a graph (or a digraph)
$\sim $
denotes an equivalence relation on the vertex set of a graph (or a digraph)
![]() $\Gamma $
we can form the quotient graph (quotient digraph)
$\Gamma $
we can form the quotient graph (quotient digraph)
![]() $\Gamma /\!\sim $
. The vertex set of
$\Gamma /\!\sim $
. The vertex set of
![]() $\Gamma/\!\thicksim$
is the set of
$\Gamma/\!\thicksim$
is the set of
![]() $\sim $
-classes. The arc set is defined as follows: if A and B are two
$\sim $
-classes. The arc set is defined as follows: if A and B are two
![]() $\sim $
-classes, then
$\sim $
-classes, then
![]() $(A,B)$
is an arc in
$(A,B)$
is an arc in
![]() $\Gamma /\!\sim $
if and only if there is a vertex
$\Gamma /\!\sim $
if and only if there is a vertex
![]() $\alpha \in A$
and a vertex
$\alpha \in A$
and a vertex
![]() $\beta \in B$
such that
$\beta \in B$
such that
![]() $(\alpha ,\beta )$
is an arc in
$(\alpha ,\beta )$
is an arc in
![]() $\Gamma $
. If H is a subgroup of
$\Gamma $
. If H is a subgroup of
![]() $\mathrm{Aut}(\Gamma )$
then
$\mathrm{Aut}(\Gamma )$
then
![]() $\Gamma /H$
denotes the quotient graph of
$\Gamma /H$
denotes the quotient graph of
![]() $\Gamma $
with respect to the equivalence relation whose classes are the H-orbits on the vertex set. If G acts on
$\Gamma $
with respect to the equivalence relation whose classes are the H-orbits on the vertex set. If G acts on
![]() $\Gamma $
and
$\Gamma $
and
![]() $\sim $
is a G-congruence then G has a natural action on the set of
$\sim $
is a G-congruence then G has a natural action on the set of
![]() $\sim $
-classes that gives an action on the quotient digraph
$\sim $
-classes that gives an action on the quotient digraph
![]() $\Gamma /\!\sim $
by automorphisms.
$\Gamma /\!\sim $
by automorphisms.
2.3 The permutation topology
When G is a group acting on a set
![]() $\Omega $
, for example the automorphism group of a graph
$\Omega $
, for example the automorphism group of a graph
![]() $\Gamma $
acting on the vertex set
$\Gamma $
acting on the vertex set
![]() $\mathrm V\Gamma $
, we can endow G with the permutation topology; see, for instance, [Reference Möller23, Reference Woess40]. One description of this topology is as follows. A neighbourhood basis of the identity element consists of all subgroups of the form
$\mathrm V\Gamma $
, we can endow G with the permutation topology; see, for instance, [Reference Möller23, Reference Woess40]. One description of this topology is as follows. A neighbourhood basis of the identity element consists of all subgroups of the form
![]() $G_{(\Phi )}$
, where
$G_{(\Phi )}$
, where
![]() $\Phi $
ranges over all finite subsets of
$\Phi $
ranges over all finite subsets of
![]() $\Omega $
. Thus a subgroup is open if and only if it contains the pointwise stabilizer of some finite subset of
$\Omega $
. Thus a subgroup is open if and only if it contains the pointwise stabilizer of some finite subset of
![]() $\Omega $
. Another way to describe this topology is to think of
$\Omega $
. Another way to describe this topology is to think of
![]() $\Omega $
as having the discrete topology and then the permutation topology is the compact-open topology on G. The compact-open topology has the property that the action map
$\Omega $
as having the discrete topology and then the permutation topology is the compact-open topology on G. The compact-open topology has the property that the action map
![]() $\Omega \times G\to \Omega; (\alpha , g)\mapsto \alpha g$
is continuous. If the group G already has a topology and the stabilizer
$\Omega \times G\to \Omega; (\alpha , g)\mapsto \alpha g$
is continuous. If the group G already has a topology and the stabilizer
![]() $G_{\alpha }$
of a point
$G_{\alpha }$
of a point
![]() $\alpha \in \Omega $
is open, then the permutation topology is a subset of the topology on G. If the action of G is faithful then G is totally disconnected.
$\alpha \in \Omega $
is open, then the permutation topology is a subset of the topology on G. If the action of G is faithful then G is totally disconnected.
Various topological properties of the permutation topology have natural descriptions in terms of the group's action. For instance, a sequence
![]() $\{g_{i}\}$
of elements in G converges to an element
$\{g_{i}\}$
of elements in G converges to an element
![]() $g\in G$
in the permutation topology if and only if for each element
$g\in G$
in the permutation topology if and only if for each element
![]() $\alpha \in \Omega $
there is a number
$\alpha \in \Omega $
there is a number
![]() $N_{\alpha }$
such that if
$N_{\alpha }$
such that if
![]() $i\geq N_{\alpha }$
then
$i\geq N_{\alpha }$
then
![]() $\alpha g_{i}=\alpha g$
. We say that G is closed in the permutation topology if
$\alpha g_{i}=\alpha g$
. We say that G is closed in the permutation topology if
![]() $G^{\Omega }$
is closed in
$G^{\Omega }$
is closed in
![]() $\mathrm {Sym}(\Omega )$
with respect to the permutation topology on
$\mathrm {Sym}(\Omega )$
with respect to the permutation topology on
![]() $\mathrm {Sym}(\Omega )$
. Compactness and cocompactness have natural descriptions in the permutation topology.
$\mathrm {Sym}(\Omega )$
. Compactness and cocompactness have natural descriptions in the permutation topology.
Lemma 2.2. Let G be a group acting transitively on a countable set
![]() $\Omega $
. Endow G with the permutation topology. Assume G is closed in the permutation topology. Assume also that all suborbits are finite. Then the following assertions hold.
$\Omega $
. Endow G with the permutation topology. Assume G is closed in the permutation topology. Assume also that all suborbits are finite. Then the following assertions hold.
-
(1) [Reference Woess40, Lemma 1] The stabilizer of a point
 $\alpha \in \Omega $
is compact.
$\alpha \in \Omega $
is compact. -
(2) [Reference Woess40, Lemma 2] A subset A in G has compact closure if and only if all orbits of A are finite.
-
(3) [Reference Nebbia25, Proposition 1], see [Reference Möller22, Lemma 7.5] A subgroup H of G is cocompact, that is,
 $G/H$
is compact, if and only if H has only finitely many orbits on
$G/H$
is compact, if and only if H has only finitely many orbits on
 $\Omega $
.
$\Omega $
.
Suppose that G already has a given topology and acts transitively on a set
![]() $\Omega $
and the stabilizers of points are compact open subgroups. Then any compact subset of G will also be compact in the permutation topology and thus have finite orbits on
$\Omega $
and the stabilizers of points are compact open subgroups. Then any compact subset of G will also be compact in the permutation topology and thus have finite orbits on
![]() $\Omega $
.
$\Omega $
.
From the above it also follows that if G is a closed subgroup of the automorphism group of a locally finite graph
![]() $\Gamma $
, then G with the permutation topology is a totally disconnected, locally compact group. The reader may also find it reassuring to know that if G is a permutation group on a countable set
$\Gamma $
, then G with the permutation topology is a totally disconnected, locally compact group. The reader may also find it reassuring to know that if G is a permutation group on a countable set
![]() $\Omega $
, then the permutation topology is metrizable. Enumerate the points in
$\Omega $
, then the permutation topology is metrizable. Enumerate the points in
![]() $\Omega $
as
$\Omega $
as
![]() $\alpha _{1}, \alpha _{2}, \ldots .$
Take two elements
$\alpha _{1}, \alpha _{2}, \ldots .$
Take two elements
![]() $g, h\in G$
. Let n be the smallest number such that
$g, h\in G$
. Let n be the smallest number such that
![]() $\alpha _{n} g\neq \alpha _{n} h$
or
$\alpha _{n} g\neq \alpha _{n} h$
or
![]() $\alpha _{n} g^{-1}\neq \alpha _{n} h^{-1}$
. Set
$\alpha _{n} g^{-1}\neq \alpha _{n} h^{-1}$
. Set
![]() $d(g,h)=1/2^{n}$
. Then d is a metric on G that induces the permutation topology.
$d(g,h)=1/2^{n}$
. Then d is a metric on G that induces the permutation topology.
2.4 Cayley–Abels graphs
Central in this work is the concept of a Cayley–Abels graph for a cgtdlc group. Recall that a fundamental theorem of van Dantzig [Reference van Dantzig35] says that every totally disconnected, locally compact group contains a compact open subgroup.
Definition 2.3. Let G be a totally disconnected, locally compact group. A connected, locally finite graph on which G acts vertex-transitively such that the stabilizers of vertices are compact open subgroups is called a Cayley–Abels graph for G.
The following graph-theoretical lemma is well known but is stated here with a sketch of a proof to assist the reader.
Lemma 2.4. Let
![]() $\Gamma $
be a locally finite connected graph. Suppose that
$\Gamma $
be a locally finite connected graph. Suppose that
![]() $\alpha $
is a vertex in
$\alpha $
is a vertex in
![]() $\Gamma $
and that there exist automorphisms
$\Gamma $
and that there exist automorphisms
![]() $g_{1}, \ldots , g_{d}$
such that
$g_{1}, \ldots , g_{d}$
such that
![]() $\{\alpha g_{1}, \ldots , \alpha g_{d}\}=\Gamma (\alpha )$
. Then the group
$\{\alpha g_{1}, \ldots , \alpha g_{d}\}=\Gamma (\alpha )$
. Then the group
![]() $H=\langle g_{1}, \ldots , g_{d}\rangle $
acts transitively on
$H=\langle g_{1}, \ldots , g_{d}\rangle $
acts transitively on
![]() $\mathrm V\Gamma $
.
$\mathrm V\Gamma $
.
Proof (Sketch). The H-orbit of
![]() $\alpha $
contains every neighbour of
$\alpha $
contains every neighbour of
![]() $\alpha $
. It follows by using conjugation that if
$\alpha $
. It follows by using conjugation that if
![]() $\beta $
is a vertex in the H-orbit of
$\beta $
is a vertex in the H-orbit of
![]() $\alpha $
then the orbit contains every neighbour of
$\alpha $
then the orbit contains every neighbour of
![]() $\beta $
. Since the graph
$\beta $
. Since the graph
![]() $\Gamma $
is connected, we conclude that the H-orbit of
$\Gamma $
is connected, we conclude that the H-orbit of
![]() $\alpha $
contains every vertex in
$\alpha $
contains every vertex in
![]() $\Gamma $
.
$\Gamma $
.
A Cayley–Abels graph for a totally disconnected, locally compact group exists if and only if the group is compactly generated. Let
![]() $\Gamma $
be a Cayley–Abels graph for G. Suppose that
$\Gamma $
be a Cayley–Abels graph for G. Suppose that
![]() $\alpha $
is a vertex and
$\alpha $
is a vertex and
![]() $g_{1}, \ldots , g_{d}$
are elements in G such that
$g_{1}, \ldots , g_{d}$
are elements in G such that
![]() $\{\alpha g_{1}, \ldots , \alpha g_{d}\}=\Gamma (\alpha )$
. By Lemma 2.4, the subgroup
$\{\alpha g_{1}, \ldots , \alpha g_{d}\}=\Gamma (\alpha )$
. By Lemma 2.4, the subgroup
![]() $H=\langle g_{1}, \ldots , g_{d}\rangle $
is vertex-transitive and the compact set
$H=\langle g_{1}, \ldots , g_{d}\rangle $
is vertex-transitive and the compact set
![]() $G_{\alpha }\cup \{g_{1}, \ldots , g_{d}\}$
generates G. As a consequence we see that if
$G_{\alpha }\cup \{g_{1}, \ldots , g_{d}\}$
generates G. As a consequence we see that if
![]() $g_{1},\ldots , g_{k}$
are elements in G such that the set
$g_{1},\ldots , g_{k}$
are elements in G such that the set
![]() $\{\alpha g_{1}, \ldots , \alpha g_{k}\}$
contains a representative of every orbit of
$\{\alpha g_{1}, \ldots , \alpha g_{k}\}$
contains a representative of every orbit of
![]() $G_{\alpha }$
on
$G_{\alpha }$
on
![]() $\Gamma (\alpha )$
, then the set
$\Gamma (\alpha )$
, then the set
![]() $G_{\alpha }\cup \{g_{1}, \ldots , g_{k}\}$
generates G. These facts are used repeatedly. Two different ways of constructing a Cayley–Abels graph for a cgtdlc group G are described below.
$G_{\alpha }\cup \{g_{1}, \ldots , g_{k}\}$
generates G. These facts are used repeatedly. Two different ways of constructing a Cayley–Abels graph for a cgtdlc group G are described below.
The first construction (see [Reference Krön and Möller19, Construction 1]) goes as follows. Start with the set
![]() $G/U$
of right cosets of some compact open subgroup U of G. This is the vertex set of our graph. Then choose group elements
$G/U$
of right cosets of some compact open subgroup U of G. This is the vertex set of our graph. Then choose group elements
![]() $g_{1}, \ldots , g_{n}$
such that
$g_{1}, \ldots , g_{n}$
such that
![]() $G=\langle U, g_{1}, \ldots , g_{n}\rangle $
and finally take some element
$G=\langle U, g_{1}, \ldots , g_{n}\rangle $
and finally take some element
![]() $\alpha \in G/U$
and let the edge set be the union of the G-orbits
$\alpha \in G/U$
and let the edge set be the union of the G-orbits
![]() $\{\alpha , \alpha g_{1}\}G, \ldots , \{\alpha , \alpha g_{n}\}G$
. The resulting graph is a Cayley–Abels graph for G.
$\{\alpha , \alpha g_{1}\}G, \ldots , \{\alpha , \alpha g_{n}\}G$
. The resulting graph is a Cayley–Abels graph for G.
The second construction is in Abels’ paper [Reference Abels1, Beispiel 5.2] (see also [Reference Krön and Möller19, Construction 2]). Start by taking a compact generating set S and a compact open subgroup U. Then construct the Cayley graph with respect to this generating set S, and finally contract the right cosets of U. After all this, we are left with a locally finite, connected graph on which G acts transitively. The stabilizers of this graph's vertices are U and its conjugates.
In both constructions the constructor has choices and thus there is always more than one possible Cayley–Abels graph. But they are all locally finite and thus the following concept is well defined.
Definition 2.5. Let G be a cgtdlc group. The number
![]() $\mathrm{md}(G)$
denotes the minimal degree of a Cayley–Abels graph for G.
$\mathrm{md}(G)$
denotes the minimal degree of a Cayley–Abels graph for G.
Remark 2.6. Any two Cayley–Abels graphs for a compactly generated, totally disconnected group G are quasi-isometric to each other (see [Reference Krön and Möller19, Theorem 2.7]). This implies that the two graphs have the same ‘large-scale’ properties; for example, any two Cayley–Abels graphs of a group G have the same number of ends. In this work we do not need the concept of quasi-isometry, except that it appears again in remarks in Sections 3 and 4.
2.5 The scale function and tidy subgroups
The pioneering paper of Willis [Reference Willis37] started a new wave of interest in totally disconnected, locally compact groups. The fundamental concepts of Willis’s theory are the scale function and tidy subgroups. In a later paper [Reference Willis38], Willis gave the following simple definitions of these fundamental concepts and showed that these new definitions are equivalent to his original definitions in [Reference Willis37].
Definition 2.7 (see [Reference Willis38, Theorem 3.1])
Let G be a totally disconnected, locally compact group. The scale function on G is defined as
A compact open subgroup U of G is said to be tidy for g if and only if this minimum is attained at U, that is, s(g) = |U: U ∩ g −1 Ug|.
The following proposition allows us to compute the scale function of elements by using an action of the group on a set.
Proposition 2.8 [Reference Möller22, Corollary 7.8]
Let G be a totally disconnected, locally compact group and let U be a compact open subgroup of G. Consider the action of G on the set of right cosets
![]() $\Omega =G/U$
. Set
$\Omega =G/U$
. Set
![]() $\alpha =U$
and think of
$\alpha =U$
and think of
![]() $\alpha $
as a point in
$\alpha $
as a point in
![]() $\Omega $
. If
$\Omega $
. If
![]() $g\in G$
then
$g\in G$
then
 $$ \begin{align*}s(g)=\lim_{n\to \infty} |(\alpha g^{n}) G_{\alpha}|^{1/n},\end{align*} $$
$$ \begin{align*}s(g)=\lim_{n\to \infty} |(\alpha g^{n}) G_{\alpha}|^{1/n},\end{align*} $$
and, furthermore,
![]() $s(g)=1$
if and only if there is a constant C such that
$s(g)=1$
if and only if there is a constant C such that
![]() $|(\alpha g^{i})G_{\alpha }|\leq C$
for all
$|(\alpha g^{i})G_{\alpha }|\leq C$
for all
![]() $i=0, 1, 2, \ldots .$
$i=0, 1, 2, \ldots .$
3 Discrete actions
Every discrete group is trivially a totally disconnected, locally compact group, but then the topology carries no information about the group. It is useful to know when the given group topology, or the permutation topology arising from the action of a group on a Cayley–Abels graph, carries additional information about the group and its action on a Cayley–Abels graph.
Definition 3.1. An action of a group G on a set
![]() $\Omega $
is said to be discrete if the stabilizers in
$\Omega $
is said to be discrete if the stabilizers in
![]() $G^{\Omega }$
of points in
$G^{\Omega }$
of points in
![]() $\Omega $
are finite.
$\Omega $
are finite.
If the action of G on
![]() $\Omega $
is discrete, then there is a finite set
$\Omega $
is discrete, then there is a finite set
![]() $\Phi \subseteq \Omega $
such that the pointwise stabilizer in
$\Phi \subseteq \Omega $
such that the pointwise stabilizer in
![]() $G^{\Omega }$
of
$G^{\Omega }$
of
![]() $\Phi $
is trivial. In particular, the permutation topology on
$\Phi $
is trivial. In particular, the permutation topology on
![]() $G^{\Omega }$
is discrete. The pointwise stabilizer in G of
$G^{\Omega }$
is discrete. The pointwise stabilizer in G of
![]() $\Phi $
is then a compact open, normal, subgroup of G, where G has the permutation topology, and is equal to K, the kernel of the action. If the action is discrete and faithful, the permutation topology on G is discrete.
$\Phi $
is then a compact open, normal, subgroup of G, where G has the permutation topology, and is equal to K, the kernel of the action. If the action is discrete and faithful, the permutation topology on G is discrete.
Definition 3.2. A topological group is said to be nearly discrete if it has a compact, open, normal subgroup.
Following Cornulier in [Reference Cornulier9], we call an action of G on a set
![]() $\Omega $
block-discrete if there is a G-congruence
$\Omega $
block-discrete if there is a G-congruence
![]() $\sim $
on
$\sim $
on
![]() $\Omega $
with finite classes such that the stabilizers in
$\Omega $
with finite classes such that the stabilizers in
![]() $G^{\Omega /\!\sim }$
of points in
$G^{\Omega /\!\sim }$
of points in
![]() $\Omega /\!\sim $
are finite.
$\Omega /\!\sim $
are finite.
Lemma 3.3 (see [Reference Cornulier9, Fact 5.6])
Let G be a topological group acting transitively on a set
![]() $\Omega $
such that the stabilizers of points are compact, open subgroups. Then G is nearly discrete if and only if the action of G on
$\Omega $
such that the stabilizers of points are compact, open subgroups. Then G is nearly discrete if and only if the action of G on
![]() $\Omega $
is block-discrete.
$\Omega $
is block-discrete.
Proof. Suppose that G is nearly discrete and that N is a compact, open, normal subgroup. The N-orbits
![]() $\omega N$
with
$\omega N$
with
![]() $\omega \in \Omega $
are finite. They form the classes of a G-congruence on
$\omega \in \Omega $
are finite. They form the classes of a G-congruence on
![]() $\Omega $
. Denote the quotient space by
$\Omega $
. Denote the quotient space by
![]() $\Omega /N$
. Let
$\Omega /N$
. Let
![]() $\omega \in \Omega $
and
$\omega \in \Omega $
and
![]() $U = G_{\omega N}$
, where
$U = G_{\omega N}$
, where
![]() $\omega N \in \Omega /N$
. Then
$\omega N \in \Omega /N$
. Then
![]() $U = G_{\{\omega N\}}$
with
$U = G_{\{\omega N\}}$
with
![]() $\omega N \subseteq \Omega $
. But
$\omega N \subseteq \Omega $
. But
![]() $\omega N$
is finite, hence U is a compact open subgroup of G. The kernel K of the action of G on
$\omega N$
is finite, hence U is a compact open subgroup of G. The kernel K of the action of G on
![]() $\Omega /N$
contains N and is contained in
$\Omega /N$
contains N and is contained in
![]() $G_{\omega N}$
. Thus K is both open and compact. In particular,
$G_{\omega N}$
. Thus K is both open and compact. In particular,
![]() $G/K$
is discrete and the image of U in
$G/K$
is discrete and the image of U in
![]() $G/K$
is finite. Hence, the action of G on
$G/K$
is finite. Hence, the action of G on
![]() $\Omega $
is block-discrete.
$\Omega $
is block-discrete.
Assume now that the action of G on
![]() $\Omega $
is block-discrete. Hence, there is a G-congruence
$\Omega $
is block-discrete. Hence, there is a G-congruence
![]() $\sim $
on
$\sim $
on
![]() $\Omega $
with finite classes such that the stabilizers in
$\Omega $
with finite classes such that the stabilizers in
![]() $G^{\Omega /\!\sim }$
are finite. Let K be the kernel of the action of G on
$G^{\Omega /\!\sim }$
are finite. Let K be the kernel of the action of G on
![]() $\Omega /\!\sim $
. The action of G on
$\Omega /\!\sim $
. The action of G on
![]() $\Omega /\!\sim $
is discrete and thus there is a finite set
$\Omega /\!\sim $
is discrete and thus there is a finite set
![]() $\Phi \subseteq \Omega /\!\sim $
such that
$\Phi \subseteq \Omega /\!\sim $
such that
![]() $G_{(\Phi )} = K$
. But
$G_{(\Phi )} = K$
. But
![]() $G_{(\Phi )}$
is a compact, open subgroup of G. Thus K is a compact, open, normal subgroup of G and G is nearly discrete.
$G_{(\Phi )}$
is a compact, open subgroup of G. Thus K is a compact, open, normal subgroup of G and G is nearly discrete.
The following nice result of Schlichting, here rephrased using our terminology, gives further connections between the action and the property that a group with the permutation topology is nearly discrete.
Theorem 3.4 [Reference Schlichting30]
Let G be a group acting transitively on a set
![]() $\Omega $
. Endow G with the permutation topology. Then G is nearly discrete if and only if there is a finite upper bound on the sizes of its suborbits.
$\Omega $
. Endow G with the permutation topology. Then G is nearly discrete if and only if there is a finite upper bound on the sizes of its suborbits.
Turning to Cayley–Abels graphs, we get the following corollary.
Corollary 3.5. Let G be a cgtdlc group. Then G is nearly discrete if and only if G has a discrete action on some Cayley–Abels graph.
Proof. Suppose that G is nearly discrete and that K is a compact, open, normal subgroup. Assume
![]() $\Gamma $
is a Cayley–Abels graph for G. Then the graph
$\Gamma $
is a Cayley–Abels graph for G. Then the graph
![]() $\Gamma /K$
is connected and locally finite (recall that by part (2) of Lemma 2.2 the orbits of K are finite). Hence,
$\Gamma /K$
is connected and locally finite (recall that by part (2) of Lemma 2.2 the orbits of K are finite). Hence,
![]() $\Gamma /K$
is also a Cayley–Abels graph for G and the action of G on
$\Gamma /K$
is also a Cayley–Abels graph for G and the action of G on
![]() $\Gamma /K$
is discrete.
$\Gamma /K$
is discrete.
Conversely, if G has a discrete action on some Cayley–Abels graph then we have already seen that G is nearly discrete.
Remark 3.6. Let G be a cgtdlc group and
![]() $\Gamma $
a Cayley–Abels graph for G. Let
$\Gamma $
a Cayley–Abels graph for G. Let
![]() $H \leq G$
be a closed, cocompact subgroup. Then H itself is compactly generated and every Cayley–Abels graph for H is quasi-isometric to
$H \leq G$
be a closed, cocompact subgroup. Then H itself is compactly generated and every Cayley–Abels graph for H is quasi-isometric to
![]() $\Gamma $
; see [Reference Krön and Möller19, Corollary 2.11]. Suppose now that K is a compact, normal subgroup of G. Then
$\Gamma $
; see [Reference Krön and Möller19, Corollary 2.11]. Suppose now that K is a compact, normal subgroup of G. Then
![]() $\Gamma /K$
is a Cayley–Abels graph for both G and
$\Gamma /K$
is a Cayley–Abels graph for both G and
![]() $G/K$
. Thus
$G/K$
. Thus
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Gamma /K$
are quasi-isometric. The conclusion is that all Cayley–Abels graphs for G, H and
$\Gamma /K$
are quasi-isometric. The conclusion is that all Cayley–Abels graphs for G, H and
![]() $G/K$
are quasi-isometric.
$G/K$
are quasi-isometric.
If G is nearly discrete then one can show by using a construction of Sabidussi [Reference Sabidussi28, Theorem 4], that there is a Cayley–Abels graph
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $G^{\Gamma }$
acts regularly on
$G^{\Gamma }$
acts regularly on
![]() $\Gamma $
.
$\Gamma $
.
In some cases one can determine from the local action on a Cayley–Abels graph that the action on the graph is discrete.
Lemma 3.7. Let G be a cgtdlc group. Let
![]() $\Gamma $
be a Cayley–Abels graph for G. If the local action of G is trivial then
$\Gamma $
be a Cayley–Abels graph for G. If the local action of G is trivial then
![]() $G^{\Gamma }$
acts regularly on
$G^{\Gamma }$
acts regularly on
![]() $\Gamma $
. If the local action of
$\Gamma $
. If the local action of
![]() $G^{\Gamma }$
is free then
$G^{\Gamma }$
is free then
![]() $G^{\Gamma }$
acts freely on the arcs of
$G^{\Gamma }$
acts freely on the arcs of
![]() $\Gamma $
and, in particular, G acts discretely on
$\Gamma $
and, in particular, G acts discretely on
![]() $\Gamma $
.
$\Gamma $
.
Proof. We first consider the case where the local action is trivial. If
![]() $\alpha \in \mathrm V\Gamma $
, then
$\alpha \in \mathrm V\Gamma $
, then
![]() $G_{\alpha }$
fixes every vertex in
$G_{\alpha }$
fixes every vertex in
![]() $\Gamma (\alpha )$
. If
$\Gamma (\alpha )$
. If
![]() $\beta \in \Gamma (\alpha )$
, then
$\beta \in \Gamma (\alpha )$
, then
![]() $G_{\alpha }$
fixes
$G_{\alpha }$
fixes
![]() $\beta $
and thus every vertex in
$\beta $
and thus every vertex in
![]() $\Gamma (\,\beta )$
is also fixed. Since the graph
$\Gamma (\,\beta )$
is also fixed. Since the graph
![]() $\Gamma $
is connected we see that
$\Gamma $
is connected we see that
![]() $G_{\alpha }$
fixes every vertex in
$G_{\alpha }$
fixes every vertex in
![]() $\Gamma $
, that is,
$\Gamma $
, that is,
![]() $G^{\Gamma }$
acts regularly.
$G^{\Gamma }$
acts regularly.
Suppose that the action of
![]() $G_{\alpha }$
on
$G_{\alpha }$
on
![]() $\Gamma (\alpha )$
is free. Let
$\Gamma (\alpha )$
is free. Let
![]() $\beta $
be a vertex in
$\beta $
be a vertex in
![]() $\Gamma (\alpha )$
. By assumption
$\Gamma (\alpha )$
. By assumption
![]() $G_{\alpha, \beta }$
fixes every vertex in
$G_{\alpha, \beta }$
fixes every vertex in
![]() $\Gamma (\alpha )$
and also every vertex in
$\Gamma (\alpha )$
and also every vertex in
![]() $\Gamma (\,\beta )$
. The conclusion now follows again from the connectivity of
$\Gamma (\,\beta )$
. The conclusion now follows again from the connectivity of
![]() $\Gamma $
.
$\Gamma $
.
Next we look at compact, normal subgroups in relation to minimal-degree Cayley–Abels graphs. The following lemma is well known.
Lemma 3.8. Let
![]() $\Gamma $
be a locally finite graph and
$\Gamma $
be a locally finite graph and
![]() $G \leq \mathrm {Aut}(\Gamma )$
a vertex-transitive subgroup. Suppose that N is a normal subgroup of G. Then the degree of
$G \leq \mathrm {Aut}(\Gamma )$
a vertex-transitive subgroup. Suppose that N is a normal subgroup of G. Then the degree of
![]() $\Gamma $
is greater than or equal to the degree of
$\Gamma $
is greater than or equal to the degree of
![]() $\Gamma /N$
. Equality holds if and only if no vertices of distance at most
$\Gamma /N$
. Equality holds if and only if no vertices of distance at most
![]() $2$
from each other lie in the same N-orbit.
$2$
from each other lie in the same N-orbit.
Proof. Consider two adjacent vertices A and B in
![]() $\Gamma /N$
. Since A and B are adjacent in
$\Gamma /N$
. Since A and B are adjacent in
![]() $\Gamma /N$
there are vertices
$\Gamma /N$
there are vertices
![]() $\alpha , \beta \in \mathrm V\Gamma $
such that
$\alpha , \beta \in \mathrm V\Gamma $
such that
![]() $\alpha \in A$
,
$\alpha \in A$
,
![]() $\beta \in B$
and
$\beta \in B$
and
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are adjacent in
$\beta $
are adjacent in
![]() $\Gamma $
. Both A and B are N-orbits in
$\Gamma $
. Both A and B are N-orbits in
![]() $\mathrm V\Gamma $
and hence we see that every vertex in A has a neighbour in B. Hence, the degree of
$\mathrm V\Gamma $
and hence we see that every vertex in A has a neighbour in B. Hence, the degree of
![]() $\Gamma /N$
is at most equal to the degree of
$\Gamma /N$
is at most equal to the degree of
![]() $\Gamma $
.
$\Gamma $
.
The degree of
![]() $\Gamma $
equals the degree of
$\Gamma $
equals the degree of
![]() $\Gamma /N$
if and only if for every vertex
$\Gamma /N$
if and only if for every vertex
![]() $\alpha \in \mathrm V\Gamma $
its neighbours belong to different N-orbits and none of them belongs to the N-orbit of
$\alpha \in \mathrm V\Gamma $
its neighbours belong to different N-orbits and none of them belongs to the N-orbit of
![]() $\alpha $
. Thus the stabilizer of
$\alpha $
. Thus the stabilizer of
![]() $\alpha $
in N must act trivially on the neighbourhood of
$\alpha $
in N must act trivially on the neighbourhood of
![]() $\alpha $
in
$\alpha $
in
![]() $\Gamma $
. The same argument as in the proof of Lemma 3.7 now shows that the stabilizer in N of a vertex in
$\Gamma $
. The same argument as in the proof of Lemma 3.7 now shows that the stabilizer in N of a vertex in
![]() $\Gamma $
acts trivially on
$\Gamma $
acts trivially on
![]() $\Gamma $
.
$\Gamma $
.
Lemma 3.8 directly implies the following result.
Corollary 3.9. Let G be a cgtdlc group. Suppose that
![]() $\Gamma $
is a Cayley–Abels graph for G with minimal degree. If N is a compact, normal subgroup of G, then the orbits of N on
$\Gamma $
is a Cayley–Abels graph for G with minimal degree. If N is a compact, normal subgroup of G, then the orbits of N on
![]() $\mathrm V\Gamma $
are finite,
$\mathrm V\Gamma $
are finite,
![]() $N^{\Gamma }$
acts freely on
$N^{\Gamma }$
acts freely on
![]() $\mathrm V\Gamma $
and no two vertices in the same N-orbit are adjacent. In particular,
$\mathrm V\Gamma $
and no two vertices in the same N-orbit are adjacent. In particular,
![]() $N^{\Gamma }$
is finite.
$N^{\Gamma }$
is finite.
Corollary 3.10. Let G be a cgtdlc group. If G is nearly discrete, then G acts discretely on some minimal-degree Cayley–Abels graph.
Proof. Let
![]() $\Gamma $
be some minimal-degree Cayley–Abels graph. If K is a compact, open, normal subgroup then
$\Gamma $
be some minimal-degree Cayley–Abels graph. If K is a compact, open, normal subgroup then
![]() $\Gamma /K$
is also a minimal-degree Cayley–Abels graph for G and G acts discretely on
$\Gamma /K$
is also a minimal-degree Cayley–Abels graph for G and G acts discretely on
![]() $\Gamma /K$
.
$\Gamma /K$
.
4 Groups with minimal degree 2 or 3
In this section we first characterize those cgtdlc groups
![]() $G$
with
$G$
with
![]() $\mathrm{md}(G)=2$
. Note that a
$\mathrm{md}(G)=2$
. Note that a
![]() $2$
-regular minimal-degree Cayley–Abels graph can only be the infinite line. We also look at the case when the minimal degree is equal to 3; for proofs of those results the reader is referred to the companion paper [Reference Árnadóttir, Lederle and Möller3].
$2$
-regular minimal-degree Cayley–Abels graph can only be the infinite line. We also look at the case when the minimal degree is equal to 3; for proofs of those results the reader is referred to the companion paper [Reference Árnadóttir, Lederle and Möller3].
Let
![]() $\Gamma $
be any graph. A ray is a one-way infinite arc such that all its vertices are different. An end of
$\Gamma $
be any graph. A ray is a one-way infinite arc such that all its vertices are different. An end of
![]() $\Gamma $
is an equivalence class of rays, where the ray
$\Gamma $
is an equivalence class of rays, where the ray
![]() $(\alpha _{0},\alpha _{1},\ldots )$
is equivalent to
$(\alpha _{0},\alpha _{1},\ldots )$
is equivalent to
![]() $(\,\beta _{0},\beta _{1},\ldots )$
if and only if there is a ray
$(\,\beta _{0},\beta _{1},\ldots )$
if and only if there is a ray
![]() $(\gamma _{0},\gamma _{1},\ldots )$
such that the intersections
$(\gamma _{0},\gamma _{1},\ldots )$
such that the intersections
![]() $\{\gamma _{i} \mid i \geq 0\} \cap \{\alpha _{i} \mid i \geq 0\}$
and
$\{\gamma _{i} \mid i \geq 0\} \cap \{\alpha _{i} \mid i \geq 0\}$
and
![]() $\{\gamma _{i} \mid i \geq 0\} \cap \{\,\beta _{i} \mid i \geq 0\}$
are both infinite.
$\{\gamma _{i} \mid i \geq 0\} \cap \{\,\beta _{i} \mid i \geq 0\}$
are both infinite.
If two graphs are quasi-isometric then they have the same number of ends; see [Reference Möller21, Proposition 1]. As any two Cayley–Abels graphs of a group G are quasi-isometric (see [Reference Krön and Möller19, Theorem 2.7]), we can define the number of ends of a cgtdlc group as the number of ends of a Cayley–Abels graph.
Theorem 4.1. For a cgtdlc group G the following assertions are equivalent.
-
(1) The minimal degree of a Cayley–Abels graph for G is
 $2$
.
$2$
. -
(2) The group G has precisely two ends.
-
(3) There is a continuous surjective homomorphism with a compact, open kernel from G onto the infinite cyclic group or the infinite dihedral group (both with the discrete topology).
-
(4) The group G has a cocompact cyclic discrete subgroup.
Proof. First note that (1) implies (2) trivially because if
![]() $\mathrm{md}(G)=2$
then the integer graph
$\mathrm{md}(G)=2$
then the integer graph
![]() $\mathbb {Z}$
is a Cayley–Abels graph for G, so G has two ends. Then (2) implies (3) by [Reference Abels1, Satz 4.5]; see also [Reference Möller and Seifter24, Proposition 3.2]. To prove that (3) implies (1), note that the groups
$\mathbb {Z}$
is a Cayley–Abels graph for G, so G has two ends. Then (2) implies (3) by [Reference Abels1, Satz 4.5]; see also [Reference Möller and Seifter24, Proposition 3.2]. To prove that (3) implies (1), note that the groups
![]() $\mathbb {Z}$
and
$\mathbb {Z}$
and
![]() $D_{\infty }$
both have regular actions on the integer graph
$D_{\infty }$
both have regular actions on the integer graph
![]() $\mathbb {Z}$
. From this we see that G has an action on the integer graph
$\mathbb {Z}$
. From this we see that G has an action on the integer graph
![]() $\mathbb {Z}$
with a compact, open kernel and thus
$\mathbb {Z}$
with a compact, open kernel and thus
![]() $\mathbb {Z}$
is a Cayley–Abels graph for G.
$\mathbb {Z}$
is a Cayley–Abels graph for G.
Finally, we note that (2) and (4) are equivalent. This can be seen, for example, from results in Section 5 in the paper by Jung and Watkins [Reference Jung and Watkins16] or in Abels’s paper [Reference Abels1, Satz 3.10]. A self-contained proof of this fact can be found in [Reference Árnadóttir, Lederle and Möller3, Appendix C].
Remark 4.2. In the case of a finitely generated group acting on a locally finite Cayley graph it follows from results of Hopf [Reference Hopf15, Satz 5] and Wall [Reference Wall36, Lemma 4.1] that conditions (2), (3) and (4) in the theorem above are equivalent.
In [Reference Árnadóttir, Lederle and Möller3] cgtdlc groups that have minimal degree 3 are studied. The first part of the following theorem was previously known by experts.
Theorem 4.3 [Reference Árnadóttir, Lederle and Möller3, Sections 3 and 4]
Let G be a cgtdlc group that is not nearly discrete. Assume that
![]() $\mathrm{md}(G)=3$
and let
$\mathrm{md}(G)=3$
and let
![]() $\Gamma $
be a minimal-degree Cayley–Abels graph for G. Then one of the following statements is true.
$\Gamma $
be a minimal-degree Cayley–Abels graph for G. Then one of the following statements is true.
-
(1) The action of G is transitive on the edges and
 $\Gamma $
is a tree.
$\Gamma $
is a tree. -
(2) The action of G has precisely two orbits on the edges of
 $\Gamma $
. For every
$\Gamma $
. For every
 $s \geq 1$
, the group G acts with precisely two orbits on the set of s-arcs whose underlying edges lie alternately in the two edge orbits of G.
$s \geq 1$
, the group G acts with precisely two orbits on the set of s-arcs whose underlying edges lie alternately in the two edge orbits of G.
A totally disconnected, locally compact group G is said to be uniscalar if the scale function is constant, that is,
![]() $s(g)=1$
for all
$s(g)=1$
for all
![]() $g\in G$
. Equivalently, every element in the group normalizes some compact, open subgroup.
$g\in G$
. Equivalently, every element in the group normalizes some compact, open subgroup.
Theorem 4.4 [Reference Árnadóttir, Lederle and Möller3, Theorem 6.2]
Suppose that G is a cgtdlc group that is not nearly discrete. If
![]() $\mathrm{md}(G)=3$
then G is not uniscalar.
$\mathrm{md}(G)=3$
then G is not uniscalar.
If a totally disconnected, locally compact group G has a compact open normal subgroup then G is uniscalar. Bhattacharjee and Macpherson [Reference Bhattacharjee and Macpherson6, Section 3] (following up on work by Kepert and Willis [Reference Kepert and Willis17]), constructed an example of a cgtdlc group that has no compact, open, normal subgroup, but every element normalizes some compact open subgroup.
Corollary 4.5 [Reference Árnadóttir, Lederle and Möller3, Corollary 6.3]
Let G be a cgtdlc group having a
![]() $3$
-regular Cayley–Abels graph. If every
$3$
-regular Cayley–Abels graph. If every
![]() $g \in G$
normalizes a compact open subgroup of G then G has a compact, open, normal subgroup.
$g \in G$
normalizes a compact open subgroup of G then G has a compact, open, normal subgroup.
5 Cayley–Abels graphs and the modular function
Let G be a locally compact group and
![]() $\mu $
a right-invariant Haar measure on G. The modular function is the map
$\mu $
a right-invariant Haar measure on G. The modular function is the map
![]() $\Delta \colon G \to \mathbb {R}^{+}$
such that for every measurable subset
$\Delta \colon G \to \mathbb {R}^{+}$
such that for every measurable subset
![]() $A \subseteq G$
and for every
$A \subseteq G$
and for every
![]() $g \in G$
we have
$g \in G$
we have
![]() $\mu (gA)=\Delta (g)\mu (A)$
; it is well known that the modular function exists and is a homomorphism. A group is unimodular if
$\mu (gA)=\Delta (g)\mu (A)$
; it is well known that the modular function exists and is a homomorphism. A group is unimodular if
![]() $\Delta (g)=1$
for all
$\Delta (g)=1$
for all
![]() $g\in G$
.
$g\in G$
.
5.1 Reading the modular function off the edges
The following result linking the modular function and sizes of suborbits was proved by Schlichting [Reference Schlichting29, Lemma 1]; see also [Reference Trofimov33, Theorem 1].
Lemma 5.1. Let G be a totally disconnected, locally compact group and
![]() $\Delta $
the modular function on G. If U is a compact open subgroup of G and
$\Delta $
the modular function on G. If U is a compact open subgroup of G and
![]() $g\in G$
then
$g\in G$
then
 $$ \begin{align*}\Delta(g)=\frac{|U:U\cap g^{-1}Ug|}{|g^{-1}Ug:U\cap g^{-1}Ug|}.\end{align*} $$
$$ \begin{align*}\Delta(g)=\frac{|U:U\cap g^{-1}Ug|}{|g^{-1}Ug:U\cap g^{-1}Ug|}.\end{align*} $$
Suppose that G acts on a set
![]() $\Omega $
with compact, open point stabilizers. If
$\Omega $
with compact, open point stabilizers. If
![]() $\alpha \in \Omega $
and
$\alpha \in \Omega $
and
![]() $g\in G$
then
$g\in G$
then
 $$ \begin{align}\Delta(g)=\frac{|G_{\alpha}:G_{\alpha}\cap g^{-1}G_{\alpha} g|}{|g^{-1}G_{\alpha} g:G_{\alpha}\cap g^{-1}G_{\alpha} g|} =\frac{|(\alpha g) G_{\alpha}|}{|\alpha G_{ \alpha g}|}. \end{align} $$
$$ \begin{align}\Delta(g)=\frac{|G_{\alpha}:G_{\alpha}\cap g^{-1}G_{\alpha} g|}{|g^{-1}G_{\alpha} g:G_{\alpha}\cap g^{-1}G_{\alpha} g|} =\frac{|(\alpha g) G_{\alpha}|}{|\alpha G_{ \alpha g}|}. \end{align} $$
Furthermore, the image of the modular function is a subgroup of the multiplicative group of positive rational numbers.
If G acts on a set
![]() $\Omega $
with compact point stabilizers and if for
$\Omega $
with compact point stabilizers and if for
![]() $g, h\in G$
there is an
$g, h\in G$
there is an
![]() $\alpha \in \Omega $
with
$\alpha \in \Omega $
with
![]() $\alpha g=\alpha h$
, then it follows from (5-1) that
$\alpha g=\alpha h$
, then it follows from (5-1) that
![]() $\Delta (g)=\Delta (h)$
. If in addition G is unimodular and its point stabilizers are open, then
$\Delta (g)=\Delta (h)$
. If in addition G is unimodular and its point stabilizers are open, then
![]() $|(\alpha g) G_{\alpha }|=|\alpha G_{\alpha g}|$
for all g in G and all
$|(\alpha g) G_{\alpha }|=|\alpha G_{\alpha g}|$
for all g in G and all
![]() $\alpha \in \Omega $
.
$\alpha \in \Omega $
.
The following idea originates from the paper by Bass and Kulkarni [Reference Bass and Kulkarni4, Section 3] and enables us to ‘read’ the values of the modular function for a cgtdlc group G off a Cayley–Abels graph
![]() $\Gamma $
. Label an arc
$\Gamma $
. Label an arc
![]() $(\alpha ,\beta )$
in
$(\alpha ,\beta )$
in
![]() $\Gamma $
with the number
$\Gamma $
with the number
 $$ \begin{align*}\Delta_{(\alpha, \beta)}=\frac{|\,\beta G_{\alpha}|}{|\alpha G_{\beta} |}.\end{align*} $$
$$ \begin{align*}\Delta_{(\alpha, \beta)}=\frac{|\,\beta G_{\alpha}|}{|\alpha G_{\beta} |}.\end{align*} $$
Note that
 $\Delta _{(\,\beta , \alpha )}=\Delta _{(\alpha , \beta )}^{-1}$
. This arc labelling is clearly invariant under the action of G on the set of arcs. Combining these observations, we see that if
$\Delta _{(\,\beta , \alpha )}=\Delta _{(\alpha , \beta )}^{-1}$
. This arc labelling is clearly invariant under the action of G on the set of arcs. Combining these observations, we see that if
![]() $\Delta _{(\alpha , \beta )}\neq 1$
then there cannot exist
$\Delta _{(\alpha , \beta )}\neq 1$
then there cannot exist
![]() $g\in G$
such that
$g\in G$
such that
![]() $(\alpha ,\beta ) g=(\,\beta ,\alpha )$
. If
$(\alpha ,\beta ) g=(\,\beta ,\alpha )$
. If
![]() $g \in G$
satisfies
$g \in G$
satisfies
![]() $\alpha g=\beta $
then Lemma 5.1 readily implies that
$\alpha g=\beta $
then Lemma 5.1 readily implies that
 $$ \begin{align} \Delta(g)= \frac{|\,\beta G_{\alpha}|}{|\alpha G_{\beta}|}=\Delta_{(\alpha, \beta)}. \end{align} $$
$$ \begin{align} \Delta(g)= \frac{|\,\beta G_{\alpha}|}{|\alpha G_{\beta}|}=\Delta_{(\alpha, \beta)}. \end{align} $$
Now let
![]() $\gamma $
be a neighbour of
$\gamma $
be a neighbour of
![]() $\beta $
and take
$\beta $
and take
![]() $h \in G$
with
$h \in G$
with
![]() $\alpha h=\gamma $
. Set
$\alpha h=\gamma $
. Set
![]() $g^{\prime }= g^{-1}h \in G$
. Then
$g^{\prime }= g^{-1}h \in G$
. Then
![]() $\beta g^{\prime }=(\alpha g)g^{-1}h=\gamma $
. Hence,
$\beta g^{\prime }=(\alpha g)g^{-1}h=\gamma $
. Hence,
![]() $\alpha h=\alpha g g^{\prime }$
and we see that
$\alpha h=\alpha g g^{\prime }$
and we see that
Inductively, we get that if
![]() $\alpha ,\beta \in \Gamma $
are arbitrary vertices,
$\alpha ,\beta \in \Gamma $
are arbitrary vertices,
![]() $g \in G$
satisfies
$g \in G$
satisfies
![]() $\alpha g=\beta $
and
$\alpha g=\beta $
and
![]() $(\alpha _{0},\ldots ,\alpha _{s})$
is an s-arc with
$(\alpha _{0},\ldots ,\alpha _{s})$
is an s-arc with
![]() $\alpha _{0}=\alpha $
and
$\alpha _{0}=\alpha $
and
![]() $\alpha _{s}=\beta $
, then
$\alpha _{s}=\beta $
, then
Thus the labelled Cayley–Abels graph completely describes the modular function on G. We have now proved the following theorem.
Theorem 5.2. Let G be a cgtdlc group,
![]() $\Delta $
the modular function on G, and
$\Delta $
the modular function on G, and
![]() $\Gamma $
a Cayley–Abels graph for G. If
$\Gamma $
a Cayley–Abels graph for G. If
![]() $g \in G$
and
$g \in G$
and
![]() $(\alpha _{0},\ldots ,\alpha _{s})$
is an s-arc in
$(\alpha _{0},\ldots ,\alpha _{s})$
is an s-arc in
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $\alpha _{0}g = \alpha _{s}$
, then
$\alpha _{0}g = \alpha _{s}$
, then
![]() $\Delta (g) = \Delta _{(\alpha _{0},\alpha _{1})} \cdots \Delta _{(\alpha _{s-1},\alpha _{s})}$
. In particular, the image of
$\Delta (g) = \Delta _{(\alpha _{0},\alpha _{1})} \cdots \Delta _{(\alpha _{s-1},\alpha _{s})}$
. In particular, the image of
![]() $\Delta $
is generated by the labels of the arcs.
$\Delta $
is generated by the labels of the arcs.
Corollary 5.3. Let G be a cgtdlc group,
![]() $\Delta $
the modular function on G and
$\Delta $
the modular function on G and
![]() $\Gamma $
a Cayley–Abels graph for G. For a vertex
$\Gamma $
a Cayley–Abels graph for G. For a vertex
![]() $\alpha $
in
$\alpha $
in
![]() $\Gamma $
, let
$\Gamma $
, let
![]() $B_{1},\ldots ,B_{n}$
be the orbits of
$B_{1},\ldots ,B_{n}$
be the orbits of
![]() $G_{\alpha }$
on the neighbours of
$G_{\alpha }$
on the neighbours of
![]() $\alpha $
and choose, for each i, an element
$\alpha $
and choose, for each i, an element
![]() $g_{i} \in G$
with
$g_{i} \in G$
with
![]() $\alpha g_{i} \in B_{i}$
. Then
$\alpha g_{i} \in B_{i}$
. Then
 $$ \begin{align*} \mathrm{im}(\Delta) = \bigg\langle \frac{|(\alpha g_{1}) G_{\alpha}|}{|(\alpha g_{1}^{-1}) G_{\alpha}|}, \ldots, \frac{|(\alpha g_{n}) G_{\alpha}|}{|(\alpha g_{n}^{-1}) G_{\alpha}|} \bigg\rangle \leq \mathbb{Q}^{+}. \end{align*} $$
$$ \begin{align*} \mathrm{im}(\Delta) = \bigg\langle \frac{|(\alpha g_{1}) G_{\alpha}|}{|(\alpha g_{1}^{-1}) G_{\alpha}|}, \ldots, \frac{|(\alpha g_{n}) G_{\alpha}|}{|(\alpha g_{n}^{-1}) G_{\alpha}|} \bigg\rangle \leq \mathbb{Q}^{+}. \end{align*} $$
The image of
![]() $\Delta $
is a finitely generated, free abelian subgroup of the multiplicative subgroup of the positive rational numbers.
$\Delta $
is a finitely generated, free abelian subgroup of the multiplicative subgroup of the positive rational numbers.
Proof. Recall that
![]() $G = \langle G_{\alpha }, g_{1}, \ldots , g_{n} \rangle $
. Lemma 5.1 implies that
$G = \langle G_{\alpha }, g_{1}, \ldots , g_{n} \rangle $
. Lemma 5.1 implies that
![]() $G_{\alpha }$
is contained in the kernel of the modular function. Thus
$G_{\alpha }$
is contained in the kernel of the modular function. Thus
![]() $\mathrm{im}(\Delta )$
is generated by
$\mathrm{im}(\Delta )$
is generated by
![]() $\Delta (g_{1}),\ldots ,\Delta (g_{n})$
. Note that
$\Delta (g_{1}),\ldots ,\Delta (g_{n})$
. Note that
 $|\alpha G_{\alpha g_{i}}|= |\alpha (g_{i}^{-1} G_{\alpha } g_{i})| =|(\alpha g_{i}^{-1}) G_{\alpha }|$
. So (5-2) gives us
$|\alpha G_{\alpha g_{i}}|= |\alpha (g_{i}^{-1} G_{\alpha } g_{i})| =|(\alpha g_{i}^{-1}) G_{\alpha }|$
. So (5-2) gives us
 $\Delta (g_{i}) = {|\alpha g_{i} G_{\alpha }|}/{|\alpha g_{i}^{-1} G_{\alpha }|}$
. The last statement follows since finitely generated subgroups of the multiplicative subgroup of positive rational numbers are free abelian.
$\Delta (g_{i}) = {|\alpha g_{i} G_{\alpha }|}/{|\alpha g_{i}^{-1} G_{\alpha }|}$
. The last statement follows since finitely generated subgroups of the multiplicative subgroup of positive rational numbers are free abelian.
5.2 Minimal degree and the modular function
The observations in the previous subsection relating the modular function and Cayley–Abels graphs allow us to get a lower bound on the minimal degree of a Cayley–Abels graph in terms of the values of the modular function.
Theorem 5.4. Let G be a noncompact, cgtdlc group. Let
![]() $H \leq \mathbb {Q}^{+}$
be the image of the modular function on G. Then every Cayley–Abels graph of G has degree at least min(A), where
$H \leq \mathbb {Q}^{+}$
be the image of the modular function on G. Then every Cayley–Abels graph of G has degree at least min(A), where
 $$ \begin{align*}A = \bigg\{\sum_{i=1}^{k}(p_{i}+q_{i}) \ \bigg| \ p_{1},\ldots,p_{k},q_{1},\ldots,q_{k} \in \mathbb{N}^{*}, \, \bigg \langle \frac{p_{1}}{q_{1}}, \ldots, \frac{p_{k}}{q_{k}} \bigg \rangle=H\bigg\}\subseteq \mathbb{N}^{*}.\end{align*} $$
$$ \begin{align*}A = \bigg\{\sum_{i=1}^{k}(p_{i}+q_{i}) \ \bigg| \ p_{1},\ldots,p_{k},q_{1},\ldots,q_{k} \in \mathbb{N}^{*}, \, \bigg \langle \frac{p_{1}}{q_{1}}, \ldots, \frac{p_{k}}{q_{k}} \bigg \rangle=H\bigg\}\subseteq \mathbb{N}^{*}.\end{align*} $$
In particular, if H is cyclic and generated by p/q, where p, q ∈ ℕ * are relatively prime, then md(G) ≥ p + q.
Proof. Let
![]() $\Gamma $
be a Cayley–Abels graph for G and let
$\Gamma $
be a Cayley–Abels graph for G and let
![]() $\alpha \in \mathrm V\Gamma $
. Think of
$\alpha \in \mathrm V\Gamma $
. Think of
![]() $\Gamma $
as a labelled digraph as in Section 5.1. The group G has finitely many orbits E
1, …, E
n
on its edges. By vertex-transitivity, we can take an edge
$\Gamma $
as a labelled digraph as in Section 5.1. The group G has finitely many orbits E
1, …, E
n
on its edges. By vertex-transitivity, we can take an edge
![]() $e_{i}=\{\alpha , \beta _{i}\}\in E_{i}$
and set
$e_{i}=\{\alpha , \beta _{i}\}\in E_{i}$
and set
![]() $p_{i}=|\,\beta _{i} G_{\alpha }|$
and
$p_{i}=|\,\beta _{i} G_{\alpha }|$
and
![]() $q_{i}=|\alpha G_{\,\beta _{i}}|$
. The label of the arc
$q_{i}=|\alpha G_{\,\beta _{i}}|$
. The label of the arc
![]() $(\alpha , \beta _{i})$
is
$(\alpha , \beta _{i})$
is
![]() $p_{i}/q_{i}$
. These numbers are independent of the choice of the representative
$p_{i}/q_{i}$
. These numbers are independent of the choice of the representative
![]() $e_{i}$
of
$e_{i}$
of
![]() $E_{i}$
. Suppose that
$E_{i}$
. Suppose that
![]() $g_{i}\in G$
is such that
$g_{i}\in G$
is such that
![]() $\alpha g_{i}=\beta _{i}$
. Set
$\alpha g_{i}=\beta _{i}$
. Set
 $\gamma _{i}=\alpha g_{i}^{-1}$
. Then
$\gamma _{i}=\alpha g_{i}^{-1}$
. Then
 $q_{i}=|\alpha G_{\,\beta _{i}}|=|(\alpha g_{i}^{-1})G_{\alpha }|=|\gamma _{i} G_{\alpha }|$
and the label of the arc
$q_{i}=|\alpha G_{\,\beta _{i}}|=|(\alpha g_{i}^{-1})G_{\alpha }|=|\gamma _{i} G_{\alpha }|$
and the label of the arc
![]() $(\alpha , \gamma _{i})$
is
$(\alpha , \gamma _{i})$
is
![]() $q_{i}/p_{i}$
. If
$q_{i}/p_{i}$
. If
![]() $p_{i}\neq q_{i}$
then the arcs
$p_{i}\neq q_{i}$
then the arcs
![]() $(\alpha , \beta _{i})$
and
$(\alpha , \beta _{i})$
and
![]() $(\alpha , \gamma _{i})$
have different labels and thus belong to different orbits of G. Therefore, the
$(\alpha , \gamma _{i})$
have different labels and thus belong to different orbits of G. Therefore, the
![]() $G_{\alpha }$
-orbits
$G_{\alpha }$
-orbits
![]() $\beta _{i} G_{\alpha }$
and
$\beta _{i} G_{\alpha }$
and
 $(\alpha g_{i}^{-1}) G_{\alpha }$
are distinct and disjoint and are both contained in
$(\alpha g_{i}^{-1}) G_{\alpha }$
are distinct and disjoint and are both contained in
![]() $\Gamma (\alpha )$
. The contribution of
$\Gamma (\alpha )$
. The contribution of
![]() $E_{i}$
to the degree of
$E_{i}$
to the degree of
![]() $\alpha $
is at least
$\alpha $
is at least
![]() $p_{i}+q_{i}$
. Hence, the degree of
$p_{i}+q_{i}$
. Hence, the degree of
![]() $\Gamma $
is at least equal to the sum of all
$\Gamma $
is at least equal to the sum of all
![]() $p_{i}+q_{i}$
with
$p_{i}+q_{i}$
with
![]() $p_{i}\neq q_{i}$
. Corollary 5.3 now says that
$p_{i}\neq q_{i}$
. Corollary 5.3 now says that
 $$ \begin{align*}H=\bigg\langle \frac{p_{1}}{q_{1}},\ldots, \frac{p_{n}}{q_{n}}\bigg\rangle\end{align*} $$
$$ \begin{align*}H=\bigg\langle \frac{p_{1}}{q_{1}},\ldots, \frac{p_{n}}{q_{n}}\bigg\rangle\end{align*} $$
and the result follows.
The lower bound provided in Theorem 5.4 is far away from being sharp in general. For a unimodular group the bound provided is
![]() $2$
but the minimal degree of a unimodular group can be arbitrarily large.
$2$
but the minimal degree of a unimodular group can be arbitrarily large.
Theorem 5.4 does not say anything about the minimal degrees of unimodular groups, such as the automorphism groups of regular or biregular trees. (A tree is said to be biregular, or more precisely
![]() $(d,d^{\prime })$
-biregular, if all the vertices in one part of the natural bipartition have degree d and all the vertices in the other part have degree
$(d,d^{\prime })$
-biregular, if all the vertices in one part of the natural bipartition have degree d and all the vertices in the other part have degree
![]() $d^{\prime }$
.) But Theorem 5.4 can be applied to the stabilizer of an end in a regular or biregular tree. Ends of graphs are defined in Section 4, but in the special case of trees the definition has a simpler form. Two rays
$d^{\prime }$
.) But Theorem 5.4 can be applied to the stabilizer of an end in a regular or biregular tree. Ends of graphs are defined in Section 4, but in the special case of trees the definition has a simpler form. Two rays
![]() $(\alpha _{0},\alpha _{1},\ldots )$
and
$(\alpha _{0},\alpha _{1},\ldots )$
and
![]() $(\,\beta _{0},\beta _{1},\ldots )$
in a tree T are said to be equivalent if and only if they have the same infinite tail, that is, there exist
$(\,\beta _{0},\beta _{1},\ldots )$
in a tree T are said to be equivalent if and only if they have the same infinite tail, that is, there exist
![]() $k,l \geq 0$
such that
$k,l \geq 0$
such that
![]() $(\alpha _{k},\alpha _{k+1},\alpha _{k+2},\ldots )=(\,\beta _{l},\beta _{l+1},\beta _{l+2},\ldots )$
. An end of a tree T is an equivalence class of rays. Given an end
$(\alpha _{k},\alpha _{k+1},\alpha _{k+2},\ldots )=(\,\beta _{l},\beta _{l+1},\beta _{l+2},\ldots )$
. An end of a tree T is an equivalence class of rays. Given an end
![]() $\omega $
of a tree, it is easy to show that for each vertex
$\omega $
of a tree, it is easy to show that for each vertex
![]() $\alpha $
in T there is a unique ray
$\alpha $
in T there is a unique ray
![]() $R_{\alpha }$
in
$R_{\alpha }$
in
![]() $\omega $
that has
$\omega $
that has
![]() $\alpha $
as its initial vertex. It is obvious that
$\alpha $
as its initial vertex. It is obvious that
![]() $\mathrm {Aut}(T)$
acts on the set of ends of T. If
$\mathrm {Aut}(T)$
acts on the set of ends of T. If
![]() $\omega $
is an end of T, then the stabilizer of the end
$\omega $
is an end of T, then the stabilizer of the end
![]() $\omega $
, the group
$\omega $
, the group
![]() $\mathrm{Aut}(T)_{\omega }$
, is a closed subgroup of
$\mathrm{Aut}(T)_{\omega }$
, is a closed subgroup of
![]() $\mathrm{Aut}(T)$
. Hence, if T is locally finite, the stabilizer in
$\mathrm{Aut}(T)$
. Hence, if T is locally finite, the stabilizer in
![]() $\mathrm{Aut}(T)$
of an end is a totally disconnected, locally compact group.
$\mathrm{Aut}(T)$
of an end is a totally disconnected, locally compact group.
Corollary 5.5.
-
(1) Let
 $T_{d}$
denote the d-regular tree and let
$T_{d}$
denote the d-regular tree and let
 $\omega $
be an end of
$\omega $
be an end of
 $T_{d}$
. Set
$T_{d}$
. Set
 $G=\mathrm{Aut}(T_{d})_{\omega }$
. Then
$G=\mathrm{Aut}(T_{d})_{\omega }$
. Then
 $\mathrm{md}(G)=d$
.
$\mathrm{md}(G)=d$
. -
(2) Let
 $T_{d,d^{\prime }}$
be a biregular tree for some distinct integers
$T_{d,d^{\prime }}$
be a biregular tree for some distinct integers
 $d, d^{\prime }\geq 2$
. Suppose that
$d, d^{\prime }\geq 2$
. Suppose that
 $\omega $
is an end of
$\omega $
is an end of
 $T_{d,d^{\prime }}$
and set
$T_{d,d^{\prime }}$
and set
 $G=\mathrm{Aut}(T_{d,d^{\prime }})_{\omega }$
. Then
$G=\mathrm{Aut}(T_{d,d^{\prime }})_{\omega }$
. Then
 $\mathrm{md}(G)= (d-1)(d^{\prime }-1)+1$
.
$\mathrm{md}(G)= (d-1)(d^{\prime }-1)+1$
. -
(3) Let
 $\mathrm{Aut}^{+}(T_{d})$
denote the index-
$\mathrm{Aut}^{+}(T_{d})$
denote the index-
 $2$
subgroup of
$2$
subgroup of
 $\mathrm{Aut}(T_{d})$
that leaves each part of the natural bipartition of
$\mathrm{Aut}(T_{d})$
that leaves each part of the natural bipartition of
 $\mathrm V T_{d}$
invariant. Suppose that
$\mathrm V T_{d}$
invariant. Suppose that
 $\omega $
is an end of
$\omega $
is an end of
 $T_{d}$
and set
$T_{d}$
and set
 $G=\mathrm{Aut}^{+}(T_{d})_{\omega }$
. Then
$G=\mathrm{Aut}^{+}(T_{d})_{\omega }$
. Then
 $\mathrm{md}(G)=(d-1)^{2}+1$
.
$\mathrm{md}(G)=(d-1)^{2}+1$
.
Proof. Clearly (3) is a special case of (2) with
![]() $d=d^{\prime }$
and (1) follows from (2) by looking at
$d=d^{\prime }$
and (1) follows from (2) by looking at
![]() $T_{d, 2}$
. It is left to prove (2).
$T_{d, 2}$
. It is left to prove (2).
Denote by
![]() $V_{1}$
one of the classes of the natural bipartition of
$V_{1}$
one of the classes of the natural bipartition of
![]() $T_{d,d^{\prime }}$
. Construct a new graph T with vertex set
$T_{d,d^{\prime }}$
. Construct a new graph T with vertex set
![]() $V_{1}$
and edge set
$V_{1}$
and edge set
![]() $\{\{\alpha ,\beta \}\mid d_{T_{d,d^{\prime }}}(\alpha , \beta )=2\mathrm{\ and\ } \beta \in R_{\alpha }\}$
. It is easy to see that this new graph is isomorphic to the
$\{\{\alpha ,\beta \}\mid d_{T_{d,d^{\prime }}}(\alpha , \beta )=2\mathrm{\ and\ } \beta \in R_{\alpha }\}$
. It is easy to see that this new graph is isomorphic to the
![]() $((d-1)(d^{\prime }-1)+1)$
-regular tree. The end
$((d-1)(d^{\prime }-1)+1)$
-regular tree. The end
![]() $\omega $
of
$\omega $
of
![]() $T_{d,d^{\prime }}$
corresponds to an end of T and G acts on T fixing that end. Clearly G acts vertex- and edge-transitively on T. So, T is a Cayley–Abels graph for G and
$T_{d,d^{\prime }}$
corresponds to an end of T and G acts on T fixing that end. Clearly G acts vertex- and edge-transitively on T. So, T is a Cayley–Abels graph for G and
![]() $\mathrm{md}(G)\leq (d-1)(d^{\prime }-1)+1$
.
$\mathrm{md}(G)\leq (d-1)(d^{\prime }-1)+1$
.
Let
![]() $\{\alpha , \beta \}$
be an edge in T such that
$\{\alpha , \beta \}$
be an edge in T such that
![]() $\beta \in R_{\alpha }$
. Suppose that
$\beta \in R_{\alpha }$
. Suppose that
![]() $g\in G$
and
$g\in G$
and
![]() $\alpha g=\beta $
. Then
$\alpha g=\beta $
. Then
 $$ \begin{align*}\Delta(g)=\frac{|\,\beta G_{\alpha}|}{|\alpha G_{\beta}|}=\frac{1}{(d-1)(d^{\prime}-1)}\end{align*} $$
$$ \begin{align*}\Delta(g)=\frac{|\,\beta G_{\alpha}|}{|\alpha G_{\beta}|}=\frac{1}{(d-1)(d^{\prime}-1)}\end{align*} $$
and by edge-transitivity this rational number generates the image of
![]() $\Delta $
. Proposition 5.3 and Theorem 5.4 say that
$\Delta $
. Proposition 5.3 and Theorem 5.4 say that
![]() $\mathrm{md}(G)\geq (d-1)(d^{\prime }-1)+1$
. We conclude that
$\mathrm{md}(G)\geq (d-1)(d^{\prime }-1)+1$
. We conclude that
![]() $\mathrm{md}(G)=(d-1)(d^{\prime }-1)+1$
.
$\mathrm{md}(G)=(d-1)(d^{\prime }-1)+1$
.
Example 5.6. Set
![]() $H=\mathrm{Aut}^{+}(T_{d})$
. We do not know the exact value of
$H=\mathrm{Aut}^{+}(T_{d})$
. We do not know the exact value of
![]() $\mathrm{md}(H)$
. But H acts transitively on the edge set of
$\mathrm{md}(H)$
. But H acts transitively on the edge set of
![]() $T_{d}$
and thus the line graph of
$T_{d}$
and thus the line graph of
![]() $T_{d}$
is a Cayley–Abels graph for H. (The line graph of a graph
$T_{d}$
is a Cayley–Abels graph for H. (The line graph of a graph
![]() $\Gamma $
has the set of edges in
$\Gamma $
has the set of edges in
![]() $\Gamma $
as a vertex set, and two vertices in the line graph, that is, edges in
$\Gamma $
as a vertex set, and two vertices in the line graph, that is, edges in
![]() $\Gamma $
, are adjacent in the line graph if and only if they have a common end vertex.) The degree of the line graph of
$\Gamma $
, are adjacent in the line graph if and only if they have a common end vertex.) The degree of the line graph of
![]() $T_{d}$
is
$T_{d}$
is
![]() $2d-2$
, and hence
$2d-2$
, and hence
![]() $\mathrm{md}(H)\leq 2d-2$
. When
$\mathrm{md}(H)\leq 2d-2$
. When
![]() $d\geq 3$
we see that
$d\geq 3$
we see that
![]() $\mathrm{md}(H)$
grows at most linearly with d and is strictly smaller than the minimal degree of the subgroup fixing an end, which grows quadratically with d.
$\mathrm{md}(H)$
grows at most linearly with d and is strictly smaller than the minimal degree of the subgroup fixing an end, which grows quadratically with d.
The line graph of
![]() $T_{d, d^{\prime }}$
is a Cayley–Abels graph for
$T_{d, d^{\prime }}$
is a Cayley–Abels graph for
![]() $H=\mathrm{Aut}(T_{d, d^{\prime }})$
. The degree of the line graph is
$H=\mathrm{Aut}(T_{d, d^{\prime }})$
. The degree of the line graph is
![]() $d+d^{\prime }-2$
, and hence
$d+d^{\prime }-2$
, and hence
![]() $\mathrm{md}(H)\leq d+d^{\prime }-2$
. If
$\mathrm{md}(H)\leq d+d^{\prime }-2$
. If
![]() $d, d^{\prime }\geq 3$
then
$d, d^{\prime }\geq 3$
then
![]() $\mathrm{md}(H)$
is strictly smaller than the minimal degree of the subgroup fixing an end.
$\mathrm{md}(H)$
is strictly smaller than the minimal degree of the subgroup fixing an end.
5.3 Digraphs and the modular function
One of the first applications of the modular function to the study of graphs and their automorphism groups was by Praeger in 1991 [Reference Praeger26]. (She does not use explicitly the term modular function but defines a function in terms of sizes of suborbits as in (5-1) in Lemma 5.1.)
Let
![]() $\vec {\mathbb {Z}}$
be the digraph with vertex set
$\vec {\mathbb {Z}}$
be the digraph with vertex set
![]() $\mathbb {Z}$
and arc set
$\mathbb {Z}$
and arc set
![]() $\{(i, i+1)\mid i\in \mathbb {Z}\}$
. Similarly, we define
$\{(i, i+1)\mid i\in \mathbb {Z}\}$
. Similarly, we define
![]() $\vec {\mathbb {Z}}^{n}$
as the digraph with vertex set
$\vec {\mathbb {Z}}^{n}$
as the digraph with vertex set
![]() $\mathbb {Z}^{n}$
, in which
$\mathbb {Z}^{n}$
, in which
![]() $((x_{1}, \ldots , x_{n}), (y_{1}, \ldots , y_{n}))$
is an arc if and only if there is
$((x_{1}, \ldots , x_{n}), (y_{1}, \ldots , y_{n}))$
is an arc if and only if there is
![]() $1 \leq j \leq n$
such that
$1 \leq j \leq n$
such that
![]() $y_{j}=x_{j}+1$
and
$y_{j}=x_{j}+1$
and
![]() $x_{i}=y_{i}$
for all
$x_{i}=y_{i}$
for all
![]() $i\neq j$
. A digraph is said to have Property Z if a surjective digraph morphism
$i\neq j$
. A digraph is said to have Property Z if a surjective digraph morphism
![]() $\Gamma \to \vec {\mathbb {Z}}$
exists. A fibre of a map is the preimage of a point.
$\Gamma \to \vec {\mathbb {Z}}$
exists. A fibre of a map is the preimage of a point.
Theorem 5.7 [Reference Praeger26]
Let
![]() $\Gamma $
be an infinite, connected, vertex- and arc-transitive digraph with finite but unequal in- and out-degrees. Then there exists a surjective graph morphism
$\Gamma $
be an infinite, connected, vertex- and arc-transitive digraph with finite but unequal in- and out-degrees. Then there exists a surjective graph morphism
 $\varphi :\Gamma \rightarrow \vec {\mathbb {Z}}$
, that is,
$\varphi :\Gamma \rightarrow \vec {\mathbb {Z}}$
, that is,
![]() $\Gamma $
has Property Z. The fibres of
$\Gamma $
has Property Z. The fibres of
![]() $\varphi $
are all infinite.
$\varphi $
are all infinite.
Note that, since
![]() $\vec {\mathbb {Z}}$
is vertex-transitive with in- and out-degree
$\vec {\mathbb {Z}}$
is vertex-transitive with in- and out-degree
![]() $1$
, a digraph morphism from a connected digraph to
$1$
, a digraph morphism from a connected digraph to
![]() $\vec {\mathbb {Z}}$
is uniquely determined by the image of one vertex and this image can be chosen arbitrarily.
$\vec {\mathbb {Z}}$
is uniquely determined by the image of one vertex and this image can be chosen arbitrarily.
Praeger’s theorem can be generalized to digraphs with more than one orbit on arcs. The proof resembles the proof of Praeger’s theorem found in Evans’s paper [Reference Evans10, Theorem 3.2].
Theorem 5.8. Let
![]() $\Gamma $
be a locally finite digraph. Let
$\Gamma $
be a locally finite digraph. Let
![]() $G\leq \mathrm{Aut}(\Gamma )$
be a closed subgroup acting vertex-transitively on
$G\leq \mathrm{Aut}(\Gamma )$
be a closed subgroup acting vertex-transitively on
![]() $\Gamma $
. Assume G is not unimodular and denote by
$\Gamma $
. Assume G is not unimodular and denote by
![]() $\Delta $
the modular function on G. Suppose that G has n orbits on the arcs of
$\Delta $
the modular function on G. Suppose that G has n orbits on the arcs of
![]() $\Gamma $
and that
$\Gamma $
and that
![]() $\mathrm{im}(\Delta )$
is a free abelian group of rank n. Then there exists a surjective digraph morphism
$\mathrm{im}(\Delta )$
is a free abelian group of rank n. Then there exists a surjective digraph morphism
 $\varphi : \Gamma \to \vec {\mathbb {Z}}^{n}$
with infinite fibres.
$\varphi : \Gamma \to \vec {\mathbb {Z}}^{n}$
with infinite fibres.
Proof. Fix a vertex
![]() $\alpha $
in
$\alpha $
in
![]() $\Gamma $
. By vertex-transitivity we can choose representatives
$\Gamma $
. By vertex-transitivity we can choose representatives
![]() $(\alpha , \beta _{1}), \ldots , (\alpha , \beta _{n})$
for the n orbits on the arcs of
$(\alpha , \beta _{1}), \ldots , (\alpha , \beta _{n})$
for the n orbits on the arcs of
![]() $\Gamma $
. Then we find elements
$\Gamma $
. Then we find elements
![]() $g_{i}\in G$
such that
$g_{i}\in G$
such that
![]() $\alpha g_{i}=\beta _{i}$
. Since
$\alpha g_{i}=\beta _{i}$
. Since
![]() $G=\langle G_{\alpha },g_{1}, \ldots ,g_{n} \rangle $
we see that
$G=\langle G_{\alpha },g_{1}, \ldots ,g_{n} \rangle $
we see that
![]() $\langle \Delta (g_{1}),\ldots ,\Delta (g_{n}) \rangle = \mathrm{im}(\Delta )\cong \mathbb {Z}^{n}$
and the Cayley digraph
$\langle \Delta (g_{1}),\ldots ,\Delta (g_{n}) \rangle = \mathrm{im}(\Delta )\cong \mathbb {Z}^{n}$
and the Cayley digraph
![]() $\Theta $
of
$\Theta $
of
![]() $\mathrm{im}(\Delta )$
with respect to this generating set is isomorphic to
$\mathrm{im}(\Delta )$
with respect to this generating set is isomorphic to
![]() $\vec {\mathbb {Z}}^{n}$
.
$\vec {\mathbb {Z}}^{n}$
.
For a vertex
![]() $\beta $
in
$\beta $
in
![]() $\Gamma $
find
$\Gamma $
find
![]() $g\in G$
such that
$g\in G$
such that
![]() $\alpha g=\beta $
and set
$\alpha g=\beta $
and set
![]() $\varphi (\,\beta )=\Delta (g)$
. By Lemma 5.1 the value of
$\varphi (\,\beta )=\Delta (g)$
. By Lemma 5.1 the value of
![]() $\varphi (\,\beta )$
is independent of the choice of g, so the map
$\varphi (\,\beta )$
is independent of the choice of g, so the map
![]() $\varphi \colon \mathrm V\Gamma \rightarrow \mathrm V\Theta $
is well defined.
$\varphi \colon \mathrm V\Gamma \rightarrow \mathrm V\Theta $
is well defined.
Let
![]() $(\,\beta , \gamma ) \in \mathrm A\Gamma $
. Find
$(\,\beta , \gamma ) \in \mathrm A\Gamma $
. Find
![]() $g\in G$
and
$g\in G$
and
![]() $1 \leq i \leq n$
such that
$1 \leq i \leq n$
such that
![]() $(\alpha , \beta _{i})g =(\,\beta , \gamma )$
. Then
$(\alpha , \beta _{i})g =(\,\beta , \gamma )$
. Then
![]() $\alpha g_{i}g=\gamma $
. Thus
$\alpha g_{i}g=\gamma $
. Thus
![]() $\varphi (\,\beta )=\Delta (g)$
and
$\varphi (\,\beta )=\Delta (g)$
and
![]() $\varphi (\gamma )=\Delta (g_{i}g)=\Delta (g_{i})\Delta (g)=\Delta (g)\Delta (g_{i})$
. The image under
$\varphi (\gamma )=\Delta (g_{i}g)=\Delta (g_{i})\Delta (g)=\Delta (g)\Delta (g_{i})$
. The image under
![]() $\varphi $
of the arc
$\varphi $
of the arc
![]() $(\,\beta , \gamma )$
is the pair
$(\,\beta , \gamma )$
is the pair
![]() $(\Delta (g), \Delta (g)\Delta (g_{i}))$
that is indeed an arc in
$(\Delta (g), \Delta (g)\Delta (g_{i}))$
that is indeed an arc in
![]() $\Theta $
. Hence,
$\Theta $
. Hence,
![]() $\varphi $
is a morphism of digraphs.
$\varphi $
is a morphism of digraphs.
Consider the digraph with vertex set
![]() $\mathrm V\Gamma $
and arc set
$\mathrm V\Gamma $
and arc set
![]() $(\alpha , \beta _{1})G$
. Set
$(\alpha , \beta _{1})G$
. Set
![]() $H=\langle G_{\alpha }, g_{1}\rangle $
. Let
$H=\langle G_{\alpha }, g_{1}\rangle $
. Let
![]() $\Gamma ^{\prime }$
be the component of this digraph that contains
$\Gamma ^{\prime }$
be the component of this digraph that contains
![]() $\alpha $
. The group H acts arc-transitively on
$\alpha $
. The group H acts arc-transitively on
![]() $\Gamma ^{\prime }$
, and
$\Gamma ^{\prime }$
, and
![]() $\varphi $
restricted to
$\varphi $
restricted to
![]() $\Gamma ^{\prime }$
gives a graph morphism whose image is isomorphic to
$\Gamma ^{\prime }$
gives a graph morphism whose image is isomorphic to
![]() $\vec {\mathbb {Z}}$
. By Theorem 5.7 and the explanation following it
$\vec {\mathbb {Z}}$
. By Theorem 5.7 and the explanation following it
![]() $\varphi $
has infinite fibers.
$\varphi $
has infinite fibers.
Corollary 5.9. Let
![]() $\Gamma $
be a digraph satisfying the conditions in Theorem 5.8. Then:
$\Gamma $
be a digraph satisfying the conditions in Theorem 5.8. Then:
-
(1) there exists a surjective digraph morphism
 $\varphi :\Gamma \rightarrow \vec {\mathbb {Z}}$
, that is to say,
$\varphi :\Gamma \rightarrow \vec {\mathbb {Z}}$
, that is to say,
 $\Gamma $
has Property Z; and
$\Gamma $
has Property Z; and -
(2)
 $\Gamma $
is bipartite.
$\Gamma $
is bipartite.
Proof. The map
 $\vec {\mathbb {Z}}^{n}\rightarrow \vec {\mathbb {Z}}; (x_{1}, \ldots , x_{n})\mapsto x_{1}+\cdots +x_{n}$
is clearly a surjective digraph morphism. The composition of this map with the digraph morphism
$\vec {\mathbb {Z}}^{n}\rightarrow \vec {\mathbb {Z}}; (x_{1}, \ldots , x_{n})\mapsto x_{1}+\cdots +x_{n}$
is clearly a surjective digraph morphism. The composition of this map with the digraph morphism
![]() $\varphi $
from Theorem 5.8 is a surjective digraph morphism
$\varphi $
from Theorem 5.8 is a surjective digraph morphism
![]() $\Gamma \to \vec {\mathbb {Z}}$
.
$\Gamma \to \vec {\mathbb {Z}}$
.
By the first part the digraph
![]() $\vec {\mathbb {Z}}$
is the image of
$\vec {\mathbb {Z}}$
is the image of
![]() $\Gamma $
under a surjective morphism. Since
$\Gamma $
under a surjective morphism. Since
![]() $\vec {\mathbb {Z}}$
is bipartite the digraph
$\vec {\mathbb {Z}}$
is bipartite the digraph
![]() $\Gamma $
must also be bipartite.
$\Gamma $
must also be bipartite.
Example 5.10. (1) Let
![]() $p,q$
be positive, coprime integers. Let T be the regular directed tree with in-degree
$p,q$
be positive, coprime integers. Let T be the regular directed tree with in-degree
![]() $2$
and out-degree
$2$
and out-degree
![]() $p+q$
. Colour its arcs red and blue such that each vertex has p red outgoing arcs, q blue outgoing arcs and one incoming arc of each colour. Clearly,
$p+q$
. Colour its arcs red and blue such that each vertex has p red outgoing arcs, q blue outgoing arcs and one incoming arc of each colour. Clearly,
![]() $\mathrm{Aut}(T)$
is vertex- and arc-transitive. Let
$\mathrm{Aut}(T)$
is vertex- and arc-transitive. Let
![]() $G\leq \mathrm{Aut}(T)$
be the subgroup that has the two colour classes as its arc orbits and let
$G\leq \mathrm{Aut}(T)$
be the subgroup that has the two colour classes as its arc orbits and let
![]() $\Delta $
denote the modular function on G. By Theorem 5.2,
$\Delta $
denote the modular function on G. By Theorem 5.2,
![]() $\mathrm{im}(\Delta )$
is generated by
$\mathrm{im}(\Delta )$
is generated by
![]() $\{p,q\}$
, and is therefore a free abelian group of rank
$\{p,q\}$
, and is therefore a free abelian group of rank
![]() $2$
. Thus, by Theorem 5.8, there is a surjective digraph morphism from T to
$2$
. Thus, by Theorem 5.8, there is a surjective digraph morphism from T to
![]() $\vec {\mathbb {Z}}^{2}$
with infinite fibres. Theorem 5.4 implies that the underlying undirected graph of T, the
$\vec {\mathbb {Z}}^{2}$
with infinite fibres. Theorem 5.4 implies that the underlying undirected graph of T, the
![]() $(p+q+2)$
-regular tree, is a minimal-degree Cayley–Abels graph for G.
$(p+q+2)$
-regular tree, is a minimal-degree Cayley–Abels graph for G.
(2) Let
![]() $T_{1},\ldots ,T_{n}$
be regular directed trees with in-degree
$T_{1},\ldots ,T_{n}$
be regular directed trees with in-degree
![]() $1$
and out-degrees
$1$
and out-degrees
![]() $d_{1},\ldots , d_{n}$
such that the
$d_{1},\ldots , d_{n}$
such that the
![]() $d_{i}$
are distinct prime numbers. Let
$d_{i}$
are distinct prime numbers. Let
![]() $\Gamma =T_{1}\square \cdots \square T_{n}$
be the Cartesian product, that is, the vertex set is
$\Gamma =T_{1}\square \cdots \square T_{n}$
be the Cartesian product, that is, the vertex set is
![]() $\mathrm V T_{1} \times \cdots \times \mathrm V T_{n}$
and
$\mathrm V T_{1} \times \cdots \times \mathrm V T_{n}$
and
![]() $((\alpha _{1},\ldots ,\alpha _{n}),(\,\beta _{1},\ldots ,\beta _{n}))$
is an arc if and only if there is i such that
$((\alpha _{1},\ldots ,\alpha _{n}),(\,\beta _{1},\ldots ,\beta _{n}))$
is an arc if and only if there is i such that
![]() $(\alpha _{i},\beta _{i})$
is an arc in
$(\alpha _{i},\beta _{i})$
is an arc in
![]() $T_{i}$
and
$T_{i}$
and
![]() $\alpha _{j} = \beta _{j}$
for all
$\alpha _{j} = \beta _{j}$
for all
![]() $j \neq i$
. In other words,
$j \neq i$
. In other words,
![]() $\Gamma$
is the
$\Gamma$
is the
![]() $1$
-skeleton of the cube complex
$1$
-skeleton of the cube complex
![]() $T_{1} \times \cdots \times T_{n}$
, remembering the directions on the factors. Let
$T_{1} \times \cdots \times T_{n}$
, remembering the directions on the factors. Let
![]() $G=\mathrm{Aut}(\Gamma )$
. It can be shown that
$G=\mathrm{Aut}(\Gamma )$
. It can be shown that
![]() $G = \mathrm{Aut}(T_{1})\times \cdots \times \mathrm{Aut}(T_{n})$
; this is a consequence of the fact that two adjacent arcs are ‘parallel to the same tree
$G = \mathrm{Aut}(T_{1})\times \cdots \times \mathrm{Aut}(T_{n})$
; this is a consequence of the fact that two adjacent arcs are ‘parallel to the same tree
![]() $T_{i}$
’ if and only if they are not sides of the same (undirected) square (see also [Reference Hammack, Imrich and Klavžar14, Corollary 6.12] for a more general version). It is easy to see that G has n orbits on the arcs of
$T_{i}$
’ if and only if they are not sides of the same (undirected) square (see also [Reference Hammack, Imrich and Klavžar14, Corollary 6.12] for a more general version). It is easy to see that G has n orbits on the arcs of
![]() $\Gamma $
. Further, if
$\Gamma $
. Further, if
![]() $\Delta $
denotes the modular function on G, then
$\Delta $
denotes the modular function on G, then
![]() $\mathrm{im}(\Delta )=\langle d_{1},\ldots ,d_{n}\rangle $
is a free abelian group of rank n (since the
$\mathrm{im}(\Delta )=\langle d_{1},\ldots ,d_{n}\rangle $
is a free abelian group of rank n (since the
![]() $d_{i}$
are distinct primes) and so there exists a surjective digraph morphism,
$d_{i}$
are distinct primes) and so there exists a surjective digraph morphism,
 $\varphi :\Gamma \to \vec {\mathbb {Z}}^{n}$
, with infinite fibres. Again, Theorem 5.4 shows that
$\varphi :\Gamma \to \vec {\mathbb {Z}}^{n}$
, with infinite fibres. Again, Theorem 5.4 shows that
![]() $\Gamma $
is a minimal-degree Cayley–Abels graph for G.
$\Gamma $
is a minimal-degree Cayley–Abels graph for G.
The following proposition can be seen as an addendum to Theorem 5.7.
Proposition 5.11. Let
![]() $\Gamma $
be a locally finite digraph and
$\Gamma $
be a locally finite digraph and
![]() $G\leq \mathrm {Aut}(\Gamma )$
a subgroup acting arc- and vertex-transitively on
$G\leq \mathrm {Aut}(\Gamma )$
a subgroup acting arc- and vertex-transitively on
![]() $\Gamma $
. If the in- and out-degrees of
$\Gamma $
. If the in- and out-degrees of
![]() $\Gamma $
are coprime then G is highly arc-transitive. Furthermore, the subdigraph induced by the set of descendants of any vertex is a tree.
$\Gamma $
are coprime then G is highly arc-transitive. Furthermore, the subdigraph induced by the set of descendants of any vertex is a tree.
Proof. We may assume that G is closed, since replacing G with its closure in
![]() $\mathrm {Aut}(\Gamma )$
does not change the orbits on vertices or s-arcs. Let q denote the in-degree of
$\mathrm {Aut}(\Gamma )$
does not change the orbits on vertices or s-arcs. Let q denote the in-degree of
![]() $\Gamma $
and let p denote the out-degree. Take vertices
$\Gamma $
and let p denote the out-degree. Take vertices
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
in
$\beta $
in
![]() $\Gamma $
such that
$\Gamma $
such that
![]() $(\alpha , \beta )$
is an arc. Choose some element
$(\alpha , \beta )$
is an arc. Choose some element
![]() $g\in G$
such that
$g\in G$
such that
![]() $\beta =\alpha g$
. The second formula for the modular function in Lemma 5.1 now says that
$\beta =\alpha g$
. The second formula for the modular function in Lemma 5.1 now says that
 $$ \begin{align*}\Delta(g)=\frac{|\,\beta G_{\alpha}|}{|\alpha G_{\beta}|} = \frac{p}{q}.\end{align*} $$
$$ \begin{align*}\Delta(g)=\frac{|\,\beta G_{\alpha}|}{|\alpha G_{\beta}|} = \frac{p}{q}.\end{align*} $$
Then
 $$ \begin{align*}\frac{|(\alpha g^{n})G_{\alpha}|}{|\alpha G_{\alpha g^{n}}|}=\Delta(g^{n})=\Delta(g)^{n}=\bigg(\frac{p}{q}\bigg)^{n}=\frac{p^{n}}{q^{n}}.\end{align*} $$
$$ \begin{align*}\frac{|(\alpha g^{n})G_{\alpha}|}{|\alpha G_{\alpha g^{n}}|}=\Delta(g^{n})=\Delta(g)^{n}=\bigg(\frac{p}{q}\bigg)^{n}=\frac{p^{n}}{q^{n}}.\end{align*} $$
Note that
![]() $(\alpha , \alpha g, \ldots , \alpha g^{n})$
is an n-arc in
$(\alpha , \alpha g, \ldots , \alpha g^{n})$
is an n-arc in
![]() $\Gamma $
. There are
$\Gamma $
. There are
![]() $p^{n}$
distinct n-arcs in
$p^{n}$
distinct n-arcs in
![]() $\Gamma $
that start at
$\Gamma $
that start at
![]() $\alpha $
, and each vertex in the orbit
$\alpha $
, and each vertex in the orbit
![]() $(\alpha g^{n})G_{\alpha }$
is the terminal vertex of such an arc. Thus
$(\alpha g^{n})G_{\alpha }$
is the terminal vertex of such an arc. Thus
![]() $|(\alpha g^{n})G_{\alpha }|\leq p^{n}$
. But since
$|(\alpha g^{n})G_{\alpha }|\leq p^{n}$
. But since
![]() $|(\alpha g^{n})G_{\alpha }|/|\alpha G_{\alpha g^{n}}|=p^{n}/q^{n}$
and p and q are coprime we see that
$|(\alpha g^{n})G_{\alpha }|/|\alpha G_{\alpha g^{n}}|=p^{n}/q^{n}$
and p and q are coprime we see that
![]() $|(\alpha g^{n})G_{\alpha }|=p^{n}$
and
$|(\alpha g^{n})G_{\alpha }|=p^{n}$
and
![]() $|\alpha G_{\alpha g^{n}}|=q^{n}$
.
$|\alpha G_{\alpha g^{n}}|=q^{n}$
.
If
![]() $\gamma $
is the terminal vertex of some n-arc starting at
$\gamma $
is the terminal vertex of some n-arc starting at
![]() $\alpha $
then the orbit of
$\alpha $
then the orbit of
![]() $\gamma $
under
$\gamma $
under
![]() $G_{\alpha }$
has precisely
$G_{\alpha }$
has precisely
![]() $p^{n}$
elements. The number of n-arcs starting at
$p^{n}$
elements. The number of n-arcs starting at
![]() $\alpha $
is
$\alpha $
is
![]() $p^{n}$
, and we see that
$p^{n}$
, and we see that
![]() $G_{\alpha }$
acts transitively on the set of n-arcs starting at
$G_{\alpha }$
acts transitively on the set of n-arcs starting at
![]() $\alpha $
. As G acts transitively on
$\alpha $
. As G acts transitively on
![]() $\mathrm V \Gamma $
we see that G acts transitively on the n-arcs in
$\mathrm V \Gamma $
we see that G acts transitively on the n-arcs in
![]() $\Gamma $
. Hence,
$\Gamma $
. Hence,
![]() $\Gamma $
is highly arc-transitive.
$\Gamma $
is highly arc-transitive.
Every arc in the subgraph induced by the set of descendants of
![]() $\alpha $
is contained in some n-arc starting at
$\alpha $
is contained in some n-arc starting at
![]() $\alpha $
. No two distinct n-arcs starting at
$\alpha $
. No two distinct n-arcs starting at
![]() $\alpha $
have a common terminal vertex. Thus the subgraph induced by the set of descendants of
$\alpha $
have a common terminal vertex. Thus the subgraph induced by the set of descendants of
![]() $\alpha $
is a tree.
$\alpha $
is a tree.
In [Reference Möller22] the scale function and tidy subgroups are analysed by using graph-theoretical concepts. A prominent role in this analysis is played by highly arc-transitive digraphs such that the subgraph induced by the set of descendants of a vertex is a tree. It is therefore not surprising that the above proposition can be interpreted as a result about tidy subgroups.
Corollary 5.12. Let G be a totally disconnected, locally compact group. Suppose that
![]() $g\in G$
and U is a compact, open subgroup of G such that
$g\in G$
and U is a compact, open subgroup of G such that
![]() $|U:U\cap g^{-1}Ug|$
and
$|U:U\cap g^{-1}Ug|$
and
![]() $|U:U\cap gUg^{-1}|$
are coprime. Then U is tidy for g and
$|U:U\cap gUg^{-1}|$
are coprime. Then U is tidy for g and
![]() $s(g)=|U:U\cap g^{-1}Ug|$
.
$s(g)=|U:U\cap g^{-1}Ug|$
.
Proof. We define a digraph
![]() $\Gamma $
such that the vertex set is the set of cosets
$\Gamma $
such that the vertex set is the set of cosets
![]() $G/U$
and the set of arcs is the G-orbit
$G/U$
and the set of arcs is the G-orbit
![]() $(\alpha , \beta )G$
where
$(\alpha , \beta )G$
where
![]() $\alpha =U$
and
$\alpha =U$
and
![]() $\beta =Ug$
. Note that
$\beta =Ug$
. Note that
![]() $G_{\alpha }=U$
. Then
$G_{\alpha }=U$
. Then
![]() $\Gamma $
is an arc- and vertex-transitive digraph. The out-degree is equal to
$\Gamma $
is an arc- and vertex-transitive digraph. The out-degree is equal to
![]() $p=|U:U\cap g^{-1}Ug|$
and the in-degree is equal to
$p=|U:U\cap g^{-1}Ug|$
and the in-degree is equal to
![]() $q=|U:U\cap gUg^{-1}|$
. Since the in- and out-degrees are coprime, by Proposition 5.11 the digraph
$q=|U:U\cap gUg^{-1}|$
. Since the in- and out-degrees are coprime, by Proposition 5.11 the digraph
![]() $\Gamma $
is highly arc-transitive and the subgraph induced by the set of descendants of a vertex is a tree. We also see that
$\Gamma $
is highly arc-transitive and the subgraph induced by the set of descendants of a vertex is a tree. We also see that
Now [Reference Möller22, Corollary 3.5] says precisely that U is tidy for g.
The following proposition is an n-dimensional version of Proposition 5.11 and can be proved in a similar way.
Proposition 5.13. Let
![]() $\Gamma $
be a connected, locally finite digraph. Let
$\Gamma $
be a connected, locally finite digraph. Let
![]() $G\leq \mathrm {Aut}(\Gamma )$
be a vertex-transitive subgroup with n orbits
$G\leq \mathrm {Aut}(\Gamma )$
be a vertex-transitive subgroup with n orbits
![]() $A_{1},\ldots ,A_{n}$
on the arcs of
$A_{1},\ldots ,A_{n}$
on the arcs of
![]() $\Gamma $
and denote by
$\Gamma $
and denote by
![]() $d_{1}^{-}, \ldots , d_{n}^{-}, d_{1}^{+}, \ldots , d_{n}^{+}$
the respective in- and out-degrees of these orbits at any given vertex. Let
$d_{1}^{-}, \ldots , d_{n}^{-}, d_{1}^{+}, \ldots , d_{n}^{+}$
the respective in- and out-degrees of these orbits at any given vertex. Let
![]() $f \colon \mathrm A\Gamma \to \{1,\ldots ,n\}$
be the unique map satisfying
$f \colon \mathrm A\Gamma \to \{1,\ldots ,n\}$
be the unique map satisfying
![]() $f(A_{i})=i$
and denote by
$f(A_{i})=i$
and denote by
![]() $f^{s}$
the induced map from the set of s-arcs of
$f^{s}$
the induced map from the set of s-arcs of
![]() $\Gamma $
to
$\Gamma $
to
![]() $\{1,\ldots ,n\}^{s}$
.
$\{1,\ldots ,n\}^{s}$
.
If each of the numbers
![]() $d_{1}^{-}, \ldots , d_{n}^{-}$
is coprime with each of the numbers
$d_{1}^{-}, \ldots , d_{n}^{-}$
is coprime with each of the numbers
![]() $d_{1}^{+}, \ldots , d_{n}^{+}$
, then G acts transitively on each fibre of
$d_{1}^{+}, \ldots , d_{n}^{+}$
, then G acts transitively on each fibre of
![]() $f^{s}$
.
$f^{s}$
.
6 Simple composition factors and the scale function
In this section we study the interplay between the structure of compact, open subgroups, the scale function and the minimal degree of a Cayley–Abels graph. In order to do so we must first prove a version of the Jordan–Hölder theorem for second countable, profinite groups and study the composition factors of compact open subgroups. For the reader not familiar with these terms it is enough to know that every compact subgroup of the automorphism group of a locally finite, connected graph is second countable and profinite.
6.1 The profinite Jordan–Hölder theorem
A composition series for a second countable, profinite group G is a countable descending subnormal series
consisting of closed subgroups such that
![]() $\bigcap _{i \geq 0} G_{i} = \{1\}$
and such that each composition factor
$\bigcap _{i \geq 0} G_{i} = \{1\}$
and such that each composition factor
![]() $G_{i-1}/G_{i}$
is simple. The number of times that a composition factor appears, up to isomorphism, is called its multiplicity. The multiplicity can be finite or countably infinite. It is well known that every profinite group has a neighbourhood basis consisting of open, normal subgroups. It is also well known that closed subgroups and Hausdorff quotients of profinite groups are again profinite. These two facts together imply that the
$G_{i-1}/G_{i}$
is simple. The number of times that a composition factor appears, up to isomorphism, is called its multiplicity. The multiplicity can be finite or countably infinite. It is well known that every profinite group has a neighbourhood basis consisting of open, normal subgroups. It is also well known that closed subgroups and Hausdorff quotients of profinite groups are again profinite. These two facts together imply that the
![]() $G_{i}$
are open subgroups of G and the composition factors are finite. By [Reference Wilson39, Lemma 0.3.1(h)] the
$G_{i}$
are open subgroups of G and the composition factors are finite. By [Reference Wilson39, Lemma 0.3.1(h)] the
![]() $G_{i}$
form a neighbourhood basis of the identity.
$G_{i}$
form a neighbourhood basis of the identity.
For finite groups, composition series and composition factors are intimately tied with the classical Jordan–Hölder theorem. An analogue of this theorem holds for profinite groups. This is well known to experts, but due to the lack of a suitable reference we give a proof here.
Remark 6.1. The only published mention we found of the Jordan–Hölder theorem for profinite groups was [Reference Klopsch and Vannacci18, Section 2.2], but without proof. The authors are grateful to Benjamin Klopsch for pointing out to us the argument presented here and to Colin Reid for some consultation concerning the theorem. For a slightly different proof, see his mathoverflow post [Reference Reid27].
A refinement of a subnormal series is a series that contains each subgroup of the original series. In particular, the series
![]() $G \triangleright \{1\}$
and
$G \triangleright \{1\}$
and
![]() $G \triangleright G \triangleright \{1\}$
are refinements of each other.
$G \triangleright G \triangleright \{1\}$
are refinements of each other.
Theorem 6.2 (Jordan–Hölder theorem for profinite groups)
Let G be a profinite group.
-
(1) Every descending subnormal series of G can be refined into a composition series. In particular, G has a composition series.
-
(2) If G is second countable, then any two composition series have, up to isomorphism and permutation, the same composition factors appearing with the same (finite or countably infinite) multiplicity.
Proof. The first part can be proven verbatim as in the finite case, together with the classical fact that G has a neighbourhood basis of the identity consisting of open, normal subgroups.
For the second part, let
![]() $G=G_{0} \triangleright G_{1} \triangleright G_{2} \triangleright \cdots $
and
$G=G_{0} \triangleright G_{1} \triangleright G_{2} \triangleright \cdots $
and
![]() $G=H_{0} \triangleright H_{1} \triangleright H_{2} \triangleright \cdots $
be two composition series for G. Let A be a finite simple group. Let
$G=H_{0} \triangleright H_{1} \triangleright H_{2} \triangleright \cdots $
be two composition series for G. Let A be a finite simple group. Let
![]() $n_{1}, n_{2} \in \mathbb {N} \cup \{\infty \}$
be the multiplicities of A in the first and the second composition series, respectively. By symmetry, it is enough to show that
$n_{1}, n_{2} \in \mathbb {N} \cup \{\infty \}$
be the multiplicities of A in the first and the second composition series, respectively. By symmetry, it is enough to show that
![]() $n_{2} \geq n_{1}$
. Let
$n_{2} \geq n_{1}$
. Let
![]() $n \in \mathbb {N}$
with
$n \in \mathbb {N}$
with
![]() $n \leq n_{1}$
. Choose
$n \leq n_{1}$
. Choose
![]() $k \geq 0$
such that A appears at least n times as a quotient in the series
$k \geq 0$
such that A appears at least n times as a quotient in the series
![]() $G_{0} \triangleright \cdots \triangleright G_{k}$
. Recall that since
$G_{0} \triangleright \cdots \triangleright G_{k}$
. Recall that since
![]() $G_{k}$
is open, it has finite index in G, so it has finitely many G-conjugates and
$G_{k}$
is open, it has finite index in G, so it has finitely many G-conjugates and
 $N= \bigcap _{g \in G} g^{-1}G_{k} g$
is an open, normal subgroup of G. Now recall that the
$N= \bigcap _{g \in G} g^{-1}G_{k} g$
is an open, normal subgroup of G. Now recall that the
![]() $H_{i}$
form a neighbourhood basis of the identity, so there exists
$H_{i}$
form a neighbourhood basis of the identity, so there exists
![]() $\ell \geq 1$
such that
$\ell \geq 1$
such that
![]() $H_{\ell } \leq N$
. Now setting
$H_{\ell } \leq N$
. Now setting
 $N^{\prime } = \bigcap _{g \in G} g^{-1}H_{\ell } g$
, we get two finite subnormal series:
$N^{\prime } = \bigcap _{g \in G} g^{-1}H_{\ell } g$
, we get two finite subnormal series:
 $$ \begin{align*} G &= G_{0} \triangleright G_{1} \triangleright G_{2} \triangleright \cdots \triangleright G_{k} \triangleright N \triangleright H_{1} \cap N \triangleright \cdots \triangleright H_{\ell} \cap N = H_{\ell} \triangleright N^{\prime}, \\ G &= H_{0} \triangleright H_{1} \triangleright H_{2} \triangleright \cdots \triangleright H_{\ell} \triangleright N^{\prime}. \end{align*} $$
$$ \begin{align*} G &= G_{0} \triangleright G_{1} \triangleright G_{2} \triangleright \cdots \triangleright G_{k} \triangleright N \triangleright H_{1} \cap N \triangleright \cdots \triangleright H_{\ell} \cap N = H_{\ell} \triangleright N^{\prime}, \\ G &= H_{0} \triangleright H_{1} \triangleright H_{2} \triangleright \cdots \triangleright H_{\ell} \triangleright N^{\prime}. \end{align*} $$
We can refine those subnormal series so that they have simple subquotients. Let
![]() $n^{\prime }$
and
$n^{\prime }$
and
![]() $n^{\prime \prime }$
be the multiplicities of A in a composition series for the finite groups
$n^{\prime \prime }$
be the multiplicities of A in a composition series for the finite groups
![]() $G/N^{\prime }$
and
$G/N^{\prime }$
and
![]() $H_{\ell }/N^{\prime }$
, respectively. By the Jordan–Hölder theorem for finite groups and the third isomorphism theorem, A has to appear
$H_{\ell }/N^{\prime }$
, respectively. By the Jordan–Hölder theorem for finite groups and the third isomorphism theorem, A has to appear
![]() $n^{\prime }$
times as a quotient in the refinement of
$n^{\prime }$
times as a quotient in the refinement of
![]() $G = H_{0} \triangleright H_{1} \triangleright H_{2} \triangleright \cdots \triangleright H_{\ell } \triangleright N^{\prime }$
and
$G = H_{0} \triangleright H_{1} \triangleright H_{2} \triangleright \cdots \triangleright H_{\ell } \triangleright N^{\prime }$
and
![]() $n^{\prime \prime }$
times in the refinement of
$n^{\prime \prime }$
times in the refinement of
![]() $H_{\ell } \triangleright N^{\prime }$
. But note that
$H_{\ell } \triangleright N^{\prime }$
. But note that
![]() $n_{2} \geq n^{\prime }-n^{\prime \prime } \geq n$
. Since
$n_{2} \geq n^{\prime }-n^{\prime \prime } \geq n$
. Since
![]() $n \leq n_{1}$
was arbitrary, we are done.
$n \leq n_{1}$
was arbitrary, we are done.
By the above theorem the following concept is well defined.
Definition 6.3. Let G be a second countable, profinite group. A finite, simple group is a composition factor of G with multiplicity
![]() $n \in \mathbb {N} \cup \{\infty \}$
if it is a composition factor with multiplicity n in one (and hence every) composition series of G.
$n \in \mathbb {N} \cup \{\infty \}$
if it is a composition factor with multiplicity n in one (and hence every) composition series of G.
6.2 The local simple content
Let G be a totally disconnected, locally compact group. We are interested in the simple groups that appear as composition factors of every open subgroup of G. The following definition is inspired by Glöckner’s concept of the local prime content; see [Reference Glöckner12], and the work of Caprace et al. in [Reference Caprace, Reid and Willis8].
Definition 6.4. The local simple content of a second countable, totally disconnected, locally compact group G is the set of finite, simple groups (up to isomorphism) that are composition factors of every compact, open subgroup of G.
The following lemma allows us to detect the local simple content by only looking at one composition series of one compact, open subgroup.
Lemma 6.5. Let A be a finite simple group. Let G be a second countable, totally disconnected, locally compact group. The following assertions are equivalent.
-
(1) The group A is in the local simple content of G.
-
(2) There exists a compact, open subgroup
 $U \leq G$
such that A is a composition factor with infinite multiplicity in U.
$U \leq G$
such that A is a composition factor with infinite multiplicity in U. -
(3) For every compact open subgroup
 $U \leq G$
, the group A is a composition factor with infinite multiplicity in U.
$U \leq G$
, the group A is a composition factor with infinite multiplicity in U.
Proof. First we prove that (1) implies (3). Assume that A is in the local simple content of G. Let U be a compact open subgroup of G and let
![]() $U = U_{0} \triangleright U_{1} \triangleright \cdots $
be a composition series for U. Then, for every
$U = U_{0} \triangleright U_{1} \triangleright \cdots $
be a composition series for U. Then, for every
![]() $k \geq 0$
, the series
$k \geq 0$
, the series
![]() $U_{k} \triangleright U_{k+1} \triangleright U_{k+2} \triangleright \cdots $
is a composition series for
$U_{k} \triangleright U_{k+1} \triangleright U_{k+2} \triangleright \cdots $
is a composition series for
![]() $U_{k}$
and A has to appear as composition factor. Consequently, A appears as composition factor of U infinitely often.
$U_{k}$
and A has to appear as composition factor. Consequently, A appears as composition factor of U infinitely often.
It is obvious that (3) implies (2).
To show that (2) implies (1), assume that U is a compact, open subgroup of G and
![]() $U = U_{0} \triangleright U_{1} \triangleright \cdots $
is a composition series for U such that A appears as composition factor infinitely often. Let V be a compact open subgroup of G and
$U = U_{0} \triangleright U_{1} \triangleright \cdots $
is a composition series for U such that A appears as composition factor infinitely often. Let V be a compact open subgroup of G and
![]() $V=V_{0} \triangleright V_{2} \triangleright \cdots $
be a composition series for V. Since the
$V=V_{0} \triangleright V_{2} \triangleright \cdots $
be a composition series for V. Since the
![]() $V_{i}$
form a neighbourhood basis of the identity, there exists
$V_{i}$
form a neighbourhood basis of the identity, there exists
![]() $m_{0} \geq 1$
with
$m_{0} \geq 1$
with
![]() $V_{m_{0}} \leq U_{0}$
. Now the series
$V_{m_{0}} \leq U_{0}$
. Now the series
is a new composition series for V. By the Jordan–Hölder theorem for profinite groups, it has the same composition factors as the original series for V. But the
![]() $U_{i}$
form a neighbourhood basis of the identity, so for large n the equality
$U_{i}$
form a neighbourhood basis of the identity, so for large n the equality
![]() $V_{m_{0}} \cap U_{n} = U_{n}$
holds. Since A appears as quotient of the subnormal series
$V_{m_{0}} \cap U_{n} = U_{n}$
holds. Since A appears as quotient of the subnormal series
![]() $U_{n} \triangleright U_{n+1} \triangleright \ldots ,$
we see that A is a composition factor of V.
$U_{n} \triangleright U_{n+1} \triangleright \ldots ,$
we see that A is a composition factor of V.
The following considerations rely heavily on the proof of [Reference Caprace, Reid and Willis8, Proposition 4.6]. A subquotient of a group H is a quotient of a subgroup of H. Let G be a cgtdlc group and let
![]() $U \leq G$
be a compact, open subgroup. Let
$U \leq G$
be a compact, open subgroup. Let
![]() $\Gamma $
be a Cayley–Abels graph for G such that
$\Gamma $
be a Cayley–Abels graph for G such that
![]() $U=G_{\alpha }$
for some vertex
$U=G_{\alpha }$
for some vertex
![]() $\alpha \in \mathrm V\Gamma $
. We can use
$\alpha \in \mathrm V\Gamma $
. We can use
![]() $\Gamma $
to produce a subnormal series for U. Namely, take subgraphs
$\Gamma $
to produce a subnormal series for U. Namely, take subgraphs
![]() $\Gamma _{0} \subseteq \Gamma _{1} \subseteq \Gamma _{2} \subseteq \cdots $
of
$\Gamma _{0} \subseteq \Gamma _{1} \subseteq \Gamma _{2} \subseteq \cdots $
of
![]() $\Gamma $
as follows.
$\Gamma $
as follows.
-
(1) The subgraph
 $\Gamma _{0}$
consists only of the vertex
$\Gamma _{0}$
consists only of the vertex
 $\alpha $
.
$\alpha $
. -
(2) For
 $i \geq 1$
, choose a vertex
$i \geq 1$
, choose a vertex
 $\alpha _{i} \in \mathrm V\Gamma _{i-1}$
satisfying the following conditions.
$\alpha _{i} \in \mathrm V\Gamma _{i-1}$
satisfying the following conditions.-
• The set of neighbours of
 $\alpha _{i}$
is not contained in
$\alpha _{i}$
is not contained in
 $\mathrm V\Gamma _{i-1}$
.
$\mathrm V\Gamma _{i-1}$
. -
•
 $\alpha _{i}$
is a vertex in
$\alpha _{i}$
is a vertex in
 $\Gamma _{i-1}$
with the above property that is closest to
$\Gamma _{i-1}$
with the above property that is closest to
 $\alpha $
.
$\alpha $
.
-
-
(3) Now define
 $\Gamma _{i}$
to be the subgraph of
$\Gamma _{i}$
to be the subgraph of
 $\Gamma $
induced by
$\Gamma $
induced by
 $\Gamma _{i-1}$
and
$\Gamma _{i-1}$
and
 $\Gamma (\alpha _{i})$
.
$\Gamma (\alpha _{i})$
.
Note that the second condition on
![]() $\alpha _{i}$
ensures that
$\alpha _{i}$
ensures that
![]() $\bigcup _{i\geq 0}\mathrm V\Gamma _{i}=\mathrm V\Gamma $
.
$\bigcup _{i\geq 0}\mathrm V\Gamma _{i}=\mathrm V\Gamma $
.
Write
![]() $G_{i} = G_{(\Gamma _{i})}$
. The sequence
$G_{i} = G_{(\Gamma _{i})}$
. The sequence
is a descending subnormal series for U. Note that there could be repetitions in the series. The condition
![]() $\bigcup _{i \geq 0} \mathrm V\Gamma _{i} = \mathrm V\Gamma $
implies that
$\bigcup _{i \geq 0} \mathrm V\Gamma _{i} = \mathrm V\Gamma $
implies that
![]() $\bigcap _{i \geq 0} G_{i} = K$
, where K is the kernel of the action of G on
$\bigcap _{i \geq 0} G_{i} = K$
, where K is the kernel of the action of G on
![]() $\Gamma $
. Note that
$\Gamma $
. Note that
![]() $G_{i-1}$
permutes those neighbours of
$G_{i-1}$
permutes those neighbours of
![]() $\alpha _{i}$
that are not already contained in
$\alpha _{i}$
that are not already contained in
![]() $\Gamma _{i-1}$
and the kernel of this action is
$\Gamma _{i-1}$
and the kernel of this action is
![]() $G_{i}$
, so for
$G_{i}$
, so for
![]() $i \geq 2$
the group
$i \geq 2$
the group
![]() $G_{i-1}/G_{i}$
is a subgroup of the symmetric group
$G_{i-1}/G_{i}$
is a subgroup of the symmetric group
![]() $S_{d-1}$
. More precisely, let
$S_{d-1}$
. More precisely, let
![]() $\beta _{i} \in \mathrm V\Gamma _{i-1}$
be a neighbour of
$\beta _{i} \in \mathrm V\Gamma _{i-1}$
be a neighbour of
![]() $\alpha _{i}$
; then
$\alpha _{i}$
; then
![]() $G_{i-1}/G_{i}$
is a subquotient of the stabilizer of
$G_{i-1}/G_{i}$
is a subquotient of the stabilizer of
![]() $\beta _{i}$
in the local action of G on
$\beta _{i}$
in the local action of G on
![]() $\Gamma $
. Quotienting every subgroup in the given subnormal series for U by K gives a subnormal series for
$\Gamma $
. Quotienting every subgroup in the given subnormal series for U by K gives a subnormal series for
![]() $U/K$
, which by the Jordan–Hölder theorem for profinite groups can be refined into a composition series for
$U/K$
, which by the Jordan–Hölder theorem for profinite groups can be refined into a composition series for
![]() $U/K$
. This provides, together with Lemma 6.5, a proof of the following theorem.
$U/K$
. This provides, together with Lemma 6.5, a proof of the following theorem.
Theorem 6.6 (see [Reference Caprace, Reid and Willis8, Proposition 4.6])
Let G be a cgtdlc group and let
![]() $\Gamma $
be a Cayley–Abels graph for G of degree d. Define K as the kernel of the action of G on
$\Gamma $
be a Cayley–Abels graph for G of degree d. Define K as the kernel of the action of G on
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $L \leq S_{d}$
be the local action of G on
$L \leq S_{d}$
be the local action of G on
![]() $\Gamma $
.
$\Gamma $
.
Suppose that A is an element of the local simple content of
![]() $G/K$
. Then A is a subquotient of a point stabilizer in L, that is, there exist
$G/K$
. Then A is a subquotient of a point stabilizer in L, that is, there exist
![]() $i \in \{1,\ldots ,d\}$
and
$i \in \{1,\ldots ,d\}$
and
![]() $N \triangleleft H \leq L_{i}$
with
$N \triangleleft H \leq L_{i}$
with
![]() $H/N \cong A$
. In particular,
$H/N \cong A$
. In particular,
![]() $H/N$
is a subquotient of
$H/N$
is a subquotient of
![]() $S_{d-1}$
.
$S_{d-1}$
.
We apply this theorem to the automorphism group of a regular tree.
Corollary 6.7. Let
![]() $d \geq 2$
be a positive integer and assume
$d \geq 2$
be a positive integer and assume
![]() $d \neq 5$
. Let
$d \neq 5$
. Let
![]() $T_{d}$
be the d-regular tree. Then
$T_{d}$
be the d-regular tree. Then
![]() $\mathrm{md}(\mathrm {Aut}(T_{d}))=d$
and
$\mathrm{md}(\mathrm {Aut}(T_{d}))=d$
and
![]() $T_{d}$
is a minimal Cayley–Abels graph for
$T_{d}$
is a minimal Cayley–Abels graph for
![]() $\mathrm {Aut}(T_{d})$
.
$\mathrm {Aut}(T_{d})$
.
Proof. First it is clear that
![]() $T_{d}$
is a Cayley–Abels graph for
$T_{d}$
is a Cayley–Abels graph for
![]() $\mathrm{Aut}(T_{d})$
.
$\mathrm{Aut}(T_{d})$
.
For
![]() $d=2$
we refer to Theorem 4.1.
$d=2$
we refer to Theorem 4.1.
Now let
![]() $d \geq 3$
, but
$d \geq 3$
, but
![]() $d \neq 5$
. We can use the method described before Theorem 6.6 with
$d \neq 5$
. We can use the method described before Theorem 6.6 with
![]() $\Gamma = T_{d}$
to obtain a subnormal series for a vertex stabilizer. The quotients of this subnormal series are all, except the first, isomorphic to
$\Gamma = T_{d}$
to obtain a subnormal series for a vertex stabilizer. The quotients of this subnormal series are all, except the first, isomorphic to
![]() $S_{d-1}$
, which has the composition factors
$S_{d-1}$
, which has the composition factors
![]() $A_{d-1}$
and
$A_{d-1}$
and
![]() $\mathbb {Z}/2\mathbb {Z}$
. By Lemma 6.5 the local simple content of
$\mathbb {Z}/2\mathbb {Z}$
. By Lemma 6.5 the local simple content of
![]() $\mathrm{Aut}(T_{d})$
consists of
$\mathrm{Aut}(T_{d})$
consists of
![]() $A_{d-1}$
and
$A_{d-1}$
and
![]() $\mathbb {Z}/2\mathbb {Z}$
. Recall, or prove as an exercise, that
$\mathbb {Z}/2\mathbb {Z}$
. Recall, or prove as an exercise, that
![]() $d-1$
is the minimal number k such that
$d-1$
is the minimal number k such that
![]() $A_{d-1}$
is a subquotient of
$A_{d-1}$
is a subquotient of
![]() $S_{k}$
. Recall as well, or prove using facts from Section 7, that
$S_{k}$
. Recall as well, or prove using facts from Section 7, that
![]() $\mathrm{Aut}(T_{d})$
does not have any nontrivial compact, normal subgroups. Now Theorem 6.6 concludes the proof.
$\mathrm{Aut}(T_{d})$
does not have any nontrivial compact, normal subgroups. Now Theorem 6.6 concludes the proof.
This argument fails for the
![]() $5$
-regular tree, because
$5$
-regular tree, because
![]() $A_{4}$
is not simple. In fact
$A_{4}$
is not simple. In fact
![]() $\mathrm {Aut}(T_{4})$
and
$\mathrm {Aut}(T_{4})$
and
![]() $\mathrm {Aut}(T_{5})$
have the same local simple content. The result also holds for
$\mathrm {Aut}(T_{5})$
have the same local simple content. The result also holds for
![]() $\mathrm {Aut}(T_{5})$
, but the proof turned out to be surprisingly tricky and is given in Section 7. The proof above also provides an alternative proof for part (1) in Corollary 5.5 for
$\mathrm {Aut}(T_{5})$
, but the proof turned out to be surprisingly tricky and is given in Section 7. The proof above also provides an alternative proof for part (1) in Corollary 5.5 for
![]() $d \neq 5$
.
$d \neq 5$
.
Remark 6.8. In Theorem 6.6 we cannot replace ‘subquotient’ by ‘subgroup’. The reason is simply that a simple subquotient of a finite, simple group might not be isomorphic to a subgroup. Concrete examples can be found, for example, among sporadic simple groups. The McLaughlin group
![]() $\mathrm {McL}$
is a subquotient of the Conway group
$\mathrm {McL}$
is a subquotient of the Conway group
![]() $\mathrm {Co_{3}}$
. In [Reference Mazurov20] Mazurov gives for each sporadic finite simple group the minimal number of points on which it admits a nontrivial action. The group
$\mathrm {Co_{3}}$
. In [Reference Mazurov20] Mazurov gives for each sporadic finite simple group the minimal number of points on which it admits a nontrivial action. The group
![]() $\mathrm {Co_{3}}$
acts nontrivially on a set with 270 points, but
$\mathrm {Co_{3}}$
acts nontrivially on a set with 270 points, but
![]() $\mathrm {McL}$
cannot act nontrivially on a set with fewer than 275 points. Then
$\mathrm {McL}$
cannot act nontrivially on a set with fewer than 275 points. Then
![]() $\mathrm {McL}$
also cannot be a subgroup of
$\mathrm {McL}$
also cannot be a subgroup of
![]() $\mathrm {Co_{3}}$
.
$\mathrm {Co_{3}}$
.
To turn this into an actual counterexample to Theorem 6.6 with ‘subgroups’ instead of ‘subquotients’, let
![]() $N \triangleleft C \leq S_{270}$
satisfy
$N \triangleleft C \leq S_{270}$
satisfy
![]() $C/N \cong \mathrm {McL}$
. It suffices to find a graph
$C/N \cong \mathrm {McL}$
. It suffices to find a graph
![]() $\Gamma $
of degree
$\Gamma $
of degree
![]() $271$
and a vertex-transitive subgroup
$271$
and a vertex-transitive subgroup
![]() $G \leq \mathrm{Aut}(\Gamma )$
such that
$G \leq \mathrm{Aut}(\Gamma )$
such that
![]() $G_{i-1}/G_{i} \cong C$
for infinitely many i. Then
$G_{i-1}/G_{i} \cong C$
for infinitely many i. Then
![]() $\mathrm {McL}$
is contained in the local simple content of G, but it is not contained in
$\mathrm {McL}$
is contained in the local simple content of G, but it is not contained in
![]() $S_{270}$
.
$S_{270}$
.
For a concrete example, we can use Burger–Mozes universal groups
![]() $U(F)$
acting on trees. The interested reader can find the definition and basic properties in [Reference Garrido, Glasner, Tornier, Caprace and Monod11]. It is not hard to see that the local simple content of
$U(F)$
acting on trees. The interested reader can find the definition and basic properties in [Reference Garrido, Glasner, Tornier, Caprace and Monod11]. It is not hard to see that the local simple content of
![]() $U(F)$
is the set of all composition factors of point stabilizers in F. Taking
$U(F)$
is the set of all composition factors of point stabilizers in F. Taking
![]() $F \cong C \times \{1\}$
, by the above
$F \cong C \times \{1\}$
, by the above
![]() $T_{271}$
is a
$T_{271}$
is a
![]() $271$
-regular Cayley–Abels graph for
$271$
-regular Cayley–Abels graph for
![]() $U(F)$
.
$U(F)$
.
6.3 The local prime content and the scale function
In this section we apply Theorem 6.6 to other invariants.
Definition 6.9 [Reference Glöckner12, Definition 6.1]
The local prime content of a totally disconnected, locally compact group G is the set of all prime numbers p such that every compact, open subgroup U of G contains a compact open subgroup
![]() $V \leq U$
with
$V \leq U$
with
![]() $p \mid |U:V|$
.
$p \mid |U:V|$
.
The following lemma gives the connection between the local prime content and the local simple content. If G is not second countable, we do not know whether 6.2(2) still holds (see [Reference Reid27]), so in the definition of composition factors, the ‘and hence every’ part needs to be left out. This subtlety is, however, not relevant for us.
Lemma 6.10. Let G be a totally disconnected, locally compact group. Then the local prime content of G contains the set of all prime numbers dividing the order of an element of the local simple content.
Equality holds if, for every compact open subgroup
![]() $U \leq G$
, every prime number in the local prime content divides the order of at most finitely many composition factors of U (without counting multiplicities). In particular, this is true if G acts faithfully on a Cayley–Abels graph.
$U \leq G$
, every prime number in the local prime content divides the order of at most finitely many composition factors of U (without counting multiplicities). In particular, this is true if G acts faithfully on a Cayley–Abels graph.
Proof. Assume that p divides the order of a finite, simple group A that is in the local simple content of G. Let U be a compact, open subgroup. Let
![]() $U = G_{0} \triangleright G_{1} \triangleright \cdots $
be a composition series of U and let
$U = G_{0} \triangleright G_{1} \triangleright \cdots $
be a composition series of U and let
![]() $n \geq 1$
be such that
$n \geq 1$
be such that
![]() $G_{n}/G_{n+1} = A$
. Then p divides the index
$G_{n}/G_{n+1} = A$
. Then p divides the index
![]() $|U:G_{n+1}|$
.
$|U:G_{n+1}|$
.
For the other direction, let p be in the local prime content. Let
![]() $U \leq G$
be a compact, open subgroup. There exist compact, open subgroups
$U \leq G$
be a compact, open subgroup. There exist compact, open subgroups
![]() $U = V_{0} \geq V_{1} \geq V_{2} \geq \cdots $
such that p divides the index
$U = V_{0} \geq V_{1} \geq V_{2} \geq \cdots $
such that p divides the index
![]() $|V_{i-1}:V_{i}|$
for all
$|V_{i-1}:V_{i}|$
for all
![]() $i \geq 1$
. By replacing
$i \geq 1$
. By replacing
![]() $V_{i}$
by
$V_{i}$
by
 $\bigcap _{g \in U} g^{-1} V_{i} g$
we can assume that
$\bigcap _{g \in U} g^{-1} V_{i} g$
we can assume that
![]() $V_{i}$
is normal in U; note that the above intersection is finite because
$V_{i}$
is normal in U; note that the above intersection is finite because
![]() $V_{i}$
has finite index in U and
$V_{i}$
has finite index in U and
![]() $\bigcap _{i \in \mathbb {N}} V_{i} = \{1\}$
. By Theorem 6.2(1) this subnormal series can be refined to a composition series. The prime number p divides infinitely many composition factors, so by assumption, these infinitely many composition factors fall into only finitely many isomorphism classes of finite simple groups. By Lemma 6.5 one of them has to be in the local simple content (note that (1) implies (3) implies (2) is also true for groups that are not second countable).
$\bigcap _{i \in \mathbb {N}} V_{i} = \{1\}$
. By Theorem 6.2(1) this subnormal series can be refined to a composition series. The prime number p divides infinitely many composition factors, so by assumption, these infinitely many composition factors fall into only finitely many isomorphism classes of finite simple groups. By Lemma 6.5 one of them has to be in the local simple content (note that (1) implies (3) implies (2) is also true for groups that are not second countable).
Example 6.11. The group
![]() $\prod _{n \geq 5} A_{n}$
, where
$\prod _{n \geq 5} A_{n}$
, where
![]() $A_{n}$
denotes the alternating group on n symbols, is compact and second countable. Its local simple content is empty, because each
$A_{n}$
denotes the alternating group on n symbols, is compact and second countable. Its local simple content is empty, because each
![]() $A_{n}$
is a composition factor with multiplicity
$A_{n}$
is a composition factor with multiplicity
![]() $1$
, but its local prime content is the set of all primes.
$1$
, but its local prime content is the set of all primes.
This lemma allows us to draw the following conclusion from Theorem 6.6.
Corollary 6.12 [Reference Caprace, Reid and Willis8, Proposition 4.6]
Let p be a prime number that is in the local prime content of
![]() $G/K$
for every compact, normal subgroup
$G/K$
for every compact, normal subgroup
![]() $K \triangleleft G$
. Then
$K \triangleleft G$
. Then
![]() ${\mathrm{md}(G) \geq p+1}$
.
${\mathrm{md}(G) \geq p+1}$
.
The connection between the scale function and the local prime content is given in the following lemma by Glöckner.
Lemma 6.13 [Reference Glöckner12, Proposition 6.2]
Let G be a totally disconnected, locally compact group. Let
![]() $g \in G$
and let p be a prime number dividing
$g \in G$
and let p be a prime number dividing
![]() $s(g)$
. Then p is contained in the local prime content of G.
$s(g)$
. Then p is contained in the local prime content of G.
The next lemma is contained in a more general statement in [Reference Bywaters, Glöckner and Tornier7, Theorem C(c)], but for completeness a proof is included here.
Lemma 6.14. Let G be a totally disconnected, locally compact group and K a compact, normal subgroup of G. Denote the scale function on G by s and the scale function on
![]() $G/K$
by
$G/K$
by
![]() $s_{G/K}$
. If
$s_{G/K}$
. If
![]() $g \in G$
, then
$g \in G$
, then
![]() $s_{G/K}(gK)=s(g)$
.
$s_{G/K}(gK)=s(g)$
.
Proof. Suppose that
![]() $\Omega $
is a set on which G acts transitively such that the stabilizers of points are compact open subgroups of G, for example
$\Omega $
is a set on which G acts transitively such that the stabilizers of points are compact open subgroups of G, for example
![]() $\Omega = G/U$
for some compact, open subgroup
$\Omega = G/U$
for some compact, open subgroup
![]() $U \leq G$
. Since K is compact in the given topology on G it is also compact in the permutation topology on G constructed from the action on
$U \leq G$
. Since K is compact in the given topology on G it is also compact in the permutation topology on G constructed from the action on
![]() $\Omega $
and thus K has finite orbits on
$\Omega $
and thus K has finite orbits on
![]() $\Omega $
; see the discussion after Lemma 2.2. Since K is normal, G has an action on
$\Omega $
; see the discussion after Lemma 2.2. Since K is normal, G has an action on
![]() $\Omega /K$
and the stabilizers in G of points in
$\Omega /K$
and the stabilizers in G of points in
![]() $\Omega /K$
are compact open subgroups of G. Let
$\Omega /K$
are compact open subgroups of G. Let
![]() $\alpha $
be a point in
$\alpha $
be a point in
![]() $\Omega /K$
. Note that the homomorphism
$\Omega /K$
. Note that the homomorphism
![]() $G \to \mathrm {Sym}(\Omega /K)$
factors through
$G \to \mathrm {Sym}(\Omega /K)$
factors through
![]() $G/K$
, thus
$G/K$
, thus
![]() $(\alpha (gK))(G/K)_{\alpha } = (\alpha g)G_{\alpha }$
for every
$(\alpha (gK))(G/K)_{\alpha } = (\alpha g)G_{\alpha }$
for every
![]() $g \in G$
. Now, by applying Proposition 2.8 to the action of
$g \in G$
. Now, by applying Proposition 2.8 to the action of
![]() $G/K$
on
$G/K$
on
![]() $\Omega /K$
and to the action of G on
$\Omega /K$
and to the action of G on
![]() $\Omega /K$
, we get
$\Omega /K$
, we get
 $$ \begin{align*}s_{G/K}(gK)=\lim_{n\to\infty} |(\alpha (gK)^{n})(G/K)_{\alpha}|^{1/n} =\lim_{n\to\infty} |(\alpha g^{n})G_{\alpha}|^{1/n}=s(g). \\[-40pt] \end{align*} $$
$$ \begin{align*}s_{G/K}(gK)=\lim_{n\to\infty} |(\alpha (gK)^{n})(G/K)_{\alpha}|^{1/n} =\lim_{n\to\infty} |(\alpha g^{n})G_{\alpha}|^{1/n}=s(g). \\[-40pt] \end{align*} $$
We are now in a position to derive a lower bound for the minimal degree in terms of the scale function.
Corollary 6.15. Let G be a cgtdlc group. If p is the largest prime that occurs as a factor of any of the values
![]() $s(g)$
for
$s(g)$
for
![]() $g\in G$
, then
$g\in G$
, then
![]() $\mathrm{md}(G)\geq p+1$
.
$\mathrm{md}(G)\geq p+1$
.
Proof. Let K be a compact normal subgroup of G. By Lemma 6.14, the prime number p is also the largest prime factor of any of the values in the image of the scale function of
![]() $G/K$
. Lemma 6.13 says that the prime p is contained in the local prime content of
$G/K$
. Lemma 6.13 says that the prime p is contained in the local prime content of
![]() $G/K$
. The result now follows from Corollary 6.12.
$G/K$
. The result now follows from Corollary 6.12.
The following is a simple application of the above results.
Corollary 6.16. Let G be a compactly generated p-adic Lie group. If G is not nearly discrete, then
![]() $\mathrm{md}(G)\geq p+1$
.
$\mathrm{md}(G)\geq p+1$
.
Proof. Glöckner and Willis have shown in [Reference Glöckner and Willis13, Theorem 5.2] that for a p-adic Lie group the condition that it is not nearly discrete is equivalent to the condition that the group is not uniscalar. From the work of Glöckner (see [Reference Glöckner and Willis13, Theorem 2.1]) we know that every value of the scale function is a nonnegative power of p. The result now follows from the previous corollary.
7 The automorphism group of a
 $5$
-regular tree
$5$
-regular tree
In Corollary 6.7 it is shown that if
![]() $d\geq 2$
and
$d\geq 2$
and
![]() $d\neq 5$
then the minimal degree of a Cayley–Abels graph for the automorphism group of the d-regular tree is d. The
$d\neq 5$
then the minimal degree of a Cayley–Abels graph for the automorphism group of the d-regular tree is d. The
![]() $1$
-regular tree consists only of a single edge, so its automorphism group is compact and
$1$
-regular tree consists only of a single edge, so its automorphism group is compact and
![]() $\mathrm{md}(\mathrm{Aut}(T_{1}))=0$
. What is left is to determine the minimal degree of
$\mathrm{md}(\mathrm{Aut}(T_{1}))=0$
. What is left is to determine the minimal degree of
![]() $\mathrm{Aut}(T_{5})$
.
$\mathrm{Aut}(T_{5})$
.
Theorem 7.1. Let
![]() $T_{5}$
be the
$T_{5}$
be the
![]() $5$
-regular tree. Then
$5$
-regular tree. Then
![]() $\mathrm{md}(\mathrm{Aut}(T_{5})) = 5$
. In particular,
$\mathrm{md}(\mathrm{Aut}(T_{5})) = 5$
. In particular,
![]() $T_{5}$
is a Cayley–Abels graph of minimal degree for
$T_{5}$
is a Cayley–Abels graph of minimal degree for
![]() $\mathrm{Aut}(T_{5})$
.
$\mathrm{Aut}(T_{5})$
.
As a preparation for the proof of this theorem, we recall a few well-known facts about groups acting on trees. First we remind the reader of the classical fact due to Tits [Reference Tits, Haefliger and Narasimhan32, Proposition 3.2] that there are three types of automorphisms of a tree.
Proposition 7.2. If g is an automorphism of a tree T, then exactly one of the following assertions is true.
-
(1) g fixes some vertex
 $\alpha $
.
$\alpha $
. -
(2) g leaves some edge
 $\{\alpha , \beta \}$
invariant and switches the vertices
$\{\alpha , \beta \}$
invariant and switches the vertices
 $\alpha $
and
$\alpha $
and
 $\beta $
.
$\beta $
. -
(3) There is a two-way infinite arc L in T invariant under g and g induces a nontrivial translation on L such that if
 $\alpha $
is a vertex in L then the unique s-arc
$\alpha $
is a vertex in L then the unique s-arc
 $(\alpha _{0}, \ldots , \alpha _{s})$
with
$(\alpha _{0}, \ldots , \alpha _{s})$
with
 $\alpha _{0}=\alpha $
and
$\alpha _{0}=\alpha $
and
 $\alpha _{s}=\alpha g$
is an s-arc in L. In this case L is called the translation axis of g and s is called the translation length of g.
$\alpha _{s}=\alpha g$
is an s-arc in L. In this case L is called the translation axis of g and s is called the translation length of g.
For an automorphism g of a tree T we denote by
![]() $\mathrm V T^{g}$
the set of vertices that are fixed by g. It is easy to see that in case (1) of Proposition 7.2 the set
$\mathrm V T^{g}$
the set of vertices that are fixed by g. It is easy to see that in case (1) of Proposition 7.2 the set
![]() $\mathrm V T^{g}$
is the vertex set of a subtree of T.
$\mathrm V T^{g}$
is the vertex set of a subtree of T.
A group G is said to act on a tree T without inversion if none of its elements satisfy case (2). If we replace T with the first barycentric division of the tree (for example, we replace
![]() $T_{5}$
by the biregular tree
$T_{5}$
by the biregular tree
![]() $T_{5,2}$
), we can be sure that we have an action without inversion.
$T_{5,2}$
), we can be sure that we have an action without inversion.
Lemma 7.3 [Reference Serre31, Proposition 26 (incl. proof)]
Let T be a tree and let g and h be automorphisms of T. Suppose that
![]() $\mathrm V T^{g}\neq \emptyset $
and
$\mathrm V T^{g}\neq \emptyset $
and
![]() $\mathrm V T^{h}\neq \emptyset $
. Then
$\mathrm V T^{h}\neq \emptyset $
. Then
![]() $gh$
fixes a vertex if and only if
$gh$
fixes a vertex if and only if
![]() $\mathrm V T^{g} \cap \mathrm V T^{h} \neq \emptyset $
. Otherwise
$\mathrm V T^{g} \cap \mathrm V T^{h} \neq \emptyset $
. Otherwise
![]() $gh$
is a translation and the unique s-arc
$gh$
is a translation and the unique s-arc
![]() $(\alpha _{0},\ldots ,\alpha _{s})$
with
$(\alpha _{0},\ldots ,\alpha _{s})$
with
![]() $\alpha _{0} \in \mathrm V T^{g}$
but
$\alpha _{0} \in \mathrm V T^{g}$
but
![]() $\alpha _{1} \notin \mathrm V T^{g}$
, and with
$\alpha _{1} \notin \mathrm V T^{g}$
, and with
![]() $\alpha _{s} \in \mathrm V T^{h}$
but
$\alpha _{s} \in \mathrm V T^{h}$
but
![]() $\alpha _{s-1} \notin \mathrm V T^{h}$
, is contained in the translation axis of
$\alpha _{s-1} \notin \mathrm V T^{h}$
, is contained in the translation axis of
![]() $gh$
.
$gh$
.
The following lemma is a consequence of the simple fact that a compact group acting continuously on a discrete set has finite orbits.
Lemma 7.4. Let T be a tree and
![]() $G \leq \mathrm{Aut}(T)$
a compact subgroup. There is a vertex or an edge in T that is stabilized by every element of G.
$G \leq \mathrm{Aut}(T)$
a compact subgroup. There is a vertex or an edge in T that is stabilized by every element of G.
We now present a lemma that can be deduced from various ‘rigidity’ results for automorphism groups of trees (for example, [Reference Bass and Lubotzky5, Corollary 4.8(c)]), but for completeness we include a direct proof.
Lemma 7.5. Let
![]() $d \neq d^{\prime }$
be nonnegative integers, greater than or equal to
$d \neq d^{\prime }$
be nonnegative integers, greater than or equal to
![]() $3$
. Then
$3$
. Then
![]() $T_{d^{\prime }}$
cannot be a Cayley–Abels graph for
$T_{d^{\prime }}$
cannot be a Cayley–Abels graph for
![]() $\mathrm{Aut}(T_{d})$
.
$\mathrm{Aut}(T_{d})$
.
Proof. Suppose that
![]() $G=\mathrm{Aut}(T_{d})$
acts transitively on
$G=\mathrm{Aut}(T_{d})$
acts transitively on
![]() $T_{d^{\prime }}$
and the stabilizers of vertices are compact open subgroups of G. Recall (or prove as an exercise using Lemma 7.4) that G does not have any nontrivial, compact, normal subgroups, so this action is faithful. As a consequence of Lemma 7.4, the automorphism group of an infinite, regular tree has two conjugacy classes of maximal compact subgroups. One conjugacy class consists of the stabilizers of vertices and the other conjugacy class consists of the stabilizers of edges. A compact open subgroup of G acting on
$T_{d^{\prime }}$
and the stabilizers of vertices are compact open subgroups of G. Recall (or prove as an exercise using Lemma 7.4) that G does not have any nontrivial, compact, normal subgroups, so this action is faithful. As a consequence of Lemma 7.4, the automorphism group of an infinite, regular tree has two conjugacy classes of maximal compact subgroups. One conjugacy class consists of the stabilizers of vertices and the other conjugacy class consists of the stabilizers of edges. A compact open subgroup of G acting on
![]() $T_{d^{\prime }}$
has to fix a vertex or stabilize an edge in
$T_{d^{\prime }}$
has to fix a vertex or stabilize an edge in
![]() $T_{d^{\prime }}$
. Thus for every vertex
$T_{d^{\prime }}$
. Thus for every vertex
![]() $\alpha \in \mathrm V T_{d}$
we can find a vertex
$\alpha \in \mathrm V T_{d}$
we can find a vertex
![]() $\alpha ^{\prime } \in \mathrm V T_{d^{\prime }}$
with
$\alpha ^{\prime } \in \mathrm V T_{d^{\prime }}$
with
![]() $G_{\alpha } \leq G_{\alpha ^{\prime }}$
or an edge
$G_{\alpha } \leq G_{\alpha ^{\prime }}$
or an edge
![]() $e^{\prime }$
in
$e^{\prime }$
in
![]() $T_{d^{\prime }}$
with
$T_{d^{\prime }}$
with
![]() $G_{\alpha } \leq G_{e^{\prime }}$
. By maximality of
$G_{\alpha } \leq G_{e^{\prime }}$
. By maximality of
![]() $G_{\alpha }$
, such an inclusion has to be an equality.
$G_{\alpha }$
, such an inclusion has to be an equality.
First we consider the case when
![]() $G_{\alpha }=G_{e^{\prime }}$
for a vertex
$G_{\alpha }=G_{e^{\prime }}$
for a vertex
![]() $\alpha $
in
$\alpha $
in
![]() $T_{d}$
and an edge
$T_{d}$
and an edge
![]() $e^{\prime }$
in
$e^{\prime }$
in
![]() $T_{d^{\prime }}$
. Let
$T_{d^{\prime }}$
. Let
![]() $\alpha ^{\prime }$
be an end vertex of
$\alpha ^{\prime }$
be an end vertex of
![]() $e^{\prime }$
. Similar considerations to those in the previous paragraph imply that there exists an edge e of
$e^{\prime }$
. Similar considerations to those in the previous paragraph imply that there exists an edge e of
![]() $T_{d}$
with
$T_{d}$
with
![]() $G_{\alpha ^{\prime }}=G_{e}$
. From the orbit–stabilizer theorem we see that
$G_{\alpha ^{\prime }}=G_{e}$
. From the orbit–stabilizer theorem we see that
![]() $|G_{e^{\prime }}:G_{\alpha ^{\prime }}\cap G_{e^{\prime }}| = |\alpha ^{\prime } G_{e^{\prime }}| \leq 2$
. However,
$|G_{e^{\prime }}:G_{\alpha ^{\prime }}\cap G_{e^{\prime }}| = |\alpha ^{\prime } G_{e^{\prime }}| \leq 2$
. However,
![]() $|G_{\alpha }:G_{e} \cap G_{\alpha }| \geq d$
and this is a contradiction.
$|G_{\alpha }:G_{e} \cap G_{\alpha }| \geq d$
and this is a contradiction.
We are left with the other case. The above allows us to construct a bijective map
![]() $\varphi \colon \mathrm V T_{d}\to \mathrm V T_{d^{\prime }}$
such that if
$\varphi \colon \mathrm V T_{d}\to \mathrm V T_{d^{\prime }}$
such that if
![]() $\alpha \in \mathrm V T_{d}$
then
$\alpha \in \mathrm V T_{d}$
then
![]() $G_{\varphi (\alpha )}=G_{\alpha }$
. In particular, for all vertices
$G_{\varphi (\alpha )}=G_{\alpha }$
. In particular, for all vertices
![]() $\alpha ,\beta \in \mathrm V T_{d}$
we have
$\alpha ,\beta \in \mathrm V T_{d}$
we have
![]() $|\,\beta G_{\alpha }| = |G_{\alpha } : G_{\alpha } \cap G_{\beta }| = |G_{\varphi (\alpha )} : G_{\varphi (\alpha )} \cap G_{\varphi (\,\beta )}| = |\varphi (\,\beta ) G_{\varphi (\alpha )}|$
. Also note that, because
$|\,\beta G_{\alpha }| = |G_{\alpha } : G_{\alpha } \cap G_{\beta }| = |G_{\varphi (\alpha )} : G_{\varphi (\alpha )} \cap G_{\varphi (\,\beta )}| = |\varphi (\,\beta ) G_{\varphi (\alpha )}|$
. Also note that, because
![]() $T_{d}$
is a tree,
$T_{d}$
is a tree,
![]() $|\gamma G_{\alpha }| \geq |\,\beta G_{\alpha }|$
whenever
$|\gamma G_{\alpha }| \geq |\,\beta G_{\alpha }|$
whenever
![]() $\beta $
lies on the unique s-arc from
$\beta $
lies on the unique s-arc from
![]() $\gamma $
to
$\gamma $
to
![]() $\alpha $
; the same statement holds for vertices in
$\alpha $
; the same statement holds for vertices in
![]() $T_{d^{\prime }}$
. In particular, fixing
$T_{d^{\prime }}$
. In particular, fixing
![]() $\alpha $
and varying
$\alpha $
and varying
![]() $\gamma \neq \alpha $
in
$\gamma \neq \alpha $
in
![]() $T_{d}$
, the cardinality
$T_{d}$
, the cardinality
![]() $|\gamma G_{\alpha }|$
is minimal if and only if
$|\gamma G_{\alpha }|$
is minimal if and only if
![]() $\gamma $
is a neighbour of
$\gamma $
is a neighbour of
![]() $\alpha $
. In
$\alpha $
. In
![]() $T_{d^{\prime }}$
we can only say that among those vertices
$T_{d^{\prime }}$
we can only say that among those vertices
![]() $\gamma ^{\prime } \neq \alpha ^{\prime }$
with
$\gamma ^{\prime } \neq \alpha ^{\prime }$
with
![]() $|\gamma ^{\prime } G_{\alpha ^{\prime }}|$
minimal there exists a neighbour of
$|\gamma ^{\prime } G_{\alpha ^{\prime }}|$
minimal there exists a neighbour of
![]() $\alpha ^{\prime }$
. These considerations imply that for every vertex
$\alpha ^{\prime }$
. These considerations imply that for every vertex
![]() $\alpha \in \mathrm V T_{d}$
the map
$\alpha \in \mathrm V T_{d}$
the map
![]() $\varphi $
sends some neighbour
$\varphi $
sends some neighbour
![]() $\beta $
of
$\beta $
of
![]() $\alpha $
to a neighbour of
$\alpha $
to a neighbour of
![]() $\varphi (\alpha )$
. Note that every element of
$\varphi (\alpha )$
. Note that every element of
![]() $\varphi (\,\beta ) G_{\varphi (\alpha )}$
has to be a neighbour of
$\varphi (\,\beta ) G_{\varphi (\alpha )}$
has to be a neighbour of
![]() $\varphi (\alpha )$
. But then
$\varphi (\alpha )$
. But then
![]() $d=|\,\beta G_{\alpha }|=|\varphi (\,\beta ) G_{\varphi (\alpha )}|$
shows that
$d=|\,\beta G_{\alpha }|=|\varphi (\,\beta ) G_{\varphi (\alpha )}|$
shows that
![]() $\varphi $
sends all neighbours of
$\varphi $
sends all neighbours of
![]() $\alpha $
to neighbours of
$\alpha $
to neighbours of
![]() $\varphi (\alpha )$
. Hence,
$\varphi (\alpha )$
. Hence,
![]() $\varphi $
defines a graph homomorphism
$\varphi $
defines a graph homomorphism
![]() $T_{d} \to T_{d^{\prime }}$
. But a graph morphism between trees that is bijective on the vertices has to be an isomorphism. This concludes the proof.
$T_{d} \to T_{d^{\prime }}$
. But a graph morphism between trees that is bijective on the vertices has to be an isomorphism. This concludes the proof.
The same proof works for automorphism groups of biregular trees and, in particular, for
![]() $\mathrm{Aut}^{+}(T_{d})$
, the index-
$\mathrm{Aut}^{+}(T_{d})$
, the index-
![]() $2$
subgroup of
$2$
subgroup of
![]() $\mathrm{Aut}(T_{d})$
fixing the bipartition on the vertices of
$\mathrm{Aut}(T_{d})$
fixing the bipartition on the vertices of
![]() $T_{d}$
. Another way to describe
$T_{d}$
. Another way to describe
![]() $\mathrm{Aut}^{+}(T_{d})$
is to say that it is the subgroup generated by the vertex stabilizers in G. It is well known that
$\mathrm{Aut}^{+}(T_{d})$
is to say that it is the subgroup generated by the vertex stabilizers in G. It is well known that
![]() $\mathrm{Aut}^{+}(T_{d})$
is the only noncompact, proper, open subgroup of
$\mathrm{Aut}^{+}(T_{d})$
is the only noncompact, proper, open subgroup of
![]() $\mathrm{Aut}(T_{d})$
and that it is simple; see [Reference Tits, Haefliger and Narasimhan32].
$\mathrm{Aut}(T_{d})$
and that it is simple; see [Reference Tits, Haefliger and Narasimhan32].
Proof of Theorem 7.1
Set
![]() $G=\mathrm{Aut}(T_{5})$
. Assume (seeking a contradiction) that
$G=\mathrm{Aut}(T_{5})$
. Assume (seeking a contradiction) that
![]() $\Gamma $
is a minimal-degree Cayley–Abels graph for G and the degree of
$\Gamma $
is a minimal-degree Cayley–Abels graph for G and the degree of
![]() $\Gamma $
is less than
$\Gamma $
is less than
![]() $5$
. Fix a vertex
$5$
. Fix a vertex
![]() $\alpha _{0}$
of
$\alpha _{0}$
of
![]() $\Gamma $
and write
$\Gamma $
and write
![]() $B = G_{\alpha _{0}}$
.
$B = G_{\alpha _{0}}$
.
Claim 1. The degree of
![]() $\Gamma $
is
$\Gamma $
is
![]() $4$
and the local action is
$4$
and the local action is
![]() $S_{3}$
. The subgroup
$S_{3}$
. The subgroup
![]() $\mathrm{Aut}^{+}(T_{5})$
of G cannot have a Cayley–Abels graph of degree less than
$\mathrm{Aut}^{+}(T_{5})$
of G cannot have a Cayley–Abels graph of degree less than
![]() $4$
.
$4$
.
Proof. Recall that G does not have any nontrivial, compact, normal subgroups. The local simple content of G consists of the cyclic groups of order
![]() $2$
and
$2$
and
![]() $3$
, so by Theorem 6.6 the degree of
$3$
, so by Theorem 6.6 the degree of
![]() $\Gamma $
is equal to
$\Gamma $
is equal to
![]() $4$
. The local simple content of
$4$
. The local simple content of
![]() $\mathrm{Aut}^{+}(T_{5})$
is the same as the local simple content of G and thus the degree of any Cayley–Abels graph for
$\mathrm{Aut}^{+}(T_{5})$
is the same as the local simple content of G and thus the degree of any Cayley–Abels graph for
![]() $\mathrm{Aut}^{+}(T_{5})$
is at least 4. By Theorem 6.6, the cyclic groups of order
$\mathrm{Aut}^{+}(T_{5})$
is at least 4. By Theorem 6.6, the cyclic groups of order
![]() $2$
and
$2$
and
![]() $3$
are composition factors of subgroups of point stabilizers of the local action. This is only possible if the local action is
$3$
are composition factors of subgroups of point stabilizers of the local action. This is only possible if the local action is
![]() $S_{3}$
or
$S_{3}$
or
![]() $S_{4}$
. However, [Reference Trofimov34, Proposition 3.1] implies that if the local action is
$S_{4}$
. However, [Reference Trofimov34, Proposition 3.1] implies that if the local action is
![]() $S_{4}$
, then
$S_{4}$
, then
![]() $\Gamma $
has to be a tree. That contradicts Lemma 7.5.
$\Gamma $
has to be a tree. That contradicts Lemma 7.5.
Let
![]() $\beta _{1}, \beta _{2}, \beta _{3}, \beta _{4}$
denote the neighbours of
$\beta _{1}, \beta _{2}, \beta _{3}, \beta _{4}$
denote the neighbours of
![]() $\alpha _{0}$
such that
$\alpha _{0}$
such that
![]() $\beta _{4}$
is the neighbour that is fixed by B.
$\beta _{4}$
is the neighbour that is fixed by B.
Claim 2. The group G has two orbits on the edges of
![]() $\Gamma $
. For
$\Gamma $
. For
![]() $i=1, 2, 3, 4$
there exists
$i=1, 2, 3, 4$
there exists
![]() $g_{i} \in G$
with
$g_{i} \in G$
with
![]() $(\alpha _{0},\beta _{i})g_{i}=(\,\beta _{i},\alpha _{0})$
. Furthermore, it is possible to choose
$(\alpha _{0},\beta _{i})g_{i}=(\,\beta _{i},\alpha _{0})$
. Furthermore, it is possible to choose
![]() $g_{1}, g_{2}$
and
$g_{1}, g_{2}$
and
![]() $g_{3}$
so that there exists
$g_{3}$
so that there exists
![]() $b \in B$
with
$b \in B$
with
![]() $g_{i+1}=b^{-1}g_{i}b$
for
$g_{i+1}=b^{-1}g_{i}b$
for
![]() $i=1,2$
.
$i=1,2$
.
Proof. Choose an element
![]() $g_{4}\in G$
such that
$g_{4}\in G$
such that
![]() $\alpha _{0} g_{4}=\beta _{4}$
. It is well known that G is unimodular and thus, by Lemma 5.1, we see that
$\alpha _{0} g_{4}=\beta _{4}$
. It is well known that G is unimodular and thus, by Lemma 5.1, we see that
![]() $|\alpha _{0} G_{\alpha _{0} g_{4}}|=|(\alpha _{0} g_{4})G_{\alpha _{0}}|=|\,\beta _{4} G_{\alpha _{0}}|=1$
. This implies that
$|\alpha _{0} G_{\alpha _{0} g_{4}}|=|(\alpha _{0} g_{4})G_{\alpha _{0}}|=|\,\beta _{4} G_{\alpha _{0}}|=1$
. This implies that
![]() $\{\alpha _{0},\beta _{4}\}$
is fixed by
$\{\alpha _{0},\beta _{4}\}$
is fixed by
![]() $G_{\,\beta _{4}}$
. But also
$G_{\,\beta _{4}}$
. But also
![]() $\{\alpha _{0},\beta _{4} \}g_{4}$
is fixed by
$\{\alpha _{0},\beta _{4} \}g_{4}$
is fixed by
 $g_{4}^{-1} G_{\alpha _{0}} g_{4} = G_{\,\beta _{4}}$
. Since there is only one fixed point in the local action, we get
$g_{4}^{-1} G_{\alpha _{0}} g_{4} = G_{\,\beta _{4}}$
. Since there is only one fixed point in the local action, we get
![]() $\{\alpha _{0},\beta _{4} \}g_{4} = \{\alpha _{0},\beta _{4}\}$
.
$\{\alpha _{0},\beta _{4} \}g_{4} = \{\alpha _{0},\beta _{4}\}$
.
From this we also see that G has two orbits on the edges, because if there did exist an element
![]() $g\in G$
such that
$g\in G$
such that
![]() $\{\alpha _{0}, \beta _{4}\}g=\{\alpha _{0}, \beta _{1}\}$
then either g or
$\{\alpha _{0}, \beta _{4}\}g=\{\alpha _{0}, \beta _{1}\}$
then either g or
![]() $g_{4}g$
would fix
$g_{4}g$
would fix
![]() $\alpha _{0}$
and take
$\alpha _{0}$
and take
![]() $\beta _{4}$
to
$\beta _{4}$
to
![]() $\beta _{1}$
contrary to assumptions. We say that the edges in the orbit
$\beta _{1}$
contrary to assumptions. We say that the edges in the orbit
![]() $\{\alpha _{0}, \beta _{4}\}G$
are red and the edges in the other orbit
$\{\alpha _{0}, \beta _{4}\}G$
are red and the edges in the other orbit
![]() $\{\alpha _{0}, \beta _{1}\}G$
are blue.
$\{\alpha _{0}, \beta _{1}\}G$
are blue.
Now let
![]() $h_{1} \in G$
be such that
$h_{1} \in G$
be such that
![]() $\alpha _{0} h_{1} = \beta _{1}$
. Because the edge
$\alpha _{0} h_{1} = \beta _{1}$
. Because the edge
![]() $\{\alpha _{0}, \beta _{4}\}h_{1}=\{\,\beta _{1},\beta _{4} h_{1}\}$
is fixed by
$\{\alpha _{0}, \beta _{4}\}h_{1}=\{\,\beta _{1},\beta _{4} h_{1}\}$
is fixed by
 $h_{1}^{-1}G_{\alpha _{0}}h_{1}=G_{\,\beta _{1}}$
, the edge
$h_{1}^{-1}G_{\alpha _{0}}h_{1}=G_{\,\beta _{1}}$
, the edge
![]() $\{\alpha _{0}, \beta _{1}\}h_{1}=\{\,\beta _{1},\beta _{1} h_{1}\}$
is not fixed by
$\{\alpha _{0}, \beta _{1}\}h_{1}=\{\,\beta _{1},\beta _{1} h_{1}\}$
is not fixed by
![]() $G_{\,\beta _{1}}$
. So there exists
$G_{\,\beta _{1}}$
. So there exists
![]() $h \in G_{\,\beta _{1}}$
with
$h \in G_{\,\beta _{1}}$
with
![]() $\beta _{1} h_{1} h = \alpha _{0}$
. We can now set
$\beta _{1} h_{1} h = \alpha _{0}$
. We can now set
![]() $g_{1} = h_{1} h$
; this element satisfies
$g_{1} = h_{1} h$
; this element satisfies
![]() $(\alpha _{0},\beta _{1})g_{1} = (\,\beta _{1},\alpha _{0})$
.
$(\alpha _{0},\beta _{1})g_{1} = (\,\beta _{1},\alpha _{0})$
.
By Claim 1 there exists
![]() $b \in B$
with
$b \in B$
with
![]() $\beta _{1} b = \beta _{2}$
and
$\beta _{1} b = \beta _{2}$
and
![]() $\beta _{1} b^{2} = \beta _{3}$
. Clearly
$\beta _{1} b^{2} = \beta _{3}$
. Clearly
![]() $g_{i} = b^{-i} g_{1} b^{i}$
satisfies
$g_{i} = b^{-i} g_{1} b^{i}$
satisfies
![]() $(\alpha _{0},\beta _{i})g_{i}= (\alpha _{0} b^{-i} g_{1} b^{i}, \beta _{i} b^{-i} g_{1} b^{i}) =(\,\beta _{i},\alpha _{0})$
for
$(\alpha _{0},\beta _{i})g_{i}= (\alpha _{0} b^{-i} g_{1} b^{i}, \beta _{i} b^{-i} g_{1} b^{i}) =(\,\beta _{i},\alpha _{0})$
for
![]() $i=1,2$
.
$i=1,2$
.
Claim 3. Write
![]() $A=\{g_{1}, g_{2}, g_{3}, g_{4}\}$
and
$A=\{g_{1}, g_{2}, g_{3}, g_{4}\}$
and
![]() $A^{\prime }=\{g_{1}, g_{2}, g_{3}\}$
. Then
$A^{\prime }=\{g_{1}, g_{2}, g_{3}\}$
. Then
![]() $BA^{\prime }B=BA^{\prime }=A^{\prime }B$
and
$BA^{\prime }B=BA^{\prime }=A^{\prime }B$
and
![]() $Bg_{4} B=Bg_{4}=g_{4} B$
. Furthermore,
$Bg_{4} B=Bg_{4}=g_{4} B$
. Furthermore,
![]() $G=\langle A, B\rangle =\langle g_{1}, g_{4}, B\rangle $
, and
$G=\langle A, B\rangle =\langle g_{1}, g_{4}, B\rangle $
, and
![]() $\langle A^{\prime }, B\rangle =\langle g_{1},B\rangle $
and
$\langle A^{\prime }, B\rangle =\langle g_{1},B\rangle $
and
![]() $\langle g_{4},B\rangle $
are compact open subgroups of G.
$\langle g_{4},B\rangle $
are compact open subgroups of G.
Proof. Note that the set of vertices
![]() $\{\,\beta _{1}, \beta _{2}, \beta _{3}\}$
is invariant under B. We show that
$\{\,\beta _{1}, \beta _{2}, \beta _{3}\}$
is invariant under B. We show that
![]() $BA^{\prime } = \{g \in G \mid \alpha _{0} g \in \{\,\beta _{1},\beta _{2},\beta _{3}\} \}$
. Indeed, if
$BA^{\prime } = \{g \in G \mid \alpha _{0} g \in \{\,\beta _{1},\beta _{2},\beta _{3}\} \}$
. Indeed, if
![]() $\alpha _{0} g= \beta _{i}$
then
$\alpha _{0} g= \beta _{i}$
then
 $g g_{i}^{-1}$
fixes
$g g_{i}^{-1}$
fixes
![]() $\alpha _{0}$
and thus
$\alpha _{0}$
and thus
 $gg_{i}^{-1} \in B$
and
$gg_{i}^{-1} \in B$
and
![]() $g\in Bg_{i}\subseteq BA^{\prime }$
. This implies
$g\in Bg_{i}\subseteq BA^{\prime }$
. This implies
![]() $BA^{\prime } B \subseteq BA^{\prime }$
, and the direction
$BA^{\prime } B \subseteq BA^{\prime }$
, and the direction
![]() $BA^{\prime } \subseteq BA^{\prime }B$
holds because B contains the identity. Note that the invariance of blue edges under G in particular implies that
$BA^{\prime } \subseteq BA^{\prime }B$
holds because B contains the identity. Note that the invariance of blue edges under G in particular implies that
![]() $BA^{\prime }=(BA^{\prime })^{-1}$
. We know that
$BA^{\prime }=(BA^{\prime })^{-1}$
. We know that
 $g_{i}^{2} \in B$
for
$g_{i}^{2} \in B$
for
![]() $i=1,2,3$
and therefore
$i=1,2,3$
and therefore
 $g_{i} B = g_{i}^{-1} B$
and
$g_{i} B = g_{i}^{-1} B$
and
![]() $(BA^{\prime })^{-1}=A^{\prime {-1}}B = A^{\prime }B$
.
$(BA^{\prime })^{-1}=A^{\prime {-1}}B = A^{\prime }B$
.
The same kind of argument can be used to show that
![]() $Bg_{4} B=Bg_{4}$
.
$Bg_{4} B=Bg_{4}$
.
Since one can move the vertex
![]() $\alpha _{0}$
to any of its neighbours by using an element from A, the standard graph-theoretical argument described in Lemma 2.4 shows that the group
$\alpha _{0}$
to any of its neighbours by using an element from A, the standard graph-theoretical argument described in Lemma 2.4 shows that the group
![]() $\langle A, B\rangle $
acts transitively on
$\langle A, B\rangle $
acts transitively on
![]() $\Gamma $
. As
$\Gamma $
. As
![]() $\langle A, B\rangle $
contains the vertex stabilizer B, we see that
$\langle A, B\rangle $
contains the vertex stabilizer B, we see that
![]() $G=\langle A, B\rangle $
. Denote by
$G=\langle A, B\rangle $
. Denote by
![]() $\Gamma ^{\prime }$
the connected component of the graph
$\Gamma ^{\prime }$
the connected component of the graph
![]() $(\mathrm V\Gamma , \{\alpha _{0}, \beta _{1}\}G)$
(the graph with the same vertex set as
$(\mathrm V\Gamma , \{\alpha _{0}, \beta _{1}\}G)$
(the graph with the same vertex set as
![]() $\Gamma $
but where the red edges have been removed) that contains
$\Gamma $
but where the red edges have been removed) that contains
![]() $\alpha _{0}$
. The group
$\alpha _{0}$
. The group
![]() $C=\langle A^{\prime }, B\rangle $
is an open subgroup of G (contains the open subgroup B) and acts transitively on the vertices of
$C=\langle A^{\prime }, B\rangle $
is an open subgroup of G (contains the open subgroup B) and acts transitively on the vertices of
![]() $\Gamma ^{\prime }$
. Thus
$\Gamma ^{\prime }$
. Thus
![]() $\Gamma ^{\prime }$
is a Cayley–Abels graph for C, and it has degree
$\Gamma ^{\prime }$
is a Cayley–Abels graph for C, and it has degree
![]() $3$
. But C is an open subgroup of G and if C is not compact then
$3$
. But C is an open subgroup of G and if C is not compact then
![]() $C=G$
or
$C=G$
or
![]() $C=\mathrm{Aut}^{+}(T_{5})$
. By Claim 1 neither of these groups can have a Cayley–Abels graph of degree 3. Thus C must be compact.
$C=\mathrm{Aut}^{+}(T_{5})$
. By Claim 1 neither of these groups can have a Cayley–Abels graph of degree 3. Thus C must be compact.
Note that
![]() $\langle g_{4}, B\rangle $
leaves the edge
$\langle g_{4}, B\rangle $
leaves the edge
![]() $\{\alpha _{0}, \beta _{4}\}$
in
$\{\alpha _{0}, \beta _{4}\}$
in
![]() $\Gamma $
invariant and is equal to its stabilizer. Hence,
$\Gamma $
invariant and is equal to its stabilizer. Hence,
![]() $\langle g_{4}, B\rangle $
is a compact open subgroup of G.
$\langle g_{4}, B\rangle $
is a compact open subgroup of G.
The next step is to relate the action of G on
![]() $\Gamma $
to the action of G on
$\Gamma $
to the action of G on
![]() $T_{5}$
. To ease the presentation we replace
$T_{5}$
. To ease the presentation we replace
![]() $T_{5}$
with its barycentric subdivision
$T_{5}$
with its barycentric subdivision
![]() $T=T_{5, 2}$
and consider the action of G on T instead of the action on
$T=T_{5, 2}$
and consider the action of G on T instead of the action on
![]() $T_{5}$
. This has the benefit that elements in G that act like inversions on
$T_{5}$
. This has the benefit that elements in G that act like inversions on
![]() $T_{5}$
now fix a vertex. An element in G that acts like a translation on
$T_{5}$
now fix a vertex. An element in G that acts like a translation on
![]() $T_{5}$
also acts like a translation on T, but an element that does not act like a translation on
$T_{5}$
also acts like a translation on T, but an element that does not act like a translation on
![]() $T_{5}$
always fixes a vertex in T. In particular, every compact subgroup of G fixes some vertex in T.
$T_{5}$
always fixes a vertex in T. In particular, every compact subgroup of G fixes some vertex in T.
Claim 4. Both groups
![]() $C=\langle g_{1}, B\rangle $
and
$C=\langle g_{1}, B\rangle $
and
![]() $D=\langle g_{4}, B\rangle $
fix a vertex in T.
$D=\langle g_{4}, B\rangle $
fix a vertex in T.
The elements
![]() $g_{1}$
and
$g_{1}$
and
![]() $g_{4}$
do not fix a common vertex in T. Therefore,
$g_{4}$
do not fix a common vertex in T. Therefore,
![]() $g_{1}g_{4}$
acts like a translation on T. Similarly,
$g_{1}g_{4}$
acts like a translation on T. Similarly,
![]() $g_{2}g_{4}$
and
$g_{2}g_{4}$
and
![]() $g_{3}g_{4}$
are also translations.
$g_{3}g_{4}$
are also translations.
Proof. The groups C and D are both compact by Claim 3 and thus each of them fixes a vertex in T.
Let
![]() $\gamma _{1}$
denote a vertex in T that is fixed by C and let
$\gamma _{1}$
denote a vertex in T that is fixed by C and let
![]() $\gamma _{4}$
denote a vertex that is fixed by D. Suppose that some vertex
$\gamma _{4}$
denote a vertex that is fixed by D. Suppose that some vertex
![]() $\gamma $
in T is fixed by both
$\gamma $
in T is fixed by both
![]() $g_{1}$
and
$g_{1}$
and
![]() $g_{4}$
. Then
$g_{4}$
. Then
![]() $g_{1}$
fixes every vertex on the unique
$g_{1}$
fixes every vertex on the unique
![]() $s_{1}$
-arc
$s_{1}$
-arc
![]() $P_{1}$
from
$P_{1}$
from
![]() $\gamma _{1}$
to
$\gamma _{1}$
to
![]() $\gamma $
and
$\gamma $
and
![]() $g_{4}$
fixes every vertex on the unique
$g_{4}$
fixes every vertex on the unique
![]() $s_{4}$
-arc
$s_{4}$
-arc
![]() $P_{4}$
from
$P_{4}$
from
![]() $\gamma _{4}$
to
$\gamma _{4}$
to
![]() $\gamma $
. But B is contained in both C and D, hence fixes both
$\gamma $
. But B is contained in both C and D, hence fixes both
![]() $\gamma _{1}$
and
$\gamma _{1}$
and
![]() $\gamma _{4}$
, and thus fixes every vertex in the unique
$\gamma _{4}$
, and thus fixes every vertex in the unique
![]() $s_{14}$
-arc
$s_{14}$
-arc
![]() $P_{14}$
from
$P_{14}$
from
![]() $\gamma _{1}$
to
$\gamma _{1}$
to
![]() $\gamma _{4}$
. Since T is a tree,
$\gamma _{4}$
. Since T is a tree,
![]() $P_{1}$
,
$P_{1}$
,
![]() $P_{4}$
and
$P_{4}$
and
![]() $P_{14}$
have a common vertex, and that common vertex is fixed by
$P_{14}$
have a common vertex, and that common vertex is fixed by
![]() $g_{1}, g_{4}$
and the group B. It is thus fixed by
$g_{1}, g_{4}$
and the group B. It is thus fixed by
![]() $G=\langle g_{1}, g_{4}, B\rangle = \mathrm{Aut}(T)$
and we reach a contradiction. From Lemma 7.3 it now follows that
$G=\langle g_{1}, g_{4}, B\rangle = \mathrm{Aut}(T)$
and we reach a contradiction. From Lemma 7.3 it now follows that
![]() $g_{1}g_{4}$
acts like a translation on T. The statements about
$g_{1}g_{4}$
acts like a translation on T. The statements about
![]() $g_{2}g_{4}$
and
$g_{2}g_{4}$
and
![]() $g_{3}g_{4}$
follow by symmetry.
$g_{3}g_{4}$
follow by symmetry.
Claim 5. For
![]() $i=1, 2, 3$
, let
$i=1, 2, 3$
, let
![]() $L_{i}$
be the translation axis of
$L_{i}$
be the translation axis of
![]() $t_{i}=g_{i}g_{4}$
and let F be the fixed tree of B. Then
$t_{i}=g_{i}g_{4}$
and let F be the fixed tree of B. Then
![]() $L_{1}\cap L_{2}\cap L_{3} \cap F$
contains at least one arc.
$L_{1}\cap L_{2}\cap L_{3} \cap F$
contains at least one arc.
Proof. Let
![]() $F_{i}$
be the fixed tree of
$F_{i}$
be the fixed tree of
![]() $g_{i}$
for
$g_{i}$
for
![]() $i=1, 2, 3,4$
. By Lemma 7.4 a tree automorphism generates a subgroup with noncompact closure if and only if it is a translation. Since C is compact, it has a nonempty fixed tree, which is contained in the intersection
$i=1, 2, 3,4$
. By Lemma 7.4 a tree automorphism generates a subgroup with noncompact closure if and only if it is a translation. Since C is compact, it has a nonempty fixed tree, which is contained in the intersection
![]() $F \cap F_{1} \cap F_{2} \cap F_{3}$
. In particular, this intersection is nonempty and
$F \cap F_{1} \cap F_{2} \cap F_{3}$
. In particular, this intersection is nonempty and
![]() $F_{1} \cup F_{2} \cup F_{3}$
is a tree. The same argument shows that
$F_{1} \cup F_{2} \cup F_{3}$
is a tree. The same argument shows that
![]() $F \cap F_{4}$
is nonempty. In the last claim we showed that
$F \cap F_{4}$
is nonempty. In the last claim we showed that
![]() $F_{i}$
and
$F_{i}$
and
![]() $F_{4}$
are disjoint for
$F_{4}$
are disjoint for
![]() $i=1,2,3$
. Thus also the s-arc from
$i=1,2,3$
. Thus also the s-arc from
![]() $F_{1} \cup F_{2} \cup F_{3}$
to
$F_{1} \cup F_{2} \cup F_{3}$
to
![]() $F_{4}$
has positive length. This s-arc is contained in F because F is connected and both
$F_{4}$
has positive length. This s-arc is contained in F because F is connected and both
![]() $F \cap F_{1} \cap F_{2} \cap F_{3}$
and
$F \cap F_{1} \cap F_{2} \cap F_{3}$
and
![]() $F \cap F_{4}$
are nonempty. Note also that by Lemma 7.3 the orientation of this arc fits with the orientation of all the translation axes.
$F \cap F_{4}$
are nonempty. Note also that by Lemma 7.3 the orientation of this arc fits with the orientation of all the translation axes.
Claim 6. There is a vertex
![]() $\gamma $
in
$\gamma $
in
![]() $L_{1}\cap L_{2}\cap L_{3}\cap F$
such that
$L_{1}\cap L_{2}\cap L_{3}\cap F$
such that
![]() $\gamma t_{1}, \gamma t_{2}$
and
$\gamma t_{1}, \gamma t_{2}$
and
![]() $\gamma t_{3}$
are all different.
$\gamma t_{3}$
are all different.
Proof. Suppose that
![]() $\gamma $
is a vertex in
$\gamma $
is a vertex in
![]() $L_{1}\cap L_{2}\cap L_{3}\cap F$
and that
$L_{1}\cap L_{2}\cap L_{3}\cap F$
and that
![]() $\gamma t_{1}=\gamma t_{2}$
. We know from Claim 2 that there is an element
$\gamma t_{1}=\gamma t_{2}$
. We know from Claim 2 that there is an element
![]() $b\in B$
such that
$b\in B$
such that
![]() $g_{2}=b^{-1}g_{1}b$
and
$g_{2}=b^{-1}g_{1}b$
and
![]() $g_{3}=b^{-2}g_{1}b^{2}$
. Then
$g_{3}=b^{-2}g_{1}b^{2}$
. Then
![]() $\gamma b = \gamma $
implies
$\gamma b = \gamma $
implies
![]() $\gamma g_{1}g_{4}=\gamma t_{1}=\gamma t_{2}=\gamma g_{2}g_{4}=\gamma b^{-1}g_{1}bg_{4}=\gamma g_{1}bg_{4}$
and thus
$\gamma g_{1}g_{4}=\gamma t_{1}=\gamma t_{2}=\gamma g_{2}g_{4}=\gamma b^{-1}g_{1}bg_{4}=\gamma g_{1}bg_{4}$
and thus
![]() $\gamma g_{1} b = \gamma g_{1}$
. Hence,
$\gamma g_{1} b = \gamma g_{1}$
. Hence,
![]() $\gamma t_{3}=\gamma g_{3}g_{4}=\gamma b^{-2}g_{1}b^{2}g_{4}=\gamma g_{1}b^{2}g_{4}=\gamma g_{1}g_{4}=\gamma t_{1}$
. This shows that
$\gamma t_{3}=\gamma g_{3}g_{4}=\gamma b^{-2}g_{1}b^{2}g_{4}=\gamma g_{1}b^{2}g_{4}=\gamma g_{1}g_{4}=\gamma t_{1}$
. This shows that
![]() $\gamma t_{1}=\gamma t_{2}=\gamma t_{3} \in L_{1} \cap L_{2} \cap L_{3}$
and we see that if any two of the vertices
$\gamma t_{1}=\gamma t_{2}=\gamma t_{3} \in L_{1} \cap L_{2} \cap L_{3}$
and we see that if any two of the vertices
![]() $\gamma t_{1}, \gamma t_{2}$
and
$\gamma t_{1}, \gamma t_{2}$
and
![]() $\gamma t_{3}$
are equal, then all three are equal. In particular, they are contained in
$\gamma t_{3}$
are equal, then all three are equal. In particular, they are contained in
![]() $L_{1} \cap L_{2} \cap L_{3}$
.
$L_{1} \cap L_{2} \cap L_{3}$
.
Next we prove that if
![]() $\gamma t_{1} = \gamma t_{2} = \gamma t_{3}$
then
$\gamma t_{1} = \gamma t_{2} = \gamma t_{3}$
then
![]() $\gamma \in F$
. Let
$\gamma \in F$
. Let
![]() $g\in B$
. By Claim 3 there are
$g\in B$
. By Claim 3 there are
![]() $g^{\prime }, g^{\prime \prime }\in B$
with
$g^{\prime }, g^{\prime \prime }\in B$
with
![]() $g_{4}g=g^{\prime }g_{4}$
and
$g_{4}g=g^{\prime }g_{4}$
and
![]() $g_{1}g^{\prime }=g^{\prime \prime }g_{i}$
for some
$g_{1}g^{\prime }=g^{\prime \prime }g_{i}$
for some
![]() $i\in \{1, 2, 3\}$
. Recall that
$i\in \{1, 2, 3\}$
. Recall that
![]() $\gamma g^{\prime \prime }=\gamma $
by definition of F. Hence
$\gamma g^{\prime \prime }=\gamma $
by definition of F. Hence
Thus
![]() $\gamma t_{1}$
is fixed by B and therefore
$\gamma t_{1}$
is fixed by B and therefore
![]() $\gamma t_{1}\in L_{1}\cap L_{2}\cap L_{3}\cap F$
.
$\gamma t_{1}\in L_{1}\cap L_{2}\cap L_{3}\cap F$
.
However,
![]() $t_{i}$
is a translation and F is finite. This implies that there exists a vertex
$t_{i}$
is a translation and F is finite. This implies that there exists a vertex
![]() $\gamma \in L_{1}\cap L_{2}\cap L_{3}\cap F$
such that
$\gamma \in L_{1}\cap L_{2}\cap L_{3}\cap F$
such that
![]() $\gamma t_{1}{\ \not \in \ } L_{1}\cap L_{2}\cap L_{3}\cap F$
. By the above
$\gamma t_{1}{\ \not \in \ } L_{1}\cap L_{2}\cap L_{3}\cap F$
. By the above
![]() $\gamma t_{1}, \gamma t_{2}$
and
$\gamma t_{1}, \gamma t_{2}$
and
![]() $\gamma t_{3}$
must all be different.
$\gamma t_{3}$
must all be different.
Claim 7 (see Figure 1). Let
![]() $\gamma $
be a vertex in
$\gamma $
be a vertex in
![]() $L_{1}\cap L_{2}\cap L_{3}\cap F$
such that
$L_{1}\cap L_{2}\cap L_{3}\cap F$
such that
![]() $\gamma t_{1}, \gamma t_{2}$
and
$\gamma t_{1}, \gamma t_{2}$
and
![]() $\gamma t_{3}$
are all different. There is a unique vertex
$\gamma t_{3}$
are all different. There is a unique vertex
![]() $\gamma ^{\prime }$
such that
$\gamma ^{\prime }$
such that
![]() $(\gamma ^{\prime },\gamma )$
is an arc which lies in the intersection
$(\gamma ^{\prime },\gamma )$
is an arc which lies in the intersection
![]() $L_{1}\cap L_{2}\cap L_{3}$
. Removing the edge
$L_{1}\cap L_{2}\cap L_{3}$
. Removing the edge
![]() $\{\gamma ,\gamma ^{\prime }\}$
would divide T into two connected components (‘half-trees’); let H be the component containing
$\{\gamma ,\gamma ^{\prime }\}$
would divide T into two connected components (‘half-trees’); let H be the component containing
![]() $\gamma $
. Set
$\gamma $
. Set
![]() $R = \{t_{1}, t_{2}, t_{3}\}$
and write
$R = \{t_{1}, t_{2}, t_{3}\}$
and write
![]() $R^{k} = \{s_{1}\cdots s_{k}\mid s_{1},\ldots , s_{k}\in \{t_{1},t_{2}, t_{3}\}\}$
for
$R^{k} = \{s_{1}\cdots s_{k}\mid s_{1},\ldots , s_{k}\in \{t_{1},t_{2}, t_{3}\}\}$
for
![]() $k \geq 0$
. Then for every
$k \geq 0$
. Then for every
![]() $r \in R^{k}$
with
$r \in R^{k}$
with
![]() $k \geq 1$
the vertex
$k \geq 1$
the vertex
![]() $\gamma r$
is contained in exactly one of
$\gamma r$
is contained in exactly one of
![]() $H t_{1}, H t_{2}$
and
$H t_{1}, H t_{2}$
and
![]() $H t_{3}$
. If
$H t_{3}$
. If
![]() $r = r^{\prime } t_{j}$
with
$r = r^{\prime } t_{j}$
with
![]() $r^{\prime } \in R^{k-1}$
, then
$r^{\prime } \in R^{k-1}$
, then
![]() $\gamma r \in H t_{j}$
.
$\gamma r \in H t_{j}$
.

Figure 1 The three translation axes splitting up.
Proof. Recall that
![]() $L_{1},L_{2}$
and
$L_{1},L_{2}$
and
![]() $L_{3}$
are two-way infinite arcs. By an abuse of notation we talk about the intersection
$L_{3}$
are two-way infinite arcs. By an abuse of notation we talk about the intersection
![]() $L_{1} \cap L_{2} \cap L_{3}$
as an s-arc for some
$L_{1} \cap L_{2} \cap L_{3}$
as an s-arc for some
![]() $s \geq 1$
. Thus
$s \geq 1$
. Thus
![]() $\gamma r^{\prime } \in H$
. Since
$\gamma r^{\prime } \in H$
. Since
![]() $\gamma t_{1}, \gamma t_{2}$
and
$\gamma t_{1}, \gamma t_{2}$
and
![]() $\gamma t_{3}$
are all different by assumption, the half-trees
$\gamma t_{3}$
are all different by assumption, the half-trees
![]() $H t_{1}$
,
$H t_{1}$
,
![]() $H t_{2}$
and
$H t_{2}$
and
![]() $H t_{3}$
are all disjoint. For every
$H t_{3}$
are all disjoint. For every
![]() $r^{\prime } \in R^{k-1}$
and
$r^{\prime } \in R^{k-1}$
and
![]() $i=1,2,3$
we have
$i=1,2,3$
we have
![]() $H r^{\prime } t_{i} \subseteq H t_{i}$
. This proves the claim.
$H r^{\prime } t_{i} \subseteq H t_{i}$
. This proves the claim.
Claim 8. For every
![]() $k\geq 0$
we have
$k\geq 0$
we have
![]() $\gamma R^{k} B = \gamma R^{k}$
.
$\gamma R^{k} B = \gamma R^{k}$
.
Proof. Note that
![]() $R^{1} = A^{\prime } g_{4}$
. The equation
$R^{1} = A^{\prime } g_{4}$
. The equation
![]() $R^{k} B = B R^{k}$
follows directly from Claim 3. Now we are done since
$R^{k} B = B R^{k}$
follows directly from Claim 3. Now we are done since
![]() $\gamma \in F$
.
$\gamma \in F$
.
Proof. Conclusion of proof
Think of T as a rooted tree with
![]() $\gamma $
as a root. We say that vertices
$\gamma $
as a root. We say that vertices
![]() $\alpha \neq \beta $
in T are siblings if they have a common neighbour, and this common neighbour is closer to
$\alpha \neq \beta $
in T are siblings if they have a common neighbour, and this common neighbour is closer to
![]() $\gamma $
than
$\gamma $
than
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. Since B is open, there exists a finite subtree
$\beta $
. Since B is open, there exists a finite subtree
![]() $F^{\prime }$
of T with
$F^{\prime }$
of T with
![]() $G_{(F^{\prime })}\leq B$
. It is possible to choose
$G_{(F^{\prime })}\leq B$
. It is possible to choose
![]() $F^{\prime }$
such that the vertex set of
$F^{\prime }$
such that the vertex set of
![]() $F^{\prime }$
consists of
$F^{\prime }$
consists of
![]() $\gamma $
and all vertices at distance at most
$\gamma $
and all vertices at distance at most
![]() $\ell $
from
$\ell $
from
![]() $\gamma $
for some number
$\gamma $
for some number
![]() $\ell $
. In particular, for all vertices
$\ell $
. In particular, for all vertices
![]() $\alpha \notin F^{\prime }$
, the orbit
$\alpha \notin F^{\prime }$
, the orbit
![]() $\alpha B$
contains all the siblings of
$\alpha B$
contains all the siblings of
![]() $\alpha $
. The automorphisms
$\alpha $
. The automorphisms
![]() $t_{1}, t_{2}, t_{3}$
are translations, so there is a number
$t_{1}, t_{2}, t_{3}$
are translations, so there is a number
![]() $k_{0} \geq 0$
such that four vertices that are siblings of each other are contained in
$k_{0} \geq 0$
such that four vertices that are siblings of each other are contained in
![]() $\gamma R^{k_{0}}B = \gamma R^{k_{0}}$
(see Claim 8). We assume that
$\gamma R^{k_{0}}B = \gamma R^{k_{0}}$
(see Claim 8). We assume that
![]() $k_{0}$
is minimal.
$k_{0}$
is minimal.
First we note that
![]() $k_{0}\neq 0$
because
$k_{0}\neq 0$
because
![]() $R^{0} = \{1\}$
. One can also exclude the possibility that
$R^{0} = \{1\}$
. One can also exclude the possibility that
![]() $k_{0}=1$
since
$k_{0}=1$
since
![]() $\gamma R^{1} = \{\gamma t_{1}, \gamma t_{2}, \gamma t_{3}\}$
has only three elements. Write
$\gamma R^{1} = \{\gamma t_{1}, \gamma t_{2}, \gamma t_{3}\}$
has only three elements. Write
![]() $\gamma _{1}, \gamma _{2}, \gamma _{3}, \gamma _{4}\in \gamma R^{k_{0}}$
for the four siblings. Thus there are elements
$\gamma _{1}, \gamma _{2}, \gamma _{3}, \gamma _{4}\in \gamma R^{k_{0}}$
for the four siblings. Thus there are elements
![]() $p_{1}, p_{2}, p_{3}, p_{4}\in R^{k_{0}-1}$
and
$p_{1}, p_{2}, p_{3}, p_{4}\in R^{k_{0}-1}$
and
![]() $s_{1}, s_{2}, s_{3}, s_{4}\in \{t_{1}, t_{2}, t_{3}\}$
such that
$s_{1}, s_{2}, s_{3}, s_{4}\in \{t_{1}, t_{2}, t_{3}\}$
such that
![]() $\gamma _{i}=\gamma p_{i} s_{i}$
. Since
$\gamma _{i}=\gamma p_{i} s_{i}$
. Since
![]() $k_{0}>1$
there is some
$k_{0}>1$
there is some
![]() $i\in \{1, 2, 3\}$
such that
$i\in \{1, 2, 3\}$
such that
![]() $\{\gamma _{1}, \gamma _{2}, \gamma _{3}, \gamma _{4}\}\subseteq H t_{i}$
; here we are using that the
$\{\gamma _{1}, \gamma _{2}, \gamma _{3}, \gamma _{4}\}\subseteq H t_{i}$
; here we are using that the
![]() $\gamma _{i}$
are siblings. Claim 7 implies that
$\gamma _{i}$
are siblings. Claim 7 implies that
![]() $s_{1}= s_{2}= s_{3}=s_{4}=t_{i}$
. Now
$s_{1}= s_{2}= s_{3}=s_{4}=t_{i}$
. Now
![]() $\gamma p_{1}, \gamma p_{2}, \gamma p_{3}, \gamma p_{4}$
are the images of the four siblings
$\gamma p_{1}, \gamma p_{2}, \gamma p_{3}, \gamma p_{4}$
are the images of the four siblings
![]() $\gamma _{1}, \gamma _{2}, \gamma _{3}, \gamma _{4}$
under the tree automorphism
$\gamma _{1}, \gamma _{2}, \gamma _{3}, \gamma _{4}$
under the tree automorphism
![]() $t_{i}^{-1}$
. In particular, because
$t_{i}^{-1}$
. In particular, because
![]() $k_{0} \geq 2$
, they are also siblings, and they are contained in
$k_{0} \geq 2$
, they are also siblings, and they are contained in
![]() $\gamma R^{k_{0}-1}$
. This means that
$\gamma R^{k_{0}-1}$
. This means that
![]() $k_{0}$
was not minimal, and we have reached our final contradiction.
$k_{0}$
was not minimal, and we have reached our final contradiction.
Acknowledgements
The seeds for this project were sown in 2014 during a visit by George Willis to the University of Iceland when he asked the third author about the minimal degree of a Cayley–Abels graph for a totally disconnected, locally compact group. Conversely, part of this work was completed when the second author was visiting George Willis at the University of Newcastle early in 2020. The second and third authors wish to thank Pierre-Emmanuel Caprace for helpful conversations.