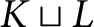1 Introduction
Let K be an abstract, finite simplicial complex. Forman’s discrete Morse theory [Reference Forman8, Reference Forman9] yields a method by which one can construct a gradient vector field on K. This can be used, for example, to compute the Betti numbers of K [Reference Forman8, Section 8]. The Morse complex of K, denoted
$\mathcal {M}(K)$
, was introduced by Chari and Joswig [Reference Chari and Joswig6] in 2005 as the simplicial complex of all gradient vector fields on K. The Morse complex of K is rich enough to reconstruct the isomorphism type of K as was shown by Capitelli and Minian [Reference Capitelli and Minian5]. Yet, it was shown by the same authors that the simple homotopy type of the Morse complex does not determine the simple homotopy type of K. In general, an explicit computation of the homotopy type of the Morse complex is known for only a handful of complexes. Kozlov determined the homotopy types of the Morse complexes of paths and cycles [Reference Kozlov12]. Other authors have looked at the complexes of discrete Morse functions generated by the maximum gradient vector fields, the so-called pure Morse complexes [Reference Ayala, Fernández, Quintero and Vilches1, Reference Chari and Joswig6]. Although some general connectivity bounds are known [Reference Scoville and Zaremsky15], determining the homotopy type of the Morse complex remains elusive, even for a complex as small as the
$3$
-simplex.
The goal of this paper is to compute the homotopy type of the Morse complex of several classes of simplicial complexes and to give a general sufficient condition that guarantees the Morse complex is collapsible. One tool we use to aid in our computation is that of a dominating vertex. If every maximal facet of vertex u also contains vertex v, then v is said to dominate u. In this case, all simplices of K containing u may be removed from K without changing the homotopy type. Such a removal is called a strong collapse. In fact, because it can be shown that a strong collapse is a sequence of collapses in Forman’s sense, removing or attaching dominated vertices creates a new notion of equivalence known as strong homotopy [Reference Barmak2, Reference Barmak and Minian3]. If there is a sequence of strong collapses from K to a vertex, then K is called strongly collapsible. We prove that the existence of two leaves attached to the same vertex on K guarantees that the resulting Morse complex is strongly collapsible and hence that its Morse complex has the homotopy type of a point. Proposition 3.6 shows that the pure Morse complex of a tree is strongly collapsible, extending a result of Ayala et al. [Reference Ayala, Fernández, Quintero and Vilches1].
We also show that the Morse complex of a disjoint union of K and L is the join of the Morse complexes of K and L. This result is used several times throughout this paper. If
$K=C_n\vee \ell $
where
$C_n$
is a cycle of length n and
$\ell $
is a leaf, we prove that the Morse complex of K collapses to the Morse complex of a disjoint union of a path of length
$n-1$
and path of length
$1$
. Using the result mentioned above along with Kozlov’s result, we then compute the homotopy type of the Morse complex of
$C_n\vee \ell $
. Furthermore, if G is any graph, we may attach a leaf to each vertex, forming a new graph
$L(G)$
. The centipede graph is one type of graph that is obtained in this way. We then show that the Morse complex of
$L(G)$
has the homotopy type of
$S^{|V(G)|-1}$
. Finally, we use the disjoint union result to compute the automorphism group of the Morse complex of the disjoint union for a large collection of complexes, continuing work begun in [Reference Lin and Scoville13], where a subset of the authors computed the automorphism group of the Morse complex of any connected simplicial complex K.
2 Background
In this section, we establish the notation, terminology, and background results that will be needed throughout this paper. All simplicial complexes are assumed to be connected unless otherwise stated. We use
$\simeq $
to denote a homotopy equivalence and
$\cong $
to denote an isomorphism.
2.1 Simplicial complexes and the Morse complex
Here, we recall some basic notions of simplicial complexes and the Morse complex. Our reference for simplicial complexes is [Reference Ferrario and Piccinini7] or [Reference Jonsson10], whereas references for discrete Morse theory and the Morse complex are found in [Reference Forman9, Reference Knudson11, Reference Scoville14]. We will also find it convenient to borrow some terms from graph theory [Reference Bickle4].
Definition 2.1 Let K be a simplicial complex. We use
$\sigma ^{(i)}$
to denote a simplex of dimension i, and we write
$\tau < \sigma ^{(i)}$
to denote any face of
$\sigma $
of dimension strictly less than i. In the special case of
$i=0$
, we write
$V(K):=\{\sigma ^{(0)}\in K\}$
and refer to
$V(K)$
as the vertex set of K. The degree of a vertex
$v\in V(K)$
, denoted
$\deg (v)$
, is the number of edges or
$1$
-simplices incident with v. If
$\deg (v)=1$
, we say that v is a leaf. The number
$\dim (\sigma )-\dim (\tau )$
is called the codimension of
$\tau $
with respect to
$\sigma $
. A simplex of K that is not properly contained in any other simplex of K is called a facet of K. If
$K,L$
are two simplicial complexes with
$v_0\in K$
and
$u_0\in L$
vertices, then the wedge or one-point union
$K\vee L$
is given by
$\frac {K\sqcup L}{v_0=u_0}$
.
We recall a few basic classes of simplicial complexes that we will utilize.
Definition 2.2 Let
$n\geq 0$
be an integer and define
$[v_n]:=\{v_0, v_1, \ldots , v_n\}$
. The simplicial complex
$\Delta ^n:=\mathcal {P}([v_n])$
is the n-simplex where
$\mathcal {P}([v_n])$
is the powerset of
$[v_n].$
Let
$P_n$
denote the simplicial complex on
$[n]$
with facets
$$ \begin{align*}\{v_0,v_1\}, \{v_1,v_2\}, \ldots, \{v_{n-1}, v_n\}, \end{align*} $$
i.e., the path of length n. A cycle of length
$n\geq 3$
on
$[v_{n-1}]$
is the simplicial complex
$C_n$
with facets
$\{v_0,v_1\}, \{v_1,v_2\}, \ldots , \{v_{n-2}, v_{n-1}\}, \{v_{n-1}, v_0\}$
.
Definition 2.3 Let K be a simplicial complex. A discrete vector field V on K is defined by
$$ \begin{align*}V:=\{(\sigma^{(p)}, \tau^{(p+1)}) : \sigma< \tau, \text{ each simplex of } K \text{ in at most one pair}\}. \end{align*} $$
Any pair in
$(\sigma ,\tau )\in V$
is called a regular pair, and
$\sigma , \tau $
are called regular simplices or just regular. If
$(\sigma ^{(p)},\tau ^{(p+1)})\in V$
, we say that
$p+1$
is the index of the regular pair. Any simplex in K which is not in V is called critical.
Definition 2.4 Let V be a discrete vector field on a simplicial complex K. A V-path or gradient path is a sequence of simplices
$$ \begin{align*}\alpha^{(p)}_0, \beta^{(p+1)}_0, \alpha^{(p)}_1, \beta^{(p+1)}_1, \alpha^{(p)}_2,\ldots , \beta^{(p+1)}_{k-1}, \alpha^{(p)}_{k}\end{align*} $$
of K such that
$(\alpha ^{(p)}_i,\beta ^{(p+1)}_i)\in V$
and
$\beta ^{(p+1)}_i>\alpha _{i+1}^{(p)}\neq \alpha _{i}^{(p)}$
for
$0\leq i\leq k-1$
. If
$k\neq 0$
, then the V-path is called non-trivial. A V-path is said to be closed if
$\alpha _{k}^{(p)}=\alpha _0^{(p)}$
. A discrete vector field V which contains no nontrivial closed V-paths is called a gradient vector field. We sometimes use f to denote a gradient vector field.
If the gradient vector field f consists of only a single element, we call f a primitive gradient vector field. Given multiple primitive gradient vector fields, we may combine them to form new gradient vector fields.
If
$f,g$
are two gradient vector fields on K, write
$g\leq f$
whenever the regular pairs of g are also regular pairs of f. In general, we say that a collection of primitive gradient vector fields
$f_0, f_1, \ldots , f_n$
is compatible if there exists a gradient vector field f such that
$f_i\leq f$
for all
$0\leq i\leq n$
.
Definition 2.5 The Morse complex of K, denoted
$\mathcal {M}(K)$
, is the simplicial complex whose vertices are given by primitive gradient vector fields and whose n-simplices are given by gradient vector fields with
$n+1$
regular pairs. A gradient vector field f is then associated with the set of
$n+1$
primitive gradient vector fields by taking their union. We write
$f:=\{f_0, \ldots , f_n\}$
and use
$f_i\leq f$
to denote
$f_i\in f$
.
Example 2.1 As a simple example, we find the Morse complex of the following complex K:
There are four primitive gradient vector fields, namely,
$(u,uv), (w,vw), (v,uv)$
, and
$(v,vw)$
along with compatibilities
$V_1=\{(u,uv), (v,vw)\}, V_2=\{(w,vw), (v,uv)\}$
, and
$V_3=\{(u,uv), (w,vw)\}$
. Hence, the Morse complex is given by
Remark 2.2 If
$(u,vu)$
is a primitive gradient vector field, we sometimes denote this as
$(u)v$
, and if
$(vw, vwu)$
is a primitive gradient vector field, we sometimes denote this as
$(vw)u$
.
Remark 2.3 There is an equivalent definition of the Morse complex. Let K be a simplicial complex and define the Hasse diagram of K, denoted
$\mathcal {H}(K)$
, to be the directed graph whose vertex set corresponds to the simplices of K and a directed edge from vertex y to vertex x whenever
$y\geq x$
and there is no z such that
$x \leq z \leq y$
. The Morse complex of K may then alternatively be defined as the simplicial complex whose simplices are given by nonempty subsets of edges of
$\mathcal {H}(K)$
such that the reverse orientation of these edges do not create a directed loop. It is not difficult to see that this definition is equivalent to Definition 2.5. We will generalize this Hasse diagram definition of the Morse complex in Definition 5.1.
2.2 Strong collapsibility
In this section, we review the basics of dominating vertices and strong collapsibility. Many of the ideas in this section are originally due to Barmak [Reference Barmak2, Reference Barmak and Minian3].
Definition 2.6 Let K be a simplicial complex. A vertex v is said to dominate
$v'$
(it is also said that
$v'$
is dominated by v) if every facet of
$v'$
also contains v.
We use the notation
$K-\{v'\}:=\{\sigma \in K: v'\not \in \sigma \}$
.
Definition 2.7 If v dominates
$v'$
, then the removal of
$v'$
from K is called an elementary strong collapse and is denoted by
$K\searrow \searrow K-\{v'\}$
. The addition of a dominated vertex is an elementary strong expansion, and is denoted
$\nearrow \nearrow $
. A sequence of elementary strong collapses or elementary strong expansions is also called a strong collapse or strong expansion, respectively, and also denoted
$\nearrow \nearrow $
or
$\searrow \searrow $
, respectively. If there is a sequence of strong collapses and expansions from K into L, then K and L are said to have the same strong homotopy type, denoted
$K\approx L.$
In particular, if
$L=*$
, then K is said to have the strong homotopy type of a point. If there is a sequence of elementary strong collapses from K to a point, K is called strongly collapsible.
Remark 2.4 Since a strong collapse is a sequence of collapses, it follows that if a complex is strongly collapsible, then it is collapsible and hence has the homotopy type of a point.
Call a simplicial complex K minimal if it contains no dominating vertices.
Example 2.5 The following simplicial complex is minimal because it has no dominating vertices.
Note, however, that K is collapsible as well as contractible.
Definition 2.8 Let K be a simplicial complex. The core of K is the minimal subcomplex
$K_0 \subseteq K$
such that
$K\searrow \searrow K_0$
.
By [Reference Barmak2, Theorem 5.1.10], the use of the definite article “the” in Definition 2.8 is justified. It follows immediately that the order in which one performs strong collapses on a complex K does not matter, as any sequence of strong collapses of K will eventually yield
$K_0$
.
One construction that is particularly well behaved with respect to strong collapses is the join.
Definition 2.9 Let
$K,L$
be two simplicial complexes with no vertices in common. Define the join of K and L, denoted
$K*L$
, by
$$ \begin{align*}K*L:= \{\sigma, \tau, \sigma\cup \tau : \sigma \in K, \tau \in L\}.\end{align*} $$
The special case when
$L=\{v,w\}$
for vertices
$v,w\not \in K$
is the suspension
$\Sigma K$
of K.
If one of the factors in the join is strongly collapsible, then the join is strongly collapsible.
Proposition 2.6 [Reference Barmak2, Proposition 5.1.16]
Let
$K, L$
be simplicial complexes. Then
$K*L$
is strongly collapsible if and only if K or L is strongly collapsible.
3 Strong Collapsibility of
$\mathcal {M}(K)$
This section is devoted to determining when the Morse complex is strongly collapsible. We first give a general condition on K that guarantees
$\mathcal {M}(K)$
is not strongly collapsible in Proposition 3.3.
3.1 Minimal Morse complexes
Lemma 3.1 Let K be a simplicial complex. If
$(\sigma _1^{(p)},\tau ^{(p+1)}) \in V(\mathcal {M}(K))$
dominates some other vertex
$(\alpha , \beta ) \in \mathcal {M}(K)$
, then
$p = 0$
.
Proof Suppose that
$p> 0$
. Since
$\tau $
is of dimension
$p+1$
, it has exactly
$p+2$
codimension 1 faces (including
$\sigma _1$
), say
$\sigma _1, \sigma _2, \ldots , \sigma _{p+2}.$
These may be paired with
$\tau $
to create a primitive vector field
$(\sigma _i,\tau )$
on K which in turn corresponds to vertices
$$ \begin{align*}(\sigma_1, \tau), (\sigma_2,\tau) ,(\sigma_3,\tau), \dots , (\sigma_{p+2},\tau) \in V(\mathcal{M}(K)).\end{align*} $$
Notice that
$(\sigma _1,\tau )$
is not compatible with any of these vertices. Thus, no facet of
$(\alpha , \beta )$
contains any of those
$p+2$
vertices so that
$(\alpha , \beta )$
must be incompatible with those
$p+2$
vertices. Since
$(\alpha ,\beta )$
is incompatible with
$(\sigma _2, \tau )$
, exactly one of the following must occur:
-
(i)
$\alpha = \sigma _2$
. -
(ii)
$\beta = \sigma _2$
. -
(iii)
$\alpha = \tau $
. -
(iv)
$\beta = \tau $
.
Now, if either (iii) or (iv) holds, then
$(\alpha , \beta )$
will not be compatible with
$(\sigma _1, \tau )$
. Therefore, either (i) or (ii) must hold. We proceed by cases.
Case 1:
$\alpha = \sigma _2$
. Then
$(\alpha , \beta ) = (\sigma _2, \beta )$
where
$\beta \neq \tau $
. This implies that
$(\alpha , \beta )$
is compatible with
$(\sigma _3, \tau )$
, a contradiction.
Case 2:
$\beta = \sigma _2$
. Then
$(\alpha , \beta ) = (\alpha , \sigma _2)$
. We must have
$\dim \alpha = \dim \sigma _2 - 1 = p-1$
. Therefore,
$\alpha \neq \sigma _3$
, so
$(\alpha , \beta )$
is compatible with
$(\sigma _3, \tau )$
, again a contradiction.
We conclude that no such vertex
$(\sigma _1,\tau )$
exists for
$p>0$
.▪
Remark 3.2 Although a dominating vertex in
$\mathcal {M}(K)$
cannot come from a vector of index greater than
$1$
, if
$\dim \sigma _1 = 0$
, it is possible for
$(\sigma _1, \tau )$
to dominate another vertex. In our proof, we required that
$\tau $
have at least three faces of codimension
$1$
, but if
$\dim \tau = 1$
, there are only two faces of codimension
$1$
. A simple example is
$K=$
We saw in Example 2.1 that the Morse complex is given by:
In this case, vertex
$(v,vw)$
dominates
$(u,uv)$
.
Proposition 3.3 Let K be a simplicial complex. If all vertices
$v \in V(K)$
have degree at least
$2$
, then
$\mathcal {M}(K)$
is minimal. In particular,
$\mathcal {M}(K)$
is not strongly collapsible.
Proof By Lemma 3.1, in order to show that no vertex in
$\mathcal {M}(K)$
dominates any other, we need only consider vertices in
$\mathcal {M}(K)$
which correspond to a primitive vector of index
$1$
. Hence, consider any vertex
$(v)a \in V(\mathcal {M}(K))$
where
$v,a \in V(K)$
. We claim that
$(v)a$
cannot dominate any other vertex of
$\mathcal {M}(K)$
. Suppose
$w \in V(\mathcal {M}(K))$
is any vertex with a facet
$\sigma $
that also contains
$(v)a$
. Since v has degree at least
$2$
, there exists a vertex
$b\in V(K)$
,
$b\neq a$
, such that
$vb$
is a simplex of K. This gives rise to the primitive vector
$(v)b$
which is also a vertex of
$\mathcal {M}(K)$
. If
$w = (b)v$
, then w is compatible with
$(a)v$
, so
$(v)a$
cannot dominate w. Now, consider
$w \neq (b)v$
. Then since w is compatible with
$(v)a$
, it must also be compatible with
$(v)b$
. Clearly,
$w \in \sigma - \{(v)a, (v)b\}$
so that there is a facet of w that contains
$\sigma - \{(v)a\} \cup \{(v)b\}$
as a face. Then w has a facet that does not contain
$(v)a$
, so
$(v)a$
does not dominate w. As this holds for any
$(v)a \in V(\mathcal {M}(K))$
, no vertex of
$\mathcal {M}(K)$
can dominate another vertex. It follows that
$\mathcal {M}(K)$
is minimal.▪
Corollary 3.4 If
$\mathcal {M}(K)$
is not minimal, there exists at least one vertex
$v \in K$
with degree
$1$
.
3.2 Leaves and strong collapsibility
By Proposition 3.3, if K does not contain a leaf, then
$\mathcal {M}(K)$
is minimal (and in particular, not strongly collapsible). On the other hand, if K has two leaves that share a common vertex,
$\mathcal {M}(K)$
is strongly collapsible.
Proposition 3.5 If K has two leaves sharing a vertex, then
$\mathcal {M}(K)$
is strongly collapsible.
Proof Call the leaves
$\{a,ab\}$
and
$\{a,ac\}$
where
$a,b,c \in V(K)$
. These correspond to vertices
$(a)b,(b)a,(a)c,(c)a \in V(\mathcal {M}(K))$
. We claim that
$(b)a$
dominates
$(a)c$
. Consider any facet
$\sigma $
of
$(a)c$
. The only vertex incompatible with
$(b)a$
is
$(a)b$
, but since
$(a)c$
and
$(a)b$
are incompatible,
$(a)b \not \in \sigma $
. Therefore, we must have
$(b)a \in \sigma $
since
$\sigma $
is maximal. Perform the strong collapse given by removing vertex
$(a)c$
. We claim that
$(c)a$
dominates every vertex in the resulting complex. Consider an arbitrary
$v \in V(\mathcal {M}(K)) - (a)c$
and a facet
$\tau $
containing v. The only vertex that
$(c)a$
is incompatible with in
$V(\mathcal {M}(K))$
is
$(a)c$
. Since
$(a)c \not \in V(\mathcal {M}(K)) - (a)c$
, we know that
$(c)a$
is compatible with every vertex in
$\tau $
, so
$(c)a \in \tau $
. Therefore,
$(c)a$
dominates v. We repeatedly apply the strong collapse removing each vertex v, strongly collapsing the Morse complex to
$(c)a$
.▪
Recall that the pure Morse complex of K, denoted
$\mathcal {M}_P(K)$
, is the subcomplex of
$\mathcal {M}(K)$
generated by the maximum facets of dimension
$\dim (\mathcal {M}(K))$
where a facet
$\sigma $
is maximum if
$\dim (\sigma )\geq \dim (\tau )$
for every simplex
$\tau $
, i.e., the complex generated by the maximum gradient vector fields on K. A simplex is maximal if it is not contained in any other simplex. Ayala et al. [Reference Ayala, Fernández, Quintero and Vilches1] showed that
$\mathcal {M}_P(T)$
is collapsible where T is a tree. We generalize this result by showing that
$\mathcal {M}_P(T)$
is strongly collapsible. The result of Ayala et al. then follows as an immediate corollary.
Proposition 3.6 Let T be a tree. Then
$\mathcal {M}_P(T)$
is strongly collapsible.
Proof Let T be a tree. By definition, T has at least one leaf, say
$\{a, ab\}$
. We will show that
$(b)a$
is dominated and that after removing
$(b)a$
from
$\mathcal {M}_P(T)$
, then
$(a)b$
dominates all remaining primitive gradient vector fields, and hence
$\mathcal {M}_P(T)$
is strongly collapsible.
Let
$bc$
be an edge incident with b with
$c\neq a$
. We claim that
$(b)a$
is dominated by
$(c)b$
in
$\mathcal {M}_P(T)$
. Suppose
$\sigma \in \mathcal {M}_P(T)$
is a facet containing
$(b)a$
. Then
$\sigma $
is a maximal gradient vector of T, and since
$\sigma $
is in the pure Morse complex,
$\sigma $
is also maximum. Since
$(b)a\in \sigma $
with a a leaf,
$\sigma $
is the only maximum gradient vector field containing
$(b)a$
and thus is dominated by
$(c)b$
(and in fact every primitive gradient vector field of
$\sigma $
). Since
$(b)a$
is dominated, we may perform a strong elementary collapse and remove it from
$\mathcal {M}_P(T)$
.
Now, we claim
$(a)b$
dominates all remaining primitive gradient vector fields. Note that since
$(b)a\not \in \mathcal {M}_P(T)-\{(b)a\}$
,
$(a)b$
is compatible with
$(\alpha )\beta \in \mathcal {M}_P(T)-\{(b)a\}$
. Thus,
$(a)b$
dominates
$(\alpha )\beta $
for all other
$(\alpha )\beta \in \mathcal {M}_P(T)-\{(b)a\}$
so that
$\mathcal {M}_P(T)-\{(b)a\}$
is a cone and thus strongly collapsible.▪
We then recover the result mentioned above.
Corollary 3.7 Let T be a tree. Then
$\mathcal {M}_P(T)$
is collapsible.
Let
$P_t$
denote the path consisting of
$t+1$
vertices
$v_0, v_1, \dots , v_{t}$
with
$v_{i}$
adjacent to
$v_{i+1}$
for
$0 \leq i \leq t-1$
. We slightly strengthen Kozlov’s computation [Reference Kozlov12, p. 119] by showing that a path on
$3n$
vertices is strongly collapsible. First a lemma that will prove useful.
Lemma 3.8 Let K be a simplicial complex with leaf
$\{a, ab\}$
and c a neighbor of b not equal to a. Then
$(b)c$
is dominated in
$\mathcal {M}(K)$
by
$(a)b$
.
Proof Consider any facet of
$(b)c$
in
$\mathcal {M}(K)$
. A facet of
$\mathcal {M}(K)$
is a maximal gradient vector field on K, and since
$(b)a$
is not compatible with
$(b)c$
and
$\{a,ab\}$
is a leaf,
$(a)b$
must be in any maximal gradient vector field containing
$(b)c$
. Thus
$(a)b$
dominates
$(b)c$
in
$\mathcal {M}(K)$
.▪
Proposition 3.9 Let
$P_{3n-1}$
be the path on
$3n$
vertices,
$n\geq 1$
. Then
$\mathcal {M}(P_t)\searrow \searrow *$
.
Proof By Lemma 3.8,
$(v_1)v_2$
dominates
$(v_2)v_3$
. After removing
$(v_2)v_3$
, we see that
$(v_3)v_2$
dominates
$(v_4)v_3$
, and so we remove
$(v_4)v_3$
. Continuing in this manner, we see that
$(v_{3k-2})v_{3k-1}$
dominates
$(v_{3k-1})v_{3k}$
for all
$1\leq k \leq n$
, and
$(v_{3k})v_{3k-1}$
dominates
$(v_{3k+1})v_{3k}$
for all
$1\leq k <n$
. Hence, we may remove each of these primitive gradient vector fields.
Now, the last primitive gradient vector field removed is
$(v_{3n-1})v_{3n}$
because it was dominated by
$(v_{3n-2})v_{3n-1}$
. We now claim that
$(v_{3n})v_{3n-1}$
dominates every remaining vertex. To see this, observe that because
$(v_{3n-1})v_{3n}$
has been removed,
$(v_{3n})v_{3n-1}$
is compatible with all remaining vertices
$(v_i)v_j$
, and no
$(v_i)v_j$
can exist in a facet of the remaining Morse complex without
$(v_{3n})v_{3n-1}$
. We remove all
$(v_i)v_j$
until we are only left with
$(v_{3n})v_{3n-1}$
. Thus
$\mathcal {M}(P_{3n-1})$
is strongly collapsible.▪
4 Morse complex of the disjoint union
Before using strong collapses to compute the homotopy type of the Morse complex of some other families of graphs, we need a result, interesting in its own right, about the Morse complex of a disjoint union. This result will be used in Section 5 as well as in Section 6 where we investigate the automorphism group of the Morse complex of a disjoint union.
Lemma 4.1 If
$A\subseteq B$
, then
$\mathcal {M}(A)\subseteq \mathcal {M}(B)$
.
Proof Consider any primitive pair
$(\sigma , \tau ) \in V(\mathcal {M}(A))$
where
$\sigma ,\tau \in A$
. Then we have
$\sigma ,\tau \in B$
, and thus
$(\sigma , \tau ) \in V(\mathcal {M}(B))$
, so
$V(\mathcal {M}(A)) \subseteq V(\mathcal {M}(B))$
. Now, consider any simplex
$\sigma = \sigma _1\sigma _2\cdots \sigma _m \in \mathcal {M}(A)$
. Since all of the vertices
$\sigma _1, \sigma _2, \dots , \sigma _m$
are compatible in
$\mathcal {M}(A)$
and are vertices in
$\mathcal {M}(B)$
, they must also be compatible in
$\mathcal {M}(B)$
. Therefore,
$\sigma \in \mathcal {M}(B)$
.▪
Proposition 4.2 Let
$K,L$
be connected simplicial complexes each with at least one edge. Then
$\mathcal {M}(K\sqcup L)= \mathcal {M}(K)\ast \mathcal {M}(L)$
.
Proof Assume without loss of generality that K and L are disjoint. We first claim that
$V(\mathcal {M}(K\cup L)) = V(\mathcal {M}(K)\ast \mathcal {M}(L))$
. Notice
$V(\mathcal {M}(K)\ast \mathcal {M}(L)) = V(\mathcal {M}(K)) \cup V(\mathcal {M}(L))$
since the join operation does not create or remove any vertices. Consider any pair
$(\sigma ,\tau ) \in V(\mathcal {M}(K\cup L))$
. Then since K and L are disjoint, we have
$\sigma ,\tau \in K$
or
$\sigma , \tau \in L$
. Therefore,
$(\sigma ,\tau ) \in V(\mathcal {M}(K))$
or
$(\sigma ,\tau )\in V(\mathcal {M}(L))$
, so
$(\sigma ,\tau ) \in V(\mathcal {M}(K))\cup V(\mathcal {M}(L))$
. Thus,
$V(\mathcal {M}(K\cup L))\subseteq V(\mathcal {M}(K)) \cup V(\mathcal {M}(L))$
.
Now, consider any
$(\alpha ,\beta ) \in V(\mathcal {M}(K)\ast \mathcal {M}(L))$
. Then
$(\alpha ,\beta ) \in V(\mathcal {M}(K)) $
or
$(\alpha ,\beta ) \in V(\mathcal {M}(L))$
. Without loss of generality suppose
$(\alpha ,\beta ) \in V(\mathcal {M}(K)) $
. By Lemma 4.1, we have
$(\alpha ,\beta ) \in V(\mathcal {M}(K\cup L))$
. Thus,
$V(\mathcal {M}(K)) \cup V(\mathcal {M}(L))\subseteq V(\mathcal {M}(K\cup L))$
, so that
$V(\mathcal {M}(K)) \cup V(\mathcal {M}(L))= V(\mathcal {M}(K\cup L))$
.
To show that
$\mathcal {M}(K \cup L) = \mathcal {M}(K) \ast \mathcal {M}(L)$
, consider any simplex
$\sigma \in \mathcal {M}(K \cup L)$
. Write
$\sigma = \alpha \cup \beta $
, where
$\alpha = \alpha _1\alpha _2\cdots \alpha _a$
and
$\beta = \beta _1\beta _2\cdots \beta _b$
, in which each
$\alpha _i = (\sigma _i, \tau _i)$
where
$\sigma _i,\tau _i \in K$
, for
$i=1, 2, \dots , a$
, and
$\beta _j = (\gamma _j, \delta _j)$
where
$\gamma _j,\delta _j \in L$
, for
$j=1, 2, \dots , b$
. Notice that
$\alpha \in \mathcal {M}(K \cup L)$
. Thus,
$\alpha $
is also a gradient vector field of
$K\cup L$
. Moreover, since all
$\alpha _i\in \alpha $
are pairs of simplices of K, this gradient vector field consists solely of primitive gradient vector fields in K. Thus,
$\alpha \in \mathcal {M}(K)$
. By the same reasoning,
$\beta \in \mathcal {M}(L)$
. Thus, it follows that
$\sigma = \alpha \cup \beta \in \mathcal {M}(K)\ast \mathcal {M}(L)$
. Hence,
$\mathcal {M}(K \cup L) \subseteq \mathcal {M}(K) \ast \mathcal {M}(L).$
Now, suppose that
$\tau \in \mathcal {M}(K) \ast \mathcal {M}(L)$
. Since
$\tau \in \mathcal {M}(K) \ast \mathcal {M}(L)$
, write
$\tau = a \cup b$
, for simplices
$a \in \mathcal {M}(K)$
and
$b \in \mathcal {M}(L)$
. This implies that all vertices in a are compatible with each other, and similarly for b. Since
$K \cap L = \emptyset $
, we know that in
$M(K\cup L)$
, every vertex in
$V(K)$
is compatible with every vertex in
$V(L)$
. It follows that all vertices in
$a\cup b$
are pairwise compatible in
$M(K \cup L)$
. It remains to show that
$a\cup b$
does not correspond to a cyclic matching of the induced directed Hasse diagram
$\mathcal {H}(K\cup L)$
. Since
$K \cap L = \emptyset $
, any cycle in
$\mathcal {H}(K\cup L)$
must be contained entirely in its subgraphs
$\mathcal {H}(K)$
or
$\mathcal {H}(L)$
. This would imply at least one of a or b corresponds to a cyclic matching of
$\mathcal {H}(K)$
or
$\mathcal {H}(L)$
, respectively. However, since
$a \in \mathcal {M}(K)$
and
$b \in \mathcal {M}(L)$
, we know that is not the case. We conclude that
$a\cup b$
corresponds to an acyclic matching of
$\mathcal {H}(K\cup L)$
, and thus
$a\cup b \in \mathcal {M}(K\cup L)$
. Hence,
$ \mathcal {M}(K) \ast \mathcal {M}(L)\subseteq \mathcal {M}(K \cup L) $
. We conclude that
$\mathcal {M}(K \cup L) = \mathcal {M}(K) \ast \mathcal {M}(L)$
.▪
Corollary 4.3 Let K be a simplicial complex. Then
$\mathcal {M}(K\sqcup P_1)\simeq \Sigma \mathcal {M}(K).$
Example 4.4 Although the collection of Morse complexes is closed under joins, not every join is realized as a Morse complex. For example, let
$K:=\{a,b,c,ab,bc\}$
and
$L:=\{u,v,uv\}$
, so that the join
$K*L$
is given by
Suppose
$K*L=\mathcal {M}(N)$
for some simplicial complex N. If N contains a
$2$
-simplex, then there are at least nine primitive gradient vector fields on N, and hence at least nine vertices in
$\mathcal {M}(N)$
, a contradiction. Hence, N must be a graph. But the number of primitive gradient vector fields on a graph is even, again a contradiction. Thus,
$K*L$
is not the Morse complex of any simplicial complex.
In addition, there are simplicial complexes K such that
$\Sigma K \neq \mathcal {M}(L)$
for any L. A similar argument to the one above shows that
$\Sigma \Delta ^2\neq \mathcal {M}(K)$
for any simplicial complex K.
5 Morse complex of some families of graphs
Our main goal in this section is to compute the homotopy type of the Morse complex of several families of graphs by strongly collapsing the Morse complex to the Morse complex of a disjoint union and applying Proposition 4.2. This is in part accomplished through an interesting observation concerning the role of strong collapses in certain Morse complexes. We begin with an example.
5.1 The Morse complex of cycles wedge a leaf
Example 5.1 Let
$C_3$
be the cycle on three vertices:
Since
$C_3$
contains no leaves,
$\mathcal {M}(C_3)$
is not strongly collapsible. However, if we attach a single leaf to any vertex, it can be shown that the resulting Morse complex strongly collapses to the Morse complex of the disjoint union of the path of length one and the path of length two which strongly collapses to a point. Evidently, the sequence of strong collapses can be written as:
We will prove in Proposition 5.6 that the Morse complex of a cycle wedged with a leaf strongly collapses to the Morse complex of a disjoint union of paths. This, along with other results, will be used in Theorem 5.8 to prove that
$$ \begin{gather*} \mathcal{M}(C_n\vee \ell) \simeq {\begin{cases} *, &\text{if } n=3k, \\ S^{2k}, &\text{if } n = 3k+1, \\ S^{2k+1}, &\text{if } n=3k+2,\\ \end{cases} } \end{gather*} $$
where
$\ell $
is a path of length 1.
Definition 5.1 Given a finite poset P, construct a simplicial complex
$f(P)$
as follows: The vertex set of
$f(P)$
is the edge set of the Hasse diagram
$\mathcal {H}(P)$
of P. Then let
$\sigma = e_1e_2 \cdots e_k$
be a simplex of
$f(P)$
if and only if the edges
$e_1, e_2, \ldots , e_k$
oriented upward and all other edges oriented downward form an acyclic matching of P.
Remark 5.2 Viewing the Morse complex as defined in Remark 2.3, note that for any simplicial complex K,
$\mathcal {M}(K) \simeq f(\mathcal {H}(K))$
. Our definition thus generalizes the notion of taking the Morse complex of Hasse diagrams not induced by a simplicial complex. We will similarly call
$f(P)$
the Morse complex of the poset P.
Given Remark 5.2 and Proposition 4.2, we also have the following.
Corollary 5.3 Let
$A,B$
be posets. Then
$f(\mathcal {H}(A)\sqcup \mathcal {H}(B)) \simeq f(\mathcal {H}(A))\ast f(\mathcal {H}(B))$
.
Let
$K\vee _v \ell $
denote attaching a leaf
$\ell $
to a vertex
$v\in K$
. We use
$K\vee \ell $
when there is no need to make reference to the vertex.
Lemma 5.4 For any simplicial complex K and vertex
$v \in V(K)$
, the Morse complex
$\mathcal {M}(K \vee _v \ell )$
strongly collapses to
$f((\mathcal {H}(K)-v) \sqcup \mathcal {H}(\ell ))$
.
Proof Write
$\ell =vw$
for some vertex w, and let
$a_1, a_2, \dots , a_k$
be the neighbors of v. By Lemma 3.8, the vertex
$(w,wv)$
dominates vertices
$(v,va_1), (v,va_2), \dots , (v,va_k)$
, leading to k strong collapses. In the Hasse diagram
$\mathcal {H}(K \vee \ell )$
, this corresponds to a removal of the edges connecting node v to nodes
$va_1,va_2, \dots , va_k$
. As these are all the edges in K that v is connected to, the Hasse diagram now consists of
$\mathcal {H}(K)$
with node v removed, together with a second component consisting of the Hasse diagram of the leaf
$vw$
. The entire Hasse diagram is
$(\mathcal {H}(K)-v) \sqcup \mathcal {H}(\ell )$
. Therefore,
$\mathcal {M}(K \vee _v \ell ) \searrow \searrow f((\mathcal {H}(K)-v) \sqcup \mathcal {H}(\ell ))$
.▪
Let
$\partial \Delta ^{n}$
be the boundary of the n-simplex on the vertices
$\{v_0, v_1, \ldots , v_n\}$
, and write
$\delta :=v_0v_1\cdots v_{n}$
. Define the reflection map [Reference Lin and Scoville13]
$\pi _n=\pi \colon \partial \Delta ^n \to \partial \Delta ^n$
by
$\pi (\sigma ) := \delta - \sigma $
. Note that the reflection map is not a simplicial map.
Proposition 5.5 Let v be a vertex of
$\partial \Delta ^n$
. Then
$$ \begin{align*}\mathcal{M}(\partial\Delta^n \vee_v \ell) \searrow \searrow \mathcal{M}( (\partial\Delta^n - \pi(v))\sqcup \ell).\end{align*} $$
Proof By Lemma 5.4,
$\mathcal {M}(\partial \Delta ^n \vee _v \ell ) \searrow \searrow f((\mathcal {H}(\partial \Delta ^n) - v) \sqcup \mathcal {H}(\ell ))$
. By Corollary 5.3, we have
$$ \begin{align*}f((\mathcal{H}(\partial\Delta^n) - v) \sqcup \mathcal{H}(\ell)) \simeq f(\mathcal{H}(\partial\Delta^n)-v) \ast f(\mathcal{H}(\ell)),\end{align*} $$
and since
$f(\mathcal {H}(\ell ))=\mathcal {M}(\ell )$
by Remark 5.2, we have
$$ \begin{align*}f(\mathcal{H}(\partial\Delta^n)-v) \ast f(\mathcal{H}(\ell))= f(\mathcal{H}(\partial\Delta^n)-v) \ast \mathcal{M}(\ell).\end{align*} $$
The same argument shows that
$\mathcal {M}( (\partial \Delta ^n - \pi (v))\sqcup \ell ) \searrow \searrow f(\mathcal {H}( \partial \Delta ^n) - \pi (v)) \ast \mathcal {M}(\ell )$
. It thus suffices to show that
$$ \begin{align*}f(\mathcal{H}(\partial\Delta^n)-v) \simeq f(\mathcal{H}( \partial\Delta^n) - \pi(v)).\end{align*} $$
Now,
$\pi _n$
is a bijection, and since all
$v\in \mathcal {H}(\partial \Delta ^n)$
are symmetric, we have
$$ \begin{align*}\mathcal{H}(\partial\Delta^n)-v \simeq \mathcal{H}(\partial\Delta^n) - \pi(v).\end{align*} $$
It thus follows that
$f(\mathcal {H}(\partial \Delta ^n)-v) \simeq f(\mathcal {H}( \partial \Delta ^n) - \pi (v))$
and hence the result.▪
Recall that in Example 5.1, we saw that
$\mathcal {M}(C_3\vee \ell )$
strongly collapses to the disjoint union of a two paths. Equipped with Lemma 5.4, we now show that this occurs for a cycle of any length.
Proposition 5.6 Let v be a vertex of
$C_n$
. Then
$\mathcal {M}(C_n \vee _v \ell ) \searrow \searrow \mathcal {M}(P_{n-1} \sqcup \ell )$
.
Proof We follow a similar method to that of the proof of Proposition 5.5. By Lemma 5.4, we know that
$\mathcal {M}(C_n \vee _v \ell ) \searrow \searrow f((\mathcal {H}(C_n)-v)\sqcup \mathcal {H}(\ell ))$
. We also have
$$ \begin{align*} f((\mathcal{H}(C_n)-v)\sqcup \mathcal{H}(\ell)) &\simeq f(\mathcal{H}(C_n)-v) \ast f(\mathcal{H}(\ell)) \\ &\simeq f(\mathcal{H}(C_n)-v)\ast \mathcal{M}(\ell). \end{align*} $$
In addition, by Proposition 4.2 and Remark 5.2,
$$ \begin{align*} \mathcal{M}(P_{n-1}\sqcup \ell) &\simeq \mathcal{M}(P_{n-1})\ast \mathcal{M}(\ell)\\ &\simeq f(\mathcal{H}(P_{n-1}))\ast \mathcal{M}(\ell). \end{align*} $$
Observe that
$\mathcal {H}(C_n)-v\simeq \mathcal {H}(P_{n-1})$
, and thus
$f(\mathcal {H}(P_{n-1})) \simeq f(\mathcal {H}(C_n)-v)$
.▪
This next result is due to Kozlov.
Proposition 5.7 [Reference Kozlov12] Let
$P_{n-1}$
be a path on n vertices. Then
$$ \begin{gather*} \mathcal{M}(P_{n-1}) \simeq {\begin{cases} *, &\text{if } n=3k, \\ S^{2k-1}, &\text{if } n = 3k+1, \\ S^{2k}, &\text{if } n=3k+2.\\ \end{cases} } \end{gather*} $$
Combining Propositions 2.6, 4.2, 5.6, and 5.7 and Corollary 4.3 yield the following theorem.
Theorem 5.8 Let
$C_n$
be a cycle of length
$n\geq 3$
. Then
$$ \begin{gather*} \mathcal{M}(C_n\vee \ell) \simeq {\begin{cases} *, &\text{if } n=3k, \\ S^{2k}, &\text{if } n = 3k+1, \\ S^{2k+1}, &\text{if } n=3k+2.\\ \end{cases} } \end{gather*} $$
5.2 The Morse complex of centipede graphs
Here, we will use Proposition 4.2 to compute the homotopy type of the Morse complex of any graph with the property that every vertex is either a leaf or adjacent to exactly one leaf. Centipede graphs satisfy this property.
Proposition 5.9 Let G be a connected graph with v vertices, and let
$L(G)$
be the complex resulting from adding a leaf to each vertex of G vertex. Then
$\mathcal {M}(L(G)) \simeq S^{v-1}$
.
Proof Let G be a connected graph, and call the leaves we add to G to obtain
$L(G)$
by
$\ell _1, \ell _2, \ldots , \ell _v$
. Let
$\{a,ab\}$
be any leaf of G. If c is any neighbor of b,
$c\neq a$
, then
$(b)c$
is dominated in
$\mathcal {M}(L(G))$
by Lemma 3.8. By adding a leaf to each vertex of G,every primitive gradient vector field on G is dominated, and thus can be removed from
$\mathcal {M}(L(G))$
. Since the Morse complex of a single leaf is
$S^0$
, we have
$$ \begin{align*} \mathcal{M}(\ell_1 \sqcup \ell_2 \sqcup\cdots \sqcup \ell_v) &= \mathcal{M}(\ell_1) * \mathcal{M}(\ell_2) * \cdots \mathcal{M}(\ell_v)\\ &\simeq S^{v-1}, \end{align*} $$
where the first equality is Proposition 4.2 and the second follows from the fact that
$\Sigma S^n \simeq S^{n+1}$
.▪
A centipede graph, denoted
$\mathcal {C}_v$
, is a graph obtained by attaching a leaf to each vertex of a path with v vertices. The following corollary is then immediate.
Corollary 5.10 Let
$\mathcal {C}_v$
be a centipede graph. Then
$\mathcal {M}(\mathcal {C}_v) \simeq S^{v-1}$
.
See Figure 1 for an illustration of Corollary 5.10.
Figure 1 On the left, we start with
$\mathcal {C}_2$
. After performing the strong collapses that Lemma 3.8 allows, we then only have to take the Morse complex of the subcomplex on the right.
5.3 Morse complex of a path with a leaf
Lemma 5.11 Let
$v_k$
be a vertex of
$P_t$
,
$1 \leq k \leq t-1$
and
$t \geq 2$
. Then
$\mathcal {M}(P_t \vee _{v_k} \ell ) \searrow \searrow \mathcal {M}(P_{k+1} \sqcup P_{t-(k+2)} \sqcup \ell )$
.
Proof Write
$\ell = v_ku$
. By Lemma 3.8,
$(u)v_k$
dominates
$(v_k)v_{k+1}$
in
$\mathcal {M}(P_t \vee _{v_k} \ell )$
. In the corresponding Hasse diagram
$\mathcal {H}(P_t \vee _{v_k} \ell )$
, this corresponds to the removal of the edge between
$v_k$
and
$v_kv_{k+1}$
.
Furthermore, by Lemma 3.8,
$(v_t)v_{t-1}$
dominates
$(v_{t-1})v_{t-2}$
. This corresponds to the removal of the edge between
$v_{t-1}$
and
$v_{t-2}v_{t-1}$
on the Hasse diagram. Upon inspection, we see that this yields three components: the Hasse diagram of the path
$P_{k+1}$
, the Hasse diagram of the path
$P_1=\ell $
, and an “upside-down” Hasse diagram of the path
$\mathcal {H}(P_{t-(k+2)})$
. Thus,
$$ \begin{align*} \mathcal{M}(P_t \vee_{v_k} \ell) \searrow \searrow f(\mathcal{H}(P_{k+1}) \sqcup \mathcal{H}(P_{t-(k+2)}) \sqcup \mathcal{H}(\ell)). \end{align*} $$
By Proposition 4.2 and Remark 5.2, we have that
$$ \begin{align*} f(\mathcal{H}(P_{k+1}) \sqcup \mathcal{H}(P_{t-(k+2)}) \sqcup \mathcal{H}(\ell)) \simeq \mathcal{M}(P_{k+1} \sqcup P_{t-(k+2)} \sqcup \ell).\\[-34pt] \end{align*} $$
▪
Combining Lemma 5.11 and Proposition 4.2, we have the following proposition.
Proposition 5.12 Let
$v_k$
be a vertex of
$P_t$
,
$1 \leq k \leq t-1$
. Then
$\mathcal {M}(P_t \vee _{v_k} \ell ) \simeq \mathcal {M}(P_{k+1}) * \mathcal {M}(P_{t-(k+2)}) * \mathcal {M}(\ell )$
.
Considering Propositions 2.6, 3.9, and 5.12, we can conclude the following corollary.
Corollary 5.13 Let
$v_k$
be a vertex of
$P_t$
,
$1 \leq k \leq t-1$
. If
$k+1 = 2j$
or
$t-(k+2) = 2j$
, then
$\mathcal {M}(P_t \vee _{v_k} l) \searrow \searrow *$
.
6 Automorphism group of the Morse complex of a disconnected complex
In this section, we give another application of Proposition 4.2. In [Reference Lin and Scoville13], a subset of the authors computed the automorphism group of the Morse complex of any connected simplicial complex. There it was shown that if K is a connected simplicial complex, then
$$ \begin{align*}\mathrm{Aut}(\mathcal{M}(K))\cong \begin{cases} \mathrm{Aut}(K), & \text{if } K\neq \partial\Delta^n,C_n, \\ \mathrm{Aut}(C_{2n}), & \text{if } K= C_n, \\ \mathrm{Aut}(K)\times \mathbb{Z}_2, & \text{if } K= \partial\Delta^n. \\ \end{cases} \end{align*} $$
Proposition 4.2 along with the results in this section allows us to compute the automorphism group of the Morse complex for certain disconnected complexes.
Definition 6.1 Let K be a simplicial complex. A subcomplex
$U\leq K$
is called fully connected in K if
$K\cong U \ast (K-U).$
Example 6.1 If
$K=\Sigma L=\{u,v\}*L$
for some complex L, then the subcomplex
$U=\{u,v\}$
of K is fully connected.
Proposition 6.2 Let
$K,L$
be simplicial complexes. Then
$\mathrm {Aut}(K\ast L) \cong \mathrm {Aut}(K) \times \mathrm {Aut}(L)$
except when there exist subcomplexes
$U_1 \leq K, U_2 \leq L$
with
$U_1 \cong U_2$
, such that
$U_1$
is fully connected in K and
$U_2$
is fully connected in L.
For example, Proposition 6.2 does not hold for
$K=\Sigma K_0$
and
$L=\Sigma L_0$
.
Proof We first show that
$\mathrm {Aut}(K) \times \mathrm {Aut}(L)$
is a subgroup of
$\mathrm {Aut}(K\ast L)$
. Define
$\phi \colon \mathrm {Aut}(K) \times \mathrm {Aut}(L)\to \mathrm {Aut}(K\ast L)$
as follows. Let
$(a,b) \in \mathrm {Aut}(K) \times \mathrm {Aut}(L)$
. For any
$\sigma \in K\ast L$
, write
$\sigma =\alpha \beta $
for
$\alpha \in K$
and
$\beta \in L$
. Let
$\phi _{(a,b)}\colon K*L\to K*L$
by
$\phi _{(a,b)} (\sigma ) = a(\alpha )b(\beta )$
, and define
$\phi (a,b)=\phi _{(a,b)}.$
Consider any simplex
$\sigma = \alpha \beta \in K \ast L$
, with
$\alpha \in K$
and
$\beta \in L$
, and any
$(a,b), (c,d) \in \mathrm {Aut}(K)\times \mathrm {Aut}(L)$
. We have
$$ \begin{align*} (\phi(a,b)\circ\phi(c,d))(\sigma)&= \phi(a,b)(\phi(c,d)(\alpha\beta))\\ &= \phi(a,b)(c(\alpha)b(\beta))\\ &= (a\circ c)(\alpha)(b\circ d)(\beta)\\ &= \phi(a\circ c, b\circ d)(\sigma)\\ &= \phi((a,b)\circ (c,d))(\sigma). \end{align*} $$
Hence,
$\phi $
is a homomorphism. We now show that
$\phi $
is injective. Consider any
$(f,g) \in \mathrm {Ker}(\phi )$
. Then
$\phi (f,g) = \mathrm {id}_{K\ast L}$
. Consider
$\sigma = \alpha \beta \in K\ast L$
, where
$\alpha \in K, \beta \in L$
. Then we have
$$ \begin{align*} \phi(f,g)(\sigma) &=\sigma,\\ f(\alpha)g(\beta)&= \alpha\beta. \end{align*} $$
It follows that
$f(\alpha )=\alpha $
, and
$g(\beta ) = \beta $
. This holds for any choice of
$\alpha \in K, \beta \in L$
, so
$f = \mathrm {id}_K$
and
$g = \mathrm {id}_L$
. Hence,
$\mathrm {Ker}(\phi )$
is trivial, so
$\phi $
is injective. Therefore,
$\mathrm {Aut}(K) \times \mathrm {Aut}(L)$
is a subgroup of
$\mathrm {Aut}(K\ast L)$
.
We now show that if the proposed conditions hold,
$|\mathrm {Aut}(K\ast L)|> |\mathrm {Aut}(K) \times \mathrm {Aut}(L)|$
. In particular, we show that there exists an automorphism in
$\mathrm {Aut}(K\ast L)$
that does not emerge from “combining” automorphisms in
$\mathrm {Aut}(K)$
and
$\mathrm {Aut}(L)$
. We build this from the hypothesis that
$U_1\cong U_2$
. Hence, let
$g\colon U_1 \to U_2$
be an isomorphism. Construct a function
$f_V: V(K\ast L) \to V(K\ast L)$
such that
$f_V(v) = g(v)$
if
$v \in U_1$
,
$f_V(v) = g^{-1}(v)$
if
$v \in U_2$
, and
$f_V(v) = v$
if
$v \not \in U_1 \cup U_2$
. It is easy to see that
$f_V$
is a bijection. Let
$f\colon K\ast L \to K\ast L$
be the induced function on the join.
We first show that f is a simplicial map. Consider any simplices
$u_1 \in U_1, u_2 \in U_2, k \in K - U_1, \ell \in L-U_2$
. Since
$U_1$
is fully connected in K and
$U_2$
is fully connected in L, we have that each of
$U_1, U_2, K-U_1, L-U_2$
is joined to each other (excluding itself) in
$K*L$
. By definition, the simplex
$u_1u_2k\ell \in K\ast L$
. Consider any simplex
$\sigma \in K\ast L$
. Write
$\sigma $
as some
$u_1u_2k\ell $
as above, in which
$u_1 \in U_1, u_2 \in U_2, k \in K - U_1, \ell \in L-U_2$
, allowing any of
$u_1, u_2, k, \ell $
to be empty. Then
$f(u_1u_2k\ell ) = f(u_1)f(u_2)f(k)f(\ell ) = f(u_1)f(u_2)k\ell $
. Since
$f(u_1) = g(u_1) \in U_2$
and
$f(u_2) =g^{-1}(u_2)\in U_1$
, we know that
$f(\sigma ) = g(u_1)g^{-1}(u_2)k\ell \in K\ast L$
. Therefore, f is a simplicial map. Since
$f_V$
is also a bijection, f is an automorphism. Thus,
$f \in \mathrm {Aut}(K\ast L)$
. However, note that f sends vertices of K to L and vice versa (namely, it swaps vertices of
$U_1$
and
$U_2$
), and therefore
$f \not \in \mathrm {Aut}(K) \times \mathrm {Aut}(L)$
.
For the other direction, we prove the contrapositive. Suppose that
$\mathrm {Aut}(K\ast L) \not \cong \mathrm {Aut}(K) \times \mathrm {Aut}(L)$
. Since
$\mathrm {Aut}(K) \times \mathrm {Aut}(L)$
is a subgroup of
$\mathrm {Aut}(K\ast L)$
,
$|\mathrm {Aut}(K) \times \mathrm {Aut}(L)| < |\mathrm {Aut}(K\ast L)|$
. Thus, there must exist some function
$f \in \mathrm {Aut}(K\ast L)$
, with
$f \not \in \mathrm {Aut}(K) \times \mathrm {Aut}(L)$
. As shown earlier,
$\mathrm {Aut}(K) \times \mathrm {Aut}(L)$
consists of isomorphisms on
$K\ast L$
that send subcomplexes of K to subcomplexes of K, and subcomplexes of L to subcomplexes of L. Therefore, f must send some subcomplex
$U_1$
of K to some subcomplex
$U_2$
of L. We first show that
$U_2$
is fully connected in L. Notice that in
$K\ast L$
, K (and thus any subcomplex of K) is joined to L. Therefore,
$U_1$
is joined to L, so it is joined to
$L-U_2$
. Since f is an isomorphism, it follows that
$U_2$
is joined to
$L-U_2$
. This means
$U_2$
is fully connected in L. By the same reasoning, since
$U_2$
is joined to K, and thus
$K-U_1$
, it follows that
$U_1$
is joined to
$K-U_1$
, so
$U_1$
is fully connected in K. Thus, the desired condition holds.▪
Theorem 6.3 Let
$K_1,K_2$
be simplicial complexes with
$K_1,K_2\neq \partial \Delta ^n$
or
$C_n$
. If
$K_1, K_2$
do not contain subcomplexes
$U_1, U_2$
satisfying the conditions of Proposition 6.2, then
$\mathrm {Aut}(\mathcal {M}(K_1\cup K_2)) \cong \mathrm {Aut}(K_1)\times \mathrm {Aut}(K_2)$
.
Proof For disjoint complexes
$K_1, K_2$
, we have
$\mathcal {M}(K_1\cup K_2) \cong \mathcal {M}(K_1)\ast \mathcal {M}(K_2)$
by Proposition 4.2, and hence
$\mathrm {Aut}(\mathcal {M}(K_1\cup K_2)) \cong \mathrm {Aut}(\mathcal {M}(K_1)\ast \mathcal {M}(K_2))$
. We then have
$\mathrm {Aut}(\mathcal {M}(K_1\cup K_2)) \cong \mathrm {Aut}(\mathcal {M}(K_1))\times \mathrm {Aut}(\mathcal {M}(K_2))$
precisely when the condition in Proposition 6.2 holds. By [Reference Lin and Scoville13, Theorem 1],
$\mathrm {Aut}(\mathcal {M}(K_1\cup K_2)) \cong \mathrm {Aut}(K_1)\times \mathrm {Aut}(K_2)$
.▪
A similar statement, which we omit here, can be made with
$K_1,K_2=\partial \Delta ^n$
or
$C_n$
.
7 Future directions and open questions
The many applications of the results found in Section 5.1 suggest a convenient way to determine the strong collapsibility of a simplicial complex’s Morse complex via a careful study of the Hasse Diagram. The following lemma further evidences this claim.
Lemma 7.1 Let X be a poset, and suppose that
$X=A \sqcup B$
. If either
$f(A)$
or
$f(B)$
is strongly collapsible, then so is
$f(X).$
Proof Without loss of generality, suppose that
$f(A)$
is strongly collapsible. Since A is disjoint from B, all of the primitive vectors in
$f(A)$
are compatible with all simplices of
$f(X)-f(A)$
. Hence, after strong collapsing
$f(A)$
to some primitive vector v, v will be compatible with all simplices of
$f(X)-f(A)$
, and thus dominates all vertices in
$f(X)-f(A)$
. Therefore,
$f(X)$
is also strongly collapsible.▪
In other words, if through the addition of leaves to a simplicial complex we encounter a disjoint section of the Hasse diagram whose Morse complex is strongly collapsible, then the original simplicial complex’s Morse complex is also strongly collapsible.
This lemma provides a potentially convenient way to determine the strong collapsibility of the Morse complex of graphs, by developing a comprehensive collection of such “disjoint sections” that are known to have strongly collapsible Morse complexes. This can be done systematically by beginning with posets of height
$2$
(corresponding to graphs) whose bottom layer has one node, two nodes, three nodes, and so on. We will show the cases for one and two nodes in the bottom layer.
Case 1: One node. The following is the only such connected poset of height
$2$
whose Morse complex is strongly collapsible, as its Morse complex is a single point:
If there is more than one node in the second layer of the poset, then its Morse complex will consist entirely of disjoint points, and thus would not be strongly collapsible.
Case 2: Two vertices. The following is the only such connected poset of height
$2$
whose Morse complex is strongly collapsible:
We now show that all other posets with two vertices in the bottom layer have Morse complexes that are not strongly collapsible. It is easy to verify that a connected poset of height
$2$
with two nodes in the bottom layer can only have one node in the second layer that is connected to both nodes in the bottom layer. We now consider the casework on the number of nodes a and b are connected to in the second layer. We have two cases.
Case 2a: One of a and b is connected to more than one node in the second layer.
The Morse complex of this poset consists of the disjoint nodes
$(a, aa_1), (a, aa_2), \dots , (a,aa_k)$
joined to the two disjoint nodes
$(b,bb_1)$
and
$(b,ab)$
, together with
$(a,ab)$
connected to
$(b,bb_1)$
. There is only one pair of dominating vertices, namely
$(b,bb_1)$
dominates
$(a,ab)$
, and it can be easily shown that no other dominating pair exists. Thus, the Morse complex of posets of this form are not strongly collapsible.
Case 2b: Both a and b are connected to more than one node in the second layer.
The Morse complex of this poset consists of the disjoint points
$(a,ab), (a,aa_1), (a,aa_2), \dots , (a,aa_k)$
joined to the disjoint points
$(b,ab),(b,bb_1),(b,bb_2), \dots , (b, bb_k)$
, together with
$(a,ab)$
joined to the disjoint points
$(b,bb_1),(b,bb_2), \dots , (b, bb_k)$
. Any point connected to a point of the form
$(a,aa_i)$
is also connected to the other
$k-1$
points of the form
$(a,aa_i)$
. Since all points of the form
$(a,aa_i)$
are disjoint,
$(a,aa_i)$
cannot dominate any other point. By symmetry, neither can be any point of the form
$(b,bb_i)$
. By similar reasoning, it can be easily seen that
$(a,ab)$
and
$(b,ab)$
cannot dominate any other points. Therefore, as there are no dominating vertices in the Morse complex, it is not strongly collapsible.
This process can be continued to determine posets with strongly collapsible Morse complexes with greater amounts of vertices in the bottom layer. For example, the following is one such poset for three vertices:
Whether this is the only such poset remains open.
If sufficiently many strongly collapsible posets of any given number of vertices in the bottom layer are computed, a simple algorithm can be used to determine the strong collapsibility of the Morse complex of any simplicial complex of dimension
$1$
:
Acknowledgment
The authors are grateful to an anonymous referee for their helpful comments and feedback.
