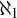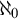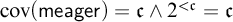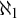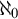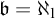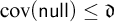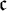1 Introduction
The method of ultrapowers is one of the most important ways to construct models. Ultrapowers are models obtained by properly equating the elements of product sets of the models using ultrafilters. We consider the problem of when there exists an ultrafilter
![]() $\mathcal {U}$
on
$\mathcal {U}$
on
![]() $\omega $
such that for two models
$\omega $
such that for two models
![]() $\mathcal {A}, \mathcal {B}$
in a countable language
$\mathcal {A}, \mathcal {B}$
in a countable language
![]() $\mathcal {L}$
, the respective ultrapowers
$\mathcal {L}$
, the respective ultrapowers
![]() $\mathcal {A}^\omega /\mathcal {U}, \mathcal {B}^\omega /\mathcal {U}$
are isomorphic. Since ultrapowers are elementary extensions of original models, if
$\mathcal {A}^\omega /\mathcal {U}, \mathcal {B}^\omega /\mathcal {U}$
are isomorphic. Since ultrapowers are elementary extensions of original models, if
![]() $\mathcal {A}^\omega /\mathcal {U}$
and
$\mathcal {A}^\omega /\mathcal {U}$
and
![]() $\mathcal {B}^\omega /\mathcal {U}$
are isomorphic, then
$\mathcal {B}^\omega /\mathcal {U}$
are isomorphic, then
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
must be elementarily equivalent. Keisler showed, under CH, conversely if
$\mathcal {B}$
must be elementarily equivalent. Keisler showed, under CH, conversely if
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
are elementarily equivalent and have size
$\mathcal {B}$
are elementarily equivalent and have size
![]() $\le \mathfrak {c}$
, then for every ultrafilter
$\le \mathfrak {c}$
, then for every ultrafilter
![]() $\mathcal {U}$
over
$\mathcal {U}$
over
![]() $\omega $
,
$\omega $
,
![]() $\mathcal {A}^\omega /\mathcal {U}$
and
$\mathcal {A}^\omega /\mathcal {U}$
and
![]() $\mathcal {B}^\omega /\mathcal {U}$
are isomorphic. The purpose of this paper is to give necessary conditions and sufficient conditions for when Keisler’s theorem holds in a model where CH does not hold, and to separate the variants of Keisler’s theorem using those conditions.
$\mathcal {B}^\omega /\mathcal {U}$
are isomorphic. The purpose of this paper is to give necessary conditions and sufficient conditions for when Keisler’s theorem holds in a model where CH does not hold, and to separate the variants of Keisler’s theorem using those conditions.
Convention. All ultrafilters considered in this paper are nonprincipal.
Definition 1.1. Let
![]() $\kappa $
be a cardinal.
$\kappa $
be a cardinal.
-
(1) We say
 $\operatorname {KT}(\kappa )$
holds if for every countable language
$\operatorname {KT}(\kappa )$
holds if for every countable language
 $\mathcal {L}$
and
$\mathcal {L}$
and
 $\mathcal {L}$
-structures
$\mathcal {L}$
-structures
 $\mathcal {A}, \mathcal {B}$
of size
$\mathcal {A}, \mathcal {B}$
of size
 $\le \kappa $
which are elementarily equivalent, there exists an ultrafilter
$\le \kappa $
which are elementarily equivalent, there exists an ultrafilter
 $\mathcal {U}$
over
$\mathcal {U}$
over
 $\omega $
such that
$\omega $
such that
 $\mathcal {A}^\omega /\mathcal {U} \simeq \mathcal {B}^\omega /\mathcal {U}$
.
$\mathcal {A}^\omega /\mathcal {U} \simeq \mathcal {B}^\omega /\mathcal {U}$
. -
(2) We say
 $\mathrm {SAT}(\kappa )$
holds if there exists an ultrafilter
$\mathrm {SAT}(\kappa )$
holds if there exists an ultrafilter
 $\mathcal {U}$
over
$\mathcal {U}$
over
 $\omega $
such that for every countable language
$\omega $
such that for every countable language
 $\mathcal {L}$
and every sequence of
$\mathcal {L}$
and every sequence of
 $\mathcal {L}$
-structures
$\mathcal {L}$
-structures
 $(\mathcal {A}_i)_{i\in \omega }$
with each
$(\mathcal {A}_i)_{i\in \omega }$
with each
 $\mathcal {A}_i$
of size
$\mathcal {A}_i$
of size
 $\le \kappa $
,
$\le \kappa $
,
 $\prod _{i \in \omega } \mathcal {A}_i / \mathcal {U}$
is saturated.
$\prod _{i \in \omega } \mathcal {A}_i / \mathcal {U}$
is saturated.
![]() $\mathrm {SAT}(\kappa )$
implies
$\mathrm {SAT}(\kappa )$
implies
![]() $\operatorname {KT}(\kappa )$
for every
$\operatorname {KT}(\kappa )$
for every
![]() $\kappa \le \mathfrak {c}$
by the fact that two saturated structures which are elementarily equivalent and have the same size are isomorphic. Golshani and Shelah [Reference Golshani and Shelah6] proved
$\kappa \le \mathfrak {c}$
by the fact that two saturated structures which are elementarily equivalent and have the same size are isomorphic. Golshani and Shelah [Reference Golshani and Shelah6] proved
![]() $\neg \operatorname {KT}(\aleph _2)$
and later we will prove
$\neg \operatorname {KT}(\aleph _2)$
and later we will prove
![]() $\neg \mathrm {SAT}(\aleph _2)$
in Theorem 2.2. So this implication
$\neg \mathrm {SAT}(\aleph _2)$
in Theorem 2.2. So this implication
![]() $\mathrm {SAT}(\kappa ) \Rightarrow \operatorname {KT}(\kappa )$
holds formally for every
$\mathrm {SAT}(\kappa ) \Rightarrow \operatorname {KT}(\kappa )$
holds formally for every
![]() $\kappa $
.
$\kappa $
.
Keisler [Reference Keisler7] proved
![]() $\mathrm {CH} \Rightarrow \mathrm {SAT}(\mathfrak {c})$
. The result
$\mathrm {CH} \Rightarrow \mathrm {SAT}(\mathfrak {c})$
. The result
![]() $\neg \operatorname {KT}(\aleph _2)$
of Golshani and Shelah implies
$\neg \operatorname {KT}(\aleph _2)$
of Golshani and Shelah implies
![]() $\operatorname {KT}(\mathfrak {c}) \Rightarrow \mathrm {CH}$
. So
$\operatorname {KT}(\mathfrak {c}) \Rightarrow \mathrm {CH}$
. So
![]() $\mathrm {CH}$
,
$\mathrm {CH}$
,
![]() $\mathrm {SAT}(\mathfrak {c})$
, and
$\mathrm {SAT}(\mathfrak {c})$
, and
![]() $\operatorname {KT}(\mathfrak {c})$
are equivalent. Golshani and Shelah also proved that
$\operatorname {KT}(\mathfrak {c})$
are equivalent. Golshani and Shelah also proved that
![]() $\operatorname {cov}(\mathsf {meager}) = \mathfrak {c} \land \operatorname {cf}(\mathfrak {c}) = \aleph _1$
implies
$\operatorname {cov}(\mathsf {meager}) = \mathfrak {c} \land \operatorname {cf}(\mathfrak {c}) = \aleph _1$
implies
![]() $\operatorname {KT}(\aleph _1)$
. Another classical result is the theorem by Ellentuck–Rucker [Reference Ellentuck and Rucker5] which shows that
$\operatorname {KT}(\aleph _1)$
. Another classical result is the theorem by Ellentuck–Rucker [Reference Ellentuck and Rucker5] which shows that
![]() $\operatorname {MA}(\sigma \text {-centered})$
implies
$\operatorname {MA}(\sigma \text {-centered})$
implies
![]() $\mathrm {SAT}(\aleph _0)$
. Moreover, Shelah [Reference Shelah9] showed
$\mathrm {SAT}(\aleph _0)$
. Moreover, Shelah [Reference Shelah9] showed
![]() $\operatorname {Con}(\neg \operatorname {KT}(\aleph _0))$
by showing that
$\operatorname {Con}(\neg \operatorname {KT}(\aleph _0))$
by showing that
![]() $\mathfrak {d} < \mathfrak {v}^\forall $
implies
$\mathfrak {d} < \mathfrak {v}^\forall $
implies
![]() $\neg \operatorname {KT}(\aleph _0)$
and that the former is consistent.
$\neg \operatorname {KT}(\aleph _0)$
and that the former is consistent.
In this paper, we prove the implications indicated by thick lines in Figure 1.

Figure 1 Implications; thick arrows indicate our results.
In the rest of this section, we recall basic notions related to cardinal invariants.
Definition 1.2.
-
(1) If
 $X, Y$
are sets and R is a subset of
$X, Y$
are sets and R is a subset of
 $X \times Y$
, we call a triple
$X \times Y$
, we call a triple
 $(X, Y, R)$
a relational system.
$(X, Y, R)$
a relational system. -
(2) For a relational system
 $\mathcal {A} = (X, Y, R)$
, define
$\mathcal {A} = (X, Y, R)$
, define
 $\mathcal {A}^\perp = (Y, X, \hat {R})$
, where
$\mathcal {A}^\perp = (Y, X, \hat {R})$
, where
 $\hat {R} = \{ (y, x) \in Y \times X : \neg (x \mathrel {R} y)\})$
.
$\hat {R} = \{ (y, x) \in Y \times X : \neg (x \mathrel {R} y)\})$
. -
(3) For a relational system
 $\mathcal {A} = (X, Y, R)$
, define
$\mathcal {A} = (X, Y, R)$
, define
 .
. -
(4) For relational systems
 $\mathcal {A} = (X, Y, R), \mathcal {B} = (X', Y', S)$
, we call a pair
$\mathcal {A} = (X, Y, R), \mathcal {B} = (X', Y', S)$
, we call a pair
 $(\varphi , \psi )$
a Galois–Tukey morphism from
$(\varphi , \psi )$
a Galois–Tukey morphism from
 $\mathcal {A}$
to
$\mathcal {A}$
to
 $\mathcal {B}$
if
$\mathcal {B}$
if
 $\varphi \colon X \to X'$
,
$\varphi \colon X \to X'$
,
 $\psi \colon Y' \to Y$
and
$\psi \colon Y' \to Y$
and
 $(\forall x \in X)(\forall y \in Y')(\varphi (x) \mathrel {S} y \implies x \mathrel {R} \psi (y))$
hold.
$(\forall x \in X)(\forall y \in Y')(\varphi (x) \mathrel {S} y \implies x \mathrel {R} \psi (y))$
hold.
Fact 1.3 [Reference Blass4, Theorem 4.9]
If there is a Galois–Tukey morphism
![]() $(\varphi , \psi )$
from
$(\varphi , \psi )$
from
![]() $\mathcal {A}$
to
$\mathcal {A}$
to
![]() $\mathcal {B}$
, then
$\mathcal {B}$
, then
![]() and
and
![]() hold.
hold.
Definition 1.4.
-
(1) For
 $f, g \in \omega ^\omega $
, define
$f, g \in \omega ^\omega $
, define
 $f <^* g$
iff
$f <^* g$
iff
 $(\forall ^\infty n) (f(n) < g(n))$
.
$(\forall ^\infty n) (f(n) < g(n))$
. -
(2) For
 $c \in (\omega +1)^\omega $
and
$c \in (\omega +1)^\omega $
and
 $h \in \omega ^\omega $
, define
$h \in \omega ^\omega $
, define
 $\prod c = \prod _{n \in \omega } c(n)$
and
$\prod c = \prod _{n \in \omega } c(n)$
and
 $S(c, h) = \prod _{n \in \omega } [c(n)]^{\le h(n)}$
.
$S(c, h) = \prod _{n \in \omega } [c(n)]^{\le h(n)}$
. -
(3) For
 $x \in \prod c$
and
$x \in \prod c$
and
 $\varphi \in S(c, h)$
, define
$\varphi \in S(c, h)$
, define
 $x \in ^* \varphi $
iff
$x \in ^* \varphi $
iff
 $(\forall ^\infty n)(x(n) \in \varphi (n))$
and define
$(\forall ^\infty n)(x(n) \in \varphi (n))$
and define
 $x \in ^\infty \varphi $
iff
$x \in ^\infty \varphi $
iff
 $(\exists ^\infty n)(x(n) \in \varphi (n))$
.
$(\exists ^\infty n)(x(n) \in \varphi (n))$
.
Definition 1.5.
-
(1) Define
 $\mathbf {D} = (\omega ^\omega , \omega ^\omega , <^*)$
,
$\mathbf {D} = (\omega ^\omega , \omega ^\omega , <^*)$
,
 and
and
 .
. -
(2) For a poset
 $(P, <)$
, define a relational system
$(P, <)$
, define a relational system
 $\mathbf {Cof}(P, <)$
by
$\mathbf {Cof}(P, <)$
by
 $\mathbf {Cof}(P, <) = (P, P, <)$
. Then we have
$\mathbf {Cof}(P, <) = (P, P, <)$
. Then we have
 .
. -
(3) For
 $c \in (\omega +1)^\omega , h \in \omega ^\omega $
, define
$c \in (\omega +1)^\omega , h \in \omega ^\omega $
, define
 $\mathbf {Lc}(c, h) = (\prod c, S(c, h), \in ^*)$
,
$\mathbf {Lc}(c, h) = (\prod c, S(c, h), \in ^*)$
,
 and
and
 .
. -
(4) Define
 $\mathbf {wLc}(c, h) = (\prod c, S(c, h), \in ^\infty )$
,
$\mathbf {wLc}(c, h) = (\prod c, S(c, h), \in ^\infty )$
,
 , and
, and
 .
. -
(5) For an ideal I on X, define
 $\mathbf {Cov}(I) = (X, I, \in )$
,
$\mathbf {Cov}(I) = (X, I, \in )$
,
 , and
, and
 .
.
By the definition of the norm
![]() , the next lemma is obvious.
, the next lemma is obvious.
Lemma 1.6.
-
(1)
 $\mathfrak {c}^\forall _{c, h} = \min \{ \left \lvert {S} \right \rvert : S \subseteq S(c, h), (\forall x \in \prod c)(\exists \varphi \in S)(\forall ^\infty n) (x(n) \in \varphi (n)) \}$
.
$\mathfrak {c}^\forall _{c, h} = \min \{ \left \lvert {S} \right \rvert : S \subseteq S(c, h), (\forall x \in \prod c)(\exists \varphi \in S)(\forall ^\infty n) (x(n) \in \varphi (n)) \}$
. -
(2)
 $\mathfrak {c}^\exists _{c, h} = \min \{ \left \lvert {S} \right \rvert : S \subseteq S(c, h), (\forall x \in \prod c)(\exists \varphi \in S)(\exists ^\infty n) (x(n) \in \varphi (n)) \}$
.
$\mathfrak {c}^\exists _{c, h} = \min \{ \left \lvert {S} \right \rvert : S \subseteq S(c, h), (\forall x \in \prod c)(\exists \varphi \in S)(\exists ^\infty n) (x(n) \in \varphi (n)) \}$
. -
(3)
 $\mathfrak {v}^\forall _{c, h} = \min \{ \left \lvert {X} \right \rvert : X \subseteq \prod c, (\forall \varphi \in S(c, h))(\exists x \in X)(\exists ^\infty n) (x(n) \not \in \varphi (n)) \}$
.
$\mathfrak {v}^\forall _{c, h} = \min \{ \left \lvert {X} \right \rvert : X \subseteq \prod c, (\forall \varphi \in S(c, h))(\exists x \in X)(\exists ^\infty n) (x(n) \not \in \varphi (n)) \}$
. -
(4)
 $\mathfrak {v}^\exists _{c, h} = \min \{ \left \lvert {X} \right \rvert : X \subseteq \prod c, (\forall \varphi \in S(c, h))(\exists x \in X)(\forall ^\infty n) (x(n) \not \in \varphi (n)) \}$
.
$\mathfrak {v}^\exists _{c, h} = \min \{ \left \lvert {X} \right \rvert : X \subseteq \prod c, (\forall \varphi \in S(c, h))(\exists x \in X)(\forall ^\infty n) (x(n) \not \in \varphi (n)) \}$
.
Definition 1.7.
-
(1) Define
 $\mathfrak {v}^\forall = \min \{ \mathfrak {v}^\forall _{c, h} : c, h \in \omega ^\omega , \lim _{n \to \infty } h(n) = \infty \}$
.
$\mathfrak {v}^\forall = \min \{ \mathfrak {v}^\forall _{c, h} : c, h \in \omega ^\omega , \lim _{n \to \infty } h(n) = \infty \}$
. -
(2) Define
 $\mathfrak {c}^\exists = \min \{ \mathfrak {c}^\exists _{c, h} : c, h \in \omega ^\omega , \sum _{n \in \omega } h(n) / c(n) < \infty \}$
.
$\mathfrak {c}^\exists = \min \{ \mathfrak {c}^\exists _{c, h} : c, h \in \omega ^\omega , \sum _{n \in \omega } h(n) / c(n) < \infty \}$
.
Fact 1.8 [Reference Bell and Slomson3, Lemma 3.5 and Theorem 3.12]
Let
![]() ${\langle \mathcal {A}_i : i \in \omega \rangle }$
be a sequence of structures in a language
${\langle \mathcal {A}_i : i \in \omega \rangle }$
be a sequence of structures in a language
![]() $\mathcal {L}$
such that each
$\mathcal {L}$
such that each
![]() $\mathcal {A}_i$
has size
$\mathcal {A}_i$
has size
![]() $\le \mathfrak {c}$
. Let
$\le \mathfrak {c}$
. Let
![]() $\mathcal {U}$
be an ultrafilter over
$\mathcal {U}$
be an ultrafilter over
![]() $\omega $
. Then the ultraproduct
$\omega $
. Then the ultraproduct
![]() $\prod _{i \in \omega } \mathcal {A}_i / \mathcal {U}$
has size either finite or
$\prod _{i \in \omega } \mathcal {A}_i / \mathcal {U}$
has size either finite or
![]() $\mathfrak {c}$
.
$\mathfrak {c}$
.
2
 $\mathrm {SAT}(\aleph _1)$
and
$\mathrm {SAT}(\aleph _1)$
and
 $\operatorname {KT}(\aleph _1)$
$\operatorname {KT}(\aleph _1)$
In this section, we prove that
![]() $\mathrm {SAT}(\aleph _1)$
is equivalent to
$\mathrm {SAT}(\aleph _1)$
is equivalent to
![]() $\mathrm {CH}$
and that
$\mathrm {CH}$
and that
![]() $\operatorname {KT}(\aleph _1)$
implies
$\operatorname {KT}(\aleph _1)$
implies
![]() $\mathfrak {b} = \aleph _1$
.
$\mathfrak {b} = \aleph _1$
.
Theorem 2.1.
![]() $\mathrm {SAT}(\aleph _1)$
implies CH.
$\mathrm {SAT}(\aleph _1)$
implies CH.
Proof Assume
![]() $\mathrm {SAT}(\aleph _1)$
and
$\mathrm {SAT}(\aleph _1)$
and
![]() $\neg \mathrm {CH}$
. Take an ultrafilter
$\neg \mathrm {CH}$
. Take an ultrafilter
![]() $\mathcal {U}$
over
$\mathcal {U}$
over
![]() $\omega $
that witnesses
$\omega $
that witnesses
![]() $\mathrm {SAT}(\aleph _1)$
. Let
$\mathrm {SAT}(\aleph _1)$
. Let
![]() $\mathcal {A}_\ast = (\omega _1, <)^\omega / \mathcal {U}$
. For
$\mathcal {A}_\ast = (\omega _1, <)^\omega / \mathcal {U}$
. For
![]() $\alpha < \omega _1$
, put
$\alpha < \omega _1$
, put
![]() $\alpha _\ast = [{\langle \alpha , \alpha , \alpha , \dots \rangle }]$
. Define a set p of formulas with a free variable x by
$\alpha _\ast = [{\langle \alpha , \alpha , \alpha , \dots \rangle }]$
. Define a set p of formulas with a free variable x by
This p is finitely satisfiable and the number of parameters occurring in p is
![]() $\aleph _1 < \mathfrak {c} = \left \lvert {\mathcal {A}_\ast } \right \rvert $
by
$\aleph _1 < \mathfrak {c} = \left \lvert {\mathcal {A}_\ast } \right \rvert $
by
![]() $\neg \mathrm {CH}$
. Thus, by
$\neg \mathrm {CH}$
. Thus, by
![]() $\mathrm {SAT}(\aleph _1)$
, we can take
$\mathrm {SAT}(\aleph _1)$
, we can take
![]() $f \colon \omega \to \omega _1$
such that
$f \colon \omega \to \omega _1$
such that
![]() $[f]$
realizes p. Put
$[f]$
realizes p. Put
![]() $\beta = \sup _{n \in \omega } f(n)$
. Now we have
$\beta = \sup _{n \in \omega } f(n)$
. Now we have
![]() $\{ n \in \omega : \beta < f(n) \} \in \mathcal {U}$
and this contradicts the definition of
$\{ n \in \omega : \beta < f(n) \} \in \mathcal {U}$
and this contradicts the definition of
![]() $\beta $
.
$\beta $
.
Theorem 2.2.
![]() $\neg \mathrm {SAT}(\aleph _2)$
holds.
$\neg \mathrm {SAT}(\aleph _2)$
holds.
Proof Take an ultrafilter
![]() $\mathcal {U}$
over
$\mathcal {U}$
over
![]() $\omega $
that witnesses
$\omega $
that witnesses
![]() $\mathrm {SAT}(\aleph _2)$
. Let
$\mathrm {SAT}(\aleph _2)$
. Let
![]() $\mathcal {A}_\ast = (\omega _2, <)^\omega / \mathcal {U}$
. For
$\mathcal {A}_\ast = (\omega _2, <)^\omega / \mathcal {U}$
. For
![]() $\alpha < \omega _1$
, put
$\alpha < \omega _1$
, put
![]() $\alpha _\ast = [{\langle \alpha , \alpha , \alpha , \dots \rangle }]$
. Define a set p of formulas with a free variable x by
$\alpha _\ast = [{\langle \alpha , \alpha , \alpha , \dots \rangle }]$
. Define a set p of formulas with a free variable x by
The remaining argument is the same as Theorem 2.1.
Definition 2.3. Let
![]() $\mathfrak {mcf} = \min \{ \operatorname {cf}(\omega ^\omega /\mathcal {U}) : \mathcal {U} \text { an ultrafilter over } \omega \}$
.
$\mathfrak {mcf} = \min \{ \operatorname {cf}(\omega ^\omega /\mathcal {U}) : \mathcal {U} \text { an ultrafilter over } \omega \}$
.
The order of
![]() $\omega ^\omega /\mathcal {U}$
is the almost domination order modulo
$\omega ^\omega /\mathcal {U}$
is the almost domination order modulo
![]() $\mathcal {U}$
and
$\mathcal {U}$
and
![]() $\operatorname {cf}(\omega ^\omega /\mathcal {U})$
is the dominating number of this relation. So it is clear that
$\operatorname {cf}(\omega ^\omega /\mathcal {U})$
is the dominating number of this relation. So it is clear that
![]() $\mathfrak {b} \le \mathfrak {mcf} \le \mathfrak {d}$
.
$\mathfrak {b} \le \mathfrak {mcf} \le \mathfrak {d}$
.
Lemma 2.4 [Reference Golshani and Shelah6, Claim 2.2]
Let
![]() $\mathcal {A}$
be a structure in a language
$\mathcal {A}$
be a structure in a language
![]() $\mathcal {L} = \{<\}$
. Suppose that
$\mathcal {L} = \{<\}$
. Suppose that
![]() $a \in \mathcal {A}$
has cofinality
$a \in \mathcal {A}$
has cofinality
![]() $\omega _1$
. Let
$\omega _1$
. Let
![]() $\mathcal {U}$
be an ultrafilter over
$\mathcal {U}$
be an ultrafilter over
![]() $\omega $
. Then
$\omega $
. Then
![]() $a_\ast = [{\langle a, a, a, \dots \rangle }]$
has cofinality
$a_\ast = [{\langle a, a, a, \dots \rangle }]$
has cofinality
![]() $\omega _1$
in
$\omega _1$
in
![]() $\mathcal {A}^\omega / \mathcal {U}$
.
$\mathcal {A}^\omega / \mathcal {U}$
.
Proof Take an increasing cofinal sequence
![]() ${\langle x_\alpha : \alpha < \omega _1\rangle }$
of points in
${\langle x_\alpha : \alpha < \omega _1\rangle }$
of points in
![]() $\mathcal {A}$
below a. Then
$\mathcal {A}$
below a. Then
![]() ${\langle x_\alpha ^* : \alpha < \omega _1\rangle }$
is an increasing cofinal sequence in
${\langle x_\alpha ^* : \alpha < \omega _1\rangle }$
is an increasing cofinal sequence in
![]() $\mathcal {A}_\ast $
, where
$\mathcal {A}_\ast $
, where
![]() $x_\alpha ^* = [{\langle x_\alpha , x_\alpha , x_\alpha , \dots \rangle }]$
for each
$x_\alpha ^* = [{\langle x_\alpha , x_\alpha , x_\alpha , \dots \rangle }]$
for each
![]() $\alpha < \omega _1$
. This can be shown by regularity of
$\alpha < \omega _1$
. This can be shown by regularity of
![]() $\omega _1$
.
$\omega _1$
.
Lemma 2.5 [Reference Golshani and Shelah6, Claim 2.4]
Let
![]() $\mathcal {U}$
be an ultrafilter over
$\mathcal {U}$
be an ultrafilter over
![]() $\omega $
and
$\omega $
and
![]() $\mathcal {B}_\ast = (\mathbb {Q}, <)^\omega /\mathcal {U}$
. Then for every
$\mathcal {B}_\ast = (\mathbb {Q}, <)^\omega /\mathcal {U}$
. Then for every
![]() $a, b \in \mathcal {B}_\ast $
, there is an automorphism on
$a, b \in \mathcal {B}_\ast $
, there is an automorphism on
![]() $\mathcal {B}_\ast $
that sends a to b.
$\mathcal {B}_\ast $
that sends a to b.
Proof Consider the map
![]() $F \colon \mathbb {Q}^3 \to \mathbb {Q}$
defined by
$F \colon \mathbb {Q}^3 \to \mathbb {Q}$
defined by
![]() $F(x, y, z) = x - y + z$
. Then we have
$F(x, y, z) = x - y + z$
. Then we have
This statement can be written by a first-order formula in the language
![]() $\mathcal {L}' = \{<, F\}$
. Thus the same statement is true in
$\mathcal {L}' = \{<, F\}$
. Thus the same statement is true in
![]() $(\mathbb {Q}, <, F)^\omega /\mathcal {U}$
. The map
$(\mathbb {Q}, <, F)^\omega /\mathcal {U}$
. The map
![]() $F_\ast : \mathcal {B}_\ast ^3 \to \mathcal {B}_\ast $
induced by F satisfies that
$F_\ast : \mathcal {B}_\ast ^3 \to \mathcal {B}_\ast $
induced by F satisfies that
 $$\begin{align*}&(\forall y, z \in \mathcal{B}_\ast) \\&\quad(\text{the map } x \mapsto F(x, y, z) \text{ is an automorphism on } (\mathcal{B}_\ast, <) \text{ that sends }y\text{ to }z).\\[-35pt] \end{align*}$$
$$\begin{align*}&(\forall y, z \in \mathcal{B}_\ast) \\&\quad(\text{the map } x \mapsto F(x, y, z) \text{ is an automorphism on } (\mathcal{B}_\ast, <) \text{ that sends }y\text{ to }z).\\[-35pt] \end{align*}$$
Theorem 2.6.
![]() $\operatorname {KT}(\aleph _1)$
implies
$\operatorname {KT}(\aleph _1)$
implies
![]() $\mathfrak {mcf} = \aleph _1$
.
$\mathfrak {mcf} = \aleph _1$
.
Proof This proof is based on [Reference Golshani and Shelah6, Theorem 2.1]. Assume that
![]() $\mathfrak {mcf} \ge \aleph _2$
. We shall show
$\mathfrak {mcf} \ge \aleph _2$
. We shall show
![]() $\neg \operatorname {KT}(\aleph _1)$
.
$\neg \operatorname {KT}(\aleph _1)$
.
Let
![]() $\mathcal {L} = \{ < \}$
,
$\mathcal {L} = \{ < \}$
,
![]() $\mathcal {A} = (\mathbb {Q}, <)$
and
$\mathcal {A} = (\mathbb {Q}, <)$
and
![]() $\mathcal {B} = (\mathbb {Q} + ((\omega _1+1) \times \mathbb {Q}_{\ge 0}), <_{\mathcal {B}})$
. Here
$\mathcal {B} = (\mathbb {Q} + ((\omega _1+1) \times \mathbb {Q}_{\ge 0}), <_{\mathcal {B}})$
. Here
![]() $<_{\mathcal {B}}$
is defined by a lexicographical order and a disjoint union order.
$<_{\mathcal {B}}$
is defined by a lexicographical order and a disjoint union order.
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
are dense linear ordered sets, so by completeness of DLO, we have
$\mathcal {B}$
are dense linear ordered sets, so by completeness of DLO, we have
![]() $\mathcal {A} \equiv \mathcal {B}$
. Take an ultrafilter
$\mathcal {A} \equiv \mathcal {B}$
. Take an ultrafilter
![]() $\mathcal {U}$
over
$\mathcal {U}$
over
![]() $\omega $
. Put
$\omega $
. Put
![]() $\mathcal {A}_* = \mathcal {A}^\omega / \mathcal {U}, \mathcal {B}_* = \mathcal {B}^\omega / \mathcal {U}$
.
$\mathcal {A}_* = \mathcal {A}^\omega / \mathcal {U}, \mathcal {B}_* = \mathcal {B}^\omega / \mathcal {U}$
.
There is a point a in
![]() $\mathcal {B}$
such that
$\mathcal {B}$
such that
![]() $\operatorname {cf}(\mathcal {B}_a) = \aleph _1$
, where
$\operatorname {cf}(\mathcal {B}_a) = \aleph _1$
, where
![]() $\mathcal {B}_a = \{ x \in \mathcal {B} : x < a \}$
. Then
$\mathcal {B}_a = \{ x \in \mathcal {B} : x < a \}$
. Then
![]() $a_* \in \mathcal {B}_*$
has cofinality
$a_* \in \mathcal {B}_*$
has cofinality
![]() $\aleph _1$
by Lemma 2.4. Here
$\aleph _1$
by Lemma 2.4. Here
![]() $a_* = [{\langle a, a, a, \dots \rangle }]$
. On the other hand, we shall show every point in
$a_* = [{\langle a, a, a, \dots \rangle }]$
. On the other hand, we shall show every point in
![]() $\mathcal {A}_*$
has cofinality
$\mathcal {A}_*$
has cofinality
![]() $\ge \mathfrak {mcf}$
. If we do this, since we assumed
$\ge \mathfrak {mcf}$
. If we do this, since we assumed
![]() $\mathfrak {mcf} \ge \aleph _2$
, we will have
$\mathfrak {mcf} \ge \aleph _2$
, we will have
![]() $\mathcal {A}_* \not \simeq \mathcal {B}_*$
.
$\mathcal {A}_* \not \simeq \mathcal {B}_*$
.
By Lemma 2.5, it suffices to consider the point
![]() $0_* = [{\langle 0, 0, 0, \dots \rangle }]$
. Since
$0_* = [{\langle 0, 0, 0, \dots \rangle }]$
. Since
![]() $\mathbb {Q}$
is symmetrical, we consider
$\mathbb {Q}$
is symmetrical, we consider
![]() $\operatorname {cf}((\mathbb {Q}_{>0})^\omega /\mathcal {U}, >_{\mathcal {U}})$
.
$\operatorname {cf}((\mathbb {Q}_{>0})^\omega /\mathcal {U}, >_{\mathcal {U}})$
.
Now we construct a Galois–Tukey morphism
![]() $(\varphi , \psi ) \colon \mathbf {Cof}(\omega ^\omega /\mathcal {U}) \kern1.2pt{\to}\kern1.2pt \mathbf {Cof}((\mathbb {Q}_{>0})^\omega /\mathcal {U}, >_{\mathcal {U}})$
by
$(\varphi , \psi ) \colon \mathbf {Cof}(\omega ^\omega /\mathcal {U}) \kern1.2pt{\to}\kern1.2pt \mathbf {Cof}((\mathbb {Q}_{>0})^\omega /\mathcal {U}, >_{\mathcal {U}})$
by
 $$ \begin{align*} \varphi &\colon \omega^\omega/\mathcal{U} \to (\mathbb{Q}_{>0})^\omega/\mathcal{U}; [f] \mapsto [{\langle1/(f(n)+1) : n \in \omega\rangle}], \\ \psi &\colon (\mathbb{Q}_{>0})^\omega/\mathcal{U} \to \omega^\omega/\mathcal{U}; [g] \mapsto [{\langle \left\lfloor {1/g(n)-1} \right\rfloor : n \in \omega\rangle}]. \end{align*} $$
$$ \begin{align*} \varphi &\colon \omega^\omega/\mathcal{U} \to (\mathbb{Q}_{>0})^\omega/\mathcal{U}; [f] \mapsto [{\langle1/(f(n)+1) : n \in \omega\rangle}], \\ \psi &\colon (\mathbb{Q}_{>0})^\omega/\mathcal{U} \to \omega^\omega/\mathcal{U}; [g] \mapsto [{\langle \left\lfloor {1/g(n)-1} \right\rfloor : n \in \omega\rangle}]. \end{align*} $$
So we have
![]() $\operatorname {cf}((\mathbb {Q}_{>0})^\omega /\mathcal {U}, >_{\mathcal {U}}) \ge \operatorname {cf}(\omega ^\omega /\mathcal {U}, <_{\mathcal {U}})$
.
$\operatorname {cf}((\mathbb {Q}_{>0})^\omega /\mathcal {U}, >_{\mathcal {U}}) \ge \operatorname {cf}(\omega ^\omega /\mathcal {U}, <_{\mathcal {U}})$
.
Thus we have
![]() $\operatorname {cf}((\mathbb {Q}_{>0})^\omega /\mathcal {U}, >_{\mathcal {U}}) \ge \mathfrak {mcf}$
. We are done.
$\operatorname {cf}((\mathbb {Q}_{>0})^\omega /\mathcal {U}, >_{\mathcal {U}}) \ge \mathfrak {mcf}$
. We are done.
Corollary 2.7.
![]() $\operatorname {KT}(\aleph _1)$
implies
$\operatorname {KT}(\aleph _1)$
implies
![]() $\mathfrak {b} = \aleph _1$
.
$\mathfrak {b} = \aleph _1$
.
Proof This follows from Theorem 2.6 and the fact that
![]() $\mathfrak {b} \le \mathfrak {mcf}$
.
$\mathfrak {b} \le \mathfrak {mcf}$
.
3
 $\mathrm {SAT}(\aleph _0)$
and
$\mathrm {SAT}(\aleph _0)$
and
 $\operatorname {KT}(\aleph _0)$
$\operatorname {KT}(\aleph _0)$
In this section, we first briefly mention consistency of
![]() $\operatorname {KT}(\aleph _0) + \neg \operatorname {KT}(\aleph _1)$
. And we prove that
$\operatorname {KT}(\aleph _0) + \neg \operatorname {KT}(\aleph _1)$
. And we prove that
![]() $\mathrm {SAT}(\aleph _0)$
is equivalent to
$\mathrm {SAT}(\aleph _0)$
is equivalent to
![]() $\operatorname {cov}(\mathsf {meager}) = \mathfrak {c} \land 2^{<\mathfrak {c}} = \mathfrak {c}$
.
$\operatorname {cov}(\mathsf {meager}) = \mathfrak {c} \land 2^{<\mathfrak {c}} = \mathfrak {c}$
.
Fact 3.1 [Reference Blass4, Theorem 7.13]
The statement
![]() $\operatorname {cov}(\mathsf {meager}) = \mathfrak {c}$
is equivalent to
$\operatorname {cov}(\mathsf {meager}) = \mathfrak {c}$
is equivalent to
![]() $\operatorname {MA}(\textrm {countable})$
, that is for every countable poset
$\operatorname {MA}(\textrm {countable})$
, that is for every countable poset
![]() $\mathbb {P}$
and a family of dense sets
$\mathbb {P}$
and a family of dense sets
![]() $\mathcal {D}$
with
$\mathcal {D}$
with
![]() $ \left \lvert {\mathcal {D}} \right \rvert < \mathfrak {c}$
there is a filter G of
$ \left \lvert {\mathcal {D}} \right \rvert < \mathfrak {c}$
there is a filter G of
![]() $\mathbb {P}$
that intersects all
$\mathbb {P}$
that intersects all
![]() $D \in \mathcal {D}$
.
$D \in \mathcal {D}$
.
Theorem 3.2.
![]() $\operatorname {cov}(\mathsf {meager}) = \mathfrak {c}$
implies
$\operatorname {cov}(\mathsf {meager}) = \mathfrak {c}$
implies
![]() $\operatorname {KT}(\aleph _0)$
.
$\operatorname {KT}(\aleph _0)$
.
Proof [Reference Golshani and Shelah6, Theorem 3.3] shows that
![]() $\operatorname {cov}(\mathsf {meager}) = \mathfrak {c} \land \operatorname {cf}(\mathfrak {c})> \aleph _1$
implies
$\operatorname {cov}(\mathsf {meager}) = \mathfrak {c} \land \operatorname {cf}(\mathfrak {c})> \aleph _1$
implies
![]() $\operatorname {KT}(\aleph _1)$
and the exact same proof works for
$\operatorname {KT}(\aleph _1)$
and the exact same proof works for
![]() $\operatorname {KT}(\aleph _0)$
without the assumption
$\operatorname {KT}(\aleph _0)$
without the assumption
![]() $\operatorname {cf}(\mathfrak {c})> \aleph _1$
.
$\operatorname {cf}(\mathfrak {c})> \aleph _1$
.
Here we sketch the proof.
Let
![]() $\mathcal {L}$
be a countable language and
$\mathcal {L}$
be a countable language and
![]() $\mathcal {A}^0$
and
$\mathcal {A}^0$
and
![]() $\mathcal {A}^1$
are countable
$\mathcal {A}^1$
are countable
![]() $\mathcal {L}$
-structures which are elementarily equivalent.
$\mathcal {L}$
-structures which are elementarily equivalent.
Enumerate
![]() $(\mathcal {A}^i)^\omega $
for
$(\mathcal {A}^i)^\omega $
for
![]() $i=0, 1$
as
$i=0, 1$
as
By a back-and-forth method, we construct a sequence of triples
![]() ${\langle (\mathcal {U}_\alpha , g^0_\alpha , g^1_\alpha ) : \alpha < \mathfrak {c}\rangle }$
satisfying:
${\langle (\mathcal {U}_\alpha , g^0_\alpha , g^1_\alpha ) : \alpha < \mathfrak {c}\rangle }$
satisfying:
-
(1)
 $g^0_\alpha \in \mathcal {A}^0$
.
$g^0_\alpha \in \mathcal {A}^0$
. -
(2)
 $g^1_\alpha \in \mathcal {A}^1$
.
$g^1_\alpha \in \mathcal {A}^1$
. -
(3)
 $\mathcal {U}_\alpha $
is a filter over
$\mathcal {U}_\alpha $
is a filter over
 $\omega $
generated by
$\omega $
generated by
 $\aleph _0 + \left \lvert {\alpha } \right \rvert $
sets.
$\aleph _0 + \left \lvert {\alpha } \right \rvert $
sets. -
(4)
 $(\mathcal {U}_\alpha : \alpha < \mathfrak {c})$
is an increasing continuous sequence.
$(\mathcal {U}_\alpha : \alpha < \mathfrak {c})$
is an increasing continuous sequence. -
(5) If
 $\varphi (x_0, \dots , x_{n-1}$
is an
$\varphi (x_0, \dots , x_{n-1}$
is an
 $\mathcal {L}$
-formula and
$\mathcal {L}$
-formula and
 $\beta _0, \dots , \beta _n \le \alpha $
, then the set
$\beta _0, \dots , \beta _n \le \alpha $
, then the set  $$\begin{align*}\{k \in \omega : \mathcal{M}^0 \models \varphi(g^0_{\beta_0}(k), \dots, g^0_{\beta_{n-1}}(k)) \iff \mathcal{M}^1 \models \varphi(g^1_{\beta_0}(k), \dots, g^1_{\beta_{n-1}}(k)) \}\end{align*}$$
$$\begin{align*}\{k \in \omega : \mathcal{M}^0 \models \varphi(g^0_{\beta_0}(k), \dots, g^0_{\beta_{n-1}}(k)) \iff \mathcal{M}^1 \models \varphi(g^1_{\beta_0}(k), \dots, g^1_{\beta_{n-1}}(k)) \}\end{align*}$$
belongs to
 $\mathcal {U}_{\alpha +1}$
.
$\mathcal {U}_{\alpha +1}$
.
In the construction, when
![]() $\alpha $
is even, we put
$\alpha $
is even, we put
![]() $g^0_\alpha = f^0_\gamma $
where
$g^0_\alpha = f^0_\gamma $
where
![]() $\gamma $
is the least ordinal
$\gamma $
is the least ordinal
![]() $f^0_\gamma \not \in \{g^0_\beta : \beta < \alpha \}$
. And
$f^0_\gamma \not \in \{g^0_\beta : \beta < \alpha \}$
. And
![]() $\mathbb {P}$
is the poset of finite partial functions from
$\mathbb {P}$
is the poset of finite partial functions from
![]() $\omega $
to
$\omega $
to
![]() $\mathcal {A}^1$
. Take a generating set
$\mathcal {A}^1$
. Take a generating set
![]() $\mathcal {F}$
of
$\mathcal {F}$
of
![]() $\mathcal {U}_\alpha $
of size
$\mathcal {U}_\alpha $
of size
![]() $\aleph _0 + \left \lvert {\alpha } \right \rvert $
. Then by using
$\aleph _0 + \left \lvert {\alpha } \right \rvert $
. Then by using
![]() $\operatorname {MA}(\textrm {countable})$
, take a
$\operatorname {MA}(\textrm {countable})$
, take a
![]() $\mathbb {P}$
-generic filter G with respect to the following family of dense sets of
$\mathbb {P}$
-generic filter G with respect to the following family of dense sets of
![]() $\mathbb {P}$
:
$\mathbb {P}$
:
and
 $$ \begin{align*} E_{X,{\langle\varphi_\iota : \iota \in I\rangle},{\langle\gamma^\iota_1,\dots,\gamma^\iota_{n_\iota} : \iota \in I\rangle}} = &\{ p \in \mathbb{P} : (\exists k \in \operatorname{dom}(p) \cap X)(\forall \iota \in I) \\ & \hspace{0.4cm} (M^0 \models \varphi_\iota(g^0_{\gamma^\iota_1}(k), \dots g^0_{\gamma^\iota_{n_\iota}}(k), g^0_\alpha(k)) \Leftrightarrow \\ & \hspace{0.54cm} M^1 \models \varphi_\iota(g^1_{\gamma^\iota_1}(k), \dots g^1_{\gamma^\iota_{n_\iota}}(k), p(k)) \}), \end{align*} $$
$$ \begin{align*} E_{X,{\langle\varphi_\iota : \iota \in I\rangle},{\langle\gamma^\iota_1,\dots,\gamma^\iota_{n_\iota} : \iota \in I\rangle}} = &\{ p \in \mathbb{P} : (\exists k \in \operatorname{dom}(p) \cap X)(\forall \iota \in I) \\ & \hspace{0.4cm} (M^0 \models \varphi_\iota(g^0_{\gamma^\iota_1}(k), \dots g^0_{\gamma^\iota_{n_\iota}}(k), g^0_\alpha(k)) \Leftrightarrow \\ & \hspace{0.54cm} M^1 \models \varphi_\iota(g^1_{\gamma^\iota_1}(k), \dots g^1_{\gamma^\iota_{n_\iota}}(k), p(k)) \}), \end{align*} $$
where
![]() $X \in \mathcal {F}$
,
$X \in \mathcal {F}$
,
![]() ${\langle \varphi _\iota : \iota \in I\rangle }$
is a finite sequence of
${\langle \varphi _\iota : \iota \in I\rangle }$
is a finite sequence of
![]() $\mathcal {L}$
-formulas and
$\mathcal {L}$
-formulas and
![]() $\gamma ^\iota _1, \dots , \gamma ^\iota _{n_\iota }$
for
$\gamma ^\iota _1, \dots , \gamma ^\iota _{n_\iota }$
for
![]() $\iota \in I$
are ordinals less than
$\iota \in I$
are ordinals less than
![]() $\alpha $
. Then putting
$\alpha $
. Then putting
![]() $g^1_\alpha = \bigcup G$
satisfies the induction hypothesis.
$g^1_\alpha = \bigcup G$
satisfies the induction hypothesis.
Then the appropriate construction guarantees that
![]() $\mathcal {U} = \bigcup _{\alpha < \mathfrak {c}} \mathcal {U}_\alpha $
is an ultrafilter and that the function
$\mathcal {U} = \bigcup _{\alpha < \mathfrak {c}} \mathcal {U}_\alpha $
is an ultrafilter and that the function
is isomorphic from
![]() $(M^0)^\omega /\mathcal {U}$
to
$(M^0)^\omega /\mathcal {U}$
to
![]() $(M^1)^\omega /\mathcal {U}$
.
$(M^1)^\omega /\mathcal {U}$
.
Corollary 3.3. Assume
![]() $\operatorname {Con}(\mathrm {ZFC})$
. Then
$\operatorname {Con}(\mathrm {ZFC})$
. Then
![]() $\operatorname {Con}(\mathrm {ZFC} + \operatorname {KT}(\aleph _0) + \neg \operatorname {KT}(\aleph _1))$
.
$\operatorname {Con}(\mathrm {ZFC} + \operatorname {KT}(\aleph _0) + \neg \operatorname {KT}(\aleph _1))$
.
Proof
![]() $\mathrm {MA} + \neg \mathrm {CH}$
implies
$\mathrm {MA} + \neg \mathrm {CH}$
implies
![]() $\operatorname {KT}(\aleph _0) \land \neg \operatorname {KT}(\aleph _1)$
by Theorems 2.6 and 3.2.
$\operatorname {KT}(\aleph _0) \land \neg \operatorname {KT}(\aleph _1)$
by Theorems 2.6 and 3.2.
Fact 3.4 [Reference Bartoszyński and Judah2, Lemma 2.4.2]
![]() $\operatorname {cov}(\mathsf {meager}) = \mathfrak {v}^\exists _{{\langle \omega : n \in \omega \rangle }, \mathrm {id}}$
. In other words,
$\operatorname {cov}(\mathsf {meager}) = \mathfrak {v}^\exists _{{\langle \omega : n \in \omega \rangle }, \mathrm {id}}$
. In other words,
![]() $\operatorname {cov}(\mathsf {meager}) \ge \kappa $
holds iff
$\operatorname {cov}(\mathsf {meager}) \ge \kappa $
holds iff
![]() $(\forall X \subseteq \omega ^\omega \text { of size } <\kappa ) (\exists S \in \prod _{i \in \omega } [\omega ]^{\le i}) (\forall x \in X) (\exists ^\infty n) (x(n) \in S(n))$
holds.
$(\forall X \subseteq \omega ^\omega \text { of size } <\kappa ) (\exists S \in \prod _{i \in \omega } [\omega ]^{\le i}) (\forall x \in X) (\exists ^\infty n) (x(n) \in S(n))$
holds.
Theorem 3.5.
![]() $\mathrm {SAT}(\aleph _0)$
implies
$\mathrm {SAT}(\aleph _0)$
implies
![]() $\operatorname {cov}(\mathsf {meager}) = \mathfrak {c}$
.
$\operatorname {cov}(\mathsf {meager}) = \mathfrak {c}$
.
Proof Take an ultrafilter
![]() $\mathcal {U}$
that witnesses
$\mathcal {U}$
that witnesses
![]() $\mathrm {SAT}(\aleph _0)$
. Fix
$\mathrm {SAT}(\aleph _0)$
. Fix
![]() $X \subseteq \omega ^\omega $
of size
$X \subseteq \omega ^\omega $
of size
![]() $< \mathfrak {c}$
. Define a language
$< \mathfrak {c}$
. Define a language
![]() $\mathcal {L}$
by
$\mathcal {L}$
by
![]() $\mathcal {L} = \{\subseteq \}$
and for each
$\mathcal {L} = \{\subseteq \}$
and for each
![]() $i \in \omega $
, define an
$i \in \omega $
, define an
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {A}_i$
by
$\mathcal {A}_i$
by
![]() $\mathcal {A}_i = ([\omega ]^{\le i}, \subseteq )$
. For each
$\mathcal {A}_i = ([\omega ]^{\le i}, \subseteq )$
. For each
![]() $x \in \omega ^\omega $
, let
$x \in \omega ^\omega $
, let
![]() $S_x = {\langle \{x(i)\} : i \in \omega \rangle }$
. In the ultraproduct
$S_x = {\langle \{x(i)\} : i \in \omega \rangle }$
. In the ultraproduct
![]() $\mathcal {A}_* = \prod _{i\in \omega } \mathcal {A}_i / \mathcal {U}$
, define a set p of formulas of one free variable S by
$\mathcal {A}_* = \prod _{i\in \omega } \mathcal {A}_i / \mathcal {U}$
, define a set p of formulas of one free variable S by
This p is finitely satisfiable. In order to check this, let
![]() $x_0, \dots , x_n$
be finitely many members of X. Define S by
$x_0, \dots , x_n$
be finitely many members of X. Define S by
![]() $S(m) = \{ x_0(m), \dots , x_n(m) \}$
for
$S(m) = \{ x_0(m), \dots , x_n(m) \}$
for
![]() $m \ge n$
. We don’t need to care about
$m \ge n$
. We don’t need to care about
![]() $S(m)$
for
$S(m)$
for
![]() $m < n$
. Then this S satisfies
$m < n$
. Then this S satisfies
![]() $[S_{x_i}] \subseteq [S]$
for all
$[S_{x_i}] \subseteq [S]$
for all
![]() $i \le n$
. Moreover, the number of parameters of p is
$i \le n$
. Moreover, the number of parameters of p is
![]() $< \mathfrak {c}$
.
$< \mathfrak {c}$
.
So by
![]() $\mathrm {SAT}(\aleph _0)$
, we can take
$\mathrm {SAT}(\aleph _0)$
, we can take
![]() $[S] \in \mathcal {A}_*$
that realizes p. Then S fulfills
$[S] \in \mathcal {A}_*$
that realizes p. Then S fulfills
![]() $(\forall x \in X) (\{ n \in \omega : x(n) \in S(n) \} \in \mathcal {U})$
. Thus
$(\forall x \in X) (\{ n \in \omega : x(n) \in S(n) \} \in \mathcal {U})$
. Thus
![]() $(\forall x \in X) (\exists ^\infty n) (x(n) \in S(n))$
.
$(\forall x \in X) (\exists ^\infty n) (x(n) \in S(n))$
.
Theorem 3.6.
![]() $\mathrm {SAT}(\aleph _0)$
implies
$\mathrm {SAT}(\aleph _0)$
implies
![]() $2^{<\mathfrak {c}} = \mathfrak {c}$
.
$2^{<\mathfrak {c}} = \mathfrak {c}$
.
Proof Take an ultrafilter
![]() $\mathcal {U}$
over
$\mathcal {U}$
over
![]() $\omega $
that witnesses
$\omega $
that witnesses
![]() $\mathrm {SAT}(\aleph _0)$
. Fix
$\mathrm {SAT}(\aleph _0)$
. Fix
![]() $\kappa < \mathfrak {c}$
.
$\kappa < \mathfrak {c}$
.
Put
![]() $\mathcal {L} = \{\subseteq \}$
and define an
$\mathcal {L} = \{\subseteq \}$
and define an
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $\mathcal {A}$
by
$\mathcal {A}$
by
![]() $\mathcal {A} = ([\omega ]^{<\omega }, \subseteq )$
. Put
$\mathcal {A} = ([\omega ]^{<\omega }, \subseteq )$
. Put
![]() $\mathcal {A}^* = \mathcal {A}^\omega /\mathcal {U}$
.
$\mathcal {A}^* = \mathcal {A}^\omega /\mathcal {U}$
.
Define a map
![]() $\iota \colon \omega ^\omega /\mathcal {U} \to \mathcal {A}^*$
by
$\iota \colon \omega ^\omega /\mathcal {U} \to \mathcal {A}^*$
by
![]() $\iota ([x]) = [{\langle \{x(n)\} : n \in \omega \rangle }]$
. By Fact 1.8, we have
$\iota ([x]) = [{\langle \{x(n)\} : n \in \omega \rangle }]$
. By Fact 1.8, we have
![]() $ \left \lvert {\omega ^\omega /\mathcal {U}} \right \rvert = \mathfrak {c}$
. Take a subset F of
$ \left \lvert {\omega ^\omega /\mathcal {U}} \right \rvert = \mathfrak {c}$
. Take a subset F of
![]() $\omega ^\omega /\mathcal {U}$
of size
$\omega ^\omega /\mathcal {U}$
of size
![]() $\kappa $
.
$\kappa $
.
For each
![]() $X \subseteq F$
, let
$X \subseteq F$
, let
![]() $p_X$
be a set of formulas with a free variable z defined by
$p_X$
be a set of formulas with a free variable z defined by
Each
![]() $p_X$
is finitely satisfiable. In order to check this, take
$p_X$
is finitely satisfiable. In order to check this, take
![]() $[x_0], \dots , [x_n] \in X$
and
$[x_0], \dots , [x_n] \in X$
and
![]() $[y_0], \dots , [y_m] \in F \smallsetminus X$
. Put
$[y_0], \dots , [y_m] \in F \smallsetminus X$
. Put
![]() $z(i) = \{ x_0(i), \dots , x_n(i) \}$
. Then
$z(i) = \{ x_0(i), \dots , x_n(i) \}$
. Then
![]() $\iota ([x_0]), \dots , \iota ([x_n]) \subseteq _{\mathcal {U}} [z]$
. In order to prove
$\iota ([x_0]), \dots , \iota ([x_n]) \subseteq _{\mathcal {U}} [z]$
. In order to prove
![]() $\iota ([y_j]) \not \subseteq _{\mathcal {U}} [z]$
for each
$\iota ([y_j]) \not \subseteq _{\mathcal {U}} [z]$
for each
![]() $j \le m$
, suppose that
$j \le m$
, suppose that
![]() $\{ i \in \omega : y_j(i) \in z(i) \} \in \mathcal {U}$
. Then for each
$\{ i \in \omega : y_j(i) \in z(i) \} \in \mathcal {U}$
. Then for each
![]() $i \in \omega $
, there is a
$i \in \omega $
, there is a
![]() $k_i \le n$
such that
$k_i \le n$
such that
![]() $\{ i \in \omega : y_j(i) = x_{k_i}(i)\} \in \mathcal {U}$
. Then there is a
$\{ i \in \omega : y_j(i) = x_{k_i}(i)\} \in \mathcal {U}$
. Then there is a
![]() $k \le n$
such that
$k \le n$
such that
![]() $\{ i \in \omega : y_j(i) = x_k(i)\} \in \mathcal {U}$
. This implies
$\{ i \in \omega : y_j(i) = x_k(i)\} \in \mathcal {U}$
. This implies
![]() $[y_j] = [x_k]$
, which is a contradiction.
$[y_j] = [x_k]$
, which is a contradiction.
By
![]() $\mathrm {SAT}(\aleph _0)$
, for each
$\mathrm {SAT}(\aleph _0)$
, for each
![]() $X \subseteq F$
, take
$X \subseteq F$
, take
![]() $[z_X] \in \mathcal {A}^*$
that realizes
$[z_X] \in \mathcal {A}^*$
that realizes
![]() $p_X$
. For
$p_X$
. For
![]() $X, Y \subseteq F$
with
$X, Y \subseteq F$
with
![]() $X \ne Y$
, we have
$X \ne Y$
, we have
![]() $[z_X] \ne [z_Y]$
. So
$[z_X] \ne [z_Y]$
. So
![]() $2^\kappa = \left \lvert {\{[z_X] : X \subseteq F\}} \right \rvert \le \left \lvert {\mathcal {A}^*} \right \rvert = \mathfrak {c}$
. Therefore we have proved
$2^\kappa = \left \lvert {\{[z_X] : X \subseteq F\}} \right \rvert \le \left \lvert {\mathcal {A}^*} \right \rvert = \mathfrak {c}$
. Therefore we have proved
![]() $2^{<\mathfrak {c}} = \mathfrak {c}$
.
$2^{<\mathfrak {c}} = \mathfrak {c}$
.
Theorem 3.7.
![]() $\operatorname {cov}(\mathsf {meager}) = \mathfrak {c} \land 2^{<\mathfrak {c}} = \mathfrak {c}$
implies
$\operatorname {cov}(\mathsf {meager}) = \mathfrak {c} \land 2^{<\mathfrak {c}} = \mathfrak {c}$
implies
![]() $\mathrm {SAT}(\aleph _0)$
.
$\mathrm {SAT}(\aleph _0)$
.
Proof This proof is based on [Reference Ellentuck and Rucker5, Theorem 1].
Let
![]() ${\langle b_\alpha : \alpha < \mathfrak {c}\rangle }$
be an enumeration of
${\langle b_\alpha : \alpha < \mathfrak {c}\rangle }$
be an enumeration of
![]() $\omega ^\omega $
. Let
$\omega ^\omega $
. Let
![]() ${\langle (\mathcal {L}_\xi , \mathcal {B}_\xi , \Delta _\xi ) : \xi < \mathfrak {c}\rangle }$
be an enumeration of triples
${\langle (\mathcal {L}_\xi , \mathcal {B}_\xi , \Delta _\xi ) : \xi < \mathfrak {c}\rangle }$
be an enumeration of triples
![]() $(\mathcal {L}, \mathcal {B}, \Delta )$
such that
$(\mathcal {L}, \mathcal {B}, \Delta )$
such that
![]() $\mathcal {L}$
is a countable language,
$\mathcal {L}$
is a countable language,
![]() $\mathcal {B} = {\langle \mathcal {A}_i : i \in \omega \rangle }$
is a sequence of
$\mathcal {B} = {\langle \mathcal {A}_i : i \in \omega \rangle }$
is a sequence of
![]() $\mathcal {L}$
-structures with universe
$\mathcal {L}$
-structures with universe
![]() $\omega $
, and
$\omega $
, and
![]() $\Delta $
is a subset of
$\Delta $
is a subset of
![]() $\operatorname {Fml}(\mathcal {L}^+)$
with
$\operatorname {Fml}(\mathcal {L}^+)$
with
![]() $ \left \lvert {\Delta } \right \rvert < \mathfrak {c}$
. Here
$ \left \lvert {\Delta } \right \rvert < \mathfrak {c}$
. Here
![]() $\mathcal {L}^+ = \mathcal {L} \cup \{ c_\alpha : \alpha < \mathfrak {c} \}$
where the
$\mathcal {L}^+ = \mathcal {L} \cup \{ c_\alpha : \alpha < \mathfrak {c} \}$
where the
![]() $c_\alpha $
’s are new constant symbols and
$c_\alpha $
’s are new constant symbols and
![]() $\operatorname {Fml}(\mathcal {L}^+)$
is the set of all
$\operatorname {Fml}(\mathcal {L}^+)$
is the set of all
![]() $\mathcal {L}^+$
formulas with one free variable. Here we used the assumption
$\mathcal {L}^+$
formulas with one free variable. Here we used the assumption
![]() $2^{<\mathfrak {c}} = \mathfrak {c}$
. And ensure each
$2^{<\mathfrak {c}} = \mathfrak {c}$
. And ensure each
![]() $(\mathcal {L}, \mathcal {B}, \Delta )$
occurs cofinally in this sequence.
$(\mathcal {L}, \mathcal {B}, \Delta )$
occurs cofinally in this sequence.
For
![]() $\mathcal {B}_\xi = {\langle \mathcal {A}^\xi _i : i \in \omega \rangle }$
, put
$\mathcal {B}_\xi = {\langle \mathcal {A}^\xi _i : i \in \omega \rangle }$
, put
![]() $\mathcal {B}_\xi (i) = (\mathcal {A}^\xi _i, b_0(i), b_1(i), \dots )$
, which is an
$\mathcal {B}_\xi (i) = (\mathcal {A}^\xi _i, b_0(i), b_1(i), \dots )$
, which is an
![]() $\mathcal {L}^+$
-structure.
$\mathcal {L}^+$
-structure.
Let
![]() ${\langle X_\xi : \xi < \mathfrak {c}\rangle }$
be an enumeration of
${\langle X_\xi : \xi < \mathfrak {c}\rangle }$
be an enumeration of
![]() $\mathcal {P}(\omega )$
.
$\mathcal {P}(\omega )$
.
We construct a sequence
![]() ${\langle F_\xi : \xi < \mathfrak {c}\rangle }$
of filters inductively so that the following properties hold:
${\langle F_\xi : \xi < \mathfrak {c}\rangle }$
of filters inductively so that the following properties hold:
-
(1)
 $F_0$
is the filter consisting of all cofinite subsets of
$F_0$
is the filter consisting of all cofinite subsets of
 $\omega $
.
$\omega $
. -
(2)
 $F_\xi \subseteq F_{\xi + 1}$
and
$F_\xi \subseteq F_{\xi + 1}$
and
 $F_\xi = \bigcup _{\alpha < \xi } F_\alpha $
for
$F_\xi = \bigcup _{\alpha < \xi } F_\alpha $
for
 $\xi $
limit.
$\xi $
limit. -
(3)
 $X_\xi \in F_{\xi +1}$
or
$X_\xi \in F_{\xi +1}$
or
 $\omega \smallsetminus X_\xi \in F_{\xi +1}$
.
$\omega \smallsetminus X_\xi \in F_{\xi +1}$
. -
(4)
 $F_\xi $
is generated by
$F_\xi $
is generated by
 $< \mathfrak {c}$
members.
$< \mathfrak {c}$
members. -
(5) If
(*) $$ \begin{align} \text{for all } \Gamma \subseteq \Delta_\xi \text{ finite, } \{i\in\omega : \Gamma \text{ is satisfiable in } \mathcal{B}_\xi(i) \} \in F_\xi, \end{align} $$
$$ \begin{align} \text{for all } \Gamma \subseteq \Delta_\xi \text{ finite, } \{i\in\omega : \Gamma \text{ is satisfiable in } \mathcal{B}_\xi(i) \} \in F_\xi, \end{align} $$
then there is an
 $f \in \omega ^\omega $
such that for all
$f \in \omega ^\omega $
such that for all
 $\varphi \in \Delta _\xi $
,
$\varphi \in \Delta _\xi $
,
 $\{ i \in \omega : f(i) \text { satisfies } \varphi \text {in } \mathcal {B}_\xi (i) \} \in F_{\xi +1}$
.
$\{ i \in \omega : f(i) \text { satisfies } \varphi \text {in } \mathcal {B}_\xi (i) \} \in F_{\xi +1}$
.
Suppose we have constructed
![]() $F_\xi $
. We construct
$F_\xi $
. We construct
![]() $F_{\xi +1}$
. Let
$F_{\xi +1}$
. Let
![]() $F_\xi '$
be a generating subset of
$F_\xi '$
be a generating subset of
![]() $F_\xi $
with
$F_\xi $
with
![]() $ \left \lvert {F_\xi '} \right \rvert < \mathfrak {c}$
. If (*) is false, let
$ \left \lvert {F_\xi '} \right \rvert < \mathfrak {c}$
. If (*) is false, let
![]() $F_{\xi +1}$
be the filter generated by
$F_{\xi +1}$
be the filter generated by
![]() $F_\xi ' \cup \{X_\xi \}$
or
$F_\xi ' \cup \{X_\xi \}$
or
![]() $F_\xi ' \cup \{\omega \smallsetminus X_\xi \}$
. Suppose (*).
$F_\xi ' \cup \{\omega \smallsetminus X_\xi \}$
. Suppose (*).
Put
![]() $\mathbb {P} = \operatorname {Fn}(\omega , \omega ) = \{ p : p\text { is a finite partial function from }\omega \text { to }\omega \}$
. For
$\mathbb {P} = \operatorname {Fn}(\omega , \omega ) = \{ p : p\text { is a finite partial function from }\omega \text { to }\omega \}$
. For
![]() $n \in \omega $
, put
$n \in \omega $
, put
For
![]() $A \in F_\xi '$
and
$A \in F_\xi '$
and
![]() $\varphi _1, \dots , \varphi _n \in \Delta _\xi $
, put
$\varphi _1, \dots , \varphi _n \in \Delta _\xi $
, put
Each
![]() $D_n$
is clearly dense. In order to show that each
$D_n$
is clearly dense. In order to show that each
![]() $E_{A,\varphi _1,\dots ,\varphi _n}$
is dense, take
$E_{A,\varphi _1,\dots ,\varphi _n}$
is dense, take
![]() $p \in \mathbb {P}$
. By (*) and the property
$p \in \mathbb {P}$
. By (*) and the property
![]() $A \in F_\xi $
, we can take
$A \in F_\xi $
, we can take
![]() $i \in A \smallsetminus \operatorname {dom} p$
and
$i \in A \smallsetminus \operatorname {dom} p$
and
![]() $k \in \omega $
such that k satisfies
$k \in \omega $
such that k satisfies
![]() $\varphi _1, \dots , \varphi _n$
in
$\varphi _1, \dots , \varphi _n$
in
![]() $\mathcal {B}_\xi (i)$
. Put
$\mathcal {B}_\xi (i)$
. Put
![]() $q = p \cup \{ (i, k) \}$
. This is an extension of p in
$q = p \cup \{ (i, k) \}$
. This is an extension of p in
![]() $E_{A,\varphi _1,\dots ,\varphi _n}$
.
$E_{A,\varphi _1,\dots ,\varphi _n}$
.
By using
![]() $\operatorname {MA}(\textrm {countable})$
, take a generic filter
$\operatorname {MA}(\textrm {countable})$
, take a generic filter
![]() $G \subseteq \mathbb {P}$
with respect to above dense sets. Put
$G \subseteq \mathbb {P}$
with respect to above dense sets. Put
![]() $f = \bigcup G$
. Then
$f = \bigcup G$
. Then
![]() $F_\xi " := F_\xi ' \cup \{ Y_\varphi : \varphi \in \Delta _\xi \}$
satisfies finite intersection property, where
$F_\xi " := F_\xi ' \cup \{ Y_\varphi : \varphi \in \Delta _\xi \}$
satisfies finite intersection property, where
![]() $Y_\varphi = \{ i \in \omega : f(i) \text { satisfies } \varphi \text { in } \mathcal {B}_\xi (i) \}$
. In order to check this, let
$Y_\varphi = \{ i \in \omega : f(i) \text { satisfies } \varphi \text { in } \mathcal {B}_\xi (i) \}$
. In order to check this, let
![]() $A \in F_\xi '$
and
$A \in F_\xi '$
and
![]() $\varphi _1, \dots , \varphi _n \in \Delta _\xi $
. Then by genericity, we can take
$\varphi _1, \dots , \varphi _n \in \Delta _\xi $
. Then by genericity, we can take
![]() $p \in G \cap E_{A,\varphi _1,\dots ,\varphi _n}$
. So we can take
$p \in G \cap E_{A,\varphi _1,\dots ,\varphi _n}$
. So we can take
![]() $i \in \operatorname {dom} p \cap A$
such that
$i \in \operatorname {dom} p \cap A$
such that
![]() $p(i) \text { satisfies } \varphi _1, \dots , \varphi _n \text { in } \mathcal {B}_\xi (i)$
. Then we have
$p(i) \text { satisfies } \varphi _1, \dots , \varphi _n \text { in } \mathcal {B}_\xi (i)$
. Then we have
![]() $i \in A \cap Y_{\varphi _1} \cap \dots \cap Y_{\varphi _n}$
.
$i \in A \cap Y_{\varphi _1} \cap \dots \cap Y_{\varphi _n}$
.
Let
![]() $F_{\xi +1}$
be the filter generated by
$F_{\xi +1}$
be the filter generated by
![]() $F_\xi '' \cup \{X_\xi \}$
or
$F_\xi '' \cup \{X_\xi \}$
or
![]() $F_\xi '' \cup \{\omega \smallsetminus X_\xi \}$
.
$F_\xi '' \cup \{\omega \smallsetminus X_\xi \}$
.
We have constructed
![]() ${\langle F_\xi : \xi < \mathfrak {c}\rangle }$
. In order to check that the resulting ultrafilter
${\langle F_\xi : \xi < \mathfrak {c}\rangle }$
. In order to check that the resulting ultrafilter
![]() $F = \bigcup _{\xi < \mathfrak {c}} F_\xi $
witnesses
$F = \bigcup _{\xi < \mathfrak {c}} F_\xi $
witnesses
![]() $\mathrm {SAT}(\aleph _0)$
, let
$\mathrm {SAT}(\aleph _0)$
, let
![]() $\mathcal {L}$
and
$\mathcal {L}$
and
![]() $\mathcal {B} = {\langle \mathcal {A}_i : i \in \omega \rangle }$
satisfy the assumption of the theorem. Let
$\mathcal {B} = {\langle \mathcal {A}_i : i \in \omega \rangle }$
satisfy the assumption of the theorem. Let
![]() $\Delta $
be a subset of
$\Delta $
be a subset of
![]() $\operatorname {Fml}(\mathcal {L}^+)$
with
$\operatorname {Fml}(\mathcal {L}^+)$
with
![]() $ \left \lvert {\Delta } \right \rvert < \mathfrak {c}$
. Assume that for all
$ \left \lvert {\Delta } \right \rvert < \mathfrak {c}$
. Assume that for all
![]() $\Gamma \subseteq \Delta $
finite,
$\Gamma \subseteq \Delta $
finite,
![]() $X_\Gamma := \{i\in \omega : \Gamma \text { is satisfiable in } \mathcal {B}_\xi (i) \} \in F$
. By the regularity of
$X_\Gamma := \{i\in \omega : \Gamma \text { is satisfiable in } \mathcal {B}_\xi (i) \} \in F$
. By the regularity of
![]() $\mathfrak {c}$
, we have
$\mathfrak {c}$
, we have
![]() $\alpha < \mathfrak {c}$
such that for all
$\alpha < \mathfrak {c}$
such that for all
![]() $\Gamma \subseteq \Delta $
finite,
$\Gamma \subseteq \Delta $
finite,
![]() $X_\Gamma \in F_\alpha $
. Let
$X_\Gamma \in F_\alpha $
. Let
![]() $\xi \ge \alpha $
be satisfying
$\xi \ge \alpha $
be satisfying
![]() $(\mathcal {L}_\xi , \mathcal {B}_\xi , \Delta _\xi ) = (\mathcal {L}, \mathcal {B}, \Delta )$
. Then by (5), there is an
$(\mathcal {L}_\xi , \mathcal {B}_\xi , \Delta _\xi ) = (\mathcal {L}, \mathcal {B}, \Delta )$
. Then by (5), there is an
![]() $f \in \omega $
such that for all
$f \in \omega $
such that for all
![]() $\varphi \in \Delta $
,
$\varphi \in \Delta $
,
![]() $\{ i \in \omega : f(i) \text { satisfies } \varphi \text { in } \mathcal {B}(i) \} \in F$
. Thus
$\{ i \in \omega : f(i) \text { satisfies } \varphi \text { in } \mathcal {B}(i) \} \in F$
. Thus
![]() $\prod _{i \in \omega } \mathcal {A}_i / F$
is saturated.
$\prod _{i \in \omega } \mathcal {A}_i / F$
is saturated.
4
 $\operatorname {KT}(\aleph _0)$
implies
$\operatorname {KT}(\aleph _0)$
implies
 $ \mathfrak {c}^\exists \le \mathfrak {d}$
$ \mathfrak {c}^\exists \le \mathfrak {d}$
In this section, we will show the following theorem. This proof is based on [Reference Shelah9, Theorem 1.1] and [Reference Abraham1, Theorem 3.7].
Theorem 4.1.
![]() $\operatorname {KT}(\aleph _0)$
implies
$\operatorname {KT}(\aleph _0)$
implies
![]() $\mathfrak {c}^\exists \le \mathfrak {d}$
.
$\mathfrak {c}^\exists \le \mathfrak {d}$
.
Definition 4.2. Define a language
![]() $\mathcal {L}$
by
$\mathcal {L}$
by
![]() $\mathcal {L} = \{E, U, V\}$
, where E is a binary predicate and
$\mathcal {L} = \{E, U, V\}$
, where E is a binary predicate and
![]() $U, V$
are unary predicates. We say an
$U, V$
are unary predicates. We say an
![]() $\mathcal {L}$
-structure
$\mathcal {L}$
-structure
![]() $M = ( \left \lvert {M} \right \rvert , E^M, U^M, V^M)$
is a bipartite directed graph if the following conditions hold:
$M = ( \left \lvert {M} \right \rvert , E^M, U^M, V^M)$
is a bipartite directed graph if the following conditions hold:
-
(1)
 $U^M \cup V^M = \left \lvert {M} \right \rvert $
.
$U^M \cup V^M = \left \lvert {M} \right \rvert $
. -
(2)
 $U^M \cap V^M = \varnothing $
.
$U^M \cap V^M = \varnothing $
. -
(3)
 $(\forall x, y \in \left \lvert {M} \right \rvert ) (x \mathrel {E^M} y \rightarrow (x \in U^M \text { and } y \in V^M))$
.
$(\forall x, y \in \left \lvert {M} \right \rvert ) (x \mathrel {E^M} y \rightarrow (x \in U^M \text { and } y \in V^M))$
.
Definition 4.3. For
![]() $n, k \in \omega $
with
$n, k \in \omega $
with
![]() $k \le n$
, define a bipartite directed graph
$k \le n$
, define a bipartite directed graph
![]() $\Delta _{n,k}$
as follows:
$\Delta _{n,k}$
as follows:
-
(1)
 $U^{\Delta _{n,k}} = \{ 1, 2, 3, \dots , n \}$
.
$U^{\Delta _{n,k}} = \{ 1, 2, 3, \dots , n \}$
. -
(2)
 $V^{\Delta _{n,k}} = [\{ 1, 2, 3, \dots , n\}]^{\le k} \smallsetminus \{\varnothing \}$
.
$V^{\Delta _{n,k}} = [\{ 1, 2, 3, \dots , n\}]^{\le k} \smallsetminus \{\varnothing \}$
. -
(3) For
 $u \in U^{\Delta _{n,k}}, v \in V^{\Delta _{n,k}}$
,
$u \in U^{\Delta _{n,k}}, v \in V^{\Delta _{n,k}}$
,
 $u \mathrel {E^{\Delta _{n,k}}} v$
iff
$u \mathrel {E^{\Delta _{n,k}}} v$
iff
 $u \in v$
.
$u \in v$
.
Definition 4.4. For
![]() $n \in \omega $
, let
$n \in \omega $
, let
![]() $G_n = \Delta _{n^3, n}$
. Let
$G_n = \Delta _{n^3, n}$
. Let
![]() $\Gamma $
be the disjoint union of
$\Gamma $
be the disjoint union of
![]() $(G_n : n \ge 2)$
.
$(G_n : n \ge 2)$
.
We define a natural order
![]() $\triangleleft $
on
$\triangleleft $
on
![]() $\Gamma $
by
$\Gamma $
by
![]() $x \triangleleft y$
if
$x \triangleleft y$
if
![]() $m < n$
for
$m < n$
for
![]() $x \in G_m, y \in G_n$
. Then
$x \in G_m, y \in G_n$
. Then
![]() $\Gamma $
is a bipartite directed graph with an order
$\Gamma $
is a bipartite directed graph with an order
![]() $\triangleleft $
. Put
$\triangleleft $
. Put
![]() $\mathcal {L}' = \mathcal {L} \cup \{ \triangleleft \}$
. From now on, we consider
$\mathcal {L}' = \mathcal {L} \cup \{ \triangleleft \}$
. From now on, we consider
![]() $\mathcal {L}'$
-structures which are elementarily equivalent to
$\mathcal {L}'$
-structures which are elementarily equivalent to
![]() $\Gamma $
.
$\Gamma $
.
Definition 4.5. Let
![]() $\Gamma _{\mathrm {NS}}$
be a countable non-standard elementary extension of
$\Gamma _{\mathrm {NS}}$
be a countable non-standard elementary extension of
![]() $\Gamma $
.
$\Gamma $
.
When we say connected components, we mean the connected components when we ignore the orientation of the edges.
Lemma 4.6. Let M be an
![]() $\mathcal {L}'$
-structure that is elementarily equivalent to
$\mathcal {L}'$
-structure that is elementarily equivalent to
![]() $\Gamma $
. Then the connected components of M are precisely the maximal antichains of M with respect to
$\Gamma $
. Then the connected components of M are precisely the maximal antichains of M with respect to
![]() $\triangleleft $
.
$\triangleleft $
.
Proof Suppose that
![]() $A \subseteq M$
is connected but not an antichain. Then we can find elements
$A \subseteq M$
is connected but not an antichain. Then we can find elements
![]() $a_0, \dots , a_n \in M$
such that
$a_0, \dots , a_n \in M$
such that
 $$ \begin{align*} M \models &(a_0 E a_1 \lor a_1 E a_0) \land \dots \land (a_{n-1} E a_n \lor a_n E a_{n-1}) \land \\ &(a_0\text{ and }a_n\text{ are comparable with respect to }\triangleleft). \end{align*} $$
$$ \begin{align*} M \models &(a_0 E a_1 \lor a_1 E a_0) \land \dots \land (a_{n-1} E a_n \lor a_n E a_{n-1}) \land \\ &(a_0\text{ and }a_n\text{ are comparable with respect to }\triangleleft). \end{align*} $$
By elementarity, we have
![]() $n+1$
many elements in
$n+1$
many elements in
![]() $\Gamma $
that satisfies the same formula. This is a contradiction. So every connected subset in M is an antichain.
$\Gamma $
that satisfies the same formula. This is a contradiction. So every connected subset in M is an antichain.
Note that any two connected vertexes in
![]() $\Gamma $
have a path of length at most
$\Gamma $
have a path of length at most
![]() $4$
. Thus we have
$4$
. Thus we have
 $$ \begin{align*} \Gamma \models (\forall a, b) &((a\text{ and }b\text{ are incomparable with respect to }\triangleleft) \\ &\rightarrow (\text{there is a path between }a\text{ and }b\text{ with length at most } 4)). \end{align*} $$
$$ \begin{align*} \Gamma \models (\forall a, b) &((a\text{ and }b\text{ are incomparable with respect to }\triangleleft) \\ &\rightarrow (\text{there is a path between }a\text{ and }b\text{ with length at most } 4)). \end{align*} $$
By elementarity, the same formula holds in M. So every antichain in M is connected.
Therefore the connected components of M are precisely the maximal antichains of M with respect to
![]() $\triangleleft $
.
$\triangleleft $
.
Therefore,
![]() $\triangleleft $
induces an order on the connected components of M and it is denoted also by
$\triangleleft $
induces an order on the connected components of M and it is denoted also by
![]() $\triangleleft $
.
$\triangleleft $
.
Lemma 4.7. Every infinite connected component C of
![]() $\Gamma _{\mathrm {NS}}$
satisfies the following:
$\Gamma _{\mathrm {NS}}$
satisfies the following:
Proof Let
![]() $F = \{ u_1, \dots , u_n \}$
. Observe that
$F = \{ u_1, \dots , u_n \}$
. Observe that
 $$ \begin{align*} \Gamma \models (\forall x_1) \dots (\forall x_n) & [ x_1, \dots, x_n \text{ are points in } U \text{ and belong to} \\ & \text {the same connected component and } \\ &\text{ the index of this connected component is } \ge n \\ & \rightarrow (\exists y) [y \text{ belongs to this component, } y \in V \text{ and } x_1, \dots, x_n \mathrel{E} y]]. \end{align*} $$
$$ \begin{align*} \Gamma \models (\forall x_1) \dots (\forall x_n) & [ x_1, \dots, x_n \text{ are points in } U \text{ and belong to} \\ & \text {the same connected component and } \\ &\text{ the index of this connected component is } \ge n \\ & \rightarrow (\exists y) [y \text{ belongs to this component, } y \in V \text{ and } x_1, \dots, x_n \mathrel{E} y]]. \end{align*} $$
By elementarity,
![]() $\Gamma _{\mathrm {NS}}$
satisfies the same formula.
$\Gamma _{\mathrm {NS}}$
satisfies the same formula.
Lemma 4.8. Let
![]() ${\langle \Delta _n : n \in \omega \rangle }$
be a sequence of bipartite directed graphs with
${\langle \Delta _n : n \in \omega \rangle }$
be a sequence of bipartite directed graphs with
![]() $ \left \lvert {U^{\Delta _n}} \right \rvert = \left \lvert {V^{\Delta _n}} \right \rvert = \aleph _0$
. Suppose that for each
$ \left \lvert {U^{\Delta _n}} \right \rvert = \left \lvert {V^{\Delta _n}} \right \rvert = \aleph _0$
. Suppose that for each
![]() $n \in \omega $
,
$n \in \omega $
,
Then for every ultraproduct
![]() $R := \prod _{n \in \omega } \Delta _n / \mathcal {V}$
, we have
$R := \prod _{n \in \omega } \Delta _n / \mathcal {V}$
, we have
Proof We may assume that each
![]() $U^{\Delta _n} = \omega $
. Let
$U^{\Delta _n} = \omega $
. Let
![]() $\{ f_i : i < \mathfrak {d} \}$
be a cofinal subset of
$\{ f_i : i < \mathfrak {d} \}$
be a cofinal subset of
![]() $(\omega ^\omega , <^*)$
. For each
$(\omega ^\omega , <^*)$
. For each
![]() $n, m \in \omega $
, take
$n, m \in \omega $
, take
![]() $v_{n, m} \in V^{\Delta _n}$
that is connected with first m points in
$v_{n, m} \in V^{\Delta _n}$
that is connected with first m points in
![]() $U^{\Delta _n}$
. For
$U^{\Delta _n}$
. For
![]() $i < \mathfrak {d}$
, put
$i < \mathfrak {d}$
, put
Let
![]() $[u] \in U^R$
. Consider u as an element of
$[u] \in U^R$
. Consider u as an element of
![]() $\omega ^\omega $
. Take
$\omega ^\omega $
. Take
![]() $f_i$
that dominates u. Then we have
$f_i$
that dominates u. Then we have
Therefore
![]() $[u] \mathrel {E^R} v_i$
.
$[u] \mathrel {E^R} v_i$
.
Lemma 4.9. Let
![]() $\mathcal {V}$
be an ultrafilter over
$\mathcal {V}$
be an ultrafilter over
![]() $\omega $
and put
$\omega $
and put
![]() $Q = (\Gamma _{\mathrm {NS}})^\omega /\mathcal {V}$
. Then there exist cofinally many connected components C with respect to
$Q = (\Gamma _{\mathrm {NS}})^\omega /\mathcal {V}$
. Then there exist cofinally many connected components C with respect to
![]() $\triangleleft $
such that
$\triangleleft $
such that
Proof Fix a connected component
![]() $C_0$
of Q and
$C_0$
of Q and
![]() $[x_0] \in C_0$
. Then for each
$[x_0] \in C_0$
. Then for each
![]() $n \in \omega $
, there is an infinite component
$n \in \omega $
, there is an infinite component
![]() $C_n$
above
$C_n$
above
![]() $x_0(n)$
. Now
$x_0(n)$
. Now
is a connected component of Q above
![]() $C_0$
. Since C can be viewed as
$C_0$
. Since C can be viewed as
![]() $C = \prod _{n \in \omega } C_n / \mathcal {V}$
, the conclusion of the lemma holds for C by Lemmas 4.7 and 4.8.
$C = \prod _{n \in \omega } C_n / \mathcal {V}$
, the conclusion of the lemma holds for C by Lemmas 4.7 and 4.8.
Lemma 4.10. Let
![]() $\kappa < \mathfrak {c}^\exists $
and
$\kappa < \mathfrak {c}^\exists $
and
![]() $\mathcal {U}$
be an ultrafilter over
$\mathcal {U}$
be an ultrafilter over
![]() $\omega $
and put
$\omega $
and put
![]() $P = \Gamma ^\omega /\mathcal {U}$
. Then for every C in a final segment of connected components of P, we have
$P = \Gamma ^\omega /\mathcal {U}$
. Then for every C in a final segment of connected components of P, we have
Proof Let
![]() $f \colon \omega \to \Gamma $
satisfy
$f \colon \omega \to \Gamma $
satisfy
![]() $f(n) \in G_n$
for all n. Let
$f(n) \in G_n$
for all n. Let
![]() $C_0$
be the connected component that
$C_0$
be the connected component that
![]() $[f]$
belongs to. Take a connected component C such that
$[f]$
belongs to. Take a connected component C such that
![]() $C_0 \triangleleft C$
and an element
$C_0 \triangleleft C$
and an element
![]() $[g] \in C$
. Take a function
$[g] \in C$
. Take a function
![]() $h \colon \omega \to \omega $
such that
$h \colon \omega \to \omega $
such that
![]() $\{ n \in \omega : g(n) \in G_{h(n)} \} \in \mathcal {U}$
. Then
$\{ n \in \omega : g(n) \in G_{h(n)} \} \in \mathcal {U}$
. Then
![]() $A := \{ n \in \omega : h(n) \ge n \} \in \mathcal {U}$
. Put
$A := \{ n \in \omega : h(n) \ge n \} \in \mathcal {U}$
. Put
![]() $h'(n) = \max \{ h(n), n\}$
.
$h'(n) = \max \{ h(n), n\}$
.
Take
![]() ${\langle [v_i] : i < \kappa \rangle }$
with each
${\langle [v_i] : i < \kappa \rangle }$
with each
![]() $[v_i] \in C \cap V^P$
. Then we have
$[v_i] \in C \cap V^P$
. Then we have
Take
![]() $v_i'$
such that
$v_i'$
such that
![]() $v_i'(n) = v_i(n)$
for
$v_i'(n) = v_i(n)$
for
![]() $n \in A \cap B_i$
and
$n \in A \cap B_i$
and
![]() $v_i'(n) \in [h'(n)^3]^{\le h'(n)}$
for
$v_i'(n) \in [h'(n)^3]^{\le h'(n)}$
for
![]() $n\in \omega $
. The assumption
$n\in \omega $
. The assumption
![]() $\kappa < \mathfrak {c}^\exists $
and the calculation
$\kappa < \mathfrak {c}^\exists $
and the calculation
 $$\begin{align*}\sum_{n \ge 1} \frac{h'(n)}{h'(n)^3} = \sum_{n \ge 1} \frac{1}{h'(n)^2} \le \sum_{n \ge 1} \frac{1}{n^2} < \infty \end{align*}$$
$$\begin{align*}\sum_{n \ge 1} \frac{h'(n)}{h'(n)^3} = \sum_{n \ge 1} \frac{1}{h'(n)^2} \le \sum_{n \ge 1} \frac{1}{n^2} < \infty \end{align*}$$
give an
![]() $x \in \prod h'$
such that for all
$x \in \prod h'$
such that for all
![]() $i < \kappa $
,
$i < \kappa $
,
![]() $(\forall ^\infty n) (x(n) \not \in v_i'(n))$
. For each
$(\forall ^\infty n) (x(n) \not \in v_i'(n))$
. For each
![]() $i < \kappa $
, take
$i < \kappa $
, take
![]() $n_i$
such that
$n_i$
such that
![]() $(\forall n \ge n_i) (x(n) \not \in v_i'(n))$
.
$(\forall n \ge n_i) (x(n) \not \in v_i'(n))$
.
Take a point
![]() $[u] \in C \cap U^P$
such that
$[u] \in C \cap U^P$
such that
![]() $u(n) = x(n)$
for all
$u(n) = x(n)$
for all
![]() $n \in A$
. Then for all
$n \in A$
. Then for all
![]() $i < \kappa $
we have
$i < \kappa $
we have
Therefore
![]() $[u] \not \mathrel{E^P} [v_i]$
for all
$[u] \not \mathrel{E^P} [v_i]$
for all
![]() $i < \kappa $
.
$i < \kappa $
.
Assume that
![]() $\mathfrak {d} < \mathfrak {c}^\exists $
. Then by Lemmas 4.10 and 4.9, for any two ultrafilters
$\mathfrak {d} < \mathfrak {c}^\exists $
. Then by Lemmas 4.10 and 4.9, for any two ultrafilters
![]() $\mathcal {U}, \mathcal {V}$
over
$\mathcal {U}, \mathcal {V}$
over
![]() $\omega $
, we have
$\omega $
, we have
![]() $\Gamma ^\omega /\mathcal {U} \not \simeq (\Gamma _{\mathrm {NS}})^\omega /\mathcal {V}$
. So
$\Gamma ^\omega /\mathcal {U} \not \simeq (\Gamma _{\mathrm {NS}})^\omega /\mathcal {V}$
. So
![]() $\neg \operatorname {KT}(\aleph _0)$
holds. We have proved Theorem 4.1.
$\neg \operatorname {KT}(\aleph _0)$
holds. We have proved Theorem 4.1.
Fact 4.11 [Reference Klausner and Mejía8, Lemma 2.3]
![]() $\operatorname {cov}(\mathsf {null}) \le \mathfrak {c}^\exists $
.
$\operatorname {cov}(\mathsf {null}) \le \mathfrak {c}^\exists $
.
Corollary 4.12. In the random model,
![]() $\neg \operatorname {KT}(\aleph _0)$
holds.
$\neg \operatorname {KT}(\aleph _0)$
holds.
Proof This corollary holds since
![]() $\aleph _1 = \mathfrak {d} < \operatorname {cov}(\mathsf {null}) = \mathfrak {c}$
in the random model.
$\aleph _1 = \mathfrak {d} < \operatorname {cov}(\mathsf {null}) = \mathfrak {c}$
in the random model.
Remark 4.13.
![]() $\mathfrak {v}^\forall \le \mathfrak {c}^\exists $
follows from [Reference Klausner and Mejía8, Lemma 2.6]. So the implication
$\mathfrak {v}^\forall \le \mathfrak {c}^\exists $
follows from [Reference Klausner and Mejía8, Lemma 2.6]. So the implication
![]() $\operatorname {KT}(\aleph _0) \implies \mathfrak {d} \ge \mathfrak {c}^\exists $
strengthens the implication
$\operatorname {KT}(\aleph _0) \implies \mathfrak {d} \ge \mathfrak {c}^\exists $
strengthens the implication
![]() $\operatorname {KT}(\aleph _0) \implies \mathfrak {d} \ge \mathfrak {v}^\forall $
.
$\operatorname {KT}(\aleph _0) \implies \mathfrak {d} \ge \mathfrak {v}^\forall $
.
Remark 4.14. In [Reference Shelah9], Shelah constructed a creature forcing that forces the following statements:
-
(1) There are a finite language
 $\mathcal {L}$
and countable
$\mathcal {L}$
and countable
 $\mathcal {L}$
-structures
$\mathcal {L}$
-structures
 $\mathcal {A}, \mathcal {B}$
with
$\mathcal {A}, \mathcal {B}$
with
 $\mathcal {A} \equiv \mathcal {B}$
such that for all ultrafilters
$\mathcal {A} \equiv \mathcal {B}$
such that for all ultrafilters
 $\mathcal {U}, \mathcal {V}$
over
$\mathcal {U}, \mathcal {V}$
over
 $\omega $
, we have
$\omega $
, we have
 $\mathcal {A}^\omega /\mathcal {U} \not \simeq \mathcal {B}^\omega /\mathcal {V}$
.
$\mathcal {A}^\omega /\mathcal {U} \not \simeq \mathcal {B}^\omega /\mathcal {V}$
. -
(2) There is an ultrafilter
 $\mathcal {U}$
over
$\mathcal {U}$
over
 $\omega $
such that for every countable language
$\omega $
such that for every countable language
 $\mathcal {L}$
and any sequence
$\mathcal {L}$
and any sequence
 ${\langle (\mathcal {A}_n, \mathcal {B}_n) : n \in \omega \rangle }$
of pairs of finite
${\langle (\mathcal {A}_n, \mathcal {B}_n) : n \in \omega \rangle }$
of pairs of finite
 $\mathcal {L}$
-structures, if
$\mathcal {L}$
-structures, if
 $\prod _{n \in \omega } \mathcal {A}_n/\mathcal {U} \equiv \prod _{n \in \omega } \mathcal {B}_n/\mathcal {U}$
, then these ultraproducts are isomorphic.
$\prod _{n \in \omega } \mathcal {A}_n/\mathcal {U} \equiv \prod _{n \in \omega } \mathcal {B}_n/\mathcal {U}$
, then these ultraproducts are isomorphic.
Shelah himself pointed out in [Reference Shelah9, Remark 2.2] item 2 holds in the random model. On the other hand, we have proved item 1 also holds in the random model. Therefore both of above two statements hold in the random model.
5
 $\operatorname {KT}(\aleph _1)$
in forcing extensions
$\operatorname {KT}(\aleph _1)$
in forcing extensions
A theorem by Golshani and Shelah [Reference Golshani and Shelah6] states that
![]() $\operatorname {cov}(\mathsf {meager}) = \mathfrak {c} \land \operatorname {cf}(\mathfrak {c}) = \aleph _1$
implies
$\operatorname {cov}(\mathsf {meager}) = \mathfrak {c} \land \operatorname {cf}(\mathfrak {c}) = \aleph _1$
implies
![]() $\operatorname {KT}(\aleph _1)$
. In [Reference Golshani and Shelah6], it was also proved that
$\operatorname {KT}(\aleph _1)$
. In [Reference Golshani and Shelah6], it was also proved that
![]() $\operatorname {cf}(\mathfrak {c}) = \aleph _1$
is not necessary for
$\operatorname {cf}(\mathfrak {c}) = \aleph _1$
is not necessary for
![]() $\operatorname {KT}(\aleph _1)$
. In this section, we prove that
$\operatorname {KT}(\aleph _1)$
. In this section, we prove that
![]() $\operatorname {cov}(\mathsf {meager}) = \mathfrak {c}$
is also not necessary for
$\operatorname {cov}(\mathsf {meager}) = \mathfrak {c}$
is also not necessary for
![]() $\operatorname {KT}(\aleph _1)$
.
$\operatorname {KT}(\aleph _1)$
.
Theorem 5.1. Let
![]() $\lambda> \aleph _1$
be a regular cardinal with
$\lambda> \aleph _1$
be a regular cardinal with
![]() $\lambda ^{<\lambda } = \lambda $
. Let
$\lambda ^{<\lambda } = \lambda $
. Let
![]() ${\langle \mathbb {P}_\alpha , \dot {\mathbb {Q}}_\alpha : \alpha < \omega _1\rangle }$
be a finite support forcing iteration. Suppose that for all
${\langle \mathbb {P}_\alpha , \dot {\mathbb {Q}}_\alpha : \alpha < \omega _1\rangle }$
be a finite support forcing iteration. Suppose that for all
![]() $\alpha < \omega _1$
,
$\alpha < \omega _1$
,
![]() $\Vdash _\alpha "\dot {\mathbb {Q}}_\alpha \text { is ccc and } \left \lvert {\dot {\mathbb {Q}}_\alpha } \right \rvert \le \lambda "$
. And suppose that for all even
$\Vdash _\alpha "\dot {\mathbb {Q}}_\alpha \text { is ccc and } \left \lvert {\dot {\mathbb {Q}}_\alpha } \right \rvert \le \lambda "$
. And suppose that for all even
![]() $\alpha < \omega _1$
,
$\alpha < \omega _1$
,
![]() $\Vdash _\alpha \dot {\mathbb {Q}}_\alpha = \mathbb {C}_\lambda $
. Here
$\Vdash _\alpha \dot {\mathbb {Q}}_\alpha = \mathbb {C}_\lambda $
. Here
![]() $\mathbb {C}_\lambda $
denotes the Cohen forcing adjoining
$\mathbb {C}_\lambda $
denotes the Cohen forcing adjoining
![]() $\lambda $
many Cohen reals. Then,
$\lambda $
many Cohen reals. Then,
![]() $\Vdash _{\omega _1} \operatorname {KT}(\aleph _1)$
.
$\Vdash _{\omega _1} \operatorname {KT}(\aleph _1)$
.
Proof This proof is based on [Reference Golshani and Shelah6, Theorem 3.3].
Let G be a
![]() $(V, \mathbb {P}_{\omega _1})$
-generic filter.
$(V, \mathbb {P}_{\omega _1})$
-generic filter.
Let
![]() $\mathcal {L}$
be a countable language and
$\mathcal {L}$
be a countable language and
![]() $M^0 \equiv M^1$
be two
$M^0 \equiv M^1$
be two
![]() $\mathcal {L}$
-structures of size
$\mathcal {L}$
-structures of size
![]() $\le \aleph _1$
in
$\le \aleph _1$
in
![]() $V[G]$
. Take sequences
$V[G]$
. Take sequences
![]() ${\langle M^l_i : i < \omega _1\rangle }$
for
${\langle M^l_i : i < \omega _1\rangle }$
for
![]() $l = 0, 1$
that are increasing and continuous such that each
$l = 0, 1$
that are increasing and continuous such that each
![]() $M^l_i$
is countable elementary substructure of
$M^l_i$
is countable elementary substructure of
![]() $M^l$
and
$M^l$
and
![]() $M^l = \bigcup _{i < \omega _1} M^l_i$
. We can take an increasing sequence
$M^l = \bigcup _{i < \omega _1} M^l_i$
. We can take an increasing sequence
![]() ${\langle \alpha _i : i < \omega _1\rangle }$
of even ordinals such that
${\langle \alpha _i : i < \omega _1\rangle }$
of even ordinals such that
![]() $M^l_i \in V[G_{\alpha _i + 1}]$
for every
$M^l_i \in V[G_{\alpha _i + 1}]$
for every
![]() $l < 2$
and
$l < 2$
and
![]() $i < \omega _1$
.
$i < \omega _1$
.
For
![]() $i < \omega _1$
and
$i < \omega _1$
and
![]() $\beta < \lambda $
, let
$\beta < \lambda $
, let
![]() $c^i_\beta $
be the
$c^i_\beta $
be the
![]() $\beta $
-th Cohen real added by
$\beta $
-th Cohen real added by
![]() $\dot {\mathbb {Q}}_{\alpha _i}$
.
$\dot {\mathbb {Q}}_{\alpha _i}$
.
Take an enumeration
![]() ${\langle X_\gamma : \gamma < \lambda \cdot \omega _1 \rangle }$
of
${\langle X_\gamma : \gamma < \lambda \cdot \omega _1 \rangle }$
of
![]() $\mathcal {P}(\omega )$
such that
$\mathcal {P}(\omega )$
such that
![]() ${\langle X_\gamma : \gamma < \lambda \cdot (i+1)\rangle } \in V[G_{\alpha _i + 1}]$
for every
${\langle X_\gamma : \gamma < \lambda \cdot (i+1)\rangle } \in V[G_{\alpha _i + 1}]$
for every
![]() $i < \omega _1$
. We can take such a sequence. The reason for this is that we can take
$i < \omega _1$
. We can take such a sequence. The reason for this is that we can take
![]() ${\langle \dot {X}_\gamma : \lambda \cdot i \le \gamma < \lambda \cdot (i+1)\rangle }$
as an enumeration of
${\langle \dot {X}_\gamma : \lambda \cdot i \le \gamma < \lambda \cdot (i+1)\rangle }$
as an enumeration of
![]() $\mathbb {P}_{\alpha _i+1}$
nice names for subsets of
$\mathbb {P}_{\alpha _i+1}$
nice names for subsets of
![]() $\omega $
and put
$\omega $
and put
![]() $X_\gamma = (\dot {X}_\gamma )^G$
.
$X_\gamma = (\dot {X}_\gamma )^G$
.
For each
![]() $l < 2$
, take an enumeration
$l < 2$
, take an enumeration
![]() ${\langle f^l_\gamma : \gamma < \lambda \cdot \omega _1\rangle }$
of
${\langle f^l_\gamma : \gamma < \lambda \cdot \omega _1\rangle }$
of
![]() $(M^l)^\omega $
such that
$(M^l)^\omega $
such that
![]() $f^l_{\lambda \cdot i + \beta } \in (M^l_i)^\omega $
for every
$f^l_{\lambda \cdot i + \beta } \in (M^l_i)^\omega $
for every
![]() $i < \omega _1$
and
$i < \omega _1$
and
![]() $\beta < \lambda $
and
$\beta < \lambda $
and
![]() ${\langle f^l_\gamma : \gamma < \lambda \cdot (i+1)\rangle } \in V[G_{\alpha _i + 1}]$
.
${\langle f^l_\gamma : \gamma < \lambda \cdot (i+1)\rangle } \in V[G_{\alpha _i + 1}]$
.
For
![]() $\lambda ' < \lambda $
, let
$\lambda ' < \lambda $
, let
![]() $G_{\alpha _i, \lambda '}$
denote
$G_{\alpha _i, \lambda '}$
denote
![]() $G \cap (\mathbb {P}_{\alpha _i} \ast \mathbb {C}_{\lambda '})$
.
$G \cap (\mathbb {P}_{\alpha _i} \ast \mathbb {C}_{\lambda '})$
.
Now we construct a sequence of quadruples
![]() ${\langle (\mathcal {U}_\gamma , g^0_\gamma , g^1_\gamma , \lambda _\gamma ) : \gamma < \lambda \cdot \omega _1\rangle }$
by induction so that the following properties hold.
${\langle (\mathcal {U}_\gamma , g^0_\gamma , g^1_\gamma , \lambda _\gamma ) : \gamma < \lambda \cdot \omega _1\rangle }$
by induction so that the following properties hold.
-
(1) Each
 $\mathcal {U}_\gamma $
is a filter over
$\mathcal {U}_\gamma $
is a filter over
 $\omega $
.
$\omega $
. -
(2) For every
 $l < 2$
,
$l < 2$
,
 $i < \omega _1$
,
$i < \omega _1$
,
 $\beta < \lambda $
, and
$\beta < \lambda $
, and
 $\gamma = \lambda \cdot i + \beta $
,
$\gamma = \lambda \cdot i + \beta $
,
 $g^l_{\gamma } \in (M^l_i)^\omega \cap V[G_{\alpha _i, \lambda _\gamma }]$
.
$g^l_{\gamma } \in (M^l_i)^\omega \cap V[G_{\alpha _i, \lambda _\gamma }]$
. -
(3) For every
 $l < 2$
and
$l < 2$
and
 $i < \omega _1$
,
$i < \omega _1$
,
 ${\langle g^l_\gamma : \gamma < \lambda \cdot (i+1)\rangle } \in V[G_{\alpha _i + 1}]$
.
${\langle g^l_\gamma : \gamma < \lambda \cdot (i+1)\rangle } \in V[G_{\alpha _i + 1}]$
. -
(4) Each
 $\lambda _\gamma $
is an ordinal below
$\lambda _\gamma $
is an ordinal below
 $ \lambda $
. For
$ \lambda $
. For
 $\lambda \cdot i \le \gamma \le \gamma ' < \lambda \cdot (i+1)$
, we have
$\lambda \cdot i \le \gamma \le \gamma ' < \lambda \cdot (i+1)$
, we have
 $\lambda _\gamma \le \lambda _{\gamma '}$
.
$\lambda _\gamma \le \lambda _{\gamma '}$
. -
(5) For
 $i < \omega _1$
and
$i < \omega _1$
and
 $l < 2$
,
$l < 2$
,
 $\{ g^l_\gamma : \gamma < \lambda \cdot i \} = \{ f^l_\gamma : \gamma < \lambda \cdot i \}$
.
$\{ g^l_\gamma : \gamma < \lambda \cdot i \} = \{ f^l_\gamma : \gamma < \lambda \cdot i \}$
. -
(6) If
 $\lambda \cdot i \le \gamma < \lambda \cdot (i+1)$
, then
$\lambda \cdot i \le \gamma < \lambda \cdot (i+1)$
, then
 $\mathcal {U}_\gamma \in V[G_{\alpha _i}, \lambda _\gamma ]$
.
$\mathcal {U}_\gamma \in V[G_{\alpha _i}, \lambda _\gamma ]$
. -
(7) If
 $\gamma < \delta < \lambda \cdot \omega _1$
, then
$\gamma < \delta < \lambda \cdot \omega _1$
, then
 $\mathcal {U}_\gamma \subseteq \mathcal {U}_\delta $
.
$\mathcal {U}_\gamma \subseteq \mathcal {U}_\delta $
. -
(8) If
 $\gamma < \lambda \cdot \omega _1$
is a limit ordinal, then
$\gamma < \lambda \cdot \omega _1$
is a limit ordinal, then
 $\mathcal {U}_\gamma = \bigcup _{\delta < \gamma } \mathcal {U}_\delta $
.
$\mathcal {U}_\gamma = \bigcup _{\delta < \gamma } \mathcal {U}_\delta $
. -
(9)
 $X_\gamma \in \mathcal {U}_{\gamma + 1}$
or
$X_\gamma \in \mathcal {U}_{\gamma + 1}$
or
 $\omega \smallsetminus X_\gamma \in \mathcal {U}_{\gamma +1}$
.
$\omega \smallsetminus X_\gamma \in \mathcal {U}_{\gamma +1}$
. -
(10) If
 $\varphi (x_1, \dots , x_n)$
is an
$\varphi (x_1, \dots , x_n)$
is an
 $\mathcal {L}$
-formula,
$\mathcal {L}$
-formula,
 $\gamma = \lambda \cdot i + \beta $
, and
$\gamma = \lambda \cdot i + \beta $
, and
 $\gamma _1, \dots , \gamma _n \le \gamma $
, then
$\gamma _1, \dots , \gamma _n \le \gamma $
, then
 $Y_{\varphi , \gamma _1, \dots , \gamma _n}$
defined below belongs to
$Y_{\varphi , \gamma _1, \dots , \gamma _n}$
defined below belongs to
 $\mathcal {U}_{\gamma +1}$
:
$\mathcal {U}_{\gamma +1}$
:  $$\begin{align*}&Y_{\varphi, \gamma_1, \dots, \gamma_n} = \{ k \in \omega : M^0_i \models \varphi(g^0_{\gamma_1}(k), \dots, g^0_{\gamma_n}(k))\\&\quad \Leftrightarrow M^1_i \models \varphi(g^1_{\gamma_1}(k), \dots, g^1_{\gamma_n}(k)) \}. \end{align*}$$
$$\begin{align*}&Y_{\varphi, \gamma_1, \dots, \gamma_n} = \{ k \in \omega : M^0_i \models \varphi(g^0_{\gamma_1}(k), \dots, g^0_{\gamma_n}(k))\\&\quad \Leftrightarrow M^1_i \models \varphi(g^1_{\gamma_1}(k), \dots, g^1_{\gamma_n}(k)) \}. \end{align*}$$
(Construction) First we let
![]() $U_0$
be the set of cofinite subsets of
$U_0$
be the set of cofinite subsets of
![]() $\omega $
.
$\omega $
.
Suppose that
![]() ${\langle \mathcal {U}_\delta : \delta \le \gamma \rangle }$
and
${\langle \mathcal {U}_\delta : \delta \le \gamma \rangle }$
and
![]() ${\langle g^0_\delta , g^1_\delta , \lambda _\delta : \delta < \gamma \rangle }$
are defined. Now we will define
${\langle g^0_\delta , g^1_\delta , \lambda _\delta : \delta < \gamma \rangle }$
are defined. Now we will define
![]() $g^0_\gamma , g^1_\gamma , \lambda _\gamma $
and
$g^0_\gamma , g^1_\gamma , \lambda _\gamma $
and
![]() $\mathcal {U}_{\gamma +1}$
. Take i and
$\mathcal {U}_{\gamma +1}$
. Take i and
![]() $\beta $
such that
$\beta $
such that
![]() $\gamma = \lambda \cdot i + \beta $
.
$\gamma = \lambda \cdot i + \beta $
.
Suppose that
![]() $\gamma $
is even.
$\gamma $
is even.
Let
![]() $g^0_\gamma = f^0_{\varepsilon _\gamma }$
, where
$g^0_\gamma = f^0_{\varepsilon _\gamma }$
, where
![]() $\varepsilon _\gamma $
is the minimum ordinal such that
$\varepsilon _\gamma $
is the minimum ordinal such that
![]() $f^0_{\varepsilon _\gamma }$
does not belong to
$f^0_{\varepsilon _\gamma }$
does not belong to
![]() $\{g^0_\delta : \delta < \gamma \}$
.
$\{g^0_\delta : \delta < \gamma \}$
.
Take
![]() $\lambda ' < \lambda $
such that
$\lambda ' < \lambda $
such that
![]() $M^0_i, M^1_i, {\langle g^0_\delta : \delta \le \gamma \rangle }, {\langle g^1_\delta : \delta < \gamma \rangle } \in V[G_{\alpha _i, \lambda '}]$
. Put
$M^0_i, M^1_i, {\langle g^0_\delta : \delta \le \gamma \rangle }, {\langle g^1_\delta : \delta < \gamma \rangle } \in V[G_{\alpha _i, \lambda '}]$
. Put
![]() $\lambda _\gamma = \lambda ' + 1$
. Take a bijection
$\lambda _\gamma = \lambda ' + 1$
. Take a bijection
![]() $\pi ^1_i \colon \omega \to M^1_i$
in
$\pi ^1_i \colon \omega \to M^1_i$
in
![]() $V[G_{\alpha _i, \lambda '}]$
. Define
$V[G_{\alpha _i, \lambda '}]$
. Define
![]() $g^1_\gamma $
by
$g^1_\gamma $
by
![]() $g^1_\gamma = \pi ^1_i \circ c^i_{\lambda '}$
.
$g^1_\gamma = \pi ^1_i \circ c^i_{\lambda '}$
.
Put
![]() $\mathcal {Y} = \{ Y_{\varphi , \gamma _1, \dots , \gamma _n} : \varphi (x_1, \dots , x_n) \text { is an } \mathcal {L}\text {-formula and }\gamma _1, \dots , \gamma _n \le \gamma \}$
. Now we show
$\mathcal {Y} = \{ Y_{\varphi , \gamma _1, \dots , \gamma _n} : \varphi (x_1, \dots , x_n) \text { is an } \mathcal {L}\text {-formula and }\gamma _1, \dots , \gamma _n \le \gamma \}$
. Now we show
![]() $\mathcal {U}_\gamma \cup \mathcal {Y}$
has the finite intersection property. In order to show it, let
$\mathcal {U}_\gamma \cup \mathcal {Y}$
has the finite intersection property. In order to show it, let
![]() $X \in \mathcal {U}_\gamma $
,
$X \in \mathcal {U}_\gamma $
,
![]() ${\langle \varphi _\iota : \iota \in I\rangle }$
is a finite sequence of
${\langle \varphi _\iota : \iota \in I\rangle }$
is a finite sequence of
![]() $\mathcal {L}$
-formulas and
$\mathcal {L}$
-formulas and
![]() $\gamma ^\iota _1, \dots , \gamma ^\iota _{n_\iota }$
for
$\gamma ^\iota _1, \dots , \gamma ^\iota _{n_\iota }$
for
![]() $\iota \in I$
are ordinals that are less than
$\iota \in I$
are ordinals that are less than
![]() $\gamma $
. It suffices to show that the set
$\gamma $
. It suffices to show that the set
![]() $D \in V[G_{\alpha _i, \lambda '}]$
defined below is a dense subset of
$D \in V[G_{\alpha _i, \lambda '}]$
defined below is a dense subset of
![]() $\mathbb {C}$
:
$\mathbb {C}$
:
 $$ \begin{align*} &D = \{ p \in \mathbb{C}:\ (\exists k \in \operatorname{dom}(p) \cap X)(\forall \iota \in I) \\ & \qquad M^0_i \models \varphi_\iota(g^0_{\gamma^\iota_1}(k), \dots g^0_{\gamma^\iota_{n_\iota}}(k), g^0_\gamma(k)) \Leftrightarrow M^1_i \models \varphi_\iota(g^1_{\gamma^\iota_1}(k), \dots g^1_{\gamma^\iota_{n_\iota}}(k), \pi^1_i(p(k))) \}. \end{align*} $$
$$ \begin{align*} &D = \{ p \in \mathbb{C}:\ (\exists k \in \operatorname{dom}(p) \cap X)(\forall \iota \in I) \\ & \qquad M^0_i \models \varphi_\iota(g^0_{\gamma^\iota_1}(k), \dots g^0_{\gamma^\iota_{n_\iota}}(k), g^0_\gamma(k)) \Leftrightarrow M^1_i \models \varphi_\iota(g^1_{\gamma^\iota_1}(k), \dots g^1_{\gamma^\iota_{n_\iota}}(k), \pi^1_i(p(k))) \}. \end{align*} $$
We now prove this. Let
![]() $p \in \mathbb {C}$
.
$p \in \mathbb {C}$
.
For each
![]() $k \in \omega $
and
$k \in \omega $
and
![]() $\iota \in I$
, put
$\iota \in I$
, put
 $$\begin{align*}v(k, \iota) = \begin{cases} 1, & \text{if }M^0_i \models \varphi_\iota(g^0_{\gamma^\iota_1}(k), \dots, g^0_{\gamma^\iota_{n_\iota}}(k), g^0_\gamma(k)), \\ 0, & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}v(k, \iota) = \begin{cases} 1, & \text{if }M^0_i \models \varphi_\iota(g^0_{\gamma^\iota_1}(k), \dots, g^0_{\gamma^\iota_{n_\iota}}(k), g^0_\gamma(k)), \\ 0, & \text{otherwise.} \end{cases} \end{align*}$$
And for each
![]() $k \in \omega $
put
$k \in \omega $
put
Then by finiteness of
![]() ${}^I 2$
, for some
${}^I 2$
, for some
![]() $v_0 \in {}^I 2$
, we have
$v_0 \in {}^I 2$
, we have
![]() $\omega \smallsetminus v^{-1}(v_0) \not \in \mathcal {U}_\gamma $
.
$\omega \smallsetminus v^{-1}(v_0) \not \in \mathcal {U}_\gamma $
.
For each
![]() $\iota \in I$
, put
$\iota \in I$
, put
 $$\begin{align*}\varphi_\iota^+(x^\iota_1, \dots, x^\iota_{n_\iota}, y) \equiv \begin{cases} \varphi_\iota(x^\iota_1, \dots, x^\iota_{n_\iota}, y), & \text{if } v_0(\iota) = 1, \\ \neg \varphi_\iota(x^\iota_1, \dots, x^\iota_{n_\iota}, y), & \text{otherwise.} \end{cases} \end{align*}$$
$$\begin{align*}\varphi_\iota^+(x^\iota_1, \dots, x^\iota_{n_\iota}, y) \equiv \begin{cases} \varphi_\iota(x^\iota_1, \dots, x^\iota_{n_\iota}, y), & \text{if } v_0(\iota) = 1, \\ \neg \varphi_\iota(x^\iota_1, \dots, x^\iota_{n_\iota}, y), & \text{otherwise.} \end{cases} \end{align*}$$
Put
Then by the induction hypothesis (10),
![]() $Y_{\psi , {\langle \gamma ^\iota _1, \dots \gamma ^\iota _{n_\iota } : \iota \in I\rangle }} \in \mathcal {U}_\gamma $
. So take
$Y_{\psi , {\langle \gamma ^\iota _1, \dots \gamma ^\iota _{n_\iota } : \iota \in I\rangle }} \in \mathcal {U}_\gamma $
. So take
![]() $k \in X \cap v^{-1}(v_0) \cap Y_{\psi , {\langle \gamma ^\iota _1, \dots \gamma ^\iota _{n_\iota } : \iota \in I\rangle }} \smallsetminus \operatorname {dom}(p)$
.
$k \in X \cap v^{-1}(v_0) \cap Y_{\psi , {\langle \gamma ^\iota _1, \dots \gamma ^\iota _{n_\iota } : \iota \in I\rangle }} \smallsetminus \operatorname {dom}(p)$
.
Since
![]() $M^0_i \models \psi ({\langle g^0_{\gamma ^\iota _1}(k), \dots g^0_{\gamma ^\iota _{n_\iota }}(k) : \iota \in I\rangle })$
, we have
$M^0_i \models \psi ({\langle g^0_{\gamma ^\iota _1}(k), \dots g^0_{\gamma ^\iota _{n_\iota }}(k) : \iota \in I\rangle })$
, we have
![]() $M^1_i \models \psi (\langle g^1_{\gamma ^\iota _1}(k), \dots g^1_{\gamma ^\iota _{n_\iota }}(k) : \iota \in I\rangle )$
.
$M^1_i \models \psi (\langle g^1_{\gamma ^\iota _1}(k), \dots g^1_{\gamma ^\iota _{n_\iota }}(k) : \iota \in I\rangle )$
.
By the definition of
![]() $\psi $
, we can take
$\psi $
, we can take
![]() $y \in M^1_i$
such that
$y \in M^1_i$
such that
![]() $M^1_i \models \varphi _\iota ^+(g^1_{\gamma ^\iota _1}(k), \dots , g^1_{\gamma ^\iota _{n_\iota }}(k), y)$
for every
$M^1_i \models \varphi _\iota ^+(g^1_{\gamma ^\iota _1}(k), \dots , g^1_{\gamma ^\iota _{n_\iota }}(k), y)$
for every
![]() $\iota \in I$
. We now put
$\iota \in I$
. We now put
![]() $q = p \cup \{ (k, (\pi ^1_i)^{-1}(y)) \} \in \mathbb {C}$
. This witnesses denseness of D.
$q = p \cup \{ (k, (\pi ^1_i)^{-1}(y)) \} \in \mathbb {C}$
. This witnesses denseness of D.
Now we define
![]() $\mathcal {U}_{\gamma +1}$
as the filter generated by
$\mathcal {U}_{\gamma +1}$
as the filter generated by
![]() $\mathcal {U}_\gamma \cup \mathcal {Y} \cup \{ X_\gamma \}$
or the filter generated by
$\mathcal {U}_\gamma \cup \mathcal {Y} \cup \{ X_\gamma \}$
or the filter generated by
![]() $\mathcal {U}_\gamma \cup \mathcal {Y} \cup \{ \omega \smallsetminus X_\gamma \}$
.
$\mathcal {U}_\gamma \cup \mathcal {Y} \cup \{ \omega \smallsetminus X_\gamma \}$
.
When
![]() $\gamma $
is odd, do the same construction above except for swapping 0 and 1. Since the above construction below
$\gamma $
is odd, do the same construction above except for swapping 0 and 1. Since the above construction below
![]() $\lambda \cdot (i+1)$
can be performed in
$\lambda \cdot (i+1)$
can be performed in
![]() $V[G_{\alpha _i + 1}]$
, (3) in the induction hypothesis holds. (End of Construction.)
$V[G_{\alpha _i + 1}]$
, (3) in the induction hypothesis holds. (End of Construction.)
Now we put
![]() $\mathcal {U} = \bigcup _{\gamma < \lambda \cdot \omega _1} \mathcal {U}_\gamma $
, which is an ultrafilter over
$\mathcal {U} = \bigcup _{\gamma < \lambda \cdot \omega _1} \mathcal {U}_\gamma $
, which is an ultrafilter over
![]() $\omega $
. Then the function
$\omega $
. Then the function
witnesses
![]() $(M^0)^\omega / \mathcal {U} \simeq (M^1)^\omega / \mathcal {U}$
.
$(M^0)^\omega / \mathcal {U} \simeq (M^1)^\omega / \mathcal {U}$
.
Corollary 5.2.
![]() $\operatorname {Con}(\mathrm {ZFC}) \rightarrow \operatorname {Con}(\mathrm {ZFC} + \operatorname {cof}(\mathsf {null}) = \aleph _1 < \mathfrak {c} + \operatorname {KT}(\aleph _1))$
.
$\operatorname {Con}(\mathrm {ZFC}) \rightarrow \operatorname {Con}(\mathrm {ZFC} + \operatorname {cof}(\mathsf {null}) = \aleph _1 < \mathfrak {c} + \operatorname {KT}(\aleph _1))$
.
Proof Let
![]() $\mathbb {A}$
denote the amoeba forcing. Let
$\mathbb {A}$
denote the amoeba forcing. Let
![]() $\lambda> \aleph _1$
be a regular cardinal with
$\lambda> \aleph _1$
be a regular cardinal with
![]() $\lambda ^{<\lambda } = \lambda $
. Let
$\lambda ^{<\lambda } = \lambda $
. Let
![]() ${\langle \mathbb {P}_\alpha , \dot {\mathbb {Q}}_\alpha : \alpha < \omega _1\rangle }$
be a finite support forcing iteration such that for all even
${\langle \mathbb {P}_\alpha , \dot {\mathbb {Q}}_\alpha : \alpha < \omega _1\rangle }$
be a finite support forcing iteration such that for all even
![]() $\alpha < \omega _1$
we have
$\alpha < \omega _1$
we have
![]() $\Vdash _\alpha \dot {\mathbb {Q}}_\alpha = \mathbb {C}_\lambda $
and for all odd
$\Vdash _\alpha \dot {\mathbb {Q}}_\alpha = \mathbb {C}_\lambda $
and for all odd
![]() $\alpha < \omega _1$
we have
$\alpha < \omega _1$
we have
![]() $\Vdash _\alpha \dot {\mathbb {Q}}_\alpha = \mathbb {A}$
.
$\Vdash _\alpha \dot {\mathbb {Q}}_\alpha = \mathbb {A}$
.
Then
![]() $\mathbb {P}_{\omega _1} \Vdash \operatorname {KT}(\aleph _1)$
by Theorem 5.1.
$\mathbb {P}_{\omega _1} \Vdash \operatorname {KT}(\aleph _1)$
by Theorem 5.1.
Moreover, we have
![]() $\operatorname {cof}(\mathsf {null}) = \aleph _1$
since the amoeba forcing
$\operatorname {cof}(\mathsf {null}) = \aleph _1$
since the amoeba forcing
![]() $\mathbb {A}$
adds a null set containing all null sets coded in the ground model (see [Reference Bartoszyński and Judah2, p. 106]).
$\mathbb {A}$
adds a null set containing all null sets coded in the ground model (see [Reference Bartoszyński and Judah2, p. 106]).
6 Open questions
The following three questions remain.
Question 6.1.
-
(1) Does
 $\operatorname {KT}(\aleph _1)$
imply a stronger hypothesis than
$\operatorname {KT}(\aleph _1)$
imply a stronger hypothesis than
 $\mathfrak {mcf} = \aleph _1$
? In particular does
$\mathfrak {mcf} = \aleph _1$
? In particular does
 $\operatorname {KT}(\aleph _1)$
imply
$\operatorname {KT}(\aleph _1)$
imply
 $\operatorname {non}(\mathsf {meager}) = \aleph _1$
?
$\operatorname {non}(\mathsf {meager}) = \aleph _1$
? -
(2) Does
 $\operatorname {KT}(\aleph _0)$
imply a stronger hypothesis than
$\operatorname {KT}(\aleph _0)$
imply a stronger hypothesis than
 $\mathfrak {c}^\exists \le \mathfrak {d}$
? In particular does
$\mathfrak {c}^\exists \le \mathfrak {d}$
? In particular does
 $\operatorname {KT}(\aleph _0)$
imply
$\operatorname {KT}(\aleph _0)$
imply
 $\operatorname {non}(\mathsf {meager}) \le \operatorname {cov}(\mathsf {meager})$
?
$\operatorname {non}(\mathsf {meager}) \le \operatorname {cov}(\mathsf {meager})$
? -
(3) In the Sacks model, does
 $\operatorname {KT}(\aleph _0)$
hold? (If in this model
$\operatorname {KT}(\aleph _0)$
hold? (If in this model
 $\neg \operatorname {KT}(\aleph _0)$
holds, we can separate
$\neg \operatorname {KT}(\aleph _0)$
holds, we can separate
 $\operatorname {KT}(\aleph _0)$
and
$\operatorname {KT}(\aleph _0)$
and
 $\mathfrak {c}^\exists \le \mathfrak {d}$
.)
$\mathfrak {c}^\exists \le \mathfrak {d}$
.)
Acknowledgments
The author is grateful to his previous supervisor Yasuo Yoshinobu and his current supervisor Jörg Brendle. Both of them gave him helpful comments. In particular, the idea of the proof of Theorem 5.1 is due to Brendle. The author would also like to thank the anonymous reviewer who appropriately mentioned points for improvement. This work was supported by JSPS KAKENHI Grant Number JP22J20021.