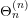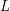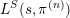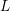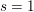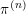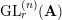1 Introduction
Let
![]() $\mathbf{A}$
denote the ring of adeles of a global field
$\mathbf{A}$
denote the ring of adeles of a global field
![]() $F$
. Assume that
$F$
. Assume that
![]() $F$
contains a full set of
$F$
contains a full set of
![]() $n$
th roots of unity. Let
$n$
th roots of unity. Let
![]() $\text{GL}_{r}^{(n)}(\mathbf{A})$
denote the
$\text{GL}_{r}^{(n)}(\mathbf{A})$
denote the
![]() $n$
-fold metaplectic cover of the group
$n$
-fold metaplectic cover of the group
![]() $\text{GL}_{r}(\mathbf{A})$
as constructed in [Reference Kazhdan and PattersonKP84]. Let
$\text{GL}_{r}(\mathbf{A})$
as constructed in [Reference Kazhdan and PattersonKP84]. Let
![]() $\unicode[STIX]{x1D70B}^{(n)}$
denote a genuine irreducible cuspidal representation of
$\unicode[STIX]{x1D70B}^{(n)}$
denote a genuine irreducible cuspidal representation of
![]() $\text{GL}_{r}^{(n)}(\mathbf{A})$
. To this representation one can attach the partial standard
$\text{GL}_{r}^{(n)}(\mathbf{A})$
. To this representation one can attach the partial standard
![]() $L$
function, denoted by
$L$
function, denoted by
![]() $L^{S}(s,\unicode[STIX]{x1D70B}^{(n)})$
.
$L^{S}(s,\unicode[STIX]{x1D70B}^{(n)})$
.
The first to consider convolutions of cuspidal representations with theta representations were Bump and Hoffstein in [Reference Bump and HoffsteinBH86, Reference Bump and HoffsteinBH87]. In these papers they considered the global construction involving the cubic theta representation and established that this construction represents an
![]() $L$
function. It was their idea that in order to study the properties of the above
$L$
function. It was their idea that in order to study the properties of the above
![]() $L$
functions, one needs to start with the well-known Rankin–Selberg convolution of two cuspidal representations of
$L$
functions, one needs to start with the well-known Rankin–Selberg convolution of two cuspidal representations of
![]() $\text{GL}_{r}(\mathbf{A})$
and
$\text{GL}_{r}(\mathbf{A})$
and
![]() $\text{GL}_{n}(\mathbf{A})$
, and adjust this construction to the covering groups.
$\text{GL}_{n}(\mathbf{A})$
, and adjust this construction to the covering groups.
In detail, let
![]() $\unicode[STIX]{x1D70B}^{(n)}$
be as defined above. Let
$\unicode[STIX]{x1D70B}^{(n)}$
be as defined above. Let
![]() $\unicode[STIX]{x1D6E9}_{n}^{(n)}$
denote the global theta representation of the group
$\unicode[STIX]{x1D6E9}_{n}^{(n)}$
denote the global theta representation of the group
![]() $\text{GL}_{n}^{(n)}(\mathbf{A})$
. The latter representation was constructed in [Reference Kazhdan and PattersonKP84]. Assume that
$\text{GL}_{n}^{(n)}(\mathbf{A})$
. The latter representation was constructed in [Reference Kazhdan and PattersonKP84]. Assume that
![]() $r>n$
. Then the proposed construction is given by
$r>n$
. Then the proposed construction is given by
Here
![]() $\unicode[STIX]{x1D719}$
is a vector in the space of
$\unicode[STIX]{x1D719}$
is a vector in the space of
![]() $\unicode[STIX]{x1D70B}^{(n)}$
, and
$\unicode[STIX]{x1D70B}^{(n)}$
, and
![]() $\unicode[STIX]{x1D703}$
is a vector in the space of
$\unicode[STIX]{x1D703}$
is a vector in the space of
![]() $\unicode[STIX]{x1D6E9}_{n}^{(n)}$
. The group
$\unicode[STIX]{x1D6E9}_{n}^{(n)}$
. The group
![]() $V_{r,n}$
and the character
$V_{r,n}$
and the character
![]() $\unicode[STIX]{x1D713}_{V_{r,n}}$
are defined in § 4. This was the starting point of [Reference Bump and FriedbergBF99]. In fact in [Reference Bump and FriedbergBF99] the authors concentrated on the case when
$\unicode[STIX]{x1D713}_{V_{r,n}}$
are defined in § 4. This was the starting point of [Reference Bump and FriedbergBF99]. In fact in [Reference Bump and FriedbergBF99] the authors concentrated on the case when
![]() $r<n$
, but up to some modifications as explained in [Reference Bump and FriedbergBF99, § 2], the idea is the same.
$r<n$
, but up to some modifications as explained in [Reference Bump and FriedbergBF99, § 2], the idea is the same.
A straightforward unfolding implies that for
![]() $\text{Re}(s)$
large, integral (1) is equal to
$\text{Re}(s)$
large, integral (1) is equal to
Here
![]() $W_{\unicode[STIX]{x1D719}}$
denotes the Whittaker coefficient of
$W_{\unicode[STIX]{x1D719}}$
denotes the Whittaker coefficient of
![]() $\unicode[STIX]{x1D719}$
, and we define
$\unicode[STIX]{x1D719}$
, and we define
![]() $W_{\unicode[STIX]{x1D703}}$
similarly.
$W_{\unicode[STIX]{x1D703}}$
similarly.
Since in general the Whittaker coefficient
![]() $W_{\unicode[STIX]{x1D719}}$
is not factorizable, it is not obvious that the above integral represents an Euler product. To show that it does, one needs to apply the method referred to as the ‘new way’ which was developed in [Reference Piatetski-Shapiro and RallisPR88]. See [Reference Bump and FriedbergBF99] for a discussion of and references for this method.
$W_{\unicode[STIX]{x1D719}}$
is not factorizable, it is not obvious that the above integral represents an Euler product. To show that it does, one needs to apply the method referred to as the ‘new way’ which was developed in [Reference Piatetski-Shapiro and RallisPR88]. See [Reference Bump and FriedbergBF99] for a discussion of and references for this method.
In our context, to deduce that integral (2) is Eulerian one proceeds in two steps. Let
![]() $F$
denote a local non-archimedean field containing a full set of
$F$
denote a local non-archimedean field containing a full set of
![]() $n$
th roots of unity. Let
$n$
th roots of unity. Let
![]() $\unicode[STIX]{x1D70B}^{(n)}$
denote a local unramified representation, and let
$\unicode[STIX]{x1D70B}^{(n)}$
denote a local unramified representation, and let
![]() $L(s,\unicode[STIX]{x1D70B}^{(n)})$
denote the corresponding local
$L(s,\unicode[STIX]{x1D70B}^{(n)})$
denote the corresponding local
![]() $L$
function. This function is defined in equation (4). The first step is to find a generating function for
$L$
function. This function is defined in equation (4). The first step is to find a generating function for
![]() $L(s,\unicode[STIX]{x1D70B}^{(n)})$
. In [Reference Bump and FriedbergBF99, p. 5], such a function was introduced and was denoted by
$L(s,\unicode[STIX]{x1D70B}^{(n)})$
. In [Reference Bump and FriedbergBF99, p. 5], such a function was introduced and was denoted by
![]() $\widetilde{\unicode[STIX]{x1D6E5}}_{s}$
. We give its definition in § 2 right after equation (4).
$\widetilde{\unicode[STIX]{x1D6E5}}_{s}$
. We give its definition in § 2 right after equation (4).
The second step is to use this function to compute a local integral which is obtained from integral (2), and to show that this local integral is independent of the choice of the local Whittaker function of the representation
![]() $\unicode[STIX]{x1D70B}^{(n)}$
. This is done as follows. First, one proves identity (5). This is done in [Reference Bump and FriedbergBF99, Proposition 1.1]. Here
$\unicode[STIX]{x1D70B}^{(n)}$
. This is done as follows. First, one proves identity (5). This is done in [Reference Bump and FriedbergBF99, Proposition 1.1]. Here
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}$
, denoted by
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}$
, denoted by
![]() $\unicode[STIX]{x1D70E}$
in [Reference Bump and FriedbergBF99], is the unique spherical function attached to
$\unicode[STIX]{x1D70E}$
in [Reference Bump and FriedbergBF99], is the unique spherical function attached to
![]() $\unicode[STIX]{x1D70B}^{(n)}$
. Then we apply the argument of [Reference Bump and FriedbergBF99, Proposition 2.1] to deduce the identity
$\unicode[STIX]{x1D70B}^{(n)}$
. Then we apply the argument of [Reference Bump and FriedbergBF99, Proposition 2.1] to deduce the identity
Here
![]() $W_{\unicode[STIX]{x1D70B}^{(n)}}(h)$
is any local unramified Whittaker function associated with the representation
$W_{\unicode[STIX]{x1D70B}^{(n)}}(h)$
is any local unramified Whittaker function associated with the representation
![]() $\unicode[STIX]{x1D70B}^{(n)}$
, normalized to equal one at the identity. The group
$\unicode[STIX]{x1D70B}^{(n)}$
, normalized to equal one at the identity. The group
![]() $V_{r}$
is the maximal unipotent subgroup of
$V_{r}$
is the maximal unipotent subgroup of
![]() $\text{GL}_{r}$
, and
$\text{GL}_{r}$
, and
![]() $\unicode[STIX]{x1D713}_{V_{r}}$
is the Whittaker character defined on
$\unicode[STIX]{x1D713}_{V_{r}}$
is the Whittaker character defined on
![]() $V_{r}$
. See equation (15).
$V_{r}$
. See equation (15).
Indeed, to obtain (3) from (5), we use the uniqueness of
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}$
. Thus, from this uniqueness we have
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}$
. Thus, from this uniqueness we have
![]() $\int _{K_{r}}W_{\unicode[STIX]{x1D70B}^{(n)}}(kh)\,dk=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}(h)W_{\unicode[STIX]{x1D70B}^{(n)}}(e)$
where
$\int _{K_{r}}W_{\unicode[STIX]{x1D70B}^{(n)}}(kh)\,dk=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}(h)W_{\unicode[STIX]{x1D70B}^{(n)}}(e)$
where
![]() $W_{\unicode[STIX]{x1D70B}^{(n)}}$
is any Whittaker function such that
$W_{\unicode[STIX]{x1D70B}^{(n)}}$
is any Whittaker function such that
![]() $W_{\unicode[STIX]{x1D70B}^{(n)}}(e)\neq 0$
. Here
$W_{\unicode[STIX]{x1D70B}^{(n)}}(e)\neq 0$
. Here
![]() $K_{r}$
is the maximal compact subgroup of
$K_{r}$
is the maximal compact subgroup of
![]() $\text{GL}_{r}$
, and if
$\text{GL}_{r}$
, and if
![]() $|n|_{F}=1$
it can be viewed as a subgroup of
$|n|_{F}=1$
it can be viewed as a subgroup of
![]() $\text{GL}_{r}^{(n)}$
. See § 2. Assuming that
$\text{GL}_{r}^{(n)}$
. See § 2. Assuming that
![]() $W_{\unicode[STIX]{x1D70B}^{(n)}}(e)=1$
, we plug this into integral (5), change variables in
$W_{\unicode[STIX]{x1D70B}^{(n)}}(e)=1$
, we plug this into integral (5), change variables in
![]() $h$
, and we obtain integral (3).
$h$
, and we obtain integral (3).
Thus we are reduced to the computation of the Whittaker function of
![]() $\widetilde{\unicode[STIX]{x1D6E5}}_{s}$
and relating this computation to the local corresponding integral of (2). This is done in [Reference Bump and FriedbergBF99] for the cases
$\widetilde{\unicode[STIX]{x1D6E5}}_{s}$
and relating this computation to the local corresponding integral of (2). This is done in [Reference Bump and FriedbergBF99] for the cases
![]() $r=2,3$
and arbitrary
$r=2,3$
and arbitrary
![]() $n$
. The general case is conjectured in [Reference Bump and FriedbergBF99, Conjecture 1.2]. This conjecture is stated in our notation as identities (20) when
$n$
. The general case is conjectured in [Reference Bump and FriedbergBF99, Conjecture 1.2]. This conjecture is stated in our notation as identities (20) when
![]() $r<n$
, and (28) when
$r<n$
, and (28) when
![]() $r\geqslant n$
.
$r\geqslant n$
.
In this paper we prove these two identities, and hence prove [Reference Bump and FriedbergBF99, Conjecture 1.2]. To do this we give a different realization for the function
![]() $\widetilde{\unicode[STIX]{x1D6E5}}_{s}$
. This realization makes the proof of the stated conjecture relatively simple. The new realization is described in § 2 and is given by a certain unique functional defined on the local theta representation
$\widetilde{\unicode[STIX]{x1D6E5}}_{s}$
. This realization makes the proof of the stated conjecture relatively simple. The new realization is described in § 2 and is given by a certain unique functional defined on the local theta representation
![]() $\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
. This last representation is defined on the group
$\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
. This last representation is defined on the group
![]() $\text{GL}_{nr}^{(n)}$
. We then use this functional to define a function on the group
$\text{GL}_{nr}^{(n)}$
. We then use this functional to define a function on the group
![]() $\text{GL}_{nr}^{(n)}$
, which we denote by
$\text{GL}_{nr}^{(n)}$
, which we denote by
![]() $W_{nr}^{(n)}(h)$
. Here
$W_{nr}^{(n)}(h)$
. Here
![]() $h\in \text{GL}_{nr}^{(n)}$
. Restricting to the group
$h\in \text{GL}_{nr}^{(n)}$
. Restricting to the group
![]() $\text{GL}_{r}^{(n)}$
, we obtain a function on that group which we use to give the new expression for
$\text{GL}_{r}^{(n)}$
, we obtain a function on that group which we use to give the new expression for
![]() $\widetilde{\unicode[STIX]{x1D6E5}}_{s}$
. Thus our result contains two parts. The first is to prove that the function
$\widetilde{\unicode[STIX]{x1D6E5}}_{s}$
. Thus our result contains two parts. The first is to prove that the function
![]() $W_{nr}^{(n)}(h)$
restricted to
$W_{nr}^{(n)}(h)$
restricted to
![]() $\text{GL}_{r}^{(n)}$
is indeed the generating function for the standard
$\text{GL}_{r}^{(n)}$
is indeed the generating function for the standard
![]() $L$
function. This we do in Proposition 2. The second, and the main result of this paper, is to obtain the desired expression for the Whittaker function of the generating function. This we do in Theorem 2, which is [Reference Bump and FriedbergBF99, Conjecture 1.2]. In both cases the computations are quite straightforward and are done by a repeated application of Lemma 1 and Corollary 1 stated and proved in § 2.1.
$L$
function. This we do in Proposition 2. The second, and the main result of this paper, is to obtain the desired expression for the Whittaker function of the generating function. This we do in Theorem 2, which is [Reference Bump and FriedbergBF99, Conjecture 1.2]. In both cases the computations are quite straightforward and are done by a repeated application of Lemma 1 and Corollary 1 stated and proved in § 2.1.
As mentioned above, the global result and some of the computations done in [Reference Bump and FriedbergBF99] assume that
![]() $r<n$
. This is just a technical point. The authors of [Reference Bump and FriedbergBF99] were well aware that their construction works for all
$r<n$
. This is just a technical point. The authors of [Reference Bump and FriedbergBF99] were well aware that their construction works for all
![]() $r$
and
$r$
and
![]() $n$
. To complete their result, in the last section we give some details in the other two cases, that is, when
$n$
. To complete their result, in the last section we give some details in the other two cases, that is, when
![]() $r>n$
and
$r>n$
and
![]() $r=n$
.
$r=n$
.
To summarize, combining [Reference Bump and FriedbergBF99] with our result, we have the following theorem.
Theorem 1. Let
![]() $\unicode[STIX]{x1D70B}^{(n)}$
denote an irreducible cuspidal representation of the group
$\unicode[STIX]{x1D70B}^{(n)}$
denote an irreducible cuspidal representation of the group
![]() $\text{GL}_{r}^{(n)}(\mathbf{A})$
. Then the partial
$\text{GL}_{r}^{(n)}(\mathbf{A})$
. Then the partial
![]() $L$
function
$L$
function
![]() $L^{S}(s,\unicode[STIX]{x1D70B}^{(n)})$
has a meromorphic continuation to the whole complex plane. When
$L^{S}(s,\unicode[STIX]{x1D70B}^{(n)})$
has a meromorphic continuation to the whole complex plane. When
![]() $r\neq n$
this partial
$r\neq n$
this partial
![]() $L$
function is holomorphic. When
$L$
function is holomorphic. When
![]() $r=n$
it can have at most a simple pole at
$r=n$
it can have at most a simple pole at
![]() $s=1$
.
$s=1$
.
As a first remark we mention that in fact we do expect that the partial
![]() $L$
function
$L$
function
![]() $L^{S}(s,\unicode[STIX]{x1D70B}^{(n)})$
will also be holomorphic in the case when
$L^{S}(s,\unicode[STIX]{x1D70B}^{(n)})$
will also be holomorphic in the case when
![]() $r=n$
. From the global integral given in § 4, see integral (26), we deduce that if this
$r=n$
. From the global integral given in § 4, see integral (26), we deduce that if this
![]() $L$
function has a simple pole at
$L$
function has a simple pole at
![]() $s=1$
, then
$s=1$
, then
![]() $\unicode[STIX]{x1D70B}^{(n)}$
will be isomorphic to
$\unicode[STIX]{x1D70B}^{(n)}$
will be isomorphic to
![]() $\unicode[STIX]{x1D6E9}_{n}^{(n)}$
. This we believe cannot happen.
$\unicode[STIX]{x1D6E9}_{n}^{(n)}$
. This we believe cannot happen.
Second, it is worthwhile mentioning that one can extend the above global constructions in two ways. First, one can replace the representation
![]() $\unicode[STIX]{x1D6E9}_{n}^{(n)}$
by the representation
$\unicode[STIX]{x1D6E9}_{n}^{(n)}$
by the representation
![]() $\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D712}}^{(n)}$
. Here
$\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D712}}^{(n)}$
. Here
![]() $\unicode[STIX]{x1D712}$
is any global character of
$\unicode[STIX]{x1D712}$
is any global character of
![]() $\text{GL}_{1}(\mathbf{A})$
such that
$\text{GL}_{1}(\mathbf{A})$
such that
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{1}^{n}$
for some character
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{1}^{n}$
for some character
![]() $\unicode[STIX]{x1D712}_{1}$
of
$\unicode[STIX]{x1D712}_{1}$
of
![]() $\text{GL}_{1}(\mathbf{A})$
. This last representation is defined as a residue of an Eisenstein series, and as
$\text{GL}_{1}(\mathbf{A})$
. This last representation is defined as a residue of an Eisenstein series, and as
![]() $\unicode[STIX]{x1D6E9}_{n}^{(n)}$
it has a unique Whittaker function. A second extension is to replace
$\unicode[STIX]{x1D6E9}_{n}^{(n)}$
it has a unique Whittaker function. A second extension is to replace
![]() $\unicode[STIX]{x1D6E9}_{n}^{(n)}$
by a cuspidal theta representation
$\unicode[STIX]{x1D6E9}_{n}^{(n)}$
by a cuspidal theta representation
![]() $\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D712}}^{(n)}$
when it exists. Here
$\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D712}}^{(n)}$
when it exists. Here
![]() $\unicode[STIX]{x1D712}$
is any global character of
$\unicode[STIX]{x1D712}$
is any global character of
![]() $\text{GL}_{1}(\mathbf{A})$
which is not of the form
$\text{GL}_{1}(\mathbf{A})$
which is not of the form
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{1}^{n}$
. For example, for
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D712}_{1}^{n}$
. For example, for
![]() $n=2$
such cuspidal representations were constructed in [Reference Gelbart and Piatetski-ShapiroGP80, Reference FlickerFli80]. For
$n=2$
such cuspidal representations were constructed in [Reference Gelbart and Piatetski-ShapiroGP80, Reference FlickerFli80]. For
![]() $n=3$
, see [Reference Patterson and Piatetski-ShapiroPP84] for the construction of such cuspidal representations. In both of these extensions we expect to get the twisted
$n=3$
, see [Reference Patterson and Piatetski-ShapiroPP84] for the construction of such cuspidal representations. In both of these extensions we expect to get the twisted
![]() $L$
function
$L$
function
![]() $L^{S}(s,\unicode[STIX]{x1D70B}^{(n)}\otimes \unicode[STIX]{x1D712}^{-1})$
. In the first case, when
$L^{S}(s,\unicode[STIX]{x1D70B}^{(n)}\otimes \unicode[STIX]{x1D712}^{-1})$
. In the first case, when
![]() $\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D712}}^{(n)}$
is not cuspidal, we expect this
$\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D712}}^{(n)}$
is not cuspidal, we expect this
![]() $L$
function to be holomorphic in all cases. However, if
$L$
function to be holomorphic in all cases. However, if
![]() $\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D712}}^{(n)}$
is cuspidal, and
$\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D712}}^{(n)}$
is cuspidal, and
![]() $r=n$
, then we do expect a simple pole at
$r=n$
, then we do expect a simple pole at
![]() $s=1$
if
$s=1$
if
![]() $\unicode[STIX]{x1D70B}^{(n)}=\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D712}}^{(n)}$
.
$\unicode[STIX]{x1D70B}^{(n)}=\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D712}}^{(n)}$
.
Finally, we mention that the result proved in this paper simplifies some of the proofs in [Reference Friedberg and GinzburgFG16]. This is explained in detail in [Reference Friedberg and GinzburgFG16] before and after equation (1).
2 Generating functions
The main references for this section are [Reference Bump and FriedbergBF99, Reference Kazhdan and PattersonKP84]. Fix a positive integer
![]() $n>1$
. Let
$n>1$
. Let
![]() $F$
denote a local non-archimedean field which contains a full set of
$F$
denote a local non-archimedean field which contains a full set of
![]() $n$
th roots of unity. Let
$n$
th roots of unity. Let
![]() $\text{GL}_{r}^{(n)}(F)$
denote the metaplectic
$\text{GL}_{r}^{(n)}(F)$
denote the metaplectic
![]() $n$
-fold cover of the group
$n$
-fold cover of the group
![]() $\text{GL}_{r}(F)$
. We realize this group as pairs
$\text{GL}_{r}(F)$
. We realize this group as pairs
![]() $\langle g,\unicode[STIX]{x1D716}\rangle$
, where
$\langle g,\unicode[STIX]{x1D716}\rangle$
, where
![]() $g\in \text{GL}_{r}(F)$
and
$g\in \text{GL}_{r}(F)$
and
![]() $\unicode[STIX]{x1D716}$
is an
$\unicode[STIX]{x1D716}$
is an
![]() $n$
th root of unity. We shall assume that
$n$
th root of unity. We shall assume that
![]() $|n|_{F}=1$
. Let
$|n|_{F}=1$
. Let
![]() $K_{r}$
denote the standard maximal compact subgroup of
$K_{r}$
denote the standard maximal compact subgroup of
![]() $\text{GL}_{r}(F)$
. Then the group
$\text{GL}_{r}(F)$
. Then the group
![]() $K_{r}$
splits under the covering, and can be viewed as a subgroup of
$K_{r}$
splits under the covering, and can be viewed as a subgroup of
![]() $\text{GL}_{r}^{(n)}(F)$
. Henceforth, we shall omit the notation of the field
$\text{GL}_{r}^{(n)}(F)$
. Henceforth, we shall omit the notation of the field
![]() $F$
. For example, we write
$F$
. For example, we write
![]() $\text{GL}_{r}$
for
$\text{GL}_{r}$
for
![]() $\text{GL}_{r}(F)$
. Let
$\text{GL}_{r}(F)$
. Let
![]() $B_{r}$
denote the standard Borel subgroup of
$B_{r}$
denote the standard Borel subgroup of
![]() $\text{GL}_{r}$
consisting of all upper triangular matrices. Let
$\text{GL}_{r}$
consisting of all upper triangular matrices. Let
![]() $T_{r}$
denote the subgroup of
$T_{r}$
denote the subgroup of
![]() $B_{r}$
consisting of all diagonal matrices, and let
$B_{r}$
consisting of all diagonal matrices, and let
![]() $V_{r}$
denote the group of all upper unipotent matrices in
$V_{r}$
denote the group of all upper unipotent matrices in
![]() $B_{r}$
.
$B_{r}$
.
Let
![]() $\unicode[STIX]{x1D70B}^{(n)}$
denote an unramified representation of
$\unicode[STIX]{x1D70B}^{(n)}$
denote an unramified representation of
![]() $\text{GL}_{r}^{(n)}$
associated to a character
$\text{GL}_{r}^{(n)}$
associated to a character
![]() $\unicode[STIX]{x1D712}$
of
$\unicode[STIX]{x1D712}$
of
![]() $T_{r}$
. These representations were defined in [Reference Kazhdan and PattersonKP84]. In detail, let
$T_{r}$
. These representations were defined in [Reference Kazhdan and PattersonKP84]. In detail, let
![]() $T_{r,n}^{(n)}$
denote the center of
$T_{r,n}^{(n)}$
denote the center of
![]() $T_{r}^{(n)}$
. This defines a genuine character of
$T_{r}^{(n)}$
. This defines a genuine character of
![]() $T_{r,n}^{(n)}$
which we will denote by
$T_{r,n}^{(n)}$
which we will denote by
![]() $\unicode[STIX]{x1D712}$
. Let
$\unicode[STIX]{x1D712}$
. Let
![]() $T_{r,0}^{(n)}$
denote any maximal abelian subgroup of
$T_{r,0}^{(n)}$
denote any maximal abelian subgroup of
![]() $T_{r}^{(n)}$
which contains the group
$T_{r}^{(n)}$
which contains the group
![]() $T_{r,n}^{(n)}$
. Choose any extension of the character
$T_{r,n}^{(n)}$
. Choose any extension of the character
![]() $\unicode[STIX]{x1D712}$
from
$\unicode[STIX]{x1D712}$
from
![]() $T_{r,n}^{(n)}$
to
$T_{r,n}^{(n)}$
to
![]() $T_{r,0}^{(n)}$
. Extend the character
$T_{r,0}^{(n)}$
. Extend the character
![]() $\unicode[STIX]{x1D712}$
trivially to
$\unicode[STIX]{x1D712}$
trivially to
![]() $V_{r}$
. Then, inducing this extension to
$V_{r}$
. Then, inducing this extension to
![]() $\text{GL}_{r}^{(n)}$
, we obtain the representation
$\text{GL}_{r}^{(n)}$
, we obtain the representation
![]() $\unicode[STIX]{x1D70B}^{(n)}=\text{Ind}_{B_{r}^{(n)}}^{\text{GL}_{r}^{(n)}}\unicode[STIX]{x1D712}\unicode[STIX]{x1D6FF}_{B_{r}}^{1/2}$
. It follows from [Reference Kazhdan and PattersonKP84] that this representation depends only on the character
$\unicode[STIX]{x1D70B}^{(n)}=\text{Ind}_{B_{r}^{(n)}}^{\text{GL}_{r}^{(n)}}\unicode[STIX]{x1D712}\unicode[STIX]{x1D6FF}_{B_{r}}^{1/2}$
. It follows from [Reference Kazhdan and PattersonKP84] that this representation depends only on the character
![]() $\unicode[STIX]{x1D712}$
. See also [Reference Bump and FriedbergBF99, p. 5]. In this paper we choose the maximal abelian subgroup
$\unicode[STIX]{x1D712}$
. See also [Reference Bump and FriedbergBF99, p. 5]. In this paper we choose the maximal abelian subgroup
![]() $T_{r,0}^{(n)}$
to be the following. It is the group generated by
$T_{r,0}^{(n)}$
to be the following. It is the group generated by
![]() $T_{r,n}^{(n)}$
and all elements
$T_{r,n}^{(n)}$
and all elements
![]() $\langle t,\unicode[STIX]{x1D716}\rangle \in T_{r}^{(n)}$
such that all diagonal entries of
$\langle t,\unicode[STIX]{x1D716}\rangle \in T_{r}^{(n)}$
such that all diagonal entries of
![]() $t$
are units. Then it follows from [Reference Kazhdan and PattersonKP84] that
$t$
are units. Then it follows from [Reference Kazhdan and PattersonKP84] that
![]() $T_{r,0}^{(n)}$
is a maximal abelian subgroup of
$T_{r,0}^{(n)}$
is a maximal abelian subgroup of
![]() $T_{r}^{(n)}$
. The extension of
$T_{r}^{(n)}$
. The extension of
![]() $\unicode[STIX]{x1D712}$
that we choose is the trivial extension.
$\unicode[STIX]{x1D712}$
that we choose is the trivial extension.
Assuming that
![]() $\unicode[STIX]{x1D712}$
is in general position, one can attach to
$\unicode[STIX]{x1D712}$
is in general position, one can attach to
![]() $\unicode[STIX]{x1D70B}^{(n)}$
the local
$\unicode[STIX]{x1D70B}^{(n)}$
the local
![]() $L$
function which is defined as
$L$
function which is defined as
Here
![]() $p$
is a generator of the maximal ideal in the ring of integers of
$p$
is a generator of the maximal ideal in the ring of integers of
![]() $F$
, and
$F$
, and
![]() $q^{-1}=|p|_{F}$
. Also,
$q^{-1}=|p|_{F}$
. Also,
![]() $s$
is a complex variable.
$s$
is a complex variable.
In [Reference Bump and FriedbergBF99, formula (1.4)] the function
![]() $\widetilde{\unicode[STIX]{x1D6E5}}_{s}(h)$
is defined. This function is a function of
$\widetilde{\unicode[STIX]{x1D6E5}}_{s}(h)$
is defined. This function is a function of
![]() $\text{GL}_{r}^{(n)}$
and is defined as follows. It is an anti-genuine
$\text{GL}_{r}^{(n)}$
and is defined as follows. It is an anti-genuine
![]() $K_{r}$
bi-invariant function, and hence it is enough to define
$K_{r}$
bi-invariant function, and hence it is enough to define
![]() $\widetilde{\unicode[STIX]{x1D6E5}}_{s}(h)$
on elements
$\widetilde{\unicode[STIX]{x1D6E5}}_{s}(h)$
on elements
![]() $h=\langle t,1\rangle$
where
$h=\langle t,1\rangle$
where
![]() $t=\text{diag}(p^{n_{1}},p^{n_{2}},\ldots ,p^{n_{r}})\in T_{r}$
. On such an element
$t=\text{diag}(p^{n_{1}},p^{n_{2}},\ldots ,p^{n_{r}})\in T_{r}$
. On such an element
![]() $h$
,
$h$
,
![]() $\widetilde{\unicode[STIX]{x1D6E5}}_{s}(h)=0$
unless all
$\widetilde{\unicode[STIX]{x1D6E5}}_{s}(h)=0$
unless all
![]() $n_{i}$
are non-negative integers, each one divisible by
$n_{i}$
are non-negative integers, each one divisible by
![]() $n$
. Finally, if all
$n$
. Finally, if all
![]() $n_{i}$
are non-negative integers, and each one of them is divisible by
$n_{i}$
are non-negative integers, and each one of them is divisible by
![]() $n$
, then
$n$
, then
Proposition 1.1 in [Reference Bump and FriedbergBF99] states that for
![]() $\text{Re}(s)$
large,
$\text{Re}(s)$
large,
Here,
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}$
, denoted by
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}$
, denoted by
![]() $\unicode[STIX]{x1D70E}$
in [Reference Bump and FriedbergBF99], is the spherical function attached to
$\unicode[STIX]{x1D70E}$
in [Reference Bump and FriedbergBF99], is the spherical function attached to
![]() $\unicode[STIX]{x1D70B}^{(n)}$
. Thus
$\unicode[STIX]{x1D70B}^{(n)}$
. Thus
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}$
is a genuine
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}$
is a genuine
![]() $K_{r}$
bi-invariant function of
$K_{r}$
bi-invariant function of
![]() $\text{GL}_{r}^{(n)}$
. As is well known, the function
$\text{GL}_{r}^{(n)}$
. As is well known, the function
![]() $\widetilde{\unicode[STIX]{x1D6E5}}_{s}(h)$
is uniquely determined by [Reference Bump and FriedbergBF99, Proposition 1.1]. This function is referred to as the generating function for the standard
$\widetilde{\unicode[STIX]{x1D6E5}}_{s}(h)$
is uniquely determined by [Reference Bump and FriedbergBF99, Proposition 1.1]. This function is referred to as the generating function for the standard
![]() $L$
function of the group
$L$
function of the group
![]() $\text{GL}_{r}^{(n)}$
.
$\text{GL}_{r}^{(n)}$
.
We will give a different realization of the function
![]() $\widetilde{\unicode[STIX]{x1D6E5}}_{s}(h)$
. To do that let
$\widetilde{\unicode[STIX]{x1D6E5}}_{s}(h)$
. To do that let
![]() $\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
denote the local unramified theta representation of
$\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
denote the local unramified theta representation of
![]() $\text{GL}_{nr}^{(n)}$
as constructed in [Reference Kazhdan and PattersonKP84]. This representation is the unramified sub-representation of
$\text{GL}_{nr}^{(n)}$
as constructed in [Reference Kazhdan and PattersonKP84]. This representation is the unramified sub-representation of
![]() $\text{Ind}_{B_{nr}^{(n)}}^{\text{GL}_{nr}^{(n)}}\unicode[STIX]{x1D6FF}_{B_{nr}}^{(n-1)/2n}=\text{Ind}_{B_{nr}^{(n)}}^{\text{GL}_{nr}^{(n)}}\unicode[STIX]{x1D6FF}_{B_{nr}}^{-1/2n}\unicode[STIX]{x1D6FF}_{B_{nr}}^{1/2}$
. Here,
$\text{Ind}_{B_{nr}^{(n)}}^{\text{GL}_{nr}^{(n)}}\unicode[STIX]{x1D6FF}_{B_{nr}}^{(n-1)/2n}=\text{Ind}_{B_{nr}^{(n)}}^{\text{GL}_{nr}^{(n)}}\unicode[STIX]{x1D6FF}_{B_{nr}}^{-1/2n}\unicode[STIX]{x1D6FF}_{B_{nr}}^{1/2}$
. Here,
![]() $B_{nr}$
is the Borel subgroup of
$B_{nr}$
is the Borel subgroup of
![]() $\text{GL}_{nr}$
. The definition of this induced representation is similar to the definition of the representation
$\text{GL}_{nr}$
. The definition of this induced representation is similar to the definition of the representation
![]() $\unicode[STIX]{x1D70B}^{(n)}$
given above, replacing the group
$\unicode[STIX]{x1D70B}^{(n)}$
given above, replacing the group
![]() $\text{GL}_{r}^{(n)}$
by
$\text{GL}_{r}^{(n)}$
by
![]() $\text{GL}_{nr}^{(n)}$
, and the character
$\text{GL}_{nr}^{(n)}$
, and the character
![]() $\unicode[STIX]{x1D712}$
by the character
$\unicode[STIX]{x1D712}$
by the character
![]() $\unicode[STIX]{x1D6FF}_{B_{nr}}^{-1/2n}$
.
$\unicode[STIX]{x1D6FF}_{B_{nr}}^{-1/2n}$
.
This representation is not generic, but it still has a certain unique functional defined on it. To describe this functional, let
![]() $U_{nr}$
denote the unipotent radical of the parabolic subgroup of
$U_{nr}$
denote the unipotent radical of the parabolic subgroup of
![]() $\text{GL}_{nr}$
whose Levi part is
$\text{GL}_{nr}$
whose Levi part is
![]() $\text{GL}_{r}\times \text{GL}_{r}\times \cdots \times \text{GL}_{r}$
. In term of matrices the group
$\text{GL}_{r}\times \text{GL}_{r}\times \cdots \times \text{GL}_{r}$
. In term of matrices the group
![]() $U_{nr}$
consists of all matrices of the form
$U_{nr}$
consists of all matrices of the form
 $$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}I & X_{1,2} & X_{1,3} & \ldots \, & X_{1,n}\\ & I & X_{2,3} & \ldots \, & X_{2,n}\\ & & I & \ddots & \vdots \\ & & & \ddots & X_{n-1,n}\\ & & & & I\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}I & X_{1,2} & X_{1,3} & \ldots \, & X_{1,n}\\ & I & X_{2,3} & \ldots \, & X_{2,n}\\ & & I & \ddots & \vdots \\ & & & \ddots & X_{n-1,n}\\ & & & & I\end{array}\right).\end{eqnarray}$$
Here
![]() $I$
is the
$I$
is the
![]() $r\times r$
identity matrix, and
$r\times r$
identity matrix, and
![]() $X_{i,j}\in \text{Mat}_{r\times r}$
.
$X_{i,j}\in \text{Mat}_{r\times r}$
.
Let
![]() $\unicode[STIX]{x1D713}$
denote an unramified character of
$\unicode[STIX]{x1D713}$
denote an unramified character of
![]() $F$
. Define a character
$F$
. Define a character
![]() $\unicode[STIX]{x1D713}_{U_{nr}}$
of
$\unicode[STIX]{x1D713}_{U_{nr}}$
of
![]() $U_{nr}$
as follows. For
$U_{nr}$
as follows. For
![]() $u\in U_{nr}$
as above, define
$u\in U_{nr}$
as above, define
![]() $\unicode[STIX]{x1D713}_{U_{nr}}(u)=\unicode[STIX]{x1D713}(\text{tr}(X_{1,2}+X_{2,3}+\cdots +X_{n-1,n}))$
. The stabilizer of
$\unicode[STIX]{x1D713}_{U_{nr}}(u)=\unicode[STIX]{x1D713}(\text{tr}(X_{1,2}+X_{2,3}+\cdots +X_{n-1,n}))$
. The stabilizer of
![]() $\unicode[STIX]{x1D713}_{U_{nr}}$
inside
$\unicode[STIX]{x1D713}_{U_{nr}}$
inside
![]() $\text{GL}_{r}\times \text{GL}_{r}\times \cdots \times \text{GL}_{r}$
is the group
$\text{GL}_{r}\times \text{GL}_{r}\times \cdots \times \text{GL}_{r}$
is the group
![]() $\text{GL}_{r}^{\unicode[STIX]{x1D6E5}}$
embedded diagonally. The embedding of
$\text{GL}_{r}^{\unicode[STIX]{x1D6E5}}$
embedded diagonally. The embedding of
![]() $\text{GL}_{r}^{\unicode[STIX]{x1D6E5}}$
inside
$\text{GL}_{r}^{\unicode[STIX]{x1D6E5}}$
inside
![]() $\text{GL}_{nr}$
is given by
$\text{GL}_{nr}$
is given by
![]() $g\mapsto \text{diag}(g,g,\ldots ,g)$
.
$g\mapsto \text{diag}(g,g,\ldots ,g)$
.
Given a representation
![]() $\unicode[STIX]{x1D70E}_{nr}^{(n)}$
of
$\unicode[STIX]{x1D70E}_{nr}^{(n)}$
of
![]() $\text{GL}_{nr}^{(n)}$
, we consider the space of all functionals on
$\text{GL}_{nr}^{(n)}$
, we consider the space of all functionals on
![]() $\unicode[STIX]{x1D70E}_{nr}^{(n)}$
which satisfies
$\unicode[STIX]{x1D70E}_{nr}^{(n)}$
which satisfies
![]() $l(\unicode[STIX]{x1D70E}_{nr}^{(n)}(u)v)=\unicode[STIX]{x1D713}_{U_{nr}}(u)l(v)$
for all
$l(\unicode[STIX]{x1D70E}_{nr}^{(n)}(u)v)=\unicode[STIX]{x1D713}_{U_{nr}}(u)l(v)$
for all
![]() $u\in U_{nr}$
and all vectors
$u\in U_{nr}$
and all vectors
![]() $v$
in the space of
$v$
in the space of
![]() $\unicode[STIX]{x1D70E}_{nr}^{(n)}$
. Given such a functional, we may consider the space of functions
$\unicode[STIX]{x1D70E}_{nr}^{(n)}$
. Given such a functional, we may consider the space of functions
![]() $W_{v}^{(n)}(h)=l(\unicode[STIX]{x1D70E}_{nr}^{(n)}(h)v)$
.
$W_{v}^{(n)}(h)=l(\unicode[STIX]{x1D70E}_{nr}^{(n)}(h)v)$
.
Henceforth we shall assume that
![]() $\unicode[STIX]{x1D70E}_{nr}^{(n)}=\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
and denote the corresponding space of functions by
$\unicode[STIX]{x1D70E}_{nr}^{(n)}=\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
and denote the corresponding space of functions by
![]() $W_{nr}^{(n)}(h)$
. Then, the following proposition is proved in [Reference CaiCai16, Theorem 1.2].
$W_{nr}^{(n)}(h)$
. Then, the following proposition is proved in [Reference CaiCai16, Theorem 1.2].
Proposition 1. The space of functionals
![]() $l$
defined as above on the representation
$l$
defined as above on the representation
![]() $\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
is one-dimensional.
$\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
is one-dimensional.
It is not hard to construct the space of functions
![]() $W_{nr}^{(n)}(h)$
explicitly on the space of
$W_{nr}^{(n)}(h)$
explicitly on the space of
![]() $\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
. Indeed, let
$\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
. Indeed, let
![]() $f\in \text{Ind}_{B_{nr}^{(n)}}^{\text{GL}_{nr}^{(n)}}\unicode[STIX]{x1D6FF}_{B_{nr}}^{(n-1)/2n}$
. Let
$f\in \text{Ind}_{B_{nr}^{(n)}}^{\text{GL}_{nr}^{(n)}}\unicode[STIX]{x1D6FF}_{B_{nr}}^{(n-1)/2n}$
. Let
![]() $U_{nr}^{0}$
denote the subgroup of
$U_{nr}^{0}$
denote the subgroup of
![]() $U_{nr}$
which consists of all matrices
$U_{nr}$
which consists of all matrices
![]() $u$
as in (6) such that
$u$
as in (6) such that
![]() $X_{i,j}\in \text{Mat}_{r\times r}^{0}$
for all
$X_{i,j}\in \text{Mat}_{r\times r}^{0}$
for all
![]() $i$
and
$i$
and
![]() $j$
. Here
$j$
. Here
![]() $\text{Mat}_{r\times r}^{0}$
is the subgroup of
$\text{Mat}_{r\times r}^{0}$
is the subgroup of
![]() $\text{Mat}_{r\times r}$
consisting of all matrices
$\text{Mat}_{r\times r}$
consisting of all matrices
![]() $X$
such that
$X$
such that
![]() $X[l_{1},l_{2}]=0$
for all
$X[l_{1},l_{2}]=0$
for all
![]() $l_{1}<l_{2}$
, where
$l_{1}<l_{2}$
, where
![]() $X[l_{1},l_{2}]$
denotes the
$X[l_{1},l_{2}]$
denotes the
![]() $(l_{1},l_{2})$
th entry of
$(l_{1},l_{2})$
th entry of
![]() $X$
. Then
$X$
. Then
defines the space of functions which satisfies the required transformation properties, provided it is not identically zero. Here
![]() $w_{J}$
is the Weyl element
$w_{J}$
is the Weyl element
![]() $w_{J}=\text{diag}(J_{n},J_{n},\ldots ,J_{n})\in \text{GL}_{nr}$
where
$w_{J}=\text{diag}(J_{n},J_{n},\ldots ,J_{n})\in \text{GL}_{nr}$
where
![]() $J_{n}$
is the longest Weyl element of
$J_{n}$
is the longest Weyl element of
![]() $\text{GL}_{n}$
. The Weyl element
$\text{GL}_{n}$
. The Weyl element
![]() $w_{0}$
is defined as the element whose
$w_{0}$
is defined as the element whose
![]() $(a+bn,(a-1)r+b+1)$
th entry is one for all
$(a+bn,(a-1)r+b+1)$
th entry is one for all
![]() $1\leqslant a\leqslant n$
and
$1\leqslant a\leqslant n$
and
![]() $0\leqslant b\leqslant r-1$
, and zero elsewhere. Matrix multiplication implies that
$0\leqslant b\leqslant r-1$
, and zero elsewhere. Matrix multiplication implies that
![]() $w_{J}w_{0}$
is the shortest Weyl element of
$w_{J}w_{0}$
is the shortest Weyl element of
![]() $\text{GL}_{nr}$
with the property that for all
$\text{GL}_{nr}$
with the property that for all
![]() $u\in U_{nr}^{0}$
, we have that
$u\in U_{nr}^{0}$
, we have that
![]() $wuw^{-1}$
is a lower unipotent matrix.
$wuw^{-1}$
is a lower unipotent matrix.
It is not hard to prove that the function
![]() $W_{nr}^{(n)}(h)$
satisfies also the property
$W_{nr}^{(n)}(h)$
satisfies also the property
![]() $W_{nr}^{(n)}(k^{\unicode[STIX]{x1D6E5}}h)=W_{nr}^{(n)}(h)$
for all
$W_{nr}^{(n)}(k^{\unicode[STIX]{x1D6E5}}h)=W_{nr}^{(n)}(h)$
for all
![]() $k^{\unicode[STIX]{x1D6E5}}\in K_{r}\subset \text{GL}_{r}^{\unicode[STIX]{x1D6E5}}$
. The group
$k^{\unicode[STIX]{x1D6E5}}\in K_{r}\subset \text{GL}_{r}^{\unicode[STIX]{x1D6E5}}$
. The group
![]() $\text{GL}_{r}^{\unicode[STIX]{x1D6E5}}$
was defined right after (6). Indeed, it follows from [Reference Cai, Friedberg, Ginzburg and KaplanCFGK16, p. 4] right after Definition 1 that
$\text{GL}_{r}^{\unicode[STIX]{x1D6E5}}$
was defined right after (6). Indeed, it follows from [Reference Cai, Friedberg, Ginzburg and KaplanCFGK16, p. 4] right after Definition 1 that
![]() $W_{nr}^{(n)}(k^{\unicode[STIX]{x1D6E5}}h)=W_{nr}^{(n)}(h)$
for all
$W_{nr}^{(n)}(k^{\unicode[STIX]{x1D6E5}}h)=W_{nr}^{(n)}(h)$
for all
![]() $k^{\unicode[STIX]{x1D6E5}}\in K_{r}\cap \operatorname{SL}_{r}^{\unicode[STIX]{x1D6E5}}$
. If
$k^{\unicode[STIX]{x1D6E5}}\in K_{r}\cap \operatorname{SL}_{r}^{\unicode[STIX]{x1D6E5}}$
. If
![]() $k^{\unicode[STIX]{x1D6E5}}$
is any diagonal matrix in
$k^{\unicode[STIX]{x1D6E5}}$
is any diagonal matrix in
![]() $K_{r}$
, then the property
$K_{r}$
, then the property
![]() $W_{nr}^{(n)}(k^{\unicode[STIX]{x1D6E5}}h)=W_{nr}^{(n)}(h)$
follows from integral (7). We mention that to derive this identity we use our choice of the maximal abelian subgroup.
$W_{nr}^{(n)}(k^{\unicode[STIX]{x1D6E5}}h)=W_{nr}^{(n)}(h)$
follows from integral (7). We mention that to derive this identity we use our choice of the maximal abelian subgroup.
By considering the function
![]() $W_{nr}^{(n)}(h)$
corresponding to the
$W_{nr}^{(n)}(h)$
corresponding to the
![]() $K_{nr}$
fixed vector
$K_{nr}$
fixed vector
![]() $f$
in the space of
$f$
in the space of
![]() $\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
, one can easily show that
$\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
, one can easily show that
![]() $W_{nr}^{(n)}(e)\neq 0$
. This will follow from the computation which we will perform in the next proposition.
$W_{nr}^{(n)}(e)\neq 0$
. This will follow from the computation which we will perform in the next proposition.
Before doing that, it will be convenient to perform a simple computation which we will refer to several times. We will do it in the following subsection.
2.1 A local computation
Let
![]() $F$
denote a local field. Given a root
$F$
denote a local field. Given a root
![]() $\unicode[STIX]{x1D6FC}$
associated with the group
$\unicode[STIX]{x1D6FC}$
associated with the group
![]() $\text{GL}_{b}$
, we will denote by
$\text{GL}_{b}$
, we will denote by
![]() $x_{\unicode[STIX]{x1D6FC}}(l)$
the one-dimensional unipotent subgroup of
$x_{\unicode[STIX]{x1D6FC}}(l)$
the one-dimensional unipotent subgroup of
![]() $\text{GL}_{b}$
associated with this root. Assume that
$\text{GL}_{b}$
associated with this root. Assume that
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
are two roots such that
$\unicode[STIX]{x1D6FD}$
are two roots such that
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}$
is also a root. Assume also that
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}$
is also a root. Assume also that
![]() $x_{\unicode[STIX]{x1D6FC}}(z)x_{\unicode[STIX]{x1D6FD}}(l)=x_{\unicode[STIX]{x1D6FD}}(l)x_{\unicode[STIX]{x1D6FC}}(z)x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(lz)$
. Let
$x_{\unicode[STIX]{x1D6FC}}(z)x_{\unicode[STIX]{x1D6FD}}(l)=x_{\unicode[STIX]{x1D6FD}}(l)x_{\unicode[STIX]{x1D6FC}}(z)x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(lz)$
. Let
![]() $h(a)$
denote a one-dimensional torus of
$h(a)$
denote a one-dimensional torus of
![]() $\text{GL}_{b}$
which satisfies the property
$\text{GL}_{b}$
which satisfies the property
![]() $h(a)^{-1}x_{\unicode[STIX]{x1D6FC}}(z)h(a)=x_{\unicode[STIX]{x1D6FC}}(a^{-1}z)$
for all
$h(a)^{-1}x_{\unicode[STIX]{x1D6FC}}(z)h(a)=x_{\unicode[STIX]{x1D6FC}}(a^{-1}z)$
for all
![]() $a\in F^{\ast }$
.
$a\in F^{\ast }$
.
Let
![]() $f$
denote a function defined on
$f$
denote a function defined on
![]() $\text{GL}_{b}(F)$
which satisfies the property
$\text{GL}_{b}(F)$
which satisfies the property
for all
![]() $k\in K_{b}$
, where
$k\in K_{b}$
, where
![]() $K_{b}$
is the standard maximal compact subgroup of
$K_{b}$
is the standard maximal compact subgroup of
![]() $\text{GL}_{b}$
.
$\text{GL}_{b}$
.
Our goal in this subsection is to compute the integral
Here
![]() $\unicode[STIX]{x1D716}=0,-1$
.
$\unicode[STIX]{x1D716}=0,-1$
.
Lemma 1. We have
![]() $I=f(h(a)x_{\unicode[STIX]{x1D6FC}}(-a^{-1}\unicode[STIX]{x1D716}))=f(x_{\unicode[STIX]{x1D6FC}}(-\unicode[STIX]{x1D716})h(a))$
.
$I=f(h(a)x_{\unicode[STIX]{x1D6FC}}(-a^{-1}\unicode[STIX]{x1D716}))=f(x_{\unicode[STIX]{x1D6FC}}(-\unicode[STIX]{x1D716})h(a))$
.
Proof. Since
![]() $f$
is right
$f$
is right
![]() $K_{b}$
invariant,
$K_{b}$
invariant,
Conjugating
![]() $x_{\unicode[STIX]{x1D6FC}}(m)$
to the left, and using the above assumptions on the commutation relations, we obtain the integral
$x_{\unicode[STIX]{x1D6FC}}(m)$
to the left, and using the above assumptions on the commutation relations, we obtain the integral
Changing variables in
![]() $z$
and using property (8), we obtain
$z$
and using property (8), we obtain
![]() $\int \unicode[STIX]{x1D713}(\mathit{lam})\,dm$
as inner integration. Here
$\int \unicode[STIX]{x1D713}(\mathit{lam})\,dm$
as inner integration. Here
![]() $m$
is integrated over
$m$
is integrated over
![]() $|m|\leqslant 1$
. Hence we may restrict the integration domain over the
$|m|\leqslant 1$
. Hence we may restrict the integration domain over the
![]() $l$
variable in integral
$l$
variable in integral
![]() $I$
to the domain
$I$
to the domain
![]() $|la|\leqslant 1$
.
$|la|\leqslant 1$
.
The next step is to conjugate
![]() $x_{\unicode[STIX]{x1D6FD}}(l)$
to the left. Using the commutation relations and property (8), we obtain
$x_{\unicode[STIX]{x1D6FD}}(l)$
to the left. Using the commutation relations and property (8), we obtain
Changing variables in
![]() $l$
, we obtain
$l$
, we obtain
Writing
![]() $a^{-1}z=a^{-1}z+\unicode[STIX]{x1D716}a^{-1}-\unicode[STIX]{x1D716}a^{-1}$
, we obtain
$a^{-1}z=a^{-1}z+\unicode[STIX]{x1D716}a^{-1}-\unicode[STIX]{x1D716}a^{-1}$
, we obtain
where the last equality is obtained from property (8), and the fact that
![]() $x_{\unicode[STIX]{x1D6FC}}(a^{-1}z+\unicode[STIX]{x1D716}a^{-1})\in K_{b}$
. From this the lemma follows.◻
$x_{\unicode[STIX]{x1D6FC}}(a^{-1}z+\unicode[STIX]{x1D716}a^{-1})\in K_{b}$
. From this the lemma follows.◻
With the above notation we prove the following corollary.
Corollary 1. Let
![]() $a=0$
, or if
$a=0$
, or if
![]() $a\in F^{\ast }$
, assume that
$a\in F^{\ast }$
, assume that
![]() $|a|\leqslant 1$
. Then
$|a|\leqslant 1$
. Then
Proof. Since
![]() $f$
is right invariant under
$f$
is right invariant under
![]() $K_{b}$
, the above integral is equal to
$K_{b}$
, the above integral is equal to
Conjugating
![]() $x_{\unicode[STIX]{x1D6FD}}(m)$
to the left, we obtain, from the left invariant property of
$x_{\unicode[STIX]{x1D6FD}}(m)$
to the left, we obtain, from the left invariant property of
![]() $f$
, the integral
$f$
, the integral
![]() $\int \unicode[STIX]{x1D713}(mz)\,dm$
as inner integration. Here
$\int \unicode[STIX]{x1D713}(mz)\,dm$
as inner integration. Here
![]() $m$
is integrated over
$m$
is integrated over
![]() $|m|\leqslant 1$
. Hence, we may restrict the integration over
$|m|\leqslant 1$
. Hence, we may restrict the integration over
![]() $z$
to the domain
$z$
to the domain
![]() $|z|\leqslant 1$
. The result follows.◻
$|z|\leqslant 1$
. The result follows.◻
2.2 On the generating function
In this subsection we will prove that the generating function can be expressed in terms of the function
![]() $W_{nr}^{(n)}$
.
$W_{nr}^{(n)}$
.
Embed
![]() $g\in \text{GL}_{r}$
in
$g\in \text{GL}_{r}$
in
![]() $\text{GL}_{nr}$
as
$\text{GL}_{nr}$
as
![]() $g\mapsto g_{0}=\text{diag}(g,I_{r},\ldots ,I_{r})$
. We have the following proposition.
$g\mapsto g_{0}=\text{diag}(g,I_{r},\ldots ,I_{r})$
. We have the following proposition.
Proposition 2. Let
![]() $W_{nr}^{(n)}(h)$
denote the function corresponding to the
$W_{nr}^{(n)}(h)$
denote the function corresponding to the
![]() $K_{nr}$
fixed vector. Then, for
$K_{nr}$
fixed vector. Then, for
![]() $s^{\prime }=s/n-(n-2)r/2-1/2n$
, we have
$s^{\prime }=s/n-(n-2)r/2-1/2n$
, we have
Proof. It follows from the discussion right after equation (7) that the function
![]() $W_{nr}^{(n)}(g_{0})$
is
$W_{nr}^{(n)}(g_{0})$
is
![]() $K_{r}$
bi-invariant. To prove the proposition it is enough to show that
$K_{r}$
bi-invariant. To prove the proposition it is enough to show that
Notice that this will also imply that the function
![]() $W_{nr}^{(n)}(h)$
as defined in (7) is not identically zero on the space of the representation
$W_{nr}^{(n)}(h)$
as defined in (7) is not identically zero on the space of the representation
![]() $\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
. Using the identity
$\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
. Using the identity
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}(g)=\int _{K_{r}}f_{\unicode[STIX]{x1D70B}^{(n)}}(kg)\,dk$
, we may, after a change of variables, replace in (10) the function
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}(g)=\int _{K_{r}}f_{\unicode[STIX]{x1D70B}^{(n)}}(kg)\,dk$
, we may, after a change of variables, replace in (10) the function
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}$
by
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}^{(n)}}$
by
![]() $f_{\unicode[STIX]{x1D70B}^{(n)}}$
. Here
$f_{\unicode[STIX]{x1D70B}^{(n)}}$
. Here
![]() $f_{\unicode[STIX]{x1D70B}^{(n)}}$
is the unramified vector in the space of
$f_{\unicode[STIX]{x1D70B}^{(n)}}$
is the unramified vector in the space of
![]() $\unicode[STIX]{x1D70B}^{(n)}$
. Performing the Iwasawa decomposition, the integral in equation (10) is equal to
$\unicode[STIX]{x1D70B}^{(n)}$
. Performing the Iwasawa decomposition, the integral in equation (10) is equal to
Here
![]() $V_{r}$
is the maximal unipotent subgroup of
$V_{r}$
is the maximal unipotent subgroup of
![]() $\text{GL}_{r}$
consisting of upper unipotent matrices. Also
$\text{GL}_{r}$
consisting of upper unipotent matrices. Also
![]() $t=\text{diag}(a_{1},a_{2},\ldots ,a_{r})$
. Plug integral (7) into integral (11). Thus, we obtain the integral
$t=\text{diag}(a_{1},a_{2},\ldots ,a_{r})$
. Plug integral (7) into integral (11). Thus, we obtain the integral
as an inner integration to integral (11). Let
![]() $U_{nr}^{1}$
denote the subgroup of
$U_{nr}^{1}$
denote the subgroup of
![]() $U_{nr}^{0}$
consisting of all matrices such that
$U_{nr}^{0}$
consisting of all matrices such that
![]() $X_{1,2}[i,j]=0$
for all
$X_{1,2}[i,j]=0$
for all
![]() $i\neq j$
. We claim that integral (12) is equal to
$i\neq j$
. We claim that integral (12) is equal to
We do this by using Lemma 1 several times. It is convenient to use the following notation. For all integers
![]() $1\leqslant a,b\leqslant nr$
and all
$1\leqslant a,b\leqslant nr$
and all
![]() $m\in F$
, let
$m\in F$
, let
![]() $x_{a,b}(m)=I_{nr}+me_{a,b}$
. Here
$x_{a,b}(m)=I_{nr}+me_{a,b}$
. Here
![]() $e_{a,b}$
is the matrix of size
$e_{a,b}$
is the matrix of size
![]() $nr$
which has a one in the
$nr$
which has a one in the
![]() $(a,b)$
th entry, and zero elsewhere.
$(a,b)$
th entry, and zero elsewhere.
In integral (12) consider the integrations over the variables
![]() $X_{1,2}[r,r-1]$
and
$X_{1,2}[r,r-1]$
and
![]() $v_{0}[r-1,r]$
, where the latter variable indicates the
$v_{0}[r-1,r]$
, where the latter variable indicates the
![]() $(r-1,r)$
th entry of
$(r-1,r)$
th entry of
![]() $v_{0}$
. In the notation of § 2.1, let
$v_{0}$
. In the notation of § 2.1, let
![]() $x_{\unicode[STIX]{x1D6FC}}(z)=x_{r,2r-1}(z)$
where
$x_{\unicode[STIX]{x1D6FC}}(z)=x_{r,2r-1}(z)$
where
![]() $z=X_{1,2}[r,r-1]$
, and let
$z=X_{1,2}[r,r-1]$
, and let
![]() $x_{\unicode[STIX]{x1D6FD}}(l)=x_{r-1,r}(l)$
where
$x_{\unicode[STIX]{x1D6FD}}(l)=x_{r-1,r}(l)$
where
![]() $l=v_{0}[r-1,r]$
. With this notation we have
$l=v_{0}[r-1,r]$
. With this notation we have
![]() $x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(m)=x_{r-1,2r-1}(m)$
, and from the definition of the character
$x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(m)=x_{r-1,2r-1}(m)$
, and from the definition of the character
![]() $\unicode[STIX]{x1D713}_{U_{nr}}$
we have
$\unicode[STIX]{x1D713}_{U_{nr}}$
we have
![]() $\unicode[STIX]{x1D713}_{U_{nr}}(x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(m))\neq 1$
. Hence, all the conditions of Lemma 1 are satisfied with
$\unicode[STIX]{x1D713}_{U_{nr}}(x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(m))\neq 1$
. Hence, all the conditions of Lemma 1 are satisfied with
![]() $\unicode[STIX]{x1D716}=0$
and
$\unicode[STIX]{x1D716}=0$
and
![]() $h(a)=h(a_{r})=\text{diag}(I_{r-1},a_{r},I_{nr-r})$
. From this we deduce that in integral (12) we may restrict the domain of integration to the group
$h(a)=h(a_{r})=\text{diag}(I_{r-1},a_{r},I_{nr-r})$
. From this we deduce that in integral (12) we may restrict the domain of integration to the group
![]() $V_{r}$
with the condition that
$V_{r}$
with the condition that
![]() $v_{0}[r-1,r]=0$
, and to the group
$v_{0}[r-1,r]=0$
, and to the group
![]() $U_{nr}^{0}$
with the condition
$U_{nr}^{0}$
with the condition
![]() $X_{1,2}[r,r-1]=0$
.
$X_{1,2}[r,r-1]=0$
.
In general, we apply this process in the following order. Fix
![]() $r+1\leqslant j\leqslant 2r-1$
. Then for all
$r+1\leqslant j\leqslant 2r-1$
. Then for all
![]() $j-r+1\leqslant i\leqslant r$
, set
$j-r+1\leqslant i\leqslant r$
, set
![]() $x_{\unicode[STIX]{x1D6FC}}(z)=x_{i,j}(z)$
with
$x_{\unicode[STIX]{x1D6FC}}(z)=x_{i,j}(z)$
with
![]() $z=X_{1,2}[i,j-r]$
, and
$z=X_{1,2}[i,j-r]$
, and
![]() $x_{\unicode[STIX]{x1D6FD}}(l)=x_{j-r,i}(l)$
with
$x_{\unicode[STIX]{x1D6FD}}(l)=x_{j-r,i}(l)$
with
![]() $l=v_{0}[j-r,i]$
. With this notation we have
$l=v_{0}[j-r,i]$
. With this notation we have
![]() $x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(m)=x_{j-r,j}(m)$
. Since
$x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(m)=x_{j-r,j}(m)$
. Since
![]() $\unicode[STIX]{x1D713}_{U_{nr}}$
is not trivial on
$\unicode[STIX]{x1D713}_{U_{nr}}$
is not trivial on
![]() $x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(m)$
, we can apply Lemma 1 with
$x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(m)$
, we can apply Lemma 1 with
![]() $\unicode[STIX]{x1D716}=0$
. The end result of this repeated process is that integral (12) is equal to integral (13).
$\unicode[STIX]{x1D716}=0$
. The end result of this repeated process is that integral (12) is equal to integral (13).
Conjugating by
![]() $w_{0}$
, write
$w_{0}$
, write
![]() $w_{0}U_{nr}^{1}w_{0}^{-1}=U_{nr}^{2}U_{nr}^{3}$
, where the groups
$w_{0}U_{nr}^{1}w_{0}^{-1}=U_{nr}^{2}U_{nr}^{3}$
, where the groups
![]() $U_{nr}^{2}$
and
$U_{nr}^{2}$
and
![]() $U_{nr}^{3}$
are defined as follows. First, identify the group
$U_{nr}^{3}$
are defined as follows. First, identify the group
![]() $U_{nr}^{2}$
with
$U_{nr}^{2}$
with
![]() $r$
copies of the group
$r$
copies of the group
![]() $V_{n}$
. Here
$V_{n}$
. Here
![]() $V_{n}$
is defined to be the group of all upper unipotent matrices of
$V_{n}$
is defined to be the group of all upper unipotent matrices of
![]() $\text{GL}_{n}$
. The embedding of
$\text{GL}_{n}$
. The embedding of
![]() $U_{nr}^{2}$
inside
$U_{nr}^{2}$
inside
![]() $\text{GL}_{nr}$
is given by
$\text{GL}_{nr}$
is given by
![]() $(v_{n,1},v_{n,2},\ldots ,v_{n,r})\mapsto \text{diag}(v_{n,1},v_{n,2},\ldots ,v_{n,r})$
. Here
$(v_{n,1},v_{n,2},\ldots ,v_{n,r})\mapsto \text{diag}(v_{n,1},v_{n,2},\ldots ,v_{n,r})$
. Here
![]() $v_{n,i}\in V_{n}$
. To define the group
$v_{n,i}\in V_{n}$
. To define the group
![]() $U_{nr}^{3}$
, consider the unipotent group generated by all matrices of the form
$U_{nr}^{3}$
, consider the unipotent group generated by all matrices of the form
 $$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}I & & & & \\ Y_{2,1} & I & & & \\ Y_{3,1} & Y_{3,2} & I & & \\ \vdots & \vdots & \ddots & I & \\ Y_{r,1} & Y_{r,2} & \ldots \, & Y_{r,r-1} & I\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}I & & & & \\ Y_{2,1} & I & & & \\ Y_{3,1} & Y_{3,2} & I & & \\ \vdots & \vdots & \ddots & I & \\ Y_{r,1} & Y_{r,2} & \ldots \, & Y_{r,r-1} & I\end{array}\right).\end{eqnarray}$$
Here
![]() $Y_{i,j}$
is in
$Y_{i,j}$
is in
![]() $\text{Mat}_{n\times n}$
. Then the group
$\text{Mat}_{n\times n}$
. Then the group
![]() $U_{nr}^{3}$
is generated by all matrices as in (14) which satisfies the conditions
$U_{nr}^{3}$
is generated by all matrices as in (14) which satisfies the conditions
![]() $Y_{i,j}[l_{1},l_{2}]=Y_{i,j}[1,2]=0$
for all
$Y_{i,j}[l_{1},l_{2}]=Y_{i,j}[1,2]=0$
for all
![]() $l_{1}\geqslant l_{2}$
.
$l_{1}\geqslant l_{2}$
.
For
![]() $v\in V_{n}$
, let
$v\in V_{n}$
, let
![]() $\unicode[STIX]{x1D713}_{V_{n}}(v)$
denote the Whittaker character of the group
$\unicode[STIX]{x1D713}_{V_{n}}(v)$
denote the Whittaker character of the group
![]() $V_{n}$
. This character is defined as follows. Given
$V_{n}$
. This character is defined as follows. Given
![]() $v=(v[i,j])\in V_{n}$
, then
$v=(v[i,j])\in V_{n}$
, then
Let
![]() $u_{2}=\text{diag}(v_{n,1},v_{n,2},\ldots ,v_{n,r})\in U_{nr}^{2}$
. Define the character
$u_{2}=\text{diag}(v_{n,1},v_{n,2},\ldots ,v_{n,r})\in U_{nr}^{2}$
. Define the character
![]() $\unicode[STIX]{x1D713}_{U_{nr}^{2}}$
of
$\unicode[STIX]{x1D713}_{U_{nr}^{2}}$
of
![]() $U_{nr}^{2}$
as
$U_{nr}^{2}$
as
![]() $\unicode[STIX]{x1D713}_{U_{nr}^{2}}(u_{2})=\unicode[STIX]{x1D713}_{V_{n}}(v_{n,1})\unicode[STIX]{x1D713}_{V_{n}}(v_{n,2})\cdots \unicode[STIX]{x1D713}_{V_{n}}(v_{n,r})$
. Then, in the notation of
$\unicode[STIX]{x1D713}_{U_{nr}^{2}}(u_{2})=\unicode[STIX]{x1D713}_{V_{n}}(v_{n,1})\unicode[STIX]{x1D713}_{V_{n}}(v_{n,2})\cdots \unicode[STIX]{x1D713}_{V_{n}}(v_{n,r})$
. Then, in the notation of
![]() $U_{nr}^{2}U_{nr}^{3}$
, the character
$U_{nr}^{2}U_{nr}^{3}$
, the character
![]() $\unicode[STIX]{x1D713}_{U_{nr}}$
transforms to the character
$\unicode[STIX]{x1D713}_{U_{nr}}$
transforms to the character
![]() $\unicode[STIX]{x1D713}_{U_{nr}^{2}}$
on the group
$\unicode[STIX]{x1D713}_{U_{nr}^{2}}$
on the group
![]() $U_{nr}^{2}$
, and is trivial on the group
$U_{nr}^{2}$
, and is trivial on the group
![]() $U_{nr}^{3}$
.
$U_{nr}^{3}$
.
Thus, integral (13) is equal to
where
We have
![]() $w_{0}t_{0}w_{0}^{-1}=\text{diag}(A_{1},A_{2},\ldots ,A_{r})$
where
$w_{0}t_{0}w_{0}^{-1}=\text{diag}(A_{1},A_{2},\ldots ,A_{r})$
where
![]() $A_{i}=\text{diag}(a_{i},I_{n-1})$
. Conjugating the matrix
$A_{i}=\text{diag}(a_{i},I_{n-1})$
. Conjugating the matrix
![]() $w_{0}t_{0}w_{0}^{-1}$
to the left in integral (16), we obtain the factor
$w_{0}t_{0}w_{0}^{-1}$
to the left in integral (16), we obtain the factor
from the change of variables in
![]() $U_{nr}^{3}$
. Thus, integral (16) is equal to
$U_{nr}^{3}$
. Thus, integral (16) is equal to
We claim that integral (17) is equal to
![]() $\unicode[STIX]{x1D6FC}(t)f_{W}(w_{0}t_{0}w_{0}^{-1})$
. This we will show by a repeated application of Corollary 1. Indeed, fix
$\unicode[STIX]{x1D6FC}(t)f_{W}(w_{0}t_{0}w_{0}^{-1})$
. This we will show by a repeated application of Corollary 1. Indeed, fix
![]() $2\leqslant i\leqslant r$
, where we first start with
$2\leqslant i\leqslant r$
, where we first start with
![]() $i=r$
, then
$i=r$
, then
![]() $i=r-1$
and so on. Let
$i=r-1$
and so on. Let
![]() $1\leqslant k\leqslant i-1$
. Assume that
$1\leqslant k\leqslant i-1$
. Assume that
![]() $l_{1}$
and
$l_{1}$
and
![]() $l_{2}$
are such that
$l_{2}$
are such that
![]() $Y_{i,k}[l_{1},l_{2}]$
is a variable in the domain of integration in integral (17). In the notation of § 2.1, let
$Y_{i,k}[l_{1},l_{2}]$
is a variable in the domain of integration in integral (17). In the notation of § 2.1, let
![]() $x_{\unicode[STIX]{x1D6FC}}(z)=x_{n(i-1)+l_{1},n(k-1)+l_{2}}(z)$
with
$x_{\unicode[STIX]{x1D6FC}}(z)=x_{n(i-1)+l_{1},n(k-1)+l_{2}}(z)$
with
![]() $z=Y_{i,k}[l_{1},l_{2}]$
, and let
$z=Y_{i,k}[l_{1},l_{2}]$
, and let
![]() $x_{\unicode[STIX]{x1D6FD}}(m)=x_{n(k-1)+l_{2},n(i-1)+l_{1}+1}(m)$
. Then
$x_{\unicode[STIX]{x1D6FD}}(m)=x_{n(k-1)+l_{2},n(i-1)+l_{1}+1}(m)$
. Then
![]() $x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(l)=x_{n(i-1)+l_{1},n(i-1)+l_{1}+1}(l)$
, and from the properties of
$x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(l)=x_{n(i-1)+l_{1},n(i-1)+l_{1}+1}(l)$
, and from the properties of
![]() $f_{W}$
we have
$f_{W}$
we have
![]() $f_{W}(x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(l)g)=\unicode[STIX]{x1D713}(-l)f_{W}(g)$
. Applying Corollary 1 several times in the indicated order, the above claim follows.
$f_{W}(x_{\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}}(l)g)=\unicode[STIX]{x1D713}(-l)f_{W}(g)$
. Applying Corollary 1 several times in the indicated order, the above claim follows.
Let
![]() $f$
be an arbitrary function in the space of
$f$
be an arbitrary function in the space of
![]() $\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
. Then the integral
$\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
. Then the integral
![]() $f_{W}(h)$
defines a functional on
$f_{W}(h)$
defines a functional on
![]() $\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
which by [Reference CaiCai16, Theorem 3.38] is unique. Applying an argument similar to that in [Reference Bump and GinzburgBG92, pp. 169–170], we deduce that for the unramified vector
$\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
which by [Reference CaiCai16, Theorem 3.38] is unique. Applying an argument similar to that in [Reference Bump and GinzburgBG92, pp. 169–170], we deduce that for the unramified vector
![]() $f$
in the space of
$f$
in the space of
![]() $\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
we have the following. First,
$\unicode[STIX]{x1D6E9}_{nr}^{(n)}$
we have the following. First,
![]() $f_{W}(w_{0}t_{0}w_{0}^{-1})=0$
unless
$f_{W}(w_{0}t_{0}w_{0}^{-1})=0$
unless
![]() $|a_{i}|\leqslant 1$
and
$|a_{i}|\leqslant 1$
and
![]() $|a_{i}|=|b_{i}|^{n}$
for some
$|a_{i}|=|b_{i}|^{n}$
for some
![]() $|b_{i}|\leqslant 1$
. On such elements
$|b_{i}|\leqslant 1$
. On such elements
![]() $f_{W}(w_{0}t_{0}w_{0}^{-1})$
is not zero and is equal to
$f_{W}(w_{0}t_{0}w_{0}^{-1})$
is not zero and is equal to
![]() $\unicode[STIX]{x1D6FF}_{B_{nr}}^{(n-1)/2n}(w_{0}t_{0}w_{0}^{-1})$
. Hence, integral (17) is equal to
$\unicode[STIX]{x1D6FF}_{B_{nr}}^{(n-1)/2n}(w_{0}t_{0}w_{0}^{-1})$
. Hence, integral (17) is equal to
When
![]() $a_{i}=b_{i}^{n}$
, we have
$a_{i}=b_{i}^{n}$
, we have
![]() $f_{\unicode[STIX]{x1D70B}^{(n)}}(t)=\prod _{i=1}^{r}\unicode[STIX]{x1D712}_{i}^{n}(b_{i})\unicode[STIX]{x1D6FF}_{B_{r}}^{n/2}(\text{diag}(1,\ldots ,1,b_{i},1,\ldots ,1))$
. Combining all this, integral (11) is equal to
$f_{\unicode[STIX]{x1D70B}^{(n)}}(t)=\prod _{i=1}^{r}\unicode[STIX]{x1D712}_{i}^{n}(b_{i})\unicode[STIX]{x1D6FF}_{B_{r}}^{n/2}(\text{diag}(1,\ldots ,1,b_{i},1,\ldots ,1))$
. Combining all this, integral (11) is equal to
From this the proposition follows. ◻
3 The Whittaker functional of the generating function
In this section we compute the Whittaker functional of the function
![]() $W_{nr}^{(n)}(g_{0})$
. Here the notation is as in § 2, but we assume that
$W_{nr}^{(n)}(g_{0})$
. Here the notation is as in § 2, but we assume that
![]() $r<n$
. We make this assumption to get a precise proof of [Reference Bump and FriedbergBF99, Conjecture 1.2]. The case when
$r<n$
. We make this assumption to get a precise proof of [Reference Bump and FriedbergBF99, Conjecture 1.2]. The case when
![]() $r\geqslant n$
is similar and will be dealt with in the next section. Embed
$r\geqslant n$
is similar and will be dealt with in the next section. Embed
![]() $g\in \text{GL}_{r}$
in
$g\in \text{GL}_{r}$
in
![]() $\text{GL}_{n}$
as
$\text{GL}_{n}$
as
![]() $g\mapsto \text{diag}(g,I_{n-r})$
. Let
$g\mapsto \text{diag}(g,I_{n-r})$
. Let
![]() $g_{0}=\text{diag}(g,I_{n-r},I_{n},\ldots ,I_{n})\in \text{GL}_{nr}$
, where
$g_{0}=\text{diag}(g,I_{n-r},I_{n},\ldots ,I_{n})\in \text{GL}_{nr}$
, where
![]() $I_{n}$
appears
$I_{n}$
appears
![]() $r-1$
times.
$r-1$
times.
Let
![]() $V_{r}$
denote the standard maximal unipotent subgroup of
$V_{r}$
denote the standard maximal unipotent subgroup of
![]() $\text{GL}_{r}$
, and let
$\text{GL}_{r}$
, and let
![]() $\unicode[STIX]{x1D713}_{V_{r}}^{-1}$
denote the Whittaker character of
$\unicode[STIX]{x1D713}_{V_{r}}^{-1}$
denote the Whittaker character of
![]() $V_{r}$
. See equation (15) for the definition of
$V_{r}$
. See equation (15) for the definition of
![]() $\unicode[STIX]{x1D713}_{V_{r}}$
. Let
$\unicode[STIX]{x1D713}_{V_{r}}$
. Let
![]() $W_{\unicode[STIX]{x1D6E9}_{n}}^{(n)}$
denote the Whittaker function of the theta function defined on
$W_{\unicode[STIX]{x1D6E9}_{n}}^{(n)}$
denote the Whittaker function of the theta function defined on
![]() $\text{GL}_{n}^{(n)}$
. Our goal is to prove the following theorem.
$\text{GL}_{n}^{(n)}$
. Our goal is to prove the following theorem.
Theorem 2. Assume that
![]() $r<n$
. With the above notation, for all
$r<n$
. With the above notation, for all
![]() $g\in \text{GL}_{r}^{(n)}$
, we have
$g\in \text{GL}_{r}^{(n)}$
, we have
Proof. We will consider the case when
![]() $r=n-1$
. This is the hardest case. When
$r=n-1$
. This is the hardest case. When
![]() $r<n-1$
the computations are similar but simpler. Since we will use some of the notation introduced in the previous sections, we will continue to write
$r<n-1$
the computations are similar but simpler. Since we will use some of the notation introduced in the previous sections, we will continue to write
![]() $r$
and
$r$
and
![]() $n$
even though we assume that
$n$
even though we assume that
![]() $r=n-1$
. By the Iwasawa decomposition, it is enough to prove identity (20) for
$r=n-1$
. By the Iwasawa decomposition, it is enough to prove identity (20) for
![]() $g=t=\text{diag}(a_{1},a_{2},\ldots ,a_{n-1})$
. Notice, that from the left invariant properties of
$g=t=\text{diag}(a_{1},a_{2},\ldots ,a_{n-1})$
. Notice, that from the left invariant properties of
![]() $W_{nr}^{(n)}$
and
$W_{nr}^{(n)}$
and
![]() $W_{\unicode[STIX]{x1D6E9}_{n}}^{(n)}$
, we may assume that
$W_{\unicode[STIX]{x1D6E9}_{n}}^{(n)}$
, we may assume that
![]() $|a_{i}|\leqslant 1$
for all
$|a_{i}|\leqslant 1$
for all
![]() $1\leqslant i\leqslant n-1$
.
$1\leqslant i\leqslant n-1$
.
We start by plugging integral (7) into the left-hand side of identity (20). Doing so, we obtain the integral
As in the proof of Proposition 2, we claim that integral (21) is equal to the integral
where
![]() $\unicode[STIX]{x1D6FF}_{0}=\prod _{i=2}^{n-1}x_{i,r+i-1}(1)$
. Here, the definitions of
$\unicode[STIX]{x1D6FF}_{0}=\prod _{i=2}^{n-1}x_{i,r+i-1}(1)$
. Here, the definitions of
![]() $U_{nr}^{0}$
and
$U_{nr}^{0}$
and
![]() $x_{a,b}(m)$
are given before and after integral (13). To prove the above claim, we follow exactly the same steps as in the proof that integral (12) is equal to integral (13). The only difference is that because of the character
$x_{a,b}(m)$
are given before and after integral (13). To prove the above claim, we follow exactly the same steps as in the proof that integral (12) is equal to integral (13). The only difference is that because of the character
![]() $\unicode[STIX]{x1D713}_{V_{r}}^{-1}$
in integral (21), for suitable variables in
$\unicode[STIX]{x1D713}_{V_{r}}^{-1}$
in integral (21), for suitable variables in
![]() $V_{r}$
, we need to use Lemma 1 with
$V_{r}$
, we need to use Lemma 1 with
![]() $\unicode[STIX]{x1D716}=-1$
and not with
$\unicode[STIX]{x1D716}=-1$
and not with
![]() $\unicode[STIX]{x1D716}=0$
as in the proof of Proposition 2. This explains the element
$\unicode[STIX]{x1D716}=0$
as in the proof of Proposition 2. This explains the element
![]() $\unicode[STIX]{x1D6FF}_{0}$
. Next we proceed as in the proof of Proposition 2. Following the exact steps which showed that integral (13) is equal to integral (17), we deduce that integral (22) is equal to
$\unicode[STIX]{x1D6FF}_{0}$
. Next we proceed as in the proof of Proposition 2. Following the exact steps which showed that integral (13) is equal to integral (17), we deduce that integral (22) is equal to
Here the group
![]() $U_{nr}^{3}$
and
$U_{nr}^{3}$
and
![]() $\unicode[STIX]{x1D6FC}(t)$
are defined before integral (17), and we remind the reader that we assume that
$\unicode[STIX]{x1D6FC}(t)$
are defined before integral (17), and we remind the reader that we assume that
![]() $r=n-1$
. Also, we have
$r=n-1$
. Also, we have
![]() $\unicode[STIX]{x1D6FF}_{1}(t)=\prod _{i=2}^{n-1}x_{(i-1)n+1,(i-2)n+2}(a_{i}^{-1})$
. This element is obtained by conjugating
$\unicode[STIX]{x1D6FF}_{1}(t)=\prod _{i=2}^{n-1}x_{(i-1)n+1,(i-2)n+2}(a_{i}^{-1})$
. This element is obtained by conjugating
![]() $\unicode[STIX]{x1D6FF}_{0}$
by
$\unicode[STIX]{x1D6FF}_{0}$
by
![]() $w_{0}$
and
$w_{0}$
and
![]() $t_{0}$
.
$t_{0}$
.
At this point, for all
![]() $2\leqslant j\leqslant n-1$
, we will introduce an integral which we denote by
$2\leqslant j\leqslant n-1$
, we will introduce an integral which we denote by
![]() $I_{j}$
. To do that we first fix some notation. Let
$I_{j}$
. To do that we first fix some notation. Let
![]() $t_{j}=\text{diag}(A_{j,j},A_{j,j+1},\ldots ,A_{j,n-1},I_{n},\ldots ,I_{n})$
denote the torus element of
$t_{j}=\text{diag}(A_{j,j},A_{j,j+1},\ldots ,A_{j,n-1},I_{n},\ldots ,I_{n})$
denote the torus element of
![]() $\text{GL}_{nr}$
where
$\text{GL}_{nr}$
where
![]() $A_{j,j}=\text{diag}(a_{1},\ldots ,a_{j},I_{n-j})$
, and for all
$A_{j,j}=\text{diag}(a_{1},\ldots ,a_{j},I_{n-j})$
, and for all
![]() $j+1\leqslant i\leqslant n-1$
we define
$j+1\leqslant i\leqslant n-1$
we define
![]() $A_{j,i}=\text{diag}(I_{j},a_{i},I_{n-j-1})$
. Notice that when
$A_{j,i}=\text{diag}(I_{j},a_{i},I_{n-j-1})$
. Notice that when
![]() $j=n-1$
, we get
$j=n-1$
, we get
![]() $t_{j}=\text{diag}(A_{n-1,n-1},I_{n},\ldots ,I_{n})=t_{0}$
. Next we define
$t_{j}=\text{diag}(A_{n-1,n-1},I_{n},\ldots ,I_{n})=t_{0}$
. Next we define
![]() $\unicode[STIX]{x1D6FC}_{j}(t)=|a_{j+1}a_{j+2}^{2}a_{j+3}^{3}\cdots a_{n-1}^{n-j-1}|^{n-2}$
, where we set
$\unicode[STIX]{x1D6FC}_{j}(t)=|a_{j+1}a_{j+2}^{2}a_{j+3}^{3}\cdots a_{n-1}^{n-j-1}|^{n-2}$
, where we set
![]() $\unicode[STIX]{x1D6FC}_{n-1}(t)=1$
. Finally, we define a set of subgroups
$\unicode[STIX]{x1D6FC}_{n-1}(t)=1$
. Finally, we define a set of subgroups
![]() $U_{n,j}$
, and a set of characters
$U_{n,j}$
, and a set of characters
![]() $\unicode[STIX]{x1D713}_{U_{n,j}}$
defined on these groups. The definition is inductive, so we start with
$\unicode[STIX]{x1D713}_{U_{n,j}}$
defined on these groups. The definition is inductive, so we start with
![]() $U_{n,2}$
. Consider the group
$U_{n,2}$
. Consider the group
![]() $U_{nr}^{3}$
with
$U_{nr}^{3}$
with
![]() $r=n-1$
, as was defined right after equation (14). Let
$r=n-1$
, as was defined right after equation (14). Let
![]() $U_{n,2}$
denote the subgroup of
$U_{n,2}$
denote the subgroup of
![]() $U_{nr}^{3}$
with the extra condition that
$U_{nr}^{3}$
with the extra condition that
![]() $Y_{n-1,i}=0$
for all
$Y_{n-1,i}=0$
for all
![]() $1\leqslant i\leqslant n-2$
. Assuming we defined
$1\leqslant i\leqslant n-2$
. Assuming we defined
![]() $U_{n,j-1}$
, we define
$U_{n,j-1}$
, we define
![]() $U_{n,j}$
as the subgroup of
$U_{n,j}$
as the subgroup of
![]() $U_{n,j-1}$
consisting of matrices of the form (14) such that
$U_{n,j-1}$
consisting of matrices of the form (14) such that
![]() $Y_{n-j+1,i}=0$
for all
$Y_{n-j+1,i}=0$
for all
![]() $1\leqslant i\leqslant n-j$
, and also satisfies the condition
$1\leqslant i\leqslant n-j$
, and also satisfies the condition
![]() $Y_{i,l}[b,j]=0$
for all
$Y_{i,l}[b,j]=0$
for all
![]() $2\leqslant i\leqslant n-j$
,
$2\leqslant i\leqslant n-j$
,
![]() $1\leqslant l\leqslant i-1$
and
$1\leqslant l\leqslant i-1$
and
![]() $1\leqslant b\leqslant n$
. The character
$1\leqslant b\leqslant n$
. The character
![]() $\unicode[STIX]{x1D713}_{U_{n,j}}$
is defined as follows. For
$\unicode[STIX]{x1D713}_{U_{n,j}}$
is defined as follows. For
![]() $u\in U_{n,j}$
written as in equation (14), we set
$u\in U_{n,j}$
written as in equation (14), we set
![]() $\unicode[STIX]{x1D713}_{U_{n,j}}(u)=\unicode[STIX]{x1D713}(\sum _{i=2}^{n-j}Y_{i,i-1}[j-1,j+1])$
.
$\unicode[STIX]{x1D713}_{U_{n,j}}(u)=\unicode[STIX]{x1D713}(\sum _{i=2}^{n-j}Y_{i,i-1}[j-1,j+1])$
.
With this notation, for all
![]() $2\leqslant j\leqslant n-1$
, we set
$2\leqslant j\leqslant n-1$
, we set
We will prove that
![]() $I_{2}=I_{1}$
, and that for all
$I_{2}=I_{1}$
, and that for all
![]() $2\leqslant j\leqslant n-1$
, we have
$2\leqslant j\leqslant n-1$
, we have
![]() $I_{j}=I_{j-1}$
. This will complete the proof of the theorem. Indeed, proving the above implies that the left-hand side of equation (20) is equal to
$I_{j}=I_{j-1}$
. This will complete the proof of the theorem. Indeed, proving the above implies that the left-hand side of equation (20) is equal to
![]() $I_{n-1}$
. Since
$I_{n-1}$
. Since
![]() $\unicode[STIX]{x1D6FC}_{n-1}(t)=1$
, the group
$\unicode[STIX]{x1D6FC}_{n-1}(t)=1$
, the group
![]() $U_{n,n-1}$
is the trivial group, and
$U_{n,n-1}$
is the trivial group, and
![]() $t_{n-1}=t_{0}$
, we deduce that
$t_{n-1}=t_{0}$
, we deduce that
![]() $I_{n-1}=f_{W}(t_{0})$
. But as in equation (18) we obtain that
$I_{n-1}=f_{W}(t_{0})$
. But as in equation (18) we obtain that
![]() $f_{W}(t_{0})$
equals the right-hand side of equation (20).
$f_{W}(t_{0})$
equals the right-hand side of equation (20).
We prove that
![]() $I_{2}=I_{1}$
. Since
$I_{2}=I_{1}$
. Since
![]() $|a_{i}|\leqslant 1$
, we obtain the Iwasawa decomposition
$|a_{i}|\leqslant 1$
, we obtain the Iwasawa decomposition
![]() $\unicode[STIX]{x1D6FF}_{1}(t)=\prod _{i=2}^{n-1}x_{(i-2)n+2,(i-1)n+1}(a_{i})\prod _{i=2}^{n-1}h_{i}(a_{i})k$
. Here
$\unicode[STIX]{x1D6FF}_{1}(t)=\prod _{i=2}^{n-1}x_{(i-2)n+2,(i-1)n+1}(a_{i})\prod _{i=2}^{n-1}h_{i}(a_{i})k$
. Here
![]() $k\in K_{nr}$
, and we have
$k\in K_{nr}$
, and we have
![]() $\prod _{i=2}^{n-1}h_{i}(a_{i})=\text{diag}(B_{2,1},B_{2,2},\ldots ,B_{2,n-1})$
. Here
$\prod _{i=2}^{n-1}h_{i}(a_{i})=\text{diag}(B_{2,1},B_{2,2},\ldots ,B_{2,n-1})$
. Here
![]() $B_{2,1}=\text{diag}(1,a_{2},I_{n-2})$
, for
$B_{2,1}=\text{diag}(1,a_{2},I_{n-2})$
, for
![]() $2\leqslant i\leqslant n-2$
we have
$2\leqslant i\leqslant n-2$
we have
![]() $B_{2,i}=\text{diag}(a_{i}^{-1},a_{i+1},I_{n-2})$
, and
$B_{2,i}=\text{diag}(a_{i}^{-1},a_{i+1},I_{n-2})$
, and
![]() $B_{2,n-1}=\text{diag}(a_{n-1}^{-1},I_{n-1})$
. Conjugating in
$B_{2,n-1}=\text{diag}(a_{n-1}^{-1},I_{n-1})$
. Conjugating in
![]() $I_{1}$
the matrix
$I_{1}$
the matrix
![]() $\unicode[STIX]{x1D6FF}_{1}(t)k^{-1}$
to the left, and using the left invariant properties of
$\unicode[STIX]{x1D6FF}_{1}(t)k^{-1}$
to the left, and using the left invariant properties of
![]() $f_{W}$
, we obtain by matrix multiplication
$f_{W}$
, we obtain by matrix multiplication
Here we use the fact that
![]() $w_{0}t_{0}w_{0}^{-1}\prod _{i=2}^{n-1}h_{i}(a_{i})=t_{2}$
. The factor of
$w_{0}t_{0}w_{0}^{-1}\prod _{i=2}^{n-1}h_{i}(a_{i})=t_{2}$
. The factor of
![]() $|a_{2}a_{3}\cdots a_{n-1}|^{-(n-2)}$
is obtained from a change of variables when we conjugate the torus
$|a_{2}a_{3}\cdots a_{n-1}|^{-(n-2)}$
is obtained from a change of variables when we conjugate the torus
![]() $\prod _{i=2}^{n-1}h_{i}(a_{i})$
across
$\prod _{i=2}^{n-1}h_{i}(a_{i})$
across
![]() $U_{nr}^{3}$
. The product of this factor by
$U_{nr}^{3}$
. The product of this factor by
![]() $\unicode[STIX]{x1D6FC}_{1}(t)$
is equal to
$\unicode[STIX]{x1D6FC}_{1}(t)$
is equal to
![]() $\unicode[STIX]{x1D6FC}_{2}(t)$
. The character
$\unicode[STIX]{x1D6FC}_{2}(t)$
. The character
![]() $\unicode[STIX]{x1D713}_{U_{nr}^{3}}$
is defined as follows. For
$\unicode[STIX]{x1D713}_{U_{nr}^{3}}$
is defined as follows. For
![]() $u_{3}\in U_{nr}^{3}$
, define
$u_{3}\in U_{nr}^{3}$
, define
![]() $\unicode[STIX]{x1D713}_{U_{nr}^{3}}(u_{3})=\unicode[STIX]{x1D713}(\sum _{i=2}^{n-1}Y_{i,i-1}[1,3])$
. To complete the proof that
$\unicode[STIX]{x1D713}_{U_{nr}^{3}}(u_{3})=\unicode[STIX]{x1D713}(\sum _{i=2}^{n-1}Y_{i,i-1}[1,3])$
. To complete the proof that
![]() $I_{2}=I_{1}$
, we need to show that we can restrict the support of integration from
$I_{2}=I_{1}$
, we need to show that we can restrict the support of integration from
![]() $U_{nr}^{3}$
to
$U_{nr}^{3}$
to
![]() $U_{n,2}$
. In other words, we need to show that for all
$U_{n,2}$
. In other words, we need to show that for all
![]() $1\leqslant i\leqslant n-2$
, the integration over all variables in
$1\leqslant i\leqslant n-2$
, the integration over all variables in
![]() $Y_{n-1,i}$
is in
$Y_{n-1,i}$
is in
![]() $K_{nr}$
. This is done as in the proof of Proposition 2 while showing that integral (17) reduces to the left-hand side of identity (18). Indeed, from the definition of the torus
$K_{nr}$
. This is done as in the proof of Proposition 2 while showing that integral (17) reduces to the left-hand side of identity (18). Indeed, from the definition of the torus
![]() $t_{2}$
, given a variable
$t_{2}$
, given a variable
![]() $Y_{n-1,i}[l_{1},l_{2}]$
, we can find a one-dimensional unipotent subgroup
$Y_{n-1,i}[l_{1},l_{2}]$
, we can find a one-dimensional unipotent subgroup
![]() $x_{\unicode[STIX]{x1D6FD}}(m)$
so that we can apply Corollary 1. Thus
$x_{\unicode[STIX]{x1D6FD}}(m)$
so that we can apply Corollary 1. Thus
![]() $I_{2}=I_{1}$
.
$I_{2}=I_{1}$
.
The next step is to prove that
![]() $I_{j}=I_{j-1}$
. The first step is to prove that we can integrate over a smaller unipotent group. Let
$I_{j}=I_{j-1}$
. The first step is to prove that we can integrate over a smaller unipotent group. Let
![]() $U_{n,j-1,1}$
denote the subgroup of
$U_{n,j-1,1}$
denote the subgroup of
![]() $U_{n,j-1}$
consisting of all matrices which also satisfies
$U_{n,j-1}$
consisting of all matrices which also satisfies
![]() $Y_{i,l}[b,j]=0$
for all
$Y_{i,l}[b,j]=0$
for all
![]() $3\leqslant i\leqslant n-j+1$
,
$3\leqslant i\leqslant n-j+1$
,
![]() $1\leqslant l\leqslant i-2$
and
$1\leqslant l\leqslant i-2$
and
![]() $1\leqslant b\leqslant j-1$
. To show that we can reduce the domain of integration from
$1\leqslant b\leqslant j-1$
. To show that we can reduce the domain of integration from
![]() $U_{n,j-1}$
to
$U_{n,j-1}$
to
![]() $U_{n,j-1,1}$
we apply Corollary 1. In the notation of this corollary, let
$U_{n,j-1,1}$
we apply Corollary 1. In the notation of this corollary, let
![]() $x_{\unicode[STIX]{x1D6FC}}(z)=x_{n(i-1)+b,n(l-1)+j}(z)$
with
$x_{\unicode[STIX]{x1D6FC}}(z)=x_{n(i-1)+b,n(l-1)+j}(z)$
with
![]() $z=Y_{i,l}[b,j]$
, and let
$z=Y_{i,l}[b,j]$
, and let
![]() $x_{\unicode[STIX]{x1D6FD}}(m)=x_{nl+j-2,n(i-1)+b}(m)$
. Notice that in this case the root
$x_{\unicode[STIX]{x1D6FD}}(m)=x_{nl+j-2,n(i-1)+b}(m)$
. Notice that in this case the root
![]() $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}$
corresponds to the one-dimensional unipotent subgroup
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}$
corresponds to the one-dimensional unipotent subgroup
![]() $x_{nl+j-2,n(l-1)+j}(c)$
, which is a subgroup of
$x_{nl+j-2,n(l-1)+j}(c)$
, which is a subgroup of
![]() $U_{n,j-1,1}$
. Moreover, the character
$U_{n,j-1,1}$
. Moreover, the character
![]() $\unicode[STIX]{x1D713}_{U_{n,j-1}}$
is not trivial on this subgroup. Hence, the conditions of the Corollary 1 are satisfied. We mention that the order for which we apply this corollary is important. We first vary
$\unicode[STIX]{x1D713}_{U_{n,j-1}}$
is not trivial on this subgroup. Hence, the conditions of the Corollary 1 are satisfied. We mention that the order for which we apply this corollary is important. We first vary
![]() $3\leqslant i\leqslant n-j+1$
and fix
$3\leqslant i\leqslant n-j+1$
and fix
![]() $l=1$
. Then we repeat the same process with
$l=1$
. Then we repeat the same process with
![]() $l=2$
and so on.
$l=2$
and so on.
The second step is to show that
![]() $I_{j-1}$
is equal to
$I_{j-1}$
is equal to
Here
![]() $U_{n,j-1,2}$
is the subgroup of
$U_{n,j-1,2}$
is the subgroup of
![]() $U_{n,j-1,1}$
which satisfies the condition that
$U_{n,j-1,1}$
which satisfies the condition that
![]() $Y_{i,i-1}[j-1,j]=0$
for all
$Y_{i,i-1}[j-1,j]=0$
for all
![]() $2\leqslant i\leqslant n-j+1$
. The matrix
$2\leqslant i\leqslant n-j+1$
. The matrix
![]() $\unicode[STIX]{x1D6FF}_{j-1}(t)=\prod _{i=2}^{n-j+1}x_{(i-1)n+j-1,n(i-2)+j}(a_{j+i-2}^{-1})$
. To derive integral (24) we apply Corollary 1 with
$\unicode[STIX]{x1D6FF}_{j-1}(t)=\prod _{i=2}^{n-j+1}x_{(i-1)n+j-1,n(i-2)+j}(a_{j+i-2}^{-1})$
. To derive integral (24) we apply Corollary 1 with
![]() $x_{\unicode[STIX]{x1D6FC}}(z)=x_{n(i-1)+j-1,n(i-2)+j}(z)$
with
$x_{\unicode[STIX]{x1D6FC}}(z)=x_{n(i-1)+j-1,n(i-2)+j}(z)$
with
![]() $z=Y_{i,i-1}[j-1,j]$
and
$z=Y_{i,i-1}[j-1,j]$
and
![]() $x_{\unicode[STIX]{x1D6FD}}(l)=x_{(i-1)n+j-2,(i-1)n+j-1}(l)$
. The next step is to perform an Iwasawa decomposition for
$x_{\unicode[STIX]{x1D6FD}}(l)=x_{(i-1)n+j-2,(i-1)n+j-1}(l)$
. The next step is to perform an Iwasawa decomposition for
![]() $\unicode[STIX]{x1D6FF}_{j-1}(t)$
in integral (24). This is done as with
$\unicode[STIX]{x1D6FF}_{j-1}(t)$
in integral (24). This is done as with
![]() $\unicode[STIX]{x1D6FF}_{1}(t)$
and we obtain
$\unicode[STIX]{x1D6FF}_{1}(t)$
and we obtain
where
![]() $k\in K_{nr}$
. Here
$k\in K_{nr}$
. Here
![]() $\prod _{i=2}^{n-j+1}h_{i}^{\prime }(a_{j+i-2})=\text{diag}(B_{j-1,1},B_{j-1,2},\ldots ,B_{j-1,n-j+1},I_{n},\ldots ,I_{n})$
, where
$\prod _{i=2}^{n-j+1}h_{i}^{\prime }(a_{j+i-2})=\text{diag}(B_{j-1,1},B_{j-1,2},\ldots ,B_{j-1,n-j+1},I_{n},\ldots ,I_{n})$
, where
![]() $B_{j-1,1}=\text{diag}(I_{j-1},a_{j},I_{n-j})$
,
$B_{j-1,1}=\text{diag}(I_{j-1},a_{j},I_{n-j})$
,
![]() $B_{j-1,i}=\text{diag}(I_{j-2},a_{j+i-2}^{-1},a_{j+i-1},I_{n-j})$
for
$B_{j-1,i}=\text{diag}(I_{j-2},a_{j+i-2}^{-1},a_{j+i-1},I_{n-j})$
for
![]() $2\leqslant i\leqslant n-j$
, and
$2\leqslant i\leqslant n-j$
, and
![]() $B_{j-1,n-j+1}=\text{diag}(I_{j-2},a_{n-1}^{-1},I_{n-j+1})$
. Plugging this into integral (24) and conjugating the matrix
$B_{j-1,n-j+1}=\text{diag}(I_{j-2},a_{n-1}^{-1},I_{n-j+1})$
. Plugging this into integral (24) and conjugating the matrix
![]() $\unicode[STIX]{x1D6FF}_{j-1}(t)k^{-1}$
to the left, we obtain
$\unicode[STIX]{x1D6FF}_{j-1}(t)k^{-1}$
to the left, we obtain
Here, we obtain the factor of
![]() $|a_{j}a_{j+1}\cdots a_{n-1}|^{-(n-2)}$
from the conjugation of the toral part of
$|a_{j}a_{j+1}\cdots a_{n-1}|^{-(n-2)}$
from the conjugation of the toral part of
![]() $\unicode[STIX]{x1D6FF}_{j-1}(t)k^{-1}$
across
$\unicode[STIX]{x1D6FF}_{j-1}(t)k^{-1}$
across
![]() $U_{n,j-1,2}$
. This combined with
$U_{n,j-1,2}$
. This combined with
![]() $\unicode[STIX]{x1D6FC}_{j-1}(t)$
gives the factor
$\unicode[STIX]{x1D6FC}_{j-1}(t)$
gives the factor
![]() $\unicode[STIX]{x1D6FC}_{j}(t)$
in integral (25). Notice also that the conjugation by the unipotent part of
$\unicode[STIX]{x1D6FC}_{j}(t)$
in integral (25). Notice also that the conjugation by the unipotent part of
![]() $\unicode[STIX]{x1D6FF}_{j-1}(t)k^{-1}$
changes the additive character to
$\unicode[STIX]{x1D6FF}_{j-1}(t)k^{-1}$
changes the additive character to
![]() $\unicode[STIX]{x1D713}_{U_{n,j}}$
. This is well defined. Indeed, notice that
$\unicode[STIX]{x1D713}_{U_{n,j}}$
. This is well defined. Indeed, notice that
![]() $U_{n,j}$
is a subgroup
$U_{n,j}$
is a subgroup
![]() $U_{n,j-1,2}$
and we can view
$U_{n,j-1,2}$
and we can view
![]() $\unicode[STIX]{x1D713}_{U_{n,j}}$
as a character of
$\unicode[STIX]{x1D713}_{U_{n,j}}$
as a character of
![]() $U_{n,j-1,2}$
by extending it trivially. Finally, we have the identity
$U_{n,j-1,2}$
by extending it trivially. Finally, we have the identity
![]() $t_{j-1}\prod _{i=2}^{n-j+1}h_{i}^{\prime }(a_{j+i-2})=t_{j}$
. To show that integral (25) equals
$t_{j-1}\prod _{i=2}^{n-j+1}h_{i}^{\prime }(a_{j+i-2})=t_{j}$
. To show that integral (25) equals
![]() $I_{j}$
, we need to show that we may restrict the domain of integration from
$I_{j}$
, we need to show that we may restrict the domain of integration from
![]() $U_{n,j-1,2}$
to
$U_{n,j-1,2}$
to
![]() $U_{n,j}$
. We do so using Corollary 1. Indeed, the group
$U_{n,j}$
. We do so using Corollary 1. Indeed, the group
![]() $U_{n,j}$
is the subgroup of
$U_{n,j}$
is the subgroup of
![]() $U_{n,j-1,2}$
obtained by setting
$U_{n,j-1,2}$
obtained by setting
![]() $Y_{n-j+1,l}=0$
for all
$Y_{n-j+1,l}=0$
for all
![]() $1\leqslant l\leqslant n-j$
and
$1\leqslant l\leqslant n-j$
and
![]() $Y_{i,i-1}[b,j]=0$
for all
$Y_{i,i-1}[b,j]=0$
for all
![]() $2\leqslant i\leqslant n-j$
and
$2\leqslant i\leqslant n-j$
and
![]() $1\leqslant b\leqslant j-2$
. To show that we may restrict the integration over
$1\leqslant b\leqslant j-2$
. To show that we may restrict the integration over
![]() $U_{n,j-1,2}$
to the subgroup obtained by setting
$U_{n,j-1,2}$
to the subgroup obtained by setting
![]() $Y_{n-j+1,l}=0$
, we argue in a similar way to the reduction from the group
$Y_{n-j+1,l}=0$
, we argue in a similar way to the reduction from the group
![]() $U_{nr}^{3}$
to
$U_{nr}^{3}$
to
![]() $U_{n,2}$
as was done right after integral (23). Then, finally, to obtain the group
$U_{n,2}$
as was done right after integral (23). Then, finally, to obtain the group
![]() $U_{n,j}$
we use Corollary 1 with
$U_{n,j}$
we use Corollary 1 with
![]() $x_{\unicode[STIX]{x1D6FC}}(z)=x_{n(i-1)+b,n(i-2)+j}(z)$
where
$x_{\unicode[STIX]{x1D6FC}}(z)=x_{n(i-1)+b,n(i-2)+j}(z)$
where
![]() $z=Y_{i,i-1}[b,j]$
and
$z=Y_{i,i-1}[b,j]$
and
![]() $x_{n(i-2)+j,n(i-1)+b+1}(m)$
. Here
$x_{n(i-2)+j,n(i-1)+b+1}(m)$
. Here
![]() $2\leqslant i\leqslant n-j$
and
$2\leqslant i\leqslant n-j$
and
![]() $1\leqslant b\leqslant j-2$
.◻
$1\leqslant b\leqslant j-2$
.◻
4 The case when
 $r\geqslant n$
$r\geqslant n$
As mentioned in the introduction, the authors of [Reference Bump and FriedbergBF99] were well aware that the situation when
![]() $r\geqslant n$
is similar. Since they do not specify this case explicitly, we briefly mention the global constructions and show how a similar result to Theorem 2 holds in this case.
$r\geqslant n$
is similar. Since they do not specify this case explicitly, we briefly mention the global constructions and show how a similar result to Theorem 2 holds in this case.
Assume first that
![]() $r>n$
. Let
$r>n$
. Let
![]() $\unicode[STIX]{x1D70B}^{(n)}$
denote a cuspidal representation of the group
$\unicode[STIX]{x1D70B}^{(n)}$
denote a cuspidal representation of the group
![]() $\text{GL}_{r}^{(n)}(\mathbf{A})$
. Let
$\text{GL}_{r}^{(n)}(\mathbf{A})$
. Let
![]() $\unicode[STIX]{x1D6E9}_{n}^{(n)}$
denote the theta representation of the group
$\unicode[STIX]{x1D6E9}_{n}^{(n)}$
denote the theta representation of the group
![]() $\text{GL}_{n}^{(n)}(\mathbf{A})$
. Then we consider the global integral (1) introduced in the introduction. The group
$\text{GL}_{n}^{(n)}(\mathbf{A})$
. Then we consider the global integral (1) introduced in the introduction. The group
![]() $V_{r,n}$
is defined as follows. Recall that
$V_{r,n}$
is defined as follows. Recall that
![]() $V_{r}$
is the standard maximal unipotent subgroup of
$V_{r}$
is the standard maximal unipotent subgroup of
![]() $\text{GL}_{r}$
. Then
$\text{GL}_{r}$
. Then
![]() $V_{r,n}$
is the subgroup of
$V_{r,n}$
is the subgroup of
![]() $V_{r}$
consisting of all matrices
$V_{r}$
consisting of all matrices
![]() $v=(v_{i,j})\in V_{r}$
such that
$v=(v_{i,j})\in V_{r}$
such that
![]() $v_{i,j}=0$
for all
$v_{i,j}=0$
for all
![]() $2\leqslant j\leqslant n+1$
. The character
$2\leqslant j\leqslant n+1$
. The character
![]() $\unicode[STIX]{x1D713}_{V_{r,n}}$
is defined by
$\unicode[STIX]{x1D713}_{V_{r,n}}$
is defined by
![]() $\unicode[STIX]{x1D713}_{V_{r,n}}(v)=\unicode[STIX]{x1D713}(v_{n+1,n+2}+v_{n+2,n+3}+\cdots +v_{r-1,r})$
. It follows from the cuspidality of
$\unicode[STIX]{x1D713}_{V_{r,n}}(v)=\unicode[STIX]{x1D713}(v_{n+1,n+2}+v_{n+2,n+3}+\cdots +v_{r-1,r})$
. It follows from the cuspidality of
![]() $\unicode[STIX]{x1D719}$
that integral (1) converges for all
$\unicode[STIX]{x1D719}$
that integral (1) converges for all
![]() $s$
. A similar unfolding to that in [Reference Bump and FriedbergBF99, § 2] implies that for
$s$
. A similar unfolding to that in [Reference Bump and FriedbergBF99, § 2] implies that for
![]() $\text{Re}(s)$
large, integral (1) is equal to integral (2).
$\text{Re}(s)$
large, integral (1) is equal to integral (2).
Next we consider the case when
![]() $r=n$
. In this case the global integral is given by
$r=n$
. In this case the global integral is given by
Here
![]() $Z_{r}$
is the subgroup of
$Z_{r}$
is the subgroup of
![]() $Z$
, the center of
$Z$
, the center of
![]() $\text{GL}_{r}$
, which consists of scalar matrices which are
$\text{GL}_{r}$
, which consists of scalar matrices which are
![]() $r$
powers. For simplicity we assume that all representations have a trivial central character. Also,
$r$
powers. For simplicity we assume that all representations have a trivial central character. Also,
![]() $E(g,s)$
is the Eisenstein series defined on the group
$E(g,s)$
is the Eisenstein series defined on the group
![]() $\text{GL}_{r}(\mathbf{A})$
and is associated with the induced representation
$\text{GL}_{r}(\mathbf{A})$
and is associated with the induced representation
![]() $\text{Ind}_{P(\mathbf{A})}^{\text{GL}_{r}(\mathbf{A})}\unicode[STIX]{x1D6FF}_{P}^{s}$
. Here
$\text{Ind}_{P(\mathbf{A})}^{\text{GL}_{r}(\mathbf{A})}\unicode[STIX]{x1D6FF}_{P}^{s}$
. Here
![]() $P$
is the maximal parabolic subgroup of
$P$
is the maximal parabolic subgroup of
![]() $\text{GL}_{r}$
whose Levi part is
$\text{GL}_{r}$
whose Levi part is
![]() $\text{GL}_{r-1}\times \text{GL}_{1}$
. Unfolding this integral, by first unfolding the Eisenstein series, we obtain for
$\text{GL}_{r-1}\times \text{GL}_{1}$
. Unfolding this integral, by first unfolding the Eisenstein series, we obtain for
![]() $\text{Re}(s)$
large that integral (26) is equal to
$\text{Re}(s)$
large that integral (26) is equal to
Here
![]() $f(g,s)$
is a section in the above induced representation.
$f(g,s)$
is a section in the above induced representation.
Next we study the local unramified computation corresponding to integrals (2) and (27). Since the Whittaker coefficient of the representation
![]() $\unicode[STIX]{x1D70B}^{(n)}$
is not factorizable, it is not clear that these integrals are Eulerian. However, as explained in [Reference Bump and FriedbergBF99], if we can prove similar results to Proposition 2 and Theorem 2, the so-called ‘new way’ would imply that these integrals are indeed factorizable. As for Proposition 2, it is clear that it holds for all values of
$\unicode[STIX]{x1D70B}^{(n)}$
is not factorizable, it is not clear that these integrals are Eulerian. However, as explained in [Reference Bump and FriedbergBF99], if we can prove similar results to Proposition 2 and Theorem 2, the so-called ‘new way’ would imply that these integrals are indeed factorizable. As for Proposition 2, it is clear that it holds for all values of
![]() $r$
and
$r$
and
![]() $n$
.
$n$
.
As for Theorem 2, this is not the case for all matrices
![]() $g\in \text{GL}_{r}^{(n)}$
. Assuming
$g\in \text{GL}_{r}^{(n)}$
. Assuming
![]() $r\geqslant n$
, denote by
$r\geqslant n$
, denote by
![]() $T_{0}$
the subgroup of
$T_{0}$
the subgroup of
![]() $\text{GL}_{r}$
which consists of all diagonal matrices
$\text{GL}_{r}$
which consists of all diagonal matrices
![]() $t=\text{diag}(a_{1},a_{2},\ldots ,a_{r})$
such that
$t=\text{diag}(a_{1},a_{2},\ldots ,a_{r})$
such that
![]() $|a_{i}|\leqslant 1$
for
$|a_{i}|\leqslant 1$
for
![]() $1\leqslant i\leqslant n$
and
$1\leqslant i\leqslant n$
and
![]() $|a_{i}|=1$
for all
$|a_{i}|=1$
for all
![]() $n+1\leqslant i\leqslant r$
. Let
$n+1\leqslant i\leqslant r$
. Let
![]() $T_{0}^{(n)}$
denote the inverse image of
$T_{0}^{(n)}$
denote the inverse image of
![]() $T_{0}$
inside
$T_{0}$
inside
![]() $\text{GL}_{r}^{(n)}$
. Let
$\text{GL}_{r}^{(n)}$
. Let
![]() $\text{GL}_{r,0}^{(n)}$
denote all elements
$\text{GL}_{r,0}^{(n)}$
denote all elements
![]() $g\in \text{GL}_{r}^{(n)}$
which can be written as
$g\in \text{GL}_{r}^{(n)}$
which can be written as
![]() $g=vtk$
where
$g=vtk$
where
![]() $v\in V_{r}$
,
$v\in V_{r}$
,
![]() $t\in T_{0}^{(n)}$
and
$t\in T_{0}^{(n)}$
and
![]() $k\in K_{r}$
. Here
$k\in K_{r}$
. Here
![]() $K_{r}$
is the standard maximal compact subgroup of
$K_{r}$
is the standard maximal compact subgroup of
![]() $\text{GL}_{r}$
. With this notation we have the following theorem.
$\text{GL}_{r}$
. With this notation we have the following theorem.
Theorem 3. Assume that
![]() $r\geqslant n$
. Then, for all
$r\geqslant n$
. Then, for all
![]() $g\in \text{GL}_{r,0}^{(n)}$
, we have
$g\in \text{GL}_{r,0}^{(n)}$
, we have
Proof. The proof of this theorem is the same as the proof of Theorem 2, and so we will only indicate the end result. Using the Iwasawa decomposition, we may assume that
![]() $g_{0}=t_{0}=\text{diag}(t,I_{r},\ldots ,I_{r})$
where
$g_{0}=t_{0}=\text{diag}(t,I_{r},\ldots ,I_{r})$
where
![]() $t=(a_{1},\ldots ,a_{r})$
. This factorization produces a factor of
$t=(a_{1},\ldots ,a_{r})$
. This factorization produces a factor of
![]() $\unicode[STIX]{x1D6FF}_{B_{r}}^{-1}(t)$
.
$\unicode[STIX]{x1D6FF}_{B_{r}}^{-1}(t)$
.
Defining similar integrals
![]() $I_{j}$
as in Theorem 2, we prove that the left-hand side of integral (28) is equal to
$I_{j}$
as in Theorem 2, we prove that the left-hand side of integral (28) is equal to
![]() $f_{W}(t_{0}^{\prime })$
where
$f_{W}(t_{0}^{\prime })$
where
![]() $t_{0}^{\prime }=\text{diag}(A_{1},A_{2},\ldots ,A_{r-n+1},I_{n},\ldots ,I_{n})$
. Here
$t_{0}^{\prime }=\text{diag}(A_{1},A_{2},\ldots ,A_{r-n+1},I_{n},\ldots ,I_{n})$
. Here
![]() $A_{1}=\text{diag}(a_{1},\ldots ,a_{n})$
, and for all
$A_{1}=\text{diag}(a_{1},\ldots ,a_{n})$
, and for all
![]() $2\leqslant i\leqslant r-n+1$
we have
$2\leqslant i\leqslant r-n+1$
we have
![]() $A_{i}=\text{diag}(I_{n-1},a_{n+i-1})$
. Applying the factorization of equation (18), we obtain the identity
$A_{i}=\text{diag}(I_{n-1},a_{n+i-1})$
. Applying the factorization of equation (18), we obtain the identity
From the properties of the Whittaker function, we deduce that for all
![]() $2\leqslant i\leqslant r-n+1$
we have
$2\leqslant i\leqslant r-n+1$
we have
![]() $W_{\unicode[STIX]{x1D6E9}_{n}}^{(n)}(A_{i})=0$
unless
$W_{\unicode[STIX]{x1D6E9}_{n}}^{(n)}(A_{i})=0$
unless
![]() $|a_{n+i-1}|=1$
. Notice that
$|a_{n+i-1}|=1$
. Notice that
![]() $\unicode[STIX]{x1D6FF}_{B_{r}}^{-1}(A_{1},I_{n-r})=\unicode[STIX]{x1D6FF}_{B_{n}}^{-1}(A_{1})|\text{det}\,A_{1}|^{n-r}$
. From this the theorem follows.◻
$\unicode[STIX]{x1D6FF}_{B_{r}}^{-1}(A_{1},I_{n-r})=\unicode[STIX]{x1D6FF}_{B_{n}}^{-1}(A_{1})|\text{det}\,A_{1}|^{n-r}$
. From this the theorem follows.◻
Notice that this theorem is enough to prove that the corresponding local versions of integrals (2) and (27) are Eulerian. Indeed, the local version of integral (2) is given by
Here
![]() $\unicode[STIX]{x1D719}$
is a vector in the local component of
$\unicode[STIX]{x1D719}$
is a vector in the local component of
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D708}}^{(n)}$
where
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D708}}^{(n)}$
where
![]() $\unicode[STIX]{x1D708}$
is a place where all data are unramified. Similarly for
$\unicode[STIX]{x1D708}$
is a place where all data are unramified. Similarly for
![]() $\unicode[STIX]{x1D703}$
. Also,
$\unicode[STIX]{x1D703}$
. Also,
![]() $W_{\unicode[STIX]{x1D719}}$
is any local Whittaker functional defined on the representation
$W_{\unicode[STIX]{x1D719}}$
is any local Whittaker functional defined on the representation
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D708}}^{(n)}$
. Similarly,
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D708}}^{(n)}$
. Similarly,
![]() $W_{\unicode[STIX]{x1D703}}$
is the Whittaker functional defined on the space of
$W_{\unicode[STIX]{x1D703}}$
is the Whittaker functional defined on the space of
![]() $\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D708}}^{(n)}$
. It is known that for the representation
$\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D708}}^{(n)}$
. It is known that for the representation
![]() $\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D708}}^{(n)}$
this Whittaker functional is unique (see [Reference Kazhdan and PattersonKP84]). However, this need not be the case for the representation
$\unicode[STIX]{x1D6E9}_{n,\unicode[STIX]{x1D708}}^{(n)}$
this Whittaker functional is unique (see [Reference Kazhdan and PattersonKP84]). However, this need not be the case for the representation
![]() $\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D708}}^{(n)}$
.
$\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D708}}^{(n)}$
.
Applying the Iwasawa decomposition to the quotient
![]() $V_{r}\backslash \text{GL}_{r}$
, the domain of integration in integral (29) is reduced to the torus
$V_{r}\backslash \text{GL}_{r}$
, the domain of integration in integral (29) is reduced to the torus
![]() $T_{r}$
of
$T_{r}$
of
![]() $\text{GL}_{r}$
. However, because of the Whittaker functional properties,
$\text{GL}_{r}$
. However, because of the Whittaker functional properties,
![]() $W_{\unicode[STIX]{x1D719}}\big(\!\begin{smallmatrix}t & \\ & I_{r-n}\end{smallmatrix}\!\big)$
is zero unless
$W_{\unicode[STIX]{x1D719}}\big(\!\begin{smallmatrix}t & \\ & I_{r-n}\end{smallmatrix}\!\big)$
is zero unless
![]() $t\in T_{0}$
. Hence, we can apply Theorem 3 to deduce that integral (2) is indeed Eulerian.
$t\in T_{0}$
. Hence, we can apply Theorem 3 to deduce that integral (2) is indeed Eulerian.
A similar argument applies to integral (27). Indeed, using the properties of the Whittaker function, we can choose representatives for the quotient
![]() $Z_{r}\backslash T_{r}$
to be in the group
$Z_{r}\backslash T_{r}$
to be in the group
![]() $T_{0}$
. Hence, once again we can apply Theorem 3.
$T_{0}$
. Hence, once again we can apply Theorem 3.