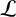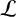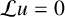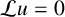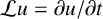1 Introduction
Let
$M^n$
be a smooth manifold of dimension n and
$(\overline {M}^{n+p},\overline {g})$
a smooth Riemannian manifold of dimension
$n+p$
. A family of immersions
$$ \begin{align*} F_t:M\to \overline{M} \end{align*} $$
is called a mean curvature flow of M in
$\overline {M}$
if it satisfies
$$ \begin{align*} \frac{\partial}{\partial t}F_t=\boldsymbol{H}_t, \end{align*} $$
where
$\boldsymbol {H}_t$
is the mean curvature vector of
$F_t(M)$
in
$\overline {M}$
.
Following Smoczyk [Reference Smoczyk7], we call M a conformal soliton to the mean curvature flow if
$$ \begin{align*} \boldsymbol{H}=\boldsymbol{X}^N \end{align*} $$
for a conformal vector field
$\boldsymbol {X}$
, where
$\boldsymbol {H}$
is the mean curvature vector of M in
$\overline {M}$
and
$\boldsymbol {X}^N$
is the normal projection of
$\boldsymbol {X}$
to the normal bundle of M in
$\overline {M}$
. A smooth vector field
$\boldsymbol {X}$
on
$\overline {M}$
is called conformal if in local coordinates,
$\overline {\nabla }_j\boldsymbol {X}_i+\overline {\nabla }_i\boldsymbol {X}_j=\lambda \overline {g}_{ij}$
for some smooth function
$\lambda $
on
$\overline {M}$
. In other words, a conformal vector field
$\boldsymbol {X}$
is a smooth vector field which satisfies
$$ \begin{align} \bar L_{\boldsymbol{X}}\overline{g}=\lambda \overline{g} \end{align} $$
for some smooth function
$\lambda $
on
$\overline {M}$
, where
$\bar L$
is the Lie derivative.
According to [Reference Smoczyk7], there exists a one-to-one correspondence between conformal solitons in a simply connected Riemannian manifold N and minimal submanifolds in
$\mathbb {R}\times N$
equipped with a warped product metric. However, based on the work in [Reference Arezzo and Sun1], conformal solitons can be regarded as generalisations of various geometric submanifolds arising from the singularities of the mean curvature flow, including self-shrinkers, self-expanders and translating solitons. Therefore, the study of conformal solitons is very important.
Let
$F:M\to (\overline {M},\overline {g})$
be a conformal soliton. We denote by
$g=F^*\overline {g}$
the induced metric on M, which makes
$F:(M,g)\to (\overline {M},\overline {g})$
an isometric immersion. Let
$\nabla $
and
$\overline {\nabla }$
be the Levi–Civita connections on M and
$\overline {M}$
, respectively. An important elliptic operator on M is defined by
$$ \begin{align} \mathcal{L}\star =\Delta\star +\langle \boldsymbol{X},\nabla \star \rangle_{\overline{g}}, \end{align} $$
where
$\Delta $
and
$\nabla $
are the Laplacian and the gradient operator on M. We call this elliptic operator the
$\mathcal {L}$
-operator for convenience. In [Reference Li and Sun5], Li and Sun considered the special conformal vector field
$\boldsymbol {X}$
satisfying
$$ \begin{align*} \overline{\nabla }_j\boldsymbol{X}_i=\lambda \overline{g}_{ij}, \end{align*} $$
which can be written as
$\boldsymbol {X}=\overline {\nabla } \omega $
for some smooth function
$\omega $
according to the Poincaré lemma, as long as
$\overline {M}$
is simply connected. Li and Sun derived gradient estimates for the positive solutions of
$\mathcal {L} u=0$
and
$\mathcal {L} u={\partial u}/{\partial t}$
. In their setting, the
$\mathcal {L}$
-operator can be written as
$\mathcal {L}\star =\Delta \star +\langle \overline {\nabla } \omega ,\nabla \star \rangle _{\overline {g}}$
, where
$\overline {\nabla }$
is the gradient operator on
$\overline {M}$
.
The gradient estimate on manifolds has been widely studied since Yau’s seminal work [Reference Yau9]. It is an important topic and tool in differential geometry, useful for deriving Harnack inequalities and Liouville theorems, as well as for applications in spectral estimates and heat kernel estimates of manifolds. We focus on the general case, considering conformal solitons given by a general conformal vector field of the form (1.1), and study gradient estimates of the eigenfunctions of the
$\mathcal {L}$
-operator. To be precise, we will study gradient estimates for positive solutions of the linear elliptic equation
$$ \begin{align} \mathcal{L} u=-\mu u, \end{align} $$
where
$\mu $
is a constant. Throughout this paper, we use
$V=\boldsymbol {X}^T$
to represent the tangential projection of
$\boldsymbol {X}$
to the tangent bundle of M. Accordingly, the
$\mathcal {L}$
-operator can be viewed as the V-Laplacian,
$$ \begin{align*} \mathcal{L}\star =\Delta\star +\langle \boldsymbol{X}^T,\nabla \star \rangle_{\overline{g}}=\Delta \star +\langle V,\nabla \star \rangle_g=:\Delta_V\star, \end{align*} $$
which is the generalised Laplacian introduced by Chen et al. [Reference Chen, Jost and Wang4]. As in [Reference Chen, Jost and Qiu3, Reference Wei and Wylie8], the Bakry–Émery Ricci tensor is defined by
$$ \begin{align*} \mathrm{Ric}_V=\mathrm{Ric} -\tfrac{1}{2}L_Vg, \end{align*} $$
where
$\mathrm {Ric} $
is the Ricci tensor and L is the Lie derivative.
In what follows, we say that M is a conformal soliton in
$(\overline {M},\overline {g})$
, meaning that M is a conformal soliton given by a conformal vector field of the form (1.1) on
$\overline {M}$
. We now state our first main result.
Theorem 1.1 (Gradient estimate).
Let
$M^n$
be a complete conformal soliton in
$(\overline {M},\overline {g})$
. Suppose that
$\overline {K}\ge -K_0$
,
$|\boldsymbol {B}|\le B_0$
,
$|\boldsymbol {X}^T|\le V_0$
and
$\lambda \le \lambda _0$
, where
$K_0,B_0$
and
$V_0$
are nonnegative constants. Let u be a positive solution to (1.3). Then, there exists a positive constant C depending on
$n,\mu , a, K_0, B_0, V_0$
and
$\lambda _0$
, such that
$$ \begin{align} \sup_{B_{a/2}(p)}\frac{|\nabla u|}{u}\le C. \end{align} $$
More explicitly, for any
$\alpha>0$
,
$$ \begin{align} \sup_{B_{a/2}(p)}\frac{|\nabla u|^2}{u^2}\le \widetilde{C}\bigg(\Lambda_0+|\Lambda_0|+|\mu |+\frac{\sqrt{K_0}+B_0+V_0}{a}+\frac{1}{a^2}\bigg), \end{align} $$
where
$\widetilde {C}$
is a positive constant depending on n and
$\alpha $
, and
$$ \begin{align*} \Lambda_0=(n-1)K_0+B_0^2+\frac{V_0^2}{\alpha (n-1)}+\frac{\lambda_0}{2}. \end{align*} $$
By letting
$\mu =0$
and taking
$a\to \infty $
in estimate (1.5), we immediately get the following Liouville type theorem for
$\mathcal {L} u=0$
.
Corollary 1.2 (Liouville type theorem).
Let
$M^n$
be a complete noncompact conformal soliton in
$(\overline {M},\overline {g})$
. Suppose that
$\overline {K}\ge -K_0$
,
$|\boldsymbol {B}|\le B_0$
,
$|\boldsymbol {X}^T|\le V_0$
and
$\lambda \le \lambda _0$
, where
$K_0,B_0$
and
$V_0$
are nonnegative constants. If there is a positive number
$\alpha $
such that
$$ \begin{align*}(n-1)K_0+B_0^2+\frac{V_0^2}{\alpha (n-1)}+\frac{\lambda_0}{2}\le 0,\end{align*} $$
then any positive or bounded solution to
$\mathcal {L} u=0$
must be constant.
Remark 1.3. Our Corollary 1.2 improves the corresponding result obtained by Li and Sun in [Reference Li and Sun5]. They obtained a Liouville type theorem for positive or bounded solutions of
$\mathcal {L} u=0$
on a conformal soliton given by a special conformal vector field of the form
$\overline {\nabla }_j\boldsymbol {X}_i=\lambda \overline {g}_{ij}$
, under the assumptions of
$\overline {K}\ge -K_0,\ |\boldsymbol {B}|\le c,\ |\nabla \omega |\le k,\ \overline {\mathrm {Hess\,}}\omega \le m\overline {g} $
and
$(n-1)K_0+c^2+{k^2}/{\alpha (n-1)}+m= 0$
, where
$\omega $
is a smooth function satisfying
$\overline {\nabla } \omega =\boldsymbol {X}$
. In this case,
$\tfrac 12\lambda \overline {g}=\tfrac 12\bar L_{\boldsymbol {X}}\overline {g}=\overline {\mathrm {Hess\,}}\omega $
, so we can take
$\tfrac 12\lambda _0=m$
.
As another application of Theorem 1.1, we can also prove a Harnack type inequality for positive eigenfunctions of the
$\mathcal {L}$
-operator.
Corollary 1.4 (Harnack type inequality).
Under the conditions of Theorem 1.1, there exists a positive constant
$\widehat {C}$
depending on
$n,\mu , a, K_0, B_0, V_0$
and
$\lambda _0$
, such that
$$ \begin{align*} \sup_{B_{a/2}(p)}u\le \widehat{C}\inf_{B_{a/2}(p)}u. \end{align*} $$
Finally, we consider conformal solitons given by some special conformal vector fields in Euclidean space. When the ambient manifold
$(\overline {M},\overline {g})$
is the Euclidean space
$(\mathbb {R}^{n+p},\delta )$
, it is easy to see that the position vector
$\boldsymbol {x}$
and any constant vector
$\boldsymbol {T}$
are conformal. As in [Reference Arezzo and Sun1], a submanifold M in Euclidean space is called a self-shrinker if it satisfies
$\boldsymbol {H}=\tfrac 12\boldsymbol {x}^N$
; it is called a translating soliton if it satisfies
$\boldsymbol {H}=\boldsymbol {T}^N$
. Therefore, conformal solitons defined by
$\boldsymbol {x}$
and
$\boldsymbol {T}$
are self-shrinkers and translating solitons, respectively.
In the case
$\boldsymbol {X}=-\tfrac 12\boldsymbol {x}$
, a simple calculation yields
$\bar L_{\boldsymbol {X}}\delta =-\tfrac 12\bar L_{\boldsymbol {x}}\delta =-\delta $
, which is the case
$\lambda \equiv -1$
in (1.1). Theorem 1.1 has the following corollary.
Corollary 1.5. Let
$\boldsymbol {x}:M^n\to \mathbb {R}^{n+p}$
be a complete self-shrinker, which satisfies
$\boldsymbol {H}=-\tfrac 12\boldsymbol {x}^N$
. Suppose that
$|\boldsymbol {B}|\le B_0$
and
$|\boldsymbol {x}^T|\le v_0$
, where
$B_0$
and
$v_0$
are nonnegative constants. Let u be a positive solution to
$\Delta u-\tfrac 12\langle \boldsymbol {x},\nabla u\rangle _\delta =-\mu u$
. Then, for any
$\alpha>0$
, there exists a positive constant
$C_1$
depending on n and
$\alpha $
, such that
$$ \begin{align*} \sup_{B_{a/2}(p)}\frac{|\nabla u|^2}{u^2}\le C_1\bigg(\max\bigg\{B_0^2+\frac{v_0^2}{4\alpha (n-1)}-\frac{1}{2},0\bigg\}+|\mu |+\frac{B_0+v_0}{a}+\frac{1}{a^2}\bigg). \end{align*} $$
We also have the following Liouville type theorem, which can be found in [Reference Zhu and Chen10], with the slight difference that our conditions are more relaxed.
Corollary 1.6. Let
$\boldsymbol {x}:M^n\to \mathbb {R}^{n+1}$
be a complete noncompact self-shrinker, which satisfies
$\boldsymbol {H}=-\tfrac 12\boldsymbol {x}^N$
. Suppose that
$|\boldsymbol {B}|\le B_0$
and
$|\boldsymbol {x}^T|\le v_0$
, where
$B_0$
and
$v_0$
are nonnegative constants. If there is a positive number
$\alpha $
such that
$B_0^2+{v_0^2}/{4\alpha (n-1)}\le \tfrac 12$
, then any positive or bounded solution to
$\Delta u-\tfrac 12\langle \boldsymbol {x},\nabla u\rangle _\delta =0$
must be constant.
In the case
$\boldsymbol {X}=\boldsymbol {T}$
, we have
$\bar L_{\boldsymbol {X}}\delta =0$
and then
$\lambda \equiv 0$
in (1.1). Theorem 1.1 has the following corollary.
Corollary 1.7. Let
$\boldsymbol {x} :M\to \mathbb {R}^{n+p}$
be a complete translating soliton, which satisfies
$\boldsymbol {H}=\boldsymbol {T}^N$
. Suppose that
$|\boldsymbol {B}|\le B_0$
and
$|\boldsymbol {T}^T|\le T_0$
. Let u be a positive solution to
$\Delta u+\langle \boldsymbol {T},\nabla u\rangle _\delta =-\mu u$
. Then for any
$\alpha>0$
, there exists a positive constant
$C_2$
depending on n and
$\alpha $
, such that
$$ \begin{align*} \sup_{B_{a/2}(p)}\frac{|\nabla u|^2}{u^2}\le C_2\bigg(B_0^2+\frac{T_0^2}{\alpha (n-1)}+|\mu |+\frac{B_0+T_0}{a}+\frac{1}{a^2}\bigg). \end{align*} $$
2 Preliminaries
Let
$(M^n,g)$
be an isometric immersed submanifold of
$(\overline {M}^{n+p},\overline {g})$
, and
$\nabla $
and
$\overline {\nabla }$
be their respective Levi–Civita connections. Here and in what follows, we equate a vector field on M with its image in
$\overline {M}$
. For any
$X,Y\in \Gamma (TM)$
, we have
$\nabla _XY=(\overline {\nabla }_XY)^T$
. We define the second fundamental form
$\boldsymbol {B}$
of M by
$\boldsymbol {B}(X,Y)=(\overline {\nabla }_XY)^N=\overline {\nabla }_XY-\nabla _XY$
, which is a symmetric bilinear form on
$TM$
with values in
$NM$
. The mean curvature vector
$\boldsymbol {H}$
of M is defined by
$\boldsymbol {H}=\mathrm {tr}_g\boldsymbol {B}=\sum _{i=1}^n\boldsymbol {B}(e_i,e_i)$
, where
$\{e_i\}_{i=1}^n$
is a local orthonormal frame field of M.
Now we compare the Lie derivatives of g and
$\overline {g}$
. For
$X,Y\in \Gamma (TM)$
, recall that we specify
$V=\boldsymbol {X}^T$
. Thus,
$$ \begin{align} L_Vg(X,Y) & =V\langle X,Y\rangle_g -\langle [V,X],Y\rangle_g -\langle X,[V,Y]\rangle_g \nonumber \\ &=\langle \nabla_XV,Y\rangle_g+\langle X,\nabla_YV\rangle_g \nonumber \\ & =X\langle V,Y\rangle_g-\langle V,\nabla_XY\rangle_g+Y\langle X,V\rangle_g-\langle \nabla_YX,V\rangle_g \nonumber\\ &=X\langle \boldsymbol{X},Y\rangle_{\overline{g}}-\langle \boldsymbol{X},\overline{\nabla }_XY\rangle_{\overline{g}}+\langle \boldsymbol{H},\boldsymbol{B}(X,Y)\rangle_{\overline{g}} \nonumber\\ &\quad +Y\langle Y,\boldsymbol{X}\rangle_{\overline{g}}-\langle \overline{\nabla }_YX,\boldsymbol{X}\rangle_{\overline{g}}+\langle \boldsymbol{B}(Y,X),\boldsymbol{H}\rangle_{\overline{g}}\nonumber \\ &=\langle \overline{\nabla }_X\boldsymbol{X},Y\rangle_{\overline{g}}+\langle X,\overline{\nabla }_YX\rangle_{\overline{g}}+2\langle \boldsymbol{X},\boldsymbol{B}(X,Y)\rangle_{\overline{g}} \nonumber\\ &=\bar L_{\boldsymbol{X}}\overline{g}(X,Y)+2\langle \boldsymbol{H},\boldsymbol{B}(X,Y)\rangle_{\overline{g}}. \end{align} $$
The curvature tensor of M is
$R(X,Y)Z=\nabla _X\nabla _YZ-\nabla _Y\nabla _XZ-\nabla _{[X,Y]}Z$
for
$X,Y,Z\in \Gamma (TM)$
. Similarly, denote the curvature tensor of
$\overline {M}$
by
$\overline {R}$
. We have the Gauss equation
$$ \begin{align*} \langle R(X,Y)Z,W\rangle_g=\langle \overline{R}(X,Y)Z,W\rangle_{\overline{g}}-\langle \boldsymbol{B}(X,Z),\boldsymbol{B}(Y,W)\rangle_{\overline{g}}+\langle \boldsymbol{B}(X,W),\boldsymbol{B}(Y,Z)\rangle_{\overline{g}}. \end{align*} $$
Choosing a local orthonormal frame field
$\{e_i\}_{i=1}^n$
of M, letting
$Y=Z=e_i$
and summing both sides of the above equation,
$$ \begin{align} \mathrm{Ric}(X,Y)=\sum_{i=1}^n\langle \overline{R}(X,e_i)e_i,Y\rangle_{\overline{g}}-\sum_{i=1}^n\langle \boldsymbol{B}(X,e_i),\boldsymbol{B}(Y,e_i)\rangle_{\overline{g}}+\langle \boldsymbol{B}(X,Y),\boldsymbol{H}\rangle_{\overline{g}}, \end{align} $$
where we replaced W with Y. From (2.1) and (2.2), the Bakry–Émery Ricci tensor is
$$\begin{align*}\mathrm{Ric}_V(X,Y) &=\mathrm{Ric}(X,Y)-\frac{1}{2}L_Vg(X,Y) \\&=\sum_{i=1}^n\langle \overline{R}(X,e_i)e_i,Y\rangle_{\overline{g}}-\sum_{i=1}^n\langle \boldsymbol{B}(X,e_i),\boldsymbol{B}(Y,e_i)\rangle_{\overline{g}}-\frac{1}{2}\bar L_{\boldsymbol{X}}\overline{g}(X,Y). \end{align*}$$
If the sectional curvature of
$\overline {M}$
has a lower bound
$-K_0$
, the second fundamental form of M has an upper bound
$B_0$
and
$\lambda \le \lambda _0$
on
$\overline {M}$
, then
$$ \begin{align} \mathrm{Ric} &\ge -(n-1)K_0-2B_0^2, \end{align} $$
$$ \begin{align} \mathrm{Ric}_V&\ge -\bigg((n-1)K_0+B_0^2+\frac{\lambda_0 }{2}\bigg). \end{align} $$
3 Proofs of the main results
To prove Theorem 1.1, we need a lemma. We first note an elementary inequality. For any
$a,b\in \mathbb {R}$
and
$\alpha>0$
,
$$ \begin{align} (a+b)^2\ge \frac{a^2}{1+\alpha }-\frac{b^2}{\alpha }, \end{align} $$
with equality if and only if
$b=-({\alpha }/{(1+\alpha ) })a$
.
Lemma 3.1. The conditions are the same as in Theorem 1.1. For
$\alpha>0$
and
$\beta>0$
,
$$ \begin{align*} |\nabla u|\Delta_V|\nabla u| & \ge \frac{|\nabla |\nabla u||^2}{(1+\alpha )(1+\beta )(n-1)}-\frac{(\mu u)^2}{\beta (1+\alpha )(n-1)}\\ &\quad -\bigg((n-1)K_0+B_0^2+\frac{\lambda_0 }{2}+\mu +\frac{V_0^2}{\alpha (n-1)}\bigg)|\nabla u|^2. \end{align*} $$
Proof. Recall that
$\mathcal {L} u=\Delta _Vu$
. From the Bochner formula
$$ \begin{align*} \tfrac{1}{2}\Delta_V|\nabla u|^2=|\mathrm{Hess\,} u|^2+\mathrm{Ric}_V(\nabla u,\nabla u)+\langle \nabla u,\nabla \Delta_Vu\rangle_g \end{align*} $$
and the identity
$$ \begin{align*} \tfrac{1}{2}\Delta_V|\nabla u|^2=|\nabla |\nabla u||^2+|\nabla u|\Delta_V|\nabla u|, \end{align*} $$
and since u is a solution of (1.3),
$$ \begin{align} |\nabla u|\Delta_V|\nabla u| =|\mathrm{Hess\,} u|^2+\mathrm{Ric}_V(\nabla u,\nabla u)-\mu |\nabla u|^2-|\nabla |\nabla u||^2. \end{align} $$
Given
$p\in M$
, choose normal coordinates around p so that
$u_i(p)=0$
for
$2\le i\le n$
and
$u_1(p)=|\nabla u|(p)$
. Then,
$$ \begin{align*} |\nabla|\nabla u||^2=|\nabla u_1|^2=\sum_{j=1}^nu_{1j}^2. \end{align*} $$
Therefore,
$$ \begin{align*} |\mathrm{Hess\,} u|^2-|\nabla |\nabla u||^2 &= \sum_{i,j=1}^nu_{ij}^2-\sum_{j=1}^nu_{1j}^2 =\sum_{i=2}^n\sum_{j=1}^nu_{ij}^2\\ & \ge \sum_{i=2}^nu_{i1}^2+\sum_{i=2}^nu_{ii}^2\\ & \ge \sum_{i=2}^nu_{i1}^2+\frac{1}{n-1}\bigg(\sum_{i=2}^nu_{ii}\bigg)^2\\ & =\sum_{i=2}^nu_{i1}^2+\frac{1}{n-1}(\mu u+u_{11}+V^1u_1). \end{align*} $$
By using (3.1) twice, for any
$\alpha>0$
and
$\beta>0$
,
$$ \begin{align*} \mu u+u_{11}+V^1u_1 & \ge \frac{(\mu u+u_{11})^2}{1+\alpha }-\frac{(V^1u_1)^2}{\alpha }\\ &\ge \frac{1}{1+\alpha }\bigg(\frac{u_{11}^2}{1+\beta }-\frac{(\mu u)^2}{\beta }\bigg)-\frac{(V^1u_1)^2}{\alpha }\\ & =\frac{u_{11}^2}{(1+\alpha )(1+\beta )}-\frac{(\mu u)^2}{\beta (1+\alpha )}-\frac{1}{\alpha }\langle V,\nabla u\rangle_g^2. \end{align*} $$
It follows that
$$ \begin{align*} |\mathrm{Hess\,} u|^2 & -|\nabla |\nabla u||^2\\ & \ge \sum_{i=2}^nu_{i1}^2+\frac{u_{11}^2}{(1+\alpha )(1+\beta )(n-1)}-\frac{(\mu u)^2}{\beta (1+\alpha )(n-1)}-\frac{1}{\alpha (n-1)}\langle V,\nabla u\rangle_g^2\\ & \ge \frac{|\nabla |\nabla u||^2}{(1+\alpha )(1+\beta )(n-1)}-\frac{(\mu u)^2}{\beta (1+\alpha )(n-1)}-\frac{|V|^2}{\alpha (n-1)}|\nabla u|^2. \end{align*} $$
Substituting this inequality and (2.4) into (3.2), using the conditions of the lemma and noting that
$\mathcal {L}=\Delta _V$
and
$V=\boldsymbol {X}^T$
completes the proof.
Proof of Theorem 1.1.
Define
$\phi :=|\nabla \ln u|={|\nabla u|}/{u}$
, so that
$$ \begin{align*} \nabla \phi =\frac{\nabla |\nabla u|}{u}-\frac{|\nabla u|\nabla u}{u^2}. \end{align*} $$
From the definition of
$\phi $
, we also have
$$ \begin{align*} \Delta_V|\nabla u| =\Delta_V(u\phi ) =u\Delta_V\phi +2\langle \nabla u,\nabla \phi \rangle_g+\phi \Delta_Vu =u\Delta_V\phi +2\langle \nabla u,\nabla \phi \rangle_g-\mu |\nabla u|. \end{align*} $$
By Lemma 3.1, for any
$\alpha>0$
and
$\beta>0$
, at any point where
$|\nabla u|\ne 0$
,
$$ \begin{align*} \Delta_V\phi & =\frac{\Delta_V|\nabla u|}{u}-\frac{2\langle \nabla u,\nabla \phi \rangle_g}{u}+\mu \phi \\ & \ge \frac{1}{u|\nabla u|}\bigg \{\frac{|\nabla |\nabla u||^2}{(1+\alpha )(1+\beta )(n-1)}-\frac{(\mu u)^2}{\beta (1+\alpha )(n-1)}\\ &\quad -\bigg((n-1)K_0+B_0^2+\frac{\lambda_0 }{2}+\mu +\frac{V_0^2}{\alpha (n-1)}\bigg)|\nabla u|^2\bigg \}-\frac{2\langle \nabla u,\nabla \phi \rangle_g}{u}+\mu \phi \\ & =\frac{|\nabla |\nabla u||^2}{(1+\alpha )(1+\beta )(n-1)u|\nabla u|}-\frac{\mu^2}{\beta (1+\alpha )(n-1)\phi }\\ &\quad -\bigg((n-1)K_0+B_0^2+\frac{V_0^2}{\alpha (n-1)}+\frac{\lambda_0 }{2}\bigg)\phi -\frac{2\langle \nabla u,\nabla \phi \rangle_g}{u}. \end{align*} $$
As in [Reference Schoen and Yau6, page 19], for any
$\epsilon>0$
,
$$ \begin{align*} -\frac{2\langle \nabla u,\nabla \phi \rangle_g}{u} & =-(2-\epsilon )\frac{\langle \nabla u,\nabla \phi \rangle_g}{u}-\epsilon \frac{\langle \nabla u,\nabla \phi \rangle_g}{u}\\ & =-(2-\epsilon )\frac{\langle \nabla u,\nabla \phi \rangle_g}{u}-\epsilon \frac{\langle \nabla |\nabla u|,\nabla u\rangle_g}{u^2}+\epsilon \frac{|\nabla u|^3}{u^3}\\ & \ge -(2-\epsilon )\frac{\langle \nabla u,\nabla \phi \rangle_g}{u}-\epsilon \frac{|\nabla |\nabla u||\cdot |\nabla u|}{u^2}+\epsilon \frac{|\nabla u|^3}{u^3}\\ & \ge -(2-\epsilon )\frac{\langle \nabla u,\nabla \phi \rangle_g}{u}-\frac{\epsilon }{2}\bigg(\frac{|\nabla |\nabla u||^2}{u|\nabla u|}+\frac{|\nabla u|^3}{u^3}\bigg)+\epsilon \frac{|\nabla u|^3}{u^3}\\ & =-(2-\epsilon )\frac{\langle \nabla u,\nabla \phi \rangle_g}{u}-\frac{\epsilon }{2}\frac{|\nabla |\nabla u||^2}{u|\nabla u|}+\frac{\epsilon }{2}\phi^3. \end{align*} $$
Taking
$\epsilon ={2}/{(1+\alpha )(1+\beta )(n-1)}$
, we arrive at
$$ \begin{align} \Delta_V\phi & \ge -\frac{\mu^2}{\beta (1+\alpha )(n-1)\phi }-\bigg((n-1)K_0+B_0^2+\frac{V_0^2}{\alpha (n-1)}+\frac{\lambda_0 }{2}\bigg)\phi \nonumber\\ &\quad -\bigg(2-\frac{2}{(1+\alpha )(1+\beta )(n-1)}\bigg)\frac{\langle \nabla u,\nabla \phi \rangle_g}{u}+\frac{\phi^3}{(1+\alpha )(1+\beta )(n-1)}. \end{align} $$
Given
$a>0$
, define the function F in
$B_a(p)$
by
$$ \begin{align*} F(x)=(a^2-r^2(x))\phi(x)=(a^2-r^2)\frac{|\nabla u|}{u}, \end{align*} $$
where
$r(x)=\mathrm {dist}(x,p)$
is the distance function from p. Without loss of generality, assume
$|\nabla u|\ne 0$
. Since
$F|_{\partial B_a(p)}=0$
and
$F>0$
, the function F attains its maximum at some point
$x_1\in B_a(p)$
. The argument of Calabi [Reference Calabi2] allows us to assume that
$x_1$
is not a cut point of p. Hence, F is smooth near
$x_1$
.
By the maximum principle, at
$x_1$
,
$$ \begin{align} 0=\nabla F=-\phi \nabla (r^2)+(a^2-r^2)\nabla \phi \end{align} $$
and
$$ \begin{align} 0\ge \Delta_VF=(a^2-r^2)\Delta_V\phi -\phi \Delta_V(r^2)-2\langle \nabla \phi ,\nabla (r^2)\rangle_g. \end{align} $$
From (3.4),
$$ \begin{align} \frac{\nabla \phi }{\phi }=\frac{\nabla (r^2)}{a^2-r^2}, \end{align} $$
and so (3.5) reduces to
$$ \begin{align} 0\ge \frac{\Delta_V\phi }{\phi }-\frac{\Delta_V(r^2)}{a^2-r^2}-\frac{2|\nabla (r^2)|^2}{(a^2-r^2)^2} =\frac{\Delta_V\phi }{\phi }-\frac{\Delta (r^2)}{a^2-r^2}-\frac{\langle V,\nabla(r^2)\rangle_g}{a^2-r^2}-\frac{8r^2}{(a^2-r^2)^2}. \end{align} $$
Since the Ricci curvature of M satisfies (2.3), the classical Laplacian comparison theorem gives
$$ \begin{align*} \Delta (r^2) =2r\Delta r+2 & \le 2r\bigg(\frac{n-1}{r}+(n-1)\sqrt{K_0+\frac{2B_0^2}{n-1}}\bigg)+2\\ & \le 2n+2(n-1)\sqrt{K_0+\frac{2B_0^2}{n-1}}a. \end{align*} $$
Therefore, it follows from (3.7) that
$$ \begin{align} 0\ge \frac{\Delta_V\phi }{\phi }-\frac{1}{a^2-r^2}\bigg(2n+2(n-1)\sqrt{K_0+\frac{2B_0^2}{n-1}}a+2V_0r\bigg)-\frac{8r^2}{(a^2-r^2)^2}. \end{align} $$
$$ \begin{align*} 0 & \ge -\frac{\mu^2}{\beta (1+\alpha )(n-1)}\phi^{-2}-\bigg((n-1)K_0+B_0^2+\frac{V_0^2}{\alpha (n-1)}+\frac{\lambda_0 }{2}\bigg)\\ &\quad -\frac{1}{a^2-r^2}\bigg(2n+2(n-1)\sqrt{K_0+\frac{2B_0^2}{n-1}}a+2V_0r\bigg)-\frac{8r^2}{(a^2-r^2)^2}\\ &\quad -\bigg(2-\frac{2}{(1+\alpha )(1+\beta )(n-1)}\bigg)\frac{\langle \nabla u,\nabla \phi \rangle_g}{u\phi }+\frac{\phi^2}{(1+\alpha )(1+\beta )(n-1)}. \end{align*} $$
By the Cauchy–Schwarz inequality and (3.6),
$$ \begin{align*} -\frac{\langle \nabla u,\nabla \phi \rangle_g}{u\phi }=-\frac{2r\langle \nabla u,\nabla r\rangle_g}{u(a^2-r^2)}\ge -\frac{2r}{a^2-r^2}\phi. \end{align*} $$
Thus,
$$ \begin{align*} 0 & \ge -\frac{\mu^2}{\beta (1+\alpha )(n-1)}\phi^{-2}-\bigg((n-1)K_0+B_0^2+\frac{V_0^2}{\alpha (n-1)}+\frac{\lambda_0 }{2}\bigg)\\ &\quad-\frac{1}{a^2-r^2}\bigg(2n+2(n-1)\sqrt{K_0+\frac{2B_0^2}{n-1}}a+2V_0r\bigg)-\frac{8r^2}{(a^2-r^2)^2}\\ &\quad -4\bigg(1-\frac{1}{(1+\alpha )(1+\beta )(n-1)}\bigg)\frac{r}{a^2-r^2}\phi +\frac{\phi^2}{(1+\alpha )(1+\beta )(n-1)}. \end{align*} $$
Multiplying through by
$(a^2-r^2)^4\phi ^2$
and noting that
$0\le r\le a$
, we arrive at
$$ \begin{align} 0 & \ge \frac{1}{(1+\alpha )(1+\beta )(n-1)}F^4 \nonumber\\ &\quad -4a\bigg(1-\frac{1}{(1+\alpha )(1+\beta )(n-1)}\bigg)F^3-C_1F^2-\frac{\mu^2a^8}{\beta (1+\alpha )(n-1)}, \end{align} $$
where
$$ \begin{align*} C_1& =\bigg((n-1)K_0+B_0^2+\frac{V_0^2}{\alpha (n-1)}+\frac{\lambda_0 }{2}\bigg)a^4 \\ &\quad+2\bigg(n+4+(n-1)\sqrt{K_0+\frac{2B_0^2}{n-1}}a+V_0a\bigg)a^2. \end{align*} $$
Consider the polynomial corresponding to the right-hand side of (3.9), that is,
$$ \begin{align*} P(y) & =\frac{1}{(1+\alpha )(1+\beta )(n-1)}y^4\\ &\quad -4a\bigg(1-\frac{1}{(1+\alpha )(1+\beta )(n-1)}\bigg)y^3-C_1y^2-\frac{\mu^2a^8}{\beta (1+\alpha )(n-1)}. \end{align*} $$
We see that
$P(y)$
is a quartic polynomial with a positive leading coefficient and negative constant term, so Vieta’s formulae tell us that it has exactly one positive real root and one negative real root. If we fix the positive numbers
$\alpha $
and
$\beta $
, there is a positive constant
$C_2$
depending on
$n,\mu , a, K_0, B_0, V_0$
and
$\lambda _0$
, such that
$F(x_1)=\sup _{B_a(p)}F\le C_2$
. Therefore, in
$B_{a/2}(p)$
,
$$ \begin{align*} \frac{3a^2}{4}\sup_{B_{a/2}(p)}\frac{|\nabla u|}{u}\le C_2. \end{align*} $$
This completes the proof of the first part of the theorem.
Now we want to make our estimate more specific. By the AM–GM inequality, for any
$\delta \in (0,1)$
,
$$ \begin{align*} -4a\bigg(1 & -\frac{1}{(1+\alpha )(1+\beta )(n-1)}\bigg)F^3 \\ & \ge -\frac{\delta }{(1+\alpha )(1+\beta )(n-1)}F^4 \\ &\quad -\frac{4}{\delta }(1+\alpha )(1+\beta )(n-1)\bigg(1-\frac{1}{(1+\alpha )(1+\beta )(n-1)}\bigg)^2a^2F^2. \end{align*} $$
Hence, (3.9) reduces to
$$ \begin{align} 0\ge \frac{1-\delta }{(1+\alpha )(1+\beta )(n-1)}F^4-\Lambda F^2-\frac{\mu^2a^8}{\beta (1+\alpha )(n-1)}, \end{align} $$
where
$\Lambda =\Lambda _0a^4+\Lambda _1a^3+\Lambda _2a^2$
with
$$ \begin{align*} \Lambda_0 &=(n-1)K_0+B_0^2+\frac{V_0^2}{\alpha (n-1)}+\frac{\lambda_0}{2}, \quad \Lambda_1=2(n-1)\sqrt{K_0+\frac{2B_0^2}{n-1}}+2V_0\ge 0,\\ \Lambda_2& =2n+8+\frac{4}{\delta }(1+\alpha )(1+\beta )(n-1)\bigg(1-\frac{1}{(1+\alpha )(1+\beta )(n-1)}\bigg)^2>0. \end{align*} $$
Note that
$\Lambda $
is not necessarily positive, because
$\Lambda _0$
can be negative and its absolute value can be large. For a positive number
$\tilde a$
and a nonnegative number
$\tilde c$
, the quadratic inequality
$\tilde ay^2-\tilde by-\tilde c\le 0$
yields
$y\le {(\tilde b+\sqrt {{\tilde b}^2+4\tilde a\tilde c})}/{2\tilde a}$
. So from (3.10),
$$ \begin{align*} (F(x_1))^2 & \le \frac{(1+\alpha )(1+\beta )(n-1)}{2(1-\delta )}\bigg\{\Lambda +\bigg(\Lambda ^2+\frac{4(1-\delta )\mu^2a^8}{\beta (1+\beta )(1+\alpha )^2(n-1)^2}\bigg)^{{1}/{2}}\bigg\}\\ & \le \frac{(1+\alpha )(1+\beta )(n-1)}{2(1-\delta )}(\Lambda +|\Lambda |)+\sqrt{\frac{1+\beta }{\beta (1-\delta )}}|\mu |a^4, \end{align*} $$
where we used the simple fact that
$\sqrt {x^2+y^2}\le |x|+|y|$
in the second inequality. It follows that
$$ \begin{align*} \frac{9a^4}{16}\sup_{B_{a/2}(p)}\frac{|\nabla u|^2}{u^2} & \le \frac{(1+\alpha )(1+\beta )(n-1)}{2(1-\delta )}(\Lambda +|\Lambda |)+\sqrt{\frac{1+\beta }{\beta (1-\delta )}}|\mu |a^4\\ & \le \frac{(1+\alpha )(1+\beta )(n-1)}{2(1-\delta )}((\Lambda_0+|\Lambda_0|)a^4+2\Lambda_1a^3+2\Lambda_2a^2)\\ &\quad+\sqrt{\frac{1+\beta }{\beta (1-\delta )}}|\mu |a^4. \end{align*} $$
Therefore, by fixing
$\beta $
and
$\delta $
, there is a positive constant
$\widetilde {C}$
depending on n and
$\alpha $
, such that (1.5) holds.
Proof of Corollary 1.4.
Choose
$x_1,x_2\in B_{a/2}(p)$
such that
$u(x_1)=\sup _{B_{a/2}(p)}u$
and
$u(x_2)=\inf _{B_{a/2}(p)}u$
. Let
$\gamma $
be a shortest geodesic connecting
$x_1$
and
$x_2$
. The triangle inequality implies
$\gamma \subset B_a(p)$
. In
$B_a(p)$
, there is also a gradient inequality such as (1.4) and integrating it over
$\gamma $
yields
$$ \begin{align*} \int_\gamma \frac{|\nabla u|}{u}\,{d} s\le C\int_\gamma \,{d} s\le 2Ca. \end{align*} $$
It follows that
$$ \begin{align*} \ln \frac{u(x_1)}{u(x_2)}\le \int_\gamma \frac{|\nabla u|}{u}\,{d} s\le 2Ca. \end{align*} $$
Hence, we obtain
$u(x_1)\le \widehat {C}u(x_2)$
, where
$\widehat {C}=e^{2Ca}$
is a constant depending on
$n,\mu , a, K_0, B_0, V_0$
and
$\lambda _0$
.
