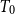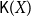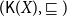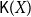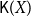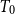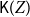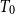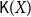1. Introduction
An important problem in domain theory is the modeling of non-deterministic features of programming languages and of parallel features treated in a non-deterministic way. If a non-deterministic program runs several times with the same input, it may produce different outputs. To describe this behavior, powerdomains were introduced by Plotkin (Reference Plotkin1976, Reference Plotkin1982) and Smyth (Reference Smyth1978) to give denotational semantics to non-deterministic choice in higher-order programming languages. The three main such powerdomains are the Smyth powerdomain for demonic non-determinism, the Hoare powerdomain for angelic non-determinism, and the Plotkin powerdomain for erratic non-determinism. This viewpoint traditionally stays with the category of dcpos, but is easily and profitably extended to general topological spaces (see, for example, Abramsky et al. Reference Abramsky and Jung1994, Sections 6.2.3 and 6.2.4 and Schalk Reference Schalk1993).
A subset A of a
![]() $T_0$
space X is called saturated if A equals the intersection of all open sets containing it (or equivalently, A is an upper set in the specialization order). We shall use
$T_0$
space X is called saturated if A equals the intersection of all open sets containing it (or equivalently, A is an upper set in the specialization order). We shall use
![]() $\mathsf{K}(X)$
to denote the set of all nonempty compact saturated subsets of X and endow it with the Smyth order
$\mathsf{K}(X)$
to denote the set of all nonempty compact saturated subsets of X and endow it with the Smyth order
![]() $\sqsubseteq$
, that is, for
$\sqsubseteq$
, that is, for
![]() $K_1,K_2\in \mathord{\mathsf{K}}(X)$
,
$K_1,K_2\in \mathord{\mathsf{K}}(X)$
,
![]() $K_1\sqsubseteq K_2$
iff
$K_1\sqsubseteq K_2$
iff
![]() $K_2\subseteq K_1$
. We call
$K_2\subseteq K_1$
. We call
![]() $(\mathord{\mathsf{K}}(X), \sqsubseteq)$
(shortly
$(\mathord{\mathsf{K}}(X), \sqsubseteq)$
(shortly
![]() $\mathsf{K}(X)$
) the Smyth power poset of X. The upper Vietoris topology on
$\mathsf{K}(X)$
) the Smyth power poset of X. The upper Vietoris topology on
![]() $\mathsf{K}(X)$
is the topology that has
$\mathsf{K}(X)$
is the topology that has
![]() $\{\Box U : U\in \mathcal O(X)\}$
as a base, where
$\{\Box U : U\in \mathcal O(X)\}$
as a base, where
![]() $\mathcal O(X)$
is the set of all open subsets of X and
$\mathcal O(X)$
is the set of all open subsets of X and
![]() $\Box U=\{K\in \mathsf{K}(X) : K\subseteq U\}$
, and the resulting space is called the Smyth power space or upper space of X and is denoted by
$\Box U=\{K\in \mathsf{K}(X) : K\subseteq U\}$
, and the resulting space is called the Smyth power space or upper space of X and is denoted by
![]() $P_S(X)$
.
$P_S(X)$
.
In domain theory and non-Hausdorff topology, we encounter numerous links between topology and order theory (cf. Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003; Goubault 2013). For a poset, the Scott topology is probably the most important one among the intrinsic topologies on it. As pointed out by Goubault (2012), there is naturally another prominent topology one can put on
![]() $\mathsf{K}(X)$
, namely the Scott topology. It is well-known that when X is well-filtered,
$\mathsf{K}(X)$
, namely the Scott topology. It is well-known that when X is well-filtered,
![]() $\mathsf{K}(X)$
is a dcpo, with least upper bounds of directed families computed as filtered intersections, and the upper Vietoris topology is coarser than the Scott topology on
$\mathsf{K}(X)$
is a dcpo, with least upper bounds of directed families computed as filtered intersections, and the upper Vietoris topology is coarser than the Scott topology on
![]() $\mathsf{K}(X)$
; when X is locally compact and well-filtered (equivalently, locally compact and sober), the two topologies coincide on
$\mathsf{K}(X)$
; when X is locally compact and well-filtered (equivalently, locally compact and sober), the two topologies coincide on
![]() $\mathsf{K}(X)$
, and
$\mathsf{K}(X)$
, and
![]() $\mathsf{K}(X)$
is then a continuous domain (see Schalk Reference Schalk1993, Proposition 7.25 and Lemma 7.26 and Xu et al. 2021c, Theorem 3.9).
$\mathsf{K}(X)$
is then a continuous domain (see Schalk Reference Schalk1993, Proposition 7.25 and Lemma 7.26 and Xu et al. 2021c, Theorem 3.9).
In this paper, we mainly discuss some basic properties of the Scott topology on Smyth power posets. The paper is organized as follows:
In Section 2, some standard definitions and notations are introduced which will be used in the whole paper. A few basic properties of irreducible sets and compact saturated sets are listed.
In Section 3, we briefly recall the concepts of Scott topology and continuous domains and some fundamental results about them.
In Section 4, we list a few important results of d-spaces, well-filtered spaces, and sober spaces that will be used in other sections.
In Section 5, we recall some concepts and results about the topological Rudin Lemma, Rudin spaces, and well-filtered determined spaces that will be used in the next four sections.
In Section 6, we mainly investigate the well-filteredness of the Scott topology on Smyth power posets. It is proved that the Scott space
![]() $\Sigma \mathsf{K}(X)$
of a well-filtered space X is still well-filtered, and a
$\Sigma \mathsf{K}(X)$
of a well-filtered space X is still well-filtered, and a
![]() $T_0$
space Y is well-filtered iff
$T_0$
space Y is well-filtered iff
![]() $\Sigma \mathsf{K}(Y)$
is well-filtered and the upper Vietoris topology is coarser than the Scott topology on
$\Sigma \mathsf{K}(Y)$
is well-filtered and the upper Vietoris topology is coarser than the Scott topology on
![]() $\mathsf{K}(Y)$
.
$\mathsf{K}(Y)$
.
In Section 10, a sober space X is constructed for which the Scott space
![]() $\Sigma \mathsf{K}(X)$
is not sober.
$\Sigma \mathsf{K}(X)$
is not sober.
In Section 8, we study the question under what conditions the Scott space
![]() $\Sigma \mathsf{K}(X)$
of a sober space X is sober. This question is related to the investigation of conditions under which the upper Vietoris topology coincides with the Scott topology on
$\Sigma \mathsf{K}(X)$
of a sober space X is sober. This question is related to the investigation of conditions under which the upper Vietoris topology coincides with the Scott topology on
![]() $\mathsf{K}(X)$
, and further it is closely related to the local compactness and first-countability of X.
$\mathsf{K}(X)$
, and further it is closely related to the local compactness and first-countability of X.
In Section 9, the Rudin property and well-filtered determinedness of Smyth power spaces and the Scott topology on Smyth power posets are discussed.
2 Preliminaries
In this section, we briefly recall some standard definitions and notations that will be used in the paper. Some basic properties of irreducible sets and compact saturated sets are presented.
For a set X,
![]() $|X|$
will denote the cardinality of X. Let
$|X|$
will denote the cardinality of X. Let
![]() $\mathbb{N}$
denote the set of all natural numbers and
$\mathbb{N}$
denote the set of all natural numbers and
![]() $\omega=|\mathbb N|$
. As a poset (indeed a chain),
$\omega=|\mathbb N|$
. As a poset (indeed a chain),
![]() $\mathbb{N}$
is always endowed with the usual order if no other explanation is given. The set of all subsets of X is denoted by
$\mathbb{N}$
is always endowed with the usual order if no other explanation is given. The set of all subsets of X is denoted by
![]() $2^X$
. Let
$2^X$
. Let
![]() $X^{(<\omega)}=\{F\subseteq X : F \mbox{~is a finite set}\}$
and
$X^{(<\omega)}=\{F\subseteq X : F \mbox{~is a finite set}\}$
and
![]() $X^{(\leq\omega)}=\{F\subseteq X : F \mbox{~is a countable set}\}$
.
$X^{(\leq\omega)}=\{F\subseteq X : F \mbox{~is a countable set}\}$
.
For a poset P and
![]() $A\subseteq P$
, let
$A\subseteq P$
, let
![]() $\mathord{\downarrow}A=\{x\in P: x\leq a \mbox{ for some }a\in A\}$
and
$\mathord{\downarrow}A=\{x\in P: x\leq a \mbox{ for some }a\in A\}$
and
![]() $\mathord{\uparrow}A=\{x\in P: x\geq a \mbox{ for some } a\in A\}$
. For
$\mathord{\uparrow}A=\{x\in P: x\geq a \mbox{ for some } a\in A\}$
. For
![]() $x\in P$
, we write
$x\in P$
, we write
![]() $\mathord{\downarrow}x$
for
$\mathord{\downarrow}x$
for
![]() $\mathord{\downarrow}\{x\}$
and
$\mathord{\downarrow}\{x\}$
and
![]() $\mathord{\uparrow}x$
for
$\mathord{\uparrow}x$
for
![]() $\mathord{\uparrow}\{x\}$
. A subset A is called a lower set (resp., an upper set) if
$\mathord{\uparrow}\{x\}$
. A subset A is called a lower set (resp., an upper set) if
![]() $A=\mathord{\downarrow}A$
(resp.,
$A=\mathord{\downarrow}A$
(resp.,
![]() $A=\mathord{\uparrow}A$
). Let
$A=\mathord{\uparrow}A$
). Let
![]() $\mathbf{Fin} P=\{\uparrow\! F : F\in P^{(<\omega)}\}$
. For a nonempty subset A of P, define
$\mathbf{Fin} P=\{\uparrow\! F : F\in P^{(<\omega)}\}$
. For a nonempty subset A of P, define
![]() $\mathrm{min} (A)=\{u\in A : u$
is a minimal element of
$\mathrm{min} (A)=\{u\in A : u$
is a minimal element of
![]() $A\}$
and
$A\}$
and
![]() $\mathrm{max} (A)=\{v\in A : v$
is a maximal element of
$\mathrm{max} (A)=\{v\in A : v$
is a maximal element of
![]() $A\}$
.
$A\}$
.
A nonempty subset D of a poset P is directed if every two elements in D have an upper bound in D. The set of all directed sets of P is denoted by
![]() $\mathcal D(P)$
.
$\mathcal D(P)$
.
![]() $I\subseteq P$
is called an ideal of P if I is a directed lower subset of P. Let
$I\subseteq P$
is called an ideal of P if I is a directed lower subset of P. Let
![]() $\mathrm{Id} (P)$
be the poset (with the order of set inclusion) of all ideals of P. Dually, we define the notion of filters and denote the poset of all filters of P by
$\mathrm{Id} (P)$
be the poset (with the order of set inclusion) of all ideals of P. Dually, we define the notion of filters and denote the poset of all filters of P by
![]() $\mathrm{Filt}(P)$
. The poset P is called a directed complete poset, or dcpo for short, if for any
$\mathrm{Filt}(P)$
. The poset P is called a directed complete poset, or dcpo for short, if for any
![]() $D\in \mathcal D(P)$
,
$D\in \mathcal D(P)$
,
![]() $\vee D$
exists in P.
$\vee D$
exists in P.
The poset P is said to be Noetherian if it satisfies the ascending chain condition (ACC for short): every ascending chain has a greatest member. Clearly, P is Noetherian iff every directed set of P has a largest element or, equivalently, every ideal of P is principal (cf. Zhao et al. 2015).
As in Erné (Reference Erné2018), a topological space X is locally hypercompact if for each
![]() $x\in X$
and each open neighborhood U of x, there is
$x\in X$
and each open neighborhood U of x, there is
![]() $\mathord{\uparrow} F\in \mathbf{Fin}X$
such that
$\mathord{\uparrow} F\in \mathbf{Fin}X$
such that
![]() $x\in{\rm int}\,\mathord{\uparrow} F\subseteq\mathord{\uparrow} F\subseteq U$
. The space X is called a c-space if for each
$x\in{\rm int}\,\mathord{\uparrow} F\subseteq\mathord{\uparrow} F\subseteq U$
. The space X is called a c-space if for each
![]() $x\in X$
and each open neighborhood U of x, there is
$x\in X$
and each open neighborhood U of x, there is
![]() $u\in X$
such that
$u\in X$
such that
![]() $x\in{\rm int}\,\mathord{\uparrow} u\subseteq\mathord{\uparrow} u\subseteq U$
). A set K of X is called supercompact if for any family
$x\in{\rm int}\,\mathord{\uparrow} u\subseteq\mathord{\uparrow} u\subseteq U$
). A set K of X is called supercompact if for any family
![]() $\{U_i : i\in I\}$
of open sets of X,
$\{U_i : i\in I\}$
of open sets of X,
![]() $K\subseteq \bigcup_{i\in I} U_i$
implies
$K\subseteq \bigcup_{i\in I} U_i$
implies
![]() $K\subseteq U$
for some
$K\subseteq U$
for some
![]() $i\in I$
. It is easy to verify that the nonempty supercompact saturated sets of X are exactly the sets
$i\in I$
. It is easy to verify that the nonempty supercompact saturated sets of X are exactly the sets
![]() $\mathord{\uparrow} x$
with
$\mathord{\uparrow} x$
with
![]() $x \in X$
(see Heckmann and Keimel Reference Heckmann and Keimel2013, Fact 2.2). It is well-known that X is a c-space iff
$x \in X$
(see Heckmann and Keimel Reference Heckmann and Keimel2013, Fact 2.2). It is well-known that X is a c-space iff
![]() $\mathcal O(X)$
is a completely distributive lattice (cf. Erné Reference Erné2009).
$\mathcal O(X)$
is a completely distributive lattice (cf. Erné Reference Erné2009).
The category of all
![]() $T_0$
spaces and continuous mappings is denoted by
$T_0$
spaces and continuous mappings is denoted by
![]() $\mathbf{Top}_0$
. For
$\mathbf{Top}_0$
. For
![]() $X\in ob(\mathbf{Top}_0)$
, we use
$X\in ob(\mathbf{Top}_0)$
, we use
![]() $\leq_X$
to denote the specialization order of X:
$\leq_X$
to denote the specialization order of X:
![]() $x\leq_X y$
iff
$x\leq_X y$
iff
![]() $x\in \overline{\{y\}}$
). In the following, when a
$x\in \overline{\{y\}}$
). In the following, when a
![]() $T_0$
space X is considered as a poset, the order always refers to the specialization order if no other explanation is given. Let
$T_0$
space X is considered as a poset, the order always refers to the specialization order if no other explanation is given. Let
![]() $\mathcal O(X)$
(resp.,
$\mathcal O(X)$
(resp.,
![]() $\mathcal C(X)$
) be the set of all open subsets (resp., closed subsets) of X, and let
$\mathcal C(X)$
) be the set of all open subsets (resp., closed subsets) of X, and let
![]() $\mathcal S^u(X)=\{\mathord{\uparrow} x : x\in X\}$
. Define
$\mathcal S^u(X)=\{\mathord{\uparrow} x : x\in X\}$
. Define
![]() $\mathcal S_c(X)=\{\overline{{\{x\}}} : x\in X\}$
and
$\mathcal S_c(X)=\{\overline{{\{x\}}} : x\in X\}$
and
![]() $\mathcal D_c(X)=\{\overline{D} : D\in \mathcal D(X)\}$
.
$\mathcal D_c(X)=\{\overline{D} : D\in \mathcal D(X)\}$
.
Remark 1. It is straightforward to verify the following.
Let X be a topological space and
![]() $A, B\subseteq X$
. Then,
$A, B\subseteq X$
. Then,
-
(1)
 $\overline{A}=\overline{B}$
if and only if for any
$\overline{A}=\overline{B}$
if and only if for any
 $U\in \mathcal O(X)$
,
$U\in \mathcal O(X)$
,
 $A\cap U\neq \emptyset$
iff
$A\cap U\neq \emptyset$
iff
 $B\cap U\neq\emptyset$
.
$B\cap U\neq\emptyset$
. -
(2) If
 $\tau_1, \tau_2$
are two topologies on the set X and
$\tau_1, \tau_2$
are two topologies on the set X and
 $\tau_1\subseteq \tau_2$
, then
$\tau_1\subseteq \tau_2$
, then
 ${\rm cl}_{\tau_2}A={\rm cl}_{\tau_2}B$
implies
${\rm cl}_{\tau_2}A={\rm cl}_{\tau_2}B$
implies
 ${\rm cl}_{\tau_1}A={\rm cl}_{\tau_1}B$
.
${\rm cl}_{\tau_1}A={\rm cl}_{\tau_1}B$
.
For a
![]() $T_0$
space X and a nonempty subset A of X, A is irreducible if for any
$T_0$
space X and a nonempty subset A of X, A is irreducible if for any
![]() $\{F_1, F_2\}\subseteq \mathcal C(X)$
,
$\{F_1, F_2\}\subseteq \mathcal C(X)$
,
![]() $A \subseteq F_1\cup F_2$
implies
$A \subseteq F_1\cup F_2$
implies
![]() $A \subseteq F_1$
or
$A \subseteq F_1$
or
![]() $A \subseteq F_2$
. Denote by
$A \subseteq F_2$
. Denote by
![]() ${\mathsf{Irr}}(X)$
(resp.,
${\mathsf{Irr}}(X)$
(resp.,
![]() ${\mathsf{Irr}}_c(X)$
) the set of all irreducible (resp., irreducible closed) subsets of X. Clearly, every subset of X that is directed under
${\mathsf{Irr}}_c(X)$
) the set of all irreducible (resp., irreducible closed) subsets of X. Clearly, every subset of X that is directed under
![]() $\leq_X$
is irreducible.
$\leq_X$
is irreducible.
The following lemma is well-known and can be easily verified.
Lemma 2. If
![]() $f : X \longrightarrow Y$
is continuous and
$f : X \longrightarrow Y$
is continuous and
![]() $A\in{\mathsf{Irr}} (X)$
, then
$A\in{\mathsf{Irr}} (X)$
, then
![]() $f(A)\in {\mathsf{Irr}} (Y)$
.
$f(A)\in {\mathsf{Irr}} (Y)$
.
For any
![]() $T_0$
space X, the lower Vietoris topology on
$T_0$
space X, the lower Vietoris topology on
![]() ${\mathsf{Irr}}_c(X)$
is the topology
${\mathsf{Irr}}_c(X)$
is the topology
![]() $\{\Diamond U : U\in \mathcal O(X)\}$
, where
$\{\Diamond U : U\in \mathcal O(X)\}$
, where
![]() $\Diamond U=\{A\in {\mathsf{Irr}}_c(X): A\cap U\neq\emptyset\}$
. The resulting space, denoted by
$\Diamond U=\{A\in {\mathsf{Irr}}_c(X): A\cap U\neq\emptyset\}$
. The resulting space, denoted by
![]() $X^s$
, with the canonical mapping
$X^s$
, with the canonical mapping
![]() $\eta_{X}: X\longrightarrow X^s, x\mapsto\overline {\{x\}}$
, is the sobrification of X (cf. Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003; Goubault 2013).
$\eta_{X}: X\longrightarrow X^s, x\mapsto\overline {\{x\}}$
, is the sobrification of X (cf. Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003; Goubault 2013).
Remark 3. For a
![]() $T_0$
space X,
$T_0$
space X,
![]() $\eta_{X}: X\longrightarrow X^s$
is a dense topological embedding (cf. Gierz et al. 2003; Goubault 2013; Schalk 1993).
$\eta_{X}: X\longrightarrow X^s$
is a dense topological embedding (cf. Gierz et al. 2003; Goubault 2013; Schalk 1993).
A subset A of a space X is called saturated if A equals the intersection of all open sets containing it (or equivalently, A is an upper set in the specialization order). We shall use
![]() $\mathsf{K}(X)$
to denote the set of all nonempty compact saturated subsets of X and endow it with the Smyth preorder
$\mathsf{K}(X)$
to denote the set of all nonempty compact saturated subsets of X and endow it with the Smyth preorder
![]() $\sqsubseteq$
, that is, for
$\sqsubseteq$
, that is, for
![]() $K_1,K_2\in \mathord{\mathsf{K}}(X)$
,
$K_1,K_2\in \mathord{\mathsf{K}}(X)$
,
![]() $K_1\sqsubseteq K_2$
iff
$K_1\sqsubseteq K_2$
iff
![]() $K_2\subseteq K_1$
. The poset
$K_2\subseteq K_1$
. The poset
![]() $(\mathord{\mathsf{K}}(X), \sqsubseteq)$
(shortly
$(\mathord{\mathsf{K}}(X), \sqsubseteq)$
(shortly
![]() $\mathsf{K}(X)$
) will be called the Smyth power poset of X. The upper Vietoris topology on
$\mathsf{K}(X)$
) will be called the Smyth power poset of X. The upper Vietoris topology on
![]() $\mathsf{K}(X)$
is the topology that has
$\mathsf{K}(X)$
is the topology that has
![]() $\{\Box U : U\in \mathcal O(X)\}$
as a base, where
$\{\Box U : U\in \mathcal O(X)\}$
as a base, where
![]() $\Box U=\{K\in \mathsf{K}(X) : K\subseteq U\}$
, and the resulting space is called the Smyth power space or upper space of X and is denoted by
$\Box U=\{K\in \mathsf{K}(X) : K\subseteq U\}$
, and the resulting space is called the Smyth power space or upper space of X and is denoted by
![]() $P_S(X)$
(cf. Heckmann Reference Heckmann1992; Schalk Reference Schalk1993). For
$P_S(X)$
(cf. Heckmann Reference Heckmann1992; Schalk Reference Schalk1993). For
![]() $A\subseteq X$
, define
$A\subseteq X$
, define
![]() $\Diamond A=\{K\in \mathsf{K}(X) : K\cap A\neq\emptyset\}$
.
$\Diamond A=\{K\in \mathsf{K}(X) : K\cap A\neq\emptyset\}$
.
Remark 4. Let X be a
![]() $T_0$
space.
$T_0$
space.
-
(1) The specialization order on
 $P_S(X)$
is the Smyth order (that is,
$P_S(X)$
is the Smyth order (that is,
 $\leq_{P_S(X)}=\sqsubseteq$
).
$\leq_{P_S(X)}=\sqsubseteq$
). -
(2) The canonical mapping
 $\xi_X: X\longrightarrow P_S(X)$
,
$\xi_X: X\longrightarrow P_S(X)$
,
 $x\mapsto\mathord{\uparrow} x$
, is an order and topological embedding Heckmann Reference Heckmann1992; Heckmann and Keimel Reference Heckmann and Keimel2013; Schalk Reference Schalk1993).
$x\mapsto\mathord{\uparrow} x$
, is an order and topological embedding Heckmann Reference Heckmann1992; Heckmann and Keimel Reference Heckmann and Keimel2013; Schalk Reference Schalk1993). -
(3) X is homeomorphic to the subspace
 $S^u(X)$
of
$S^u(X)$
of
 $P_S(X)$
by means of
$P_S(X)$
by means of
 $\xi_X$
.
$\xi_X$
.
Lemma 5. For a
![]() $T_0$
space X and
$T_0$
space X and
![]() $A\subseteq X$
,
$A\subseteq X$
,
![]() ${\rm cl}_{\mathcal O(P_S(X))}\xi_X(A)=\Diamond \overline{A}$
.
${\rm cl}_{\mathcal O(P_S(X))}\xi_X(A)=\Diamond \overline{A}$
.
Proof. Clearly,
![]() $\Diamond \overline{A}=\mathsf{K}(X)\setminus \Box (X\setminus \overline{A})$
is closed in
$\Diamond \overline{A}=\mathsf{K}(X)\setminus \Box (X\setminus \overline{A})$
is closed in
![]() $P_S(X),$
and hence,
$P_S(X),$
and hence,
![]() ${\rm cl}_{\mathcal O(P_S(X))}\xi_X(A)\subseteq\Diamond \overline{A}$
. Since
${\rm cl}_{\mathcal O(P_S(X))}\xi_X(A)\subseteq\Diamond \overline{A}$
. Since
![]() $\{\Diamond C : C\in \mathcal C(X)\}$
is a (closed) base of
$\{\Diamond C : C\in \mathcal C(X)\}$
is a (closed) base of
![]() $P_S(X)$
, there is a family
$P_S(X)$
, there is a family
![]() $\{C_i : i\in I\}\subseteq \mathcal C(X)$
such that
$\{C_i : i\in I\}\subseteq \mathcal C(X)$
such that
![]() ${\rm cl}_{\mathcal O(P_S(X))}\xi_X(A)=\bigcap_{i\in I} \Diamond C_i$
. Then for each
${\rm cl}_{\mathcal O(P_S(X))}\xi_X(A)=\bigcap_{i\in I} \Diamond C_i$
. Then for each
![]() $i\in I$
,
$i\in I$
,
![]() $\xi_X(A)\subseteq \Diamond C_i$
, and consequently,
$\xi_X(A)\subseteq \Diamond C_i$
, and consequently,
![]() $\mathord{\uparrow} a\cap C_i\neq \emptyset$
for each
$\mathord{\uparrow} a\cap C_i\neq \emptyset$
for each
![]() $a\in A$
; whence, for each
$a\in A$
; whence, for each
![]() $a\in A$
,
$a\in A$
,
![]() $a\in C_i$
as
$a\in C_i$
as
![]() $C_i=\mathord{\downarrow} C_i$
. It follow that
$C_i=\mathord{\downarrow} C_i$
. It follow that
![]() $\overline{A}\subseteq C_i$
for each
$\overline{A}\subseteq C_i$
for each
![]() $i\in I,$
and hence,
$i\in I,$
and hence,
![]() $\Diamond \overline{A}\subseteq \bigcap_{i\in I}\Diamond C_i={\rm cl}_{\mathcal O(P_S(X))}\xi_X(A)$
. Thus,
$\Diamond \overline{A}\subseteq \bigcap_{i\in I}\Diamond C_i={\rm cl}_{\mathcal O(P_S(X))}\xi_X(A)$
. Thus,
![]() ${\rm cl}_{\mathcal O(P_S(X))}\xi_X(A)=\Diamond \overline{A}$
.
${\rm cl}_{\mathcal O(P_S(X))}\xi_X(A)=\Diamond \overline{A}$
.
Proposition 6.
(Xu Reference Xu2021, Lemma 2.19)
![]() $P_S : \mathbf{Top}_0 \longrightarrow \mathbf{Top}_0$
is a covariant functor, where for any
$P_S : \mathbf{Top}_0 \longrightarrow \mathbf{Top}_0$
is a covariant functor, where for any
![]() $f : X \longrightarrow Y$
in
$f : X \longrightarrow Y$
in
![]() $\mathbf{Top}_0$
,
$\mathbf{Top}_0$
,
![]() $P_S(f) : P_S(X) \longrightarrow P_S(Y)$
is defined by
$P_S(f) : P_S(X) \longrightarrow P_S(Y)$
is defined by
![]() $P_S(f)(K)=\uparrow f(K)$
for all
$P_S(f)(K)=\uparrow f(K)$
for all
![]() $ K\in\mathsf{K}(X)$
.
$ K\in\mathsf{K}(X)$
.
Corollary 7. Let X and Y be two
![]() $T_0$
spaces. If Y is a retract of X, then
$T_0$
spaces. If Y is a retract of X, then
![]() $P_S(Y)$
is a retract of
$P_S(Y)$
is a retract of
![]() $P_S(X)$
.
$P_S(X)$
.
For a nonempty subset C of a
![]() $T_0$
space X, it is easy to see that C is compact iff
$T_0$
space X, it is easy to see that C is compact iff
![]() $\mathord{\uparrow} C\in \mathord{\mathsf{K}} (X)$
. Furthermore, we have the following useful result (see, e.g., Erné Reference Erné2009, pp. 2068).
$\mathord{\uparrow} C\in \mathord{\mathsf{K}} (X)$
. Furthermore, we have the following useful result (see, e.g., Erné Reference Erné2009, pp. 2068).
Lemma 8. Let X be a
![]() $T_0$
space and
$T_0$
space and
![]() $C\in \mathord{\mathsf{K}} (X)$
. Then,
$C\in \mathord{\mathsf{K}} (X)$
. Then,
![]() $C=\mathord{\uparrow} \mathrm{min}(C)$
and
$C=\mathord{\uparrow} \mathrm{min}(C)$
and
![]() $\mathrm{min}(C)$
is compact.
$\mathrm{min}(C)$
is compact.
Lemma 9. Let X be a
![]() $T_0$
space. For any nonempty family
$T_0$
space. For any nonempty family
![]() $\{K_i : i\in I\}\subseteq \mathord{\mathsf{K}} (X)$
,
$\{K_i : i\in I\}\subseteq \mathord{\mathsf{K}} (X)$
,
![]() $\bigvee_{i\in I} K_i$
exists in
$\bigvee_{i\in I} K_i$
exists in
![]() $\mathord{\mathsf{K}} (X)$
iff
$\mathord{\mathsf{K}} (X)$
iff
![]() $\bigcap_{i\in I} K_i\in \mathord{\mathsf{K}} (X)$
. In this case,
$\bigcap_{i\in I} K_i\in \mathord{\mathsf{K}} (X)$
. In this case,
![]() $\bigvee_{i\in I} K_i=\bigcap_{i\in I} K_i$
.
$\bigvee_{i\in I} K_i=\bigcap_{i\in I} K_i$
.
Proof. Suppose that
![]() $\{K_i : i\in I\}\subseteq \mathord{\mathsf{K}} (X)$
is a nonempty family and
$\{K_i : i\in I\}\subseteq \mathord{\mathsf{K}} (X)$
is a nonempty family and
![]() $\bigvee_{i\in I} K_i$
exists in
$\bigvee_{i\in I} K_i$
exists in
![]() $\mathord{\mathsf{K}} (X)$
. Let
$\mathord{\mathsf{K}} (X)$
. Let
![]() $K=\bigvee_{i\in I} K_i$
. Then,
$K=\bigvee_{i\in I} K_i$
. Then,
![]() $K\subseteq K_i$
for all
$K\subseteq K_i$
for all
![]() $i\in I$
, and hence,
$i\in I$
, and hence,
![]() $K\subseteq \bigcap_{i\in I} K_i$
. For any
$K\subseteq \bigcap_{i\in I} K_i$
. For any
![]() $x\in \bigcap_{i\in I} K_i$
,
$x\in \bigcap_{i\in I} K_i$
,
![]() $\mathord{\uparrow} x$
is a upper bound of
$\mathord{\uparrow} x$
is a upper bound of
![]() $\{K_i : i\in I\}\subseteq \mathord{\mathsf{K}} (X)$
, whence
$\{K_i : i\in I\}\subseteq \mathord{\mathsf{K}} (X)$
, whence
![]() $K\sqsubseteq \mathord{\uparrow} x$
or, equivalently,
$K\sqsubseteq \mathord{\uparrow} x$
or, equivalently,
![]() $\mathord{\uparrow} x \subseteq K$
. Therefore,
$\mathord{\uparrow} x \subseteq K$
. Therefore,
![]() $\bigcap_{i\in I} K_i\subseteq K$
. Thus,
$\bigcap_{i\in I} K_i\subseteq K$
. Thus,
![]() $\bigcap_{i\in I} K_i=K\in \mathord{\mathsf{K}} (X)$
.
$\bigcap_{i\in I} K_i=K\in \mathord{\mathsf{K}} (X)$
.
Conversely, if
![]() $\bigcap_{i\in I} K_i\in \mathord{\mathsf{K}} (X)$
, then
$\bigcap_{i\in I} K_i\in \mathord{\mathsf{K}} (X)$
, then
![]() $\bigcap_{i\in I} K_i$
is an upper bound of
$\bigcap_{i\in I} K_i$
is an upper bound of
![]() $\{K_i : i\in I\}$
in
$\{K_i : i\in I\}$
in
![]() $\mathord{\mathsf{K}} (X)$
. Let
$\mathord{\mathsf{K}} (X)$
. Let
![]() $G\in \mathord{\mathsf{K}} (X)$
be another upper bound of
$G\in \mathord{\mathsf{K}} (X)$
be another upper bound of
![]() $\{K_i : i\in I\}$
, then
$\{K_i : i\in I\}$
, then
![]() $G\subseteq K_i$
for all
$G\subseteq K_i$
for all
![]() $i\in I$
, and hence,
$i\in I$
, and hence,
![]() $G\subseteq \bigcap_{i\in I} K_i$
, that is,
$G\subseteq \bigcap_{i\in I} K_i$
, that is,
![]() $\bigcap_{i\in I} K_i\sqsubseteq G$
, proving that
$\bigcap_{i\in I} K_i\sqsubseteq G$
, proving that
![]() $\bigvee_{i\in I} K_i=\bigcap_{i\in I} K_i$
.
$\bigvee_{i\in I} K_i=\bigcap_{i\in I} K_i$
.
Similarly, we have the following.
Lemma 10. Let P be a poset. For any nonempty family
![]() $\{\mathord{\uparrow} F_i : i\in I\}\subseteq \mathbf{Fin}~\!P$
,
$\{\mathord{\uparrow} F_i : i\in I\}\subseteq \mathbf{Fin}~\!P$
,
![]() $\bigvee_{i\in I} \mathord{\uparrow} F_i$
exists in
$\bigvee_{i\in I} \mathord{\uparrow} F_i$
exists in
![]() $\mathbf{Fin}~\!P$
iff
$\mathbf{Fin}~\!P$
iff
![]() $\bigcap_{i\in I} \mathord{\uparrow} F_i\in \mathbf{Fin}~\!P$
. In this case
$\bigcap_{i\in I} \mathord{\uparrow} F_i\in \mathbf{Fin}~\!P$
. In this case
![]() $\bigvee_{i\in I} \mathord{\uparrow} F_i=\bigcap_{i\in I} \mathord{\uparrow} F_i$
.
$\bigvee_{i\in I} \mathord{\uparrow} F_i=\bigcap_{i\in I} \mathord{\uparrow} F_i$
.
Lemma 11. (Schalk Reference Schalk1993, Proposition 7.21) Let X be a
![]() $T_0$
space.
$T_0$
space.
-
(1) If
 $\mathcal K\in\mathord{\mathsf{K}}(P_S(X))$
, then
$\mathcal K\in\mathord{\mathsf{K}}(P_S(X))$
, then
 $\bigcup \mathcal K\in\mathord{\mathsf{K}}(X)$
.
$\bigcup \mathcal K\in\mathord{\mathsf{K}}(X)$
. -
(2) The mapping
 $\bigcup : P_S(P_S(X)) \longrightarrow P_S(X)$
,
$\bigcup : P_S(P_S(X)) \longrightarrow P_S(X)$
,
 $\mathcal K\mapsto \bigcup \mathcal K$
, is continuous.
$\mathcal K\mapsto \bigcup \mathcal K$
, is continuous.
3. Scott Topology and Continuous Domains
For a poset P, a subset U of P is Scott open if (i)
![]() $U=\mathord{\uparrow}U$
and (ii) for any directed subset D with
$U=\mathord{\uparrow}U$
and (ii) for any directed subset D with
![]() $\vee D$
existing,
$\vee D$
existing,
![]() $\vee D\in U$
implies
$\vee D\in U$
implies
![]() $D\cap U\neq\emptyset$
. All Scott open subsets of P form a topology, called the Scott topology on P and denoted by
$D\cap U\neq\emptyset$
. All Scott open subsets of P form a topology, called the Scott topology on P and denoted by
![]() $\sigma(P)$
. The space
$\sigma(P)$
. The space
![]() $\Sigma~\!\! P=(P,\sigma(P))$
is called the Scott space of P. For the chain
$\Sigma~\!\! P=(P,\sigma(P))$
is called the Scott space of P. For the chain
![]() $2=\{0, 1\}$
(with the order
$2=\{0, 1\}$
(with the order
![]() $0<1$
), we have
$0<1$
), we have
![]() $\sigma(2)=\{\emptyset, \{1\}, \{0,1\}\}$
. The space
$\sigma(2)=\{\emptyset, \{1\}, \{0,1\}\}$
. The space
![]() $\Sigma~\!\!2$
is well-known under the name of Sierpiński space. The upper topology on P, generated by the complements of the principal ideals of P, is denoted by
$\Sigma~\!\!2$
is well-known under the name of Sierpiński space. The upper topology on P, generated by the complements of the principal ideals of P, is denoted by
![]() $\upsilon (P)$
. The upper sets of P form the (upper) Alexandroff topology
$\upsilon (P)$
. The upper sets of P form the (upper) Alexandroff topology
![]() $\alpha (P)$
.
$\alpha (P)$
.
Lemma 12. (Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Proposition II-2.1) For posets P, Q, and
![]() $f : P \longrightarrow Q$
, the following two conditions are equivalent:
$f : P \longrightarrow Q$
, the following two conditions are equivalent:
-
(1)
 $f : \Sigma~\!\! P \longrightarrow \Sigma~\!\! Q$
is continuous.
$f : \Sigma~\!\! P \longrightarrow \Sigma~\!\! Q$
is continuous. -
(2) For each
 $D\in \mathcal D(P)$
for which
$D\in \mathcal D(P)$
for which
 $\vee D$
exists in P,
$\vee D$
exists in P,
 $\vee f(D)$
exists in Q and
$\vee f(D)$
exists in Q and
 $f(\vee D)=\vee f(D)$
.
$f(\vee D)=\vee f(D)$
.
A mapping
![]() $f : P \longrightarrow Q$
satisfying the equivalent conditions (1) and (2) of Lemma 12 is said to be Scott continuous. Let
$f : P \longrightarrow Q$
satisfying the equivalent conditions (1) and (2) of Lemma 12 is said to be Scott continuous. Let
![]() $\mathbf{DCPO}$
denote the category of all dcpos and Scott continuous mappings.
$\mathbf{DCPO}$
denote the category of all dcpos and Scott continuous mappings.
For a dcpo P and
![]() $A, B\subseteq P$
, we say A is way below B, written
$A, B\subseteq P$
, we say A is way below B, written
![]() $A\ll B$
, if for each
$A\ll B$
, if for each
![]() $D\in \mathcal D(P)$
,
$D\in \mathcal D(P)$
,
![]() $\vee D\in \mathord{\uparrow} B$
implies
$\vee D\in \mathord{\uparrow} B$
implies
![]() $D\cap \mathord{\uparrow} A\neq \emptyset$
. For
$D\cap \mathord{\uparrow} A\neq \emptyset$
. For
![]() $B=\{x\}$
, a singleton,
$B=\{x\}$
, a singleton,
![]() $A\ll B$
is written
$A\ll B$
is written
![]() $A\ll x$
for short. For
$A\ll x$
for short. For
![]() $x\in P$
, let
$x\in P$
, let
![]() $w(x)=\{F\in P^{(<\omega)} : F\ll x\}$
,
$w(x)=\{F\in P^{(<\omega)} : F\ll x\}$
,
![]() $\Downarrow x = \{u\in P : u\ll x\}$
and
$\Downarrow x = \{u\in P : u\ll x\}$
and
![]() $K(P)=\{k\in P : k\ll k\}$
. Points in K(P) are called compact elements of P.
$K(P)=\{k\in P : k\ll k\}$
. Points in K(P) are called compact elements of P.
For the following definition and related conceptions, please refer to Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003).
Definition 13. Let P be a dcpo and X a
![]() $T_0$
space.
$T_0$
space.
-
(1) P is called a continuous domain, if for each
 $x\in P$
,
$x\in P$
,
 $\Downarrow x$
is directed and
$\Downarrow x$
is directed and
 $x=\vee\Downarrow x$
. When a complete lattice L is continuous, we call L a continuous lattice.
$x=\vee\Downarrow x$
. When a complete lattice L is continuous, we call L a continuous lattice. -
(2) P is called an algebraic domain, if for each
 $x\in P$
,
$x\in P$
,
 $\{k\in K(P) : k\leq x\}$
is directed and
$\{k\in K(P) : k\leq x\}$
is directed and
 $x=\vee \{k\in K(P) : k\leq x\}$
. When a complete lattice L is algebraic, we call L an algebraic lattice.
$x=\vee \{k\in K(P) : k\leq x\}$
. When a complete lattice L is algebraic, we call L an algebraic lattice. -
(3) P is called a quasicontinuous domain, if for each
 $x\in P$
,
$x\in P$
,
 $\{\mathord{\uparrow} F : F\in w(x)\}$
is filtered and
$\{\mathord{\uparrow} F : F\in w(x)\}$
is filtered and
 $\mathord{\uparrow} x=\bigcap\{\mathord{\uparrow} F : F\in w(x)\}$
.
$\mathord{\uparrow} x=\bigcap\{\mathord{\uparrow} F : F\in w(x)\}$
. -
(4) X is called core-compact if
 $\mathcal O(X)$
is a continuous lattice.
$\mathcal O(X)$
is a continuous lattice.
A topological space X is said to be a Noetherian space if every open subset is compact (see Goubault 2013, Definition 9.7.1) or, equivalently, if
![]() $U\ll U$
in
$U\ll U$
in
![]() $\mathcal O(X)$
for any open subset U of X. Clearly, if X is a Noetherian space, then
$\mathcal O(X)$
for any open subset U of X. Clearly, if X is a Noetherian space, then
![]() $\mathcal O(X)$
is an algebraic lattice.
$\mathcal O(X)$
is an algebraic lattice.
It is well-known that if a topological space X is locally compact, then it is core-compact (see, e.g., Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Examples I-1.7). (1978, Section 7) (see also Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Exercise V-5.25), Hofmann and Lawson gave a second-countable core-compact
![]() $T_0$
space X in which every compact subset of X has empty interior, and hence, it is not locally compact.
$T_0$
space X in which every compact subset of X has empty interior, and hence, it is not locally compact.
The following result is well-known (see Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003).
Theorem 15. Let P be a dcpo.
-
(1) If P is algebraic, then it is continuous.
-
(2) If P is continuous, then it is quasicontinuous.
-
(3) P is continuous iff
 $\Sigma ~\!\! P$
is a c-space.
$\Sigma ~\!\! P$
is a c-space.
-
(4) P is quasicontinuous iff
 $\Sigma ~\!\! P$
is locally hypercompact.
$\Sigma ~\!\! P$
is locally hypercompact.
4. d-spaces, Well-Filtered Spaces, and Sober Spaces
A
![]() $T_0$
space X is called a d-space (or monotone convergence space) if X (with the specialization order) is a dcpo and
$T_0$
space X is called a d-space (or monotone convergence space) if X (with the specialization order) is a dcpo and
![]() $\mathcal O(X) \subseteq \sigma(X)$
(cf. Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003; Wyler Reference Wyler1981).
$\mathcal O(X) \subseteq \sigma(X)$
(cf. Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003; Wyler Reference Wyler1981).
It is easy to verify the following result (cf. Gierz et al. 2003; Xu et al. 2020b).
Proposition 16. For a
![]() $T_0$
space X, the following conditions are equivalent:
$T_0$
space X, the following conditions are equivalent:
-
(1) X is a d-space.
-
(2)
 $\mathcal D_c(X)=\mathcal S_c(X)$
.
$\mathcal D_c(X)=\mathcal S_c(X)$
. -
(3) X is a dcpo, and
 $\overline{D}=\overline{\{\vee D\}}$
for any
$\overline{D}=\overline{\{\vee D\}}$
for any
 $D\in \mathcal D(X)$
.
$D\in \mathcal D(X)$
. -
(4) For any
 $D\in \mathcal D(X)$
and
$D\in \mathcal D(X)$
and
 $U\in \mathcal O(X)$
,
$U\in \mathcal O(X)$
,
 $\bigcap\limits\limits_{d\in D}\mathord{\uparrow} d\subseteq U$
implies
$\bigcap\limits\limits_{d\in D}\mathord{\uparrow} d\subseteq U$
implies
 $\mathord{\uparrow} d \subseteq U$
(i.e.,
$\mathord{\uparrow} d \subseteq U$
(i.e.,
 $d\in U$
) for some
$d\in U$
) for some
 $d\in D$
.
$d\in D$
.
Lemma 17. (Xu et al. 2021d, Lemma 2.1) Let X be a d-space. Then for any nonempty closed subset A of X,
![]() $A=\mathord{\downarrow} \mathrm{max}(A)$
, and hence,
$A=\mathord{\downarrow} \mathrm{max}(A)$
, and hence,
![]() $\mathrm{max}(A)\neq\emptyset$
.
$\mathrm{max}(A)\neq\emptyset$
.
A topological space X is called sober, if for any
![]() $F\in{\mathsf{Irr}}_c(X)$
, there is a unique point
$F\in{\mathsf{Irr}}_c(X)$
, there is a unique point
![]() $a\in X$
such that
$a\in X$
such that
![]() $F=\overline{\{a\}}$
. Hausdorff spaces are always sober (see, e.g., Goubault 2013, Proposition 8.2.12), and sober spaces are always
$F=\overline{\{a\}}$
. Hausdorff spaces are always sober (see, e.g., Goubault 2013, Proposition 8.2.12), and sober spaces are always
![]() $T_0$
since
$T_0$
since
![]() $\overline{\{x\}}=\overline{\{y\}}$
always implies
$\overline{\{x\}}=\overline{\{y\}}$
always implies
![]() $x=y$
. The Sierpinski space
$x=y$
. The Sierpinski space
![]() $\Sigma~\!\!2$
is sober but not
$\Sigma~\!\!2$
is sober but not
![]() $T_1,$
and an infinite set with the co-finite topology is
$T_1,$
and an infinite set with the co-finite topology is
![]() $T_1$
but not sober (see Example 57).
$T_1$
but not sober (see Example 57).
The following conclusion is well-known (see, e.g., Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Reference Gierz, Lawson and Stralka1983; Heckmann Reference Heckmann1992).
Proposition 18. For a quasicontinuous domain P,
![]() $\Sigma ~\!\! P$
is sober.
$\Sigma ~\!\! P$
is sober.
For the sobriety of the Smyth power spaces, we have the following well-known result.
Theorem 19.
(Heckmann-Keimel-Schalk Theorem) (
Heckmann and Keimel Reference Heckmann and Keimel2013
, Theorem 3.13) (Schalk Reference Schalk1993, Lemma 7.20) For a
![]() $T_0$
space X, the following conditions are equivalent:
$T_0$
space X, the following conditions are equivalent:
-
(1) X is sober.
-
(2) For any
 $\mathcal A\in {\mathsf{Irr}}(P_S(X))$
and
$\mathcal A\in {\mathsf{Irr}}(P_S(X))$
and
 $U\in \mathcal O(X)$
,
$U\in \mathcal O(X)$
,
 $\bigcap\mathcal A\subseteq U$
implies
$\bigcap\mathcal A\subseteq U$
implies
 $K \subseteq U$
for some
$K \subseteq U$
for some
 $K\in \mathcal A$
.
$K\in \mathcal A$
. -
(3)
 $P_S(X)$
is sober.
$P_S(X)$
is sober.
A
![]() $T_0$
space X is called well-filtered if for any filtered family
$T_0$
space X is called well-filtered if for any filtered family
![]() $\mathcal{K}\subseteq \mathord{\mathsf{K}}(X)$
and open set U,
$\mathcal{K}\subseteq \mathord{\mathsf{K}}(X)$
and open set U,
![]() $\bigcap\mathcal{K}{\subseteq} U$
implies
$\bigcap\mathcal{K}{\subseteq} U$
implies
![]() $K{\subseteq} U$
for some
$K{\subseteq} U$
for some
![]() $K{\in}\mathcal{K}$
. The full subcategory of
$K{\in}\mathcal{K}$
. The full subcategory of
![]() $\mathbf{Top}_0$
of well-filtered spaces is denoted by
$\mathbf{Top}_0$
of well-filtered spaces is denoted by
![]() $\mathbf{Top}_w$
.
$\mathbf{Top}_w$
.
Remark 20. The following implications are well-known (which are irreversible) (cf. Gierz et al. 2003):
In Xu et al. (2020b), Xu et al. obtained the following equational characterization of well-filtered spaces.
Proposition 21.
(
Reference Xu, Shen, Xi and Zhao
Xu et al. 2020b
, Theorem 5.1) Let X be a
![]() $T_0$
space and
$T_0$
space and
![]() $\mathbf{K}$
a full subcategory of
$\mathbf{K}$
a full subcategory of
![]() $\mathbf{Top}_0$
containing
$\mathbf{Top}_0$
containing
![]() $\mathbf{Sob}$
. Then, the following conditions are equivalent:
$\mathbf{Sob}$
. Then, the following conditions are equivalent:
-
(1) X is well-filtered.
-
(2) For every continuous mapping
 $f : X\longrightarrow Y$
from X to a
$f : X\longrightarrow Y$
from X to a
 $T_0$
space Y and a filtered family
$T_0$
space Y and a filtered family
 $\mathcal K\subseteq \mathord{\mathsf{K}}(X)$
,
$\mathcal K\subseteq \mathord{\mathsf{K}}(X)$
,
 $\mathord{\uparrow} f\left(\bigcap\mathcal K\right)=\bigcap\limits_{K\in\mathcal K}\mathord{\uparrow} f(K)$
.
$\mathord{\uparrow} f\left(\bigcap\mathcal K\right)=\bigcap\limits_{K\in\mathcal K}\mathord{\uparrow} f(K)$
. -
(3) For every continuous mapping
 $f : X\longrightarrow Y$
from X to a well-filtered space Y and a filtered family
$f : X\longrightarrow Y$
from X to a well-filtered space Y and a filtered family
 $\mathcal K\subseteq \mathord{\mathsf{K}}(X)$
,
$\mathcal K\subseteq \mathord{\mathsf{K}}(X)$
,
 $\mathord{\uparrow} f\left(\bigcap\mathcal K\right)=\bigcap\limits_{K\in\mathcal K}\mathord{\uparrow} f(K)$
.
$\mathord{\uparrow} f\left(\bigcap\mathcal K\right)=\bigcap\limits_{K\in\mathcal K}\mathord{\uparrow} f(K)$
. -
(4) For every continuous mapping
 $f : X\longrightarrow Y$
from X to a sober space Y and a filtered family
$f : X\longrightarrow Y$
from X to a sober space Y and a filtered family
 $\mathcal K\subseteq \mathord{\mathsf{K}}(X)$
,
$\mathcal K\subseteq \mathord{\mathsf{K}}(X)$
,
 $\mathord{\uparrow} f\left(\bigcap\mathcal K\right)=\bigcap\limits_{K\in\mathcal K}\mathord{\uparrow} f(K)$
.
$\mathord{\uparrow} f\left(\bigcap\mathcal K\right)=\bigcap\limits_{K\in\mathcal K}\mathord{\uparrow} f(K)$
.
In Xi et al. (2017), Hofmann et al. (1978), and Kou (Reference Kou2001), the following two useful results were given.
Proposition 22. (Xi et al. 2017, Corollary 3.2) If a dcpo P endowed with the Lawson topology is compact (in particular, P is a complete lattice), then
![]() $\Sigma P$
is well-filtered.
$\Sigma P$
is well-filtered.
Theorem 23. (Hofmann et al. 1978, Corollary 4.6) (
Kou Reference Kou2001
, Theorem 2.3) For a
![]() $T_0$
space X, the following conditions are equivalent:
$T_0$
space X, the following conditions are equivalent:
-
(1) X locally compact and sober.
-
(2) X is locally compact and well-filtered.
-
(3) X is core-compact and sober.
For the well-filteredness of topological spaces, a similar result to Theorem 19 was proved in Xu et al. (2021b) (see also Xu et al. 2020b).
Theorem 24. (Xu et al. 2020b, Theorem 5.3) (Xu et al. 2021b, Theorem 4) For a
![]() $T_0$
space, the following conditions are equivalent:
$T_0$
space, the following conditions are equivalent:
-
(1) X is well-filtered.
-
(2)
 $P_S(X)$
is a d-space.
$P_S(X)$
is a d-space.
-
(3)
 $P_S(X)$
is well-filtered.
$P_S(X)$
is well-filtered.
Corollary 25. For a well-filtered space (especially, a sober space) X,
![]() $\mathsf{K}(X)$
(with the Smyth order) is a dcpo and the upper Vietoris topology is coarser than the Scott topology on
$\mathsf{K}(X)$
(with the Smyth order) is a dcpo and the upper Vietoris topology is coarser than the Scott topology on
![]() $\mathsf{K}(X)$
.
$\mathsf{K}(X)$
.
By Theorem 24 and Corollary 25, we know that for a
![]() $T_0$
space X, if
$T_0$
space X, if
![]() $P_S(X)$
is a d-space (equivalently, X is a well-filtered space), then
$P_S(X)$
is a d-space (equivalently, X is a well-filtered space), then
![]() $\Sigma~\!\!\mathsf{K}(X)$
is a d-space. Example 68 below shows that
$\Sigma~\!\!\mathsf{K}(X)$
is a d-space. Example 68 below shows that
![]() $\Sigma~\!\!\mathsf{K}(X)$
is a sober space does not imply that X is well-filtered (i.e.,
$\Sigma~\!\!\mathsf{K}(X)$
is a sober space does not imply that X is well-filtered (i.e.,
![]() $P_S(X)$
is a d-space) in general.
$P_S(X)$
is a d-space) in general.
The following example shows that there is a
![]() $T_0$
space X such that
$T_0$
space X such that
![]() $\mathsf{K}(X)$
(with the Smyth order) is a dcpo but X is not well-filtered.
$\mathsf{K}(X)$
(with the Smyth order) is a dcpo but X is not well-filtered.
Example 26. (Johnstone’s dcpo adding a top element) Let
![]() $\mathbb{J}=\mathbb{N}\times (\mathbb{N}\cup \{\infty\})$
with ordering defined by
$\mathbb{J}=\mathbb{N}\times (\mathbb{N}\cup \{\infty\})$
with ordering defined by
![]() $(j, k)\leq (m, n)$
iff
$(j, k)\leq (m, n)$
iff
![]() $j = m$
and
$j = m$
and
![]() $k \leq n$
, or
$k \leq n$
, or
![]() $n =\infty$
and
$n =\infty$
and
![]() $k\leq m$
.
$k\leq m$
.
![]() $\mathbb{J}$
is a well-known dcpo constructed by Johnstone (Reference Johnstone1981) (see Fig. 1).
$\mathbb{J}$
is a well-known dcpo constructed by Johnstone (Reference Johnstone1981) (see Fig. 1).

Figure 1. Johnstone’s dcpo
![]() $\mathbb{J}$
.
$\mathbb{J}$
.
The set
![]() $\mathbb{J}_{max}=\{(n, \infty) : n\in\mathbb N \}$
is the set of all maximal elements of
$\mathbb{J}_{max}=\{(n, \infty) : n\in\mathbb N \}$
is the set of all maximal elements of
![]() $\mathbb{J}$
. Adding top
$\mathbb{J}$
. Adding top
![]() $\top$
to
$\top$
to
![]() $\mathbb{J}$
yields a dcpo
$\mathbb{J}$
yields a dcpo
![]() $\mathbb{J}_{\top}=\mathbb{J}\cup \{\top\}$
(
$\mathbb{J}_{\top}=\mathbb{J}\cup \{\top\}$
(
![]() $x\leq \top$
for any
$x\leq \top$
for any
![]() $x\in \mathbb{J}$
). Then,
$x\in \mathbb{J}$
). Then,
![]() $\top$
is the largest element of
$\top$
is the largest element of
![]() $\mathbb{J}_{\top}$
and
$\mathbb{J}_{\top}$
and
![]() $\{\top\}\in \sigma (\mathbb{J}_{\top})$
. The following three conclusions about
$\{\top\}\in \sigma (\mathbb{J}_{\top})$
. The following three conclusions about
![]() $\Sigma~\!\!\mathbb{J}$
are known (see, e.g., Lu et al. 2017, Example 3.1 and Miao et al. Reference Miao, Li and Zhao2021, Lemma 3.1):
$\Sigma~\!\!\mathbb{J}$
are known (see, e.g., Lu et al. 2017, Example 3.1 and Miao et al. Reference Miao, Li and Zhao2021, Lemma 3.1):
-
(i)
 ${\mathsf{Irr}}_c (\Sigma~\!\!\mathbb{J})=\{\overline{\{x\}}=\mathord{\downarrow}_{\mathbb{J}} x : x\in \mathbb{J}\}\cup \{\mathbb{J}\}$
.
${\mathsf{Irr}}_c (\Sigma~\!\!\mathbb{J})=\{\overline{\{x\}}=\mathord{\downarrow}_{\mathbb{J}} x : x\in \mathbb{J}\}\cup \{\mathbb{J}\}$
. -
(ii)
 $\mathsf{K}(\Sigma~\!\!\mathbb{J})=(2^{\mathbb{J}_{max}} \setminus \{\emptyset\})\bigcup \mathbf{Fin}~\!\mathbb{J}$
.
$\mathsf{K}(\Sigma~\!\!\mathbb{J})=(2^{\mathbb{J}_{max}} \setminus \{\emptyset\})\bigcup \mathbf{Fin}~\!\mathbb{J}$
. -
(iii)
 $\Sigma~\!\!\mathbb{J}$
is not well-filtered.
$\Sigma~\!\!\mathbb{J}$
is not well-filtered.
Hence, we have
1.
![]() ${\mathsf{Irr}}_c (\Sigma~\!\!\mathbb{J}_\top)=\{\overline{\{x\}}=\mathord{\downarrow}_{\mathbb{J}_{\top}} x : x\in \mathbb{J}_\top\}\cup \{\mathbb{J}\}$
by (i).
${\mathsf{Irr}}_c (\Sigma~\!\!\mathbb{J}_\top)=\{\overline{\{x\}}=\mathord{\downarrow}_{\mathbb{J}_{\top}} x : x\in \mathbb{J}_\top\}\cup \{\mathbb{J}\}$
by (i).
2.
![]() $\mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)=\{\mathord{\uparrow}_{\mathbb{J}_{\top}} G : G \mbox{~is nonempty and~} G\subseteq \mathbb{J}_{max}\cup\{\top\}\}\bigcup \mathbf{Fin}~\!\mathbb{J}_\top$
by (ii).
$\mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)=\{\mathord{\uparrow}_{\mathbb{J}_{\top}} G : G \mbox{~is nonempty and~} G\subseteq \mathbb{J}_{max}\cup\{\top\}\}\bigcup \mathbf{Fin}~\!\mathbb{J}_\top$
by (ii).
3.
![]() $\mathsf{K}(\Sigma~\!\!\mathbb{J})$
is not a dcpo.
$\mathsf{K}(\Sigma~\!\!\mathbb{J})$
is not a dcpo.
Let
![]() $\mathcal G=\{\mathbb{J}_{max}\setminus F : F\in (\mathbb{J}_{max})^{(<\omega)}\}$
. Then by (ii),
$\mathcal G=\{\mathbb{J}_{max}\setminus F : F\in (\mathbb{J}_{max})^{(<\omega)}\}$
. Then by (ii),
![]() $\mathcal G\subseteq \mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
is a filtered family and
$\mathcal G\subseteq \mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
is a filtered family and
![]() $\bigcap\mathcal{G}=\bigcap_{F\in (\mathbb{J}_{max})^{(<\omega)}} (\mathbb{J}_{max}\setminus F)=\mathbb{J}_{max}\setminus \bigcup (\mathbb{J}_{max})^{(<\omega)}=\emptyset$
, whence by Lemma 9
$\bigcap\mathcal{G}=\bigcap_{F\in (\mathbb{J}_{max})^{(<\omega)}} (\mathbb{J}_{max}\setminus F)=\mathbb{J}_{max}\setminus \bigcup (\mathbb{J}_{max})^{(<\omega)}=\emptyset$
, whence by Lemma 9
![]() $\mathcal G$
has no least upper bound in
$\mathcal G$
has no least upper bound in
![]() $\mathsf{K}(X)$
. Thus
$\mathsf{K}(X)$
. Thus
![]() $\mathsf{K}(\Sigma~\!\!\mathbb{J})$
is not a dcpo.
$\mathsf{K}(\Sigma~\!\!\mathbb{J})$
is not a dcpo.
4.
![]() $\mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
is a dcpo.
$\mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
is a dcpo.
Suppose that
![]() $\{K_d : d\in D\}$
is directed in
$\{K_d : d\in D\}$
is directed in
![]() $\mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
(with the Smyth order). Then,
$\mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
(with the Smyth order). Then,
![]() $\top \in\bigcap_{d\in D}K_d,$
and hence,
$\top \in\bigcap_{d\in D}K_d,$
and hence,
![]() $\bigcap_{d\in D}K_d\neq\emptyset$
. Now we show that
$\bigcap_{d\in D}K_d\neq\emptyset$
. Now we show that
![]() $\bigcap_{d\in D}K_d\in \mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
. If
$\bigcap_{d\in D}K_d\in \mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
. If
![]() $\bigcap_{d\in D}K_d=\{\top\}$
, then obviously
$\bigcap_{d\in D}K_d=\{\top\}$
, then obviously
![]() $\bigcap_{d\in D}K_d\in \mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
. Now we assume
$\bigcap_{d\in D}K_d\in \mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
. Now we assume
![]() $\bigcap_{d\in D}K_d\neq \{\top\}$
and
$\bigcap_{d\in D}K_d\neq \{\top\}$
and
![]() $\{V_i : i\in I\}\subseteq \mathcal \sigma(\mathbb{J}_\top))$
is an open cover of
$\{V_i : i\in I\}\subseteq \mathcal \sigma(\mathbb{J}_\top))$
is an open cover of
![]() $\bigcap_{d\in D}K_d$
. For each
$\bigcap_{d\in D}K_d$
. For each
![]() $d\in D$
and
$d\in D$
and
![]() $i\in I$
, let
$i\in I$
, let
![]() $H_d=K_d\setminus \{\top\}$
and
$H_d=K_d\setminus \{\top\}$
and
![]() $U_i=V_i\setminus \{\top\}$
. Then,
$U_i=V_i\setminus \{\top\}$
. Then,
![]() $H_d\in \mathsf{K}(\Sigma~\!\!\mathbb{J})$
(
$H_d\in \mathsf{K}(\Sigma~\!\!\mathbb{J})$
(
![]() $d\in D$
),
$d\in D$
),
![]() $U_i\in \sigma(\mathbb{J})$
(
$U_i\in \sigma(\mathbb{J})$
(
![]() $i\in I$
) and
$i\in I$
) and
![]() $\emptyset\neq\bigcap_{d\in D}H_d=\bigcap_{d\in D}K_{d_0}\setminus \{\top\}\subseteq \bigcup_{i\in I}V_i\setminus \{\top\}=\bigcup_{i\in I}U_i$
. By Lu et al. (2017, Example 3.1), there is
$\emptyset\neq\bigcap_{d\in D}H_d=\bigcap_{d\in D}K_{d_0}\setminus \{\top\}\subseteq \bigcup_{i\in I}V_i\setminus \{\top\}=\bigcup_{i\in I}U_i$
. By Lu et al. (2017, Example 3.1), there is
![]() $d_0\in D$
such that
$d_0\in D$
such that
![]() $H_{d_0}\in \bigcup_{i\in I}U_i$
, and consequently, there is
$H_{d_0}\in \bigcup_{i\in I}U_i$
, and consequently, there is
![]() $J\in I^{(<\omega)}$
such that
$J\in I^{(<\omega)}$
such that
![]() $H_d\subseteq \bigcup_{i\in J}U_i$
. It follows that
$H_d\subseteq \bigcup_{i\in J}U_i$
. It follows that
![]() $\bigcap_{d\in D}K_d\subseteq K_{d_0}\subseteq \bigcup_{i\in J}V_i$
. Thus
$\bigcap_{d\in D}K_d\subseteq K_{d_0}\subseteq \bigcup_{i\in J}V_i$
. Thus
![]() $,\bigcap_{d\in D}K_d\in \mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
. By Lemma 9,
$,\bigcap_{d\in D}K_d\in \mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
. By Lemma 9,
![]() $\mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
is a dcpo.
$\mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
is a dcpo.
5.
![]() $\Sigma~\!\!\mathbb{J}_\top$
is not well-filtered.
$\Sigma~\!\!\mathbb{J}_\top$
is not well-filtered.
Indeed, let
![]() $\mathcal K=\{\mathord{\uparrow}_{\mathbb{J}_\top} (\mathbb{J}_{max}\setminus F) : F\in (\mathbb{J}_{max})^{(<\omega)}\}$
. Then by (b),
$\mathcal K=\{\mathord{\uparrow}_{\mathbb{J}_\top} (\mathbb{J}_{max}\setminus F) : F\in (\mathbb{J}_{max})^{(<\omega)}\}$
. Then by (b),
![]() $\mathcal K\subseteq \mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
is a filtered family and
$\mathcal K\subseteq \mathsf{K}(\Sigma~\!\!\mathbb{J}_\top)$
is a filtered family and
![]() $\bigcap\mathcal{K}=\bigcap_{F\in (\mathbb{J}_{max})^{(<\omega)}} \mathord{\uparrow}_{\mathbb{J}_\top} (\mathbb{J}_{max}\setminus F)=\bigcap_{F\in (\mathbb{J}_{max})^{(<\omega)}} ((\mathbb{J}_{max}\setminus F)\cup\{\top\})=\{\top\}\cup(\mathbb{J}_{max}\setminus \bigcup (\mathbb{J}_{max})^{(<\omega)})=\{\top\}\in \sigma (\mathbb{J}_\top)$
, but there is no
$\bigcap\mathcal{K}=\bigcap_{F\in (\mathbb{J}_{max})^{(<\omega)}} \mathord{\uparrow}_{\mathbb{J}_\top} (\mathbb{J}_{max}\setminus F)=\bigcap_{F\in (\mathbb{J}_{max})^{(<\omega)}} ((\mathbb{J}_{max}\setminus F)\cup\{\top\})=\{\top\}\cup(\mathbb{J}_{max}\setminus \bigcup (\mathbb{J}_{max})^{(<\omega)})=\{\top\}\in \sigma (\mathbb{J}_\top)$
, but there is no
![]() $F\in (\mathbb{J}_{max})^{(<\omega)}$
with
$F\in (\mathbb{J}_{max})^{(<\omega)}$
with
![]() $\mathord{\uparrow}_{\mathbb{J}_\top} (\mathbb{J}_{max}\setminus F)\subseteq \{\top\}$
. Therefore,
$\mathord{\uparrow}_{\mathbb{J}_\top} (\mathbb{J}_{max}\setminus F)\subseteq \{\top\}$
. Therefore,
![]() $\Sigma~\!\!\mathbb{J}_\top$
is not well-filtered.
$\Sigma~\!\!\mathbb{J}_\top$
is not well-filtered.
5. Topological Rudin Lemma, Rudin Spaces, and Well-Filtered Determined Spaces
In Section 5, we recall some concepts and results about the topological Rudin Lemma, Rudin spaces,
![]() $\omega$
-Rudin spaces, well-filtered determined spaces, and
$\omega$
-Rudin spaces, well-filtered determined spaces, and
![]() $\omega$
-well-filtered determined spaces that will be used in the next four sections.
$\omega$
-well-filtered determined spaces that will be used in the next four sections.
Rudin’s Lemma is a useful tool in non-Hausdorff topology and plays a crucial role in domain theory (see Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Reference Gierz, Lawson and Stralka1983; Heckmann Reference Heckmann1992). Rudin (1980) proved her lemma by transfinite methods, using the Axiom of Choice. Heckmann and Keimel (Reference Heckmann and Keimel2013) presented the following topological variant of Rudin’s Lemma.
Lemma 27. (Topological Rudin Lemma) Let X be a topological space and
![]() $\mathcal{A}$
an irreducible subset of the Smyth power space
$\mathcal{A}$
an irreducible subset of the Smyth power space
![]() $P_S(X)$
. Then, every closed set
$P_S(X)$
. Then, every closed set
![]() $C {\subseteq} X$
that meets all members of
$C {\subseteq} X$
that meets all members of
![]() $\mathcal{A}$
contains a minimal irreducible closed subset A that still meets all members of
$\mathcal{A}$
contains a minimal irreducible closed subset A that still meets all members of
![]() $\mathcal{A}$
.
$\mathcal{A}$
.
Applying Lemma 27 to the Alexandroff topology on a poset P, one obtains the original Rudin’s Lemma.
Corollary 28. (Rudin’s Lemma) Let P be a poset, C a nonempty lower subset of P, and
![]() $\mathcal F\in \mathbf{Fin} P$
a filtered family with
$\mathcal F\in \mathbf{Fin} P$
a filtered family with
![]() $\mathcal F\subseteq\Diamond C$
. Then, there exists a directed subset D of C such that
$\mathcal F\subseteq\Diamond C$
. Then, there exists a directed subset D of C such that
![]() $\mathcal F\subseteq \Diamond\mathord{\downarrow} D$
.
$\mathcal F\subseteq \Diamond\mathord{\downarrow} D$
.
For a
![]() $T_0$
space X and
$T_0$
space X and
![]() $\mathcal{K}\subseteq \mathord{\mathsf{K}}(X)$
, let
$\mathcal{K}\subseteq \mathord{\mathsf{K}}(X)$
, let
![]() $M(\mathcal{K})=\{A\in \mathcal C(X) : K\bigcap A\neq\emptyset \mbox{~for all~} K\in \mathcal{K}\}$
(that is,
$M(\mathcal{K})=\{A\in \mathcal C(X) : K\bigcap A\neq\emptyset \mbox{~for all~} K\in \mathcal{K}\}$
(that is,
![]() $\mathcal K\subseteq \Diamond A$
) and
$\mathcal K\subseteq \Diamond A$
) and
![]() $m(\mathcal{K})=\{A\in \mathcal C(X) : A \mbox{~is a minimal member of~} M(\mathcal{K})\}$
.
$m(\mathcal{K})=\{A\in \mathcal C(X) : A \mbox{~is a minimal member of~} M(\mathcal{K})\}$
.
In Shen et al. (Reference Shen, Xi, Xu and Zhao2019) and Reference Xu, Shen, Xi and ZhaoXu et al. (2020b
), based on topological Rudin’s Lemma, Rudin spaces and well-filtered determined spaces (
![]() $\mathord{\mathsf{WD}}$
spaces for short) were introduced and investigated. These two spaces are closely related to sober spaces and well-filtered spaces (see Shen et al. Reference Shen, Xi, Xu and Zhao2019; Reference Xu, Shen, Xi and ZhaoXu et al. 2020b
).
$\mathord{\mathsf{WD}}$
spaces for short) were introduced and investigated. These two spaces are closely related to sober spaces and well-filtered spaces (see Shen et al. Reference Shen, Xi, Xu and Zhao2019; Reference Xu, Shen, Xi and ZhaoXu et al. 2020b
).
Definition 29. (Shen et al. 2019; Xu et al. 2020b) Let X be a
![]() $T_0$
space.
$T_0$
space.
-
(1) A nonempty subset A of X is said to have the Rudin property , if there exists a filtered family
 $\mathcal K\subseteq \mathord{\mathsf{K}}(X)$
such that
$\mathcal K\subseteq \mathord{\mathsf{K}}(X)$
such that
 $\overline{A}\in m(\mathcal K)$
(i.e.,
$\overline{A}\in m(\mathcal K)$
(i.e.,
 $\overline{A}$
is a minimal closed set that intersects all members of
$\overline{A}$
is a minimal closed set that intersects all members of
 $\mathcal K$
). Let
$\mathcal K$
). Let
 $\mathsf{RD}(X)=\{A\in \mathcal C(X) : A\mbox{~has Rudin property}\}$
. The sets in
$\mathsf{RD}(X)=\{A\in \mathcal C(X) : A\mbox{~has Rudin property}\}$
. The sets in
 $\mathsf{RD}(X)$
will also be called Rudin sets.
$\mathsf{RD}(X)$
will also be called Rudin sets. -
(2) X is called a Rudin space,
 $\mathsf{RD}$
space for short, if
$\mathsf{RD}$
space for short, if
 ${\mathsf{Irr}}_c(X)=\mathsf{RD}(X)$
, that is, all irreducible closed sets of X are Rudin sets.
${\mathsf{Irr}}_c(X)=\mathsf{RD}(X)$
, that is, all irreducible closed sets of X are Rudin sets.
The Rudin property is called the compactly filtered property in Shen et al. (Reference Shen, Xi, Xu and Zhao2019). In order to emphasize its origin from (topological) Rudin’s Lemma, such a property was called the Rudin property in Reference Xu, Shen, Xi and ZhaoXu et al. (2020b). Clearly, A has Rudin property iff
![]() $\overline{A}$
has Rudin property (that is,
$\overline{A}$
has Rudin property (that is,
![]() $\overline{A}$
is a Rudin set).
$\overline{A}$
is a Rudin set).
Proposition 30. (Shen et al. 2019; Xu et al. 2020b) Let X be a
![]() $T_0$
space and Y a well-filtered space. If
$T_0$
space and Y a well-filtered space. If
![]() $f : X\longrightarrow Y$
is continuous and
$f : X\longrightarrow Y$
is continuous and
![]() $A\subseteq X$
has Rudin property, then there exists a unique
$A\subseteq X$
has Rudin property, then there exists a unique
![]() $y_A\in X$
such that
$y_A\in X$
such that
![]() $\overline{f(A)}=\overline{\{y_A\}}$
.
$\overline{f(A)}=\overline{\{y_A\}}$
.
Motivated by Proposition 30, the following concept was introduced in Xu et al. (Reference Xu, Shen, Xi and Zhao2020b).
Definition 31. (Xu et al. 2020b) Let X be a
![]() $T_0$
space.
$T_0$
space.
-
(1) A subset A of X is called a well-filtered determined set,
 $\mathord{\mathsf{WD}}$
set for short, if for any continuous mapping
$\mathord{\mathsf{WD}}$
set for short, if for any continuous mapping
 $ f:X\longrightarrow Y$
to a well-filtered space Y, there exists a unique
$ f:X\longrightarrow Y$
to a well-filtered space Y, there exists a unique
 $y_A\in Y$
such that
$y_A\in Y$
such that
 $\overline{f(A)}=\overline{\{y_A\}}$
. Denote by
$\overline{f(A)}=\overline{\{y_A\}}$
. Denote by
 $\mathsf{WD}(X)$
the set of all closed well-filtered determined subsets of X.
$\mathsf{WD}(X)$
the set of all closed well-filtered determined subsets of X.
-
(2) X is called a well-filtered determined space,
 $\mathsf{WD}$
space for short, if all irreducible closed subsets of X are well-filtered determined, that is,
$\mathsf{WD}$
space for short, if all irreducible closed subsets of X are well-filtered determined, that is,
 ${\mathsf{Irr}}_c(X)=\mathord{\mathsf{WD}} (X)$
.
${\mathsf{Irr}}_c(X)=\mathord{\mathsf{WD}} (X)$
.
Obviously, a subset A of a space X is well-filtered determined iff
![]() $\overline{A}$
is well-filtered determined.
$\overline{A}$
is well-filtered determined.
Proposition 32. (Shen et al. 2019; Xu et al. 2020b) Let X be a
![]() $T_0$
space. Then,
$T_0$
space. Then,
![]() $\mathcal S_c(X)\subseteq\mathcal{D}_c(X)\subseteq \mathsf{RD}(X)\subseteq\mathsf{WD}(X)\subseteq{\mathsf{Irr}}_c(X)$
.
$\mathcal S_c(X)\subseteq\mathcal{D}_c(X)\subseteq \mathsf{RD}(X)\subseteq\mathsf{WD}(X)\subseteq{\mathsf{Irr}}_c(X)$
.
Definition 33.
(Xu et al. 2020b) A
![]() $T_0$
space X is called a directed closure space,
$T_0$
space X is called a directed closure space,
![]() $\mathsf{DC}$
space for short, if
$\mathsf{DC}$
space for short, if
![]() ${\mathsf{Irr}}_c(X)=\mathcal{D}_c(X)$
, that is, for each
${\mathsf{Irr}}_c(X)=\mathcal{D}_c(X)$
, that is, for each
![]() $A\in {\mathsf{Irr}}_c(X)$
, there exists a directed subset of X such that
$A\in {\mathsf{Irr}}_c(X)$
, there exists a directed subset of X such that
![]() $A=\overline{D}$
.
$A=\overline{D}$
.
Corollary 34. (Xu et al. 2020b, Corollary 6.3) Sober
![]() $\Rightarrow$
$\Rightarrow$
![]() $\mathsf{DC}$
$\mathsf{DC}$
![]() $\Rightarrow$
$\Rightarrow$
![]() $\mathsf{RD}$
$\mathsf{RD}$
![]() $\Rightarrow$
$\Rightarrow$
![]() $\mathsf{WD}$
.
$\mathsf{WD}$
.
Proposition 35. (Xu et al. 2020b, Corollary 7.11) For a
![]() $T_0$
space X, the following conditions are equivalent:
$T_0$
space X, the following conditions are equivalent:
-
(1) X is well-filtered.
-
(2)
 $\mathsf{RD}(X)=\mathcal S_c(X)$
.
$\mathsf{RD}(X)=\mathcal S_c(X)$
. -
(3)
 $\mathord{\mathsf{WD}} (X)=\mathcal S_c(X)$
.
$\mathord{\mathsf{WD}} (X)=\mathcal S_c(X)$
.
Theorem 36.
(Xu et al. 2020b, Theorem 6.6) For a
![]() $T_0$
space X, the following conditions are equivalent:
$T_0$
space X, the following conditions are equivalent:
-
(1) X is sober.
-
(2) X is a
 $\mathsf{DC}$
d-space.
$\mathsf{DC}$
d-space.
-
(3) X is a well-filtered
 $\mathsf{DC}$
space.
$\mathsf{DC}$
space.
-
(4) X is a well-filtered Rudin space.
-
(5) X is a well-filtered
 $\mathsf{WD}$
space.
$\mathsf{WD}$
space.
Proposition 37.
(Erné 2018, Proposition 3.2) Let X be a locally hypercompact
![]() $T_0$
space and
$T_0$
space and
![]() $A\in{\mathsf{Irr}}(X)$
. Then, there exists a directed subset
$A\in{\mathsf{Irr}}(X)$
. Then, there exists a directed subset
![]() $D\subseteq\mathord{\downarrow} A$
such that
$D\subseteq\mathord{\downarrow} A$
such that
![]() $\overline{A}=\overline{D}$
. Therefore, X is a
$\overline{A}=\overline{D}$
. Therefore, X is a
![]() $\mathsf{DC}$
space.
$\mathsf{DC}$
space.
Proposition 38.
(Xu et al. 2020b, Theorems 6.10 and 6.15) Let X be a
![]() $T_0$
space.
$T_0$
space.
-
(1) If X is locally compact, then X is a Rudin space.
-
(2) If X is core-compact, then X is a
 $\mathsf{WD}$
space.
$\mathsf{WD}$
space.
It is still not known whether every core-compact
![]() $T_0$
space is a Rudin space (see Xu et al. 2021d, Question 5.14).
$T_0$
space is a Rudin space (see Xu et al. 2021d, Question 5.14).
Question 39. For a core-compact
![]() $T_0$
space X, is the Smyth power space
$T_0$
space X, is the Smyth power space
![]() $P_S(X)$
a
$P_S(X)$
a
![]() $\mathsf{WD}$
space? Is the Scott space
$\mathsf{WD}$
space? Is the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
a
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
a
![]() $\mathsf{WD}$
space?
$\mathsf{WD}$
space?
From Theorem 36 and Proposition 38, one can immediately get the following result, which was first proved by Lawson et al. (2020) using a different method.
Corollary 40. (Lawson et al. 2020; Xu et al. 2020b) Every core-compact well-filtered space is sober.
By Corollary 40, Theorem23 can be strengthened into the following one.
Theorem 41.
For a
![]() $T_0$
space X, the following conditions are equivalent:
$T_0$
space X, the following conditions are equivalent:
-
(1) X locally compact and sober.
-
(2) X is locally compact and well-filtered.
-
(3) X is core-compact and sober.
-
(4) X is core-compact and well-filtered.

Figure 2. Certain relations among some kinds of spaces.
Fig. 2 shows certain relations among some kinds of spaces.
In order to emphasize the Scott topology, we introduce the following notions.
Definition 42.
A poset P is called a sober dcpo (resp., a well-filtered dcpo) if
![]() $\Sigma~\!\! P$
is a sober space (resp., well-filtered space).
$\Sigma~\!\! P$
is a sober space (resp., well-filtered space).
Clearly, a sober dcpo is a well-filtered dcpo. For Isbell’s lattice L constructed in Isbell (Reference Isbell1982),
![]() $\Sigma~\!\! L$
is non-sober, namely L is not a sober dcpo, and by Proposition 22, L is well-filtered. The Johnstone’s dcpo
$\Sigma~\!\! L$
is non-sober, namely L is not a sober dcpo, and by Proposition 22, L is well-filtered. The Johnstone’s dcpo
![]() $\mathbb{J}$
(see Example 26) is not well-filtered.
$\mathbb{J}$
(see Example 26) is not well-filtered.
Definition 43. Let P be a poset.
-
(1) P is said to be a
 $\mathsf{DC}$
poset if
$\mathsf{DC}$
poset if
 $\Sigma~\!\!P$
is a
$\Sigma~\!\!P$
is a
 $\mathsf{DC}$
space.
$\mathsf{DC}$
space.
-
(2) P is said to be a Rudin poset if
 $\Sigma~\!\! P$
is a Rudin space.
$\Sigma~\!\! P$
is a Rudin space.
-
(3) P is said to be a well-filtered determined poset, a
 $\mathord{\mathsf{WD }}$
poset for short, if
$\mathord{\mathsf{WD }}$
poset for short, if
 $\Sigma~\!\! P$
is a well-filtered determined space.
$\Sigma~\!\! P$
is a well-filtered determined space.
-
(4) When a dcpo P is a Rudin poset (resp., a well-filtered determined poset), we will call P a Rudin dcpo (resp., a well-filtered determined dcpo).
The following corollary follows directly from Theorem 36.
Corollary 44. For a poset P, the following conditions are equivalent:
-
(1) P is a sober dcpo.
-
(2) P is a
 $\mathsf{DC}$
dcpo.
$\mathsf{DC}$
dcpo.
-
(3) P is a
 $\mathsf{DC}$
well-filtered dcpo.
$\mathsf{DC}$
well-filtered dcpo.
-
(4) P is a Rudin well-filtered dcpo.
-
(5) P is a
 $\mathord{\mathsf{WD}}$
well-filtered dcpo.
$\mathord{\mathsf{WD}}$
well-filtered dcpo.
In Xu et al. (Reference Xu, Shen, Xi and Zhao2020a), the following countable versions of Rudin spaces and
![]() $\mathsf{WD}$
spaces were introduced and studied.
$\mathsf{WD}$
spaces were introduced and studied.
Definition 45. (Xu et al. 2020a, Definition 5.1) Let X be a
![]() $T_0$
space and A a nonempty subset of X.
$T_0$
space and A a nonempty subset of X.
-
(a) The set A is said to be an
 $\omega$
-Rudin set, if there exists a countable filtered family
$\omega$
-Rudin set, if there exists a countable filtered family
 $\mathcal K\subseteq \mathord{\mathsf{K}}(X)$
such that
$\mathcal K\subseteq \mathord{\mathsf{K}}(X)$
such that
 $\overline{A}\in m(\mathcal K)$
. Let
$\overline{A}\in m(\mathcal K)$
. Let
 $\mathsf{RD}_\omega(X)$
denote the set of all closed
$\mathsf{RD}_\omega(X)$
denote the set of all closed
 $\omega$
-Rudin sets of X.
$\omega$
-Rudin sets of X.
-
(b) The space X is called
 $\omega$
-Rudin space, if
$\omega$
-Rudin space, if
 ${\mathsf{Irr}}_c(X)=\mathsf{RD}_\omega(X)$
or, equivalently, all irreducible (closed) subsets of X are
${\mathsf{Irr}}_c(X)=\mathsf{RD}_\omega(X)$
or, equivalently, all irreducible (closed) subsets of X are
 $\omega$
-Rudin sets.
$\omega$
-Rudin sets.
Definition 46. (Xu et al. 2020a, Definition 3.9) A
![]() $T_0$
space X is called
$T_0$
space X is called
![]() $\omega$
-well-filtered, if for any countable filtered family
$\omega$
-well-filtered, if for any countable filtered family
![]() $\{K_n : n<\omega\}\subseteq \mathord{\mathsf{K}} (X)$
and
$\{K_n : n<\omega\}\subseteq \mathord{\mathsf{K}} (X)$
and
![]() $U\in\mathcal O(X)$
, it holds that
$U\in\mathcal O(X)$
, it holds that
Definition 47. (Xu et al. 2020a, Definition 5.4) Let X be a
![]() $T_0$
space and A a nonempty subset of X.
$T_0$
space and A a nonempty subset of X.
-
(a) The set A is called an
 $\omega$
-well-filtered determined set,
$\omega$
-well-filtered determined set,
 $\omega$
-
$\omega$
-
 $\mathord{\mathsf{WD}}$
set for short, if for any continuous mapping
$\mathord{\mathsf{WD}}$
set for short, if for any continuous mapping
 $ f:X\longrightarrow Y$
to an
$ f:X\longrightarrow Y$
to an
 $\omega$
-well-filtered space Y, there exists a (unique)
$\omega$
-well-filtered space Y, there exists a (unique)
 $y_A\in Y$
such that
$y_A\in Y$
such that
 $\overline{f(A)}=\overline{\{y_A\}}$
. Denote by
$\overline{f(A)}=\overline{\{y_A\}}$
. Denote by
 $\mathsf{WD}_\omega(X)$
the set of all closed
$\mathsf{WD}_\omega(X)$
the set of all closed
 $\omega$
-well-filtered determined subsets of X.
$\omega$
-well-filtered determined subsets of X.
-
(b) The space X is called
 $\omega$
-well-filtered determined,
$\omega$
-well-filtered determined,
 $\omega$
-
$\omega$
-
 $\mathsf{WD}$
space for short, if
$\mathsf{WD}$
space for short, if
 ${\mathsf{Irr}}_c(X)=\mathsf{WD}_\omega(X)$
or, equivalently, all irreducible (closed) subsets of X are
${\mathsf{Irr}}_c(X)=\mathsf{WD}_\omega(X)$
or, equivalently, all irreducible (closed) subsets of X are
 $\omega$
-well-filtered determined.
$\omega$
-well-filtered determined.
For a
![]() $T_0$
space X, it was proved in Reference Xu, Shen, Xi and ZhaoXu et al. (2020a
, Proposition 5.5) that
$T_0$
space X, it was proved in Reference Xu, Shen, Xi and ZhaoXu et al. (2020a
, Proposition 5.5) that
![]() $\mathcal{S}_c(X)\subseteq \mathsf{RD}_\omega(X)\subseteq\mathsf{WD}_\omega(X)\subseteq{\mathsf{Irr}}_c(X)$
. Therefore, every
$\mathcal{S}_c(X)\subseteq \mathsf{RD}_\omega(X)\subseteq\mathsf{WD}_\omega(X)\subseteq{\mathsf{Irr}}_c(X)$
. Therefore, every
![]() $\omega$
-Rudin space is
$\omega$
-Rudin space is
![]() $\omega$
-well-filtered determined.
$\omega$
-well-filtered determined.
The following result is a countable version of Theorem 36.
Proposition 48. (Xu et al. 2020a, Theorem 5.11) For a
![]() $T_0$
space X, the following conditions are equivalent:
$T_0$
space X, the following conditions are equivalent:
-
(1) X is sober.
-
(2) X is an
 $\omega$
-Rudin and
$\omega$
-Rudin and
 $\omega$
-well-filtered space.
$\omega$
-well-filtered space.
-
(3) X is an
 $\omega$
-well-filtered determined and
$\omega$
-well-filtered determined and
 $\omega$
-well-filtered space.
$\omega$
-well-filtered space.
Theorem 49. (Xu et al. 2021a, Theorems 5.6 and 6.12) Let X be a
![]() $T_0$
space.
$T_0$
space.
If the sobrification
![]() $X^s$
of X is first-countable, then X is an
$X^s$
of X is first-countable, then X is an
![]() $\omega$
-Rudin space.
$\omega$
-Rudin space.
-
(1) If X is first-countable, then X is a
 $\mathsf{WD}$
space.
$\mathsf{WD}$
space.
From Theorems 36 and 49, we immediately deduce the following result.
Corollary 50. (Xu et al. 2020a, Theorem 4.2) Every first-countable well-filtered
![]() $T_0$
space is sober.
$T_0$
space is sober.
It is still not known whether a first-countable
![]() $T_0$
space is a Rudin space (see Reference Xu, Shen, Xi and ZhaoXu et al. 2021a
, Problem 6.15). Since the first-countability is a hereditary property, from Remark 4 and Theorem 49 we know that if the Smyth power space
$T_0$
space is a Rudin space (see Reference Xu, Shen, Xi and ZhaoXu et al. 2021a
, Problem 6.15). Since the first-countability is a hereditary property, from Remark 4 and Theorem 49 we know that if the Smyth power space
![]() $P_S(X)$
of a
$P_S(X)$
of a
![]() $T_0$
space X is first-countable, then X is a
$T_0$
space X is first-countable, then X is a
![]() $\mathsf{WD}$
space.
$\mathsf{WD}$
space.
So naturally, we ask the following question.
Question 51. Is a
![]() $T_0$
space with a first-countable Smyth power space a Rudin space?
$T_0$
space with a first-countable Smyth power space a Rudin space?
In Example 67, a
![]() $T_0$
space X is given for which the Scott space
$T_0$
space X is given for which the Scott space
![]() $\Sigma~\!\!\mathsf{K}(X)$
is a first-countable sober c-space but X is not a
$\Sigma~\!\!\mathsf{K}(X)$
is a first-countable sober c-space but X is not a
![]() $\mathsf{WD}$
space (and hence not a Rudin space).
$\mathsf{WD}$
space (and hence not a Rudin space).
By Proposition 48 and Theorem 49, we have the following result.
Corollary 52. (Xu et al. 2021a, Theorem 5.9) Every
![]() $\omega$
-well-filtered space with a first-countable sobrification is sober.
$\omega$
-well-filtered space with a first-countable sobrification is sober.
In Theorem 49 and Corollary 52, the first-countability of
![]() $X^s$
cannot be weakened to that of X as shown in the following example. It also shows that the first-countability of a
$X^s$
cannot be weakened to that of X as shown in the following example. It also shows that the first-countability of a
![]() $T_0$
space X does not imply the first-countability of
$T_0$
space X does not imply the first-countability of
![]() $X^s$
in general.
$X^s$
in general.
Example 53. Let
![]() $\omega_1$
be the first uncountable ordinal number and
$\omega_1$
be the first uncountable ordinal number and
![]() $P=[0, \omega_1)$
. Then,
$P=[0, \omega_1)$
. Then,
-
(a)
 $\mathcal C(\Sigma P)=\{\mathord{\downarrow} t : t\in P\}\cup\{\emptyset, P\}$
.
$\mathcal C(\Sigma P)=\{\mathord{\downarrow} t : t\in P\}\cup\{\emptyset, P\}$
. -
(b)
 $\Sigma P$
is first-countable and compact (since P has a least element 0).
$\Sigma P$
is first-countable and compact (since P has a least element 0). -
(c)
 $(\Sigma P)^s$
is not first-countable.
$(\Sigma P)^s$
is not first-countable.In fact, it is easy to verify that
 $(\Sigma P)^s$
is homeomorphic to
$(\Sigma P)^s$
is homeomorphic to
 $\Sigma [0, \omega_1]$
. Since sup of a countable family of countable ordinal numbers is still a countable ordinal number,
$\Sigma [0, \omega_1]$
. Since sup of a countable family of countable ordinal numbers is still a countable ordinal number,
 $\Sigma [0, \omega_1]$
has no countable base at the point
$\Sigma [0, \omega_1]$
has no countable base at the point
 $\omega_1$
.
$\omega_1$
. -
(d)
 $\mathsf{K}(\Sigma P)=\{\mathord{\uparrow} x : x\in P\}$
and
$\mathsf{K}(\Sigma P)=\{\mathord{\uparrow} x : x\in P\}$
and
 $\Sigma P$
is not an
$\Sigma P$
is not an
 $\omega$
-Rudin space.
$\omega$
-Rudin space.
For
![]() $K\in \mathsf{K}(\Sigma P)$
, we have
$K\in \mathsf{K}(\Sigma P)$
, we have
![]() $\mathrm{inf}~K\in K$
, and hence
$\mathrm{inf}~K\in K$
, and hence
![]() $K=\mathord{\uparrow} \mathrm{inf}~K$
. So
$K=\mathord{\uparrow} \mathrm{inf}~K$
. So
![]() $\mathsf{K}(\Sigma P)=\{\mathord{\uparrow} x : x\in P\}$
. Now we show that the irreducible closed set P is not an
$\mathsf{K}(\Sigma P)=\{\mathord{\uparrow} x : x\in P\}$
. Now we show that the irreducible closed set P is not an
![]() $\omega$
-Rudin set. For any countable filtered family
$\omega$
-Rudin set. For any countable filtered family
![]() $\{\mathord{\uparrow} \alpha_n : n\in\mathbb N \}\subseteq \mathsf{K}(\Sigma P)$
, let
$\{\mathord{\uparrow} \alpha_n : n\in\mathbb N \}\subseteq \mathsf{K}(\Sigma P)$
, let
![]() $\beta=\mathrm{sup}\{\alpha_n : n\in\mathbb N\}$
. Then,
$\beta=\mathrm{sup}\{\alpha_n : n\in\mathbb N\}$
. Then,
![]() $\beta$
is still a countable ordinal number. Clearly,
$\beta$
is still a countable ordinal number. Clearly,
![]() $\mathord{\downarrow} \beta \in M(\{\mathord{\uparrow} \alpha_n : n\in \mathbb N\})$
and
$\mathord{\downarrow} \beta \in M(\{\mathord{\uparrow} \alpha_n : n\in \mathbb N\})$
and
![]() $P\neq \mathord{\downarrow} \beta$
. Therefore,
$P\neq \mathord{\downarrow} \beta$
. Therefore,
![]() $P\notin m(\{\mathord{\uparrow} \alpha_n : n\in \mathbb N\})$
. Thus, P is not an
$P\notin m(\{\mathord{\uparrow} \alpha_n : n\in \mathbb N\})$
. Thus, P is not an
![]() $\omega$
-Rudin set, and hence,
$\omega$
-Rudin set, and hence,
![]() $\Sigma P$
is not an
$\Sigma P$
is not an
![]() $\omega$
-Rudin space.
$\omega$
-Rudin space.
-
(e)
 $\Sigma P$
is a Rudin space.
$\Sigma P$
is a Rudin space.
It is easy to check that
![]() ${\mathsf{Irr}}_c(\Sigma P)=\{\downarrow x : x\in P\}\cup \{P\}$
. Clearly,
${\mathsf{Irr}}_c(\Sigma P)=\{\downarrow x : x\in P\}\cup \{P\}$
. Clearly,
![]() $\downarrow x$
is a Rudin set for each
$\downarrow x$
is a Rudin set for each
![]() $x\in P$
. Now we show that P is a Rudin set. First,
$x\in P$
. Now we show that P is a Rudin set. First,
![]() $\{\mathord{\uparrow} s : s\in P\}$
is filtered. Second,
$\{\mathord{\uparrow} s : s\in P\}$
is filtered. Second,
![]() $P\in M(\{\mathord{\uparrow} s : s\in P\})$
. For a closed subset B of
$P\in M(\{\mathord{\uparrow} s : s\in P\})$
. For a closed subset B of
![]() $\Sigma P$
, if
$\Sigma P$
, if
![]() $B\neq P$
, then
$B\neq P$
, then
![]() $B=\mathord{\downarrow} t$
for some
$B=\mathord{\downarrow} t$
for some
![]() $t\in P$
, and hence,
$t\in P$
, and hence,
![]() $\mathord{\uparrow} (t+1)\cap\mathord{\downarrow} t=\emptyset$
. Thus,
$\mathord{\uparrow} (t+1)\cap\mathord{\downarrow} t=\emptyset$
. Thus,
![]() $B\notin M(\{\mathord{\uparrow} s : s\in P\})$
, proving that P is a Rudin set.
$B\notin M(\{\mathord{\uparrow} s : s\in P\})$
, proving that P is a Rudin set.
-
(f) P is not a dcpo (note that P is directed and
 $\vee P$
does not exist). So
$\vee P$
does not exist). So
 $\Sigma P$
is not a d-space, and hence,
$\Sigma P$
is not a d-space, and hence,
 $\Sigma P$
is neither well-filtered nor sober (see Remark 20).
$\Sigma P$
is neither well-filtered nor sober (see Remark 20). -
(g)
 $\Sigma P$
is
$\Sigma P$
is
 $\omega$
-well-filtered.
$\omega$
-well-filtered.
If
![]() $\{\mathord{\uparrow} x_n : n\in \mathbb N\}\subseteq \mathsf{K}(\Sigma P)$
is countable filtered family and
$\{\mathord{\uparrow} x_n : n\in \mathbb N\}\subseteq \mathsf{K}(\Sigma P)$
is countable filtered family and
![]() $U\in \sigma (P)$
with
$U\in \sigma (P)$
with
![]() $\bigcap_{n\in \mathbb N}\mathord{\uparrow} x_n\subseteq U$
, then
$\bigcap_{n\in \mathbb N}\mathord{\uparrow} x_n\subseteq U$
, then
![]() $\{x_n : i\in\mathbb N\}$
is a countable subset of
$\{x_n : i\in\mathbb N\}$
is a countable subset of
![]() $P=[0, \omega_1)$
. Since sup of a countable family of countable ordinal numbers is still a countable ordinal number, we have
$P=[0, \omega_1)$
. Since sup of a countable family of countable ordinal numbers is still a countable ordinal number, we have
![]() $\beta=\mathrm{sup}\{x_n : n\in \mathbb N\}\in P$
, and hence,
$\beta=\mathrm{sup}\{x_n : n\in \mathbb N\}\in P$
, and hence,
![]() $\mathord{\uparrow} \beta=\bigcap_{n\in \mathbb N}\mathord{\uparrow} x_n\subseteq U$
. Therefore,
$\mathord{\uparrow} \beta=\bigcap_{n\in \mathbb N}\mathord{\uparrow} x_n\subseteq U$
. Therefore,
![]() $\beta\in U$
, and consequently,
$\beta\in U$
, and consequently,
![]() $x_n\in U$
for some
$x_n\in U$
for some
![]() $n\in \mathbb N$
or, equivalently,
$n\in \mathbb N$
or, equivalently,
![]() $\mathord{\uparrow} x_n\subseteq U$
, proving that
$\mathord{\uparrow} x_n\subseteq U$
, proving that
![]() $\Sigma P$
is
$\Sigma P$
is
![]() $\omega$
-well-filtered.
$\omega$
-well-filtered.
6 Well-Filteredness of Scott Topology on Smyth Power Posets
In this section, we mainly discuss the following two questions:
Question 1. Is the Scott space
![]() $\Sigma~\!\! \mathord{\mathsf{K}}(X)$
of a d-space X a d-space?
$\Sigma~\!\! \mathord{\mathsf{K}}(X)$
of a d-space X a d-space?
Question 2. Is the Scott space
![]() $\Sigma~\!\! \mathord{\mathsf{K}}(X)$
of a well-filtered space X well-filtered?
$\Sigma~\!\! \mathord{\mathsf{K}}(X)$
of a well-filtered space X well-filtered?
First, Example 57 below shows that there is a second-countable Noetherian d-space X for which
![]() $\mathord{\mathsf{K}} (X)$
is not a dcpo, and hence, neither the Smyth power space
$\mathord{\mathsf{K}} (X)$
is not a dcpo, and hence, neither the Smyth power space
![]() $P_S(X)$
nor the Scott space
$P_S(X)$
nor the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a d-space, which gives a negative answer to Question 1.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a d-space, which gives a negative answer to Question 1.
In order to present the example, we need the following lemma.
Lemma 54. (Schalk 1993, Lemma 7.26) For a locally compact
![]() $T_0$
space X, the Scott topology is coarser than the upper Vietoris topology on
$T_0$
space X, the Scott topology is coarser than the upper Vietoris topology on
![]() $\mathsf{K}(X)$
, that is,
$\mathsf{K}(X)$
, that is,
![]() $\sigma(\mathsf{K}(X))\subseteq \mathcal O(P_S(X))$
.
$\sigma(\mathsf{K}(X))\subseteq \mathcal O(P_S(X))$
.
Proof. It was proved by Schalk (Reference Schalk1993, the proof of Lemma 7.26). We present a more direct proof here.
Suppose that
![]() $\mathcal U\in \sigma(\mathsf{K}(X))$
and
$\mathcal U\in \sigma(\mathsf{K}(X))$
and
![]() $K\in \mathcal U$
. Let
$K\in \mathcal U$
. Let
![]() $\mathcal K=\{G\in \mathsf{K}(X) : K\subseteq {\rm int} ~\!G\}$
. Now we show that
$\mathcal K=\{G\in \mathsf{K}(X) : K\subseteq {\rm int} ~\!G\}$
. Now we show that
![]() $\mathcal K$
is filtered and
$\mathcal K$
is filtered and
![]() $G=\bigcap \mathcal K$
.
$G=\bigcap \mathcal K$
.
![]() $1^{\circ}$
For each
$1^{\circ}$
For each
![]() $U\in \mathcal O(X)$
with
$U\in \mathcal O(X)$
with
![]() $K\subseteq U$
, there is
$K\subseteq U$
, there is
![]() $G_U\in \mathcal K$
with
$G_U\in \mathcal K$
with
![]() $G_U\subseteq U$
.
$G_U\subseteq U$
.
If
![]() $U\in \mathcal O(X)$
for which
$U\in \mathcal O(X)$
for which
![]() $K\subseteq U$
, then for each
$K\subseteq U$
, then for each
![]() $x\in K$
, there is
$x\in K$
, there is
![]() $K_x\in \mathsf{K}(X)$
such that
$K_x\in \mathsf{K}(X)$
such that
![]() $x\in {\rm int}~\!K_x\subseteq K_x\subseteq U$
since X is locally compact. By the compactness of K, there is
$x\in {\rm int}~\!K_x\subseteq K_x\subseteq U$
since X is locally compact. By the compactness of K, there is
![]() $\{x_1, x_2, ..., x_n\}\subseteq K$
such that
$\{x_1, x_2, ..., x_n\}\subseteq K$
such that
![]() $K\subseteq \bigcup\limits_{i=1}^{n} {\rm int}~\!K_{x_i}$
. Let
$K\subseteq \bigcup\limits_{i=1}^{n} {\rm int}~\!K_{x_i}$
. Let
![]() $G_U=\bigcup\limits_{i=1}^{n} K_{x_i}$
. Then,
$G_U=\bigcup\limits_{i=1}^{n} K_{x_i}$
. Then,
![]() $K\subseteq {\rm int}~\!G_U\subseteq G_U\subseteq U$
, whence
$K\subseteq {\rm int}~\!G_U\subseteq G_U\subseteq U$
, whence
![]() $G_U\in \mathcal K$
and
$G_U\in \mathcal K$
and
![]() $G_U\subseteq U$
.
$G_U\subseteq U$
.
![]() $2^{\circ}$
$2^{\circ}$
![]() $\mathcal K$
is filtered.
$\mathcal K$
is filtered.
Suppose that
![]() $G_1, G_2\in \mathcal K$
. Then,
$G_1, G_2\in \mathcal K$
. Then,
![]() $K\subseteq {\rm int}~\!G_1\cap {\rm int}~\!G_2$
. Hence, by what was shown above, there is
$K\subseteq {\rm int}~\!G_1\cap {\rm int}~\!G_2$
. Hence, by what was shown above, there is
![]() $G_3\in \mathcal K$
with
$G_3\in \mathcal K$
with
![]() $G_3\subseteq {\rm int}~\!G_1\cap {\rm int}~\!G_2\subseteq G_1\cap G_2$
, proving the filteredness of
$G_3\subseteq {\rm int}~\!G_1\cap {\rm int}~\!G_2\subseteq G_1\cap G_2$
, proving the filteredness of
![]() $\mathcal K$
.
$\mathcal K$
.
By
![]() $1^{\circ}$
and
$1^{\circ}$
and
![]() $2^{\circ}$
,
$2^{\circ}$
,
![]() $K\subseteq \bigcap \mathcal K\subseteq \{U\in \mathcal O(X) : K\subseteq U\}=K$
, whence
$K\subseteq \bigcap \mathcal K\subseteq \{U\in \mathcal O(X) : K\subseteq U\}=K$
, whence
![]() $K=\bigcap \mathcal K=\bigvee_{\mathsf{K}(X)}\mathcal K$
by Lemma 9. Since
$K=\bigcap \mathcal K=\bigvee_{\mathsf{K}(X)}\mathcal K$
by Lemma 9. Since
![]() $K\in \mathcal U\in \sigma(\mathsf{K}(X))$
,
$K\in \mathcal U\in \sigma(\mathsf{K}(X))$
,
![]() $G\in \mathcal U$
for some
$G\in \mathcal U$
for some
![]() $G\in \mathcal K$
. Hence,
$G\in \mathcal K$
. Hence,
![]() $K\in \Box_{\mathsf{K}(X)}{\rm int}~\!G\subseteq \mathcal U$
. Thus,
$K\in \Box_{\mathsf{K}(X)}{\rm int}~\!G\subseteq \mathcal U$
. Thus,
![]() $\mathcal U\in \mathcal O(P_S(X))$
.
$\mathcal U\in \mathcal O(P_S(X))$
.
By Corollary 25 and Lemma 54, we get the following corollary.
Corollary 55. (Schalk 1993, Lemma 7.26) If X is a locally compact sober space (equivalently, a locally compact well-filtered space or a core-compact well-filtered space), then the upper Vietoris topology and the Scott topology on
![]() $\mathord{\mathsf{K}} (X)$
coincide.
$\mathord{\mathsf{K}} (X)$
coincide.
Considering Remark 14 and Lemma 54, we have the following question.
Question 56. For a core-compact
![]() $T_0$
space X, is the Scott topology coarser than the upper Vietoris topology on
$T_0$
space X, is the Scott topology coarser than the upper Vietoris topology on
![]() $\mathsf{K}(X)$
?
$\mathsf{K}(X)$
?
Example 57. Let X be a countably infinite set (for example,
![]() $X=\mathbb{N}$
) and
$X=\mathbb{N}$
) and
![]() $X_{cof}$
the space equipped with the co-finite topology (the empty set and the complements of finite subsets of X are open). Then
$X_{cof}$
the space equipped with the co-finite topology (the empty set and the complements of finite subsets of X are open). Then
-
(a)
 $\mathcal C(X_{cof})=\{\emptyset, X\}\cup X^{(<\omega)}$
,
$\mathcal C(X_{cof})=\{\emptyset, X\}\cup X^{(<\omega)}$
,
 $X_{cof}$
is
$X_{cof}$
is
 $T_1$
and hence a d-space.
$T_1$
and hence a d-space. -
(b)
 ${\mathsf{Irr}}_c (X_{cof})=\{\{x\} : x\in X\}\cup \{X\}$
.
${\mathsf{Irr}}_c (X_{cof})=\{\{x\} : x\in X\}\cup \{X\}$
. -
(c)
 $\mathord{\mathsf{K}} (X_{cof})=2^X\setminus \{\emptyset\}$
.
$\mathord{\mathsf{K}} (X_{cof})=2^X\setminus \{\emptyset\}$
. -
(d)
 $X_{cof}$
is second-countable.
$X_{cof}$
is second-countable.
Clearly,
![]() $\mathcal O(X_{cof})$
is countable, and hence,
$\mathcal O(X_{cof})$
is countable, and hence,
![]() $X_{cof}$
is second-countable.
$X_{cof}$
is second-countable.
-
(e)
 $X_{cof}$
is Noetherian and hence locally compact.
$X_{cof}$
is Noetherian and hence locally compact.
Since every subset of X is compact in
![]() $X_{cof}$
, the space
$X_{cof}$
, the space
![]() $X_{cof}$
is a Noetherian space and hence a locally compact space.
$X_{cof}$
is a Noetherian space and hence a locally compact space.
-
(f)
 $X_{cof}$
is a Rudin space.
$X_{cof}$
is a Rudin space.
By (e) and Proposition 38 (or by (d) and Corollary 108 below),
![]() $X_{cof}$
is a Rudin space.
$X_{cof}$
is a Rudin space.
-
(g)
 $\mathord{\mathsf{K}} (X_{cof})$
is not a dcpo, and hence,
$\mathord{\mathsf{K}} (X_{cof})$
is not a dcpo, and hence,
 $X_{cof}$
is neither well-filtered nor sober.
$X_{cof}$
is neither well-filtered nor sober.
![]() $\mathcal{K}=\{X\setminus F : F\in X^{(<\omega)}\}\subseteq\mathord{\mathsf{K}} (X_{cof})$
is countable filtered and
$\mathcal{K}=\{X\setminus F : F\in X^{(<\omega)}\}\subseteq\mathord{\mathsf{K}} (X_{cof})$
is countable filtered and
![]() $\bigcap \mathcal{K}_X=X\setminus \bigcup X^{(<\omega)}=X\setminus X=\emptyset$
, whence
$\bigcap \mathcal{K}_X=X\setminus \bigcup X^{(<\omega)}=X\setminus X=\emptyset$
, whence
![]() $\bigvee \mathcal K$
does not exist in
$\bigvee \mathcal K$
does not exist in
![]() $\mathord{\mathsf{K}} (X_{cof})$
by Lemma 9. Thus,
$\mathord{\mathsf{K}} (X_{cof})$
by Lemma 9. Thus,
![]() $\mathord{\mathsf{K}} (X_{cof})$
is not a dcpo, whence by Remark 20 and Theorem 24,
$\mathord{\mathsf{K}} (X_{cof})$
is not a dcpo, whence by Remark 20 and Theorem 24,
![]() $X_{cof}$
is neither well-filtered nor sober.
$X_{cof}$
is neither well-filtered nor sober.
-
(h) The upper Vietoris topology and the Scott topology on
 $\mathord{\mathsf{K}} (X_{cof})$
agree.
$\mathord{\mathsf{K}} (X_{cof})$
agree.
By the local compactness of
![]() $X_{cof}$
and Lemma 54, we have
$X_{cof}$
and Lemma 54, we have
![]() $\sigma (\mathord{\mathsf{K}} (X_{cof})\subseteq \mathcal O(P_S(X_{cof}))$
. Now we show that
$\sigma (\mathord{\mathsf{K}} (X_{cof})\subseteq \mathcal O(P_S(X_{cof}))$
. Now we show that
![]() $\Box U\in \sigma (\mathsf{K}(X_{cof})$
for each
$\Box U\in \sigma (\mathsf{K}(X_{cof})$
for each
![]() $U\in \mathcal O(X_{cof})\setminus \{\emptyset\}$
. Clearly,
$U\in \mathcal O(X_{cof})\setminus \{\emptyset\}$
. Clearly,
![]() $\Box U=\mathord{\uparrow}_{\mathsf{K}(X_{cof})}\Box U$
. Suppose that
$\Box U=\mathord{\uparrow}_{\mathsf{K}(X_{cof})}\Box U$
. Suppose that
![]() $\mathcal K_D=\{K_d : d\in D\}\in \mathcal D(\mathord{\mathsf{K}} (X_{cof})$
and
$\mathcal K_D=\{K_d : d\in D\}\in \mathcal D(\mathord{\mathsf{K}} (X_{cof})$
and
![]() $\bigvee_{\mathord{\mathsf{K}} (X_{cof})} \mathcal K_D\in \Box U$
. Then by Lemma 9
$\bigvee_{\mathord{\mathsf{K}} (X_{cof})} \mathcal K_D\in \Box U$
. Then by Lemma 9
![]() $\bigcap_{d\in D}K_d=\bigvee_{\mathord{\mathsf{K}} (X_{cof})} \mathcal K_D\subseteq U$
or, equivalently,
$\bigcap_{d\in D}K_d=\bigvee_{\mathord{\mathsf{K}} (X_{cof})} \mathcal K_D\subseteq U$
or, equivalently,
![]() $X\setminus U\subseteq \bigcup_{d\in D}(X\setminus K_d)$
. Since
$X\setminus U\subseteq \bigcup_{d\in D}(X\setminus K_d)$
. Since
![]() $X\setminus U$
is finite and
$X\setminus U$
is finite and
![]() $ \{X\setminus K_d : d\in D\}$
is directed, there is
$ \{X\setminus K_d : d\in D\}$
is directed, there is
![]() $d_0\in D$
with
$d_0\in D$
with
![]() $X\setminus U\subseteq X\setminus K_{d_0}$
, whence
$X\setminus U\subseteq X\setminus K_{d_0}$
, whence
![]() $K_{d_0}\subseteq U$
. Thus,
$K_{d_0}\subseteq U$
. Thus,
![]() $\Box U\in \sigma (\mathsf{K}(X_{cof})$
. Therefore,
$\Box U\in \sigma (\mathsf{K}(X_{cof})$
. Therefore,
![]() $\mathcal O(P_S(X_{cof}))\subseteq\sigma (\mathord{\mathsf{K}} (X_{cof}),$
and hence,
$\mathcal O(P_S(X_{cof}))\subseteq\sigma (\mathord{\mathsf{K}} (X_{cof}),$
and hence,
![]() $\sigma (\mathord{\mathsf{K}} (X_{cof})=\mathcal O(P_S(X_{cof}))$
.
$\sigma (\mathord{\mathsf{K}} (X_{cof})=\mathcal O(P_S(X_{cof}))$
.
-
(i)
 $\Sigma~\!\!\mathord{\mathsf{K}} (X_{cof})$
is not a d-space, and hence, it is neither a well-filtered space nor a sober space.
$\Sigma~\!\!\mathord{\mathsf{K}} (X_{cof})$
is not a d-space, and hence, it is neither a well-filtered space nor a sober space.
Since
![]() $\mathord{\mathsf{K}} (X_{cof})$
is not a dcpo,
$\mathord{\mathsf{K}} (X_{cof})$
is not a dcpo,
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X_{cof})$
is not a d-space. By Remark 20,
$\Sigma~\!\!\mathord{\mathsf{K}} (X_{cof})$
is not a d-space. By Remark 20,
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X_{cof})$
is neither a well-filtered space nor a sober space.
$\Sigma~\!\!\mathord{\mathsf{K}} (X_{cof})$
is neither a well-filtered space nor a sober space.
Now we investigate Question 2. First, as one of the main results of this paper, we have the following conclusion.
Theorem 58.
For a well-filtered space X,
![]() $\Sigma~\!\! \mathsf{K}(X)$
is well-filtered.
$\Sigma~\!\! \mathsf{K}(X)$
is well-filtered.
Proof. By Corollary 25,
![]() $\mathord{\mathsf{K}} (X)$
is a dcpo and
$\mathord{\mathsf{K}} (X)$
is a dcpo and
![]() $\mathcal O(P_S(X))\subseteq \sigma (\mathord{\mathsf{K}} (X))$
(i.e.,
$\mathcal O(P_S(X))\subseteq \sigma (\mathord{\mathsf{K}} (X))$
(i.e.,
![]() $\Box U\in \sigma (\mathord{\mathsf{K}} (X))$
for all
$\Box U\in \sigma (\mathord{\mathsf{K}} (X))$
for all
![]() $U\in O(X)$
). Suppose that
$U\in O(X)$
). Suppose that
![]() $\{\mathcal K_d : d\in D\}\subseteq \mathord{\mathsf{K}}(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
is filtered,
$\{\mathcal K_d : d\in D\}\subseteq \mathord{\mathsf{K}}(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
is filtered,
![]() $\mathcal U\in \sigma (\mathord{\mathsf{K}} (X))$
and
$\mathcal U\in \sigma (\mathord{\mathsf{K}} (X))$
and
![]() $\bigcap\limits_{d\in D} \mathcal K_d \subseteq \mathcal U$
. If
$\bigcap\limits_{d\in D} \mathcal K_d \subseteq \mathcal U$
. If
![]() $\mathcal K_d\not\subseteq \mathcal U$
for each
$\mathcal K_d\not\subseteq \mathcal U$
for each
![]() $d\in D$
, that is,
$d\in D$
, that is,
![]() $\mathcal K_d\bigcap (\mathord{\mathsf{K}} (X)\setminus \mathcal U)\neq\emptyset$
, then
$\mathcal K_d\bigcap (\mathord{\mathsf{K}} (X)\setminus \mathcal U)\neq\emptyset$
, then
![]() $\{\mathcal K_d : d\in D\}\in {\mathsf{Irr}} (P_S(\mathord{\mathsf{K}}(\Sigma~\!\! \mathord{\mathsf{K}} (X)))),$
and hence by Lemma 27,
$\{\mathcal K_d : d\in D\}\in {\mathsf{Irr}} (P_S(\mathord{\mathsf{K}}(\Sigma~\!\! \mathord{\mathsf{K}} (X)))),$
and hence by Lemma 27,
![]() $\mathord{\mathsf{K}} (X)\setminus \mathcal U$
contains a minimal irreducible closed subset
$\mathord{\mathsf{K}} (X)\setminus \mathcal U$
contains a minimal irreducible closed subset
![]() $\mathcal A$
that still meets all members
$\mathcal A$
that still meets all members
![]() $\mathcal K_d$
. For each
$\mathcal K_d$
. For each
![]() $d\in D$
, let
$d\in D$
, let
![]() $K_d=\bigcup \mathord{\uparrow}_{\mathsf{K}(X)} (\mathcal K_d\cap \mathcal A)$
.
$K_d=\bigcup \mathord{\uparrow}_{\mathsf{K}(X)} (\mathcal K_d\cap \mathcal A)$
.
Claim 1: For each
![]() $d\in D$
,
$d\in D$
,
![]() $K_d\in \mathord{\mathsf{K}} (X)$
and
$K_d\in \mathord{\mathsf{K}} (X)$
and
![]() $K_d\in \mathcal A$
.
$K_d\in \mathcal A$
.
By
![]() $\mathcal K_d\in \mathord{\mathsf{K}}(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
and
$\mathcal K_d\in \mathord{\mathsf{K}}(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
and
![]() $\mathcal A\in \mathcal C(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
, we have that
$\mathcal A\in \mathcal C(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
, we have that
![]() $\mathord{\uparrow}_{\mathsf{K}(X)} (\mathcal K_d\cap \mathcal A)\in \mathord{\mathsf{K}}(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
, and hence,
$\mathord{\uparrow}_{\mathsf{K}(X)} (\mathcal K_d\cap \mathcal A)\in \mathord{\mathsf{K}}(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
, and hence,
![]() $\mathord{\uparrow}_{\mathsf{K}(X)} (\mathcal K_d\cap \mathcal A)\in \mathord{\mathsf{K}} (P_s(X))$
by
$\mathord{\uparrow}_{\mathsf{K}(X)} (\mathcal K_d\cap \mathcal A)\in \mathord{\mathsf{K}} (P_s(X))$
by
![]() $\mathcal O(P_S(X))\subseteq \sigma (\mathord{\mathsf{K}} (X))$
. By Lemma 11,
$\mathcal O(P_S(X))\subseteq \sigma (\mathord{\mathsf{K}} (X))$
. By Lemma 11,
![]() $K_d=\bigcup \mathord{\uparrow}_{\mathsf{K}(X)} (\mathcal K_d\cap \mathcal A)=\bigcup (\mathcal K_d\cap \mathcal A)\in \mathord{\mathsf{K}} (X)$
. Since
$K_d=\bigcup \mathord{\uparrow}_{\mathsf{K}(X)} (\mathcal K_d\cap \mathcal A)=\bigcup (\mathcal K_d\cap \mathcal A)\in \mathord{\mathsf{K}} (X)$
. Since
![]() $\mathcal A=\mathord{\downarrow}_{\mathord{\mathsf{K}} (X)}\mathcal A$
and
$\mathcal A=\mathord{\downarrow}_{\mathord{\mathsf{K}} (X)}\mathcal A$
and
![]() $\mathcal K_d\cap \mathcal A\neq\emptyset$
, we have
$\mathcal K_d\cap \mathcal A\neq\emptyset$
, we have
![]() $K_d\in\mathcal A$
.
$K_d\in\mathcal A$
.
Claim 2:
![]() $\{K_d : d\in D\}\subseteq \mathord{\mathsf{K}} (X)$
is filtered (by Claim 1 and the filteredness of
$\{K_d : d\in D\}\subseteq \mathord{\mathsf{K}} (X)$
is filtered (by Claim 1 and the filteredness of
![]() $\{\mathcal K_d : d\in D\}$
).
$\{\mathcal K_d : d\in D\}$
).
Claim 3:
![]() $K=\bigcap_{d\in D}K_d\in \mathord{\mathsf{K}} (X)$
and
$K=\bigcap_{d\in D}K_d\in \mathord{\mathsf{K}} (X)$
and
![]() $K\in \mathcal A$
.
$K\in \mathcal A$
.
By the well-filteredness of X,
![]() $K=\bigcap_{d\in D}K_d\in \mathord{\mathsf{K}} (X)$
. By Claims 1, 2 and Lemma 9,
$K=\bigcap_{d\in D}K_d\in \mathord{\mathsf{K}} (X)$
. By Claims 1, 2 and Lemma 9,
![]() $K=\bigvee_{\mathord{\mathsf{K}} (X)} \{K_d : d\in D\}\in \mathcal A$
since
$K=\bigvee_{\mathord{\mathsf{K}} (X)} \{K_d : d\in D\}\in \mathcal A$
since
![]() $\mathcal A\in \mathcal C(\Sigma \mathord{\mathsf{K}} (X))$
.
$\mathcal A\in \mathcal C(\Sigma \mathord{\mathsf{K}} (X))$
.
Claim 4: For each
![]() $k\in K$
,
$k\in K$
,
![]() $\mathcal A\subseteq \Diamond_{\mathord{\mathsf{K}} (X)}\overline{\{k\}}$
.
$\mathcal A\subseteq \Diamond_{\mathord{\mathsf{K}} (X)}\overline{\{k\}}$
.
For each
![]() $d\in D$
, we have
$d\in D$
, we have
![]() $k\in K\subseteq K_d=\bigcup (\mathcal K_d\cap \mathcal A)$
, whence there is
$k\in K\subseteq K_d=\bigcup (\mathcal K_d\cap \mathcal A)$
, whence there is
![]() $G_d\in \mathcal K_d\cap \mathcal A$
such that
$G_d\in \mathcal K_d\cap \mathcal A$
such that
![]() $k\in G_d$
, and consequently,
$k\in G_d$
, and consequently,
![]() $G_d\in \mathcal K_d\cap \mathcal A\cap \Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}$
. Therefore,
$G_d\in \mathcal K_d\cap \mathcal A\cap \Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}$
. Therefore,
![]() $\mathcal A\cap \Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}\in M(\{\mathcal K_d : d\in D\})$
. By the minimality of
$\mathcal A\cap \Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}\in M(\{\mathcal K_d : d\in D\})$
. By the minimality of
![]() $\mathcal A$
and
$\mathcal A$
and
![]() $\Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}\in \mathcal C(P_S(X))\subseteq \mathcal C(\Sigma~\!\!\mathord{\mathsf{K}} (X))$
, we have
$\Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}\in \mathcal C(P_S(X))\subseteq \mathcal C(\Sigma~\!\!\mathord{\mathsf{K}} (X))$
, we have
![]() $\mathcal A=\Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}\bigcap\mathcal A$
, that is,
$\mathcal A=\Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}\bigcap\mathcal A$
, that is,
![]() $\mathcal A\subseteq \Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}$
.
$\mathcal A\subseteq \Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}$
.
Claim 5:
![]() $\mathcal A=\mathord{\downarrow}_{\mathord{\mathsf{K}} (X)}K$
.
$\mathcal A=\mathord{\downarrow}_{\mathord{\mathsf{K}} (X)}K$
.
By Claims 3 and 4,
![]() $\mathord{\downarrow}_{\mathord{\mathsf{K}} (X)}K\subseteq\mathcal A\subseteq \bigcap_{k\in K} \Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}$
. Clearly,
$\mathord{\downarrow}_{\mathord{\mathsf{K}} (X)}K\subseteq\mathcal A\subseteq \bigcap_{k\in K} \Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}$
. Clearly,
 $$\begin{array}{lll} G\in \bigcap_{k\in K} \Diamond_{\mathord{\mathsf{K}} (X)}\overline{\{k\}} &\Leftrightarrow& \forall k\in K, G \in \Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}\\ &\Leftrightarrow&\forall k\in K, G\cap \overline{\{k\}}\neq\emptyset\\ &\Leftrightarrow& \forall k\in K, k\in G\\ &\Leftrightarrow& K\subseteq G. \end{array}$$
$$\begin{array}{lll} G\in \bigcap_{k\in K} \Diamond_{\mathord{\mathsf{K}} (X)}\overline{\{k\}} &\Leftrightarrow& \forall k\in K, G \in \Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}\\ &\Leftrightarrow&\forall k\in K, G\cap \overline{\{k\}}\neq\emptyset\\ &\Leftrightarrow& \forall k\in K, k\in G\\ &\Leftrightarrow& K\subseteq G. \end{array}$$
This implies that
![]() $\bigcap_{k\in K} \Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}=\mathord{\downarrow}_{\mathord{\mathsf{K}} (X)}K$
, and hence,
$\bigcap_{k\in K} \Diamond_{\mathord{\mathsf{K}} (K)}\overline{\{k\}}=\mathord{\downarrow}_{\mathord{\mathsf{K}} (X)}K$
, and hence,
![]() $\mathcal A=\mathord{\downarrow}_{\mathord{\mathsf{K}} (X)}K$
.
$\mathcal A=\mathord{\downarrow}_{\mathord{\mathsf{K}} (X)}K$
.
Claim 6:
![]() $K\in \bigcap_{d\in D}\mathcal K_d$
.
$K\in \bigcap_{d\in D}\mathcal K_d$
.
For each
![]() $d\in D$
, by
$d\in D$
, by
![]() $\mathcal K_d\bigcap \mathcal A\neq\emptyset$
,
$\mathcal K_d\bigcap \mathcal A\neq\emptyset$
,
![]() $\mathcal K_d=\mathord{\uparrow}_{\mathord{\mathsf{K}} (X)}\mathcal K_d$
and
$\mathcal K_d=\mathord{\uparrow}_{\mathord{\mathsf{K}} (X)}\mathcal K_d$
and
![]() $\mathcal A=\mathord{\downarrow}_{\mathord{\mathsf{K}} (X)}K$
, we have
$\mathcal A=\mathord{\downarrow}_{\mathord{\mathsf{K}} (X)}K$
, we have
![]() $K\in \mathcal K_d$
, whence
$K\in \mathcal K_d$
, whence
![]() $K\in \bigcap_{d\in D}\mathcal K_d\subseteq \mathcal U$
, being a contradiction with
$K\in \bigcap_{d\in D}\mathcal K_d\subseteq \mathcal U$
, being a contradiction with
![]() $K\in \mathcal A\subseteq \mathord{\mathsf{K}} (X)\setminus \mathcal U$
.
$K\in \mathcal A\subseteq \mathord{\mathsf{K}} (X)\setminus \mathcal U$
.
Therefore, there is
![]() $d_0\in D$
such that
$d_0\in D$
such that
![]() $\mathcal K_{d_0}\subseteq\mathcal U$
, proving that
$\mathcal K_{d_0}\subseteq\mathcal U$
, proving that
![]() $\Sigma~\!\! \mathord{\mathsf{K}} (X)$
is well-filtered.
$\Sigma~\!\! \mathord{\mathsf{K}} (X)$
is well-filtered.
Definition 59.
A poset P is called a well-filtered dcpo if its Scott space
![]() $\Sigma P$
is well-filtered. Let
$\Sigma P$
is well-filtered. Let
![]() $\mathbf{DCPO}_w$
denote the full subcategory of
$\mathbf{DCPO}_w$
denote the full subcategory of
![]() $\mathbf{DCPO}$
of well-filtered dcpos.
$\mathbf{DCPO}$
of well-filtered dcpos.
Proposition 60.
For any well-filtered space X, let
![]() $\Phi(X)=\mathord{\mathsf{K}}(X)$
. Then
$\Phi(X)=\mathord{\mathsf{K}}(X)$
. Then
![]() $\Phi : \mathbf{Top}_w \longrightarrow \mathbf{DCPO}_w$
is a covariant functor, where for any
$\Phi : \mathbf{Top}_w \longrightarrow \mathbf{DCPO}_w$
is a covariant functor, where for any
![]() $f : X \longrightarrow Y$
in
$f : X \longrightarrow Y$
in
![]() $\mathbf{Top}_w$
,
$\mathbf{Top}_w$
,
![]() $\Phi(f) : \Phi(X) \longrightarrow \Phi(Y)$
is defined by
$\Phi(f) : \Phi(X) \longrightarrow \Phi(Y)$
is defined by
![]() $\Phi(f)(K)=\mathord{\uparrow} f(K)$
for all
$\Phi(f)(K)=\mathord{\uparrow} f(K)$
for all
![]() $ K\in\Phi(X)$
.
$ K\in\Phi(X)$
.
Proof. Let
![]() $f : X \longrightarrow Y$
be a morphism in
$f : X \longrightarrow Y$
be a morphism in
![]() $\mathbf{Top}_w$
.
$\mathbf{Top}_w$
.
Claim 1:
![]() $\Phi(f) : \Phi(X) \longrightarrow \Phi(Y)$
is well-defined.
$\Phi(f) : \Phi(X) \longrightarrow \Phi(Y)$
is well-defined.
By Theorem 58,
![]() $\Phi(X)$
and
$\Phi(X)$
and
![]() $\Phi(Y)$
are well-filtered dcpos. For any
$\Phi(Y)$
are well-filtered dcpos. For any
![]() $ K\in\Phi(X)$
, since
$ K\in\Phi(X)$
, since
![]() $f : X \longrightarrow Y$
is continuous,
$f : X \longrightarrow Y$
is continuous,
![]() $\Phi(f)(K)=\mathord{\uparrow} f(K)\in \Phi(Y)$
. Thus,
$\Phi(f)(K)=\mathord{\uparrow} f(K)\in \Phi(Y)$
. Thus,
![]() $\Phi(f) : \Phi(X) \longrightarrow \Phi(Y)$
is well-defined.
$\Phi(f) : \Phi(X) \longrightarrow \Phi(Y)$
is well-defined.
Claim 2:
![]() $\Phi(f) : \Phi(X) \longrightarrow \Phi(Y)$
is Scott continuous.
$\Phi(f) : \Phi(X) \longrightarrow \Phi(Y)$
is Scott continuous.
Let
![]() $\{K_d : d\in D\}\in \mathcal{D}(\Phi(X))$
(note that
$\{K_d : d\in D\}\in \mathcal{D}(\Phi(X))$
(note that
![]() $\Phi(X)$
is endowed with the Smyth order). Then by Lemma 9 and Proposition 21, we have that
$\Phi(X)$
is endowed with the Smyth order). Then by Lemma 9 and Proposition 21, we have that
![]() $\bigvee_{\Phi(X)} \{K_d : d\in D\}=\bigcap_{d\in D}K_d$
and
$\bigvee_{\Phi(X)} \{K_d : d\in D\}=\bigcap_{d\in D}K_d$
and
 $$\begin{array}{lll}\Phi(f)(\bigvee_{\Phi(X)} \{K_d : d\in D\})&=&\Phi(f)(\bigcap_{d\in D}K_d)\\&=&\mathord{\uparrow} f(\bigcap_{d\in D}K_d)\\&=&\mathord{\uparrow} \bigcap_{d\in D}\mathord{\uparrow} f(K_d)\\&=&\bigvee_{\Phi(Y)} \{\Phi(f)(K_d) : d\in D\}.\end{array}$$
$$\begin{array}{lll}\Phi(f)(\bigvee_{\Phi(X)} \{K_d : d\in D\})&=&\Phi(f)(\bigcap_{d\in D}K_d)\\&=&\mathord{\uparrow} f(\bigcap_{d\in D}K_d)\\&=&\mathord{\uparrow} \bigcap_{d\in D}\mathord{\uparrow} f(K_d)\\&=&\bigvee_{\Phi(Y)} \{\Phi(f)(K_d) : d\in D\}.\end{array}$$
It follows that
![]() $\Phi(f) : \Phi(X) \longrightarrow \Phi(Y)$
is Scott continuous by Lemma 12.
$\Phi(f) : \Phi(X) \longrightarrow \Phi(Y)$
is Scott continuous by Lemma 12.
Claim 3:
![]() $\Phi(id_X)=id_{\Phi(X)}$
$\Phi(id_X)=id_{\Phi(X)}$
For each
![]() $K\in \Phi(X)$
,
$K\in \Phi(X)$
,
![]() $P_S(id_X)(K)=\mathord{\uparrow} id_X(K)=\mathord{\uparrow} K=K$
.
$P_S(id_X)(K)=\mathord{\uparrow} id_X(K)=\mathord{\uparrow} K=K$
.
Claim 4: For any morphism
![]() $g : Y \longrightarrow Z$
in
$g : Y \longrightarrow Z$
in
![]() $\mathbf{Top}_w$
,
$\mathbf{Top}_w$
,
![]() $\Phi(g\circ f)=\Phi(g)\circ \Phi(f)$
.
$\Phi(g\circ f)=\Phi(g)\circ \Phi(f)$
.
For any
![]() $K\in \Phi(X)$
,
$K\in \Phi(X)$
,
![]() $\Phi(g\circ f)(K)=\mathord{\uparrow} g\circ f(K)=\mathord{\uparrow} g(f(K))=\mathord{\uparrow} g(\mathord{\uparrow} f(K))=\Phi(g)\circ \Phi(f)(K)$
. So
$\Phi(g\circ f)(K)=\mathord{\uparrow} g\circ f(K)=\mathord{\uparrow} g(f(K))=\mathord{\uparrow} g(\mathord{\uparrow} f(K))=\Phi(g)\circ \Phi(f)(K)$
. So
![]() $\Phi(g\circ f)=\Phi(g)\circ \Phi(f)$
.
$\Phi(g\circ f)=\Phi(g)\circ \Phi(f)$
.
Thus,
![]() $\Phi : \mathbf{Top}_w \longrightarrow \mathbf{DCPO}_w$
is a covariant functor.
$\Phi : \mathbf{Top}_w \longrightarrow \mathbf{DCPO}_w$
is a covariant functor.
Corollary 61.
For any well-filtered dcpo P, let
![]() $\Phi_S(P)=\mathord{\mathsf{K}}(\Sigma P)$
. Then,
$\Phi_S(P)=\mathord{\mathsf{K}}(\Sigma P)$
. Then,
![]() $\Phi_S : \mathbf{DCPO}_w \longrightarrow \mathbf{DCPO}_w$
is a covariant functor, where for any
$\Phi_S : \mathbf{DCPO}_w \longrightarrow \mathbf{DCPO}_w$
is a covariant functor, where for any
![]() $f : P \longrightarrow Q$
in
$f : P \longrightarrow Q$
in
![]() $\mathbf{DCPO}_w$
,
$\mathbf{DCPO}_w$
,
![]() $\Phi_S(f) : \Phi_S(P) \longrightarrow \Phi_S(Q)$
is defined by
$\Phi_S(f) : \Phi_S(P) \longrightarrow \Phi_S(Q)$
is defined by
![]() $\Phi_S(f)(K)=\mathord{\uparrow} f(K)$
for all
$\Phi_S(f)(K)=\mathord{\uparrow} f(K)$
for all
![]() $K\in\Phi_S(P)$
.
$K\in\Phi_S(P)$
.
Example 68 shows that unlike Smyth power spaces (see Theorem 24), the converse of Theorem 58 does not hold.
From Theorems 41 and 58, we deduce the following result.
Corollary 62. For a well-filtered space X, the following two conditions are equivalent:
-
(1)
 $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is core-compact.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is core-compact.
-
(2)
 $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is locally compact.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is locally compact.
By Theorems 36 and 58, we have the following corollary.
Corollary 63. For a well-filtered space X, the following three conditions are equivalent:
-
(1)
 $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is sober.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is sober.
-
(2)
 $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is Rudin.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is Rudin.
-
(3)
 $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is well-filtered determined.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is well-filtered determined.
Proposition 64. Let X be a well-filtered space.
-
(1) If
 $\mathcal K\in\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))$
, then
$\mathcal K\in\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))$
, then
 $\bigcup \mathcal K\in\mathord{\mathsf{K}}(X)$
.
$\bigcup \mathcal K\in\mathord{\mathsf{K}}(X)$
. -
(2) The mapping
 $\bigcup : \Sigma~\!\!\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X)) \longrightarrow \Sigma~\!\!\mathord{\mathsf{K}} (X)$
,
$\bigcup : \Sigma~\!\!\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X)) \longrightarrow \Sigma~\!\!\mathord{\mathsf{K}} (X)$
,
 $\mathcal K\mapsto \bigcup \mathcal K$
, is continuous.
$\mathcal K\mapsto \bigcup \mathcal K$
, is continuous.
Proof. (1): By Corollary 25,
![]() $\mathcal O(P_S(X))\subseteq \sigma (\mathord{\mathsf{K}} (X))$
. For
$\mathcal O(P_S(X))\subseteq \sigma (\mathord{\mathsf{K}} (X))$
. For
![]() $\mathcal K\in \mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))$
, we have
$\mathcal K\in \mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))$
, we have
![]() $\mathcal K\in \mathord{\mathsf{K}}(P_S(X))$
since
$\mathcal K\in \mathord{\mathsf{K}}(P_S(X))$
since
![]() $\mathcal O(P_S(X))\subseteq \sigma (\mathord{\mathsf{K}} (X))$
. Then by Lemma 11,
$\mathcal O(P_S(X))\subseteq \sigma (\mathord{\mathsf{K}} (X))$
. Then by Lemma 11,
![]() $\bigcup \mathcal K\in\mathord{\mathsf{K}}(X)$
.
$\bigcup \mathcal K\in\mathord{\mathsf{K}}(X)$
.
(2): Suppose that
![]() $\{\mathcal K_d : d\in D\}\subseteq \mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))$
is directed (with the Smyth order) for which
$\{\mathcal K_d : d\in D\}\subseteq \mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))$
is directed (with the Smyth order) for which
![]() $\bigvee_{\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))}\{\mathcal K_d : d\in D\}$
exists. Then by Lemma 9,
$\bigvee_{\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))}\{\mathcal K_d : d\in D\}$
exists. Then by Lemma 9,
![]() $\bigvee_{\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))}\{\mathcal K_d : d\in D\}=\bigcap_{d\in D}\mathcal K_d$
. It follows that
$\bigvee_{\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))}\{\mathcal K_d : d\in D\}=\bigcap_{d\in D}\mathcal K_d$
. It follows that
![]() $\bigcup \bigvee_{\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))}\{\mathcal K_d : d\in D\}=\bigcup \bigcap_{d\in D}\mathcal K_d$
and
$\bigcup \bigvee_{\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))}\{\mathcal K_d : d\in D\}=\bigcup \bigcap_{d\in D}\mathcal K_d$
and
![]() $\bigvee_{d\in D} \bigcup \mathcal K_d=\bigcap_{d\in D}\bigcup \mathcal K_d=\bigcup_{\varphi\in \prod_{d\in D}\mathcal K_d}\bigcap_{d\in D}\varphi(d)$
by Lemma 9. For each
$\bigvee_{d\in D} \bigcup \mathcal K_d=\bigcap_{d\in D}\bigcup \mathcal K_d=\bigcup_{\varphi\in \prod_{d\in D}\mathcal K_d}\bigcap_{d\in D}\varphi(d)$
by Lemma 9. For each
![]() $K\in \bigcap_{d\in D}\mathcal K_d$
, define
$K\in \bigcap_{d\in D}\mathcal K_d$
, define
![]() $\varphi_{K}\in \prod_{d\in D}\mathcal K_d$
by
$\varphi_{K}\in \prod_{d\in D}\mathcal K_d$
by
![]() $\varphi_K(d)\equiv K$
for all
$\varphi_K(d)\equiv K$
for all
![]() $d\in D$
. Then,
$d\in D$
. Then,
![]() $\bigcap_{d\in D}\varphi_K(d)=K$
. Hence
$\bigcap_{d\in D}\varphi_K(d)=K$
. Hence
![]() $\bigcup \bigcap_{d\in D}\mathcal K_d\subseteq \bigcup_{\varphi\in \prod_{d\in D}\mathcal K_d}\bigcap_{d\in D}\varphi(d)$
.
$\bigcup \bigcap_{d\in D}\mathcal K_d\subseteq \bigcup_{\varphi\in \prod_{d\in D}\mathcal K_d}\bigcap_{d\in D}\varphi(d)$
.
Conversely, for each
![]() $\varphi\in \prod_{d\in D}\mathcal K_d$
,
$\varphi\in \prod_{d\in D}\mathcal K_d$
,
![]() $x\in \bigcap_{d\in D}\varphi(d),$
and
$x\in \bigcap_{d\in D}\varphi(d),$
and
![]() $d^{\prime}\in D$
, we have that
$d^{\prime}\in D$
, we have that
![]() $\mathord{\uparrow} x\sqsupseteq\varphi (d^{\prime})\in \mathcal K_{d^{\prime}}=\mathord{\uparrow}_{\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))}\mathcal K_d^{\prime}$
, and consequently,
$\mathord{\uparrow} x\sqsupseteq\varphi (d^{\prime})\in \mathcal K_{d^{\prime}}=\mathord{\uparrow}_{\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))}\mathcal K_d^{\prime}$
, and consequently,
![]() $\mathord{\uparrow} x\in \bigcap_{d^{\prime}\in D}\mathcal K_d^{\prime}$
and hence,
$\mathord{\uparrow} x\in \bigcap_{d^{\prime}\in D}\mathcal K_d^{\prime}$
and hence,
![]() $\mathord{\uparrow} x\subseteq \bigcup \bigcap_{d\in D}\mathcal K_d$
. It follows that
$\mathord{\uparrow} x\subseteq \bigcup \bigcap_{d\in D}\mathcal K_d$
. It follows that
![]() $\bigcap_{d\in D}\varphi(d)\subseteq \bigcup \bigcap_{d\in D}\mathcal K_d$
. Therefore,
$\bigcap_{d\in D}\varphi(d)\subseteq \bigcup \bigcap_{d\in D}\mathcal K_d$
. Therefore,
![]() $\bigcup_{\varphi\in \prod_{d\in D}\mathcal K_d}\bigcap_{d\in D}\varphi(d)\subseteq \bigcup \bigcap_{d\in D}\mathcal K_d$
.
$\bigcup_{\varphi\in \prod_{d\in D}\mathcal K_d}\bigcap_{d\in D}\varphi(d)\subseteq \bigcup \bigcap_{d\in D}\mathcal K_d$
.
Thus,
![]() $\bigcup \bigvee_{\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))}\{\mathcal K_d : d\in D\}=\bigvee_{d\in D} \bigcup \mathcal K_d$
. By Lemma 12,
$\bigcup \bigvee_{\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X))}\{\mathcal K_d : d\in D\}=\bigvee_{d\in D} \bigcup \mathcal K_d$
. By Lemma 12,
![]() $\bigcup : \Sigma~\!\!\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X)) \longrightarrow \Sigma~\!\!\mathord{\mathsf{K}} (X)$
is continuous.
$\bigcup : \Sigma~\!\!\mathord{\mathsf{K}}(\Sigma~\!\!\mathord{\mathsf{K}} (X)) \longrightarrow \Sigma~\!\!\mathord{\mathsf{K}} (X)$
is continuous.
Proposition 65.
Let X be a
![]() $T_0$
space. If the upper Vietoris topology is coarser than the Scott topology on
$T_0$
space. If the upper Vietoris topology is coarser than the Scott topology on
![]() $\mathsf{K}(X)$
(i.e.,
$\mathsf{K}(X)$
(i.e.,
![]() $\mathcal O(P_S(X))\subseteq \sigma (\mathsf{K}(X))$
), and
$\mathcal O(P_S(X))\subseteq \sigma (\mathsf{K}(X))$
), and
![]() $\Sigma~\!\! \mathsf{K}(X)$
is well-filtered, then X is well-filtered.
$\Sigma~\!\! \mathsf{K}(X)$
is well-filtered, then X is well-filtered.
Proof. Suppose that
![]() $\{K_d : d\in D\}\subseteq \mathsf{K}(X)$
is filtered and
$\{K_d : d\in D\}\subseteq \mathsf{K}(X)$
is filtered and
![]() $U\in \mathcal O(X)$
with
$U\in \mathcal O(X)$
with
![]() $\bigcap_{d\in D}K_d\subseteq U$
. Then,
$\bigcap_{d\in D}K_d\subseteq U$
. Then,
![]() $\{\mathord{\uparrow}_{\mathsf{K}(X)}K_d : d\in D\}\subseteq \mathsf{K}(\Sigma~\!\! \mathsf{K}(X))$
is filtered,
$\{\mathord{\uparrow}_{\mathsf{K}(X)}K_d : d\in D\}\subseteq \mathsf{K}(\Sigma~\!\! \mathsf{K}(X))$
is filtered,
![]() $\Box U\in \mathcal O(P_S(X))\subseteq \sigma (\mathsf{K}(X))$
and
$\Box U\in \mathcal O(P_S(X))\subseteq \sigma (\mathsf{K}(X))$
and
![]() $\bigcap_{d\in D}\mathord{\uparrow}_{\mathsf{K}(X)}K_d\subseteq \Box U$
. By the well-filteredness of
$\bigcap_{d\in D}\mathord{\uparrow}_{\mathsf{K}(X)}K_d\subseteq \Box U$
. By the well-filteredness of
![]() $\Sigma~\!\! \mathsf{K}(X)$
, there is
$\Sigma~\!\! \mathsf{K}(X)$
, there is
![]() $d\in D$
such that
$d\in D$
such that
![]() $\mathord{\uparrow}_{\mathsf{K}(X)}K_d\subseteq \Box U$
, and hence,
$\mathord{\uparrow}_{\mathsf{K}(X)}K_d\subseteq \Box U$
, and hence,
![]() $K_d\subseteq U$
. Thus, X is well-filtered.
$K_d\subseteq U$
. Thus, X is well-filtered.
Example 68 below shows that when X lacks the condition of
![]() $\mathcal O(P_S(X))\subseteq \sigma (\mathsf{K}(X))$
, Proposition 65 may not hold.
$\mathcal O(P_S(X))\subseteq \sigma (\mathsf{K}(X))$
, Proposition 65 may not hold.
Corollary 66.
For a
![]() $T_0$
space X, the following conditions are equivalent:
$T_0$
space X, the following conditions are equivalent:
-
(1) X is well-filtered.
-
(2) The upper Vietoris topology is coarser than the Scott topology on
 $\mathsf{K}(X)$
, and
$\mathsf{K}(X)$
, and
 $\Sigma~\!\! \mathsf{K}(X)$
is well-filtered.
$\Sigma~\!\! \mathsf{K}(X)$
is well-filtered.
-
(3) The upper Vietoris topology is coarser than the Scott topology on
 $\mathsf{K}(X)$
, and
$\mathsf{K}(X)$
, and
 $\Sigma~\!\! \mathsf{K}(X)$
is a d-space.
$\Sigma~\!\! \mathsf{K}(X)$
is a d-space.
-
(4)
 $\mathsf{K}(X)$
is a dcpo, and the upper Vietoris topology is coarser than the Scott topology on
$\mathsf{K}(X)$
is a dcpo, and the upper Vietoris topology is coarser than the Scott topology on
 $\mathsf{K}(X)$
.
$\mathsf{K}(X)$
.
Proof. (1)
![]() $\Rightarrow$
(2): By Corollary 25 and Theorem 58.
$\Rightarrow$
(2): By Corollary 25 and Theorem 58.
(2)
![]() $\Rightarrow$
(3): By Remark 20.
$\Rightarrow$
(3): By Remark 20.
(3)
![]() $\Rightarrow$
(4): Trivial.
$\Rightarrow$
(4): Trivial.
(4)
![]() $\Rightarrow$
(1): By (4),
$\Rightarrow$
(1): By (4),
![]() $P_S(X)$
is a d-space, whence X is well-filtered by Theorem 24.
$P_S(X)$
is a d-space, whence X is well-filtered by Theorem 24.
7. Non-sobriety of Scott Topology on Smyth Power Poset of a Sober Space
In this section, we investigate the following question:
Question 3. Is the Scott space
![]() $\Sigma~\!\! \mathord{\mathsf{K}}(X)$
of a sober space X sober?
$\Sigma~\!\! \mathord{\mathsf{K}}(X)$
of a sober space X sober?
First, the following example shows that there is a well-filtered space X for which the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a first-countable sober c-space, but X is not sober although the Scott space
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a first-countable sober c-space, but X is not sober although the Scott space
![]() $\Sigma~\!\! \mathord{\mathsf{K}} (X)$
is sober by Corollary 94. Hence, by Corollaries 40 and 50, X is neither core-compact nor first-countable. So the sobriety of the Scott space
$\Sigma~\!\! \mathord{\mathsf{K}} (X)$
is sober by Corollary 94. Hence, by Corollaries 40 and 50, X is neither core-compact nor first-countable. So the sobriety of the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
of a
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
of a
![]() $T_0$
space X does not imply the sobriety of X in general.
$T_0$
space X does not imply the sobriety of X in general.
Example 67. Let X be an uncountably infinite set and
![]() $X_{coc}$
the space equipped with the co-countable topology (the empty set and the complements of countable subsets of X are open). Then
$X_{coc}$
the space equipped with the co-countable topology (the empty set and the complements of countable subsets of X are open). Then
(a)
![]() $\mathcal C(X_{coc})=\{\emptyset, X\}\bigcup X^{(\leq\omega)}$
,
$\mathcal C(X_{coc})=\{\emptyset, X\}\bigcup X^{(\leq\omega)}$
,
![]() $X_{coc}$
is
$X_{coc}$
is
![]() $T_1$
and hence a d-space, and the specialization order on
$T_1$
and hence a d-space, and the specialization order on
![]() $X_{coc}$
is the discrete order.
$X_{coc}$
is the discrete order.
(b) Neither
![]() $X_{coc}$
nor
$X_{coc}$
nor
![]() $P_S(X_{coc})$
is first-countable.
$P_S(X_{coc})$
is first-countable.
For a point
![]() $x\in X$
, suppose that there is a countable base
$x\in X$
, suppose that there is a countable base
![]() $\{X\setminus C_n : n\in \mathbb{N}, C_n\in X^{(\leq\omega)}\}$
at x in
$\{X\setminus C_n : n\in \mathbb{N}, C_n\in X^{(\leq\omega)}\}$
at x in
![]() $X_{coc}$
. Let
$X_{coc}$
. Let
![]() $C=\bigcup_{n\in \mathbb{N}}C_n$
. Then,
$C=\bigcup_{n\in \mathbb{N}}C_n$
. Then,
![]() $C\in X^{(\leq\omega)}$
. Select
$C\in X^{(\leq\omega)}$
. Select
![]() $t\in X\setminus (C\cup\{x\})$
and let
$t\in X\setminus (C\cup\{x\})$
and let
![]() $U=X\setminus \{t\}$
. Then,
$U=X\setminus \{t\}$
. Then,
![]() $x\in U\in \mathcal O(X_{coc})$
. But
$x\in U\in \mathcal O(X_{coc})$
. But
![]() $X\setminus C_n\not\subseteq U$
for every
$X\setminus C_n\not\subseteq U$
for every
![]() $n\in \mathbb{N}$
, a contradiction. Thus,
$n\in \mathbb{N}$
, a contradiction. Thus,
![]() $X_{coc}$
is not first-countable. Since the first-countability is a hereditary property and
$X_{coc}$
is not first-countable. Since the first-countability is a hereditary property and
![]() $X_{coc}$
is homeomorphic to the subspace
$X_{coc}$
is homeomorphic to the subspace
![]() $\mathcal S^u(X_{coc})$
of
$\mathcal S^u(X_{coc})$
of
![]() $P_S(X_{coc})$
(see Remark 4 or Proposition 102 below),
$P_S(X_{coc})$
(see Remark 4 or Proposition 102 below),
![]() $P_S(X_{coc})$
is not first-countable.
$P_S(X_{coc})$
is not first-countable.
(c)
![]() ${\mathsf{Irr}}_c(X_{coc})=\{\overline{\{x\}} : x\in X\}\cup\{X\}=\{\{x\} : x\in X\}\cup\{X\}$
. Therefore,
${\mathsf{Irr}}_c(X_{coc})=\{\overline{\{x\}} : x\in X\}\cup\{X\}=\{\{x\} : x\in X\}\cup\{X\}$
. Therefore,
![]() $X_{coc}$
is not sober.
$X_{coc}$
is not sober.
(d)
![]() $\mathord{\mathsf{K}} (X_{coc})=X^{(<\omega)}\setminus \{\emptyset\}$
and
$\mathord{\mathsf{K}} (X_{coc})=X^{(<\omega)}\setminus \{\emptyset\}$
and
![]() ${\rm int}\ K=\emptyset$
for all
${\rm int}\ K=\emptyset$
for all
![]() $K\in \mathord{\mathsf{K}} (X_{coc})$
, and hence,
$K\in \mathord{\mathsf{K}} (X_{coc})$
, and hence,
![]() $X_{coc}$
is not locally compact.
$X_{coc}$
is not locally compact.
Clearly, every finite subset is compact. Conversely, if
![]() $C\subseteq X$
is infinite, then C has an infinite countable subset
$C\subseteq X$
is infinite, then C has an infinite countable subset
![]() $\{c_n : n\in\mathbb N\}$
. Let
$\{c_n : n\in\mathbb N\}$
. Let
![]() $C_0=\{c_n : n\in\mathbb N\}$
and
$C_0=\{c_n : n\in\mathbb N\}$
and
![]() $U_m=(X\setminus C_0)\cup \{c_m\}$
for each
$U_m=(X\setminus C_0)\cup \{c_m\}$
for each
![]() $m\in \mathbb N$
. Then,
$m\in \mathbb N$
. Then,
![]() $\{U_n : n\in\mathbb N\}$
is an open cover of C, but has no finite subcover. Hence, C is not compact. Thus,
$\{U_n : n\in\mathbb N\}$
is an open cover of C, but has no finite subcover. Hence, C is not compact. Thus,
![]() $\mathord{\mathsf{K}} (X_{coc})=X^{(<\omega)}\setminus \{\emptyset\}$
. Clearly,
$\mathord{\mathsf{K}} (X_{coc})=X^{(<\omega)}\setminus \{\emptyset\}$
. Clearly,
![]() ${\rm int}~\!K=\emptyset$
for all
${\rm int}~\!K=\emptyset$
for all
![]() $K\in \mathord{\mathsf{K}} (X_{coc})$
. Hence,
$K\in \mathord{\mathsf{K}} (X_{coc})$
. Hence,
![]() $X_{coc}$
is not locally compact.
$X_{coc}$
is not locally compact.
(e)
![]() $X_{coc}$
is well-filtered and not core-compact.
$X_{coc}$
is well-filtered and not core-compact.
Suppose that
![]() $\{F_d : d\in D\}\subseteq \mathord{\mathsf{K}} (X_{coc})$
is a filtered family and
$\{F_d : d\in D\}\subseteq \mathord{\mathsf{K}} (X_{coc})$
is a filtered family and
![]() $U\in \mathcal O(X_{coc})$
with
$U\in \mathcal O(X_{coc})$
with
![]() $\bigcap_{d\in D}F_d\subseteq U$
. As
$\bigcap_{d\in D}F_d\subseteq U$
. As
![]() $\{F_d : d\in D\}$
is filtered and all
$\{F_d : d\in D\}$
is filtered and all
![]() $F_d$
are finite,
$F_d$
are finite,
![]() $\{F_d : d\in D\}$
has a least element
$\{F_d : d\in D\}$
has a least element
![]() $F_{d_0}$
, and hence,
$F_{d_0}$
, and hence,
![]() $F_{d_0}=\bigcap_{d\in D}F_d\subseteq U$
, proving that
$F_{d_0}=\bigcap_{d\in D}F_d\subseteq U$
, proving that
![]() $X_{coc}$
is well-filtered. By (d) and Theorem 41,
$X_{coc}$
is well-filtered. By (d) and Theorem 41,
![]() $X_{coc}$
is not core-compact.
$X_{coc}$
is not core-compact.
(f)
![]() $\mathord{\mathsf{K}} (X_{coc})$
is a Noetherian dcpo, and hence,
$\mathord{\mathsf{K}} (X_{coc})$
is a Noetherian dcpo, and hence,
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X_{coc})=(\mathord{\mathsf{K}} (X_{coc}), \alpha(\mathord{\mathsf{K}} (X_{coc}))$
is first-countable.
$\Sigma~\!\!\mathord{\mathsf{K}} (X_{coc})=(\mathord{\mathsf{K}} (X_{coc}), \alpha(\mathord{\mathsf{K}} (X_{coc}))$
is first-countable.
Clearly,
![]() $\mathord{\mathsf{K}} (X_{coc})=X^{(<\omega)}\setminus \{\emptyset\}$
(with the Smyth order) is a Noetherian dcpo and
$\mathord{\mathsf{K}} (X_{coc})=X^{(<\omega)}\setminus \{\emptyset\}$
(with the Smyth order) is a Noetherian dcpo and
![]() $\sigma(\mathord{\mathsf{K}} (X_{coc}))=\alpha(\mathord{\mathsf{K}} (X_{coc}))$
. For any
$\sigma(\mathord{\mathsf{K}} (X_{coc}))=\alpha(\mathord{\mathsf{K}} (X_{coc}))$
. For any
![]() $F\in \mathord{\mathsf{K}} (X_{coc})=X^{(<\omega)}\setminus \{\emptyset\}$
,
$F\in \mathord{\mathsf{K}} (X_{coc})=X^{(<\omega)}\setminus \{\emptyset\}$
,
![]() $\{\mathord{\uparrow}_{\mathord{\mathsf{K}} (X_{coc})}F\}$
is a base at F in
$\{\mathord{\uparrow}_{\mathord{\mathsf{K}} (X_{coc})}F\}$
is a base at F in
![]() $\Sigma~\!\! \mathord{\mathsf{K}}(X_{coc})$
. Hence
$\Sigma~\!\! \mathord{\mathsf{K}}(X_{coc})$
. Hence
![]() $\Sigma~\!\! \mathord{\mathsf{K}}(X_{coc})$
is first-countable.
$\Sigma~\!\! \mathord{\mathsf{K}}(X_{coc})$
is first-countable.
(g) The upper Vietoris topology and the Scott topology on
![]() $\mathord{\mathsf{K}} (X_{coc})$
do not agree.
$\mathord{\mathsf{K}} (X_{coc})$
do not agree.
By (e) and Corollary 25,
![]() $\mathcal O(P_S(X_{coc}))\subseteq \sigma (\mathord{\mathsf{K}} (X_{coc})$
. For
$\mathcal O(P_S(X_{coc}))\subseteq \sigma (\mathord{\mathsf{K}} (X_{coc})$
. For
![]() $F\in X^{(<\omega)}\setminus \{\emptyset\}$
,
$F\in X^{(<\omega)}\setminus \{\emptyset\}$
,
![]() $\mathord{\uparrow}_{\mathord{\mathsf{K}} (X_{coc})}F\in \alpha(\mathord{\mathsf{K}} (X_{coc}))=\sigma(\mathord{\mathsf{K}} (X_{coc}))$
but
$\mathord{\uparrow}_{\mathord{\mathsf{K}} (X_{coc})}F\in \alpha(\mathord{\mathsf{K}} (X_{coc}))=\sigma(\mathord{\mathsf{K}} (X_{coc}))$
but
![]() $\mathord{\uparrow}_{\mathord{\mathsf{K}} (X_{coc})}F\not\in \mathcal O(P_S(X_{coc}))$
since there is no
$\mathord{\uparrow}_{\mathord{\mathsf{K}} (X_{coc})}F\not\in \mathcal O(P_S(X_{coc}))$
since there is no
![]() $G\in X^{(<\omega)}$
with
$G\in X^{(<\omega)}$
with
![]() $F\in \Box (X\setminus G)=(X\setminus G)^{(<\omega)}\setminus \{\emptyset\}\subseteq \mathord{\uparrow}_{\mathord{\mathsf{K}} (X_{coc})}F$
. Thus,
$F\in \Box (X\setminus G)=(X\setminus G)^{(<\omega)}\setminus \{\emptyset\}\subseteq \mathord{\uparrow}_{\mathord{\mathsf{K}} (X_{coc})}F$
. Thus,
![]() $\sigma(\mathord{\mathsf{K}} (X_{coc}))\not\subseteq\mathcal O(P_S(X_{coc}))$
.
$\sigma(\mathord{\mathsf{K}} (X_{coc}))\not\subseteq\mathcal O(P_S(X_{coc}))$
.
(h) The Scott space
![]() $\Sigma~\!\! \mathord{\mathsf{K}}(X_{coc})$
is a sober c-space. So it is Rudin and well-filtered determined.
$\Sigma~\!\! \mathord{\mathsf{K}}(X_{coc})$
is a sober c-space. So it is Rudin and well-filtered determined.
![]() $\mathord{\mathsf{K}} (X_{coc})=X^{(<\omega)}\setminus \{\emptyset\}$
(with the Smyth order) is a Noetherian dcpo, and hence, it is an algebraic domain. By Theorem 15 and Proposition 18,
$\mathord{\mathsf{K}} (X_{coc})=X^{(<\omega)}\setminus \{\emptyset\}$
(with the Smyth order) is a Noetherian dcpo, and hence, it is an algebraic domain. By Theorem 15 and Proposition 18,
![]() $\Sigma~\!\! \mathord{\mathsf{K}}(X)$
is a sober c-space. Hence by Theorem 36,
$\Sigma~\!\! \mathord{\mathsf{K}}(X)$
is a sober c-space. Hence by Theorem 36,
![]() $\Sigma~\!\! \mathord{\mathsf{K}}(X)$
is Rudin and well-filtered determined.
$\Sigma~\!\! \mathord{\mathsf{K}}(X)$
is Rudin and well-filtered determined.
(i)
![]() $X_{coc}$
is neither a Rudin space nor a
$X_{coc}$
is neither a Rudin space nor a
![]() $\mathsf{WD}$
space.
$\mathsf{WD}$
space.
By (c), (e) and Theorem 36,
![]() $X_{coc}$
is neither a Rudin space nor a
$X_{coc}$
is neither a Rudin space nor a
![]() $\mathsf{WD}$
space.
$\mathsf{WD}$
space.
(j) The Smyth power space
![]() $P_S(X_{coc})$
is well-filtered but non-sober. Hence, it is neither a Rudin space nor a
$P_S(X_{coc})$
is well-filtered but non-sober. Hence, it is neither a Rudin space nor a
![]() $\mathsf{WD}$
space.
$\mathsf{WD}$
space.
By (c), (e), Theorems 19 and 24,
![]() $P_S(X_{coc})$
is well-filtered and non-sober. Hence,
$P_S(X_{coc})$
is well-filtered and non-sober. Hence,
![]() $P_S(X_{coc})$
is neither a Rudin space nor a
$P_S(X_{coc})$
is neither a Rudin space nor a
![]() $\mathsf{WD}$
space by Theorem 36.
$\mathsf{WD}$
space by Theorem 36.
(k)
![]() $P_S(X_{coc})$
is not core-compact.
$P_S(X_{coc})$
is not core-compact.
By (j) and Corollary 40 (or Theorem 41),
![]() $P_S(X_{coc})$
is not core-compact.
$P_S(X_{coc})$
is not core-compact.
The following example shows there is even a second-countable Noetherian
![]() $T_0$
space X such that the Scott space
$T_0$
space X such that the Scott space
![]() $\Sigma ~\!\!\mathord{\mathsf{K}} (X)$
is a second-countable sober space but X is not well-filtered (and hence not sober).
$\Sigma ~\!\!\mathord{\mathsf{K}} (X)$
is a second-countable sober space but X is not well-filtered (and hence not sober).
Example 68. Let
![]() $P=\mathbb{N}\cup\{\infty\}$
and define an order on P by
$P=\mathbb{N}\cup\{\infty\}$
and define an order on P by
![]() $x\leq_P y$
iff
$x\leq_P y$
iff
![]() $x=y$
or
$x=y$
or
![]() $x\in\mathbb{N}$
and
$x\in\mathbb{N}$
and
![]() $y=\infty$
(see Fig. 3).
$y=\infty$
(see Fig. 3).

Figure 3. The poset P.
Let
![]() $\tau=\{(\mathbb{N}\setminus F)\cup \{\infty\} : F\in \mathbb{N}^{(<\omega)}\}\cup\{\emptyset, P\}\cup \{\{\infty\}\}$
. It is straightforward to verify that
$\tau=\{(\mathbb{N}\setminus F)\cup \{\infty\} : F\in \mathbb{N}^{(<\omega)}\}\cup\{\emptyset, P\}\cup \{\{\infty\}\}$
. It is straightforward to verify that
![]() $\tau$
is a
$\tau$
is a
![]() $T_0$
topology on P and the specialization order of
$T_0$
topology on P and the specialization order of
![]() $(P, \tau)$
agrees with the original order on P. Now we have
$(P, \tau)$
agrees with the original order on P. Now we have
1.
![]() $\mathcal C((P, \tau))=\mathbb{N}^{(<\omega)}\cup \{\emptyset, P\}\cup \{\mathbb{N}\}$
.
$\mathcal C((P, \tau))=\mathbb{N}^{(<\omega)}\cup \{\emptyset, P\}\cup \{\mathbb{N}\}$
.
2.
![]() ${\mathsf{Irr}}_c((P, \tau))=\{\overline{\{n\}}=\{n\} : n\in \mathbb{N}\}\cup\{\overline{\{\infty\}}=P\}\cup\{\mathbb{N}\}$
and hence
${\mathsf{Irr}}_c((P, \tau))=\{\overline{\{n\}}=\{n\} : n\in \mathbb{N}\}\cup\{\overline{\{\infty\}}=P\}\cup\{\mathbb{N}\}$
and hence
![]() $(P, \tau)$
is not sober.
$(P, \tau)$
is not sober.
3.
![]() $\mathord{\mathsf{K}} ((P, \tau))=\{A\cup \{\infty\} : A\subseteq \mathbb{N}\}$
.
$\mathord{\mathsf{K}} ((P, \tau))=\{A\cup \{\infty\} : A\subseteq \mathbb{N}\}$
.
4.
![]() $(P, \tau)$
is not well-filtered.
$(P, \tau)$
is not well-filtered.
Let
![]() $\mathcal K=\{(\mathbb{N}\setminus F)\cup\{\infty\} : F\in \mathbb{N}^{(<\omega)}\}$
. Then,
$\mathcal K=\{(\mathbb{N}\setminus F)\cup\{\infty\} : F\in \mathbb{N}^{(<\omega)}\}$
. Then,
![]() $\mathcal K\subseteq \mathord{\mathsf{K}} ((P, \tau))$
is a filtered family and
$\mathcal K\subseteq \mathord{\mathsf{K}} ((P, \tau))$
is a filtered family and
![]() $\bigcap \mathcal K=\{\infty\}\in \tau$
. But there is no
$\bigcap \mathcal K=\{\infty\}\in \tau$
. But there is no
![]() $F\in \mathbb{N}^{(<\omega)}$
with
$F\in \mathbb{N}^{(<\omega)}$
with
![]() $(\mathbb{N}\setminus F)\cup\{\infty\}=\{\infty\}$
. Thus,
$(\mathbb{N}\setminus F)\cup\{\infty\}=\{\infty\}$
. Thus,
![]() $(P, \tau)$
is not well-filtered. In fact,
$(P, \tau)$
is not well-filtered. In fact,
![]() $(P, \tau)$
is not weak well-filtered in the sense of Lu et al. (2017).
$(P, \tau)$
is not weak well-filtered in the sense of Lu et al. (2017).
5.
![]() $(P, \tau)$
is Noetherian and second-countable, and hence, it is a Rudin space.
$(P, \tau)$
is Noetherian and second-countable, and hence, it is a Rudin space.
Since
![]() $|\tau|=\omega$
,
$|\tau|=\omega$
,
![]() $(P, \tau)$
is second-countable. As every subset of P is compact in
$(P, \tau)$
is second-countable. As every subset of P is compact in
![]() $(P, \tau)$
, the space
$(P, \tau)$
, the space
![]() $(P, \tau)$
is a Noetherian space (and hence a locally compact space). Hence by Proposition 38,
$(P, \tau)$
is a Noetherian space (and hence a locally compact space). Hence by Proposition 38,
![]() $(P, \tau)$
is a Rudin space.
$(P, \tau)$
is a Rudin space.
6.
![]() $\Sigma~\!\!\mathord{\mathsf{K}} ((P, \tau))$
is a second-countable sober space.
$\Sigma~\!\!\mathord{\mathsf{K}} ((P, \tau))$
is a second-countable sober space.
Clearly,
![]() $\mathord{\mathsf{K}} ((P, \tau))$
is isomorphic with the algebraic lattice
$\mathord{\mathsf{K}} ((P, \tau))$
is isomorphic with the algebraic lattice
![]() $2^{\mathbb{N}}$
(with the order of set inclusion) via the poset isomorphism
$2^{\mathbb{N}}$
(with the order of set inclusion) via the poset isomorphism
![]() $\varphi : \mathord{\mathsf{K}} ((P, \tau))\rightarrow 2^{\mathbb{N}}$
defined by
$\varphi : \mathord{\mathsf{K}} ((P, \tau))\rightarrow 2^{\mathbb{N}}$
defined by
![]() $\varphi (A\cup \{\infty\})=\mathbb{N}\setminus A$
for each
$\varphi (A\cup \{\infty\})=\mathbb{N}\setminus A$
for each
![]() $A\in 2^{\mathbb{N}}$
(note that the order on
$A\in 2^{\mathbb{N}}$
(note that the order on
![]() $\mathord{\mathsf{K}} ((P, \tau))$
is the Smyth order). Hence
$\mathord{\mathsf{K}} ((P, \tau))$
is the Smyth order). Hence
![]() $\Sigma~\!\!\mathord{\mathsf{K}} ((P, \tau))\cong \Sigma~\!\!2^{\mathbb{N}}$
. Clearly,
$\Sigma~\!\!\mathord{\mathsf{K}} ((P, \tau))\cong \Sigma~\!\!2^{\mathbb{N}}$
. Clearly,
![]() $2^{\mathbb{N}}$
is an algebraic lattice, whence by Theorem 15 and Proposition 18,
$2^{\mathbb{N}}$
is an algebraic lattice, whence by Theorem 15 and Proposition 18,
![]() $\Sigma~\!\!2^{\mathbb{N}}$
is sober and hence
$\Sigma~\!\!2^{\mathbb{N}}$
is sober and hence
![]() $\Sigma~\!\!\mathord{\mathsf{K}} ((P, \tau))$
is sober. Clearly,
$\Sigma~\!\!\mathord{\mathsf{K}} ((P, \tau))$
is sober. Clearly,
![]() $\Sigma~\!\!2^{\mathbb{N}}$
is second-countable since
$\Sigma~\!\!2^{\mathbb{N}}$
is second-countable since
![]() $\{\mathord{\uparrow}_{2^{\mathbb{N}}} F : F\in (2^{\mathbb{N}})^{(<\omega)}\}$
is a countable base of
$\{\mathord{\uparrow}_{2^{\mathbb{N}}} F : F\in (2^{\mathbb{N}})^{(<\omega)}\}$
is a countable base of
![]() $\Sigma~\!\!2^{\mathbb{N}}$
. So
$\Sigma~\!\!2^{\mathbb{N}}$
. So
![]() $\Sigma~\!\!\mathord{\mathsf{K}} ((P, \tau))$
is second-countable.
$\Sigma~\!\!\mathord{\mathsf{K}} ((P, \tau))$
is second-countable.
7.
![]() $P_S((P, \tau))$
is second-countable.
$P_S((P, \tau))$
is second-countable.
Clearly,
![]() $\{\Box U : U\in \tau\}$
is a countable base of
$\{\Box U : U\in \tau\}$
is a countable base of
![]() $P_S((P, \tau))$
(note that
$P_S((P, \tau))$
(note that
![]() $|\tau|=\omega$
). Hence
$|\tau|=\omega$
). Hence
![]() $P_S((P, \tau))$
is second-countable.
$P_S((P, \tau))$
is second-countable.
8.
![]() $\sigma(\mathsf{K}((P, \tau))\subseteq \mathcal O(P_S((P, \tau)))$
but
$\sigma(\mathsf{K}((P, \tau))\subseteq \mathcal O(P_S((P, \tau)))$
but
![]() $\mathcal O(P_S((P, \tau))\not\subseteq \sigma(\mathsf{K}((P, \tau)))$
.
$\mathcal O(P_S((P, \tau))\not\subseteq \sigma(\mathsf{K}((P, \tau)))$
.
Since
![]() $(P, \tau)$
is locally compact,
$(P, \tau)$
is locally compact,
![]() $\sigma(\mathsf{K}((P, \tau))\subseteq \mathcal O(P_S((P, \tau)))$
by Lemma 54. Clearly,
$\sigma(\mathsf{K}((P, \tau))\subseteq \mathcal O(P_S((P, \tau)))$
by Lemma 54. Clearly,
![]() $\Box \{\infty\}=\{\{\infty\}\}\in \mathcal O(P_S((P, \tau))$
. Now we show that
$\Box \{\infty\}=\{\{\infty\}\}\in \mathcal O(P_S((P, \tau))$
. Now we show that
![]() $\Box \{\infty\}\not\in \sigma(\mathsf{K}((P, \tau)))$
. By Lemma 9,
$\Box \{\infty\}\not\in \sigma(\mathsf{K}((P, \tau)))$
. By Lemma 9,
![]() $\bigvee \{F\cup\{\infty\} : F\in (\mathbb{N})^{(<\omega)}\setminus \{\emptyset\}\}=\bigcap \{F\cup\{\infty\} : F\in (\mathbb{N})^{(<\omega)}\setminus \{\emptyset\}\}=\{\infty\}\in \Box \{\infty\}$
, but there is no
$\bigvee \{F\cup\{\infty\} : F\in (\mathbb{N})^{(<\omega)}\setminus \{\emptyset\}\}=\bigcap \{F\cup\{\infty\} : F\in (\mathbb{N})^{(<\omega)}\setminus \{\emptyset\}\}=\{\infty\}\in \Box \{\infty\}$
, but there is no
![]() $F\in (\mathbb{N})^{(<\omega)}\setminus \{\emptyset\}$
with
$F\in (\mathbb{N})^{(<\omega)}\setminus \{\emptyset\}$
with
![]() $F\cup\{\infty\}\in \Box \{\infty\}=\{\{\infty\}\}$
. Thus,
$F\cup\{\infty\}\in \Box \{\infty\}=\{\{\infty\}\}$
. Thus,
![]() $\Box \{\infty\}\not\in \sigma(\mathsf{K}((P, \tau)))$
.
$\Box \{\infty\}\not\in \sigma(\mathsf{K}((P, \tau)))$
.
In the following, we will construct a sober space X for which the Scott space
![]() $\Sigma~\!\!\mathsf{K}(X)$
is non-sober (see Theorem 91 below).
$\Sigma~\!\!\mathsf{K}(X)$
is non-sober (see Theorem 91 below).
Let
![]() $\mathcal{L}=\mathbb{N}\times \mathbb{N}\times (\mathbb{N}\cup \{\infty\})$
, where
$\mathcal{L}=\mathbb{N}\times \mathbb{N}\times (\mathbb{N}\cup \{\infty\})$
, where
![]() $\mathbb{N}$
is the set of natural numbers with the usual order. Define an order
$\mathbb{N}$
is the set of natural numbers with the usual order. Define an order
![]() $\leq$
on
$\leq$
on
![]() $\mathcal L$
as follows:
$\mathcal L$
as follows:
![]() $(i_1, j_1, k_1)\leq (i_2, j_2, k_2)$
if and only if:
$(i_1, j_1, k_1)\leq (i_2, j_2, k_2)$
if and only if:
(1)
![]() $i_1=i_2, j_1=j_2, k_1\leq k_2\leq \infty$
; or
$i_1=i_2, j_1=j_2, k_1\leq k_2\leq \infty$
; or
(2)
![]() $i_2=i_1+1, k_1\leq j_2, k_2=\infty$
.
$i_2=i_1+1, k_1\leq j_2, k_2=\infty$
.
![]() $\mathcal L$
is a known dcpo constructed by Jia in Jia (Reference Jia2018, Example 2.6.1). It can be easily depicted as in Fig. 4 taken from Jia (Reference Jia2018).
$\mathcal L$
is a known dcpo constructed by Jia in Jia (Reference Jia2018, Example 2.6.1). It can be easily depicted as in Fig. 4 taken from Jia (Reference Jia2018).

Figure 4. A non-sober well-filtered dcpo
![]() $\mathcal L$
.
$\mathcal L$
.
For each
![]() $(n, m)\in \mathbb{N}\times \mathbb{N}$
, let
$(n, m)\in \mathbb{N}\times \mathbb{N}$
, let
![]() $\mathcal L_{(n,m)}=\{(n, , l) : l\in \mathbb{N}\cup \{\infty\}$
(the (n, m)th line of
$\mathcal L_{(n,m)}=\{(n, , l) : l\in \mathbb{N}\cup \{\infty\}$
(the (n, m)th line of
![]() $\mathcal L$
),
$\mathcal L$
),
![]() $\mathcal L_n=\bigcup_{j\in \mathbb{N}}\mathcal L_{(n,j)}$
(the nth row of
$\mathcal L_n=\bigcup_{j\in \mathbb{N}}\mathcal L_{(n,j)}$
(the nth row of
![]() $\mathcal L$
) and
$\mathcal L$
) and
![]() $\mathcal L_0=\emptyset$
,
$\mathcal L_0=\emptyset$
,
![]() $\mathcal L_n^{\infty}=\{(n, j, \infty) : j\in \mathbb{N}\}$
(the set of all maximal elements of
$\mathcal L_n^{\infty}=\{(n, j, \infty) : j\in \mathbb{N}\}$
(the set of all maximal elements of
![]() $\mathcal L_n$
),
$\mathcal L_n$
),
![]() $\mathcal L_n^{<\infty}=\mathcal L_n\setminus \mathcal L_n^{\infty}$
(the set of all finite height elements of
$\mathcal L_n^{<\infty}=\mathcal L_n\setminus \mathcal L_n^{\infty}$
(the set of all finite height elements of
![]() $\mathcal L_n$
),
$\mathcal L_n$
),
![]() $\mathcal L^{\infty}=\bigcup_{n\in \mathbb{N}}\mathcal L_n^{\infty}=\{(i, j, \infty) : (i, j)\in \mathbb{N}\times\mathbb{N}\}$
(the set of all maximal elements of
$\mathcal L^{\infty}=\bigcup_{n\in \mathbb{N}}\mathcal L_n^{\infty}=\{(i, j, \infty) : (i, j)\in \mathbb{N}\times\mathbb{N}\}$
(the set of all maximal elements of
![]() $\mathcal L$
),
$\mathcal L$
),
![]() $\mathcal L^{<\infty}=\mathcal L\setminus \mathcal L^{\infty}$
(the set of all elements of finite height),
$\mathcal L^{<\infty}=\mathcal L\setminus \mathcal L^{\infty}$
(the set of all elements of finite height),
![]() $\mathcal L_{(\leq n)}=\bigcup\limits_{i=1}^{n}\mathcal L_i=\{(i, j, l) : i\leq n, j\in \mathbb{N}, l\in \mathbb{N}\cup\{\infty\}\}$
,
$\mathcal L_{(\leq n)}=\bigcup\limits_{i=1}^{n}\mathcal L_i=\{(i, j, l) : i\leq n, j\in \mathbb{N}, l\in \mathbb{N}\cup\{\infty\}\}$
,
![]() $\mathcal L_{(\geq n)}=\bigcup\limits_{i\geq n}\mathcal L_i=\{(i, j, l) : i\geq n, j\in \mathbb{N}, l\in \mathbb{N}\cup\{\infty\}\}$
,
$\mathcal L_{(\geq n)}=\bigcup\limits_{i\geq n}\mathcal L_i=\{(i, j, l) : i\geq n, j\in \mathbb{N}, l\in \mathbb{N}\cup\{\infty\}\}$
,
![]() $\mathcal L_{(< n+1)}^{\infty}=\mathcal L_{(\leq n)}^{\infty}=\bigcup\limits_{i=1}^{n}\mathcal L_i^{\infty}=\{(i, j, \infty) : i\leq n, j\in \mathbb{N}\}$
,
$\mathcal L_{(< n+1)}^{\infty}=\mathcal L_{(\leq n)}^{\infty}=\bigcup\limits_{i=1}^{n}\mathcal L_i^{\infty}=\{(i, j, \infty) : i\leq n, j\in \mathbb{N}\}$
,
![]() $\mathcal L_{(> n)}^{\infty}=\mathcal L_{(\geq n+1)}^{\infty}=\bigcup\limits_{i\geq n}\mathcal L_i^{\infty}=\{(i, j, \infty) : i> n, j\in \mathbb{N}\}$
, and
$\mathcal L_{(> n)}^{\infty}=\mathcal L_{(\geq n+1)}^{\infty}=\bigcup\limits_{i\geq n}\mathcal L_i^{\infty}=\{(i, j, \infty) : i> n, j\in \mathbb{N}\}$
, and
![]() $\mathcal L_{(n, \geq m)}^{\infty}=\{(n, j, \infty) : j\geq m\}$
.
$\mathcal L_{(n, \geq m)}^{\infty}=\{(n, j, \infty) : j\geq m\}$
.
Definition 69.
For
![]() $x=(i, j, k)\in \mathcal L$
, k is called the height of x and is denoted by h(x) (i.e.,
$x=(i, j, k)\in \mathcal L$
, k is called the height of x and is denoted by h(x) (i.e.,
![]() $h(x)=k$
). If
$h(x)=k$
). If
![]() $k\in \mathbb{N}$
(resp.,
$k\in \mathbb{N}$
(resp.,
![]() $k=\infty$
), then we say that x is a point of finite height (resp., point of infinite height). For a nonempty subset A of
$k=\infty$
), then we say that x is a point of finite height (resp., point of infinite height). For a nonempty subset A of
![]() $\mathcal L$
, if there is
$\mathcal L$
, if there is
![]() $n\in \mathbb{N}$
with
$n\in \mathbb{N}$
with
![]() $\{h(a) : a\in A\}\subseteq \downarrow n$
, then A is said a subset of finite height; otherwise,A is said to be a subset of infinite height. The height of A is defined by
$\{h(a) : a\in A\}\subseteq \downarrow n$
, then A is said a subset of finite height; otherwise,A is said to be a subset of infinite height. The height of A is defined by
 $$h(A)= \begin{cases} \mathrm{max} \{h(a) : a\in A\},& \mathrm{if~} A \mathrm{~is~finite~height}\\ \infty,& \mathrm{otherwise}. \end{cases}$$
$$h(A)= \begin{cases} \mathrm{max} \{h(a) : a\in A\},& \mathrm{if~} A \mathrm{~is~finite~height}\\ \infty,& \mathrm{otherwise}. \end{cases}$$
For simplicity, let
![]() $h(\emptyset)=0$
.
$h(\emptyset)=0$
.
Lemma 70.
Let
![]() $i\in \mathbb{N}$
and U be a nonempty Scott open set of
$i\in \mathbb{N}$
and U be a nonempty Scott open set of
![]() $\mathcal L$
. If
$\mathcal L$
. If
![]() $U\cap \mathcal L_i\neq\emptyset$
, then there is
$U\cap \mathcal L_i\neq\emptyset$
, then there is
![]() $j^{\prime}\in \mathbb{N}$
such that
$j^{\prime}\in \mathbb{N}$
such that
![]() $\mathcal L_{(i+1, \geq j^{\prime})}^{\infty}=\{(i+1, j, \infty) : j\geq j^{\prime}\}\subseteq U$
.
$\mathcal L_{(i+1, \geq j^{\prime})}^{\infty}=\{(i+1, j, \infty) : j\geq j^{\prime}\}\subseteq U$
.
Proof. Since
![]() $U=\uparrow U$
and
$U=\uparrow U$
and
![]() $U\cap \mathcal L_i\neq\emptyset$
, we can assume that
$U\cap \mathcal L_i\neq\emptyset$
, we can assume that
![]() $(i, j(i), \infty)\in U$
for some
$(i, j(i), \infty)\in U$
for some
![]() $j(i)\in \mathbb{N}$
. As
$j(i)\in \mathbb{N}$
. As
![]() $\bigvee_{l\in \mathbb{N}}(i, j(i), l)=(i, j(i), \infty)\in U\in\sigma (\mathcal L)$
, there is
$\bigvee_{l\in \mathbb{N}}(i, j(i), l)=(i, j(i), \infty)\in U\in\sigma (\mathcal L)$
, there is
![]() $l(i)\in \mathbb{N}$
such that
$l(i)\in \mathbb{N}$
such that
![]() $(i, j(i), l(i))\in U$
. Let
$(i, j(i), l(i))\in U$
. Let
![]() $j^{\prime}=l(i)$
. Then,
$j^{\prime}=l(i)$
. Then,
![]() $\mathcal L_{(i+1, \geq j^{\prime})}^{\infty}\subseteq \uparrow (i, j(i), l(i))\subseteq U$
.
$\mathcal L_{(i+1, \geq j^{\prime})}^{\infty}\subseteq \uparrow (i, j(i), l(i))\subseteq U$
.
Lemma 71.
Suppose that D is an infinite directed subset of
![]() $\mathcal L$
. Then, there is a unique
$\mathcal L$
. Then, there is a unique
![]() $(i_D, j_D, \infty)\in \mathcal L^{\infty}$
such that
$(i_D, j_D, \infty)\in \mathcal L^{\infty}$
such that
![]() $(i_D, j_D, \infty)$
is a largest element of D or the following three conditions are satisfied:
$(i_D, j_D, \infty)$
is a largest element of D or the following three conditions are satisfied:
-
(i)
 $(i_D, j_D, \infty)\not\in D$
,
$(i_D, j_D, \infty)\not\in D$
, -
(ii)
 $D\subseteq \{(i_D, j_D, l) : l\in \mathbb{N}\}$
, and
$D\subseteq \{(i_D, j_D, l) : l\in \mathbb{N}\}$
, and -
(iii)
 $(i_D, j_D, \infty)=\bigvee_{\mathcal L} D$
.
$(i_D, j_D, \infty)=\bigvee_{\mathcal L} D$
.
Hence,
![]() $\mathcal L$
is a dcpo.
$\mathcal L$
is a dcpo.
Proof. If there is
![]() $(i_0, j_0, \infty)\in D\cap \mathcal L^{\infty}$
, then for each
$(i_0, j_0, \infty)\in D\cap \mathcal L^{\infty}$
, then for each
![]() $d=(i_d, j_d, l_d)\in D$
, there is
$d=(i_d, j_d, l_d)\in D$
, there is
![]() $d^*=(i_{d^*}, j_{d^*}, l_{d^*})\in D$
such that
$d^*=(i_{d^*}, j_{d^*}, l_{d^*})\in D$
such that
![]() $(i_0, j_0, \infty)\leq d^*=(i_{d^*}, j_{d^*}, l_{d^*})$
and
$(i_0, j_0, \infty)\leq d^*=(i_{d^*}, j_{d^*}, l_{d^*})$
and
![]() $d=(i_d, j_d, l_d)\leq d^*=(i_{d^*}, j_{d^*}, l_{d^*})$
, whence
$d=(i_d, j_d, l_d)\leq d^*=(i_{d^*}, j_{d^*}, l_{d^*})$
, whence
![]() $l_{d^*}=\infty, i_{d^*}=i_0, j_{d^*}=j_0$
(i.e.,
$l_{d^*}=\infty, i_{d^*}=i_0, j_{d^*}=j_0$
(i.e.,
![]() $d^*=(i_0, j_0, \infty)$
) and
$d^*=(i_0, j_0, \infty)$
) and
![]() $d\leq d^*=(i_0, j_0, \infty)$
. Hence,
$d\leq d^*=(i_0, j_0, \infty)$
. Hence,
![]() $(i_D, j_D, \infty)=(i_0, j_0, \infty)$
is the (unique) largest element of D.
$(i_D, j_D, \infty)=(i_0, j_0, \infty)$
is the (unique) largest element of D.
Now suppose that
![]() $D\cap \mathcal L^{\infty}=\emptyset$
, that is,
$D\cap \mathcal L^{\infty}=\emptyset$
, that is,
![]() $D\subseteq \mathbb{N}\times \mathbb{N}\times \mathbb{N}$
. Select a
$D\subseteq \mathbb{N}\times \mathbb{N}\times \mathbb{N}$
. Select a
![]() $d_1=(i_{d_1}, j_{d_1}, l_{d_1})\in D$
. Then for each
$d_1=(i_{d_1}, j_{d_1}, l_{d_1})\in D$
. Then for each
![]() $d=(i_d, j_d, l_d)\in D$
, by the directedness of D, there is
$d=(i_d, j_d, l_d)\in D$
, by the directedness of D, there is
![]() $d^{\prime}=(i_{d^{\prime}}, j_{d^{\prime}}, l_{d^{\prime}})\in D$
such that
$d^{\prime}=(i_{d^{\prime}}, j_{d^{\prime}}, l_{d^{\prime}})\in D$
such that
![]() $d_1=(i_{d_1}, j_{d_1}, l_{d_1})\leq d^{\prime}=(i_{d^{\prime}}, j_{d^{\prime}}, l_{d^{\prime}})$
and
$d_1=(i_{d_1}, j_{d_1}, l_{d_1})\leq d^{\prime}=(i_{d^{\prime}}, j_{d^{\prime}}, l_{d^{\prime}})$
and
![]() $d=(i_d, j_d, l_d)\leq d^{\prime}=(i_{d^{\prime}}, j_{d^{\prime}}, l_{d^{\prime}})$
. Hence,
$d=(i_d, j_d, l_d)\leq d^{\prime}=(i_{d^{\prime}}, j_{d^{\prime}}, l_{d^{\prime}})$
. Hence,
![]() $i_{d^{\prime}}=i_d=i_{d_0}, j_{d^{\prime}}=j_d=j_{d_0}$
and
$i_{d^{\prime}}=i_d=i_{d_0}, j_{d^{\prime}}=j_d=j_{d_0}$
and
![]() $l_{d_0}\leq l_{d^{\prime}}, l_d\leq l_{d^{\prime}}$
. Let
$l_{d_0}\leq l_{d^{\prime}}, l_d\leq l_{d^{\prime}}$
. Let
![]() $i_D=i_{d_1}$
and
$i_D=i_{d_1}$
and
![]() $j_D=j_{d_1}$
. Then,
$j_D=j_{d_1}$
. Then,
![]() $D\subseteq \{(i_D, j_D, l) : l\in \mathbb{N}\}$
. Clearly,
$D\subseteq \{(i_D, j_D, l) : l\in \mathbb{N}\}$
. Clearly,
![]() $(i_D, j_D, \infty)$
is the unique element of
$(i_D, j_D, \infty)$
is the unique element of
![]() $\mathcal L^{\infty}$
satisfying Conditions (i)–(iii).
$\mathcal L^{\infty}$
satisfying Conditions (i)–(iii).
For any
![]() $D\in \mathcal D(\mathcal L)$
, if D has a largest element s, then
$D\in \mathcal D(\mathcal L)$
, if D has a largest element s, then
![]() $s=\vee D$
; if D has no largest element, then D is infinite directed subset of
$s=\vee D$
; if D has no largest element, then D is infinite directed subset of
![]() $\mathcal L$
, whence there is a unique
$\mathcal L$
, whence there is a unique
![]() $(i, j, \infty)\in \mathcal L^{\infty}$
such that Conditions (i)–(iii) are satisfied. Then,
$(i, j, \infty)\in \mathcal L^{\infty}$
such that Conditions (i)–(iii) are satisfied. Then,
![]() $(i, j, \infty)=\bigvee_{\mathcal L} D$
. Hence,
$(i, j, \infty)=\bigvee_{\mathcal L} D$
. Hence,
![]() $\mathcal L$
is a dcpo.
$\mathcal L$
is a dcpo.
Corollary 72.
Suppose that A is a nonempty subset of
![]() $\mathcal L$
with
$\mathcal L$
with
![]() $A=\mathord{\downarrow} \mathrm{max}(A)$
and D is an infinite directed subset of A having no largest element. Let
$A=\mathord{\downarrow} \mathrm{max}(A)$
and D is an infinite directed subset of A having no largest element. Let
![]() $(i_D, j_D, \infty)\in \mathcal L^{\infty}$
be the unique maximal element of
$(i_D, j_D, \infty)\in \mathcal L^{\infty}$
be the unique maximal element of
![]() $\mathcal L$
satisfying Conditions (i)–(iii) in Lemma 71. Then,
$\mathcal L$
satisfying Conditions (i)–(iii) in Lemma 71. Then,
![]() $(i_D, j_D, \infty)\in \mathrm{max}(A)$
or
$(i_D, j_D, \infty)\in \mathrm{max}(A)$
or
![]() $|\mathrm{max}(A)\cap \mathcal L_{i_D+1}^{\infty}|=\omega$
.
$|\mathrm{max}(A)\cap \mathcal L_{i_D+1}^{\infty}|=\omega$
.
Proof. Since D has no largest element, by Lemma 71, there is a unique
![]() $(i_D, j_D, \infty)\in \mathcal L^{\infty}$
such that the following three conditions are satisfied:
$(i_D, j_D, \infty)\in \mathcal L^{\infty}$
such that the following three conditions are satisfied:
-
(i)
 $(i_D, j_D, \infty)\not\in D$
,
$(i_D, j_D, \infty)\not\in D$
, -
(ii)
 $D\subseteq \{(i_D, j_D, l) : l\in \mathbb{N}\}$
, and
$D\subseteq \{(i_D, j_D, l) : l\in \mathbb{N}\}$
, and -
(iii)
 $(i_D, j_D, \infty)=\bigvee_{\mathcal L} D$
.
$(i_D, j_D, \infty)=\bigvee_{\mathcal L} D$
.
Suppose that
![]() $(i_D, j_D, \infty)\not\in \mathrm{max}(A)$
. We will show that
$(i_D, j_D, \infty)\not\in \mathrm{max}(A)$
. We will show that
![]() $\mathrm{max}(A)\cap \mathcal L_{i_D+1}^{\infty}$
is infinite. For each
$\mathrm{max}(A)\cap \mathcal L_{i_D+1}^{\infty}$
is infinite. For each
![]() $d=(i_D, j_D, l_d)\in D$
, by
$d=(i_D, j_D, l_d)\in D$
, by
![]() $A=\mathord{\downarrow} \mathrm{max}(A)$
, there is
$A=\mathord{\downarrow} \mathrm{max}(A)$
, there is
![]() $(i(d), j(d), l(d))\in \mathrm{max}(A)$
with
$(i(d), j(d), l(d))\in \mathrm{max}(A)$
with
![]() $d=(i_D, j_D, l_d)\leq (i(d), j(d), l(d))$
. If
$d=(i_D, j_D, l_d)\leq (i(d), j(d), l(d))$
. If
![]() $i(d)=i_D$
, then
$i(d)=i_D$
, then
![]() $j(d)=j_D$
and
$j(d)=j_D$
and
![]() $l_d\leq l(d)$
. Since
$l_d\leq l(d)$
. Since
![]() $D\subseteq A\cap \{(i_D, j_D, l) : l\in \mathbb{N}\}$
is infinite,
$D\subseteq A\cap \{(i_D, j_D, l) : l\in \mathbb{N}\}$
is infinite,
![]() $\{l_{d^{\prime}} : d^{\prime}=(i_D, j_D, l_{d^{\prime}})\in D\}\subseteq \mathbb{N}$
is infinite and
$\{l_{d^{\prime}} : d^{\prime}=(i_D, j_D, l_{d^{\prime}})\in D\}\subseteq \mathbb{N}$
is infinite and
![]() $(i_D, j_D, l(d))=(i(d), j(d), l(d))\in \mathrm{max}(A)$
, we have that
$(i_D, j_D, l(d))=(i(d), j(d), l(d))\in \mathrm{max}(A)$
, we have that
![]() $l(d)=\infty$
, which is in contradiction with
$l(d)=\infty$
, which is in contradiction with
![]() $(i_D, j_D, \infty)\not\in \mathrm{max}(A)$
. Therefore,
$(i_D, j_D, \infty)\not\in \mathrm{max}(A)$
. Therefore,
![]() $i(d)=i_D+1$
and hence
$i(d)=i_D+1$
and hence
![]() $l(d)=\infty$
and
$l(d)=\infty$
and
![]() $l_d\leq j(d)$
by
$l_d\leq j(d)$
by
![]() $(i_D, j_D, l_d)\leq (i(d), j(d), l(d))=(i_D+1, j(d), l(d))$
. Since
$(i_D, j_D, l_d)\leq (i(d), j(d), l(d))=(i_D+1, j(d), l(d))$
. Since
![]() $\{l_d : d=(i_D, j_D, l_d)\in D\}\subseteq \mathbb{N}$
is infinite,
$\{l_d : d=(i_D, j_D, l_d)\in D\}\subseteq \mathbb{N}$
is infinite,
![]() $\{(i(d), j(d), l(d))=(i_D+1, j(d), \infty) : d\in D\}\subseteq \mathrm{max}(A)\cap \mathcal L^{\infty}$
is infinite (note that
$\{(i(d), j(d), l(d))=(i_D+1, j(d), \infty) : d\in D\}\subseteq \mathrm{max}(A)\cap \mathcal L^{\infty}$
is infinite (note that
![]() $l_d\leq j(d)$
for each
$l_d\leq j(d)$
for each
![]() $d=(i_D, j_D, l_d)\in D$
). Thus,
$d=(i_D, j_D, l_d)\in D$
). Thus,
![]() $\mathrm{max}(A)\cap \mathcal L_{i_D+1}^{\infty}$
is infinite.
$\mathrm{max}(A)\cap \mathcal L_{i_D+1}^{\infty}$
is infinite.
Corollary 73.
Suppose that A is a nonempty subset of
![]() $\mathcal L$
with
$\mathcal L$
with
![]() $A=\mathord{\downarrow} \mathrm{max}(A)$
and D is an infinite directed subset of A for which
$A=\mathord{\downarrow} \mathrm{max}(A)$
and D is an infinite directed subset of A for which
![]() $\vee D$
does not exist in A. Let
$\vee D$
does not exist in A. Let
![]() $(i_D, j_D, \infty)\in \mathcal L^{\infty}$
be the unique maximal element of
$(i_D, j_D, \infty)\in \mathcal L^{\infty}$
be the unique maximal element of
![]() $\mathcal L$
satisfying Conditions (i)–(iii) in Lemma 71. Then,
$\mathcal L$
satisfying Conditions (i)–(iii) in Lemma 71. Then,
![]() $(i_D, j_D, \infty)\not\in \mathrm{max}(A)$
and
$(i_D, j_D, \infty)\not\in \mathrm{max}(A)$
and
![]() $|\mathrm{max}(A)\cap \mathcal L_{i_D+1}^{\infty}|=\omega$
.
$|\mathrm{max}(A)\cap \mathcal L_{i_D+1}^{\infty}|=\omega$
.
Remark 74. Suppose that A is a nonempty subset of
![]() $\mathcal L$
with
$\mathcal L$
with
![]() $A=\mathord{\downarrow} \mathrm{max}(A)$
. Since
$A=\mathord{\downarrow} \mathrm{max}(A)$
. Since
![]() $\mathrm{max}(A)=(\mathrm{max}(A)\cap \mathcal L^{\infty})\cup (\mathrm{max}(A)\cap \mathcal L^{<\infty})$
, we have
$\mathrm{max}(A)=(\mathrm{max}(A)\cap \mathcal L^{\infty})\cup (\mathrm{max}(A)\cap \mathcal L^{<\infty})$
, we have
![]() $A=\mathord{\downarrow} \mathrm{max}(A)=\downarrow (\mathrm{max}(A)\cap \mathcal L^{\infty})\cup \downarrow (\mathrm{max}(A)\cap \mathcal L^{<\infty})$
. Clearly,
$A=\mathord{\downarrow} \mathrm{max}(A)=\downarrow (\mathrm{max}(A)\cap \mathcal L^{\infty})\cup \downarrow (\mathrm{max}(A)\cap \mathcal L^{<\infty})$
. Clearly,
![]() $\mathrm{max}(A)\cap \mathcal L^{<\infty}\cap \downarrow (\mathrm{max}(A)\cap \mathcal L^{\infty})=\emptyset$
and
$\mathrm{max}(A)\cap \mathcal L^{<\infty}\cap \downarrow (\mathrm{max}(A)\cap \mathcal L^{\infty})=\emptyset$
and
![]() $\mathrm{max}(A)\cap \mathcal L^{\infty}\cap \downarrow (\mathrm{max}(A)\cap \mathcal L^{<\infty})=\emptyset$
.
$\mathrm{max}(A)\cap \mathcal L^{\infty}\cap \downarrow (\mathrm{max}(A)\cap \mathcal L^{<\infty})=\emptyset$
.
Lemma 75.
Let
![]() $A\subseteq \mathcal L$
be a nonempty set and
$A\subseteq \mathcal L$
be a nonempty set and
![]() $A\neq \mathcal L$
. Then, A is Scott closed if and only if
$A\neq \mathcal L$
. Then, A is Scott closed if and only if
![]() $A=\mathord{\downarrow} \mathrm{max}(A)$
and one of the following three conditions is satisfied:
$A=\mathord{\downarrow} \mathrm{max}(A)$
and one of the following three conditions is satisfied:
-
(1)
 $A\subseteq \mathcal L^{<\infty}$
(or equivalently,
$A\subseteq \mathcal L^{<\infty}$
(or equivalently,
 $\mathrm{max}(A)\subseteq \mathcal L^{<\infty}$
).
$\mathrm{max}(A)\subseteq \mathcal L^{<\infty}$
). -
(2)
 $A\cap \mathcal L^{\infty}\neq \emptyset$
and
$A\cap \mathcal L^{\infty}\neq \emptyset$
and
 $|A\cap \mathcal L_n^{\infty}|<\omega$
for each
$|A\cap \mathcal L_n^{\infty}|<\omega$
for each
 $n\in \mathbb{N}$
.
$n\in \mathbb{N}$
. -
(3)
 $i(A)=\mathrm{max}\{i\in \mathbb{N} : |A\cap L_i^{\infty}|=\omega \}$
exists and
$i(A)=\mathrm{max}\{i\in \mathbb{N} : |A\cap L_i^{\infty}|=\omega \}$
exists and
 $\mathcal L_{n}\subseteq A$
for each
$\mathcal L_{n}\subseteq A$
for each
 $n\leq i(A)-1$
.
$n\leq i(A)-1$
.
Proof. Suppose that A is Scott closed. Then,
![]() $A=\mathord{\downarrow} \mathrm{max} (A)$
by Lemma 17. Now we show that A satisfies one of Conditions (1)–(3). If neither Condition (1) nor Condition (2) holds, then there is some
$A=\mathord{\downarrow} \mathrm{max} (A)$
by Lemma 17. Now we show that A satisfies one of Conditions (1)–(3). If neither Condition (1) nor Condition (2) holds, then there is some
![]() $i_0\in \mathbb{N}$
such that
$i_0\in \mathbb{N}$
such that
![]() $A\cap L_{i_0}^{\infty}$
is infinite. We first show that A satisfies the following property Q:
$A\cap L_{i_0}^{\infty}$
is infinite. We first show that A satisfies the following property Q:
(Q) For
![]() $n\in \mathbb{N}$
, if
$n\in \mathbb{N}$
, if
![]() $A\cap L_{n}^{\infty}$
is infinite, then
$A\cap L_{n}^{\infty}$
is infinite, then
![]() $\mathcal L_{i}\subseteq A$
for each
$\mathcal L_{i}\subseteq A$
for each
![]() $i\leq n-1$
.
$i\leq n-1$
.
If
![]() $n=1$
, then
$n=1$
, then
![]() $\mathcal L_{n-1}=\mathcal L_0=\emptyset\subseteq A$
. Now we assume
$\mathcal L_{n-1}=\mathcal L_0=\emptyset\subseteq A$
. Now we assume
![]() $2\leq n$
. For each
$2\leq n$
. For each
![]() $(j, l)\in \mathbb{N}\times \mathbb{N}$
, since
$(j, l)\in \mathbb{N}\times \mathbb{N}$
, since
![]() $A\cap L_{n}^{\infty}$
is infinite (i.e.,
$A\cap L_{n}^{\infty}$
is infinite (i.e.,
![]() $\{j^{\prime}\in \mathbb{N} : (n, j^{\prime}, \infty)\in A\}$
is infinite), there is
$\{j^{\prime}\in \mathbb{N} : (n, j^{\prime}, \infty)\in A\}$
is infinite), there is
![]() $j^{\prime}\in \mathbb{N}$
such that
$j^{\prime}\in \mathbb{N}$
such that
![]() $(n, j^{\prime}, \infty)\in A$
and
$(n, j^{\prime}, \infty)\in A$
and
![]() $l\leq j^{\prime}$
, whence
$l\leq j^{\prime}$
, whence
![]() $(n-1, j, l)\leq (n, j^{\prime}, \infty)$
. Thus,
$(n-1, j, l)\leq (n, j^{\prime}, \infty)$
. Thus,
![]() $\{(n-1, j, l) : (j, l)\in \mathbb{N}\times \mathbb{N}\}\subseteq \mathord{\downarrow} (A\cap L_{n}^{\infty})\subseteq \mathord{\downarrow} A=A$
. For each
$\{(n-1, j, l) : (j, l)\in \mathbb{N}\times \mathbb{N}\}\subseteq \mathord{\downarrow} (A\cap L_{n}^{\infty})\subseteq \mathord{\downarrow} A=A$
. For each
![]() $j\in \mathbb{N}$
, since
$j\in \mathbb{N}$
, since
![]() $(n-1, j, \infty)=\bigvee_{l\in \mathbb{N}}(n-1, j, l)$
and A is Scott closed, we have
$(n-1, j, \infty)=\bigvee_{l\in \mathbb{N}}(n-1, j, l)$
and A is Scott closed, we have
![]() $(n-1, j, \infty)\in A$
. Hence,
$(n-1, j, \infty)\in A$
. Hence,
![]() $\mathcal L_{n-1}\subseteq A$
. In particular,
$\mathcal L_{n-1}\subseteq A$
. In particular,
![]() $\mathcal L_{n-1}^{\infty}\subseteq A$
. Then by induction, we get that
$\mathcal L_{n-1}^{\infty}\subseteq A$
. Then by induction, we get that
![]() $\mathcal L_i\subseteq A$
for any
$\mathcal L_i\subseteq A$
for any
![]() $1\leq i\leq n-1$
.
$1\leq i\leq n-1$
.
By property Q, if
![]() $\{i\in \mathbb{N} : |A\cap L_i^{\infty}|=\omega \}$
is infinite, then for each
$\{i\in \mathbb{N} : |A\cap L_i^{\infty}|=\omega \}$
is infinite, then for each
![]() $n\in \mathbb{N}$
,
$n\in \mathbb{N}$
,
![]() $\mathcal L_{n-1}\subseteq A$
. Hence,
$\mathcal L_{n-1}\subseteq A$
. Hence,
![]() $\mathcal L=\bigcup_{n\in \mathbb{N}}\mathcal L_n\subseteq A$
, which contradicts
$\mathcal L=\bigcup_{n\in \mathbb{N}}\mathcal L_n\subseteq A$
, which contradicts
![]() $A\neq \mathcal L$
. Hence
$A\neq \mathcal L$
. Hence
![]() $\{i\in \mathbb{N} : |A\cap L_i^{\infty}|=\omega \}$
is a nonempty finite subset of
$\{i\in \mathbb{N} : |A\cap L_i^{\infty}|=\omega \}$
is a nonempty finite subset of
![]() $\mathbb{N}$
, and consequently,
$\mathbb{N}$
, and consequently,
![]() $i(A)=\mathrm{max}\{i\in \mathbb{N} : |A\cap L_i^{\infty}|=\omega \}$
exists. By property Q, we have
$i(A)=\mathrm{max}\{i\in \mathbb{N} : |A\cap L_i^{\infty}|=\omega \}$
exists. By property Q, we have
![]() $\mathcal L_{i}\subseteq A$
for each
$\mathcal L_{i}\subseteq A$
for each
![]() $i\leq i(A)-1$
. This completes the proof of Condition (3).
$i\leq i(A)-1$
. This completes the proof of Condition (3).
Conversely, assume that
![]() $A=\mathord{\downarrow} \mathrm{max}(A)$
and one of Conditions (1)–(3) is satisfied. We will show that A is Scott closed.
$A=\mathord{\downarrow} \mathrm{max}(A)$
and one of Conditions (1)–(3) is satisfied. We will show that A is Scott closed.
Case 1. Condition (1) or Condition (2) holds.
Suppose that D is a directed subset of A. If D has a largest element s, then
![]() $\vee D=s\in A$
. Now suppose that D has no largest element. Then, D is infinite, whence by Lemma 71, there is a unique
$\vee D=s\in A$
. Now suppose that D has no largest element. Then, D is infinite, whence by Lemma 71, there is a unique
![]() $(i_D, j_D, \infty)\in \mathcal L^{\infty}$
such that the following three conditions are satisfied:
$(i_D, j_D, \infty)\in \mathcal L^{\infty}$
such that the following three conditions are satisfied:
-
(i)
 $(i_D, j_D, \infty)\not\in D$
,
$(i_D, j_D, \infty)\not\in D$
, -
(ii)
 $D\subseteq \{(i_D, j_D, l) : l\in \mathbb{N}\}$
, and
$D\subseteq \{(i_D, j_D, l) : l\in \mathbb{N}\}$
, and -
(iii)
 $(i_D, j_D, \infty)=\bigvee_{\mathcal L} D$
.
$(i_D, j_D, \infty)=\bigvee_{\mathcal L} D$
.
If
![]() $(i_D, j_D, \infty)\not\in A$
, then by Corollary 72,
$(i_D, j_D, \infty)\not\in A$
, then by Corollary 72,
![]() $\mathrm{max}(A)\cap \mathcal L_{i_D+1}^{\infty}$
is infinite, which is a contradiction with Condition (1) or Condition (2). So
$\mathrm{max}(A)\cap \mathcal L_{i_D+1}^{\infty}$
is infinite, which is a contradiction with Condition (1) or Condition (2). So
![]() $\bigvee_{\mathcal L} D=(i_D, j_D, \infty)\in A$
. Thus, A is Scott closed.
$\bigvee_{\mathcal L} D=(i_D, j_D, \infty)\in A$
. Thus, A is Scott closed.
Case 2.
![]() $i(A)=\mathrm{max}\{i\in \mathbb{N} : |A\cap L_i^{\infty}|=\omega \}$
exists and
$i(A)=\mathrm{max}\{i\in \mathbb{N} : |A\cap L_i^{\infty}|=\omega \}$
exists and
![]() $\mathcal L_{n}\subseteq A$
for each
$\mathcal L_{n}\subseteq A$
for each
![]() $n\leq i(A)-1$
.
$n\leq i(A)-1$
.
Suppose that D is a directed subset of A. When D has a largest element, we clearly have
![]() $\bigvee_{\mathcal L} D\in A$
. Now we assume that D has no largest element. Then, D is infinite, whence by Lemma71, there is a unique
$\bigvee_{\mathcal L} D\in A$
. Now we assume that D has no largest element. Then, D is infinite, whence by Lemma71, there is a unique
![]() $(i_D, j_, \infty)\in \mathcal L^{\infty}$
satisfying Conditions (i)–(iii) in Lemma 71. If
$(i_D, j_, \infty)\in \mathcal L^{\infty}$
satisfying Conditions (i)–(iii) in Lemma 71. If
![]() $(i_D, j_D, \infty)\in A$
or
$(i_D, j_D, \infty)\in A$
or
![]() $i_D\leq i(A)-1$
, then
$i_D\leq i(A)-1$
, then
![]() $\bigvee_{\mathcal L} D=(i_D, j_D, \infty)\in A$
or
$\bigvee_{\mathcal L} D=(i_D, j_D, \infty)\in A$
or
![]() $\bigvee_{\mathcal L} D=(i_D, j_D, \infty)\in \mathcal L_{i_D}\subseteq A$
. If
$\bigvee_{\mathcal L} D=(i_D, j_D, \infty)\in \mathcal L_{i_D}\subseteq A$
. If
![]() $i_D\geq i(A)$
and
$i_D\geq i(A)$
and
![]() $(i_D, j_D, \infty)\not\in A$
, then by Corollary 72,
$(i_D, j_D, \infty)\not\in A$
, then by Corollary 72,
![]() $\mathrm{max}(A)\cap \mathcal L_{i_D+1}^{\infty}$
is infinite. It follows that
$\mathrm{max}(A)\cap \mathcal L_{i_D+1}^{\infty}$
is infinite. It follows that
![]() $i_D+1\leq i(A)$
, which is a contradiction with
$i_D+1\leq i(A)$
, which is a contradiction with
![]() $i_D\geq i(A)$
. So
$i_D\geq i(A)$
. So
![]() $A\in \mathcal C(\Sigma~\!\! \mathcal L)$
.
$A\in \mathcal C(\Sigma~\!\! \mathcal L)$
.
Remark 76. The condition
![]() $A=\mathord{\downarrow} \mathrm{max}(A)$
is necessary. For example, for any
$A=\mathord{\downarrow} \mathrm{max}(A)$
is necessary. For example, for any
![]() $(i, j)\in \mathbb{N}\times \mathbb{N}$
the set
$(i, j)\in \mathbb{N}\times \mathbb{N}$
the set
![]() $A_{(i,j)}=\{(i, j, l) : l\in \mathbb{N}\}$
is a lower set and
$A_{(i,j)}=\{(i, j, l) : l\in \mathbb{N}\}$
is a lower set and
![]() $\mathrm{max}(A)=\emptyset$
, whence
$\mathrm{max}(A)=\emptyset$
, whence
![]() $A\neq\mathord{\downarrow} \mathrm{max}(A)$
. Clearly,
$A\neq\mathord{\downarrow} \mathrm{max}(A)$
. Clearly,
![]() $A_{(i,j)}\subseteq \mathcal L^{<\infty}$
and
$A_{(i,j)}\subseteq \mathcal L^{<\infty}$
and
![]() $\vee \{(i, j, l) : l\in \mathbb{N}\}=(i, j, \infty)\not\in A_{(i,j)}$
. So
$\vee \{(i, j, l) : l\in \mathbb{N}\}=(i, j, \infty)\not\in A_{(i,j)}$
. So
![]() $A_{(i,j)}$
is not Scott closed.
$A_{(i,j)}$
is not Scott closed.
Proposition 77.
Let
![]() $A\subseteq \mathcal L$
be a nonempty lower set. Then, the following four conditions are equivalent:
$A\subseteq \mathcal L$
be a nonempty lower set. Then, the following four conditions are equivalent:
-
(1) A is Scott closed.
-
(2) For each
 $(i, j)\in \mathbb{N}\times \mathbb{N}$
, if
$(i, j)\in \mathbb{N}\times \mathbb{N}$
, if
 $(i, j, \infty)\not\in A$
, then
$(i, j, \infty)\not\in A$
, then
 $A\cap\{(i, j, l) : l\in \mathbb{N}\}$
is finite.
$A\cap\{(i, j, l) : l\in \mathbb{N}\}$
is finite.
-
(3) For each
 $(i, j)\in \mathbb{N}\times \mathbb{N}$
,
$(i, j)\in \mathbb{N}\times \mathbb{N}$
,
 $\mathcal L_{(i, j)}\subseteq A$
or
$\mathcal L_{(i, j)}\subseteq A$
or
 $(i, j, \infty)\not\in A$
and
$(i, j, \infty)\not\in A$
and
 $A\cap\{(i, j, l) : l\in \mathbb{N}\}$
is finite.
$A\cap\{(i, j, l) : l\in \mathbb{N}\}$
is finite.
-
(4) For each
 $(i, j)\in \mathbb{N}\times \mathbb{N}$
,
$(i, j)\in \mathbb{N}\times \mathbb{N}$
,
 $\mathcal L_{(i, j)}\subseteq A$
or
$\mathcal L_{(i, j)}\subseteq A$
or
 $A\cap\mathcal L_{(i, j)}$
is finite.
$A\cap\mathcal L_{(i, j)}$
is finite.
Proof. (1)
![]() $\Rightarrow$
(2): Trivial. (2)
$\Rightarrow$
(2): Trivial. (2)
![]() $\Leftrightarrow$
(3)
$\Leftrightarrow$
(3)
![]() $\Leftrightarrow$
(4): Trivial (since A is a lower set).
$\Leftrightarrow$
(4): Trivial (since A is a lower set).
(2)
![]() $\Rightarrow$
(1): Suppose that D is a directed subset of A. When D has a largest element, then
$\Rightarrow$
(1): Suppose that D is a directed subset of A. When D has a largest element, then
![]() $\bigvee_{\mathcal L} D\in A$
. Now assume that D has no largest element. Then, D is infinite, whence by Lemma 71, there is a unique
$\bigvee_{\mathcal L} D\in A$
. Now assume that D has no largest element. Then, D is infinite, whence by Lemma 71, there is a unique
![]() $(i_D, j_D, \infty)\in \mathcal L^{\infty}$
satisfying Conditions (i)-(iii) in Lemma 4. Since
$(i_D, j_D, \infty)\in \mathcal L^{\infty}$
satisfying Conditions (i)-(iii) in Lemma 4. Since
![]() $D\subseteq A\cap \{(i_D, j_D, l) : l\in \mathbb{N}\}$
is infinite, by (2),
$D\subseteq A\cap \{(i_D, j_D, l) : l\in \mathbb{N}\}$
is infinite, by (2),
![]() $\bigvee_{\mathcal L}D=(i_D, j_D, \infty)\in A$
. Thus, A is Scott closed.
$\bigvee_{\mathcal L}D=(i_D, j_D, \infty)\in A$
. Thus, A is Scott closed.
Dually, as a direct corollary of Proposition 77, we have the following.
Corollary 78.
Let
![]() $U\subseteq \mathcal L$
be an upper set. Then, the following four conditions are equivalent:
$U\subseteq \mathcal L$
be an upper set. Then, the following four conditions are equivalent:
-
(1) U is Scott open.
-
(2) For each
 $(i, j)\in \mathbb{N}\times \mathbb{N}$
, if
$(i, j)\in \mathbb{N}\times \mathbb{N}$
, if
 $(i, j, \infty)\in U$
, then
$(i, j, \infty)\in U$
, then
 $U\cap \mathcal L_{(i, j)}$
is infinite.
$U\cap \mathcal L_{(i, j)}$
is infinite.
-
(3) For each
 $(i, j)\in \mathbb{N}\times \mathbb{N}$
,
$(i, j)\in \mathbb{N}\times \mathbb{N}$
,
 $U\cap\mathcal L_{(i, j)}=\emptyset$
or
$U\cap\mathcal L_{(i, j)}=\emptyset$
or
 $(i, j, \infty)\in U$
and
$(i, j, \infty)\in U$
and
 $U\cap \mathcal L_{(i, j)}$
is infinite.
$U\cap \mathcal L_{(i, j)}$
is infinite.
-
(4) For each
 $(i, j)\in \mathbb{N}\times \mathbb{N}$
,
$(i, j)\in \mathbb{N}\times \mathbb{N}$
,
 $U\cap\mathcal L_{(i, j)}=\emptyset$
or
$U\cap\mathcal L_{(i, j)}=\emptyset$
or
 $U\cap \mathcal L_{(i, j)}$
is infinite.
$U\cap \mathcal L_{(i, j)}$
is infinite.
By Lemma 75 and Proposition 77, we get the following.
Corollary 79.
Let
![]() $A\subseteq \mathcal L$
be a nonempty lower set and
$A\subseteq \mathcal L$
be a nonempty lower set and
![]() $A\neq \mathcal L$
. Then, A is Scott closed if and only if one of the following three conditions is satisfied:
$A\neq \mathcal L$
. Then, A is Scott closed if and only if one of the following three conditions is satisfied:
-
(1)
 $A\subseteq \mathcal L^{<\infty}$
(or equivalently,
$A\subseteq \mathcal L^{<\infty}$
(or equivalently,
 $\mathrm{max}(A)\subseteq \mathcal L^{<\infty}$
) and
$\mathrm{max}(A)\subseteq \mathcal L^{<\infty}$
) and
 $A\cap \{(i, j, l) : l\in \mathbb{N}\}$
is finite for each
$A\cap \{(i, j, l) : l\in \mathbb{N}\}$
is finite for each
 $(i, j)\in \mathbb{N}\times \mathbb{N}$
.
$(i, j)\in \mathbb{N}\times \mathbb{N}$
. -
(2)
 $A\cap \mathcal L^{\infty}\neq \emptyset$
,
$A\cap \mathcal L^{\infty}\neq \emptyset$
,
 $|A\cap \mathcal L_i^{\infty}|<\omega$
for each
$|A\cap \mathcal L_i^{\infty}|<\omega$
for each
 $i\in \mathbb{N}$
and
$i\in \mathbb{N}$
and
 $A\cap \{(i, j, l) : l\in \mathbb{N}\}$
is finite for each
$A\cap \{(i, j, l) : l\in \mathbb{N}\}$
is finite for each
 $(i, j)\in \mathbb{N}\times \mathbb{N}$
with
$(i, j)\in \mathbb{N}\times \mathbb{N}$
with
 $(i, j, \infty)\not\in A$
.
$(i, j, \infty)\not\in A$
. -
(3)
 $i(A)=\mathrm{max}\{i\in \mathbb{N} : |A\cap L_i^{\infty}|=\omega \}$
exists,
$i(A)=\mathrm{max}\{i\in \mathbb{N} : |A\cap L_i^{\infty}|=\omega \}$
exists,
 $\mathcal L_{n}\subseteq A$
for each
$\mathcal L_{n}\subseteq A$
for each
 $n\leq i(A)-1$
, and
$n\leq i(A)-1$
, and
 $A\cap \{(i, j, l) : l\in \mathbb{N}\}$
is finite for each
$A\cap \{(i, j, l) : l\in \mathbb{N}\}$
is finite for each
 $(i, j)\in \mathbb{N}$
with
$(i, j)\in \mathbb{N}$
with
 $(i, j, \infty)\not\in A$
.
$(i, j, \infty)\not\in A$
.
Lemma 80.
![]() ${\mathsf{Irr}}_c(\Sigma~\!\!\mathcal L)=\{\overline{\{x\}}=\mathord{\downarrow} x : x\in \mathcal L\}\cup\{\mathcal L\}$
.
${\mathsf{Irr}}_c(\Sigma~\!\!\mathcal L)=\{\overline{\{x\}}=\mathord{\downarrow} x : x\in \mathcal L\}\cup\{\mathcal L\}$
.
Proof. Clearly,
![]() $\{\overline{\{x\}}=\mathord{\downarrow} x : x\in \mathcal L\}\subseteq {\mathsf{Irr}}_c(\Sigma~\!\!\mathcal L)$
. It was shown in Jia (Reference Jia2018, Example 2.6.1) that
$\{\overline{\{x\}}=\mathord{\downarrow} x : x\in \mathcal L\}\subseteq {\mathsf{Irr}}_c(\Sigma~\!\!\mathcal L)$
. It was shown in Jia (Reference Jia2018, Example 2.6.1) that
![]() $\mathcal L\in {\mathsf{Irr}}_c(\Sigma~\!\!\mathcal L)$
. This can be easily proved by Lemma 75. Suppose that
$\mathcal L\in {\mathsf{Irr}}_c(\Sigma~\!\!\mathcal L)$
. This can be easily proved by Lemma 75. Suppose that
![]() $B, C\in \mathcal C(\Sigma~\!\!\mathcal L)$
and
$B, C\in \mathcal C(\Sigma~\!\!\mathcal L)$
and
![]() $\mathcal L=B\cup C$
. Let
$\mathcal L=B\cup C$
. Let
![]() $\mathbb{N}_B=\{n\in \mathbb{N} : |B\cap L_n^{\infty}|=\omega\}$
and
$\mathbb{N}_B=\{n\in \mathbb{N} : |B\cap L_n^{\infty}|=\omega\}$
and
![]() $\mathbb{N}_C=\{n\in \mathbb{N} : |C\cap L_n^{\infty}|=\omega\}$
. As
$\mathbb{N}_C=\{n\in \mathbb{N} : |C\cap L_n^{\infty}|=\omega\}$
. As
![]() $\mathcal L=B\cup C$
, we have
$\mathcal L=B\cup C$
, we have
![]() $\mathbb{N}=\mathbb{N}_B\cup \mathbb{N}_C,$
and hence, at least one of
$\mathbb{N}=\mathbb{N}_B\cup \mathbb{N}_C,$
and hence, at least one of
![]() $\mathbb{N}_B$
and
$\mathbb{N}_B$
and
![]() $\mathbb{N}_C$
is infinite. Without loss of generality, assume
$\mathbb{N}_C$
is infinite. Without loss of generality, assume
![]() $\mathbb{N}_B$
is infinite. Then by property Q in the proof of Lemma 75, we have
$\mathbb{N}_B$
is infinite. Then by property Q in the proof of Lemma 75, we have
![]() $B=\mathcal L$
. Thus,
$B=\mathcal L$
. Thus,
![]() $\mathcal L\in {\mathsf{Irr}}_c(\Sigma~\!\!\mathcal L)$
.
$\mathcal L\in {\mathsf{Irr}}_c(\Sigma~\!\!\mathcal L)$
.
Conversely, suppose that
![]() $A\in {\mathsf{Irr}}_c(\Sigma~\!\!\mathcal L)$
and
$A\in {\mathsf{Irr}}_c(\Sigma~\!\!\mathcal L)$
and
![]() $A\neq \mathcal L$
.
$A\neq \mathcal L$
.
Case 1.
![]() $\mathrm{max}(A)\cap \mathcal L^{<\infty}\neq \emptyset$
(i.e., A has a maximal point of finite height).
$\mathrm{max}(A)\cap \mathcal L^{<\infty}\neq \emptyset$
(i.e., A has a maximal point of finite height).
Select an
![]() $(i, j, l)\in \mathrm{max}(A)\cap \mathcal L^{<\infty}$
. Then,
$(i, j, l)\in \mathrm{max}(A)\cap \mathcal L^{<\infty}$
. Then,
![]() $l\in \mathbb{N}$
. Let
$l\in \mathbb{N}$
. Let
![]() $B=\downarrow (\mathrm{max}(A)\setminus \{(i, j, l)\})$
(B may be the empty set). Then,
$B=\downarrow (\mathrm{max}(A)\setminus \{(i, j, l)\})$
(B may be the empty set). Then,
![]() $A=B\cup \downarrow (i, j, l)$
. Clearly,
$A=B\cup \downarrow (i, j, l)$
. Clearly,
![]() $\downarrow (i, j, l)$
is Scott closed. By Lemma 75 or Proposition 77, it is easy to verify that B is Scott closed. Indeed, we can give a direct proof of the Scott closedness of B. Suppose that D is a directed subset of B. When D has a largest element, we clearly have
$\downarrow (i, j, l)$
is Scott closed. By Lemma 75 or Proposition 77, it is easy to verify that B is Scott closed. Indeed, we can give a direct proof of the Scott closedness of B. Suppose that D is a directed subset of B. When D has a largest element, we clearly have
![]() $\bigvee_{\mathcal L} D\in D\subseteq B$
. Now we assume that D has no largest element. Then, D is infinite, whence by Lemma 71, there is a unique
$\bigvee_{\mathcal L} D\in D\subseteq B$
. Now we assume that D has no largest element. Then, D is infinite, whence by Lemma 71, there is a unique
![]() $(i_D, j_, \infty)\in \mathcal L^{\infty}$
satisfying Conditions (i)-(iii) in Lemma 71. Since A is Scott closed,
$(i_D, j_, \infty)\in \mathcal L^{\infty}$
satisfying Conditions (i)-(iii) in Lemma 71. Since A is Scott closed,
![]() $(i_D, j_D, \infty)=\bigvee_{\mathcal L} D\in A$
. As
$(i_D, j_D, \infty)=\bigvee_{\mathcal L} D\in A$
. As
![]() $l\in \mathbb{N}$
,
$l\in \mathbb{N}$
,
![]() $(i_D, j_D, \infty)\not\in \downarrow (i, j, l)$
, whence
$(i_D, j_D, \infty)\not\in \downarrow (i, j, l)$
, whence
![]() $(i_D, j_D, \infty)\in \mathrm{max}(A)\setminus \{(i, j, l)\}\subseteq B$
. Thus, B is Scott closed. By the irreducibility of A, we have
$(i_D, j_D, \infty)\in \mathrm{max}(A)\setminus \{(i, j, l)\}\subseteq B$
. Thus, B is Scott closed. By the irreducibility of A, we have
![]() $A=B$
or
$A=B$
or
![]() $A=\downarrow (i, j, l)$
. If
$A=\downarrow (i, j, l)$
. If
![]() $A=B$
, then there is
$A=B$
, then there is
![]() $(i^{\ast}, j^{\ast}, l^{\ast})\in \mathrm{max}(A)\setminus \{(i, j, l)\}$
with
$(i^{\ast}, j^{\ast}, l^{\ast})\in \mathrm{max}(A)\setminus \{(i, j, l)\}$
with
![]() $(i, j, l)\leq (i^{\ast}, j^{\ast}, l^{\ast})$
. Hence,
$(i, j, l)\leq (i^{\ast}, j^{\ast}, l^{\ast})$
. Hence,
![]() $(i, j, l)=(i^{\ast}, j^{\ast}, l^{\ast})$
by
$(i, j, l)=(i^{\ast}, j^{\ast}, l^{\ast})$
by
![]() $(i, j, l)\in \mathrm{max}(A)$
, a contradiction. Therefore,
$(i, j, l)\in \mathrm{max}(A)$
, a contradiction. Therefore,
![]() $A=\downarrow (i, j, l)={\rm cl}_{\sigma (\mathcal L)}\{(i, j, l)\}$
.
$A=\downarrow (i, j, l)={\rm cl}_{\sigma (\mathcal L)}\{(i, j, l)\}$
.
Case 2.
![]() $\mathrm{max}(A)\subseteq \mathcal L^{\infty}$
(i.e., every maximal point of A is a point of infinite height).
$\mathrm{max}(A)\subseteq \mathcal L^{\infty}$
(i.e., every maximal point of A is a point of infinite height).
Since
![]() $A\neq \emptyset$
,
$A\neq \emptyset$
,
![]() $A=\downarrow \mathrm{max}(A)$
and
$A=\downarrow \mathrm{max}(A)$
and
![]() $\mathrm{max}(A)\subseteq \mathcal L^{\infty}$
, we have that
$\mathrm{max}(A)\subseteq \mathcal L^{\infty}$
, we have that
![]() $\mathrm{max}(A)\cap\mathcal L^{\infty}\neq\emptyset$
. If
$\mathrm{max}(A)\cap\mathcal L^{\infty}\neq\emptyset$
. If
![]() $|A\cap L_n^{\infty}|<\omega$
for all
$|A\cap L_n^{\infty}|<\omega$
for all
![]() $n\in \mathbb{N}$
, then select any point
$n\in \mathbb{N}$
, then select any point
![]() $(i, j, \infty)\in \mathrm{max}(A)$
and let
$(i, j, \infty)\in \mathrm{max}(A)$
and let
![]() $n(A)=i$
. We clearly have that
$n(A)=i$
. We clearly have that
![]() $|A\cap L_{n(A)+1}^{\infty}|<\omega$
. If
$|A\cap L_{n(A)+1}^{\infty}|<\omega$
. If
![]() $|A\cap L_m^{\infty}|=\omega$
for some
$|A\cap L_m^{\infty}|=\omega$
for some
![]() $m\in \mathbb{N}$
, then by property Q in the proof of Lemma 75, the set
$m\in \mathbb{N}$
, then by property Q in the proof of Lemma 75, the set
![]() $\{n\in\mathbb{N} : |A\cap L_n^{\infty}|=\omega\}$
is a nonempty finite set, whence
$\{n\in\mathbb{N} : |A\cap L_n^{\infty}|=\omega\}$
is a nonempty finite set, whence
![]() $n(A)=\mathrm{max}\{n\in\mathbb{N} : |A\cap L_n^{\infty}|=\omega\}$
exists. Then,
$n(A)=\mathrm{max}\{n\in\mathbb{N} : |A\cap L_n^{\infty}|=\omega\}$
exists. Then,
![]() $A\cap L_{n(A)+1}^{\infty}$
is finite. Select an
$A\cap L_{n(A)+1}^{\infty}$
is finite. Select an
![]() $(n(A), j, \infty)\in A\cap L_{n(A)}^{\infty}$
. Let
$(n(A), j, \infty)\in A\cap L_{n(A)}^{\infty}$
. Let
![]() $B=\downarrow (\mathrm{max}(A)\setminus \{(n(A), j, \infty)\})$
. Then,
$B=\downarrow (\mathrm{max}(A)\setminus \{(n(A), j, \infty)\})$
. Then,
![]() $A=B\cup \downarrow (n(A), j, \infty)$
. Clearly,
$A=B\cup \downarrow (n(A), j, \infty)$
. Clearly,
![]() $\downarrow (n(A), j, \infty)$
is Scott closed. Now we show that B is Scott closed. Suppose that D is a directed subset of B. If D has a largest element s, then
$\downarrow (n(A), j, \infty)$
is Scott closed. Now we show that B is Scott closed. Suppose that D is a directed subset of B. If D has a largest element s, then
![]() $\bigvee_{\mathcal L} D=s\in D\subseteq B$
; if D has no largest element, then D is infinite, whence by Lemma 71, there is a unique
$\bigvee_{\mathcal L} D=s\in D\subseteq B$
; if D has no largest element, then D is infinite, whence by Lemma 71, there is a unique
![]() $(i_D, j_D, \infty)\in \mathcal L^{\infty}$
such that the following three conditions are satisfied:
$(i_D, j_D, \infty)\in \mathcal L^{\infty}$
such that the following three conditions are satisfied:
-
(i)
 $(i_D, j_D, \infty)\not\in D$
,
$(i_D, j_D, \infty)\not\in D$
, -
(ii)
 $D\subseteq \{(i_D, j_D, l) : l\in \mathbb{N}\}$
, and
$D\subseteq \{(i_D, j_D, l) : l\in \mathbb{N}\}$
, and -
(iii)
 $(i_D, j_D, \infty)=\bigvee_{\mathcal L} D$
.
$(i_D, j_D, \infty)=\bigvee_{\mathcal L} D$
.
Since A is Scott closed,
![]() $(i_D, j_D, \infty)=\bigvee_{\mathcal L} D\in A$
, whence
$(i_D, j_D, \infty)=\bigvee_{\mathcal L} D\in A$
, whence
![]() $(i_D, j_D, \infty)\in \mathrm{max}(A)$
. Now we show that
$(i_D, j_D, \infty)\in \mathrm{max}(A)$
. Now we show that
![]() $(i_D, j_D, \infty)\neq (n(A), j, \infty)$
. Suppose, on the contrary, that
$(i_D, j_D, \infty)\neq (n(A), j, \infty)$
. Suppose, on the contrary, that
![]() $(i_D, j_D, \infty)=(n(A), j, \infty)$
. For each
$(i_D, j_D, \infty)=(n(A), j, \infty)$
. For each
![]() $d=(i_D, j_D, l_d)\in D$
, there is an
$d=(i_D, j_D, l_d)\in D$
, there is an
![]() $(i_d, j_d, \infty)\in \mathrm{max}(A)\setminus \{(n(A), j, \infty)\}$
such that
$(i_d, j_d, \infty)\in \mathrm{max}(A)\setminus \{(n(A), j, \infty)\}$
such that
![]() $d=(i_D, j_D, l_d)\leq (i_d, j_d, \infty)$
. Since
$d=(i_D, j_D, l_d)\leq (i_d, j_d, \infty)$
. Since
![]() $(i_d, j_d, \infty)\neq (n(A), j, \infty)=(i_D, j_D, \infty)$
, we have that
$(i_d, j_d, \infty)\neq (n(A), j, \infty)=(i_D, j_D, \infty)$
, we have that
![]() $i_d=i_D+1=n(A)+1$
and
$i_d=i_D+1=n(A)+1$
and
![]() $l_d\leq j_d$
. As
$l_d\leq j_d$
. As
![]() $D\subseteq \{(i_D, j_D, l) : l\in \mathbb{N}\}$
is infinite, the set
$D\subseteq \{(i_D, j_D, l) : l\in \mathbb{N}\}$
is infinite, the set
![]() $\{(n(A)+1, l_d, \infty)=(i_D+1, l_d, \infty) : d\in D\}$
is infinite, and consequently,
$\{(n(A)+1, l_d, \infty)=(i_D+1, l_d, \infty) : d\in D\}$
is infinite, and consequently,
![]() $A\cap L_{n(A)+1}^{\infty}$
is infinite, a contradiction. So
$A\cap L_{n(A)+1}^{\infty}$
is infinite, a contradiction. So
![]() $(i_D, j_D, \infty)\neq (n(A), j, \infty)$
and hence
$(i_D, j_D, \infty)\neq (n(A), j, \infty)$
and hence
![]() $\bigvee_{\mathcal L} D=(i_D, j_D, \infty)\in \mathrm{max}(A)\setminus \{(n(A), j, \infty)\}\subseteq B$
. Thus, B is Scott closed.
$\bigvee_{\mathcal L} D=(i_D, j_D, \infty)\in \mathrm{max}(A)\setminus \{(n(A), j, \infty)\}\subseteq B$
. Thus, B is Scott closed.
By the irreducibility of A, we have
![]() $A=B$
or
$A=B$
or
![]() $A=\downarrow (n(A), j, \infty)$
. It follows from
$A=\downarrow (n(A), j, \infty)$
. It follows from
![]() $(n(A), j, \infty)\not\in B$
that
$(n(A), j, \infty)\not\in B$
that
![]() $A=\downarrow (n(A), j, \infty)={\rm cl}_{\sigma (\mathcal L)}\{(n(A), j, \infty)\}$
.
$A=\downarrow (n(A), j, \infty)={\rm cl}_{\sigma (\mathcal L)}\{(n(A), j, \infty)\}$
.
All these together deduce that
![]() ${\mathsf{Irr}}_c(\Sigma~\!\!\mathcal L)=\{\overline{\{x\}}=\mathord{\downarrow} x : x\in \mathcal L\}\cup\{\mathcal L\}$
.
${\mathsf{Irr}}_c(\Sigma~\!\!\mathcal L)=\{\overline{\{x\}}=\mathord{\downarrow} x : x\in \mathcal L\}\cup\{\mathcal L\}$
.
Lemma 81.
(Jia Reference Jia2018, Example 2.6.1) For a nonempty saturated subset
![]() $K\subseteq \mathcal L$
, K is compact in
$K\subseteq \mathcal L$
, K is compact in
![]() $\Sigma~\!\!\mathcal L$
if and only if the following three conditions are satisfied:
$\Sigma~\!\!\mathcal L$
if and only if the following three conditions are satisfied:
-
(1)
 $\mathrm{min}(K)\cap \mathcal L^{<\infty}$
is finite,
$\mathrm{min}(K)\cap \mathcal L^{<\infty}$
is finite,
-
(2)
 $\{n\in \mathbb{N} : \mathcal L_n^{\infty}\cap K\neq\emptyset\}$
is finite, and
$\{n\in \mathbb{N} : \mathcal L_n^{\infty}\cap K\neq\emptyset\}$
is finite, and
-
(3) there is a unique
 $(i_K, j_K)\in \mathbb{N}\times \mathbb{N}$
such that
$(i_K, j_K)\in \mathbb{N}\times \mathbb{N}$
such that
 $K\cap (\mathcal L_{(<{i_K})}^{\infty}\cup \mathcal L_{(i_K, \geq j_K)}^{\infty})=\{(i_K, j_K, \infty)\}$
(or equivalently,
$K\cap (\mathcal L_{(<{i_K})}^{\infty}\cup \mathcal L_{(i_K, \geq j_K)}^{\infty})=\{(i_K, j_K, \infty)\}$
(or equivalently,
 $K\cap (\mathcal L_{(<{i_K})}\cup \mathcal L_{(i_K, \geq j_K)}^{\infty})=\{(i_K, j_K, \infty)\}$
).
$K\cap (\mathcal L_{(<{i_K})}\cup \mathcal L_{(i_K, \geq j_K)}^{\infty})=\{(i_K, j_K, \infty)\}$
).
Corollary 82.
For any filtered family
![]() $\{K_d : d\in D\}\subseteq \mathord{\mathsf{K}} (\Sigma~\!\!\mathcal L)$
,
$\{K_d : d\in D\}\subseteq \mathord{\mathsf{K}} (\Sigma~\!\!\mathcal L)$
,
![]() $\bigcap_{d\in D}K_d\neq\emptyset$
.
$\bigcap_{d\in D}K_d\neq\emptyset$
.
Proof. We can assume that D is directed and
![]() $K_{d_2}\subseteq K_{d_1}$
iff
$K_{d_2}\subseteq K_{d_1}$
iff
![]() $d_1\leq d_2$
(indeed, D can be defined an order by
$d_1\leq d_2$
(indeed, D can be defined an order by
![]() $d_1\leq d_2$
iff
$d_1\leq d_2$
iff
![]() $K_{d_2}\subseteq K_{d_1}$
). For each
$K_{d_2}\subseteq K_{d_1}$
). For each
![]() $d\in D$
, by Lemma 81, there exists a unique
$d\in D$
, by Lemma 81, there exists a unique
![]() $(i_d, j_d)\in \mathbb{N}\times \mathbb{N}$
such that
$(i_d, j_d)\in \mathbb{N}\times \mathbb{N}$
such that
![]() $(\mathcal L_{(<i_d)}^{\infty}\cup \mathcal L_{(i_d, \geq j_d)}^{\infty})\cap K_d=\{(i_d, j_d, \infty)\}$
and the set
$(\mathcal L_{(<i_d)}^{\infty}\cup \mathcal L_{(i_d, \geq j_d)}^{\infty})\cap K_d=\{(i_d, j_d, \infty)\}$
and the set
![]() $\mathbb{N}_d=\{n\in \mathbb{N} : \mathcal L_n^{\infty}\cap K_d\neq\emptyset\}$
is finite. Select a
$\mathbb{N}_d=\{n\in \mathbb{N} : \mathcal L_n^{\infty}\cap K_d\neq\emptyset\}$
is finite. Select a
![]() $d_0\in D$
. Then for each
$d_0\in D$
. Then for each
![]() $d\in D$
with
$d\in D$
with
![]() $d_0\leq d$
(whence
$d_0\leq d$
(whence
![]() $K_d\subseteq K_{d_0}$
), we have that
$K_d\subseteq K_{d_0}$
), we have that
![]() $i_d\in \mathbb{N}_d\subseteq \mathbb{N}_{d_0}$
and
$i_d\in \mathbb{N}_d\subseteq \mathbb{N}_{d_0}$
and
![]() $i_{d_0}\leq i_d$
(otherwise,
$i_{d_0}\leq i_d$
(otherwise,
![]() $i_{d_0}> i_d$
would imply that
$i_{d_0}> i_d$
would imply that
![]() $(i_d, j_d, \infty)\in (\mathcal L_{(<i_d)}^{\infty}\cup \mathcal L_{(i_d, \geq j_d)}^{\infty})\cap K_d\subseteq L_{(<i_{d_0})}^{\infty}\cap K_{d_0}$
, which contradicts
$(i_d, j_d, \infty)\in (\mathcal L_{(<i_d)}^{\infty}\cup \mathcal L_{(i_d, \geq j_d)}^{\infty})\cap K_d\subseteq L_{(<i_{d_0})}^{\infty}\cap K_{d_0}$
, which contradicts
![]() $L_{(<i_{d_0})}^{\infty}\cap K_{d_0}=\emptyset$
). Let
$L_{(<i_{d_0})}^{\infty}\cap K_{d_0}=\emptyset$
). Let
![]() $D_{d_0}=\{d\in D : d_0\leq d\}$
and
$D_{d_0}=\{d\in D : d_0\leq d\}$
and
![]() $D_i=\{d\in D_{d_0} : i_d=i\}$
for each
$D_i=\{d\in D_{d_0} : i_d=i\}$
for each
![]() $i\in \mathbb{N}_{d_0}$
. Since
$i\in \mathbb{N}_{d_0}$
. Since
![]() $\mathbb{N}_{d_0}$
is finite,
$\mathbb{N}_{d_0}$
is finite,
![]() $D_{d_0}$
is directed and
$D_{d_0}$
is directed and
![]() $D_{d_0}=\bigcup_{i\in\mathbb{N}_{d_0}} D_i$
, there is
$D_{d_0}=\bigcup_{i\in\mathbb{N}_{d_0}} D_i$
, there is
![]() $i_0\in \mathbb{N}_{d_0}$
such that
$i_0\in \mathbb{N}_{d_0}$
such that
![]() $D_{i_0}$
is a cofinal subset of
$D_{i_0}$
is a cofinal subset of
![]() $D_{d_0}$
and hence a cofinal subset of D, more precisely, for each
$D_{d_0}$
and hence a cofinal subset of D, more precisely, for each
![]() $d\in D$
, there is
$d\in D$
, there is
![]() $d^*\in D$
such that
$d^*\in D$
such that
![]() $d^*\in \mathord{\uparrow} d_0\cap \mathord{\uparrow} d$
and
$d^*\in \mathord{\uparrow} d_0\cap \mathord{\uparrow} d$
and
![]() $i_{d^*}=i_0$
.
$i_{d^*}=i_0$
.
Clearly,
![]() $D_{i_0}$
is also directed. Select a
$D_{i_0}$
is also directed. Select a
![]() $d_1\in D_{i_0}$
. Then,
$d_1\in D_{i_0}$
. Then,
![]() $D_{d_1}=\{d\in D_{i_0} : d_1\leq d\}$
is a directed and cofinal subset of
$D_{d_1}=\{d\in D_{i_0} : d_1\leq d\}$
is a directed and cofinal subset of
![]() $D_{i_0}$
and hence a directed and cofinal subset of D. For each
$D_{i_0}$
and hence a directed and cofinal subset of D. For each
![]() $d\in D_{d_1}$
(note that
$d\in D_{d_1}$
(note that
![]() $K_d\subseteq K_{d_1}$
), we have that
$K_d\subseteq K_{d_1}$
), we have that
![]() $i_{d_1}=i_d=i_0$
,
$i_{d_1}=i_d=i_0$
,
![]() $(i_d=i_0, j_d, \infty)\in K_d\subseteq K_{d_1}$
and
$(i_d=i_0, j_d, \infty)\in K_d\subseteq K_{d_1}$
and
![]() $\mathcal L_{(i_0, \geq j_{d_1})}^{\infty}\cap K_{d_1}=\{(i_0, j_{d_1}, \infty)\}$
. It follows that
$\mathcal L_{(i_0, \geq j_{d_1})}^{\infty}\cap K_{d_1}=\{(i_0, j_{d_1}, \infty)\}$
. It follows that
![]() $j_d\leq j_{d_1}$
. For each
$j_d\leq j_{d_1}$
. For each
![]() $1\leq j\leq j_{d_1}$
, let
$1\leq j\leq j_{d_1}$
, let
![]() $\widetilde{D}_{j}=\{d\in D_{d_1} : j_d=j\}$
. Since
$\widetilde{D}_{j}=\{d\in D_{d_1} : j_d=j\}$
. Since
![]() $\{1, 2, ..., j_{d_1}\}$
is finite,
$\{1, 2, ..., j_{d_1}\}$
is finite,
![]() $D_{d_1}$
is directed and
$D_{d_1}$
is directed and
![]() $D_{d_1}=\bigcup_{i\in\mathbb{N}_{d_0}} \widetilde{D}_{j}$
, there is
$D_{d_1}=\bigcup_{i\in\mathbb{N}_{d_0}} \widetilde{D}_{j}$
, there is
![]() $1\leq j_0\leq j_{d_1}$
such that
$1\leq j_0\leq j_{d_1}$
such that
![]() $\widetilde{D}_{j_0}$
is a cofinal subset of
$\widetilde{D}_{j_0}$
is a cofinal subset of
![]() $D_{d_1}$
and hence a cofinal subset of D; more precisely, for each
$D_{d_1}$
and hence a cofinal subset of D; more precisely, for each
![]() $d\in D$
, there is
$d\in D$
, there is
![]() $d^{\prime}\in D$
such that
$d^{\prime}\in D$
such that
![]() $d^{\prime}\in \mathord{\uparrow} d_0\cap \mathord{\uparrow} d_1\cap \mathord{\uparrow} d$
,
$d^{\prime}\in \mathord{\uparrow} d_0\cap \mathord{\uparrow} d_1\cap \mathord{\uparrow} d$
,
![]() $i_{d^{\prime}}=i_0$
and
$i_{d^{\prime}}=i_0$
and
![]() $j_{d^{\prime}}=j_0$
. It follows that
$j_{d^{\prime}}=j_0$
. It follows that
![]() $(i_0, j_0, \infty)\in \bigcap_{d\in D}K_d$
.
$(i_0, j_0, \infty)\in \bigcap_{d\in D}K_d$
.
Proposition 83.
(Jia Reference Jia2018, Example 2.6.1)
![]() $\Sigma~\!\!\mathcal L$
is well-filtered but non-sober.
$\Sigma~\!\!\mathcal L$
is well-filtered but non-sober.
Proof. By Lemma 80,
![]() $\mathcal L$
is an irreducible closed subset of
$\mathcal L$
is an irreducible closed subset of
![]() $\Sigma~\!\!\mathcal L$
but has no largest element, so
$\Sigma~\!\!\mathcal L$
but has no largest element, so
![]() $\Sigma~\!\!\mathcal L$
is non-sober.
$\Sigma~\!\!\mathcal L$
is non-sober.
The well-filteredness of
![]() $\Sigma~\!\!\mathcal L$
was proved in Jia (Reference Jia2018) (see Jia Reference Jia2018, the proof of Claim 2.6.4). Using Topological Rudin Lemma, Lemma 80 and Corollary 82, we can give a short proof of the well-filteredness of
$\Sigma~\!\!\mathcal L$
was proved in Jia (Reference Jia2018) (see Jia Reference Jia2018, the proof of Claim 2.6.4). Using Topological Rudin Lemma, Lemma 80 and Corollary 82, we can give a short proof of the well-filteredness of
![]() $\Sigma~\!\!\mathcal L$
. Suppose that
$\Sigma~\!\!\mathcal L$
. Suppose that
![]() $\{K_d : d\in D\}\subseteq \mathord{\mathsf{K}} (\Sigma~\!\!\mathcal L)$
is a filtered family and
$\{K_d : d\in D\}\subseteq \mathord{\mathsf{K}} (\Sigma~\!\!\mathcal L)$
is a filtered family and
![]() $U\in \sigma (\mathcal L)$
with
$U\in \sigma (\mathcal L)$
with
![]() $\bigcap_{d\in D}K_d\subseteq U$
. Assume, on the contrary, that
$\bigcap_{d\in D}K_d\subseteq U$
. Assume, on the contrary, that
![]() $K_d\not\subseteq U$
for each
$K_d\not\subseteq U$
for each
![]() $d\in D$
(whence
$d\in D$
(whence
![]() $U\neq \mathcal L$
). Then by Lemma 27,
$U\neq \mathcal L$
). Then by Lemma 27,
![]() $\mathcal L\setminus U$
contains a minimal irreducible closed subset A that still meets all members
$\mathcal L\setminus U$
contains a minimal irreducible closed subset A that still meets all members
![]() $K_d$
. By Corollary 82,
$K_d$
. By Corollary 82,
![]() $\bigcap_{d\in D}K_d\neq\emptyset$
, whence
$\bigcap_{d\in D}K_d\neq\emptyset$
, whence
![]() $U\neq\emptyset$
and
$U\neq\emptyset$
and
![]() $A\neq \mathcal L$
. It follows from Lemma 80 that
$A\neq \mathcal L$
. It follows from Lemma 80 that
![]() $A=\overline{\{x\}}$
for some
$A=\overline{\{x\}}$
for some
![]() $x\in \mathcal L$
. Then,
$x\in \mathcal L$
. Then,
![]() $x\in \bigcap_{d\in D}K_d\subseteq U$
, which contradicts
$x\in \bigcap_{d\in D}K_d\subseteq U$
, which contradicts
![]() $x\in A\subseteq \mathcal L \setminus U$
. Thus
$x\in A\subseteq \mathcal L \setminus U$
. Thus
![]() $\Sigma~\!\!\mathcal L$
is well-filtered.
$\Sigma~\!\!\mathcal L$
is well-filtered.
Definition 84.
Let X be a
![]() $T_0$
space for which X is irreducible (i.e.,
$T_0$
space for which X is irreducible (i.e.,
![]() $X\in{\mathsf{Irr}}_c(X)$
). Choose a point
$X\in{\mathsf{Irr}}_c(X)$
). Choose a point
![]() $\top$
such that
$\top$
such that
![]() $\top\not\in X$
. Then,
$\top\not\in X$
. Then,
![]() $(\mathcal C(X)\setminus \{X\})\cup \{X\cup\{\top\}\}$
(as the set of all closed sets) is a topology on
$(\mathcal C(X)\setminus \{X\})\cup \{X\cup\{\top\}\}$
(as the set of all closed sets) is a topology on
![]() $X\cup\{\top\}$
. The resulting space is denoted by
$X\cup\{\top\}$
. The resulting space is denoted by
![]() $X_{\top}$
. Define a mapping
$X_{\top}$
. Define a mapping
![]() $\zeta_{X}: X\rightarrow X_{\top}$
by
$\zeta_{X}: X\rightarrow X_{\top}$
by
![]() $\zeta_{X}(x)=x$
for each
$\zeta_{X}(x)=x$
for each
![]() $x\in X$
. Clearly,
$x\in X$
. Clearly,
![]() $\eta_{X}$
is a topological embedding.
$\eta_{X}$
is a topological embedding.
As X is
![]() $T_0$
,
$T_0$
,
![]() $X_{\top}$
is also
$X_{\top}$
is also
![]() $T_0$
and
$T_0$
and
![]() $\overline{\{\top\}}=X\cup\{\top\}$
in
$\overline{\{\top\}}=X\cup\{\top\}$
in
![]() $X_{\top}$
. Hence,
$X_{\top}$
. Hence,
![]() $\top$
is a largest element of
$\top$
is a largest element of
![]() $X_{\top}$
and for
$X_{\top}$
and for
![]() $x, y\in X$
,
$x, y\in X$
,
![]() $x\leq_X y$
iff
$x\leq_X y$
iff
![]() $x\leq y$
in
$x\leq y$
in
![]() $X_{\top}$
. It is worthy noting that the set
$X_{\top}$
. It is worthy noting that the set
![]() $\{\top\}$
is not open in
$\{\top\}$
is not open in
![]() $X_{\top}$
.
$X_{\top}$
.
Remark 85. If X is not irreducible, then there exist
![]() $A, B\in \mathcal C(X)\setminus \{X\}$
such that
$A, B\in \mathcal C(X)\setminus \{X\}$
such that
![]() $X=A\cup B$
, whence
$X=A\cup B$
, whence
![]() $(\mathcal C(X)\setminus \{X\})\cup \{X\cup\{\top\}\}$
is not a topology on
$(\mathcal C(X)\setminus \{X\})\cup \{X\cup\{\top\}\}$
is not a topology on
![]() $X\cup\{\top\}$
.
$X\cup\{\top\}$
.
Lemma 86.
Let X be a
![]() $T_0$
space for which X is irreducible. Then,
$T_0$
space for which X is irreducible. Then,
![]() $\mathsf{K}(X_{\top})=\{G\cup\{\top\} : G\in \mathsf{K}(X)\}\cup\{\{\top\}\}$
.
$\mathsf{K}(X_{\top})=\{G\cup\{\top\} : G\in \mathsf{K}(X)\}\cup\{\{\top\}\}$
.
Proof. Clearly,
![]() $\mathcal O(X_{\top})=\{U\cup\{\top\} : U\in \mathcal O(X)\setminus \{\emptyset\}\}\cup\{\emptyset\}$
.
$\mathcal O(X_{\top})=\{U\cup\{\top\} : U\in \mathcal O(X)\setminus \{\emptyset\}\}\cup\{\emptyset\}$
.
First, if
![]() $K\in \mathsf{K}(X_{\top})\setminus \{\{\top\}\}$
, then
$K\in \mathsf{K}(X_{\top})\setminus \{\{\top\}\}$
, then
![]() $G=K\setminus \{\top\}$
is a nonempty saturated subset of X. Now we verify that G is a compact subset of X. Suppose that
$G=K\setminus \{\top\}$
is a nonempty saturated subset of X. Now we verify that G is a compact subset of X. Suppose that
![]() $\{U_i : i\in I\}\subseteq \mathcal O(X)\setminus \{\emptyset\}$
is an open cover of G. Then,
$\{U_i : i\in I\}\subseteq \mathcal O(X)\setminus \{\emptyset\}$
is an open cover of G. Then,
![]() $\{U_i\cup\{\top\} : i\in I\}\subseteq \mathcal O(X_{\top})$
is an open cover of
$\{U_i\cup\{\top\} : i\in I\}\subseteq \mathcal O(X_{\top})$
is an open cover of
![]() $K=G\cup \{\top\}$
. By the compactness of K, there is
$K=G\cup \{\top\}$
. By the compactness of K, there is
![]() $I_0\in I^{(<\omega)}$
such that
$I_0\in I^{(<\omega)}$
such that
![]() $K\subseteq \bigcup_{i\in I_0}U_i\cup\{\top\}$
, whence
$K\subseteq \bigcup_{i\in I_0}U_i\cup\{\top\}$
, whence
![]() $G=K\setminus \{\top\}\subseteq \bigcup_{i\in I_0}U_i$
, proving that
$G=K\setminus \{\top\}\subseteq \bigcup_{i\in I_0}U_i$
, proving that
![]() $G\in \mathsf{K}(X)$
.
$G\in \mathsf{K}(X)$
.
Conversely, assume that
![]() $G\in \mathsf{K}(X)$
and
$G\in \mathsf{K}(X)$
and
![]() $\{W_j : j\in J\}\subseteq \mathcal O(X_{\top})\setminus \{\emptyset\}$
is an open cover of
$\{W_j : j\in J\}\subseteq \mathcal O(X_{\top})\setminus \{\emptyset\}$
is an open cover of
![]() $K=G\cup \{\top\}$
. Then, K is saturated and for each
$K=G\cup \{\top\}$
. Then, K is saturated and for each
![]() $j\in J$
, there is
$j\in J$
, there is
![]() $V_j\in \mathcal O(X)$
such that
$V_j\in \mathcal O(X)$
such that
![]() $W_j=V_j\cup\{\top\}$
. Hence,
$W_j=V_j\cup\{\top\}$
. Hence,
![]() $\{V_j : j\in J\}\subseteq \mathcal O(X)$
is an open cover of G. By the compactness of G, there is
$\{V_j : j\in J\}\subseteq \mathcal O(X)$
is an open cover of G. By the compactness of G, there is
![]() $J_0\in J^{(<\omega)}$
such that
$J_0\in J^{(<\omega)}$
such that
![]() $G\subseteq \bigcup_{j\in J_0}V_j$
, whence
$G\subseteq \bigcup_{j\in J_0}V_j$
, whence
![]() $K=G\cup\{\top\}\subseteq \bigcup_{j\in J_0}W_j$
. So
$K=G\cup\{\top\}\subseteq \bigcup_{j\in J_0}W_j$
. So
![]() $K\in \mathsf{K}(X_{\top})$
.
$K\in \mathsf{K}(X_{\top})$
.
Thus,
![]() $\mathsf{K}(X_{\top})=\{G\cup\{\top\} : G\in \mathsf{K}(X)\}\cup\{\{\top\}\}$
.
$\mathsf{K}(X_{\top})=\{G\cup\{\top\} : G\in \mathsf{K}(X)\}\cup\{\{\top\}\}$
.
Lemma 87.
Suppose that X is a non-sober
![]() $T_0$
space for which
$T_0$
space for which
![]() ${\mathsf{Irr}}_c(X)=\{\overline{\{x\}} : x\in X\}\cup\{X\}$
. Then,
${\mathsf{Irr}}_c(X)=\{\overline{\{x\}} : x\in X\}\cup\{X\}$
. Then,
![]() $\langle X_{\top},\zeta_{X} \rangle$
is a sobrification of X.
$\langle X_{\top},\zeta_{X} \rangle$
is a sobrification of X.
Proof. Since X is non-sober and
![]() ${\mathsf{Irr}}_c(X)=\{\overline{\{x\}} : x\in X\}\bigcup\{X\}$
,
${\mathsf{Irr}}_c(X)=\{\overline{\{x\}} : x\in X\}\bigcup\{X\}$
,
![]() $X\neq\overline{\{x\}}$
for every
$X\neq\overline{\{x\}}$
for every
![]() $x\in X$
. It is well-known that the space
$x\in X$
. It is well-known that the space
![]() $X^s$
with the canonical mapping
$X^s$
with the canonical mapping
![]() $\eta_{X}: X\longrightarrow X^s$
,
$\eta_{X}: X\longrightarrow X^s$
,
![]() $\eta_{X}(x)=x$
, is a sobrification of X (see, e.g., Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Exercise V-4.9). For
$\eta_{X}(x)=x$
, is a sobrification of X (see, e.g., Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Exercise V-4.9). For
![]() $C\in \mathcal C(X)$
, we have
$C\in \mathcal C(X)$
, we have
 $$\Box_{{\mathsf{Irr}}_c(X)} C=\{A\in {\mathsf{Irr}}_c(X) : A\subseteq C\}=\begin{cases}\{\overline{\{c\}} : c\in C\},& C\neq X,\\\{\overline{\{x\}} : x\in X\}\cup\{X\},& C=X. \end{cases}$$
$$\Box_{{\mathsf{Irr}}_c(X)} C=\{A\in {\mathsf{Irr}}_c(X) : A\subseteq C\}=\begin{cases}\{\overline{\{c\}} : c\in C\},& C\neq X,\\\{\overline{\{x\}} : x\in X\}\cup\{X\},& C=X. \end{cases}$$
Define a mapping
![]() $f : X^s \rightarrow X_{\top}$
by
$f : X^s \rightarrow X_{\top}$
by
 $$f (A)=\begin{cases} x & A=\overline{\{x\}}, x\in X,\\\top & A=X. \end{cases}$$
$$f (A)=\begin{cases} x & A=\overline{\{x\}}, x\in X,\\\top & A=X. \end{cases}$$
For each
![]() $C\in (\mathcal C(X)\setminus \{X\})\bigcup \{X_{\top}\}$
and
$C\in (\mathcal C(X)\setminus \{X\})\bigcup \{X_{\top}\}$
and
![]() $B\in \mathcal C(X)$
, we have
$B\in \mathcal C(X)$
, we have
![]() $f^{-1}(C)=\Box_{{\mathsf{Irr}}_c(X)} C$
and
$f^{-1}(C)=\Box_{{\mathsf{Irr}}_c(X)} C$
and
 $$f(\Box_{{\mathsf{Irr}}_c(X)} B)=\begin{cases} B& B\neq X,\\X\cup\{\top\}& B=X. \end{cases}$$
$$f(\Box_{{\mathsf{Irr}}_c(X)} B)=\begin{cases} B& B\neq X,\\X\cup\{\top\}& B=X. \end{cases}$$
Thus, f is a homeomorphism.

So
![]() $\langle X_{\top},\zeta_{X}=f\circ\eta_X\rangle$
is a sobrification of X.
$\langle X_{\top},\zeta_{X}=f\circ\eta_X\rangle$
is a sobrification of X.
The following corollary is straightforward from Lemma 80, Proposition 83, and Lemma 87.
Corollary 88.
![]() $\langle (\Sigma~\!\!\mathcal L)_{\top},\zeta_{\mathcal L} \rangle$
is a sobrification of
$\langle (\Sigma~\!\!\mathcal L)_{\top},\zeta_{\mathcal L} \rangle$
is a sobrification of
![]() $\Sigma~\!\!\mathcal L$
, where
$\Sigma~\!\!\mathcal L$
, where
![]() $\zeta_{\mathcal L}: \Sigma~\!\!\mathcal L\rightarrow (\Sigma~\!\!\mathcal L)_{\top}$
is defined by
$\zeta_{\mathcal L}: \Sigma~\!\!\mathcal L\rightarrow (\Sigma~\!\!\mathcal L)_{\top}$
is defined by
![]() $\zeta_{\mathcal L}(x)=x$
for each
$\zeta_{\mathcal L}(x)=x$
for each
![]() $x\in \mathcal L$
.
$x\in \mathcal L$
.
Note that although the set
![]() $\{\top\}$
is open in
$\{\top\}$
is open in
![]() $\Sigma~\!\!\mathcal L_{\top}$
(or equivalently,
$\Sigma~\!\!\mathcal L_{\top}$
(or equivalently,
![]() $\top$
is a compact element of the dcpo
$\top$
is a compact element of the dcpo
![]() $\mathcal L\cup\{\top\}$
), it is not open in
$\mathcal L\cup\{\top\}$
), it is not open in
![]() $(\Sigma~\!\!\mathcal L)_{\top}$
.
$(\Sigma~\!\!\mathcal L)_{\top}$
.
By Lemmas 80 and 86, we get the following.
Corollary 89.
![]() $\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})=\{G\cup\{\top\} : G\in \mathsf{K}(\Sigma~\!\!\mathcal L))\}\cup\{\{\top\}\}$
.
$\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})=\{G\cup\{\top\} : G\in \mathsf{K}(\Sigma~\!\!\mathcal L))\}\cup\{\{\top\}\}$
.
Lemma 90.
![]() $\{\top\}$
is a compact element in the dcpo
$\{\top\}$
is a compact element in the dcpo
![]() $\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
. Hence,
$\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
. Hence,
![]() $\{\{\top\}\}$
is open in the Scott space
$\{\{\top\}\}$
is open in the Scott space
![]() $\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
.
$\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
.
Proof. By Proposition 83,
![]() $\Sigma~\!\!\mathcal L$
is well-filtered, whence
$\Sigma~\!\!\mathcal L$
is well-filtered, whence
![]() $\mathsf{K}(\Sigma~\!\!\mathcal L)$
(with the Smyth order) is a dcpo. So by Corollary 89,
$\mathsf{K}(\Sigma~\!\!\mathcal L)$
(with the Smyth order) is a dcpo. So by Corollary 89,
![]() $\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
is a dcpo. Now we show that
$\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
is a dcpo. Now we show that
![]() $\{\top\}\ll \{\top\}$
in
$\{\top\}\ll \{\top\}$
in
![]() $\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
. Suppose that
$\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
. Suppose that
![]() $\{K_d : d\in D\}$
is a directed subset of
$\{K_d : d\in D\}$
is a directed subset of
![]() $\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
and
$\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
and
![]() $\{\top\}\sqsubseteq \bigvee_{d\in D}K_d$
. Then by Lemma 9,
$\{\top\}\sqsubseteq \bigvee_{d\in D}K_d$
. Then by Lemma 9,
![]() $\bigvee_{d\in D}K_d=\bigcap_{d\in D}K_d,$
and hence,
$\bigvee_{d\in D}K_d=\bigcap_{d\in D}K_d,$
and hence,
![]() $\bigcap_{d\in D}K_d\subseteq \{\top\}$
. It follows that
$\bigcap_{d\in D}K_d\subseteq \{\top\}$
. It follows that
![]() $\bigcap_{d\in D}(K_d\setminus \{\top\})=\emptyset$
. By Corollaries 82 and 89, there is
$\bigcap_{d\in D}(K_d\setminus \{\top\})=\emptyset$
. By Corollaries 82 and 89, there is
![]() $d\in D$
such that
$d\in D$
such that
![]() $K_d\setminus \{\top\}=\emptyset$
, that is,
$K_d\setminus \{\top\}=\emptyset$
, that is,
![]() $K_d=\{\top\}$
. Thus,
$K_d=\{\top\}$
. Thus,
![]() $\{\top\}$
is a compact element in
$\{\top\}$
is a compact element in
![]() $\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
. Hence,
$\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
. Hence,
![]() $\{\{\top\}\}\in \sigma(\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top}))$
.
$\{\{\top\}\}\in \sigma(\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top}))$
.
Theorem 91.
The Scott space
![]() $\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
of the sober space
$\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
of the sober space
![]() $(\Sigma~\!\!\mathcal L)_{\top}$
is non-sober.
$(\Sigma~\!\!\mathcal L)_{\top}$
is non-sober.
Proof. For simplicity, let
![]() $\mathcal A=\{G\cup\{\top\} : G\in \mathsf{K}(\Sigma~\!\!\mathcal L)\}$
.
$\mathcal A=\{G\cup\{\top\} : G\in \mathsf{K}(\Sigma~\!\!\mathcal L)\}$
.
Claim 1:
![]() $\mathcal A$
is a closed subset of
$\mathcal A$
is a closed subset of
![]() $\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
.
$\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
.
By Corollary 89 and Lemma 90,
![]() $\mathcal A$
is Scott closed.
$\mathcal A$
is Scott closed.
Claim 2:
![]() $\mathcal A$
is irreducible.
$\mathcal A$
is irreducible.
Suppose that
![]() $\mathcal U, \mathcal V\in \sigma(\mathsf{K}((\Sigma \mathcal L)_{\top}))$
and
$\mathcal U, \mathcal V\in \sigma(\mathsf{K}((\Sigma \mathcal L)_{\top}))$
and
![]() $\mathcal A\bigcap \mathcal U\neq \emptyset \neq \mathcal A\bigcap \mathcal V$
. Then by Corollary 89, there are some
$\mathcal A\bigcap \mathcal U\neq \emptyset \neq \mathcal A\bigcap \mathcal V$
. Then by Corollary 89, there are some
![]() $G_1, G_2\in \mathsf{K}(\Sigma~\!\!\mathcal L))$
such that
$G_1, G_2\in \mathsf{K}(\Sigma~\!\!\mathcal L))$
such that
![]() $G_1\cup\{\top\}\in \mathcal A\bigcap \mathcal U$
and
$G_1\cup\{\top\}\in \mathcal A\bigcap \mathcal U$
and
![]() $G_2\cup\{\top\}\in \mathcal A\bigcap \mathcal V$
, whence
$G_2\cup\{\top\}\in \mathcal A\bigcap \mathcal V$
, whence
![]() $(i_1, j_1, \infty)\in G_1$
and
$(i_1, j_1, \infty)\in G_1$
and
![]() $(i_2, j_2, \infty)\in G_2$
for some
$(i_2, j_2, \infty)\in G_2$
for some
![]() $(i_1, j_1), (i_2, j_2)\in \mathbb{N}\times \mathbb{N}$
. Hence by Corollary 89,
$(i_1, j_1), (i_2, j_2)\in \mathbb{N}\times \mathbb{N}$
. Hence by Corollary 89,
![]() $\mathord{\uparrow} (i_1, j_1, \infty)\cup \{\top\}\in \mathcal A\bigcap \mathcal U$
and
$\mathord{\uparrow} (i_1, j_1, \infty)\cup \{\top\}\in \mathcal A\bigcap \mathcal U$
and
![]() $\mathord{\uparrow} (i_2, j_2, \infty)\cup \{\top\}\in \mathcal A\bigcap \mathcal V$
(note that
$\mathord{\uparrow} (i_2, j_2, \infty)\cup \{\top\}\in \mathcal A\bigcap \mathcal V$
(note that
![]() $\mathcal U, \mathcal V$
are upper sets and
$\mathcal U, \mathcal V$
are upper sets and
![]() $G_1\cup\{\top\}\sqsubseteq \mathord{\uparrow} (i_1, j_1, \infty)\cup \{\top\}, G_2\cup\{\top\}\sqsubseteq \mathord{\uparrow} (i_2, j_2, \infty)\cup \{\top\}$
). Without loss of generality, we assume
$G_1\cup\{\top\}\sqsubseteq \mathord{\uparrow} (i_1, j_1, \infty)\cup \{\top\}, G_2\cup\{\top\}\sqsubseteq \mathord{\uparrow} (i_2, j_2, \infty)\cup \{\top\}$
). Without loss of generality, we assume
![]() $i_1\leq i_2$
. Since
$i_1\leq i_2$
. Since
![]() $\bigvee_{l\in \mathbb{N}}(\mathord{\uparrow} (i_1, j_1, l)\cup \{\top\})=\bigcap_{l\in \mathbb{N}}(\mathord{\uparrow} (i_1, j_1, l)\cup \{\top\})=\mathord{\uparrow} (i_1, j_1, \infty)\cup \{\top\}\in \mathcal U\in \sigma(\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top}))$
, we have some
$\bigvee_{l\in \mathbb{N}}(\mathord{\uparrow} (i_1, j_1, l)\cup \{\top\})=\bigcap_{l\in \mathbb{N}}(\mathord{\uparrow} (i_1, j_1, l)\cup \{\top\})=\mathord{\uparrow} (i_1, j_1, \infty)\cup \{\top\}\in \mathcal U\in \sigma(\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top}))$
, we have some
![]() $l_1\in\mathbb{N}$
such that
$l_1\in\mathbb{N}$
such that
![]() $\mathord{\uparrow} (i_1, j_1, l_1)\in \mathcal U$
. So by Corollary 89,
$\mathord{\uparrow} (i_1, j_1, l_1)\in \mathcal U$
. So by Corollary 89,
![]() $\mathord{\uparrow} (i_1+1, l_1, \infty)\cup\{\top\}\in \mathcal U$
since
$\mathord{\uparrow} (i_1+1, l_1, \infty)\cup\{\top\}\in \mathcal U$
since
![]() $(i_1, j_1, l_1)\leq (i_1+1, l_1, \infty)$
and
$(i_1, j_1, l_1)\leq (i_1+1, l_1, \infty)$
and
![]() $\mathcal U$
is an upper set. Then by induction, we have
$\mathcal U$
is an upper set. Then by induction, we have
![]() $\mathord{\uparrow} (i_2, j^{\prime}, \infty)\cup\{\top\}\in \mathcal U$
for some
$\mathord{\uparrow} (i_2, j^{\prime}, \infty)\cup\{\top\}\in \mathcal U$
for some
![]() $j^{\prime}\in \mathbb{N}$
. Again, since
$j^{\prime}\in \mathbb{N}$
. Again, since
![]() $\bigvee_{l\in \mathbb{N}}(\mathord{\uparrow} (i_2, j^{\prime}, l)\cup \{\top\})=\bigcap_{l\in \mathbb{N}}(\mathord{\uparrow} (i_2, j^{\prime}, l)\cup \{\top\})=\mathord{\uparrow} (i_2, j^{\prime}, l)\cup \{\top\}\in \mathcal U\in \sigma(\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top}))$
and
$\bigvee_{l\in \mathbb{N}}(\mathord{\uparrow} (i_2, j^{\prime}, l)\cup \{\top\})=\bigcap_{l\in \mathbb{N}}(\mathord{\uparrow} (i_2, j^{\prime}, l)\cup \{\top\})=\mathord{\uparrow} (i_2, j^{\prime}, l)\cup \{\top\}\in \mathcal U\in \sigma(\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top}))$
and
![]() $\bigvee_{l\in \mathbb{N}}(\mathord{\uparrow} (i_2, j_2, l)\cup \{\top\})=\bigcap_{l\in \mathbb{N}}(\mathord{\uparrow} (i_2, j_2, l)\cup \{\top\})=\mathord{\uparrow} (i_2, j_2, \infty)\cup \{\top\}\in \mathcal V\in \sigma(\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top}))$
, we have some
$\bigvee_{l\in \mathbb{N}}(\mathord{\uparrow} (i_2, j_2, l)\cup \{\top\})=\bigcap_{l\in \mathbb{N}}(\mathord{\uparrow} (i_2, j_2, l)\cup \{\top\})=\mathord{\uparrow} (i_2, j_2, \infty)\cup \{\top\}\in \mathcal V\in \sigma(\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top}))$
, we have some
![]() $k_1, k_2\in\mathbb{N}$
such that
$k_1, k_2\in\mathbb{N}$
such that
![]() $\mathord{\uparrow} (i_2, j^{\prime}, k_1)\in \mathcal U$
and
$\mathord{\uparrow} (i_2, j^{\prime}, k_1)\in \mathcal U$
and
![]() $\mathord{\uparrow} (i_2, j_2, k_2)\in \mathcal V$
. Take
$\mathord{\uparrow} (i_2, j_2, k_2)\in \mathcal V$
. Take
![]() $m=\mathrm{max}\{k_1, k_2\}$
. Then,
$m=\mathrm{max}\{k_1, k_2\}$
. Then,
![]() $\mathord{\uparrow} (i_2, m, \infty)\cup\{\top\}\in \mathcal A\bigcap \mathcal U\bigcap \mathcal V$
. Thus,
$\mathord{\uparrow} (i_2, m, \infty)\cup\{\top\}\in \mathcal A\bigcap \mathcal U\bigcap \mathcal V$
. Thus,
![]() $\mathcal A\in {\mathsf{Irr}}_c(\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top}))$
.
$\mathcal A\in {\mathsf{Irr}}_c(\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top}))$
.
Claim 3:
![]() $\mathcal A$
has no largest element.
$\mathcal A$
has no largest element.
Clearly,
![]() $\{\mathord{\uparrow} (i, j, \infty)\cup \{\top\} : i, j\in\mathbb{N}\}$
is the set of all maximal elements of
$\{\mathord{\uparrow} (i, j, \infty)\cup \{\top\} : i, j\in\mathbb{N}\}$
is the set of all maximal elements of
![]() $\mathcal A,$
and hence,
$\mathcal A,$
and hence,
![]() $\mathcal A$
has no largest element.
$\mathcal A$
has no largest element.
By Claims 1–3, the Scott space
![]() $\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
is non-sober.
$\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
is non-sober.
Question 92. For a dcpo (especially, a complete lattice) P with the sober Scott topology, is the Scott space
![]() $\Sigma~\!\!\mathsf{K}(\Sigma~\!\!P)$
sober?
$\Sigma~\!\!\mathsf{K}(\Sigma~\!\!P)$
sober?
We know that every
![]() $T_2$
space is sober, and hence, the Scott space
$T_2$
space is sober, and hence, the Scott space
![]() $\Sigma~\!\!\mathsf{K}(X)$
is well-filtered by Theorem 58. In the next section, we will show that for a locally compact (especially, compact)
$\Sigma~\!\!\mathsf{K}(X)$
is well-filtered by Theorem 58. In the next section, we will show that for a locally compact (especially, compact)
![]() $T_2$
space X, the Soctt space
$T_2$
space X, the Soctt space
![]() $\Sigma~\!\!\mathsf{K}(X)$
is sober (see Corollary 99 below).
$\Sigma~\!\!\mathsf{K}(X)$
is sober (see Corollary 99 below).
By Theorem 19, Corollary 25, Theorem 91, and Corollary 99 below, we naturally pose the following question.
Question 93. For a
![]() $T_2$
space X, is the Scott space
$T_2$
space X, is the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
sober?
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
sober?
8. Local Compactness, First-Countability, and Sobriety of Scott Topology on Smyth Power Posets
In this section, we study the question under what conditions the Scott space
![]() $\Sigma \mathsf{K}(X)$
of a sober space X is sober. This question is related to the investigation of conditions under which the upper Vietoris topology coincides with the Scott topology on
$\Sigma \mathsf{K}(X)$
of a sober space X is sober. This question is related to the investigation of conditions under which the upper Vietoris topology coincides with the Scott topology on
![]() $\mathord{\mathsf{K}} (X)$
, and further, it is closely related to the local compactness and first-countability of X.
$\mathord{\mathsf{K}} (X)$
, and further, it is closely related to the local compactness and first-countability of X.
First, by Corollaries 40, 50 and Theorem 58, we get the following.
Corollary 94.
If X is a well-filtered space for which the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is first-countable or core-compact (especially, locally compact), then
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is first-countable or core-compact (especially, locally compact), then
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is sober.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is sober.
For the local compactness of Smyth power spaces, we have the following.
Lemma 95.
(Lyu et al. Reference Lyu, Chen and Jia2022, Theorem 3.1) For a
![]() $T_0$
space X, the following conditions are equivalent:
$T_0$
space X, the following conditions are equivalent:
-
(1) X is locally compact.
-
(2)
 $P_S(X)$
is core-compact.
$P_S(X)$
is core-compact.
-
(3)
 $P_S(X)$
is locally compact.
$P_S(X)$
is locally compact.
-
(4)
 $P_S(X)$
is locally hypercompact.
$P_S(X)$
is locally hypercompact.
-
(5)
 $P_S(X)$
is a c-space.
$P_S(X)$
is a c-space.
The following corollary follows directly from Proposition 37 and Lemma 95.
Corollary 96.
For a locally compact
![]() $T_0$
space X, the Smyth power space
$T_0$
space X, the Smyth power space
![]() $P_S(X)$
is a
$P_S(X)$
is a
![]() $\mathsf{DC}$
space.
$\mathsf{DC}$
space.
Concerning the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
of a locally compact
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
of a locally compact
![]() $T_0$
space X, we have the following question.
$T_0$
space X, we have the following question.
Question 97. For a locally compact
![]() $T_0$
space X, is the Scott space
$T_0$
space X, is the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
a Rudin space or a
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
a Rudin space or a
![]() $\mathsf{WD}$
space?
$\mathsf{WD}$
space?
Proposition 98. Let X be a locally compact sober space. Then,
-
(1) the Scott space
 $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
and the Symth power space of X coincide, that is,
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
and the Symth power space of X coincide, that is,
 $\Sigma~\!\!\mathsf{K}(X)=P_S(X)$
.
$\Sigma~\!\!\mathsf{K}(X)=P_S(X)$
. -
(2)
 $\mathord{\mathsf{K}} (X)$
is a continuous domain.
$\mathord{\mathsf{K}} (X)$
is a continuous domain.
-
(3)
 $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a sober c-space.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a sober c-space.
Proof. By Corollary 25 and Lemma 54,
![]() $\Sigma~\!\!\mathsf{K}(X)=P_S(X)$
. By Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Proposition I-1.24.2),
$\Sigma~\!\!\mathsf{K}(X)=P_S(X)$
. By Gierz et al. (Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Proposition I-1.24.2),
![]() $\mathsf{K}(X)$
is a continuous semilattice, and hence by Theorem 15 and Proposition 18,
$\mathsf{K}(X)$
is a continuous semilattice, and hence by Theorem 15 and Proposition 18,
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a sober c-space.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a sober c-space.
Corollary 99.
If X is a locally compact
![]() $T_2$
(especially, a compact
$T_2$
(especially, a compact
![]() $T_2$
) space, then
$T_2$
) space, then
-
(1)
 $\Sigma~\!\!\mathsf{K}(X)=P_S(X)$
.
$\Sigma~\!\!\mathsf{K}(X)=P_S(X)$
. -
(2)
 $\mathord{\mathsf{K}} (X)$
is a continuous domain.
$\mathord{\mathsf{K}} (X)$
is a continuous domain.
-
(3)
 $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a sober c-space.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a sober c-space.
By Theorem 15, Propositions 18 and 98, we have the following corollary.
Corollary 100. Let P be a quasicontinuous domain. Then
-
(1) the upper Vietoris topology agrees with the Scott topology on
 $\mathord{\mathsf{K}} (\Sigma~\!\!P)$
.
$\mathord{\mathsf{K}} (\Sigma~\!\!P)$
. -
(2)
 $\mathord{\mathsf{K}} (\Sigma~\!\!P)$
is a continuous semilattice.
$\mathord{\mathsf{K}} (\Sigma~\!\!P)$
is a continuous semilattice.
-
(3) the Scott space
 $\Sigma~\!\!\mathord{\mathsf{K}}(\Sigma~\!\!P)$
is a sober c-space.
$\Sigma~\!\!\mathord{\mathsf{K}}(\Sigma~\!\!P)$
is a sober c-space.
Now we discuss the first-countability of the Scott topology on Smyth power posets. First, for the Smyth power spaces and sobrifications of
![]() $T_0$
spaces, we have the following conclusion. ZZZ
$T_0$
spaces, we have the following conclusion. ZZZ
Proposition 101.
(Brecht et al. 2019; Xu et al. Reference Xu, Shen, Xi and Zhao2021
a,c) For a
![]() $T_0$
space, the following conditions are equivalent:
$T_0$
space, the following conditions are equivalent:
-
(1) X is second-countable.
-
(2)
 $P_S(X)$
is second-countable.
$P_S(X)$
is second-countable.
-
(3)
 $X^s$
is second-countable.
$X^s$
is second-countable.
Since first-countability is a hereditary property, by Remarks 3 and 4, we get the following result.
Proposition 102.
Let X be a
![]() $T_0$
space. If
$T_0$
space. If
![]() $X^s$
is first-countable or
$X^s$
is first-countable or
![]() $P_S(X)$
is first-countable, then X is first-countable.
$P_S(X)$
is first-countable, then X is first-countable.
Example 67 shows that unlike the Smyth power space, the first-countability of the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
of a
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
of a
![]() $T_0$
space X does not imply the first-countability of X in general.
$T_0$
space X does not imply the first-countability of X in general.
The converse of Proposition 102 does not hold in general, as shown in Example 53 and the following example. It also shows that even for a compact Hausdorff first-countable space X, the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
and the Smyth power space of X may not be first-countable.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
and the Smyth power space of X may not be first-countable.
There is even a
![]() $T_0$
space X for which the Scott space
$T_0$
space X for which the Scott space
![]() $\Sigma~\!\!\mathsf{K}(X)$
is second-countable but X is not fist-countable (see Example 120 below). So for the Scott topology on Smyth power posets, the analogous results to Propositions 101 and 102 do not hold.
$\Sigma~\!\!\mathsf{K}(X)$
is second-countable but X is not fist-countable (see Example 120 below). So for the Scott topology on Smyth power posets, the analogous results to Propositions 101 and 102 do not hold.
Example 103. Consider in the plane
![]() $\mathbb{R}^2$
two concentric circles
$\mathbb{R}^2$
two concentric circles
![]() $C_i=\{(x,y)\in \mathbb{R}^2 :x^2+y^2=i\}$
, where
$C_i=\{(x,y)\in \mathbb{R}^2 :x^2+y^2=i\}$
, where
![]() $i=1, 2$
, and their union
$i=1, 2$
, and their union
![]() $X=C_1\cup C_2$
; the projection of
$X=C_1\cup C_2$
; the projection of
![]() $C_1$
onto
$C_1$
onto
![]() $C_2$
from the point (0,0) is denoted by p. On the set X, we generate a topology by defining a neighborhood system
$C_2$
from the point (0,0) is denoted by p. On the set X, we generate a topology by defining a neighborhood system
![]() $\{B(z): z\in X\}$
as follows:
$\{B(z): z\in X\}$
as follows:
![]() $B(z)=\{{z}\}$
for
$B(z)=\{{z}\}$
for
![]() $z\in C_2$
and
$z\in C_2$
and
![]() $B(z)=\{U_j(z): j\in \mathbb{N}\}$
for
$B(z)=\{U_j(z): j\in \mathbb{N}\}$
for
![]() $z\in C_1$
, where
$z\in C_1$
, where
![]() $U_j=V_j\bigcup p(V_j\setminus \{z\})$
and
$U_j=V_j\bigcup p(V_j\setminus \{z\})$
and
![]() $V_j$
is the arc of
$V_j$
is the arc of
![]() $C_1$
with center at z and of length
$C_1$
with center at z and of length
![]() $1/j$
. The space X is called the Alexandroff double circle (cf. Engelking Reference Engelking1989). The following conclusions about X are known (see, for example, Engelking Reference Engelking1989, Example 3.1.26).
$1/j$
. The space X is called the Alexandroff double circle (cf. Engelking Reference Engelking1989). The following conclusions about X are known (see, for example, Engelking Reference Engelking1989, Example 3.1.26).
-
(a) X is Hausdorff and first-countable.
-
(b) X is compact and locally compact.
-
(c) X is not separable, and hence not second-countable.
-
(d)
 $C_1$
is a compact subspace of X.
$C_1$
is a compact subspace of X. -
(e)
 $C_2$
is a discrete subspace of X.
$C_2$
is a discrete subspace of X.
There is no countable base at
![]() $C_1$
in
$C_1$
in
![]() $P_S(X)$
. Thus,
$P_S(X)$
. Thus,
![]() $P_S(X)$
is not first-countable. For details, see Xu et al. (2021c, Example 4.4). By Corollary 99,
$P_S(X)$
is not first-countable. For details, see Xu et al. (2021c, Example 4.4). By Corollary 99,
![]() $\Sigma~\!\!\mathsf{K}(X)=P_S(X)$
, whence the Scott space
$\Sigma~\!\!\mathsf{K}(X)=P_S(X)$
, whence the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is not first-countable.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is not first-countable.
Proposition 104.
(Xu et al. 2021c, Proposition 4.5) Let X be a first-countable
![]() $T_0$
space. If
$T_0$
space. If
![]() $\mathrm{min}(K)$
is countable for any
$\mathrm{min}(K)$
is countable for any
![]() $K\in \mathord{\mathsf{K}} (X)$
, then
$K\in \mathord{\mathsf{K}} (X)$
, then
![]() $P_S(X)$
is first-countable.
$P_S(X)$
is first-countable.
For a metric space (X, d),
![]() $x\in X$
and a positive number r, let
$x\in X$
and a positive number r, let
![]() $B(x, r)=\{y\in Y : d(x, y)<r\}$
be the r-ball about x. For a set
$B(x, r)=\{y\in Y : d(x, y)<r\}$
be the r-ball about x. For a set
![]() $A\subseteq X$
and a positive number r, by the r-ball about A we mean the set
$A\subseteq X$
and a positive number r, by the r-ball about A we mean the set
![]() $B(A, r)=\bigcup_{a\in A}B(a, r)$
.
$B(A, r)=\bigcup_{a\in A}B(a, r)$
.
The following result is well-known (cf. Engelking Reference Engelking1989).
Lemma 105.
Let (X, d) be a metric space and K a compact set of X. Then for any open set U containing K, there is an
![]() $r>0$
such that
$r>0$
such that
![]() $K\subseteq B(K, r)\subseteq U$
.
$K\subseteq B(K, r)\subseteq U$
.
Proposition 106.
For a metric space (X, d),
![]() $P_S((X, d))$
is first-countable.
$P_S((X, d))$
is first-countable.
Proof. For
![]() $K\in \mathord{\mathsf{K}} ((X, d))$
, let
$K\in \mathord{\mathsf{K}} ((X, d))$
, let
![]() $\mathcal B_K=\{B(K, 1/n) : n\in \mathbb{N}\}$
. Then by Lemma 105,
$\mathcal B_K=\{B(K, 1/n) : n\in \mathbb{N}\}$
. Then by Lemma 105,
![]() $\mathcal B_K=\{B(K, 1/n) : n\in \mathbb{N}\}$
is a countable base at K in
$\mathcal B_K=\{B(K, 1/n) : n\in \mathbb{N}\}$
is a countable base at K in
![]() $P_S((X, d))$
. Thus,
$P_S((X, d))$
. Thus,
![]() $P_S((X, d))$
is first-countable.
$P_S((X, d))$
is first-countable.
For a countable
![]() $T_0$
space X, it is easy to see that X is second-countable iff X is first-countable. Indeed, let
$T_0$
space X, it is easy to see that X is second-countable iff X is first-countable. Indeed, let
![]() $X=\{x_n : n\in \mathbb N\}$
. If X is first-countable, then for each
$X=\{x_n : n\in \mathbb N\}$
. If X is first-countable, then for each
![]() $n\in \mathbb N$
, there is a countable base
$n\in \mathbb N$
, there is a countable base
![]() $\mathcal B_n$
at
$\mathcal B_n$
at
![]() $x_n$
. Let
$x_n$
. Let
![]() $\mathcal B=\bigcup_{n\in \mathbb N}\mathcal B_n$
. Then,
$\mathcal B=\bigcup_{n\in \mathbb N}\mathcal B_n$
. Then,
![]() $\mathcal B$
is a countable base of X. Thus, X is second-countable. Therefore, by Propositions 101 and 102, we have the following.
$\mathcal B$
is a countable base of X. Thus, X is second-countable. Therefore, by Propositions 101 and 102, we have the following.
Corollary 107.
For a countable
![]() $T_0$
space X, the following conditions are equivalent:
$T_0$
space X, the following conditions are equivalent:
-
(1) X is first-countable.
-
(2) X is second-countable.
-
(3)
 $X^s$
is first-countable.
$X^s$
is first-countable.
-
(4)
 $X^s$
is second-countable.
$X^s$
is second-countable.
-
(5)
 $P_S(X)$
is first-countable.
$P_S(X)$
is first-countable.
-
(6)
 $P_S(X)$
is second-countable.
$P_S(X)$
is second-countable.
It is worth noting that the Scott topology on a countable complete lattice may not be first-countable, see Reference Xu, Shen, Xi and ZhaoXu et al. (2020a , Example 4.8).
By Proposition 48, Theorem 49, Proposition 101, and Corollary 107, we deduce the following two results.
Corollary 108. (Xu et al. 2021a, Corollaries 5.7 and 5.8) Every second-countable (especially, countable first-countable)
![]() $T_0$
space is an
$T_0$
space is an
![]() $\omega$
-Rudin space.
$\omega$
-Rudin space.
Corollary 109.
Every second-countable (especially, countable first-countable)
![]() $\omega$
-well-filtered space is sober.
$\omega$
-well-filtered space is sober.
For a
![]() $T_0$
space X with a first-countable Smyth power space, we have a similar result to Lemma 54.
$T_0$
space X with a first-countable Smyth power space, we have a similar result to Lemma 54.
Lemma 110.
Let X be a
![]() $T_0$
space for which the Smyth power space
$T_0$
space for which the Smyth power space
![]() $P_S(X)$
is first-countable. Then, the Scott topology is coarser than the upper Vietoris topology on
$P_S(X)$
is first-countable. Then, the Scott topology is coarser than the upper Vietoris topology on
![]() $\mathsf{K}(X)$
.
$\mathsf{K}(X)$
.
Proof. See the proof of Xu et al. (2021c, Theorem 5.7).
The following conclusion is straightforward from Theorem 24, Corollaries 25, 50, and Lemma 110.
Corollary 111.
(Xu et al. 2021c, Theorem 5.7) Let X be a well-filtered space for which the Smyth power space
![]() $P_S(X)$
is first-countable. Then
$P_S(X)$
is first-countable. Then
-
(1) the upper Vietoris topology agrees with the Scott topology on
 $\mathord{\mathsf{K}} (X)$
.
$\mathord{\mathsf{K}} (X)$
. -
(2) the Scott space
 $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a first-countable sober space.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a first-countable sober space.
By Proposition 104 and Corollary 111, we obtain the following.
Corollary 112.
(Xu et al. 2021c, Corollary 5.10) Let X be a first-countable well-filtered space X in which all compact subsets are countable (especially,
![]() $|X|\leq\omega$
). Then
$|X|\leq\omega$
). Then
-
(1) the upper Vietoris topology agrees with the Scott topology on
 $\mathord{\mathsf{K}} (X)$
.
$\mathord{\mathsf{K}} (X)$
. -
(2) the Scott space
 $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a first-countable sober space.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a first-countable sober space.
Let
![]() $X_{coc}$
be the space in Example 67. Then,
$X_{coc}$
be the space in Example 67. Then,
![]() $X_{coc}$
is well-filtered and not first-countable, and the Scott space
$X_{coc}$
is well-filtered and not first-countable, and the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a first-countable sober c-space, but
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a first-countable sober c-space, but
![]() $\sigma (\mathord{\mathsf{K}} (X_{coc})\not\subseteq \mathcal O(P_S(X_{coc}))$
.
$\sigma (\mathord{\mathsf{K}} (X_{coc})\not\subseteq \mathcal O(P_S(X_{coc}))$
.
By Example 67, Lemma 110, and Corollary 111, we naturally pose the following four questions.
Question 113. For a first-countable
![]() $T_0$
space X, is the Scott topology coarser than the upper Vietoris topology on
$T_0$
space X, is the Scott topology coarser than the upper Vietoris topology on
![]() $\mathsf{K}(X)$
?
$\mathsf{K}(X)$
?
Question 114. For a first-countable well-filtered (or equivalently, a first-countable sober) space X, does the upper Vietoris topology and the Scott topology on
![]() $\mathord{\mathsf{K}} (X)$
coincide?
$\mathord{\mathsf{K}} (X)$
coincide?
Question 115. For a first-countable
![]() $T_2$
space X, does the upper Vietoris topology and the Scott topology on
$T_2$
space X, does the upper Vietoris topology and the Scott topology on
![]() $\mathord{\mathsf{K}} (X)$
coincide?
$\mathord{\mathsf{K}} (X)$
coincide?
Question 116. For a first-countable well-filtered (or equivalently, a first-countable sober) space X, is the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
sober?
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
sober?
Since every metric space is
![]() $T_2$
(and hence sober), by Propositions 98, 106, and Corollary 111, we get the following conclusion.
$T_2$
(and hence sober), by Propositions 98, 106, and Corollary 111, we get the following conclusion.
Corollary 117. Let (X, d) be a metric space. Then,
-
(1) the upper Vietoris topology agrees with the Scott topology on
 $\mathord{\mathsf{K}} ((X, d))$
.
$\mathord{\mathsf{K}} ((X, d))$
. -
(2) the Scott space
 $\Sigma~\!\!\mathord{\mathsf{K}}((X, d))$
is a first-countable sober space.
$\Sigma~\!\!\mathord{\mathsf{K}}((X, d))$
is a first-countable sober space.
If, in addition, (X, d) is locally compact (especially, compact), then
(3)
![]() $\mathord{\mathsf{K}} ((X, d))$
is a continuous semilattice.
$\mathord{\mathsf{K}} ((X, d))$
is a continuous semilattice.
(4) the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}}((X, d))$
is a c-space.
$\Sigma~\!\!\mathord{\mathsf{K}}((X, d))$
is a c-space.
The following two conclusions follow directly from Proposition 101, Lemma 110, and Corollary 111.
Corollary 118.
Let X be a second-countable
![]() $T_0$
space. Then, the Scott topology is coarser than the upper Vietoris topology on
$T_0$
space. Then, the Scott topology is coarser than the upper Vietoris topology on
![]() $\mathsf{K}(X)$
.
$\mathsf{K}(X)$
.
Corollary 119. Let X be a second-countable well-filtered space (or equivalently, a second-countable sober space). Then,
-
(1) the Scott topology agrees with the upper Vietoris topology on
 $\mathsf{K}(X)$
.
$\mathsf{K}(X)$
. -
(2) the Scott space
 $\Sigma~\!\!\mathord{\mathsf{K}}(X)$
is a second-countable sober space.
$\Sigma~\!\!\mathord{\mathsf{K}}(X)$
is a second-countable sober space.
The following example shows that there is a countable Hausdorff space X for which the Scott space
![]() $\Sigma ~\!\!\mathord{\mathsf{K}} (X)$
is second-countable but X is not first-countable (and hence
$\Sigma ~\!\!\mathord{\mathsf{K}} (X)$
is second-countable but X is not first-countable (and hence
![]() $P_S(X)$
is not first-countable).
$P_S(X)$
is not first-countable).
Example 120. Let p be a point in
![]() $\beta (\mathbb{N})\setminus \mathbb{N}$
, where
$\beta (\mathbb{N})\setminus \mathbb{N}$
, where
![]() $\beta (\mathbb{N})$
is the Stone-Cěch compactification of the discrete space of natural numbers, and consider on
$\beta (\mathbb{N})$
is the Stone-Cěch compactification of the discrete space of natural numbers, and consider on
![]() $X=\mathbb{N}\cup\{p\}$
the induced topology. (cf. Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Example II-1.25).Then
$X=\mathbb{N}\cup\{p\}$
the induced topology. (cf. Gierz et al. Reference Gierz, Hofmann, Keimel, Lawson, Mislove and Scott2003, Example II-1.25).Then
1.
![]() $|X|=\omega$
and X is a non-discrete Hausdorff space and hence a sober space.
$|X|=\omega$
and X is a non-discrete Hausdorff space and hence a sober space.
2.
![]() $\mathord{\mathsf{K}} (X)=X^{(<\omega)}\setminus \{\emptyset\}$
and
$\mathord{\mathsf{K}} (X)=X^{(<\omega)}\setminus \{\emptyset\}$
and
![]() $\mathrm{int}K=\emptyset$
for each
$\mathrm{int}K=\emptyset$
for each
![]() $K\in \mathord{\mathsf{K}} (X)$
with
$K\in \mathord{\mathsf{K}} (X)$
with
![]() $p\in K$
. So X is not locally compact.
$p\in K$
. So X is not locally compact.
3.
![]() $\mathord{\mathsf{K}} (X)$
is a Noetherian poset and
$\mathord{\mathsf{K}} (X)$
is a Noetherian poset and
![]() $|\mathord{\mathsf{K}} (X)|=\omega$
. Hence, the Scott space
$|\mathord{\mathsf{K}} (X)|=\omega$
. Hence, the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a second-countable sober c-space.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a second-countable sober c-space.
Clearly,
![]() $\mathord{\mathsf{K}} (X)=X^{(<\omega)}\setminus \{\emptyset\}$
(with the Smyth order) is Noetherian (and hence algebraic) and
$\mathord{\mathsf{K}} (X)=X^{(<\omega)}\setminus \{\emptyset\}$
(with the Smyth order) is Noetherian (and hence algebraic) and
![]() $|\mathord{\mathsf{K}} (X)|=\omega$
since
$|\mathord{\mathsf{K}} (X)|=\omega$
since
![]() $|X|=\omega$
. Therefore,
$|X|=\omega$
. Therefore,
![]() $\sigma(\mathord{\mathsf{K}} (X))=\alpha(\mathord{\mathsf{K}} (X))$
and
$\sigma(\mathord{\mathsf{K}} (X))=\alpha(\mathord{\mathsf{K}} (X))$
and
![]() $\{\uparrow_{\mathord{\mathsf{K}} (X)} F : F\in X^{(<\omega)}\setminus \{\emptyset\}\}$
is a countable base of
$\{\uparrow_{\mathord{\mathsf{K}} (X)} F : F\in X^{(<\omega)}\setminus \{\emptyset\}\}$
is a countable base of
![]() $\Sigma \mathord{\mathsf{K}} (X)$
. By Theorem 15 and Proposition 18,
$\Sigma \mathord{\mathsf{K}} (X)$
. By Theorem 15 and Proposition 18,
![]() $\Sigma \mathord{\mathsf{K}} (X)$
is a sober c-space.
$\Sigma \mathord{\mathsf{K}} (X)$
is a sober c-space.
4. the upper Vietoris topology and the Scott topology on
![]() $\mathord{\mathsf{K}} (X)$
does not coincide, or more precisely,
$\mathord{\mathsf{K}} (X)$
does not coincide, or more precisely,
![]() $\sigma (\mathord{\mathsf{K}} (X))\not\subseteq \mathcal O(P_S(X))$
.
$\sigma (\mathord{\mathsf{K}} (X))\not\subseteq \mathcal O(P_S(X))$
.
By Corollary 25,
![]() $\mathcal O(P_S(X))\subseteq \sigma (\mathord{\mathsf{K}} (X))$
. Clearly, for any
$\mathcal O(P_S(X))\subseteq \sigma (\mathord{\mathsf{K}} (X))$
. Clearly, for any
![]() $F\in X^{(<\omega)}\setminus \{\emptyset\}$
,
$F\in X^{(<\omega)}\setminus \{\emptyset\}$
,
![]() $\uparrow_{\mathord{\mathsf{K}} (X)} F\in \sigma(\mathord{\mathsf{K}} (X))$
but
$\uparrow_{\mathord{\mathsf{K}} (X)} F\in \sigma(\mathord{\mathsf{K}} (X))$
but
![]() $\uparrow_{\mathord{\mathsf{K}} (X)} G\not\in \mathcal O(P_S(X))$
for any
$\uparrow_{\mathord{\mathsf{K}} (X)} G\not\in \mathcal O(P_S(X))$
for any
![]() $G\in \sigma(\mathord{\mathsf{K}} (X))$
with
$G\in \sigma(\mathord{\mathsf{K}} (X))$
with
![]() $p\in G$
, proving that
$p\in G$
, proving that
![]() $\sigma (\mathord{\mathsf{K}} (X))\not\subseteq \mathcal O(P_S(X))$
. We can also get this result by (b), (c) and Xu et al. (2021c, Theorem 3.10).
$\sigma (\mathord{\mathsf{K}} (X))\not\subseteq \mathcal O(P_S(X))$
. We can also get this result by (b), (c) and Xu et al. (2021c, Theorem 3.10).
5. Neither X nor
![]() $P_S(X)$
is first-countable.
$P_S(X)$
is first-countable.
By (d), Proposition 104 and Lemma 110, neither
![]() $P_S(X)$
nor X is first-countable (cf. Engelking Reference Engelking1989, Corollary 3.6.17).
$P_S(X)$
nor X is first-countable (cf. Engelking Reference Engelking1989, Corollary 3.6.17).
The above example also shows that if the Smyth power space
![]() $P_S(X)$
is replaced with the Scott space
$P_S(X)$
is replaced with the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}}(X)$
in the conditions of Lemma 110 and Corollary 111, the analogous results to Lemma 110 and Corollary 111 do not hold.By Proposition 101, Lemma 110, Corollaries 111 and 119, we raise the following question.
$\Sigma~\!\!\mathord{\mathsf{K}}(X)$
in the conditions of Lemma 110 and Corollary 111, the analogous results to Lemma 110 and Corollary 111 do not hold.By Proposition 101, Lemma 110, Corollaries 111 and 119, we raise the following question.
Question 121. For a second-countable
![]() $T_0$
space X, is the Scott space
$T_0$
space X, is the Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}}(X)$
second-countable?
$\Sigma~\!\!\mathord{\mathsf{K}}(X)$
second-countable?
9. Rudin Property and Well-Filtered Determinedness of Smyth Power Spaces and Scott Topology on Smyth Power Posets
Firstly, we discuss the Rudin property and well-filtered determinedness of Smyth power spaces. The following result was proved in Reference Xu, Shen, Xi and ZhaoXu et al. (2020b ).
Proposition 122.
(Xu et al. Reference Xu, Shen, Xi and Zhao2020
b, Theorem 7.21) Let X be a
![]() $T_0$
space. If
$T_0$
space. If
![]() $P_S(X)$
is well-filtered determined, then X is well-filtered determined.
$P_S(X)$
is well-filtered determined, then X is well-filtered determined.
By Theorems 24 and 36, we have the following.
Proposition 123. Let X be a well-filtered space. Then, the following conditions are equivalent:
-
(1) X is a Rudin space.
-
(2) X is a
 $\mathsf{WD}$
space.
$\mathsf{WD}$
space.
-
(3)
 $P_S(X)$
is a Rudin space.
$P_S(X)$
is a Rudin space.
-
(4)
 $P_S(X)$
is a
$P_S(X)$
is a
 $\mathsf{WD}$
space.
$\mathsf{WD}$
space.
It is still not known whether the converse of Proposition 122 holds (i.e., whether the Smyth power space
![]() $P_S(X)$
of a well-filtered determined
$P_S(X)$
of a well-filtered determined
![]() $T_0$
space X is well-filtered determined) (see Reference Xu, Shen, Xi and ZhaoXu et al. 2020b
, Question 8.6).
$T_0$
space X is well-filtered determined) (see Reference Xu, Shen, Xi and ZhaoXu et al. 2020b
, Question 8.6).
Theorem 124.
Let X be a
![]() $T_0$
space. If
$T_0$
space. If
![]() $P_S(X)$
is a Rudin space, then X is a Rudin space.
$P_S(X)$
is a Rudin space, then X is a Rudin space.
Proof. Let
![]() $A\in{\mathsf{Irr}}_c(X)$
. Then by Lemma 5,
$A\in{\mathsf{Irr}}_c(X)$
. Then by Lemma 5,
![]() $\overline{\xi_X(A)}=\Diamond A\in{\mathsf{Irr}}_c(P_S(X))$
, where
$\overline{\xi_X(A)}=\Diamond A\in{\mathsf{Irr}}_c(P_S(X))$
, where
![]() $\xi_X : X \longrightarrow P_S(X)$
is the canonical embedding (see Remark 4). Since
$\xi_X : X \longrightarrow P_S(X)$
is the canonical embedding (see Remark 4). Since
![]() $P_S(X)$
is a Rudin space, there is a filtered family
$P_S(X)$
is a Rudin space, there is a filtered family
![]() $\{\mathcal{K}_d : d\in D\}\subseteq \mathsf{K}(P_S(X))$
such that
$\{\mathcal{K}_d : d\in D\}\subseteq \mathsf{K}(P_S(X))$
such that
![]() $\Diamond A\in m(\{\mathcal{K}_d : d\in D\})$
. For each
$\Diamond A\in m(\{\mathcal{K}_d : d\in D\})$
. For each
![]() $d\in D$
, let
$d\in D$
, let
![]() $K_d=\bigcup \mathcal{K}_d$
. Then by Lemma 11,
$K_d=\bigcup \mathcal{K}_d$
. Then by Lemma 11,
![]() $\{K_d : d\in D\}\subseteq \mathsf{K}(X)$
is filtered. Clearly,
$\{K_d : d\in D\}\subseteq \mathsf{K}(X)$
is filtered. Clearly,
![]() $A\in M(\{K_d : d\in D\})$
. For any proper closed subset B of A, we have that
$A\in M(\{K_d : d\in D\})$
. For any proper closed subset B of A, we have that
![]() $\Diamond B\in\mathcal C(P_S(X))$
and
$\Diamond B\in\mathcal C(P_S(X))$
and
![]() $\Diamond B$
is a proper closed subset of
$\Diamond B$
is a proper closed subset of
![]() $\Diamond A$
(for any
$\Diamond A$
(for any
![]() $a\in A\setminus B$
,
$a\in A\setminus B$
,
![]() $\mathord{\uparrow} a\in \Diamond A\setminus \Diamond B$
). By the minimality of
$\mathord{\uparrow} a\in \Diamond A\setminus \Diamond B$
). By the minimality of
![]() $\Diamond A$
, there is a
$\Diamond A$
, there is a
![]() $d\in D$
such that
$d\in D$
such that
![]() $\Diamond B\cap \mathcal{K}_d=\emptyset$
, and consequently,
$\Diamond B\cap \mathcal{K}_d=\emptyset$
, and consequently,
![]() $B\cap K_d=\emptyset$
. Thus
$B\cap K_d=\emptyset$
. Thus
![]() $B\notin M(\{K_d : d\in D\})$
, and hence,
$B\notin M(\{K_d : d\in D\})$
, and hence,
![]() $A\in m(\{K_d : d\in D\})$
.
$A\in m(\{K_d : d\in D\})$
.
Question 125. Is the Smyth power space
![]() $P_S(X)$
of a Rudin space X still a Rudin space?
$P_S(X)$
of a Rudin space X still a Rudin space?
Now we discuss the Rudin property and well-filtered determinedness of the Scott topology on Smyth power posets.
First, even for a sober space X (whence it is both a Rudin space and a
![]() $\mathsf{WD}$
space by Theorem 36), the Scott space
$\mathsf{WD}$
space by Theorem 36), the Scott space
![]() $\Sigma~\!\!\mathsf{K}(X)$
may not be a
$\Sigma~\!\!\mathsf{K}(X)$
may not be a
![]() $\mathsf{WD}$
space (and hence not a Rudin space). Indeed, let
$\mathsf{WD}$
space (and hence not a Rudin space). Indeed, let
![]() $(\Sigma~\!\!\mathcal L)_{\top}$
be as in Theorem 91. Then,
$(\Sigma~\!\!\mathcal L)_{\top}$
be as in Theorem 91. Then,
![]() $(\Sigma~\!\!\mathcal L)_{\top}$
is a sober space. By Theorems 58 and 91, the Scott space
$(\Sigma~\!\!\mathcal L)_{\top}$
is a sober space. By Theorems 58 and 91, the Scott space
![]() $\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
is well-filtered but non-sober. Hence by Theorem 36,
$\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
is well-filtered but non-sober. Hence by Theorem 36,
![]() $\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
is neither a Rudin space nor a
$\Sigma~\!\!\mathsf{K}((\Sigma~\!\!\mathcal L)_{\top})$
is neither a Rudin space nor a
![]() $\mathsf{WD}$
space.
$\mathsf{WD}$
space.
Conversely, Example 67 shows that there is a well-filtered space X such that
-
(a) the Scott space
 $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a first-countable sober c-space, and hence,
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a first-countable sober c-space, and hence,
 $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is both Rudin and
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is both Rudin and
 $\mathsf{WD}$
.
$\mathsf{WD}$
. -
(b) X is neither a Rudin space nor a
 $\mathsf{WD}$
space.
$\mathsf{WD}$
space. -
(c) the Smyth power space
 $P_S(X)$
is neither a Rudin space nor a
$P_S(X)$
is neither a Rudin space nor a
 $\mathsf{WD}$
space.
$\mathsf{WD}$
space.
Then for a
![]() $T_0$
space X, we investigate some sufficient conditions under which the well-filtered determinedness (resp. the Rudin property) of Scott space
$T_0$
space X, we investigate some sufficient conditions under which the well-filtered determinedness (resp. the Rudin property) of Scott space
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
implies that of X.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
implies that of X.
Definition 126.
A
![]() $T_0$
space X is said to have property S if for each
$T_0$
space X is said to have property S if for each
![]() $A\in {\mathsf{Irr}}_c(X)$
,
$A\in {\mathsf{Irr}}_c(X)$
,
![]() $\{\mathord{\uparrow} a : a\in A\}\in {\mathsf{Irr}} (\Sigma~\!\! \mathord{\mathsf{K}} (X))$
or
$\{\mathord{\uparrow} a : a\in A\}\in {\mathsf{Irr}} (\Sigma~\!\! \mathord{\mathsf{K}} (X))$
or
![]() $\Diamond A\in {\mathsf{Irr}}_c(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
. A poset P is said to have property S if
$\Diamond A\in {\mathsf{Irr}}_c(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
. A poset P is said to have property S if
![]() $\Sigma~\!\! P$
has property S.
$\Sigma~\!\! P$
has property S.
Remark 127. Let X be a
![]() $T_0$
space and
$T_0$
space and
![]() $A\in {\mathsf{Irr}}_c(X)$
.
$A\in {\mathsf{Irr}}_c(X)$
.
1. Since
![]() $\xi_X : X \longrightarrow P_S(\mathord{\mathsf{K}} (X)), x\mapsto \mathord{\uparrow} x$
, is continuous, by Lemmas 2 and 5, we have that
$\xi_X : X \longrightarrow P_S(\mathord{\mathsf{K}} (X)), x\mapsto \mathord{\uparrow} x$
, is continuous, by Lemmas 2 and 5, we have that
![]() $\{\mathord{\uparrow} a : a\in A\}\in {\mathsf{Irr}} (P_S(X))$
and
$\{\mathord{\uparrow} a : a\in A\}\in {\mathsf{Irr}} (P_S(X))$
and
![]() ${\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} a : a\in A\}=\Diamond A\in {\mathsf{Irr}}_c(P_S(X))$
${\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} a : a\in A\}=\Diamond A\in {\mathsf{Irr}}_c(P_S(X))$
2. If
![]() $\xi_X^\sigma : X \longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (X), x\mapsto \mathord{\uparrow} x$
, is continuous, then by Lemma 2, X has property S.
$\xi_X^\sigma : X \longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (X), x\mapsto \mathord{\uparrow} x$
, is continuous, then by Lemma 2, X has property S.
3. If
![]() $\sigma (\mathord{\mathsf{K}} (X))\subseteq \mathcal O(P_S(X))$
, then
$\sigma (\mathord{\mathsf{K}} (X))\subseteq \mathcal O(P_S(X))$
, then
![]() $\xi_X^\sigma : X \longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (X)$
is continuous by Remark 4, and hence, X has property S.
$\xi_X^\sigma : X \longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (X)$
is continuous by Remark 4, and hence, X has property S.
4. For a poset P, by Lemmas 12 and 19, the mapping
![]() $\xi_P^\sigma : \Sigma~\!\! P \longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (\Sigma~\!\! P), x\mapsto \mathord{\uparrow} x$
, is continuous. Therefore, P has property S.
$\xi_P^\sigma : \Sigma~\!\! P \longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (\Sigma~\!\! P), x\mapsto \mathord{\uparrow} x$
, is continuous. Therefore, P has property S.
Proposition 128.
Suppose that a
![]() $T_0$
space X has property S and
$T_0$
space X has property S and
![]() $\mathcal O(P_S(X))\subseteq\sigma (\mathord{\mathsf{K}} (X))$
. If
$\mathcal O(P_S(X))\subseteq\sigma (\mathord{\mathsf{K}} (X))$
. If
![]() $\Sigma~\!\!\mathsf{K}(X)$
is a Rudin space, then X is a Rudin space.
$\Sigma~\!\!\mathsf{K}(X)$
is a Rudin space, then X is a Rudin space.
Proof. Let
![]() $A\in{\mathsf{Irr}}_c(X)$
. Then by the property S of X,
$A\in{\mathsf{Irr}}_c(X)$
. Then by the property S of X,
![]() $\{\mathord{\uparrow} a : a\in A\}\in {\mathsf{Irr}} (\Sigma~\!\! \mathord{\mathsf{K}} (X))$
or
$\{\mathord{\uparrow} a : a\in A\}\in {\mathsf{Irr}} (\Sigma~\!\! \mathord{\mathsf{K}} (X))$
or
![]() $\Diamond A\in {\mathsf{Irr}}_c(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
.
$\Diamond A\in {\mathsf{Irr}}_c(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
.
Case 1:
![]() $\{\mathord{\uparrow} a : a\in A\}\in {\mathsf{Irr}} (\Sigma~\!\! \mathord{\mathsf{K}} (X))$
.
$\{\mathord{\uparrow} a : a\in A\}\in {\mathsf{Irr}} (\Sigma~\!\! \mathord{\mathsf{K}} (X))$
.
Since
![]() $\Sigma~\!\!\mathsf{K}(X)$
is a Rudin space, there is a filtered family
$\Sigma~\!\!\mathsf{K}(X)$
is a Rudin space, there is a filtered family
![]() $\{\mathcal{K}_d : d\in D\}\subseteq \mathsf{K}(\Sigma ~\!\!\mathsf{K}(X))$
such that
$\{\mathcal{K}_d : d\in D\}\subseteq \mathsf{K}(\Sigma ~\!\!\mathsf{K}(X))$
such that
![]() ${\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} a : a\in A\}\in m(\{\mathcal{K}_d : d\in D\})$
. As
${\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} a : a\in A\}\in m(\{\mathcal{K}_d : d\in D\})$
. As
![]() $\mathcal O(P_S(X))\subseteq \sigma (\mathsf{K}(X))$
, we have that
$\mathcal O(P_S(X))\subseteq \sigma (\mathsf{K}(X))$
, we have that
![]() ${\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} a : a\in A\}\subseteq \Diamond A\in \mathcal C(P_S(X))\subseteq \mathcal C(\Sigma~\!\!\mathord{\mathsf{K}} (X))$
and
${\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} a : a\in A\}\subseteq \Diamond A\in \mathcal C(P_S(X))\subseteq \mathcal C(\Sigma~\!\!\mathord{\mathsf{K}} (X))$
and
![]() $\{\mathcal{K}_d : d\in D\}\subseteq \mathsf{K}(P_S(X))$
. Therefore,
$\{\mathcal{K}_d : d\in D\}\subseteq \mathsf{K}(P_S(X))$
. Therefore,
![]() $\Diamond A\in M(\{\mathcal{K}_d : d\in D\})$
. For each
$\Diamond A\in M(\{\mathcal{K}_d : d\in D\})$
. For each
![]() $d\in D$
, let
$d\in D$
, let
![]() $K_d=\bigcup \mathcal{K}_d$
. Then by Lemma 11,
$K_d=\bigcup \mathcal{K}_d$
. Then by Lemma 11,
![]() $\{K_d : d\in D\}\subseteq \mathsf{K}(X)$
is filtered. Since
$\{K_d : d\in D\}\subseteq \mathsf{K}(X)$
is filtered. Since
![]() $\Diamond A\in M(\{\mathcal{K}_d : d\in D\})$
,
$\Diamond A\in M(\{\mathcal{K}_d : d\in D\})$
,
![]() $A\in M(\{K_d : d\in D\})$
. Now we show that
$A\in M(\{K_d : d\in D\})$
. Now we show that
![]() $A\in m(\{K_d : d\in D\})$
. Suppose that B is a proper closed subset B of A. Then, there is
$A\in m(\{K_d : d\in D\})$
. Suppose that B is a proper closed subset B of A. Then, there is
![]() $a\in A\cap (X\setminus B)$
, and hence
$a\in A\cap (X\setminus B)$
, and hence
![]() $\mathord{\uparrow} a\in \Box (X\setminus B)\in \mathcal O(P_S(X)\subseteq \sigma (\mathord{\mathsf{K}} (X))$
. Clearly,
$\mathord{\uparrow} a\in \Box (X\setminus B)\in \mathcal O(P_S(X)\subseteq \sigma (\mathord{\mathsf{K}} (X))$
. Clearly,
![]() $\{\mathord{\uparrow} b : b\in B\}\cap \Box (X\setminus B)=\emptyset$
, and consequently,
$\{\mathord{\uparrow} b : b\in B\}\cap \Box (X\setminus B)=\emptyset$
, and consequently,
![]() $\mathord{\uparrow} a\notin {\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} b : b\in B\}$
. Therefore,
$\mathord{\uparrow} a\notin {\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} b : b\in B\}$
. Therefore,
![]() ${\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} b : b\in B\}$
is a proper subset of
${\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} b : b\in B\}$
is a proper subset of
![]() ${\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} a : a\in A\}$
. By
${\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} a : a\in A\}$
. By
![]() ${\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} a : a\in A\}\in m(\{\mathcal{K}_d : d\in D\})$
, there is
${\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} a : a\in A\}\in m(\{\mathcal{K}_d : d\in D\})$
, there is
![]() $d_0\in D$
such that
$d_0\in D$
such that
![]() ${\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} b : b\in B\}\cap \mathcal K_{d_0}=\emptyset$
, and hence
${\rm cl}_{\sigma (\mathord{\mathsf{K}} (X))}\{\mathord{\uparrow} b : b\in B\}\cap \mathcal K_{d_0}=\emptyset$
, and hence
![]() $\{\mathord{\uparrow} b : b\in B\}\cap \mathcal K_{d_0}=\emptyset$
. Since
$\{\mathord{\uparrow} b : b\in B\}\cap \mathcal K_{d_0}=\emptyset$
. Since
![]() $\mathcal K_{d_0}=\mathord{\uparrow}_{\mathord{\mathsf{K}} (X)} \mathcal K_{d_0}$
, we have that
$\mathcal K_{d_0}=\mathord{\uparrow}_{\mathord{\mathsf{K}} (X)} \mathcal K_{d_0}$
, we have that
![]() $B\cap K_{d_0}=B\cap (\bigcup \mathcal K_{d_0})=\emptyset$
. Thus,
$B\cap K_{d_0}=B\cap (\bigcup \mathcal K_{d_0})=\emptyset$
. Thus,
![]() $A\in m(\{K_d : d\in D\})$
.
$A\in m(\{K_d : d\in D\})$
.
Case 2:
![]() $\Diamond A\in {\mathsf{Irr}}_c(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
.
$\Diamond A\in {\mathsf{Irr}}_c(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
.
Since
![]() $\Sigma~\!\!\mathsf{K}(X)$
is a Rudin space, there is a filtered family
$\Sigma~\!\!\mathsf{K}(X)$
is a Rudin space, there is a filtered family
![]() $\{\mathcal{K}_d : d\in D\}\subseteq \mathsf{K}(\Sigma~\!\!\mathsf{K}(X))$
such that
$\{\mathcal{K}_d : d\in D\}\subseteq \mathsf{K}(\Sigma~\!\!\mathsf{K}(X))$
such that
![]() $\Diamond A\in m(\{\mathcal{K}_d : d\in D\})$
. As carried out in the proof of Case 1, A is a Rudin set of X.
$\Diamond A\in m(\{\mathcal{K}_d : d\in D\})$
. As carried out in the proof of Case 1, A is a Rudin set of X.
Thus, X is a Rudin space.
Corollary 129.
Suppose that X is a well-filtered space with property S. If
![]() $\Sigma~\!\!\mathsf{K}(X)$
is a
$\Sigma~\!\!\mathsf{K}(X)$
is a
![]() $\mathsf{WD}$
space (especially, a Rudin space), then both
$\mathsf{WD}$
space (especially, a Rudin space), then both
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
and X are sober.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
and X are sober.
Proof. By Theorem 58,
![]() $\Sigma~\!\!\mathsf{K}(X)$
is well-filtered. As
$\Sigma~\!\!\mathsf{K}(X)$
is well-filtered. As
![]() $\Sigma~\!\!\mathsf{K}(X)$
is
$\Sigma~\!\!\mathsf{K}(X)$
is
![]() $\mathsf{WD}$
(if
$\mathsf{WD}$
(if
![]() $\Sigma~\!\!\mathsf{K}(X)$
is Rudin, then by Proposition 34 it is
$\Sigma~\!\!\mathsf{K}(X)$
is Rudin, then by Proposition 34 it is
![]() $\mathsf{WD}$
), by Theorem 36,
$\mathsf{WD}$
), by Theorem 36,
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is sober. Hence, by Theorem 36 and Corollary 25,
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is sober. Hence, by Theorem 36 and Corollary 25,
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is Rudin and
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is Rudin and
![]() $\mathcal O(P_S(X))\subseteq\sigma (\mathord{\mathsf{K}} (X))$
, and consequently, X is Rudin by Proposition 128. It follows from Theorem 36 that X is sober.
$\mathcal O(P_S(X))\subseteq\sigma (\mathord{\mathsf{K}} (X))$
, and consequently, X is Rudin by Proposition 128. It follows from Theorem 36 that X is sober.
By Remark 127 and Corollary 129, we have the following corollary.
Corollary 130.
Let X be a well-filtered space. If
![]() $\xi_X^\sigma : X \longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (X)$
is continuous and
$\xi_X^\sigma : X \longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (X)$
is continuous and
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
is a
![]() $\mathsf{WD}$
space (especially, a Rudin space), then both
$\mathsf{WD}$
space (especially, a Rudin space), then both
![]() $\Sigma~\!\!\mathord{\mathsf{K}} (X)$
and X are sober.
$\Sigma~\!\!\mathord{\mathsf{K}} (X)$
and X are sober.
As an immediate corollary of Corollary 130, we get one the main results of Reference Xu, Xi and ZhaoXu et al. (2021b ).
Corollary 131.
(Xu et al. 2021b, Theorem 2) Suppose that X is a well-filtered space and
![]() $\xi_X^\sigma : X \longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (X)$
is continuous. If
$\xi_X^\sigma : X \longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (X)$
is continuous. If
![]() $\Sigma~\!\!\mathsf{K}(X)$
is sober, then X is sober. Therefore, if X is non-sober, then the Scott space
$\Sigma~\!\!\mathsf{K}(X)$
is sober, then X is sober. Therefore, if X is non-sober, then the Scott space
![]() $\Sigma~\!\!\mathsf{K}(X)$
is non-sober.
$\Sigma~\!\!\mathsf{K}(X)$
is non-sober.
Example 67 shows that when X lacks the property S or the continuity of
![]() $\xi_X^\sigma : X \longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (X)$
, Proposition 128, Corollaries 129, 130, and 131 may not hold.
$\xi_X^\sigma : X \longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (X)$
, Proposition 128, Corollaries 129, 130, and 131 may not hold.
By Remark 127, Proposition 128, Corollaries 129 and 131, we deduce the following three corollaries.
Corollary 132.
Let P be a poset. If
![]() $\mathcal O(P_S(\Sigma~\!\!P))\subseteq\sigma (\mathord{\mathsf{K}} (\Sigma~\!\!P))$
and
$\mathcal O(P_S(\Sigma~\!\!P))\subseteq\sigma (\mathord{\mathsf{K}} (\Sigma~\!\!P))$
and
![]() $\mathsf{K}(\Sigma~\!\!P)$
is a Rudin poset, then P is a Rudin dcpo.
$\mathsf{K}(\Sigma~\!\!P)$
is a Rudin poset, then P is a Rudin dcpo.
Corollary 133.
Let P be a well-filtered dcpo. If
![]() $\mathsf{K}(\Sigma~\!\!P)$
is a
$\mathsf{K}(\Sigma~\!\!P)$
is a
![]() $\mathsf{WD}$
dcpo (especially, a Rudin dcpo), then both
$\mathsf{WD}$
dcpo (especially, a Rudin dcpo), then both
![]() $\mathord{\mathsf{K}} (\Sigma~\!\!P)$
and P are sober dcpos.
$\mathord{\mathsf{K}} (\Sigma~\!\!P)$
and P are sober dcpos.
Corollary 134.
Let P be a well-filtered dcpo. If
![]() $\mathsf{K}(\Sigma~\!\!P)$
is a sober dcpo, then P is a sober dcpo. Therefore, if P is not a sober dcpo, then
$\mathsf{K}(\Sigma~\!\!P)$
is a sober dcpo, then P is a sober dcpo. Therefore, if P is not a sober dcpo, then
![]() $\mathsf{K}(\Sigma~\!\!P)$
is not a sober dcpo.
$\mathsf{K}(\Sigma~\!\!P)$
is not a sober dcpo.
Example 135. Let L be the Isbell’s lattice constructed in Isbell (Reference Isbell1982). Then,
-
(a) L is not a sober dcpo (see Isbell Reference Isbell1982).
-
(b) L is a well-filtered dcpo by Proposition 22
-
(c) L is neither a Rudin dcpo nor a
 $\mathord{\mathsf{WD}}$
dcpo by (a), (b) and Corollary 44.
$\mathord{\mathsf{WD}}$
dcpo by (a), (b) and Corollary 44. -
(d)
 $\mathsf{K}(\Sigma~\!\!L)$
is a well-filtered dcpo by Theorem 58.
$\mathsf{K}(\Sigma~\!\!L)$
is a well-filtered dcpo by Theorem 58. -
(e)
 $\mathsf{K}(\Sigma~\!\!L)$
is a spatial frame (see Xu et al. Reference Xu, Xi and Zhao2021b, Lemma 1).
$\mathsf{K}(\Sigma~\!\!L)$
is a spatial frame (see Xu et al. Reference Xu, Xi and Zhao2021b, Lemma 1). -
(f)
 $\mathsf{K}(\Sigma~\!\!L)$
is not a sober dcpo by (a) and Corollary 134.
$\mathsf{K}(\Sigma~\!\!L)$
is not a sober dcpo by (a) and Corollary 134. -
(g)
 $\mathsf{K}(\Sigma~\!\!L)$
is neither a Rudin dcpo nor a
$\mathsf{K}(\Sigma~\!\!L)$
is neither a Rudin dcpo nor a
 $\mathord{\mathsf{WD}}$
dcpo by (a), (b) and Corollary 133.
$\mathord{\mathsf{WD}}$
dcpo by (a), (b) and Corollary 133.
Proposition 136.
Suppose that X is a
![]() $T_0$
space for which
$T_0$
space for which
![]() $\sigma (\mathord{\mathsf{K}} (X))\subseteq\mathcal O(P_S(X))$
. If
$\sigma (\mathord{\mathsf{K}} (X))\subseteq\mathcal O(P_S(X))$
. If
![]() $\Sigma~\!\! \mathord{\mathsf{K}} (X)$
is well-filtered determined, then X is well-filtered determined.
$\Sigma~\!\! \mathord{\mathsf{K}} (X)$
is well-filtered determined, then X is well-filtered determined.
Proof. By Remark 127, X has property S. Let
![]() $A\in{\mathsf{Irr}}_c(X)$
, Y a well-filtered space and
$A\in{\mathsf{Irr}}_c(X)$
, Y a well-filtered space and
![]() $f:X\longrightarrow Y$
a continuous mapping. Then by
$f:X\longrightarrow Y$
a continuous mapping. Then by
![]() $\sigma (\mathord{\mathsf{K}} (X))\subseteq\mathcal O(P_S(X))$
, Lemma 6 and Theorem 58,
$\sigma (\mathord{\mathsf{K}} (X))\subseteq\mathcal O(P_S(X))$
, Lemma 6 and Theorem 58,
![]() $\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
is well-filtered and
$\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
is well-filtered and
![]() $P_S^{\sigma}(f): P_S(X)\longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (Y)$
is continuous, where
$P_S^{\sigma}(f): P_S(X)\longrightarrow \Sigma~\!\! \mathord{\mathsf{K}} (Y)$
is continuous, where
![]() $P_S^\sigma (f)(K)=\mathord{\uparrow} f(K)$
for all
$P_S^\sigma (f)(K)=\mathord{\uparrow} f(K)$
for all
![]() $K\in \mathord{\mathsf{K}} (X)$
. By assumption,
$K\in \mathord{\mathsf{K}} (X)$
. By assumption,
![]() $\{\mathord{\uparrow} a : a\in A\}\in {\mathsf{Irr}} (\Sigma~\!\! \mathord{\mathsf{K}} (X))$
or
$\{\mathord{\uparrow} a : a\in A\}\in {\mathsf{Irr}} (\Sigma~\!\! \mathord{\mathsf{K}} (X))$
or
![]() $\Diamond A\in {\mathsf{Irr}}_c(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
, and hence by the well-filtered determinedness of
$\Diamond A\in {\mathsf{Irr}}_c(\Sigma~\!\! \mathord{\mathsf{K}} (X))$
, and hence by the well-filtered determinedness of
![]() $\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
and the continuity of
$\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
and the continuity of
![]() $P_S^\sigma (f)$
, there exists a unique
$P_S^\sigma (f)$
, there exists a unique
![]() $Q\in \mathord{\mathsf{K}}(Y)$
such that
$Q\in \mathord{\mathsf{K}}(Y)$
such that
![]() $\overline{\{\mathord{\uparrow} f(a) : a\in A\}}=\overline{P_S^\sigma(f)(\{\mathord{\uparrow} a : a\in A\})}=\overline{\{Q\}}=\downarrow_{\mathord{\mathsf{K}} (Y)} Q$
in
$\overline{\{\mathord{\uparrow} f(a) : a\in A\}}=\overline{P_S^\sigma(f)(\{\mathord{\uparrow} a : a\in A\})}=\overline{\{Q\}}=\downarrow_{\mathord{\mathsf{K}} (Y)} Q$
in
![]() $\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
or
$\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
or
![]() $\overline{P_S^\sigma(f)(\Diamond A)}=\overline{\{Q\}}=\downarrow_{\mathord{\mathsf{K}} (Y)} Q$
in
$\overline{P_S^\sigma(f)(\Diamond A)}=\overline{\{Q\}}=\downarrow_{\mathord{\mathsf{K}} (Y)} Q$
in
![]() $\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
. For the case of
$\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
. For the case of
![]() $\overline{P_S^\sigma(f)(\Diamond A)}=\overline{\{Q\}}$
in
$\overline{P_S^\sigma(f)(\Diamond A)}=\overline{\{Q\}}$
in
![]() $\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
, since
$\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
, since
![]() $\overline{P_S^\sigma(f)(\Diamond A)}=\overline{P_S^\sigma(f)({\rm cl}_{\mathcal O(P_S(X))}\xi_X (A))}=\overline{P_S^\sigma(f)(\xi_X (A))}=\overline{\{\mathord{\uparrow} f(a) : a\in A\}}$
in
$\overline{P_S^\sigma(f)(\Diamond A)}=\overline{P_S^\sigma(f)({\rm cl}_{\mathcal O(P_S(X))}\xi_X (A))}=\overline{P_S^\sigma(f)(\xi_X (A))}=\overline{\{\mathord{\uparrow} f(a) : a\in A\}}$
in
![]() $\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
, we also have
$\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
, we also have
![]() $\overline{\{\mathord{\uparrow} f(a) : a\in A\}}=\overline{\{Q\}}$
in
$\overline{\{\mathord{\uparrow} f(a) : a\in A\}}=\overline{\{Q\}}$
in
![]() $\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
. Since Y is well-filtered, by Corollary 25,
$\Sigma~\!\! \mathord{\mathsf{K}} (Y)$
. Since Y is well-filtered, by Corollary 25,
![]() $\mathcal O(P_S(Y))\subseteq \sigma(\mathord{\mathsf{K}} (Y))$
. Hence by Remark 2,
$\mathcal O(P_S(Y))\subseteq \sigma(\mathord{\mathsf{K}} (Y))$
. Hence by Remark 2,
![]() ${\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} f(a) : a\in A\}={\rm cl}_{\mathcal O(P_S(X))}\{Q\}$
.
${\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} f(a) : a\in A\}={\rm cl}_{\mathcal O(P_S(X))}\{Q\}$
.
Claim 1: Q is supercompact.
Let
![]() $\{V_j:j\in J\}\subseteq\mathcal O(Y)$
with
$\{V_j:j\in J\}\subseteq\mathcal O(Y)$
with
![]() $Q\subseteq \bigcup_{j\in J}V_j$
, i.e.,
$Q\subseteq \bigcup_{j\in J}V_j$
, i.e.,
![]() $Q\in\Box \bigcup_{j\in J}V_j$
. Since
$Q\in\Box \bigcup_{j\in J}V_j$
. Since
![]() ${\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} f(a) : a\in A\}=cl_{\mathcal O(P_S(X))}\{Q\}$
, we have
${\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} f(a) : a\in A\}=cl_{\mathcal O(P_S(X))}\{Q\}$
, we have
![]() $\{\mathord{\uparrow} f(a):a\in A\}\cap \Box \bigcup_{j\in J}V_j\neq\emptyset$
. Then, there exists
$\{\mathord{\uparrow} f(a):a\in A\}\cap \Box \bigcup_{j\in J}V_j\neq\emptyset$
. Then, there exists
![]() $a_0\in A$
and
$a_0\in A$
and
![]() $j_0\in J$
such that
$j_0\in J$
such that
![]() $\mathord{\uparrow} f(a_0)\subseteq V_{j_0}$
, and consequently,
$\mathord{\uparrow} f(a_0)\subseteq V_{j_0}$
, and consequently,
![]() $\{\mathord{\uparrow} a : a\in A\}\cap \Box U_{j_0}\neq\emptyset$
. By
$\{\mathord{\uparrow} a : a\in A\}\cap \Box U_{j_0}\neq\emptyset$
. By
![]() ${\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} f(a) : a\in A\}={\rm cl}_{\mathcal O(P_S(X))}\{Q\}$
again, we have
${\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} f(a) : a\in A\}={\rm cl}_{\mathcal O(P_S(X))}\{Q\}$
again, we have
![]() $Q\in \Box U_{j_0}$
, that is,
$Q\in \Box U_{j_0}$
, that is,
![]() $Q\subseteq U_{j_0}$
.
$Q\subseteq U_{j_0}$
.
Hence, by Heckmann and Keimel (Reference Heckmann and Keimel2013, Fact 2.2), there exists
![]() $y_Q\in Y$
such that
$y_Q\in Y$
such that
![]() $Q=\mathord{\uparrow} y_Q$
.
$Q=\mathord{\uparrow} y_Q$
.
Claim 2:
![]() $\overline{f(A)}=\overline{\{y_Q\}}$
in Y.
$\overline{f(A)}=\overline{\{y_Q\}}$
in Y.
For each
![]() $y\in f(A)$
, by
$y\in f(A)$
, by
![]() ${\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} f(a) : a\in A\}=cl_{\mathcal O(P_S(X))}\{\mathord{\uparrow} y_Q\}$
, we have that
${\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} f(a) : a\in A\}=cl_{\mathcal O(P_S(X))}\{\mathord{\uparrow} y_Q\}$
, we have that
![]() $\mathord{\uparrow} y\in {\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} y_Q\}=$
$\mathord{\uparrow} y\in {\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} y_Q\}=$
![]() $\downarrow_{\mathord{\mathsf{K}} (Y)}\mathord{\uparrow} y_Q$
, whence
$\downarrow_{\mathord{\mathsf{K}} (Y)}\mathord{\uparrow} y_Q$
, whence
![]() $\mathord{\uparrow} y_Q\subseteq \mathord{\uparrow} y$
, i.e.,
$\mathord{\uparrow} y_Q\subseteq \mathord{\uparrow} y$
, i.e.,
![]() $y\in\overline{\{y_Q\}}$
. This implies that
$y\in\overline{\{y_Q\}}$
. This implies that
![]() $f(A)\subseteq \overline{\{y_Q\}}$
. In addition, since
$f(A)\subseteq \overline{\{y_Q\}}$
. In addition, since
![]() $\mathord{\uparrow} y_Q\in$
$\mathord{\uparrow} y_Q\in$
![]() ${\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} f(a) : a\in A\}\subseteq \Diamond \overline{f(A)}$
,
${\rm cl}_{\mathcal O(P_S(X))}\{\mathord{\uparrow} f(a) : a\in A\}\subseteq \Diamond \overline{f(A)}$
,
![]() $\mathord{\uparrow} y_Q\cap\overline{f(A)}\neq\emptyset$
. It follows that
$\mathord{\uparrow} y_Q\cap\overline{f(A)}\neq\emptyset$
. It follows that
![]() $y_Q\in \overline{f(A)}$
. Therefore,
$y_Q\in \overline{f(A)}$
. Therefore,
![]() $\overline{f(A)}=\overline{\{y_Q\}}$
.
$\overline{f(A)}=\overline{\{y_Q\}}$
.
By Claim 2,
![]() $A\in \mathord{\mathsf{WD}} (X)$
, proving that X is well-filtered determined.
$A\in \mathord{\mathsf{WD}} (X)$
, proving that X is well-filtered determined.
Corollary 137.
For a poset P, if
![]() $\sigma (\mathord{\mathsf{K}} (\Sigma~\!\!P))\subseteq \mathcal O(P_S(\Sigma~\!\!P))$
and
$\sigma (\mathord{\mathsf{K}} (\Sigma~\!\!P))\subseteq \mathcal O(P_S(\Sigma~\!\!P))$
and
![]() $\mathord{\mathsf{K}} (\Sigma~\!\!P))$
is a
$\mathord{\mathsf{K}} (\Sigma~\!\!P))$
is a
![]() $\mathord{\mathsf{WD}}$
poset, then P is a
$\mathord{\mathsf{WD}}$
poset, then P is a
![]() $\mathord{\mathsf{WD}}$
poset.
$\mathord{\mathsf{WD}}$
poset.
From Corollaries 44 and 137, we deduce the following result.
Corollary 138.
If P is a well-filtered dcpo,
![]() $\sigma (\mathord{\mathsf{K}} (\Sigma~\!\!P))\subseteq \mathcal O(P_S(\Sigma~\!\!P))$
and
$\sigma (\mathord{\mathsf{K}} (\Sigma~\!\!P))\subseteq \mathcal O(P_S(\Sigma~\!\!P))$
and
![]() $\mathord{\mathsf{K}} (\Sigma~\!\!P)$
is a
$\mathord{\mathsf{K}} (\Sigma~\!\!P)$
is a
![]() $\mathord{\mathsf{WD}}$
dcpo (especially, a Rudin dcpo), then both
$\mathord{\mathsf{WD}}$
dcpo (especially, a Rudin dcpo), then both
![]() $\mathord{\mathsf{K}} (\Sigma~\!\!P)$
and P are sober dcpos.
$\mathord{\mathsf{K}} (\Sigma~\!\!P)$
and P are sober dcpos.
Acknowledgements
The authors would like to thank the referee for the numerous and very helpful suggestions that have improved this paper substantially.