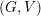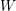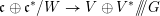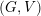1 Introduction
The quotient of a symplectic complex vector space
$(M,\unicode[STIX]{x1D714})$
by a reductive group
$G$
does not naturally inherit a symplectic structure, even if the group action preserves the symplectic form
$\unicode[STIX]{x1D714}$
. The classical approach is to consider the moment map
$\unicode[STIX]{x1D707}:M\rightarrow \mathfrak{g}^{\ast }$
and the quotient of its null-fibre
$M/\!\!/\!\!/G:=\unicode[STIX]{x1D707}^{-1}(0)/\!\!/G$
instead, the so-called Marsden–Weinstein reduction or symplectic reduction. Such symplectic reductions arise naturally as local models for the singularities of certain quiver varieties or moduli of sheaves on K3 surfaces. Symplectic reductions are, in general, rather singular spaces and often fail to satisfy Beauville’s criteria for a symplectic singularity [Reference BeauvilleBea00]. They do, however, always carry natural Poisson structures.
In this article, we study a particularly interesting class of symplectic reductions which in many cases turn out to be isomorphic to quotients of finite groups. Dadok and Kac [Reference Dadok and KacDK85] introduced the concept of a polar representation
$(G,V)$
of a reductive group. One feature of polar representations is the existence of a linear subspace
$\mathfrak{c}\subseteq V$
with an action of a finite subfactor
$W$
of
$G$
such that the inclusion
$\mathfrak{c}\rightarrow V$
induces an isomorphism
$\mathfrak{c}/W\rightarrow V/\!\!/G$
. A classical example for such a situation is the adjoint action of
$G$
on its Lie algebra
$\mathfrak{g}$
: if
$W$
denotes its Weyl group and
$\mathfrak{h}$
a Cartan subalgebra of
$\mathfrak{g}$
, then
$\mathfrak{h}/W\cong \mathfrak{g}/\!\!/G$
by Chevalley’s theorem. Now the representations
$\mathfrak{c}\oplus \mathfrak{c}^{\ast }$
and
$V\oplus V^{\ast }$
carry natural symplectic structures that are equivariant for the actions of
$W$
and
$G$
, respectively. As a first technical result we construct a morphism of Poisson schemes
$$\begin{eqnarray}\displaystyle r:\mathfrak{c}\oplus \mathfrak{c}^{\ast }/W\rightarrow V\oplus V^{\ast }/\!\!/\!\!/G. & & \displaystyle\end{eqnarray}$$
This can be seen as a symplectic analogue of Chevalley’s isomorphism, and it is natural to seek conditions for
$r$
to actually be an isomorphism.
Conjecture 1.1. Let
$(G,V)$
be a visible polar representation of a reductive algebraic group
$G$
. Then
$r:\mathfrak{c}\oplus \mathfrak{c}^{\ast }/W\rightarrow (V\oplus V^{\ast }/\!\!/\!\!/G)_{\text{red}}$
is an isomorphism of Poisson varieties, where
$(V\oplus V^{\ast }/\!\!/\!\!/G)_{\text{red}}$
denotes the reduced scheme associated to the symplectic reduction
$V\oplus V^{\ast }/\!\!/\!\!/G$
.
Here a representation
$(G,V)$
is said to be visible if each fibre of the quotient map
$V\rightarrow V/\!\!/G$
consists of only finitely many orbits. The morphism
$r:\mathfrak{c}\oplus \mathfrak{c}^{\ast }/W\rightarrow (V\oplus V^{\ast }/\!\!/\!\!/G)_{\text{red}}$
is known to be an isomorphism for the adjoint representation by results of Richardson [Reference RichardsonRic79], Hunziker [Reference HunzikerHun97] (for simple groups) and Joseph [Reference JosephJos97] (for semisimple groups), and for isotropy representations associated to symmetric spaces by the work of Panyushev [Reference PanyushevPan94, §§ 3–4] (for the locally free case) and Tevelev [Reference TevelevTev00] (for the general case). These are special cases of visible polar representations and belong to the class of
$\unicode[STIX]{x1D703}$
-representations studied by Vinberg in [Reference VinbergVin76]. We will review this concept in § 5. In the framework of quiver representations, Crawley-Boevey [Reference Crawley-BoeveyCra03] has shown that the symplectic reduction is normal, which implies the conjecture for the
$\unicode[STIX]{x1D703}$
-representations obtained from quivers. Finally,
$r$
is also known to be an isomorphism in some special cases considered in [Reference LehnLeh07, Reference BeckerBec09, Reference TerpereauTer14].
In support of the conjecture, we cover the following new cases.
Theorem 1.2. Let
$(G,V)$
be a visible stable locally free polar representation with Cartan subspace
$\mathfrak{c}$
and Weyl group
$W$
. Then the restriction morphism
$r:\mathfrak{c}\oplus \mathfrak{c}^{\ast }/W\longrightarrow V\oplus V^{\ast }/\!\!/\!\!/G$
is an isomorphism of Poisson schemes.
A representation
$(G,V)$
is said to be locally free if the stabiliser subgroup of a general point in
$V$
is finite, and stable if there is a closed orbit whose dimension is maximal among all orbit dimensions. The
$\unicode[STIX]{x1D703}$
-representations are always visible and polar, but are not necessarily locally free or stable. One might wonder how special a visible stable polar representation is, e.g. whether such a representation is automatically a
$\unicode[STIX]{x1D703}$
-representation. It turns out that this is not the case: in Example 8.6 we provide a family of examples of visible stable locally free polar representations which are not
$\unicode[STIX]{x1D703}$
-representations.
We first obtained a proof of Theorem 1.2 for
$\unicode[STIX]{x1D703}$
-representations by using their classification, but the proof we present here is more elegant and classification free, which is why we are convinced that the framework of polar representations is the one where Conjecture 1.1 should be posed. Further evidence for Conjecture 1.1 is provided in this paper through a number of examples where we are able to verify the conjecture or, in some cases, even the stronger statement where the symplectic reduction is reduced. For instance, we prove that the conjecture holds for
$\unicode[STIX]{x1D703}$
-representations with a Cartan subspace of dimension at most
$1$
(see Corollary 5.2); this case is the generic case and could be of major importance in an inductive approach to proving the conjecture for
$\unicode[STIX]{x1D703}$
-representations.
We will show by counterexamples that the conjecture does not hold in general if the visibility assumption is dropped; see Proposition 8.5 and Example 8.7. Also, the
$16$
-dimensional spin representation of
$\text{Spin}_{9}$
, which is the isotropy representation of a symmetric space, provides an example (see § 8) where the symplectic reduction is irreducible but non-reduced, whereas, of course,
$\mathfrak{c}\oplus \mathfrak{c}^{\ast }/W$
is always reduced. So, unless stronger hypotheses on
$(G,V)$
are imposed, the symplectic reduction has to be taken with its reduced structure.
Let us note that the question of whether the symplectic reduction
$\mathfrak{g}\oplus \mathfrak{g}^{\ast }/\!\!/\!\!/G$
in the adjoint case is reduced (respectively normal) from the start is closely related to the classical problem of whether the commuting scheme
$$\begin{eqnarray}\unicode[STIX]{x1D707}^{-1}(0)=\{(x,y)\in \mathfrak{g}^{2}\mid [x,y]=0\}\end{eqnarray}$$
is reduced (respectively normal) or not; see, for example, [Reference PopovPop08, Reference ProcesiPro15] for results in this direction.
Notation
We call an integral separated scheme of finite type over
$\mathbb{C}$
a variety; in particular, varieties are always irreducible. If
$X$
is a scheme, then we denote by
$X_{\text{red}}$
the corresponding reduced subscheme. We always denote by
$G$
a reductive algebraic group and by
$\mathfrak{g}$
its Lie algebra.
2 Symplectic reductions
Let
$M$
be a finite-dimensional complex vector space with a symplectic bilinear form
$\unicode[STIX]{x1D714}$
, and let
$G$
be a reductive group that acts linearly on
$M$
and preserves the symplectic structure. Such an action is always Hamiltonian, i.e. it admits a moment map
$\unicode[STIX]{x1D707}:M\rightarrow \mathfrak{g}^{\ast }$
, namely
$\unicode[STIX]{x1D707}(m)(A)=\unicode[STIX]{x1D707}^{A}(m)=\frac{1}{2}\unicode[STIX]{x1D714}(m,Am)$
for all
$m\in M$
and
$A\in \mathfrak{g}$
, where
$\mathfrak{g}$
denotes the Lie algebra of
$G$
. Since
$\unicode[STIX]{x1D707}$
is
$G$
-equivariant,
$G$
acts on the fibre
$\unicode[STIX]{x1D707}^{-1}(\unicode[STIX]{x1D701})$
for any
$\unicode[STIX]{x1D701}\in (\mathfrak{g}^{\ast })^{G}$
. The quotient
$\unicode[STIX]{x1D707}^{-1}(\unicode[STIX]{x1D701})/\!\!/G$
is referred to as the symplectic reduction or Marsden–Weinstein reduction. In this paper, we are interested only in the
$\unicode[STIX]{x1D701}=0$
case, which is the only choice for semisimple groups anyway, and we write
$M/\!\!/\!\!/G:=\unicode[STIX]{x1D707}^{-1}(0)/\!\!/G$
. If the group
$G$
is finite, the moment map vanishes identically and the symplectic reduction coincides with the ordinary quotient,
$M/\!\!/\!\!/G=M/G$
.
The symplectic reduction tends to be rather singular. Despite its name, it fails in general to satisfy the criteria of a symplectic singularity in the sense of Beauville, since
$M/\!\!/\!\!/G$
can be reducible or even non-reduced, as several of the examples we discuss in this paper show. However,
$M/\!\!/\!\!/G$
always carries a canonical Poisson structure.
Recall that a Poisson bracket on a
$\mathbb{C}$
-algebra
$A$
is a
$\mathbb{C}$
-bilinear Lie bracket
$\{-,-\}:A\times A\rightarrow A$
that satisfies the Leibniz rule
$\{fg,h\}=f\{g,h\}+g\{f,h\}$
. An ideal
$I\subseteq A$
is a Poisson ideal if
$\{I,A\}\subseteq I$
. Kaledin [Reference KaledinKal06] showed that all minimal primes of
$A$
and the nilradical
$\text{nil}(A)$
are Poisson ideals. A Poisson scheme is a scheme
$X$
together with a Poisson bracket on its structure sheaf.
A symplectic form on a smooth variety induces a Poisson structure in the following way. The Hamilton vector field
$H_{f}$
associated to a regular function
$f$
is defined by the relation
$df(\unicode[STIX]{x1D709})=\unicode[STIX]{x1D714}(H_{f},\unicode[STIX]{x1D709})$
for all tangent vectors
$\unicode[STIX]{x1D709}$
. Then
$\{f,f^{\prime }\}:=df(H_{f^{\prime }})=-df^{\prime }(H_{f})$
. The skew-symmetry of the bracket is immediate, and the Jacobi identity follows from
$d\unicode[STIX]{x1D714}=0$
. If
$X$
is a normal symplectic variety, the bracket
$\{f,f^{\prime }\}$
is defined as the unique regular extension of the function
$\{f|_{X_{\text{reg}}},f^{\prime }|_{X_{\text{reg}}}\}$
. For a symplectic vector space
$(M,\unicode[STIX]{x1D714})$
with a basis
$x_{1},\ldots ,x_{2n}$
and a dual basis
$y_{1},\ldots ,y_{2n}$
characterised by
$\unicode[STIX]{x1D714}(x_{i},y_{j})=\unicode[STIX]{x1D6FF}_{ij}$
, the Poisson bracket is given by
$\{f,f^{\prime }\}=\sum _{i}(\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{i})(\unicode[STIX]{x2202}f^{\prime }/\unicode[STIX]{x2202}y_{i})$
.
The ideal
$I\subseteq \mathbb{C}[M]$
of the null-fibre
$\unicode[STIX]{x1D707}^{-1}(0)$
of the moment map is generated by the functions
$\unicode[STIX]{x1D707}^{A}(m)=\frac{1}{2}\unicode[STIX]{x1D714}(m,Am)$
. Their differentials equal
$d\unicode[STIX]{x1D707}_{m}^{A}(\unicode[STIX]{x1D709})=\unicode[STIX]{x1D714}(\unicode[STIX]{x1D709},Am)$
. Hence, for any regular function
$f$
, one has
$\{f,\unicode[STIX]{x1D707}^{A}\}(m)=-\unicode[STIX]{x1D714}(H_{f},Am)=-df_{m}(Am)$
. If
$f$
is assumed to be
$G$
-equivariant, then its derivative vanishes in the orbit directions, so that
$\{f,\unicode[STIX]{x1D707}^{A}\}=0$
for all
$f\in \mathbb{C}[M]^{G}$
and all
$A\in \mathfrak{g}$
. The Leibniz rule now implies
$\{I,\mathbb{C}[M]^{G}\}\subseteq I$
and hence
$\{I^{G},\mathbb{C}[M]^{G}\}=I^{G}$
as the bracket is
$G$
-invariant. This signifies that
$I^{G}$
is a Poisson ideal in the invariant ring
$\mathbb{C}[M]^{G}$
and, consequently, that
$W/\!\!/\!\!/G=\text{Spec}((\mathbb{C}[M]/I)^{G})$
inherits a canonical Poisson structure. Note that
$(\mathbb{C}[M]/I)^{G}=\mathbb{C}[M]^{G}/I^{G}$
due to the linear reductivity of
$G$
.
In this paper, the relevant symplectic representations take the special form
$M=V\oplus V^{\ast }$
with symplectic form
$\unicode[STIX]{x1D714}(v+\unicode[STIX]{x1D711},v^{\prime }+\unicode[STIX]{x1D711}^{\prime }):=\unicode[STIX]{x1D711}(v^{\prime })-\unicode[STIX]{x1D711}^{\prime }(v)$
. Then, for any linear action of
$G$
on
$V$
and the corresponding contragredient action on the dual space
$V^{\ast }$
, the diagonal action on
$V\oplus V^{\ast }$
preserves the symplectic structure. The moment map takes the special form
$\unicode[STIX]{x1D707}^{A}(v+\unicode[STIX]{x1D711})=\unicode[STIX]{x1D711}(Av)$
for
$v+\unicode[STIX]{x1D711}\in V\oplus V^{\ast }$
. We refer to
$V\oplus V^{\ast }$
as the symplectic double of
$V$
.
3 Symplectic double of polar representations
The concept of a polar representation was developed and thoroughly investigated by Dadok and Kac. As this notion is central for our purposes, we briefly recall here the main concepts and results but refer to [Reference Dadok and KacDK85] for all proofs.
Let
$V$
be a representation of a reductive group
$G$
. A vector
$v\in V$
is semisimple if its orbit is closed. Such orbits are affine, and by Matsushima’s criterion the stabiliser subgroup
$G_{v}\subseteq G$
of
$v$
is again reductive. A semisimple
$v$
is regular if its orbit dimension is maximal among all semisimple orbits. For a regular
$v$
consider the linear space
$\mathfrak{c}_{v}:=\{x\in V\mid \mathfrak{g}x\subseteq \mathfrak{g}v\}$
. Obviously,
$\mathfrak{c}_{v}=\mathfrak{c}_{w}$
for all regular semisimple elements
$w\in \mathfrak{g}_{v}$
.
Dadok and Kac showed that
$\mathfrak{c}_{v}$
consists of semisimple elements only and that it is annihilated by the Lie algebra
$\mathfrak{g}_{v}$
of the stabiliser subgroup of
$v$
[Reference Dadok and KacDK85, Lemma 2.1]. Moreover, the natural projection
$\mathfrak{c}_{v}\rightarrow V/\!\!/G$
is finite [Reference Dadok and KacDK85, Proposition 2.2], so that in particular its dimension is bounded by
$\dim \mathfrak{c}_{v}\leqslant \dim V/\!\!/G$
. A representation
$V$
is said to be polar if there is a regular element
$v$
such that
$\dim \mathfrak{c}_{v}=\dim V/\!\!/G$
. The space
$\mathfrak{c}_{v}$
is then called a Cartan subspace of
$V$
.
For instance, if
$\dim V/\!\!/G\leqslant 1$
, then
$V$
is polar and any non-zero semisimple element generates a Cartan subspace. The adjoint representation
$\mathfrak{g}$
of a semisimple Lie group
$G$
is polar, and any Cartan subalgebra
$\mathfrak{h}\subseteq \mathfrak{g}$
is a Cartan subspace. The natural representation of
$\text{SL}_{3}$
on the space
$S^{3}\mathbb{C}^{3}=\mathbb{C}[x,y,z]_{3}$
of ternary cubic forms is polar, and the Hesse family
$\langle x^{3}+y^{3}+z^{3},xyz\rangle$
is a Cartan subspace.
Assume now that
$V$
is a polar representation of
$G$
. By [Reference Dadok and KacDK85, Theorem 2.3], all Cartan subspaces are
$G$
-conjugate. Let
$\mathfrak{c}\subseteq V$
be a fixed Cartan subspace, and let
$v\in \mathfrak{c}$
denote a regular semisimple element. Dadok and Kac further proved that there is a maximal compact Lie group
$K\subseteq G$
and a
$K$
-equivariant Hermitian scalar product
$\langle -,-\rangle$
on
$V$
such that all vectors of
$\mathfrak{c}$
have minimal length in their orbit, and
$\mathfrak{c}$
and
$\mathfrak{g}\mathfrak{c}=\mathfrak{g}v$
are orthogonal to each other [Reference Dadok and KacDK85, Lemma 2.1]. The quotient of the normaliser subgroup
$N_{G}(\mathfrak{c})=\{g\in G\mid g(\mathfrak{c})=\mathfrak{c}\}$
and the centraliser subgroup
$Z_{G}(\mathfrak{c})=\{g\in G\mid g(x)=x\text{ for all }x\in \mathfrak{c}\}$
is a finite group
$W=N_{G}(\mathfrak{c})/Z_{G}(\mathfrak{c})$
which, in analogy to the case of adjoint representations, is called the Weyl group of the polar representation;
$W$
is generated by complex reflections when
$G$
is connected. Theorem 2.10 of [Reference Dadok and KacDK85] states that the inclusion
$\mathfrak{c}\rightarrow V$
induces an isomorphism
$$\begin{eqnarray}\displaystyle \mathfrak{c}/W\xrightarrow[{}]{\;\cong \;}V/\!\!/G & & \displaystyle\end{eqnarray}$$
or, equivalently,
$\mathbb{C}[V]^{G}\cong \mathbb{C}[\mathfrak{c}]^{W}$
. This generalises the Chevalley isomorphism in the case of adjoint representations. Since
$G_{v}$
stabilises the tangent space
$\mathfrak{g}v$
to the
$G$
-orbit of
$v$
and since the definition of
$\mathfrak{c}=\mathfrak{c}_{v}$
depends only on
$\mathfrak{g}v$
, the stabiliser subgroup acts on
$\mathfrak{c}$
, so there are natural inclusions
$Z_{G}(\mathfrak{c})\subseteq G_{v}\subseteq N_{G}(\mathfrak{c})$
of finite index. All three groups are reductive.
Our goal is to construct a morphism
$$\begin{eqnarray}\displaystyle r:\mathfrak{c}\oplus \mathfrak{c}^{\ast }/W\longrightarrow V\oplus V^{\ast }/\!\!/\!\!/G & & \displaystyle\end{eqnarray}$$
and to give conditions for
$r$
to be an isomorphism. As the functorial projection
$V^{\ast }\rightarrow \mathfrak{c}^{\ast }$
points in the wrong direction, the first task is to identify an appropriate subspace
$\mathfrak{c}^{\vee }\subseteq V^{\ast }$
that splits the projection.
Let
$U\subseteq V$
be the orthogonal complement to
$\mathfrak{c}\oplus \mathfrak{g}\mathfrak{c}$
. By [Reference Dadok and KacDK85, Proposition 1.3(ii)], the orthogonal decomposition
$$\begin{eqnarray}\displaystyle V=\mathfrak{c}\oplus \mathfrak{g}\mathfrak{c}\oplus U & & \displaystyle\end{eqnarray}$$
is
$G_{v}$
-stable, and by [Reference Dadok and KacDK85, Corollary 2.5],
$\dim U/\!\!/G_{v}=0$
. As
$N_{G}(\mathfrak{c})$
normalises
$Z_{G}(\mathfrak{c})$
, the decomposition is also preserved by the normaliser group
$N_{G}(\mathfrak{c})$
. Let
$$\begin{eqnarray}\displaystyle \mathfrak{c}^{\vee }:=\{\unicode[STIX]{x1D711}\in V^{\ast }\mid \unicode[STIX]{x1D711}(\mathfrak{g}\mathfrak{c}\oplus U)=0\}. & & \displaystyle\end{eqnarray}$$
Lemma 3.1. The subspace
$\mathfrak{c}^{\vee }\subseteq V^{\ast }$
depends only on
$\mathfrak{c}$
. It is stable under the action of
$N_{G}(\mathfrak{c})$
and pointwise invariant under the action of
$Z_{G}(\mathfrak{c})$
. The natural pairing
$\mathfrak{c}\times \mathfrak{c}^{\vee }\rightarrow \mathbb{C}$
is non-degenerate and induces an
$N_{G}(\mathfrak{c})$
-equivariant isomorphism
$\mathfrak{c}^{\vee }\rightarrow \mathfrak{c}^{\ast }$
.
Proof. There is a unique
$Z_{G}(\mathfrak{c})$
-stable complement
$V_{1}$
to the invariant subspace
$V_{0}=V^{Z_{G}(\mathfrak{c})}$
. By definition,
$\mathfrak{c}\subseteq V_{0}$
, and since
$\dim U/\!\!/G_{v}=0$
, one has
$U\subseteq V_{1}$
. Hence
$\mathfrak{g}\mathfrak{c}\oplus U=\mathfrak{g}\mathfrak{c}+V_{1}$
. This shows that
$\mathfrak{c}^{\vee }$
is independent of the choice of the Hermitian scalar product. By definition,
$\mathfrak{c}^{\vee }$
pairs trivially with
$\mathfrak{g}\mathfrak{c}\oplus U$
, so the pairing with
$\mathfrak{c}$
is non-degenerate. The statements about the action of
$N_{G}(\mathfrak{c})$
and
$Z_{G}(\mathfrak{c})$
follow from the
$N_{G}(\mathfrak{c})$
-equivariance of the decomposition (4).◻
Proposition 3.2. Let
$V$
be a polar representation of a reductive group
$G$
with Cartan subspace
$\mathfrak{c}$
. Then the contragredient representation
$V^{\ast }$
is also polar, and
$\mathfrak{c}^{\vee }$
is a Cartan subspace for
$V^{\ast }$
. The action of the Weyl group
$W$
on
$\mathfrak{c}^{\vee }$
defines an isomorphism of
$W$
with the Weyl group of
$\mathfrak{c}^{\vee }$
.
Proof. The Hermitian scalar product
$\langle -,-\rangle$
defines a
$K$
-equivariant semilinear isomorphism
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}:V\rightarrow V^{\ast },\;\;v\mapsto \langle v,-\rangle . & & \displaystyle\end{eqnarray}$$
Via
$\unicode[STIX]{x1D6F7}$
,
$V^{\ast }$
inherits a
$K$
-equivariant Hermitian scalar product
$\langle \unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\rangle :=\langle \unicode[STIX]{x1D6F7}^{-1}(\unicode[STIX]{x1D713}),\unicode[STIX]{x1D6F7}^{-1}(\unicode[STIX]{x1D711})\rangle$
. The orthogonality of the decomposition (4) implies that
$\mathfrak{c}^{\vee }=\unicode[STIX]{x1D6F7}(\mathfrak{c})$
. Let
$\mathfrak{k}$
denote the Lie algebra of
$K$
. The
$K$
-equivariance of the Hermitian product implies
$\unicode[STIX]{x1D6F7}(\mathfrak{k}w)=\mathfrak{k}\unicode[STIX]{x1D6F7}(w)$
for any
$w\in V$
. And since
$\mathfrak{g}=\mathbb{C}\mathfrak{k}$
, one also has
$\mathfrak{g}\unicode[STIX]{x1D6F7}(w)=\unicode[STIX]{x1D6F7}(\mathfrak{g}w)$
. In particular, for all
$w\in \mathfrak{c}$
,
$\langle \unicode[STIX]{x1D6F7}(w),\mathfrak{g}\unicode[STIX]{x1D6F7}(w)\rangle =0$
, so
$\unicode[STIX]{x1D6F7}(w)$
is semisimple and of minimal length in its orbit by the Kempf–Ness theorem [Reference Dadok and KacDK85, Theorem 1.1]. We also deduce that
$\unicode[STIX]{x1D6F7}(v)$
is regular and that
$\mathfrak{c}^{\vee }=\{\unicode[STIX]{x1D711}\in V^{\ast }\mid \mathfrak{g}\unicode[STIX]{x1D711}\subseteq \mathfrak{g}\unicode[STIX]{x1D6F7}(v)\}=\mathfrak{c}_{\unicode[STIX]{x1D6F7}(v)}$
. Any element
$g\in G$
may be written in the form
$g=k\exp (i\unicode[STIX]{x1D709})$
with
$k\in K$
and
$\unicode[STIX]{x1D709}\in \mathfrak{k}$
. The
$K$
-equivariance and semilinearity of
$\unicode[STIX]{x1D6F7}$
yield
$\unicode[STIX]{x1D6F7}(gw)=\unicode[STIX]{x1D6F7}(k\exp (i\unicode[STIX]{x1D709})w)=k\exp (-i\unicode[STIX]{x1D709})\unicode[STIX]{x1D6F7}(w)$
and hence
$\unicode[STIX]{x1D6F7}(Gw)=G\unicode[STIX]{x1D6F7}(w)$
for every
$w\in V$
. In particular,
$\unicode[STIX]{x1D6F7}$
provides a bijection between closed orbits in
$V$
and
$V^{\ast }$
. Necessarily, all closed orbits in
$V^{\ast }$
meet
$\mathfrak{c}^{\vee }$
. This implies
$\dim \mathfrak{c}^{\vee }\geqslant \dim V^{\ast }/\!\!/G$
and hence that
$V^{\ast }$
is polar. The statement about the action of
$W$
follows from the fact that the Weyl group can be seen as the quotient
$N_{K}(\mathfrak{c})/Z_{K}(\mathfrak{c})$
according to [Reference Dadok and KacDK85, Lemma 2.7].◻
We continue to use the
$K$
-equivariant semilinear automorphism
$\unicode[STIX]{x1D6F7}:V\rightarrow V^{\ast }$
of (6). The proof of the proposition shows that
$\unicode[STIX]{x1D6F7}(\mathfrak{c})=\mathfrak{c}^{\vee }$
and
$\unicode[STIX]{x1D6F7}(\mathfrak{g}\mathfrak{c})=\mathfrak{g}\mathfrak{c}^{\vee }$
. One obtains a
$K$
-equivariant orthogonal decomposition
$$\begin{eqnarray}\displaystyle V^{\ast }=\mathfrak{c}^{\vee }\oplus \mathfrak{g}\mathfrak{c}^{\vee }\oplus U^{\vee } & & \displaystyle\end{eqnarray}$$
with
$U^{\vee }:=\unicode[STIX]{x1D6F7}(U)$
dual to (4). As before, we consider the symplectic form
$\unicode[STIX]{x1D714}(v+\unicode[STIX]{x1D711},v^{\prime }+\unicode[STIX]{x1D711}^{\prime }):=\unicode[STIX]{x1D711}(v^{\prime })-\unicode[STIX]{x1D711}^{\prime }(v)$
on
$V\oplus V^{\ast }$
. The symplectic vector space
$(V\oplus V^{\ast },\unicode[STIX]{x1D714})$
splits into the direct sum of symplectic subspaces
$\mathfrak{c}\oplus \mathfrak{c}^{\vee }$
,
$\mathfrak{g}\mathfrak{c}\oplus \mathfrak{g}\mathfrak{c}^{\vee }$
and
$U\oplus U^{\vee }$
. As
$\unicode[STIX]{x1D714}(\mathfrak{c}\oplus \mathfrak{c}^{\vee },\mathfrak{g}\mathfrak{c}\oplus \mathfrak{g}\mathfrak{c}^{\vee })=0$
, it follows that
$$\begin{eqnarray}\displaystyle \mathfrak{c}\oplus \mathfrak{c}^{\vee }\subseteq \unicode[STIX]{x1D707}^{-1}(0), & & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D707}:V\oplus V^{\ast }\rightarrow \mathfrak{g}^{\ast }$
denotes the moment map.
Polar representations behave well under taking slices [Reference Dadok and KacDK85, § 2]. Let
$w\in \mathfrak{c}$
be any element. The orthogonal complement
$N_{w}$
to the tangent space
$\mathfrak{g}w\subseteq \mathfrak{g}\mathfrak{c}$
is stable under
$G_{w}$
and contains
$\mathfrak{c}$
. The representation of
$G_{w}$
on
$N_{w}$
is called the slice representation at
$w$
, and Dadok and Kac have shown that
$N_{w}$
is again polar and that
$\mathfrak{c}$
is a Cartan subspace.
Proposition 3.3. Let
$V$
be a polar representation of
$G$
with a Cartan subspace
$\mathfrak{c}\subseteq V$
and corresponding Weyl group
$W$
. Let
$\mathfrak{c}^{\vee }\subseteq V^{\ast }$
denote the dual Cartan subspace. Then every
$m\in \mathfrak{c}\oplus \mathfrak{c}^{\vee }$
has a closed
$G$
-orbit in
$V\oplus V^{\ast }$
and
$Gm\cap (\mathfrak{c}\oplus \mathfrak{c}^{\vee })=Wm$
. Also, the morphism
$$\begin{eqnarray}r:\mathfrak{c}\oplus \mathfrak{c}^{\vee }/W\longrightarrow V\oplus V^{\ast }/\!\!/\!\!/G\end{eqnarray}$$
is injective and finite.
Proof. The symplectic double
$V\oplus V^{\ast }$
comes with a
$K$
-equivariant Hermitian scalar product
$$\begin{eqnarray}\langle w+\unicode[STIX]{x1D711},w^{\prime }+\unicode[STIX]{x1D711}^{\prime }\rangle =\langle w,w^{\prime }\rangle +\langle \unicode[STIX]{x1D711},\unicode[STIX]{x1D711}^{\prime }\rangle\end{eqnarray}$$
inherited from the scalar products on its direct summands. The orthogonality of the decompositions (4) and (7) implies that
$\langle m,\mathfrak{g}m\rangle =0$
for any
$m\in \mathfrak{c}\oplus \mathfrak{c}^{\vee }$
. It follows from the Kempf–Ness criterion [Reference Dadok and KacDK85, Theorem 1.1] that
$m$
is semisimple and of minimal length in its
$G$
-orbit, and that
$$\begin{eqnarray}Gm\cap (\mathfrak{c}\oplus \mathfrak{c}^{\vee })=Km\cap (\mathfrak{c}\oplus \mathfrak{c}^{\vee }).\end{eqnarray}$$
Assume now that
$(w,\unicode[STIX]{x1D711}),(w^{\prime },\unicode[STIX]{x1D711}^{\prime })\in \mathfrak{c}\oplus \mathfrak{c}^{\vee }$
belong to the same
$G$
-orbit and hence the same
$K$
-orbit, say
$w^{\prime }=kw$
and
$\unicode[STIX]{x1D711}^{\prime }=k\unicode[STIX]{x1D711}$
for some
$k\in K$
. Up to the action of
$W$
, we may assume
$w^{\prime }=w$
, so that
$k\in K_{w}=G_{w}\cap K$
. Let
$x=\unicode[STIX]{x1D6F7}^{-1}(\unicode[STIX]{x1D711}),x^{\prime }=\unicode[STIX]{x1D6F7}^{-1}(\unicode[STIX]{x1D711}^{\prime })\in \mathfrak{c}$
. As
$\unicode[STIX]{x1D6F7}$
is
$K$
-equivariant, it follows that
$kx=x^{\prime }$
. Now
$x$
and
$x^{\prime }$
are elements in the same
$G_{w}$
-orbit and contained in a Cartan subspace
$\mathfrak{c}$
of the slice representation
$N_{w}$
. By [Reference Dadok and KacDK85, Theorem 2.8],
$x$
and
$x^{\prime }$
also belong to the same orbit under the normaliser subgroup
$N_{G_{w}}(\mathfrak{c})\subseteq N_{G}(\mathfrak{c})$
. Hence, there is an element
$\unicode[STIX]{x1D6FE}\in W$
with
$w^{\prime }=\unicode[STIX]{x1D6FE}w=w$
and
$x^{\prime }=\unicode[STIX]{x1D6FE}x$
. In particular, the natural morphism
$r:\mathfrak{c}\oplus \mathfrak{c}^{\vee }/W\rightarrow V\oplus V^{\ast }/\!\!/G$
is injective. The same arguments as in the proof of [Reference Dadok and KacDK85, Proposition 2.2] show that
$r$
is finite.◻
If the Cartan subspace is one-dimensional, a simple argument gives something much stronger.
Proposition 3.4. Let
$(G,V)$
be a polar representation with a one-dimensional Cartan subspace. Then
$r:\mathfrak{c}\oplus \mathfrak{c}^{\vee }/W\rightarrow V\oplus V^{\ast }/\!\!/\!\!/G$
is a closed immersion.
Proof. If
$\dim \mathfrak{c}=1$
, the Weyl group
$W$
is cyclic, say of order
$m$
, and a generator acts on
$\mathfrak{c}\,\oplus \,\mathfrak{c}^{\vee }=\mathbb{C}^{2}$
via
$(x,y)\mapsto (\unicode[STIX]{x1D701}x,\unicode[STIX]{x1D701}^{-1}y)$
for some primitive
$m$
th root of unity
$\unicode[STIX]{x1D701}$
. Hence
$\mathbb{C}[\mathfrak{c}\oplus \mathfrak{c}^{\vee }]^{W}\cong \mathbb{C}[x^{m},xy,y^{m}]$
. We have to show that the restriction morphism
$(\mathbb{C}[V]\,\otimes \,\mathbb{C}[V^{\ast }])^{G}\cong (\mathbb{C}[V\,\oplus \,V^{\ast }])^{G}\rightarrow \mathbb{C}[\mathfrak{c}\oplus \mathfrak{c}^{\vee }]^{W}$
is surjective. Since
$V$
is a polar representation, there are isomorphisms
$\mathbb{C}[V]^{G}\rightarrow \mathbb{C}[\mathfrak{c}]^{W}$
and
$\mathbb{C}[V^{\ast }]^{G}\rightarrow \mathbb{C}[\mathfrak{c}^{\vee }]^{W}$
. Also, the
$G$
-invariant pairing
$V\otimes V^{\ast }\rightarrow \mathbb{C}$
restricts to the invariant
$xy$
. This shows that
$\mathbb{C}[V\oplus V^{\ast }]^{G}\rightarrow \mathbb{C}[\mathfrak{c}\oplus \mathfrak{c}^{\vee }]^{W}$
is surjective.◻
The null-fibre
$\unicode[STIX]{x1D707}^{-1}(0)$
of the momentum map contains the
$G$
-variety
$$\begin{eqnarray}C_{0}:=\overline{G.(\mathfrak{c}\oplus \mathfrak{c}^{\vee })},\end{eqnarray}$$
which will play a key role in our analysis.
Proposition 3.5. The quotient
$C_{0}/\!\!/G$
is a Poisson subscheme in
$(V\oplus V^{\ast })/\!\!/G$
and hence also in the symplectic reduction
$(V\oplus V^{\ast })/\!\!/\!\!/G$
. Moreover,
$r:\mathfrak{c}\oplus \mathfrak{c}^{\vee }/W\rightarrow C_{0}/\!\!/G$
is a bijective morphism of Poisson schemes.
Proof. Let
$J\subseteq \mathbb{C}[V\oplus V^{\ast }]$
denote the vanishing ideal of
$C_{0}$
. If we can show that
$\{h,f\}|_{C_{0}}=0$
for all
$h\in J$
and all
$f\in \mathbb{C}[V\oplus V^{\ast }]^{G}$
, then the Leibniz rule implies
$\{J,\mathbb{C}[V\oplus V^{\ast }]^{G}\}\subseteq J$
, and hence
$\{J^{G},\mathbb{C}[V\oplus V^{\ast }]^{G}\}\subseteq J^{G}$
, which covers the first assertion. Moreover, as
$J$
is a
$G$
-equivariant ideal sheaf and
$G(\mathfrak{c}\oplus \mathfrak{c}^{\vee })$
is dense in
$C_{0}$
by definition, it suffices to show that
$\{h,f\}$
vanishes in a general point
$m=w+\unicode[STIX]{x1D711}$
of
$\mathfrak{c}\oplus \mathfrak{c}^{\vee }$
for all
$h\in J$
and
$f\in \mathbb{C}[V\oplus V^{\ast }]^{G}$
. Now the tangent space of
$V\oplus V^{\ast }$
decomposes into symplectic subspaces
$\mathfrak{c}\oplus \mathfrak{c}^{\vee }$
,
$\mathfrak{g}\mathfrak{c}\oplus \mathfrak{g}\mathfrak{c}^{\vee }$
and
$U\oplus U^{\vee }$
, and this decomposition is stable under
$G_{w}$
. According to a result of Dadok and Kac mentioned above, the quotient
$U/\!\!/G_{w}$
is zero-dimensional. This implies that any
$G$
-invariant function
$f$
is constant on subsets
$m+U$
and
$m+U^{\bot }$
. In particular, all derivatives of
$f$
in
$m$
in the directions
$U\oplus U^{\vee }$
vanish. On the other hand,
$h$
vanishes on
$C_{0}$
so that all derivatives of
$h$
vanish in the directions
$\mathfrak{c}\oplus \mathfrak{c}^{\vee }$
. Thus, the calculation of the Poisson bracket is reduced to
$$\begin{eqnarray}\displaystyle \{h,f\}=\mathop{\sum }_{i=1}^{2\ell }\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x_{i}}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}y_{i}}, & & \displaystyle\end{eqnarray}$$
where the
$x_{i}$
and the
$y_{i}$
run through a basis and the dual basis of
$\mathfrak{g}\mathfrak{c}\oplus \mathfrak{g}\mathfrak{c}^{\vee }$
, respectively. For a general
$m$
, the tangent space
$\mathfrak{g}m\subseteq \mathfrak{g}\mathfrak{c}\oplus \mathfrak{g}\mathfrak{c}^{\vee }$
is a Lagrangian subspace; as it is half-dimensional, it suffices to verify that it is isotropic. Indeed, for any
$A,B\in \mathfrak{g}$
, one has
$$\begin{eqnarray}\displaystyle \{Am,Bm\}=\{Aw+A\unicode[STIX]{x1D711},Bw+B\unicode[STIX]{x1D711}\}=A\unicode[STIX]{x1D711}(Bw)-B\unicode[STIX]{x1D711}(Aw)=\unicode[STIX]{x1D711}([B,A]w)=0, & & \displaystyle\end{eqnarray}$$
since
$\mathfrak{c}^{\vee }$
annihilates
$\mathfrak{g}\mathfrak{c}$
by construction. Let
$x_{1},\ldots ,x_{\ell }$
be a basis of
$\mathfrak{g}m$
and augment it by
$x_{\ell +1},\ldots ,x_{2\ell }$
to form a symplectic basis of
$\mathfrak{g}\mathfrak{c}\oplus \mathfrak{g}\mathfrak{c}^{\vee }$
. Then
$$\begin{eqnarray}\displaystyle \{h,f\}=\mathop{\sum }_{i=1}^{\ell }\biggl(\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x_{i}}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}x_{\ell +i}}-\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}x_{i}}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x_{\ell +i}}\biggr). & & \displaystyle\end{eqnarray}$$
Since both functions
$f$
and
$h$
are constant along
$Gm$
, the partial derivatives
$\unicode[STIX]{x2202}f/\unicode[STIX]{x2202}x_{i}$
and
$\unicode[STIX]{x2202}h/\unicode[STIX]{x2202}x_{i}$
vanish in
$m$
, so that finally
$\{h,f\}(m)=0$
.
For the last statement, it suffices to show that for any two functions
$f,f^{\prime }\in \mathbb{C}[V\oplus V^{\ast }]^{G}$
one has
$$\begin{eqnarray}\{f,f^{\prime }\}|_{\mathfrak{ c}\oplus \mathfrak{c}^{\vee }}=\{f|_{\mathfrak{c}\oplus \mathfrak{c}^{\vee }},f^{\prime }|_{\mathfrak{ c}\oplus \mathfrak{c}^{\vee }}\},\end{eqnarray}$$
where the bracket on the left is that in
$\mathbb{C}[V\oplus V^{\ast }]$
and the bracket on the right is that in
$\mathbb{C}[\mathfrak{c}\oplus \mathfrak{c}^{\vee }]$
. Splitting the sum
$$\begin{eqnarray}\{f,f^{\prime }\}=\mathop{\sum }_{i}\frac{\unicode[STIX]{x2202}f}{\unicode[STIX]{x2202}x_{i}}\frac{\unicode[STIX]{x2202}f^{\prime }}{\unicode[STIX]{x2202}y_{i}}\end{eqnarray}$$
into contributions from
$\mathfrak{c}\oplus \mathfrak{c}^{\vee }$
,
$\mathfrak{g}\mathfrak{c}\oplus \mathfrak{g}\mathfrak{c}^{\vee }$
and
$U\oplus U^{\vee }$
, this amounts to proving that the latter two summands only contribute trivially. But this follows from the same arguments as before: the derivatives of both
$f$
and
$f^{\prime }$
vanish in the directions
$U\oplus U^{\vee }\oplus \mathfrak{g}m$
due to their
$G$
-equivariance.
The bijectivity of
$r$
is obvious from Proposition 3.3 and the definition of
$C_{0}$
.◻
From the two propositions above it follows that the conjecture holds if and only if the following assertions are true.
-
(i) The inclusion
$C_{0}\subseteq \unicode[STIX]{x1D707}^{-1}(0)$
induces an isomorphism
$C_{0}/\!\!/G\rightarrow (V\oplus V^{\ast }/\!\!/\!\!/G)_{\text{red}}$
. This is equivalent to saying that
$r:\mathfrak{c}\oplus \mathfrak{c}^{\vee }/W\rightarrow V\oplus V^{\ast }/\!\!/\!\!/G$
is bijective. -
(ii) The variety
$C_{0}/\!\!/G$
is normal.
Remark 3.6. If
$(G,V)$
is a stable polar representation such that
$\unicode[STIX]{x1D707}^{-1}(0)$
is a normal variety, then the conjecture holds (see Lemma 4.5). However, in general
$\unicode[STIX]{x1D707}^{-1}(0)$
is not even irreducible; see, for instance, [Reference Panyushev and YakimovaPY07, § 4] for examples where
$\unicode[STIX]{x1D707}^{-1}(0)$
has an arbitrarily large number of irreducible components.
4 The structure of the null-fibre of the moment map
As before, let
$V$
denote a representation of a reductive group
$G$
, let
$\unicode[STIX]{x1D70B}:V\rightarrow V/\!\!/G$
be the quotient map, and let
$\unicode[STIX]{x1D707}:V\oplus V^{\ast }\rightarrow \mathfrak{g}^{\ast }$
be the moment map. The aim of this section is to highlight some properties of the null-fibre
$\unicode[STIX]{x1D707}^{-1}(0)$
. Part of this content is directly inspired by [Reference PanyushevPan94].
Consider the linear map
$f:V\times \mathfrak{g}\rightarrow V\times V$
,
$(x,A)\mapsto (x,Ax)$
of trivial vector bundles on
$V$
. For each point
$x\in A$
, one has
$\text{rk}(f(x))=\dim \mathfrak{g}x=\dim Gx$
. A sheet
$S$
of
$V$
is an irreducible component of any of the strata
$\{x\in V\mid \text{rk}(f(x))=r\}$
,
$r\in \mathbb{N}_{0}$
, and one puts
$r_{S}:=\text{rk}(f(x))$
for any
$x\in S$
. The number
$\text{mod}(G,S)=\dim S-r_{S}$
is called the modality of
$S$
. The restriction
$f|_{S}$
of
$f$
to a sheet
$S$
with its reduced subscheme structure has constant rank. Hence its image and its kernel are subbundles of rank
$r_{S}$
and rank
$\dim \mathfrak{g}-r_{S}$
, respectively. Let
$\text{pr}_{1}:\unicode[STIX]{x1D707}^{-1}(0)\rightarrow V$
denote the projection to the first component of
$V\oplus V^{\ast }$
. Then
$$\begin{eqnarray}\text{pr}_{1}^{-1}(S)=\{(x,\unicode[STIX]{x1D711})\in S\times V\mid \unicode[STIX]{x1D711}\bot \mathfrak{g}x=\text{Im}f(x)\}\end{eqnarray}$$
is a subbundle in
$S\times V^{\ast }$
of rank
$\dim V^{\ast }-r_{S}$
. In particular, it is an irreducible locally closed subset of
$\unicode[STIX]{x1D707}^{-1}(0)$
of dimension
$$\begin{eqnarray}\displaystyle \dim \text{pr}_{1}^{-1}(S)=\dim S+\dim V^{\ast }-r_{S}=\dim V+\text{mod}(G,S). & & \displaystyle\end{eqnarray}$$
Clearly,
$\unicode[STIX]{x1D707}^{-1}(0)=\bigcup _{S}\text{pr}_{1}^{-1}(S)$
, and since the set of sheets
$S$
of
$V$
is finite, it follows that
$$\begin{eqnarray}\dim \unicode[STIX]{x1D707}^{-1}(0)=\dim V+\max _{S}\,\text{mod}(G,S).\end{eqnarray}$$
A representation
$(G,V)$
is said to be visible if each fibre of
$\unicode[STIX]{x1D70B}$
has only finitely many orbits. It is well known that it suffices to require that the special fibre
$\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D70B}(0))$
have only finitely many orbits.
Lemma 4.1. If
$V$
is visible, then
$\text{mod}(G,S)=\dim \unicode[STIX]{x1D70B}(S)$
for each sheet
$S$
of
$V$
.
Proof. Visibility of
$V$
implies that the fibres of the restriction
$\unicode[STIX]{x1D70B}|_{S}$
have only finitely many orbits, all of dimension
$r_{S}$
. Hence, all fibres of
$\unicode[STIX]{x1D70B}|_{S}$
have dimension
$r_{S}$
, so that
$\dim S=r_{S}+\dim \unicode[STIX]{x1D70B}(S)$
.◻
Let
$(G,V)$
be a polar representation with Cartan subspace
$\mathfrak{c}$
. The space
$V$
always contains two special sheets, as described below.
Let
$r^{\prime }$
be the maximal dimension of an orbit in
$V$
. By semicontinuity, the set
$S^{\prime }$
of points with
$r^{\prime }$
-dimensional orbits is an open and hence irreducible subset of
$V$
, the open sheet of
$V$
. If follows that
$C^{\prime }:=\overline{\text{pr}_{1}^{-1}(S^{\prime })}$
is an irreducible component of the null-fibre
$\unicode[STIX]{x1D707}^{-1}(0)$
of dimension
$2\dim V-r^{\prime }$
.
On the other hand, let
$r_{0}$
denote the maximal dimension of a closed orbit. Let
$S_{0}$
be a sheet that contains the open subset
$\mathfrak{g}_{\text{reg}}\subseteq \mathfrak{c}$
of regular semisimple elements, i.e. those with
$r_{0}$
-dimensional orbits. Since
$\unicode[STIX]{x1D70B}:\mathfrak{c}_{\text{reg}}\rightarrow V/\!\!/G$
is dominant, so is
$\unicode[STIX]{x1D70B}:S_{0}\rightarrow V/\!\!/G$
. Hence, for a general point
$s\in S_{0}$
there exists a point
$x\in \mathfrak{c}_{\text{reg}}$
with
$\unicode[STIX]{x1D70B}(s)=\unicode[STIX]{x1D70B}(x)$
, where
$\mathfrak{c}_{\text{reg}}$
denotes the dense open subset of
$\mathfrak{c}$
formed by regular elements. The orbit of
$x$
is closed and hence contained in the closure of the orbit of
$s$
. But the two orbits have the same dimension and thus must be equal. This shows that
$G\mathfrak{c}_{\text{reg}}\subseteq S_{0}\subseteq \overline{G\mathfrak{c}}$
. In particular, the sheet
$S_{0}$
is uniquely determined.
In general, we have
$r_{0}\leqslant r^{\prime }$
. A representation
$(G,V)$
is said to be stable if the maximal orbit dimension is attained by orbits of regular semisimple elements, i.e. if
$r_{0}=r^{\prime }$
.
Lemma 4.2. Let
$(G,V)$
be a stable polar representation. Then
$C_{0}$
is an irreducible component of
$\unicode[STIX]{x1D707}^{-1}(0)$
of dimension
$\dim V+\dim \mathfrak{c}$
.
Proof. If
$(G,V)$
is stable, the regular sheet
$S_{0}$
and the open sheet
$S^{\prime }$
coincide. Also, in this case the general fibre of the quotient
$\unicode[STIX]{x1D70B}:V\rightarrow V/\!\!/G$
is closed. Therefore, the modality of the sheet
$S_{0}$
equals
$\dim \mathfrak{c}$
. Hence,
$\overline{\text{pr}_{1}^{-1}(S_{0})}$
is an irreducible component of
$\unicode[STIX]{x1D707}^{-1}(0)$
of dimension
$\dim V+\dim \mathfrak{c}$
. It remains to show that the inclusion
$C_{0}\subseteq \text{pr}_{1}^{-1}(S_{0})$
is an equality. Indeed, if
$V$
is stable, the space
$U$
in the decomposition (4) is trivial according to [Reference Dadok and KacDK85, Corollary 2.5]. Thus,
$G(\mathfrak{c}_{\text{reg}}\times \mathfrak{c}^{\vee })$
is a dense subset of
$\text{pr}^{-1}(S_{0})$
, and
$C_{0}=\overline{\text{pr}^{-1}(S_{0})}$
.◻
Proposition 4.3. Let
$(G,V)$
be a visible polar representation. Then the following properties hold.
-
(i)
$\dim \unicode[STIX]{x1D707}^{-1}(0)=\dim V+\dim \mathfrak{c}$
. -
(ii) The irreducible components of
$\unicode[STIX]{x1D707}^{-1}(0)$
of maximal dimension are in bijection with sheets
$S$
such that
$\unicode[STIX]{x1D70B}(S)\subseteq V/\!\!/G$
is dense. -
(iii) If
$(G,V)$
is stable, then
$C_{0}$
is the only irreducible component of
$\unicode[STIX]{x1D707}^{-1}(0)$
of maximal dimension. -
(iv) If
$(G,V)$
is unstable, then
$\unicode[STIX]{x1D707}^{-1}(0)$
has several irreducible components of maximal dimension.
Proof. The first assertion is a consequence of Panyushev’s results [Reference PanyushevPan94, Theorem 2.3, Corollary 2.5, Theorem 3.1]. Alternatively, it follows from Lemma 4.1 that the modality of each sheet is bounded by
$\dim V/\!\!/G=\dim \mathfrak{c}$
. This bound is attained by
$S_{0}$
. The same argument proves the second assertion.
If in addition
$V$
is stable, then
$S_{0}$
is the only sheet whose image under
$\unicode[STIX]{x1D70B}$
is dense in
$V/\!\!/G$
. If, on the other hand,
$V$
is unstable, then
$S^{\prime }$
and
$S_{0}$
are distinct and dominate
$V/\!\!/G$
, contributing two different irreducible components of maximal dimension
$d$
.◻
Example 4.4. We list a few examples that illustrate the decomposition of the null-fibre into irreducible components.
-
(1) The standard representation of
$\text{Sp}(V)$
on
$V$
is polar with zero-dimensional Cartan subspace. There are only two sheets: the regular sheet
$S_{0}=\{0\}$
and the open sheet
$S_{1}=V\setminus \{0\}$
, each forming a single orbit, so that
$V$
is certainly visible. Both sheets contribute an irreducible component of maximal dimension to
$\unicode[STIX]{x1D707}^{-1}(0)=V\times \{0\}\cup \{0\}\times V^{\ast }$
, and
$C_{0}=\{(0,0)\}$
is their intersection. -
(2) Let
$V=V_{0}\oplus V_{1}\oplus V_{2}$
be a
$\mathbb{Z}/3\mathbb{Z}$
-graded vector space with components of dimensions
$\dim V_{0}=1$
and
$\dim V_{1}=\dim V_{2}=2$
, and consider the corresponding decomposition of the Lie algebra
$\mathfrak{g}\mathfrak{l}(V)=\mathfrak{g}_{0}\oplus \mathfrak{g}_{1}\oplus \mathfrak{g}_{2}$
. Then
$\mathfrak{g}_{0}$
is the Lie algebra of
$G_{0}=\text{GL}(V_{0})\times \text{GL}(V_{1})\times \text{GL}(V_{2})$
, and
$\mathfrak{g}_{1}=\text{Hom}(V_{0},V_{1})\oplus \text{Hom}(V_{1},V_{2})\oplus \text{Hom}(V_{2},V_{0})$
is a visible unstable polar representation of
$G_{0}$
. This is an example of a
$\unicode[STIX]{x1D703}$
-representation to be discussed in § 5. The invariant ring
$\mathbb{C}[\mathfrak{g}_{1}]^{G_{0}}$
is generated by the function
$(a,b,c)\mapsto \text{tr}(abc)$
, and if
$a:V_{0}\rightarrow V_{1}$
,
$b:V_{1}\rightarrow V_{2}$
and
$c:V_{2}\rightarrow V_{0}$
are rank-one maps such that
$\text{tr}(abc)$
is non-zero, then the space spanned by
$(a,b,c)$
is a Cartan subspace. An explicit calculation shows that
$\unicode[STIX]{x1D707}^{-1}(0)$
has eight irreducible components, six of dimension 8 and two of dimension 9. The latter two intersect in
$C_{0}$
, which is of dimension
$8$
. The symplectic reduction
$V\oplus V^{\ast }/\!\!/\!\!/G$
is an
$A_{2}$
-singularity. Since
$\mathfrak{g}_{1}$
can also be seen as a space of representations of a quiver, the results of Crawley-Boevey apply and the normality of
$V\oplus V^{\ast }/\!\!/\!\!/G$
is given by [Reference Crawley-BoeveyCra03, Theorem 1.1]. -
(3) The representation of
$\text{SL}_{3}$
on
$V=\mathbb{C}^{3\times 3}$
is stable and polar but non-visible. The null-fibre of the moment map equals the space of pairs of
$3\times 3$
matrices
$(a,b)$
such that
$ab=\frac{1}{3}\,\text{tr}(ab)I_{3}$
. It is 11-dimensional with two components of dimension 11 and one component
$C_{0}$
of dimension 10. The symplectic reduction
$V\oplus V^{\ast }/\!\!/\!\!/\text{SL}_{3}$
is non-reduced. It has two irreducible components of dimensions 4 and 2, the latter being
$C_{0}/\!\!/\text{SL}_{3}$
, an
$A_{2}$
-surface singularity. In particular, the normality result of [Reference Crawley-BoeveyCra03] no longer holds in the general setting of polar representations.
Lemma 4.5. Let
$(G,V)$
be a stable polar representation. If
$V\oplus V^{\ast }/\!\!/\!\!/G$
is irreducible, then
$C_{0}/\!\!/G=(V\oplus V^{\ast }/\!\!/\!\!/G)_{\text{red}}$
.
Proof. Assume that
$V\,\oplus \,V^{\ast }/\!\!/\!\!/G$
is irreducible. Then there is an irreducible component
$C_{1}\subseteq \unicode[STIX]{x1D707}^{-1}(0)$
dominating the symplectic reduction. Since every fibre of the quotient map
$\unicode[STIX]{x1D70B}$
contains exactly one closed orbit, all closed orbits must be contained in
$C_{1}$
. As closed orbits are dense in
$C_{0}$
, one has
$C_{0}\subseteq C_{1}$
. Since by assumption
$(G,V)$
is stable polar,
$C_{0}$
is itself an irreducible component and hence equals
$C_{1}$
.◻
Example 4.6. Without the stability assumption, the conclusion of the lemma can be wrong as the following example shows:
$(\text{SL}_{3},\mathbb{C}^{3}\oplus \mathbb{C}^{3})$
is a non-visible and unstable polar representation with trivial Cartan subspace. Consequently,
$C_{0}=\{0\}$
. However,
$\unicode[STIX]{x1D707}^{-1}(0)/\!\!/\text{SL}_{3}$
is an irreducible non-reduced surface, and its reduction is an
$A_{1}$
-singularity.
Lemma 4.7. Let
$(G,V)$
be a polar representation with Cartan subspace
$\mathfrak{c}\subseteq V$
and dual Cartan subspace
$\mathfrak{c}^{\vee }\subseteq V^{\ast }$
. If
$(x,y)\in \unicode[STIX]{x1D707}^{-1}(0)$
with semisimple elements
$x\in V$
and
$y\in V^{\ast }$
, then there is an element
$g\in G$
such that
$(gx,gy)\in \mathfrak{c}\oplus \mathfrak{c}^{\vee }$
.
Proof. As
$x$
is semisimple, there is an element
$h\in G$
such that
$hx\in \mathfrak{c}$
. Replacing
$(x,y)$
by
$(hx,hy)$
, we may assume that
$x\in \mathfrak{c}$
. According to the definition of the moment map,
$\unicode[STIX]{x1D707}(x,y)=0$
means that
$y$
is contained in the annihilator of the tangent space
$\mathfrak{g}x$
, which is exactly the dual
$N_{x}^{\ast }$
of the slice representation
$N_{x}$
. As
$y$
is semisimple and since the slice representation has
$\mathfrak{c}$
as a Cartan subspace, there is an element
$g\in G_{x}$
such that
$gy\in \mathfrak{c}^{\vee }$
.◻
5 Recapitulation of
$\unicode[STIX]{x1D703}$
-representations
A particular class of polar representations is formed by the so-called
$\unicode[STIX]{x1D703}$
-representations, as introduced by Vinberg [Reference VinbergVin76]. Let
$G$
be a connected reductive group with Lie algebra
$\mathfrak{g}$
. Let
$\unicode[STIX]{x1D703}$
denote both an automorphism of
$G$
of finite order
$m$
and the induced automorphism of
$\mathfrak{g}$
. After fixing a primitive
$m$
th root of unity
$\unicode[STIX]{x1D709}$
, the action of
$\unicode[STIX]{x1D703}$
gives rise to a
$\mathbb{Z}/m\mathbb{Z}$
-grading
$\mathfrak{g}=\bigoplus _{i\in \mathbb{Z}/m\mathbb{Z}}\mathfrak{g}_{i}$
with components
$\mathfrak{g}_{i}=\text{ker}(\unicode[STIX]{x1D703}-\unicode[STIX]{x1D709}^{i}\,\text{id})$
. Then
$\mathfrak{g}_{0}$
is a reductive Lie algebra, each
$\mathfrak{g}_{i}$
is a
$\mathfrak{g}_{0}$
representation, and
$\mathfrak{g}_{i}$
is dual to
$\mathfrak{g}_{-i}$
via the Killing form. Let
$G_{0}\subseteq G$
be the connected algebraic subgroup with Lie algebra
$\mathfrak{g}_{0}$
. Then
$G_{0}$
is reductive and acts linearly on
$\mathfrak{g}_{1}$
. The representation
$(G_{0},\mathfrak{g}_{1})$
is called the
$\unicode[STIX]{x1D703}$
-representation obtained from the pair
$(\mathfrak{g},\unicode[STIX]{x1D703})$
. These representations are visible and polar but not always stable. A complete list of irreducible
$\unicode[STIX]{x1D703}$
-representations with their main features can be found in the paper [Reference KacKac80] of Kac.
A Cartan subspace
$\mathfrak{c}\subseteq \mathfrak{g}_{1}$
is defined as a maximal abelian subspace consisting of semisimple elements. The subspace
$\mathfrak{c}$
lies in some
$\unicode[STIX]{x1D703}$
-invariant Cartan subalgebra
$\mathfrak{h}$
of
$\mathfrak{g}$
, and the dual Cartan subspace is
$\mathfrak{c}^{\vee }=\mathfrak{h}_{-1}\subseteq \mathfrak{g}_{-1}$
. The dual Cartan subspace can also be described as the space of all semisimple elements in
$\mathfrak{g}_{-1}$
that commute with
$\mathfrak{c}$
. Note that the moment map
$\unicode[STIX]{x1D707}:\mathfrak{g}_{1}\oplus \mathfrak{g}_{-1}\rightarrow \mathfrak{g}_{0}$
is, up to the identification via the Killing form, the ordinary commutator. Hence
$\unicode[STIX]{x1D707}(x,y)=0$
if and only if
$x$
and
$y$
commute.
If
$\mathfrak{g}$
is a reductive algebra and
$x\in \mathfrak{g}$
is any element, the centraliser of
$x$
in
$\mathfrak{g}$
will be denoted by
$\mathfrak{g}^{x}=\{y\in \mathfrak{g}\mid [x,y]=0\}$
.
In [Reference PanyushevPan94, § 3.8, Theorem], Panyushev outlines the proof of the next proposition. However, he assumes the stability of the
$\unicode[STIX]{x1D703}$
-representation without actually using it for the part of the proof relevant to our proposition and he considers the component
$C_{0}$
instead of
$\unicode[STIX]{x1D707}^{-1}(0)$
. Therefore, we have opted to reformulate his theorem in our setting and write out the details.
Proposition 5.1. Let
$(G_{0},\mathfrak{g}_{1})$
be a
$\unicode[STIX]{x1D703}$
-representation with Cartan subspace
$\mathfrak{c}$
and let
$$\begin{eqnarray}C_{0}=\overline{G_{0}(\mathfrak{c}\oplus \mathfrak{c}^{\vee })}.\end{eqnarray}$$
Then
$C_{0}/\!\!/G_{0}=\unicode[STIX]{x1D707}^{-1}(0)_{\text{red}}/\!\!/G_{0}$
.
Proof. For any
$x\in \mathfrak{g}$
, denote by
$x_{s}$
and
$x_{n}$
its semisimple and nilpotent parts, respectively. One can check that
$x_{s},x_{n}\in \mathfrak{g}_{i}$
if
$x\in \mathfrak{g}_{i}$
.
Assume now that
$\unicode[STIX]{x1D707}(x,y)=0$
, i.e. that
$[x,y]=0$
. Then all components
$x_{s}$
,
$x_{n}$
,
$y_{s}$
and
$y_{n}$
mutually commute. According to Lemma 4.7,
$(x_{s},y_{s})\in G_{0}(\mathfrak{c}\times \mathfrak{c}^{\vee })$
. Therefore, in order to prove the proposition, it suffices to show that
$(x_{s},y_{s})\in \overline{G_{0}(x,y)}$
. The Lie subalgebra
$\mathfrak{l}=\mathfrak{g}^{x_{s}}\cap \mathfrak{g}^{y_{s}}$
is reductive by Matsuhima’s criterion, and since
$x_{s}$
and
$y_{s}$
are homogeneous,
$\mathfrak{l}$
is a graded subalgebra,
$\mathfrak{l}=\bigoplus _{i\in \mathbb{Z}/m\mathbb{Z}}\mathfrak{l}_{i}$
. Let
$L_{0}\subseteq G_{0}$
be the connected subgroup of
$G_{0}$
with Lie algebra
$\mathfrak{l}_{0}$
. We claim that
$(0,0)\in \overline{L_{0}(x_{n},y_{n})}$
. The assertion will then follow since
$\overline{L_{0}(x,y)}=(x_{s},y_{s})+\overline{L_{0}(x_{n},y_{n})}$
.
By the graded version of the Jacobson–Morozov theorem [Reference KacKac80, § 2], there exist elements
$h\in \mathfrak{l}_{0}$
and
$y^{\prime }\in \mathfrak{l}_{-1}$
such that
$(x_{n},h,y^{\prime })$
is an
$\mathfrak{s}\mathfrak{l}_{2}$
-triplet. Consider the corresponding weight space decomposition
$$\begin{eqnarray}\mathfrak{l}=\bigoplus _{j\in \mathbb{Z}}\mathfrak{l}_{h}(j),\quad \mathfrak{l}_{h}(j)=\{z\in \mathfrak{l}\mid [h,z]=jz\}\end{eqnarray}$$
and the associated one-parameter subgroup
$\unicode[STIX]{x1D719}:\mathbb{G}_{m}\rightarrow L_{0}$
with
$\unicode[STIX]{x1D719}(t)|_{\mathfrak{l}_{h}(j)}=t^{j}\,\text{id}_{\mathfrak{l}_{h}(j)}$
. Since
$x_{n}\in \mathfrak{l}_{h}(2)$
, we have
$\lim _{t\rightarrow 0}\unicode[STIX]{x1D719}(t).x_{n}=0$
. On the other hand, the centraliser of
$x_{n}$
in
$\mathfrak{l}$
, including
$y_{n}$
, must be contained in
$\bigoplus _{j\geqslant 0}\mathfrak{l}_{h}(j)$
, and so
$\lim _{t\rightarrow 0}\unicode[STIX]{x1D719}(t).y_{n}=:y_{0}$
equals the weight-
$0$
component of
$y_{n}$
. This shows that
$(0,y_{0})\in \overline{L_{0}(x_{n},y_{n})}$
. Finally, since
$y_{n}$
is nilpotent, the same is true for
$y_{0}$
, so that
$(0,0)\in \overline{L_{0}(0,y_{0})}$
.◻
Corollary 5.2. Conjecture 1.1 holds whenever
$(G_{0},\mathfrak{g}_{1})$
has a Cartan subspace of dimension at most
$1$
.
Proof. If
$\dim \mathfrak{c}=0$
, then the symplectic reduction associated to
$(G_{0},\mathfrak{g}_{1})$
is a point. If
$\dim \mathfrak{c}=1$
, then the result follows from Propositions 3.4 and 5.1.◻
Remark 5.3. For visible polar representations, such as all
$\unicode[STIX]{x1D703}$
-representations, having a zero-dimensional Cartan subspace is equivalent to having a finite number of orbits. A list of all irreducible visible representations with a finite number of orbits can be found in the paper [Reference KacKac80, § 3] of Kac.
Remark 5.4. In contrast to the cases of Lie algebras and symmetric Lie algebras, there exist many stable and locally free
$\unicode[STIX]{x1D703}$
-representations with a one-dimensional Cartan subspace. It turns out that
$\unicode[STIX]{x1D707}^{-1}(0)$
is non-normal only in five of these cases. It is remarkable that, except in these five sporadic cases, the null-fibre of the moment map of a stable and locally free
$\unicode[STIX]{x1D703}$
-representation obtained from a simple Lie algebra is always normal. Let us describe these
$\unicode[STIX]{x1D703}$
-representations in terms of their Kac diagrams. Here the number
$m$
is the order of the automorphism
$\unicode[STIX]{x1D703}$
.
-
(i)
$m=9$
,
-
(ii)
$m=14$
,
-
(iii)
$m=24$
,
-
(iv)
$m=20$
,
-
(v)
$m=15$
,
Details on the interpretation of Kac diagrams can be found in the papers of Kac [Reference KacKac90] and Vinberg [Reference VinbergVin76]. Details of the claims made here will be given in a forthcoming paper by the first author.
Example 5.5. All
$\unicode[STIX]{x1D703}$
-representations obtained from automorphisms
$\unicode[STIX]{x1D703}$
of order
$m=2$
are known to be stable. If they are in addition locally free, then they are of maximal rank, i.e.
$\unicode[STIX]{x1D711}(m)\dim \mathfrak{c}=\dim \mathfrak{h}$
, where
$\unicode[STIX]{x1D711}$
denotes Euler’s
$\unicode[STIX]{x1D711}$
-function and
$\mathfrak{h}\subseteq \mathfrak{g}$
is a Cartan subalgebra of
$\mathfrak{g}$
. Thus, for
$m=2$
, maximality of rank is equivalent to the existence of a Cartan subalgebra
$\mathfrak{h}$
that is completely contained in
$\mathfrak{g}_{1}$
; see [Reference VinbergVin76, § 3.1].
An example of a locally free stable
$\unicode[STIX]{x1D703}$
-representation which is not of maximal rank can be obtained as follows: let
$\mathfrak{g}=\mathfrak{s}\mathfrak{l}_{m}$
and let
$\unicode[STIX]{x1D703}$
be conjugation by
$a=\text{diag}(1,\unicode[STIX]{x1D709},\ldots ,\unicode[STIX]{x1D709}^{m-1})$
for some primitive
$m$
th root of unity. Then
$G_{0}\subseteq \text{SL}_{m}$
is the diagonal torus and
$\mathfrak{g}_{1}$
is the span of all elementary matrices
$E_{i,i+1}$
, for
$i=1,\ldots ,m-1$
, and
$E_{m,1}$
. If
$m$
is not prime, then
$(G_{0},\mathfrak{g}_{1})$
is not of maximal rank.
Example 5.6. The motivating example for this paper is the representation
$(\text{SL}_{3},S^{3}\mathbb{C}^{3})$
. This is a stable locally free
$\unicode[STIX]{x1D703}$
-representation for an automorphism of order
$m=3$
on
$\mathfrak{s}\mathfrak{o}_{8}$
. If
$S^{3}\mathbb{C}^{3}$
is viewed as the space of plane cubic curves, a Cartan subspace is provided by the Hesse pencil
$\langle x^{3}+y^{3}+z^{3},xyz\rangle$
. The corresponding Weyl group is the binary tetrahedral group. The quotient
$\mathfrak{c}\oplus \mathfrak{c}^{\vee }/W$
is among the small list of finite symplectic quotients that do admit a symplectic resolution. Explicit resolutions were given in [Reference Lehn, Sorger and BrionLS12].
6 Slices
In the proof of our main theorem we will need an induction argument that is based on the passage from a polar representation
$(G,V)$
to the slice representation
$(G_{x},N)$
of a semisimple element
$x\in \mathfrak{c}$
in the Cartan subspace. The reduction argument splits into two parts: a Luna-type slice theorem for symplectic reductions, and a formal Darboux theorem. We treat the slice theorem first. For the special case of a linear action of the group of units in a semisimple algebra, the theorem is due to Crawley-Boevey [Reference Crawley-BoeveyCra03, § 4]; the general case is due to Jung [Reference JungJun09]. As Jung’s paper is unpublished, we give a simplified proof as follows.
Let
$(X,\unicode[STIX]{x1D714})$
be a smooth affine symplectic variety with a Hamiltonian action by a reductive group
$G$
, i.e. an action that preserves the symplectic structure and admits a moment map
$\unicode[STIX]{x1D707}:X\rightarrow \mathfrak{g}^{\ast }$
. Let
$x\in \unicode[STIX]{x1D707}^{-1}(0)$
be a point with closed orbit and therefore reductive stabiliser subgroup
$H=G_{x}$
. The defining property of the moment map,
$d\unicode[STIX]{x1D707}_{x}(\unicode[STIX]{x1D709})(A)=\unicode[STIX]{x1D714}(\unicode[STIX]{x1D709},Ax)$
for all
$A\in \mathfrak{g}$
and
$\unicode[STIX]{x1D709}\in T_{x}X$
, directly implies that
$\text{Im}(d\unicode[STIX]{x1D707}_{x})=\mathfrak{h}^{\bot }=(\mathfrak{g}/\mathfrak{h})^{\ast }$
and
$\text{ker}(d\unicode[STIX]{x1D707}_{x})=(\mathfrak{g}x)^{\bot }\subseteq T_{x}X$
.
Choose a
$G$
-equivariant closed embedding
$X\subseteq V$
into a linear representation of
$G$
and
$H$
-equivariant splittings
$V=\mathfrak{g}x\oplus V^{\prime }$
and
$\mathfrak{g}^{\ast }=\mathfrak{h}^{\bot }\oplus \mathfrak{h}^{\ast }$
. The second splitting yields a decomposition
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D707}^{\bot }\oplus \bar{\unicode[STIX]{x1D707}}$
into two components. The fact that
$\text{Im}(d\unicode[STIX]{x1D707}_{x})=\mathfrak{h}^{\bot }$
implies that the component
$\unicode[STIX]{x1D707}^{\bot }:X\rightarrow \mathfrak{h}^{\bot }$
is smooth at
$x$
and hence
$Y:=(\unicode[STIX]{x1D707}^{\bot })^{-1}(0)=\unicode[STIX]{x1D707}^{-1}(\mathfrak{h}^{\ast })$
is smooth at
$x$
of dimension
$\dim _{x}Y=\dim X-\dim \mathfrak{g}x$
. In fact,
$T_{x}Y=\text{ker}(d\unicode[STIX]{x1D707}_{x})$
. Now
$S_{X}:=(x+V^{\prime })\cap X$
and
$S_{Y}:=(x+V^{\prime })\cap Y$
are transverse slices at
$x$
to the orbit of
$x$
in
$X$
and
$Y$
, respectively, and the natural projection
$T_{x}S_{Y}\rightarrow (\mathfrak{g}x)^{\bot }/\mathfrak{g}x$
is an isomorphism. In particular, there is an
$H$
-stable open affine neighbourhood
$U$
of
$x$
in
$S_{Y}$
such that
$U$
is smooth and the restriction of
$\unicode[STIX]{x1D714}$
to
$U$
is symplectic. Moreover, the composite map
$\unicode[STIX]{x1D707}^{\prime }:S_{Y}\rightarrow X\xrightarrow[{}]{\;\unicode[STIX]{x1D707}\;}\mathfrak{g}^{\ast }\rightarrow \mathfrak{h}^{\ast }$
is a moment map for the action of
$H$
on
$S_{Y}$
. By construction,
$\unicode[STIX]{x1D707}^{-1}(0)\cap S_{X}={\unicode[STIX]{x1D707}^{\prime }}^{-1}(0)$
. Hence, the inclusion induces a natural morphism
$$\begin{eqnarray}U/\!\!/\!\!/H\subseteq (\unicode[STIX]{x1D707}^{-1}(0)\cap S_{X})/\!\!/H\rightarrow \unicode[STIX]{x1D707}^{-1}(0)/\!\!/G=X/\!\!/\!\!/G,\end{eqnarray}$$
and Luna’s slice theorem implies the following result.
Theorem 6.1 (Symplectic slice theorem).
The morphism
$U/\!\!/\!\!/H\rightarrow X/\!\!/\!\!/G$
is étale at
$[x]$
.
It remains to compare the symplectic reductions of
$U$
and its tangent space
$T_{x}U=\mathfrak{g}x^{\bot }/\mathfrak{g}x$
at
$x$
, endowed with the linearised action of
$H$
.
Let
$\mathfrak{m}\subseteq \widehat{{\mathcal{O}}}_{S_{Y},x}$
denote the maximal ideal of the completion of the local ring of
$S_{Y}$
at
$x$
. Any choice of regular parameters
$\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n}\in \mathfrak{m}$
induces an isomorphism
$u:\widehat{{\mathcal{O}}}_{\mathfrak{g}x^{\bot }/\mathfrak{g}x,0}\rightarrow R$
that is characterised by
$z_{i}=(\unicode[STIX]{x1D709}_{i}\,\text{mod}\,\mathfrak{m}^{2})\mapsto \unicode[STIX]{x1D709}_{i}$
,
$i=1,\ldots ,n$
. Let
$\unicode[STIX]{x1D714}$
denote the symplectic form on
$S_{Y}$
and
$\unicode[STIX]{x1D714}^{(0)}$
its value at
$x$
, i.e. the corresponding constant symplectic form on
$T_{x}S_{Y}$
.
Theorem 6.2 (Formal Darboux theorem).
There exist regular parameters
$\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n}\in \widehat{{\mathcal{O}}}_{S_{Y},x}$
,
$n=\dim _{x}S_{Y}$
, such that the induced isomorphism
$u:\widehat{{\mathcal{O}}}_{\mathfrak{g}x^{\bot }/\mathfrak{g}x,0}\rightarrow \widehat{{\mathcal{O}}}_{S_{Y},x}$
satisfies
$u^{\ast }\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}^{(0)}$
.
Proof. Let
$z_{1},\ldots ,z_{n}\in \mathfrak{m}$
be any set of regular parameters. Since
$\unicode[STIX]{x1D714}$
is closed, the Poincaré lemma allows one to find
$1$
-forms
$\unicode[STIX]{x1D713}^{(m)}$
,
$m\geqslant 2$
, with homogeneous coefficients of degree
$m$
, such that
$\unicode[STIX]{x1D714}$
may be written as
$$\begin{eqnarray}\unicode[STIX]{x1D714}=\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}dz_{\unicode[STIX]{x1D6FC}}\wedge dz_{\unicode[STIX]{x1D6FD}}+d\unicode[STIX]{x1D713}^{(2)}+d\unicode[STIX]{x1D713}^{(3)}+\cdots\end{eqnarray}$$
for some non-degenerate skew-symmetric matrix
$\unicode[STIX]{x1D6FA}$
. We need to find power series
$$\begin{eqnarray}\unicode[STIX]{x1D709}_{i}:=z_{i}+\mathop{\sum }_{m\geqslant 2}\unicode[STIX]{x1D709}_{i}^{(m)},\end{eqnarray}$$
where each
$\unicode[STIX]{x1D709}_{i}^{(m)}$
is a homogeneous polynomial in
$z_{1},\ldots ,z_{n}$
of degree
$m$
, such that
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}=\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}d\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FC}}\wedge d\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}. & & \displaystyle\end{eqnarray}$$
This equation is certainly satisfied if the
$\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}^{(m)}$
satisfy the relations
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D713}^{(m)}-\mathop{\sum }_{i=1}^{m-2}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FC}}^{(m-i)}d\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}^{(i+1)}=2\mathop{\sum }_{p,q}\unicode[STIX]{x1D6FA}_{pq}\unicode[STIX]{x1D709}_{p}^{(m)}dz_{q} & & \displaystyle\end{eqnarray}$$
for
$m\geqslant 2$
. Let
$\unicode[STIX]{x1D704}_{\unicode[STIX]{x2202}_{q}}$
denote the partial evaluation along the vector field
$\unicode[STIX]{x2202}_{q}$
satisfying
$\unicode[STIX]{x2202}_{q}(z_{p})=\unicode[STIX]{x1D6FF}_{pq}$
. Then (14) may be recast into the form
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D709}_{p}^{(m)}=\frac{1}{2}\mathop{\sum }_{q}\unicode[STIX]{x1D6FA}_{pq}^{-1}\unicode[STIX]{x1D704}_{\unicode[STIX]{x2202}_{q}}\biggl(\unicode[STIX]{x1D713}^{(m)}-\mathop{\sum }_{i=1}^{m-2}\mathop{\sum }_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FC}}^{(m-i)}d\unicode[STIX]{x1D709}_{\unicode[STIX]{x1D6FD}}^{(i+1)}\biggr), & & \displaystyle\end{eqnarray}$$
which provides a means of computing the
$\unicode[STIX]{x1D709}^{(m)}$
,
$m\geqslant 2$
, recursively.◻
Lemma 6.3. Let
$(G,V)$
be a representation of a reductive algebraic group, let
$w\in V$
be a semisimple element, and let
$(G_{w},N)$
denote the slice representation associated to
$w$
. If
$(G,V)$
satisfies any of the properties of being:
-
(i) visible;
-
(ii) locally free; or
-
(iii) stable;
then the same property holds for
$(G_{w},N)$
.
Note that slice representations are defined for an arbitrary representation thanks to [Reference Popov and VinbergPV94, § 6.5] and that these coincide with slice representations of [Reference Dadok and KacDK85, § 2].
Proof. (i) This is contained in the Encyclopaedia article [Reference Popov and VinbergPV94, Theorem 8.2] by Popov and Vinberg.
(ii) The image of the differential of the morphism
$\unicode[STIX]{x1D6FE}:G\times N\rightarrow V$
,
$(g,n)\mapsto gn$
at
$(e,w)$
equals
$\mathfrak{g}.w+N=V$
. Consequently,
$\unicode[STIX]{x1D6FE}$
is dominant. Thus, for a general element
$n$
in
$N$
, the stabiliser subgroup in
$G$
is finite, and a fortiori its stabiliser in
$G_{w}$
is finite. Hence
$(G_{w},N)$
is locally free.
(iii) A representation is stable if and only if the set of semisimple elements contains a dense open subset. We deduce the existence of a non-empty (and hence dense) open subset
$U\subseteq N$
consisting of closed orbits for the
$G_{w}$
action from Luna’s fundamental lemma [Reference LunaLun73, II.2] and [Reference LunaLun73, I.3 Lemme].◻
Remark 6.4. We will not use this fact in the following, but it is worth noting that if the morphism
$r:\mathfrak{c}\oplus \mathfrak{c}^{\ast }/W\rightarrow (V\oplus V^{\ast }/\!\!/\!\!/G)_{\text{red}}$
is bijective, then so is the induced morphism
$\mathfrak{c}\oplus \mathfrak{c}^{\ast }/W_{w}\rightarrow (N\oplus N^{\ast }/\!\!/\!\!/G_{w})_{\text{red}}$
, where
$W_{w}=N_{G_{w}}(\mathfrak{c})/Z_{G_{w}}(\mathfrak{c})$
.
Proposition 6.5. Let
$(G,V)$
be a polar representation with Cartan subspace
$\mathfrak{c}$
. Let
$N$
denote a
$G_{x}$
-stable complement to
$\mathfrak{g}x$
for a point
$x\in \mathfrak{c}$
. Then
$\widehat{{\mathcal{O}}}_{N\oplus N^{\ast }/\!\!/\!\!/G_{x},[0,0]}\cong \widehat{{\mathcal{O}}}_{V\oplus V^{\ast }/\!\!/\!\!/G,[(x,0)]}.$
Proof. The stabiliser of the point
$(x,0)\in V\oplus V^{\ast }$
is
$G_{x}$
, and
$N\oplus V^{\ast }$
is a
$G_{x}$
-stable slice to the orbit. The annihilator of
$\mathfrak{g}x$
with respect to the symplectic structure is
$(\mathfrak{g}x)^{\bot }=\mathfrak{g}x\oplus N^{\ast }$
, so that
$(N\oplus V^{\ast })\cap (\mathfrak{g}x)^{\bot }=N\oplus N^{\ast }$
. Hence, the assertion follows from the symplectic slice theorem and the formal Darboux theorem.◻
7 Proof of Theorem 1.2
We will now prove Theorem 1.2 from the introduction. Let
$(G,V)$
denote a stable locally free and visible polar representation.
Panyushev [Reference PanyushevPan94, Theorem 3.2] showed that for locally free, stable, visible polar representations the null-fibre
$\unicode[STIX]{x1D707}^{-1}(0)$
is a reduced and irreducible complete intersection of expected dimension
$2\dim V-\dim G=\dim V+\dim \mathfrak{c}$
. In particular, the symplectic reduction is a variety, i.e. reduced and irreducible. According to Propositions 3.3 and 3.5 and Lemma 4.5, the morphism
$r:\mathfrak{c}\oplus \mathfrak{c}^{\vee }/W\rightarrow V\oplus V^{\ast }/\!\!/\!\!/G$
is the normalisation of the symplectic reduction. Hence, showing that
$r$
is an isomorphism is equivalent to proving that
$V\oplus V^{\ast }/\!\!/\!\!/G$
is normal. (Unfortunately, it is not true in general that the null-fibre itself is normal; see Remark 5.4.)
We will argue by induction on the rank
$$\begin{eqnarray}\text{rk}(G,V)=\dim \mathfrak{c}-\dim (\mathfrak{c}\cap V^{G}).\end{eqnarray}$$
Because of the stability assumption,
$\text{rk}(G,V)=0$
is equivalent to
$V$
being a trivial representation. Note that we can in fact always assume that
$V$
contains no trivial summand; for otherwise we may decompose
$V$
as
$V=\mathbb{C}^{\ell }\oplus V_{0}$
with a representation
$V_{0}$
that is again stable, locally free, visible and polar. Clearly, the corresponding Cartan subspaces are related by
$\mathfrak{c}=\mathbb{C}^{\ell }\oplus \mathfrak{c}_{0}$
, and the symplectic reductions by
$V\oplus V^{\ast }/\!\!/\!\!/G=\mathbb{C}^{2\ell }\times (V_{0}\oplus V_{0}^{\ast })/\!\!/\!\!/G$
.
If
$\text{rk}(G,V)=1$
, the assertion follows from Proposition 3.4.
Assume now that
$\text{rk}(G,V)\geqslant 2$
, that
$V$
contains no trivial summand, and that the assertion has been proved for all stable, locally free, visible polar representations of lower rank.
Let
$(G_{w},N)$
denote the slice representation for some point
$w\in \mathfrak{c}\setminus \{0\}$
. According to Lemma 6.3, the slice representation is again visible, locally free and stable. Since
$w\in \mathfrak{c}\cap N^{G_{w}}$
, one has
$$\begin{eqnarray}\text{rk}(G_{w},N)=\dim \mathfrak{c}-\dim (\mathfrak{c}\cap N^{G_{w}})<\dim \mathfrak{c}=\text{rk}(G,V).\end{eqnarray}$$
By our induction hypothesis,
$N\oplus N^{\ast }/\!\!/\!\!/G_{w}$
is normal. By Zariski’s theorem [Reference Zariski and SamuelZS58, Vol. II, p. 320], the completion of the local ring
${\mathcal{O}}_{N\oplus N^{\ast }/\!\!/\!\!/G_{w},[0,0]}$
is normal. By Proposition 6.5, the completion of
${\mathcal{O}}_{V\oplus V^{\ast }/\!\!/\!\!/G,[w,0]}$
is normal. Hence, the symplectic reduction is normal in a neighbourhood
$B$
of the image of
$(\mathfrak{c}\setminus \{0\})\times \{0\}$
and, for symmetry reasons, also in a neighbourhood
$B^{\prime }$
of the image of
$\{0\}\times (\mathfrak{c}^{\vee }\setminus \{0\})$
.
Consider the action of
$\mathbb{C}^{\ast }\times \mathbb{C}^{\ast }$
on
$V\,\oplus \,V^{\ast }$
given by
$(t_{1},t_{2})\cdot (x,\unicode[STIX]{x1D711})=(t_{1}x,t_{2}\unicode[STIX]{x1D711})$
. It commutes with the
$G$
-action and preserves the null-fibre. Therefore, it descends to an action on the symplectic reduction. Clearly, the orbit of any point other than the origin in the symplectic reduction meets
$B$
or
$B^{\prime }$
. This implies that
$(V\oplus V^{\ast }/\!\!/\!\!/G)\setminus \{[0,0]\}$
is normal.
Since the rank of
$(G,V)$
is at least
$2$
, the codimension of the origin in the symplectic reduction is at least
$4$
, so the symplectic reduction is regular in codimension 1. Using Serre’s criterion for normality, it suffices to show that the symplectic reduction satisfies condition
$(S_{2})$
. According to a theorem of Crawley-Boevey [Reference Crawley-BoeveyCra03, Theorem 7.1], it suffices to verify the following assumptions in order to conclude that
$V\,\oplus \,V^{\ast }/\!\!/\!\!/G$
has property
$(S_{2})$
: (i)
$\unicode[STIX]{x1D707}^{-1}(0)$
has property
$(S_{2})$
; (ii)
$(V\oplus V^{\ast }/\!\!/\!\!/G)\setminus \{0\}$
has property
$(S_{2})$
; (iii)
$Z:=q^{-1}(0)\cap \unicode[STIX]{x1D707}^{-1}(0)$
has codimension at least
$2$
in
$\unicode[STIX]{x1D707}^{-1}(0)$
, where
$q:V\oplus V^{\ast }\rightarrow V\oplus V^{\ast }/\!\!/G$
denotes the quotient map.
As we have already seen that (i) and (ii) hold, it suffices to bound the codimension of
$Z:=q^{-1}(0)\cap \unicode[STIX]{x1D707}^{-1}(0)$
. Any point in
$Z$
is of the form
$(n,\unicode[STIX]{x1D711})$
, where
$n\in V$
is nilpotent, i.e.
$0\in \overline{Gn}$
and
$\unicode[STIX]{x1D711}\in (\mathfrak{g}n)^{\bot }$
. Since
$V$
is visible, there are only finitely many nilpotent orbits
$Gn_{1},\ldots ,Gn_{s}$
in
$V$
, so
$Z\subseteq \bigcup _{i=1}^{s}G.(\{n_{i}\}\times (\mathfrak{g}n_{i})^{\bot })$
and
$\dim Z\leqslant \max \{\dim \mathfrak{g}n_{i}+(\dim V-\dim \mathfrak{g}n_{i})\}=\dim V$
. As
$\dim \unicode[STIX]{x1D707}^{-1}(0)=\dim V+\dim \mathfrak{c}\geqslant \dim V+2$
, the theorem is proved.
Remark 7.1. The proof above can be adapted to show that for a visible polar representation
$(G,V)$
, if the morphism
$r:\mathfrak{c}\oplus \mathfrak{c}^{\ast }/W\rightarrow (V\oplus V^{\ast }/\!\!/\!\!/G)_{\text{red}}$
is bijective, then
$(V\oplus V^{\ast }/\!\!/\!\!/G)_{\text{red}}$
is smooth in codimension
$1$
. In particular, by Proposition 5.1, the conjecture holds for an arbitrary
$\unicode[STIX]{x1D703}$
-representation if and only if
$(V\oplus V^{\ast }/\!\!/\!\!/G)_{\text{red}}$
satisfies Serre’s condition
$(S_{2})$
.
8 Examples and counterexamples
We first discuss several cases where the conjecture holds but which are not covered by general results. The tools are representation theory and classical invariant theory.
Example 8.1. The conjecture holds for the representations
$(\text{SL}_{n},S^{2}\mathbb{C}^{n})$
and
$(\text{SL}_{n},\unicode[STIX]{x1D6EC}^{2}\mathbb{C}^{n})$
. These are polar but not
$\unicode[STIX]{x1D703}$
-representations. The cases are very similar, and we will give details only for
$(\text{SL}_{n},\unicode[STIX]{x1D6EC}^{2}\mathbb{C}^{n})$
with
$n$
even.
Let
$n=2m$
and identify both
$V=\unicode[STIX]{x1D6EC}^{2}\mathbb{C}^{n}$
and its dual
$V^{\ast }$
with the space of skew-symmetric matrices, so that the action of
$\text{SL}_{n}$
on
$V\,\oplus \,V^{\ast }$
is given by
$g.(A,B)=(gAg^{t},(g^{t})^{-1}Bg^{-1})$
. Through this identification, the moment map becomes
$\unicode[STIX]{x1D707}(A,B)=AB-(1/n)\,\text{tr}(AB)I_{n}$
, so that
$$\begin{eqnarray}\unicode[STIX]{x1D707}^{-1}(0)=\biggl\{(A,B)\biggl|AB=\frac{1}{n}\,\text{tr}(AB)I_{n}\biggr\}.\end{eqnarray}$$
On the other hand, we see from Schwarz’s Table 1a in [Reference SchwarzSch78] that the invariant algebra is generated by the Pfaffians
$X=\text{pf}(A)$
and
$Y=\text{pf}(B)$
and the traces
$Z_{i}=(1/n)\,\text{tr}((AB)^{i})$
for
$1\leqslant i\leqslant m-1$
. In the coordinate ring
$\mathbb{C}[\unicode[STIX]{x1D707}^{-1}(0)]$
of the null-fibre, the restrictions of these invariants satisfy the relations
$Z_{i}=Z_{1}^{i}$
and
$XY=Z_{1}^{m}$
, and no more. It follows that
$V\,\oplus \,V^{\ast }/\!\!/\!\!/\text{SL}_{n}$
is a normal surface singularity of type
$A_{m-1}$
. So the conjecture holds.
Example 8.2. The conjecture holds for the standard representations
$(G_{2},\mathbb{C}^{7})$
and
$(F_{4},\mathbb{C}^{26})$
and the spin representation
$(\text{Spin}_{7},\mathbb{C}^{8})$
. In all cases, the null-fibre of the moment map is non-reduced, but the symplectic reduction is normal. Again, the cases are very similar, and we give details only for the eight-dimensional spin representation
$V$
. As
$V$
has a
$\text{Spin}_{7}$
-invariant non-degenerate quadratic form
$q$
, the representation is self-dual,
$V\cong V^{\ast }$
. According to Schwarz [Reference SchwarzSch07, Theorem 4.3], the invariant algebra
$\mathbb{C}[V\oplus V]^{\text{Spin}_{7}}$
is generated by the invariants
$A(v+v^{\prime })=q(v)$
and
$B(v+v^{\prime })=q(v,v^{\prime })$
, the polarisation of
$v$
, and
$C(v+v^{\prime })=q(v^{\prime })$
. The quadratic part of the coordinate ring
$\mathbb{C}[V\oplus V]$
equals
$S^{2}V\oplus V\otimes V\oplus S^{2}V$
, and the summand
$V\otimes V$
that contains the generators of the ideal
$I$
of the null-fibre
$\unicode[STIX]{x1D707}^{-1}(0)$
further decomposes into
$$\begin{eqnarray}V\otimes V=S^{2}V\oplus \unicode[STIX]{x1D6EC}^{2}V\cong (V_{(0,0,0)}\oplus V_{(0,0,2)})\oplus (V_{(0,1,0)}\oplus V_{(1,0,0)}),\end{eqnarray}$$
where
$V_{(k_{1},k_{2},k_{3})}$
denotes the irreducible representation with highest weight
$k_{1}\unicode[STIX]{x1D71B}_{1}+k_{2}\unicode[STIX]{x1D71B}_{2}+k_{3}\unicode[STIX]{x1D71B}_{3}$
. One can check that
$I$
is in fact generated by
$V_{(0,1,0)}$
, and that
$J^{2}\subseteq I\subsetneq J$
, where
$J$
is the ideal generated by
$V_{(0,1,0)}\oplus V_{(0,0,2)}$
. In particular,
$\unicode[STIX]{x1D707}^{-1}(0)$
is non-reduced. A direct computation with Singular [Reference Decker, Greuel, Pfister and SchönemannDGPS15] or Macaulay2 [Reference Grayson and StillmanGS] shows that
$\mathbb{C}[\unicode[STIX]{x1D707}^{-1}(0)]^{\text{Spin}_{7}}=\mathbb{C}[A,B,C]/(AC-B^{2})$
is a normal ring.
Example 8.3. The conjecture holds for the spin representation
$(\text{Spin}_{9},V=\mathbb{C}^{16})$
. In this example, even the symplectic reduction is non-reduced, but
$(V\oplus V^{\ast }/\!\!/\!\!/\text{Spin}_{9})_{\text{red}}$
is normal. As before,
$V_{(k_{1},k_{2},k_{3},k_{4})}$
will denote the irreducible representation of highest weight
$k_{1}\unicode[STIX]{x1D71B}_{1}+k_{2}\unicode[STIX]{x1D71B}_{2}+k_{3}\unicode[STIX]{x1D71B}_{3}+k_{4}\unicode[STIX]{x1D71B}_{4}$
. In particular, the spin representation is
$V=V_{(0,0,0,1)}$
. As for
$\text{Spin}_{7}$
, there is an invariant quadratic form
$q$
on
$V$
that allows the identification of
$V$
and
$V^{\ast }$
, and whose polarisations provide invariants of bidegree
$(2,0)$
,
$(1,1)$
and
$(0,2)$
in
$\mathbb{C}[V\oplus V]^{\text{Spin}_{9}}$
. It is well known that the null-fibre
$\unicode[STIX]{x1D707}^{-1}(0)$
has two irreducible components (cf. [Reference PanyushevPan04, § 4]). Let
$I\subseteq \mathbb{C}[V\oplus V]$
denote the vanishing ideal of the null-fibre. It is generated by the 36-dimensional summand
$V_{(0,1,0,0)}(\cong \mathfrak{s}\mathfrak{o}_{9})$
in the decomposition
$$\begin{eqnarray}\mathbb{C}[V\oplus V]_{2}\supseteq V\otimes V\cong (V_{(0,0,0,0)}\oplus V_{(0,0,0,2)}\oplus V_{(1,0,0,0)})\oplus (V_{(0,0,1,0)}\oplus V_{0,1,0,0}).\end{eqnarray}$$
Moreover, according to Schwarz [Reference SchwarzSch78, Table 3a], the invariant ring
$\mathbb{C}[V\oplus V]^{\text{Spin}_{9}}$
is generated by the aforementioned invariants
$A$
,
$B$
and
$C$
together with an invariant
$D$
of bidegree
$(2,2)$
. The explicit description of
$D$
is more involved. It arises as the unique invariant quadratic form on
$V_{0,1,0,0}\cong \unicode[STIX]{x1D6EC}^{3}\mathbb{C}^{9}$
.
Using Singular or Macaulay2, one can check that the invariant
$P=AC-B^{2}$
satisfies
$P\not \in I$
but
$P^{2}\in I$
, so that
$V\oplus V^{\ast }/\!\!/\!\!/\text{Spin}_{9}$
is not reduced.
From Tevelev’s theorem [Reference TevelevTev00] we already know that the conjecture holds for the spin representation of
$\text{Spin}_{9}$
, since it can be realized as the isotropy representation of the symmetric space
$F_{4}/\text{Spin}_{9}$
, i.e. a
$\unicode[STIX]{x1D703}$
-representation of order
$m=2$
. Explicitly, this can be seen as follows. First, one verifies (for instance by using the software LiE [Reference van Leeuwen, Cohen and LisservLCL92]) that
$V\otimes V\otimes V_{(0,1,0,0)}$
contains a unique copy of the trivial representation, and thus the bidegree-
$(2,2)$
component
$I_{(2,2)}$
of the ideal
$I$
contains at most one invariant. Using Macaulay2, one computes the rank of the multiplication map
$\unicode[STIX]{x1D705}:I_{(1,1)}\otimes I_{(1,1)}\rightarrow I_{(2,2)}$
to be 666. The only dimension match for a submodule in
$V\otimes V\otimes V_{(0,1,0,0)}$
is
$\text{Im}(\unicode[STIX]{x1D705})=V_{(0,0,0,0)}\oplus V_{(0,0,0,2)}\oplus V_{(0,2,0,0)}\oplus V_{(2,0,0,0)}$
. In particular,
$I_{(2,2)}^{\text{Spin}_{9}}=\mathbb{C}Q$
for some linear combination
$Q=\unicode[STIX]{x1D6FC}D\,\oplus \,\unicode[STIX]{x1D6FD}AC+\unicode[STIX]{x1D6FE}B^{2}$
with
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in \mathbb{C}$
. A Macaulay2 calculation gives
$I\cap \mathbb{C}[A,B,C]=(A,B,C)(AC-B^{2})$
. Hence, the coefficient
$\unicode[STIX]{x1D6FC}$
must be non-zero. It follows that
$I^{\text{Spin}_{9}}=(Q,A(AC-B^{2}),B(AC-B^{2}),C(AC-B^{2}))$
and
$\sqrt{I^{\text{Spin}_{9}}}=(Q,AC-B^{2})$
, whence
$$\begin{eqnarray}\mathbb{C}[\unicode[STIX]{x1D707}^{-1}(0)_{\text{red}}]^{\text{Spin}_{9}}=\mathbb{C}[A,B,C,D]/(Q,AC-B^{2})=\mathbb{C}[A,B,C]/(AC-B^{2}),\end{eqnarray}$$
a normal ring.
Remark 8.4. One of the features of the representation
$\text{Spin}_{9}$
is that
$\unicode[STIX]{x1D707}^{-1}(0)$
is reducible. Hence, one might ask whether for every isotropy representation
$(G,V)$
of a symmetric space whose commuting scheme
$\unicode[STIX]{x1D707}^{-1}(0)$
is reducible we always have that
$V\oplus V^{\ast }/\!\!/\!\!/G$
is non-reduced. The answer is actually negative. For instance, if
$$\begin{eqnarray}(G,V)=(\text{GL}(V_{1})\times \text{GL}(V_{2}),\,\text{Hom}(V_{1},V_{2})\times \text{Hom}(V_{2},V_{1}))\end{eqnarray}$$
with
$\dim V_{1}=1<\dim V_{2}$
, then
$(G,V)$
is the isotropy representation of a symmetric space [Reference Panyushev and YakimovaPY07, Example 4.3],
$\unicode[STIX]{x1D707}^{-1}(0)$
is reduced and has three irreducible components [Reference TerpereauTer12, § 2.2.1], and
$V\oplus V^{\ast }/\!\!/\!\!/G$
is a normal variety [Reference TerpereauTer12, § 2.2.2].
The following proposition indicates that the visibility assumption in Conjecture 1.1 should not be dropped.
Proposition 8.5. Let
$(G,V)$
be a polar representation of a reductive algebraic group
$G$
such that
$V$
contains a non-trivial representation
$E$
with multiplicity greater than or equal to
$2$
. Then
$V$
is non-visible and
$\mathfrak{c}\oplus \mathfrak{c}^{\vee }/W$
maps to a proper closed subset of
$(V\oplus V^{\ast }/\!\!/\!\!/G)_{\text{red}}$
.
Proof. Consider a decomposition
$V=E\oplus E\oplus V^{\prime }$
. Since
$E$
is a non-trivial representation, the general fibre, and hence every fibre, of the quotient map
$E\rightarrow E/\!\!/G$
has positive dimension. In particular, there exists a nilpotent element
$y\in E\setminus \{0\}$
, i.e. an element with
$0\in \overline{Gy}$
. For different values of
$t\in \mathbb{C}$
, the pairs
$(y,ty)$
belong to different nilpotent
$G$
-orbits in
$E\,\oplus \,E$
. Thus, the number of orbits in the null-fibre of
$V\rightarrow V/\!\!/G$
is infinite, and
$V$
is not visible.
By the Hilbert–Mumford criterion [Reference Mumford and FogartyMF82, ch. 2, § 1], there exists a one-parameter subgroup
$\unicode[STIX]{x1D706}:\mathbb{G}_{m}\rightarrow G$
such that
$\lim _{t\rightarrow 0}\unicode[STIX]{x1D706}(t)y=0$
. If
$E=\bigoplus _{n\in \mathbb{Z}}E_{\unicode[STIX]{x1D706}}(n)$
and
$E^{\ast }=\bigoplus _{n\in \mathbb{Z}}E_{\unicode[STIX]{x1D706}}(n)^{\ast }$
are the associated weight space decompositions of
$E$
and
$E^{\ast }$
, one has
$y\in \bigoplus _{n>0}E_{\unicode[STIX]{x1D706}}(n)$
. We may choose
$\unicode[STIX]{x1D713}\in \bigoplus _{n>0}E_{\unicode[STIX]{x1D706}}^{\ast }(n)$
with
$\unicode[STIX]{x1D713}(y)\neq 0$
. Then
$\unicode[STIX]{x1D713}$
is nilpotent as well. Consider the elements
$w=(y,y,0)\in V$
and
$\unicode[STIX]{x1D711}=(\unicode[STIX]{x1D713},-\unicode[STIX]{x1D713},0)\in V^{\ast }$
. By construction,
$w+\unicode[STIX]{x1D711}\in \unicode[STIX]{x1D707}^{-1}(0)$
. The invariant
$V\oplus V^{\ast }\ni (a,b,c)+(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})\mapsto \unicode[STIX]{x1D6FC}(a)$
takes the non-zero value
$\unicode[STIX]{x1D713}(y)$
at the point
$w+\unicode[STIX]{x1D711}$
, so that
$w+\unicode[STIX]{x1D711}$
cannot be nilpotent. Let
$w^{\prime }+\unicode[STIX]{x1D711}^{\prime }$
be a representative of the closed orbit in
$\overline{G(w+\unicode[STIX]{x1D711})}$
. Then
$w^{\prime }$
and
$\unicode[STIX]{x1D711}^{\prime }$
must have the forms
$w^{\prime }=(y^{\prime },y^{\prime },0)$
and
$\unicode[STIX]{x1D711}^{\prime }=(\unicode[STIX]{x1D713}^{\prime },\unicode[STIX]{x1D713}^{\prime },0)$
with nilpotent elements
$y^{\prime }$
and
$\unicode[STIX]{x1D713}^{\prime }$
satisfying
$\unicode[STIX]{x1D713}^{\prime }(y^{\prime })=\unicode[STIX]{x1D713}(y)\neq 0$
. In particular, the orbit
$w^{\prime }+\unicode[STIX]{x1D711}^{\prime }$
does not meet
$\mathfrak{c}\,\oplus \,\mathfrak{c}^{\vee }$
. Hence
$C_{0}/\!\!/G$
is a proper closed subset of the symplectic reduction.◻
Example 8.6. Here we construct a family of examples of visible stable locally free polar representations which are not
$\unicode[STIX]{x1D703}$
-representations.
Fix
$n\geqslant 1$
. Take an
$n$
-dimensional torus
$G=\mathbb{G}_{m}^{n}$
acting on
$V=\mathbb{C}^{n+1}$
with weights
$(a_{1},a_{2},\ldots ,a_{n},-\sum _{i=1}^{n}\,a_{i})$
, where
$a_{1},\ldots ,a_{n}$
are linearly independent. It is easily checked that the representation
$(G,V)$
is visible, stable and locally free. As the invariant ring
$k[V]^{G}$
is generated by a single polynomial (the product of the
$n+1$
coordinate vectors), it is automatically polar (every non-zero semisimple element spans a Cartan space). Using Vinberg’s theory [Reference VinbergVin76], one can check that if
$(G,V)$
is a
$\unicode[STIX]{x1D703}$
-representation, then there is a simple graded Lie algebra
$(\tilde{\mathfrak{g}},\unicode[STIX]{x1D703})$
such that
$G=\tilde{G}_{0}$
and
$V=\tilde{\mathfrak{g}}_{1}$
. From the classification of
$\unicode[STIX]{x1D703}$
-representations by Kac diagrams, one deduces that there are only finitely many possibilities for
$(\tilde{G}_{0},\tilde{\mathfrak{g}}_{1})$
up to isomorphism, but there is certainly an infinite number of weights
$a_{1},\ldots ,a_{n}$
as above. For instance, for
$n=1$
the representation
$(G,V)$
is a
$\unicode[STIX]{x1D703}$
-representation if and only if
$a_{1}=\pm 2$
.
This family of examples provides a hint that the class of polar representations for a general reductive Lie algebra should be much richer than the class of
$\unicode[STIX]{x1D703}$
-representations, and underlines the importance of working in the general context of polar representations.
Example 8.7. Here are several examples of non-visible polar representations to which Proposition 8.5 applies.
-
(i) Let
$(G,V)=(\text{Sp}_{n},\mathbb{C}^{n}\oplus \mathbb{C}^{n})$
with
$n\geqslant 2$
even. Then
$V\oplus V^{\ast }/\!\!/\!\!/G$
is the union of two irreducible normal surfaces
$C_{0}/\!\!/G$
and
$F$
; see [Reference TerpereauTer12, § 3.5] for details. -
(ii) Let
$(G,V)=(\text{SL}_{2},\mathbb{C}^{2}\oplus \mathbb{C}^{2})$
, which is a stable representation with a locally free action. Then one may check that
$\unicode[STIX]{x1D707}^{-1}(0)$
is a five-dimensional complete intersection with two irreducible components (meeting in the four-dimensional singular locus) and that
$V\oplus V^{\ast }/\!\!/\!\!/G$
is the union of two normal surfaces
$C_{0}/\!\!/G$
and
$F$
with a single isolated
$A_{1}$
-singularity each and meeting in the singular point; see [Reference BeckerBec09, § 3] for details. More generally, we can consider
$(G,V)=(\text{SL}_{n},(\mathbb{C}^{n})^{\oplus n})$
, but then the general description of
$\unicode[STIX]{x1D707}^{-1}(0)$
is more involved. -
(iii) Let
$(G,V)=(\text{Spin}_{10},E\oplus E)$
, where
$E$
is the spin representation. Then
$V\oplus V^{\ast }/\!\!/\!\!/G$
is of dimension at least
$4$
while
$C_{0}/\!\!/G$
is of dimension
$2$
.
Remark 8.8. The previous example suggests that a weaker form of the conjecture might be true for arbitrary polar representations provided that we replace
$(V\oplus V^{\ast }/\!\!/\!\!/G)_{\text{red}}$
by
$C_{0}/\!\!/G$
in the statement.
Acknowledgements
We would like to thank Dmitry Kaledin, Peter Littelmann, Dimitri Panyushev, and Christoph Sorger for interesting discussions related to this work. We also thank the referee for useful remarks, in particular for pointing out that some previously made assumptions in Lemma 6.3 were unnecessary. The second author gratefully acknowledges the support of the DFG through the research grants Le 3093/2-1 and Le 3093/3-1. The third author was supported by SFB Transregio 45 ‘Periods, Moduli Spaces and Arithmetic of Algebraic Varieties’. The fourth author is grateful to the Max-Planck-Institut für Mathematik of Bonn for the warm hospitality and support provided during the writing of this paper. Part of the genesis of this paper occurred during the half-semester programme Algebraic Groups and Representations supported by Labex MILYON/ANR-10-LABX-0070.
