3.1. Upper bound on heat transport

We choose $Z=v_z \theta = -\theta \varDelta _2 \phi$ so that $\delta \int Z \,\mathrm {d}V = -\int \{ \varDelta _2 \theta \delta \phi + \varDelta _2 \phi \delta \theta \} \,\mathrm {d}V$. The Euler–Lagrange equations resulting from the variations with respect to $\theta$, $\psi$ and $\phi$ are therefore, respectively

(3.8)\begin{gather} -\varDelta_2 \phi + {\textit{Ra}} \varDelta_2 \mu_1 - 2 \lambda \theta = 0 , \end{gather}

(3.9)\begin{gather}\sqrt{{\textit{Ta}}} \partial_z \varDelta_2 \mu_1 + \nabla^2 \varDelta_2 \mu_2 = 0 , \end{gather}

(3.10)\begin{gather}-\varDelta_2 \theta - \nabla^2 \nabla^2 \varDelta_2 \mu_1 + \sqrt{{\textit{Ta}}} \partial_z \varDelta_2 \mu_2 = 0 . \end{gather}

The last two equations combine to

(3.11)\begin{equation} {\mathcal{D}} \varDelta_2 \mu_1 ={-} \nabla^2 \varDelta_2 \theta. \end{equation}

On the boundaries $z=0$ and $z=1$, we required $\mu _1 = \partial _z^2 \mu _1 = \partial _z \mu _2 = 0$ and we already know that $\phi =\partial _z^2 \phi = \partial _z^4 \phi = \partial _z \psi = \theta = \partial _z^2 \theta = 0$. It follows from (3.10) that $\partial _z^4 \mu _1 = 0$ and from (3.11) that $\partial _z^6 \mu _1 = 0$, and applying $\partial _z^4$ to (3.8) leads to $\partial _z^4 \theta = 0$. One can now go in loops and take two additional derivatives of (3.4), (3.11) and again (3.8) to conclude that all even derivatives of $\theta$, $\phi$ and $\mu _1$ are zero at $z=0$ and $z=1$.

We next eliminate from (3.2), (3.3), (3.8), (3.9), (3.10) all spatially dependent variables except one to obtain

(3.12)\begin{equation} \frac{\lambda}{{\textit{Ra}}} {\mathcal{D}} \nabla^2 \varDelta_2 \theta ={-}\nabla^2 \nabla^2 \varDelta_2 \varDelta_2 \theta. \end{equation}

The eigenfunction compatible with all boundary conditions is of the form

(3.13)\begin{equation} \theta \propto \sin(n {\rm \pi}z) \exp({\mathrm{i}(k_x x + k_y y)}), \quad n=1,2,3 \ldots. \end{equation}

Upon insertion into (3.12) and after the substitutions $k^2=k_x^2+k_y^2=n^2 {\rm \pi}^2 \xi$ and $\tau = {{\textit {Ta}}}/{n^4 {\rm \pi}^4}$ one finds that the eigenvalues have the form

(3.14)\begin{equation} \frac{\lambda}{{\textit{Ra}}} = \frac{1}{n^2{\rm \pi}^2} \frac{(1+\xi)\xi}{(1+\xi)^3+\tau}. \end{equation}

To find $\lambda _1$, the largest of these eigenvalues, we may first optimize the fraction over $\xi$. A necessary condition for a maximum is

(3.15)\begin{equation} (1+\xi)^3 (1-\xi) + \tau (1+2\xi) = 0 . \end{equation}

The largest root of this polynomial will obey $\xi \gg 1$ for $\tau \gg 1$ so that asymptotically, $\xi ^3=2\tau$. Inserting this into the expression for $\lambda /{\textit {Ra}}$ shows that the largest $\lambda$ is realized for $n=1$ so that asymptotically,

(3.16)\begin{equation} \lambda_1 = \frac{1}{3} \left( \frac{4}{{\rm \pi}^2} \right)^{1/3} {\textit{Ra}} {\textit{Ta}}^{{-}1/3}. \end{equation}

This asymptotic expression for $\lambda _1$ also serves as an upper bound for $\lambda _1$ for ${\textit {Ta}}$ not too small. Figure 1(a) plots the largest root of the polynomial in (3.15) as a function of $\tau$. The asymptotic expression ceases to be an upper bound for $\lambda _1$ at Taylor numbers too small to be of practical interest. The situation is similar for the variational problems that follow and we simply agree to be interested in ${\textit {Ta}} \geqslant 130$ only. With this restriction, the bound on the heat advection is

(3.17)\begin{align} \langle v_z \theta \rangle & \leqslant \frac{1}{3} \left( \frac{4}{{\rm \pi}^2} \right)^{1/3} {\textit{Ra}} {\textit{Ta}}^{{-}1/3} \langle \theta^2 \rangle\nonumber\\ & \leqslant \frac{7}{36} \left( \frac{4}{{\rm \pi}^2} \right)^{1/3} {\textit{Ra}} {\textit{Ta}}^{{-}1/3}. \end{align}

Figure 1. The largest root of the polynomials in (3.15) (a), (3.29) (b), (3.34) (c) and (4.18) (d) as a function of $\tau$ together with the asymptotic dependences $(2 \tau )^{1/3}$ (a), $(\tau /2)^{1/3}$ (b), $(\tau /3)^{1/4}$ (c) and $(2 \tau )^{1/3}$ (d) shown with dashed lines.

We may note that we could have obtained the same result from a Fourier technique. If we start from the outset with a mode decomposition of the form

(3.18)\begin{equation} \theta = \sum_{n,k_x,k_y} \hat{\theta}_{n,k_x,k_y} \sin(n {\rm \pi}z) \exp({\mathrm{i}(k_x x + k_y y)}), \end{equation}

and similarly for $\phi$ with coefficients $\hat {\phi }_{n,k_x,k_y}$ and insert the sum into (3.4), we find that the amplitudes are related by

(3.19)\begin{equation} \hat{\phi}_{n,k_x,k_y} = {\textit{Ra}} \frac{n^2{\rm \pi}^2+k^2} {(n^2{\rm \pi}^2+k^2)^3 +{\textit{Ta}} \, n^2{\rm \pi}^2} \hat{\theta}_{n,k_x,k_y}. \end{equation}

The advective heat transport is then given by

(3.20)\begin{align} \langle v_z \theta \rangle &= \sum_{n,k_x,k_y} \frac{1}{2} k^2 (\hat{\phi}_{n,k_x,k_y} \hat{\theta}_{n,k_x,k_y}^* + \hat{\phi}_{n,k_x,k_y}^* \hat{\theta}_{n,k_x,k_y})\nonumber\\ & = \sum_{n,k_x,k_y} {\textit{Ra}} \frac{(n^2{\rm \pi}^2+k^2)k^2} {(n^2{\rm \pi}^2+k^2)^3 +{\textit{Ta}} \, n^2{\rm \pi}^2} \frac{1}{2} |\hat{\theta}_{n,k_x,k_y}|^2, \end{align}

with $\sum _{n,k_x,k_y} \frac {1}{2} |\hat {\theta }_{n,k_x,k_y}|^2 = \frac {7}{12}$. It now is enough to find the mode $n,k_x,k_y$ which optimizes $\langle v_z \theta \rangle$ for the available $\langle \theta ^2 \rangle =7/12$. This optimization is algebraically identical with the optimization of $\lambda$ given by (3.14). The Fourier technique appears to be simpler than the variational problem for the optimization of the heat transport, but the advantage is less clear for the following problems, and the variational formulation promises to be more convenient for other boundary conditions and geometries. That is why we will stick to the variational calculus. However, because of the connection with the mode decomposition, we will not discuss in detail the boundary conditions for $\theta$ and $\phi$ that derive from the Euler–Lagrange equations of the upcoming variational problems and simply assume an eigenfunction with a sinusoidal dependence on $z$.

3.2. Bounds on the kinetic energy

Poloidal and toroidal fields are orthogonal in the sense of $\langle (\boldsymbol {\nabla } \times \boldsymbol {\nabla } \times \phi \hat {\boldsymbol {z}}) \boldsymbol {\cdot } (\boldsymbol {\nabla } \times \psi \hat {\boldsymbol {z}}) \rangle = 0$ so that

(3.21)\begin{equation} \langle |\boldsymbol{v}|^2 \rangle = \langle |\boldsymbol{\nabla} \times \boldsymbol{\nabla} \times \phi \hat{\boldsymbol{z}}|^2 \rangle + \langle |\boldsymbol{\nabla} \times \psi \hat{\boldsymbol{z}}|^2 \rangle. \end{equation}

We note that $\langle \boldsymbol {a} \boldsymbol {\cdot } [(\hat {\boldsymbol {z}} \times \boldsymbol {\nabla }) \times \boldsymbol {b} ] \rangle = \langle \boldsymbol {b} \boldsymbol {\cdot } [(\hat {\boldsymbol {z}} \times \boldsymbol {\nabla }) \times \boldsymbol {a} ] \rangle$ for any two vector fields $\boldsymbol {a}(\boldsymbol {r})$ and $\boldsymbol {b}(\boldsymbol {r})$ satisfying periodic boundary conditions in the horizontal directions and $\boldsymbol {\nabla } \times \boldsymbol {\nabla } \times \phi \hat {\boldsymbol {z}} = (\hat {\boldsymbol {z}} \times \boldsymbol {\nabla }) \times \boldsymbol {\nabla } \phi$. This helps to derive

(3.22)\begin{align} \delta \int |\boldsymbol{\nabla}\times \boldsymbol{\nabla}\times \phi \hat{\boldsymbol{z}}|^2 \,\mathrm{d}V &={-}2 \int \boldsymbol{\nabla}\boldsymbol{\cdot} \left\{ (\hat{\boldsymbol{z}} \times \boldsymbol{\nabla}) \times [ (\hat{\boldsymbol{z}} \times \boldsymbol{\nabla}) \times \boldsymbol{\nabla}\phi ] \right\} \delta \phi \,\mathrm{d}V \nonumber\\ &= 2 \int \left( \nabla^2 \varDelta_2 \phi \right) \delta \phi \,\mathrm{d}V , \end{align}

while

(3.23)\begin{equation} \delta \int |\boldsymbol{\nabla}\times \psi \hat{\boldsymbol{z}}|^2 \,\mathrm{d}V ={-}2 \int \varDelta_2 \psi \delta \psi \,\mathrm{d}V. \end{equation}

The variations of the Lagrangian (3.5) for $Z=|\boldsymbol {v}|^2$ with respect to $\theta$, $\psi$ and $\phi$ yield, respectively,

(3.24)\begin{gather} {\textit{Ra}} \varDelta_2 \mu_1 - 2 \lambda \theta = 0 , \end{gather}

(3.25)\begin{gather}2 \varDelta_2 \psi + \sqrt{{\textit{Ta}}} \partial_z \varDelta_2 \mu_1 + \nabla^2 \varDelta_2\mu_2 = 0 , \end{gather}

(3.26)\begin{gather}2 \nabla^2 \varDelta_2 \phi - \nabla^2 \nabla^2 \varDelta_2 \mu_1 + \sqrt{{\textit{Ta}}} \partial_z \varDelta_2 \mu_2 = 0 . \end{gather}

We again eliminate from (3.2), (3.3), (3.24), (3.25), (3.26) all variables except $\theta$ to find

(3.27)\begin{equation} \frac{\lambda}{{\textit{Ra}}^2} {\mathcal{D}} \theta = \varDelta_2 \theta. \end{equation}

Inserting the eigenfunction $\theta \propto \sin (n {\rm \pi}z) \exp ({\mathrm {i}(k_x x + k_y y)})$ and substituting $k^2=k_x^2+k_y^2=n^2 {\rm \pi}^2 \xi$ and $\tau = {{\textit {Ta}}}/{n^4 {\rm \pi}^4}$ yields

(3.28)\begin{equation} \frac{\lambda}{{\textit{Ra}}^2} = \frac{1}{n^4 {\rm \pi}^4} \frac{\xi}{(1+\xi)^3 + \tau}. \end{equation}

A necessary condition for a maximum in $\xi$ is that $\xi$ satisfies

(3.29)\begin{equation} \tau + (1+\xi)^2 (1-2\xi) = 0, \end{equation}

which for large $\xi$ leads to the solution $\xi ^3=\tau /2$. The maximal eigenvalue $\lambda _2$ is realized for $n=1$ which leads to the asymptotic expression

(3.30)\begin{equation} \lambda_2 = \frac{1}{3 {\rm \pi}} \left( \frac{4}{\rm \pi} \right)^{1/3} {\textit{Ra}}^2 {\textit{Ta}}^{{-}2/3}, \end{equation}

which is also an upper bound for any ${\textit {Ta}}$ of interest (see figure 1b) so that

(3.31)\begin{align} \langle |\boldsymbol{v}|^2 \rangle & \leqslant \frac{1}{3 {\rm \pi}} \left( \frac{4}{\rm \pi} \right)^{1/3} {\textit{Ra}}^2 {\textit{Ta}}^{{-}2/3} \langle \theta^2 \rangle\nonumber\\ & \leqslant \frac{7}{36 {\rm \pi}} \left( \frac{4}{\rm \pi} \right)^{1/3} {\textit{Ra}}^2 {\textit{Ta}}^{{-}2/3}. \end{align}

Another result arises if one bounds $\langle |\boldsymbol {v}|^2 \rangle$ in terms of $\langle |\boldsymbol {\nabla }\theta |^2 \rangle$. To this end, one has to replace in the Lagrangian (3.5) the last term $-\lambda \theta ^2$ by $-\lambda |\boldsymbol {\nabla }\theta |^2$. Since $\delta \int |\boldsymbol {\nabla }\theta |^2 \,\mathrm {d}V = -2 \int \nabla ^2 \theta \delta \theta \,\mathrm {d}V$, the only change to the Euler–Lagrange equations (3.24), (3.25), (3.26) is that $\lambda \theta$ needs to be replaced by $-\lambda \nabla ^2 \theta$, so that the calculation ends with

(3.32)\begin{equation} -\frac{\lambda}{{\textit{Ra}}^2} {\mathcal{D}} \nabla^2 \theta = \varDelta_2 \theta \end{equation}

in place of (3.27). The same ansatz for the eigenfunction and the same substitutions as before now lead to

(3.33)\begin{equation} \frac{\lambda}{{\textit{Ra}}^2} = \frac{1}{n^6 {\rm \pi}^6} \frac{\xi}{(1+\xi) [(1+\xi)^3 + \tau]}. \end{equation}

The necessary condition for a maximum in $\xi$ becomes

(3.34)\begin{equation} \tau + (1-3\xi) (1+\xi)^3 = 0, \end{equation}

which has a root for large $\xi$ at $\xi ^4=\tau /3$, which leads after the selection $n=1$ and with figure 1(c) to

(3.35)\begin{equation} \langle |\boldsymbol{v}|^2 \rangle \leqslant \frac{1}{{\rm \pi}^2} \frac{{\textit{Ra}}^2}{{\textit{Ta}}} \langle |\boldsymbol{\nabla}\theta|^2 \rangle. \end{equation}

The inequalities in the abstract result from (3.31) and (3.35) and $E_{kin}=\langle |\boldsymbol {v}|^2 \rangle / 2$.

3.3. Maximal velocity

This section determines the largest possible velocity in rotating convection at infinite ${\textit {Pr}}$. To this end, we compute the Green's function $\boldsymbol {v}_G(\boldsymbol {r}, \boldsymbol {r}')$ from

(3.36a,b)\begin{equation} \sqrt{{\textit{Ta}}} \hat{\boldsymbol{z}} \times \boldsymbol{v}_G ={-} \boldsymbol{\nabla}p + \nabla^2 \boldsymbol{v}_G +\delta(\boldsymbol{r}-\boldsymbol{r}') \hat{\boldsymbol{z}} , \quad \boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{v}_G = 0, \end{equation}

so that, for any temperature distribution $\theta (\boldsymbol {r})$, the velocity is given by

(3.37)\begin{equation} \boldsymbol{v}(\boldsymbol{r}) = \int \boldsymbol{v}_G(\boldsymbol{r}, \boldsymbol{r}') {\textit{Ra}} \theta(\boldsymbol{r}') \,\mathrm{d}^3 \boldsymbol{r}'. \end{equation}

Because of the maximum principle $|\theta | \leqslant 1$, $|\boldsymbol {v}|$ is bounded by

(3.38)\begin{equation} |\boldsymbol{v}(\boldsymbol{r})| \leqslant {\textit{Ra}} \int |\boldsymbol{v}_G(\boldsymbol{r}, \boldsymbol{r}')| \,\mathrm{d}^3 \boldsymbol{r}'. \end{equation}

We now decompose $\boldsymbol {v}_G$ into poloidal and toroidal scalars

(3.39)\begin{equation} \boldsymbol{v}_G = \boldsymbol{\nabla}\times \boldsymbol{\nabla}\times \phi_G \hat{\boldsymbol{z}} + \boldsymbol{\nabla}\times \psi_G \hat{\boldsymbol{z}}, \end{equation}

and introduce the pair of Fourier transforms with respect to the horizontal coordinates

(3.40)\begin{gather} \phi_G(\boldsymbol{r}, \boldsymbol{r}') = \left( \frac{1}{2{\rm \pi}} \right)^2 \int \int \mathrm{d}k_x \,\mathrm{d}k_y \hat{\phi}_G(k_x,k_y,z,\boldsymbol{r}') \exp({-\mathrm{i}k_x x}) \exp({-\mathrm{i}k_y y}), \end{gather}

(3.41)\begin{gather}\hat{\phi}_G(k_x,k_y,z,\boldsymbol{r}') = \int \int \mathrm{d} x \,\mathrm{d} y \phi_G(\boldsymbol{r}, \boldsymbol{r}') \exp({\mathrm{i}k_x x}) \exp({\mathrm{i}k_y y}), \end{gather}

and similarly for $\psi _G$ and $\hat {\psi }_G$; $\hat {\phi }_G$ and $\hat {\psi }_G$ have to obey

(3.42)\begin{gather} (\partial_z^2 - k^2)^2 \hat{\phi}_G - \sqrt{{\textit{Ta}}} \partial_z \hat{\psi}_G = \delta(z-z') , \end{gather}

(3.43)\begin{gather}\sqrt{{\textit{Ta}}} \partial_z \hat{\phi}_G + (\partial_z^2 - k^2) \hat{\psi}_G = 0, \end{gather}

for a source placed at $\boldsymbol {r}' = (0,0,z')$. The homogeneous equations, valid for $z \neq z'$, are solved by

(3.44)\begin{equation} \left\{ (\partial_z^2 - k^2)^3 + {\textit{Ta}} \partial_z^2 \right\} \hat{\phi}_G = 0. \end{equation}

In both regions, $z < z'$ and $z > z'$, $\hat {\phi }_G$ may be written as a linear combination

(3.45)\begin{equation} \hat{\phi}_G = \sum_{j=1}^6 c_j \mathrm{e}^{\alpha_j z} \end{equation}

with six coefficients $c_j$ and where the $\alpha _j$ are the six roots of the following polynomial in $\alpha$:

(3.46)\begin{equation} (\alpha^2 - k^2)^3 + {\textit{Ta}} \alpha^2 = 0. \end{equation}

Because of (3.43), $\hat {\psi }_G$ is given by

(3.47)\begin{equation} \hat{\psi}_G ={-} \sqrt{{\textit{Ta}}} \sum_{j=1}^6 c_j \frac{\alpha_j}{\alpha_j^2-k^2} \mathrm{e}^{\alpha_j z}. \end{equation}

There are six coefficients $c_j$ for $z< z'$ and another six for $z>z'$ so that 12 conditions are necessary to determine them all. These are the six boundary conditions $\hat {\phi }_G=\partial _z^2 \hat {\phi }_G = \partial _z \hat {\psi }_G = 0$ at $z=0$ and $z=1$ together with six conditions at $z=z'$. If we denote with square brackets the jump of a variable at $z=z'$, (3.42) and (3.43) require that $[\hat {\phi }_G] = [\partial _z \hat {\phi }_G] = [\partial _z^2 \hat {\phi }_G] = [\hat {\psi }_G] = [\partial _z \hat {\psi }_G] = 0$ and $[\partial _z^3 \hat {\phi }_G] = 1$.

Because of the translational and rotational invariance of the system, $\phi _G$ and $\psi _G$ can only depend on $z$, $z'$, and the horizontal distance $s=\sqrt {(x-x')^2+(y-y)^2}$ between the points at $\boldsymbol {r}$ and $\boldsymbol {r}'$. We therefore change the list of arguments to $\phi _G = \phi _G(s,z,z')$ and $\hat {\phi }_G=\hat {\phi }_G(k,z,z')$ and note that for an axisymmetric function

(3.48)\begin{equation} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \mathrm{d}k_x \,\mathrm{d}k_y \exp({-\mathrm{i}(k_x x+k_y y)}) \hat{\phi}_G =2 {\rm \pi}\int_0^{\infty} k \textrm{J}_0(ks) \hat{\phi}_G \,\mathrm{d}k. \end{equation}

The response $\boldsymbol {v}_G$ to a source located at $(0,0,z')$ is then given in cylindrical coordinates $(s,\varphi,z)$ by

(3.49)\begin{gather} v_{Gs}={-} \frac{1}{2{\rm \pi}} \int_0^{\infty} k^2 \textrm{J}_1(ks) \partial_z \hat{\phi}_G(k,z,z') \,\mathrm{d}k , \end{gather}

(3.50)\begin{gather}v_{G \varphi}= \frac{1}{2{\rm \pi}} \int_0^{\infty} k^2 \textrm{J}_1(ks) \hat{\psi}_G(k,z,z')\, \mathrm{d}k , \end{gather}

(3.51)\begin{gather}v_{Gz}= \frac{1}{2{\rm \pi}} \int_0^{\infty} k^3 \textrm{J}_0(ks) \hat{\phi}_G(k,z,z') \,\mathrm{d}k, \end{gather}

with the usual symbols $\textrm {J}_0$ and $\textrm {J}_1$ for Bessel functions of the first kind.

In order to prepare for (3.38) we first consider the height dependent suprema $s_s$, $s_\varphi$, $s_z$ computed as

(3.52)\begin{equation} \begin{pmatrix} s_s \\ s_\varphi \\ s_z \end{pmatrix} (z) = \int_0^\infty \mathrm{d}s 2 {\rm \pi}s \int_0^1 \mathrm{d}z' \begin{pmatrix} |v_{Gs}| \\ |v_{G\varphi}| \\ |v_{Gz}| \end{pmatrix} (s,z,z'). \end{equation}

Several properties of $s_s$, $s_\varphi$, $s_z$ are now deduced from numerical evaluations of $\boldsymbol {v}_G$. Figure 2 shows these functions for an exemplary Ta. All three functions are symmetric about $z=1/2$; $s_s$ and $s_\varphi$ are maximal at $z=0$ while $s_z=0$ there. At the ${\textit {Ta}}$ of figure 2 and all other inspected ${\textit {Ta}}$, the function $\sqrt {s_s^2 + s_\varphi ^2 + s_z^2}$ still is maximal at $z=0$, so that

(3.53)\begin{equation} \frac{1}{{\textit{Ra}}} \| \boldsymbol{v} \|_\infty \leqslant s_s(0)+s_\varphi(0), \end{equation}

where $\| \boldsymbol {v} \|_\infty$ denotes the supremum of $| \boldsymbol {v}|$ taken over the entire volume. In a next step, $s_s(0)$ and $s_\varphi (0)$ are computed for different Ta. The result is shown in figure 3. At large ${\textit {Ta}}$, $s_s(0) \ll s_\varphi (0)$ because $s_s(0)$ asymptotes to $s_s(0)=9 {\textit {Ta}}^{-1/2}$, whereas $s_\varphi (0)$ approaches $s_\varphi (0) = 1.23 {\textit {Ta}}^{-1/3}$. The exponents are familiar from vertical shear layers in rotating flows (Stewartson Reference Stewartson1957). As seen in the figure, these power laws are approached from below so that they can be used as upper bounds. We conclude that

(3.54)\begin{equation} \| \boldsymbol{v} \|_\infty \leqslant 1.23 {\textit{Ra}} {\textit{Ta}}^{{-}1/3}. \end{equation}

Figure 2. Values of $s_s$ (dot dashed), $s_\varphi$ (dotted) and $s_z$ (dashed) as functions of height $z$ for ${\textit {Ta}}=10^6$. The solid line shows $\sqrt {s_s^2 + s_\varphi ^2 + s_z^2}$.

Figure 3. Values of $s_\varphi (0)$ (circles) and $s_s(0)$ (squares) together with the functions $1.23 {\textit {Ta}}^{-1/3}$ (solid) and $9 {\textit {Ta}}^{-1/2}$ (dashed).

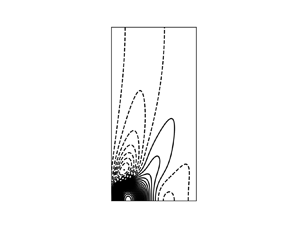
This bound is entirely obtained from numerical evaluation of the Green's function and is not supported by an analytical calculation in an asymptotic limit as the other results in this paper. An analytical treatment of (3.52) is arduous because of the absolute values in the integrand which are essential even at $z=0$. This is due to an interesting point about the structure of $\boldsymbol {v}_G$ shown for an example in figure 4. The source term in (3.42) corresponds to an upward pointing force. The upwelling driven by this force, in conjunction with the boundaries, generates a converging flow below the source and a diverging flow above it. The Coriolis force then gives rise to a cyclonic circulation below the source and an anticyclonic swirl above it. These are indeed the main features observed in figure 4. However, there is also an anticyclonic ring that develops at some distance from the source near $z=0$. This anticyclonic ring weakens as the source moves away from the boundary and is clearly the result of the interaction with the boundary. This ring also causes a change of sign in $v_{G\varphi }$ on $z=0$ as a function of $s$ and makes the absolute value in (3.52) indispensable. Figure 4 plots the product $s v_{G,\varphi }$ rather than $v_{G,\varphi }$ alone to clearly display the change of sign.

Figure 4. Contour plot of the circulation $s v_{G,\varphi }$ (a) and the streamlines of the meridional part of $\boldsymbol {v}_G$, $(v_{G,s},0,v_{G,z})$ (b) in a vertical plane for a source located at height $z=0.1$ on the axis $s=0$ for ${\textit {Ta}}=10^6$. Dashed contour lines indicate anticyclonic circulation.

4.1. The additional constraint

The previous section derived bounds on the heat advection and the kinetic energy of the field $\boldsymbol {v}$ defined by (2.12). These are simultaneously bounds on Nusselt number and total kinetic energy for convection at infinite ${\textit {Pr}}$. At finite ${\textit {Pr}}$, the velocity field is $\boldsymbol {v} + \boldsymbol {u}$. A bound on $\boldsymbol {u}$ is provided by the time average of (2.14)

(4.1)\begin{equation} \langle \overline{ |\boldsymbol{\nabla}\boldsymbol{u}|^2 } \rangle ={-}\frac{1}{{\textit{Pr}}} \langle \overline{ \boldsymbol{u} \boldsymbol{\cdot} \partial_t \boldsymbol{v} } \rangle +\frac{1}{{\textit{Pr}}} \langle \overline{\boldsymbol{v} \boldsymbol{\cdot} \left[ (\boldsymbol{u} + \boldsymbol{v}) \boldsymbol{\cdot} \boldsymbol{\nabla}\right] \boldsymbol{u}} \rangle ,\end{equation}

where $\langle \boldsymbol {u} \boldsymbol {\cdot } [ (\boldsymbol {u} + \boldsymbol {v}) \boldsymbol {\cdot } \boldsymbol {\nabla }] \boldsymbol {v} \rangle =-\langle \boldsymbol {v} \boldsymbol {\cdot } [ (\boldsymbol {u} + \boldsymbol {v}) \boldsymbol {\cdot } \boldsymbol {\nabla }] \boldsymbol {u} \rangle$ was used. One readily bounds the last term from

(4.2)\begin{align} |\langle \overline{\boldsymbol{v} \boldsymbol{\cdot} \left[ (\boldsymbol{u} + \boldsymbol{v}) \boldsymbol{\cdot} \boldsymbol{\nabla}\right] \boldsymbol{u}} \rangle| & \leqslant \left\langle \overline{ \sqrt{\sum_{ij} v_i^2(u_j+v_j)^2} \sqrt{\sum_{ij} (\partial_j u_i)^2} } \right\rangle\nonumber\\ & \leqslant \| \boldsymbol{v} \|_\infty \left\langle \overline{ \sqrt{|\boldsymbol{u} + \boldsymbol{v}|^2} \sqrt{|\boldsymbol{\nabla}\boldsymbol{u}|^2} }\right\rangle\nonumber\\ & \leqslant \| \boldsymbol{v} \|_\infty \sqrt{\langle \overline{|\boldsymbol{u} + \boldsymbol{v}|^2} \rangle } \sqrt{\langle \overline{|\boldsymbol{\nabla}\boldsymbol{u}|^2} \rangle }. \end{align}

The term with the time derivative on the other hand gives rise to another variational problem; $\partial _t \boldsymbol {v}$ has a decomposition in poloidal and toroidal scalars $\tilde {\phi }$ and $\tilde {\psi }$ with $\partial _t \boldsymbol {v} = \boldsymbol {\nabla }\times \boldsymbol {\nabla }\times \tilde {\phi } \hat {\boldsymbol {z}} + \boldsymbol {\nabla }\times \tilde {\psi } \hat {\boldsymbol {z}}$, $\tilde {\phi } = \partial _t \phi$, $\tilde {\psi } = \partial _t \psi$ and $\phi$ and $\psi$ are the scalars for the decomposition of $\boldsymbol {v}$ itself; $\tilde {\phi }$ and $\tilde {\psi }$ obey the same boundary conditions as $\phi$ and $\psi$. The relation

(4.3)\begin{equation} \langle \boldsymbol{u} \boldsymbol{\cdot} \partial_t \boldsymbol{v} \rangle =\langle (\boldsymbol{\nabla}\times \boldsymbol{u}) \boldsymbol{\cdot} (\boldsymbol{\nabla}\times \tilde{\phi} \hat{\boldsymbol{z}} + \tilde{\psi} \hat{\boldsymbol{z}} ) \rangle, \end{equation}

holds if $\boldsymbol {v}$ obeys no-penetration boundary conditions. The transformation

(4.4)\begin{align} \int\boldsymbol{u} \boldsymbol{\cdot} (\boldsymbol{\nabla}\times \boldsymbol{\nabla}\times \tilde{\phi} \hat{\boldsymbol{z}} + \boldsymbol{\nabla}\times \tilde{\psi} \hat{\boldsymbol{z}}) \,\mathrm{d}V &= \int (\boldsymbol{\nabla}\times \boldsymbol{u}) \boldsymbol{\cdot} (\boldsymbol{\nabla}\times \tilde{\phi} \hat{\boldsymbol{z}} + \tilde{\psi} \hat{\boldsymbol{z}} ) \,\mathrm{d}V\nonumber\\ &\quad + \oint \hat{\boldsymbol{n}} \boldsymbol{\cdot} \left[ \boldsymbol{u} \times \begin{pmatrix} \partial_y \tilde{\phi} \\ -\partial_x \tilde{\phi} \\ 0 \end{pmatrix} \right] \mathrm{d}A \!+\! \oint \hat{\boldsymbol{n}} \boldsymbol{\cdot} \left[ \boldsymbol{u} \!\times\! \tilde{\psi} \hat{\boldsymbol{z}} \right] \mathrm{d}A, \end{align}

is independent of boundary conditions; $\hat {\boldsymbol {n}}$ is the outward pointing normal vector to the surface bounding a periodicity volume. The contribution to the boundary integrals from the vertical faces of the periodicity volume cancel because of periodicity; $\hat {\boldsymbol {n}} \propto \hat {\boldsymbol {z}}$ on the remaining faces. The second boundary integral is zero for $\hat {\boldsymbol {n}} \propto \hat {\boldsymbol {z}}$ independently of the behaviour of $\tilde {\psi }$, and the first integral is zero because $\tilde {\phi }=0$ on $z=0$ and $z=1$.

The Schwarz inequality

(4.5)\begin{equation} |\langle \overline{\boldsymbol{u} \boldsymbol{\cdot} \partial_t \boldsymbol{v} } \rangle| \leqslant \sqrt{\langle \overline{|\boldsymbol{\nabla}\times \boldsymbol{u}|^2} \rangle } \sqrt{\langle \overline{|\boldsymbol{\nabla}\times \tilde{\phi} \hat{\boldsymbol{z}}|^2} \rangle +\langle \overline{ \tilde{\psi}^2} \rangle} \end{equation}

motivates us to seek bounds for $\langle |\boldsymbol {\nabla }\times \tilde {\phi } \hat {\boldsymbol {z}}|^2 \rangle$ and $\langle \tilde {\psi }^2 \rangle$. The time variation of $\phi$ and $\psi$ derives from the time dependence of $\theta$. Let us rewrite (2.5) as ${\textit {Ra}} \partial _t \theta = \boldsymbol {\nabla }\boldsymbol {\cdot } \boldsymbol {q}$ with $\boldsymbol {q} = {\textit {Ra}} \boldsymbol {\nabla }\theta -{\textit {Ra}} (\boldsymbol {u} + \boldsymbol {v}) (T-\frac {1}{2})$ and take time derivatives of (3.2) and (3.3) to find

(4.6)\begin{gather} \nabla^2 \nabla^2 \varDelta_2 \tilde{\phi} -\sqrt{{\textit{Ta}}} \partial_z \varDelta_2 \tilde{\psi} = \varDelta_2 \boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{q} , \end{gather}

(4.7)\begin{gather}\nabla^2 \varDelta_2 \tilde{\psi} + \sqrt{{\textit{Ta}}} \partial_z \varDelta_2 \tilde{\phi} = 0 . \end{gather}

Before starting the next variational problem, we first note that the preceding equations may alternatively be written as a direct time derivative of (2.12) as

(4.8)\begin{equation} 0 ={-} \boldsymbol{\nabla}\tilde p_\infty + \nabla^2 \tilde{\boldsymbol{v}} + \hat{\boldsymbol{z}} (\boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{q} ) -\sqrt{{\textit{Ta}}} \hat{\boldsymbol{z}} \times \tilde{\boldsymbol{v}}, \end{equation}

with $\tilde p_\infty = \partial _t p_\infty$ and $\tilde {\boldsymbol {v}} = \partial _t \boldsymbol {v}$. Taking the scalar product of this equation with $\tilde {\boldsymbol {v}}$ and averaging over all space leads to

(4.9)\begin{equation} \langle |\boldsymbol{\nabla}\tilde{\boldsymbol{v}}|^2 \rangle = \langle \tilde{v}_z (\boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{q} ) \rangle ={-} \langle (\boldsymbol{\nabla}\tilde{v}_z) \boldsymbol{\cdot} \boldsymbol{q} \rangle \leqslant \sqrt{\langle |\boldsymbol{\nabla}\tilde{v}_z|^2 \rangle} \sqrt{\langle |\boldsymbol{q}|^2 \rangle} \leqslant \sqrt{\langle |\boldsymbol{\nabla}\tilde{\boldsymbol{v}}|^2 \rangle} \sqrt{\langle |\boldsymbol{q}|^2 \rangle}, \end{equation}

and hence $\langle |\boldsymbol {\nabla }\tilde {\boldsymbol {v}}|^2 \rangle \leqslant \langle |\boldsymbol {q}|^2 \rangle$. Both $\langle |\boldsymbol {\nabla }\times \tilde {\phi } \hat {\boldsymbol {z}}|^2 \rangle$ and $\langle \tilde {\psi }^2 \rangle$ are bounded in terms of $\langle |\boldsymbol {\nabla }\tilde {\boldsymbol {v}}|^2 \rangle$ because of the Poincaré inequality, which means that both quantities are smaller than some finite factor multiplied by $\langle |\boldsymbol {q}|^2 \rangle$. The existence of such finite factors being established, we now proceed to determine ${\textit {Ta}}$ dependent values for these factors from a variational problem.

The source term $\boldsymbol {q}$ obeys $\boldsymbol {\nabla }\boldsymbol {\cdot } {\boldsymbol {q}} =0$ at $z=0$ and $z=1$, which from (4.6) implies $\partial _z^4 \tilde {\phi } =0$ on those boundaries. Taking the second derivative of (2.5) also leads to $\partial _z^2 \boldsymbol {\nabla }\boldsymbol {\cdot } {\boldsymbol {q}}=0$, so that $\boldsymbol {\nabla }\boldsymbol {\cdot } {\boldsymbol {q}}$ obeys the same boundary conditions as $\theta$ and we can set up a variational problem similar to those of the previous sections for maximizing an objective $Z$ subject to (4.6), (4.7) and $\langle |{\boldsymbol {q}}|^2 \rangle$ fixed to any arbitrary value. This leads to a Lagrangian analogous to (3.5):

(4.10)\begin{align} {{\mathcal{L}}} &= \int \left\{ Z - \mu_1(\boldsymbol{r}) \left[ \nabla^2 \nabla^2 \varDelta_2 \tilde{\phi} -\sqrt{{\textit{Ta}}} \partial_z \varDelta_2 \tilde{\psi} -\varDelta_2 \boldsymbol{\nabla}\boldsymbol{\cdot} {\boldsymbol{q}} \right]\right.\nonumber\\ &\quad \left.- \mu_2(\boldsymbol{r}) \left[ \nabla^2 \varDelta_2 \tilde{\psi} + \sqrt{{\textit{Ta}}} \partial_z \varDelta_2 \tilde{\phi} \right]- \lambda |{\boldsymbol{q}}|^2\right\} \mathrm{d}V . \end{align}

The Euler–Lagrange equations again lead to an eigenvalue problem for $\lambda$ and the largest eigenvalue $\lambda _{max}$ provides us with the inequality $\langle Z \rangle \leqslant \lambda _{max} \langle |{\boldsymbol {q}}|^2 \rangle$.

To simplify the algebra, it is convenient to choose $Z=a |\boldsymbol {\nabla }\times \tilde {\phi } \hat {\boldsymbol {z}}|^2 + b \tilde {\psi }^2$ in which we can set the coefficients $a$ and $b$ alternatively to 0 and 1. The variations with respect to ${\boldsymbol {q}}$, $\tilde {\psi }$, and $\tilde {\phi }$, respectively yield,

(4.11)\begin{gather} \boldsymbol{\nabla}\varDelta_2 \mu_1 + 2 \lambda {\boldsymbol{q}} = 0 , \end{gather}

(4.12)\begin{gather}2 b \tilde{\psi} - \sqrt{{\textit{Ta}}} \partial_z \varDelta_2 \mu_1 - \nabla^2 \varDelta_2 \mu_2 = 0 , \end{gather}

(4.13)\begin{gather}-2 a \varDelta_2 \tilde{\phi} - \nabla^2 \nabla^2 \varDelta_2 \mu_1 + \sqrt{{\textit{Ta}}} \partial_z \varDelta_2 \mu_2 = 0, \end{gather}

from which one deduces

(4.14)\begin{equation} \lambda {\mathcal{D}} {\mathcal{D}} \varDelta_2 \tilde{\phi} = a \nabla^2 \nabla^2 \nabla^2 \varDelta_2 \varDelta_2 \tilde{\phi} +b {\textit{Ta}} \partial_z^2 \nabla^2 \varDelta_2 \tilde{\phi}. \end{equation}

Insertion of the sinusoidal eigenfunction and the substitutions $k^2=k_x^2+k_y^2=n^2 {\rm \pi}^2 \xi$ and $\tau = {{\textit {Ta}}}/{n^4 {\rm \pi}^4}$ lead to

(4.15)\begin{equation} \lambda = \frac{1}{n^4 {\rm \pi}^4} \frac{(1+\xi) [b \tau + a\xi(1+\xi)^2]}{[(1+\xi)^3+\tau]^2}. \end{equation}

Let us first select $a=0$ and $b=1$. The necessary condition for the maximizing $\xi$ becomes

(4.16)\begin{equation} \tau [\tau - 5(1+\xi)^3] = 0, \end{equation}

which is solved by $\xi =(\tau /5)^{1/3}-1$ without any asymptotic approximation and from which we can deduce

(4.17)\begin{equation} \langle \tilde{\psi}^2 \rangle \leqslant \frac{5^{5/3}}{36 {\rm \pi}^{4/3}} {\textit{Ta}}^{{-}2/3} \langle |{\boldsymbol{q}}|^2 \rangle. \end{equation}

In the opposite case $a=1$, $b=0$, the necessary condition for the maximizing $\xi$ becomes

(4.18)\begin{equation} (1+\xi)^3 (1-2\xi) + \tau (1+4\xi) = 0, \end{equation}

which requires for $\xi \gg 1$ that $\xi ^3 = 2\tau$. The maximal eigenvalue $\lambda _4$ is realized for $n=1$ and is asymptotically

(4.19)\begin{equation} \lambda_4 = \frac{2}{9} \left(\frac{2}{{\rm \pi}^4} \right)^{1/3} {\textit{Ta}}^{{-}2/3}, \end{equation}

which also constitutes an upper bound for the largest root of (4.18) for reasonably large ${\textit {Ta}}$ (see figure 1d) so that we arrive at

(4.20)\begin{equation} \langle |\boldsymbol{\nabla}\times \tilde{\phi} \hat{\boldsymbol{z}}|^2 \rangle + \langle \tilde{\psi}^2 \rangle \leqslant \left( \frac{5^{5/3}}{36}+\frac{2^{4/3}}{9} \right) \frac{1}{{\rm \pi}^{4/3}} {\textit{Ta}}^{{-}2/3} \langle |{\boldsymbol{q}}|^2 \rangle \lesssim 0.15 {\textit{Ta}}^{{-}2/3} \langle |{\boldsymbol{q}}|^2 \rangle. \end{equation}

With the maximum principle, $\langle |(\boldsymbol {u} + \boldsymbol {v})(T-\frac {1}{2})|^2 \rangle \leqslant \frac {1}{4} \langle |(\boldsymbol {u} + \boldsymbol {v})|^2 \rangle$, and the triangle inequality in the form $\langle |(\boldsymbol {a} + \boldsymbol {b})|^2 \rangle \leqslant 2 \langle |\boldsymbol {a}|^2 \rangle + 2 \langle |\boldsymbol {b}|^2 \rangle$, it follows from the definition of ${\boldsymbol {q}}$ that

(4.21)\begin{equation} \frac{1}{{\textit{Ra}}^2} \langle |{\boldsymbol{q}}|^2 \rangle \leqslant 2 \langle |\boldsymbol{\nabla}\theta|^2 \rangle + \frac{1}{2} \langle |(\boldsymbol{u} + \boldsymbol{v})|^2 \rangle, \end{equation}

and we finally arrive at

(4.22)\begin{equation} |\langle \overline{\boldsymbol{u} \boldsymbol{\cdot} \partial_t \boldsymbol{v} } \rangle| \leqslant \sqrt{\langle \overline{|\boldsymbol{\nabla}\boldsymbol{u}|^2} \rangle } \sqrt{0.15} {\textit{Ra}} {\textit{Ta}}^{{-}1/3} \left( \sqrt{2 \langle \overline{|\boldsymbol{\nabla}\theta|^2} \rangle} + \sqrt{\frac{1}{2} \langle \overline{|(\boldsymbol{u} + \boldsymbol{v})|^2} \rangle} \right), \end{equation}

where $\langle \overline {|\boldsymbol {\nabla }\times \boldsymbol {u}|^2} \rangle = \langle \overline {|\boldsymbol {\nabla }\boldsymbol {u}|^2} \rangle$ was used.

We can now return to (4.1) and insert (4.2), (3.54), (4.22) to find

(4.23)\begin{equation} \left.\begin{gathered} \sqrt{\langle \overline{|\boldsymbol{\nabla}\boldsymbol{u}|^2} \rangle } \leqslant c_1 \sqrt{\langle \overline{|\boldsymbol{\nabla}\theta|^2} \rangle} + c_2 \sqrt{\langle \overline{|(\boldsymbol{u} + \boldsymbol{v})|^2} \rangle} ,\\ c_1 = \sqrt{0.3} \frac{1}{{\textit{Pr}}} {\textit{Ra}} {\textit{Ta}}^{{-}1/3} , \\ c_2 = (\sqrt{0.075}+1.23) \frac{1}{{\textit{Pr}}} {\textit{Ra}} {\textit{Ta}}^{{-}1/3} . \end{gathered}\right\} \end{equation}

With $c_0=\max \{1,{L}/{2} \}$ and the Poincaré inequality $\sqrt {\langle \overline {|(\boldsymbol {u} \!+\! \boldsymbol {v})|^2} \rangle } \!\leqslant\! ({1}/{{\rm \pi} } )c_0 \sqrt {\langle \overline {|\boldsymbol {\nabla }(\boldsymbol {u} \!+\! \boldsymbol {v})|^2} \rangle }$ from (2.15), and (2.10) and (2.11), this can be rewritten as

(4.24)\begin{equation} \sqrt{\langle \overline{|\boldsymbol{\nabla}\boldsymbol{u}|^2} \rangle } \leqslant \left(c_1 + \frac{c_2}{\rm \pi} c_0 {\textit{Ra}}^{1/2} \right)\sqrt{\langle \overline{|\boldsymbol{\nabla}\theta|^2} \rangle}. \end{equation}

4.2. Bound on the Nusselt number

Equations (2.11) and (2.8) lead to

(4.25)\begin{equation} \langle \overline{|\boldsymbol{\nabla}\theta|^2} \rangle = \langle \overline{v_z \theta } \rangle + \langle \overline{u_z \theta } \rangle \leqslant \langle \overline{v_z \theta } \rangle +\sqrt{\frac{7}{12}} \sqrt{\langle \overline{u_z^2} \rangle }, \end{equation}

in which we may insert the Poincaré inequality $\sqrt {\langle \overline {u_z^2} \rangle } \leqslant {1}/{{\rm \pi} } \sqrt {\langle \overline {(\partial _z u_z)^2} \rangle }$ and $\langle (\partial _z u_z)^2 \rangle \leqslant \frac {1}{4} \langle |\boldsymbol {\nabla }\boldsymbol {u}|^2 \rangle$ (Doering & Constantin Reference Doering and Constantin1996) together with (4.24) and (3.17) to find

(4.26)\begin{equation} \langle \overline{|\boldsymbol{\nabla}\theta|^2} \rangle - \frac{1}{2{\rm \pi}} \sqrt{\frac{7}{12}} \left(c_1 + \frac{c_2}{\rm \pi} c_0 {\textit{Ra}}^{1/2} \right)\sqrt{\langle \overline{|\boldsymbol{\nabla}\theta|^2} \rangle} \leqslant \frac{7}{36} \left(\frac{4}{{\rm \pi}^2} \right)^{1/3} {\textit{Ra}} {\textit{Ta}}^{{-}1/3}. \end{equation}

We finally deduce

(4.27)\begin{equation} \left.\begin{gathered} {\textit{Nu}}-1 = \langle \overline{|\boldsymbol{\nabla}\theta|^2} \rangle \leqslant \frac{7}{36} \left(\frac{4}{{\rm \pi}^2} \right)^{1/3} {\textit{Ra}} {\textit{Ta}}^{{-}1/3} (\sqrt{1+A^2}+A)^2 ,\\ A = [0.088+0.077 c_0 {\textit{Ra}}^{1/2}] {\textit{Pr}}^{{-}1} {\textit{Ra}}^{1/2} {\textit{Ta}}^{{-}1/6}. \end{gathered}\right\}\end{equation}

It is found that $A \rightarrow 0$ for ${\textit {Pr}} \rightarrow \infty$ and (3.17) is recovered as a special case of (4.27).

4.3. Bounds on the velocity field

With the triangle and Poincaré inequalities,

(4.28)\begin{equation} \sqrt{\langle \overline{|(\boldsymbol{u} + \boldsymbol{v})|^2} \rangle} \leqslant \sqrt{\langle \overline{|\boldsymbol{v}|^2} \rangle} + \frac{1}{\rm \pi} c_0 \sqrt{\langle \overline{|\boldsymbol{\nabla}\boldsymbol{u}|^2} \rangle } ,\end{equation}

which becomes with (4.23), (2.11), (2.8) and (3.31)

(4.29)\begin{align} &\sqrt{\langle \overline{|(\boldsymbol{u} + \boldsymbol{v})|^2} \rangle} -\frac{1}{\rm \pi} c_0 \left(c_1 + \frac{c_2}{\rm \pi} c_0 {\textit{Ra}}^{1/2} \right) \left( \frac{7}{12} \right)^{1/4} \langle \overline{|(\boldsymbol{u} + \boldsymbol{v})|^2} \rangle^{1/4} \nonumber\\ &\quad \leqslant \sqrt{\frac{7}{36}} \left( \frac{4}{\rm \pi} \right)^{1/6} \frac{1}{\sqrt{\rm \pi}} {\textit{Ra}} {\textit{Ta}}^{{-}1/3}, \end{align}

from which we can conclude that

(4.30)\begin{equation} \left.\begin{gathered} \sqrt{\langle \overline{|(\boldsymbol{u} + \boldsymbol{v})|^2} \rangle} \leqslant \frac{\sqrt{7}}{6} 4^{1/6} {\rm \pi}^{{-}2/3} {\textit{Ra}} {\textit{Ta}}^{{-}1/3} (\sqrt{1+B^2}+B)^2 ,\\ B = c_0 [0.15+0.13 c_0 {\textit{Ra}}^{1/2}] {\textit{Pr}}^{{-}1} {\textit{Ra}}^{1/2} {\textit{Ta}}^{{-}1/6}. \end{gathered}\right\}\end{equation}

Once again, this formula includes the result (3.31) for infinite Prandtl number convection because $B \rightarrow 0$ for ${\textit {Pr}} \rightarrow \infty$.

It is also possible to generalize (3.35). Start again from (4.28) and substitute (4.24) and (3.35) to obtain

(4.31)\begin{equation} \sqrt{\langle \overline{|(\boldsymbol{u} + \boldsymbol{v})|^2} \rangle} \leqslant \left\{ 1+ c_0 [0.55 + 0.48 c_0 {\textit{Ra}}^{1/2}] \frac{{\textit{Ta}}^{1/6}}{{\textit{Pr}}} \right\} \frac{{\textit{Ra}} {\textit{Ta}}^{{-}1/2}}{\rm \pi} \sqrt{ \langle \overline{|\boldsymbol{\nabla}\theta|^2} \rangle }. \end{equation}