No CrossRef data available.
Published online by Cambridge University Press: 09 June 2023
We show that for a fixed 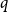 $q$, the number of
$q$, the number of 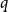 $q$-ary
$q$-ary 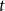 $t$-error correcting codes of length
$t$-error correcting codes of length  $n$ is at most
$n$ is at most 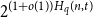 $2^{(1 + o(1)) H_q(n,t)}$ for all
$2^{(1 + o(1)) H_q(n,t)}$ for all 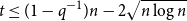 $t \leq (1 - q^{-1})n - 2\sqrt{n \log n}$, where
$t \leq (1 - q^{-1})n - 2\sqrt{n \log n}$, where 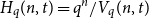 $H_q(n, t) = q^n/ V_q(n,t)$ is the Hamming bound and
$H_q(n, t) = q^n/ V_q(n,t)$ is the Hamming bound and 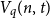 $V_q(n,t)$ is the cardinality of the radius
$V_q(n,t)$ is the cardinality of the radius 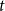 $t$ Hamming ball. This proves a conjecture of Balogh, Treglown, and Wagner, who showed the result for
$t$ Hamming ball. This proves a conjecture of Balogh, Treglown, and Wagner, who showed the result for 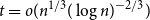 $t = o(n^{1/3} (\log n)^{-2/3})$.
$t = o(n^{1/3} (\log n)^{-2/3})$.
Mani was supported by the NSF Graduate Research Fellowship Program and a Hertz Graduate Fellowship.
Zhao was supported by NSF CAREER award DMS-2044606, a Sloan Research Fellowship, and the MIT Solomon Buchsbaum Fund.