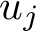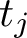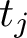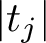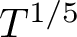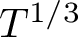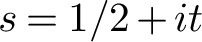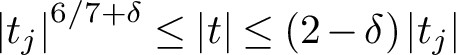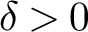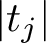1. Introduction
1.1. Background
The widely studied subconvexity problem for automorphic L-functions is completely resolved for degree
![]() $\le 2$
. For uniform bounds, over arbitrary number fields, this is due to Michel and Venkatesh [Reference Michel and Venkatesh25]; for superior-quality bounds in various special cases, this is due to many authors (e.g., [Reference Jutila and Motohashi17, Reference Blomer and Harcos6, Reference Bourgain9, Reference Blomer, Humphries, Khan and Milinovich7, Reference Petrow and Young29]. The next frontier is degree
$\le 2$
. For uniform bounds, over arbitrary number fields, this is due to Michel and Venkatesh [Reference Michel and Venkatesh25]; for superior-quality bounds in various special cases, this is due to many authors (e.g., [Reference Jutila and Motohashi17, Reference Blomer and Harcos6, Reference Bourgain9, Reference Blomer, Humphries, Khan and Milinovich7, Reference Petrow and Young29]. The next frontier is degree
![]() $3$
, but here the subconvexity problem remains a great challenge, save for a few spectacular successes. The first breakthrough is due to Xiaoqing Li [Reference Li23], who established subconvexity for
$3$
, but here the subconvexity problem remains a great challenge, save for a few spectacular successes. The first breakthrough is due to Xiaoqing Li [Reference Li23], who established subconvexity for
![]() $L(f,1/2+it)$
on the critical line (t-aspect), where f is a fixed self-dual Hecke–Maass cusp form for
$L(f,1/2+it)$
on the critical line (t-aspect), where f is a fixed self-dual Hecke–Maass cusp form for
![]() $SL_3(\mathbb {Z})$
. This result was generalized by Munshi [Reference Munshi26], by a very different method, to forms f that are not necessarily self-dual. Munshi [Reference Munshi27] also established subconvexity for twists
$SL_3(\mathbb {Z})$
. This result was generalized by Munshi [Reference Munshi26], by a very different method, to forms f that are not necessarily self-dual. Munshi [Reference Munshi27] also established subconvexity for twists
![]() $L(f\times \chi , 1/2)$
in the p-aspect, where
$L(f\times \chi , 1/2)$
in the p-aspect, where
![]() $\chi $
is a primitive Dirichlet character of prime modulus p. Subconvexity in the spectral aspect of f itself is much harder, and even more so when f is self-dual due to a conductor-dropping phenomenon. Blomer and Buttcane [Reference Blomer and Buttcane5], Kumar, Mallesham, and Singh [Reference Kumar, Mallesham and Singh21], and Sharma [Reference Sharma30] have established subconvexity for
$\chi $
is a primitive Dirichlet character of prime modulus p. Subconvexity in the spectral aspect of f itself is much harder, and even more so when f is self-dual due to a conductor-dropping phenomenon. Blomer and Buttcane [Reference Blomer and Buttcane5], Kumar, Mallesham, and Singh [Reference Kumar, Mallesham and Singh21], and Sharma [Reference Sharma30] have established subconvexity for
![]() $L(1/2, f)$
in the spectral aspect of f in many cases, but excluding the self-dual forms.
$L(1/2, f)$
in the spectral aspect of f in many cases, but excluding the self-dual forms.
A self-dual
![]() $GL_3$
Hecke–Maass cusp form is known to be a symmetric-square lift from
$GL_3$
Hecke–Maass cusp form is known to be a symmetric-square lift from
![]() $GL_2$
[Reference Soudry31]. Let
$GL_2$
[Reference Soudry31]. Let
![]() $u_j$
be a Hecke–Maass cusp form for the full modular group
$u_j$
be a Hecke–Maass cusp form for the full modular group
![]() $SL_2(\mathbb Z)$
, with Laplace eigenvalue
$SL_2(\mathbb Z)$
, with Laplace eigenvalue
 $1/4 + t_j^2$
. It is an outstanding open problem to prove subconvexity for the associated symmetric-square L-function
$1/4 + t_j^2$
. It is an outstanding open problem to prove subconvexity for the associated symmetric-square L-function
 $L\left (\mathrm {sym}^2 u_j, 1/2\right )$
in the
$L\left (\mathrm {sym}^2 u_j, 1/2\right )$
in the
![]() $t_j$
-aspect. Such a bound would represent major progress in the problem of obtaining a power-saving rate of decay in the quantum unique ergodicity problem [Reference Iwaniec and Sarnak15]. A related problem is that of establishing the Lindelöf-on-average bound
$t_j$
-aspect. Such a bound would represent major progress in the problem of obtaining a power-saving rate of decay in the quantum unique ergodicity problem [Reference Iwaniec and Sarnak15]. A related problem is that of establishing the Lindelöf-on-average bound
 $$ \begin{align} \sum_{T\le t_j\le T+\Delta} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2 +it\right)\right\rvert^2 \ll \Delta T^{1+\epsilon}, \end{align} $$
$$ \begin{align} \sum_{T\le t_j\le T+\Delta} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2 +it\right)\right\rvert^2 \ll \Delta T^{1+\epsilon}, \end{align} $$
where we assume throughout that
![]() $T^\epsilon \le \Delta \le T^{1-\epsilon }$
, and we generally aim to take
$T^\epsilon \le \Delta \le T^{1-\epsilon }$
, and we generally aim to take
![]() $\Delta $
as small as possible. Such an estimate is interesting in its own right, and also yields by positivity a bound for each L-value in the sum. At the central point (
$\Delta $
as small as possible. Such an estimate is interesting in its own right, and also yields by positivity a bound for each L-value in the sum. At the central point (
![]() $t=0$
), if formula (1.1) can be established for
$t=0$
), if formula (1.1) can be established for
![]() $\Delta =T^\epsilon $
, it would give the convexity bound for
$\Delta =T^\epsilon $
, it would give the convexity bound for
 $L\left (\mathrm {sym}^2 u_j, 1/2\right )$
; the hope would then be to insert an amplifier in order to prove subconvexity. While a second moment bound which implies convexity at the central point is known in the level aspect by the work of Iwaniec and Michel [Reference Iwaniec and Michel14], in the spectral aspect the problem is much more difficult. The best known result until now for formula (1.1) was
$L\left (\mathrm {sym}^2 u_j, 1/2\right )$
; the hope would then be to insert an amplifier in order to prove subconvexity. While a second moment bound which implies convexity at the central point is known in the level aspect by the work of Iwaniec and Michel [Reference Iwaniec and Michel14], in the spectral aspect the problem is much more difficult. The best known result until now for formula (1.1) was
![]() $\Delta =T^{1/3+\epsilon }$
by Lam [Reference Lam22]. (Lam’s work actually involves symmetric-square L-functions attached to holomorphic Hecke eigenforms, but his method should apply equally well to Hecke–Maass forms.) Other works involving moments of symmetric square L-functions include [Reference Blomer3, Reference Khan18, Reference Jung16, Reference Khan and Das19, Reference Balkanova and Frolenkov2, Reference Balkanova1, Reference Nelson28].
$\Delta =T^{1/3+\epsilon }$
by Lam [Reference Lam22]. (Lam’s work actually involves symmetric-square L-functions attached to holomorphic Hecke eigenforms, but his method should apply equally well to Hecke–Maass forms.) Other works involving moments of symmetric square L-functions include [Reference Blomer3, Reference Khan18, Reference Jung16, Reference Khan and Das19, Reference Balkanova and Frolenkov2, Reference Balkanova1, Reference Nelson28].
1.2. Main results
One of the main results of this paper is an approximate version of the subconvexity bound for
 $L\left (\mathrm {sym}^2 u_j, 1/2\right )$
. Namely, we establish subconvexity for
$L\left (\mathrm {sym}^2 u_j, 1/2\right )$
. Namely, we establish subconvexity for
 $L\left (\mathrm {sym}^2 u_j, 1/2+it\right )$
for t small, but not too small, compared to
$L\left (\mathrm {sym}^2 u_j, 1/2+it\right )$
for t small, but not too small, compared to
![]() $2t_j$
. This hybrid bound (stated precisely later) seems to be the first subconvexity bound for symmetric-square L-functions in which the dominant aspect is the spectral parameter
$2t_j$
. This hybrid bound (stated precisely later) seems to be the first subconvexity bound for symmetric-square L-functions in which the dominant aspect is the spectral parameter
![]() $t_j$
. For comparison, note that bookkeeping the proofs of Li [Reference Li23] or Munshi [Reference Munshi26] would yield hybrid subconvexity bounds for
$t_j$
. For comparison, note that bookkeeping the proofs of Li [Reference Li23] or Munshi [Reference Munshi26] would yield hybrid subconvexity bounds for
![]() $t_j$
(very) small compared to t. Our method also yields a hybrid subconvexity bound for
$t_j$
(very) small compared to t. Our method also yields a hybrid subconvexity bound for
 $L\left (\mathrm {sym}^2 u_j, 1/2+it\right )$
when t is larger (but not too much larger) than
$L\left (\mathrm {sym}^2 u_j, 1/2+it\right )$
when t is larger (but not too much larger) than
![]() $2t_j$
, but for simplicity we refrain from making precise statements. We do not prove anything when t is close to
$2t_j$
, but for simplicity we refrain from making precise statements. We do not prove anything when t is close to
![]() $2t_j$
, for in this case the analytic conductor of the L-function drops. In fact, it is then the same size as the analytic conductor at
$2t_j$
, for in this case the analytic conductor of the L-function drops. In fact, it is then the same size as the analytic conductor at
![]() $t=0$
, where the subconvexity problem is the hardest.
$t=0$
, where the subconvexity problem is the hardest.
Our approach is to establish a sharp estimate for the second moment as in formula (1.1), which is strong enough to yield subconvexity in certain ranges.
Theorem 1.1. Let
![]() $0<\delta <2$
be fixed, and let
$0<\delta <2$
be fixed, and let
![]() $U,T,\Delta>1$
be such that
$U,T,\Delta>1$
be such that
 $$ \begin{align} \frac{T^{3/2+\delta}}{\Delta^{3/2}} \le U\le (2-\delta) T. \end{align} $$
$$ \begin{align} \frac{T^{3/2+\delta}}{\Delta^{3/2}} \le U\le (2-\delta) T. \end{align} $$
We have
 $$ \begin{align} \sum_{T < t_j <T+\Delta} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2+iU\right)\right\rvert^2 \ll \Delta T^{1+\epsilon}. \end{align} $$
$$ \begin{align} \sum_{T < t_j <T+\Delta} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2+iU\right)\right\rvert^2 \ll \Delta T^{1+\epsilon}. \end{align} $$
Corollary 1.2. Let
![]() $0<\delta <2$
be fixed. For
$0<\delta <2$
be fixed. For
![]() $|t_j|^{6/7+\delta } \leq U \leq (2-\delta ) |t_j|$
, we have the hybrid subconvexity bound
$|t_j|^{6/7+\delta } \leq U \leq (2-\delta ) |t_j|$
, we have the hybrid subconvexity bound
 $$ \begin{align} L\left(\mathrm{sym}^2 u_j, 1/2+iU\right) \ll \left\lvert t_j\right\rvert^{1+\epsilon} U^{-1/3}. \end{align} $$
$$ \begin{align} L\left(\mathrm{sym}^2 u_j, 1/2+iU\right) \ll \left\lvert t_j\right\rvert^{1+\epsilon} U^{-1/3}. \end{align} $$
Proof. The bound follows by taking
![]() $\Delta = T^{1+\delta }U^{-2/3}$
in Theorem 1.1 with
$\Delta = T^{1+\delta }U^{-2/3}$
in Theorem 1.1 with
![]() $\delta $
chosen small enough. When
$\delta $
chosen small enough. When
![]() $U\ge T^{6/7+\delta }$
, this bound is subconvex.
$U\ge T^{6/7+\delta }$
, this bound is subconvex.
Note that in Theorem 1.1, we are able to take
![]() $\Delta $
as small as
$\Delta $
as small as
![]() $T^{1/3}$
at best. This requires
$T^{1/3}$
at best. This requires
![]() $T \ll U \leq (2-\delta ) T$
and for instance yields the subconvexity bound
$T \ll U \leq (2-\delta ) T$
and for instance yields the subconvexity bound
 $L\left (\mathrm {sym}^2 u_j, 1/2+it_j\right )\ll \left \lvert t_j\right \rvert ^{2/3+\epsilon }$
.
$L\left (\mathrm {sym}^2 u_j, 1/2+it_j\right )\ll \left \lvert t_j\right \rvert ^{2/3+\epsilon }$
.
We might also speculate that the lower bound in formula (1.2) could plausibly be relaxed to
![]() $\Delta U \gg T^{1+\delta }$
(possibly with an additional term on the right-hand side of formula (1.3), as in formula (12.10)) which would give subconvexity in the wider range
$\Delta U \gg T^{1+\delta }$
(possibly with an additional term on the right-hand side of formula (1.3), as in formula (12.10)) which would give subconvexity in the wider range
![]() $ T^{2/3+\delta } \le U\leq (2-\delta )T$
. For some reasoning on this, see the remarks following formula (9.16).
$ T^{2/3+\delta } \le U\leq (2-\delta )T$
. For some reasoning on this, see the remarks following formula (9.16).
For the central values we do not get subconvexity, but we are able to improve the state of the art for the second moment. This is the other main result of this paper: We establish a Lindelöf-on-average estimate for the second moment with
![]() $\Delta $
as small as
$\Delta $
as small as
![]() $T^{1/5+\epsilon }$
:
$T^{1/5+\epsilon }$
:
Theorem 1.3. For
![]() $\Delta \ge T^{1/5+\varepsilon }$
and
$\Delta \ge T^{1/5+\varepsilon }$
and
![]() $0\leq U \ll T^{\varepsilon }$
, we have
$0\leq U \ll T^{\varepsilon }$
, we have
 $$ \begin{align} \sum_{T < t_j <T+\Delta} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2 +iU\right)\right\rvert^2 \ll \Delta T^{1+\varepsilon}. \end{align} $$
$$ \begin{align} \sum_{T < t_j <T+\Delta} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2 +iU\right)\right\rvert^2 \ll \Delta T^{1+\varepsilon}. \end{align} $$
It is a standing challenge to prove a Lindelöf-on-average bound in formula (1.5) with
![]() $\Delta = 1$
.
$\Delta = 1$
.
Theorem 1.3 also has implications for the quantum variance problem. To explain this, recall that quantum unique ergodicity [Reference Lindenstrauss24, Reference Soundararajan32] says that for any smooth, bounded function
![]() $\psi $
on
$\psi $
on
![]() $\Gamma \backslash \mathbb H$
, we have that
$\Gamma \backslash \mathbb H$
, we have that
 $\langle \lvert u_j\rvert ^2, \psi \rangle \to \frac {3}{\pi }\langle 1,\psi \rangle $
as
$\langle \lvert u_j\rvert ^2, \psi \rangle \to \frac {3}{\pi }\langle 1,\psi \rangle $
as
![]() $t_j\to \infty $
. By spectrally decomposing
$t_j\to \infty $
. By spectrally decomposing
![]() $\psi $
, this is equivalent to demonstrating the decay of
$\psi $
, this is equivalent to demonstrating the decay of
![]() $\langle \lvert u_j \rvert ^2, \varphi \rangle $
and
$\langle \lvert u_j \rvert ^2, \varphi \rangle $
and
![]() $\langle \lvert u_j \rvert ^2, E_U \rangle $
, where
$\langle \lvert u_j \rvert ^2, E_U \rangle $
, where
![]() $\varphi $
is a fixed Hecke–Maass cusp form and
$\varphi $
is a fixed Hecke–Maass cusp form and
 $E_U=E\left (\cdot , \frac {1}{2}+iU\right )$
is the standard Eisenstein series with U fixed. The quantum variance problem is the problem of understanding the variance of these crucial quantitites. More precisely, the quantum variance problem asks for nontrivial bounds on
$E_U=E\left (\cdot , \frac {1}{2}+iU\right )$
is the standard Eisenstein series with U fixed. The quantum variance problem is the problem of understanding the variance of these crucial quantitites. More precisely, the quantum variance problem asks for nontrivial bounds on
 $$ \begin{align} \sum_{T < t_j <T+\Delta} \left\lvert\left\langle u_j^2, \varphi \right\rangle\right\rvert^2, \end{align} $$
$$ \begin{align} \sum_{T < t_j <T+\Delta} \left\lvert\left\langle u_j^2, \varphi \right\rangle\right\rvert^2, \end{align} $$
as well as the Eisenstein contribution
 $$ \begin{align} \sum_{T < t_j <T+\Delta} \left\lvert\left\langle u_j^2, E_U \right\rangle\right\rvert^2. \end{align} $$
$$ \begin{align} \sum_{T < t_j <T+\Delta} \left\lvert\left\langle u_j^2, E_U \right\rangle\right\rvert^2. \end{align} $$
Our Theorem 1.3 gives, by classical Rankin–Selberg theory, a sharp bound on expression (1.7) for
![]() $\Delta \ge T^{1/5+\epsilon }$
. In turn, by Watson’s formula [Reference Watson33], a sharp estimate for expression (1.6) boils down to establishing
$\Delta \ge T^{1/5+\epsilon }$
. In turn, by Watson’s formula [Reference Watson33], a sharp estimate for expression (1.6) boils down to establishing
 $$ \begin{align} \sum_{T < t_j <T+\Delta} L\left(\mathrm{sym}^2 u_j \otimes \varphi,1/2\right) \ll \Delta T^{1+\varepsilon}. \end{align} $$
$$ \begin{align} \sum_{T < t_j <T+\Delta} L\left(\mathrm{sym}^2 u_j \otimes \varphi,1/2\right) \ll \Delta T^{1+\varepsilon}. \end{align} $$
It is plausible that the methods used to prove Theorem 1.3 should also generalize to show formula (1.8) for
![]() $\Delta \ge T^{1/5+\epsilon }$
, which would improve on [Reference Jung16], but this requires a rigorous proof. For quantum variance in the level aspect, see [Reference Nelson28].
$\Delta \ge T^{1/5+\epsilon }$
, which would improve on [Reference Jung16], but this requires a rigorous proof. For quantum variance in the level aspect, see [Reference Nelson28].
1.3. Overview
We now give a rough sketch of our ideas for Theorems 1.1 and 1.3, both of which consider the second moment of the symmetric-square L-function. Let
![]() $h(t)$
be a smooth function supported essentially on
$h(t)$
be a smooth function supported essentially on
![]() $T <\lvert t\rvert <T+\Delta $
, such as the one given in equation (6.2). For
$T <\lvert t\rvert <T+\Delta $
, such as the one given in equation (6.2). For
![]() $0\le U\le (2-\delta )T$
, the analytic conductor of
$0\le U\le (2-\delta )T$
, the analytic conductor of
 $L\left (\mathrm {sym}^2 u_j, 1/2+iU\right )$
is of size
$L\left (\mathrm {sym}^2 u_j, 1/2+iU\right )$
is of size
![]() $T^2(U+1)$
, so using an approximate functional equation, we have roughly
$T^2(U+1)$
, so using an approximate functional equation, we have roughly
 $$ \begin{align*} \sum_{j\ge 1} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2+iU\right)\right\rvert^2 h\left(t_j\right)= \sum_{j\ge 1} \ \sum_{m,n \le T^{1+\epsilon}(U+1)^{1/2} } \frac{\lambda_j\left(m^2\right)\lambda_j\left(n^2\right)}{m^{1/2+iU}n^{1/2-iU}} h\left(t_j\right), \end{align*} $$
$$ \begin{align*} \sum_{j\ge 1} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2+iU\right)\right\rvert^2 h\left(t_j\right)= \sum_{j\ge 1} \ \sum_{m,n \le T^{1+\epsilon}(U+1)^{1/2} } \frac{\lambda_j\left(m^2\right)\lambda_j\left(n^2\right)}{m^{1/2+iU}n^{1/2-iU}} h\left(t_j\right), \end{align*} $$
which we need to show is bounded by
![]() $T^{1+\epsilon }\Delta $
. Applying the Kuznetsov formula, the diagonal contribution is of size
$T^{1+\epsilon }\Delta $
. Applying the Kuznetsov formula, the diagonal contribution is of size
 $O\left (T^{1+\epsilon }\Delta \right )$
, while the off-diagonal contribution is roughly
$O\left (T^{1+\epsilon }\Delta \right )$
, while the off-diagonal contribution is roughly
 $$ \begin{align*} \sum_{m,n \le T^{1+\epsilon}(U+1)^{1/2} } \frac{1}{m^{1/2+iU}n^{1/2-iU}} \sum_{c\ge 1} \frac{S\left(m^2,n^2,c\right)}{c} H\left(\frac{4\pi mn}{c}\right) \end{align*} $$
$$ \begin{align*} \sum_{m,n \le T^{1+\epsilon}(U+1)^{1/2} } \frac{1}{m^{1/2+iU}n^{1/2-iU}} \sum_{c\ge 1} \frac{S\left(m^2,n^2,c\right)}{c} H\left(\frac{4\pi mn}{c}\right) \end{align*} $$
for some transform H of h, given in equation (6.6). By developing equation (6.12), we have that
![]() $H(x)$
is essentially supported on
$H(x)$
is essentially supported on
![]() $x\ge T^{1-\epsilon }\Delta $
and roughly has the shape
$x\ge T^{1-\epsilon }\Delta $
and roughly has the shape
 $H(x)=\frac {T\Delta }{x^{1/2}} e^{i\left (x - T^2/x\right )}$
. Thus in the generic ranges
$H(x)=\frac {T\Delta }{x^{1/2}} e^{i\left (x - T^2/x\right )}$
. Thus in the generic ranges
![]() $m,n\sim T(U+1)^{1/2}$
and
$m,n\sim T(U+1)^{1/2}$
and
![]() $c\sim \frac {mn}{T\Delta }$
, writing
$c\sim \frac {mn}{T\Delta }$
, writing
![]() $(n/m)^{i U}=e(U\log (n/m)/2\pi )$
and not being very careful about factors of
$(n/m)^{i U}=e(U\log (n/m)/2\pi )$
and not being very careful about factors of
![]() $\pi $
and such, the off-diagonal is
$\pi $
and such, the off-diagonal is
 $$ \begin{align} \frac{\Delta^{3/2}}{U^{3/2}T^{3/2}} \sum_{m,n \sim T(U+1)^{1/2} } \sum_{c\sim T(U+1)/\Delta} S\left(m^2,n^2,c\right) e\left( \frac{2 mn}{c}\right)e\left(-\frac{T^2c}{mn} +U \log (n/m) \right). \end{align} $$
$$ \begin{align} \frac{\Delta^{3/2}}{U^{3/2}T^{3/2}} \sum_{m,n \sim T(U+1)^{1/2} } \sum_{c\sim T(U+1)/\Delta} S\left(m^2,n^2,c\right) e\left( \frac{2 mn}{c}\right)e\left(-\frac{T^2c}{mn} +U \log (n/m) \right). \end{align} $$
The oscillatory factor
 $e\left ( -\frac {T^2c}{nm} +U \log (n/ m)\right )$
behaves differently according to whether U is large or small. When U is large, the dominant phase is
$e\left ( -\frac {T^2c}{nm} +U \log (n/ m)\right )$
behaves differently according to whether U is large or small. When U is large, the dominant phase is
![]() $U \log (n/ m)$
, whereas when U is small, the dominant phase is
$U \log (n/ m)$
, whereas when U is small, the dominant phase is
 $-\frac {T^2c}{nm} \sim - \frac {T}{\Delta }$
.
$-\frac {T^2c}{nm} \sim - \frac {T}{\Delta }$
.
Consider one extreme end of our problem: the case
![]() $U=T$
(covered by Theorem 1.1), so that the convexity bound is
$U=T$
(covered by Theorem 1.1), so that the convexity bound is
![]() $T^{3/4+\epsilon }$
. Since the diagonal after Kuznetsov is
$T^{3/4+\epsilon }$
. Since the diagonal after Kuznetsov is
 $O\left (T^{1+\epsilon }\Delta \right )$
, the largest we can take
$O\left (T^{1+\epsilon }\Delta \right )$
, the largest we can take
![]() $\Delta $
to establish subconvexity is
$\Delta $
to establish subconvexity is
![]() $\Delta =T^{1/2-\delta }$
for some
$\Delta =T^{1/2-\delta }$
for some
![]() $\delta>0$
. Thus for the off-diagonal, what we need to prove is roughly (specializing expression (1.9) to
$\delta>0$
. Thus for the off-diagonal, what we need to prove is roughly (specializing expression (1.9) to
![]() $U= T, \Delta =T^{1/2}$
, and retaining only the dominant phase)
$U= T, \Delta =T^{1/2}$
, and retaining only the dominant phase)
 $$ \begin{align} \frac{1}{T^{9/4}} \sum_{m,n\sim T^{3/2} } \sum_{c\sim T^{3/2} } S\left(m^2,n^2,c\right) e\left( \frac{2mn}{c}\right) e(T \log (n/m) )\ll T^{3/2}. \end{align} $$
$$ \begin{align} \frac{1}{T^{9/4}} \sum_{m,n\sim T^{3/2} } \sum_{c\sim T^{3/2} } S\left(m^2,n^2,c\right) e\left( \frac{2mn}{c}\right) e(T \log (n/m) )\ll T^{3/2}. \end{align} $$
We split the n and m sums into residue classes modulo c and apply Poisson summation to each. The off-diagonal then equals
 $$ \begin{align*} \frac{1}{T^{9/4}} \sum_{c\sim T^{3/2} } \ \sum_{k,\ell\in \mathbb{Z} } \frac{1}{c^2} T(k,\ell,c) I(k,\ell,c), \end{align*} $$
$$ \begin{align*} \frac{1}{T^{9/4}} \sum_{c\sim T^{3/2} } \ \sum_{k,\ell\in \mathbb{Z} } \frac{1}{c^2} T(k,\ell,c) I(k,\ell,c), \end{align*} $$
where
 $$ \begin{align*} I(k,\ell, c) = \iint e\left(\frac{-kx-\ell y}{c}+T\log x-T\log y\right)w\left(\frac{x}{T^{3/2}},\frac{y}{T^{3/2}}\right) dxdy \end{align*} $$
$$ \begin{align*} I(k,\ell, c) = \iint e\left(\frac{-kx-\ell y}{c}+T\log x-T\log y\right)w\left(\frac{x}{T^{3/2}},\frac{y}{T^{3/2}}\right) dxdy \end{align*} $$
for some smooth weight function w which restricts support to
![]() $x\sim T^{3/2}, y\sim T^{3/2}$
, and
$x\sim T^{3/2}, y\sim T^{3/2}$
, and
 $$ \begin{align*} T(k,\ell,c) =\sum_{a,b \bmod c} S\left(a^2, b^2, c\right)e\left(\frac{2ab+ak+b\ell}{c}\right). \end{align*} $$
$$ \begin{align*} T(k,\ell,c) =\sum_{a,b \bmod c} S\left(a^2, b^2, c\right)e\left(\frac{2ab+ak+b\ell}{c}\right). \end{align*} $$
We compute this arithmetic sum in §5 and roughly get
 $T(k,\ell , c) = c^{3/2} \left (\frac {k\ell }{c}\right ) e\left (\frac {-k\ell }{4c} \right )$
. The integral is computed using stationary phase (see §4 and §8). We see that it is negligibly small unless
$T(k,\ell , c) = c^{3/2} \left (\frac {k\ell }{c}\right ) e\left (\frac {-k\ell }{4c} \right )$
. The integral is computed using stationary phase (see §4 and §8). We see that it is negligibly small unless
![]() $k,\ell \sim T$
, in which case we get roughly
$k,\ell \sim T$
, in which case we get roughly
 $I(k,\ell ,c)= T^2e\left (\frac {k\ell }{c}\right ) (k/\ell )^{iT}$
(see Lemma 9.3 for the rigorous statement). Thus we need to show
$I(k,\ell ,c)= T^2e\left (\frac {k\ell }{c}\right ) (k/\ell )^{iT}$
(see Lemma 9.3 for the rigorous statement). Thus we need to show
 $$ \begin{align*} \frac{1}{T} \sum_{k,\ell\sim T} \sum_{c\sim T^{3/2}} \left(\frac{k}{\ell}\right)^{iT} e\left(\frac{ 3 k\ell}{4 c}\right) \left(\frac{k\ell}{c}\right)\ll T^{3/2}. \end{align*} $$
$$ \begin{align*} \frac{1}{T} \sum_{k,\ell\sim T} \sum_{c\sim T^{3/2}} \left(\frac{k}{\ell}\right)^{iT} e\left(\frac{ 3 k\ell}{4 c}\right) \left(\frac{k\ell}{c}\right)\ll T^{3/2}. \end{align*} $$
At this point we go beyond previous approaches to the second moment problem [Reference Iwaniec and Michel14, Reference Lam22] by finding cancellation in the c sum. We split the c sum into arithmetic progresssions modulo
![]() $k\ell $
by quadratic reciprocity and apply Poisson summation, getting that the off-diagonal equals
$k\ell $
by quadratic reciprocity and apply Poisson summation, getting that the off-diagonal equals
 $$ \begin{align} \frac{1}{T} \sum_{k,\ell\sim T} \left(\frac{k}{\ell}\right)^{iT} \sum_{q\in\mathbb{Z}} \frac{1}{k\ell} \sum_{a\bmod k\ell} \left(\frac{a}{k\ell}\right)e\left( \frac{-aq}{k\ell}\right) \int e\left(\frac{ 3k\ell}{4x}+\frac{qx}{k\ell} \right) w\left(\frac{x}{T^{3/2}}\right)dx. \end{align} $$
$$ \begin{align} \frac{1}{T} \sum_{k,\ell\sim T} \left(\frac{k}{\ell}\right)^{iT} \sum_{q\in\mathbb{Z}} \frac{1}{k\ell} \sum_{a\bmod k\ell} \left(\frac{a}{k\ell}\right)e\left( \frac{-aq}{k\ell}\right) \int e\left(\frac{ 3k\ell}{4x}+\frac{qx}{k\ell} \right) w\left(\frac{x}{T^{3/2}}\right)dx. \end{align} $$
This Poisson summation step may be viewed as the key new ingredient in our paper. It leads to a simpler expression in two ways. First, an integration-by-parts argument shows that the q sum can be restricted to
![]() $q \sim T$
, which is significantly shorter than the earlier c sum of length
$q \sim T$
, which is significantly shorter than the earlier c sum of length
![]() $T^{3/2}$
. A more elaborate stationary-phase analysis of the integral shows that the integral is essentially independent of k and
$T^{3/2}$
. A more elaborate stationary-phase analysis of the integral shows that the integral is essentially independent of k and
![]() $\ell $
, which can be seen in rough form by the substitution
$\ell $
, which can be seen in rough form by the substitution
![]() $x\to xk\ell $
in expression (1.11). The reader will not actually find an expression like (1.11) in the paper, because we execute Poisson summation in c in the language of Dirichlet series and functional equations. This allows us to more effectively deal with some of the more delicate features of this step (see, e.g., Remark 11.5).
$x\to xk\ell $
in expression (1.11). The reader will not actually find an expression like (1.11) in the paper, because we execute Poisson summation in c in the language of Dirichlet series and functional equations. This allows us to more effectively deal with some of the more delicate features of this step (see, e.g., Remark 11.5).
Evaluating the arithmetic sum and using stationary phase to compute the integral in expression (1.11), we get that the off-diagonal equals
 $$ \begin{align} \frac{1}{T^{3/4}}\sum_{k,\ell\sim T} \sum_{q\sim T} e\left(\sqrt{q}\right)\left(\frac{q}{k\ell}\right)\left(\frac{k}{\ell}\right)^{iT} = \frac{1}{T^{3/4}} \sum_{q\sim T} e\left(\sqrt{q}\right) \left\lvert \sum_{k\sim T} \left(\frac{q}{k}\right)k^{iT}\right\rvert^2. \end{align} $$
$$ \begin{align} \frac{1}{T^{3/4}}\sum_{k,\ell\sim T} \sum_{q\sim T} e\left(\sqrt{q}\right)\left(\frac{q}{k\ell}\right)\left(\frac{k}{\ell}\right)^{iT} = \frac{1}{T^{3/4}} \sum_{q\sim T} e\left(\sqrt{q}\right) \left\lvert \sum_{k\sim T} \left(\frac{q}{k}\right)k^{iT}\right\rvert^2. \end{align} $$
Finally, applying Heath-Brown’s [Reference Heath-Brown12] large sieve for quadratic characters, we get that the off-diagonal is
 $O\left (T^{5/4+\epsilon }\right )$
, which is better than the required bound in expresion (1.10).
$O\left (T^{5/4+\epsilon }\right )$
, which is better than the required bound in expresion (1.10).
Now consider Theorem 1.3, which deals with the other extreme end of our problem, where U is small. The treatment of this follows the same plan as just sketched for large values of U, but the details are changed a bit, because the oscillatory factor in expression (1.9) behaves differently. Consider the case
![]() $U=0$
(the central point) and
$U=0$
(the central point) and
![]() $\Delta =T^{1/5}$
, which is the best we can do in Theorem 1.3. In the end, instead of equation (1.12), one arrives roughly at an expression of the form
$\Delta =T^{1/5}$
, which is the best we can do in Theorem 1.3. In the end, instead of equation (1.12), one arrives roughly at an expression of the form
 $$ \begin{align} \sum_{q \sim T^{6/5}} e\left(T^{1/2}q^{1/4}\right) \left\lvert\sum_{k \sim T^{3/5}} \frac{ \left(\frac{k}{q}\right) }{\sqrt{k}} \right\rvert^2. \end{align} $$
$$ \begin{align} \sum_{q \sim T^{6/5}} e\left(T^{1/2}q^{1/4}\right) \left\lvert\sum_{k \sim T^{3/5}} \frac{ \left(\frac{k}{q}\right) }{\sqrt{k}} \right\rvert^2. \end{align} $$
Again, Heath-Brown’s quadratic large sieve is the endgame, giving a bound of
![]() $\Delta T^{1+\epsilon }=T^{6/5+\epsilon }$
. It is a curious difference that the q sum in expression (1.13) is now actually longer than the c sum from which it arose via Poisson summation, in contrast to the situation with
$\Delta T^{1+\epsilon }=T^{6/5+\epsilon }$
. It is a curious difference that the q sum in expression (1.13) is now actually longer than the c sum from which it arose via Poisson summation, in contrast to the situation with
![]() $U = T$
presented earlier. However, the gain is that the variables q and k become separated in the exponential-phase factor (indeed, k is completely removed from the phase in expression (1.13)).
$U = T$
presented earlier. However, the gain is that the variables q and k become separated in the exponential-phase factor (indeed, k is completely removed from the phase in expression (1.13)).
1.4. Notational conventions
Throughout, we will follow the epsilon convention, in which
![]() $\epsilon $
always denotes an arbitrarily small positive constant, but not necessarily the same one from one occurrence to another. As usual, we will write
$\epsilon $
always denotes an arbitrarily small positive constant, but not necessarily the same one from one occurrence to another. As usual, we will write
![]() $e(x)=e^{2\pi i x}$
and
$e(x)=e^{2\pi i x}$
and
![]() $e_c(x) = e(x/c)$
. For n a positive odd integer, we let
$e_c(x) = e(x/c)$
. For n a positive odd integer, we let
 $\chi _n(m) = \left (\frac {m}{n}\right )$
denote the Jacobi symbol. If s is complex, an expression of the form
$\chi _n(m) = \left (\frac {m}{n}\right )$
denote the Jacobi symbol. If s is complex, an expression of the form
![]() $O(p^{-s})$
should be interpreted to mean
$O(p^{-s})$
should be interpreted to mean
 $O\left (p^{-\mathrm {Re}(s)}\right )$
. This abuse of notation will only be used on occasion with Euler products. We may also write
$O\left (p^{-\mathrm {Re}(s)}\right )$
. This abuse of notation will only be used on occasion with Euler products. We may also write
 $O\left (p^{- \min (s,u)}\right )$
in place of
$O\left (p^{- \min (s,u)}\right )$
in place of
 $O\left (p^{-\min (\mathrm {Re}(s), \mathrm {Re}(u))}\right )$
.
$O\left (p^{-\min (\mathrm {Re}(s), \mathrm {Re}(u))}\right )$
.
Upper bounds in terms of the size of U are usually expressed, since U may be
![]() $0$
, in terms of
$0$
, in terms of
![]() $1+U$
. However, to save clutter, such upper bounds will be written in terms of U only. This is justified at the start of §6.
$1+U$
. However, to save clutter, such upper bounds will be written in terms of U only. This is justified at the start of §6.
2. Automorphic forms
2.1. Symmetric-square L-functions
Let
![]() $u_j$
be a Hecke–Maass cusp form for the modular group
$u_j$
be a Hecke–Maass cusp form for the modular group
![]() $SL_2(\mathbb Z)$
with Laplace eigenvalue
$SL_2(\mathbb Z)$
with Laplace eigenvalue
 $1/4 + t_j^2$
and nth Hecke eigenvalue
$1/4 + t_j^2$
and nth Hecke eigenvalue
![]() $\lambda _j(n)$
. It has an associated symmetric-square L-function defined by
$\lambda _j(n)$
. It has an associated symmetric-square L-function defined by
 $L\left (\mathrm {sym}^2 u_j, s\right ) = \sum _{n \geq 1} \lambda _{\mathrm {sym}^2 u_j}(n) n^{-s}$
, with
$L\left (\mathrm {sym}^2 u_j, s\right ) = \sum _{n \geq 1} \lambda _{\mathrm {sym}^2 u_j}(n) n^{-s}$
, with
 $\lambda _{\mathrm {sym}^2 u_j}(n) = \sum _{a^2 b = n} \lambda _j\left (b^2\right )$
. Let
$\lambda _{\mathrm {sym}^2 u_j}(n) = \sum _{a^2 b = n} \lambda _j\left (b^2\right )$
. Let
![]() $\Gamma _{\mathbb R}(s) = \pi ^{-s/2} \Gamma (s/2)$
and
$\Gamma _{\mathbb R}(s) = \pi ^{-s/2} \Gamma (s/2)$
and
 $\gamma \left (\mathrm {sym}^2 u_j, s\right ) = \Gamma _{\mathbb R}(s) \Gamma _{\mathbb R}\left (s+2it_j\right ) \Gamma _{\mathbb R}\left (s-2it_j\right )$
. Then
$\gamma \left (\mathrm {sym}^2 u_j, s\right ) = \Gamma _{\mathbb R}(s) \Gamma _{\mathbb R}\left (s+2it_j\right ) \Gamma _{\mathbb R}\left (s-2it_j\right )$
. Then
 $L\left (\mathrm {sym}^2 u_j, s\right )$
has an analytic continuation to
$L\left (\mathrm {sym}^2 u_j, s\right )$
has an analytic continuation to
![]() $\mathbb C$
and satisfies the functional equation
$\mathbb C$
and satisfies the functional equation
 $\gamma \left (\mathrm {sym}^2 u_j, s\right ) L\left (\mathrm {sym}^2 u_j, s\right ) = \gamma \left (\mathrm {sym}^2 u_j, 1-s\right ) L\left (\mathrm {sym}^2 u_j, 1-s\right )$
, where the notation for
$\gamma \left (\mathrm {sym}^2 u_j, s\right ) L\left (\mathrm {sym}^2 u_j, s\right ) = \gamma \left (\mathrm {sym}^2 u_j, 1-s\right ) L\left (\mathrm {sym}^2 u_j, 1-s\right )$
, where the notation for
![]() $\gamma (f,s)$
agrees with [Reference Iwaniec and Kowalski13, Chapter 5]. In particular, the analytic conductor of
$\gamma (f,s)$
agrees with [Reference Iwaniec and Kowalski13, Chapter 5]. In particular, the analytic conductor of
 $L\left (\mathrm {sym}^2 u_j, 1/2 + it\right )$
equals
$L\left (\mathrm {sym}^2 u_j, 1/2 + it\right )$
equals
2.2. The Kuznetsov formula
Let
![]() $h(z)$
be an even, holomorphic function on
$h(z)$
be an even, holomorphic function on
 $\lvert \Im (z)\rvert <\frac 12 +\delta $
, with decay
$\lvert \Im (z)\rvert <\frac 12 +\delta $
, with decay
![]() $\lvert h(z)\rvert \ll (1+\lvert z\rvert )^{2-\delta }$
, for some
$\lvert h(z)\rvert \ll (1+\lvert z\rvert )^{2-\delta }$
, for some
![]() $\delta>0$
. Let
$\delta>0$
. Let
![]() $\left \{u_j: j\ge 1\right \}$
denote an orthonormal basis of Maass cusp forms of level q with Laplace eigenvalue
$\left \{u_j: j\ge 1\right \}$
denote an orthonormal basis of Maass cusp forms of level q with Laplace eigenvalue
 $\frac 14+t_j^2$
and Fourier expansion
$\frac 14+t_j^2$
and Fourier expansion
 $$ \begin{align*} u_j(z)=y^{\frac12} \sum_{n\neq 0} \rho_j(n) K_{it_j}(2\pi \lvert n\rvert y)e(nx), \end{align*} $$
$$ \begin{align*} u_j(z)=y^{\frac12} \sum_{n\neq 0} \rho_j(n) K_{it_j}(2\pi \lvert n\rvert y)e(nx), \end{align*} $$
where
![]() $z=x+iy$
and
$z=x+iy$
and
![]() $K_{it_j}$
is the K-Bessel function. At each inequivalent cusp
$K_{it_j}$
is the K-Bessel function. At each inequivalent cusp
![]() $\mathfrak {a}$
of
$\mathfrak {a}$
of
![]() $\Gamma _0(q)$
, let
$\Gamma _0(q)$
, let
 $E_{\mathfrak {a}}\left (\cdot , \frac 12+it\right )$
be the associated Eisenstein series with Fourier expansion
$E_{\mathfrak {a}}\left (\cdot , \frac 12+it\right )$
be the associated Eisenstein series with Fourier expansion
 $$ \begin{align*} E_{\mathfrak{a}}\left(z, \tfrac12+it\right)=\delta_{\mathfrak{a}=\infty} y^{\frac12+it} + \varphi_{\mathfrak{a}}\left(\tfrac12+it\right)y^{\frac12-it}+y^{\frac12} \sum_{n\neq 0} \tau_{\mathfrak{a}}(n,t) K_{it}(2\pi \lvert n\rvert y)e(nx), \end{align*} $$
$$ \begin{align*} E_{\mathfrak{a}}\left(z, \tfrac12+it\right)=\delta_{\mathfrak{a}=\infty} y^{\frac12+it} + \varphi_{\mathfrak{a}}\left(\tfrac12+it\right)y^{\frac12-it}+y^{\frac12} \sum_{n\neq 0} \tau_{\mathfrak{a}}(n,t) K_{it}(2\pi \lvert n\rvert y)e(nx), \end{align*} $$
where
![]() $\varphi _{\mathfrak {a}}(s)$
is meromorphic on
$\varphi _{\mathfrak {a}}(s)$
is meromorphic on
![]() $\mathbb C$
. These expansions may be found in [Reference Iwaniec and Kowalski13, equations (16.19) and (16.22)].
$\mathbb C$
. These expansions may be found in [Reference Iwaniec and Kowalski13, equations (16.19) and (16.22)].
Lemma 2.1 Kuznetsov’s formula[Reference Iwaniec and Kowalski13, Theorem 16.3]
For any
![]() $n,m>0$
, we have
$n,m>0$
, we have
 $$ \begin{align*} &\sum_{j\ge 1} \rho_j(n)\overline{\rho}_j(m)\frac{h\left(t_j\right)}{\cosh\left(\pi t_j\right)}+\sum_{\mathfrak{a}}\frac{1}{4\pi}\int_{-\infty}^{\infty} \tau_{\mathfrak{a}}(n,t)\overline{\tau}_{\mathfrak{a}}(m,t) \frac{h(t)dt}{\cosh(\pi t)}\\ &\quad =\delta_{(n=m)}\int_{-\infty}^\infty h(t) t \tanh(\pi t) \frac{dt}{\pi^2} \\ &\qquad + \frac{i}{\pi} \sum_{c\equiv 0 \bmod q}\frac{S(n,m,c)}{c} \int_{-\infty}^\infty J\left(\frac{4\pi\sqrt{nm}}{c},t\right)h(t) t\tanh(\pi t)dt, \end{align*} $$
$$ \begin{align*} &\sum_{j\ge 1} \rho_j(n)\overline{\rho}_j(m)\frac{h\left(t_j\right)}{\cosh\left(\pi t_j\right)}+\sum_{\mathfrak{a}}\frac{1}{4\pi}\int_{-\infty}^{\infty} \tau_{\mathfrak{a}}(n,t)\overline{\tau}_{\mathfrak{a}}(m,t) \frac{h(t)dt}{\cosh(\pi t)}\\ &\quad =\delta_{(n=m)}\int_{-\infty}^\infty h(t) t \tanh(\pi t) \frac{dt}{\pi^2} \\ &\qquad + \frac{i}{\pi} \sum_{c\equiv 0 \bmod q}\frac{S(n,m,c)}{c} \int_{-\infty}^\infty J\left(\frac{4\pi\sqrt{nm}}{c},t\right)h(t) t\tanh(\pi t)dt, \end{align*} $$
where
 $\displaystyle J(x,t) =\frac {J_{2it}(x) - J_{-2it}(x)}{\sinh (\pi t)}$
.
$\displaystyle J(x,t) =\frac {J_{2it}(x) - J_{-2it}(x)}{\sinh (\pi t)}$
.
Later we will need to use the Kuznetsov formula for level
![]() $2^4$
. We will choose our orthonormal basis to include the level
$2^4$
. We will choose our orthonormal basis to include the level
![]() $1$
Hecke–Maass forms, for which we may write
$1$
Hecke–Maass forms, for which we may write
 $$ \begin{align*} \rho_j(n)\overline{\rho}_j(m)\frac{h\left(t_j\right)}{\cosh\left(\pi t_j\right)}=\lambda_j(n)\overline{\lambda}_j(m) \frac{h\left(t_j\right) \left\lvert p_j(1)\right\rvert^2}{\cosh\left(\pi t_j\right)}, \end{align*} $$
$$ \begin{align*} \rho_j(n)\overline{\rho}_j(m)\frac{h\left(t_j\right)}{\cosh\left(\pi t_j\right)}=\lambda_j(n)\overline{\lambda}_j(m) \frac{h\left(t_j\right) \left\lvert p_j(1)\right\rvert^2}{\cosh\left(\pi t_j\right)}, \end{align*} $$
and note that
 $t_j^{-\epsilon }\ll \frac {\left \lvert \rho _j(1)\right \rvert ^2}{\cosh \left (\pi t_j\right )}\ll t_j^\epsilon $
by [Reference Harcos and Michel11, equation (30)] together with the fact that
$t_j^{-\epsilon }\ll \frac {\left \lvert \rho _j(1)\right \rvert ^2}{\cosh \left (\pi t_j\right )}\ll t_j^\epsilon $
by [Reference Harcos and Michel11, equation (30)] together with the fact that
![]() $L^2$
-normalization in
$L^2$
-normalization in
 $\Gamma _0\left (2^4\right )$
and
$\Gamma _0\left (2^4\right )$
and
![]() $\Gamma _0(1)$
is the same up to a constant factor.
$\Gamma _0(1)$
is the same up to a constant factor.
3. The quadratic large sieve
We will have need of Heath-Brown’s large sieve inequality for quadratic characters:
Theorem 3.1 Heath-Brown [Reference Heath-Brown12]
Set
![]() $M, N \gg 1$
. Then
$M, N \gg 1$
. Then
 $$ \begin{align} \sideset{}{^*}\sum_{m \leq M} \left\lvert \sideset{}{^*}\sum_{n \leq N} a_n \left(\frac{n}{m}\right)\right\rvert^2 \ll (M+N)(MN)^{\varepsilon} \sum_{n \leq N} \lvert a_n\rvert^2, \end{align} $$
$$ \begin{align} \sideset{}{^*}\sum_{m \leq M} \left\lvert \sideset{}{^*}\sum_{n \leq N} a_n \left(\frac{n}{m}\right)\right\rvert^2 \ll (M+N)(MN)^{\varepsilon} \sum_{n \leq N} \lvert a_n\rvert^2, \end{align} $$
where the sums are restricted to odd square-free integers.
We will need a corollary of Heath-Brown’s result, namely
 $$ \begin{align} \sum_{m \leq M} \lvert L(1/2 + it, \chi_{m})\rvert^2 \ll \left(M+ \sqrt{M(1+\lvert t\rvert)}\right) (M(1+\lvert t\rvert))^{\varepsilon}. \end{align} $$
$$ \begin{align} \sum_{m \leq M} \lvert L(1/2 + it, \chi_{m})\rvert^2 \ll \left(M+ \sqrt{M(1+\lvert t\rvert)}\right) (M(1+\lvert t\rvert))^{\varepsilon}. \end{align} $$
This follows from an approximate functional equation and a simple observation that the square parts of the inner and outer variables are harmless. Similarly, we obtain
 $$ \begin{align} \sum_{m \leq M} m^{-1/2} \lvert L(1/2 + it, \chi_{m})\rvert^2 \ll \left(M^{1/2} + (1+\lvert t\rvert)^{1/2} \right) (M(1+\lvert t\rvert))^{\varepsilon}. \end{align} $$
$$ \begin{align} \sum_{m \leq M} m^{-1/2} \lvert L(1/2 + it, \chi_{m})\rvert^2 \ll \left(M^{1/2} + (1+\lvert t\rvert)^{1/2} \right) (M(1+\lvert t\rvert))^{\varepsilon}. \end{align} $$
4. Oscillatory integrals
Throughout this paper we will make extensive use of estimates for oscillatory integrals. We will largely rely on the results of [Reference Kıral, Petrow and Young20] (built on [Reference Blomer, Khan and Young8]), which use the language of families of inert functions. This language gives a concise way to track bounds on derivatives of weight functions. It also has the pleasant property that, loosely speaking, the class of inert functions is closed under application of the stationary-phase method (the precise statement is in Lemma 4.3). We refer the reader to [Reference Kıral, Petrow and Young20] for a more thorough discussion, including examples of applying stationary phase using this language.
Let
![]() $\mathcal {F}$
be an index set and
$\mathcal {F}$
be an index set and
![]() $X=X_T: \mathcal {F} \to \mathbb R_{\geq 1}$
be a function of
$X=X_T: \mathcal {F} \to \mathbb R_{\geq 1}$
be a function of
![]() $T \in \mathcal {F}$
.
$T \in \mathcal {F}$
.
Definition 4.1. A family
![]() $\{w_T\}_{T\in \mathcal {F}}$
of smooth functions supported on a product of dyadic intervals in
$\{w_T\}_{T\in \mathcal {F}}$
of smooth functions supported on a product of dyadic intervals in
 $\mathbb R_{>0}^d$
is called X -inert if for each
$\mathbb R_{>0}^d$
is called X -inert if for each
 $j=(j_1,\dotsc ,j_d) \in \mathbb Z_{\geq 0}^d$
we have
$j=(j_1,\dotsc ,j_d) \in \mathbb Z_{\geq 0}^d$
we have
 $$ \begin{align} C_{\mathcal{F}}(j_1,\dotsc,j_d) := \sup_{T \in \mathcal{F}} \sup_{\left(x_1, \dotsc, x_d\right) \in \mathbb R_{>0}^d} X_T^{-j_1- \dotsb -j_d}\left\lvert x_{1}^{j_1} \dotsm x_{d}^{j_d} w_T^{\left(j_1,\cdots,j_d\right)}(x_1,\dotsc,x_d) \right\rvert < \infty. \end{align} $$
$$ \begin{align} C_{\mathcal{F}}(j_1,\dotsc,j_d) := \sup_{T \in \mathcal{F}} \sup_{\left(x_1, \dotsc, x_d\right) \in \mathbb R_{>0}^d} X_T^{-j_1- \dotsb -j_d}\left\lvert x_{1}^{j_1} \dotsm x_{d}^{j_d} w_T^{\left(j_1,\cdots,j_d\right)}(x_1,\dotsc,x_d) \right\rvert < \infty. \end{align} $$
As an abuse, we might say that a single function is
![]() $1$
-inert (or simply inert), by which we should mean that it is a member of a family of
$1$
-inert (or simply inert), by which we should mean that it is a member of a family of
![]() $1$
-inert functions.
$1$
-inert functions.
Lemma 4.2 Integration-by-parts bound [Reference Blomer, Khan and Young8]
Suppose that
![]() $w = w_T(t)$
is a family of X-inert functions, with compact support on
$w = w_T(t)$
is a family of X-inert functions, with compact support on
![]() $[Z, 2Z]$
, so that for all
$[Z, 2Z]$
, so that for all
![]() $j=0,1,\dotsc $
we have the bound
$j=0,1,\dotsc $
we have the bound
![]() $w^{\left (j\right )}(t) \ll (Z/X)^{-j}$
. Also suppose that
$w^{\left (j\right )}(t) \ll (Z/X)^{-j}$
. Also suppose that
![]() $\phi $
is smooth and satisfies, for
$\phi $
is smooth and satisfies, for
![]() $j=2,3, \dotsc $
,
$j=2,3, \dotsc $
,
 $\phi ^{\left (j\right )}(t) \ll \frac {Y}{Z^j}$
for some
$\phi ^{\left (j\right )}(t) \ll \frac {Y}{Z^j}$
for some
![]() $R \geq 1$
with
$R \geq 1$
with
![]() $Y/X \geq R$
and all t in the support of w. Let
$Y/X \geq R$
and all t in the support of w. Let
 $$ \begin{align*} I = \int_{-\infty}^{\infty} w(t) e^{i \phi(t)} dt. \end{align*} $$
$$ \begin{align*} I = \int_{-\infty}^{\infty} w(t) e^{i \phi(t)} dt. \end{align*} $$
If
 $\lvert \phi '(t)\rvert \gg \frac {Y}{Z}$
for all t in the support of w, then
$\lvert \phi '(t)\rvert \gg \frac {Y}{Z}$
for all t in the support of w, then
![]() $I \ll _A Z R^{-A}$
for A arbitrarily large.
$I \ll _A Z R^{-A}$
for A arbitrarily large.
Lemma 4.3 stationary phase [Reference Blomer, Khan and Young8, Reference Kıral, Petrow and Young20]
Suppose
![]() $w_T$
is X-inert in
$w_T$
is X-inert in
![]() $t_1, \dotsc , t_d$
, supported on
$t_1, \dotsc , t_d$
, supported on
![]() $t_1 \asymp Z$
and
$t_1 \asymp Z$
and
![]() $t_i \asymp X_i$
for
$t_i \asymp X_i$
for
![]() $i=2,\dotsc , d$
. Suppose that on the support of
$i=2,\dotsc , d$
. Suppose that on the support of
![]() $w_T$
,
$w_T$
,
![]() $\phi = \phi _T$
satisfies
$\phi = \phi _T$
satisfies
 $$ \begin{align} \frac{\partial^{a_1 + a_2 + \dotsb + a_d}}{\partial t_1^{a_1} \dotsm \partial t_d^{a_d}} \phi(t_1, t_2, \dotsc, t_d) \ll_{C_{\mathcal{F}}} \frac{Y}{Z^{a_1}} \frac{1}{X_2^{a_2} \dotsm X_d^{a_d}}, \end{align} $$
$$ \begin{align} \frac{\partial^{a_1 + a_2 + \dotsb + a_d}}{\partial t_1^{a_1} \dotsm \partial t_d^{a_d}} \phi(t_1, t_2, \dotsc, t_d) \ll_{C_{\mathcal{F}}} \frac{Y}{Z^{a_1}} \frac{1}{X_2^{a_2} \dotsm X_d^{a_d}}, \end{align} $$
for all
![]() $a_1, \dotsc , a_d \in \mathbb {N}$
with
$a_1, \dotsc , a_d \in \mathbb {N}$
with
![]() $a_1\ge 1$
. Suppose
$a_1\ge 1$
. Suppose
 $\phi ''(t_1, t_2, \dotsc , t_d) \gg \frac {Y}{Z^2}$
(here and later,
$\phi ''(t_1, t_2, \dotsc , t_d) \gg \frac {Y}{Z^2}$
(here and later,
![]() $\phi '$
and
$\phi '$
and
![]() $\phi ''$
denote the derivative with respect to
$\phi ''$
denote the derivative with respect to
![]() $t_1$
), for all
$t_1$
), for all
![]() $t_1, t_2, \dotsc , t_d$
in the support of
$t_1, t_2, \dotsc , t_d$
in the support of
![]() $w_T$
, and for each
$w_T$
, and for each
![]() $t_2, \dotsc , t_d$
in the support of
$t_2, \dotsc , t_d$
in the support of
![]() $\phi $
there exists
$\phi $
there exists
![]() $t_0 \asymp Z$
such that
$t_0 \asymp Z$
such that
![]() $\phi '(t_0, t_2, \dotsc , t_d) = 0$
. Suppose that
$\phi '(t_0, t_2, \dotsc , t_d) = 0$
. Suppose that
![]() $Y/X^2 \geq R$
for some
$Y/X^2 \geq R$
for some
![]() $R\geq 1$
. Then
$R\geq 1$
. Then
 $$ \begin{align} I = \int_{\mathbb{R}} e^{i \phi\left(t_1, \dotsc, t_d\right)} w_T(t_1, \dotsc, t_d) dt_1 = \frac{Z}{\sqrt{Y}} e^{i \phi\left(t_0, t_2, \dotsc, t_d\right)} W_T(t_2, \dotsc, t_d) + O_{A}\left(ZR^{-A}\right), \end{align} $$
$$ \begin{align} I = \int_{\mathbb{R}} e^{i \phi\left(t_1, \dotsc, t_d\right)} w_T(t_1, \dotsc, t_d) dt_1 = \frac{Z}{\sqrt{Y}} e^{i \phi\left(t_0, t_2, \dotsc, t_d\right)} W_T(t_2, \dotsc, t_d) + O_{A}\left(ZR^{-A}\right), \end{align} $$
for some X-inert family of functions
![]() $W_T$
, and where
$W_T$
, and where
![]() $A>0$
may be taken to be arbitrarily large. The implied constant in equation (4.3) depends only on A and on
$A>0$
may be taken to be arbitrarily large. The implied constant in equation (4.3) depends only on A and on
![]() $C_{\mathcal {F}}$
defined in formula (4.1).
$C_{\mathcal {F}}$
defined in formula (4.1).
The fact that
![]() $W_T$
is inert with respect to the same variables as
$W_T$
is inert with respect to the same variables as
![]() $w_T$
(with the exception of
$w_T$
(with the exception of
![]() $t_1$
, of course) is highly convenient. In practice, we may often temporarily suppress certain variables from the notation. This is justified, provided that the functions satisfy the inertness condition in terms of these variables. We also remark that if
$t_1$
, of course) is highly convenient. In practice, we may often temporarily suppress certain variables from the notation. This is justified, provided that the functions satisfy the inertness condition in terms of these variables. We also remark that if
![]() $d=1$
, then
$d=1$
, then
![]() $W_T(t_{2}, \dotsc , t_d)$
is a constant.
$W_T(t_{2}, \dotsc , t_d)$
is a constant.
The following remark will be helpful for using Lemma 4.3 in an iterative fashion. First note that
![]() $t_0$
is the unique function of
$t_0$
is the unique function of
![]() $t_2, \dotsc , t_d$
which solves
$t_2, \dotsc , t_d$
which solves
![]() $\phi '(t_1, \dotsc , t_d) = 0$
when viewed as an equation in
$\phi '(t_1, \dotsc , t_d) = 0$
when viewed as an equation in
![]() $t_1$
. In other words,
$t_1$
. In other words,
![]() $t_0$
is defined implicitly by
$t_0$
is defined implicitly by
![]() $\phi '(t_0, \dotsc , t_d) = 0$
. In practice it might be an unwelcome task to explicitly solve for
$\phi '(t_0, \dotsc , t_d) = 0$
. In practice it might be an unwelcome task to explicitly solve for
![]() $t_0$
, and the following discussion will aid in avoiding this issue. Let
$t_0$
, and the following discussion will aid in avoiding this issue. Let
so by the chain rule,
 $$ \begin{align} \frac{\partial}{\partial t_j} \Phi(t_2, \dotsc, t_d) = \phi'(t_0, t_2, \dotsc, t_d) \frac{\partial t_0}{\partial t_j} + \frac{\partial }{\partial t_j} \phi\left(t_0, \dotsc, t_j\right) = \frac{\partial}{\partial t_j} \phi\left(t_0, \dotsc, t_j\right), \end{align} $$
$$ \begin{align} \frac{\partial}{\partial t_j} \Phi(t_2, \dotsc, t_d) = \phi'(t_0, t_2, \dotsc, t_d) \frac{\partial t_0}{\partial t_j} + \frac{\partial }{\partial t_j} \phi\left(t_0, \dotsc, t_j\right) = \frac{\partial}{\partial t_j} \phi\left(t_0, \dotsc, t_j\right), \end{align} $$
and so on for higher derivatives. Hence the derivatives of
![]() $\Phi $
have the same bounds as those on
$\Phi $
have the same bounds as those on
![]() $\phi $
(supposing uniformity with respect to the first variable
$\phi $
(supposing uniformity with respect to the first variable
![]() $t_1$
).
$t_1$
).
As a simple yet useful consequence of this, if
![]() $\phi $
satisfies formula (4.2) (with Z replaced by
$\phi $
satisfies formula (4.2) (with Z replaced by
![]() $X_1$
, say) as well as
$X_1$
, say) as well as
 $\frac {\partial ^2}{\partial t_j^2} \phi (t_1, \dotsc , t_d) \gg \frac {Y}{X_j^2} \geq R \geq 1$
for
$\frac {\partial ^2}{\partial t_j^2} \phi (t_1, \dotsc , t_d) \gg \frac {Y}{X_j^2} \geq R \geq 1$
for
![]() $j=1,2,\dotsc , k$
, uniformly for all
$j=1,2,\dotsc , k$
, uniformly for all
![]() $t_1, \dotsc , t_d$
in the support of
$t_1, \dotsc , t_d$
in the support of
![]() $w_T$
, then
$w_T$
, then
 $$ \begin{align} & \int_{\mathbb R^k} e^{i\phi\left(t_1, \dotsc, t_d\right)} w_T(t_1, \dotsc, t_d) dt_1 \dotsm dt_k \nonumber \\ &\quad = \frac{X_1 \dotsm X_k}{Y^{k/2}} e^{i \phi\left(\mathbf{v_0}; t_{k+1}, \dotsc, t_d\right)} W_T(t_{k+1}, \dotsc, t_d) + O\left(\frac{X_1 \dotsm X_k}{R^A}\right), \end{align} $$
$$ \begin{align} & \int_{\mathbb R^k} e^{i\phi\left(t_1, \dotsc, t_d\right)} w_T(t_1, \dotsc, t_d) dt_1 \dotsm dt_k \nonumber \\ &\quad = \frac{X_1 \dotsm X_k}{Y^{k/2}} e^{i \phi\left(\mathbf{v_0}; t_{k+1}, \dotsc, t_d\right)} W_T(t_{k+1}, \dotsc, t_d) + O\left(\frac{X_1 \dotsm X_k}{R^A}\right), \end{align} $$
where
![]() $\mathbf {v_0} \in \mathbb R^k$
is the solution to
$\mathbf {v_0} \in \mathbb R^k$
is the solution to
![]() $\nabla \phi (\mathbf {v_0};t_{k+1}, \dotsc , t_d) = 0$
, with the derivative being with respect to the first k variables only (i.e., the first k entries of
$\nabla \phi (\mathbf {v_0};t_{k+1}, \dotsc , t_d) = 0$
, with the derivative being with respect to the first k variables only (i.e., the first k entries of
![]() $\nabla \phi $
are zero). Here we have trivially integrated each error term over any remaining variables of integration; the arbitrarily large power of R savings nicely allows for this crude treatment of the error terms.
$\nabla \phi $
are zero). Here we have trivially integrated each error term over any remaining variables of integration; the arbitrarily large power of R savings nicely allows for this crude treatment of the error terms.
The following is an Archimedean analogue of the well-known change-of-basis formula from additive to multiplicative characters (compare with [Reference Iwaniec and Kowalski13, equation (3.11)]):
Lemma 4.4. Suppose that
![]() $w_T$
is
$w_T$
is
![]() $1$
-inert, supported on
$1$
-inert, supported on
![]() $x \asymp X$
where
$x \asymp X$
where
![]() $X\gg 1$
. Then
$X\gg 1$
. Then
 $$ \begin{align} e^{-ix} w_T(x) = X^{-1/2} \int_{-t \asymp X} v(t) x^{it} dt + O\left(X^{-100}\right), \end{align} $$
$$ \begin{align} e^{-ix} w_T(x) = X^{-1/2} \int_{-t \asymp X} v(t) x^{it} dt + O\left(X^{-100}\right), \end{align} $$
where
![]() $v(t) = v_{X}(t)$
is some smooth function satisfying
$v(t) = v_{X}(t)$
is some smooth function satisfying
![]() $v(t) \ll 1$
. Moreover,
$v(t) \ll 1$
. Moreover,
![]() $v(t) = e^{-it \log \left (\lvert t\rvert /e\right )} W(t)$
for some
$v(t) = e^{-it \log \left (\lvert t\rvert /e\right )} W(t)$
for some
![]() $1$
-inert function W supported on
$1$
-inert function W supported on
![]() $-t \asymp X$
.
$-t \asymp X$
.
Proof. Let
![]() $f(x) = e^{-ix} w_T(x)$
. By Mellin inversion,
$f(x) = e^{-ix} w_T(x)$
. By Mellin inversion,
 $$ \begin{align} f(x) = \int_{(\sigma)} \frac{\widetilde{f}(-s)}{2\pi i} x^s ds, \quad \text{where} \quad \widetilde{f}(-s) = \int_0^{\infty} e^{-ix} x^{-s} w_T(x) \frac{dx}{x}. \end{align} $$
$$ \begin{align} f(x) = \int_{(\sigma)} \frac{\widetilde{f}(-s)}{2\pi i} x^s ds, \quad \text{where} \quad \widetilde{f}(-s) = \int_0^{\infty} e^{-ix} x^{-s} w_T(x) \frac{dx}{x}. \end{align} $$
Take
![]() $\sigma = 0$
, so
$\sigma = 0$
, so
![]() $s=it$
. Lemma 4.2 implies that
$s=it$
. Lemma 4.2 implies that
 $\widetilde {f}(-it)$
is very small outside of the interval
$\widetilde {f}(-it)$
is very small outside of the interval
![]() $-t \asymp X$
. For
$-t \asymp X$
. For
![]() $-t \asymp X$
, Lemma 4.3 gives
$-t \asymp X$
, Lemma 4.3 gives
 $$ \begin{align} \widetilde{f}(-it) = X^{-1/2} e^{-it \log\left(\lvert t\rvert/e\right)} W(t) + O\left(X^{-200}\right), \end{align} $$
$$ \begin{align} \widetilde{f}(-it) = X^{-1/2} e^{-it \log\left(\lvert t\rvert/e\right)} W(t) + O\left(X^{-200}\right), \end{align} $$
where W is a
![]() $1$
-inert function supported on
$1$
-inert function supported on
![]() $-t \asymp X$
.
$-t \asymp X$
.
For later use, we record some simple consequences of the previous lemmas.
Lemma 4.5. Let
![]() $v(t) = e^{-it \log \left (\lvert t\rvert /e\right )} W(t)$
for some
$v(t) = e^{-it \log \left (\lvert t\rvert /e\right )} W(t)$
for some
![]() $1$
-inert function W supported on
$1$
-inert function W supported on
![]() $-t \asymp X$
with
$-t \asymp X$
with
![]() $X\gg 1$
. Let
$X\gg 1$
. Let
 $\gamma (s) = \pi ^{-s/2} \Gamma \left (\frac {s+\kappa }{2}\right )$
for
$\gamma (s) = \pi ^{-s/2} \Gamma \left (\frac {s+\kappa }{2}\right )$
for
![]() $\kappa \in \{0, 1 \}$
. Let
$\kappa \in \{0, 1 \}$
. Let
![]() $D(s) = \sum _{n=1}^{\infty } a_n n^{-s}$
be a Dirichlet series absolutely convergent for
$D(s) = \sum _{n=1}^{\infty } a_n n^{-s}$
be a Dirichlet series absolutely convergent for
![]() $\mathrm {Re}(s) = 0$
with
$\mathrm {Re}(s) = 0$
with
![]() $\max _{t \in \mathbb R} \lvert D(it)\rvert \leq A$
for some
$\max _{t \in \mathbb R} \lvert D(it)\rvert \leq A$
for some
![]() $A\ge 0$
. Let
$A\ge 0$
. Let
![]() $c_1,c_2,c_3$
be some real numbers (which may vary with X) with
$c_1,c_2,c_3$
be some real numbers (which may vary with X) with
![]() $0 \le c_1\ll 1$
and
$0 \le c_1\ll 1$
and
![]() $ \lvert c_2\rvert X^3+\lvert c_3\rvert \ll X^{1-\delta }$
for some
$ \lvert c_2\rvert X^3+\lvert c_3\rvert \ll X^{1-\delta }$
for some
![]() $\delta>0$
. For any
$\delta>0$
. For any
![]() $Y> 0$
, we have
$Y> 0$
, we have
 $$ \begin{align} X^{-1/2} \int_{-\infty}^{\infty} v(t) e^{-c_1 it\log\lvert t\rvert+c_2it^3} Y^{it} D(it) dt \ll_{v,A} 1 \end{align} $$
$$ \begin{align} X^{-1/2} \int_{-\infty}^{\infty} v(t) e^{-c_1 it\log\lvert t\rvert+c_2it^3} Y^{it} D(it) dt \ll_{v,A} 1 \end{align} $$
and
 $$ \begin{align} X^{-1/2} \int_{-\infty}^{\infty} v(t) e^{-c_1i t\log\lvert t\rvert+c_2it^3} \frac{\gamma(1/2-i(t+c_3))}{\gamma(1/2+i(t+c_3))} Y^{it} D(it) dt \ll_{v,A} 1. \end{align} $$
$$ \begin{align} X^{-1/2} \int_{-\infty}^{\infty} v(t) e^{-c_1i t\log\lvert t\rvert+c_2it^3} \frac{\gamma(1/2-i(t+c_3))}{\gamma(1/2+i(t+c_3))} Y^{it} D(it) dt \ll_{v,A} 1. \end{align} $$
The bounds depend only on v and A.
Proof. Expanding out the Dirichlet series, and exchanging summation and integration, it suffices to prove the result with
![]() $D(s)=1$
. We first consider formula (4.10), which is an oscillatory integral with phase
$D(s)=1$
. We first consider formula (4.10), which is an oscillatory integral with phase
Note that the leading phase points in the direction
![]() $-t\log \lvert t\rvert $
. For
$-t\log \lvert t\rvert $
. For
![]() $\lvert t\rvert \asymp X$
we have
$\lvert t\rvert \asymp X$
we have
 $\phi '(t) = -(1+c_1) \log {\lvert t\rvert } + \log (Y) -c_1 + O\left (X^{-\delta }\right )$
. Lemma 4.2 shows that the left-hand side of formula (4.10) is very small unless
$\phi '(t) = -(1+c_1) \log {\lvert t\rvert } + \log (Y) -c_1 + O\left (X^{-\delta }\right )$
. Lemma 4.2 shows that the left-hand side of formula (4.10) is very small unless
![]() $\log {Y} = (1+c_1) \log {X} + O(1)$
, for a sufficiently large implied constant. On the other hand, if
$\log {Y} = (1+c_1) \log {X} + O(1)$
, for a sufficiently large implied constant. On the other hand, if
![]() $\log {Y} = (1+c_1) \log {X} + O(1)$
, then
$\log {Y} = (1+c_1) \log {X} + O(1)$
, then
![]() $\phi '(t) = -(1+c_1) \log (\lvert t\rvert /X) - (1+c_1) \log {X} + \log (Y) +O(1)= O(1)$
. We may then use Lemma 4.3 to show the claimed bound (4.10).
$\phi '(t) = -(1+c_1) \log (\lvert t\rvert /X) - (1+c_1) \log {X} + \log (Y) +O(1)= O(1)$
. We may then use Lemma 4.3 to show the claimed bound (4.10).
For the second bound (4.11), we first observe that by Stirling’s formula we have
 $$ \begin{align*} \frac{\gamma(1/2-i(t+c_3))}{\gamma(1/2+i(t+c_3))} = W(t) e^{- i \left(t+c_3\right) \log\left\lvert t+c_3\right\rvert + cit} + O\left(X^{-200}\right) \end{align*} $$
$$ \begin{align*} \frac{\gamma(1/2-i(t+c_3))}{\gamma(1/2+i(t+c_3))} = W(t) e^{- i \left(t+c_3\right) \log\left\lvert t+c_3\right\rvert + cit} + O\left(X^{-200}\right) \end{align*} $$
for some
![]() $1$
-inert function W and some
$1$
-inert function W and some
![]() $c \in \mathbb R$
. With the phase of this gamma ratio pointing in the same direction as
$c \in \mathbb R$
. With the phase of this gamma ratio pointing in the same direction as
![]() $-t\log \lvert t\rvert $
, we can repeat the same argument as before to show square-root cancellation.
$-t\log \lvert t\rvert $
, we can repeat the same argument as before to show square-root cancellation.
We end this section with some heuristic motivation for the bound in formula (4.11), and how it is related to expression (1.11) from the sketch. Let w be a fixed inert function,
![]() $C \gg 1$
, and
$C \gg 1$
, and
![]() $P:=A/C \gg 1$
. By Poisson summation, we have
$P:=A/C \gg 1$
. By Poisson summation, we have
 $$ \begin{align} S := \sum_{c=1}^{\infty} e\left(-\frac{A}{c}\right) w(c/C) = \sum_q \int_{-\infty}^{\infty} e\left(-\frac{A}{t} - qt \right) w(t/C) dt. \end{align} $$
$$ \begin{align} S := \sum_{c=1}^{\infty} e\left(-\frac{A}{c}\right) w(c/C) = \sum_q \int_{-\infty}^{\infty} e\left(-\frac{A}{t} - qt \right) w(t/C) dt. \end{align} $$
Integration by parts and stationary phase tells us that the sum is essentially supported on
 $q \asymp \frac {A}{C^2}$
, in which case the integral is bounded by
$q \asymp \frac {A}{C^2}$
, in which case the integral is bounded by
 $\frac {C}{\sqrt {P}}$
. An alternative (and admittedly more roundabout!) way to accomplish this same goal is to use Lemma 4.4 with
$\frac {C}{\sqrt {P}}$
. An alternative (and admittedly more roundabout!) way to accomplish this same goal is to use Lemma 4.4 with
 $x = 2 \pi \frac {A}{c}$
and the functional equation of the Riemann zeta function (shifting contours appropriately). The dual sum will have a test function of the form on the left-hand side of formula (4.11) (with
$x = 2 \pi \frac {A}{c}$
and the functional equation of the Riemann zeta function (shifting contours appropriately). The dual sum will have a test function of the form on the left-hand side of formula (4.11) (with
![]() $c_3=0$
, in fact), and the bound in formula (4.11) is consistent with the simpler Fourier analysis just presented. The reader may wonder, then, why we have proceeded in this more complicated fashion if the Fourier approach is simpler. The answer is that the actual sums we encounter in this paper are arithmetically much more intricate than the simplified one presented in formula (4.12). The Mellin-transform approach is better suited to handling the more complicated arithmetical features that are present in our problem, so on the whole, taking into account both the analytic and arithmetic aspects of the problem, it is simpler.
$c_3=0$
, in fact), and the bound in formula (4.11) is consistent with the simpler Fourier analysis just presented. The reader may wonder, then, why we have proceeded in this more complicated fashion if the Fourier approach is simpler. The answer is that the actual sums we encounter in this paper are arithmetically much more intricate than the simplified one presented in formula (4.12). The Mellin-transform approach is better suited to handling the more complicated arithmetical features that are present in our problem, so on the whole, taking into account both the analytic and arithmetic aspects of the problem, it is simpler.
5. Character sum evaluations
We need the following elementary character sum calculations. Define the Gauss sum
 $$ \begin{align} G\left(\frac{a}{c}\right) = \sum_{x \negthickspace \negthickspace \pmod{c}} e_c\left(ax^2\right). \end{align} $$
$$ \begin{align} G\left(\frac{a}{c}\right) = \sum_{x \negthickspace \negthickspace \pmod{c}} e_c\left(ax^2\right). \end{align} $$
We need to evaluate
![]() $G(a/c)$
. It is well known (see, e.g., [Reference Iwaniec and Kowalski13, equations (3.22) and (3.38)]) that
$G(a/c)$
. It is well known (see, e.g., [Reference Iwaniec and Kowalski13, equations (3.22) and (3.38)]) that
 $$ \begin{align} G\left(\frac{a}{c}\right) = \left(\frac{a}{c}\right) \epsilon_c \sqrt{c}, \qquad \epsilon_c = \begin{cases} 1, & c \equiv 1 \pmod{4}, \\ i, & c \equiv 3 \pmod{4}, \end{cases} \end{align} $$
$$ \begin{align} G\left(\frac{a}{c}\right) = \left(\frac{a}{c}\right) \epsilon_c \sqrt{c}, \qquad \epsilon_c = \begin{cases} 1, & c \equiv 1 \pmod{4}, \\ i, & c \equiv 3 \pmod{4}, \end{cases} \end{align} $$
provided
![]() $(2a,c) = 1$
. The case with c even is treated as follows. Let
$(2a,c) = 1$
. The case with c even is treated as follows. Let
![]() $\delta \in \{0,1\}$
indicate the parity of the highest power of
$\delta \in \{0,1\}$
indicate the parity of the highest power of
![]() $2$
dividing c, as follows: If
$2$
dividing c, as follows: If
![]() $2^{v_2}\Vert c$
then let
$2^{v_2}\Vert c$
then let
From the context, this should not be confused with usages where
![]() $\delta $
is a small positive constant or the
$\delta $
is a small positive constant or the
![]() $\delta (P)$
function, which equals
$\delta (P)$
function, which equals
![]() $1$
when a statement P is true and
$1$
when a statement P is true and
![]() $0$
otherwise.
$0$
otherwise.
Lemma 5.1. Suppose
![]() $c=2^k c_o$
with
$c=2^k c_o$
with
![]() $k \geq 2$
,
$k \geq 2$
,
![]() $c_o$
odd, and
$c_o$
odd, and
![]() $\delta $
is as in equation (5.3). Suppose also
$\delta $
is as in equation (5.3). Suppose also
![]() $(a,c)=1$
. Then
$(a,c)=1$
. Then
 $$ \begin{align} G\left(\frac{a}{c}\right) = \epsilon_{c_o} c^{1/2} \left(\frac{a 2^{\delta}}{c_o}\right) \begin{cases} 1 + e_4(a c_o), & \delta=0, \\ 2^{1/2} e_8(a c_o), & \delta=1. \end{cases} \end{align} $$
$$ \begin{align} G\left(\frac{a}{c}\right) = \epsilon_{c_o} c^{1/2} \left(\frac{a 2^{\delta}}{c_o}\right) \begin{cases} 1 + e_4(a c_o), & \delta=0, \\ 2^{1/2} e_8(a c_o), & \delta=1. \end{cases} \end{align} $$
Proof. First we note that if
![]() $c = c_1 c_2$
with
$c = c_1 c_2$
with
![]() $(c_1, c_2) = 1$
, then
$(c_1, c_2) = 1$
, then
 $$ \begin{align} G\left(\frac{a}{c_1 c_2}\right) = G\left(\frac{a c_2}{c_1 }\right) G\left(\frac{a c_1}{c_2 }\right). \end{align} $$
$$ \begin{align} G\left(\frac{a}{c_1 c_2}\right) = G\left(\frac{a c_2}{c_1 }\right) G\left(\frac{a c_1}{c_2 }\right). \end{align} $$
Suppose that
![]() $c= 2^k$
with
$c= 2^k$
with
![]() $k \geq 2$
. Let j be an integer so that
$k \geq 2$
. Let j be an integer so that
![]() $2j \geq k$
, and write
$2j \geq k$
, and write
![]() $x = u + 2^j v$
with u running modulo
$x = u + 2^j v$
with u running modulo
![]() $2^j$
and v running modulo
$2^j$
and v running modulo
![]() $2^{k-j}$
. Then
$2^{k-j}$
. Then
 $$ \begin{align} G\left(\frac{a}{2^k}\right) = \sum_{u \negthickspace \negthickspace \pmod{2^j}} e_{2^k}\left(au^2\right) \sum_{v \negthickspace \negthickspace \pmod{2^{k-j}}} e_{2^{k-j-1}}(a uv). \end{align} $$
$$ \begin{align} G\left(\frac{a}{2^k}\right) = \sum_{u \negthickspace \negthickspace \pmod{2^j}} e_{2^k}\left(au^2\right) \sum_{v \negthickspace \negthickspace \pmod{2^{k-j}}} e_{2^{k-j-1}}(a uv). \end{align} $$
The inner sum over v vanishes unless
![]() $u \equiv 0 \pmod {2^{k-j-1}}$
, so we change variables
$u \equiv 0 \pmod {2^{k-j-1}}$
, so we change variables
![]() $u = 2^{k-j-1} r$
, with r now running modulo
$u = 2^{k-j-1} r$
, with r now running modulo
![]() $2^{2j-k+1}$
. This gives
$2^{2j-k+1}$
. This gives
 $$ \begin{align} G\left(\frac{a}{2^k}\right) = 2^{k-j} \sum_{r \negthickspace \negthickspace \pmod{2^{2j-k+1}}} e_{2^{2j-k+2}}\left(ar^2\right). \end{align} $$
$$ \begin{align} G\left(\frac{a}{2^k}\right) = 2^{k-j} \sum_{r \negthickspace \negthickspace \pmod{2^{2j-k+1}}} e_{2^{2j-k+2}}\left(ar^2\right). \end{align} $$
In the case that k is even, we make the choice
![]() $j=k/2$
, giving
$j=k/2$
, giving
 $$ \begin{align} G\left(\frac{a}{2^k}\right) = 2^{k/2} \sum_{r \negthickspace \negthickspace \pmod{2}} e_4\left(ar^2\right) = 2^{k/2}(1 + e_4(a)). \end{align} $$
$$ \begin{align} G\left(\frac{a}{2^k}\right) = 2^{k/2} \sum_{r \negthickspace \negthickspace \pmod{2}} e_4\left(ar^2\right) = 2^{k/2}(1 + e_4(a)). \end{align} $$
If k is odd, we take
 $j = \frac {k+1}{2}$
, giving now
$j = \frac {k+1}{2}$
, giving now
 $$ \begin{align} G\left(\frac{a}{2^k}\right) = 2^{\frac{k-1}{2}} \sum_{r \negthickspace \negthickspace \pmod{2^2}} e_{2^3}\left(ar^2\right) = 2^{\frac{k+1}{2}} e_{8}(a). \end{align} $$
$$ \begin{align} G\left(\frac{a}{2^k}\right) = 2^{\frac{k-1}{2}} \sum_{r \negthickspace \negthickspace \pmod{2^2}} e_{2^3}\left(ar^2\right) = 2^{\frac{k+1}{2}} e_{8}(a). \end{align} $$
Assembling these facts and using equation (5.2) completes the proof.
Lemma 5.2. Let
![]() $\chi $
be a Dirichlet character modulo q, and suppose
$\chi $
be a Dirichlet character modulo q, and suppose
![]() $d\mid q$
and
$d\mid q$
and
![]() $(a,d) = 1$
. Let
$(a,d) = 1$
. Let
 $$ \begin{align} S_{\chi}(a,d,q) = \sum_{\substack{n \negthickspace \negthickspace \pmod{q} \\ n \equiv a \negthickspace \negthickspace \pmod{d}}} \chi(n). \end{align} $$
$$ \begin{align} S_{\chi}(a,d,q) = \sum_{\substack{n \negthickspace \negthickspace \pmod{q} \\ n \equiv a \negthickspace \negthickspace \pmod{d}}} \chi(n). \end{align} $$
Suppose that
![]() $\chi $
is induced by the primitive character
$\chi $
is induced by the primitive character
![]() $\chi ^*$
modulo
$\chi ^*$
modulo
![]() $q^*$
, and write
$q^*$
, and write
![]() $\chi = \chi ^* \chi _0$
where
$\chi = \chi ^* \chi _0$
where
![]() $\chi _0$
is trivial modulo
$\chi _0$
is trivial modulo
![]() $q_0$
, with
$q_0$
, with
![]() $(q_0, q^*) = 1$
. Then
$(q_0, q^*) = 1$
. Then
![]() $S_{\chi }(a,d,q) = 0$
unless
$S_{\chi }(a,d,q) = 0$
unless
![]() $q^*\mid d$
, in which case
$q^*\mid d$
, in which case
 $$ \begin{align} S_{\chi}(a,d,q) = \frac{q}{d} \chi^*(a) \prod_{\substack{p \mid q_0 \\ p \nmid d}} \left(1-\frac{1}{p}\right). \end{align} $$
$$ \begin{align} S_{\chi}(a,d,q) = \frac{q}{d} \chi^*(a) \prod_{\substack{p \mid q_0 \\ p \nmid d}} \left(1-\frac{1}{p}\right). \end{align} $$
Proof. Suppose
![]() $q = q_1 q_2$
with
$q = q_1 q_2$
with
![]() $(q_1, q_2) = 1$
and correspondingly factor
$(q_1, q_2) = 1$
and correspondingly factor
![]() $d = d_1 d_2$
and
$d = d_1 d_2$
and
![]() $\chi = \chi _1 \chi _2$
with
$\chi = \chi _1 \chi _2$
with
![]() $\chi _i$
modulo
$\chi _i$
modulo
![]() $q_i$
. The Chinese remainder theorem gives
$q_i$
. The Chinese remainder theorem gives
![]() $S_{\chi }(a,d,q) = S_{\chi _1}(a, d_1, q_1) S_{\chi _2}(a, d_2, q_2)$
. Writing
$S_{\chi }(a,d,q) = S_{\chi _1}(a, d_1, q_1) S_{\chi _2}(a, d_2, q_2)$
. Writing
![]() $d= d^* d_0$
where
$d= d^* d_0$
where
![]() $d^* \mid q^*$
and
$d^* \mid q^*$
and
![]() $d_0 \mid q_0$
, we apply this with
$d_0 \mid q_0$
, we apply this with
![]() $q_1 = q^*$
,
$q_1 = q^*$
,
![]() $q_2 = q_0$
,
$q_2 = q_0$
,
![]() $\chi _1 = \chi ^*$
,
$\chi _1 = \chi ^*$
,
![]() $\chi _2 = \chi _0$
,
$\chi _2 = \chi _0$
,
![]() $d_1 = d^*$
, and
$d_1 = d^*$
, and
![]() $d_2 = d_0$
. By the multiplicativity of the right-hand side of equation (5.11), it suffices to prove it for
$d_2 = d_0$
. By the multiplicativity of the right-hand side of equation (5.11), it suffices to prove it for
![]() $\chi ^*$
and
$\chi ^*$
and
![]() $\chi _0$
.
$\chi _0$
.
By [Reference Iwaniec and Kowalski13, equation (3.9)],
![]() $S_{\chi ^*}(a, d^*, q^*) = 0$
unless
$S_{\chi ^*}(a, d^*, q^*) = 0$
unless
![]() $q^*\mid d^*$
, in which case it is given by equation (5.11), so this case is done.
$q^*\mid d^*$
, in which case it is given by equation (5.11), so this case is done.
For the
![]() $\chi _0$
part, we simply use Möbius inversion, giving
$\chi _0$
part, we simply use Möbius inversion, giving
 $$ \begin{align} S_{\chi_0}(a, d_0, q_0) = \sum_{\ell \mid q_0} \mu(\ell) \sum_{\substack{n \negthickspace \negthickspace \pmod{q_0/\ell} \\ \ell n \equiv a \negthickspace \negthickspace \pmod{d_0}}} 1. \end{align} $$
$$ \begin{align} S_{\chi_0}(a, d_0, q_0) = \sum_{\ell \mid q_0} \mu(\ell) \sum_{\substack{n \negthickspace \negthickspace \pmod{q_0/\ell} \\ \ell n \equiv a \negthickspace \negthickspace \pmod{d_0}}} 1. \end{align} $$
Since
![]() $(a,d_0) = 1$
by assumption, this means that we may assume
$(a,d_0) = 1$
by assumption, this means that we may assume
![]() $(\ell , d_0) = 1$
, and then n is uniquely determined modulo
$(\ell , d_0) = 1$
, and then n is uniquely determined modulo
![]() $d_0$
, which divides
$d_0$
, which divides
![]() $q_0/\ell $
, giving
$q_0/\ell $
, giving
 $$ \begin{align} S_{\chi_0}(a, d_0, q_0) = \frac{q_0}{d_0} \sum_{\substack{\ell \mid q_0 \\ (\ell, d_0) =1}} \frac{\mu(\ell)}{\ell} = \frac{q_0}{d_0} \prod_{\substack{p \mid q_0 \\ p \nmid d_0}} \left(1-\frac{1}{p}\right).\end{align} $$
$$ \begin{align} S_{\chi_0}(a, d_0, q_0) = \frac{q_0}{d_0} \sum_{\substack{\ell \mid q_0 \\ (\ell, d_0) =1}} \frac{\mu(\ell)}{\ell} = \frac{q_0}{d_0} \prod_{\substack{p \mid q_0 \\ p \nmid d_0}} \left(1-\frac{1}{p}\right).\end{align} $$
For
![]() $a,b,c \in \mathbb Z$
with
$a,b,c \in \mathbb Z$
with
![]() $c \geq 1$
, define
$c \geq 1$
, define
 $$ \begin{align} T(a,b;c) = \sum_{x,y \negthickspace \negthickspace \pmod{c}} S\left(x^2, y^2;c\right) e_c(2xy + ax + b y). \end{align} $$
$$ \begin{align} T(a,b;c) = \sum_{x,y \negthickspace \negthickspace \pmod{c}} S\left(x^2, y^2;c\right) e_c(2xy + ax + b y). \end{align} $$
For
![]() $c_o$
odd, write its prime factorization as
$c_o$
odd, write its prime factorization as
 $c_o = \prod _{p} p^{a_p} \prod _q q^{b_q}$
, where each
$c_o = \prod _{p} p^{a_p} \prod _q q^{b_q}$
, where each
![]() $a_p$
is odd and each
$a_p$
is odd and each
![]() $b_q$
is even. Let
$b_q$
is even. Let
 $c^* = \prod _p p$
and
$c^* = \prod _p p$
and
 $c_{\square } = \prod _q q$
. Then
$c_{\square } = \prod _q q$
. Then
![]() $c^*$
is the conductor of the Jacobi symbol
$c^*$
is the conductor of the Jacobi symbol
 $\left (\tfrac {\cdot }{c_o}\right )$
.
$\left (\tfrac {\cdot }{c_o}\right )$
.
Lemma 5.3. Set
![]() $a, b, c \in \mathbb Z$
, with
$a, b, c \in \mathbb Z$
, with
![]() $c \geq 1$
. Suppose
$c \geq 1$
. Suppose
![]() $c= 2^j c_o$
with
$c= 2^j c_o$
with
![]() $j \geq 4$
and
$j \geq 4$
and
![]() $c_o$
odd, with
$c_o$
odd, with
![]() $\delta $
defined as in equation (5.3). Define
$\delta $
defined as in equation (5.3). Define
 $a' = \frac {a}{(a,c)}$
,
$a' = \frac {a}{(a,c)}$
,
 $b' = \frac {b}{(b,c)}$
. Then
$b' = \frac {b}{(b,c)}$
. Then
![]() $T(a,b;c) = 0$
unless
$T(a,b;c) = 0$
unless
![]() $4\mid (a,b)$
and
$4\mid (a,b)$
and
![]() $(a,c) = (b,c)$
, in which case
$(a,c) = (b,c)$
, in which case
 $$ \begin{align} T(a,b;c) = \left(a,\frac{c}{2^{2+\delta}}\right) c^{3/2} e_c(-ab/4) \left(\frac{a'b'}{c^*}\right)\! g_{\delta}(a',b', c_o) \delta\left(c^*\mid\frac{c_o}{(a,c_o)}\right)\! \prod_{\substack{p \mid c_{\square}, \thinspace p \nmid \frac{c_o}{(a,c_o)}}} (1-p^{-1}), \end{align} $$
$$ \begin{align} T(a,b;c) = \left(a,\frac{c}{2^{2+\delta}}\right) c^{3/2} e_c(-ab/4) \left(\frac{a'b'}{c^*}\right)\! g_{\delta}(a',b', c_o) \delta\left(c^*\mid\frac{c_o}{(a,c_o)}\right)\! \prod_{\substack{p \mid c_{\square}, \thinspace p \nmid \frac{c_o}{(a,c_o)}}} (1-p^{-1}), \end{align} $$
where
![]() $g_{\delta }$
is some function depending on
$g_{\delta }$
is some function depending on
![]() $a',b',c_o$
modulo
$a',b',c_o$
modulo
![]() $2^{2+\delta }$
that additionally depends on
$2^{2+\delta }$
that additionally depends on
 $\left (\frac {2^j}{\left (a,2^j\right )}, 2^{2+\delta }\right )$
. In particular, we have
$\left (\frac {2^j}{\left (a,2^j\right )}, 2^{2+\delta }\right )$
. In particular, we have
![]() $T(0,b;c) \ll c^{5/2} \delta (c^* = 1) \delta (c\mid b)$
.
$T(0,b;c) \ll c^{5/2} \delta (c^* = 1) \delta (c\mid b)$
.
Proof. We have
 $$ \begin{align} T(a,b;c) = \sideset{}{^*}\sum_{t \negthickspace \negthickspace \pmod{c}} \sum_{x,y \negthickspace \negthickspace \pmod{c}} e_c\left(t\left(x + \overline{t} y\right)^2 + ax + by\right). \end{align} $$
$$ \begin{align} T(a,b;c) = \sideset{}{^*}\sum_{t \negthickspace \negthickspace \pmod{c}} \sum_{x,y \negthickspace \negthickspace \pmod{c}} e_c\left(t\left(x + \overline{t} y\right)^2 + ax + by\right). \end{align} $$
Changing variables
![]() $x \rightarrow x- \overline {t} y$
and evaluating the resulting y sum by orthogonality, we deduce
$x \rightarrow x- \overline {t} y$
and evaluating the resulting y sum by orthogonality, we deduce
 $$ \begin{align} T(a,b;c) = c \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c} \\ bt \equiv a \negthickspace \negthickspace \pmod{c}}} \sum_{x \negthickspace \negthickspace \pmod{c}} e_c\left(tx^2 + ax\right). \end{align} $$
$$ \begin{align} T(a,b;c) = c \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c} \\ bt \equiv a \negthickspace \negthickspace \pmod{c}}} \sum_{x \negthickspace \negthickspace \pmod{c}} e_c\left(tx^2 + ax\right). \end{align} $$
The congruence in the sum implies that
![]() $T(a,b;c) = 0$
unless
$T(a,b;c) = 0$
unless
![]() $(a,c) = (b,c)$
, a condition that we henceforth assume. Changing variables
$(a,c) = (b,c)$
, a condition that we henceforth assume. Changing variables
![]() $x \rightarrow x + c/2$
also shows that
$x \rightarrow x + c/2$
also shows that
![]() $T(a,b;c) = 0$
unless
$T(a,b;c) = 0$
unless
![]() $2\mid a$
, so we assume this condition also.
$2\mid a$
, so we assume this condition also.
Write c uniquely as
![]() $c = c_1 c_2$
, where
$c = c_1 c_2$
, where
![]() $c\mid c_1^2$
,
$c\mid c_1^2$
,
![]() $c_2 \mid c_1$
, and
$c_2 \mid c_1$
, and
![]() $c_1/c_2$
is square-free (another way to see this factorization is by writing c uniquely as
$c_1/c_2$
is square-free (another way to see this factorization is by writing c uniquely as
![]() $AB^2$
with A square-free; then
$AB^2$
with A square-free; then
![]() $c_1 = AB$
and
$c_1 = AB$
and
![]() $c_2 = B$
). Observe that
$c_2 = B$
). Observe that
![]() $2^2\mid c_2$
from
$2^2\mid c_2$
from
![]() $2^4\mid c$
. Let
$2^4\mid c$
. Let
![]() $x = x_1 + c_1 x_2$
, and let
$x = x_1 + c_1 x_2$
, and let
![]() $Q(x) = tx^2 + ax$
. Note that
$Q(x) = tx^2 + ax$
. Note that
 $$ \begin{align} Q(x_1 + c_1 x_2) = Q(x_1) + Q'(x_1) c_1 x_2 + \tfrac{Q''\left(x_1\right)}{2} c_1^2 x_2^2 \equiv Q(x_1) + Q'(x_1) c_1 x_2 \pmod{c}. \end{align} $$
$$ \begin{align} Q(x_1 + c_1 x_2) = Q(x_1) + Q'(x_1) c_1 x_2 + \tfrac{Q''\left(x_1\right)}{2} c_1^2 x_2^2 \equiv Q(x_1) + Q'(x_1) c_1 x_2 \pmod{c}. \end{align} $$
Thus
 $$ \begin{align} \sum_{x \negthickspace \negthickspace \pmod{c}} e_c(Q(x)) &= \sum_{x_1 \negthickspace \negthickspace \pmod{c_1}} e_c(Q(x_1)) \sum_{x_2 \negthickspace \negthickspace \pmod{c_2}} e_{c_2}(Q'(x_1) x_2) \nonumber \\ &= c_2 \sum_{\substack{x_1 \negthickspace \negthickspace \pmod{c_1} \\ Q'(x_1) \equiv 0 \negthickspace \negthickspace \pmod{c_2}}} e_c(Q(x_1)). \end{align} $$
$$ \begin{align} \sum_{x \negthickspace \negthickspace \pmod{c}} e_c(Q(x)) &= \sum_{x_1 \negthickspace \negthickspace \pmod{c_1}} e_c(Q(x_1)) \sum_{x_2 \negthickspace \negthickspace \pmod{c_2}} e_{c_2}(Q'(x_1) x_2) \nonumber \\ &= c_2 \sum_{\substack{x_1 \negthickspace \negthickspace \pmod{c_1} \\ Q'(x_1) \equiv 0 \negthickspace \negthickspace \pmod{c_2}}} e_c(Q(x_1)). \end{align} $$
In our case,
![]() $Q'(x_1) = 2tx_1 + a$
, so the congruence means
$Q'(x_1) = 2tx_1 + a$
, so the congruence means
![]() $2x_1 \equiv - \overline {t} a \pmod {c_2}$
. Since
$2x_1 \equiv - \overline {t} a \pmod {c_2}$
. Since
![]() $2\mid a$
and
$2\mid a$
and
![]() $2\mid c_2$
, this is equivalent to
$2\mid c_2$
, this is equivalent to
![]() $x_1 \equiv - \overline {t} \frac {a}{2} \pmod {c_2/2}$
. Writing
$x_1 \equiv - \overline {t} \frac {a}{2} \pmod {c_2/2}$
. Writing
![]() $x_1 = - \overline {t} \frac {a}{2} + \frac {c_2}{2} v$
, with v running modulo
$x_1 = - \overline {t} \frac {a}{2} + \frac {c_2}{2} v$
, with v running modulo
![]() $2 \frac {c_1}{c_2}$
, we obtain
$2 \frac {c_1}{c_2}$
, we obtain
 $$ \begin{align} \sum_{x \negthickspace \negthickspace \pmod{c}} e_c(Q(x)) = c_2 e_c\left(- \overline{t} a^2/4\right) \sum_{v \negthickspace \negthickspace \pmod{2 \frac{c_1}{c_2}}} e\left(\frac{t v^2}{4 c_1/c_2}\right). \end{align} $$
$$ \begin{align} \sum_{x \negthickspace \negthickspace \pmod{c}} e_c(Q(x)) = c_2 e_c\left(- \overline{t} a^2/4\right) \sum_{v \negthickspace \negthickspace \pmod{2 \frac{c_1}{c_2}}} e\left(\frac{t v^2}{4 c_1/c_2}\right). \end{align} $$
While the exponential in the inner sum has modulus
![]() $4c_1/c_2$
, the sum is only over
$4c_1/c_2$
, the sum is only over
![]() $0 \le v \le 2(c_1/c_2) -1$
. However, observe that the exponential has the same values at
$0 \le v \le 2(c_1/c_2) -1$
. However, observe that the exponential has the same values at
![]() $1\le -v \le 2(c_1/c_2)$
, so that the inner sum is half of a Gauss sum. Thus
$1\le -v \le 2(c_1/c_2)$
, so that the inner sum is half of a Gauss sum. Thus
 $$ \begin{align} T(a,b;c) = c \frac{c_2}{2} \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c} \\ bt \equiv a \negthickspace \negthickspace \pmod{c}}} e_c\left(- \overline{t} a^2/4\right) G\left(\frac{t}{4 c_1/c_2}\right). \end{align} $$
$$ \begin{align} T(a,b;c) = c \frac{c_2}{2} \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c} \\ bt \equiv a \negthickspace \negthickspace \pmod{c}}} e_c\left(- \overline{t} a^2/4\right) G\left(\frac{t}{4 c_1/c_2}\right). \end{align} $$
By Lemma 5.1, we deduce
 $$ \begin{align} T(a,b;c) = c^{3/2} \epsilon_{c_o} \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c} \\ bt \equiv a \negthickspace \negthickspace \pmod{c}}} e_c\left(- \overline{t} a^2/4\right) \left(\frac{t 2^{\delta}}{c_{o}}\right) \begin{cases} 1 + e_4(t c_o), & \delta=0, \\ 2^{1/2} e_8(t c_o), & \delta=1. \end{cases} \end{align} $$
$$ \begin{align} T(a,b;c) = c^{3/2} \epsilon_{c_o} \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c} \\ bt \equiv a \negthickspace \negthickspace \pmod{c}}} e_c\left(- \overline{t} a^2/4\right) \left(\frac{t 2^{\delta}}{c_{o}}\right) \begin{cases} 1 + e_4(t c_o), & \delta=0, \\ 2^{1/2} e_8(t c_o), & \delta=1. \end{cases} \end{align} $$
This formulation contains a few additional observations. We have used the fact that the Jacobi symbol
 $\left (\frac {t}{\left (c_1/c_2\right )_o}\right )$
agrees with
$\left (\frac {t}{\left (c_1/c_2\right )_o}\right )$
agrees with
 $\left (\frac {t}{c_o}\right )$
for t coprime to c, where
$\left (\frac {t}{c_o}\right )$
for t coprime to c, where
![]() $n_o$
is the odd part of an integer n. We have also used the fact that
$n_o$
is the odd part of an integer n. We have also used the fact that
![]() $(c_1/c_2)_o$
and
$(c_1/c_2)_o$
and
![]() $c_o$
have the same values modulo
$c_o$
have the same values modulo
![]() $8$
. Thus we can replace
$8$
. Thus we can replace
![]() $\epsilon _{\left (c_1/c_2\right )_o}$
,
$\epsilon _{\left (c_1/c_2\right )_o}$
,
![]() $e_4(t (c_1/c_2)_o)$
, and
$e_4(t (c_1/c_2)_o)$
, and
![]() $e_8(t (c_1/c_2)_o)$
with
$e_8(t (c_1/c_2)_o)$
with
![]() $\epsilon _{c_o}$
,
$\epsilon _{c_o}$
,
![]() $e_4(t c_o)$
, and
$e_4(t c_o)$
, and
![]() $e_8(t c_o)$
, respectively. These observations can easily be checked by using multiplicativity to reduce to the case when c is a power of an odd prime. If
$e_8(t c_o)$
, respectively. These observations can easily be checked by using multiplicativity to reduce to the case when c is a power of an odd prime. If
![]() $c=p^l$
, then
$c=p^l$
, then
![]() $c_1/c_2=1$
when l is even and
$c_1/c_2=1$
when l is even and
![]() $c_1/c_2=p$
when l is odd.
$c_1/c_2=p$
when l is odd.
Next we turn to the t sum in equation (5.22). Suppose first that
![]() $2\Vert a$
. Let
$2\Vert a$
. Let
 $a' = \frac {a}{(a,c)}$
and
$a' = \frac {a}{(a,c)}$
and
 $b' = \frac {b}{(a,c)}$
. The congruence
$b' = \frac {b}{(a,c)}$
. The congruence
![]() $bt \equiv a \pmod {c}$
uniquely determines t modulo
$bt \equiv a \pmod {c}$
uniquely determines t modulo
![]() $c/(a,c)$
, since it is equivalent to
$c/(a,c)$
, since it is equivalent to
![]() $\overline {t} \equiv b'\overline {a'} \pmod {c/(a,c)}$
. Now in the t sum, one can pair up
$\overline {t} \equiv b'\overline {a'} \pmod {c/(a,c)}$
. Now in the t sum, one can pair up
![]() $\overline {t}$
with
$\overline {t}$
with
![]() $\overline {t}+c/2$
and observe that the corresponding values of the exponential
$\overline {t}+c/2$
and observe that the corresponding values of the exponential
 $e_c\left (- \overline {t} a^2/4\right )$
will cancel out, since
$e_c\left (- \overline {t} a^2/4\right )$
will cancel out, since
 $e_c\left (- (c/2) a^2/4\right )=-1$
. Also, the values of
$e_c\left (- (c/2) a^2/4\right )=-1$
. Also, the values of
 $\left (\frac {t}{c_o}\right )=\left (\frac {\overline {t}}{c_o}\right )$
,
$\left (\frac {t}{c_o}\right )=\left (\frac {\overline {t}}{c_o}\right )$
,
 $e_4(t c_o)=e_4\left (\overline {t} c_o\right )$
, and
$e_4(t c_o)=e_4\left (\overline {t} c_o\right )$
, and
 $e_8(t c_o)=e_8\left (\overline {t} c_o\right )$
remain the same under
$e_8(t c_o)=e_8\left (\overline {t} c_o\right )$
remain the same under
![]() $\overline {t}\to \overline {t}+c/2$
, since by assumption
$\overline {t}\to \overline {t}+c/2$
, since by assumption
![]() $2^4\mid c$
. Therefore,
$2^4\mid c$
. Therefore,
![]() $T(a,b,c)$
vanishes unless
$T(a,b,c)$
vanishes unless
![]() $4\mid a$
(and hence
$4\mid a$
(and hence
![]() $4\mid b$
), which we now assume to be the case. This allows the convenient simplification
$4\mid b$
), which we now assume to be the case. This allows the convenient simplification
 $e_c\left (-\overline {t} a^2/4\right ) = e_c(-ab/4)$
.
$e_c\left (-\overline {t} a^2/4\right ) = e_c(-ab/4)$
.
Breaking up the t sum into congruence classes modulo
![]() $2^{2+\delta }$
, to uniquely determine
$2^{2+\delta }$
, to uniquely determine
![]() $e_{2^{2+\delta }}(t c_o)$
, we obtain
$e_{2^{2+\delta }}(t c_o)$
, we obtain
 $$ \begin{align} T(a,b;c) = c^{3/2} \epsilon_{c_o} e_c(- ab/4) \sideset{}{^*}\sum_{v \negthickspace \negthickspace \pmod{2^{2+\delta}}} \left \{ \begin{aligned} 1 + e_4(v c_o) \\ 2^{1/2} e_8(v c_o) \end{aligned}\right\} \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c} \\ t \equiv \overline{b'} a' \negthickspace \negthickspace \pmod{\frac{c}{(a,c)}} \\ t \equiv v \negthickspace \negthickspace \pmod{2^{2+\delta}} }} \left(\frac{t 2^{\delta}}{c_{o}}\right). \end{align} $$
$$ \begin{align} T(a,b;c) = c^{3/2} \epsilon_{c_o} e_c(- ab/4) \sideset{}{^*}\sum_{v \negthickspace \negthickspace \pmod{2^{2+\delta}}} \left \{ \begin{aligned} 1 + e_4(v c_o) \\ 2^{1/2} e_8(v c_o) \end{aligned}\right\} \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c} \\ t \equiv \overline{b'} a' \negthickspace \negthickspace \pmod{\frac{c}{(a,c)}} \\ t \equiv v \negthickspace \negthickspace \pmod{2^{2+\delta}} }} \left(\frac{t 2^{\delta}}{c_{o}}\right). \end{align} $$
For the congruence
 $t \equiv \overline {b'}a' \pmod {\frac {c}{(a,c)}}$
to be consistent with
$t \equiv \overline {b'}a' \pmod {\frac {c}{(a,c)}}$
to be consistent with
![]() $t \equiv v \pmod {2^{2+\delta }}$
, it is necessary and sufficient that
$t \equiv v \pmod {2^{2+\delta }}$
, it is necessary and sufficient that
 $v \equiv \overline {b'}a' \pmod {\left (\frac {c}{(a,c)}, 2^{2+\delta }\right )}$
.
$v \equiv \overline {b'}a' \pmod {\left (\frac {c}{(a,c)}, 2^{2+\delta }\right )}$
.
Recall that
![]() $c = 2^j c_o$
, where
$c = 2^j c_o$
, where
![]() $j \geq 4$
. Factoring the moduli in the sum, we have
$j \geq 4$
. Factoring the moduli in the sum, we have
 $$ \begin{align} \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c} \\ t \equiv \overline{b'} a' \negthickspace \negthickspace \pmod{\frac{c}{\left(a,c\right)}} \\ t \equiv v \negthickspace \negthickspace \pmod{2^{2+\delta}} }} \left(\frac{t}{c_{o}}\right) = \left(\ \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c_o} \\ t \equiv \overline{b'} a' \negthickspace \negthickspace \pmod{\frac{c_o}{\left(a,c_o\right)}}}} \left(\frac{t}{c_{o}}\right) \right) \left(\sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{2^j} \\ t \equiv \overline{b'} a' \negthickspace \negthickspace \pmod{\frac{2^j}{\left(a,2^j\right)}} \\ t \equiv v \negthickspace \negthickspace \pmod{2^{2+\delta}}}} 1 \right). \end{align} $$
$$ \begin{align} \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c} \\ t \equiv \overline{b'} a' \negthickspace \negthickspace \pmod{\frac{c}{\left(a,c\right)}} \\ t \equiv v \negthickspace \negthickspace \pmod{2^{2+\delta}} }} \left(\frac{t}{c_{o}}\right) = \left(\ \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c_o} \\ t \equiv \overline{b'} a' \negthickspace \negthickspace \pmod{\frac{c_o}{\left(a,c_o\right)}}}} \left(\frac{t}{c_{o}}\right) \right) \left(\sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{2^j} \\ t \equiv \overline{b'} a' \negthickspace \negthickspace \pmod{\frac{2^j}{\left(a,2^j\right)}} \\ t \equiv v \negthickspace \negthickspace \pmod{2^{2+\delta}}}} 1 \right). \end{align} $$
The sum modulo
![]() $2^j$
, by the Chinese remainder theorem and the fact that the condition
$2^j$
, by the Chinese remainder theorem and the fact that the condition
![]() $(t,2)=1$
is automatic because
$(t,2)=1$
is automatic because
![]() $(v,2)=1$
, equals
$(v,2)=1$
, equals
 $$ \begin{align*} \frac{2^j}{\left[\frac{2^j}{\left(a,2^j\right)}, 2^{2+\delta}\right]} = \frac{2^j \left(\frac{2^j}{\left(a,2^j\right)}, 2^{2+\delta}\right)}{\frac{2^j}{\left(a,2^j\right)} 2^{2+\delta}} = \left(a,2^{j-2-\delta}\right), \end{align*} $$
$$ \begin{align*} \frac{2^j}{\left[\frac{2^j}{\left(a,2^j\right)}, 2^{2+\delta}\right]} = \frac{2^j \left(\frac{2^j}{\left(a,2^j\right)}, 2^{2+\delta}\right)}{\frac{2^j}{\left(a,2^j\right)} 2^{2+\delta}} = \left(a,2^{j-2-\delta}\right), \end{align*} $$
provided of course that
 $v \equiv \overline {b'} a' \pmod {\left (\frac {2^j}{\left (a,2^j\right )}, 2^{2+\delta }\right )}$
. Therefore, we have that
$v \equiv \overline {b'} a' \pmod {\left (\frac {2^j}{\left (a,2^j\right )}, 2^{2+\delta }\right )}$
. Therefore, we have that
![]() $T(a,b;c)$
equals
$T(a,b;c)$
equals
 $$ \begin{align} c^{3/2} \epsilon_{c_o} e_c(- ab/4) \left(a, 2^{j-2-\delta}\right) \sideset{}{^*}\sum_{\substack{v \negthickspace \negthickspace \pmod{2^{2+\delta}} \\ v \equiv \overline{b'} a' \negthickspace \negthickspace \pmod{\left(\frac{2^j}{\left(a,2^j\right)}, 2^{2+\delta}\right)}}} \left \{ \begin{aligned} 1 + e_4(v c_o) \\ 2^{1/2} e_8(v c_o) \end{aligned}\right\} \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c_o} \\ t \equiv \overline{b'}a' \negthickspace \negthickspace \pmod{\frac{c_o}{\left(a,c_o\right)}} }} \left(\frac{t 2^{\delta}}{c_{o}}\right). \end{align} $$
$$ \begin{align} c^{3/2} \epsilon_{c_o} e_c(- ab/4) \left(a, 2^{j-2-\delta}\right) \sideset{}{^*}\sum_{\substack{v \negthickspace \negthickspace \pmod{2^{2+\delta}} \\ v \equiv \overline{b'} a' \negthickspace \negthickspace \pmod{\left(\frac{2^j}{\left(a,2^j\right)}, 2^{2+\delta}\right)}}} \left \{ \begin{aligned} 1 + e_4(v c_o) \\ 2^{1/2} e_8(v c_o) \end{aligned}\right\} \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c_o} \\ t \equiv \overline{b'}a' \negthickspace \negthickspace \pmod{\frac{c_o}{\left(a,c_o\right)}} }} \left(\frac{t 2^{\delta}}{c_{o}}\right). \end{align} $$
By Lemma 5.2, with
![]() $q= c_o$
,
$q= c_o$
,
 $d = \frac {c_o}{\left (a,c_o\right )}$
,
$d = \frac {c_o}{\left (a,c_o\right )}$
,
![]() $a = \overline {b'} a'$
,
$a = \overline {b'} a'$
,
![]() $q^* = c^*$
, and
$q^* = c^*$
, and
![]() $q_0 = c_{\square }$
, we have
$q_0 = c_{\square }$
, we have
 $$ \begin{align} \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c_o} \\ t \equiv \overline{b'}a' \negthickspace \negthickspace \pmod{\frac{c_o}{\left(a,c_o\right)}} }} \left(\frac{t}{c_{o}}\right) = (a,c_o) \left(\frac{a' b'}{c^*}\right) \delta\left(c^*\mid\frac{c_o}{(a,c_o)}\right) \prod_{\substack{p \mid c_{\square} \\ p \nmid \frac{c_o}{\left(a,c_o\right)}}} \left(1-p^{-1}\right). \end{align} $$
$$ \begin{align} \sideset{}{^*}\sum_{\substack{t \negthickspace \negthickspace \pmod{c_o} \\ t \equiv \overline{b'}a' \negthickspace \negthickspace \pmod{\frac{c_o}{\left(a,c_o\right)}} }} \left(\frac{t}{c_{o}}\right) = (a,c_o) \left(\frac{a' b'}{c^*}\right) \delta\left(c^*\mid\frac{c_o}{(a,c_o)}\right) \prod_{\substack{p \mid c_{\square} \\ p \nmid \frac{c_o}{\left(a,c_o\right)}}} \left(1-p^{-1}\right). \end{align} $$
Inserting equation (5.26) into expression (5.25) and simplifying a bit using
 $(a, c_o)\left (a, 2^{j-2-\delta }\right ) = \left (a, \frac {c}{2^{2+\delta }}\right )$
, we deduce that
$(a, c_o)\left (a, 2^{j-2-\delta }\right ) = \left (a, \frac {c}{2^{2+\delta }}\right )$
, we deduce that
![]() $T(a,b;c)$
equals
$T(a,b;c)$
equals
 $$ \begin{align} c^{3/2} \epsilon_{c_o} e_c(- ab/4) \left(a,\tfrac{c}{2^{2+\delta}}\right) \left(\frac{a' b' 2^{\delta}}{c^*}\right) \prod_{\substack{p\mid c_{\square} \\ p \nmid \frac{c_o}{\left(a,c_o\right)}}} \left(1-p^{-1}\right) \sideset{}{^*}\sum_{\substack{v \negthickspace \negthickspace \pmod{2^{2+\delta}} \\ v \equiv \overline{b'} a' \negthickspace \negthickspace \pmod{\left(\frac{2^j}{\left(a,2^j\right)}, 2^{2+\delta}\right)}}} \begin{cases} 1 + e_4(v c_o) \\ 2^{1/2} e_8(v c_o) \end{cases} \end{align} $$
$$ \begin{align} c^{3/2} \epsilon_{c_o} e_c(- ab/4) \left(a,\tfrac{c}{2^{2+\delta}}\right) \left(\frac{a' b' 2^{\delta}}{c^*}\right) \prod_{\substack{p\mid c_{\square} \\ p \nmid \frac{c_o}{\left(a,c_o\right)}}} \left(1-p^{-1}\right) \sideset{}{^*}\sum_{\substack{v \negthickspace \negthickspace \pmod{2^{2+\delta}} \\ v \equiv \overline{b'} a' \negthickspace \negthickspace \pmod{\left(\frac{2^j}{\left(a,2^j\right)}, 2^{2+\delta}\right)}}} \begin{cases} 1 + e_4(v c_o) \\ 2^{1/2} e_8(v c_o) \end{cases} \end{align} $$
times the delta function that
![]() $c^*$
divides
$c^*$
divides
 $\frac {c_o}{\left (a,c_o\right )}$
. The inner sum over v is a function of
$\frac {c_o}{\left (a,c_o\right )}$
. The inner sum over v is a function of
![]() $a', b', c_o$
modulo
$a', b', c_o$
modulo
![]() $2^{2+\delta }$
that additionally depends on
$2^{2+\delta }$
that additionally depends on
 $\left (\frac {2^j}{\left (a,2^j\right )}, 2^{2+\delta }\right )$
. In addition,
$\left (\frac {2^j}{\left (a,2^j\right )}, 2^{2+\delta }\right )$
. In addition,
 $\left (\frac {2^{\delta }}{c^*}\right )$
is a function of
$\left (\frac {2^{\delta }}{c^*}\right )$
is a function of
![]() $c_o$
modulo
$c_o$
modulo
![]() $2^{2+\delta }$
.
$2^{2+\delta }$
.
6. Start of proof
Set
![]() $0\le U \le (2-\delta )T$
. By an approximate functional equation, dyadic decomposition of unity, and Cauchy’s inequality, we have
$0\le U \le (2-\delta )T$
. By an approximate functional equation, dyadic decomposition of unity, and Cauchy’s inequality, we have
 $$ \begin{align} \mathcal{M}:= \sum_{T < t_j <T + \Delta} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2+iU\right)\right\rvert^2 \ll \max_{1 \ll N \ll N_{\text{max}}} \frac{ T^{\varepsilon}}{N} \sum_{T < t_j <T + \Delta} \left\lvert \sum_{n} \frac{\lambda_j\left(n^2\right)}{n^{iU}} w_N(n) \right\rvert^2, \end{align} $$
$$ \begin{align} \mathcal{M}:= \sum_{T < t_j <T + \Delta} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2+iU\right)\right\rvert^2 \ll \max_{1 \ll N \ll N_{\text{max}}} \frac{ T^{\varepsilon}}{N} \sum_{T < t_j <T + \Delta} \left\lvert \sum_{n} \frac{\lambda_j\left(n^2\right)}{n^{iU}} w_N(n) \right\rvert^2, \end{align} $$
where
![]() $w_N(x)$
is supported on
$w_N(x)$
is supported on
![]() $x \asymp N$
and satisfies
$x \asymp N$
and satisfies
 $w_N^{\left (j\right )}(x) \ll _j N^{-j}$
and
$w_N^{\left (j\right )}(x) \ll _j N^{-j}$
and
![]() $N_{\text {max}} = (U+1)^{1/2} T^{1+\varepsilon }$
. To save some clutter in the notation, we want to simply write U instead of
$N_{\text {max}} = (U+1)^{1/2} T^{1+\varepsilon }$
. To save some clutter in the notation, we want to simply write U instead of
![]() $U+1$
in all estimates involving U. The reader may accept this as a convention or, when
$U+1$
in all estimates involving U. The reader may accept this as a convention or, when
![]() $0\le U\le 1$
, we can write
$0\le U\le 1$
, we can write
![]() $n^{-iU} w_N(n) = n^{-i(U+1)} n^{i} w_N(n)$
and absorb
$n^{-iU} w_N(n) = n^{-i(U+1)} n^{i} w_N(n)$
and absorb
![]() $n^i$
into
$n^i$
into
![]() $w_N(n)$
by redefining the weight function. Thus we can henceforth assume that
$w_N(n)$
by redefining the weight function. Thus we can henceforth assume that
![]() $U\ge 1$
.
$U\ge 1$
.
Next we insert a weight
 $$ \begin{align} h(t) = \frac{t^2 + \frac14}{T^2} \left[ \exp\left(-\frac{(t-T)^2}{\Delta^2} \right) + \exp\left(-\frac{(t+T)^2}{\Delta^2} \right) \right], \end{align} $$
$$ \begin{align} h(t) = \frac{t^2 + \frac14}{T^2} \left[ \exp\left(-\frac{(t-T)^2}{\Delta^2} \right) + \exp\left(-\frac{(t+T)^2}{\Delta^2} \right) \right], \end{align} $$
write
 $\lambda _j\left (n^2\right )=\rho _j\left (n^2\right )/\rho _j(1)$
, and overextend (by positivity) the spectral sum to an orthonormal basis of all cusp forms of level
$\lambda _j\left (n^2\right )=\rho _j\left (n^2\right )/\rho _j(1)$
, and overextend (by positivity) the spectral sum to an orthonormal basis of all cusp forms of level
![]() $2^4$
, embedding the level
$2^4$
, embedding the level
![]() $1$
forms. This embedding trick, introduced for the purpose of simplifying the
$1$
forms. This embedding trick, introduced for the purpose of simplifying the
![]() $2$
-part of the exponential sum in Lemma 5.3, is motivated from [Reference Blomer4, p. 4]. We also form the obvious Eisenstein series variant on the sum. This leads to the following inequality (see the remarks following Lemma 2.1):
$2$
-part of the exponential sum in Lemma 5.3, is motivated from [Reference Blomer4, p. 4]. We also form the obvious Eisenstein series variant on the sum. This leads to the following inequality (see the remarks following Lemma 2.1):
 $$ \begin{align} \mathcal{M} \ll \max_{1 \ll N \ll N_{\text{max}}} \frac{T^{\varepsilon}}{N} \left( \sum_{u_j \text{ level }2^4} \frac{h\left(t_j\right)}{\cosh\left(\pi t_j\right)} \left\lvert \sum_{n} \frac{\rho_j\left(n^2\right)}{n^{iU}} w_N(n) \right\rvert^2 \right. \nonumber\\ \left. + \sum_{\mathfrak{a}} \frac{1}{4 \pi} \int_{-\infty}^{\infty} \frac{h(t)}{\cosh(\pi t)} \left\lvert \sum_{n} \frac{\tau_{\mathfrak{a}, it}\left(n^2\right)}{n^{iU}} w_N(n) \right\rvert^2 dt \right). \end{align} $$
$$ \begin{align} \mathcal{M} \ll \max_{1 \ll N \ll N_{\text{max}}} \frac{T^{\varepsilon}}{N} \left( \sum_{u_j \text{ level }2^4} \frac{h\left(t_j\right)}{\cosh\left(\pi t_j\right)} \left\lvert \sum_{n} \frac{\rho_j\left(n^2\right)}{n^{iU}} w_N(n) \right\rvert^2 \right. \nonumber\\ \left. + \sum_{\mathfrak{a}} \frac{1}{4 \pi} \int_{-\infty}^{\infty} \frac{h(t)}{\cosh(\pi t)} \left\lvert \sum_{n} \frac{\tau_{\mathfrak{a}, it}\left(n^2\right)}{n^{iU}} w_N(n) \right\rvert^2 dt \right). \end{align} $$
Opening the square and applying the Kuznetsov formula, we obtain
 $$ \begin{align} \mathcal{M} \ll \Delta T^{1+\varepsilon} + \max_{1 \ll N \ll N_{\max}} T^{\varepsilon} \lvert \mathcal{S}(H)\rvert, \end{align} $$
$$ \begin{align} \mathcal{M} \ll \Delta T^{1+\varepsilon} + \max_{1 \ll N \ll N_{\max}} T^{\varepsilon} \lvert \mathcal{S}(H)\rvert, \end{align} $$
where
 $$ \begin{align} \mathcal{S}(H) = \frac{1}{N} \sum_{c \equiv 0 \negthickspace \negthickspace \pmod{2^4}} \sum_{m,n} \frac{S\left(m^2, n^2;c\right)}{c m^{iU} n^{-iU}} w_N(m) w_N(n) H\left(\frac{4 \pi mn}{c}\right), \end{align} $$
$$ \begin{align} \mathcal{S}(H) = \frac{1}{N} \sum_{c \equiv 0 \negthickspace \negthickspace \pmod{2^4}} \sum_{m,n} \frac{S\left(m^2, n^2;c\right)}{c m^{iU} n^{-iU}} w_N(m) w_N(n) H\left(\frac{4 \pi mn}{c}\right), \end{align} $$
 $$ \begin{align} H(x) = i \int_{-\infty}^{\infty} J(x,t) t \tanh(\pi t) h(t) dt, \end{align} $$
$$ \begin{align} H(x) = i \int_{-\infty}^{\infty} J(x,t) t \tanh(\pi t) h(t) dt, \end{align} $$
and
![]() $J(x,t)$
is as defined in Lemma 2.1.
$J(x,t)$
is as defined in Lemma 2.1.
By [Reference Jutila and Motohashi17, equation (3.10)], we get
 $H(x) \ll \frac {\Delta }{T} x^{2}$
for
$H(x) \ll \frac {\Delta }{T} x^{2}$
for
![]() $x\le 1$
. Using this with
$x\le 1$
. Using this with
![]() $x=4\pi mn/c$
, we can truncate c at some large power of T, say
$x=4\pi mn/c$
, we can truncate c at some large power of T, say
![]() $c \le T^{100}$
, with an acceptable error term.
$c \le T^{100}$
, with an acceptable error term.
Using [Reference Gradshteyn, Ryzhik, Jeffrey and Zwillinger10, section 8.411 equation 11] and the fact that the integrand in equation (6.6) is an even function of t, one can derive as in [Reference Jutila and Motohashi17, eqaution (3.13)] that
 $H(x) = \frac {2}{\pi } \mathrm {Re}(H_{0}(x))$
, where
$H(x) = \frac {2}{\pi } \mathrm {Re}(H_{0}(x))$
, where
 $$ \begin{align} H_0(x) = \int_{-\infty}^{\infty} e^{ix \cosh{v}}\int_{-\infty}^{\infty} e^{-2ivt} t \tanh(\pi t) h(t) dt dv. \end{align} $$
$$ \begin{align} H_0(x) = \int_{-\infty}^{\infty} e^{ix \cosh{v}}\int_{-\infty}^{\infty} e^{-2ivt} t \tanh(\pi t) h(t) dt dv. \end{align} $$
The inner t-integral is
 $$ \begin{align} \int_{-\infty}^{\infty} e^{-2ivt} t \tanh(\pi t) \frac{t^2 + \frac14}{T^2} \left(\exp\left(-\frac{(t-T)^2}{\Delta^2}\right)+\exp\left(-\frac{(t+T)^2}{\Delta^2} \right)\right) dt \nonumber\\ = \Delta T\left( e^{-2ivT}+e^{2ivT}\right) g(\Delta v), \end{align} $$
$$ \begin{align} \int_{-\infty}^{\infty} e^{-2ivt} t \tanh(\pi t) \frac{t^2 + \frac14}{T^2} \left(\exp\left(-\frac{(t-T)^2}{\Delta^2}\right)+\exp\left(-\frac{(t+T)^2}{\Delta^2} \right)\right) dt \nonumber\\ = \Delta T\left( e^{-2ivT}+e^{2ivT}\right) g(\Delta v), \end{align} $$
where
![]() $g(y) = g_{\Delta , T}(y)$
behaves like a fixed (even) Schwartz-class function; namely, it satisfies the derivative bounds
$g(y) = g_{\Delta , T}(y)$
behaves like a fixed (even) Schwartz-class function; namely, it satisfies the derivative bounds
![]() $g^{\left (j\right )}(y) \ll _{j,A} (1+\lvert y\rvert )^{-A}$
, for any
$g^{\left (j\right )}(y) \ll _{j,A} (1+\lvert y\rvert )^{-A}$
, for any
![]() $j, A \in \mathbb {Z}_{\geq 0}$
. Hence
$j, A \in \mathbb {Z}_{\geq 0}$
. Hence
 $$ \begin{align} H_{0}(x) = 2 \Delta T \int_{-\infty}^{\infty} e^{ix \cosh{v}} e^{-2ivT} g(\Delta v) dv. \end{align} $$
$$ \begin{align} H_{0}(x) = 2 \Delta T \int_{-\infty}^{\infty} e^{ix \cosh{v}} e^{-2ivT} g(\Delta v) dv. \end{align} $$
From this, we can write the real part of
![]() $H_0(x)$
as a linear combination of
$H_0(x)$
as a linear combination of
![]() $H_{\pm }(x)$
, where
$H_{\pm }(x)$
, where
 $$ \begin{align} H_{\pm}(x) = \Delta T \int_{-\infty}^{\infty} e^{\pm i x \cosh{v} - 2ivT} g(\Delta v) dv = \Delta T e^{\pm ix} \int_{-\infty}^{\infty} e^{\pm ix (\cosh{v} - 1) - 2ivT} g(\Delta v) dv. \end{align} $$
$$ \begin{align} H_{\pm}(x) = \Delta T \int_{-\infty}^{\infty} e^{\pm i x \cosh{v} - 2ivT} g(\Delta v) dv = \Delta T e^{\pm ix} \int_{-\infty}^{\infty} e^{\pm ix (\cosh{v} - 1) - 2ivT} g(\Delta v) dv. \end{align} $$
Then formula (6.4) becomes
 $$ \begin{align} \mathcal{M} \ll \Delta T^{1+\varepsilon} + \max_{\substack{1 \ll N \ll N_{\text{max}}\\ \pm }} T^{\varepsilon} \left\lvert\mathcal{S}\left(H_\pm\right)\right\rvert. \end{align} $$
$$ \begin{align} \mathcal{M} \ll \Delta T^{1+\varepsilon} + \max_{\substack{1 \ll N \ll N_{\text{max}}\\ \pm }} T^{\varepsilon} \left\lvert\mathcal{S}\left(H_\pm\right)\right\rvert. \end{align} $$
It suffices to bound
![]() $\mathcal {S}\left (H_{+}\right )$
, as the argument for
$\mathcal {S}\left (H_{+}\right )$
, as the argument for
![]() $\mathcal {S}(H_{-})$
is similar. For convenience, let us write this as
$\mathcal {S}(H_{-})$
is similar. For convenience, let us write this as
![]() $H_{+}(x) = \Delta T e^{ix} K_{+}(x)$
, where
$H_{+}(x) = \Delta T e^{ix} K_{+}(x)$
, where
 $$ \begin{align} K_{+}(x) = \int_{-\infty}^{\infty} e^{ix (\cosh{v} - 1) - 2ivT} g(\Delta v) dv. \end{align} $$
$$ \begin{align} K_{+}(x) = \int_{-\infty}^{\infty} e^{ix (\cosh{v} - 1) - 2ivT} g(\Delta v) dv. \end{align} $$
Finally, we apply a dyadic partition of unity to the c sum. To summarize, we have shown
 $$ \begin{align} \mathcal{S}(H_{+}) = \frac{\Delta T}{N} \sum_{C } \sum_{c \equiv 0 \negthickspace \negthickspace \pmod{2^4}} \sum_{m,n} \frac{S\left(m^2, n^2;c\right) e_c(2mn)}{c m^{iU} n^{-iU}} w(m,n,c) K_{+} \!\left(\frac{4 \pi mn}{c}\right) + O(T^{-100}), \end{align} $$
$$ \begin{align} \mathcal{S}(H_{+}) = \frac{\Delta T}{N} \sum_{C } \sum_{c \equiv 0 \negthickspace \negthickspace \pmod{2^4}} \sum_{m,n} \frac{S\left(m^2, n^2;c\right) e_c(2mn)}{c m^{iU} n^{-iU}} w(m,n,c) K_{+} \!\left(\frac{4 \pi mn}{c}\right) + O(T^{-100}), \end{align} $$
where the first sum is a sum over integers C equal to
![]() $2^{j/2}$
for
$2^{j/2}$
for
![]() $0\le j\leq 300 \log T$
and
$0\le j\leq 300 \log T$
and
![]() $w(x_1,x_2,x_3)=w_{N,C}(x_1,x_2,x_3)$
is 1-inert and supported on
$w(x_1,x_2,x_3)=w_{N,C}(x_1,x_2,x_3)$
is 1-inert and supported on
![]() $x_1\asymp x_2\asymp N$
and
$x_1\asymp x_2\asymp N$
and
![]() $c\asymp C$
.
$c\asymp C$
.
We may approximate
![]() $H_{+}(x)$
quite well by truncating the integral at
$H_{+}(x)$
quite well by truncating the integral at
![]() $\lvert v\rvert \leq \Delta ^{-1} T^{\varepsilon }$
, and then use an integration-by-parts argument to see that
$\lvert v\rvert \leq \Delta ^{-1} T^{\varepsilon }$
, and then use an integration-by-parts argument to see that
![]() $H_{+}(x)$
is very small unless
$H_{+}(x)$
is very small unless
For more details of an alternative approach, see [Reference Jutila and Motohashi17, pp. 76–77]. In our situation, where
 $x \asymp \frac {N^2}{C}$
, we conclude that we may assume
$x \asymp \frac {N^2}{C}$
, we conclude that we may assume
 $$ \begin{align} C \ll T^{\varepsilon} \frac{N^2}{\Delta T^{}} \ll T^{\varepsilon} \frac{UT}{\Delta}. \end{align} $$
$$ \begin{align} C \ll T^{\varepsilon} \frac{N^2}{\Delta T^{}} \ll T^{\varepsilon} \frac{UT}{\Delta}. \end{align} $$
For our purposes it is inconvenient to develop the v-integral further at this early stage. However, we do record the following slight refinement that is useful for large values of x:
Lemma 6.1. Suppose that
Then
 $$ \begin{align} K_{+}(x) = \int_{\lvert v\rvert \ll x^{-1/2} T^{\varepsilon}} e^{ix(\cosh(v) - 1) - 2iTv} g(\Delta v) \eta(v) dv + O\left((xT)^{-100}\right), \end{align} $$
$$ \begin{align} K_{+}(x) = \int_{\lvert v\rvert \ll x^{-1/2} T^{\varepsilon}} e^{ix(\cosh(v) - 1) - 2iTv} g(\Delta v) \eta(v) dv + O\left((xT)^{-100}\right), \end{align} $$
where
![]() $\eta $
is supported on
$\eta $
is supported on
![]() $\lvert v\rvert \ll x^{-1/2}T^{\varepsilon }$
and satisfies property (4.1) for a
$\lvert v\rvert \ll x^{-1/2}T^{\varepsilon }$
and satisfies property (4.1) for a
![]() $1$
-inert function.
$1$
-inert function.
Proof. This follows from the integration-by-parts lemma 4.2.
7. Double Poisson summation
Next we apply Poisson summation to the m and n sums in equation (6.13), giving
 $$ \begin{align} \mathcal{S}(H_{+}) = \frac{\Delta T}{N} \sum_C \sum_{c \equiv 0 \negthickspace \negthickspace \pmod{2^4}} \sum_{k,\ell} \frac{T(-k,\ell;c)}{c^3} I(k,\ell,c) + O\left(T^{-100}\right), \end{align} $$
$$ \begin{align} \mathcal{S}(H_{+}) = \frac{\Delta T}{N} \sum_C \sum_{c \equiv 0 \negthickspace \negthickspace \pmod{2^4}} \sum_{k,\ell} \frac{T(-k,\ell;c)}{c^3} I(k,\ell,c) + O\left(T^{-100}\right), \end{align} $$
where
 $$ \begin{align} I(k,\ell,c) = \int_0^{\infty} \int_0^{\infty} x^{-iU} y^{iU} e_c(kx - \ell y) K_{+}\left(\frac{4 \pi xy}{c}\right) w(x,y,c) dx dy. \end{align} $$
$$ \begin{align} I(k,\ell,c) = \int_0^{\infty} \int_0^{\infty} x^{-iU} y^{iU} e_c(kx - \ell y) K_{+}\left(\frac{4 \pi xy}{c}\right) w(x,y,c) dx dy. \end{align} $$
By Lemma 5.3,
![]() $T(-k,\ell ;c) = 0$
unless
$T(-k,\ell ;c) = 0$
unless
![]() $(k,c) = (\ell , c)$
and
$(k,c) = (\ell , c)$
and
![]() $4\mid (k,\ell )$
, in which case
$4\mid (k,\ell )$
, in which case
 $$ \begin{align} & T(-k,\ell,c) \nonumber \\ &\quad = c^{3/2} \left(k, 2^{-2-\delta} c\right) e_c(k\ell/4) \left(\frac{k' \ell'}{c^*}\right) g_{\delta}(k',\ell', c_o) \delta\left(c^*\mid\frac{c_o}{(k,c_o)}\right) \prod_{\substack{p \mid c_{\square}, \thinspace p \nmid \frac{c_o}{\left(k,c_o\right)}}} \left(1-p^{-1}\right) , \end{align} $$
$$ \begin{align} & T(-k,\ell,c) \nonumber \\ &\quad = c^{3/2} \left(k, 2^{-2-\delta} c\right) e_c(k\ell/4) \left(\frac{k' \ell'}{c^*}\right) g_{\delta}(k',\ell', c_o) \delta\left(c^*\mid\frac{c_o}{(k,c_o)}\right) \prod_{\substack{p \mid c_{\square}, \thinspace p \nmid \frac{c_o}{\left(k,c_o\right)}}} \left(1-p^{-1}\right) , \end{align} $$
where
 $k' = \frac {k}{\left (k,c\right )}$
,
$k' = \frac {k}{\left (k,c\right )}$
,
 $\ell ' = \frac {\ell }{\left (\ell ,c\right )}$
,
$\ell ' = \frac {\ell }{\left (\ell ,c\right )}$
,
![]() $\delta $
was defined in equation (5.3), and other notation is carried over from Lemma 5.3 (here the function
$\delta $
was defined in equation (5.3), and other notation is carried over from Lemma 5.3 (here the function
![]() $g_{\delta }$
has the same properties as the one appearing in Lemma 5.3, but may not agree with it).
$g_{\delta }$
has the same properties as the one appearing in Lemma 5.3, but may not agree with it).
Write
with
![]() $(k_o \ell _o c_o, 2) = 1$
. The condition
$(k_o \ell _o c_o, 2) = 1$
. The condition
![]() $(k,c) = (\ell , c)$
now becomes
$(k,c) = (\ell , c)$
now becomes
![]() $\min (\lambda , \nu ) = \min (\lambda , \gamma )$
, and
$\min (\lambda , \nu ) = \min (\lambda , \gamma )$
, and
![]() $(k_o, c_o) = (\ell _o, c_o)$
. The condition
$(k_o, c_o) = (\ell _o, c_o)$
. The condition
![]() $4\mid (k,\ell )$
now means
$4\mid (k,\ell )$
now means
![]() $\nu , \gamma \geq 2$
. We also write
$\nu , \gamma \geq 2$
. We also write
where q is square-free,
![]() $r_1 \mid q^{\infty }$
, and
$r_1 \mid q^{\infty }$
, and
![]() $(q,r_2) = 1$
. With this notation,
$(q,r_2) = 1$
. With this notation,
![]() $c^* = q$
and
$c^* = q$
and
![]() $c_{\square }$
shares the same prime factors as
$c_{\square }$
shares the same prime factors as
![]() $r_2$
. Note that
$r_2$
. Note that
 $\frac {c_o}{\left (k, c_o\right )} = \frac {q r_1^2}{\left (k_o, q r_1^2\right )} \frac {r_2^2}{\left (k_o, r_2^2\right )}$
. Thus the condition
$\frac {c_o}{\left (k, c_o\right )} = \frac {q r_1^2}{\left (k_o, q r_1^2\right )} \frac {r_2^2}{\left (k_o, r_2^2\right )}$
. Thus the condition
 $ c^* \mid \frac {c_o}{\left (k,c_o\right )}$
means
$ c^* \mid \frac {c_o}{\left (k,c_o\right )}$
means
 $q \mid \frac {q r_1^2}{\left (k_o, q r_1^2\right )}$
, which is equivalent to
$q \mid \frac {q r_1^2}{\left (k_o, q r_1^2\right )}$
, which is equivalent to
 $\left (k_o, q r_1^2\right ) \mid r_1^2$
. Then
$\left (k_o, q r_1^2\right ) \mid r_1^2$
. Then
 $$ \begin{align} \mathcal{S}(H_{+}) = \sum_C \frac{\Delta T}{NC^{3/2}} \sum_{\substack{\nu, \gamma \geq 2, \thinspace \lambda \geq 4 \\ \min(\lambda, \nu) = \min\left(\lambda, \gamma\right)}} \left(2^{\nu}, 2^{\lambda-2-\delta}\right) \sum_{\substack{ \left(r_1 r_2, 2\right) = 1}} \sideset{}{^*}\sum_{\substack{q: r_1 \mid q^{\infty} \\ \left(q,2r_2\right) = 1}} \sum_{\substack{(k_o \ell_o, 2)=1 \\ (k_o, c_o) = (\ell_o, c_o) \\ \left(k_o, q r_1^2\right) \mid r_1^2}} \nonumber\\ \left(\prod_{\substack{p \mid r_2, \thinspace p \nmid \frac{r_2^2}{\left(k_o,r_2^2\right)}}} \left(1-p^{-1}\right) \right) \left(\frac{k' \ell'}{c^*}\right) (k_o, c_o) e_c(k \ell/4) g_{\delta}(k',\ell', c_o) I(k,\ell,c) + O\left(T^{-100}\right), \end{align} $$
$$ \begin{align} \mathcal{S}(H_{+}) = \sum_C \frac{\Delta T}{NC^{3/2}} \sum_{\substack{\nu, \gamma \geq 2, \thinspace \lambda \geq 4 \\ \min(\lambda, \nu) = \min\left(\lambda, \gamma\right)}} \left(2^{\nu}, 2^{\lambda-2-\delta}\right) \sum_{\substack{ \left(r_1 r_2, 2\right) = 1}} \sideset{}{^*}\sum_{\substack{q: r_1 \mid q^{\infty} \\ \left(q,2r_2\right) = 1}} \sum_{\substack{(k_o \ell_o, 2)=1 \\ (k_o, c_o) = (\ell_o, c_o) \\ \left(k_o, q r_1^2\right) \mid r_1^2}} \nonumber\\ \left(\prod_{\substack{p \mid r_2, \thinspace p \nmid \frac{r_2^2}{\left(k_o,r_2^2\right)}}} \left(1-p^{-1}\right) \right) \left(\frac{k' \ell'}{c^*}\right) (k_o, c_o) e_c(k \ell/4) g_{\delta}(k',\ell', c_o) I(k,\ell,c) + O\left(T^{-100}\right), \end{align} $$
where in places to simplify the notation we have not displayed the substituted values, such as
![]() $c_o = q r_1^2 r_2^2$
. We remark that the statement that
$c_o = q r_1^2 r_2^2$
. We remark that the statement that
![]() $g_{\delta }(k', \ell ', c_o)$
depends additionally on
$g_{\delta }(k', \ell ', c_o)$
depends additionally on
 $\left (\frac {c}{\left (a,c\right )}, 2^{2+\delta }\right )$
means it depends on
$\left (\frac {c}{\left (a,c\right )}, 2^{2+\delta }\right )$
means it depends on
 $\left (2^{\lambda -\min \left (\lambda ,\nu \right )}, 2^{2+\delta }\right )$
. In particular,
$\left (2^{\lambda -\min \left (\lambda ,\nu \right )}, 2^{2+\delta }\right )$
. In particular,
![]() $g_{\delta }$
depends additionally on
$g_{\delta }$
depends additionally on
![]() $\lambda , \nu $
, but only lightly, in the sense that it falls into the four following cases:
$\lambda , \nu $
, but only lightly, in the sense that it falls into the four following cases:
Next we want to give a variable name to
![]() $(k_o, c_o)$
, etc. We have
$(k_o, c_o)$
, etc. We have
 $(k_o, c_o) = \left (k_o, q r_1^2\right ) \left (k_o, r_2^2\right )$
, and similarly
$(k_o, c_o) = \left (k_o, q r_1^2\right ) \left (k_o, r_2^2\right )$
, and similarly
 $(\ell _o, c_o) = \left (\ell _o, qr_1^2\right )\left (k_o, r_2^2\right )$
. Let
$(\ell _o, c_o) = \left (\ell _o, qr_1^2\right )\left (k_o, r_2^2\right )$
. Let
 $$ \begin{align} \left(k_o, q r_1^2\right) = \left(\ell_o, q r_1^2\right) = g_1 \quad \text{and} \quad \left(k_o, r_2^2\right) = \left(\ell_o, r_2^2\right) = g_2. \end{align} $$
$$ \begin{align} \left(k_o, q r_1^2\right) = \left(\ell_o, q r_1^2\right) = g_1 \quad \text{and} \quad \left(k_o, r_2^2\right) = \left(\ell_o, r_2^2\right) = g_2. \end{align} $$
Here
![]() $g_1$
runs over divisors of
$g_1$
runs over divisors of
![]() $r_1^2$
and
$r_1^2$
and
![]() $g_2$
runs over divisors of
$g_2$
runs over divisors of
![]() $r_2^2$
. Let
$r_2^2$
. Let
where
 $\left (k_o' \ell _o', q \frac {r_1^2}{g_1}\right ) = 1$
and
$\left (k_o' \ell _o', q \frac {r_1^2}{g_1}\right ) = 1$
and
 $\left (k_o' \ell _o', \frac {r_2^2}{g_2}\right ) = 1$
. In our context, the presence of the Jacobi symbol
$\left (k_o' \ell _o', \frac {r_2^2}{g_2}\right ) = 1$
. In our context, the presence of the Jacobi symbol
 $\left (\frac {k' \ell '}{q}\right )$
means that we may automatically assume
$\left (\frac {k' \ell '}{q}\right )$
means that we may automatically assume
![]() $\left (k_o' \ell _o', q\right ) = 1$
, which implies
$\left (k_o' \ell _o', q\right ) = 1$
, which implies
 $\left (k_o' \ell _o', q \frac {r_1^2}{g_1}\right ) = 1$
. Note that
$\left (k_o' \ell _o', q \frac {r_1^2}{g_1}\right ) = 1$
. Note that
![]() $k' = k_o' 2^{\nu - \min \left (\nu , \lambda \right )}$
and
$k' = k_o' 2^{\nu - \min \left (\nu , \lambda \right )}$
and
![]() $\ell ' = \ell _o' 2^{\gamma - \min \left (\gamma , \lambda \right )}$
. We also apply quadratic reciprocity, giving
$\ell ' = \ell _o' 2^{\gamma - \min \left (\gamma , \lambda \right )}$
. We also apply quadratic reciprocity, giving
 $\left (\frac {k_o' \ell _o'}{q}\right ) = \left (\frac {q}{k_o' \ell _o'}\right )$
times a function depending on
$\left (\frac {k_o' \ell _o'}{q}\right ) = \left (\frac {q}{k_o' \ell _o'}\right )$
times a function depending on
![]() $k_o', \ell _o', q'$
modulo
$k_o', \ell _o', q'$
modulo
![]() $8$
(which alters only the definition of g). Making these substitutions, we obtain
$8$
(which alters only the definition of g). Making these substitutions, we obtain
 $$ \begin{align} \mathcal{S}(H_{+}) = \sum_C \frac{\Delta T}{NC^{3/2}} \sum_{\substack{\nu, \gamma \geq 2, \thinspace \lambda \geq 4 \\ \min\left(\lambda, \nu\right) = \min\left(\lambda, \gamma\right)}} \left(2^{\nu}, 2^{\lambda-2-\delta}\right) \sum_{\substack{ \left(r_1 r_2, 2\right) = 1}} \sum_{\substack{g_1 \mid r_1^2 \\ g_2 \mid r_2^2}} g_1 g_2 \prod_{\substack{p \mid r_2, \thinspace p \nmid \frac{r_2^2}{g_2}}} \left(1-p^{-1}\right) \nonumber\\ \sideset{}{^*}\sum_{\substack{q: r_1 \mid q^{\infty} \\ \left(q,2r_2\right) = 1}} \sum_{\substack{\left(k_o' \ell_o', 2\right)=1 \\ \left(k_o' \ell_o', \frac{r_2^2}{g_2}\right) = 1}} \left(\frac{q}{k_o' \ell_o'}\right) e_c(k \ell/4) g_{\lambda, \nu, \gamma, \delta}\left(k_o',\ell_o', q\right) I(k,\ell,c) + O\left(T^{-100}\right), \end{align} $$
$$ \begin{align} \mathcal{S}(H_{+}) = \sum_C \frac{\Delta T}{NC^{3/2}} \sum_{\substack{\nu, \gamma \geq 2, \thinspace \lambda \geq 4 \\ \min\left(\lambda, \nu\right) = \min\left(\lambda, \gamma\right)}} \left(2^{\nu}, 2^{\lambda-2-\delta}\right) \sum_{\substack{ \left(r_1 r_2, 2\right) = 1}} \sum_{\substack{g_1 \mid r_1^2 \\ g_2 \mid r_2^2}} g_1 g_2 \prod_{\substack{p \mid r_2, \thinspace p \nmid \frac{r_2^2}{g_2}}} \left(1-p^{-1}\right) \nonumber\\ \sideset{}{^*}\sum_{\substack{q: r_1 \mid q^{\infty} \\ \left(q,2r_2\right) = 1}} \sum_{\substack{\left(k_o' \ell_o', 2\right)=1 \\ \left(k_o' \ell_o', \frac{r_2^2}{g_2}\right) = 1}} \left(\frac{q}{k_o' \ell_o'}\right) e_c(k \ell/4) g_{\lambda, \nu, \gamma, \delta}\left(k_o',\ell_o', q\right) I(k,\ell,c) + O\left(T^{-100}\right), \end{align} $$
where
![]() $g_{\lambda ,\nu ,\gamma ,\delta }$
is some new function modulo
$g_{\lambda ,\nu ,\gamma ,\delta }$
is some new function modulo
![]() $8$
.
$8$
.
Finally, we decompose g into Dirichlet characters modulo
![]() $8$
and break up the sum according to the four cases in formula (7.7), leading to a formula of the form
$8$
and break up the sum according to the four cases in formula (7.7), leading to a formula of the form
 $$ \begin{align} \left\lvert\mathcal{S}\left(H_{+}\right)\right\rvert \ll \max_{\substack{\eta_1, \eta_2, \eta_3 \\ \text{cases in } (7.7)}} \left\lvert\mathcal{S}_{\eta}\left(H_{+}\right)\right\rvert, \end{align} $$
$$ \begin{align} \left\lvert\mathcal{S}\left(H_{+}\right)\right\rvert \ll \max_{\substack{\eta_1, \eta_2, \eta_3 \\ \text{cases in } (7.7)}} \left\lvert\mathcal{S}_{\eta}\left(H_{+}\right)\right\rvert, \end{align} $$
where
 $$ \begin{align} \mathcal{S}_{\eta}\left(H_{+}\right) = \sum_C \frac{\Delta T}{NC^{3/2}} \sum_{\substack{\nu, \gamma \geq 2, \thinspace \lambda \geq 4 \\ \min\left(\lambda, \nu\right) = \min\left(\lambda, \gamma\right) \\ \text{one of (7.7) holds}}} \left(2^{\nu}, 2^{\lambda-2-\delta}\right) \sum_{\substack{ \left(r_1 r_2, 2\right) = 1}} \sum_{\substack{g_1 \mid r_1^2 \\ g_2 \mid r_2^2}} g_1 g_2 \prod_{\substack{p \mid r_2, \thinspace p \nmid \frac{r_2^2}{g_2}}} \left(1-p^{-1}\right) \nonumber\\ \sideset{}{^*}\sum_{\substack{q: r_1 \mid q^{\infty} \\ \left(q,2r_2\right) = 1}} \sum_{\substack{\left(k_o' \ell_o', 2\right)=1 \\ \left(k_o' \ell_o', \frac{r_2^2}{g_2}\right) = 1}} \eta_1\left(k_o'\right) \eta_2\left(\ell_o'\right) \eta_3(q) \left(\frac{q}{k_o' \ell_o'}\right) e_c(k \ell/4) I(k,\ell,c) + O\left(T^{-100}\right). \end{align} $$
$$ \begin{align} \mathcal{S}_{\eta}\left(H_{+}\right) = \sum_C \frac{\Delta T}{NC^{3/2}} \sum_{\substack{\nu, \gamma \geq 2, \thinspace \lambda \geq 4 \\ \min\left(\lambda, \nu\right) = \min\left(\lambda, \gamma\right) \\ \text{one of (7.7) holds}}} \left(2^{\nu}, 2^{\lambda-2-\delta}\right) \sum_{\substack{ \left(r_1 r_2, 2\right) = 1}} \sum_{\substack{g_1 \mid r_1^2 \\ g_2 \mid r_2^2}} g_1 g_2 \prod_{\substack{p \mid r_2, \thinspace p \nmid \frac{r_2^2}{g_2}}} \left(1-p^{-1}\right) \nonumber\\ \sideset{}{^*}\sum_{\substack{q: r_1 \mid q^{\infty} \\ \left(q,2r_2\right) = 1}} \sum_{\substack{\left(k_o' \ell_o', 2\right)=1 \\ \left(k_o' \ell_o', \frac{r_2^2}{g_2}\right) = 1}} \eta_1\left(k_o'\right) \eta_2\left(\ell_o'\right) \eta_3(q) \left(\frac{q}{k_o' \ell_o'}\right) e_c(k \ell/4) I(k,\ell,c) + O\left(T^{-100}\right). \end{align} $$
8. The behavior of
 $I(k,\ell ,c)$
$I(k,\ell ,c)$
The purpose of this section is to develop the analytic properties of
![]() $I(k, \ell , c)$
. We begin with a few reduction steps. Inserting equation (6.12) into equation (7.2), we have
$I(k, \ell , c)$
. We begin with a few reduction steps. Inserting equation (6.12) into equation (7.2), we have
 $$ \begin{align} I(k,\ell,c) = \!\int_{-\infty}^{\infty} g(\Delta v) e^{-2ivT} \!\int_0^{\infty} \!\int_0^{\infty} \! x^{-iU} y^{iU} e_c(kx - \ell y + 2 xy(\cosh{v} - 1)) w(x,y,c) dx dy dv. \end{align} $$
$$ \begin{align} I(k,\ell,c) = \!\int_{-\infty}^{\infty} g(\Delta v) e^{-2ivT} \!\int_0^{\infty} \!\int_0^{\infty} \! x^{-iU} y^{iU} e_c(kx - \ell y + 2 xy(\cosh{v} - 1)) w(x,y,c) dx dy dv. \end{align} $$
Let
![]() $A,B>0$
,
$A,B>0$
,
![]() $\epsilon \ge 0$
be real numbers and N and U as before, and consider the integral
$\epsilon \ge 0$
be real numbers and N and U as before, and consider the integral
 $$ \begin{align} I(A, B, U, \epsilon, N) = \int_{\mathbb R^2} e^{i \phi\left(x,y\right)} w_N(x,y, \cdot)dx dy, \end{align} $$
$$ \begin{align} I(A, B, U, \epsilon, N) = \int_{\mathbb R^2} e^{i \phi\left(x,y\right)} w_N(x,y, \cdot)dx dy, \end{align} $$
where
![]() $w_N$
is
$w_N$
is
![]() $1$
-inert, supported on
$1$
-inert, supported on
![]() $x \asymp y \asymp N$
with
$x \asymp y \asymp N$
with
![]() $N\gg 1$
, and
$N\gg 1$
, and
In our case,
 $$ \begin{align} A = \frac{2 \pi k}{c}, \qquad B = \frac{2\pi \ell}{c}, \qquad \epsilon = \epsilon(v) = 4 \pi \frac{\cosh{v} -1}{c}, \end{align} $$
$$ \begin{align} A = \frac{2 \pi k}{c}, \qquad B = \frac{2\pi \ell}{c}, \qquad \epsilon = \epsilon(v) = 4 \pi \frac{\cosh{v} -1}{c}, \end{align} $$
and then
 $$ \begin{align} I(k, \ell, c) = \int_{-\infty}^{\infty} g(\Delta v) e^{-2ivT} I(A,B,U,\epsilon(v), N) dv. \end{align} $$
$$ \begin{align} I(k, \ell, c) = \int_{-\infty}^{\infty} g(\Delta v) e^{-2ivT} I(A,B,U,\epsilon(v), N) dv. \end{align} $$
Note that in our study of
![]() $I(A, B, U, \epsilon , N)$
, we may assume throughout that
$I(A, B, U, \epsilon , N)$
, we may assume throughout that
![]() $\epsilon>0$
, because
$\epsilon>0$
, because
![]() $\epsilon (v)=0$
if and only if
$\epsilon (v)=0$
if and only if
![]() $v=0$
, a set of measure
$v=0$
, a set of measure
![]() $0$
for the v-integral of
$0$
for the v-integral of
![]() $I(k, \ell , c)$
.
$I(k, \ell , c)$
.
Moreover, we may wish to assume that
![]() $w_N(x,y) = w_N(x,y, \cdot )$
depends on some unspecified finite list of additional variables that are held suppressed in the notation. In this situation we will assume that
$w_N(x,y) = w_N(x,y, \cdot )$
depends on some unspecified finite list of additional variables that are held suppressed in the notation. In this situation we will assume that
![]() $w_N$
is
$w_N$
is
![]() $1$
-inert in terms of all the variables, not just x and y.
$1$
-inert in terms of all the variables, not just x and y.
Lemma 8.1. Suppose that
![]() $\epsilon N^2 = o(U)$
, with
$\epsilon N^2 = o(U)$
, with
![]() $U \rightarrow \infty $
.
$U \rightarrow \infty $
.
-
1. Then
 $I(A,B,U,\epsilon ,N) \ll _C N U^{-C}$
with
$I(A,B,U,\epsilon ,N) \ll _C N U^{-C}$
with
 $C>0$
arbitrarily large, unless (8.6)
$C>0$
arbitrarily large, unless (8.6) $$ \begin{align} A \asymp B \asymp \frac{U}{N}. \end{align} $$
$$ \begin{align} A \asymp B \asymp \frac{U}{N}. \end{align} $$
-
2. In the range (8.6), we have
(8.7)where $$ \begin{align} I = \frac{N^2}{U} e^{i\phi\left(x_0, y_0\right)} W(\cdot) + O\left(N^2 U^{-C}\right), \end{align} $$
$$ \begin{align} I = \frac{N^2}{U} e^{i\phi\left(x_0, y_0\right)} W(\cdot) + O\left(N^2 U^{-C}\right), \end{align} $$
 $(x_0, y_0)$
is the unique solution to
$(x_0, y_0)$
is the unique solution to
 $\nabla \phi (x_0,y_0) = \mathbf {0}$
and W is
$\nabla \phi (x_0,y_0) = \mathbf {0}$
and W is
 $1$
-inert in terms of any suppressed variables on which
$1$
-inert in terms of any suppressed variables on which
 $w_N$
may depend.
$w_N$
may depend.
-
3. Supposing formula (8.6) holds,
 $\phi (x_0, y_0)$
has the asymptotic expansion (8.8)for some absolute constants
$\phi (x_0, y_0)$
has the asymptotic expansion (8.8)for some absolute constants $$ \begin{align} \phi(x_0, y_0) = U \log(A/B) + \sum_{j=0}^{J} c_j U \left(\frac{\epsilon U}{AB}\right)^{1+2j} + O\left(U \left(\frac{\epsilon U}{AB}\right)^{3+2J} \right), \end{align} $$
$$ \begin{align} \phi(x_0, y_0) = U \log(A/B) + \sum_{j=0}^{J} c_j U \left(\frac{\epsilon U}{AB}\right)^{1+2j} + O\left(U \left(\frac{\epsilon U}{AB}\right)^{3+2J} \right), \end{align} $$
 $c_j$
.
$c_j$
.
Note that formula (8.6) implies
 $\frac {\epsilon U}{AB} \asymp \frac {\epsilon N^2}{U} = o(1)$
, so that equation (8.8) is an asymptotic expansion. We also remark that the assumption
$\frac {\epsilon U}{AB} \asymp \frac {\epsilon N^2}{U} = o(1)$
, so that equation (8.8) is an asymptotic expansion. We also remark that the assumption
![]() $\epsilon N^2 = o(U)$
means that the dominant part of
$\epsilon N^2 = o(U)$
means that the dominant part of
![]() $\phi $
comes from
$\phi $
comes from
![]() $-U \log {x} + U \log {y}$
, and
$-U \log {x} + U \log {y}$
, and
![]() $\epsilon xy$
is a smaller perturbation.
$\epsilon xy$
is a smaller perturbation.
Proof. The integration-by-parts lemma (Lemma 4.2) shows that the integral is small unless formula (8.6) holds. Assuming it does hold, Lemma 4.3 may be iteratively applied (using the remarks following Lemma 4.3), which gives the form (8.7), with a
![]() $1$
-inert function W.
$1$
-inert function W.
It only remains to derive the Taylor expansion for
![]() $\phi (x_0, y_0)$
. We have
$\phi (x_0, y_0)$
. We have
where
 $$ \begin{align} \Phi(x,y) = -\log{x} + \log{y} + x-y + \delta xy \quad \text{and} \quad \delta = \frac{\epsilon U}{AB} = o(1). \end{align} $$
$$ \begin{align} \Phi(x,y) = -\log{x} + \log{y} + x-y + \delta xy \quad \text{and} \quad \delta = \frac{\epsilon U}{AB} = o(1). \end{align} $$
By a simple calculation, we have
![]() $\nabla \Phi (x_0,y_0)=\bf {0}$
if and only if
$\nabla \Phi (x_0,y_0)=\bf {0}$
if and only if
![]() $x_0 = 1 - \delta x_0 y_0$
and
$x_0 = 1 - \delta x_0 y_0$
and
![]() $y_0 = 1 + \delta x_0 y_0$
. Thus
$y_0 = 1 + \delta x_0 y_0$
. Thus
Letting
![]() $r_0 = x_0 y_0$
, we see that it satisfies the relation
$r_0 = x_0 y_0$
, we see that it satisfies the relation
![]() $r_0 = (1- \delta r_0)(1+\delta r_0) = 1 - \delta ^2 r_0^2$
. Solving this explicitly, we see that
$r_0 = (1- \delta r_0)(1+\delta r_0) = 1 - \delta ^2 r_0^2$
. Solving this explicitly, we see that
![]() $r_0$
is an even function of
$r_0$
is an even function of
![]() $\delta $
, analytic for
$\delta $
, analytic for
![]() $\lvert \delta \rvert < 1/2$
. Note that
$\lvert \delta \rvert < 1/2$
. Note that
 $r_0 = 1 - \delta ^2 + O\left (\delta ^4\right )$
. Then we have
$r_0 = 1 - \delta ^2 + O\left (\delta ^4\right )$
. Then we have
 $$ \begin{align} \Phi(x_0, y_0) = \log(y_0/x_0) + x_0 - y_0 + \delta x_0 y_0 = \log\left(\frac{1+\delta r_0}{1-\delta r_0}\right) - \delta r_0, \end{align} $$
$$ \begin{align} \Phi(x_0, y_0) = \log(y_0/x_0) + x_0 - y_0 + \delta x_0 y_0 = \log\left(\frac{1+\delta r_0}{1-\delta r_0}\right) - \delta r_0, \end{align} $$
which is an odd function of
![]() $\delta $
, with power series expansion of the form
$\delta $
, with power series expansion of the form
 $\Phi (x_0, y_0) = \delta - \frac 13 \delta ^3 + \dotsb $
. Translating back to the original notation gives equation (8.8).
$\Phi (x_0, y_0) = \delta - \frac 13 \delta ^3 + \dotsb $
. Translating back to the original notation gives equation (8.8).
Lemma 8.2. Suppose that
 $\frac {U}{\epsilon N^2} = o(1)$
.
$\frac {U}{\epsilon N^2} = o(1)$
.
-
1. Then
 $I(A,B,U,\epsilon ,N) \ll _C N^{-C}$
with
$I(A,B,U,\epsilon ,N) \ll _C N^{-C}$
with
 $C>0$
arbitrarily large, unless (8.13)
$C>0$
arbitrarily large, unless (8.13) $$ \begin{align} \lvert A\rvert \asymp \lvert B\rvert \asymp \epsilon N, \quad A < 0, \ B> 0. \end{align} $$
$$ \begin{align} \lvert A\rvert \asymp \lvert B\rvert \asymp \epsilon N, \quad A < 0, \ B> 0. \end{align} $$
-
2. Assuming formula (8.13), then
(8.14)where $$ \begin{align} I = \frac{1}{\epsilon} e^{i\phi\left(x_0, y_0\right)} W(\cdot) + O\left(N^2 U^{-C}\right), \end{align} $$
$$ \begin{align} I = \frac{1}{\epsilon} e^{i\phi\left(x_0, y_0\right)} W(\cdot) + O\left(N^2 U^{-C}\right), \end{align} $$
 $(x_0, y_0)$
is the unique solution to
$(x_0, y_0)$
is the unique solution to
 $\nabla \phi (x_0,y_0) = \mathbf {0}$
and W is
$\nabla \phi (x_0,y_0) = \mathbf {0}$
and W is
 $1$
-inert in terms of any suppressed variables on which
$1$
-inert in terms of any suppressed variables on which
 $w_N$
may depend.
$w_N$
may depend.
-
3. Finally,
 $\phi (x_0, y_0)$
has the following Taylor expansion: (8.15)with certain absolute constants
$\phi (x_0, y_0)$
has the following Taylor expansion: (8.15)with certain absolute constants $$ \begin{align} \phi(x_0, y_0) = \frac{AB}{\epsilon} \left[ \sum_{j=0}^{J} c_j \left(\frac{U \varepsilon}{AB}\right)^{2j} + O\left(\frac{U \varepsilon}{AB}\right)^{2J+2} \right] + U \log\left(\frac{-A}{B}\right), \end{align} $$
$$ \begin{align} \phi(x_0, y_0) = \frac{AB}{\epsilon} \left[ \sum_{j=0}^{J} c_j \left(\frac{U \varepsilon}{AB}\right)^{2j} + O\left(\frac{U \varepsilon}{AB}\right)^{2J+2} \right] + U \log\left(\frac{-A}{B}\right), \end{align} $$
 $c_j$
.
$c_j$
.
The condition
![]() $U = o(\epsilon N^2)$
means that the dominant phase in
$U = o(\epsilon N^2)$
means that the dominant phase in
![]() $\phi $
is
$\phi $
is
![]() $\epsilon xy$
, and the phase
$\epsilon xy$
, and the phase
![]() $-U\log {x} + U\log {y}$
is a perturbation.
$-U\log {x} + U\log {y}$
is a perturbation.
Proof. Considering the x-integral, Lemma 4.2 shows that
![]() $I \ll N^{-C}$
unless
$I \ll N^{-C}$
unless
 $$ \begin{align} \left\lvert\frac{A}{\epsilon N} + \frac{y}{N} \right\rvert \ll \frac{U}{\epsilon N^2} = o(1). \end{align} $$
$$ \begin{align} \left\lvert\frac{A}{\epsilon N} + \frac{y}{N} \right\rvert \ll \frac{U}{\epsilon N^2} = o(1). \end{align} $$
Since
![]() $1 \ll \frac {y}{N} \ll 1$
(with certain absolute implied constants), this means that
$1 \ll \frac {y}{N} \ll 1$
(with certain absolute implied constants), this means that
![]() $\lvert A\rvert \asymp \lvert \epsilon \rvert N$
, with A having the opposite sign of
$\lvert A\rvert \asymp \lvert \epsilon \rvert N$
, with A having the opposite sign of
![]() $\epsilon $
(i.e.,
$\epsilon $
(i.e.,
![]() $A <0$
). Similarly, considering the y-integral shows that I is small unless
$A <0$
). Similarly, considering the y-integral shows that I is small unless
![]() $\lvert B\rvert \asymp \epsilon N$
, with B having the same sign as
$\lvert B\rvert \asymp \epsilon N$
, with B having the same sign as
![]() $\epsilon $
(i.e.,
$\epsilon $
(i.e.,
![]() $B> 0$
).
$B> 0$
).
Next we wish to apply Lemma 4.3 to I. There is a minor technical issue from the fact that the second derivative with respect to x (or y) of
![]() $\epsilon xy$
vanishes, even though this should be viewed as the dominant phase. This issue may be circumvented by a simple change of variable to diagonalize this quadratic form. Precisely, if we let
$\epsilon xy$
vanishes, even though this should be viewed as the dominant phase. This issue may be circumvented by a simple change of variable to diagonalize this quadratic form. Precisely, if we let
![]() $x = u+v$
and
$x = u+v$
and
![]() $y=u-v$
, then
$y=u-v$
, then
 $$ \begin{align} \varphi(u,v):= \phi(u+v, u-v) = \epsilon u^2 + \alpha u - \epsilon v^2 + \beta v + U \log \left(\frac{u-v}{u+v} \right), \end{align} $$
$$ \begin{align} \varphi(u,v):= \phi(u+v, u-v) = \epsilon u^2 + \alpha u - \epsilon v^2 + \beta v + U \log \left(\frac{u-v}{u+v} \right), \end{align} $$
for certain
![]() $\alpha ,\beta $
whose values are immaterial. Then a simple calculation gives
$\alpha ,\beta $
whose values are immaterial. Then a simple calculation gives
 $$ \begin{align} \frac{\partial^2}{\partial u^2} \varphi(u,v) = 2 \epsilon + U\left(\frac{-1}{(u-v)^2} + \frac{1}{(u+v)^2}\right) = 2 \epsilon \left(1 + O\left(\epsilon^{-1} N^{-2} U\right)\right) \gg \lvert\epsilon\rvert. \end{align} $$
$$ \begin{align} \frac{\partial^2}{\partial u^2} \varphi(u,v) = 2 \epsilon + U\left(\frac{-1}{(u-v)^2} + \frac{1}{(u+v)^2}\right) = 2 \epsilon \left(1 + O\left(\epsilon^{-1} N^{-2} U\right)\right) \gg \lvert\epsilon\rvert. \end{align} $$
A similar calculation shows
 $\left \lvert \frac {\partial ^2}{\partial v^2} \varphi (u,v) \right \rvert \gg \lvert \epsilon \rvert $
. Once we know that stationary phase can be applied after this linear change of variables, we can then revert back to the original variables
$\left \lvert \frac {\partial ^2}{\partial v^2} \varphi (u,v) \right \rvert \gg \lvert \epsilon \rvert $
. Once we know that stationary phase can be applied after this linear change of variables, we can then revert back to the original variables
![]() $x,y$
, giving
$x,y$
, giving
 $$ \begin{align} I = \frac{1}{\epsilon} e^{i\phi\left(x_0, y_0\right)} W_T(\cdot) + O\left(N^{-C}\right), \end{align} $$
$$ \begin{align} I = \frac{1}{\epsilon} e^{i\phi\left(x_0, y_0\right)} W_T(\cdot) + O\left(N^{-C}\right), \end{align} $$
where
![]() $\nabla \phi (x_0, y_0) = \mathbf {0}$
. We have
$\nabla \phi (x_0, y_0) = \mathbf {0}$
. We have
 $$ \begin{align} \phi(Bx/\epsilon, -Ay/\epsilon) = \frac{-AB}{\epsilon} \Phi(x,y) + U \log\left(\frac{-A}{B}\right), \end{align} $$
$$ \begin{align} \phi(Bx/\epsilon, -Ay/\epsilon) = \frac{-AB}{\epsilon} \Phi(x,y) + U \log\left(\frac{-A}{B}\right), \end{align} $$
where
 $$ \begin{align} \Phi(x,y) = xy - x -y + \delta \log(y/x) \quad \text{and} \quad \delta = \frac{U \epsilon}{AB} \asymp \frac{U}{\epsilon N^2} = o(1). \end{align} $$
$$ \begin{align} \Phi(x,y) = xy - x -y + \delta \log(y/x) \quad \text{and} \quad \delta = \frac{U \epsilon}{AB} \asymp \frac{U}{\epsilon N^2} = o(1). \end{align} $$
A simple calculation shows
![]() $\nabla \Phi (x_0, y_0) = \mathbf {0}$
if and only if
$\nabla \Phi (x_0, y_0) = \mathbf {0}$
if and only if
 $$ \begin{align} x_0 = 1- \frac{\delta}{y_0}, \qquad y_0 = 1 + \frac{\delta}{x_0}. \end{align} $$
$$ \begin{align} x_0 = 1- \frac{\delta}{y_0}, \qquad y_0 = 1 + \frac{\delta}{x_0}. \end{align} $$
Solving these explicitly, we obtain
 $$ \begin{align} x_0 = \frac{1-2 \delta + \sqrt{1+4\delta^2}}{2}, \qquad y_0 = \frac{1+2 \delta + \sqrt{1+4\delta^2}}{2}, \end{align} $$
$$ \begin{align} x_0 = \frac{1-2 \delta + \sqrt{1+4\delta^2}}{2}, \qquad y_0 = \frac{1+2 \delta + \sqrt{1+4\delta^2}}{2}, \end{align} $$
and thus
 $$ \begin{align} \Phi(x_0, y_0) = - \frac{1 + \sqrt{1 + 4\delta^2}}{2} - \delta \log\left(\frac{1 + 2 \delta + \sqrt{1+4 \delta^2}}{1- 2 \delta + \sqrt{1+4\delta^2}}\right) = -\sum_{j=0}^{\infty} c_j \delta^{j}, \end{align} $$
$$ \begin{align} \Phi(x_0, y_0) = - \frac{1 + \sqrt{1 + 4\delta^2}}{2} - \delta \log\left(\frac{1 + 2 \delta + \sqrt{1+4 \delta^2}}{1- 2 \delta + \sqrt{1+4\delta^2}}\right) = -\sum_{j=0}^{\infty} c_j \delta^{j}, \end{align} $$
which is analytic in
![]() $\delta $
for
$\delta $
for
![]() $\lvert \delta \rvert < 1/2$
, and also even with respect to
$\lvert \delta \rvert < 1/2$
, and also even with respect to
![]() $\delta $
.
$\delta $
.
Remark. Lemmas 8.1 and 8.2 have some close similarities. In both cases, the stationary-phase method may be applied, and the stationary point can be explicitly found by solving a quadratic equation. In each case, only one of the two roots is relevant, and the other is outside the support of the test function. We expect, but did not confirm rigorously, that when
![]() $U \asymp \epsilon N^2$
, which is a range that is not needed in this paper, then both roots of the quadratic equation are relevant. This situation is more complicated because the two roots may approach each other, in which case a cubic Taylor approximation to the phase function is more applicable (as with the Airy function, for instance).
$U \asymp \epsilon N^2$
, which is a range that is not needed in this paper, then both roots of the quadratic equation are relevant. This situation is more complicated because the two roots may approach each other, in which case a cubic Taylor approximation to the phase function is more applicable (as with the Airy function, for instance).
9 Cleaning up some terms
In this section we take the opportunity to deal with some ranges of parameters for which relatively easy methods suffice. This will simplify our exposition for the more difficult cases.
With the aid of the analysis from §8 we can now treat some ranges of c.
Lemma 9.1. The contribution to
![]() $ \mathcal {S}\left (H_{+}\right )$
from
$ \mathcal {S}\left (H_{+}\right )$
from
 $C \ll \frac {N^2}{T^2} T^{\varepsilon }$
is bounded by
$C \ll \frac {N^2}{T^2} T^{\varepsilon }$
is bounded by
![]() $\Delta T^{1+\varepsilon }$
.
$\Delta T^{1+\varepsilon }$
.
Proof. Let
![]() $\mathcal {S}$
be the contribution to
$\mathcal {S}$
be the contribution to
![]() $ \mathcal {S}\left (H_{+}\right )$
from
$ \mathcal {S}\left (H_{+}\right )$
from
 $C \ll \frac {N^2}{T^2} T^{\varepsilon }$
. Since
$C \ll \frac {N^2}{T^2} T^{\varepsilon }$
. Since
 $x \asymp \frac {N^2}{C}$
, the assumed upper bound on C means
$x \asymp \frac {N^2}{C}$
, the assumed upper bound on C means
![]() $x \gg T^{2-\varepsilon }$
, so that the conditions to apply Lemma 6.1 are in effect. Applying equation (6.17) to equation (7.2), we deduce
$x \gg T^{2-\varepsilon }$
, so that the conditions to apply Lemma 6.1 are in effect. Applying equation (6.17) to equation (7.2), we deduce
 $$ \begin{align} I(k, \ell, c) = \int_{\lvert v\rvert \ll x^{-1/2} T^{\varepsilon}} e^{- 2iTv} g(\Delta v) \eta(v) I(A, B, U, \epsilon(v), N) dv + O\left(T^{-50}\right), \end{align} $$
$$ \begin{align} I(k, \ell, c) = \int_{\lvert v\rvert \ll x^{-1/2} T^{\varepsilon}} e^{- 2iTv} g(\Delta v) \eta(v) I(A, B, U, \epsilon(v), N) dv + O\left(T^{-50}\right), \end{align} $$
with parameters as given in equation (8.4). Under the present assumptions, we have
 $\epsilon \ll \frac {v^2}{c} \ll \frac {T^{2\varepsilon }}{x c} \asymp \frac {T^{2\varepsilon }}{N^2}$
. Therefore, in the notation of equation (8.4), we have
$\epsilon \ll \frac {v^2}{c} \ll \frac {T^{2\varepsilon }}{x c} \asymp \frac {T^{2\varepsilon }}{N^2}$
. Therefore, in the notation of equation (8.4), we have
![]() $\epsilon N^2 \ll T^{2\varepsilon }$
.
$\epsilon N^2 \ll T^{2\varepsilon }$
.
First consider the case where
![]() $U \gg T^{3\varepsilon }$
. In this case,
$U \gg T^{3\varepsilon }$
. In this case,
![]() $\epsilon N^2 = o(U)$
, and so Lemma 8.1 implies that
$\epsilon N^2 = o(U)$
, and so Lemma 8.1 implies that
![]() $I(A,B,U, \epsilon , N) \ll U^{-1} N^2$
and is very small unless
$I(A,B,U, \epsilon , N) \ll U^{-1} N^2$
and is very small unless
 $A \asymp B \asymp \frac {U}{N}$
. Translating notation, we may assume
$A \asymp B \asymp \frac {U}{N}$
. Translating notation, we may assume
 $\lvert k\rvert \asymp \lvert \ell \rvert \asymp \frac {CU}{N}$
, and in particular k and
$\lvert k\rvert \asymp \lvert \ell \rvert \asymp \frac {CU}{N}$
, and in particular k and
![]() $\ell $
are nonzero. Integrating trivially over v, we deduce
$\ell $
are nonzero. Integrating trivially over v, we deduce
 $$ \begin{align} I(k,\ell,c) \ll \frac{N C^{1/2} T^{\varepsilon}}{U} \left(1 + \frac{\lvert k\rvert N}{CU}\right)^{-100} \left(1 + \frac{\lvert\ell\rvert N}{CU}\right)^{-100}. \end{align} $$
$$ \begin{align} I(k,\ell,c) \ll \frac{N C^{1/2} T^{\varepsilon}}{U} \left(1 + \frac{\lvert k\rvert N}{CU}\right)^{-100} \left(1 + \frac{\lvert\ell\rvert N}{CU}\right)^{-100}. \end{align} $$
Inserting this bound into equation (7.10), we obtain
 $$ \begin{align} &\lvert\mathcal{S}\rvert \ll \frac{\Delta T T^{\varepsilon}}{UC} \sum_{\substack{\nu, \gamma \geq 2, \thinspace \lambda \geq 4 \\ \min\left(\lambda, \nu\right) = \min\left(\lambda, \gamma\right)}} \left(2^{\nu}, 2^{\lambda-2-\delta}\right) \nonumber\\ &\quad \sum_{k_o', \ell_o' \neq 0} \sum_{r_1, r_2} \sum_{\substack{g_1\mid r_1^2 \\ g_2 \mid r_2^2}} g_1 g_2 \sum_{\substack{q^{\infty} \equiv 0 \negthickspace \negthickspace \pmod{r_1} \\ q \asymp \frac{C}{2^{\lambda} r_1^2 r_2^2}}} \left(1 + \frac{\left\lvert k_o' 2^{\nu} g_1 g_2\right\rvert N}{CU}\right)^{-100} \left(1 + \frac{\left\lvert\ell_o' 2^{\gamma} g_1 g_2\right\rvert N}{CU}\right)^{-100}. \end{align} $$
$$ \begin{align} &\lvert\mathcal{S}\rvert \ll \frac{\Delta T T^{\varepsilon}}{UC} \sum_{\substack{\nu, \gamma \geq 2, \thinspace \lambda \geq 4 \\ \min\left(\lambda, \nu\right) = \min\left(\lambda, \gamma\right)}} \left(2^{\nu}, 2^{\lambda-2-\delta}\right) \nonumber\\ &\quad \sum_{k_o', \ell_o' \neq 0} \sum_{r_1, r_2} \sum_{\substack{g_1\mid r_1^2 \\ g_2 \mid r_2^2}} g_1 g_2 \sum_{\substack{q^{\infty} \equiv 0 \negthickspace \negthickspace \pmod{r_1} \\ q \asymp \frac{C}{2^{\lambda} r_1^2 r_2^2}}} \left(1 + \frac{\left\lvert k_o' 2^{\nu} g_1 g_2\right\rvert N}{CU}\right)^{-100} \left(1 + \frac{\left\lvert\ell_o' 2^{\gamma} g_1 g_2\right\rvert N}{CU}\right)^{-100}. \end{align} $$
Estimating the sum trivially, and simplifying using
 $C \ll \frac {N^2}{T^2} T^{\varepsilon }$
and
$C \ll \frac {N^2}{T^2} T^{\varepsilon }$
and
![]() $N \ll N_{\text {max}} \ll U^{1/2} T^{1+\varepsilon }$
, we deduce
$N \ll N_{\text {max}} \ll U^{1/2} T^{1+\varepsilon }$
, we deduce
 $$ \begin{align} \lvert\mathcal{S}\rvert \ll \frac{\Delta T}{N} \frac{C^2 U}{N} T^{\varepsilon} \ll \frac{\Delta U N^2}{T^3} T^{\varepsilon} \ll \Delta T \frac{U^2}{T^2} T^{\varepsilon}, \end{align} $$
$$ \begin{align} \lvert\mathcal{S}\rvert \ll \frac{\Delta T}{N} \frac{C^2 U}{N} T^{\varepsilon} \ll \frac{\Delta U N^2}{T^3} T^{\varepsilon} \ll \Delta T \frac{U^2}{T^2} T^{\varepsilon}, \end{align} $$
which is acceptable, since
![]() $U \ll T$
.
$U \ll T$
.
Next we indicate the changes needed to handle the case
![]() $U \ll T^{3\varepsilon }$
. Integration by parts (Lemma 4.2) shows that
$U \ll T^{3\varepsilon }$
. Integration by parts (Lemma 4.2) shows that
![]() $I(A, B, U, \epsilon , N)$
is very small unless
$I(A, B, U, \epsilon , N)$
is very small unless
 $A, B \ll \frac {T^{3 \varepsilon }}{N}$
, or equivalently,
$A, B \ll \frac {T^{3 \varepsilon }}{N}$
, or equivalently,
 $\lvert k\rvert , \lvert \ell \rvert \ll \frac {C}{N} T^{3 \varepsilon }$
. Using
$\lvert k\rvert , \lvert \ell \rvert \ll \frac {C}{N} T^{3 \varepsilon }$
. Using
 $C \ll \frac {N^2}{T^2} T^{\varepsilon }$
and
$C \ll \frac {N^2}{T^2} T^{\varepsilon }$
and
![]() $N \ll N_{\max } \ll T^{1+3 \varepsilon }$
, this means that we only need to consider
$N \ll N_{\max } \ll T^{1+3 \varepsilon }$
, this means that we only need to consider
![]() $k = \ell = 0$
. A trivial bound implies
$k = \ell = 0$
. A trivial bound implies
![]() $I(0, 0, c) \ll N C^{1/2} T^{\varepsilon }$
.
$I(0, 0, c) \ll N C^{1/2} T^{\varepsilon }$
.
Using the final sentence of Lemma 5.3, we see that the contribution to
![]() $ \mathcal {S}$
from
$ \mathcal {S}$
from
![]() $k=\ell =0$
is bounded by
$k=\ell =0$
is bounded by
 $$ \begin{align} \frac{\Delta T}{N C^{3/2}} \frac{N C^{1/2} T^{\varepsilon}}{U} \sum_{r_2 \asymp C^{1/2}} C \ll \frac{\Delta T}{U} T^{\varepsilon} C^{1/2} \ll \frac{\Delta N}{U} T^{\varepsilon} \ll \Delta T^{1+\varepsilon}. \end{align} $$
$$ \begin{align} \frac{\Delta T}{N C^{3/2}} \frac{N C^{1/2} T^{\varepsilon}}{U} \sum_{r_2 \asymp C^{1/2}} C \ll \frac{\Delta T}{U} T^{\varepsilon} C^{1/2} \ll \frac{\Delta N}{U} T^{\varepsilon} \ll \Delta T^{1+\varepsilon}. \end{align} $$
In light of Lemma 9.1, for the rest of the paper we can assume that
 $$ \begin{align} C \gg \frac{N^2}{T^2} T^{\varepsilon}. \end{align} $$
$$ \begin{align} C \gg \frac{N^2}{T^2} T^{\varepsilon}. \end{align} $$
Lemma 9.2. Suppose formula (9.6) holds, and let
 $$ \begin{align} V_0 = \frac{TC}{N^2}. \end{align} $$
$$ \begin{align} V_0 = \frac{TC}{N^2}. \end{align} $$
Then with
 $x = \frac {4 \pi mn}{c} \asymp \frac {N^2}{C}$
, we have
$x = \frac {4 \pi mn}{c} \asymp \frac {N^2}{C}$
, we have
 $$ \begin{align} K_{+}(x) = \int_{v \asymp V_0} e^{ix(\cosh(v) - 1) - 2iTv} g(\Delta v) \eta(v) dv + O\left((xT)^{-100}\right), \end{align} $$
$$ \begin{align} K_{+}(x) = \int_{v \asymp V_0} e^{ix(\cosh(v) - 1) - 2iTv} g(\Delta v) \eta(v) dv + O\left((xT)^{-100}\right), \end{align} $$
where
![]() $\eta $
is a
$\eta $
is a
![]() $1$
-inert function supported on
$1$
-inert function supported on
![]() $v \asymp V_0$
.
$v \asymp V_0$
.
Before proving the lemma, we record a simple consequence of it which follows from inserting equation (9.8) into equation (7.2) (valid under the assumption (9.6), which is in effect):
 $$ \begin{align} I(k,\ell,c) = \int_{v \asymp V_0} e^{ix(\cosh(v) - 1) - 2iTv} g(\Delta v) \eta(v) I(A, B, U, \epsilon(v), N) dv + O\left(T^{-50}\right). \end{align} $$
$$ \begin{align} I(k,\ell,c) = \int_{v \asymp V_0} e^{ix(\cosh(v) - 1) - 2iTv} g(\Delta v) \eta(v) I(A, B, U, \epsilon(v), N) dv + O\left(T^{-50}\right). \end{align} $$
Proof. In the definition of
![]() $K_{+}(x)$
given by equation (6.12), we first apply a smooth dyadic partition of unity to the region
$K_{+}(x)$
given by equation (6.12), we first apply a smooth dyadic partition of unity to the region
![]() $100 V_0 \leq \lvert v\rvert \ll \Delta ^{-1} T^{\varepsilon } = o(1)$
. Consider a piece of this partition, with, say,
$100 V_0 \leq \lvert v\rvert \ll \Delta ^{-1} T^{\varepsilon } = o(1)$
. Consider a piece of this partition, with, say,
![]() $Z \leq \lvert v\rvert \leq 2Z$
. We may apply Lemma 4.2 with both Y and R taking the value
$Z \leq \lvert v\rvert \leq 2Z$
. We may apply Lemma 4.2 with both Y and R taking the value
![]() $x Z^2$
(and
$x Z^2$
(and
 $x \asymp \frac {N^2}{C}$
). Note that
$x \asymp \frac {N^2}{C}$
). Note that
 $x Z^2 \gg \frac {N^2 V_0^2}{C} \gg T^{\varepsilon }$
, so any such dyadic piece is very small.
$x Z^2 \gg \frac {N^2 V_0^2}{C} \gg T^{\varepsilon }$
, so any such dyadic piece is very small.
Next we consider the portion of the integral with
 $\lvert v\rvert \leq \frac {V_0}{100}$
. The version of the integration-by-parts bound stated in Lemma 4.2 is a simplified variant of [Reference Blomer, Khan and Young8, Lemma 8.1] (localized to a dyadic interval, etc.) which does not directly apply. However, the more general [Reference Blomer, Khan and Young8, Lemma 8.1] can be used to show that this portion of the integral is also small. The statement of [Reference Blomer, Khan and Young8, Lemma 8.1] contains a list of parameters
$\lvert v\rvert \leq \frac {V_0}{100}$
. The version of the integration-by-parts bound stated in Lemma 4.2 is a simplified variant of [Reference Blomer, Khan and Young8, Lemma 8.1] (localized to a dyadic interval, etc.) which does not directly apply. However, the more general [Reference Blomer, Khan and Young8, Lemma 8.1] can be used to show that this portion of the integral is also small. The statement of [Reference Blomer, Khan and Young8, Lemma 8.1] contains a list of parameters
![]() $(X, U, R, Y, Q)$
– not to be confused with the notation from this paper – which in our present context take the values
$(X, U, R, Y, Q)$
– not to be confused with the notation from this paper – which in our present context take the values
 $\left (1, V_0, T, N^2/C, 1\right )$
. It suffices to use [Reference Blomer, Khan and Young8, Lemma 8.1] to show that the integral is very small, provided
$\left (1, V_0, T, N^2/C, 1\right )$
. It suffices to use [Reference Blomer, Khan and Young8, Lemma 8.1] to show that the integral is very small, provided
 $\frac {QR}{\sqrt {Y}} \rightarrow \infty $
and
$\frac {QR}{\sqrt {Y}} \rightarrow \infty $
and
![]() $RU \rightarrow \infty $
. Here
$RU \rightarrow \infty $
. Here
![]() $QR/\sqrt {Y}$
takes the form
$QR/\sqrt {Y}$
takes the form
 $\frac {T \sqrt {C}}{N} \gg T^{\varepsilon /2}$
, and
$\frac {T \sqrt {C}}{N} \gg T^{\varepsilon /2}$
, and
![]() $RU = V_0 T \gg T^{\varepsilon }$
, using the assumption (9.6). The remaining part of the integral is displayed in equation (9.8).
$RU = V_0 T \gg T^{\varepsilon }$
, using the assumption (9.6). The remaining part of the integral is displayed in equation (9.8).
Lemma 9.3. Suppose that the conditions of Theorem 1.1 hold, along with formula (6.15). Then
 $$ \begin{align} I(k,\ell,c) = \frac{N C^{1/2}}{U} \left(\frac{k}{\ell}\right)^{iU} \exp\left(-\frac{2\pi i T^2 k \ell}{U^2 c} \right) W(\cdot) + O\left(T^{-100}\right), \end{align} $$
$$ \begin{align} I(k,\ell,c) = \frac{N C^{1/2}}{U} \left(\frac{k}{\ell}\right)^{iU} \exp\left(-\frac{2\pi i T^2 k \ell}{U^2 c} \right) W(\cdot) + O\left(T^{-100}\right), \end{align} $$
where W is
![]() $1$
-inert (in k,
$1$
-inert (in k,
![]() $\ell $
, and c, as well as all suppressed variables), and supported on
$\ell $
, and c, as well as all suppressed variables), and supported on
 $$ \begin{align} k \asymp \ell \asymp \frac{CU}{N}. \end{align} $$
$$ \begin{align} k \asymp \ell \asymp \frac{CU}{N}. \end{align} $$
Proof. We begin by making some simple deductions from the conditions of Theorem 1.1. First we note that formula (1.2) directly implies
![]() $U \Delta \geq T^{1+\delta }$
. Since formula (6.15) holds, we additionally deduce
$U \Delta \geq T^{1+\delta }$
. Since formula (6.15) holds, we additionally deduce
 $$ \begin{align} C \ll \frac{U N^2}{T^2} T^{-\delta}, \end{align} $$
$$ \begin{align} C \ll \frac{U N^2}{T^2} T^{-\delta}, \end{align} $$
for some
![]() $\delta> 0$
. Another consequence of formula (1.2) is that
$\delta> 0$
. Another consequence of formula (1.2) is that
 $$ \begin{align} \frac{T^3}{U^2 \Delta^3} \ll T^{-2\delta}. \end{align} $$
$$ \begin{align} \frac{T^3}{U^2 \Delta^3} \ll T^{-2\delta}. \end{align} $$
From the fact that
![]() $U \ll T$
, we also deduce that (for some
$U \ll T$
, we also deduce that (for some
![]() $\delta> 0$
)
$\delta> 0$
)
Now we pick up with equation (9.9). Using equation (9.7), the condition (9.12) means that
 $\frac {\epsilon N^2}{U} \asymp \frac {V_0^2 N^2}{CU} \asymp \frac {T^2 C}{UN^2} \ll T^{-\delta }$
, so that the conditions of Lemma 8.1 are met. This gives an asymptotic formula for the inner integral
$\frac {\epsilon N^2}{U} \asymp \frac {V_0^2 N^2}{CU} \asymp \frac {T^2 C}{UN^2} \ll T^{-\delta }$
, so that the conditions of Lemma 8.1 are met. This gives an asymptotic formula for the inner integral
![]() $I(A,B, U, \epsilon (v), N)$
for all
$I(A,B, U, \epsilon (v), N)$
for all
![]() $v \asymp V_0$
. In particular, we deduce that
$v \asymp V_0$
. In particular, we deduce that
![]() $I(k, \ell , c)$
is very small unless formula (9.11) holds, a condition that we henceforth assume is in place. Note that by formula (8.6),
$I(k, \ell , c)$
is very small unless formula (9.11) holds, a condition that we henceforth assume is in place. Note that by formula (8.6),
 $$ \begin{align} \frac{\epsilon U}{AB} = \frac{ (\cosh v -1) Uc}{\pi k \ell } \asymp \frac{UC V_0^2}{k \ell} \asymp \frac{UC \left(T C/N^2\right)^2 }{(CU/N)^2} = \frac{T^2 C}{U N^2} \ll \frac{T}{U \Delta } T^{\varepsilon} , \end{align} $$
$$ \begin{align} \frac{\epsilon U}{AB} = \frac{ (\cosh v -1) Uc}{\pi k \ell } \asymp \frac{UC V_0^2}{k \ell} \asymp \frac{UC \left(T C/N^2\right)^2 }{(CU/N)^2} = \frac{T^2 C}{U N^2} \ll \frac{T}{U \Delta } T^{\varepsilon} , \end{align} $$
since
 $k \asymp \ell \asymp \frac {CU}{N}$
,
$k \asymp \ell \asymp \frac {CU}{N}$
,
![]() $v \asymp V_0$
, and
$v \asymp V_0$
, and
 $C \ll \frac {N^2}{\Delta T} T^{\varepsilon }$
(recalling formula (6.15)). Therefore,
$C \ll \frac {N^2}{\Delta T} T^{\varepsilon }$
(recalling formula (6.15)). Therefore,
 $$ \begin{align} U \left(\frac{\epsilon U}{AB}\right)^3 \ll U \left(\frac{T}{U \Delta}\right)^3 T^{\varepsilon} \ll \frac{T^3}{U^2 \Delta^3} T^{\varepsilon} \ll T^{-\delta'}, \end{align} $$
$$ \begin{align} U \left(\frac{\epsilon U}{AB}\right)^3 \ll U \left(\frac{T}{U \Delta}\right)^3 T^{\varepsilon} \ll \frac{T^3}{U^2 \Delta^3} T^{\varepsilon} \ll T^{-\delta'}, \end{align} $$
for some
![]() $\delta '>0$
. This calculation shows that in equation (8.8), the terms with
$\delta '>0$
. This calculation shows that in equation (8.8), the terms with
![]() $j \geq 1$
can be absorbed into the inert weight function. This is where we use the condition (1.2), which can likely be relaxed to
$j \geq 1$
can be absorbed into the inert weight function. This is where we use the condition (1.2), which can likely be relaxed to
![]() $U \Delta \gg T^{1+\delta }$
, since this condition is sufficient to show that equation (8.8) is a good asymptotic expansion. Therefore,
$U \Delta \gg T^{1+\delta }$
, since this condition is sufficient to show that equation (8.8) is a good asymptotic expansion. Therefore,
 $$ \begin{align} I(k,\ell,c) = \frac{N^2}{U} \left(\frac{k}{\ell}\right)^{iU} \int_{v \asymp V_0} \exp\left(-2iTv + i\frac{U^2 c(\cosh v -1)}{\pi k \ell}\right) W(v, \cdot) dv, \end{align} $$
$$ \begin{align} I(k,\ell,c) = \frac{N^2}{U} \left(\frac{k}{\ell}\right)^{iU} \int_{v \asymp V_0} \exp\left(-2iTv + i\frac{U^2 c(\cosh v -1)}{\pi k \ell}\right) W(v, \cdot) dv, \end{align} $$
plus a small error term, where
![]() $W(v, \cdot )$
is
$W(v, \cdot )$
is
![]() $1$
-inert with respect to
$1$
-inert with respect to
![]() $k, \ell , c$
, and all other suppressed variables. Next we can apply
$k, \ell , c$
, and all other suppressed variables. Next we can apply
 $\cosh (v) - 1 = v^2/2 + O\left (v^4\right )$
and absorb the
$\cosh (v) - 1 = v^2/2 + O\left (v^4\right )$
and absorb the
![]() $v^4$
terms into the inert weight function, using formulas (6.15) and (9.14) as follows:
$v^4$
terms into the inert weight function, using formulas (6.15) and (9.14) as follows:
 $$ \begin{align} \frac{U^2 C V_0^4}{k \ell} \asymp \frac{C^3 T^4}{N^6} \ll \frac{T}{\Delta^3} T^{3\varepsilon} \ll T^{-\delta'}. \end{align} $$
$$ \begin{align} \frac{U^2 C V_0^4}{k \ell} \asymp \frac{C^3 T^4}{N^6} \ll \frac{T}{\Delta^3} T^{3\varepsilon} \ll T^{-\delta'}. \end{align} $$
Finally, by stationary phase we obtain the desired estimate.
Next we simplify our expression for
![]() $I(k,\ell ,c)$
under the conditions of Theorem 1.3, when U is small.
$I(k,\ell ,c)$
under the conditions of Theorem 1.3, when U is small.
Lemma 9.4. Suppose that the conditions of Theorem 1.3 hold, as well as formula (9.6). Then
![]() $I(k,\ell ,c)$
is very small unless
$I(k,\ell ,c)$
is very small unless
 $$ \begin{align} -k \asymp \ell \asymp \frac{C^2 T^2}{N^3}, \end{align} $$
$$ \begin{align} -k \asymp \ell \asymp \frac{C^2 T^2}{N^3}, \end{align} $$
in which case
 $$ \begin{align} I(k,\ell, c) = \frac{N^4}{CT^2} (-k/\ell)^{iU} e_c(-k \ell/12) \int_{v \asymp V_0} e^{-2ivT + \frac{2\pi i k \ell}{cv^2}} W(v,\cdot) dv + O\left(T^{-100}\right), \end{align} $$
$$ \begin{align} I(k,\ell, c) = \frac{N^4}{CT^2} (-k/\ell)^{iU} e_c(-k \ell/12) \int_{v \asymp V_0} e^{-2ivT + \frac{2\pi i k \ell}{cv^2}} W(v,\cdot) dv + O\left(T^{-100}\right), \end{align} $$
for some function
![]() $W(v, \cdot )$
that is
$W(v, \cdot )$
that is
![]() $1$
-inert with respect to k,
$1$
-inert with respect to k,
![]() $\ell $
, c, and all other suppressed variables.
$\ell $
, c, and all other suppressed variables.
Remark. Although it is possible to also evaluate the asymptotic of the v-integral in equation (9.20), we prefer to save this step for later (§10).
Proof. We again pick up with equation (9.9) (recall also the definition (8.2)), which takes the form
 $$ \begin{align} I(k,\ell,c) = \int_{v \asymp V_0} \eta(v) g(\Delta v) e^{-2ivT} I\left(\frac{2 \pi k}{c}, \frac{2 \pi \ell}{c}, U, \epsilon, N\right) dv, \end{align} $$
$$ \begin{align} I(k,\ell,c) = \int_{v \asymp V_0} \eta(v) g(\Delta v) e^{-2ivT} I\left(\frac{2 \pi k}{c}, \frac{2 \pi \ell}{c}, U, \epsilon, N\right) dv, \end{align} $$
with
 $\epsilon =\epsilon (v) = 4\pi \frac {\cosh (v) - 1}{c} \asymp \frac {V_0^2}{C} \asymp \frac {C T^2}{N^4}$
, for all
$\epsilon =\epsilon (v) = 4\pi \frac {\cosh (v) - 1}{c} \asymp \frac {V_0^2}{C} \asymp \frac {C T^2}{N^4}$
, for all
![]() $v \asymp V_0$
. Since formula (9.6) holds, this means that
$v \asymp V_0$
. Since formula (9.6) holds, this means that
 $\frac {U}{\epsilon N^2} \asymp \frac {U N^2}{T^2 C} \ll T^{-\varepsilon }$
, so that the conditions of Lemma 8.2 are met. This directly implies that
$\frac {U}{\epsilon N^2} \asymp \frac {U N^2}{T^2 C} \ll T^{-\varepsilon }$
, so that the conditions of Lemma 8.2 are met. This directly implies that
![]() $I(k,\ell ,c)$
is very small unless formula (9.19) holds. Note that
$I(k,\ell ,c)$
is very small unless formula (9.19) holds. Note that
 $$ \begin{align} \frac{AB}{\epsilon} = \frac{\pi k \ell}{c (\cosh v -1)}, \qquad \left\lvert\frac{AB}{\epsilon} \right\rvert \left(\frac{U \epsilon}{AB}\right)^2 = \left\lvert\frac{U^2 \epsilon}{AB} \right\rvert \asymp \frac{U^2 N^2}{CT^2} \ll T^{-\varepsilon}. \end{align} $$
$$ \begin{align} \frac{AB}{\epsilon} = \frac{\pi k \ell}{c (\cosh v -1)}, \qquad \left\lvert\frac{AB}{\epsilon} \right\rvert \left(\frac{U \epsilon}{AB}\right)^2 = \left\lvert\frac{U^2 \epsilon}{AB} \right\rvert \asymp \frac{U^2 N^2}{CT^2} \ll T^{-\varepsilon}. \end{align} $$
The latter calculation shows that the terms with
![]() $j \geq 1$
in equation (8.15) may be absorbed into the inert weight function. We thus conclude that
$j \geq 1$
in equation (8.15) may be absorbed into the inert weight function. We thus conclude that
 $$ \begin{align} I(k,\ell, c) = \frac{N^4}{CT^2} (-k/\ell)^{iU} \int_{v \asymp V_0} e^{-2ivT + \frac{\pi i k \ell}{c(\cosh v - 1)}} W(v,\cdot) dv + O\left(T^{-100}\right). \end{align} $$
$$ \begin{align} I(k,\ell, c) = \frac{N^4}{CT^2} (-k/\ell)^{iU} \int_{v \asymp V_0} e^{-2ivT + \frac{\pi i k \ell}{c(\cosh v - 1)}} W(v,\cdot) dv + O\left(T^{-100}\right). \end{align} $$
Finally we observe the Taylor/Laurent approximation
 $$ \begin{align} \frac{1}{\cosh v -1} = \frac{2}{v^2} - \frac{1}{6} + O\left(v^2\right), \end{align} $$
$$ \begin{align} \frac{1}{\cosh v -1} = \frac{2}{v^2} - \frac{1}{6} + O\left(v^2\right), \end{align} $$
and that
 $$ \begin{align} \frac{k \ell}{c} v^2 \asymp \frac{C^5 T^6}{N^{10}} \ll \frac{T}{\Delta^5} T^{\varepsilon} \ll T^{-\delta'} \end{align} $$
$$ \begin{align} \frac{k \ell}{c} v^2 \asymp \frac{C^5 T^6}{N^{10}} \ll \frac{T}{\Delta^5} T^{\varepsilon} \ll T^{-\delta'} \end{align} $$
for some
![]() $\delta '>0$
, where we have used
$\delta '>0$
, where we have used
 $C \ll \frac {N^2}{\Delta T} T^{\varepsilon }$
from formula (6.15). This lets us absorb the lower-order terms in the Taylor expansion into the inert weight function. Therefore, equation (9.20) holds.
$C \ll \frac {N^2}{\Delta T} T^{\varepsilon }$
from formula (6.15). This lets us absorb the lower-order terms in the Taylor expansion into the inert weight function. Therefore, equation (9.20) holds.
10 Mellin inversion
We recall that we have the expression (7.10), which contains a smooth (yet oscillatory) weight function of the form
In the conditions of Theorem 1.1, I is given by Lemma 9.3, whereas in the conditions of Theorem 1.3, I is given by Lemma 9.4. In both cases, the function f is very small except when k and
![]() $\ell $
are fixed into dyadic intervals. We may therefore freely insert an inert weight function that enforces this condition.
$\ell $
are fixed into dyadic intervals. We may therefore freely insert an inert weight function that enforces this condition.
First consider the setting relevant for Theorem 1.1. The function f has phase as given in Lemma 9.3, modified to include
![]() $e_c(k \ell /4)$
, which is strictly smaller in size due to the assumption
$e_c(k \ell /4)$
, which is strictly smaller in size due to the assumption
![]() $U \leq (2-\delta )T$
. We apply Lemma 4.4 to the phase function and Mellin inversion to the inert part. We therefore obtain
$U \leq (2-\delta )T$
. We apply Lemma 4.4 to the phase function and Mellin inversion to the inert part. We therefore obtain
 $$ \begin{align} f(k,\ell,c) &= \frac{\Phi}{\sqrt{P}} \!\left(\frac{2^{\nu} k_o'}{2^{\gamma} \ell_o'}\right)^{iU} \! \int_{-t \asymp P} \int \int \int \!\left(\frac{T^2 g_1^2 g_2^2 k_o' \ell_o'}{U^2 q r_1^2 r_2^2 2^{\lambda-\nu-\gamma}}\right)^s \!\left(1-\frac{U^2}{4T^2}\right)^s v(t) \widetilde{w}(u_1, u_2, u_3) \nonumber\\ &\quad \times \left(\frac{C}{q r_1^2 r_2^2 2^{\lambda}}\right)^{u_1} \left(\frac{K}{k_o' g_1 g_2 2^{\nu}}\right)^{u_2} \left(\frac{K}{\ell_o' g_1 g_2 2^{\gamma}} \right)^{u_3} du_1 du_2 du_3 ds, \end{align} $$
$$ \begin{align} f(k,\ell,c) &= \frac{\Phi}{\sqrt{P}} \!\left(\frac{2^{\nu} k_o'}{2^{\gamma} \ell_o'}\right)^{iU} \! \int_{-t \asymp P} \int \int \int \!\left(\frac{T^2 g_1^2 g_2^2 k_o' \ell_o'}{U^2 q r_1^2 r_2^2 2^{\lambda-\nu-\gamma}}\right)^s \!\left(1-\frac{U^2}{4T^2}\right)^s v(t) \widetilde{w}(u_1, u_2, u_3) \nonumber\\ &\quad \times \left(\frac{C}{q r_1^2 r_2^2 2^{\lambda}}\right)^{u_1} \left(\frac{K}{k_o' g_1 g_2 2^{\nu}}\right)^{u_2} \left(\frac{K}{\ell_o' g_1 g_2 2^{\gamma}} \right)^{u_3} du_1 du_2 du_3 ds, \end{align} $$
plus a small error term, where
![]() $s=it$
and
$s=it$
and
 $$ \begin{align} \Phi = \frac{N \sqrt{C}}{U}, \qquad P = \frac{C T^2}{N^2}, \qquad K = \frac{CU}{N}. \end{align} $$
$$ \begin{align} \Phi = \frac{N \sqrt{C}}{U}, \qquad P = \frac{C T^2}{N^2}, \qquad K = \frac{CU}{N}. \end{align} $$
By standard Mellin inversion of an inert function, the function
![]() $\widetilde {w}$
is entire and has rapid decay on any vertical line. However, we do not specify the vertical contour in this integral (or in several instances to follow). Also, we have absorbed constants such as
$\widetilde {w}$
is entire and has rapid decay on any vertical line. However, we do not specify the vertical contour in this integral (or in several instances to follow). Also, we have absorbed constants such as
 $\frac {1}{2\pi i}$
and the like into the weight functions. We recall that
$\frac {1}{2\pi i}$
and the like into the weight functions. We recall that
![]() $k = 2^{\nu } g_1 g_2 k_o'$
,
$k = 2^{\nu } g_1 g_2 k_o'$
,
![]() $\ell = 2^{\gamma } g_1 g_2 \ell _o'$
, and
$\ell = 2^{\gamma } g_1 g_2 \ell _o'$
, and
![]() $c = 2^{\lambda } q r_1^2 r_2^2$
. We recall from Lemma 4.4 that
$c = 2^{\lambda } q r_1^2 r_2^2$
. We recall from Lemma 4.4 that
![]() $v(t)$
is supported on
$v(t)$
is supported on
![]() $-t \asymp P$
, is
$-t \asymp P$
, is
![]() $O(1)$
, and has phase
$O(1)$
, and has phase
![]() $e^{-it \log \left (\lvert t\rvert /e\right )}$
.
$e^{-it \log \left (\lvert t\rvert /e\right )}$
.
We can also apply these steps to I given by Lemma 9.4, which will have a similar structure but with an extra v-integral. We obtain
 $$ \begin{align} f(k,\ell,c) &= \frac{\Phi_0}{\sqrt{P}} \int_{v \asymp V_0} e^{-2ivT} \left(\frac{-2^{\nu} k_o'}{2^{\gamma} \ell_o'}\right)^{iU} \int_{-t \asymp P} \int \int \int \left(\frac{g_1^2 g_2^2 \left\lvert k_o'\right\rvert \ell_o'}{q r_1^2 r_2^2 2^{\lambda-\nu-\gamma}}\right)^s \nonumber \\ &\quad \times \left(\frac{1}{v^2} + \frac{1}{6} \right)^s v(t) \widetilde{w}(u_1, u_2, u_3) \nonumber\\ &\quad \times \left(\frac{C}{q r_1^2 r_2^2 2^{\lambda}}\right)^{u_1} \left(\frac{K}{\left\lvert k_o'\right\rvert g_1 g_2 2^{\nu}}\right)^{u_2} \left(\frac{K}{\ell_o' g_1 g_2 2^{\gamma}} \right)^{u_3} du_1 du_2 du_3 ds dv, \end{align} $$
$$ \begin{align} f(k,\ell,c) &= \frac{\Phi_0}{\sqrt{P}} \int_{v \asymp V_0} e^{-2ivT} \left(\frac{-2^{\nu} k_o'}{2^{\gamma} \ell_o'}\right)^{iU} \int_{-t \asymp P} \int \int \int \left(\frac{g_1^2 g_2^2 \left\lvert k_o'\right\rvert \ell_o'}{q r_1^2 r_2^2 2^{\lambda-\nu-\gamma}}\right)^s \nonumber \\ &\quad \times \left(\frac{1}{v^2} + \frac{1}{6} \right)^s v(t) \widetilde{w}(u_1, u_2, u_3) \nonumber\\ &\quad \times \left(\frac{C}{q r_1^2 r_2^2 2^{\lambda}}\right)^{u_1} \left(\frac{K}{\left\lvert k_o'\right\rvert g_1 g_2 2^{\nu}}\right)^{u_2} \left(\frac{K}{\ell_o' g_1 g_2 2^{\gamma}} \right)^{u_3} du_1 du_2 du_3 ds dv, \end{align} $$
plus a small error term, where this time
 $$ \begin{align} \Phi_0 = \frac{N^4}{C T^2}, \qquad P = \frac{C T^2}{N^2}, \qquad K = \frac{C^2 T^2}{N^3}, \qquad V_0 = \frac{CT}{N^2}. \end{align} $$
$$ \begin{align} \Phi_0 = \frac{N^4}{C T^2}, \qquad P = \frac{C T^2}{N^2}, \qquad K = \frac{C^2 T^2}{N^3}, \qquad V_0 = \frac{CT}{N^2}. \end{align} $$
Here,
![]() $\widetilde {w}(u_1, u_2, u_3)$
is implicitly an inert function of v. It is the Mellin transform (in the suppressed variables, but not in v) of the function
$\widetilde {w}(u_1, u_2, u_3)$
is implicitly an inert function of v. It is the Mellin transform (in the suppressed variables, but not in v) of the function
![]() $W(v,\cdot )$
which was introduced in Lemma 9.4.
$W(v,\cdot )$
which was introduced in Lemma 9.4.
At this point, we finally asymptotically evaluate the v-integral. We are considering
 $$ \begin{align} \int_{v \asymp V_0} e^{-2ivT - 2s \log{v} + s\log\left(1+\frac{v^2}{6}\right)} W(v,\cdot) dv, \end{align} $$
$$ \begin{align} \int_{v \asymp V_0} e^{-2ivT - 2s \log{v} + s\log\left(1+\frac{v^2}{6}\right)} W(v,\cdot) dv, \end{align} $$
where we recall
![]() $s=it$
and
$s=it$
and
![]() $-t \asymp P$
. We first observe that
$-t \asymp P$
. We first observe that
 $s \log \left (1+\frac {v^2}{6}\right ) = s v^2/6 + O\left (sv^4\right )$
, and note that
$s \log \left (1+\frac {v^2}{6}\right ) = s v^2/6 + O\left (sv^4\right )$
, and note that
 $$ \begin{align} \left\lvert sv^4\right\rvert \asymp P V_0^4 \ll \frac{T^{1+\varepsilon}}{\Delta^5} \ll T^{-\delta}, \end{align} $$
$$ \begin{align} \left\lvert sv^4\right\rvert \asymp P V_0^4 \ll \frac{T^{1+\varepsilon}}{\Delta^5} \ll T^{-\delta}, \end{align} $$
by the assumption
![]() $\Delta \gg T^{1/5+\varepsilon }$
. Therefore, the term with
$\Delta \gg T^{1/5+\varepsilon }$
. Therefore, the term with
![]() $sv^4$
can be absorbed into the inert weight function at no cost. We are therefore considering an oscillatory integral with phase
$sv^4$
can be absorbed into the inert weight function at no cost. We are therefore considering an oscillatory integral with phase
![]() $\phi (v) = -2vT - 2t \log {v} + t v^2/6$
. It is easy to see that
$\phi (v) = -2vT - 2t \log {v} + t v^2/6$
. It is easy to see that
 $\lvert \phi ''(v)\rvert \asymp \frac {P}{V_0^2}$
throughout the support of the test function, and that there exists a stationary point at
$\lvert \phi ''(v)\rvert \asymp \frac {P}{V_0^2}$
throughout the support of the test function, and that there exists a stationary point at
![]() $v_0$
satisfying
$v_0$
satisfying
 $$ \begin{align} -2T - \frac{2t}{v_0} + \frac{t v_0}{3} = 0. \end{align} $$
$$ \begin{align} -2T - \frac{2t}{v_0} + \frac{t v_0}{3} = 0. \end{align} $$
We explicitly calculate
 $$ \begin{align} v_0 = \frac{2T - 2T \sqrt{1+ \frac{2 t^2}{3T^2}}}{2t/3} = \frac{-t}{T} + a' \frac{t^3}{T^3} + O\left(\frac{P^5}{T^5}\right) \end{align} $$
$$ \begin{align} v_0 = \frac{2T - 2T \sqrt{1+ \frac{2 t^2}{3T^2}}}{2t/3} = \frac{-t}{T} + a' \frac{t^3}{T^3} + O\left(\frac{P^5}{T^5}\right) \end{align} $$
for some constant
![]() $a'$
. We observe that
$a'$
. We observe that
 $\frac {P^5}{T^4} \ll \frac {T^{1+\varepsilon }}{\Delta ^5} \ll T^{-\delta }$
, so quantities of this size (or smaller) may be safely discarded. For later use, we note in passing that
$\frac {P^5}{T^4} \ll \frac {T^{1+\varepsilon }}{\Delta ^5} \ll T^{-\delta }$
, so quantities of this size (or smaller) may be safely discarded. For later use, we note in passing that
 $\frac {P^2}{T^2} \ll \frac {T^{\varepsilon }}{\Delta ^2} \ll T^{-\delta }$
. We conclude
$\frac {P^2}{T^2} \ll \frac {T^{\varepsilon }}{\Delta ^2} \ll T^{-\delta }$
. We conclude
 $$ \begin{align} \phi(v_0) = -2 t \log\left(\lvert s\rvert/T\right) + 2t + a \frac{t^3}{T^2} +O\left(\frac{P^5}{T^4}\right) \end{align} $$
$$ \begin{align} \phi(v_0) = -2 t \log\left(\lvert s\rvert/T\right) + 2t + a \frac{t^3}{T^2} +O\left(\frac{P^5}{T^4}\right) \end{align} $$
for some new constant a. Therefore,
 $$ \begin{align} \int_{v \asymp V_0} e^{-2ivT - 2 it \log{v} + it \log\left(1+\frac{v^2}{6}\right)} w(v, \cdot) dv = \frac{V_0}{\sqrt{P}} e^{-2it \log\left(\frac{\lvert t\rvert}{eT}\right)} e^{ia \frac{t^3}{T^2}} W(\cdot) \end{align} $$
$$ \begin{align} \int_{v \asymp V_0} e^{-2ivT - 2 it \log{v} + it \log\left(1+\frac{v^2}{6}\right)} w(v, \cdot) dv = \frac{V_0}{\sqrt{P}} e^{-2it \log\left(\frac{\lvert t\rvert}{eT}\right)} e^{ia \frac{t^3}{T^2}} W(\cdot) \end{align} $$
for some inert function W and constant a. We deduce a formula for f in the form
 $$ \begin{align} f(k,\ell,c) &= \frac{\Phi}{\sqrt{P}} \!\left(\frac{-k_o'}{\ell_o'}\right)^{iU} \!\!\int_{-t \asymp P} \int\! \int\! \int \!\left(\frac{g_1^2 g_2^2 \lvert k_o'\rvert \ell_o'}{q r_1^2 r_2^2 2^{\lambda-\nu-\gamma}}\right)^s \! v(t) e^{-2it \log\left(\frac{\lvert t\rvert}{eT}\right) + ia\frac{t^3}{T^2}} \widetilde{w}(u_1, u_2, u_3) \nonumber\\ &\quad \times \left(\frac{C}{q r_1^2 r_2^2 2^{\lambda}}\right)^{u_1} \left(\frac{K}{\left\lvert k_o'\right\rvert g_1 g_2 2^{\nu}}\right)^{u_2} \left(\frac{K}{\ell_o' g_1 g_2 2^{\gamma}} \right)^{u_3} du_1 du_2 du_3 ds dv, \end{align} $$
$$ \begin{align} f(k,\ell,c) &= \frac{\Phi}{\sqrt{P}} \!\left(\frac{-k_o'}{\ell_o'}\right)^{iU} \!\!\int_{-t \asymp P} \int\! \int\! \int \!\left(\frac{g_1^2 g_2^2 \lvert k_o'\rvert \ell_o'}{q r_1^2 r_2^2 2^{\lambda-\nu-\gamma}}\right)^s \! v(t) e^{-2it \log\left(\frac{\lvert t\rvert}{eT}\right) + ia\frac{t^3}{T^2}} \widetilde{w}(u_1, u_2, u_3) \nonumber\\ &\quad \times \left(\frac{C}{q r_1^2 r_2^2 2^{\lambda}}\right)^{u_1} \left(\frac{K}{\left\lvert k_o'\right\rvert g_1 g_2 2^{\nu}}\right)^{u_2} \left(\frac{K}{\ell_o' g_1 g_2 2^{\gamma}} \right)^{u_3} du_1 du_2 du_3 ds dv, \end{align} $$
where now
 $$ \begin{align} \Phi = \frac{N^4 V_0}{C T^2 P^{1/2}} = \frac{N^3}{C^{1/2} T^2}, \qquad P = \frac{C T^2}{N^2}, \qquad K = \frac{C^2 T^2}{N^3}, \qquad V_0 = \frac{CT}{N^2}. \end{align} $$
$$ \begin{align} \Phi = \frac{N^4 V_0}{C T^2 P^{1/2}} = \frac{N^3}{C^{1/2} T^2}, \qquad P = \frac{C T^2}{N^2}, \qquad K = \frac{C^2 T^2}{N^3}, \qquad V_0 = \frac{CT}{N^2}. \end{align} $$
This expression for
![]() $f(k,\ell ,c)$
is similar enough to equation (10.2) that we can proceed in parallel. We mainly focus on the proof of Theorem 1.1.
$f(k,\ell ,c)$
is similar enough to equation (10.2) that we can proceed in parallel. We mainly focus on the proof of Theorem 1.1.
Inserting equation (10.2) into equation (7.12), we obtain
 $$ \begin{align} \mathcal{S}_{\eta}\left(H_{+}\right) = \sum_C \frac{\Delta T}{NC^{3/2}} \frac{\Phi}{\sqrt{P}} \int_{-t \asymp P} \int \int \int \left(\frac{T^2}{U^2} - \frac{1}{4}\right)^s v(t) \widetilde{w}(u_1, u_2, u_3) \nonumber\\ C^{u_1} K^{u_2 + u_3} Z(s,u_1,u_2,u_3) du_1 du_2 du_3 ds, \end{align} $$
$$ \begin{align} \mathcal{S}_{\eta}\left(H_{+}\right) = \sum_C \frac{\Delta T}{NC^{3/2}} \frac{\Phi}{\sqrt{P}} \int_{-t \asymp P} \int \int \int \left(\frac{T^2}{U^2} - \frac{1}{4}\right)^s v(t) \widetilde{w}(u_1, u_2, u_3) \nonumber\\ C^{u_1} K^{u_2 + u_3} Z(s,u_1,u_2,u_3) du_1 du_2 du_3 ds, \end{align} $$
where
![]() $Z = Z_{\eta }$
is defined by
$Z = Z_{\eta }$
is defined by
 $$ \begin{align} Z(s, u_1, u_2, u_3) = \sum_{\substack{\nu, \gamma \geq 2, \thinspace \lambda \geq 4 \\ \min\left(\lambda, \nu\right) = \min\left(\lambda, \gamma\right) \\ \text{one of (7.7) holds}}} \frac{\left(2^{\nu}, 2^{\lambda-2-\delta}\right)}{2^{\lambda\left(u_1+s\right) + \nu\left(u_2-iU-s\right) + \gamma\left(u_3+iU-s\right)}} \sum_{\substack{ \left(r_1 r_2, 2\right) = 1}} \sum_{\substack{g_1 \mid r_1^2 \\ g_2 \mid r_2^2}} \nonumber\\ \sideset{}{^*}\sum_{\substack{q: r_1 \mid q^{\infty} \\ \left(q,2r_2\right) = 1}} \sum_{\substack{\left(k_o' \ell_o', 2\right)=1 \\ \left(k_o' \ell_o', \frac{r_2^2}{g_2}\right) = 1}} \frac{\left(\frac{q}{k_o' \ell_o'}\right) \eta_1\left(k_o'\right) \eta_2\left(\ell_o'\right) \eta_3(q) \prod_{\substack{p \mid r_2, \thinspace p \nmid \frac{r_2^2}{g_2}}} \left(1-p^{-1}\right)} {\left(k_o'\right)^{u_2-iU -s} \left(\ell_o'\right)^{u_3+iU-s} q^{u_1+s} \left(r_1^2 r_2^2\right)^{u_1+s} (g_1 g_2)^{u_2+u_3-2s-1}}. \end{align} $$
$$ \begin{align} Z(s, u_1, u_2, u_3) = \sum_{\substack{\nu, \gamma \geq 2, \thinspace \lambda \geq 4 \\ \min\left(\lambda, \nu\right) = \min\left(\lambda, \gamma\right) \\ \text{one of (7.7) holds}}} \frac{\left(2^{\nu}, 2^{\lambda-2-\delta}\right)}{2^{\lambda\left(u_1+s\right) + \nu\left(u_2-iU-s\right) + \gamma\left(u_3+iU-s\right)}} \sum_{\substack{ \left(r_1 r_2, 2\right) = 1}} \sum_{\substack{g_1 \mid r_1^2 \\ g_2 \mid r_2^2}} \nonumber\\ \sideset{}{^*}\sum_{\substack{q: r_1 \mid q^{\infty} \\ \left(q,2r_2\right) = 1}} \sum_{\substack{\left(k_o' \ell_o', 2\right)=1 \\ \left(k_o' \ell_o', \frac{r_2^2}{g_2}\right) = 1}} \frac{\left(\frac{q}{k_o' \ell_o'}\right) \eta_1\left(k_o'\right) \eta_2\left(\ell_o'\right) \eta_3(q) \prod_{\substack{p \mid r_2, \thinspace p \nmid \frac{r_2^2}{g_2}}} \left(1-p^{-1}\right)} {\left(k_o'\right)^{u_2-iU -s} \left(\ell_o'\right)^{u_3+iU-s} q^{u_1+s} \left(r_1^2 r_2^2\right)^{u_1+s} (g_1 g_2)^{u_2+u_3-2s-1}}. \end{align} $$
We initially suppose that
![]() $\mathrm {Re}(s) = 0$
and
$\mathrm {Re}(s) = 0$
and
![]() $\mathrm {Re}(u_i) = 2$
for each i, securing absolute convergence of the sum. An obvious modification, using equation (10.12) in place of equation (10.4), gives the corresponding formula for U small, namely
$\mathrm {Re}(u_i) = 2$
for each i, securing absolute convergence of the sum. An obvious modification, using equation (10.12) in place of equation (10.4), gives the corresponding formula for U small, namely
 $$ \begin{align} \mathcal{S}_{\eta}\left(H_{+}\right) = \sum_C \frac{\Delta T}{NC^{3/2}} \frac{\Phi}{\sqrt{P}} \int_{-t \asymp P} \int \int \int e^{-2it \log\left(\frac{\lvert t\rvert}{eT}\right) + ia\frac{t^3}{T^2}} v(t) \widetilde{w}(u_1, u_2, u_3) \nonumber\\ C^{u_1} K^{u_2 + u_3} Z(s,u_1,u_2,u_3) du_1 du_2 du_3 ds, \end{align} $$
$$ \begin{align} \mathcal{S}_{\eta}\left(H_{+}\right) = \sum_C \frac{\Delta T}{NC^{3/2}} \frac{\Phi}{\sqrt{P}} \int_{-t \asymp P} \int \int \int e^{-2it \log\left(\frac{\lvert t\rvert}{eT}\right) + ia\frac{t^3}{T^2}} v(t) \widetilde{w}(u_1, u_2, u_3) \nonumber\\ C^{u_1} K^{u_2 + u_3} Z(s,u_1,u_2,u_3) du_1 du_2 du_3 ds, \end{align} $$
where the parameters correspond with equation (10.13) and the formula for Z is slightly different (multiplied by
![]() $\eta _1(-1)$
to account for changing variables
$\eta _1(-1)$
to account for changing variables
![]() $k_o' \rightarrow -k$
, with
$k_o' \rightarrow -k$
, with
![]() $k \geq 1$
).
$k \geq 1$
).
11 Properties of the Dirichlet series Z
In this section, we pause the development of
![]() $S_{\eta }\left (H_{+}\right )$
and entirely focus on the Dirichlet series Z.
$S_{\eta }\left (H_{+}\right )$
and entirely focus on the Dirichlet series Z.
11.1 Initial factorization
Throughout this section we assume that
![]() $\mathrm {Re}(s) = 0$
. For simplicity of notation only, we also take
$\mathrm {Re}(s) = 0$
. For simplicity of notation only, we also take
![]() $\eta = (\eta _1, \eta _2, \eta _3)$
to be trivial, as the same proof works in the general case.
$\eta = (\eta _1, \eta _2, \eta _3)$
to be trivial, as the same proof works in the general case.
Definition 11.1. Let
![]() $\mathcal {D}_0$
be the set of
$\mathcal {D}_0$
be the set of
![]() $(s,u_1, u_2, u_3) \in \mathbb C^4$
with
$(s,u_1, u_2, u_3) \in \mathbb C^4$
with
![]() $\mathrm {Re}(s) = 0$
, and
$\mathrm {Re}(s) = 0$
, and
It is easy to see that the multiple sum (10.15) defining Z converges absolutely on
![]() $\mathcal {D}_0$
. We will work initially in
$\mathcal {D}_0$
. We will work initially in
![]() $\mathcal {D}_0$
, and progressively develop analytic properties (meromorphic continuation, bounds, etc.) to larger regions. The largest domain in which we work is the following:
$\mathcal {D}_0$
, and progressively develop analytic properties (meromorphic continuation, bounds, etc.) to larger regions. The largest domain in which we work is the following:
Definition 11.2. Let
![]() $\mathcal {D}_{\infty }$
be the set of
$\mathcal {D}_{\infty }$
be the set of
![]() $(s,u_1, u_2, u_3) \in \mathbb C^4$
with
$(s,u_1, u_2, u_3) \in \mathbb C^4$
with
![]() $\mathrm {Re}(s) = 0$
, and
$\mathrm {Re}(s) = 0$
, and
Obviously,
![]() $\mathcal {D}_0 \subset \mathcal {D}_{\infty }$
.
$\mathcal {D}_0 \subset \mathcal {D}_{\infty }$
.
The following notation will be useful throughout this section. Suppose that
![]() $\mathcal {D}$
is a subset of
$\mathcal {D}$
is a subset of
![]() $(s,u_1,u_2,u_3) \in \mathbb C^{4}$
defined by
$(s,u_1,u_2,u_3) \in \mathbb C^{4}$
defined by
![]() $\mathrm {Re}(s) = 0$
and by finitely many equations of the form
$\mathrm {Re}(s) = 0$
and by finitely many equations of the form
![]() $L(\mathrm {Re}(u_1), \mathrm {Re}(u_2), \mathrm {Re}(u_3))> c$
, where
$L(\mathrm {Re}(u_1), \mathrm {Re}(u_2), \mathrm {Re}(u_3))> c$
, where
![]() $c \in \mathbb R$
and L is linear with nonnegative coefficients. For
$c \in \mathbb R$
and L is linear with nonnegative coefficients. For
![]() $\sigma> 0$
, define
$\sigma> 0$
, define
![]() $\mathcal {D}^{\sigma }$
by replacing each such equation by
$\mathcal {D}^{\sigma }$
by replacing each such equation by
![]() $L(\mathrm {Re}(u_1), \mathrm {Re}(u_2), \mathrm {Re}(u_3)) \geq c + \sigma $
. The nonnegativity condition means
$L(\mathrm {Re}(u_1), \mathrm {Re}(u_2), \mathrm {Re}(u_3)) \geq c + \sigma $
. The nonnegativity condition means
![]() $\mathcal {D}^{\sigma } \subseteq \mathcal {D}$
for any
$\mathcal {D}^{\sigma } \subseteq \mathcal {D}$
for any
![]() $\sigma> 0$
.
$\sigma> 0$
.
As a notational convenience, we write k and
![]() $\ell $
instead of
$\ell $
instead of
![]() $k_0'$
and
$k_0'$
and
![]() $\ell _0'$
in equation (10.15) (since there should be no danger of confusion with the original k and
$\ell _0'$
in equation (10.15) (since there should be no danger of confusion with the original k and
![]() $\ell $
variables). In the domain
$\ell $
variables). In the domain
![]() $\mathcal {D}_0$
, we may take the sums over k and
$\mathcal {D}_0$
, we may take the sums over k and
![]() $\ell $
to the outside, giving
$\ell $
to the outside, giving
 $$ \begin{align} Z(s,u_1,u_2,u_3) = Z^{(2)}(s,u_1,u_2, u_3) \sum_{\left(k \ell, 2\right) = 1} \frac{Z_{k, \ell}(s,u_1,u_2,u_3)}{k^{u_2-iU-s} \ell^{u_3+iU-s}} , \end{align} $$
$$ \begin{align} Z(s,u_1,u_2,u_3) = Z^{(2)}(s,u_1,u_2, u_3) \sum_{\left(k \ell, 2\right) = 1} \frac{Z_{k, \ell}(s,u_1,u_2,u_3)}{k^{u_2-iU-s} \ell^{u_3+iU-s}} , \end{align} $$
where
 $$ \begin{align} Z_{k, \ell}(s,u_1,u_2,u_3) = \sum_{\substack{\left( r_1 r_2, 2\right) = 1 }} \sum_{\substack{g_1 \mid r_1^2 \\ g_2 \mid r_2^2 \\ \left(\frac{r_2^2}{g_2}, k \ell \right) = 1}} \sideset{}{^*}\sum_{\substack{q: r_1 \mid q^{\infty} \\ \left(q,2r_2\right) = 1}} \frac{\left(\frac{q}{k \ell}\right) \prod_{\substack{p \mid r_2, \thinspace p \nmid \frac{r_2^2}{g_2}}} \left(1-p^{-1}\right)} {q^{u_1+s} \left(r_1^2 r_2^2\right)^{u_1+s} (g_1 g_2)^{u_2+u_3-2s-1}} \end{align} $$
$$ \begin{align} Z_{k, \ell}(s,u_1,u_2,u_3) = \sum_{\substack{\left( r_1 r_2, 2\right) = 1 }} \sum_{\substack{g_1 \mid r_1^2 \\ g_2 \mid r_2^2 \\ \left(\frac{r_2^2}{g_2}, k \ell \right) = 1}} \sideset{}{^*}\sum_{\substack{q: r_1 \mid q^{\infty} \\ \left(q,2r_2\right) = 1}} \frac{\left(\frac{q}{k \ell}\right) \prod_{\substack{p \mid r_2, \thinspace p \nmid \frac{r_2^2}{g_2}}} \left(1-p^{-1}\right)} {q^{u_1+s} \left(r_1^2 r_2^2\right)^{u_1+s} (g_1 g_2)^{u_2+u_3-2s-1}} \end{align} $$
and
 $$ \begin{align} Z^{(2)}(s, u_1, u_2, u_3) = \sum_{\substack{\nu, \gamma \geq 2, \thinspace \lambda \geq 4 \\ \min\left(\lambda, \nu\right) = \min\left(\lambda, \gamma\right) \\ \text{one of (7.7) holds}}} \frac{\left(2^{\nu}, 2^{\lambda-2-\delta}\right)}{2^{\lambda\left(u_1+s\right) + \nu\left(u_2-iU-s\right) + \gamma\left(u_3+iU-s\right)}}. \end{align} $$
$$ \begin{align} Z^{(2)}(s, u_1, u_2, u_3) = \sum_{\substack{\nu, \gamma \geq 2, \thinspace \lambda \geq 4 \\ \min\left(\lambda, \nu\right) = \min\left(\lambda, \gamma\right) \\ \text{one of (7.7) holds}}} \frac{\left(2^{\nu}, 2^{\lambda-2-\delta}\right)}{2^{\lambda\left(u_1+s\right) + \nu\left(u_2-iU-s\right) + \gamma\left(u_3+iU-s\right)}}. \end{align} $$
We first focus on properties of
![]() $Z_{k, \ell }$
, and then turn to
$Z_{k, \ell }$
, and then turn to
![]() $Z^{(2)}$
.
$Z^{(2)}$
.
11.2 Continuation of
 $Z_{k, \ell }$
$Z_{k, \ell }$
Note that
![]() $Z_{k,\ell }$
has an Euler product, say
$Z_{k,\ell }$
has an Euler product, say
 $Z_{k,\ell } = \prod _{p \neq 2} Z_{k,\ell }^{\left (p\right )}$
. It is convenient to define
$Z_{k,\ell } = \prod _{p \neq 2} Z_{k,\ell }^{\left (p\right )}$
. It is convenient to define
Note that formula (11.1) implies
![]() $\mathrm {Re}(\alpha )> 1$
and
$\mathrm {Re}(\alpha )> 1$
and
![]() $\mathrm {Re}(\beta )> 1$
. It is also convenient to observe that
$\mathrm {Re}(\beta )> 1$
. It is also convenient to observe that
We evaluate
 $Z_{k,\ell }^{\left (p\right )}$
explicitly as follows.
$Z_{k,\ell }^{\left (p\right )}$
explicitly as follows.
Lemma 11.3. Suppose that
![]() $\mathrm {Re}(\beta )> 0$
and
$\mathrm {Re}(\beta )> 0$
and
![]() $\mathrm {Re}(\alpha + \beta )> 0$
. For
$\mathrm {Re}(\alpha + \beta )> 0$
. For
![]() $p \nmid 2 k \ell $
, we have
$p \nmid 2 k \ell $
, we have
 $$ \begin{align} Z_{k, \ell}^{\left(p\right)}(s,u_1,u_2,u_3) = \frac{1+p^{-\alpha - 2\beta} - p^{-1-2\alpha-2\beta} + \chi(p) p^{-1-2\alpha-3\beta}}{\left(1- \chi(p) p^{-\beta}\right)\left(1-p^{-2\alpha-2\beta}\right)}, \end{align} $$
$$ \begin{align} Z_{k, \ell}^{\left(p\right)}(s,u_1,u_2,u_3) = \frac{1+p^{-\alpha - 2\beta} - p^{-1-2\alpha-2\beta} + \chi(p) p^{-1-2\alpha-3\beta}}{\left(1- \chi(p) p^{-\beta}\right)\left(1-p^{-2\alpha-2\beta}\right)}, \end{align} $$
where
 $\chi (n) = \chi _{k \ell }(n) = \left (\frac {n}{k \ell }\right )$
. For
$\chi (n) = \chi _{k \ell }(n) = \left (\frac {n}{k \ell }\right )$
. For
![]() $p \mid k \ell $
, we have
$p \mid k \ell $
, we have
 $$ \begin{align} Z_{k, \ell}^{\left(p\right)}(s,u_1,u_2,u_3) = \frac{1-p^{-1-2\alpha - 2\beta}}{1-p^{-2 \alpha - 2\beta}}. \end{align} $$
$$ \begin{align} Z_{k, \ell}^{\left(p\right)}(s,u_1,u_2,u_3) = \frac{1-p^{-1-2\alpha - 2\beta}}{1-p^{-2 \alpha - 2\beta}}. \end{align} $$
Proof. For
![]() $(p, 2k \ell ) = 1$
, we have, using the convention
$(p, 2k \ell ) = 1$
, we have, using the convention
![]() $\infty \cdot 0 = 0$
,
$\infty \cdot 0 = 0$
,
 $$ \begin{align} Z^{\left(p\right)}(\alpha,\beta) = \sum_{\min\left(r_1, r_2\right) = 0} \sum_{\substack{0 \leq g_1 \leq 2r_1 \\ 0 \leq g_2 \leq 2 r_2}} \left(1-p^{-1}\right)^{\delta_{g_2 = 2r_2> 0}} \sum_{\substack{ 0 \leq q \leq 1 \\ \infty \cdot q \geq r_1 \\ \min\left(q, r_2\right) = 0}} \frac{\chi\left(p^q\right)}{p^{\beta\left(q + 2 r_1 + 2r_2\right) + \alpha\left(g_1 + g_2\right)}}. \end{align} $$
$$ \begin{align} Z^{\left(p\right)}(\alpha,\beta) = \sum_{\min\left(r_1, r_2\right) = 0} \sum_{\substack{0 \leq g_1 \leq 2r_1 \\ 0 \leq g_2 \leq 2 r_2}} \left(1-p^{-1}\right)^{\delta_{g_2 = 2r_2> 0}} \sum_{\substack{ 0 \leq q \leq 1 \\ \infty \cdot q \geq r_1 \\ \min\left(q, r_2\right) = 0}} \frac{\chi\left(p^q\right)}{p^{\beta\left(q + 2 r_1 + 2r_2\right) + \alpha\left(g_1 + g_2\right)}}. \end{align} $$
We write this as
 $\sum _{r_2=0} + \sum _{r_2 \geq 1}$
, where the latter terms force
$\sum _{r_2=0} + \sum _{r_2 \geq 1}$
, where the latter terms force
![]() $q=r_1=0$
. We have
$q=r_1=0$
. We have
 $$ \begin{align} \sum_{r_2 \geq 1} &= \sum_{r_2=1}^{\infty} p^{-2 \beta r_2} \left( \sum_{0 \leq g_2 \leq 2r_2-1} p^{-\alpha g_2} + \left(1-p^{-1}\right) p^{-2 \alpha r_2} \right) \nonumber \\ &= \sum_{r_2=1}^{\infty} p^{-2 \beta r_2} \left(\frac{1-p^{-2\alpha r_2}}{1-p^{-\alpha}} + \left(1-p^{-1}\right) p^{-2 \alpha r_2}\right). \end{align} $$
$$ \begin{align} \sum_{r_2 \geq 1} &= \sum_{r_2=1}^{\infty} p^{-2 \beta r_2} \left( \sum_{0 \leq g_2 \leq 2r_2-1} p^{-\alpha g_2} + \left(1-p^{-1}\right) p^{-2 \alpha r_2} \right) \nonumber \\ &= \sum_{r_2=1}^{\infty} p^{-2 \beta r_2} \left(\frac{1-p^{-2\alpha r_2}}{1-p^{-\alpha}} + \left(1-p^{-1}\right) p^{-2 \alpha r_2}\right). \end{align} $$
This evaluates as
 $$ \begin{align} \left(1-p^{-\alpha}\right)^{-1} \left( \frac{p^{-2\beta}}{1-p^{-2\beta}} - \frac{p^{-2\beta-2\alpha}}{1-p^{-2\alpha-2\beta}}\right) + \left(1-p^{-1}\right) \frac{p^{-2\alpha - 2 \beta}}{1-p^{-2\alpha - 2\beta}}, \end{align} $$
$$ \begin{align} \left(1-p^{-\alpha}\right)^{-1} \left( \frac{p^{-2\beta}}{1-p^{-2\beta}} - \frac{p^{-2\beta-2\alpha}}{1-p^{-2\alpha-2\beta}}\right) + \left(1-p^{-1}\right) \frac{p^{-2\alpha - 2 \beta}}{1-p^{-2\alpha - 2\beta}}, \end{align} $$
which simplifies as
 $$ \begin{align} p^{-2 \beta} \frac{1+p^{-\alpha}}{\left(1-p^{-2\beta}\right)\left(1-p^{-2\alpha - 2\beta}\right)} + \left(1-p^{-1}\right) \frac{p^{-2\alpha - 2\beta} \left(1-p^{-2\beta}\right)}{\left(1-p^{-2\alpha-2\beta}\right)\left(1-p^{-2\beta}\right)}. \end{align} $$
$$ \begin{align} p^{-2 \beta} \frac{1+p^{-\alpha}}{\left(1-p^{-2\beta}\right)\left(1-p^{-2\alpha - 2\beta}\right)} + \left(1-p^{-1}\right) \frac{p^{-2\alpha - 2\beta} \left(1-p^{-2\beta}\right)}{\left(1-p^{-2\alpha-2\beta}\right)\left(1-p^{-2\beta}\right)}. \end{align} $$
In turn, this becomes
 $$ \begin{align} \frac{p^{-2 \beta}}{\left(1-p^{-2\alpha-2\beta}\right)\left(1-p^{-2\beta}\right)} \left[ 1 + p^{-\alpha} + \left(1-p^{-1}\right) p^{-2\alpha}\left(1-p^{-2\beta}\right)\right]. \end{align} $$
$$ \begin{align} \frac{p^{-2 \beta}}{\left(1-p^{-2\alpha-2\beta}\right)\left(1-p^{-2\beta}\right)} \left[ 1 + p^{-\alpha} + \left(1-p^{-1}\right) p^{-2\alpha}\left(1-p^{-2\beta}\right)\right]. \end{align} $$
Likewise, we compute
 $$ \begin{align} \sum_{r_2=0} = \sum_{r_1=0}^{\infty} \sum_{\substack{0 \leq g_1 \leq 2r_1 }} \sum_{\substack{ 0 \leq q \leq 1 \\ \infty \cdot q \geq r_1 }} \frac{\chi(p^q)}{p^{\beta\left(q + 2 r_1 \right) + \alpha g_1}} = 1 + \sum_{r_1=0}^{\infty} \sum_{\substack{0 \leq g_1 \leq 2r_1 }} \frac{\chi(p)}{p^{\beta\left(1 + 2 r_1 \right) + \alpha g_1}}, \end{align} $$
$$ \begin{align} \sum_{r_2=0} = \sum_{r_1=0}^{\infty} \sum_{\substack{0 \leq g_1 \leq 2r_1 }} \sum_{\substack{ 0 \leq q \leq 1 \\ \infty \cdot q \geq r_1 }} \frac{\chi(p^q)}{p^{\beta\left(q + 2 r_1 \right) + \alpha g_1}} = 1 + \sum_{r_1=0}^{\infty} \sum_{\substack{0 \leq g_1 \leq 2r_1 }} \frac{\chi(p)}{p^{\beta\left(1 + 2 r_1 \right) + \alpha g_1}}, \end{align} $$
by separating out the cases
![]() $q=0$
and
$q=0$
and
![]() $q=1$
. We calculate this as
$q=1$
. We calculate this as
 $$ \begin{align} 1 + \chi(p) p^{-\beta} \sum_{r_1=0}^{\infty} p^{-2\beta r_1} \frac{1-p^{-\alpha\left(2r_1 + 1\right)}}{1-p^{-\alpha}}, \end{align} $$
$$ \begin{align} 1 + \chi(p) p^{-\beta} \sum_{r_1=0}^{\infty} p^{-2\beta r_1} \frac{1-p^{-\alpha\left(2r_1 + 1\right)}}{1-p^{-\alpha}}, \end{align} $$
which can be expressed as
 $$ \begin{align} 1 + \frac{\chi(p) p^{-\beta}}{1-p^{-\alpha}} \left(\frac{1}{1-p^{-2\beta}} - \frac{p^{-\alpha}}{1-p^{-2\alpha-2\beta}}\right) =1 + \frac{\chi(p) p^{-\beta} \left(1+p^{-\alpha-2\beta}\right)}{\left(1-p^{-2\beta}\right)\left(1-p^{-2\alpha-2\beta}\right)}. \end{align} $$
$$ \begin{align} 1 + \frac{\chi(p) p^{-\beta}}{1-p^{-\alpha}} \left(\frac{1}{1-p^{-2\beta}} - \frac{p^{-\alpha}}{1-p^{-2\alpha-2\beta}}\right) =1 + \frac{\chi(p) p^{-\beta} \left(1+p^{-\alpha-2\beta}\right)}{\left(1-p^{-2\beta}\right)\left(1-p^{-2\alpha-2\beta}\right)}. \end{align} $$
Putting the two calculations together, we obtain
 $$ \begin{align*} &Z^{\left(p\right)}(\alpha,\beta)\\ &=\frac{\left(1-p^{-2\beta}\right)\left(1-p^{-2\alpha-2\beta}\right) + \chi(p) p^{-\beta}\left(1+p^{-\alpha-2\beta}\right) + p^{-2\beta}\left(1+p^{-\alpha} + \left(1-p^{-1}\right)\left(p^{-2\alpha} - p^{-2\alpha-2\beta}\right)\right) }{\left(1-p^{-2\beta}\right)\left(1-p^{-2\alpha-2\beta}\right)}. \end{align*} $$
$$ \begin{align*} &Z^{\left(p\right)}(\alpha,\beta)\\ &=\frac{\left(1-p^{-2\beta}\right)\left(1-p^{-2\alpha-2\beta}\right) + \chi(p) p^{-\beta}\left(1+p^{-\alpha-2\beta}\right) + p^{-2\beta}\left(1+p^{-\alpha} + \left(1-p^{-1}\right)\left(p^{-2\alpha} - p^{-2\alpha-2\beta}\right)\right) }{\left(1-p^{-2\beta}\right)\left(1-p^{-2\alpha-2\beta}\right)}. \end{align*} $$
Distributing out the numerator and canceling like terms, we obtain
 $$ \begin{align} Z^{\left(p\right)}(\alpha,\beta) = \frac{\left(1+ \chi(p) p^{-\beta}\right)\left(1+p^{-\alpha-2\beta}\right) - p^{-1-2\alpha-2\beta}\left(1-p^{-2\beta}\right) }{\left(1-p^{-2\beta}\right)\left(1-p^{-2\alpha-2\beta}\right)}. \end{align} $$
$$ \begin{align} Z^{\left(p\right)}(\alpha,\beta) = \frac{\left(1+ \chi(p) p^{-\beta}\right)\left(1+p^{-\alpha-2\beta}\right) - p^{-1-2\alpha-2\beta}\left(1-p^{-2\beta}\right) }{\left(1-p^{-2\beta}\right)\left(1-p^{-2\alpha-2\beta}\right)}. \end{align} $$
Simplifying gives equation (11.8).
Next we need to consider the primes
![]() $p \mid k \ell $
. At such a prime we must have
$p \mid k \ell $
. At such a prime we must have
![]() $(q,p)=1$
(or else
$(q,p)=1$
(or else
 $\left (\frac {q}{k \ell }\right )=0$
), which implies
$\left (\frac {q}{k \ell }\right )=0$
), which implies
![]() $r_1 = 1$
and
$r_1 = 1$
and
![]() $g_2 = r_2^2$
. Thus
$g_2 = r_2^2$
. Thus
 $$ \begin{align} Z^{\left(p\right)}(s,u_1,u_2,u_3) = \sum_{r_2\ge 0 } \frac{\left(1-p^{-1}\right)^{\delta_{r_2>0}}} { p^{r_2\left(2\beta + 2\alpha\right)} } = \frac{1-p^{-1-2\alpha - 2\beta}}{1-p^{-2 \alpha - 2\beta}}. \end{align} $$
$$ \begin{align} Z^{\left(p\right)}(s,u_1,u_2,u_3) = \sum_{r_2\ge 0 } \frac{\left(1-p^{-1}\right)^{\delta_{r_2>0}}} { p^{r_2\left(2\beta + 2\alpha\right)} } = \frac{1-p^{-1-2\alpha - 2\beta}}{1-p^{-2 \alpha - 2\beta}}. \end{align} $$
Define the Dirichlet series
 $$ \begin{align} D(\alpha, \beta, \chi_{k \ell}) = \sum_{\left(n,2\right) = 1} \frac{\mu^2(n)}{n^{\alpha + 2\beta}} \sum_{abc=n} \frac{\mu(b) \chi_{k \ell}(c)}{b^{1+\alpha} c^{1+\alpha+\beta}}, \end{align} $$
$$ \begin{align} D(\alpha, \beta, \chi_{k \ell}) = \sum_{\left(n,2\right) = 1} \frac{\mu^2(n)}{n^{\alpha + 2\beta}} \sum_{abc=n} \frac{\mu(b) \chi_{k \ell}(c)}{b^{1+\alpha} c^{1+\alpha+\beta}}, \end{align} $$
which is absolutely convergent for
![]() $\mathrm {Re}(\alpha + 2 \beta )> 1$
and
$\mathrm {Re}(\alpha + 2 \beta )> 1$
and
![]() $\mathrm {Re}(\alpha + \beta )> 0$
(observe that these conditions hold on
$\mathrm {Re}(\alpha + \beta )> 0$
(observe that these conditions hold on
![]() $\mathcal {D}_{\infty }$
, by formula (11.7)). Note the Euler product formula
$\mathcal {D}_{\infty }$
, by formula (11.7)). Note the Euler product formula
 $$ \begin{align} D(\alpha, \beta, \chi_{k \ell}) = \prod_{p \neq 2} \left(1 + p^{-\alpha - 2\beta}\left(1- p^{-1-\alpha} + \chi_{k \ell}(p) p^{-1-\alpha-\beta}\right)\right). \end{align} $$
$$ \begin{align} D(\alpha, \beta, \chi_{k \ell}) = \prod_{p \neq 2} \left(1 + p^{-\alpha - 2\beta}\left(1- p^{-1-\alpha} + \chi_{k \ell}(p) p^{-1-\alpha-\beta}\right)\right). \end{align} $$
Putting together equations (11.8) and (11.9), we deduce (initially) in the region
![]() $\mathcal {D}_0$
$\mathcal {D}_0$
 $$ \begin{align} Z_{k,\ell}(s, u_1, u_2, u_3) = L(\beta, \chi_{k \ell}) \frac{\zeta(2\alpha + 2\beta)}{\left(1-2^{-2\alpha - 2\beta}\right)^{-1}} D(\alpha, \beta, \chi_{k \ell}) \left(1- \chi_{k\ell}(2) 2^{-\beta}\right) \prod_{p \mid k \ell} a_p , \end{align} $$
$$ \begin{align} Z_{k,\ell}(s, u_1, u_2, u_3) = L(\beta, \chi_{k \ell}) \frac{\zeta(2\alpha + 2\beta)}{\left(1-2^{-2\alpha - 2\beta}\right)^{-1}} D(\alpha, \beta, \chi_{k \ell}) \left(1- \chi_{k\ell}(2) 2^{-\beta}\right) \prod_{p \mid k \ell} a_p , \end{align} $$
where
 $$ \begin{align} a_p = \frac{1 - p^{-1-2\alpha-2\beta}}{1 + p^{-\alpha - 2\beta} - p^{-1-2\alpha - 2\beta}}. \end{align} $$
$$ \begin{align} a_p = \frac{1 - p^{-1-2\alpha-2\beta}}{1 + p^{-\alpha - 2\beta} - p^{-1-2\alpha - 2\beta}}. \end{align} $$
Note that in
![]() $\mathcal {D}_{\infty }$
, we have
$\mathcal {D}_{\infty }$
, we have
 $$ \begin{align} a_p = 1 + O\left(p^{-1}\right). \end{align} $$
$$ \begin{align} a_p = 1 + O\left(p^{-1}\right). \end{align} $$
Lemma 11.4. The series
![]() $Z_{k,\ell }(s,u_1, u_2, u_3)$
has meromorphic continuation to the domain
$Z_{k,\ell }(s,u_1, u_2, u_3)$
has meromorphic continuation to the domain
![]() $\mathcal {D}_{\infty }$
. In this region,
$\mathcal {D}_{\infty }$
. In this region,
![]() $Z_{k,\ell }$
has a polar line only at
$Z_{k,\ell }$
has a polar line only at
![]() $\beta = 1$
which occurs if and only if
$\beta = 1$
which occurs if and only if
![]() $\chi _{k \ell }$
is trivial.
$\chi _{k \ell }$
is trivial.
Remark 11.5. Observe the nice simplification in the passage from equation (11.18) to equation (11.8), in which a factor of
 $\left (1-p^{-2\beta }\right )$
is canceled from the numerator and denominator. This reveals that there is no
$\left (1-p^{-2\beta }\right )$
is canceled from the numerator and denominator. This reveals that there is no
![]() $\zeta (2\beta )^{-1}$
-type factor in equation (11.22), which would have infinitely many poles in the domain
$\zeta (2\beta )^{-1}$
-type factor in equation (11.22), which would have infinitely many poles in the domain
![]() $\mathcal {D}_{\infty }$
.
$\mathcal {D}_{\infty }$
.
11.3 Evaluation of
 $Z^{(2)}$
$Z^{(2)}$
Recall that
![]() $Z^{(2)}$
has four cases, corresponding to formula (7.7).
$Z^{(2)}$
has four cases, corresponding to formula (7.7).
Lemma 11.6. In cases (i)–(iii) of formula (7.7), the function
![]() $Z^{(2)}$
initially defined by equation (11.5) in the region (11.1) extends to a bounded analytic function on
$Z^{(2)}$
initially defined by equation (11.5) in the region (11.1) extends to a bounded analytic function on
![]() $\mathcal {D}_{\infty }$
.
$\mathcal {D}_{\infty }$
.
Proof. This follows from brute-force computation with geometric series. For case (i), we have
 $$ \begin{align} Z^{(2)} = \frac{\left(1-2^{-\left(u_2-iU-s\right)}\right)^{-1} \left(1-2^{-\left(u_3+iU-s\right)}\right)^{-1}}{2^{2+\delta} 2^{4(\alpha+\beta)} \left(1-2^{-\alpha-\beta}\right)}, \end{align} $$
$$ \begin{align} Z^{(2)} = \frac{\left(1-2^{-\left(u_2-iU-s\right)}\right)^{-1} \left(1-2^{-\left(u_3+iU-s\right)}\right)^{-1}}{2^{2+\delta} 2^{4(\alpha+\beta)} \left(1-2^{-\alpha-\beta}\right)}, \end{align} $$
which satisfies the claimed properties by inspection. Cases (ii) and (iii) are easier, and give
 $Z^{(2)} = 2^{-1-\delta -3 \alpha - 4\beta } \left (1-2^{-\alpha -\beta }\right )^{-1}$
and
$Z^{(2)} = 2^{-1-\delta -3 \alpha - 4\beta } \left (1-2^{-\alpha -\beta }\right )^{-1}$
and
 $Z^{(2)} = 2^{-\delta -2 \alpha - 4\beta } \left (1-2^{-\alpha -\beta }\right )^{-1}$
, respectively. In case (ii), to see the boundedness on
$Z^{(2)} = 2^{-\delta -2 \alpha - 4\beta } \left (1-2^{-\alpha -\beta }\right )^{-1}$
, respectively. In case (ii), to see the boundedness on
![]() $\mathcal {D}_{\infty }$
, note
$\mathcal {D}_{\infty }$
, note
![]() $2^{-3\alpha - 4\beta } = 2^{-2 \alpha - 2\beta } 2^{-\alpha - 2 \beta }$
, and recall formula (11.7).
$2^{-3\alpha - 4\beta } = 2^{-2 \alpha - 2\beta } 2^{-\alpha - 2 \beta }$
, and recall formula (11.7).
When
![]() $Z^{(2)}$
is given by case (iv) – which, recall, restricts the summation to
$Z^{(2)}$
is given by case (iv) – which, recall, restricts the summation to
![]() $\lambda \geq \nu +3$
– it is convenient to split the sum into two pieces according to the size of
$\lambda \geq \nu +3$
– it is convenient to split the sum into two pieces according to the size of
![]() $\lambda - \nu $
. For any integer
$\lambda - \nu $
. For any integer
![]() $L \geq 3$
, write
$L \geq 3$
, write
 $Z^{(2)} = Z^{(2)}_{\leq L} + Z^{(2)}_{>L}$
, where
$Z^{(2)} = Z^{(2)}_{\leq L} + Z^{(2)}_{>L}$
, where
 $Z^{(2)}_{\leq L}$
restricts to
$Z^{(2)}_{\leq L}$
restricts to
![]() $\lambda - \nu \leq L$
and
$\lambda - \nu \leq L$
and
 $Z^{(2)}_{>L}$
restricts to
$Z^{(2)}_{>L}$
restricts to
![]() $\lambda - \nu> L$
.
$\lambda - \nu> L$
.
Lemma 11.7. In case (iv),
 $Z_{\leq L}^{(2)}$
extends to an analytic function on
$Z_{\leq L}^{(2)}$
extends to an analytic function on
![]() $\mathcal {D}_{\infty }$
, wherein it satisfies the bound
$\mathcal {D}_{\infty }$
, wherein it satisfies the bound
 $$ \begin{align} \left\lvert Z^{(2)}_{\leq L}\right\rvert \ll L \left(2^{- L \beta} + 1\right). \end{align} $$
$$ \begin{align} \left\lvert Z^{(2)}_{\leq L}\right\rvert \ll L \left(2^{- L \beta} + 1\right). \end{align} $$
The tail
 $Z_{> L}^{(2)}$
is analytic on
$Z_{> L}^{(2)}$
is analytic on
![]() $\mathcal {D}_0$
, wherein it satisfies the bound
$\mathcal {D}_0$
, wherein it satisfies the bound
 $$ \begin{align} \left\lvert Z^{(2)}_{> L}\right\rvert \ll 2^{-L \beta}. \end{align} $$
$$ \begin{align} \left\lvert Z^{(2)}_{> L}\right\rvert \ll 2^{-L \beta}. \end{align} $$
Proof. Since
![]() $\lambda \geq \nu + 3$
, then
$\lambda \geq \nu + 3$
, then
![]() $\min (\lambda , \nu ) = \nu $
, and the condition
$\min (\lambda , \nu ) = \nu $
, and the condition
![]() $\min (\lambda , \nu ) = \min (\lambda , \gamma )$
means
$\min (\lambda , \nu ) = \min (\lambda , \gamma )$
means
![]() $\gamma = \nu $
. Therefore,
$\gamma = \nu $
. Therefore,
 $$ \begin{align} Z^{(2)}_{\leq L} = \sum_{\nu \geq 2} \sum_{\nu + 3 \leq \lambda \leq \nu + L} \frac{2^{\nu}}{2^{\lambda \beta + \nu (\alpha + 1)}} = \sum_{\nu \geq 2} \sum_{ 3 \leq \mu \leq L} \frac{1}{2^{(\nu + \mu) \beta + \nu \alpha}} = \frac{2^{-2\alpha - 2 \beta}}{\left(1-2^{-\alpha-\beta}\right)} \sum_{3 \leq \mu \leq L} 2^{-\mu \beta}. \end{align} $$
$$ \begin{align} Z^{(2)}_{\leq L} = \sum_{\nu \geq 2} \sum_{\nu + 3 \leq \lambda \leq \nu + L} \frac{2^{\nu}}{2^{\lambda \beta + \nu (\alpha + 1)}} = \sum_{\nu \geq 2} \sum_{ 3 \leq \mu \leq L} \frac{1}{2^{(\nu + \mu) \beta + \nu \alpha}} = \frac{2^{-2\alpha - 2 \beta}}{\left(1-2^{-\alpha-\beta}\right)} \sum_{3 \leq \mu \leq L} 2^{-\mu \beta}. \end{align} $$
From this representation we easily read off its analytic continuation and the bound (11.26). For the tail, we may modify the previous calculation to give
 $$ \begin{align} Z^{(2)}_{> L} = \frac{2^{-2\alpha - 2 \beta}}{\left(1-2^{-\alpha-\beta}\right)} \sum_{\mu \geq L+1} 2^{-\mu \beta} = \frac{2^{-2\alpha - 2 \beta}}{\left(1-2^{-\alpha-\beta}\right)} \frac{2^{-\beta(L+1)}}{\left(1-2^{-\beta}\right)}, \end{align} $$
$$ \begin{align} Z^{(2)}_{> L} = \frac{2^{-2\alpha - 2 \beta}}{\left(1-2^{-\alpha-\beta}\right)} \sum_{\mu \geq L+1} 2^{-\mu \beta} = \frac{2^{-2\alpha - 2 \beta}}{\left(1-2^{-\alpha-\beta}\right)} \frac{2^{-\beta(L+1)}}{\left(1-2^{-\beta}\right)}, \end{align} $$
from which we immediately read off the desired properties.
Remark. Note that
 $Z^{(2)}_{>L}$
does not analytically continue to
$Z^{(2)}_{>L}$
does not analytically continue to
![]() $\mathcal {D}_{\infty }$
, since equation (11.29) has poles on the line
$\mathcal {D}_{\infty }$
, since equation (11.29) has poles on the line
![]() $\mathrm {Re}(\beta ) = 0$
. This explains the reason for splitting
$\mathrm {Re}(\beta ) = 0$
. This explains the reason for splitting
![]() $Z^{(2)}$
into these two pieces.
$Z^{(2)}$
into these two pieces.
To unify the notation, in cases (i)–(iii) we define
 $Z_{>L}^{(2)} = 0$
and
$Z_{>L}^{(2)} = 0$
and
 $Z_{\leq L}^{(2)} = Z^{(2)}$
. Corresponding to this decomposition of
$Z_{\leq L}^{(2)} = Z^{(2)}$
. Corresponding to this decomposition of
![]() $Z^{(2)}$
, we likewise write
$Z^{(2)}$
, we likewise write
With this definition, the statement of Lemma 11.7 holds in cases (i)–(iii) as well. In this way we may henceforth unify the exposition for all four cases.
11.4 Continuation of
 $Z_{\leq L}$
$Z_{\leq L}$
It is now useful to define another domain.
Definition 11.8. Let
![]() $\mathcal {D}_1$
be the set of
$\mathcal {D}_1$
be the set of
![]() $(s,u_1, u_2, u_3) \in \mathbb C^4$
with
$(s,u_1, u_2, u_3) \in \mathbb C^4$
with
![]() $\mathrm {Re}(s) =0$
,
$\mathrm {Re}(s) =0$
,
![]() $\mathrm {Re}(u_2)> 1$
, and
$\mathrm {Re}(u_2)> 1$
, and
![]() $\mathrm {Re}(u_3)> 1$
, and satisfying
$\mathrm {Re}(u_3)> 1$
, and satisfying
 $$ \begin{align} \quad \begin{cases} \mathrm{Re}(u_1) + \min(\mathrm{Re}(u_2), \mathrm{Re}(u_3))> 3/2 \\ \mathrm{Re}(u_1) + 2 \min(\mathrm{Re}(u_2), \mathrm{Re}(u_3)) ) > 3. \end{cases} \end{align} $$
$$ \begin{align} \quad \begin{cases} \mathrm{Re}(u_1) + \min(\mathrm{Re}(u_2), \mathrm{Re}(u_3))> 3/2 \\ \mathrm{Re}(u_1) + 2 \min(\mathrm{Re}(u_2), \mathrm{Re}(u_3)) ) > 3. \end{cases} \end{align} $$
Note that
![]() $\mathcal {D}_0 \subset \mathcal {D}_1 \subset \mathcal {D}_{\infty }$
.
$\mathcal {D}_0 \subset \mathcal {D}_1 \subset \mathcal {D}_{\infty }$
.
Lemma 11.9. The series (11.3) converges absolutely on
![]() $\mathcal {D}_1 \cap \{ \beta \neq 1 \}$
(and uniformly on compact subsets), which furnishes meromorphic continuation of the function
$\mathcal {D}_1 \cap \{ \beta \neq 1 \}$
(and uniformly on compact subsets), which furnishes meromorphic continuation of the function
![]() $Z_{\leq L}$
to this domain. Moreoever, the residue at
$Z_{\leq L}$
to this domain. Moreoever, the residue at
![]() $\beta = 1$
of
$\beta = 1$
of
![]() $Z_{\leq L}$
is bounded for
$Z_{\leq L}$
is bounded for
![]() $\mathrm {Re}(u_2), \mathrm {Re}(u_3)> 1$
.
$\mathrm {Re}(u_2), \mathrm {Re}(u_3)> 1$
.
Proof. We return to equation (11.3) and use the representation (11.22), valid in
![]() $\mathcal {D}_0$
. The results from §11.3 give the analytic continuation of
$\mathcal {D}_0$
. The results from §11.3 give the analytic continuation of
 $Z^{(2)}_{\leq L}$
to
$Z^{(2)}_{\leq L}$
to
![]() $\mathcal {D}_{\infty }$
(and hence,
$\mathcal {D}_{\infty }$
(and hence,
![]() $\mathcal {D}_1$
). Since
$\mathcal {D}_1$
). Since
![]() $L(\beta , \chi _{k \ell })$
has a pole at
$L(\beta , \chi _{k \ell })$
has a pole at
![]() $\beta = 1$
when
$\beta = 1$
when
![]() $\chi _{k \ell }$
is trivial, we suppose
$\chi _{k \ell }$
is trivial, we suppose
![]() $\lvert \beta - 1\rvert \geq \sigma> 0$
, and will claim bounds with an implied constant that may depend on
$\lvert \beta - 1\rvert \geq \sigma> 0$
, and will claim bounds with an implied constant that may depend on
![]() $\sigma $
. For
$\sigma $
. For
![]() $0 \leq \mathrm {Re}(\beta ) = \mathrm {Re}(u_1) \leq 1$
, we have the convexity bound
$0 \leq \mathrm {Re}(\beta ) = \mathrm {Re}(u_1) \leq 1$
, we have the convexity bound
 $\lvert L(\beta , \chi _{k \ell })\rvert \ll _{\mathrm {Im}\left (\beta \right ), \sigma , \varepsilon } (kl)^{ \frac {1-\mathrm {Re}\left (\beta \right )}{2} + \varepsilon }$
(with an implied constant depending at most polynomially on
$\lvert L(\beta , \chi _{k \ell })\rvert \ll _{\mathrm {Im}\left (\beta \right ), \sigma , \varepsilon } (kl)^{ \frac {1-\mathrm {Re}\left (\beta \right )}{2} + \varepsilon }$
(with an implied constant depending at most polynomially on
![]() $\beta $
). One easily checks that equation (11.3) converges absolutely for
$\beta $
). One easily checks that equation (11.3) converges absolutely for
 $\min (\mathrm {Re}(u_2), \mathrm {Re}(u_3)) + \frac {\mathrm {Re}(\beta )}{2}> \frac 32$
, which is one of the inequalities stated in formula (11.31). Similarly, for
$\min (\mathrm {Re}(u_2), \mathrm {Re}(u_3)) + \frac {\mathrm {Re}(\beta )}{2}> \frac 32$
, which is one of the inequalities stated in formula (11.31). Similarly, for
![]() $\mathrm {Re}(\beta ) \leq 0$
we use the convexity bound
$\mathrm {Re}(\beta ) \leq 0$
we use the convexity bound
 $\lvert L(\beta , \chi _{k \ell })\rvert \ll (k \ell )^{\frac 12 - \text {Re}\left (\beta \right ) + \varepsilon }$
to see the absolute convergence for
$\lvert L(\beta , \chi _{k \ell })\rvert \ll (k \ell )^{\frac 12 - \text {Re}\left (\beta \right ) + \varepsilon }$
to see the absolute convergence for
![]() $\mathrm {Re}(u_1) + \min (\mathrm {Re}(u_2), \mathrm {Re}(u_3))> 3/2$
. The uniform convergence on compact subsets is immediate, and so the meromorphic continuation follows.
$\mathrm {Re}(u_1) + \min (\mathrm {Re}(u_2), \mathrm {Re}(u_3))> 3/2$
. The uniform convergence on compact subsets is immediate, and so the meromorphic continuation follows.
Finally, to see the size of the residue, we simply note from equation (11.22) that
![]() $\text {Res}_{\beta = 1} Z_{k, \ell } \ll (k \ell )^{\varepsilon }$
for
$\text {Res}_{\beta = 1} Z_{k, \ell } \ll (k \ell )^{\varepsilon }$
for
![]() $\mathrm {Re}(u_2), \mathrm {Re}(u_3) \geq 1$
. In addition, the pole exists only if
$\mathrm {Re}(u_2), \mathrm {Re}(u_3) \geq 1$
. In addition, the pole exists only if
![]() $k \ell $
is a square. Moreover,
$k \ell $
is a square. Moreover,
 $Z_{\leq L}^{(2)}$
is bounded at this point. From equation (11.3) we may then easily see the absolute convergence of the sum of these residues over
$Z_{\leq L}^{(2)}$
is bounded at this point. From equation (11.3) we may then easily see the absolute convergence of the sum of these residues over
![]() $k, \ell $
.
$k, \ell $
.
11.5 Functional equation
Next we investigate how
![]() $Z_{k, \ell }$
and
$Z_{k, \ell }$
and
![]() $Z_{\leq L}$
behave after an application of the functional equation of
$Z_{\leq L}$
behave after an application of the functional equation of
![]() $L(\beta , \chi _{k \ell })$
. Suppose that
$L(\beta , \chi _{k \ell })$
. Suppose that
![]() $\chi _{k \ell }$
is induced by the primitive character
$\chi _{k \ell }$
is induced by the primitive character
![]() $\chi ^*$
of conductor
$\chi ^*$
of conductor
![]() $(k \ell )^*$
. We have
$(k \ell )^*$
. We have
 $$ \begin{align} \Lambda(s,\chi^*) = ((k \ell)^*)^{s/2} \gamma(s) L(s, \chi^*) = \Lambda(1-s, \chi^*), \end{align} $$
$$ \begin{align} \Lambda(s,\chi^*) = ((k \ell)^*)^{s/2} \gamma(s) L(s, \chi^*) = \Lambda(1-s, \chi^*), \end{align} $$
where
 $\gamma (s) = \pi ^{-s/2} \Gamma \left (\frac {s+\kappa }{2}\right )$
, with
$\gamma (s) = \pi ^{-s/2} \Gamma \left (\frac {s+\kappa }{2}\right )$
, with
![]() $\kappa \in \{0, 1\}$
reflecting the parity of
$\kappa \in \{0, 1\}$
reflecting the parity of
![]() $\chi $
. We therefore deduce the asymmetric form of the functional equation:
$\chi $
. We therefore deduce the asymmetric form of the functional equation:
 $$ \begin{align} L(s,\chi_{k \ell}) =((k \ell)^*)^{\frac12 - s} \frac{\gamma(1-s)}{\gamma(s)} L(1-s,\chi_{k \ell}) \prod_{p\mid k \ell} \frac{(1-\chi^*(p) p^{-s})}{\left(1-\chi^*(p) p^{s-1}\right)}. \end{align} $$
$$ \begin{align} L(s,\chi_{k \ell}) =((k \ell)^*)^{\frac12 - s} \frac{\gamma(1-s)}{\gamma(s)} L(1-s,\chi_{k \ell}) \prod_{p\mid k \ell} \frac{(1-\chi^*(p) p^{-s})}{\left(1-\chi^*(p) p^{s-1}\right)}. \end{align} $$
Lemma 11.10. In
![]() $\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(\beta ) < 0 \}$
, we have
$\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(\beta ) < 0 \}$
, we have
 $$ \begin{align} Z_{k, \ell} = ((k \ell)^*)^{\frac12 - \beta} \frac{\gamma(1-\beta)}{\gamma(\beta)} D(\alpha, \beta, \chi_{k \ell}) \frac{\zeta(2\alpha + 2\beta)}{\left(1-2^{-2\alpha - 2\beta}\right)^{-1}} \left(1- 2^{-\beta} \chi_{k \ell}(2)\right) \nonumber\\ \sum_{q=1}^{\infty} \frac{\left(\frac{q}{k \ell}\right)}{q^{1-\beta}} \prod_{p\mid k \ell} \frac{\left(1-\chi^*(p) p^{-\beta}\right)}{\left(1-\chi^*(p) p^{\beta-1}\right)} \prod_{p \mid k \ell} a_p. \end{align} $$
$$ \begin{align} Z_{k, \ell} = ((k \ell)^*)^{\frac12 - \beta} \frac{\gamma(1-\beta)}{\gamma(\beta)} D(\alpha, \beta, \chi_{k \ell}) \frac{\zeta(2\alpha + 2\beta)}{\left(1-2^{-2\alpha - 2\beta}\right)^{-1}} \left(1- 2^{-\beta} \chi_{k \ell}(2)\right) \nonumber\\ \sum_{q=1}^{\infty} \frac{\left(\frac{q}{k \ell}\right)}{q^{1-\beta}} \prod_{p\mid k \ell} \frac{\left(1-\chi^*(p) p^{-\beta}\right)}{\left(1-\chi^*(p) p^{\beta-1}\right)} \prod_{p \mid k \ell} a_p. \end{align} $$
Proof. Lemma 11.4 implies that the expression (11.22) for
![]() $Z_{k, \ell }$
is analytic on
$Z_{k, \ell }$
is analytic on
![]() $\mathcal {D}_{\infty } \cap \{ \beta \neq 1\}$
. With the assumption
$\mathcal {D}_{\infty } \cap \{ \beta \neq 1\}$
. With the assumption
![]() $\mathrm {Re}(\beta ) < 0$
, we may apply the functional equation and express
$\mathrm {Re}(\beta ) < 0$
, we may apply the functional equation and express
![]() $L(1-\beta , \chi _{k \ell })$
in terms of its absolutely convergent Dirichlet series, which is equation (11.34).
$L(1-\beta , \chi _{k \ell })$
in terms of its absolutely convergent Dirichlet series, which is equation (11.34).
Having applied the functional equation to
![]() $Z_{k, \ell }$
, the plan of action is to now insert this expression into the definition of
$Z_{k, \ell }$
, the plan of action is to now insert this expression into the definition of
![]() $Z_{\leq L}$
and reverse the orders of summation, bringing k and
$Z_{\leq L}$
and reverse the orders of summation, bringing k and
![]() $\ell $
to the inside. The outcome of this step is recorded with the following:
$\ell $
to the inside. The outcome of this step is recorded with the following:
Lemma 11.11. On
![]() $\mathcal {D}_1 \cap \{\mathrm {Re}(\beta ) < 0 \}$
,
$\mathcal {D}_1 \cap \{\mathrm {Re}(\beta ) < 0 \}$
,
![]() $Z_{\leq L}$
is a finite linear combination of absolutely convergent expressions of the form
$Z_{\leq L}$
is a finite linear combination of absolutely convergent expressions of the form
 $$ \begin{align} Z^{(2)}_{\leq L} \frac{\gamma(1-\beta)}{\gamma(\beta)} \frac{\zeta(2\alpha + 2\beta)}{\left(1-2^{-2\alpha - 2\beta}\right)^{-1}} \frac{\left(1 \pm 2^{-\beta}\right)}{\left(1 \pm 2^{\beta-1}\right)} \sum_{\left(q,2\right) = 1} q^{\beta -1} \nu_1(q) A_q, \end{align} $$
$$ \begin{align} Z^{(2)}_{\leq L} \frac{\gamma(1-\beta)}{\gamma(\beta)} \frac{\zeta(2\alpha + 2\beta)}{\left(1-2^{-2\alpha - 2\beta}\right)^{-1}} \frac{\left(1 \pm 2^{-\beta}\right)}{\left(1 \pm 2^{\beta-1}\right)} \sum_{\left(q,2\right) = 1} q^{\beta -1} \nu_1(q) A_q, \end{align} $$
with
![]() $A_q = A_q(s, u_1, u_2, u_3, U, \nu _2, \dotsc , \nu _6)$
defined by
$A_q = A_q(s, u_1, u_2, u_3, U, \nu _2, \dotsc , \nu _6)$
defined by
 $$ \begin{align} A_q = \sum_{\left(abc,2\right) = 1} \frac{\mu^2(abc) \nu_2(c) }{(abc)^{\alpha + 2\beta}} \frac{\mu(b)}{b^{1+\alpha} c^{1+\alpha+\beta}} \nonumber\\[-2pt] \sum_{\left(k \ell, 2\right)=1} \frac{ \left(\frac{k \ell}{cq}\right) \nu_3(k) \nu_4(\ell)((k \ell)^*)^{\frac12 - \beta}}{k^{u_2-iU-s} \ell^{u_3+iU-s}} \prod_{p\mid k \ell} \frac{\left(1-\chi_p((k\ell)^*) \nu_5(p) p^{-\beta}\right)}{\left(1- \chi_p((k\ell)^* \nu_6(p)) p^{\beta-1}\right)} \prod_{p \mid k \ell} a_p, \end{align} $$
$$ \begin{align} A_q = \sum_{\left(abc,2\right) = 1} \frac{\mu^2(abc) \nu_2(c) }{(abc)^{\alpha + 2\beta}} \frac{\mu(b)}{b^{1+\alpha} c^{1+\alpha+\beta}} \nonumber\\[-2pt] \sum_{\left(k \ell, 2\right)=1} \frac{ \left(\frac{k \ell}{cq}\right) \nu_3(k) \nu_4(\ell)((k \ell)^*)^{\frac12 - \beta}}{k^{u_2-iU-s} \ell^{u_3+iU-s}} \prod_{p\mid k \ell} \frac{\left(1-\chi_p((k\ell)^*) \nu_5(p) p^{-\beta}\right)}{\left(1- \chi_p((k\ell)^* \nu_6(p)) p^{\beta-1}\right)} \prod_{p \mid k \ell} a_p, \end{align} $$
and where the
![]() $\nu _i$
run over Dirichlet characters modulo
$\nu _i$
run over Dirichlet characters modulo
![]() $8$
.
$8$
.
Observe that equation (11.36) converges absolutely on
![]() $\mathcal {D}_1$
.
$\mathcal {D}_1$
.
Proof. Applying Lemma 11.10 into equation (11.3), which is valid on
![]() $\mathcal {D}_1 \cap \{ \mathrm {Re}(\beta ) < 0 \}$
by Lemma 11.9, and applying the Dirichlet series expansion of
$\mathcal {D}_1 \cap \{ \mathrm {Re}(\beta ) < 0 \}$
by Lemma 11.9, and applying the Dirichlet series expansion of
![]() $D(\alpha , \beta , \chi _{k \ell })$
given in equation (11.20), we deduce
$D(\alpha , \beta , \chi _{k \ell })$
given in equation (11.20), we deduce
 $$ \begin{align} Z_{\leq L}(s,u_1,u_2,u_3) = Z^{(2)}_{\leq L} \frac{\zeta(2\alpha + 2\beta)}{\left(1-2^{-2\alpha - 2\beta}\right)^{-1}} \sum_{\left(k \ell, 2\right) = 1} \frac{((k \ell)^*)^{\frac12 - \beta}}{k^{u_2-iU-s} \ell^{u_3+iU-s}} \frac{\gamma(1-\beta)}{\gamma(\beta)} \nonumber\\ \left(1 - \chi_{k \ell}(2) 2^{-\beta}\right) \sum_{\left(abc,2\right) = 1} \frac{\mu^2(abc)}{(abc)^{\alpha + 2\beta}} \frac{\mu(b)}{b^{1+\alpha} c^{1+\alpha+\beta}} \sum_{q=1}^{\infty} \frac{\left(\frac{qc}{k \ell}\right)}{q^{1-\beta}} \prod_{p\mid k \ell} \frac{\left(1-\chi^*(p) p^{-\beta}\right)}{\left(1-\chi^*(p) p^{\beta-1}\right)} \prod_{p \mid k \ell} a_p, \end{align} $$
$$ \begin{align} Z_{\leq L}(s,u_1,u_2,u_3) = Z^{(2)}_{\leq L} \frac{\zeta(2\alpha + 2\beta)}{\left(1-2^{-2\alpha - 2\beta}\right)^{-1}} \sum_{\left(k \ell, 2\right) = 1} \frac{((k \ell)^*)^{\frac12 - \beta}}{k^{u_2-iU-s} \ell^{u_3+iU-s}} \frac{\gamma(1-\beta)}{\gamma(\beta)} \nonumber\\ \left(1 - \chi_{k \ell}(2) 2^{-\beta}\right) \sum_{\left(abc,2\right) = 1} \frac{\mu^2(abc)}{(abc)^{\alpha + 2\beta}} \frac{\mu(b)}{b^{1+\alpha} c^{1+\alpha+\beta}} \sum_{q=1}^{\infty} \frac{\left(\frac{qc}{k \ell}\right)}{q^{1-\beta}} \prod_{p\mid k \ell} \frac{\left(1-\chi^*(p) p^{-\beta}\right)}{\left(1-\chi^*(p) p^{\beta-1}\right)} \prod_{p \mid k \ell} a_p, \end{align} $$
where recall
 $a_p = 1 + O\left (p^{-1}\right )$
on
$a_p = 1 + O\left (p^{-1}\right )$
on
![]() $\mathcal {D}_{\infty }$
, and
$\mathcal {D}_{\infty }$
, and
![]() $\chi ^* = \chi _{k \ell }^*$
is the primitive character induced by
$\chi ^* = \chi _{k \ell }^*$
is the primitive character induced by
 $\chi _{k \ell }(n) = \left (\frac {n}{k \ell }\right ) \left (\text {so }\chi ^*(n) = \left (\frac {n}{(k \ell )^*}\right )\right )$
.
$\chi _{k \ell }(n) = \left (\frac {n}{k \ell }\right ) \left (\text {so }\chi ^*(n) = \left (\frac {n}{(k \ell )^*}\right )\right )$
.
We next wish to focus on the sums over k and
![]() $\ell $
. One small issue is that the parity of the character
$\ell $
. One small issue is that the parity of the character
![]() $\chi _{k \ell }$
(and hence the formula for
$\chi _{k \ell }$
(and hence the formula for
![]() $\gamma (s)$
) may vary. However, the parity depends only on k and
$\gamma (s)$
) may vary. However, the parity depends only on k and
![]() $\ell $
modulo
$\ell $
modulo
![]() $8$
. Also, q may be even, but we can factor out the
$8$
. Also, q may be even, but we can factor out the
![]() $2$
-part of q and directly evaluate its summation. Likewise, we can apply quadratic reciprocity (again!) to give that
$2$
-part of q and directly evaluate its summation. Likewise, we can apply quadratic reciprocity (again!) to give that
 $\left (\frac {qc}{k \ell }\right )$
equals
$\left (\frac {qc}{k \ell }\right )$
equals
 $\left (\frac {k \ell }{qc}\right )$
times a function that depends only on
$\left (\frac {k \ell }{qc}\right )$
times a function that depends only on
![]() $q,c, k,\ell $
modulo
$q,c, k,\ell $
modulo
![]() $4$
. Similarly, we have that
$4$
. Similarly, we have that
![]() $\chi _{k \ell }^*(p)$
equals
$\chi _{k \ell }^*(p)$
equals
![]() $\chi _p((k \ell )^*)$
up to a function modulo
$\chi _p((k \ell )^*)$
up to a function modulo
![]() $4$
. We can then use multiplicative Fourier/Mellin decomposition modulo
$4$
. We can then use multiplicative Fourier/Mellin decomposition modulo
![]() $8$
to express
$8$
to express
![]() $Z_{\leq L}$
as a finite linear combination, with bounded coefficients, of sums of the form claimed in the statement of the lemma.
$Z_{\leq L}$
as a finite linear combination, with bounded coefficients, of sums of the form claimed in the statement of the lemma.
Next we develop some of the analytic properties of
![]() $A_q$
. For notational convenience, we consider the case with all
$A_q$
. For notational convenience, we consider the case with all
![]() $\nu _i = 1$
, as the general case is no more difficult. We expand the Euler product over
$\nu _i = 1$
, as the general case is no more difficult. We expand the Euler product over
![]() $p\mid k \ell $
involving
$p\mid k \ell $
involving
![]() $\chi ^*$
into its Dirichlet series and reverse the orders of summation (taking
$\chi ^*$
into its Dirichlet series and reverse the orders of summation (taking
![]() $k, \ell $
to the inside), giving
$k, \ell $
to the inside), giving
 $$ \begin{align} A_q = \sum_{\left(abc d e, 2\right)=1} \frac{\mu^2(abc) \mu(b) \mu(d)}{(abc)^{\alpha + 2\beta} b^{1 + \alpha} c^{1 + \alpha + \beta} d^{\beta} e^{1-\beta}} A_{q,c,d,e}, \end{align} $$
$$ \begin{align} A_q = \sum_{\left(abc d e, 2\right)=1} \frac{\mu^2(abc) \mu(b) \mu(d)}{(abc)^{\alpha + 2\beta} b^{1 + \alpha} c^{1 + \alpha + \beta} d^{\beta} e^{1-\beta}} A_{q,c,d,e}, \end{align} $$
where
 $$ \begin{align} A_{q,c,d,e} = \sum_{\substack{k \ell \equiv 0 \negthickspace \negthickspace \pmod{d} \\ (k \ell)^{\infty} \equiv 0 \negthickspace \negthickspace \pmod{e} \\ \left(k\ell, 2\right)=1}} \frac{ \left(\frac{k \ell}{cq}\right)\left(\frac{(k \ell)^*}{de}\right)((k \ell)^*)^{\frac12 - \beta}}{k^{u_2-iU-s} \ell^{u_3+iU-s}} \prod_{p | k \ell} a_p. \end{align} $$
$$ \begin{align} A_{q,c,d,e} = \sum_{\substack{k \ell \equiv 0 \negthickspace \negthickspace \pmod{d} \\ (k \ell)^{\infty} \equiv 0 \negthickspace \negthickspace \pmod{e} \\ \left(k\ell, 2\right)=1}} \frac{ \left(\frac{k \ell}{cq}\right)\left(\frac{(k \ell)^*}{de}\right)((k \ell)^*)^{\frac12 - \beta}}{k^{u_2-iU-s} \ell^{u_3+iU-s}} \prod_{p | k \ell} a_p. \end{align} $$
Lemma 11.12. The function
![]() $A_{q,c,d,e}$
has meromorphic continuation to
$A_{q,c,d,e}$
has meromorphic continuation to
![]() $\mathcal {D}_{\infty }$
, in the form
$\mathcal {D}_{\infty }$
, in the form
 $$ \begin{align} A_{q,c,d,e} = L\left(u_1 + u_2 - iU - \tfrac12, \chi_{qcde}\right) L\left(u_1 + u_3 - iU - \tfrac12, \chi_{qcde}\right) C(\cdot), \end{align} $$
$$ \begin{align} A_{q,c,d,e} = L\left(u_1 + u_2 - iU - \tfrac12, \chi_{qcde}\right) L\left(u_1 + u_3 - iU - \tfrac12, \chi_{qcde}\right) C(\cdot), \end{align} $$
where
![]() $C = C_q(c,d,e, s,u_1,u_2,u_3, U)$
is a Dirichlet series analytic on
$C = C_q(c,d,e, s,u_1,u_2,u_3, U)$
is a Dirichlet series analytic on
![]() $\mathcal {D}_{\infty }$
and satisfying the bound
$\mathcal {D}_{\infty }$
and satisfying the bound
![]() $C \ll ((de)')^{-2 \min \mathrm {Re} \left (u_2, u_3\right ) + \varepsilon }$
on
$C \ll ((de)')^{-2 \min \mathrm {Re} \left (u_2, u_3\right ) + \varepsilon }$
on
![]() $\mathcal {D}_{\infty }$
.
$\mathcal {D}_{\infty }$
.
Proof. We initially work on
![]() $\mathcal {D}_1$
, where the sum defining
$\mathcal {D}_1$
, where the sum defining
![]() $A_{q,c,d,e}$
converges absolutely. Now
$A_{q,c,d,e}$
converges absolutely. Now
![]() $A_{q,c,d,e}$
has an Euler product, taking the form
$A_{q,c,d,e}$
has an Euler product, taking the form
 $A_{q,c,d,e} = \prod _{\left (p,2\right )=1} A_{q,c,d,e}^{\left (p\right )}$
, say, where
$A_{q,c,d,e} = \prod _{\left (p,2\right )=1} A_{q,c,d,e}^{\left (p\right )}$
, say, where
 $$ \begin{align} A_{q,c,d,e}^{\left(p\right)} = \sum_{\substack{k + \ell \geq v_p(d) \\ \infty \cdot (k+\ell) \geq v_p(e)} } \frac{\left(\frac{p^{k+\ell}}{cq}\right)\left(\frac{\left(p^{k+\ell}\right)^*}{de}\right) \left(\left(p^{k+\ell}\right)^*\right)^{\frac12-\beta}}{p^{k\left(u_2-iU-s\right) + \ell\left(u_3 + iU - s\right)}} a_{p^{k+\ell}} , \end{align} $$
$$ \begin{align} A_{q,c,d,e}^{\left(p\right)} = \sum_{\substack{k + \ell \geq v_p(d) \\ \infty \cdot (k+\ell) \geq v_p(e)} } \frac{\left(\frac{p^{k+\ell}}{cq}\right)\left(\frac{\left(p^{k+\ell}\right)^*}{de}\right) \left(\left(p^{k+\ell}\right)^*\right)^{\frac12-\beta}}{p^{k\left(u_2-iU-s\right) + \ell\left(u_3 + iU - s\right)}} a_{p^{k+\ell}} , \end{align} $$
where
![]() $v_p$
is the p-adic valuation and where we set
$v_p$
is the p-adic valuation and where we set
![]() $a_{p^{0}} = 1$
and
$a_{p^{0}} = 1$
and
![]() $a_{p^j} = a_p$
for
$a_{p^j} = a_p$
for
![]() $j \geq 1$
.
$j \geq 1$
.
For the forthcoming estimates, we recall our convention from §1.4 that an expression of the form
![]() $O(p^{-s})$
should be interpreted to mean
$O(p^{-s})$
should be interpreted to mean
 $O\left (p^{-\mathrm {Re}(s)}\right )$
. If
$O\left (p^{-\mathrm {Re}(s)}\right )$
. If
![]() $p \nmid de$
, then by separating the cases with
$p \nmid de$
, then by separating the cases with
![]() $k+ \ell $
odd and
$k+ \ell $
odd and
![]() $k+\ell $
even we obtain
$k+\ell $
even we obtain
 $$ \begin{align*} A_{q,c,d,e}^{\left(p\right)} &= 1 + \left(\frac{p}{qcde}\right) \left[ \frac{1}{p^{u_1 + u_2 -iU -\frac12}} + \frac{1}{p^{u_1+u_3 +iU -\frac12}} \right] a_p + O\left(p^{-\min\left(2u_2, 2 u_3\right)}\right) \\ &= 1 + \left(\frac{p}{qcde}\right) \left[ \frac{1}{p^{u_1 + u_2 -iU -\frac12}} + \frac{1}{p^{u_1+u_3 +iU -\frac12}} \right]\\ &\quad + O\left(p^{-\min\left(2u_2, 2 u_3\right)}\right) + O\left(\frac{p^{-1}}{p^{u_1 + \min\left(u_2, u_3\right) - \frac12}}\right) \\ & = \frac{1 + O\left(p^{-\min\left(2u_2, 2 u_3\right)}\right) + O\left(\frac{p^{-1}}{p^{u_1 + \min\left(u_2, u_3\right) - \frac12}}\right) + O\left(p^{-2\left(u_1 + \min\left(u_2, u_3\right) - \frac12\right)}\right)}{ \left(1- \chi_{qcde}(p) p^{-u_1-u_2+iU+\frac12}\right) \left(1- \chi_{qcde}(p) p^{-u_1-u_3-iU+\frac12}\right) }. \end{align*} $$
$$ \begin{align*} A_{q,c,d,e}^{\left(p\right)} &= 1 + \left(\frac{p}{qcde}\right) \left[ \frac{1}{p^{u_1 + u_2 -iU -\frac12}} + \frac{1}{p^{u_1+u_3 +iU -\frac12}} \right] a_p + O\left(p^{-\min\left(2u_2, 2 u_3\right)}\right) \\ &= 1 + \left(\frac{p}{qcde}\right) \left[ \frac{1}{p^{u_1 + u_2 -iU -\frac12}} + \frac{1}{p^{u_1+u_3 +iU -\frac12}} \right]\\ &\quad + O\left(p^{-\min\left(2u_2, 2 u_3\right)}\right) + O\left(\frac{p^{-1}}{p^{u_1 + \min\left(u_2, u_3\right) - \frac12}}\right) \\ & = \frac{1 + O\left(p^{-\min\left(2u_2, 2 u_3\right)}\right) + O\left(\frac{p^{-1}}{p^{u_1 + \min\left(u_2, u_3\right) - \frac12}}\right) + O\left(p^{-2\left(u_1 + \min\left(u_2, u_3\right) - \frac12\right)}\right)}{ \left(1- \chi_{qcde}(p) p^{-u_1-u_2+iU+\frac12}\right) \left(1- \chi_{qcde}(p) p^{-u_1-u_3-iU+\frac12}\right) }. \end{align*} $$
Note that on
![]() $\mathcal {D}_{\infty }^{\sigma }$
, the O-term is of size
$\mathcal {D}_{\infty }^{\sigma }$
, the O-term is of size
 $O\left (p^{-1-\sigma }\right )$
, and hence
$O\left (p^{-1-\sigma }\right )$
, and hence
 $$ \begin{align} \prod_{p \nmid de} A_{q,c,d,e}^{\left(p\right)} = L\left(u_1 + u_2 - iU - \tfrac12, \chi_{qcde}\right) L\left(u_1 + u_3 - iU - \tfrac12, \chi_{qcde}\right) B, \end{align} $$
$$ \begin{align} \prod_{p \nmid de} A_{q,c,d,e}^{\left(p\right)} = L\left(u_1 + u_2 - iU - \tfrac12, \chi_{qcde}\right) L\left(u_1 + u_3 - iU - \tfrac12, \chi_{qcde}\right) B, \end{align} $$
where
![]() $B = B(q,c,d,e, s,u_1, u_2, u_3, U)$
is an Euler product that is absolutely convergent and bounded on
$B = B(q,c,d,e, s,u_1, u_2, u_3, U)$
is an Euler product that is absolutely convergent and bounded on
![]() $\mathcal {D}_{\infty }^{\sigma }$
.
$\mathcal {D}_{\infty }^{\sigma }$
.
If
![]() $p \mid de$
, then
$p \mid de$
, then
 $\left (\frac {\left (p^{k+\ell }\right )^*}{de}\right )=0$
unless
$\left (\frac {\left (p^{k+\ell }\right )^*}{de}\right )=0$
unless
 $\left (p^{k+\ell }\right )^* = 1$
, so we can assume that
$\left (p^{k+\ell }\right )^* = 1$
, so we can assume that
![]() $k+\ell $
is even (and positive, hence
$k+\ell $
is even (and positive, hence
![]() $\geq 2$
). From such primes we obtain
$\geq 2$
). From such primes we obtain
 $ A_{q,c,d,e}^{\left (p\right )} = O\left (p^{-\min \left (2u_2, 2 u_3\right )}\right ) $
, and hence
$ A_{q,c,d,e}^{\left (p\right )} = O\left (p^{-\min \left (2u_2, 2 u_3\right )}\right ) $
, and hence
 $$ \begin{align} \prod_{p\mid de} A_{q,c,d,e}^{(p)} \ll ((de)')^{-2 \min \mathrm{Re} \left(u_2, u_3\right) + \varepsilon}, \end{align} $$
$$ \begin{align} \prod_{p\mid de} A_{q,c,d,e}^{(p)} \ll ((de)')^{-2 \min \mathrm{Re} \left(u_2, u_3\right) + \varepsilon}, \end{align} $$
where
 $(de)' = \prod _{p\mid de} p$
. Putting the estimates together, we deduce (initially in
$(de)' = \prod _{p\mid de} p$
. Putting the estimates together, we deduce (initially in
![]() $\mathcal {D}_1$
) the representation (11.40), where C is analytic on
$\mathcal {D}_1$
) the representation (11.40), where C is analytic on
![]() $\mathcal {D}_{\infty }$
. Thus
$\mathcal {D}_{\infty }$
. Thus
![]() $A_{q,c,d,e}$
inherits the meromorphic continuation to
$A_{q,c,d,e}$
inherits the meromorphic continuation to
![]() $\mathcal {D}_{\infty }$
as well.
$\mathcal {D}_{\infty }$
as well.
Definition 11.13. Let
![]() $\mathcal {D}_2$
be the set of
$\mathcal {D}_2$
be the set of
![]() $(s,u_1, u_2, u_3) \in \mathbb C^4$
with
$(s,u_1, u_2, u_3) \in \mathbb C^4$
with
![]() $\mathrm {Re}(s) =0$
,
$\mathrm {Re}(s) =0$
,
![]() $\mathrm {Re}(u_2)> 1/2$
,
$\mathrm {Re}(u_2)> 1/2$
,
![]() $\mathrm {Re}(u_3)> 1/2$
, and satisfying
$\mathrm {Re}(u_3)> 1/2$
, and satisfying
One easily checks that
![]() $\mathcal {D}_1 \subset \mathcal {D}_2 \subset \mathcal {D}_{\infty }.$
$\mathcal {D}_1 \subset \mathcal {D}_2 \subset \mathcal {D}_{\infty }.$
Lemma 11.14. The function
![]() $A_q$
has meromorphic continuation to
$A_q$
has meromorphic continuation to
![]() $\mathcal {D}_2 \cap \{\mathrm {Re}(u_1) < 1/2 \}$
.
$\mathcal {D}_2 \cap \{\mathrm {Re}(u_1) < 1/2 \}$
.
Proof. We (initially) work in the domain
![]() $\mathcal {D}_1$
, where the absolute convergence is ensured. Substituting equation (11.40) into equation (11.36) and letting
$\mathcal {D}_1$
, where the absolute convergence is ensured. Substituting equation (11.40) into equation (11.36) and letting
![]() $cde = r$
, we obtain
$cde = r$
, we obtain
 $$ \begin{align} A_q = \sum_{\left(r,2\right) = 1 } L\left(u_1 + u_2 - iU-\tfrac12, \chi_{qr}\right) L\left(u_1 + u_3 + iU-\tfrac12, \chi_{qr}\right) D(q,r) , \end{align} $$
$$ \begin{align} A_q = \sum_{\left(r,2\right) = 1 } L\left(u_1 + u_2 - iU-\tfrac12, \chi_{qr}\right) L\left(u_1 + u_3 + iU-\tfrac12, \chi_{qr}\right) D(q,r) , \end{align} $$
where
 $$ \begin{align} D(q,r) = \sum_{\substack{\left(ab,2\right)=1 \\ cde = r}} \frac{\mu^2(abc) \mu(b) \mu(d)}{(abc)^{\alpha + 2\beta} b^{1 + \alpha} c^{1 + \alpha + \beta} d^{\beta} e^{1-\beta}} C_q(\cdot). \end{align} $$
$$ \begin{align} D(q,r) = \sum_{\substack{\left(ab,2\right)=1 \\ cde = r}} \frac{\mu^2(abc) \mu(b) \mu(d)}{(abc)^{\alpha + 2\beta} b^{1 + \alpha} c^{1 + \alpha + \beta} d^{\beta} e^{1-\beta}} C_q(\cdot). \end{align} $$
We claim that
![]() $D(q,r)$
is analytic on
$D(q,r)$
is analytic on
![]() $\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(u_1) < 1/2 \}$
and therein satisfies the bound
$\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(u_1) < 1/2 \}$
and therein satisfies the bound
 $$ \begin{align} D(q,r) \ll q^{\varepsilon} r^{\beta - 1 + \varepsilon} \prod_{p|r} p^{-2 u_1 - 2 \min\left(u_2, u_3\right)+1}. \end{align} $$
$$ \begin{align} D(q,r) \ll q^{\varepsilon} r^{\beta - 1 + \varepsilon} \prod_{p|r} p^{-2 u_1 - 2 \min\left(u_2, u_3\right)+1}. \end{align} $$
We now prove this claim. Recall formula (11.7), which in particular immediately shows the absolute convergence in
![]() $\mathcal {D}_{\infty }$
of the free sum over
$\mathcal {D}_{\infty }$
of the free sum over
![]() $a,b$
in equation (11.46). Hence
$a,b$
in equation (11.46). Hence
 $$ \begin{align} \lvert D(q,r)\rvert \ll r^{\varepsilon} \sum_{cde=r} \frac{\mu^2(c) \mu^2(d) ((de)')^{-2 \min\left(u_2, u_3\right)}}{ c^{1 + 2\alpha + 3\beta} d^{\beta} e^{1-\beta} } = \sum_{cd | r} \frac{\mu^2(c) \mu^2(d) ((r/c)')^{-2 \min\left(u_2, u_3\right)}}{ c^{1 + 2\alpha + 3\beta} d^{\beta} \left(\frac{r}{cd}\right)^{1-\beta}}. \end{align} $$
$$ \begin{align} \lvert D(q,r)\rvert \ll r^{\varepsilon} \sum_{cde=r} \frac{\mu^2(c) \mu^2(d) ((de)')^{-2 \min\left(u_2, u_3\right)}}{ c^{1 + 2\alpha + 3\beta} d^{\beta} e^{1-\beta} } = \sum_{cd | r} \frac{\mu^2(c) \mu^2(d) ((r/c)')^{-2 \min\left(u_2, u_3\right)}}{ c^{1 + 2\alpha + 3\beta} d^{\beta} \left(\frac{r}{cd}\right)^{1-\beta}}. \end{align} $$
One may now check formula (11.47) by brute force, prime by prime (by multiplicativity).
A consequence of formula (11.47) is that on
![]() $\mathcal {D}_{\infty } \cap \{\mathrm {Re}(u_1) < 1/2 \}$
we have the bound
$\mathcal {D}_{\infty } \cap \{\mathrm {Re}(u_1) < 1/2 \}$
we have the bound
 $D\left (q, p^k\right ) \ll p^{k \varepsilon } p^{-1-\frac {k}{2}}$
, for p prime and
$D\left (q, p^k\right ) \ll p^{k \varepsilon } p^{-1-\frac {k}{2}}$
, for p prime and
![]() $k \geq 1$
, which extends multiplicatively. Therefore,
$k \geq 1$
, which extends multiplicatively. Therefore,
![]() $\sum _{r} \lvert D(q,r)\rvert < \infty $
on
$\sum _{r} \lvert D(q,r)\rvert < \infty $
on
![]() $\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(u_1) < 1/2 \}$
. The Dirichlet L-functions appearing in equation (11.45) are at most
$\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(u_1) < 1/2 \}$
. The Dirichlet L-functions appearing in equation (11.45) are at most
![]() $O((qr)^{\varepsilon })$
on
$O((qr)^{\varepsilon })$
on
![]() $\mathcal {D}_2$
. Therefore, equation (11.45) gives the meromorphic continuation of
$\mathcal {D}_2$
. Therefore, equation (11.45) gives the meromorphic continuation of
![]() $A_q$
as stated in the lemma.
$A_q$
as stated in the lemma.
Lemma 11.15. On
![]() $\mathcal {D}_2 \cap \{ \mathrm {Re}(u_1) < 0 \}$
, the function
$\mathcal {D}_2 \cap \{ \mathrm {Re}(u_1) < 0 \}$
, the function
![]() $Z_{\leq L}$
extends to a meromorphic function, on which it is a finite linear combination of absolutely convergent sums of the form
$Z_{\leq L}$
extends to a meromorphic function, on which it is a finite linear combination of absolutely convergent sums of the form
 $$ \begin{align} Z_{\leq L}^{(2)} \frac{\gamma(1-\beta)}{\gamma(\beta)} \sideset{}{^*}\sum_{ \left(r,2\right)=1} \sideset{}{^*}\sum_{\left(q,2\right)=1} \frac{c_{q,r}}{q^{1-\beta}} L\left(u_1 + u_2 - iU - \tfrac12, \chi_{qr} \nu\right) L\left(u_1 + u_3 - iU - \tfrac12, \chi_{qr} \nu'\right), \end{align} $$
$$ \begin{align} Z_{\leq L}^{(2)} \frac{\gamma(1-\beta)}{\gamma(\beta)} \sideset{}{^*}\sum_{ \left(r,2\right)=1} \sideset{}{^*}\sum_{\left(q,2\right)=1} \frac{c_{q,r}}{q^{1-\beta}} L\left(u_1 + u_2 - iU - \tfrac12, \chi_{qr} \nu\right) L\left(u_1 + u_3 - iU - \tfrac12, \chi_{qr} \nu'\right), \end{align} $$
where
![]() $\nu $
,
$\nu $
,
![]() $\nu '$
are Dirichlet characters modulo
$\nu '$
are Dirichlet characters modulo
![]() $8$
and
$8$
and
![]() $\sum ^*$
means that the sum runs only over square-free integers. Here
$\sum ^*$
means that the sum runs only over square-free integers. Here
![]() $c_{q,r}$
is a Dirichlet series depending on
$c_{q,r}$
is a Dirichlet series depending on
![]() $s, u_1, u_2, u_3, U$
that is analytic on
$s, u_1, u_2, u_3, U$
that is analytic on
![]() $\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(u_1) < 1/2 \}$
, wherein it satisfies the bound
$\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(u_1) < 1/2 \}$
, wherein it satisfies the bound
 $$ \begin{align} c_{q,r} \ll r^{-u_1 - 2 \min\left(u_2, u_3\right)} (qr)^{\varepsilon}. \end{align} $$
$$ \begin{align} c_{q,r} \ll r^{-u_1 - 2 \min\left(u_2, u_3\right)} (qr)^{\varepsilon}. \end{align} $$
Proof. We work initially on the domain
![]() $\mathcal {D}_1 \cap \{ \mathrm {Re}(u_1) < 0 \}$
, so that Lemma 11.11 may be applied, giving expression (11.35). Now Lemma 11.14 may be invoked to give that
$\mathcal {D}_1 \cap \{ \mathrm {Re}(u_1) < 0 \}$
, so that Lemma 11.11 may be applied, giving expression (11.35). Now Lemma 11.14 may be invoked to give that
![]() $Z_{\leq L}$
is a linear combination of terms of the form
$Z_{\leq L}$
is a linear combination of terms of the form
 $$ \begin{align} &Z^{(2)}_{\leq L} \frac{\gamma(1-\beta)}{\gamma(\beta)} \frac{\zeta(2\alpha + 2\beta)}{\left(1-2^{-2\alpha - 2\beta}\right)^{-1}} \frac{\left(1 \pm 2^{-\beta}\right)}{\left(1 \pm 2^{\beta-1}\right)} \nonumber\\ &\sum_{\left(q,2\right) = 1} q^{\beta -1} \sum_{\left(r,2\right) = 1 } L\left(u_1 + u_2 - iU-\tfrac12, \chi_{qr} \nu\right) L\left(u_1 + u_3 + iU-\tfrac12, \chi_{qr} \nu'\right) D(q,r), \end{align} $$
$$ \begin{align} &Z^{(2)}_{\leq L} \frac{\gamma(1-\beta)}{\gamma(\beta)} \frac{\zeta(2\alpha + 2\beta)}{\left(1-2^{-2\alpha - 2\beta}\right)^{-1}} \frac{\left(1 \pm 2^{-\beta}\right)}{\left(1 \pm 2^{\beta-1}\right)} \nonumber\\ &\sum_{\left(q,2\right) = 1} q^{\beta -1} \sum_{\left(r,2\right) = 1 } L\left(u_1 + u_2 - iU-\tfrac12, \chi_{qr} \nu\right) L\left(u_1 + u_3 + iU-\tfrac12, \chi_{qr} \nu'\right) D(q,r), \end{align} $$
which converges absolutely on
![]() $\mathcal {D}_2 \cap \{ \mathrm {Re}(\beta ) < 0 \}$
. This gives the claimed meromorphic continuation of
$\mathcal {D}_2 \cap \{ \mathrm {Re}(\beta ) < 0 \}$
. This gives the claimed meromorphic continuation of
![]() $Z_{\leq L}$
.
$Z_{\leq L}$
.
Next we show the claimed form (11.49), which closely resembles expression (11.51) except that we need to restrict q and r to be square-free. Toward this end, replace q by
![]() $q q_2^2$
and r by
$q q_2^2$
and r by
![]() $r r_2^2$
, where the new q and r are square-free. Note that
$r r_2^2$
, where the new q and r are square-free. Note that
 $L\left (s, \chi _{q r q_2^2 r_2^2}\right )$
agrees with
$L\left (s, \chi _{q r q_2^2 r_2^2}\right )$
agrees with
![]() $L\left (s, \chi _{qr}\right )$
up to finitely many Euler factors that are bounded by
$L\left (s, \chi _{qr}\right )$
up to finitely many Euler factors that are bounded by
![]() $O((qr)^{\varepsilon })$
for
$O((qr)^{\varepsilon })$
for
![]() $\mathrm {Re}(s)> 1/2$
. These finite Euler products can be incorporated into the definition of
$\mathrm {Re}(s)> 1/2$
. These finite Euler products can be incorporated into the definition of
![]() $D(q,r)$
, which still satisfies formula (11.47) on
$D(q,r)$
, which still satisfies formula (11.47) on
![]() $\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(u_1) < 1/2 \}$
. Then we need to check the convergence in the sums over
$\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(u_1) < 1/2 \}$
. Then we need to check the convergence in the sums over
![]() $q_2$
and
$q_2$
and
![]() $r_2$
. To this end, we first note simply that
$r_2$
. To this end, we first note simply that
 $\sum _{\left (q_2,2\right )=1} q_2^{2\left (\beta - 1\right )}=\zeta (2 - 2 \beta ) \left (1- 2^{-2+2 \beta }\right )$
, which is analytic and bounded for
$\sum _{\left (q_2,2\right )=1} q_2^{2\left (\beta - 1\right )}=\zeta (2 - 2 \beta ) \left (1- 2^{-2+2 \beta }\right )$
, which is analytic and bounded for
![]() $\mathrm {Re}(u_1) \leq 1/2 - \sigma $
. For
$\mathrm {Re}(u_1) \leq 1/2 - \sigma $
. For
![]() $r_2$
, we have from formula (11.47) that
$r_2$
, we have from formula (11.47) that
 $$ \begin{align} \sum_{r_2} \left\lvert D\left(q, r r_2^2\right)\right\rvert \ll \sum_{r_2} q^{\varepsilon} \left(r r_2^2\right)^{\beta - 1 + \varepsilon} \prod_{p\mid r} p^{-2 u_1 - 2 \min\left(u_2, u_3\right)+1} \ll (qr)^{\varepsilon} r^{- u_1 - 2 \min\left(u_2, u_3\right)}. \end{align} $$
$$ \begin{align} \sum_{r_2} \left\lvert D\left(q, r r_2^2\right)\right\rvert \ll \sum_{r_2} q^{\varepsilon} \left(r r_2^2\right)^{\beta - 1 + \varepsilon} \prod_{p\mid r} p^{-2 u_1 - 2 \min\left(u_2, u_3\right)+1} \ll (qr)^{\varepsilon} r^{- u_1 - 2 \min\left(u_2, u_3\right)}. \end{align} $$
Finally, this gives the meromorphic continuation of
![]() $Z_{\leq L}$
to
$Z_{\leq L}$
to
![]() $\mathcal {D}_2 \cap \{\mathrm {Re}(u_1) < 0\}$
with the coefficients
$\mathcal {D}_2 \cap \{\mathrm {Re}(u_1) < 0\}$
with the coefficients
![]() $c_{q,r}$
analytic on
$c_{q,r}$
analytic on
![]() $\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(u_1) < 1/2 \}$
and satisfying formula (11.50).
$\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(u_1) < 1/2 \}$
and satisfying formula (11.50).
12 Completion of the proof of Theorem 1.1
Recall that the off-diagonal of
 $\sum _{T < t_j <T + \Delta } \left \lvert L\left (\mathrm {sym}^2 u_j, 1/2+iU\right )\right \rvert ^2$
is a sum which we have been studying in dyadic intervals
$\sum _{T < t_j <T + \Delta } \left \lvert L\left (\mathrm {sym}^2 u_j, 1/2+iU\right )\right \rvert ^2$
is a sum which we have been studying in dyadic intervals
![]() $n\asymp m\asymp N$
and
$n\asymp m\asymp N$
and
![]() $c\asymp C$
. Recall that
$c\asymp C$
. Recall that
![]() $N \ll U^{1/2} T^{1+\varepsilon }$
,
$N \ll U^{1/2} T^{1+\varepsilon }$
,
 $C \ll \frac {N^2 T^{\varepsilon }}{\Delta T}$
, and
$C \ll \frac {N^2 T^{\varepsilon }}{\Delta T}$
, and
 $C \gg \frac {N^2 T^{\varepsilon }}{T^2}$
, originating from formulas (6.1), (6.15), and (9.6). We also defined certain parameters
$C \gg \frac {N^2 T^{\varepsilon }}{T^2}$
, originating from formulas (6.1), (6.15), and (9.6). We also defined certain parameters
![]() $\Phi , P, K$
which can be found in equation (10.3), but for convenience we recall here
$\Phi , P, K$
which can be found in equation (10.3), but for convenience we recall here
 $\Phi = \frac {N \sqrt {C}}{U}$
,
$\Phi = \frac {N \sqrt {C}}{U}$
,
 $P = \frac {CT^2}{N^2}$
,
$P = \frac {CT^2}{N^2}$
,
 $K = \frac {CU}{N}$
. Aided by the properties of Z developed in the previous section, we are now ready to finish the proof of Theorem 1.1. We pick up from expression (10.14), where we begin with
$K = \frac {CU}{N}$
. Aided by the properties of Z developed in the previous section, we are now ready to finish the proof of Theorem 1.1. We pick up from expression (10.14), where we begin with
![]() $\mathrm {Re}(u_1) = \mathrm {Re}(u_2) = \mathrm {Re}(u_3) = 2$
. Next we write
$\mathrm {Re}(u_1) = \mathrm {Re}(u_2) = \mathrm {Re}(u_3) = 2$
. Next we write
![]() $Z = Z_{\leq L} + Z_{>L}$
, and choose L so that
$Z = Z_{\leq L} + Z_{>L}$
, and choose L so that
![]() $2^{L} \asymp C T^{\varepsilon }$
. To bound the contribution from
$2^{L} \asymp C T^{\varepsilon }$
. To bound the contribution from
![]() $Z_{>L}$
, we shift
$Z_{>L}$
, we shift
![]() $u_1$
far to the right, and use the bound (11.27). In terms of
$u_1$
far to the right, and use the bound (11.27). In terms of
![]() $u_1$
, we get a bound of size
$u_1$
, we get a bound of size
 $O\left (\left (C/2^L\right )^{\mathrm {Re}\left (u_1\right )}\right) \ll T^{-\varepsilon \mathrm {Re}\left (u_1\right )}$
which is negligible. Next we focus on
$O\left (\left (C/2^L\right )^{\mathrm {Re}\left (u_1\right )}\right) \ll T^{-\varepsilon \mathrm {Re}\left (u_1\right )}$
which is negligible. Next we focus on
![]() $Z_{\leq L}$
.
$Z_{\leq L}$
.
We begin by shifting
![]() $u_1$
to the line
$u_1$
to the line
![]() $-\varepsilon $
, which is allowed by Lemma 11.9. There is a pole of
$-\varepsilon $
, which is allowed by Lemma 11.9. There is a pole of
![]() $Z_{\leq L}$
at
$Z_{\leq L}$
at
![]() $\beta = u_1 + s = 1$
, with bounded residue. However, since
$\beta = u_1 + s = 1$
, with bounded residue. However, since
![]() $\mathrm {Im}(s) \asymp P$
and
$\mathrm {Im}(s) \asymp P$
and
![]() $P\gg T^\epsilon $
, the weight function is very small at this height and the contribution from such poles are negligible. Thus we obtain
$P\gg T^\epsilon $
, the weight function is very small at this height and the contribution from such poles are negligible. Thus we obtain
 $$ \begin{align} &\mathcal{S}\left(H_{+}\right) \nonumber \\ &\quad = \sum_C \frac{\Delta T}{NC^{3/2}} \frac{\Phi}{\sqrt{P}} \int_{-t \asymp P} \int \int \int \left(\frac{T^2}{U^2} - \frac{1}{4}\right)^s v(t) \widetilde{w}(u_1, u_2, u_3) C^{u_1} K^{u_2 + u_3} \frac{\gamma(1-u_1-s)}{\gamma(u_1+s)} \nonumber \\ & Z^{(2)}_{\leq L} \sideset{}{^*}\sum_{r} \sideset{}{^*}\sum_{q} q^{u_1+s-1}c_{q,r} L\left(u_1 + u_2 - iU - \tfrac12, \chi_{qr}\right) L\left(u_1 + u_3 - iU - \tfrac12, \chi_{qr}\right) du_1 du_2 du_3 ds, \end{align} $$
$$ \begin{align} &\mathcal{S}\left(H_{+}\right) \nonumber \\ &\quad = \sum_C \frac{\Delta T}{NC^{3/2}} \frac{\Phi}{\sqrt{P}} \int_{-t \asymp P} \int \int \int \left(\frac{T^2}{U^2} - \frac{1}{4}\right)^s v(t) \widetilde{w}(u_1, u_2, u_3) C^{u_1} K^{u_2 + u_3} \frac{\gamma(1-u_1-s)}{\gamma(u_1+s)} \nonumber \\ & Z^{(2)}_{\leq L} \sideset{}{^*}\sum_{r} \sideset{}{^*}\sum_{q} q^{u_1+s-1}c_{q,r} L\left(u_1 + u_2 - iU - \tfrac12, \chi_{qr}\right) L\left(u_1 + u_3 - iU - \tfrac12, \chi_{qr}\right) du_1 du_2 du_3 ds, \end{align} $$
plus a small error term, as well as additional terms with the characters twisted modulo
![]() $8$
. Since all our estimates hold verbatim for these additional twists, we suppress this from the notation. Next we want to truncate the sums over q and r. To do so, we move
$8$
. Since all our estimates hold verbatim for these additional twists, we suppress this from the notation. Next we want to truncate the sums over q and r. To do so, we move
![]() $u_1$
far to the left, keeping
$u_1$
far to the left, keeping
![]() $\mathrm {Re}(u_2) = \mathrm {Re}(u_3) = -\mathrm {Re}(u_1) + 100$
. Note that this remains in the domain
$\mathrm {Re}(u_2) = \mathrm {Re}(u_3) = -\mathrm {Re}(u_1) + 100$
. Note that this remains in the domain
![]() $\mathcal {D}_{2}'$
and that
$\mathcal {D}_{2}'$
and that
![]() $\mathrm {Re}(u_1) < 0$
, so that the conditions of Lemma 11.15 remain in place to apply expression (11.49). Also, note that the coefficients
$\mathrm {Re}(u_1) < 0$
, so that the conditions of Lemma 11.15 remain in place to apply expression (11.49). Also, note that the coefficients
![]() $c_{q,r}$
are
$c_{q,r}$
are
 $O\left (r^{-100}\right )$
here. Moreover, we observe by Stirling that
$O\left (r^{-100}\right )$
here. Moreover, we observe by Stirling that
 $$ \begin{align} \left\lvert\frac{\gamma(1-u_1-s)}{\gamma(u_1+s)}\right\rvert \ll P^{\frac12 - \mathrm{Re}\left(u_1\right)}. \end{align} $$
$$ \begin{align} \left\lvert\frac{\gamma(1-u_1-s)}{\gamma(u_1+s)}\right\rvert \ll P^{\frac12 - \mathrm{Re}\left(u_1\right)}. \end{align} $$
In terms of the
![]() $u_1$
-variable, the integrand in equation (12.1) is bounded by some fixed polynomial in T times
$u_1$
-variable, the integrand in equation (12.1) is bounded by some fixed polynomial in T times
 $$ \begin{align} \left(\frac{Cq}{PK^2} \right)^{\mathrm{Re}\left(u_1\right)}. \end{align} $$
$$ \begin{align} \left(\frac{Cq}{PK^2} \right)^{\mathrm{Re}\left(u_1\right)}. \end{align} $$
Therefore, we may truncate q at
![]() $q \leq Q$
, where
$q \leq Q$
, where
 $$ \begin{align} Q = \frac{P K^2}{C} T^{\varepsilon}. \end{align} $$
$$ \begin{align} Q = \frac{P K^2}{C} T^{\varepsilon}. \end{align} $$
After enforcing this condition and reversing the orders of summation (taking
![]() $r,q$
to the outside of the integrals), we shift the contours of integration so that
$r,q$
to the outside of the integrals), we shift the contours of integration so that
![]() $\mathrm {Re}(u_1) = 1/2-\varepsilon $
and
$\mathrm {Re}(u_1) = 1/2-\varepsilon $
and
![]() $\mathrm {Re}(u_2) = \mathrm {Re}(u_3) = 1/2 + \varepsilon $
; this is allowed by Lemma 11.15, as these contour shifts may be done in such a way that we remain in the domain
$\mathrm {Re}(u_2) = \mathrm {Re}(u_3) = 1/2 + \varepsilon $
; this is allowed by Lemma 11.15, as these contour shifts may be done in such a way that we remain in the domain
![]() $\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(u_1) < 1/2 \}$
, on which
$\mathcal {D}_{\infty } \cap \{ \mathrm {Re}(u_1) < 1/2 \}$
, on which
![]() $c_{q,r}$
is analytic. Moreover, we observe from formula (11.26) that
$c_{q,r}$
is analytic. Moreover, we observe from formula (11.26) that
 $Z_{\leq L}^{(2)} \ll L \ll T^{\varepsilon }$
on this contour. We then bound everything with absolute values, obtaining
$Z_{\leq L}^{(2)} \ll L \ll T^{\varepsilon }$
on this contour. We then bound everything with absolute values, obtaining
 $$ \begin{align} \mathcal{S}\left(H_{+}\right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{NC^{3/2}} \frac{\Phi}{\sqrt{P}} \int \int \int \max_{\substack{x> 0 \\ q,r \ll Q}} \left\lvert \int_{-t \asymp P} x^{it} \frac{\gamma(1-u_1-it)}{\gamma(u_1+it)} v(t) c_{q,r} dt \right\rvert \nonumber\\ \left\lvert\widetilde{w}(u_1, u_2, u_3)\right\rvert C^{1/2} K \sideset{}{^*}\sum_{q \leq Q} q^{-1/2} \left\lvert L\left(u_1 + u_2 - iU - \tfrac12, \chi_{q}\right)\right\rvert^2 du_1 du_2 du_3. \end{align} $$
$$ \begin{align} \mathcal{S}\left(H_{+}\right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{NC^{3/2}} \frac{\Phi}{\sqrt{P}} \int \int \int \max_{\substack{x> 0 \\ q,r \ll Q}} \left\lvert \int_{-t \asymp P} x^{it} \frac{\gamma(1-u_1-it)}{\gamma(u_1+it)} v(t) c_{q,r} dt \right\rvert \nonumber\\ \left\lvert\widetilde{w}(u_1, u_2, u_3)\right\rvert C^{1/2} K \sideset{}{^*}\sum_{q \leq Q} q^{-1/2} \left\lvert L\left(u_1 + u_2 - iU - \tfrac12, \chi_{q}\right)\right\rvert^2 du_1 du_2 du_3. \end{align} $$
By Lemma 4.5, keeping in mind that
![]() $c_{q,r}$
is given by a Dirichlet series uniformly bounded in t by formula (11.50), we have
$c_{q,r}$
is given by a Dirichlet series uniformly bounded in t by formula (11.50), we have
 $$ \begin{align} \max_{x> 0} \left\lvert P^{-1/2} \int x^{it} \frac{\gamma(1-u_1-it)}{\gamma(u_1+it)} v(t) c_{q,r} dt \right\rvert \ll 1. \end{align} $$
$$ \begin{align} \max_{x> 0} \left\lvert P^{-1/2} \int x^{it} \frac{\gamma(1-u_1-it)}{\gamma(u_1+it)} v(t) c_{q,r} dt \right\rvert \ll 1. \end{align} $$
Applying formula (3.3), we then obtain
 $$ \begin{align} \mathcal{S}\left(H_{+}\right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{NC^{}} \Phi K \left(Q^{1/2} + U^{1/2}\right), \qquad Q = \frac{PK^2}{C} T^{\varepsilon}. \end{align} $$
$$ \begin{align} \mathcal{S}\left(H_{+}\right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{NC^{}} \Phi K \left(Q^{1/2} + U^{1/2}\right), \qquad Q = \frac{PK^2}{C} T^{\varepsilon}. \end{align} $$
Therefore, we obtain
 $$ \begin{align} \mathcal{S}\left(H_{+}\right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{NC} \Phi K \left( \frac{P^{1/2} K }{C^{1/2}} + U^{1/2} \right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{NC} \frac{N \sqrt{C}}{U} \frac{CU}{N} \left( \frac{ T CU }{N^2} + U^{1/2} \right). \end{align} $$
$$ \begin{align} \mathcal{S}\left(H_{+}\right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{NC} \Phi K \left( \frac{P^{1/2} K }{C^{1/2}} + U^{1/2} \right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{NC} \frac{N \sqrt{C}}{U} \frac{CU}{N} \left( \frac{ T CU }{N^2} + U^{1/2} \right). \end{align} $$
Using
 $C \ll \frac {N^2}{\Delta T} T^{\varepsilon }$
, this simplifies as
$C \ll \frac {N^2}{\Delta T} T^{\varepsilon }$
, this simplifies as
 $$ \begin{align} \mathcal{S}\left(H_{+}\right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{N} \sqrt{C} \left( \frac{ T CU }{N^2} + U^{1/2} \right) \ll T^{\varepsilon} \left(\frac{T^{1/2} U }{\Delta^{1/2}} + (\Delta T U)^{1/2} \right). \end{align} $$
$$ \begin{align} \mathcal{S}\left(H_{+}\right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{N} \sqrt{C} \left( \frac{ T CU }{N^2} + U^{1/2} \right) \ll T^{\varepsilon} \left(\frac{T^{1/2} U }{\Delta^{1/2}} + (\Delta T U)^{1/2} \right). \end{align} $$
By formula (6.11) and the remark following it, this implies
 $$ \begin{align} \sum_{T < t_j <T+\Delta} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2+iU\right)\right\rvert^2 \ll T^{\varepsilon}\left(\Delta T + \frac{T^{1/2} U }{\Delta^{1/2}}\right). \end{align} $$
$$ \begin{align} \sum_{T < t_j <T+\Delta} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2+iU\right)\right\rvert^2 \ll T^{\varepsilon}\left(\Delta T + \frac{T^{1/2} U }{\Delta^{1/2}}\right). \end{align} $$
We have
 $\Delta T\gg \frac {T^{1/2} U }{\Delta ^{1/2}}$
if and only if
$\Delta T\gg \frac {T^{1/2} U }{\Delta ^{1/2}}$
if and only if
 $\Delta \gg \frac {U^{2/3}}{T^{1/3}}$
. This inequality holds because one of the conditions of Theorem 1.1 requires
$\Delta \gg \frac {U^{2/3}}{T^{1/3}}$
. This inequality holds because one of the conditions of Theorem 1.1 requires
 $\Delta \gg \frac {T}{U^{2/3}}$
, and
$\Delta \gg \frac {T}{U^{2/3}}$
, and
 $\frac {T}{U^{2/3}}\gg \frac {U^{2/3}}{T^{1/3}}$
because
$\frac {T}{U^{2/3}}\gg \frac {U^{2/3}}{T^{1/3}}$
because
![]() $T\gg U$
.
$T\gg U$
.
13 Proving Theorem 1.3
For the proof of Theorem 1.3, the parameters
![]() $\Phi , P, K$
are given in equation (10.13), which for convenience we recall take the form
$\Phi , P, K$
are given in equation (10.13), which for convenience we recall take the form
 $\Phi = \frac {N^3}{\sqrt {C} T^2}$
,
$\Phi = \frac {N^3}{\sqrt {C} T^2}$
,
 $P = \frac {C T^2}{N^2}$
,
$P = \frac {C T^2}{N^2}$
,
 $K = \frac {C^2 T^2}{N^3}$
. The bounds on N and C are the same as recollected in §12. The overall idea is to follow the same steps as in §12, but picking up with equation (10.16) instead of equation (10.14). The only structural difference between the two formulas is the additional phase of the form
$K = \frac {C^2 T^2}{N^3}$
. The bounds on N and C are the same as recollected in §12. The overall idea is to follow the same steps as in §12, but picking up with equation (10.16) instead of equation (10.14). The only structural difference between the two formulas is the additional phase of the form
 $$ \begin{align} e^{-2it \log\left(\frac{\lvert t\rvert}{eT}\right) + i a\frac{t^3}{T^2}}. \end{align} $$
$$ \begin{align} e^{-2it \log\left(\frac{\lvert t\rvert}{eT}\right) + i a\frac{t^3}{T^2}}. \end{align} $$
Here the cubic term is of size
 $O\left (P T^{-\delta }\right )$
, as mentioned after equation (10.9). This affects only the argument in bounding formula (12.6), but Lemma 4.5 is applicable (using the previous remark that the cubic term is of lower order) and gives the same bound with the additional phase from before. Referring to formula (12.7), we thus obtain
$O\left (P T^{-\delta }\right )$
, as mentioned after equation (10.9). This affects only the argument in bounding formula (12.6), but Lemma 4.5 is applicable (using the previous remark that the cubic term is of lower order) and gives the same bound with the additional phase from before. Referring to formula (12.7), we thus obtain
 $$ \begin{align} \mathcal{S}\left(H_{+}\right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{NC^{}} \Phi K \left( \frac{P^{1/2} K}{C^{1/2}} + U^{1/2} \right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{NC} \frac{N^3}{C^{1/2} T^2} \frac{C^2 T^2}{N^3} \left( \frac{ T^3 C^2 }{N^4} + 1 \right). \end{align} $$
$$ \begin{align} \mathcal{S}\left(H_{+}\right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{NC^{}} \Phi K \left( \frac{P^{1/2} K}{C^{1/2}} + U^{1/2} \right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{NC} \frac{N^3}{C^{1/2} T^2} \frac{C^2 T^2}{N^3} \left( \frac{ T^3 C^2 }{N^4} + 1 \right). \end{align} $$
Using
 $C \ll \frac {N^2}{\Delta T} T^{\varepsilon }$
, this simplifies as
$C \ll \frac {N^2}{\Delta T} T^{\varepsilon }$
, this simplifies as
 $$ \begin{align} \mathcal{S}\left(H_{+}\right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{N} C^{1/2} \left(\frac{ T^3 C^2 }{N^4} + 1 \right) \ll T^{\varepsilon} \left(\frac{T^{3/2} }{\Delta^{3/2}} + (\Delta T)^{1/2} \right). \end{align} $$
$$ \begin{align} \mathcal{S}\left(H_{+}\right) \ll T^{\varepsilon} \max_C \frac{\Delta T}{N} C^{1/2} \left(\frac{ T^3 C^2 }{N^4} + 1 \right) \ll T^{\varepsilon} \left(\frac{T^{3/2} }{\Delta^{3/2}} + (\Delta T)^{1/2} \right). \end{align} $$
Thus in all, by formula (6.11) and the remark following it, we obtain
 $$ \begin{align} \sum_{T < t_j <T+\Delta} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2\right)\right\rvert^2 \ll T^{\varepsilon} \left(\Delta T + \frac{T^{3/2}}{\Delta^{3/2}} \right). \end{align} $$
$$ \begin{align} \sum_{T < t_j <T+\Delta} \left\lvert L\left(\mathrm{sym}^2 u_j, 1/2\right)\right\rvert^2 \ll T^{\varepsilon} \left(\Delta T + \frac{T^{3/2}}{\Delta^{3/2}} \right). \end{align} $$
The second term is smaller than the first term if and only if
![]() $\Delta \gg T^{1/5}$
.
$\Delta \gg T^{1/5}$
.
Acknowledgments
This material is based upon work supported by the National Science Foundation under agreements DMS-2001183 (R.K.) and DMS-1702221 (M.Y.), and by the Simons Foundation under award 630985 (R.K.). Any opinions, findings, conclusions, or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. We are grateful to the anonymous referee for an exceptionally thorough and helpful review.
Competing Interest
The author(s) declare none.