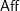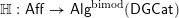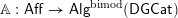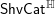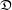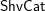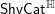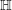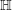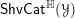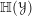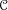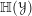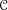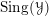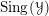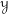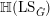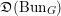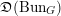1 Introduction
1.1 Overview
The present paper is a contribution to the field of categorical algebraic geometry. In this field one studies schemes and stacks via their categorical invariants, as opposed to their usual linear invariants. Among the usual invariants, typical examples are the coherent cohomology, the de Rham cohomology, the Picard group. An example of a categorical invariant is the symmetric monoidal category of quasi-coherent sheaves; other examples, including the invariant
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
appearing in the title of this paper, will be given below.
$\mathsf{ShvCat}^{\mathbb{H}}$
appearing in the title of this paper, will be given below.
The extra level of categorical abstraction might appear unjustified at first sight, but it turns out to be quite useful in several concrete situations. In this paper we will encounter a few, for instance in §§ 1.2.6, 1.4.1 and 1.11.
The interplay between categorical and ordinary algebraic geometry is likely to be very fruitful. For more on the comparison between the two points of view, we recommend the discussion and the dictionary appearing in [Reference LurieLur18, p. 720].
In the rest of this overview, after discussing some illuminating examples, we will roughly state the goals and the main results of this paper. These results and goals will be further clarified in the later sections of the introduction.
1.1.1
As mentioned earlier, given a scheme or an algebraic stack
![]() ${\mathcal{Y}}$
, its most basic categorical invariant is the symmetric monoidal differential graded (DG) category
${\mathcal{Y}}$
, its most basic categorical invariant is the symmetric monoidal differential graded (DG) category
![]() $\operatorname{QCoh}({\mathcal{Y}})$
.
$\operatorname{QCoh}({\mathcal{Y}})$
.
It turns out that there are strong analogies between the behaviour of
![]() $\operatorname{QCoh}({\mathcal{Y}})$
for an algebraic stack
$\operatorname{QCoh}({\mathcal{Y}})$
for an algebraic stack
![]() ${\mathcal{Y}}$
and the behaviour of
${\mathcal{Y}}$
and the behaviour of
![]() $H^{\ast }(Y,{\mathcal{O}}_{Y})$
for an affine schemeFootnote
1
$H^{\ast }(Y,{\mathcal{O}}_{Y})$
for an affine schemeFootnote
1
![]() $Y$
. In other words, categorical algebraic geometry has many more affine objects than ordinary algebraic geometry. Let us illustrate this principle with three examples.
$Y$
. In other words, categorical algebraic geometry has many more affine objects than ordinary algebraic geometry. Let us illustrate this principle with three examples.
1.1.2 Tannaka duality
For
![]() ${\mathcal{Y}}$
an algebraic stack satisfying mild conditions, Tannaka duality [Reference LurieLur18, ch. 9] allows one to ‘recover’
${\mathcal{Y}}$
an algebraic stack satisfying mild conditions, Tannaka duality [Reference LurieLur18, ch. 9] allows one to ‘recover’
![]() ${\mathcal{Y}}$
from the symmetric monoidal DG category
${\mathcal{Y}}$
from the symmetric monoidal DG category
![]() $\operatorname{QCoh}({\mathcal{Y}})$
. On the other hand, the DG algebra
$\operatorname{QCoh}({\mathcal{Y}})$
. On the other hand, the DG algebra
![]() $H^{\ast }({\mathcal{Y}},{\mathcal{O}}_{{\mathcal{Y}}})$
does not recover
$H^{\ast }({\mathcal{Y}},{\mathcal{O}}_{{\mathcal{Y}}})$
does not recover
![]() ${\mathcal{Y}}$
, unless
${\mathcal{Y}}$
, unless
![]() ${\mathcal{Y}}$
is an affine DG scheme.
${\mathcal{Y}}$
is an affine DG scheme.
1.1.3 Tensor products
Given a diagram
![]() $X\rightarrow Z\leftarrow Y$
of (DG) affine schemes, one has
$X\rightarrow Z\leftarrow Y$
of (DG) affine schemes, one has
Note that it is essential that the fibre product is taken in the derived sense. This formula obviously fails for very simple non-affine schemes and stacks. On the other hand, the categorical counterpart is the tensor product formula
which holds true for most algebraic stacks
![]() ${\mathcal{X}}$
,
${\mathcal{X}}$
,
![]() ${\mathcal{Y}}$
,
${\mathcal{Y}}$
,
![]() ${\mathcal{Z}}$
that one encounters in practice; see, for instance, [Reference Ben-Zvi, Francis and NadlerBFN10].
${\mathcal{Z}}$
that one encounters in practice; see, for instance, [Reference Ben-Zvi, Francis and NadlerBFN10].
The right-hand side of the above formula involves the tensor product of DG categories [Reference LurieLur17], which plays a crucial role in the theory. Note that
![]() $\operatorname{QCoh}({\mathcal{Z}})$
acts on
$\operatorname{QCoh}({\mathcal{Z}})$
acts on
![]() $\operatorname{QCoh}({\mathcal{X}})$
and on
$\operatorname{QCoh}({\mathcal{X}})$
and on
![]() $\operatorname{QCoh}({\mathcal{Y}})$
by pullback along the given maps
$\operatorname{QCoh}({\mathcal{Y}})$
by pullback along the given maps
![]() ${\mathcal{X}}\xrightarrow[{}]{f}{\mathcal{Z}}\xleftarrow[{}]{g}{\mathcal{Y}}$
.
${\mathcal{X}}\xrightarrow[{}]{f}{\mathcal{Z}}\xleftarrow[{}]{g}{\mathcal{Y}}$
.
1.1.4
 $1$
-affineness
$1$
-affineness
In the categorical context, one considers categorified quasi-coherent sheaves over a scheme or a stack
![]() ${\mathcal{Y}}$
. These categorified sheaves are defined in [Reference GaitsgoryGai15b] under the name of ‘sheaves of categories’, and in [Reference LurieLur18, ch. 10] under the name of ‘quasi-coherent stacks’. They assemble into an
${\mathcal{Y}}$
. These categorified sheaves are defined in [Reference GaitsgoryGai15b] under the name of ‘sheaves of categories’, and in [Reference LurieLur18, ch. 10] under the name of ‘quasi-coherent stacks’. They assemble into an
![]() $\infty$
-category denoted
$\infty$
-category denoted
![]() $\mathsf{ShvCat}({\mathcal{Y}})$
. We will recall and generalize the notion of
$\mathsf{ShvCat}({\mathcal{Y}})$
. We will recall and generalize the notion of
![]() $\mathsf{ShvCat}$
in § 1.6.
$\mathsf{ShvCat}$
in § 1.6.
In the above papers it is proven that most algebraic stacks, while far from being affine schemes, are nevertheless
![]() $1$
-affine: by definition,
$1$
-affine: by definition,
![]() ${\mathcal{Y}}$
is
${\mathcal{Y}}$
is
![]() $1$
-affine if the
$1$
-affine if the
![]() $\infty$
-category
$\infty$
-category
![]() $\mathsf{ShvCat}({\mathcal{Y}})$
is equivalent to the
$\mathsf{ShvCat}({\mathcal{Y}})$
is equivalent to the
![]() $\infty$
-category of modules DG categories for
$\infty$
-category of modules DG categories for
![]() $\operatorname{QCoh}({\mathcal{Y}})$
. This categorifies the classical fact that, for
$\operatorname{QCoh}({\mathcal{Y}})$
. This categorifies the classical fact that, for
![]() $Y$
an affine DG scheme, a quasi-coherent sheaf is the same as a module over
$Y$
an affine DG scheme, a quasi-coherent sheaf is the same as a module over
![]() $H^{\ast }(Y,{\mathcal{O}}_{Y})$
.
$H^{\ast }(Y,{\mathcal{O}}_{Y})$
.
1.1.5
The above examples illustrate the point of view that
![]() $\operatorname{QCoh}({\mathcal{Y}})$
is the categorical counterpart of the algebra of functions on an affine DG scheme.
$\operatorname{QCoh}({\mathcal{Y}})$
is the categorical counterpart of the algebra of functions on an affine DG scheme.
In [Reference BeraldoBer17b] we introduced another monoidal DG category,
![]() $\mathbb{H}({\mathcal{Y}})$
, which is the categorical counterpart of the algebra of differential operators on an affine DG scheme.
$\mathbb{H}({\mathcal{Y}})$
, which is the categorical counterpart of the algebra of differential operators on an affine DG scheme.
In a nutshell, the goal of the present paper is to develop the tensor product formula and the
![]() $1$
-affineness result with
$1$
-affineness result with
![]() $\mathbb{H}({\mathcal{Y}})$
in place of
$\mathbb{H}({\mathcal{Y}})$
in place of
![]() $\operatorname{QCoh}({\mathcal{Y}})$
.
$\operatorname{QCoh}({\mathcal{Y}})$
.
1.1.6 Tensor products for
 $\mathbb{H}$
$\mathbb{H}$
The tensor product formula in the
![]() $\mathbb{H}$
situation is by necessity slightly different from (1.1). Indeed, as explained in detail later, there is no natural action of
$\mathbb{H}$
situation is by necessity slightly different from (1.1). Indeed, as explained in detail later, there is no natural action of
![]() $\mathbb{H}({\mathcal{Z}})$
on
$\mathbb{H}({\mathcal{Z}})$
on
![]() $\mathbb{H}({\mathcal{X}})$
. Rather, these two monoidal DG categories are connected by a transfer bimodule category
$\mathbb{H}({\mathcal{X}})$
. Rather, these two monoidal DG categories are connected by a transfer bimodule category
![]() $\mathbb{H}_{{\mathcal{X}}\rightarrow {\mathcal{Z}}}$
. (This is in perfect agreement with the situation of rings of differential operators, from which the notation is borrowed.) Under some conditions to be discussed later, the tensor product formula reads
$\mathbb{H}_{{\mathcal{X}}\rightarrow {\mathcal{Z}}}$
. (This is in perfect agreement with the situation of rings of differential operators, from which the notation is borrowed.) Under some conditions to be discussed later, the tensor product formula reads
For some pleasing applications of this formula, the reader might look ahead at §§ 1.10 and 1.11.
1.1.7
 $1$
-affineness for
$1$
-affineness for
 $\mathbb{H}$
(or
$\mathbb{H}$
(or
 $\mathbb{H}$
-affineness)
$\mathbb{H}$
-affineness)
The
![]() $1$
-affineness mentioned in § 1.1.4 corresponds, in the
$1$
-affineness mentioned in § 1.1.4 corresponds, in the
![]() $\mathbb{H}$
setup, to our main Theorem 1.7.4, which establishes a tight link between modules categories for
$\mathbb{H}$
setup, to our main Theorem 1.7.4, which establishes a tight link between modules categories for
![]() $\mathbb{H}({\mathcal{Y}})$
and categorified D-modules on
$\mathbb{H}({\mathcal{Y}})$
and categorified D-modules on
![]() ${\mathcal{Y}}$
. The latter are also called sheaves of categories over
${\mathcal{Y}}$
. The latter are also called sheaves of categories over
![]() ${\mathcal{Y}}$
with local actions of Hochschild cochains, and denoted by
${\mathcal{Y}}$
with local actions of Hochschild cochains, and denoted by
![]() $\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
. As we explain in the following sections, the objects of
$\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
. As we explain in the following sections, the objects of
![]() $\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
are the sheaves of categories for which a notion of singular support is defined and well behaved.
$\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
are the sheaves of categories for which a notion of singular support is defined and well behaved.
1.2 Singular support via the
 $\mathbb{H}$
-action
$\mathbb{H}$
-action
1.2.1
In [Reference BeraldoBer17b] we introduced a monoidal DG category
![]() $\mathbb{H}({\mathcal{Y}})$
attached to a quasi-smooth stack
$\mathbb{H}({\mathcal{Y}})$
attached to a quasi-smooth stack
![]() ${\mathcal{Y}}$
. In contrast to
${\mathcal{Y}}$
. In contrast to
![]() $\operatorname{QCoh}({\mathcal{Y}})$
, which can be defined in vast generality, the construction of
$\operatorname{QCoh}({\mathcal{Y}})$
, which can be defined in vast generality, the construction of
![]() $\mathbb{H}({\mathcal{Y}})$
requires some (mild) conditions on
$\mathbb{H}({\mathcal{Y}})$
requires some (mild) conditions on
![]() ${\mathcal{Y}}$
. The definition of
${\mathcal{Y}}$
. The definition of
![]() $\mathbb{H}({\mathcal{Y}})$
and the necessary conditions on
$\mathbb{H}({\mathcal{Y}})$
and the necessary conditions on
![]() ${\mathcal{Y}}$
are recalled in § 1.3. For now, let us just say that any quasi-smooth stack
${\mathcal{Y}}$
are recalled in § 1.3. For now, let us just say that any quasi-smooth stack
![]() ${\mathcal{Y}}$
satisfies those conditions.
${\mathcal{Y}}$
satisfies those conditions.
1.2.2
As a brief reminder of the notion of quasi-smoothness: an algebraic stack
![]() ${\mathcal{Y}}$
is quasi-smooth if it is smooth locally a global complete intersection. It follows that, for any geometric point
${\mathcal{Y}}$
is quasi-smooth if it is smooth locally a global complete intersection. It follows that, for any geometric point
![]() $y\in {\mathcal{Y}}$
, the
$y\in {\mathcal{Y}}$
, the
![]() $y$
-fibre
$y$
-fibre
![]() $\mathbb{L}_{{\mathcal{Y}},y}:=\left.\mathbb{L}_{{\mathcal{Y}}}\right|_{y}$
of the contangent complex has cohomologies concentrated in degrees
$\mathbb{L}_{{\mathcal{Y}},y}:=\left.\mathbb{L}_{{\mathcal{Y}}}\right|_{y}$
of the contangent complex has cohomologies concentrated in degrees
![]() $[-1,1]$
.
$[-1,1]$
.
Thus, to a quasi-smooth stack
![]() ${\mathcal{Y}}$
we associate the stack
${\mathcal{Y}}$
we associate the stack
![]() $\operatorname{Sing}({\mathcal{Y}})$
that parametrizes pairs
$\operatorname{Sing}({\mathcal{Y}})$
that parametrizes pairs
![]() $(y,\unicode[STIX]{x1D709})$
with
$(y,\unicode[STIX]{x1D709})$
with
![]() $y\in {\mathcal{Y}}$
and
$y\in {\mathcal{Y}}$
and
![]() $\unicode[STIX]{x1D709}\in H^{-1}(\mathbb{L}_{{\mathcal{Y}},y})$
. This is the space that controls the singularities of
$\unicode[STIX]{x1D709}\in H^{-1}(\mathbb{L}_{{\mathcal{Y}},y})$
. This is the space that controls the singularities of
![]() ${\mathcal{Y}}$
(see [Reference Arinkin and GaitsgoryAG15]), and it is equipped with a
${\mathcal{Y}}$
(see [Reference Arinkin and GaitsgoryAG15]), and it is equipped with a
![]() $\mathbb{G}_{m}$
-action that rescales the fibres of the projection
$\mathbb{G}_{m}$
-action that rescales the fibres of the projection
![]() $\operatorname{Sing}({\mathcal{Y}})\rightarrow {\mathcal{Y}}$
.
$\operatorname{Sing}({\mathcal{Y}})\rightarrow {\mathcal{Y}}$
.
1.2.3
Suppose that a DG category
![]() ${\mathcal{C}}$
carries an action of
${\mathcal{C}}$
carries an action of
![]() $\mathbb{H}({\mathcal{Y}})$
. The goal of this paper is to explain how rich this structure is. As an example, let us informally state here the most important consequence of our main results.
$\mathbb{H}({\mathcal{Y}})$
. The goal of this paper is to explain how rich this structure is. As an example, let us informally state here the most important consequence of our main results.
Theorem 1.2.4. Let
![]() ${\mathcal{Y}}$
be a quasi-smooth stack and
${\mathcal{Y}}$
be a quasi-smooth stack and
![]() ${\mathcal{C}}$
a left
${\mathcal{C}}$
a left
![]() $\mathbb{H}({\mathcal{Y}})$
-module. Then
$\mathbb{H}({\mathcal{Y}})$
-module. Then
![]() ${\mathcal{C}}$
is equipped with a singular support theory relative to
${\mathcal{C}}$
is equipped with a singular support theory relative to
![]() $\operatorname{Sing}({\mathcal{Y}})$
.
$\operatorname{Sing}({\mathcal{Y}})$
.
1.2.5
To make sense of this, we need to explain what we mean by ‘singular support theory’. First and foremost, this means that there is a map (the singular support map) from objects of
![]() ${\mathcal{C}}$
to closed conical subsets of
${\mathcal{C}}$
to closed conical subsets of
![]() $\operatorname{Sing}({\mathcal{Y}})$
. For each such subset
$\operatorname{Sing}({\mathcal{Y}})$
. For each such subset
![]() ${\mathcal{N}}\subseteq \operatorname{Sing}({\mathcal{Y}})$
, we set
${\mathcal{N}}\subseteq \operatorname{Sing}({\mathcal{Y}})$
, we set
![]() ${\mathcal{C}}_{{\mathcal{N}}}$
to be the full subcategory of
${\mathcal{C}}_{{\mathcal{N}}}$
to be the full subcategory of
![]() ${\mathcal{C}}$
spanned by those objects with singular support contained in
${\mathcal{C}}$
spanned by those objects with singular support contained in
![]() ${\mathcal{N}}$
.
${\mathcal{N}}$
.
The second feature of a singular support theory is that any inclusion
![]() ${\mathcal{N}}\subseteq {\mathcal{N}}^{\prime }$
yields a colocalization (that is, an adjunction whose left adjoint is fully faithful)
${\mathcal{N}}\subseteq {\mathcal{N}}^{\prime }$
yields a colocalization (that is, an adjunction whose left adjoint is fully faithful)
![]() ${\mathcal{C}}_{{\mathcal{N}}}\rightleftarrows {\mathcal{C}}_{{\mathcal{N}}^{\prime }}$
.
${\mathcal{C}}_{{\mathcal{N}}}\rightleftarrows {\mathcal{C}}_{{\mathcal{N}}^{\prime }}$
.
1.2.6
Thus, the datum of an action of
![]() $\mathbb{H}({\mathcal{Y}})$
on
$\mathbb{H}({\mathcal{Y}})$
on
![]() ${\mathcal{C}}$
immediately produces a multitude of semi-orthogonal decompositions of
${\mathcal{C}}$
immediately produces a multitude of semi-orthogonal decompositions of
![]() ${\mathcal{C}}$
, one for each closed conical subset of
${\mathcal{C}}$
, one for each closed conical subset of
![]() $\operatorname{Sing}({\mathcal{Y}})$
. Obviously, these decompositions help compute Hom spaces between objects of
$\operatorname{Sing}({\mathcal{Y}})$
. Obviously, these decompositions help compute Hom spaces between objects of
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
More generally, the philosophyFootnote
2
is that, in the presence of an
![]() $\mathbb{H}({\mathcal{Y}})$
-action on
$\mathbb{H}({\mathcal{Y}})$
-action on
![]() ${\mathcal{C}}$
, any decomposition of
${\mathcal{C}}$
, any decomposition of
![]() $\operatorname{Sing}({\mathcal{Y}})$
into atomic blocks induces a decomposition of
$\operatorname{Sing}({\mathcal{Y}})$
into atomic blocks induces a decomposition of
![]() ${\mathcal{C}}$
into atomic blocks. By ‘atomic blocks’ we mean closed conical subsets of
${\mathcal{C}}$
into atomic blocks. By ‘atomic blocks’ we mean closed conical subsets of
![]() $\operatorname{Sing}({\mathcal{Y}})$
that are of a particular significance or simplicity, such as the zero section, a particular fibre, or more generally the conormal bundle of a closed subset of
$\operatorname{Sing}({\mathcal{Y}})$
that are of a particular significance or simplicity, such as the zero section, a particular fibre, or more generally the conormal bundle of a closed subset of
![]() ${\mathcal{Y}}$
. See [Reference Arinkin and GaitsgoryAG18, Reference BeraldoBer18] for applications of this principle.
${\mathcal{Y}}$
. See [Reference Arinkin and GaitsgoryAG18, Reference BeraldoBer18] for applications of this principle.
1.2.7
It is also natural to require that singular support be functorial in
![]() ${\mathcal{C}}$
. Namely, given an
${\mathcal{C}}$
. Namely, given an
![]() $\mathbb{H}({\mathcal{Y}})$
-linear functor
$\mathbb{H}({\mathcal{Y}})$
-linear functor
![]() $F:{\mathcal{C}}\rightarrow {\mathcal{D}}$
and
$F:{\mathcal{C}}\rightarrow {\mathcal{D}}$
and
![]() ${\mathcal{N}}\subseteq \operatorname{Sing}({\mathcal{Y}})$
, we would like
${\mathcal{N}}\subseteq \operatorname{Sing}({\mathcal{Y}})$
, we would like
![]() $F$
to restrict to a functor
$F$
to restrict to a functor
![]() ${\mathcal{C}}_{{\mathcal{N}}}\rightarrow {\mathcal{D}}_{{\mathcal{N}}}$
. Fortunately, this is also guaranteed by our theory. Hence the informal statement of Theorem 1.2.4 could be improved as follows.
${\mathcal{C}}_{{\mathcal{N}}}\rightarrow {\mathcal{D}}_{{\mathcal{N}}}$
. Fortunately, this is also guaranteed by our theory. Hence the informal statement of Theorem 1.2.4 could be improved as follows.
Theorem 1.2.8. For
![]() ${\mathcal{Y}}$
a quasi-smooth stack,
${\mathcal{Y}}$
a quasi-smooth stack,
![]() $\mathbb{H}({\mathcal{Y}})$
-module categories admit a singular support theory relative to
$\mathbb{H}({\mathcal{Y}})$
-module categories admit a singular support theory relative to
![]() $\operatorname{Sing}({\mathcal{Y}})$
.
$\operatorname{Sing}({\mathcal{Y}})$
.
Remark 1.2.9. The proof of this theorem is an easy consequence of the construction of
![]() $\mathbb{H}({\mathcal{Y}})$
(namely, the relation with Hochschild cochains as in § 1.5) and our
$\mathbb{H}({\mathcal{Y}})$
(namely, the relation with Hochschild cochains as in § 1.5) and our
![]() $\mathbb{H}$
-affineness theorem, Theorem 1.7.4.
$\mathbb{H}$
-affineness theorem, Theorem 1.7.4.
Remark 1.2.10. Our expectation on possible usages of this theorem is the following. It is generally difficult to directly equip
![]() ${\mathcal{C}}$
with a singular support theory relative to
${\mathcal{C}}$
with a singular support theory relative to
![]() $\operatorname{Sing}({\mathcal{Y}})$
; instead, one should try to exhibit an action of
$\operatorname{Sing}({\mathcal{Y}})$
; instead, one should try to exhibit an action of
![]() $\mathbb{H}({\mathcal{Y}})$
on
$\mathbb{H}({\mathcal{Y}})$
on
![]() ${\mathcal{C}}$
. In § 1.4 we will illustrate a concrete application of this point of view on the geometric Langlands programme.
${\mathcal{C}}$
. In § 1.4 we will illustrate a concrete application of this point of view on the geometric Langlands programme.
1.2.11
There exists a monoidal functor
![]() $\operatorname{QCoh}({\mathcal{Y}})\rightarrow \mathbb{H}({\mathcal{Y}})$
; hence, an
$\operatorname{QCoh}({\mathcal{Y}})\rightarrow \mathbb{H}({\mathcal{Y}})$
; hence, an
![]() $\mathbb{H}({\mathcal{Y}})$
-action on
$\mathbb{H}({\mathcal{Y}})$
-action on
![]() ${\mathcal{C}}$
means in particular that
${\mathcal{C}}$
means in particular that
![]() ${\mathcal{C}}$
admits a
${\mathcal{C}}$
admits a
![]() $\operatorname{QCoh}({\mathcal{Y}})$
-action. Thus, our theorem above can be regarded as an improvement of the following one in the setting of quasi-smooth stacks.
$\operatorname{QCoh}({\mathcal{Y}})$
-action. Thus, our theorem above can be regarded as an improvement of the following one in the setting of quasi-smooth stacks.
Theorem 1.2.12. Let
![]() ${\mathcal{Y}}$
be an algebraic stack (not necessarily quasi-smooth). Then left
${\mathcal{Y}}$
be an algebraic stack (not necessarily quasi-smooth). Then left
![]() $\operatorname{QCoh}({\mathcal{Y}})$
-modules are equipped with a support theory relative to
$\operatorname{QCoh}({\mathcal{Y}})$
-modules are equipped with a support theory relative to
![]() ${\mathcal{Y}}$
.
${\mathcal{Y}}$
.
1.3 The monoidal category
 $\mathbb{H}({\mathcal{Y}})$
$\mathbb{H}({\mathcal{Y}})$
Let us now recall the elements that go into the definition of
![]() $\mathbb{H}({\mathcal{Y}})$
, following [Reference Arinkin and GaitsgoryAG18] and [Reference BeraldoBer17b]. Although the applications of this theory so far concern only
$\mathbb{H}({\mathcal{Y}})$
, following [Reference Arinkin and GaitsgoryAG18] and [Reference BeraldoBer17b]. Although the applications of this theory so far concern only
![]() ${\mathcal{Y}}$
quasi-smooth, the natural set-up for
${\mathcal{Y}}$
quasi-smooth, the natural set-up for
![]() $\mathbb{H}({\mathcal{Y}})$
is more general. Namely, we assume that
$\mathbb{H}({\mathcal{Y}})$
is more general. Namely, we assume that
![]() ${\mathcal{Y}}$
is a quasi-compact algebraic stack which is perfect, bounded (eventually coconnective) and locally of finite presentation (lfp). See [Reference Ben-Zvi, Francis and NadlerBFN10] for the notion of ‘perfect stack’.
${\mathcal{Y}}$
is a quasi-compact algebraic stack which is perfect, bounded (eventually coconnective) and locally of finite presentation (lfp). See [Reference Ben-Zvi, Francis and NadlerBFN10] for the notion of ‘perfect stack’.
1.3.1
The definition of
![]() $\mathbb{H}$
requires some familiarity with the theory of ind-coherent sheaves on formal completions. We refer to [Reference Gaitsgory and RozenblyumGR17, ch. III] or [Reference BeraldoBer17b] for a quick review.
$\mathbb{H}$
requires some familiarity with the theory of ind-coherent sheaves on formal completions. We refer to [Reference Gaitsgory and RozenblyumGR17, ch. III] or [Reference BeraldoBer17b] for a quick review.
Nevertheless, let us recall the most important concepts. First,
![]() ${\mathcal{Y}}_{\operatorname{dR}}$
denotes the de Rham prestack of
${\mathcal{Y}}_{\operatorname{dR}}$
denotes the de Rham prestack of
![]() ${\mathcal{Y}}$
, whence
${\mathcal{Y}}$
, whence
![]() ${\mathcal{Y}}\times _{{\mathcal{Y}}_{\operatorname{dR}}}{\mathcal{Y}}$
is the formal completion of the diagonal
${\mathcal{Y}}\times _{{\mathcal{Y}}_{\operatorname{dR}}}{\mathcal{Y}}$
is the formal completion of the diagonal
![]() $\unicode[STIX]{x1D6E5}:{\mathcal{Y}}\rightarrow {\mathcal{Y}}\times {\mathcal{Y}}$
. Second, we have the standard functor
$\unicode[STIX]{x1D6E5}:{\mathcal{Y}}\rightarrow {\mathcal{Y}}\times {\mathcal{Y}}$
. Second, we have the standard functor
which is the functor of acting on the dualizing sheaf
![]() $\unicode[STIX]{x1D714}_{{\mathcal{Y}}}\in \operatorname{IndCoh}({\mathcal{Y}})$
. The boundedness condition on
$\unicode[STIX]{x1D714}_{{\mathcal{Y}}}\in \operatorname{IndCoh}({\mathcal{Y}})$
. The boundedness condition on
![]() ${\mathcal{Y}}$
is imposed so that
${\mathcal{Y}}$
is imposed so that
![]() $\unicode[STIX]{x1D6F6}_{{\mathcal{Y}}}$
is fully faithful.
$\unicode[STIX]{x1D6F6}_{{\mathcal{Y}}}$
is fully faithful.
1.3.2
We define
![]() $\mathbb{H}({\mathcal{Y}})$
to be the full subcategory of
$\mathbb{H}({\mathcal{Y}})$
to be the full subcategory of
![]() $\operatorname{IndCoh}({\mathcal{Y}}\times _{{\mathcal{Y}}_{\operatorname{dR}}}{\mathcal{Y}})$
cut out by the requirement that the image of the pullback functor
$\operatorname{IndCoh}({\mathcal{Y}}\times _{{\mathcal{Y}}_{\operatorname{dR}}}{\mathcal{Y}})$
cut out by the requirement that the image of the pullback functor
![]() $\unicode[STIX]{x1D6E5}^{!}:\operatorname{IndCoh}({\mathcal{Y}}\times _{{\mathcal{Y}}_{\operatorname{dR}}}{\mathcal{Y}})\rightarrow \operatorname{IndCoh}({\mathcal{Y}})$
be contained in the subcategory
$\unicode[STIX]{x1D6E5}^{!}:\operatorname{IndCoh}({\mathcal{Y}}\times _{{\mathcal{Y}}_{\operatorname{dR}}}{\mathcal{Y}})\rightarrow \operatorname{IndCoh}({\mathcal{Y}})$
be contained in the subcategory
![]() $\unicode[STIX]{x1D6F6}_{{\mathcal{Y}}}(\operatorname{QCoh}({\mathcal{Y}}))\subseteq \operatorname{IndCoh}({\mathcal{Y}})$
. Now,
$\unicode[STIX]{x1D6F6}_{{\mathcal{Y}}}(\operatorname{QCoh}({\mathcal{Y}}))\subseteq \operatorname{IndCoh}({\mathcal{Y}})$
. Now,
![]() $\operatorname{IndCoh}({\mathcal{Y}}\times _{{\mathcal{Y}}_{\operatorname{dR}}}{\mathcal{Y}})$
has a monoidal structure given by convolution, that is, pull-push along the correspondence
$\operatorname{IndCoh}({\mathcal{Y}}\times _{{\mathcal{Y}}_{\operatorname{dR}}}{\mathcal{Y}})$
has a monoidal structure given by convolution, that is, pull-push along the correspondence
The lfp assumption on
![]() ${\mathcal{Y}}$
is crucial: it ensures that
${\mathcal{Y}}$
is crucial: it ensures that
![]() $\mathbb{H}({\mathcal{Y}})$
is preserved by this multiplication, thereby inheriting a monoidal structure.
$\mathbb{H}({\mathcal{Y}})$
is preserved by this multiplication, thereby inheriting a monoidal structure.
Example 1.3.3. Of course,
![]() $\mathbb{H}({\mathcal{Y}})$
admits two obvious module categories:
$\mathbb{H}({\mathcal{Y}})$
admits two obvious module categories:
![]() $\operatorname{IndCoh}({\mathcal{Y}})$
and
$\operatorname{IndCoh}({\mathcal{Y}})$
and
![]() $\operatorname{QCoh}({\mathcal{Y}})$
. For
$\operatorname{QCoh}({\mathcal{Y}})$
. For
![]() $\operatorname{IndCoh}({\mathcal{Y}})$
, the theory of singular support of Theorem 1.2.4 reduces to the one developed by [Reference Arinkin and GaitsgoryAG15] and before by [Reference Benson, Iyengar and KrauseBIK08].
$\operatorname{IndCoh}({\mathcal{Y}})$
, the theory of singular support of Theorem 1.2.4 reduces to the one developed by [Reference Arinkin and GaitsgoryAG15] and before by [Reference Benson, Iyengar and KrauseBIK08].
Example 1.3.4. By [Reference Arinkin and GaitsgoryAG15], objects of
![]() $\operatorname{QCoh}({\mathcal{Y}})$
have singular support contained in the zero section of
$\operatorname{QCoh}({\mathcal{Y}})$
have singular support contained in the zero section of
![]() $\operatorname{Sing}({\mathcal{Y}})$
: in our language, this is expressed by the fact that the action of
$\operatorname{Sing}({\mathcal{Y}})$
: in our language, this is expressed by the fact that the action of
![]() $\mathbb{H}({\mathcal{Y}})$
on
$\mathbb{H}({\mathcal{Y}})$
on
![]() $\operatorname{QCoh}({\mathcal{Y}})$
factors through the monoidal localization
$\operatorname{QCoh}({\mathcal{Y}})$
factors through the monoidal localization
The construction and study of this monoidal localization are deferred to another publication. For now, let us say that we will call
![]() ${\mathcal{C}}\in \mathbb{H}({\mathcal{Y}})\operatorname{ -}\mathbf{mod}$
tempered if the
${\mathcal{C}}\in \mathbb{H}({\mathcal{Y}})\operatorname{ -}\mathbf{mod}$
tempered if the
![]() $\mathbb{H}({\mathcal{Y}})$
-action factors through the above monoidal quotient.
$\mathbb{H}({\mathcal{Y}})$
-action factors through the above monoidal quotient.
1.4
 $\mathbb{H}$
for Hecke
$\mathbb{H}$
for Hecke
In this section, we anticipate a future application of Theorem 1.2.4. The reader not interested in geometric Langlands might skip ahead to § 1.5.
1.4.1
Let us recall the rough statement of the geometric Langlands conjecture (see [Reference Arinkin and GaitsgoryAG15]): there is a canonical equivalence
![]() $\mathfrak{D}(\operatorname{Bun}_{G})\simeq \operatorname{IndCoh}_{{\mathcal{N}}}(\operatorname{LS}_{{\check{G}}})$
. This conjecture predicts in particular that any
$\mathfrak{D}(\operatorname{Bun}_{G})\simeq \operatorname{IndCoh}_{{\mathcal{N}}}(\operatorname{LS}_{{\check{G}}})$
. This conjecture predicts in particular that any
![]() ${\mathcal{F}}\in \mathfrak{D}(\operatorname{Bun}_{G})$
has a (nilpotent) singular support in
${\mathcal{F}}\in \mathfrak{D}(\operatorname{Bun}_{G})$
has a (nilpotent) singular support in
![]() $\operatorname{Sing}(\operatorname{LS}_{{\check{G}}})$
. The question that prompted the writing of this paper and the study of
$\operatorname{Sing}(\operatorname{LS}_{{\check{G}}})$
. The question that prompted the writing of this paper and the study of
![]() $\mathbb{H}$
is the following: is it possible to exhibit this structure on
$\mathbb{H}$
is the following: is it possible to exhibit this structure on
![]() $\mathfrak{D}(\operatorname{Bun}_{G})$
independently of the geometric Langlands conjecture?
$\mathfrak{D}(\operatorname{Bun}_{G})$
independently of the geometric Langlands conjecture?
Having such a notion is evidently desirable, as it allows us to cut out
![]() $\mathfrak{D}(\operatorname{Bun}_{G})$
into several subcategories by imposing singular support conditions. For instance, the zero section
$\mathfrak{D}(\operatorname{Bun}_{G})$
into several subcategories by imposing singular support conditions. For instance, the zero section
![]() $O_{\operatorname{LS}_{{\check{G}}}}\subseteq \operatorname{Sing}(\operatorname{LS}_{{\check{G}}})$
ought to give rise to the DG category
$O_{\operatorname{LS}_{{\check{G}}}}\subseteq \operatorname{Sing}(\operatorname{LS}_{{\check{G}}})$
ought to give rise to the DG category
![]() $\mathfrak{D}(\operatorname{Bun}_{G})_{O_{\operatorname{LS}_{{\check{G}}}}}$
of tempered
$\mathfrak{D}(\operatorname{Bun}_{G})_{O_{\operatorname{LS}_{{\check{G}}}}}$
of tempered
![]() $\mathfrak{D}$
-modules.
$\mathfrak{D}$
-modules.
1.4.2
Our Theorem 1.2.4 gives a way to answer the above question. We make the following claim, which we plan to address elsewhere: there is a canonical action of
![]() $\mathbb{H}(\operatorname{LS}_{{\check{G}}})$
on
$\mathbb{H}(\operatorname{LS}_{{\check{G}}})$
on
![]() $\mathfrak{D}(\operatorname{Bun}_{G})$
.
$\mathfrak{D}(\operatorname{Bun}_{G})$
.
Modulo technical and foundational details, the construction of such action goes as follows.
– Consider the action of the renormalized spherical category
 $\operatorname{Sph}_{G,\mathsf{Ran}}^{\text{ren}}$
on
$\operatorname{Sph}_{G,\mathsf{Ran}}^{\text{ren}}$
on
 $\mathfrak{D}(\operatorname{Bun}_{G})$
.Footnote
3
$\mathfrak{D}(\operatorname{Bun}_{G})$
.Footnote
3
– Derived geometric Satake over
 $\mathsf{Ran}$
yields a monoidal equivalence between
$\mathsf{Ran}$
yields a monoidal equivalence between
 $\operatorname{Sph}_{G,\mathsf{Ran}}^{\text{ren}}$
and the (not yet defined) convolution monoidal DG category
$\operatorname{Sph}_{G,\mathsf{Ran}}^{\text{ren}}$
and the (not yet defined) convolution monoidal DG category  $$\begin{eqnarray}\operatorname{Sph}_{{\check{G}},\mathsf{Ran}}^{\text{spec},\text{ren}}:=\operatorname{IndCoh}\big(\big(\operatorname{LS}_{{\check{G}}}(D)\times _{\operatorname{LS}_{{\check{G}}}(D^{\times })}\operatorname{LS}_{{\check{G}}}(D)\big)_{\operatorname{LS}_{{\check{G}}}(D)}^{\wedge }\big)_{\mathsf{Ran}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sph}_{{\check{G}},\mathsf{Ran}}^{\text{spec},\text{ren}}:=\operatorname{IndCoh}\big(\big(\operatorname{LS}_{{\check{G}}}(D)\times _{\operatorname{LS}_{{\check{G}}}(D^{\times })}\operatorname{LS}_{{\check{G}}}(D)\big)_{\operatorname{LS}_{{\check{G}}}(D)}^{\wedge }\big)_{\mathsf{Ran}}.\end{eqnarray}$$
– The argument of [Reference RozenblyumRoz11] yields a monoidal localization
with kernel denoted by $$\begin{eqnarray}\operatorname{Sph}_{{\check{G}},\mathsf{Ran}}^{\text{spec},\text{ren}}{\twoheadrightarrow}\mathbb{H}(\operatorname{LS}_{{\check{G}}}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sph}_{{\check{G}},\mathsf{Ran}}^{\text{spec},\text{ren}}{\twoheadrightarrow}\mathbb{H}(\operatorname{LS}_{{\check{G}}}),\end{eqnarray}$$
 ${\mathcal{K}}$
.
${\mathcal{K}}$
.– Now consider the spherical category
 $\operatorname{Sph}_{G,\mathsf{Ran}}^{\text{spec},\text{naive}}$
, the monoidal localization with kernel denoted
$\operatorname{Sph}_{G,\mathsf{Ran}}^{\text{spec},\text{naive}}$
, the monoidal localization with kernel denoted $$\begin{eqnarray}\operatorname{Sph}_{G,\mathsf{Ran}}^{\text{spec},\text{naive}}{\twoheadrightarrow}\operatorname{QCoh}(\operatorname{LS}_{{\check{G}}})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sph}_{G,\mathsf{Ran}}^{\text{spec},\text{naive}}{\twoheadrightarrow}\operatorname{QCoh}(\operatorname{LS}_{{\check{G}}})\end{eqnarray}$$
 ${\mathcal{K}}^{\text{naive}}$
, and the monoidal functor
${\mathcal{K}}^{\text{naive}}$
, and the monoidal functor  $$\begin{eqnarray}\operatorname{Sph}_{G,\mathsf{Ran}}^{\text{spec},\text{naive}}\longrightarrow \operatorname{Sph}_{{\check{G}},\mathsf{Ran}}^{\text{spec},\text{ren}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sph}_{G,\mathsf{Ran}}^{\text{spec},\text{naive}}\longrightarrow \operatorname{Sph}_{{\check{G}},\mathsf{Ran}}^{\text{spec},\text{ren}}.\end{eqnarray}$$
– By construction, the essential image of the resulting functor
 ${\mathcal{K}}^{\text{naive}}\rightarrow {\mathcal{K}}$
generates the target under colimits.
${\mathcal{K}}^{\text{naive}}\rightarrow {\mathcal{K}}$
generates the target under colimits.– The vanishing theorem [Reference GaitsgoryGai15a] states that objects of
 ${\mathcal{K}}^{\text{naive}}$
act by zero on
${\mathcal{K}}^{\text{naive}}$
act by zero on
 $\mathfrak{D}(\operatorname{Bun}_{G})$
, whence the same is true for objects of
$\mathfrak{D}(\operatorname{Bun}_{G})$
, whence the same is true for objects of
 ${\mathcal{K}}$
l in other words, the
${\mathcal{K}}$
l in other words, the
 $\operatorname{Sph}_{G,\mathsf{Ran}}^{\text{ren}}$
-action on
$\operatorname{Sph}_{G,\mathsf{Ran}}^{\text{ren}}$
-action on
 $\mathfrak{D}(\operatorname{Bun}_{G})$
factors through an action of
$\mathfrak{D}(\operatorname{Bun}_{G})$
factors through an action of
 $\mathbb{H}(\operatorname{LS}_{{\check{G}}})$
.
$\mathbb{H}(\operatorname{LS}_{{\check{G}}})$
.
In particular, the construction implies that
![]() $\mathbb{H}(\operatorname{LS}_{{\check{G}}})$
acts on
$\mathbb{H}(\operatorname{LS}_{{\check{G}}})$
acts on
![]() $\mathfrak{D}(\operatorname{Bun}_{G})$
by Hecke functors.
$\mathfrak{D}(\operatorname{Bun}_{G})$
by Hecke functors.
1.5
 $\mathbb{H}$
for Hochschild
$\mathbb{H}$
for Hochschild
To motivate the definition of
![]() $\mathbb{H}({\mathcal{Y}})$
and to explain the connection with singular support, it is instructive to look at the case where
$\mathbb{H}({\mathcal{Y}})$
and to explain the connection with singular support, it is instructive to look at the case where
![]() ${\mathcal{Y}}=S$
is an affine DG scheme. Under our standing assumptions,
${\mathcal{Y}}=S$
is an affine DG scheme. Under our standing assumptions,
![]() $S$
is of finite type, bounded and with perfect cotangent complex. (Hereafter, we denote by
$S$
is of finite type, bounded and with perfect cotangent complex. (Hereafter, we denote by
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
the
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
the
![]() $\infty$
-category of such affine schemes.) In this case, the monoidal category
$\infty$
-category of such affine schemes.) In this case, the monoidal category
![]() $\mathbb{H}(S)$
is very explicit: it is the monoidal DG category of right modules over the
$\mathbb{H}(S)$
is very explicit: it is the monoidal DG category of right modules over the
![]() $E_{2}$
-algebra
$E_{2}$
-algebra
of Hochschild cochains on
![]() $S$
. Under the equivalence
$S$
. Under the equivalence
![]() $\mathbb{H}(S)\simeq \operatorname{HC}(S)^{\operatorname{op}}\operatorname{ -}\!\mathsf{mod}$
, the monoidal functor
$\mathbb{H}(S)\simeq \operatorname{HC}(S)^{\operatorname{op}}\operatorname{ -}\!\mathsf{mod}$
, the monoidal functor
![]() $\operatorname{QCoh}(S)\rightarrow \mathbb{H}(S)$
corresponds to induction along the
$\operatorname{QCoh}(S)\rightarrow \mathbb{H}(S)$
corresponds to induction along the
![]() $E_{2}$
-algebra map
$E_{2}$
-algebra map
![]() $\unicode[STIX]{x1D6E4}(S,{\mathcal{O}}_{S})\rightarrow \operatorname{HC}(S)^{\operatorname{op}}$
.
$\unicode[STIX]{x1D6E4}(S,{\mathcal{O}}_{S})\rightarrow \operatorname{HC}(S)^{\operatorname{op}}$
.
1.5.1
From this description, one observes that Theorem 1.2.4 is obvious in the affine case. Indeed, as we have just seen, the datum of
![]() ${\mathcal{C}}\in \mathbb{H}(S)\operatorname{ -}\mathbf{mod}$
means that
${\mathcal{C}}\in \mathbb{H}(S)\operatorname{ -}\mathbf{mod}$
means that
![]() ${\mathcal{C}}$
is enriched over
${\mathcal{C}}$
is enriched over
![]() $\operatorname{HC}(S)^{\operatorname{op}}$
. Now, the Hochschild–Kostant–Rosenberg theorem yields a graded algebra map
$\operatorname{HC}(S)^{\operatorname{op}}$
. Now, the Hochschild–Kostant–Rosenberg theorem yields a graded algebra map
and, by definition, singular support for objects of
![]() ${\mathcal{C}}$
is computed just using the action of the left-hand side on
${\mathcal{C}}$
is computed just using the action of the left-hand side on
![]() $H^{\bullet }({\mathcal{C}})$
.
$H^{\bullet }({\mathcal{C}})$
.
1.5.2
In summary, there is a hierarchy of structures that a DG category
![]() ${\mathcal{C}}$
might carry:
${\mathcal{C}}$
might carry:
– an action of the
 $E_{2}$
-algebra
$E_{2}$
-algebra
 $\operatorname{HC}(S)^{\operatorname{op}}$
;
$\operatorname{HC}(S)^{\operatorname{op}}$
;– an action of the commutative graded algebra
 $\operatorname{Sym}_{H^{0}(S,{\mathcal{O}}_{S})}H^{1}(S,\mathbb{T}_{S})[-2]$
on
$\operatorname{Sym}_{H^{0}(S,{\mathcal{O}}_{S})}H^{1}(S,\mathbb{T}_{S})[-2]$
on
 $H^{\bullet }({\mathcal{C}})$
;
$H^{\bullet }({\mathcal{C}})$
;– an action of the commutative algebra
 $H^{0}(S,{\mathcal{O}}_{S})$
on
$H^{0}(S,{\mathcal{O}}_{S})$
on
 $H^{\bullet }({\mathcal{C}})$
.
$H^{\bullet }({\mathcal{C}})$
.
The first two data endow objects of
![]() ${\mathcal{C}}$
with singular support, which is a closed conical subset of
${\mathcal{C}}$
with singular support, which is a closed conical subset of
![]() $\operatorname{Sing}(S)$
; see [Reference Arinkin and GaitsgoryAG15]. The third datum only allows us to define ordinary support in
$\operatorname{Sing}(S)$
; see [Reference Arinkin and GaitsgoryAG15]. The third datum only allows us to define ordinary support in
![]() $S$
.
$S$
.
1.6 Sheaves of categories
Next, we would like to generalize the above constructions to non-affine schemes and then to algebraic stacks. The key hint is that singular support of quasi-coherent and ind-coherent sheaves can be computed smooth locally. Thus, we hope to be able to glue the local
![]() $\operatorname{HC}$
-actions as well.
$\operatorname{HC}$
-actions as well.
1.6.1
The first step towards this goal is to understand the functoriality of
![]() $\mathbb{H}(S)\operatorname{ -}\mathbf{mod}$
along maps of affine schemes. This is not immediate, as
$\mathbb{H}(S)\operatorname{ -}\mathbf{mod}$
along maps of affine schemes. This is not immediate, as
![]() $\operatorname{HC}(S)$
is not functorial in
$\operatorname{HC}(S)$
is not functorial in
![]() $S$
. In particular, for
$S$
. In particular, for
![]() $f:S\rightarrow T$
a morphism in
$f:S\rightarrow T$
a morphism in
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, there is no natural monoidal functor between
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, there is no natural monoidal functor between
![]() $\mathbb{H}(T)$
and
$\mathbb{H}(T)$
and
![]() $\mathbb{H}(S)$
. However, these two monoidal categories are connected by a canonical bimodule
$\mathbb{H}(S)$
. However, these two monoidal categories are connected by a canonical bimodule
Example 1.6.2. Observe that
![]() $\mathbb{H}_{S\rightarrow \operatorname{pt}}\simeq \operatorname{QCoh}(S)$
and
$\mathbb{H}_{S\rightarrow \operatorname{pt}}\simeq \operatorname{QCoh}(S)$
and
![]() $\mathbb{H}_{S\rightarrow S}=\mathbb{H}(S)$
.
$\mathbb{H}_{S\rightarrow S}=\mathbb{H}(S)$
.
1.6.3
Moreover, for any string
![]() $S\rightarrow T\rightarrow U$
in
$S\rightarrow T\rightarrow U$
in
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, there is a natural functor
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, there is a natural functor
given by convolution along the obvious correspondence
We will prove in Theorem 4.3.4 that (1.2) is an equivalence of
![]() $(\mathbb{H}(S),\mathbb{H}(U))$
-bimodules. It follows that the assignment
$(\mathbb{H}(S),\mathbb{H}(U))$
-bimodules. It follows that the assignment
![]() $[S\rightarrow T]{\rightsquigarrow}\mathbb{H}_{S\rightarrow T}$
upgrades to a functor
$[S\rightarrow T]{\rightsquigarrow}\mathbb{H}_{S\rightarrow T}$
upgrades to a functor
where
![]() $\mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
is the
$\mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
is the
![]() $\infty$
-category whose objects are monoidal DG categories and whose morphisms are bimodules.
$\infty$
-category whose objects are monoidal DG categories and whose morphisms are bimodules.
1.6.4
A functor
(or a slight variation, for example the functor
![]() $\mathbb{H}:\mathsf{Aff}_{\text{lfp}}^{{<}\infty }\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
) will be called a coefficient system in this paper. Informally,
$\mathbb{H}:\mathsf{Aff}_{\text{lfp}}^{{<}\infty }\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
) will be called a coefficient system in this paper. Informally,
![]() $\mathbb{A}$
consists of the following pieces of data:
$\mathbb{A}$
consists of the following pieces of data:
– for an affine scheme
 $S$
, a monoidal DG category
$S$
, a monoidal DG category
 $\mathbb{A}(S)$
;
$\mathbb{A}(S)$
;– for a map of affine schemes
 $f:S\rightarrow T$
, an
$f:S\rightarrow T$
, an
 $(\mathbb{A}(S),\mathbb{A}(T))$
-bimodule
$(\mathbb{A}(S),\mathbb{A}(T))$
-bimodule
 $\mathbb{A}_{S\rightarrow T}$
;
$\mathbb{A}_{S\rightarrow T}$
;– for any string of affine schemes
 $S\rightarrow T\rightarrow U$
, an
$S\rightarrow T\rightarrow U$
, an
 $(\mathbb{A}(S),\mathbb{A}(U))$
-bilinear equivalence
$(\mathbb{A}(S),\mathbb{A}(U))$
-bilinear equivalence  $$\begin{eqnarray}\mathbb{A}_{S\rightarrow T}\underset{\mathbb{A}(T)}{\otimes }\mathbb{A}_{T\rightarrow U}\longrightarrow \mathbb{A}_{S\rightarrow U};\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{A}_{S\rightarrow T}\underset{\mathbb{A}(T)}{\otimes }\mathbb{A}_{T\rightarrow U}\longrightarrow \mathbb{A}_{S\rightarrow U};\end{eqnarray}$$
– a system of coherent compatibilities for higher compositions.
The reason for the terminology is that each
![]() $\mathbb{A}$
is the coefficient system for a sheaf of categories attached to it. More precisely, the datum of
$\mathbb{A}$
is the coefficient system for a sheaf of categories attached to it. More precisely, the datum of
![]() $\mathbb{A}$
as above allows us to define a functor
$\mathbb{A}$
as above allows us to define a functor
as follows:
– for
 $S$
affine, we set
$S$
affine, we set
 $\mathsf{ShvCat}^{\mathbb{A}}(S)=\mathbb{A}(S)\operatorname{ -}\mathbf{mod}$
;
$\mathsf{ShvCat}^{\mathbb{A}}(S)=\mathbb{A}(S)\operatorname{ -}\mathbf{mod}$
;– for
 $f:S\rightarrow T$
a map in
$f:S\rightarrow T$
a map in
 $\mathsf{Aff}$
, we have a structure pullback functor
$\mathsf{Aff}$
, we have a structure pullback functor  $$\begin{eqnarray}f^{\ast ,\mathbb{A}}:\mathsf{ShvCat}^{\mathbb{A}}(T)=\mathbb{A}(T)\operatorname{ -}\mathbf{mod}\xrightarrow[{}]{\mathbb{A}_{S\rightarrow T}\underset{\mathbb{A}(T)}{\otimes }-}\mathsf{ShvCat}^{\mathbb{A}}(S)=\mathbb{A}(S)\operatorname{ -}\mathbf{mod};\end{eqnarray}$$
$$\begin{eqnarray}f^{\ast ,\mathbb{A}}:\mathsf{ShvCat}^{\mathbb{A}}(T)=\mathbb{A}(T)\operatorname{ -}\mathbf{mod}\xrightarrow[{}]{\mathbb{A}_{S\rightarrow T}\underset{\mathbb{A}(T)}{\otimes }-}\mathsf{ShvCat}^{\mathbb{A}}(S)=\mathbb{A}(S)\operatorname{ -}\mathbf{mod};\end{eqnarray}$$
– for
 ${\mathcal{Y}}$
a prestack, we define
${\mathcal{Y}}$
a prestack, we define
 $\mathsf{ShvCat}^{\mathbb{A}}({\mathcal{Y}})$
as a right Kan extension along the inclusion
$\mathsf{ShvCat}^{\mathbb{A}}({\mathcal{Y}})$
as a right Kan extension along the inclusion
 $\mathsf{Aff}{\hookrightarrow}\mathsf{PreStk}$
, that is,
$\mathsf{Aff}{\hookrightarrow}\mathsf{PreStk}$
, that is,  $$\begin{eqnarray}\mathsf{ShvCat}^{\mathbb{A}}({\mathcal{Y}})=\lim _{S\in (\mathsf{Aff}_{/{\mathcal{Y}}})^{\operatorname{op}}}\mathbb{A}(S)\operatorname{ -}\mathbf{mod}.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{ShvCat}^{\mathbb{A}}({\mathcal{Y}})=\lim _{S\in (\mathsf{Aff}_{/{\mathcal{Y}}})^{\operatorname{op}}}\mathbb{A}(S)\operatorname{ -}\mathbf{mod}.\end{eqnarray}$$
Thus, an object of
![]() $\mathsf{ShvCat}^{\mathbb{A}}({\mathcal{Y}})$
is a collection of
$\mathsf{ShvCat}^{\mathbb{A}}({\mathcal{Y}})$
is a collection of
![]() $\mathbb{A}(S)$
-modules
$\mathbb{A}(S)$
-modules
![]() ${\mathcal{C}}_{S}$
, one for each
${\mathcal{C}}_{S}$
, one for each
![]() $S$
mapping to
$S$
mapping to
![]() ${\mathcal{Y}}$
, together with compatible equivalences
${\mathcal{Y}}$
, together with compatible equivalences
![]() $\mathbb{A}_{S\rightarrow T}\otimes _{\mathbb{A}(T)}{\mathcal{C}}_{T}\simeq {\mathcal{C}}_{S}$
.
$\mathbb{A}_{S\rightarrow T}\otimes _{\mathbb{A}(T)}{\mathcal{C}}_{T}\simeq {\mathcal{C}}_{S}$
.
Example 1.6.5. The easiest non-trivial example of coefficient system is arguably the one denoted by
![]() $\mathbb{Q}$
and defined as
$\mathbb{Q}$
and defined as
The theory of sheaves of categories associated to
![]() $\mathbb{Q}$
is the ‘original one’, developed by D. Gaitsgory in [Reference GaitsgoryGai15b]. There such theory was denoted by
$\mathbb{Q}$
is the ‘original one’, developed by D. Gaitsgory in [Reference GaitsgoryGai15b]. There such theory was denoted by
![]() $\mathsf{ShvCat}$
; in this paper, for the sake of uniformity, we will instead denote it by
$\mathsf{ShvCat}$
; in this paper, for the sake of uniformity, we will instead denote it by
![]() $\mathsf{ShvCat}^{\mathbb{Q}}$
.
$\mathsf{ShvCat}^{\mathbb{Q}}$
.
Example 1.6.6. Parallel to the above, consider the coefficient system
![]() $\mathbb{D}:\mathsf{Aff}_{\text{aft}}\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
defined by
$\mathbb{D}:\mathsf{Aff}_{\text{aft}}\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
defined by
The theory
![]() $\mathsf{ShvCat}^{\mathbb{D}}$
is the theory of crystals of categories, also discussed in [Reference GaitsgoryGai15b].
$\mathsf{ShvCat}^{\mathbb{D}}$
is the theory of crystals of categories, also discussed in [Reference GaitsgoryGai15b].
Remark 1.6.7. The following list of analogies is sometimes helpful:
![]() $\mathsf{ShvCat}^{\mathbb{Q}}$
categorifies quasi-coherent sheaves,
$\mathsf{ShvCat}^{\mathbb{Q}}$
categorifies quasi-coherent sheaves,
![]() $\mathsf{ShvCat}^{\mathbb{D}}$
categorifies locally constant sheaves,
$\mathsf{ShvCat}^{\mathbb{D}}$
categorifies locally constant sheaves,
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
categorifies
$\mathsf{ShvCat}^{\mathbb{H}}$
categorifies
![]() $\mathfrak{D}$
-modules.
$\mathfrak{D}$
-modules.
1.7
 $\mathbb{H}$
-affineness
$\mathbb{H}$
-affineness
In line with the first of the above analogies, the foundational paper [Reference GaitsgoryGai15b] constructs an explicit adjunction
In line with the analogy again, a prestack
![]() ${\mathcal{Y}}$
is said to be
${\mathcal{Y}}$
is said to be
![]() $1$
-affine if these adjoints are mutually inverse equivalences. This is tautologically true in the case where
$1$
-affine if these adjoints are mutually inverse equivalences. This is tautologically true in the case where
![]() ${\mathcal{Y}}$
is an affine scheme. However, there are several other examples: most notably many algebraic stacks (specifically, quasi-compact bounded algebraic stacks of finite type and with affine diagonal) are
${\mathcal{Y}}$
is an affine scheme. However, there are several other examples: most notably many algebraic stacks (specifically, quasi-compact bounded algebraic stacks of finite type and with affine diagonal) are
![]() $1$
-affine; see [Reference GaitsgoryGai15b, Theorem 2.2.6].
$1$
-affine; see [Reference GaitsgoryGai15b, Theorem 2.2.6].
For the sake of uniformity, we take the liberty to rename ‘
![]() $1$
-affineness’ as ‘
$1$
-affineness’ as ‘
![]() $\mathbb{Q}$
-affineness’.
$\mathbb{Q}$
-affineness’.
1.7.1
One of our main constructions is the adjunction
sketched below (and discussed thoroughly in § 6.2). Contrarily to the
![]() $\mathbb{Q}$
-case, in the
$\mathbb{Q}$
-case, in the
![]() $\mathbb{H}$
-case we do not allow
$\mathbb{H}$
-case we do not allow
![]() ${\mathcal{Y}}$
to be an arbitrary prestack, but we need
${\mathcal{Y}}$
to be an arbitrary prestack, but we need
![]() ${\mathcal{Y}}$
to be an algebraic stack satisfying the conditions that make
${\mathcal{Y}}$
to be an algebraic stack satisfying the conditions that make
![]() $\mathbb{H}({\mathcal{Y}})$
well defined; see § 1.3.
$\mathbb{H}({\mathcal{Y}})$
well defined; see § 1.3.
1.7.2
The definition of the left adjoint
![]() $\mathbf{Loc}_{{\mathcal{Y}}}^{\mathbb{H}}$
is easy. For a map
$\mathbf{Loc}_{{\mathcal{Y}}}^{\mathbb{H}}$
is easy. For a map
![]() $S\rightarrow {\mathcal{Y}}$
with
$S\rightarrow {\mathcal{Y}}$
with
![]() $S\in \mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, look at the
$S\in \mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, look at the
![]() $(\mathbb{H}(S),\mathbb{H}({\mathcal{Y}}))$
-bimodule
$(\mathbb{H}(S),\mathbb{H}({\mathcal{Y}}))$
-bimodule
![]() $\mathbb{H}_{S\rightarrow {\mathcal{Y}}}:=\operatorname{IndCoh}_{0}((S\times {\mathcal{Y}})_{S}^{\wedge })$
. Given
$\mathbb{H}_{S\rightarrow {\mathcal{Y}}}:=\operatorname{IndCoh}_{0}((S\times {\mathcal{Y}})_{S}^{\wedge })$
. Given
![]() ${\mathcal{C}}\in \mathbb{H}({\mathcal{Y}})\operatorname{ -}\mathbf{mod}$
, we form the
${\mathcal{C}}\in \mathbb{H}({\mathcal{Y}})\operatorname{ -}\mathbf{mod}$
, we form the
![]() $\mathbb{H}$
-sheaf of categories
$\mathbb{H}$
-sheaf of categories
To define the right adjoint
![]() $\unicode[STIX]{x1D71E}_{{\mathcal{Y}}}^{\mathbb{H}}$
, we need to make sure that each bimodule
$\unicode[STIX]{x1D71E}_{{\mathcal{Y}}}^{\mathbb{H}}$
, we need to make sure that each bimodule
![]() $\mathbb{H}_{S\rightarrow {\mathcal{Y}}}$
admits a right dual. Such right dual exists and it is fortunately the obvious
$\mathbb{H}_{S\rightarrow {\mathcal{Y}}}$
admits a right dual. Such right dual exists and it is fortunately the obvious
![]() $(\mathbb{H}({\mathcal{Y}}),\mathbb{H}(S))$
-bimodule
$(\mathbb{H}({\mathcal{Y}}),\mathbb{H}(S))$
-bimodule
From this, it is straightforward to see that
with its natural left
![]() $\mathbb{H}({\mathcal{Y}})$
-module structure.
$\mathbb{H}({\mathcal{Y}})$
-module structure.
1.7.3
We can now state our main theorem.
Theorem 1.7.4. Any
![]() ${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
is
${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
is
![]() $\mathbb{H}$
-affine, that is, the adjoint functors in (1.3) are equivalences.
$\mathbb{H}$
-affine, that is, the adjoint functors in (1.3) are equivalences.
In the rest of this introduction, we will explain our two applications of this theorem: the relation with singular support as in Theorem 1.2.4, and the functoriality of
![]() $\mathbb{H}$
for algebraic stacks.
$\mathbb{H}$
for algebraic stacks.
1.8 Change of coefficients
Coefficient systems form an
![]() $\infty$
-category. By definition, a morphism
$\infty$
-category. By definition, a morphism
![]() $\mathbb{A}\rightarrow \mathbb{B}$
consists of an
$\mathbb{A}\rightarrow \mathbb{B}$
consists of an
![]() $(\mathbb{A}(S),\mathbb{B}(S))$
-bimodule
$(\mathbb{A}(S),\mathbb{B}(S))$
-bimodule
![]() $M(S)$
for any
$M(S)$
for any
![]() $S\in \mathsf{Aff}$
, and of a system of compatible equivalences
$S\in \mathsf{Aff}$
, and of a system of compatible equivalences
Under mild conditions, a morphism of coefficient systems
![]() $\mathbb{A}\rightarrow \mathbb{B}$
gives rise to an adjunction
$\mathbb{A}\rightarrow \mathbb{B}$
gives rise to an adjunction
which may be regarded as a categorified version of the usual ‘extension/restriction of scalars’ adjunction.
Example 1.8.1. For instance,
![]() $\operatorname{QCoh}$
yields a morphism
$\operatorname{QCoh}$
yields a morphism
![]() $\mathbb{H}\rightarrow \mathbb{D}$
; that is,
$\mathbb{H}\rightarrow \mathbb{D}$
; that is,
![]() $\operatorname{QCoh}(S)$
is naturally an
$\operatorname{QCoh}(S)$
is naturally an
![]() $(\mathbb{H}(S),\mathfrak{D}(S))$
-bimodule and there are natural equivalences
$(\mathbb{H}(S),\mathfrak{D}(S))$
-bimodule and there are natural equivalences
for any
![]() $S\rightarrow T$
. In fact, both sides are obviously equivalent to
$S\rightarrow T$
. In fact, both sides are obviously equivalent to
![]() $\operatorname{QCoh}(S)$
.
$\operatorname{QCoh}(S)$
.
Example 1.8.2. Similarly,
![]() $\operatorname{IndCoh}$
gives rise to a morphism
$\operatorname{IndCoh}$
gives rise to a morphism
![]() $\mathbb{D}\rightarrow \mathbb{H}$
; indeed, both sides of
$\mathbb{D}\rightarrow \mathbb{H}$
; indeed, both sides of
are equivalent to
![]() $\operatorname{IndCoh}(T_{S}^{\wedge })$
, as shown in the main body of the paper.
$\operatorname{IndCoh}(T_{S}^{\wedge })$
, as shown in the main body of the paper.
Remark 1.8.3. Continuing the analogies of Remark 1.6.7, one may think of
![]() $\operatorname{QCoh}({\mathcal{Y}})$
as a categorification of the algebra
$\operatorname{QCoh}({\mathcal{Y}})$
as a categorification of the algebra
![]() ${\mathcal{O}}_{{\mathcal{Y}}}$
of functions on
${\mathcal{O}}_{{\mathcal{Y}}}$
of functions on
![]() ${\mathcal{Y}}$
(a left
${\mathcal{Y}}$
(a left
![]() $\mathfrak{D}$
-module). Likewise,
$\mathfrak{D}$
-module). Likewise,
![]() $\operatorname{IndCoh}({\mathcal{Y}})$
categorifies the space of distributions on
$\operatorname{IndCoh}({\mathcal{Y}})$
categorifies the space of distributions on
![]() ${\mathcal{Y}}$
(a right
${\mathcal{Y}}$
(a right
![]() $\mathfrak{D}$
-module). Then the
$\mathfrak{D}$
-module). Then the
![]() $\mathbb{H}$
-affineness theorem states that
$\mathbb{H}$
-affineness theorem states that
![]() $\mathbb{H}$
categorifies the algebra of differential operators on
$\mathbb{H}$
categorifies the algebra of differential operators on
![]() ${\mathcal{Y}}$
. These observations help remember/explain the directions of the morphisms
${\mathcal{Y}}$
. These observations help remember/explain the directions of the morphisms
![]() $\mathbb{H}\rightarrow \mathbb{D}$
and
$\mathbb{H}\rightarrow \mathbb{D}$
and
![]() $\mathbb{D}\rightarrow \mathbb{H}$
in the two examples above:
$\mathbb{D}\rightarrow \mathbb{H}$
in the two examples above:
![]() $\operatorname{QCoh}$
is naturally a left
$\operatorname{QCoh}$
is naturally a left
![]() $\mathbb{H}$
-module, while
$\mathbb{H}$
-module, while
![]() $\operatorname{IndCoh}$
is naturally a right
$\operatorname{IndCoh}$
is naturally a right
![]() $\mathbb{H}$
-module.
$\mathbb{H}$
-module.
Remark 1.8.4. Our Theorem 1.9.2 shows that the morphism
![]() $\operatorname{QCoh}:\mathbb{H}\rightarrow \mathbb{D}$
is ‘optimal’ in that the natural monoidal functor
$\operatorname{QCoh}:\mathbb{H}\rightarrow \mathbb{D}$
is ‘optimal’ in that the natural monoidal functor
is an equivalence for any
![]() $Y\in \mathsf{Sch}_{\text{lfp}}^{{<}\infty }$
. On the other hand, the morphism
$Y\in \mathsf{Sch}_{\text{lfp}}^{{<}\infty }$
. On the other hand, the morphism
![]() $\operatorname{IndCoh}:\mathbb{D}\rightarrow \mathbb{H}$
is not optimal; in another work (see [Reference BeraldoBer18] for more in this direction), we plan to show that
$\operatorname{IndCoh}:\mathbb{D}\rightarrow \mathbb{H}$
is not optimal; in another work (see [Reference BeraldoBer18] for more in this direction), we plan to show that
where ‘
![]() $\mathfrak{D}$
’
$\mathfrak{D}$
’
![]() $(LY)$
is the monoidal DG category introduced in [Reference BeraldoBer17b]. For
$(LY)$
is the monoidal DG category introduced in [Reference BeraldoBer17b]. For
![]() $Y$
quasi-smooth, ‘
$Y$
quasi-smooth, ‘
![]() $\mathfrak{D}$
’
$\mathfrak{D}$
’
![]() $(LY)$
is closely related to
$(LY)$
is closely related to
![]() $\mathfrak{D}(\operatorname{Sing}(Y))$
. We remark that the above equivalence (1.6) would provide an answer to the question ‘What acts on
$\mathfrak{D}(\operatorname{Sing}(Y))$
. We remark that the above equivalence (1.6) would provide an answer to the question ‘What acts on
![]() $\operatorname{IndCoh}$
?’ raised in [Reference Arinkin and GaitsgoryAG18, Remark 1.4.3].
$\operatorname{IndCoh}$
?’ raised in [Reference Arinkin and GaitsgoryAG18, Remark 1.4.3].
Example 1.8.5. Another morphism of coefficient systems of interest in this paper is
![]() $\mathbb{Q}\rightarrow \mathbb{H}$
, the one induced by the monoidal functor
$\mathbb{Q}\rightarrow \mathbb{H}$
, the one induced by the monoidal functor
![]() $\operatorname{QCoh}(S)\rightarrow \mathbb{H}(S)$
. In this case, the adjunction (1.5) categorifies the induction/forgetful adjunction between quasi-coherent sheaves and left
$\operatorname{QCoh}(S)\rightarrow \mathbb{H}(S)$
. In this case, the adjunction (1.5) categorifies the induction/forgetful adjunction between quasi-coherent sheaves and left
![]() $\mathfrak{D}$
-modules.
$\mathfrak{D}$
-modules.
1.8.6
Here is how the
![]() $\mathbb{H}$
-affineness theorem (Theorem 1.7.4) implies Theorem 1.2.4. The datum of a left
$\mathbb{H}$
-affineness theorem (Theorem 1.7.4) implies Theorem 1.2.4. The datum of a left
![]() $\mathbb{H}({\mathcal{Y}})$
-action
$\mathbb{H}({\mathcal{Y}})$
-action
![]() ${\mathcal{C}}$
corresponds the datum of an object
${\mathcal{C}}$
corresponds the datum of an object
![]() $\widetilde{{\mathcal{C}}}\in \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
. Now, on the one hand
$\widetilde{{\mathcal{C}}}\in \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
. Now, on the one hand
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
satisfies smooth descent; see Theorem 6.1.2. On the other hand, singular support is computed smooth locally. Hence, we are back to Theorem 1.2.4 for affine schemes, which has already been discussed.
$\mathsf{ShvCat}^{\mathbb{H}}$
satisfies smooth descent; see Theorem 6.1.2. On the other hand, singular support is computed smooth locally. Hence, we are back to Theorem 1.2.4 for affine schemes, which has already been discussed.
1.9 Functoriality of
 $\mathbb{H}$
for algebraic stacks
$\mathbb{H}$
for algebraic stacks
The
![]() $\mathbb{H}$
-affineness theorem has another consequence: it allows to extend the assignment
$\mathbb{H}$
-affineness theorem has another consequence: it allows to extend the assignment
![]() ${\mathcal{Y}}{\rightsquigarrow}\mathbb{H}({\mathcal{Y}})$
to a functor out of a certain
${\mathcal{Y}}{\rightsquigarrow}\mathbb{H}({\mathcal{Y}})$
to a functor out of a certain
![]() $\infty$
-category of correspondences of stacks.
$\infty$
-category of correspondences of stacks.
1.9.1
Indeed, as we prove in this paper,
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
enjoys a rich functoriality: besides the structure pullbacks
$\mathsf{ShvCat}^{\mathbb{H}}$
enjoys a rich functoriality: besides the structure pullbacks
![]() $f^{\ast ,\mathbb{H}}:\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Z}})\rightarrow \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
associated to
$f^{\ast ,\mathbb{H}}:\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Z}})\rightarrow \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
associated to
![]() $f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
, there are also pushforward functors
$f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
, there are also pushforward functors
![]() $f_{\ast ,\mathbb{H}}$
(right adjoint to pullbacks) satisfying base-change along cartesian squares.
$f_{\ast ,\mathbb{H}}$
(right adjoint to pullbacks) satisfying base-change along cartesian squares.
Now, Theorem 1.7.4 guarantees that the assignment
![]() ${\mathcal{Y}}{\rightsquigarrow}\mathbb{H}({\mathcal{Y}})$
enjoys a parallel functoriality, as stated in the following theorem.
${\mathcal{Y}}{\rightsquigarrow}\mathbb{H}({\mathcal{Y}})$
enjoys a parallel functoriality, as stated in the following theorem.
Theorem 1.9.2. There is a natural functor
that sends
Here
![]() $\mathsf{Corr}(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })_{\text{bdd};\operatorname{all}}$
is the
$\mathsf{Corr}(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })_{\text{bdd};\operatorname{all}}$
is the
![]() $\infty$
-category whose objects are objects of
$\infty$
-category whose objects are objects of
![]() $\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
and whose
$\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
and whose
![]() $1$
-morphisms are given by correspondences
$1$
-morphisms are given by correspondences
![]() $[{\mathcal{X}}\leftarrow {\mathcal{W}}\rightarrow {\mathcal{Y}}]$
with bounded left leg.
$[{\mathcal{X}}\leftarrow {\mathcal{W}}\rightarrow {\mathcal{Y}}]$
with bounded left leg.
1.10
 $\mathbb{H}$
for Harish-Chandra
$\mathbb{H}$
for Harish-Chandra
For
![]() ${\mathcal{Y}}$
smooth,
${\mathcal{Y}}$
smooth,
![]() $\mathbb{H}({\mathcal{Y}})$
is equivalent to
$\mathbb{H}({\mathcal{Y}})$
is equivalent to
![]() $\operatorname{IndCoh}({\mathcal{Y}}\times _{{\mathcal{Y}}_{\operatorname{dR}}}{\mathcal{Y}})$
, with its natural convolution monoidal structure. For instance, if
$\operatorname{IndCoh}({\mathcal{Y}}\times _{{\mathcal{Y}}_{\operatorname{dR}}}{\mathcal{Y}})$
, with its natural convolution monoidal structure. For instance, if
![]() $G$
is an affine algebraic group, we have
$G$
is an affine algebraic group, we have
This is the monoidal category of Harish-Chandra bimodules for the group
![]() $G$
; see [Reference BeraldoBer17a, § 2.3] for the connection with the theory of weak/strong actions on categories. Likewise,
$G$
; see [Reference BeraldoBer17a, § 2.3] for the connection with the theory of weak/strong actions on categories. Likewise,
is the DG category
![]() $\mathfrak{g}\operatorname{ -}\!\mathsf{mod}$
of modules for the Lie algebra
$\mathfrak{g}\operatorname{ -}\!\mathsf{mod}$
of modules for the Lie algebra
![]() $\mathfrak{g}=\operatorname{Lie}(G)$
. More generally, for a group morphism
$\mathfrak{g}=\operatorname{Lie}(G)$
. More generally, for a group morphism
![]() $H\rightarrow G$
, we have
$H\rightarrow G$
, we have
This is the correct derived enhancement of the ordinary category of Harish-Chandra
![]() $(\mathfrak{g},H)$
-modules.
$(\mathfrak{g},H)$
-modules.
1.10.1
Theorem 1.9.2 yields the following equivalences:
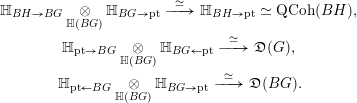 $$\begin{eqnarray}\displaystyle & \displaystyle \mathbb{H}_{BH\rightarrow BG}\underset{\mathbb{H}(BG)}{\otimes }\mathbb{H}_{BG\rightarrow \operatorname{pt}}\xrightarrow[{}]{\;\;\simeq \;\;}\mathbb{H}_{BH\rightarrow \operatorname{pt}}\simeq \operatorname{QCoh}(BH), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbb{H}_{\operatorname{pt}\rightarrow BG}\underset{\mathbb{H}(BG)}{\otimes }\mathbb{H}_{BG\leftarrow \operatorname{pt}}\xrightarrow[{}]{\;\;\simeq \;\;}\mathfrak{D}(G), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbb{H}_{\operatorname{pt}\leftarrow BG}\underset{\mathbb{H}(BG)}{\otimes }\mathbb{H}_{BG\rightarrow \operatorname{pt}}\xrightarrow[{}]{\;\;\simeq \;\;}\mathfrak{D}(BG). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathbb{H}_{BH\rightarrow BG}\underset{\mathbb{H}(BG)}{\otimes }\mathbb{H}_{BG\rightarrow \operatorname{pt}}\xrightarrow[{}]{\;\;\simeq \;\;}\mathbb{H}_{BH\rightarrow \operatorname{pt}}\simeq \operatorname{QCoh}(BH), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbb{H}_{\operatorname{pt}\rightarrow BG}\underset{\mathbb{H}(BG)}{\otimes }\mathbb{H}_{BG\leftarrow \operatorname{pt}}\xrightarrow[{}]{\;\;\simeq \;\;}\mathfrak{D}(G), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \mathbb{H}_{\operatorname{pt}\leftarrow BG}\underset{\mathbb{H}(BG)}{\otimes }\mathbb{H}_{BG\rightarrow \operatorname{pt}}\xrightarrow[{}]{\;\;\simeq \;\;}\mathfrak{D}(BG). & \displaystyle \nonumber\end{eqnarray}$$
1.10.2
Another way to prove these is via the theory of DG categories with
![]() $G$
-action; see [Reference BeraldoBer17a, § 2]. For instance, it was proven there that, for any category
$G$
-action; see [Reference BeraldoBer17a, § 2]. For instance, it was proven there that, for any category
![]() ${\mathcal{C}}$
equipped with a right strong action of
${\mathcal{C}}$
equipped with a right strong action of
![]() $G$
, there are natural equivalences
$G$
, there are natural equivalences
Now, let
![]() ${\mathcal{C}}=^{H,w}\mathfrak{D}(G)$
,
${\mathcal{C}}=^{H,w}\mathfrak{D}(G)$
,
![]() ${\mathcal{C}}=\mathfrak{D}(G)$
and
${\mathcal{C}}=\mathfrak{D}(G)$
and
![]() ${\mathcal{C}}=\operatorname{Vect}$
, respectively.
${\mathcal{C}}=\operatorname{Vect}$
, respectively.
1.10.3
For generalizations of these computations to the topological setting, the reader may consult [Reference BeraldoBer19b].
1.11 The gluing theorems in geometric Langlands
More interesting than
![]() $\mathbb{H}(BG)$
is the monoidal DG category
$\mathbb{H}(BG)$
is the monoidal DG category
![]() $\mathbb{H}(\operatorname{LS}_{G})$
, to which we now turn our attention. Observe that, by construction, we have
$\mathbb{H}(\operatorname{LS}_{G})$
, to which we now turn our attention. Observe that, by construction, we have
With this notation, the spectral gluing theorem of [Reference Arinkin and GaitsgoryAG18] may be rephrased as follows: there is an explicit
![]() $\mathbb{H}(\operatorname{LS}_{{\check{G}}})$
-linear localization adjunction
$\mathbb{H}(\operatorname{LS}_{{\check{G}}})$
-linear localization adjunction
Here we have switched to the Langlands dual
![]() ${\check{G}}$
as we are going to discuss Langlands duality, and it is customary to have Langlands dual groups on the spectral side.
${\check{G}}$
as we are going to discuss Langlands duality, and it is customary to have Langlands dual groups on the spectral side.
1.11.1
Let
![]() $\check{M}$
be the Levi quotient of a parabolic
$\check{M}$
be the Levi quotient of a parabolic
![]() $\check{P}$
. By Theorem 1.9.2, we can rewrite
$\check{P}$
. By Theorem 1.9.2, we can rewrite
By the
![]() $\mathbb{H}$
-affineness theorem, we reinterpret the bimodule
$\mathbb{H}$
-affineness theorem, we reinterpret the bimodule
![]() $\mathbb{H}_{\operatorname{LS}_{{\check{G}}}\leftarrow \operatorname{LS}_{\check{P}}\rightarrow \operatorname{LS}_{\check{M}}}$
, or better the functor
$\mathbb{H}_{\operatorname{LS}_{{\check{G}}}\leftarrow \operatorname{LS}_{\check{P}}\rightarrow \operatorname{LS}_{\check{M}}}$
, or better the functor
attached to it, as an Eisenstein series functor in the setting of
![]() $\mathbb{H}$
-sheaves of categories.
$\mathbb{H}$
-sheaves of categories.
1.11.2
These considerations shed light on the left-hand side of (1.7). Coupled with the construction of § 1.4.2, they allow us to formulate a conjecture on the automorphic side of geometric Langlands. This conjecture explains how
![]() $\mathfrak{D}(\operatorname{Bun}_{G})$
can be reconstructed algorithmically out of tempered
$\mathfrak{D}(\operatorname{Bun}_{G})$
can be reconstructed algorithmically out of tempered
![]() $\mathfrak{D}$
-modules for all the Levis of
$\mathfrak{D}$
-modules for all the Levis of
![]() $G$
, including
$G$
, including
![]() $G$
itself.
$G$
itself.
Conjecture 1.11.3 (Automorphic gluing).
There is an explicit
![]() $\mathbb{H}(\operatorname{LS}_{{\check{G}}})$
-linear localization adjunction
$\mathbb{H}(\operatorname{LS}_{{\check{G}}})$
-linear localization adjunction
1.11.4
We make some comments on this conjecture and on some future research directions.
(i) We will construct the adjunction (1.8) in a follow-up paper; this will be relatively easy. The difficult part is to show that the right adjoint is fully faithful.
(ii) Actually, the conjecture can be pushed even further, as it is possible to guess what the essential image
 $\unicode[STIX]{x1D6FE}$
is. This follows from an explicit description of the essential image of
$\unicode[STIX]{x1D6FE}$
is. This follows from an explicit description of the essential image of
 $\unicode[STIX]{x1D6FE}^{\text{spec}}$
; see [Reference BeraldoBer18].
$\unicode[STIX]{x1D6FE}^{\text{spec}}$
; see [Reference BeraldoBer18].(iii) Clearly, Conjecture 1.11.3 is related to the extended Whittaker conjecture; see [Reference GaitsgoryGai15a, Reference BeraldoBer19a]. The left-hand side of (1.8) is expected to be smaller than the extended Whittaker category.
1.12 Conventions
We refer to [Reference Gaitsgory and RozenblyumGR17], [Reference GaitsgoryGai15b] or [Reference BeraldoBer17b] for a review of our conventions concerning category theory and algebraic geometry. In particular:
– we always work over an algebraically closed field
 $k$
of characteristic
$k$
of characteristic
 $0$
;
$0$
;– we denote by
 $\mathsf{DGCat}$
the (large) symmetric monoidal
$\mathsf{DGCat}$
the (large) symmetric monoidal
 $\infty$
-category of small cocomplete DG categories over
$\infty$
-category of small cocomplete DG categories over
 $k$
and continuous functors; see [Reference LurieLur17] or [Reference Gaitsgory and RozenblyumGR17].
$k$
and continuous functors; see [Reference LurieLur17] or [Reference Gaitsgory and RozenblyumGR17].
1.13 Structure of the paper
Section 2 is devoted to recalling some higher algebra: a few facts about rigid monoidal DG categories and their module categories, as well as several
![]() $(\infty ,2)$
-categorical constructions (correspondences, lax
$(\infty ,2)$
-categorical constructions (correspondences, lax
![]() $(\infty ,2)$
-functors, algebras and bimodules).
$(\infty ,2)$
-functors, algebras and bimodules).
The first part of § 3 is a reminder of the theory of
![]() $\operatorname{IndCoh}_{0}$
, as developed in [Reference BeraldoBer17b]. In the second part of the same section, we discuss the
$\operatorname{IndCoh}_{0}$
, as developed in [Reference BeraldoBer17b]. In the second part of the same section, we discuss the
![]() $(\infty ,2)$
-categorical functoriality of
$(\infty ,2)$
-categorical functoriality of
![]() $\mathbb{H}$
.
$\mathbb{H}$
.
Section 4 introduces the notion of coefficient system, providing several examples of interest in present, as well as future, applications. In particular, we define the (a priori lax) coefficient system
![]() $\mathbb{H}$
and prove it is strict.
$\mathbb{H}$
and prove it is strict.
In § 5 we discuss the (left, right, ambidextrous) Beck–Chevalley conditions for coefficient systems. These conditions (which are satisfied in the examples of interest) guarantee that the resulting theory of sheaves of categories is very rich functorially; for example, it has pushforwards and base-change.
Finally, in § 6, we define
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
, the theory of sheaves of categories with local actions of Hochschild cochains, and prove the
$\mathsf{ShvCat}^{\mathbb{H}}$
, the theory of sheaves of categories with local actions of Hochschild cochains, and prove the
![]() $\mathbb{H}$
-affineness of algebraic stacks.
$\mathbb{H}$
-affineness of algebraic stacks.
2 Some categorical algebra
In this section we recall some
![]() $(\infty ,1)$
- and
$(\infty ,1)$
- and
![]() $(\infty ,2)$
-categorical algebra needed later in the main sections of the paper. All the results we need concern the theory of algebras and bimodules. More specifically, we first need criteria for dualizability of bimodule categories; furthermore, we need some abstract constructions that relate ‘algebras and bimodules’ with
$(\infty ,2)$
-categorical algebra needed later in the main sections of the paper. All the results we need concern the theory of algebras and bimodules. More specifically, we first need criteria for dualizability of bimodule categories; furthermore, we need some abstract constructions that relate ‘algebras and bimodules’ with
![]() $(\infty ,2)$
-categories of correspondences.
$(\infty ,2)$
-categories of correspondences.
We advise the reader to skip this material and refer to it only if necessary.
2.1 Dualizability of bimodule categories
Recall that
![]() $\mathsf{DGCat}$
admits colimits (as well as limits) and its tensor product preserves colimits in each variable [Reference LurieLur17]. Hence, by [Reference LurieLur17] again, we have a good theory of dualizability of algebras and bimodules in
$\mathsf{DGCat}$
admits colimits (as well as limits) and its tensor product preserves colimits in each variable [Reference LurieLur17]. Hence, by [Reference LurieLur17] again, we have a good theory of dualizability of algebras and bimodules in
![]() $\mathsf{DGCat}$
, whose main points we record below. We will need a criterion that relates the dualizability of a bimodule to the dualizability of its underlying DG category.
$\mathsf{DGCat}$
, whose main points we record below. We will need a criterion that relates the dualizability of a bimodule to the dualizability of its underlying DG category.
2.1.1
First, let us fix some terminology. Algebra objects in a symmetric monoidal
![]() $\infty$
-category are always unital in this paper. In particular, monoidal DG categories are unital. Given
$\infty$
-category are always unital in this paper. In particular, monoidal DG categories are unital. Given
![]() $A$
an algebra, denote by
$A$
an algebra, denote by
![]() $A^{\operatorname{rev}}$
the algebra obtained by reversing the order of the multiplication. For a left
$A^{\operatorname{rev}}$
the algebra obtained by reversing the order of the multiplication. For a left
![]() $A$
-module
$A$
-module
![]() $M$
and a right
$M$
and a right
![]() $A$
-module
$A$
-module
![]() $N$
, we denote by
$N$
, we denote by
![]() $\mathsf{pr}:N\otimes M\rightarrow N\otimes _{A}M$
the tautological functor.
$\mathsf{pr}:N\otimes M\rightarrow N\otimes _{A}M$
the tautological functor.
Our conventions regarding bimodules are as follows: an
![]() $(A,B)$
-bimodule
$(A,B)$
-bimodule
![]() $M$
is acted on on the left by
$M$
is acted on on the left by
![]() $A$
and on the right by
$A$
and on the right by
![]() $B$
. Hence, endowing
$B$
. Hence, endowing
![]() $C\in \mathsf{DGCat}$
with the structure of an
$C\in \mathsf{DGCat}$
with the structure of an
![]() $(A,B)$
-bimodule amounts to endowing it with the structure of a left
$(A,B)$
-bimodule amounts to endowing it with the structure of a left
![]() $A\otimes B^{\operatorname{rev}}$
-module.
$A\otimes B^{\operatorname{rev}}$
-module.
2.1.2
Let
![]() $M$
be an
$M$
be an
![]() $(A,B)$
-bimodule. We say that
$(A,B)$
-bimodule. We say that
![]() $M$
is left dualizable (as an
$M$
is left dualizable (as an
![]() $(A,B)$
-bimodule) if there exists a
$(A,B)$
-bimodule) if there exists a
![]() $(B,A)$
-bimodule
$(B,A)$
-bimodule
![]() $M^{L}$
(called the left dual of
$M^{L}$
(called the left dual of
![]() $M$
) realizing an adjunction
$M$
) realizing an adjunction
Similarly,
![]() $M$
is right dualizable if there exists
$M$
is right dualizable if there exists
![]() $M^{R}\in (B,A)\operatorname{ -}\mathsf{bimod}$
(the right dual of
$M^{R}\in (B,A)\operatorname{ -}\mathsf{bimod}$
(the right dual of
![]() $M$
) realizing an adjunction
$M$
) realizing an adjunction
We say that an
![]() $(A,B)$
-bimodule
$(A,B)$
-bimodule
![]() $M$
is ambidextrous if both
$M$
is ambidextrous if both
![]() $M^{L}$
and
$M^{L}$
and
![]() $M^{R}$
exist and are equivalent as
$M^{R}$
exist and are equivalent as
![]() $(B,A)$
-bimodules.
$(B,A)$
-bimodules.
Remark 2.1.3. Being (left or right) dualizable as a
![]() $(\operatorname{Vect},\operatorname{Vect})$
-bimodule is equivalent to being dualizable as a DG category. By definition, being ‘left (or right) dualizable as a right
$(\operatorname{Vect},\operatorname{Vect})$
-bimodule is equivalent to being dualizable as a DG category. By definition, being ‘left (or right) dualizable as a right
![]() $A$
-module’ means being ‘left (or right) dualizable as a
$A$
-module’ means being ‘left (or right) dualizable as a
![]() $(\operatorname{Vect},A)$
-module’. Similarly for left
$(\operatorname{Vect},A)$
-module’. Similarly for left
![]() $A$
-modules.
$A$
-modules.
2.1.4
Let
![]() $M$
be an
$M$
be an
![]() $(A,B)$
-bimodule which is dualizable as a DG category. Then we can contemplate three
$(A,B)$
-bimodule which is dualizable as a DG category. Then we can contemplate three
![]() $(B,A)$
-bimodules:
$(B,A)$
-bimodules:
![]() $M^{L},M^{R}$
(if they exist) as well as
$M^{L},M^{R}$
(if they exist) as well as
![]() $M^{\ast }$
, the dual of
$M^{\ast }$
, the dual of
![]() $\mathsf{oblv}_{A,B}(M)$
equipped with the dual actions.
$\mathsf{oblv}_{A,B}(M)$
equipped with the dual actions.
In particular, a monoidal DG category
![]() $A$
is called proper if it is dualizable as a plain DG category. In this case, we denote by
$A$
is called proper if it is dualizable as a plain DG category. In this case, we denote by
![]() $S_{A}:=A^{\ast }$
its dual, equipped with the tautological
$S_{A}:=A^{\ast }$
its dual, equipped with the tautological
![]() $(A,A)$
-bimodule structure.
$(A,A)$
-bimodule structure.
2.1.5
Recall the notion of rigid monoidal DG category; see [Reference GaitsgoryGai15b, Appendix D]. Any rigid
![]() $A$
is automatically proper. Furthermore, its dual
$A$
is automatically proper. Furthermore, its dual
![]() $S_{A}:=A^{\ast }$
comes equipped with the canonical object
$S_{A}:=A^{\ast }$
comes equipped with the canonical object
![]() $1_{A}^{\text{fake}}:=(u^{R})^{\vee }(k)$
, where
$1_{A}^{\text{fake}}:=(u^{R})^{\vee }(k)$
, where
![]() $u^{R}$
is the (continuous) right adjoint to the unit functor
$u^{R}$
is the (continuous) right adjoint to the unit functor
![]() $u:\operatorname{Vect}\rightarrow A$
. The left
$u:\operatorname{Vect}\rightarrow A$
. The left
![]() $A$
-linear functor
$A$
-linear functor
is an equivalence; in particular, any rigid monoidal category is self-dual. We say that
![]() $A$
is very rigid if the canonical equivalence
$A$
is very rigid if the canonical equivalence
![]() $\unicode[STIX]{x1D70E}_{A}:A\rightarrow S_{A}$
admits a lift to an equivalence of
$\unicode[STIX]{x1D70E}_{A}:A\rightarrow S_{A}$
admits a lift to an equivalence of
![]() $(A,A)$
-bimodules.Footnote
4
$(A,A)$
-bimodules.Footnote
4
Proposition 2.1.6. Let
![]() $A,B$
be rigid monoidal DG categories and
$A,B$
be rigid monoidal DG categories and
![]() $M$
an
$M$
an
![]() $(A,B)$
-bimodule which is dualizable as a DG category. Then
$(A,B)$
-bimodule which is dualizable as a DG category. Then
![]() $M$
is right dualizable as an
$M$
is right dualizable as an
![]() $(A,B)$
-bimodule and
$(A,B)$
-bimodule and
![]() $M^{R}\simeq M^{\ast }\otimes _{A}S_{A}$
. Likewise,
$M^{R}\simeq M^{\ast }\otimes _{A}S_{A}$
. Likewise,
![]() $M$
is left dualizable and
$M$
is left dualizable and
![]() $M^{L}\simeq S_{B}\otimes _{B}M^{\ast }$
.
$M^{L}\simeq S_{B}\otimes _{B}M^{\ast }$
.
Proof. The formula for
![]() $M^{R}$
is proven as in the ‘if’ direction of [Reference GaitsgoryGai15b, Proposition D.5.4], which in turn is a consequence of [Reference GaitsgoryGai15b, Corollary D.4.5]. In the notation there, the twist
$M^{R}$
is proven as in the ‘if’ direction of [Reference GaitsgoryGai15b, Proposition D.5.4], which in turn is a consequence of [Reference GaitsgoryGai15b, Corollary D.4.5]. In the notation there, the twist
![]() $(-)_{\unicode[STIX]{x1D713}_{A}}$
corresponds to our
$(-)_{\unicode[STIX]{x1D713}_{A}}$
corresponds to our
![]() $-\otimes _{A}S_{A}$
. The formula for
$-\otimes _{A}S_{A}$
. The formula for
![]() $M^{L}$
follows similarly.◻
$M^{L}$
follows similarly.◻
Corollary 2.1.7. Let
![]() $A,B$
be very rigid and
$A,B$
be very rigid and
![]() $M$
an
$M$
an
![]() $(A,B)$
-bimodule which is dualizable as a DG category. Then we have canonical
$(A,B)$
-bimodule which is dualizable as a DG category. Then we have canonical
![]() $(B,A)$
-linear equivalences
$(B,A)$
-linear equivalences
![]() $M^{R}\simeq M^{\ast }\simeq M^{L}$
.
$M^{R}\simeq M^{\ast }\simeq M^{L}$
.
2.2 Some
 $(\infty ,2)$
-categorical algebra
$(\infty ,2)$
-categorical algebra
In this section we recall some abstract
![]() $(\infty ,2)$
-categorical nonsense and provide some examples of
$(\infty ,2)$
-categorical nonsense and provide some examples of
![]() $(\infty ,2)$
-categories and of lax
$(\infty ,2)$
-categories and of lax
![]() $(\infty ,2)$
-functors between them. All the statements below look obvious enough and no proof will be given.
$(\infty ,2)$
-functors between them. All the statements below look obvious enough and no proof will be given.
2.2.1
We assume familiarity with the notion of
![]() $(\infty ,2)$
-category and with the notion of (lax)
$(\infty ,2)$
-category and with the notion of (lax)
![]() $(\infty ,2)$
-functor between
$(\infty ,2)$
-functor between
![]() $(\infty ,2)$
-categories; see, for example, [Reference Gaitsgory and RozenblyumGR17, Appendix A]. For an
$(\infty ,2)$
-categories; see, for example, [Reference Gaitsgory and RozenblyumGR17, Appendix A]. For an
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathbf{C}$
, we denote by
$\mathbf{C}$
, we denote by
![]() $\mathbf{C}^{1-\operatorname{op}}$
the
$\mathbf{C}^{1-\operatorname{op}}$
the
![]() $(\infty ,2)$
-category obtained from
$(\infty ,2)$
-category obtained from
![]() $\mathbf{C}$
by flipping the
$\mathbf{C}$
by flipping the
![]() $1$
-arrows. Similarly, we denote by
$1$
-arrows. Similarly, we denote by
![]() $\mathbf{C}^{2-\operatorname{op}}$
the
$\mathbf{C}^{2-\operatorname{op}}$
the
![]() $(\infty ,2)$
-category obtained by flipping the directions of the
$(\infty ,2)$
-category obtained by flipping the directions of the
![]() $2$
-arrows.
$2$
-arrows.
2.2.2 Correspondences
Let
![]() ${\mathcal{C}}$
be an
${\mathcal{C}}$
be an
![]() $\infty$
-category equipped with fibre products. We refer to [Reference Gaitsgory and RozenblyumGR17, ch. V.1] for the construction of the
$\infty$
-category equipped with fibre products. We refer to [Reference Gaitsgory and RozenblyumGR17, ch. V.1] for the construction of the
![]() $\infty$
-category of correspondences associated to
$\infty$
-category of correspondences associated to
![]() ${\mathcal{C}}$
. In particular, for
${\mathcal{C}}$
. In particular, for
![]() $\text{vert}$
and
$\text{vert}$
and
![]() $\text{horiz}$
two subsets of the space morphisms of
$\text{horiz}$
two subsets of the space morphisms of
![]() ${\mathcal{C}}$
satisfying some natural requirements, one considers the
${\mathcal{C}}$
satisfying some natural requirements, one considers the
![]() $\infty$
-category
$\infty$
-category
![]() $\mathsf{Corr}({\mathcal{C}})_{\text{vert};\text{horiz}}$
, defined in the usual way: objects of
$\mathsf{Corr}({\mathcal{C}})_{\text{vert};\text{horiz}}$
, defined in the usual way: objects of
![]() $\mathsf{Corr}({\mathcal{C}})_{\text{vert};\text{horiz}}$
coincide with the objects of
$\mathsf{Corr}({\mathcal{C}})_{\text{vert};\text{horiz}}$
coincide with the objects of
![]() ${\mathcal{C}}$
, while
${\mathcal{C}}$
, while
![]() $1$
-morphisms in
$1$
-morphisms in
![]() $\mathsf{Corr}({\mathcal{C}})_{\text{vert};\text{horiz}}$
are given by correspondences
$\mathsf{Corr}({\mathcal{C}})_{\text{vert};\text{horiz}}$
are given by correspondences
with left leg in
![]() $\text{vert}$
and right leg in
$\text{vert}$
and right leg in
![]() $\text{horiz}$
.
$\text{horiz}$
.
To enhance
![]() $\mathsf{Corr}({\mathcal{C}})_{\text{vert};\text{horiz}}$
to an
$\mathsf{Corr}({\mathcal{C}})_{\text{vert};\text{horiz}}$
to an
![]() $(\infty ,2)$
-category, we must further choose a subset
$(\infty ,2)$
-category, we must further choose a subset
![]() $\text{adm}\subset \text{vert}\cap \text{horiz}$
of admissible arrows, closed under composition. Then, following [Reference Gaitsgory and RozenblyumGR17, ch. V.1], we define the
$\text{adm}\subset \text{vert}\cap \text{horiz}$
of admissible arrows, closed under composition. Then, following [Reference Gaitsgory and RozenblyumGR17, ch. V.1], we define the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
This is one of the most important
![]() $(\infty ,2)$
-categories of the present paper.
$(\infty ,2)$
-categories of the present paper.
To fix notation, recall that a
![]() $2$
-arrow
$2$
-arrow
in
![]() $\mathsf{Corr}({\mathcal{C}})_{\text{vert};\text{horiz}}^{\text{adm}}$
is by definition an admissible arrow
$\mathsf{Corr}({\mathcal{C}})_{\text{vert};\text{horiz}}^{\text{adm}}$
is by definition an admissible arrow
![]() $h\rightarrow h^{\prime }$
compatible with the maps to
$h\rightarrow h^{\prime }$
compatible with the maps to
![]() $c\times d$
.
$c\times d$
.
As explained in [Reference Gaitsgory and RozenblyumGR17, ch. V.3],
![]() $\mathsf{Corr}({\mathcal{C}})_{\text{vert};\text{horiz}}^{\text{adm}}$
is symmetric monoidal with tensor product induced by the cartesian symmetric monoidal product on
$\mathsf{Corr}({\mathcal{C}})_{\text{vert};\text{horiz}}^{\text{adm}}$
is symmetric monoidal with tensor product induced by the cartesian symmetric monoidal product on
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
2.2.3 Algebras and bimodules
The other important
![]() $(\infty ,2)$
-category of this paper is
$(\infty ,2)$
-category of this paper is
![]() $\mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
, the
$\mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
, the
![]() $(\infty ,2)$
-category of monoidal DG categories, bimodules, and natural transformations. We refer to [Reference HaugsengHau17] for a rigorous construction. More generally, that paper gives a construction of
$(\infty ,2)$
-category of monoidal DG categories, bimodules, and natural transformations. We refer to [Reference HaugsengHau17] for a rigorous construction. More generally, that paper gives a construction of
![]() $\mathsf{ALG}^{\text{bimod}}({\mathcal{S}})$
for any (nice enough) symmetric monoidal
$\mathsf{ALG}^{\text{bimod}}({\mathcal{S}})$
for any (nice enough) symmetric monoidal
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() ${\mathcal{S}}$
.
${\mathcal{S}}$
.
We denote by
![]() $\mathsf{Alg}^{\text{bimod}}({\mathcal{S}})$
the
$\mathsf{Alg}^{\text{bimod}}({\mathcal{S}})$
the
![]() $(\infty ,1)$
-category underlying
$(\infty ,1)$
-category underlying
![]() $\mathsf{ALG}^{\text{bimod}}({\mathcal{S}})$
: that is, the former is obtained from the latter by discarding non-invertible
$\mathsf{ALG}^{\text{bimod}}({\mathcal{S}})$
: that is, the former is obtained from the latter by discarding non-invertible
![]() $2$
-morphisms.
$2$
-morphisms.
2.2.4
There is an obvious functor
that is the identity on objects and that sends a monoidal functor
![]() $A\rightarrow B$
to the
$A\rightarrow B$
to the
![]() $(B,A)$
-bimodule
$(B,A)$
-bimodule
![]() $B$
.
$B$
.
The tautological functor
upgrades to a (strict)
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
where now
![]() $\mathsf{Cat}_{\infty }$
is considered as an
$\mathsf{Cat}_{\infty }$
is considered as an
![]() $(\infty ,2)$
-category.
$(\infty ,2)$
-category.
2.2.5
Let
![]() ${\mathcal{C}}$
denote an
${\mathcal{C}}$
denote an
![]() $(\infty ,1)$
-category admitting fibre products and equipped with the cartesian symmetric monoidal structure. Let
$(\infty ,1)$
-category admitting fibre products and equipped with the cartesian symmetric monoidal structure. Let
![]() $F:{\mathcal{C}}^{\operatorname{op}}\longrightarrow \mathsf{DGCat}$
be a lax-monoidal functor. (The example we have in mind is
$F:{\mathcal{C}}^{\operatorname{op}}\longrightarrow \mathsf{DGCat}$
be a lax-monoidal functor. (The example we have in mind is
![]() ${\mathcal{C}}=\mathsf{PreStk}$
and
${\mathcal{C}}=\mathsf{PreStk}$
and
![]() $F=\operatorname{QCoh}$
.)
$F=\operatorname{QCoh}$
.)
These data give rise to a lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
described informally as follows:
– an object
 $c\in {\mathcal{C}}$
gets sent to
$c\in {\mathcal{C}}$
gets sent to
 $F(c)$
, with its natural monoidal structure;
$F(c)$
, with its natural monoidal structure;– a correspondence
 $[c\leftarrow h\rightarrow d]$
gets sent to the
$[c\leftarrow h\rightarrow d]$
gets sent to the
 $(F(c),F(d))$
-bimodule
$(F(c),F(d))$
-bimodule
 $F(h)$
;
$F(h)$
;– a map between correspondences, given by an arrow
 $h^{\prime }\rightarrow h$
over
$h^{\prime }\rightarrow h$
over
 $c\times d$
, gets sent to the associated
$c\times d$
, gets sent to the associated
 $(F(c),F(d))$
-linear arrow
$(F(c),F(d))$
-linear arrow
 $F(h)\rightarrow F(h^{\prime })$
;
$F(h)\rightarrow F(h^{\prime })$
;– for two correspondences
 $[c\leftarrow h\rightarrow d]$
and
$[c\leftarrow h\rightarrow d]$
and
 $[d\leftarrow k\rightarrow e]$
, the lax composition is encoded by the natural
$[d\leftarrow k\rightarrow e]$
, the lax composition is encoded by the natural
 $(F(c),F(e))$
-linear arrow
$(F(c),F(e))$
-linear arrow  $$\begin{eqnarray}F(h)\underset{F(d)}{\otimes }F(k)\longrightarrow F(h\times _{d}k).\end{eqnarray}$$
$$\begin{eqnarray}F(h)\underset{F(d)}{\otimes }F(k)\longrightarrow F(h\times _{d}k).\end{eqnarray}$$
2.2.6
Here is another example of the interaction between lax-monoidal functors and lax
![]() $(\infty ,2)$
-functors. Let
$(\infty ,2)$
-functors. Let
![]() $F:{\mathcal{C}}\rightarrow {\mathcal{D}}$
be a lax-monoidal functor between ‘well-behaved’ monoidal
$F:{\mathcal{C}}\rightarrow {\mathcal{D}}$
be a lax-monoidal functor between ‘well-behaved’ monoidal
![]() $(\infty ,1)$
-categories. Then
$(\infty ,1)$
-categories. Then
![]() $F$
induces a lax
$F$
induces a lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
To define it, it suffices to recall that, since
![]() $F$
is lax monoidal, it preserves algebra and bimodule objects. The fact that
$F$
is lax monoidal, it preserves algebra and bimodule objects. The fact that
![]() $\widetilde{F}$
is a lax
$\widetilde{F}$
is a lax
![]() $(\infty ,2)$
-functor comes from the natural map (not necessarily an isomorphism)
$(\infty ,2)$
-functor comes from the natural map (not necessarily an isomorphism)
2.2.7
Recall the
![]() $\infty$
-category
$\infty$
-category
![]() $\operatorname{Mod}(\mathsf{DGCat})$
whose objects are pairs
$\operatorname{Mod}(\mathsf{DGCat})$
whose objects are pairs
![]() $(A,M)$
with
$(A,M)$
with
![]() $A$
a monoidal DG category and
$A$
a monoidal DG category and
![]() $M$
an
$M$
an
![]() $A$
-module. Morphisms
$A$
-module. Morphisms
![]() $(A,M)\rightarrow (B,N)$
consist of pairs
$(A,M)\rightarrow (B,N)$
consist of pairs
![]() $(\unicode[STIX]{x1D719},f)$
where
$(\unicode[STIX]{x1D719},f)$
where
![]() $\unicode[STIX]{x1D719}:A\rightarrow B$
is a monoidal functor and
$\unicode[STIX]{x1D719}:A\rightarrow B$
is a monoidal functor and
![]() $f:M\rightarrow N$
an
$f:M\rightarrow N$
an
![]() $A$
-linear functor.
$A$
-linear functor.
There is a lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
described informally as follows:
– an object
 $(A,M)\in \operatorname{Mod}(\mathsf{DGCat})$
goes to the monoidal DG category
$(A,M)\in \operatorname{Mod}(\mathsf{DGCat})$
goes to the monoidal DG category
 $\mathsf{End}_{A}(M):=\mathsf{Fun}_{A}(M,M)$
;
$\mathsf{End}_{A}(M):=\mathsf{Fun}_{A}(M,M)$
;– a morphism
 $(A,M)\xrightarrow[{}]{(\unicode[STIX]{x1D719},f)}(B,N)$
gets sent to the
$(A,M)\xrightarrow[{}]{(\unicode[STIX]{x1D719},f)}(B,N)$
gets sent to the
 $(\mathsf{End}_{B}(N),\mathsf{End}_{A}(M))$
-bimodule
$(\mathsf{End}_{B}(N),\mathsf{End}_{A}(M))$
-bimodule
 $\mathsf{Fun}_{A}(M,N)$
;
$\mathsf{Fun}_{A}(M,N)$
;– a composition
 $(A,M)\xrightarrow[{}]{(\unicode[STIX]{x1D719},f)}(B,N)\xrightarrow[{}]{(\unicode[STIX]{x1D713},g)}(C,P)$
goes over to the
$(A,M)\xrightarrow[{}]{(\unicode[STIX]{x1D719},f)}(B,N)\xrightarrow[{}]{(\unicode[STIX]{x1D713},g)}(C,P)$
goes over to the
 $(\mathsf{End}_{C}(P),\mathsf{End}_{A}(M))$
-bimodule
$(\mathsf{End}_{C}(P),\mathsf{End}_{A}(M))$
-bimodule $$\begin{eqnarray}\mathsf{Fun}_{B}(N,P)\underset{\mathsf{End}_{B}(N)}{\otimes }\mathsf{Fun}_{A}(M,N);\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Fun}_{B}(N,P)\underset{\mathsf{End}_{B}(N)}{\otimes }\mathsf{Fun}_{A}(M,N);\end{eqnarray}$$
– the lax structure comes from the tautological morphism (not invertible, in general)
(2.3)induced by composition. $$\begin{eqnarray}\mathsf{Fun}_{B}(N,P)\underset{\mathsf{End}_{B}(N)}{\otimes }\mathsf{Fun}_{A}(M,N)\longrightarrow \mathsf{Fun}_{A}(M,P)\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{Fun}_{B}(N,P)\underset{\mathsf{End}_{B}(N)}{\otimes }\mathsf{Fun}_{A}(M,N)\longrightarrow \mathsf{Fun}_{A}(M,P)\end{eqnarray}$$
2.2.8
For later use, we record here the following tautological observation. Let
![]() ${\mathcal{I}}$
be an
${\mathcal{I}}$
be an
![]() $(\infty ,1)$
-category and
$(\infty ,1)$
-category and
![]() $\mathbb{A}:{\mathcal{I}}\rightarrow \mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
be a lax
$\mathbb{A}:{\mathcal{I}}\rightarrow \mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
be a lax
![]() $(\infty ,2)$
-functor. Assume given the following data:
$(\infty ,2)$
-functor. Assume given the following data:
– for each
 $i\in {\mathcal{I}}$
, a monoidal subcategory
$i\in {\mathcal{I}}$
, a monoidal subcategory
 $\mathbb{A}^{\prime }(i){\hookrightarrow}\mathbb{A}(i)$
;
$\mathbb{A}^{\prime }(i){\hookrightarrow}\mathbb{A}(i)$
;– for each
 $i\rightarrow j$
, a full subcategory
$i\rightarrow j$
, a full subcategory
 $\mathbb{A}_{i\rightarrow j}^{\prime }{\hookrightarrow}\mathbb{A}_{i\rightarrow j}$
preserved by the
$\mathbb{A}_{i\rightarrow j}^{\prime }{\hookrightarrow}\mathbb{A}_{i\rightarrow j}$
preserved by the
 $(\mathbb{A}^{\prime }(i),\mathbb{A}^{\prime }(j))$
-action.
$(\mathbb{A}^{\prime }(i),\mathbb{A}^{\prime }(j))$
-action.
Assume also that, for each string
![]() $i\rightarrow j\rightarrow k$
, the functor
$i\rightarrow j\rightarrow k$
, the functor
lands in
![]() $\mathbb{A}_{i\rightarrow k}^{\prime }\subseteq \mathbb{A}_{i\rightarrow k}$
. Then the assignment
$\mathbb{A}_{i\rightarrow k}^{\prime }\subseteq \mathbb{A}_{i\rightarrow k}$
. Then the assignment
naturally upgrades to a lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
![]() $\mathbb{A}^{\prime }:{\mathcal{I}}\rightarrow \mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
.
$\mathbb{A}^{\prime }:{\mathcal{I}}\rightarrow \mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
.
3
 $\operatorname{IndCoh}_{0}$
on formal moduli problems
$\operatorname{IndCoh}_{0}$
on formal moduli problems
In the section we study the sheaf theory
![]() $\operatorname{IndCoh}_{0}$
from which
$\operatorname{IndCoh}_{0}$
from which
![]() $\mathbb{H}$
originates. As mentioned in the introduction to [Reference BeraldoBer17b],
$\mathbb{H}$
originates. As mentioned in the introduction to [Reference BeraldoBer17b],
![]() $\operatorname{IndCoh}_{0}$
enjoys
$\operatorname{IndCoh}_{0}$
enjoys
![]() $(\infty ,1)$
-categorical functoriality as well as
$(\infty ,1)$
-categorical functoriality as well as
![]() $(\infty ,2)$
-categorical functoriality. The former was developed in [Reference BeraldoBer17b], and is recalled here in Theorem 3.1.6. The latter is one of the main subjects of the present paper: it consists of an extension of the assignment
$(\infty ,2)$
-categorical functoriality. The former was developed in [Reference BeraldoBer17b], and is recalled here in Theorem 3.1.6. The latter is one of the main subjects of the present paper: it consists of an extension of the assignment
![]() ${\mathcal{Y}}{\rightsquigarrow}\mathbb{H}({\mathcal{Y}})$
to a lax
${\mathcal{Y}}{\rightsquigarrow}\mathbb{H}({\mathcal{Y}})$
to a lax
![]() $(\infty ,2)$
-functor from a certain
$(\infty ,2)$
-functor from a certain
![]() $(\infty ,2)$
-category of correspondences to
$(\infty ,2)$
-category of correspondences to
![]() $\mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
.
$\mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
.
3.1
 $(\infty ,1)$
-categorical functoriality
$(\infty ,1)$
-categorical functoriality
In this section we review the definition of the assignment
![]() $\operatorname{IndCoh}_{0}$
and its basic functoriality. We follow [Reference BeraldoBer17b] closely.
$\operatorname{IndCoh}_{0}$
and its basic functoriality. We follow [Reference BeraldoBer17b] closely.
3.1.1
Let
![]() $\mathsf{Stk}$
denote the
$\mathsf{Stk}$
denote the
![]() $\infty$
-category of perfect quasi-compact algebraic stacks of finite type and with affine diagonal; see, for example, [Reference Ben-Zvi, Francis and NadlerBFN10]. Inside
$\infty$
-category of perfect quasi-compact algebraic stacks of finite type and with affine diagonal; see, for example, [Reference Ben-Zvi, Francis and NadlerBFN10]. Inside
![]() $\mathsf{Stk}$
, we single out the subcategory
$\mathsf{Stk}$
, we single out the subcategory
![]() $\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
consisting of those stacks that are bounded and with perfect cotangent complex (both properties can be checked on an atlas).
$\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
consisting of those stacks that are bounded and with perfect cotangent complex (both properties can be checked on an atlas).
3.1.2
For
![]() ${\mathcal{C}}$
an
${\mathcal{C}}$
an
![]() $\infty$
-category, denote by
$\infty$
-category, denote by
![]() $\mathsf{Arr}({\mathcal{C}}):={\mathcal{C}}^{\unicode[STIX]{x1D6E5}^{1}}$
the
$\mathsf{Arr}({\mathcal{C}}):={\mathcal{C}}^{\unicode[STIX]{x1D6E5}^{1}}$
the
![]() $\infty$
-category whose objects are arrows in
$\infty$
-category whose objects are arrows in
![]() ${\mathcal{C}}$
and whose
${\mathcal{C}}$
and whose
![]() $1$
-morphisms are commutative squares. We will be interested in the
$1$
-morphisms are commutative squares. We will be interested in the
![]() $\infty$
-category
$\infty$
-category
![]() $\mathsf{Arr}(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })$
and in the functor
$\mathsf{Arr}(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })$
and in the functor
defined by
Recall from [Reference Arinkin and GaitsgoryAG18] or [Reference BeraldoBer17b] that
![]() $\operatorname{IndCoh}_{0}({\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge })$
is defined by the pullback square
$\operatorname{IndCoh}_{0}({\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge })$
is defined by the pullback square
In particular, when writing
![]() $\operatorname{IndCoh}_{0}({\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge })$
we are committing a potentially dangerous abuse of notation: it would be better to write
$\operatorname{IndCoh}_{0}({\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge })$
we are committing a potentially dangerous abuse of notation: it would be better to write
![]() $\operatorname{IndCoh}_{0}({\mathcal{Y}}\rightarrow {\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge })$
, as the latter category depends on the formal moduli problem
$\operatorname{IndCoh}_{0}({\mathcal{Y}}\rightarrow {\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge })$
, as the latter category depends on the formal moduli problem
![]() ${\mathcal{Y}}\rightarrow {\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge }$
and in particular on the derived structure of
${\mathcal{Y}}\rightarrow {\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge }$
and in particular on the derived structure of
![]() ${\mathcal{Y}}$
.
${\mathcal{Y}}$
.
3.1.3
For two objects
![]() $[{\mathcal{Y}}_{1}\rightarrow {\mathcal{Z}}_{1}]$
and
$[{\mathcal{Y}}_{1}\rightarrow {\mathcal{Z}}_{1}]$
and
![]() $[{\mathcal{Y}}_{2}\rightarrow {\mathcal{Z}}_{2}]$
in
$[{\mathcal{Y}}_{2}\rightarrow {\mathcal{Z}}_{2}]$
in
![]() $\mathsf{Arr}(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })$
, a morphism
$\mathsf{Arr}(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })$
, a morphism
![]() $\unicode[STIX]{x1D709}$
from the former to the latter is given by a commutative square
$\unicode[STIX]{x1D709}$
from the former to the latter is given by a commutative square
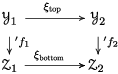
The structure pullback functor
is the obvious one induced by the pullback functor
![]() $\unicode[STIX]{x1D709}^{!}:\operatorname{IndCoh}(({\mathcal{Z}}_{2})_{{\mathcal{Y}}_{2}}^{\wedge })\rightarrow \operatorname{IndCoh}(({\mathcal{Z}}_{1})_{{\mathcal{Y}}_{1}}^{\wedge })$
, where we are abusing notation again by confusing
$\unicode[STIX]{x1D709}^{!}:\operatorname{IndCoh}(({\mathcal{Z}}_{2})_{{\mathcal{Y}}_{2}}^{\wedge })\rightarrow \operatorname{IndCoh}(({\mathcal{Z}}_{1})_{{\mathcal{Y}}_{1}}^{\wedge })$
, where we are abusing notation again by confusing
![]() $\unicode[STIX]{x1D709}$
with the map
$\unicode[STIX]{x1D709}$
with the map
![]() $({\mathcal{Z}}_{1})_{{\mathcal{Y}}_{1}}^{\wedge }\rightarrow ({\mathcal{Z}}_{2})_{{\mathcal{Y}}_{2}}^{\wedge }$
. We will do this throughout the paper, and hope it will not be too unpleasant for the reader.
$({\mathcal{Z}}_{1})_{{\mathcal{Y}}_{1}}^{\wedge }\rightarrow ({\mathcal{Z}}_{2})_{{\mathcal{Y}}_{2}}^{\wedge }$
. We will do this throughout the paper, and hope it will not be too unpleasant for the reader.
3.1.4
Let us now recall the extension of (3.1) to a functor out of a category of correspondences. Notice that
![]() $\mathsf{Arr}(\mathsf{PreStk})$
admits fibre products, computed objectwise; its subcategory
$\mathsf{Arr}(\mathsf{PreStk})$
admits fibre products, computed objectwise; its subcategory
![]() $\mathsf{Arr}(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })$
is closed under products, but not under fibre products. Thus, to have a well-defined category of correspondences, we must choose appropriate classes of horizontal and vertical arrows.
$\mathsf{Arr}(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })$
is closed under products, but not under fibre products. Thus, to have a well-defined category of correspondences, we must choose appropriate classes of horizontal and vertical arrows.
We say that a commutative diagram (3.1.3), thought of as a morphism in
![]() $\mathsf{Arr}(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })$
, is schematic (or bounded, or proper) if so is the top horizontal map. It is clear that
$\mathsf{Arr}(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })$
, is schematic (or bounded, or proper) if so is the top horizontal map. It is clear that
is well defined.
For the theorem below, we will need to further upgrade (3.4) to an
![]() $(\infty ,2)$
-category by allowing as admissible arrows (see § 2.2.2 for the terminology) those
$(\infty ,2)$
-category by allowing as admissible arrows (see § 2.2.2 for the terminology) those
![]() $\unicode[STIX]{x1D709}$
that are schematic, bounded and proper. We denote by
$\unicode[STIX]{x1D709}$
that are schematic, bounded and proper. We denote by
the resulting
![]() $(\infty ,2)$
-category.
$(\infty ,2)$
-category.
3.1.5
If
![]() $\unicode[STIX]{x1D709}$
is bounded and schematic in the above sense, then the pushforward
$\unicode[STIX]{x1D709}$
is bounded and schematic in the above sense, then the pushforward
![]() $\unicode[STIX]{x1D709}_{\ast }^{\operatorname{IndCoh}}:\operatorname{IndCoh}(({\mathcal{Z}}_{1})_{{\mathcal{Y}}_{1}}^{\wedge })\rightarrow \operatorname{IndCoh}(({\mathcal{Z}}_{2})_{{\mathcal{Y}}_{2}}^{\wedge })$
is continuous and preserves the
$\unicode[STIX]{x1D709}_{\ast }^{\operatorname{IndCoh}}:\operatorname{IndCoh}(({\mathcal{Z}}_{1})_{{\mathcal{Y}}_{1}}^{\wedge })\rightarrow \operatorname{IndCoh}(({\mathcal{Z}}_{2})_{{\mathcal{Y}}_{2}}^{\wedge })$
is continuous and preserves the
![]() $\operatorname{IndCoh}_{0}$
-subcategories, thereby descending to a functor
$\operatorname{IndCoh}_{0}$
-subcategories, thereby descending to a functor
![]() $\unicode[STIX]{x1D709}_{\ast ,0}$
. For the proof, see [Reference BeraldoBer17b].
$\unicode[STIX]{x1D709}_{\ast ,0}$
. For the proof, see [Reference BeraldoBer17b].
Theorem 3.1.6. The above pushforward functors upgrade the functor
![]() $\operatorname{IndCoh}_{0}^{!}$
of (3.1) to an
$\operatorname{IndCoh}_{0}^{!}$
of (3.1) to an
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
where
![]() $\mathsf{DGCat}$
is viewed as an
$\mathsf{DGCat}$
is viewed as an
![]() $(\infty ,2)$
-category in the obvious way.
$(\infty ,2)$
-category in the obvious way.
Remark 3.1.7. The existence of the above
![]() $(\infty ,2)$
-functor is deduced (essentially formally) by the
$(\infty ,2)$
-functor is deduced (essentially formally) by the
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
constructed in [Reference Gaitsgory and RozenblyumGR17, ch. III.3]. For later use, we will also need another fact from the same book: the above
![]() $(\infty ,2)$
-category of correspondences possesses a symmetric monoidal structure, and (3.5) is naturally symmetric monoidal; see [Reference Gaitsgory and RozenblyumGR17, ch. V.3]. It follows that the
$(\infty ,2)$
-category of correspondences possesses a symmetric monoidal structure, and (3.5) is naturally symmetric monoidal; see [Reference Gaitsgory and RozenblyumGR17, ch. V.3]. It follows that the
![]() $(\infty ,2)$
-functor on Theorem 3.1.6 is symmetric monoidal, too.
$(\infty ,2)$
-functor on Theorem 3.1.6 is symmetric monoidal, too.
3.1.8 Example
For
![]() $f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
, the admissible arrow
$f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
, the admissible arrow
![]() ${\mathcal{Y}}\rightarrow {\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge }$
yields an adjuction
${\mathcal{Y}}\rightarrow {\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge }$
yields an adjuction
Let us also recall that
![]() $\operatorname{IndCoh}_{0}({\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge })$
is self-dual and that these two adjoints
$\operatorname{IndCoh}_{0}({\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge })$
is self-dual and that these two adjoints
![]() $(\text{}^{\prime }f)_{\ast ,0}$
and
$(\text{}^{\prime }f)_{\ast ,0}$
and
![]() $(\text{}^{\prime }f)^{!,0}$
are dual to each other.
$(\text{}^{\prime }f)^{!,0}$
are dual to each other.
3.2
 $(\infty ,2)$
-categorical functoriality
$(\infty ,2)$
-categorical functoriality
In this section we enhance the assignment
to a lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
which we will prove is strict towards the end of the paper (Theorem 6.5.3). Here we have used the notation
![]() $\mathbb{H}^{\text{geom}}$
for emphasis, as later we will encounter a categorical construction producing a lax
$\mathbb{H}^{\text{geom}}$
for emphasis, as later we will encounter a categorical construction producing a lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
![]() $\mathbb{H}^{\text{cat}}$
. We will eventually show that these two lax
$\mathbb{H}^{\text{cat}}$
. We will eventually show that these two lax
![]() $(\infty ,2)$
-functors are identified and then denoted simply by
$(\infty ,2)$
-functors are identified and then denoted simply by
![]() $\mathbb{H}$
.
$\mathbb{H}$
.
Remark 3.2.1. The condition of boundedness of the horizontal arrows is necessary to have a well-defined
![]() $\infty$
-category of correspondences.
$\infty$
-category of correspondences.
3.2.2
We begin by observing that, for any
![]() ${\mathcal{X}}\in \mathsf{Stk}$
, the DG category
${\mathcal{X}}\in \mathsf{Stk}$
, the DG category
possesses a convolution monoidal structure and that, for any correspondence
![]() $[{\mathcal{Y}}\leftarrow {\mathcal{W}}\rightarrow {\mathcal{Z}}]$
in
$[{\mathcal{Y}}\leftarrow {\mathcal{W}}\rightarrow {\mathcal{Z}}]$
in
![]() $\mathsf{Stk}$
, the DG category
$\mathsf{Stk}$
, the DG category
admits the structure of an
![]() $(\mathbb{I}^{\wedge ,\text{geom}}({\mathcal{Y}}),\mathbb{I}^{\wedge ,\text{geom}}({\mathcal{Z}}))$
-bimodule.
$(\mathbb{I}^{\wedge ,\text{geom}}({\mathcal{Y}}),\mathbb{I}^{\wedge ,\text{geom}}({\mathcal{Z}}))$
-bimodule.
3.2.3
Let us now enhance the assignment
to a lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
To construct this, we first appeal to the lax symmetric monoidal structure on (3.5): § 2.2.6 yields a lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
All that remains is to precompose with the lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
that sends
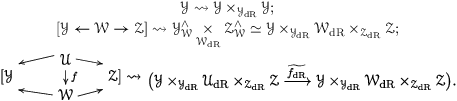
Observe that the requirement that
![]() $f$
be schematic and proper implies that
$f$
be schematic and proper implies that
![]() $f_{\operatorname{dR}}$
, and hence
$f_{\operatorname{dR}}$
, and hence
![]() $\widetilde{f_{\operatorname{dR}}}$
, is inf-schematic and ind-proper.
$\widetilde{f_{\operatorname{dR}}}$
, is inf-schematic and ind-proper.
3.2.5
Let us now turn to the construction of
![]() $\mathbb{H}^{\text{geom}}$
. For
$\mathbb{H}^{\text{geom}}$
. For
![]() ${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, the canonical inclusion
${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, the canonical inclusion
is monoidal. Moreover, the left action of
![]() $\operatorname{IndCoh}_{0}({\mathcal{Y}}\times _{{\mathcal{Y}}_{\operatorname{dR}}}{\mathcal{Y}})$
on
$\operatorname{IndCoh}_{0}({\mathcal{Y}}\times _{{\mathcal{Y}}_{\operatorname{dR}}}{\mathcal{Y}})$
on
![]() $\operatorname{IndCoh}(({\mathcal{Y}}\times {\mathcal{Z}})_{{\mathcal{W}}}^{\wedge })$
preserves the subcategory
$\operatorname{IndCoh}(({\mathcal{Y}}\times {\mathcal{Z}})_{{\mathcal{W}}}^{\wedge })$
preserves the subcategory
![]() $\operatorname{IndCoh}_{0}(({\mathcal{Y}}\times {\mathcal{Z}})_{{\mathcal{W}}}^{\wedge })$
. This is an easy diagram chase left to the reader.
$\operatorname{IndCoh}_{0}(({\mathcal{Y}}\times {\mathcal{Z}})_{{\mathcal{W}}}^{\wedge })$
. This is an easy diagram chase left to the reader.
Thus, we are in a position to apply the paradigm of § 2.2.8 to obtain a lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
as desired. We repeat here that one of the aims of this paper is to show that such lax
![]() $(\infty ,2)$
-functor is actually strict: this is accomplished in Theorem 6.5.3. In the next section, we give an overview of the strategy of the proof of such theorem. This could serve as a guide through the constructions of the remainder of the present paper.
$(\infty ,2)$
-functor is actually strict: this is accomplished in Theorem 6.5.3. In the next section, we give an overview of the strategy of the proof of such theorem. This could serve as a guide through the constructions of the remainder of the present paper.
3.3 Outline of the proof of Theorem 6.5.3
It suffices to prove that the lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
![]() $\mathbb{H}^{\text{geom}}:\mathsf{Corr}\big(\mathsf{Stk}_{\text{lfp}}^{{<}\infty }\big)_{\text{bdd};\operatorname{all}}\rightarrow \mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
is strict. We will proceed in stages.
$\mathbb{H}^{\text{geom}}:\mathsf{Corr}\big(\mathsf{Stk}_{\text{lfp}}^{{<}\infty }\big)_{\text{bdd};\operatorname{all}}\rightarrow \mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
is strict. We will proceed in stages.
3.3.1
First, we look at the restriction of
![]() $\mathbb{H}^{\text{geom}}$
along the functor
$\mathbb{H}^{\text{geom}}$
along the functor
which is the natural inclusion on objects, and
![]() $[S\rightarrow T]{\rightsquigarrow}[S\xleftarrow[{}]{=}S\rightarrow T]$
on
$[S\rightarrow T]{\rightsquigarrow}[S\xleftarrow[{}]{=}S\rightarrow T]$
on
![]() $1$
-morphisms.
$1$
-morphisms.
Using results from the theory of ind-coherent sheaves, we show in Theorem 4.3.4 that such lax
![]() $(\infty ,2)$
-functor is strict. By definition, this is simply the functor
$(\infty ,2)$
-functor is strict. By definition, this is simply the functor
![]() $\mathbb{H}:\mathsf{Aff}_{\text{lfp}}^{{<}\infty }\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
discussed in § 1.6.3.
$\mathbb{H}:\mathsf{Aff}_{\text{lfp}}^{{<}\infty }\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
discussed in § 1.6.3.
3.3.2
Next, we show that the restriction of
![]() $\mathbb{H}^{\text{geom}}$
to
$\mathbb{H}^{\text{geom}}$
to
![]() $\mathsf{Corr}(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{\text{bdd};\operatorname{all}}$
is strict (Corollary 5.2.13). We do so in an indirect way, by establishing some important duality properties of
$\mathsf{Corr}(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{\text{bdd};\operatorname{all}}$
is strict (Corollary 5.2.13). We do so in an indirect way, by establishing some important duality properties of
![]() $\mathbb{H}$
. Namely, we show that, for each map
$\mathbb{H}$
. Namely, we show that, for each map
![]() $U\rightarrow T$
in
$U\rightarrow T$
in
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, the bimodule
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, the bimodule
![]() $\mathbb{H}_{U\rightarrow T}$
admits a right dual (which happens to be a left dual as well), denoted by
$\mathbb{H}_{U\rightarrow T}$
admits a right dual (which happens to be a left dual as well), denoted by
![]() $\mathbb{H}_{T\leftarrow U}$
. Having such right duals allows us to form the bimodules
$\mathbb{H}_{T\leftarrow U}$
. Having such right duals allows us to form the bimodules
We also show that
![]() $\mathbb{H}_{S\rightarrow V\leftarrow T}\simeq \mathbb{H}_{S\leftarrow S\times _{V}T\rightarrow T}$
naturally, provided that at least one arrow between
$\mathbb{H}_{S\rightarrow V\leftarrow T}\simeq \mathbb{H}_{S\leftarrow S\times _{V}T\rightarrow T}$
naturally, provided that at least one arrow between
![]() $S\rightarrow V$
and
$S\rightarrow V$
and
![]() $T\rightarrow V$
is bounded. This is enough to extend
$T\rightarrow V$
is bounded. This is enough to extend
![]() $\mathbb{H}$
to a strict functor
$\mathbb{H}$
to a strict functor
By inspection, such functor coincides with the restriction of
![]() $\mathbb{H}^{\text{geom}}$
to
$\mathbb{H}^{\text{geom}}$
to
![]() $\mathsf{Corr}(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{\text{bdd};\operatorname{all}}$
, whence the latter is also strict.
$\mathsf{Corr}(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{\text{bdd};\operatorname{all}}$
, whence the latter is also strict.
Remark 3.3.3. The fact that left and right duals coincide implies that we could also have defined
![]() $\mathbb{H}^{\mathsf{Corr}}$
on
$\mathbb{H}^{\mathsf{Corr}}$
on
![]() $\mathsf{Corr}(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{\operatorname{all};\text{bdd}}$
. These two versions of
$\mathsf{Corr}(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{\operatorname{all};\text{bdd}}$
. These two versions of
![]() $\mathbb{H}^{\mathsf{Corr}}$
, exchanged by duality, agree on
$\mathbb{H}^{\mathsf{Corr}}$
, exchanged by duality, agree on
![]() $\mathsf{Corr}(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{\text{bdd};\text{bdd}}$
.
$\mathsf{Corr}(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{\text{bdd};\text{bdd}}$
.
3.3.4
To study
![]() $\mathbb{H}^{\text{geom}}$
on stacks, we introduce the sheaf theory
$\mathbb{H}^{\text{geom}}$
on stacks, we introduce the sheaf theory
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
, which is the right Kan extension of the functor
$\mathsf{ShvCat}^{\mathbb{H}}$
, which is the right Kan extension of the functor
Note that Theorem 4.3.4 is essential to make this well defined.
In principle,
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
comes equipped only with pullback functors. However, thanks to the existence of the right duals
$\mathsf{ShvCat}^{\mathbb{H}}$
comes equipped only with pullback functors. However, thanks to the existence of the right duals
![]() $\mathbb{H}_{T\leftarrow S}$
, there are also
$\mathbb{H}_{T\leftarrow S}$
, there are also
![]() $\ast$
-pushforward functors (right adjoints to pullbacks), which turn out to satisfy base-change against pullbacks. Symmetrically, the existence of the left duals provides
$\ast$
-pushforward functors (right adjoints to pullbacks), which turn out to satisfy base-change against pullbacks. Symmetrically, the existence of the left duals provides
![]() $!$
-pushforward functors (left adjoints to pullbacks), also satisfying base-change against pullbacks.Footnote
5
$!$
-pushforward functors (left adjoints to pullbacks), also satisfying base-change against pullbacks.Footnote
5
3.3.5
In Theorem 6.5.1, we prove the
![]() $\mathbb{H}$
-affineness theorem, which states that, for any
$\mathbb{H}$
-affineness theorem, which states that, for any
![]() ${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, the
${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, the
![]() $\infty$
-category
$\infty$
-category
![]() $\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
is equivalent to
$\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
is equivalent to
![]() $\mathbb{H}^{\text{geom}}({\mathcal{Y}})\operatorname{ -}\mathbf{mod}$
. This theorem, together with the above base-change properties, automatically upgrades the assignment
$\mathbb{H}^{\text{geom}}({\mathcal{Y}})\operatorname{ -}\mathbf{mod}$
. This theorem, together with the above base-change properties, automatically upgrades the assignment
![]() ${\mathcal{Y}}{\rightsquigarrow}\mathbb{H}^{\text{geom}}({\mathcal{Y}})$
to a strict
${\mathcal{Y}}{\rightsquigarrow}\mathbb{H}^{\text{geom}}({\mathcal{Y}})$
to a strict
![]() $(\infty ,2)$
-functor out of
$(\infty ,2)$
-functor out of
![]() $\mathsf{Corr}(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })_{\text{bdd};\operatorname{all}}$
. Fortunately, such functor is easily seen to match with
$\mathsf{Corr}(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })_{\text{bdd};\operatorname{all}}$
. Fortunately, such functor is easily seen to match with
![]() $\mathbb{H}^{\text{geom}}$
, thereby proving that the latter is strict, too.
$\mathbb{H}^{\text{geom}}$
, thereby proving that the latter is strict, too.
3.3.6
An important technical result, which we use frequently, is the smooth descent property for
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
, proven in § 6.1: any object
$\mathsf{ShvCat}^{\mathbb{H}}$
, proven in § 6.1: any object
![]() ${\mathcal{C}}\in \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
is determined by its restrictions along smooth maps
${\mathcal{C}}\in \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
is determined by its restrictions along smooth maps
![]() $S\rightarrow {\mathcal{Y}}$
, with
$S\rightarrow {\mathcal{Y}}$
, with
![]() $S$
affine. This is a very convenient simplification. For instance, let
$S$
affine. This is a very convenient simplification. For instance, let
![]() $\operatorname{IndCoh}_{/{\mathcal{Y}}}\in \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
be the sheaf corresponding to
$\operatorname{IndCoh}_{/{\mathcal{Y}}}\in \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
be the sheaf corresponding to
![]() $\operatorname{IndCoh}({\mathcal{Y}})\in \mathbb{H}^{\text{geom}}({\mathcal{Y}})\operatorname{ -}\mathbf{mod}$
via
$\operatorname{IndCoh}({\mathcal{Y}})\in \mathbb{H}^{\text{geom}}({\mathcal{Y}})\operatorname{ -}\mathbf{mod}$
via
![]() $\mathbb{H}$
-affineness. In § 6.6 we will show that the restriction of
$\mathbb{H}$
-affineness. In § 6.6 we will show that the restriction of
![]() $\operatorname{IndCoh}_{/{\mathcal{Y}}}$
along a smooth map
$\operatorname{IndCoh}_{/{\mathcal{Y}}}$
along a smooth map
![]() $S\rightarrow {\mathcal{Y}}$
is the
$S\rightarrow {\mathcal{Y}}$
is the
![]() $\mathbb{H}(S)$
-module
$\mathbb{H}(S)$
-module
![]() $\operatorname{IndCoh}(S)$
, whereas the restriction along a non-smooth map does not admit such a simple description.
$\operatorname{IndCoh}(S)$
, whereas the restriction along a non-smooth map does not admit such a simple description.
4 Coefficient systems for sheaves of categories
In this section we introduce one of the central notions of this paper, the notion of coefficient system, together with its companion notion of lax coefficient system.
We present a list of examples, and, in particular, we define the coefficient system
![]() $\mathbb{H}$
related to Hochschild cochains. Let us anticipate that
$\mathbb{H}$
related to Hochschild cochains. Let us anticipate that
![]() $\mathbb{H}$
arises naturally as a lax coefficient system and some work is needed in order to prove that it is actually strict. (Here and later, the adjective ‘strict’ is used to emphasize that a certain coefficient system is a genuine one, not a lax one.)
$\mathbb{H}$
arises naturally as a lax coefficient system and some work is needed in order to prove that it is actually strict. (Here and later, the adjective ‘strict’ is used to emphasize that a certain coefficient system is a genuine one, not a lax one.)
4.1 Definition and examples
Consider the
![]() $(\infty ,2)$
-category
$(\infty ,2)$
-category
![]() $\mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
, whose objects are monoidal DG categories, whose
$\mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
, whose objects are monoidal DG categories, whose
![]() $1$
-morphisms are bimodule categories, and whose
$1$
-morphisms are bimodule categories, and whose
![]() $2$
-morphisms are functors of bimodules. Recall that the
$2$
-morphisms are functors of bimodules. Recall that the
![]() $(\infty ,1)$
-category underlying
$(\infty ,1)$
-category underlying
![]() $\mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
will be denoted by
$\mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
will be denoted by
![]() $\mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
.
$\mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
.
A coefficient system is a functor
A lax coefficient system is a lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
4.1.1
Thus, a lax coefficient system
![]() $\mathbb{A}$
consists of:
$\mathbb{A}$
consists of:
– a monoidal category
 $\mathbb{A}(S)$
, for each affine scheme
$\mathbb{A}(S)$
, for each affine scheme
 $S$
;
$S$
;– an
 $(\mathbb{A}(S),\mathbb{A}(T))$
-bimodule
$(\mathbb{A}(S),\mathbb{A}(T))$
-bimodule
 $\mathbb{A}_{S\rightarrow T}$
for any map of affine schemes
$\mathbb{A}_{S\rightarrow T}$
for any map of affine schemes
 $S\rightarrow T$
;
$S\rightarrow T$
;– an
 $(\mathbb{A}(S),\mathbb{A}(U))$
-linear functor for any string
$(\mathbb{A}(S),\mathbb{A}(U))$
-linear functor for any string $$\begin{eqnarray}\unicode[STIX]{x1D702}_{S\rightarrow T\rightarrow U}:\mathbb{A}_{S\rightarrow T}\underset{\mathbb{A}(T)}{\otimes }\mathbb{A}_{T\rightarrow U}\longrightarrow \mathbb{A}_{S\rightarrow U}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{S\rightarrow T\rightarrow U}:\mathbb{A}_{S\rightarrow T}\underset{\mathbb{A}(T)}{\otimes }\mathbb{A}_{T\rightarrow U}\longrightarrow \mathbb{A}_{S\rightarrow U}\end{eqnarray}$$
 $S\rightarrow T\rightarrow U$
of affine schemes;
$S\rightarrow T\rightarrow U$
of affine schemes;– natural compatibilities for higher compositions.
Clearly, such
![]() $\mathbb{A}$
is a strict (i.e. non-lax) coefficient system if and only if all functors
$\mathbb{A}$
is a strict (i.e. non-lax) coefficient system if and only if all functors
![]() $\unicode[STIX]{x1D702}_{S\rightarrow T\rightarrow U}$
are equivalences.
$\unicode[STIX]{x1D702}_{S\rightarrow T\rightarrow U}$
are equivalences.
4.1.2
One obtains variants of the above definitions by replacing the source
![]() $\infty$
-category
$\infty$
-category
![]() $\mathsf{Aff}$
with a subcategory
$\mathsf{Aff}$
with a subcategory
![]() $\mathsf{Aff}_{\text{type}}$
, where ‘
$\mathsf{Aff}_{\text{type}}$
, where ‘
![]() $\text{type}$
’ is a property of affine schemes. For instance, we will often consider
$\text{type}$
’ is a property of affine schemes. For instance, we will often consider
![]() $\mathsf{Aff}_{\text{aft}}$
(the full subcategory of affine schemes almost of finite type) or
$\mathsf{Aff}_{\text{aft}}$
(the full subcategory of affine schemes almost of finite type) or
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
(affine schemes that are bounded and locally of finite presentation).
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
(affine schemes that are bounded and locally of finite presentation).
We now give a list of examples of (lax) coefficient systems, in decreasing order of simplicity.
4.1.3 Example 1
Any monoidal DG category
![]() ${\mathcal{A}}$
yields a ‘constant’ coefficient system
${\mathcal{A}}$
yields a ‘constant’ coefficient system
![]() $\text{}\underline{{\mathcal{A}}}$
whose value on
$\text{}\underline{{\mathcal{A}}}$
whose value on
![]() $S\rightarrow T$
is
$S\rightarrow T$
is
![]() ${\mathcal{A}}$
, considered as a bimodule over itself.
${\mathcal{A}}$
, considered as a bimodule over itself.
4.1.4 Example 2
Slightly less trivial: coefficient systems induced by a functor
![]() $\mathsf{Aff}\rightarrow \mathsf{Alg}(\mathsf{DGCat})^{\operatorname{op}}$
via the functor
$\mathsf{Aff}\rightarrow \mathsf{Alg}(\mathsf{DGCat})^{\operatorname{op}}$
via the functor
![]() $\unicode[STIX]{x1D704}_{\mathsf{Alg}\rightarrow \mathsf{Bimod}}$
defined in (2.1). These coefficient systems are automatically strict.
$\unicode[STIX]{x1D704}_{\mathsf{Alg}\rightarrow \mathsf{Bimod}}$
defined in (2.1). These coefficient systems are automatically strict.
For instance, we have the coefficient system
![]() $\mathbb{Q}$
which sends
$\mathbb{Q}$
which sends
Similarly, we have
![]() $\mathbb{D}$
, obtained as above using
$\mathbb{D}$
, obtained as above using
![]() $\mathfrak{D}$
-modules rather than quasi-coherent sheaves. This coefficient system is defined only out of
$\mathfrak{D}$
-modules rather than quasi-coherent sheaves. This coefficient system is defined only out of
![]() $\mathsf{Aff}_{\text{aft}}\subset \mathsf{Aff}$
.
$\mathsf{Aff}_{\text{aft}}\subset \mathsf{Aff}$
.
4.1.5 Example 3
Let us precompose the lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
of § 2.2.7 with the functor
that encodes the action of
![]() $\mathfrak{D}$
-modules on ind-coherent sheaves. Since
$\mathfrak{D}$
-modules on ind-coherent sheaves. Since
![]() $\operatorname{IndCoh}(S)$
is self-dual as a
$\operatorname{IndCoh}(S)$
is self-dual as a
![]() $\mathfrak{D}(S)$
-module (Corollary 4.2.2), we obtain a lax coefficient system
$\mathfrak{D}(S)$
-module (Corollary 4.2.2), we obtain a lax coefficient system
described informally by
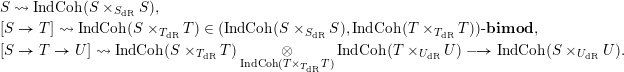 $$\begin{eqnarray}\displaystyle & & \displaystyle S{\rightsquigarrow}\operatorname{IndCoh}(S\times _{S_{\operatorname{dR}}}S),\nonumber\\ \displaystyle & & \displaystyle [S\rightarrow T]{\rightsquigarrow}\operatorname{IndCoh}(S\times _{T_{\operatorname{dR}}}T)\in (\operatorname{IndCoh}(S\times _{S_{\operatorname{dR}}}S),\operatorname{IndCoh}(T\times _{T_{\operatorname{dR}}}T))\!\operatorname{ -}\!\mathbf{bimod},\nonumber\\ \displaystyle & & \displaystyle [S\rightarrow T\rightarrow U]{\rightsquigarrow}\operatorname{IndCoh}(S\times _{T_{\operatorname{dR}}}T)\underset{\operatorname{IndCoh}(T\times _{T_{\operatorname{dR}}}T)}{\otimes }\operatorname{IndCoh}(T\times _{U_{\operatorname{dR}}}U)\longrightarrow \operatorname{IndCoh}(S\times _{U_{\operatorname{dR}}}U).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle S{\rightsquigarrow}\operatorname{IndCoh}(S\times _{S_{\operatorname{dR}}}S),\nonumber\\ \displaystyle & & \displaystyle [S\rightarrow T]{\rightsquigarrow}\operatorname{IndCoh}(S\times _{T_{\operatorname{dR}}}T)\in (\operatorname{IndCoh}(S\times _{S_{\operatorname{dR}}}S),\operatorname{IndCoh}(T\times _{T_{\operatorname{dR}}}T))\!\operatorname{ -}\!\mathbf{bimod},\nonumber\\ \displaystyle & & \displaystyle [S\rightarrow T\rightarrow U]{\rightsquigarrow}\operatorname{IndCoh}(S\times _{T_{\operatorname{dR}}}T)\underset{\operatorname{IndCoh}(T\times _{T_{\operatorname{dR}}}T)}{\otimes }\operatorname{IndCoh}(T\times _{U_{\operatorname{dR}}}U)\longrightarrow \operatorname{IndCoh}(S\times _{U_{\operatorname{dR}}}U).\nonumber\end{eqnarray}$$
In other words,
![]() $\mathbb{I}^{\wedge }$
is obtained by restricting the very general
$\mathbb{I}^{\wedge }$
is obtained by restricting the very general
![]() $\mathbb{I}^{\wedge ,\text{geom}}$
defined in § 3.2.3 to
$\mathbb{I}^{\wedge ,\text{geom}}$
defined in § 3.2.3 to
![]() $\mathsf{Aff}_{\text{aft}}$
. We will prove that
$\mathsf{Aff}_{\text{aft}}$
. We will prove that
![]() $\mathbb{I}^{\wedge }$
is strict in Proposition 4.2.5.
$\mathbb{I}^{\wedge }$
is strict in Proposition 4.2.5.
4.1.6 Example 4
As a variation on the above example, let
![]() $\mathbb{H}$
be the lax coefficient system
$\mathbb{H}$
be the lax coefficient system
defined by
 $$\begin{eqnarray}\displaystyle & & \displaystyle S{\rightsquigarrow}\mathbb{H}(S):=\operatorname{IndCoh}_{0}(S\times _{S_{\operatorname{dR}}}S),\nonumber\\ \displaystyle & & \displaystyle [S\rightarrow T]{\rightsquigarrow}\mathbb{H}_{S\rightarrow T}:=\operatorname{IndCoh}_{0}(S\times _{T_{\operatorname{dR}}}T)\in (\mathbb{H}(S),\mathbb{H}(T))\!\operatorname{ -}\!\mathbf{bimod},\nonumber\\ \displaystyle & & \displaystyle [S\rightarrow T\rightarrow U]{\rightsquigarrow}\mathbb{H}_{S\rightarrow T}\underset{\mathbb{H}(T)}{\otimes }\mathbb{H}_{T\rightarrow U}\longrightarrow \mathbb{H}_{S\rightarrow U}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle S{\rightsquigarrow}\mathbb{H}(S):=\operatorname{IndCoh}_{0}(S\times _{S_{\operatorname{dR}}}S),\nonumber\\ \displaystyle & & \displaystyle [S\rightarrow T]{\rightsquigarrow}\mathbb{H}_{S\rightarrow T}:=\operatorname{IndCoh}_{0}(S\times _{T_{\operatorname{dR}}}T)\in (\mathbb{H}(S),\mathbb{H}(T))\!\operatorname{ -}\!\mathbf{bimod},\nonumber\\ \displaystyle & & \displaystyle [S\rightarrow T\rightarrow U]{\rightsquigarrow}\mathbb{H}_{S\rightarrow T}\underset{\mathbb{H}(T)}{\otimes }\mathbb{H}_{T\rightarrow U}\longrightarrow \mathbb{H}_{S\rightarrow U}.\nonumber\end{eqnarray}$$
Similarly to
![]() $\mathbb{I}^{\wedge }$
, this is the restriction of (3.9) to affine schemes. We will show that
$\mathbb{I}^{\wedge }$
, this is the restriction of (3.9) to affine schemes. We will show that
![]() $\mathbb{H}$
is strict too.
$\mathbb{H}$
is strict too.
The importance of
![]() $\mathbb{H}$
comes from the monoidal equivalence
$\mathbb{H}$
comes from the monoidal equivalence
To be precise, we have the following. First, the equivalence
![]() $\mathbb{H}(S)\simeq \operatorname{HC}(\operatorname{IndCoh}(S))^{\operatorname{op}}\operatorname{ -}\!\mathsf{mod}$
is obvious. Second, [Reference Arinkin and GaitsgoryAG15, Proposition F.1.5] provides a natural isomorphism
$\mathbb{H}(S)\simeq \operatorname{HC}(\operatorname{IndCoh}(S))^{\operatorname{op}}\operatorname{ -}\!\mathsf{mod}$
is obvious. Second, [Reference Arinkin and GaitsgoryAG15, Proposition F.1.5] provides a natural isomorphism
![]() $\operatorname{HC}(\operatorname{IndCoh}(S))\simeq \operatorname{HC}(\operatorname{QCoh}(S))=:\operatorname{HC}(S)$
of
$\operatorname{HC}(\operatorname{IndCoh}(S))\simeq \operatorname{HC}(\operatorname{QCoh}(S))=:\operatorname{HC}(S)$
of
![]() $E_{2}$
-algebras.
$E_{2}$
-algebras.
4.1.7 Example 5
One last example arising in a geometric fashion. Let
![]() ${\mathcal{Y}}:\mathsf{Aff}\rightarrow \mathsf{Corr}(\mathsf{PreStk})_{\operatorname{all};\operatorname{all}}^{\operatorname{all}}$
be an arbitrary lax
${\mathcal{Y}}:\mathsf{Aff}\rightarrow \mathsf{Corr}(\mathsf{PreStk})_{\operatorname{all};\operatorname{all}}^{\operatorname{all}}$
be an arbitrary lax
![]() $(\infty ,2)$
-functor, described informally by the assignments
$(\infty ,2)$
-functor, described informally by the assignments
The lax structure amounts to the data of maps
over
![]() ${\mathcal{Y}}_{S}\times {\mathcal{Y}}_{U}$
, for any string
${\mathcal{Y}}_{S}\times {\mathcal{Y}}_{U}$
, for any string
![]() $S\rightarrow T\rightarrow U$
. Recalling now the paradigm of § 2.2.5, we obtain a lax
$S\rightarrow T\rightarrow U$
. Recalling now the paradigm of § 2.2.5, we obtain a lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
defined by sending
The combination of this with
![]() ${\mathcal{Y}}$
yields a lax coefficient system, which is strict if the maps (4.1) are isomorphisms and the prestacks
${\mathcal{Y}}$
yields a lax coefficient system, which is strict if the maps (4.1) are isomorphisms and the prestacks
![]() ${\mathcal{Y}}_{S\rightarrow T}$
are nice enough.Footnote
6
${\mathcal{Y}}_{S\rightarrow T}$
are nice enough.Footnote
6
4.1.8 Sub-example: singular support
The theory of singular support provides an important example of the above construction: the assignment
where
![]() $\operatorname{Sing}(U):=\operatorname{Spec}(\operatorname{Sym}_{H^{0}(U,{\mathcal{O}}_{U})}H^{1}(U,\mathbb{T}_{U}))$
is equipped with the obvious weight-
$\operatorname{Sing}(U):=\operatorname{Spec}(\operatorname{Sym}_{H^{0}(U,{\mathcal{O}}_{U})}H^{1}(U,\mathbb{T}_{U}))$
is equipped with the obvious weight-
![]() $2$
dilation action.
$2$
dilation action.
We obtain a coefficient system
![]() $\mathbb{S}^{\prime }:\mathsf{Aff}_{\text{q-smooth}}\longrightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
defined on quasi-smooth affine schemes. By construction, if
$\mathbb{S}^{\prime }:\mathsf{Aff}_{\text{q-smooth}}\longrightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
defined on quasi-smooth affine schemes. By construction, if
![]() ${\mathcal{C}}$
is a module category over
${\mathcal{C}}$
is a module category over
![]() $\mathbb{S}^{\prime }(U)$
, then objects of
$\mathbb{S}^{\prime }(U)$
, then objects of
![]() ${\mathcal{C}}$
are equipped with a notion of support in
${\mathcal{C}}$
are equipped with a notion of support in
![]() $\operatorname{Sing}(U)$
; see [Reference Arinkin and GaitsgoryAG15] for more details.
$\operatorname{Sing}(U)$
; see [Reference Arinkin and GaitsgoryAG15] for more details.
4.2 The coefficient system
 $\mathbb{I}^{\wedge }$
$\mathbb{I}^{\wedge }$
Let us prove that
![]() $\mathbb{I}^{\wedge }$
and
$\mathbb{I}^{\wedge }$
and
![]() $\mathbb{H}$
are strict coefficient systems. We will need to use the following fact.
$\mathbb{H}$
are strict coefficient systems. We will need to use the following fact.
Lemma 4.2.1. For any diagram
![]() $Y\rightarrow W\leftarrow Z$
in
$Y\rightarrow W\leftarrow Z$
in
![]() $\mathsf{Sch}_{\text{aft}}$
, the exterior tensor product yields the equivalence
$\mathsf{Sch}_{\text{aft}}$
, the exterior tensor product yields the equivalence
Proof. Note that
![]() $Y\times _{W_{\operatorname{dR}}}Z\simeq (Y\times Z)_{Y\times _{W}Z}^{\wedge }$
. Hence, by [Reference Arinkin and GaitsgoryAG18, Proposition 3.1.2], the right-hand side is equivalent to
$Y\times _{W_{\operatorname{dR}}}Z\simeq (Y\times Z)_{Y\times _{W}Z}^{\wedge }$
. Hence, by [Reference Arinkin and GaitsgoryAG18, Proposition 3.1.2], the right-hand side is equivalent to
while the left-hand side is obviously equivalent to
Now the statement reduces to the analogous statement with
![]() $\operatorname{IndCoh}$
replaced by
$\operatorname{IndCoh}$
replaced by
![]() $\operatorname{QCoh}$
, which is well known.◻
$\operatorname{QCoh}$
, which is well known.◻
Corollary 4.2.2. For
![]() $Y\in \mathsf{Sch}_{\text{aft}}$
, the DG category
$Y\in \mathsf{Sch}_{\text{aft}}$
, the DG category
![]() $\operatorname{IndCoh}(Y)$
is self-dual as a
$\operatorname{IndCoh}(Y)$
is self-dual as a
![]() $\mathfrak{D}(Y)$
-module.
$\mathfrak{D}(Y)$
-module.
Proof. One uses the equivalence of the above lemma to write the evaluation and coevaluation as standard pull-push formulas. ◻
Corollary 4.2.3. For any map
![]() $Y\rightarrow Z$
in
$Y\rightarrow Z$
in
![]() $\mathsf{Sch}_{\text{aft}}$
, we obtain a natural equivalence
$\mathsf{Sch}_{\text{aft}}$
, we obtain a natural equivalence
In the special case
![]() $Y=Z$
, the ‘composition’ monoidal structure on the right-hand side corresponds to the ‘convolution’ monoidal structure on the left-hand side.
$Y=Z$
, the ‘composition’ monoidal structure on the right-hand side corresponds to the ‘convolution’ monoidal structure on the left-hand side.
4.2.4
The lax-coefficient system
![]() $\mathbb{I}^{\wedge }$
is the restriction of the lax
$\mathbb{I}^{\wedge }$
is the restriction of the lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
![]() $\operatorname{IndCoh}^{\wedge ,\text{geom}}$
to
$\operatorname{IndCoh}^{\wedge ,\text{geom}}$
to
![]() $\mathsf{Aff}_{\text{aft}}$
. Consider now the intermediate lax
$\mathsf{Aff}_{\text{aft}}$
. Consider now the intermediate lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
![]() $\mathsf{Sch}_{\text{aft}}\rightarrow \mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
, also denoted by
$\mathsf{Sch}_{\text{aft}}\rightarrow \mathsf{ALG}^{\text{bimod}}(\mathsf{DGCat})$
, also denoted by
![]() $\mathbb{I}^{\wedge }$
by an abuse of notation. Our present aim is to prove the following result.
$\mathbb{I}^{\wedge }$
by an abuse of notation. Our present aim is to prove the following result.
Proposition 4.2.5. The lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
is strict.
The proof of the above proposition will be given after some preparation.
4.2.6
For
![]() $Y\in \mathsf{Sch}_{\text{aft}}$
, Corollary 4.2.3 shows that
$Y\in \mathsf{Sch}_{\text{aft}}$
, Corollary 4.2.3 shows that
![]() $\operatorname{IndCoh}(Y)$
admits the structure of an
$\operatorname{IndCoh}(Y)$
admits the structure of an
![]() $(\operatorname{IndCoh}(Y\times _{Y_{\operatorname{dR}}}Y),\mathfrak{D}(Y))$
-bimodule, as well as the structure of a
$(\operatorname{IndCoh}(Y\times _{Y_{\operatorname{dR}}}Y),\mathfrak{D}(Y))$
-bimodule, as well as the structure of a
![]() $(\mathfrak{D}(Y),\operatorname{IndCoh}(Y\times _{Y_{\operatorname{dR}}}Y))$
-bimodule. Now, one verifies directly that the latter bimodule is left dual to the former, that is, there is an adjunction
$(\mathfrak{D}(Y),\operatorname{IndCoh}(Y\times _{Y_{\operatorname{dR}}}Y))$
-bimodule. Now, one verifies directly that the latter bimodule is left dual to the former, that is, there is an adjunction
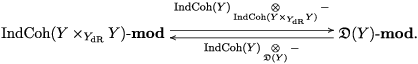
Lemma 4.2.7. These two adjoint functors form a pair of mutually inverse equivalences. In particular, we also have an adjunction in the other direction:
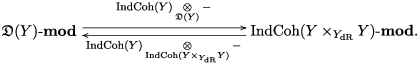
Proof. The left adjoint in (4.3) is fully faithful by (4.2) and the right adjoint is colimit-preserving. By the Barr–Beck theorem, it suffices to show that the right adjoint in (4.3) is conservative, a statement which is the content of the next lemma. ◻
Lemma 4.2.8. For
![]() $Y\in \mathsf{Sch}_{\text{aft}}$
, the functor
$Y\in \mathsf{Sch}_{\text{aft}}$
, the functor
is conservative.
Proof. Let
![]() $f:{\mathcal{M}}\rightarrow {\mathcal{N}}$
be a
$f:{\mathcal{M}}\rightarrow {\mathcal{N}}$
be a
![]() $\mathfrak{D}(Y)$
-linear functor with the property that
$\mathfrak{D}(Y)$
-linear functor with the property that
is an equivalence. We need to show that
![]() $f$
itself is an equivalence.
$f$
itself is an equivalence.
Denote by
![]() $\widehat{Y}_{\bullet }$
the Čech nerve of
$\widehat{Y}_{\bullet }$
the Čech nerve of
![]() $q:Y\rightarrow Y_{\operatorname{dR}}$
. Recall that the natural arrow
$q:Y\rightarrow Y_{\operatorname{dR}}$
. Recall that the natural arrow
is an equivalence and that each of the structure functors composing the above cosimplicial category admits a left adjoint (indeed, each structure map
![]() $\widehat{Y}_{m}\rightarrow \widehat{Y}_{n}$
is a nil-isomorphism between inf-schemes). Consequently, the tautological functor
$\widehat{Y}_{m}\rightarrow \widehat{Y}_{n}$
is a nil-isomorphism between inf-schemes). Consequently, the tautological functor
is an equivalence for any
![]() ${\mathcal{C}}\in \mathfrak{D}(S)\operatorname{ -}\mathbf{mod}$
. Under these identifications, our functor
${\mathcal{C}}\in \mathfrak{D}(S)\operatorname{ -}\mathbf{mod}$
. Under these identifications, our functor
![]() $f:{\mathcal{M}}\rightarrow {\mathcal{N}}$
is the limit of the equivalences
$f:{\mathcal{M}}\rightarrow {\mathcal{N}}$
is the limit of the equivalences
whence it is itself an equivalence. ◻
4.2.9
We are now ready for the proof of the proposition left open above.
Proof of Proposition 4.2.5.
Thanks to (4.2), it suffices to prove that, for any
![]() $Y\in \mathsf{Sch}_{\text{aft}}$
, the obvious functor
$Y\in \mathsf{Sch}_{\text{aft}}$
, the obvious functor
![]() $q_{\ast }^{\operatorname{IndCoh}}\circ \unicode[STIX]{x1D6E5}^{!}:\operatorname{IndCoh}(Y)\otimes \operatorname{IndCoh}(Y)\rightarrow \mathfrak{D}(Y)$
induces an equivalence
$q_{\ast }^{\operatorname{IndCoh}}\circ \unicode[STIX]{x1D6E5}^{!}:\operatorname{IndCoh}(Y)\otimes \operatorname{IndCoh}(Y)\rightarrow \mathfrak{D}(Y)$
induces an equivalence
The latter is precisely the counit of the adjunction (4.3), which we have shown to be an equivalence. ◻
4.3 The coefficient system
 $\mathbb{H}$
$\mathbb{H}$
Our present aim is to prove Theorem 4.3.4, which states that the lax coefficient system
is strict. Actually, the theorem proves something slightly stronger, namely, the parallel statement for schemes that are not necessarily affine.
4.3.1
We need a preliminary result, which is of interest in its own right.
Proposition 4.3.2. Let
![]() $f:X\rightarrow Y$
be a map in
$f:X\rightarrow Y$
be a map in
![]() $\mathsf{Sch}_{\text{lfp}}^{{<}\infty }$
. Then the
$\mathsf{Sch}_{\text{lfp}}^{{<}\infty }$
. Then the
![]() $(\mathfrak{D}(X),\mathbb{H}(Y))$
-linear functor
$(\mathfrak{D}(X),\mathbb{H}(Y))$
-linear functor
obtained as the composition
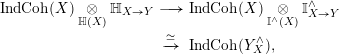 $$\begin{eqnarray}\displaystyle \operatorname{IndCoh}(X)\underset{\mathbb{H}(X)}{\otimes }\mathbb{H}_{X\rightarrow Y} & \longrightarrow & \displaystyle \operatorname{IndCoh}(X)\underset{\mathbb{I}^{\wedge }(X)}{\otimes }\mathbb{I}_{X\rightarrow Y}^{\wedge }\nonumber\\ \displaystyle & \xrightarrow[{}]{\simeq } & \displaystyle \operatorname{IndCoh}(Y_{X}^{\wedge }),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{IndCoh}(X)\underset{\mathbb{H}(X)}{\otimes }\mathbb{H}_{X\rightarrow Y} & \longrightarrow & \displaystyle \operatorname{IndCoh}(X)\underset{\mathbb{I}^{\wedge }(X)}{\otimes }\mathbb{I}_{X\rightarrow Y}^{\wedge }\nonumber\\ \displaystyle & \xrightarrow[{}]{\simeq } & \displaystyle \operatorname{IndCoh}(Y_{X}^{\wedge }),\nonumber\end{eqnarray}$$
is an equivalence of categories.
Proof. The source category is compactly generated by objects of the form
![]() $[C_{X},(\text{}^{\prime }f)_{\ast }^{\operatorname{IndCoh}}(\unicode[STIX]{x1D714}_{X})]$
for
$[C_{X},(\text{}^{\prime }f)_{\ast }^{\operatorname{IndCoh}}(\unicode[STIX]{x1D714}_{X})]$
for
![]() $C_{X}\in \operatorname{Coh}(X)$
. Hence, it is clear that the functor in question (let us denote it by
$C_{X}\in \operatorname{Coh}(X)$
. Hence, it is clear that the functor in question (let us denote it by
![]() $\unicode[STIX]{x1D719}$
) admits a continuous and conservative right adjoint: indeed,
$\unicode[STIX]{x1D719}$
) admits a continuous and conservative right adjoint: indeed,
![]() $\unicode[STIX]{x1D719}$
sends
$\unicode[STIX]{x1D719}$
sends
whence it preserves compactness and generates the target under colimits. It remains to show that
![]() $\unicode[STIX]{x1D719}$
is fully faithful on objects of the form
$\unicode[STIX]{x1D719}$
is fully faithful on objects of the form
![]() $[C_{X},(\text{}^{\prime }f)_{\ast }^{\operatorname{IndCoh}}(\unicode[STIX]{x1D714}_{X})]$
. The nil-isomorphism
$[C_{X},(\text{}^{\prime }f)_{\ast }^{\operatorname{IndCoh}}(\unicode[STIX]{x1D714}_{X})]$
. The nil-isomorphism
![]() $\unicode[STIX]{x1D6FD}:(X\times X)_{X}^{\wedge }\rightarrow (X\times Y)_{X}^{\wedge }$
induces the adjunction
$\unicode[STIX]{x1D6FD}:(X\times X)_{X}^{\wedge }\rightarrow (X\times Y)_{X}^{\wedge }$
induces the adjunction
Observe that both functors are
![]() $\operatorname{IndCoh}((X\times X)_{X}^{\wedge })$
-linear and preserve the
$\operatorname{IndCoh}((X\times X)_{X}^{\wedge })$
-linear and preserve the
![]() $\operatorname{IndCoh}_{0}$
-subcategories. To conclude the proof, just note that
$\operatorname{IndCoh}_{0}$
-subcategories. To conclude the proof, just note that
![]() $(\text{}^{\prime }f)_{\ast }^{\operatorname{IndCoh}}(\unicode[STIX]{x1D714}_{X})$
is the image of the unit of
$(\text{}^{\prime }f)_{\ast }^{\operatorname{IndCoh}}(\unicode[STIX]{x1D714}_{X})$
is the image of the unit of
![]() $\mathbb{H}(X)$
under
$\mathbb{H}(X)$
under
![]() $\unicode[STIX]{x1D6FD}_{\ast }^{\operatorname{IndCoh}}$
, and use the above adjunction.◻
$\unicode[STIX]{x1D6FD}_{\ast }^{\operatorname{IndCoh}}$
, and use the above adjunction.◻
Corollary 4.3.3. For
![]() $f:X\rightarrow Y$
as above and
$f:X\rightarrow Y$
as above and
![]() ${\mathcal{C}}$
a right
${\mathcal{C}}$
a right
![]() $\mathbb{I}^{\wedge }(X)$
-module, the natural functor
$\mathbb{I}^{\wedge }(X)$
-module, the natural functor
is an equivalence.
Proof. It suffices to prove the assertion for
![]() ${\mathcal{C}}=\mathbb{I}^{\wedge }(X)$
, viewed as a right module over itself. Thanks to the right
${\mathcal{C}}=\mathbb{I}^{\wedge }(X)$
, viewed as a right module over itself. Thanks to the right
![]() $\mathbb{I}^{\wedge }(X)$
-linear equivalence
$\mathbb{I}^{\wedge }(X)$
-linear equivalence
the assertion reduces to the proposition above. ◻
Theorem 4.3.4. The lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
obtained by restricting
![]() $\mathbb{H}^{\text{geom}}$
to schemes, is strict.
$\mathbb{H}^{\text{geom}}$
to schemes, is strict.
Proof. Let
![]() $U\rightarrow X\rightarrow Y$
be a string in
$U\rightarrow X\rightarrow Y$
be a string in
![]() $\mathsf{Sch}_{\text{lfp}}^{{<}\infty }$
. We need to prove that the convolution functor
$\mathsf{Sch}_{\text{lfp}}^{{<}\infty }$
. We need to prove that the convolution functor
is an equivalence onto the subcategory
![]() $\mathbb{H}_{U\rightarrow Y}\subseteq \mathbb{I}_{U\rightarrow Y}^{\wedge }$
. One easily checks that the essential image of the functor is indeed
$\mathbb{H}_{U\rightarrow Y}\subseteq \mathbb{I}_{U\rightarrow Y}^{\wedge }$
. One easily checks that the essential image of the functor is indeed
![]() $\mathbb{H}_{U\rightarrow Y}$
, whence it remains to prove fully faithfulness. By construction, (4.7) factors as the composition
$\mathbb{H}_{U\rightarrow Y}$
, whence it remains to prove fully faithfulness. By construction, (4.7) factors as the composition
Now the first arrow is obviously fully faithful, while the second one is an equivalence by the above corollary. ◻
4.4 Morphisms between coefficient systems
Coefficient systems assemble into an
![]() $\infty$
-category:
$\infty$
-category:
Hence, it makes sense to consider morphisms of coefficient systems. This notion has already been discussed in § 1.8, where some examples have been given. Here we just recall the only morphism of interest in this paper, the arrow
![]() $\mathbb{Q}\rightarrow \mathbb{H}$
.
$\mathbb{Q}\rightarrow \mathbb{H}$
.
4.4.1
Let
![]() $\mathbb{A}$
and
$\mathbb{A}$
and
![]() $\mathbb{B}$
be two coefficient systems. Consider the following pieces of data:
$\mathbb{B}$
be two coefficient systems. Consider the following pieces of data:
– for each
 $S\in \mathsf{Aff}$
, a monoidal functor
$S\in \mathsf{Aff}$
, a monoidal functor
 $\mathbb{A}(S)\rightarrow \mathbb{B}(S)$
;
$\mathbb{A}(S)\rightarrow \mathbb{B}(S)$
;– for each
 $S\rightarrow T$
, an
$S\rightarrow T$
, an
 $(\mathbb{A}(S),\mathbb{A}(T))$
-linear functor (4.8)that induces an
$(\mathbb{A}(S),\mathbb{A}(T))$
-linear functor (4.8)that induces an $$\begin{eqnarray}\unicode[STIX]{x1D702}_{S\rightarrow T}:\mathbb{A}_{S\rightarrow T}\longrightarrow \mathbb{B}_{S\rightarrow T}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{S\rightarrow T}:\mathbb{A}_{S\rightarrow T}\longrightarrow \mathbb{B}_{S\rightarrow T}\end{eqnarray}$$
 $(\mathbb{A}(S),\mathbb{B}(T))$
-equivalence
$(\mathbb{A}(S),\mathbb{B}(T))$
-equivalence
 $\mathbb{A}_{S\rightarrow T}\otimes _{\mathbb{A}(T)}\mathbb{B}(T)\rightarrow \mathbb{B}_{S\rightarrow T}$
;
$\mathbb{A}_{S\rightarrow T}\otimes _{\mathbb{A}(T)}\mathbb{B}(T)\rightarrow \mathbb{B}_{S\rightarrow T}$
;– natural higher compatibilities with respect to strings of affine schemes.
These data give rise to a morphism
![]() $\mathbb{A}\rightarrow \mathbb{B}$
.
$\mathbb{A}\rightarrow \mathbb{B}$
.
4.4.2
It is easy to see that the morphism
![]() $\mathbb{Q}\rightarrow \mathbb{H}$
(defined on
$\mathbb{Q}\rightarrow \mathbb{H}$
(defined on
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
) falls under this rubric. Indeed, we just need to verify that the tautological
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
) falls under this rubric. Indeed, we just need to verify that the tautological
![]() $(\operatorname{QCoh}(S),\mathbb{H}(T))$
-linear functor
$(\operatorname{QCoh}(S),\mathbb{H}(T))$
-linear functor
is an equivalence, for any
![]() $S\rightarrow T$
in
$S\rightarrow T$
in
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
. This has been proven in [Reference BeraldoBer17b] in greater generality.
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
. This has been proven in [Reference BeraldoBer17b] in greater generality.
5 Coefficient systems: dualizability and base-change
As mentioned in the introduction, a coefficient system
![]() $\mathbb{A}:\mathsf{Aff}_{\text{type}}\longrightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
yields a functor
$\mathbb{A}:\mathsf{Aff}_{\text{type}}\longrightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
yields a functor
and then, by right Kan extension, a functor
where
![]() $\mathsf{Stk}_{\text{type}}$
denotes the
$\mathsf{Stk}_{\text{type}}$
denotes the
![]() $\infty$
-category of algebraic stacks with affine diagonal and with an atlas in
$\infty$
-category of algebraic stacks with affine diagonal and with an atlas in
![]() $\mathsf{Aff}_{\text{type}}$
.
$\mathsf{Aff}_{\text{type}}$
.
This is only half of what we need to accomplish though: it is not enough to just have pullbacks functors in
![]() $\mathsf{ShvCat}^{\mathbb{A}}$
, we want pushforwards too. To put it more formally, we wish to extend
$\mathsf{ShvCat}^{\mathbb{A}}$
, we want pushforwards too. To put it more formally, we wish to extend
![]() $\mathsf{ShvCat}^{\mathbb{A}}$
to a functor out of
$\mathsf{ShvCat}^{\mathbb{A}}$
to a functor out of
for an appropriate choice of vertical and horizontal arrows. In this section we examine this possibility for affine schemes. Actually, we will look for something stronger: we check under what conditions the coefficient system
![]() $\mathbb{A}$
itself admits an extension to a functor
$\mathbb{A}$
itself admits an extension to a functor
or even better to an
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
5.1 The Beck–Chevalley conditions
As we now explain, the (left or right) Beck–Chevalley conditions are conditions on a coefficient system
![]() $\mathbb{A}$
that automatically guarantee the existence of an
$\mathbb{A}$
that automatically guarantee the existence of an
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
![]() $\mathbb{A}^{\mathsf{Corr}}$
extending
$\mathbb{A}^{\mathsf{Corr}}$
extending
![]() $\mathbb{A}$
.
$\mathbb{A}$
.
5.1.1
We say that
![]() $\mathbb{A}$
satisfies the right Beck–Chevalley condition if the two requirements of §§ 5.1.2 and 5.1.5 are met.
$\mathbb{A}$
satisfies the right Beck–Chevalley condition if the two requirements of §§ 5.1.2 and 5.1.5 are met.
5.1.2 The first requirement
We ask that, for any arrow
![]() $S\rightarrow T$
in
$S\rightarrow T$
in
![]() $\mathsf{Aff}_{\text{type}}$
, the
$\mathsf{Aff}_{\text{type}}$
, the
![]() $(\mathbb{A}(S),\mathbb{A}(T))$
-bimodule
$(\mathbb{A}(S),\mathbb{A}(T))$
-bimodule
![]() $\mathbb{A}_{S\rightarrow T}$
be right dualizable; see § 2.1.2 for our conventions. Let us denote by
$\mathbb{A}_{S\rightarrow T}$
be right dualizable; see § 2.1.2 for our conventions. Let us denote by
![]() $\mathbb{A}_{T\leftarrow S}$
such right dual.
$\mathbb{A}_{T\leftarrow S}$
such right dual.
5.1.3
Assume now that
![]() $\mathbb{A}$
satisfies the above requirement, so that the bimodules
$\mathbb{A}$
satisfies the above requirement, so that the bimodules
![]() $\mathbb{A}_{?\leftarrow ?}$
are defined. Before formulating the second requirement, we need to fix some notation. For a commutative (but not necessarily cartesian) diagram
$\mathbb{A}_{?\leftarrow ?}$
are defined. Before formulating the second requirement, we need to fix some notation. For a commutative (but not necessarily cartesian) diagram

in
![]() $\mathsf{Aff}_{\text{type}}$
, define
$\mathsf{Aff}_{\text{type}}$
, define
Denote by
![]() $\mathit{u}\!\operatorname{ -}\!\text{type}$
the largest class of arrows in
$\mathit{u}\!\operatorname{ -}\!\text{type}$
the largest class of arrows in
![]() $\mathsf{Aff}_{\text{type}}$
that makes
$\mathsf{Aff}_{\text{type}}$
that makes
![]() $\mathsf{Corr}(\mathsf{Aff}_{\text{type}})_{\operatorname{all};\mathit{u}\!\operatorname{-}\!\text{type}}$
well defined.Footnote
7
Namely, an arrow
$\mathsf{Corr}(\mathsf{Aff}_{\text{type}})_{\operatorname{all};\mathit{u}\!\operatorname{-}\!\text{type}}$
well defined.Footnote
7
Namely, an arrow
![]() $S\rightarrow T$
in
$S\rightarrow T$
in
![]() $\mathsf{Aff}_{\text{type}}$
belongs to
$\mathsf{Aff}_{\text{type}}$
belongs to
![]() $\mathit{u}\!\operatorname{ -}\!\text{type}$
if, for any
$\mathit{u}\!\operatorname{ -}\!\text{type}$
if, for any
![]() $T^{\prime }\rightarrow T$
in
$T^{\prime }\rightarrow T$
in
![]() $\mathsf{Aff}_{\text{type}}$
, the scheme
$\mathsf{Aff}_{\text{type}}$
, the scheme
![]() $S\times _{T}T^{\prime }$
belongs to
$S\times _{T}T^{\prime }$
belongs to
![]() $\mathsf{Aff}_{\text{type}}$
.
$\mathsf{Aff}_{\text{type}}$
.
5.1.4
Consider a commutative diagram like (5.3). The resulting commutative diagram
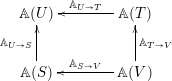
in
![]() $\mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
gives rise, by changing the vertical arrows with their right duals, to a lax commutative diagram
$\mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
gives rise, by changing the vertical arrows with their right duals, to a lax commutative diagram
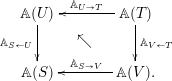
In other words, any commutative diagram (5.3) yields a canonical
![]() $(\mathbb{A}(S),\mathbb{A}(T))$
-linear functor
$(\mathbb{A}(S),\mathbb{A}(T))$
-linear functor
5.1.5 The second requirement
In particular, for
![]() $S\rightarrow V\in \mathit{u}\!\operatorname{ -}\!\text{type}$
and
$S\rightarrow V\in \mathit{u}\!\operatorname{ -}\!\text{type}$
and
![]() $T\rightarrow V$
arbitrary, we have
$T\rightarrow V$
arbitrary, we have
and we require that such functor be an equivalence.
5.1.6
Let us now explain what the right Beck–Chevalley condition is good for. Tautologically, if
![]() $\mathbb{A}$
satisfies the right Beck–Chevalley condition, the assignment
$\mathbb{A}$
satisfies the right Beck–Chevalley condition, the assignment
extends to a functor
Further, thanks to [Reference Gaitsgory and RozenblyumGR17, ch. V.1, Theorem 3.2.2], the latter automatically extends further to an
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
Thus, for
![]() $\mathbb{A}$
satisfying the right Beck–Chevalley condition, the corresponding sheaf theory
$\mathbb{A}$
satisfying the right Beck–Chevalley condition, the corresponding sheaf theory
![]() $\left.\mathsf{ShvCat}^{\mathbb{A}}\right|_{\mathsf{Aff}_{\text{type}}^{\operatorname{op}}}$
admits
$\left.\mathsf{ShvCat}^{\mathbb{A}}\right|_{\mathsf{Aff}_{\text{type}}^{\operatorname{op}}}$
admits
![]() $\ast$
-pushforwards (defined to be right adjoint to pullbacks). Moreover, these pushforwards satisfy base-change against pullbacks along the appropriate fibre squares.
$\ast$
-pushforwards (defined to be right adjoint to pullbacks). Moreover, these pushforwards satisfy base-change against pullbacks along the appropriate fibre squares.
5.1.7
The definition of left Beck–Chevalley condition for
![]() $\mathbb{A}$
is totally symmetric: each
$\mathbb{A}$
is totally symmetric: each
![]() $\mathbb{A}_{S\rightarrow T}$
must admit a left dual
$\mathbb{A}_{S\rightarrow T}$
must admit a left dual
![]() $\mathbb{A}_{T\leftarrow S}^{L}$
and, for any cartesian diagram (5.3) with
$\mathbb{A}_{T\leftarrow S}^{L}$
and, for any cartesian diagram (5.3) with
![]() $T\rightarrow V$
in
$T\rightarrow V$
in
![]() $\mathit{u}\!\operatorname{ -}\!\text{type}$
, the structure functor
$\mathit{u}\!\operatorname{ -}\!\text{type}$
, the structure functor
must be an equivalence. Thus, if
![]() $\mathbb{A}$
satisfies the left Beck–Chevalley condition, the sheaf theory
$\mathbb{A}$
satisfies the left Beck–Chevalley condition, the sheaf theory
![]() $\mathsf{ShvCat}^{\mathbb{A}}|_{\mathsf{Aff}_{\text{type}}^{\operatorname{op}}}$
admits
$\mathsf{ShvCat}^{\mathbb{A}}|_{\mathsf{Aff}_{\text{type}}^{\operatorname{op}}}$
admits
![]() $!$
-pushforwards (defined to be left adjoint to pullbacks), again, satisfying base-change against pullbacks along the appropriate fibre squares.
$!$
-pushforwards (defined to be left adjoint to pullbacks), again, satisfying base-change against pullbacks along the appropriate fibre squares.
5.1.8
A coefficient system
![]() $\mathbb{A}$
is said to be ambidextrous if it satisfies the right Beck–Chevalley condition and, for any
$\mathbb{A}$
is said to be ambidextrous if it satisfies the right Beck–Chevalley condition and, for any
![]() $S\rightarrow T\in \mathsf{Aff}_{\text{type}}$
, the
$S\rightarrow T\in \mathsf{Aff}_{\text{type}}$
, the
![]() $(\mathbb{A}(T),\mathbb{A}(S))$
-bimodule
$(\mathbb{A}(T),\mathbb{A}(S))$
-bimodule
![]() $\mathbb{A}_{S\rightarrow T}$
is ambidextrous (see § 2.1.2 for the definition). Any ambidextrous
$\mathbb{A}_{S\rightarrow T}$
is ambidextrous (see § 2.1.2 for the definition). Any ambidextrous
![]() $\mathbb{A}$
automatically satisfies the left Beck–Chevalley condition as well. Thus, for
$\mathbb{A}$
automatically satisfies the left Beck–Chevalley condition as well. Thus, for
![]() $\mathbb{A}$
ambidextrous, we obtain two extensions of
$\mathbb{A}$
ambidextrous, we obtain two extensions of
![]() $\mathbb{A}$
,
$\mathbb{A}$
,
that are exchanged by duality.
5.1.9
Let us spell out these pieces of structure in more detail. First, up to switching vertical and horizontal arrows in
![]() $\mathbb{A}^{\operatorname{R-BC}}$
(see Remark 3.3.3), the two
$\mathbb{A}^{\operatorname{R-BC}}$
(see Remark 3.3.3), the two
![]() $(\infty ,2)$
-functors
$(\infty ,2)$
-functors
![]() $\mathbb{A}^{\operatorname{R-BC}},\mathbb{A}^{\operatorname{L-BC}}$
have a common underlying
$\mathbb{A}^{\operatorname{R-BC}},\mathbb{A}^{\operatorname{L-BC}}$
have a common underlying
![]() $(\infty ,1)$
-functor
$(\infty ,1)$
-functor
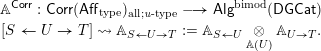 $$\begin{eqnarray}\displaystyle & \displaystyle \mathbb{A}^{\mathsf{Corr}}:\mathsf{Corr}(\mathsf{Aff}_{\text{type}})_{\operatorname{all};\mathit{u}\!\operatorname{-}\!\text{type}}\longrightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle [S\leftarrow U\rightarrow T]{\rightsquigarrow}\mathbb{A}_{S\leftarrow U\rightarrow T}:=\mathbb{A}_{S\leftarrow U}\underset{\mathbb{A}(U)}{\otimes }\mathbb{A}_{U\rightarrow T}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \mathbb{A}^{\mathsf{Corr}}:\mathsf{Corr}(\mathsf{Aff}_{\text{type}})_{\operatorname{all};\mathit{u}\!\operatorname{-}\!\text{type}}\longrightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat}) & \displaystyle \nonumber\\ \displaystyle & \displaystyle [S\leftarrow U\rightarrow T]{\rightsquigarrow}\mathbb{A}_{S\leftarrow U\rightarrow T}:=\mathbb{A}_{S\leftarrow U}\underset{\mathbb{A}(U)}{\otimes }\mathbb{A}_{U\rightarrow T}. & \displaystyle \nonumber\end{eqnarray}$$
Secondly, the two enhancements of
![]() $\mathbb{A}^{\mathsf{Corr}}$
to
$\mathbb{A}^{\mathsf{Corr}}$
to
![]() $\mathbb{A}^{\operatorname{L-BC}}$
and
$\mathbb{A}^{\operatorname{L-BC}}$
and
![]() $\mathbb{A}^{\operatorname{R-BC}}$
amount to the following data: for
$\mathbb{A}^{\operatorname{R-BC}}$
amount to the following data: for
![]() $U^{\prime }\rightarrow U$
of
$U^{\prime }\rightarrow U$
of
![]() $\mathit{u}\!\operatorname{ -}\!\text{type}$
over
$\mathit{u}\!\operatorname{ -}\!\text{type}$
over
![]() $S\times T$
, there are two mutually dual structure functors
$S\times T$
, there are two mutually dual structure functors
![]() $\mathbb{A}_{S\leftarrow U^{\prime }\rightarrow T}\rightleftarrows \mathbb{A}_{S\leftarrow U\rightarrow T}$
, compatible in
$\mathbb{A}_{S\leftarrow U^{\prime }\rightarrow T}\rightleftarrows \mathbb{A}_{S\leftarrow U\rightarrow T}$
, compatible in
![]() $U$
in the natural way. Such enhancements will be used in §§ 6.3.1 and 6.3.2 to construct the two kinds of pushforwards in the setting of
$U$
in the natural way. Such enhancements will be used in §§ 6.3.1 and 6.3.2 to construct the two kinds of pushforwards in the setting of
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
on stacks.
$\mathsf{ShvCat}^{\mathbb{H}}$
on stacks.
5.1.10 Easy examples
It is obvious that
![]() $\mathbb{Q}$
and
$\mathbb{Q}$
and
![]() $\mathbb{D}$
are ambidextrous. For instance, for the former,
$\mathbb{D}$
are ambidextrous. For instance, for the former,
is defined on
![]() $1$
-arrows by
$1$
-arrows by
![]() $\mathbb{Q}_{S\leftarrow U\rightarrow T}\simeq \operatorname{QCoh}(U)$
, the latter equipped with its obvious
$\mathbb{Q}_{S\leftarrow U\rightarrow T}\simeq \operatorname{QCoh}(U)$
, the latter equipped with its obvious
![]() $(\operatorname{QCoh}(S),\operatorname{QCoh}(T))$
-bimodule structure. The two mutually dual structure functors
$(\operatorname{QCoh}(S),\operatorname{QCoh}(T))$
-bimodule structure. The two mutually dual structure functors
![]() $\mathbb{Q}_{S\leftarrow U^{\prime }\rightarrow T}\rightleftarrows \mathbb{Q}_{S\leftarrow U\rightarrow T}$
are simply the pullback and pushforward functors along
$\mathbb{Q}_{S\leftarrow U^{\prime }\rightarrow T}\rightleftarrows \mathbb{Q}_{S\leftarrow U\rightarrow T}$
are simply the pullback and pushforward functors along
![]() $U^{\prime }\rightarrow U$
.
$U^{\prime }\rightarrow U$
.
We leave it as an exercise to show that the coefficient system
![]() $\mathbb{S}^{\prime }$
responsible for singular support is ambidextrous: it extends to a functor out of
$\mathbb{S}^{\prime }$
responsible for singular support is ambidextrous: it extends to a functor out of
![]() $\mathsf{Corr}(\mathsf{Aff}_{\text{q-smooth}})_{\operatorname{all};\text{smooth}}^{\text{smooth}}$
.
$\mathsf{Corr}(\mathsf{Aff}_{\text{q-smooth}})_{\operatorname{all};\text{smooth}}^{\text{smooth}}$
.
5.1.11
Let us now turn to
![]() $\mathbb{I}^{\wedge }$
. We have the following result, which will later help us understand base-change for
$\mathbb{I}^{\wedge }$
. We have the following result, which will later help us understand base-change for
![]() $\mathbb{H}$
.
$\mathbb{H}$
.
Proposition 5.1.12. The functor
![]() $\mathbb{I}^{\wedge }:\mathsf{Sch}_{\text{aft}}\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
satisfies the right Beck–Chevalley condition, so that it extends to an
$\mathbb{I}^{\wedge }:\mathsf{Sch}_{\text{aft}}\rightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
satisfies the right Beck–Chevalley condition, so that it extends to an
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
Proof. We start by setting up some notation. For
![]() $X\rightarrow Y$
in
$X\rightarrow Y$
in
![]() $\mathsf{Sch}_{\text{aft}}$
, consider the maps
$\mathsf{Sch}_{\text{aft}}$
, consider the maps
where
![]() $\unicode[STIX]{x1D701}$
is induced by
$\unicode[STIX]{x1D701}$
is induced by
![]() $\unicode[STIX]{x1D6E5}_{X/Y}:X\rightarrow X\times _{Y}X$
. With the help of Lemma 4.2.1, one can easily check that the functors
$\unicode[STIX]{x1D6E5}_{X/Y}:X\rightarrow X\times _{Y}X$
. With the help of Lemma 4.2.1, one can easily check that the functors
exhibit
![]() $\mathbb{I}_{Y\leftarrow X}^{\wedge }:=\operatorname{IndCoh}(Y\times _{Y_{\operatorname{dR}}}X)$
as the right dual of the
$\mathbb{I}_{Y\leftarrow X}^{\wedge }:=\operatorname{IndCoh}(Y\times _{Y_{\operatorname{dR}}}X)$
as the right dual of the
![]() $(\mathbb{I}^{\wedge }(X),\mathbb{I}^{\wedge }(Y))$
-bimodule
$(\mathbb{I}^{\wedge }(X),\mathbb{I}^{\wedge }(Y))$
-bimodule
![]() $\mathbb{I}_{X\rightarrow Y}^{\wedge }$
.
$\mathbb{I}_{X\rightarrow Y}^{\wedge }$
.
Now let
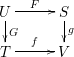
be a commutative square in
![]() $\mathsf{Sch}_{\text{aft}}$
. By Lemma 4.2.1, one easily gets equivalences
$\mathsf{Sch}_{\text{aft}}$
. By Lemma 4.2.1, one easily gets equivalences
compatible with the natural
![]() $(\mathbb{I}^{\wedge }(S),\mathbb{I}^{\wedge }(T))$
-bimodule structures on both sides. Further, the structure arrow induced by the right Beck–Chevalley condition
$(\mathbb{I}^{\wedge }(S),\mathbb{I}^{\wedge }(T))$
-bimodule structures on both sides. Further, the structure arrow induced by the right Beck–Chevalley condition
is the
![]() $!$
-pullback functor along the natural map
$!$
-pullback functor along the natural map
![]() $U_{\operatorname{dR}}\rightarrow (S\times _{V}T)_{\operatorname{dR}}$
, whence it is an equivalence whenever the square is nil-cartesian (i.e. cartesian at the level of reduced schemes).◻
$U_{\operatorname{dR}}\rightarrow (S\times _{V}T)_{\operatorname{dR}}$
, whence it is an equivalence whenever the square is nil-cartesian (i.e. cartesian at the level of reduced schemes).◻
Remark 5.1.13. The same argument with the functors
![]() $\unicode[STIX]{x1D701}_{\ast }^{\operatorname{IndCoh}}$
and
$\unicode[STIX]{x1D701}_{\ast }^{\operatorname{IndCoh}}$
and
![]() $\unicode[STIX]{x1D702}_{\ast }^{\operatorname{IndCoh}}$
shows that
$\unicode[STIX]{x1D702}_{\ast }^{\operatorname{IndCoh}}$
shows that
![]() $\mathbb{I}^{\wedge }$
satisfies the left Beck–Chevalley condition, too. It follows that
$\mathbb{I}^{\wedge }$
satisfies the left Beck–Chevalley condition, too. It follows that
![]() $\mathbb{I}^{\wedge }$
is ambidextrous.
$\mathbb{I}^{\wedge }$
is ambidextrous.
5.2 Base-change for
 $\mathbb{H}$
$\mathbb{H}$
The aim of this section is to show that
![]() $\mathbb{H}$
is ambidextrous (Theorem 5.2.10). After this is proven, we will summarize the important consequences of this result.
$\mathbb{H}$
is ambidextrous (Theorem 5.2.10). After this is proven, we will summarize the important consequences of this result.
5.2.1
Observe that, for any
![]() $S\in \mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, the monoidal category
$S\in \mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, the monoidal category
![]() $\mathbb{H}(S)$
is rigid and compactly generated. Recall now the definition of
$\mathbb{H}(S)$
is rigid and compactly generated. Recall now the definition of
![]() $1_{\mathbb{H}(S)}^{\text{fake}}\in \mathbb{H}(S)^{\ast }$
and the notion of very rigid monoidal category; see § 2.1.5.
$1_{\mathbb{H}(S)}^{\text{fake}}\in \mathbb{H}(S)^{\ast }$
and the notion of very rigid monoidal category; see § 2.1.5.
Proposition 5.2.2. For any
![]() $S\in \mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, the monoidal DG category
$S\in \mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, the monoidal DG category
![]() $\mathbb{H}(S)$
is very rigid.
$\mathbb{H}(S)$
is very rigid.
Proof. It suffices to show that
![]() $1_{\mathbb{H}(S)}^{\text{fake}}\in \mathbb{H}(S)^{\ast }$
admits a lift through the forgetful functor
$1_{\mathbb{H}(S)}^{\text{fake}}\in \mathbb{H}(S)^{\ast }$
admits a lift through the forgetful functor
Recall from [Reference BeraldoBer17b] that the functor
factors as the composition
where the DG category in the middle is by definition the Drinfeld centre of
![]() $\mathbb{H}(S)$
. A variation of the argument there shows that
$\mathbb{H}(S)$
. A variation of the argument there shows that
factors as the composition
Finally, one computes
![]() $1_{\mathbb{H}(S)}^{\text{fake}}\in \mathbb{H}(S)^{\ast }$
explicitly: it is readily checked that
$1_{\mathbb{H}(S)}^{\text{fake}}\in \mathbb{H}(S)^{\ast }$
explicitly: it is readily checked that
a fact that concludes the proof. ◻
5.2.3
Coupling this with Corollary 2.1.7, we obtain that each bimodule
![]() $\mathbb{H}_{S\rightarrow T}$
is ambidextrous: moreover, its left and right duals are canonically identified with
$\mathbb{H}_{S\rightarrow T}$
is ambidextrous: moreover, its left and right duals are canonically identified with
![]() $(\mathbb{H}_{S\rightarrow T})^{\ast }$
.
$(\mathbb{H}_{S\rightarrow T})^{\ast }$
.
Let us now determine the right dual to
![]() $\mathbb{H}_{S\rightarrow T}$
explicitly. By the above, we already know what the DG category underlying
$\mathbb{H}_{S\rightarrow T}$
explicitly. By the above, we already know what the DG category underlying
![]() $\mathbb{H}_{T\leftarrow S}:=(\mathbb{H}_{S\rightarrow T})^{R}$
must be: it is the dual of the DG category
$\mathbb{H}_{T\leftarrow S}:=(\mathbb{H}_{S\rightarrow T})^{R}$
must be: it is the dual of the DG category
![]() $\operatorname{IndCoh}_{0}((S\times T)_{S}^{\wedge })$
. The latter is self-dual as a plain DG category, so we are just searching for the correct
$\operatorname{IndCoh}_{0}((S\times T)_{S}^{\wedge })$
. The latter is self-dual as a plain DG category, so we are just searching for the correct
![]() $(\mathbb{H}(T),\mathbb{H}(S))$
-bimodule structure on
$(\mathbb{H}(T),\mathbb{H}(S))$
-bimodule structure on
![]() $\operatorname{IndCoh}_{0}((S\times T)_{S}^{\wedge })$
.
$\operatorname{IndCoh}_{0}((S\times T)_{S}^{\wedge })$
.
We claim that
![]() $\mathbb{H}_{T\leftarrow S}$
is equivalent to
$\mathbb{H}_{T\leftarrow S}$
is equivalent to
![]() $\operatorname{IndCoh}_{0}((T\times S)_{S}^{\wedge })$
, equipped with the obvious
$\operatorname{IndCoh}_{0}((T\times S)_{S}^{\wedge })$
, equipped with the obvious
![]() $(\mathbb{H}(T),\mathbb{H}(S))$
-bimodule structure. We will establish this fact directly, by constructing the evaluation and coevaluation that make
$(\mathbb{H}(T),\mathbb{H}(S))$
-bimodule structure. We will establish this fact directly, by constructing the evaluation and coevaluation that make
![]() $\operatorname{IndCoh}_{0}((T\times S)_{S}^{\wedge })$
right dual to
$\operatorname{IndCoh}_{0}((T\times S)_{S}^{\wedge })$
right dual to
![]() $\mathbb{H}_{S\rightarrow T}$
.
$\mathbb{H}_{S\rightarrow T}$
.
Lemma 5.2.4. For
![]() $S\rightarrow T$
a map in
$S\rightarrow T$
a map in
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, the natural functor
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, the natural functor
lands into the full subcategory
![]() $\mathbb{H}(S)\subseteq \mathbb{I}^{\wedge }(S)$
.
$\mathbb{H}(S)\subseteq \mathbb{I}^{\wedge }(S)$
.
Proof. We will use the commutative diagram
with cartesian square. The DG category
is generated by a single canonical compact object, which is sent by our functor to
![]() $\unicode[STIX]{x1D701}^{!}\circ \unicode[STIX]{x1D709}_{\ast }^{\operatorname{IndCoh}}(\unicode[STIX]{x1D714}_{S\times _{T}S})\in \mathbb{I}^{\wedge }(S)$
. Hence, it suffices to show that the object
$\unicode[STIX]{x1D701}^{!}\circ \unicode[STIX]{x1D709}_{\ast }^{\operatorname{IndCoh}}(\unicode[STIX]{x1D714}_{S\times _{T}S})\in \mathbb{I}^{\wedge }(S)$
. Hence, it suffices to show that the object
belongs to the image of
![]() $\unicode[STIX]{x1D6F6}_{S}:\operatorname{QCoh}(S){\hookrightarrow}\operatorname{IndCoh}(S)$
. This is clear:
$\unicode[STIX]{x1D6F6}_{S}:\operatorname{QCoh}(S){\hookrightarrow}\operatorname{IndCoh}(S)$
. This is clear:
![]() $\unicode[STIX]{x1D70B}_{\ast }^{\operatorname{IndCoh}}\unicode[STIX]{x1D70B}^{!}$
is equivalent as a functor to the universal envelope of the Lie algebroid
$\unicode[STIX]{x1D70B}_{\ast }^{\operatorname{IndCoh}}\unicode[STIX]{x1D70B}^{!}$
is equivalent as a functor to the universal envelope of the Lie algebroid
![]() $\mathbb{T}_{S/S\times T}\rightarrow \mathbb{T}_{S}$
, and by assumption
$\mathbb{T}_{S/S\times T}\rightarrow \mathbb{T}_{S}$
, and by assumption
![]() $\mathbb{T}_{S/S\times T}$
belongs to
$\mathbb{T}_{S/S\times T}$
belongs to
![]() $\unicode[STIX]{x1D6F6}_{S}(\mathsf{Perf}(S))$
. We conclude as in [Reference Arinkin and GaitsgoryAG18, Proposition 3.2.3].◻
$\unicode[STIX]{x1D6F6}_{S}(\mathsf{Perf}(S))$
. We conclude as in [Reference Arinkin and GaitsgoryAG18, Proposition 3.2.3].◻
5.2.5
Hence, we have constructed an
![]() $(\mathbb{H}(S),\mathbb{H}(S))$
-linear functor
$(\mathbb{H}(S),\mathbb{H}(S))$
-linear functor
which will be our evaluation. To construct the coevaluation, we need another lemma.
Lemma 5.2.6. For a diagram
![]() $S\leftarrow U\rightarrow T$
in
$S\leftarrow U\rightarrow T$
in
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, the functor
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, the functor
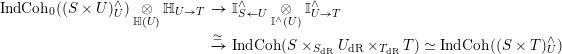 $$\begin{eqnarray}\displaystyle \operatorname{IndCoh}_{0}((S\times U)_{U}^{\wedge })\underset{\mathbb{H}(U)}{\otimes }\mathbb{H}_{U\rightarrow T} & \rightarrow & \displaystyle \mathbb{I}_{S\leftarrow U}^{\wedge }\underset{\mathbb{I}^{\wedge }(U)}{\otimes }\mathbb{I}_{U\rightarrow T}^{\wedge }\nonumber\\ \displaystyle & \xrightarrow[{}]{\simeq } & \displaystyle \operatorname{IndCoh}(S\times _{S_{\operatorname{dR}}}U_{\operatorname{dR}}\times _{T_{\operatorname{dR}}}T)\simeq \operatorname{IndCoh}((S\times T)_{U}^{\wedge })\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{IndCoh}_{0}((S\times U)_{U}^{\wedge })\underset{\mathbb{H}(U)}{\otimes }\mathbb{H}_{U\rightarrow T} & \rightarrow & \displaystyle \mathbb{I}_{S\leftarrow U}^{\wedge }\underset{\mathbb{I}^{\wedge }(U)}{\otimes }\mathbb{I}_{U\rightarrow T}^{\wedge }\nonumber\\ \displaystyle & \xrightarrow[{}]{\simeq } & \displaystyle \operatorname{IndCoh}(S\times _{S_{\operatorname{dR}}}U_{\operatorname{dR}}\times _{T_{\operatorname{dR}}}T)\simeq \operatorname{IndCoh}((S\times T)_{U}^{\wedge })\nonumber\end{eqnarray}$$
is an equivalence onto the subcategory
![]() $\operatorname{IndCoh}_{0}((S\times T)_{U}^{\wedge })\subseteq \operatorname{IndCoh}((S\times T)_{U}^{\wedge })$
.
$\operatorname{IndCoh}_{0}((S\times T)_{U}^{\wedge })\subseteq \operatorname{IndCoh}((S\times T)_{U}^{\wedge })$
.
Proof. Denote by
![]() $\unicode[STIX]{x1D719}:U\rightarrow S\times T$
and by
$\unicode[STIX]{x1D719}:U\rightarrow S\times T$
and by
![]() $^{\prime }\unicode[STIX]{x1D719}:U\rightarrow (S\times T)_{U}^{\wedge }$
the obvious maps. The source DG category is compactly generated by a single canonical object. Base-change along the pullback square
$^{\prime }\unicode[STIX]{x1D719}:U\rightarrow (S\times T)_{U}^{\wedge }$
the obvious maps. The source DG category is compactly generated by a single canonical object. Base-change along the pullback square
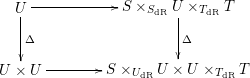
shows that such object is sent to
![]() $^{\prime }\unicode[STIX]{x1D719}_{\ast }^{\operatorname{IndCoh}}(\unicode[STIX]{x1D714}_{U})\in \operatorname{IndCoh}((S\times T)_{U}^{\wedge })$
, which is a compact generator of
$^{\prime }\unicode[STIX]{x1D719}_{\ast }^{\operatorname{IndCoh}}(\unicode[STIX]{x1D714}_{U})\in \operatorname{IndCoh}((S\times T)_{U}^{\wedge })$
, which is a compact generator of
![]() $\operatorname{IndCoh}_{0}((S\times T)_{U}^{\wedge })$
. All that remains is to show that the functor
$\operatorname{IndCoh}_{0}((S\times T)_{U}^{\wedge })$
. All that remains is to show that the functor
is fully faithful. This is evident: the functor in question arises as the composition
where the second arrow is an equivalence thanks to Corollary 4.3.3. ◻
5.2.7
We now use
![]() $\unicode[STIX]{x1D702}^{!}:\operatorname{IndCoh}((T\times T)_{T}^{\wedge })\longrightarrow \operatorname{IndCoh}((T\times T)_{S}^{\wedge })$
as in (5.8), together with the equivalence
$\unicode[STIX]{x1D702}^{!}:\operatorname{IndCoh}((T\times T)_{T}^{\wedge })\longrightarrow \operatorname{IndCoh}((T\times T)_{S}^{\wedge })$
as in (5.8), together with the equivalence
of the above lemma, to construct the functor
As the next proposition shows, this is the coevaluation we were looking for.
Proposition 5.2.8. Let
![]() $f:S\rightarrow T$
be a map in
$f:S\rightarrow T$
be a map in
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
. Then the functors (5.10) and (5.11) exhibit
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
. Then the functors (5.10) and (5.11) exhibit
![]() $\operatorname{IndCoh}_{0}((T\times S)_{S}^{\wedge })$
, with its natural
$\operatorname{IndCoh}_{0}((T\times S)_{S}^{\wedge })$
, with its natural
![]() $(\mathbb{H}(T),\mathbb{H}(S))$
-bimodule structure, as the right dual of
$(\mathbb{H}(T),\mathbb{H}(S))$
-bimodule structure, as the right dual of
![]() $\mathbb{H}_{S\rightarrow T}$
.
$\mathbb{H}_{S\rightarrow T}$
.
Proof. This follows formally from the analogous statement for
![]() $\mathbb{I}_{S\rightarrow T}^{\wedge }$
.◻
$\mathbb{I}_{S\rightarrow T}^{\wedge }$
.◻
5.2.9
Henceforth, we will freely use the
![]() $(\mathbb{H}(T),\mathbb{H}(S))$
-linear equivalence
$(\mathbb{H}(T),\mathbb{H}(S))$
-linear equivalence
![]() $\mathbb{H}_{T\leftarrow S}\simeq \operatorname{IndCoh}_{0}((T\times S)_{S}^{\wedge })$
. We are finally ready to settle the ambidexterity of the coefficient system
$\mathbb{H}_{T\leftarrow S}\simeq \operatorname{IndCoh}_{0}((T\times S)_{S}^{\wedge })$
. We are finally ready to settle the ambidexterity of the coefficient system
![]() $\mathbb{H}$
.
$\mathbb{H}$
.
Theorem 5.2.10. The coefficient system
![]() $\mathbb{H}:\mathsf{Aff}_{\text{lfp}}^{{<}\infty }\longrightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
is ambidextrous.
$\mathbb{H}:\mathsf{Aff}_{\text{lfp}}^{{<}\infty }\longrightarrow \mathsf{Alg}^{\text{bimod}}(\mathsf{DGCat})$
is ambidextrous.
Half of the proof of this theorem has been done in Lemma 5.2.6. All that remains is to add the following statement.
Lemma 5.2.11. Let
![]() $S\rightarrow V\leftarrow T$
be a diagram in
$S\rightarrow V\leftarrow T$
be a diagram in
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, with either
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, with either
![]() $S\rightarrow V$
or
$S\rightarrow V$
or
![]() $T\rightarrow V$
bounded.Footnote
8
Then the functor
$T\rightarrow V$
bounded.Footnote
8
Then the functor
is an equivalence onto the subcategory
Proof. Let
![]() $\unicode[STIX]{x1D709}:S\times _{V}T\rightarrow (S\times T)_{S\times _{V}T}^{\wedge }\simeq S\times _{V_{\operatorname{dR}}}T$
be the canonical map. As before,
$\unicode[STIX]{x1D709}:S\times _{V}T\rightarrow (S\times T)_{S\times _{V}T}^{\wedge }\simeq S\times _{V_{\operatorname{dR}}}T$
be the canonical map. As before,
![]() $\mathbb{H}_{S\rightarrow V}\underset{\mathbb{H}(V)}{\otimes }\mathbb{H}_{V\leftarrow T}$
is compactly generated by its canonical object. Now, the functor in question sends such object to
$\mathbb{H}_{S\rightarrow V}\underset{\mathbb{H}(V)}{\otimes }\mathbb{H}_{V\leftarrow T}$
is compactly generated by its canonical object. Now, the functor in question sends such object to
![]() $\unicode[STIX]{x1D709}_{\ast }^{\operatorname{IndCoh}}(\unicode[STIX]{x1D714}_{S\times _{V}T})$
, which is a compact generator of
$\unicode[STIX]{x1D709}_{\ast }^{\operatorname{IndCoh}}(\unicode[STIX]{x1D714}_{S\times _{V}T})$
, which is a compact generator of
![]() $\operatorname{IndCoh}_{0}((S\times T)_{S\times _{V}T}^{\wedge })$
. Hence, all that remains is to verify that the functor
$\operatorname{IndCoh}_{0}((S\times T)_{S\times _{V}T}^{\wedge })$
. Hence, all that remains is to verify that the functor
is fully faithful. Assume that
![]() $S\rightarrow V$
is bounded; the argument for the other case is symmetric. We have the following sequence of left
$S\rightarrow V$
is bounded; the argument for the other case is symmetric. We have the following sequence of left
![]() $\operatorname{QCoh}(S)$
-linear fully faithful functors:
$\operatorname{QCoh}(S)$
-linear fully faithful functors:
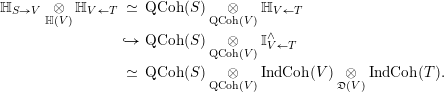 $$\begin{eqnarray}\displaystyle \mathbb{H}_{S\rightarrow V}\underset{\mathbb{H}(V)}{\otimes }\mathbb{H}_{V\leftarrow T} & \simeq & \displaystyle \operatorname{QCoh}(S)\underset{\operatorname{QCoh}(V)}{\otimes }\mathbb{H}_{V\leftarrow T}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \operatorname{QCoh}(S)\underset{\operatorname{QCoh}(V)}{\otimes }\mathbb{I}_{V\leftarrow T}^{\wedge }\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{QCoh}(S)\underset{\operatorname{QCoh}(V)}{\otimes }\operatorname{IndCoh}(V)\underset{\mathfrak{D}(V)}{\otimes }\operatorname{IndCoh}(T).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{H}_{S\rightarrow V}\underset{\mathbb{H}(V)}{\otimes }\mathbb{H}_{V\leftarrow T} & \simeq & \displaystyle \operatorname{QCoh}(S)\underset{\operatorname{QCoh}(V)}{\otimes }\mathbb{H}_{V\leftarrow T}\nonumber\\ \displaystyle & {\hookrightarrow} & \displaystyle \operatorname{QCoh}(S)\underset{\operatorname{QCoh}(V)}{\otimes }\mathbb{I}_{V\leftarrow T}^{\wedge }\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{QCoh}(S)\underset{\operatorname{QCoh}(V)}{\otimes }\operatorname{IndCoh}(V)\underset{\mathfrak{D}(V)}{\otimes }\operatorname{IndCoh}(T).\nonumber\end{eqnarray}$$
To conclude, recall [Reference GaitsgoryGai13, Proposition 4.4.2] that the tautological functor
![]() $\operatorname{QCoh}(S)\otimes _{\operatorname{QCoh}(V)}\operatorname{IndCoh}(V)\rightarrow \operatorname{IndCoh}(S)$
is fully faithful whenever
$\operatorname{QCoh}(S)\otimes _{\operatorname{QCoh}(V)}\operatorname{IndCoh}(V)\rightarrow \operatorname{IndCoh}(S)$
is fully faithful whenever
![]() $S\rightarrow V$
is bounded.◻
$S\rightarrow V$
is bounded.◻
5.2.12
Following the template of § 5.1.9, let us summarize the consequences of the ambidexterity of
![]() $\mathbb{H}$
. First, we obtain that
$\mathbb{H}$
. First, we obtain that
![]() $\mathbb{H}$
extends to a functor
$\mathbb{H}$
extends to a functor
which has been shown to send
In other words,
![]() $\mathbb{H}^{\mathsf{Corr}}$
coincides with the restriction of
$\mathbb{H}^{\mathsf{Corr}}$
coincides with the restriction of
![]() $\mathbb{H}^{\text{geom}}$
on
$\mathbb{H}^{\text{geom}}$
on
![]() $\mathsf{Corr}(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{\operatorname{all};\text{bdd}}$
. Therefore, we have the following result.
$\mathsf{Corr}(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{\operatorname{all};\text{bdd}}$
. Therefore, we have the following result.
Corollary 5.2.13. The lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
![]() $\mathbb{H}^{\text{geom}}$
is strict when restricted to
$\mathbb{H}^{\text{geom}}$
is strict when restricted to
![]() $\mathsf{Corr}(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{\operatorname{all};\text{bdd}}$
.
$\mathsf{Corr}(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{\operatorname{all};\text{bdd}}$
.
5.2.14
Secondly,
![]() $\mathbb{H}^{\mathsf{Corr}}$
admits two extensions to
$\mathbb{H}^{\mathsf{Corr}}$
admits two extensions to
![]() $(\infty ,2)$
-functors,
$(\infty ,2)$
-functors,
and
described as follows. To a
![]() $2$
-morphism
$2$
-morphism
induced by
![]() $U^{\prime }\rightarrow U$
bounded,
$U^{\prime }\rightarrow U$
bounded,
![]() $\mathbb{H}^{\operatorname{R-BC}}$
assigns the
$\mathbb{H}^{\operatorname{R-BC}}$
assigns the
![]() $!$
-pullback
$!$
-pullback
while the
![]() $\mathbb{H}^{\operatorname{L-BC}}$
assigns the dual
$\mathbb{H}^{\operatorname{L-BC}}$
assigns the dual
![]() $(\ast ,0)$
-pushforward
$(\ast ,0)$
-pushforward
which is well defined thanks to boundedness; see Theorem 3.1.6.
6 Sheaves of categories relative to
 $\mathbb{H}$
$\mathbb{H}$
The coefficient system
![]() $\mathbb{H}$
allows us to define the
$\mathbb{H}$
allows us to define the
![]() $\infty$
-category
$\infty$
-category
![]() $\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{X}})$
, for any prestack
$\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{X}})$
, for any prestack
![]() ${\mathcal{X}}\in \mathsf{Fun}((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })^{\operatorname{op}},\mathsf{Grpd}_{\infty })$
. As we are only interested in studying
${\mathcal{X}}\in \mathsf{Fun}((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })^{\operatorname{op}},\mathsf{Grpd}_{\infty })$
. As we are only interested in studying
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
on algebraic stacks, we only consider the functor
$\mathsf{ShvCat}^{\mathbb{H}}$
on algebraic stacks, we only consider the functor
where
![]() $\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
consists of those bounded algebraic stacks that have affine diagonal and perfect cotangent complex.
$\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
consists of those bounded algebraic stacks that have affine diagonal and perfect cotangent complex.
In this section we explain several constructions regarding
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
, which we then use to prove our main theorems. We first show that
$\mathsf{ShvCat}^{\mathbb{H}}$
, which we then use to prove our main theorems. We first show that
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
satisfies smooth descent. Secondly, we discuss pushforwards and base-change as follows: by Theorem 5.2.10,
$\mathsf{ShvCat}^{\mathbb{H}}$
satisfies smooth descent. Secondly, we discuss pushforwards and base-change as follows: by Theorem 5.2.10,
![]() $\mathbb{H}$
is ambidextrous; accordingly,
$\mathbb{H}$
is ambidextrous; accordingly,
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
will admit extensions to categories of correspondences in two mutually dual ways. Next, we discuss the notion of
$\mathsf{ShvCat}^{\mathbb{H}}$
will admit extensions to categories of correspondences in two mutually dual ways. Next, we discuss the notion of
![]() $\mathbb{H}$
-affineness of objects of
$\mathbb{H}$
-affineness of objects of
![]() $\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
: we show that
$\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
: we show that
![]() $\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
is the
$\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
is the
![]() $\infty$
-category of modules over the monoidal DG category
$\infty$
-category of modules over the monoidal DG category
![]() $\mathbb{H}^{\text{geom}}({\mathcal{Y}})$
. Finally, we deduce that the lax
$\mathbb{H}^{\text{geom}}({\mathcal{Y}})$
. Finally, we deduce that the lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
![]() $\mathbb{H}^{\text{geom}}$
is actually strict.
$\mathbb{H}^{\text{geom}}$
is actually strict.
6.1 Descent
Define
to be the right Kan extension of
along the inclusion
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }{\hookrightarrow}\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
. The purpose of this section is to show that the functor
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }{\hookrightarrow}\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
. The purpose of this section is to show that the functor
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
satisfies smooth descent.
$\mathsf{ShvCat}^{\mathbb{H}}$
satisfies smooth descent.
6.1.1
Objects of
will be often represented simply by
![]() ${\mathcal{C}}\simeq \{{{\mathcal{C}}_{S}\}}_{S\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}}}}$
, leaving the coherent system of compatibilities
${\mathcal{C}}\simeq \{{{\mathcal{C}}_{S}\}}_{S\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}}}}$
, leaving the coherent system of compatibilities
![]() $\mathbb{H}_{S\rightarrow T}\otimes _{\mathbb{H}(T)}{\mathcal{C}}_{T}\simeq {\mathcal{C}}_{S}$
implicit. For any
$\mathbb{H}_{S\rightarrow T}\otimes _{\mathbb{H}(T)}{\mathcal{C}}_{T}\simeq {\mathcal{C}}_{S}$
implicit. For any
![]() $f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
in
$f:{\mathcal{X}}\rightarrow {\mathcal{Y}}$
in
![]() $\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, denote by
$\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, denote by
![]() $f^{\ast ,\mathbb{H}}$
the structure functor. Explicitly (and tautologically),
$f^{\ast ,\mathbb{H}}$
the structure functor. Explicitly (and tautologically),
![]() $f^{\ast ,\mathbb{H}}$
sends
$f^{\ast ,\mathbb{H}}$
sends
In what follows, elements of
![]() $S\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}}}$
will be denoted by
$S\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}}}$
will be denoted by
![]() $\unicode[STIX]{x1D719}_{S\rightarrow {\mathcal{Y}}}:S\rightarrow {\mathcal{Y}}$
. It is obvious that
$\unicode[STIX]{x1D719}_{S\rightarrow {\mathcal{Y}}}:S\rightarrow {\mathcal{Y}}$
. It is obvious that
![]() $(\unicode[STIX]{x1D719}_{S\rightarrow {\mathcal{Y}}})^{\ast ,\mathbb{H}}({\mathcal{C}})={\mathcal{C}}_{S}$
.
$(\unicode[STIX]{x1D719}_{S\rightarrow {\mathcal{Y}}})^{\ast ,\mathbb{H}}({\mathcal{C}})={\mathcal{C}}_{S}$
.
Theorem 6.1.2. The functor
![]() $\mathsf{ShvCat}^{\mathbb{H}}:(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })^{\operatorname{op}}\rightarrow \mathsf{Cat}_{\infty }$
satisfies smooth descent. In particular, for any
$\mathsf{ShvCat}^{\mathbb{H}}:(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })^{\operatorname{op}}\rightarrow \mathsf{Cat}_{\infty }$
satisfies smooth descent. In particular, for any
![]() ${\mathcal{Y}}$
, the restriction functor
${\mathcal{Y}}$
, the restriction functor
is an equivalence. Here,
![]() $(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}}$
is the subcategory of
$(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}}$
is the subcategory of
![]() $(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}}}$
whose objects are smooth maps
$(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}}}$
whose objects are smooth maps
![]() $S\rightarrow {\mathcal{Y}}$
and whose morphisms are triangles
$S\rightarrow {\mathcal{Y}}$
and whose morphisms are triangles
![]() $S\rightarrow T\rightarrow {\mathcal{Y}}$
with all maps smooth.
$S\rightarrow T\rightarrow {\mathcal{Y}}$
with all maps smooth.
6.1.3
We will need a few preliminary results that will be stated and proven after having fixed some notation.
Let
![]() $\unicode[STIX]{x1D719}:U\rightarrow S$
be a smooth cover in
$\unicode[STIX]{x1D719}:U\rightarrow S$
be a smooth cover in
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
and let
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
and let
![]() $U_{\bullet }$
be its associated Čech simplicial scheme. For any arrow
$U_{\bullet }$
be its associated Čech simplicial scheme. For any arrow
![]() $[m]\rightarrow [n]$
in
$[m]\rightarrow [n]$
in
![]() $\unicode[STIX]{x1D71F}^{\operatorname{op}}$
, denote by
$\unicode[STIX]{x1D71F}^{\operatorname{op}}$
, denote by
![]() $\unicode[STIX]{x1D719}_{[m]\rightarrow [n]}:U_{m}\rightarrow U_{n}$
and
$\unicode[STIX]{x1D719}_{[m]\rightarrow [n]}:U_{m}\rightarrow U_{n}$
and
![]() $\unicode[STIX]{x1D719}_{n}:U_{n}\rightarrow S$
the induced (smooth) maps.
$\unicode[STIX]{x1D719}_{n}:U_{n}\rightarrow S$
the induced (smooth) maps.
Now let
![]() ${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
be a stack under
${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
be a stack under
![]() $S$
. The above maps induce functors
$S$
. The above maps induce functors
We obtain a functor
Lemma 6.1.4. The functor (6.1) is an equivalence.
Proof. Denote by
the colimit category appearing in the left-hand side of (6.1). We will proceed in several steps.
Step 1. We need to introduce an auxiliary category. Denote by
![]() $(\unicode[STIX]{x1D6F7}_{n})^{?}$
and
$(\unicode[STIX]{x1D6F7}_{n})^{?}$
and
![]() $(\unicode[STIX]{x1D6F7}_{[m]\rightarrow [n]})^{?}$
the possibly discontinuous right adjoints to
$(\unicode[STIX]{x1D6F7}_{[m]\rightarrow [n]})^{?}$
the possibly discontinuous right adjoints to
![]() $(\unicode[STIX]{x1D6F7}_{n})_{\ast ,0}$
and
$(\unicode[STIX]{x1D6F7}_{n})_{\ast ,0}$
and
![]() $(\unicode[STIX]{x1D6F7}_{[m]\rightarrow [n]})_{\ast ,0}$
. Consider the cosimplicial DG category
$(\unicode[STIX]{x1D6F7}_{[m]\rightarrow [n]})_{\ast ,0}$
. Consider the cosimplicial DG category
and define
![]() $\operatorname{IndCoh}_{0}({\mathcal{Y}}_{S}^{\wedge })^{[U,?]}$
to be its totalization. Of course,
$\operatorname{IndCoh}_{0}({\mathcal{Y}}_{S}^{\wedge })^{[U,?]}$
to be its totalization. Of course,
via the usual limit–colimit procedure. However, the former interpretation allows us to write
![]() $\unicode[STIX]{x1D700}^{R}$
as the functor
$\unicode[STIX]{x1D700}^{R}$
as the functor
given by the limit of the
![]() $(\unicode[STIX]{x1D6F7}_{n})^{?}$
.
$(\unicode[STIX]{x1D6F7}_{n})^{?}$
.
Step 2. We will prove the lemma by showing that
![]() $\unicode[STIX]{x1D700}^{R}$
is an equivalence. By a standard argument, it suffices to check two facts:
$\unicode[STIX]{x1D700}^{R}$
is an equivalence. By a standard argument, it suffices to check two facts:
– the (discontinuous) forgetful functor
is monadic; $$\begin{eqnarray}(\unicode[STIX]{x1D6F7}_{0})^{?}:\operatorname{IndCoh}_{0}({\mathcal{Y}}_{S}^{\wedge })^{[U,?]}\longrightarrow \operatorname{IndCoh}_{0}({\mathcal{Y}}_{U}^{\wedge })\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D6F7}_{0})^{?}:\operatorname{IndCoh}_{0}({\mathcal{Y}}_{S}^{\wedge })^{[U,?]}\longrightarrow \operatorname{IndCoh}_{0}({\mathcal{Y}}_{U}^{\wedge })\end{eqnarray}$$
– the cosimplicial category (6.2) satisfies the monadic Beck–Chevalley condition.
Step 3. In this step, we will prove the first item above. To this end, we define
where
![]() $(\unicode[STIX]{x1D719}_{[m]\rightarrow [n]})^{?}$
is the discontinuous right adjoint to
$(\unicode[STIX]{x1D719}_{[m]\rightarrow [n]})^{?}$
is the discontinuous right adjoint to
![]() $(\unicode[STIX]{x1D719}_{[m]\rightarrow [n]})_{\ast }$
. It is easy to see that there is a commutative square
$(\unicode[STIX]{x1D719}_{[m]\rightarrow [n]})_{\ast }$
. It is easy to see that there is a commutative square
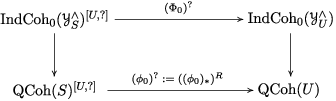
where the vertical arrows are the structure (conservative) functors induced by the morphism
![]() $\mathbb{Q}\rightarrow \mathbb{H}$
. Hence, it suffices to show that the bottom horizontal arrow is monadic, and the latter has been established in [Reference GaitsgoryGai15b, § 8.1].
$\mathbb{Q}\rightarrow \mathbb{H}$
. Hence, it suffices to show that the bottom horizontal arrow is monadic, and the latter has been established in [Reference GaitsgoryGai15b, § 8.1].
Step 4. All that remains is to verify the second item of Step 2 above. This is a particular case of the lemma below. ◻
Lemma 6.1.5. Consider a diagram
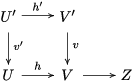
in
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, where the square is cartesian with all maps smooth. We do not require that
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, where the square is cartesian with all maps smooth. We do not require that
![]() $V\rightarrow Z$
be smooth. Then the natural lax commutative diagram
$V\rightarrow Z$
be smooth. Then the natural lax commutative diagram
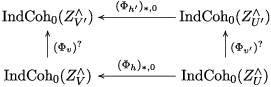
is commutative.Footnote 9
Proof. We proceed in steps here as well.
Step 1. For
![]() $f:X\rightarrow V$
a map in
$f:X\rightarrow V$
a map in
![]() $\mathsf{Sch}_{\text{aft}}$
, denote the induced functor by
$\mathsf{Sch}_{\text{aft}}$
, denote the induced functor by
![]() $\unicode[STIX]{x1D6F7}_{f}:Z_{X}^{\wedge }\rightarrow Z_{V}^{\wedge }$
. Recall the equivalence
$\unicode[STIX]{x1D6F7}_{f}:Z_{X}^{\wedge }\rightarrow Z_{V}^{\wedge }$
. Recall the equivalence
given by exterior tensor product (Lemma 4.2.1). One immediately checks that, under such equivalence,
![]() $(\unicode[STIX]{x1D6F7}_{f})_{\ast }^{\operatorname{IndCoh}}$
goes over to the functor
$(\unicode[STIX]{x1D6F7}_{f})_{\ast }^{\operatorname{IndCoh}}$
goes over to the functor
Thus, whenever
![]() $f$
is smooth,
$f$
is smooth,
![]() $(\unicode[STIX]{x1D6F7}_{f})_{\ast }^{\operatorname{IndCoh}}$
admits a left adjoint which we denote by
$(\unicode[STIX]{x1D6F7}_{f})_{\ast }^{\operatorname{IndCoh}}$
admits a left adjoint which we denote by
![]() $(\unicode[STIX]{x1D6F7}_{f})^{\ast ,\operatorname{IndCoh}}$
; this is obtained from the
$(\unicode[STIX]{x1D6F7}_{f})^{\ast ,\operatorname{IndCoh}}$
; this is obtained from the
![]() $\mathfrak{D}$
-module
$\mathfrak{D}$
-module
![]() $\ast$
-pullback
$\ast$
-pullback
![]() $f^{\ast ,\operatorname{dR}}\simeq f^{!,\operatorname{dR}}[-2\dim _{f}]$
by tensoring up. Hence, for
$f^{\ast ,\operatorname{dR}}\simeq f^{!,\operatorname{dR}}[-2\dim _{f}]$
by tensoring up. Hence, for
![]() $f$
smooth, we have an equivalence
$f$
smooth, we have an equivalence
Step 2. Applying the above to
![]() $h$
and
$h$
and
![]() $h^{\prime }$
, we see that the functors
$h^{\prime }$
, we see that the functors
![]() $(\unicode[STIX]{x1D6F7}_{h})^{\ast ,\operatorname{IndCoh}}$
and
$(\unicode[STIX]{x1D6F7}_{h})^{\ast ,\operatorname{IndCoh}}$
and
![]() $(\unicode[STIX]{x1D6F7}_{h^{\prime }})^{\ast ,\operatorname{IndCoh}}$
preserve the
$(\unicode[STIX]{x1D6F7}_{h^{\prime }})^{\ast ,\operatorname{IndCoh}}$
preserve the
![]() $\operatorname{IndCoh}_{0}$
-subcategories. We thus have a diagram
$\operatorname{IndCoh}_{0}$
-subcategories. We thus have a diagram
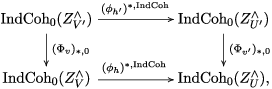
which is immediately seen to be commutative thanks to (6.5) and base-change for
![]() $\operatorname{IndCoh}_{0}$
.
$\operatorname{IndCoh}_{0}$
.
Step 3. We leave it to the reader to check that the horizontal arrows in the commutative diagram (6.6) are left adjoint to the horizontal arrows of (6.3). Hence, we obtain the desired assertion by passing to the diagram right adjoint to (6.6). ◻
6.1.6
Let us finally prove Theorem 6.1.2.
Proof of Theorem 6.1.2.
It suffices to prove that the functor
![]() $\mathsf{ShvCat}^{\mathbb{H}}:(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })^{\operatorname{op}}\rightarrow \mathsf{Cat}_{\infty }$
satisfies smooth descent. For
$\mathsf{ShvCat}^{\mathbb{H}}:(\mathsf{Aff}_{\text{lfp}}^{{<}\infty })^{\operatorname{op}}\rightarrow \mathsf{Cat}_{\infty }$
satisfies smooth descent. For
![]() $S\in \mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, let
$S\in \mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, let
![]() $f:U\rightarrow S$
be a smooth cover and
$f:U\rightarrow S$
be a smooth cover and
![]() $U_{\bullet }$
the corresponding Čech resolution. Denote by
$U_{\bullet }$
the corresponding Čech resolution. Denote by
![]() $f_{n}:U_{n}\rightarrow S$
the structure maps. We are to show that the natural functor
$f_{n}:U_{n}\rightarrow S$
the structure maps. We are to show that the natural functor
is an equivalence.
Note that
![]() $\unicode[STIX]{x1D6FC}$
admits a left adjoint,
$\unicode[STIX]{x1D6FC}$
admits a left adjoint,
![]() $\unicode[STIX]{x1D6FC}^{L}$
, which sends
$\unicode[STIX]{x1D6FC}^{L}$
, which sends
where we have used the left dualizability of the
![]() $\mathbb{H}_{U_{n}\rightarrow S}$
. We will show that
$\mathbb{H}_{U_{n}\rightarrow S}$
. We will show that
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FC}^{L}$
are both fully faithful.
$\unicode[STIX]{x1D6FC}^{L}$
are both fully faithful.
For
![]() $\unicode[STIX]{x1D6FC}$
, it suffices to verify that the natural functor
$\unicode[STIX]{x1D6FC}$
, it suffices to verify that the natural functor
![]() $\unicode[STIX]{x1D6FC}^{L}\circ \unicode[STIX]{x1D6FC}(\mathbb{H}(S))\rightarrow \mathbb{H}(S)$
is an equivalence. Such functor is readily rewritten as
$\unicode[STIX]{x1D6FC}^{L}\circ \unicode[STIX]{x1D6FC}(\mathbb{H}(S))\rightarrow \mathbb{H}(S)$
is an equivalence. Such functor is readily rewritten as
By Lemma 5.2.6, our claim is exactly the content of Lemma 6.1.4 applied to
![]() ${\mathcal{Y}}=S\times S$
.
${\mathcal{Y}}=S\times S$
.
Next, we prove
![]() $\unicode[STIX]{x1D6FC}^{L}$
is fully faithful: it suffices to check that the natural functor
$\unicode[STIX]{x1D6FC}^{L}$
is fully faithful: it suffices to check that the natural functor
is an equivalence. Using base-change for
![]() $\mathbb{H}$
, this reduces to proving that
$\mathbb{H}$
, this reduces to proving that
is an equivalence. This is again an instance of Lemma 6.1.4. ◻
6.2 Localization and global sections
Let
![]() ${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
. In this section we equip
${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
. In this section we equip
![]() $\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
with a canonical object that we denote by
$\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
with a canonical object that we denote by
![]() $\mathbb{H}_{/{\mathcal{Y}}}$
. We then use such object to define a fundamental adjunction and the notion of
$\mathbb{H}_{/{\mathcal{Y}}}$
. We then use such object to define a fundamental adjunction and the notion of
![]() $\mathbb{H}$
-affineness.
$\mathbb{H}$
-affineness.
6.2.1
For
![]() $S\in \mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
mapping to
$S\in \mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
mapping to
![]() ${\mathcal{Y}}$
, consider the left
${\mathcal{Y}}$
, consider the left
![]() $\mathbb{H}(S)$
-module
$\mathbb{H}(S)$
-module
Let
![]() $U\rightarrow {\mathcal{Y}}$
be an affine atlas with induced Čech complex
$U\rightarrow {\mathcal{Y}}$
be an affine atlas with induced Čech complex
![]() $U_{\bullet }$
. By [Reference BeraldoBer17b], there is a natural left
$U_{\bullet }$
. By [Reference BeraldoBer17b], there is a natural left
![]() $\mathbb{H}(S)$
-linear equivalence
$\mathbb{H}(S)$
-linear equivalence
from which we obtain a left
![]() $\mathbb{H}(S)$
-linear equivalence
$\mathbb{H}(S)$
-linear equivalence
where the limit on the right-hand side is formed using the
![]() $(!,0)$
-pullbacks. We now show that the same category
$(!,0)$
-pullbacks. We now show that the same category
![]() $\mathbb{H}_{S\rightarrow {\mathcal{Y}}}$
can be expressed as a colimit.
$\mathbb{H}_{S\rightarrow {\mathcal{Y}}}$
can be expressed as a colimit.
Lemma 6.2.2. Let
![]() $S$
,
$S$
,
![]() ${\mathcal{Y}}$
,
${\mathcal{Y}}$
,
![]() $U_{\bullet }$
be as above. Then the natural functor
$U_{\bullet }$
be as above. Then the natural functor
given by the
![]() $(\ast ,0)$
-pushforward functors is an equivalence.
$(\ast ,0)$
-pushforward functors is an equivalence.
Proof. Under the equivalence (6.7), the left-hand side becomes
where the colimit on the right-hand side is taken with respect to the
![]() $\ast$
-pushforward functors. It suffices to recall again that the obvious functor
$\ast$
-pushforward functors. It suffices to recall again that the obvious functor
is a
![]() $\operatorname{QCoh}({\mathcal{Y}})$
-linear equivalence; see [Reference GaitsgoryGai15b, Proposition 6.2.7].◻
$\operatorname{QCoh}({\mathcal{Y}})$
-linear equivalence; see [Reference GaitsgoryGai15b, Proposition 6.2.7].◻
Lemma 6.2.3. The collection
![]() $\{{\mathbb{H}_{S\rightarrow {\mathcal{Y}}}\}}_{S\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}}}}$
assembles to an object of
$\{{\mathbb{H}_{S\rightarrow {\mathcal{Y}}}\}}_{S\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}}}}$
assembles to an object of
![]() $\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
that we shall denote by
$\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
that we shall denote by
![]() $\mathbb{H}_{/{\mathcal{Y}}}$
.
$\mathbb{H}_{/{\mathcal{Y}}}$
.
Proof. We need to prove that, for
![]() $S^{\prime }\rightarrow S$
a map in
$S^{\prime }\rightarrow S$
a map in
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, the canonical arrow
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
, the canonical arrow
is an equivalence. We use the canonical left
![]() $\mathbb{H}(S)$
-linear equivalence
$\mathbb{H}(S)$
-linear equivalence
discussed above. Since the left leg of each correspondence above is smooth, base-change for
![]() $\mathbb{H}$
can be applied to yield
$\mathbb{H}$
can be applied to yield
The latter is
![]() $\mathbb{H}_{S^{\prime }\rightarrow {\mathcal{Y}}}$
, as desired.◻
$\mathbb{H}_{S^{\prime }\rightarrow {\mathcal{Y}}}$
, as desired.◻
6.2.4
Set
![]() $\mathbb{H}({\mathcal{Y}}):=\mathbb{H}^{\text{geom}}({\mathcal{Y}})$
. Recall that the left
$\mathbb{H}({\mathcal{Y}}):=\mathbb{H}^{\text{geom}}({\mathcal{Y}})$
. Recall that the left
![]() $\mathbb{H}(S)$
-module category
$\mathbb{H}(S)$
-module category
![]() $\mathbb{H}_{S\rightarrow {\mathcal{Y}}}:=\mathbb{H}_{S\rightarrow {\mathcal{Y}}}^{\text{geom}}$
is actually an
$\mathbb{H}_{S\rightarrow {\mathcal{Y}}}:=\mathbb{H}_{S\rightarrow {\mathcal{Y}}}^{\text{geom}}$
is actually an
![]() $(\mathbb{H}(S),\mathbb{H}({\mathcal{Y}}))$
-bimodule, where both actions are given by convolution. Since
$(\mathbb{H}(S),\mathbb{H}({\mathcal{Y}}))$
-bimodule, where both actions are given by convolution. Since
![]() $\mathbb{H}_{S\rightarrow {\mathcal{Y}}}$
is dualizable as a DG category and the monoidal DG categories
$\mathbb{H}_{S\rightarrow {\mathcal{Y}}}$
is dualizable as a DG category and the monoidal DG categories
![]() $\mathbb{H}(S)$
and
$\mathbb{H}(S)$
and
![]() $\mathbb{H}({\mathcal{Y}})$
are both very rigid, Corollary 2.1.7 implies that
$\mathbb{H}({\mathcal{Y}})$
are both very rigid, Corollary 2.1.7 implies that
![]() $\mathbb{H}_{S\rightarrow {\mathcal{Y}}}$
is ambidextrous.
$\mathbb{H}_{S\rightarrow {\mathcal{Y}}}$
is ambidextrous.
By Lemma 6.2.2 and the ambidexterity of
![]() $\mathbb{H}$
, its (right, as well as left) dual is easily seen to be the obvious
$\mathbb{H}$
, its (right, as well as left) dual is easily seen to be the obvious
![]() $(\mathbb{H}({\mathcal{Y}}),\mathbb{H}(S))$
-bimodule
$(\mathbb{H}({\mathcal{Y}}),\mathbb{H}(S))$
-bimodule
6.2.5
We can now introduce the fundamental adjunction
The left adjoint sends
![]() ${\mathcal{C}}\in \mathbb{H}({\mathcal{Y}})\operatorname{ -}\mathbf{mod}$
to the
${\mathcal{C}}\in \mathbb{H}({\mathcal{Y}})\operatorname{ -}\mathbf{mod}$
to the
![]() $\mathbb{H}$
-sheaf of categories represented by
$\mathbb{H}$
-sheaf of categories represented by
This makes sense in view of Lemma 6.2.3. The right adjoint sends
![]() ${\mathcal{C}}=\{{{\mathcal{C}}_{S}\}}_{S}\in \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
to the
${\mathcal{C}}=\{{{\mathcal{C}}_{S}\}}_{S}\in \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
to the
![]() $\mathbb{H}({\mathcal{Y}})$
-module
$\mathbb{H}({\mathcal{Y}})$
-module
where we have used Theorem 6.1.2.
We say that
![]() ${\mathcal{Y}}$
is
${\mathcal{Y}}$
is
![]() $\mathbb{H}$
-affine if the adjoint functors (6.9) are mutually inverse equivalences.
$\mathbb{H}$
-affine if the adjoint functors (6.9) are mutually inverse equivalences.
Remark 6.2.6. Note that
![]() $\unicode[STIX]{x1D71E}_{{\mathcal{Y}}}^{\mathbb{H}}({\mathcal{C}})$
can be computed as
$\unicode[STIX]{x1D71E}_{{\mathcal{Y}}}^{\mathbb{H}}({\mathcal{C}})$
can be computed as
where
![]() $\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
is regarded as an
$\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
is regarded as an
![]() $(\infty ,2)$
-category and
$(\infty ,2)$
-category and
![]() ${\mathcal{H}}om$
denotes the
${\mathcal{H}}om$
denotes the
![]() $(\infty ,1)$
-category of
$(\infty ,1)$
-category of
![]() $1$
-arrows in an
$1$
-arrows in an
![]() $(\infty ,2)$
-category.
$(\infty ,2)$
-category.
6.3 Pushforwards and the Beck–Chevalley conditions
For any arrow
![]() $f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
in
$f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
in
![]() $\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, the functor
$\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, the functor
![]() $f^{\ast ,\mathbb{H}}$
commutes with colimits, whence it admits a right adjoint, denoted by
$f^{\ast ,\mathbb{H}}$
commutes with colimits, whence it admits a right adjoint, denoted by
![]() $f_{\ast ,\mathbb{H}}$
. Moreover, since
$f_{\ast ,\mathbb{H}}$
. Moreover, since
![]() $\mathbb{H}$
satisfies the left Beck–Chevalley condition,
$\mathbb{H}$
satisfies the left Beck–Chevalley condition,
![]() $f^{\ast ,\mathbb{H}}$
commutes with limits as well, whence it also admits a left adjoint, denoted by
$f^{\ast ,\mathbb{H}}$
commutes with limits as well, whence it also admits a left adjoint, denoted by
![]() $f_{!,\mathbb{H}}$
.
$f_{!,\mathbb{H}}$
.
In this section we give formulas for these pushforward functors and discuss base-change for
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
.
$\mathsf{ShvCat}^{\mathbb{H}}$
.
6.3.1
Let
![]() $f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
be an arrow in
$f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
be an arrow in
![]() $\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
. For
$\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
. For
![]() ${\mathcal{C}}\in \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
, we will compute the
${\mathcal{C}}\in \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
, we will compute the
![]() $\mathbb{H}$
-sheaf of categories
$\mathbb{H}$
-sheaf of categories
![]() $f_{\ast ,\mathbb{H}}({\mathcal{C}})$
. By Theorem 6.1.2, it suffices to specify the value of
$f_{\ast ,\mathbb{H}}({\mathcal{C}})$
. By Theorem 6.1.2, it suffices to specify the value of
![]() $f_{\ast ,\mathbb{H}}({\mathcal{C}})$
on affine schemes
$f_{\ast ,\mathbb{H}}({\mathcal{C}})$
on affine schemes
![]() $U\in \mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
mapping smoothly to
$U\in \mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
mapping smoothly to
![]() ${\mathcal{Z}}$
. For each such
${\mathcal{Z}}$
. For each such
![]() $\unicode[STIX]{x1D719}_{U\rightarrow {\mathcal{Y}}}:U\rightarrow {\mathcal{Y}}$
, consider the
$\unicode[STIX]{x1D719}_{U\rightarrow {\mathcal{Y}}}:U\rightarrow {\mathcal{Y}}$
, consider the
![]() $\mathbb{H}(U)$
-module
$\mathbb{H}(U)$
-module
The limit is well defined thanks to the left Beck–Chevalley condition, that is, exploiting the
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
![]() $\mathbb{H}^{\operatorname{L-BC}}$
of § 5.2.14. Next, using the right Beck–Chevalley condition, one readily checks that the natural functor
$\mathbb{H}^{\operatorname{L-BC}}$
of § 5.2.14. Next, using the right Beck–Chevalley condition, one readily checks that the natural functor
is an equivalence for any smooth map
![]() $U^{\prime }\rightarrow U$
in
$U^{\prime }\rightarrow U$
in
![]() $\mathsf{Aff}$
. This guarantees that
$\mathsf{Aff}$
. This guarantees that
![]() $\{{{\mathcal{E}}_{U}\}}_{U\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Z}},\text{smooth}}}$
is a well-defined object of
$\{{{\mathcal{E}}_{U}\}}_{U\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Z}},\text{smooth}}}$
is a well-defined object of
![]() $\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Z}})$
. We leave it to the reader to verify that such object in the required pushforward
$\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Z}})$
. We leave it to the reader to verify that such object in the required pushforward
![]() $f_{\ast ,\mathbb{H}}({\mathcal{C}})$
.
$f_{\ast ,\mathbb{H}}({\mathcal{C}})$
.
6.3.2
Similarly, the
![]() $!$
-pushforward of
$!$
-pushforward of
![]() ${\mathcal{C}}$
is written as
${\mathcal{C}}$
is written as
where
![]() ${\mathcal{D}}_{U}$
is defined, using the
${\mathcal{D}}_{U}$
is defined, using the
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
![]() $\mathbb{H}^{\operatorname{R-BC}}$
, as
$\mathbb{H}^{\operatorname{R-BC}}$
, as
6.3.3
It is then tautological to verify that the
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
has the right Beck–Chevalley condition with respect to bounded arrows, that is, the assignment
$\mathsf{ShvCat}^{\mathbb{H}}$
has the right Beck–Chevalley condition with respect to bounded arrows, that is, the assignment
upgrades to an
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
with
![]() $\mathsf{Cat}_{\infty }$
being regarded here as an
$\mathsf{Cat}_{\infty }$
being regarded here as an
![]() $(\infty ,2)$
-category. Symmetrically, the assignment
$(\infty ,2)$
-category. Symmetrically, the assignment
upgrades to an
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
Remark 6.3.4. Combining the two functors together, we deduce that we have base-change isomorphisms
as soon as at least one between
![]() $f$
and
$f$
and
![]() $g$
is bounded.
$g$
is bounded.
Remark 6.3.5. We will show later that
![]() $!$
- and
$!$
- and
![]() $\ast$
-pushforwards of
$\ast$
-pushforwards of
![]() $\mathbb{H}$
-sheaves of categories are naturally identified; see Corollary 6.5.5.
$\mathbb{H}$
-sheaves of categories are naturally identified; see Corollary 6.5.5.
6.4 Extension/restriction of coefficients
In this section we relate
![]() $\mathbb{H}$
-sheaves of categories with the more familiar quasi-coherent sheaves of categories developed in [Reference GaitsgoryGai15b]. The latter are the ones obtained from the coefficient system
$\mathbb{H}$
-sheaves of categories with the more familiar quasi-coherent sheaves of categories developed in [Reference GaitsgoryGai15b]. The latter are the ones obtained from the coefficient system
![]() $\mathbb{Q}$
.
$\mathbb{Q}$
.
6.4.1
The relation between
![]() $\mathsf{ShvCat}^{\mathbb{H}}$
and
$\mathsf{ShvCat}^{\mathbb{H}}$
and
![]() $\mathsf{ShvCat}^{\mathbb{Q}}$
is induced by the map
$\mathsf{ShvCat}^{\mathbb{Q}}$
is induced by the map
![]() $\mathbb{Q}\rightarrow \mathbb{H}$
of coefficient systems on
$\mathbb{Q}\rightarrow \mathbb{H}$
of coefficient systems on
![]() $\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
. Specifically,
$\mathsf{Aff}_{\text{lfp}}^{{<}\infty }$
. Specifically,
![]() $\mathbb{Q}\rightarrow \mathbb{H}$
induces a natural transformation
$\mathbb{Q}\rightarrow \mathbb{H}$
induces a natural transformation
between functors out of
![]() $(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })^{\operatorname{op}}$
. In other words, this means that
$(\mathsf{Stk}_{\text{lfp}}^{{<}\infty })^{\operatorname{op}}$
. In other words, this means that
![]() $\mathsf{oblv}^{\mathbb{Q}\rightarrow \mathbb{H}}$
is compatible with the pullback functors.
$\mathsf{oblv}^{\mathbb{Q}\rightarrow \mathbb{H}}$
is compatible with the pullback functors.
Lemma 6.4.2. For
![]() ${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, the functor
${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, the functor
![]() $\mathsf{oblv}_{{\mathcal{Y}}}^{\mathbb{Q}\rightarrow \mathbb{H}}:\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})\rightarrow \mathsf{ShvCat}^{\mathbb{Q}}({\mathcal{Y}})$
is conservative and admits a left adjoint, which we will call
$\mathsf{oblv}_{{\mathcal{Y}}}^{\mathbb{Q}\rightarrow \mathbb{H}}:\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})\rightarrow \mathsf{ShvCat}^{\mathbb{Q}}({\mathcal{Y}})$
is conservative and admits a left adjoint, which we will call
![]() $\mathsf{ind}_{{\mathcal{Y}}}^{\mathbb{Q}\rightarrow \mathbb{H}}$
.
$\mathsf{ind}_{{\mathcal{Y}}}^{\mathbb{Q}\rightarrow \mathbb{H}}$
.
Proof. Conservativeness is obvious. The existence of the left adjoint is clear thanks to the fact that
![]() $\mathsf{oblv}_{{\mathcal{Y}}}^{\mathbb{Q}\rightarrow \mathbb{H}}$
commutes with limits.◻
$\mathsf{oblv}_{{\mathcal{Y}}}^{\mathbb{Q}\rightarrow \mathbb{H}}$
commutes with limits.◻
6.4.3
The functor
is really easy to describe explicitly. Namely,
Lemma 6.4.4. The induction functor
![]() $\mathsf{ind}_{{\mathcal{Y}}}^{\mathbb{Q}\rightarrow \mathbb{H}}:\mathsf{ShvCat}^{\mathbb{Q}}({\mathcal{Y}})\rightarrow \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
sends
$\mathsf{ind}_{{\mathcal{Y}}}^{\mathbb{Q}\rightarrow \mathbb{H}}:\mathsf{ShvCat}^{\mathbb{Q}}({\mathcal{Y}})\rightarrow \mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})$
sends
![]() $\mathbb{Q}_{/{\mathcal{Y}}}$
to
$\mathbb{Q}_{/{\mathcal{Y}}}$
to
![]() $\mathbb{H}_{/{\mathcal{Y}}}$
.
$\mathbb{H}_{/{\mathcal{Y}}}$
.
Proof. The above formula and § 6.3.2 yield
 $$\begin{eqnarray}\displaystyle \mathsf{ind}_{{\mathcal{Y}}}^{\mathbb{Q}\rightarrow \mathbb{H}}(\mathbb{Q}_{/{\mathcal{Y}}}) & \simeq & \displaystyle \underset{S\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}}}}{\operatorname{colim}}(\unicode[STIX]{x1D719}_{S\rightarrow {\mathcal{Y}}})_{!,\mathbb{H}}(\mathbb{H}(S))\nonumber\\ \displaystyle & \simeq & \displaystyle \underset{S\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}}}{\operatorname{colim}}\left\{\underset{V\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/U\times _{{\mathcal{Y}}}S,\text{smooth}}}{\operatorname{colim}}\mathbb{H}_{U\leftarrow V}\underset{\mathbb{H}(V)}{\otimes }\mathbb{H}_{V\rightarrow S}\right\}_{U}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathsf{ind}_{{\mathcal{Y}}}^{\mathbb{Q}\rightarrow \mathbb{H}}(\mathbb{Q}_{/{\mathcal{Y}}}) & \simeq & \displaystyle \underset{S\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}}}}{\operatorname{colim}}(\unicode[STIX]{x1D719}_{S\rightarrow {\mathcal{Y}}})_{!,\mathbb{H}}(\mathbb{H}(S))\nonumber\\ \displaystyle & \simeq & \displaystyle \underset{S\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}}}{\operatorname{colim}}\left\{\underset{V\in (\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/U\times _{{\mathcal{Y}}}S,\text{smooth}}}{\operatorname{colim}}\mathbb{H}_{U\leftarrow V}\underset{\mathbb{H}(V)}{\otimes }\mathbb{H}_{V\rightarrow S}\right\}_{U}.\nonumber\end{eqnarray}$$
We now apply Lemma 6.1.4 twice. Firstly,
is equivalent to
![]() $\operatorname{IndCoh}_{0}((U\times S)_{U\times _{{\mathcal{Y}}}S}^{\wedge })$
. Secondly,
$\operatorname{IndCoh}_{0}((U\times S)_{U\times _{{\mathcal{Y}}}S}^{\wedge })$
. Secondly,
This concludes the computation. ◻
6.5
 $\mathbb{H}$
-affineness
$\mathbb{H}$
-affineness
In this section we prove our main theorem, the
![]() $\mathbb{H}$
-affineness of algebraic stacks, and deduce that
$\mathbb{H}$
-affineness of algebraic stacks, and deduce that
![]() $\mathbb{H}^{\text{geom}}$
is a strict
$\mathbb{H}^{\text{geom}}$
is a strict
![]() $(\infty ,2)$
-functor.
$(\infty ,2)$
-functor.
Theorem 6.5.1. Any
![]() ${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
is
${\mathcal{Y}}\in \mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
is
![]() $\mathbb{H}$
-affine, that is, the adjunction
$\mathbb{H}$
-affine, that is, the adjunction
is an equivalence of
![]() $\infty$
-categories.
$\infty$
-categories.
Proof. Our strategy is to reduce to the known
![]() $\mathbb{Q}$
-affineness of such stacks (see [Reference GaitsgoryGai15b, Theorem 2.2.6]) using the adjunction
$\mathbb{Q}$
-affineness of such stacks (see [Reference GaitsgoryGai15b, Theorem 2.2.6]) using the adjunction
Step 1. For a monoidal functor
![]() $f:{\mathcal{A}}\rightarrow {\mathcal{B}}$
, we denote by
$f:{\mathcal{A}}\rightarrow {\mathcal{B}}$
, we denote by
![]() $\mathsf{ind}[f]:{\mathcal{A}}\operatorname{ -}\mathbf{mod}\rightleftarrows {\mathcal{B}}\operatorname{-}\mathbf{mod}:\mathsf{oblv}[f]$
the standard adjunction. Let
$\mathsf{ind}[f]:{\mathcal{A}}\operatorname{ -}\mathbf{mod}\rightleftarrows {\mathcal{B}}\operatorname{-}\mathbf{mod}:\mathsf{oblv}[f]$
the standard adjunction. Let
![]() $\unicode[STIX]{x1D6FF}_{{\mathcal{Y}}}:\operatorname{QCoh}({\mathcal{Y}})\rightarrow \mathbb{H}({\mathcal{Y}})$
be the usual monoidal functor.
$\unicode[STIX]{x1D6FF}_{{\mathcal{Y}}}:\operatorname{QCoh}({\mathcal{Y}})\rightarrow \mathbb{H}({\mathcal{Y}})$
be the usual monoidal functor.
By Lemma 6.4.4, the diagram
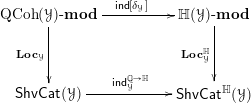
is commutative. It follows that the square

is commutative too.
Step 2. By changing the vertical arrows with their left adjoints, we obtain a lax commutative diagram
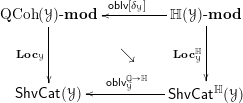
However, this diagram is genuinely commutative thanks to the canonical
![]() $(\operatorname{QCoh}(S),\mathbb{H}({\mathcal{Y}}))$
-linear equivalence
$(\operatorname{QCoh}(S),\mathbb{H}({\mathcal{Y}}))$
-linear equivalence
Step 3. We are now ready to prove the theorem by checking that the two compositions
![]() $\mathbf{Loc}_{{\mathcal{Y}}}^{\mathbb{H}}\circ \unicode[STIX]{x1D71E}_{{\mathcal{Y}}}^{\mathbb{H}}$
and
$\mathbf{Loc}_{{\mathcal{Y}}}^{\mathbb{H}}\circ \unicode[STIX]{x1D71E}_{{\mathcal{Y}}}^{\mathbb{H}}$
and
![]() $\unicode[STIX]{x1D71E}_{{\mathcal{Y}}}^{\mathbb{H}}\circ \mathbf{Loc}_{{\mathcal{Y}}}^{\mathbb{H}}$
are isomorphic to the corresponding identity functors. This is easily done by using the commutative diagrams (6.15) and (6.16), the conservativity of the functors
$\unicode[STIX]{x1D71E}_{{\mathcal{Y}}}^{\mathbb{H}}\circ \mathbf{Loc}_{{\mathcal{Y}}}^{\mathbb{H}}$
are isomorphic to the corresponding identity functors. This is easily done by using the commutative diagrams (6.15) and (6.16), the conservativity of the functors
and the
![]() $\mathbb{Q}$
-affineness of
$\mathbb{Q}$
-affineness of
![]() ${\mathcal{Y}}$
.◻
${\mathcal{Y}}$
.◻
6.5.2
Combining the
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
of (6.11) with Theorem 6.5.1, we obtain another strict
![]() $(\infty ,2)$
-functor,
$(\infty ,2)$
-functor,
defined by
Theorem 6.5.3. The lax
![]() $(\infty ,2)$
-functor
$(\infty ,2)$
-functor
of § 3.2 is naturally equivalent to the restriction of
![]() $\mathbb{H}^{\text{cat}}$
to
$\mathbb{H}^{\text{cat}}$
to
![]() $\mathsf{Corr}\big(\mathsf{Stk}_{\text{lfp}}^{{<}\infty }\big)_{\text{bdd};\operatorname{all}}^{\text{schem}\& \text{bdd}\& \text{proper}}$
. Hence,
$\mathsf{Corr}\big(\mathsf{Stk}_{\text{lfp}}^{{<}\infty }\big)_{\text{bdd};\operatorname{all}}^{\text{schem}\& \text{bdd}\& \text{proper}}$
. Hence,
![]() $\mathbb{H}^{\text{geom}}$
is strict.
$\mathbb{H}^{\text{geom}}$
is strict.
Henceforth, we will denote both
![]() $(\infty ,2)$
-functors simply by
$(\infty ,2)$
-functors simply by
![]() $\mathbb{H}$
.
$\mathbb{H}$
.
Proof. By Remark 6.2.6, the DG category underlying
![]() $\mathbb{H}_{{\mathcal{X}}\leftarrow {\mathcal{W}}\rightarrow {\mathcal{Y}}}^{\text{cat}}$
is computed as follows:
$\mathbb{H}_{{\mathcal{X}}\leftarrow {\mathcal{W}}\rightarrow {\mathcal{Y}}}^{\text{cat}}$
is computed as follows:
 $$\begin{eqnarray}\displaystyle \mathbb{H}_{{\mathcal{X}}\leftarrow {\mathcal{W}}\rightarrow {\mathcal{Y}}}^{\text{cat}} & \simeq & \displaystyle {\mathcal{H}}om_{\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})}\big(\mathbb{H}_{/{\mathcal{Y}}},h_{\ast ,\mathbb{H}}\circ v^{\ast ,\mathbb{H}}(\mathbb{H}_{/{\mathcal{X}}})\big)\nonumber\\ \displaystyle & \simeq & \displaystyle {\mathcal{H}}om_{\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{W}})}\big(h^{\ast ,\mathbb{H}}(\mathbb{H}_{/{\mathcal{X}}}),v^{\ast ,\mathbb{H}}(\mathbb{H}_{/{\mathcal{Y}}})\big)\nonumber\\ \displaystyle & \simeq & \displaystyle \lim _{U\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{W}},\text{smooth}})^{\operatorname{op}}}{\mathcal{H}}om_{\mathbb{H}(U)}\big(\mathbb{H}_{U\rightarrow {\mathcal{X}}},\mathbb{H}_{U\rightarrow {\mathcal{Y}}}\big)\nonumber\\ \displaystyle & \simeq & \displaystyle \lim _{U\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{W}},\text{smooth}})^{\operatorname{op}}}\mathbb{H}_{{\mathcal{X}}\leftarrow U}\underset{\mathbb{H}(U)}{\otimes }\mathbb{H}_{U\rightarrow {\mathcal{Y}}}\nonumber\\ \displaystyle & \simeq & \displaystyle \lim _{U\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{W}},\text{smooth}})^{\operatorname{op}}}\lim _{S\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{X}},\text{smooth}})^{\operatorname{op}}}\lim _{T\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}})^{\operatorname{op}}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathbb{H}_{S\leftarrow S\times _{{\mathcal{X}}}U\rightarrow U}\underset{\mathbb{H}(U)}{\otimes }\mathbb{H}_{U\leftarrow U\times _{{\mathcal{Y}}}T\rightarrow T}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbb{H}_{{\mathcal{X}}\leftarrow {\mathcal{W}}\rightarrow {\mathcal{Y}}}^{\text{cat}} & \simeq & \displaystyle {\mathcal{H}}om_{\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{Y}})}\big(\mathbb{H}_{/{\mathcal{Y}}},h_{\ast ,\mathbb{H}}\circ v^{\ast ,\mathbb{H}}(\mathbb{H}_{/{\mathcal{X}}})\big)\nonumber\\ \displaystyle & \simeq & \displaystyle {\mathcal{H}}om_{\mathsf{ShvCat}^{\mathbb{H}}({\mathcal{W}})}\big(h^{\ast ,\mathbb{H}}(\mathbb{H}_{/{\mathcal{X}}}),v^{\ast ,\mathbb{H}}(\mathbb{H}_{/{\mathcal{Y}}})\big)\nonumber\\ \displaystyle & \simeq & \displaystyle \lim _{U\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{W}},\text{smooth}})^{\operatorname{op}}}{\mathcal{H}}om_{\mathbb{H}(U)}\big(\mathbb{H}_{U\rightarrow {\mathcal{X}}},\mathbb{H}_{U\rightarrow {\mathcal{Y}}}\big)\nonumber\\ \displaystyle & \simeq & \displaystyle \lim _{U\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{W}},\text{smooth}})^{\operatorname{op}}}\mathbb{H}_{{\mathcal{X}}\leftarrow U}\underset{\mathbb{H}(U)}{\otimes }\mathbb{H}_{U\rightarrow {\mathcal{Y}}}\nonumber\\ \displaystyle & \simeq & \displaystyle \lim _{U\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{W}},\text{smooth}})^{\operatorname{op}}}\lim _{S\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{X}},\text{smooth}})^{\operatorname{op}}}\lim _{T\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}})^{\operatorname{op}}}\nonumber\\ \displaystyle & & \displaystyle \times \,\mathbb{H}_{S\leftarrow S\times _{{\mathcal{X}}}U\rightarrow U}\underset{\mathbb{H}(U)}{\otimes }\mathbb{H}_{U\leftarrow U\times _{{\mathcal{Y}}}T\rightarrow T}.\nonumber\end{eqnarray}$$
By base-change for
![]() $\mathbb{H}$
, we have
$\mathbb{H}$
, we have
By taking the limit, we obtain
as desired. ◻
Corollary 6.5.4. For
![]() $f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
in
$f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
in
![]() $\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
. Then the functors
$\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
. Then the functors
![]() $f_{\ast ,\mathbb{H}}$
and
$f_{\ast ,\mathbb{H}}$
and
![]() $f^{\ast ,\mathbb{H}}$
correspond under
$f^{\ast ,\mathbb{H}}$
correspond under
![]() $\mathbb{H}$
-affineness to the functors of
$\mathbb{H}$
-affineness to the functors of
![]() $\mathbb{H}_{{\mathcal{Z}}\leftarrow {\mathcal{Y}}}\otimes _{\mathbb{H}({\mathcal{Y}})}-$
and
$\mathbb{H}_{{\mathcal{Z}}\leftarrow {\mathcal{Y}}}\otimes _{\mathbb{H}({\mathcal{Y}})}-$
and
![]() $\mathbb{H}_{{\mathcal{Y}}\rightarrow {\mathcal{Z}}}\otimes _{\mathbb{H}({\mathcal{Z}})}-$
, respectively.
$\mathbb{H}_{{\mathcal{Y}}\rightarrow {\mathcal{Z}}}\otimes _{\mathbb{H}({\mathcal{Z}})}-$
, respectively.
Proof. Let
![]() ${\mathcal{C}}\in \mathbb{H}({\mathcal{Y}})\operatorname{ -}\mathbf{mod}$
. We need to exhibit a natural equivalence
${\mathcal{C}}\in \mathbb{H}({\mathcal{Y}})\operatorname{ -}\mathbf{mod}$
. We need to exhibit a natural equivalence
This easily reduces to the case
![]() ${\mathcal{C}}=\mathbb{H}({\mathcal{Y}})$
, where it holds true by construction. The assertion for
${\mathcal{C}}=\mathbb{H}({\mathcal{Y}})$
, where it holds true by construction. The assertion for
![]() $f^{\ast ,\mathbb{H}}$
is proven similarly.◻
$f^{\ast ,\mathbb{H}}$
is proven similarly.◻
Corollary 6.5.5. Pullbacks of
![]() $\mathbb{H}$
-sheaves of categories are ambidextrous: for any
$\mathbb{H}$
-sheaves of categories are ambidextrous: for any
![]() $f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
in
$f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
in
![]() $\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, there is a canonical equivalence
$\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, there is a canonical equivalence
![]() $f_{!,\mathbb{H}}\simeq f_{\ast ,\mathbb{H}}$
.
$f_{!,\mathbb{H}}\simeq f_{\ast ,\mathbb{H}}$
.
Proof. Recall the formulas for
![]() $f_{!,\mathbb{H}}$
and
$f_{!,\mathbb{H}}$
and
![]() $f_{\ast ,\mathbb{H}}$
from §§ 6.3.1 and 6.3.2. By
$f_{\ast ,\mathbb{H}}$
from §§ 6.3.1 and 6.3.2. By
![]() $\mathbb{H}$
-affineness, it suffices to exhibit a natural equivalence
$\mathbb{H}$
-affineness, it suffices to exhibit a natural equivalence
![]() $f_{!,\mathbb{H}}(\mathbb{H}_{/{\mathcal{Y}}})\simeq f_{\ast ,\mathbb{H}}(\mathbb{H}_{/{\mathcal{Y}}})$
. The latter is constructed as in Lemma 6.1.4.◻
$f_{!,\mathbb{H}}(\mathbb{H}_{/{\mathcal{Y}}})\simeq f_{\ast ,\mathbb{H}}(\mathbb{H}_{/{\mathcal{Y}}})$
. The latter is constructed as in Lemma 6.1.4.◻
6.6 The
 $\mathbb{H}$
-action on
$\mathbb{H}$
-action on
 $\operatorname{IndCoh}$
$\operatorname{IndCoh}$
This final section contains an example of our techniques. We view
![]() $\operatorname{IndCoh}({\mathcal{Y}})$
as a left module for
$\operatorname{IndCoh}({\mathcal{Y}})$
as a left module for
![]() $\mathbb{H}({\mathcal{Y}})$
and compute
$\mathbb{H}({\mathcal{Y}})$
and compute
![]() $\mathbb{H}$
-pullbacks along smooth maps, as well as
$\mathbb{H}$
-pullbacks along smooth maps, as well as
![]() $\mathbb{H}$
-pushforwards along arbitrary maps.
$\mathbb{H}$
-pushforwards along arbitrary maps.
Lemma 6.6.1. For a smooth map
![]() ${\mathcal{X}}\rightarrow {\mathcal{Y}}$
in
${\mathcal{X}}\rightarrow {\mathcal{Y}}$
in
![]() $\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, the natural
$\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, the natural
![]() $\mathbb{H}({\mathcal{X}})$
-linear functor
$\mathbb{H}({\mathcal{X}})$
-linear functor
is an equivalence.
Proof. This is just a consequence of the
![]() $(\operatorname{QCoh}({\mathcal{X}}),\mathbb{H}({\mathcal{Y}}))$
-bilinear equivalence
$(\operatorname{QCoh}({\mathcal{X}}),\mathbb{H}({\mathcal{Y}}))$
-bilinear equivalence
together with [Reference GaitsgoryGai13, Proposition 4.5.3]. ◻
Remark 6.6.2. The example of
![]() ${\mathcal{Y}}=\operatorname{pt}$
shows that we should not expect this result to be true for non-smooth maps.
${\mathcal{Y}}=\operatorname{pt}$
shows that we should not expect this result to be true for non-smooth maps.
Proposition 6.6.3. For a map
![]() $f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
in
$f:{\mathcal{Y}}\rightarrow {\mathcal{Z}}$
in
![]() $\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, the natural
$\mathsf{Stk}_{\text{lfp}}^{{<}\infty }$
, the natural
![]() $\mathbb{H}({\mathcal{Z}})$
-linear functor
$\mathbb{H}({\mathcal{Z}})$
-linear functor
is an equivalence.
Proof. Let
Lemma 6.6.1 gives the equivalence
![]() $(\unicode[STIX]{x1D719}_{V\rightarrow {\mathcal{Y}}})^{\ast ,\mathbb{H}}(\operatorname{IndCoh}_{/{\mathcal{Y}}})\simeq \operatorname{IndCoh}(V)$
for any affine scheme
$(\unicode[STIX]{x1D719}_{V\rightarrow {\mathcal{Y}}})^{\ast ,\mathbb{H}}(\operatorname{IndCoh}_{/{\mathcal{Y}}})\simeq \operatorname{IndCoh}(V)$
for any affine scheme
![]() $V$
mapping smoothly to
$V$
mapping smoothly to
![]() ${\mathcal{Y}}$
. We then have
${\mathcal{Y}}$
. We then have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D71E}_{{\mathcal{Z}}}^{\mathbb{H}}f_{\ast ,\mathbb{H}}(\operatorname{IndCoh}_{/{\mathcal{Y}}}) & \simeq & \displaystyle \lim _{V\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}})^{\operatorname{op}}}\mathbb{H}_{{\mathcal{Z}}\leftarrow V}\underset{\mathbb{H}(V)}{\otimes }\operatorname{IndCoh}(V)\nonumber\\ \displaystyle & \simeq & \displaystyle \lim _{V\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}})^{\operatorname{op}}}\lim _{U\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Z}},\text{smooth}})^{\operatorname{op}}}\mathbb{H}_{U\leftarrow U\times _{{\mathcal{Z}}}V\rightarrow V}\underset{\mathbb{H}(V)}{\otimes }\operatorname{IndCoh}(V)\nonumber\\ \displaystyle & \simeq & \displaystyle \lim _{V\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}})^{\operatorname{op}}}\lim _{U\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Z}},\text{smooth}})^{\operatorname{op}}}\operatorname{IndCoh}(U_{U\times _{{\mathcal{Z}}}V}^{\wedge })\nonumber\\ \displaystyle & \simeq & \displaystyle \lim _{V\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}})^{\operatorname{op}}}\operatorname{IndCoh}({\mathcal{Z}}_{V}^{\wedge })\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{IndCoh}({\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D71E}_{{\mathcal{Z}}}^{\mathbb{H}}f_{\ast ,\mathbb{H}}(\operatorname{IndCoh}_{/{\mathcal{Y}}}) & \simeq & \displaystyle \lim _{V\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}})^{\operatorname{op}}}\mathbb{H}_{{\mathcal{Z}}\leftarrow V}\underset{\mathbb{H}(V)}{\otimes }\operatorname{IndCoh}(V)\nonumber\\ \displaystyle & \simeq & \displaystyle \lim _{V\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}})^{\operatorname{op}}}\lim _{U\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Z}},\text{smooth}})^{\operatorname{op}}}\mathbb{H}_{U\leftarrow U\times _{{\mathcal{Z}}}V\rightarrow V}\underset{\mathbb{H}(V)}{\otimes }\operatorname{IndCoh}(V)\nonumber\\ \displaystyle & \simeq & \displaystyle \lim _{V\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}})^{\operatorname{op}}}\lim _{U\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Z}},\text{smooth}})^{\operatorname{op}}}\operatorname{IndCoh}(U_{U\times _{{\mathcal{Z}}}V}^{\wedge })\nonumber\\ \displaystyle & \simeq & \displaystyle \lim _{V\in ((\mathsf{Aff}_{\text{lfp}}^{{<}\infty })_{/{\mathcal{Y}},\text{smooth}})^{\operatorname{op}}}\operatorname{IndCoh}({\mathcal{Z}}_{V}^{\wedge })\nonumber\\ \displaystyle & \simeq & \displaystyle \operatorname{IndCoh}({\mathcal{Z}}_{{\mathcal{Y}}}^{\wedge }).\nonumber\end{eqnarray}$$
Here we have used the self-duality of
![]() $\operatorname{IndCoh}(S)$
, the rigidity of
$\operatorname{IndCoh}(S)$
, the rigidity of
![]() $\mathbb{H}(S)$
, Proposition 4.3.2 (i.e. the special case of the assertion for affine schemes), Lemma 6.6.1 and smooth descent for
$\mathbb{H}(S)$
, Proposition 4.3.2 (i.e. the special case of the assertion for affine schemes), Lemma 6.6.1 and smooth descent for
![]() $\operatorname{IndCoh}$
. The conclusion now follows from Corollary 6.5.4.◻
$\operatorname{IndCoh}$
. The conclusion now follows from Corollary 6.5.4.◻
Acknowledgements
The main idea behind the present paper was conceived as a result of five illuminating conversations with Dennis Gaitsgory (Paris, August 2015). It is a pleasure to thank him for his generosity in explaining and donating his ideas. Thanks are also due to Dima Arinkin, David Ben-Zvi, Ian Grojnowski, David Jordan, Tony Pantev, Sam Raskin and Pavel Safronov for their interest and influence. Finally, I am grateful to the referee for a very helpful technical report.