1. Introduction
Dissipative anomaly states that ![]() $\varepsilon$, the rate of turbulent energy dissipation (per unit mass) away from boundaries, remains finite as viscosity tends to zero (Taylor Reference Taylor1935). As a basic hypothesis of the K41 turbulence theory (Kolmogorov Reference Kolmogorov1941a,Reference Kolmogorovb,Reference Kolmogorovc; Frisch Reference Frisch1995), it is of fundamental importance and is often deemed as the ‘zeroth law of turbulence’. Understanding dissipative anomaly was primarily phenomenological until the pioneering theoretical study of Onsager (Reference Onsager1949). His work established a crucial connection between finite dissipation in hydrodynamic (HD) turbulence and the inherent roughness of velocity field. Onsager's conjecture was then proved rigorously under different assumptions (Constantin, Weinan & Titi Reference Constantin, Weinan and Titi1994; Eyink Reference Eyink1994; Duchon & Robert Reference Duchon and Robert2000), and extended to diverse turbulence systems as well, including incompressible magnetohydrodynamic (IMHD) turbulence (Aluie Reference Aluie2017), incompressible Hall magnetohydrodynamic (MHD) turbulence (Galtier Reference Galtier2018), and compressible HD turbulence (Eyink & Drivas Reference Eyink and Drivas2018).
$\varepsilon$, the rate of turbulent energy dissipation (per unit mass) away from boundaries, remains finite as viscosity tends to zero (Taylor Reference Taylor1935). As a basic hypothesis of the K41 turbulence theory (Kolmogorov Reference Kolmogorov1941a,Reference Kolmogorovb,Reference Kolmogorovc; Frisch Reference Frisch1995), it is of fundamental importance and is often deemed as the ‘zeroth law of turbulence’. Understanding dissipative anomaly was primarily phenomenological until the pioneering theoretical study of Onsager (Reference Onsager1949). His work established a crucial connection between finite dissipation in hydrodynamic (HD) turbulence and the inherent roughness of velocity field. Onsager's conjecture was then proved rigorously under different assumptions (Constantin, Weinan & Titi Reference Constantin, Weinan and Titi1994; Eyink Reference Eyink1994; Duchon & Robert Reference Duchon and Robert2000), and extended to diverse turbulence systems as well, including incompressible magnetohydrodynamic (IMHD) turbulence (Aluie Reference Aluie2017), incompressible Hall magnetohydrodynamic (MHD) turbulence (Galtier Reference Galtier2018), and compressible HD turbulence (Eyink & Drivas Reference Eyink and Drivas2018).
Dissipative anomaly has been well explored by experiments and simulations in HD turbulence (Sreenivasan Reference Sreenivasan1984, Reference Sreenivasan1998; Kaneda et al. Reference Kaneda, Ishihara, Yokokawa, Itakura and Uno2003; Pearson et al. Reference Pearson, Yousef, Haugen, Brandenburg and Krogstad2004; Mazellier & Vassilicos Reference Mazellier and Vassilicos2008; Goto & Vassilicos Reference Goto and Vassilicos2009; McComb et al. Reference McComb, Berera, Yoffe and Linkmann2015; Vassilicos Reference Vassilicos2015; John, Donzis & Sreenivasan Reference John, Donzis and Sreenivasan2021) and IMHD turbulence (Mininni & Pouquet Reference Mininni and Pouquet2009; Dallas & Alexakis Reference Dallas and Alexakis2014; Linkmann et al. Reference Linkmann, Berera, McComb and McKay2015; Linkmann, Berera & Goldstraw Reference Linkmann, Berera and Goldstraw2017; Bandyopadhyay et al. Reference Bandyopadhyay, Oughton, Wan, Matthaeus, Chhiber and Parashar2018). In practice, the interest centres on the dimensionless dissipation rate
and its asymptotic value ![]() $\mathcal {C}_{\varepsilon,\infty }$ as Reynolds number tends to infinity, where
$\mathcal {C}_{\varepsilon,\infty }$ as Reynolds number tends to infinity, where ![]() $\mathcal {U}, \mathcal {L}$ denote the characteristic values of velocity and length, respectively. Non-universality of
$\mathcal {U}, \mathcal {L}$ denote the characteristic values of velocity and length, respectively. Non-universality of ![]() $\mathcal {C}_{\varepsilon,\infty }$ was investigated in various turbulent flows, with varying vector field correlations (Linkmann et al. Reference Linkmann, Berera, McComb and McKay2015, Reference Linkmann, Berera and Goldstraw2017) and anisotropy (Bandyopadhyay et al. Reference Bandyopadhyay, Oughton, Wan, Matthaeus, Chhiber and Parashar2018).
$\mathcal {C}_{\varepsilon,\infty }$ was investigated in various turbulent flows, with varying vector field correlations (Linkmann et al. Reference Linkmann, Berera, McComb and McKay2015, Reference Linkmann, Berera and Goldstraw2017) and anisotropy (Bandyopadhyay et al. Reference Bandyopadhyay, Oughton, Wan, Matthaeus, Chhiber and Parashar2018).
In turbulent flows with more intricate configurations, the energy dissipation properties can be notably influenced by a variety of phenomena and structures. For instance, in oceanic or stratified geophysical flows, interactions between eddies, waves, drafts and fronts in these environments contribute to the complexity of energy dissipation dynamics (Pearson & Fox-Kemper Reference Pearson and Fox-Kemper2018; Pouquet, Rosenberg & Marino Reference Pouquet, Rosenberg and Marino2019; Marino et al. Reference Marino, Feraco, Primavera, Pumir, Pouquet, Rosenberg and Mininni2022). Similarly, in compressible MHD turbulence, the interplay between vortices, shocks and Alfvén waves adds additional complexity, leading to a significantly expanded parameter space. As a result, the understanding of dissipative anomaly in compressible MHD turbulence remains limited.
In this paper, we study the dissipative anomaly in compressible MHD turbulence by performing direct numerical simulations of forced compressible MHD turbulence, without background magnetic field and cross-helicity. The compressibility effect on the dissipative anomaly is explored quantitatively. We propose a unified model that explains the normalized dissipation rate and its variation with compressibility.
2. Equations and numerical simulations
By introducing the reference scales ![]() $\rho _0$ for density,
$\rho _0$ for density, ![]() $U_0$ for velocity,
$U_0$ for velocity, ![]() $B_0$ for magnetic induction,
$B_0$ for magnetic induction, ![]() $L_0$ for length,
$L_0$ for length, ![]() $T_0$ for temperature,
$T_0$ for temperature, ![]() $\rho _0U_0^2$ for pressure,
$\rho _0U_0^2$ for pressure, ![]() $\mu _0$ for dynamic viscosity,
$\mu _0$ for dynamic viscosity, ![]() $\eta _0$ for magnetic diffusivity, and
$\eta _0$ for magnetic diffusivity, and ![]() $\kappa _0$ for thermal conductivity, the compressible MHD system involves five dimensionless parameters: the Reynolds number
$\kappa _0$ for thermal conductivity, the compressible MHD system involves five dimensionless parameters: the Reynolds number ![]() ${Re} = \rho _0U_0L_0/\mu _0$, the magnetic Reynolds number
${Re} = \rho _0U_0L_0/\mu _0$, the magnetic Reynolds number ![]() ${Re}_{m} = U_0L_0/\eta _0$, the Mach number
${Re}_{m} = U_0L_0/\eta _0$, the Mach number ![]() ${M} = U_0/\sqrt {\gamma R T_0}$, the Alfvén Mach number
${M} = U_0/\sqrt {\gamma R T_0}$, the Alfvén Mach number ![]() ${M}_{m} = U_0\sqrt {\rho _0}/B_0$, and the Prandtl number
${M}_{m} = U_0\sqrt {\rho _0}/B_0$, and the Prandtl number ![]() ${Pr} = \mu _0 C_p/\kappa _0,$ where
${Pr} = \mu _0 C_p/\kappa _0,$ where ![]() $\gamma =1.4$ denotes the adiabatic index,
$\gamma =1.4$ denotes the adiabatic index, ![]() $R$ the gas constant, and
$R$ the gas constant, and ![]() $C_p = \gamma R/(\gamma - 1)$ the specific heat at constant pressure. The dimensionless governing equations are
$C_p = \gamma R/(\gamma - 1)$ the specific heat at constant pressure. The dimensionless governing equations are
 $$\begin{gather} \partial_t E + \boldsymbol{\nabla}\boldsymbol{\cdot}\left[(E + p_t)\boldsymbol{u} - \frac{(\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{b})\boldsymbol{b}}{{M}_{m}^2}\right] = \frac{\boldsymbol{\nabla}\boldsymbol{\cdot}(\boldsymbol{\sigma}\boldsymbol{\cdot}\boldsymbol{u})}{{Re}} + \frac{\boldsymbol{\nabla}\boldsymbol{\cdot}(\boldsymbol{b}\boldsymbol{\times}\eta\,\boldsymbol{j})}{{Re}_{m}\,{M}_{m}^2} + \frac{\boldsymbol{\nabla}\boldsymbol{\cdot}(\kappa\,\boldsymbol{\nabla}{T})}{{Pr}\,{Re}\, (\gamma-1){M}^2} \nonumber\\ \qquad + \,\mathcal{F}\boldsymbol{\cdot}\boldsymbol{u} - \varLambda , \end{gather}$$
$$\begin{gather} \partial_t E + \boldsymbol{\nabla}\boldsymbol{\cdot}\left[(E + p_t)\boldsymbol{u} - \frac{(\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{b})\boldsymbol{b}}{{M}_{m}^2}\right] = \frac{\boldsymbol{\nabla}\boldsymbol{\cdot}(\boldsymbol{\sigma}\boldsymbol{\cdot}\boldsymbol{u})}{{Re}} + \frac{\boldsymbol{\nabla}\boldsymbol{\cdot}(\boldsymbol{b}\boldsymbol{\times}\eta\,\boldsymbol{j})}{{Re}_{m}\,{M}_{m}^2} + \frac{\boldsymbol{\nabla}\boldsymbol{\cdot}(\kappa\,\boldsymbol{\nabla}{T})}{{Pr}\,{Re}\, (\gamma-1){M}^2} \nonumber\\ \qquad + \,\mathcal{F}\boldsymbol{\cdot}\boldsymbol{u} - \varLambda , \end{gather}$$
where ![]() $\rho$,
$\rho$, ![]() $\boldsymbol {u}$,
$\boldsymbol {u}$, ![]() $\boldsymbol {b}$ and
$\boldsymbol {b}$ and ![]() $T$ are the density, velocity, magnetic and temperature fields, respectively. Here,
$T$ are the density, velocity, magnetic and temperature fields, respectively. Here, ![]() $E = \rho \boldsymbol {u}^2/2 + p/(\gamma - 1) + \boldsymbol {b}^2/(2{M}_{m}^2)$ denotes the total energy,
$E = \rho \boldsymbol {u}^2/2 + p/(\gamma - 1) + \boldsymbol {b}^2/(2{M}_{m}^2)$ denotes the total energy, ![]() $p_t = p + \boldsymbol {b}^2/(2{M}_{m}^2)$ the total pressure,
$p_t = p + \boldsymbol {b}^2/(2{M}_{m}^2)$ the total pressure, ![]() $\boldsymbol {\sigma } = 2\mu (\boldsymbol{\mathsf{S}} - \theta \boldsymbol {I}/3)$ the viscous stress tensor,
$\boldsymbol {\sigma } = 2\mu (\boldsymbol{\mathsf{S}} - \theta \boldsymbol {I}/3)$ the viscous stress tensor, ![]() $\boldsymbol{\mathsf{S}} = (\boldsymbol {\nabla }\boldsymbol {u} + \boldsymbol {\nabla }\boldsymbol {u}^{\rm T})/2$ the strain rate tensor,
$\boldsymbol{\mathsf{S}} = (\boldsymbol {\nabla }\boldsymbol {u} + \boldsymbol {\nabla }\boldsymbol {u}^{\rm T})/2$ the strain rate tensor, ![]() $\theta = \boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {u}$ the dilatation,
$\theta = \boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {u}$ the dilatation, ![]() $\boldsymbol {I}$ the unit tensor, and
$\boldsymbol {I}$ the unit tensor, and ![]() $\boldsymbol {j} = \boldsymbol {\nabla }\boldsymbol {\times }\boldsymbol {b}$ the current density. Closure is achieved using the ideal gas law
$\boldsymbol {j} = \boldsymbol {\nabla }\boldsymbol {\times }\boldsymbol {b}$ the current density. Closure is achieved using the ideal gas law ![]() $p = \rho T/(\gamma {M}^2)$. For simplicity, we set
$p = \rho T/(\gamma {M}^2)$. For simplicity, we set ![]() ${Pr} = 0.704$,
${Pr} = 0.704$, ![]() ${Pr}_{m} = {Re}_{m}/{Re} = 1$ and
${Pr}_{m} = {Re}_{m}/{Re} = 1$ and ![]() ${M}_{m} = 1$. The dimensionless constitutive coefficients
${M}_{m} = 1$. The dimensionless constitutive coefficients ![]() $\mu, \kappa, \eta$ obey Sutherland's law of air with reference temperature
$\mu, \kappa, \eta$ obey Sutherland's law of air with reference temperature ![]() $T_0=273.15\,{\rm K}$,
$T_0=273.15\,{\rm K}$, ![]() $\mu = \kappa = {1.40417T^{3/2}}/{(T + 0.40417)}$ and
$\mu = \kappa = {1.40417T^{3/2}}/{(T + 0.40417)}$ and ![]() $\eta = \nu = {\mu }/{\rho }$, where
$\eta = \nu = {\mu }/{\rho }$, where ![]() $\nu$ is the kinematic viscosity. To attain a statistically steady state, a large-scale force
$\nu$ is the kinematic viscosity. To attain a statistically steady state, a large-scale force ![]() $\mathcal {F}$ and cooling function
$\mathcal {F}$ and cooling function ![]() $\varLambda$ are imposed in the momentum and energy equations, respectively.
$\varLambda$ are imposed in the momentum and energy equations, respectively.
Direct numerical simulations (DNS) of compressible MHD turbulence are performed in a periodic ![]() $(2{\rm \pi} )^3$ cubic domain, using a hybrid compact-WENO scheme (Wang et al. Reference Wang, Wang, Xiao, Shi and Chen2010; Yang et al. Reference Yang, Wan, Shi, Yang and Chen2016b). This hybrid scheme, known for its high accuracy and efficiency in handling shock–turbulence interaction in compressible turbulent flows, generates negligible numerical dissipation (Yang et al. Reference Yang, Wan, Matthaeus and Chen2021), thus guarantees the reliability of the numerical results presented in this study. To control the compressibility, the large-scale force
$(2{\rm \pi} )^3$ cubic domain, using a hybrid compact-WENO scheme (Wang et al. Reference Wang, Wang, Xiao, Shi and Chen2010; Yang et al. Reference Yang, Wan, Shi, Yang and Chen2016b). This hybrid scheme, known for its high accuracy and efficiency in handling shock–turbulence interaction in compressible turbulent flows, generates negligible numerical dissipation (Yang et al. Reference Yang, Wan, Matthaeus and Chen2021), thus guarantees the reliability of the numerical results presented in this study. To control the compressibility, the large-scale force ![]() $\mathcal {F}$ modifies the compressive (dilatational) velocity field
$\mathcal {F}$ modifies the compressive (dilatational) velocity field ![]() $\boldsymbol {u}_c$ and solenoidal velocity field
$\boldsymbol {u}_c$ and solenoidal velocity field ![]() $\boldsymbol {u}_s$ in the first two wavenumber shells. These are defined by the Helmholtz decomposition (Wang et al. Reference Wang, Shi, Wang, Xiao, He and Chen2012; Yang et al. Reference Yang, Wan, Shi, Yang and Chen2016b, Reference Yang, Matthaeus, Shi, Wan and Chen2017)
$\boldsymbol {u}_s$ in the first two wavenumber shells. These are defined by the Helmholtz decomposition (Wang et al. Reference Wang, Shi, Wang, Xiao, He and Chen2012; Yang et al. Reference Yang, Wan, Shi, Yang and Chen2016b, Reference Yang, Matthaeus, Shi, Wan and Chen2017)
The parameter ![]() $r_c$ regulates the fraction of the energy input into the compressive field
$r_c$ regulates the fraction of the energy input into the compressive field ![]() $\boldsymbol {u}_c$. The limiting conditions
$\boldsymbol {u}_c$. The limiting conditions ![]() $r_c = 1$ and 0 represent pure dilatational and pure solenoidal forcing, respectively. For more simulation details, see Yang et al. (Reference Yang, Wan, Shi, Yang and Chen2016b).
$r_c = 1$ and 0 represent pure dilatational and pure solenoidal forcing, respectively. For more simulation details, see Yang et al. (Reference Yang, Wan, Shi, Yang and Chen2016b).
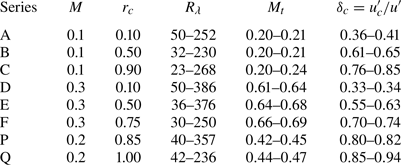
A number of simulations with resolution up to ![]() $768^3$ were performed, and grouped into eight different series, based on Mach number
$768^3$ were performed, and grouped into eight different series, based on Mach number ![]() ${M}$ and forcing parameter
${M}$ and forcing parameter ![]() $r_c$. All statistical quantities are obtained by averaging (denoted by
$r_c$. All statistical quantities are obtained by averaging (denoted by ![]() $\langle \ \rangle$) over 80 snapshots spanning at least 6 large-eddy turnover times, after the flow reaches the statistically steady state. Basic simulation parameters are the Taylor microscale Reynolds number
$\langle \ \rangle$) over 80 snapshots spanning at least 6 large-eddy turnover times, after the flow reaches the statistically steady state. Basic simulation parameters are the Taylor microscale Reynolds number ![]() $R_\lambda = 23\unicode{x2013}386$, the turbulent Mach number
$R_\lambda = 23\unicode{x2013}386$, the turbulent Mach number ![]() $M_t = 0.2\unicode{x2013}0.69$, and
$M_t = 0.2\unicode{x2013}0.69$, and ![]() $\delta _c = u_c^\prime /u^\prime = 0.36\unicode{x2013}0.94$. The parameter
$\delta _c = u_c^\prime /u^\prime = 0.36\unicode{x2013}0.94$. The parameter ![]() $\delta _c$ represents the relative magnitude of the compressive velocity and the flow compressibility, where
$\delta _c$ represents the relative magnitude of the compressive velocity and the flow compressibility, where ![]() $u^\prime = \sqrt {\langle \boldsymbol {u}^2 \rangle /3}$ and
$u^\prime = \sqrt {\langle \boldsymbol {u}^2 \rangle /3}$ and ![]() $u_c^\prime$ denote the root mean square (r.m.s.) values of the components of the vectors
$u_c^\prime$ denote the root mean square (r.m.s.) values of the components of the vectors ![]() $\boldsymbol {u}$ and
$\boldsymbol {u}$ and ![]() $\boldsymbol {u}_c$, respectively. All simulations are fully resolved such that
$\boldsymbol {u}_c$, respectively. All simulations are fully resolved such that ![]() $k_{max} \eta _u \ge 2$, where
$k_{max} \eta _u \ge 2$, where ![]() $k_{max}$ is the maximum resolved wavenumber, and
$k_{max}$ is the maximum resolved wavenumber, and ![]() $\eta _u$ denotes the Kolmogorov length scale. The magnetic and cross helicities remain small in all simulation cases, to eliminate their impacts and emphasize the compressibility effect.
$\eta _u$ denotes the Kolmogorov length scale. The magnetic and cross helicities remain small in all simulation cases, to eliminate their impacts and emphasize the compressibility effect.
Simulation parameters are summarized in table 1. More simulation details can be found in tables I and II of the supplementary material available at https://doi.org/10.1017/jfm.2024.545. We note that the variations of ![]() $M_t$ and
$M_t$ and ![]() $\delta _c$ within each series are small, implying their weak dependence on Reynolds number. It is also clear that the forcing parameter
$\delta _c$ within each series are small, implying their weak dependence on Reynolds number. It is also clear that the forcing parameter ![]() $r_c$ has little impact on
$r_c$ has little impact on ![]() $M_t$ for fixed Mach number, and
$M_t$ for fixed Mach number, and ![]() $M_t/{M} \approx 2$ holds for all cases, whereas the parameter
$M_t/{M} \approx 2$ holds for all cases, whereas the parameter ![]() $\delta _c$ obviously increases as
$\delta _c$ obviously increases as ![]() $r_c$ increases, and is almost independent of Mach number. Therefore, as in compressible HD turbulence (Donzis & John Reference Donzis and John2020), the nature of forcing has to be considered in addition to
$r_c$ increases, and is almost independent of Mach number. Therefore, as in compressible HD turbulence (Donzis & John Reference Donzis and John2020), the nature of forcing has to be considered in addition to ![]() $R_\lambda$ and
$R_\lambda$ and ![]() $M_t$.
$M_t$.
Table 1. Basic parameters and statistics of simulation series: ![]() ${M}$ denotes the Mach number,
${M}$ denotes the Mach number, ![]() $r_c$ the forcing parameter,
$r_c$ the forcing parameter, ![]() $R_\lambda = {Re}\,\langle \rho \rangle \,u^\prime \lambda /\left \langle \mu \right \rangle$ the Taylor scale Reynolds number,
$R_\lambda = {Re}\,\langle \rho \rangle \,u^\prime \lambda /\left \langle \mu \right \rangle$ the Taylor scale Reynolds number, ![]() $M_t = {M} u^\prime /\langle \sqrt {T/3} \rangle$ the turbulent Mach number, and
$M_t = {M} u^\prime /\langle \sqrt {T/3} \rangle$ the turbulent Mach number, and ![]() $\delta _c = u_c^\prime /u^\prime$ the flow compressibility parameter.
$\delta _c = u_c^\prime /u^\prime$ the flow compressibility parameter.
3. Results
By analysing selective DNS cases (see figure 1 in the supplementary material), it is found that the velocity field spectrum follows a classical incompressible ![]() $k^{-5/3}$ law for low to moderate
$k^{-5/3}$ law for low to moderate ![]() $\delta _c$, but shows
$\delta _c$, but shows ![]() $k^{-2}$ behaviour for cases with high
$k^{-2}$ behaviour for cases with high ![]() $\delta _c$, due to the shock effects (Wang et al. Reference Wang, Yang, Shi, Xiao, He and Chen2013; Yang et al. Reference Yang, Shi, Wan, Matthaeus and Chen2016a). This different scaling behaviour suggests that the large-scale force can strongly influence the cascade process, and implies non-universality of compressible MHD turbulence associated with the dimensionless parameter
$\delta _c$, due to the shock effects (Wang et al. Reference Wang, Yang, Shi, Xiao, He and Chen2013; Yang et al. Reference Yang, Shi, Wan, Matthaeus and Chen2016a). This different scaling behaviour suggests that the large-scale force can strongly influence the cascade process, and implies non-universality of compressible MHD turbulence associated with the dimensionless parameter ![]() $\delta _c = u_c^\prime /u^\prime$.
$\delta _c = u_c^\prime /u^\prime$.
3.1. The scaling of the relative dissipation rates
The total dissipation consists of the viscous dissipation ![]() $\varepsilon _k = {Re}^{-1}\,\langle \sigma _{ij}S_{ij}/\rho \rangle$ and Ohmic dissipation
$\varepsilon _k = {Re}^{-1}\,\langle \sigma _{ij}S_{ij}/\rho \rangle$ and Ohmic dissipation ![]() $\varepsilon _m = {Re}_{m}^{-1}\,\langle \eta\,\boldsymbol {j}^2/\rho \rangle$. Moreover, the viscous dissipation
$\varepsilon _m = {Re}_{m}^{-1}\,\langle \eta\,\boldsymbol {j}^2/\rho \rangle$. Moreover, the viscous dissipation ![]() $\varepsilon _k$ can be decomposed as
$\varepsilon _k$ can be decomposed as ![]() $\varepsilon _k = \varepsilon _s + \varepsilon _c + \varepsilon _n$. Here, the first term,
$\varepsilon _k = \varepsilon _s + \varepsilon _c + \varepsilon _n$. Here, the first term, ![]() $\varepsilon _s = {Re}^{-1}\,\langle \nu \boldsymbol {\omega }^2 \rangle$, represents contributions by the solenoidal velocity field
$\varepsilon _s = {Re}^{-1}\,\langle \nu \boldsymbol {\omega }^2 \rangle$, represents contributions by the solenoidal velocity field ![]() $\boldsymbol {u}_s$. The second component,
$\boldsymbol {u}_s$. The second component, ![]() $\varepsilon _c = (4/3)\,{Re}^{-1}\,\langle \nu \theta ^2 \rangle$, denotes the dilatational dissipation and is exclusively due to the dilatational motion
$\varepsilon _c = (4/3)\,{Re}^{-1}\,\langle \nu \theta ^2 \rangle$, denotes the dilatational dissipation and is exclusively due to the dilatational motion ![]() $\boldsymbol {u}_c$. The mixed term
$\boldsymbol {u}_c$. The mixed term ![]() $\varepsilon _n = 2\,{Re}^{-1}\,\langle \nu \boldsymbol {\nabla }\boldsymbol {\cdot }(\boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {\nabla } \boldsymbol {u} - \theta \boldsymbol {u}) \rangle$ vanishes if
$\varepsilon _n = 2\,{Re}^{-1}\,\langle \nu \boldsymbol {\nabla }\boldsymbol {\cdot }(\boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {\nabla } \boldsymbol {u} - \theta \boldsymbol {u}) \rangle$ vanishes if ![]() $\nu$ is uniform over the whole domain. The magnitude of
$\nu$ is uniform over the whole domain. The magnitude of ![]() $\varepsilon _n/\varepsilon _k$ remains small for all the simulation cases, hence the dissipation due to dilatational and shear motions can be viewed as decoupled.
$\varepsilon _n/\varepsilon _k$ remains small for all the simulation cases, hence the dissipation due to dilatational and shear motions can be viewed as decoupled.
The scaling of ![]() $\varepsilon _c/\varepsilon _s$ versus the parameter
$\varepsilon _c/\varepsilon _s$ versus the parameter ![]() $\varLambda _c = E_c/E_s$ is shown in figure 1(a), where
$\varLambda _c = E_c/E_s$ is shown in figure 1(a), where ![]() $E_s = \langle \rho \boldsymbol {u}_s^2 / 2 \rangle$ and
$E_s = \langle \rho \boldsymbol {u}_s^2 / 2 \rangle$ and ![]() $E_c = \langle \rho \boldsymbol {u}_c^2 / 2 \rangle$ denote the turbulent total energy of the solenoidal and compressive fields, respectively. One can see that all data points follow a simple scaling
$E_c = \langle \rho \boldsymbol {u}_c^2 / 2 \rangle$ denote the turbulent total energy of the solenoidal and compressive fields, respectively. One can see that all data points follow a simple scaling
especially for the cases with high Reynolds number ![]() $R_\lambda \ge 150$. This scaling was also observed in compressible HD turbulence (Donzis & John Reference Donzis and John2020).
$R_\lambda \ge 150$. This scaling was also observed in compressible HD turbulence (Donzis & John Reference Donzis and John2020).
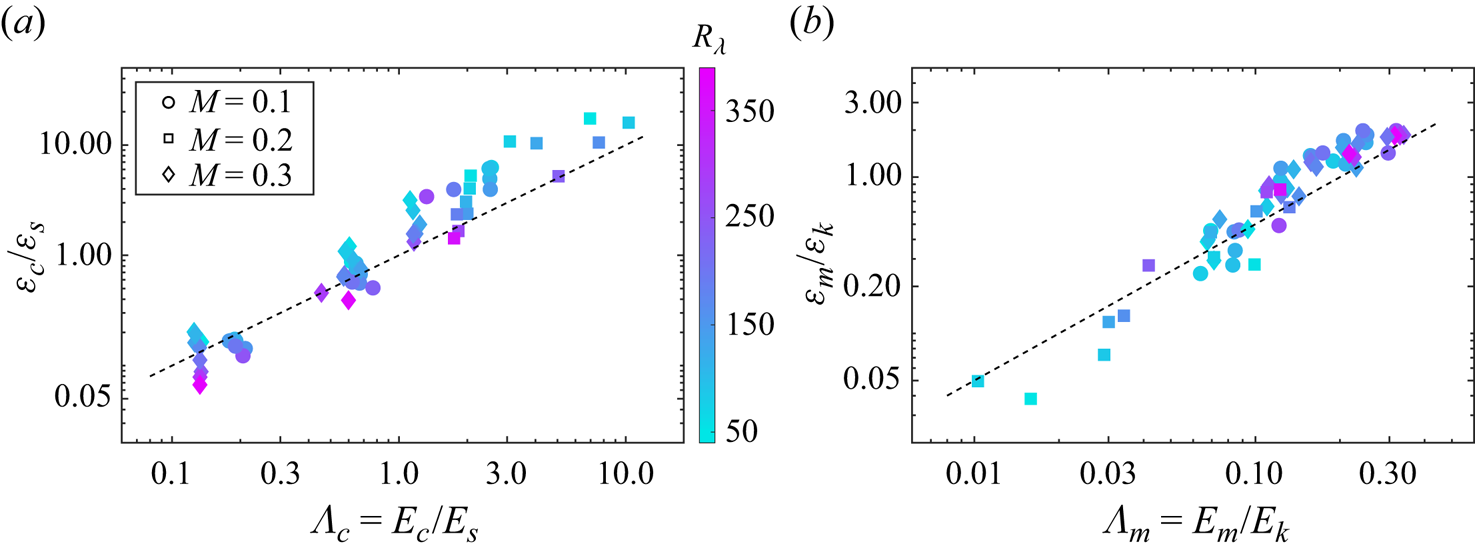
Figure 1. (a) The ratio of dilatational to solenoidal dissipation rate ![]() $\varepsilon _c/\varepsilon _s$ versus
$\varepsilon _c/\varepsilon _s$ versus ![]() $\varLambda _c = E_c/E_s$, the ratio of solenoidal to dilatational energy. (b) The ratio of Ohmic to viscous dissipation
$\varLambda _c = E_c/E_s$, the ratio of solenoidal to dilatational energy. (b) The ratio of Ohmic to viscous dissipation ![]() $\varepsilon _m/\varepsilon _k$ versus
$\varepsilon _m/\varepsilon _k$ versus ![]() $\varLambda _m = E_m/E_k$, the ratio of magnetic to kinetic energy. Here, only simulation cases with
$\varLambda _m = E_m/E_k$, the ratio of magnetic to kinetic energy. Here, only simulation cases with ![]() $R_\lambda \ge 50$ are taken into account, and the dashed lines indicate the linear scaling.
$R_\lambda \ge 50$ are taken into account, and the dashed lines indicate the linear scaling.
Figure 1(b) shows the scaling of ![]() $\varepsilon _m/\varepsilon _k$, the ratio of Ohmic to viscous dissipation, as a function of
$\varepsilon _m/\varepsilon _k$, the ratio of Ohmic to viscous dissipation, as a function of ![]() $\varLambda _m = E_m/E_k$, where
$\varLambda _m = E_m/E_k$, where ![]() $E_m$ and
$E_m$ and ![]() $E_k$ denote the magnetic and kinetic energy, respectively. All simulations in our study are mechanically driven; hence the magnetic energy, maintained by the dynamo process, is much smaller than the kinetic energy (
$E_k$ denote the magnetic and kinetic energy, respectively. All simulations in our study are mechanically driven; hence the magnetic energy, maintained by the dynamo process, is much smaller than the kinetic energy (![]() $\varLambda _m \lessapprox 0.3$ here). However, the magnetic dissipation can surpass the viscous dissipation when
$\varLambda _m \lessapprox 0.3$ here). However, the magnetic dissipation can surpass the viscous dissipation when ![]() $\varLambda _m \gtrapprox 0.2$, suggesting that the magnetic field is dominated by the strong turbulent shear motions at small scales, such as current sheets. Moreover, all data points fit well with
$\varLambda _m \gtrapprox 0.2$, suggesting that the magnetic field is dominated by the strong turbulent shear motions at small scales, such as current sheets. Moreover, all data points fit well with
with ![]() $g_m \approx 5.0$. This scaling remains robust over two orders of magnitude in
$g_m \approx 5.0$. This scaling remains robust over two orders of magnitude in ![]() $\varepsilon _m/\varepsilon _k$, implying that the characteristic time scales of magnetic and kinetic energy dissipation are of similar order. Figure 1(b) also shows that
$\varepsilon _m/\varepsilon _k$, implying that the characteristic time scales of magnetic and kinetic energy dissipation are of similar order. Figure 1(b) also shows that ![]() $\varepsilon _m/\varepsilon _k$ approximately increases as
$\varepsilon _m/\varepsilon _k$ approximately increases as ![]() $R_\lambda$ increases, implying that the nonlinear dynamo process is more efficient in maintaining small-scale magnetic field fluctuations at higher Reynolds number than at lower Reynolds number. Similar conclusions have been reached for IMHD turbulence (Linkmann et al. Reference Linkmann, Berera and Goldstraw2017).
$R_\lambda$ increases, implying that the nonlinear dynamo process is more efficient in maintaining small-scale magnetic field fluctuations at higher Reynolds number than at lower Reynolds number. Similar conclusions have been reached for IMHD turbulence (Linkmann et al. Reference Linkmann, Berera and Goldstraw2017).
3.2. The normalized total dissipation rate
As used in IMHD turbulence (Linkmann et al. Reference Linkmann, Berera, McComb and McKay2015, Reference Linkmann, Berera and Goldstraw2017), the Elsässer variables ![]() $\boldsymbol {z}_\pm = \boldsymbol {u} \pm \boldsymbol {v}_A$ are introduced, where
$\boldsymbol {z}_\pm = \boldsymbol {u} \pm \boldsymbol {v}_A$ are introduced, where ![]() $\boldsymbol {v}_A = \boldsymbol {b}/\sqrt {\rho }$ denotes the magnetic fluctuations in Alfvén velocity unit. The r.m.s. values and integral length scales defined with respect to the Elsässer variables are
$\boldsymbol {v}_A = \boldsymbol {b}/\sqrt {\rho }$ denotes the magnetic fluctuations in Alfvén velocity unit. The r.m.s. values and integral length scales defined with respect to the Elsässer variables are ![]() $Z_\pm = \sqrt {(\langle \boldsymbol {z}_\pm ^2 \rangle - \langle \boldsymbol {z}_\pm \rangle ^2)/3}$ and
$Z_\pm = \sqrt {(\langle \boldsymbol {z}_\pm ^2 \rangle - \langle \boldsymbol {z}_\pm \rangle ^2)/3}$ and ![]() $L_\pm = {\rm \pi}/(2Z_\pm ^2) \int _0^\infty k^{-1}\,E^\pm (k)\,\mathrm {d}{k}$, where
$L_\pm = {\rm \pi}/(2Z_\pm ^2) \int _0^\infty k^{-1}\,E^\pm (k)\,\mathrm {d}{k}$, where ![]() $E^\pm (k)$ denotes the Elsässer energy spectrum such that
$E^\pm (k)$ denotes the Elsässer energy spectrum such that ![]() $\int _0^\infty E^\pm (k)\,\mathrm {d}{k} = 3 Z_\pm ^2/2$. In analogy with the IMHD case (Linkmann et al. Reference Linkmann, Berera, McComb and McKay2015, Reference Linkmann, Berera and Goldstraw2017), we define the dimensionless dissipation rate
$\int _0^\infty E^\pm (k)\,\mathrm {d}{k} = 3 Z_\pm ^2/2$. In analogy with the IMHD case (Linkmann et al. Reference Linkmann, Berera, McComb and McKay2015, Reference Linkmann, Berera and Goldstraw2017), we define the dimensionless dissipation rate ![]() $\mathcal {C}_{\varepsilon }^\pm$ and the generalized large-scale Reynolds number
$\mathcal {C}_{\varepsilon }^\pm$ and the generalized large-scale Reynolds number ![]() $R_L^\pm$ as
$R_L^\pm$ as
In our simulations ![]() $Z_+ \approx Z_-$ and
$Z_+ \approx Z_-$ and ![]() $L_+ \approx L_-$ since the cross-helicity
$L_+ \approx L_-$ since the cross-helicity ![]() $H_c = \langle \boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {b} \rangle$ remains negligible. Then
$H_c = \langle \boldsymbol {u}\boldsymbol {\cdot }\boldsymbol {b} \rangle$ remains negligible. Then ![]() $R_L^+ \approx R_L^-$ and
$R_L^+ \approx R_L^-$ and ![]() $\mathcal {C}_{\varepsilon }^+ \approx \mathcal {C}_{\varepsilon }^-$ also hold (see figure 2 in the supplementary material). We focus on the relation between
$\mathcal {C}_{\varepsilon }^+ \approx \mathcal {C}_{\varepsilon }^-$ also hold (see figure 2 in the supplementary material). We focus on the relation between
and ![]() $R_L^-$ to explore the dissipative anomaly in this paper.
$R_L^-$ to explore the dissipative anomaly in this paper.
The model equation
is often used to describe quantitatively the trend of dimensionless dissipation rate as Reynolds number increases (Linkmann et al. Reference Linkmann, Berera, McComb and McKay2015, Reference Linkmann, Berera and Goldstraw2017; McComb et al. Reference McComb, Berera, Yoffe and Linkmann2015; Bandyopadhyay et al. Reference Bandyopadhyay, Oughton, Wan, Matthaeus, Chhiber and Parashar2018), where ![]() $\mathcal {C}_{\varepsilon,\infty }$ is the asymptotic value of
$\mathcal {C}_{\varepsilon,\infty }$ is the asymptotic value of ![]() $\mathcal {C}_{\varepsilon }$ as
$\mathcal {C}_{\varepsilon }$ as ![]() $R_L^-$ tends to infinity, and
$R_L^-$ tends to infinity, and ![]() $\mathcal {D}$ is the coefficient of the first-order term. As suggested in Linkmann et al. (Reference Linkmann, Berera, McComb and McKay2015, Reference Linkmann, Berera and Goldstraw2017), the higher-order terms become important only for low Reynolds number cases, which is further discussed in the supplementary material.
$\mathcal {D}$ is the coefficient of the first-order term. As suggested in Linkmann et al. (Reference Linkmann, Berera, McComb and McKay2015, Reference Linkmann, Berera and Goldstraw2017), the higher-order terms become important only for low Reynolds number cases, which is further discussed in the supplementary material.
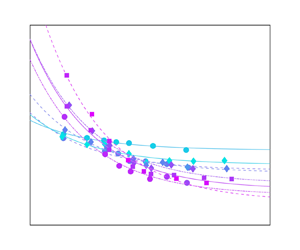
The dimensionless dissipation rate ![]() $\mathcal {C}_{\varepsilon }$ as a function of generalized large-scale Reynolds number
$\mathcal {C}_{\varepsilon }$ as a function of generalized large-scale Reynolds number ![]() $R_L^-$ is scattered in figure 2 for all simulation cases with
$R_L^-$ is scattered in figure 2 for all simulation cases with ![]() $R_L^- \ge 150$, which fits well with the model (3.5). Here, the data points and fitting curves are coloured by the parameter
$R_L^- \ge 150$, which fits well with the model (3.5). Here, the data points and fitting curves are coloured by the parameter ![]() $\delta _c$ to highlight the flow compressibility effect. The asymptotic dissipation rates
$\delta _c$ to highlight the flow compressibility effect. The asymptotic dissipation rates ![]() $\mathcal {C}_{\varepsilon,\infty }$ remain positive, hence the dissipative anomaly holds generally in compressible MHD turbulence, even for flows with high compressibility.
$\mathcal {C}_{\varepsilon,\infty }$ remain positive, hence the dissipative anomaly holds generally in compressible MHD turbulence, even for flows with high compressibility.
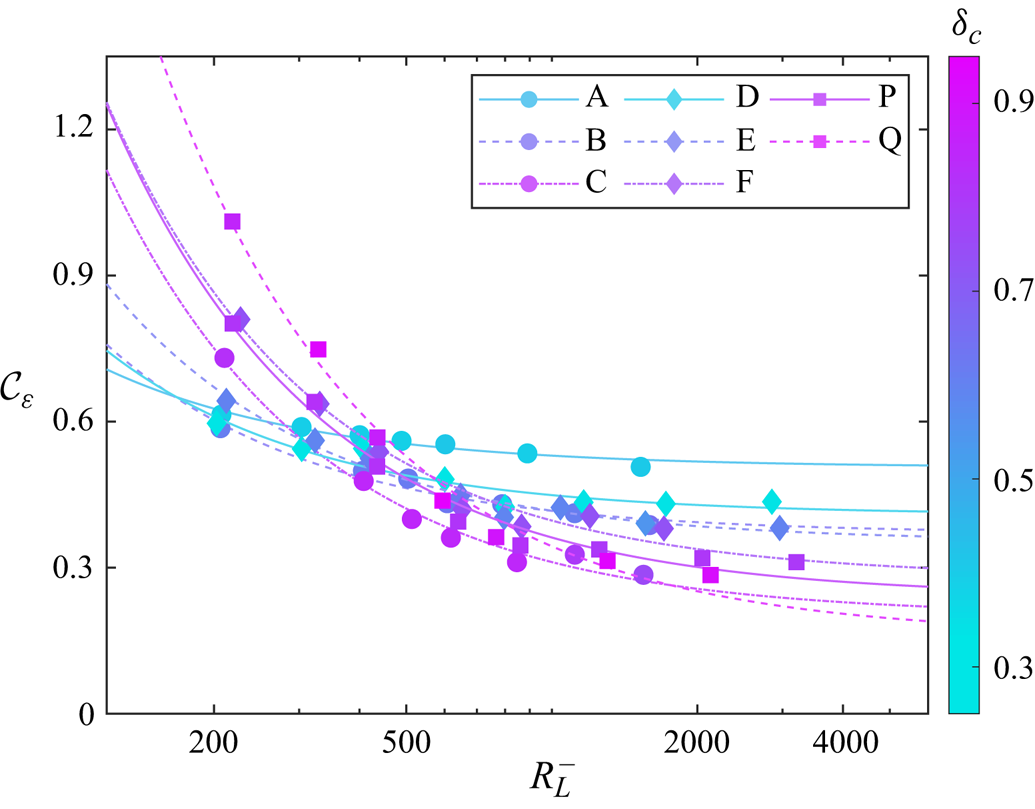
Figure 2. The normalized dissipation rate ![]() $\mathcal {C}_{\varepsilon }$ versus the generalized large-scale Reynolds number
$\mathcal {C}_{\varepsilon }$ versus the generalized large-scale Reynolds number ![]() $R_L^-$ for all simulation series, along with corresponding fitting curves (3.5). Here, the markers and lines are coloured by the values of compressibility parameter
$R_L^-$ for all simulation series, along with corresponding fitting curves (3.5). Here, the markers and lines are coloured by the values of compressibility parameter ![]() $\delta _c$.
$\delta _c$.
3.3. The compressibility effect on the dissipative anomaly
As shown in figure 2, the compressibility depresses the normalized dissipation rate ![]() $\mathcal {C}_{\varepsilon }$ at high Reynolds number yet enhances it at low Reynolds number, indicating that
$\mathcal {C}_{\varepsilon }$ at high Reynolds number yet enhances it at low Reynolds number, indicating that ![]() $\mathcal {C}_{\varepsilon,\infty }$ decreases with increasing compressibility, but the coefficient
$\mathcal {C}_{\varepsilon,\infty }$ decreases with increasing compressibility, but the coefficient ![]() $\mathcal {D}$ increases with the increase of flow compressibility. The estimated values of model coefficients
$\mathcal {D}$ increases with the increase of flow compressibility. The estimated values of model coefficients ![]() $\mathcal {C}_{\varepsilon,\infty }, \mathcal {D}$ and the corresponding standard errors
$\mathcal {C}_{\varepsilon,\infty }, \mathcal {D}$ and the corresponding standard errors ![]() $\sigma _C, \sigma _D$ are summarized in table 2. The values of
$\sigma _C, \sigma _D$ are summarized in table 2. The values of ![]() $\overline {\delta _c}$, denoting the mean value of
$\overline {\delta _c}$, denoting the mean value of ![]() $\delta _c$ within each DNS series, are also reported to clearly show the level of compressibility of each simulation series. Moreover, the results of incompressible isotropic driven HD turbulence (McComb et al. Reference McComb, Berera, Yoffe and Linkmann2015) and MHD turbulence (Bandyopadhyay et al. Reference Bandyopadhyay, Oughton, Wan, Matthaeus, Chhiber and Parashar2018) are included for comparison. (Here, the result from Bandyopadhyay et al. (Reference Bandyopadhyay, Oughton, Wan, Matthaeus, Chhiber and Parashar2018) is multiplied by factor 2 due to the different definitions of
$\delta _c$ within each DNS series, are also reported to clearly show the level of compressibility of each simulation series. Moreover, the results of incompressible isotropic driven HD turbulence (McComb et al. Reference McComb, Berera, Yoffe and Linkmann2015) and MHD turbulence (Bandyopadhyay et al. Reference Bandyopadhyay, Oughton, Wan, Matthaeus, Chhiber and Parashar2018) are included for comparison. (Here, the result from Bandyopadhyay et al. (Reference Bandyopadhyay, Oughton, Wan, Matthaeus, Chhiber and Parashar2018) is multiplied by factor 2 due to the different definitions of ![]() $\mathcal {C}_{\varepsilon }$.) One can see that the values of
$\mathcal {C}_{\varepsilon }$.) One can see that the values of ![]() $\mathcal {C}_{\varepsilon,\infty }$ and
$\mathcal {C}_{\varepsilon,\infty }$ and ![]() $\mathcal {D}$ of series A (with weak compressibility) are quite close to those in incompressible cases. Also, the standard errors are significantly small compared to the estimated values, for all simulation series, indicating the credibility of the fitting model (3.5). Based on the von Kármán–Howarth (vKH) equation (de Kármán & Howarth Reference de Kármán and Howarth1938; Chandrasekhar Reference Chandrasekhar1951; Politano & Pouquet Reference Politano and Pouquet1998) that describes the evolution of correlation functions in turbulence, the asymptotic value
$\mathcal {D}$ of series A (with weak compressibility) are quite close to those in incompressible cases. Also, the standard errors are significantly small compared to the estimated values, for all simulation series, indicating the credibility of the fitting model (3.5). Based on the von Kármán–Howarth (vKH) equation (de Kármán & Howarth Reference de Kármán and Howarth1938; Chandrasekhar Reference Chandrasekhar1951; Politano & Pouquet Reference Politano and Pouquet1998) that describes the evolution of correlation functions in turbulence, the asymptotic value ![]() $\mathcal {C}_{\varepsilon,\infty }$ represents the flux of total energy across scales in a well scale-separated inertial range (Linkmann et al. Reference Linkmann, Berera, McComb and McKay2015, Reference Linkmann, Berera and Goldstraw2017; McComb et al. Reference McComb, Berera, Yoffe and Linkmann2015). Our results show that the flow compressibility can strongly depress the energy flux, and again indicate the non-universality of energy transfer and dissipation processes in compressible MHD turbulence.
$\mathcal {C}_{\varepsilon,\infty }$ represents the flux of total energy across scales in a well scale-separated inertial range (Linkmann et al. Reference Linkmann, Berera, McComb and McKay2015, Reference Linkmann, Berera and Goldstraw2017; McComb et al. Reference McComb, Berera, Yoffe and Linkmann2015). Our results show that the flow compressibility can strongly depress the energy flux, and again indicate the non-universality of energy transfer and dissipation processes in compressible MHD turbulence.
Table 2. Summary of estimated values for the asymptotic dimensionless dissipation rate ![]() $\mathcal {C}_{\varepsilon,\infty }$ and model coefficient
$\mathcal {C}_{\varepsilon,\infty }$ and model coefficient ![]() $\mathcal {D}$ from different simulation series and references. Here,
$\mathcal {D}$ from different simulation series and references. Here, ![]() $\sigma _C, \sigma _D$ refer to the standard errors of
$\sigma _C, \sigma _D$ refer to the standard errors of ![]() $\mathcal {C}_{\varepsilon,\infty }, \mathcal {D}$ in the fitting procedure, respectively, and
$\mathcal {C}_{\varepsilon,\infty }, \mathcal {D}$ in the fitting procedure, respectively, and ![]() $\overline {\delta _c}$ denotes the mean value of
$\overline {\delta _c}$ denotes the mean value of ![]() $\delta _c$ within each simulation series. The results of HD turbulence (McComb et al. Reference McComb, Berera, Yoffe and Linkmann2015) and MHD turbulence (Bandyopadhyay et al. Reference Bandyopadhyay, Oughton, Wan, Matthaeus, Chhiber and Parashar2018) are included for comparison.
$\delta _c$ within each simulation series. The results of HD turbulence (McComb et al. Reference McComb, Berera, Yoffe and Linkmann2015) and MHD turbulence (Bandyopadhyay et al. Reference Bandyopadhyay, Oughton, Wan, Matthaeus, Chhiber and Parashar2018) are included for comparison.
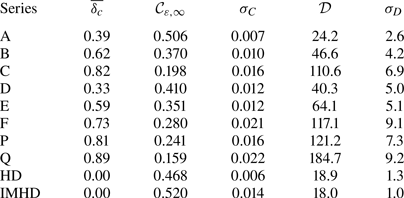
To quantify the compressibility effect on the dissipative anomaly in compressible MHD (CMHD) turbulence, the asymptotic dimensionless dissipation rate ![]() $\mathcal {C}_{\varepsilon,\infty }$ and model coefficient
$\mathcal {C}_{\varepsilon,\infty }$ and model coefficient ![]() $\mathcal {D}$ from all simulation series are scattered. Figure 3(a) shows the trend of
$\mathcal {D}$ from all simulation series are scattered. Figure 3(a) shows the trend of ![]() $\mathcal {C}_{\varepsilon,\infty }$ versus
$\mathcal {C}_{\varepsilon,\infty }$ versus ![]() $\overline {\delta _c}^2 \approx \overline {E_c/E_k}$, along with the incompressible values. Surprisingly, a simple scaling
$\overline {\delta _c}^2 \approx \overline {E_c/E_k}$, along with the incompressible values. Surprisingly, a simple scaling
is observed, where ![]() $\mathcal {C}_0 = 0.517 \pm 0.021$ is quite close to the asymptotic value in the IMHD case, and
$\mathcal {C}_0 = 0.517 \pm 0.021$ is quite close to the asymptotic value in the IMHD case, and ![]() $\mathcal {C}_1 = 0.436 \pm 0.042$ denotes the fitting coefficient. Also, the positivity of the limiting value
$\mathcal {C}_1 = 0.436 \pm 0.042$ denotes the fitting coefficient. Also, the positivity of the limiting value ![]() $\mathcal {C}_{\varepsilon,\infty }(\overline {\delta _c} \rightarrow 1) = \mathcal {C}_0 - \mathcal {C}_1 = 0.081 \pm 0.027$ suggests that the dissipative anomaly still holds even in the MHD turbulence with extremely high compressibility. Figure 3(b) depicts the scaling of
$\mathcal {C}_{\varepsilon,\infty }(\overline {\delta _c} \rightarrow 1) = \mathcal {C}_0 - \mathcal {C}_1 = 0.081 \pm 0.027$ suggests that the dissipative anomaly still holds even in the MHD turbulence with extremely high compressibility. Figure 3(b) depicts the scaling of ![]() $\mathcal {D}/\mathcal {D}_0$, the normalized model coefficient as flow compressibility increases, where
$\mathcal {D}/\mathcal {D}_0$, the normalized model coefficient as flow compressibility increases, where ![]() $\mathcal {D}_0 = 18.0$ denotes the model coefficient in the IMHD case. The plot indicates that the scaling
$\mathcal {D}_0 = 18.0$ denotes the model coefficient in the IMHD case. The plot indicates that the scaling
holds approximately, with fitting parameter ![]() $\mathcal {D}_1 = 13.5$.
$\mathcal {D}_1 = 13.5$.
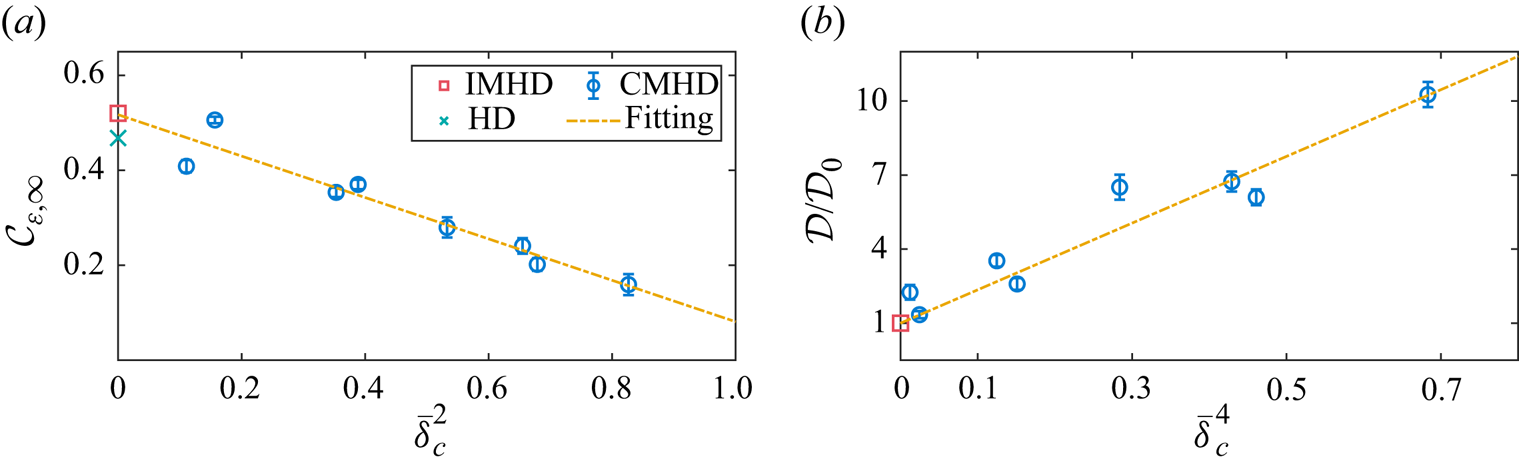
Figure 3. The trend of the asymptotic normalized dissipation rate ![]() $\mathcal {C}_{\varepsilon,\infty }$ and model coefficient
$\mathcal {C}_{\varepsilon,\infty }$ and model coefficient ![]() $\mathcal {D}$ as flow compressibility changes: (a)
$\mathcal {D}$ as flow compressibility changes: (a) ![]() $\mathcal {C}_{\varepsilon,\infty }$ versus
$\mathcal {C}_{\varepsilon,\infty }$ versus ![]() $\overline {\delta _c}^2$; (b)
$\overline {\delta _c}^2$; (b) ![]() $\mathcal {D}/\mathcal {D}_0$ versus
$\mathcal {D}/\mathcal {D}_0$ versus ![]() $\overline {\delta _c}^4$. The dashed lines indicate the linear regression, and the error bars represent the standard errors in fitting procedure.
$\overline {\delta _c}^4$. The dashed lines indicate the linear regression, and the error bars represent the standard errors in fitting procedure.
Based on the above simple scaling of ![]() $\mathcal {C}_{\varepsilon,\infty }, \mathcal {D}$ versus
$\mathcal {C}_{\varepsilon,\infty }, \mathcal {D}$ versus ![]() $\delta _c$, the model equation (3.5) that expresses the dimensionless dissipation rate
$\delta _c$, the model equation (3.5) that expresses the dimensionless dissipation rate ![]() $\mathcal {C}_{\varepsilon }$ in terms of the generalized Reynolds number
$\mathcal {C}_{\varepsilon }$ in terms of the generalized Reynolds number ![]() $R_L^-$ can be transformed into a unified form,
$R_L^-$ can be transformed into a unified form,
similar in form to the model for the IMHD case. In particular, the modified dimensionless dissipation rate ![]() $\mathcal {C}_{\varepsilon }^\prime$ and the modified large-scale Reynolds number
$\mathcal {C}_{\varepsilon }^\prime$ and the modified large-scale Reynolds number ![]() $R_L^\prime$ are defined as
$R_L^\prime$ are defined as
in which the correction from compressibility is implemented. To emphasize the efficacy of this re-scaling, the values of ![]() $\mathcal {C}_{\varepsilon }^\prime$ and
$\mathcal {C}_{\varepsilon }^\prime$ and ![]() $R_L^\prime$ for all DNS cases are scattered in figure 4. Notably, all data points, regardless of their level of flow compressibility, collapse along the model equation (3.8).
$R_L^\prime$ for all DNS cases are scattered in figure 4. Notably, all data points, regardless of their level of flow compressibility, collapse along the model equation (3.8).

Figure 4. Modified normalized dissipation rate ![]() $\mathcal {C}_{\varepsilon }^\prime$ versus modified Reynolds number
$\mathcal {C}_{\varepsilon }^\prime$ versus modified Reynolds number ![]() $R_L^\prime$ for all simulations. The dashed line corresponds to (3.8), the same form as in the IMHD case.
$R_L^\prime$ for all simulations. The dashed line corresponds to (3.8), the same form as in the IMHD case.
However, it is essential to highlight that the aforementioned results cannot be considered as universal. In particular, the unified model equation was obtained under the specific conditions of isotropy and zero helicities, and fixed fluid parameters, including ![]() $Pr=0.704$ and
$Pr=0.704$ and ![]() $T_0=273.15\,{\rm K}$. While these conditions and parameters may not alter the qualitative form of the basic model equation (3.5), the model coefficients
$T_0=273.15\,{\rm K}$. While these conditions and parameters may not alter the qualitative form of the basic model equation (3.5), the model coefficients ![]() $\mathcal {C}_{\varepsilon,\infty }, \mathcal {D}$ will likely depend on various flow parameters and may not follow simple scaling laws similar to (3.6)–(3.7). For instance, prior studies have showed notable dependencies of the asymptotic dissipation rate
$\mathcal {C}_{\varepsilon,\infty }, \mathcal {D}$ will likely depend on various flow parameters and may not follow simple scaling laws similar to (3.6)–(3.7). For instance, prior studies have showed notable dependencies of the asymptotic dissipation rate ![]() $\mathcal {C}_{\varepsilon,\infty }$ on cross-helicity, magnetic helicity (Linkmann et al. Reference Linkmann, Berera, McComb and McKay2015, Reference Linkmann, Berera and Goldstraw2017) and mean magnetic field (Bandyopadhyay et al. Reference Bandyopadhyay, Oughton, Wan, Matthaeus, Chhiber and Parashar2018) in IMHD turbulence. Therefore, in this study, the unified (3.8) serves as an alternative representation to illustrate the scaling relations between model coefficients and compressibility parameters, and does not imply the universality of dissipation in compressible MHD turbulence. We expect that exploring compressible MHD turbulence under more general configurations may yield further intriguing findings.
$\mathcal {C}_{\varepsilon,\infty }$ on cross-helicity, magnetic helicity (Linkmann et al. Reference Linkmann, Berera, McComb and McKay2015, Reference Linkmann, Berera and Goldstraw2017) and mean magnetic field (Bandyopadhyay et al. Reference Bandyopadhyay, Oughton, Wan, Matthaeus, Chhiber and Parashar2018) in IMHD turbulence. Therefore, in this study, the unified (3.8) serves as an alternative representation to illustrate the scaling relations between model coefficients and compressibility parameters, and does not imply the universality of dissipation in compressible MHD turbulence. We expect that exploring compressible MHD turbulence under more general configurations may yield further intriguing findings.
4. Conclusions
In conclusion, by direct numerical simulation, we explored the non-universality in compressible MHD turbulence, emphasizing the effect of compressibility (which is mainly controlled by the forcing scheme) on the dissipative anomaly, a feature of substantial importance in turbulence theory and modelling. By studying the scaling between the ratio of dissipation rates and the ratio of energy, it is found that the characteristic time scales of viscous dissipation and magnetic dissipation are of the same order of magnitude, and a similar result was verified for the kinetic dissipation process induced by dilatation and shearing processes.
In the compressible MHD turbulence, the dimensionless total dissipation rate ![]() $\mathcal {C}_{\varepsilon }$ approaches asymptotically a non-zero value
$\mathcal {C}_{\varepsilon }$ approaches asymptotically a non-zero value ![]() $\mathcal {C}_{\varepsilon,\infty }$ for increasing generalized large-scale Reynolds number
$\mathcal {C}_{\varepsilon,\infty }$ for increasing generalized large-scale Reynolds number ![]() $R_L^-$. That is, as in HD and IMHD turbulence, the dissipative anomaly is present in compressible MHD turbulence as well. Moreover, the relation between
$R_L^-$. That is, as in HD and IMHD turbulence, the dissipative anomaly is present in compressible MHD turbulence as well. Moreover, the relation between ![]() $\mathcal {C}_{\varepsilon }$ and
$\mathcal {C}_{\varepsilon }$ and ![]() $R_L^-$ can be described by the simple model equation (3.5). The values of
$R_L^-$ can be described by the simple model equation (3.5). The values of ![]() $\mathcal {C}_{\varepsilon,\infty }$ and model coefficient
$\mathcal {C}_{\varepsilon,\infty }$ and model coefficient ![]() $\mathcal {D}$ of simulation series show obvious differences, suggesting the non-universality of compressible MHD turbulence induced by different levels of flow compressibility. Specifically, a decreasing trend was found for
$\mathcal {D}$ of simulation series show obvious differences, suggesting the non-universality of compressible MHD turbulence induced by different levels of flow compressibility. Specifically, a decreasing trend was found for ![]() $\mathcal {C}_{\varepsilon,\infty }$ with the increase of
$\mathcal {C}_{\varepsilon,\infty }$ with the increase of ![]() $\delta _c$, implying that the compressibility can strongly depress the energy flux in compressible MHD turbulence. It was also found that the model coefficient
$\delta _c$, implying that the compressibility can strongly depress the energy flux in compressible MHD turbulence. It was also found that the model coefficient ![]() $\mathcal {D}$ would increase dramatically for enhanced flow compressibility. Further numerical results find that
$\mathcal {D}$ would increase dramatically for enhanced flow compressibility. Further numerical results find that ![]() $\mathcal {C}_{\varepsilon,\infty }$ and
$\mathcal {C}_{\varepsilon,\infty }$ and ![]() $\mathcal {D}$ exhibit simple scaling with respect to the compressibility parameter
$\mathcal {D}$ exhibit simple scaling with respect to the compressibility parameter ![]() $\delta _c$. Based on this finding, we introduced a modified normalized dissipation rate
$\delta _c$. Based on this finding, we introduced a modified normalized dissipation rate ![]() $\mathcal {C}_{\varepsilon }^\prime$ and a modified large-scale Reynolds number
$\mathcal {C}_{\varepsilon }^\prime$ and a modified large-scale Reynolds number ![]() $R_L^\prime$, which incorporate the compressibility effect. In terms of these, we find the quantitative relation (3.5) transformed into one unified equation (3.8), in which the asymptotic value and model coefficient correspond to the IMHD case. These results inform understanding of the relationship between incompressible and compressible MHD flow models, and provide a quantitative assessment of the influence of compressibility on energy transfer. Our findings hold potential relevance to various studies focusing on real physics systems, particularly in plasma turbulence domains like the solar wind. For instance, our numerical results could provide valuable guidance to simplify the complex formulations of exact laws in compressible MHD turbulence (Banerjee & Galtier Reference Banerjee and Galtier2013; Andrés & Sahraoui Reference Andrés and Sahraoui2017). Moreover, these exact relations are frequently utilized to estimate energy dissipation and particle heating in spacecraft observations (Sorriso-Valvo et al. Reference Sorriso-Valvo, Marino, Carbone, Noullez, Lepreti, Veltri, Bruno, Bavassano and Pietropaolo2007; Wan et al. Reference Wan, Matthaeus, Karimabadi, Roytershteyn, Shay, Wu, Daughton, Loring and Chapman2012, Reference Wan, Matthaeus, Roytershteyn, Parashar, Wu and Karimabadi2016; Andrés et al. Reference Andrés, Sahraoui, Galtier, Hadid, Dmitruk and Mininni2018; Hadid et al. Reference Hadid, Sahraoui, Galtier and Huang2018; Simon & Sahraoui Reference Simon and Sahraoui2021; Yang et al. Reference Yang, Matthaeus, Roy, Roytershteyn, Parashar, Bandyopadhyay and Wan2022; Jiang et al. Reference Jiang, Li, Yang, Zhou, Matthaeus and Wan2023; Marino & Sorriso-Valvo Reference Marino and Sorriso-Valvo2023). This is especially pertinent in collisionless plasmas where classical definitions of viscosity and resistivity are inapplicable, making direct dissipation rate calculations from observational data unfeasible.
$R_L^\prime$, which incorporate the compressibility effect. In terms of these, we find the quantitative relation (3.5) transformed into one unified equation (3.8), in which the asymptotic value and model coefficient correspond to the IMHD case. These results inform understanding of the relationship between incompressible and compressible MHD flow models, and provide a quantitative assessment of the influence of compressibility on energy transfer. Our findings hold potential relevance to various studies focusing on real physics systems, particularly in plasma turbulence domains like the solar wind. For instance, our numerical results could provide valuable guidance to simplify the complex formulations of exact laws in compressible MHD turbulence (Banerjee & Galtier Reference Banerjee and Galtier2013; Andrés & Sahraoui Reference Andrés and Sahraoui2017). Moreover, these exact relations are frequently utilized to estimate energy dissipation and particle heating in spacecraft observations (Sorriso-Valvo et al. Reference Sorriso-Valvo, Marino, Carbone, Noullez, Lepreti, Veltri, Bruno, Bavassano and Pietropaolo2007; Wan et al. Reference Wan, Matthaeus, Karimabadi, Roytershteyn, Shay, Wu, Daughton, Loring and Chapman2012, Reference Wan, Matthaeus, Roytershteyn, Parashar, Wu and Karimabadi2016; Andrés et al. Reference Andrés, Sahraoui, Galtier, Hadid, Dmitruk and Mininni2018; Hadid et al. Reference Hadid, Sahraoui, Galtier and Huang2018; Simon & Sahraoui Reference Simon and Sahraoui2021; Yang et al. Reference Yang, Matthaeus, Roy, Roytershteyn, Parashar, Bandyopadhyay and Wan2022; Jiang et al. Reference Jiang, Li, Yang, Zhou, Matthaeus and Wan2023; Marino & Sorriso-Valvo Reference Marino and Sorriso-Valvo2023). This is especially pertinent in collisionless plasmas where classical definitions of viscosity and resistivity are inapplicable, making direct dissipation rate calculations from observational data unfeasible.
Supplementary material
Supplementary material is available at https://doi.org/10.1017/jfm.2024.545.
Funding
This work was supported by NSFC (grant nos 12225204 and 11902138), Department of Science and Technology of Guangdong Province (grant nos 2019B21203001 and 2020B1212030001), and the Shenzhen Science and Technology Program (grant no. KQTD20180411143441009). Y.Y. and W.H.M. were partially supported by US NSF grant AGS-2108834. Numerical simulations were supported by the Center for Computational Science and Engineering of Southern University of Science and Technology.
Declaration of interests
The authors report no conflict of interest.