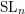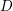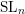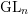1 Introduction
Let
![]() $C$
be a nonsingular projective and integral curve of genus
$C$
be a nonsingular projective and integral curve of genus
![]() $g$
over an algebraically closed field of characteristic zero. Let
$g$
over an algebraically closed field of characteristic zero. Let
![]() $D$
be a line bundle on
$D$
be a line bundle on
![]() $C$
, with
$C$
, with
 $d:=\deg (D)>2g-2$
.
$d:=\deg (D)>2g-2$
.
Fix a pair of coprime positive integers
![]() $(n,e)$
. The
$(n,e)$
. The
![]() $\text{GL}_{n}$
moduli space we consider is the moduli space [Reference NitsureNit91] of stable, rank
$\text{GL}_{n}$
moduli space we consider is the moduli space [Reference NitsureNit91] of stable, rank
![]() $n$
, degree
$n$
, degree
![]() $e$
,
$e$
,
![]() $D$
-twisted Higgs bundles
$D$
-twisted Higgs bundles
 $(E,\unicode[STIX]{x1D719}:E\rightarrow E(D))$
on
$(E,\unicode[STIX]{x1D719}:E\rightarrow E(D))$
on
![]() $C$
; it is an integral, quasi projective and nonsingular variety. There is the projective Hitchin morphism
$C$
; it is an integral, quasi projective and nonsingular variety. There is the projective Hitchin morphism
 $h_{n}:M_{n}\rightarrow A_{n}=\bigoplus _{i=1}^{n}H^{0}(C,iD)$
onto the affine space of the possible characteristic polynomials of
$h_{n}:M_{n}\rightarrow A_{n}=\bigoplus _{i=1}^{n}H^{0}(C,iD)$
onto the affine space of the possible characteristic polynomials of
![]() $\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}$
.
The decomposition theorem [Reference Beilinson, Bernstein and DeligneBBD81] predicts that the direct image complex
 ${Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell }$
splits into a finite direct sum of shifted simple perverse sheaves, each supported on an integral closed subvariety
${Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell }$
splits into a finite direct sum of shifted simple perverse sheaves, each supported on an integral closed subvariety
![]() $S\subseteq A_{n}$
. These subvarieties are called the supports of
$S\subseteq A_{n}$
. These subvarieties are called the supports of
 ${Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell }$
. The socle of
${Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell }$
. The socle of
 ${Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell }$
, denoted by
${Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell }$
, denoted by
 $\text{Socle}({Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })$
, is the finite subset of
$\text{Socle}({Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })$
, is the finite subset of
![]() $A_{n}$
of generic points
$A_{n}$
of generic points
![]() $\unicode[STIX]{x1D702}_{S}$
of the supports
$\unicode[STIX]{x1D702}_{S}$
of the supports
![]() $S$
of
$S$
of
 ${Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell }$
.
${Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell }$
.
One of the main geometric ingredients of Ngô’s proof [Reference NgôNgô10] of the Langlands–Shelstad fundamental lemma for reductive Lie groups
![]() $G$
, is his support theorem [Reference NgôNgô10, Theorem 7.2.1]. This is a statement concerning the socle of the direct image complex via the Hitchin morphism
$G$
, is his support theorem [Reference NgôNgô10, Theorem 7.2.1]. This is a statement concerning the socle of the direct image complex via the Hitchin morphism
 $M_{G}\rightarrow A_{G}$
associated with
$M_{G}\rightarrow A_{G}$
associated with
 $(G,C,D)$
, after restriction to a certain large open subset of the target
$(G,C,D)$
, after restriction to a certain large open subset of the target
![]() $A_{G}$
. In the special case
$A_{G}$
. In the special case
 $G=\text{GL}_{n}$
, one considers the elliptic locus, i.e. the dense open subvariety
$G=\text{GL}_{n}$
, one considers the elliptic locus, i.e. the dense open subvariety
 $A_{n}^{\text{ell}}\subseteq A_{n}$
corresponding to those points
$A_{n}^{\text{ell}}\subseteq A_{n}$
corresponding to those points
![]() $a\in A_{n}$
for which the associated spectral curve is geometrically integral. Then the Ngô support theorem implies that
$a\in A_{n}$
for which the associated spectral curve is geometrically integral. Then the Ngô support theorem implies that
 $\text{Socle}(Rh_{n,\ast }\overline{\mathbb{Q}}_{\ell })\,\cap \,A_{n}^{\text{ell}}=\{\unicode[STIX]{x1D702}_{A_{n}}\}$
, the generic point of the target
$\text{Socle}(Rh_{n,\ast }\overline{\mathbb{Q}}_{\ell })\,\cap \,A_{n}^{\text{ell}}=\{\unicode[STIX]{x1D702}_{A_{n}}\}$
, the generic point of the target
![]() $A_{n}$
. In other words, over the elliptic locus, the simple summands appearing in the decomposition theorem are the intermediate extensions to
$A_{n}$
. In other words, over the elliptic locus, the simple summands appearing in the decomposition theorem are the intermediate extensions to
![]() $A_{n}^{\text{ell}}$
of the direct image lisse sheaves over the locus
$A_{n}^{\text{ell}}$
of the direct image lisse sheaves over the locus
 $A_{n}^{\text{smooth}}$
of regular values of
$A_{n}^{\text{smooth}}$
of regular values of
![]() $h_{n}$
. This has striking consequences for the handling of orbital integrals over the elliptic locus (for every
$h_{n}$
. This has striking consequences for the handling of orbital integrals over the elliptic locus (for every
![]() $G$
), which thus become more tractable: the ones corresponding to points in
$G$
), which thus become more tractable: the ones corresponding to points in
 $A_{n}^{\text{ell}}\setminus A^{\text{smooth}}$
can be related to the ones over
$A_{n}^{\text{ell}}\setminus A^{\text{smooth}}$
can be related to the ones over
 $A_{n}^{\text{ smooth}}$
by a principle of continuity on
$A_{n}^{\text{ smooth}}$
by a principle of continuity on
![]() $A_{n}^{\text{ell}}$
; this is precisely because there are no new supports on the boundary
$A_{n}^{\text{ell}}$
; this is precisely because there are no new supports on the boundary
 $A_{n}^{\text{ ell}}\setminus A_{n}^{\text{smooth}}$
(cf. [Reference NgôNgô11, § 1]).
$A_{n}^{\text{ ell}}\setminus A_{n}^{\text{smooth}}$
(cf. [Reference NgôNgô11, § 1]).
Support-type theorems have been appearing in the related geometric contexts of relative Hilbert schemes and of relative compactified Jacobians of families of reduced planar curves in [Reference Maulik and YunMY14, Reference Migliorini and ShendeMS13, Reference Migliorini and ShendeMS13, Reference Migliorini, Shende and VivianiMSV15, Reference ShendeShe12], also in connection with Bogomol’nyi–Prasad–Sommerfield (BPS) states.
It is thus interesting, important, and seemingly nontrivial, to ‘go beyond the elliptic locus’. Chaudouard and Laumon have extended [Reference Chaudouard and LaumonCL12] Ngô’s result on
![]() $A_{n}^{\text{ell}}$
(which holds for every
$A_{n}^{\text{ell}}$
(which holds for every
![]() $G$
), by proving that (and here we specialize their result to
$G$
), by proving that (and here we specialize their result to
 $G=\text{GL}_{n}$
)
$G=\text{GL}_{n}$
)
 $\text{Socle}(Rh_{n,\ast }\overline{\mathbb{Q}}_{\ell })\,\cap \,A_{n}^{\text{grss}}=\{\unicode[STIX]{x1D702}_{A_{n}}\}$
, where
$\text{Socle}(Rh_{n,\ast }\overline{\mathbb{Q}}_{\ell })\,\cap \,A_{n}^{\text{grss}}=\{\unicode[STIX]{x1D702}_{A_{n}}\}$
, where
 $A_{n}^{\text{ell}}\subseteq A_{n}^{\text{grss}}$
is the larger open locus for which the associated spectral curves are reduced. They have also subsequently extended this result to the whole base
$A_{n}^{\text{ell}}\subseteq A_{n}^{\text{grss}}$
is the larger open locus for which the associated spectral curves are reduced. They have also subsequently extended this result to the whole base
![]() $A_{n}$
of the
$A_{n}$
of the
![]() $D$
-twisted
$D$
-twisted
![]() $\text{GL}_{n}$
Hitchin fibration in [Reference Chaudouard and LaumonCL16], where they prove the following.
$\text{GL}_{n}$
Hitchin fibration in [Reference Chaudouard and LaumonCL16], where they prove the following.
Theorem 1.0.1 (
 $\text{GL}_{n}$
socle [Reference Chaudouard and LaumonCL16]).
$\text{GL}_{n}$
socle [Reference Chaudouard and LaumonCL16]).
 $\text{Socle}({Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })=\{\unicode[STIX]{x1D702}_{A_{n}}\}$
.
$\text{Socle}({Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })=\{\unicode[STIX]{x1D702}_{A_{n}}\}$
.
In particular, there are no new supports as one passes from the regular locus
 $A_{n}^{\text{smooth}}$
, to the elliptic locus
$A_{n}^{\text{smooth}}$
, to the elliptic locus
![]() $A_{n}^{\text{ ell}}$
, to
$A_{n}^{\text{ ell}}$
, to
![]() $A_{n}^{\text{grss}}$
and, finally, to the whole of
$A_{n}^{\text{grss}}$
and, finally, to the whole of
![]() $A_{n}$
. The decomposition theorem then takes the form of an isomorphism
$A_{n}$
. The decomposition theorem then takes the form of an isomorphism
 ${Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell }\cong \bigoplus _{q\geqslant 0}{\mathcal{I}}{\mathcal{C}}_{A_{n}}(R^{q})[-q]$
, where
${Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell }\cong \bigoplus _{q\geqslant 0}{\mathcal{I}}{\mathcal{C}}_{A_{n}}(R^{q})[-q]$
, where
![]() $R^{q}$
is the lisse restriction of the
$R^{q}$
is the lisse restriction of the
![]() $\overline{\mathbb{Q}}_{\ell }$
-constructible sheaf
$\overline{\mathbb{Q}}_{\ell }$
-constructible sheaf
 ${Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell }$
to
${Rh_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell }$
to
 $A_{n}^{\text{smooth}}$
, and where
$A_{n}^{\text{smooth}}$
, and where
![]() ${\mathcal{I}}{\mathcal{C}}$
denotes the intermediate extension functor shifted so as to ‘start’ in cohomological degree zero. Since the general fibers of
${\mathcal{I}}{\mathcal{C}}$
denotes the intermediate extension functor shifted so as to ‘start’ in cohomological degree zero. Since the general fibers of
![]() $h_{n}$
are (connected) abelian varieties, we even have
$h_{n}$
are (connected) abelian varieties, we even have
 $R^{q}\cong \bigwedge ^{q}R^{1}$
for every
$R^{q}\cong \bigwedge ^{q}R^{1}$
for every
 $0\leqslant q\leqslant 2d_{h_{n}}$
, where
$0\leqslant q\leqslant 2d_{h_{n}}$
, where
![]() $d_{h_{n}}$
is the relative dimension of
$d_{h_{n}}$
is the relative dimension of
![]() $h_{n}$
.
$h_{n}$
.
When
 $G=\text{SL}_{n}$
, we have the following picture, which goes back, at least implicitly, to [Reference NitsureNit91]; see § 2.2. Our
$G=\text{SL}_{n}$
, we have the following picture, which goes back, at least implicitly, to [Reference NitsureNit91]; see § 2.2. Our
![]() $\text{SL}_{n}$
moduli space
$\text{SL}_{n}$
moduli space
 $\check{M}_{n}\subseteq M_{n}$
consists of those stable pairs with fixed
$\check{M}_{n}\subseteq M_{n}$
consists of those stable pairs with fixed
 $\unicode[STIX]{x1D716}=\det (E)$
and trivial trace
$\unicode[STIX]{x1D716}=\det (E)$
and trivial trace
 $\text{tr}(\unicode[STIX]{x1D719})=0$
. Then
$\text{tr}(\unicode[STIX]{x1D719})=0$
. Then
![]() $\check{M}_{n}$
is an integral, quasi projective and nonsingular variety. The restriction of the Hitchin morphism
$\check{M}_{n}$
is an integral, quasi projective and nonsingular variety. The restriction of the Hitchin morphism
![]() $h_{n}$
, yields the Hitchin morphism
$h_{n}$
, yields the Hitchin morphism
 $\check{h}_{n}:\check{M}_{n}\rightarrow {\check{A}}_{n}:=\bigoplus _{i=2}^{n}H^{0}(X,iD)$
, whose socle is the object of study of this paper.
$\check{h}_{n}:\check{M}_{n}\rightarrow {\check{A}}_{n}:=\bigoplus _{i=2}^{n}H^{0}(X,iD)$
, whose socle is the object of study of this paper.
This socle is known over the elliptic locus
 ${\check{A}}_{n}^{\text{ell}}={\check{A}}_{n}\,\cap \,A_{n}^{\text{ell}}$
: by work of Ngô [Reference NgôNgô06, Reference NgôNgô10], we have that
${\check{A}}_{n}^{\text{ell}}={\check{A}}_{n}\,\cap \,A_{n}^{\text{ell}}$
: by work of Ngô [Reference NgôNgô06, Reference NgôNgô10], we have that
 $\text{socle}({R\check{h}_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })\,\cap \,{\check{A}}_{n}^{\text{ ell}}$
is given by the generic point
$\text{socle}({R\check{h}_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })\,\cap \,{\check{A}}_{n}^{\text{ ell}}$
is given by the generic point
![]() $\unicode[STIX]{x1D702}_{{\check{A}}_{n}}$
, union a finite set of points (66), directly related to the endoscopy theory of
$\unicode[STIX]{x1D702}_{{\check{A}}_{n}}$
, union a finite set of points (66), directly related to the endoscopy theory of
![]() $\text{SL}_{n}$
.
$\text{SL}_{n}$
.
The purpose of this paper is to prove the following theorem, to the effect that there are no new supports in
![]() ${\check{A}}_{n}\setminus {\check{A}}_{n}^{\text{ell}}$
, beyond the ones (66) already known to dwell in
${\check{A}}_{n}\setminus {\check{A}}_{n}^{\text{ell}}$
, beyond the ones (66) already known to dwell in
![]() ${\check{A}}_{n}^{\text{ell}}$
.
${\check{A}}_{n}^{\text{ell}}$
.
Theorem 1.0.2 (
 $\text{SL}_{n}$
socle).
$\text{SL}_{n}$
socle).
 $\text{Socle}({R\check{h}_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })\subseteq {\check{A}}_{n}^{ell}$
.
$\text{Socle}({R\check{h}_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })\subseteq {\check{A}}_{n}^{ell}$
.
At first sight, the proof of our main Theorem 1.0.2 for the
![]() $\text{SL}_{n}$
socle runs in parallel with the one of Theorem 1.0.1 for the
$\text{SL}_{n}$
socle runs in parallel with the one of Theorem 1.0.1 for the
![]() $\text{GL}_{n}$
socle in [Reference Chaudouard and LaumonCL16, § 9], where the authors use: Ngô support inequality over the whole base
$\text{GL}_{n}$
socle in [Reference Chaudouard and LaumonCL16, § 9], where the authors use: Ngô support inequality over the whole base
![]() $A_{n}$
; a multi-variable
$A_{n}$
; a multi-variable
![]() $\unicode[STIX]{x1D6FF}$
-regularity inequality for the Jacobi group scheme acting on the Hitchin fibers over the elliptic locus; the identity between the abelian variety parts of the Jacobian of an arbitrary spectral curve, and the Jacobian of the normalization of its reduction.
$\unicode[STIX]{x1D6FF}$
-regularity inequality for the Jacobi group scheme acting on the Hitchin fibers over the elliptic locus; the identity between the abelian variety parts of the Jacobian of an arbitrary spectral curve, and the Jacobian of the normalization of its reduction.
The situation over
![]() $\text{SL}_{n}$
presents some substantial differences, which we now summarize.
$\text{SL}_{n}$
presents some substantial differences, which we now summarize.
-
(1) We need to prove the support inequality Theorem 3.4.1(1) over the whole
 $\text{SL}_{n}$
base
$\text{SL}_{n}$
base
 ${\check{A}}_{n}$
. This had been known [Reference NgôNgô10] over
${\check{A}}_{n}$
. This had been known [Reference NgôNgô10] over
 ${\check{A}}_{n}^{\text{ell}}$
only.
${\check{A}}_{n}^{\text{ell}}$
only. -
(2) In order to achieve the
 $\text{SL}_{n}$
support inequality, we need to establish the polarizability Theorem 4.7.2 of the Tate module of the Prym group scheme over
$\text{SL}_{n}$
support inequality, we need to establish the polarizability Theorem 4.7.2 of the Tate module of the Prym group scheme over
 ${\check{A}}_{n}$
.
${\check{A}}_{n}$
. -
(3) In turn, this required that: we determine the explicit form (38) of a natural polarization of the Tate module of the Jacobian of an arbitrary spectral curve (see the
 $\text{GL}_{n}$
polarizability Theorem 3.3.1); we combine the explicit (38) with the identification (47) of the affine parts of the fibers of the Jacobi and Prym groups schemes. At this juncture, the
$\text{GL}_{n}$
polarizability Theorem 3.3.1); we combine the explicit (38) with the identification (47) of the affine parts of the fibers of the Jacobi and Prym groups schemes. At this juncture, the
 $\text{SL}_{n}$
polarizability result follows by first exhibiting the Prym Tate module as a natural direct summand of the Jacobi Tate module, and then by using that pull-back and push-forward (norm) are adjoint for the cup product.
$\text{SL}_{n}$
polarizability result follows by first exhibiting the Prym Tate module as a natural direct summand of the Jacobi Tate module, and then by using that pull-back and push-forward (norm) are adjoint for the cup product. -
(4) The
 $\unicode[STIX]{x1D6FF}$
-regularity inequality over
$\unicode[STIX]{x1D6FF}$
-regularity inequality over
 ${\check{A}}_{n}^{\text{ell}}$
afforded by (58) is not useful towards proving our main result Theorem 1.0.2. However, the method of proof is: we use a product formula for the Hitchin fibration, and the identification (47) of the affine parts of the Jacobi and Prym varieties, to show that the codimensions of the
${\check{A}}_{n}^{\text{ell}}$
afforded by (58) is not useful towards proving our main result Theorem 1.0.2. However, the method of proof is: we use a product formula for the Hitchin fibration, and the identification (47) of the affine parts of the Jacobi and Prym varieties, to show that the codimensions of the
 $\unicode[STIX]{x1D6FF}$
-loci are preserved when passing from the elliptic locus
$\unicode[STIX]{x1D6FF}$
-loci are preserved when passing from the elliptic locus
 $A_{n}^{\text{ell}}$
, to the traceless elliptic locus
$A_{n}^{\text{ell}}$
, to the traceless elliptic locus
 ${\check{A}}_{n}^{\text{ell}}$
, so that (58) holds.
${\check{A}}_{n}^{\text{ell}}$
, so that (58) holds. -
(5) We pursue the same line of argument to reach the correct
 $\text{SL}_{n}$
replacement (76) of the
$\text{SL}_{n}$
replacement (76) of the
 $\text{GL}_{n}$
multi-variable
$\text{GL}_{n}$
multi-variable
 $\unicode[STIX]{x1D6FF}$
-regularity inequality used in [Reference Chaudouard and LaumonCL16, § 9]. This is done by first considering a multi-variable Hitchin base, then by slicing it using linear weighted conditions on the traces, and finally by verifying that the codimensions of the
$\unicode[STIX]{x1D6FF}$
-regularity inequality used in [Reference Chaudouard and LaumonCL16, § 9]. This is done by first considering a multi-variable Hitchin base, then by slicing it using linear weighted conditions on the traces, and finally by verifying that the codimensions of the
 $\unicode[STIX]{x1D6FF}$
-loci are un-effected by the slicing.
$\unicode[STIX]{x1D6FF}$
-loci are un-effected by the slicing. -
(6) We fix a minor inaccuracy in [Reference Chaudouard and LaumonCL16]. See Remark 5.4.3.
As to the structure of the paper, we refer the reader to the summaries at the beginning of each of the five sections.
2 Preliminaries
This section is a collection of preliminary constructions, results and definitions. Sections 2.1, 2.2 introduce the
![]() $D$
-twisted
$D$
-twisted
![]() $\text{SL}_{n}$
Hitchin morphism
$\text{SL}_{n}$
Hitchin morphism
 $\check{h}_{n}:\check{M}_{n}\rightarrow {\check{A}}_{n}$
which is the focus of this paper. The
$\check{h}_{n}:\check{M}_{n}\rightarrow {\check{A}}_{n}$
which is the focus of this paper. The
![]() $\text{GL}_{n}$
case plays an important role, and is thus discussed as well. Section 2.3 discusses spectral curves and covers: diagram (2) plays a recurrent role in the paper. Spectral curves afford an important alternative interpretation of the fibers of the Hitchin morphism via the Hitchin, Beauville–Narasimhan–Ramanan, Schaub correspondence, which is discussed in § 2.4, together with some essential properties of the Hitchin morphism and of its fibers: connectivity, action of the Prym variety (8), irreducible components over the elliptic locus. This leads to a discussion in § 2.5 of the endoscopic locus for
$\text{GL}_{n}$
case plays an important role, and is thus discussed as well. Section 2.3 discusses spectral curves and covers: diagram (2) plays a recurrent role in the paper. Spectral curves afford an important alternative interpretation of the fibers of the Hitchin morphism via the Hitchin, Beauville–Narasimhan–Ramanan, Schaub correspondence, which is discussed in § 2.4, together with some essential properties of the Hitchin morphism and of its fibers: connectivity, action of the Prym variety (8), irreducible components over the elliptic locus. This leads to a discussion in § 2.5 of the endoscopic locus for
![]() $\text{SL}_{n}$
, which can be described with the aid of the
$\text{SL}_{n}$
, which can be described with the aid of the
![]() $n$
-torsion in
$n$
-torsion in
 $\text{ Pic}^{0}(C)$
. Section 2.6 discusses Ngô’s notion of
$\text{ Pic}^{0}(C)$
. Section 2.6 discusses Ngô’s notion of
![]() $\unicode[STIX]{x1D6FF}$
-regular weak abelian fibration, which is a very important tool in the study of Hitchin systems, and an essential one for this paper; two highlights are Ngô support inequality, and its ‘opposite’, the
$\unicode[STIX]{x1D6FF}$
-regular weak abelian fibration, which is a very important tool in the study of Hitchin systems, and an essential one for this paper; two highlights are Ngô support inequality, and its ‘opposite’, the
![]() $\unicode[STIX]{x1D6FF}$
-regularity inequality.
$\unicode[STIX]{x1D6FF}$
-regularity inequality.
Unless otherwise mentioned, we work with varieties, separated schemes of finite type, over a field of characteristic zero. Let
![]() $C$
be an integral and nonsingular curve of genus
$C$
be an integral and nonsingular curve of genus
![]() $g$
and let
$g$
and let
 $D\in \text{Pic}^{d}(C)$
be a fixed line bundle on
$D\in \text{Pic}^{d}(C)$
be a fixed line bundle on
![]() $C$
of degree
$C$
of degree
 $d>2g-2$
. We fix two coprime integers
$d>2g-2$
. We fix two coprime integers
![]() $(n,e)$
and a degree
$(n,e)$
and a degree
![]() $e$
line bundle
$e$
line bundle
 $\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
. Recall that the coprimality condition ensures that the two notions of stability and of semistability coincide, so that the (coarse
$\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
. Recall that the coprimality condition ensures that the two notions of stability and of semistability coincide, so that the (coarse
![]() $=$
fine) moduli spaces of Higgs bundles we consider are nonsingular.
$=$
fine) moduli spaces of Higgs bundles we consider are nonsingular.
2.1
 $\text{GL}_{n}$
and
$\text{GL}_{n}$
and
 $\text{SL}_{n}$
Hitchin fibrations
$\text{SL}_{n}$
Hitchin fibrations
A standard reference for what follows is [Reference NitsureNit91].
The
![]() $\text{GL}_{n}$
case. Let
$\text{GL}_{n}$
case. Let
![]() $\mathscr{M}$
be the moduli space of stable,
$\mathscr{M}$
be the moduli space of stable,
![]() $D$
-twisted,
$D$
-twisted,
![]() $\text{GL}_{n}$
Higgs bundles of rank
$\text{GL}_{n}$
Higgs bundles of rank
![]() $n$
and degree
$n$
and degree
![]() $e$
on the curve
$e$
on the curve
![]() $C$
. Then
$C$
. Then
![]() $\mathscr{M}$
is a nonsingular and quasi-projective variety of pure dimension
$\mathscr{M}$
is a nonsingular and quasi-projective variety of pure dimension
![]() $n^{2}d+1$
. It parameterizes stable pairs
$n^{2}d+1$
. It parameterizes stable pairs
![]() $(E,\unicode[STIX]{x1D719})$
, where:
$(E,\unicode[STIX]{x1D719})$
, where:
![]() $E$
is a rank
$E$
is a rank
![]() $n$
and degree
$n$
and degree
![]() $e$
vector bundle on the curve
$e$
vector bundle on the curve
![]() $C$
, and
$C$
, and
 $\unicode[STIX]{x1D719}:E\rightarrow E(D)$
is a morphism of
$\unicode[STIX]{x1D719}:E\rightarrow E(D)$
is a morphism of
![]() ${\mathcal{O}}_{C}$
-modules. The notion of stability is the usual one: for every
${\mathcal{O}}_{C}$
-modules. The notion of stability is the usual one: for every
![]() $\unicode[STIX]{x1D719}$
-invariant proper sub-bundle
$\unicode[STIX]{x1D719}$
-invariant proper sub-bundle
![]() $F\subseteq E$
, the slopes
$F\subseteq E$
, the slopes
 $\unicode[STIX]{x1D707}:=\deg /\text{rk}$
satisfy the inequality
$\unicode[STIX]{x1D707}:=\deg /\text{rk}$
satisfy the inequality
 $\unicode[STIX]{x1D707}(F)<\unicode[STIX]{x1D707}(E)$
. There is the projective characteristic morphism
$\unicode[STIX]{x1D707}(F)<\unicode[STIX]{x1D707}(E)$
. There is the projective characteristic morphism
 $$\begin{eqnarray}h:\mathscr{M}\rightarrow \mathscr{A}:=\bigoplus _{i=1}^{n}H^{0}(C,iD),\end{eqnarray}$$
$$\begin{eqnarray}h:\mathscr{M}\rightarrow \mathscr{A}:=\bigoplus _{i=1}^{n}H^{0}(C,iD),\end{eqnarray}$$
sending
![]() $(E,\unicode[STIX]{x1D719})$
to the coefficients
$(E,\unicode[STIX]{x1D719})$
to the coefficients
 $(-\text{tr}(\unicode[STIX]{x1D719}),+\text{ tr}(\wedge ^{2}\unicode[STIX]{x1D719}),\ldots ,(-1)^{n}\det (\unicode[STIX]{x1D719}))$
of the characteristic polynomial of
$(-\text{tr}(\unicode[STIX]{x1D719}),+\text{ tr}(\wedge ^{2}\unicode[STIX]{x1D719}),\ldots ,(-1)^{n}\det (\unicode[STIX]{x1D719}))$
of the characteristic polynomial of
![]() $\unicode[STIX]{x1D719}$
. The elements of
$\unicode[STIX]{x1D719}$
. The elements of
![]() $\mathscr{A}$
are called characteristics.
$\mathscr{A}$
are called characteristics.
The pure-dimensional nonsingular variety
![]() $\mathscr{M}$
is connected, hence irreducible. One way to see this, is to couple the fact that the proper characteristic morphism is of pure relative dimension [Reference Chaudouard and LaumonCL16, Corollaire 8.2] with the fact (Remark 2.4.4) that the general fiber, being the Jacobian of a nonsingular and connected spectral curve, is connected. I thank the anonymous referee for bringing this to my attention.
$\mathscr{M}$
is connected, hence irreducible. One way to see this, is to couple the fact that the proper characteristic morphism is of pure relative dimension [Reference Chaudouard and LaumonCL16, Corollaire 8.2] with the fact (Remark 2.4.4) that the general fiber, being the Jacobian of a nonsingular and connected spectral curve, is connected. I thank the anonymous referee for bringing this to my attention.
The moduli space
![]() $N$
of rank
$N$
of rank
![]() $n$
and degree
$n$
and degree
![]() $e$
vector bundles on
$e$
vector bundles on
![]() $C$
sits naturally in
$C$
sits naturally in
![]() $\mathscr{M}$
(take
$\mathscr{M}$
(take
![]() $\unicode[STIX]{x1D719}:=0$
). It is well known that
$\unicode[STIX]{x1D719}:=0$
). It is well known that
![]() $N$
is integral, nonsingular, projective and of dimension
$N$
is integral, nonsingular, projective and of dimension
 $n^{2}(g-1)+1$
. We have inclusions
$n^{2}(g-1)+1$
. We have inclusions
 $\mathscr{M}=\overline{T}\supseteq T\supseteq N$
, where
$\mathscr{M}=\overline{T}\supseteq T\supseteq N$
, where
![]() $T$
is the total space of the vector bundle of rank
$T$
is the total space of the vector bundle of rank
 $n^{2}[d-(g-1)]$
over
$n^{2}[d-(g-1)]$
over
![]() $N$
with fiber at
$N$
with fiber at
![]() $E$
given by
$E$
given by
 $H^{0}(C,\text{End}(E)(D))$
; see [Reference NitsureNit91, Proposition 7.1 and the formula above it]. Then
$H^{0}(C,\text{End}(E)(D))$
; see [Reference NitsureNit91, Proposition 7.1 and the formula above it]. Then
![]() $T$
is integral, nonsingular, of dimension
$T$
is integral, nonsingular, of dimension
![]() $n^{2}d+1$
, and it is a Zariski-dense open subvariety of
$n^{2}d+1$
, and it is a Zariski-dense open subvariety of
![]() $\mathscr{M}$
; see [Reference NitsureNit91, pp. 297–298].
$\mathscr{M}$
; see [Reference NitsureNit91, pp. 297–298].
The
![]() $\text{GL}_{n}$
traceless case. We need the following simple traceless variant of the
$\text{GL}_{n}$
traceless case. We need the following simple traceless variant of the
![]() $D$
-twisted
$D$
-twisted
![]() $\text{GL}_{n}$
moduli space: geometrically, it is the pre-image via the morphism
$\text{GL}_{n}$
moduli space: geometrically, it is the pre-image via the morphism
 $h:\mathscr{M}\rightarrow \mathscr{A}$
of the locus
$h:\mathscr{M}\rightarrow \mathscr{A}$
of the locus
 $\mathscr{A}(0)\subseteq \mathscr{A}$
of traceless characteristics. Let
$\mathscr{A}(0)\subseteq \mathscr{A}$
of traceless characteristics. Let
 $\mathscr{M}(0)\subseteq \mathscr{M}$
be the moduli space of stable pairs
$\mathscr{M}(0)\subseteq \mathscr{M}$
be the moduli space of stable pairs
![]() $(E,\unicode[STIX]{x1D719})$
as above, subject to the additional traceless constraint
$(E,\unicode[STIX]{x1D719})$
as above, subject to the additional traceless constraint
 $\text{tr}(\unicode[STIX]{x1D719})=0$
. By repeating the arguments in [Reference NitsureNit91] concerning
$\text{tr}(\unicode[STIX]{x1D719})=0$
. By repeating the arguments in [Reference NitsureNit91] concerning
![]() $\mathscr{M}$
, but with the traceless constraint, we see that
$\mathscr{M}$
, but with the traceless constraint, we see that
![]() $\mathscr{M}(0)$
is a nonsingular and quasi-projective variety, of pure dimension
$\mathscr{M}(0)$
is a nonsingular and quasi-projective variety, of pure dimension
 $nd^{2}+1-h^{0}(D)$
. Moreover, we have a natural isomorphism
$nd^{2}+1-h^{0}(D)$
. Moreover, we have a natural isomorphism
 $\mathscr{M}\cong H^{0}(C,D)\times \mathscr{M}(0)$
(see § 4.3, (51)), implying that the nonsingular
$\mathscr{M}\cong H^{0}(C,D)\times \mathscr{M}(0)$
(see § 4.3, (51)), implying that the nonsingular
![]() $\mathscr{M}(0)$
is connected and irreducible.
$\mathscr{M}(0)$
is connected and irreducible.
As above, we have inclusions
 $\mathscr{M}(0)=\overline{T(0)}\supseteq T(0)\supseteq N$
, with the same properties listed above, except that we take traceless endomorphisms, and the rank of the corresponding vector bundle on
$\mathscr{M}(0)=\overline{T(0)}\supseteq T(0)\supseteq N$
, with the same properties listed above, except that we take traceless endomorphisms, and the rank of the corresponding vector bundle on
![]() $N$
equals
$N$
equals
 $h^{0}(C,\text{End}^{0}(E)(D))=n^{2}[d-(g-1)]-h^{0}(D)$
. We have the projective characteristic morphism
$h^{0}(C,\text{End}^{0}(E)(D))=n^{2}[d-(g-1)]-h^{0}(D)$
. We have the projective characteristic morphism
 $$\begin{eqnarray}h(0):\mathscr{M}(0)\rightarrow \mathscr{A}(0):=\bigoplus _{i=2}^{n}H^{0}(C,iD).\end{eqnarray}$$
$$\begin{eqnarray}h(0):\mathscr{M}(0)\rightarrow \mathscr{A}(0):=\bigoplus _{i=2}^{n}H^{0}(C,iD).\end{eqnarray}$$
The
![]() $\text{SL}_{n}$
case. Finally, we introduce the moduli space to which this paper is devoted. Fix a line bundle
$\text{SL}_{n}$
case. Finally, we introduce the moduli space to which this paper is devoted. Fix a line bundle
 $\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
on
$\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
on
![]() $C$
, of degree
$C$
, of degree
![]() $e$
. Let
$e$
. Let
 $\mathscr{M}(0,\unicode[STIX]{x1D716})\subseteq \mathscr{M}(0)\subseteq \mathscr{M}$
be the moduli space of stable pairs
$\mathscr{M}(0,\unicode[STIX]{x1D716})\subseteq \mathscr{M}(0)\subseteq \mathscr{M}$
be the moduli space of stable pairs
![]() $(E,\unicode[STIX]{x1D719})$
as above, subject to
$(E,\unicode[STIX]{x1D719})$
as above, subject to
 $\text{ tr}(\unicode[STIX]{x1D719})=0$
and to
$\text{ tr}(\unicode[STIX]{x1D719})=0$
and to
 $\det (E)=\unicode[STIX]{x1D716}$
. By repeating the arguments in [Reference NitsureNit91], but with the traceless and fixed-determinant constraints, we see that the variety
$\det (E)=\unicode[STIX]{x1D716}$
. By repeating the arguments in [Reference NitsureNit91], but with the traceless and fixed-determinant constraints, we see that the variety
 $\mathscr{M}(0,\unicode[STIX]{x1D716})$
is nonsingular and quasi-projective, of pure dimension
$\mathscr{M}(0,\unicode[STIX]{x1D716})$
is nonsingular and quasi-projective, of pure dimension
 $n^{2}d+1-h^{0}(D)-g$
. We have the projective characteristic map
$n^{2}d+1-h^{0}(D)-g$
. We have the projective characteristic map
 $$\begin{eqnarray}h(0,\unicode[STIX]{x1D716}):\mathscr{M}(0,\unicode[STIX]{x1D716})\rightarrow \mathscr{A}(0):=\bigoplus _{i=2}^{n}H^{0}(C,iD).\end{eqnarray}$$
$$\begin{eqnarray}h(0,\unicode[STIX]{x1D716}):\mathscr{M}(0,\unicode[STIX]{x1D716})\rightarrow \mathscr{A}(0):=\bigoplus _{i=2}^{n}H^{0}(C,iD).\end{eqnarray}$$
Let
 $\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}$
be the irreducible (also a connected) component containing the moduli space
$\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}$
be the irreducible (also a connected) component containing the moduli space
![]() $N(\unicode[STIX]{x1D716})$
of stable rank
$N(\unicode[STIX]{x1D716})$
of stable rank
![]() $n$
and degree
$n$
and degree
![]() $e$
bundles on
$e$
bundles on
![]() $C$
with fixed determinant
$C$
with fixed determinant
 $\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
. It is well known that the variety
$\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
. It is well known that the variety
![]() $N(\unicode[STIX]{x1D716})$
is integral, nonsingular, projective, and of dimension
$N(\unicode[STIX]{x1D716})$
is integral, nonsingular, projective, and of dimension
 $(n^{2}-1)(g-1)$
. As above, we have inclusions
$(n^{2}-1)(g-1)$
. As above, we have inclusions
 $\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}=\overline{T(0,\unicode[STIX]{x1D716})}\supseteq T(0,\unicode[STIX]{x1D716})\supseteq N(\unicode[STIX]{x1D716})$
, with the same properties listed above (again, we take traceless endomorphisms).
$\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}=\overline{T(0,\unicode[STIX]{x1D716})}\supseteq T(0,\unicode[STIX]{x1D716})\supseteq N(\unicode[STIX]{x1D716})$
, with the same properties listed above (again, we take traceless endomorphisms).
Note that
 $\mathscr{M}(0,\unicode[STIX]{x1D716})=\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}$
and that the isomorphism class of
$\mathscr{M}(0,\unicode[STIX]{x1D716})=\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}$
and that the isomorphism class of
 $\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}$
is independent of
$\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}$
is independent of
 $\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
. This can be seen as in the proof of the following simple lemma.
$\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
. This can be seen as in the proof of the following simple lemma.
Lemma 2.1.1. The variety
 $\mathscr{M}(0,\unicode[STIX]{x1D716})$
is connected, i.e.
$\mathscr{M}(0,\unicode[STIX]{x1D716})$
is connected, i.e.
 $\mathscr{M}(0,\unicode[STIX]{x1D716})=\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}$
. The variety
$\mathscr{M}(0,\unicode[STIX]{x1D716})=\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}$
. The variety
 $\mathscr{M}(0,\unicode[STIX]{x1D716})$
is the fiber over
$\mathscr{M}(0,\unicode[STIX]{x1D716})$
is the fiber over
 $\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
of the determinant map
$\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
of the determinant map
 $\det :\mathscr{M}(0)\rightarrow \text{Pic}^{e}(C)$
, as well as the fiber over
$\det :\mathscr{M}(0)\rightarrow \text{Pic}^{e}(C)$
, as well as the fiber over
 $(0,\unicode[STIX]{x1D716})\in H^{0}(C,D)\times \text{Pic}^{e}(C)$
of the trace-determinant map
$(0,\unicode[STIX]{x1D716})\in H^{0}(C,D)\times \text{Pic}^{e}(C)$
of the trace-determinant map
 $\text{tr}\times \det :\mathscr{M}\rightarrow H^{0}(C,D)\times \text{Pic}^{e}(C)$
.
$\text{tr}\times \det :\mathscr{M}\rightarrow H^{0}(C,D)\times \text{Pic}^{e}(C)$
.
Proof. The map
![]() $\det$
is equivariant with respect to the action of
$\det$
is equivariant with respect to the action of
 $\text{ Pic}^{0}(C)$
given by
$\text{ Pic}^{0}(C)$
given by
 $L\cdot (E,\unicode[STIX]{x1D719}):=(E\otimes L,\unicode[STIX]{x1D719}\otimes \text{Id}_{L})$
on the domain, and by
$L\cdot (E,\unicode[STIX]{x1D719}):=(E\otimes L,\unicode[STIX]{x1D719}\otimes \text{Id}_{L})$
on the domain, and by
 $L\cdot M:=M\otimes L^{\otimes n}$
on the target. It follows that
$L\cdot M:=M\otimes L^{\otimes n}$
on the target. It follows that
![]() $\det$
is smooth of relative dimension
$\det$
is smooth of relative dimension
 $\dim (\mathscr{M}(0,\unicode[STIX]{x1D716}))$
, and that all of its fibers are mutually isomorphic to each other. The same is true of the restriction of
$\dim (\mathscr{M}(0,\unicode[STIX]{x1D716}))$
, and that all of its fibers are mutually isomorphic to each other. The same is true of the restriction of
![]() $\det$
to the
$\det$
to the
 $\text{Pic}^{0}(C)$
-invariant open subvariety
$\text{Pic}^{0}(C)$
-invariant open subvariety
 $T(0)\subseteq \mathscr{M}(0)$
. Let
$T(0)\subseteq \mathscr{M}(0)$
. Let
 $Z:=\mathscr{M}(0)\setminus T(0)$
be the closed complement. The resulting map
$Z:=\mathscr{M}(0)\setminus T(0)$
be the closed complement. The resulting map
 $Z\rightarrow \text{Pic}^{0}(C)$
is also
$Z\rightarrow \text{Pic}^{0}(C)$
is also
 $\text{ Pic}^{0}(C)$
-invariant, so that all of its fibers have the same dimension, which must be strictly smaller than
$\text{ Pic}^{0}(C)$
-invariant, so that all of its fibers have the same dimension, which must be strictly smaller than
 $\dim (\mathscr{M}(0,\unicode[STIX]{x1D716}))$
. It is clear that
$\dim (\mathscr{M}(0,\unicode[STIX]{x1D716}))$
. It is clear that
 $\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}$
is contained in
$\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}$
is contained in
 $\det ^{-1}(\unicode[STIX]{x1D716})=\mathscr{M}(0\,e)$
and that, by the smoothness of
$\det ^{-1}(\unicode[STIX]{x1D716})=\mathscr{M}(0\,e)$
and that, by the smoothness of
![]() $\det$
, it must constitute a connected component of such fiber. Since the fiber
$\det$
, it must constitute a connected component of such fiber. Since the fiber
 $\det ^{-1}(\unicode[STIX]{x1D716})$
is of pure dimension
$\det ^{-1}(\unicode[STIX]{x1D716})$
is of pure dimension
 $\dim (\mathscr{M}(0,\unicode[STIX]{x1D716}))$
, the variety
$\dim (\mathscr{M}(0,\unicode[STIX]{x1D716}))$
, the variety
![]() $Z$
cannot contain any other connected component of the smooth fiber
$Z$
cannot contain any other connected component of the smooth fiber
 $\det ^{-1}(\unicode[STIX]{x1D716})$
. We have thus proved that
$\det ^{-1}(\unicode[STIX]{x1D716})$
. We have thus proved that
 $\det ^{-1}(\unicode[STIX]{x1D716})=\mathscr{M}(0,\unicode[STIX]{x1D716})=\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}$
, which are thus all connected, for the third one is by construction. The assertion concerning
$\det ^{-1}(\unicode[STIX]{x1D716})=\mathscr{M}(0,\unicode[STIX]{x1D716})=\mathscr{M}(0,\unicode[STIX]{x1D716})_{o}$
, which are thus all connected, for the third one is by construction. The assertion concerning
 $\text{tr}\times \det$
is proved in a similar way.◻
$\text{tr}\times \det$
is proved in a similar way.◻
2.2 Simplified notation for Hitchin fibrations
We want to simplify our notation, while emphasizing the role of the rank
![]() $n$
.
$n$
.
Fix
 $(n,e,\unicode[STIX]{x1D716},D)$
. Denote the characteristic Hitchin morphisms
$(n,e,\unicode[STIX]{x1D716},D)$
. Denote the characteristic Hitchin morphisms
 $$\begin{eqnarray}h:\mathscr{M}\rightarrow \mathscr{A},\quad h(0):\mathscr{M}(0)\rightarrow \mathscr{A}(0),\quad h(0,e):\mathscr{M}(0,\unicode[STIX]{x1D716})\rightarrow \mathscr{A}(0)\end{eqnarray}$$
$$\begin{eqnarray}h:\mathscr{M}\rightarrow \mathscr{A},\quad h(0):\mathscr{M}(0)\rightarrow \mathscr{A}(0),\quad h(0,e):\mathscr{M}(0,\unicode[STIX]{x1D716})\rightarrow \mathscr{A}(0)\end{eqnarray}$$
as follows:
 $$\begin{eqnarray}h_{n}:M_{n}\rightarrow A_{n},\quad h_{n}(0):M_{n}(0)\rightarrow A_{n}(0),\quad \check{h}_{n}:\check{M}_{n}\rightarrow {\check{A}}_{n}:=A_{n}(0).\end{eqnarray}$$
$$\begin{eqnarray}h_{n}:M_{n}\rightarrow A_{n},\quad h_{n}(0):M_{n}(0)\rightarrow A_{n}(0),\quad \check{h}_{n}:\check{M}_{n}\rightarrow {\check{A}}_{n}:=A_{n}(0).\end{eqnarray}$$
We are denoting the same object
 ${\check{A}}_{n}=A_{n}(0)$
in two different ways: we prefer to use the notation
${\check{A}}_{n}=A_{n}(0)$
in two different ways: we prefer to use the notation
![]() $A_{n}(0)$
when dealing with
$A_{n}(0)$
when dealing with
![]() $M_{n}(0)$
, and to use
$M_{n}(0)$
, and to use
![]() ${\check{A}}_{n}$
when dealing with
${\check{A}}_{n}$
when dealing with
![]() $\check{M}_{n}$
.
$\check{M}_{n}$
.
The projective morphisms
![]() $h_{n}$
and
$h_{n}$
and
![]() $\check{h}_{n}$
are known as the
$\check{h}_{n}$
are known as the
![]() $D$
-twisted, Hitchin
$D$
-twisted, Hitchin
![]() $\text{GL}_{n}$
and
$\text{GL}_{n}$
and
![]() $\text{SL}_{n}$
fibrations. The morphism
$\text{SL}_{n}$
fibrations. The morphism
![]() $h_{n}(0)$
plays an important auxiliary role in this paper.
$h_{n}(0)$
plays an important auxiliary role in this paper.
We shall also need to consider two several-variable-variants of these Hitchin fibrations, namely
 $h_{n_{\bullet }}:M_{n_{\bullet }}\rightarrow A_{\bullet }$
, and
$h_{n_{\bullet }}:M_{n_{\bullet }}\rightarrow A_{\bullet }$
, and
 $h_{n_{\bullet }m_{\bullet }}(0):M_{n_{\bullet }m_{\bullet }}(0)\rightarrow A_{n_{\bullet }m_{\bullet }}(0)$
(cf. §§ 5.1 and 5.3).
$h_{n_{\bullet }m_{\bullet }}(0):M_{n_{\bullet }m_{\bullet }}(0)\rightarrow A_{n_{\bullet }m_{\bullet }}(0)$
(cf. §§ 5.1 and 5.3).
An important locus inside the base of the Hitchin fibration is the elliptic locus. In the case of
![]() $\text{GL}_{n}$
and
$\text{GL}_{n}$
and
![]() $\text{SL}_{n}$
we define it as follows.
$\text{SL}_{n}$
we define it as follows.
Definition 2.2.1 (Elliptic locus).
The elliptic loci
 $A_{n}^{\text{ell}}\subseteq A_{n}$
and
$A_{n}^{\text{ell}}\subseteq A_{n}$
and
 ${\check{A}}_{n}^{\text{ ell}}\subseteq {\check{A}}_{n}$
are the respective Zariski-dense open subvarieties of points such that the associated spectral curves are geometrically integral.
${\check{A}}_{n}^{\text{ ell}}\subseteq {\check{A}}_{n}$
are the respective Zariski-dense open subvarieties of points such that the associated spectral curves are geometrically integral.
Clearly,
 ${\check{A}}_{n}^{\text{ell}}=A_{n}^{\text{ell}}\,\cap \,{\check{A}}_{n}$
.
${\check{A}}_{n}^{\text{ell}}=A_{n}^{\text{ell}}\,\cap \,{\check{A}}_{n}$
.
2.3 Spectral covers and the norm map
Let
 $\unicode[STIX]{x1D70B}:V(D)\rightarrow C$
be the surface total space of the line bundle
$\unicode[STIX]{x1D70B}:V(D)\rightarrow C$
be the surface total space of the line bundle
![]() $D$
on
$D$
on
![]() $C$
. Let
$C$
. Let
![]() $t$
be the universal section of
$t$
be the universal section of
![]() $\unicode[STIX]{x1D70B}^{\ast }D$
, with zero set on
$\unicode[STIX]{x1D70B}^{\ast }D$
, with zero set on
![]() $V(D)$
given by
$V(D)$
given by
![]() $C$
, viewed as the zero section on
$C$
, viewed as the zero section on
![]() $V(D)$
. Let
$V(D)$
. Let
 ${\mathcal{C}}={\mathcal{C}}_{n}\subseteq V(D)\times A_{n}$
be the universal spectral curve, that is the relative curve over
${\mathcal{C}}={\mathcal{C}}_{n}\subseteq V(D)\times A_{n}$
be the universal spectral curve, that is the relative curve over
![]() $A_{n}$
with fiber
$A_{n}$
with fiber
![]() ${\mathcal{C}}_{a}$
over a closed point
${\mathcal{C}}_{a}$
over a closed point
 $a=(a(1),\ldots ,a(n))\in A_{n}$
, given by the zero set in
$a=(a(1),\ldots ,a(n))\in A_{n}$
, given by the zero set in
 $V(D)\times \{a\}$
of the section
$V(D)\times \{a\}$
of the section
 $P_{a}(t):=t^{n}+\unicode[STIX]{x1D70B}^{\ast }a(1)t^{n-1}+\unicode[STIX]{x1D70B}^{\ast }a(2)t^{n-2}+\cdots +\unicode[STIX]{x1D70B}^{\ast }a(n)$
of the line bundle
$P_{a}(t):=t^{n}+\unicode[STIX]{x1D70B}^{\ast }a(1)t^{n-1}+\unicode[STIX]{x1D70B}^{\ast }a(2)t^{n-2}+\cdots +\unicode[STIX]{x1D70B}^{\ast }a(n)$
of the line bundle
![]() $\unicode[STIX]{x1D70B}^{\ast }(nD)$
on
$\unicode[STIX]{x1D70B}^{\ast }(nD)$
on
 $V(D)\times \{a\}$
. Note that
$V(D)\times \{a\}$
. Note that
![]() $A_{n}$
is an affine space inside the projective space given by the linear system
$A_{n}$
is an affine space inside the projective space given by the linear system
![]() $|nC|$
on the standard projective completion
$|nC|$
on the standard projective completion
 $\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{O}}_{C}(-D))$
of
$\mathbb{P}_{C}({\mathcal{O}}_{C}\oplus {\mathcal{O}}_{C}(-D))$
of
![]() $V(D)$
, where
$V(D)$
, where
![]() $C$
sits as the zero section. Let
$C$
sits as the zero section. Let
 $p:{\mathcal{C}}\rightarrow A_{n}$
be the natural ensuing morphism. For
$p:{\mathcal{C}}\rightarrow A_{n}$
be the natural ensuing morphism. For
![]() $a\in A_{n}$
, the spectral curve
$a\in A_{n}$
, the spectral curve
![]() ${\mathcal{C}}_{a}$
is geometrically connected and maps
${\mathcal{C}}_{a}$
is geometrically connected and maps
![]() $n:1$
onto
$n:1$
onto
 $C_{a}:=C\otimes k(a)$
via the flat finite morphism
$C_{a}:=C\otimes k(a)$
via the flat finite morphism
 $p_{a}:=p_{|{\mathcal{C}}_{a}}:{\mathcal{C}}_{a}\rightarrow C_{a}$
. The total space of the family
$p_{a}:=p_{|{\mathcal{C}}_{a}}:{\mathcal{C}}_{a}\rightarrow C_{a}$
. The total space of the family
![]() ${\mathcal{C}}$
is integral and nonsingular, and the natural morphism
${\mathcal{C}}$
is integral and nonsingular, and the natural morphism
 ${\mathcal{C}}\rightarrow C\times A_{n}$
is finite, flat and of degree
${\mathcal{C}}\rightarrow C\times A_{n}$
is finite, flat and of degree
![]() $n$
.
$n$
.
When we view each spectral curve
![]() ${\mathcal{C}}_{a}$
over a geometric point
${\mathcal{C}}_{a}$
over a geometric point
![]() $a$
of
$a$
of
![]() $A_{n}$
, as an effective Cartier divisor on
$A_{n}$
, as an effective Cartier divisor on
 $V(D)\otimes k(a)$
, we may write
$V(D)\otimes k(a)$
, we may write
 ${\mathcal{C}}_{a}=\sum _{k=1}^{s}m_{k,a}{\mathcal{C}}_{k,a}$
, where each
${\mathcal{C}}_{a}=\sum _{k=1}^{s}m_{k,a}{\mathcal{C}}_{k,a}$
, where each
![]() ${\mathcal{C}}_{k,a}$
is geometrically integral, each integer
${\mathcal{C}}_{k,a}$
is geometrically integral, each integer
 $m_{k,a}>0$
, and the expression is unique. Each curve
$m_{k,a}>0$
, and the expression is unique. Each curve
![]() ${\mathcal{C}}_{k,a}$
maps finitely onto
${\mathcal{C}}_{k,a}$
maps finitely onto
![]() $C_{a}$
; denote the corresponding degree by
$C_{a}$
; denote the corresponding degree by
![]() $n_{k,a}$
. Clearly,
$n_{k,a}$
. Clearly,
 $n=\sum _{k}m_{k,a}n_{k,a}$
. By considering the coefficients
$n=\sum _{k}m_{k,a}n_{k,a}$
. By considering the coefficients
![]() $a(i)$
above as the
$a(i)$
above as the
![]() $i$
th symmetric functions of the
$i$
th symmetric functions of the
![]() $D$
-valued roots of the polynomial equation
$D$
-valued roots of the polynomial equation
![]() $P_{a}(t)$
, we obtain the unique factorization
$P_{a}(t)$
, we obtain the unique factorization
 $P_{a}(t)=\prod _{k}P_{a_{k}}^{m_{k,a}}(t)$
, where each
$P_{a}(t)=\prod _{k}P_{a_{k}}^{m_{k,a}}(t)$
, where each
 $a_{k}(i)\in H^{0}(C,iD)$
,
$a_{k}(i)\in H^{0}(C,iD)$
,
 $1\leqslant i\leqslant n_{k}$
, is the
$1\leqslant i\leqslant n_{k}$
, is the
![]() $i$
th symmetric function of the
$i$
th symmetric function of the
![]() $D$
-valued roots of
$D$
-valued roots of
![]() $P_{a}(t)$
that lie on
$P_{a}(t)$
that lie on
![]() ${\mathcal{C}}_{k,a}$
. In particular, we have that
${\mathcal{C}}_{k,a}$
. In particular, we have that
![]() $a_{k}$
is a geometric point of
$a_{k}$
is a geometric point of
![]() $A_{n_{k}}$
(base of the Hitchin fibration for
$A_{n_{k}}$
(base of the Hitchin fibration for
 $(n_{k},e,D)$
), and that
$(n_{k},e,D)$
), and that
![]() ${\mathcal{C}}_{k,a}$
is a spectral curve for the
${\mathcal{C}}_{k,a}$
is a spectral curve for the
![]() $D$
-twisted
$D$
-twisted
![]() $\text{GL}_{n_{k}}$
Hitchin fibration.
$\text{GL}_{n_{k}}$
Hitchin fibration.
Let
![]() $a\in A_{n}$
. We need to list the various covers of the curve
$a\in A_{n}$
. We need to list the various covers of the curve
 $C_{a}=C\otimes k(a)$
that arise from the given spectral cover
$C_{a}=C\otimes k(a)$
that arise from the given spectral cover
 $p_{a}:{\mathcal{C}}_{a}\rightarrow C_{a}$
. In doing so, we also simplify and abuse the notation a little bit. We do not assume the point
$p_{a}:{\mathcal{C}}_{a}\rightarrow C_{a}$
. In doing so, we also simplify and abuse the notation a little bit. We do not assume the point
![]() $a\in A_{n}$
to be a geometric one, so that the intervening integral curves may not be geometrically integral.
$a\in A_{n}$
to be a geometric one, so that the intervening integral curves may not be geometrically integral.
We denote the curve
 ${\mathcal{C}}_{a}=\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}$
, where: each
${\mathcal{C}}_{a}=\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}$
, where: each
![]() $\unicode[STIX]{x1D6E4}_{k}$
is a spectral curve, zero-set of a section
$\unicode[STIX]{x1D6E4}_{k}$
is a spectral curve, zero-set of a section
![]() $\mathfrak{s}_{k}$
of the line bundle
$\mathfrak{s}_{k}$
of the line bundle
 $\unicode[STIX]{x1D70B}^{\ast }(n_{k}D)$
on the surface
$\unicode[STIX]{x1D70B}^{\ast }(n_{k}D)$
on the surface
 $V(D)\otimes k(a)$
; the
$V(D)\otimes k(a)$
; the
![]() $n_{k}>0$
are uniquely-determined positive integers, and we have
$n_{k}>0$
are uniquely-determined positive integers, and we have
 $n=\sum n_{k}m_{k}$
. Scheme-theoretically,
$n=\sum n_{k}m_{k}$
. Scheme-theoretically,
![]() $m_{k}\unicode[STIX]{x1D6E4}_{k}$
is the zero set of the
$m_{k}\unicode[STIX]{x1D6E4}_{k}$
is the zero set of the
![]() $m_{k}$
th power
$m_{k}$
th power
![]() $\mathfrak{s}^{m_{k}}$
, and
$\mathfrak{s}^{m_{k}}$
, and
 ${\mathcal{C}}_{a}=\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}$
is the zero set of the product
${\mathcal{C}}_{a}=\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}$
is the zero set of the product
![]() $\prod _{k}\mathfrak{s}_{k}^{m_{k}}$
. We denote by
$\prod _{k}\mathfrak{s}_{k}^{m_{k}}$
. We denote by
 $\unicode[STIX]{x1D709}_{3,k}:\widetilde{\unicode[STIX]{x1D6E4}_{k}}\rightarrow \unicode[STIX]{x1D6E4}_{k}$
the normalization morphism.
$\unicode[STIX]{x1D709}_{3,k}:\widetilde{\unicode[STIX]{x1D6E4}_{k}}\rightarrow \unicode[STIX]{x1D6E4}_{k}$
the normalization morphism.
We have the following commutative diagram of finite surjective morphisms of curves.

Fact 2.3.1 (The Jacobian of a spectral curve).
Let
![]() $\overline{a}$
be a geometric point of
$\overline{a}$
be a geometric point of
![]() $A_{n}$
with underlying Zariski point
$A_{n}$
with underlying Zariski point
![]() $a\in A_{n}$
. Then the identity connected component
$a\in A_{n}$
. Then the identity connected component
 $\text{Pic}^{0}({\mathcal{C}}_{a})$
of the degree zero component of
$\text{Pic}^{0}({\mathcal{C}}_{a})$
of the degree zero component of
![]() $\text{Pic}({\mathcal{C}}_{a})$
consists of the isomorphism classes of line bundles on the spectral curve
$\text{Pic}({\mathcal{C}}_{a})$
consists of the isomorphism classes of line bundles on the spectral curve
![]() ${\mathcal{C}}_{a}$
whose restriction to each irreducible component of
${\mathcal{C}}_{a}$
whose restriction to each irreducible component of
![]() ${\mathcal{C}}_{\overline{a}}$
have degree zero; see [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 9.3, Corollary 13].
${\mathcal{C}}_{\overline{a}}$
have degree zero; see [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 9.3, Corollary 13].
Each of the morphisms to
![]() $C_{a}$
in diagram (2) comes with an associated norm morphism into
$C_{a}$
in diagram (2) comes with an associated norm morphism into
 $\text{Pic}(C_{a})$
, and with an associated pull-back morphism from
$\text{Pic}(C_{a})$
, and with an associated pull-back morphism from
 $\text{Pic}(C_{a})$
. Similarly, if we replace
$\text{Pic}(C_{a})$
. Similarly, if we replace
![]() $\text{Pic}$
with
$\text{Pic}$
with
![]() $\text{Pic}^{0}$
. For the definition and properties of the norm morphism, see [Reference GrothendieckEGAII, § 6.5] and [Reference GrothendieckEGAIV.4, § 21.5]. For a quick reference for the facts we use in this paper, see also [Reference Hausel and PaulyHP12, § 3]. See also Fact 2.4.5. We have the norm morphism
$\text{Pic}^{0}$
. For the definition and properties of the norm morphism, see [Reference GrothendieckEGAII, § 6.5] and [Reference GrothendieckEGAIV.4, § 21.5]. For a quick reference for the facts we use in this paper, see also [Reference Hausel and PaulyHP12, § 3]. See also Fact 2.4.5. We have the norm morphism
 $$\begin{eqnarray}N_{p}:\text{Pic}({\mathcal{C}}_{a})\longrightarrow \text{Pic}(C),\quad \text{Pic}^{0}({\mathcal{C}}_{a})\longrightarrow \text{Pic}^{0}(C_{a}).\end{eqnarray}$$
$$\begin{eqnarray}N_{p}:\text{Pic}({\mathcal{C}}_{a})\longrightarrow \text{Pic}(C),\quad \text{Pic}^{0}({\mathcal{C}}_{a})\longrightarrow \text{Pic}^{0}(C_{a}).\end{eqnarray}$$
We also have the norm morphisms
![]() $N_{\widetilde{p}},N_{p^{\prime }}$
and
$N_{\widetilde{p}},N_{p^{\prime }}$
and
![]() $N_{p^{\prime \prime }}$
, as well as the pull-back morphisms
$N_{p^{\prime \prime }}$
, as well as the pull-back morphisms
![]() $\widetilde{p}^{\ast },{p^{\prime }}^{\ast }$
and
$\widetilde{p}^{\ast },{p^{\prime }}^{\ast }$
and
![]() ${p^{\prime \prime }}^{\ast }$
; similarly, for each of their
${p^{\prime \prime }}^{\ast }$
; similarly, for each of their
![]() $k$
th components.
$k$
th components.
We end this section with the following consideration that will play a role later.
Fact 2.3.2. Since
![]() $D$
has positive degree
$D$
has positive degree
 $d>2g-2$
on
$d>2g-2$
on
![]() $C$
, we have that, on each
$C$
, we have that, on each
![]() $\unicode[STIX]{x1D6E4}_{k}$
, the line bundle
$\unicode[STIX]{x1D6E4}_{k}$
, the line bundle
 $({p^{\prime \prime }}^{\ast }n_{k}D)_{|\unicode[STIX]{x1D6E4}_{k}}$
admits some nontrivial section
$({p^{\prime \prime }}^{\ast }n_{k}D)_{|\unicode[STIX]{x1D6E4}_{k}}$
admits some nontrivial section
![]() $z_{k}$
with zero subscheme
$z_{k}$
with zero subscheme
![]() $\unicode[STIX]{x1D701}_{k}$
supported at a closed finite nonempty subset of
$\unicode[STIX]{x1D701}_{k}$
supported at a closed finite nonempty subset of
![]() $\unicode[STIX]{x1D6E4}_{k}$
. We fix such a section, and we obtain the short exact sequences of
$\unicode[STIX]{x1D6E4}_{k}$
. We fix such a section, and we obtain the short exact sequences of
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6E4}_{k}}$
-modules
${\mathcal{O}}_{\unicode[STIX]{x1D6E4}_{k}}$
-modules
 $$\begin{eqnarray}0\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D6E4}_{k}}(-\unicode[STIX]{x1D6E4}_{k})\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D6E4}_{k}}\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D701}_{k}}\longrightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D6E4}_{k}}(-\unicode[STIX]{x1D6E4}_{k})\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D6E4}_{k}}\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D701}_{k}}\longrightarrow 0.\end{eqnarray}$$
2.4 The fibers of the Hitchin fibrations
Let
![]() $a\in A_{n}$
and let
$a\in A_{n}$
and let
 $p:{\mathcal{C}}_{a}=:\unicode[STIX]{x1D6E4}=\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}\rightarrow C_{a}$
be the corresponding spectral cover, with
$p:{\mathcal{C}}_{a}=:\unicode[STIX]{x1D6E4}=\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}\rightarrow C_{a}$
be the corresponding spectral cover, with
 $n=n_{\unicode[STIX]{x1D6E4}}=\deg (p)=\sum _{k}n_{k}m_{k}=\text{rk}_{C}(p_{\ast }{\mathcal{O}}_{\unicode[STIX]{x1D6E4}})$
; see (2). Let
$n=n_{\unicode[STIX]{x1D6E4}}=\deg (p)=\sum _{k}n_{k}m_{k}=\text{rk}_{C}(p_{\ast }{\mathcal{O}}_{\unicode[STIX]{x1D6E4}})$
; see (2). Let
 $j_{k}:\unicode[STIX]{x1D702}_{k}\rightarrow \unicode[STIX]{x1D6E4}$
be the finitely many generic points in
$j_{k}:\unicode[STIX]{x1D702}_{k}\rightarrow \unicode[STIX]{x1D6E4}$
be the finitely many generic points in
![]() $\unicode[STIX]{x1D6E4}$
, one for each irreducible component
$\unicode[STIX]{x1D6E4}$
, one for each irreducible component
![]() $m_{k}\unicode[STIX]{x1D6E4}_{k}$
. A coherent sheaf
$m_{k}\unicode[STIX]{x1D6E4}_{k}$
. A coherent sheaf
![]() ${\mathcal{E}}$
on
${\mathcal{E}}$
on
![]() $\unicode[STIX]{x1D6E4}$
is torsion free if and only if the natural map
$\unicode[STIX]{x1D6E4}$
is torsion free if and only if the natural map
 ${\mathcal{E}}\rightarrow \prod _{k}{\mathcal{E}}_{k}$
is injective, where
${\mathcal{E}}\rightarrow \prod _{k}{\mathcal{E}}_{k}$
is injective, where
 ${\mathcal{E}}_{k}={j_{k}}_{\ast }j_{k}^{\ast }{\mathcal{E}}$
; see [Reference SchaubSch98, Definition 1.1. and Proposition 1.1]. A torsion-free
${\mathcal{E}}_{k}={j_{k}}_{\ast }j_{k}^{\ast }{\mathcal{E}}$
; see [Reference SchaubSch98, Definition 1.1. and Proposition 1.1]. A torsion-free
![]() ${\mathcal{E}}$
is said to have
${\mathcal{E}}$
is said to have
 $\text{Rk}_{\unicode[STIX]{x1D6E4}}({\mathcal{E}})=r$
if its lengths at the generic points satisfy
$\text{Rk}_{\unicode[STIX]{x1D6E4}}({\mathcal{E}})=r$
if its lengths at the generic points satisfy
 $l_{k}({\mathcal{E}}):=l_{{\mathcal{O}}_{\unicode[STIX]{x1D702}_{k}}}({\mathcal{E}}_{\unicode[STIX]{x1D702}_{k}})=r\,m_{k}$
, for every
$l_{k}({\mathcal{E}}):=l_{{\mathcal{O}}_{\unicode[STIX]{x1D702}_{k}}}({\mathcal{E}}_{\unicode[STIX]{x1D702}_{k}})=r\,m_{k}$
, for every
![]() $k$
; such a rank is then a nonnegative rational number, which is zero if and only if
$k$
; such a rank is then a nonnegative rational number, which is zero if and only if
![]() ${\mathcal{E}}=0$
. A torsion free
${\mathcal{E}}=0$
. A torsion free
![]() ${\mathcal{E}}$
may fail to have a well-defined
${\mathcal{E}}$
may fail to have a well-defined
![]() $\text{Rk}_{\unicode[STIX]{x1D6E4}}({\mathcal{E}})$
. When this rank is well defined, one defines the degree by setting
$\text{Rk}_{\unicode[STIX]{x1D6E4}}({\mathcal{E}})$
. When this rank is well defined, one defines the degree by setting
 $\text{Deg}_{\unicode[STIX]{x1D6E4}}({\mathcal{E}}):=\unicode[STIX]{x1D712}({\mathcal{E}})-\text{Rk}_{\unicode[STIX]{x1D6E4}}({\mathcal{E}})\unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6E4}})$
.
$\text{Deg}_{\unicode[STIX]{x1D6E4}}({\mathcal{E}}):=\unicode[STIX]{x1D712}({\mathcal{E}})-\text{Rk}_{\unicode[STIX]{x1D6E4}}({\mathcal{E}})\unicode[STIX]{x1D712}({\mathcal{O}}_{\unicode[STIX]{x1D6E4}})$
.
Let
 $P_{\unicode[STIX]{x1D6E4}}=\prod _{k}P_{\unicode[STIX]{x1D6E4}_{k}}^{m_{k}}$
be the characteristic equation defining
$P_{\unicode[STIX]{x1D6E4}}=\prod _{k}P_{\unicode[STIX]{x1D6E4}_{k}}^{m_{k}}$
be the characteristic equation defining
![]() $\unicode[STIX]{x1D6E4}$
. A torsion-free coherent sheaf
$\unicode[STIX]{x1D6E4}$
. A torsion-free coherent sheaf
![]() ${\mathcal{E}}$
on
${\mathcal{E}}$
on
![]() $\unicode[STIX]{x1D6E4}$
corresponds, via
$\unicode[STIX]{x1D6E4}$
corresponds, via
![]() $p_{\ast }$
, to a pair
$p_{\ast }$
, to a pair
 $(E,\unicode[STIX]{x1D719}:E\rightarrow E(D))$
on
$(E,\unicode[STIX]{x1D719}:E\rightarrow E(D))$
on
![]() $C$
, where:
$C$
, where:
 $E=p_{\ast }{\mathcal{E}}$
is locally free of rank
$E=p_{\ast }{\mathcal{E}}$
is locally free of rank
 $\text{rk}_{C}(E)=\sum _{k}n_{k}l_{k}$
;
$\text{rk}_{C}(E)=\sum _{k}n_{k}l_{k}$
;
![]() $\unicode[STIX]{x1D719}$
is the twisted endomorphism corresponding to multiplication by
$\unicode[STIX]{x1D719}$
is the twisted endomorphism corresponding to multiplication by
![]() $t$
on
$t$
on
![]() ${\mathcal{E}}$
. Then
${\mathcal{E}}$
. Then
![]() $\unicode[STIX]{x1D719}$
has characteristic polynomial
$\unicode[STIX]{x1D719}$
has characteristic polynomial
 $P_{\unicode[STIX]{x1D719}}=\prod _{k}P_{\unicode[STIX]{x1D6E4}_{k}}^{l_{k}}$
. It follows that
$P_{\unicode[STIX]{x1D719}}=\prod _{k}P_{\unicode[STIX]{x1D6E4}_{k}}^{l_{k}}$
. It follows that
 $P_{\unicode[STIX]{x1D719}}=P_{\unicode[STIX]{x1D6E4}}$
if and only if
$P_{\unicode[STIX]{x1D719}}=P_{\unicode[STIX]{x1D6E4}}$
if and only if
![]() $\text{Rk}_{\unicode[STIX]{x1D6E4}}({\mathcal{E}})$
is well defined and equals
$\text{Rk}_{\unicode[STIX]{x1D6E4}}({\mathcal{E}})$
is well defined and equals
![]() $1$
(this is the content of [Reference SchaubSch98, Proposition 2.1]).
$1$
(this is the content of [Reference SchaubSch98, Proposition 2.1]).
Note that [Reference Hausel and PaulyHP12, § 3.3] introduces, via the Riemann–Roch theorem, a different notion of rank and degree for every coherent
![]() ${\mathcal{O}}_{\unicode[STIX]{x1D6E4}}$
-module, even for those torsion-free ones for which the notion of degree given above is not well defined. In this paper, we use the notion of rank and degree given above [Reference SchaubSch98], not the one in [Reference Hausel and PaulyHP12]. The forthcoming modular description of the fibers of the Hitchin fibration is given in terms of the notions employed in this paper, and the torsion-free sheaves on spectral curves that arise are, by necessity, the ones for which the rank is well defined and it has value one.
${\mathcal{O}}_{\unicode[STIX]{x1D6E4}}$
-module, even for those torsion-free ones for which the notion of degree given above is not well defined. In this paper, we use the notion of rank and degree given above [Reference SchaubSch98], not the one in [Reference Hausel and PaulyHP12]. The forthcoming modular description of the fibers of the Hitchin fibration is given in terms of the notions employed in this paper, and the torsion-free sheaves on spectral curves that arise are, by necessity, the ones for which the rank is well defined and it has value one.
Example 2.4.1. Let
 $nC={\mathcal{C}}_{0}$
be the spectral curve for the characteristic polynomial
$nC={\mathcal{C}}_{0}$
be the spectral curve for the characteristic polynomial
![]() $t^{n}$
, i.e. for
$t^{n}$
, i.e. for
 $a=0\in A_{n}$
. See § 2.3 for the notation.
$a=0\in A_{n}$
. See § 2.3 for the notation.
For
 $1\leqslant m\leqslant n$
, we consider the curves
$1\leqslant m\leqslant n$
, we consider the curves
![]() $mC$
, their structural sheaves
$mC$
, their structural sheaves
![]() ${\mathcal{O}}_{mC}$
and their ideal sheaves
${\mathcal{O}}_{mC}$
and their ideal sheaves
 ${\mathcal{I}}_{mC,nC}\subseteq {\mathcal{O}}_{nC}$
. We have
${\mathcal{I}}_{mC,nC}\subseteq {\mathcal{O}}_{nC}$
. We have
 $\unicode[STIX]{x1D712}({\mathcal{O}}_{mC})=-\binom{m}{2}d-m(g-1)$
; see (7). We then have:
$\unicode[STIX]{x1D712}({\mathcal{O}}_{mC})=-\binom{m}{2}d-m(g-1)$
; see (7). We then have:
 $\text{Rk}_{nC}({\mathcal{O}}_{mC})=m/n$
;
$\text{Rk}_{nC}({\mathcal{O}}_{mC})=m/n$
;
 $\text{Rk}_{nC}({\mathcal{I}}_{mC,nC})=1-m/n$
;
$\text{Rk}_{nC}({\mathcal{I}}_{mC,nC})=1-m/n$
;
 $\text{Deg}_{nC}({\mathcal{O}}_{mC})=(m/2)(n-m)d$
;
$\text{Deg}_{nC}({\mathcal{O}}_{mC})=(m/2)(n-m)d$
;
 $\text{Deg}_{nC}({\mathcal{I}}_{mC,nC})=-(m/2)(n-m)d$
. We have
$\text{Deg}_{nC}({\mathcal{I}}_{mC,nC})=-(m/2)(n-m)d$
. We have
 $P({\mathcal{O}}_{mC})=P_{C}^{m}$
,
$P({\mathcal{O}}_{mC})=P_{C}^{m}$
,
 $P({\mathcal{I}}_{mC,nC})=P_{C}^{m-n}$
.
$P({\mathcal{I}}_{mC,nC})=P_{C}^{m-n}$
.
Let
![]() $E$
be a stable vector bundle of rank
$E$
be a stable vector bundle of rank
![]() $n$
and degree
$n$
and degree
![]() $e$
on
$e$
on
![]() $C$
; let
$C$
; let
 $i:C\rightarrow nC$
be the natural map induced by the zero section
$i:C\rightarrow nC$
be the natural map induced by the zero section
 $C\rightarrow C\subseteq V$
, followed by the closed embedding
$C\rightarrow C\subseteq V$
, followed by the closed embedding
 $C=(nC)_{\text{red}}\rightarrow nC$
; we have that
$C=(nC)_{\text{red}}\rightarrow nC$
; we have that
 $\text{Rk}_{nC}(i_{\ast }E)=1$
and
$\text{Rk}_{nC}(i_{\ast }E)=1$
and
 $\text{Deg}_{nC}(i_{\ast }E)=e+\binom{n}{2}d$
. We have
$\text{Deg}_{nC}(i_{\ast }E)=e+\binom{n}{2}d$
. We have
 $P(i_{\ast }E)=P_{nC}=P_{C}^{n}$
.
$P(i_{\ast }E)=P_{nC}=P_{C}^{n}$
.
It is easy to show that in the context of torsion-free and
 $\text{ Rk}_{\unicode[STIX]{x1D6E4}}(-)=r$
coherent sheaves on
$\text{ Rk}_{\unicode[STIX]{x1D6E4}}(-)=r$
coherent sheaves on
![]() $\unicode[STIX]{x1D6E4}$
, the notion of slope in [Reference SimpsonSim94, p. 55] and [Reference SimpsonSim95, Corollary 6.9] and the notion of slope
$\unicode[STIX]{x1D6E4}$
, the notion of slope in [Reference SimpsonSim94, p. 55] and [Reference SimpsonSim95, Corollary 6.9] and the notion of slope
 $\text{Deg}_{\unicode[STIX]{x1D6E4}}/\text{Rk}_{\unicode[STIX]{x1D6E4}}$
yield coinciding notions of slope stability. In turn, this coincides with the notion of slope-stable Higgs pair
$\text{Deg}_{\unicode[STIX]{x1D6E4}}/\text{Rk}_{\unicode[STIX]{x1D6E4}}$
yield coinciding notions of slope stability. In turn, this coincides with the notion of slope-stable Higgs pair
 $(p_{\ast }{\mathcal{E}},\unicode[STIX]{x1D719})$
, with slopes defined by taking
$(p_{\ast }{\mathcal{E}},\unicode[STIX]{x1D719})$
, with slopes defined by taking
 $\deg _{C}/\text{rk}_{C}$
. By working with quotients, instead of with subobjects, the stability condition takes the form (6) below. Define
$\deg _{C}/\text{rk}_{C}$
. By working with quotients, instead of with subobjects, the stability condition takes the form (6) below. Define
 $$\begin{eqnarray}e^{\prime }:=e+\binom{n}{2}d.\end{eqnarray}$$
$$\begin{eqnarray}e^{\prime }:=e+\binom{n}{2}d.\end{eqnarray}$$
Remark 2.4.2. As pointed out in [Reference Chaudouard and LaumonCL16, Remark 4.2], the statement of [Reference SchaubSch98, Theorem 3.1], which characterizes stability, needs to be slightly modified (cf. (6)).
Remark 2.4.3. Let us point out that one has also to correct some minor inaccuracies at the end of the proof of [Reference SchaubSch98, Proposition 2.1, p. 303, from the top, to the end of the proof]: the degrees on the finite maps from the reduced irreducible components of the spectral curve are omitted from the first two displayed equalities; the inequality on the lengths implying that the rank should be
![]() $1$
is not justified. One remedies this minor inaccuracies by means of the discussion at the beginning of this section involving the role of the characteristic polynomials.
$1$
is not justified. One remedies this minor inaccuracies by means of the discussion at the beginning of this section involving the role of the characteristic polynomials.
Modular description of the Hitchin fiber
 $M_{n,a}:=h_{n}^{-1}(a)$
,
$M_{n,a}:=h_{n}^{-1}(a)$
,
![]() $a\in A_{n}$
. The discussion that follows does not require that one first proves that
$a\in A_{n}$
. The discussion that follows does not require that one first proves that
![]() $M_{n}$
is irreducible; in particular, it can be used in order to establish this fact, as it has been done in § 2.1. The Hitchin fiber
$M_{n}$
is irreducible; in particular, it can be used in order to establish this fact, as it has been done in § 2.1. The Hitchin fiber
 $M_{n,a}:=h_{n}^{-1}(a)$
, i.e. the moduli space of stable
$M_{n,a}:=h_{n}^{-1}(a)$
, i.e. the moduli space of stable
![]() $D$
-twisted Higgs pairs with rank
$D$
-twisted Higgs pairs with rank
![]() $n$
and degree
$n$
and degree
![]() $e$
and with characteristic
$e$
and with characteristic
![]() $a\in A_{n}$
, is isomorphic to the moduli space of torsion-free sheaves
$a\in A_{n}$
, is isomorphic to the moduli space of torsion-free sheaves
![]() ${\mathcal{E}}$
on the spectral curve
${\mathcal{E}}$
on the spectral curve
![]() ${\mathcal{C}}_{a}$
with
${\mathcal{C}}_{a}$
with
 $\text{ Rk}_{{\mathcal{C}}_{a}}({\mathcal{E}})=1$
(and hence with associated characteristic polynomial
$\text{ Rk}_{{\mathcal{C}}_{a}}({\mathcal{E}})=1$
(and hence with associated characteristic polynomial
 $P_{\unicode[STIX]{x1D719}}=P_{{\mathcal{C}}_{a}}$
) and
$P_{\unicode[STIX]{x1D719}}=P_{{\mathcal{C}}_{a}}$
) and
 $\text{Deg}_{{\mathcal{C}}_{a}}({\mathcal{E}})=e^{\prime }$
, subject to the following stability condition: for every closed subscheme
$\text{Deg}_{{\mathcal{C}}_{a}}({\mathcal{E}})=e^{\prime }$
, subject to the following stability condition: for every closed subscheme
 $i_{Z}:Z\rightarrow {\mathcal{C}}_{a}$
of pure dimension one, for every torsion-free quotient
$i_{Z}:Z\rightarrow {\mathcal{C}}_{a}$
of pure dimension one, for every torsion-free quotient
![]() ${\mathcal{O}}_{Z}$
-module
${\mathcal{O}}_{Z}$
-module  with
with
 $\text{Rk}_{Z}({\mathcal{E}}_{Z})=1$
, we have
$\text{Rk}_{Z}({\mathcal{E}}_{Z})=1$
, we have
 $$\begin{eqnarray}\frac{\text{Deg}_{Z}({\mathcal{E}}_{Z})}{\text{Rk}_{C}(p_{\ast }{\mathcal{O}}_{Z})}+\frac{1}{2}(n-\text{Rk}_{C}(p_{\ast }{\mathcal{O}}_{Z}))d>\frac{e^{\prime }}{n}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\text{Deg}_{Z}({\mathcal{E}}_{Z})}{\text{Rk}_{C}(p_{\ast }{\mathcal{O}}_{Z})}+\frac{1}{2}(n-\text{Rk}_{C}(p_{\ast }{\mathcal{O}}_{Z}))d>\frac{e^{\prime }}{n}.\end{eqnarray}$$
The isomorphism is given by the push-forward morphism
![]() ${p_{a}}_{\ast }$
on coherent sheaves under the finite, flat, degree
${p_{a}}_{\ast }$
on coherent sheaves under the finite, flat, degree
![]() $n$
, spectral cover morphism
$n$
, spectral cover morphism
 $p_{a}:{\mathcal{C}}_{a}\rightarrow C_{a}=C\otimes k(a)$
.
$p_{a}:{\mathcal{C}}_{a}\rightarrow C_{a}=C\otimes k(a)$
.
Remark 2.4.4. If the spectral curve
![]() ${\mathcal{C}}_{a}$
is smooth, i.e. for
${\mathcal{C}}_{a}$
is smooth, i.e. for
![]() $a\in A_{n}$
general, then the fiber
$a\in A_{n}$
general, then the fiber
![]() $M_{n,a}$
is geometrically connected, for, in view of its modular description, it coincides with
$M_{n,a}$
is geometrically connected, for, in view of its modular description, it coincides with
 $\text{ Pic}^{e^{\prime }}({\mathcal{C}}_{a})$
.
$\text{ Pic}^{e^{\prime }}({\mathcal{C}}_{a})$
.
Let us record the properties of the norm map that we need.
Fact 2.4.5. Let
 $p_{a}:{\mathcal{C}}_{a}\rightarrow C_{a}$
be a spectral cover (of degree
$p_{a}:{\mathcal{C}}_{a}\rightarrow C_{a}$
be a spectral cover (of degree
![]() $n$
) with norm map
$n$
) with norm map
 $N_{p_{a}}:\text{Pic}^{0}({\mathcal{C}}_{a})\rightarrow \text{Pic}^{0}(C_{a})$
and pull-back map
$N_{p_{a}}:\text{Pic}^{0}({\mathcal{C}}_{a})\rightarrow \text{Pic}^{0}(C_{a})$
and pull-back map
 $p_{a}^{\ast }:\text{Pic}^{0}(C_{a})\rightarrow \text{Pic}^{0}({\mathcal{C}}_{a})$
. For what follows, see [Reference Hausel and PaulyHP12, Corollary 1.3 and § 3].
$p_{a}^{\ast }:\text{Pic}^{0}(C_{a})\rightarrow \text{Pic}^{0}({\mathcal{C}}_{a})$
. For what follows, see [Reference Hausel and PaulyHP12, Corollary 1.3 and § 3].
-
(1) For every
 $L\in \text{Pic}(C_{a})$
, we have
$L\in \text{Pic}(C_{a})$
, we have
 $N_{p_{a}}(p_{a}^{\ast }L)=L^{\otimes n}$
; in particular,
$N_{p_{a}}(p_{a}^{\ast }L)=L^{\otimes n}$
; in particular,
 $N_{p_{a}}$
is surjective.
$N_{p_{a}}$
is surjective. -
(2) Let
 ${\mathcal{E}}$
be a torsion-free
${\mathcal{E}}$
be a torsion-free
 ${\mathcal{O}}_{{\mathcal{C}}_{a}}$
-module of some integral rank
${\mathcal{O}}_{{\mathcal{C}}_{a}}$
-module of some integral rank
 $\text{Rk}_{{\mathcal{C}}_{a}}({\mathcal{E}})=:r$
and let
$\text{Rk}_{{\mathcal{C}}_{a}}({\mathcal{E}})=:r$
and let
 ${\mathcal{L}}\in \text{Pic}({\mathcal{C}}_{a})$
; then
${\mathcal{L}}\in \text{Pic}({\mathcal{C}}_{a})$
; then
 $\det ({p_{a}}_{\ast }({\mathcal{E}}\otimes {\mathcal{L}}))=\det ({p_{a}}_{\ast }{\mathcal{E}})\otimes N_{p_{a}}({\mathcal{L}})^{\otimes r}$
.
$\det ({p_{a}}_{\ast }({\mathcal{E}}\otimes {\mathcal{L}}))=\det ({p_{a}}_{\ast }{\mathcal{E}})\otimes N_{p_{a}}({\mathcal{L}})^{\otimes r}$
. -
(3) If
 $a\in A_{n}$
is general, then
$a\in A_{n}$
is general, then
 $\text{Ker}(N_{p_{a}})$
is a (connected) abelian variety (see § 2.5).
$\text{Ker}(N_{p_{a}})$
is a (connected) abelian variety (see § 2.5).
Proposition 2.4.6. The projective,
![]() $D$
-twisted,
$D$
-twisted,
![]() $\text{GL}_{n}$
Hitchin morphism
$\text{GL}_{n}$
Hitchin morphism
 $h_{n}:M_{n}\rightarrow A_{n}$
is surjective, with geometrically connected fibers, flat of pure relative dimension
$h_{n}:M_{n}\rightarrow A_{n}$
is surjective, with geometrically connected fibers, flat of pure relative dimension
 $$\begin{eqnarray}d_{h_{n}}=\binom{n}{2}d+n(g-1)+1.\end{eqnarray}$$
$$\begin{eqnarray}d_{h_{n}}=\binom{n}{2}d+n(g-1)+1.\end{eqnarray}$$
Let
![]() $a\in A_{n}$
. Then
$a\in A_{n}$
. Then
 $\text{Pic}^{0}({\mathcal{C}}_{a})$
acts on the Hitchin fiber
$\text{Pic}^{0}({\mathcal{C}}_{a})$
acts on the Hitchin fiber
![]() $M_{n,a}$
. If the spectral curve
$M_{n,a}$
. If the spectral curve
![]() ${\mathcal{C}}_{a}$
is smooth, then the corresponding Hitchin fiber
${\mathcal{C}}_{a}$
is smooth, then the corresponding Hitchin fiber
 $M_{n,a}\cong \text{Pic}^{e^{\prime }}({\mathcal{C}}_{a})$
is smooth, and a
$M_{n,a}\cong \text{Pic}^{e^{\prime }}({\mathcal{C}}_{a})$
is smooth, and a
 $\text{Pic}^{0}({\mathcal{C}}_{a})$
-torsor via tensor product.
$\text{Pic}^{0}({\mathcal{C}}_{a})$
-torsor via tensor product.
Proof. In view of the modular description of
![]() $M_{n,a}$
, it is clear that Fact 2.4.5(2) implies that, for every
$M_{n,a}$
, it is clear that Fact 2.4.5(2) implies that, for every
![]() $a\in A_{n}$
,
$a\in A_{n}$
,
 $\text{ Pic}^{0}({\mathcal{C}}_{a})$
acts on
$\text{ Pic}^{0}({\mathcal{C}}_{a})$
acts on
![]() $M_{n,a}$
via tensor product (degree and stability are preserved), and that, when
$M_{n,a}$
via tensor product (degree and stability are preserved), and that, when
![]() ${\mathcal{C}}_{a}$
is smooth, this action turns
${\mathcal{C}}_{a}$
is smooth, this action turns
![]() $M_{n,a}$
into the
$M_{n,a}$
into the
 $\text{Pic}^{0}({\mathcal{C}}_{a})$
-torsor
$\text{Pic}^{0}({\mathcal{C}}_{a})$
-torsor
 $\text{ Pic}^{e^{\prime }}({\mathcal{C}}_{a})$
. Since the locus of characteristics in
$\text{ Pic}^{e^{\prime }}({\mathcal{C}}_{a})$
. Since the locus of characteristics in
![]() $A_{n}$
yielding a smooth spectral curve is open and dense in
$A_{n}$
yielding a smooth spectral curve is open and dense in
![]() $A_{n}$
, we conclude that
$A_{n}$
, we conclude that
![]() $h_{n}$
is dominant. Since
$h_{n}$
is dominant. Since
![]() $h_{n}$
is projective, it is also surjective. The same line of argument implies that the general fiber of
$h_{n}$
is projective, it is also surjective. The same line of argument implies that the general fiber of
![]() $h_{n}$
is geometrically connected. On the other hand, since
$h_{n}$
is geometrically connected. On the other hand, since
![]() $A_{n}$
is nonsingular, hence normal, Zariski’s main theorem implies that
$A_{n}$
is nonsingular, hence normal, Zariski’s main theorem implies that
![]() $h_{n}$
has geometrically connected fibers. In view of [Reference Chaudouard and LaumonCL16, § 8, Corollary], the morphism
$h_{n}$
has geometrically connected fibers. In view of [Reference Chaudouard and LaumonCL16, § 8, Corollary], the morphism
 $h_{n}:M_{n}\rightarrow A_{n}$
is of pure relative dimension equal to the arithmetic genus of the spectral curves, which can be easily shown to be (7). Since
$h_{n}:M_{n}\rightarrow A_{n}$
is of pure relative dimension equal to the arithmetic genus of the spectral curves, which can be easily shown to be (7). Since
![]() $M_{n}$
and
$M_{n}$
and
![]() $A_{n}$
are nonsingular, the pure-relative-dimension morphism
$A_{n}$
are nonsingular, the pure-relative-dimension morphism
![]() $h_{n}$
is flat.◻
$h_{n}$
is flat.◻
Remark 2.4.7 (No line bundles in the nilpotent cone when
 $(e,n)=1$
).
$(e,n)=1$
).
The fiber
![]() $M_{n,0}$
over the origin does not contain line bundles. In fact, the spectral curve is of the form
$M_{n,0}$
over the origin does not contain line bundles. In fact, the spectral curve is of the form
![]() $nC$
(given by
$nC$
(given by
![]() $t^{n}=0$
on the surface
$t^{n}=0$
on the surface
![]() $V(D)$
), a nonreduced curve with multiple structure of multiplicity
$V(D)$
), a nonreduced curve with multiple structure of multiplicity
![]() $n$
, and with reduced curve
$n$
, and with reduced curve
![]() $C$
; it follows that every line bundle on it has degree
$C$
; it follows that every line bundle on it has degree
![]() $\text{Deg}_{nC}$
a multiple of
$\text{Deg}_{nC}$
a multiple of
![]() $n$
; since the required degree is
$n$
; since the required degree is
 $e^{\prime }=e+\binom{n}{2}d$
and
$e^{\prime }=e+\binom{n}{2}d$
and
 $(e,n)=1$
, in general, there is no such line bundle (e.g. if
$(e,n)=1$
, in general, there is no such line bundle (e.g. if
![]() $n$
is odd or if
$n$
is odd or if
![]() $d$
is even). By way of contrast, if the spectral curve
$d$
is even). By way of contrast, if the spectral curve
![]() ${\mathcal{C}}_{a}$
is geometrically integral, then
${\mathcal{C}}_{a}$
is geometrically integral, then
 $\text{Pic}^{e^{\prime }}({\mathcal{C}}_{a})\subseteq M_{n,a}$
is an integral, Zariski-dense, open subvariety. Finally, if we arrange for
$\text{Pic}^{e^{\prime }}({\mathcal{C}}_{a})\subseteq M_{n,a}$
is an integral, Zariski-dense, open subvariety. Finally, if we arrange for
![]() $e^{\prime }=0$
(in which case, we may not have the coprimality of the pair
$e^{\prime }=0$
(in which case, we may not have the coprimality of the pair
![]() $(e,n)$
), one sees that, for every
$(e,n)$
), one sees that, for every
![]() $a\in A_{n}$
, the variety
$a\in A_{n}$
, the variety
 $\text{Pic}^{0}({\mathcal{C}}_{a})$
is open in
$\text{Pic}^{0}({\mathcal{C}}_{a})$
is open in
![]() $M_{n,a}$
; see [Reference SchaubSch98, Corollary 5.2].
$M_{n,a}$
; see [Reference SchaubSch98, Corollary 5.2].
Modular description of the Hitchin fiber
![]() $\check{h}_{n}^{-1}(a)$
,
$\check{h}_{n}^{-1}(a)$
,
![]() $a\in {\check{A}}_{n}$
. The description in question is the same as the modular description given above, except for the added constraint on the determinant
$a\in {\check{A}}_{n}$
. The description in question is the same as the modular description given above, except for the added constraint on the determinant
 $\det ({p_{a}}_{\ast }{\mathcal{E}})=\unicode[STIX]{x1D716}$
, where
$\det ({p_{a}}_{\ast }{\mathcal{E}})=\unicode[STIX]{x1D716}$
, where
 $\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
is the fixed line bundle involved in the definition (1) of
$\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
is the fixed line bundle involved in the definition (1) of
![]() $\check{M}_{n}$
.
$\check{M}_{n}$
.
Definition 2.4.8 (The Prym variety of a spectral cover).
Let
![]() $a\in A_{n}$
and set
$a\in A_{n}$
and set
 $$\begin{eqnarray}\text{Prym}_{a}:=\text{Ker}\{N_{p_{a}}:\text{Pic}^{0}({\mathcal{C}}_{a})\rightarrow \text{Pic}^{0}(C_{a})\}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Prym}_{a}:=\text{Ker}\{N_{p_{a}}:\text{Pic}^{0}({\mathcal{C}}_{a})\rightarrow \text{Pic}^{0}(C_{a})\}.\end{eqnarray}$$
In general, the Prym variety
![]() $\text{Prym}_{a}$
is a disconnected group scheme with finitely many components; see [Reference Hausel and PaulyHP12] for a description of these components at geometric points of
$\text{Prym}_{a}$
is a disconnected group scheme with finitely many components; see [Reference Hausel and PaulyHP12] for a description of these components at geometric points of
![]() $A_{n}$
. We also call Prym variety the corresponding identity connected component. In a given context, we shall make it clear which Prym variety we are using.
$A_{n}$
. We also call Prym variety the corresponding identity connected component. In a given context, we shall make it clear which Prym variety we are using.
If
![]() $a\in A_{n}$
is general, then
$a\in A_{n}$
is general, then
![]() $\text{Prym}_{a}$
is geometrically connected (Fact 2.4.5(3)).
$\text{Prym}_{a}$
is geometrically connected (Fact 2.4.5(3)).
Proposition 2.4.9. The projective,
![]() $D$
-twisted,
$D$
-twisted,
![]() $\text{SL}_{n}$
Hitchin morphism
$\text{SL}_{n}$
Hitchin morphism
 $\check{h}_{n}:\check{M}_{n}\rightarrow {\check{A}}_{n}$
is surjective, with geometrically connected fibers, flat of pure relative dimension
$\check{h}_{n}:\check{M}_{n}\rightarrow {\check{A}}_{n}$
is surjective, with geometrically connected fibers, flat of pure relative dimension
 $$\begin{eqnarray}d_{\check{h}_{n}}=d_{h_{n}}-g=\binom{n}{2}d+(n-1)(g-1).\end{eqnarray}$$
$$\begin{eqnarray}d_{\check{h}_{n}}=d_{h_{n}}-g=\binom{n}{2}d+(n-1)(g-1).\end{eqnarray}$$
Let
![]() $a\in {\check{A}}_{n}$
. Then
$a\in {\check{A}}_{n}$
. Then
![]() $\text{Prym}_{a}$
acts on the Hitchin fiber
$\text{Prym}_{a}$
acts on the Hitchin fiber
![]() $\check{M}_{n,a}$
. If the spectral curve
$\check{M}_{n,a}$
. If the spectral curve
![]() ${\mathcal{C}}_{a}$
is smooth, then
${\mathcal{C}}_{a}$
is smooth, then
![]() $\text{Prym}_{a}$
is connected, the corresponding
$\text{Prym}_{a}$
is connected, the corresponding
![]() $\text{SL}_{n}$
Hitchin fiber
$\text{SL}_{n}$
Hitchin fiber
![]() $\check{M}_{n,a}$
is smooth, and a
$\check{M}_{n,a}$
is smooth, and a
![]() $\text{Prym}_{a}$
-torsor via tensor product.
$\text{Prym}_{a}$
-torsor via tensor product.
Proof. By Proposition 2.4.6, for every
![]() $a\in {\check{A}}_{n}$
, the
$a\in {\check{A}}_{n}$
, the
![]() $\text{GL}_{n}$
Hitchin fiber
$\text{GL}_{n}$
Hitchin fiber
 $M_{n,a}\neq \emptyset$
. There is the natural morphism
$M_{n,a}\neq \emptyset$
. There is the natural morphism
 $$\begin{eqnarray}\mathfrak{p}_{a}:=\det \circ {p_{a}}_{\ast }:M_{n,a}\longrightarrow \text{Pic}^{e}(C).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{p}_{a}:=\det \circ {p_{a}}_{\ast }:M_{n,a}\longrightarrow \text{Pic}^{e}(C).\end{eqnarray}$$
In view of the modular description of the
![]() $\text{SL}_{n}$
Hitchin fiber
$\text{SL}_{n}$
Hitchin fiber
![]() $\check{M}_{n,a}$
, we have that
$\check{M}_{n,a}$
, we have that
 $\check{M}_{n,a}=\mathfrak{p}_{a}^{-1}(\unicode[STIX]{x1D716})$
.
$\check{M}_{n,a}=\mathfrak{p}_{a}^{-1}(\unicode[STIX]{x1D716})$
.
The morphism
![]() $\mathfrak{p}_{a}$
is equivariant for the
$\mathfrak{p}_{a}$
is equivariant for the
 $\text{ Pic}^{0}(C)$
-actions given by
$\text{ Pic}^{0}(C)$
-actions given by
 $L\cdot {\mathcal{E}}:={\mathcal{E}}\otimes L$
on the domain and by
$L\cdot {\mathcal{E}}:={\mathcal{E}}\otimes L$
on the domain and by
 $L\cdot M:=M\cdot L^{\otimes n}$
on the target (Fact 2.4.5(2),(1)). It follows that
$L\cdot M:=M\cdot L^{\otimes n}$
on the target (Fact 2.4.5(2),(1)). It follows that
![]() $\mathfrak{p}_{a}$
is surjective. In particular, for every
$\mathfrak{p}_{a}$
is surjective. In particular, for every
![]() $a\in {\check{A}}_{n}$
,
$a\in {\check{A}}_{n}$
,
 $\check{M}_{n,a}\neq \emptyset$
, so that
$\check{M}_{n,a}\neq \emptyset$
, so that
![]() $\check{h}_{n}$
is surjective.
$\check{h}_{n}$
is surjective.
By Zariski’s main theorem, in order to check that
![]() $\check{h}_{n}$
has geometrically connected fibers, it is enough to do so at a general point. We do this next.
$\check{h}_{n}$
has geometrically connected fibers, it is enough to do so at a general point. We do this next.
Since
 $\check{M}_{n,a}=\mathfrak{p}_{a}^{-1}(\unicode[STIX]{x1D716})$
, Fact 2.4.5(2) implies that
$\check{M}_{n,a}=\mathfrak{p}_{a}^{-1}(\unicode[STIX]{x1D716})$
, Fact 2.4.5(2) implies that
 $\text{Prym}_{a}\subseteq \text{Pic}^{0}({\mathcal{C}}_{a})$
is the largest subgroup acting on
$\text{Prym}_{a}\subseteq \text{Pic}^{0}({\mathcal{C}}_{a})$
is the largest subgroup acting on
![]() $\check{M}_{n,a}$
. More precisely, if
$\check{M}_{n,a}$
. More precisely, if
 ${\mathcal{E}}\in \check{M}_{n,a}$
and
${\mathcal{E}}\in \check{M}_{n,a}$
and
 $L\in \text{Pic}^{0}({\mathcal{C}}_{a})$
, then
$L\in \text{Pic}^{0}({\mathcal{C}}_{a})$
, then
 ${\mathcal{E}}\otimes {\mathcal{L}}\in \check{M}_{n,a}$
if and only if
${\mathcal{E}}\otimes {\mathcal{L}}\in \check{M}_{n,a}$
if and only if
 ${\mathcal{L}}\in \text{Prym}_{a}$
.
${\mathcal{L}}\in \text{Prym}_{a}$
.
Let
![]() $a\in {\check{A}}_{n}$
be a traceless characteristic yielding a nonsingular spectral curve
$a\in {\check{A}}_{n}$
be a traceless characteristic yielding a nonsingular spectral curve
![]() ${\mathcal{C}}_{a}$
. Since
${\mathcal{C}}_{a}$
. Since
![]() $M_{n,a}$
is a
$M_{n,a}$
is a
 $\text{ Pic}^{0}({\mathcal{C}}_{a})$
-torsor by Proposition 2.4.6, we deduce that
$\text{ Pic}^{0}({\mathcal{C}}_{a})$
-torsor by Proposition 2.4.6, we deduce that
![]() $\check{M}_{n,a}$
is s a
$\check{M}_{n,a}$
is s a
![]() $\text{Prym}_{a}$
-torsor. For
$\text{Prym}_{a}$
-torsor. For
![]() $a\in {\check{A}}_{n}$
general,
$a\in {\check{A}}_{n}$
general,
![]() $\text{Prym}_{a}$
is geometrically connected by Fact 2.4.5(3), so that so is the general fiber
$\text{Prym}_{a}$
is geometrically connected by Fact 2.4.5(3), so that so is the general fiber
![]() $\check{M}_{n,a}$
, and, as anticipated,
$\check{M}_{n,a}$
, and, as anticipated,
![]() $\check{h}_{n}$
has thus geometrically connected fibers.
$\check{h}_{n}$
has thus geometrically connected fibers.
Since all fibers of
![]() $\check{h}_{n}$
are now known to be geometrically connected, so is the fiber
$\check{h}_{n}$
are now known to be geometrically connected, so is the fiber
![]() $\check{M}_{n,a}$
corresponding to a smooth spectral curve. Since such a fiber is a
$\check{M}_{n,a}$
corresponding to a smooth spectral curve. Since such a fiber is a
![]() $\text{Prym}_{a}$
-torsor, the Prym variety
$\text{Prym}_{a}$
-torsor, the Prym variety
![]() $\text{Prym}_{a}$
is also geometrically connected.
$\text{Prym}_{a}$
is also geometrically connected.
Finally, since the morphism
![]() $\mathfrak{p}_{a}$
is flat, and the morphism
$\mathfrak{p}_{a}$
is flat, and the morphism
![]() $h_{n}$
is of pure dimension (7), all the fibers of
$h_{n}$
is of pure dimension (7), all the fibers of
![]() $\check{h}_{n}$
are of pure dimension (7) minus
$\check{h}_{n}$
are of pure dimension (7) minus
![]() $g$
, and hence (9) holds. The flatness of
$g$
, and hence (9) holds. The flatness of
![]() $\check{h}_{n}$
follows by this and by the smoothness of
$\check{h}_{n}$
follows by this and by the smoothness of
![]() $\check{M}_{n}$
and of
$\check{M}_{n}$
and of
![]() ${\check{A}}_{n}$
.◻
${\check{A}}_{n}$
.◻
2.5 Endoscopy loci of the Hitchin
 $\text{SL}_{n}$
fibration
$\text{SL}_{n}$
fibration
Let
![]() $a$
be a geometric point of
$a$
be a geometric point of
![]() $A_{n}^{\text{ell}}$
, so that the spectral curve
$A_{n}^{\text{ell}}$
, so that the spectral curve
![]() ${\mathcal{C}}_{a}$
is (geometrically) integral. The
${\mathcal{C}}_{a}$
is (geometrically) integral. The
![]() $D$
-twisted,
$D$
-twisted,
![]() $\text{GL}_{n}$
Hitchin fiber
$\text{GL}_{n}$
Hitchin fiber
![]() $M_{n,a}$
is also integral: it is isomorphic to the compactified Jacobian of the integral locally planar spectral curve, parameterizing rank one and degree
$M_{n,a}$
is also integral: it is isomorphic to the compactified Jacobian of the integral locally planar spectral curve, parameterizing rank one and degree
![]() $e^{\prime }$
torsion-free coherent sheaves on it. In particular, the regular part
$e^{\prime }$
torsion-free coherent sheaves on it. In particular, the regular part
 $\text{Pic}^{e^{\prime }}({\mathcal{C}}_{a})\cong M_{n,a}^{\text{reg}}\subseteq M_{n,a}$
of this fiber is integral, Zariski open and dense in the whole fiber, and it is a
$\text{Pic}^{e^{\prime }}({\mathcal{C}}_{a})\cong M_{n,a}^{\text{reg}}\subseteq M_{n,a}$
of this fiber is integral, Zariski open and dense in the whole fiber, and it is a
 $\text{ Pic}^{0}({\mathcal{C}}_{a})$
-torsor.
$\text{ Pic}^{0}({\mathcal{C}}_{a})$
-torsor.
Let
![]() $a$
be a geometric point of
$a$
be a geometric point of
![]() ${\check{A}}_{n}$
. Then the
${\check{A}}_{n}$
. Then the
![]() $D$
-twisted,
$D$
-twisted,
![]() $\text{SL}_{n}$
Hitchin fiber
$\text{SL}_{n}$
Hitchin fiber
 $\check{M}_{n,a}=\mathfrak{p}_{a}^{-1}(\unicode[STIX]{x1D716})$
(cf. (10)), and it is (geometrically) connected. Since the morphism
$\check{M}_{n,a}=\mathfrak{p}_{a}^{-1}(\unicode[STIX]{x1D716})$
(cf. (10)), and it is (geometrically) connected. Since the morphism
![]() $\check{h}_{n}$
is flat and
$\check{h}_{n}$
is flat and
![]() ${\check{A}}_{n}$
is nonsingular, every fiber of
${\check{A}}_{n}$
is nonsingular, every fiber of
![]() $\check{h}_{n}$
is a local complete intersection (l.c.i).
$\check{h}_{n}$
is a local complete intersection (l.c.i).
Assume, in addition, that
![]() $a$
is a geometric point of
$a$
is a geometric point of
![]() ${\check{A}}_{n}^{\text{ell}}$
. By the
${\check{A}}_{n}^{\text{ell}}$
. By the
 $\text{Pic}^{0}(C)$
-equivariance of
$\text{Pic}^{0}(C)$
-equivariance of
![]() $\mathfrak{p}_{a}$
, the regular part of
$\mathfrak{p}_{a}$
, the regular part of
![]() $\check{M}_{n,a}$
satisfies
$\check{M}_{n,a}$
satisfies
 $\check{M}_{n,a}^{\text{reg}}=M_{n,a}^{\text{reg}}\,\cap \,\check{M}_{n,a}$
, and it is Zariski open and dense. Since the fiber
$\check{M}_{n,a}^{\text{reg}}=M_{n,a}^{\text{reg}}\,\cap \,\check{M}_{n,a}$
, and it is Zariski open and dense. Since the fiber
![]() $\check{M}_{n,a}$
is a l.c.i., we have that, being smooth on a Zariski-dense open subset, it is also reduced. The regular part
$\check{M}_{n,a}$
is a l.c.i., we have that, being smooth on a Zariski-dense open subset, it is also reduced. The regular part
![]() $\check{M}_{n,a}^{\text{reg}}$
is made of line bundles
$\check{M}_{n,a}^{\text{reg}}$
is made of line bundles
![]() ${\mathcal{E}}$
on the spectral curve with
${\mathcal{E}}$
on the spectral curve with
 $\mathfrak{p}_{a}({\mathcal{E}})=\unicode[STIX]{x1D716}$
. It is clear that
$\mathfrak{p}_{a}({\mathcal{E}})=\unicode[STIX]{x1D716}$
. It is clear that
![]() $\check{M}_{n,a}^{\text{reg}}$
is then a
$\check{M}_{n,a}^{\text{reg}}$
is then a
![]() $\text{Prym}_{a}$
-torsor.
$\text{Prym}_{a}$
-torsor.
Fact 2.5.1. Let
![]() $a\in {\check{A}}_{n}^{\text{ell}}$
. The discussion above implies that the number of irreducible components of the pure dimensional and reduced
$a\in {\check{A}}_{n}^{\text{ell}}$
. The discussion above implies that the number of irreducible components of the pure dimensional and reduced
![]() $\check{M}_{n,a}$
coincides with the number of connected components of
$\check{M}_{n,a}$
coincides with the number of connected components of
![]() $\text{Prym}_{a}$
.
$\text{Prym}_{a}$
.
For every
![]() $a\in A_{n}$
, the group of connected components
$a\in A_{n}$
, the group of connected components
 $\unicode[STIX]{x1D70B}_{0}(\text{ Prim}_{a})$
is described in [Reference Hausel and PaulyHP12, Theorem 1.1]. The locus
$\unicode[STIX]{x1D70B}_{0}(\text{ Prim}_{a})$
is described in [Reference Hausel and PaulyHP12, Theorem 1.1]. The locus
 ${\check{A}}_{n,\text{endo}}\subseteq {\check{A}}_{n}$
over which
${\check{A}}_{n,\text{endo}}\subseteq {\check{A}}_{n}$
over which
![]() $\text{ Prym}_{a}$
is disconnected is called the endoscopic locus of the
$\text{ Prym}_{a}$
is disconnected is called the endoscopic locus of the
![]() $\text{SL}_{n}$
Hitchin fibration and it is described in [Reference Hausel and PaulyHP12, § 5, especially Lemmas 5.1; 7.1]:
$\text{SL}_{n}$
Hitchin fibration and it is described in [Reference Hausel and PaulyHP12, § 5, especially Lemmas 5.1; 7.1]:
 $$\begin{eqnarray}{\check{A}}_{n,\text{endo}}=\mathop{\bigcup }_{\unicode[STIX]{x1D6E4}}{\check{A}}_{n,\unicode[STIX]{x1D6E4}},\end{eqnarray}$$
$$\begin{eqnarray}{\check{A}}_{n,\text{endo}}=\mathop{\bigcup }_{\unicode[STIX]{x1D6E4}}{\check{A}}_{n,\unicode[STIX]{x1D6E4}},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6E4}$
ranges over the finite set of cyclic subgroups of
$\unicode[STIX]{x1D6E4}$
ranges over the finite set of cyclic subgroups of
 $\text{Pic}^{0}(C)[n]$
of prime number order. Each
$\text{Pic}^{0}(C)[n]$
of prime number order. Each
 ${\check{A}}_{n,\unicode[STIX]{x1D6E4}}\subseteq {\check{A}}_{n}$
is a geometrically integral subvariety. The codimension of each
${\check{A}}_{n,\unicode[STIX]{x1D6E4}}\subseteq {\check{A}}_{n}$
is a geometrically integral subvariety. The codimension of each
![]() ${\check{A}}_{n,\unicode[STIX]{x1D6E4}}$
can be computed in the same way as in the proof of [Reference Hausel and PaulyHP12, Lemma 7.1], whose proof in the case
${\check{A}}_{n,\unicode[STIX]{x1D6E4}}$
can be computed in the same way as in the proof of [Reference Hausel and PaulyHP12, Lemma 7.1], whose proof in the case
 $D=K_{C}$
, remains valid for
$D=K_{C}$
, remains valid for
![]() $D$
: we need the knowledge of
$D$
: we need the knowledge of
![]() $d_{{\check{A}}_{n}}$
(78), obtained by the Riemann–Roch theorem, and the formula directly above [Reference Hausel and PaulyHP12, Lemma 5.1]. The resulting value
$d_{{\check{A}}_{n}}$
(78), obtained by the Riemann–Roch theorem, and the formula directly above [Reference Hausel and PaulyHP12, Lemma 5.1]. The resulting value
 $$\begin{eqnarray}\text{codim}_{{\check{A}}_{n}}({\check{A}}_{n,\unicode[STIX]{x1D6E4}})={\textstyle \frac{1}{2}}(n-\unicode[STIX]{x1D708})\{(n+\unicode[STIX]{x1D708})d+[d-2(g-1)]\},\quad (\unicode[STIX]{x1D708}:=n/\#(\unicode[STIX]{x1D6E4})),\end{eqnarray}$$
$$\begin{eqnarray}\text{codim}_{{\check{A}}_{n}}({\check{A}}_{n,\unicode[STIX]{x1D6E4}})={\textstyle \frac{1}{2}}(n-\unicode[STIX]{x1D708})\{(n+\unicode[STIX]{x1D708})d+[d-2(g-1)]\},\quad (\unicode[STIX]{x1D708}:=n/\#(\unicode[STIX]{x1D6E4})),\end{eqnarray}$$
is strictly positive in view, for example, of our assumption
 $d>2(g-1)$
.
$d>2(g-1)$
.
The subvarieties
 ${\check{A}}_{n,\unicode[STIX]{x1D6E4}}^{\text{ell}}:={\check{A}}_{n,\unicode[STIX]{x1D6E4}}\,\cap \,{\check{A}}_{n}^{\text{ell}}\subseteq {\check{A}}_{n}^{\text{ell}}$
are nonsingular and mutually disjoint [Reference NgôNgô06, Proposition 10.3]. By construction, the number
${\check{A}}_{n,\unicode[STIX]{x1D6E4}}^{\text{ell}}:={\check{A}}_{n,\unicode[STIX]{x1D6E4}}\,\cap \,{\check{A}}_{n}^{\text{ell}}\subseteq {\check{A}}_{n}^{\text{ell}}$
are nonsingular and mutually disjoint [Reference NgôNgô06, Proposition 10.3]. By construction, the number
 $$\begin{eqnarray}o(\unicode[STIX]{x1D6E4}):=\#(\unicode[STIX]{x1D70B}_{0}(\text{Prym}_{a}))\end{eqnarray}$$
$$\begin{eqnarray}o(\unicode[STIX]{x1D6E4}):=\#(\unicode[STIX]{x1D70B}_{0}(\text{Prym}_{a}))\end{eqnarray}$$
of connected components of
![]() $\text{Prym}_{a}$
is independent of
$\text{Prym}_{a}$
is independent of
 $a\in {\check{A}}_{n,\unicode[STIX]{x1D6E4}}^{\text{ell}}$
.
$a\in {\check{A}}_{n,\unicode[STIX]{x1D6E4}}^{\text{ell}}$
.
A point
 $a\in {\check{A}}_{n,\unicode[STIX]{x1D6E4}}^{\text{ell}}$
if and only if the spectral cover
$a\in {\check{A}}_{n,\unicode[STIX]{x1D6E4}}^{\text{ell}}$
if and only if the spectral cover
 $p_{a}:{\mathcal{C}}_{a}\rightarrow C$
has the property that the induced morphism from the normalization of the integral spectral curve
$p_{a}:{\mathcal{C}}_{a}\rightarrow C$
has the property that the induced morphism from the normalization of the integral spectral curve
 $\widetilde{p_{a}}=\widetilde{{\mathcal{C}}_{a}}\rightarrow C$
factors through the étale cyclic cover of
$\widetilde{p_{a}}=\widetilde{{\mathcal{C}}_{a}}\rightarrow C$
factors through the étale cyclic cover of
![]() $C$
associated with
$C$
associated with
![]() $\unicode[STIX]{x1D6E4}$
(cf. [Reference Hausel and PaulyHP12, Proof of Theorem 5.3]).
$\unicode[STIX]{x1D6E4}$
(cf. [Reference Hausel and PaulyHP12, Proof of Theorem 5.3]).
The locus
 $$\begin{eqnarray}{\check{A}}_{n,\text{endo}}^{\text{ell}}=\coprod _{\unicode[STIX]{x1D6E4}}{\check{A}}_{n,\unicode[STIX]{x1D6E4}}^{\text{ell}}\end{eqnarray}$$
$$\begin{eqnarray}{\check{A}}_{n,\text{endo}}^{\text{ell}}=\coprod _{\unicode[STIX]{x1D6E4}}{\check{A}}_{n,\unicode[STIX]{x1D6E4}}^{\text{ell}}\end{eqnarray}$$
is the
 $G=\text{SL}_{n}$
endoscopic locus introduced by Ngô in [Reference NgôNgô06, § 10] for
$G=\text{SL}_{n}$
endoscopic locus introduced by Ngô in [Reference NgôNgô06, § 10] for
![]() $D$
-twisted,
$D$
-twisted,
![]() $G$
Hitchin fibrations (
$G$
Hitchin fibrations (
![]() $G$
reductive). It determines the socle
$G$
reductive). It determines the socle
 $\text{Socle}({R\check{h}_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })\,\cap \,{\check{A}}_{n}^{\text{ell}}$
over the elliptic locus; see § 4.9.
$\text{Socle}({R\check{h}_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })\,\cap \,{\check{A}}_{n}^{\text{ell}}$
over the elliptic locus; see § 4.9.
2.6 Weak abelian fibrations and
 $\unicode[STIX]{x1D6FF}$
-regularity
$\unicode[STIX]{x1D6FF}$
-regularity
The notion of
![]() $\unicode[STIX]{x1D6FF}$
-regular weak abelian fibration has been introduced in [Reference NgôNgô10] as an encapsulation of some important features of the Hitchin fibration over the elliptic locus: presence of the action of a commutative smooth group scheme with affine stabilizers, polarizability of the associated Tate module, and
$\unicode[STIX]{x1D6FF}$
-regular weak abelian fibration has been introduced in [Reference NgôNgô10] as an encapsulation of some important features of the Hitchin fibration over the elliptic locus: presence of the action of a commutative smooth group scheme with affine stabilizers, polarizability of the associated Tate module, and
![]() $\unicode[STIX]{x1D6FF}$
-regularity of the group scheme. See also [Reference NgôNgô11] for an introduction to this circle of ideas.
$\unicode[STIX]{x1D6FF}$
-regularity of the group scheme. See also [Reference NgôNgô11] for an introduction to this circle of ideas.
In this section, let
 $g:J\rightarrow A$
be a smooth commutative group scheme over an irreducible variety
$g:J\rightarrow A$
be a smooth commutative group scheme over an irreducible variety
![]() $A$
such that
$A$
such that
![]() $g$
has geometrically connected fibers.
$g$
has geometrically connected fibers.
Chevalley devissage. References for what follows are, for example, [Reference MilneMil, Theorem 10.25, Propositions 10.24, 10.5 (and its proof), Proposition 10.3] and [Reference ConradCon02].
Let
![]() $\overline{a}$
be a geometric point on
$\overline{a}$
be a geometric point on
![]() $A$
with underlying point a Zariski point
$A$
with underlying point a Zariski point
![]() $a\in A$
. Let
$a\in A$
. Let
![]() $J_{\overline{a}}$
be the fiber of
$J_{\overline{a}}$
be the fiber of
![]() $J$
at
$J$
at
![]() $\overline{a}$
. There is a canonical short exact sequence of commutative connected group schemes over the residue field of
$\overline{a}$
. There is a canonical short exact sequence of commutative connected group schemes over the residue field of
![]() $\overline{a}$
:
$\overline{a}$
:
 $$\begin{eqnarray}0\rightarrow J_{\overline{a}}^{\text{aff}}\rightarrow J_{\overline{a}}\rightarrow J_{\overline{a}}^{\text{ab}}\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow J_{\overline{a}}^{\text{aff}}\rightarrow J_{\overline{a}}\rightarrow J_{\overline{a}}^{\text{ab}}\rightarrow 0,\end{eqnarray}$$
where
 $J_{\overline{a}}^{\text{aff}}\subseteq J_{\overline{a}}$
is the maximal connected affine linear subgroup of
$J_{\overline{a}}^{\text{aff}}\subseteq J_{\overline{a}}$
is the maximal connected affine linear subgroup of
![]() $J_{\overline{a}}$
, and
$J_{\overline{a}}$
, and
![]() $J_{\overline{a}}^{\text{ ab}}$
is an abelian variety. The dimensions of these varieties depend only on the Zariski point
$J_{\overline{a}}^{\text{ ab}}$
is an abelian variety. The dimensions of these varieties depend only on the Zariski point
![]() $a\in A$
, and are denoted by
$a\in A$
, and are denoted by
![]() $d_{a}^{\text{aff}}(J)$
and
$d_{a}^{\text{aff}}(J)$
and
![]() $d_{a}^{\text{ab}}(J)$
, respectively. Clearly,
$d_{a}^{\text{ab}}(J)$
, respectively. Clearly,
 $$\begin{eqnarray}d_{a}(J)=d_{a}^{\text{aff}}(J)+d_{a}^{\text{ab}}(J).\end{eqnarray}$$
$$\begin{eqnarray}d_{a}(J)=d_{a}^{\text{aff}}(J)+d_{a}^{\text{ab}}(J).\end{eqnarray}$$
The notion of
![]() $\unicode[STIX]{x1D6FF}$
-regularity. The function
$\unicode[STIX]{x1D6FF}$
-regularity. The function
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}:A\longrightarrow \mathbb{Z}^{{\geqslant}0},\quad a\mapsto \unicode[STIX]{x1D6FF}_{a}:=d_{a}^{\text{aff}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}:A\longrightarrow \mathbb{Z}^{{\geqslant}0},\quad a\mapsto \unicode[STIX]{x1D6FF}_{a}:=d_{a}^{\text{aff}}\end{eqnarray}$$
is upper semicontinuous (jumps up on closed subsets); see [Reference Grothendieck and DemazureSGA3.II, X, Remark 8.7]. We have the disjoint union decomposition
 $$\begin{eqnarray}A=\coprod _{\unicode[STIX]{x1D6FF}\geqslant 0}S_{\unicode[STIX]{x1D6FF}},\quad S_{\unicode[STIX]{x1D6FF}}=S_{\unicode[STIX]{x1D6FF}}(J/A):=\{a\in A\mid \unicode[STIX]{x1D6FF}_{a}=\unicode[STIX]{x1D6FF}\}\end{eqnarray}$$
$$\begin{eqnarray}A=\coprod _{\unicode[STIX]{x1D6FF}\geqslant 0}S_{\unicode[STIX]{x1D6FF}},\quad S_{\unicode[STIX]{x1D6FF}}=S_{\unicode[STIX]{x1D6FF}}(J/A):=\{a\in A\mid \unicode[STIX]{x1D6FF}_{a}=\unicode[STIX]{x1D6FF}\}\end{eqnarray}$$
of
![]() $A$
into locally closed subvarieties of
$A$
into locally closed subvarieties of
![]() $A$
. We call
$A$
. We call
![]() $S_{\unicode[STIX]{x1D6FF}}$
the
$S_{\unicode[STIX]{x1D6FF}}$
the
![]() $\unicode[STIX]{x1D6FF}$
-locus of
$\unicode[STIX]{x1D6FF}$
-locus of
![]() $J/A$
.
$J/A$
.
Definition 2.6.1 (
 $\unicode[STIX]{x1D6FF}$
-regularity).
$\unicode[STIX]{x1D6FF}$
-regularity).
We say that
 $g:J\rightarrow A$
is
$g:J\rightarrow A$
is
![]() $\unicode[STIX]{x1D6FF}$
-regular if
$\unicode[STIX]{x1D6FF}$
-regular if
 $$\begin{eqnarray}\text{codim}_{A}(S_{\unicode[STIX]{x1D6FF}})\geqslant \unicode[STIX]{x1D6FF},\quad \forall \unicode[STIX]{x1D6FF}\geqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}\text{codim}_{A}(S_{\unicode[STIX]{x1D6FF}})\geqslant \unicode[STIX]{x1D6FF},\quad \forall \unicode[STIX]{x1D6FF}\geqslant 0,\end{eqnarray}$$
where one requires the inequality to hold for every irreducible component of
![]() $S_{\unicode[STIX]{x1D6FF}}$
.
$S_{\unicode[STIX]{x1D6FF}}$
.
The following lemma is an immediate consequence of the upper-semicontinuity of the function
![]() $\unicode[STIX]{x1D6FF}$
and of the identity (16).
$\unicode[STIX]{x1D6FF}$
and of the identity (16).
Lemma 2.6.2. A group scheme
 $g:J\rightarrow A$
as above is
$g:J\rightarrow A$
as above is
![]() $\unicode[STIX]{x1D6FF}$
-regular if and only if either of the two following equivalent conditions hold.
$\unicode[STIX]{x1D6FF}$
-regular if and only if either of the two following equivalent conditions hold.
-
(1) For every closed irreducible subvariety
 $Z\subseteq A$
, let
$Z\subseteq A$
, let
 $\unicode[STIX]{x1D6FF}_{Z}$
be the minimum value of
$\unicode[STIX]{x1D6FF}_{Z}$
be the minimum value of
 $\unicode[STIX]{x1D6FF}$
on
$\unicode[STIX]{x1D6FF}$
on
 $Z$
(it is attained at general points of
$Z$
(it is attained at general points of
 $Z$
, as well as at the generic point of
$Z$
, as well as at the generic point of
 $Z$
); then
$Z$
); then
 $\text{ codim}_{A}(Z)\geqslant \unicode[STIX]{x1D6FF}_{Z}$
.
$\text{ codim}_{A}(Z)\geqslant \unicode[STIX]{x1D6FF}_{Z}$
. -
(2) For every point
 $a\in A$
, let
$a\in A$
, let
 $d_{a}:=\dim \overline{\{a\}}$
and let
$d_{a}:=\dim \overline{\{a\}}$
and let
 $d_{A}:=\dim (A)$
; then (20)
$d_{A}:=\dim (A)$
; then (20) $$\begin{eqnarray}d_{a}^{\text{ab}}(J)\geqslant d_{a}(J)-d_{A}+d_{a}.\end{eqnarray}$$
$$\begin{eqnarray}d_{a}^{\text{ab}}(J)\geqslant d_{a}(J)-d_{A}+d_{a}.\end{eqnarray}$$
The Tate module
![]() $T_{\overline{\mathbb{Q}}_{\ell }}(J)$
and the notion of its polarizability. Let
$T_{\overline{\mathbb{Q}}_{\ell }}(J)$
and the notion of its polarizability. Let
 $g:J\rightarrow A$
be as above and let
$g:J\rightarrow A$
be as above and let
 $d_{g}:=\dim (J)-\dim (A)$
be the pure relative dimension of
$d_{g}:=\dim (J)-\dim (A)$
be the pure relative dimension of
![]() $g$
. The Tate module of
$g$
. The Tate module of
![]() $J$
is the
$J$
is the
![]() $\overline{\mathbb{Q}}_{\ell }$
-adic sheaf [Reference NgôNgô10, § 4.12]
$\overline{\mathbb{Q}}_{\ell }$
-adic sheaf [Reference NgôNgô10, § 4.12]
 $$\begin{eqnarray}T_{\overline{\mathbb{Q}}_{\ell }}(J):=R^{2d_{g}-1}g_{!}\overline{\mathbb{Q}}_{\ell }(d_{g}).\end{eqnarray}$$
$$\begin{eqnarray}T_{\overline{\mathbb{Q}}_{\ell }}(J):=R^{2d_{g}-1}g_{!}\overline{\mathbb{Q}}_{\ell }(d_{g}).\end{eqnarray}$$
Its stalk at any geometric point
![]() $\overline{a}$
of
$\overline{a}$
of
![]() $A$
is given by the Tate module
$A$
is given by the Tate module
![]() $T_{\overline{\mathbb{Q}}_{\ell }}(J_{\overline{a}})$
, i.e. the inverse limit, with respect to
$T_{\overline{\mathbb{Q}}_{\ell }}(J_{\overline{a}})$
, i.e. the inverse limit, with respect to
![]() $i\in \mathbb{N}$
, of the
$i\in \mathbb{N}$
, of the
![]() $\ell ^{i}$
-torsion points on
$\ell ^{i}$
-torsion points on
![]() $J_{\overline{a}}$
, tensored with
$J_{\overline{a}}$
, tensored with
![]() $\overline{\mathbb{Q}}_{\ell }$
over
$\overline{\mathbb{Q}}_{\ell }$
over
![]() $\mathbb{Z}_{\ell }$
. The Chevalley devissage at the stalks yields the natural short exact sequence
$\mathbb{Z}_{\ell }$
. The Chevalley devissage at the stalks yields the natural short exact sequence
 $$\begin{eqnarray}0\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{\overline{a}}^{\text{aff}})\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{\overline{a}})\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{\overline{a}}^{\text{ab}})\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{\overline{a}}^{\text{aff}})\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{\overline{a}})\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{\overline{a}}^{\text{ab}})\rightarrow 0.\end{eqnarray}$$
The Tate module
![]() $T_{\overline{\mathbb{Q}}_{\ell }}(J)$
is said to be polarizable if it admits a polarization, i.e. an alternating bilinear pairing
$T_{\overline{\mathbb{Q}}_{\ell }}(J)$
is said to be polarizable if it admits a polarization, i.e. an alternating bilinear pairing
 $$\begin{eqnarray}\unicode[STIX]{x1D713}:T_{\overline{\mathbb{Q}}_{\ell }}(J)\otimes _{\overline{\mathbb{Q}}_{\ell }}T_{\overline{\mathbb{Q}}_{\ell }}(J)\longrightarrow \overline{\mathbb{Q}}_{\ell }(1),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}:T_{\overline{\mathbb{Q}}_{\ell }}(J)\otimes _{\overline{\mathbb{Q}}_{\ell }}T_{\overline{\mathbb{Q}}_{\ell }}(J)\longrightarrow \overline{\mathbb{Q}}_{\ell }(1),\end{eqnarray}$$
such that, for every geometric point
![]() $\overline{a}$
of
$\overline{a}$
of
![]() $A$
, we have that the kernel of
$A$
, we have that the kernel of
![]() $\unicode[STIX]{x1D713}_{\overline{a}}$
is exactly
$\unicode[STIX]{x1D713}_{\overline{a}}$
is exactly
 $T_{\overline{\mathbb{Q}}_{\ell }}(J_{\overline{a}}^{\text{ aff}})$
. In this case, the pairings
$T_{\overline{\mathbb{Q}}_{\ell }}(J_{\overline{a}}^{\text{ aff}})$
. In this case, the pairings
![]() $\unicode[STIX]{x1D713}_{\overline{a}}$
descend to nondegenerate, alternating, bilinear parings on the
$\unicode[STIX]{x1D713}_{\overline{a}}$
descend to nondegenerate, alternating, bilinear parings on the
 $T_{\overline{\mathbb{Q}}_{\ell }}(J_{\overline{a}}^{\text{ab}})$
.
$T_{\overline{\mathbb{Q}}_{\ell }}(J_{\overline{a}}^{\text{ab}})$
.
Note that by general principles (cf. [Reference Grothendieck, Raynaud and RimSGA7.I, VIII, Corollary 4.10]), the alternating bilinear pairings we consider in this paper are automatically trivial on the ‘affine’ part, and do descend to the ‘abelian’ part. We do verify this fact along the way to proving the key fact that, in the cases we deal with, they in fact descend to nondegenerate pairings.
Affine stabilizers. Let
 $h:M\rightarrow A$
be a morphism of varieties and let
$h:M\rightarrow A$
be a morphism of varieties and let
![]() $J\rightarrow A$
be a group scheme acting on
$J\rightarrow A$
be a group scheme acting on
![]() $M/A$
. We say that the action has affine stabilizers if for every geometric point
$M/A$
. We say that the action has affine stabilizers if for every geometric point
![]() $m$
of
$m$
of
![]() $M$
, we have that the stabilizer subgroup
$M$
, we have that the stabilizer subgroup
 $\text{St}_{\text{m}}\subseteq J_{h(m)}$
is affine.
$\text{St}_{\text{m}}\subseteq J_{h(m)}$
is affine.
![]() $\unicode[STIX]{x1D6FF}$
-regular weak abelian fibrations. See [Reference NgôNgô10, Reference NgôNgô11]. Let
$\unicode[STIX]{x1D6FF}$
-regular weak abelian fibrations. See [Reference NgôNgô10, Reference NgôNgô11]. Let
 $h:M\rightarrow A\leftarrow J:g$
be a pair of morphisms of varieties, where
$h:M\rightarrow A\leftarrow J:g$
be a pair of morphisms of varieties, where
![]() $g$
is as in the beginning of this section (smooth commutative group scheme, with geometrically connected fibers over an irreducible
$g$
is as in the beginning of this section (smooth commutative group scheme, with geometrically connected fibers over an irreducible
![]() $A$
),
$A$
),
![]() $h$
is proper, and
$h$
is proper, and
![]() $J/A$
acts on
$J/A$
acts on
![]() $M/A$
. We denote this situation simply by
$M/A$
. We denote this situation simply by
 $(M,A,J)$
; the context will make it clear which morphisms
$(M,A,J)$
; the context will make it clear which morphisms
![]() $h,g$
are being used.
$h,g$
are being used.
Definition 2.6.3 (Weak abelian fibration).
We say that
 $(M,A,J)$
is a weak abelian fibration if
$(M,A,J)$
is a weak abelian fibration if
![]() $g$
and
$g$
and
![]() $h$
have the same pure relative dimension, the Tate module
$h$
have the same pure relative dimension, the Tate module
![]() $T_{\overline{\mathbb{Q}}_{\ell }}(J)$
is polarizable and the action has affine stabilizers. (
$T_{\overline{\mathbb{Q}}_{\ell }}(J)$
is polarizable and the action has affine stabilizers. (
![]() $\unicode[STIX]{x1D6FF}$
-regular weak abelian fibration) A weak abelian fibration
$\unicode[STIX]{x1D6FF}$
-regular weak abelian fibration) A weak abelian fibration
 $(M,A,J)$
is said to be
$(M,A,J)$
is said to be
![]() $\unicode[STIX]{x1D6FF}$
-regular if
$\unicode[STIX]{x1D6FF}$
-regular if
 $g:J\rightarrow A$
is
$g:J\rightarrow A$
is
![]() $\unicode[STIX]{x1D6FF}$
-regular as in Definition 2.6.1 (equation (19)), or equivalently as in Lemma 2.6.2 (equation (20)).
$\unicode[STIX]{x1D6FF}$
-regular as in Definition 2.6.1 (equation (19)), or equivalently as in Lemma 2.6.2 (equation (20)).
Ngô support inequality. The following is a remarkable, and remarkably useful, topological restriction on the dimensions of the supports appearing in the context of weak abelian fibrations. If
![]() $a\in A$
, then
$a\in A$
, then
 $d_{a}:=\dim \overline{\{a\}}$
is the dimension of the closed subvariety of
$d_{a}:=\dim \overline{\{a\}}$
is the dimension of the closed subvariety of
![]() $A$
with generic point
$A$
with generic point
![]() $a$
. For the notion of socle, see § 1. The celebrated Ngô support theorem [Reference NgôNgô10, Theorem 7.2.1] is a more refined restriction on the geometry of the supports, and it is proved also by using the support inequality.
$a$
. For the notion of socle, see § 1. The celebrated Ngô support theorem [Reference NgôNgô10, Theorem 7.2.1] is a more refined restriction on the geometry of the supports, and it is proved also by using the support inequality.
Theorem 2.6.4 (Nĝo’s support inequality [Reference NgôNgô10, Theorem 7.2.2]).
Let
 $(M,A,J)$
be a weak abelian fibration with
$(M,A,J)$
be a weak abelian fibration with
![]() $M$
and
$M$
and
![]() $A$
nonsingular and with
$A$
nonsingular and with
![]() $h$
projective of pure relative dimension
$h$
projective of pure relative dimension
![]() $d_{h}$
. If
$d_{h}$
. If
 $a\in \text{Socle}(Rh_{\ast }\overline{\mathbb{Q}}_{\ell })$
, then
$a\in \text{Socle}(Rh_{\ast }\overline{\mathbb{Q}}_{\ell })$
, then
 $$\begin{eqnarray}d_{h}-d_{A}+d_{a}\geqslant d_{a}^{\text{ab}}(J).\end{eqnarray}$$
$$\begin{eqnarray}d_{h}-d_{A}+d_{a}\geqslant d_{a}^{\text{ab}}(J).\end{eqnarray}$$
Given that we are assuming
 $d_{h}=d_{g}$
, we may re-formulate (24) as follows via (16):
$d_{h}=d_{g}$
, we may re-formulate (24) as follows via (16):
 $$\begin{eqnarray}d_{a}^{\text{aff}}(J)\geqslant \text{codim}(\overline{\{a\}}).\end{eqnarray}$$
$$\begin{eqnarray}d_{a}^{\text{aff}}(J)\geqslant \text{codim}(\overline{\{a\}}).\end{eqnarray}$$
3 The
 $\text{GL}_{n}$
weak abelian fibration
$\text{GL}_{n}$
weak abelian fibration
This section is devoted to a detailed study of the
![]() $\unicode[STIX]{x1D6FF}$
-regular weak abelian fibration
$\unicode[STIX]{x1D6FF}$
-regular weak abelian fibration
 $(M_{n},A_{n},J_{n})$
, arising from the action of the Jacobi group scheme
$(M_{n},A_{n},J_{n})$
, arising from the action of the Jacobi group scheme
![]() $J_{n}/A_{n}$
, associated with the family of spectral curves of the
$J_{n}/A_{n}$
, associated with the family of spectral curves of the
![]() $\text{GL}_{n}$
Hitchin fibration
$\text{GL}_{n}$
Hitchin fibration
![]() $M_{n}/A_{n}$
. Section 3.1 introduces the Jacobi group scheme
$M_{n}/A_{n}$
. Section 3.1 introduces the Jacobi group scheme
![]() $J_{n}/A_{n}$
and its action on
$J_{n}/A_{n}$
and its action on
![]() $M_{n}/A_{n}$
: its fibers are the Jacobians of the spectral curves. Section 3.2 shows that the stabilizers for this action are affine. I am not aware of an explicit reference in the literature for this result over the whole base
$M_{n}/A_{n}$
: its fibers are the Jacobians of the spectral curves. Section 3.2 shows that the stabilizers for this action are affine. I am not aware of an explicit reference in the literature for this result over the whole base
![]() $A_{n}$
; [Reference NgôNgô10, 4.15.2] deals with a suitable open proper subset of
$A_{n}$
; [Reference NgôNgô10, 4.15.2] deals with a suitable open proper subset of
![]() $A_{n}$
, and for every
$A_{n}$
, and for every
![]() $G$
reductive. Section 3.3 is devoted to the lengthy proof that the Tate module associated with
$G$
reductive. Section 3.3 is devoted to the lengthy proof that the Tate module associated with
![]() $J_{n}/A_{n}$
is polarizable over the whole base
$J_{n}/A_{n}$
is polarizable over the whole base
![]() $A_{n}$
. Again, I am not aware of an explicit reference in the literature for this result over the whole base
$A_{n}$
. Again, I am not aware of an explicit reference in the literature for this result over the whole base
![]() $A_{n}$
; the standard reference for this important-for-us technical fact is [Reference NgôNgô10, § 4.12], which deals with the situation over the elliptic locus
$A_{n}$
; the standard reference for this important-for-us technical fact is [Reference NgôNgô10, § 4.12], which deals with the situation over the elliptic locus
 $A_{n}^{\text{ell}}\subseteq A_{n}$
. Following this preparation, § 3.4 contains the main result of this section, namely Theorem 3.4.1, to the effect that
$A_{n}^{\text{ell}}\subseteq A_{n}$
. Following this preparation, § 3.4 contains the main result of this section, namely Theorem 3.4.1, to the effect that
 $(M_{n},A_{n},J_{n})$
is a weak abelian fibration that is
$(M_{n},A_{n},J_{n})$
is a weak abelian fibration that is
![]() $\unicode[STIX]{x1D6FF}$
-regular over the elliptic locus
$\unicode[STIX]{x1D6FF}$
-regular over the elliptic locus
![]() $A_{n}^{\text{ell}}$
; this affords the support inequality over the whole
$A_{n}^{\text{ell}}$
; this affords the support inequality over the whole
![]() $A_{n}$
, and the
$A_{n}$
, and the
![]() $\unicode[STIX]{x1D6FF}$
-regularity inequality over the elliptic locus
$\unicode[STIX]{x1D6FF}$
-regularity inequality over the elliptic locus
![]() $A_{n}^{\text{ell}}$
. We need some of these explicit details of this
$A_{n}^{\text{ell}}$
. We need some of these explicit details of this
![]() $\text{GL}_{n}$
, especially in connection with nonreduced spectral curves, in view of our main Theorem 1.0.2 on the
$\text{GL}_{n}$
, especially in connection with nonreduced spectral curves, in view of our main Theorem 1.0.2 on the
![]() $\text{SL}_{n}$
socle.
$\text{SL}_{n}$
socle.
3.1 The action of the Jacobi group scheme
 $J_{n}$
$J_{n}$
For what follows, see [Reference Chaudouard and LaumonCL16, § 5]. Let
 $J_{n}\rightarrow A_{n}$
be the identity connected component of the degree zero component of the relative Picard stack
$J_{n}\rightarrow A_{n}$
be the identity connected component of the degree zero component of the relative Picard stack
![]() $\text{Pic}_{{\mathcal{C}}/A_{n}}$
. This is a connected, smooth, commutative group scheme over
$\text{Pic}_{{\mathcal{C}}/A_{n}}$
. This is a connected, smooth, commutative group scheme over
![]() $A_{n}$
, whose fiber
$A_{n}$
, whose fiber
![]() $J_{n,a}$
over a point
$J_{n,a}$
over a point
![]() $a\in A_{n}$
is
$a\in A_{n}$
is
 $\text{Pic}^{0}({\mathcal{C}}_{a})$
; see Fact 2.3.1 for a description of this group. In particular, the structural morphism
$\text{Pic}^{0}({\mathcal{C}}_{a})$
; see Fact 2.3.1 for a description of this group. In particular, the structural morphism
 $g_{n}:J_{n}\rightarrow A_{n}$
is of pure relative dimension, call it
$g_{n}:J_{n}\rightarrow A_{n}$
is of pure relative dimension, call it
![]() $d_{g_{n}}$
, the arithmetic genus of the spectral curves, which coincides with the pure relative dimension
$d_{g_{n}}$
, the arithmetic genus of the spectral curves, which coincides with the pure relative dimension
![]() $d_{h_{n}}$
(7) of
$d_{h_{n}}$
(7) of
 $h_{n}:M_{n}\rightarrow A_{n}$
, i.e. we have
$h_{n}:M_{n}\rightarrow A_{n}$
, i.e. we have
 $$\begin{eqnarray}d_{g_{n}}=d_{h_{n}}.\end{eqnarray}$$
$$\begin{eqnarray}d_{g_{n}}=d_{h_{n}}.\end{eqnarray}$$
The group scheme
![]() $J_{n}/A_{n}$
acts on the Hitchin fibration
$J_{n}/A_{n}$
acts on the Hitchin fibration
![]() $M_{n}/A_{n}$
; see Proposition 2.4.9.
$M_{n}/A_{n}$
; see Proposition 2.4.9.
3.2 Affine stabilizers for the action of the Jacobi group scheme
Proposition 3.2.1. The action of
![]() $J_{n}/A$
on
$J_{n}/A$
on
![]() $M_{n}/A_{n}$
has affine stabilizers.
$M_{n}/A_{n}$
has affine stabilizers.
Proof. Let
![]() $a$
be a geometric point of
$a$
be a geometric point of
![]() $A_{n}$
and let
$A_{n}$
and let
 ${\mathcal{E}}\in M_{n,a}$
. Recall that
${\mathcal{E}}\in M_{n,a}$
. Recall that
 $\text{Rk}_{{\mathcal{C}}_{a}}({\mathcal{E}})=1$
means that, with the notation of § 2.3, if
$\text{Rk}_{{\mathcal{C}}_{a}}({\mathcal{E}})=1$
means that, with the notation of § 2.3, if
 ${\mathcal{C}}_{a}=\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}$
, with
${\mathcal{C}}_{a}=\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}$
, with
![]() $m_{k}\geqslant 1$
for every
$m_{k}\geqslant 1$
for every
![]() $k$
, then the length of
$k$
, then the length of
![]() ${\mathcal{E}}$
at the stalk of the generic point of
${\mathcal{E}}$
at the stalk of the generic point of
![]() $\unicode[STIX]{x1D6E4}_{k}$
is
$\unicode[STIX]{x1D6E4}_{k}$
is
![]() $m_{k}$
, for every
$m_{k}$
, for every
![]() $k$
. Let
$k$
. Let
 $\unicode[STIX]{x1D709}:\widetilde{{\mathcal{C}}_{a,\text{red}}}=\coprod _{k}\widetilde{\unicode[STIX]{x1D6E4}_{k}}\rightarrow {\mathcal{C}}_{a}$
be the morphism from the normalization of
$\unicode[STIX]{x1D709}:\widetilde{{\mathcal{C}}_{a,\text{red}}}=\coprod _{k}\widetilde{\unicode[STIX]{x1D6E4}_{k}}\rightarrow {\mathcal{C}}_{a}$
be the morphism from the normalization of
![]() ${\mathcal{C}}_{a,\text{red}}$
(cf. (2)). Let
${\mathcal{C}}_{a,\text{red}}$
(cf. (2)). Let
 $0\rightarrow \text{Tors}(\unicode[STIX]{x1D709}^{\ast }{\mathcal{E}})\rightarrow \unicode[STIX]{x1D709}^{\ast }{\mathcal{E}}\rightarrow \unicode[STIX]{x1D709}^{\ast }{\mathcal{E}}/\text{Tors}(\unicode[STIX]{x1D709}^{\ast }{\mathcal{E}})=:\mathscr{E}\rightarrow 0$
be the canonical devissage of the torsion of
$0\rightarrow \text{Tors}(\unicode[STIX]{x1D709}^{\ast }{\mathcal{E}})\rightarrow \unicode[STIX]{x1D709}^{\ast }{\mathcal{E}}\rightarrow \unicode[STIX]{x1D709}^{\ast }{\mathcal{E}}/\text{Tors}(\unicode[STIX]{x1D709}^{\ast }{\mathcal{E}})=:\mathscr{E}\rightarrow 0$
be the canonical devissage of the torsion of
![]() $\unicode[STIX]{x1D709}^{\ast }{\mathcal{E}}$
on the nonsingular projective curve
$\unicode[STIX]{x1D709}^{\ast }{\mathcal{E}}$
on the nonsingular projective curve
![]() $\coprod _{k}\widetilde{\unicode[STIX]{x1D6E4}_{k}}$
. Let
$\coprod _{k}\widetilde{\unicode[STIX]{x1D6E4}_{k}}$
. Let
 ${\mathcal{L}}\in \text{Pic}^{0}({\mathcal{C}}_{a})$
. Assume that
${\mathcal{L}}\in \text{Pic}^{0}({\mathcal{C}}_{a})$
. Assume that
![]() ${\mathcal{L}}$
stabilizes
${\mathcal{L}}$
stabilizes
![]() ${\mathcal{E}}$
. Then
${\mathcal{E}}$
. Then
![]() $\unicode[STIX]{x1D709}^{\ast }{\mathcal{L}}$
stabilizes every term in the canonical torsion devissage of
$\unicode[STIX]{x1D709}^{\ast }{\mathcal{L}}$
stabilizes every term in the canonical torsion devissage of
 $\unicode[STIX]{x1D709}^{\ast }({\mathcal{E}})\otimes \unicode[STIX]{x1D709}^{\ast }{\mathcal{L}}$
. In particular,
$\unicode[STIX]{x1D709}^{\ast }({\mathcal{E}})\otimes \unicode[STIX]{x1D709}^{\ast }{\mathcal{L}}$
. In particular,
![]() $\unicode[STIX]{x1D709}^{\ast }{\mathcal{L}}$
stabilizes the vector bundle
$\unicode[STIX]{x1D709}^{\ast }{\mathcal{L}}$
stabilizes the vector bundle
![]() $\mathscr{E}$
, which has rank
$\mathscr{E}$
, which has rank
![]() $m_{k}$
on each
$m_{k}$
on each
![]() $\widetilde{\unicode[STIX]{x1D6E4}_{k}}$
. By considerations of determinants, we see that
$\widetilde{\unicode[STIX]{x1D6E4}_{k}}$
. By considerations of determinants, we see that
 $\unicode[STIX]{x1D709}^{\ast }{\mathcal{L}}\in \prod _{k}\text{Pic}^{0}(\widetilde{\unicode[STIX]{x1D6E4}_{k}})[m_{k}]$
, a finite group. The natural morphism
$\unicode[STIX]{x1D709}^{\ast }{\mathcal{L}}\in \prod _{k}\text{Pic}^{0}(\widetilde{\unicode[STIX]{x1D6E4}_{k}})[m_{k}]$
, a finite group. The natural morphism
 $\unicode[STIX]{x1D709}^{\ast }:\text{Pic}^{0}({\mathcal{C}}_{a,\text{red}})\rightarrow \text{Pic}^{0}(\widetilde{{\mathcal{C}}_{a}})=\prod _{k}\text{Pic}^{0}(\widetilde{\unicode[STIX]{x1D6E4}_{k}})$
is surjective, with affine (connected) kernel (cf. [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 9]). It follows that the stabilizer of
$\unicode[STIX]{x1D709}^{\ast }:\text{Pic}^{0}({\mathcal{C}}_{a,\text{red}})\rightarrow \text{Pic}^{0}(\widetilde{{\mathcal{C}}_{a}})=\prod _{k}\text{Pic}^{0}(\widetilde{\unicode[STIX]{x1D6E4}_{k}})$
is surjective, with affine (connected) kernel (cf. [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 9]). It follows that the stabilizer of
![]() ${\mathcal{E}}$
is an extension of a finite group by an affine subgroup, so that it is affine.◻
${\mathcal{E}}$
is an extension of a finite group by an affine subgroup, so that it is affine.◻
3.3 The Tate module of the Jacobi group scheme is polarizable
We refer to § 2.6 for the terminology. Let
 $g_{n}:J_{n}\rightarrow A_{n}$
be the structural morphism for Picard. The Tate module is the
$g_{n}:J_{n}\rightarrow A_{n}$
be the structural morphism for Picard. The Tate module is the
![]() $\overline{\mathbb{Q}}_{\ell }$
-adic sheaf (22)
$\overline{\mathbb{Q}}_{\ell }$
-adic sheaf (22)
 $T_{\overline{\mathbb{Q}}_{\ell }}(J_{n}):=R^{2d_{h_{n}}-1}{g_{n}}_{!}\overline{\mathbb{Q}}_{\ell }(d_{h_{n}})$
. If
$T_{\overline{\mathbb{Q}}_{\ell }}(J_{n}):=R^{2d_{h_{n}}-1}{g_{n}}_{!}\overline{\mathbb{Q}}_{\ell }(d_{h_{n}})$
. If
![]() $a$
is a geometric point of
$a$
is a geometric point of
![]() $A_{n}$
, then the Chevalley devissage yields the natural short exact sequences
$A_{n}$
, then the Chevalley devissage yields the natural short exact sequences
 $$\begin{eqnarray}0\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{aff}})\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a})\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{aff}})\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a})\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})\rightarrow 0.\end{eqnarray}$$
Note that: (i)
 $\dim _{\overline{\mathbb{Q}}_{\ell }}T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})=2\dim J_{n,a}^{\text{ab}}$
; (ii)
$\dim _{\overline{\mathbb{Q}}_{\ell }}T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})=2\dim J_{n,a}^{\text{ab}}$
; (ii)
 $\dim _{\overline{\mathbb{Q}}_{\ell }}T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{aff}})\leqslant \dim J_{n,a}^{\text{aff}}$
, and that the strict inequality can occur: this is due to the fact that the affine part
$\dim _{\overline{\mathbb{Q}}_{\ell }}T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{aff}})\leqslant \dim J_{n,a}^{\text{aff}}$
, and that the strict inequality can occur: this is due to the fact that the affine part
![]() $J_{n,a}^{\text{aff}}$
is an iterated extension of the additive and of the multiplicative group
$J_{n,a}^{\text{aff}}$
is an iterated extension of the additive and of the multiplicative group
![]() $\mathbb{G}_{a}$
and
$\mathbb{G}_{a}$
and
![]() $\mathbb{G}_{m}$
[Reference Bosch, Lütkebohmert and RaynaudBLR90, § 9], and only the latter contribute to the Tate module.
$\mathbb{G}_{m}$
[Reference Bosch, Lütkebohmert and RaynaudBLR90, § 9], and only the latter contribute to the Tate module.
The goal of this section is to prove the following polarizability result, which has been proved over the elliptic locus
![]() $A_{n}^{\text{ell}}$
in [Reference NgôNgô10], and is stated implicitly over the whole base
$A_{n}^{\text{ell}}$
in [Reference NgôNgô10], and is stated implicitly over the whole base
![]() $A_{n}$
and then used in [Reference Chaudouard and LaumonCL16, § 9].
$A_{n}$
and then used in [Reference Chaudouard and LaumonCL16, § 9].
Theorem 3.3.1. The Tate module
 $T_{\overline{\mathbb{Q}}_{\ell }}(J_{n})$
on
$T_{\overline{\mathbb{Q}}_{\ell }}(J_{n})$
on
![]() $A_{n}$
is polarizable.
$A_{n}$
is polarizable.
Proof. Let
 $p:{\mathcal{C}}\rightarrow A_{n}$
be the family of spectral curves: it is proper, flat, with geometrically connected fibers, with nonsingular total space, and with nonsingular general fiber. As in [Reference NgôNgô10, § 4.12], the pairing is defined by constructing it over the strict henselianization of the local ring of any Zariski point
$p:{\mathcal{C}}\rightarrow A_{n}$
be the family of spectral curves: it is proper, flat, with geometrically connected fibers, with nonsingular total space, and with nonsingular general fiber. As in [Reference NgôNgô10, § 4.12], the pairing is defined by constructing it over the strict henselianization of the local ring of any Zariski point
![]() $a\in A_{n}$
, for the construction yields a canonical outcome. We denote these new shrunken families by
$a\in A_{n}$
, for the construction yields a canonical outcome. We denote these new shrunken families by
 $p:{\mathcal{C}}\rightarrow A$
,
$p:{\mathcal{C}}\rightarrow A$
,
 $g:J\rightarrow A$
. For a coherent sheaf
$g:J\rightarrow A$
. For a coherent sheaf
![]() $F$
on
$F$
on
![]() ${\mathcal{C}}$
, set
${\mathcal{C}}$
, set
 $\unicode[STIX]{x1D6E5}(F):=\det (Rp_{\ast }F)$
, where we are taking the determinant of cohomology [Reference DeligneDel87, Reference SouléSou92, especially, § 1.4] and the result is a graded line bundle on
$\unicode[STIX]{x1D6E5}(F):=\det (Rp_{\ast }F)$
, where we are taking the determinant of cohomology [Reference DeligneDel87, Reference SouléSou92, especially, § 1.4] and the result is a graded line bundle on
![]() $A$
. If
$A$
. If
![]() $F$
is
$F$
is
![]() ${\mathcal{O}}_{A}$
-flat, then the degree of this graded line bundle is the Euler characteristic of
${\mathcal{O}}_{A}$
-flat, then the degree of this graded line bundle is the Euler characteristic of
![]() $F$
along the fibers
$F$
along the fibers
![]() ${\mathcal{C}}_{a}$
. The Weil pairing construction associates with
${\mathcal{C}}_{a}$
. The Weil pairing construction associates with
 $L,M\in \text{Pic}^{0}({\mathcal{C}}/A)$
the graded line bundle on
$L,M\in \text{Pic}^{0}({\mathcal{C}}/A)$
the graded line bundle on
![]() $A$
given by the formula
$A$
given by the formula
 $$\begin{eqnarray}\langle L,M\rangle _{{\mathcal{C}}/A}:=P(L,M):=\unicode[STIX]{x1D6E5}(L\otimes M)\otimes \unicode[STIX]{x1D6E5}({\mathcal{O}}_{A})\otimes \unicode[STIX]{x1D6E5}(L)^{\vee }\otimes \unicode[STIX]{x1D6E5}(M)^{\vee }.\end{eqnarray}$$
$$\begin{eqnarray}\langle L,M\rangle _{{\mathcal{C}}/A}:=P(L,M):=\unicode[STIX]{x1D6E5}(L\otimes M)\otimes \unicode[STIX]{x1D6E5}({\mathcal{O}}_{A})\otimes \unicode[STIX]{x1D6E5}(L)^{\vee }\otimes \unicode[STIX]{x1D6E5}(M)^{\vee }.\end{eqnarray}$$
Note that both of the terms defined by (28) make sense for any pair of coherent sheaves on
![]() ${\mathcal{C}}$
. However, we shall use
${\mathcal{C}}$
. However, we shall use
![]() $\langle -,-\rangle$
when dealing with line bundles, whereas we shall use
$\langle -,-\rangle$
when dealing with line bundles, whereas we shall use
 $P(-,-)$
also for other coherent sheaves, and hence the two distinct pieces of notation.
$P(-,-)$
also for other coherent sheaves, and hence the two distinct pieces of notation.
Let
 $L,M\in \text{Pic}^{0}({\mathcal{C}}/A)[\ell ^{i}]$
be
$L,M\in \text{Pic}^{0}({\mathcal{C}}/A)[\ell ^{i}]$
be
![]() $\ell ^{i}$
-torsion line bundles. The formalism of the determinant of cohomology yields two distinguished isomorphisms
$\ell ^{i}$
-torsion line bundles. The formalism of the determinant of cohomology yields two distinguished isomorphisms
 $i_{L},i_{M}:\langle L,M\rangle _{{\mathcal{C}}/A}^{\otimes \ell ^{i}}\longrightarrow {\mathcal{O}}_{S}$
whose difference
$i_{L},i_{M}:\langle L,M\rangle _{{\mathcal{C}}/A}^{\otimes \ell ^{i}}\longrightarrow {\mathcal{O}}_{S}$
whose difference
![]() $\unicode[STIX]{x1D716}_{L,M}$
is an
$\unicode[STIX]{x1D716}_{L,M}$
is an
![]() $\ell ^{i}$
th root of unity in the ground field and which depends only on the isomorphism classes of
$\ell ^{i}$
th root of unity in the ground field and which depends only on the isomorphism classes of
![]() $L$
and of
$L$
and of
![]() $M$
. By taking inverse limits with respect to
$M$
. By taking inverse limits with respect to
![]() $i$
, and then by tensoring with
$i$
, and then by tensoring with
![]() $\overline{\mathbb{Q}}_{\ell }$
, we obtain a pairing, let us call it the Tate–Weil pairing
$\overline{\mathbb{Q}}_{\ell }$
, we obtain a pairing, let us call it the Tate–Weil pairing
 $$\begin{eqnarray}\mathit{TW}:T_{\overline{\mathbb{Q}}_{\ell }}(J)\otimes _{\overline{\mathbb{Q}}_{\ell }}T_{\overline{\mathbb{Q}}_{\ell }}(J)\longrightarrow T_{\overline{\mathbb{Q}}_{\ell }}(\mathbb{G}_{m})=\overline{\mathbb{Q}}_{\ell }(1),\quad \{L_{i},M_{i}\}_{i\in \mathbb{N}}\mapsto \{\unicode[STIX]{x1D716}_{L_{i},M_{i}}\}_{i\in \mathbb{N}}\in \mathbb{Z}_{\ell }(1).\end{eqnarray}$$
$$\begin{eqnarray}\mathit{TW}:T_{\overline{\mathbb{Q}}_{\ell }}(J)\otimes _{\overline{\mathbb{Q}}_{\ell }}T_{\overline{\mathbb{Q}}_{\ell }}(J)\longrightarrow T_{\overline{\mathbb{Q}}_{\ell }}(\mathbb{G}_{m})=\overline{\mathbb{Q}}_{\ell }(1),\quad \{L_{i},M_{i}\}_{i\in \mathbb{N}}\mapsto \{\unicode[STIX]{x1D716}_{L_{i},M_{i}}\}_{i\in \mathbb{N}}\in \mathbb{Z}_{\ell }(1).\end{eqnarray}$$
The Weil and the Tate–Weil pairing are compatible with base change.
Let
![]() $a$
be a geometric point of
$a$
be a geometric point of
![]() $A$
. Consider the diagram (2) of maps of curves, and extract the following morphisms:
$A$
. Consider the diagram (2) of maps of curves, and extract the following morphisms:

 $$\begin{eqnarray}\unicode[STIX]{x1D709}:\widetilde{{\mathcal{C}}_{a,\text{red}}}\stackrel{\unicode[STIX]{x1D708}}{\longrightarrow }{\mathcal{C}}_{a,\text{red}}\stackrel{\unicode[STIX]{x1D70C}}{\longrightarrow }{\mathcal{C}}_{a},\quad \unicode[STIX]{x1D709}=\coprod _{k}\unicode[STIX]{x1D709}_{k}:\coprod _{k}\widetilde{\unicode[STIX]{x1D6E4}_{k}}\stackrel{\unicode[STIX]{x1D708}=\coprod _{k}\unicode[STIX]{x1D708}_{k}}{\longrightarrow }\mathop{\sum }_{k}\unicode[STIX]{x1D6E4}_{k}\stackrel{\unicode[STIX]{x1D70C}}{\longrightarrow }\mathop{\sum }_{k}m_{k}\unicode[STIX]{x1D6E4}_{k}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D709}:\widetilde{{\mathcal{C}}_{a,\text{red}}}\stackrel{\unicode[STIX]{x1D708}}{\longrightarrow }{\mathcal{C}}_{a,\text{red}}\stackrel{\unicode[STIX]{x1D70C}}{\longrightarrow }{\mathcal{C}}_{a},\quad \unicode[STIX]{x1D709}=\coprod _{k}\unicode[STIX]{x1D709}_{k}:\coprod _{k}\widetilde{\unicode[STIX]{x1D6E4}_{k}}\stackrel{\unicode[STIX]{x1D708}=\coprod _{k}\unicode[STIX]{x1D708}_{k}}{\longrightarrow }\mathop{\sum }_{k}\unicode[STIX]{x1D6E4}_{k}\stackrel{\unicode[STIX]{x1D70C}}{\longrightarrow }\mathop{\sum }_{k}m_{k}\unicode[STIX]{x1D6E4}_{k}.\end{eqnarray}$$
Claim. Let
 $L,M\in J_{a}=\text{Pic}(\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k})$
. Then
$L,M\in J_{a}=\text{Pic}(\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k})$
. Then
 $$\begin{eqnarray}\langle L,M\rangle _{\mathop{\sum }_{k}m_{k}\unicode[STIX]{x1D6E4}_{k}}=\bigotimes _{k}\langle \unicode[STIX]{x1D709}_{4,k}^{\ast }L,\unicode[STIX]{x1D709}_{4,k}^{\ast }M\rangle _{\unicode[STIX]{x1D6E4}_{k}}^{\otimes m_{k}}=\bigotimes _{k}\langle \unicode[STIX]{x1D709}_{k}^{\ast }L,\unicode[STIX]{x1D709}_{k}^{\ast }M\rangle _{\widetilde{\unicode[STIX]{x1D6E4}_{k}}}^{\otimes m_{k}}.\end{eqnarray}$$
$$\begin{eqnarray}\langle L,M\rangle _{\mathop{\sum }_{k}m_{k}\unicode[STIX]{x1D6E4}_{k}}=\bigotimes _{k}\langle \unicode[STIX]{x1D709}_{4,k}^{\ast }L,\unicode[STIX]{x1D709}_{4,k}^{\ast }M\rangle _{\unicode[STIX]{x1D6E4}_{k}}^{\otimes m_{k}}=\bigotimes _{k}\langle \unicode[STIX]{x1D709}_{k}^{\ast }L,\unicode[STIX]{x1D709}_{k}^{\ast }M\rangle _{\widetilde{\unicode[STIX]{x1D6E4}_{k}}}^{\otimes m_{k}}.\end{eqnarray}$$
In order to prove this claim, we first list the three short exact sequences below.
The ideal sheaf of
![]() ${\mathcal{C}}_{a}$
in
${\mathcal{C}}_{a}$
in
 ${\mathcal{O}}_{V(D)\otimes k(a)}$
is locally generated by the product
${\mathcal{O}}_{V(D)\otimes k(a)}$
is locally generated by the product
 $\prod _{k=1}^{s}\mathfrak{s}_{k}^{m_{k}}$
(cf. § 2.3) of powers of sections of the line bundle
$\prod _{k=1}^{s}\mathfrak{s}_{k}^{m_{k}}$
(cf. § 2.3) of powers of sections of the line bundle
![]() $\unicode[STIX]{x1D70B}^{\ast }D$
on the surface
$\unicode[STIX]{x1D70B}^{\ast }D$
on the surface
 $V(D)\otimes k(a)$
. Fix any index
$V(D)\otimes k(a)$
. Fix any index
 $1\leqslant k_{o}\leqslant s$
; fix any sequence
$1\leqslant k_{o}\leqslant s$
; fix any sequence
 $\{\unicode[STIX]{x1D707}_{k}\}_{k=1}^{s}$
, with
$\{\unicode[STIX]{x1D707}_{k}\}_{k=1}^{s}$
, with
 $0\leqslant \unicode[STIX]{x1D707}_{k}\leqslant m_{k}$
for every
$0\leqslant \unicode[STIX]{x1D707}_{k}\leqslant m_{k}$
for every
![]() $k$
, with
$k$
, with
![]() $1\leqslant \unicode[STIX]{x1D707}_{k_{o}}$
, and with
$1\leqslant \unicode[STIX]{x1D707}_{k_{o}}$
, and with
 $\sum _{k}\unicode[STIX]{x1D707}_{k}\geqslant 2$
(these conditions are simply to ensure that (33) below is meaningful as written). We have the following system of short exact sequences on the curve
$\sum _{k}\unicode[STIX]{x1D707}_{k}\geqslant 2$
(these conditions are simply to ensure that (33) below is meaningful as written). We have the following system of short exact sequences on the curve
 $\sum _{k}\unicode[STIX]{x1D707}_{k}\unicode[STIX]{x1D6E4}_{k}$
(see [Reference ReidRei97, Lemma 3.10], for example)
$\sum _{k}\unicode[STIX]{x1D707}_{k}\unicode[STIX]{x1D6E4}_{k}$
(see [Reference ReidRei97, Lemma 3.10], for example)
 $$\begin{eqnarray}0\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D6E4}_{k_{o}}}(-\unicode[STIX]{x1D6E4}_{k_{o}})\longrightarrow {\mathcal{O}}_{\mathop{\sum }_{k}\unicode[STIX]{x1D707}_{k}\unicode[STIX]{x1D6E4}_{k}}\longrightarrow {\mathcal{O}}_{(\unicode[STIX]{x1D707}_{k_{o}}-1)\unicode[STIX]{x1D6E4}_{k_{o}}+\mathop{\sum }_{k\neq k_{o}}\unicode[STIX]{x1D707}_{k}\unicode[STIX]{x1D6E4}_{k}}\longrightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D6E4}_{k_{o}}}(-\unicode[STIX]{x1D6E4}_{k_{o}})\longrightarrow {\mathcal{O}}_{\mathop{\sum }_{k}\unicode[STIX]{x1D707}_{k}\unicode[STIX]{x1D6E4}_{k}}\longrightarrow {\mathcal{O}}_{(\unicode[STIX]{x1D707}_{k_{o}}-1)\unicode[STIX]{x1D6E4}_{k_{o}}+\mathop{\sum }_{k\neq k_{o}}\unicode[STIX]{x1D707}_{k}\unicode[STIX]{x1D6E4}_{k}}\longrightarrow 0.\end{eqnarray}$$
We have the short exact sequences (4) on the curves
![]() $\unicode[STIX]{x1D6E4}_{k}$
$\unicode[STIX]{x1D6E4}_{k}$
 $$\begin{eqnarray}0\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D6E4}_{k}}(-\unicode[STIX]{x1D6E4}_{k})\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D6E4}_{k}}\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D701}_{k}}\longrightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D6E4}_{k}}(-\unicode[STIX]{x1D6E4}_{k})\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D6E4}_{k}}\longrightarrow {\mathcal{O}}_{\unicode[STIX]{x1D701}_{k}}\longrightarrow 0.\end{eqnarray}$$
We have a natural short exact sequence on
![]() $\coprod _{k}\unicode[STIX]{x1D6E4}_{k}$
arising from the normalization map
$\coprod _{k}\unicode[STIX]{x1D6E4}_{k}$
arising from the normalization map
![]() $\unicode[STIX]{x1D709}_{3}$
$\unicode[STIX]{x1D709}_{3}$
 $$\begin{eqnarray}0\longrightarrow {\mathcal{O}}_{\coprod _{k}\unicode[STIX]{x1D6E4}_{k}}\longrightarrow {\mathcal{O}}_{\coprod _{k}\widetilde{\unicode[STIX]{x1D6E4}_{k}}}\longrightarrow \unicode[STIX]{x1D6F4}\longrightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow {\mathcal{O}}_{\coprod _{k}\unicode[STIX]{x1D6E4}_{k}}\longrightarrow {\mathcal{O}}_{\coprod _{k}\widetilde{\unicode[STIX]{x1D6E4}_{k}}}\longrightarrow \unicode[STIX]{x1D6F4}\longrightarrow 0,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6F4}$
is supported at finitely many points on
$\unicode[STIX]{x1D6F4}$
is supported at finitely many points on
![]() $\sum _{k}\unicode[STIX]{x1D6E4}_{k}$
.
$\sum _{k}\unicode[STIX]{x1D6E4}_{k}$
.
Since
![]() $\unicode[STIX]{x1D6F4}$
is supported at finitely many points, it follows from the definition that, for every pair of line bundles
$\unicode[STIX]{x1D6F4}$
is supported at finitely many points, it follows from the definition that, for every pair of line bundles
![]() $L,M$
on the curve
$L,M$
on the curve
![]() $\sum _{k}\unicode[STIX]{x1D6E4}_{k}$
, we have that
$\sum _{k}\unicode[STIX]{x1D6E4}_{k}$
, we have that
 $P(\unicode[STIX]{x1D6F4}\otimes L,\unicode[STIX]{x1D6F4}\otimes M)$
is canonically isomorphic to the trivially trivialized, trivial line bundle on the spectrum of the residue field of
$P(\unicode[STIX]{x1D6F4}\otimes L,\unicode[STIX]{x1D6F4}\otimes M)$
is canonically isomorphic to the trivially trivialized, trivial line bundle on the spectrum of the residue field of
![]() $a$
; see [Reference NgôNgô10, proof of Lemma 4.12.2]. We call this circumstance the
$a$
; see [Reference NgôNgô10, proof of Lemma 4.12.2]. We call this circumstance the
![]() $P$
-triviality property of
$P$
-triviality property of
![]() $\unicode[STIX]{x1D6F4}$
. The same holds true for
$\unicode[STIX]{x1D6F4}$
. The same holds true for
 $P({\mathcal{O}}_{\unicode[STIX]{x1D701}_{k}}\otimes L,{\mathcal{O}}_{\unicode[STIX]{x1D701}_{k}}\otimes M)$
, i.e. we have the
$P({\mathcal{O}}_{\unicode[STIX]{x1D701}_{k}}\otimes L,{\mathcal{O}}_{\unicode[STIX]{x1D701}_{k}}\otimes M)$
, i.e. we have the
![]() $P$
-triviality property of
$P$
-triviality property of
![]() $\unicode[STIX]{x1D701}_{k}$
.
$\unicode[STIX]{x1D701}_{k}$
.
By what we have said above, and by using the multiplicativity property of the determinant of cohomology with respect to short exact sequences, and hence of the operation
 $P(-,-)$
, we see that the second equality of the claim (32) follows from the short exact sequence (35) on
$P(-,-)$
, we see that the second equality of the claim (32) follows from the short exact sequence (35) on
![]() $\coprod _{k}\unicode[STIX]{x1D6E4}_{k}$
, by using the
$\coprod _{k}\unicode[STIX]{x1D6E4}_{k}$
, by using the
![]() $P$
-triviality property of
$P$
-triviality property of
![]() $\unicode[STIX]{x1D6F4}$
, and the fact that
$\unicode[STIX]{x1D6F4}$
, and the fact that
 $\unicode[STIX]{x1D709}_{k}^{\ast }=\unicode[STIX]{x1D709}_{3,k}^{\ast }\circ \unicode[STIX]{x1D709}_{4,k}^{\ast }$
; in fact, we get, the identity
$\unicode[STIX]{x1D709}_{k}^{\ast }=\unicode[STIX]{x1D709}_{3,k}^{\ast }\circ \unicode[STIX]{x1D709}_{4,k}^{\ast }$
; in fact, we get, the identity
 $$\begin{eqnarray}P(\unicode[STIX]{x1D709}_{3,k}^{\ast }\unicode[STIX]{x1D709}_{4,k}^{\ast },\unicode[STIX]{x1D709}_{3,k}^{\ast }\unicode[STIX]{x1D709}_{4.k}^{\ast }M)=P(\unicode[STIX]{x1D709}_{4,k}^{\ast }L,\unicode[STIX]{x1D709}_{4,k}^{\ast }M)\otimes P(\unicode[STIX]{x1D6F4}\otimes \unicode[STIX]{x1D709}_{4,k}^{\ast }L,\unicode[STIX]{x1D6F4}\otimes \unicode[STIX]{x1D709}_{4,k}^{\ast }M)=P(\unicode[STIX]{x1D709}_{4,k}^{\ast }L,\unicode[STIX]{x1D709}_{4,k}^{\ast }M).\end{eqnarray}$$
$$\begin{eqnarray}P(\unicode[STIX]{x1D709}_{3,k}^{\ast }\unicode[STIX]{x1D709}_{4,k}^{\ast },\unicode[STIX]{x1D709}_{3,k}^{\ast }\unicode[STIX]{x1D709}_{4.k}^{\ast }M)=P(\unicode[STIX]{x1D709}_{4,k}^{\ast }L,\unicode[STIX]{x1D709}_{4,k}^{\ast }M)\otimes P(\unicode[STIX]{x1D6F4}\otimes \unicode[STIX]{x1D709}_{4,k}^{\ast }L,\unicode[STIX]{x1D6F4}\otimes \unicode[STIX]{x1D709}_{4,k}^{\ast }M)=P(\unicode[STIX]{x1D709}_{4,k}^{\ast }L,\unicode[STIX]{x1D709}_{4,k}^{\ast }M).\end{eqnarray}$$
(N.B. there is no need for the exponents
![]() $m_{k}$
, for this second equality in (32).)
$m_{k}$
, for this second equality in (32).)
The first equality of the claim (32), and here the exponents
![]() $m_{k}$
are essential, follows in the same way (by using the
$m_{k}$
are essential, follows in the same way (by using the
![]() $P$
-triviality property for
$P$
-triviality property for
![]() $\unicode[STIX]{x1D701}_{k}$
) from (33) and (34) by means of a simple descending induction on the multiplicities
$\unicode[STIX]{x1D701}_{k}$
) from (33) and (34) by means of a simple descending induction on the multiplicities
 $\unicode[STIX]{x1D707}_{k}\leqslant m_{k}$
, based on the following equalities (where we denote line bundles and their restrictions in the same way, and we instead add a subfix to
$\unicode[STIX]{x1D707}_{k}\leqslant m_{k}$
, based on the following equalities (where we denote line bundles and their restrictions in the same way, and we instead add a subfix to
 $P(-,-)$
)
$P(-,-)$
)
 $$\begin{eqnarray}\displaystyle & \displaystyle P_{\mathop{\sum }_{k}\unicode[STIX]{x1D707}_{k}\unicode[STIX]{x1D6E4}_{k}}(L,M)=P_{(\unicode[STIX]{x1D707}_{k_{o}}-1)\unicode[STIX]{x1D6E4}_{k_{o}}+\sum k\neq k_{o}\unicode[STIX]{x1D707}_{k}\unicode[STIX]{x1D6E4}_{k}}(L,M)\otimes P_{\unicode[STIX]{x1D6E4}_{k_{o}}}(L-\unicode[STIX]{x1D6E4}_{k_{o}},M-\unicode[STIX]{x1D6E4}_{k_{o}}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle P_{\unicode[STIX]{x1D6E4}_{k_{o}}}(L-\unicode[STIX]{x1D6E4}_{k_{o}},M-\unicode[STIX]{x1D6E4}_{k_{o}})=P_{\unicode[STIX]{x1D6E4}_{k_{o}}}(L,M)\otimes P_{\unicode[STIX]{x1D701}_{k_{o}}}(L,M)=P_{\unicode[STIX]{x1D6E4}_{k_{o}}}(L,M). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle P_{\mathop{\sum }_{k}\unicode[STIX]{x1D707}_{k}\unicode[STIX]{x1D6E4}_{k}}(L,M)=P_{(\unicode[STIX]{x1D707}_{k_{o}}-1)\unicode[STIX]{x1D6E4}_{k_{o}}+\sum k\neq k_{o}\unicode[STIX]{x1D707}_{k}\unicode[STIX]{x1D6E4}_{k}}(L,M)\otimes P_{\unicode[STIX]{x1D6E4}_{k_{o}}}(L-\unicode[STIX]{x1D6E4}_{k_{o}},M-\unicode[STIX]{x1D6E4}_{k_{o}}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle P_{\unicode[STIX]{x1D6E4}_{k_{o}}}(L-\unicode[STIX]{x1D6E4}_{k_{o}},M-\unicode[STIX]{x1D6E4}_{k_{o}})=P_{\unicode[STIX]{x1D6E4}_{k_{o}}}(L,M)\otimes P_{\unicode[STIX]{x1D701}_{k_{o}}}(L,M)=P_{\unicode[STIX]{x1D6E4}_{k_{o}}}(L,M). & \displaystyle \nonumber\end{eqnarray}$$
We now use the just-proved claim (32) to verify that the Tate–Weil pairing
![]() $\mathit{TW}$
(29) has, at every geometric point
$\mathit{TW}$
(29) has, at every geometric point
![]() $a$
of
$a$
of
![]() $A_{n}$
, kernel given precisely by the ‘affine part’
$A_{n}$
, kernel given precisely by the ‘affine part’
 $T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{aff}})$
, so that it descends to a nondegenerate pairing on
$T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{aff}})$
, so that it descends to a nondegenerate pairing on
 $T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})$
.
$T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})$
.
By [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 9.3, Corollary 11], we have the canonical short exact sequence
 $$\begin{eqnarray}0\longrightarrow \text{Ker}\,\unicode[STIX]{x1D709}^{\ast }\longrightarrow J_{n,a}=\text{Pic}^{0}\biggl({\mathcal{C}}_{a}=\mathop{\sum }_{k}m_{k}\unicode[STIX]{x1D6E4}_{k}\biggr)\longrightarrow \text{Pic}^{0}(\widetilde{{\mathcal{C}}_{a,\text{red}}})=\mathop{\prod }_{k}\text{Pic}^{0}(\widetilde{\unicode[STIX]{x1D6E4}_{k}})\longrightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow \text{Ker}\,\unicode[STIX]{x1D709}^{\ast }\longrightarrow J_{n,a}=\text{Pic}^{0}\biggl({\mathcal{C}}_{a}=\mathop{\sum }_{k}m_{k}\unicode[STIX]{x1D6E4}_{k}\biggr)\longrightarrow \text{Pic}^{0}(\widetilde{{\mathcal{C}}_{a,\text{red}}})=\mathop{\prod }_{k}\text{Pic}^{0}(\widetilde{\unicode[STIX]{x1D6E4}_{k}})\longrightarrow 0,\end{eqnarray}$$
with quotient an abelian variety and with affine and connected
![]() $\text{Ker}\,\unicode[STIX]{x1D709}^{\ast }$
, an iterated extension of groups of type
$\text{Ker}\,\unicode[STIX]{x1D709}^{\ast }$
, an iterated extension of groups of type
![]() $\mathbb{G}_{a}$
and
$\mathbb{G}_{a}$
and
![]() $\mathbb{G}_{m}$
. It follows that the above short exact sequence is the ‘abelian-by-affine’ Chevalley devissage (§ 2.6) of
$\mathbb{G}_{m}$
. It follows that the above short exact sequence is the ‘abelian-by-affine’ Chevalley devissage (§ 2.6) of
![]() $J_{n,a}$
. By passing to Tate modules, we get the short exact sequence
$J_{n,a}$
. By passing to Tate modules, we get the short exact sequence
 $$\begin{eqnarray}0\longrightarrow T_{\overline{\mathbb{Q}}_{\ell }}(\text{Ker}\,\unicode[STIX]{x1D709}^{\ast })=T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{aff}})\longrightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a})\longrightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})=\bigoplus _{k}T_{\overline{\mathbb{Q}}_{\ell }}(\text{Pic}^{0}(\widetilde{\unicode[STIX]{x1D6E4}_{k}}))\longrightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow T_{\overline{\mathbb{Q}}_{\ell }}(\text{Ker}\,\unicode[STIX]{x1D709}^{\ast })=T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{aff}})\longrightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a})\longrightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})=\bigoplus _{k}T_{\overline{\mathbb{Q}}_{\ell }}(\text{Pic}^{0}(\widetilde{\unicode[STIX]{x1D6E4}_{k}}))\longrightarrow 0.\end{eqnarray}$$
In view of (32), and of the definition of the Tate–Weil pairing via the Weil pairing, we see that the kernel of the Tate–Weil pairing contains
 $T_{\overline{\mathbb{Q}}_{\ell }}(\text{Ker}\,\unicode[STIX]{x1D709}^{\ast })$
, so that the Tate–Weil pairing
$T_{\overline{\mathbb{Q}}_{\ell }}(\text{Ker}\,\unicode[STIX]{x1D709}^{\ast })$
, so that the Tate–Weil pairing
 $\mathit{TW}:=\mathit{TW}_{\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}}$
descends to a paring
$\mathit{TW}:=\mathit{TW}_{\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}}$
descends to a paring
![]() $\mathit{TW}^{\text{ab}}$
on the abelian part
$\mathit{TW}^{\text{ab}}$
on the abelian part
 $T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})$
where, again in view of (32), it is the direct sum of the Tate–Weil pairing
$T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})$
where, again in view of (32), it is the direct sum of the Tate–Weil pairing
![]() $\mathit{TW}_{\widetilde{\unicode[STIX]{x1D6E4}_{k}}}$
on the individual nonsingular projective curves
$\mathit{TW}_{\widetilde{\unicode[STIX]{x1D6E4}_{k}}}$
on the individual nonsingular projective curves
![]() $\widetilde{\unicode[STIX]{x1D6E4}_{k}}$
, multiplied by the integer
$\widetilde{\unicode[STIX]{x1D6E4}_{k}}$
, multiplied by the integer
![]() $m_{k}$
$m_{k}$
 $$\begin{eqnarray}\mathit{TW}^{\text{ab}}=\mathop{\sum }_{k}m_{k}\mathit{TW}_{\widetilde{\unicode[STIX]{x1D6E4}_{k}}}.\end{eqnarray}$$
$$\begin{eqnarray}\mathit{TW}^{\text{ab}}=\mathop{\sum }_{k}m_{k}\mathit{TW}_{\widetilde{\unicode[STIX]{x1D6E4}_{k}}}.\end{eqnarray}$$
Each
![]() $\mathit{TW}_{\widetilde{\unicode[STIX]{x1D6E4}_{k}}}$
is nondegenerate: in fact, it is the Tate–Weil pairing on the Tate module of the Jacobian of a nonsingular projective curve over an algebraically closed field, which, in turn, can be identified with the cup product on the first étale
$\mathit{TW}_{\widetilde{\unicode[STIX]{x1D6E4}_{k}}}$
is nondegenerate: in fact, it is the Tate–Weil pairing on the Tate module of the Jacobian of a nonsingular projective curve over an algebraically closed field, which, in turn, can be identified with the cup product on the first étale
![]() $\overline{\mathbb{Q}}_{\ell }$
-adic cohomology group of the curve; see [Reference MilneMil80, ch. V, Remark 2.4(f), and references therein]. It follows that their
$\overline{\mathbb{Q}}_{\ell }$
-adic cohomology group of the curve; see [Reference MilneMil80, ch. V, Remark 2.4(f), and references therein]. It follows that their
![]() $m_{k}$
-weighted direct sum
$m_{k}$
-weighted direct sum
![]() $\mathit{TW}^{\text{ab}}$
is nondegenerate as well.◻
$\mathit{TW}^{\text{ab}}$
is nondegenerate as well.◻
Remark 3.3.2. [Reference Bosch, Lütkebohmert and RaynaudBLR90, § 9.2, Theorem 11] gives a precise structure theorem for the Jacobians of curves which immediately yields the following description of their abelian variety parts. Let
![]() $a$
be a geometric point of
$a$
be a geometric point of
![]() $A_{n}$
and let
$A_{n}$
and let
 ${\mathcal{C}}_{a}=\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}$
be corresponding spectral curve. Then we have natural isomorphisms of abelian varieties
${\mathcal{C}}_{a}=\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}$
be corresponding spectral curve. Then we have natural isomorphisms of abelian varieties
 $$\begin{eqnarray}\text{Pic}^{0}({\mathcal{C}}_{a})^{\text{ab}}=\text{Pic}^{0}({\mathcal{C}}_{a,\text{red}})^{\text{ab}}=\mathop{\prod }_{k}\text{Pic}^{0}(\unicode[STIX]{x1D6E4}_{k})^{\text{ab}}=\mathop{\prod }_{k}\text{Pic}^{0}(\widetilde{\unicode[STIX]{x1D6E4}_{k}}).\end{eqnarray}$$
$$\begin{eqnarray}\text{Pic}^{0}({\mathcal{C}}_{a})^{\text{ab}}=\text{Pic}^{0}({\mathcal{C}}_{a,\text{red}})^{\text{ab}}=\mathop{\prod }_{k}\text{Pic}^{0}(\unicode[STIX]{x1D6E4}_{k})^{\text{ab}}=\mathop{\prod }_{k}\text{Pic}^{0}(\widetilde{\unicode[STIX]{x1D6E4}_{k}}).\end{eqnarray}$$
3.4
 $\unicode[STIX]{x1D6FF}$
-regularity of the action of the Jacobi group scheme over the elliptic locus
$\unicode[STIX]{x1D6FF}$
-regularity of the action of the Jacobi group scheme over the elliptic locus
Theorem 3.4.1. The triple
 $(M_{n},A_{n},J_{n})$
is a weak abelian fibration and its restriction over
$(M_{n},A_{n},J_{n})$
is a weak abelian fibration and its restriction over
![]() $A_{n}^{\text{ell}}$
is a
$A_{n}^{\text{ell}}$
is a
![]() $\unicode[STIX]{x1D6FF}$
-regular weak abelian fibration. In particular, we have the following.
$\unicode[STIX]{x1D6FF}$
-regular weak abelian fibration. In particular, we have the following.
-
(i) If
 $a\in \text{Socle}(R{h_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })$
, then (40)
$a\in \text{Socle}(R{h_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })$
, then (40)
-
(ii) If
 $a\in A_{n}^{\text{ell}}$
, then (41)
$a\in A_{n}^{\text{ell}}$
, then (41) $$\begin{eqnarray}d_{a}^{\text{ab}}(J_{n})\geqslant d_{h_{n}}-d_{A_{n}}+d_{a}\quad (\text{GL}_{n}\;\unicode[STIX]{x1D6FF}\text{-regularity inequality}).\end{eqnarray}$$
$$\begin{eqnarray}d_{a}^{\text{ab}}(J_{n})\geqslant d_{h_{n}}-d_{A_{n}}+d_{a}\quad (\text{GL}_{n}\;\unicode[STIX]{x1D6FF}\text{-regularity inequality}).\end{eqnarray}$$
Proof. The two morphisms
![]() $h_{n}$
and
$h_{n}$
and
![]() $g_{n}$
have the same pure relative dimension (26). The stabilizers of the action are affine by Proposition 3.2.1. The Tate module is polarizable by Theorem 3.3.1. It follows that the triple is indeed a weak abelian fibration. Since
$g_{n}$
have the same pure relative dimension (26). The stabilizers of the action are affine by Proposition 3.2.1. The Tate module is polarizable by Theorem 3.3.1. It follows that the triple is indeed a weak abelian fibration. Since
![]() $h_{n}$
is projective and
$h_{n}$
is projective and
![]() $M_{n}$
is nonsingular, (40) follows from Ngô support inequality Theorem 2.6.4. The inequality (41) is known as ‘Severi’s inequality’; see [Reference Chaudouard and LaumonCL16, Theorem 7.3] for references; see also [Reference Fantechi, Gottsche and van StratenFGvS99, the paragraph following Theorem 2 on p. 3]. The
$M_{n}$
is nonsingular, (40) follows from Ngô support inequality Theorem 2.6.4. The inequality (41) is known as ‘Severi’s inequality’; see [Reference Chaudouard and LaumonCL16, Theorem 7.3] for references; see also [Reference Fantechi, Gottsche and van StratenFGvS99, the paragraph following Theorem 2 on p. 3]. The
![]() $\unicode[STIX]{x1D6FF}$
-regularity assertion (41) then follows from Lemma 2.6.2, equation (20).◻
$\unicode[STIX]{x1D6FF}$
-regularity assertion (41) then follows from Lemma 2.6.2, equation (20).◻
4 The
 $\text{SL}_{n}$
weak abelian fibration
$\text{SL}_{n}$
weak abelian fibration
Section 4 is devoted to proving Theorem 4.8.1, i.e. the
![]() $\text{SL}_{n}$
counterpart to Theorem 3.4.1 for
$\text{SL}_{n}$
counterpart to Theorem 3.4.1 for
![]() $\text{GL}_{n}$
. Section 4.1 introduces the group scheme
$\text{GL}_{n}$
. Section 4.1 introduces the group scheme
![]() $\check{J}_{n}/{\check{A}}_{n}$
of identity components of the Prym group scheme, which, in turn, has fibers (8) that become disconnected precisely over the endoscopic locus (11). Section 4.2 establishes the precise relation between the abelian-variety-parts of the fibers of the Jacobi group scheme
$\check{J}_{n}/{\check{A}}_{n}$
of identity components of the Prym group scheme, which, in turn, has fibers (8) that become disconnected precisely over the endoscopic locus (11). Section 4.2 establishes the precise relation between the abelian-variety-parts of the fibers of the Jacobi group scheme
![]() $J_{n}/A_{n}$
, and the ones of the Prym-like group scheme
$J_{n}/A_{n}$
, and the ones of the Prym-like group scheme
![]() $\check{J}_{n}/{\check{A}}_{n}$
; this is a key step in establishing the
$\check{J}_{n}/{\check{A}}_{n}$
; this is a key step in establishing the
![]() $\unicode[STIX]{x1D6FF}$
-regularity of
$\unicode[STIX]{x1D6FF}$
-regularity of
![]() $\check{J}_{n}$
over the elliptic locus. Section 4.3 establishes the expected product structure of
$\check{J}_{n}$
over the elliptic locus. Section 4.3 establishes the expected product structure of
![]() $M_{n}$
, with factors
$M_{n}$
, with factors
![]() $M_{n}(0)$
(traceless Higgs bundles) and
$M_{n}(0)$
(traceless Higgs bundles) and
 $H^{0}(C,D)$
(space of possible traces); this is another key step towards the
$H^{0}(C,D)$
(space of possible traces); this is another key step towards the
![]() $\unicode[STIX]{x1D6FF}$
-regularity above. These factorizations are further pursued in § 4.4, where one factors
$\unicode[STIX]{x1D6FF}$
-regularity above. These factorizations are further pursued in § 4.4, where one factors
![]() $J_{n}$
in the same way. Section 4.5 establishes the
$J_{n}$
in the same way. Section 4.5 establishes the
![]() $\unicode[STIX]{x1D6FF}$
-regularity of
$\unicode[STIX]{x1D6FF}$
-regularity of
![]() $\check{J}_{n}/{\check{A}}_{n}$
over the elliptic locus
$\check{J}_{n}/{\check{A}}_{n}$
over the elliptic locus
![]() ${\check{A}}_{n}^{\text{ell}}$
. Section 4.6 studies in detail the norm morphism associated with arbitrary (not necessarily irreducible, nor reduced) spectral curves. Section 4.7 establishes the key polarizability of the Tate module of
${\check{A}}_{n}^{\text{ell}}$
. Section 4.6 studies in detail the norm morphism associated with arbitrary (not necessarily irreducible, nor reduced) spectral curves. Section 4.7 establishes the key polarizability of the Tate module of
![]() $\check{J}_{n}$
over the whole base
$\check{J}_{n}$
over the whole base
![]() ${\check{A}}_{n}$
by using: the explicit form (38) of the polarization of the Tate module of
${\check{A}}_{n}$
by using: the explicit form (38) of the polarization of the Tate module of
![]() $J_{n}$
; the explicit form (61) of the norm map; a formal reduction of the
$J_{n}$
; the explicit form (61) of the norm map; a formal reduction of the
![]() $\text{SL}_{n}$
polarizability result to the classical fact that, at the level of Tate modules of Jacobians, the maps induced by the pull-back and by the norm are adjoint for the Tate–Weil pairing. Section 4.8 is devoted to binding-up the results of this section by establishing Theorem 4.8.1, i.e. the
$\text{SL}_{n}$
polarizability result to the classical fact that, at the level of Tate modules of Jacobians, the maps induced by the pull-back and by the norm are adjoint for the Tate–Weil pairing. Section 4.8 is devoted to binding-up the results of this section by establishing Theorem 4.8.1, i.e. the
![]() $\text{SL}_{n}$
counterpart to Theorem 3.4.1 for
$\text{SL}_{n}$
counterpart to Theorem 3.4.1 for
![]() $\text{GL}_{n}$
, to the effect that
$\text{GL}_{n}$
, to the effect that
 $(\check{M}_{n},{\check{A}}_{n},\check{J}_{n})$
is a weak abelian fibration which is
$(\check{M}_{n},{\check{A}}_{n},\check{J}_{n})$
is a weak abelian fibration which is
![]() $\unicode[STIX]{x1D6FF}$
-regular over the elliptic locus; this yields the support inequality over the whole base
$\unicode[STIX]{x1D6FF}$
-regular over the elliptic locus; this yields the support inequality over the whole base
![]() ${\check{A}}_{n}$
, and the
${\check{A}}_{n}$
, and the
![]() $\unicode[STIX]{x1D6FF}$
-regularity inequality over the elliptic locus
$\unicode[STIX]{x1D6FF}$
-regularity inequality over the elliptic locus
![]() ${\check{A}}_{n}^{\text{ell}}$
. Section 4.9 is devoted to spelling-out the supports for the
${\check{A}}_{n}^{\text{ell}}$
. Section 4.9 is devoted to spelling-out the supports for the
![]() $\text{SL}_{n}$
Hitchin fibration over the elliptic locus
$\text{SL}_{n}$
Hitchin fibration over the elliptic locus
![]() ${\check{A}}_{n}^{\text{ell}}$
; the results over the elliptic locus in § 4.9, and for every
${\check{A}}_{n}^{\text{ell}}$
; the results over the elliptic locus in § 4.9, and for every
![]() $G$
, are due to Ngô [Reference NgôNgô10].
$G$
, are due to Ngô [Reference NgôNgô10].
4.1 The action of the Prym group scheme
 $\check{J}_{n}$
$\check{J}_{n}$
Let
 $p:{\mathcal{C}}\rightarrow A_{n}$
be the family of spectral curves as in § 2.3. The norm morphism (3) defines a morphism of group schemes over
$p:{\mathcal{C}}\rightarrow A_{n}$
be the family of spectral curves as in § 2.3. The norm morphism (3) defines a morphism of group schemes over
![]() $A_{n}$
(cf. [Reference Hausel and PaulyHP12, Corollary 3.12], for example)
$A_{n}$
(cf. [Reference Hausel and PaulyHP12, Corollary 3.12], for example)
 $$\begin{eqnarray}N_{p}:J_{n}\longrightarrow \text{Pic}^{0}(C)\times A_{n},\quad L\mapsto \det (p_{\ast }L)\otimes [\det (p_{\ast }({\mathcal{O}}_{{\mathcal{C}}}))]^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}N_{p}:J_{n}\longrightarrow \text{Pic}^{0}(C)\times A_{n},\quad L\mapsto \det (p_{\ast }L)\otimes [\det (p_{\ast }({\mathcal{O}}_{{\mathcal{C}}}))]^{-1}.\end{eqnarray}$$
The
![]() $A_{n}$
-morphism
$A_{n}$
-morphism
 $p:{\mathcal{C}}\rightarrow A_{n}$
induces the morphism
$p:{\mathcal{C}}\rightarrow A_{n}$
induces the morphism
 $p^{\ast }:\text{Pic}(C)\times A\rightarrow J_{n}$
of group schemes over
$p^{\ast }:\text{Pic}(C)\times A\rightarrow J_{n}$
of group schemes over
![]() $A_{n}$
. One verifies that
$A_{n}$
. One verifies that
 $N_{p}(p^{\ast }(-))=(-)^{\otimes n}$
; see Fact 2.4.5(1). In particular, the morphism
$N_{p}(p^{\ast }(-))=(-)^{\otimes n}$
; see Fact 2.4.5(1). In particular, the morphism
![]() $N_{p}$
is surjective. The differential of the composition
$N_{p}$
is surjective. The differential of the composition
![]() $N_{p}\circ p^{\ast }$
along the identity section is multiplication by
$N_{p}\circ p^{\ast }$
along the identity section is multiplication by
![]() $n$
, so that the morphism
$n$
, so that the morphism
![]() $N_{p}$
is smooth. The kernel
$N_{p}$
is smooth. The kernel
 $\text{Ker}(N_{p})$
of
$\text{Ker}(N_{p})$
of
![]() $N_{p}$
is a closed subgroup scheme that is smooth over
$N_{p}$
is a closed subgroup scheme that is smooth over
![]() $A_{n}$
. We call it the Prym group scheme. Its fibers are precisely the Prym varieties (8). Then, by [Reference Grothendieck and DemazureSGA3.I, Exp VI-B, Theorem 3.10], there is the open subgroup scheme over
$A_{n}$
. We call it the Prym group scheme. Its fibers are precisely the Prym varieties (8). Then, by [Reference Grothendieck and DemazureSGA3.I, Exp VI-B, Theorem 3.10], there is the open subgroup scheme over
![]() $A_{n}$
$A_{n}$
 $$\begin{eqnarray}J_{n}^{\prime }:=(\text{Ker}(N_{p}))^{0}\end{eqnarray}$$
$$\begin{eqnarray}J_{n}^{\prime }:=(\text{Ker}(N_{p}))^{0}\end{eqnarray}$$
of the kernel, which (set-theoretically) is the union of the identity connected components of the fibers of this kernel group scheme over
![]() $A_{n}$
. Since this whole construction is compatible with arbitrary base change, the fiber
$A_{n}$
. Since this whole construction is compatible with arbitrary base change, the fiber
![]() $J_{n,a}^{\prime }$
over
$J_{n,a}^{\prime }$
over
![]() $a\in A_{n}$
is precisely the identity connected component of the kernel of the norm morphism associated with the spectral cover
$a\in A_{n}$
is precisely the identity connected component of the kernel of the norm morphism associated with the spectral cover
 ${\mathcal{C}}_{a}\rightarrow C_{a}=C\otimes k(a)$
.
${\mathcal{C}}_{a}\rightarrow C_{a}=C\otimes k(a)$
.
We restrict this whole picture to the
![]() $\text{SL}_{n}$
Hitchin base
$\text{SL}_{n}$
Hitchin base
 ${\check{A}}_{n}=A_{n}(0)\subseteq A_{n}$
and set
${\check{A}}_{n}=A_{n}(0)\subseteq A_{n}$
and set
 $$\begin{eqnarray}\check{J}_{n}:={J_{n}^{\prime }}_{|{\check{A}}_{n}},\end{eqnarray}$$
$$\begin{eqnarray}\check{J}_{n}:={J_{n}^{\prime }}_{|{\check{A}}_{n}},\end{eqnarray}$$
which we also call the Prym group scheme.
Then
![]() $\check{J}_{n}/{\check{A}}_{n}$
is a smooth connected group scheme with connected fibers over
$\check{J}_{n}/{\check{A}}_{n}$
is a smooth connected group scheme with connected fibers over
![]() ${\check{A}}_{n}$
that acts on
${\check{A}}_{n}$
that acts on
 $M_{n}(0)/A_{n}(0)$
(trace zero) preserving
$M_{n}(0)/A_{n}(0)$
(trace zero) preserving
![]() $\check{M}_{n}/{\check{A}}_{n}$
(trace zero and fixed determinant
$\check{M}_{n}/{\check{A}}_{n}$
(trace zero and fixed determinant
![]() $\unicode[STIX]{x1D716}$
); see Fact 2.4.5(3) and the proof of Proposition 2.4.9. It follows that
$\unicode[STIX]{x1D716}$
); see Fact 2.4.5(3) and the proof of Proposition 2.4.9. It follows that
![]() $\check{J}_{n}/{\check{A}}_{n}$
acts on
$\check{J}_{n}/{\check{A}}_{n}$
acts on
![]() $\check{M}_{n}/{\check{A}}_{n}$
.
$\check{M}_{n}/{\check{A}}_{n}$
.
According to Proposition 2.4.9, on each fiber
![]() $\check{M}_{n,a}$
, this action is free on the open part given by those rank one torsion-free sheaves which are locally free. The Hitchin fibers
$\check{M}_{n,a}$
, this action is free on the open part given by those rank one torsion-free sheaves which are locally free. The Hitchin fibers
![]() $\check{M}_{n,a}$
corresponding to nonsingular spectral curves are
$\check{M}_{n,a}$
corresponding to nonsingular spectral curves are
![]() $\check{J}_{n,a}$
-torsors via this action.
$\check{J}_{n,a}$
-torsors via this action.
4.2 The abelian variety parts
Let
![]() $a$
be a geometric point of
$a$
be a geometric point of
![]() $A_{n}$
(
$A_{n}$
(
![]() ${\check{A}}_{n}$
, respectively). Recalling the Chevalley devissage § 2.6 for
${\check{A}}_{n}$
, respectively). Recalling the Chevalley devissage § 2.6 for
![]() $J_{n,a}$
(
$J_{n,a}$
(
![]() $\check{J}_{n,a}$
, respectively), we set, by taking dimensions as varieties over the algebraically closed residue field of
$\check{J}_{n,a}$
, respectively), we set, by taking dimensions as varieties over the algebraically closed residue field of
![]() $a$
,
$a$
,

these dimensions depend only on the Zariski point underlying
![]() $a$
.
$a$
.
Lemma 4.2.1. For every point
![]() $a\in {\check{A}}_{n}$
, we have
$a\in {\check{A}}_{n}$
, we have
 $$\begin{eqnarray}d_{a}^{\text{ab}}(\check{J}_{n})\geqslant d_{a}^{\text{ab}}(J_{n})-g.\end{eqnarray}$$
$$\begin{eqnarray}d_{a}^{\text{ab}}(\check{J}_{n})\geqslant d_{a}^{\text{ab}}(J_{n})-g.\end{eqnarray}$$
Proof. Since
![]() $J_{n,a}^{\text{aff}}$
is the biggest affine normal connected group subscheme inside
$J_{n,a}^{\text{aff}}$
is the biggest affine normal connected group subscheme inside
![]() $J_{n,a}$
, we must have
$J_{n,a}$
, we must have
 $d_{a}^{\text{aff}}(\check{J}_{n})\leqslant d_{a}^{\text{aff}}(J_{n})$
. Since
$d_{a}^{\text{aff}}(\check{J}_{n})\leqslant d_{a}^{\text{aff}}(J_{n})$
. Since
 $\dim (J_{n,a})=\dim (\check{J}_{n,a})+g$
, the conclusion follows.◻
$\dim (J_{n,a})=\dim (\check{J}_{n,a})+g$
, the conclusion follows.◻
In fact, as Proposition 4.2.2 below shows, the inequality of Lemma 4.2.1 is an equality.
Proposition 4.2.2. For every geometric point
![]() $a$
of
$a$
of
![]() ${\check{A}}_{n}$
, we have that:
${\check{A}}_{n}$
, we have that:
 $$\begin{eqnarray}d_{a}^{\text{ab}}(\check{J}_{n})=d_{a}^{\text{ab}}(J_{n})-g.\end{eqnarray}$$
$$\begin{eqnarray}d_{a}^{\text{ab}}(\check{J}_{n})=d_{a}^{\text{ab}}(J_{n})-g.\end{eqnarray}$$
More precisely, we have
 $$\begin{eqnarray}\displaystyle & \displaystyle \check{J}_{n,a}^{\text{aff}}=J_{n,a}^{\text{aff}}\subseteq J_{n,a}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \check{J}_{n,a}^{\text{aff}}=J_{n,a}^{\text{aff}}\subseteq J_{n,a}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle J_{n,a}/\check{J}_{n,a}\cong J_{n,a}^{\text{ab}}/\check{J}_{n,a}^{\text{ab}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle J_{n,a}/\check{J}_{n,a}\cong J_{n,a}^{\text{ab}}/\check{J}_{n,a}^{\text{ab}}, & \displaystyle\end{eqnarray}$$
and a natural isogeny
 $$\begin{eqnarray}J_{n,a}^{\text{ab}}/\check{J}_{n,a}^{\text{ab}}\longrightarrow \text{Pic}^{0}(C_{a}).\end{eqnarray}$$
$$\begin{eqnarray}J_{n,a}^{\text{ab}}/\check{J}_{n,a}^{\text{ab}}\longrightarrow \text{Pic}^{0}(C_{a}).\end{eqnarray}$$
Proof. Recall that we have the surjective norm morphism
 $N_{p}:J_{n,a}=\text{Pic}^{0}({\mathcal{C}}_{a})\rightarrow \text{Pic}^{0}(C_{a})$
and that
$N_{p}:J_{n,a}=\text{Pic}^{0}({\mathcal{C}}_{a})\rightarrow \text{Pic}^{0}(C_{a})$
and that
 $\check{J}_{n,a}:=(\text{Ker}(N_{p}))^{0}$
. We thus obtain the natural isogeny
$\check{J}_{n,a}:=(\text{Ker}(N_{p}))^{0}$
. We thus obtain the natural isogeny
 $J_{n,a}/\check{J}_{n,a}\rightarrow \text{Pic}^{0}(C_{a})$
. In particular,
$J_{n,a}/\check{J}_{n,a}\rightarrow \text{Pic}^{0}(C_{a})$
. In particular,
 $J_{n,a}/\check{J}_{n,a}$
is an abelian variety of dimension
$J_{n,a}/\check{J}_{n,a}$
is an abelian variety of dimension
![]() $g$
.
$g$
.
In view of the Chevalley devissage construction, we have the commutative diagram of short exact sequences of morphisms

where:
![]() $v$
is the natural inclusion;
$v$
is the natural inclusion;
![]() $u$
, also an inclusion, arises from the fact that in the Chevalley devissage,
$u$
, also an inclusion, arises from the fact that in the Chevalley devissage,
![]() $J_{n,a}^{\text{aff}}$
is the biggest connected affine subgroup of
$J_{n,a}^{\text{aff}}$
is the biggest connected affine subgroup of
![]() $J_{n,a}$
, so that it contains all other connected affine subgroups of
$J_{n,a}$
, so that it contains all other connected affine subgroups of
![]() $J_{n,a}$
, so that it contains
$J_{n,a}$
, so that it contains
![]() $\check{J}_{n,a}^{\text{aff}}$
;
$\check{J}_{n,a}^{\text{aff}}$
;
![]() $w$
is the natural map induced by the commutativity of the left-hand square.
$w$
is the natural map induced by the commutativity of the left-hand square.
The snake lemma yields a natural exact sequence:
 $$\begin{eqnarray}0\rightarrow \text{Ker}\,u\rightarrow \text{Ker}\,v\rightarrow \text{Ker}\,w\rightarrow \text{Coker}\,u\rightarrow \text{Coker}\,v\rightarrow \text{Coker}\,w\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{Ker}\,u\rightarrow \text{Ker}\,v\rightarrow \text{Ker}\,w\rightarrow \text{Coker}\,u\rightarrow \text{Coker}\,v\rightarrow \text{Coker}\,w\rightarrow 0,\end{eqnarray}$$
which, in view of the fact that
![]() $u,v$
are injective, reduces to
$u,v$
are injective, reduces to
 $$\begin{eqnarray}0\rightarrow \text{Coker}\,u/\text{Ker}\,w\rightarrow J_{n,a}/\check{J}_{n,a}\rightarrow J_{n,a}^{\text{ab}}/(\check{J}_{n,a}^{\text{ab}}/\text{Ker}\,w)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{Coker}\,u/\text{Ker}\,w\rightarrow J_{n,a}/\check{J}_{n,a}\rightarrow J_{n,a}^{\text{ab}}/(\check{J}_{n,a}^{\text{ab}}/\text{Ker}\,w)\rightarrow 0.\end{eqnarray}$$
Since
![]() $\text{Ker}\,w$
sits inside the abelian variety
$\text{Ker}\,w$
sits inside the abelian variety
![]() $\check{J}^{\text{ab}}$
and inside the affine
$\check{J}^{\text{ab}}$
and inside the affine
 $\text{Coker}\,u$
, it is a finite group.
$\text{Coker}\,u$
, it is a finite group.
Since
 $\text{Coker}\,u/\text{Ker}\,w$
is affine, connected, and sits inside the abelian variety
$\text{Coker}\,u/\text{Ker}\,w$
is affine, connected, and sits inside the abelian variety
 $J_{n,a}/\check{J}_{n,a}$
, it is trivial. It follows that
$J_{n,a}/\check{J}_{n,a}$
, it is trivial. It follows that
 $\text{Coker}\,u=\text{Ker}\,w$
, and since
$\text{Coker}\,u=\text{Ker}\,w$
, and since
 $\text{Coker}\,u$
is connected, so is the finite
$\text{Coker}\,u$
is connected, so is the finite
![]() $\text{Ker}\,w$
which is thus trivial. In particular,
$\text{Ker}\,w$
which is thus trivial. In particular,
 $\text{Coker}\,u$
is also trivial and
$\text{Coker}\,u$
is also trivial and
 $\check{J}_{n,a}^{\text{aff}}=J_{n,a}^{\text{aff}}$
.
$\check{J}_{n,a}^{\text{aff}}=J_{n,a}^{\text{aff}}$
.
It follows that
 $J_{n,a}/\check{J}_{n,a}=J_{n,a}^{\text{ab}}/\check{J}_{n,a}^{\text{ab}}$
, and we are done.◻
$J_{n,a}/\check{J}_{n,a}=J_{n,a}^{\text{ab}}/\check{J}_{n,a}^{\text{ab}}$
, and we are done.◻
4.3 Product structures
Lemma 4.3.1. There is the following cartesian diagram with
![]() $q,q^{\prime }$
isomorphisms.
$q,q^{\prime }$
isomorphisms.

Proof. The map
![]() $q^{\prime }$
is defined by the assignment
$q^{\prime }$
is defined by the assignment
 $(\unicode[STIX]{x1D70E},(E,\unicode[STIX]{x1D719}))\mapsto (E,\unicode[STIX]{x1D719}+\unicode[STIX]{x1D70E}\text{Id}_{E})$
. Since
$(\unicode[STIX]{x1D70E},(E,\unicode[STIX]{x1D719}))\mapsto (E,\unicode[STIX]{x1D719}+\unicode[STIX]{x1D70E}\text{Id}_{E})$
. Since
![]() $\unicode[STIX]{x1D719}$
preserves a subsheaf of
$\unicode[STIX]{x1D719}$
preserves a subsheaf of
![]() $E$
if and only if
$E$
if and only if
 $\unicode[STIX]{x1D719}+\unicode[STIX]{x1D70E}\text{Id}_{E}$
does the same, we have that
$\unicode[STIX]{x1D719}+\unicode[STIX]{x1D70E}\text{Id}_{E}$
does the same, we have that
![]() $q^{\prime }$
preserves stability. The inverse assignment to
$q^{\prime }$
preserves stability. The inverse assignment to
![]() $q^{\prime }$
is
$q^{\prime }$
is
 $(E,\unicode[STIX]{x1D719})\mapsto (\text{tr}(\unicode[STIX]{x1D719})/n,(E,\unicode[STIX]{x1D719}-(\text{tr}(\unicode[STIX]{x1D719})/n)\text{Id}_{E}))$
.
$(E,\unicode[STIX]{x1D719})\mapsto (\text{tr}(\unicode[STIX]{x1D719})/n,(E,\unicode[STIX]{x1D719}-(\text{tr}(\unicode[STIX]{x1D719})/n)\text{Id}_{E}))$
.
Let
 $p(M)(t)=\det (t\text{Id}-M)=\sum _{i=0}^{n}(-1)^{i}m_{i}t^{n-i}$
be the characteristic polynomial of an
$p(M)(t)=\det (t\text{Id}-M)=\sum _{i=0}^{n}(-1)^{i}m_{i}t^{n-i}$
be the characteristic polynomial of an
![]() $n\times n$
matrix
$n\times n$
matrix
![]() $M$
. Let
$M$
. Let
![]() $s$
be a scalar. Then a simple calculation shows that
$s$
be a scalar. Then a simple calculation shows that
 $$\begin{eqnarray}p(M+s\text{Id})(t)=\mathop{\sum }_{i=0}^{n}(-1)^{i}\biggl[m_{i}+\mathop{\sum }_{j=1}^{i-1}\binom{n-i+j}{j}m_{i-j}s^{j}+\binom{n}{i}s^{i}\biggr]t^{n-i},\end{eqnarray}$$
$$\begin{eqnarray}p(M+s\text{Id})(t)=\mathop{\sum }_{i=0}^{n}(-1)^{i}\biggl[m_{i}+\mathop{\sum }_{j=1}^{i-1}\binom{n-i+j}{j}m_{i-j}s^{j}+\binom{n}{i}s^{i}\biggr]t^{n-i},\end{eqnarray}$$
where we have broken up the summation in square bracket to emphasize that the coefficients of
![]() $t^{n-i}$
is linear in
$t^{n-i}$
is linear in
![]() $m_{i}$
, and to identify the coefficient of
$m_{i}$
, and to identify the coefficient of
![]() $s^{i}$
.
$s^{i}$
.
The shape of
![]() $q$
is dictated by the desire to have (51) commutative and by the relation (52) between the characteristic polynomial of
$q$
is dictated by the desire to have (51) commutative and by the relation (52) between the characteristic polynomial of
![]() $\unicode[STIX]{x1D719}$
and the one of
$\unicode[STIX]{x1D719}$
and the one of
 $\unicode[STIX]{x1D719}+\unicode[STIX]{x1D70E}\text{Id}_{E}$
. We thus define
$\unicode[STIX]{x1D719}+\unicode[STIX]{x1D70E}\text{Id}_{E}$
. We thus define
![]() $q$
by the assignment (N.B. there is no
$q$
by the assignment (N.B. there is no
![]() $u_{1}$
, so
$u_{1}$
, so
 $j\neq i-1$
, hence the upper bound
$j\neq i-1$
, hence the upper bound
 $j=i-2$
in the summation below)
$j=i-2$
in the summation below)
 $$\begin{eqnarray}(\unicode[STIX]{x1D70E},u_{2},\ldots u_{n})\longmapsto \biggl(n\unicode[STIX]{x1D70E},\biggl\{u_{i}+\mathop{\sum }_{j=1}^{i-2}\binom{n-i+j}{j}\unicode[STIX]{x1D70E}^{j}u_{i-j}+\binom{n}{i}\unicode[STIX]{x1D70E}^{i}\biggr\}_{i=2}^{n}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70E},u_{2},\ldots u_{n})\longmapsto \biggl(n\unicode[STIX]{x1D70E},\biggl\{u_{i}+\mathop{\sum }_{j=1}^{i-2}\binom{n-i+j}{j}\unicode[STIX]{x1D70E}^{j}u_{i-j}+\binom{n}{i}\unicode[STIX]{x1D70E}^{i}\biggr\}_{i=2}^{n}\biggr).\end{eqnarray}$$
For example,
 $q:(\unicode[STIX]{x1D70E},u_{2},u_{3})\mapsto (3\unicode[STIX]{x1D70E},u_{2}+3\unicode[STIX]{x1D70E}^{2},u_{3}+u_{2}\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{3})$
. A simple recursion, based on the fact that
$q:(\unicode[STIX]{x1D70E},u_{2},u_{3})\mapsto (3\unicode[STIX]{x1D70E},u_{2}+3\unicode[STIX]{x1D70E}^{2},u_{3}+u_{2}\unicode[STIX]{x1D70E}+\unicode[STIX]{x1D70E}^{3})$
. A simple recursion, based on the fact that
![]() $u_{i}$
appears linearly in the component labelled by
$u_{i}$
appears linearly in the component labelled by
![]() $i$
, shows that the assignment above can be inverted and that
$i$
, shows that the assignment above can be inverted and that
![]() $q$
is an isomorphism.
$q$
is an isomorphism.
It is immediate to verify that the square diagram is commutative. Since the morphisms
![]() $q$
and
$q$
and
![]() $q^{\prime }$
are isomorphisms, the diagram is cartesian.◻
$q^{\prime }$
are isomorphisms, the diagram is cartesian.◻
Lemma 4.3.2. There is a natural commutative diagram of proper morphisms with cartesian square

with
![]() $r$
and
$r$
and
![]() $r^{\prime }$
proper Galois étale covers with Galois group the finite subgroup
$r^{\prime }$
proper Galois étale covers with Galois group the finite subgroup
 $\text{Pic}^{0}[n]\subseteq \text{Pic}^{0}(C)$
of line bundles of order
$\text{Pic}^{0}[n]\subseteq \text{Pic}^{0}(C)$
of line bundles of order
![]() $n$
.
$n$
.
Proof. The map
![]() $r$
is defined by the assignment
$r$
is defined by the assignment
 $(L,(E,\unicode[STIX]{x1D719}))\mapsto (E\otimes L,\unicode[STIX]{x1D719}\otimes \text{Id}_{L})$
. Since
$(L,(E,\unicode[STIX]{x1D719}))\mapsto (E\otimes L,\unicode[STIX]{x1D719}\otimes \text{Id}_{L})$
. Since
![]() $\check{M}_{n}$
is the closure of the loci of stable Higgs pairs with stable underlying vector bundle, it is clear that, as indicated in (54),
$\check{M}_{n}$
is the closure of the loci of stable Higgs pairs with stable underlying vector bundle, it is clear that, as indicated in (54),
![]() $r$
maps into the closure
$r$
maps into the closure
![]() $M_{n}(0)$
of the loci of stable Higgs pairs with stable underlying vector bundle.
$M_{n}(0)$
of the loci of stable Higgs pairs with stable underlying vector bundle.
The map
![]() $r^{\prime }$
is defined by the assignment
$r^{\prime }$
is defined by the assignment
 $(L\mapsto \unicode[STIX]{x1D716}\otimes L^{\otimes n})$
(rem:
$(L\mapsto \unicode[STIX]{x1D716}\otimes L^{\otimes n})$
(rem:
 $\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
is the fixed line bundle used to define
$\unicode[STIX]{x1D716}\in \text{Pic}^{e}(C)$
is the fixed line bundle used to define
![]() $\check{M}_{n}$
). The map
$\check{M}_{n}$
). The map
![]() $r^{\prime }$
is finite, étale and Galois, with Galois group the subgroup
$r^{\prime }$
is finite, étale and Galois, with Galois group the subgroup
 $\text{Pic}^{0}(C)[n]\subseteq \text{Pic}(C)$
of
$\text{Pic}^{0}(C)[n]\subseteq \text{Pic}(C)$
of
![]() $n$
-torsion points.
$n$
-torsion points.
By construction, (54) is commutative. We need to show that the square is cartesian.
Let
![]() $F$
be the fiber product of
$F$
be the fiber product of
![]() $r^{\prime }$
and
$r^{\prime }$
and
![]() $\det$
. Since
$\det$
. Since
![]() $r^{\prime }$
is étale and
$r^{\prime }$
is étale and
![]() $M_{n}(0)$
is nonsingular,
$M_{n}(0)$
is nonsingular,
![]() $F$
is nonsingular. Since, by virtue of Lemma 2.1.1,
$F$
is nonsingular. Since, by virtue of Lemma 2.1.1,
![]() $\det$
is smooth with integral fibers, then so is the natural projection
$\det$
is smooth with integral fibers, then so is the natural projection
 $F\rightarrow \text{Pic}^{0}(C)$
, and
$F\rightarrow \text{Pic}^{0}(C)$
, and
![]() $F$
is integral. By the universal property of fibre products, we have a natural map
$F$
is integral. By the universal property of fibre products, we have a natural map
 $u:\text{Pic}^{0}(C)\times \check{M}_{n}\rightarrow F$
making the evident diagram commutative. This map is bijective on closed points, where the inverse is given by
$u:\text{Pic}^{0}(C)\times \check{M}_{n}\rightarrow F$
making the evident diagram commutative. This map is bijective on closed points, where the inverse is given by
 $(L,(E,\unicode[STIX]{x1D719}))\mapsto (L,(E\otimes L^{-1},\unicode[STIX]{x1D719}\,\otimes \,\text{Id}_{L^{-1}}))$
. Since the domain and range of
$(L,(E,\unicode[STIX]{x1D719}))\mapsto (L,(E\otimes L^{-1},\unicode[STIX]{x1D719}\,\otimes \,\text{Id}_{L^{-1}}))$
. Since the domain and range of
![]() $u$
are nonsingular and
$u$
are nonsingular and
![]() $u$
is bijective, we conclude that
$u$
is bijective, we conclude that
![]() $u$
is an isomorphism: factor
$u$
is an isomorphism: factor
 $u=f\circ j$
, with
$u=f\circ j$
, with
![]() $j$
an open immersion and
$j$
an open immersion and
![]() $f$
finite and birational, so that
$f$
finite and birational, so that
![]() $f$
is necessarily an isomorphism, and
$f$
is necessarily an isomorphism, and
![]() $j$
is bijective, hence an isomorphism as well.◻
$j$
is bijective, hence an isomorphism as well.◻
4.4 Product structures, re-mixed
In analogy with Lemma 4.3.1, and keeping in mind the construction of spectral curves § 2.3 as the universal divisor inside of
 $V(D)\times A_{n}$
, we have the cartesian square diagram with
$V(D)\times A_{n}$
, we have the cartesian square diagram with
![]() $q,q^{\prime \prime }$
isomorphisms
$q,q^{\prime \prime }$
isomorphisms

where
 $(\unicode[STIX]{x1D70E},u_{\bullet }=(u_{2},\ldots ,u_{n}))\in H^{0}(C,D)\times A(0)$
and
$(\unicode[STIX]{x1D70E},u_{\bullet }=(u_{2},\ldots ,u_{n}))\in H^{0}(C,D)\times A(0)$
and
 $(x,v)\in V(D)_{x}$
is the line fiber of
$(x,v)\in V(D)_{x}$
is the line fiber of
![]() $V(D)$
over a point
$V(D)$
over a point
![]() $x\in C$
. For every fixed
$x\in C$
. For every fixed
![]() $(\unicode[STIX]{x1D70E},u_{\bullet })$
, the resulting morphism
$(\unicode[STIX]{x1D70E},u_{\bullet })$
, the resulting morphism
 $q^{\prime \prime }:V(D)\stackrel{{\sim}}{\rightarrow }V(D)$
is, fiber-by-fiber, the translation in the line direction by the amount
$q^{\prime \prime }:V(D)\stackrel{{\sim}}{\rightarrow }V(D)$
is, fiber-by-fiber, the translation in the line direction by the amount
![]() $\unicode[STIX]{x1D70E}$
(linear change of coordinates
$\unicode[STIX]{x1D70E}$
(linear change of coordinates
 $t\mapsto t+\unicode[STIX]{x1D70E}$
) (cf. [Reference Hausel and PaulyHP12, Remark 2.5]).
$t\mapsto t+\unicode[STIX]{x1D70E}$
) (cf. [Reference Hausel and PaulyHP12, Remark 2.5]).
Consider the spectral curve family
 ${\mathcal{C}}\subseteq A_{n}\times V(D)$
and the pre-image
${\mathcal{C}}\subseteq A_{n}\times V(D)$
and the pre-image
![]() ${\mathcal{C}}(0)$
of
${\mathcal{C}}(0)$
of
![]() $A_{n}(0)$
. Then, by restricting
$A_{n}(0)$
. Then, by restricting
![]() $q^{\prime \prime }$
to
$q^{\prime \prime }$
to
![]() ${\mathcal{C}}$
, we obtain a cartesian square diagram
${\mathcal{C}}$
, we obtain a cartesian square diagram

with
![]() $q,q^{\prime \prime \prime }$
isomorphisms. For every fixed
$q,q^{\prime \prime \prime }$
isomorphisms. For every fixed
 $(\unicode[STIX]{x1D70E},u_{\bullet })\in H^{0}(C,D)\times A_{n}(0)$
, we have the spectral curve
$(\unicode[STIX]{x1D70E},u_{\bullet })\in H^{0}(C,D)\times A_{n}(0)$
, we have the spectral curve
 $(\text{Id}\times p(0))^{-1}(\unicode[STIX]{x1D70E},u_{\bullet })=p(0)^{-1}(u_{\bullet })={\mathcal{C}}_{0,u_{\bullet }}$
. The morphism
$(\text{Id}\times p(0))^{-1}(\unicode[STIX]{x1D70E},u_{\bullet })=p(0)^{-1}(u_{\bullet })={\mathcal{C}}_{0,u_{\bullet }}$
. The morphism
![]() $q^{\prime \prime }$
maps
$q^{\prime \prime }$
maps
![]() ${\mathcal{C}}_{0,u_{\bullet }}$
isomorphically onto
${\mathcal{C}}_{0,u_{\bullet }}$
isomorphically onto
![]() ${\mathcal{C}}_{q(\unicode[STIX]{x1D70E},u_{\bullet })}$
, via the fiber-by-fiber translation by the amount
${\mathcal{C}}_{q(\unicode[STIX]{x1D70E},u_{\bullet })}$
, via the fiber-by-fiber translation by the amount
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
By recalling that
 $J_{n}(0)={J_{n}}_{|A_{n}(0)}$
, and by setting
$J_{n}(0)={J_{n}}_{|A_{n}(0)}$
, and by setting
 $q^{iv}:=((q^{\prime \prime \prime })^{-1})^{\ast }$
, we obtain a cartesian square diagram with
$q^{iv}:=((q^{\prime \prime \prime })^{-1})^{\ast }$
, we obtain a cartesian square diagram with
![]() $q,q^{iv}$
isomorphisms.
$q,q^{iv}$
isomorphisms.

4.5
 $\unicode[STIX]{x1D6FF}$
-regularity of Prym over the elliptic locus
$\unicode[STIX]{x1D6FF}$
-regularity of Prym over the elliptic locus
Recall that the elliptic locus
 $A_{n}^{\text{ell}}\subseteq A_{n}$
is the locus of characteristics
$A_{n}^{\text{ell}}\subseteq A_{n}$
is the locus of characteristics
![]() $a\in A_{n}$
yielding geometrically integral spectral curves
$a\in A_{n}$
yielding geometrically integral spectral curves
![]() ${\mathcal{C}}_{a}$
. We denote by
${\mathcal{C}}_{a}$
. We denote by
![]() $A_{n}^{\text{ell}}(0)$
and by
$A_{n}^{\text{ell}}(0)$
and by
![]() ${\check{A}}_{n}^{\text{ell}}$
the restriction of the elliptic locus to
${\check{A}}_{n}^{\text{ell}}$
the restriction of the elliptic locus to
 $A_{n}(0)={\check{A}}_{n}$
. Recall Definition 2.6.1 (
$A_{n}(0)={\check{A}}_{n}$
. Recall Definition 2.6.1 (
![]() $\unicode[STIX]{x1D6FF}$
-regularity).
$\unicode[STIX]{x1D6FF}$
-regularity).
Proposition 4.5.1. The group scheme
 $J_{n}(0)/A_{n}(0)$
is
$J_{n}(0)/A_{n}(0)$
is
![]() $\unicode[STIX]{x1D6FF}$
-regular over
$\unicode[STIX]{x1D6FF}$
-regular over
![]() $A_{n}^{\text{ell}}(0)$
. The group scheme
$A_{n}^{\text{ell}}(0)$
. The group scheme
![]() $\check{J}_{n}/{\check{A}}_{n}$
is
$\check{J}_{n}/{\check{A}}_{n}$
is
![]() $\unicode[STIX]{x1D6FF}$
-regular over
$\unicode[STIX]{x1D6FF}$
-regular over
![]() ${\check{A}}_{n}^{\text{ell}}$
, i.e. if
${\check{A}}_{n}^{\text{ell}}$
, i.e. if
![]() $a\in {\check{A}}_{n}^{\text{ell}}$
, then
$a\in {\check{A}}_{n}^{\text{ell}}$
, then
 $$\begin{eqnarray}d_{a}^{\text{ab}}(\check{J}_{n})\geqslant d_{\check{h}_{n}}-d_{{\check{A}}_{n}}+d_{a}\quad (\text{SL}_{n}\;\unicode[STIX]{x1D6FF}\text{-regularity inequality}).\end{eqnarray}$$
$$\begin{eqnarray}d_{a}^{\text{ab}}(\check{J}_{n})\geqslant d_{\check{h}_{n}}-d_{{\check{A}}_{n}}+d_{a}\quad (\text{SL}_{n}\;\unicode[STIX]{x1D6FF}\text{-regularity inequality}).\end{eqnarray}$$
Proof. Consider the locally closed ‘strata’ with invariant
 $d_{a}^{\text{aff}}(-)=\unicode[STIX]{x1D6FF}$
:
$d_{a}^{\text{aff}}(-)=\unicode[STIX]{x1D6FF}$
:
 $$\begin{eqnarray}S_{\unicode[STIX]{x1D6FF}}:=S_{\unicode[STIX]{x1D6FF}}(J_{n}/A_{n})\subseteq A_{n},\quad S_{\unicode[STIX]{x1D6FF}}(0):=S_{\unicode[STIX]{x1D6FF}}(J_{n}(0)/A_{n}(0))\subseteq A_{n}(0)\quad {\check{S}}_{\unicode[STIX]{x1D6FF}}:=S_{\unicode[STIX]{x1D6FF}}(\check{J}_{n}/{\check{A}}_{n})\subseteq {\check{A}}_{n}.\end{eqnarray}$$
$$\begin{eqnarray}S_{\unicode[STIX]{x1D6FF}}:=S_{\unicode[STIX]{x1D6FF}}(J_{n}/A_{n})\subseteq A_{n},\quad S_{\unicode[STIX]{x1D6FF}}(0):=S_{\unicode[STIX]{x1D6FF}}(J_{n}(0)/A_{n}(0))\subseteq A_{n}(0)\quad {\check{S}}_{\unicode[STIX]{x1D6FF}}:=S_{\unicode[STIX]{x1D6FF}}(\check{J}_{n}/{\check{A}}_{n})\subseteq {\check{A}}_{n}.\end{eqnarray}$$
By Proposition 4.2.2(47), we have that
 ${\check{S}}_{\unicode[STIX]{x1D6FF}}=S_{\unicode[STIX]{x1D6FF}}\,\cap \,A_{n}(0)=S_{\unicode[STIX]{x1D6FF}}(0)$
. It follows that the two conclusions of the proposition are equivalent to each other, and that it is enough to prove the codimension assertion for
${\check{S}}_{\unicode[STIX]{x1D6FF}}=S_{\unicode[STIX]{x1D6FF}}\,\cap \,A_{n}(0)=S_{\unicode[STIX]{x1D6FF}}(0)$
. It follows that the two conclusions of the proposition are equivalent to each other, and that it is enough to prove the codimension assertion for
![]() $S_{\unicode[STIX]{x1D6FF}}(0)$
.
$S_{\unicode[STIX]{x1D6FF}}(0)$
.
By Lemma 2.6.2, since we already know that
 $\text{codim}_{A_{n}}(S_{\unicode[STIX]{x1D6FF}})\geqslant \unicode[STIX]{x1D6FF}$
, for every
$\text{codim}_{A_{n}}(S_{\unicode[STIX]{x1D6FF}})\geqslant \unicode[STIX]{x1D6FF}$
, for every
![]() $\unicode[STIX]{x1D6FF}\geqslant 0$
(see Lemma 2.6.2(20) and the Severi inequality in the proof of Theorem 3.4.1), we need to make sure that intersecting with
$\unicode[STIX]{x1D6FF}\geqslant 0$
(see Lemma 2.6.2(20) and the Severi inequality in the proof of Theorem 3.4.1), we need to make sure that intersecting with
![]() $A_{n}(0)$
does not spoil codimensions. This follows from (57), for it implies that
$A_{n}(0)$
does not spoil codimensions. This follows from (57), for it implies that
 $$\begin{eqnarray}q^{-1}(S_{\unicode[STIX]{x1D6FF}})=H^{0}(C,D)\times S_{\unicode[STIX]{x1D6FF}}(0),\end{eqnarray}$$
$$\begin{eqnarray}q^{-1}(S_{\unicode[STIX]{x1D6FF}})=H^{0}(C,D)\times S_{\unicode[STIX]{x1D6FF}}(0),\end{eqnarray}$$
so that the codimensions of
![]() $S_{\unicode[STIX]{x1D6FF}}$
in
$S_{\unicode[STIX]{x1D6FF}}$
in
 $A_{n}=H^{0}(C,D)\times A_{n}(0)$
, and of
$A_{n}=H^{0}(C,D)\times A_{n}(0)$
, and of
![]() $S_{\unicode[STIX]{x1D6FF}}(0)$
in
$S_{\unicode[STIX]{x1D6FF}}(0)$
in
![]() $A_{n}(0)$
, coincide.◻
$A_{n}(0)$
, coincide.◻
4.6 The norm morphism
 $N_{p}^{\text{ab}}$
$N_{p}^{\text{ab}}$
Fix a geometric point
![]() $a$
of
$a$
of
![]() ${\check{A}}_{n}$
. Recall the diagram (2) of finite morphisms of curves and let us focus on
${\check{A}}_{n}$
. Recall the diagram (2) of finite morphisms of curves and let us focus on
![]() $\unicode[STIX]{x1D709},p,\widetilde{p}$
. We have the surjection (36)
$\unicode[STIX]{x1D709},p,\widetilde{p}$
. We have the surjection (36)
 $\unicode[STIX]{x1D709}^{\ast }:J_{n,a}=\text{Pic}^{0}({\mathcal{C}}_{a}=:\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k})\rightarrow \text{Pic}^{0}(\widetilde{{\mathcal{C}}_{a,\text{red}}}=\coprod _{k}\widetilde{\unicode[STIX]{x1D6E4}_{k}})$
. Keeping in mind the Chevalley devissage, we have the following commutative diagram of short exact sequences completing the right-hand square in (50) (recall that
$\unicode[STIX]{x1D709}^{\ast }:J_{n,a}=\text{Pic}^{0}({\mathcal{C}}_{a}=:\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k})\rightarrow \text{Pic}^{0}(\widetilde{{\mathcal{C}}_{a,\text{red}}}=\coprod _{k}\widetilde{\unicode[STIX]{x1D6E4}_{k}})$
. Keeping in mind the Chevalley devissage, we have the following commutative diagram of short exact sequences completing the right-hand square in (50) (recall that
 $C_{a}:=C\otimes k(a)$
)
$C_{a}:=C\otimes k(a)$
)

where
![]() $N_{p}^{\text{ab}}$
is the arrow induced by
$N_{p}^{\text{ab}}$
is the arrow induced by
![]() $N_{p}$
, in view of the fact that, since
$N_{p}$
, in view of the fact that, since
![]() $N_{p}$
has target an abelian variety, it must be trivial when restricted to the connected and affine
$N_{p}$
has target an abelian variety, it must be trivial when restricted to the connected and affine
 $\text{Ker}\,\unicode[STIX]{x1D709}^{\ast }=J_{n,a}^{\text{aff}}\subseteq J_{n,a}$
.
$\text{Ker}\,\unicode[STIX]{x1D709}^{\ast }=J_{n,a}^{\text{aff}}\subseteq J_{n,a}$
.
The arrow
![]() $N_{p}^{\text{ab}}$
is not the norm
$N_{p}^{\text{ab}}$
is not the norm
![]() $N_{\widetilde{p}}$
associated with the morphism
$N_{\widetilde{p}}$
associated with the morphism
![]() $\widetilde{p}$
. In fact, we have the following lemma.
$\widetilde{p}$
. In fact, we have the following lemma.
Lemma 4.6.1. For every
 $L\in J_{n,a}$
, we have
$L\in J_{n,a}$
, we have
 $$\begin{eqnarray}\displaystyle & \displaystyle N_{p}^{\text{ab}}(\unicode[STIX]{x1D709}^{\ast }L)=\bigotimes _{k}N_{\widetilde{p}_{k}}(\unicode[STIX]{x1D709}_{k}^{\ast }L)^{\otimes m_{k}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle N_{p}^{\text{ab}}(\unicode[STIX]{x1D709}^{\ast }L)=\bigotimes _{k}N_{\widetilde{p}_{k}}(\unicode[STIX]{x1D709}_{k}^{\ast }L)^{\otimes m_{k}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle N_{\widetilde{p}}(\unicode[STIX]{x1D709}^{\ast }L)=\bigotimes _{k}N_{\widetilde{p}_{k}}(\unicode[STIX]{x1D709}_{k}^{\ast }L). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle N_{\widetilde{p}}(\unicode[STIX]{x1D709}^{\ast }L)=\bigotimes _{k}N_{\widetilde{p}_{k}}(\unicode[STIX]{x1D709}_{k}^{\ast }L). & \displaystyle\end{eqnarray}$$
Proof. Again, recall diagram (2). We have the following chain of identities:
 $$\begin{eqnarray}N_{p}^{\text{ab}}(\unicode[STIX]{x1D709}^{\ast }L)=N_{p}(L)=\bigotimes _{k}N_{p_{k}^{\prime }}(\unicode[STIX]{x1D709}_{1,k}^{\ast }L)=\bigotimes _{k}N_{p_{k}^{\prime \prime }}(\unicode[STIX]{x1D709}_{2,k}^{\ast }\unicode[STIX]{x1D709}_{1,k}^{\ast }L)^{\otimes m_{k}}=\bigotimes _{k}N_{\widetilde{p}_{k}}(\unicode[STIX]{x1D709}^{\ast }L)^{\otimes m_{k}},\end{eqnarray}$$
$$\begin{eqnarray}N_{p}^{\text{ab}}(\unicode[STIX]{x1D709}^{\ast }L)=N_{p}(L)=\bigotimes _{k}N_{p_{k}^{\prime }}(\unicode[STIX]{x1D709}_{1,k}^{\ast }L)=\bigotimes _{k}N_{p_{k}^{\prime \prime }}(\unicode[STIX]{x1D709}_{2,k}^{\ast }\unicode[STIX]{x1D709}_{1,k}^{\ast }L)^{\otimes m_{k}}=\bigotimes _{k}N_{\widetilde{p}_{k}}(\unicode[STIX]{x1D709}^{\ast }L)^{\otimes m_{k}},\end{eqnarray}$$
where: the first identity is by the definition of
![]() $N_{p}^{\text{ab}}$
, for
$N_{p}^{\text{ab}}$
, for
![]() $N_{p}$
has descended via the surjective
$N_{p}$
has descended via the surjective
 $\unicode[STIX]{x1D709}^{\ast }:J_{n,a}\rightarrow J_{n,a}^{\text{ab}}$
, which has
$\unicode[STIX]{x1D709}^{\ast }:J_{n,a}\rightarrow J_{n,a}^{\text{ab}}$
, which has
 $\text{Ker}\,\unicode[STIX]{x1D709}^{\ast }=J_{n,a}^{\text{aff}}$
; the second identity follows from [Reference Hausel and PaulyHP12, Lemma 3.5], applied to the morphisms
$\text{Ker}\,\unicode[STIX]{x1D709}^{\ast }=J_{n,a}^{\text{aff}}$
; the second identity follows from [Reference Hausel and PaulyHP12, Lemma 3.5], applied to the morphisms
![]() $\unicode[STIX]{x1D709}_{1,k}$
, by keeping in mind that the norm from a disjoint union is the tensor product of the norms from the individual connected components; the third identity follows from [Reference Hausel and PaulyHP12, Lemma 3.6], applied to the morphisms
$\unicode[STIX]{x1D709}_{1,k}$
, by keeping in mind that the norm from a disjoint union is the tensor product of the norms from the individual connected components; the third identity follows from [Reference Hausel and PaulyHP12, Lemma 3.6], applied to the morphisms
![]() $\unicode[STIX]{x1D709}_{2,k}$
; the fourth identity follows from [Reference Hausel and PaulyHP12, Lemma 3.4], applied to the morphisms
$\unicode[STIX]{x1D709}_{2,k}$
; the fourth identity follows from [Reference Hausel and PaulyHP12, Lemma 3.4], applied to the morphisms
![]() $\unicode[STIX]{x1D709}_{3,k}$
. This proves (61).
$\unicode[STIX]{x1D709}_{3,k}$
. This proves (61).
The identity (62) can be proved in the same way (without recourse to [Reference Hausel and PaulyHP12, Lemma 3.6]). ◻
4.7 The Tate module of Prym is polarizable
Lemma 4.7.1. Let
![]() $a$
be any geometric point of
$a$
be any geometric point of
![]() ${\check{A}}_{n}$
. Let
${\check{A}}_{n}$
. Let
![]() $\widetilde{p}_{a}$
, etc. be the corresponding morphisms in (2). Then we have:
$\widetilde{p}_{a}$
, etc. be the corresponding morphisms in (2). Then we have:
-
(1)
 $T_{\overline{\mathbb{Q}}_{\ell }}(\widetilde{p}_{a}^{\ast })$
and
$T_{\overline{\mathbb{Q}}_{\ell }}(\widetilde{p}_{a}^{\ast })$
and
 $T_{\overline{\mathbb{Q}}_{\ell }}(N_{p_{a}}^{\text{ab}})$
are adjoint with respect to the bilinear forms
$T_{\overline{\mathbb{Q}}_{\ell }}(N_{p_{a}}^{\text{ab}})$
are adjoint with respect to the bilinear forms
 $\mathit{TW}_{a}^{\text{ab}}$
and
$\mathit{TW}_{a}^{\text{ab}}$
and
 $\mathit{TW}_{C_{a}}$
;
$\mathit{TW}_{C_{a}}$
; -
(2)
 $\text{Ker}\,(T_{\overline{\mathbb{Q}}_{\ell }}(N_{p_{a}}^{\text{ab}}))=T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{a}^{\text{ab}})$
;
$\text{Ker}\,(T_{\overline{\mathbb{Q}}_{\ell }}(N_{p_{a}}^{\text{ab}}))=T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{a}^{\text{ab}})$
; -
(3)
 $N_{p_{a}}^{\text{ab}}\circ \widetilde{p}_{a}^{\ast }=n\,\text{Id}_{\text{Pic}^{0}(C_{a})}$
.
$N_{p_{a}}^{\text{ab}}\circ \widetilde{p}_{a}^{\ast }=n\,\text{Id}_{\text{Pic}^{0}(C_{a})}$
.
Proof. Recall that we have the spectral cover
 ${\mathcal{C}}_{a}=\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}\rightarrow C_{a}=C\otimes k(a)$
. We start with part (1). For every
${\mathcal{C}}_{a}=\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}\rightarrow C_{a}=C\otimes k(a)$
. We start with part (1). For every
 $\widetilde{\unicode[STIX]{x1D6FE}}=\sum _{k}\widetilde{\unicode[STIX]{x1D6FE}}_{k}\in T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})=\bigoplus _{k}T_{\overline{\mathbb{Q}}_{\ell }}(\text{Pic}^{0}(\widetilde{\unicode[STIX]{x1D6E4}}_{k}))$
, and for every
$\widetilde{\unicode[STIX]{x1D6FE}}=\sum _{k}\widetilde{\unicode[STIX]{x1D6FE}}_{k}\in T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})=\bigoplus _{k}T_{\overline{\mathbb{Q}}_{\ell }}(\text{Pic}^{0}(\widetilde{\unicode[STIX]{x1D6E4}}_{k}))$
, and for every
 $c\in T_{\overline{\mathbb{Q}}_{\ell }}(\text{Pic}^{0}(C_{a}))$
, we have that
$c\in T_{\overline{\mathbb{Q}}_{\ell }}(\text{Pic}^{0}(C_{a}))$
, we have that
 $$\begin{eqnarray}\displaystyle \mathit{TW}^{\text{ab}}(\widetilde{\unicode[STIX]{x1D6FE}},T_{\overline{\mathbb{Q}}_{\ell }}(\widetilde{p}^{\ast })(c)) & = & \displaystyle \mathit{TW}^{\text{ab}}\biggl(\mathop{\sum }_{k}\widetilde{\unicode[STIX]{x1D6FE}}_{k},\mathop{\sum }_{k}T_{\overline{\mathbb{Q}}_{\ell }}(\widetilde{p}_{k}^{\ast })(c)\biggr)=\mathop{\sum }_{k}m_{k}\,\mathit{TW}_{\widetilde{\unicode[STIX]{x1D6E4}}_{k}}(\widetilde{\unicode[STIX]{x1D6FE}}_{k},T_{\overline{\mathbb{Q}}_{\ell }}(\widetilde{p}_{k}^{\ast })(c))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k}m_{k}\,\mathit{TW}_{C}(T_{\overline{\mathbb{Q}}_{\ell }}(N_{\widetilde{p}_{k}})(\widetilde{\unicode[STIX]{x1D6FE}_{k}}),c)=\mathit{TW}_{C}\biggl(\mathop{\sum }_{k}m_{k}\,T_{\overline{\mathbb{Q}}_{\ell }}(N_{\widetilde{p}_{k}})(\widetilde{\unicode[STIX]{x1D6FE}_{k}}),c\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathit{TW}_{C}(T_{\overline{\mathbb{Q}}_{\ell }}(N_{p}^{\text{ab}})(\widetilde{\unicode[STIX]{x1D6FE}}),c),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathit{TW}^{\text{ab}}(\widetilde{\unicode[STIX]{x1D6FE}},T_{\overline{\mathbb{Q}}_{\ell }}(\widetilde{p}^{\ast })(c)) & = & \displaystyle \mathit{TW}^{\text{ab}}\biggl(\mathop{\sum }_{k}\widetilde{\unicode[STIX]{x1D6FE}}_{k},\mathop{\sum }_{k}T_{\overline{\mathbb{Q}}_{\ell }}(\widetilde{p}_{k}^{\ast })(c)\biggr)=\mathop{\sum }_{k}m_{k}\,\mathit{TW}_{\widetilde{\unicode[STIX]{x1D6E4}}_{k}}(\widetilde{\unicode[STIX]{x1D6FE}}_{k},T_{\overline{\mathbb{Q}}_{\ell }}(\widetilde{p}_{k}^{\ast })(c))\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{k}m_{k}\,\mathit{TW}_{C}(T_{\overline{\mathbb{Q}}_{\ell }}(N_{\widetilde{p}_{k}})(\widetilde{\unicode[STIX]{x1D6FE}_{k}}),c)=\mathit{TW}_{C}\biggl(\mathop{\sum }_{k}m_{k}\,T_{\overline{\mathbb{Q}}_{\ell }}(N_{\widetilde{p}_{k}})(\widetilde{\unicode[STIX]{x1D6FE}_{k}}),c\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathit{TW}_{C}(T_{\overline{\mathbb{Q}}_{\ell }}(N_{p}^{\text{ab}})(\widetilde{\unicode[STIX]{x1D6FE}}),c),\nonumber\end{eqnarray}$$
where: the first identity follows simply by consideration of components; the second identity follows from the fact that
![]() $\mathit{TW}^{\text{ab}}$
is obtained from
$\mathit{TW}^{\text{ab}}$
is obtained from
![]() $\mathit{TW}$
, which is the direct sum of the individual
$\mathit{TW}$
, which is the direct sum of the individual
![]() $\mathit{TW}_{\widetilde{p}_{k}}$
, weighted by
$\mathit{TW}_{\widetilde{p}_{k}}$
, weighted by
![]() $m_{k}$
(see the end of the proof of Proposition 3.3.1); the third identity is the classical adjunction relation (cf. [Reference MumfordMum70, p. 186, equation I] and [Reference Lange and BirkenhakeLB92, Corollary 11.4.2, especially p. 331, equation (2)]) between norm and pull-back for the morphism
$m_{k}$
(see the end of the proof of Proposition 3.3.1); the third identity is the classical adjunction relation (cf. [Reference MumfordMum70, p. 186, equation I] and [Reference Lange and BirkenhakeLB92, Corollary 11.4.2, especially p. 331, equation (2)]) between norm and pull-back for the morphism
 $\widetilde{p}_{k}:\widetilde{\unicode[STIX]{x1D6E4}}_{k}\rightarrow C_{a}$
; the last equality is obtained by applying the functor
$\widetilde{p}_{k}:\widetilde{\unicode[STIX]{x1D6E4}}_{k}\rightarrow C_{a}$
; the last equality is obtained by applying the functor
![]() $T_{\overline{\mathbb{Q}}_{\ell }}$
to the identity (61), and part (1) is proved.
$T_{\overline{\mathbb{Q}}_{\ell }}$
to the identity (61), and part (1) is proved.
We prove part (2). The lower line in (60) yields, in view of the isogeny (49), the short exact sequence

so that the resulting arrow
 $T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}}/\check{J}_{n,a}^{\text{ab}})$
gets identified with
$T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})\rightarrow T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}}/\check{J}_{n,a}^{\text{ab}})$
gets identified with
 $$\begin{eqnarray}T_{\overline{\mathbb{Q}}_{\ell }}(N_{p}^{\text{ab}}):T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})\longrightarrow T_{\overline{\mathbb{Q}}_{\ell }}(\text{Pic}^{0}(C_{a})).\end{eqnarray}$$
$$\begin{eqnarray}T_{\overline{\mathbb{Q}}_{\ell }}(N_{p}^{\text{ab}}):T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})\longrightarrow T_{\overline{\mathbb{Q}}_{\ell }}(\text{Pic}^{0}(C_{a})).\end{eqnarray}$$
We prove part (3). Recall the standard identity
 $N_{\widetilde{p}_{k}}\circ \widetilde{p}_{k}^{\ast }=n_{k}\text{Id}$
, and that
$N_{\widetilde{p}_{k}}\circ \widetilde{p}_{k}^{\ast }=n_{k}\text{Id}$
, and that
 $n=\sum _{k}n_{k}m_{k}$
. Then part (3) follows from Lemma 4.6.1: for every
$n=\sum _{k}n_{k}m_{k}$
. Then part (3) follows from Lemma 4.6.1: for every
 $L\in \text{Pic}^{0}(C_{a})$
, we have
$L\in \text{Pic}^{0}(C_{a})$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle N_{p}^{\text{ab}}(\widetilde{p}^{\ast }L)=N_{p}^{\text{ab}}(\unicode[STIX]{x1D709}^{\ast }p^{\ast }L)=\bigotimes _{k}N_{\widetilde{p}_{k}}(\unicode[STIX]{x1D709}_{k}^{\ast }p_{k}^{\ast }L)^{\otimes m_{k}}\nonumber\\ \displaystyle & & \displaystyle =\bigotimes _{k}N_{\widetilde{p}_{k}}(\widetilde{p}_{k}^{\ast }L)^{\otimes m_{k}}=\bigotimes _{k}L^{\otimes n_{k}m_{k}}=L^{\otimes n}.\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle N_{p}^{\text{ab}}(\widetilde{p}^{\ast }L)=N_{p}^{\text{ab}}(\unicode[STIX]{x1D709}^{\ast }p^{\ast }L)=\bigotimes _{k}N_{\widetilde{p}_{k}}(\unicode[STIX]{x1D709}_{k}^{\ast }p_{k}^{\ast }L)^{\otimes m_{k}}\nonumber\\ \displaystyle & & \displaystyle =\bigotimes _{k}N_{\widetilde{p}_{k}}(\widetilde{p}_{k}^{\ast }L)^{\otimes m_{k}}=\bigotimes _{k}L^{\otimes n_{k}m_{k}}=L^{\otimes n}.\Box \nonumber\end{eqnarray}$$
Theorem 4.7.2 (Polarizability of the Tate module of Prym).
The restriction
 $$\begin{eqnarray}\check{\mathit{TW}}:T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n})\otimes T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n})\rightarrow \overline{\mathbb{Q}}_{\ell }(1)\end{eqnarray}$$
$$\begin{eqnarray}\check{\mathit{TW}}:T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n})\otimes T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n})\rightarrow \overline{\mathbb{Q}}_{\ell }(1)\end{eqnarray}$$
of the Tate–Weil pairing
 $\mathit{TW}:T_{\overline{\mathbb{Q}}_{\ell }}(J_{n})\otimes T_{\overline{\mathbb{Q}}_{\ell }}(J_{n})\rightarrow \overline{\mathbb{Q}}_{\ell }(1)$
is a polarization of the Tate module
$\mathit{TW}:T_{\overline{\mathbb{Q}}_{\ell }}(J_{n})\otimes T_{\overline{\mathbb{Q}}_{\ell }}(J_{n})\rightarrow \overline{\mathbb{Q}}_{\ell }(1)$
is a polarization of the Tate module
 $T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n})$
on
$T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n})$
on
![]() ${\check{A}}_{n}$
.
${\check{A}}_{n}$
.
Proof. We fix an arbitrary geometric point
![]() $a$
of
$a$
of
![]() ${\check{A}}_{n}$
. By Proposition 4.2.2, we have that
${\check{A}}_{n}$
. By Proposition 4.2.2, we have that
 $\check{J}_{n,a}^{\text{aff}}=J_{n,a}^{\text{aff}}$
. We have already verified that
$\check{J}_{n,a}^{\text{aff}}=J_{n,a}^{\text{aff}}$
. We have already verified that
![]() $\mathit{TW}$
is trivial on the ‘affine part’
$\mathit{TW}$
is trivial on the ‘affine part’
 $J_{n,a}^{\text{aff}}=\check{J}_{n,a}^{\text{aff}}$
(see the proof of Proposition 3.3.1 and (47)). It follows that
$J_{n,a}^{\text{aff}}=\check{J}_{n,a}^{\text{aff}}$
(see the proof of Proposition 3.3.1 and (47)). It follows that
![]() $\mathit{TW}$
is trivial on
$\mathit{TW}$
is trivial on
 $T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n,a}^{\text{aff}})$
. We need to show that the descended nondegenerate
$T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n,a}^{\text{aff}})$
. We need to show that the descended nondegenerate
![]() $\mathit{TW}^{\text{ab}}$
(cf. Theorem 3.3.1) on
$\mathit{TW}^{\text{ab}}$
(cf. Theorem 3.3.1) on
 $T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})$
stays nondegenerate on
$T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})$
stays nondegenerate on
 $T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n,a}^{\text{ab}})$
.
$T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n,a}^{\text{ab}})$
.
By Lemma 4.7.1(3), we have that
 $$\begin{eqnarray}T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})=\text{Ker}\,(T_{\overline{\mathbb{Q}}_{\ell }}(N_{p}^{\text{ab}}))\oplus \text{Im}\,(\widetilde{p}^{\ast }).\end{eqnarray}$$
$$\begin{eqnarray}T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})=\text{Ker}\,(T_{\overline{\mathbb{Q}}_{\ell }}(N_{p}^{\text{ab}}))\oplus \text{Im}\,(\widetilde{p}^{\ast }).\end{eqnarray}$$
By Lemma 4.7.1(1), the direct sum decomposition is orthogonal with respect to
![]() $\mathit{TW}^{\text{ab}}$
.
$\mathit{TW}^{\text{ab}}$
.
By Lemma 4.7.1(2), we may re-write the orthogonal direct sum decomposition above as
 $$\begin{eqnarray}T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})=T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n,a}^{\text{ab}})\bigoplus ^{\bot _{\mathit{TW}^{\text{ab}}}}\text{Im}\,(\widetilde{p}^{\ast }),\end{eqnarray}$$
$$\begin{eqnarray}T_{\overline{\mathbb{Q}}_{\ell }}(J_{n,a}^{\text{ab}})=T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n,a}^{\text{ab}})\bigoplus ^{\bot _{\mathit{TW}^{\text{ab}}}}\text{Im}\,(\widetilde{p}^{\ast }),\end{eqnarray}$$
so that the nondegenerate form
![]() $\mathit{TW}^{\text{ab}}$
restricts to a nondegenerate form on
$\mathit{TW}^{\text{ab}}$
restricts to a nondegenerate form on
 $T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n,a}^{\text{ab}})$
.◻
$T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n,a}^{\text{ab}})$
.◻
4.8 Recap for the
 $\text{SL}_{n}$
weak abelian fibration
$\text{SL}_{n}$
weak abelian fibration
Theorem 3.4.1 tells us that in the
![]() $D$
-twisted,
$D$
-twisted,
![]() $\text{GL}_{n}$
case, the triple
$\text{GL}_{n}$
case, the triple
 $(M_{n},A_{n},J_{n})$
is a weak abelian fibration that is
$(M_{n},A_{n},J_{n})$
is a weak abelian fibration that is
![]() $\unicode[STIX]{x1D6FF}$
-regular over the elliptic locus.
$\unicode[STIX]{x1D6FF}$
-regular over the elliptic locus.
Proposition 4.5.1 implies that the analogous conclusion holds for (
 $M_{n}(0),A_{n}(0),J_{n}(0)$
). In fact, the polarizability of the Tate module is automatic when restricting from
$M_{n}(0),A_{n}(0),J_{n}(0)$
). In fact, the polarizability of the Tate module is automatic when restricting from
![]() $A_{n}$
to
$A_{n}$
to
![]() $A_{n}(0)$
: because
$A_{n}(0)$
: because
 $J_{n}(0)={J_{n}}_{|A_{n}(0)}$
, and the Tate module is the restriction of the Tate module. Similarly, the stabilizers are the same and they are thus affine. Even though the Chevalley devissages are un-effected when passing from
$J_{n}(0)={J_{n}}_{|A_{n}(0)}$
, and the Tate module is the restriction of the Tate module. Similarly, the stabilizers are the same and they are thus affine. Even though the Chevalley devissages are un-effected when passing from
![]() $A_{n}$
to
$A_{n}$
to
![]() $A_{n}(0)$
, it is not a priori evident that the
$A_{n}(0)$
, it is not a priori evident that the
![]() $\unicode[STIX]{x1D6FF}$
-regularity should be preserved (intersecting may spoil codimensions), and this is precisely what Proposition 4.5.1 ensures.
$\unicode[STIX]{x1D6FF}$
-regularity should be preserved (intersecting may spoil codimensions), and this is precisely what Proposition 4.5.1 ensures.
The
![]() $D$
-twisted
$D$
-twisted
![]() $\text{SL}_{n}$
case, i.e.
$\text{SL}_{n}$
case, i.e.
 $(\check{M}_{n},{\check{A}}_{n},\check{J}_{n})$
, is slightly trickier because, in addition to the discussion in the previous paragraph, the polarizability Theorem 4.7.2 for the Tate module
$(\check{M}_{n},{\check{A}}_{n},\check{J}_{n})$
, is slightly trickier because, in addition to the discussion in the previous paragraph, the polarizability Theorem 4.7.2 for the Tate module
 $T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n})$
did not follow immediately from the
$T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n})$
did not follow immediately from the
![]() $\text{GL}_{n}$
analogous Theorem 3.3.1.
$\text{GL}_{n}$
analogous Theorem 3.3.1.
We record for future use the following result.
Theorem 4.8.1. The triple
 $(\check{M}_{n},{\check{A}}_{n},\check{J}_{n})$
is a weak abelian fibration which is
$(\check{M}_{n},{\check{A}}_{n},\check{J}_{n})$
is a weak abelian fibration which is
![]() $\unicode[STIX]{x1D6FF}$
-regular over
$\unicode[STIX]{x1D6FF}$
-regular over
![]() ${\check{A}}_{n}^{\text{ell}}$
. In particular, we have the following.
${\check{A}}_{n}^{\text{ell}}$
. In particular, we have the following.
-
(i) If
 $a\in \text{Socle}({R\check{h}_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })$
, then (63)
$a\in \text{Socle}({R\check{h}_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })$
, then (63)
-
(ii) If
 $a\in {\check{A}}_{n}^{\text{ell}}$
, then (64)
$a\in {\check{A}}_{n}^{\text{ell}}$
, then (64) $$\begin{eqnarray}d_{{\check{a}}}^{\text{ab}}(\check{J}_{n})\geqslant d_{\check{h}_{n}}-d_{{\check{A}}_{n}}+d_{{\check{a}}}\quad (\unicode[STIX]{x1D6FF}\text{-regularity inequality}).\end{eqnarray}$$
$$\begin{eqnarray}d_{{\check{a}}}^{\text{ab}}(\check{J}_{n})\geqslant d_{\check{h}_{n}}-d_{{\check{A}}_{n}}+d_{{\check{a}}}\quad (\unicode[STIX]{x1D6FF}\text{-regularity inequality}).\end{eqnarray}$$
Proof. The projective morphism
 $\check{h}_{n}:\check{M}_{n}\rightarrow {\check{A}}_{n}$
is of pure relative dimension
$\check{h}_{n}:\check{M}_{n}\rightarrow {\check{A}}_{n}$
is of pure relative dimension
 $d_{\check{h}_{n}}=d_{h_{n}}-g$
(Proposition 2.4.9). By (26), the pure relative dimension
$d_{\check{h}_{n}}=d_{h_{n}}-g$
(Proposition 2.4.9). By (26), the pure relative dimension
 $d_{g_{n}}=d_{h_{n}}$
. By the very construction § 4.1 of
$d_{g_{n}}=d_{h_{n}}$
. By the very construction § 4.1 of
![]() $\check{J}_{n}$
, the pure relative dimension of
$\check{J}_{n}$
, the pure relative dimension of
 ${\check{g}}_{n}:\check{J}_{n}\rightarrow {\check{A}}_{n}$
is
${\check{g}}_{n}:\check{J}_{n}\rightarrow {\check{A}}_{n}$
is
 $d_{{\check{g}}_{n}}=d_{g_{n}}-g$
. It follows that
$d_{{\check{g}}_{n}}=d_{g_{n}}-g$
. It follows that
 $d_{\check{h}_{n}}=d_{{\check{g}}_{n}}$
. The stabilizers of the
$d_{\check{h}_{n}}=d_{{\check{g}}_{n}}$
. The stabilizers of the
![]() $\check{J}_{n}$
-action are affine because they are closed subgroups of the stabilizers of the
$\check{J}_{n}$
-action are affine because they are closed subgroups of the stabilizers of the
![]() $J_{n}$
-action, which are affine by virtue of Proposition 3.2.1. The Tate module
$J_{n}$
-action, which are affine by virtue of Proposition 3.2.1. The Tate module
 $T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n})$
is polarizable by virtue of Theorem 4.7.2. We have thus verified that the triple is a weak abelian fibration. In particular, Ngô support inequality 2.6.4 implies (63). The
$T_{\overline{\mathbb{Q}}_{\ell }}(\check{J}_{n})$
is polarizable by virtue of Theorem 4.7.2. We have thus verified that the triple is a weak abelian fibration. In particular, Ngô support inequality 2.6.4 implies (63). The
![]() $\unicode[STIX]{x1D6FF}$
-regularity assertion is contained in Proposition 4.5.1.◻
$\unicode[STIX]{x1D6FF}$
-regularity assertion is contained in Proposition 4.5.1.◻
4.9 Endoscopy and the
 $\text{SL}_{n}$
socle over the elliptic locus
$\text{SL}_{n}$
socle over the elliptic locus
We employ the notation and results in § 2.5, especially Fact 2.5.1.
According to [Reference NgôNgô10, Proposition 6.5.1], we have

In view of Theorem 4.8.1, the triple
 $(\check{M}_{n},{\check{A}}_{n},\check{J}_{n})$
is a weak abelian fibration that is
$(\check{M}_{n},{\check{A}}_{n},\check{J}_{n})$
is a weak abelian fibration that is
![]() $\unicode[STIX]{x1D6FF}$
-regular over
$\unicode[STIX]{x1D6FF}$
-regular over
![]() ${\check{A}}_{n}^{\text{ell}}$
, so that we may use Ngô support theorem [Reference NgôNgô10, Theorem 7.2.1], to the effect that the supports over the elliptic locus must also be the supports appearing in (65), and conclude that
${\check{A}}_{n}^{\text{ell}}$
, so that we may use Ngô support theorem [Reference NgôNgô10, Theorem 7.2.1], to the effect that the supports over the elliptic locus must also be the supports appearing in (65), and conclude that
 $$\begin{eqnarray}\text{Socle}(R\check{h}_{n\ast }\overline{\mathbb{Q}}_{\ell })\cap {\check{A}}_{n}^{\text{ell}}=\{\unicode[STIX]{x1D702}_{{\check{A}}_{n}}\}\coprod \coprod _{\unicode[STIX]{x1D6E4}}\{\unicode[STIX]{x1D702}_{{\check{A}}_{n,\unicode[STIX]{x1D6E4}}}\}.\end{eqnarray}$$
$$\begin{eqnarray}\text{Socle}(R\check{h}_{n\ast }\overline{\mathbb{Q}}_{\ell })\cap {\check{A}}_{n}^{\text{ell}}=\{\unicode[STIX]{x1D702}_{{\check{A}}_{n}}\}\coprod \coprod _{\unicode[STIX]{x1D6E4}}\{\unicode[STIX]{x1D702}_{{\check{A}}_{n,\unicode[STIX]{x1D6E4}}}\}.\end{eqnarray}$$
5 Multi-variable weak abelian fibrations
While the
![]() $\text{SL}_{n}$
support inequality is used in the proof of our main Theorem 1.0.2 on the
$\text{SL}_{n}$
support inequality is used in the proof of our main Theorem 1.0.2 on the
![]() $\text{SL}_{n}$
socle, the
$\text{SL}_{n}$
socle, the
![]() $\text{SL}_{n}$
$\text{SL}_{n}$
![]() $\unicode[STIX]{x1D6FF}$
-regularity inequality is of no use in that respect. Section 5 is devoted to establish the
$\unicode[STIX]{x1D6FF}$
-regularity inequality is of no use in that respect. Section 5 is devoted to establish the
![]() $\unicode[STIX]{x1D6FF}$
-regularity-type inequality that we need instead, i.e. (76). To this end, § 5.1 introduces the multi-variable
$\unicode[STIX]{x1D6FF}$
-regularity-type inequality that we need instead, i.e. (76). To this end, § 5.1 introduces the multi-variable
![]() $\text{GL}_{n}$
weak abelian fibration
$\text{GL}_{n}$
weak abelian fibration
 $(M_{n_{\bullet }},A_{n_{\bullet }},J_{n_{\bullet }})$
. Section 5.3 introduces its
$(M_{n_{\bullet }},A_{n_{\bullet }},J_{n_{\bullet }})$
. Section 5.3 introduces its
![]() $m_{\bullet }$
-weighted-traceless counterpart
$m_{\bullet }$
-weighted-traceless counterpart
 $(M_{n_{\bullet }m_{\bullet }}(0),A_{n_{\bullet }m_{\bullet }}(0),J_{n_{\bullet }}(0))$
, and establishes a series of product-decomposition-formulae of the form
$(M_{n_{\bullet }m_{\bullet }}(0),A_{n_{\bullet }m_{\bullet }}(0),J_{n_{\bullet }}(0))$
, and establishes a series of product-decomposition-formulae of the form
 $H^{0}(C,D)\times (-)_{n_{\bullet }m_{\bullet }}(0)\cong (-)_{n_{\bullet }}$
. This construction yields the group scheme
$H^{0}(C,D)\times (-)_{n_{\bullet }m_{\bullet }}(0)\cong (-)_{n_{\bullet }}$
. This construction yields the group scheme
 $J_{n_{\bullet }m_{\bullet }}(0)/A_{n_{\bullet }m_{\bullet }}(0)$
with the useful
$J_{n_{\bullet }m_{\bullet }}(0)/A_{n_{\bullet }m_{\bullet }}(0)$
with the useful
![]() $\unicode[STIX]{x1D6FF}$
-regularity-type inequality that we need. Extracting it, as it is done in § 5.4, is not a priori completely evident: one has trivially a
$\unicode[STIX]{x1D6FF}$
-regularity-type inequality that we need. Extracting it, as it is done in § 5.4, is not a priori completely evident: one has trivially a
![]() $\unicode[STIX]{x1D6FF}$
-regularity-type inequality for the multi-variable Jacobi groups scheme
$\unicode[STIX]{x1D6FF}$
-regularity-type inequality for the multi-variable Jacobi groups scheme
 $J_{n_{\bullet }m_{\bullet }}/A_{n_{\bullet }m_{\bullet }}$
, which takes the form of an inequality for codimensions of
$J_{n_{\bullet }m_{\bullet }}/A_{n_{\bullet }m_{\bullet }}$
, which takes the form of an inequality for codimensions of
![]() $\unicode[STIX]{x1D6FF}$
-loci in
$\unicode[STIX]{x1D6FF}$
-loci in
![]() $A_{n_{\bullet }m_{\bullet }}$
; however, one needs instead to control the codimensions of the
$A_{n_{\bullet }m_{\bullet }}$
; however, one needs instead to control the codimensions of the
![]() $\unicode[STIX]{x1D6FF}$
-loci after restriction to the linear subspace
$\unicode[STIX]{x1D6FF}$
-loci after restriction to the linear subspace
 $A_{n_{\bullet }m_{\bullet }}(0)$
, which is not meeting the
$A_{n_{\bullet }m_{\bullet }}(0)$
, which is not meeting the
![]() $\unicode[STIX]{x1D6FF}$
-loci transversally.
$\unicode[STIX]{x1D6FF}$
-loci transversally.
5.1 The weak abelian fibration
 $(M_{n_{\bullet }},A_{n_{\bullet }},J_{n_{\bullet }})$
$(M_{n_{\bullet }},A_{n_{\bullet }},J_{n_{\bullet }})$
Let
 $n_{\bullet }=(n_{1},\ldots ,n_{s})$
be a finite sequence of positive integers. Define
$n_{\bullet }=(n_{1},\ldots ,n_{s})$
be a finite sequence of positive integers. Define
 $$\begin{eqnarray}\displaystyle & \displaystyle (M_{n_{\bullet }},A_{n_{\bullet }},J_{n_{\bullet }}):=\biggl(\mathop{\prod }_{k}M_{n_{k}},\mathop{\prod }_{k}A_{n_{k}},\mathop{\prod }_{k}J_{n_{k}}\biggr) & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (M_{n_{\bullet }},A_{n_{\bullet }},J_{n_{\bullet }}):=\biggl(\mathop{\prod }_{k}M_{n_{k}},\mathop{\prod }_{k}A_{n_{k}},\mathop{\prod }_{k}J_{n_{k}}\biggr) & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle A_{n_{\bullet }}^{\text{ell}}:=\mathop{\prod }_{k}A_{n_{k}}^{\text{ell}}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle A_{n_{\bullet }}^{\text{ell}}:=\mathop{\prod }_{k}A_{n_{k}}^{\text{ell}}. & \displaystyle\end{eqnarray}$$
A geometric point of
![]() $A_{n_{\bullet }}^{\text{ell}}$
correspond to an ordered
$A_{n_{\bullet }}^{\text{ell}}$
correspond to an ordered
![]() $s$
-tuple of geometrically integral spectral curves
$s$
-tuple of geometrically integral spectral curves
 $(\unicode[STIX]{x1D6E4}_{1},\ldots ,\unicode[STIX]{x1D6E4}_{s})$
of respective spectral degrees
$(\unicode[STIX]{x1D6E4}_{1},\ldots ,\unicode[STIX]{x1D6E4}_{s})$
of respective spectral degrees
 $(n_{1},\ldots ,n_{s})$
.
$(n_{1},\ldots ,n_{s})$
.
The requirements of Definition 2.6.3 (same pure relative dimensions, affine stabilizers, polarizability of Tate modules,
![]() $\unicode[STIX]{x1D6FF}$
-regularity on the elliptic locus) are met on each factor separately by virtue of Theorem 3.4.1. (In verifying
$\unicode[STIX]{x1D6FF}$
-regularity on the elliptic locus) are met on each factor separately by virtue of Theorem 3.4.1. (In verifying
![]() $\unicode[STIX]{x1D6FF}$
-regularity, one needs a simple application of Lemma 2.6.2(2) to each factor: let
$\unicode[STIX]{x1D6FF}$
-regularity, one needs a simple application of Lemma 2.6.2(2) to each factor: let
 $a\in A_{n_{\bullet }}^{\text{ell}}$
; let
$a\in A_{n_{\bullet }}^{\text{ell}}$
; let
![]() $x_{\bullet }$
be a closed general point in
$x_{\bullet }$
be a closed general point in
![]() $\overline{\{a\}}$
; let
$\overline{\{a\}}$
; let
![]() $a_{k}$
be the projection of
$a_{k}$
be the projection of
![]() $a$
to the
$a$
to the
![]() $k$
th factor; then
$k$
th factor; then
 $a_{k}\in A_{n_{k}}^{\text{ell}}$
,
$a_{k}\in A_{n_{k}}^{\text{ell}}$
,
![]() $x_{k}$
is a closed general point of
$x_{k}$
is a closed general point of
![]() $\overline{\{a_{k}\}}$
, and
$\overline{\{a_{k}\}}$
, and
 $\sum _{k}d_{a_{k}}\geqslant d_{a}$
(because
$\sum _{k}d_{a_{k}}\geqslant d_{a}$
(because
 $\overline{\{a\}}\subseteq \prod _{k}\overline{\{a_{k}\}}$
); we have
$\overline{\{a\}}\subseteq \prod _{k}\overline{\{a_{k}\}}$
); we have
 $d_{a}^{\text{ab}}(J_{n_{\bullet }})=d_{x_{\bullet }}^{\text{ab}}(J_{n_{\bullet }})=\sum _{k}d_{x_{k}}^{\text{ab}}(J_{n_{k}})=\sum _{k}d_{a_{k}}^{\text{ab}}(J_{n_{k}})\geqslant \sum _{k}(d_{a_{k}}(J_{n_{k}})-d_{A_{n_{k}}}+d_{a_{k}})=\sum _{k}d_{a_{k}}(J_{n_{k}})-d_{A_{n_{\bullet }}}+\sum _{k}d_{a_{k}}\geqslant \sum _{k}d_{a_{k}}(J_{n_{k}})-d_{A_{n_{\bullet }}}+d_{a}=\sum _{k}d_{x_{k}}(J_{n_{k}})-d_{A_{n_{\bullet }}}+d_{a}=d_{a}(J_{n_{\bullet }})-d_{A_{n_{\bullet }}}+d_{a}$
.) It follows immediately that they are met on the product, so that (67) is a weak abelian fibration which is
$d_{a}^{\text{ab}}(J_{n_{\bullet }})=d_{x_{\bullet }}^{\text{ab}}(J_{n_{\bullet }})=\sum _{k}d_{x_{k}}^{\text{ab}}(J_{n_{k}})=\sum _{k}d_{a_{k}}^{\text{ab}}(J_{n_{k}})\geqslant \sum _{k}(d_{a_{k}}(J_{n_{k}})-d_{A_{n_{k}}}+d_{a_{k}})=\sum _{k}d_{a_{k}}(J_{n_{k}})-d_{A_{n_{\bullet }}}+\sum _{k}d_{a_{k}}\geqslant \sum _{k}d_{a_{k}}(J_{n_{k}})-d_{A_{n_{\bullet }}}+d_{a}=\sum _{k}d_{x_{k}}(J_{n_{k}})-d_{A_{n_{\bullet }}}+d_{a}=d_{a}(J_{n_{\bullet }})-d_{A_{n_{\bullet }}}+d_{a}$
.) It follows immediately that they are met on the product, so that (67) is a weak abelian fibration which is
![]() $\unicode[STIX]{x1D6FF}$
-regular over
$\unicode[STIX]{x1D6FF}$
-regular over
![]() $A_{n_{\bullet }}^{\text{ell}}$
.
$A_{n_{\bullet }}^{\text{ell}}$
.
5.2 Stratification by type of the
 $\text{GL}_{n}$
Hitchin base
$\text{GL}_{n}$
Hitchin base
 $A_{n}$
$A_{n}$
Let
 $n\in \mathbb{Z}^{{\geqslant}1}$
and let
$n\in \mathbb{Z}^{{\geqslant}1}$
and let
 $s\in \mathbb{Z}^{{\geqslant}1}$
with
$s\in \mathbb{Z}^{{\geqslant}1}$
with
 $1\leqslant s\leqslant n$
. We consider the set
$1\leqslant s\leqslant n$
. We consider the set
![]() $NM(s)$
of pairs
$NM(s)$
of pairs
 $(n_{\bullet },m_{\bullet })$
subject to the following requirements: (1)
$(n_{\bullet },m_{\bullet })$
subject to the following requirements: (1)
 $n_{1}\geqslant \ldots \geqslant n_{s}$
; (2)
$n_{1}\geqslant \ldots \geqslant n_{s}$
; (2)
 $m_{k}\geqslant m_{k+1}$
whenever
$m_{k}\geqslant m_{k+1}$
whenever
 $n_{k}=n_{k+1}$
; (3)
$n_{k}=n_{k+1}$
; (3)
 $\sum _{k=1}^{s}m_{k}n_{k}=n$
. There is the partition of the integral variety
$\sum _{k=1}^{s}m_{k}n_{k}=n$
. There is the partition of the integral variety
 $$\begin{eqnarray}A_{n}=\coprod _{1\leqslant s\leqslant n}\,\coprod _{(n_{\bullet },m_{\bullet })\in MN(s)}S_{n_{\bullet }m_{\bullet }}\end{eqnarray}$$
$$\begin{eqnarray}A_{n}=\coprod _{1\leqslant s\leqslant n}\,\coprod _{(n_{\bullet },m_{\bullet })\in MN(s)}S_{n_{\bullet }m_{\bullet }}\end{eqnarray}$$
into the locally closed integral subvarieties
 $$\begin{eqnarray}S_{n_{\bullet }m_{\bullet }}:=\biggl\{a\in A_{n}\mid {\mathcal{C}}_{\overline{a}}=\mathop{\sum }_{k=1}^{s}m_{k}{\mathcal{C}}_{k,\overline{a}}\biggr\}\subseteq A_{n},\end{eqnarray}$$
$$\begin{eqnarray}S_{n_{\bullet }m_{\bullet }}:=\biggl\{a\in A_{n}\mid {\mathcal{C}}_{\overline{a}}=\mathop{\sum }_{k=1}^{s}m_{k}{\mathcal{C}}_{k,\overline{a}}\biggr\}\subseteq A_{n},\end{eqnarray}$$
where
![]() $\overline{a}\rightarrow a$
is given by an algebraic closure
$\overline{a}\rightarrow a$
is given by an algebraic closure
 $k(a)\subseteq \overline{k(a)}$
, and each spectral curve
$k(a)\subseteq \overline{k(a)}$
, and each spectral curve
![]() ${\mathcal{C}}_{k,\overline{a}}$
is irreducible of spectral curve degree
${\mathcal{C}}_{k,\overline{a}}$
is irreducible of spectral curve degree
![]() $n_{k}$
. The closure
$n_{k}$
. The closure
 $\overline{S_{n_{\bullet },m_{\bullet }}}\subseteq A_{n}$
is the image of the finite morphism [Reference Chaudouard and LaumonCL16, § 9]
$\overline{S_{n_{\bullet },m_{\bullet }}}\subseteq A_{n}$
is the image of the finite morphism [Reference Chaudouard and LaumonCL16, § 9]
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{m_{\bullet }n_{\bullet }}:A_{n_{\bullet }}\rightarrow A_{n},\quad \text{Im}\,(\unicode[STIX]{x1D706}_{n_{\bullet }m_{\bullet }})=\overline{S_{n_{\bullet }m_{\bullet }}}\subseteq A_{n},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{m_{\bullet }n_{\bullet }}:A_{n_{\bullet }}\rightarrow A_{n},\quad \text{Im}\,(\unicode[STIX]{x1D706}_{n_{\bullet }m_{\bullet }})=\overline{S_{n_{\bullet }m_{\bullet }}}\subseteq A_{n},\end{eqnarray}$$
which on closed points is defined as follows:
 $(a_{1},\ldots ,a_{s})\mapsto a$
, where we view
$(a_{1},\ldots ,a_{s})\mapsto a$
, where we view
![]() $a_{k}$
as a characteristic polynomial
$a_{k}$
as a characteristic polynomial
![]() $P_{a_{k}}$
of degree
$P_{a_{k}}$
of degree
![]() $n_{k}$
, we consider the degree
$n_{k}$
, we consider the degree
![]() $n$
polynomial
$n$
polynomial
 $\prod _{k=1}^{s}P_{a_{k}}^{m_{k}}$
, and we take
$\prod _{k=1}^{s}P_{a_{k}}^{m_{k}}$
, and we take
![]() $a$
to be the corresponding closed point on
$a$
to be the corresponding closed point on
![]() $A_{n}$
. The stratum
$A_{n}$
. The stratum
![]() $S_{n_{\bullet }m_{\bullet }}$
is the image of a suitable Zariski-dense open subvariety inside the Zariski-dense open subvariety
$S_{n_{\bullet }m_{\bullet }}$
is the image of a suitable Zariski-dense open subvariety inside the Zariski-dense open subvariety
 $\prod _{k=1}^{s}A_{n_{k}}^{\text{ell}}\subseteq A_{n_{\bullet }}$
. Given a point
$\prod _{k=1}^{s}A_{n_{k}}^{\text{ell}}\subseteq A_{n_{\bullet }}$
. Given a point
![]() $a\in A_{n}$
, we have
$a\in A_{n}$
, we have
 $a\in S_{n_{\bullet }m_{\bullet }}$
for a unique triple
$a\in S_{n_{\bullet }m_{\bullet }}$
for a unique triple
 $(s,(n_{\bullet },m_{\bullet }))$
, with
$(s,(n_{\bullet },m_{\bullet }))$
, with
 $1\leqslant s\leqslant n$
the number of irreducible components of
$1\leqslant s\leqslant n$
the number of irreducible components of
![]() ${\mathcal{C}}_{\overline{a}}$
, and with
${\mathcal{C}}_{\overline{a}}$
, and with
 $(n_{\bullet },m_{\bullet })\in NM(s)$
, which we call the type of
$(n_{\bullet },m_{\bullet })\in NM(s)$
, which we call the type of
![]() $a\in A_{n}$
. Since the spectral curve
$a\in A_{n}$
. Since the spectral curve
![]() ${\mathcal{C}}_{a}$
may have a strictly smaller number of components than
${\mathcal{C}}_{a}$
may have a strictly smaller number of components than
![]() ${\mathcal{C}}_{\overline{a}}$
, the type of
${\mathcal{C}}_{\overline{a}}$
, the type of
![]() $a$
is observed on
$a$
is observed on
![]() ${\mathcal{C}}_{\overline{a}}$
.
${\mathcal{C}}_{\overline{a}}$
.
Geometrically, we may think of the morphism
![]() $\unicode[STIX]{x1D706}_{n_{\bullet }m_{\bullet }}$
as sending an ordered
$\unicode[STIX]{x1D706}_{n_{\bullet }m_{\bullet }}$
as sending an ordered
![]() $s$
-tuple of integral curves
$s$
-tuple of integral curves
 $(\unicode[STIX]{x1D6E4}_{1},\ldots ,\unicode[STIX]{x1D6E4}_{s})$
, to the spectral curve denoted (§ 2.3) by
$(\unicode[STIX]{x1D6E4}_{1},\ldots ,\unicode[STIX]{x1D6E4}_{s})$
, to the spectral curve denoted (§ 2.3) by
 $\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}$
. As it is already clear in the case
$\sum _{k}m_{k}\unicode[STIX]{x1D6E4}_{k}$
. As it is already clear in the case
![]() $s=2$
, with
$s=2$
, with
 $(n_{1},n_{2};m_{1},m_{2})=(1,1;1,1)$
, in general, the finite morphisms
$(n_{1},n_{2};m_{1},m_{2})=(1,1;1,1)$
, in general, the finite morphisms
![]() $\unicode[STIX]{x1D706}_{n_{\bullet }m_{\bullet }}$
are not birational.
$\unicode[STIX]{x1D706}_{n_{\bullet }m_{\bullet }}$
are not birational.
The morphisms (71) are introduced in [Reference Chaudouard and LaumonCL16, § 9] in order to exploit the
![]() $\text{GL}_{n}$
$\text{GL}_{n}$
![]() $\unicode[STIX]{x1D6FF}$
-regularity inequalities for each
$\unicode[STIX]{x1D6FF}$
-regularity inequalities for each
 $J_{n_{k}}^{\text{ell}}/A_{n_{k}}^{\text{ell}}$
,
$J_{n_{k}}^{\text{ell}}/A_{n_{k}}^{\text{ell}}$
,
 $k=1,\ldots ,s$
(however, see Remark 5.4.3).
$k=1,\ldots ,s$
(however, see Remark 5.4.3).
The resulting inequalities are of no use to us for the
![]() $\text{SL}_{n}$
case: they are too weak. One may be tempted to replace them by taking the multi-variable counterpart to the
$\text{SL}_{n}$
case: they are too weak. One may be tempted to replace them by taking the multi-variable counterpart to the
![]() $\text{SL}_{n}$
$\text{SL}_{n}$
![]() $\unicode[STIX]{x1D6FF}$
-regularity inequality (64). As it turns out, these
$\unicode[STIX]{x1D6FF}$
-regularity inequality (64). As it turns out, these
![]() $\text{SL}_{n}$
inequalities are also of no use to us towards the proof of Theorem 1.0.2 on the
$\text{SL}_{n}$
inequalities are also of no use to us towards the proof of Theorem 1.0.2 on the
![]() $\text{SL}_{n}$
socle: they are not relevant in the proof given in § 6.2 of Theorem 1.0.2 (the
$\text{SL}_{n}$
socle: they are not relevant in the proof given in § 6.2 of Theorem 1.0.2 (the
![]() $\text{SL}_{n}$
support inequality (63) plays a crucial role, though).
$\text{SL}_{n}$
support inequality (63) plays a crucial role, though).
The multi-variable
![]() $\unicode[STIX]{x1D6FF}$
-regularity inequalities that we need for the proof of Theorem 1.0.2 on the
$\unicode[STIX]{x1D6FF}$
-regularity inequalities that we need for the proof of Theorem 1.0.2 on the
![]() $\text{SL}_{n}$
socle are given by Corollary 5.4.4(76), and are to be extracted from the constructions of § 5.3.
$\text{SL}_{n}$
socle are given by Corollary 5.4.4(76), and are to be extracted from the constructions of § 5.3.
5.3 The weak abelian fibration (
 $M_{n_{\bullet }m_{\bullet }}(0),A_{n_{\bullet }m_{\bullet }}(0),J_{n_{\bullet }m_{\bullet }}(0)$
)
$M_{n_{\bullet }m_{\bullet }}(0),A_{n_{\bullet }m_{\bullet }}(0),J_{n_{\bullet }m_{\bullet }}(0)$
)
Define what we may call the subspace of multi-weighted-traceless characteristics by setting (recall that
![]() $a(1)$
is the trace-component of a characteristic)
$a(1)$
is the trace-component of a characteristic)
 $$\begin{eqnarray}A_{n_{\bullet }m_{\bullet }}(0):=\biggl\{(a_{1},\ldots ,a_{s})\biggm\vert\mathop{\sum }_{k}m_{k}a_{k}(1)=0\biggr\}\subseteq A_{n_{\bullet }}.\end{eqnarray}$$
$$\begin{eqnarray}A_{n_{\bullet }m_{\bullet }}(0):=\biggl\{(a_{1},\ldots ,a_{s})\biggm\vert\mathop{\sum }_{k}m_{k}a_{k}(1)=0\biggr\}\subseteq A_{n_{\bullet }}.\end{eqnarray}$$
This is a vector subspace of codimension
 $h^{0}(C,D)=d-(g-1)$
. Define
$h^{0}(C,D)=d-(g-1)$
. Define
 $M_{n_{\bullet }m_{\bullet }}(0):=h_{n_{\bullet }}^{-1}(A_{n_{\bullet }m_{\bullet }}(0))\subseteq M_{n_{\bullet }}$
(given its reduced structure; we are about to verify the statement associated with (73), so that, a posteriori, this pre-image is indeed automatically reduced).
$M_{n_{\bullet }m_{\bullet }}(0):=h_{n_{\bullet }}^{-1}(A_{n_{\bullet }m_{\bullet }}(0))\subseteq M_{n_{\bullet }}$
(given its reduced structure; we are about to verify the statement associated with (73), so that, a posteriori, this pre-image is indeed automatically reduced).
What follows is in direct analogy with the constructions in the proof of Lemma 4.3.1, and in its re-mixed version in § 4.4. We have the cartesian square diagram

with
![]() $\mathfrak{q},\mathfrak{q}^{\prime }$
isomorphisms, where we have the following.
$\mathfrak{q},\mathfrak{q}^{\prime }$
isomorphisms, where we have the following.
-
(i) In analogy with (53), and by keeping in mind that here the entries
 $u_{k1}$
are not necessarily zero, the map
$u_{k1}$
are not necessarily zero, the map
 $\mathfrak{q}$
is given by the assignment sending to (having set
$\mathfrak{q}$
is given by the assignment sending to (having set $$\begin{eqnarray}(\unicode[STIX]{x1D70E},(u_{11},\ldots ,u_{1n_{1}}),\ldots (u_{s1},\ldots ,u_{sn_{s}})),\quad \text{subject to }\mathop{\sum }_{k}m_{k}u_{k1}=0,\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70E},(u_{11},\ldots ,u_{1n_{1}}),\ldots (u_{s1},\ldots ,u_{sn_{s}})),\quad \text{subject to }\mathop{\sum }_{k}m_{k}u_{k1}=0,\end{eqnarray}$$
 $u_{k0}:=1$
, for convenience)
$u_{k0}:=1$
, for convenience)  $$\begin{eqnarray}\biggl(\biggl\{\mathop{\sum }_{j=0}^{i}\binom{n_{1}-i+j}{j}\unicode[STIX]{x1D70E}^{j}u_{1,i-j}\biggr\}_{i=1}^{n_{1}},\ldots ,\biggl\{\mathop{\sum }_{j=0}^{i}\binom{n_{s}-i+j}{j}\unicode[STIX]{x1D70E}^{j}u_{s,i-j}\biggr\}_{i=1}^{n_{s}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\biggl\{\mathop{\sum }_{j=0}^{i}\binom{n_{1}-i+j}{j}\unicode[STIX]{x1D70E}^{j}u_{1,i-j}\biggr\}_{i=1}^{n_{1}},\ldots ,\biggl\{\mathop{\sum }_{j=0}^{i}\binom{n_{s}-i+j}{j}\unicode[STIX]{x1D70E}^{j}u_{s,i-j}\biggr\}_{i=1}^{n_{s}}\biggr).\end{eqnarray}$$
-
(ii) The isomorphism
 $\mathfrak{q}^{\prime }$
is defined by the assignment
$\mathfrak{q}^{\prime }$
is defined by the assignment $$\begin{eqnarray}(\unicode[STIX]{x1D70E},(E_{1},\unicode[STIX]{x1D719}_{1}),\ldots ,(E_{s},\unicode[STIX]{x1D719}_{s}))\longmapsto ((E_{1},\unicode[STIX]{x1D719}_{1}+\unicode[STIX]{x1D70E}\text{Id}),\ldots ,(E_{s},\unicode[STIX]{x1D719}_{s}+\unicode[STIX]{x1D70E}\text{Id})).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70E},(E_{1},\unicode[STIX]{x1D719}_{1}),\ldots ,(E_{s},\unicode[STIX]{x1D719}_{s}))\longmapsto ((E_{1},\unicode[STIX]{x1D719}_{1}+\unicode[STIX]{x1D70E}\text{Id}),\ldots ,(E_{s},\unicode[STIX]{x1D719}_{s}+\unicode[STIX]{x1D70E}\text{Id})).\end{eqnarray}$$
As in the proof Lemma 4.3.1, a simple recursion yields the map inverse to
![]() $\mathfrak{q}$
, whereas the one inverse to
$\mathfrak{q}$
, whereas the one inverse to
![]() $\mathfrak{q}^{\prime }$
is given by the assignment (remember that
$\mathfrak{q}^{\prime }$
is given by the assignment (remember that
 $n=\sum _{k}m_{k}n_{k}$
)
$n=\sum _{k}m_{k}n_{k}$
)
 $$\begin{eqnarray}\{(E_{k},\unicode[STIX]{x1D713}_{k})\}_{k=1}^{s}\longmapsto \biggl(\frac{\mathop{\sum }_{j}m_{j}\text{tr}(\unicode[STIX]{x1D713}_{j})}{n},\biggl\{\biggl(E_{k},\unicode[STIX]{x1D713}_{k}-\mathop{\sum }_{j}\frac{m_{j}}{n}\text{tr}(\unicode[STIX]{x1D713}_{j})\text{Id}\biggr)\biggr\}_{k=1}^{s}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\{(E_{k},\unicode[STIX]{x1D713}_{k})\}_{k=1}^{s}\longmapsto \biggl(\frac{\mathop{\sum }_{j}m_{j}\text{tr}(\unicode[STIX]{x1D713}_{j})}{n},\biggl\{\biggl(E_{k},\unicode[STIX]{x1D713}_{k}-\mathop{\sum }_{j}\frac{m_{j}}{n}\text{tr}(\unicode[STIX]{x1D713}_{j})\text{Id}\biggr)\biggr\}_{k=1}^{s}\biggr).\end{eqnarray}$$
Finally, by setting
 $J_{n_{\bullet }m_{\bullet }}(0):={J_{n_{\bullet }}}_{|A_{n_{\bullet }m_{\bullet }}(0)}$
, we have the cartesian square diagram with
$J_{n_{\bullet }m_{\bullet }}(0):={J_{n_{\bullet }}}_{|A_{n_{\bullet }m_{\bullet }}(0)}$
, we have the cartesian square diagram with
![]() $\mathfrak{q}^{\prime \prime }$
and
$\mathfrak{q}^{\prime \prime }$
and
![]() $\mathfrak{q}$
isomorphisms
$\mathfrak{q}$
isomorphisms

obtained in the same way as (57).
5.4 Multi-variable
 $\unicode[STIX]{x1D6FF}$
-regularity over the elliptic loci
$\unicode[STIX]{x1D6FF}$
-regularity over the elliptic loci
Recalling the definition of
 $S_{\unicode[STIX]{x1D6FF}}(J/A)$
in (19), we have the following identification of
$S_{\unicode[STIX]{x1D6FF}}(J/A)$
in (19), we have the following identification of
![]() $\unicode[STIX]{x1D6FF}$
-loci
$\unicode[STIX]{x1D6FF}$
-loci
Proposition 5.4.1.
 $\mathfrak{q}^{-1}(S_{\unicode[STIX]{x1D6FF}}(J_{n_{\bullet }}/A_{n_{\bullet }}))=H^{0}(C,D)\times S_{\unicode[STIX]{x1D6FF}}(J_{n_{\bullet }m_{\bullet }}(0)/A_{n_{\bullet }m_{\bullet }}(0))$
.
$\mathfrak{q}^{-1}(S_{\unicode[STIX]{x1D6FF}}(J_{n_{\bullet }}/A_{n_{\bullet }}))=H^{0}(C,D)\times S_{\unicode[STIX]{x1D6FF}}(J_{n_{\bullet }m_{\bullet }}(0)/A_{n_{\bullet }m_{\bullet }}(0))$
.
Proof. Keeping in mind that
 $S_{\unicode[STIX]{x1D6FF}}(J_{n_{\bullet }}/A_{n_{\bullet }})$
is naturally stratified by products of individual
$S_{\unicode[STIX]{x1D6FF}}(J_{n_{\bullet }}/A_{n_{\bullet }})$
is naturally stratified by products of individual
 $S_{\unicode[STIX]{x1D6FF}_{k}}(J_{n_{k}}/A_{n_{k}})$
with
$S_{\unicode[STIX]{x1D6FF}_{k}}(J_{n_{k}}/A_{n_{k}})$
with
 $\sum _{k}\unicode[STIX]{x1D6FF}_{k}=\unicode[STIX]{x1D6FF}$
, the proof runs parallel to the one of Proposition 4.5.1, with (74) playing the role of (57).◻
$\sum _{k}\unicode[STIX]{x1D6FF}_{k}=\unicode[STIX]{x1D6FF}$
, the proof runs parallel to the one of Proposition 4.5.1, with (74) playing the role of (57).◻
Theorem 5.4.2. The weak abelian fibrations
 $$\begin{eqnarray}\displaystyle & \displaystyle (M_{n},A_{n},J_{n}),\quad (M_{n}(0),A_{n}(0),J_{n}(0)),\quad (\check{M}_{n},{\check{A}}_{n},\check{J}_{n}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (M_{n_{\bullet }},A_{n_{\bullet }},J_{n_{\bullet }}),\quad (M_{n_{\bullet }m_{\bullet }}(0),A_{n_{\bullet }m_{\bullet }}(0),J_{n_{\bullet }m_{\bullet }}(0)) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle (M_{n},A_{n},J_{n}),\quad (M_{n}(0),A_{n}(0),J_{n}(0)),\quad (\check{M}_{n},{\check{A}}_{n},\check{J}_{n}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (M_{n_{\bullet }},A_{n_{\bullet }},J_{n_{\bullet }}),\quad (M_{n_{\bullet }m_{\bullet }}(0),A_{n_{\bullet }m_{\bullet }}(0),J_{n_{\bullet }m_{\bullet }}(0)) & \displaystyle \nonumber\end{eqnarray}$$
are
![]() $\unicode[STIX]{x1D6FF}$
-regular when restricted to their respective elliptic loci
$\unicode[STIX]{x1D6FF}$
-regular when restricted to their respective elliptic loci
 $$\begin{eqnarray}\displaystyle & \displaystyle A_{n}^{\text{ell}},\quad A_{n}^{\text{ell}}(0):=A_{n}(0)\cap A_{n}^{\text{ell}},\quad {\check{A}}_{n}^{\text{ell}}:={\check{A}}_{n}\cap A_{n}^{\text{ell}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle A_{n_{\bullet }}^{\text{ell}}:=\mathop{\prod }_{k}A_{n_{k}}^{\text{ell}},\quad A_{n_{\bullet }m_{\bullet }}^{\text{ell}}(0):=A_{n_{\bullet }m_{\bullet }}(0)\cap \mathop{\prod }_{k}A_{n_{k}}^{\text{ell}}. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle A_{n}^{\text{ell}},\quad A_{n}^{\text{ell}}(0):=A_{n}(0)\cap A_{n}^{\text{ell}},\quad {\check{A}}_{n}^{\text{ell}}:={\check{A}}_{n}\cap A_{n}^{\text{ell}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle A_{n_{\bullet }}^{\text{ell}}:=\mathop{\prod }_{k}A_{n_{k}}^{\text{ell}},\quad A_{n_{\bullet }m_{\bullet }}^{\text{ell}}(0):=A_{n_{\bullet }m_{\bullet }}(0)\cap \mathop{\prod }_{k}A_{n_{k}}^{\text{ell}}. & \displaystyle \nonumber\end{eqnarray}$$
Proof. We have already proved all the conclusions in the single-variable case: we have displayed them for emphasis only. We have already observed in § 5.1 that the single-variable case implies that
 $(M_{n_{\bullet }},A_{n_{\bullet }},J_{n_{\bullet }})$
is a weak abelian fibration which is
$(M_{n_{\bullet }},A_{n_{\bullet }},J_{n_{\bullet }})$
is a weak abelian fibration which is
![]() $\unicode[STIX]{x1D6FF}$
-regular over its elliptic locus
$\unicode[STIX]{x1D6FF}$
-regular over its elliptic locus
![]() $A_{n_{\bullet }}^{\text{ell}}$
.
$A_{n_{\bullet }}^{\text{ell}}$
.
By virtue of (73) and of (74), we see that
 $(M_{n_{\bullet }m_{\bullet }}(0),A_{n_{\bullet }m_{\bullet }}(0),J_{n_{\bullet }m_{\bullet }}(0))$
is a weak abelian fibration as well, which, by virtue of Proposition 5.4.1, is
$(M_{n_{\bullet }m_{\bullet }}(0),A_{n_{\bullet }m_{\bullet }}(0),J_{n_{\bullet }m_{\bullet }}(0))$
is a weak abelian fibration as well, which, by virtue of Proposition 5.4.1, is
![]() $\unicode[STIX]{x1D6FF}$
-regular over its elliptic locus
$\unicode[STIX]{x1D6FF}$
-regular over its elliptic locus
 $A_{n_{\bullet }m_{\bullet }}^{\text{ell}}(0)$
(cf. the proof of Proposition 4.5.1).◻
$A_{n_{\bullet }m_{\bullet }}^{\text{ell}}(0)$
(cf. the proof of Proposition 4.5.1).◻
Remark 5.4.3. The following claim does not hold: given a point
 $a\in S_{n_{\bullet }m_{\bullet }}\subseteq A_{n}$
, we can write
$a\in S_{n_{\bullet }m_{\bullet }}\subseteq A_{n}$
, we can write
 $a=\unicode[STIX]{x1D706}_{n_{\bullet }m_{\bullet }}(a_{1},\ldots a_{s})$
for a suitable
$a=\unicode[STIX]{x1D706}_{n_{\bullet }m_{\bullet }}(a_{1},\ldots a_{s})$
for a suitable
![]() $s$
-tuple
$s$
-tuple
 $a_{k}\in A_{n_{k}}$
. This is true if
$a_{k}\in A_{n_{k}}$
. This is true if
![]() $a$
is a closed point, but it fails in general. This claim has been used in [Reference Chaudouard and LaumonCL16, § 9, proof of main theorem].
$a$
is a closed point, but it fails in general. This claim has been used in [Reference Chaudouard and LaumonCL16, § 9, proof of main theorem].
Corollary 5.4.4, equation (75) below remedies the minor inaccuracy in the proof of [Reference Chaudouard and LaumonCL16, § 9, proof of main theorem] pointed out in Remark 5.4.3. It also establishes the
![]() $\text{SL}_{n}$
-variant (76) that we need in the course of the proof of Theorem 1.0.2 in § 6.2.
$\text{SL}_{n}$
-variant (76) that we need in the course of the proof of Theorem 1.0.2 in § 6.2.
Corollary 5.4.4 (Multi-variable
 $\unicode[STIX]{x1D6FF}$
-inequalities).
$\unicode[STIX]{x1D6FF}$
-inequalities).
Let
![]() $a\in A_{n}$
and let
$a\in A_{n}$
and let
 $(n_{\bullet },m_{\bullet })\in NM(s)$
be its type (§ 5.3). Then we have the following multi-variable
$(n_{\bullet },m_{\bullet })\in NM(s)$
be its type (§ 5.3). Then we have the following multi-variable
![]() $\text{GL}_{n}$
$\text{GL}_{n}$
![]() $\unicode[STIX]{x1D6FF}$
-inequality:
$\unicode[STIX]{x1D6FF}$
-inequality:
 $$\begin{eqnarray}d_{a}^{\text{ab}}(J_{n})\geqslant \mathop{\sum }_{k}(d_{h_{n_{k}}}-d_{A_{n_{k}}})+d_{a}.\end{eqnarray}$$
$$\begin{eqnarray}d_{a}^{\text{ab}}(J_{n})\geqslant \mathop{\sum }_{k}(d_{h_{n_{k}}}-d_{A_{n_{k}}})+d_{a}.\end{eqnarray}$$
If, in addition,
 $a\in A_{n}(0)={\check{A}}_{n}$
, then we have the following multi-variable
$a\in A_{n}(0)={\check{A}}_{n}$
, then we have the following multi-variable
![]() $\text{SL}_{n}$
$\text{SL}_{n}$
![]() $\unicode[STIX]{x1D6FF}$
-inequality:
$\unicode[STIX]{x1D6FF}$
-inequality:
 $$\begin{eqnarray}d_{a}^{\text{ab}}(J_{n})\geqslant \mathop{\sum }_{k}(d_{h_{n_{k}}}-d_{A_{n_{k}}})+[d-(g-1)]+d_{a}.\end{eqnarray}$$
$$\begin{eqnarray}d_{a}^{\text{ab}}(J_{n})\geqslant \mathop{\sum }_{k}(d_{h_{n_{k}}}-d_{A_{n_{k}}})+[d-(g-1)]+d_{a}.\end{eqnarray}$$
Proof. Let
![]() $a\in A_{n}$
and let
$a\in A_{n}$
and let
 $V(a):=\overline{\{a\}}\subseteq A_{n}$
be the associated integral closed subvariety. Let
$V(a):=\overline{\{a\}}\subseteq A_{n}$
be the associated integral closed subvariety. Let
 $(n_{\bullet },m_{\bullet })\in NM(s)$
be the type of
$(n_{\bullet },m_{\bullet })\in NM(s)$
be the type of
![]() $a$
. Let
$a$
. Let
![]() $\unicode[STIX]{x1D6FC}$
be any point in the non empty fiber
$\unicode[STIX]{x1D6FC}$
be any point in the non empty fiber
 $\unicode[STIX]{x1D706}_{n_{\bullet }m_{\bullet }}^{-1}(a)$
. Then
$\unicode[STIX]{x1D706}_{n_{\bullet }m_{\bullet }}^{-1}(a)$
. Then
 $d_{a}:=\dim (\overline{\{a\}})=\dim (\overline{\{\unicode[STIX]{x1D6FC}\}})=d_{\unicode[STIX]{x1D6FC}}$
.
$d_{a}:=\dim (\overline{\{a\}})=\dim (\overline{\{\unicode[STIX]{x1D6FC}\}})=d_{\unicode[STIX]{x1D6FC}}$
.
We choose an algebraic closure of
![]() $k(a)$
that contains the finite field extension
$k(a)$
that contains the finite field extension
 $k(a)\subseteq k(\unicode[STIX]{x1D6FC})$
. We can identify the curves
$k(a)\subseteq k(\unicode[STIX]{x1D6FC})$
. We can identify the curves
 ${\mathcal{C}}_{\overline{\unicode[STIX]{x1D6FC}}}={\mathcal{C}}_{\overline{a},\text{red}}$
, so that the two curves have the same number
${\mathcal{C}}_{\overline{\unicode[STIX]{x1D6FC}}}={\mathcal{C}}_{\overline{a},\text{red}}$
, so that the two curves have the same number
![]() $s$
of geometrically irreducible components. It follows that
$s$
of geometrically irreducible components. It follows that
 $\unicode[STIX]{x1D6FC}\in A_{n_{\bullet }}^{\text{ell}}$
. By virtue of (39), it also follows that
$\unicode[STIX]{x1D6FC}\in A_{n_{\bullet }}^{\text{ell}}$
. By virtue of (39), it also follows that
 $d_{a}^{\text{ab}}(J_{n})=d_{\unicode[STIX]{x1D6FC}}^{\text{ab}}(J_{n_{\bullet }})$
.
$d_{a}^{\text{ab}}(J_{n})=d_{\unicode[STIX]{x1D6FC}}^{\text{ab}}(J_{n_{\bullet }})$
.
The
![]() $\unicode[STIX]{x1D6FF}$
-regularity inequality for
$\unicode[STIX]{x1D6FF}$
-regularity inequality for
![]() $J_{n_{\bullet }}$
over
$J_{n_{\bullet }}$
over
![]() $A_{n_{\bullet }}^{\text{ell}}$
implies that
$A_{n_{\bullet }}^{\text{ell}}$
implies that
 $d_{\unicode[STIX]{x1D6FC}}^{\text{ab}}(J_{n_{\bullet }})\geqslant d_{h_{n_{\bullet }}}-d_{A_{n_{\bullet }}}+d_{\unicode[STIX]{x1D6FC}}$
, and (75) follows.
$d_{\unicode[STIX]{x1D6FC}}^{\text{ab}}(J_{n_{\bullet }})\geqslant d_{h_{n_{\bullet }}}-d_{A_{n_{\bullet }}}+d_{\unicode[STIX]{x1D6FC}}$
, and (75) follows.
Since
![]() $a$
has type
$a$
has type
 $(n_{\bullet },m_{\bullet })$
, we have that
$(n_{\bullet },m_{\bullet })$
, we have that
![]() $\unicode[STIX]{x1D6FC}$
satisfies the weighted trace constraint (72) that defines
$\unicode[STIX]{x1D6FC}$
satisfies the weighted trace constraint (72) that defines
![]() $A_{n_{\bullet }m_{\bullet }}^{\text{ell}}$
, so that
$A_{n_{\bullet }m_{\bullet }}^{\text{ell}}$
, so that
 $\unicode[STIX]{x1D6FC}\in A_{n_{\bullet }m_{\bullet }}^{\text{ell}}(0)$
. Then (76) is proved in the same way as (75) by using the
$\unicode[STIX]{x1D6FC}\in A_{n_{\bullet }m_{\bullet }}^{\text{ell}}(0)$
. Then (76) is proved in the same way as (75) by using the
![]() $\unicode[STIX]{x1D6FF}$
-regularity of
$\unicode[STIX]{x1D6FF}$
-regularity of
 $J_{n_{\bullet }m_{\bullet }}(0)$
over
$J_{n_{\bullet }m_{\bullet }}(0)$
over
 $A_{n_{\bullet }m_{\bullet }}^{\text{ell}}(0)$
, and the facts that
$A_{n_{\bullet }m_{\bullet }}^{\text{ell}}(0)$
, and the facts that
 $d_{h_{n_{\bullet }}}=\sum _{k}d_{h_{n_{k}}}$
, and (cf. (72))
$d_{h_{n_{\bullet }}}=\sum _{k}d_{h_{n_{k}}}$
, and (cf. (72))
 $d_{A_{n_{\bullet }m_{\bullet }}}(0)=\dim (A_{n_{\bullet }})-h^{0}(C,D)=\sum _{k}d_{A_{n_{k}}}-[d-(g-1)]$
.◻
$d_{A_{n_{\bullet }m_{\bullet }}}(0)=\dim (A_{n_{\bullet }})-h^{0}(C,D)=\sum _{k}d_{A_{n_{k}}}-[d-(g-1)]$
.◻
6 Proof of the main Theorem 1.0.2 on the
 $\text{SL}_{n}$
socle
$\text{SL}_{n}$
socle
This section is devoted to the proof of our main Theorem 1.0.2 on the
![]() $\text{SL}_{n}$
socle. Section 6.1 collects some formulae. Section 6.2 contains the proof of Theorem 1.0.2.
$\text{SL}_{n}$
socle. Section 6.1 collects some formulae. Section 6.2 contains the proof of Theorem 1.0.2.
6.1 A list of dimension formulae
We first list some dimensional formulae in the
![]() $\text{GL}_{n}$
case. We set
$\text{GL}_{n}$
case. We set
 $d_{M_{n}}:=\dim M_{n}$
,
$d_{M_{n}}:=\dim M_{n}$
,
 $d_{A_{n}}:=\dim A_{n}$
, and
$d_{A_{n}}:=\dim A_{n}$
, and
 $d_{h_{n}}:=d_{M_{n}}-d_{A_{n}}$
. The dimension of
$d_{h_{n}}:=d_{M_{n}}-d_{A_{n}}$
. The dimension of
![]() $M_{n}$
is given by [Reference NitsureNit91, Proposition 7.1]; the dimension of
$M_{n}$
is given by [Reference NitsureNit91, Proposition 7.1]; the dimension of
 $A_{n}=\bigoplus _{i=1}^{n}h^{0}(C,iD)$
is computed via Riemann–Roch; the relative dimension
$A_{n}=\bigoplus _{i=1}^{n}h^{0}(C,iD)$
is computed via Riemann–Roch; the relative dimension
![]() $d_{h_{n}}$
is given by (7). We thus have
$d_{h_{n}}$
is given by (7). We thus have
 $$\begin{eqnarray}\displaystyle & \displaystyle d_{M_{n}}=n^{2}d+1,\quad d_{A_{n}}=\frac{n(n+1)}{2}d-n(g-1), & \displaystyle \nonumber\\ \displaystyle & \displaystyle d_{h_{n}}=\frac{n(n-1)}{2}d+n(g-1)+1,\quad d_{h_{n}}-d_{A_{n}}=-nd+2n(g-1)+1. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle d_{M_{n}}=n^{2}d+1,\quad d_{A_{n}}=\frac{n(n+1)}{2}d-n(g-1), & \displaystyle \nonumber\\ \displaystyle & \displaystyle d_{h_{n}}=\frac{n(n-1)}{2}d+n(g-1)+1,\quad d_{h_{n}}-d_{A_{n}}=-nd+2n(g-1)+1. & \displaystyle\end{eqnarray}$$
The corresponding formula for
![]() $\text{SL}_{n}$
follow easily, for example, from the above, remembering that, in view of lemmata 4.3.1 and 4.3.2, we have that
$\text{SL}_{n}$
follow easily, for example, from the above, remembering that, in view of lemmata 4.3.1 and 4.3.2, we have that
 $\dim (M_{n})=\dim (\check{M}_{n})+h^{0}(D)+g$
:
$\dim (M_{n})=\dim (\check{M}_{n})+h^{0}(D)+g$
:
 $$\begin{eqnarray}\displaystyle & \displaystyle d_{\check{M}_{n}}=n^{2}d-d,\quad d_{{\check{A}}_{n}}=\frac{n(n+1)}{2}d-d-(n-1)(g-1), & \displaystyle \nonumber\\ \displaystyle & \displaystyle d_{\check{h}_{n}}=\frac{n(n-1)}{2}d+(n-1)(g-1),\quad d_{\check{h}_{n}}-d_{{\check{A}}_{n}}=-(n-1)d+2(n-1)(g-1). & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle d_{\check{M}_{n}}=n^{2}d-d,\quad d_{{\check{A}}_{n}}=\frac{n(n+1)}{2}d-d-(n-1)(g-1), & \displaystyle \nonumber\\ \displaystyle & \displaystyle d_{\check{h}_{n}}=\frac{n(n-1)}{2}d+(n-1)(g-1),\quad d_{\check{h}_{n}}-d_{{\check{A}}_{n}}=-(n-1)d+2(n-1)(g-1). & \displaystyle\end{eqnarray}$$
Recall that, given
![]() $a\in A_{n}$
, we have been denoting the dimensions of
$a\in A_{n}$
, we have been denoting the dimensions of
 $J_{n,a},J_{n,a}^{\text{aff}}$
and
$J_{n,a},J_{n,a}^{\text{aff}}$
and
![]() $J_{n,a}^{\text{ab}}$
by
$J_{n,a}^{\text{ab}}$
by
 $d_{a}(J_{n}),d_{a}^{\text{aff}}(J_{n})$
and
$d_{a}(J_{n}),d_{a}^{\text{aff}}(J_{n})$
and
![]() $d_{a}^{\text{ab}}(J_{n})$
, respectively, and have been doing the same for
$d_{a}^{\text{ab}}(J_{n})$
, respectively, and have been doing the same for
 ${\check{a}}\in {\check{A}}_{n}\subseteq A_{n}$
,
${\check{a}}\in {\check{A}}_{n}\subseteq A_{n}$
,
![]() $\check{J}_{n,a}$
etc. (Recall that the Chevalley devissage is defined at geometric points, but the indicated dimensions depend only on the underlying Zariski point; as it is about to become clear, it is better to keep track of Zariski points.)
$\check{J}_{n,a}$
etc. (Recall that the Chevalley devissage is defined at geometric points, but the indicated dimensions depend only on the underlying Zariski point; as it is about to become clear, it is better to keep track of Zariski points.)
6.2 Proof of Theorem 1.0.2
Having done all the necessary preparation, the proof of Theorem 1.0.2 for the
![]() $\text{SL}_{n}$
socle, can now proceed parallel to the proof of Theorem 1.0.1 for the
$\text{SL}_{n}$
socle, can now proceed parallel to the proof of Theorem 1.0.1 for the
![]() $\text{GL}_{n}$
socle in [Reference Chaudouard and LaumonCL16, § 9].
$\text{GL}_{n}$
socle in [Reference Chaudouard and LaumonCL16, § 9].
Let
![]() $a\in {\check{A}}_{n}$
belong to
$a\in {\check{A}}_{n}$
belong to
 $\text{Socle}({R\check{h}_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })$
. Apply the support inequality (63) for the Zariski points in the socle:
$\text{Socle}({R\check{h}_{n}}_{\ast }\overline{\mathbb{Q}}_{\ell })$
. Apply the support inequality (63) for the Zariski points in the socle:
 $$\begin{eqnarray}d_{\check{h}_{n}}-d_{{\check{A}}_{n}}+d_{a}\geqslant d_{a}^{\text{ab}}(\check{J}_{n}).\end{eqnarray}$$
$$\begin{eqnarray}d_{\check{h}_{n}}-d_{{\check{A}}_{n}}+d_{a}\geqslant d_{a}^{\text{ab}}(\check{J}_{n}).\end{eqnarray}$$
By Lemma (4.2.1), we have
 $d_{a}^{\text{ab}}(\check{J}_{n})=d_{a}^{\text{ab}}(J_{n})-g$
, so that
$d_{a}^{\text{ab}}(\check{J}_{n})=d_{a}^{\text{ab}}(J_{n})-g$
, so that
 $$\begin{eqnarray}d_{\check{h}_{n}}-d_{{\check{A}}_{n}}+d_{a}\geqslant d_{a}^{\text{ab}}(J_{n})-g.\end{eqnarray}$$
$$\begin{eqnarray}d_{\check{h}_{n}}-d_{{\check{A}}_{n}}+d_{a}\geqslant d_{a}^{\text{ab}}(J_{n})-g.\end{eqnarray}$$
By combining (80) with (76), we get
 $$\begin{eqnarray}d_{\check{h}_{n}}-d_{{\check{A}}_{n}}\geqslant \mathop{\sum }_{k=1}^{s}(d_{h_{n_{k}}}-d_{A_{n_{k}}})+[d-(g-1)]-g.\end{eqnarray}$$
$$\begin{eqnarray}d_{\check{h}_{n}}-d_{{\check{A}}_{n}}\geqslant \mathop{\sum }_{k=1}^{s}(d_{h_{n_{k}}}-d_{A_{n_{k}}})+[d-(g-1)]-g.\end{eqnarray}$$
By using (78) for the left-hand side, and (77) for each
![]() $n_{k}$
for the right-hand side, we re-write (81) as follows:
$n_{k}$
for the right-hand side, we re-write (81) as follows:
 $$\begin{eqnarray}-(n-1)d+2(n-1)(g-1)\geqslant \mathop{\sum }_{k}[-n_{k}d+2n_{k}(g-1)+1]+[d-(g-1)]-g,\end{eqnarray}$$
$$\begin{eqnarray}-(n-1)d+2(n-1)(g-1)\geqslant \mathop{\sum }_{k}[-n_{k}d+2n_{k}(g-1)+1]+[d-(g-1)]-g,\end{eqnarray}$$
i.e.
 $$\begin{eqnarray}0\geqslant \biggl(n-\mathop{\sum }_{k}n_{k}\biggr)[d-2(g-1)]+(s-1).\end{eqnarray}$$
$$\begin{eqnarray}0\geqslant \biggl(n-\mathop{\sum }_{k}n_{k}\biggr)[d-2(g-1)]+(s-1).\end{eqnarray}$$
Since
 $d>2(g-1)$
(by assumption) and
$d>2(g-1)$
(by assumption) and
![]() $s\geqslant 1$
(by construction), we must have
$s\geqslant 1$
(by construction), we must have
 $\sum _{k}m_{k}n_{k}=n=\sum _{k}n_{k}$
and
$\sum _{k}m_{k}n_{k}=n=\sum _{k}n_{k}$
and
![]() $s=1$
.
$s=1$
.
The first condition forces all
![]() $m_{k}=1$
, so that the corresponding geometric spectral curve
$m_{k}=1$
, so that the corresponding geometric spectral curve
![]() ${\mathcal{C}}_{\overline{a}}$
is reduced.
${\mathcal{C}}_{\overline{a}}$
is reduced.
The second condition
![]() $s=1$
means that in addition to being reduced, the geometric spectral curve
$s=1$
means that in addition to being reduced, the geometric spectral curve
![]() ${\mathcal{C}}_{\overline{a}}$
must be integral, i.e.
${\mathcal{C}}_{\overline{a}}$
must be integral, i.e.
![]() $a\in {\check{A}}_{n}^{\text{ell}}$
.◻
$a\in {\check{A}}_{n}^{\text{ell}}$
.◻
We conclude with two remarks.
Remark 6.2.1 (Positive characteristic).
Chaudouard has informed us that the main Theorem 1.0.1 for the
![]() $\text{GL}_{n}$
socle in [Reference Chaudouard and LaumonCL16], should also hold over an algebraically closed field of positive characteristic bigger than
$\text{GL}_{n}$
socle in [Reference Chaudouard and LaumonCL16], should also hold over an algebraically closed field of positive characteristic bigger than
![]() $n$
. This should be the case in view of the fact that one major obstacle in proving such theorem in positive characteristic had been the lack of the positive-characteristic analogue of the Severi inequality (41). At least as far as the corresponding inequality at the level of the semiuniversal (miniversal) deformation for integral (even reduced) locally planar curves, this obstacle has been removed in [Reference Rapagnetta, Melo and VivianiRMV12, Theorem 3.3]. The restriction on the characteristic seems natural in view of the fact that the spectral covers have order
$n$
. This should be the case in view of the fact that one major obstacle in proving such theorem in positive characteristic had been the lack of the positive-characteristic analogue of the Severi inequality (41). At least as far as the corresponding inequality at the level of the semiuniversal (miniversal) deformation for integral (even reduced) locally planar curves, this obstacle has been removed in [Reference Rapagnetta, Melo and VivianiRMV12, Theorem 3.3]. The restriction on the characteristic seems natural in view of the fact that the spectral covers have order
![]() $n$
, and also because of formulae such as (53). We did not verify whether all of our arguments could be easily modified to yield the positive characteristic
$n$
, and also because of formulae such as (53). We did not verify whether all of our arguments could be easily modified to yield the positive characteristic
![]() $({>}n)$
cases of Theorems 1.0.1 and 1.0.2, on the
$({>}n)$
cases of Theorems 1.0.1 and 1.0.2, on the
![]() $\text{GL}_{n}$
and
$\text{GL}_{n}$
and
![]() $\text{SL}_{n}$
socles.
$\text{SL}_{n}$
socles.
Remark 6.2.2 (
 $D=K_{C}$
).
$D=K_{C}$
).
The methods of proofs of [Reference Chaudouard and LaumonCL16] for
![]() $\text{GL}_{n}$
, and of this paper for
$\text{GL}_{n}$
, and of this paper for
![]() $\text{SL}_{n}$
, do not work in the very interesting case when
$\text{SL}_{n}$
, do not work in the very interesting case when
 $D=K_{C}$
. There is even more geometry at play in that symplectic/integrable case. See [Reference Chaudouard and LaumonCL16, § 11] for a short discussion of the
$D=K_{C}$
. There is even more geometry at play in that symplectic/integrable case. See [Reference Chaudouard and LaumonCL16, § 11] for a short discussion of the
 $D=K_{C}$
case.
$D=K_{C}$
case.
Acknowledgements
I thank Pierre-Henri Chaudouard, Brian Conrad, Jochen Heinloth, Andrea Maffei, Eyal Markman, Luca Migliorini, Mircea Mustaţă, Christian Pauly, Giulia Saccà and Jason Starr for very stimulating conversations. I am very grateful to the anonymous referee for suggestions on improving the article.