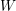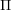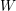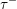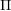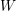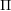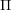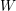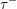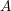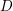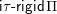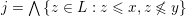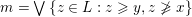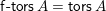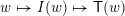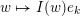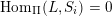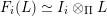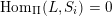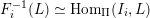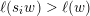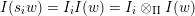1 Introduction
Let
![]() $\unicode[STIX]{x1D6E5}$
be a simply laced Dynkin diagram and
$\unicode[STIX]{x1D6E5}$
be a simply laced Dynkin diagram and
![]() $W$
the corresponding Weyl group. Once we fix an orientation
$W$
the corresponding Weyl group. Once we fix an orientation
![]() $Q$
of
$Q$
of
![]() $\unicode[STIX]{x1D6E5}$
, then the representation theory of
$\unicode[STIX]{x1D6E5}$
, then the representation theory of
![]() $Q$
categorifies the root system associated with
$Q$
categorifies the root system associated with
![]() $\unicode[STIX]{x1D6E5}$
in the sense that we have Gabriel’s bijection between positive roots and indecomposable representations of
$\unicode[STIX]{x1D6E5}$
in the sense that we have Gabriel’s bijection between positive roots and indecomposable representations of
![]() $Q$
. Throughout this paper, we denote by
$Q$
. Throughout this paper, we denote by
![]() $\unicode[STIX]{x1D6F1}$
the preprojective algebra of
$\unicode[STIX]{x1D6F1}$
the preprojective algebra of
![]() $\unicode[STIX]{x1D6E5}$
over an arbitrary field
$\unicode[STIX]{x1D6E5}$
over an arbitrary field
![]() $k$
. It unifies the representation theory of different quivers with the same underlying graph
$k$
. It unifies the representation theory of different quivers with the same underlying graph
![]() $\unicode[STIX]{x1D6E5}$
, and its various aspects have been studied, e.g. [Reference Baumann, Kamnitzer and TingleyBKT14, Reference Baer, Geigle and LenzingBGL87, Reference Buan, Iyama, Reiten and ScottBIRS09, Reference Crawley-Boevey and HollandCH98, Reference Dlab and RingelDR80, Reference Geiss, Leclerc and SchröerGLS11, Reference LusztigLus91, Reference Kashiwara and SaitoKS97, Reference NakajimaNak94]. Mizuno [Reference MizunoMiz14] showed that the support
$\unicode[STIX]{x1D6E5}$
, and its various aspects have been studied, e.g. [Reference Baumann, Kamnitzer and TingleyBKT14, Reference Baer, Geigle and LenzingBGL87, Reference Buan, Iyama, Reiten and ScottBIRS09, Reference Crawley-Boevey and HollandCH98, Reference Dlab and RingelDR80, Reference Geiss, Leclerc and SchröerGLS11, Reference LusztigLus91, Reference Kashiwara and SaitoKS97, Reference NakajimaNak94]. Mizuno [Reference MizunoMiz14] showed that the support
![]() $\unicode[STIX]{x1D70F}$
-tilting theory of
$\unicode[STIX]{x1D70F}$
-tilting theory of
![]() $\unicode[STIX]{x1D6F1}$
categorifies the Weyl group
$\unicode[STIX]{x1D6F1}$
categorifies the Weyl group
![]() $W$
with the weak order in the following sense: there exists a bijection
$W$
with the weak order in the following sense: there exists a bijection
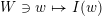 $W\ni w\mapsto I(w)$
from
$W\ni w\mapsto I(w)$
from
![]() $W$
to the set
$W$
to the set
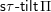 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
of support
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
of support
![]() $\unicode[STIX]{x1D70F}$
-tilting
$\unicode[STIX]{x1D70F}$
-tilting
![]() $\unicode[STIX]{x1D6F1}$
-modules with the property that
$\unicode[STIX]{x1D6F1}$
-modules with the property that
![]() $v\leqslant w$
in the weak order on
$v\leqslant w$
in the weak order on
![]() $W$
if and only if
$W$
if and only if
 $I(v)\geqslant I(w)$
in the generation order on
$I(v)\geqslant I(w)$
in the generation order on
 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
. The ideal
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
. The ideal
![]() $I(w)$
was introduced in [Reference Iyama and ReitenIR08, Reference Buan, Iyama, Reiten and ScottBIRS09] and has been studied by several authors, e.g. [Reference Aihara and MizunoAM17, Reference AmiotAmi09, Reference Amiot, Iyama, Reiten and TodorovAIRT12, Reference Baumann, Kamnitzer and TingleyBKT14, Reference Geiss, Leclerc and SchröerGLS11, Reference KimuraKim18, Reference LeclercLec16, Reference MarksMar17, Reference Oppermann, Reiten and ThomasORT15, Reference Sekiya and YamauraSY13]. In what follows, we will overload the symbol
$I(w)$
was introduced in [Reference Iyama and ReitenIR08, Reference Buan, Iyama, Reiten and ScottBIRS09] and has been studied by several authors, e.g. [Reference Aihara and MizunoAM17, Reference AmiotAmi09, Reference Amiot, Iyama, Reiten and TodorovAIRT12, Reference Baumann, Kamnitzer and TingleyBKT14, Reference Geiss, Leclerc and SchröerGLS11, Reference KimuraKim18, Reference LeclercLec16, Reference MarksMar17, Reference Oppermann, Reiten and ThomasORT15, Reference Sekiya and YamauraSY13]. In what follows, we will overload the symbol
![]() $W$
to denote not only the group
$W$
to denote not only the group
![]() $W$
, but also the weak order on
$W$
, but also the weak order on
![]() $W$
.
$W$
.
The weak order on
![]() $W$
is a lattice [Reference Björner and BrentiBB05]: a partial order such that meets (greatest lower bounds) and joins (least upper bounds) exist. It is enlightening to take a more algebraic point of view of lattices, viewing a lattice as a set with two binary operations (meet and join). Seen in this light, the categorification of
$W$
is a lattice [Reference Björner and BrentiBB05]: a partial order such that meets (greatest lower bounds) and joins (least upper bounds) exist. It is enlightening to take a more algebraic point of view of lattices, viewing a lattice as a set with two binary operations (meet and join). Seen in this light, the categorification of
![]() $W$
by support
$W$
by support
![]() $\unicode[STIX]{x1D70F}$
-tilting theory is the categorification of an algebraic object (a lattice) in terms of another algebraic object (a finite-dimensional algebra). In both of these algebraic settings, there is an important algebraic quotient operation. Quotients of the weak order are governed by lattice congruences, while quotients of the preprojective algebra are governed by ideals. A natural question is whether these two notions of quotient are related. The answer is yes, and the relationship turns out to be very nice.
$\unicode[STIX]{x1D70F}$
-tilting theory is the categorification of an algebraic object (a lattice) in terms of another algebraic object (a finite-dimensional algebra). In both of these algebraic settings, there is an important algebraic quotient operation. Quotients of the weak order are governed by lattice congruences, while quotients of the preprojective algebra are governed by ideals. A natural question is whether these two notions of quotient are related. The answer is yes, and the relationship turns out to be very nice.
This paper and a companion paper [Reference Demonet, Iyama, Reiten, Reading and ThomasDIRRT17] concern the relationship between the two notions of quotient. In the other paper, we observe, for a more general algebra
![]() $A$
and an ideal
$A$
and an ideal
![]() $I$
of
$I$
of
![]() $A$
, that
$A$
, that
 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}(A/I)$
is a lattice quotient of
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}(A/I)$
is a lattice quotient of
 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
and we give necessary conditions for lattice congruences which arise in this way from quotients of
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
and we give necessary conditions for lattice congruences which arise in this way from quotients of
![]() $\unicode[STIX]{x1D6F1}$
. We study the combinatorics of such algebraic quotients of the weak order in general, and in the special case where
$\unicode[STIX]{x1D6F1}$
. We study the combinatorics of such algebraic quotients of the weak order in general, and in the special case where
![]() $\unicode[STIX]{x1D6F1}/I$
is hereditary. We also work out, in detail, the combinatorics of algebraic quotients in type A.
$\unicode[STIX]{x1D6F1}/I$
is hereditary. We also work out, in detail, the combinatorics of algebraic quotients in type A.
Whereas [Reference Demonet, Iyama, Reiten, Reading and ThomasDIRRT17] starts with algebra quotients and determines what happens to the corresponding lattices, this paper starts from the other direction. Here, we start with the rich combinatorics of (arbitrary, not necessarily algebraic) lattice congruences of
![]() $W$
and find that it appears naturally within the representation theory of
$W$
and find that it appears naturally within the representation theory of
![]() $\unicode[STIX]{x1D6F1}$
.
$\unicode[STIX]{x1D6F1}$
.
The set of all lattice congruences of
![]() $L$
form a lattice
$L$
form a lattice
![]() $\mathsf{Con}\,L$
, and the join-irreducible elements of
$\mathsf{Con}\,L$
, and the join-irreducible elements of
![]() $\mathsf{Con}\,L$
are called the join-irreducible congruences (see § 2.1 for details). The combinatorial approach to congruences of a finite lattice
$\mathsf{Con}\,L$
are called the join-irreducible congruences (see § 2.1 for details). The combinatorial approach to congruences of a finite lattice
![]() $L$
begins with the connection between arrows in the Hasse quiver of
$L$
begins with the connection between arrows in the Hasse quiver of
![]() $L$
, join-irreducible elements of
$L$
, join-irreducible elements of
![]() $L$
, and join-irreducible congruences on
$L$
, and join-irreducible congruences on
![]() $L$
. We will overload the symbol
$L$
. We will overload the symbol
![]() $W$
, using it to denote the Hasse quiver of the weak order on
$W$
, using it to denote the Hasse quiver of the weak order on
![]() $W$
.
$W$
.
Our first main theorem connects join-irreducible elements of
![]() $W$
and join-irreducible congruences on
$W$
and join-irreducible congruences on
![]() $W$
to layers of
$W$
to layers of
![]() $\unicode[STIX]{x1D6F1}$
. A
$\unicode[STIX]{x1D6F1}$
. A
![]() $\unicode[STIX]{x1D6F1}$
-module is called a layer if it is isomorphic to
$\unicode[STIX]{x1D6F1}$
-module is called a layer if it is isomorphic to
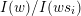 $I(w)/I(ws_{i})$
for an arrow
$I(w)/I(ws_{i})$
for an arrow
 $ws_{i}\rightarrow w$
in the Hasse quiver of
$ws_{i}\rightarrow w$
in the Hasse quiver of
![]() $W$
, see [Reference Amiot, Iyama, Reiten and TodorovAIRT12].
$W$
, see [Reference Amiot, Iyama, Reiten and TodorovAIRT12].
Theorem 1.1. There exist bijections between the following sets.
∙ The set
 $\mathsf{j}\text{-}\mathsf{Irr}\,W$
of join-irreducible elements of
$\mathsf{j}\text{-}\mathsf{Irr}\,W$
of join-irreducible elements of
 $W$
.
$W$
.∙ The set
 $\mathsf{m}\text{-}\mathsf{Irr}\,W$
of meet-irreducible elements of
$\mathsf{m}\text{-}\mathsf{Irr}\,W$
of meet-irreducible elements of
 $W$
.
$W$
.∙ The set
 $\mathsf{Con}_{\mathsf{JI}}(W)$
of join-irreducible congruences of
$\mathsf{Con}_{\mathsf{JI}}(W)$
of join-irreducible congruences of
 $W$
.
$W$
.∙ The set
 $\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}$
of indecomposable
$\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}$
of indecomposable
 $\unicode[STIX]{x1D70F}$
-rigid
$\unicode[STIX]{x1D70F}$
-rigid
 $\unicode[STIX]{x1D6F1}$
-modules.
$\unicode[STIX]{x1D6F1}$
-modules.∙ The set
 $\mathsf{i}\unicode[STIX]{x1D70F}^{{-}}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}$
of indecomposable
$\mathsf{i}\unicode[STIX]{x1D70F}^{{-}}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}$
of indecomposable
 $\unicode[STIX]{x1D70F}^{-}$
-rigid
$\unicode[STIX]{x1D70F}^{-}$
-rigid
 $\unicode[STIX]{x1D6F1}$
-modules.
$\unicode[STIX]{x1D6F1}$
-modules.∙ The set
 $\mathsf{layer}\,\unicode[STIX]{x1D6F1}$
of layers of
$\mathsf{layer}\,\unicode[STIX]{x1D6F1}$
of layers of
 $\unicode[STIX]{x1D6F1}$
.
$\unicode[STIX]{x1D6F1}$
.
We prove Theorem 1.1 and give explicit bijections as part of Theorem 4.1. The fact that join-irreducible elements, meet-irreducible elements, and join-irreducible congruences of
![]() $W$
are all in bijection is known, and this property of a lattice is called congruence uniformity (in the sense of Day [Reference DayDay94]). This was proved in [Reference Caspard, Le Conte de Poly-Barbut and MorvanCLM04] (where in fact an equivalent property called boundedness was established).
$W$
are all in bijection is known, and this property of a lattice is called congruence uniformity (in the sense of Day [Reference DayDay94]). This was proved in [Reference Caspard, Le Conte de Poly-Barbut and MorvanCLM04] (where in fact an equivalent property called boundedness was established).
The main content of Theorem 1.1 is the unexpectedly deep link between the representation theory of the preprojective algebra and the lattice theory of weak order on the corresponding Weyl group. As part of establishing this link, we have also proved some new results within the representation theory of preprojective algebras which we believe to be of independent interest. Our second main theorem gives two additional algebraic descriptions of layers of
![]() $\unicode[STIX]{x1D6F1}$
. We say that a
$\unicode[STIX]{x1D6F1}$
. We say that a
![]() $\unicode[STIX]{x1D6F1}$
-module
$\unicode[STIX]{x1D6F1}$
-module
![]() $L$
is a brick if
$L$
is a brick if
 $\operatorname{End}_{\unicode[STIX]{x1D6F1}}(L)$
is a division algebra, and a stone if
$\operatorname{End}_{\unicode[STIX]{x1D6F1}}(L)$
is a division algebra, and a stone if
![]() $L$
is a brick satisfying
$L$
is a brick satisfying
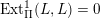 $\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(L,L)=0$
[Reference Happel, Hartlieb, Kerner and UngerHHKU96, Reference Kerner and LukasKL94]. Let
$\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(L,L)=0$
[Reference Happel, Hartlieb, Kerner and UngerHHKU96, Reference Kerner and LukasKL94]. Let
![]() $\widehat{\unicode[STIX]{x1D6F1}}$
be the preprojective algebra of the extended Dynkin type corresponding to
$\widehat{\unicode[STIX]{x1D6F1}}$
be the preprojective algebra of the extended Dynkin type corresponding to
![]() $\unicode[STIX]{x1D6F1}$
. Let
$\unicode[STIX]{x1D6F1}$
. Let
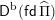 $\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
be the bounded derived category of finite-dimensional
$\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
be the bounded derived category of finite-dimensional
![]() $\widehat{\unicode[STIX]{x1D6F1}}$
-modules. An object
$\widehat{\unicode[STIX]{x1D6F1}}$
-modules. An object
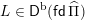 $L\in \mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
is called 2-spherical if
$L\in \mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
is called 2-spherical if
 $\dim _{k}\operatorname{Hom}_{\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})}(L,L[i])$
is
$\dim _{k}\operatorname{Hom}_{\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})}(L,L[i])$
is
![]() $1$
for
$1$
for
![]() $i=0,2$
and 0 otherwise. (See [Reference Seidel and ThomasST01].)
$i=0,2$
and 0 otherwise. (See [Reference Seidel and ThomasST01].)
Theorem 1.2. The following classes of
![]() $\unicode[STIX]{x1D6F1}$
-modules are the same.
$\unicode[STIX]{x1D6F1}$
-modules are the same.
∙ Layers of
 $\unicode[STIX]{x1D6F1}$
.
$\unicode[STIX]{x1D6F1}$
.∙ Bricks of
 $\unicode[STIX]{x1D6F1}$
.
$\unicode[STIX]{x1D6F1}$
.∙ Stones of
 $\unicode[STIX]{x1D6F1}$
.
$\unicode[STIX]{x1D6F1}$
.∙
 $\unicode[STIX]{x1D6F1}$
-modules which are 2-spherical as
$\unicode[STIX]{x1D6F1}$
-modules which are 2-spherical as
 $\widehat{\unicode[STIX]{x1D6F1}}$
-modules.
$\widehat{\unicode[STIX]{x1D6F1}}$
-modules.
Moreover any module
![]() $L$
in these classes satisfies
$L$
in these classes satisfies
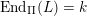 $\operatorname{End}_{\unicode[STIX]{x1D6F1}}(L)=k$
.
$\operatorname{End}_{\unicode[STIX]{x1D6F1}}(L)=k$
.
It was shown by Bolten [Reference BoltenBol10] that layers and bricks are the same. Also a related observation was given by Sekiya and Yamaura (private communication).
Our third main result concerns the interplay between arrows in the Hasse quiver of
![]() $W$
, join-irreducible elements of
$W$
, join-irreducible elements of
![]() $W$
, and join-irreducible congruences on
$W$
, and join-irreducible congruences on
![]() $W$
. We refer to § 2.1 for details about the following notions. Given any arrow
$W$
. We refer to § 2.1 for details about the following notions. Given any arrow
![]() $x\rightarrow y$
in the Hasse quiver of an arbitrary finite lattice
$x\rightarrow y$
in the Hasse quiver of an arbitrary finite lattice
![]() $L$
, define
$L$
, define
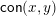 $\mathsf{con}(x,y)$
to be the smallest congruence on
$\mathsf{con}(x,y)$
to be the smallest congruence on
![]() $L$
such that
$L$
such that
![]() $x\equiv y$
. This is a join-irreducible congruence. If
$x\equiv y$
. This is a join-irreducible congruence. If
![]() $j$
is a join-irreducible element of
$j$
is a join-irreducible element of
![]() $L$
, we write
$L$
, we write
![]() $j_{\ast }$
for the unique element covered by
$j_{\ast }$
for the unique element covered by
![]() $j$
in
$j$
in
![]() $L$
. The congruence
$L$
. The congruence
 $\mathsf{con}(j,j_{\ast })$
is thus join-irreducible, and it turns out that every join-irreducible element is
$\mathsf{con}(j,j_{\ast })$
is thus join-irreducible, and it turns out that every join-irreducible element is
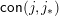 $\mathsf{con}(j,j_{\ast })$
for some
$\mathsf{con}(j,j_{\ast })$
for some
![]() $j$
. When
$j$
. When
![]() $L$
is the weak order on
$L$
is the weak order on
![]() $W$
, the map
$W$
, the map
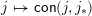 $j\mapsto \mathsf{con}(j,j_{\ast })$
is the bijection from join-irreducible elements of
$j\mapsto \mathsf{con}(j,j_{\ast })$
is the bijection from join-irreducible elements of
![]() $W$
to join-irreducible congruences from Theorem 1.1. Since each Hasse arrow of
$W$
to join-irreducible congruences from Theorem 1.1. Since each Hasse arrow of
![]() $W$
specifies a join-irreducible congruence, and since join-irreducible congruences are in bijection with join-irreducible elements, we obtain a labelling of the Hasse arrows of
$W$
specifies a join-irreducible congruence, and since join-irreducible congruences are in bijection with join-irreducible elements, we obtain a labelling of the Hasse arrows of
![]() $W$
by join-irreducible elements. We call this the join-irreducible labelling of
$W$
by join-irreducible elements. We call this the join-irreducible labelling of
![]() $W$
. Besides this labelling coming from lattice theory, there is a labelling of the Hasse quiver coming from representation theory, namely the layer labelling. This labels a Hasse arrow
$W$
. Besides this labelling coming from lattice theory, there is a labelling of the Hasse quiver coming from representation theory, namely the layer labelling. This labels a Hasse arrow
 $ws_{i}\rightarrow w$
by the layer
$ws_{i}\rightarrow w$
by the layer
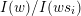 $I(w)/I(ws_{i})$
. The layer labellings for type
$I(w)/I(ws_{i})$
. The layer labellings for type
![]() $A_{2}$
and
$A_{2}$
and
![]() $A_{3}$
are given in Figures 1 and 2.
$A_{3}$
are given in Figures 1 and 2.

Figure 1. Layer labelling for
![]() $A_{2}$
.
$A_{2}$
.

Figure 2. Layer labelling for
![]() $A_{3}$
.
$A_{3}$
.
Theorem 1.3. The map
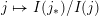 $j\mapsto I(j_{\ast })/I(j)$
takes the join-irreducible labelling of
$j\mapsto I(j_{\ast })/I(j)$
takes the join-irreducible labelling of
![]() $W$
to the layer labelling on
$W$
to the layer labelling on
![]() $W$
. That is, given a Hasse arrow
$W$
. That is, given a Hasse arrow
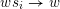 $ws_{i}\rightarrow w$
labelled by the join-irreducible element
$ws_{i}\rightarrow w$
labelled by the join-irreducible element
![]() $j$
, which covers the element
$j$
, which covers the element
![]() $j_{\ast }$
, the layer label on
$j_{\ast }$
, the layer label on
 $ws_{i}\rightarrow w$
is
$ws_{i}\rightarrow w$
is
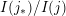 $I(j_{\ast })/I(j)$
.
$I(j_{\ast })/I(j)$
.
This is also proved as part of Theorem 4.1, which gives a commutative diagram shown in Figure 3 between important objects. We include this diagram here, although some elements of it have not yet been explained, as a road map to the major results of the paper. The maps are bijections or surjections as marked with tildes ‘
![]() ${\sim}$
’ or double-headed arrows.
${\sim}$
’ or double-headed arrows.

Figure 3. The correspondences established in Theorem 4.1.
Given two Hasse arrows
![]() $x\rightarrow y$
and
$x\rightarrow y$
and
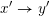 $x^{\prime }\rightarrow y^{\prime }$
of a lattice
$x^{\prime }\rightarrow y^{\prime }$
of a lattice
![]() $L$
, we say that
$L$
, we say that
![]() $x\rightarrow y$
forces
$x\rightarrow y$
forces
 $x^{\prime }\rightarrow y^{\prime }$
if
$x^{\prime }\rightarrow y^{\prime }$
if
 $\mathsf{con}(x,y)\geqslant \mathsf{con}(x^{\prime },y^{\prime })$
in
$\mathsf{con}(x,y)\geqslant \mathsf{con}(x^{\prime },y^{\prime })$
in
![]() $\mathsf{Con}(L)$
. In other words,
$\mathsf{Con}(L)$
. In other words,
![]() $x\rightarrow y$
forces
$x\rightarrow y$
forces
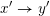 $x^{\prime }\rightarrow y^{\prime }$
if every congruence setting
$x^{\prime }\rightarrow y^{\prime }$
if every congruence setting
![]() $x\equiv y$
also sets
$x\equiv y$
also sets
![]() $x^{\prime }\equiv y^{\prime }$
. In the weak order on
$x^{\prime }\equiv y^{\prime }$
. In the weak order on
![]() $W$
, the forcing order on Hasse arrows restricts to a partial order on Hasse arrows of the form
$W$
, the forcing order on Hasse arrows restricts to a partial order on Hasse arrows of the form
![]() $j\rightarrow j_{\ast }$
such that
$j\rightarrow j_{\ast }$
such that
![]() $j$
is join-irreducible. We think of this as a partial order on join-irreducible elements and call it the forcing order on join-irreducible elements of
$j$
is join-irreducible. We think of this as a partial order on join-irreducible elements and call it the forcing order on join-irreducible elements of
![]() $W$
.
$W$
.
We say that a pair of layer modules
![]() $X,Y$
form a doubleton if
$X,Y$
form a doubleton if
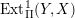 $\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(Y,X)$
and
$\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(Y,X)$
and
 $\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(X,Y)$
are one-dimensional, and the corresponding extensions are again layer modules. We define the doubleton extension order on layer modules to be the transitive closure of the relation with
$\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(X,Y)$
are one-dimensional, and the corresponding extensions are again layer modules. We define the doubleton extension order on layer modules to be the transitive closure of the relation with
![]() $A>B$
if there exists a doubleton
$A>B$
if there exists a doubleton
![]() $A,C$
such that
$A,C$
such that
![]() $B$
is the extension of
$B$
is the extension of
![]() $A$
by
$A$
by
![]() $C$
or of
$C$
or of
![]() $C$
by
$C$
by
![]() $A$
. Our fourth main result is the following.
$A$
. Our fourth main result is the following.
Theorem 1.4. The map
 $j\mapsto I(j_{\ast })/I(j)$
is an isomorphism from the forcing order on join-irreducible elements of
$j\mapsto I(j_{\ast })/I(j)$
is an isomorphism from the forcing order on join-irreducible elements of
![]() $W$
to the doubleton extension order on layer modules of
$W$
to the doubleton extension order on layer modules of
![]() $\unicode[STIX]{x1D6F1}$
.
$\unicode[STIX]{x1D6F1}$
.
In addition to these general results, we show that in type
![]() $A_{n}$
, the doubleton extension order coincides with the reverse of the subfactor order (see Theorem 5.5). In § 6, we give an explicit combinatorial description of the indecomposable
$A_{n}$
, the doubleton extension order coincides with the reverse of the subfactor order (see Theorem 5.5). In § 6, we give an explicit combinatorial description of the indecomposable
![]() $\unicode[STIX]{x1D70F}$
-rigid modules in types
$\unicode[STIX]{x1D70F}$
-rigid modules in types
![]() $A_{n}$
and
$A_{n}$
and
![]() $D_{n}$
. For these cases, elements of the Weyl group
$D_{n}$
. For these cases, elements of the Weyl group
![]() $W$
are given by (signed) permutations, and join-irreducible elements in
$W$
are given by (signed) permutations, and join-irreducible elements in
![]() $W$
have simple characterizations. We prove in Theorems 6.1, 6.5 and 6.12 that the indecomposable
$W$
have simple characterizations. We prove in Theorems 6.1, 6.5 and 6.12 that the indecomposable
![]() $\unicode[STIX]{x1D70F}$
-rigid
$\unicode[STIX]{x1D70F}$
-rigid
![]() $\unicode[STIX]{x1D6F1}$
-modules have direct combinatorial descriptions in terms of the corresponding (signed) permutations. These concrete examples complement the general theory worked out in the previous sections.
$\unicode[STIX]{x1D6F1}$
-modules have direct combinatorial descriptions in terms of the corresponding (signed) permutations. These concrete examples complement the general theory worked out in the previous sections.
2 Preliminaries
In this section, we review the necessary background on lattices, the weak order, and finite-dimensional algebras.
2.1 Lattice-theoretic preliminaries
Proofs and additional details for the material reviewed here can be found in [Reference ReadingRea16a, §§ 9–5 and 9–6].
For any poset
![]() $P$
, we say that
$P$
, we say that
![]() $x$
covers
$x$
covers
![]() $y$
, and we write
$y$
, and we write
![]() $x\gtrdot y$
, if
$x\gtrdot y$
, if
![]() $x>y$
, and there is no
$x>y$
, and there is no
![]() $z\in P$
such that
$z\in P$
such that
 $x>z>y$
. We represent
$x>z>y$
. We represent
![]() $P$
by its Hasse quiver
$P$
by its Hasse quiver
 $\mathsf{Hasse}(P)=(P,\mathsf{Hasse}_{1}(P))$
, whose vertex set is
$\mathsf{Hasse}(P)=(P,\mathsf{Hasse}_{1}(P))$
, whose vertex set is
![]() $P$
, and whose arrow set
$P$
, and whose arrow set
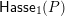 $\mathsf{Hasse}_{1}(P)$
consists of all arrows
$\mathsf{Hasse}_{1}(P)$
consists of all arrows
![]() $v\rightarrow w$
where
$v\rightarrow w$
where
![]() $v$
covers
$v$
covers
![]() $w$
.
$w$
.
Given a subset
![]() $S$
of
$S$
of
![]() $P$
, if there is a unique smallest element which is greater than or equal to all elements in
$P$
, if there is a unique smallest element which is greater than or equal to all elements in
![]() $S$
, then this least upper bound is called the join of
$S$
, then this least upper bound is called the join of
![]() $S$
and denoted
$S$
and denoted
![]() $\vee S$
. Similarly, if there is a unique largest element in
$\vee S$
. Similarly, if there is a unique largest element in
![]() $P$
that is less than or equal to all elements in
$P$
that is less than or equal to all elements in
![]() $S$
, then this element is called the meet of
$S$
, then this element is called the meet of
![]() $S$
and denoted
$S$
and denoted
![]() $\bigwedge S$
. A lattice
$\bigwedge S$
. A lattice
![]() $L$
is a poset in which every pair
$L$
is a poset in which every pair
![]() $a,b$
of elements in
$a,b$
of elements in
![]() $L$
has both a meet
$L$
has both a meet
![]() $a\wedge b$
and a join
$a\wedge b$
and a join
![]() $a\vee b$
, and a complete lattice
$a\vee b$
, and a complete lattice
![]() $L$
is a poset in which every subset
$L$
is a poset in which every subset
![]() $S$
of
$S$
of
![]() $L$
has both a meet and a join. (Every finite subset of a lattice
$L$
has both a meet and a join. (Every finite subset of a lattice
![]() $L$
has both a meet and a join, but an infinite lattice fails to be complete if it has some infinite subset without a meet or without a join.)
$L$
has both a meet and a join, but an infinite lattice fails to be complete if it has some infinite subset without a meet or without a join.)
We restrict our attention to finite lattices in this paper. Some of the assertions made here for finite lattices hold for infinite lattice as well, but some do not.
An element
![]() $j$
of a finite lattice
$j$
of a finite lattice
![]() $L$
is called join-irreducible, whenever
$L$
is called join-irreducible, whenever
 $j=a\vee b$
for some
$j=a\vee b$
for some
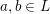 $a,b\in L$
, either
$a,b\in L$
, either
![]() $a=j$
or
$a=j$
or
![]() $b=j$
or both, and
$b=j$
or both, and
![]() $j$
is not the minimum element of
$j$
is not the minimum element of
![]() $L$
. Equivalently,
$L$
. Equivalently,
![]() $j$
is join-irreducible if and only if it covers exactly one element of
$j$
is join-irreducible if and only if it covers exactly one element of
![]() $L$
. We write
$L$
. We write
![]() $j_{\ast }$
for the unique element covered by a join-irreducible element
$j_{\ast }$
for the unique element covered by a join-irreducible element
![]() $j$
. Dually, a meet-irreducible element of
$j$
. Dually, a meet-irreducible element of
![]() $L$
is an element
$L$
is an element
![]() $m$
that is covered by a unique element
$m$
that is covered by a unique element
![]() $m^{\ast }$
. The set of join-irreducible (respectively, meet-irreducible) elements of
$m^{\ast }$
. The set of join-irreducible (respectively, meet-irreducible) elements of
![]() $L$
is denoted
$L$
is denoted
![]() $\mathsf{j}\text{-}\mathsf{Irr}\,L$
(respectively,
$\mathsf{j}\text{-}\mathsf{Irr}\,L$
(respectively,
![]() $\mathsf{m}\text{-}\mathsf{Irr}\,L$
).
$\mathsf{m}\text{-}\mathsf{Irr}\,L$
).
A (lattice) congruence on a lattice
![]() $L$
is an equivalence relation
$L$
is an equivalence relation
![]() $\unicode[STIX]{x1D6E9}$
having the property that the
$\unicode[STIX]{x1D6E9}$
having the property that the
![]() $\unicode[STIX]{x1D6E9}$
-class of
$\unicode[STIX]{x1D6E9}$
-class of
![]() $a\vee b$
depends only on the
$a\vee b$
depends only on the
![]() $\unicode[STIX]{x1D6E9}$
-class of
$\unicode[STIX]{x1D6E9}$
-class of
![]() $a$
and the
$a$
and the
![]() $\unicode[STIX]{x1D6E9}$
-class of
$\unicode[STIX]{x1D6E9}$
-class of
![]() $b$
, and having the same property for meets. Given a congruence
$b$
, and having the same property for meets. Given a congruence
![]() $\unicode[STIX]{x1D6E9}$
on
$\unicode[STIX]{x1D6E9}$
on
![]() $L$
, the set
$L$
, the set
![]() $L/\unicode[STIX]{x1D6E9}$
of
$L/\unicode[STIX]{x1D6E9}$
of
![]() $\unicode[STIX]{x1D6E9}$
-classes has a well-defined meet and join operation, making
$\unicode[STIX]{x1D6E9}$
-classes has a well-defined meet and join operation, making
![]() $L/\unicode[STIX]{x1D6E9}$
a lattice called the quotient of
$L/\unicode[STIX]{x1D6E9}$
a lattice called the quotient of
![]() $L$
modulo
$L$
modulo
![]() $\unicode[STIX]{x1D6E9}$
.
$\unicode[STIX]{x1D6E9}$
.
The set of all equivalence relations on a given set
![]() $L$
forms a lattice, where the meet of two relations is given by the intersection of relations and the join of two relations is given by the transitive closure of union of relations. When
$L$
forms a lattice, where the meet of two relations is given by the intersection of relations and the join of two relations is given by the transitive closure of union of relations. When
![]() $L$
is a lattice, the set
$L$
is a lattice, the set
![]() $\mathsf{Con}(L)$
consisting of congruences of
$\mathsf{Con}(L)$
consisting of congruences of
![]() $L$
is a sublattice of the lattice of equivalence relations. Furthermore,
$L$
is a sublattice of the lattice of equivalence relations. Furthermore,
![]() $\mathsf{Con}(L)$
is a distributive lattice. We denote by
$\mathsf{Con}(L)$
is a distributive lattice. We denote by
 $\mathsf{Con}_{\mathsf{JI}}(L)$
the set of all join-irreducible congruences. As mentioned in the introduction, we have a surjective map
$\mathsf{Con}_{\mathsf{JI}}(L)$
the set of all join-irreducible congruences. As mentioned in the introduction, we have a surjective map
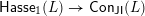 $\mathsf{Hasse}_{1}(L)\rightarrow \mathsf{Con}_{\mathsf{JI}}(L)$
sending an arrow
$\mathsf{Hasse}_{1}(L)\rightarrow \mathsf{Con}_{\mathsf{JI}}(L)$
sending an arrow
![]() $x\rightarrow y$
to
$x\rightarrow y$
to
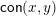 $\mathsf{con}(x,y)$
. Here
$\mathsf{con}(x,y)$
. Here
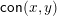 $\mathsf{con}(x,y)$
is the meet, in
$\mathsf{con}(x,y)$
is the meet, in
![]() $\mathsf{Con}(L)$
, of all congruences with
$\mathsf{Con}(L)$
, of all congruences with
![]() $x\equiv y$
. A congruence
$x\equiv y$
. A congruence
![]() $\unicode[STIX]{x1D6E9}$
on a finite lattice
$\unicode[STIX]{x1D6E9}$
on a finite lattice
![]() $L$
is determined completely by the set of cover relations
$L$
is determined completely by the set of cover relations
![]() $x\gtrdot y$
in
$x\gtrdot y$
in
![]() $L$
such that
$L$
such that
![]() $x\equiv y$
modulo
$x\equiv y$
modulo
![]() $\unicode[STIX]{x1D6E9}$
. It is also determined uniquely by the set of join-irreducible elements
$\unicode[STIX]{x1D6E9}$
. It is also determined uniquely by the set of join-irreducible elements
![]() $j$
in
$j$
in
![]() $L$
such that
$L$
such that
![]() $j\equiv j_{\ast }$
modulo
$j\equiv j_{\ast }$
modulo
![]() $\unicode[STIX]{x1D6E9}$
, and thus we have an injective map
$\unicode[STIX]{x1D6E9}$
, and thus we have an injective map
 $\mathsf{Con}(L)\rightarrow 2^{\mathsf{j}\text{-}\mathsf{Irr}(L)}$
.
$\mathsf{Con}(L)\rightarrow 2^{\mathsf{j}\text{-}\mathsf{Irr}(L)}$
.
The map from cover relations
![]() $x\gtrdot y$
to join-irreducible congruences is typically not one-to-one. The restriction of the map to cover relations of the form
$x\gtrdot y$
to join-irreducible congruences is typically not one-to-one. The restriction of the map to cover relations of the form
![]() $j\gtrdot j_{\ast }$
is also surjective onto join-irreducible congruences, but may still fail to be one-to-one. A lattice is called congruence uniform if the map
$j\gtrdot j_{\ast }$
is also surjective onto join-irreducible congruences, but may still fail to be one-to-one. A lattice is called congruence uniform if the map
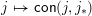 $j\mapsto \mathsf{con}(j,j_{\ast })$
is injective (and thus a bijection) from join-irreducible elements to join-irreducible congruences and the map
$j\mapsto \mathsf{con}(j,j_{\ast })$
is injective (and thus a bijection) from join-irreducible elements to join-irreducible congruences and the map
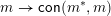 $m\rightarrow \mathsf{con}(m^{\ast },m)$
is injective (and thus a bijection) from meet-irreducible elements to join-irreducible congruences. A finite congruence uniform lattice is always semidistributive. This means that if
$m\rightarrow \mathsf{con}(m^{\ast },m)$
is injective (and thus a bijection) from meet-irreducible elements to join-irreducible congruences. A finite congruence uniform lattice is always semidistributive. This means that if
 $x\vee y=x\vee z$
then
$x\vee y=x\vee z$
then
 $x\vee (y\wedge z)=x\vee y$
and if
$x\vee (y\wedge z)=x\vee y$
and if
 $x\wedge y=x\wedge z$
then
$x\wedge y=x\wedge z$
then
 $x\wedge (y\vee z)=x\wedge y$
.
$x\wedge (y\vee z)=x\wedge y$
.
Since
![]() $\mathsf{Con}(L)$
is a finite distributive lattice, the Fundamental Theorem of Finite Distributive Lattices says that its elements are naturally identified with order ideals in the subposet
$\mathsf{Con}(L)$
is a finite distributive lattice, the Fundamental Theorem of Finite Distributive Lattices says that its elements are naturally identified with order ideals in the subposet
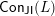 $\mathsf{Con}_{\mathsf{JI}}(L)$
of
$\mathsf{Con}_{\mathsf{JI}}(L)$
of
![]() $\mathsf{Con}(L)$
. When
$\mathsf{Con}(L)$
. When
![]() $L$
is congruence uniform, the subposet
$L$
is congruence uniform, the subposet
 $\mathsf{Con}_{\mathsf{JI}}(L)$
induces a partial order on the join-irreducible elements of
$\mathsf{Con}_{\mathsf{JI}}(L)$
induces a partial order on the join-irreducible elements of
![]() $L$
, which we call the forcing order. A congruence
$L$
, which we call the forcing order. A congruence
 $\unicode[STIX]{x1D6E9}\in \mathsf{Con}(L)$
corresponds to the order ideal in
$\unicode[STIX]{x1D6E9}\in \mathsf{Con}(L)$
corresponds to the order ideal in
 $\mathsf{Con}_{\mathsf{JI}}(L)$
consisting of those join-irreducible congruences below
$\mathsf{Con}_{\mathsf{JI}}(L)$
consisting of those join-irreducible congruences below
![]() $\unicode[STIX]{x1D6E9}$
in
$\unicode[STIX]{x1D6E9}$
in
![]() $\mathsf{Con}(L)$
(i.e. finer than
$\mathsf{Con}(L)$
(i.e. finer than
![]() $\unicode[STIX]{x1D6E9}$
as equivalence relations). These are the join-irreducible congruences
$\unicode[STIX]{x1D6E9}$
as equivalence relations). These are the join-irreducible congruences
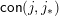 $\mathsf{con}(j,j_{\ast })$
such that
$\mathsf{con}(j,j_{\ast })$
such that
![]() $j\equiv j_{\ast }$
modulo
$j\equiv j_{\ast }$
modulo
![]() $\unicode[STIX]{x1D6E9}$
. The forcing order on join-irreducible elements sets
$\unicode[STIX]{x1D6E9}$
. The forcing order on join-irreducible elements sets
![]() $j\leqslant j^{\prime }$
if and only if
$j\leqslant j^{\prime }$
if and only if
![]() $j\equiv j_{\ast }$
modulo
$j\equiv j_{\ast }$
modulo
 $\mathsf{con}(j^{\prime },j_{\ast }^{\prime })$
.
$\mathsf{con}(j^{\prime },j_{\ast }^{\prime })$
.
As mentioned above, each cover relation
![]() $x\gtrdot y$
in a finite lattice defines a join-irreducible congruence of
$x\gtrdot y$
in a finite lattice defines a join-irreducible congruence of
![]() $L$
. In a finite congruence uniform lattice
$L$
. In a finite congruence uniform lattice
![]() $L$
, each join-irreducible congruence is
$L$
, each join-irreducible congruence is
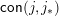 $\mathsf{con}(j,j_{\ast })$
for a unique join-irreducible element
$\mathsf{con}(j,j_{\ast })$
for a unique join-irreducible element
![]() $j$
of
$j$
of
![]() $L$
. The map
$L$
. The map
 $\mathsf{Hasse}_{1}(L)\rightarrow \mathsf{j}\text{-}\mathsf{Irr}(L)$
sending the arrow
$\mathsf{Hasse}_{1}(L)\rightarrow \mathsf{j}\text{-}\mathsf{Irr}(L)$
sending the arrow
![]() $x\rightarrow y$
to the unique
$x\rightarrow y$
to the unique
![]() $j$
with
$j$
with
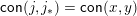 $\mathsf{con}(j,j_{\ast })=\mathsf{con}(x,y)$
is called the join-irreducible labelling of
$\mathsf{con}(j,j_{\ast })=\mathsf{con}(x,y)$
is called the join-irreducible labelling of
![]() $L$
. Each join-irreducible congruence is also
$L$
. Each join-irreducible congruence is also
 $\mathsf{con}(m^{\ast },m)$
for a unique meet-irreducible element
$\mathsf{con}(m^{\ast },m)$
for a unique meet-irreducible element
![]() $m$
, and the map
$m$
, and the map
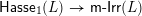 $\mathsf{Hasse}_{1}(L)\rightarrow \mathsf{m}\text{-}\mathsf{Irr}(L)$
sending
$\mathsf{Hasse}_{1}(L)\rightarrow \mathsf{m}\text{-}\mathsf{Irr}(L)$
sending
![]() $x\rightarrow y$
to the unique
$x\rightarrow y$
to the unique
![]() $m$
with
$m$
with
 $\mathsf{con}(m^{\ast },m)=\mathsf{con}(x,y)$
is called the meet-irreducible labelling of
$\mathsf{con}(m^{\ast },m)=\mathsf{con}(x,y)$
is called the meet-irreducible labelling of
![]() $L$
. These labellings are described explicitly as follows.
$L$
. These labellings are described explicitly as follows.
The following proposition is [Reference ReadingRea16a, Propositions 9–5.20]. Since that proposition’s proof is left to an exercise, we give a proof here.
Proposition 2.1. Let
![]() $L$
be a finite congruence uniform lattice and let
$L$
be a finite congruence uniform lattice and let
![]() $x\rightarrow y$
be an arrow in
$x\rightarrow y$
be an arrow in
 $\mathsf{Hasse}(L)$
.
$\mathsf{Hasse}(L)$
.
(a) The join-irreducible label on
 $x\rightarrow y$
is
$x\rightarrow y$
is
 $j=\bigwedge \{z\in L:z\leqslant x,z\not \leqslant y\}$
. Furthermore,
$j=\bigwedge \{z\in L:z\leqslant x,z\not \leqslant y\}$
. Furthermore,
 $j\leqslant x$
but
$j\leqslant x$
but
 $j\not \leqslant y$
.
$j\not \leqslant y$
.(b) The meet-irreducible label on
 $x\rightarrow y$
is
$x\rightarrow y$
is
 $m=\vee \{z\in L:z\geqslant y,z\not \geqslant x\}$
. Furthermore,
$m=\vee \{z\in L:z\geqslant y,z\not \geqslant x\}$
. Furthermore,
 $m\geqslant y$
but
$m\geqslant y$
but
 $m\not \geqslant x$
.
$m\not \geqslant x$
.
In particular, if
![]() $j$
is a join-irreducible element and
$j$
is a join-irreducible element and
![]() $m$
is a meet-irreducible element with
$m$
is a meet-irreducible element with
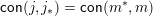 $\mathsf{con}(j,j_{\ast })=\mathsf{con}(m^{\ast },m)$
, then
$\mathsf{con}(j,j_{\ast })=\mathsf{con}(m^{\ast },m)$
, then
 $j=\bigwedge \{z\in L:z\leqslant m^{\ast },z\not \leqslant m\}$
and
$j=\bigwedge \{z\in L:z\leqslant m^{\ast },z\not \leqslant m\}$
and
 $m=\vee \{z\in L:z\geqslant j_{\ast },z\not \geqslant j\}$
.
$m=\vee \{z\in L:z\geqslant j_{\ast },z\not \geqslant j\}$
.
Proof. The last statements are special cases of assertions (a) and (b). Assertions (a) and (b) are dual to each other, so by symmetry it is enough to prove (a). To do so, it is enough to show that
![]() $j$
is join-irreducible and that
$j$
is join-irreducible and that
 $\mathsf{con}(j,j_{\ast })=\mathsf{con}(x,y)$
.
$\mathsf{con}(j,j_{\ast })=\mathsf{con}(x,y)$
.
Recall that a congruence uniform finite lattice is also semidistributive. Every element
![]() $z$
of
$z$
of
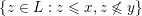 $\{z\in L:z\leqslant x,z\not \leqslant y\}$
has
$\{z\in L:z\leqslant x,z\not \leqslant y\}$
has
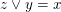 $z\vee y=x$
, so applying semidistributivity several times, we see that
$z\vee y=x$
, so applying semidistributivity several times, we see that
 $j\vee y=x$
, so in particular
$j\vee y=x$
, so in particular
![]() $j\not \leqslant y$
. It is immediate that
$j\not \leqslant y$
. It is immediate that
![]() $j\leqslant x$
. If
$j\leqslant x$
. If
![]() $j$
covers elements
$j$
covers elements
![]() $a$
and
$a$
and
![]() $b$
, then
$b$
, then
![]() $a\leqslant y$
and
$a\leqslant y$
and
![]() $b\leqslant y$
. But if
$b\leqslant y$
. But if
![]() $a\neq b$
, then
$a\neq b$
, then
![]() $j$
is a minimal upper bound for
$j$
is a minimal upper bound for
![]() $a$
and
$a$
and
![]() $b$
, so it must equal
$b$
, so it must equal
![]() $a\vee b$
. Since
$a\vee b$
. Since
![]() $y$
is another upper bound for
$y$
is another upper bound for
![]() $a$
and
$a$
and
![]() $b$
, we reach the contradiction
$b$
, we reach the contradiction
![]() $j\leqslant y$
. We conclude that
$j\leqslant y$
. We conclude that
![]() $j$
covers at most one element. If
$j$
covers at most one element. If
![]() $j$
covers no element, then
$j$
covers no element, then
![]() $j$
is the minimal element of
$j$
is the minimal element of
![]() $L$
, contradicting again the fact that
$L$
, contradicting again the fact that
![]() $j\not \leqslant y$
. We see that
$j\not \leqslant y$
. We see that
![]() $j$
is join-irreducible.
$j$
is join-irreducible.
We saw that
 $j\vee y=x$
and we also verify easily that
$j\vee y=x$
and we also verify easily that
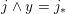 $j\wedge y=j_{\ast }$
. If
$j\wedge y=j_{\ast }$
. If
![]() $\unicode[STIX]{x1D6E9}$
is a congruence with
$\unicode[STIX]{x1D6E9}$
is a congruence with
![]() $j\equiv j_{\ast }$
, then
$j\equiv j_{\ast }$
, then
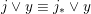 $j\vee y\equiv j_{\ast }\vee y$
, or in other words
$j\vee y\equiv j_{\ast }\vee y$
, or in other words
![]() $x\equiv y$
. Conversely, if
$x\equiv y$
. Conversely, if
![]() $\unicode[STIX]{x1D6E9}$
has
$\unicode[STIX]{x1D6E9}$
has
![]() $x\equiv y$
, then
$x\equiv y$
, then
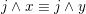 $j\wedge x\equiv j\wedge y$
, or in other words
$j\wedge x\equiv j\wedge y$
, or in other words
![]() $j\equiv j_{\ast }$
. We see that
$j\equiv j_{\ast }$
. We see that
![]() $\unicode[STIX]{x1D6E9}$
has
$\unicode[STIX]{x1D6E9}$
has
![]() $j\equiv j_{\ast }$
if and only if
$j\equiv j_{\ast }$
if and only if
![]() $x\equiv y$
, so that
$x\equiv y$
, so that
 $\mathsf{con}(j,j_{\ast })=\mathsf{con}(x,y)$
.◻
$\mathsf{con}(j,j_{\ast })=\mathsf{con}(x,y)$
.◻
We summarize some of what we know about join-irreducible elements, meet-irreducible elements, and congruences in a finite congruence uniform lattice in Figure 4. If
![]() $L$
is a finite congruence uniform lattice with Hasse quiver
$L$
is a finite congruence uniform lattice with Hasse quiver
 $\mathsf{Hasse}(L)$
, join-irreducible elements
$\mathsf{Hasse}(L)$
, join-irreducible elements
![]() $\mathsf{j}\text{-}\mathsf{Irr}(L)$
, meet-irreducible elements
$\mathsf{j}\text{-}\mathsf{Irr}(L)$
, meet-irreducible elements
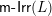 $\mathsf{m}\text{-}\mathsf{Irr}(L)$
, and join-irreducible congruences
$\mathsf{m}\text{-}\mathsf{Irr}(L)$
, and join-irreducible congruences
 $\mathsf{Con}_{\mathsf{JI}}(L)$
, then the diagram in Figure 4 commutes and the maps are bijections or surjections as marked with tildes ‘
$\mathsf{Con}_{\mathsf{JI}}(L)$
, then the diagram in Figure 4 commutes and the maps are bijections or surjections as marked with tildes ‘
![]() ${\sim}$
’ or double-headed arrows.
${\sim}$
’ or double-headed arrows.

Figure 4. Join-irreducible elements, meet-irreducible elements, and congruences in a finite congruence uniform lattice.
Let
![]() $x$
be an element of a finite lattice
$x$
be an element of a finite lattice
![]() $L$
. The expression
$L$
. The expression
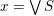 $x=\vee S$
is the canonical join representation of
$x=\vee S$
is the canonical join representation of
![]() $x$
if no proper subset of
$x$
if no proper subset of
![]() $S$
joins to
$S$
joins to
![]() $x$
and if every join-representation
$x$
and if every join-representation
 $x=\vee T$
has the property that for all
$x=\vee T$
has the property that for all
![]() $s\in S$
, there exists
$s\in S$
, there exists
![]() $t\in T$
with
$t\in T$
with
![]() $s\leqslant t$
. An element
$s\leqslant t$
. An element
![]() $x$
may fail to have a canonical join representation, but the canonical join representation of
$x$
may fail to have a canonical join representation, but the canonical join representation of
![]() $x$
is unique if it exists. The canonical meet representation is defined dually. The semidistributive property of a finite lattice
$x$
is unique if it exists. The canonical meet representation is defined dually. The semidistributive property of a finite lattice
![]() $L$
, described above, is equivalent to the property that every element of
$L$
, described above, is equivalent to the property that every element of
![]() $L$
has a canonical join representation and a canonical meet representation. A finite congruence uniform lattice is in particular semidistributive, and canonical join and meet representations can be described in terms of the join-irreducible labelling and meet-irreducible labelling as follows.
$L$
has a canonical join representation and a canonical meet representation. A finite congruence uniform lattice is in particular semidistributive, and canonical join and meet representations can be described in terms of the join-irreducible labelling and meet-irreducible labelling as follows.
The following proposition is [Reference ReadingRea16a, Proposition 9–5.30]. Since that proposition’s proof is also left to an exercise, we give a proof here.
Proposition 2.2. If
![]() $L$
is a finite congruence uniform lattice, then the canonical join representation of
$L$
is a finite congruence uniform lattice, then the canonical join representation of
![]() $x\in L$
is
$x\in L$
is
 $x=\vee J$
, where
$x=\vee J$
, where
![]() $J$
is the set of join-irreducible labels on arrows starting at
$J$
is the set of join-irreducible labels on arrows starting at
![]() $x$
in
$x$
in
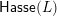 $\mathsf{Hasse}(L)$
. The canonical meet representation is
$\mathsf{Hasse}(L)$
. The canonical meet representation is
 $x=\bigwedge M$
, where
$x=\bigwedge M$
, where
![]() $M$
is the set of meet-irreducible labels on arrows ending at
$M$
is the set of meet-irreducible labels on arrows ending at
![]() $x$
in
$x$
in
 $\mathsf{Hasse}(L)$
.
$\mathsf{Hasse}(L)$
.
Proof. We prove the statement for canonical join representations, using Proposition 2.1 throughout. The other statement is dual.
First, we check that
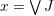 $x=\vee J$
. On the one hand, each
$x=\vee J$
. On the one hand, each
![]() $j\in J$
is below
$j\in J$
is below
![]() $x$
by Proposition 2.1, so
$x$
by Proposition 2.1, so
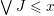 $\vee J\leqslant x$
. If
$\vee J\leqslant x$
. If
 $\vee J<x$
, then there exists
$\vee J<x$
, then there exists
![]() $y$
with
$y$
with
 $x\gtrdot y\geqslant \vee J$
. But the label of
$x\gtrdot y\geqslant \vee J$
. But the label of
![]() $x\rightarrow y$
is in
$x\rightarrow y$
is in
![]() $J$
and is not below
$J$
and is not below
![]() $y$
, which is a contradiction.
$y$
, which is a contradiction.
Next, we show that no proper subset of
![]() $J$
joins to
$J$
joins to
![]() $x$
. Let
$x$
. Let
![]() $x\rightarrow y$
be an arrow with join-irreducible label
$x\rightarrow y$
be an arrow with join-irreducible label
![]() $j\in J$
. For any other arrow
$j\in J$
. For any other arrow
![]() $x\rightarrow y^{\prime }$
with join-irreducible label
$x\rightarrow y^{\prime }$
with join-irreducible label
![]() $j^{\prime }\in J$
, we have
$j^{\prime }\in J$
, we have
![]() $y^{\prime }\not \leqslant y$
and
$y^{\prime }\not \leqslant y$
and
![]() $y^{\prime }\leqslant x$
, from which it follows that
$y^{\prime }\leqslant x$
, from which it follows that
![]() $j\leqslant y^{\prime }$
by Proposition 2.1. By symmetry,
$j\leqslant y^{\prime }$
by Proposition 2.1. By symmetry,
![]() $j^{\prime }\leqslant y$
holds, and hence
$j^{\prime }\leqslant y$
holds, and hence
 $\vee (J\setminus \{j\})\leqslant y<x$
as desired.
$\vee (J\setminus \{j\})\leqslant y<x$
as desired.
Finally, we show that, if
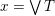 $x=\vee T$
for some
$x=\vee T$
for some
![]() $T\subseteq L$
, then for all
$T\subseteq L$
, then for all
![]() $j\in J$
, there exists
$j\in J$
, there exists
![]() $t\in T$
with
$t\in T$
with
![]() $j\leqslant t$
. Let
$j\leqslant t$
. Let
![]() $y$
have
$y$
have
![]() $x\rightarrow y$
and
$x\rightarrow y$
and
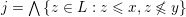 $j=\bigwedge \{z\in L:z\leqslant x,z\not \leqslant y\}$
. Every element of
$j=\bigwedge \{z\in L:z\leqslant x,z\not \leqslant y\}$
. Every element of
![]() $T$
is
$T$
is
![]() ${\leqslant}x$
, and if every element of
${\leqslant}x$
, and if every element of
![]() $T$
is
$T$
is
![]() ${\leqslant}y$
, then
${\leqslant}y$
, then
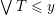 $\vee T\leqslant y$
, contradicting the assumption that
$\vee T\leqslant y$
, contradicting the assumption that
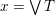 $x=\vee T$
. Thus there exists some element
$x=\vee T$
. Thus there exists some element
![]() $t$
of
$t$
of
![]() $T$
with
$T$
with
![]() $t\leqslant x$
and
$t\leqslant x$
and
![]() $t\not \leqslant y$
, and this element is above
$t\not \leqslant y$
, and this element is above
![]() $j$
by definition.◻
$j$
by definition.◻
A polygon in a finite lattice
![]() $L$
is an interval
$L$
is an interval
![]() $[x,y]$
such that
$[x,y]$
such that
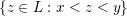 $\{z\in L:x<z<y\}$
consists of two disjoint non-empty chains. (Thus the Hasse quiver of
$\{z\in L:x<z<y\}$
consists of two disjoint non-empty chains. (Thus the Hasse quiver of
![]() $[x,y]$
is a cycle with one source and one sink.) The lattice
$[x,y]$
is a cycle with one source and one sink.) The lattice
![]() $L$
is polygonal if the following two conditions hold: first, if distinct elements
$L$
is polygonal if the following two conditions hold: first, if distinct elements
![]() $y_{1}$
and
$y_{1}$
and
![]() $y_{2}$
both cover an element
$y_{2}$
both cover an element
![]() $x$
, then
$x$
, then
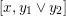 $[x,y_{1}\vee y_{2}]$
is a polygon; and second, if an element
$[x,y_{1}\vee y_{2}]$
is a polygon; and second, if an element
![]() $y$
covers distinct elements
$y$
covers distinct elements
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{2}$
, then
$x_{2}$
, then
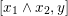 $[x_{1}\wedge x_{2},y]$
is a polygon.
$[x_{1}\wedge x_{2},y]$
is a polygon.
If
![]() $L$
is a polygonal lattice, then we define a quiver
$L$
is a polygonal lattice, then we define a quiver
 $\mathsf{FPoly}(L)$
whose set of vertices is
$\mathsf{FPoly}(L)$
whose set of vertices is
 $\mathsf{Hasse}_{1}(L)$
, with arrows defined in every polygon
$\mathsf{Hasse}_{1}(L)$
, with arrows defined in every polygon
![]() $P$
of
$P$
of
![]() $L$
as follows. The two arrows into the bottom element of
$L$
as follows. The two arrows into the bottom element of
![]() $P$
are called bottom arrows, while the two arrows from the top element of
$P$
are called bottom arrows, while the two arrows from the top element of
![]() $P$
are called top arrows, and all other arrows of
$P$
are called top arrows, and all other arrows of
![]() $P$
are called side arrows. Every bottom arrow of
$P$
are called side arrows. Every bottom arrow of
![]() $P$
has an arrow (in
$P$
has an arrow (in
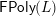 $\mathsf{FPoly}(L)$
) to the opposite top arrow in
$\mathsf{FPoly}(L)$
) to the opposite top arrow in
![]() $P$
(i.e. the top arrow in the opposite chain) and has an arrow to every side arrow in
$P$
(i.e. the top arrow in the opposite chain) and has an arrow to every side arrow in
![]() $P$
. Every top arrow of
$P$
. Every top arrow of
![]() $P$
has an arrow to the opposite bottom arrow and every side arrow in
$P$
has an arrow to the opposite bottom arrow and every side arrow in
![]() $P$
. For example, a square and hexagon in
$P$
. For example, a square and hexagon in
![]() $L$
would contribute to
$L$
would contribute to
 $\mathsf{FPoly}(L)$
as indicated below.
$\mathsf{FPoly}(L)$
as indicated below.

The following is [Reference ReadingRea16a, Theorem 9–6.5].
Theorem 2.3. If
![]() $L$
is a finite polygonal lattice, and
$L$
is a finite polygonal lattice, and
![]() $x\rightarrow y$
and
$x\rightarrow y$
and
 $x^{\prime }\rightarrow y^{\prime }$
are arrows in
$x^{\prime }\rightarrow y^{\prime }$
are arrows in
 $\mathsf{Hasse}(L)$
, then
$\mathsf{Hasse}(L)$
, then
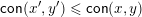 $\mathsf{con}(x^{\prime },y^{\prime })\leqslant \mathsf{con}(x,y)$
if and only if there is a directed path from
$\mathsf{con}(x^{\prime },y^{\prime })\leqslant \mathsf{con}(x,y)$
if and only if there is a directed path from
![]() $x\rightarrow y$
to
$x\rightarrow y$
to
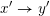 $x^{\prime }\rightarrow y^{\prime }$
in
$x^{\prime }\rightarrow y^{\prime }$
in
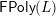 $\mathsf{FPoly}(L)$
.
$\mathsf{FPoly}(L)$
.
When
![]() $L$
is also congruence uniform, the quiver
$L$
is also congruence uniform, the quiver
 $\mathsf{FPoly}(L)$
is closely related to the forcing order on join-irreducible elements of
$\mathsf{FPoly}(L)$
is closely related to the forcing order on join-irreducible elements of
![]() $L$
, as described in the following corollary, which is immediate by combining Theorem 2.3 with facts about finite congruence uniform lattices already given in this section. We say that a quiver
$L$
, as described in the following corollary, which is immediate by combining Theorem 2.3 with facts about finite congruence uniform lattices already given in this section. We say that a quiver
![]() $Q$
is strongly connected if given any two vertices
$Q$
is strongly connected if given any two vertices
![]() $x$
and
$x$
and
![]() $y$
of the quiver, there exists a path from
$y$
of the quiver, there exists a path from
![]() $x$
to
$x$
to
![]() $y$
and a path from
$y$
and a path from
![]() $y$
to
$y$
to
![]() $x$
. A strongly connected component of
$x$
. A strongly connected component of
![]() $Q$
is a set of vertices of
$Q$
is a set of vertices of
![]() $Q$
that is maximal with respect to inducing a strongly connected subquiver.
$Q$
that is maximal with respect to inducing a strongly connected subquiver.
Corollary 2.4. Suppose
![]() $L$
is a finite, polygonal, congruence uniform lattice. Then each strongly connected component of
$L$
is a finite, polygonal, congruence uniform lattice. Then each strongly connected component of
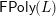 $\mathsf{FPoly}(L)$
contains exactly one arrow in
$\mathsf{FPoly}(L)$
contains exactly one arrow in
 $\mathsf{Hasse}(L)$
of the form
$\mathsf{Hasse}(L)$
of the form
![]() $j\rightarrow j_{\ast }$
where
$j\rightarrow j_{\ast }$
where
![]() $j$
is join-irreducible. This bijection between join-irreducible elements of
$j$
is join-irreducible. This bijection between join-irreducible elements of
![]() $L$
and strongly connected components of
$L$
and strongly connected components of
 $\mathsf{FPoly}(L)$
is an isomorphism from the forcing order on join-irreducible elements of
$\mathsf{FPoly}(L)$
is an isomorphism from the forcing order on join-irreducible elements of
![]() $L$
to the partial order induced by
$L$
to the partial order induced by
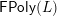 $\mathsf{FPoly}(L)$
on its strongly connected components.
$\mathsf{FPoly}(L)$
on its strongly connected components.
Informally, the corollary says that all forcing in a finite polygonal, congruence uniform lattice comes from forcing in polygons. Indeed, the notation
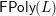 $\mathsf{FPoly}(L)$
suggests the phrase ‘forcing in polygons.’
$\mathsf{FPoly}(L)$
suggests the phrase ‘forcing in polygons.’
We define another quiver
 $\mathsf{SFPoly}(L)$
, again with the set of vertices given by
$\mathsf{SFPoly}(L)$
, again with the set of vertices given by
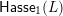 $\mathsf{Hasse}_{1}(L)$
, but with strictly fewer arrows than
$\mathsf{Hasse}_{1}(L)$
, but with strictly fewer arrows than
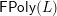 $\mathsf{FPoly}(L)$
. The notation
$\mathsf{FPoly}(L)$
. The notation
 $\mathsf{SFPoly}(L)$
suggests the phrase ‘strong forcing in polygons.’ In
$\mathsf{SFPoly}(L)$
suggests the phrase ‘strong forcing in polygons.’ In
 $\mathsf{SFPoly}(L)$
, every bottom arrow of a polygon
$\mathsf{SFPoly}(L)$
, every bottom arrow of a polygon
![]() $P$
has an arrow only to the opposite top arrow in
$P$
has an arrow only to the opposite top arrow in
![]() $P$
and every top arrow of
$P$
and every top arrow of
![]() $P$
has an arrow only to the opposite bottom arrow in
$P$
has an arrow only to the opposite bottom arrow in
![]() $P$
. Thus from the square and hexagon as labelled above,
$P$
. Thus from the square and hexagon as labelled above,
 $\mathsf{SFPoly}(L)$
gets arrows as indicated below:
$\mathsf{SFPoly}(L)$
gets arrows as indicated below:
 $$\begin{eqnarray}\begin{array}{@{}ccccc@{}}a\leftrightarrow d & b\leftrightarrow c & \qquad & e\leftrightarrow j & g\leftrightarrow h.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccccc@{}}a\leftrightarrow d & b\leftrightarrow c & \qquad & e\leftrightarrow j & g\leftrightarrow h.\end{array}\end{eqnarray}$$
Strong forcing in polygons controls whether two Hasse arrows in a finite polygonal, congruence uniform lattice determine the same congruence, as described in the following corollary.
Corollary 2.5. Suppose
![]() $L$
is a finite polygonal, congruence uniform lattice and let
$L$
is a finite polygonal, congruence uniform lattice and let
![]() $x\rightarrow y$
and
$x\rightarrow y$
and
 $x^{\prime }\rightarrow y^{\prime }$
be arrows of
$x^{\prime }\rightarrow y^{\prime }$
be arrows of
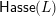 $\mathsf{Hasse}(L)$
. Then
$\mathsf{Hasse}(L)$
. Then
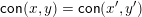 $\mathsf{con}(x,y)=\mathsf{con}(x^{\prime },y^{\prime })$
if and only if there is a directed path (or equivalently a path) in
$\mathsf{con}(x,y)=\mathsf{con}(x^{\prime },y^{\prime })$
if and only if there is a directed path (or equivalently a path) in
 $\mathsf{SFPoly}(L)$
from
$\mathsf{SFPoly}(L)$
from
![]() $x\rightarrow y$
to
$x\rightarrow y$
to
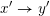 $x^{\prime }\rightarrow y^{\prime }$
.
$x^{\prime }\rightarrow y^{\prime }$
.
Proof. The ‘if’ direction is immediate by Theorem 2.3, the fact that every arrow is
 $\mathsf{SFPoly}(L)$
is also an arrow in
$\mathsf{SFPoly}(L)$
is also an arrow in
 $\mathsf{FPoly}(L)$
, and the fact that arrows in
$\mathsf{FPoly}(L)$
, and the fact that arrows in
 $\mathsf{SFPoly}(L)$
come in opposite pairs. We prove the converse by proving that for every Hasse arrow
$\mathsf{SFPoly}(L)$
come in opposite pairs. We prove the converse by proving that for every Hasse arrow
![]() $x\rightarrow y$
, there is a directed path in
$x\rightarrow y$
, there is a directed path in
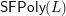 $\mathsf{SFPoly}(L)$
from
$\mathsf{SFPoly}(L)$
from
![]() $x\rightarrow y$
to
$x\rightarrow y$
to
![]() $j\rightarrow j_{\ast }$
, where
$j\rightarrow j_{\ast }$
, where
![]() $j$
is the unique join-irreducible element with
$j$
is the unique join-irreducible element with
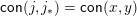 $\mathsf{con}(j,j_{\ast })=\mathsf{con}(x,y)$
. Proposition 2.1 says in particular that
$\mathsf{con}(j,j_{\ast })=\mathsf{con}(x,y)$
. Proposition 2.1 says in particular that
![]() $x\geqslant j$
, so we can argue by induction on the length of a longest maximal chain from
$x\geqslant j$
, so we can argue by induction on the length of a longest maximal chain from
![]() $j$
to
$j$
to
![]() $x$
. Choose
$x$
. Choose
![]() $z$
with
$z$
with
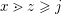 $x\gtrdot z\geqslant j$
and set
$x\gtrdot z\geqslant j$
and set
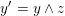 $y^{\prime }=y\wedge z$
. Since
$y^{\prime }=y\wedge z$
. Since
![]() $L$
is polygonal,
$L$
is polygonal,
![]() $[y^{\prime },x]$
is a polygon
$[y^{\prime },x]$
is a polygon
![]() $P$
, and
$P$
, and
![]() $x\rightarrow y$
is a top arrow in
$x\rightarrow y$
is a top arrow in
![]() $P$
. Choosing
$P$
. Choosing
![]() $x^{\prime }$
so that
$x^{\prime }$
so that
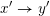 $x^{\prime }\rightarrow y^{\prime }$
is the bottom arrow opposite
$x^{\prime }\rightarrow y^{\prime }$
is the bottom arrow opposite
![]() $x\rightarrow y$
(i.e. in the other chain of
$x\rightarrow y$
(i.e. in the other chain of
![]() $P$
), we have
$P$
), we have
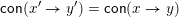 $\mathsf{con}(x^{\prime }\rightarrow y^{\prime })=\mathsf{con}(x\rightarrow y)$
by Theorem 2.3. Thus
$\mathsf{con}(x^{\prime }\rightarrow y^{\prime })=\mathsf{con}(x\rightarrow y)$
by Theorem 2.3. Thus
 $\mathsf{con}(j,j_{\ast })=\mathsf{con}(x^{\prime },y^{\prime })$
, and thus
$\mathsf{con}(j,j_{\ast })=\mathsf{con}(x^{\prime },y^{\prime })$
, and thus
![]() $x^{\prime }\geqslant j$
. By induction, there is a directed path in
$x^{\prime }\geqslant j$
. By induction, there is a directed path in
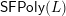 $\mathsf{SFPoly}(L)$
from
$\mathsf{SFPoly}(L)$
from
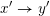 $x^{\prime }\rightarrow y^{\prime }$
to
$x^{\prime }\rightarrow y^{\prime }$
to
![]() $j\rightarrow j_{\ast }$
, and using an arrow in
$j\rightarrow j_{\ast }$
, and using an arrow in
![]() $P$
, we obtain a directed path in
$P$
, we obtain a directed path in
 $\mathsf{SFPoly}(L)$
from
$\mathsf{SFPoly}(L)$
from
![]() $x\rightarrow y$
to
$x\rightarrow y$
to
![]() $j\rightarrow j_{\ast }$
.◻
$j\rightarrow j_{\ast }$
.◻
2.2 Weak order preliminaries
Fix a simply-laced Dynkin type (i.e., one of
![]() $A_{n}$
for
$A_{n}$
for
![]() $n\geqslant 1$
,
$n\geqslant 1$
,
![]() $D_{n}$
for
$D_{n}$
for
![]() $n\geqslant 4$
,
$n\geqslant 4$
,
![]() $E_{6}$
,
$E_{6}$
,
![]() $E_{7}$
, or
$E_{7}$
, or
![]() $E_{8}$
). Let
$E_{8}$
). Let
![]() $W$
be the finite Weyl group of that type. For background on Weyl groups, see [Reference Björner and BrentiBB05].
$W$
be the finite Weyl group of that type. For background on Weyl groups, see [Reference Björner and BrentiBB05].
Let
 $S=\{s_{1},\ldots ,s_{n}\}$
be the set of simple reflections of
$S=\{s_{1},\ldots ,s_{n}\}$
be the set of simple reflections of
![]() $W$
. By definition, any element
$W$
. By definition, any element
![]() $w$
of
$w$
of
![]() $W$
can be written as a product of the simple reflections. Such an expression for
$W$
can be written as a product of the simple reflections. Such an expression for
![]() $w$
of minimal length is called reduced. The length of a reduced expression is the length of
$w$
of minimal length is called reduced. The length of a reduced expression is the length of
![]() $w$
, denoted
$w$
, denoted
![]() $\ell (w)$
.
$\ell (w)$
.
The (right) weak order on
![]() $W$
is the partial order with
$W$
is the partial order with
![]() $u\geqslant v$
if
$u\geqslant v$
if
 $\ell (u)=\ell (v)+\ell (v^{-1}u)$
. We write
$\ell (u)=\ell (v)+\ell (v^{-1}u)$
. We write
 $\mathsf{Hasse}(W)$
for the Hasse quiver of the weak order on
$\mathsf{Hasse}(W)$
for the Hasse quiver of the weak order on
![]() $W$
. The arrows of
$W$
. The arrows of
 $\mathsf{Hasse}(W)$
are all arrows
$\mathsf{Hasse}(W)$
are all arrows
 $ws_{i}\rightarrow w$
such that
$ws_{i}\rightarrow w$
such that
![]() $w\in W$
,
$w\in W$
,
![]() $s_{i}\in S$
, and
$s_{i}\in S$
, and
 $\ell (ws_{i})>\ell (w)$
, or equivalently
$\ell (ws_{i})>\ell (w)$
, or equivalently
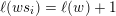 $\ell (ws_{i})=\ell (w)+1$
. For
$\ell (ws_{i})=\ell (w)+1$
. For
![]() $w\in W$
, we denote by
$w\in W$
, we denote by
![]() $w^{+}$
(respectively,
$w^{+}$
(respectively,
![]() $w^{-}$
) the set of arrows in
$w^{-}$
) the set of arrows in
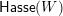 $\mathsf{Hasse}(W)$
starting (respectively, ending) at
$\mathsf{Hasse}(W)$
starting (respectively, ending) at
![]() $w$
.
$w$
.
The weak order on
![]() $W$
is a finite lattice. In particular, it has a maximal element, denoted
$W$
is a finite lattice. In particular, it has a maximal element, denoted
![]() $w_{0}$
and often called the longest element of
$w_{0}$
and often called the longest element of
![]() $W$
. For our purposes, the most important properties of the weak order are the following.
$W$
. For our purposes, the most important properties of the weak order are the following.
Theorem 2.6.
![]() $W$
is congruence uniform [Reference Caspard, Le Conte de Poly-Barbut and MorvanCLM04] and polygonal [Reference ReadingRea16b, Theorem 10–3.7].
$W$
is congruence uniform [Reference Caspard, Le Conte de Poly-Barbut and MorvanCLM04] and polygonal [Reference ReadingRea16b, Theorem 10–3.7].
2.3 Algebraic preliminaries
Fix a base field
![]() $k$
, and let
$k$
, and let
![]() $A$
be a finite-dimensional
$A$
be a finite-dimensional
![]() $k$
-algebra. We write
$k$
-algebra. We write
![]() $\mathsf{mod}\,A$
for the finite-dimensional left
$\mathsf{mod}\,A$
for the finite-dimensional left
![]() $A$
-modules. We denote by
$A$
-modules. We denote by
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D70F}^{-}$
the Auslander–Reiten translations of
$\unicode[STIX]{x1D70F}^{-}$
the Auslander–Reiten translations of
![]() $A$
. They give mutually inverse bijections between isomorphism classes of indecomposable non-projective
$A$
. They give mutually inverse bijections between isomorphism classes of indecomposable non-projective
![]() $A$
-modules and those of indecomposable non-injective
$A$
-modules and those of indecomposable non-injective
![]() $A$
-modules.
$A$
-modules.
We say that a full subcategory
![]() $\mathscr{T}$
of
$\mathscr{T}$
of
![]() $\mathsf{mod}\,A$
is a torsion class if it is closed under factors, isomorphisms and extensions. Torsion-free classes are defined dually. We write
$\mathsf{mod}\,A$
is a torsion class if it is closed under factors, isomorphisms and extensions. Torsion-free classes are defined dually. We write
![]() $\mathsf{tors}\,A$
for the torsion classes of
$\mathsf{tors}\,A$
for the torsion classes of
![]() $A$
, and
$A$
, and
![]() $\mathsf{torf}\,A$
for its torsion-free classes. We view
$\mathsf{torf}\,A$
for its torsion-free classes. We view
![]() $\mathsf{tors}\,A$
and
$\mathsf{tors}\,A$
and
![]() $\mathsf{torf}\,A$
as posets under the inclusion order. Then we have an anti-isomorphism given by
$\mathsf{torf}\,A$
as posets under the inclusion order. Then we have an anti-isomorphism given by
 $\mathscr{T}\mapsto \mathscr{T}^{\bot }=\{X\in \mathsf{mod}\,A\mid \operatorname{Hom}_{A}(\mathscr{T},X)=0\}$
$\mathscr{T}\mapsto \mathscr{T}^{\bot }=\{X\in \mathsf{mod}\,A\mid \operatorname{Hom}_{A}(\mathscr{T},X)=0\}$
 $$\begin{eqnarray}\mathsf{tors}\,A\rightarrow \mathsf{torf}\,A,\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{tors}\,A\rightarrow \mathsf{torf}\,A,\end{eqnarray}$$
whose inverse is given by
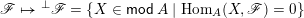 $\mathscr{F}\mapsto ^{\bot }\mathscr{F}=\{X\in \mathsf{mod}\,A\mid \operatorname{Hom}_{A}(X,\mathscr{F})=0\}$
.
$\mathscr{F}\mapsto ^{\bot }\mathscr{F}=\{X\in \mathsf{mod}\,A\mid \operatorname{Hom}_{A}(X,\mathscr{F})=0\}$
.
We recall that a torsion class
![]() $\mathscr{T}$
of
$\mathscr{T}$
of
![]() $\mathsf{mod}\,A$
is functorially finite if there exists
$\mathsf{mod}\,A$
is functorially finite if there exists
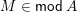 $M\in \mathsf{mod}\,A$
such that
$M\in \mathsf{mod}\,A$
such that
 $\mathscr{T}=\mathsf{Fac}\,M$
, where
$\mathscr{T}=\mathsf{Fac}\,M$
, where
![]() $\mathsf{Fac}\,M$
is the full subcategory of
$\mathsf{Fac}\,M$
is the full subcategory of
![]() $\mathsf{mod}\,A$
consisting of factor modules of finite direct sums of copies of
$\mathsf{mod}\,A$
consisting of factor modules of finite direct sums of copies of
![]() $M$
[Reference Auslander and SmaloAS81]. We denote by
$M$
[Reference Auslander and SmaloAS81]. We denote by
![]() $\mathsf{f}\text{-}\mathsf{tors}\,A$
(respectively,
$\mathsf{f}\text{-}\mathsf{tors}\,A$
(respectively,
![]() $\mathsf{f}\text{-}\mathsf{torf}\,A$
) the set of all functorially finite torsion (respectively, torsionfree) classes in
$\mathsf{f}\text{-}\mathsf{torf}\,A$
) the set of all functorially finite torsion (respectively, torsionfree) classes in
![]() $\mathsf{mod}\,A$
. We view
$\mathsf{mod}\,A$
. We view
![]() $\mathsf{f}\text{-}\mathsf{tors}\,A$
also as a poset under inclusion. The above anti-isomorphism restricts to an anti-isomorphism
$\mathsf{f}\text{-}\mathsf{tors}\,A$
also as a poset under inclusion. The above anti-isomorphism restricts to an anti-isomorphism
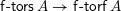 $\mathsf{f}\text{-}\mathsf{tors}\,A\rightarrow \mathsf{f}\text{-}\mathsf{torf}\,A$
[Reference SmaløSma84].
$\mathsf{f}\text{-}\mathsf{tors}\,A\rightarrow \mathsf{f}\text{-}\mathsf{torf}\,A$
[Reference SmaløSma84].
There is a bijection between
![]() $\mathsf{f}\text{-}\mathsf{tors}\,A$
and a certain class of
$\mathsf{f}\text{-}\mathsf{tors}\,A$
and a certain class of
![]() $A$
-modules. Recall that a module
$A$
-modules. Recall that a module
 $M\in \mathsf{mod}\,A$
is called
$M\in \mathsf{mod}\,A$
is called
![]() $\unicode[STIX]{x1D70F}$
-rigid if
$\unicode[STIX]{x1D70F}$
-rigid if
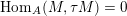 $\operatorname{Hom}_{A}(M,\unicode[STIX]{x1D70F}M)=0$
, and
$\operatorname{Hom}_{A}(M,\unicode[STIX]{x1D70F}M)=0$
, and
![]() $\unicode[STIX]{x1D70F}^{-}$
-rigid if
$\unicode[STIX]{x1D70F}^{-}$
-rigid if
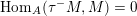 $\operatorname{Hom}_{A}(\unicode[STIX]{x1D70F}^{-}M,M)=0$
. A module
$\operatorname{Hom}_{A}(\unicode[STIX]{x1D70F}^{-}M,M)=0$
. A module
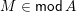 $M\in \mathsf{mod}\,A$
is called
$M\in \mathsf{mod}\,A$
is called
![]() $\unicode[STIX]{x1D70F}$
-tilting if it is
$\unicode[STIX]{x1D70F}$
-tilting if it is
![]() $\unicode[STIX]{x1D70F}$
-rigid and
$\unicode[STIX]{x1D70F}$
-rigid and
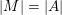 $|M|=|A|$
holds, where
$|M|=|A|$
holds, where
![]() $|M|$
is the number of non-isomorphic indecomposable direct summands of
$|M|$
is the number of non-isomorphic indecomposable direct summands of
![]() $M$
. A module
$M$
. A module
 $M\in \mathsf{mod}\,A$
is called support
$M\in \mathsf{mod}\,A$
is called support
![]() $\unicode[STIX]{x1D70F}$
-tilting if there exists an idempotent
$\unicode[STIX]{x1D70F}$
-tilting if there exists an idempotent
![]() $e$
of
$e$
of
![]() $A$
such that
$A$
such that
![]() $M$
is a
$M$
is a
![]() $\unicode[STIX]{x1D70F}$
-tilting
$\unicode[STIX]{x1D70F}$
-tilting
![]() $(A/\langle e\rangle )$
-module. We denote by
$(A/\langle e\rangle )$
-module. We denote by
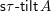 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
the set of isomorphism classes of basic support
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
the set of isomorphism classes of basic support
![]() $\unicode[STIX]{x1D70F}$
-tilting
$\unicode[STIX]{x1D70F}$
-tilting
![]() $A$
-modules, and by
$A$
-modules, and by
 $\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,A$
(respectively,
$\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,A$
(respectively,
 $\mathsf{i}\unicode[STIX]{x1D70F}^{{-}}\text{-}\mathsf{rigid}\,A$
) the set of isomorphism classes of indecomposable
$\mathsf{i}\unicode[STIX]{x1D70F}^{{-}}\text{-}\mathsf{rigid}\,A$
) the set of isomorphism classes of indecomposable
![]() $\unicode[STIX]{x1D70F}$
-rigid (respectively,
$\unicode[STIX]{x1D70F}$
-rigid (respectively,
![]() $\unicode[STIX]{x1D70F}^{-}$
-rigid)
$\unicode[STIX]{x1D70F}^{-}$
-rigid)
![]() $A$
-modules. (See [Reference Adachi, Iyama and ReitenAIR14] for more background on these notions.) By [Reference Adachi, Iyama and ReitenAIR14, 2.7], we have a surjection
$A$
-modules. (See [Reference Adachi, Iyama and ReitenAIR14] for more background on these notions.) By [Reference Adachi, Iyama and ReitenAIR14, 2.7], we have a surjection
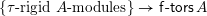 $\{\unicode[STIX]{x1D70F}\text{-}\text{rigid}~A\text{-}\text{modules}\}\rightarrow \mathsf{f}\text{-}\mathsf{tors}\,A$
given by
$\{\unicode[STIX]{x1D70F}\text{-}\text{rigid}~A\text{-}\text{modules}\}\rightarrow \mathsf{f}\text{-}\mathsf{tors}\,A$
given by
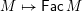 $M\mapsto \mathsf{Fac}\,M$
, which induces a bijection
$M\mapsto \mathsf{Fac}\,M$
, which induces a bijection
 $$\begin{eqnarray}\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A\xrightarrow[{}]{{\sim}}\mathsf{f}\text{-}\mathsf{tors}\,A.\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A\xrightarrow[{}]{{\sim}}\mathsf{f}\text{-}\mathsf{tors}\,A.\end{eqnarray}$$
Recall that
![]() $A$
is
$A$
is
![]() $\unicode[STIX]{x1D70F}$
-tilting finite if
$\unicode[STIX]{x1D70F}$
-tilting finite if
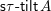 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
is a finite set, or equivalently,
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
is a finite set, or equivalently,
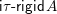 $\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,A$
is a finite set. It is shown in [Reference Demonet, Iyama and JassoDIJ15] and [Reference Iyama, Reiten, Thomas and TodorovIRTT15, 1.2] that the following conditions are equivalent:
$\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,A$
is a finite set. It is shown in [Reference Demonet, Iyama and JassoDIJ15] and [Reference Iyama, Reiten, Thomas and TodorovIRTT15, 1.2] that the following conditions are equivalent:
∙
 $A$
is
$A$
is
 $\unicode[STIX]{x1D70F}$
-tilting finite;
$\unicode[STIX]{x1D70F}$
-tilting finite;∙
 $\mathsf{f}\text{-}\mathsf{tors}\,A$
is a finite set;
$\mathsf{f}\text{-}\mathsf{tors}\,A$
is a finite set;∙
 $\mathsf{f}\text{-}\mathsf{tors}\,A$
(respectively,
$\mathsf{f}\text{-}\mathsf{tors}\,A$
(respectively,
 $\mathsf{f}\text{-}\mathsf{torf}\,A$
) forms a complete lattice;
$\mathsf{f}\text{-}\mathsf{torf}\,A$
) forms a complete lattice;∙
 $\mathsf{f}\text{-}\mathsf{tors}\,A=\mathsf{tors}\,A$
.
$\mathsf{f}\text{-}\mathsf{tors}\,A=\mathsf{tors}\,A$
.
Via the bijection between
![]() $\mathsf{f}\text{-}\mathsf{tors}\,A$
and
$\mathsf{f}\text{-}\mathsf{tors}\,A$
and
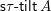 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
, we obtain a partial order on
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
, we obtain a partial order on
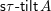 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
. We refer to the poset on
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
. We refer to the poset on
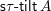 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
as generation order. The arrows of the Hasse diagram of this poset are mutations (see [Reference Adachi, Iyama and ReitenAIR14, Theorem 0.6]).
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
as generation order. The arrows of the Hasse diagram of this poset are mutations (see [Reference Adachi, Iyama and ReitenAIR14, Theorem 0.6]).
Using
![]() $\unicode[STIX]{x1D70F}$
-tilting theory, we have the following description of join-irreducible elements in
$\unicode[STIX]{x1D70F}$
-tilting theory, we have the following description of join-irreducible elements in
![]() $\mathsf{tors}\,A$
.
$\mathsf{tors}\,A$
.
Theorem 2.7. Let
![]() $A$
be a finite-dimensional
$A$
be a finite-dimensional
![]() $k$
-algebra which is
$k$
-algebra which is
![]() $\unicode[STIX]{x1D70F}$
-tilting finite. Then we have a bijection given by
$\unicode[STIX]{x1D70F}$
-tilting finite. Then we have a bijection given by
 $M\mapsto \mathsf{Fac}\,M$
$M\mapsto \mathsf{Fac}\,M$
 $$\begin{eqnarray}\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,A\rightarrow \mathsf{j}\text{-}\mathsf{Irr}(\mathsf{tors}\,A).\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,A\rightarrow \mathsf{j}\text{-}\mathsf{Irr}(\mathsf{tors}\,A).\end{eqnarray}$$
The inverse map is given by
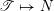 $\mathscr{T}\mapsto N$
, where
$\mathscr{T}\mapsto N$
, where
 $M\in \mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
satisfies
$M\in \mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
satisfies
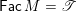 $\mathsf{Fac}\,M=\mathscr{T}$
and
$\mathsf{Fac}\,M=\mathscr{T}$
and
![]() $N$
is a unique indecomposable direct summand of
$N$
is a unique indecomposable direct summand of
![]() $M$
satisfying
$M$
satisfying
 $\mathsf{Fac}\,N=\mathsf{Fac}\,M$
.
$\mathsf{Fac}\,N=\mathsf{Fac}\,M$
.
Proof. Since
![]() $A$
is
$A$
is
![]() $\unicode[STIX]{x1D70F}$
-tilting finite, we have
$\unicode[STIX]{x1D70F}$
-tilting finite, we have
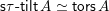 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A\simeq \mathsf{tors}\,A$
. For
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A\simeq \mathsf{tors}\,A$
. For
 $\mathscr{T}\in \mathsf{tors}\,A$
, we take
$\mathscr{T}\in \mathsf{tors}\,A$
, we take
 $M\in \mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
such that
$M\in \mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,A$
such that
 $\mathscr{T}=\mathsf{Fac}\,M$
, and an idempotent
$\mathscr{T}=\mathsf{Fac}\,M$
, and an idempotent
![]() $e\in A$
such that
$e\in A$
such that
![]() $M$
is a
$M$
is a
![]() $\unicode[STIX]{x1D70F}$
-tilting
$\unicode[STIX]{x1D70F}$
-tilting
![]() $(A/(e))$
-module. Take a basic module
$(A/(e))$
-module. Take a basic module
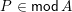 $P\in \mathsf{mod}\,A$
such that
$P\in \mathsf{mod}\,A$
such that
 $\mathsf{add}\,P=\mathsf{add}\,Ae$
. Then we can write
$\mathsf{add}\,P=\mathsf{add}\,Ae$
. Then we can write
 $M=M_{1}\oplus \cdots \oplus M_{m}$
and
$M=M_{1}\oplus \cdots \oplus M_{m}$
and
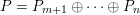 $P=P_{m+1}\oplus \cdots \oplus P_{n}$
, where
$P=P_{m+1}\oplus \cdots \oplus P_{n}$
, where
![]() $n=|A|$
and each
$n=|A|$
and each
![]() $M_{k}$
and
$M_{k}$
and
![]() $P_{k}$
is indecomposable. It is shown in [Reference Adachi, Iyama and ReitenAIR14] that adjacent vertices to
$P_{k}$
is indecomposable. It is shown in [Reference Adachi, Iyama and ReitenAIR14] that adjacent vertices to
![]() $\mathscr{T}$
in the Hasse quiver of
$\mathscr{T}$
in the Hasse quiver of
![]() $\mathsf{tors}\,A$
are given by
$\mathsf{tors}\,A$
are given by
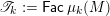 $\mathscr{T}_{k}:=\mathsf{Fac}\,\unicode[STIX]{x1D707}_{k}(M)$
for
$\mathscr{T}_{k}:=\mathsf{Fac}\,\unicode[STIX]{x1D707}_{k}(M)$
for
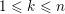 $1\leqslant k\leqslant n$
, where
$1\leqslant k\leqslant n$
, where
![]() $\unicode[STIX]{x1D707}_{k}(M)$
is the mutation of
$\unicode[STIX]{x1D707}_{k}(M)$
is the mutation of
![]() $M$
at
$M$
at
![]() $M_{k}$
for
$M_{k}$
for
 $1\leqslant k\leqslant m$
, and at
$1\leqslant k\leqslant m$
, and at
![]() $P_{k}$
for
$P_{k}$
for
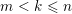 $m<k\leqslant n$
. In particular, either
$m<k\leqslant n$
. In particular, either
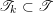 $\mathscr{T}_{k}\subset \mathscr{T}$
or
$\mathscr{T}_{k}\subset \mathscr{T}$
or
 $\mathscr{T}_{k}\supset \mathscr{T}$
holds.
$\mathscr{T}_{k}\supset \mathscr{T}$
holds.
We claim that
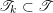 $\mathscr{T}_{k}\subset \mathscr{T}$
holds if and only if
$\mathscr{T}_{k}\subset \mathscr{T}$
holds if and only if
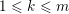 $1\leqslant k\leqslant m$
and
$1\leqslant k\leqslant m$
and
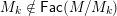 $M_{k}\notin \mathsf{Fac}(M/M_{k})$
. If
$M_{k}\notin \mathsf{Fac}(M/M_{k})$
. If
 $m<k\leqslant n$
, then
$m<k\leqslant n$
, then
 $M\in \mathsf{add}\,\unicode[STIX]{x1D707}_{k}(M)$
, and hence
$M\in \mathsf{add}\,\unicode[STIX]{x1D707}_{k}(M)$
, and hence
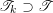 $\mathscr{T}_{k}\supset \mathscr{T}$
. Assume
$\mathscr{T}_{k}\supset \mathscr{T}$
. Assume
 $1\leqslant k\leqslant m$
. Then
$1\leqslant k\leqslant m$
. Then
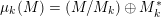 $\unicode[STIX]{x1D707}_{k}(M)=(M/M_{k})\oplus M_{k}^{\ast }$
holds for some
$\unicode[STIX]{x1D707}_{k}(M)=(M/M_{k})\oplus M_{k}^{\ast }$
holds for some
![]() $M_{k}^{\ast }$
which is either indecomposable or zero. In this case, precisely one of
$M_{k}^{\ast }$
which is either indecomposable or zero. In this case, precisely one of
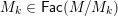 $M_{k}\in \mathsf{Fac}(M/M_{k})$
and
$M_{k}\in \mathsf{Fac}(M/M_{k})$
and
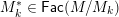 $M_{k}^{\ast }\in \mathsf{Fac}(M/M_{k})$
holds, and the former condition holds if and only if
$M_{k}^{\ast }\in \mathsf{Fac}(M/M_{k})$
holds, and the former condition holds if and only if
 $\mathscr{T}_{k}\supset \mathscr{T}$
. Thus the claim follows.
$\mathscr{T}_{k}\supset \mathscr{T}$
. Thus the claim follows.
Therefore
![]() $\mathscr{T}$
is join-irreducible if and only if there exists a unique
$\mathscr{T}$
is join-irreducible if and only if there exists a unique
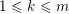 $1\leqslant k\leqslant m$
satisfying
$1\leqslant k\leqslant m$
satisfying
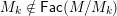 $M_{k}\notin \mathsf{Fac}(M/M_{k})$
. This holds if and only if
$M_{k}\notin \mathsf{Fac}(M/M_{k})$
. This holds if and only if
 $\mathscr{T}=\mathsf{Fac}\,M_{k}$
for some
$\mathscr{T}=\mathsf{Fac}\,M_{k}$
for some
![]() $k$
. In fact, the ‘if’ part is clear, and the ‘only if’ part follows from the general fact that all minimal direct summands
$k$
. In fact, the ‘if’ part is clear, and the ‘only if’ part follows from the general fact that all minimal direct summands
![]() $N$
of
$N$
of
![]() $M$
satisfying
$M$
satisfying
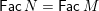 $\mathsf{Fac}\,N=\mathsf{Fac}\,M$
are isomorphic. Since
$\mathsf{Fac}\,N=\mathsf{Fac}\,M$
are isomorphic. Since
![]() $M_{k}$
is an indecomposable
$M_{k}$
is an indecomposable
![]() $\unicode[STIX]{x1D70F}$
-rigid
$\unicode[STIX]{x1D70F}$
-rigid
![]() $A$
-module, we have the assertion.◻
$A$
-module, we have the assertion.◻
For a complete lattice
![]() $L$
, we denote by
$L$
, we denote by
![]() $\mathsf{j}\text{-}\mathsf{Irr}^{\mathsf{c}}\,L$
the set of completely join-irreducible elements, that is, elements
$\mathsf{j}\text{-}\mathsf{Irr}^{\mathsf{c}}\,L$
the set of completely join-irreducible elements, that is, elements
![]() $a\in L$
such that
$a\in L$
such that
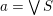 $a=\vee S$
for a subset
$a=\vee S$
for a subset
![]() $S$
of
$S$
of
![]() $L$
implies
$L$
implies
![]() $a\in S$
. If we drop the
$a\in S$
. If we drop the
![]() $\unicode[STIX]{x1D70F}$
-tilting finiteness assumption on
$\unicode[STIX]{x1D70F}$
-tilting finiteness assumption on
![]() $A$
, then we still have a bijection
$A$
, then we still have a bijection
 $\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,A\rightarrow \mathsf{f}\text{-}\mathsf{tors}\,A\cap \mathsf{j}\text{-}\mathsf{Irr}^{\mathsf{c}}(\mathsf{tors}\,A)$
given by
$\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,A\rightarrow \mathsf{f}\text{-}\mathsf{tors}\,A\cap \mathsf{j}\text{-}\mathsf{Irr}^{\mathsf{c}}(\mathsf{tors}\,A)$
given by
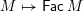 $M\mapsto \mathsf{Fac}\,M$
. The proof is the same, we only need to use [Reference Demonet, Iyama and JassoDIJ15, Theorem 3.1]. Note that completely join-irreducible elements in
$M\mapsto \mathsf{Fac}\,M$
. The proof is the same, we only need to use [Reference Demonet, Iyama and JassoDIJ15, Theorem 3.1]. Note that completely join-irreducible elements in
![]() $\mathsf{tors}\,A$
are not necessarily functorially finite. For example, consider
$\mathsf{tors}\,A$
are not necessarily functorially finite. For example, consider
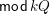 $\mathsf{mod}\,kQ$
for a Kronecker quiver
$\mathsf{mod}\,kQ$
for a Kronecker quiver
![]() $Q$
. Then all preinjective modules together with one tube form such a torsion class.
$Q$
. Then all preinjective modules together with one tube form such a torsion class.
We denote by
![]() $\mathsf{brick}\,A$
the set of isomorphism classes of bricks of
$\mathsf{brick}\,A$
the set of isomorphism classes of bricks of
![]() $A$
. A full subcategory
$A$
. A full subcategory
![]() $\mathscr{W}$
of
$\mathscr{W}$
of
![]() $\mathsf{mod}\,A$
is called wide if it is closed under kernels, cokernels and extensions. In this case,
$\mathsf{mod}\,A$
is called wide if it is closed under kernels, cokernels and extensions. In this case,
![]() $\mathscr{W}$
forms an abelian category and the inclusion functor
$\mathscr{W}$
forms an abelian category and the inclusion functor
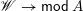 $\mathscr{W}\rightarrow \mathsf{mod}\,A$
is exact. A wide subcategory
$\mathscr{W}\rightarrow \mathsf{mod}\,A$
is exact. A wide subcategory
![]() $\mathscr{W}$
is called local if it contains a unique simple object up to isomorphism. We denote by
$\mathscr{W}$
is called local if it contains a unique simple object up to isomorphism. We denote by
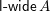 $\mathsf{l}\text{-}\mathsf{wide}\,A$
the set of local wide subcategories of
$\mathsf{l}\text{-}\mathsf{wide}\,A$
the set of local wide subcategories of
![]() $\mathsf{mod}\,A$
. We have the following easy observation.
$\mathsf{mod}\,A$
. We have the following easy observation.
Proposition 2.8. Let
![]() $A$
be a finite-dimensional
$A$
be a finite-dimensional
![]() $k$
-algebra. Then we have a bijection
$k$
-algebra. Then we have a bijection
 $$\begin{eqnarray}\mathsf{brick}\,A\rightarrow \mathsf{l}\text{-}\mathsf{wide}\,A\quad \text{given by}~S\mapsto \mathsf{Filt}\,S,\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{brick}\,A\rightarrow \mathsf{l}\text{-}\mathsf{wide}\,A\quad \text{given by}~S\mapsto \mathsf{Filt}\,S,\end{eqnarray}$$
where
![]() $\mathsf{Filt}\,S$
consists of
$\mathsf{Filt}\,S$
consists of
![]() $A$
-modules
$A$
-modules
![]() $X$
which have a filtration
$X$
which have a filtration
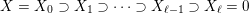 $X=X_{0}\supset X_{1}\supset \cdots \supset X_{\ell -1}\supset X_{\ell }=0$
with
$X=X_{0}\supset X_{1}\supset \cdots \supset X_{\ell -1}\supset X_{\ell }=0$
with
![]() $\ell \geqslant 0$
such that
$\ell \geqslant 0$
such that
 $X_{i}/X_{i+1}\simeq S$
for any
$X_{i}/X_{i+1}\simeq S$
for any
 $0\leqslant i<\ell$
.
$0\leqslant i<\ell$
.
Proof. Let
![]() $S$
be a brick of
$S$
be a brick of
![]() $A$
. Then
$A$
. Then
![]() $\mathsf{Filt}\,S$
is a wide subcategory by [Reference RingelRi76, 1.2]. Clearly
$\mathsf{Filt}\,S$
is a wide subcategory by [Reference RingelRi76, 1.2]. Clearly
![]() $\mathsf{Filt}\,S$
has a unique simple object
$\mathsf{Filt}\,S$
has a unique simple object
![]() $S$
. Conversely, let
$S$
. Conversely, let
![]() $\mathscr{W}$
be a local wide subcategory of
$\mathscr{W}$
be a local wide subcategory of
![]() $\mathsf{mod}\,A$
with a simple object
$\mathsf{mod}\,A$
with a simple object
![]() $S$
. For any endomorphism
$S$
. For any endomorphism
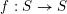 $f:S\rightarrow S$
of
$f:S\rightarrow S$
of
![]() $S$
, its image belongs to
$S$
, its image belongs to
![]() $\mathscr{W}$
. Therefore it is either
$\mathscr{W}$
. Therefore it is either
![]() $0$
or
$0$
or
![]() $S$
, and
$S$
, and
![]() $f$
is an isomorphism in the latter case. Therefore
$f$
is an isomorphism in the latter case. Therefore
![]() $S$
is a brick and we have
$S$
is a brick and we have
 $\mathscr{W}=\mathsf{Filt}\,S$
.◻
$\mathscr{W}=\mathsf{Filt}\,S$
.◻
2.4 Preliminaries on preprojective algebras
Let
 $\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D6F1}(W)$
be a preprojective algebra of the same Dynkin type as
$\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D6F1}(W)$
be a preprojective algebra of the same Dynkin type as
![]() $W$
. To construct
$W$
. To construct
![]() $\unicode[STIX]{x1D6F1}$
, take the Dynkin diagram and replace each edge by a pair of opposite arrows
$\unicode[STIX]{x1D6F1}$
, take the Dynkin diagram and replace each edge by a pair of opposite arrows
![]() $a,a^{\ast }$
to obtain the quiver
$a,a^{\ast }$
to obtain the quiver
![]() $\overline{Q}$
. Then
$\overline{Q}$
. Then
![]() $\unicode[STIX]{x1D6F1}(W)$
is the path algebra of
$\unicode[STIX]{x1D6F1}(W)$
is the path algebra of
![]() $\overline{Q}$
modulo the ideal generated by
$\overline{Q}$
modulo the ideal generated by
 $\sum _{a}(aa^{\ast }-a^{\ast }a)$
. It is a finite-dimensional self-injective algebra. We write
$\sum _{a}(aa^{\ast }-a^{\ast }a)$
. It is a finite-dimensional self-injective algebra. We write
![]() $S_{i}$
for the simple module corresponding to vertex
$S_{i}$
for the simple module corresponding to vertex
![]() $i$
.
$i$
.
We let
![]() $e_{i}$
be the idempotent corresponding to the vertex
$e_{i}$
be the idempotent corresponding to the vertex
![]() $i$
. Let
$i$
. Let
![]() $I_{i}$
be the two-sided ideal
$I_{i}$
be the two-sided ideal
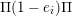 $\unicode[STIX]{x1D6F1}(1-e_{i})\unicode[STIX]{x1D6F1}$
. It is maximal as a left ideal and as a right ideal. For each
$\unicode[STIX]{x1D6F1}(1-e_{i})\unicode[STIX]{x1D6F1}$
. It is maximal as a left ideal and as a right ideal. For each
![]() $w\in W$
, we take a reduced word
$w\in W$
, we take a reduced word
 $w=s_{i_{1}}\ldots s_{i_{k}}$
, and we define
$w=s_{i_{1}}\ldots s_{i_{k}}$
, and we define
 $$\begin{eqnarray}I(w)=I_{i_{1}}\ldots I_{i_{k}},\quad \mathsf{T}(w):=\mathsf{Fac}\,I(w)\quad \text{and}\quad \mathsf{F}(w):=\mathsf{Sub}(\unicode[STIX]{x1D6F1}/I(w)).\end{eqnarray}$$
$$\begin{eqnarray}I(w)=I_{i_{1}}\ldots I_{i_{k}},\quad \mathsf{T}(w):=\mathsf{Fac}\,I(w)\quad \text{and}\quad \mathsf{F}(w):=\mathsf{Sub}(\unicode[STIX]{x1D6F1}/I(w)).\end{eqnarray}$$
Here
![]() $\mathsf{Sub}\,X$
refers to the subcategory consisting of subobjects of direct sums of copies of
$\mathsf{Sub}\,X$
refers to the subcategory consisting of subobjects of direct sums of copies of
![]() $X$
.
$X$
.
The following result due to Mizuno is fundamental.
Theorem 2.9 [Reference MizunoMiz14, 2.14, 2.21].
(a)
 $I(w)$
does not depend on the choice of the reduced word for
$I(w)$
does not depend on the choice of the reduced word for
 $w$
.
$w$
.(b) We have bijections given by
 $w\mapsto I(w)\mapsto \mathsf{T}(w)$
: (2.1)
$w\mapsto I(w)\mapsto \mathsf{T}(w)$
: (2.1) $$\begin{eqnarray}W\xrightarrow[{}]{{\sim}}\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}\xrightarrow[{}]{{\sim}}\mathsf{tors}\,\unicode[STIX]{x1D6F1}.\end{eqnarray}$$
$$\begin{eqnarray}W\xrightarrow[{}]{{\sim}}\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}\xrightarrow[{}]{{\sim}}\mathsf{tors}\,\unicode[STIX]{x1D6F1}.\end{eqnarray}$$
(c) The bijection above from
 $W$
to
$W$
to
 $\mathsf{tors}\,\unicode[STIX]{x1D6F1}$
is an anti-isomorphism from weak order on
$\mathsf{tors}\,\unicode[STIX]{x1D6F1}$
is an anti-isomorphism from weak order on
 $W$
to inclusion order on torsion classes.
$W$
to inclusion order on torsion classes.
We remark that Mizuno uses right modules, while we use left modules, and therefore his results need to be suitably translated to account for this difference. (In particular, this has the effect that he uses left weak order while we use right weak order.) We also remark here that [Reference Adachi, Iyama and ReitenAIR14] uses right modules, but writes
![]() $I_{w}$
for the ideal which we would refer to as
$I_{w}$
for the ideal which we would refer to as
![]() $I(w^{-1})$
.
$I(w^{-1})$
.
Thus
 $I(e)=\unicode[STIX]{x1D6F1}$
gives the maximum torsion class
$I(e)=\unicode[STIX]{x1D6F1}$
gives the maximum torsion class
 $\mathsf{T}(e)=\mathsf{mod}\,\unicode[STIX]{x1D6F1}$
and
$\mathsf{T}(e)=\mathsf{mod}\,\unicode[STIX]{x1D6F1}$
and
 $I(w_{0})=0$
gives the minimum torsion class
$I(w_{0})=0$
gives the minimum torsion class
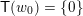 $\mathsf{T}(w_{0})=\{0\}$
, where
$\mathsf{T}(w_{0})=\{0\}$
, where
![]() $e\in W$
is the identity and
$e\in W$
is the identity and
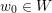 $w_{0}\in W$
is the longest element.
$w_{0}\in W$
is the longest element.
The following is an easy consequence of (2.1).
Lemma 2.10. Let
 $w,v\in W$
. Then
$w,v\in W$
. Then
 $\ell (wv)=\ell (w)+\ell (v)$
holds if and only if
$\ell (wv)=\ell (w)+\ell (v)$
holds if and only if
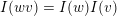 $I(wv)=I(w)I(v)$
holds. If this holds, then we have
$I(wv)=I(w)I(v)$
holds. If this holds, then we have
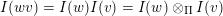 $I(wv)=I(w)I(v)=I(w)\otimes _{\unicode[STIX]{x1D6F1}}I(v)$
.
$I(wv)=I(w)I(v)=I(w)\otimes _{\unicode[STIX]{x1D6F1}}I(v)$
.
We prepare the following results on indecomposable
![]() $\unicode[STIX]{x1D70F}$
-rigid
$\unicode[STIX]{x1D70F}$
-rigid
![]() $\unicode[STIX]{x1D6F1}$
-modules.
$\unicode[STIX]{x1D6F1}$
-modules.
Corollary 2.11.
(a) We have a surjection given by
 $(w,i)\mapsto I(w)e_{i}$
$(w,i)\mapsto I(w)e_{i}$
 $$\begin{eqnarray}W\times Q_{0}\rightarrow (\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1})\sqcup \{0\}.\end{eqnarray}$$
$$\begin{eqnarray}W\times Q_{0}\rightarrow (\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1})\sqcup \{0\}.\end{eqnarray}$$
(b) We have a bijection
given by $$\begin{eqnarray}\mathsf{m}\text{-}\mathsf{Irr}\,W\xrightarrow[{}]{{\sim}}\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{m}\text{-}\mathsf{Irr}\,W\xrightarrow[{}]{{\sim}}\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}\end{eqnarray}$$
 $w\mapsto I(w)e_{k}$
, where
$w\mapsto I(w)e_{k}$
, where
 $k$
is the unique vertex satisfying
$k$
is the unique vertex satisfying
 $\ell (ws_{k})=\ell (w)+1$
.
$\ell (ws_{k})=\ell (w)+1$
.
Proof. (a) Since
![]() $I(w)e_{i}$
is a direct summand of a support
$I(w)e_{i}$
is a direct summand of a support
![]() $\unicode[STIX]{x1D70F}$
-tilting module
$\unicode[STIX]{x1D70F}$
-tilting module
![]() $I(w)$
, it is
$I(w)$
, it is
![]() $\unicode[STIX]{x1D70F}$
-rigid. It is either indecomposable or zero since it is a submodule of
$\unicode[STIX]{x1D70F}$
-rigid. It is either indecomposable or zero since it is a submodule of
![]() $\unicode[STIX]{x1D6F1}e_{i}$
and hence its socle is either simple or zero. The map is surjective since any
$\unicode[STIX]{x1D6F1}e_{i}$
and hence its socle is either simple or zero. The map is surjective since any
![]() $\unicode[STIX]{x1D70F}$
-rigid module is a direct summand of a
$\unicode[STIX]{x1D70F}$
-rigid module is a direct summand of a
![]() $\unicode[STIX]{x1D70F}$
-tilting module.
$\unicode[STIX]{x1D70F}$
-tilting module.
(b) By Theorem 2.9, there is a bijection
 $\mathsf{m}\text{-}\mathsf{Irr}\,W\simeq \mathsf{j}\text{-}\mathsf{Irr}(\mathsf{tors}\,\unicode[STIX]{x1D6F1})$
given by
$\mathsf{m}\text{-}\mathsf{Irr}\,W\simeq \mathsf{j}\text{-}\mathsf{Irr}(\mathsf{tors}\,\unicode[STIX]{x1D6F1})$
given by
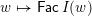 $w\mapsto \mathsf{Fac}\,I(w)$
. Applying Theorem 2.7 to
$w\mapsto \mathsf{Fac}\,I(w)$
. Applying Theorem 2.7 to
![]() $\unicode[STIX]{x1D6F1}$
, we have a bijection
$\unicode[STIX]{x1D6F1}$
, we have a bijection
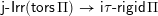 $\mathsf{j}\text{-}\mathsf{Irr}(\mathsf{tors}\,\unicode[STIX]{x1D6F1})\rightarrow \mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}$
sending
$\mathsf{j}\text{-}\mathsf{Irr}(\mathsf{tors}\,\unicode[STIX]{x1D6F1})\rightarrow \mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}$
sending
 $\mathsf{Fac}\,I(w)$
to
$\mathsf{Fac}\,I(w)$
to
![]() $I(w)e_{k}$
, where
$I(w)e_{k}$
, where
![]() $k$
is the unique vertex satisfying
$k$
is the unique vertex satisfying
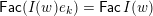 $\mathsf{Fac}(I(w)e_{k})=\mathsf{Fac}\,I(w)$
. This equality is equivalent to
$\mathsf{Fac}(I(w)e_{k})=\mathsf{Fac}\,I(w)$
. This equality is equivalent to
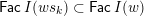 $\mathsf{Fac}\,I(ws_{k})\subset \mathsf{Fac}\,I(w)$
, and also to
$\mathsf{Fac}\,I(ws_{k})\subset \mathsf{Fac}\,I(w)$
, and also to
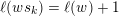 $\ell (ws_{k})=\ell (w)+1$
. Thus the assertion follows.◻
$\ell (ws_{k})=\ell (w)+1$
. Thus the assertion follows.◻
We show a few examples. Following the usual convention, we describe
![]() $\unicode[STIX]{x1D6F1}$
-modules
$\unicode[STIX]{x1D6F1}$
-modules
![]() $X$
in terms of their composition factors. Thus the numbers
$X$
in terms of their composition factors. Thus the numbers
![]() $i$
give a basis of the
$i$
give a basis of the
![]() $k$
-vector space
$k$
-vector space
![]() $e_{i}X$
, and the action of arrows is shown by the relative position of these numbers. For example,
$e_{i}X$
, and the action of arrows is shown by the relative position of these numbers. For example,
![]() $\begin{smallmatrix}1 & & \\ & 2 & \\ & & 3\end{smallmatrix}$
refers to the indecomposable
$\begin{smallmatrix}1 & & \\ & 2 & \\ & & 3\end{smallmatrix}$
refers to the indecomposable
![]() $\unicode[STIX]{x1D6F1}$
-module with composition factors
$\unicode[STIX]{x1D6F1}$
-module with composition factors
 $S_{1},S_{2},S_{3}$
from top to bottom.
$S_{1},S_{2},S_{3}$
from top to bottom.
Example 2.12. The left picture in Figure 5 shows the weak order on permutations in
![]() $S_{3}$
(the Weyl group of type
$S_{3}$
(the Weyl group of type
![]() $A_{2}$
). The right picture in Figure 5 shows the set
$A_{2}$
). The right picture in Figure 5 shows the set
 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
for
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
for
![]() $\unicode[STIX]{x1D6F1}$
of type
$\unicode[STIX]{x1D6F1}$
of type
![]() $A_{2}$
, arranged in generation order, where bars mean direct sums. We show in grey (red online) the meet-irreducible elements of
$A_{2}$
, arranged in generation order, where bars mean direct sums. We show in grey (red online) the meet-irreducible elements of
![]() $W$
and the join-irreducible elements of
$W$
and the join-irreducible elements of
 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
. The two pictures are arranged so that the map
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
. The two pictures are arranged so that the map
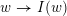 $w\rightarrow I(w)$
is accomplished by a translation of the page.
$w\rightarrow I(w)$
is accomplished by a translation of the page.

Figure 5. (Colour online) The weak order and
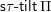 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
in type
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
in type
![]() $A_{2}$
.
$A_{2}$
.
Example 2.13. Figure 6 shows the weak order on permutations in
![]() $S_{4}$
(the Weyl group of type
$S_{4}$
(the Weyl group of type
![]() $A_{3}$
) and
$A_{3}$
) and
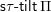 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
for
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
for
![]() $\unicode[STIX]{x1D6F1}$
of type
$\unicode[STIX]{x1D6F1}$
of type
![]() $A_{3}$
, with the same conventions as described in Example 2.12.
$A_{3}$
, with the same conventions as described in Example 2.12.

Figure 6. (Colour online) The weak order and
 $\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
in type
$\mathsf{s}\unicode[STIX]{x1D70F}\text{-}\mathsf{tilt}\,\unicode[STIX]{x1D6F1}$
in type
![]() $A_{3}$
.
$A_{3}$
.
Let
![]() $\widehat{\unicode[STIX]{x1D6F1}}$
be the preprojective algebra of the extended Dynkin type corresponding to
$\widehat{\unicode[STIX]{x1D6F1}}$
be the preprojective algebra of the extended Dynkin type corresponding to
![]() $\unicode[STIX]{x1D6F1}$
. We identify
$\unicode[STIX]{x1D6F1}$
. We identify
![]() $\unicode[STIX]{x1D6F1}$
-modules with
$\unicode[STIX]{x1D6F1}$
-modules with
![]() $\widehat{\unicode[STIX]{x1D6F1}}$
-modules annihilated by
$\widehat{\unicode[STIX]{x1D6F1}}$
-modules annihilated by
![]() $e_{0}$
, where
$e_{0}$
, where
![]() $e_{0}$
is an idempotent of
$e_{0}$
is an idempotent of
![]() $\widehat{\unicode[STIX]{x1D6F1}}$
satisfying
$\widehat{\unicode[STIX]{x1D6F1}}$
satisfying
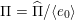 $\unicode[STIX]{x1D6F1}=\widehat{\unicode[STIX]{x1D6F1}}/\langle e_{0}\rangle$
. Then the category
$\unicode[STIX]{x1D6F1}=\widehat{\unicode[STIX]{x1D6F1}}/\langle e_{0}\rangle$
. Then the category
![]() $\mathsf{mod}\,\unicode[STIX]{x1D6F1}$
can be regarded as a full subcategory of
$\mathsf{mod}\,\unicode[STIX]{x1D6F1}$
can be regarded as a full subcategory of
![]() $\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}}$
which is closed under extensions. Therefore we have
$\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}}$
which is closed under extensions. Therefore we have
 $$\begin{eqnarray}\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,Y)=\operatorname{Hom}_{\widehat{\unicode[STIX]{x1D6F1}}}(X,Y)\quad \text{and}\quad \operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(X,Y)=\operatorname{Ext}_{\widehat{\unicode[STIX]{x1D6F1}}}^{1}(X,Y)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,Y)=\operatorname{Hom}_{\widehat{\unicode[STIX]{x1D6F1}}}(X,Y)\quad \text{and}\quad \operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(X,Y)=\operatorname{Ext}_{\widehat{\unicode[STIX]{x1D6F1}}}^{1}(X,Y)\end{eqnarray}$$
for any
 $X,Y\in \mathsf{mod}\,\unicode[STIX]{x1D6F1}$
. On the other hand,
$X,Y\in \mathsf{mod}\,\unicode[STIX]{x1D6F1}$
. On the other hand,
![]() $\widehat{\unicode[STIX]{x1D6F1}}$
is a 2-Calabi–Yau algebra [Reference KellerKel08, § 4.2] and hence there exists a functorial isomorphism
$\widehat{\unicode[STIX]{x1D6F1}}$
is a 2-Calabi–Yau algebra [Reference KellerKel08, § 4.2] and hence there exists a functorial isomorphism
 $$\begin{eqnarray}\operatorname{Hom}_{\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})}(X,Y)\simeq D\operatorname{Hom}_{\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})}(Y,X[2])\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})}(X,Y)\simeq D\operatorname{Hom}_{\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})}(Y,X[2])\end{eqnarray}$$
for any
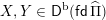 $X,Y\in \mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
[Reference KellerKel08, 4.1], where
$X,Y\in \mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
[Reference KellerKel08, 4.1], where
![]() $D$
is the
$D$
is the
![]() $k$
-dual.
$k$
-dual.
3 Homological characterizations of layers
In this section we prove Theorem 1.2, the homological characterization of layer modules of the preprojective algebra
![]() $\unicode[STIX]{x1D6F1}$
. The assertion that every layer module
$\unicode[STIX]{x1D6F1}$
. The assertion that every layer module
![]() $L$
is a stone satisfying
$L$
is a stone satisfying
 $\operatorname{End}_{\unicode[STIX]{x1D6F1}}(L)=k$
was shown in [Reference Amiot, Iyama, Reiten and TodorovAIRT12, 2.3]. (Although
$\operatorname{End}_{\unicode[STIX]{x1D6F1}}(L)=k$
was shown in [Reference Amiot, Iyama, Reiten and TodorovAIRT12, 2.3]. (Although
![]() $k$
was assumed to be algebraically closed in [Reference Amiot, Iyama, Reiten and TodorovAIRT12], this assumption was never used.) It is also easy to show that the stones
$k$
was assumed to be algebraically closed in [Reference Amiot, Iyama, Reiten and TodorovAIRT12], this assumption was never used.) It is also easy to show that the stones
![]() $L$
of
$L$
of
![]() $\unicode[STIX]{x1D6F1}$
satisfying
$\unicode[STIX]{x1D6F1}$
satisfying
 $\operatorname{End}_{\unicode[STIX]{x1D6F1}}(L)=k$
are exactly the
$\operatorname{End}_{\unicode[STIX]{x1D6F1}}(L)=k$
are exactly the
![]() $\unicode[STIX]{x1D6F1}$
-modules which are
$\unicode[STIX]{x1D6F1}$
-modules which are
![]() $2$
-spherical as
$2$
-spherical as
![]() $\widehat{\unicode[STIX]{x1D6F1}}$
-modules. Indeed, for any
$\widehat{\unicode[STIX]{x1D6F1}}$
-modules. Indeed, for any
![]() $\unicode[STIX]{x1D6F1}$
-module
$\unicode[STIX]{x1D6F1}$
-module
![]() $L$
, we have
$L$
, we have
 $\operatorname{Ext}_{\widehat{\unicode[STIX]{x1D6F1}}}^{1}(L,L)=\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(L,L)$
and
$\operatorname{Ext}_{\widehat{\unicode[STIX]{x1D6F1}}}^{1}(L,L)=\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(L,L)$
and
 $\operatorname{Ext}_{\widehat{\unicode[STIX]{x1D6F1}}}^{2}(L,L)=D\operatorname{End}_{\unicode[STIX]{x1D6F1}}(L)$
by (2.2) and (2.3), and the assertion follows.
$\operatorname{Ext}_{\widehat{\unicode[STIX]{x1D6F1}}}^{2}(L,L)=D\operatorname{End}_{\unicode[STIX]{x1D6F1}}(L)$
by (2.2) and (2.3), and the assertion follows.
To complete the proof, we will show that every brick is a layer. As before,
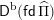 $\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
is the bounded derived category of finite-dimensional
$\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
is the bounded derived category of finite-dimensional
![]() $\widehat{\unicode[STIX]{x1D6F1}}$
-modules. For a vertex
$\widehat{\unicode[STIX]{x1D6F1}}$
-modules. For a vertex
![]() $i\in Q_{0}$
, let
$i\in Q_{0}$
, let
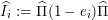 $\widehat{I}_{i}:=\widehat{\unicode[STIX]{x1D6F1}}(1-e_{i})\widehat{\unicode[STIX]{x1D6F1}}$
be an ideal of
$\widehat{I}_{i}:=\widehat{\unicode[STIX]{x1D6F1}}(1-e_{i})\widehat{\unicode[STIX]{x1D6F1}}$
be an ideal of
![]() $\widehat{\unicode[STIX]{x1D6F1}}$
. Then we have an exact sequence
$\widehat{\unicode[STIX]{x1D6F1}}$
. Then we have an exact sequence
 $$\begin{eqnarray}0\rightarrow \widehat{I}_{i}\rightarrow \widehat{\unicode[STIX]{x1D6F1}}\rightarrow S_{i}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \widehat{I}_{i}\rightarrow \widehat{\unicode[STIX]{x1D6F1}}\rightarrow S_{i}\rightarrow 0\end{eqnarray}$$
of
![]() $\widehat{\unicode[STIX]{x1D6F1}}$
-bimodules. Moreover we have an autoequivalence
$\widehat{\unicode[STIX]{x1D6F1}}$
-bimodules. Moreover we have an autoequivalence
 $$\begin{eqnarray}F_{i}:=\widehat{I}_{i}\{_{\widehat{\unicode[STIX]{x1D6F1}}}-:\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})\rightarrow \mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})\end{eqnarray}$$
$$\begin{eqnarray}F_{i}:=\widehat{I}_{i}\{_{\widehat{\unicode[STIX]{x1D6F1}}}-:\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})\rightarrow \mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})\end{eqnarray}$$
with quasi-inverse
 $$\begin{eqnarray}F_{i}^{-1}:=\mathbf{R}\text{Hom}_{\widehat{\unicode[STIX]{x1D6F1}}}(\widehat{I}_{i},-):\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})\rightarrow \mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}}).\end{eqnarray}$$
$$\begin{eqnarray}F_{i}^{-1}:=\mathbf{R}\text{Hom}_{\widehat{\unicode[STIX]{x1D6F1}}}(\widehat{I}_{i},-):\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})\rightarrow \mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}}).\end{eqnarray}$$
The following assertions are easy to check.
Lemma 3.1. Let
![]() $L$
be a finite-dimensional
$L$
be a finite-dimensional
![]() $\unicode[STIX]{x1D6F1}$
-module.
$\unicode[STIX]{x1D6F1}$
-module.
(a) We have
 $I_{i}=\widehat{I}_{i}\otimes _{\widehat{\unicode[STIX]{x1D6F1}}}\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D6F1}\otimes _{\widehat{\unicode[STIX]{x1D6F1}}}\widehat{I}_{i}$
.
$I_{i}=\widehat{I}_{i}\otimes _{\widehat{\unicode[STIX]{x1D6F1}}}\unicode[STIX]{x1D6F1}=\unicode[STIX]{x1D6F1}\otimes _{\widehat{\unicode[STIX]{x1D6F1}}}\widehat{I}_{i}$
.(b) We have
 $I_{i}\otimes _{\unicode[STIX]{x1D6F1}}L=\widehat{I}_{i}\otimes _{\widehat{\unicode[STIX]{x1D6F1}}}L$
and
$I_{i}\otimes _{\unicode[STIX]{x1D6F1}}L=\widehat{I}_{i}\otimes _{\widehat{\unicode[STIX]{x1D6F1}}}L$
and
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(I_{i},L)=\operatorname{Hom}_{\widehat{\unicode[STIX]{x1D6F1}}}(\widehat{I}_{i},L)$
.
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(I_{i},L)=\operatorname{Hom}_{\widehat{\unicode[STIX]{x1D6F1}}}(\widehat{I}_{i},L)$
.
The following observation plays a key role.
Proposition 3.2. Let
![]() $L$
be a brick of
$L$
be a brick of
![]() $\unicode[STIX]{x1D6F1}$
and
$\unicode[STIX]{x1D6F1}$
and
![]() $i$
a vertex of
$i$
a vertex of
![]() $\overline{Q}$
.
$\overline{Q}$
.
(a) If
 $L\not \simeq S_{i}$
, then at least one of
$L\not \simeq S_{i}$
, then at least one of
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},L)=0$
or
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},L)=0$
or
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(L,S_{i})=0$
holds.
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(L,S_{i})=0$
holds.(b) If
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},L)=0$
, then
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},L)=0$
, then
 $F_{i}(L)\simeq I_{i}\otimes _{\unicode[STIX]{x1D6F1}}L$
is a brick of
$F_{i}(L)\simeq I_{i}\otimes _{\unicode[STIX]{x1D6F1}}L$
is a brick of
 $\unicode[STIX]{x1D6F1}$
.
$\unicode[STIX]{x1D6F1}$
.(c) If
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(L,S_{i})=0$
, then
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(L,S_{i})=0$
, then
 $F_{i}^{-1}(L)\simeq \operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(I_{i},L)$
is a brick of
$F_{i}^{-1}(L)\simeq \operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(I_{i},L)$
is a brick of
 $\unicode[STIX]{x1D6F1}$
.
$\unicode[STIX]{x1D6F1}$
.
Proof. (a) If both
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},L)$
and
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},L)$
and
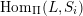 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(L,S_{i})$
are non-zero, the composition
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(L,S_{i})$
are non-zero, the composition
 $L\rightarrow S_{i}\rightarrow L$
is a non-zero non-isomorphic endomorphism of
$L\rightarrow S_{i}\rightarrow L$
is a non-zero non-isomorphic endomorphism of
![]() $L$
. This is a contradiction since
$L$
. This is a contradiction since
 $\operatorname{End}_{\unicode[STIX]{x1D6F1}}(L)$
is a division algebra.
$\operatorname{End}_{\unicode[STIX]{x1D6F1}}(L)$
is a division algebra.
(b) We show that
![]() $F_{i}(L)$
is a
$F_{i}(L)$
is a
![]() $\widehat{\unicode[STIX]{x1D6F1}}$
-module, that is,
$\widehat{\unicode[STIX]{x1D6F1}}$
-module, that is,
 $\operatorname{Tor}_{j}^{\widehat{\unicode[STIX]{x1D6F1}}}(\widehat{I}_{i},L)=0$
holds for any
$\operatorname{Tor}_{j}^{\widehat{\unicode[STIX]{x1D6F1}}}(\widehat{I}_{i},L)=0$
holds for any
![]() $j\neq 0$
. Since the
$j\neq 0$
. Since the
![]() $\widehat{\unicode[STIX]{x1D6F1}}$
-module
$\widehat{\unicode[STIX]{x1D6F1}}$
-module
![]() $\widehat{I}_{i}$
has projective dimension at most one [Reference Buan, Iyama, Reiten and ScottBIRS09, Proposition III.1.4], we only have to check the case
$\widehat{I}_{i}$
has projective dimension at most one [Reference Buan, Iyama, Reiten and ScottBIRS09, Proposition III.1.4], we only have to check the case
![]() $j=1$
. We have
$j=1$
. We have

by our assumption, where the second isomorphism follows from a functorial isomorphism
 $-\otimes _{\widehat{\unicode[STIX]{x1D6F1}}}L\simeq D\operatorname{Hom}_{\widehat{\unicode[STIX]{x1D6F1}}}(L,D(-))$
. Thus we have
$-\otimes _{\widehat{\unicode[STIX]{x1D6F1}}}L\simeq D\operatorname{Hom}_{\widehat{\unicode[STIX]{x1D6F1}}}(L,D(-))$
. Thus we have
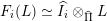 $F_{i}(L)\simeq \widehat{I}_{i}\otimes _{\widehat{\unicode[STIX]{x1D6F1}}}L$
, which is isomorphic to
$F_{i}(L)\simeq \widehat{I}_{i}\otimes _{\widehat{\unicode[STIX]{x1D6F1}}}L$
, which is isomorphic to
![]() $I_{i}\otimes _{\unicode[STIX]{x1D6F1}}L$
by Lemma 3.1. Since
$I_{i}\otimes _{\unicode[STIX]{x1D6F1}}L$
by Lemma 3.1. Since
![]() $F_{i}$
is an autoequivalence of
$F_{i}$
is an autoequivalence of
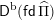 $\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
,
$\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
,
![]() $F_{i}(L)$
is a brick of
$F_{i}(L)$
is a brick of
![]() $\unicode[STIX]{x1D6F1}$
.
$\unicode[STIX]{x1D6F1}$
.
(c) Similar to (b). ◻
We need the following observation.
Lemma 3.3. Let
![]() $w\in W$
and let
$w\in W$
and let
![]() $L$
be a brick of
$L$
be a brick of
![]() $\unicode[STIX]{x1D6F1}$
which belongs to
$\unicode[STIX]{x1D6F1}$
which belongs to
![]() $\mathsf{T}(w)$
. For any
$\mathsf{T}(w)$
. For any
![]() $i$
satisfying
$i$
satisfying
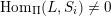 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(L,S_{i})\neq 0$
, the following assertions hold.
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(L,S_{i})\neq 0$
, the following assertions hold.
(a)
 $\ell (s_{i}w)>\ell (w)$
and
$\ell (s_{i}w)>\ell (w)$
and
 $I(s_{i}w)=I_{i}I(w)=I_{i}\otimes _{\unicode[STIX]{x1D6F1}}I(w)$
.
$I(s_{i}w)=I_{i}I(w)=I_{i}\otimes _{\unicode[STIX]{x1D6F1}}I(w)$
.(b) If
 $L\not \simeq S_{i}$
, then
$L\not \simeq S_{i}$
, then
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},L)=0$
and
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},L)=0$
and
 $F_{i}(L)$
is a brick of
$F_{i}(L)$
is a brick of
 $\unicode[STIX]{x1D6F1}$
which belongs to
$\unicode[STIX]{x1D6F1}$
which belongs to
 $\mathsf{T}(s_{i}w)$
.
$\mathsf{T}(s_{i}w)$
.
Proof. (a) Since
 $L\in \mathsf{T}(w)$
and
$L\in \mathsf{T}(w)$
and
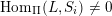 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(L,S_{i})\neq 0$
, we have
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(L,S_{i})\neq 0$
, we have
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(I(w),S_{i})\neq 0$
. Thus
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(I(w),S_{i})\neq 0$
. Thus
 $I_{i}I(w)\neq I(w)$
holds. Thus we have the assertions by Lemma 2.10.
$I_{i}I(w)\neq I(w)$
holds. Thus we have the assertions by Lemma 2.10.
(b) By Proposition 3.2,
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},L)=0$
holds, and
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},L)=0$
holds, and
![]() $F_{i}(L)$
is a brick of
$F_{i}(L)$
is a brick of
![]() $\unicode[STIX]{x1D6F1}$
. Since we have a surjection
$\unicode[STIX]{x1D6F1}$
. Since we have a surjection
 $I(w)^{\oplus m}\rightarrow L$
, we have a surjection
$I(w)^{\oplus m}\rightarrow L$
, we have a surjection
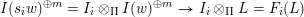 $I(s_{i}w)^{\oplus m}=I_{i}\otimes _{\unicode[STIX]{x1D6F1}}I(w)^{\oplus m}\rightarrow I_{i}\otimes _{\unicode[STIX]{x1D6F1}}L=F_{i}(L)$
. Thus
$I(s_{i}w)^{\oplus m}=I_{i}\otimes _{\unicode[STIX]{x1D6F1}}I(w)^{\oplus m}\rightarrow I_{i}\otimes _{\unicode[STIX]{x1D6F1}}L=F_{i}(L)$
. Thus
![]() $F_{i}(L)$
belongs to
$F_{i}(L)$
belongs to
![]() $\mathsf{T}(s_{i}w)$
.◻
$\mathsf{T}(s_{i}w)$
.◻
For
![]() $w\in W$
, we have an ideal
$w\in W$
, we have an ideal
![]() $\widehat{I}(w)$
of
$\widehat{I}(w)$
of
![]() $\widehat{\unicode[STIX]{x1D6F1}}$
satisfying
$\widehat{\unicode[STIX]{x1D6F1}}$
satisfying
 $\widehat{I}(w)\supseteq \langle e_{0}\rangle$
and
$\widehat{I}(w)\supseteq \langle e_{0}\rangle$
and
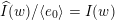 $\widehat{I}(w)/\langle e_{0}\rangle =I(w)$
. Let
$\widehat{I}(w)/\langle e_{0}\rangle =I(w)$
. Let
 $$\begin{eqnarray}F(w):=\widehat{I}(w)\{_{\widehat{\unicode[STIX]{x1D6F1}}}-:\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})\rightarrow \mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}}).\end{eqnarray}$$
$$\begin{eqnarray}F(w):=\widehat{I}(w)\{_{\widehat{\unicode[STIX]{x1D6F1}}}-:\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})\rightarrow \mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}}).\end{eqnarray}$$
For any reduced expression
 $w=s_{i_{1}}\cdots s_{i_{\ell }}$
, we have
$w=s_{i_{1}}\cdots s_{i_{\ell }}$
, we have
 $$\begin{eqnarray}\widehat{I}(w)=\widehat{I}_{i_{1}}\cdots \widehat{I}_{i_{\ell }}\quad \text{and}\quad F(w)=F_{i_{1}}\circ \cdots \circ F_{i_{\ell }}.\end{eqnarray}$$
$$\begin{eqnarray}\widehat{I}(w)=\widehat{I}_{i_{1}}\cdots \widehat{I}_{i_{\ell }}\quad \text{and}\quad F(w)=F_{i_{1}}\circ \cdots \circ F_{i_{\ell }}.\end{eqnarray}$$
Lemma 3.4. Let
![]() $L$
be a brick of
$L$
be a brick of
![]() $\unicode[STIX]{x1D6F1}$
. Then there exists
$\unicode[STIX]{x1D6F1}$
. Then there exists
![]() $v\in W$
such that
$v\in W$
such that
 $F(v)(L)$
is a simple
$F(v)(L)$
is a simple
![]() $\unicode[STIX]{x1D6F1}$
-module
$\unicode[STIX]{x1D6F1}$
-module
![]() $S_{i}$
.
$S_{i}$
.
Proof. Assume that
![]() $L$
is not simple. Taking
$L$
is not simple. Taking
![]() $i_{1}$
such that
$i_{1}$
such that
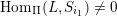 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(L,S_{i_{1}})\neq 0$
and applying Lemma 3.3 to the brick
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(L,S_{i_{1}})\neq 0$
and applying Lemma 3.3 to the brick
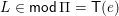 $L\in \mathsf{mod}\,\unicode[STIX]{x1D6F1}=\mathsf{T}(e)$
, we have that
$L\in \mathsf{mod}\,\unicode[STIX]{x1D6F1}=\mathsf{T}(e)$
, we have that
![]() $F_{i_{1}}(L)$
is a brick in
$F_{i_{1}}(L)$
is a brick in
![]() $\mathsf{Fac}\,I_{i_{1}}$
.
$\mathsf{Fac}\,I_{i_{1}}$
.
Assume that
![]() $F_{i_{1}}(L)$
is not simple. Taking
$F_{i_{1}}(L)$
is not simple. Taking
![]() $i_{2}$
such that
$i_{2}$
such that
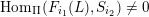 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(F_{i_{1}}(L),S_{i_{2}})\neq 0$
and applying Lemma 3.3 to the brick
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(F_{i_{1}}(L),S_{i_{2}})\neq 0$
and applying Lemma 3.3 to the brick
 $F_{i_{1}}(L)\in \mathsf{Fac}\,I_{i_{1}}$
, we have that
$F_{i_{1}}(L)\in \mathsf{Fac}\,I_{i_{1}}$
, we have that
 $F_{i_{2}}F_{i_{1}}(L)$
is a brick in
$F_{i_{2}}F_{i_{1}}(L)$
is a brick in
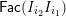 $\mathsf{Fac}(I_{i_{2}}I_{i_{1}})$
and
$\mathsf{Fac}(I_{i_{2}}I_{i_{1}})$
and
 $\ell (s_{i_{2}}s_{i_{1}})=2$
holds.
$\ell (s_{i_{2}}s_{i_{1}})=2$
holds.
We repeat this process. Since the lengths of elements in
![]() $W$
are bounded by
$W$
are bounded by
![]() $\ell (w_{0})$
, the process must stop, that is, there exists
$\ell (w_{0})$
, the process must stop, that is, there exists
![]() $v\in W$
such that
$v\in W$
such that
 $F(v)(L)$
is a simple
$F(v)(L)$
is a simple
![]() $\unicode[STIX]{x1D6F1}$
-module
$\unicode[STIX]{x1D6F1}$
-module
![]() $S_{i}$
.◻
$S_{i}$
.◻
We need the following general observation.
Lemma 3.5. For any
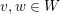 $v,w\in W$
satisfying
$v,w\in W$
satisfying
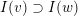 $I(v)\supset I(w)$
, we have an isomorphism
$I(v)\supset I(w)$
, we have an isomorphism
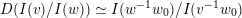 $D(I(v)/I(w))\simeq I(w^{-1}w_{0})/I(v^{-1}w_{0})$
of
$D(I(v)/I(w))\simeq I(w^{-1}w_{0})/I(v^{-1}w_{0})$
of
![]() $\unicode[STIX]{x1D6F1}$
-modules.
$\unicode[STIX]{x1D6F1}$
-modules.
Proof. Applying
![]() $D$
to the exact sequence
$D$
to the exact sequence
 $0\rightarrow I(w)\rightarrow I(v)\rightarrow I(v)/I(w)\rightarrow 0$
of
$0\rightarrow I(w)\rightarrow I(v)\rightarrow I(v)/I(w)\rightarrow 0$
of
![]() $\unicode[STIX]{x1D6F1}^{\operatorname{op}}$
-modules, we have an exact sequence
$\unicode[STIX]{x1D6F1}^{\operatorname{op}}$
-modules, we have an exact sequence
 $$\begin{eqnarray}0\rightarrow D(I(v)/I(w))\rightarrow D(I(v))\rightarrow D(I(w))\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow D(I(v)/I(w))\rightarrow D(I(v))\rightarrow D(I(w))\rightarrow 0\end{eqnarray}$$
of
![]() $\unicode[STIX]{x1D6F1}$
-modules. On the other hand, we have an exact sequence
$\unicode[STIX]{x1D6F1}$
-modules. On the other hand, we have an exact sequence
 $$\begin{eqnarray}0\rightarrow I(w^{-1}w_{0})/I(v^{-1}w_{0})\rightarrow \unicode[STIX]{x1D6F1}/I(v^{-1}w_{0})\rightarrow \unicode[STIX]{x1D6F1}/I(w^{-1}w_{0})\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow I(w^{-1}w_{0})/I(v^{-1}w_{0})\rightarrow \unicode[STIX]{x1D6F1}/I(v^{-1}w_{0})\rightarrow \unicode[STIX]{x1D6F1}/I(w^{-1}w_{0})\rightarrow 0\end{eqnarray}$$
of
![]() $\unicode[STIX]{x1D6F1}$
-modules. Using an isomorphism
$\unicode[STIX]{x1D6F1}$
-modules. Using an isomorphism
 $D(I(w))\simeq \unicode[STIX]{x1D6F1}/I(w^{-1}w_{0})$
of
$D(I(w))\simeq \unicode[STIX]{x1D6F1}/I(w^{-1}w_{0})$
of
![]() $\unicode[STIX]{x1D6F1}$
-modules for any
$\unicode[STIX]{x1D6F1}$
-modules for any
![]() $w\in W$
[Reference Oppermann, Reiten and ThomasORT15] and comparing (3.2) and (3.3), we have the assertion.◻
$w\in W$
[Reference Oppermann, Reiten and ThomasORT15] and comparing (3.2) and (3.3), we have the assertion.◻
Now we are ready to finish the proof of Theorem 1.2.
Proof of Theorem 1.2.
As shown in the first paragraph of this section, we can complete the proof by showing that every brick is a layer. Let
![]() $L$
be a brick of
$L$
be a brick of
![]() $\unicode[STIX]{x1D6F1}$
. By Lemma 3.4, there exists
$\unicode[STIX]{x1D6F1}$
. By Lemma 3.4, there exists
![]() $v\in W$
such that
$v\in W$
such that
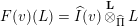 $F(v)(L)=\widehat{I}(v)\{_{\widehat{\unicode[STIX]{x1D6F1}}}L$
is a simple
$F(v)(L)=\widehat{I}(v)\{_{\widehat{\unicode[STIX]{x1D6F1}}}L$
is a simple
![]() $\unicode[STIX]{x1D6F1}$
-module
$\unicode[STIX]{x1D6F1}$
-module
![]() $S_{i}$
. Thus
$S_{i}$
. Thus
![]() $L$
equals
$L$
equals

This is a layer of
![]() $\unicode[STIX]{x1D6F1}$
by Lemma 3.5. ◻
$\unicode[STIX]{x1D6F1}$
by Lemma 3.5. ◻
4 Bijections: Theorems 1.1 and 1.3
Throughout this section, let
![]() $\unicode[STIX]{x1D6F1}$
be a preprojective algebra of Dynkin type and
$\unicode[STIX]{x1D6F1}$
be a preprojective algebra of Dynkin type and
![]() $W$
the corresponding Weyl group. The main result of this section is that Figure 3 is commutative. Commutativity of that diagram includes Theorems 1.1 and 1.3.
$W$
the corresponding Weyl group. The main result of this section is that Figure 3 is commutative. Commutativity of that diagram includes Theorems 1.1 and 1.3.
For an arrow
 $a:ws_{i}\rightarrow w$
in
$a:ws_{i}\rightarrow w$
in
![]() $H$
, we have a natural inclusion
$H$
, we have a natural inclusion
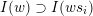 $I(w)\supset I(ws_{i})$
of ideals of
$I(w)\supset I(ws_{i})$
of ideals of
![]() $\unicode[STIX]{x1D6F1}$
, and we associate to
$\unicode[STIX]{x1D6F1}$
, and we associate to
![]() $a$
the
$a$
the
![]() $\unicode[STIX]{x1D6F1}$
-module
$\unicode[STIX]{x1D6F1}$
-module
 $$\begin{eqnarray}L(a):=I(w)/I(ws_{i})=(I(w)e_{i})/(I(w)I_{i}e_{i}),\end{eqnarray}$$
$$\begin{eqnarray}L(a):=I(w)/I(ws_{i})=(I(w)e_{i})/(I(w)I_{i}e_{i}),\end{eqnarray}$$
where the right equality follows from
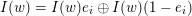 $I(w)=I(w)e_{i}\oplus I(w)(1-e_{i})$
,
$I(w)=I(w)e_{i}\oplus I(w)(1-e_{i})$
,
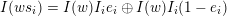 $I(ws_{i})=I(w)I_{i}e_{i}\oplus I(w)I_{i}(1-e_{i})$
and
$I(ws_{i})=I(w)I_{i}e_{i}\oplus I(w)I_{i}(1-e_{i})$
and
 $I_{i}(1-e_{i})=\unicode[STIX]{x1D6F1}(1-e_{i})$
. We also define maps
$I_{i}(1-e_{i})=\unicode[STIX]{x1D6F1}(1-e_{i})$
. We also define maps
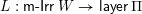 $L:\mathsf{m}\text{-}\mathsf{Irr}\,W\rightarrow \mathsf{layer}\,\unicode[STIX]{x1D6F1}$
and
$L:\mathsf{m}\text{-}\mathsf{Irr}\,W\rightarrow \mathsf{layer}\,\unicode[STIX]{x1D6F1}$
and
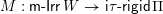 $M:\mathsf{m}\text{-}\mathsf{Irr}\,W\rightarrow \mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}$
as
$M:\mathsf{m}\text{-}\mathsf{Irr}\,W\rightarrow \mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}$
as
 $$\begin{eqnarray}L(m):=L(a)\quad \text{and}\quad M(m):=I(m)e_{i}\end{eqnarray}$$
$$\begin{eqnarray}L(m):=L(a)\quad \text{and}\quad M(m):=I(m)e_{i}\end{eqnarray}$$
for
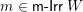 $m\in \mathsf{m}\text{-}\mathsf{Irr}\,W$
and
$m\in \mathsf{m}\text{-}\mathsf{Irr}\,W$
and
 $a:m^{\ast }=ms_{i}\rightarrow m$
in
$a:m^{\ast }=ms_{i}\rightarrow m$
in
![]() $H$
(see Proposition 2.11 for
$H$
(see Proposition 2.11 for
![]() $M(m)$
).
$M(m)$
).
Theorem 4.1. Let
![]() $\unicode[STIX]{x1D6F1}$
be a preprojective algebra of Dynkin type and
$\unicode[STIX]{x1D6F1}$
be a preprojective algebra of Dynkin type and
![]() $W$
the corresponding Weyl group. Then we have the commutative diagram shown in Figure 3. The maps are bijections or surjections as marked with tildes ‘
$W$
the corresponding Weyl group. Then we have the commutative diagram shown in Figure 3. The maps are bijections or surjections as marked with tildes ‘
![]() ${\sim}$
’ or double-headed arrows.
${\sim}$
’ or double-headed arrows.
We start with the following simple observation, where
 $\mathsf{rad}\,M(m)_{\operatorname{End}_{\unicode[STIX]{x1D6F1}}(M(m))}$
is the radical of the
$\mathsf{rad}\,M(m)_{\operatorname{End}_{\unicode[STIX]{x1D6F1}}(M(m))}$
is the radical of the
 $\operatorname{End}_{\unicode[STIX]{x1D6F1}}(M(m))^{\operatorname{op}}$
-module
$\operatorname{End}_{\unicode[STIX]{x1D6F1}}(M(m))^{\operatorname{op}}$
-module
![]() $M(m)$
.
$M(m)$
.
Lemma 4.2.
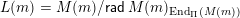 $L(m)=M(m)/\mathsf{rad}\,M(m)_{\operatorname{End}_{\unicode[STIX]{x1D6F1}}(M(m))}$
holds for any
$L(m)=M(m)/\mathsf{rad}\,M(m)_{\operatorname{End}_{\unicode[STIX]{x1D6F1}}(M(m))}$
holds for any
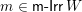 $m\in \mathsf{m}\text{-}\mathsf{Irr}\,W$
.
$m\in \mathsf{m}\text{-}\mathsf{Irr}\,W$
.
Proof. We have
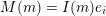 $M(m)=I(m)e_{i}$
and
$M(m)=I(m)e_{i}$
and
 $L(m)=I(m)e_{i}/I(m)I_{i}e_{i}$
. Thus we only have to show
$L(m)=I(m)e_{i}/I(m)I_{i}e_{i}$
. Thus we only have to show
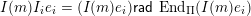 $I(m)I_{i}e_{i}=(I(m)e_{i})\mathsf{rad}\,\operatorname{End}_{\unicode[STIX]{x1D6F1}}(I(m)e_{i})$
.
$I(m)I_{i}e_{i}=(I(m)e_{i})\mathsf{rad}\,\operatorname{End}_{\unicode[STIX]{x1D6F1}}(I(m)e_{i})$
.
Since
 $\mathsf{T}(m)=\mathsf{Fac}\,I(m)$
is join-irreducible, we have
$\mathsf{T}(m)=\mathsf{Fac}\,I(m)$
is join-irreducible, we have
 $I(m)\in \mathsf{Fac}(I(m)e_{i})$
. Thus
$I(m)\in \mathsf{Fac}(I(m)e_{i})$
. Thus
 $$\begin{eqnarray}\displaystyle (I(m)e_{i})\mathsf{rad}\,\operatorname{End}_{\unicode[STIX]{x1D6F1}}(I(m)e_{i}) & = & \displaystyle \mathop{\sum }_{f\in \mathsf{rad}\,\operatorname{End}_{\unicode[STIX]{x1D6F1}}(I(m)e_{i})}\operatorname{Im}(f:I(m)e_{i}\rightarrow I(m)e_{i})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{g\in \mathsf{rad}_{\unicode[STIX]{x1D6F1}}(I(m),I(m)e_{i})}\operatorname{Im}(g:I(m)\rightarrow I(m)e_{i}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (I(m)e_{i})\mathsf{rad}\,\operatorname{End}_{\unicode[STIX]{x1D6F1}}(I(m)e_{i}) & = & \displaystyle \mathop{\sum }_{f\in \mathsf{rad}\,\operatorname{End}_{\unicode[STIX]{x1D6F1}}(I(m)e_{i})}\operatorname{Im}(f:I(m)e_{i}\rightarrow I(m)e_{i})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{g\in \mathsf{rad}_{\unicode[STIX]{x1D6F1}}(I(m),I(m)e_{i})}\operatorname{Im}(g:I(m)\rightarrow I(m)e_{i}),\nonumber\end{eqnarray}$$
where
![]() $\mathsf{rad}_{\unicode[STIX]{x1D6F1}}$
is the radical of the category
$\mathsf{rad}_{\unicode[STIX]{x1D6F1}}$
is the radical of the category
![]() $\mathsf{mod}\,\unicode[STIX]{x1D6F1}$
and hence
$\mathsf{mod}\,\unicode[STIX]{x1D6F1}$
and hence
 $\mathsf{rad}_{\unicode[STIX]{x1D6F1}}(I(m),I(m)e_{i})$
consists of morphisms which are not split epimorphisms.
$\mathsf{rad}_{\unicode[STIX]{x1D6F1}}(I(m),I(m)e_{i})$
consists of morphisms which are not split epimorphisms.
By [Reference MizunoMiz14, Lemma 2.7], we have a surjection
 $\unicode[STIX]{x1D6F1}\rightarrow \operatorname{End}_{\unicode[STIX]{x1D6F1}}(I(m))$
given by
$\unicode[STIX]{x1D6F1}\rightarrow \operatorname{End}_{\unicode[STIX]{x1D6F1}}(I(m))$
given by
 $x\mapsto (y\mapsto yx)$
. This induces surjections
$x\mapsto (y\mapsto yx)$
. This induces surjections
 $\unicode[STIX]{x1D6F1}e_{i}\rightarrow \operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(I(m),I(m)e_{i})$
and
$\unicode[STIX]{x1D6F1}e_{i}\rightarrow \operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(I(m),I(m)e_{i})$
and
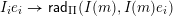 $I_{i}e_{i}\rightarrow \mathsf{rad}_{\unicode[STIX]{x1D6F1}}(I(m),I(m)e_{i})$
. Therefore we have
$I_{i}e_{i}\rightarrow \mathsf{rad}_{\unicode[STIX]{x1D6F1}}(I(m),I(m)e_{i})$
. Therefore we have
 $$\begin{eqnarray}\mathop{\sum }_{g\in \mathsf{rad}_{\unicode[STIX]{x1D6F1}}(I(m),I(m)e_{i})}\operatorname{Im}(g:I(m)\rightarrow I(m)e_{i})=I(m)I_{i}e_{i},\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{g\in \mathsf{rad}_{\unicode[STIX]{x1D6F1}}(I(m),I(m)e_{i})}\operatorname{Im}(g:I(m)\rightarrow I(m)e_{i})=I(m)I_{i}e_{i},\end{eqnarray}$$
which completes the proof. ◻
In § 2.1 (particularly Theorem 2.3 and Corollary 2.4), we described how the forcing order on join-irreducible elements interacts with the polygons (squares and rectangles) in
![]() $W$
. One ingredient in the proof of Theorem 4.1 is a similar description of how the layer labelling interacts with polygons.
$W$
. One ingredient in the proof of Theorem 4.1 is a similar description of how the layer labelling interacts with polygons.
Recall from the introduction that a pair of layer modules
![]() $X,Y$
form a doubleton if
$X,Y$
form a doubleton if
 $\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(Y,X)$
and
$\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(Y,X)$
and
 $\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(X,Y)$
are one-dimensional, and the corresponding extensions are again layer modules. Recall also that the doubleton extension order on layer modules is the transitive closure of the relation with
$\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(X,Y)$
are one-dimensional, and the corresponding extensions are again layer modules. Recall also that the doubleton extension order on layer modules is the transitive closure of the relation with
![]() $A>B$
if there exists a doubleton
$A>B$
if there exists a doubleton
![]() $A,C$
such that
$A,C$
such that
![]() $B$
is the extension of
$B$
is the extension of
![]() $A$
by
$A$
by
![]() $C$
or of
$C$
or of
![]() $C$
by
$C$
by
![]() $A$
.
$A$
.
Proposition 4.3. For a polygon in
![]() $W$
(necessarily a square or hexagon), the layer labelling has the following configuration:
$W$
(necessarily a square or hexagon), the layer labelling has the following configuration:

Moreover, in the hexagon case the layers
![]() $X$
and
$X$
and
![]() $Y$
form a doubleton and there exist short exact sequences of
$Y$
form a doubleton and there exist short exact sequences of
![]() $\unicode[STIX]{x1D6F1}$
-modules:
$\unicode[STIX]{x1D6F1}$
-modules:
 $$\begin{eqnarray}0\rightarrow X\rightarrow E\rightarrow Y\rightarrow 0\quad \text{and}\quad 0\rightarrow Y\rightarrow F\rightarrow X\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow X\rightarrow E\rightarrow Y\rightarrow 0\quad \text{and}\quad 0\rightarrow Y\rightarrow F\rightarrow X\rightarrow 0.\end{eqnarray}$$
Thus
![]() $X\geqslant E$
,
$X\geqslant E$
,
![]() $X\geqslant F$
,
$X\geqslant F$
,
![]() $Y\geqslant E$
, and
$Y\geqslant E$
, and
![]() $Y\geqslant F$
in the doubleton extension order.
$Y\geqslant F$
in the doubleton extension order.
Proof. Of the two diagrams in the statement of the theorem, the hexagon occurs if and only if
![]() $i$
and
$i$
and
![]() $j$
are neighbouring in
$j$
are neighbouring in
![]() $\overline{Q}$
. We argue the hexagon case. The square case is similar but simpler. What we need to show is the following.
$\overline{Q}$
. We argue the hexagon case. The square case is similar but simpler. What we need to show is the following.
(i) There are isomorphisms of
 $\unicode[STIX]{x1D6F1}$
-modules:
$\unicode[STIX]{x1D6F1}$
-modules:  $$\begin{eqnarray}I(u)/I(u)I_{i}\simeq I(u)I_{j}I_{i}/I(u)I_{i}I_{j}I_{i}\quad \text{and}\quad I(u)/I(u)I_{j}\simeq I(u)I_{i}I_{j}/I(u)I_{i}I_{j}I_{i}.\end{eqnarray}$$
$$\begin{eqnarray}I(u)/I(u)I_{i}\simeq I(u)I_{j}I_{i}/I(u)I_{i}I_{j}I_{i}\quad \text{and}\quad I(u)/I(u)I_{j}\simeq I(u)I_{i}I_{j}/I(u)I_{i}I_{j}I_{i}.\end{eqnarray}$$
(ii) There are short exact sequences of
 $\unicode[STIX]{x1D6F1}$
-modules:
$\unicode[STIX]{x1D6F1}$
-modules:  $$\begin{eqnarray}\displaystyle & 0\rightarrow I(u)/I(u)I_{i}\rightarrow I(u)I_{i}/I(u)I_{i}I_{j}\rightarrow I(u)I_{i}I_{j}/I(u)I_{i}I_{j}I_{i}\rightarrow 0, & \displaystyle \nonumber\\ \displaystyle & 0\rightarrow I(u)/I(u)I_{j}\rightarrow I(u)I_{j}/I(u)I_{j}I_{i}\rightarrow I(u)I_{j}I_{i}/I(u)I_{i}I_{j}I_{i}\rightarrow 0. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & 0\rightarrow I(u)/I(u)I_{i}\rightarrow I(u)I_{i}/I(u)I_{i}I_{j}\rightarrow I(u)I_{i}I_{j}/I(u)I_{i}I_{j}I_{i}\rightarrow 0, & \displaystyle \nonumber\\ \displaystyle & 0\rightarrow I(u)/I(u)I_{j}\rightarrow I(u)I_{j}/I(u)I_{j}I_{i}\rightarrow I(u)I_{j}I_{i}/I(u)I_{i}I_{j}I_{i}\rightarrow 0. & \displaystyle \nonumber\end{eqnarray}$$
We first show (i). The partial order tells us, by Lemma 2.10, that we have
 $$\begin{eqnarray}I(u)/I(u)I_{i}=I(u)\otimes _{\unicode[STIX]{x1D6F1}}(\unicode[STIX]{x1D6F1}/I_{i})\quad \text{and}\quad I(u)I_{j}I_{i}/I(u)I_{i}I_{j}I_{i}=I(u)\otimes _{\unicode[STIX]{x1D6F1}}(I_{j}I_{i}/I_{i}I_{j}I_{i}).\end{eqnarray}$$
$$\begin{eqnarray}I(u)/I(u)I_{i}=I(u)\otimes _{\unicode[STIX]{x1D6F1}}(\unicode[STIX]{x1D6F1}/I_{i})\quad \text{and}\quad I(u)I_{j}I_{i}/I(u)I_{i}I_{j}I_{i}=I(u)\otimes _{\unicode[STIX]{x1D6F1}}(I_{j}I_{i}/I_{i}I_{j}I_{i}).\end{eqnarray}$$
Since
 $\unicode[STIX]{x1D6F1}/I_{i}\simeq S_{i}\simeq I_{j}I_{i}/I_{i}I_{j}I_{i}$
holds by an easy calculation for the preprojective algebra
$\unicode[STIX]{x1D6F1}/I_{i}\simeq S_{i}\simeq I_{j}I_{i}/I_{i}I_{j}I_{i}$
holds by an easy calculation for the preprojective algebra
 $\unicode[STIX]{x1D6F1}/I_{i}I_{j}I_{i}$
of type
$\unicode[STIX]{x1D6F1}/I_{i}I_{j}I_{i}$
of type
![]() $A_{2}$
(see Figure 5), we have
$A_{2}$
(see Figure 5), we have
 $$\begin{eqnarray}I(u)/I(u)I_{i}=I(u)\otimes _{\unicode[STIX]{x1D6F1}}(\unicode[STIX]{x1D6F1}/I_{i})\simeq I(u)\otimes _{\unicode[STIX]{x1D6F1}}(I_{j}I_{i}/I_{i}I_{j}I_{i})=I(u)I_{j}I_{i}/I(u)I_{i}I_{j}I_{i}.\end{eqnarray}$$
$$\begin{eqnarray}I(u)/I(u)I_{i}=I(u)\otimes _{\unicode[STIX]{x1D6F1}}(\unicode[STIX]{x1D6F1}/I_{i})\simeq I(u)\otimes _{\unicode[STIX]{x1D6F1}}(I_{j}I_{i}/I_{i}I_{j}I_{i})=I(u)I_{j}I_{i}/I(u)I_{i}I_{j}I_{i}.\end{eqnarray}$$
The other isomorphism follows by interchanging
![]() $i$
and
$i$
and
![]() $j$
.
$j$
.
Now we show (ii). Again by an easy calculation for the preprojective algebra
 $\unicode[STIX]{x1D6F1}/I_{i}I_{j}I_{i}$
of type
$\unicode[STIX]{x1D6F1}/I_{i}I_{j}I_{i}$
of type
![]() $A_{2}$
(see Figure 5), we have
$A_{2}$
(see Figure 5), we have
 $\unicode[STIX]{x1D6F1}/I_{i}\simeq S_{i}$
,
$\unicode[STIX]{x1D6F1}/I_{i}\simeq S_{i}$
,
 $I_{i}/I_{i}I_{j}\simeq \binom{S_{j}}{S_{i}}$
and
$I_{i}/I_{i}I_{j}\simeq \binom{S_{j}}{S_{i}}$
and
 $I_{i}I_{j}/I_{i}I_{j}I_{i}\simeq S_{j}$
. Thus there exists an exact sequence
$I_{i}I_{j}/I_{i}I_{j}I_{i}\simeq S_{j}$
. Thus there exists an exact sequence
 $$\begin{eqnarray}0\rightarrow \unicode[STIX]{x1D6F1}/I_{i}\rightarrow I_{i}/I_{i}I_{j}\rightarrow I_{i}I_{j}/I_{i}I_{j}I_{i}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \unicode[STIX]{x1D6F1}/I_{i}\rightarrow I_{i}/I_{i}I_{j}\rightarrow I_{i}I_{j}/I_{i}I_{j}I_{i}\rightarrow 0\end{eqnarray}$$
of
![]() $\unicode[STIX]{x1D6F1}$
-modules. Applying
$\unicode[STIX]{x1D6F1}$
-modules. Applying
 $I(u)\otimes _{\unicode[STIX]{x1D6F1}}-$
and using
$I(u)\otimes _{\unicode[STIX]{x1D6F1}}-$
and using
 $\operatorname{Tor}_{1}^{\unicode[STIX]{x1D6F1}}(I(u),S_{j})=0$
(which follows from
$\operatorname{Tor}_{1}^{\unicode[STIX]{x1D6F1}}(I(u),S_{j})=0$
(which follows from
 $\ell (us_{j})=\ell (u)+1$
and Lemma 2.10), we obtain the first sequence. The second one follows by interchanging
$\ell (us_{j})=\ell (u)+1$
and Lemma 2.10), we obtain the first sequence. The second one follows by interchanging
![]() $i$
and
$i$
and
![]() $j$
.
$j$
.
We verify that
![]() $X$
and
$X$
and
![]() $Y$
form a doubleton in the hexagon case. If the labels are simple, then the extension groups are certainly one-dimensional, and the extensions are layers by
$Y$
form a doubleton in the hexagon case. If the labels are simple, then the extension groups are certainly one-dimensional, and the extensions are layers by
 $\binom{S_{j}}{S_{i}}\simeq I_{i}/I_{i}I_{j}$
. Any hexagon is obtained by applying
$\binom{S_{j}}{S_{i}}\simeq I_{i}/I_{i}I_{j}$
. Any hexagon is obtained by applying
 $I(u)\otimes _{\unicode[STIX]{x1D6F1}}-$
to such a hexagon, as above. This implies the desired result once we note that, by Lemma 3.1, we can instead consider applying
$I(u)\otimes _{\unicode[STIX]{x1D6F1}}-$
to such a hexagon, as above. This implies the desired result once we note that, by Lemma 3.1, we can instead consider applying
 $\widehat{I}(u)\{_{\widehat{\unicode[STIX]{x1D6F1}}}-$
, which is an auto-equivalence of
$\widehat{I}(u)\{_{\widehat{\unicode[STIX]{x1D6F1}}}-$
, which is an auto-equivalence of
 $\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
by [Reference Buan, Iyama, Reiten and ScottBIRS09].
$\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
by [Reference Buan, Iyama, Reiten and ScottBIRS09].
Now
![]() $X\geqslant E$
,
$X\geqslant E$
,
![]() $X\geqslant F$
,
$X\geqslant F$
,
![]() $Y\geqslant E$
, and
$Y\geqslant E$
, and
![]() $Y\geqslant F$
because there exist short exact sequences
$Y\geqslant F$
because there exist short exact sequences
 $0\rightarrow X\rightarrow E\rightarrow Y\rightarrow 0$
and
$0\rightarrow X\rightarrow E\rightarrow Y\rightarrow 0$
and
 $0\rightarrow Y\rightarrow F\rightarrow X\rightarrow 0$
.◻
$0\rightarrow Y\rightarrow F\rightarrow X\rightarrow 0$
.◻
The ideas in the proof above also lead to the following lemma. For vertices
![]() $i\neq j$
in
$i\neq j$
in
![]() $\overline{Q}$
, let
$\overline{Q}$
, let
 $W_{i,j}:=\langle s_{i},s_{j}\rangle \subset W$
be a parabolic subgroup of
$W_{i,j}:=\langle s_{i},s_{j}\rangle \subset W$
be a parabolic subgroup of
![]() $W$
. For
$W$
. For
![]() $w\in W$
, the coset
$w\in W$
, the coset
![]() $wW_{i,j}$
is an interval in the weak order on
$wW_{i,j}$
is an interval in the weak order on
![]() $W$
. We write
$W$
. We write
![]() $H|_{wW_{i,j}}$
for the restriction of
$H|_{wW_{i,j}}$
for the restriction of
 $\mathsf{Hasse}(W)$
to
$\mathsf{Hasse}(W)$
to
![]() $wW_{i,j}$
. Define
$wW_{i,j}$
. Define
![]() $w^{+}$
(respectively,
$w^{+}$
(respectively,
![]() $w^{-}$
) to be the set of arrows in
$w^{-}$
) to be the set of arrows in
 $\mathsf{Hasse}(W)$
starting (respectively, ending) at
$\mathsf{Hasse}(W)$
starting (respectively, ending) at
![]() $w$
. For a set
$w$
. For a set
![]() $S$
of
$S$
of
![]() $\unicode[STIX]{x1D6F1}$
-modules, we denote by
$\unicode[STIX]{x1D6F1}$
-modules, we denote by
![]() $\mathsf{T}(S)$
(respectively,
$\mathsf{T}(S)$
(respectively,
![]() $\mathsf{F}(S)$
) the smallest torsion (respectively, torsionfree) class in
$\mathsf{F}(S)$
) the smallest torsion (respectively, torsionfree) class in
![]() $\mathsf{mod}\,\unicode[STIX]{x1D6F1}$
containing
$\mathsf{mod}\,\unicode[STIX]{x1D6F1}$
containing
![]() $S$
. For convenience and brevity, we will omit set braces inside the operator
$S$
. For convenience and brevity, we will omit set braces inside the operator
![]() $\mathsf{T}(\bullet )$
, so that, for example
$\mathsf{T}(\bullet )$
, so that, for example
 $\mathsf{T}(L_{0},M_{i}\mid i\in I)$
would mean
$\mathsf{T}(L_{0},M_{i}\mid i\in I)$
would mean
 $\mathsf{T}(\{L_{0}\}\cup \{M_{i}\mid i\in I\})$
. Recall that the layer labelling of
$\mathsf{T}(\{L_{0}\}\cup \{M_{i}\mid i\in I\})$
. Recall that the layer labelling of
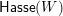 $\mathsf{Hasse}(W)$
maps each Hasse arrow
$\mathsf{Hasse}(W)$
maps each Hasse arrow
![]() $x\rightarrow y$
to the isomorphism class of the corresponding concrete layer
$x\rightarrow y$
to the isomorphism class of the corresponding concrete layer
 $L(x\rightarrow y):=I(y)/I(x)$
.
$L(x\rightarrow y):=I(y)/I(x)$
.
Lemma 4.4. If
 $a:ws_{i}\rightarrow w$
is an arrow in
$a:ws_{i}\rightarrow w$
is an arrow in
 $\mathsf{Hasse}(W)$
, and
$\mathsf{Hasse}(W)$
, and
![]() $j\neq i$
is a vertex in
$j\neq i$
is a vertex in
![]() $\overline{Q}$
, then
$\overline{Q}$
, then
 $$\begin{eqnarray}\mathsf{T}(L(b)\mid b\in w^{-}\cap H|_{wW_{i,j}})=\mathsf{T}(L(a),L(b)\mid b\in (ws_{i})^{-}\cap H|_{wW_{i,j}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{T}(L(b)\mid b\in w^{-}\cap H|_{wW_{i,j}})=\mathsf{T}(L(a),L(b)\mid b\in (ws_{i})^{-}\cap H|_{wW_{i,j}}).\end{eqnarray}$$
Proof. We have either the square or the hexagon in Proposition 4.3. We argue the hexagon case. The square case is similar but simpler. If
![]() $w$
coincides with
$w$
coincides with
![]() $u$
in Proposition 4.3, the desired equality reduces to an identity
$u$
in Proposition 4.3, the desired equality reduces to an identity
 $\mathsf{T}(X,Y)=\mathsf{T}(X,E)$
, which follows from the exact sequence
$\mathsf{T}(X,Y)=\mathsf{T}(X,E)$
, which follows from the exact sequence
 $0\rightarrow X\rightarrow E\rightarrow Y\rightarrow 0$
. If
$0\rightarrow X\rightarrow E\rightarrow Y\rightarrow 0$
. If
![]() $w$
coincides with
$w$
coincides with
![]() $us_{j}$
in Proposition 4.3, the desired equality reduces to an identity
$us_{j}$
in Proposition 4.3, the desired equality reduces to an identity
 $\mathsf{T}(F)=\mathsf{T}(F,X)$
, which follows from the exact sequence
$\mathsf{T}(F)=\mathsf{T}(F,X)$
, which follows from the exact sequence
 $0\rightarrow Y\rightarrow F\rightarrow X\rightarrow 0$
. If
$0\rightarrow Y\rightarrow F\rightarrow X\rightarrow 0$
. If
![]() $w$
coincides with
$w$
coincides with
![]() $us_{i}s_{j}$
in Proposition 4.3, the desired equality reduces to an identity
$us_{i}s_{j}$
in Proposition 4.3, the desired equality reduces to an identity
 $\mathsf{T}(Y)=\mathsf{T}(Y)$
, which clearly holds.◻
$\mathsf{T}(Y)=\mathsf{T}(Y)$
, which clearly holds.◻
Another ingredient in the proof of Theorem 4.1 is a precise connection between torsion classes and layer modules.
Theorem 4.5. For any
![]() $w\in W$
, we have
$w\in W$
, we have
 $$\begin{eqnarray}\mathsf{T}(w)=\mathsf{T}(L(a)\mid a\in w^{-})\quad \text{and}\quad \mathsf{F}(w)=\mathsf{F}(L(a)\mid a\in w^{+}).\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{T}(w)=\mathsf{T}(L(a)\mid a\in w^{-})\quad \text{and}\quad \mathsf{F}(w)=\mathsf{F}(L(a)\mid a\in w^{+}).\end{eqnarray}$$
Proof. We only prove the first equality since the second one is proved similarly. We use decreasing induction on
![]() $W$
. The statement is clear for the longest element
$W$
. The statement is clear for the longest element
![]() $w_{0}$
since both sides are
$w_{0}$
since both sides are
![]() $\{0\}$
in this case.
$\{0\}$
in this case.
Let
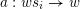 $a:ws_{i}\rightarrow w$
be an arrow in
$a:ws_{i}\rightarrow w$
be an arrow in
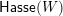 $\mathsf{Hasse}(W)$
. Assume that the assertion holds for
$\mathsf{Hasse}(W)$
. Assume that the assertion holds for
![]() $ws_{i}$
, that is,
$ws_{i}$
, that is,
 $$\begin{eqnarray}\mathsf{T}(ws_{i})=\mathsf{T}(L(b)\mid b\in (ws_{i})^{-}).\end{eqnarray}$$
$$\begin{eqnarray}\mathsf{T}(ws_{i})=\mathsf{T}(L(b)\mid b\in (ws_{i})^{-}).\end{eqnarray}$$
Using obvious decompositions
 $$\begin{eqnarray}w^{-}=\mathop{\bigcup }_{j\neq i}(w^{-}\cap H|_{wW_{i,j}})\quad \text{and}\quad (ws_{i})^{-}=\mathop{\bigcup }_{j\neq i}((ws_{i})^{-}\cap H|_{wW_{i,j}}),\end{eqnarray}$$
$$\begin{eqnarray}w^{-}=\mathop{\bigcup }_{j\neq i}(w^{-}\cap H|_{wW_{i,j}})\quad \text{and}\quad (ws_{i})^{-}=\mathop{\bigcup }_{j\neq i}((ws_{i})^{-}\cap H|_{wW_{i,j}}),\end{eqnarray}$$
we have

where the last equality follows from having an exact sequence
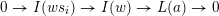 $0\rightarrow I(ws_{i})\rightarrow I(w)\rightarrow L(a)\rightarrow 0$
and
$0\rightarrow I(ws_{i})\rightarrow I(w)\rightarrow L(a)\rightarrow 0$
and
 $I(ws_{i})\in \mathsf{T}(w)$
.◻
$I(ws_{i})\in \mathsf{T}(w)$
.◻
Proposition 4.6. Two arrows
![]() $x\rightarrow y$
and
$x\rightarrow y$
and
 $x^{\prime }\rightarrow y^{\prime }$
in
$x^{\prime }\rightarrow y^{\prime }$
in
 $\mathsf{Hasse}(W)$
have
$\mathsf{Hasse}(W)$
have
 $\mathsf{con}(x,y)=\mathsf{con}(x^{\prime },y^{\prime })$
if and only if they have the same layer label.
$\mathsf{con}(x,y)=\mathsf{con}(x^{\prime },y^{\prime })$
if and only if they have the same layer label.
Proof. Proposition 4.3 implies in particular that the map
 $(x\rightarrow y)\mapsto I(y)/I(x)$
is constant on components of
$(x\rightarrow y)\mapsto I(y)/I(x)$
is constant on components of
 $\mathsf{SFPoly}(W)$
. Thus by Corollary 2.5, if
$\mathsf{SFPoly}(W)$
. Thus by Corollary 2.5, if
![]() $x\rightarrow y$
and
$x\rightarrow y$
and
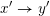 $x^{\prime }\rightarrow y^{\prime }$
have
$x^{\prime }\rightarrow y^{\prime }$
have
 $\mathsf{con}(x,y)=\mathsf{con}(x^{\prime },y^{\prime })$
, then they have the same layer labelling.
$\mathsf{con}(x,y)=\mathsf{con}(x^{\prime },y^{\prime })$
, then they have the same layer labelling.
If
![]() $x\rightarrow y$
and
$x\rightarrow y$
and
 $x^{\prime }\rightarrow y^{\prime }$
have the same layer labelling, let
$x^{\prime }\rightarrow y^{\prime }$
have the same layer labelling, let
![]() $m$
be the unique meet-irreducible element with
$m$
be the unique meet-irreducible element with
 $\mathsf{con}(m^{\ast },m)=\mathsf{con}(x,y)$
, and similarly let
$\mathsf{con}(m^{\ast },m)=\mathsf{con}(x,y)$
, and similarly let
![]() $m^{\prime }$
be the meet-irreducible corresponding to
$m^{\prime }$
be the meet-irreducible corresponding to
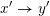 $x^{\prime }\rightarrow y^{\prime }$
. Then
$x^{\prime }\rightarrow y^{\prime }$
. Then
 $L(m^{\ast }\rightarrow m)=L((m^{\prime })^{\ast }\rightarrow m^{\prime })$
, so by Theorem 4.5,
$L(m^{\ast }\rightarrow m)=L((m^{\prime })^{\ast }\rightarrow m^{\prime })$
, so by Theorem 4.5,
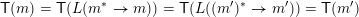 $\mathsf{T}(m)=\mathsf{T}(L(m^{\ast }\rightarrow m))=\mathsf{T}(L((m^{\prime })^{\ast }\rightarrow m^{\prime }))=\mathsf{T}(m^{\prime })$
. Since
$\mathsf{T}(m)=\mathsf{T}(L(m^{\ast }\rightarrow m))=\mathsf{T}(L((m^{\prime })^{\ast }\rightarrow m^{\prime }))=\mathsf{T}(m^{\prime })$
. Since
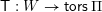 $\mathsf{T}:W\rightarrow \mathsf{tors}\,\unicode[STIX]{x1D6F1}$
is a bijection, we see that
$\mathsf{T}:W\rightarrow \mathsf{tors}\,\unicode[STIX]{x1D6F1}$
is a bijection, we see that
 $m=m^{\prime }$
, so that
$m=m^{\prime }$
, so that
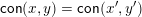 $\mathsf{con}(x,y)=\mathsf{con}(x^{\prime },y^{\prime })$
.◻
$\mathsf{con}(x,y)=\mathsf{con}(x^{\prime },y^{\prime })$
.◻
Proof of Theorem 4.1.
Commutativity of the two triangles involving
 $\mathsf{m}\text{-}\mathsf{Irr}(W)$
,
$\mathsf{m}\text{-}\mathsf{Irr}(W)$
,
 $\mathsf{j}\text{-}\mathsf{Irr}(W)$
,
$\mathsf{j}\text{-}\mathsf{Irr}(W)$
,
 $\mathsf{Con}_{\mathsf{JI}}(W)$
, and
$\mathsf{Con}_{\mathsf{JI}}(W)$
, and
 $\mathsf{Hasse}_{1}(W)$
, and correctness of the markings of the arrows as bijections or surjections was established in § 2.1 in the more general context of congruence uniform lattices. (See especially Figure 4.)
$\mathsf{Hasse}_{1}(W)$
, and correctness of the markings of the arrows as bijections or surjections was established in § 2.1 in the more general context of congruence uniform lattices. (See especially Figure 4.)
The map from
 $\mathsf{Hasse}_{1}(W)$
to
$\mathsf{Hasse}_{1}(W)$
to
![]() $\mathsf{layer}\,\unicode[STIX]{x1D6F1}$
is surjective by definition. Proposition 4.6, together with the commutativity of the triangles containing
$\mathsf{layer}\,\unicode[STIX]{x1D6F1}$
is surjective by definition. Proposition 4.6, together with the commutativity of the triangles containing
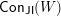 $\mathsf{Con}_{\mathsf{JI}}(W)$
, then implies the commutativity of the two triangles containing the map from
$\mathsf{Con}_{\mathsf{JI}}(W)$
, then implies the commutativity of the two triangles containing the map from
 $\mathsf{Hasse}_{1}(W)$
to
$\mathsf{Hasse}_{1}(W)$
to
![]() $\mathsf{layer}\,\unicode[STIX]{x1D6F1}$
and also implies that the map from
$\mathsf{layer}\,\unicode[STIX]{x1D6F1}$
and also implies that the map from
 $\mathsf{m}\text{-}\mathsf{Irr}(W)$
to
$\mathsf{m}\text{-}\mathsf{Irr}(W)$
to
![]() $\mathsf{layer}\,\unicode[STIX]{x1D6F1}$
is a bijection. The triangle containing
$\mathsf{layer}\,\unicode[STIX]{x1D6F1}$
is a bijection. The triangle containing
 $\mathsf{m}\text{-}\mathsf{Irr}(W)$
,
$\mathsf{m}\text{-}\mathsf{Irr}(W)$
,
 $\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}$
and
$\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}$
and
![]() $\mathsf{layer}\,\unicode[STIX]{x1D6F1}$
commutes by Lemma 4.2, and the left bottom square commutes by Theorem 4.5. The remaining part of the diagram commutes dually. The maps
$\mathsf{layer}\,\unicode[STIX]{x1D6F1}$
commutes by Lemma 4.2, and the left bottom square commutes by Theorem 4.5. The remaining part of the diagram commutes dually. The maps
 $M:\mathsf{m}\text{-}\mathsf{Irr}\,W\rightarrow \mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}$
,
$M:\mathsf{m}\text{-}\mathsf{Irr}\,W\rightarrow \mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}$
,
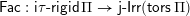 $\mathsf{Fac}:\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}\rightarrow \mathsf{j}\text{-}\mathsf{Irr}(\mathsf{tors}\,\unicode[STIX]{x1D6F1})$
and
$\mathsf{Fac}:\mathsf{i}\unicode[STIX]{x1D70F}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}\rightarrow \mathsf{j}\text{-}\mathsf{Irr}(\mathsf{tors}\,\unicode[STIX]{x1D6F1})$
and
 $\mathsf{Filt}:\mathsf{brick}\,\unicode[STIX]{x1D6F1}\rightarrow \mathsf{l}\text{-}\mathsf{wide}\,\unicode[STIX]{x1D6F1}$
are bijections by Corollary 2.11, Theorem 2.7 and Proposition 2.8. The bijectivity of the other maps follows from commutativity.◻
$\mathsf{Filt}:\mathsf{brick}\,\unicode[STIX]{x1D6F1}\rightarrow \mathsf{l}\text{-}\mathsf{wide}\,\unicode[STIX]{x1D6F1}$
are bijections by Corollary 2.11, Theorem 2.7 and Proposition 2.8. The bijectivity of the other maps follows from commutativity.◻
The bijections
 $\mathsf{j}\text{-}\mathsf{Irr}\,W\simeq \mathsf{layer}\,\unicode[STIX]{x1D6F1}\simeq \mathsf{m}\text{-}\mathsf{Irr}\,W$
given in Theorem 4.1, combined with Proposition 2.2, imply the following corollary.
$\mathsf{j}\text{-}\mathsf{Irr}\,W\simeq \mathsf{layer}\,\unicode[STIX]{x1D6F1}\simeq \mathsf{m}\text{-}\mathsf{Irr}\,W$
given in Theorem 4.1, combined with Proposition 2.2, imply the following corollary.
Corollary 4.7.
![]() $\mathsf{T}(w)$
is the smallest subcategory of
$\mathsf{T}(w)$
is the smallest subcategory of
![]() $\unicode[STIX]{x1D6F1}$
-mod which is closed under extensions and quotients and contains the layers corresponding to the canonical meet representation of
$\unicode[STIX]{x1D6F1}$
-mod which is closed under extensions and quotients and contains the layers corresponding to the canonical meet representation of
![]() $w$
.
$w$
.
![]() $\mathsf{F}(w)$
is the smallest subcategory of
$\mathsf{F}(w)$
is the smallest subcategory of
![]() $\unicode[STIX]{x1D6F1}$
-mod which is closed under extensions and subobjects and contains the layers corresponding to the canonical join representation of
$\unicode[STIX]{x1D6F1}$
-mod which is closed under extensions and subobjects and contains the layers corresponding to the canonical join representation of
![]() $w$
.
$w$
.
Remark 4.8. Let
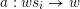 $a:ws_{i}\rightarrow w$
be an arrow in
$a:ws_{i}\rightarrow w$
be an arrow in
![]() $H$
. One might wonder if
$H$
. One might wonder if
![]() $L(a)$
is a unique brick of
$L(a)$
is a unique brick of
![]() $\unicode[STIX]{x1D6F1}$
which belongs to
$\unicode[STIX]{x1D6F1}$
which belongs to
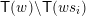 $\mathsf{T}(w)\backslash \mathsf{T}(ws_{i})$
.
$\mathsf{T}(w)\backslash \mathsf{T}(ws_{i})$
.
This has an easy counterexample: let
![]() $\unicode[STIX]{x1D6F1}$
be of type
$\unicode[STIX]{x1D6F1}$
be of type
![]() $A_{2}$
, and let
$A_{2}$
, and let
![]() $w:=e$
and
$w:=e$
and
![]() $s_{i}:=s_{1}$
. Then both layer modules
$s_{i}:=s_{1}$
. Then both layer modules
![]() $S_{1}$
and
$S_{1}$
and
![]() $P_{1}$
belong to
$P_{1}$
belong to
 $(\mathsf{mod}\,\unicode[STIX]{x1D6F1})\backslash (\mathsf{Fac}\,I_{1})$
.
$(\mathsf{mod}\,\unicode[STIX]{x1D6F1})\backslash (\mathsf{Fac}\,I_{1})$
.
On the other hand,
![]() $L(a)$
is a unique brick in
$L(a)$
is a unique brick in
 ${\mathcal{T}}(w)\cap {\mathcal{F}}(ws_{i})$
[Reference Demonet, Iyama, Reiten, Reading and ThomasDIRRT17].
${\mathcal{T}}(w)\cap {\mathcal{F}}(ws_{i})$
[Reference Demonet, Iyama, Reiten, Reading and ThomasDIRRT17].
5 Doubleton extension order on layer modules
In this section, we prove Theorem 1.4 and a characterization of the doubleton extension order on layer modules. The last ingredient needed is the following proposition.
Proposition 5.1. Suppose
![]() $A$
,
$A$
,
![]() $B$
, and
$B$
, and
![]() $C$
are layers of
$C$
are layers of
![]() $\unicode[STIX]{x1D6F1}$
such that
$\unicode[STIX]{x1D6F1}$
such that
![]() $A,C$
is a doubleton and
$A,C$
is a doubleton and
![]() $B$
is the extension of
$B$
is the extension of
![]() $C$
by
$C$
by
![]() $A$
. Then there exists a hexagon in weak order such that the layer ordering of one of its chains is
$A$
. Then there exists a hexagon in weak order such that the layer ordering of one of its chains is
 $(A,B,C)$
, read either from bottom to top or from top to bottom.
$(A,B,C)$
, read either from bottom to top or from top to bottom.
Before proving Proposition 5.1, we show how it completes the proof of Theorem 1.4.
Proof of Theorem 1.4.
Theorem 4.1 already states that the map
 $j\mapsto I(j_{\ast })/I(j)$
is a bijection from the set of join-irreducible elements of
$j\mapsto I(j_{\ast })/I(j)$
is a bijection from the set of join-irreducible elements of
![]() $W$
to the set of layer modules of
$W$
to the set of layer modules of
![]() $\unicode[STIX]{x1D6F1}$
. Proposition 4.3 implies that every arrow in the quiver
$\unicode[STIX]{x1D6F1}$
. Proposition 4.3 implies that every arrow in the quiver
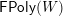 $\mathsf{FPoly}(W)$
(defined in § 2.1) gives rise to an order relation in the doubleton extension order. Proposition 5.1 shows that each doubleton extension comes from some arrow in
$\mathsf{FPoly}(W)$
(defined in § 2.1) gives rise to an order relation in the doubleton extension order. Proposition 5.1 shows that each doubleton extension comes from some arrow in
 $\mathsf{FPoly}(W)$
. Corollary 2.4 (which applies in light of Theorem 2.6) thus implies that
$\mathsf{FPoly}(W)$
. Corollary 2.4 (which applies in light of Theorem 2.6) thus implies that
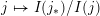 $j\mapsto I(j_{\ast })/I(j)$
is an isomorphism from the forcing order on join-irreducible elements of
$j\mapsto I(j_{\ast })/I(j)$
is an isomorphism from the forcing order on join-irreducible elements of
![]() $W$
to the doubleton extension order on layers.◻
$W$
to the doubleton extension order on layers.◻
We now prepare to prove Proposition 5.1.
Lemma 5.2. If
![]() $X,Y$
is a doubleton, then
$X,Y$
is a doubleton, then
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,Y)=\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(Y,X)=0$
.
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,Y)=\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(Y,X)=0$
.
Proof. Let
![]() $\langle -,-\rangle$
be the Euler form on
$\langle -,-\rangle$
be the Euler form on
 $K_{0}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
. Since the extensions
$K_{0}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
. Since the extensions
![]() $E$
of
$E$
of
![]() $X,Y$
are layers by assumption, we have
$X,Y$
are layers by assumption, we have
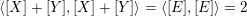 $\langle [X]+[Y],[X]+[Y]\rangle =\langle [E],[E]\rangle =2$
. Thus
$\langle [X]+[Y],[X]+[Y]\rangle =\langle [E],[E]\rangle =2$
. Thus
 $$\begin{eqnarray}2\langle [X],[Y]\rangle =\langle [X]+[Y],[X]+[Y]\rangle -\langle [X],[X]\rangle -\langle [Y],[Y]\rangle =-2.\end{eqnarray}$$
$$\begin{eqnarray}2\langle [X],[Y]\rangle =\langle [X]+[Y],[X]+[Y]\rangle -\langle [X],[X]\rangle -\langle [Y],[Y]\rangle =-2.\end{eqnarray}$$
Since
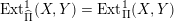 $\operatorname{Ext}_{\widehat{\unicode[STIX]{x1D6F1}}}^{1}(X,Y)=\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(X,Y)$
is one-dimensional by assumption, it follows that
$\operatorname{Ext}_{\widehat{\unicode[STIX]{x1D6F1}}}^{1}(X,Y)=\operatorname{Ext}_{\unicode[STIX]{x1D6F1}}^{1}(X,Y)$
is one-dimensional by assumption, it follows that
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,Y)=\operatorname{Hom}_{\widehat{\unicode[STIX]{x1D6F1}}}(X,Y)=0$
and
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,Y)=\operatorname{Hom}_{\widehat{\unicode[STIX]{x1D6F1}}}(X,Y)=0$
and
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(Y,X)=D\operatorname{Ext}_{\widehat{\unicode[STIX]{x1D6F1}}}^{2}(X,Y)=0$
.◻
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(Y,X)=D\operatorname{Ext}_{\widehat{\unicode[STIX]{x1D6F1}}}^{2}(X,Y)=0$
.◻
The following lemma is an analogue for doubletons of Lemma 3.3.
Lemma 5.3. If
![]() $X,Y$
is a doubleton contained in
$X,Y$
is a doubleton contained in
![]() $\mathsf{T}(w)$
, and
$\mathsf{T}(w)$
, and
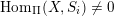 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,S_{i})\neq 0$
and
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,S_{i})\neq 0$
and
![]() $X\not \simeq S_{i}$
, then
$X\not \simeq S_{i}$
, then
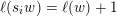 $\ell (s_{i}w)=\ell (w)+1$
and
$\ell (s_{i}w)=\ell (w)+1$
and
 $F_{i}(X),F_{i}(Y)$
form a doubleton contained in
$F_{i}(X),F_{i}(Y)$
form a doubleton contained in
![]() $\mathsf{T}(s_{i}w)$
.
$\mathsf{T}(s_{i}w)$
.
Proof. Since
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,S_{i})\neq 0$
, we have
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,S_{i})\neq 0$
, we have
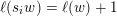 $\ell (s_{i}w)=\ell (w)+1$
by Lemma 3.3 and
$\ell (s_{i}w)=\ell (w)+1$
by Lemma 3.3 and
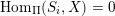 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},X)=0$
by Proposition 3.2(a). Since
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},X)=0$
by Proposition 3.2(a). Since
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,Y)=0$
by Lemma 5.2, then
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,Y)=0$
by Lemma 5.2, then
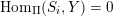 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},Y)=0$
also. Thus, by Proposition 3.2(b),
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},Y)=0$
also. Thus, by Proposition 3.2(b),
![]() $F_{i}(X)$
and
$F_{i}(X)$
and
![]() $F_{i}(Y)$
are layer modules. Since
$F_{i}(Y)$
are layer modules. Since
![]() $F_{i}$
is an auto-equivalence of
$F_{i}$
is an auto-equivalence of
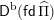 $\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
, it follows that
$\mathsf{D}^{\operatorname{b}}(\mathsf{fd}\,\widehat{\unicode[STIX]{x1D6F1}})$
, it follows that
![]() $F_{i}(X)$
,
$F_{i}(X)$
,
![]() $F_{i}(Y)$
still form a doubleton.
$F_{i}(Y)$
still form a doubleton.
![]() $F_{i}(X)$
belongs to
$F_{i}(X)$
belongs to
![]() $\mathsf{T}(s_{i}w)$
by Lemma 3.3(b). If
$\mathsf{T}(s_{i}w)$
by Lemma 3.3(b). If
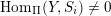 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(Y,S_{i})\neq 0$
, then Lemma 3.3 is also directly applicable to
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(Y,S_{i})\neq 0$
, then Lemma 3.3 is also directly applicable to
![]() $Y$
, and tells us that
$Y$
, and tells us that
![]() $F_{i}(Y)$
also belongs to
$F_{i}(Y)$
also belongs to
![]() $\mathsf{T}(s_{i}w)$
. In fact, the proof of Lemma 3.3(b) is actually applicable to
$\mathsf{T}(s_{i}w)$
. In fact, the proof of Lemma 3.3(b) is actually applicable to
![]() $Y$
even if
$Y$
even if
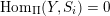 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(Y,S_{i})=0$
. All that is really needed is that
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(Y,S_{i})=0$
. All that is really needed is that
 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},Y)=0$
, and we have this. Thus,
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(S_{i},Y)=0$
, and we have this. Thus,
![]() $F_{i}(Y)$
also belongs to
$F_{i}(Y)$
also belongs to
![]() $\mathsf{T}(s_{i}w)$
.◻
$\mathsf{T}(s_{i}w)$
.◻
The following lemma is an analogue for doubletons of Lemma 3.4.
Lemma 5.4. If
![]() $X,Y$
is a doubleton, then there exists
$X,Y$
is a doubleton, then there exists
![]() $v\in W$
such that
$v\in W$
such that
 $F(v)(X)$
and
$F(v)(X)$
and
 $F(v)(Y)$
are simple modules.
$F(v)(Y)$
are simple modules.
Proof. Suppose that at least one of
![]() $X$
and
$X$
and
![]() $Y$
is not simple. Without loss of generality, suppose that
$Y$
is not simple. Without loss of generality, suppose that
![]() $X$
is not simple. Choose
$X$
is not simple. Choose
![]() $S_{i}$
so that
$S_{i}$
so that
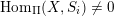 $\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,S_{i})\neq 0$
. Applying Lemma 5.3, we see that
$\operatorname{Hom}_{\unicode[STIX]{x1D6F1}}(X,S_{i})\neq 0$
. Applying Lemma 5.3, we see that
![]() $F_{i}(X)$
and
$F_{i}(X)$
and
![]() $F_{i}(Y)$
are a doubleton in
$F_{i}(Y)$
are a doubleton in
![]() $\mathsf{Fac}\,I_{s_{i}}$
. Assume that one of
$\mathsf{Fac}\,I_{s_{i}}$
. Assume that one of
![]() $F_{i}(X)$
and
$F_{i}(X)$
and
![]() $F_{i}(Y)$
is not simple. Repeat the previous procedure. As in the proof of Lemma 3.4, the procedure must terminate, at which point we have obtained a doubleton of simple modules.◻
$F_{i}(Y)$
is not simple. Repeat the previous procedure. As in the proof of Lemma 3.4, the procedure must terminate, at which point we have obtained a doubleton of simple modules.◻
Proof of Proposition 5.1.
Suppose that we have a doubleton
![]() $A,C$
, with
$A,C$
, with
![]() $B$
the extension of
$B$
the extension of
![]() $C$
by
$C$
by
![]() $A$
. We will establish that there exists a hexagon in weak order such that one side of it is labelled
$A$
. We will establish that there exists a hexagon in weak order such that one side of it is labelled
 $(A,B,C)$
. By Lemma 5.4, there exists
$(A,B,C)$
. By Lemma 5.4, there exists
![]() $v\in W$
such that
$v\in W$
such that
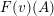 $F(v)(A)$
,
$F(v)(A)$
,
 $F(v)(C)$
form a doubleton of simple modules, say
$F(v)(C)$
form a doubleton of simple modules, say
![]() $S_{i},S_{j}$
. As in the proof of Theorem 1.2, we conclude that
$S_{i},S_{j}$
. As in the proof of Theorem 1.2, we conclude that
![]() $A,C$
are isomorphic to
$A,C$
are isomorphic to
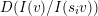 $D(I(v)/I(s_{i}v))$
and
$D(I(v)/I(s_{i}v))$
and
 $D(I(v)/I(s_{j}v))$
. By Lemma 3.5, these are the labels of the Hasse arrows
$D(I(v)/I(s_{j}v))$
. By Lemma 3.5, these are the labels of the Hasse arrows
 $v^{-1}w_{0}\rightarrow v^{-1}s_{i}w_{0}$
and
$v^{-1}w_{0}\rightarrow v^{-1}s_{i}w_{0}$
and
 $v^{-1}w_{0}\rightarrow v^{-1}s_{i}w_{0}$
which form the two top arrows of the desired hexagon. Since the extension groups between
$v^{-1}w_{0}\rightarrow v^{-1}s_{i}w_{0}$
which form the two top arrows of the desired hexagon. Since the extension groups between
![]() $A$
and
$A$
and
![]() $C$
are one-dimensional, the side of the hexagon whose arrows are labelled
$C$
are one-dimensional, the side of the hexagon whose arrows are labelled
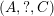 $(A,?,C)$
, has
$(A,?,C)$
, has
![]() $B$
as the label of its middle side.◻
$B$
as the label of its middle side.◻
It is immediate from the definition that if
![]() $A\geqslant B$
in the doubleton extension order, then
$A\geqslant B$
in the doubleton extension order, then
![]() $A$
is a subfactor of
$A$
is a subfactor of
![]() $B$
. The converse does not hold in general. In § 6, we define conventions regarding modules over the preprojective algebra of type
$B$
. The converse does not hold in general. In § 6, we define conventions regarding modules over the preprojective algebra of type
![]() $D_{n}$
. In the notation of that section, in type
$D_{n}$
. In the notation of that section, in type
![]() $D_{4}$
,
$D_{4}$
,

even though the first of these modules is a subfactor of the second.
We now show that the converse does hold in type
![]() $A_{n}$
. We denote by
$A_{n}$
. We denote by
![]() $\mathscr{S}$
the set of non-revisiting walks on the double quiver
$\mathscr{S}$
the set of non-revisiting walks on the double quiver
![]() $\overline{Q}$
. By definition, these are walks in
$\overline{Q}$
. By definition, these are walks in
![]() $Q$
which follow a sequence of arrows either with or against the direction of the arrow and which do not visit any vertex more than once. We identify a walk and its reverse walk.
$Q$
which follow a sequence of arrows either with or against the direction of the arrow and which do not visit any vertex more than once. We identify a walk and its reverse walk.
Let
![]() $I_{\operatorname{cyc}}$
denote the ideal of
$I_{\operatorname{cyc}}$
denote the ideal of
![]() $\unicode[STIX]{x1D6F1}$
generated by all 2-cycles and let
$\unicode[STIX]{x1D6F1}$
generated by all 2-cycles and let
 $\overline{\unicode[STIX]{x1D6F1}}:=\unicode[STIX]{x1D6F1}/I_{\operatorname{cyc}}$
. To any
$\overline{\unicode[STIX]{x1D6F1}}:=\unicode[STIX]{x1D6F1}/I_{\operatorname{cyc}}$
. To any
![]() $p\in \mathscr{S}$
, we can associate an indecomposable
$p\in \mathscr{S}$
, we can associate an indecomposable
![]() $\overline{\unicode[STIX]{x1D6F1}}$
-module
$\overline{\unicode[STIX]{x1D6F1}}$
-module
![]() $X_{p}$
called a string module, and these exhaust the indecomposable
$X_{p}$
called a string module, and these exhaust the indecomposable
![]() $\overline{\unicode[STIX]{x1D6F1}}$
-modules, see [Reference Wald and WaschbüschWW85].
$\overline{\unicode[STIX]{x1D6F1}}$
-modules, see [Reference Wald and WaschbüschWW85].
Theorem 5.5. Suppose
![]() $\unicode[STIX]{x1D6F1}$
is the preprojective algebra of type
$\unicode[STIX]{x1D6F1}$
is the preprojective algebra of type
![]() $A_{n}$
.
$A_{n}$
.
(a) The layer modules for
 $\unicode[STIX]{x1D6F1}$
are exactly the indecomposable
$\unicode[STIX]{x1D6F1}$
are exactly the indecomposable
 $\overline{\unicode[STIX]{x1D6F1}}$
-modules (which are exactly the string modules).
$\overline{\unicode[STIX]{x1D6F1}}$
-modules (which are exactly the string modules).(b) The doubleton extension order on layer modules is the opposite of subfactor order.
Proof. (a) For each
![]() $i\in Q_{0}$
, let
$i\in Q_{0}$
, let
![]() $x_{i}\in \unicode[STIX]{x1D6F1}$
be the 2-cycle at the vertex
$x_{i}\in \unicode[STIX]{x1D6F1}$
be the 2-cycle at the vertex
![]() $i$
. It follows from relations of
$i$
. It follows from relations of
![]() $\unicode[STIX]{x1D6F1}$
that
$\unicode[STIX]{x1D6F1}$
that
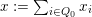 $x:=\sum _{i\in Q_{0}}x_{i}$
is a central element, and
$x:=\sum _{i\in Q_{0}}x_{i}$
is a central element, and
![]() $I_{\text{cyc}}$
is generated by
$I_{\text{cyc}}$
is generated by
![]() $x$
. If
$x$
. If
![]() $X$
is a
$X$
is a
![]() $\unicode[STIX]{x1D6F1}$
-module, then multiplication by
$\unicode[STIX]{x1D6F1}$
-module, then multiplication by
![]() $x$
is a surjective morphism onto
$x$
is a surjective morphism onto
 $I_{\text{cyc}}X\subset X$
. Therefore, if
$I_{\text{cyc}}X\subset X$
. Therefore, if
![]() $X$
is a brick,
$X$
is a brick,
![]() $I_{\text{cyc}}X$
must be zero. Conversely, it is easy to see that any string module for
$I_{\text{cyc}}X$
must be zero. Conversely, it is easy to see that any string module for
![]() $\overline{\unicode[STIX]{x1D6F1}}$
is a brick.
$\overline{\unicode[STIX]{x1D6F1}}$
is a brick.
(b) As mentioned above, we need only show that if
![]() $A$
is a subfactor of
$A$
is a subfactor of
![]() $B$
, then
$B$
, then
![]() $A\geqslant B$
. It suffices to consider the case when
$A\geqslant B$
. It suffices to consider the case when
![]() $A$
is a submodule or a quotient module of
$A$
is a submodule or a quotient module of
![]() $B$
such that
$B$
such that
 $\dim _{k}A=\dim _{k}B-1$
. In this case, it is clear from the shape of string modules that there is a doubleton
$\dim _{k}A=\dim _{k}B-1$
. In this case, it is clear from the shape of string modules that there is a doubleton
![]() $A,S$
for some simple
$A,S$
for some simple
![]() $\unicode[STIX]{x1D6F1}$
-module
$\unicode[STIX]{x1D6F1}$
-module
![]() $S$
such that
$S$
such that
![]() $B$
is one of its two extensions. Thus
$B$
is one of its two extensions. Thus
![]() $A\geqslant B$
.◻
$A\geqslant B$
.◻
Example 5.6. Let
![]() $n=3$
. Then the Hasse quiver of
$n=3$
. Then the Hasse quiver of
![]() $\mathscr{S}$
with respect to the opposite of subfactor order is the following:
$\mathscr{S}$
with respect to the opposite of subfactor order is the following:

In light of Theorems 1.4 and 5.5, this quiver is the Hasse quiver of the forcing order on join-irreducible elements in type
![]() $A_{3}$
. Compare [Reference ReadingRea04, Figure 4].
$A_{3}$
. Compare [Reference ReadingRea04, Figure 4].
6 Combinatorial description of indecomposable
 $\unicode[STIX]{x1D70F}$
-rigid modules
$\unicode[STIX]{x1D70F}$
-rigid modules
Let
![]() $\unicode[STIX]{x1D6F1}$
be a preprojective algebra of Dynkin type and
$\unicode[STIX]{x1D6F1}$
be a preprojective algebra of Dynkin type and
![]() $W$
the corresponding Weyl group. A combinatorial description of join-irreducible elements in
$W$
the corresponding Weyl group. A combinatorial description of join-irreducible elements in
![]() $W$
is well known for type
$W$
is well known for type
![]() $A$
and
$A$
and
![]() $D$
. We refer to [Reference Björner and BrentiBB05, §§ 1.5, 2.1, 2.4, and 2.6] for type A, and [Reference Björner and BrentiBB05, § 8.2] for type D. (The description of join-irreducible elements is not given explicitly in [Reference Björner and BrentiBB05], but it is easily worked out from the combinatorial models developed there.) On the other hand, recall from Theorem 4.1 that we have a bijection
$D$
. We refer to [Reference Björner and BrentiBB05, §§ 1.5, 2.1, 2.4, and 2.6] for type A, and [Reference Björner and BrentiBB05, § 8.2] for type D. (The description of join-irreducible elements is not given explicitly in [Reference Björner and BrentiBB05], but it is easily worked out from the combinatorial models developed there.) On the other hand, recall from Theorem 4.1 that we have a bijection
 $$\begin{eqnarray}J:\mathsf{j}\text{-}\mathsf{Irr}\,W\rightarrow \mathsf{i}\unicode[STIX]{x1D70F}^{{-}}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}\end{eqnarray}$$
$$\begin{eqnarray}J:\mathsf{j}\text{-}\mathsf{Irr}\,W\rightarrow \mathsf{i}\unicode[STIX]{x1D70F}^{{-}}\text{-}\mathsf{rigid}\,\unicode[STIX]{x1D6F1}\end{eqnarray}$$
given by
 $J(w):=(\unicode[STIX]{x1D6F1}/I(w))e_{i}$
for a unique arrow
$J(w):=(\unicode[STIX]{x1D6F1}/I(w))e_{i}$
for a unique arrow
 $w\rightarrow ws_{i}$
in the Hasse quiver of
$w\rightarrow ws_{i}$
in the Hasse quiver of
![]() $W$
starting at
$W$
starting at
![]() $w$
.
$w$
.
The main result of this section is to give a combinatorial description of the
![]() $\unicode[STIX]{x1D6F1}$
-module
$\unicode[STIX]{x1D6F1}$
-module
![]() $J(w)$
for each join-irreducible element
$J(w)$
for each join-irreducible element
![]() $w\in W$
in type
$w\in W$
in type
![]() $A$
or
$A$
or
![]() $D$
. See Theorem 6.1 for type
$D$
. See Theorem 6.1 for type
![]() $A$
and Theorems 6.5 and 6.12 for type
$A$
and Theorems 6.5 and 6.12 for type
![]() $D$
. It will be interesting to compare our results with Bongartz’s description of bricks for type
$D$
. It will be interesting to compare our results with Bongartz’s description of bricks for type
![]() $A$
and
$A$
and
![]() $D$
[Reference BongartzBon15].
$D$
[Reference BongartzBon15].
6.1 Type
 $A$
$A$
Let
![]() $\unicode[STIX]{x1D6F1}$
be a preprojective algebra of type
$\unicode[STIX]{x1D6F1}$
be a preprojective algebra of type
![]() $A_{n}$
. It is given by a quiver
$A_{n}$
. It is given by a quiver

with relations
 $x_{1}y_{2}=0$
,
$x_{1}y_{2}=0$
,
 $x_{i}y_{i+1}=y_{i}x_{i-1}$
for
$x_{i}y_{i+1}=y_{i}x_{i-1}$
for
 $2\leqslant i\leqslant n-1$
and
$2\leqslant i\leqslant n-1$
and
 $y_{n}x_{n-1}=0$
. We denote by
$y_{n}x_{n-1}=0$
. We denote by
![]() $S_{\ell }$
the simple
$S_{\ell }$
the simple
![]() $\unicode[STIX]{x1D6F1}$
-module corresponding to the vertex
$\unicode[STIX]{x1D6F1}$
-module corresponding to the vertex
![]() $\ell$
, and by
$\ell$
, and by
![]() $P_{\ell }$
the projective cover of
$P_{\ell }$
the projective cover of
![]() $S_{\ell }$
.
$S_{\ell }$
.
Let
 $W=\mathfrak{S}_{n+1}$
be the Weyl group of
$W=\mathfrak{S}_{n+1}$
be the Weyl group of
![]() $\unicode[STIX]{x1D6F1}$
. We use the convention that the product
$\unicode[STIX]{x1D6F1}$
. We use the convention that the product
![]() $ww^{\prime }$
of elements
$ww^{\prime }$
of elements
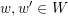 $w,w^{\prime }\in W$
is given by
$w,w^{\prime }\in W$
is given by
 $(ww^{\prime })(i)=w(w^{\prime }(i))$
for
$(ww^{\prime })(i)=w(w^{\prime }(i))$
for
 $i\in \{1,\ldots ,n+1\}$
. The elements of
$i\in \{1,\ldots ,n+1\}$
. The elements of
![]() $W$
are the permutations
$W$
are the permutations
 $$\begin{eqnarray}w=[i_{1},\ldots ,i_{n+1}].\end{eqnarray}$$
$$\begin{eqnarray}w=[i_{1},\ldots ,i_{n+1}].\end{eqnarray}$$
This is join-irreducible if and only if there exists
 $\ell \in \{1,\ldots ,n\}$
such that
$\ell \in \{1,\ldots ,n\}$
such that
 $$\begin{eqnarray}i_{1}<\cdots <i_{\ell }>i_{\ell +1}<\cdots <i_{n+1}.\end{eqnarray}$$
$$\begin{eqnarray}i_{1}<\cdots <i_{\ell }>i_{\ell +1}<\cdots <i_{n+1}.\end{eqnarray}$$
In this case, we say that
![]() $w$
is of type
$w$
is of type
![]() $\ell$
. There exists a unique arrow
$\ell$
. There exists a unique arrow
 $w\rightarrow ws_{\ell }$
starting at
$w\rightarrow ws_{\ell }$
starting at
![]() $w$
in the Hasse quiver of
$w$
in the Hasse quiver of
![]() $W$
. The number of join-irreducible elements of type
$W$
. The number of join-irreducible elements of type
![]() $\ell$
is given by
$\ell$
is given by
 $$\begin{eqnarray}\binom{n+1}{\ell }-1,\end{eqnarray}$$
$$\begin{eqnarray}\binom{n+1}{\ell }-1,\end{eqnarray}$$
and therefore
 $\#\mathsf{j}\text{-}\mathsf{Irr}\,W=2^{n+1}-n-2$
.
$\#\mathsf{j}\text{-}\mathsf{Irr}\,W=2^{n+1}-n-2$
.
As a quiver representation,
![]() $P_{\ell }$
is given by
$P_{\ell }$
is given by

where each number
![]() $i$
shows a
$i$
shows a
![]() $k$
-vector space
$k$
-vector space
![]() $k$
lying on the vertex
$k$
lying on the vertex
![]() $i$
, and each arrow is the identity map of
$i$
, and each arrow is the identity map of
![]() $k$
. Submodules (respectively, factor modules) of
$k$
. Submodules (respectively, factor modules) of
![]() $P_{\ell }$
correspond bijectively to subquivers that are closed under successors (respectively, predecessors).
$P_{\ell }$
correspond bijectively to subquivers that are closed under successors (respectively, predecessors).
We represent
![]() $P_{\ell }$
in abbreviated form as an array of numbers in rows as follows:
$P_{\ell }$
in abbreviated form as an array of numbers in rows as follows:

Submodules and factor modules are similarly represented by sub-arrays of
![]() $P_{\ell }$
, as, for example, in the following theorem.
$P_{\ell }$
, as, for example, in the following theorem.
Theorem 6.1. Let
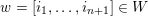 $w=[i_{1},\ldots ,i_{n+1}]\in W$
be a join-irreducible element of type
$w=[i_{1},\ldots ,i_{n+1}]\in W$
be a join-irreducible element of type
![]() $\ell$
. Then
$\ell$
. Then
![]() $J(w)$
is a factor module of
$J(w)$
is a factor module of
![]() $P_{\ell }$
which has the form
$P_{\ell }$
which has the form

In particular, any factor module of
![]() $P_{\ell }$
is indecomposable
$P_{\ell }$
is indecomposable
![]() $\unicode[STIX]{x1D70F}^{-}$
-rigid.
$\unicode[STIX]{x1D70F}^{-}$
-rigid.
Note that
 $i_{m}\leqslant m$
holds for any
$i_{m}\leqslant m$
holds for any
 $m\in \{\ell +1,\ldots ,n+1\}$
, and if
$m\in \{\ell +1,\ldots ,n+1\}$
, and if
 $i_{m}=m$
holds, then the row starting at
$i_{m}=m$
holds, then the row starting at
![]() $m-1$
is empty. For example, for
$m-1$
is empty. For example, for
![]() $n=5$
and
$n=5$
and
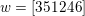 $w=[351246]$
, then
$w=[351246]$
, then
![]() $\ell =2$
and
$\ell =2$
and

To prove this, we need the following easy observation.
Lemma 6.2. Let
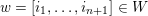 $w=[i_{1},\ldots ,i_{n+1}]\in W$
be a join-irreducible element of type
$w=[i_{1},\ldots ,i_{n+1}]\in W$
be a join-irreducible element of type
![]() $\ell$
. Then we have a reduced expression
$\ell$
. Then we have a reduced expression
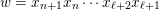 $w=x_{n+1}x_{n}\cdots x_{\ell +2}x_{\ell +1}$
, where
$w=x_{n+1}x_{n}\cdots x_{\ell +2}x_{\ell +1}$
, where
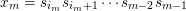 $x_{m}=s_{i_{m}}s_{i_{m}+1}\cdots s_{m-2}s_{m-1}$
for
$x_{m}=s_{i_{m}}s_{i_{m}+1}\cdots s_{m-2}s_{m-1}$
for
 $m\in \{\ell +1,\ldots ,n+1\}$
.
$m\in \{\ell +1,\ldots ,n+1\}$
.
Proof. If
![]() $\ell =n$
, then
$\ell =n$
, then
 $w=[1,2,\ldots ,i-1,i+1,\ldots ,n+1,i]$
holds for some
$w=[1,2,\ldots ,i-1,i+1,\ldots ,n+1,i]$
holds for some
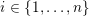 $i\in \{1,\ldots ,n\}$
. Thus
$i\in \{1,\ldots ,n\}$
. Thus
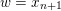 $w=x_{n+1}$
holds clearly. In the rest, assume
$w=x_{n+1}$
holds clearly. In the rest, assume
![]() $\ell \neq n$
, and let
$\ell \neq n$
, and let
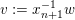 $v:=x_{n+1}^{-1}w$
. Since
$v:=x_{n+1}^{-1}w$
. Since
![]() $x_{n+1}^{-1}$
is a cyclic permutation
$x_{n+1}^{-1}$
is a cyclic permutation
 $(n+1,n,\ldots ,i_{n+1}+1,i_{n+1})$
, it preserves the total order on
$(n+1,n,\ldots ,i_{n+1}+1,i_{n+1})$
, it preserves the total order on
 $\{i_{1},\ldots ,i_{n}\}$
, and therefore
$\{i_{1},\ldots ,i_{n}\}$
, and therefore
![]() $v$
is a join-irreducible element of type
$v$
is a join-irreducible element of type
![]() $\ell$
and clearly satisfies
$\ell$
and clearly satisfies
 $v(n+1)=n+1$
. Since
$v(n+1)=n+1$
. Since
![]() $x_{n+1}^{-1}$
fixes any element in
$x_{n+1}^{-1}$
fixes any element in
 $\{i_{\ell +1},\ldots ,i_{n}\}$
, we have
$\{i_{\ell +1},\ldots ,i_{n}\}$
, we have
 $v(m)=i_{m}$
for any
$v(m)=i_{m}$
for any
 $m\in \{\ell +1,\ldots ,n\}$
and
$m\in \{\ell +1,\ldots ,n\}$
and
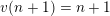 $v(n+1)=n+1$
. Inductively on
$v(n+1)=n+1$
. Inductively on
![]() $n$
, we have
$n$
, we have
 $v=x_{n}\cdots x_{\ell +1}$
, and therefore
$v=x_{n}\cdots x_{\ell +1}$
, and therefore
 $w=x_{n+1}x_{n}\cdots x_{\ell +1}$
.◻
$w=x_{n+1}x_{n}\cdots x_{\ell +1}$
.◻
Now we are ready to prove Theorem 6.1.
Proof of Theorem 6.1.
Clearly we have

and

Repeating similar calculations, we have

Therefore
 $J(w)=(\unicode[STIX]{x1D6F1}/I(w))e_{\ell }$
has the desired form.◻
$J(w)=(\unicode[STIX]{x1D6F1}/I(w))e_{\ell }$
has the desired form.◻
Example 6.3. Let
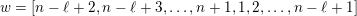 $w=[n-\ell +2,n-\ell +3,\ldots ,n+1,1,2,\ldots ,n-\ell +1]$
be a join-irreducible element of type
$w=[n-\ell +2,n-\ell +3,\ldots ,n+1,1,2,\ldots ,n-\ell +1]$
be a join-irreducible element of type
![]() $\ell$
. Then we have a reduced expression
$\ell$
. Then we have a reduced expression
 $$\begin{eqnarray}w=x_{n+1}x_{n}\cdots x_{\ell +2}x_{\ell +1}\quad \text{for}~x_{m}=s_{m-\ell }\cdots s_{m-2}s_{m-1},\end{eqnarray}$$
$$\begin{eqnarray}w=x_{n+1}x_{n}\cdots x_{\ell +2}x_{\ell +1}\quad \text{for}~x_{m}=s_{m-\ell }\cdots s_{m-2}s_{m-1},\end{eqnarray}$$
and the corresponding indecomposable
![]() $\unicode[STIX]{x1D70F}^{-}$
-rigid
$\unicode[STIX]{x1D70F}^{-}$
-rigid
![]() $\unicode[STIX]{x1D6F1}$
-module is
$\unicode[STIX]{x1D6F1}$
-module is
 $J(w)=P_{\ell }$
.
$J(w)=P_{\ell }$
.
Example 6.4. Consider type
![]() $A_{3}$
. Below we show the expression given in Lemma 6.2 by using dots:
$A_{3}$
. Below we show the expression given in Lemma 6.2 by using dots:
 $w=x_{n+1}\cdot x_{n}\cdot \cdots \cdot x_{\ell +2}\cdot x_{\ell +1}$
.
$w=x_{n+1}\cdot x_{n}\cdot \cdots \cdot x_{\ell +2}\cdot x_{\ell +1}$
.
We have the following 3 join-irreducible elements of type 1:

We have the following 5 join-irreducible elements of type 2:


We have the following 3 join-irreducible elements of type 3:


6.2 Type
 $D$
$D$
Let
![]() $\unicode[STIX]{x1D6F1}$
be a preprojective algebra of type
$\unicode[STIX]{x1D6F1}$
be a preprojective algebra of type
![]() $D_{n}$
. Then
$D_{n}$
. Then
![]() $\unicode[STIX]{x1D6F1}$
is given by a quiver
$\unicode[STIX]{x1D6F1}$
is given by a quiver

with relations
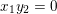 $x_{1}y_{2}=0$
,
$x_{1}y_{2}=0$
,
 $x_{1}^{\prime }y_{2}^{\prime }=0$
,
$x_{1}^{\prime }y_{2}^{\prime }=0$
,
 $x_{2}y_{3}=y_{2}x_{1}+y_{2}^{\prime }x_{1}^{\prime }$
,
$x_{2}y_{3}=y_{2}x_{1}+y_{2}^{\prime }x_{1}^{\prime }$
,
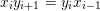 $x_{i}y_{i+1}=y_{i}x_{i-1}$
for
$x_{i}y_{i+1}=y_{i}x_{i-1}$
for
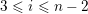 $3\leqslant i\leqslant n-2$
and
$3\leqslant i\leqslant n-2$
and
 $y_{n-1}x_{n-2}=0$
. Let
$y_{n-1}x_{n-2}=0$
. Let
![]() $S_{\ell }$
be the simple
$S_{\ell }$
be the simple
![]() $\unicode[STIX]{x1D6F1}$
-module corresponding to the vertex
$\unicode[STIX]{x1D6F1}$
-module corresponding to the vertex
![]() $\ell$
, and let
$\ell$
, and let
![]() $P_{\ell }$
be the projective cover of
$P_{\ell }$
be the projective cover of
![]() $S_{\ell }$
.
$S_{\ell }$
.
The Weyl group
![]() $W$
of
$W$
of
![]() $\unicode[STIX]{x1D6F1}$
is the group of automorphisms
$\unicode[STIX]{x1D6F1}$
is the group of automorphisms
![]() $w$
of the set
$w$
of the set
 $\{\pm 1,\ldots ,\pm n\}$
satisfying
$\{\pm 1,\ldots ,\pm n\}$
satisfying
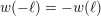 $w(-\ell )=-w(\ell )$
for any
$w(-\ell )=-w(\ell )$
for any
![]() $\ell$
and
$\ell$
and
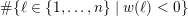 $\#\{\ell \in \{1,\ldots ,n\}\mid w(\ell )<0\}$
is even. Setting
$\#\{\ell \in \{1,\ldots ,n\}\mid w(\ell )<0\}$
is even. Setting
 $i_{\ell }=w(\ell )$
for
$i_{\ell }=w(\ell )$
for
 $\ell \in \{1,\ldots ,n\}$
, we write
$\ell \in \{1,\ldots ,n\}$
, we write
![]() $w\in W$
as a sequence
$w\in W$
as a sequence
 $$\begin{eqnarray}w=[i_{1},\ldots ,i_{n}]\in \{\pm 1,\ldots ,\pm n\}^{n}\end{eqnarray}$$
$$\begin{eqnarray}w=[i_{1},\ldots ,i_{n}]\in \{\pm 1,\ldots ,\pm n\}^{n}\end{eqnarray}$$
satisfying the following two conditions.
∙
 $|i_{1}|,\ldots ,|i_{n}|$
is a permutation of
$|i_{1}|,\ldots ,|i_{n}|$
is a permutation of
 $1,\ldots ,n$
.
$1,\ldots ,n$
.∙ The number of negative integers is even.
We often denote
![]() $-i$
by
$-i$
by
![]() $\text{}\underline{i}$
. The simple reflections in
$\text{}\underline{i}$
. The simple reflections in
![]() $W$
are given by
$W$
are given by
 $$\begin{eqnarray}s_{-1}=[\text{}\underline{2},\text{}\underline{1},3,4,\ldots ,n]\quad \text{and}\quad s_{\ell }=[1,\ldots ,\ell -1,\ell +1,\ell ,\ell +2,\ldots ,n]\end{eqnarray}$$
$$\begin{eqnarray}s_{-1}=[\text{}\underline{2},\text{}\underline{1},3,4,\ldots ,n]\quad \text{and}\quad s_{\ell }=[1,\ldots ,\ell -1,\ell +1,\ell ,\ell +2,\ldots ,n]\end{eqnarray}$$
with
 $\ell \in \{1,\ldots ,n-1\}$
. The length of
$\ell \in \{1,\ldots ,n-1\}$
. The length of
 $w=[i_{1},\ldots ,i_{n}]$
is given by
$w=[i_{1},\ldots ,i_{n}]$
is given by
 $$\begin{eqnarray}\ell (w)=\#\{1\leqslant \ell <m\leqslant n\mid i_{\ell }>i_{m}\}+\#\{1\leqslant \ell <m\leqslant n\mid -i_{\ell }>i_{m}\}.\end{eqnarray}$$
$$\begin{eqnarray}\ell (w)=\#\{1\leqslant \ell <m\leqslant n\mid i_{\ell }>i_{m}\}+\#\{1\leqslant \ell <m\leqslant n\mid -i_{\ell }>i_{m}\}.\end{eqnarray}$$
For
 $\ell \in \{1,\ldots ,n-1\}$
,
$\ell \in \{1,\ldots ,n-1\}$
,
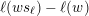 $\ell (ws_{\ell })-\ell (w)$
is
$\ell (ws_{\ell })-\ell (w)$
is
![]() $1$
if
$1$
if
 $i_{\ell }<i_{\ell +1}$
, and
$i_{\ell }<i_{\ell +1}$
, and
![]() $-1$
otherwise. Moreover
$-1$
otherwise. Moreover
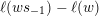 $\ell (ws_{-1})-\ell (w)$
is
$\ell (ws_{-1})-\ell (w)$
is
![]() $1$
if
$1$
if
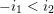 $-i_{1}<i_{2}$
, and
$-i_{1}<i_{2}$
, and
![]() $-1$
otherwise. Therefore an element
$-1$
otherwise. Therefore an element
 $w=[i_{1},\ldots ,i_{n}]\in W$
is join-irreducible if and only if one of the following conditions is satisfied.
$w=[i_{1},\ldots ,i_{n}]\in W$
is join-irreducible if and only if one of the following conditions is satisfied.
∙
 $i_{1}<\cdots <i_{n}$
and
$i_{1}<\cdots <i_{n}$
and
 $-i_{1}>i_{2}$
.
$-i_{1}>i_{2}$
.∙ There exists
 $\ell \in \{1,\ldots ,n-1\}$
such that
$\ell \in \{1,\ldots ,n-1\}$
such that
 $i_{1}<\cdots <i_{\ell }>i_{\ell +1}<\cdots <i_{n}$
and
$i_{1}<\cdots <i_{\ell }>i_{\ell +1}<\cdots <i_{n}$
and
 $-i_{1}<i_{2}$
.
$-i_{1}<i_{2}$
.
We say that
![]() $w$
is of type
$w$
is of type
![]() $-1$
(respectively, type
$-1$
(respectively, type
![]() $\ell$
) if the first (respectively, second) condition is satisfied. Then there exists a unique arrow
$\ell$
) if the first (respectively, second) condition is satisfied. Then there exists a unique arrow
 $w\rightarrow ws_{\ell }$
starting at
$w\rightarrow ws_{\ell }$
starting at
![]() $w$
in the Hasse quiver of
$w$
in the Hasse quiver of
![]() $W$
. The number of join-irreducible elements of type
$W$
. The number of join-irreducible elements of type
![]() $\ell \neq \pm 1$
(respectively, 1,
$\ell \neq \pm 1$
(respectively, 1,
![]() $-1$
) is
$-1$
) is
 $$\begin{eqnarray}2^{n-\ell }\binom{n}{\ell }-1\quad (\text{respectively},2^{n-1}-1,2^{n-1}-1),\end{eqnarray}$$
$$\begin{eqnarray}2^{n-\ell }\binom{n}{\ell }-1\quad (\text{respectively},2^{n-1}-1,2^{n-1}-1),\end{eqnarray}$$
and therefore
 $\#\mathsf{j}\text{-}\mathsf{Irr}\,W=3^{n}-n2^{n-1}-n-1$
.
$\#\mathsf{j}\text{-}\mathsf{Irr}\,W=3^{n}-n2^{n-1}-n-1$
.
As a quiver representation,
![]() $P_{\ell }$
for
$P_{\ell }$
for
![]() $\ell =\pm 1$
is given by
$\ell =\pm 1$
is given by

where each number
![]() $i$
shows a
$i$
shows a
![]() $k$
-vector space
$k$
-vector space
![]() $k$
lying on the vertex
$k$
lying on the vertex
![]() $i$
, and each arrow is the identity map of
$i$
, and each arrow is the identity map of
![]() $k$
. Again, submodules (respectively, factor modules) of
$k$
. Again, submodules (respectively, factor modules) of
![]() $P_{\ell }$
correspond bijectively to subquivers that are closed under successors (respectively, predecessors).
$P_{\ell }$
correspond bijectively to subquivers that are closed under successors (respectively, predecessors).
We represent
![]() $P_{\ell }$
in abbreviated form as an array of numbers in rows as follows:
$P_{\ell }$
in abbreviated form as an array of numbers in rows as follows:

Submodules and factor modules of
![]() $P_{\ell }$
are again represented by subarrays.
$P_{\ell }$
are again represented by subarrays.
Theorem 6.5. Let
 $w=[i_{1},\ldots ,i_{n}]\in W$
be a join-irreducible element of type
$w=[i_{1},\ldots ,i_{n}]\in W$
be a join-irreducible element of type
![]() $\ell =\pm 1$
. Then
$\ell =\pm 1$
. Then
![]() $J(w)$
is a factor module of
$J(w)$
is a factor module of
![]() $P_{\ell }$
which has the form
$P_{\ell }$
which has the form

where
 $i_{m}^{\prime }:=\max \{i_{m},(-1)^{m}\ell \}$
for
$i_{m}^{\prime }:=\max \{i_{m},(-1)^{m}\ell \}$
for
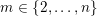 $m\in \{2,\ldots ,n\}$
.
$m\in \{2,\ldots ,n\}$
.
Note that
 $i_{m}^{\prime }\leqslant m$
holds for any
$i_{m}^{\prime }\leqslant m$
holds for any
 $m\in \{2,\ldots ,n\}$
, and if
$m\in \{2,\ldots ,n\}$
, and if
 $i_{m}^{\prime }=m$
holds, then the row starting at
$i_{m}^{\prime }=m$
holds, then the row starting at
![]() $m-1$
is empty. For example, for
$m-1$
is empty. For example, for
![]() $n=6$
and
$n=6$
and
 $w=[5\text{}\underline{3}\text{}\underline{1}246]$
, then
$w=[5\text{}\underline{3}\text{}\underline{1}246]$
, then
![]() $\ell =1$
and
$\ell =1$
and

To prove this, we need the following observation.
Lemma 6.6. Let
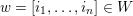 $w=[i_{1},\ldots ,i_{n}]\in W$
be a join-irreducible element of type
$w=[i_{1},\ldots ,i_{n}]\in W$
be a join-irreducible element of type
![]() $\ell =\pm 1$
. Then we have a reduced expression
$\ell =\pm 1$
. Then we have a reduced expression
 $w=x_{n}x_{n-1}\cdots x_{3}x_{2}$
, where
$w=x_{n}x_{n-1}\cdots x_{3}x_{2}$
, where
 $$\begin{eqnarray}x_{m}=\left\{\begin{array}{@{}ll@{}}s_{i_{m}}s_{i_{m}+1}\cdots s_{m-2}s_{m-1} & \text{if}~i_{m}\geqslant 2\\ s_{(-1)^{m}\ell }s_{2}\cdots s_{m-2}s_{m-1} & \text{if}~i_{m}<2\end{array}\right.\quad \text{for}~m\in \{2,\ldots ,n\}.\end{eqnarray}$$
$$\begin{eqnarray}x_{m}=\left\{\begin{array}{@{}ll@{}}s_{i_{m}}s_{i_{m}+1}\cdots s_{m-2}s_{m-1} & \text{if}~i_{m}\geqslant 2\\ s_{(-1)^{m}\ell }s_{2}\cdots s_{m-2}s_{m-1} & \text{if}~i_{m}<2\end{array}\right.\quad \text{for}~m\in \{2,\ldots ,n\}.\end{eqnarray}$$
Proof. The case
![]() $n=2$
can be checked directly. In the rest, we assume
$n=2$
can be checked directly. In the rest, we assume
![]() $n\geqslant 3$
. Assume that the assertion holds for
$n\geqslant 3$
. Assume that the assertion holds for
![]() $n-1$
. Again, let
$n-1$
. Again, let
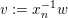 $v:=x_{n}^{-1}w$
.
$v:=x_{n}^{-1}w$
.
Assume
![]() $i_{n}>0$
. Then
$i_{n}>0$
. Then
![]() $v$
is obtained from
$v$
is obtained from
![]() $w$
by replacing
$w$
by replacing
![]() $i_{n}$
with
$i_{n}$
with
![]() $n$
and then, for each
$n$
and then, for each
![]() $i_{j}$
with
$i_{j}$
with
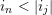 $i_{n}<|i_{j}|$
replacing
$i_{n}<|i_{j}|$
replacing
![]() $i_{j}$
by an entry with the same sign but absolute value
$i_{j}$
by an entry with the same sign but absolute value
![]() $|i_{j}|-1$
. In particular,
$|i_{j}|-1$
. In particular,
![]() $v$
is a join-irreducible element of type
$v$
is a join-irreducible element of type
![]() $\ell$
and satisfies
$\ell$
and satisfies
 $v(n)=n$
. Fix
$v(n)=n$
. Fix
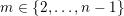 $m\in \{2,\ldots ,n-1\}$
. If
$m\in \{2,\ldots ,n-1\}$
. If
![]() $i_{m}>0$
, then
$i_{m}>0$
, then
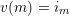 $v(m)=i_{m}$
holds, and if
$v(m)=i_{m}$
holds, and if
![]() $i_{m}<0$
, then
$i_{m}<0$
, then
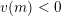 $v(m)<0$
holds. By our assumption on induction, we have
$v(m)<0$
holds. By our assumption on induction, we have
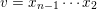 $v=x_{n-1}\cdots x_{2}$
, and therefore
$v=x_{n-1}\cdots x_{2}$
, and therefore
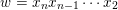 $w=x_{n}x_{n-1}\cdots x_{2}$
.
$w=x_{n}x_{n-1}\cdots x_{2}$
.
Assume
![]() $i_{n}<0$
. In this case, we have
$i_{n}<0$
. In this case, we have
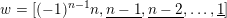 $w=[(-1)^{n-1}n,\text{}\underline{n-1},\text{}\underline{n-2},\ldots ,\text{}\underline{1}]$
and
$w=[(-1)^{n-1}n,\text{}\underline{n-1},\text{}\underline{n-2},\ldots ,\text{}\underline{1}]$
and
 $\ell =(-1)^{n-1}$
. Thus
$\ell =(-1)^{n-1}$
. Thus
 $x_{n}^{-1}=[\text{}\underline{n},\text{}\underline{1},2,\ldots ,n-1]$
and
$x_{n}^{-1}=[\text{}\underline{n},\text{}\underline{1},2,\ldots ,n-1]$
and
 $v=[(-1)^{n-1}(n-1),\text{}\underline{n-2},\ldots ,\text{}\underline{2},1,n]$
hold. Therefore
$v=[(-1)^{n-1}(n-1),\text{}\underline{n-2},\ldots ,\text{}\underline{2},1,n]$
hold. Therefore
![]() $v$
is a join-irreducible element of type
$v$
is a join-irreducible element of type
![]() $\ell$
and satisfies
$\ell$
and satisfies
 $v(n)=n$
. Since
$v(n)=n$
. Since
 $v(m)<2$
holds for any
$v(m)<2$
holds for any
 $m\in \{2,\ldots ,n-1\}$
, we have
$m\in \{2,\ldots ,n-1\}$
, we have
 $v=x_{n-1}\cdots x_{2}$
by our assumption on induction, and therefore
$v=x_{n-1}\cdots x_{2}$
by our assumption on induction, and therefore
 $w=x_{n}x_{n-1}\cdots x_{2}$
.◻
$w=x_{n}x_{n-1}\cdots x_{2}$
.◻
Now we are ready to prove Theorem 6.5.
Proof of Theorem 6.5.
Using Lemma 6.6, one can calculate
![]() $I(w)$
as in the proof of Theorem 6.1, and we obtain the desired assertion.◻
$I(w)$
as in the proof of Theorem 6.1, and we obtain the desired assertion.◻
Example 6.7. Let
 $w=[n,\text{}\underline{n-1},\text{}\underline{n-2},\ldots ,\text{}\underline{2},(-1)^{n}]$
be a join-irreducible element of type 1. Then we have a reduced expression
$w=[n,\text{}\underline{n-1},\text{}\underline{n-2},\ldots ,\text{}\underline{2},(-1)^{n}]$
be a join-irreducible element of type 1. Then we have a reduced expression
 $$\begin{eqnarray}w=x_{n}x_{n-1}\cdots x_{3}x_{2}\quad \text{for}~x_{m}=s_{(-1)^{m}}s_{2}s_{3}\cdots s_{m-1},\end{eqnarray}$$
$$\begin{eqnarray}w=x_{n}x_{n-1}\cdots x_{3}x_{2}\quad \text{for}~x_{m}=s_{(-1)^{m}}s_{2}s_{3}\cdots s_{m-1},\end{eqnarray}$$
and the corresponding indecomposable
![]() $\unicode[STIX]{x1D70F}^{-}$
-rigid
$\unicode[STIX]{x1D70F}^{-}$
-rigid
![]() $\unicode[STIX]{x1D6F1}$
-module is
$\unicode[STIX]{x1D6F1}$
-module is
 $J(w)=P_{1}$
.
$J(w)=P_{1}$
.
Similarly, let
 $w=[\text{}\underline{n},\text{}\underline{n-1},\text{}\underline{n-2},\ldots ,\text{}\underline{2},(-1)^{n+1}]$
be a join-irreducible element of type
$w=[\text{}\underline{n},\text{}\underline{n-1},\text{}\underline{n-2},\ldots ,\text{}\underline{2},(-1)^{n+1}]$
be a join-irreducible element of type
![]() $-1$
. Then we have a reduced expression
$-1$
. Then we have a reduced expression
 $$\begin{eqnarray}w=x_{n}x_{n-1}\cdots x_{3}x_{2}\quad \text{for}~x_{m}=s_{(-1)^{m+1}}s_{2}s_{3}\cdots s_{m-1},\end{eqnarray}$$
$$\begin{eqnarray}w=x_{n}x_{n-1}\cdots x_{3}x_{2}\quad \text{for}~x_{m}=s_{(-1)^{m+1}}s_{2}s_{3}\cdots s_{m-1},\end{eqnarray}$$
and the corresponding indecomposable
![]() $\unicode[STIX]{x1D70F}^{-}$
-rigid
$\unicode[STIX]{x1D70F}^{-}$
-rigid
![]() $\unicode[STIX]{x1D6F1}$
-module is
$\unicode[STIX]{x1D6F1}$
-module is
 $J(w)=P_{-1}$
.
$J(w)=P_{-1}$
.
Example 6.8. Consider type
![]() $D_{4}$
. Below we show the expression given in Lemma 6.6 by using dots:
$D_{4}$
. Below we show the expression given in Lemma 6.6 by using dots:
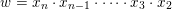 $w=x_{n}\cdot x_{n-1}\cdot \cdots \cdot x_{3}\cdot x_{2}$
.
$w=x_{n}\cdot x_{n-1}\cdot \cdots \cdot x_{3}\cdot x_{2}$
.
We have the following 7 join-irreducible elements of type 1:




We have the following 7 join-irreducible elements of type
![]() $-1$
:
$-1$
:




In the rest of this section, let
![]() $w$
be a join-irreducible element
$w$
be a join-irreducible element
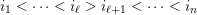 $i_{1}<\cdots <i_{\ell }>i_{\ell +1}<\cdots <i_{n}$
of type
$i_{1}<\cdots <i_{\ell }>i_{\ell +1}<\cdots <i_{n}$
of type
![]() $\ell \neq \pm 1$
. Note that all integers in
$\ell \neq \pm 1$
. Note that all integers in
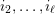 $i_{2},\ldots ,i_{\ell }$
must be positive, and therefore
$i_{2},\ldots ,i_{\ell }$
must be positive, and therefore
![]() $w$
can be recovered from the latter part
$w$
can be recovered from the latter part
 $i_{\ell +1},\ldots ,i_{n}$
.
$i_{\ell +1},\ldots ,i_{n}$
.
We need the following preparation on the structure of
![]() $P_{\ell }$
.
$P_{\ell }$
.
Lemma 6.9. Let
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
be scalars satisfying
$\unicode[STIX]{x1D6FD}$
be scalars satisfying
 $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=1$
. As a quiver representation,
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=1$
. As a quiver representation,
![]() $P_{\ell }$
with
$P_{\ell }$
with
![]() $\ell \neq \pm 1$
is given by Figure 7 where each number
$\ell \neq \pm 1$
is given by Figure 7 where each number
![]() $i$
shows a
$i$
shows a
![]() $k$
-vector space
$k$
-vector space
![]() $k$
lying on the vertex
$k$
lying on the vertex
![]() $i$
if
$i$
if
![]() $i\geqslant -1$
and
$i\geqslant -1$
and
![]() $-i$
if
$-i$
if
![]() $i\leqslant -2$
. Each unlabelled arrow is the identity map of
$i\leqslant -2$
. Each unlabelled arrow is the identity map of
![]() $k$
, and each arrow labelled by a scalar
$k$
, and each arrow labelled by a scalar
![]() $\unicode[STIX]{x1D6FE}$
is a linear map multiplying by
$\unicode[STIX]{x1D6FE}$
is a linear map multiplying by
![]() $\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D6FE}$
.

Figure 7. The indecomposable projective
![]() $\unicode[STIX]{x1D6F1}$
-module
$\unicode[STIX]{x1D6F1}$
-module
![]() $P_{\ell }$
.
$P_{\ell }$
.
Proof. Since all relations of
![]() $\unicode[STIX]{x1D6F1}$
are satisfied, this gives a
$\unicode[STIX]{x1D6F1}$
are satisfied, this gives a
![]() $\unicode[STIX]{x1D6F1}$
-module
$\unicode[STIX]{x1D6F1}$
-module
![]() $X$
. It is easy to check that
$X$
. It is easy to check that
![]() $X$
is generated by
$X$
is generated by
![]() $\ell$
in the upper left corner. Thus we have a surjective morphism
$\ell$
in the upper left corner. Thus we have a surjective morphism
 $\unicode[STIX]{x1D70B}:P_{\ell }\rightarrow X$
of
$\unicode[STIX]{x1D70B}:P_{\ell }\rightarrow X$
of
![]() $\unicode[STIX]{x1D6F1}$
-modules. On the other hand, it is well known that the Loewy length of any indecomposable projective
$\unicode[STIX]{x1D6F1}$
-modules. On the other hand, it is well known that the Loewy length of any indecomposable projective
![]() $\unicode[STIX]{x1D6F1}$
-module is equal to
$\unicode[STIX]{x1D6F1}$
-module is equal to
![]() $h-1$
, where
$h-1$
, where
![]() $h$
is the Coxeter number. For type
$h$
is the Coxeter number. For type
![]() $D_{n}$
, we have
$D_{n}$
, we have
 $h-1=2n-3$
. Since the length of the path from
$h-1=2n-3$
. Since the length of the path from
![]() $\ell$
in the left corner to
$\ell$
in the left corner to
![]() $-\ell$
in the lower right corner is
$-\ell$
in the lower right corner is
![]() $2n-4$
, the above
$2n-4$
, the above
![]() $\unicode[STIX]{x1D70B}$
must be an isomorphism.◻
$\unicode[STIX]{x1D70B}$
must be an isomorphism.◻
Example 6.10. Let
![]() $n=6$
. Then
$n=6$
. Then
![]() $P_{2}$
is given by the following quiver representations, where the left one is the case
$P_{2}$
is given by the following quiver representations, where the left one is the case
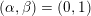 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})=(0,1)$
, and the right one is the case
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})=(0,1)$
, and the right one is the case
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})=(1,0)$
.
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})=(1,0)$
.

We write the quiver
![]() $P_{\ell }$
of Figure 7 in abbreviated form as the following array of numbers:
$P_{\ell }$
of Figure 7 in abbreviated form as the following array of numbers:

The description of factor
![]() $P_{\pm 1}$
was no more complicated than the analogous description in type
$P_{\pm 1}$
was no more complicated than the analogous description in type
![]() $A$
. However, for
$A$
. However, for
![]() $\ell >1$
, the description of factor modules of
$\ell >1$
, the description of factor modules of
![]() $P_{\ell }$
is much more complicated in type
$P_{\ell }$
is much more complicated in type
![]() $D$
. For example, consider the direct sum
$D$
. For example, consider the direct sum
![]() $k^{2}$
of two copies of
$k^{2}$
of two copies of
![]() $k$
corresponding to
$k$
corresponding to
![]() $-2$
in the first row and
$-2$
in the first row and
![]() $2$
in the second row. Then subspaces of
$2$
in the second row. Then subspaces of
![]() $k^{2}$
generate distinct submodules of
$k^{2}$
generate distinct submodules of
![]() $P_{\ell }$
. Fortunately, to describe
$P_{\ell }$
. Fortunately, to describe
![]() $J(w)$
for
$J(w)$
for
![]() $w$
join-irreducible, we only need the following special class of factor modules.
$w$
join-irreducible, we only need the following special class of factor modules.
Definition 6.11. Let
![]() $S$
be a subarray (that is, an arbitrary subset of the entries) of the array (6.1). We say that
$S$
be a subarray (that is, an arbitrary subset of the entries) of the array (6.1). We say that
![]() $S$
is predecessor-closed if it is closed under predecessors in the quiver Figure 7.
$S$
is predecessor-closed if it is closed under predecessors in the quiver Figure 7.
Now we fix scalars
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
satisfying
$\unicode[STIX]{x1D6FD}$
satisfying
 $\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=1$
. We say that
$\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}=1$
. We say that
![]() $S$
is
$S$
is
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
-predecessor-closed if it is closed under predecessors in the subquiver of Figure 7 obtained by removing all arrows indexed by the scalar
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
-predecessor-closed if it is closed under predecessors in the subquiver of Figure 7 obtained by removing all arrows indexed by the scalar
![]() $0$
. An
$0$
. An
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
-predecessor-closed subarray
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
-predecessor-closed subarray
![]() $S$
gives a factor module of
$S$
gives a factor module of
![]() $P_{\ell }$
in a natural way. Clearly, if
$P_{\ell }$
in a natural way. Clearly, if
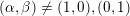 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\neq (1,0),(0,1)$
, then
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\neq (1,0),(0,1)$
, then
![]() $S$
is
$S$
is
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
-predecessor-closed if and only if it is predecessor-closed.
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
-predecessor-closed if and only if it is predecessor-closed.
For
 $m\in \{2,\ldots ,n-1\}$
, let
$m\in \{2,\ldots ,n-1\}$
, let
 $C(m,j)$
be the following subset of numbers in the row of (6.1) starting at
$C(m,j)$
be the following subset of numbers in the row of (6.1) starting at
![]() $m$
:
$m$
:

We simply write
 $C(m,j)$
as
$C(m,j)$
as  where
where
![]() $j^{\prime }:=j$
if
$j^{\prime }:=j$
if
![]() $j\geqslant -1$
and
$j\geqslant -1$
and
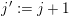 $j^{\prime }:=j+1$
if
$j^{\prime }:=j+1$
if
![]() $j\leqslant -2$
.
$j\leqslant -2$
.
Let
![]() $S(w)$
be the subarray of the array (6.1) given by
$S(w)$
be the subarray of the array (6.1) given by

Note that
 $i_{m}^{\prime }\leqslant m$
holds for any
$i_{m}^{\prime }\leqslant m$
holds for any
 $m\in \{\ell +1,\ldots ,n\}$
, and if
$m\in \{\ell +1,\ldots ,n\}$
, and if
 $i_{m}^{\prime }=m$
holds, then the row starting at
$i_{m}^{\prime }=m$
holds, then the row starting at
![]() $m-1$
is empty.
$m-1$
is empty.
Theorem 6.12. Let
 $w=[i_{1},\ldots ,i_{n}]\in W$
be a join-irreducible element of type
$w=[i_{1},\ldots ,i_{n}]\in W$
be a join-irreducible element of type
![]() $\ell \neq \pm 1$
, and
$\ell \neq \pm 1$
, and
![]() $S(w)$
subarray of the array (6.1) described in (6.2).
$S(w)$
subarray of the array (6.1) described in (6.2).
(a) If
 $\{1,2\}\not \subset \{|i_{\ell +1}|,\ldots ,|i_{n}|\}$
, then
$\{1,2\}\not \subset \{|i_{\ell +1}|,\ldots ,|i_{n}|\}$
, then
 $S(w)$
is predecessor-closed.
$S(w)$
is predecessor-closed.(b) If
 $\{1,2\}\subset \{|i_{\ell +1}|,\ldots ,|i_{n}|\}$
, then
$\{1,2\}\subset \{|i_{\ell +1}|,\ldots ,|i_{n}|\}$
, then
 $S(w)$
is
$S(w)$
is
 $(1,0)$
or
$(1,0)$
or
 $(0,1)$
-predecessor-closed.
$(0,1)$
-predecessor-closed.
In either case, we have a factor module of
![]() $P_{\ell }$
corresponding to
$P_{\ell }$
corresponding to
![]() $S(w)$
.
$S(w)$
.
(c)
 $J(w)$
is the factor module of
$J(w)$
is the factor module of
 $P_{\ell }$
corresponding to
$P_{\ell }$
corresponding to
 $S(w)$
.
$S(w)$
.
For example, let
![]() $n=6$
and
$n=6$
and
 $w=[\text{}\underline{3}4\text{}\underline{5}126]$
and
$w=[\text{}\underline{3}4\text{}\underline{5}126]$
and
 $w^{\prime }=[34\text{}\underline{5}\text{}\underline{2}16]$
. Then
$w^{\prime }=[34\text{}\underline{5}\text{}\underline{2}16]$
. Then

Thus
![]() $S(w)$
is
$S(w)$
is
![]() $(0,1)$
-predecessor-closed and
$(0,1)$
-predecessor-closed and
![]() $S(w^{\prime })$
is
$S(w^{\prime })$
is
![]() $(1,0)$
-predecessor-closed, and
$(1,0)$
-predecessor-closed, and

To prove Theorem 6.12, we need some preparation. Let
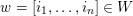 $w=[i_{1},\ldots ,i_{n}]\in W$
be a join-irreducible element of type
$w=[i_{1},\ldots ,i_{n}]\in W$
be a join-irreducible element of type
![]() $\ell$
. For each
$\ell$
. For each
 $m\in \{\ell +1,\ldots ,n\}$
, let
$m\in \{\ell +1,\ldots ,n\}$
, let
 $$\begin{eqnarray}j_{m}:=i_{m}+\#\{m^{\prime }\mid m\leqslant m^{\prime }\leqslant n,~|i_{m^{\prime }}|\leqslant |i_{m}|\}.\end{eqnarray}$$
$$\begin{eqnarray}j_{m}:=i_{m}+\#\{m^{\prime }\mid m\leqslant m^{\prime }\leqslant n,~|i_{m^{\prime }}|\leqslant |i_{m}|\}.\end{eqnarray}$$
Clearly
![]() $i_{m}>0$
implies
$i_{m}>0$
implies
 $j_{m}=i_{m}+1>1$
, and
$j_{m}=i_{m}+1>1$
, and
![]() $i_{m}<0$
implies
$i_{m}<0$
implies
![]() $j_{m}\leqslant 0$
. In the latter case, we have
$j_{m}\leqslant 0$
. In the latter case, we have
 $j_{m}=-\#\{m^{\prime }\mid 1\leqslant m^{\prime }\leqslant \ell ,~|i_{m^{\prime }}|\leqslant |i_{m}|\}$
. Therefore
$j_{m}=-\#\{m^{\prime }\mid 1\leqslant m^{\prime }\leqslant \ell ,~|i_{m^{\prime }}|\leqslant |i_{m}|\}$
. Therefore
 $j_{\ell +1}\leqslant j_{\ell +2}\leqslant \cdots \leqslant j_{n}$
holds.
$j_{\ell +1}\leqslant j_{\ell +2}\leqslant \cdots \leqslant j_{n}$
holds.
Lemma 6.13. Let
 $w=[i_{1},\ldots ,i_{n}]\in W$
be a join-irreducible element of type
$w=[i_{1},\ldots ,i_{n}]\in W$
be a join-irreducible element of type
![]() $\ell \neq \pm 1$
. Then we have a reduced expression
$\ell \neq \pm 1$
. Then we have a reduced expression
 $w=x_{n}x_{n-1}\cdots x_{\ell +2}x_{\ell +1}$
, where
$w=x_{n}x_{n-1}\cdots x_{\ell +2}x_{\ell +1}$
, where
![]() $x_{m}$
for
$x_{m}$
for
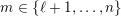 $m\in \{\ell +1,\ldots ,n\}$
is given by
$m\in \{\ell +1,\ldots ,n\}$
is given by
 $$\begin{eqnarray}x_{m}=\left\{\begin{array}{@{}ll@{}}s_{i_{m}}s_{i_{m}+1}\cdots s_{m-1} & \text{if}~j_{m}>0,\\ s_{\unicode[STIX]{x1D716}_{m}}s_{2}s_{3}\cdots s_{m-1}~\text{for}~\unicode[STIX]{x1D716}_{m}:=(-1)^{\#\{m^{\prime }\mid m\leqslant m^{\prime }\leqslant n,~i_{m^{\prime }}<0\}} & \text{if}~j_{m}=0,\\ s_{-1}s_{1}s_{2}s_{3}\cdots s_{m-1} & \text{if}~j_{m}=-1,\\ s_{-j_{m}}s_{-j_{m}-1}\cdots s_{3}s_{2}s_{-1}s_{1}s_{2}s_{3}\cdots s_{m-1} & \text{if}~j_{m}<-1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}x_{m}=\left\{\begin{array}{@{}ll@{}}s_{i_{m}}s_{i_{m}+1}\cdots s_{m-1} & \text{if}~j_{m}>0,\\ s_{\unicode[STIX]{x1D716}_{m}}s_{2}s_{3}\cdots s_{m-1}~\text{for}~\unicode[STIX]{x1D716}_{m}:=(-1)^{\#\{m^{\prime }\mid m\leqslant m^{\prime }\leqslant n,~i_{m^{\prime }}<0\}} & \text{if}~j_{m}=0,\\ s_{-1}s_{1}s_{2}s_{3}\cdots s_{m-1} & \text{if}~j_{m}=-1,\\ s_{-j_{m}}s_{-j_{m}-1}\cdots s_{3}s_{2}s_{-1}s_{1}s_{2}s_{3}\cdots s_{m-1} & \text{if}~j_{m}<-1.\end{array}\right.\end{eqnarray}$$
Proof. Since
![]() $i_{1}<i_{2}$
and
$i_{1}<i_{2}$
and
 $-i_{1}<i_{2}$
, we have
$-i_{1}<i_{2}$
, we have
 $0<i_{2}<\cdots <i_{\ell }$
. Let
$0<i_{2}<\cdots <i_{\ell }$
. Let
 $h_{1}<\cdots <h_{\ell +1}$
be the reordering of
$h_{1}<\cdots <h_{\ell +1}$
be the reordering of
∙
 $i_{1},i_{2},\ldots ,i_{\ell },i_{\ell +1}$
if
$i_{1},i_{2},\ldots ,i_{\ell },i_{\ell +1}$
if
 $j_{\ell +1}>0$
or (
$j_{\ell +1}>0$
or (
 $j_{\ell +1}=0$
and
$j_{\ell +1}=0$
and
 $i_{1}>0$
),
$i_{1}>0$
),∙
 $-i_{1},i_{2},\ldots ,i_{\ell },-i_{\ell +1}$
if
$-i_{1},i_{2},\ldots ,i_{\ell },-i_{\ell +1}$
if
 $j_{\ell +1}<0$
or (
$j_{\ell +1}<0$
or (
 $j_{\ell +1}=0$
and
$j_{\ell +1}=0$
and
 $i_{1}<0$
),
$i_{1}<0$
),
and let
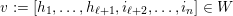 $v:=[h_{1},\ldots ,h_{\ell +1},i_{\ell +2},\ldots ,i_{n}]\in W$
. It is easy to check that
$v:=[h_{1},\ldots ,h_{\ell +1},i_{\ell +2},\ldots ,i_{n}]\in W$
. It is easy to check that
![]() $v$
is either an identity or join-irreducible of type
$v$
is either an identity or join-irreducible of type
![]() $\ell +1$
. We will show
$\ell +1$
. We will show
 $$\begin{eqnarray}wx_{\ell +1}^{-1}=v\quad \text{and}\quad \ell (w)-\ell (x_{\ell +1})=\ell (v).\end{eqnarray}$$
$$\begin{eqnarray}wx_{\ell +1}^{-1}=v\quad \text{and}\quad \ell (w)-\ell (x_{\ell +1})=\ell (v).\end{eqnarray}$$
Then the assertion follows inductively.
Let
![]() $t$
be the unique integer satisfying
$t$
be the unique integer satisfying
 $h_{t}=|i_{\ell +1}|$
.
$h_{t}=|i_{\ell +1}|$
.
Assume
 $j_{\ell +1}>0$
and so
$j_{\ell +1}>0$
and so
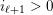 $i_{\ell +1}>0$
. Since all positive integers smaller than
$i_{\ell +1}>0$
. Since all positive integers smaller than
![]() $i_{\ell +1}$
appear in
$i_{\ell +1}$
appear in
 $|i_{1}|,\ldots ,|i_{\ell }|$
we have
$|i_{1}|,\ldots ,|i_{\ell }|$
we have
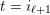 $t=i_{\ell +1}$
. Thus (6.4) follows from
$t=i_{\ell +1}$
. Thus (6.4) follows from
 $x_{\ell +1}=s_{t}s_{t+1}\cdots s_{\ell }$
.
$x_{\ell +1}=s_{t}s_{t+1}\cdots s_{\ell }$
.
Assume
 $j_{\ell +1}=0$
and so
$j_{\ell +1}=0$
and so
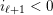 $i_{\ell +1}<0$
. Since all positive integers smaller than
$i_{\ell +1}<0$
. Since all positive integers smaller than
![]() $|i_{\ell +1}|$
appear in
$|i_{\ell +1}|$
appear in
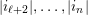 $|i_{\ell +2}|,\ldots ,|i_{n}|$
, we have
$|i_{\ell +2}|,\ldots ,|i_{n}|$
, we have
![]() $t=1$
. If
$t=1$
. If
![]() $i_{1}>0$
, then
$i_{1}>0$
, then
 $\unicode[STIX]{x1D716}_{\ell +1}=1$
holds, and (6.4) follows from
$\unicode[STIX]{x1D716}_{\ell +1}=1$
holds, and (6.4) follows from
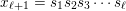 $x_{\ell +1}=s_{1}s_{2}s_{3}\cdots s_{\ell }$
. If
$x_{\ell +1}=s_{1}s_{2}s_{3}\cdots s_{\ell }$
. If
![]() $i_{1}<0$
, then
$i_{1}<0$
, then
 $\unicode[STIX]{x1D716}_{\ell +1}=-1$
holds, and (6.4) follows from
$\unicode[STIX]{x1D716}_{\ell +1}=-1$
holds, and (6.4) follows from
 $x_{\ell +1}=s_{-1}s_{2}s_{3}\cdots s_{\ell }$
.
$x_{\ell +1}=s_{-1}s_{2}s_{3}\cdots s_{\ell }$
.
Assume
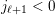 $j_{\ell +1}<0$
and so
$j_{\ell +1}<0$
and so
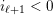 $i_{\ell +1}<0$
. Then
$i_{\ell +1}<0$
. Then
 $t=1-j_{\ell +1}$
holds, and (6.4) follows easily from
$t=1-j_{\ell +1}$
holds, and (6.4) follows easily from
 $x_{\ell +1}=s_{t-1}s_{t-2}\cdots s_{3}s_{2}s_{-1}s_{1}s_{2}s_{3}\cdots s_{\ell }$
.◻
$x_{\ell +1}=s_{t-1}s_{t-2}\cdots s_{3}s_{2}s_{-1}s_{1}s_{2}s_{3}\cdots s_{\ell }$
.◻
Now we are ready to prove Theorem 6.12.
Proof of Theorem 6.12.
(a) and (b) are easily checked.
(c) Choose scalars
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
such that
$\unicode[STIX]{x1D6FD}$
such that
![]() $S(w)$
is
$S(w)$
is
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
-predecessor-closed. Using the quiver representation of
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})$
-predecessor-closed. Using the quiver representation of
![]() $P_{\ell }$
given in Figure 7 and the reduced expression of
$P_{\ell }$
given in Figure 7 and the reduced expression of
![]() $w$
given in Lemma 6.13, we calculate
$w$
given in Lemma 6.13, we calculate
![]() $I(w)e_{\ell }$
. Dividing into three cases, we show that the first row of
$I(w)e_{\ell }$
. Dividing into three cases, we show that the first row of
![]() $J(w)$
coincides with that of
$J(w)$
coincides with that of
![]() $S(w)$
.
$S(w)$
.
Assume
 $j_{\ell +1}>0$
. By (6.3), the first row of
$j_{\ell +1}>0$
. By (6.3), the first row of
 $I(x_{\ell +1})e_{\ell }$
is given by
$I(x_{\ell +1})e_{\ell }$
is given by

Since
 $0<i_{\ell +1}<i_{\ell +2}<\cdots <i_{n}$
holds, both
$0<i_{\ell +1}<i_{\ell +2}<\cdots <i_{n}$
holds, both
![]() $s_{i_{\ell +1}-1}$
(when
$s_{i_{\ell +1}-1}$
(when
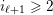 $i_{\ell +1}\geqslant 2$
) and
$i_{\ell +1}\geqslant 2$
) and
![]() $s_{-1}$
(when
$s_{-1}$
(when
 $i_{\ell +1}=1$
) do not appear in
$i_{\ell +1}=1$
) do not appear in
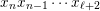 $x_{n}x_{n-1}\cdots x_{\ell +2}$
by (6.3). Thus the first row of
$x_{n}x_{n-1}\cdots x_{\ell +2}$
by (6.3). Thus the first row of
![]() $I(w)e_{\ell }$
coincides with that of
$I(w)e_{\ell }$
coincides with that of
 $I(x_{\ell +1})e_{\ell }$
, and the first row of
$I(x_{\ell +1})e_{\ell }$
, and the first row of
![]() $J(w)$
coincides with that of
$J(w)$
coincides with that of
![]() $S(w)$
.
$S(w)$
.
Assume
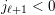 $j_{\ell +1}<0$
. By (6.3), the first row of
$j_{\ell +1}<0$
. By (6.3), the first row of
 $I(x_{\ell +1})e_{\ell }$
is given by
$I(x_{\ell +1})e_{\ell }$
is given by

Let
 $m_{0}:=\max \{m\mid \ell +1\leqslant m\leqslant n,|i_{m}|\leqslant |i_{\ell +1}|\}$
, which equals
$m_{0}:=\max \{m\mid \ell +1\leqslant m\leqslant n,|i_{m}|\leqslant |i_{\ell +1}|\}$
, which equals
 $j_{\ell +1}-i_{\ell +1}+\ell$
. We show that, for any
$j_{\ell +1}-i_{\ell +1}+\ell$
. We show that, for any
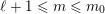 $\ell +1\leqslant m\leqslant m_{0}$
, the first row of
$\ell +1\leqslant m\leqslant m_{0}$
, the first row of
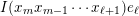 $I(x_{m}x_{m-1}\cdots x_{\ell +1})e_{\ell }$
is
$I(x_{m}x_{m-1}\cdots x_{\ell +1})e_{\ell }$
is

The case
 $m=\ell +1$
was shown above. Assume that this is the case for
$m=\ell +1$
was shown above. Assume that this is the case for
 $m-1({<}m_{0})$
. It suffices to show that
$m-1({<}m_{0})$
. It suffices to show that
 $s_{-j_{\ell +1}+m-1-\ell }$
appears in
$s_{-j_{\ell +1}+m-1-\ell }$
appears in
![]() $x_{m}$
, and that
$x_{m}$
, and that
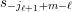 $s_{-j_{\ell +1}+m-\ell }$
does not appear in the left side of
$s_{-j_{\ell +1}+m-\ell }$
does not appear in the left side of
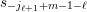 $s_{-j_{\ell +1}+m-1-\ell }$
in
$s_{-j_{\ell +1}+m-1-\ell }$
in
![]() $x_{m}$
. Since
$x_{m}$
. Since
 $-j_{\ell +1}\leqslant \ell$
holds, we have
$-j_{\ell +1}\leqslant \ell$
holds, we have
 $$\begin{eqnarray}2\leqslant -j_{\ell +1}+m-1-\ell \leqslant m-1.\end{eqnarray}$$
$$\begin{eqnarray}2\leqslant -j_{\ell +1}+m-1-\ell \leqslant m-1.\end{eqnarray}$$
If
![]() $j_{m}\geqslant 0$
, then the assertion follows from (6.3) and
$j_{m}\geqslant 0$
, then the assertion follows from (6.3) and
 $$\begin{eqnarray}i_{m}\leqslant i_{m_{0}}-m_{0}+m\leqslant -i_{\ell +1}-m_{0}+m-1=-j_{\ell +1}+m-1-\ell .\end{eqnarray}$$
$$\begin{eqnarray}i_{m}\leqslant i_{m_{0}}-m_{0}+m\leqslant -i_{\ell +1}-m_{0}+m-1=-j_{\ell +1}+m-1-\ell .\end{eqnarray}$$
If
![]() $j_{m}<0$
, then the assertion follows from (6.3) and
$j_{m}<0$
, then the assertion follows from (6.3) and
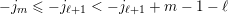 $-j_{m}\leqslant -j_{\ell +1}<-j_{\ell +1}+m-1-\ell$
. Inductively, we have shown that the first row of
$-j_{m}\leqslant -j_{\ell +1}<-j_{\ell +1}+m-1-\ell$
. Inductively, we have shown that the first row of
 $I(x_{m_{0}}x_{m_{0}-1}\cdots x_{\ell +1})e_{\ell }$
is
$I(x_{m_{0}}x_{m_{0}-1}\cdots x_{\ell +1})e_{\ell }$
is

since
 $j_{\ell +1}-m_{0}+\ell =i_{\ell +1}$
. Since
$j_{\ell +1}-m_{0}+\ell =i_{\ell +1}$
. Since
 $0<-i_{\ell +1}<i_{m_{0}+1}<\cdots <i_{n}$
holds,
$0<-i_{\ell +1}<i_{m_{0}+1}<\cdots <i_{n}$
holds,
![]() $s_{-i_{\ell +1}}$
does not appear in
$s_{-i_{\ell +1}}$
does not appear in
 $x_{n}x_{n-1}\cdots x_{m_{0}+1}$
. Thus the first row of
$x_{n}x_{n-1}\cdots x_{m_{0}+1}$
. Thus the first row of
![]() $I(w)e_{\ell }$
coincides with (6.5), and the first row of
$I(w)e_{\ell }$
coincides with (6.5), and the first row of
![]() $J(w)$
coincides with that of
$J(w)$
coincides with that of
![]() $S(w)$
.
$S(w)$
.
Assume
 $j_{\ell +1}=0$
. By (6.3), the first row of
$j_{\ell +1}=0$
. By (6.3), the first row of
 $I(x_{\ell +1})e_{\ell }$
is given by
$I(x_{\ell +1})e_{\ell }$
is given by

By a similar argument as in the case
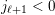 $j_{\ell +1}<0$
, one can check that the first row of
$j_{\ell +1}<0$
, one can check that the first row of
![]() $J(w)$
coincides with that of
$J(w)$
coincides with that of
![]() $S(w)$
.
$S(w)$
.
We have completed to show that the first row of
![]() $J(w)$
coincides with that of
$J(w)$
coincides with that of
![]() $S(w)$
. All rows of
$S(w)$
. All rows of
 $I(x_{\ell +1})e_{\ell }$
except the first one coincide with those of
$I(x_{\ell +1})e_{\ell }$
except the first one coincide with those of
![]() $P_{\ell }$
since
$P_{\ell }$
since
![]() $s_{\ell +1}$
does not appear in
$s_{\ell +1}$
does not appear in
![]() $x_{\ell +1}$
. Repeating the same calculation, all rows of
$x_{\ell +1}$
. Repeating the same calculation, all rows of
![]() $J(w)$
coincide with that of
$J(w)$
coincide with that of
![]() $S(w)$
.◻
$S(w)$
.◻
Example 6.14. Let
 $w=[(-1)^{n-\ell },2,\ldots ,\ell ,\text{}\underline{n},\text{}\underline{n-1},\ldots ,\text{}\underline{\ell +1}]$
be a join-irreducible element of type
$w=[(-1)^{n-\ell },2,\ldots ,\ell ,\text{}\underline{n},\text{}\underline{n-1},\ldots ,\text{}\underline{\ell +1}]$
be a join-irreducible element of type
![]() $\ell$
. Then we have a reduced expression
$\ell$
. Then we have a reduced expression
 $$\begin{eqnarray}w=x_{n}x_{n-1}\cdots x_{\ell +2}x_{\ell +1}\quad \text{for}~x_{m}=s_{\ell }\cdots s_{3}s_{2}s_{-1}s_{1}s_{2}s_{3}\cdots s_{m-1},\end{eqnarray}$$
$$\begin{eqnarray}w=x_{n}x_{n-1}\cdots x_{\ell +2}x_{\ell +1}\quad \text{for}~x_{m}=s_{\ell }\cdots s_{3}s_{2}s_{-1}s_{1}s_{2}s_{3}\cdots s_{m-1},\end{eqnarray}$$
and the corresponding indecomposable
![]() $\unicode[STIX]{x1D70F}^{-}$
-rigid
$\unicode[STIX]{x1D70F}^{-}$
-rigid
![]() $\unicode[STIX]{x1D6F1}$
-module is
$\unicode[STIX]{x1D6F1}$
-module is
 $J(w)=P_{\ell }$
.
$J(w)=P_{\ell }$
.
Example 6.15. Consider type
![]() $D_{4}$
. Below we show the expression given in Lemma 6.13 by using dots:
$D_{4}$
. Below we show the expression given in Lemma 6.13 by using dots:
 $w=x_{n}\cdot x_{n-1}\cdot \cdots \cdot x_{\ell +2}\cdot x_{\ell +1}$
.
$w=x_{n}\cdot x_{n-1}\cdot \cdots \cdot x_{\ell +2}\cdot x_{\ell +1}$
.
We have the following 7 join-irreducible elements of type 3:




We have the following 23 join-irreducible elements of type 2. They are predecessor-closed unless otherwise specified.