No CrossRef data available.
Published online by Cambridge University Press: 20 April 2023
In this paper we study the asymptotic behaviour of a random uniform parking function 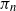 $\pi_n$ of size n. We show that the first
$\pi_n$ of size n. We show that the first 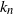 $k_n$ places
$k_n$ places 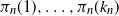 $\pi_n(1),\ldots,\pi_n(k_n)$ of
$\pi_n(1),\ldots,\pi_n(k_n)$ of 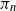 $\pi_n$ are asymptotically independent and identically distributed (i.i.d.) and uniform on
$\pi_n$ are asymptotically independent and identically distributed (i.i.d.) and uniform on 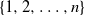 $\{1,2,\ldots,n\}$, for the total variation distance when
$\{1,2,\ldots,n\}$, for the total variation distance when 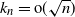 $k_n = {\rm{o}}(\sqrt{n})$, and for the Kolmogorov distance when
$k_n = {\rm{o}}(\sqrt{n})$, and for the Kolmogorov distance when 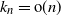 $k_n={\rm{o}}(n)$, improving results of Diaconis and Hicks. Moreover, we give bounds for the rate of convergence, as well as limit theorems for certain statistics such as the sum or the maximum of the first
$k_n={\rm{o}}(n)$, improving results of Diaconis and Hicks. Moreover, we give bounds for the rate of convergence, as well as limit theorems for certain statistics such as the sum or the maximum of the first 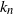 $k_n$ parking places. The main tool is a reformulation using conditioned random walks.
$k_n$ parking places. The main tool is a reformulation using conditioned random walks.