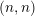1 Introduction
Triply graded Khovanov–Rozansky homology is a link homology theory which was originally introduced by Khovanov and Rozansky [Reference Khovanov and RozanskyKR08] using matrix factorizations, but was soon after reinterpreted by Khovanov [Reference KhovanovKho07] using the Hochschild homology of Soergel bimodules. It has generated a great deal of interest, admitting spectral sequences which converge to various
![]() $\mathfrak{s}\mathfrak{l}_{n}$
-link homology theories [Reference RasmussenRas15], and having deep connections to the representation theory of Hecke algebras in type
$\mathfrak{s}\mathfrak{l}_{n}$
-link homology theories [Reference RasmussenRas15], and having deep connections to the representation theory of Hecke algebras in type
![]() $A$
.
$A$
.
Khovanov’s construction begins with a braid
![]() $\unicode[STIX]{x1D6FD}$
on
$\unicode[STIX]{x1D6FD}$
on
![]() $n$
strands. To such a braid, Rouquier [Reference RouquierRou04] has associated a complex (up to homotopy)
$n$
strands. To such a braid, Rouquier [Reference RouquierRou04] has associated a complex (up to homotopy)
![]() $F(\unicode[STIX]{x1D6FD})$
of Soergel bimodules, which are certain graded bimodules [Reference SoergelSoe07] over the polynomial ring
$F(\unicode[STIX]{x1D6FD})$
of Soergel bimodules, which are certain graded bimodules [Reference SoergelSoe07] over the polynomial ring
![]() $R=R_{n}=\mathbb{Q}[x_{1},\ldots ,x_{n}]$
in
$R=R_{n}=\mathbb{Q}[x_{1},\ldots ,x_{n}]$
in
![]() $n$
variables. More precisely, Rouquier associates a complex to each braid generator (e.g. over- or under-crossing). From this, one obtains a complex for any braid diagram by taking the tensor product of these elementary complexes. Rouquier proves that two braid diagrams for the same braid yield complexes which are canonically isomorphic in the homotopy category of
$n$
variables. More precisely, Rouquier associates a complex to each braid generator (e.g. over- or under-crossing). From this, one obtains a complex for any braid diagram by taking the tensor product of these elementary complexes. Rouquier proves that two braid diagrams for the same braid yield complexes which are canonically isomorphic in the homotopy category of
![]() $R$
-bimodules.
$R$
-bimodules.
Khovanov [Reference KhovanovKho07] observed that taking the closure
![]() $\overline{\unicode[STIX]{x1D6FD}}$
of a braid
$\overline{\unicode[STIX]{x1D6FD}}$
of a braid
![]() $\unicode[STIX]{x1D6FD}$
should correspond to identifying the right and left actions of
$\unicode[STIX]{x1D6FD}$
should correspond to identifying the right and left actions of
![]() $R$
, or rather the higher derived functors of this operation. These higher derived functors are known as Hochschild homology and are denoted by
$R$
, or rather the higher derived functors of this operation. These higher derived functors are known as Hochschild homology and are denoted by
![]() $\operatorname{HH}_{i}(R;M)$
, where
$\operatorname{HH}_{i}(R;M)$
, where
![]() $M$
is an
$M$
is an
![]() $(R,R)$
bimodule; when
$(R,R)$
bimodule; when
![]() $R$
is understood we write
$R$
is understood we write
![]() $\operatorname{HH}_{i}(M)=\operatorname{HH}_{i}(R;M)$
. Khovanov proved that the complex obtained by applying
$\operatorname{HH}_{i}(M)=\operatorname{HH}_{i}(R;M)$
. Khovanov proved that the complex obtained by applying
![]() $\operatorname{HH}_{i}$
to each Soergel bimodule in a Rouquier complex
$\operatorname{HH}_{i}$
to each Soergel bimodule in a Rouquier complex
![]() $F(\unicode[STIX]{x1D6FD})$
yields a complex of vector spaces which (up to homotopy) depends only on the closure
$F(\unicode[STIX]{x1D6FD})$
yields a complex of vector spaces which (up to homotopy) depends only on the closure
![]() $\overline{\unicode[STIX]{x1D6FD}}$
, and thus the homology groups of this complex are link invariants of
$\overline{\unicode[STIX]{x1D6FD}}$
, and thus the homology groups of this complex are link invariants of
![]() $\overline{\unicode[STIX]{x1D6FD}}$
. The three gradings come from the Hochschild homological grading, the usual homological grading, and the internal grading of the Soergel bimodules.
$\overline{\unicode[STIX]{x1D6FD}}$
. The three gradings come from the Hochschild homological grading, the usual homological grading, and the internal grading of the Soergel bimodules.
It is well known (see [Reference KhovanovKho07] and references therein) that if
![]() $R=R_{n}$
is a polynomial ring and
$R=R_{n}$
is a polynomial ring and
![]() $M$
is an
$M$
is an
![]() $R$
-bimodule, then there is an isomorphism between Hochschild homology group
$R$
-bimodule, then there is an isomorphism between Hochschild homology group
![]() $\operatorname{HH}_{i}(R;M)$
, and the Hochschild cohomology group
$\operatorname{HH}_{i}(R;M)$
, and the Hochschild cohomology group
![]() $\operatorname{HH}^{n-i}(R;M)$
. The Hochschild cohomology groups are the higher derived functors of
$\operatorname{HH}^{n-i}(R;M)$
. The Hochschild cohomology groups are the higher derived functors of
![]() $M\mapsto \text{Hom}_{(R,R)}(R,M)$
, the space of
$M\mapsto \text{Hom}_{(R,R)}(R,M)$
, the space of
![]() $R$
-bimodule maps from the monoidal identity
$R$
-bimodule maps from the monoidal identity
![]() $R$
. For the remainder of this paper, we work exclusively with Hochschild cohomology.
$R$
. For the remainder of this paper, we work exclusively with Hochschild cohomology.
The Khovanov–Rozansky homology of torus links has deep connections to Hilbert schemes, rational Cherednik algebras, and refined Chern–Simons theory [Reference Gorsky, Oblomkov, Rasmussen and ShendeGORS14, Reference Gorsky and NeguțGN15, Reference Gorsky, Neguț and RasmussenGNR16]. At the moment these connections are purely conjectural, but they suggest that the Khovanov–Rozansky homologies of torus links are quite interesting objects. Up until now, however, the connection with other subjects has been difficult to verify, since the computation of Khovanov–Rozansky homology is quite challenging in practice. In this paper we introduce a new method for computing Khovanov–Rozansky homology which seems particularly well adapted to compute homologies of torus links. In particular, we provide a remarkably simple description of the triply graded homology of the
![]() $(n,n)$
torus links, in Theorem 1.6.Footnote
1
$(n,n)$
torus links, in Theorem 1.6.Footnote
1
In § 1.5 we compare our results with the predictions of Gorsky and Negut [Reference Gorsky and NeguțGN15] (also Gorsky, Negut and Rasmussen [Reference Gorsky, Neguț and RasmussenGNR16])Footnote
2
coming from flag Hilbert schemes; in every case we have checked, they match identically. Previous checks of the connection with Hilbert schemes have been limited to the cases
![]() $n=2,3$
, but with our method we are able to verify the predictions of [Reference Gorsky, Neguț and RasmussenGNR16] for
$n=2,3$
, but with our method we are able to verify the predictions of [Reference Gorsky, Neguț and RasmussenGNR16] for
![]() $n\leqslant 4$
.
$n\leqslant 4$
.
On the other hand, it is difficult to compare our results on
![]() $(n,n)$
torus links with the conjectures of Gorsky et al. [Reference Gorsky, Oblomkov and RasmussenGOR13] since they focus on the case of the
$(n,n)$
torus links with the conjectures of Gorsky et al. [Reference Gorsky, Oblomkov and RasmussenGOR13] since they focus on the case of the
![]() $(n,m)$
-torus knots, that is, when
$(n,m)$
-torus knots, that is, when
![]() $n$
and
$n$
and
![]() $m$
are coprime, and much less is known about the link case. Nonetheless, from Etingof we learned that the ring of
$m$
are coprime, and much less is known about the link case. Nonetheless, from Etingof we learned that the ring of
![]() $k$
-quasi-invariants for
$k$
-quasi-invariants for
![]() $S_{n}$
acting on
$S_{n}$
acting on
![]() $\mathbb{Q}[x_{1},\ldots ,x_{n}]$
(see [Reference Etingof and StricklandES02] for a survey) is a representation of the rational Cherednik algebra for
$\mathbb{Q}[x_{1},\ldots ,x_{n}]$
(see [Reference Etingof and StricklandES02] for a survey) is a representation of the rational Cherednik algebra for
![]() $\mathfrak{s}\mathfrak{l}_{n}$
, and is the correct replacement for the simple module
$\mathfrak{s}\mathfrak{l}_{n}$
, and is the correct replacement for the simple module
![]() $L_{m/n}$
which appears in [Reference Gorsky, Oblomkov, Rasmussen and ShendeGORS14] when
$L_{m/n}$
which appears in [Reference Gorsky, Oblomkov, Rasmussen and ShendeGORS14] when
![]() $m=kn$
. Thus, the minimal Hochschild degree part of the Poincaré series of the
$m=kn$
. Thus, the minimal Hochschild degree part of the Poincaré series of the
![]() $(n,nk)$
torus links is expected to equal the Hilbert series for a certain filtration on the ring of
$(n,nk)$
torus links is expected to equal the Hilbert series for a certain filtration on the ring of
![]() $k$
-quasi-invariants. However, it is not clear how to filter the ring of quasi-invariants in an appropriate way, so we will not say more about this connection in this paper.
$k$
-quasi-invariants. However, it is not clear how to filter the ring of quasi-invariants in an appropriate way, so we will not say more about this connection in this paper.
In Appendix A we include some additional computations. We found that the Poincaré polynomial of
![]() $\operatorname{HH}^{0}$
of the
$\operatorname{HH}^{0}$
of the
![]() $(n,n+1)$
torus knot is given by the
$(n,n+1)$
torus knot is given by the
![]() $q,t$
Catalan number for
$q,t$
Catalan number for
![]() $n=2,3,4$
, which verifies a conjecture of Gorsky’s [Reference GorskyGor12] for these knots.
$n=2,3,4$
, which verifies a conjecture of Gorsky’s [Reference GorskyGor12] for these knots.
Our particular interest in the homology of the
![]() $(n,n)$
torus links stems from the fact that this triply graded vector space parametrizes maps from the identity Soergel bimodule
$(n,n)$
torus links stems from the fact that this triply graded vector space parametrizes maps from the identity Soergel bimodule
![]() $R$
to the Rouquier complex associated to the full twist braid
$R$
to the Rouquier complex associated to the full twist braid
![]() $\text{FT}_{n}$
. The computation above is used in forthcoming work of the authors, in which we decompose the Soergel category into its ‘eigencategories’ for the action of
$\text{FT}_{n}$
. The computation above is used in forthcoming work of the authors, in which we decompose the Soergel category into its ‘eigencategories’ for the action of
![]() $\text{FT}_{n}$
, thereby laying the groundwork for the study of the categorical representation theory of Hecke algebras.
$\text{FT}_{n}$
, thereby laying the groundwork for the study of the categorical representation theory of Hecke algebras.
1.1 Motivation from categorical representation theory
It was shown by Khovanov and Thomas [Reference Khovanov and ThomasKT07] that Rouquier complexes give a faithful action of the braid group on the homotopy category of Soergel bimodules. For this reason, the collection of Rouquier complexes is often referred to as a categorification of the braid group, but this is somewhat misleading, as this particular action of the braid group is intricately tied to its Hecke quotient. Soergel [Reference SoergelSoe07] proved that Soergel bimodules over
![]() $R_{n}$
categorify the Hecke algebra
$R_{n}$
categorify the Hecke algebra
![]() $\mathbf{H}=\mathbf{H}_{n}$
of the symmetric group
$\mathbf{H}=\mathbf{H}_{n}$
of the symmetric group
![]() $S_{n}$
. Note that
$S_{n}$
. Note that
![]() $\mathbf{H}$
is linear over the ring
$\mathbf{H}$
is linear over the ring
![]() $\mathbb{Z}[Q,Q^{-1}]$
, where
$\mathbb{Z}[Q,Q^{-1}]$
, where
![]() $Q$
is categorified by the grading shift of an
$Q$
is categorified by the grading shift of an
![]() $R$
-bimodule;Footnote
3
for this to work correctly,
$R$
-bimodule;Footnote
3
for this to work correctly,
![]() $R$
is graded so that
$R$
is graded so that
![]() $\deg x_{i}=2$
for all
$\deg x_{i}=2$
for all
![]() $1\leqslant i\leqslant n$
. Taking the image of a Rouquier complex in this Grothendieck group yields the familiar quotient map from the braid group (or its group algebra over
$1\leqslant i\leqslant n$
. Taking the image of a Rouquier complex in this Grothendieck group yields the familiar quotient map from the braid group (or its group algebra over
![]() $\mathbb{Z}[Q,Q^{-1}]$
) to the Hecke algebra. However, the fact that Rouquier complexes only reflect the ‘Hecke-type’ actions of the braid group is an advantage, not a limitation, as one can lift results from the representation theory of Hecke algebras to study the homotopy category of Soergel bimodules. This paper can be understood and appreciated without a foray into categorical representation theory, but we provide some brief motivation here.
$\mathbb{Z}[Q,Q^{-1}]$
) to the Hecke algebra. However, the fact that Rouquier complexes only reflect the ‘Hecke-type’ actions of the braid group is an advantage, not a limitation, as one can lift results from the representation theory of Hecke algebras to study the homotopy category of Soergel bimodules. This paper can be understood and appreciated without a foray into categorical representation theory, but we provide some brief motivation here.
The Hecke algebra admits a sign representation
![]() $\operatorname{sgn}_{n}$
, on which each of its standard generators (the images of the overcrossings) acts by
$\operatorname{sgn}_{n}$
, on which each of its standard generators (the images of the overcrossings) acts by
![]() $-Q^{-1}$
. The projection from an arbitrary Hecke algebra representation to its isotypic component for the sign representation is an idempotent often known as a (generalized) Jones–Wenzl projector, after the corresponding idempotent in the Temperley–Lieb algebra [Reference JonesJon01, Reference WenzlWen87]. This projection can not be defined in
$-Q^{-1}$
. The projection from an arbitrary Hecke algebra representation to its isotypic component for the sign representation is an idempotent often known as a (generalized) Jones–Wenzl projector, after the corresponding idempotent in the Temperley–Lieb algebra [Reference JonesJon01, Reference WenzlWen87]. This projection can not be defined in
![]() $\mathbf{H}$
itself, requiring certain scalars to be inverted (like
$\mathbf{H}$
itself, requiring certain scalars to be inverted (like
![]() $Q+Q^{-1}$
, for example). It can be defined in the base change
$Q+Q^{-1}$
, for example). It can be defined in the base change
![]() $\mathbf{H}\otimes _{\mathbb{Z}[Q,Q^{-1}]}\mathbb{Z}((Q))$
.
$\mathbf{H}\otimes _{\mathbb{Z}[Q,Q^{-1}]}\mathbb{Z}((Q))$
.
In [Reference HogancampHog18], the second author constructs an infinite complex of Soergel bimodules
![]() $P_{n}$
which categorifies this Jones–Wenzl projector. In this paper we study a finite complex
$P_{n}$
which categorifies this Jones–Wenzl projector. In this paper we study a finite complex
![]() $K_{n}$
which categorifies the ‘renormalized’ Jones–Wenzl projector, a rescaling of the projector which is actually defined within
$K_{n}$
which categorifies the ‘renormalized’ Jones–Wenzl projector, a rescaling of the projector which is actually defined within
![]() $\mathbf{H}$
before base change. The fact that the Jones–Wenzl idempotent projects to the sign representation is categorified by the fact that the Rouquier complex for an overcrossing, acting by tensor product on
$\mathbf{H}$
before base change. The fact that the Jones–Wenzl idempotent projects to the sign representation is categorified by the fact that the Rouquier complex for an overcrossing, acting by tensor product on
![]() $K_{n}$
, will simply act by a homological and a grading shift.
$K_{n}$
, will simply act by a homological and a grading shift.
The inductive construction of
![]() $K_{n}$
itself also is motivated by the representation theory of the Hecke algebra. When
$K_{n}$
itself also is motivated by the representation theory of the Hecke algebra. When
![]() $\operatorname{sgn}_{n}$
is induced from
$\operatorname{sgn}_{n}$
is induced from
![]() $\mathbf{H}_{n}$
to
$\mathbf{H}_{n}$
to
![]() $\mathbf{H}_{n+1}$
, it splits into two irreducible representations,
$\mathbf{H}_{n+1}$
, it splits into two irreducible representations,
![]() $\operatorname{sgn}_{n+1}$
and another representation
$\operatorname{sgn}_{n+1}$
and another representation
![]() $V$
. This splitting is actually the eigenspace decomposition for the Young–Jucys–Murphy operator
$V$
. This splitting is actually the eigenspace decomposition for the Young–Jucys–Murphy operator
![]() $y_{n+1}$
, a certain element of the braid group on
$y_{n+1}$
, a certain element of the braid group on
![]() $n+1$
strands which commutes with any braid on the first
$n+1$
strands which commutes with any braid on the first
![]() $n$
strands. If
$n$
strands. If
![]() $\unicode[STIX]{x1D6FE}$
is the eigenvalue corresponding to
$\unicode[STIX]{x1D6FE}$
is the eigenvalue corresponding to
![]() $V$
, then
$V$
, then
![]() $y_{n+1}-\unicode[STIX]{x1D6FE}$
kills
$y_{n+1}-\unicode[STIX]{x1D6FE}$
kills
![]() $V$
, and thus is equal to the projection to
$V$
, and thus is equal to the projection to
![]() $\operatorname{sgn}_{n+1}$
up to scalar. If
$\operatorname{sgn}_{n+1}$
up to scalar. If
![]() $k_{n}\in \mathbf{H}_{n}\subset \mathbf{H}_{n+1}$
denotes the renormalized projection onto the sign representation, then by the previous discussion there is a linear relation
$k_{n}\in \mathbf{H}_{n}\subset \mathbf{H}_{n+1}$
denotes the renormalized projection onto the sign representation, then by the previous discussion there is a linear relation
On the categorical level, this relation becomes an exact triangle. More precisely, there is a grading shift
![]() $\unicode[STIX]{x1D6E4}$
and a chain map
$\unicode[STIX]{x1D6E4}$
and a chain map
![]() $\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6E4}K_{n}\rightarrow K_{n}F(y_{n+1})$
such that
$\unicode[STIX]{x1D711}:\unicode[STIX]{x1D6E4}K_{n}\rightarrow K_{n}F(y_{n+1})$
such that
![]() $K_{n+1}:=\text{Cone}(\unicode[STIX]{x1D711})$
categorifies the renormalized projection to
$K_{n+1}:=\text{Cone}(\unicode[STIX]{x1D711})$
categorifies the renormalized projection to
![]() $\operatorname{sgn}_{n+1}$
. Recall that
$\operatorname{sgn}_{n+1}$
. Recall that
![]() $F(y_{n+1})$
indicates the Rouquier complex associated to
$F(y_{n+1})$
indicates the Rouquier complex associated to
![]() $y_{n+1}$
. It turns out that
$y_{n+1}$
. It turns out that
![]() $\unicode[STIX]{x1D6FE}=Q^{2}$
, and
$\unicode[STIX]{x1D6FE}=Q^{2}$
, and
![]() $\unicode[STIX]{x1D6E4}=Q^{2}$
is simply the functor which shifts internal degree up by 2. This chain map is constructed in [Reference HogancampHog18], and we recall the basics in § 2.6.
$\unicode[STIX]{x1D6E4}=Q^{2}$
is simply the functor which shifts internal degree up by 2. This chain map is constructed in [Reference HogancampHog18], and we recall the basics in § 2.6.
This is an example of categorical diagonalization, a concept which is developed in forthcoming work.Footnote
4
The chain map
![]() $\unicode[STIX]{x1D711}$
mentioned above is an eigenmap; in our categorification of various concepts in linear algebra, the cones of eigenmaps are used to categorify the operators
$\unicode[STIX]{x1D711}$
mentioned above is an eigenmap; in our categorification of various concepts in linear algebra, the cones of eigenmaps are used to categorify the operators
![]() $(A-\unicode[STIX]{x1D706}I)$
for an eigenvalue
$(A-\unicode[STIX]{x1D706}I)$
for an eigenvalue
![]() $\unicode[STIX]{x1D706}$
of an operator
$\unicode[STIX]{x1D706}$
of an operator
![]() $A$
. This makes the computation of
$A$
. This makes the computation of
![]() $\operatorname{HH}^{0}$
of a braid particularly significant, because it describes the space of maps from the (shifted) monoidal identity, which are potential eigenmaps. In fact, the main result of this paper is used as a lemma in [Reference Elias and HogancampEH18] to prove that the full twist in the braid group has enough eigenmaps and therefore is categorically diagonalizable. We use this to construct categorical projections to arbitrary irreducible representations of the Hecke algebra, not just the sign representation.
$\operatorname{HH}^{0}$
of a braid particularly significant, because it describes the space of maps from the (shifted) monoidal identity, which are potential eigenmaps. In fact, the main result of this paper is used as a lemma in [Reference Elias and HogancampEH18] to prove that the full twist in the braid group has enough eigenmaps and therefore is categorically diagonalizable. We use this to construct categorical projections to arbitrary irreducible representations of the Hecke algebra, not just the sign representation.
In this paper, our focus is on computation: the existence of
![]() $K_{n}$
is known by other means, and we use the recursive definition of
$K_{n}$
is known by other means, and we use the recursive definition of
![]() $K_{n}$
to compute link invariants. This strategy is outlined below.
$K_{n}$
to compute link invariants. This strategy is outlined below.
1.2 Our method, decategorified
The Hecke algebra
![]() $\mathbf{H}_{n}$
is isomorphic to a quotient of the group algebra
$\mathbf{H}_{n}$
is isomorphic to a quotient of the group algebra
![]() $\mathbb{Z}[Q,Q^{-1}][\operatorname{Br}_{n}]$
where we identify
$\mathbb{Z}[Q,Q^{-1}][\operatorname{Br}_{n}]$
where we identify
The Jones–Ocneanu trace
![]() $\operatorname{Tr}:\mathbf{H}_{n}\rightarrow \mathbb{Z}[Q^{\pm },A^{\pm }]$
is such that
$\operatorname{Tr}:\mathbf{H}_{n}\rightarrow \mathbb{Z}[Q^{\pm },A^{\pm }]$
is such that
![]() $\operatorname{Tr}(\unicode[STIX]{x1D6FD})$
is the Homfly polynomial of the braid closure
$\operatorname{Tr}(\unicode[STIX]{x1D6FD})$
is the Homfly polynomial of the braid closure
![]() $\hat{\unicode[STIX]{x1D6FD}}$
. Using the skein relation above, and the formula which defines
$\hat{\unicode[STIX]{x1D6FD}}$
. Using the skein relation above, and the formula which defines
![]() $\operatorname{Tr}$
, one can in principal compute the Homfly polynomial for any link. In (1.2) we introduce another skein-like relation which is often useful.
$\operatorname{Tr}$
, one can in principal compute the Homfly polynomial for any link. In (1.2) we introduce another skein-like relation which is often useful.
There are elements
![]() $k_{n}\in \mathbf{H}_{n}$
defined inductively by
$k_{n}\in \mathbf{H}_{n}$
defined inductively by
![]() $k_{1}=1\in \mathbf{H}_{n}$
, and
$k_{1}=1\in \mathbf{H}_{n}$
, and

The element
![]() $k_{n}$
is a renormalized projection onto the sign representation:
$k_{n}$
is a renormalized projection onto the sign representation:
![]() $k_{n}\unicode[STIX]{x1D70E}_{i}^{\pm }=-Q^{\mp }k_{n}=\unicode[STIX]{x1D70E}_{i}^{\pm }k_{n}$
for all
$k_{n}\unicode[STIX]{x1D70E}_{i}^{\pm }=-Q^{\mp }k_{n}=\unicode[STIX]{x1D70E}_{i}^{\pm }k_{n}$
for all
![]() $1\leqslant i\leqslant n-1$
, where
$1\leqslant i\leqslant n-1$
, where
![]() $\unicode[STIX]{x1D70E}_{i}$
denotes the elementary braid generator. This implies that
$\unicode[STIX]{x1D70E}_{i}$
denotes the elementary braid generator. This implies that

The Jones–Ocneanu trace
![]() $\operatorname{Tr}(k_{n})$
can easily be computed inductively from this equation using the invariance of
$\operatorname{Tr}(k_{n})$
can easily be computed inductively from this equation using the invariance of
![]() $\operatorname{Tr}$
under the Markov moves together with the fact that
$\operatorname{Tr}$
under the Markov moves together with the fact that
![]() $k_{n}$
absorbs crossings. We can use
$k_{n}$
absorbs crossings. We can use
![]() $k_{n}$
to compute link invariants as follows.
$k_{n}$
to compute link invariants as follows.
– Assume
 $\unicode[STIX]{x1D6FD}$
is given. Choose a crossing
$\unicode[STIX]{x1D6FD}$
is given. Choose a crossing
 $x$
in
$x$
in
 $\unicode[STIX]{x1D6FD}$
. Place
$\unicode[STIX]{x1D6FD}$
. Place
 $k_{1}$
somewhere in the vicinity of this crossing. Since
$k_{1}$
somewhere in the vicinity of this crossing. Since
 $k_{1}$
is the identity element of
$k_{1}$
is the identity element of
 $\mathbf{H}_{1}$
, this does not change the element
$\mathbf{H}_{1}$
, this does not change the element
 $\unicode[STIX]{x1D6FD}\in \mathbf{H}_{n}$
.
$\unicode[STIX]{x1D6FD}\in \mathbf{H}_{n}$
.– Apply the relation (1.2); one of the terms will involve the switched crossing
 $x^{-1}$
, and in the other term
$x^{-1}$
, and in the other term
 $k_{1}$
will have grown to
$k_{1}$
will have grown to
 $k_{2}$
, which now has the potential to absorb some crossings.
$k_{2}$
, which now has the potential to absorb some crossings.– Repeat. That is, assume that
 $\unicode[STIX]{x1D6FD}$
is a braid with a
$\unicode[STIX]{x1D6FD}$
is a braid with a
 $k_{\ell }$
inserted somewhere. After manipulating the diagram, if necessary, arrange the picture so that (1.2) can be applied. In one of the resulting terms, some crossings will be switched, which in good situations will simplify
$k_{\ell }$
inserted somewhere. After manipulating the diagram, if necessary, arrange the picture so that (1.2) can be applied. In one of the resulting terms, some crossings will be switched, which in good situations will simplify
 $\unicode[STIX]{x1D6FD}$
. In the other term,
$\unicode[STIX]{x1D6FD}$
. In the other term,
 $k_{\ell }$
grows in size and can now absorb more crossings, also resulting in a simpler diagram.
$k_{\ell }$
grows in size and can now absorb more crossings, also resulting in a simpler diagram.
If one is lucky, this process can be repeated until the trace
![]() $\operatorname{Tr}$
of the resulting terms is trivial to compute. Torus links seem especially well adapted to the application of this trick.
$\operatorname{Tr}$
of the resulting terms is trivial to compute. Torus links seem especially well adapted to the application of this trick.
Example 1.1. Let
![]() $x=\unicode[STIX]{x1D70E}_{1}\in \mathbf{H}_{2}$
denote the crossing. The trefoil is the
$x=\unicode[STIX]{x1D70E}_{1}\in \mathbf{H}_{2}$
denote the crossing. The trefoil is the
![]() $(2,3)$
torus knot, and can be presented as the closure of
$(2,3)$
torus knot, and can be presented as the closure of
![]() $x^{3}$
. Equation (1.2) says that
$x^{3}$
. Equation (1.2) says that
![]() $x=-Qk_{2}+Q^{2}x^{-1}$
. Multiplying by
$x=-Qk_{2}+Q^{2}x^{-1}$
. Multiplying by
![]() $x$
gives
$x$
gives
Multiplying by
![]() $x$
again gives
$x$
again gives
The trace of
![]() $k_{2}$
is easy to compute, and the trace of
$k_{2}$
is easy to compute, and the trace of
![]() $x$
is the Homfly polynomial of the unknot, up to normalization. Thus, the trace of
$x$
is the Homfly polynomial of the unknot, up to normalization. Thus, the trace of
![]() $x^{3}$
is expressed in terms of known quantities. We can continue in this manner, obtaining
$x^{3}$
is expressed in terms of known quantities. We can continue in this manner, obtaining
and
from which the Homfly polynomials of the
![]() $(2,m)$
torus links are readily computed.
$(2,m)$
torus links are readily computed.
1.3 Our method, categorified
In this paper we categorify the method outlined in the previous section. As alluded to earlier in this introduction, the element
![]() $k_{n}\in \mathbf{H}_{n}$
gets replaced by a finite complex
$k_{n}\in \mathbf{H}_{n}$
gets replaced by a finite complex
![]() $K_{n}$
of Soergel bimodules, and the relations (1.1) and (1.2) become exact triangles. More precisely, there is a chain map constructed in [Reference HogancampHog18] from
$K_{n}$
of Soergel bimodules, and the relations (1.1) and (1.2) become exact triangles. More precisely, there is a chain map constructed in [Reference HogancampHog18] from
![]() $Q^{2}K_{n}\rightarrow K_{n}F(y_{n+1})$
, and
$Q^{2}K_{n}\rightarrow K_{n}F(y_{n+1})$
, and
![]() $K_{n+1}$
is defined to be the mapping cone on this map. The fact that
$K_{n+1}$
is defined to be the mapping cone on this map. The fact that
![]() $k_{n}$
absorbs crossings becomes the fact that
$k_{n}$
absorbs crossings becomes the fact that
![]() $K_{n}F(\unicode[STIX]{x1D70E}_{i})\simeq TQ^{-1}K_{n}\simeq F(\unicode[STIX]{x1D70E}_{i})K_{n}$
. Here and throughout we use
$K_{n}F(\unicode[STIX]{x1D70E}_{i})\simeq TQ^{-1}K_{n}\simeq F(\unicode[STIX]{x1D70E}_{i})K_{n}$
. Here and throughout we use
![]() $T$
and
$T$
and
![]() $Q$
to denote the functors which increase homological degree and bimodule degree respectively. We have, for instance, an equivalence
$Q$
to denote the functors which increase homological degree and bimodule degree respectively. We have, for instance, an equivalence

where the notation
![]() $A\simeq (B\rightarrow C)$
means that there is an exact triangle
$A\simeq (B\rightarrow C)$
means that there is an exact triangle
The distinguished triangle (1.3) will be essentially the only weapon we need to attack our computations. Suppose
![]() $F(\unicode[STIX]{x1D6FD})$
is a Rouquier complex that we would like to study. Iterated application of the above exact triangle results in a certain kind of filtered complex (a convolution of a twisted complex; see below) which is homotopy equivalent to
$F(\unicode[STIX]{x1D6FD})$
is a Rouquier complex that we would like to study. Iterated application of the above exact triangle results in a certain kind of filtered complex (a convolution of a twisted complex; see below) which is homotopy equivalent to
![]() $F(\unicode[STIX]{x1D6FD})$
, and whose subquotients are tensor products of Rouquier complexes and some
$F(\unicode[STIX]{x1D6FD})$
, and whose subquotients are tensor products of Rouquier complexes and some
![]() $K_{\ell }$
. In favorable situations these have Hochschild cohomologies which are easy to compute. There then arises the problem of recovering the homology of the total complex from the homology of its constituents. For certain computations, we will see that this very serious complication is nullified by an equally serious miracle: the miracle of parity.
$K_{\ell }$
. In favorable situations these have Hochschild cohomologies which are easy to compute. There then arises the problem of recovering the homology of the total complex from the homology of its constituents. For certain computations, we will see that this very serious complication is nullified by an equally serious miracle: the miracle of parity.
We first explain what sorts of filtered complexes we will use. Suppose
![]() $A_{i}$
(
$A_{i}$
(
![]() $i\in I$
) is a family of complexes, indexed by a finite partially ordered set
$i\in I$
) is a family of complexes, indexed by a finite partially ordered set
![]() $I$
. Suppose
$I$
. Suppose
![]() $d_{ij}:A_{j}\rightarrow A_{i}$
are a collection of linear maps such that:
$d_{ij}:A_{j}\rightarrow A_{i}$
are a collection of linear maps such that:
–
 $d_{ij}$
increases homological degree by 1;
$d_{ij}$
increases homological degree by 1;–
 $d_{ii}$
is the given differential on
$d_{ii}$
is the given differential on
 $A_{i}$
;
$A_{i}$
;–
 $d_{ij}=0$
unless
$d_{ij}=0$
unless
 $i\geqslant j$
;
$i\geqslant j$
;– the total differential
 $d_{\text{tot}}:=\sum _{i\geqslant j}d_{ij}$
satisfies
$d_{\text{tot}}:=\sum _{i\geqslant j}d_{ij}$
satisfies
 $d_{\text{tot}}^{2}=0$
.
$d_{\text{tot}}^{2}=0$
.
Then
![]() $C:=(\bigoplus _{i\in I}A_{i},d_{\text{tot}})$
is a chain complex, which we call a convolution of the
$C:=(\bigoplus _{i\in I}A_{i},d_{\text{tot}})$
is a chain complex, which we call a convolution of the
![]() $A_{i}$
. More precisely, this is the convolution of a one-sided twisted complex; see [Reference Bondal and KapranovBK90] for more details on this construction in homological algebra. We will also say that
$A_{i}$
. More precisely, this is the convolution of a one-sided twisted complex; see [Reference Bondal and KapranovBK90] for more details on this construction in homological algebra. We will also say that
![]() $C=\bigoplus _{i}A_{i}$
with twisted differential, to indicate that the differential is not merely the sum of the differentials on the
$C=\bigoplus _{i}A_{i}$
with twisted differential, to indicate that the differential is not merely the sum of the differentials on the
![]() $A_{i}$
. The differential on this complex may be quite complicated, possibly sending terms in homological degree
$A_{i}$
. The differential on this complex may be quite complicated, possibly sending terms in homological degree
![]() $m$
inside
$m$
inside
![]() $A_{j}$
to terms in homological degree
$A_{j}$
to terms in homological degree
![]() $m+1$
inside many different
$m+1$
inside many different
![]() $A_{i}$
, but it does respect the order on
$A_{i}$
, but it does respect the order on
![]() $I$
. Thus, convolutions can also be thought of as certain kinds of filtered complexes, whose subquotients are the
$I$
. Thus, convolutions can also be thought of as certain kinds of filtered complexes, whose subquotients are the
![]() $A_{i}$
.
$A_{i}$
.
Note that any exact triangle
gives rise to an equivalence
![]() $C\simeq (A_{1}\oplus A_{2})$
with twisted differential. Iterated mapping cones can be regarded as convolutions in a similar way.
$C\simeq (A_{1}\oplus A_{2})$
with twisted differential. Iterated mapping cones can be regarded as convolutions in a similar way.
Our main application is to the Rouquier complex
![]() $\text{FT}_{n}$
associated to the full twist braids. In § 3 we iterate the equivalence (1.3), obtaining a convolution description of
$\text{FT}_{n}$
associated to the full twist braids. In § 3 we iterate the equivalence (1.3), obtaining a convolution description of
![]() $F(y_{n})$
, the Rouquier complex associated to the Young–Jucys–Murphy braid. Using the relation
$F(y_{n})$
, the Rouquier complex associated to the Young–Jucys–Murphy braid. Using the relation
![]() $\text{FT}_{n}=\text{FT}_{n-1}F(y_{n})$
, we then prove the following.
$\text{FT}_{n}=\text{FT}_{n-1}F(y_{n})$
, we then prove the following.
Theorem 1.2. We have
![]() $\text{FT}_{n}\simeq \bigoplus _{v}q^{k}D_{v}$
with twisted differential. The sum is over sequences
$\text{FT}_{n}\simeq \bigoplus _{v}q^{k}D_{v}$
with twisted differential. The sum is over sequences
![]() $v\in \{0,1\}^{n}$
such that
$v\in \{0,1\}^{n}$
such that
![]() $v_{n}=1$
. Here,
$v_{n}=1$
. Here,
![]() $q=Q^{2}$
indicates a grading shift,
$q=Q^{2}$
indicates a grading shift,
![]() $k$
is the number of zeroes in
$k$
is the number of zeroes in
![]() $v$
, and
$v$
, and
![]() $D_{v}$
is described below. The differential respects the anti-lexicographic order on sequences.
$D_{v}$
is described below. The differential respects the anti-lexicographic order on sequences.
In the antilexicographic order we regard
![]() $(\ast ,1)$
as larger than
$(\ast ,1)$
as larger than
![]() $(\ast ,0)$
, where
$(\ast ,0)$
, where
![]() $\ast$
denotes any sequence of zeroes and ones. For each sequence
$\ast$
denotes any sequence of zeroes and ones. For each sequence
![]() $v\in \{0,1\}^{n}$
, which we will call a shuffle, there is a complex which we call
$v\in \{0,1\}^{n}$
, which we will call a shuffle, there is a complex which we call
![]() $D_{v}$
. For example, here is
$D_{v}$
. For example, here is
![]() $D_{10101101}$
, which occurs (up to shift) in the expression of
$D_{10101101}$
, which occurs (up to shift) in the expression of
![]() $\text{FT}_{8}$
:
$\text{FT}_{8}$
:

Inside
![]() $v$
, the zeroes indicate which strands are connected to the full twist
$v$
, the zeroes indicate which strands are connected to the full twist
![]() $\text{FT}_{k}$
, and the ones indicate which are connected to
$\text{FT}_{k}$
, and the ones indicate which are connected to
![]() $K_{\ell }$
, for
$K_{\ell }$
, for
![]() $k+\ell =n$
.
$k+\ell =n$
.
Then, of course, one wants to compute the Hochschild homology of the complexes
![]() $D_{v}$
. Let us be precise. Given a complex
$D_{v}$
. Let us be precise. Given a complex
![]() $F$
of Soergel bimodules, let
$F$
of Soergel bimodules, let
![]() $\operatorname{HH}^{i}(C)$
denote the complex obtained by applying the functor
$\operatorname{HH}^{i}(C)$
denote the complex obtained by applying the functor
![]() $\operatorname{HH}^{i}$
to each bimodule, and let
$\operatorname{HH}^{i}$
to each bimodule, and let
![]() $\operatorname{HH}(C)=\oplus \operatorname{HH}^{i}(C)$
. Let
$\operatorname{HH}(C)=\oplus \operatorname{HH}^{i}(C)$
. Let
![]() $\operatorname{HHH}(C)$
denote the cohomology of the complex
$\operatorname{HHH}(C)$
denote the cohomology of the complex
![]() $\operatorname{HH}(C)$
.
$\operatorname{HH}(C)$
.
Because Hochschild cohomology of a complex
![]() $C$
is unchanged by conjugation
$C$
is unchanged by conjugation
![]() $C\mapsto FCF^{-1}$
for any invertible complex
$C\mapsto FCF^{-1}$
for any invertible complex
![]() $F$
, we can move part of
$F$
, we can move part of
![]() $D_{v}$
from the bottom to the top, yielding the complex
$D_{v}$
from the bottom to the top, yielding the complex
![]() $C_{v}^{\prime }$
:
$C_{v}^{\prime }$
:

Note that
![]() $\text{FT}_{n}=C_{00\cdots 0}^{\prime }$
.
$\text{FT}_{n}=C_{00\cdots 0}^{\prime }$
.
For purely combinatorial reasons, we work instead with a similar complex
![]() $C_{v}$
, which is defined by the same expression as
$C_{v}$
, which is defined by the same expression as
![]() $C_{v}^{\prime }$
, but with
$C_{v}^{\prime }$
, but with
![]() $K_{\ell }$
replaced by its reduced version
$K_{\ell }$
replaced by its reduced version
![]() $\hat{K}_{\ell }$
. Reduced complexes are discussed in § 4.3. The effect this has on Poincaré polynomials is multiplication by a factor of
$\hat{K}_{\ell }$
. Reduced complexes are discussed in § 4.3. The effect this has on Poincaré polynomials is multiplication by a factor of
![]() $(1-Q^{2})$
.
$(1-Q^{2})$
.
Let
![]() $v\cdot w$
denote the concatenation of two shuffles (sequences of zeroes and ones). For any shuffle
$v\cdot w$
denote the concatenation of two shuffles (sequences of zeroes and ones). For any shuffle
![]() $v$
, we can use our distinguished triangle for
$v$
, we can use our distinguished triangle for
![]() $K_{n}$
to prove the following.
$K_{n}$
to prove the following.
Proposition 1.3. We have
![]() $\operatorname{HH}(C_{v\cdot 0})\simeq (\operatorname{HH}(C_{1\cdot v})\rightarrow Q^{2}\operatorname{HH}(C_{0\cdot v}))$
.
$\operatorname{HH}(C_{v\cdot 0})\simeq (\operatorname{HH}(C_{1\cdot v})\rightarrow Q^{2}\operatorname{HH}(C_{0\cdot v}))$
.
Next, we can use some relatively easy arguments involving the complex
![]() $K_{n}$
to prove that
$K_{n}$
to prove that
![]() $\operatorname{HH}(C_{v\cdot 1})$
is just a direct sum of shifted copies of
$\operatorname{HH}(C_{v\cdot 1})$
is just a direct sum of shifted copies of
![]() $\operatorname{HH}(C_{v})$
. For readers familiar with knot theory, this last statement should be thought of as analogous to the Markov move; it allows us to reduce the number of strands by
$\operatorname{HH}(C_{v})$
. For readers familiar with knot theory, this last statement should be thought of as analogous to the Markov move; it allows us to reduce the number of strands by
![]() $1$
. Finally, a simple observation (pertaining to reduced complexes) allows one to replace the computation of
$1$
. Finally, a simple observation (pertaining to reduced complexes) allows one to replace the computation of
![]() $\operatorname{HH}(C_{000\cdots 0})$
with
$\operatorname{HH}(C_{000\cdots 0})$
with
![]() $\operatorname{HH}(C_{100\cdots 0})$
. Combining these three operations, we obtain a recursive convolution description of any
$\operatorname{HH}(C_{100\cdots 0})$
. Combining these three operations, we obtain a recursive convolution description of any
![]() $\operatorname{HH}(C_{v})$
. This is the main result of § 4.5.
$\operatorname{HH}(C_{v})$
. This is the main result of § 4.5.
Let us return to the computation of the Hochschild cohomology of the Rouquier complex for the full twist
![]() $\text{FT}_{n}$
on
$\text{FT}_{n}$
on
![]() $n$
strands.
$n$
strands.
We are interested in the cohomology
![]() $\operatorname{HHH}(C_{v})$
of the complexes
$\operatorname{HHH}(C_{v})$
of the complexes
![]() $\operatorname{HH}(C_{v})$
. However, in general, the cohomology of a convolution of complexes is not the direct sum of the cohomology of the individual complexes; instead, there is a spectral sequence relating the two. Our final argument comes from observing a parity miracle! We prove inductively that
$\operatorname{HH}(C_{v})$
. However, in general, the cohomology of a convolution of complexes is not the direct sum of the cohomology of the individual complexes; instead, there is a spectral sequence relating the two. Our final argument comes from observing a parity miracle! We prove inductively that
![]() $\operatorname{HHH}(C_{v})$
is concentrated in even homological degrees. This forces every spectral sequence in sight to degenerate at the
$\operatorname{HHH}(C_{v})$
is concentrated in even homological degrees. This forces every spectral sequence in sight to degenerate at the
![]() $E_{1}$
page, and implies that our convolution description of
$E_{1}$
page, and implies that our convolution description of
![]() $\operatorname{HH}(C_{v})$
gives a direct sum description of
$\operatorname{HH}(C_{v})$
gives a direct sum description of
![]() $\operatorname{HHH}(C_{v})$
. See Theorem 4.22 and its proof for further discussion of this parity argument.
$\operatorname{HHH}(C_{v})$
. See Theorem 4.22 and its proof for further discussion of this parity argument.
Thus, we have a recursive formula for the triply graded cohomologies
![]() $\operatorname{HHH}(C_{v})$
, and as a special case, a formula for
$\operatorname{HHH}(C_{v})$
, and as a special case, a formula for
![]() $\operatorname{HHH}(\text{FT}_{n})$
. We discuss this formula in the next section.
$\operatorname{HHH}(\text{FT}_{n})$
. We discuss this formula in the next section.
Let us pause to point out one of the subtleties we have ignored above. One can conjugate a complex by a braid and obtain a non-isomorphic complex with the same Hochschild cohomology. We begin to apply this operation freely in § 4. Above, we have stated that
![]() $\operatorname{HH}(C_{v\cdot 0})$
is a convolution of
$\operatorname{HH}(C_{v\cdot 0})$
is a convolution of
![]() $\operatorname{HH}(C_{0\cdot v})$
and
$\operatorname{HH}(C_{0\cdot v})$
and
![]() $\operatorname{HH}(C_{1\cdot v})$
, but the same statement does not hold for the original complexes. Instead, some conjugate of
$\operatorname{HH}(C_{1\cdot v})$
, but the same statement does not hold for the original complexes. Instead, some conjugate of
![]() $C_{v\cdot 0}$
is a convolution of a conjugate of
$C_{v\cdot 0}$
is a convolution of a conjugate of
![]() $C_{0\cdot v}$
and a conjugate of
$C_{0\cdot v}$
and a conjugate of
![]() $C_{1\cdot v}$
(conjugating by different braids for each term). For purposes of Hochschild cohomology, this imprecision is harmless. However, were one to try to actually construct a chain map from
$C_{1\cdot v}$
(conjugating by different braids for each term). For purposes of Hochschild cohomology, this imprecision is harmless. However, were one to try to actually construct a chain map from
![]() $R$
to
$R$
to
![]() $C_{v}$
using this computation of
$C_{v}$
using this computation of
![]() $\operatorname{HHH}^{0}(C_{v})$
, then one would need to keep track of conjugation more carefully, which would be rather difficult.
$\operatorname{HHH}^{0}(C_{v})$
, then one would need to keep track of conjugation more carefully, which would be rather difficult.
On the other hand, the work done in § 3 describes full twist as a genuine convolution of complexes
![]() $D_{v}$
, not complexes up to conjugation. This result is not actually needed or used in the recursive computation of
$D_{v}$
, not complexes up to conjugation. This result is not actually needed or used in the recursive computation of
![]() $\operatorname{HHH}(C_{v})$
which is our main result. We include this auxiliary result because it can be used to construct chain maps from
$\operatorname{HHH}(C_{v})$
which is our main result. We include this auxiliary result because it can be used to construct chain maps from
![]() $R$
to
$R$
to
![]() $\text{FT}_{n}$
. Our main theorem implies that the complexes
$\text{FT}_{n}$
. Our main theorem implies that the complexes
![]() $D_{v}$
satisfy a parity condition, and therefore our convolution description of
$D_{v}$
satisfy a parity condition, and therefore our convolution description of
![]() $\text{FT}_{n}$
induces a direct sum decompositions on Hochschild cohomology. In particular, any chain map (up to homotopy) from
$\text{FT}_{n}$
induces a direct sum decompositions on Hochschild cohomology. In particular, any chain map (up to homotopy) from
![]() $R$
to the complex
$R$
to the complex
![]() $D_{v}$
(an element of
$D_{v}$
(an element of
![]() $\operatorname{HHH}^{0}(D_{v})$
) can be extended uniquely (up to homotopy) to a chain map from
$\operatorname{HHH}^{0}(D_{v})$
) can be extended uniquely (up to homotopy) to a chain map from
![]() $R$
to the entire complex
$R$
to the entire complex
![]() $\text{FT}_{n}$
. We use this fact to construct eigenmaps to the full twist in [Reference Elias and HogancampEH18].
$\text{FT}_{n}$
. We use this fact to construct eigenmaps to the full twist in [Reference Elias and HogancampEH18].
In addition, the convolution description involving
![]() $D_{v}$
from § 3 can be adapted to other torus links, whereas the results § 4 are fundamentally tied to the case of
$D_{v}$
from § 3 can be adapted to other torus links, whereas the results § 4 are fundamentally tied to the case of
![]() $(n,n)$
-torus links.
$(n,n)$
-torus links.
Remark 1.4. Suppose that one were interested in computing the Hochschild cohomologies of
![]() $\text{FT}_{n}^{-1}$
. One can produce a convolution description of
$\text{FT}_{n}^{-1}$
. One can produce a convolution description of
![]() $\text{FT}_{n}^{-1}$
similar to the description of
$\text{FT}_{n}^{-1}$
similar to the description of
![]() $\text{FT}_{n}$
above, but the parity miracle no longer holds! The corresponding spectral sequence is far from degenerate, and consequently there are extremely few (non-nulhomotopic) chain maps from
$\text{FT}_{n}$
above, but the parity miracle no longer holds! The corresponding spectral sequence is far from degenerate, and consequently there are extremely few (non-nulhomotopic) chain maps from
![]() $R$
to
$R$
to
![]() $\text{FT}_{n}^{-1}$
. This lack of symmetry between
$\text{FT}_{n}^{-1}$
. This lack of symmetry between
![]() $\text{FT}_{n}$
and
$\text{FT}_{n}$
and
![]() $\text{FT}_{n}^{-1}$
is an interesting and complicating feature in categorical representation theory.
$\text{FT}_{n}^{-1}$
is an interesting and complicating feature in categorical representation theory.
1.4 The recursive formula
We will find it convenient to use a non-standard choice of variables for our Poincaré series. We let
![]() $t=T^{2}Q^{-2}$
,
$t=T^{2}Q^{-2}$
,
![]() $q=Q^{2}$
, and
$q=Q^{2}$
, and
![]() $a=Q^{-2}A$
, where
$a=Q^{-2}A$
, where
![]() $T$
denotes the usual homological degree,
$T$
denotes the usual homological degree,
![]() $Q$
the bimodule degree (also called internal degree, or quantum degree), and
$Q$
the bimodule degree (also called internal degree, or quantum degree), and
![]() $A$
the Hochschild degree. For instance, the Poincaré series of the polynomial ring
$A$
the Hochschild degree. For instance, the Poincaré series of the polynomial ring
![]() $R=\mathbb{Q}[x_{1},\ldots ,x_{n}]$
is written
$R=\mathbb{Q}[x_{1},\ldots ,x_{n}]$
is written
![]() $1/(1-q)^{n}$
, and the Poincaré series of its Hochschild cohomology is
$1/(1-q)^{n}$
, and the Poincaré series of its Hochschild cohomology is
![]() $(1-q)^{-n}(1+a)^{n}$
. In general, all our Poincaré series will be power series in the variables
$(1-q)^{-n}(1+a)^{n}$
. In general, all our Poincaré series will be power series in the variables
![]() $q$
,
$q$
,
![]() $a$
, and
$a$
, and
![]() $t^{1/2}$
.
$t^{1/2}$
.
Proposition 1.5. There is a unique family of polynomials
![]() $f_{v}(q,a,t)$
, indexed by integers
$f_{v}(q,a,t)$
, indexed by integers
![]() $n\geqslant 0$
and binary sequences
$n\geqslant 0$
and binary sequences
![]() $v\in \{0,1\}^{n}$
, satisfying
$v\in \{0,1\}^{n}$
, satisfying
![]() $f_{\emptyset }=1$
together with
$f_{\emptyset }=1$
together with
The following theorem, together with the fact that the
![]() $f_{v}$
are rational functions in
$f_{v}$
are rational functions in
![]() $q,a,t$
rather than
$q,a,t$
rather than
![]() $q,a,t^{1/2}$
implies that the parity miracle holds.
$q,a,t^{1/2}$
implies that the parity miracle holds.
Theorem 1.6. The Poincaré series of
![]() $\operatorname{HHH}(C_{v})$
is
$\operatorname{HHH}(C_{v})$
is
![]() $f_{v}(q,a,t)$
, where
$f_{v}(q,a,t)$
, where
![]() $C_{v}$
are the complexes from Definition 4.8. In particular, the Hochschild cohomology
$C_{v}$
are the complexes from Definition 4.8. In particular, the Hochschild cohomology
![]() $\operatorname{HHH}(\text{FT})$
is given by
$\operatorname{HHH}(\text{FT})$
is given by
![]() $f_{v}(q,a,t)$
for
$f_{v}(q,a,t)$
for
![]() $v=(00\cdots 0)$
. These homologies are all supported in even homological degrees.
$v=(00\cdots 0)$
. These homologies are all supported in even homological degrees.
These results are restated and proved in § 4.6. The proof of Theorem 1.6 comes from the convolution description of
![]() $\operatorname{HH}(C_{v})$
discussed in the previous section.
$\operatorname{HH}(C_{v})$
discussed in the previous section.
For the reader’s edification, here are the complete power series for
![]() $\operatorname{HHH}(\text{FT}_{n})$
for
$\operatorname{HHH}(\text{FT}_{n})$
for
![]() $n=1,2,3$
:
$n=1,2,3$
:
 $$\begin{eqnarray}\displaystyle & \displaystyle f_{0}(q,a,t)=\frac{1+a}{1-q}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle f_{00}(q,a,t)=\frac{1+a}{(1-q)^{2}}(q+t-qt+a), & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle f_{0}(q,a,t)=\frac{1+a}{1-q}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle f_{00}(q,a,t)=\frac{1+a}{(1-q)^{2}}(q+t-qt+a), & \displaystyle \nonumber\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle f_{000}(q,a,t) & = & \displaystyle \frac{1+a}{(1-q)^{3}} (\,(t^{3}q^{2}+q^{3}t^{2}-2t^{2}q^{2}-2tq^{3}-2qt^{3}+t^{3}+q^{3}+tq^{2}+qt^{2}+tq)\nonumber\\ \displaystyle & & \displaystyle +\,(t^{2}q^{2}-2tq^{2}-2qt^{2}+t^{2}+q^{2}+tq+t+q)a+a^{2} ).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle f_{000}(q,a,t) & = & \displaystyle \frac{1+a}{(1-q)^{3}} (\,(t^{3}q^{2}+q^{3}t^{2}-2t^{2}q^{2}-2tq^{3}-2qt^{3}+t^{3}+q^{3}+tq^{2}+qt^{2}+tq)\nonumber\\ \displaystyle & & \displaystyle +\,(t^{2}q^{2}-2tq^{2}-2qt^{2}+t^{2}+q^{2}+tq+t+q)a+a^{2} ).\nonumber\end{eqnarray}$$
The recursion can be unraveled into the equivalent recursion below, which is more complicated but faster to implement.
Definition 1.7. For each integer
![]() $n\geqslant 0$
, we let
$n\geqslant 0$
, we let
![]() $[n]:=\{1,\ldots ,n\}$
. We identify subsets
$[n]:=\{1,\ldots ,n\}$
. We identify subsets
![]() $v\subset [n]$
with binary sequences
$v\subset [n]$
with binary sequences
![]() $v\in \{0,1\}^{n}$
. For each such
$v\in \{0,1\}^{n}$
. For each such
![]() $v\subset [n]$
, we define a rational function
$v\subset [n]$
, we define a rational function
![]() $f_{v}(q,a,t)$
by
$f_{v}(q,a,t)$
by
![]() $f_{\emptyset }=1$
, together with the following rules:
$f_{\emptyset }=1$
, together with the following rules:
The equivalence between these recursions is proven in § 5, which contains various such numerological considerations. For example, one can show that both rule (1.5a) and (1.5b) are actually just consequences of rule (1.5c) when applied verbatim, although this is not obvious.
Remark 1.8. In our original version of this manuscript, our convolution argument categorified the recursive formula of Definition 1.7 rather than Proposition 1.5, thus proving that this complicated recursion does compute
![]() $\operatorname{HHH}(C_{v})$
. Then we discovered the simpler recursion of Proposition 1.5, drastically simplifying our arguments.
$\operatorname{HHH}(C_{v})$
. Then we discovered the simpler recursion of Proposition 1.5, drastically simplifying our arguments.
Note that the contribution to higher Hochschild gradings comes only from a factor in rule (1.5b) and the factor
![]() ${\mathcal{P}}_{v,w}(a,t)$
in rule (1.5c); both of these become explicit monomials in
${\mathcal{P}}_{v,w}(a,t)$
in rule (1.5c); both of these become explicit monomials in
![]() $t$
upon setting
$t$
upon setting
![]() $a=0$
. Thus, to understand the zeroth Hochschild degree coefficient, i.e. the polynomial
$a=0$
. Thus, to understand the zeroth Hochschild degree coefficient, i.e. the polynomial
![]() $f_{v}(q,0,t)$
, one use a simplified recursion relation. Using this, we prove the following closed formula for the power series
$f_{v}(q,0,t)$
, one use a simplified recursion relation. Using this, we prove the following closed formula for the power series
![]() $f_{00\cdots 0}(q,0,t)$
, also known as the Poincaré series of the zeroth Hochschild cohomology
$f_{00\cdots 0}(q,0,t)$
, also known as the Poincaré series of the zeroth Hochschild cohomology
![]() $\operatorname{HHH}^{0}(\text{FT})$
.
$\operatorname{HHH}^{0}(\text{FT})$
.
Theorem 1.9. The Hochschild degree zero part of the unreduced triply graded homology of
![]() $(n,n)$
torus links has Poincaré series equal to
$(n,n)$
torus links has Poincaré series equal to
where the sum is over functions
![]() $\unicode[STIX]{x1D70E}:\{1,\ldots ,n\}\rightarrow \mathbb{Z}_{{\geqslant}0}$
, and the integers
$\unicode[STIX]{x1D70E}:\{1,\ldots ,n\}\rightarrow \mathbb{Z}_{{\geqslant}0}$
, and the integers
![]() $a(\unicode[STIX]{x1D70E})$
,
$a(\unicode[STIX]{x1D70E})$
,
![]() $b(\unicode[STIX]{x1D70E})$
,
$b(\unicode[STIX]{x1D70E})$
,
![]() $c(\unicode[STIX]{x1D70E})$
are defined by:
$c(\unicode[STIX]{x1D70E})$
are defined by:
(i)
 $a(\unicode[STIX]{x1D70E})=\sum _{k\geqslant 0}\binom{|\unicode[STIX]{x1D70E}^{-1}(k)|}{2}$
;
$a(\unicode[STIX]{x1D70E})=\sum _{k\geqslant 0}\binom{|\unicode[STIX]{x1D70E}^{-1}(k)|}{2}$
;(ii)
 $b(\unicode[STIX]{x1D70E})$
is the number of pairs
$b(\unicode[STIX]{x1D70E})$
is the number of pairs
 $(i,j)\in \{1,\ldots ,n\}$
such that
$(i,j)\in \{1,\ldots ,n\}$
such that
 $i<j$
and
$i<j$
and
 $\unicode[STIX]{x1D70E}(j)=\unicode[STIX]{x1D70E}(i)+1$
;
$\unicode[STIX]{x1D70E}(j)=\unicode[STIX]{x1D70E}(i)+1$
;(iii)
 $c(\unicode[STIX]{x1D70E})=\sum _{i=1}^{n}\unicode[STIX]{x1D70E}(i)$
.
$c(\unicode[STIX]{x1D70E})=\sum _{i=1}^{n}\unicode[STIX]{x1D70E}(i)$
.
Example 1.10. In case
![]() $n=1$
we have
$n=1$
we have
![]() $F_{1}(q,t)=1+q+q^{2}+\cdots =1/(1-q)$
.
$F_{1}(q,t)=1+q+q^{2}+\cdots =1/(1-q)$
.
Example 1.11. In case
![]() $n=2$
,
$n=2$
,
![]() $F_{2}(q,t)$
is the sum of monomials appearing in the following diagram.
$F_{2}(q,t)$
is the sum of monomials appearing in the following diagram.

After rearranging, this becomes
![]() $F_{2}(q,t)=t/(1-q)+q/(1-q)^{2}$
, agreeing with
$F_{2}(q,t)=t/(1-q)+q/(1-q)^{2}$
, agreeing with
![]() $f_{00}(q,0,t)$
which was computed above.
$f_{00}(q,0,t)$
which was computed above.
The proof of this closed formula from Theorem 1.6 is a simple combinatorial argument, and is found in § 5. Unfortunately, the polynomials
![]() ${\mathcal{P}}_{v,w}(q,a,t)$
are sufficiently complicated so that we have been unable to produce a closed formula for the higher Hochschild degrees along these lines.
${\mathcal{P}}_{v,w}(q,a,t)$
are sufficiently complicated so that we have been unable to produce a closed formula for the higher Hochschild degrees along these lines.
We conclude with a recursion for the normalized polynomials
![]() $\widetilde{f}_{v}(q,a,t):=(1-q)^{k}f_{v}(q,a,t)$
, where
$\widetilde{f}_{v}(q,a,t):=(1-q)^{k}f_{v}(q,a,t)$
, where
![]() $k$
is the number of zeroes in
$k$
is the number of zeroes in
![]() $v$
. The recursion of Proposition 1.5 immediately gives rise to
$v$
. The recursion of Proposition 1.5 immediately gives rise to
Remark 1.12. A clumsy card dealer has a deck of
![]() $n$
cards, some face up and some face down. When the dealer encounters a face down card, he deals it. When the dealer encounters a face up card, he puts it back on the bottom of the deck, sometimes remembering to flip it face down. Eventually, the deck is dealt (with probability
$n$
cards, some face up and some face down. When the dealer encounters a face down card, he deals it. When the dealer encounters a face up card, he puts it back on the bottom of the deck, sometimes remembering to flip it face down. Eventually, the deck is dealt (with probability
![]() $1$
). Every time the dealer deals a card, you, the player, choose whether to receive 1 silver coin, or a number of dollars equal to the number of face-up cards in the deck. Then the coefficient of
$1$
). Every time the dealer deals a card, you, the player, choose whether to receive 1 silver coin, or a number of dollars equal to the number of face-up cards in the deck. Then the coefficient of
![]() $a^{k}t^{\ell }$
in
$a^{k}t^{\ell }$
in
![]() $\widetilde{f}_{v}(q,a,t)$
is the number of ways of ending up with
$\widetilde{f}_{v}(q,a,t)$
is the number of ways of ending up with
![]() $k$
silver coins and
$k$
silver coins and
![]() $\ell$
dollars, weighted by their probability of occurring. In particular, the coefficient on
$\ell$
dollars, weighted by their probability of occurring. In particular, the coefficient on
![]() $a^{n}$
is 1.
$a^{n}$
is 1.
Computer experiments suggest the following.
Conjecture 1.13. We have the following symmetry:
![]() $\widetilde{f}_{00\cdots 0}(q,a,t)=\widetilde{f}_{00\cdots 0}(t,a,q)$
.
$\widetilde{f}_{00\cdots 0}(q,a,t)=\widetilde{f}_{00\cdots 0}(t,a,q)$
.
This symmetry would follow from a formula of Gorsky, Negut, and Rasmussen, which we discuss now.
1.5 Flag Hilbert schemes and a magic formula
According to the remarkable work of Gorsky, Negut, and Rasmussen [Reference Gorsky and NeguțGN15, Reference Gorsky, Neguț and RasmussenGNR16], triply graded link homology can be extracted from flag Hilbert schemes.Footnote
5
Roughly, the picture looks like this: there is a space
![]() $\operatorname{FHilb}_{n}(\mathbb{C}^{2})$
, which parametrizes flags of ideals
$\operatorname{FHilb}_{n}(\mathbb{C}^{2})$
, which parametrizes flags of ideals
![]() $I_{1}\subset \cdots \subset I_{n}\in \mathbb{C}[x,y]$
such that
$I_{1}\subset \cdots \subset I_{n}\in \mathbb{C}[x,y]$
such that
![]() $I_{i}/I_{i-1}$
is 1-dimensional. Associated to each
$I_{i}/I_{i-1}$
is 1-dimensional. Associated to each
![]() $n$
-strand braid, Gorsky, Negut, and Rasmussen conjecture that there exists a line bundle (or sheaf, or complex of sheaves) on
$n$
-strand braid, Gorsky, Negut, and Rasmussen conjecture that there exists a line bundle (or sheaf, or complex of sheaves) on
![]() $\operatorname{FHilb}_{n}(\mathbb{C}^{2})$
whose space of global sections recovers
$\operatorname{FHilb}_{n}(\mathbb{C}^{2})$
whose space of global sections recovers
![]() $\operatorname{HHH}^{0}(F(\unicode[STIX]{x1D6FD}))$
. The sheaves are meant to be equivariant with respect to an obvious action of
$\operatorname{HHH}^{0}(F(\unicode[STIX]{x1D6FD}))$
. The sheaves are meant to be equivariant with respect to an obvious action of
![]() $\mathbb{C}^{\ast }\times \mathbb{C}^{\ast }$
, and the variables
$\mathbb{C}^{\ast }\times \mathbb{C}^{\ast }$
, and the variables
![]() $q,t$
correspond to weights with respect to this action. The variable
$q,t$
correspond to weights with respect to this action. The variable
![]() $a$
can also be accounted for with more work. A combination of Atiyah–Bott localization and careful analysis of the flag Hilbert scheme near its torus fixed points yields a remarkably simple combinatorial formula which, given their conjecture, will describe the knot homology of positive torus links. Now we state the formulas, and we will make no further mention of the geometric foundations which motivate them.
$a$
can also be accounted for with more work. A combination of Atiyah–Bott localization and careful analysis of the flag Hilbert scheme near its torus fixed points yields a remarkably simple combinatorial formula which, given their conjecture, will describe the knot homology of positive torus links. Now we state the formulas, and we will make no further mention of the geometric foundations which motivate them.
Let
![]() $\unicode[STIX]{x1D706}$
be a Young diagram, drawn in the ‘English style’ as in the following.
$\unicode[STIX]{x1D706}$
be a Young diagram, drawn in the ‘English style’ as in the following.
Suppose a box
![]() $c$
is in the
$c$
is in the
![]() $i$
th column and
$i$
th column and
![]() $j$
th row. Here columns and rows are counted left-to-right and top-to-bottom, starting at zero. To such a box we associated the monomial
$j$
th row. Here columns and rows are counted left-to-right and top-to-bottom, starting at zero. To such a box we associated the monomial
![]() $z_{c}=t^{i}q^{j}$
.Footnote
6
To a Young diagram, we let
$z_{c}=t^{i}q^{j}$
.Footnote
6
To a Young diagram, we let
![]() $z_{\unicode[STIX]{x1D706}}=z_{\unicode[STIX]{x1D706}}(q,t)$
be the product of
$z_{\unicode[STIX]{x1D706}}=z_{\unicode[STIX]{x1D706}}(q,t)$
be the product of
![]() $z_{c}$
as
$z_{c}$
as
![]() $c$
ranges over all the boxes of
$c$
ranges over all the boxes of
![]() $\unicode[STIX]{x1D706}$
. Note that
$\unicode[STIX]{x1D706}$
. Note that
![]() $z_{\unicode[STIX]{x1D706}}(q,t)=z_{\unicode[STIX]{x1D706}^{t}}(t,q)$
, where
$z_{\unicode[STIX]{x1D706}}(q,t)=z_{\unicode[STIX]{x1D706}^{t}}(t,q)$
, where
![]() $\unicode[STIX]{x1D706}^{t}$
is the transposed partition.
$\unicode[STIX]{x1D706}^{t}$
is the transposed partition.
A box in
![]() $\unicode[STIX]{x1D706}$
is removable if
$\unicode[STIX]{x1D706}$
is removable if
![]() $\unicode[STIX]{x1D706}\smallsetminus c$
is a Young diagram. Now we discuss boxes, i.e. coordinates
$\unicode[STIX]{x1D706}\smallsetminus c$
is a Young diagram. Now we discuss boxes, i.e. coordinates
![]() $(i,j)$
, which need not be in the given Young diagram
$(i,j)$
, which need not be in the given Young diagram
![]() $\unicode[STIX]{x1D706}$
. We call
$\unicode[STIX]{x1D706}$
. We call
![]() $c\notin \unicode[STIX]{x1D706}$
an outer corner of
$c\notin \unicode[STIX]{x1D706}$
an outer corner of
![]() $\unicode[STIX]{x1D706}$
if the top left corner of
$\unicode[STIX]{x1D706}$
if the top left corner of
![]() $c$
coincides with the bottom right corner of a removable box in
$c$
coincides with the bottom right corner of a removable box in
![]() $\unicode[STIX]{x1D706}$
. We call a box
$\unicode[STIX]{x1D706}$
. We call a box
![]() $c\notin \unicode[STIX]{x1D706}$
an inner corner of
$c\notin \unicode[STIX]{x1D706}$
an inner corner of
![]() $\unicode[STIX]{x1D706}$
if
$\unicode[STIX]{x1D706}$
if
![]() $\unicode[STIX]{x1D706}\cup c$
is a Young diagram. Pictorially, we have the following.
$\unicode[STIX]{x1D706}\cup c$
is a Young diagram. Pictorially, we have the following.

The inner corners are darkly shaded, and the outer corners are lightly shaded. Let
![]() $\operatorname{In}(\unicode[STIX]{x1D706})$
and
$\operatorname{In}(\unicode[STIX]{x1D706})$
and
![]() $\operatorname{Out}(\unicode[STIX]{x1D706})$
denote the sets of inner and outer corners of
$\operatorname{Out}(\unicode[STIX]{x1D706})$
denote the sets of inner and outer corners of
![]() $\unicode[STIX]{x1D706}$
. If
$\unicode[STIX]{x1D706}$
. If
![]() $c\in \operatorname{In}(\unicode[STIX]{x1D706})$
, then we define
$c\in \operatorname{In}(\unicode[STIX]{x1D706})$
, then we define
It is easy to observe that
![]() $f_{\unicode[STIX]{x1D706},c}(q,t)=f_{\unicode[STIX]{x1D706}^{t},c^{t}}(t,q)$
, where
$f_{\unicode[STIX]{x1D706},c}(q,t)=f_{\unicode[STIX]{x1D706}^{t},c^{t}}(t,q)$
, where
![]() $c^{t}$
is the corresponding transposed inner corner of
$c^{t}$
is the corresponding transposed inner corner of
![]() $\unicode[STIX]{x1D706}^{t}$
.
$\unicode[STIX]{x1D706}^{t}$
.
Remark 1.14. Let
![]() $\{x_{1},\ldots ,x_{n}\}$
and
$\{x_{1},\ldots ,x_{n}\}$
and
![]() $\{y_{1},\ldots ,y_{n+1}\}$
be two families of abstract variables. It is not a hard exercise to show that
$\{y_{1},\ldots ,y_{n+1}\}$
be two families of abstract variables. It is not a hard exercise to show that
Applying this general formula to the definition above, one obtains
a fact which has nothing to do with the combinatorics of partitions.
A standard tableau
![]() $T$
can be thought of as a sequence of Young diagrams
$T$
can be thought of as a sequence of Young diagrams
![]() $T=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})$
such that
$T=(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{n})$
such that
![]() $\unicode[STIX]{x1D706}_{1}=\Box$
and
$\unicode[STIX]{x1D706}_{1}=\Box$
and
![]() $\unicode[STIX]{x1D706}_{i+1}\smallsetminus \unicode[STIX]{x1D706}_{i}=\Box$
. Let
$\unicode[STIX]{x1D706}_{i+1}\smallsetminus \unicode[STIX]{x1D706}_{i}=\Box$
. Let
![]() $\operatorname{Sh}(T)=\unicode[STIX]{x1D706}_{n}$
denote the shape of
$\operatorname{Sh}(T)=\unicode[STIX]{x1D706}_{n}$
denote the shape of
![]() $T$
. To each tableau we set
$T$
. To each tableau we set
where
![]() $c_{i}\in \operatorname{In}(\unicode[STIX]{x1D706}_{i})$
is the box such that
$c_{i}\in \operatorname{In}(\unicode[STIX]{x1D706}_{i})$
is the box such that
![]() $\unicode[STIX]{x1D706}_{i+1}=\unicode[STIX]{x1D706}_{i}\cup c_{i}$
. Once more,
$\unicode[STIX]{x1D706}_{i+1}=\unicode[STIX]{x1D706}_{i}\cup c_{i}$
. Once more,
![]() $f_{T}(q,t)=f_{T^{t}}(t,q)$
, where
$f_{T}(q,t)=f_{T^{t}}(t,q)$
, where
![]() $T^{t}$
is the transposed tableau.
$T^{t}$
is the transposed tableau.
Finally, associated to a Young diagram
![]() $\unicode[STIX]{x1D706}$
, let
$\unicode[STIX]{x1D706}$
, let
![]() $g_{\unicode[STIX]{x1D706}}(q,a,t)$
denote the product over all boxes
$g_{\unicode[STIX]{x1D706}}(q,a,t)$
denote the product over all boxes
![]() $c\in \unicode[STIX]{x1D706}$
of
$c\in \unicode[STIX]{x1D706}$
of
![]() $(1+az_{c}^{-1})$
.
$(1+az_{c}^{-1})$
.
Conjecture 1.15 (Magic formula).
Let
![]() $F_{n,r}(q,a,t)$
denote the Poincaré series of
$F_{n,r}(q,a,t)$
denote the Poincaré series of
![]() $\operatorname{HHH}^{0}(\text{FT}_{n}^{\otimes r})$
. Then
$\operatorname{HHH}^{0}(\text{FT}_{n}^{\otimes r})$
. Then
a sum over all tableaux with
![]() $n$
boxes. In particular, the right-hand side is symmetric under replacing
$n$
boxes. In particular, the right-hand side is symmetric under replacing
![]() $q$
with
$q$
with
![]() $t$
, and thus so is the left-hand side. We remind the reader that
$t$
, and thus so is the left-hand side. We remind the reader that
![]() $z_{\operatorname{Sh}(T)}$
and
$z_{\operatorname{Sh}(T)}$
and
![]() $f_{T}$
are functions of
$f_{T}$
are functions of
![]() $q$
and
$q$
and
![]() $t$
, while
$t$
, while
![]() $g_{\operatorname{Sh}(T)}$
is a function of
$g_{\operatorname{Sh}(T)}$
is a function of
![]() $q$
,
$q$
,
![]() $a$
, and
$a$
, and
![]() $t$
.
$t$
.
When
![]() $r=0$
, the formula yields
$r=0$
, the formula yields
![]() $1=\sum _{T}g_{\operatorname{Sh}(\unicode[STIX]{x1D706})}(q,a,t)f_{T}(q,t)$
, whose
$1=\sum _{T}g_{\operatorname{Sh}(\unicode[STIX]{x1D706})}(q,a,t)f_{T}(q,t)$
, whose
![]() $a$
-degree zero part follows from (1.7). We have verified the magic formula for
$a$
-degree zero part follows from (1.7). We have verified the magic formula for
![]() $r=1$
and for
$r=1$
and for
![]() $1\leqslant n\leqslant 4$
, using a Mathematica notebook which is available upon request.
$1\leqslant n\leqslant 4$
, using a Mathematica notebook which is available upon request.
According to the magic formula, the
![]() $a$
-degree
$a$
-degree
![]() $n$
part of the Poincaré series of the
$n$
part of the Poincaré series of the
![]() $(n,n)$
torus link is supposed to be
$(n,n)$
torus link is supposed to be
![]() $(1-q)^{-n}$
times
$(1-q)^{-n}$
times
The factor
![]() $z_{\operatorname{Sh}(T)}^{-1}$
comes from taking the
$z_{\operatorname{Sh}(T)}^{-1}$
comes from taking the
![]() $a$
-degree
$a$
-degree
![]() $n$
part of
$n$
part of
![]() $g_{\operatorname{Sh}(T)}(q,a,t)$
. This instance of the magic formula can be proved directly from our recursive description of this series (see Remark 1.12).
$g_{\operatorname{Sh}(T)}(q,a,t)$
. This instance of the magic formula can be proved directly from our recursive description of this series (see Remark 1.12).
Another consequence of the magic formula concerns the sub-maximal part of the Poincaré series of full twists.
Conjecture 1.16. The
![]() $a$
-degree
$a$
-degree
![]() $n-1$
part of the Poincaré series of
$n-1$
part of the Poincaré series of
![]() $\operatorname{HHH}(\text{FT}_{n})$
is a geometric progression
$\operatorname{HHH}(\text{FT}_{n})$
is a geometric progression
We expect that this is not difficult to prove, but we do not do so here. We have verified this conjecture up to
![]() $n=7$
using computer calculations.
$n=7$
using computer calculations.
In the algorithm to compute
![]() $f_{00\cdots 0}(q,a,t)$
using (1.5c), one travels from the zero sequence
$f_{00\cdots 0}(q,a,t)$
using (1.5c), one travels from the zero sequence
![]() $(00\cdots 0)\in \{0,1\}^{n}$
to the sequence
$(00\cdots 0)\in \{0,1\}^{n}$
to the sequence
![]() $\emptyset \in \{0,1\}^{0}$
by repeatedly choosing subsets (i.e. smaller sequences in
$\emptyset \in \{0,1\}^{0}$
by repeatedly choosing subsets (i.e. smaller sequences in
![]() $\{0,1\}^{k}$
) of the previous set of zeroes. Our instinct indicates that such a sequence of sequences can be thought of as encoding the entries in a Robinson–Shensted row-bumping algorithm, and can thus be assigned a tableau. The contribution to
$\{0,1\}^{k}$
) of the previous set of zeroes. Our instinct indicates that such a sequence of sequences can be thought of as encoding the entries in a Robinson–Shensted row-bumping algorithm, and can thus be assigned a tableau. The contribution to
![]() $f_{00\cdots 0}(q,a,t)$
coming from this sequence of sequences and the contribution to
$f_{00\cdots 0}(q,a,t)$
coming from this sequence of sequences and the contribution to
![]() $\sum _{T}z_{\operatorname{Sh}(T)}g_{\operatorname{Sh}(T)}f_{T}$
coming from the tableau
$\sum _{T}z_{\operatorname{Sh}(T)}g_{\operatorname{Sh}(T)}f_{T}$
coming from the tableau
![]() $T$
have many superficial similarities, but no direct relation has yet been found.
$T$
have many superficial similarities, but no direct relation has yet been found.
1.6 Organization of the paper
In § 2 we provide some background. We describe various elements of the braid group, including full twists, Young–Jucys–Murphy elements, shuffle braids, and shuffle twists. In § 2.4 we briefly recall Soergel’s categorification of the Hecke algebra and Rouquier’s categorification of the braid group. In § 2.5 we define convolutions of complexes, and give the crucial argument involving the degeneration of a spectral sequence thanks to parity considerations. In § 2.6 we recall the main result of [Reference HogancampHog18], a complex which categorifies a renormalized Jones–Wenzl projector, and state its properties. The specifics of the Soergel–Rouquier construction need not concern the reader, as all we will use in this paper are facts about the braid group and the results of [Reference HogancampHog18].
In § 3 we find a convolution description of the full twist
![]() $\text{FT}_{n}$
in terms of certain complexes
$\text{FT}_{n}$
in terms of certain complexes
![]() $D_{v}$
associated to
$D_{v}$
associated to
![]() $v\in \{0,1\}^{n}$
.
$v\in \{0,1\}^{n}$
.
In § 4 we switch to a Hochschild frame of mind. Since Hochschild cohomology of a complex is invariant under conjugation by Rouquier complexes of braids, we will allow ourselves to freely conjugate complexes. In § 4.2 we discuss another result of [Reference HogancampHog18] which is an analog of the Markov move on braid closures: a relationship between the Hochschild homologies of the Jones–Wenzl projector on
![]() $n$
strands and the projector on
$n$
strands and the projector on
![]() $n-1$
strands. We also discuss reduced complexes in § 4.3, finally describing complexes
$n-1$
strands. We also discuss reduced complexes in § 4.3, finally describing complexes
![]() $C_{v}$
in § 4.4 which may be thought of as reduced versions of conjugates of
$C_{v}$
in § 4.4 which may be thought of as reduced versions of conjugates of
![]() $D_{v}$
. Finally, in §§ 4.5 and 4.6 we state and prove the main result, which is a convolution description of the Hochschild cohomology of
$D_{v}$
. Finally, in §§ 4.5 and 4.6 we state and prove the main result, which is a convolution description of the Hochschild cohomology of
![]() $C_{v}$
in terms of the Hochschild cohomologies of smaller
$C_{v}$
in terms of the Hochschild cohomologies of smaller
![]() $C_{w}$
, which is an analogue of the recursion of Proposition 1.5.
$C_{w}$
, which is an analogue of the recursion of Proposition 1.5.
In § 5 we prove some combinatorial results which justify Theorem 1.9, our closed form solution for
![]() $\operatorname{HHH}^{0}(\text{FT})$
, and show that the two recursive formulas agree.
$\operatorname{HHH}^{0}(\text{FT})$
, and show that the two recursive formulas agree.
In the appendix, we include without proof some computations for other
![]() $(n,m)$
torus links. These were obtained by techniques entirely analogous to the computation for
$(n,m)$
torus links. These were obtained by techniques entirely analogous to the computation for
![]() $(n,n)$
torus links, and many of them have not appeared in the literature before.
$(n,n)$
torus links, and many of them have not appeared in the literature before.
1.7 Notation
We collect here some of our notational conventions, for the reader’s convenience. Unfamiliar concepts will be explained in due course. Soergel bimodules are graded. We denote by
![]() $(1)$
the grading shift, so that
$(1)$
the grading shift, so that
![]() $M(1)^{i}=M^{i+1}$
. We let
$M(1)^{i}=M^{i+1}$
. We let
![]() $Q=(-1)$
denote the functor which increases the degree of each element. Complexes of Soergel bimodules are bigraded. The differentials always preserve the bimodule degree, and increase homological degree by 1. The shift in homological degree is denoted by
$Q=(-1)$
denote the functor which increases the degree of each element. Complexes of Soergel bimodules are bigraded. The differentials always preserve the bimodule degree, and increase homological degree by 1. The shift in homological degree is denoted by
![]() $\langle 1\rangle$
, so that
$\langle 1\rangle$
, so that
![]() $C(a)\langle b\rangle ^{i,j}=C^{i+a,j+b}$
. We denote by
$C(a)\langle b\rangle ^{i,j}=C^{i+a,j+b}$
. We denote by
![]() ${\mathcal{K}}^{b}({\mathcal{A}})$
the homotopy category of finite complexes over an additive category
${\mathcal{K}}^{b}({\mathcal{A}})$
the homotopy category of finite complexes over an additive category
![]() ${\mathcal{A}}$
. Isomorphism in
${\mathcal{A}}$
. Isomorphism in
![]() ${\mathcal{K}}^{b}({\mathcal{A}})$
, that is, chain homotopy equivalence, is denoted by
${\mathcal{K}}^{b}({\mathcal{A}})$
, that is, chain homotopy equivalence, is denoted by
![]() $\simeq$
. The existence of a distinguished triangle
$\simeq$
. The existence of a distinguished triangle
will be indicated by writing
![]() $B\simeq (C\overset{\unicode[STIX]{x1D6FF}}{\rightarrow }A)$
. We also let
$B\simeq (C\overset{\unicode[STIX]{x1D6FF}}{\rightarrow }A)$
. We also let
![]() $T=\langle -1\rangle$
denote the functor which increases homological degree by 1. If
$T=\langle -1\rangle$
denote the functor which increases homological degree by 1. If
![]() $\unicode[STIX]{x1D6FD}$
is a braid, we denote the braid exponent by
$\unicode[STIX]{x1D6FD}$
is a braid, we denote the braid exponent by
![]() $e(\unicode[STIX]{x1D6FD})$
; this is the signed number of crossings in a diagram representing
$e(\unicode[STIX]{x1D6FD})$
; this is the signed number of crossings in a diagram representing
![]() $\unicode[STIX]{x1D6FD}$
. The Rouquier complex
$\unicode[STIX]{x1D6FD}$
. The Rouquier complex
![]() $F(\unicode[STIX]{x1D6FD})$
is normalized so that if
$F(\unicode[STIX]{x1D6FD})$
is normalized so that if
![]() $\unicode[STIX]{x1D6FD}$
is a positive braid, then there is a chain map
$\unicode[STIX]{x1D6FD}$
is a positive braid, then there is a chain map
![]() $(TQ^{-1})^{e(\unicode[STIX]{x1D6FD})}R\rightarrow F(\unicode[STIX]{x1D6FD})$
which is the inclusion of the degree
$(TQ^{-1})^{e(\unicode[STIX]{x1D6FD})}R\rightarrow F(\unicode[STIX]{x1D6FD})$
which is the inclusion of the degree
![]() $e(\unicode[STIX]{x1D6FD})$
chain bimodule, whereas if
$e(\unicode[STIX]{x1D6FD})$
chain bimodule, whereas if
![]() $\unicode[STIX]{x1D6FD}$
is a negative braid, there is a chain map
$\unicode[STIX]{x1D6FD}$
is a negative braid, there is a chain map
![]() $F(\unicode[STIX]{x1D6FD})\rightarrow (TQ^{-1})^{e(\unicode[STIX]{x1D6FD})}R$
which is the projection onto the degree
$F(\unicode[STIX]{x1D6FD})\rightarrow (TQ^{-1})^{e(\unicode[STIX]{x1D6FD})}R$
which is the projection onto the degree
![]() $e(\unicode[STIX]{x1D6FD})$
bimodule. Note, in [Reference Abel and HogancampAH15] and [Reference HogancampHog18], the shifts
$e(\unicode[STIX]{x1D6FD})$
bimodule. Note, in [Reference Abel and HogancampAH15] and [Reference HogancampHog18], the shifts
![]() $(k)$
and
$(k)$
and
![]() $\langle \ell \rangle$
would have been denoted
$\langle \ell \rangle$
would have been denoted
![]() $(-k)$
and
$(-k)$
and
![]() $\langle -\ell \rangle$
, respectively.
$\langle -\ell \rangle$
, respectively.
Hochschild cohomology gives rise to a functor
![]() $\operatorname{HH}$
whose input is a graded bimodule, and whose output is a bigraded vector space. The additional grading is called the Hochschild grading, and shifts in the Hochschild grading are denoted by
$\operatorname{HH}$
whose input is a graded bimodule, and whose output is a bigraded vector space. The additional grading is called the Hochschild grading, and shifts in the Hochschild grading are denoted by
![]() $A$
. Extending to complexes gives a functor from complexes of graded bimodules to complexes of bigraded vector spaces. These are triply graded objects, so all together we have the shift functors
$A$
. Extending to complexes gives a functor from complexes of graded bimodules to complexes of bigraded vector spaces. These are triply graded objects, so all together we have the shift functors
![]() $Q,A,T$
. If
$Q,A,T$
. If
![]() $C$
is a complex of bimodules, then the homology of
$C$
is a complex of bimodules, then the homology of
![]() $\operatorname{HH}(C)$
is denoted by
$\operatorname{HH}(C)$
is denoted by
![]() $\operatorname{HHH}(C)$
.
$\operatorname{HHH}(C)$
.
We also find it convenient to introduce
![]() $t=T^{2}Q^{-2}$
,
$t=T^{2}Q^{-2}$
,
![]() $q=Q^{2}$
, and
$q=Q^{2}$
, and
![]() $a=AQ^{-2}$
. One might call these the geometric variables, since they appear most naturally in the connection with Hilbert schemes. When convenient, we express our degree shifts and Poincaré series in terms of these variables.
$a=AQ^{-2}$
. One might call these the geometric variables, since they appear most naturally in the connection with Hilbert schemes. When convenient, we express our degree shifts and Poincaré series in terms of these variables.
2 Background and key tools
2.1 Braids
Let
![]() $\operatorname{Br}_{n}$
denote the braid group with
$\operatorname{Br}_{n}$
denote the braid group with
![]() $n$
strands. The generators will be denoted by
$n$
strands. The generators will be denoted by
![]() $\unicode[STIX]{x1D70E}_{i}$
, for
$\unicode[STIX]{x1D70E}_{i}$
, for
![]() $1\leqslant i\leqslant n-1$
, and drawn as an overcrossing of the
$1\leqslant i\leqslant n-1$
, and drawn as an overcrossing of the
![]() $i$
th and
$i$
th and
![]() $(i+1)$
st strands. The overcrossing
$(i+1)$
st strands. The overcrossing
![]() $\unicode[STIX]{x1D70E}_{i}$
and its inverse, the undercrossing
$\unicode[STIX]{x1D70E}_{i}$
and its inverse, the undercrossing
![]() $\unicode[STIX]{x1D70E}_{i}^{-1}$
, are depicted as
$\unicode[STIX]{x1D70E}_{i}^{-1}$
, are depicted as
A labeled strand denotes the corresponding number of parallel copies of that strand. We will always draw our braids in a rectangle, with
![]() $n$
boundary points on the top and bottom. Composition of braids is given by vertical stacking, so that
$n$
boundary points on the top and bottom. Composition of braids is given by vertical stacking, so that
![]() $\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FD}^{\prime }$
is
$\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FD}^{\prime }$
is
![]() $\unicode[STIX]{x1D6FD}$
on top of
$\unicode[STIX]{x1D6FD}$
on top of
![]() $\unicode[STIX]{x1D6FD}^{\prime }$
. There is a group homomorphism
$\unicode[STIX]{x1D6FD}^{\prime }$
. There is a group homomorphism
![]() $e:\operatorname{Br}_{n}\rightarrow \mathbb{Z}$
sending
$e:\operatorname{Br}_{n}\rightarrow \mathbb{Z}$
sending
![]() $\unicode[STIX]{x1D70E}_{i}^{\pm }\mapsto \pm 1$
. The integer
$\unicode[STIX]{x1D70E}_{i}^{\pm }\mapsto \pm 1$
. The integer
![]() $e(\unicode[STIX]{x1D6FD})$
is called the braid exponent of
$e(\unicode[STIX]{x1D6FD})$
is called the braid exponent of
![]() $\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}$
.
A braid is positive if it has an expression only involving overcrossings, and negative if it has an expression only involving undercrossings. Given an element
![]() $w$
of the symmetric group
$w$
of the symmetric group
![]() $S_{n}$
, its positive braid lift in
$S_{n}$
, its positive braid lift in
![]() $\operatorname{Br}_{n}$
is the product
$\operatorname{Br}_{n}$
is the product
![]() $\unicode[STIX]{x1D70E}_{i_{1}}\unicode[STIX]{x1D70E}_{i_{2}}\cdots \unicode[STIX]{x1D70E}_{i_{d}}$
, where
$\unicode[STIX]{x1D70E}_{i_{1}}\unicode[STIX]{x1D70E}_{i_{2}}\cdots \unicode[STIX]{x1D70E}_{i_{d}}$
, where
![]() $s_{i_{1}}s_{i_{2}}\cdots s_{i_{d}}$
is a reduced expression for
$s_{i_{1}}s_{i_{2}}\cdots s_{i_{d}}$
is a reduced expression for
![]() $w$
in terms of the usual Coxeter generators
$w$
in terms of the usual Coxeter generators
![]() $\{s_{i}\}$
of
$\{s_{i}\}$
of
![]() $S_{n}$
. This element is independent of the choice of reduced expression. Its negative braid lift is
$S_{n}$
. This element is independent of the choice of reduced expression. Its negative braid lift is
![]() $\unicode[STIX]{x1D70E}_{i_{1}}^{-1}\cdots \unicode[STIX]{x1D70E}_{i_{d}}^{-1}$
.
$\unicode[STIX]{x1D70E}_{i_{1}}^{-1}\cdots \unicode[STIX]{x1D70E}_{i_{d}}^{-1}$
.
Definition 2.1. We define the following symmetries of
![]() $\operatorname{Br}_{n}$
.
$\operatorname{Br}_{n}$
.
(i) Rotation about the vertical axis: Let
 $\unicode[STIX]{x1D70F}:\operatorname{Br}_{n}\rightarrow \operatorname{Br}_{n}$
satisfy
$\unicode[STIX]{x1D70F}:\operatorname{Br}_{n}\rightarrow \operatorname{Br}_{n}$
satisfy
 $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D70E}_{i})=\unicode[STIX]{x1D70E}_{n-i}$
and
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D70E}_{i})=\unicode[STIX]{x1D70E}_{n-i}$
and
 $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FD})$
. Then
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FD})$
. Then
 $\unicode[STIX]{x1D70F}$
is an involution.
$\unicode[STIX]{x1D70F}$
is an involution.(ii) Rotation about the horizontal axis: Let
 $\unicode[STIX]{x1D714}:\operatorname{Br}_{n}\rightarrow \operatorname{Br}_{n}$
satisfy
$\unicode[STIX]{x1D714}:\operatorname{Br}_{n}\rightarrow \operatorname{Br}_{n}$
satisfy
 $\unicode[STIX]{x1D714}(\unicode[STIX]{x1D70E}_{i})=\unicode[STIX]{x1D70E}_{i}$
and
$\unicode[STIX]{x1D714}(\unicode[STIX]{x1D70E}_{i})=\unicode[STIX]{x1D70E}_{i}$
and
 $\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FC})$
. Then
$\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FC})$
. Then
 $\unicode[STIX]{x1D714}$
is an anti-involution.
$\unicode[STIX]{x1D714}$
is an anti-involution.(iii) Reflection across a horizontal plane: Let
 $(-)^{\vee }:\operatorname{Br}_{n}\rightarrow \operatorname{Br}_{n}$
satisfy
$(-)^{\vee }:\operatorname{Br}_{n}\rightarrow \operatorname{Br}_{n}$
satisfy
 $\unicode[STIX]{x1D70E}_{i}^{\vee }=\unicode[STIX]{x1D70E}_{i}^{-1}$
and
$\unicode[STIX]{x1D70E}_{i}^{\vee }=\unicode[STIX]{x1D70E}_{i}^{-1}$
and
 $(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})^{\vee }=\unicode[STIX]{x1D6FD}^{\vee }\unicode[STIX]{x1D6FC}^{\vee }$
. Then
$(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})^{\vee }=\unicode[STIX]{x1D6FD}^{\vee }\unicode[STIX]{x1D6FC}^{\vee }$
. Then
 $(-)^{\vee }$
is an anti-involution, and is just another notation for taking the inverse braid.
$(-)^{\vee }$
is an anti-involution, and is just another notation for taking the inverse braid.(iv) Crossing swap: Let
 $(-)^{L}:\operatorname{Br}_{n}\rightarrow \operatorname{Br}_{n}$
satisfy
$(-)^{L}:\operatorname{Br}_{n}\rightarrow \operatorname{Br}_{n}$
satisfy
 $\unicode[STIX]{x1D70E}_{i}^{L}=\unicode[STIX]{x1D70E}_{i}^{-1}$
and
$\unicode[STIX]{x1D70E}_{i}^{L}=\unicode[STIX]{x1D70E}_{i}^{-1}$
and
 $(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})^{L}=(\unicode[STIX]{x1D6FC})^{L}(\unicode[STIX]{x1D6FD})^{L}$
. Then
$(\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FD})^{L}=(\unicode[STIX]{x1D6FC})^{L}(\unicode[STIX]{x1D6FD})^{L}$
. Then
 $(-)^{L}$
is an involution, and
$(-)^{L}$
is an involution, and
 $(\unicode[STIX]{x1D6FD})^{L}=\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD})^{\vee }$
.
$(\unicode[STIX]{x1D6FD})^{L}=\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD})^{\vee }$
.
The letter
![]() $L$
indicates that
$L$
indicates that
![]() $\unicode[STIX]{x1D6FD}^{L}$
this is the left-handed version of the braid
$\unicode[STIX]{x1D6FD}^{L}$
this is the left-handed version of the braid
![]() $\unicode[STIX]{x1D6FD}$
. This swaps the positive and negative braid lifts of an element of
$\unicode[STIX]{x1D6FD}$
. This swaps the positive and negative braid lifts of an element of
![]() $S_{n}$
. Note that
$S_{n}$
. Note that
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D714}$
preserve positive braids, while
$\unicode[STIX]{x1D714}$
preserve positive braids, while
![]() $(-)^{\vee }$
and
$(-)^{\vee }$
and
![]() $(-)^{L}$
swap positive braids and negative braids. These symmetries all commute with each other.
$(-)^{L}$
swap positive braids and negative braids. These symmetries all commute with each other.
We let
![]() $\sqcup :\operatorname{Br}_{k}\times \operatorname{Br}_{l}\rightarrow \operatorname{Br}_{k+l}$
denote the homomorphism given by horizontal concatenation.
$\sqcup :\operatorname{Br}_{k}\times \operatorname{Br}_{l}\rightarrow \operatorname{Br}_{k+l}$
denote the homomorphism given by horizontal concatenation.
2.2 Shuffle braids
Definition 2.2. A shuffle permutation is a permutation
![]() $\unicode[STIX]{x1D70B}\in S_{n}$
which is a minimal length coset representative for some coset in
$\unicode[STIX]{x1D70B}\in S_{n}$
which is a minimal length coset representative for some coset in
![]() $S_{n}/(S_{k}\times S_{\ell })$
, for some
$S_{n}/(S_{k}\times S_{\ell })$
, for some
![]() $0\leqslant k,\ell \leqslant n$
with
$0\leqslant k,\ell \leqslant n$
with
![]() $k+\ell =n$
. Said differently, a shuffle permutation preserves the ordering of
$k+\ell =n$
. Said differently, a shuffle permutation preserves the ordering of
![]() $\{1,\ldots ,k\}$
and
$\{1,\ldots ,k\}$
and
![]() $\{k+1,\ldots ,n\}$
for some
$\{k+1,\ldots ,n\}$
for some
![]() $k$
, but ‘shuffles’ these two sets together.
$k$
, but ‘shuffles’ these two sets together.
Let
![]() $v\in \{0,1\}^{n}$
be a sequence with
$v\in \{0,1\}^{n}$
be a sequence with
![]() $k$
zeroes and
$k$
zeroes and
![]() $\ell$
ones. We call
$\ell$
ones. We call
![]() $v$
a shuffle. There is a corresponding shuffle permutation
$v$
a shuffle. There is a corresponding shuffle permutation
![]() $\unicode[STIX]{x1D70B}_{v}$
, a minimal coset representation for
$\unicode[STIX]{x1D70B}_{v}$
, a minimal coset representation for
![]() $S_{n}/(S_{k}\times S_{\ell })$
, for which
$S_{n}/(S_{k}\times S_{\ell })$
, for which
![]() $\unicode[STIX]{x1D70B}_{v}(\{1,\ldots ,k\})$
gives the locations of the zeroes, and
$\unicode[STIX]{x1D70B}_{v}(\{1,\ldots ,k\})$
gives the locations of the zeroes, and
![]() $\unicode[STIX]{x1D70B}_{v}(\{k+1,\ldots ,n\})$
gives the locations of the ones.
$\unicode[STIX]{x1D70B}_{v}(\{k+1,\ldots ,n\})$
gives the locations of the ones.
Note that a shuffle permutation can come from a shuffle in multiple different ways. For example, the identity element is a minimal coset representative for
![]() $S_{k}\times S_{\ell }$
for every
$S_{k}\times S_{\ell }$
for every
![]() $k$
and
$k$
and
![]() $l$
with
$l$
with
![]() $k+\ell =n$
; whenever all the zeroes come before all the ones,
$k+\ell =n$
; whenever all the zeroes come before all the ones,
![]() $\unicode[STIX]{x1D70B}_{0\cdots 01\cdots 1}$
is the identity. When the shuffle
$\unicode[STIX]{x1D70B}_{0\cdots 01\cdots 1}$
is the identity. When the shuffle
![]() $v\in \{0,1\}^{n}$
is understood,
$v\in \{0,1\}^{n}$
is understood,
![]() $k$
will always refer to the number of zeroes, and
$k$
will always refer to the number of zeroes, and
![]() $\ell$
to the number of ones.
$\ell$
to the number of ones.
Example 2.3. The shuffle permutation
![]() $\unicode[STIX]{x1D70B}_{1\cdots 10}$
is the
$\unicode[STIX]{x1D70B}_{1\cdots 10}$
is the
![]() $n$
-cycle
$n$
-cycle
![]() $(n,n-1,\ldots ,2,1)$
.
$(n,n-1,\ldots ,2,1)$
.
Definition 2.4. For each
![]() $v\in \{0,1\}^{n}$
, let
$v\in \{0,1\}^{n}$
, let
![]() $\unicode[STIX]{x1D6FD}_{v}$
denote the positive braid lift of
$\unicode[STIX]{x1D6FD}_{v}$
denote the positive braid lift of
![]() $\unicode[STIX]{x1D70B}_{v}$
. Let
$\unicode[STIX]{x1D70B}_{v}$
. Let
![]() $\operatorname{Tw}_{v}:=\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v})\unicode[STIX]{x1D6FD}_{v}$
, the shuffle twist, denote the positive pure braid obtained by gluing
$\operatorname{Tw}_{v}:=\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v})\unicode[STIX]{x1D6FD}_{v}$
, the shuffle twist, denote the positive pure braid obtained by gluing
![]() $\unicode[STIX]{x1D6FD}_{v}$
with its rotation.
$\unicode[STIX]{x1D6FD}_{v}$
with its rotation.
Example 2.5. If
![]() $v=(0101100)$
, then the shuffle permutation
$v=(0101100)$
, then the shuffle permutation
![]() $\unicode[STIX]{x1D70B}_{v}$
, its positive braid lift, and the associated pure braid are pictured as
$\unicode[STIX]{x1D70B}_{v}$
, its positive braid lift, and the associated pure braid are pictured as

Note that
![]() $v$
partitions the strands in these diagrams into two subsets: the 0-strands and the 1-strands. In
$v$
partitions the strands in these diagrams into two subsets: the 0-strands and the 1-strands. In
![]() $\unicode[STIX]{x1D6FD}_{v}$
the 0-strands cross over the 1-strands. In the
$\unicode[STIX]{x1D6FD}_{v}$
the 0-strands cross over the 1-strands. In the
![]() $\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v})$
portion of
$\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v})$
portion of
![]() $\operatorname{Tw}_{v}$
, they cross back under.
$\operatorname{Tw}_{v}$
, they cross back under.
The following gives a useful recursive description of the braids
![]() $\operatorname{Tw}_{v}$
.
$\operatorname{Tw}_{v}$
.
Proposition 2.6. Let
![]() $v$
be a shuffle with
$v$
be a shuffle with
![]() $k$
zeroes and
$k$
zeroes and
![]() $\ell$
ones, with
$\ell$
ones, with
![]() $k+\ell =n$
. Let
$k+\ell =n$
. Let
![]() $\cdot$
denote concatenation of shuffles, so that
$\cdot$
denote concatenation of shuffles, so that
![]() $v\cdot 0$
and
$v\cdot 0$
and
![]() $v\cdot 1$
are the two shuffles of length
$v\cdot 1$
are the two shuffles of length
![]() $n+1$
which extend
$n+1$
which extend
![]() $v$
. Then
$v$
. Then

Here a strand labeled
![]() $\ell$
actually represents
$\ell$
actually represents
![]() $\ell$
strands cabled together in the usual way, so that the ‘thick crossings’ in the expression for
$\ell$
strands cabled together in the usual way, so that the ‘thick crossings’ in the expression for
![]() $\operatorname{Tw}_{v\cdot 0}$
each represent
$\operatorname{Tw}_{v\cdot 0}$
each represent
![]() $\ell$
ordinary crossings. This recursion, together with the base cases
$\ell$
ordinary crossings. This recursion, together with the base cases
![]() $\operatorname{Tw}_{0}=\operatorname{Tw}_{1}=1$
, produces all the shuffle twists
$\operatorname{Tw}_{0}=\operatorname{Tw}_{1}=1$
, produces all the shuffle twists
![]() $\operatorname{Tw}_{v}$
. There is a similar such recursion which describes
$\operatorname{Tw}_{v}$
. There is a similar such recursion which describes
![]() $\operatorname{Tw}_{0\cdot v}$
and
$\operatorname{Tw}_{0\cdot v}$
and
![]() $\operatorname{Tw}_{1\cdot v}$
.
$\operatorname{Tw}_{1\cdot v}$
.
Proof. The proof is graphically obvious.◻
We now discuss the behavior of the shuffle braids with respect to the symmetries of the braid group.
Definition 2.7. For each
![]() $v\in \{0,1\}^{n}$
, let
$v\in \{0,1\}^{n}$
, let
![]() $r(v)$
denote the sequence obtained by reversing the order, so that
$r(v)$
denote the sequence obtained by reversing the order, so that
![]() $r(v)_{i}=v_{n+1-i}$
. Let
$r(v)_{i}=v_{n+1-i}$
. Let
![]() $v^{\ast }$
be the sequence obtained by swapping the ones with zeros and vice versa:
$v^{\ast }$
be the sequence obtained by swapping the ones with zeros and vice versa:
![]() $(v^{\ast })_{i}=1-v_{i}$
.
$(v^{\ast })_{i}=1-v_{i}$
.
Proposition 2.8. Let
![]() $v\in \{0,1\}^{n}$
be given. Then
$v\in \{0,1\}^{n}$
be given. Then
(i)
 $\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FD}_{v})=\unicode[STIX]{x1D6FD}_{r(v)^{\ast }}$
,
$\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FD}_{v})=\unicode[STIX]{x1D6FD}_{r(v)^{\ast }}$
,(ii)
 $\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v}^{-1})=\unicode[STIX]{x1D6FD}_{v}^{L}$
.
$\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v}^{-1})=\unicode[STIX]{x1D6FD}_{v}^{L}$
.
Proof. The proof is clear.◻
2.3 Half twists and shuffle braids
Let
![]() $\text{HT}=\text{HT}_{n}\in \operatorname{Br}_{n}$
denote the half twist braid
$\text{HT}=\text{HT}_{n}\in \operatorname{Br}_{n}$
denote the half twist braid
The full twist is
![]() $\text{FT}_{n}=\text{HT}_{n}^{2}$
, and is central in the braid group. This implies that the mapping
$\text{FT}_{n}=\text{HT}_{n}^{2}$
, and is central in the braid group. This implies that the mapping
![]() $\unicode[STIX]{x1D6FD}\mapsto \text{HT}\unicode[STIX]{x1D6FD}\text{HT}^{-1}$
defines an involution on the braid group. Indeed,
$\unicode[STIX]{x1D6FD}\mapsto \text{HT}\unicode[STIX]{x1D6FD}\text{HT}^{-1}$
defines an involution on the braid group. Indeed,
![]() $\text{HT}\unicode[STIX]{x1D6FD}\text{HT}^{-1}=\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FD})$
. We leave the proof of this fact to this reader, as it is elementary. It is also elementary that
$\text{HT}\unicode[STIX]{x1D6FD}\text{HT}^{-1}=\unicode[STIX]{x1D70F}(\unicode[STIX]{x1D6FD})$
. We leave the proof of this fact to this reader, as it is elementary. It is also elementary that
![]() $\text{HT}_{n}$
is fixed by
$\text{HT}_{n}$
is fixed by
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\unicode[STIX]{x1D714}$
.
$\unicode[STIX]{x1D714}$
.
We will need to know how the shuffle braids interact with
![]() $\text{HT}$
and
$\text{HT}$
and
![]() $\text{FT}$
.
$\text{FT}$
.
Proposition 2.9. Let
![]() $v\in \{0,1\}^{n}$
be given. Let
$v\in \{0,1\}^{n}$
be given. Let
![]() $k$
and
$k$
and
![]() $\ell$
be the number of zeroes and ones in
$\ell$
be the number of zeroes and ones in
![]() $v$
, respectively. Then:
$v$
, respectively. Then:
(i)
 $\text{HT}_{n}\unicode[STIX]{x1D6FE}_{v}=\unicode[STIX]{x1D6FE}_{r(v)^{\ast }}\text{HT}_{n}$
, where
$\text{HT}_{n}\unicode[STIX]{x1D6FE}_{v}=\unicode[STIX]{x1D6FE}_{r(v)^{\ast }}\text{HT}_{n}$
, where
 $\unicode[STIX]{x1D6FE}_{v}$
is any of the braids
$\unicode[STIX]{x1D6FE}_{v}$
is any of the braids
 $\unicode[STIX]{x1D6FD}_{v}$
,
$\unicode[STIX]{x1D6FD}_{v}$
,
 $\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v})$
,
$\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v})$
,
 $\unicode[STIX]{x1D6FD}_{v}^{L}$
, or
$\unicode[STIX]{x1D6FD}_{v}^{L}$
, or
 $\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v})^{L}$
;
$\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v})^{L}$
;(ii)
 $\text{HT}_{n}\unicode[STIX]{x1D6FD}_{v}^{L}=\unicode[STIX]{x1D6FD}_{r(v)}(\text{HT}_{k}\sqcup \text{HT}_{\ell })$
;
$\text{HT}_{n}\unicode[STIX]{x1D6FD}_{v}^{L}=\unicode[STIX]{x1D6FD}_{r(v)}(\text{HT}_{k}\sqcup \text{HT}_{\ell })$
;(iii)
 $\text{FT}_{n}\operatorname{Tw}_{v}^{L}\sim \operatorname{Tw}_{r(v)}(\text{FT}_{k}\sqcup \text{FT}_{\ell })$
.
$\text{FT}_{n}\operatorname{Tw}_{v}^{L}\sim \operatorname{Tw}_{r(v)}(\text{FT}_{k}\sqcup \text{FT}_{\ell })$
.
Here
![]() ${\sim}$
denotes that the given braids are equivalent modulo conjugation.
${\sim}$
denotes that the given braids are equivalent modulo conjugation.
Proof. Statement (1) follows from Proposition 2.8, since conjugation by
![]() $\text{HT}_{n}$
acts on the braid group by
$\text{HT}_{n}$
acts on the braid group by
![]() $\unicode[STIX]{x1D70F}$
(180 degree rotation about a vertical axis).
$\unicode[STIX]{x1D70F}$
(180 degree rotation about a vertical axis).
The idea of the proof of (2) is best illustrated with an example. For instance, when
![]() $v=(1100101)$
we have
$v=(1100101)$
we have

In the second diagram, the left-handed shuffle braid corresponds to
![]() $r(v)^{\ast }=(0101100)$
by statement (1) of the proposition. In the third diagram we have simply rewritten the half twist in terms of the ‘thick crossing’ between four cabled strands and three cabled strands. This is a well-known identity in the braid group. In the last diagram we have performed an isotopy.
$r(v)^{\ast }=(0101100)$
by statement (1) of the proposition. In the third diagram we have simply rewritten the half twist in terms of the ‘thick crossing’ between four cabled strands and three cabled strands. This is a well-known identity in the braid group. In the last diagram we have performed an isotopy.
Finally, statement (3) follows from (2). First, note that an application of
![]() $\unicode[STIX]{x1D714}$
to statement (2) yields
$\unicode[STIX]{x1D714}$
to statement (2) yields
Then observe:
 $$\begin{eqnarray}\displaystyle \text{FT}\operatorname{Tw}_{v}^{L} & = & \displaystyle \text{FT}\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v}^{L})\unicode[STIX]{x1D6FD}_{v}^{L}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v}^{L})\text{FT}\unicode[STIX]{x1D6FD}_{v}^{L}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v}^{L})\text{HT}\text{HT}\unicode[STIX]{x1D6FD}_{v}^{L}\nonumber\\ \displaystyle & = & \displaystyle (\text{HT}_{k}\sqcup \text{HT}_{\ell })\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{r(v)})\unicode[STIX]{x1D6FD}_{r(v)}(\text{HT}_{k}\sqcup \text{HT}_{\ell })\nonumber\\ \displaystyle & {\sim} & \displaystyle \unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{r(v)})\unicode[STIX]{x1D6FD}_{r(v)}(\text{FT}_{k}\sqcup \text{FT}_{\ell }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{FT}\operatorname{Tw}_{v}^{L} & = & \displaystyle \text{FT}\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v}^{L})\unicode[STIX]{x1D6FD}_{v}^{L}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v}^{L})\text{FT}\unicode[STIX]{x1D6FD}_{v}^{L}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v}^{L})\text{HT}\text{HT}\unicode[STIX]{x1D6FD}_{v}^{L}\nonumber\\ \displaystyle & = & \displaystyle (\text{HT}_{k}\sqcup \text{HT}_{\ell })\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{r(v)})\unicode[STIX]{x1D6FD}_{r(v)}(\text{HT}_{k}\sqcup \text{HT}_{\ell })\nonumber\\ \displaystyle & {\sim} & \displaystyle \unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{r(v)})\unicode[STIX]{x1D6FD}_{r(v)}(\text{FT}_{k}\sqcup \text{FT}_{\ell }).\nonumber\end{eqnarray}$$
The second equality holds since
![]() $\text{FT}_{n}\in \operatorname{Br}_{n}$
is central. The third holds since
$\text{FT}_{n}\in \operatorname{Br}_{n}$
is central. The third holds since
![]() $\text{FT}=\text{HT}\text{HT}$
. The fourth holds by (1) and (2). Finally the last
$\text{FT}=\text{HT}\text{HT}$
. The fourth holds by (1) and (2). Finally the last
![]() ${\sim}$
holds by transferring the
${\sim}$
holds by transferring the
![]() $(\text{HT}_{k}\sqcup \text{HT}_{\ell })$
to the right-hand side (recall that
$(\text{HT}_{k}\sqcup \text{HT}_{\ell })$
to the right-hand side (recall that
![]() $\unicode[STIX]{x1D6FD}\sim \unicode[STIX]{x1D6FD}^{\prime }$
means
$\unicode[STIX]{x1D6FD}\sim \unicode[STIX]{x1D6FD}^{\prime }$
means
![]() $\unicode[STIX]{x1D6FD}$
is conjugate to
$\unicode[STIX]{x1D6FD}$
is conjugate to
![]() $\unicode[STIX]{x1D6FD}^{\prime }$
). This completes the proof.◻
$\unicode[STIX]{x1D6FD}^{\prime }$
). This completes the proof.◻
2.4 Rouquier complexes
Let
![]() $R=R_{n}=\mathbb{Q}[x_{1},\ldots ,x_{n}]$
be the polynomial ring in
$R=R_{n}=\mathbb{Q}[x_{1},\ldots ,x_{n}]$
be the polynomial ring in
![]() $n$
variables, graded so that
$n$
variables, graded so that
![]() $\deg x_{i}=2$
. This is the polynomial ring associated to the standard
$\deg x_{i}=2$
. This is the polynomial ring associated to the standard
![]() $n$
-dimensional representation of
$n$
-dimensional representation of
![]() $S_{n}$
over
$S_{n}$
over
![]() $\mathbb{Q}$
. Given a graded
$\mathbb{Q}$
. Given a graded
![]() $R$
-bimodule
$R$
-bimodule
![]() $M$
, we let
$M$
, we let
![]() $M(1)$
denote the shifted bimodule for which
$M(1)$
denote the shifted bimodule for which
![]() $M(1)^{d}=M^{1+d}$
, where
$M(1)^{d}=M^{1+d}$
, where
![]() $M^{d}$
denotes the degree
$M^{d}$
denotes the degree
![]() $d$
part of
$d$
part of
![]() $M$
. We denote tensor product of graded bimodules over
$M$
. We denote tensor product of graded bimodules over
![]() $R$
simply by juxtaposition:
$R$
simply by juxtaposition:
![]() $M\otimes _{R}N=MN$
. We often let
$M\otimes _{R}N=MN$
. We often let
![]() $\unicode[STIX]{x1D7D9}=\unicode[STIX]{x1D7D9}_{n}$
denote the bimodule
$\unicode[STIX]{x1D7D9}=\unicode[STIX]{x1D7D9}_{n}$
denote the bimodule
![]() $R$
, which is the monoidal identity.
$R$
, which is the monoidal identity.
For each
![]() $i$
with
$i$
with
![]() $1\leqslant i\leqslant n-1$
, let
$1\leqslant i\leqslant n-1$
, let
![]() $B_{i}$
denote the graded
$B_{i}$
denote the graded
![]() $R$
-bimodule
$R$
-bimodule
where
![]() $R^{i}$
denotes the subring of polynomials invariant under the reflection
$R^{i}$
denotes the subring of polynomials invariant under the reflection
![]() $s_{i}=(i,i+1)$
. A Bott–Samelson bimodule is any tensor product of the bimodules
$s_{i}=(i,i+1)$
. A Bott–Samelson bimodule is any tensor product of the bimodules
![]() $B_{1},\ldots ,B_{n-1}$
. Let
$B_{1},\ldots ,B_{n-1}$
. Let
![]() $\mathbb{S}\text{Bim}_{n}$
denote the category of Soergel bimodules associated to
$\mathbb{S}\text{Bim}_{n}$
denote the category of Soergel bimodules associated to
![]() $R$
. This is the full graded monoidal additive Karoubian subcategory of graded
$R$
. This is the full graded monoidal additive Karoubian subcategory of graded
![]() $R$
-bimodules generated by
$R$
-bimodules generated by
![]() $B_{i}$
for
$B_{i}$
for
![]() $1\leqslant i\leqslant n-1$
. Thus, its objects are those objects isomorphic to direct sums of direct summands of grading shifts of Bott–Samelson bimodules.
$1\leqslant i\leqslant n-1$
. Thus, its objects are those objects isomorphic to direct sums of direct summands of grading shifts of Bott–Samelson bimodules.
Let
![]() ${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
denote the homotopy category of bounded complexes of Soergel bimodules. Objects of
${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
denote the homotopy category of bounded complexes of Soergel bimodules. Objects of
![]() ${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
are finite complexes with differentials of degree
${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
are finite complexes with differentials of degree
![]() $+1$
$+1$
and morphisms in
![]() ${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
are chain maps modulo homotopy.
${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
are chain maps modulo homotopy.
Associated to each braid word
![]() $\unicode[STIX]{x1D6FD}$
we have the Rouquier complex
$\unicode[STIX]{x1D6FD}$
we have the Rouquier complex
![]() $F(\unicode[STIX]{x1D6FD})$
in
$F(\unicode[STIX]{x1D6FD})$
in
![]() ${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
, defined by
${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
, defined by
together with
![]() $F(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FD}^{\prime })=F(\unicode[STIX]{x1D6FD})F(\unicode[STIX]{x1D6FD}^{\prime })$
. The underline indicates which object lies in homological degree
$F(\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6FD}^{\prime })=F(\unicode[STIX]{x1D6FD})F(\unicode[STIX]{x1D6FD}^{\prime })$
. The underline indicates which object lies in homological degree
![]() $0$
. Rouquier proved that there is a canonical homotopy equivalence between
$0$
. Rouquier proved that there is a canonical homotopy equivalence between
![]() $F(\unicode[STIX]{x1D6FD})$
and
$F(\unicode[STIX]{x1D6FD})$
and
![]() $F(\unicode[STIX]{x1D6FD}^{\prime })$
when
$F(\unicode[STIX]{x1D6FD}^{\prime })$
when
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D6FD}^{\prime }$
are braid words expressing the same braid. A more direct proof which works over
$\unicode[STIX]{x1D6FD}^{\prime }$
are braid words expressing the same braid. A more direct proof which works over
![]() $\mathbb{Z}$
can also be found in [Reference Elias and KrasnerEK10].
$\mathbb{Z}$
can also be found in [Reference Elias and KrasnerEK10].
Remark 2.10. Recall the notation
![]() $Q,T$
for gradings shifts (see § 1.7). One reason why
$Q,T$
for gradings shifts (see § 1.7). One reason why
![]() $t$
is more natural that
$t$
is more natural that
![]() $T$
is that any Rouquier complex
$T$
is that any Rouquier complex
![]() $F(\unicode[STIX]{x1D6FD})$
always has a unique copy of
$F(\unicode[STIX]{x1D6FD})$
always has a unique copy of
![]() $R$
which appears in homological degree
$R$
which appears in homological degree
![]() $e(\unicode[STIX]{x1D6FD})$
and internal degree
$e(\unicode[STIX]{x1D6FD})$
and internal degree
![]() $-e(\unicode[STIX]{x1D6FD})$
, so that this copy of
$-e(\unicode[STIX]{x1D6FD})$
, so that this copy of
![]() $R$
appears with shift
$R$
appears with shift
![]() $t^{(1/2)e(\unicode[STIX]{x1D6FD})}$
, where
$t^{(1/2)e(\unicode[STIX]{x1D6FD})}$
, where
![]() $e(\unicode[STIX]{x1D6FD})$
is the braid exponent. It was proven in [Reference Elias and WilliamsonEW14] that Rouquier complexes for reduced expressions are perverse (when one works in characteristic zero). A complex is perverse if each indecomposable bimodule in the complex appears with a grading shift equal to its homological degree, or equivalently, that the grading and homological shifts are described only as powers of
$e(\unicode[STIX]{x1D6FD})$
is the braid exponent. It was proven in [Reference Elias and WilliamsonEW14] that Rouquier complexes for reduced expressions are perverse (when one works in characteristic zero). A complex is perverse if each indecomposable bimodule in the complex appears with a grading shift equal to its homological degree, or equivalently, that the grading and homological shifts are described only as powers of
![]() $(TQ^{-1})$
. Note that the Rouquier complex for the full twist is not perverse, nor are shuffle twists. We will not use any perversity results in this paper. Nonetheless, we will express our shifts using the variables
$(TQ^{-1})$
. Note that the Rouquier complex for the full twist is not perverse, nor are shuffle twists. We will not use any perversity results in this paper. Nonetheless, we will express our shifts using the variables
![]() $t=T^{2}Q^{-2}$
and
$t=T^{2}Q^{-2}$
and
![]() $q=Q^{2}$
.
$q=Q^{2}$
.
The symmetries of the braid group lift to symmetries of
![]() $\mathbb{S}\text{Bim}_{n}$
and its homotopy category. Let
$\mathbb{S}\text{Bim}_{n}$
and its homotopy category. Let
![]() $\unicode[STIX]{x1D70F}:R\rightarrow R$
denote the map sending
$\unicode[STIX]{x1D70F}:R\rightarrow R$
denote the map sending
![]() $x_{i}\mapsto x_{n+1-i}$
.
$x_{i}\mapsto x_{n+1-i}$
.
Definition 2.11. We define the following symmetries of
![]() $\mathbb{S}\text{Bim}_{n}$
.
$\mathbb{S}\text{Bim}_{n}$
.
(i) Rotation about vertical axis: Let
 $\unicode[STIX]{x1D70F}:\mathbb{S}\text{Bim}_{n}\rightarrow \mathbb{S}\text{Bim}_{n}$
denote the covariant graded monoidal functor induced by the Dynkin automorphism of
$\unicode[STIX]{x1D70F}:\mathbb{S}\text{Bim}_{n}\rightarrow \mathbb{S}\text{Bim}_{n}$
denote the covariant graded monoidal functor induced by the Dynkin automorphism of
 $S_{n}$
. That is,
$S_{n}$
. That is,
 $\unicode[STIX]{x1D70F}:B_{i}\mapsto B_{n-i}$
, and satisfies
$\unicode[STIX]{x1D70F}:B_{i}\mapsto B_{n-i}$
, and satisfies
 $\unicode[STIX]{x1D70F}(MN)=\unicode[STIX]{x1D70F}(M)\unicode[STIX]{x1D70F}(N)$
and
$\unicode[STIX]{x1D70F}(MN)=\unicode[STIX]{x1D70F}(M)\unicode[STIX]{x1D70F}(N)$
and
 $\unicode[STIX]{x1D70F}(M(1))=\unicode[STIX]{x1D70F}(M)(1)$
.
$\unicode[STIX]{x1D70F}(M(1))=\unicode[STIX]{x1D70F}(M)(1)$
.(ii) Rotation about horizontal axis: Let
 $\unicode[STIX]{x1D714}:\mathbb{S}\text{Bim}_{n}\rightarrow \mathbb{S}\text{Bim}_{n}$
denote the covariant graded anti-monoidal functor which sends
$\unicode[STIX]{x1D714}:\mathbb{S}\text{Bim}_{n}\rightarrow \mathbb{S}\text{Bim}_{n}$
denote the covariant graded anti-monoidal functor which sends
 $B_{i}\mapsto B_{i}$
and satisfies
$B_{i}\mapsto B_{i}$
and satisfies
 $\unicode[STIX]{x1D714}(MN)=\unicode[STIX]{x1D714}(N)\unicode[STIX]{x1D714}(M)$
and
$\unicode[STIX]{x1D714}(MN)=\unicode[STIX]{x1D714}(N)\unicode[STIX]{x1D714}(M)$
and
 $\unicode[STIX]{x1D714}(M(1))=\unicode[STIX]{x1D714}(M)(1)$
.
$\unicode[STIX]{x1D714}(M(1))=\unicode[STIX]{x1D714}(M)(1)$
.(iii) Reflection across a horizontal plane: Let
 $(-)^{\vee }:\mathbb{S}\text{Bim}_{n}\rightarrow \mathbb{S}\text{Bim}_{n}^{\text{op}}$
denote the contravariant anti-graded anti-monoidal ‘duality’ functor on
$(-)^{\vee }:\mathbb{S}\text{Bim}_{n}\rightarrow \mathbb{S}\text{Bim}_{n}^{\text{op}}$
denote the contravariant anti-graded anti-monoidal ‘duality’ functor on
 $\mathbb{S}\text{Bim}_{n}$
, which sends
$\mathbb{S}\text{Bim}_{n}$
, which sends
 $B_{i}\mapsto B_{i}$
and satisfies
$B_{i}\mapsto B_{i}$
and satisfies
 $(MN)^{\vee }=N^{\vee }M^{\vee }$
and
$(MN)^{\vee }=N^{\vee }M^{\vee }$
and
 $M(1)^{\vee }=M^{\vee }(-1)$
.
$M(1)^{\vee }=M^{\vee }(-1)$
.(iv) Crossing swap: Let
 $(-)^{L}:\mathbb{S}\text{Bim}_{n}\rightarrow \mathbb{S}\text{Bim}_{n}$
denote the contravariant anti-graded monoidal functor
$(-)^{L}:\mathbb{S}\text{Bim}_{n}\rightarrow \mathbb{S}\text{Bim}_{n}$
denote the contravariant anti-graded monoidal functor
 $(-)^{\vee }\circ \unicode[STIX]{x1D714}$
.
$(-)^{\vee }\circ \unicode[STIX]{x1D714}$
.
These symmetries commute up to canonical isomorphism.
Proposition 2.12. These symmetries intertwine the braid symmetries from Definition 2.1, under Rouquier’s map
![]() $F$
, via a canonical isomorphism. In particular,
$F$
, via a canonical isomorphism. In particular,
![]() $F(\unicode[STIX]{x1D6FD})^{\vee }\cong F(\unicode[STIX]{x1D6FD}^{-1})$
.
$F(\unicode[STIX]{x1D6FD})^{\vee }\cong F(\unicode[STIX]{x1D6FD}^{-1})$
.
Proof. This is easy. Although we have not stated explicitly what the differentials in
![]() $F(\unicode[STIX]{x1D70E}_{i})$
and
$F(\unicode[STIX]{x1D70E}_{i})$
and
![]() $F(\unicode[STIX]{x1D70E}_{i}^{-1})$
are, they live in one-dimensional morphism spaces, and are interchanged by duality.◻
$F(\unicode[STIX]{x1D70E}_{i}^{-1})$
are, they live in one-dimensional morphism spaces, and are interchanged by duality.◻
There is an isomorphism of rings
![]() $R_{k}\boxtimes R_{l}\rightarrow R_{k+l}$
given by renaming the variables, where
$R_{k}\boxtimes R_{l}\rightarrow R_{k+l}$
given by renaming the variables, where
![]() $\boxtimes$
denotes tensor product over
$\boxtimes$
denotes tensor product over
![]() $\mathbb{Q}$
. Correspondingly, there is an inclusion functor
$\mathbb{Q}$
. Correspondingly, there is an inclusion functor
![]() $\sqcup :\mathbb{S}\text{Bim}_{k}\boxtimes \mathbb{S}\text{Bim}_{l}\rightarrow \mathbb{S}\text{Bim}_{k+l}$
, which sends
$\sqcup :\mathbb{S}\text{Bim}_{k}\boxtimes \mathbb{S}\text{Bim}_{l}\rightarrow \mathbb{S}\text{Bim}_{k+l}$
, which sends
![]() $B_{i}\boxtimes \unicode[STIX]{x1D7D9}_{l}$
to
$B_{i}\boxtimes \unicode[STIX]{x1D7D9}_{l}$
to
![]() $B_{i}$
and sends
$B_{i}$
and sends
![]() $\unicode[STIX]{x1D7D9}_{k}\boxtimes B_{i}$
to
$\unicode[STIX]{x1D7D9}_{k}\boxtimes B_{i}$
to
![]() $B_{k+i}$
. This intertwines with the map
$B_{k+i}$
. This intertwines with the map
![]() $\sqcup :\operatorname{Br}_{k}\times \operatorname{Br}_{l}\rightarrow \operatorname{Br}_{k+l}$
after applying Rouquier’s map
$\sqcup :\operatorname{Br}_{k}\times \operatorname{Br}_{l}\rightarrow \operatorname{Br}_{k+l}$
after applying Rouquier’s map
![]() $F$
.
$F$
.
It was proven by Soergel that morphisms between objects in
![]() $\mathbb{S}\text{Bim}_{n}$
are free as left or right modules over
$\mathbb{S}\text{Bim}_{n}$
are free as left or right modules over
![]() $R_{n}$
. Using Soergel’s Hom formula [Reference SoergelSoe07, Theorem 5.15], one can prove that
$R_{n}$
. Using Soergel’s Hom formula [Reference SoergelSoe07, Theorem 5.15], one can prove that
![]() $\sqcup$
is actually fully faithful, after identifying
$\sqcup$
is actually fully faithful, after identifying
![]() $R_{k}\boxtimes R_{l}$
with
$R_{k}\boxtimes R_{l}$
with
![]() $R_{n}$
. Another way of phrasing this result is that the inclusion
$R_{n}$
. Another way of phrasing this result is that the inclusion
![]() $\mathbb{S}\text{Bim}_{i}\rightarrow \mathbb{S}\text{Bim}_{n}$
for
$\mathbb{S}\text{Bim}_{i}\rightarrow \mathbb{S}\text{Bim}_{n}$
for
![]() $i<n$
, which comes from the functor
$i<n$
, which comes from the functor
![]() $(-)\sqcup \unicode[STIX]{x1D7D9}_{n-i}$
, is fully faithful after base change along the inclusion from
$(-)\sqcup \unicode[STIX]{x1D7D9}_{n-i}$
, is fully faithful after base change along the inclusion from
![]() $R_{i}$
to
$R_{i}$
to
![]() $R_{n}$
. See [Reference Elias and WilliamsonEW13, Remark 3.19] for further discussion.
$R_{n}$
. See [Reference Elias and WilliamsonEW13, Remark 3.19] for further discussion.
2.5 Complexes and convolutions
We may write
![]() $\langle 1\rangle$
for the homological shift of a complex, so that the homological degree
$\langle 1\rangle$
for the homological shift of a complex, so that the homological degree
![]() $d$
part of
$d$
part of
![]() $F\langle 1\rangle$
is the homological degree
$F\langle 1\rangle$
is the homological degree
![]() $d+1$
part of
$d+1$
part of
![]() $F$
. By convention,
$F$
. By convention,
![]() $\langle 1\rangle$
also negates the differential.
$\langle 1\rangle$
also negates the differential.
We now introduce some notation which we will be used exhaustively throughout. To motivate it, we begin with an example. Suppose
![]() $A$
and
$A$
and
![]() $B$
are complexes, and
$B$
are complexes, and
![]() $f:A\rightarrow B$
is a chain map. The mapping cone
$f:A\rightarrow B$
is a chain map. The mapping cone
![]() $C_{f}$
is the chain complex
$C_{f}$
is the chain complex
![]() $(C_{f})_{k}=A_{k+1}\oplus B_{k}$
with differential given by the matrix
$(C_{f})_{k}=A_{k+1}\oplus B_{k}$
with differential given by the matrix
![]() $\left[\!\begin{smallmatrix}-d_{A} & 0\\ f & d_{B}\end{smallmatrix}\!\right]$
. In other words
$\left[\!\begin{smallmatrix}-d_{A} & 0\\ f & d_{B}\end{smallmatrix}\!\right]$
. In other words
![]() $C_{f}=A\langle 1\rangle \oplus B$
with an additional component of the differential from
$C_{f}=A\langle 1\rangle \oplus B$
with an additional component of the differential from
![]() $A\langle 1\rangle$
to
$A\langle 1\rangle$
to
![]() $B$
, given by
$B$
, given by
![]() $f$
. Note that the additional sign on the differential of
$f$
. Note that the additional sign on the differential of
![]() $A\langle 1\rangle$
is necessary for the differential on
$A\langle 1\rangle$
is necessary for the differential on
![]() $C_{f}$
to satisfy
$C_{f}$
to satisfy
![]() $d^{2}=0$
. We prefer to keep track of the homological degree shift explicitly, so that the mapping cone can be written as
$d^{2}=0$
. We prefer to keep track of the homological degree shift explicitly, so that the mapping cone can be written as
We will also say that
![]() $C_{f}=A\langle 1\rangle \oplus B$
with twisted differential. This notation will come in handy when we later consider mapping cones of mapping cones, and so on.
$C_{f}=A\langle 1\rangle \oplus B$
with twisted differential. This notation will come in handy when we later consider mapping cones of mapping cones, and so on.
For instance, this notation allows us to use explicit shifts instead of underlines in a complex, so that we may write
The general way to describe an iterated cone is using the idea of a convolution of complexes. Let
![]() $F_{j}$
(
$F_{j}$
(
![]() $j\in J$
) be complexes of
$j\in J$
) be complexes of
![]() $R$
-bimodules indexed by a finite partially-ordered set
$R$
-bimodules indexed by a finite partially-ordered set
![]() $J$
. Let
$J$
. Let
![]() $d_{j}$
denote the differential on the complex
$d_{j}$
denote the differential on the complex
![]() $F_{j}$
(which, in our notation, is a map of bigraded
$F_{j}$
(which, in our notation, is a map of bigraded
![]() $R$
-bimodules of homological degree
$R$
-bimodules of homological degree
![]() $+1$
and graded degree
$+1$
and graded degree
![]() $0$
). Let
$0$
). Let
![]() $E=\bigoplus _{j\in J}F_{j}$
be a bigraded
$E=\bigoplus _{j\in J}F_{j}$
be a bigraded
![]() $R$
-bimodule, and let
$R$
-bimodule, and let
![]() $d$
be a differential on
$d$
be a differential on
![]() $E$
such that
$E$
such that
– restricted to a map
 $F_{j}\rightarrow F_{j}$
,
$F_{j}\rightarrow F_{j}$
,
 $d$
agrees with
$d$
agrees with
 $d_{j}$
, and
$d_{j}$
, and– restricted to a map
 $F_{j}\rightarrow F_{j^{\prime }}$
,
$F_{j}\rightarrow F_{j^{\prime }}$
,
 $d$
is zero unless
$d$
is zero unless
 $j\leqslant j^{\prime }$
.
$j\leqslant j^{\prime }$
.
Then
![]() $E$
is called a convolution of the complexes
$E$
is called a convolution of the complexes
![]() $F_{j}$
, as is any complex which is homotopy equivalent to
$F_{j}$
, as is any complex which is homotopy equivalent to
![]() $E$
. We may write
$E$
. We may write
![]() $d=\sum _{i\leqslant j}d_{ji}$
, where
$d=\sum _{i\leqslant j}d_{ji}$
, where
![]() $d_{ji}$
is the component of the differential mapping
$d_{ji}$
is the component of the differential mapping
![]() $F_{i}$
to
$F_{i}$
to
![]() $F_{j}$
.
$F_{j}$
.
We refer to
![]() $F_{j}$
as the subquotients of the convolution
$F_{j}$
as the subquotients of the convolution
![]() $E$
. We say that
$E$
. We say that
![]() $E=\bigoplus _{j\in J}F_{j}$
with twisted differential, indicating that the differential is not just the direct sum of the differentials on each summand. We say that this twisted differential respects the partial order on
$E=\bigoplus _{j\in J}F_{j}$
with twisted differential, indicating that the differential is not just the direct sum of the differentials on each summand. We say that this twisted differential respects the partial order on
![]() $J$
because
$J$
because
![]() $d_{ji}=0$
for
$d_{ji}=0$
for
![]() $i\not \leqslant j$
.
$i\not \leqslant j$
.
Remark 2.13. By abuse of language, we will refer to a two term convolution
![]() $E=(A\overset{f}{\longrightarrow }B)$
as a mapping cone. Note that, strictly speaking
$E=(A\overset{f}{\longrightarrow }B)$
as a mapping cone. Note that, strictly speaking
![]() $f$
is not a chain map from
$f$
is not a chain map from
![]() $A$
to
$A$
to
![]() $B$
, but rather a chain map
$B$
, but rather a chain map
![]() $A\langle -1\rangle \rightarrow B$
. Here
$A\langle -1\rangle \rightarrow B$
. Here
![]() $J$
has two elements, with the order determined by the arrow. A general convolution can be described as an iterated cone of complexes, where each
$J$
has two elements, with the order determined by the arrow. A general convolution can be described as an iterated cone of complexes, where each
![]() $F_{j}$
is added one at a time.
$F_{j}$
is added one at a time.
In practice, one can often show indirectly that a complex
![]() $E$
is a convolution of other complexes
$E$
is a convolution of other complexes
![]() $F_{j}$
, in which case the components
$F_{j}$
, in which case the components
![]() $d_{ji}$
of the differential may be difficult to write down for
$d_{ji}$
of the differential may be difficult to write down for
![]() $i\neq j$
(the task is complicated further by the presence of homotopy equivalences). In particular, this makes it difficult to compute the homology
$i\neq j$
(the task is complicated further by the presence of homotopy equivalences). In particular, this makes it difficult to compute the homology
![]() $H(E)$
. Thankfully, a parity argument will come to the rescue in this paper.
$H(E)$
. Thankfully, a parity argument will come to the rescue in this paper.
Proposition 2.14. Suppose
![]() $E=\bigoplus _{j\in J}F_{j}$
with twisted differential, for some finite partially ordered set
$E=\bigoplus _{j\in J}F_{j}$
with twisted differential, for some finite partially ordered set
![]() $J$
. Suppose the homology
$J$
. Suppose the homology
![]() $H(F_{j})$
is supported in even homological degrees, for all
$H(F_{j})$
is supported in even homological degrees, for all
![]() $j\in J$
. Then
$j\in J$
. Then
![]() $H(E)\cong \bigoplus _{j}H(F_{j})$
.
$H(E)\cong \bigoplus _{j}H(F_{j})$
.
Proof. We induct on the cardinality of
![]() $J$
. In the base case
$J$
. In the base case
![]() $J=\{j\}$
, we have
$J=\{j\}$
, we have
![]() $E=F_{j}$
, and the statement is trivial. Now, assume by induction that we have proved the result for partially ordered sets of cardinality
$E=F_{j}$
, and the statement is trivial. Now, assume by induction that we have proved the result for partially ordered sets of cardinality
![]() $r$
, and let
$r$
, and let
![]() $J$
be a partially ordered set of cardinality
$J$
be a partially ordered set of cardinality
![]() $r+1$
. Let
$r+1$
. Let
![]() $j\in J$
be maximal. Set
$j\in J$
be maximal. Set
![]() $B:=F_{j}$
and
$B:=F_{j}$
and
![]() $A=\bigoplus _{i\in J\smallsetminus \{j\}}F_{j}$
with twisted differential. Note that
$A=\bigoplus _{i\in J\smallsetminus \{j\}}F_{j}$
with twisted differential. Note that
![]() $E=A\oplus B$
with twisted differential:
$E=A\oplus B$
with twisted differential:
for some map
![]() $\unicode[STIX]{x1D6FF}$
of homological degree
$\unicode[STIX]{x1D6FF}$
of homological degree
![]() $+1$
. We have
$+1$
. We have
![]() $H(A)\cong \bigoplus _{i\neq j}H(F_{i})$
by induction, so we must prove that
$H(A)\cong \bigoplus _{i\neq j}H(F_{i})$
by induction, so we must prove that
![]() $H(E)\cong H(A)\oplus H(B)$
.
$H(E)\cong H(A)\oplus H(B)$
.
The short exact sequence
![]() $0\rightarrow B\rightarrow E\rightarrow A\rightarrow 0$
gives rise to a long exact sequence
$0\rightarrow B\rightarrow E\rightarrow A\rightarrow 0$
gives rise to a long exact sequence
Our parity assumption implies that
![]() $H^{k}(A)=H^{k}(B)=0$
when
$H^{k}(A)=H^{k}(B)=0$
when
![]() $k$
is odd. Thus
$k$
is odd. Thus
![]() $H^{k}(E)=0$
when
$H^{k}(E)=0$
when
![]() $k$
is odd. When
$k$
is odd. When
![]() $k$
is even we have a short exact sequence
$k$
is even we have a short exact sequence
If we work over a field, then this short exact sequence splits. This completes the inductive step, and completes the proof.◻
Remark 2.15. In general, there is a spectral sequence converging to
![]() $H(E)$
, whose
$H(E)$
, whose
![]() $E_{2}$
page is
$E_{2}$
page is
![]() $\bigoplus _{j}H(F_{j})$
. If
$\bigoplus _{j}H(F_{j})$
. If
![]() $H(F_{i})$
is even, then the subsequent differentials (which have odd homological degree) must all vanish. This gives an alternate proof of the above.
$H(F_{i})$
is even, then the subsequent differentials (which have odd homological degree) must all vanish. This gives an alternate proof of the above.
Remark 2.16. The above presents a ‘computation-free and serendipitous’ approach to computing homology groups. Suppose we wish to compute the homology of a chain complex
![]() $E$
. We may get lucky and discover a filtration on
$E$
. We may get lucky and discover a filtration on
![]() $E$
whose successive quotients are supported in even homological degrees. In this case, Proposition 2.14 says that
$E$
whose successive quotients are supported in even homological degrees. In this case, Proposition 2.14 says that
![]() $H(E)$
simply splits as a direct sum of these homology groups. In this paper we are extraordinarily lucky in this regard.
$H(E)$
simply splits as a direct sum of these homology groups. In this paper we are extraordinarily lucky in this regard.
2.6 Categorified symmetrizers
In this subsection we recall the constructions of the second author in [Reference HogancampHog18], and extract from them a finite complex
![]() $K_{n}\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
which will play an essential role in this paper. First, define the following complexes.
$K_{n}\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
which will play an essential role in this paper. First, define the following complexes.
Definition 2.17. Let
![]() $X=X_{n}=F(\unicode[STIX]{x1D70E}_{n-1}\cdots \unicode[STIX]{x1D70E}_{1})$
and
$X=X_{n}=F(\unicode[STIX]{x1D70E}_{n-1}\cdots \unicode[STIX]{x1D70E}_{1})$
and
![]() $Y=Y_{n}=F(\unicode[STIX]{x1D70E}_{n-1}^{-1}\cdots \unicode[STIX]{x1D70E}_{1}^{-1})$
denote the Rouquier complexes associated to the positive and negative braid lifts of the standard
$Y=Y_{n}=F(\unicode[STIX]{x1D70E}_{n-1}^{-1}\cdots \unicode[STIX]{x1D70E}_{1}^{-1})$
denote the Rouquier complexes associated to the positive and negative braid lifts of the standard
![]() $n$
-cycle
$n$
-cycle
![]() $(n,n-1,\ldots ,2,1)$
. In other words,
$(n,n-1,\ldots ,2,1)$
. In other words,
![]() $X=F(\unicode[STIX]{x1D6FD}_{v})$
and
$X=F(\unicode[STIX]{x1D6FD}_{v})$
and
![]() $Y=F(\unicode[STIX]{x1D6FD}_{v}^{L})$
for
$Y=F(\unicode[STIX]{x1D6FD}_{v}^{L})$
for
![]() $v=(11\cdots 10)$
. Note that
$v=(11\cdots 10)$
. Note that
![]() $\unicode[STIX]{x1D70F}(X)=\unicode[STIX]{x1D714}(X)=Y^{-1}$
,
$\unicode[STIX]{x1D70F}(X)=\unicode[STIX]{x1D714}(X)=Y^{-1}$
,
![]() $\unicode[STIX]{x1D70F}(Y)=\unicode[STIX]{x1D714}(Y)=X^{-1}$
.
$\unicode[STIX]{x1D70F}(Y)=\unicode[STIX]{x1D714}(Y)=X^{-1}$
.
In this paper we adopt a graphical notation for certain complexes of Soergel bimodules. We will denote a braid and its Rouquier complex similarly, so for example pictures such as
will denote the complexes
![]() $X_{n}$
and
$X_{n}$
and
![]() $Y_{n}$
of Definition 2.17. The tensor product of complexes corresponds to vertical stacking. For example we have
$Y_{n}$
of Definition 2.17. The tensor product of complexes corresponds to vertical stacking. For example we have

Complexes of the form
![]() $XY^{-1}$
play a very special role in this paper. They are the Rouquier complexes associated to the Young–Jucys–Murphy braids. Note that braids corresponding to
$XY^{-1}$
play a very special role in this paper. They are the Rouquier complexes associated to the Young–Jucys–Murphy braids. Note that braids corresponding to
![]() $X_{k}Y_{k}^{-1}$
generate a commutative subgroup of the braid group, and their product is the full twist. The following defines a family of complexes
$X_{k}Y_{k}^{-1}$
generate a commutative subgroup of the braid group, and their product is the full twist. The following defines a family of complexes
![]() $K_{n}$
which are compatible with these braids, in a particular sense.
$K_{n}$
which are compatible with these braids, in a particular sense.
Proposition 2.18. There exists a family of finite complexes
![]() $K_{n}\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
(
$K_{n}\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
(
![]() $n\geqslant 1$
) such that we have the following.
$n\geqslant 1$
) such that we have the following.
(i)
 $K_{1}=R$
.
$K_{1}=R$
.(ii) We have
 $K_{n-1}XY^{-1}\simeq (K_{n}\rightarrow qK_{n-1})$
. Graphically this is (2.2)
$K_{n-1}XY^{-1}\simeq (K_{n}\rightarrow qK_{n-1})$
. Graphically this is (2.2)
(iii)
 $K_{n}$
kills all generating Bott–Samelson bimodules in
$K_{n}$
kills all generating Bott–Samelson bimodules in
 $\mathbb{S}\text{Bim}_{n}$
. That is,
$\mathbb{S}\text{Bim}_{n}$
. That is,
 $K_{n}B_{i}\simeq 0\simeq B_{i}K_{n}$
for
$K_{n}B_{i}\simeq 0\simeq B_{i}K_{n}$
for
 $1\leqslant i\leqslant n-1$
.
$1\leqslant i\leqslant n-1$
.
Note that finiteness of the
![]() $K_{n}$
follows from the recursion (2).
$K_{n}$
follows from the recursion (2).
Proof. In [Reference HogancampHog18] the second author defined a family of complexes
![]() $P_{n}\in {\mathcal{K}}^{-}(\mathbb{S}\text{Bim}_{n})$
such that:
$P_{n}\in {\mathcal{K}}^{-}(\mathbb{S}\text{Bim}_{n})$
such that:
–
 $P_{n}$
kills all Bott–Samelson bimodules:
$P_{n}$
kills all Bott–Samelson bimodules:
 $P_{n}\otimes B_{i}\simeq 0\simeq B_{i}\otimes P_{n}$
for all
$P_{n}\otimes B_{i}\simeq 0\simeq B_{i}\otimes P_{n}$
for all
 $1\leqslant i\leqslant n-1$
;
$1\leqslant i\leqslant n-1$
;– any other complex
 $M\in {\mathcal{K}}^{-}(\mathbb{S}\text{Bim}_{n})$
kills Bott–Samelson bimodules if and only if
$M\in {\mathcal{K}}^{-}(\mathbb{S}\text{Bim}_{n})$
kills Bott–Samelson bimodules if and only if
 $P_{n}\otimes M\simeq M\simeq P_{n}\otimes M$
.
$P_{n}\otimes M\simeq M\simeq P_{n}\otimes M$
.
Further,
![]() $P_{n}$
is uniquely characterized up to homotopy equivalence by these properties. The complexes
$P_{n}$
is uniquely characterized up to homotopy equivalence by these properties. The complexes
![]() $P_{n}$
can be thought of as categorical projections onto the sign representation of the Hecke algebra.
$P_{n}$
can be thought of as categorical projections onto the sign representation of the Hecke algebra.
We will construct the complexes
![]() $K_{n}$
inductively. First, set
$K_{n}$
inductively. First, set
![]() $K_{1}=R_{1}$
. Now, assume
$K_{1}=R_{1}$
. Now, assume
![]() $K_{n-1}$
has been constructed for
$K_{n-1}$
has been constructed for
![]() $n\geqslant 2$
. In § 4 of [Reference HogancampHog18] it was shown that there is a chain map
$n\geqslant 2$
. In § 4 of [Reference HogancampHog18] it was shown that there is a chain map
![]() $\unicode[STIX]{x1D713}:qP_{n-1}\rightarrow P_{n-1}XY^{-1}$
such that the mapping cone
$\unicode[STIX]{x1D713}:qP_{n-1}\rightarrow P_{n-1}XY^{-1}$
such that the mapping cone
![]() $Q_{n}:=\text{Cone}(\unicode[STIX]{x1D713})$
kills Bott–Samelson bimodules.Footnote
7
Graphically, this is
$Q_{n}:=\text{Cone}(\unicode[STIX]{x1D713})$
kills Bott–Samelson bimodules.Footnote
7
Graphically, this is

From the above characterization of
![]() $P_{n-1}$
, the fact that
$P_{n-1}$
, the fact that
![]() $K_{n-1}$
kills the Bott–Samelson bimodules in
$K_{n-1}$
kills the Bott–Samelson bimodules in
![]() $\mathbb{S}\text{Bim}_{n-1}$
implies that
$\mathbb{S}\text{Bim}_{n-1}$
implies that
![]() $K_{n-1}P_{n-1}\simeq K_{n-1}$
. We define
$K_{n-1}P_{n-1}\simeq K_{n-1}$
. We define
![]() $K_{n}$
by tensoring (2.3) on the left with
$K_{n}$
by tensoring (2.3) on the left with
![]() $K_{n-1}$
and applying the equivalence
$K_{n-1}$
and applying the equivalence
![]() $K_{n-1}P_{n-1}\simeq K_{n-1}$
. Note that
$K_{n-1}P_{n-1}\simeq K_{n-1}$
. Note that
![]() $K_{n}\simeq K_{n-1}Q_{n}$
. The recursion (2) is satisfied after rotating triangles. Clearly
$K_{n}\simeq K_{n-1}Q_{n}$
. The recursion (2) is satisfied after rotating triangles. Clearly
![]() $K_{n}$
kills all Bott–Samelson bimodules on the right since
$K_{n}$
kills all Bott–Samelson bimodules on the right since
![]() $Q_{n}$
does. It was shown in [Reference HogancampHog18] that a complex kills Bott–Samelson bimodules from the right if and only if it kills all Bott–Samelson bimodules from the left. This gives statement (3).◻
$Q_{n}$
does. It was shown in [Reference HogancampHog18] that a complex kills Bott–Samelson bimodules from the right if and only if it kills all Bott–Samelson bimodules from the left. This gives statement (3).◻
Lemma 2.19. The complex
![]() $K_{n}$
absorbs Rouquier complexes: if
$K_{n}$
absorbs Rouquier complexes: if
![]() $\unicode[STIX]{x1D6FD}$
is a braid, then
$\unicode[STIX]{x1D6FD}$
is a braid, then
![]() $K_{n}F(\unicode[STIX]{x1D6FD})\simeq t^{(1/2)e(\unicode[STIX]{x1D6FD})}K_{n}\simeq F(\unicode[STIX]{x1D6FD})K_{n}$
. Recall that
$K_{n}F(\unicode[STIX]{x1D6FD})\simeq t^{(1/2)e(\unicode[STIX]{x1D6FD})}K_{n}\simeq F(\unicode[STIX]{x1D6FD})K_{n}$
. Recall that
![]() $e(\unicode[STIX]{x1D6FD})$
is the braid exponent, which records the number of overcrossings minus the number of undercrossings in a braid word.
$e(\unicode[STIX]{x1D6FD})$
is the braid exponent, which records the number of overcrossings minus the number of undercrossings in a braid word.
Proof. It suffices to prove the result for
![]() $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70E}_{i}^{\pm }$
. In this case the claim is obvious since
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D70E}_{i}^{\pm }$
. In this case the claim is obvious since
![]() $K_{n}$
kills
$K_{n}$
kills
![]() $B_{i}$
, hence the only term of
$B_{i}$
, hence the only term of
![]() $K_{n}F(\unicode[STIX]{x1D70E}_{i}^{\pm })$
which survives is
$K_{n}F(\unicode[STIX]{x1D70E}_{i}^{\pm })$
which survives is
![]() $K_{n}(\pm 1)\langle \mp 1\rangle$
.◻
$K_{n}(\pm 1)\langle \mp 1\rangle$
.◻
Remark 2.20. It is sometimes also useful to consider the following equivalence:

This follows from (2.2) by tensoring on the right with
![]() $Y$
, applying the equivalence
$Y$
, applying the equivalence
![]() $K_{n}Y\simeq t^{(1/2)(1-n)}K_{n}$
.
$K_{n}Y\simeq t^{(1/2)(1-n)}K_{n}$
.
Example 2.21. There is a chain map
![]() $qF(\unicode[STIX]{x1D70E}_{1}^{-1})\rightarrow F(\unicode[STIX]{x1D70E}_{1})$
whose mapping cone is the 4-term complex
$qF(\unicode[STIX]{x1D70E}_{1}^{-1})\rightarrow F(\unicode[STIX]{x1D70E}_{1})$
whose mapping cone is the 4-term complex
There is a projection map
![]() $K_{2}\rightarrow R(-2)\langle 1\rangle$
, the mapping cone on which is
$K_{2}\rightarrow R(-2)\langle 1\rangle$
, the mapping cone on which is
By (2.4), this is homotopy equivalent to the full twist
![]() $\text{FT}_{2}=F(\unicode[STIX]{x1D70E}_{1}^{2})$
on two strands. This fact is also straightforward to check directly.
$\text{FT}_{2}=F(\unicode[STIX]{x1D70E}_{1}^{2})$
on two strands. This fact is also straightforward to check directly.
The construction of
![]() $K_{n}$
appears to be asymmetric. However,
$K_{n}$
appears to be asymmetric. However,
![]() $K_{n}$
is preserved by the symmetries of the Soergel category up to homotopy.
$K_{n}$
is preserved by the symmetries of the Soergel category up to homotopy.
Proposition 2.22. We have
Further,
3 Resolving the full twist
In this section we give a new expression for the Rouquier complex associated to the full twist braid
![]() $\text{FT}_{n}$
. Our main result is that
$\text{FT}_{n}$
. Our main result is that
![]() $\text{FT}_{n}\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
is homotopy equivalent to a convolution whose subquotients are described in terms of shuffle braids and the complexes
$\text{FT}_{n}\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
is homotopy equivalent to a convolution whose subquotients are described in terms of shuffle braids and the complexes
![]() $K_{n}$
.
$K_{n}$
.
3.1 Young–Jucys–Murphy braids
First, we describe the Rouquier complexes for Young–Jucys–Murphy braids as convolutions. We write
![]() $y_{i}=\unicode[STIX]{x1D70E}_{i-1}\cdots \unicode[STIX]{x1D70E}_{2}\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}\cdots \unicode[STIX]{x1D70E}_{i-1}$
for the
$y_{i}=\unicode[STIX]{x1D70E}_{i-1}\cdots \unicode[STIX]{x1D70E}_{2}\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{1}\unicode[STIX]{x1D70E}_{2}\cdots \unicode[STIX]{x1D70E}_{i-1}$
for the
![]() $i$
th Young–Jucys–Murphy braid, which is an element of
$i$
th Young–Jucys–Murphy braid, which is an element of
![]() $\operatorname{Br}_{i}$
. For example,
$\operatorname{Br}_{i}$
. For example,
![]() $y_{4}$
is picture in (2.1). We may also view
$y_{4}$
is picture in (2.1). We may also view
![]() $y_{i}$
as an element of
$y_{i}$
as an element of
![]() $\operatorname{Br}_{n}$
for any
$\operatorname{Br}_{n}$
for any
![]() $n\geqslant i$
, which acts on the first
$n\geqslant i$
, which acts on the first
![]() $i$
strands; this comes from the inclusion
$i$
strands; this comes from the inclusion
![]() $\operatorname{Br}_{i}=\operatorname{Br}_{i}\times 1_{n-i}\subset \operatorname{Br}_{i}\times \operatorname{Br}_{n-i}\rightarrow \operatorname{Br}_{n}$
.
$\operatorname{Br}_{i}=\operatorname{Br}_{i}\times 1_{n-i}\subset \operatorname{Br}_{i}\times \operatorname{Br}_{n-i}\rightarrow \operatorname{Br}_{n}$
.
Definition 3.1. Let
![]() $v\in \{0,1\}^{n}$
be a shuffle on
$v\in \{0,1\}^{n}$
be a shuffle on
![]() $n$
letters, with
$n$
letters, with
![]() $k$
zeroes and
$k$
zeroes and
![]() $\ell$
ones, so that
$\ell$
ones, so that
![]() $k+\ell =n$
. Let
$k+\ell =n$
. Let
![]() $E_{v}\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim})$
be defined as follows:
$E_{v}\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim})$
be defined as follows:
Note that the shuffle braids involved here are left-handed.
Example 3.2. For example, when
![]() $v=(1011001)$
, the complex
$v=(1011001)$
, the complex
![]() $E_{v}$
looks like
$E_{v}$
looks like

In this section the only complexes that concern us are those of the form
![]() $E_{v\cdot 1}$
. Recall that
$E_{v\cdot 1}$
. Recall that
![]() $\cdot$
denotes concatenation of sequences, so that
$\cdot$
denotes concatenation of sequences, so that
![]() $v\cdot 1$
ranges over all sequences which end in 1. Note that (analogously to Proposition 2.6)
$v\cdot 1$
ranges over all sequences which end in 1. Note that (analogously to Proposition 2.6)
![]() $\unicode[STIX]{x1D6FD}_{v\cdot 1}$
is equal to
$\unicode[STIX]{x1D6FD}_{v\cdot 1}$
is equal to
![]() $\unicode[STIX]{x1D6FD}_{v}\sqcup \unicode[STIX]{x1D7D9}_{1}$
, and the right-most strand in
$\unicode[STIX]{x1D6FD}_{v}\sqcup \unicode[STIX]{x1D7D9}_{1}$
, and the right-most strand in
![]() $E_{v\cdot 1}$
is a straight vertical line which does not cross over or under any other strands.
$E_{v\cdot 1}$
is a straight vertical line which does not cross over or under any other strands.
Proposition 3.3. The Rouquier complex
![]() $F(y_{n})$
satisfies
$F(y_{n})$
satisfies
with twisted differential. As usual,
![]() $k$
is the number of zeroes in
$k$
is the number of zeroes in
![]() $v$
and
$v$
and
![]() $\ell$
is the number of ones, with
$\ell$
is the number of ones, with
![]() $k+\ell =n-1$
. The partial order in this convolution is the antilexicographic order on sequences.
$k+\ell =n-1$
. The partial order in this convolution is the antilexicographic order on sequences.
Remark 3.4. Consider the ‘thick crossing’ between
![]() $K_{m}$
and
$K_{m}$
and
![]() $n-m$
parallel strands, which one might picture as
$n-m$
parallel strands, which one might picture as

There is an expression of this complex as a direct sum (with twisted differential) of complexes
![]() $E_{v\cdot 1^{m}}$
with shifts, where
$E_{v\cdot 1^{m}}$
with shifts, where
![]() $v\in \{0,1\}^{n-m}$
. Proposition 3.3 corresponds to the case
$v\in \{0,1\}^{n-m}$
. Proposition 3.3 corresponds to the case
![]() $m=1$
. This is the only case that concerns us, so we leave the statement (and proof) for
$m=1$
. This is the only case that concerns us, so we leave the statement (and proof) for
![]() $m>1$
to the reader.
$m>1$
to the reader.
Proof. We prove this by induction on
![]() $n\geqslant 1$
. In the base case we have
$n\geqslant 1$
. In the base case we have
![]() $y_{1}=1$
and
$y_{1}=1$
and
![]() $F(y_{1})=K_{1}$
. There is exactly one element of
$F(y_{1})=K_{1}$
. There is exactly one element of
![]() $\{0,1\}^{0}$
, the empty sequence, so that the sum on the right-hand side has one term
$\{0,1\}^{0}$
, the empty sequence, so that the sum on the right-hand side has one term
![]() $E_{\emptyset \cdot 1}$
, and that term is
$E_{\emptyset \cdot 1}$
, and that term is
![]() $K_{1}$
. This establishes the base case.
$K_{1}$
. This establishes the base case.
Assume by induction that the result holds for
![]() $n\geqslant 1$
. Note that
$n\geqslant 1$
. Note that
![]() $y_{n+1}=\unicode[STIX]{x1D70E}_{n}y_{n}\unicode[STIX]{x1D70E}_{n}$
. By induction, we have
$y_{n+1}=\unicode[STIX]{x1D70E}_{n}y_{n}\unicode[STIX]{x1D70E}_{n}$
. By induction, we have
with twisted differential, for some grading shifts
![]() $G_{v}$
. Each of the above summands can be rewritten as follows: for fixed
$G_{v}$
. Each of the above summands can be rewritten as follows: for fixed
![]() $v\in \{0,1\}^{n-1}$
, let
$v\in \{0,1\}^{n-1}$
, let
![]() $k$
denote the number of zeroes in
$k$
denote the number of zeroes in
![]() $v$
and
$v$
and
![]() $\ell$
the number of ones. Then the summand corresponding to
$\ell$
the number of ones. Then the summand corresponding to
![]() $v$
is
$v$
is

The first equality (or rather, homotopy equivalence) is a simple isotopy, pulling one strand past the cable of
![]() $l$
strands. In the second equality we have used (2.4). Applying Lemma 2.19 to the first complex on the right,
$l$
strands. In the second equality we have used (2.4). Applying Lemma 2.19 to the first complex on the right,
![]() $K_{\ell +2}$
absorbs the
$K_{\ell +2}$
absorbs the
![]() $\ell$
negative crossings (in the cabled crossing below
$\ell$
negative crossings (in the cabled crossing below
![]() $K_{\ell +2}$
) and one positive crossing (above), gaining an additional grading shift of
$K_{\ell +2}$
) and one positive crossing (above), gaining an additional grading shift of
![]() $t^{1/2-(1/2)\ell }$
. After absorbing these crossings and applying an isotopy to the right-most complex, we obtain
$t^{1/2-(1/2)\ell }$
. After absorbing these crossings and applying an isotopy to the right-most complex, we obtain

The first term is just
![]() $E_{v\cdot 1\cdot 1}$
, and the second is
$E_{v\cdot 1\cdot 1}$
, and the second is
![]() $E_{v\cdot 0\cdot 1}$
. Applying this simplification to each term of the right-hand side of (3.2) completes the inductive step. It remains to verify that the grading shifts and partial order on the convolution are as claimed.
$E_{v\cdot 0\cdot 1}$
. Applying this simplification to each term of the right-hand side of (3.2) completes the inductive step. It remains to verify that the grading shifts and partial order on the convolution are as claimed.
The grading shifts are determined recursively by
![]() $G_{v\cdot 1}=t^{-|v|}G_{v}$
and
$G_{v\cdot 1}=t^{-|v|}G_{v}$
and
![]() $G_{v\cdot 0}=qG_{v}$
, from which the formula
$G_{v\cdot 0}=qG_{v}$
, from which the formula
![]() $G_{v}=t^{-\binom{|v|}{2}}q^{n-1-|v|}$
follows easily.
$G_{v}=t^{-\binom{|v|}{2}}q^{n-1-|v|}$
follows easily.
Suppose that, for two sequences
![]() $v,w\in \{0,1\}^{n-1}$
, the differential from the summand
$v,w\in \{0,1\}^{n-1}$
, the differential from the summand
![]() $E_{v\cdot 1}$
to the summand
$E_{v\cdot 1}$
to the summand
![]() $E_{w\cdot 1}$
is zero in the twisted differential for
$E_{w\cdot 1}$
is zero in the twisted differential for
![]() $F(y_{n})$
. Then replacing
$F(y_{n})$
. Then replacing
![]() $F(\unicode[STIX]{x1D70E}_{n})(E_{v\cdot 1}\sqcup \unicode[STIX]{x1D7D9}_{1})F(\unicode[STIX]{x1D70E}_{n})$
and
$F(\unicode[STIX]{x1D70E}_{n})(E_{v\cdot 1}\sqcup \unicode[STIX]{x1D7D9}_{1})F(\unicode[STIX]{x1D70E}_{n})$
and
![]() $F(\unicode[STIX]{x1D70E}_{n})(E_{w\cdot 1}\sqcup \unicode[STIX]{x1D7D9}_{1})F(\unicode[STIX]{x1D70E}_{n})$
by the equivalent complexes in the right-hand side of (3.3) does not introduce any differential between any of the corresponding terms in the twisted differential for
$F(\unicode[STIX]{x1D70E}_{n})(E_{w\cdot 1}\sqcup \unicode[STIX]{x1D7D9}_{1})F(\unicode[STIX]{x1D70E}_{n})$
by the equivalent complexes in the right-hand side of (3.3) does not introduce any differential between any of the corresponding terms in the twisted differential for
![]() $F(y_{n+1})$
. Moreover, there is no differential from
$F(y_{n+1})$
. Moreover, there is no differential from
![]() $E_{v\cdot 0\cdot 1}$
to
$E_{v\cdot 0\cdot 1}$
to
![]() $E_{v\cdot 1\cdot 1}$
. Therefore, induction implies that the twisted differential respects the antilexicographic order.◻
$E_{v\cdot 1\cdot 1}$
. Therefore, induction implies that the twisted differential respects the antilexicographic order.◻
3.2 The full twist
It is fairly easy to bootstrap this convolution description of the Young–Jucys–Murphy elements into a convolution description of the full twist.
Definition 3.5. Let
![]() $v\in \{0,1\}^{n}$
be a shuffle, with
$v\in \{0,1\}^{n}$
be a shuffle, with
![]() $k$
zeroes and
$k$
zeroes and
![]() $\ell$
ones, so that
$\ell$
ones, so that
![]() $k+\ell =n$
. Then let
$k+\ell =n$
. Then let
![]() $D_{v}\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim})$
be defined as follows:
$D_{v}\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim})$
be defined as follows:
Note that the shuffle braids involved here are right-handed.
Example 3.6. Here is
![]() $D_{v}$
for
$D_{v}$
for
![]() $v=(10101101)$
:
$v=(10101101)$
:

In this example, the last index in
![]() $v$
is a one, so the rightmost strand in
$v$
is a one, so the rightmost strand in
![]() $D_{v}$
does not cross the strands coming from the full twist.
$D_{v}$
does not cross the strands coming from the full twist.
Theorem 3.7. Let
![]() $\text{FT}_{n}$
denote the full right-handed twist on
$\text{FT}_{n}$
denote the full right-handed twist on
![]() $n$
-strands. We have
$n$
-strands. We have
with twisted differential, respecting the antilexicographic order on
![]() $\{0,1\}^{n-1}$
. Here
$\{0,1\}^{n-1}$
. Here
![]() $k$
is the number of zeroes in
$k$
is the number of zeroes in
![]() $v$
.
$v$
.
We have omitted the functor
![]() $F$
from the notation, identifying a braid with its Rouquier complex. We employ this abuse of notation frequently henceforth.
$F$
from the notation, identifying a braid with its Rouquier complex. We employ this abuse of notation frequently henceforth.
Proof. Note that the full twist braid factors as
![]() $\text{FT}_{n+1}=\text{FT}_{n}y_{n+1}$
, where as usual
$\text{FT}_{n+1}=\text{FT}_{n}y_{n+1}$
, where as usual
![]() $\text{FT}_{n}$
is viewed as an element inside
$\text{FT}_{n}$
is viewed as an element inside
![]() $\operatorname{Br}_{n+1}$
via the inclusion
$\operatorname{Br}_{n+1}$
via the inclusion
![]() $\operatorname{Br}_{n}\rightarrow \operatorname{Br}_{n+1}$
. Actually it will be more useful to write
$\operatorname{Br}_{n}\rightarrow \operatorname{Br}_{n+1}$
. Actually it will be more useful to write
Proposition 3.3 gives an expression of the Jucys–Murphy complex
![]() $F(y_{n+1})$
. Tensoring on the left and right with
$F(y_{n+1})$
. Tensoring on the left and right with
![]() $\text{HT}_{n}=\text{HT}_{n}\sqcup \unicode[STIX]{x1D7D9}_{1}$
gives
$\text{HT}_{n}=\text{HT}_{n}\sqcup \unicode[STIX]{x1D7D9}_{1}$
gives
 $$\begin{eqnarray}\displaystyle \text{FT}_{n+1} & \simeq & \displaystyle \bigoplus _{v}G_{v}(\text{HT}_{n}\sqcup \unicode[STIX]{x1D7D9}_{1})(\unicode[STIX]{x1D6FD}_{v}^{L}\sqcup \unicode[STIX]{x1D7D9}_{1})(\unicode[STIX]{x1D7D9}_{k}\sqcup K_{\ell +1})(\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v}^{L})\sqcup \unicode[STIX]{x1D7D9}_{1})(\text{HT}_{n}\sqcup \unicode[STIX]{x1D7D9}_{1})\nonumber\\ \displaystyle & \simeq & \displaystyle \bigoplus _{v}G_{v}((\text{HT}_{n}\unicode[STIX]{x1D6FD}_{v}^{L})\sqcup \unicode[STIX]{x1D7D9}_{1})(\unicode[STIX]{x1D7D9}_{k}\sqcup K_{\ell +1})((\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v}^{L})\text{HT}_{n})\sqcup \unicode[STIX]{x1D7D9}_{1})\nonumber\\ \displaystyle & \simeq & \displaystyle \bigoplus _{v}G_{v}(\unicode[STIX]{x1D6FD}_{r(v)}\sqcup \unicode[STIX]{x1D7D9}_{1})(\text{HT}_{k}\sqcup \text{HT}_{\ell }\sqcup \unicode[STIX]{x1D7D9}_{1})(\unicode[STIX]{x1D7D9}_{k}\sqcup K_{\ell +1})(\text{HT}_{k}\sqcup \text{HT}_{\ell }\sqcup \unicode[STIX]{x1D7D9}_{1})(\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{r(v)})\sqcup \unicode[STIX]{x1D7D9})\nonumber\\ \displaystyle & \simeq & \displaystyle \bigoplus _{v}G_{v}t^{\binom{\ell }{2}}(\unicode[STIX]{x1D6FD}_{r(v)}\sqcup \unicode[STIX]{x1D7D9}_{1})(\text{FT}_{k}\sqcup K_{\ell +1})(\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{r(v)})\sqcup \unicode[STIX]{x1D7D9}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{FT}_{n+1} & \simeq & \displaystyle \bigoplus _{v}G_{v}(\text{HT}_{n}\sqcup \unicode[STIX]{x1D7D9}_{1})(\unicode[STIX]{x1D6FD}_{v}^{L}\sqcup \unicode[STIX]{x1D7D9}_{1})(\unicode[STIX]{x1D7D9}_{k}\sqcup K_{\ell +1})(\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v}^{L})\sqcup \unicode[STIX]{x1D7D9}_{1})(\text{HT}_{n}\sqcup \unicode[STIX]{x1D7D9}_{1})\nonumber\\ \displaystyle & \simeq & \displaystyle \bigoplus _{v}G_{v}((\text{HT}_{n}\unicode[STIX]{x1D6FD}_{v}^{L})\sqcup \unicode[STIX]{x1D7D9}_{1})(\unicode[STIX]{x1D7D9}_{k}\sqcup K_{\ell +1})((\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{v}^{L})\text{HT}_{n})\sqcup \unicode[STIX]{x1D7D9}_{1})\nonumber\\ \displaystyle & \simeq & \displaystyle \bigoplus _{v}G_{v}(\unicode[STIX]{x1D6FD}_{r(v)}\sqcup \unicode[STIX]{x1D7D9}_{1})(\text{HT}_{k}\sqcup \text{HT}_{\ell }\sqcup \unicode[STIX]{x1D7D9}_{1})(\unicode[STIX]{x1D7D9}_{k}\sqcup K_{\ell +1})(\text{HT}_{k}\sqcup \text{HT}_{\ell }\sqcup \unicode[STIX]{x1D7D9}_{1})(\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{r(v)})\sqcup \unicode[STIX]{x1D7D9})\nonumber\\ \displaystyle & \simeq & \displaystyle \bigoplus _{v}G_{v}t^{\binom{\ell }{2}}(\unicode[STIX]{x1D6FD}_{r(v)}\sqcup \unicode[STIX]{x1D7D9}_{1})(\text{FT}_{k}\sqcup K_{\ell +1})(\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6FD}_{r(v)})\sqcup \unicode[STIX]{x1D7D9}).\nonumber\end{eqnarray}$$
Here,
![]() $G_{v}=t^{-\binom{\ell }{2}}q^{k}$
is the shift determined by Proposition 3.3. The second equivalence is simply given by reassociating. The third equivalence holds by Proposition 2.9, which describes how
$G_{v}=t^{-\binom{\ell }{2}}q^{k}$
is the shift determined by Proposition 3.3. The second equivalence is simply given by reassociating. The third equivalence holds by Proposition 2.9, which describes how
![]() $\text{HT}_{n}$
interacts with shuffle braids. The last equivalence holds since
$\text{HT}_{n}$
interacts with shuffle braids. The last equivalence holds since
![]() $K_{\ell +1}$
absorbs the two copies of
$K_{\ell +1}$
absorbs the two copies of
![]() $\text{HT}_{\ell }$
(each of which has
$\text{HT}_{\ell }$
(each of which has
![]() $\binom{\ell }{2}$
crossings), and the two copies of
$\binom{\ell }{2}$
crossings), and the two copies of
![]() $\text{HT}_{k}$
contribute a factor of
$\text{HT}_{k}$
contribute a factor of
![]() $\text{FT}_{k}$
. The grading shift on each summand is
$\text{FT}_{k}$
. The grading shift on each summand is
![]() $G_{v}t^{\binom{\ell }{2}}=q^{k}$
, as claimed. This completes the proof.◻
$G_{v}t^{\binom{\ell }{2}}=q^{k}$
, as claimed. This completes the proof.◻
Remark 3.8. One can construct convolution descriptions of other torus links in much the same way. At the moment, we have done this ad hoc for small torus links, and have neglected to write it down here for reasons of space. It would be interesting to find a combinatorial framework (analogous to shuffles) in order to treat the general torus link in a more holistic fashion. The results of the next chapter, including the parity miracle which makes these convolution descriptions useful, can also be adapted to our small examples in a straightforward way. The fruits of this labor are presented in the appendix.
4 Resolving the Hochschild homology of the full twist
In this section we introduce Hochschild cohomology
![]() $\operatorname{HH}$
, and we compute
$\operatorname{HH}$
, and we compute
![]() $\operatorname{HH}(\text{FT}_{n})$
for all
$\operatorname{HH}(\text{FT}_{n})$
for all
![]() $n\geqslant 1$
. Our strategy is recursive. The main result of the previous section expresses
$n\geqslant 1$
. Our strategy is recursive. The main result of the previous section expresses
![]() $\text{FT}_{n}$
as a filtered complex whose subquotients are of the form
$\text{FT}_{n}$
as a filtered complex whose subquotients are of the form
![]() $D_{v}$
. In this section we show that
$D_{v}$
. In this section we show that
![]() $\operatorname{HH}(D_{v})$
has a filtration in terms of other
$\operatorname{HH}(D_{v})$
has a filtration in terms of other
![]() $\operatorname{HH}(D_{w})$
, with smaller
$\operatorname{HH}(D_{w})$
, with smaller
![]() $w$
. However, we will find it convenient to work instead with related complexes
$w$
. However, we will find it convenient to work instead with related complexes
![]() $C_{v}$
, to be defined in § 4.4.
$C_{v}$
, to be defined in § 4.4.
4.1 Hochschild cohomology
The zeroth Hochschild cohomology functor
![]() $\operatorname{HH}^{0}$
is the functor which takes a graded
$\operatorname{HH}^{0}$
is the functor which takes a graded
![]() $R$
-bimodule
$R$
-bimodule
![]() $M$
to the graded vector space
$M$
to the graded vector space
![]() $\bigoplus _{m\in \mathbb{Z}}\text{Hom}(R,M(m))$
of bimodule maps of all degrees. Its higher derived functors
$\bigoplus _{m\in \mathbb{Z}}\text{Hom}(R,M(m))$
of bimodule maps of all degrees. Its higher derived functors
![]() $\operatorname{HH}^{k}$
are packaged together in a single functor
$\operatorname{HH}^{k}$
are packaged together in a single functor
![]() $\operatorname{HH}=\bigoplus _{k\geqslant 0}\operatorname{HH}^{k}:\mathbb{S}\text{Bim}_{n}\rightarrow \mathbb{Q}\text{-}\mathbf{vect}^{\mathbb{Z}\times \mathbb{Z}}$
, where this latter category is the category of bigraded vector spaces. The two gradings are the internal grading of the bimodule (the
$\operatorname{HH}=\bigoplus _{k\geqslant 0}\operatorname{HH}^{k}:\mathbb{S}\text{Bim}_{n}\rightarrow \mathbb{Q}\text{-}\mathbf{vect}^{\mathbb{Z}\times \mathbb{Z}}$
, where this latter category is the category of bigraded vector spaces. The two gradings are the internal grading of the bimodule (the
![]() $m$
in the direct sum above), and the Hochschild cohomological grading
$m$
in the direct sum above), and the Hochschild cohomological grading
![]() $k$
, which we call the Hochschild grading.
$k$
, which we call the Hochschild grading.
Extending to complexes gives a functor
![]() $\operatorname{HH}:{\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})\rightarrow {\mathcal{K}}^{b}(\mathbb{Q}\text{-}\mathbf{vect}^{\mathbb{Z}\times \mathbb{Z}})$
. Given a complex
$\operatorname{HH}:{\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})\rightarrow {\mathcal{K}}^{b}(\mathbb{Q}\text{-}\mathbf{vect}^{\mathbb{Z}\times \mathbb{Z}})$
. Given a complex
![]() $C$
,
$C$
,
![]() $\operatorname{HH}^{0}(C)$
is the complex
$\operatorname{HH}^{0}(C)$
is the complex
![]() $\operatorname{RHom}(R,C)$
used to compute maps of all internal and homological degrees from the complex
$\operatorname{RHom}(R,C)$
used to compute maps of all internal and homological degrees from the complex
![]() $R$
(concentrated in a single homological degree) to
$R$
(concentrated in a single homological degree) to
![]() $C$
. The homology of
$C$
. The homology of
![]() $\operatorname{HH}(C)$
and
$\operatorname{HH}(C)$
and
![]() $\operatorname{HH}^{0}(C)$
are denoted by
$\operatorname{HH}^{0}(C)$
are denoted by
![]() $\operatorname{HHH}(C)$
and
$\operatorname{HHH}(C)$
and
![]() $\operatorname{HHH}^{0}(C)$
. When we wish to emphasize the index
$\operatorname{HHH}^{0}(C)$
. When we wish to emphasize the index
![]() $n$
(which is not a degree, but the number of strands) we will write
$n$
(which is not a degree, but the number of strands) we will write
![]() $\operatorname{HH}(R_{n};C)$
,
$\operatorname{HH}(R_{n};C)$
,
![]() $\operatorname{HH}^{0}(R_{n};C)$
, and so on.
$\operatorname{HH}^{0}(R_{n};C)$
, and so on.
Note that
![]() $\operatorname{HH}(C)$
is triply graded. We will denote shifts in the tridegree by
$\operatorname{HH}(C)$
is triply graded. We will denote shifts in the tridegree by
![]() $Q^{i}A^{j}T^{k}\operatorname{HH}(C)$
, where
$Q^{i}A^{j}T^{k}\operatorname{HH}(C)$
, where
![]() $Q$
is the usual degree,
$Q$
is the usual degree,
![]() $A$
is Hochschild degree, and
$A$
is Hochschild degree, and
![]() $T$
is homological degree. In previous sections we found it useful to introduce the variables (or grading shifts)
$T$
is homological degree. In previous sections we found it useful to introduce the variables (or grading shifts)
![]() $t=T^{2}Q^{-2}$
and
$t=T^{2}Q^{-2}$
and
![]() $q=Q^{2}$
. In what follows it will prove convenient to package the Hochschild and
$q=Q^{2}$
. In what follows it will prove convenient to package the Hochschild and
![]() $q$
-degrees together by introducing
$q$
-degrees together by introducing
![]() $a=AQ^{-2}$
. We write
$a=AQ^{-2}$
. We write
![]() ${\mathcal{P}}_{C}(q,a,t)$
for the Poincaré series of
${\mathcal{P}}_{C}(q,a,t)$
for the Poincaré series of
![]() $\operatorname{HHH}(C)$
.
$\operatorname{HHH}(C)$
.
The experienced reader may wish to orient himself or herself by observing that in these conventions, we have
which is the Hochschild cohomology of the ring
![]() $\mathbb{Q}[x]$
as a bimodule over itself. The reader should think of
$\mathbb{Q}[x]$
as a bimodule over itself. The reader should think of
![]() $(1-q)^{-1}$
as the Poincaré series of
$(1-q)^{-1}$
as the Poincaré series of
![]() $\mathbb{Q}[x]$
itself, and
$\mathbb{Q}[x]$
itself, and
![]() $(1+a)$
as the Poincaré series of the exterior algebra in one variable. Similarly,
$(1+a)$
as the Poincaré series of the exterior algebra in one variable. Similarly,
![]() ${\mathcal{P}}_{R_{n}}=(1+a)^{n}(1-q)^{-n}$
.
${\mathcal{P}}_{R_{n}}=(1+a)^{n}(1-q)^{-n}$
.
Example 4.1. We have
![]() ${\mathcal{P}}_{B_{s}}=(1-Q^{2})^{-n}(1+Q^{-2}A)^{n-1}(Q+Q^{-3}A)$
. Here is a brief conceptual explanation. Consider the Koszul complex which resolves
${\mathcal{P}}_{B_{s}}=(1-Q^{2})^{-n}(1+Q^{-2}A)^{n-1}(Q+Q^{-3}A)$
. Here is a brief conceptual explanation. Consider the Koszul complex which resolves
![]() $R$
by free
$R$
by free
![]() $R$
-bimodules. Applying
$R$
-bimodules. Applying
![]() $\text{Hom}$
to
$\text{Hom}$
to
![]() $R$
, the differentials all become zero, yielding
$R$
, the differentials all become zero, yielding
![]() $(1+Q^{-2}A)^{n}$
times the Poincaré series of
$(1+Q^{-2}A)^{n}$
times the Poincaré series of
![]() $R$
, as for
$R$
, as for
![]() ${\mathcal{P}}_{R}$
above. Applying
${\mathcal{P}}_{R}$
above. Applying
![]() $\text{Hom}$
to
$\text{Hom}$
to
![]() $B_{s}$
instead, one of the differentials in the Kozsul complex is non-zero, becoming the middle differential in Example 2.21, except dualized. Thus this differential yields a factor of
$B_{s}$
instead, one of the differentials in the Kozsul complex is non-zero, becoming the middle differential in Example 2.21, except dualized. Thus this differential yields a factor of
![]() $(Q+Q^{-3}A)$
instead. We will not use this computation.
$(Q+Q^{-3}A)$
instead. We will not use this computation.
Definition 4.2. We say that two complexes
![]() $A,B\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
are
$A,B\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
are
![]() $\operatorname{HH}$
-equivalent if
$\operatorname{HH}$
-equivalent if
![]() $\operatorname{HH}(A)\simeq \operatorname{HH}(B)$
as complexes of triply graded vector spaces. In this case we will write
$\operatorname{HH}(A)\simeq \operatorname{HH}(B)$
as complexes of triply graded vector spaces. In this case we will write
![]() $A\sim B$
.
$A\sim B$
.
The basic property of Hochschild cohomology which motivates its relationship with braid closures is that
![]() $\operatorname{HH}(CD)\cong \operatorname{HH}(DC)$
whenever these tensor products make sense (e.g. if
$\operatorname{HH}(CD)\cong \operatorname{HH}(DC)$
whenever these tensor products make sense (e.g. if
![]() $C,D\in {\mathcal{K}}(\mathbb{S}\text{Bim}_{n})$
are simultaneously bounded above or below). Thus, any complex
$C,D\in {\mathcal{K}}(\mathbb{S}\text{Bim}_{n})$
are simultaneously bounded above or below). Thus, any complex
![]() $C$
is
$C$
is
![]() $\operatorname{HH}$
-equivalent to
$\operatorname{HH}$
-equivalent to
![]() $F(\unicode[STIX]{x1D6FD})CF(\unicode[STIX]{x1D6FD}^{-1})$
for any braid
$F(\unicode[STIX]{x1D6FD})CF(\unicode[STIX]{x1D6FD}^{-1})$
for any braid
![]() $\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}$
.
Note that
![]() $\operatorname{HH}^{i}$
can actually be viewed as a map from
$\operatorname{HH}^{i}$
can actually be viewed as a map from
![]() $R$
-bimodules to the subcategory of
$R$
-bimodules to the subcategory of
![]() $R$
-bimodules for which the left and right actions agree, which can be identified with
$R$
-bimodules for which the left and right actions agree, which can be identified with
![]() $R$
-modules. However, the isomorphism
$R$
-modules. However, the isomorphism
![]() $\operatorname{HH}(CD)\cong \operatorname{HH}(DC)$
is not an isomorphism of (complexes of)
$\operatorname{HH}(CD)\cong \operatorname{HH}(DC)$
is not an isomorphism of (complexes of)
![]() $R$
-bimodules, only of their underlying vector spaces. Nonetheless, there is still an action of
$R$
-bimodules, only of their underlying vector spaces. Nonetheless, there is still an action of
![]() $R_{n}$
on any Hochschild complex
$R_{n}$
on any Hochschild complex
![]() $\operatorname{HH}^{i}(R_{n};C)$
.
$\operatorname{HH}^{i}(R_{n};C)$
.
Remark 4.3. The isomorphism
![]() $\operatorname{HH}(R_{n};CD)\cong \operatorname{HH}(R_{n};DC)$
of complexes of vector spaces does actually lift to an isomorphism of modules over the invariant subring
$\operatorname{HH}(R_{n};CD)\cong \operatorname{HH}(R_{n};DC)$
of complexes of vector spaces does actually lift to an isomorphism of modules over the invariant subring
![]() $R^{S_{n}}$
.
$R^{S_{n}}$
.
4.2 The Markov move for Jones–Wenzl projectors
The Markov move states that the closure of a braid
![]() $\unicode[STIX]{x1D6FD}$
on
$\unicode[STIX]{x1D6FD}$
on
![]() $n-1$
strands is isotopic (as a link) to the closure of the braid
$n-1$
strands is isotopic (as a link) to the closure of the braid
![]() $\unicode[STIX]{x1D70E}_{n-1}^{\pm }(\unicode[STIX]{x1D6FD}\sqcup \unicode[STIX]{x1D7D9}_{1})$
on
$\unicode[STIX]{x1D70E}_{n-1}^{\pm }(\unicode[STIX]{x1D6FD}\sqcup \unicode[STIX]{x1D7D9}_{1})$
on
![]() $n$
strands. To prove that
$n$
strands. To prove that
![]() $\operatorname{HHH}$
is a link invariant, Khovanov [Reference KhovanovKho07] proved a result comparing
$\operatorname{HHH}$
is a link invariant, Khovanov [Reference KhovanovKho07] proved a result comparing
![]() $\operatorname{HH}(R_{n-1};\unicode[STIX]{x1D6FD})$
and
$\operatorname{HH}(R_{n-1};\unicode[STIX]{x1D6FD})$
and
![]() $\operatorname{HH}(R_{n};\unicode[STIX]{x1D70E}_{n-1}^{\pm }(\unicode[STIX]{x1D6FD}\sqcup \unicode[STIX]{x1D7D9}_{1}))$
. In this paper, we will need a similar result, comparing
$\operatorname{HH}(R_{n};\unicode[STIX]{x1D70E}_{n-1}^{\pm }(\unicode[STIX]{x1D6FD}\sqcup \unicode[STIX]{x1D7D9}_{1}))$
. In this paper, we will need a similar result, comparing
![]() $\operatorname{HH}(R_{n-1};K_{n-1})$
and
$\operatorname{HH}(R_{n-1};K_{n-1})$
and
![]() $\operatorname{HH}(R_{n};K_{n})$
.
$\operatorname{HH}(R_{n};K_{n})$
.
Proposition 4.4. Suppose that
![]() $2\leqslant n$
. Let
$2\leqslant n$
. Let
![]() $C\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n-1})$
be viewed as a complex in
$C\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n-1})$
be viewed as a complex in
![]() ${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
via the usual inclusion functor. We have
${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
via the usual inclusion functor. We have
This can also be described as
where
![]() $\deg (\unicode[STIX]{x1D709}_{n})=t^{1-n}a$
. Hence
$\deg (\unicode[STIX]{x1D709}_{n})=t^{1-n}a$
. Hence
![]() ${\mathcal{P}}_{CK_{n}}=(t^{n-1}+a){\mathcal{P}}_{CK_{n-1}}$
.
${\mathcal{P}}_{CK_{n}}=(t^{n-1}+a){\mathcal{P}}_{CK_{n-1}}$
.
Proof. We use results in [Reference HogancampHog18]. Let
![]() ${\mathcal{C}}_{n}$
denote the bounded derived category of graded
${\mathcal{C}}_{n}$
denote the bounded derived category of graded
![]() $(R_{n},R_{n})$
-bimodules, where
$(R_{n},R_{n})$
-bimodules, where
![]() $R_{n}=\mathbb{Q}[x_{1},\ldots ,x_{n}]$
as usual. Let
$R_{n}=\mathbb{Q}[x_{1},\ldots ,x_{n}]$
as usual. Let
![]() ${\mathcal{D}}_{n}={\mathcal{K}}^{b}({\mathcal{C}}_{n})$
denote the homotopy category of
${\mathcal{D}}_{n}={\mathcal{K}}^{b}({\mathcal{C}}_{n})$
denote the homotopy category of
![]() ${\mathcal{C}}_{n}$
. Note that
${\mathcal{C}}_{n}$
. Note that
![]() $\mathbb{S}\text{Bim}_{n}$
includes as a full subcategory of
$\mathbb{S}\text{Bim}_{n}$
includes as a full subcategory of
![]() ${\mathcal{C}}_{n}$
, and
${\mathcal{C}}_{n}$
, and
![]() ${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
includes as a full subcategory of
${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
includes as a full subcategory of
![]() ${\mathcal{D}}_{n}$
. In case
${\mathcal{D}}_{n}$
. In case
![]() $n=0$
,
$n=0$
,
![]() ${\mathcal{D}}_{0}$
is equivalent to the category
${\mathcal{D}}_{0}$
is equivalent to the category
![]() $\mathbb{Q}^{\mathbb{Z}\times \mathbb{Z}\times \mathbb{Z}}$
of triply graded vector spaces.
$\mathbb{Q}^{\mathbb{Z}\times \mathbb{Z}\times \mathbb{Z}}$
of triply graded vector spaces.
There is a partial Hochschild cohomology functor
![]() $T_{n}\,:\,{\mathcal{D}}_{n}\rightarrow {\mathcal{D}}_{n-1}$
, such that
$T_{n}\,:\,{\mathcal{D}}_{n}\rightarrow {\mathcal{D}}_{n-1}$
, such that
![]() $\operatorname{HH}=T_{1}\circ \cdots \circ \,T_{n}$
. These can be defined as the right adjoints to the standard inclusions
$\operatorname{HH}=T_{1}\circ \cdots \circ \,T_{n}$
. These can be defined as the right adjoints to the standard inclusions
![]() $I_{n}:{\mathcal{D}}_{n-1}\rightarrow {\mathcal{D}}_{n}$
. We usually abuse notation, and write
$I_{n}:{\mathcal{D}}_{n-1}\rightarrow {\mathcal{D}}_{n}$
. We usually abuse notation, and write
![]() $C$
when we mean
$C$
when we mean
![]() $I(C)$
. For each
$I(C)$
. For each
![]() $C\in {\mathcal{D}}_{n-1}$
and each
$C\in {\mathcal{D}}_{n-1}$
and each
![]() $D\in {\mathcal{D}}_{n}$
we have
$D\in {\mathcal{D}}_{n}$
we have
Recall from the proof of Proposition 2.18 that
![]() $K_{n}\simeq K_{n-1}Q_{n}$
, so that
$K_{n}\simeq K_{n-1}Q_{n}$
, so that
![]() $T_{n}(K_{n})\simeq K_{n-1}T_{n}(Q_{n})$
. It was proven in § 4 of [Reference HogancampHog18] that
$T_{n}(K_{n})\simeq K_{n-1}T_{n}(Q_{n})$
. It was proven in § 4 of [Reference HogancampHog18] that
![]() $T_{n}(Q_{n})\simeq t^{n-1}P_{n-1}\otimes \unicode[STIX]{x1D6EC}[\unicode[STIX]{x1D709}_{n}]$
. Since
$T_{n}(Q_{n})\simeq t^{n-1}P_{n-1}\otimes \unicode[STIX]{x1D6EC}[\unicode[STIX]{x1D709}_{n}]$
. Since
![]() $K_{n-1}P_{n-1}\simeq K_{n-1}$
, we conclude that
$K_{n-1}P_{n-1}\simeq K_{n-1}$
, we conclude that
From this, the proposition follows from the observation that
![]() $\operatorname{HH}=T_{1}\circ \cdots \circ T_{n}$
.◻
$\operatorname{HH}=T_{1}\circ \cdots \circ T_{n}$
.◻
In our reduction algorithm to come, we need a relative version of the above proposition.
Corollary 4.5. Suppose that
![]() $2\leqslant \ell \leqslant n$
, with
$2\leqslant \ell \leqslant n$
, with
![]() $n=k+\ell$
. Let
$n=k+\ell$
. Let
![]() $C\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n-1})$
be viewed as a complex in
$C\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n-1})$
be viewed as a complex in
![]() ${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
via the usual inclusion functor. We have
${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
via the usual inclusion functor. We have
Hence
![]() ${\mathcal{P}}_{C(\unicode[STIX]{x1D7D9}_{k}\sqcup K_{\ell })}=(t^{\ell -1}+a){\mathcal{P}}_{C(\unicode[STIX]{x1D7D9}_{k}\sqcup K_{\ell -1})}$
.
${\mathcal{P}}_{C(\unicode[STIX]{x1D7D9}_{k}\sqcup K_{\ell })}=(t^{\ell -1}+a){\mathcal{P}}_{C(\unicode[STIX]{x1D7D9}_{k}\sqcup K_{\ell -1})}$
.
Proof. We picture the partial trace
![]() $T_{n}:{\mathcal{D}}_{n}\rightarrow {\mathcal{D}}_{n-1}$
graphically as identifying the top right and bottom right strands. The statement of the Lemma then becomes
$T_{n}:{\mathcal{D}}_{n}\rightarrow {\mathcal{D}}_{n-1}$
graphically as identifying the top right and bottom right strands. The statement of the Lemma then becomes

whose proof is immediate given (4.2).◻
This corollary allows one to slowly shrink copies of
![]() $K_{\ell }$
that appear, reducing the number of strands in the process. However, the case
$K_{\ell }$
that appear, reducing the number of strands in the process. However, the case
![]() $\ell =1$
is separate; diagrammatically, this corresponds to taking the complex
$\ell =1$
is separate; diagrammatically, this corresponds to taking the complex
![]() $C$
and adding a circle, since
$C$
and adding a circle, since
![]() $K_{1}$
is the identity.
$K_{1}$
is the identity.
Proposition 4.6. Let
![]() $C\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n-1})$
be viewed as a complex in
$C\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n-1})$
be viewed as a complex in
![]() ${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
via the usual inclusion functor. We have
${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
via the usual inclusion functor. We have
where
![]() $\deg (\unicode[STIX]{x1D709}_{1})=Q^{-2}A=a$
. Hence
$\deg (\unicode[STIX]{x1D709}_{1})=Q^{-2}A=a$
. Hence
![]() ${\mathcal{P}}_{C\sqcup K_{1}}=(1-q)^{-1}(1+a){\mathcal{P}}_{C}$
.
${\mathcal{P}}_{C\sqcup K_{1}}=(1-q)^{-1}(1+a){\mathcal{P}}_{C}$
.
Proof. In general,
![]() $\operatorname{HHH}(A\sqcup B)\cong \operatorname{HHH}(A)\otimes \operatorname{HHH}(B)$
. Hence this proposition just amounts to the observation that
$\operatorname{HHH}(A\sqcup B)\cong \operatorname{HHH}(A)\otimes \operatorname{HHH}(B)$
. Hence this proposition just amounts to the observation that
![]() $\operatorname{HHH}(\mathbb{Q}[x_{n}])\cong \mathbb{Q}[x_{n}]\otimes \unicode[STIX]{x1D6EC}[\unicode[STIX]{x1D709}_{1}]$
. This may be pictured as
$\operatorname{HHH}(\mathbb{Q}[x_{n}])\cong \mathbb{Q}[x_{n}]\otimes \unicode[STIX]{x1D6EC}[\unicode[STIX]{x1D709}_{1}]$
. This may be pictured as

We will also call results like these
![]() $\operatorname{HH}$
-equivalences.
$\operatorname{HH}$
-equivalences.
Definition 4.7. We extend Definition 4.2 above to say that two complexes
![]() $A\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
and
$A\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
and
![]() $B\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{k})$
are
$B\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{k})$
are
![]() $\operatorname{HH}$
-equivalent, written
$\operatorname{HH}$
-equivalent, written
![]() $A\sim B$
, if
$A\sim B$
, if
![]() $\operatorname{HH}(A)\simeq \operatorname{HH}(B)$
as complexes of triply graded vector spaces. Note that
$\operatorname{HH}(A)\simeq \operatorname{HH}(B)$
as complexes of triply graded vector spaces. Note that
![]() $n$
and
$n$
and
![]() $k$
need not be equal. The complexes
$k$
need not be equal. The complexes
![]() $A$
and
$A$
and
![]() $B$
are allowed to have built-in formal Hochschild grading shifts.
$B$
are allowed to have built-in formal Hochschild grading shifts.
4.3 Reduced complexes
Observe that the formulas for
![]() ${\mathcal{P}}_{C(\unicode[STIX]{x1D7D9}_{k}\sqcup K_{\ell })}$
for
${\mathcal{P}}_{C(\unicode[STIX]{x1D7D9}_{k}\sqcup K_{\ell })}$
for
![]() $\ell \geqslant 2$
and
$\ell \geqslant 2$
and
![]() $\ell =1$
do not follow the same pattern, as the
$\ell =1$
do not follow the same pattern, as the
![]() $\ell =1$
case has an extra factor of
$\ell =1$
case has an extra factor of
![]() $(1-q)^{-1}$
. We will need to use both (4.3) and (4.5) in our recursion for
$(1-q)^{-1}$
. We will need to use both (4.3) and (4.5) in our recursion for
![]() $\operatorname{HHH}(\text{FT}_{n})$
, and the differences between these two formulas lead to a bookkeeping nightmare. Instead, we will introduce the reduced complexes
$\operatorname{HHH}(\text{FT}_{n})$
, and the differences between these two formulas lead to a bookkeeping nightmare. Instead, we will introduce the reduced complexes
![]() $\hat{K}_{\ell }$
, which admit a streamlined formula which works for
$\hat{K}_{\ell }$
, which admit a streamlined formula which works for
![]() $\ell =1$
as well as for
$\ell =1$
as well as for
![]() $\ell \geqslant 2$
.
$\ell \geqslant 2$
.
Definition 4.8. For each complex
![]() $C\in {\mathcal{K}}(\mathbb{S}\text{Bim}_{n})$
and each element
$C\in {\mathcal{K}}(\mathbb{S}\text{Bim}_{n})$
and each element
![]() $f\in R_{n}$
of the ground ring, let
$f\in R_{n}$
of the ground ring, let
![]() $f\operatorname{Id}_{C}$
and
$f\operatorname{Id}_{C}$
and
![]() $\operatorname{Id}_{C}f$
denote the endomorphisms of
$\operatorname{Id}_{C}f$
denote the endomorphisms of
![]() $C$
given by left and right multiplication by
$C$
given by left and right multiplication by
![]() $f$
, respectively. Set
$f$
, respectively. Set
![]() ${\hat{C}}:=\text{Cone}(x_{n}\operatorname{Id}_{C})$
.
${\hat{C}}:=\text{Cone}(x_{n}\operatorname{Id}_{C})$
.
Remark 4.9. Effectively,
![]() ${\hat{C}}$
is the result of killing the left action of
${\hat{C}}$
is the result of killing the left action of
![]() $x_{n}$
on
$x_{n}$
on
![]() $C$
. Indeed, since
$C$
. Indeed, since
![]() $R_{n}$
acts freely on Soergel bimodules, standard arguments imply that
$R_{n}$
acts freely on Soergel bimodules, standard arguments imply that
![]() ${\hat{C}}\simeq C/x_{n}C$
. Thus, one may think of
${\hat{C}}\simeq C/x_{n}C$
. Thus, one may think of
![]() ${\hat{C}}$
as a reduced version of
${\hat{C}}$
as a reduced version of
![]() $C$
. The usual reduced complex is the mapping cone on
$C$
. The usual reduced complex is the mapping cone on
![]() $e_{1}\operatorname{Id}_{C}$
(equivalently, the quotient
$e_{1}\operatorname{Id}_{C}$
(equivalently, the quotient
![]() $C/e_{1}C$
), where
$C/e_{1}C$
), where
![]() $e_{1}=x_{1}+\cdots +x_{n}$
. The two notions are related, but generally different. Our sole reason for introducing
$e_{1}=x_{1}+\cdots +x_{n}$
. The two notions are related, but generally different. Our sole reason for introducing
![]() ${\hat{C}}$
is have a functorial way of converting expressions involving
${\hat{C}}$
is have a functorial way of converting expressions involving
![]() $K_{n}$
to expressions involving
$K_{n}$
to expressions involving
![]() $\hat{K}_{n}$
.
$\hat{K}_{n}$
.
The relationship between
![]() $\hat{K}_{n}$
and
$\hat{K}_{n}$
and
![]() $K_{n}$
is best understood as follows. Let
$K_{n}$
is best understood as follows. Let
![]() $P_{n}$
be the complex introduced in [Reference HogancampHog18], whose definition is recalled in the proof of Proposition 2.18. Let
$P_{n}$
be the complex introduced in [Reference HogancampHog18], whose definition is recalled in the proof of Proposition 2.18. Let
![]() $\text{END}(P_{n})$
denote the bigraded ring spanned by all homogeneous chain maps
$\text{END}(P_{n})$
denote the bigraded ring spanned by all homogeneous chain maps
![]() $Q^{i}T^{j}P_{n}\rightarrow P_{n}$
modulo homotopy. In [Reference HogancampHog18] the second author showed that
$Q^{i}T^{j}P_{n}\rightarrow P_{n}$
modulo homotopy. In [Reference HogancampHog18] the second author showed that
![]() $\text{END}(P_{n})\cong \mathbb{Q}[u_{1},u_{2},\ldots ,u_{n}]$
, where the
$\text{END}(P_{n})\cong \mathbb{Q}[u_{1},u_{2},\ldots ,u_{n}]$
, where the
![]() $u_{k}$
are variables of bidegree
$u_{k}$
are variables of bidegree
![]() $\deg (u_{k})=Q^{2k}T^{2-2k}=qt^{1-k}$
. In particular,
$\deg (u_{k})=Q^{2k}T^{2-2k}=qt^{1-k}$
. In particular,
![]() $u_{1}$
has degree
$u_{1}$
has degree
![]() $q$
, and is represented by left or right multiplication by
$q$
, and is represented by left or right multiplication by
![]() $x_{i}\in R$
in the ground ring (in [Reference HogancampHog18] it is shown that all such maps are homotopic; see also the proof of Lemma 4.10 below).
$x_{i}\in R$
in the ground ring (in [Reference HogancampHog18] it is shown that all such maps are homotopic; see also the proof of Lemma 4.10 below).
The complex
![]() $K_{n}$
can be interpreted as the total complex of the Koszul complex associated to the action of
$K_{n}$
can be interpreted as the total complex of the Koszul complex associated to the action of
![]() $u_{2},\ldots ,u_{n}$
acting on
$u_{2},\ldots ,u_{n}$
acting on
![]() $P_{n}$
. Precisely:
$P_{n}$
. Precisely:
![]() $K_{n}\simeq \text{Cone}(u_{2})\text{Cone}(u_{3})\cdots \text{Cone}(u_{n})$
, where concatenation denotes tensor product. This description clarifies the manner in which our definition of
$K_{n}\simeq \text{Cone}(u_{2})\text{Cone}(u_{3})\cdots \text{Cone}(u_{n})$
, where concatenation denotes tensor product. This description clarifies the manner in which our definition of
![]() $K_{n}$
gives special treatment to the case
$K_{n}$
gives special treatment to the case
![]() $n=1$
. A more equitable construction would also include a factor of
$n=1$
. A more equitable construction would also include a factor of
![]() $\text{Cone}(u_{1})$
. By our comments above, this is precisely what
$\text{Cone}(u_{1})$
. By our comments above, this is precisely what
![]() $\hat{K}_{n}$
does:
$\hat{K}_{n}$
does:
![]() $\hat{K}_{n}\simeq \text{Cone}(u_{1})\text{Cone}(u_{2})\cdots \text{Cone}(u_{n})$
.
$\hat{K}_{n}\simeq \text{Cone}(u_{1})\text{Cone}(u_{2})\cdots \text{Cone}(u_{n})$
.
Lemma 4.10. We have
![]() $\hat{K}_{n}\simeq \hat{K}_{1}K_{n}$
.
$\hat{K}_{n}\simeq \hat{K}_{1}K_{n}$
.
Proof. It is clear that
![]() $\hat{K}_{1}K_{n}=\text{Cone}(x_{1}\operatorname{Id}_{K_{n}})$
, while
$\hat{K}_{1}K_{n}=\text{Cone}(x_{1}\operatorname{Id}_{K_{n}})$
, while
![]() $\hat{K}_{n}=\text{Cone}(x_{n}\operatorname{Id}_{K_{n}})$
by definition. Thus, it suffices to prove that
$\hat{K}_{n}=\text{Cone}(x_{n}\operatorname{Id}_{K_{n}})$
by definition. Thus, it suffices to prove that
![]() $x_{1}\operatorname{Id}_{K_{n}}\simeq x_{n}\operatorname{Id}_{K_{n}}$
, and the lemma will follow by homotopy invariance of mapping cones. It is a standard fact that there are canonical maps
$x_{1}\operatorname{Id}_{K_{n}}\simeq x_{n}\operatorname{Id}_{K_{n}}$
, and the lemma will follow by homotopy invariance of mapping cones. It is a standard fact that there are canonical maps
![]() $R(-1)\rightarrow B_{i}$
and
$R(-1)\rightarrow B_{i}$
and
![]() $B_{i}(-1)\rightarrow R$
whose composition is
$B_{i}(-1)\rightarrow R$
whose composition is
![]() $\unicode[STIX]{x1D6FC}_{i}:=x_{i}-x_{i+1}$
. Thus,
$\unicode[STIX]{x1D6FC}_{i}:=x_{i}-x_{i+1}$
. Thus,
![]() $B_{i}K_{n}\simeq 0$
implies that
$B_{i}K_{n}\simeq 0$
implies that
![]() $\unicode[STIX]{x1D6FC}_{i}\operatorname{Id}_{K_{n}}$
factors through a contractible complex, and hence is null-homotopic for all
$\unicode[STIX]{x1D6FC}_{i}\operatorname{Id}_{K_{n}}$
factors through a contractible complex, and hence is null-homotopic for all
![]() $1\leqslant i\leqslant n-1$
. This implies that
$1\leqslant i\leqslant n-1$
. This implies that
![]() $x_{1}\operatorname{Id}_{K_{n}}\simeq x_{n}\operatorname{Id}_{K_{n}}$
, and completes the proof.◻
$x_{1}\operatorname{Id}_{K_{n}}\simeq x_{n}\operatorname{Id}_{K_{n}}$
, and completes the proof.◻
Remark 4.11. Applying the functor
![]() $C\mapsto {\hat{C}}$
to the result of Theorem 3.7 yields an equivalence
$C\mapsto {\hat{C}}$
to the result of Theorem 3.7 yields an equivalence
![]() $\hat{\text{FT}}_{n}\simeq \bigoplus _{v\in \{0,1\}^{n-1}}q^{k}\hat{D}_{v\cdot 1}$
with twisted differential. Further,
$\hat{\text{FT}}_{n}\simeq \bigoplus _{v\in \{0,1\}^{n-1}}q^{k}\hat{D}_{v\cdot 1}$
with twisted differential. Further,
![]() $\hat{D}_{v\cdot 1}$
is given by the same formula as
$\hat{D}_{v\cdot 1}$
is given by the same formula as
![]() $D_{v\cdot 1}$
, except with
$D_{v\cdot 1}$
, except with
![]() $K_{\ell }$
replaced by
$K_{\ell }$
replaced by
![]() $\hat{K}_{\ell }$
.
$\hat{K}_{\ell }$
.
Our next result will later be used to show that the computation of
![]() $\operatorname{HHH}(\text{FT}_{n})$
reduces to a computation of
$\operatorname{HHH}(\text{FT}_{n})$
reduces to a computation of
![]() $\operatorname{HHH}(\hat{\text{FT}}_{n})$
. In particular
$\operatorname{HHH}(\hat{\text{FT}}_{n})$
. In particular
![]() ${\mathcal{P}}_{\text{FT}_{n}}=(1/(1-q)){\mathcal{P}}_{\hat{\text{FT}}_{n}}$
.
${\mathcal{P}}_{\text{FT}_{n}}=(1/(1-q)){\mathcal{P}}_{\hat{\text{FT}}_{n}}$
.
Proposition 4.12. If
![]() $C\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
is such that
$C\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
is such that
![]() $\operatorname{HHH}({\hat{C}})$
is supported in even homological degrees, then so is
$\operatorname{HHH}({\hat{C}})$
is supported in even homological degrees, then so is
![]() $\operatorname{HHH}(C)$
, and
$\operatorname{HHH}(C)$
, and
![]() $\operatorname{HHH}(C)\cong \mathbb{Q}[x_{n}]\otimes \operatorname{HHH}({\hat{C}})$
. In particular, if
$\operatorname{HHH}(C)\cong \mathbb{Q}[x_{n}]\otimes \operatorname{HHH}({\hat{C}})$
. In particular, if
![]() ${\mathcal{P}}_{C}(q,a,t)$
denotes the Poincaré series of
${\mathcal{P}}_{C}(q,a,t)$
denotes the Poincaré series of
![]() $\operatorname{HHH}(C)$
, then
$\operatorname{HHH}(C)$
, then
Proof. Consider a more general situation in which
![]() $M$
is a chain complex on which some polynomial ring
$M$
is a chain complex on which some polynomial ring
![]() $\mathbb{Q}[x]$
acts. Let
$\mathbb{Q}[x]$
acts. Let
![]() $Z$
denote the dg algebra
$Z$
denote the dg algebra
![]() $\mathbb{Q}[x,y,\unicode[STIX]{x1D703}]$
with
$\mathbb{Q}[x,y,\unicode[STIX]{x1D703}]$
with
![]() $d(\unicode[STIX]{x1D703})=x-y$
,
$d(\unicode[STIX]{x1D703})=x-y$
,
![]() $d(x)=0$
, and
$d(x)=0$
, and
![]() $d(y)=0$
. Here,
$d(y)=0$
. Here,
![]() $\unicode[STIX]{x1D703}$
is an odd variable, and hence we assume that
$\unicode[STIX]{x1D703}$
is an odd variable, and hence we assume that
![]() $\unicode[STIX]{x1D703}^{2}=0$
. The differential ensures that
$\unicode[STIX]{x1D703}^{2}=0$
. The differential ensures that
![]() $y\simeq x$
. More precisely, there is a chain map
$y\simeq x$
. More precisely, there is a chain map
![]() $Z\rightarrow \mathbb{Q}[x]$
sending
$Z\rightarrow \mathbb{Q}[x]$
sending
![]() $\unicode[STIX]{x1D703}\mapsto 0$
,
$\unicode[STIX]{x1D703}\mapsto 0$
,
![]() $x\mapsto x$
, and
$x\mapsto x$
, and
![]() $y\mapsto x$
. This map is a homotopy equivalence
$y\mapsto x$
. This map is a homotopy equivalence
![]() $Z\rightarrow \mathbb{Q}[x]$
. Further, the inverse map and the relevant homotopies can all be chosen to be
$Z\rightarrow \mathbb{Q}[x]$
. Further, the inverse map and the relevant homotopies can all be chosen to be
![]() $\mathbb{Q}[x]$
-equivariant.
$\mathbb{Q}[x]$
-equivariant.
Consider the chain complex
![]() $M^{\prime }\simeq Z\otimes _{\mathbb{Q}[x]}M$
. This is regarded as a dg
$M^{\prime }\simeq Z\otimes _{\mathbb{Q}[x]}M$
. This is regarded as a dg
![]() $\mathbb{Q}[x]$
-module in a slightly non-standard way, where
$\mathbb{Q}[x]$
-module in a slightly non-standard way, where
![]() $x$
acts by multiplication by
$x$
acts by multiplication by
![]() $y$
on the first tensor factor. The above paragraph implies that there is a homotopy equivalence
$y$
on the first tensor factor. The above paragraph implies that there is a homotopy equivalence
![]() $M^{\prime }\simeq M$
which commutes the
$M^{\prime }\simeq M$
which commutes the
![]() $\mathbb{Q}[x]$
actions up to homotopy. Now,
$\mathbb{Q}[x]$
actions up to homotopy. Now,
![]() $M^{\prime }\cong \mathbb{Q}[y,\unicode[STIX]{x1D703}]\otimes M$
with twisted differential:
$M^{\prime }\cong \mathbb{Q}[y,\unicode[STIX]{x1D703}]\otimes M$
with twisted differential:
–
 $d(y\otimes m)=y\otimes d(m)$
;
$d(y\otimes m)=y\otimes d(m)$
;–
 $d(\unicode[STIX]{x1D703}\otimes m)=1\otimes xm-y\otimes m-\unicode[STIX]{x1D703}\otimes d(m)$
.
$d(\unicode[STIX]{x1D703}\otimes m)=1\otimes xm-y\otimes m-\unicode[STIX]{x1D703}\otimes d(m)$
.
After rearranging, we see that
![]() $M\simeq M^{\prime }\simeq \mathbb{Q}[y]\otimes \hat{M}$
with twisted differential, where
$M\simeq M^{\prime }\simeq \mathbb{Q}[y]\otimes \hat{M}$
with twisted differential, where
![]() $\hat{M}$
denotes the ‘reduced complex’
$\hat{M}$
denotes the ‘reduced complex’
![]() $\hat{M}:=\text{Cone}(M\overset{x}{\rightarrow }M)$
. This construction is formally analogous to the fact that if
$\hat{M}:=\text{Cone}(M\overset{x}{\rightarrow }M)$
. This construction is formally analogous to the fact that if
![]() $X$
is a topological space on which a group
$X$
is a topological space on which a group
![]() $G$
acts, then there is a space
$G$
acts, then there is a space
![]() $X^{\prime }$
on which
$X^{\prime }$
on which
![]() $G$
acts freely, such that
$G$
acts freely, such that
![]() $X\simeq X^{\prime }$
via a
$X\simeq X^{\prime }$
via a
![]() $G$
-equivariant homotopy equivalence.
$G$
-equivariant homotopy equivalence.
Now we apply this construction to the case of interest. Since
![]() $\operatorname{HH}$
is a linear functor which is extended to complexes, we have that
$\operatorname{HH}$
is a linear functor which is extended to complexes, we have that
![]() $\operatorname{HH}$
commutes with mapping cones. In particular
$\operatorname{HH}$
commutes with mapping cones. In particular
![]() $\operatorname{HH}({\hat{C}})$
is the mapping cone of
$\operatorname{HH}({\hat{C}})$
is the mapping cone of
![]() $x_{n}$
acting on
$x_{n}$
acting on
![]() $\operatorname{HH}(C)$
. The above construction then produces a twisted differential on
$\operatorname{HH}(C)$
. The above construction then produces a twisted differential on
![]() $\mathbb{Q}[x_{n}]\otimes \operatorname{HH}({\hat{C}})$
such that the resulting complex is homotopy equivalent to
$\mathbb{Q}[x_{n}]\otimes \operatorname{HH}({\hat{C}})$
such that the resulting complex is homotopy equivalent to
![]() $\operatorname{HH}(C)$
. Thus we may regard
$\operatorname{HH}(C)$
. Thus we may regard
![]() $\operatorname{HH}(C)$
as a convolution of complexes
$\operatorname{HH}(C)$
as a convolution of complexes
![]() $q^{k}\operatorname{HH}({\hat{C}})$
, indexed by
$q^{k}\operatorname{HH}({\hat{C}})$
, indexed by
![]() $k\in \mathbb{Z}_{{\geqslant}0}$
. The result now follows by the parity miracle (Proposition 2.14). Strictly speaking the parity miracle does not directly apply, because the indexing set is not finite. To fix this problem we fix
$k\in \mathbb{Z}_{{\geqslant}0}$
. The result now follows by the parity miracle (Proposition 2.14). Strictly speaking the parity miracle does not directly apply, because the indexing set is not finite. To fix this problem we fix
![]() $r$
and consider the subcomplex of
$r$
and consider the subcomplex of
![]() $\operatorname{HH}(C)$
consisting of chains with
$\operatorname{HH}(C)$
consisting of chains with
![]() $q$
-degree
$q$
-degree
![]() $r$
. Each of these is a convolution with only finitely many terms, since
$r$
. Each of these is a convolution with only finitely many terms, since
![]() $q^{k}\operatorname{HH}({\hat{C}})$
is supported in large
$q^{k}\operatorname{HH}({\hat{C}})$
is supported in large
![]() $q$
-degrees for
$q$
-degrees for
![]() $k$
large. Thus, the parity miracle can be applied separately to each
$k$
large. Thus, the parity miracle can be applied separately to each
![]() $q$
-degree. The details are straightforward, so we omit them.◻
$q$
-degree. The details are straightforward, so we omit them.◻
Proposition 4.13. The complexes
![]() $\hat{K}_{n}$
satisfy the same recursion as
$\hat{K}_{n}$
satisfy the same recursion as
![]() $K_{n}$
. That is,
$K_{n}$
. That is,

This holds for all
![]() $n\geqslant 1$
, where by convention we set
$n\geqslant 1$
, where by convention we set
![]() $\hat{K}_{0}=\mathbb{Q}\in \mathbb{S}\text{Bim}_{0}$
.
$\hat{K}_{0}=\mathbb{Q}\in \mathbb{S}\text{Bim}_{0}$
.
Proof. For
![]() $n\geqslant 2$
simply tensor (2.2) on the left with
$n\geqslant 2$
simply tensor (2.2) on the left with
![]() $\hat{K}_{1}$
and use Lemma 4.10. For the somewhat degenerate case
$\hat{K}_{1}$
and use Lemma 4.10. For the somewhat degenerate case
![]() $n=1$
, the result follows from the following argument. Note that when
$n=1$
, the result follows from the following argument. Note that when
![]() $n=1$
, the left-hand side of (4.6) is
$n=1$
, the left-hand side of (4.6) is
![]() $\mathbb{Q}[x_{1}]$
, and the second term on the right-hand side can be identified with
$\mathbb{Q}[x_{1}]$
, and the second term on the right-hand side can be identified with
![]() $x_{1}\mathbb{Q}[x_{1}]$
. Then the result follows from the observation that
$x_{1}\mathbb{Q}[x_{1}]$
. Then the result follows from the observation that
![]() $\hat{K}_{1}\simeq \mathbb{Q}$
, and
$\hat{K}_{1}\simeq \mathbb{Q}$
, and
![]() $\mathbb{Q}[x_{1}]\cong \mathbb{Q}\,\oplus \,x_{1}\mathbb{Q}[x_{1}]$
.◻
$\mathbb{Q}[x_{1}]\cong \mathbb{Q}\,\oplus \,x_{1}\mathbb{Q}[x_{1}]$
.◻
We have the following streamlined version of the Markov move for the reduced Jones–Wenzl complexes.
Corollary 4.14. Suppose that
![]() $1\leqslant \ell \leqslant n$
, with
$1\leqslant \ell \leqslant n$
, with
![]() $n=k+\ell$
. Let
$n=k+\ell$
. Let
![]() $C\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n-1})$
be viewed as a complex in
$C\in {\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n-1})$
be viewed as a complex in
![]() ${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
via the usual inclusion functor. We have
${\mathcal{K}}^{b}(\mathbb{S}\text{Bim}_{n})$
via the usual inclusion functor. We have
where
![]() $\unicode[STIX]{x1D6EC}$
denotes an exterior algebra, and
$\unicode[STIX]{x1D6EC}$
denotes an exterior algebra, and
![]() $\deg \unicode[STIX]{x1D709}_{i}=t^{1-i}a$
. Hence
$\deg \unicode[STIX]{x1D709}_{i}=t^{1-i}a$
. Hence
![]() ${\mathcal{P}}_{C(\unicode[STIX]{x1D7D9}_{k}\sqcup \hat{K}_{\ell })}=(t^{\ell -1}+a){\mathcal{P}}_{C(\unicode[STIX]{x1D7D9}_{k}\sqcup \hat{K}_{\ell -1})}$
.
${\mathcal{P}}_{C(\unicode[STIX]{x1D7D9}_{k}\sqcup \hat{K}_{\ell })}=(t^{\ell -1}+a){\mathcal{P}}_{C(\unicode[STIX]{x1D7D9}_{k}\sqcup \hat{K}_{\ell -1})}$
.
Proof. For
![]() $\ell >1$
this follows by the same argument in the proof of Corollary 4.5. For
$\ell >1$
this follows by the same argument in the proof of Corollary 4.5. For
![]() $\ell =1$
this follows from the fact that
$\ell =1$
this follows from the fact that
![]() $\operatorname{HH}(\hat{K}_{1})$
is the mapping cone of
$\operatorname{HH}(\hat{K}_{1})$
is the mapping cone of
![]() $x_{1}$
acting on
$x_{1}$
acting on
![]() $\operatorname{HH}(\mathbb{Q}[x_{1}];\mathbb{Q}[x_{1}])=\mathbb{Q}[x_{1}]\otimes \unicode[STIX]{x1D6EC}[\unicode[STIX]{x1D709}_{1}]$
. Since
$\operatorname{HH}(\mathbb{Q}[x_{1}];\mathbb{Q}[x_{1}])=\mathbb{Q}[x_{1}]\otimes \unicode[STIX]{x1D6EC}[\unicode[STIX]{x1D709}_{1}]$
. Since
![]() $x_{1}$
acts freely, standard arguments imply that this mapping cone is equivalent to the quotient
$x_{1}$
acts freely, standard arguments imply that this mapping cone is equivalent to the quotient
![]() $\unicode[STIX]{x1D6EC}[\unicode[STIX]{x1D709}_{1}]$
, which has Poincaré polynomial
$\unicode[STIX]{x1D6EC}[\unicode[STIX]{x1D709}_{1}]$
, which has Poincaré polynomial
![]() $1+a$
.◻
$1+a$
.◻
Corollary 4.15. Let
![]() $\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6EC}[\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n}]$
be the exterior algebra, where
$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6EC}[\unicode[STIX]{x1D709}_{1},\ldots ,\unicode[STIX]{x1D709}_{n}]$
be the exterior algebra, where
![]() $\deg (\unicode[STIX]{x1D709}_{i})=at^{1-i}$
. Let
$\deg (\unicode[STIX]{x1D709}_{i})=at^{1-i}$
. Let
![]() ${\mathcal{P}}_{\unicode[STIX]{x1D6EC}}$
denote its Poincaré polynomial. Then
${\mathcal{P}}_{\unicode[STIX]{x1D6EC}}$
denote its Poincaré polynomial. Then
![]() ${\mathcal{P}}_{\hat{K}_{n}}=t^{\binom{n}{2}}{\mathcal{P}}_{\unicode[STIX]{x1D6EC}}$
.
${\mathcal{P}}_{\hat{K}_{n}}=t^{\binom{n}{2}}{\mathcal{P}}_{\unicode[STIX]{x1D6EC}}$
.
Note that
4.4 The complexes we use
Now let us return to the convolution description of the full twist.
Definition 4.16. For each
![]() $v\in \{0,1\}^{n}$
with
$v\in \{0,1\}^{n}$
with
![]() $k$
zeroes and
$k$
zeroes and
![]() $\ell$
ones, let
$\ell$
ones, let
![]() $C_{v}=\operatorname{Tw}_{v}(\text{FT}_{k}\sqcup \hat{K}_{\ell })$
. Recall that the shuffle twist
$C_{v}=\operatorname{Tw}_{v}(\text{FT}_{k}\sqcup \hat{K}_{\ell })$
. Recall that the shuffle twist
![]() $\operatorname{Tw}_{v}$
was described in Definition 2.4. Again, we identify a braid with its Rouquier complex.
$\operatorname{Tw}_{v}$
was described in Definition 2.4. Again, we identify a braid with its Rouquier complex.
Example 4.17. If
![]() $v=(0101100)$
, then we have
$v=(0101100)$
, then we have

It is clear that
![]() $C_{v}$
is conjugate to
$C_{v}$
is conjugate to
![]() $\hat{D}_{v}$
, where
$\hat{D}_{v}$
, where
![]() $D_{v}$
is as in Definition 3.5. These will be the complexes we use in our inductive computation of Hochschild cohomology.
$D_{v}$
is as in Definition 3.5. These will be the complexes we use in our inductive computation of Hochschild cohomology.
Example 4.18. We have
![]() $C_{00\cdots 0}=\text{FT}_{n}$
while
$C_{00\cdots 0}=\text{FT}_{n}$
while
![]() $C_{10\cdots 0}=\hat{\text{FT}}_{n}$
. In general
$C_{10\cdots 0}=\hat{\text{FT}}_{n}$
. In general
![]() $C_{1\cdots 10\cdots \,,0}$
is given by a diagram of the form
$C_{1\cdots 10\cdots \,,0}$
is given by a diagram of the form

exemplified here in the case of
![]() $v=(1111000)$
. The empty white box represents
$v=(1111000)$
. The empty white box represents
![]() $\hat{K}_{4}$
.
$\hat{K}_{4}$
.
We now present a simple convolution recursion for
![]() $\operatorname{HH}(C_{v})$
.
$\operatorname{HH}(C_{v})$
.
4.5 The key recursion
Lemma 4.19. Let
![]() $v\in \{0,1\}^{n}$
be a sequence with
$v\in \{0,1\}^{n}$
be a sequence with
![]() $k$
zeroes and
$k$
zeroes and
![]() $\ell =n-k$
ones. Then
$\ell =n-k$
ones. Then

Proof. This is simply the result of Proposition 2.6, followed by an isotopy.◻
Proposition 4.20. We have
![]() $\operatorname{HH}(C_{v\cdot 0})\simeq (\operatorname{HH}(C_{1\cdot v})\rightarrow q\operatorname{HH}(C_{0\cdot v}))$
.
$\operatorname{HH}(C_{v\cdot 0})\simeq (\operatorname{HH}(C_{1\cdot v})\rightarrow q\operatorname{HH}(C_{0\cdot v}))$
.
Proof. Let
![]() $v\in \{0,1\}^{n}$
be a sequence with
$v\in \{0,1\}^{n}$
be a sequence with
![]() $k$
zeroes and
$k$
zeroes and
![]() $\ell =n-k$
ones. Observe that
$\ell =n-k$
ones. Observe that
![]() $C_{v\cdot 0}$
can be written
$C_{v\cdot 0}$
can be written

where we have used Lemma 4.19 to rewrite
![]() $\operatorname{Tw}_{v\cdot 0}$
. Now, the exact triangle for
$\operatorname{Tw}_{v\cdot 0}$
. Now, the exact triangle for
![]() $K_{n}$
(2.2) says that this complex is homotopy equivalent to a convolution of the form
$K_{n}$
(2.2) says that this complex is homotopy equivalent to a convolution of the form

To prove the Proposition, we must show that the term on the left is
![]() $\operatorname{HH}$
-equivalent to
$\operatorname{HH}$
-equivalent to
![]() $C_{1\cdot v}$
, and the term on the right is
$C_{1\cdot v}$
, and the term on the right is
![]() $\operatorname{HH}$
-equivalent to
$\operatorname{HH}$
-equivalent to
![]() $C_{0\cdot v}$
. For the term on the right, simply slide the left-handed crossing (rather, the cabled crossing between 1 strand and
$C_{0\cdot v}$
. For the term on the right, simply slide the left-handed crossing (rather, the cabled crossing between 1 strand and
![]() $k$
parallel strands) from the top to the bottom, through the full twist, where it meets and annihilates the right-handed crossing. The resulting complex is
$k$
parallel strands) from the top to the bottom, through the full twist, where it meets and annihilates the right-handed crossing. The resulting complex is
![]() $C_{0\cdot v}$
. For the term on the left, we have the following sequence of simplifications:
$C_{0\cdot v}$
. For the term on the left, we have the following sequence of simplifications:

The first equivalence is obtained by rewriting the full-twist as
![]() $\text{FT}_{k+1}=\text{FT}_{k}J_{k+1}$
, where
$\text{FT}_{k+1}=\text{FT}_{k}J_{k+1}$
, where
![]() $J_{k+1}$
is the Jucys–Murphy braid. The second is an
$J_{k+1}$
is the Jucys–Murphy braid. The second is an
![]() $\operatorname{HH}$
-equivalence which slides the Jucys–Murphy braid from the bottom to the top. The final equivalence is an obvious isotopy. The braid on the top of the resulting complex is
$\operatorname{HH}$
-equivalence which slides the Jucys–Murphy braid from the bottom to the top. The final equivalence is an obvious isotopy. The braid on the top of the resulting complex is
![]() $\operatorname{Tw}_{1\cdot v}$
(similar to the statement of Proposition 2.6 for
$\operatorname{Tw}_{1\cdot v}$
(similar to the statement of Proposition 2.6 for
![]() $\operatorname{Tw}_{v\cdot 0}$
). The resulting complex is therefore
$\operatorname{Tw}_{v\cdot 0}$
). The resulting complex is therefore
![]() $C_{1\cdot v}$
. Each of the above equivalences corresponds to an honest homotopy equivalence after applying the functor
$C_{1\cdot v}$
. Each of the above equivalences corresponds to an honest homotopy equivalence after applying the functor
![]() $\operatorname{HH}(-)$
. This completes the proof.◻
$\operatorname{HH}(-)$
. This completes the proof.◻
4.6 Our main result
In this section we prove our main theorem, which gives a recursion formula for the Poincaré series for
![]() $\operatorname{HHH}(C_{v})$
.
$\operatorname{HHH}(C_{v})$
.
Proposition 4.21. There is a unique family of rational functions
![]() $f_{v}(q,a,t)$
, indexed by binary sequences
$f_{v}(q,a,t)$
, indexed by binary sequences
![]() $v\in \{0,1\}^{n}$
with
$v\in \{0,1\}^{n}$
with
![]() $n\in \mathbb{Z}_{{\geqslant}0}$
, satisfying
$n\in \mathbb{Z}_{{\geqslant}0}$
, satisfying
Proof. Let us first prove uniqueness. Note that (4.9b) applied to the sequence
![]() $v=(00\cdots 0)$
yields
$v=(00\cdots 0)$
yields
![]() $f_{00\cdots 0}=qf_{00\cdots 0}+f_{10\cdots 0}$
. In other words,
$f_{00\cdots 0}=qf_{00\cdots 0}+f_{10\cdots 0}$
. In other words,
Now, define a partial order on the set of binary sequences as follows. Given
![]() $v\in \{0,1\}^{n}$
and
$v\in \{0,1\}^{n}$
and
![]() $w\in \{0,1\}^{m}$
, write
$w\in \{0,1\}^{m}$
, write
![]() $v<w$
if one of the following conditions is met:
$v<w$
if one of the following conditions is met:
–
 $n<m$
;
$n<m$
;–
 $n=m$
and
$n=m$
and
 $v$
has fewer zeroes than
$v$
has fewer zeroes than
 $w$
;
$w$
;–
 $n=m$
,
$n=m$
,
 $v$
and
$v$
and
 $w$
have the same number of zeroes, and the number of inversions in the shuffle permutation
$w$
have the same number of zeroes, and the number of inversions in the shuffle permutation
 $\unicode[STIX]{x1D70B}_{v}$
is less than the number of inversions in
$\unicode[STIX]{x1D70B}_{v}$
is less than the number of inversions in
 $\unicode[STIX]{x1D70B}_{w}$
.
$\unicode[STIX]{x1D70B}_{w}$
.
Then
![]() ${<}$
defines a partial order on the set of binary sequences. The number of inversions in
${<}$
defines a partial order on the set of binary sequences. The number of inversions in
![]() $\unicode[STIX]{x1D70B}_{v}$
is the number of pairs
$\unicode[STIX]{x1D70B}_{v}$
is the number of pairs
![]() $(i<j)$
where
$(i<j)$
where
![]() $v_{i}=1$
and
$v_{i}=1$
and
![]() $v_{j}=0$
. Thus,
$v_{j}=0$
. Thus,
![]() $0\cdot v\leqslant v\cdot 0$
with equality if and only if
$0\cdot v\leqslant v\cdot 0$
with equality if and only if
![]() $v=(00\cdots 0)$
. Clearly the empty sequence is the unique minimum with respect to this partial order, and relations (4.9a), (4.9b) (where we use (4.10) to rewrite the all zeroes sequence) for express any
$v=(00\cdots 0)$
. Clearly the empty sequence is the unique minimum with respect to this partial order, and relations (4.9a), (4.9b) (where we use (4.10) to rewrite the all zeroes sequence) for express any
![]() $f_{v}$
in terms of
$f_{v}$
in terms of
![]() $f_{w}$
with
$f_{w}$
with
![]() $w<v$
. This proves uniqueness.
$w<v$
. This proves uniqueness.
For existence, we need to prove consistency of the relations (4.9a), (4.9b). However, this is clear since for each
![]() $v$
, exactly one of the relations (4.9a) or (4.9b) can be applied.◻
$v$
, exactly one of the relations (4.9a) or (4.9b) can be applied.◻
We now have our main theorem.
Theorem 4.22. The Poincaré series for
![]() $\operatorname{HHH}(C_{v})$
equals the rational function
$\operatorname{HHH}(C_{v})$
equals the rational function
![]() $f_{v}(q,a,t)$
from Proposition 4.21. In particular,
$f_{v}(q,a,t)$
from Proposition 4.21. In particular,
![]() $\operatorname{HHH}(C_{v})$
is supported in even homological degrees. As a special case we have that
$\operatorname{HHH}(C_{v})$
is supported in even homological degrees. As a special case we have that
![]() $\operatorname{HHH}(\text{FT}_{n})=f_{00\cdots 0}(q,a,t)$
is the Poincaré series of the triply graded homology of the
$\operatorname{HHH}(\text{FT}_{n})=f_{00\cdots 0}(q,a,t)$
is the Poincaré series of the triply graded homology of the
![]() $(n,n)$
torus link, up to an overall shift.
$(n,n)$
torus link, up to an overall shift.
Proof. Let
![]() ${\mathcal{P}}_{v}={\mathcal{P}}_{C_{v}}$
denote the Poincaré series for
${\mathcal{P}}_{v}={\mathcal{P}}_{C_{v}}$
denote the Poincaré series for
![]() $\operatorname{HHH}(C_{v})$
. We will show that
$\operatorname{HHH}(C_{v})$
. We will show that
![]() ${\mathcal{P}}_{v}=f_{v}$
by induction on
${\mathcal{P}}_{v}=f_{v}$
by induction on
![]() $v$
, using the partial order on the set of binary sequences introduced in the proof of Proposition 4.21.
$v$
, using the partial order on the set of binary sequences introduced in the proof of Proposition 4.21.
In case
![]() $v=\emptyset$
, we have
$v=\emptyset$
, we have
![]() $C_{\emptyset }=\mathbb{Q}$
, which satisfies
$C_{\emptyset }=\mathbb{Q}$
, which satisfies
![]() $\operatorname{HHH}(R_{0};\mathbb{Q})=\operatorname{HHH}(\mathbb{Q};\mathbb{Q})=\mathbb{Q}$
. Thus
$\operatorname{HHH}(R_{0};\mathbb{Q})=\operatorname{HHH}(\mathbb{Q};\mathbb{Q})=\mathbb{Q}$
. Thus
![]() ${\mathcal{P}}_{\emptyset }=1=f_{\emptyset }$
.
${\mathcal{P}}_{\emptyset }=1=f_{\emptyset }$
.
Now, fix
![]() $v\in \{0,1\}^{n}$
, and assume by induction that
$v\in \{0,1\}^{n}$
, and assume by induction that
![]() ${\mathcal{P}}_{w}=f_{w}$
for all
${\mathcal{P}}_{w}=f_{w}$
for all
![]() $w<v$
. If
$w<v$
. If
![]() $v=(00\cdots 0)$
, then
$v=(00\cdots 0)$
, then
![]() ${\mathcal{P}}_{10\cdots 0}=f_{10\cdots 0}$
by induction. Further,
${\mathcal{P}}_{10\cdots 0}=f_{10\cdots 0}$
by induction. Further,
![]() $C_{10\cdots 0}={\hat{C}}_{00\cdots 0}$
, so Proposition 4.12 says that
$C_{10\cdots 0}={\hat{C}}_{00\cdots 0}$
, so Proposition 4.12 says that
![]() ${\mathcal{P}}_{00\cdots 0}=(1/(1-q)){\mathcal{P}}_{10\cdots 0}$
, which equals
${\mathcal{P}}_{00\cdots 0}=(1/(1-q)){\mathcal{P}}_{10\cdots 0}$
, which equals
![]() $f_{00\cdots 0}$
by (4.10). This takes care of the case where
$f_{00\cdots 0}$
by (4.10). This takes care of the case where
![]() $v$
is the zero sequence. Thus, we assume below that
$v$
is the zero sequence. Thus, we assume below that
![]() $v$
is non-zero.
$v$
is non-zero.
There are two cases: either
![]() $v=w\cdot 1$
or
$v=w\cdot 1$
or
![]() $w\cdot 0$
for some
$w\cdot 0$
for some
![]() $w$
. In the first case, then Corollary 4.14 says that
$w$
. In the first case, then Corollary 4.14 says that
![]() ${\mathcal{P}}_{w\cdot 1}=(t^{|v|}+a){\mathcal{P}}_{w}$
, hence
${\mathcal{P}}_{w\cdot 1}=(t^{|v|}+a){\mathcal{P}}_{w}$
, hence
![]() ${\mathcal{P}}_{w\cdot 1}=f_{w\cdot 1}$
by (4.9a) and induction. Thus, we may assume that
${\mathcal{P}}_{w\cdot 1}=f_{w\cdot 1}$
by (4.9a) and induction. Thus, we may assume that
![]() $v=w\cdot 0$
. Since
$v=w\cdot 0$
. Since
![]() $v$
is non-zero, we have
$v$
is non-zero, we have
![]() $1\cdot w<w\cdot 0$
(fewer zeroes) and
$1\cdot w<w\cdot 0$
(fewer zeroes) and
![]() $0\cdot w<w\cdot 0$
(fewer inversions). Thus, by induction, we have
$0\cdot w<w\cdot 0$
(fewer inversions). Thus, by induction, we have
![]() ${\mathcal{P}}_{1\cdot w}=f_{1\cdot w}$
and
${\mathcal{P}}_{1\cdot w}=f_{1\cdot w}$
and
![]() ${\mathcal{P}}_{0\cdot w}=f_{0\cdot w}$
. Also by induction, we may assume that
${\mathcal{P}}_{0\cdot w}=f_{0\cdot w}$
. Also by induction, we may assume that
![]() $\operatorname{HHH}(C_{1\cdot w})$
and
$\operatorname{HHH}(C_{1\cdot w})$
and
![]() $\operatorname{HHH}(C_{0\cdot w})$
are supported in even homological degrees. Thus, the terms of the convolution Proposition 4.20 have the same parity after taking
$\operatorname{HHH}(C_{0\cdot w})$
are supported in even homological degrees. Thus, the terms of the convolution Proposition 4.20 have the same parity after taking
![]() $\operatorname{HHH}$
. Proposition 2.14 implies that
$\operatorname{HHH}$
. Proposition 2.14 implies that
![]() $\operatorname{HHH}(C_{w\cdot 0})$
splits as a direct sum
$\operatorname{HHH}(C_{w\cdot 0})$
splits as a direct sum
Taking Poincaré series, we see that
![]() ${\mathcal{P}}_{w\cdot 0}=q{\mathcal{P}}_{0\cdot w}+{\mathcal{P}}_{1\cdot w}$
. It follows that
${\mathcal{P}}_{w\cdot 0}=q{\mathcal{P}}_{0\cdot w}+{\mathcal{P}}_{1\cdot w}$
. It follows that
![]() ${\mathcal{P}}_{v}=f_{v}$
, by induction and the uniqueness statement of Proposition 4.21.◻
${\mathcal{P}}_{v}=f_{v}$
, by induction and the uniqueness statement of Proposition 4.21.◻
5 Numerological considerations
Below, we give an alternate recursive formula for the power series
![]() $f_{v}(q,a,t)$
for sequences
$f_{v}(q,a,t)$
for sequences
![]() $v\in \{0,1\}^{n}$
. We then give a closed formula for
$v\in \{0,1\}^{n}$
. We then give a closed formula for
![]() $a=0$
specialization
$a=0$
specialization
![]() $f_{00\cdots 0}(q,0,t)$
.
$f_{00\cdots 0}(q,0,t)$
.
5.1 An alternate recursive formula
The recursion described in this section was actually discovered before the recursion that appears in Proposition 4.21. We originally proved our main result (Theorem 4.22) using this recursion, and later found a much more elegant route which now appears in our § 4.6. Nonetheless this alternate recursion is quite useful, and will lead us to a closed formula for the
![]() $a$
-degree zero part of
$a$
-degree zero part of
![]() $\operatorname{HHH}(\text{FT}_{n})$
in § 5.3. We introduce some combinatorial notions which will be relevant below.
$\operatorname{HHH}(\text{FT}_{n})$
in § 5.3. We introduce some combinatorial notions which will be relevant below.
Definition 5.1. Fix a sequence
![]() $v\in \{0,1\}^{n}$
. We will call a pair of sequences
$v\in \{0,1\}^{n}$
. We will call a pair of sequences
![]() $(v,w)$
compatible if
$(v,w)$
compatible if
![]() $w\in \{0,1\}^{k}$
, where
$w\in \{0,1\}^{k}$
, where
![]() $k$
is the number of zeroes in
$k$
is the number of zeroes in
![]() $v$
. If
$v$
. If
![]() $(v,w)$
is a compatible pair, we define a sequence
$(v,w)$
is a compatible pair, we define a sequence
![]() $v\circ w$
by ‘inserting
$v\circ w$
by ‘inserting
![]() $w$
into the zeroes of
$w$
into the zeroes of
![]() $v$
.’ That is, let
$v$
.’ That is, let
![]() $(v\circ w)_{i}=1$
if either
$(v\circ w)_{i}=1$
if either
![]() $v_{i}=1$
, or if
$v_{i}=1$
, or if
![]() $v_{i}$
is the
$v_{i}$
is the
![]() $j$
th zero in
$j$
th zero in
![]() $v$
and
$v$
and
![]() $w_{j}=1$
. We let
$w_{j}=1$
. We let
![]() $I_{v,w}\subset \{1,\ldots ,n\}$
denote the subset of indices such that
$I_{v,w}\subset \{1,\ldots ,n\}$
denote the subset of indices such that
![]() $v_{i}=0$
but
$v_{i}=0$
but
![]() $(v\circ w)_{i}=1$
. We say that
$(v\circ w)_{i}=1$
. We say that
![]() $i$
is a one in
$i$
is a one in
![]() $v$
if
$v$
if
![]() $v_{i}=1$
, and
$v_{i}=1$
, and
![]() $i$
is a one in
$i$
is a one in
![]() $w$
(relative to
$w$
(relative to
![]() $v$
) if
$v$
) if
![]() $v_{i}=0$
but
$v_{i}=0$
but
![]() $(v\circ w)_{i}=1$
. When
$(v\circ w)_{i}=1$
. When
![]() $v$
is understood, we omit the phrase relative to
$v$
is understood, we omit the phrase relative to
![]() $v$
.
$v$
.
Example 5.2. Let
![]() $v=(1101001)$
and
$v=(1101001)$
and
![]() $w=(001)$
. In this case we have
$w=(001)$
. In this case we have
![]() $v\circ w=(11\text{}\underline{0}1\text{}\underline{0}\text{}\underline{1}1)$
, where the underlined terms indicate where we have inserted
$v\circ w=(11\text{}\underline{0}1\text{}\underline{0}\text{}\underline{1}1)$
, where the underlined terms indicate where we have inserted
![]() $w$
into
$w$
into
![]() $v$
.
$v$
.
Definition 5.3. Fix
![]() $v\in \{0,1\}^{n}$
and
$v\in \{0,1\}^{n}$
and
![]() $w\in \{0,1\}^{k}$
as above. For each index
$w\in \{0,1\}^{k}$
as above. For each index
![]() $i$
, let
$i$
, let
![]() $\ell (i)$
denote the number of ones of
$\ell (i)$
denote the number of ones of
![]() $v$
strictly to the left of
$v$
strictly to the left of
![]() $i$
, and let
$i$
, and let
![]() $m(i)$
denote the number of ones in
$m(i)$
denote the number of ones in
![]() $w$
strictly to the right of
$w$
strictly to the right of
![]() $i$
. Let
$i$
. Let
![]() ${\mathcal{P}}_{v,w,i}$
denote
${\mathcal{P}}_{v,w,i}$
denote
![]() $(t^{\ell (i)+m(i)}+a)$
if
$(t^{\ell (i)+m(i)}+a)$
if
![]() $v_{i}=1$
and
$v_{i}=1$
and
![]() $P_{v,w,i}=1$
otherwise. Set
$P_{v,w,i}=1$
otherwise. Set
![]() ${\mathcal{P}}_{v,w}:=\prod _{i=1}^{n}{\mathcal{P}}_{v,w,i}$
.
${\mathcal{P}}_{v,w}:=\prod _{i=1}^{n}{\mathcal{P}}_{v,w,i}$
.
Lemma 5.4. The following relations hold:
(i)
 ${\mathcal{P}}_{v\cdot 1,w}=(t^{|v|}+a){\mathcal{P}}_{v,w}$
;
${\mathcal{P}}_{v\cdot 1,w}=(t^{|v|}+a){\mathcal{P}}_{v,w}$
;(ii)
 ${\mathcal{P}}_{v\cdot 0,w\cdot 0}={\mathcal{P}}_{v,w}$
;
${\mathcal{P}}_{v\cdot 0,w\cdot 0}={\mathcal{P}}_{v,w}$
;(iii)
 ${\mathcal{P}}_{1\cdot v,w}=(t^{|w|}+a){\mathcal{P}}_{v\cdot 0,w\cdot 1}$
;
${\mathcal{P}}_{1\cdot v,w}=(t^{|w|}+a){\mathcal{P}}_{v\cdot 0,w\cdot 1}$
;(iv)
 ${\mathcal{P}}_{0\cdot v,0\cdot w}={\mathcal{P}}_{v,w}$
;
${\mathcal{P}}_{0\cdot v,0\cdot w}={\mathcal{P}}_{v,w}$
;(v)
 ${\mathcal{P}}_{0\cdot v,1\cdot w}={\mathcal{P}}_{v,w}$
.
${\mathcal{P}}_{0\cdot v,1\cdot w}={\mathcal{P}}_{v,w}$
.
Proof. These are easily verified directly from the definition.◻
Proposition 5.5. The functions
![]() $f_{v}(q,a,t)$
defined in Proposition 4.21 can also be defined by the recursion:
$f_{v}(q,a,t)$
defined in Proposition 4.21 can also be defined by the recursion:
Note that we regard
![]() $\{0,1\}^{0}$
as the set containing the empty set. Thus, (5.1b) gives
$\{0,1\}^{0}$
as the set containing the empty set. Thus, (5.1b) gives
as a special case.
Proof. Both recursions uniquely pin down a collection of functions
![]() $f_{v}(q,a,t)$
. Therefore, if one of these definitions satisfies the other’s recursive formula, then they are equivalent definitions. The recursions are clearly equivalent when computing
$f_{v}(q,a,t)$
. Therefore, if one of these definitions satisfies the other’s recursive formula, then they are equivalent definitions. The recursions are clearly equivalent when computing
![]() $f_{v}$
for sequences of length
$f_{v}$
for sequences of length
![]() $n\leqslant 1$
. Let us temporarily denote by
$n\leqslant 1$
. Let us temporarily denote by
![]() $g_{v}$
the family of functions determined by (5.1a) and (5.1b). We will show that the
$g_{v}$
the family of functions determined by (5.1a) and (5.1b). We will show that the
![]() $g_{v}$
also satisfy the recursion which defines
$g_{v}$
also satisfy the recursion which defines
![]() $f_{v}$
(equations (4.9a) and (4.9b)).
$f_{v}$
(equations (4.9a) and (4.9b)).
First, note that
![]() $g_{v\cdot 1}=\sum _{w\in \{0,1\}^{k}}{\mathcal{P}}_{v\cdot 1,w}q^{k_{1}}g_{w}$
, where
$g_{v\cdot 1}=\sum _{w\in \{0,1\}^{k}}{\mathcal{P}}_{v\cdot 1,w}q^{k_{1}}g_{w}$
, where
![]() $k_{1}$
is the number of zeroes in
$k_{1}$
is the number of zeroes in
![]() $w$
. By part (1) of Lemma 5.4, we have
$w$
. By part (1) of Lemma 5.4, we have
![]() ${\mathcal{P}}_{v\cdot 1,w}=(t^{|v|}+a)g_{w}$
, which implies that
${\mathcal{P}}_{v\cdot 1,w}=(t^{|v|}+a)g_{w}$
, which implies that
Thus, the rule (4.9a) is satisfied by
![]() $g_{v}$
.
$g_{v}$
.
We now check that
![]() $g_{v\cdot 0}$
satisfies (4.9b). If
$g_{v\cdot 0}$
satisfies (4.9b). If
![]() $v=(00\cdots 0)$
, then this translates precisely to rule (5.1a), which we are assuming is valid. Thus, we may assume that
$v=(00\cdots 0)$
, then this translates precisely to rule (5.1a), which we are assuming is valid. Thus, we may assume that
![]() $v$
is non-zero. We must show that
$v$
is non-zero. We must show that
![]() $g_{v\cdot 0}=qg_{0\cdot v}+g_{1\cdot v}$
. To do this, fix
$g_{v\cdot 0}=qg_{0\cdot v}+g_{1\cdot v}$
. To do this, fix
![]() $v\in \{0,1\}^{n}$
, let
$v\in \{0,1\}^{n}$
, let
![]() $\ell =|v|$
the number of ones in
$\ell =|v|$
the number of ones in
![]() $v$
and
$v$
and
![]() $k=n-\ell$
the number of zeroes. Below, we let
$k=n-\ell$
the number of zeroes. Below, we let
![]() $k_{1}$
denote the number of zeroes in
$k_{1}$
denote the number of zeroes in
![]() $w$
, so that
$w$
, so that
Let us expand
![]() $g_{v\cdot 0}(q,a,t)$
using the rule (5.1b). Because of the extra zero, there are twice as many terms in this sum as there were for
$g_{v\cdot 0}(q,a,t)$
using the rule (5.1b). Because of the extra zero, there are twice as many terms in this sum as there were for
![]() $g_{v}$
, corresponding to sequences
$g_{v}$
, corresponding to sequences
![]() $w\cdot 0$
and sequences
$w\cdot 0$
and sequences
![]() $w\cdot 1$
. We obtain
$w\cdot 1$
. We obtain
For the sequence
![]() $w\cdot 0$
relative to
$w\cdot 0$
relative to
![]() $w$
, there is an extra zero yielding an extra factor of
$w$
, there is an extra zero yielding an extra factor of
![]() $q$
. By Lemma 5.4, we have
$q$
. By Lemma 5.4, we have
![]() ${\mathcal{P}}_{v\cdot 0,w\cdot 0}={\mathcal{P}}_{v,w}$
, and by (5.2), we have
${\mathcal{P}}_{v\cdot 0,w\cdot 0}={\mathcal{P}}_{v,w}$
, and by (5.2), we have
![]() $g_{w\cdot 1}=(t^{|w|}+a)g_{w}$
. This yields
$g_{w\cdot 1}=(t^{|w|}+a)g_{w}$
. This yields
Recall that we are assuming
![]() $v$
is not the zero-sequence, hence
$v$
is not the zero-sequence, hence
![]() $k<n$
. Now we apply induction on
$k<n$
. Now we apply induction on
![]() $n$
, assuming (4.9a) and (4.9b) hold for
$n$
, assuming (4.9a) and (4.9b) hold for
![]() $g_{w}$
. Applying both of these equations to the right-hand side of (5.3) we obtain
$g_{w}$
. Applying both of these equations to the right-hand side of (5.3) we obtain
Similarly,
and
Lemma 5.4 says
![]() ${\mathcal{P}}_{0\cdot v,0\cdot w}={\mathcal{P}}_{v,w}={\mathcal{P}}_{0\cdot v,1\cdot w}$
and
${\mathcal{P}}_{0\cdot v,0\cdot w}={\mathcal{P}}_{v,w}={\mathcal{P}}_{0\cdot v,1\cdot w}$
and
![]() ${\mathcal{P}}_{1\cdot v,w}=(t^{|w|}+a){\mathcal{P}}_{v\cdot 0,w\cdot 1}$
. Thus,
${\mathcal{P}}_{1\cdot v,w}=(t^{|w|}+a){\mathcal{P}}_{v\cdot 0,w\cdot 1}$
. Thus,
Comparing (5.4) to (5.5), we have shown that
![]() $g_{v\cdot 0}=qg_{0\cdot v}+g_{1\cdot v}$
, as desired.◻
$g_{v\cdot 0}=qg_{0\cdot v}+g_{1\cdot v}$
, as desired.◻
5.2 The redundancy of rule (5.1a)
Proposition 5.6. Equation (5.1a) follows from a verbatim application of (5.1b) to the case of the zero sequence
![]() $v=(00\cdots 0)$
.
$v=(00\cdots 0)$
.
Proof. Let
![]() $v$
be the zero sequence of length
$v$
be the zero sequence of length
![]() $n$
. When we expand
$n$
. When we expand
![]() $f_{00\cdots 0}$
using (5.1b), we obtain a sum of
$f_{00\cdots 0}$
using (5.1b), we obtain a sum of
![]() $2^{n}$
terms, indexed by sequences
$2^{n}$
terms, indexed by sequences
![]() $w\in \{0,1\}^{n}$
. We claim that the sum of the terms with
$w\in \{0,1\}^{n}$
. We claim that the sum of the terms with
![]() $w$
ending in
$w$
ending in
![]() $1$
is actually just
$1$
is actually just
![]() $f_{10\cdots 0}$
; that the sum of the terms with
$f_{10\cdots 0}$
; that the sum of the terms with
![]() $w$
ending in
$w$
ending in
![]() $10$
is actually just
$10$
is actually just
![]() $qf_{10\cdots 0}$
; the sum of the terms with
$qf_{10\cdots 0}$
; the sum of the terms with
![]() $w$
ending in
$w$
ending in
![]() $100$
is
$100$
is
![]() $q^{2}f_{10\cdots 0}$
; and so forth. Of course, the unique term where
$q^{2}f_{10\cdots 0}$
; and so forth. Of course, the unique term where
![]() $w$
ends in
$w$
ends in
![]() $10\cdot 0$
(length
$10\cdot 0$
(length
![]() $n$
) is just
$n$
) is just
![]() $q^{n-1}f_{10\cdots 0}$
, because
$q^{n-1}f_{10\cdots 0}$
, because
![]() $q^{n-1}$
is easy observed to be the coefficient of
$q^{n-1}$
is easy observed to be the coefficient of
![]() $f_{10\cdots 0}$
in this expansion.
$f_{10\cdots 0}$
in this expansion.
Given this claim, we have
which immediately implies (5.1a). So it is enough to show the claim.
The claim is proven by an easy induction, using (4.9b). For instance,
by one application of (4.9b). These are the two terms which end in
![]() $(10\cdots 0)$
(length
$(10\cdots 0)$
(length
![]() $n-1$
). This proves one statement of the claim. For the next, we apply (4.9b) again and decrease the power of
$n-1$
). This proves one statement of the claim. For the next, we apply (4.9b) again and decrease the power of
![]() $q$
, obtaining
$q$
, obtaining
These are the four terms which end in
![]() $10\cdots 0$
(length
$10\cdots 0$
(length
![]() $n-2$
), and each appears with the correct power of
$n-2$
), and each appears with the correct power of
![]() $q$
. This proves the second statement of our claim. The remaining parts of the claim follow by repeating this argument. We leave the details to the reader.◻
$q$
. This proves the second statement of our claim. The remaining parts of the claim follow by repeating this argument. We leave the details to the reader.◻
5.3 The closed form of
 $\operatorname{HHH}^{0}(\text{FT}_{n})$
$\operatorname{HHH}^{0}(\text{FT}_{n})$
One useful consequence of the alternate recursion is that it leads to a simple derivation of Theorem 1.9. To remind the reader, this theorem stated that
where the sum is over functions
![]() $\unicode[STIX]{x1D70E}:\{1,\ldots ,n\}\rightarrow \mathbb{Z}_{{\geqslant}0}$
, and the integers
$\unicode[STIX]{x1D70E}:\{1,\ldots ,n\}\rightarrow \mathbb{Z}_{{\geqslant}0}$
, and the integers
![]() $a(\unicode[STIX]{x1D70E})$
,
$a(\unicode[STIX]{x1D70E})$
,
![]() $b(\unicode[STIX]{x1D70E})$
,
$b(\unicode[STIX]{x1D70E})$
,
![]() $c(\unicode[STIX]{x1D70E})$
are defined by:
$c(\unicode[STIX]{x1D70E})$
are defined by:
(i)
 $a(\unicode[STIX]{x1D70E})=\sum _{k\geqslant 0}\binom{|\unicode[STIX]{x1D70E}^{-1}(k)|}{2}$
;
$a(\unicode[STIX]{x1D70E})=\sum _{k\geqslant 0}\binom{|\unicode[STIX]{x1D70E}^{-1}(k)|}{2}$
;(ii)
 $b(\unicode[STIX]{x1D70E})$
is the number of pairs
$b(\unicode[STIX]{x1D70E})$
is the number of pairs
 $(i,j)\in \{1,\ldots ,n\}$
such that
$(i,j)\in \{1,\ldots ,n\}$
such that
 $i<j$
and
$i<j$
and
 $\unicode[STIX]{x1D70E}(j)=\unicode[STIX]{x1D70E}(i)+1$
;
$\unicode[STIX]{x1D70E}(j)=\unicode[STIX]{x1D70E}(i)+1$
;(iii)
 $c(\unicode[STIX]{x1D70E})=\sum _{i=1}^{n}\unicode[STIX]{x1D70E}(i)$
.
$c(\unicode[STIX]{x1D70E})=\sum _{i=1}^{n}\unicode[STIX]{x1D70E}(i)$
.
Definition 5.7. Recall Definition 5.1. If
![]() $(v,w)$
is a compatible pair of sequences, let
$(v,w)$
is a compatible pair of sequences, let
![]() $c(v,w)$
denote the number of pairs of indices
$c(v,w)$
denote the number of pairs of indices
![]() $i<j$
such that
$i<j$
such that
![]() $i$
is a one in
$i$
is a one in
![]() $v$
and
$v$
and
![]() $j$
is a one in
$j$
is a one in
![]() $w$
(relative to
$w$
(relative to
![]() $v$
).
$v$
).
Example 5.8. Let
![]() $v=(1101000101)$
and
$v=(1101000101)$
and
![]() $w=(10110)$
. In this case we have
$w=(10110)$
. In this case we have
![]() $v\circ w=(11\text{}\underline{1}1\text{}\underline{0}\text{}\underline{1}\text{}\underline{1}1\text{}\underline{0}1)$
, where the underlined terms indicate where we have inserted
$v\circ w=(11\text{}\underline{1}1\text{}\underline{0}\text{}\underline{1}\text{}\underline{1}1\text{}\underline{0}1)$
, where the underlined terms indicate where we have inserted
![]() $w$
into
$w$
into
![]() $v$
. Then
$v$
. Then
![]() $c(v,w)=8$
. We interpret
$c(v,w)=8$
. We interpret
![]() $c(v,w)$
as the number of crossings in a certain diagram associated to
$c(v,w)$
as the number of crossings in a certain diagram associated to
![]() $(v,w)$
. First, draw the shuffle permutation associated to
$(v,w)$
. First, draw the shuffle permutation associated to
![]() $v$
.
$v$
.

The ones in the sequence
![]() $w$
tell us which strands corresponding to zeroes of
$w$
tell us which strands corresponding to zeroes of
![]() $v$
are ‘on’. We will indicate the ‘on’ and ‘off’ strands by dotted [green] lines and dashed [red] lines, respectively, in the case of
$v$
are ‘on’. We will indicate the ‘on’ and ‘off’ strands by dotted [green] lines and dashed [red] lines, respectively, in the case of
![]() $w=(10110)$
.
$w=(10110)$
.

Then
![]() $c(v,w)$
is the total number of crossings between the 1-strands and the ‘on’ 0-strands, shown here as dots.
$c(v,w)$
is the total number of crossings between the 1-strands and the ‘on’ 0-strands, shown here as dots.
We now prove the following.
Lemma 5.9. Let
![]() $v\in \{0,1\}^{n}$
be a sequence with
$v\in \{0,1\}^{n}$
be a sequence with
![]() $\ell _{0}$
ones and
$\ell _{0}$
ones and
![]() $k_{0}=n-\ell _{0}$
zeroes. The functions
$k_{0}=n-\ell _{0}$
zeroes. The functions
![]() $f_{v}(q,0,t)$
satisfy the recursion
$f_{v}(q,0,t)$
satisfy the recursion
![]() $f_{\emptyset }(q,0,t)=1$
and
$f_{\emptyset }(q,0,t)=1$
and
where
![]() $w$
has
$w$
has
![]() $k_{1}$
zeroes.
$k_{1}$
zeroes.
Proof. Setting
![]() $a=0$
in Definition 5.3, we see that
$a=0$
in Definition 5.3, we see that
![]() ${\mathcal{P}}_{v,w}(q,0,t)$
is the product of
${\mathcal{P}}_{v,w}(q,0,t)$
is the product of
![]() $t^{\ell (i)+m(i)}$
over all indices
$t^{\ell (i)+m(i)}$
over all indices
![]() $i$
such that
$i$
such that
![]() $v_{i}=1$
. The
$v_{i}=1$
. The
![]() $t^{\ell (i)}$
factors contribute
$t^{\ell (i)}$
factors contribute
![]() $t^{\binom{\ell _{0}}{2}}$
and the
$t^{\binom{\ell _{0}}{2}}$
and the
![]() $t^{m(i)}$
factors contribute
$t^{m(i)}$
factors contribute
![]() $t^{c(v,w)}$
. Thus, setting
$t^{c(v,w)}$
. Thus, setting
![]() $a=0$
in the alternate recursion Proposition 5.5 gives the statement. We are also using the result of Proposition 5.6 in the special case where
$a=0$
in the alternate recursion Proposition 5.5 gives the statement. We are also using the result of Proposition 5.6 in the special case where
![]() $v$
is the zero sequence.◻
$v$
is the zero sequence.◻
Proof of Theorem 1.9.
Consider a sequence
![]() $\mathbf{v}=(v^{(0)},v^{(1)},\ldots ,)$
of sequences
$\mathbf{v}=(v^{(0)},v^{(1)},\ldots ,)$
of sequences
![]() $v^{(r)}\in \{0,1\}^{n}$
such that
$v^{(r)}\in \{0,1\}^{n}$
such that
![]() $v_{i}^{(r)}\leqslant v_{i}^{(r+1)}$
for all
$v_{i}^{(r)}\leqslant v_{i}^{(r+1)}$
for all
![]() $i\in \{1,\ldots ,n\}$
and all
$i\in \{1,\ldots ,n\}$
and all
![]() $r\geqslant 0$
. Assume that
$r\geqslant 0$
. Assume that
![]() $v^{(r)}=(1,1,\ldots ,1)$
for
$v^{(r)}=(1,1,\ldots ,1)$
for
![]() $r\gg 0$
. Then
$r\gg 0$
. Then
![]() $\mathbf{v}$
defines a function
$\mathbf{v}$
defines a function
![]() $\unicode[STIX]{x1D70E}:\{1,\ldots ,n\}\rightarrow \mathbb{Z}_{{\geqslant}0}$
, where
$\unicode[STIX]{x1D70E}:\{1,\ldots ,n\}\rightarrow \mathbb{Z}_{{\geqslant}0}$
, where
![]() $\unicode[STIX]{x1D70E}(i)$
is the smallest
$\unicode[STIX]{x1D70E}(i)$
is the smallest
![]() $r$
such that
$r$
such that
![]() $v_{i}^{(r)}=1$
. It is easy to see that this yields a bijection between sequences
$v_{i}^{(r)}=1$
. It is easy to see that this yields a bijection between sequences
![]() $\mathbf{v}$
and functions
$\mathbf{v}$
and functions
![]() $\unicode[STIX]{x1D70E}$
.
$\unicode[STIX]{x1D70E}$
.
Let
![]() $k(r)$
denote the number of zeroes of
$k(r)$
denote the number of zeroes of
![]() $v^{(r)}$
, and let
$v^{(r)}$
, and let
![]() $w^{(r)}\in \{0,1\}^{k(r)}$
denote the sequence such that
$w^{(r)}\in \{0,1\}^{k(r)}$
denote the sequence such that
![]() $w^{(0)}=v^{(0)}$
and
$w^{(0)}=v^{(0)}$
and
![]() $v^{(r-1)}\circ w^{(r)}=v^{(r)}$
for
$v^{(r-1)}\circ w^{(r)}=v^{(r)}$
for
![]() $r\geqslant 1$
. Clearly this establishes a bijection between increasing sequences
$r\geqslant 1$
. Clearly this establishes a bijection between increasing sequences
![]() $\mathbf{v}$
and eventually empty sequences
$\mathbf{v}$
and eventually empty sequences
![]() $\mathbf{w}=(w^{(1)},w^{(2)},\ldots )$
such that
$\mathbf{w}=(w^{(1)},w^{(2)},\ldots )$
such that
![]() $(w^{(r)},w^{(r+1)})$
are compatible for all
$(w^{(r)},w^{(r+1)})$
are compatible for all
![]() $r$
.
$r$
.
With these notions in place, we apply Lemma 5.9 to
![]() $f_{(00\cdots 0)}$
iteratively. After one application, we see that
$f_{(00\cdots 0)}$
iteratively. After one application, we see that
![]() $f_{00\cdots 0}$
is a sum over sequences
$f_{00\cdots 0}$
is a sum over sequences
![]() $w^{(0)}$
of
$w^{(0)}$
of
![]() $f_{w^{(0)}}$
, weighted by some monomials in
$f_{w^{(0)}}$
, weighted by some monomials in
![]() $q$
and
$q$
and
![]() $t$
. We apply the recursion again. The result can be viewed as a sum over sequences
$t$
. We apply the recursion again. The result can be viewed as a sum over sequences
![]() $w^{(0)}$
and
$w^{(0)}$
and
![]() $w^{(1)}$
with
$w^{(1)}$
with
![]() $(w^{(0)},w^{(1)})$
compatible. Iterating indefinitely, we see that
$(w^{(0)},w^{(1)})$
compatible. Iterating indefinitely, we see that
![]() $f_{00\cdots 0}$
can be expressed as a sum over all sequences
$f_{00\cdots 0}$
can be expressed as a sum over all sequences
![]() $\mathbf{w}$
of some monomials in
$\mathbf{w}$
of some monomials in
![]() $q$
and
$q$
and
![]() $t$
. Using the bijection between the
$t$
. Using the bijection between the
![]() $\mathbf{w}$
sequences and the
$\mathbf{w}$
sequences and the
![]() $\mathbf{v}$
sequences, we regard this as a sum over all sequences
$\mathbf{v}$
sequences, we regard this as a sum over all sequences
![]() $\mathbf{v}$
of some monomials
$\mathbf{v}$
of some monomials
![]() $g_{\mathbf{v}}$
computed from
$g_{\mathbf{v}}$
computed from
![]() $\mathbf{v}$
. We claim that
$\mathbf{v}$
. We claim that
![]() $g_{\mathbf{v}}=t^{a(\unicode[STIX]{x1D70E})+b(\unicode[STIX]{x1D70E})}q^{c(\unicode[STIX]{x1D70E})}$
, which would prove the theorem.
$g_{\mathbf{v}}=t^{a(\unicode[STIX]{x1D70E})+b(\unicode[STIX]{x1D70E})}q^{c(\unicode[STIX]{x1D70E})}$
, which would prove the theorem.
Suppose an index
![]() $i$
is such that
$i$
is such that
![]() $v^{(r-1)}=0$
but
$v^{(r-1)}=0$
but
![]() $v^{(r)}=1$
, with
$v^{(r)}=1$
, with
![]() $r\geqslant 1$
. Then the
$r\geqslant 1$
. Then the
![]() $t$
contribution at the
$t$
contribution at the
![]() $r$
th step is
$r$
th step is
![]() $t^{c(w^{(r-1)},w^{(r)})+\binom{\unicode[STIX]{x1D70E}^{-1}(r)}{2}}$
by Lemma 5.9. Taking the product over all
$t^{c(w^{(r-1)},w^{(r)})+\binom{\unicode[STIX]{x1D70E}^{-1}(r)}{2}}$
by Lemma 5.9. Taking the product over all
![]() $r\geqslant 1$
accounts for the factor of
$r\geqslant 1$
accounts for the factor of
![]() $t^{a(\unicode[STIX]{x1D70E})+b(\unicode[STIX]{x1D70E})}$
.
$t^{a(\unicode[STIX]{x1D70E})+b(\unicode[STIX]{x1D70E})}$
.
Finally, the number of zeroes in
![]() $w^{(r)}$
equals the number of indices
$w^{(r)}$
equals the number of indices
![]() $i\in \{1,\ldots ,n\}$
such that
$i\in \{1,\ldots ,n\}$
such that
![]() $\unicode[STIX]{x1D70E}(i)>r$
, that is,
$\unicode[STIX]{x1D70E}(i)>r$
, that is,
![]() $\sum _{s>r}|\unicode[STIX]{x1D70E}^{-1}(s)|$
. Each of these contributes a factor of
$\sum _{s>r}|\unicode[STIX]{x1D70E}^{-1}(s)|$
. Each of these contributes a factor of
![]() $q$
. Taking the product over all
$q$
. Taking the product over all
![]() $r\geqslant 0$
yields
$r\geqslant 0$
yields
![]() $q$
to the power of
$q$
to the power of
This accounts for the factor of
![]() $q^{c(\unicode[STIX]{x1D70E})}$
.◻
$q^{c(\unicode[STIX]{x1D70E})}$
.◻
Acknowledgements
The authors would like to thank Eugene Gorsky, Alee Oblocutor, Pave Eringo, and Andre Negus for enlightening conversations. A substantial amount of this work was completed during the second author’s visit to the University of Oregon during the summer of 2015; we are indebted to the UO math department for its hospitality and support, and apologize for filling the lounge chalkboard with half twists. Both authors would like to thank Yeppie for her excellent sandwiches, which kept us full of hope and inspiration.
Appendix A Miscellaneous computations
In this appendix we illustrate the usefulness of our method with a few computations of triply graded homology for certain torus knots. For the reader’s convenience we present our results with the proper normalization, and we state how to obtain classical invariants from them.
Let
![]() ${\mathcal{P}}_{\unicode[STIX]{x1D6FD}}(Q,A,T)$
denote the Poincaré series of
${\mathcal{P}}_{\unicode[STIX]{x1D6FD}}(Q,A,T)$
denote the Poincaré series of
![]() $\operatorname{HHH}(F(\unicode[STIX]{x1D6FD}))$
, where
$\operatorname{HHH}(F(\unicode[STIX]{x1D6FD}))$
, where
![]() $Q,A,T$
denote the usual quantum degree, homological degree, and Hochschild degree, respectively. This
$Q,A,T$
denote the usual quantum degree, homological degree, and Hochschild degree, respectively. This
![]() ${\mathcal{P}}_{\unicode[STIX]{x1D6FD}}$
is an invariant of the braid closure
${\mathcal{P}}_{\unicode[STIX]{x1D6FD}}$
is an invariant of the braid closure
![]() $L=\hat{\unicode[STIX]{x1D6FD}}$
up to multiplication by a unit in
$L=\hat{\unicode[STIX]{x1D6FD}}$
up to multiplication by a unit in
![]() $\mathbb{Z}[A^{\pm },Q^{\pm },T^{\pm }]$
. The precise normalization which yields a link invariant requires that we introduce half-integral powers of
$\mathbb{Z}[A^{\pm },Q^{\pm },T^{\pm }]$
. The precise normalization which yields a link invariant requires that we introduce half-integral powers of
![]() $A$
and
$A$
and
![]() $T$
:
$T$
:
where
![]() $e(\unicode[STIX]{x1D6FD})$
is the braid exponent (signed number of crossings). The decategorification corresponds to specializing
$e(\unicode[STIX]{x1D6FD})$
is the braid exponent (signed number of crossings). The decategorification corresponds to specializing
![]() $T=-1$
. To avoid choosing a square root of
$T=-1$
. To avoid choosing a square root of
![]() $-1$
, we first rewrite
$-1$
, we first rewrite
![]() ${\mathcal{P}}_{L}$
in terms of
${\mathcal{P}}_{L}$
in terms of
![]() $Q,T$
, and the Homfly variable
$Q,T$
, and the Homfly variable
![]() $\unicode[STIX]{x1D6FC}=A^{1/2}T^{1/2}Q^{-1}$
:
$\unicode[STIX]{x1D6FC}=A^{1/2}T^{1/2}Q^{-1}$
:
We call
![]() ${\mathcal{P}}_{L}$
the super polynomial. Setting
${\mathcal{P}}_{L}$
the super polynomial. Setting
![]() $T=-1$
recovers the Homfly polynomial in variables
$T=-1$
recovers the Homfly polynomial in variables
![]() $\unicode[STIX]{x1D6FC},Q$
. The
$\unicode[STIX]{x1D6FC},Q$
. The
![]() $\mathfrak{s}\mathfrak{l}_{N}$
specialization is then obtained by setting
$\mathfrak{s}\mathfrak{l}_{N}$
specialization is then obtained by setting
![]() $\unicode[STIX]{x1D6FC}=Q^{N}$
. For reference, the invariant of the unknot is
$\unicode[STIX]{x1D6FC}=Q^{N}$
. For reference, the invariant of the unknot is
Recall that we prefer the variables
![]() $t=T^{2}Q^{-2}$
,
$t=T^{2}Q^{-2}$
,
![]() $q=Q^{2}$
,
$q=Q^{2}$
,
![]() $a=AQ^{-2}$
. Thus, we will usually rewrite
$a=AQ^{-2}$
. Thus, we will usually rewrite
![]() $P_{L}$
in terms of these variables. The decategorification is obtained by setting
$P_{L}$
in terms of these variables. The decategorification is obtained by setting
![]() $t^{1/2}=-q^{-1/2}$
; if one wishes to avoid working in a ring with
$t^{1/2}=-q^{-1/2}$
; if one wishes to avoid working in a ring with
![]() $\sqrt{-1}$
, then one should also set
$\sqrt{-1}$
, then one should also set
![]() $a^{1/2}(tq)^{1/4}=-\unicode[STIX]{x1D6FC}$
. For knots, it turns out that the reduced superpolynomial
$a^{1/2}(tq)^{1/4}=-\unicode[STIX]{x1D6FC}$
. For knots, it turns out that the reduced superpolynomial
![]() $\widetilde{P}_{L}(q,a,t):=P_{L}(q,a,t)/P_{U}(q,a,t)$
is a Laurent polynomial in
$\widetilde{P}_{L}(q,a,t):=P_{L}(q,a,t)/P_{U}(q,a,t)$
is a Laurent polynomial in
![]() $q^{1/2},a,t^{1/2}$
, so no technical issue arises from the decategorification
$q^{1/2},a,t^{1/2}$
, so no technical issue arises from the decategorification
![]() $t^{1/2}\mapsto -q^{-1/2}$
. The
$t^{1/2}\mapsto -q^{-1/2}$
. The
![]() $\mathfrak{s}\mathfrak{l}_{N}$
specialization is then obtained by setting
$\mathfrak{s}\mathfrak{l}_{N}$
specialization is then obtained by setting
![]() $a=-q^{N}$
. The following computations were all done by hand. We omit their derivations, in the interest of readability and length.
$a=-q^{N}$
. The following computations were all done by hand. We omit their derivations, in the interest of readability and length.
Example A.1. The reduced superpolynomial of the
![]() $(2,2k+1)$
torus knot is
$(2,2k+1)$
torus knot is
In particular, the superpolynomial of the right-handed trefoil, that is, the
![]() $(2,3)$
torus knot, is
$(2,3)$
torus knot, is
![]() $a(tq)^{-1/2}(q+t+a)$
. The decategorification is
$a(tq)^{-1/2}(q+t+a)$
. The decategorification is
![]() $-a(q+q^{-1}+a)$
, and the
$-a(q+q^{-1}+a)$
, and the
![]() $\mathfrak{s}\mathfrak{l}_{N}$
specialization is
$\mathfrak{s}\mathfrak{l}_{N}$
specialization is
![]() $q^{N-1}+q^{N+1}-q^{2N}$
.
$q^{N-1}+q^{N+1}-q^{2N}$
.
Example A.2. The reduced superpolynomial of the
![]() $(3,4)$
torus knot is
$(3,4)$
torus knot is
The decategorification is
Setting
![]() $a=-q^{2}$
and
$a=-q^{2}$
and
![]() $tq=1$
gives the correct
$tq=1$
gives the correct
![]() $\mathfrak{s}\mathfrak{l}_{2}$
specialization (Jones polynomial):
$\mathfrak{s}\mathfrak{l}_{2}$
specialization (Jones polynomial):
Example A.3. The reduced superpolynomial of the
![]() $(3,5)$
torus knot is
$(3,5)$
torus knot is
![]() $a^{4}(tq)^{-2}$
times
$a^{4}(tq)^{-2}$
times
Example A.4. The reduced superpolynomial of the
![]() $(4,5)$
torus knot is
$(4,5)$
torus knot is
 $$\begin{eqnarray}\displaystyle & & \displaystyle a^{6}(tq)^{-3} (t^{6}+qt^{5}+qt^{4}+qt^{3}+q^{2}t^{4}+q^{3}t^{2}+q^{2}t^{3}+q^{2}t^{2}+q^{3}t+q^{3}t^{3}+q^{4}t^{2}+q^{4}t+q^{5}t+q^{6}\nonumber\\ \displaystyle & & \displaystyle \quad +\,a(t^{5}+t^{4}+t^{3}+qt^{4}+q^{2}t^{3}+2qt^{3}+2qt^{2}+qt+2q^{2}t^{2}+2q^{2}t+2q^{3}t+q^{3}t^{2}\nonumber\\ \displaystyle & & \displaystyle \quad +\,q^{4}t+q^{3}+q^{4}+q^{5} )+\,a^{2}(t^{3}+t^{2}+t+qt^{2}+qt+q^{2}t+q+q^{2}+q^{3})+a^{3} ).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle a^{6}(tq)^{-3} (t^{6}+qt^{5}+qt^{4}+qt^{3}+q^{2}t^{4}+q^{3}t^{2}+q^{2}t^{3}+q^{2}t^{2}+q^{3}t+q^{3}t^{3}+q^{4}t^{2}+q^{4}t+q^{5}t+q^{6}\nonumber\\ \displaystyle & & \displaystyle \quad +\,a(t^{5}+t^{4}+t^{3}+qt^{4}+q^{2}t^{3}+2qt^{3}+2qt^{2}+qt+2q^{2}t^{2}+2q^{2}t+2q^{3}t+q^{3}t^{2}\nonumber\\ \displaystyle & & \displaystyle \quad +\,q^{4}t+q^{3}+q^{4}+q^{5} )+\,a^{2}(t^{3}+t^{2}+t+qt^{2}+qt+q^{2}t+q+q^{2}+q^{3})+a^{3} ).\nonumber\end{eqnarray}$$
Observation A.5. Each of the above polynomials is symmetric with respect to exchanging
![]() $q$
and
$q$
and
![]() $t$
. Further, the smallest
$t$
. Further, the smallest
![]() $a$
-degree summands of the Poincaré series of the
$a$
-degree summands of the Poincaré series of the
![]() $(n,n+1)$
torus knots are the
$(n,n+1)$
torus knots are the
![]() $q,t$
Catalan numbers, for
$q,t$
Catalan numbers, for
![]() $n=2,3,4$
. This verifies a conjecture in [Reference Gorsky, Oblomkov, Rasmussen and ShendeGORS14] in these cases.
$n=2,3,4$
. This verifies a conjecture in [Reference Gorsky, Oblomkov, Rasmussen and ShendeGORS14] in these cases.