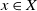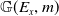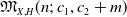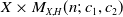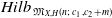1. Introduction
Let X be a nonsingular irreducible complex projective variety of dimension d. Let E be a vector bundle of rank n and fixed Chern classes
![]() $c_i \in H^{2i}(X, \mathbb{Z})$
on X. The m-elementary transformation E ′ of E at the point
$c_i \in H^{2i}(X, \mathbb{Z})$
on X. The m-elementary transformation E ′ of E at the point
![]() $x \in X$
is defined as the kernel of a surjection
$x \in X$
is defined as the kernel of a surjection
![]() $\alpha\,:\,E \longrightarrow \mathcal{O}_x^m$
which fits the exact sequence
$\alpha\,:\,E \longrightarrow \mathcal{O}_x^m$
which fits the exact sequence
It is not hard to check that the class of such extensions is parameterized by
![]() $\mathbb{G}(E_x,m)$
. This elementary transformation coincides with those defined by Maruyama, when X is a curve (see, [Reference Maruyama17]) but differs when
$\mathbb{G}(E_x,m)$
. This elementary transformation coincides with those defined by Maruyama, when X is a curve (see, [Reference Maruyama17]) but differs when
![]() $\dim\, X\geq 2$
, because the point
$\dim\, X\geq 2$
, because the point
![]() $x\in X$
is not a divisor anymore.
$x\in X$
is not a divisor anymore.
Maruyama used his definition of elementary transformation to construct vector bundles on nonsingular projective varieties. Since then these elementary transformations have been a powerful tool in order to get topological and geometric properties of the moduli space of sheaves, for instance:
When X is a curve and
![]() $m=1$
, the elementary transformation E ′ of E is a vector bundle. Moreover, if E is a general stable vector bundle then E ′ is stable, and under this condition, Narasimhan and Ramanan used elementary transformations to determine certain subvarieties (called Hecke cycles) in the moduli space of vector bundles on curves, see [Reference Narasimhan and Ramanan20, Reference Narasimhan and Ramanan21]. These Hecke cycles are contained in a component of the Hilbert scheme of the moduli space of vector bundles on curves (called Hecke component). Hence, Narasimhan and Ramanan computed a bound for the dimension of the Hecke component and proved that is nonsingular in those points defined by Hecke cycles. Moreover, when X is a curve and
$m=1$
, the elementary transformation E ′ of E is a vector bundle. Moreover, if E is a general stable vector bundle then E ′ is stable, and under this condition, Narasimhan and Ramanan used elementary transformations to determine certain subvarieties (called Hecke cycles) in the moduli space of vector bundles on curves, see [Reference Narasimhan and Ramanan20, Reference Narasimhan and Ramanan21]. These Hecke cycles are contained in a component of the Hilbert scheme of the moduli space of vector bundles on curves (called Hecke component). Hence, Narasimhan and Ramanan computed a bound for the dimension of the Hecke component and proved that is nonsingular in those points defined by Hecke cycles. Moreover, when X is a curve and
![]() $m\geq2,$
Brambila-Paz and Mata-Gutiérrez in [Reference Brambila-Paz and Mata-Gutiérrez2] generalized the construction of Hecke cycles using Grassmannians and defined Hecke Grassmannians. They proved that the corresponding Hecke component is nonsingular and a bound for its dimension was given.
$m\geq2,$
Brambila-Paz and Mata-Gutiérrez in [Reference Brambila-Paz and Mata-Gutiérrez2] generalized the construction of Hecke cycles using Grassmannians and defined Hecke Grassmannians. They proved that the corresponding Hecke component is nonsingular and a bound for its dimension was given.
In case that X is a surface and
![]() $m=1$
, Coskun and Huizenga [Reference Coskun and Huizenga3] used elementary transformations to determine a component of the moduli space of vector bundles of rank two and compute a bound for its dimension. Also, Costa and Miró-Roig used priority sheaves and elementary transformations in the sense of Maruyama in order to establish maps between certain moduli spaces over
$m=1$
, Coskun and Huizenga [Reference Coskun and Huizenga3] used elementary transformations to determine a component of the moduli space of vector bundles of rank two and compute a bound for its dimension. Also, Costa and Miró-Roig used priority sheaves and elementary transformations in the sense of Maruyama in order to establish maps between certain moduli spaces over
![]() $\mathbb{P}^2$
with the same rank and different Chern classes (see [7]).
$\mathbb{P}^2$
with the same rank and different Chern classes (see [7]).
The aim of this paper is to consider the case when X is a surface and
![]() $m\geq 1$
, we use m-elementary transformations to determine Hecke cycles in the moduli space of stable torsion-free sheaves and determine geometrical aspects of a component of its Hilbert scheme. Specifically, we prove the following result (see Theorem 3.10):
$m\geq 1$
, we use m-elementary transformations to determine Hecke cycles in the moduli space of stable torsion-free sheaves and determine geometrical aspects of a component of its Hilbert scheme. Specifically, we prove the following result (see Theorem 3.10):
Theorem 1.1.
The Hilbert scheme
![]() $\text{Hilb}_{\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)}$
of the moduli space of stable torsion-free sheaves has an irreducible component of dimension at least
$\text{Hilb}_{\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)}$
of the moduli space of stable torsion-free sheaves has an irreducible component of dimension at least
![]() $2+\dim\, M_{X,H}(n;\,c_1,c_2)$
.
$2+\dim\, M_{X,H}(n;\,c_1,c_2)$
.
The proof of this Theorem follows some ideas and techniques of [Reference Brambila-Paz and Mata-Gutiérrez2, Reference Narasimhan and Ramanan20]. For a fixed vector bundle E and a point
![]() $x\in X$
, we determine a closed embedding
$x\in X$
, we determine a closed embedding
![]() $\phi_z\,:\, \mathbb{G}(E_x,m) \mapsto \mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
(see Proposition 3.4). We use the closed embedding
$\phi_z\,:\, \mathbb{G}(E_x,m) \mapsto \mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
(see Proposition 3.4). We use the closed embedding
![]() $\phi_z$
to define the injective morphism
$\phi_z$
to define the injective morphism
Additionally, we establish the following morphism
where
![]() $\mathcal{U}$
denotes the universal family parameterized by
$\mathcal{U}$
denotes the universal family parameterized by
![]() $M_{X,H}(n;\,c_1,c_2)$
. This morphism allows us to determine an irreducible projective variety of
$M_{X,H}(n;\,c_1,c_2)$
. This morphism allows us to determine an irreducible projective variety of
![]() $\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)-M_{X,H}(n;\,c_1,c_2+m)$
and we get the following result (see Theorem 3.6):
$\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)-M_{X,H}(n;\,c_1,c_2+m)$
and we get the following result (see Theorem 3.6):
Theorem 1.2.
Let m, n natural integers with
![]() $1\leq m \lt n $
. Then
$1\leq m \lt n $
. Then
![]() $\mathfrak{M}_{X,H}(n;\,c_1,c_2)-M_{X,H}(n;\,c_1,c_2+m)$
contains an irreducible projective variety Y of dimension
$\mathfrak{M}_{X,H}(n;\,c_1,c_2)-M_{X,H}(n;\,c_1,c_2+m)$
contains an irreducible projective variety Y of dimension
![]() $3+\dim\, M_{X,H}(n;\,c_1,c_2)$
such that the general element
$3+\dim\, M_{X,H}(n;\,c_1,c_2)$
such that the general element
![]() $F \in Y$
fits into exact sequence
$F \in Y$
fits into exact sequence
where
![]() $E\in M_{X,H}(n;\,c_1,c_2)$
,
$E\in M_{X,H}(n;\,c_1,c_2)$
,
![]() $W\in\mathbb{G}(E_x, m)$
and
$W\in\mathbb{G}(E_x, m)$
and
![]() $x\in X$
. In particular, if
$x\in X$
. In particular, if
![]() $n=2 $
then
$n=2 $
then
![]() $\Phi$
is injective and Y is a divisor.
$\Phi$
is injective and Y is a divisor.
As an application of the previous result, we compute the Hilbert polynomial of the Hilbert scheme
![]() $\text{Hilb}^P_{\mathfrak{M}_{X,H}(n;\,c_1,c_2)}$
which contains the cycle
$\text{Hilb}^P_{\mathfrak{M}_{X,H}(n;\,c_1,c_2)}$
which contains the cycle
![]() $\phi_z(\mathbb{G}(E_x,m))$
when X is the projective plane. In particular, we prove the following (see Theorem 4.3);
$\phi_z(\mathbb{G}(E_x,m))$
when X is the projective plane. In particular, we prove the following (see Theorem 4.3);
Theorem 1.3.
Assume that
![]() $c_1=-1$
(resp.
$c_1=-1$
(resp.
![]() $c_1=0$
) and that
$c_1=0$
) and that
![]() $c_2 \geq 2$
(resp.
$c_2 \geq 2$
(resp.
![]() $c_2 \geq 3$
is odd). Let
$c_2 \geq 3$
is odd). Let
![]() $L= a\epsilon + b\delta$
, (resp.
$L= a\epsilon + b\delta$
, (resp.
![]() $a\varphi+b\psi$
) be an ample line bundle in
$a\varphi+b\psi$
) be an ample line bundle in
![]() $Pic(\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2))$
. Then,
$Pic(\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2))$
. Then,
![]() $\mathcal{H}\mathcal{G}$
is the component of the Hilbert scheme
$\mathcal{H}\mathcal{G}$
is the component of the Hilbert scheme
![]() $\text{Hilb}^P_{\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)}$
where P is the Hilbert polynomial defined as;
$\text{Hilb}^P_{\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)}$
where P is the Hilbert polynomial defined as;
The paper is organized as follows: Section 2 contains a brief summary of the main results of Grassmannians of vector bundles, moduli space of torsion-free sheaves, and m-elementary transformations. In Section 3, we give some technical results which allow us to prove our main results: Theorems 1.1 and 1.2. In Section 4, an application of the previous results is indicated for the Hilbert scheme of moduli space of rank 2 sheaves on the projective plane.
2. Preliminaries
Let X be a nonsingular irreducible complex projective algebraic surface. This section contains a brief summary about stable torsion-free sheaves on surfaces, and we recall some basic facts on Grasmannians of vector bundles and m-elementary transformations see [Reference Fantechi9, Reference Friedman10, Reference Huybrechts and Lehn14] for more details.
2.1. Grassmannian
We will collect here the principal properties of Grassmannians of vector bundles necessary for our purpose. For a fuller treatment, we refer the reader to [Reference Eisenbud and Harris8, Reference Tyurin25].
Let E be a vector bundle of rank n on X. Let
![]() $p_E\,:\, \mathbb{G}(E,m)\rightarrow X$
be the Grassmannian bundle of rank m quotients of E whose fiber at
$p_E\,:\, \mathbb{G}(E,m)\rightarrow X$
be the Grassmannian bundle of rank m quotients of E whose fiber at
![]() $x\in X$
is the Grassmannian
$x\in X$
is the Grassmannian
![]() $\mathbb{G}(E_{x},m)$
of m-dimensional quotients of
$\mathbb{G}(E_{x},m)$
of m-dimensional quotients of
![]() $E_x$
, that is
$E_x$
, that is
Let
be the tautological exact sequence over
![]() $\mathbb{G}(E,m)$
where
$\mathbb{G}(E,m)$
where
![]() $S_E$
and
$S_E$
and
![]() $Q_E$
denote the universal subbundle of rank
$Q_E$
denote the universal subbundle of rank
![]() $n-m$
and universal quotient of rank m, respectively. The tangent bundle of
$n-m$
and universal quotient of rank m, respectively. The tangent bundle of
![]() $\mathbb{G}(E,m)$
is the vector bundle
$\mathbb{G}(E,m)$
is the vector bundle
![]() $T\mathbb{G}(E,m)=Hom(S_E,Q_E)$
and hence
$T\mathbb{G}(E,m)=Hom(S_E,Q_E)$
and hence
![]() $T_x\mathbb{G}(E,m)=Hom(S_{E_x},Q_{E_x})$
. Moreover, we have the following exact sequence:
$T_x\mathbb{G}(E,m)=Hom(S_{E_x},Q_{E_x})$
. Moreover, we have the following exact sequence:
where
![]() $T_{p_E}$
is the relative tangent bundle to the fibers and
$T_{p_E}$
is the relative tangent bundle to the fibers and
![]() $T_{p_E}=S^{*}_E\otimes Q_E$
.
$T_{p_E}=S^{*}_E\otimes Q_E$
.
2.2. Torsion-Free sheaves
Let H be an ample divisor on X. For a torsion-free sheaf
![]() $\mathcal{E}$
on X with Chern classes
$\mathcal{E}$
on X with Chern classes
![]() $c_i \in H^{2i}(X,\mathbb{Z})$
,
$c_i \in H^{2i}(X,\mathbb{Z})$
,
![]() $i=1,2$
one sets
$i=1,2$
one sets
where
![]() $\text{deg}_H(\mathcal{E})$
is the degree of
$\text{deg}_H(\mathcal{E})$
is the degree of
![]() $\mathcal{E}$
defined by
$\mathcal{E}$
defined by
![]() $c_1(\mathcal{E}).H$
and
$c_1(\mathcal{E}).H$
and
![]() $\chi(\mathcal{E} \otimes H^m)$
denotes the Hilbert polynomial defined by
$\chi(\mathcal{E} \otimes H^m)$
denotes the Hilbert polynomial defined by
![]() $\sum ({-}1)^ih^i(X, \mathcal{E} \otimes H^m)$
.
$\sum ({-}1)^ih^i(X, \mathcal{E} \otimes H^m)$
.
Definition 2.1. Let H be an ample divisor on X. A torsion-free sheaf
![]() $\mathcal{E}$
on X is H-stable (resp. stable) if for all nonzero subsheaf
$\mathcal{E}$
on X is H-stable (resp. stable) if for all nonzero subsheaf
![]() $\mathcal{F}\subset \mathcal{E}$
$\mathcal{F}\subset \mathcal{E}$
We want to emphasize that both notions of stability depend on the ample divisor we fix on the underlying surface X and it is easily seen that H-stability implies stability.Footnote 1
Recall that any H-stable (resp. stable) torsion-free sheaf is simple, i.e. if
![]() $\mathcal{E}$
is H-stable (resp. stable), then
$\mathcal{E}$
is H-stable (resp. stable), then
![]() $\dim Hom(\mathcal{E},\mathcal{E})=1$
. We will denote by
$\dim Hom(\mathcal{E},\mathcal{E})=1$
. We will denote by
![]() $M_{X,H}(n;\, c_1,c_2)$
the moduli space of H-stable vector bundles on X of rank n and fixed Chern classes
$M_{X,H}(n;\, c_1,c_2)$
the moduli space of H-stable vector bundles on X of rank n and fixed Chern classes
![]() $c_1, c_2$
and by
$c_1, c_2$
and by
![]() $\mathfrak{M}_{X,H}(n;\,c_1,c_2)$
the moduli space of stable torsion-free sheaves on X. Since locally free is an open property and H-stability implies stability, it follows that
$\mathfrak{M}_{X,H}(n;\,c_1,c_2)$
the moduli space of stable torsion-free sheaves on X. Since locally free is an open property and H-stability implies stability, it follows that
![]() $M_{X,H}(n;\, c_1,c_2)$
is an open subset of
$M_{X,H}(n;\, c_1,c_2)$
is an open subset of
![]() $\mathfrak{M}_{X,H}(n;\,c_1,c_2)$
. In general an universal family on
$\mathfrak{M}_{X,H}(n;\,c_1,c_2)$
. In general an universal family on
![]() $X \times M_{X,H}(n;\,c_1,c_2)$
(resp. on
$X \times M_{X,H}(n;\,c_1,c_2)$
(resp. on
![]() $X \times \mathfrak{M}_{X,H}(n;\,c_1,c_2)$
) does not exist, the existence of such universal family is guaranteed by the following criterion.
$X \times \mathfrak{M}_{X,H}(n;\,c_1,c_2)$
) does not exist, the existence of such universal family is guaranteed by the following criterion.
Lemma 2.2. [Reference Huybrechts and Lehn14, Corollary 4.6.7] Let X be a nonsingular surface and let H be an ample divisor on X. Let
![]() $n,c_1, c_2$
fixed values for the rank and Chern classes. If
$n,c_1, c_2$
fixed values for the rank and Chern classes. If
![]() $gcd(n, c_1.H, \frac{1}{2}c_1.(c_1-K_X)-c_2)=1$
, then there is an universal family on
$gcd(n, c_1.H, \frac{1}{2}c_1.(c_1-K_X)-c_2)=1$
, then there is an universal family on
![]() $X \times M_{X,H}(n;\,c_1,c_2)$
(resp.
$X \times M_{X,H}(n;\,c_1,c_2)$
(resp.
![]() $X \times \mathfrak{M}_{X,H}(n;\,c_1,c_2)$
).
$X \times \mathfrak{M}_{X,H}(n;\,c_1,c_2)$
).
2.3. m-elementary transformations
Definition 2.3. Let E be a locally free sheaf on X of rank n and Chern classes
![]() $c_1, c_2$
and let
$c_1, c_2$
and let
be an exact sequence of sheaves, where
![]() $\mathcal{O}^{m}_{x}=\oplus_{i=1}^{m} \mathcal{O}_{x}$
is the sum of skyscraper sheaf with support on
$\mathcal{O}^{m}_{x}=\oplus_{i=1}^{m} \mathcal{O}_{x}$
is the sum of skyscraper sheaf with support on
![]() $x\in X.$
The coherent sheaf E ′ is called the m-elementary transformation of E at
$x\in X.$
The coherent sheaf E ′ is called the m-elementary transformation of E at
![]() $x \in X$
.
$x \in X$
.
Notice that even though E is locally free, its elementary transformation E ′ is a torsion free sheaf not locally free. Moreover if E is H-stable then E ′ is also H-stable. However, if E is stable then E ′ is not necessarily stable (see for instance [Reference Coskun and Huizenga6, Remark 1]).
The m-elementary transformations have been used for several authors to construct many vector bundles on a higher dimensional projective variety and to determine topological and geometric properties of the moduli space of sheaves. For instance, Maruyama did a general study of elementary transformations of sheaves in his master’s and doctoral theses [Reference Maruyama16, Reference Maruyama17]. In [Reference Narasimhan and Ramanan20] Narasimhan and Ramanan used elementary transformations of vector bundles on curves to introduce certain subvarieties in the moduli space of vector bundles which they called Hecke cycles. Brambila-Paz and the first author also used m-elementary transformations to describe a nonsingular open set of the Hilbert scheme of the moduli space of vector bundles on a curve [Reference Brambila-Paz and Mata-Gutiérrez2]. Coskun and Huizenga have used elementary transformations to study priority sheaves since that they are well-behaved under elementary modifications [Reference Coskun and Huizenga3–Reference Coskun and Huizenga5].
We now collect some other basic properties related with m-elementary transformations in the following result.
Proposition 2.4.
Let H be an ample divisor on X. Let E be a vector bundle on X of rank n and Chern classes
![]() $c_1,c_2$
,and let E′ be a m-elementary transformation of E at
$c_1,c_2$
,and let E′ be a m-elementary transformation of E at
![]() $x \in X,$
i.e. we have
$x \in X,$
i.e. we have
Then,
-
(i)
 $rk(E^{\prime})=n$
,
$rk(E^{\prime})=n$
,
 $c_1(E^{\prime})=c_1$
,
$c_1(E^{\prime})=c_1$
,
 $c_2(E^{\prime})= c_2+m$
and
$c_2(E^{\prime})= c_2+m$
and
 $\chi(E^{\prime})=\chi(E)-m.$
$\chi(E^{\prime})=\chi(E)-m.$
-
(ii) E′ is a torsion-free sheaf not locally free.
-
(iii) If E is H-stable, then E′ is H-stable. Hence, E′ is stable.
Proof.
-
(i) The proof follows directly from the exact sequence and Riemann–Roch Theorem.
-
(ii) Clearly E ′ is torsion free since E is a vector bundle. Now, suppose that E ′ is locally free, by [Reference Friedman10, Chapter 4, Lemma 3], it follows that
 $E =E^{\prime}$
which is impossible because
$E =E^{\prime}$
which is impossible because
 $c_2(E^{\prime}) =c_2+m$
. Therefore E ′ is a torsion-free sheaf not locally free.
$c_2(E^{\prime}) =c_2+m$
. Therefore E ′ is a torsion-free sheaf not locally free. -
(iii) Let F be subsheaf of E ′ and assume that E is H-stable. It is clear that F is a subsheaf of E and by item (i), it follows that
Hence E ′ is H-stable and therefore stable. \begin{equation*}\mu_H(F) \lt \mu_H(E) = \mu_H(E^{\prime}).\end{equation*}
\begin{equation*}\mu_H(F) \lt \mu_H(E) = \mu_H(E^{\prime}).\end{equation*}
Remark 2.5. The class of extensions (2.2) are parameterized by
![]() $\mathbb{G}(E_x,m)$
. Furthermore, any
$\mathbb{G}(E_x,m)$
. Furthermore, any
![]() $W \in \mathbb{G}(E_x,m)$
defines a surjective linear transformation
$W \in \mathbb{G}(E_x,m)$
defines a surjective linear transformation
![]() $\tilde{\alpha}_{W}\,:\,E_{x}\rightarrow W\rightarrow 0$
which determines a surjective morphism of sheaves
$\tilde{\alpha}_{W}\,:\,E_{x}\rightarrow W\rightarrow 0$
which determines a surjective morphism of sheaves
![]() $\alpha_{W}\,:\,E\rightarrow \mathcal{O}^{m}_{x}$
. If
$\alpha_{W}\,:\,E\rightarrow \mathcal{O}^{m}_{x}$
. If
![]() $E^W$
denotes
$E^W$
denotes
![]() $\text{ker}(\alpha_W)$
then we have the exact sequence:
$\text{ker}(\alpha_W)$
then we have the exact sequence:
The following result will be used in the next sections:
Lemma 2.6.
Let E be a vector bundle on X and let
![]() $\mathcal{O}_{x}$
be the skyscraper sheaf with support on
$\mathcal{O}_{x}$
be the skyscraper sheaf with support on
![]() $x\in X$
. Then, for any integer
$x\in X$
. Then, for any integer
![]() $m\geq 1$
we have
$m\geq 1$
we have
For a deeper discussion of m-elementary transformations, we refer to reader to [Reference Brambila-Paz and Mata-Gutiérrez2, Reference Coskun and Huizenga3].
2.4. Hecke cycles on the moduli space of vector bundles on curves
Let X be a smooth projective curve, and let
![]() $x \in X$
be a point. For any vector bundle E on X, the m-elementary transformation
$x \in X$
be a point. For any vector bundle E on X, the m-elementary transformation
determines a vector bundle E ′, where
![]() $\text{deg}(E^{\prime})=\text{deg}(E)-m$
and
$\text{deg}(E^{\prime})=\text{deg}(E)-m$
and
![]() $\text{rk}(E^{\prime})=\text{rk}(E)$
. If E is general in the moduli space
$\text{rk}(E^{\prime})=\text{rk}(E)$
. If E is general in the moduli space
![]() $M_X(n,d)$
of stable vector bundles of rank n and degree d, then E ′ is stable (see [Reference Brambila-Paz and Mata-Gutiérrez2, Proposition 2.4]).
$M_X(n,d)$
of stable vector bundles of rank n and degree d, then E ′ is stable (see [Reference Brambila-Paz and Mata-Gutiérrez2, Proposition 2.4]).
In [Reference Narasimhan and Ramanan20] Narasimhan and Ramanan considered the m-elementary transformations of type
to prove that, for a general
![]() $E\in M_X(n,d)$
(for an explicit description of the general open set in
$E\in M_X(n,d)$
(for an explicit description of the general open set in
![]() $M_X(n,d)$
see [Reference Narasimhan and Ramanan20, Lemma 5.5]), the pair (E, x) determines a closed embedding
$M_X(n,d)$
see [Reference Narasimhan and Ramanan20, Lemma 5.5]), the pair (E, x) determines a closed embedding
(see, [Reference Narasimhan and Ramanan20, Lemma 5.8]) and therefore
![]() $\mathbb{P}\left(E^{*}_x\right)$
can be considered as a subscheme of the moduli space
$\mathbb{P}\left(E^{*}_x\right)$
can be considered as a subscheme of the moduli space
![]() $M_X(n,d-1)$
. These projective subschemes are called Hecke cycles. Every Hecke cycle determines a point in the Hilbert scheme
$M_X(n,d-1)$
. These projective subschemes are called Hecke cycles. Every Hecke cycle determines a point in the Hilbert scheme
![]() $\text{Hilb}_{M_X(n,d-1)}$
. Narasimhan and Ramanan proved that there is an open subscheme in
$\text{Hilb}_{M_X(n,d-1)}$
. Narasimhan and Ramanan proved that there is an open subscheme in
![]() $M_X(n,d)$
which is isomorphic to an open subscheme of
$M_X(n,d)$
which is isomorphic to an open subscheme of
![]() $\text{Hilb}_{M_X(n,d-1)}$
(see, [Reference Narasimhan and Ramanan20, Theorem 5.13]).
$\text{Hilb}_{M_X(n,d-1)}$
(see, [Reference Narasimhan and Ramanan20, Theorem 5.13]).
Later, in [Reference Brambila-Paz and Mata-Gutiérrez2] the authors generalize the ideas of Narasimhan and Ramanan and they considered m-elementary transformations,
![]() $m\gt1$
in order to prove that, if
$m\gt1$
in order to prove that, if
![]() $E\in M_X(n,d)$
is general (for an explicit description of the general open set in
$E\in M_X(n,d)$
is general (for an explicit description of the general open set in
![]() $M_X(n,d)$
see [Reference Brambila-Paz and Mata-Gutiérrez2, Proposition 2.4]), then E ′ is stable. Moreover, every pair (E, x) determines a closed embedding
$M_X(n,d)$
see [Reference Brambila-Paz and Mata-Gutiérrez2, Proposition 2.4]), then E ′ is stable. Moreover, every pair (E, x) determines a closed embedding
(see [Reference Brambila-Paz and Mata-Gutiérrez2, Proposition 3.1]) and therefore
![]() $\mathbb{G}(E_x,m)$
can be considered as a Grassmannian subvariety in the moduli space
$\mathbb{G}(E_x,m)$
can be considered as a Grassmannian subvariety in the moduli space
![]() $M_X(n,d-m)$
which is called m-Hecke cycles. Hence, they concluded that
$M_X(n,d-m)$
which is called m-Hecke cycles. Hence, they concluded that
![]() $\text{Hilb}_{M(n,d-m)}$
has an irreducible component
$\text{Hilb}_{M(n,d-m)}$
has an irreducible component
![]() $\mathcal{HG}$
of dimension
$\mathcal{HG}$
of dimension
![]() $(n^2-1)(g-1)+1$
where every m-Hecke cycle determines a smooth point (see, [Reference Brambila-Paz and Mata-Gutiérrez2, Theorem 1.1]).
$(n^2-1)(g-1)+1$
where every m-Hecke cycle determines a smooth point (see, [Reference Brambila-Paz and Mata-Gutiérrez2, Theorem 1.1]).
The principal significance of [Reference Narasimhan and Ramanan20, Lemma 5.8] and [Reference Brambila-Paz and Mata-Gutiérrez2, Proposition 3.1] is that the morphisms (2.5) and (2.6) are closed embeddings. It allows determine m-Hecke cycles and geometric and topological properties of the Hilbert scheme
![]() $\text{Hilb}_{M_X(n,d-m)}$
.
$\text{Hilb}_{M_X(n,d-m)}$
.
3. On the moduli space of torsion free sheaves
The aim of this section is to define an embedding from
![]() $\mathbb{G}(E_x,m)$
into the moduli space
$\mathbb{G}(E_x,m)$
into the moduli space
![]() $\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
of torsion-free sheaves. Generalizing some techniques of [Reference Brambila-Paz and Mata-Gutiérrez2, Reference Narasimhan and Ramanan20] we establish a closed embedding
$\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
of torsion-free sheaves. Generalizing some techniques of [Reference Brambila-Paz and Mata-Gutiérrez2, Reference Narasimhan and Ramanan20] we establish a closed embedding
![]() $\phi_z\,:\, \mathbb{G}(E_x, m) \to \mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
and an injective algebraic morphism
$\phi_z\,:\, \mathbb{G}(E_x, m) \to \mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
and an injective algebraic morphism
![]() $\Psi\,:\,X \times M_{X,H}(n;\,c_1, c_2) \to \text{Hilb}_{\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)},$
where
$\Psi\,:\,X \times M_{X,H}(n;\,c_1, c_2) \to \text{Hilb}_{\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)},$
where
![]() $z =(x,E) \in X \times M_{X, H}(n;\,c_1,c_2)$
and
$z =(x,E) \in X \times M_{X, H}(n;\,c_1,c_2)$
and
![]() $Hilb_{\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)}$
denotes the Hilbert scheme of the moduli space
$Hilb_{\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)}$
denotes the Hilbert scheme of the moduli space
![]() $\mathfrak{M}_{X,H}(n;\,c_1,c_2)$
. Moreover, we construct an irreducible variety properly contained in
$\mathfrak{M}_{X,H}(n;\,c_1,c_2)$
. Moreover, we construct an irreducible variety properly contained in
![]() $\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)-M_{X,H}(n;\,c_1,c_2+m)$
.
$\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)-M_{X,H}(n;\,c_1,c_2+m)$
.
The following Lemma deals with m-elementary transformations, specifically we compute the dimension of the morphisms of a m-elementary transformation E ′ of E. The important point to note here is that E is a vector bundle. Here and subsequently, E denotes a vector bundle on X.
Lemma 3.1.
Let H be an ample divisor on X. Let E′ be a torsion-free sheaf of rank n and let E be an H-stable vector bundle of rank n. If
![]() $c_1(E^{\prime})= c_1(E)$
, then
$c_1(E^{\prime})= c_1(E)$
, then
![]() $\dim \, Hom (E^{\prime},E) \leq 1.$
$\dim \, Hom (E^{\prime},E) \leq 1.$
Proof. Let
![]() $f\,:\,E^{\prime}\rightarrow E$
be a not zero homomorphism. By [Reference Friedman10, Proposition 7, Chapter 4] the morphism f is injective and hence we have the sequence
$f\,:\,E^{\prime}\rightarrow E$
be a not zero homomorphism. By [Reference Friedman10, Proposition 7, Chapter 4] the morphism f is injective and hence we have the sequence
By [Reference Hartshorne12, Proposition 6.4.], we have the following long exact sequence
Note that
![]() $E/E^{\prime}$
has support in a finite number of points because
$E/E^{\prime}$
has support in a finite number of points because
![]() $c_1(E)=c_1(E^{\prime})$
, hence
$c_1(E)=c_1(E^{\prime})$
, hence
![]() $\text{Hom}(E/E^{\prime},E)=0.$
On the other hand Lemma 2.6, implies that
$\text{Hom}(E/E^{\prime},E)=0.$
On the other hand Lemma 2.6, implies that
![]() $\text{Ext}^{1}(E/E^{\prime},E)=0$
. Since E is a H-stable vector bundle, it follows that
$\text{Ext}^{1}(E/E^{\prime},E)=0$
. Since E is a H-stable vector bundle, it follows that
as we desired.
Set
![]() $z\,:\!=\,(x,E)\in X \times M_{X,H}(n;\,c_1,c_2)$
and let m be a fixed natural number with
$z\,:\!=\,(x,E)\in X \times M_{X,H}(n;\,c_1,c_2)$
and let m be a fixed natural number with
![]() $m\lt n$
. Let
$m\lt n$
. Let
![]() $\pi_E\,:\, \mathbb{G}(E,m) \rightarrow X$
be the Grassmannian bundle associated to E and for any
$\pi_E\,:\, \mathbb{G}(E,m) \rightarrow X$
be the Grassmannian bundle associated to E and for any
![]() $x \in X$
denote by
$x \in X$
denote by
![]() $\mathbb{G}(E_x,m)$
the Grassmannian of m-quotients of
$\mathbb{G}(E_x,m)$
the Grassmannian of m-quotients of
![]() $E_x$
. On
$E_x$
. On
![]() $\mathbb{G}(E,m)$
, we have the tautological exact sequence
$\mathbb{G}(E,m)$
, we have the tautological exact sequence
where
![]() $S_E$
is the universal subbundle and
$S_E$
is the universal subbundle and
![]() $Q_E$
is the universal quotient bundle. Note that for any
$Q_E$
is the universal quotient bundle. Note that for any
![]() $x \in X$
, if we restrict (3.1) to
$x \in X$
, if we restrict (3.1) to
![]() $\mathbb{G}(E_x,m)$
then we obtain
$\mathbb{G}(E_x,m)$
then we obtain
Let us denote by
![]() $\mathbb{G}(z) \,:\!=\, \mathbb{G}(E_x,m)$
. Consider on
$\mathbb{G}(z) \,:\!=\, \mathbb{G}(E_x,m)$
. Consider on
![]() $X \times \mathbb{G}(z)$
, the surjective morphism
$X \times \mathbb{G}(z)$
, the surjective morphism
![]() $\alpha\,:\, p_1^*E \longrightarrow p_1^*\mathcal{O}_x \otimes p_2^*Q_{E_x}$
associated to the canonical surjective morphism
$\alpha\,:\, p_1^*E \longrightarrow p_1^*\mathcal{O}_x \otimes p_2^*Q_{E_x}$
associated to the canonical surjective morphism
![]() $\alpha_x\,:\, \mathcal{O}_{\mathbb{G}} \times E_{x} \rightarrow Q_{E_x}$
in (3.2) under the isomorphism:
$\alpha_x\,:\, \mathcal{O}_{\mathbb{G}} \times E_{x} \rightarrow Q_{E_x}$
in (3.2) under the isomorphism:
 \begin{eqnarray*}H^0\left(X \times \mathbb{G}(z), p_1^{*}E^* \otimes p_1^{*}\mathcal{O}_x \otimes p_{2}^*Q_{E_x}\right)&\cong & H^0\left( \mathbb{G}(z), p_{2_*} (p_1^{*}E^* \otimes p_1^*\mathcal{O}_x ) \otimes Q_{E_x}\right)\\[3pt]&\cong & H^0\left( \mathbb{G}(z), p_{2_*}p_1^*(E_{{x}}^*) \otimes Q_{E_x}\right) \\[3pt]&\cong & H^0\left( \mathbb{G}(z), \left(\mathcal{O}_{\mathbb{G}} \times E_x^*\right) \otimes Q_{E_x}\right) \\[3pt]&\cong & H^0\left( \mathbb{G}(z), \mathcal{H}om\left(\mathcal{O}_{\mathbb{G}} \times E_x, Q_{E_x}\right)\right),\end{eqnarray*}
\begin{eqnarray*}H^0\left(X \times \mathbb{G}(z), p_1^{*}E^* \otimes p_1^{*}\mathcal{O}_x \otimes p_{2}^*Q_{E_x}\right)&\cong & H^0\left( \mathbb{G}(z), p_{2_*} (p_1^{*}E^* \otimes p_1^*\mathcal{O}_x ) \otimes Q_{E_x}\right)\\[3pt]&\cong & H^0\left( \mathbb{G}(z), p_{2_*}p_1^*(E_{{x}}^*) \otimes Q_{E_x}\right) \\[3pt]&\cong & H^0\left( \mathbb{G}(z), \left(\mathcal{O}_{\mathbb{G}} \times E_x^*\right) \otimes Q_{E_x}\right) \\[3pt]&\cong & H^0\left( \mathbb{G}(z), \mathcal{H}om\left(\mathcal{O}_{\mathbb{G}} \times E_x, Q_{E_x}\right)\right),\end{eqnarray*}
where the second isomorphism is given by projection formula (see, [Reference Mumford19], p. 76). Here, taking the kernel of the surjective morphism
![]() $\alpha\,:\, p_1^*E \longrightarrow p_1^*\mathcal{O}_x \otimes p_2^*Q_{E_x},$
we get the exact sequence
$\alpha\,:\, p_1^*E \longrightarrow p_1^*\mathcal{O}_x \otimes p_2^*Q_{E_x},$
we get the exact sequence
on
![]() $X \times \mathbb{G}(z)$
.
$X \times \mathbb{G}(z)$
.
Lemma 3.2.
Let
![]() $z=(x,E)\in X\times M_{X,H}(n;\, c_1,c_2)$
and
$z=(x,E)\in X\times M_{X,H}(n;\, c_1,c_2)$
and
![]() $W\in\mathbb{G}(z)$
, then
$W\in\mathbb{G}(z)$
, then
Proof. Restricting the exact sequence
to
![]() $X \times \{W\}$
, we get
$X \times \{W\}$
, we get
As is well-known
![]() $p_1^{*}I_x\cong I_{\{x\}\times \mathbb{G}}$
and
$p_1^{*}I_x\cong I_{\{x\}\times \mathbb{G}}$
and
![]() $ I_{\{x\} \times \mathbb{G}}\vert_{X\times \{W\}}\cong I_x$
. Then it follows that
$ I_{\{x\} \times \mathbb{G}}\vert_{X\times \{W\}}\cong I_x$
. Then it follows that
With the above notation and as consequence of Lemma 3.2, we have the following result.
Proposition 3.3.
If E is H-stable, then
![]() $\mathcal{F}_z$
is a family of stable torsion-free sheaves parameterized by
$\mathcal{F}_z$
is a family of stable torsion-free sheaves parameterized by
![]() $\mathbb{G}(z)$
.
$\mathbb{G}(z)$
.
Proof. Let
![]() $W\in \mathbb{G}(z)$
. Restricting the exact sequence (3.3) to
$W\in \mathbb{G}(z)$
. Restricting the exact sequence (3.3) to
![]() $X\times \{W\}$
, we get the exact sequence
$X\times \{W\}$
, we get the exact sequence
over X. Hence,
![]() $E^{W}$
is a torsion-free sheaf of rank n called the m-elementary transformation of E in x defined by W. Since
$E^{W}$
is a torsion-free sheaf of rank n called the m-elementary transformation of E in x defined by W. Since
![]() $c_1( \mathcal{O}_x \otimes W)=0$
and E is H-stable, it follows that
$c_1( \mathcal{O}_x \otimes W)=0$
and E is H-stable, it follows that
![]() $E^W$
is H-stable and therefore stable with
$E^W$
is H-stable and therefore stable with
![]() $c_1(E^W)=c_1(E)$
(see Proposition 2.4). Moreover, by Whitney sum and
$c_1(E^W)=c_1(E)$
(see Proposition 2.4). Moreover, by Whitney sum and
![]() $c_2( \mathcal{O}_x \otimes W)=-\dim\, (W)=-m$
we get
$c_2( \mathcal{O}_x \otimes W)=-\dim\, (W)=-m$
we get
![]() $c_2(E^{W})=c_2(E)+m$
which completes the proof.
$c_2(E^{W})=c_2(E)+m$
which completes the proof.
The classification map of
![]() $\mathcal{F}_z$
is given by
$\mathcal{F}_z$
is given by
where
![]() $E^W$
was defined in the above Proposition. The following result shows that the morphism
$E^W$
was defined in the above Proposition. The following result shows that the morphism
![]() $\phi_z$
is a closed embedding. For the proof of the proposition, we follow the techniques and ideas of [Reference Narasimhan and Ramanan20, Lemma 5.10], and [Reference Brambila-Paz and Mata-Gutiérrez2, Proposition 3.1] who proved a similar result for vector bundles on curves.
$\phi_z$
is a closed embedding. For the proof of the proposition, we follow the techniques and ideas of [Reference Narasimhan and Ramanan20, Lemma 5.10], and [Reference Brambila-Paz and Mata-Gutiérrez2, Proposition 3.1] who proved a similar result for vector bundles on curves.
Proposition 3.4.
For any point
![]() $z=(x,E)\in X\times M_{X,H}(n;\,c_1,c_2)$
, the morphism
$z=(x,E)\in X\times M_{X,H}(n;\,c_1,c_2)$
, the morphism
![]() $\phi_z\,:\, \mathbb{G}(z)\rightarrow \mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
is a closed embedding.
$\phi_z\,:\, \mathbb{G}(z)\rightarrow \mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
is a closed embedding.
Proof. We first prove that the morphism
![]() $\phi_z$
is injective. Assume that there exist
$\phi_z$
is injective. Assume that there exist
![]() $W_1,W_2\in \mathbb{G}(z) $
such that
$W_1,W_2\in \mathbb{G}(z) $
such that
![]() $\psi\,:\, E^{W_1}\rightarrow E^{W_{2}}$
is an isomorphism, we claim that
$\psi\,:\, E^{W_1}\rightarrow E^{W_{2}}$
is an isomorphism, we claim that
![]() $W_1=W_2$
. Recall that for any
$W_1=W_2$
. Recall that for any
![]() $i=1,2$
, we have the following exact sequence
$i=1,2$
, we have the following exact sequence

By Lemma 3.1 we have
![]() $\dim\,\text{Hom}(E^{W_1},E)=1$
, it follows that there exist
$\dim\,\text{Hom}(E^{W_1},E)=1$
, it follows that there exist
![]() $\lambda \in \mathbb{C}^{*}$
such that
$\lambda \in \mathbb{C}^{*}$
such that
![]() $ \lambda f_1=f_2\circ \psi $
. Hence,
$ \lambda f_1=f_2\circ \psi $
. Hence,
![]() $\text{Im}\,f_{1,x}=\text{Im}\,f_{2,x}$
which implies
$\text{Im}\,f_{1,x}=\text{Im}\,f_{2,x}$
which implies
![]() $W_{1}=W_{2}$
. Therefore,
$W_{1}=W_{2}$
. Therefore,
![]() $\phi_{z}$
is injective.
$\phi_{z}$
is injective.
We now proceed to show the injectivity of the differential map
![]() $d\phi_z\,:\, T_W\mathbb{G}(z) \to \mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
. By [Reference Narasimhan and Ramanan20, Lemma 5.10], its infinitesimal deformation map in
$d\phi_z\,:\, T_W\mathbb{G}(z) \to \mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
. By [Reference Narasimhan and Ramanan20, Lemma 5.10], its infinitesimal deformation map in
![]() $W\in \mathbb{G}(z)$
is, up to the sign, the composition of the natural map
$W\in \mathbb{G}(z)$
is, up to the sign, the composition of the natural map
![]() $T_W\mathbb{G}(z) \rightarrow \text{Hom} \left(E^{W}, \mathcal{O}_{x}\otimes W\right)$
with the boundary map
$T_W\mathbb{G}(z) \rightarrow \text{Hom} \left(E^{W}, \mathcal{O}_{x}\otimes W\right)$
with the boundary map
![]() $\text{Hom} \left(E^{W}, \mathcal{O}_{x}\otimes W\right)\rightarrow \text{Ext}^{1}(X, E^{W},E^{W})$
given by the long exact sequence
$\text{Hom} \left(E^{W}, \mathcal{O}_{x}\otimes W\right)\rightarrow \text{Ext}^{1}(X, E^{W},E^{W})$
given by the long exact sequence
obtained from (3.4). Notice that
![]() $\text{Hom}\left(E^{W},E^{W}\right)\cong \mathbb{C}$
because
$\text{Hom}\left(E^{W},E^{W}\right)\cong \mathbb{C}$
because
![]() $E^{W}$
is an H-stable free torsion sheaf. Moreover,
$E^{W}$
is an H-stable free torsion sheaf. Moreover,
![]() $\text{Hom}(E^{W},E)\cong \mathbb{C}$
by Lemma 3.1. Therefore, the coboundary morphism
$\text{Hom}(E^{W},E)\cong \mathbb{C}$
by Lemma 3.1. Therefore, the coboundary morphism
is injective.
As in [Reference Brambila-Paz and Mata-Gutiérrez2, Reference Narasimhan and Ramanan20], a consequence of the above result is that we determine a collection of closed subschemes in
![]() $\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
and a collection of points in its Hilbert scheme (see, [Reference Narasimhan and Ramanan20, Definition 5.12]). From a stable vector bundle E on X, we constructed the family
$\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
and a collection of points in its Hilbert scheme (see, [Reference Narasimhan and Ramanan20, Definition 5.12]). From a stable vector bundle E on X, we constructed the family
![]() $\mathcal{F}_z$
of stable torsion-free sheaves. Analogously, if we start with a family
$\mathcal{F}_z$
of stable torsion-free sheaves. Analogously, if we start with a family
![]() $\mathcal{E}$
of stable vector bundles on X parameterized by T, then we can construct a family of of stable torsion-free sheaves
$\mathcal{E}$
of stable vector bundles on X parameterized by T, then we can construct a family of of stable torsion-free sheaves
![]() $\mathcal{F}$
. In the next paragraphs, we describe the construction when
$\mathcal{F}$
. In the next paragraphs, we describe the construction when
![]() $\mathcal{E}$
is the universal family of stable vector bundles parameterized by
$\mathcal{E}$
is the universal family of stable vector bundles parameterized by
![]() $M_{X,H}(n;\,c_1, c_2)$
.
$M_{X,H}(n;\,c_1, c_2)$
.
Let H be an ample divisor on X. As is well-known if
![]() $\text{gcd}\left(n, c_1.H, \frac{1}{2}c_1.(c_1-K_X)-c_2\right)=1,$
then there exists a universal family
$\text{gcd}\left(n, c_1.H, \frac{1}{2}c_1.(c_1-K_X)-c_2\right)=1,$
then there exists a universal family
![]() $\mathcal{U}$
of vector bundles parameterized by
$\mathcal{U}$
of vector bundles parameterized by
![]() $M_{X,H}(n;\,c_1,c_2)$
(see Lemma 2.2). Under this conditions, we will determine a family
$M_{X,H}(n;\,c_1,c_2)$
(see Lemma 2.2). Under this conditions, we will determine a family
![]() $\mathcal{F}$
of stable torsion-free sheaves parameterized by
$\mathcal{F}$
of stable torsion-free sheaves parameterized by
![]() $\mathbb{G}(\mathcal{U},m)$
which extends to
$\mathbb{G}(\mathcal{U},m)$
which extends to
![]() $\mathcal{F}_z$
(see Proposition 3.3).
$\mathcal{F}_z$
(see Proposition 3.3).
Let
![]() $\mathcal{U}$
be the universal family of vector bundles parameterized by
$\mathcal{U}$
be the universal family of vector bundles parameterized by
![]() $M_{X,H}(n;\,c_1,c_2)$
, hence
$M_{X,H}(n;\,c_1,c_2)$
, hence
![]() $p\,:\,\mathcal{U}\rightarrow X\times M_{X,H}(n;\,c_1, c_2)$
is a vector bundle. We denote by
$p\,:\,\mathcal{U}\rightarrow X\times M_{X,H}(n;\,c_1, c_2)$
is a vector bundle. We denote by
![]() $\pi_{\mathcal{U}}\,:\,\mathbb{G}(\mathcal{U},m) \rightarrow X\times M_{X,H}(n;\, c_1, c_2) $
the Grassmannian bundle of quotients associated to
$\pi_{\mathcal{U}}\,:\,\mathbb{G}(\mathcal{U},m) \rightarrow X\times M_{X,H}(n;\, c_1, c_2) $
the Grassmannian bundle of quotients associated to
![]() $\mathcal{U}$
. An element of
$\mathcal{U}$
. An element of
![]() $\mathbb{G}(\mathcal{U}, m)$
is a pair ((x, E),W), where
$\mathbb{G}(\mathcal{U}, m)$
is a pair ((x, E),W), where
![]() $(x,E) \in X \times M_{X,H}(n;\,c_1,c_2)$
and
$(x,E) \in X \times M_{X,H}(n;\,c_1,c_2)$
and
![]() $W\in \mathbb{G}(E_x,m)$
. The tautological exact sequence over
$W\in \mathbb{G}(E_x,m)$
. The tautological exact sequence over
![]() $\mathbb{G}(\mathcal{U}, m)$
is
$\mathbb{G}(\mathcal{U}, m)$
is
where
![]() $Q_{\mathcal{U}}$
denotes the universal quotient bundle of rank m over
$Q_{\mathcal{U}}$
denotes the universal quotient bundle of rank m over
![]() $\mathbb{G}(\mathcal{U},m)$
. We now consider the graph of the following composition
$\mathbb{G}(\mathcal{U},m)$
. We now consider the graph of the following composition

![]() $\Gamma\,:\!=\,\Gamma_{p_{1}\circ \pi_{U}}$
as a subvariety of
$\Gamma\,:\!=\,\Gamma_{p_{1}\circ \pi_{U}}$
as a subvariety of
![]() $X\times \mathbb{G}(\mathcal{U},m)$
. Then we have the following result.
$X\times \mathbb{G}(\mathcal{U},m)$
. Then we have the following result.
Lemma 3.5.
Let
![]() $g\in \mathbb{G}(\mathcal{U},m)$
. Then
$g\in \mathbb{G}(\mathcal{U},m)$
. Then
-
(a)
 $\mathcal{T}or^1(I_{X\times \{g\}}, \mathcal{O}_{\Gamma})=0.$
$\mathcal{T}or^1(I_{X\times \{g\}}, \mathcal{O}_{\Gamma})=0.$
-
(b) There exists a canonical surjective morphism of sheaves
(3.6)over \begin{equation}(id \times p_2 \circ \pi_{\mathcal{U}}) ^{*}\,\mathcal{U}\rightarrow \mathcal{O}_{\Gamma}\otimes p_{\mathbb{G}(\mathcal{U})}^{*}Q_{\mathcal{U}}\rightarrow 0,\end{equation}
\begin{equation}(id \times p_2 \circ \pi_{\mathcal{U}}) ^{*}\,\mathcal{U}\rightarrow \mathcal{O}_{\Gamma}\otimes p_{\mathbb{G}(\mathcal{U})}^{*}Q_{\mathcal{U}}\rightarrow 0,\end{equation}
 $X\times \mathbb{G}(\mathcal{U},m),$
determined by
$X\times \mathbb{G}(\mathcal{U},m),$
determined by
 $\alpha$
, where
$\alpha$
, where
 $p_{\mathbb{G}(\mathcal{U})}\,:\,X\times \mathbb{G}(\mathcal{U},m) \rightarrow \mathbb{G}(\mathcal{U},m)$
and
$p_{\mathbb{G}(\mathcal{U})}\,:\,X\times \mathbb{G}(\mathcal{U},m) \rightarrow \mathbb{G}(\mathcal{U},m)$
and
 $p_2\,:\,X\times M_{X,H}(n;\,c_1,c_2) \rightarrow M_{X,H}(n;\,c_1, c_2)$
are the respective second projections.
$p_2\,:\,X\times M_{X,H}(n;\,c_1,c_2) \rightarrow M_{X,H}(n;\,c_1, c_2)$
are the respective second projections.
Proof. Taking
![]() $\beta\,:\!=\,p_{\mathbb{G}(\mathcal{U})}|_\Gamma$
as the restriction of the projection, we have the following commutative diagram
$\beta\,:\!=\,p_{\mathbb{G}(\mathcal{U})}|_\Gamma$
as the restriction of the projection, we have the following commutative diagram

where
![]() $i\,:\,\Gamma \to X\times \mathbb{G}(\mathcal{U})$
is the inclusion map, hence
$i\,:\,\Gamma \to X\times \mathbb{G}(\mathcal{U})$
is the inclusion map, hence
![]() $I_{X \times {g}}\vert_{\Gamma}= i^{*}p_{\mathbb{G}(\mathcal{U})}^{*}(I_{g})=\beta^{*}(I_g).$
$I_{X \times {g}}\vert_{\Gamma}= i^{*}p_{\mathbb{G}(\mathcal{U})}^{*}(I_{g})=\beta^{*}(I_g).$
From the exact sequence
we get
Therefore,
![]() $\mathcal{T}or^1(I_{X\times \{g\}}, \mathcal{O}_{\Gamma})=0$
and this prove (a).
$\mathcal{T}or^1(I_{X\times \{g\}}, \mathcal{O}_{\Gamma})=0$
and this prove (a).
Now, to prove (b) consider the surjective map
![]() $\alpha\,:\, \pi_\mathcal{U}^{*}\,\mathcal{U}\rightarrow Q_{\mathcal{U}}$
given in (3.5) and notice that
$\alpha\,:\, \pi_\mathcal{U}^{*}\,\mathcal{U}\rightarrow Q_{\mathcal{U}}$
given in (3.5) and notice that
![]() $\beta^{*}\alpha\,:\,\beta^{*}\pi_\mathcal{U}^{*}\,\mathcal{U}\rightarrow \beta^{*}Q_{\mathcal{U}}$
is also surjective. Since
$\beta^{*}\alpha\,:\,\beta^{*}\pi_\mathcal{U}^{*}\,\mathcal{U}\rightarrow \beta^{*}Q_{\mathcal{U}}$
is also surjective. Since
![]() $\beta^{*} \pi_U^{*}(\mathcal{U})\cong (id \times p_{2} \circ \pi_{\mathcal{U}})^{*}\,(\mathcal{U})\vert_{\Gamma}$
and
$\beta^{*} \pi_U^{*}(\mathcal{U})\cong (id \times p_{2} \circ \pi_{\mathcal{U}})^{*}\,(\mathcal{U})\vert_{\Gamma}$
and
![]() $\beta^{*}Q_{\mathcal{U}}\cong p_{\mathbb{G}((\mathcal{U})}^{*}(Q_{\mathcal{U}})\vert_{\Gamma}$
, we get a surjective morphism
$\beta^{*}Q_{\mathcal{U}}\cong p_{\mathbb{G}((\mathcal{U})}^{*}(Q_{\mathcal{U}})\vert_{\Gamma}$
, we get a surjective morphism
Hence, from the exact sequence
and the morphism (3.7) we get the surjective map
![]() $(id \times p_{2} \circ \pi_{\mathcal{U}})^{*}\,\mathcal{U}\rightarrow \mathcal{O}_{\Gamma}\otimes p_{\mathbb{G}(\mathcal{U})}^{*}Q_{\mathcal{U}}$
which completes the proof.
$(id \times p_{2} \circ \pi_{\mathcal{U}})^{*}\,\mathcal{U}\rightarrow \mathcal{O}_{\Gamma}\otimes p_{\mathbb{G}(\mathcal{U})}^{*}Q_{\mathcal{U}}$
which completes the proof.
According to the above Lemma, let us denote by
![]() $\mathcal{F}$
the kernel of the surjective morphism (3.6). Hence, we get the exact sequence
$\mathcal{F}$
the kernel of the surjective morphism (3.6). Hence, we get the exact sequence
Note that
![]() $(id \times p_{2} \circ \pi_{\mathcal{U}})^{*}\,(\mathcal{U}) \vert_{X\times ((x,E),W)}=E$
and
$(id \times p_{2} \circ \pi_{\mathcal{U}})^{*}\,(\mathcal{U}) \vert_{X\times ((x,E),W)}=E$
and
![]() $\mathcal{O}_{\Gamma}\otimes p_{\mathbb{G}(\mathcal{U})}^*Q_{\mathcal{U}}\vert_{X \times ((x,E),W)}=\mathcal{O}_x \otimes W$
. Since
$\mathcal{O}_{\Gamma}\otimes p_{\mathbb{G}(\mathcal{U})}^*Q_{\mathcal{U}}\vert_{X \times ((x,E),W)}=\mathcal{O}_x \otimes W$
. Since
![]() $ p_{\mathbb{G}(\mathcal{U})}^*Q_{\mathcal{U}}$
is a vector bundle and
$ p_{\mathbb{G}(\mathcal{U})}^*Q_{\mathcal{U}}$
is a vector bundle and
![]() $\mathcal{T}or^1(I_{X\times \{g\}}, \mathcal{O}_{\Gamma})=0,$
it follows that
$\mathcal{T}or^1(I_{X\times \{g\}}, \mathcal{O}_{\Gamma})=0,$
it follows that
![]() $\mathcal{T}or^1(I_{X\times \{g\}}, \mathcal{O}_{\Gamma}\otimes p_{\mathbb{G}(\mathcal{U})}^*Q_{\mathcal{U}} )=p_{\mathbb{G}(\mathcal{U})}^*Q_{\mathcal{U}}\otimes \mathcal{T}or^1(I_{X\times \{g\}}, \mathcal{O}_{\Gamma})=0.$
Therefore, restricting the exact sequence (3.8) to
$\mathcal{T}or^1(I_{X\times \{g\}}, \mathcal{O}_{\Gamma}\otimes p_{\mathbb{G}(\mathcal{U})}^*Q_{\mathcal{U}} )=p_{\mathbb{G}(\mathcal{U})}^*Q_{\mathcal{U}}\otimes \mathcal{T}or^1(I_{X\times \{g\}}, \mathcal{O}_{\Gamma})=0.$
Therefore, restricting the exact sequence (3.8) to
![]() $X\times \{((x,E),W)\}$
, we get the exact sequence
$X\times \{((x,E),W)\}$
, we get the exact sequence
over X. Moreover, if we restrict (3.8) to
![]() $X\times \mathbb{G}(z)$
, we obtain (3.3).
$X\times \mathbb{G}(z)$
, we obtain (3.3).
Hence by similar arguments to Proposition 3.3, we have that
![]() $\mathcal{F}$
is a family of stable torsion-free sheaves of rank n of type
$\mathcal{F}$
is a family of stable torsion-free sheaves of rank n of type
![]() $(c_1, c_2+m)$
which determines a morphism
$(c_1, c_2+m)$
which determines a morphism
Note that
![]() $\text{Im}\,\Phi$
lies in
$\text{Im}\,\Phi$
lies in
![]() $\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)- M_{X,H}(n;\,c_1,c_2+m)$
. In the following theorem, we compute the dimension of
$\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)- M_{X,H}(n;\,c_1,c_2+m)$
. In the following theorem, we compute the dimension of
![]() $\text{Im}\,\Phi$
.
$\text{Im}\,\Phi$
.
Theorem 3.6.
Let m, n natural integers with
![]() $1\leq m \lt n $
. Then
$1\leq m \lt n $
. Then
![]() $\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)-M_{X,H}(n;\,c_1,c_2+m)$
contains an irreducible projective variety Y of dimension
$\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)-M_{X,H}(n;\,c_1,c_2+m)$
contains an irreducible projective variety Y of dimension
![]() $3+\dim\, M_{X,H}(n;\,c_1,c_2)$
such that the general element
$3+\dim\, M_{X,H}(n;\,c_1,c_2)$
such that the general element
![]() $F \in Y$
fits into exact sequence
$F \in Y$
fits into exact sequence
where
![]() $E\in M_{X,H}(n;\,c_1,c_2)$
,
$E\in M_{X,H}(n;\,c_1,c_2)$
,
![]() $W\in\mathbb{G}(E_x, m)$
and
$W\in\mathbb{G}(E_x, m)$
and
![]() $x\in X$
. In particular, if
$x\in X$
. In particular, if
![]() $n=2 $
then
$n=2 $
then
![]() $\Phi$
is injective and Y is a divisor.
$\Phi$
is injective and Y is a divisor.
Proof. We will prove that image of
![]() $\Phi$
is an irreducible variety of dimension
$\Phi$
is an irreducible variety of dimension
![]() $3 + \dim\, M_{X,H}(n;\,c_1,c_2)$
. For this, it will thus be sufficient to compute the dimension of the fibers of
$3 + \dim\, M_{X,H}(n;\,c_1,c_2)$
. For this, it will thus be sufficient to compute the dimension of the fibers of
![]() $\Phi$
. Let
$\Phi$
. Let
![]() $F \in \text{Im} \,\Phi$
, then there exists
$F \in \text{Im} \,\Phi$
, then there exists
![]() $((x,E),W)\in \mathbb{G}(\mathcal{U},m)$
such that F fits into the following exact sequence
$((x,E),W)\in \mathbb{G}(\mathcal{U},m)$
such that F fits into the following exact sequence
where E is a vector bundle and
![]() $W\in \mathbb{G}(E_x,m)$
. We claim
$W\in \mathbb{G}(E_x,m)$
. We claim
![]() $\dim\, \text{Ext}^1(\mathcal{O}_{X,x}\otimes W,F)=m^2$
.
$\dim\, \text{Ext}^1(\mathcal{O}_{X,x}\otimes W,F)=m^2$
.
From the exact sequence (3.10), we get the long exact sequence
Since
![]() $\text{Hom}(\mathcal{O}_{X,x},E)=0$
and by Lemma 2.6
$\text{Hom}(\mathcal{O}_{X,x},E)=0$
and by Lemma 2.6
![]() $\text{Ext}^1(\mathcal{O}_{X,x},E)=0$
, it follows that
$\text{Ext}^1(\mathcal{O}_{X,x},E)=0$
, it follows that
Thus,
![]() $\dim\,\text{Ext}^1(\mathcal{O}_{X,x}\otimes W,F)=m^2$
.
$\dim\,\text{Ext}^1(\mathcal{O}_{X,x}\otimes W,F)=m^2$
.
We now proceed to compute the dimension of
![]() $\text{Im} \, \Phi$
. Let
$\text{Im} \, \Phi$
. Let
![]() $p_i$
be denote the canonical projection of
$p_i$
be denote the canonical projection of
![]() $X\times \mathbb{G}(E_x, m)$
for
$X\times \mathbb{G}(E_x, m)$
for
![]() $i=1,2$
and consider the sheaf
$i=1,2$
and consider the sheaf
![]() $\mathcal{H}om(p_{1}^*\mathcal{O}_{x}\otimes p_2^{*}\mathcal{Q}_{E_{x}},p_{1}^*F )$
. Taking higher direct image, we obtain on
$\mathcal{H}om(p_{1}^*\mathcal{O}_{x}\otimes p_2^{*}\mathcal{Q}_{E_{x}},p_{1}^*F )$
. Taking higher direct image, we obtain on
![]() $\mathbb{G}(E_x, m)$
the sheaf:
$\mathbb{G}(E_x, m)$
the sheaf:
This
![]() $\Lambda$
is locally free over
$\Lambda$
is locally free over
![]() $\mathbb{G}(E_x, m)$
because
$\mathbb{G}(E_x, m)$
because
for any
![]() $W\in \mathbb{G}(E_x, m)$
. Hence, the fiber of
$W\in \mathbb{G}(E_x, m)$
. Hence, the fiber of
![]() $\Lambda$
at
$\Lambda$
at
![]() $W \in \mathbb{G}(E_x, m)$
is
$W \in \mathbb{G}(E_x, m)$
is
![]() $\text{Ext}^1(\mathcal{O}_{X,x} \otimes W,F)$
.
$\text{Ext}^1(\mathcal{O}_{X,x} \otimes W,F)$
.
Let
![]() $\pi \,:\,\mathbb{P}\Lambda \to \mathbb{G}(E_x, m)$
denote the projectivization of the sheaf
$\pi \,:\,\mathbb{P}\Lambda \to \mathbb{G}(E_x, m)$
denote the projectivization of the sheaf
![]() $\Lambda$
. By [Reference Gottsche11, Lemma 3.2] there exists an exact sequence:
$\Lambda$
. By [Reference Gottsche11, Lemma 3.2] there exists an exact sequence:
on
![]() $X \times \mathbb{P}\Lambda$
such that, for each
$X \times \mathbb{P}\Lambda$
such that, for each
![]() $p\in \mathbb{P}\Lambda$
, its restriction to
$p\in \mathbb{P}\Lambda$
, its restriction to
![]() $X \times \{p\}$
is the extension
$X \times \{p\}$
is the extension
where
![]() $\mathcal{E}_{|_p}\,:\!=\,\mathcal{E}_{|_{X\times\{p\}}}$
.
$\mathcal{E}_{|_p}\,:\!=\,\mathcal{E}_{|_{X\times\{p\}}}$
.
The set
is irreducible open set of dimension
![]() $ m(n-m)+m^2-1=mn-1.$
Therefore, the dimension of the fiber of
$ m(n-m)+m^2-1=mn-1.$
Therefore, the dimension of the fiber of
![]() $\Phi$
is
$\Phi$
is
![]() $mn-1-m^2=m(n-m)-1$
and then we have
$mn-1-m^2=m(n-m)-1$
and then we have
Note that for rank two case, the morphism
![]() $\phi$
is injective because the dimension of
$\phi$
is injective because the dimension of
![]() $\mathbb{P}\text{Ext}^1(\mathcal{O}_{X,x}\otimes W, F)=0$
and
$\mathbb{P}\text{Ext}^1(\mathcal{O}_{X,x}\otimes W, F)=0$
and
![]() $\mathbb{P}\text{Ext}^1(\mathcal{O}_{X,x}\otimes W, F)$
is irreducible.
$\mathbb{P}\text{Ext}^1(\mathcal{O}_{X,x}\otimes W, F)$
is irreducible.
By functorial construction, we also have the following algebraic morphism
with
![]() $\mathbb{G}(z)\,:\!=\, \phi_z(\mathbb{G}(E_x,m))$
. This construction is essentially the same as the one carried out in [Reference Brambila-Paz and Mata-Gutiérrez2, Reference Narasimhan and Ramanan20].
$\mathbb{G}(z)\,:\!=\, \phi_z(\mathbb{G}(E_x,m))$
. This construction is essentially the same as the one carried out in [Reference Brambila-Paz and Mata-Gutiérrez2, Reference Narasimhan and Ramanan20].
The injectivity of the function
![]() $\Psi\,:\,X \times M_{X,H}(n;\,c_1, c_2)\rightarrow \text{Hilb}_{\ \mathfrak{M}_{X,H}(n;\,c_1,c_2+m)}$
is established in the next proposition. The proof proceeds as [Reference Brambila-Paz and Mata-Gutiérrez2, Proposition 3.2] and we use the following two lemmas.
$\Psi\,:\,X \times M_{X,H}(n;\,c_1, c_2)\rightarrow \text{Hilb}_{\ \mathfrak{M}_{X,H}(n;\,c_1,c_2+m)}$
is established in the next proposition. The proof proceeds as [Reference Brambila-Paz and Mata-Gutiérrez2, Proposition 3.2] and we use the following two lemmas.
Lemma 3.7. Let X be an irreducible variety and let
be an exact sequence of sheaves over X. If E and G are locally free sheaves, then F is locally free.
Proof. Let H be a sheaf on X. We claim that for any locally free sheaf E on X
![]() $\mathcal{E}xt^{i}(E,H)=0$
. By [Reference Hartshorne12, Proposition 6.8], we have
$\mathcal{E}xt^{i}(E,H)=0$
. By [Reference Hartshorne12, Proposition 6.8], we have
which is zero for any
![]() $x\in X$
because [Reference Friedman10, Theorem 17]. Consider the exact sequence
$x\in X$
because [Reference Friedman10, Theorem 17]. Consider the exact sequence
where E and G are locally free sheaves. Applying the functor
![]() $\mathcal{H}om({-},H)$
to the exact sequence (3.12), we get
$\mathcal{H}om({-},H)$
to the exact sequence (3.12), we get
Note that
![]() $\mathcal{E}xt^i(G,H) = \mathcal{E}xt^i(E,H) = 0$
for
$\mathcal{E}xt^i(G,H) = \mathcal{E}xt^i(E,H) = 0$
for
![]() $i\gt 0$
. Therefore,
$i\gt 0$
. Therefore,
![]() $\mathcal{E}xt^1(F,H) =0$
from which we conclude that F is locally free as we desired.
$\mathcal{E}xt^1(F,H) =0$
from which we conclude that F is locally free as we desired.
Lemma 3.8 ([Reference Huybrechts and Lehn14], Lemma 8.2.12). Let
![]() $F_1$
and
$F_1$
and
![]() $F_2$
be
$F_2$
be
![]() $\mu$
-semistable sheaves on X. If a is sufficiently large integer and
$\mu$
-semistable sheaves on X. If a is sufficiently large integer and
![]() $C\in|aH|$
a general nonsingular curve, then
$C\in|aH|$
a general nonsingular curve, then
![]() $F_1|_C$
and
$F_1|_C$
and
![]() $F_2|_C$
are S-equivalent if and only if
$F_2|_C$
are S-equivalent if and only if
![]() $F_1^{**}\cong F_2^{**}$
$F_1^{**}\cong F_2^{**}$
Proposition 3.9.
The morphism
![]() $\Psi\,:\,X \times M_{X,H}(n;\,c_1, c_2)\rightarrow \text{Hilb}_{\ \mathfrak{M}_{X,H}(n;\,c_1, c_2+m)}$
defined as above is injective.
$\Psi\,:\,X \times M_{X,H}(n;\,c_1, c_2)\rightarrow \text{Hilb}_{\ \mathfrak{M}_{X,H}(n;\,c_1, c_2+m)}$
defined as above is injective.
Proof. Assume that for
![]() $i=1,2$
, there exist
$i=1,2$
, there exist
![]() $z_i=(x_i,E_i)\in X\times M_{X,H}(n;\,c_1,c_2)$
such that
$z_i=(x_i,E_i)\in X\times M_{X,H}(n;\,c_1,c_2)$
such that
![]() $\mathbb{G}(z_1)= \mathbb{G}(z_2)$
, we want to prove that
$\mathbb{G}(z_1)= \mathbb{G}(z_2)$
, we want to prove that
![]() $E_1\cong E_2$
and
$E_1\cong E_2$
and
![]() $x_1=x_2$
. We recall that for any
$x_1=x_2$
. We recall that for any
![]() $z_i=(x_i,E_i)$
there exists a family
$z_i=(x_i,E_i)$
there exists a family
![]() $\mathcal{F}_{z_i}$
of stable torsion-free sheaves parameterized by
$\mathcal{F}_{z_i}$
of stable torsion-free sheaves parameterized by
![]() $\mathbb{G}(z_i),$
and
$\mathbb{G}(z_i),$
and
![]() $\mathcal{F}_{z_i}$
fits into the following exact sequence
$\mathcal{F}_{z_i}$
fits into the following exact sequence
of sheaves over
![]() $X\times \mathbb{G}(z_i),$
where
$X\times \mathbb{G}(z_i),$
where
![]() $p_j$
denotes the j-projection over
$p_j$
denotes the j-projection over
![]() $X\times \mathbb{G}(z_i)$
. From universal properties of moduli space
$X\times \mathbb{G}(z_i)$
. From universal properties of moduli space
![]() $\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
, there exists an isomorphism
$\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
, there exists an isomorphism
![]() $\beta\,:\,\mathbb{G}(z_1)\rightarrow \mathbb{G}({z_2})$
that induces the following commutative diagrams
$\beta\,:\,\mathbb{G}(z_1)\rightarrow \mathbb{G}({z_2})$
that induces the following commutative diagrams

and

i.e.
![]() $\phi_{z_1}=\phi_{z_2}\circ\beta$
and
$\phi_{z_1}=\phi_{z_2}\circ\beta$
and
![]() $p_1 = p^{\prime}_{1} \circ \, (id_{X} \times \beta)$
. By the universal property of
$p_1 = p^{\prime}_{1} \circ \, (id_{X} \times \beta)$
. By the universal property of
![]() $\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
, we have
$\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)$
, we have
for some line bundle L on
![]() $\mathbb{G}({z_1)}$
. The following properties are satisfied:
$\mathbb{G}({z_1)}$
. The following properties are satisfied:
-
(1) L is trivial.
-
(2)
 $ R^1 {p_1}_*\left(\mathcal{F}_{z_1}\right)= R^1 {p^{\prime}_1}_*\left(\mathcal{F}_{z_2}\right)= 0$
.
$ R^1 {p_1}_*\left(\mathcal{F}_{z_1}\right)= R^1 {p^{\prime}_1}_*\left(\mathcal{F}_{z_2}\right)= 0$
. -
(3)
 ${p_1}_{*}\mathcal{F}_{z_1}= {p^{\prime}_1}_{*} \mathcal{F}_{z_2}$
.
${p_1}_{*}\mathcal{F}_{z_1}= {p^{\prime}_1}_{*} \mathcal{F}_{z_2}$
.
First we proved that
![]() $\mathcal{F}_{z_i}|_{\{y\}\times \mathbb{G}(z_i)}\cong E_y\otimes \mathcal{O}_{\mathbb{G}(z_i)}$
is trivial for any
$\mathcal{F}_{z_i}|_{\{y\}\times \mathbb{G}(z_i)}\cong E_y\otimes \mathcal{O}_{\mathbb{G}(z_i)}$
is trivial for any
![]() $y\neq x_i$
. Restricting the exact sequence (3.13), we obtain
$y\neq x_i$
. Restricting the exact sequence (3.13), we obtain
Note that
![]() $p_1^{*}(E_i)|_{y\times \mathbb{G}(z_i)}\cong E_y \otimes \mathcal{O}_{\mathbb{G}(z_i)}$
and
$p_1^{*}(E_i)|_{y\times \mathbb{G}(z_i)}\cong E_y \otimes \mathcal{O}_{\mathbb{G}(z_i)}$
and
![]() $\mathcal{F}_{z_i}|_{y\times \mathbb{G}(z_i)}$
are vector bundle of the same rank, then by Lemma 3.7 we have
$\mathcal{F}_{z_i}|_{y\times \mathbb{G}(z_i)}$
are vector bundle of the same rank, then by Lemma 3.7 we have
![]() $\mathcal{T}or^1\left(\mathcal{O}_{\mathbb{G}},p_1^*\mathcal{O}_{x_i} \otimes p_2^*Q_{E_{x_i}}\right)=0$
and
$\mathcal{T}or^1\left(\mathcal{O}_{\mathbb{G}},p_1^*\mathcal{O}_{x_i} \otimes p_2^*Q_{E_{x_i}}\right)=0$
and
![]() $\mathcal{F}_{z_i}|_{y\times \mathbb{G}(z_i)}\cong E_y \otimes \mathcal{O}_{\mathbb{G}(z_i)}$
. On the other hand
$\mathcal{F}_{z_i}|_{y\times \mathbb{G}(z_i)}\cong E_y \otimes \mathcal{O}_{\mathbb{G}(z_i)}$
. On the other hand
Therefore,
Thus, L is trivial [Reference Newstead22, p. 12] and this prove (1). Moreover
And for any
![]() $y \in X$
we have
$y \in X$
we have
Similarly, we can prove that
![]() $\mathcal{F}_{z_2}|_{x_2 \times \mathbb{G}(z_2)}\cong E_{x_2}\otimes \mathcal{O}_{\mathbb{G}(z_2)}$
and
$\mathcal{F}_{z_2}|_{x_2 \times \mathbb{G}(z_2)}\cong E_{x_2}\otimes \mathcal{O}_{\mathbb{G}(z_2)}$
and
![]() $R^1 {p_1}^{\prime}_*\left(\mathcal{F}_{z_2}\right)=0$
and this prove (2). Since
$R^1 {p_1}^{\prime}_*\left(\mathcal{F}_{z_2}\right)=0$
and this prove (2). Since
![]() $p_1=p_1^{\prime}\circ (id \times \beta)$
and
$p_1=p_1^{\prime}\circ (id \times \beta)$
and
![]() $\left(id_X \times \beta\right)$
is an isomorphism, we get
$\left(id_X \times \beta\right)$
is an isomorphism, we get
 \begin{eqnarray*}p_{1*}\left(\mathcal{F}_{z_1}\right)=p_{1*}(id \times \beta)^{*}\left(\mathcal{F}_{z_2}\right)&=&\left.(p^{\prime}_1 \circ (id \times \beta))_{*} (id\times \beta)^{*} \mathcal{F}_{z_2}\right)\\&=& \left. p^{\prime}_{1*}((id \times \beta)_{*}(id \times \beta)^{*}\left(\mathcal{F}_{z_2}\right)\right)\\&=& p^{\prime}_{1_*}\left(\mathcal{F}_{z_2}\right),\end{eqnarray*}
\begin{eqnarray*}p_{1*}\left(\mathcal{F}_{z_1}\right)=p_{1*}(id \times \beta)^{*}\left(\mathcal{F}_{z_2}\right)&=&\left.(p^{\prime}_1 \circ (id \times \beta))_{*} (id\times \beta)^{*} \mathcal{F}_{z_2}\right)\\&=& \left. p^{\prime}_{1*}((id \times \beta)_{*}(id \times \beta)^{*}\left(\mathcal{F}_{z_2}\right)\right)\\&=& p^{\prime}_{1_*}\left(\mathcal{F}_{z_2}\right),\end{eqnarray*}
and this proves (3). We now proceed to show that
![]() $E_1\cong E_2$
and
$E_1\cong E_2$
and
![]() $x_1=x_2$
. The proof will be divided into three steps:
$x_1=x_2$
. The proof will be divided into three steps:
Step 1: We will show that
![]() $E_1\otimes I_{x_1}\cong E_2\otimes I_{x_2}$
.
$E_1\otimes I_{x_1}\cong E_2\otimes I_{x_2}$
.
Taking the direct image of (3.13) by
![]() $p_1$
we obtain the following exact sequence:
$p_1$
we obtain the following exact sequence:
because
![]() $ R^1 {p_1}_*\left(\mathcal{F}_{z_1}\right)=0$
. And we can complete the diagram
$ R^1 {p_1}_*\left(\mathcal{F}_{z_1}\right)=0$
. And we can complete the diagram

Since
![]() ${p_1}_*p_1^*(E_1)\cong E_1$
and
${p_1}_*p_1^*(E_1)\cong E_1$
and
![]() ${p_1}_*\left(p_1^*\mathcal{O}_{x_1}\otimes p_2^*Q_{E_{1,x_1}}\right)\cong E_{1}\otimes \mathcal{O}_{x_1}$
by projection formula, it follows that
${p_1}_*\left(p_1^*\mathcal{O}_{x_1}\otimes p_2^*Q_{E_{1,x_1}}\right)\cong E_{1}\otimes \mathcal{O}_{x_1}$
by projection formula, it follows that
![]() ${p_1}_*\mathcal{F}_{z_1}\cong E_1\otimes I_{x_1}$
. We can now proceed analogously to obtain
${p_1}_*\mathcal{F}_{z_1}\cong E_1\otimes I_{x_1}$
. We can now proceed analogously to obtain
![]() ${p^{\prime}_1}_{*}\mathcal{F}_{z_2}\cong E_2\otimes I_{x_2}$
. Therefore,
${p^{\prime}_1}_{*}\mathcal{F}_{z_2}\cong E_2\otimes I_{x_2}$
. Therefore,
Step 2: We will show that
![]() $E_1 \cong E_2$
;
$E_1 \cong E_2$
;
Note that the general curve on X does not goes through the points
![]() $x_1$
and
$x_1$
and
![]() $x_2$
, hence
$x_2$
, hence
![]() $E_1|_C\cong (E_1\otimes I_{x_1})|_{C}\cong (E_2\otimes I_{x_1})|_{C}\cong E_2|_C$
for the general curve
$E_1|_C\cong (E_1\otimes I_{x_1})|_{C}\cong (E_2\otimes I_{x_1})|_{C}\cong E_2|_C$
for the general curve
![]() $C\in |aH|$
. From Lemma 3.8, we conclude that
$C\in |aH|$
. From Lemma 3.8, we conclude that
![]() $E_1\cong E_2$
which is the desired conclusion.
$E_1\cong E_2$
which is the desired conclusion.
Step 3: We show will that
![]() $x_1=x_2$
;
$x_1=x_2$
;
Notice that by step 1 there exists an isomorphism
![]() $\lambda\,:\,E_1\otimes I_{x_1} \to E_2\otimes I_{x_2}$
. On the other hand, step 2 provided us an isomorphism
$\lambda\,:\,E_1\otimes I_{x_1} \to E_2\otimes I_{x_2}$
. On the other hand, step 2 provided us an isomorphism
![]() $\phi\,:\,E_1\rightarrow E_2$
. Considering the exact sequence
$\phi\,:\,E_1\rightarrow E_2$
. Considering the exact sequence

for
![]() $i=1,2$
. Moreover
$i=1,2$
. Moreover
![]() $\phi\circ f_{1},$
$\phi\circ f_{1},$
![]() $f_{2}\circ \lambda\in \text{Hom}(E_1\otimes I_{x_1},E_2)$
, and hence by Lemma 3.1,
$f_{2}\circ \lambda\in \text{Hom}(E_1\otimes I_{x_1},E_2)$
, and hence by Lemma 3.1,
![]() $\phi\circ f_{1}=t(f_{2}\circ \lambda)$
for some
$\phi\circ f_{1}=t(f_{2}\circ \lambda)$
for some
![]() $t\in \mathbb{C}^{*}$
. Without loss of generality, we suppose that
$t\in \mathbb{C}^{*}$
. Without loss of generality, we suppose that
![]() $t=1$
therefore we have the following commutative diagram
$t=1$
therefore we have the following commutative diagram

where
![]() $\alpha$
is an isomorphism of skyscraper sheaves supported at
$\alpha$
is an isomorphism of skyscraper sheaves supported at
![]() $x_1$
and
$x_1$
and
![]() $x_2$
, respectively. Hence
$x_2$
, respectively. Hence
![]() $x_1=x_2$
. Therefore,
$x_1=x_2$
. Therefore,
![]() $\Psi$
is injective which establishes the proposition.
$\Psi$
is injective which establishes the proposition.
We can now state our main result. The theorem computes a bound of the dimension of an irreducible subvariety of the Hilbert scheme
![]() $\text{Hilb}_{\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)}$
.
$\text{Hilb}_{\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)}$
.
Theorem 3.10.
The Hilbert scheme
![]() ${Hilb}_{\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)}$
of the moduli space of stable vector bundles has an irreducible component of dimension at least
${Hilb}_{\mathfrak{M}_{X,H}(n;\,c_1,c_2+m)}$
of the moduli space of stable vector bundles has an irreducible component of dimension at least
![]() $2+\dim\, M_{X,H}(n;\,c_1,c_2)$
.
$2+\dim\, M_{X,H}(n;\,c_1,c_2)$
.
Proof. The proof follows from Proposition 3.9.
4. Application to the moduli space of sheaves on the projective plane
Let us denote by
![]() $\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)$
the moduli space of rank 2 stable sheaves on the projective plane
$\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)$
the moduli space of rank 2 stable sheaves on the projective plane
![]() $\mathbb{P}^2$
with respect to the ample line bundle
$\mathbb{P}^2$
with respect to the ample line bundle
![]() $\mathcal{O}_{\mathbb{P}^2}(1)$
. By Proposition 3.4, the image
$\mathcal{O}_{\mathbb{P}^2}(1)$
. By Proposition 3.4, the image
![]() $\phi_{z}(\mathbb{P}(z))$
defines a cycle in the Hilbert scheme of
$\phi_{z}(\mathbb{P}(z))$
defines a cycle in the Hilbert scheme of
![]() $\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)$
$\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)$
In this section, we will describe the component of the Hilbert scheme which contains the cycles
![]() $\phi_z(\mathbb{P}(E_x))$
. Our computations use some results and techniques of [Reference Hirshowitz and Hulek13, Reference Stromme24].
$\phi_z(\mathbb{P}(E_x))$
. Our computations use some results and techniques of [Reference Hirshowitz and Hulek13, Reference Stromme24].
Definition 4.1. Let E be a normalized rank 2 sheaf on
![]() $\mathbb{P}^2$
. A line L (resp. a conic C)
$\mathbb{P}^2$
. A line L (resp. a conic C)
![]() $\subset \mathbb{P}^2$
is jumping line (resp. jumping conic) if
$\subset \mathbb{P}^2$
is jumping line (resp. jumping conic) if
![]() $h^1 (L,E({-}c_1-1) \vert_L)\neq 0$
(resp.
$h^1 (L,E({-}c_1-1) \vert_L)\neq 0$
(resp.
![]() $h^1 (C,E\vert_C) \neq 0)$
.
$h^1 (C,E\vert_C) \neq 0)$
.
The following theorem was proved in [Reference Stromme24]
Theorem 4.2.
Assume that
![]() $c_1=-1$
(resp.
$c_1=-1$
(resp.
![]() $c_1=0$
) and that
$c_1=0$
) and that
![]() $c_2= n \geq 2$
(resp.
$c_2= n \geq 2$
(resp.
![]() $c_2= n\geq 3$
is odd). Then
$c_2= n\geq 3$
is odd). Then
-
(i)
 $Pic(\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2))$
is freely generated by two generators denoted by
$Pic(\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2))$
is freely generated by two generators denoted by
 $\epsilon$
and
$\epsilon$
and
 $\delta$
(resp.
$\delta$
(resp.
 $\varphi$
and
$\varphi$
and
 $\psi$
).
$\psi$
). -
(ii) An integral linear combination
 $a\epsilon + b\delta$
(resp.
$a\epsilon + b\delta$
(resp.
 $a \varphi +b\psi$
) is ample if and only if
$a \varphi +b\psi$
) is ample if and only if
 $a \gt 0$
and
$a \gt 0$
and
 $b \gt 0$
.
$b \gt 0$
. -
(iii) Consider the following sets in
 $ \mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)$
:Then
$ \mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)$
:Then \begin{eqnarray*} D_1 &=&\{sheaves\ with\ a\ given\ jumping\ conic\ (resp- line)\}.\\ D_2&=&\{sheaves\ with\ a\ given\ jumping\ line\ (resp. conic)\ passing\ through\ 1\ (resp. 3)\ given\ points\}. \end{eqnarray*}
\begin{eqnarray*} D_1 &=&\{sheaves\ with\ a\ given\ jumping\ conic\ (resp- line)\}.\\ D_2&=&\{sheaves\ with\ a\ given\ jumping\ line\ (resp. conic)\ passing\ through\ 1\ (resp. 3)\ given\ points\}. \end{eqnarray*}
 $D_1$
is the support of a reduced divisor in the linear system
$D_1$
is the support of a reduced divisor in the linear system
 $ \vert \epsilon \vert$
(resp.
$ \vert \epsilon \vert$
(resp.
 $ \vert \varphi \vert$
) and
$ \vert \varphi \vert$
) and
 $D_2$
is the support of a reduced divisor in the linear system
$D_2$
is the support of a reduced divisor in the linear system
 $\vert\delta \vert$
(resp.
$\vert\delta \vert$
(resp.
 $ \vert \frac{1}{2}(n-1)\psi\vert $
).
$ \vert \frac{1}{2}(n-1)\psi\vert $
).
Following the construction given in Section 3, if
![]() $z=(x,E) \in \mathbb{P}^2 \times M_{\mathbb{P}^2}(2;\,c_1,c_2-1)$
then, Proposition 3.3, we have a family
$z=(x,E) \in \mathbb{P}^2 \times M_{\mathbb{P}^2}(2;\,c_1,c_2-1)$
then, Proposition 3.3, we have a family
![]() $\mathcal{F}_z$
of H-stable torsion-free sheaves rank two on
$\mathcal{F}_z$
of H-stable torsion-free sheaves rank two on
![]() $\mathbb{P}^2$
parameterized by
$\mathbb{P}^2$
parameterized by
![]() $\mathbb{P}(E_x)$
or
$\mathbb{P}(E_x)$
or
![]() $\mathbb{P}(z)$
for short. Such family fits in the following exact sequence
$\mathbb{P}(z)$
for short. Such family fits in the following exact sequence
defined on
![]() $\mathbb{P}^2\times \mathbb{P}(z).$
The classification map of
$\mathbb{P}^2\times \mathbb{P}(z).$
The classification map of
![]() $\mathcal{F}_z$
is the morphism
$\mathcal{F}_z$
is the morphism
defined as
![]() $\phi_z(W)=E^{W}$
.
$\phi_z(W)=E^{W}$
.
We now use the exact sequence (4.1) and the morphism (4.2) to determine the irreducible component of the Hilbert scheme
![]() $\text{Hilb}_{\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)}$
of the moduli space
$\text{Hilb}_{\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)}$
of the moduli space
![]() $\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)$
,
$\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)$
,
![]() $c_1=0$
or
$c_1=0$
or
![]() $-1$
which contains the cycles
$-1$
which contains the cycles
![]() $\phi_z(\mathbb{P}(z))$
. This component is denoted by
$\phi_z(\mathbb{P}(z))$
. This component is denoted by
![]() $\mathcal{H}\mathcal{G}$
.
$\mathcal{H}\mathcal{G}$
.
For the proof of the theorem, we first establish the result for two particular cases:
![]() $c_1=-1$
and
$c_1=-1$
and
![]() $c_1=0$
.
$c_1=0$
.
Theorem 4.3. Under the notation of Theorem 4.2
-
(1) Assume that
 $c_1=-1$
and let
$c_1=-1$
and let
 $c_2 \geq 2$
. Let
$c_2 \geq 2$
. Let
 $\mathfrak{L}\,:\!=\, a\epsilon + b\delta$
be an ample line bundle in
$\mathfrak{L}\,:\!=\, a\epsilon + b\delta$
be an ample line bundle in
 $Pic(\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2))$
. Then,
$Pic(\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2))$
. Then,
 $\mathcal{H}\mathcal{G}$
is the component of the Hilbert scheme
$\mathcal{H}\mathcal{G}$
is the component of the Hilbert scheme
 ${Hilb}^P_{\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)}$
where P is the Hilbert polynomial defined as;
${Hilb}^P_{\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)}$
where P is the Hilbert polynomial defined as; \begin{equation*}P(m) = \chi\left(\mathbb{P}(z), \phi^{*}_z(\mathfrak{L}) \right) = \chi\left(\mathbb{P}(z), \mathcal{O}_{\mathbb{P}(z)}(mb)\right).\end{equation*}
\begin{equation*}P(m) = \chi\left(\mathbb{P}(z), \phi^{*}_z(\mathfrak{L}) \right) = \chi\left(\mathbb{P}(z), \mathcal{O}_{\mathbb{P}(z)}(mb)\right).\end{equation*}
-
(2) Assume that
 $c_1=0$
and let
$c_1=0$
and let
 $c_2 \geq 3$
odd number. Let
$c_2 \geq 3$
odd number. Let
 $\mathfrak{L}\,:\!=\, a\varphi+b\psi$
be an ample line bundle in
$\mathfrak{L}\,:\!=\, a\varphi+b\psi$
be an ample line bundle in
 $Pic(\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2))$
. Then,
$Pic(\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2))$
. Then,
 $\mathcal{H}\mathcal{G}$
is the component of the Hilbert scheme
$\mathcal{H}\mathcal{G}$
is the component of the Hilbert scheme
 ${Hilb}^P_{\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)}$
where P is the Hilbert polynomial defined as;
${Hilb}^P_{\mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2)}$
where P is the Hilbert polynomial defined as; \begin{equation*}P(m) = \chi\left(\mathbb{P}(z), \phi^{*}_z(\mathfrak{L}) \right) = \left.\chi\left(\mathbb{P}(z), \mathcal{O}_{\mathbb{P}(z)}\left(m\left(c_2-1\right)b\right)\right)\right).\end{equation*}
\begin{equation*}P(m) = \chi\left(\mathbb{P}(z), \phi^{*}_z(\mathfrak{L}) \right) = \left.\chi\left(\mathbb{P}(z), \mathcal{O}_{\mathbb{P}(z)}\left(m\left(c_2-1\right)b\right)\right)\right).\end{equation*}
Proof.
-
(1) Let
 $z=(x,E) \in \mathbb{P}^2 \times M_{\mathbb{P}^2}(2;\,c_1,r)$
,
$z=(x,E) \in \mathbb{P}^2 \times M_{\mathbb{P}^2}(2;\,c_1,r)$
,
 $c_1=-1$
and
$c_1=-1$
and
 $r \geq 1.$
Consider the family
$r \geq 1.$
Consider the family
 $\mathcal{F}_z$
of stable sheaves of rank two given by the exact sequence (4.1). Then,
$\mathcal{F}_z$
of stable sheaves of rank two given by the exact sequence (4.1). Then,
 $\mathcal{F}_{z_t} \,:\!=\,(\mathcal{F}_{z})\vert_{\mathbb{P}^2 \times \{t\}}$
is stable for any
$\mathcal{F}_{z_t} \,:\!=\,(\mathcal{F}_{z})\vert_{\mathbb{P}^2 \times \{t\}}$
is stable for any
 $t\in \mathbb{P}(z)$
and by Proposition 2.4 its Chern classes are
$t\in \mathbb{P}(z)$
and by Proposition 2.4 its Chern classes are
 $c_1(\mathcal{F}_{z_t})=-1$
and
$c_1(\mathcal{F}_{z_t})=-1$
and
 $c_2\,:\!=\, c_2(\mathcal{F}_{z_t})=r+1 \geq 2$
. Therefore, we have the morphism
$c_2\,:\!=\, c_2(\mathcal{F}_{z_t})=r+1 \geq 2$
. Therefore, we have the morphism \begin{equation*}\phi_z\,:\, \mathbb{P}(E_x) \longrightarrow \mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2), \,\,\,\, t \mapsto \mathcal{F}_z \vert_t\end{equation*}
\begin{equation*}\phi_z\,:\, \mathbb{P}(E_x) \longrightarrow \mathfrak{M}_{\mathbb{P}^2}(2;\,c_1,c_2), \,\,\,\, t \mapsto \mathcal{F}_z \vert_t\end{equation*}
and set
 $\tau = p_1^*(\mathcal{O}_{\mathbb{P}^2}(1))$
.
$\tau = p_1^*(\mathcal{O}_{\mathbb{P}^2}(1))$
.Now we will compute
 $\phi_z^* \epsilon$
and
$\phi_z^* \epsilon$
and
 $\phi_z^* \delta$
.
$\phi_z^* \delta$
.Let
 $l \geq 0 $
, from the exact sequence (4.1) we have
$l \geq 0 $
, from the exact sequence (4.1) we have \begin{equation*}\begin{aligned}0 \to & p_{2_*}\mathcal{F}({-}l\tau) \to p_{2_*}p_1^*E({-}l\tau) \to p_{2_*}p_1^*\mathcal{O}_x({-}l\tau) \otimes p_2^*Q_{E_x} \to \\ & R^1p_{2_*}\mathcal{F}({-}l\tau) \to R^1p_{2_*}p_1^*E({-}l\tau) \to R^1p_{2_*}\left(p_1^*\mathcal{O}_x({-}l\tau) \otimes p_2^*Q_{E_x}\right) \to 0.\end{aligned}\end{equation*}
\begin{equation*}\begin{aligned}0 \to & p_{2_*}\mathcal{F}({-}l\tau) \to p_{2_*}p_1^*E({-}l\tau) \to p_{2_*}p_1^*\mathcal{O}_x({-}l\tau) \otimes p_2^*Q_{E_x} \to \\ & R^1p_{2_*}\mathcal{F}({-}l\tau) \to R^1p_{2_*}p_1^*E({-}l\tau) \to R^1p_{2_*}\left(p_1^*\mathcal{O}_x({-}l\tau) \otimes p_2^*Q_{E_x}\right) \to 0.\end{aligned}\end{equation*}
Using the projection formula, we get
 \begin{eqnarray*}R^ip_{2_*}p_1^*E({-}l\tau) = \mathcal{O}_{\mathbb{P}(E_x)}\otimes H^i(\mathbb{P}^2,E({-}l)).\end{eqnarray*}
\begin{eqnarray*}R^ip_{2_*}p_1^*E({-}l\tau) = \mathcal{O}_{\mathbb{P}(E_x)}\otimes H^i(\mathbb{P}^2,E({-}l)).\end{eqnarray*}
Since
 $E({-}l)$
is a stable vector bundle on
$E({-}l)$
is a stable vector bundle on
 $\mathbb{P}^2$
with
$\mathbb{P}^2$
with
 $c_1\leq 0,$
it follows that
$c_1\leq 0,$
it follows that
 $p_{2_*}p_1^*E({-}l\tau) =0$
and
$p_{2_*}p_1^*E({-}l\tau) =0$
and
 $R^ip_{2_*}p_1^*E({-}l\tau)$
is a trivial bundle. Moreover, by similar arguments we have
$R^ip_{2_*}p_1^*E({-}l\tau)$
is a trivial bundle. Moreover, by similar arguments we have \begin{eqnarray*}R^ip_{2_*}\left(p_1^*\mathcal{O}_x({-}l\tau) \otimes p_2^*Q_{E_x}\right) \cong Q_{E_x} \otimes p_{2_*}p_1^*\mathcal{O}_x({-}l\tau) \cong Q_{E_x}\otimes H^i\left(\mathbb{P}^2,\mathcal{O}_{\mathbb{P}^2}({-}l)_x\right).\end{eqnarray*}
\begin{eqnarray*}R^ip_{2_*}\left(p_1^*\mathcal{O}_x({-}l\tau) \otimes p_2^*Q_{E_x}\right) \cong Q_{E_x} \otimes p_{2_*}p_1^*\mathcal{O}_x({-}l\tau) \cong Q_{E_x}\otimes H^i\left(\mathbb{P}^2,\mathcal{O}_{\mathbb{P}^2}({-}l)_x\right).\end{eqnarray*}
Hence
 $R^1p_{2_*}p_1^*\mathcal{O}_x({-}l\tau) \otimes p_2^*Q_{E_x}=0$
and
$R^1p_{2_*}p_1^*\mathcal{O}_x({-}l\tau) \otimes p_2^*Q_{E_x}=0$
and
 $p_{2_*}p_1^*\mathcal{O}_x({-}l\tau) \otimes p_2^*Q_{E_x}=Q_{E_x}$
. Therefore, we have the exact sequencewhere we conclude that
$p_{2_*}p_1^*\mathcal{O}_x({-}l\tau) \otimes p_2^*Q_{E_x}=Q_{E_x}$
. Therefore, we have the exact sequencewhere we conclude that \begin{eqnarray*}0 \to Q_{E_x} \to R^1p_{2_*}\mathcal{F}({-}l\tau) \to R^1p_{2_*}p_1^*E({-}l\tau) \to 0 \end{eqnarray*}
\begin{eqnarray*}0 \to Q_{E_x} \to R^1p_{2_*}\mathcal{F}({-}l\tau) \to R^1p_{2_*}p_1^*E({-}l\tau) \to 0 \end{eqnarray*}
 $ c_1(R^1p_{2_*}\mathcal{F}({-}l\tau)) = 1$
for any
$ c_1(R^1p_{2_*}\mathcal{F}({-}l\tau)) = 1$
for any
 $l\geq 0$
.
$l\geq 0$
.
According to [Reference Hirshowitz and Hulek13, Lemmas 3.3 and 3.4], it follows that
and \begin{equation*} \phi_z^*(\epsilon) = c_1\left(R^1p_{2_*}\mathcal{F}\right)- c_1(R^1p_{2_*}\mathcal{F}({-}2\tau)=0 \end{equation*}
\begin{equation*} \phi_z^*(\epsilon) = c_1\left(R^1p_{2_*}\mathcal{F}\right)- c_1(R^1p_{2_*}\mathcal{F}({-}2\tau)=0 \end{equation*}
 \begin{equation*} \phi_z^*(\delta) = (r+1)c_1\left(R^1p_{2_*}\mathcal{F}\right)-rc_1\left(R^1p_{2_*}\mathcal{F}({-}\tau)\right)= 1. \end{equation*}
\begin{equation*} \phi_z^*(\delta) = (r+1)c_1\left(R^1p_{2_*}\mathcal{F}\right)-rc_1\left(R^1p_{2_*}\mathcal{F}({-}\tau)\right)= 1. \end{equation*}
Hence, we conclude that
 \begin{equation*}P(m) = \chi(\mathbb{P}(z), \phi^{*}_z(a\epsilon+b\delta) ) = \chi(\mathbb{P}(z), \mathcal{O}_{\mathbb{P}(E_x)}(mb))\end{equation*}
\begin{equation*}P(m) = \chi(\mathbb{P}(z), \phi^{*}_z(a\epsilon+b\delta) ) = \chi(\mathbb{P}(z), \mathcal{O}_{\mathbb{P}(E_x)}(mb))\end{equation*}
as we desired.
-
(2) For the case,
 $c_1=0$
and
$c_1=0$
and
 $c_2 \geq 3$
odd. Consider
$c_2 \geq 3$
odd. Consider
 $z=(x,E) \in \mathbb{P}^2 \times M_{\mathbb{P}^2}(2;\,c_1,r)$
,
$z=(x,E) \in \mathbb{P}^2 \times M_{\mathbb{P}^2}(2;\,c_1,r)$
,
 $c_1= 0$
and
$c_1= 0$
and
 $r \geq 2$
even. From the exact sequence (4.1), we get
$r \geq 2$
even. From the exact sequence (4.1), we get
 $\mathcal{F}_{z_t} \,:\!=\,\mathcal{F}_{z_{\vert_{\mathbb{P}^2 \times \{t\}}}}$
is stable for all
$\mathcal{F}_{z_t} \,:\!=\,\mathcal{F}_{z_{\vert_{\mathbb{P}^2 \times \{t\}}}}$
is stable for all
 $t \in \mathbb{P}(E_x)$
and
$t \in \mathbb{P}(E_x)$
and
 $c_1(\mathcal{F}_{z_t})=0$
,
$c_1(\mathcal{F}_{z_t})=0$
,
 $c_2\,:\!=\, c_2(\mathcal{F}_{z_t})=r+1 \geq 3$
odd. By [Reference Hirshowitz and Hulek13, Lemmas 3.3 and 3.4] we have that
$c_2\,:\!=\, c_2(\mathcal{F}_{z_t})=r+1 \geq 3$
odd. By [Reference Hirshowitz and Hulek13, Lemmas 3.3 and 3.4] we have that \begin{equation*}\phi_z^*(\varphi) = c_1\left(R^1p_{2_*}\mathcal{F}({-}\tau)\right)- c_1(R^1p_{2_*}\mathcal{F}({-}2\tau))=0,\end{equation*}
\begin{equation*}\phi_z^*(\varphi) = c_1\left(R^1p_{2_*}\mathcal{F}({-}\tau)\right)- c_1(R^1p_{2_*}\mathcal{F}({-}2\tau))=0,\end{equation*}
and
 \begin{equation*} \phi_z^*(\psi) = \frac{1}{2}r\left((r+1)c_1\left(R^1p_{2_*}\mathcal{F}\right)-(r-1)c_1\left(R^1p_{2_*}\mathcal{F}({-}\tau)\right)\right)=c_2-1.\end{equation*}
\begin{equation*} \phi_z^*(\psi) = \frac{1}{2}r\left((r+1)c_1\left(R^1p_{2_*}\mathcal{F}\right)-(r-1)c_1\left(R^1p_{2_*}\mathcal{F}({-}\tau)\right)\right)=c_2-1.\end{equation*}
which implies
 \begin{equation*}P(m) = \chi(\mathbb{P}(z), \phi^{*}_z(a\varphi+b\psi) ) = \chi(\mathbb{P}(z), \mathcal{O}_{\mathbb{P}(E_x)}(m(c_2-1)b)))\end{equation*}
\begin{equation*}P(m) = \chi(\mathbb{P}(z), \phi^{*}_z(a\varphi+b\psi) ) = \chi(\mathbb{P}(z), \mathcal{O}_{\mathbb{P}(E_x)}(m(c_2-1)b)))\end{equation*}
and the proof is complete.
Acknowledgment
The first author acknowledges the financial support of Universidad de Guadalajara via PROSNI programme.