1. Introduction
The emergence of a unified constitutive law is a hallmark of gravity-induced convective turbulence (Ahlers, Grossmann & Lohse Reference Ahlers, Grossmann and Lohse2009; Sreenivasan Reference Sreenivasan2019; Wang, Mathai & Sun Reference Wang, Mathai and Sun2019; Chen, Wang & Xi Reference Chen, Wang and Xi2020; Jiang et al. Reference Jiang, Zhu, Wang, Huisman and Sun2020; Wang et al. Reference Wang, Calzavarini, Sun and Toschi2021; Li et al. Reference Li, Chen, Xu and Xi2022; Zhao et al. Reference Zhao, Wang, Wu, Chong and Zhou2022; Ecke & Shishkina Reference Ecke and Shishkina2023), e.g. 
$Nu \sim Ra^\beta$ with 
$\beta \approx 0.3$ in the classical regime (Ahlers et al. Reference Ahlers, Grossmann and Lohse2009; Huang & Zhou Reference Huang and Zhou2013; Xi et al. Reference Xi, Zhang, Hao and Xia2016; Zhang, Zhou & Sun Reference Zhang, Zhou and Sun2017; Plumley & Julien Reference Plumley and Julien2019; Iyer et al. Reference Iyer, Scheel, Schumacher and Sreenivasan2020; Ahlers et al. Reference Ahlers2022; Xu, Xu & Xi Reference Xu, Xu and Xi2023; Li, Chen & Xi Reference Li, Chen and Xi2024) and 
$\beta =1/2$ in the ultimate regime for paradigmatic Rayleigh–Bénard (RB) convection (Grossmann & Lohse Reference Grossmann and Lohse2011; He et al. Reference He, Funfschilling, Nobach, Bodenschatz and Ahlers2012; Toppaladoddi, Succi & Wettlaufer Reference Toppaladoddi, Succi and Wettlaufer2017; Lepot, Aumaître & Gallet Reference Lepot, Aumaître and Gallet2018; Wang, Zhou & Sun Reference Wang, Zhou and Sun2020; Zou & Yang Reference Zou and Yang2021; Jiang et al. Reference Jiang, Wang, Liu and Sun2022), where the Nusselt number 
$Nu$ quantifies the heat transport efficiency and the Rayleigh number 
$Ra$ quantifies the strength of buoyancy forcing. However, in microgravity, as the gravity effect is, however, almost absent, gravity-induced convection becomes too feeble to transport matter and heat. Vibration, omnipresent in science and technology, has been shown to be an attractive way to operate fluids, modulate convective patterns and control heat transport by creating an ‘artificial gravity’ (Beysens et al. Reference Beysens, Chatain, Evesque and Garrabos2005; Beysens Reference Beysens2006), e.g. vibration shapes liquid interfaces in an arbitrary direction (Gaponenko et al. Reference Gaponenko, Torregrosa, Yasnou, Mialdun and Shevtsova2015; Sánchez et al. Reference Sánchez, Yasnou, Gaponenko, Mialdun, Porter and Shevtsova2019, Reference Sánchez, Gaponenko, Yasnou, Mialdun, Porter and Shevtsova2020; Apffel et al. Reference Apffel, Hidalgo-Caballero, Eddi and Fort2021), vibration levitates a fluid layer upon a gas layer (Apffel et al. Reference Apffel, Novkoski, Eddi and Fort2020), vibration selects patterns through the parametric response (Rogers et al. Reference Rogers, Schatz, Bougie and Swift2000a,Reference Rogers, Schatz, Brausch and Peschb; Pesch et al. Reference Pesch, Palaniappan, Tao and Busse2008; Salgado Sánchez et al. Reference Salgado Sánchez, Gaponenko, Porter and Shevtsova2019), vibration significantly enhances or suppresses heat transport depending on the mutual direction of vibration and temperature gradient (Swaminathan et al. Reference Swaminathan, Garrett, Poese and Smith2018; Wang et al. Reference Wang, Zhou and Sun2020; Wu et al. Reference Wu, Dong, Wang and Zhou2021, Reference Wu, Wang, Chong, Dong, Sun and Zhou2022a; Guo et al. Reference Guo, Wang, Wu, Chong and Zhou2022; Wu, Wang & Zhou Reference Wu, Wang and Zhou2022b). Vibroconvection, resulting directly from a non-isothermal fluid subjected to the external vibration, is very pronounced under microgravity conditions and provides a potential mechanism of heat and mass transport in the absence of gravity-induced convection (Gershuni & Lyubimov Reference Gershuni and Lyubimov1998; Mialdun et al. Reference Mialdun, Ryzhkov, Melnikov and Shevtsova2008; Shevtsova et al. Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010). Elucidating the potential constitutive law of vibroconvective turbulence and its underlying mechanism is not only of great importance in microgravity science, but also provides practical guiding significance for space missions (Monti, Savino & Lappa Reference Monti, Savino and Lappa2001) and microfluidic technologies (Daniel, Chaudhury & De Gennes Reference Daniel, Chaudhury and De Gennes2005; Brunet, Eggers & Deegan Reference Brunet, Eggers and Deegan2007).
In past decades, due to the difficulty of conducting microgravity experiments, the experimental studies on vibroconvection at low gravity were limited. An experiment was carried out with the ALICE-2 instrument onboard the Mir space station, which revealed the vibrational influence on the propagation of a temperature wave from a heat source in near-critical fluids (Zyuzgin et al. Reference Zyuzgin, Ivanov, Polezhaev, Putin and Soboleva2001; Garrabos et al. Reference Garrabos, Beysens, Lecoutre, Dejoan, Polezhaev and Emelianov2007). The other known experiment was conducted in the parabolic flights during the 46th campaign organized by the European Space Agency, which reported the first direct experimental evidence of vibroconvection in low gravity (Mialdun et al. Reference Mialdun, Ryzhkov, Melnikov and Shevtsova2008; Shevtsova et al. Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010). There are extensive theoretical and numerical investigations of vibroconvection under weightlessness conditions. In the limiting case of high-frequencies and small amplitudes, the averaging technique was applied to theoretically deduce the dynamical equation of the mean flows (Gershuni & Lyubimov Reference Gershuni and Lyubimov1998). Based on the averaged equations, the onset and bifurcation scenarios of vibroconvection were widely investigated in square, rectangular and cubic enclosures (Savino, Monti & Piccirillo Reference Savino, Monti and Piccirillo1998; Cissé, Bardan & Mojtabi Reference Cissé, Bardan and Mojtabi2004). The synchronous, subharmonic and non-periodic responses to external vibration were observed in vibroconvection from a parametric study over a wide range of frequencies and amplitudes (Hirata, Sasaki & Tanigawa Reference Hirata, Sasaki and Tanigawa2001; Crewdson & Lappa Reference Crewdson and Lappa2021). The parametric and Rayleigh-vibrational instability were examined in vibroconvection in the absence of gravity (Amiroudine & Beysens Reference Amiroudine and Beysens2008; Sharma et al. Reference Sharma, Erriguible, Gandikota, Beysens and Amiroudine2019). The heat transport enhancement near the onset of vibroconvection were also investigated (Gershuni & Lyubimov Reference Gershuni and Lyubimov1998; Shevtsova et al. Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010). However, the basic properties of constitutive law in vibroconvective turbulence have been rarely addressed.
In this paper, we carried out a series of direct numerical simulations on vibroconvection in a wide range of vibration amplitudes and frequencies. Then we theoretically and numerically unveil the emergence of a unified constitutive law and underlying mechanism of vibroconvective turbulence. In § 2, the governing equations and numerical approach of microgravity vibroconvection are described. In § 3, flow structure in vibroconvection is analysed and the unified scaling law of vibroconvective heat transport is revealed theoretically and examined numerically. Finally, the conclusion is given in § 4.
2. Direct numerical simulation
We consider the microgravity vibroconvection set-up of the convective flows in an enclosure heated from below by a hot wall and cooled from above by a cold wall, and subjected to the harmonic vibration 
$A \cos (\varOmega t)$ in the horizontal direction. Here, 
$\varOmega$ and 
$A$ are the angular frequency and pulsating displacement. In the non-inertial frame associated with the imposed vibration, an inertial acceleration of 
$A\varOmega ^2 \cos (\varOmega t) \boldsymbol {e}_x$ is added to the system, where 
$\boldsymbol {e}_x$ is the unit vector in the 
$x$-direction. The governing equations for vibroconvective turbulence can then be written as
$$\begin{gather} \partial_t \boldsymbol{u} + (\boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla}) \boldsymbol{u} ={-}{\boldsymbol{\nabla}}{p} + \nu \nabla^2 \boldsymbol{u} - \alpha A \varOmega^2 \cos(\varOmega t) T \boldsymbol{e}_{x}, \end{gather}$$
$$\begin{gather}\partial_t T + (\boldsymbol{u} \boldsymbol{\cdot} \boldsymbol{\nabla}) T =\kappa \nabla^2 T, \end{gather}$$
in addition to 
$\boldsymbol {\nabla } \boldsymbol {\cdot } \boldsymbol {u}=0$, where 
$\boldsymbol {u}$ is the fluid velocity, 
$T$ the temperature, 
$p$ the modified pressure, 
$\nu$ the kinematic viscosity, 
$\kappa$ thermal diffusivity and 
$\alpha$ thermal expansion coefficient, respectively. Here, the modified pressure is expressed as 
$p = \tilde {p}-\alpha A \varOmega ^2 \cos (\varOmega t) T_0 x$ where 
$\tilde {p}$ is the fluid pressure and 
$T_0$ is the reference temperature (Shevtsova et al. Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010). All quantities used in our simulations have been made dimensionless with respect to the cell's height 
$H$, the temperature difference across the fluid layer 
$\varDelta$ and the viscous diffusion velocity 
$\nu /H$. Based on these choices, the relevant control parameters for the vibroconvection system are the dimensionless vibration amplitude 
${\textit {a}} = \alpha \Delta A/H$, the dimensionless vibration frequency 
$\omega = \varOmega H^2/\nu$ and the Prandtl number 
${\textit {Pr}} = \nu /\kappa$.
We performed direct numerical simulation of microgravity vibroconvection in a rectangular enclosure with aspect ratio of 
$W:D:H = 1:0.3:1$ in three-dimensional (3-D) cases and of 
$W:H=1:1$ in two-dimensional (2-D) cases, where 
$W$, 
$D$, 
$H$ are, respectively, the width, depth and height of the convection cell. The governing equations are numerically solved by a second-order finite difference code, which has been validated many times in the single-phase turbulent convection (Zhang et al. Reference Zhang, Sun, Bao and Zhou2018; Wang et al. Reference Wang, Zhou and Sun2020; Guo et al. Reference Guo, Wang, Wu, Chong and Zhou2022, Reference Guo, Wu, Wang, Zhou and Chong2023; Wu et al. Reference Wu, Wang, Chong, Dong, Sun and Zhou2022a,Reference Wu, Wang and Zhoub; Huang et al. Reference Huang, Guo, Wu, Wang, Chong and Zhou2023; Chong et al. Reference Chong, Qiao, Wu and Wang2024; Zhang & Zhou Reference Zhang and Zhou2024) and multiphase flow (Meng et al. Reference Meng, Zhao, Wu, Wang, Zhou and Chong2024; Zhao et al. Reference Zhao, Wu, Wang, Chang, Zhou and Chong2024). Furthermore, the comparison between our simulation results and experimental data reported in Shevtsova et al. (Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010) is given in Appendix A. The agreement on the growth of the heat flux validates our in-house code. At all solid boundaries, no-slip boundary conditions are applied for the velocity. At the top and bottom plates, the dimensionless temperature is adopted as constant 
$T_{top}=0$ and 
$T_{bot}=1$; and at all sidewalls, the adiabatic conditions are adopted. We performed a series of direct numerical simulations of microgravity vibroconvective turbulence over the vibration amplitude range 
$0.001 \le {\textit {a}} \le 0.1$ and the frequency range 
$10^5 \le \omega \le 10^7$ for 3-D cases, and over the vibration amplitude range 
$0.001 \le {\textit {a}} \le 0.3$ and the frequency range 
$10^3 \le \omega \le 10^7$ for 2-D cases at fixed Prandtl number 
${\textit {Pr}} = 4.38$. For all simulations, the computational mesh size is chosen to adequately resolve the dynamics both the thermal and oscillating boundary layers (BLs), and the time step is chosen to not only fulfil the Courant–Friedrichs–Lewy conditions, but also resolve the time scale of 1 % of the vibration period.
3. Results and discussion
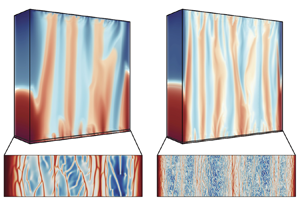
Figure 1(a) shows the typical snapshots of flow structures in vibroconvection with different dimensionless frequencies 
$\omega =10^5$, 
$10^6$ and 
$10^7$ at fixed dimensionless amplitude 
${\textit {a}}=0.01$ and fixed Prandtl number 
${\textit {Pr}} = 4.38$. It is seen that the shaking by external vibration strongly destabilizes the conductive state and generates large distortion of the temperature field in bulk regions by creating an artificial gravity (Beysens et al. Reference Beysens, Chatain, Evesque and Garrabos2005; Beysens Reference Beysens2006). With increasing 
$\omega$, it is vibration-induced artificial gravity that becomes strong enough to destabilize the TBL and trigger abundant thermal plumes. Those plumes are transported into bulk regions and self-organized into columnar structures. This indicates that the feature of the main structures responsible for heat transport in microgravity vibroconvection are different from those in the gravity-induced RB convection. The vertical columnar structure in the bulk is very similar to the columnar pattern observed in experiments on the interface between two miscible liquids under vibration in microgravity (Gaponenko et al. Reference Gaponenko, Torregrosa, Yasnou, Mialdun and Shevtsova2015).
Figure 1. Flow structure in microgravity vibroconvection. (a) Instantaneous 3-D flow structure visualized by the volume rendering of the instantaneous temperature field (see supplementary movies available at https://doi.org/10.1017/jfm.2024.368) under different vibration frequencies 
$\omega = 10^5$ (a i), 
$10^6$ (a ii) and 
$10^7$ (a iii) at fixed amplitude 
${\textit {a}} = 0.01$ and Prandtl number 
${\textit {Pr}} = 4.38$. The subpanels below show the corresponding temperature contours extracted on the horizontal slice at the edge of TBL. (b) Power spectrum of fluctuating temperature in bulk zones. (c) The variation of the characteristic wavenumber 
$k_m$ as functions of 
$\omega$. (d) Percentage of BL (solid symbols) and bulk (hollow symbols) to the global averaged thermal dissipation rate, as functions of vibration frequency.
To quantitatively analyse the feature of columnar structures, we extract the instantaneous temperature field in bulk zones and calculate the power spectrum 
$P(k)$ of temperature fluctuations by applying the Fourier transform in the vibrational direction as shown in figure 1(b). It is found that there exists a characteristic wavenumber 
$k_{m}$, at which the wavenumber distribution function 
$P(k)$ is maximal. Indeed, 
$k_{m}$ characterizes the number of columnar structures in vibroconvection. We then plot the variation of 
$k_{m}$ as functions of 
$\omega$ in figure 1(c). It is shown that 
$k_m$ monotonically increases with increasing 
$\omega$, indicating that more columnar structures are formed under a stronger vibrational driving force. Such a kind of relation for the columnar structures was experimentally established while vibrating two miscible liquids (see figure 5 in the work of Gaponenko et al. (Reference Gaponenko, Torregrosa, Yasnou, Mialdun and Shevtsova2015)). This is consistent with the fact that larger heat transport enhancement occurs at larger 
$\omega$. Further, to examine the role of the TBL in vibroconvective heat transport processes, we decompose the globally averaged thermal dissipation rate 
$\epsilon _T = \kappa \lvert \boldsymbol {\nabla } T \rvert ^2$ into their boundary layer (BL) and bulk contributions, and then plot the variation of relative contributions as functions of 
$\omega$ in figure 1(d), as suggested by the Grossmann–Lohse theory (Ahlers et al. Reference Ahlers, Grossmann and Lohse2009; Stevens et al. Reference Stevens, van der Poel, Grossmann and Lohse2013). It is seen in figure 1(d) that the BL contribution of 
$\epsilon _T$ is much larger than the bulk one, suggesting the BL-dominant thermal dissipation. This reveals that the dynamics of BLs plays a crucial role on the underlying mechanism of heat transport in vibroconvective turbulence.
Next, we address the question of how the global heat transport depends on the control parameters of vibroconvection. First, we examine the dependence of heat transport on the vibration frequency. Figure 2(a,d) shows the measured 
${\textit {Nu}}$ as functions of frequency 
$\omega$ in a log–log plot for different amplitudes 
${\textit {a}}$ in 3-D and 2-D cases. Here, the 
${\textit {Nu}}$ number, as the non-dimensional ratio of the measured heat flux to the conductive one, is calculated by 
${\textit {Nu}} = \langle w T - \kappa \partial _z T\rangle /(\kappa \varDelta /H)$, where 
$w$ is the vertical velocity and 
$\langle {\cdot } \rangle$ denotes the time and space averaging. It is observed that the 
${\textit {Nu}}$–
$\omega$ scaling relation is not unique for a specific amplitude, namely, there seems to be a transition from 
${\textit {Nu}} \sim \omega$ to 
${\textit {Nu}} \sim \omega ^{2/3}$ in both 3-D and 2-D cases, as shown by the dashed lines or in figure 5 in Appendix B. Note that the precise values of scaling exponents are obtained from the physical model we proposed below, not adjusted from the fitting with the numerical data.
Figure 2. Heat transport scaling in vibroconvective turbulence. (a–c) The measured Nusselt number 
${\textit {Nu}}$ as functions of vibration frequency 
$\omega$, vibrational Rayleigh number 
${\textit {Ra}}_{vib}$, oscillational Rayleigh number 
${\textit {Ra}}_{os}$ for 3-D cases. (d–f) The measured Nusselt number 
${\textit {Nu}}$ as functions of vibration frequency 
$\omega$, vibrational Rayleigh number 
${\textit {Ra}}_{vib}$, oscillational Rayleigh number 
${\textit {Ra}}_{os}$ for 2-D cases. The dashed lines in the panels are 
${\textit {Nu}} \sim \omega$ (lower), 
${\textit {Nu}} \sim \omega ^{2/3}$ (upper) in (a,d), 
${\textit {Nu}} \sim {\textit {Ra}}_{vib}^{1/2}$ in (b,e), 
${\textit {Nu}} \sim {\textit {Ra}}_{os}^{1/3}$ in (c,f). Those precise scaling relations are theoretically deduced by our proposed physical model in the paper. Note that the vibration amplitude range in the 3-D cases is from 
${\textit {a}}=10^{-3}$ to 
${\textit {a}}=10^{-1}$ and in the 2-D cases is from 
${\textit {a}}=10^{-3}$ to 
${\textit {a}}=3 \times 10^{-1}$.
Further, we examine the dependency of heat transport on the two important analogous Rayleigh numbers in vibroconvective turbulence, which are the vibrational Rayleigh number 
${\textit {Ra}}_{vib}$ and oscillational Rayleigh number 
${\textit {Ra}}_{os}$. The first one is the vibrational Rayleigh number 
${\textit {Ra}}_{vib} = (\alpha A \varOmega \Delta H)^2/(2\nu \kappa )$, i.e. 
${\textit {Ra}}_{vib} = \tfrac {1}{2}{\textit {a}}^2\omega ^2 {\textit {Pr}}$, which is obtained from applying the averaged approach on vibroconvective equations in the limit of small amplitudes and high frequencies, and quantifies the intensity of the external vibrational source. Figure 2(b,e) depict, respectively, the measured 
${\textit {Nu}}$ as functions of 
${\textit {Ra}}_{vib}$ in a log–log plot at different amplitudes for 3-D and 2-D cases. We find that at small 
${\textit {Ra}}_{vib}$, numerical data almost collapse together on the same scaling law, i.e. 
${\textit {Nu}} \sim {\textit {Ra}}_{vib}^{1/2}$, as shown by the dashed lines. However, at large 
${\textit {Ra}}_{vib}$, a significant departure from this scaling behaviour is observed for large amplitudes. The other is the oscillational Rayleigh number 
${\textit {Ra}}_{os} = \alpha A \varOmega ^2 \Delta H^3/(\nu \kappa )$, i.e. 
${\textit {Ra}}_{os} = {\textit {a}} \omega ^2 {\textit {Pr}}$, which is analogous to Rayleigh number in RB convection but replacing the gravitation by the vibration-induced acceleration. Figure 2(c,f) shows the variation of 
${\textit {Nu}}$ as functions of 
${\textit {Ra}}_{os}$ for various amplitudes in 3-D and 2-D cases. We find that at large 
${\textit {Ra}}_{os}$, numerical data almost collapse onto the same scaling relation 
${\textit {Nu}} \sim {\textit {Ra}}_{os}^{1/3}$ as shown by the dashed line, but at small 
${\textit {Ra}}_{os}$, numerical data points deviate considerably from this scaling for small amplitudes. Both scaling relations 
${\textit {Nu}} \sim {\textit {Ra}}_{vib}^{1/2}$ for small 
${\textit {Ra}}_{vib}$ and 
${\textit {Nu}} \sim {\textit {Ra}}_{os}^{1/3}$ for large 
${\textit {Ra}}_{os}$ can be further confirmed from the compensated plots in figure 6 in Appendix C. From above, using solely the common control parameters like 
$\omega$, 
${\textit {Ra}}_{vib}$ or 
${\textit {Ra}}_{os}$, unifying the heat transport scaling in vibroconvective turbulence cannot be achieved.
Now, there are two important questions remaining to be answered in vibroconvective turbulence: one is why there exists two different heat transport scaling laws, i.e. 
${\textit {Nu}} \sim {\textit {Ra}}_{vib}^{1/2}$ and 
${\textit {Nu}} \sim {\textit {Ra}}_{os}^{1/3}$; the other is whether a unified constitutive law emerges in vibroconvective turbulence. Hereafter, we propose a physical model to address the first question. From the analysis above, we know that the BL-contribution to the global thermal dissipation rate is dominant, implying that the BL dynamics plays a crucial role in the heat transport mechanism. In vibroconvective turbulence, there are two types of BL: the thermal boundary layer (TBL) with the thickness of 
$\delta _{th}$, which is estimated by 
$\delta _{th}\approx H/(2{\textit {Nu}})$; the other is the oscillating boundary layer (OBL) induced by the external vibration. The modulation depth of OBL referring to 
$\delta _{os}$ is defined as the depth, at which the delaying rate of the intensity of vibration-induced shear effect is equal to 
$99\,\%$. Considering the intensity of vibrational modulation falling off exponentially from the surface, one easily obtains 
$\delta _{os} = -\ln (1-0.99) \delta _S \approx 4.605 \delta _S$ where 
$\delta _S = \sqrt {2\nu /\varOmega }$ is the Stokes layer thickness. First, when 
$\delta _{th} > \delta _{os}$ as sketched in figure 3(ai), by taking into account the balance between the convective and conductive transports within TBL, the dimensional analysis of the governing equation of the temperature field gives rise to 
$w {\varDelta }/{\delta _{th}} \sim \kappa {\varDelta }/{\delta ^2_{th}}$. And, in the momentum equation, the balance between the vibration-induced buoyancy and the viscous dissipation leads to 
$\alpha A\varOmega ^2 \varDelta \sim \nu {u}/{\delta ^2_{os}}$ with 
$u$ the horizontal velocity. Using both above relations, assuming that the magnitude of velocity components 
$u$ and 
$w$ follows a similar scaling behaviour, i.e. the ratio 
$w/u$ is approximately constant, together with 
$\delta _{os} \sim \sqrt {\nu /\varOmega }$ and 
$\delta _{th} \sim H/{\textit {Nu}}$, one obtains the scaling relation between 
${\textit {Nu}}$ and 
${\textit {Ra}}_{vib}$,
\begin{equation} {\textit{Nu}} \sim {\textit{Ra}}_{vib}^{1/2} {\textit{Pr}}^{1/2}. \end{equation}
The scaling relation in (3.1) shows that vibroconvective heat transport is independent of viscosity 
$\nu$, but depends on thermal diffusion coefficient 
$\kappa$. This implies that the dynamics of TBL is dominant to heat transport in cases of 
$\delta _{th} > \delta _{os}$.
Figure 3. Unified constitutive law in vibroconvective turbulence. (a) Sketch of the (a i) TBL-dominant regime and the (a ii) OBL-dominant regime. (b,d) The TBL thickness 
$\delta _{th}$ (symbols) and the critical modulation depth 
$\delta _{os}$ (solid line) of OBL as a function of the oscillational Reynolds number 
${\textit {Re}}_{os}$ for 3-D and 2-D cases. The insets in (b,d) show the ratio 
$\delta _{os}/\delta _{th}$ as a function of the oscillational Reynolds number 
${\textit {Re}}_{os}$. The solid dashed line indicates 
$\delta _{os}/\delta _{th} = 1$. (d,e) The unified scaling law exhibited between 
$a {\textit {Nu}}$ and the oscillational Reynolds number 
${\textit {Re}}_{os}$ for 3-D and 2-D cases. The emergence of a universal constitutive law of vibroconvective turbulence is clearly observed. Here, the TBL-dominated regime is coloured light purple and OBL-dominated regime light cyan in (b–e). The coloured symbols have the same meaning as those in figure 2.
When 
$\delta _{th} < \delta _{os}$ as sketched in figure 3(a ii), the balance between the vibration-induced buoyancy and the viscous dissipation within TBL allows one to rewrite the momentum equation using dimensional analysis: 
$\alpha A\varOmega ^2 \varDelta \sim \nu {u}/{\delta ^2_{th}}$. Combining the above equation and 
$w {\varDelta }/{\delta _{th}} \sim \kappa {\varDelta }/{\delta ^2_{th}}$ for the temperature equation, together with the above assumption that the ratio 
$w/u$ is approximately constant, 
$\delta _{os} \sim \sqrt {\nu /\varOmega }$ and 
$\delta _{th} \sim H/{\textit {Nu}}$, one deduces the scaling relation between 
${\textit {Nu}}$ and 
${\textit {Ra}}_{os}$,
\begin{equation} {\textit{Nu}} \sim {\textit{Ra}}_{os}^{1/3}. \end{equation}
The heat transport scaling in (3.2) is similar to that of RB convection in the classical regime through replacing the gravitation by vibration-induced acceleration. Both heat transport scalings predicted in (3.1) and (3.2) agree well with numerical results shown in figure 2. The competition between TBL and OBL results in the two different heat transport scaling relations, namely, 
${\textit {Nu}} \sim {\textit {Ra}}_{vib}^{1/2}$ and 
${\textit {Nu}} \sim {\textit {Ra}}_{os}^{1/3}$.
Furthermore, we address the second question of whether the universal constitutive law of vibroconvective turbulence emerges. First, to quantify the dynamics of OBL, we define the oscillational Reynolds number 
${\textit {Re}}_{os} = \alpha \Delta A \varOmega \delta _{os}/\nu$, which is related to the vibrational velocity with the Boussinesq parameter 
$\alpha \Delta A \varOmega$ and the modulation depth 
$\delta _{os}$ and obeys the relation 
${\textit {Re}}_{os} = 4.605 {\textit {a}} (2\omega )^{1/2}$. Second, we study the dependency of 
${\textit {Nu}}$ on 
${\textit {Re}}_{os}$. It is intriguing to find that both 
${\textit {Nu}} \sim {\textit {Ra}}_{vib}^{1/2}$ and 
${\textit {Nu}} \sim {\textit {Ra}}_{os}^{1/3}$ scaling laws can be rewritten as 
${\textit {Nu}} \sim {\textit {a}}^{-1} {\textit {Re}}_{os}^\beta$ with 
$\beta =2$ for the TBL-dominant heat transport regime (
$\delta _{th}>\delta _{os}$), and 
$\beta =4/3$ for the OBL-dominant heat transport regime (
$\delta _{th}<\delta _{os}$). Therefore, we conclude that due to the competition between the dynamics TBL and OBL on heat transport, the underlying mechanism of heat transport in vibroconvective turbulence can be categorized into the two following regimes.
(i) The TBL-dominant regime (
$\delta _{th} > \delta _{os}$): the OBL is submerged into TBL. Thermal plumes facilitated by vibration-induced strong shear detach from OBL and move into TBL. The plume dynamics is then mainly dominant by the molecular diffusion between OBL and TBL. Those plumes thermally diffuse and then self-organize into columnar structures in bulk zones, which transport heat from the bottom hot plate to the top cold one. The heat transport scaling exhibits the scaling ${\textit {Nu}} \sim {\textit {a}}^{-1} {\textit {Re}}_{os}^{2}$.(ii) The OBL-dominant regime (
$\delta _{os} > \delta _{th}$): the TBL is nested into OBL. The OBL dominates the dynamics of thermal plumes ejected from TBL by vibration-induced strong shear. Between OBL and TBL, the shear effect mixes those plumes and sweep away some of them (Scagliarini, Gylfason & Toschi Reference Scagliarini, Gylfason and Toschi2014; Blass et al. Reference Blass, Zhu, Verzicco, Lohse and Stevens2020; Jin et al. Reference Jin, Wu, Zhang, Liu and Zhou2022). The remaining plumes then move into bulk zones and self-organize into columnar structures. In this regime, due to the plume-sweeping mechanism between OBL and TBL, the heat transport is depleted and obeys the scaling with a smaller scaling relation exponent ${\textit {Nu}} \sim {\textit {a}}^{-1} {\textit {Re}}_{os}^{4/3}$.
Finally, we use the simulated data to confirm the theoretically deduced unified constitutive law. First, we plot in figure 3(b,d) the variation of both 
${\textit {a}} \delta _{th}$ and 
${\textit {a}} \delta _{os}$ as functions of 
${\textit {Re}}_{os}$. It is shown that for all fixed amplitudes, the value of both 
$\delta _{th}$ and 
$\delta _{os}$ monotonically decreases as increasing 
${\textit {Re}}_{os}$, and 
$\delta _{th}$ decreases faster than 
$\delta _{os}$. The intersection point between the curves of 
${\textit {a}} \delta _{th}$ and 
${\textit {a}} \delta _{os}$ divides the plane into two regions, which corresponds to the TBL-dominant regime in the left-hand side (
$\delta _{th} > \delta _{os}$) and OBL-dominant regime in the right-hand side (
$\delta _{th} > \delta _{os}$). As depicted in the inset of figure 3(b,d), the dividing line between TBL-dominant and OBL-dominant regimes is nearly at the position of 
$\delta _{os}/\delta _{th} = 1$. This confirms that the underlying mechanism of vibroconvective heat transport is attributed to the competition between the dynamics of TBL and OBL. Second, we plot the calculated 
${\textit {a}} {\textit {Nu}}$ as functions of 
${\textit {Re}}_{os}$ as shown in figure 3(c,e). It is expected that all numerical data collapse together onto the derived universal constitutive law. Evidently, the numerical data and theoretical model show an excellent agreement. This confirms the emergence of the universal constitutive law of vibroconvective turbulence in microgravity. The evidence of this unified heat transport heat scaling is also shown from the compensated plots in figure 7 in Appendix D.
4. Conclusions
In summary, we have conducted direct numerical simulations of both 2-D and 3-D microgravity vibroconvective turbulence over a wide range of dimensionless vibration amplitude and frequency at fixed 
${\textit {Pr}} = 4.38$. It is shown that in the absence of gravitational acceleration, vibration creates an ‘artificial gravity’ in microgravity to destabilize TBL and trigger a massive eruption of thermal plumes. We find that those plumes are finally self-organized into columnar structures in bulk zones to transport heat from the bottom hot plate to the top cold one. This is different from the gravity-induced convection, like RB convection, in which large-scale circulation is formed in the bulk and dominates heat transport. By analysing the basic properties of heat transport, we find the heat transport exhibits two different power-low relations, i.e. 
${\textit {Nu}} \sim {\textit {Ra}}_{vib}^{1/2}$ at small amplitudes and 
${\textit {Nu}} \sim {\textit {Ra}}_{os}^{1/3}$ at large amplitudes. Both 
${\textit {Nu}}$-relations show that the global heat flux is independent of the cell height. We also find that the BL-contribution is dominant to the global thermal dissipation rate, implying that the dynamics of BL plays an essential role in vibroconvective heat transport. We then propose a physical model to theoretically deduce both 
${\textit {Nu}}$-scaling-relations, and explain the distinct properties of vibroconvective heat transport, based on the competition between the TBL and OBL induced by the external vibration. To look for the universal features, we define the oscillational Reynolds number 
${\textit {Re}}_{os}$ quantifying the dynamics of OBL, and study the dependency of heat transport on 
${\textit {Re}}_{os}$. Both theoretical results and numerical data shows the emergence of the universal constitutive law in vibroconvective turbulence, i.e. 
${\textit {Nu}} \sim {\textit {a}}^{-1} {\textit {Re}}_{os}^{\beta }$, where 
$\beta$ is the universal scaling exponent. We also find that the exponent 
$\beta$ is determined by the relative importance between the dynamics of TBL and of OBL to heat transport, and identify 
$\beta = 2$ in TBL-dominant regime and 
$\beta = 4/3$ in OBL-dominant regime. It is concluded that the type of vibroconvective turbulence in microgravity owns a universal constitutive law with its underlying heat transport mechanism different from that in gravity-induced convective turbulence. The emergence of universal constitutive laws in vibroconvective turbulence provides a powerful basis for generating a controllable heat transport under microgravity conditions or in a microfluidic environment.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2024.368.
Funding
This work was supported by the Natural Science Foundation of China under grant nos. 11988102, 92052201, 12032016, 12102246 and 11972220.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Comparison with the experimental results
To further validate our simulation, we compared our simulated Nusselt number with the experimentally measured data in parabolic flight reported in Shevtsova et al. (Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010). Note that in the validation case, a linear temperature profile is applied on the lateral boundaries and the residual gravity also remained, which is different from the fact that lateral boundaries are adiabatic and the gravity vanishes in the main text. The main numerical control parameters are given in table 1. More details of set-up are given in Melnikov et al. (Reference Melnikov, Ryzhkov, Mialdun and Shevtsova2008) and Shevtsova et al. (Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010). Both the time series of simulated Nusselt number and the experimentally measured one are shown in figure 4. Here, the simulated Nusselt number is calculated using the summation of the normal gradient of the instantaneous temperature over the whole boundaries. The instantaneous temperature field of thermal vibrational convection is extracted at the time of integer multiples of the vibration period. It is shown in figure 4 that the general trend in the growth of the Nusselt number is the same in 2-D/3-D simulations and experiment, although one can see the difference between the value of experimental and numerical results. This result is consistent with the comparison reported in Shevtsova et al. (Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010). And, Shevtsova et al. (Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010) reported that this difference is attributed to the different heat flux through the lateral walls between the numerical and experimental set-up.
Table 1. Numerical parameters for the validation case. The dimensional cell size is 
$H=0.005\,{\rm m}$. The magnitude of gravitation is 
$g=9.81\,{\rm m}\,{\rm s}^{-2}$. The Rayleigh numbers corresponding to the residual gravity are given by 
$Ra_x = \alpha g_x \Delta H^3/(\nu \kappa )$, 
$Ra_y = \alpha g_y \Delta H^3/(\nu \kappa )$ and 
$Ra_z = \alpha g_z \Delta H^3/(\nu \kappa )$. Note that the direction of the residual gravity is the same as with that in Shevtsova et al. (Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010).
Figure 4. Comparison between the time series of the simulated Nusselt number and experimentally measured data in the parabolic flight reported in the work of Shevtsova et al. (Reference Shevtsova, Ryzhkov, Melnikov, Gaponenko and Mialdun2010). Here, the horizontal axis is denoted by the dimensional time.
Appendix B. Transition from $Nu \sim \omega$ to $Nu\sim \omega ^{2/3}$ for fixed $a = 0.03$
To clearly show the transition of scaling relation from 
$Nu \sim \omega$ to 
$Nu\sim \omega ^{2/3}$, we carried out a series of direct numerical simulations for a fixed amplitude 
$a = 0.03$ and plot the measured 
$Nu$ number as a function of 
$\omega$ in figure 5(a). A transition from 
$Nu \sim \omega$ to 
$Nu\sim \omega ^{2/3}$ is observed. And, the compensated plots shown in figure 5(b,c) further confirm this transition of scaling relations.
Figure 5. Transition of the 
$Nu$–
$\omega$ relation from 
$Nu\sim \omega$ to 
$Nu\sim \omega ^{2/3}$ for 
$a = 0.03$. (a) The measured 
$Nu$ number as a function of vibration frequency 
$\omega$. (b,c) The compensated plots of the scaling relations 
$Nu\sim \omega$ and 
$Nu\sim \omega ^{2/3}$.
Appendix C. Compensated plots for $Nu\sim Ra_{vib}^{1/2}$ and $Nu \sim Ra_{os}^{1/3}$
Figure 6 shows the compensated plots of the heat transport scaling relations 
$Nu \sim Ra_{vib}^{1/2}$ and 
$Nu \sim Ra_{os}^{1/3}$ using numerical data of both 3-D and 2-D cases, which correspond to figure 2. Those compensated plots shown in figure 6(a–d) further confirm the scaling relations 
$Nu\sim Ra_{vib}^{1/2}$ and 
$Nu \sim Ra_{os}^{1/3}$ observed in figure 2.
Figure 6. Compensated plots for scaling relations (a) 
$Nu \sim Ra_{vib}^{1/2}$ and (b) 
$Nu \sim Ra_{os}^{1/3}$ for 3-D cases, (c) 
$Nu \sim Ra_{vib}^{1/2}$ and (d) 
$Nu \sim Ra_{os}^{1/3}$ for 2-D cases. Here, the coloured symbols have the same meaning as with those in figure 2.
Appendix D. Compensated plots for the unified scaling $Nu\sim a^{-1}Re_{os}^{\beta }$
Figure 7 shows the compensated plots of the unified heat transport scaling law 
$Nu \sim a^{-1} Re_{os}^{\beta }$ with 
$\beta = 2$ in the TBL-dominant regime and 
$\beta = 4/3$ in the OBL-dominant regime using numerical data of both 3-D and 2-D cases, which correspond to figure 3. Those compensated plots shown in figure 7(a–d) further confirm the unified scaling laws we have obtained theoretically and numerically in the main text.
Figure 7. Compensated plots for unified scaling relation (a) 
$Nu \sim a^{-1}Re_{os}^{2}$ and (b) 
$Nu \sim a^{-1}Re_{os}^{4/3}$ for 3-D cases, (c) 
$Nu \sim a^{-1}Re_{os}^{2}$ and (d) 
$Nu \sim a^{-1}Re_{os}^{4/3}$ for 2-D cases. Here, the TBL-dominated regime is coloured light purple and the OBL-dominated regime light cyan in (a–d). The coloured symbols have the same meaning as those in figure 2.
