1 Introduction
Along a degeneration of a smooth algebraic curve
$C$
to a nodal curve, there is a simple closed curve in
$C$
that gets contracted to the nodal point. This simple closed curve, well-defined up to isotopy, is called the vanishing cycle of the degeneration.
If the question of contracting simple closed curves abstractly in
$\overline{{\mathcal{M}}}_{g}$
leaves no mystery, the embedded case is still open. In particular, we may ask what are the possible vanishing cycles of a curve
$C$
embedded in a toric surface
$X$
, where the underlying degenerations are constrained in a fixed complete linear system
$|{\mathcal{L}}|$
on
$X$
. As simply as it is stated, this question, suggested by Donaldson [Reference DonaldsonDon00], admits no definitive answer. Another approach is to study the monodromy map from the fundamental group of the complement of the discriminant
${\mathcal{D}}\subset |{\mathcal{L}}|$
to the mapping class group
$\text{MCG}(C)$
. The study of such fundamental groups was suggested by Dolgachev and Libgober [Reference Dolgachev and LibgoberDL81] and is still an active field of investigation (see, for example, [Reference LönneLön09]). From a wider perspective, the description of the monodromy map gives an insight into the universal map
$|{\mathcal{L}}|\setminus {\mathcal{D}}\rightarrow {\mathcal{M}}_{g}$
which is far from being understood (see e.g. [Reference Castryck and VoightCV09]).
We know from [Reference WajnrybWaj77] that, for a smooth plane curve
$C$
of genus
$g$
, we can contract
$2g$
simple closed curves whose complement in
$C$
is a disc. It leads in particular to the topological classification of smooth projective surfaces in
$\mathbb{C}P^{3}$
given in [Reference Mandelbaum and MoishezonMM76]. In [Reference BeauvilleBea86], Beauville determines the image of the algebraic monodromy map for hypersurfaces of degree
$d$
in
$\mathbb{C}P^{m}$
, for any
$m$
and
$d$
.
In this paper, we focus on the case of curves but investigate any complete linear system
$|{\mathcal{L}}|$
on any smooth toric surface
$X$
. We point out the obstructions to contracting cycles in the curve
$C$
. They mainly arise from the roots of the adjoint line bundle
$K_{X}\otimes {\mathcal{L}}$
. Square roots of
$K_{X}\otimes {\mathcal{L}}$
were already considered in [Reference BeauvilleBea86]. The obstructions provided by higher-order roots of
$K_{X}\otimes {\mathcal{L}}$
were studied in [Reference Earle and SipeES91] and [Reference SipeSip82] but were somehow forgotten in the common literature until recently. In particular, they do not show up in the work of Beauville [Reference BeauvilleBea86] as the obstructions they provide are undetectable at the homological level. It might also happen that all the curves in
$|{\mathcal{L}}|$
are hyperelliptic. In such a case, the monodromy map has to preserve the hyperelliptic involution.
We show that there are no other obstructions than the ones mentioned above.
Theorem 1. Let
$X$
be a smooth complete toric surface,
${\mathcal{L}}$
an ample line bundle on
$X$
and
$C\in |{\mathcal{L}}|$
a generic smooth curve. Then, the monodromy map
$$\begin{eqnarray}\unicode[STIX]{x1D707}:\unicode[STIX]{x1D70B}_{1}(|{\mathcal{L}}|\setminus {\mathcal{D}})\rightarrow \text{MCG}(C)\end{eqnarray}$$
is surjective if and only if
$C$
is not hyperelliptic and if the adjoint line bundle of
${\mathcal{L}}$
admits no root. In this case, any non-separating simple closed curve in
$C$
is a vanishing cycle.
Let us mention, on the one hand, a very recent independent work by Salter [Reference SalterSal16], in which he proves this result in the particular case of
$\mathbb{C}P^{2}$
and, on the other hand, a work by Bolognesi and Lönne [Reference Bolognesi and LönneBL16] in which they prove this result in the case of ample linear systems of trisections on Hirzebruch surfaces.
As suggested by Beauville [Reference BeauvilleBea86], some of the latter obstructions persist in homology. In the following statement,
$\text{Sp}(H_{1}(C,\mathbb{Z}))$
denotes the group of automorphisms preserving the intersection form.
Theorem 2. Let
$X$
be a smooth complete toric surface,
${\mathcal{L}}$
an ample line bundle on
$X$
and
$C\in |{\mathcal{L}}|$
a generic smooth curve. Then the algebraic monodromy map
$$\begin{eqnarray}[\unicode[STIX]{x1D707}]:\unicode[STIX]{x1D70B}_{1}(|{\mathcal{L}}|\setminus {\mathcal{D}})\rightarrow \text{Sp}(H_{1}(C,\mathbb{Z}))\end{eqnarray}$$
is surjective if and only if
$C$
is not hyperelliptic and if the adjoint line bundle of
${\mathcal{L}}$
admits no root of even order. In this case, any non-separating simple closed curve in
$C$
is homologous to a vanishing cycle.
We introduce new techniques to determine the image of the monodromy map
$\unicode[STIX]{x1D707}$
. We first use the intensively studied simple Harnack curves (see [Reference MikhalkinMik00, Reference Kenyon and OkounkovKO06]), for which all possible degenerations are known. From them, we then construct loops in
$|{\mathcal{L}}|\setminus {\mathcal{D}}$
with explicit monodromy in
$\text{MCG}(C)$
using tropical methods. With this aim, we consider partial phase-tropical compactifications of
${\mathcal{M}}_{g}$
. According to [Reference LangLan15b], we have a proper understanding of the closure of
$|{\mathcal{L}}|\setminus {\mathcal{D}}$
in this compactification in terms of Fenchel–Nielsen coordinates. Using these coordinates, we construct loops with prescribed monodromy in the closure. We then push these loops back to
$|{\mathcal{L}}|\setminus {\mathcal{D}}$
with the help of Mikhalkin’s approximation theorem, see Theorem 5. The efficiency of such a technique suggests that the discriminant nicely intersects the boundary of a globally well-defined phase-tropical compactification of
${\mathcal{M}}_{g}$
. It also has the advantage of being explicit in the sense that we can actually draw the cycles that we can contract on our reference curve
$C$
.
In [Reference Crétois and LangCL17], we will use this technique further to determine the image of the (algebraic) monodromy in the hyperelliptic and spin cases. Motivated by these results and the constructions given in § 7.5, we give a conjecture about the image of
$\unicode[STIX]{x1D707}$
in the general case (see Conjecture 1). In [Reference SalterSal16], Salter proves this conjecture for degree
$5$
curves in
$\mathbb{C}P^{2}$
. Note that during a review of the present paper, Salter answered Donaldson’s question in the present context by proving Conjecture 1 in almost full generality, see [Reference SalterSal17]. By introducing elegant techniques in mapping class group theory, he showed that the constructions of the present paper suffice to generate the whole group
$\text{im}(\unicode[STIX]{x1D707})$
. Coming back to the broader question asked in [Reference DonaldsonDon00], we believe that the tropical approach could be carried to the case of smooth surfaces in toric
$3$
-folds. Another interesting and fundamental variation of the problem is the study of the contraction of cycles along degenerations of real curves.
This paper is organized as follows. In § 2, we introduce the obstructions and the main results more precisely. In § 3, we recall some basic facts about toric surfaces and how to detect the obstructions on a Newton polygon corresponding to the linear system. In § 4, we generalize some results of Kenyon and Okounkov [Reference Kenyon and OkounkovKO06] in order to produce our first vanishing cycles (see Theorem 3). Moreover, we provide a trivialization of the universal curve over the space of simple Harnack curves (see Proposition 4.6). It allows us to describe the vanishing cycles in a combinatorial fashion on the Newton polygon (see Corollary 4.7). In § 5, we use a
$1$
-parameter version of Mikhalkin’s approximation theorem (see Theorem 5) to produce elements of
$\text{im}(\unicode[STIX]{x1D707})$
given as some particular weighted graphs in the Newton polygon. In § 6, we play with this combinatorics to prepare the proofs of Theorems 1 and 2, which we give in § 7. At the end of the paper, we motivate Conjecture 1 with some additional constructions.
2 Setting and statements
2.1 Setting
Let
$X$
be a smooth complete toric surface. Take an ample line bundle
${\mathcal{L}}$
on
$X$
and denote by
$|{\mathcal{L}}|=\mathbb{P}(H^{0}(X,{\mathcal{L}}))$
the complete linear system associated with it.
Definition 2.1. The discriminant of the linear system
$|{\mathcal{L}}|$
is the subset
${\mathcal{D}}\subset |{\mathcal{L}}|$
consisting of all the singular curves in
$|{\mathcal{L}}|$
.
Notice that since
$X$
is toric,
${\mathcal{L}}$
is in fact very ample (see [Reference OdaOda88, Corollary 2.15]) and the embedding of
$X$
in the dual
$|{\mathcal{L}}|^{\ast }$
of the linear system identifies
${\mathcal{D}}$
with the dual variety of
$X$
. In particular, we have the following classical facts.
Proposition 2.2 [Reference Degtyarev, Itenberg and KharlamovDIK00, § 6.5.1].
If
${\mathcal{L}}$
is an ample line bundle on a smooth complete toric surface
$X$
, then the discriminant
${\mathcal{D}}$
is an irreducible subvariety of
$|{\mathcal{L}}|$
of codimension at least
$1$
. It is of codimension
$1$
if and only if there exists a curve in
${\mathcal{D}}$
whose only singularity is a nodal point. In this case, the smooth set of
${\mathcal{D}}$
is exactly the set of such curves.
From now on, we will assume that the discriminant
${\mathcal{D}}$
is a hypersurface in
$|{\mathcal{L}}|$
. Let
$C^{\prime }\in {\mathcal{D}}$
be a curve whose only singularity is a node, which we denote
$p\in C^{\prime }\subset X$
. Then, from [Reference Arbarello, Cornalba and GriffithsACG11, Proposition 2.1] we deduce that there exist a neighborhood
$U\subset X$
of
$p$
and a neighborhood
$B\subset |{\mathcal{L}}|$
of
$C^{\prime }$
such that the restriction of the universal curve
$$\begin{eqnarray}\{(x,C)\in U\times B~|~x\in C\}\rightarrow B\end{eqnarray}$$
is isomorphic to
$$\begin{eqnarray}\{(z,w,t_{1},\ldots ,t_{\dim (|{\mathcal{L}}|)})\in \mathbb{C}^{2}\times \mathbb{C}^{\dim (|{\mathcal{L}}|)}~|~z^{2}+w^{2}=t_{1}\}\rightarrow \mathbb{C}^{\dim (|{\mathcal{L}}|)}\end{eqnarray}$$
in a neighborhood of
$(0,\ldots ,0)$
. The restriction of the previous map to the locus where
$t_{1}\neq 0$
and
$z^{2}/t_{1},w^{2}/t_{1}\geqslant 0$
is fibered in circles whose radius goes to
$0$
as
$t_{1}$
goes to
$0$
.
Now take
$C_{0}\in |{\mathcal{L}}|$
a smooth curve and
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow |{\mathcal{L}}|$
a smooth path, such that
$\unicode[STIX]{x1D6FE}(0)=C_{0}$
and
$\unicode[STIX]{x1D6FE}^{-1}({\mathcal{D}})=\{1\}$
, with
$\unicode[STIX]{x1D6FE}(1)=C^{\prime }$
. We can find
$\unicode[STIX]{x1D716}>0$
such that
$\unicode[STIX]{x1D6FE}([1-\unicode[STIX]{x1D716},1])$
is included in
$B$
. From Ehresmann’s theorem [Reference VoisinVoi07a, Theorem 9.3], the universal curve over
$|{\mathcal{L}}|\setminus {\mathcal{D}}$
is a smooth locally trivial fibration. In particular, we can trivialize its pullback to
$[0,1-\unicode[STIX]{x1D716}]$
via
$\unicode[STIX]{x1D6FE}$
. Using this trivialization and the local form of the universal curve over
$B$
, the circles obtained in the local form (1) of the universal curve induce a smooth simple closed curve
$\unicode[STIX]{x1D6FF}$
on
$C_{0}$
. The isotopy class of this curve does not depend on the choices made (see [Reference Arbarello, Cornalba and GriffithsACG11, § 10.9]).
Definition 2.3. We call the isotopy class of
$\unicode[STIX]{x1D6FF}$
in
$C_{0}$
a vanishing cycle of
$C_{0}$
in the linear system
$|{\mathcal{L}}|$
.
The present paper is motivated by a question of Donaldson [Reference DonaldsonDon00, Question 1], which we formulate as follows.
Question 1. Which isotopy classes of smooth simple closed curves on
$C_{0}\in |{\mathcal{L}}|$
are vanishing cycles in
$|{\mathcal{L}}|$
?
Starting from a vanishing cycle
$\unicode[STIX]{x1D6FF}$
on
$C_{0}$
, one can construct another one using the geometric monodromy map, which is defined as follows. Taking a path
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow |{\mathcal{L}}|\setminus {\mathcal{D}}$
from
$C_{0}$
to itself, the pullback of the universal curve over
$\unicode[STIX]{x1D6FE}$
is trivializable and a choice of trivialization induces an orientation preserving diffeomorphism
$\unicode[STIX]{x1D719}$
of
$C_{0}$
. In fact, the class of
$\unicode[STIX]{x1D719}$
in the mapping class group
$\text{MCG}(C_{0})$
of
$C_{0}$
only depends on the homotopy class of
$\unicode[STIX]{x1D6FE}$
. Thus, we obtain the geometric monodromy morphism
$$\begin{eqnarray}\unicode[STIX]{x1D707}:\unicode[STIX]{x1D70B}_{1}(|{\mathcal{L}}|\setminus {\mathcal{D}},C_{0})\rightarrow \text{MCG}(C_{0}).\end{eqnarray}$$
If
$\unicode[STIX]{x1D6FF}$
is a vanishing cycle on
$C_{0}$
, it follows from the definitions that for any element
$\unicode[STIX]{x1D719}\in \text{im}(\unicode[STIX]{x1D707})$
,
$\unicode[STIX]{x1D719}(\unicode[STIX]{x1D6FF})$
is also a vanishing cycle. Moreover, the irreducibility of
${\mathcal{D}}$
implies the following.
Lemma 2.4 [Reference VoisinVoi07b, Proposition 3.23].
If
$\unicode[STIX]{x1D6FF}$
is a vanishing cycle of
$C_{0}$
in
$|{\mathcal{L}}|$
, then all the other vanishing cycles are obtained from
$\unicode[STIX]{x1D6FF}$
under the action of the image of the geometric monodromy map. In particular, if
$\unicode[STIX]{x1D6FF}$
and
$\unicode[STIX]{x1D6FF}^{\prime }$
are two vanishing cycles of
$C_{0}$
in
$|{\mathcal{L}}|$
, then the pairs
$(C_{0},\unicode[STIX]{x1D6FF})$
and
$(C_{0},\unicode[STIX]{x1D6FF}^{\prime })$
are homeomorphic.
For an ample line bundle
${\mathcal{L}}$
, there always exists a non-separating vanishing cycle on
$C_{0}$
as soon as the genus of
$C_{0}$
is at least
$1$
(see Theorem 3). By non-separating we mean that the complement of the vanishing cycle in
$C_{0}$
is connected. It then follows from Lemma 2.4 that all the other vanishing cycles have the same property. If
${\mathcal{I}}$
denotes the set of isotopy classes of non-separating simple closed curves on
$C_{0}$
, Question 1 now becomes: are all the elements of
${\mathcal{I}}$
vanishing cycles?
In the converse spirit to Lemma 2.4, we can construct elements of the monodromy from vanishing cycles.
Proposition 2.5 [Reference Arbarello, Cornalba and GriffithsACG11, § 10.9].
If a simple closed curve
$\unicode[STIX]{x1D6FF}\in {\mathcal{I}}$
is a vanishing cycle in
$|{\mathcal{L}}|$
, then the Dehn twist
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FF}}$
along
$\unicode[STIX]{x1D6FF}$
is in the image of
$\unicode[STIX]{x1D707}$
.
The construction of an element
$\ell \in \unicode[STIX]{x1D70B}_{1}(|{\mathcal{L}}|\setminus {\mathcal{D}},C_{0})$
such that
$\unicode[STIX]{x1D707}(\ell )=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FF}}$
is rather explicit. Since
$\unicode[STIX]{x1D6FF}\in {\mathcal{I}}$
is a vanishing cycle, we can find a path
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow |{\mathcal{L}}|$
joining
$C_{0}$
to
${\mathcal{D}}$
and defining
$\unicode[STIX]{x1D6FF}$
. Then the loop
$\ell$
is obtained from
$\unicode[STIX]{x1D6FE}$
by replacing the end of
$\unicode[STIX]{x1D6FE}$
itself with the boundary of a small disk transverse to
${\mathcal{D}}$
, with appropriate orientation.
We do not know if the converse to Proposition 2.5 is true in general. However, Lemma 2.4 shows that if the geometric monodromy is surjective then all the elements of
${\mathcal{I}}$
are vanishing cycles. Conversely, if all the elements of
${\mathcal{I}}$
are vanishing cycles, the geometric monodromy is surjective since
$\text{MCG}(C_{0})$
is generated by the Dehn twists around the elements of
${\mathcal{I}}$
, see, for example, [Reference HumphriesHum79]. This suggests the following analogue to Question 1, which we will study in the rest of the paper.
Question 2. When is the geometric monodromy map
$\unicode[STIX]{x1D707}$
surjective? More generally, describe the subgroup
$\text{im}(\unicode[STIX]{x1D707})$
.
2.2 Roots of the canonical bundle and monodromy
In some cases, the smooth curves in
$|{\mathcal{L}}|$
will inherit some geometric structure from the ambient toric surface. As a partial answer to Question 2, we will see how this structure might prevent the map
$\unicode[STIX]{x1D707}$
from being surjective. To make this more precise, we introduce subgroups of the mapping class group which will come into play.
Let
$\unicode[STIX]{x1D70B}:{\mathcal{C}}\rightarrow B$
be a holomorphic family of compact Riemann surfaces of genus
$g>1$
and
$n>0$
be an integer that divides
$2g-2$
. An
$n\text{th}$
root of the relative canonical bundle
$K_{\text{rel}}({\mathcal{C}})$
of
${\mathcal{C}}$
is a holomorphic line bundle
${\mathcal{S}}$
on
${\mathcal{C}}$
, such that
${\mathcal{S}}^{\otimes n}=K_{\text{rel}}({\mathcal{C}})$
. Denote by
$R_{n}({\mathcal{C}})$
the set of
$n\text{th}$
roots of
$K_{\text{rel}}({\mathcal{C}})$
. If the base
$B$
is a point,
$R_{n}({\mathcal{C}})$
is finite of order
$n^{2g}$
.
Choose a base point
$b_{0}\in B$
, and let
$C_{0}=\unicode[STIX]{x1D70B}^{-1}(b_{0})$
. On the one hand, there is a restriction map from
$R_{n}({\mathcal{C}})$
to
$R_{n}(C_{0})$
; on the other hand, there is a monodromy morphism
$\unicode[STIX]{x1D707}_{{\mathcal{C}}}:\unicode[STIX]{x1D70B}_{1}(B,b_{0})\rightarrow \text{MCG}(C_{0})$
, defined as in § 2.1. Recall from [Reference SipeSip82, Corollary p. 73] that the group
$\text{MCG}(C_{0})$
acts on
$R_{n}(C_{0})$
. Moreover, we have the following result.
Proposition 2.6 [Reference Earle and SipeES91, Theorem 2].
If
${\mathcal{S}}\in R_{n}({\mathcal{C}})$
, then all the elements in
$\text{im}(\unicode[STIX]{x1D707}_{{\mathcal{C}}})$
preserve
${\mathcal{S}}_{|C_{0}}\in R_{n}(C_{0})$
.
If
$S\in R_{n}(C_{0})$
, denote by
$\text{MCG}(C_{0},S)$
the subgroup of
$\text{MCG}(C_{0})$
that preserves
$S$
. It is a subgroup of finite index which is proper in general (see [Reference SipeSip82]).
Coming back to our problem, we obtain the following.
Proposition 2.7. Let
$|{\mathcal{L}}|$
be an ample complete linear system on
$X$
, such that its generic element is a curve of genus at least
$2$
. Suppose that the adjoint line bundle
$K_{X}\otimes {\mathcal{L}}$
admits a root of order
$n\geqslant 2$
, i.e. a line bundle
${\mathcal{S}}$
over
$X$
such that
${\mathcal{S}}^{\otimes n}=K_{X}\otimes {\mathcal{L}}$
. Then the restriction of
${\mathcal{S}}$
to
$C_{0}$
is a root of order
$n$
of
$K_{C_{0}}$
and the image of
$\unicode[STIX]{x1D707}$
is a subgroup of
$\text{MCG}(C_{0},{\mathcal{S}}_{|C_{0}})$
.
Proof. The fact that the restriction of
${\mathcal{S}}$
to
$C_{0}$
is a root of order
$n$
of
$C_{0}$
comes from the adjunction formula (see [Reference Griffiths and HarrisGH94])
$$\begin{eqnarray}(K_{X})_{|C_{0}}=K_{C_{0}}\otimes {\mathcal{L}}_{|C_{0}}^{\ast }.\end{eqnarray}$$
To prove the rest of the proposition, we show that this formula is true in families. To that end, choose a hyperplane
$H$
in
$|{\mathcal{L}}|$
that does not contain
$C_{0}$
. Let
$$\begin{eqnarray}{\mathcal{C}}=\{(x,C)\in X\times |{\mathcal{L}}|\setminus ({\mathcal{D}}\cup H)~|~x\in C\}\end{eqnarray}$$
be the universal curve with projection
$\unicode[STIX]{x1D70B}:{\mathcal{C}}\rightarrow |{\mathcal{L}}|\setminus ({\mathcal{D}}\cup H)$
and evaluation map
$\text{ev}:{\mathcal{C}}\rightarrow X$
. Then the pullback of
$K_{X}\otimes {\mathcal{L}}$
to
${\mathcal{C}}$
by
$\text{ev}$
is isomorphic to the relative canonical bundle of
${\mathcal{C}}$
. Indeed, denote by
$T_{\text{rel}}{\mathcal{C}}$
the kernel of
$\text{d}\unicode[STIX]{x1D70B}$
. By definition,
$K_{\text{rel}}({\mathcal{C}})$
is the dual of
$T_{\text{rel}}{\mathcal{C}}$
. Moreover, since all the curves in
$|{\mathcal{L}}|\setminus {\mathcal{D}}$
are smooth, the differential of the evaluation map induces an injective morphism
$T_{\text{rel}}{\mathcal{C}}\rightarrow \text{ev}^{\ast }TX$
. Conversely, since we removed
$H$
from
$|{\mathcal{L}}|$
, we can choose a section
$s$
of the pullback of
${\mathcal{L}}$
over
$X\times |{\mathcal{L}}|\setminus ({\mathcal{D}}\cup H)$
that vanishes along
${\mathcal{C}}$
. Its derivative is well-defined along
${\mathcal{C}}$
and induces a morphism
$\text{ev}^{\ast }TX\rightarrow \text{ev}^{\ast }{\mathcal{L}}$
, which is surjective since the curves in
$|{\mathcal{L}}|\setminus {\mathcal{D}}$
are transversally cut. It follows also that we have an exact sequence
$$\begin{eqnarray}0\rightarrow T_{\text{rel}}{\mathcal{C}}\rightarrow \text{ev}^{\ast }TX\rightarrow \text{ev}^{\ast }{\mathcal{L}}\rightarrow 0.\end{eqnarray}$$
Thus
$\text{ev}^{\ast }K_{X}\otimes \text{ev}^{\ast }{\mathcal{L}}=K_{\text{rel}}({\mathcal{C}})$
. In particular,
$\text{ev}^{\ast }{\mathcal{S}}^{\otimes n}=K_{\text{rel}}({\mathcal{C}})$
, and
$\text{ev}^{\ast }{\mathcal{S}}$
is an element of
$R_{n}({\mathcal{C}})$
. The result follows from Proposition 2.6 and the fact that the morphism
$\unicode[STIX]{x1D70B}_{1}(|{\mathcal{L}}|\setminus ({\mathcal{D}}\cup H),C_{0})\rightarrow \unicode[STIX]{x1D70B}_{1}(|{\mathcal{L}}|\setminus {\mathcal{D}},C_{0})$
is surjective.◻
Earle and Sipe showed in [Reference Earle and SipeES91, Corollary 5.3] that, for any Riemann surface of genus
$g>2$
, there exists an element of its mapping class group that does not preserve any
$n\text{th}$
root of its canonical bundle for all
$n>2$
dividing
$2g-2$
. In particular, Proposition 2.7 gives the following.
Corollary 2.8. Let
$X$
be a smooth and complete toric surface and let
${\mathcal{L}}$
be an ample line bundle on
$X$
. Assume that the curves in
$|{\mathcal{L}}|$
are of arithmetic genus at least
$3$
. Fix a smooth curve
$C_{0}$
in
$|{\mathcal{L}}|$
.
If
$K_{X}\otimes {\mathcal{L}}$
admits an
$n\text{th}$
root with
$n>2$
, the geometric monodromy
$\unicode[STIX]{x1D707}$
is not surjective. In particular, there exists a non-separating simple closed curve on
$C_{0}$
that is not a vanishing cycle.
Remark 2.9. Since the Picard group of
$X$
is free [Reference FultonFul93, proposition p. 63], the
$n\text{th}$
root of
$K_{X}\otimes {\mathcal{L}}$
is unique when it exists.
2.3 Main results
In the following theorems,
$X$
is a smooth and complete toric surface and
${\mathcal{L}}$
is an ample line bundle on
$X$
. We assume that the curves in
$|{\mathcal{L}}|$
are of arithmetic genus at least
$1$
. This implies that the adjoint line bundle
$K_{X}\otimes {\mathcal{L}}$
of
${\mathcal{L}}$
has an empty base locus (see Proposition 3.3). Finally, we denote by
$d$
the dimension of the image of the map
$X\rightarrow |K_{X}\otimes {\mathcal{L}}|^{\ast }$
and we fix a smooth curve
$C_{0}$
in
$|{\mathcal{L}}|$
.
Theorem 1. The monodromy map
$\unicode[STIX]{x1D707}$
is surjective if and only if one of the following is satisfied:
(i)
$d=0$
;(ii)
$d=2$
and
$K_{X}\otimes {\mathcal{L}}$
admits no root of order greater or equal to
$2$
.
The case
$d=1$
corresponds to the hyperelliptic case and will be treated in the follow-up paper [Reference Crétois and LangCL17]. In the case
$d=2$
, the parity of the largest order
$n$
of a root
${\mathcal{S}}$
of
$K_{X}\otimes {\mathcal{L}}$
plays an important role.
When
$n$
is even, the restriction of
${\mathcal{S}}^{\otimes n/2}$
to
$C_{0}$
is a spin structure on
$C_{0}$
. We also treat this case in [Reference Crétois and LangCL17]. Let us simply say that the non-surjectivity of the monodromy already appears through the algebraic monodromy map
$$\begin{eqnarray}[\unicode[STIX]{x1D707}]:\unicode[STIX]{x1D70B}_{1}(|{\mathcal{L}}|\setminus {\mathcal{D}},C_{0})\rightarrow \text{Sp}(H_{1}(C_{0},\mathbb{Z})),\end{eqnarray}$$
obtained by composing
$\unicode[STIX]{x1D707}$
with the natural map
$\text{MCG}(C_{0})\rightarrow \text{Sp}(H_{1}(C_{0},\mathbb{Z}))$
, where
$\text{Sp}(H_{1}(C_{0},\mathbb{Z}))$
is the group of automorphisms of
$H_{1}(C_{0},\mathbb{Z})$
that preserve the intersection form.
When
$n$
is odd, the obstruction described in Corollary 2.8 is not detected by the algebraic monodromy. More precisely, we have the following.
Theorem 2. The algebraic monodromy map
$[\unicode[STIX]{x1D707}]$
is surjective if and only one of the following is satisfied:
(i)
$\unicode[STIX]{x1D707}$
is surjective;(ii)
$d=2$
and
$K_{X}\otimes {\mathcal{L}}$
admits no root of order
$2$
.
In the general case, we conjecture the following.
Conjecture 1. Assume that
$d=2$
. Let
$n$
be the largest order of a root
${\mathcal{S}}$
of
$K_{X}\otimes {\mathcal{L}}$
. The image of
$\unicode[STIX]{x1D707}$
is exactly
$\text{MCG}(C_{0},{\mathcal{S}}_{|C_{0}})$
.
We motivate this conjecture in this paper (see § 7.5) and the follow-up paper [Reference Crétois and LangCL17]. We give the proofs of Theorems 1 and 2 in §§ 6.3 and 7, where we treat the cases
$d=0$
and
$d=2$
separately.
Remark 2.10. (i) The amplitude and genus requirements in Theorems 1 and 2 guarantee that the discriminant
${\mathcal{D}}$
is of codimension
$1$
in
$|{\mathcal{L}}|$
and that the vanishing cycles are non-separating (see Theorem 3).
(ii) Question 1 can also be stated in a symplectic setting. That is, if one allows the almost-complex structure on
$X$
to vary along a degeneration of
$C_{0}$
, can one obtain more vanishing cycles than in the algebraic case? Does the obstruction coming from the root of
$K_{X}\otimes {\mathcal{L}}$
survive in this setting?
To prove Theorems 1 and 2, we use techniques from tropical geometry, namely a version of Mikhalkin’s approximation theorem (Theorem 5). It allows the construction of explicit
$1$
-parameter families of curves in
$|{\mathcal{L}}|\setminus {\mathcal{D}}$
whose images by
$\unicode[STIX]{x1D707}$
are rather simple and explicit elements of
$\text{MCG}(C_{0})$
. If no root of
$K_{X}\otimes {\mathcal{L}}$
appears, we show that we can recover Humphries’ generating set for
$\text{MCG}(C_{0})$
, see § 7.3. If no even root of
$K_{X}\otimes {\mathcal{L}}$
appears, we recover the image of Humphries’ generating set in
$\text{Sp}(H_{1}(C_{0},\mathbb{Z}))$
, see § 7.4.
3 Toric surfaces, line bundles, and polygons
We recall some facts about toric surfaces (for more details, see, for example, [Reference FultonFul93] or [Reference Gelfand, Kapranov and ZelevinskyGKZ08]). Let
$X$
be a smooth complete toric surface associated with the fan
$\unicode[STIX]{x1D6F4}\subset \mathbb{Z}^{2}\otimes \mathbb{R}$
. Denote by
$\unicode[STIX]{x1D6F4}(1)$
the set of one-dimensional cones in
$\unicode[STIX]{x1D6F4}$
. For each element
$\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D6F4}(1)$
, let
$u_{\unicode[STIX]{x1D716}}$
be the primitive integer vector in
$\unicode[STIX]{x1D716}$
and
$D_{\unicode[STIX]{x1D716}}\subset X$
the associated toric divisor.
Take a line bundle
${\mathcal{L}}={\mathcal{O}}_{X}(\sum _{\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D6F4}(1)}a_{\unicode[STIX]{x1D716}}D_{\unicode[STIX]{x1D716}})$
on
$X$
and define
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{{\mathcal{L}}}=\{v\in \mathbb{R}^{2}\mid \unicode[STIX]{x1D716}\in \unicode[STIX]{x1D6F4}(1),\langle v,u_{\unicode[STIX]{x1D716}}\rangle \geqslant -a_{\unicode[STIX]{x1D716}}\}.\end{eqnarray}$$
Notice that
$\unicode[STIX]{x1D6E5}_{{\mathcal{L}}}$
is, in fact, only well-defined up to translation by an integer vector.
If
${\mathcal{L}}$
is nef,
$\unicode[STIX]{x1D6E5}_{{\mathcal{L}}}$
is a convex lattice polygon (in this paper, lattice polygons are bounded by convention) and
$\unicode[STIX]{x1D6F4}$
is a refinement of its normal fan. More precisely,
$\unicode[STIX]{x1D6E5}_{{\mathcal{L}}}$
has one edge for each
$\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D6F4}(1)$
and the integer length
$l_{\unicode[STIX]{x1D716}}$
of this edge is equal to the intersection product
$(\sum _{\unicode[STIX]{x1D716}^{\prime }\in \unicode[STIX]{x1D6F4}(1)}a_{\unicode[STIX]{x1D716}^{\prime }}D_{\unicode[STIX]{x1D716}^{\prime }})\bullet D_{\unicode[STIX]{x1D716}}$
, which can be
$0$
. In particular, we have the following proposition.
Proposition 3.1. Let
${\mathcal{L}}$
be a nef line bundle on a smooth complete toric surface
$X$
with fan
$\unicode[STIX]{x1D6F4}$
. Let
$n$
be the largest order of a root of
${\mathcal{L}}$
. Then
$$\begin{eqnarray}n=\gcd (\{l_{\unicode[STIX]{x1D716}}\mid \unicode[STIX]{x1D716}\in \unicode[STIX]{x1D6F4}(1)\}).\end{eqnarray}$$
Proof. Let
$m=\gcd (\{l_{\unicode[STIX]{x1D716}}\mid \unicode[STIX]{x1D716}\in \unicode[STIX]{x1D6F4}(1)\})$
and let
${\mathcal{S}}$
be a root of order
$n$
of
${\mathcal{L}}$
. Then, for any
$\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D6F4}(1)$
,
$$\begin{eqnarray}l_{\unicode[STIX]{x1D716}}={\mathcal{L}}\bullet D_{\unicode[STIX]{x1D716}}=n({\mathcal{S}}\bullet D_{\unicode[STIX]{x1D716}}).\end{eqnarray}$$
Thus
$n$
divides
$m$
.
Conversely, let
$U$
be the matrix whose rows are given by the vectors
$u_{\unicode[STIX]{x1D716}}$
. Up to translation, we can assume that
$0$
is a vertex of
$\unicode[STIX]{x1D6E5}_{{\mathcal{L}}}$
. In particular,
$(1/m)\unicode[STIX]{x1D6E5}_{{\mathcal{L}}}$
is still a convex lattice polygon. Moreover, if
$\unicode[STIX]{x1D6E5}_{{\mathcal{L}}}$
is given by the system
$Uv\geqslant -a$
, then
$(1/m)\unicode[STIX]{x1D6E5}_{{\mathcal{L}}}$
is given by
$Uv\geqslant -(a/m)$
. In particular,
$m$
divides all the coordinates of
$a$
. Thus, we can write
$$\begin{eqnarray}{\mathcal{L}}=\mathop{\sum }_{\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D6F4}(1)}a_{\unicode[STIX]{x1D716}}D_{\unicode[STIX]{x1D716}}=m\mathop{\sum }_{\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D6F4}(1)}\frac{a_{\unicode[STIX]{x1D716}}}{m}D_{\unicode[STIX]{x1D716}},\end{eqnarray}$$
and
${\mathcal{L}}$
has a root of order
$m$
. Thus
$m$
divides
$n$
.◻
Definition 3.2. A convex lattice polygon
$\unicode[STIX]{x1D6E5}$
is even (respectively odd, respectively prime) if the integer
$\gcd (\{l_{\unicode[STIX]{x1D716}}\mid \unicode[STIX]{x1D716}\text{ edge of }\unicode[STIX]{x1D6E5}\})$
is even (respectively odd, respectively equal to
$1$
).
A nef line bundle
${\mathcal{L}}$
on a smooth complete toric surface
$X$
is even (respectively odd, respectively prime) if the polygon
$\unicode[STIX]{x1D6E5}_{{\mathcal{L}}}$
is even (respectively odd, respectively prime).
If
${\mathcal{L}}$
is ample, the normal fan of
$\unicode[STIX]{x1D6E5}_{{\mathcal{L}}}$
is
$\unicode[STIX]{x1D6F4}$
. Moreover, since
$X$
is smooth, the polygon
$\unicode[STIX]{x1D6E5}_{{\mathcal{L}}}$
is also smooth, i.e. any pair of primitive integer vectors directing two consecutive edges of
$\unicode[STIX]{x1D6E5}_{{\mathcal{L}}}$
generates the lattice. Conversely, a smooth convex lattice polygon
$\unicode[STIX]{x1D6E5}$
of dimension 2 defines a smooth complete toric surface
$X$
as follows: label the elements of
$\unicode[STIX]{x1D6E5}\cap \mathbb{Z}^{2}=\{(a_{1},b_{1}),\ldots (a_{m},b_{m})\}$
and consider the monomial embedding
$(\mathbb{C}^{\ast })^{2}\rightarrow \mathbb{C}P^{m}$
given by
$$\begin{eqnarray}(z,w)\mapsto [z^{a_{1}}w^{b_{1}},\ldots ,z^{a_{m}}w^{b_{m}}].\end{eqnarray}$$
Then
$X$
is defined as the closure of
$(\mathbb{C}^{\ast })^{2}$
in
$\mathbb{C}P^{m}$
. In particular, it always comes with
$(z,w)$
-coordinates and the associated complex conjugation. The line bundle
${\mathcal{L}}$
on
$X$
given by the inclusion in
$\mathbb{C}P^{m}$
is such that
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{{\mathcal{L}}}$
. If
$\unicode[STIX]{x1D6E5}^{\prime }$
is obtained from
$\unicode[STIX]{x1D6E5}$
by an invertible affine transformation
$A:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$
preserving the lattice, then
$A$
induces an isomorphism between the two toric surfaces obtained from
$\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}^{\prime }$
, which pulls back
${\mathcal{L}}^{\prime }$
to
${\mathcal{L}}$
. Indeed, the lattice
$\mathbb{Z}^{2}\subset \mathbb{R}^{2}$
is naturally isomorphic to the space of characters on
$(\mathbb{C}^{\ast })^{2}$
via the
$(z,w)$
-coordinates. The map
$A^{\vee }:(\mathbb{C}^{\ast })^{2}\rightarrow (\mathbb{C}^{\ast })^{2}$
dual to
$A$
induces the desired isomorphism of toric surfaces.
When
$\text{int}(\unicode[STIX]{x1D6E5})\cap \mathbb{Z}^{2}$
is non-empty, we can consider the adjoint polygon
$\unicode[STIX]{x1D6E5}_{a}$
of
$\unicode[STIX]{x1D6E5}$
defined as the convex hull of the interior lattice points of
$\unicode[STIX]{x1D6E5}$
. The number of lattice points of
$\unicode[STIX]{x1D6E5}_{a}$
is equal to the arithmetic genus of the curves in
$|{\mathcal{L}}|$
, which we denote
$g_{{\mathcal{L}}}$
, see [Reference KhovanskiiKho78]. Denote also by
$b_{{\mathcal{L}}}$
the number of lattice points on
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
. The integer
$b_{{\mathcal{L}}}$
is then equal to the intersection multiplicity of the curves in
$|{\mathcal{L}}|$
with the divisor
$(\sum _{\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D6F4}(1)}D_{\unicode[STIX]{x1D716}})$
.
Proposition 3.3. Let
$X$
be a smooth complete toric surface with fan
$\unicode[STIX]{x1D6F4}$
and let
${\mathcal{L}}$
be an ample line bundle on
$X$
such that
$g_{{\mathcal{L}}}\geqslant 1$
.
(i) The adjoint line bundle
$K_{X}\otimes {\mathcal{L}}$
is nef with empty base locus and
$\unicode[STIX]{x1D6E5}_{K_{X}\otimes {\mathcal{L}}}=\unicode[STIX]{x1D6E5}_{a}$
. In particular, for each
$\unicode[STIX]{x1D716}\in \unicode[STIX]{x1D6F4}(1)$
, the associated edge of
$\unicode[STIX]{x1D6E5}_{a}$
has length
$l_{\unicode[STIX]{x1D716}}-D_{\unicode[STIX]{x1D716}}^{2}-2$
([Reference KoelmanKoe91, Lemma 2.3.1 and Proposition 2.4.2], [Reference OdaOda88, Theorem 2.7]).(ii) Let
$\unicode[STIX]{x1D719}_{K_{X}\otimes {\mathcal{L}}}:X\rightarrow |K_{X}\otimes {\mathcal{L}}|^{\ast }$
be the natural map. We have
$\dim (\text{im}(\unicode[STIX]{x1D719}_{K_{X}\otimes {\mathcal{L}}}))=\dim (\unicode[STIX]{x1D6E5}_{a})$
.(iii) If
$\dim (\unicode[STIX]{x1D6E5}_{a})=2$
, then
$\unicode[STIX]{x1D6E5}_{a}$
is smooth [Reference OgataOga07, Lemma 5].◻
If
$\unicode[STIX]{x1D6E5}$
is a smooth convex lattice polygon, we call its extremal points vertices.
4 Simple Harnack curves
Let
$\unicode[STIX]{x1D6E5}\subset \mathbb{Z}^{2}\otimes \mathbb{R}$
be a smooth two-dimensional convex lattice polygon,
$X$
the associated toric surface, and
${\mathcal{L}}$
the line bundle on
$X$
given by
$\unicode[STIX]{x1D6E5}$
. Recall that
$X$
comes with an open dense torus
$(\mathbb{C}^{\ast })^{2}\subset X$
with coordinates
$(z,w)$
. These coordinates induce a complex conjugation on
$X$
. A curve
$C\in |{\mathcal{L}}|$
is real if it is invariant by complex conjugation. Define the amoeba map
${\mathcal{A}}:(\mathbb{C}^{\ast })^{2}\rightarrow \mathbb{R}^{2}$
by
$$\begin{eqnarray}{\mathcal{A}}(z,w)=(\log |z|,\log |w|).\end{eqnarray}$$
For any algebraic curve
$C\subset X$
, denote
$C^{\circ }:=C\cap (\mathbb{C}^{\ast })^{2}$
and
$\mathbb{R}C^{\circ }:=C\cap (\mathbb{R}^{\ast })^{2}$
.
Definition 4.1. A real curve
$C\in |{\mathcal{L}}|$
is a (possibly singular) simple Harnack curve if
$C\setminus C^{\circ }$
is a finite set and if the amoeba map
${\mathcal{A}}:C^{\circ }\rightarrow \mathbb{R}^{2}$
is at most 2-to-1.
Remark 4.2. The original definition of simple Harnack curves can be found in [Reference MikhalkinMik00]. The equivalence to the definition given here is proven in [Reference Mikhalkin and RullgårdMR01, Theorem 1]. We seize the occasion to slightly clarify [Reference Mikhalkin and RullgårdMR01, Theorem 1]. For the latter theorem to be true, one has to stress in [Reference Mikhalkin and RullgårdMR01, Definition 2] that the intersection
$\unicode[STIX]{x1D6FC}_{k}\,\cap \,l_{k}$
consists of
$d_{k}$
points, counted with multiplicities. Whether Mikhalkin and Rullgård [Reference Mikhalkin and RullgårdMR01] meant Definition
$2$
this way or not, it is, in any case, a minor issue.
From the present perspective, simple Harnack curves have two remarkable properties. First, the topological type of
$(\mathbb{R}X,\mathbb{R}C,\bigcup _{\unicode[STIX]{x1D716}}\mathbb{R}D_{\unicode[STIX]{x1D716}})$
is unique, see [Reference MikhalkinMik00]. Second, the space of simple Harnack curves admits a very simple set of coordinates, see [Reference Kenyon and OkounkovKO06] and [Reference OlarteOla17]. In particular, all the possible deformations of simple Harnack curves to singular curves are known. The topology of
$\mathbb{R}C\subset \mathbb{R}X$
can be recovered from Definition 4.1. The real part
$\mathbb{R}C$
consists of
$g_{{\mathcal{L}}}+1$
ovals. One of these ovals intersects all the toric divisors
$D_{\unicode[STIX]{x1D716}}$
in the maximal number of points (with multiplicities) in the cyclical order induced by the fan
$\unicode[STIX]{x1D6F4}$
. The remaining
$g_{{\mathcal{L}}}$
ovals are mutually non-nested. The amoeba of
$C^{\circ }$
is a closed domain of
$\mathbb{R}^{2}$
bounded by
${\mathcal{A}}(\mathbb{R}C^{\circ })$
. In particular, it has
$g_{{\mathcal{L}}}$
holes and one tentacle going off to infinity for any intersection point of
$\mathbb{R}C$
with
$X\setminus (\mathbb{C}^{\ast })^{2}$
. These properties are illustrated, for instance, in [Reference LangLan15a, Figures 1 and 2]. Next, we use these properties to construct a rigid and combinatorial model for simple Harnack curves, see Proposition 4.6 and Figure 1. The latter model will be very helpful in keeping track of vanishing cycles or monodromy along 1-parameter families of curves.
Figure 1. Construction of
$C_{\unicode[STIX]{x1D6E5}}^{\circ }$
from
$\unicode[STIX]{x1D6E5}$
.
For a simple Harnack curve
$C$
, the amoeba map
${\mathcal{A}}$
is 1-to-1 on
$\mathbb{R}C^{\circ }$
and
${\mathcal{A}}(C^{\circ })$
determines
$C$
up to sign. We get rid of this sign ambiguity as follows. Choose a vertex
$v\in \unicode[STIX]{x1D6E5}$
with adjacent edges
$\unicode[STIX]{x1D716}_{1}$
and
$\unicode[STIX]{x1D716}_{2}$
. By [Reference Mikhalkin and RullgårdMR01, Definition 2], there is a unique connected arc
$\unicode[STIX]{x1D6FC}\subset \mathbb{R}C^{\circ }$
joining
$\unicode[STIX]{x1D716}_{1}$
to
$\unicode[STIX]{x1D716}_{2}$
. We restrict ourselves to the set of smooth simple Harnack curves for which
$\unicode[STIX]{x1D6FC}$
sits in the
$(+,+)$
-quadrant of
$\mathbb{R}^{2}$
. For technical reasons, we also assume that
$C$
intersects the divisor
$X\setminus (\mathbb{C}^{\ast })^{2}$
transversally, implying that
$C^{\circ }$
is a compact Riemann surface with
$b_{{\mathcal{L}}}$
points removed. The latter is a Zariski-open condition in the linear system
$|{\mathcal{L}}|$
, see, for example, [Reference ViroVir84, § 1.1]. We denote by
${\mathcal{H}}_{\unicode[STIX]{x1D6E5}}\subset |{\mathcal{L}}|$
the set of such simple Harnack curves. In the following, we refer to the
$g_{{\mathcal{L}}}$
ovals of
$\mathbb{R}C$
contained in
$(\mathbb{C}^{\ast })^{2}$
as the
$A$
-cycles of
$C$
.
Theorem 3. Any
$A$
-cycle of a curve
$C_{0}\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
is a vanishing cycle in the linear system
$|{\mathcal{L}}|$
.
Theorem 4. The set
${\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
is connected.
These theorems are given in [Reference Kenyon and OkounkovKO06] for the case
$X=\mathbb{C}P^{2}$
. The proofs we provide here rely mainly on [Reference Kenyon and OkounkovKO06]. We only provide the extra arguments that we require. Before doing so, we recall one of the main ingredients. We identify
$H^{0}(X,{\mathcal{L}})$
with the space of Laurent polynomials with support inside
$\unicode[STIX]{x1D6E5}\cap \mathbb{Z}^{2}$
. For any
$f\in H^{0}(X,{\mathcal{L}})$
and
$C:=\overline{f^{-1}(0)}\subset X$
, the Ronkin function
$N_{f}:\mathbb{R}^{2}\rightarrow \mathbb{R}$
given by
$$\begin{eqnarray}N_{f}(x,y)=\frac{1}{(2i\unicode[STIX]{x1D70B})^{2}}\iint _{\substack{ |z|=e^{x} \\ |w|=e^{y}}}\log |f(z,w)|\frac{dz\,dw}{zw}\end{eqnarray}$$
is convex, piecewise linear with integer slope on every connected component of
$\mathbb{R}^{2}\setminus {\mathcal{A}}(C^{\circ })$
. It induces the order map
$$\begin{eqnarray}\begin{array}{@{}rcl@{}}\unicode[STIX]{x1D70B}_{0}(\mathbb{R}^{2}\setminus {\mathcal{A}}(C^{\circ }))\ & \rightarrow \ & \unicode[STIX]{x1D6E5}\cap \mathbb{Z}^{2}\\ U\ & \mapsto \ & \text{grad}\,N_{f}(U).\end{array}\end{eqnarray}$$
For a curve
$C\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
, the latter map is a bijection, mapping any compact connected component of
$\mathbb{R}^{2}\setminus {\mathcal{A}}(C^{\circ })$
to
$\unicode[STIX]{x1D6E5}_{a}\cap \mathbb{Z}^{2}$
. Note that for two polynomials defining the same fixed curve
$C$
, the associated Ronkin functions differ only by an additive constant. It follows that the map
$(\text{grad}\,N_{f})\circ {\mathcal{A}}:C^{\circ }\rightarrow \mathbb{R}^{2}$
does not depend on the choice of
$f$
. We refer to [Reference Forsberg, Passare and TsikhFPT00] and [Reference Passare and RullgårdPR04] for more details.
The proof of Theorem 3 relies on the fact that [Reference Kenyon and OkounkovKO06, Proposition 6] extends to the present case. To show this, we need an explicit description of the space of holomorphic differentials on a curve
$C\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
.
Lemma 4.3. Let
$C\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
and
$f\in H^{0}(X,{\mathcal{L}}_{\unicode[STIX]{x1D6E5}})$
, such that
$C=\overline{\{f=0\}}$
. The space of holomorphic differentials on
$C$
is isomorphic to the space of sections of
${\mathcal{L}}_{\unicode[STIX]{x1D6E5}_{a}}$
via the map
$$\begin{eqnarray}h(z,w)\mapsto {\displaystyle \frac{h(z,w)}{\unicode[STIX]{x2202}_{w}f(z,w)\,zw}}\,dz.\end{eqnarray}$$
Proof. The space of sections of
${\mathcal{L}}_{\unicode[STIX]{x1D6E5}_{a}}$
has the expected dimension
$g_{{\mathcal{L}}}$
and two such meromorphic differentials are linearly independent for different
$h$
. It remains to show that they are in fact holomorphic. We proceed in two steps.
Assume first that
$\unicode[STIX]{x1D6E5}\subset \mathbb{N}^{2}$
has a vertex at the origin with adjacent edges given by the coordinates axes. Then, the plane
$\mathbb{C}^{2}$
given by the coordinates
$(z,w)$
provides a chart of
$X_{\unicode[STIX]{x1D6E5}}$
at this vertex. In such a case,
$h(z,w)/zw$
is a polynomial and the poles of
$1/\unicode[STIX]{x2202}_{w}f(z,w)$
are compensated by the vanishing of
$dz$
on
$\mathbb{C}^{2}\cap C$
. The latter fact follows from a straightforward computation, using a local parametrization of
$C$
. It implies that any differential
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}={\displaystyle \frac{h(z,w)}{\unicode[STIX]{x2202}_{w}f(z,w)\,zw}}\,dz\end{eqnarray}$$
is holomorphic on
$\mathbb{C}^{2}\cap C$
.
We now show that one can apply the following argument at any vertex of
$\unicode[STIX]{x1D6E5}$
, to conclude the proof. It relies on the following claim: for any lattice-preserving transformation
$A:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$
sending
$\unicode[STIX]{x1D6E5}$
to some
$\unicode[STIX]{x1D6E5}^{\prime }$
and dual map
$A^{\vee }:(\mathbb{C}^{\ast })^{2}\rightarrow (\mathbb{C}^{\ast })^{2}$
, then
$$\begin{eqnarray}A_{\ast }^{\vee }\unicode[STIX]{x1D6FA}={\displaystyle \frac{h^{\prime }(s,t)}{\unicode[STIX]{x2202}_{t}f^{\prime }(s,t)\,st}}\,ds\,,\end{eqnarray}$$
where
$h^{\prime }:=A_{\ast }h\in {\mathcal{L}}_{\unicode[STIX]{x1D6E5}_{a}^{\prime }}$
,
$f^{\prime }:=A_{\ast }f\in {\mathcal{L}}_{\unicode[STIX]{x1D6E5}^{\prime }}$
, and
$(s,t):=A^{\vee }(z,w)$
. Any such map
$A$
can be decomposed into an integer translation and an
$Sl_{2}(\mathbb{Z})$
-linear map. If
$A$
is a translation by some vector
$(a,b)\in \mathbb{Z}^{2}$
, the map
$A^{\vee }$
is the identity. We have
$h^{\prime }=z^{a}w^{b}h$
,
$f^{\prime }=z^{a}w^{b}f$
. On the curve
$C$
, we have
$\unicode[STIX]{x2202}_{w}f^{\prime }(z,w)=z^{a}w^{b}\unicode[STIX]{x2202}_{w}f(z,w)$
as
$f_{|C}=0$
. It follows that
$$\begin{eqnarray}{\displaystyle \frac{h^{\prime }(z,w)}{\unicode[STIX]{x2202}_{w}f^{\prime }(z,w)\,zw}}\,dz=\unicode[STIX]{x1D6FA}.\end{eqnarray}$$
If
$A(n,m)=(dn-bm,\,-cn+am)$
, then
$A^{\vee }(z,w)=(z^{a}w^{b},z^{c}w^{d})$
and, by definition,
$h(z,w)=h^{\prime }(s,t)$
. Set the logarithmic coordinates
$(\mathbf{z},\mathbf{w})=(\log (z),\log (w))$
and
$(\mathbf{s},\mathbf{t})=(\log (s),\log (t))$
and define
$\mathbf{f}(\mathbf{z},\mathbf{w}):=f(z,w)$
and
$\mathbf{f}^{\prime }(\mathbf{z},\mathbf{w}):=f^{\prime }(z,w)$
. Observing that
$\mathbf{f}^{\prime }(\mathbf{s},\mathbf{t})=\mathbf{f}(d\mathbf{s}-b\mathbf{t},-c\mathbf{s}+a\mathbf{t})$
and that
$$\begin{eqnarray}{\displaystyle \frac{d\mathbf{z}}{\unicode[STIX]{x2202}_{\mathbf{w}}\mathbf{f}(\mathbf{z},\mathbf{w})}}=-{\displaystyle \frac{d\mathbf{w}}{\unicode[STIX]{x2202}_{\mathbf{z}}\mathbf{f}(\mathbf{z},\mathbf{w})}}\end{eqnarray}$$
on
$\{\mathbf{f}=0\}$
, we compute
$$\begin{eqnarray}{\displaystyle \frac{ds}{\unicode[STIX]{x2202}_{t}f^{\prime }(s,t)\,st}}={\displaystyle \frac{d\mathbf{s}}{\unicode[STIX]{x2202}_{\mathbf{t}}\mathbf{f}^{\prime }(\mathbf{s},\mathbf{t})}}={\displaystyle \frac{a\,d\mathbf{z}+b\,d\mathbf{w}}{-b\,\unicode[STIX]{x2202}_{\mathbf{z}}\mathbf{f}(\mathbf{z},\mathbf{w})+a\,\unicode[STIX]{x2202}_{\mathbf{w}}\mathbf{f}(\mathbf{z},\mathbf{w})}}={\displaystyle \frac{d\mathbf{z}}{\unicode[STIX]{x2202}_{\mathbf{w}}\mathbf{f}(\mathbf{z},\mathbf{w})}}={\displaystyle \frac{dz}{\unicode[STIX]{x2202}_{w}f(z,w)\,zw}}.\square\end{eqnarray}$$
Proof of Theorem 3.
To begin with, we briefly describe the setting of [Reference Kenyon and OkounkovKO06, Propositions 6 and 10]. Consider the space
$H$
of simple Harnack curves in
$|{\mathcal{L}}|$
with fixed intersection points with
$X\setminus (\mathbb{C}^{\ast })^{2}$
. Note that
$H$
is closed and has dimension
$g_{{\mathcal{L}}}$
, and the only singular curves in
$H$
have isolated real double points (see [Reference Mikhalkin and RullgårdMR01]).
Consider then the continuous and proper map
$\text{Area}:H\rightarrow \mathbb{R}_{{\geqslant}0}^{g_{{\mathcal{L}}}}$
that associates with any curve
$C$
the area of the holes of
${\mathcal{A}}(C^{\circ })$
. We show next that the map
$\text{Area}$
is a local diffeomorphism. In particular, it is a covering map. Now, for any curve
$C\in H$
, denote
$\text{Area}(C)=:(a_{1},a_{2},\ldots ,a_{g_{{\mathcal{L}}}})$
and
$T_{j}:=\{(a_{1},\ldots ,ta_{j},\ldots ,a_{g_{{\mathcal{L}}}})\mid t\in [0,1]\}$
, for
$1\leqslant j\leqslant g_{{\mathcal{L}}}$
. As the map
$\text{Area}$
is a covering map, we can lift the segment
$T_{j}$
to a path in
$|{\mathcal{L}}|$
starting at
$C$
. By construction, this path ends at a curve whose only singularity is a node and the corresponding vanishing cycle is the
$j\text{th}$
$A$
-cycle of
$C$
.
Let us now show that
$\text{Area}$
is a local diffeomorphism. With this aim, we show that [Reference Kenyon and OkounkovKO06, Proposition 6] holds true in the present case. Namely, fixing a simple Harnack curve
$C\in H$
defined by a polynomial
$f$
, we check that the intercepts of the
$g_{{\mathcal{L}}}$
affine linear functions supporting
$N_{f}$
on the compact connected component of
$\mathbb{R}^{2}\setminus {\mathcal{A}}(C^{\circ })$
provide local coordinates on
$H$
near
$C$
. We reproduce the computation of [Reference Kenyon and OkounkovKO06]: from Lemma 4.3, we know that for a defining polynomial
$f\in H^{0}(X,{\mathcal{L}})$
of
$C$
, any holomorphic differential on
$C$
has the form
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}={\displaystyle \frac{h(z,w)}{\unicode[STIX]{x2202}_{w}f(z,w)\,zw}}\,dz,\end{eqnarray}$$
where
$h\in H^{0}(X,{\mathcal{L}}_{\unicode[STIX]{x1D6E5}_{a}})$
. Taking
$f$
to be a real polynomial, the tangent space of
$H$
at
$C$
is identified with the space of real polynomials
$h$
in
$H^{0}(X,{\mathcal{L}}_{\unicode[STIX]{x1D6E5}_{a}})$
. For any points
$(x,y)$
contained in a compact component of
$\mathbb{R}^{2}\setminus {\mathcal{A}}(C^{\circ })$
, we can compute the variation of
$N_{f}$
as in [Reference Kenyon and OkounkovKO06, Proposition 6]
$$\begin{eqnarray}\displaystyle \displaystyle {\displaystyle \frac{d}{dt}}N_{f+th}(x,y)\biggr|_{t=0} & = & \displaystyle \mathfrak{Re}\frac{1}{(2i\unicode[STIX]{x1D70B})^{2}}\iint _{\substack{ |z|=e^{x} \\ |w|=e^{y}}}{\displaystyle \frac{h(z,w)}{f(z,w)}}\frac{dz\,dw}{zw}\nonumber\\ \displaystyle & = & \displaystyle \mathfrak{Re}\frac{1}{2i\unicode[STIX]{x1D70B}}\int _{|z|=e^{x}}\mathop{\sum }_{\substack{ f(z,w)=0 \\ |w|<e^{y}}}{\displaystyle \frac{h(z,w)}{\unicode[STIX]{x2202}_{w}f(z,w)}}\frac{dz}{zw}=\frac{1}{2i\unicode[STIX]{x1D70B}}\int _{\unicode[STIX]{x1D6FD}}{\displaystyle \frac{h(z,w)}{\unicode[STIX]{x2202}_{w}f(z,w)}}\frac{dz}{zw},\nonumber\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FD}$
is the
$B$
-cycle
$\{|z|=e^{x},|w|<e^{y}\}\,\cap \,C$
. The latter is anti-invariant by complex conjugation, justifying that we can omit
$\mathfrak{Re}$
in the last equality. Hence, the differential of the map giving the intercepts in terms of the coefficients of
$f$
is the period matrix of
$C$
, which is invertible.
Now the variational principle of Proposition 8 and the discussion opening [Reference Kenyon and OkounkovKO06, § 4.5] hold true in the present case as no argument depends on
$\unicode[STIX]{x1D6E5}$
. It implies that the map giving the areas of the holes of
${\mathcal{A}}(C^{\circ })$
in terms of the intercepts is a local diffeomorphism. We conclude that the map
$\text{Area}$
is a local diffeomorphism.◻
Proof of Theorem 4.
The strategy of the proof is as follows: we first show that any two curves
$C_{0}$
,
$C_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
can be continuously degenerated to rational simple Harnack curves
$C_{0}^{\ast }$
and
$C_{1}^{\ast }$
. Then we show that the space of rational simple Harnack curves is path connected, and construct a path inside the latter space joining
$C_{0}^{\ast }$
to
$C_{1}^{\ast }$
. Finally, we show that the resulting path joining
$C_{0}$
to
$C_{1}$
can be deformed in
${\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
.
First, we use the same argument as in the proof of Theorem 3 involving [Reference Kenyon and OkounkovKO06, Proposition 10]. If
$(a_{j,1},a_{j,2},\ldots ,a_{j,g_{{\mathcal{L}}}})$
is the vector of the area of the holes of
${\mathcal{A}}(C_{j}^{\circ })$
,
$j=0,1$
, we can construct two continuous paths of simple Harnack curves
$\{C_{j,s}|s\in [0,1]\}$
such that
$C_{j,1}=C_{j}$
and the area of the holes of
${\mathcal{A}}(C_{j,s}^{\circ })$
is
$s\cdot (a_{j,1},\ldots ,a_{j,g_{{\mathcal{L}}}})$
. Notice that
$C_{j,s}\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
for
$s>0$
. The curves
$C_{j,0}$
are the curves
$C_{j}^{\ast }$
announced already.
The space of rational Harnack curves admits a parametrization similar to that given in [Reference Kenyon and OkounkovKO06, § 4.1]. Label the edges of
$\unicode[STIX]{x1D6E5}$
counterclockwise as
$\unicode[STIX]{x1D716}_{1},\ldots ,\unicode[STIX]{x1D716}_{n}$
, with respective primitive integer normal vectors
$v_{1}=(a_{1},b_{1}),\ldots ,v_{n}=(a_{n},b_{n})$
pointing outwards, and finally
$l_{j}:=l_{\unicode[STIX]{x1D716}_{j}}$
. Real rational curves with Newton polygon
$\unicode[STIX]{x1D6E5}$
can always be parametrized by
$$\begin{eqnarray}\displaystyle t\in \mathbb{C}P^{1}\mapsto \biggl(\unicode[STIX]{x1D6FC}\mathop{\prod }_{j=1}^{n}\mathop{\prod }_{k=1}^{l_{j}}(t-c_{jk})^{a_{j}},\unicode[STIX]{x1D6FD}\mathop{\prod }_{j=1}^{n}\mathop{\prod }_{k=1}^{l_{j}}(t-c_{jk})^{b_{j}}\biggr)\in X & & \displaystyle\end{eqnarray}$$
with
$\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FD}\in \mathbb{R}^{\ast }$
; the
$c_{jk}$
are either real or appear in complex conjugated pairs. Such a representation is unique up to the action of
$\text{PGL}_{2}(\mathbb{R})$
on the parameter
$t$
. The same arguments as in [Reference Kenyon and OkounkovKO06, Proposition 4] apply so that the curve (2) is a rational simple Harnack curve if and only if all the
$c_{jk}$
are real and
$$\begin{eqnarray}\displaystyle c_{11}\leqslant \cdots \leqslant c_{1l_{1}}<c_{21}\leqslant \cdots \leqslant c_{2l_{2}}<\cdots <c_{n1}\leqslant \cdots \leqslant c_{nl_{n}}. & & \displaystyle\end{eqnarray}$$
For a curve in
$\unicode[STIX]{x2202}{\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
, the signs of
$\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FD}$
are determined by the sign convention made on
${\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
. The space of parameters
$\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FD}$
, and
$c_{jk}$
satisfying (3) is connected. This implies that the space of rational simple Harnack curves in
$\unicode[STIX]{x2202}{\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
is connected. Hence, one can construct a continuous path
$\{C_{t}^{\ast }\mid t\in [0,1]\}$
in this space joining
$C_{0}^{\ast }$
to
$C_{1}^{\ast }$
.
The deformations of
$C_{t}^{\ast }$
towards
${\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
with fixed points on
$X\setminus (\mathbb{C}^{\ast })^{2}$
are given by real polynomials
$h\in H^{0}(X,{\mathcal{L}}_{\unicode[STIX]{x1D6E5}_{a}})$
having prescribed signs at the nodes of
$C_{t}^{\ast }$
, once we choose a continuous path of defining real polynomials
$f_{t}$
for
$C_{t}^{\ast }$
. Indeed,
$h$
and
$f_{t}$
need to have opposite signs around each node for an oval to appear. This sign distribution does not depend on
$t$
, as the topological pair
$((\mathbb{R}^{\ast })^{2},\mathbb{R}(C_{t}^{\ast })^{\circ })$
does not depend on
$t$
either. The vanishing of the polynomials of
$\mathbb{R}H^{0}(X,{\mathcal{L}}_{\unicode[STIX]{x1D6E5}_{a}})$
at each of the nodes of
$C_{t}^{\ast }$
imposes independent conditions, cutting
$\mathbb{R}H^{0}(X,{\mathcal{L}}_{\unicode[STIX]{x1D6E5}_{a}})$
into
$2^{g_{{\mathcal{L}}}}$
orthant. Only the orthant corresponding to the sign prescription above leads to deformations into
${\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
. It induces a continuous family of orthant in
$t$
, inside of which
$\{C_{t}^{\ast }\}_{t}$
can be continuously deformed to a path in
${\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
with endpoints on
$\{C_{0,s}\}_{s}$
and
$\{C_{1,s}\}_{s}$
. The result follows.◻
Remark 4.4. In his recent work [Reference OlarteOla17], Olarte generalized the parametrization of the space of simple Harnack curves given in [Reference Kenyon and OkounkovKO06] to any Newton polygon. In particular, Olarte shows that the space
${\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
is contractible, generalizing Theorem 4.
We now show that
$\mathbf{H}_{\unicode[STIX]{x1D6E5}}:=\{((z,w),C)\in (\mathbb{C}^{\ast })^{2}\times {\mathcal{H}}_{\unicode[STIX]{x1D6E5}},\mid (z,w)\in C\}$
is a trivial fibration over
${\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
. For this purpose, we will again make use of the Ronkin function. It is shown in [Reference Passare and RullgårdPR04] that, for
$C\in |{\mathcal{L}}|$
and
$f$
a defining polynomial, the map
$(\text{grad}\,N_{f})\circ {\mathcal{A}}:C^{\circ }\rightarrow \mathbb{R}^{2}$
takes values in
$\unicode[STIX]{x1D6E5}$
. In the Harnack case, we have the following stronger statement.
Lemma 4.5. For a polynomial
$f$
defining a curve
$C\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
, the map
$(\text{grad}\,N_{f}):\text{int}({\mathcal{A}}(C^{\circ }))\rightarrow \unicode[STIX]{x1D6E5}$
is a diffeomorphism onto
$\text{int}(\unicode[STIX]{x1D6E5}\setminus \mathbb{Z}^{2})$
.
Proof. This lemma follows from [Reference KricheverKri13, Lemma 4.4]. We choose to give an alternative proof here.
First, it is shown in [Reference Passare and RullgårdPR04, Theorem 7] that the Hessian of
$N_{f}$
is symmetric positive definite on
$\text{int}({\mathcal{A}}(C^{\circ }))$
, implying both that
$\text{grad}\,N_{f}$
is a local diffeomorphism and that
$N_{f}$
is strictly convex on
$\text{int}({\mathcal{A}}(C^{\circ }))$
. Let us show that
$\text{grad}\,N_{f}$
is injective on
$\text{int}({\mathcal{A}}(C^{\circ }))$
. Suppose there are two points
$p,q\in \mathbb{R}^{2}$
such that
$\text{grad}\,N_{f}(p)=\text{grad}\,N_{f}(q)$
. By the convexity of
$N_{f}$
, it implies that
$N_{f}$
is affine linear on the segment joining
$p$
to
$q$
. By the strict convexity of
$N_{f}$
on
$\text{int}({\mathcal{A}}(C^{\circ }))$
, it follows that both
$p$
and
$q$
sit outside
$\text{int}({\mathcal{A}}(C^{\circ }))$
. This proves injectivity.
Now, it is shown in [Reference Passare and RullgårdPR04, Theorem 4] that
$\overline{\text{im}(\text{grad}\,N_{f})}=\unicode[STIX]{x1D6E5}$
. Suppose there is a point
$p\in \text{int}(\unicode[STIX]{x1D6E5}\setminus \mathbb{Z}^{2})$
not in
$\text{im}(\text{grad}\,N_{f})$
and consider a sequence
$\{p_{n}\}_{n\in \mathbb{N}}\subset \text{im}(\text{grad}\,N_{f})$
converging to
$p$
. All the limit points of
$\{(\text{grad}\,N_{f})^{-1}(p_{n})\}_{n\in \mathbb{N}}$
are either in
$\unicode[STIX]{x2202}{\mathcal{A}}(C^{\circ })$
or escape to infinity along the tentacles of
${\mathcal{A}}(C^{\circ })$
. This implies that
$p_{n}$
converges either to
$\unicode[STIX]{x1D6E5}\cap \mathbb{Z}^{2}$
or to
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
. This leads to a contradiction. The surjectivity follows.◻
We now show that this map provides a trivialization of the fibration
$\mathbf{H}_{\unicode[STIX]{x1D6E5}}\rightarrow {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
via the following construction. First, consider the real oriented blow-up of
$\mathbb{R}^{2}$
at
$\mathbb{Z}^{2}$
. This operation replaces the neighborhood of any lattice point
$p$
with
$\{x\in \mathbb{R}^{2}\mid \Vert x\Vert \geqslant \unicode[STIX]{x1D700}\}$
for an arbitrarily small
$\unicode[STIX]{x1D700}>0$
. Define
$\tilde{\unicode[STIX]{x1D6E5}}$
to be the closure of
$\text{int}(\unicode[STIX]{x1D6E5})\setminus \mathbb{Z}^{2}$
inside the latter blow-up of
$\mathbb{R}^{2}$
minus the closure of
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}\setminus \mathbb{Z}^{2}$
. Now, consider a copy
$\tilde{\unicode[STIX]{x1D6E5}}^{\prime }$
of
$\tilde{\unicode[STIX]{x1D6E5}}$
given with opposite orientation and define
$$\begin{eqnarray}C_{\unicode[STIX]{x1D6E5}}^{\circ }:=\tilde{\unicode[STIX]{x1D6E5}}^{\prime }\cup \tilde{\unicode[STIX]{x1D6E5}}/\sim ,\end{eqnarray}$$
where
${\sim}$
is the identification of the boundary of
$\tilde{\unicode[STIX]{x1D6E5}}^{\prime }$
to that of
$\tilde{\unicode[STIX]{x1D6E5}}$
. It follows that
$C_{\unicode[STIX]{x1D6E5}}^{\circ }$
is a compact oriented surface of genus
$g_{{\mathcal{L}}}$
with
$b_{{\mathcal{L}}}$
points removed. The construction of
$C_{\unicode[STIX]{x1D6E5}}^{\circ }$
is illustrated in Figure 1. Denote by
$\text{pr}:C_{\unicode[STIX]{x1D6E5}}^{\circ }\rightarrow \tilde{\unicode[STIX]{x1D6E5}}$
the 2-to-1 projection and by
$\text{conj}:C_{\unicode[STIX]{x1D6E5}}^{\circ }\rightarrow C_{\unicode[STIX]{x1D6E5}}^{\circ }$
the associated deck transformation. By Lemma 4.5, we can define an orientation-preserving and equivariant map
$R_{C}:C^{\circ }\setminus \mathbb{R}C^{\circ }\rightarrow C_{\unicode[STIX]{x1D6E5}}^{\circ }$
such that
$\text{pr}\circ R_{C}=(\text{grad}\,N_{f})\circ {\mathcal{A}}$
. The map
$R_{C}$
is unique.
Proposition 4.6. The map
$R_{C}$
extends to a diffeomorphism
$R_{C}:C^{\circ }\rightarrow C_{\unicode[STIX]{x1D6E5}}^{\circ }$
. Moreover, the map
$R:=(R_{C},\text{id}):\mathbf{H}_{\unicode[STIX]{x1D6E5}}\rightarrow C_{\unicode[STIX]{x1D6E5}}^{\circ }\times {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
is a trivialization of the fibration
$\mathbf{H}_{\unicode[STIX]{x1D6E5}}\rightarrow {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
.
Before getting into the proof, recall that the logarithmic Gauss map
$\unicode[STIX]{x1D6FE}:C^{\circ }\rightarrow \mathbb{C}P^{1}$
is the composition of any branch of the complex logarithm with the standard Gauss map. In coordinates
$(z,w)\in (\mathbb{C}^{\ast })^{2}$
,
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}(z,w)=[z\unicode[STIX]{x2202}_{z}f(z,w):w\unicode[STIX]{x2202}_{w}f(z,w)]\,,\end{eqnarray}$$
where
$f$
is a defining polynomial for
$C$
.
Proof. For the first part of the statement, we show that
$R_{C}$
extends to a diffeomorphism on one half of the curve
$C^{\circ }$
and use the equivariance to conclude.
Consider the affine chart
$[u:v]\rightarrow u/v$
of
$\mathbb{C}P^{1}$
and define the half
$C^{+}$
of
$C^{\circ }$
to be the closure of
$\{q\in C^{\circ }\mid \mathfrak{Im}(\unicode[STIX]{x1D6FE}(q))\geqslant 0\}$
. Notice that it induces an orientation on
$\mathbb{R}C^{\circ }$
and a lift
$\unicode[STIX]{x1D6FE}^{+}:\mathbb{R}C^{\circ }\rightarrow S^{1}$
of
$\unicode[STIX]{x1D6FE}$
. By the computation of the Hessian of
$N_{f}$
in [Reference Passare and RullgårdPR04, (19)], we deduce that the restriction to
$C^{+}$
of
$(\text{grad}\,N_{f})\circ {\mathcal{A}}$
is a lift of the argument map
$\text{Arg}:C^{\circ }\rightarrow (S^{1})^{2}$
to its universal covering
$\mathbb{R}^{2}$
after a rotation of
$\unicode[STIX]{x1D70B}/2$
. Now let
$p\in \mathbb{R}C^{\circ }$
. Up to permutation of the coordinates and sign change, we can assume that
$\unicode[STIX]{x1D6FE}(p)=[\unicode[STIX]{x1D6FC}:1]$
and that
$p$
sits in the positive quadrant. We prove next that the restriction of
$\text{Arg}$
to a neighborhood of
$p$
in
$C^{+}$
lifts to the real oriented blow-up of
$(S^{1})^{2}$
at
$(0,0)$
.
By [Reference MikhalkinMik00, Corollary 6], the logarithmic Gauss map
$\unicode[STIX]{x1D6FE}$
has no critical point on
$\mathbb{R}C^{\circ }$
. Then
$\unicode[STIX]{x1D6FE}$
is 1-to-1 around
$p$
and can be used as a local coordinate for
$C$
around
$p$
. The local parametrization
$\operatorname{Log}\circ \unicode[STIX]{x1D6FE}^{-1}:t:=u/v\mapsto (\mathbf{z}(t),\mathbf{w}(t))$
of
$\operatorname{Log}(C)$
around
$\operatorname{Log}(p)$
satisfies
$$\begin{eqnarray}-\mathbf{w}^{\prime }(t)/\mathbf{z}^{\prime }(t)=t,\end{eqnarray}$$
where the left-hand side is the map
$\unicode[STIX]{x1D6FE}$
seen via the affine chart of
$\mathbb{C}P^{1}$
chosen above. It follows that
$$\begin{eqnarray}\mathbf{z}(t)=a_{\mathbf{z}}+\mathop{\sum }_{j\geqslant 1}a_{j}t^{j}\quad \text{and}\quad \mathbf{w}(t)=a_{\boldsymbol{ w}}-\mathop{\sum }_{j\geqslant 1}\frac{j}{j+1}a_{j}t^{j+1},\end{eqnarray}$$
where
$a_{\mathbf{z}},a_{\mathbf{w}},a_{j}\in \mathbb{R}$
. Recall that
$\text{Arg}$
is the projection on
$i\mathbb{R}^{2}$
in logarithmic coordinates. Hence, in the coordinate
$t$
, we have
$$\begin{eqnarray}\text{Arg}(t)=(\mathfrak{Im}(\mathbf{z}(t)),\mathfrak{Im}(\mathbf{w}(t)))=\biggl(\mathop{\sum }_{j\geqslant 1}a_{j}\mathfrak{Im}(t^{j}),-\mathop{\sum }_{j\geqslant 1}\frac{j}{j+1}a_{j}\mathfrak{Im}(t^{j+1})\biggr).\end{eqnarray}$$
Now, let us denote
$t=\unicode[STIX]{x1D6FC}+i\unicode[STIX]{x1D6FD}$
. A direct computation shows that
$$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6FD}\rightarrow 0}\unicode[STIX]{x1D6FC}\frac{\mathfrak{Im}(t^{j})}{\unicode[STIX]{x1D6FD}}=\lim _{\unicode[STIX]{x1D6FD}\rightarrow 0}\frac{j}{j+1}\frac{\mathfrak{Im}(t^{j+1})}{\unicode[STIX]{x1D6FD}}=j\unicode[STIX]{x1D6FC}^{j}\,,\end{eqnarray}$$
providing the following explicit formula
$$\begin{eqnarray}\lim _{\unicode[STIX]{x1D6FD}\rightarrow 0^{+}}{\displaystyle \frac{\text{Arg}(t)}{\Vert \text{Arg}(t)\Vert }}={\displaystyle \frac{\mathbf{z}^{\prime }(\unicode[STIX]{x1D6FC})}{|\mathbf{z}^{\prime }(\unicode[STIX]{x1D6FC})|}}{\displaystyle \frac{(1,-\unicode[STIX]{x1D6FC})}{\Vert (1,-\unicode[STIX]{x1D6FC})\Vert }}\end{eqnarray}$$
for the extension of
$\text{Arg}$
to the real oriented blow-up at
$(0,0)$
. The same computation shows that
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FD}}\,\text{Arg}(\unicode[STIX]{x1D6FC})=\mathbf{z}^{\prime }(\unicode[STIX]{x1D6FC})(1,-\unicode[STIX]{x1D6FC})$
.
Applying a rotation of
$\unicode[STIX]{x1D70B}/2$
, we deduce that
$R_{C}$
extends to
$C^{+}$
and that its restriction to
$\mathbb{R}C^{\circ }$
is given by
$\unicode[STIX]{x1D6FE}^{+}$
. Together with Lemma 4.5, It implies that
$R_{C}$
is differentiable and then induces a diffeomorphism from
$C^{+}$
to
$\tilde{\unicode[STIX]{x1D6E5}}$
. From the equality
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FD}}\,\text{Arg}(\unicode[STIX]{x1D6FC})=\mathbf{z}^{\prime }(\unicode[STIX]{x1D6FC})(1,-\unicode[STIX]{x1D6FC})$
, we deduce, moreover, that the partial derivative
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D6FD}}R_{C}$
at any point of
$\mathbb{R}C^{\circ }$
is normal to
$\unicode[STIX]{x2202}\tilde{\unicode[STIX]{x1D6E5}}$
. Hence, it extends to an equivariant diffeomorphism on the whole
$C^{\circ }$
.
From the computation led above and Lemma 4.5, we deduce that the map
$R:=(R_{C},\text{id}):\mathbf{H}_{\unicode[STIX]{x1D6E5}}\rightarrow C_{\unicode[STIX]{x1D6E5}}^{\circ }\times {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
is a differentiable map, and therefore a trivialization of the fibration
$\mathbf{H}_{\unicode[STIX]{x1D6E5}}\rightarrow {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
. Indeed,
$R_{C}$
is given by the lift of the argument map to its universal covering on
$C^{\circ }\setminus \mathbb{R}C^{\circ }$
and extended by the logarithmic Gauss map on
$\mathbb{R}C^{\circ }$
. Both maps depend analytically on the coefficients of the defining polynomial of
$C\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
.◻
We define a primitive integer segment to be a segment in
$\unicode[STIX]{x1D6E5}$
that joins two integer points and is of integer length 1. For a primitive integer segment
$\unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6E5}$
, denote by
$\tilde{\unicode[STIX]{x1D70E}}$
its lift in
$\tilde{\unicode[STIX]{x1D6E5}}$
. It follows from Proposition 4.6 that for any primitive integer segment
$\unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6E5}$
,
$(\text{pr}\circ R_{C})^{-1}(\tilde{\unicode[STIX]{x1D70E}})\subset C$
is a loop invariant by complex conjugation. Similarly, denote by
$\tilde{v}\subset \tilde{\unicode[STIX]{x1D6E5}}$
the boundary circle projecting down to
$v\in \unicode[STIX]{x1D6E5}_{a}\cap \mathbb{Z}^{2}$
. Then
$(\text{pr}\circ R_{C})^{-1}(\tilde{v})\subset \mathbb{R}C$
is one of the A-cycles of
$C$
.
Corollary 4.7. Let
$C_{0},C_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
and
$\unicode[STIX]{x1D711}:C_{0}\rightarrow C_{1}$
be the diffeomorphism induced by the trivialization
$R$
. Also, let
$\unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6E5}$
be a primitive integer segment and
$v\in \unicode[STIX]{x1D6E5}_{a}\cap \mathbb{Z}^{2}$
. Then, the pullback by
$\unicode[STIX]{x1D711}$
of the Dehn twist along the loop
$(\text{pr}\circ R_{C_{1}})^{-1}(\tilde{\unicode[STIX]{x1D70E}})$
(respectively
$(\text{pr}\circ R_{C_{1}})^{-1}(\tilde{v})$
) in
$C_{1}$
is the Dehn twist along the loop
$(\text{pr}\circ R_{C_{0}})^{-1}(\tilde{\unicode[STIX]{x1D70E}})$
(respectively
$(\text{pr}\circ R_{C_{0}})^{-1}(\tilde{v})$
) in
$C_{0}$
.
Definition 4.8. For any primitive integer segment
$\unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6E5}$
and any curve
$C\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
, define the loop
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}:=(\text{pr}\circ R_{C})^{-1}(\tilde{\unicode[STIX]{x1D70E}})\subset C$
and
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{MCG}(C)$
to be the Dehn twist along
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}$
.
For any
$v\in \unicode[STIX]{x1D6E5}_{a}\cap \mathbb{Z}^{2}$
, define the A-cycle
$\unicode[STIX]{x1D6FF}_{v}:=(\text{pr}\circ R_{C})^{-1}(\tilde{v})\subset \mathbb{R}C$
and
$\unicode[STIX]{x1D70F}_{v}\in \text{MCG}(C)$
to be the Dehn twist along
$\unicode[STIX]{x1D6FF}_{v}$
.
Remark 4.9. The loops
$\unicode[STIX]{x1D6FF}_{v}$
and
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}$
intersect if and only if
$v$
is an end point of
$\unicode[STIX]{x1D70E}$
. In this case,
$\unicode[STIX]{x1D6FF}_{v}$
intersects
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}$
transversally at one point.
5 Tropical curves
In this section, we recall some definitions for tropical and phase-tropical curves, following [Reference Itenberg, Mikhalkin and ShustinIMS09] and [Reference LangLan15b]. For the sake of pragmatism and simplicity, some definitions are given in a restrictive context. The expert reader should not be disturbed. The main goal of this section is the statement and proof of Theorem 5, as a corollary of Mikhalkin’s approximation theorem, see [Reference LangLan15b, Theorem 5]. Namely, we construct explicit elements in the image of the monodromy map
$\unicode[STIX]{x1D707}$
by approximating well-chosen loops in the relevant moduli space of phase-tropical curves.
A tropical polynomial in two variables
$x$
and
$y$
is a function
where
$A\subset \mathbb{N}^{2}$
is a finite set and
$c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}\in \mathbb{R}$
.
Definition 5.1. The tropical zero set of a tropical polynomial
$f(x,y)$
is defined by
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{f}:=\{(x,y)\in \mathbb{R}^{2}\mid f\text{ is not smooth at }(x,y)\}\end{eqnarray}$$
A subset
$\unicode[STIX]{x1D6E4}\subset \mathbb{R}^{2}$
is a tropical curve if
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{f}$
for some tropical polynomial
$f$
. We denote by
$E(\unicode[STIX]{x1D6E4})$
the set of its bounded edges and by
$V(\unicode[STIX]{x1D6E4})$
the set of its vertices.
It follows from the definition that a tropical curve
$\unicode[STIX]{x1D6E4}\subset \mathbb{R}^{2}$
is a piecewise-linear graph with rational slopes. The Newton polygon of a tropical polynomial
$f$
is defined as the convex hull of its support
$A$
. The Newton polygon of a tropical curve is only defined up to translation as the multiplication of tropical polynomial by a tropical monomial does not affect its zero set. Tropical curves are intimately related to subdivision on their Newton polygon. For a finite set
$A\subset \unicode[STIX]{x1D6E5}\cap \mathbb{N}^{2}$
, denote by
$\unicode[STIX]{x1D6E5}$
the lattice polygon
$\unicode[STIX]{x1D6E5}:=\text{conv}(A)$
. For any function
$h:A\rightarrow \mathbb{R}$
, define
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{h}:=\text{conv}\{((\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}),t)\in \mathbb{R}^{3}\mid (\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\in A,\hspace{2.22198pt}t\geqslant h(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\},\end{eqnarray}$$
i.e.
$\unicode[STIX]{x1D6E5}_{h}$
is the convex hull of the epigraph of
$h$
. The bounded faces of
$\unicode[STIX]{x1D6E5}_{h}$
define a piecewise-linear convex function
$\unicode[STIX]{x1D708}_{h}:\unicode[STIX]{x1D6E5}\rightarrow \mathbb{R}$
. Finally, define
$S_{h}$
to be the subdivision
$\unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D6E5}_{1}\cup \unicode[STIX]{x1D6E5}_{2}\cup \cdots \cup \unicode[STIX]{x1D6E5}_{N}$
given by the domains of linearity
$\unicode[STIX]{x1D6E5}_{i}$
of
$\unicode[STIX]{x1D708}_{h}$
. The subdivision
$S_{h}$
is a union of 0-, 1- and 2-cells. For practical matters, we will often consider
$S_{h}$
as a graph. The set of its vertices is
$V(S_{h})=\bigcup _{i}(\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}_{i}\cap \mathbb{N}^{2})$
and the set of its edges
$E(S_{h})$
is the union over
$i$
of all the primitive integer segments contained in
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}_{i}$
.
Definition 5.2. A convex subdivision
$S$
of
$\unicode[STIX]{x1D6E5}$
is a graph
$S=S_{h}$
for some function
$h:A\rightarrow \mathbb{R}$
. The subdivision
$S$
is unimodular if any connected component of
$\unicode[STIX]{x1D6E5}\setminus S$
has Euclidean area 1/2.
Notice that by Pick’s formula, a subdivision is unimodular if it decomposes
$\unicode[STIX]{x1D6E5}$
into triangles, whose vertices generate the lattice
$\mathbb{Z}^{2}$
. Now any tropical polynomial
$f$
as in (4) can be considered as the function
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\mapsto c_{\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}}$
on
$A$
, and hence induces a convex subdivision
$S_{f}$
on its Newton polygon
$\unicode[STIX]{x1D6E5}$
. We have the following duality, see [Reference Itenberg, Mikhalkin and ShustinIMS09].
Proposition 5.3. Let
$f(x,y)$
be a tropical polynomial. The subdivision
$(\mathbb{R}^{2},\unicode[STIX]{x1D6E4}_{f})$
is dual to the subdivision
$(\unicode[STIX]{x1D6E5},S_{f})$
in the following sense.
(a)
$i$
-cells of
$(\mathbb{R}^{2},\unicode[STIX]{x1D6E4}_{f})$
are in 1-to-1 correspondence with
$(2-i)$
-cells of
$(\unicode[STIX]{x1D6E5},S_{f})$
, and the linear spans of corresponding cells are orthogonal to each other.(b) The latter correspondence reverses the incidence relations.
For any edge
$e\in E(\unicode[STIX]{x1D6E4}_{f})$
, denote its dual edge by
$e^{\vee }\in E(S_{f})$
. Define the order of any connected component of
$\mathbb{R}^{2}\setminus \unicode[STIX]{x1D6E4}_{f}$
to be its corresponding lattice point in
$\unicode[STIX]{x1D6E5}$
.
Remark 5.4. A unimodular convex subdivision
$S$
of
$\unicode[STIX]{x1D6E5}$
induces a pair of pants decomposition of any curve
$C\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
by considering the union of the loops
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}$
for all
$\unicode[STIX]{x1D70E}\in E(S)$
, see Definition 4.8.
Definition 5.5. A tropical curve
$\unicode[STIX]{x1D6E4}_{f}\subset \mathbb{R}^{2}$
is smooth if its dual subdivision
$S_{f}$
is unimodular.
In particular, a smooth tropical curve has only 3-valent vertices. Now, we introduce some material in order to define smooth phase-tropical curves. Consider the family of diffeomorphism on
$(\mathbb{C}^{\ast })^{2}$
given by
$$\begin{eqnarray}H_{t}(z,w)=\biggl(|z|^{1/\log (t)}\frac{z}{|z|},|w|^{1/\log (t)}\frac{w}{|w|}\biggr).\end{eqnarray}$$
Define the phase-tropical line
$L\subset (\mathbb{C}^{\ast })^{2}$
as the Hausdorff limit of
$H_{t}(\{1+z+w=0\})\subset (\mathbb{C}^{\ast })^{2}$
when
$t$
tends to
$+\infty$
. If we denote by 
the tropical line centered at the origin,
$L$
is a topological pair of pants such that
${\mathcal{A}}(L)=\unicode[STIX]{x1D6EC}$
. The tropical line
$\unicode[STIX]{x1D6EC}$
consists of
$3$
infinite rays merging at the origin. The preimages by
${\mathcal{A}}$
in
$L$
of the
$3$
open rays of
$\unicode[STIX]{x1D6EC}$
are the cylinders
$$\begin{eqnarray}\{z=1,|w|<1\},\quad \{w=1,|z|<1\}\quad \text{and}\quad \{z=w,|z|>1\}.\end{eqnarray}$$
These cylinders are glued to the coamoeba
$\text{Arg}(\{1+z+w=0\})$
over the vertex of
$\unicode[STIX]{x1D6EC}$
.
A toric transformation
$A:(\mathbb{C}^{\ast })^{2}\rightarrow (\mathbb{C}^{\ast })^{2}$
is a diffeomorphism of the form
$$\begin{eqnarray}(z,w)\mapsto (b_{1}z^{a_{11}}w^{a_{12}},b_{2}z^{a_{21}}w^{a_{22}}),\end{eqnarray}$$
where
$(b_{1},b_{2})\in (\mathbb{C}^{\ast })^{2}$
and
$(a_{ij})_{i,j}\in Sl_{2}(\mathbb{Z})$
. The composition of
$A$
with the projection
${\mathcal{A}}$
(respectively
$\text{Arg}$
) is an affine linear transformation on
$\mathbb{R}^{2}$
(respectively on
$(S^{1})^{2}$
) that we still denote by
$A$
. Notice that the group of toric transformations fixing
$L$
is generated by
$(z,w)\mapsto (w,z)$
and
$(z,w)\mapsto (w,(zw)^{-1})$
. It descends to the group of symmetries of
$\unicode[STIX]{x1D6EC}$
via
${\mathcal{A}}$
.
Definition 5.6. A smooth phase-tropical curve
$V\subset (\mathbb{C}^{\ast })^{2}$
is a topological surface such that:
(i) its amoeba
${\mathcal{A}}(V)$
is a smooth tropical curve
$\unicode[STIX]{x1D6E4}\subset \mathbb{R}^{2}$
;(ii) for any open set
$U\subset \mathbb{R}^{2}$
such that
$U\cap \unicode[STIX]{x1D6E4}$
is connected and contains exactly one vertex
$v$
of
$\unicode[STIX]{x1D6E4}$
, there exists a toric transformation
$A$
such that
$V\cap {\mathcal{A}}^{-1}(U)=A(L)\cap {\mathcal{A}}^{-1}(U)$
.
We will say that the map
$A$
is a chart of
$V$
at the vertex
$v$
.
Remark 5.7. It follows from the definition that the topology of
$V$
is determined by its underlying tropical curve
${\mathcal{A}}(V)$
.
$V$
is an oriented genus
$g$
surface with
$b$
punctures, where
$g$
and
$b$
are, respectively, the genus and the number of infinite rays of
${\mathcal{A}}(V)$
.
Smooth phase-tropical curves enjoy a description very similar to the one of Riemann surfaces in terms of Fenchel–Nielsen coordinates, see [Reference LangLan15b]. Let
$V$
be a smooth phase-tropical curve and
$\unicode[STIX]{x1D6E4}:={\mathcal{A}}(V)$
. Up to toric translation, the phase-tropical curve
$V$
can be encoded by the pair
$(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E9})$
where
$\unicode[STIX]{x1D6E9}:E(\unicode[STIX]{x1D6E4})\rightarrow S^{1}$
is defined in the following way. For any
$e\in E(\unicode[STIX]{x1D6E4})$
bounded by
$v_{1},v_{2}\in V(\unicode[STIX]{x1D6E4})$
, consider any two charts
$A_{1},A_{2}:(\mathbb{C}^{\ast })^{2}\rightarrow (\mathbb{C}^{\ast })^{2}$
at
$v_{1}$
and
$v_{2}$
overlapping on
$e$
such that
$A_{1}$
and
$A_{2}$
map
$e$
on the same edge of
$\unicode[STIX]{x1D6EC}$
and exactly one of the
$A_{i}:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$
is orientation-preserving. Without restriction, we can assume that the cylinder of
$V$
over the edge
$e$
is mapped to the cylinder
$\{w=1,\unicode[STIX]{x1D700}<|z|<1\}$
by both
$A_{1}$
and
$A_{2}$
. The induced automorphism
$A_{2}\circ A_{1}^{-1}$
on the latter cylinder is given in coordinates by
$z\mapsto \unicode[STIX]{x1D717}/z$
for a unique
$\unicode[STIX]{x1D717}\in \mathbb{C}^{\ast }$
. We can check that the quantity
$\text{arg}(\unicode[STIX]{x1D717})\in S^{1}$
is an intrinsic datum of
$V$
, see [Reference LangLan15b, Proposition 2.36].
Definition 5.8. For a phase-tropical curve
$V\subset (\mathbb{C}^{\ast })^{2}$
and
$\unicode[STIX]{x1D6E4}:={\mathcal{A}}(V)$
, the associated twist function
$\unicode[STIX]{x1D6E9}:E(\unicode[STIX]{x1D6E4})\rightarrow S^{1}$
is defined by
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}(e):=\text{arg}(\unicode[STIX]{x1D717})\end{eqnarray}$$
for any
$e\in E(\unicode[STIX]{x1D6E4})$
and
$\unicode[STIX]{x1D717}\in \mathbb{C}^{\ast }$
, as constructed above.
Remark 5.9. If any smooth phase-tropical curve
$V\subset (\mathbb{C}^{\ast })^{2}$
can be described by a pair
$(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E9})$
, there are conditions on the twist function
$\unicode[STIX]{x1D6E9}$
for the pair
$(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E9})$
to correspond to a phase-tropical curve in
$(\mathbb{C}^{\ast })^{2}$
. These conditions are given in [Reference LangLan15b, (5)]. Notice also that any tropical curve
$\unicode[STIX]{x1D6E4}$
induces a length function
$l$
on
$E(\unicode[STIX]{x1D6E4})$
. The Fenchel–Nielsen coordinates of a phase-tropical curve
$(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E9})$
consist of the pair
$(l,\unicode[STIX]{x1D6E9})$
, see [Reference LangLan15b].
Phase-tropical Harnack curves are the phase-tropical counterpart of the simple Harnack curves that we reviewed in the previous section.
Definition 5.10. A phase-tropical Harnack curve is a smooth phase-tropical curve
$V\subset (\mathbb{C}^{\ast })^{2}$
invariant by complex conjugation and with associated twist function
$\unicode[STIX]{x1D6E9}\equiv 1$
.
It follows from the definition that, for a given smooth tropical curve
$\unicode[STIX]{x1D6E4}$
, there are exactly four phase-tropical Harnack curves
$V\subset (\mathbb{C}^{\ast })^{2}$
such that
${\mathcal{A}}(v)=\unicode[STIX]{x1D6E4}$
and that they are all obtained from each other by sign changes of the coordinates. The map
${\mathcal{A}}$
is
$2$
-to-
$1$
from the real part
$\mathbb{R}V$
onto
$\unicode[STIX]{x1D6E4}$
. In particular, the topological type of
$(\mathbb{R}X,\mathbb{R}V)$
can be recovered from
$\unicode[STIX]{x1D6E4}$
. If
$\unicode[STIX]{x1D6E5}$
is the Newton polygon of
$\unicode[STIX]{x1D6E4}$
, it follows from [Reference LangLan15a, Theorem 2] that the approximation of
$\unicode[STIX]{x1D6E4}$
in
${\mathcal{L}}_{\unicode[STIX]{x1D6E5}}$
is a simple Harnack curve whose amoeba can be made arbitrarily close to
$\unicode[STIX]{x1D6E4}$
.
We now introduce some necessary terminology for the statement of Theorem 5.
Definition 5.11. A weighted graph of
$\unicode[STIX]{x1D6E5}$
is a pair
$(G,m)$
, where
$G$
is a graph whose edges are primitive integer segments contained in
$\unicode[STIX]{x1D6E5}$
and
$m:E(G)\rightarrow \mathbb{Z}$
. A weighted graph
$(G,m)$
is balanced if, for any vertex
$v\in V(G)\cap \text{int}(\unicode[STIX]{x1D6E5})$
,
$$\begin{eqnarray}\mathop{\sum }_{\vec{e}\in E(G,v)}m(e)\cdot \vec{e}=0\,,\end{eqnarray}$$
where
$E(G,v)\subset E(G)$
is the set of edges adjacent to
$v$
oriented outwards. A weighted graph
$(G,m)$
is admissible if it is balanced and if it is a subgraph of a unimodular convex subdivision of
$\unicode[STIX]{x1D6E5}$
.
Definition 5.12. For a weighted graph
${\mathcal{G}}:=(G,m)$
of
$\unicode[STIX]{x1D6E5}$
, and any curve
$C_{0}\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
, define
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\mathcal{G}}}:=\mathop{\prod }_{\unicode[STIX]{x1D70E}\in E(G)}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}^{m(\unicode[STIX]{x1D70E})}\in \text{MCG}(C_{0})\,,\end{eqnarray}$$
where
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}$
is given in Definition 4.8.
Theorem 5. For any curve
$C_{0}\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
and any admissible graph
${\mathcal{G}}=(G,m)$
of
$\unicode[STIX]{x1D6E5}$
, we have
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\in \text{im}(\unicode[STIX]{x1D707}).\end{eqnarray}$$
Proof. Let
$S$
be a unimodular convex subdivision containing
$G$
and
$\unicode[STIX]{x1D6E4}\subset \mathbb{R}^{2}$
be a tropical curve of dual subdivision
$S$
. Among the four phase-tropical Harnack curves supported on
$\unicode[STIX]{x1D6E4}$
, consider the one,
$V$
, that is coherent with the sign convention made for
${\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
.
The admissible graph
${\mathcal{G}}=(G,m)$
induces the following family
$\{V_{t}:=(\unicode[STIX]{x1D6E4},\unicode[STIX]{x1D6E9}_{t})\mid 0\leqslant t\leqslant 2\unicode[STIX]{x1D70B}\}$
of phase-tropical curves: for any
$\unicode[STIX]{x1D716}\in E(\unicode[STIX]{x1D6E4})$
such that
$\unicode[STIX]{x1D716}^{\vee }\in E(G)$
, define
$\unicode[STIX]{x1D6E9}_{t}(\unicode[STIX]{x1D716})=e^{it\cdot m(\unicode[STIX]{x1D716}^{\vee })}$
and
$\unicode[STIX]{x1D6E9}_{t}(\unicode[STIX]{x1D716})=1$
otherwise. One easily checks that
$\unicode[STIX]{x1D6E9}_{t}$
satisfies
$(5)$
in [Reference LangLan15b] for any parameter
$t$
, so that it actually defines a loop of smooth phase-tropical curves in
$(\mathbb{C}^{\ast })^{2}$
based at
$V_{0}=V_{2\unicode[STIX]{x1D70B}}=V$
.
We now want to use Mikhalkin’s approximation theorem in families (see [Reference LangLan15b, Theorem 5]). For this, we briefly reproduce a construction that can be found in [Reference LangLan15b, § 4.2]. Consider the Teichmüller space
${\mathcal{T}}(C)$
pointed at a fixed curve
$C\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
. The pair of pants decomposition of
$C$
given by
$\{\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}\mid \unicode[STIX]{x1D70E}\in E(S)\}$
induces Fenchel–Nielsen coordinates on
${\mathcal{T}}(C)$
, see, for example, [Reference BuserBus10, ch. 6, §3]. The partial quotient
${\mathcal{T}}(C)\rightarrow (\mathbb{C}^{\ast })^{E(\unicode[STIX]{x1D6E4})}\rightarrow {\mathcal{M}}_{g_{{\mathcal{L}}},b_{{\mathcal{L}}}}$
by the group generated by the set of Dehn twists
$\{\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\mid \unicode[STIX]{x1D70E}\in E(S)\}$
inherits Fenchel–Nielsen coordinates
$\mathbb{R}_{{>}0}^{E(\unicode[STIX]{x1D6E4})}\times (S^{1})^{E(\unicode[STIX]{x1D6E4})}\simeq (\mathbb{C}^{\ast })^{E(\unicode[STIX]{x1D6E4})}$
. In particular, the latter quotient parametrizes actual genus
$g_{{\mathcal{L}}}$
Riemann surfaces with
$b_{{\mathcal{L}}}$
punctures, see, for example, [Reference BuserBus10, ch. 3, §6]. Using these coordinates, we consider the partial compactification
$F$
of
$(\mathbb{C}^{\ast })^{E(\unicode[STIX]{x1D6E4})}$
obtained by considering the real oriented blow-up of its
$\mathbb{R}_{{>}0}$
-factor at the origin. Namely, we replace
$\mathbb{R}_{{>}0}^{E(\unicode[STIX]{x1D6E4})}$
with
$\{l\in \mathbb{R}_{{>}0}^{E(\unicode[STIX]{x1D6E4})}\mid \Vert l\Vert \geqslant \unicode[STIX]{x1D700}\}$
. We then identify the boundary points of the blow-up with phase-tropical curves of coordinates
$(l,\unicode[STIX]{x1D6E9})$
up to positive rescaling of
$l$
, see Remark 5.9. Hence, the 1-parameter family
$\{V_{t}\}_{0\leqslant t\leqslant 2\unicode[STIX]{x1D70B}}$
induces a loop in
$\unicode[STIX]{x2202}F$
.
By [Reference LangLan15b, Proposition 4.9], there exists a smooth analytic subset
$U\subset \mathbb{R}_{{>}0}^{E(\unicode[STIX]{x1D6E4})}\times \{\unicode[STIX]{x1D6E9}_{t}\}_{0\leqslant t\leqslant 2\unicode[STIX]{x1D70B}}$
of real codimension
$g_{{\mathcal{L}}}$
, such that
$\overline{U}\subset F$
intersects transversally
$\unicode[STIX]{x2202}F$
along a smooth locus containing
$\{V_{t}\}_{0\leqslant t\leqslant 2\unicode[STIX]{x1D70B}}$
. This implies that one can find a loop
$\{(l_{t},\unicode[STIX]{x1D6E9}_{t})\}_{0\leqslant t\leqslant 2\unicode[STIX]{x1D70B}}\subset U$
isotopic to
$\{V_{t}\}_{0\leqslant t\leqslant 2\unicode[STIX]{x1D70B}}$
in
$\overline{U}$
. By [Reference LangLan15b, Proposition 4.9] again, the set
$U$
comes with a smooth map
$s:U\rightarrow |{\mathcal{L}}|$
, such that the Riemann surface parametrized by
$u\in U$
is isomorphic to
$s(u)\in |{\mathcal{L}}|$
. Define
$C_{t}^{\mathbb{T}}:=s(l_{t},\unicode[STIX]{x1D6E9}_{t})$
. According to [Reference LangLan15a, Theorem 2], the loop
$\{(l_{t},\unicode[STIX]{x1D6E9}_{t})\}_{0\leqslant t\leqslant 2\unicode[STIX]{x1D70B}}$
can be chosen so that
$C_{0}^{\mathbb{T}}=C_{2\unicode[STIX]{x1D70B}}^{\mathbb{T}}\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
. Moreover, it follows from the construction of the map
$s$
that the pair of pants decomposition of
$C_{0}^{\mathbb{T}}$
induced by
$s$
is the decomposition given by
$\{\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}\mid \unicode[STIX]{x1D70E}\in E(S)\}$
. Together with the definition of
$\unicode[STIX]{x1D6E9}_{t}$
, it implies that the monodromy induced by the closed path
$\{C_{t}^{\mathbb{T}}\}_{0\leqslant t\leqslant 2\unicode[STIX]{x1D70B}}$
is
$$\begin{eqnarray}\mathop{\prod }_{\unicode[STIX]{x1D70E}\in E(G)}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}^{m(\unicode[STIX]{x1D70E})}=\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\in \text{MCG}(C_{0}^{\mathbb{T}}).\end{eqnarray}$$
Now, by the connectedness of
${\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
, see Theorem 4, we can conjugate the closed path
$\{C_{t}^{\mathbb{T}}\}_{0\leqslant t\leqslant 2\unicode[STIX]{x1D70B}}$
by a continuous path in
${\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
joining
$C_{0}$
to
$C_{0}^{\mathbb{T}}$
in order to get a loop
$\ell$
based at
$C_{0}$
. By Corollary 4.7, we deduce that
$\unicode[STIX]{x1D707}(\ell )=\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\in \text{MCG}(C_{0})$
.◻
6 Combinatorial tools
6.1 Unimodular convex subdivisions
To apply Theorem 5, we need to be able to construct unimodular convex subdivisions of a polygon. We give an extension lemma and a refinement lemma, which will be our main construction tools.
Lemma 6.1. Let
$\unicode[STIX]{x1D6E5}^{\prime }\subset \unicode[STIX]{x1D6E5}$
be two convex lattice polygons and take a convex subdivision
$S^{\prime }$
of
$\unicode[STIX]{x1D6E5}^{\prime }$
. There exists a convex subdivision of
$\unicode[STIX]{x1D6E5}$
that extends
$S^{\prime }$
.
Proof. By assumption, we can associate a piecewise-linear convex function
$\unicode[STIX]{x1D708}:\unicode[STIX]{x1D6E5}^{\prime }\rightarrow \mathbb{R}$
with the subdivision
$S^{\prime }$
. We may also assume that
$\unicode[STIX]{x1D708}$
only takes positive values. Denote by
$K$
the set of vertices of
$\unicode[STIX]{x1D6E5}$
that are not in
$\unicode[STIX]{x1D6E5}^{\prime }$
. For each
$h\in \mathbb{R}$
, consider the convex hull of the union of the epigraph of
$\unicode[STIX]{x1D708}$
and of the rays
$K\times [h,+\infty ]$
; this convex set is the epigraph of a piecewise-linear function
$\unicode[STIX]{x1D708}_{h}:\unicode[STIX]{x1D6E5}\rightarrow \mathbb{R}$
. By definition, the function
$\unicode[STIX]{x1D708}_{h}$
is convex so it defines a convex subdivision of
$\unicode[STIX]{x1D6E5}$
. To prove the statement, we show that we can choose
$h$
such that the subdivision
$S_{\unicode[STIX]{x1D708}_{h}}$
of
$\unicode[STIX]{x1D6E5}$
associated with
$\unicode[STIX]{x1D708}_{h}$
coincides with the subdivision
$S^{\prime }$
on
$\unicode[STIX]{x1D6E5}^{\prime }$
.
First, we note that there exists a value
$h_{0}\in \mathbb{R}$
such that for any
$h\geqslant h_{0}$
, the subdivisions
$S_{\unicode[STIX]{x1D708}_{h}}$
and
$S^{\prime }$
coincide on the interior of
$\unicode[STIX]{x1D6E5}^{\prime }$
. Indeed, we can take
$h_{0}$
such that for any
$h\geqslant h_{0}$
, the set
$K\times \{h\}\subset \unicode[STIX]{x1D6E5}\times \mathbb{R}$
is above all the supporting hyperplanes of the epigraph of
$\unicode[STIX]{x1D708}$
; in other words, the epigraphs of the functions
$\unicode[STIX]{x1D708}$
and
$\unicode[STIX]{x1D708}_{h}$
coincide over
$\unicode[STIX]{x1D6E5}^{\prime }$
.
However, we still need to ensure that we can choose
$h\geqslant h_{0}$
such that the boundary of
$\unicode[STIX]{x1D6E5}^{\prime }$
is supported on
$S_{\unicode[STIX]{x1D708}_{h}}$
. To this end, we check that if we take
$h$
to be large enough, the piecewise affine linear function
$\unicode[STIX]{x1D708}_{h}$
has to break on each edge of the boundary of
$\unicode[STIX]{x1D6E5}^{\prime }$
in
$\unicode[STIX]{x1D6E5}$
.
More precisely, for each pair of lattice points
$v$
,
$w$
that are consecutive on the boundary of
$\unicode[STIX]{x1D6E5}^{\prime }$
and not both in the boundary of
$\unicode[STIX]{x1D6E5}$
, consider the points
$P_{\pm \unicode[STIX]{x1D700}}=(v+w)/2\pm \unicode[STIX]{x1D700}n$
, where
$n$
is the exterior normal unit vector to
$\unicode[STIX]{x1D6E5}^{\prime }$
on the segment
$[v,w]$
. Since
$S_{\unicode[STIX]{x1D708}_{h}}$
and
$S^{\prime }$
coincide on the interior of
$\unicode[STIX]{x1D6E5}^{\prime }$
, the only possible segment of
$S_{\unicode[STIX]{x1D708}_{h}}$
passing through the point
$(v+w)/2$
is
$[v,w]$
. Thus, we can take an
$\unicode[STIX]{x1D700}_{0}>0$
, such that, for any
$0<\unicode[STIX]{x1D700}\leqslant \unicode[STIX]{x1D700}_{0}$
and for any
$h\geqslant h_{0}$
, the segment
$[P_{-\unicode[STIX]{x1D700}},P_{\unicode[STIX]{x1D700}}]$
intersects the subdivision
$S_{\unicode[STIX]{x1D708}_{h}}$
at most once. This intersection is non-empty exactly when the segment
$[v,w]$
is in
$S_{\unicode[STIX]{x1D708}_{h}}$
. Since
$\unicode[STIX]{x1D6E5}^{\prime }$
has only a finite number of lattice points, we can repeat the same construction for all such pairs of points
$v$
and
$w$
to obtain a finite set of points
$P_{\pm \unicode[STIX]{x1D700}}^{i}$
,
$i\in I$
, such that, for all
$i\in I$
and
$h\geqslant h_{0}$
, the segment
$[P_{-\unicode[STIX]{x1D700}}^{i},P_{\unicode[STIX]{x1D700}}^{i}]$
intersects the subdivision
$S_{\unicode[STIX]{x1D708}_{h}}$
at most once.
The restriction of
$\unicode[STIX]{x1D708}$
over the segment
$[P_{-\unicode[STIX]{x1D700}}^{i},P_{\unicode[STIX]{x1D700}}^{i}]\cap \unicode[STIX]{x1D6E5}^{\prime }$
coincides with
$\unicode[STIX]{x1D708}$
so it is affine linear of slope
$\unicode[STIX]{x1D6FC}_{i}$
, independent of
$h$
. We need to find
$h\geqslant h_{0}$
such that
$\unicode[STIX]{x1D708}$
is not affine linear along the whole segment
$[P_{-\unicode[STIX]{x1D700}}^{i},P_{\unicode[STIX]{x1D700}}^{i}]$
.
For any
$i\in I$
and any
$h\geqslant h_{0}$
, the point
$(P_{\unicode[STIX]{x1D700}}^{i},\unicode[STIX]{x1D708}_{h}(P_{\unicode[STIX]{x1D700}}^{i}))\in \unicode[STIX]{x1D6E5}\times \mathbb{R}$
is a convex combination
$\sum _{A\in \unicode[STIX]{x1D6E5}^{\prime }\cap \mathbb{Z}^{2}}\unicode[STIX]{x1D706}_{A}(A,\unicode[STIX]{x1D708}(A))+\sum _{B\in K}\unicode[STIX]{x1D707}_{B}(B,h)$
. The coefficients
$\unicode[STIX]{x1D706}_{A}\in [0,1]$
and
$\unicode[STIX]{x1D707}_{B}\in [0,1]$
are not uniquely defined. However, since the points
$P_{\unicode[STIX]{x1D700}}^{i}$
are outside
$\unicode[STIX]{x1D6E5}^{\prime }$
, there exists a
$\unicode[STIX]{x1D707}_{0}>0$
such that, for any such convex combination giving some point
$P_{\unicode[STIX]{x1D700}}^{i}$
, there exists
$B\in K$
with
$\unicode[STIX]{x1D707}_{B}\geqslant \unicode[STIX]{x1D707}_{0}$
. Take
$$\begin{eqnarray}h=\max \biggl(h_{0},\frac{\max (\unicode[STIX]{x1D708})+2\unicode[STIX]{x1D700}\max _{i\in I}(\unicode[STIX]{x1D6FC}_{i})}{\unicode[STIX]{x1D707}_{0}}+1\biggr).\end{eqnarray}$$
Then, since
$\unicode[STIX]{x1D708}$
takes only positive values, for any
$i\in I$
,
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{h}(P_{\unicode[STIX]{x1D700}}^{i}) & = & \displaystyle \mathop{\sum }_{A\in \unicode[STIX]{x1D6E5}^{\prime }\cap \mathbb{Z}^{2}}\unicode[STIX]{x1D706}_{A}\unicode[STIX]{x1D708}(A)+\mathop{\sum }_{B\in K}\unicode[STIX]{x1D707}_{B}h\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \unicode[STIX]{x1D707}_{0}h\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \max (\unicode[STIX]{x1D708})+2\unicode[STIX]{x1D700}\max (\unicode[STIX]{x1D6FC}_{i})+\unicode[STIX]{x1D707}_{0}.\nonumber\end{eqnarray}$$
If the function
$\unicode[STIX]{x1D708}_{h}$
were to be affine linear along any of the segments
$[P_{-\unicode[STIX]{x1D700}}^{i},P_{\unicode[STIX]{x1D700}}^{i}]$
, we would have
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{h}(P_{\unicode[STIX]{x1D700}}^{i}) & = & \displaystyle \unicode[STIX]{x1D708}(P_{-\unicode[STIX]{x1D700}}^{i})+2\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}_{i}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \max (\unicode[STIX]{x1D708})+2\unicode[STIX]{x1D700}\max (\unicode[STIX]{x1D6FC}_{i})\nonumber\\ \displaystyle & {<} & \displaystyle \max (\unicode[STIX]{x1D708})+2\unicode[STIX]{x1D700}\max (\unicode[STIX]{x1D6FC}_{i})+\unicode[STIX]{x1D707}_{0}.\nonumber\end{eqnarray}$$
Thus, the function
$\unicode[STIX]{x1D708}_{h}$
is not affine linear along any of the segments
$[P_{-\unicode[STIX]{x1D700}}^{i},P_{\unicode[STIX]{x1D700}}^{i}]$
. The subdivision
$S_{\unicode[STIX]{x1D708}_{h}}$
has to contain all the segments of the boundary of
$\unicode[STIX]{x1D6E5}^{\prime }$
and coincides with
$S^{\prime }$
on the interior of
$\unicode[STIX]{x1D6E5}^{\prime }$
. It is the extension of
$S^{\prime }$
that we wanted.◻
Lemma 6.2 [Reference Haase, Paffenholz, Piechnik and SantosHPPS14, Lemma 2.1].
Let
$S$
be a convex subdivision of a convex lattice polygon
$\unicode[STIX]{x1D6E5}$
. There exists a refinement of
$S$
, which is a unimodular convex subdivision of
$\unicode[STIX]{x1D6E5}$
.
6.2 Constructing Dehn twists
We give some applications of Theorem 5 that will be useful in the rest of the paper. In particular, the following constructions are enough to treat the case
$d<2$
. Let
$\unicode[STIX]{x1D6E5}$
be a smooth convex lattice polygon and
$(X,{\mathcal{L}})$
the associated polarized toric surface. Fix a curve
$C_{0}\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
.
Lemma 6.3. Let
${\mathcal{G}}=(G,m)$
be a weighted graph of
$\unicode[STIX]{x1D6E5}$
such that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{{\mathcal{G}}}]\in \text{im}([\unicode[STIX]{x1D707}])$
). Assume that
${\mathcal{G}}$
has a vertex
$v\in V(G)\cap \text{int}(\unicode[STIX]{x1D6E5})$
of valency
$1$
and let
$\unicode[STIX]{x1D70E}\in E(G)$
be the edge ending at
$v$
. Denote by
${\mathcal{G}}^{\prime }$
the weighted graph obtained from
${\mathcal{G}}$
by removing
$\unicode[STIX]{x1D70E}$
. If
$m(\unicode[STIX]{x1D70E})=\pm 1$
then
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
and
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}^{\prime }}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}]\in \text{im}([\unicode[STIX]{x1D707}])$
and
$[\unicode[STIX]{x1D70F}_{{\mathcal{G}}^{\prime }}]\in \text{im}([\unicode[STIX]{x1D707}])$
).
Proof. Assume first that
$m(\unicode[STIX]{x1D70E})=1$
. We know from Theorem 3 that
$\unicode[STIX]{x1D70F}_{v}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
. Since
$\unicode[STIX]{x1D6FF}_{v}$
and
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}$
intersect transversely in only one point,
$\unicode[STIX]{x1D70F}_{v}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D6FF}_{v})$
is isotopic to
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}$
. Moreover
$\unicode[STIX]{x1D70F}_{v}$
and
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}$
commute with
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}^{\prime }}$
. Thus we obtain
$$\begin{eqnarray}(\unicode[STIX]{x1D70F}_{v}\unicode[STIX]{x1D70F}_{{\mathcal{G}}})\unicode[STIX]{x1D70F}_{v}(\unicode[STIX]{x1D70F}_{v}\unicode[STIX]{x1D70F}_{{\mathcal{G}}})^{-1}=(\unicode[STIX]{x1D70F}_{v}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70F}_{{\mathcal{G}}^{\prime }})\unicode[STIX]{x1D70F}_{v}(\unicode[STIX]{x1D70F}_{v}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\unicode[STIX]{x1D70F}_{{\mathcal{G}}^{\prime }})^{-1}=(\unicode[STIX]{x1D70F}_{v}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}})\unicode[STIX]{x1D70F}_{v}(\unicode[STIX]{x1D70F}_{v}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}})^{-1}=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707}).\end{eqnarray}$$
The case when
$m(\unicode[STIX]{x1D70E})=-1$
follows immediately.
Since the map
$\text{MCG}(C_{0})\rightarrow \text{Sp}(H_{1}(C_{0},\mathbb{Z}))$
is a morphism, the homological statement follows from the previous argument.◻
Notation 1. In the rest of the paper, we will draw weighted graphs using two different line styles: the dashed lines will be for segments for which we know that the associated Dehn twist is in the image of the monodromy and the plain lines will be for the other segments.
Let us introduce a type of primitive integer segment that will appear often in the rest of the paper.
Definition 6.4. A primitive integer segment
$\unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6E5}$
is a bridge if it joins a lattice point of
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
to a lattice point of
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}_{a}$
and does not intersect
$\text{int}(\unicode[STIX]{x1D6E5}_{a})$
.
Lemma 6.5. Let
$v$
be a lattice point on
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}_{a}$
and
$\unicode[STIX]{x1D70E}^{\prime }$
be a bridge ending at
$v$
. Assume that
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }})^{m}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}]^{m}\in \text{im}([\unicode[STIX]{x1D707}])$
) for some integer
$m\in \mathbb{Z}$
. Then we have
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}})^{m}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}]^{m}\in \text{im}([\unicode[STIX]{x1D707}])$
) for any bridge
$\unicode[STIX]{x1D70E}$
ending at
$v$
.
Proof. This follows from the fact that, for any two bridges
$\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}^{\prime }$
ending at the same point of
$\unicode[STIX]{x1D6E5}_{a}$
, the loops
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}$
and
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}^{\prime }}$
are isotopic in
$C_{0}$
.◻
Proposition 6.6. Let
$\unicode[STIX]{x1D705}\in \unicode[STIX]{x1D6E5}_{a}$
be a vertex. If
$\unicode[STIX]{x1D70E}$
is a bridge ending at
$\unicode[STIX]{x1D705}$
, then
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
.
Proof. Using an invertible affine transformation that preserves the lattice, we may assume that
$\unicode[STIX]{x1D705}$
is the point
$(1,1)$
, that the origin is a vertex of
$\unicode[STIX]{x1D6E5}$
and that the two edges of
$\unicode[STIX]{x1D6E5}$
meeting at this point are directed by
$(1,0)$
and
$(0,1)$
.
Using Lemma 6.5, we may assume that
$\unicode[STIX]{x1D70E}$
is the segment joining
$(0,0)$
to
$(1,1)$
. Denote by
$\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{2}$
the segments joining
$(1,1)$
to
$(1,0)$
and
$(0,1)$
, respectively. Define the weighted graph
${\mathcal{G}}=(G,m)$
given by Figure 2.
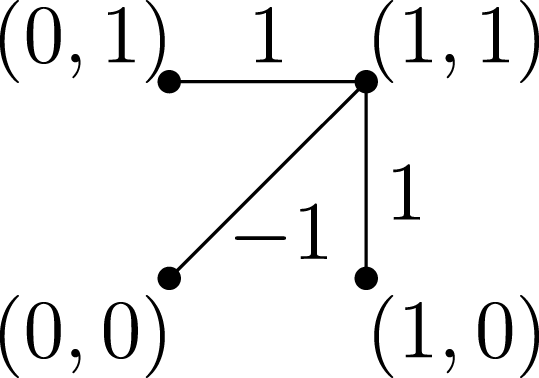
Figure 2. Weighted graph
${\mathcal{G}}$
.
It satisfies the balancing condition at the point
$(1,1)$
. To prove that it is admissible, we only need to find a unimodular convex subdivision of
$\unicode[STIX]{x1D6E5}$
supporting
$G$
. To that end, take the subdivision of the square consisting of
$G$
and the segments joining
$(0,0)$
to
$(1,0)$
and
$(0,0)$
to
$(0,1)$
. It is convex as it can be obtained from the function taking value
$0$
on
$(0,0)$
and
$(1,1)$
and
$1$
on
$(0,1)$
and
$(1,0)$
. Using Lemmas 6.1 and 6.2, we obtain a unimodular convex subdivision of
$\unicode[STIX]{x1D6E5}$
that contains
$G$
.
Thus
${\mathcal{G}}$
is an admissible graph of
$\unicode[STIX]{x1D6E5}$
. We apply Theorem 5 to deduce that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
. However, the loops
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}$
,
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}_{1}}$
, and
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}_{2}}$
are all isotopic. It follows that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}$
and the statement is proved.◻
Proposition 6.7. Let
$\unicode[STIX]{x1D70E}$
be a primitive integer vector lying on an edge of
$\unicode[STIX]{x1D6E5}_{a}$
. The Dehn twist
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
.
Proof. By Proposition 3.3, we may use an invertible affine transformation of
$\mathbb{R}^{2}$
, preserving the lattice such that
$\unicode[STIX]{x1D6E5}$
has a vertex at
$(-1,-1)$
with adjacent edges going through
$(-1,0)$
and
$(0,-1)$
and such that the edge of
$\unicode[STIX]{x1D6E5}_{a}$
containing
$\unicode[STIX]{x1D70E}$
is the segment joining
$(0,0)$
to
$(l,0)$
for some
$l\geqslant 1$
. Notice that the points
$(-1,0)$
and
$(l+1,0)$
are on the boundary of
$\unicode[STIX]{x1D6E5}$
. For
$i$
from
$0$
to
$l+1$
, denote by
$\unicode[STIX]{x1D70E}_{i}$
the segment joining
$(i-1,0)$
to
$(i,0)$
.
We know from Proposition 6.6 that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{0}}$
and
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{l+1}}$
are in
$\text{im}(\unicode[STIX]{x1D707})$
. Define the weighted graph
${\mathcal{G}}=(G,m)$
given by Figure 3.
Figure 3. Weighted graph
${\mathcal{G}}$
.
This graph is balanced at all the vertices in
$\unicode[STIX]{x1D6E5}_{a}$
. Conversely, we can take a convex function on
$\unicode[STIX]{x1D6E5}$
that is affine linear on each component of
$\unicode[STIX]{x1D6E5}\setminus G$
. The associated convex subdivision contains
$G$
. Using Lemma 6.2, it follows that
${\mathcal{G}}$
is an admissible graph.
From Theorem 5, we deduce that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}=\prod \unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{i}}\in \text{im}(\unicode[STIX]{x1D707})$
. We now apply Lemma 6.3 several times; this shows that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{i}}\in \text{im}(\unicode[STIX]{x1D707})$
for all
$i$
between
$1$
and
$l$
.◻
6.3 The elliptic case
Proof of Theorem 1, case
$d=0$
.
Let
$X$
be a smooth and complete toric surface and let
${\mathcal{L}}$
be an ample line bundle on
$X$
with
$d=0$
. Denote by
$\unicode[STIX]{x1D6E5}$
the associated lattice polygon and fix a curve
$C_{0}\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
. By assumption, the polygon
$\unicode[STIX]{x1D6E5}$
has only one interior lattice point
$\unicode[STIX]{x1D705}$
. Take
$\unicode[STIX]{x1D70E}$
to be one of the bridges ending at
$\unicode[STIX]{x1D705}$
. We know from Proposition 6.6 and Theorem 3 that both
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D705}}$
and
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}$
are in
$\text{im}(\unicode[STIX]{x1D707})$
. Since
$C_{0}$
is of genus
$1$
, the group
$\text{MCG}(C_{0})$
is generated by
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D705}}$
and
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}$
. Thus,
$\text{im}(\unicode[STIX]{x1D707})=\text{MCG}(C_{0})$
.◻
7 Proof of Theorems 1 and 2
In the rest of the paper,
$X$
is a smooth and complete toric surface equipped with an ample line bundle
${\mathcal{L}}$
. The associated polygon is denoted by
$\unicode[STIX]{x1D6E5}$
and its interior polygon by
$\unicode[STIX]{x1D6E5}_{a}$
. Since we already took care of the elliptic case in § 6.3, we assume that
$\dim (\unicode[STIX]{x1D6E5}_{a})=2$
and fix a curve
$C_{0}\in {\mathcal{H}}_{\unicode[STIX]{x1D6E5}}$
.
7.1 Normalizations
We first give a description of
$\unicode[STIX]{x1D6E5}$
near a vertex of
$\unicode[STIX]{x1D6E5}_{a}$
.
Definition 7.1. If
$\unicode[STIX]{x1D705}$
is a vertex of
$\unicode[STIX]{x1D6E5}_{a}$
, a normalization of
$\unicode[STIX]{x1D6E5}$
at
$\unicode[STIX]{x1D705}$
is an invertible affine transformation
$A:\mathbb{R}^{2}\rightarrow \mathbb{R}^{2}$
preserving the lattice and mapping
$\unicode[STIX]{x1D705}$
to
$(0,0)$
and its adjacent edges in
$\unicode[STIX]{x1D6E5}_{a}$
to the edges directed by
$(1,0)$
and
$(0,1)$
.
We will usually abuse notation and keep calling
$\unicode[STIX]{x1D6E5}$
the image of
$\unicode[STIX]{x1D6E5}$
under a normalization. It follows from Proposition 3.3 that after a normalization at
$\unicode[STIX]{x1D705}$
, there are two possibilities for the polygon
$\unicode[STIX]{x1D6E5}$
near
$\unicode[STIX]{x1D705}$
, as depicted in Figure 4.
Figure 4. The polygon
$\unicode[STIX]{x1D6E5}$
near
$\unicode[STIX]{x1D705}$
.
Indeed, since the normal fan of
$\unicode[STIX]{x1D6E5}$
is a refinement of that of
$\unicode[STIX]{x1D6E5}_{a}$
, there is an edge of
$\unicode[STIX]{x1D6E5}$
supported on the line
$y=-1$
and one supported on the line
$x=-1$
. The two cases are as follows.
(i) Those two edges meet; then we have the left case of Figure 4.
(ii) There is at least one other edge between those two. Let us call it
$\unicode[STIX]{x1D70C}$
. Since
$\unicode[STIX]{x1D70C}$
has no corresponding edge in
$\unicode[STIX]{x1D6E5}_{a}$
, we have
$l_{\unicode[STIX]{x1D70C}}-D_{\unicode[STIX]{x1D70C}}^{2}-2=0$
. Since
$\dim (\unicode[STIX]{x1D6E5}_{a})=2$
, this can only happen if
$l_{\unicode[STIX]{x1D70C}}=1$
and
$D_{\unicode[STIX]{x1D70C}}^{2}=-1$
(see [Reference KoelmanKoe91], Lemma 2.3.1). The assumption that
$\unicode[STIX]{x1D6E5}_{a}$
has dimension 2 also ensures that there cannot be two consecutive edges satisfying those two equalities. Geometrically, the primitive integer vector supporting
$\unicode[STIX]{x1D70C}$
has to be the sum of the two primitive integer vectors supporting its adjacent edges (see [Reference FultonFul93, § 2.5]). We obtain the right case of Figure 4.
After a normalization of
$\unicode[STIX]{x1D6E5}$
at
$\unicode[STIX]{x1D705}$
, it follows from this discussion that the points
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}=(0,-1)$
and
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}^{\prime }=(-1,0)$
always belong to
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
. Moreover, if the edge of
$\unicode[STIX]{x1D6E5}_{a}$
directed by
$(0,1)$
(respectively by
$(1,0)$
) is of length
$l$
(respectively of length
$l^{\prime }$
), then the point
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}=(0,l+1)$
(respectively
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}^{\prime }=(l^{\prime }+1,0)$
) belongs to
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
.
7.2 Constructions
Let us start with some technical definitions. Fix a vertex
$\unicode[STIX]{x1D705}$
of
$\unicode[STIX]{x1D6E5}_{a}$
and choose a boundary lattice point
$\unicode[STIX]{x1D705}^{\prime }$
of
$\unicode[STIX]{x1D6E5}_{a}$
such that
$\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}^{\prime }$
are consecutive on
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}_{a}$
(the orientation does not matter). Denote by
$\unicode[STIX]{x1D716}$
the edge of
$\unicode[STIX]{x1D6E5}_{a}$
containing
$\unicode[STIX]{x1D705}^{\prime }$
. Choose a bridge
$\unicode[STIX]{x1D70E}^{\prime }$
, which joins
$\unicode[STIX]{x1D705}^{\prime }$
to any boundary lattice point of
$\unicode[STIX]{x1D6E5}$
. We aim to prove the following.
Lemma 7.2. Assume that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}]\in \text{im}([\unicode[STIX]{x1D707}])$
). Then for any bridge
$\unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6E5}$
, we have
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}]\in \text{im}([\unicode[STIX]{x1D707}])$
).
Remark 7.3. In the rest of § 7, we will make constant use of admissible graphs in the proofs of the various statements. Most of the time, we will only show that the weighted graph
${\mathcal{G}}=(G,m)$
under consideration is balanced and leave the proof of the admissibility for the reader. Note that we only need to exhibit a convex subdivision supporting the graph
$G$
and obtain a unimodular one by Lemma 6.2.
Proof of Lemma 7.2.
Consider the normalization of
$\unicode[STIX]{x1D6E5}$
at
$\unicode[STIX]{x1D705}$
mapping
$\unicode[STIX]{x1D705}^{\prime }$
to
$(0,1)$
. The edge
$\unicode[STIX]{x1D716}$
is then vertical.
We claim the following: if
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}\in \text{im}(\unicode[STIX]{x1D707})$
and
$\unicode[STIX]{x1D705}^{\prime \prime }$
is a lattice point on the edge of
$\unicode[STIX]{x1D6E5}_{a}$
adjacent to
$\unicode[STIX]{x1D716}$
and containing
$\unicode[STIX]{x1D705}$
, then there is a bridge
$\unicode[STIX]{x1D70E}$
ending at
$\unicode[STIX]{x1D705}^{\prime \prime }$
such that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
.
By Lemma 6.5, we can assume, without loss of generality, that
$\unicode[STIX]{x1D70E}^{\prime }$
joins
$\unicode[STIX]{x1D705}^{\prime }$
to
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}^{\prime }=(-1,0)$
. By Proposition 6.6, there is nothing to prove if
$\unicode[STIX]{x1D705}^{\prime \prime }$
is a vertex of
$\unicode[STIX]{x1D6E5}_{a}$
. Therefore, we can assume that
$\unicode[STIX]{x1D705}^{\prime \prime }=(a,0)$
is not a vertex. Now consider the admissible graph
${\mathcal{G}}$
of Figure 5, where the horizontal edges have weight
$-2a$
and the vertical edges have weight
$-a-1$
. By Theorem 5, we have
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\in \text{im}(\unicode[STIX]{x1D707})$
. By Proposition 7.6 applied to
${\mathcal{G}}$
and the assumption
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}\in \text{im}(\unicode[STIX]{x1D707})$
, Lemma 6.3 allows us to chase any primitive integer segment of
${\mathcal{G}}$
except
$\unicode[STIX]{x1D70E}$
and conclude that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
. This proves the claim.
By applying this claim and Lemma 6.5 to any
$\unicode[STIX]{x1D705}^{\prime \prime }$
, we show that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
for any bridge ending on the edge of
$\unicode[STIX]{x1D6E5}_{a}$
adjacent to
$\unicode[STIX]{x1D716}$
and containing
$\unicode[STIX]{x1D705}$
. By induction on the edges of
$\unicode[STIX]{x1D6E5}_{a}$
, it follows that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
for any bridge of
$\unicode[STIX]{x1D6E5}$
.
The homological statement follows from the previous arguments and the fact that Lemma 6.3 and Proposition 6.6 hold in homology.◻
Figure 5. Admissible graph
${\mathcal{G}}$
.
Remark 7.4. If
$\unicode[STIX]{x1D6E5}_{a}$
has a side of integer length 1, it follows from Lemma 7.2 and Proposition 6.6 that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
for any bridge
$\unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6E5}$
.
In the rest of this section, we explain how to construct a Dehn twist around a loop corresponding to a primitive integer segment
$\unicode[STIX]{x1D70E}$
joining any two points of
$\unicode[STIX]{x1D6E5}$
(see Proposition 7.6). To that end, we will construct an admissible graph containing
$\unicode[STIX]{x1D70E}$
with multiplicity
$1$
and such that the Dehn twists corresponding to the edges of the graph adjacent to
$\unicode[STIX]{x1D70E}$
are in
$\text{im}(\unicode[STIX]{x1D707})$
. We will construct this graph by parts.
Let us choose again a vertex
$\unicode[STIX]{x1D705}$
of
$\unicode[STIX]{x1D6E5}_{a}$
and a boundary lattice point
$\unicode[STIX]{x1D705}^{\prime }$
of
$\unicode[STIX]{x1D6E5}_{a}$
such that
$\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}^{\prime }$
are consecutive on
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}_{a}$
. Take a point
$v\in \text{int}(\unicode[STIX]{x1D6E5}_{a})\cap \mathbb{Z}^{2}$
and choose two integers
$m_{1}$
and
$m_{2}$
. We construct two weighted graphs
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}=(G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v},m_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}})$
and
${\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}^{m_{1},m_{2}}=(G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v},m_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}^{m_{1},m_{2}})$
associated with these data as follows.
First, consider once again the normalization of
$\unicode[STIX]{x1D6E5}$
at
$\unicode[STIX]{x1D705}$
mapping
$\unicode[STIX]{x1D705}^{\prime }$
to
$(0,1)$
. Let us also recall from § 7.1 that the points
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}=(0,-1)$
and
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}^{\prime }=(-1,0)$
are boundary points of
$\unicode[STIX]{x1D6E5}$
. The set of edges of
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}$
is the union of two subsets, as well as that of
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}$
.
The first subset is constructed by induction. We start with
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}$
. Take
$v_{0}^{\prime }=v$
and define
$v_{1}^{\prime }$
as follows. We call
$\unicode[STIX]{x1D70E}_{1,0}$
the primitive integer segment starting at
$v_{0}^{\prime }$
and directing
$[v_{0}^{\prime },\unicode[STIX]{x1D705}^{\prime }]$
. Consider the ray starting at
$v_{0}^{\prime }$
and directed by
$\unicode[STIX]{x1D70E}_{1,0}$
and make it rotate counterclockwise around
$v_{0}^{\prime }$
until it hits a lattice point in
$\text{conv}(v_{0}^{\prime },\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705})$
. Denote by
$l$
this new ray and by
$\unicode[STIX]{x1D70E}_{2,0}$
the primitive integer segment directing it (see Figure 6, on the left).
Figure 6. Sketch of the construction of
$v_{1}^{\prime }$
for the graphs
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}$
(on the left) and
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}$
(on the right). There is no lattice point inside the triangles.
Take
$v_{1}^{\prime }$
to be the lattice point in
$l\cap \text{conv}(v_{0}^{\prime },\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705})$
that is farthest away from
$v_{0}^{\prime }$
. Take all the primitive integer segments on the segment
$[v_{0}^{\prime },\unicode[STIX]{x1D705}^{\prime }]$
with weight
$m_{1,0}=m_{1}$
and all the primitive integer segments on the segment
$[v_{0}^{\prime },v_{1}^{\prime }]$
with weight
$m_{2,0}=m_{2}$
to be edges of
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}$
.
Suppose we have constructed
$v_{0}^{\prime },\ldots ,v_{k}^{\prime }$
for some
$k\geqslant 1$
and that the edges on
$[v_{k-1}^{\prime },\unicode[STIX]{x1D705}^{\prime }]$
are weighted with
$m_{1,k-1}$
and that those on
$[v_{k-1}^{\prime },v_{k}^{\prime }]$
have weight
$m_{2,k-1}$
. If
$v_{k}^{\prime }=\unicode[STIX]{x1D705}$
, we are done. If not, replacing
$v_{0}^{\prime }$
with
$v_{k}^{\prime }$
in the previous case, we construct
$v_{k+1}^{\prime }\in \text{conv}(v_{k}^{\prime },\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705})$
and the primitive integer segments
$\unicode[STIX]{x1D70E}_{1,k}$
on
$[v_{k}^{\prime },\unicode[STIX]{x1D705}^{\prime }]$
and
$\unicode[STIX]{x1D70E}_{2,k}$
on
$[v_{k}^{\prime },v_{k+1}^{\prime }]$
. By construction,
$\unicode[STIX]{x1D70E}_{1,k}$
and
$\unicode[STIX]{x1D70E}_{2,k}$
generate the lattice. Thus we can find integers
$m_{1,k}$
and
$m_{2,k}$
such that
$$\begin{eqnarray}m_{2,k-1}\unicode[STIX]{x1D70E}_{2,k-1}+m_{1,k}\unicode[STIX]{x1D70E}_{1,k}+m_{2,k}\unicode[STIX]{x1D70E}_{2,k}=0.\end{eqnarray}$$
Here we identify the segments with the vectors of
$\mathbb{Z}^{2}$
they induce once we orient them going out of
$v_{k}^{\prime }$
. We take all the primitive integer segments on the segments
$[v_{k}^{\prime },\unicode[STIX]{x1D705}^{\prime }]$
and
$[v_{k}^{\prime },v_{k+1}^{\prime }]$
, weighted by
$m_{1,k}$
and
$m_{2,k}$
, respectively, to be edges of
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}$
.
After a finite number of steps
$t\geqslant 1$
, we obtain
$v_{t}^{\prime }=\unicode[STIX]{x1D705}$
. The graph we obtain looks like the left graph in Figure 7.
Figure 7. Rough sketch of the graphs
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}$
(on the left) and
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}$
(on the right). There is no lattice point in any of the small triangles.
The construction for
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}$
is the same, except we exchange the roles of
$\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D705}^{\prime }$
; that is, we use the ray starting at
$v$
and going through
$\unicode[STIX]{x1D705}$
to sweep-out the triangle
$v,\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime }$
, and we stop when we encounter
$\unicode[STIX]{x1D705}^{\prime }$
(see Figures 6 and 7). We use the same notations for both graphs.
The second set of edges for both graphs consists of the four segments
$\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{4}$
joining, respectively,
$\unicode[STIX]{x1D705}^{\prime }$
to
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}^{\prime }=(-1,0)$
and
$\unicode[STIX]{x1D705}$
to
$\unicode[STIX]{x1D705}^{\prime }$
,
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}^{\prime }$
and
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}=(0,-1)$
. The first two generate the lattice. Thus we can find two integers
$a_{1}$
and
$a_{2}$
such that
$m_{1,0}\unicode[STIX]{x1D70E}_{1,0}+\cdots +m_{1,n-1}\unicode[STIX]{x1D70E}_{1,n-1}+a_{1}\unicode[STIX]{x1D70C}_{1}+a_{2}\unicode[STIX]{x1D70C}_{2}=0$
(where the segments are oriented going out of
$\unicode[STIX]{x1D705}^{\prime }$
). We set
$m_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}(\unicode[STIX]{x1D70C}_{1})=a_{1}$
and
$m_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}(\unicode[STIX]{x1D70C}_{2})=a_{2}$
. The segments
$\unicode[STIX]{x1D70C}_{3}$
and
$\unicode[STIX]{x1D70C}_{4}$
also generate the lattice. Hence, we can find two integers
$a_{3}$
and
$a_{4}$
such that
$m_{2,n-1}\unicode[STIX]{x1D70E}_{2,n-1}+a_{2}\unicode[STIX]{x1D70C}_{2}+a_{3}\unicode[STIX]{x1D70C}_{3}+a_{4}\unicode[STIX]{x1D70C}_{4}=0$
(where the segments are oriented going out of
$\unicode[STIX]{x1D705}$
). We set
$m_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}(\unicode[STIX]{x1D70C}_{3})=a_{3}$
and
$m_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}(\unicode[STIX]{x1D70C}_{4})=a_{4}$
.
Notice that, by construction, the graphs
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}$
and
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}$
do not depend on
$m_{1}$
and
$m_{2}$
and that the weighted graph
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v_{k}^{\prime }}^{m_{1,k},m_{2,k}}$
(respectively
${\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v_{k}^{\prime }}^{m_{1,k},m_{2,k}}$
) is a subgraph of
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}$
(respectively
${\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}^{m_{1},m_{2}}$
) for any
$0\leqslant k<t-1$
, although the weights on the segments
$\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{4}$
may differ from one to the other.
We give a complete example, taking
$v=(16,4)$
and weights
$m_{1}=m_{2}=1$
, in Figure 8.
Figure 8. Weighted graphs
${\mathcal{G}}_{(0,0),(0,1),(16,4)}^{(1,1)}$
(top) and
${\mathcal{G}}_{(0,1),(0,0),(16,4)}^{(1,1)}$
(bottom).
Lemma 7.5. The weighted graphs
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}$
and
${\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}^{m_{1},m_{2}}$
satisfy the following properties:
(i) the edges
$\unicode[STIX]{x1D70E}_{1}=\unicode[STIX]{x1D70E}_{1,0}$
and
$\unicode[STIX]{x1D70E}_{2}=\unicode[STIX]{x1D70E}_{2,0}$
generate the lattice;(ii) the weight function
$m_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}$
(respectively
$m_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}^{m_{1},m_{2}}$
) satisfies the balancing condition (5) at every element of
$V(G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v})\cap \text{int}\unicode[STIX]{x1D6E5}$
(respectively
$V(G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v})\cap \text{int}\unicode[STIX]{x1D6E5}$
) except at
$v$
.
Assume, moreover, that there is a bridge
$\unicode[STIX]{x1D70E}^{\prime }$
ending at
$\unicode[STIX]{x1D705}^{\prime }$
, such that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}]$
is in
$\text{im}([\unicode[STIX]{x1D707}])$
). Then
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}}$
and
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}$
are in
$\text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}}]$
and
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}]$
are in
$\text{im}([\unicode[STIX]{x1D707}])$
).
Proof. The two properties of
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}$
and
${\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}^{m_{1},m_{2}}$
follow from the construction.
For the second part of the lemma, we start with the weighted graph
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}$
and show how to adapt the proof for the other one.
The strategy is to include the graph
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}$
in another one, called
$G$
, which will be supported by a unimodular convex subdivision of
$\unicode[STIX]{x1D6E5}$
. Moreover, we will be able to put two weight functions on
$G$
, such that
$\unicode[STIX]{x1D70E}_{1}$
appears with weight
$1$
for one and
$\unicode[STIX]{x1D70E}_{2}$
appears with weight
$1$
for the other and such that both functions satisfy the balancing condition at every interior vertex of
$G$
. To conclude, we apply Theorem 5 and Lemma 6.3.
Let us give the details of the proof. Denote by
$\unicode[STIX]{x1D709}$
the vertex of
$\unicode[STIX]{x1D6E5}_{a}$
next to
$\unicode[STIX]{x1D705}$
such that
$\unicode[STIX]{x1D705}^{\prime }$
is not on
$[\unicode[STIX]{x1D709},\unicode[STIX]{x1D705}]$
and take
$\unicode[STIX]{x1D709}^{\prime }$
to be the boundary point of
$\unicode[STIX]{x1D6E5}_{a}$
next to
$\unicode[STIX]{x1D709}$
and outside
$[\unicode[STIX]{x1D709},\unicode[STIX]{x1D705}]$
. In the coordinates chosen previously, the point
$\unicode[STIX]{x1D709}$
is of the form
$(l,0)$
and
$\unicode[STIX]{x1D709}^{\prime }$
is given by
$(l+s,1)$
, for some integers
$l$
and
$s$
. The points
$(l-s,-1)$
and
$(l+1,0)$
are boundary lattice points of
$\unicode[STIX]{x1D6E5}$
. Define the graph
$G$
as the union of
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}$
and
$G_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },v}$
(see Figure 9).
Figure 9. Rough sketch of the graph
$G$
(with
$s=0$
). There is no lattice point in the small triangles. The dashed lines indicate the edges of
$G$
for which we know that the associated Dehn twist is in the image of the monodromy.
Let us show that
$G$
is supported by a unimodular convex subdivision of
$\unicode[STIX]{x1D6E5}$
. First, we construct the subdivision on the pentagon
$Q$
with vertices
$\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },v$
, which is convex. To this end, let us call
$w_{i}^{\prime }$
the counterparts of the points
$v_{i}^{\prime }$
used in the construction of
$G_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },v}$
. Define also the function
$h$
taking value
$0$
on the points
$v,\unicode[STIX]{x1D705},v_{1}^{\prime },\ldots ,v_{t-1}^{\prime },\unicode[STIX]{x1D709},w_{1}^{\prime },\ldots ,w_{p-1}^{\prime }$
and
$1$
on
$\unicode[STIX]{x1D705}^{\prime }$
and
$\unicode[STIX]{x1D709}^{\prime }$
. The subdivision
$S_{h}$
is a convex subdivision of
$Q$
(see Definition 5.2). Moreover, if we call
$\unicode[STIX]{x1D708}_{h}:Q\rightarrow \mathbb{R}$
the associated convex function, then
$\unicode[STIX]{x1D708}_{h}$
is affine linear along
$[\unicode[STIX]{x1D705}^{\prime },v]$
. Moreover, the subdivision associated with
$\unicode[STIX]{x1D708}$
contains the part of the graph
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}$
in
$Q$
since the angles
$v_{i-1}^{\prime }v_{i}^{\prime }v_{i+1}^{\prime }$
facing
$\unicode[STIX]{x1D705}^{\prime }$
are all greater than
$\unicode[STIX]{x1D70B}$
for
$i=1,\ldots ,t-1$
. By similar arguments, this subdivision also contains the part of the graph
$G_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },v}$
in
$Q$
.
Extend the convex subdivision obtained on
$Q$
to the polygon
$\text{conv}(Q,(0,-1),(l-s,-1))$
using Lemma 6.1. Since the edges
$[\unicode[STIX]{x1D705},(0,-1)]$
and
$[\unicode[STIX]{x1D709},(l-s,-1)]$
are on the boundary of the polygon, the graph
$G$
is still supported by the extended subdivision.
Extend the subdivision once again to the convex polygon
$\text{conv}(v,\unicode[STIX]{x1D705}^{\prime },(-1,0),(0,-1),(l-s,-1),(l+1,0),\unicode[STIX]{x1D709}^{\prime })$
. The subdivision that we obtain does not necessarily support the graph
$G$
, the only possibly missing edges being
$[(-1,0),\unicode[STIX]{x1D705}]$
,
$[(-1,0),\unicode[STIX]{x1D705}^{\prime }]$
,
$[(l+1,0),\unicode[STIX]{x1D709}]$
and
$[(l+1,0),\unicode[STIX]{x1D709}^{\prime }]$
. However, once we refine it using Lemma 6.2, the unimodular convex subdivision of
$\text{conv}(v,\unicode[STIX]{x1D705}^{\prime },(-1,0),(0,-1),(l-s,-1),(l+1,0),\unicode[STIX]{x1D709}^{\prime })$
necessarily contains the whole graph
$G$
. Extending this last subdivision to the whole
$\unicode[STIX]{x1D6E5}$
and refining it, we conclude that
$G$
is supported by a unimodular convex subdivision of
$\unicode[STIX]{x1D6E5}$
.
Now, let us assume that there is a bridge
$\unicode[STIX]{x1D70E}^{\prime }$
ending at
$\unicode[STIX]{x1D705}^{\prime }$
such that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}]$
is in
$\text{im}([\unicode[STIX]{x1D707}])$
). Using Lemma 6.5, we know that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70C}_{1}}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70C}_{1}}]$
is in
$\text{im}([\unicode[STIX]{x1D707}])$
).
We first show that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}}]$
is in
$\text{im}([\unicode[STIX]{x1D707}])$
). Let us call
$\unicode[STIX]{x1D702}_{1}$
and
$\unicode[STIX]{x1D702}_{2}$
the two edges of
$G_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },v}$
going out of
$v$
. Since
$\unicode[STIX]{x1D702}_{1}$
and
$\unicode[STIX]{x1D702}_{2}$
generate the lattice, take
$m_{1}$
and
$m_{2}$
such that
$\unicode[STIX]{x1D70E}_{1}+m_{1}\unicode[STIX]{x1D702}_{1}+m_{2}\unicode[STIX]{x1D702}_{2}=0$
(the vectors being oriented going out of
$v$
). Let
$m:E(G)\rightarrow \mathbb{Z}$
be the sum of
$m_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{1,0}$
and
$m_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },v}^{m_{1},m_{2}}$
(both extended by
$0$
where they are not defined) and define the weighted graph
${\mathcal{G}}=(G,m)$
. It is admissible, so from Theorem 5 we know that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\in \text{im}(\unicode[STIX]{x1D707})$
. From Proposition 6.7, we have
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70C}_{2}}\in \text{im}(\unicode[STIX]{x1D707})$
. By assumption, we also know that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70C}_{1}}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70C}_{1}}]\in \text{im}([\unicode[STIX]{x1D707}])$
). Applying Lemma 6.3 repeatedly, we obtain that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}}]$
is in
$\text{im}([\unicode[STIX]{x1D707}])$
).
We now show that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}]$
is in
$\text{im}([\unicode[STIX]{x1D707}])$
). We proceed by induction on the number
$t$
of steps required to construct
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}$
. Let us first assume that
$t=1$
. Take
$m_{1}$
and
$m_{2}$
such that
$\unicode[STIX]{x1D70E}_{2}+m_{1}\unicode[STIX]{x1D702}_{1}+m_{2}\unicode[STIX]{x1D702}_{2}=0$
(the vectors being oriented going out of
$v$
). Let
$m:E(G)\rightarrow \mathbb{Z}$
be the sum of
$m_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{0,1}$
and
$m_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },v}^{m_{1},m_{2}}$
and define the weighted graph
${\mathcal{G}}=(G,m)$
. It is admissible, so from Theorem 5 we know that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\in \text{im}(\unicode[STIX]{x1D707})$
. From Proposition 6.6, we have
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70C}_{3}},\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70C}_{4}}\in \text{im}(\unicode[STIX]{x1D707})$
. Applying Lemma 6.3 repeatedly, we obtain that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}]$
is in
$\text{im}([\unicode[STIX]{x1D707}])$
).
Assume that
$t>1$
and that the result is true for
$t-1$
. Once again, take
$m_{1}$
and
$m_{2}$
such that
$\unicode[STIX]{x1D70E}_{2}+m_{1}\unicode[STIX]{x1D702}_{1}+m_{2}\unicode[STIX]{x1D702}_{2}=0$
(the vectors being oriented going out of
$v$
). Let
$m:E(G)\rightarrow \mathbb{Z}$
be the sum of
$m_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{0,1}$
and
$m_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },v}^{m_{1},m_{2}}$
and define the weighted graph
${\mathcal{G}}=(G,m)$
. It is admissible, so from Theorem 5 we know that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\in \text{im}(\unicode[STIX]{x1D707})$
. Since the graph
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v_{1}^{\prime }}$
is constructed in
$t-1$
steps, we use the induction hypothesis and the first part of the lemma to deduce that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1,1}},\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2,1}}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1,1}}],[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2,1}}]\in \text{im}([\unicode[STIX]{x1D707}])$
). Applying Lemma 6.3, we obtain that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}]$
is in
$\text{im}([\unicode[STIX]{x1D707}])$
). We conclude by induction on
$t$
that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}]$
is in
$\text{im}([\unicode[STIX]{x1D707}])$
).
The case of the graph
${\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}^{m_{1},m_{2}}$
is very similar. The graph
$G$
differs a little to ensure that it is supported by a convex subdivision. Indeed, there are two cases.
(i) The first one is if
$\unicode[STIX]{x1D705}^{\prime }$
is not itself a vertex of
$\unicode[STIX]{x1D6E5}_{a}$
. Then we denote by
$\unicode[STIX]{x1D709}$
the vertex of
$\unicode[STIX]{x1D6E5}_{a}$
next to
$\unicode[STIX]{x1D705}$
such that
$\unicode[STIX]{x1D705}^{\prime }$
is on
$[\unicode[STIX]{x1D709},\unicode[STIX]{x1D705}]$
and take
$\unicode[STIX]{x1D709}^{\prime }$
to be the boundary point of
$\unicode[STIX]{x1D6E5}_{a}$
next to
$\unicode[STIX]{x1D709}$
and outside
$[\unicode[STIX]{x1D709},\unicode[STIX]{x1D705}]$
. In the coordinates chosen previously, the point
$\unicode[STIX]{x1D709}$
is of the form
$(0,l)$
and
$\unicode[STIX]{x1D709}^{\prime }$
is given by
$(1,l+s)$
for some integers
$l$
and
$s$
. The points
$(-1,l-s)$
and
$(0,l+1)$
are boundary lattice points of
$\unicode[STIX]{x1D6E5}$
.(ii) In the second case, the point
$\unicode[STIX]{x1D705}^{\prime }$
is a vertex of
$\unicode[STIX]{x1D6E5}_{a}$
and we take
$\unicode[STIX]{x1D709}\neq \unicode[STIX]{x1D705}$
the vertex of
$\unicode[STIX]{x1D6E5}_{a}$
next to
$\unicode[STIX]{x1D705}^{\prime }$
and
$\unicode[STIX]{x1D709}^{\prime }$
the boundary point of
$\unicode[STIX]{x1D6E5}_{a}$
next to
$\unicode[STIX]{x1D709}$
and not in
$[\unicode[STIX]{x1D709},\unicode[STIX]{x1D705}^{\prime }]$
.
In both cases, the graph
$G$
is the union of
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}$
and
$G_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },v}$
. The rest of the proof follows along the same lines as for
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}$
so we omit it.◻
We can now use the graphs we constructed to show the following proposition, which provides us with a lot of Dehn twists in the image of the monodromy.
Proposition 7.6. Let
$\unicode[STIX]{x1D70E}^{\prime }$
be a bridge ending at
$\unicode[STIX]{x1D705}^{\prime }$
. Assume that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}]\in \text{im}([\unicode[STIX]{x1D707}])$
). Then for any primitive integer segment
$\unicode[STIX]{x1D70E}$
joining two points of
$\unicode[STIX]{x1D6E5}\cap \mathbb{Z}^{2}$
not both on the boundary of
$\unicode[STIX]{x1D6E5}$
, we have
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}]\in \text{im}([\unicode[STIX]{x1D707}])$
).
Proof. Let us first note that, using Lemma 7.2, we may move the vertex
$\unicode[STIX]{x1D705}$
without changing the assumptions of the proposition.
Take any primitive integer segment
$\unicode[STIX]{x1D70E}$
in
$\unicode[STIX]{x1D6E5}$
. The idea of the proof is to construct an admissible graph containing
$\unicode[STIX]{x1D70E}$
with weight
$1$
using the graphs introduced in the beginning of the section and then to apply Lemmas 7.5 and 6.3 to conclude.
Let
$v$
and
$w$
in
$\unicode[STIX]{x1D6E5}\cap \mathbb{Z}^{2}$
be the two ends of
$\unicode[STIX]{x1D70E}$
. We distinguish between four cases: when
$v$
and
$w$
are both in the interior of
$\unicode[STIX]{x1D6E5}_{a}$
, when exactly one of them is on the boundary of
$\unicode[STIX]{x1D6E5}_{a}$
, when both of them are on the boundary of
$\unicode[STIX]{x1D6E5}_{a}$
, and when one of them is on the boundary of
$\unicode[STIX]{x1D6E5}$
.
Let us first assume that both
$v$
and
$w$
are in
$\text{int}(\unicode[STIX]{x1D6E5}_{a})\cap \mathbb{Z}^{2}$
. Up to renaming
$v$
and
$w$
, we may choose two consecutive vertices
$\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D709}$
of
$\unicode[STIX]{x1D6E5}_{a}$
and boundary points,
$\unicode[STIX]{x1D705}^{\prime }$
on
$[\unicode[STIX]{x1D705},\unicode[STIX]{x1D709}]$
next to
$\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D709}^{\prime }$
next to
$\unicode[STIX]{x1D709}$
outside of
$[\unicode[STIX]{x1D705},\unicode[STIX]{x1D709}]$
, such that the pentagon
$\unicode[STIX]{x1D705},v,w,\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709}$
is convex with its vertices arranged in this order. It can happen that
$\unicode[STIX]{x1D705}^{\prime }=\unicode[STIX]{x1D709}$
. Consider the graph
$G$
to be the reunion of the graphs
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}$
and
$G_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}$
and the segment
$\unicode[STIX]{x1D70E}$
(see Figure 10). It can be shown, as in the proof of Lemma 7.5, that
$G$
is supported by a unimodular convex subdivision.
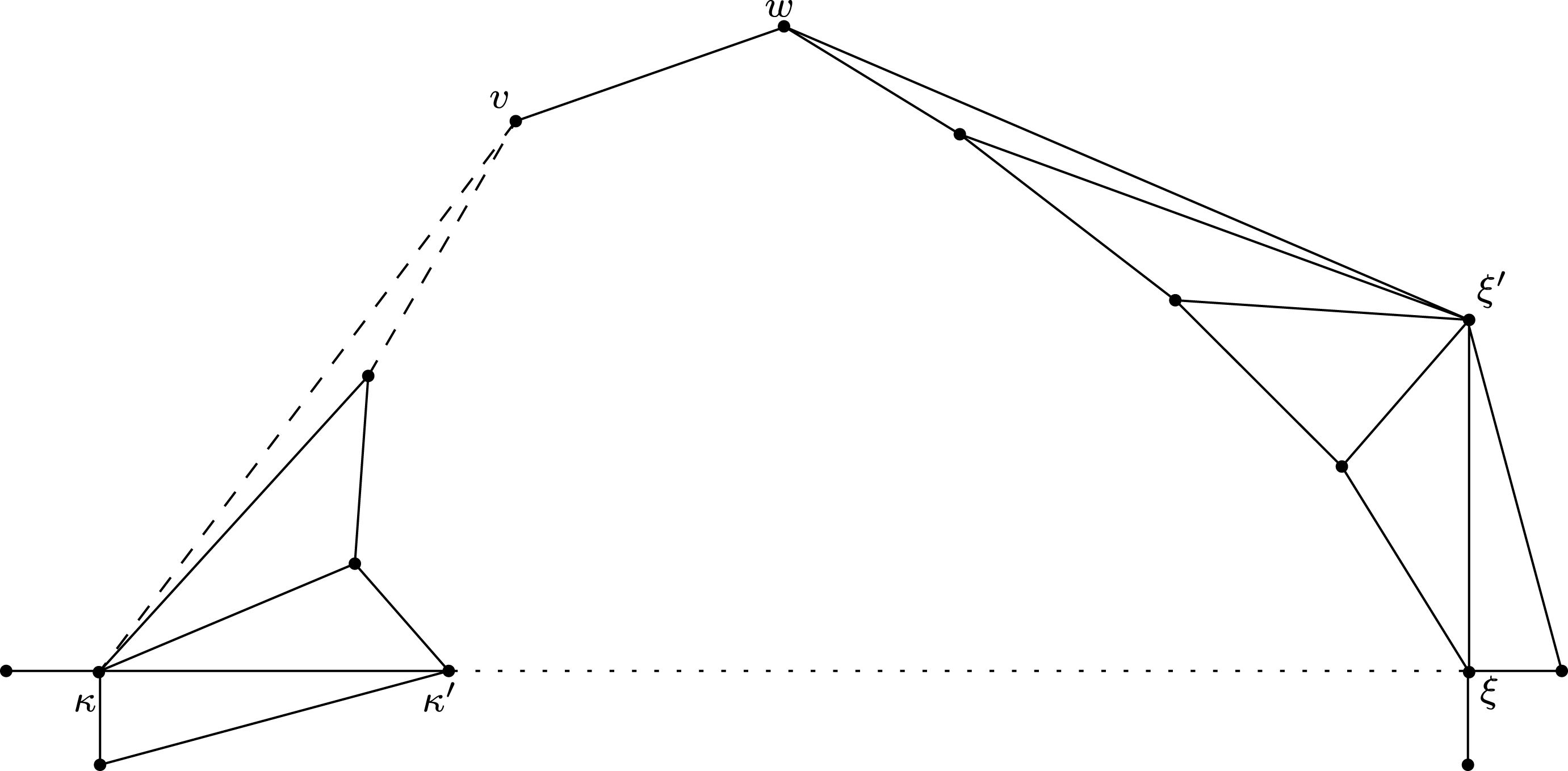
Figure 10. Rough sketch of the graph
$G$
. There is no lattice point in the small triangles. Dashed lines indicate the edges of
$G$
for which we know that the associated Dehn twist is in the image of the monodromy.
We now define the weight function on
$G$
. Let
$\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{2}$
(respectively
$\unicode[STIX]{x1D702}_{1}$
and
$\unicode[STIX]{x1D702}_{2}$
) be the primitive integer segments in
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}$
(respectively in
$G_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}$
) going out of
$v$
(respectively out of
$w$
). Since
$\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{2}$
generate the lattice, choose
$m_{1}$
and
$m_{2}$
such that
$\unicode[STIX]{x1D70E}+m_{1}\unicode[STIX]{x1D70E}_{1}+m_{2}\unicode[STIX]{x1D70E}_{2}=0$
(where the orientations go out of
$v$
). In the same manner, choose
$m_{1}^{\prime }$
and
$m_{2}^{\prime }$
such that
$\unicode[STIX]{x1D70E}+m_{1}^{\prime }\unicode[STIX]{x1D702}_{1}+m_{2}^{\prime }\unicode[STIX]{x1D702}_{2}=0$
(where the orientations go out of
$w$
). Let
$m:E(G)\rightarrow \mathbb{Z}$
be the function given by
$m_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}^{m_{1},m_{2}}$
(respectively
$m_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}^{m_{1}^{\prime },m_{2}^{\prime }}$
) on
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}$
(respectively
$G_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}$
) and equal to
$1$
on
$\unicode[STIX]{x1D70E}$
. Define the weighted graph
${\mathcal{G}}=(G,m)$
. It is admissible, so, from Theorem 5, we know that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\in \text{im}(\unicode[STIX]{x1D707})$
.
By assumption, we have that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}]\in \text{im}([\unicode[STIX]{x1D707}])$
). We know from Lemma 7.5 that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}},\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}}],[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}]\in \text{im}([\unicode[STIX]{x1D707}])$
). Using Lemma 6.3 once, we obtain that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}]\in \text{im}([\unicode[STIX]{x1D707}])$
).
For the last three cases, we only construct the graph
$G$
and leave the end of the proof to the reader as it follows, word for word, that of the first case.
Let us now assume that exactly one of the two ends of
$\unicode[STIX]{x1D70E}$
, say
$v$
, is on the boundary of
$\unicode[STIX]{x1D6E5}_{a}$
. In this case, take three consecutive vertices
$\unicode[STIX]{x1D701}$
,
$\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D709}$
of
$\unicode[STIX]{x1D6E5}_{a}$
and the boundary point
$\unicode[STIX]{x1D709}^{\prime }$
of
$\unicode[STIX]{x1D6E5}_{a}$
next to
$\unicode[STIX]{x1D709}$
outside of
$[\unicode[STIX]{x1D705},\unicode[STIX]{x1D709}]$
, such that
$v$
is on
$[\unicode[STIX]{x1D701},\unicode[STIX]{x1D705}]$
and the pentagon
$\unicode[STIX]{x1D705},v,w,\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709}$
is convex with its vertices arranged in this order. It can happen that
$v=\unicode[STIX]{x1D705}$
. Consider the graph
$G$
to be the reunion of the graph
$G_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}$
, the segment from
$v$
to
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
going through
$\unicode[STIX]{x1D705}$
, any bridge ending at
$v$
and the segment
$\unicode[STIX]{x1D70E}$
. Once again, it can be shown that
$G$
is supported by a unimodular convex subdivision.
Just like in the first case, we may define a balanced weight function on
$G$
such that
$\unicode[STIX]{x1D70E}$
has weight
$1$
: we only replace
$\unicode[STIX]{x1D70E}_{1}$
by the bridge ending at
$v$
and
$\unicode[STIX]{x1D70E}_{2}$
by the primitive integer of the ray starting at
$v$
.
Assume now that both
$v$
and
$w$
are on the boundary of
$\unicode[STIX]{x1D6E5}_{a}$
. By Proposition 6.7, we can assume that they are not on the same edge of
$\unicode[STIX]{x1D6E5}_{a}$
. Take
$\unicode[STIX]{x1D705}\neq v,w$
and
$\unicode[STIX]{x1D709}\neq v,w$
to be the ends of the edges of
$\unicode[STIX]{x1D6E5}_{a}$
containing, respectively,
$v$
and
$w$
and such that
$\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D709}$
are on the same side of the line joining
$v$
and
$w$
. It can happen that
$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D709}$
. Take the graph
$G$
to be the reunion of the segment from
$v$
to
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
going through
$\unicode[STIX]{x1D705}$
and any bridge ending at
$v$
, the segment from
$w$
to
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
going through
$\unicode[STIX]{x1D709}$
and any bridge ending at
$w$
, and the segment
$\unicode[STIX]{x1D70E}$
. This graph is still supported by a unimodular convex subdivision.
To define the weight function on
$G$
, we proceed as in the second case but we replace
$\unicode[STIX]{x1D702}_{1}$
with the bridge ending at
$w$
and
$\unicode[STIX]{x1D702}_{2}$
with the primitive integer of the ray starting at
$w$
.
Finally assume that one of the two ends of
$\unicode[STIX]{x1D70E}$
, say
$v$
is on the boundary of
$\unicode[STIX]{x1D6E5}$
. If
$w$
is in
$\text{int}(\unicode[STIX]{x1D6E5}_{a})$
, take a vertex
$\unicode[STIX]{x1D709}$
of
$\unicode[STIX]{x1D6E5}_{a}$
and a boundary point
$\unicode[STIX]{x1D709}^{\prime }$
next to
$\unicode[STIX]{x1D709}$
such that the line generated by
$\unicode[STIX]{x1D70E}$
and the graph
$G_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}$
intersect only at
$w$
. Define
$G$
to be the reunion of
$G_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}$
and
$\unicode[STIX]{x1D70E}$
. If
$w$
is on the boundary of
$\unicode[STIX]{x1D6E5}_{a}$
, we may assume that
$\unicode[STIX]{x1D70E}$
is not a bridge and take
$\unicode[STIX]{x1D709}$
to be one of the end of the edge of
$\unicode[STIX]{x1D6E5}_{a}$
containing
$w$
. Define
$G$
to be the reunion of the segment from
$w$
to
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}$
going through
$\unicode[STIX]{x1D709}$
and any bridge ending at
$w$
and the segment
$\unicode[STIX]{x1D70E}$
. In those two cases, the graph
$G$
is supported by a unimodular convex subdivision and one can define a balanced weight function such that
$\unicode[STIX]{x1D70E}$
has weight
$1$
.
Once again, the proof of the homological statement is the same as this one, so we omit it. ◻
7.3
$K_{X}\otimes {\mathcal{L}}$
prime
In this section, we prove the second case of Theorem 1, that is when
$d=2$
and
$n=1$
. One of the cornerstones of the proof is the following.
Proposition 7.7. Let
$s:=\gcd (\{l_{\unicode[STIX]{x1D716}}\mid \unicode[STIX]{x1D716}\text{ edge of }\unicode[STIX]{x1D6E5}_{a}\})$
. Then for any bridge
$\unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6E5}$
, we have
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}})^{s}\in \text{im}(\unicode[STIX]{x1D707})$
.
To prove this statement, we will need the following lemmas.
Lemma 7.8. Let
$\unicode[STIX]{x1D705}$
be a vertex of
$\unicode[STIX]{x1D6E5}_{a}$
and
$\unicode[STIX]{x1D716}_{1},\unicode[STIX]{x1D716}_{2}\subset \unicode[STIX]{x1D6E5}_{a}$
be the edges adjacent to
$\unicode[STIX]{x1D705}$
. Take
$\unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6E5}$
to be a bridge ending at the point of
$\unicode[STIX]{x1D716}_{1}$
at integer distance
$m$
of
$\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D70E}^{\prime }\subset \unicode[STIX]{x1D6E5}$
to be a bridge ending at the point of
$\unicode[STIX]{x1D716}_{2}$
at integer distance
$l$
of
$\unicode[STIX]{x1D705}$
, for some
$m,l\geqslant 1$
.
Assume that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
. Then we have
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }})^{m/(m\wedge l)}\in \text{im}(\unicode[STIX]{x1D707})$
.
Proof. Using a normalization of
$\unicode[STIX]{x1D6E5}$
at
$\unicode[STIX]{x1D705}$
if necessary, we can assume that
$\unicode[STIX]{x1D705}=(0,0)$
, that
$\unicode[STIX]{x1D716}_{1}$
is supported by the horizontal axis and that
$\unicode[STIX]{x1D70E}$
ends at
$(m,0)$
. By Lemma 6.5, we can assume, without loss of generality, that
$\unicode[STIX]{x1D70E}$
starts at
$(-1,0)$
. Consider the admissible graph
${\mathcal{G}}$
of Figure 11, where the vertical edges have weight
$-(l(m/(m\wedge l))+l/(m\wedge l))$
and the horizontal edges have weight
$-(m(l/(m\wedge l))+m/(m\wedge l))$
.
Figure 11. Admissible graph
${\mathcal{G}}$
.
As
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
, so is
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}})^{l/(m\wedge l)}$
. By Theorem 5, we have
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\in \text{im}(\unicode[STIX]{x1D707})$
. Now using Proposition 6.7 and Lemma 6.3, we can chase any primitive integer segment of
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\circ (\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}})^{-(l/(m\wedge l))}\in \text{im}(\unicode[STIX]{x1D707})$
except
$\unicode[STIX]{x1D70E}^{\prime }$
and deduce that
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }})^{m/(m\wedge l)}\in \text{im}(\unicode[STIX]{x1D707})$
.◻
Lemma 7.9. Let
$\unicode[STIX]{x1D705}$
be a vertex of
$\unicode[STIX]{x1D6E5}_{a}$
and denote by
$\unicode[STIX]{x1D716}_{1}$
and
$\unicode[STIX]{x1D716}_{2}$
the two edges of
$\unicode[STIX]{x1D6E5}_{a}$
adjacent to
$\unicode[STIX]{x1D705}$
. Also, let
$\unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6E5}$
be a bridge ending at the point next to
$\unicode[STIX]{x1D705}$
on
$\unicode[STIX]{x1D716}_{1}$
. For any positive integer
$m\leqslant \min \{l_{\unicode[STIX]{x1D716}_{1}},l_{\unicode[STIX]{x1D716}_{2}}\}$
and any bridge
$\unicode[STIX]{x1D70E}^{\prime }\subset \unicode[STIX]{x1D6E5}$
ending on
$\unicode[STIX]{x1D716}_{2}$
, then
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }})^{m}\in \text{im}(\unicode[STIX]{x1D707})$
if
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}})^{m}\in \text{im}(\unicode[STIX]{x1D707})$
.
Proof. Using a normalization of
$\unicode[STIX]{x1D6E5}$
at
$\unicode[STIX]{x1D705}$
if necessary, we can assume that
$\unicode[STIX]{x1D705}=(0,0)$
and that
$\unicode[STIX]{x1D716}_{1}$
is supported by the vertical axis. By Lemma 6.5, we can assume, without loss of generality, that
$\unicode[STIX]{x1D70E}$
joins
$(-1,0)$
to
$(0,1)$
. Consider the admissible graphs
${\mathcal{G}}$
and
${\mathcal{G}}^{\prime }$
of Figure 12, where the vertical edges have weight
$-m-1$
and the horizontal edges have weight
$-2m$
for
${\mathcal{G}}$
and
$-m-1$
for
${\mathcal{G}}^{\prime }$
. By Theorem 5, we have
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}},\unicode[STIX]{x1D70F}_{{\mathcal{G}}^{\prime }}\in \text{im}(\unicode[STIX]{x1D707})$
. Using Proposition 6.7 and Lemma 6.3, we can chase any primitive integer segment of
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\circ (\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}})^{-1}\in \text{im}(\unicode[STIX]{x1D707})$
except
$\unicode[STIX]{x1D70E}^{\prime }$
and deduce that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}\in \text{im}(\unicode[STIX]{x1D707})$
. Using, again, Proposition 6.7 and Lemma 6.3, we can chase any primitive integer segment of
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}^{\prime }}\circ (\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }})^{-1}\in \text{im}(\unicode[STIX]{x1D707})$
except
$\unicode[STIX]{x1D70E}^{\prime \prime }$
and deduce that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime \prime }}\in \text{im}(\unicode[STIX]{x1D707})$
. To conclude, we can apply Lemma 7.8 to the vertex
$\unicode[STIX]{x1D705}$
and the primitive integer segment
$\unicode[STIX]{x1D70E}^{\prime \prime }$
.◻
Figure 12. Admissible graphs
${\mathcal{G}}$
(left) and
${\mathcal{G}}^{\prime }$
(right).
Proof of Proposition 7.7.
Let
$\unicode[STIX]{x1D716}_{1}$
and
$\unicode[STIX]{x1D716}_{2}$
be two consecutive edges of
$\unicode[STIX]{x1D6E5}_{a}$
intersecting at the vertex
$\unicode[STIX]{x1D705}$
. We first claim that, for any bridge
$\unicode[STIX]{x1D70E}$
ending on
$\unicode[STIX]{x1D716}_{1}\cup \unicode[STIX]{x1D716}_{2}$
, we have
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}})^{l_{\unicode[STIX]{x1D716}_{1}}\wedge l_{\unicode[STIX]{x1D716}_{2}}}\in \text{im}(\unicode[STIX]{x1D707})$
. Without loss of generality, we may assume that
$l_{\unicode[STIX]{x1D716}_{1}}\geqslant l_{\unicode[STIX]{x1D716}_{2}}$
and consider the normalization of
$\unicode[STIX]{x1D6E5}$
at
$\unicode[STIX]{x1D705}$
such that
$\unicode[STIX]{x1D716}_{1}$
is horizontal. Let
$\unicode[STIX]{x1D709}$
be the other end of
$\unicode[STIX]{x1D716}_{2}$
.
Since
$\unicode[STIX]{x1D709}$
is a vertex, we know from Proposition 6.6 that if
$\unicode[STIX]{x1D70E}^{\prime }$
is a bridge ending at
$\unicode[STIX]{x1D709}$
then
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}\in \text{im}(\unicode[STIX]{x1D707})$
. Using Lemma 7.8 and then Lemma 7.9, we deduce that for any bridge
$\unicode[STIX]{x1D70E}$
ending on
$\unicode[STIX]{x1D716}_{1}\cup \unicode[STIX]{x1D716}_{2}$
, we have
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}})^{l_{\unicode[STIX]{x1D716}_{2}}}\in \text{im}(\unicode[STIX]{x1D707})$
.
Now consider the weighted graph
${\mathcal{G}}^{\prime \prime }$
given in Figure 13 where the horizontal edges have weight
$-2l_{\unicode[STIX]{x1D716}_{1}}$
and the vertical edges have weight
$-2$
.
Figure 13. Admissible graph
${\mathcal{G}}^{\prime \prime }$
.
This graph is admissible, so by Theorem 5, we know that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}^{\prime \prime }}\in \text{im}(\unicode[STIX]{x1D707})$
. Using Propositions 6.6 and 6.7, as well as Lemma 6.3, we obtain that
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime \prime }})^{l_{\unicode[STIX]{x1D716}_{1}}}\in \text{im}(\unicode[STIX]{x1D707})$
and thus
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime \prime }})^{l_{\unicode[STIX]{x1D716}_{1}}\wedge l_{\unicode[STIX]{x1D716}_{2}}}\in \text{im}(\unicode[STIX]{x1D707})$
. Applying Lemma 7.9 twice, we deduce that, for any bridge
$\unicode[STIX]{x1D70E}$
ending on
$\unicode[STIX]{x1D716}_{1}\cup \unicode[STIX]{x1D716}_{2}$
, we have that
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}})^{l_{\unicode[STIX]{x1D716}_{1}}\wedge l_{\unicode[STIX]{x1D716}_{2}}}\in \text{im}(\unicode[STIX]{x1D707})$
; this proves the claim.
Using this claim and Lemma 7.9, we show by induction that, for any
$k$
consecutive edges
$\unicode[STIX]{x1D716}_{1},\ldots \unicode[STIX]{x1D716}_{k}$
of
$\unicode[STIX]{x1D6E5}_{a}$
, we have
$(\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}})^{l_{\unicode[STIX]{x1D716}_{1}}\wedge \cdots \wedge l_{\unicode[STIX]{x1D716}_{k}}}\in \text{im}(\unicode[STIX]{x1D707})$
for all bridges
$\unicode[STIX]{x1D70E}$
ending on
$\unicode[STIX]{x1D716}_{1}\cup \cdots \cup \unicode[STIX]{x1D716}_{k}$
. The result follows.◻
The proof of the case
$d=2$
in Theorem 1 involves finding a family of Dehn twists in the image of the monodromy, which generates the mapping class group. This family will appear as a ‘snake’ in
$\unicode[STIX]{x1D6E5}$
.
Definition 7.10. A snake in the polygon
$\unicode[STIX]{x1D6E5}$
is a family of primitive integer segments
$\unicode[STIX]{x1D70E}_{1}=[v_{0},v_{1}],\unicode[STIX]{x1D70E}_{2}=[v_{1},v_{2}],\ldots ,\unicode[STIX]{x1D70E}_{g_{{\mathcal{L}}}}=[v_{g_{{\mathcal{L}}}-1},v_{g_{{\mathcal{L}}}}],\unicode[STIX]{x1D70E}$
in
$\unicode[STIX]{x1D6E5}$
, such that:
(i) the point
$v_{0}$
is a boundary point of
$\unicode[STIX]{x1D6E5}$
, while the points
$v_{1},\ldots ,v_{g_{{\mathcal{L}}}}$
are distinct points of
$\unicode[STIX]{x1D6E5}_{a}$
such that
$v_{1}$
is a vertex of
$\unicode[STIX]{x1D6E5}_{a}$
and
$v_{2}$
sits on
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}_{a}$
;(ii) two segments
$\unicode[STIX]{x1D70E}_{i}$
and
$\unicode[STIX]{x1D70E}_{i}$
intersect if and only if
$|i-j|=1$
;(iii) the segment
$\unicode[STIX]{x1D70E}$
is a bridge ending at
$v_{2}$
and disjoint from
$\unicode[STIX]{x1D70E}_{1}$
.
Given a snake in
$\unicode[STIX]{x1D6E5}$
, the loops
$\unicode[STIX]{x1D6FF}_{v_{i}}$
and
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}_{i}}$
are arranged as in Figure 14.
Figure 14. Loops
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}_{1}},\ldots ,\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}_{g_{{\mathcal{L}}}}}$
and
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}$
in
$C_{0}$
.
Lemma 7.11. There always exists a snake
$\unicode[STIX]{x1D70E}_{1}=[v_{0},v_{1}],\unicode[STIX]{x1D70E}_{2}=[v_{1},v_{2}],\ldots ,\unicode[STIX]{x1D70E}_{g_{{\mathcal{L}}}}=[v_{g_{{\mathcal{L}}}-1},v_{g_{{\mathcal{L}}}}],\unicode[STIX]{x1D70E}$
in
$\unicode[STIX]{x1D6E5}$
. Moreover, if
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}},\ldots ,\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{g_{{\mathcal{L}}}}},\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}$
are in
$\text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}}],\ldots ,[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{g_{{\mathcal{L}}}}}],[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}]$
are in
$\text{im}([\unicode[STIX]{x1D707}])$
, the map
$\unicode[STIX]{x1D707}$
(respectively
$[\unicode[STIX]{x1D707}]$
) is surjective.
Proof. To prove the existence of a snake, choose a vertex
$\unicode[STIX]{x1D705}$
of
$\unicode[STIX]{x1D6E5}_{a}$
and take a normalization of
$\unicode[STIX]{x1D6E5}$
at
$\unicode[STIX]{x1D705}$
. Let
$v_{0}=(-1,0)$
,
$v_{1}=\unicode[STIX]{x1D705}$
,
$v_{2}=(1,0)$
and
$\unicode[STIX]{x1D70E}=[(0,-1),(1,0)]$
. We number the rest of the lattice points in
$\unicode[STIX]{x1D6E5}_{a}$
by going through them in colexicographic order.
We know from Theorem 3 that, for
$i=1,\ldots ,g_{{\mathcal{L}}}$
, the Dehn twist
$\unicode[STIX]{x1D70F}_{v_{i}}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
. The second part of the lemma then follows from Humphries’ theorem [Reference HumphriesHum79], which states that the family
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}},\unicode[STIX]{x1D70F}_{v_{1}},\ldots ,\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{g_{{\mathcal{L}}}}},\unicode[STIX]{x1D70F}_{v_{g_{{\mathcal{L}}}}}$
, and
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}$
generates the group
$\text{MCG}(C_{0})$
.◻
Proof of Theorem 1, case
$d=2$
and
$n=1$
.
Assume that the largest order of a root of
$K_{X}\otimes {\mathcal{L}}$
is
$1$
. We know from Proposition 3.1 that
$\gcd (\{l_{\unicode[STIX]{x1D716}}\mid \unicode[STIX]{x1D716}\text{ edge of }\unicode[STIX]{x1D6E5}_{a}\})=1$
. Thus it follows from Proposition 7.7 that, for any bridge, the associated Dehn twist is in
$\text{im}(\unicode[STIX]{x1D707})$
. Proposition 7.6 then implies that, for any primitive integer segment
$\unicode[STIX]{x1D70E}$
joining two points of
$\unicode[STIX]{x1D6E5}\cap \mathbb{Z}^{2}$
not both on the boundary of
$\unicode[STIX]{x1D6E5}$
, we have
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
. In particular, taking any snake in
$\unicode[STIX]{x1D6E5}$
, all the corresponding Dehn twists are in
$\text{im}(\unicode[STIX]{x1D707})$
. Lemma 7.11 then gives the result we wanted.◻
7.4
$K_{X}\otimes {\mathcal{L}}$
odd
Proof of Theorem 2, case
$d=2$
and
$n$
odd.
Since
$K_{X}\otimes {\mathcal{L}}$
does not have a square root, the largest order of one of its roots is odd. Let us show that the algebraic monodromy
$[\unicode[STIX]{x1D707}]$
is surjective on
$\text{Sp}(H_{1}(C_{0},\mathbb{Z}))$
.
Notice first that since
$n$
is odd, we know from Proposition 3.1 that the greatest common divisor
$s$
of the lengths of the edges of
$\unicode[STIX]{x1D6E5}_{a}$
is odd.
Using Lemma 7.11, take a snake
$\unicode[STIX]{x1D70E}_{1}=[v_{0},v_{1}],\unicode[STIX]{x1D70E}_{2}=[v_{1},v_{2}],\ldots ,\unicode[STIX]{x1D70E}_{g_{{\mathcal{L}}}}=[v_{g_{{\mathcal{L}}}-1},v_{g_{{\mathcal{L}}}}],\unicode[STIX]{x1D70E}$
in
$\unicode[STIX]{x1D6E5}$
. We know from Proposition 7.7 that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}^{s}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
.
Conversely,
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}]^{2}$
is in
$\text{im}([\unicode[STIX]{x1D707}])$
. Indeed, we know from Propositions 6.6 and 6.7 and Theorem 3 that
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}}]$
,
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}]$
, and
$[\unicode[STIX]{x1D70F}_{v_{1}}]$
are in
$\text{im}([\unicode[STIX]{x1D707}])$
. Since both boundary components of a closed regular neighborhood of
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}_{1}}\cup \unicode[STIX]{x1D6FF}_{v_{1}}\cup \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}_{2}}$
are homologous to
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}}$
in
$C_{0}$
if one orients them carefully, using the chain rule (see [Reference Farb and MargalitFM11, Proposition 4.12]), we have
$$\begin{eqnarray}([\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}}][\unicode[STIX]{x1D70F}_{v_{1}}][\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}])^{4}=[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}]^{2}\in \text{im}([\unicode[STIX]{x1D707}]).\end{eqnarray}$$
Since
$s$
is odd, we deduce that
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}]$
is in
$\text{im}([\unicode[STIX]{x1D707}])$
. We apply Proposition 7.6 to deduce that, for any
$i=1,\ldots ,g_{{\mathcal{L}}}$
,
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{i}}]$
is in
$\text{im}([\unicode[STIX]{x1D707}])$
. Lemma 7.11 provides the last piece of the proof.◻
7.5 About Conjecture 1
We show in this section that, when the adjoint bundle of
${\mathcal{L}}$
admits a non-trivial root
${\mathcal{S}}$
, we can still exhibit a lot of (powers of) Dehn twists in
$\text{im}(\unicode[STIX]{x1D707})$
and
$\text{im}([\unicode[STIX]{x1D707}])$
. This is a motivation for Conjecture 1 as well as a preparation for the results of [Reference Crétois and LangCL17]. Indeed, we will show in [Reference Crétois and LangCL17] that the conjecture is true when the highest order of a root of
$K_{X}\otimes {\mathcal{L}}$
is
$2$
.
Let
$d\geqslant 1$
be an integer and
$h_{1/d,\unicode[STIX]{x1D705}}$
be the homothety of ratio
$1/d$
and centered at
$\unicode[STIX]{x1D705}$
. When
$h_{1/d,\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D6E5}_{a})$
is again a lattice polygon, we say that
$\unicode[STIX]{x1D6E5}_{a}$
is divisible by
$d$
and we denote by
$\unicode[STIX]{x1D6E5}_{a}(d)$
the subset
$h_{1/d,\unicode[STIX]{x1D705}}^{-1}(h_{1/d,\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D6E5}_{a})\cap \mathbb{Z})$
. Note that neither
$d$
nor
$\unicode[STIX]{x1D6E5}_{a}(d)$
depend on the choice of the vertex
$\unicode[STIX]{x1D705}$
. In this case, we introduce a variation of the graphs
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}$
and
${\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}^{m_{1},m_{2}}$
, which we will use to motivate conjecture 1.
Assume that
$v=h_{1/d,\unicode[STIX]{x1D705}}^{-1}(u)\in \unicode[STIX]{x1D6E5}_{a}(d)$
and denote by
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}(d)$
(respectively
${\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}^{m_{1},m_{2}}(d)$
) the following weighted graphs. The graph
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}(d)$
(respectively
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}(d)$
) is given as the reunion of
$h_{1/d,\unicode[STIX]{x1D705}}^{-1}(G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },u}\cap \unicode[STIX]{x1D6E5}_{a})$
(respectively of
$h_{1/d,\unicode[STIX]{x1D705}}^{-1}(G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},u}\cap \unicode[STIX]{x1D6E5}_{a})$
) and of the segments
$[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}^{\prime },h_{1/d,\unicode[STIX]{x1D705}}^{-1}(\unicode[STIX]{x1D705}^{\prime })]$
,
$[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}^{\prime },\unicode[STIX]{x1D705}]$
, and
$[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D705}]$
. The weight function on
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}(d)$
(respectively on
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}(d)$
) is equal to
$m_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },u}^{m_{1},m_{2}}\circ h_{1/d,\unicode[STIX]{x1D705}}$
(respectively to
$m_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},u}^{m_{1},m_{2}}\circ h_{1/d,\unicode[STIX]{x1D705}}$
) inside
$\unicode[STIX]{x1D6E5}_{a}$
and adjusted on the last three segments to be balanced at
$\unicode[STIX]{x1D705}$
and
$h_{1/d,\unicode[STIX]{x1D705}}^{-1}(\unicode[STIX]{x1D705}^{\prime })$
. We denote by
$\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{2}$
the two primitive integer segments in
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}(d)$
(respectively in
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}(d)$
) that have an end at
$v$
.
We have the analogue of Lemma 7.5. We omit its proof, as it is the same as that of Lemma 7.5.
Lemma 7.12. Let
$d\geqslant 1$
be an integer and assume that
$\unicode[STIX]{x1D6E5}_{a}$
is divisible by
$d$
. Let
$v\in \unicode[STIX]{x1D6E5}_{a}(d)$
.
The weighted graphs
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}(d)$
and
${\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}^{m_{1},m_{2}}(d)$
satisfy the following properties.
(i) The edges
$\unicode[STIX]{x1D70E}_{1}=\unicode[STIX]{x1D70E}_{1,0}$
and
$\unicode[STIX]{x1D70E}_{2}=\unicode[STIX]{x1D70E}_{2,0}$
generate the lattice.(ii) The weight function
$m_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}^{m_{1},m_{2}}$
(respectively
$m_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}^{m_{1},m_{2}}$
) satisfies the balancing condition (5) at every element of
$V(G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },v}(d))\cap \text{int}\unicode[STIX]{x1D6E5}$
(respectively
$V(G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}(d))\cap \text{int}\unicode[STIX]{x1D6E5}$
), except at
$v$
.
Assume, moreover, that there is a bridge
$\unicode[STIX]{x1D70E}^{\prime }$
ending at
$h_{1/d,\unicode[STIX]{x1D705}}^{-1}(\unicode[STIX]{x1D705}^{\prime })$
, such that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}]$
is in
$\text{im}([\unicode[STIX]{x1D707}])$
). Then
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}}$
and
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}$
are in
$\text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}}]$
and
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}]$
are in
$\text{im}([\unicode[STIX]{x1D707}])$
).◻
Proposition 7.13. Let
$d\geqslant 1$
be an integer and assume that
$\unicode[STIX]{x1D6E5}_{a}$
is divisible by
$d$
. Assume that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}]\in \text{im}([\unicode[STIX]{x1D707}])$
) for any bridge
$\unicode[STIX]{x1D70E}^{\prime }$
ending at a point in
$\unicode[STIX]{x1D6E5}_{a}(d)$
. Then we have
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}]\in \text{im}([\unicode[STIX]{x1D707}])$
) for any primitive integer segment
$\unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6E5}$
such that the line supported by
$\unicode[STIX]{x1D70E}$
intersects
$\unicode[STIX]{x1D6E5}_{a}(d)$
.
Proof. The proof uses the same ideas as that of Proposition 7.6. Namely, let
$v$
and
$w$
be the two ends of
$\unicode[STIX]{x1D70E}$
. Let us denote by
$L$
the line supported by
$\unicode[STIX]{x1D70E}$
and
$u$
, a point in
$\unicode[STIX]{x1D6E5}_{a}(d)\cap L$
. We may assume that
$v$
is on the segment
$[u,w]$
and that
$[u,w]\cap \unicode[STIX]{x1D6E5}_{a}(d)=\{u\}$
. We will only give the proof in the case where both
$u$
and
$w$
are in the interior of
$\unicode[STIX]{x1D6E5}_{a}$
, as the other cases follow the same pattern as in Proposition 7.6.
To this end, choose
$\unicode[STIX]{x1D705}$
and
$\unicode[STIX]{x1D709}$
two consecutive vertices of
$\unicode[STIX]{x1D6E5}_{a}$
that are on the same side of
$L$
and such that the points
$u$
,
$w$
,
$\unicode[STIX]{x1D709}$
, and
$\unicode[STIX]{x1D705}$
appear in this order when following the boundary of their convex hull in the clockwise orientation. Take a normalization of
$\unicode[STIX]{x1D6E5}$
at
$\unicode[STIX]{x1D705}$
such that the edge
$[\unicode[STIX]{x1D705},\unicode[STIX]{x1D709}]$
is horizontal.
Since the roles of
$v$
and
$w$
are not the same, we will need to consider two cases. If the line
$L$
intersects the vertical line though
$\unicode[STIX]{x1D705}$
in the interval
$[\unicode[STIX]{x1D705},(0,d))$
, take
$\unicode[STIX]{x1D705}^{\prime }=(1,0)$
and
$\unicode[STIX]{x1D709}^{\prime }$
the boundary lattice point of
$\unicode[STIX]{x1D6E5}_{a}$
adjacent to
$\unicode[STIX]{x1D709}$
and not on the segment
$[\unicode[STIX]{x1D705},\unicode[STIX]{x1D709}]$
. In the other case, take
$\unicode[STIX]{x1D705}^{\prime }=(0,1)$
and
$\unicode[STIX]{x1D709}^{\prime }$
the boundary point of
$\unicode[STIX]{x1D6E5}_{a}$
adjacent to
$\unicode[STIX]{x1D709}$
and on the segment
$[\unicode[STIX]{x1D705},\unicode[STIX]{x1D709}]$
. Now consider the graph
$G$
to be the reunion of
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},u}(d)$
,
$[u,w]$
and
$G_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}$
in the first case and the reunion of
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },u}(d)$
,
$[u,w]$
and
$G_{\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709},w}$
in the second case (see Figure 15). Notice that, in the first case, the pentagon
$\unicode[STIX]{x1D705},u,w,\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709}$
is convex and, in the second case, the pentagon
$\unicode[STIX]{x1D705},h_{1/d,\unicode[STIX]{x1D705}}^{-1}(\unicode[STIX]{x1D705}^{\prime }),u,w,\unicode[STIX]{x1D709}$
is convex. It can be shown, as in the proof of Proposition 7.6, that
$G$
is supported by a unimodular convex subdivision.
Figure 15. Rough sketch of the admissible graph
${\mathcal{G}}$
in the two cases.
We next define a weighted graph
${\mathcal{G}}=(G,m)$
. Let
$\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{2}$
(respectively
$\unicode[STIX]{x1D702}_{1}$
and
$\unicode[STIX]{x1D702}_{2}$
) be the primitive integer segments in
$G$
going out of
$u$
(respectively out of
$w$
). Since
$\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{2}$
generate the lattice, choose
$m_{1}$
and
$m_{2}$
such that
$\unicode[STIX]{x1D70E}+m_{1}\unicode[STIX]{x1D70E}_{1}+m_{2}\unicode[STIX]{x1D70E}_{2}=0$
(where the orientations go out of
$u$
). In the same manner, choose
$m_{1}^{\prime }$
and
$m_{2}^{\prime }$
such that
$\unicode[STIX]{x1D70E}+m_{1}^{\prime }\unicode[STIX]{x1D702}_{1}+m_{2}^{\prime }\unicode[STIX]{x1D702}_{2}=0$
(where the orientations go out of
$w$
). In the first case, take the weight function
$m$
to be that of
${\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},u}^{m_{1},m_{2}}(d)$
on
$G_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},u}(d)$
, that of
${\mathcal{G}}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}^{m_{1}^{\prime },m_{2}^{\prime }}$
on
$G_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}$
, and equal to
$1$
on
$[u,w]$
. In the second case, take the weight function of
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },u}^{m_{1},m_{2}}(d)$
on
$G_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },u}(d)$
, that of
${\mathcal{G}}_{\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709},w}^{m_{1}^{\prime },m_{2}^{\prime }}$
on
$G_{\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709},w}$
, and equal to
$1$
on
$[u,w]$
. The weighted graph
${\mathcal{G}}$
is admissible, so from Theorem 5, we know that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\in \text{im}(\unicode[STIX]{x1D707})$
. The conclusion is the same as in Proposition7.6.
The cases where at least one of the ends of
$[u,w]$
is not in
$\text{int}(\unicode[STIX]{x1D6E5})$
can be treated in the same way as in Proposition 7.6.◻
As we noticed in Corollary 2.8, when
$\unicode[STIX]{x1D6E5}_{a}$
is divisible by an integer
$d>1$
, we cannot have
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
for all primitive integer segments in
$\unicode[STIX]{x1D6E5}$
. However, we have the following two statements.
Lemma 7.14. Let
$d>1$
be an integer and assume that
$\unicode[STIX]{x1D6E5}_{a}$
is divisible by
$d$
. Assume that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}]\in \text{im}([\unicode[STIX]{x1D707}])$
) for any bridge
$\unicode[STIX]{x1D70E}^{\prime }$
ending at a point in
$\unicode[STIX]{x1D6E5}_{a}(d)$
. Let
$w\in \unicode[STIX]{x1D6E5}_{a}$
be an interior lattice point,
$\unicode[STIX]{x1D705}$
any vertex of
$\unicode[STIX]{x1D6E5}_{a}$
, and
$\unicode[STIX]{x1D705}^{\prime }$
and
$\unicode[STIX]{x1D705}^{\prime \prime }$
the lattice points of
$\unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}_{a}$
next to
$\unicode[STIX]{x1D705}$
on each side. Then, for any integers
$m_{1}$
and
$m_{2}$
,
$$\begin{eqnarray}(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{m_{1},m_{2}}})^{d},(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},w}^{m_{1},m_{2}}})^{d},(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime \prime },w}^{m_{1},m_{2}}})^{d},(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime \prime },\unicode[STIX]{x1D705},w}^{m_{1},m_{2}}})^{d}\in \text{im}(\unicode[STIX]{x1D707}).\end{eqnarray}$$
We prove this lemma after the following proposition.
Proposition 7.15. Let
$d>1$
be an integer and assume that
$\unicode[STIX]{x1D6E5}_{a}$
is divisible by
$d$
. Assume that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}]\in \text{im}([\unicode[STIX]{x1D707}])$
) for any bridge
$\unicode[STIX]{x1D70E}^{\prime }$
ending at a point in
$\unicode[STIX]{x1D6E5}_{a}(d)$
. Then for any primitive integer segment
$\unicode[STIX]{x1D70E}\subset \unicode[STIX]{x1D6E5}$
, we have
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}^{d}\in \text{im}(\unicode[STIX]{x1D707})$
(respectively
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}]^{d}\in \text{im}([\unicode[STIX]{x1D707}])$
).
Proof. The idea of the proof is similar to that of Proposition 7.6. Namely, if
$v$
and
$w$
denote the two ends of
$\unicode[STIX]{x1D70E}$
, we first assume that they are both in the interior of
$\unicode[STIX]{x1D6E5}_{a}$
and we consider exactly the same weighted graph
${\mathcal{G}}=(G,m)$
as in Proposition 7.6. Recall that it contains two subgraphs,
${\mathcal{G}}_{1}={\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},v}^{m_{1},m_{2}}$
and
${\mathcal{G}}_{2}={\mathcal{G}}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}^{m_{1}^{\prime },m_{2}^{\prime }}$
. From Theorem 5, we know that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{1}}\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{2}}\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
. Lemma 7.14 gives us the conclusion we want.
The cases where one of the ends is not in the interior of
$\unicode[STIX]{x1D6E5}_{a}$
can be proved in the same way. We leave it to the reader.◻
Proof of Lemma 7.14.
Recall that
$\unicode[STIX]{x1D70E}_{1}$
and
$\unicode[STIX]{x1D70E}_{2}$
are the two primitive integer segments in
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{m_{1},m_{2}}$
going out of
$w$
. Let us first show that if
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{m_{1},m_{2}}}\in \text{im}(\unicode[STIX]{x1D707})$
then for any vertex
$\unicode[STIX]{x1D709}$
of
$\unicode[STIX]{x1D6E5}_{a}$
,
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}^{a_{1},a_{2}}},\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime \prime },w}^{b_{1},b_{2}}},\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709},w}^{c_{1},c_{2}}},\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D709}^{\prime \prime },\unicode[STIX]{x1D709},w}^{d_{1},d_{2}}}\in \text{im}(\unicode[STIX]{x1D707}),\end{eqnarray}$$
where the weights are chosen so that adding
$m_{1}\unicode[STIX]{x1D70E}_{1}+m_{2}\unicode[STIX]{x1D70E}_{2}$
balances each graph at
$w$
.
To this end, we can assume that
$\unicode[STIX]{x1D709}$
is a vertex next to
$\unicode[STIX]{x1D705}$
, so that
$\unicode[STIX]{x1D705}^{\prime \prime }$
and
$\unicode[STIX]{x1D709}^{\prime \prime }$
are on
$[\unicode[STIX]{x1D705},\unicode[STIX]{x1D709}]$
.
(i) The weighted graph obtained by concatenating
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{m_{1},m_{2}}$
and
${\mathcal{G}}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}^{a_{1},a_{2}}$
is admissible, so, by Theorem 5,
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{m_{1},m_{2}}}\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}^{a_{1},a_{2}}}\in \text{im}(\unicode[STIX]{x1D707})$
.(ii) The weighted graph obtained by concatenating
${\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{m_{1},m_{2}}$
and
${\mathcal{G}}_{\unicode[STIX]{x1D709}^{\prime \prime },\unicode[STIX]{x1D709},w}^{d_{1},d_{2}}$
is admissible, so, by Theorem 5,
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{m_{1},m_{2}}}\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D709}^{\prime \prime },\unicode[STIX]{x1D709},w}^{d_{1},d_{2}}}\in \text{im}(\unicode[STIX]{x1D707})$
.(iii) The weighted graph obtained by concatenating
${\mathcal{G}}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}^{a_{1},a_{2}}$
and
${\mathcal{G}}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime \prime },w}^{b_{1},b_{2}}$
is admissible, so, by Theorem 5,
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}^{a_{1},a_{2}}}\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime \prime },w}^{b_{1},b_{2}}}\in \text{im}(\unicode[STIX]{x1D707})$
.
To prove that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709},w}^{c_{1},c_{2}}}\in \text{im}(\unicode[STIX]{x1D707})$
, we consider the vertex
$\unicode[STIX]{x1D701}$
next to
$\unicode[STIX]{x1D709}$
such that
$\unicode[STIX]{x1D709}^{\prime }$
and
$\unicode[STIX]{x1D701}^{\prime }$
are on
$[\unicode[STIX]{x1D709},\unicode[STIX]{x1D701}]$
. We choose weights so that adding
$m_{1}\unicode[STIX]{x1D70E}_{1}+m_{2}\unicode[STIX]{x1D70E}_{2}$
balances the graph
${\mathcal{G}}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D701},w}^{e_{1},e_{2}}$
at
$w$
.
(i) The weighted graph obtained by concatenating
${\mathcal{G}}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime \prime },w}^{b_{1},b_{2}}$
and
${\mathcal{G}}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D701},w}^{e_{1},e_{2}}$
is admissible, so, by Theorem 5,
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime \prime },w}^{b_{1},b_{2}}}\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D701},w}^{e_{1},e_{2}}}\in \text{im}(\unicode[STIX]{x1D707})$
.(ii) The weighted graph obtained by concatenating
${\mathcal{G}}_{\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709},w}^{c_{1},c_{2}}$
and
${\mathcal{G}}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D701},w}^{e_{1},e_{2}}$
is admissible, so, by Theorem 5,
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709},w}^{c_{1},c_{2}}}\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D701}^{\prime },\unicode[STIX]{x1D701},w}^{e_{1},e_{2}}}\in \text{im}(\unicode[STIX]{x1D707})$
.
Thus, we obtain the result we wanted. Notice that the previous claim is still true if we assume that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},w}^{m_{1},m_{2}}}$
is in
$\text{im}(\unicode[STIX]{x1D707})$
instead of
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{m_{1},m_{2}}}$
.
Now, choose a unimodular convex subdivision of
$h_{1/d,\unicode[STIX]{x1D705}}(\unicode[STIX]{x1D6E5}_{a})$
. The point
$h_{1/d,\unicode[STIX]{x1D705}}(w)$
is in at least one of the triangles of this subdivision, possibly on its boundary. Let
$x$
,
$y$
, and
$z$
be the three vertices of the image of such a triangle by
$h_{1/d,\unicode[STIX]{x1D705}}^{-1}$
. Denote by
$\unicode[STIX]{x1D6FE}_{1}$
,
$\unicode[STIX]{x1D6FE}_{2}$
, and
$\unicode[STIX]{x1D6FE}_{3}$
, respectively, the primitive integer segments on
$[x,w]$
,
$[y,w]$
, and
$[z,w]$
ending at
$w$
.
Let us now show that
$(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{m_{1},m_{2}}})^{d}\in \text{im}(\unicode[STIX]{x1D707})$
. We proceed as in the proof of Proposition 7.13, using
$\unicode[STIX]{x1D6FE}_{1}$
in place of
$\unicode[STIX]{x1D70E}$
. Using the same notation, we obtain that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\prime },w}^{m_{1}^{\prime },m_{2}^{\prime }}}\in \text{im}(\unicode[STIX]{x1D707})$
in the first case, and
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D709}^{\prime },\unicode[STIX]{x1D709},w}^{m_{1}^{\prime },m_{2}^{\prime }}}\in \text{im}(\unicode[STIX]{x1D707})$
in the second case for some vertex
$\unicode[STIX]{x1D709}$
of
$\unicode[STIX]{x1D6E5}_{a}$
. Using the claim we proved in the beginning, we have that
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{a_{1},a_{2}}},\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},w}^{b_{1},b_{2}}},\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime \prime },w}^{c_{1},c_{2}}},\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime \prime },\unicode[STIX]{x1D705},w}^{d_{1},d_{2}}}\in \text{im}(\unicode[STIX]{x1D707}),\end{eqnarray}$$
where the weights are chosen so that adding
$\unicode[STIX]{x1D6FE}_{1}$
with weight
$1$
balances the graph at
$w$
.
We do the same for
$\unicode[STIX]{x1D6FE}_{2}$
to prove that
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{a_{1}^{\prime },a_{2}^{\prime }}},\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},w}^{b_{1}^{\prime },b_{2}^{\prime }}},\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime \prime },w}^{c_{1}^{\prime },c_{2}^{\prime }}},\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime \prime },\unicode[STIX]{x1D705},w}^{d_{1}^{\prime },d_{2}^{\prime }}}\in \text{im}(\unicode[STIX]{x1D707}),\end{eqnarray}$$
where the weights are chosen so that adding
$\unicode[STIX]{x1D6FE}_{2}$
with weight
$1$
balances the graph at
$w$
, and for
$\unicode[STIX]{x1D6FE}_{3}$
to obtain that
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{a_{1}^{\prime \prime },a_{2}^{\prime \prime }}},\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime },\unicode[STIX]{x1D705},w}^{b_{1}^{\prime \prime },b_{2}^{\prime \prime }}},\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime \prime },w}^{c_{1}^{\prime \prime },c_{2}^{\prime \prime }}},\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705}^{\prime \prime },\unicode[STIX]{x1D705},w}^{d_{1}^{\prime \prime },d_{2}^{\prime \prime }}}\in \text{im}(\unicode[STIX]{x1D707}),\end{eqnarray}$$
where the weights are chosen so that adding
$\unicode[STIX]{x1D6FE}_{3}$
with weight
$1$
balances the graph at
$w$
.
Since
$d\mathbb{Z}$
is included in the lattice generated by
$\unicode[STIX]{x1D6FE}_{1}$
,
$\unicode[STIX]{x1D6FE}_{2}$
, and
$\unicode[STIX]{x1D6FE}_{3}$
, we can find integer combinations
$\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FE}_{1}+\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FE}_{2}+\unicode[STIX]{x1D6FC}_{3}\unicode[STIX]{x1D6FE}_{3}+d\unicode[STIX]{x1D70E}_{1}=0$
and
$\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FE}_{1}+\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D6FE}_{2}+\unicode[STIX]{x1D6FD}_{3}\unicode[STIX]{x1D6FE}_{3}+d\unicode[STIX]{x1D70E}_{2}=0$
. Thus,
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{d,0}}=(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{a_{1},a_{2}}})^{\unicode[STIX]{x1D6FC}_{1}}(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{a_{1}^{\prime },a_{2}^{\prime }}})^{\unicode[STIX]{x1D6FC}_{2}}(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{a_{1}^{\prime \prime },a_{2}^{\prime \prime }}})^{\unicode[STIX]{x1D6FC}_{3}}\in \text{im}(\unicode[STIX]{x1D707})\end{eqnarray}$$
and
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{0,d}}=(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{a_{1},a_{2}}})^{\unicode[STIX]{x1D6FD}_{1}}(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{a_{1}^{\prime },a_{2}^{\prime }}})^{\unicode[STIX]{x1D6FD}_{2}}(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{a_{1}^{\prime \prime },a_{2}^{\prime \prime }}})^{\unicode[STIX]{x1D6FD}_{3}}\in \text{im}(\unicode[STIX]{x1D707}).\end{eqnarray}$$
This implies that
$$\begin{eqnarray}(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{m_{1},m_{2}}})^{d}=(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{d,0}})^{m_{1}}(\unicode[STIX]{x1D70F}_{{\mathcal{G}}_{\unicode[STIX]{x1D705},\unicode[STIX]{x1D705}^{\prime },w}^{0,d}})^{m_{2}}\in \text{im}(\unicode[STIX]{x1D707}).\end{eqnarray}$$
We conclude the proof of Lemma 7.14 using the same argument for the three other graphs. ◻
To be able to apply Propositions 7.13 and 7.15, we need to be able to say something about the bridges ending at a point of
$\unicode[STIX]{x1D6E5}_{a}(d)$
.
Proposition 7.16. Let
$s=\gcd (\{l_{\unicode[STIX]{x1D716}}\mid \unicode[STIX]{x1D716}\text{ edge of }\unicode[STIX]{x1D6E5}_{a}\})$
. If
$v\in \unicode[STIX]{x1D6E5}_{a}(s)\cap \unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}_{a}$
, then, for any bridge
$\unicode[STIX]{x1D70E}$
ending at
$v$
, we have
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
. Moreover, if
$s$
is even and
$v\in \unicode[STIX]{x1D6E5}_{a}(2)$
, then, for any bridge
$\unicode[STIX]{x1D70E}$
ending at
$v$
, we have
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}]\in \text{im}([\unicode[STIX]{x1D707}])$
.
Proof. We may assume that
$v$
is not a vertex, as this case is taken care of by Proposition 6.6. Let
$v\in \unicode[STIX]{x2202}\unicode[STIX]{x1D6E5}_{a}$
and let
$\unicode[STIX]{x1D705}$
be a vertex of
$\unicode[STIX]{x1D6E5}_{a}$
next to
$v$
. Using a normalization at
$\unicode[STIX]{x1D705}$
, we may assume that
$v$
is of the form
$(l,0)$
for some integer
$l\geqslant 1$
. Using Lemma 6.5, we may assume that
$\unicode[STIX]{x1D70E}$
joins
$v$
to
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}=(0,-1)$
. Now consider the weighted graph
${\mathcal{G}}$
given in Figure 16, where the horizontal edges have weight
$-2l$
. This graph is admissible so, by Theorem 5, we know that
$\unicode[STIX]{x1D70F}_{{\mathcal{G}}}\in \text{im}(\unicode[STIX]{x1D707})$
.
Figure 16. Weighted graph
${\mathcal{G}}$
.
If
$v\in \unicode[STIX]{x1D6E5}_{a}(s)$
, we have
$l=as$
for some integer
$a\geqslant 1$
. We know from Proposition 7.7 that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}^{as}\in \text{im}(\unicode[STIX]{x1D707})$
. Thus, applying Propositions 6.6 and 6.7 as well as Lemma 6.3, we obtain that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}\in \text{im}(\unicode[STIX]{x1D707})$
.
If
$s$
is even and
$v\in \unicode[STIX]{x1D6E5}_{a}(2)$
, then
$l=2a$
for some integer
$a\geqslant 1$
. Let
$\unicode[STIX]{x1D70E}^{\prime }$
be the bridge joining
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}}^{\prime }=(-1,0)$
to
$(0,1)$
. We do not have, in general, that
$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}^{2}\in \text{im}(\unicode[STIX]{x1D707})$
. However, if we define
$\unicode[STIX]{x1D70E}_{1}=[\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D705}},\unicode[STIX]{x1D705}]$
and
$\unicode[STIX]{x1D70E}_{2}=[\unicode[STIX]{x1D705},(0,1)]$
, the boundary of a regular neighborhood of
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}_{1}}\cup \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D705}}\cup \unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}_{2}}$
has two connected components both homologous to
$\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70E}^{\prime }}$
if one orients them carefully. Using the chain rule (see [Reference Farb and MargalitFM11, Proposition 4.12]) we obtain that
$$\begin{eqnarray}([\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{1}}][\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D705}}][\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}_{2}}])^{4}=[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}]^{2}.\end{eqnarray}$$
It follows then from Propositions 6.6 and 6.7, as well as Theorem 3, that
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}^{\prime }}]^{2}\in \text{im}([\unicode[STIX]{x1D707}])$
. Using the previous construction, we conclude that
$[\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D70E}}]\in \text{im}([\unicode[STIX]{x1D707}])$
.◻
Acknowledgements
We are grateful to Denis Auroux, Sylvain Courte, Simon K. Donaldson, Christian Haase, Tobias Ekholm, Ilia Itenberg, Grigory Mikhalkin, and all the participants of the learning seminar on Lefschetz fibrations of Uppsala. Finally, we are grateful to the reviewer for helpful comments.
R.C. and L.L. were supported by the Knut and Alice Wallenberg Foundation.
