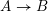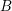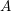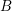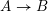Notations. If
$A$
is a local ring, we denote by
$\mathfrak{m}_{A}$
its maximal ideal and by
$\unicode[STIX]{x1D705}(A)$
its residue field. The embedding dimension of
$A$
, i.e. the minimal number of generators of
$\mathfrak{m}_{A}$
, is denoted by
$\operatorname{edim}(A)$
. A local morphism
$A\rightarrow B$
of Noetherian local rings is a relative complete intersection if the ring
$B/\mathfrak{m}_{A}B$
is a complete intersection.
1 Introduction
A crucial step in the proof of the modularity of semistable elliptic curves over
$\mathbb{Q}$
by Taylor and Wiles is to show that certain Hecke algebras are complete intersections. Their method, now commonly referred to as a ‘patching method’, heuristically consists of considering the limit of algebras arising from forms of different levels. In their construction, they used in particular the following (fundamental) ‘multiplicity one’ result: the homology of the modular curve is a free module over the Hecke algebra (after localization at some maximal ideal). Diamond reversed the argument in [Reference DiamondDia97]: ‘multiplicity one’ becomes a byproduct of the proof rather than an ingredient. The key input from commutative algebra that allowed Diamond’s improvement was the freeness criterion [Reference DiamondDia97, Theorem 2.1]. Its proof still relies on a patching argument.
In the hypotheses of Diamond’s freeness criterion, there is a condition that has to hold for all positive integers
$n$
. The condition for
$n$
implies the condition for all smaller integers. In [Reference DiamondDia97, Remark 2.2], Diamond asks whether a sufficiently large
$n$
would be enough, and whether there could exist a lower bound for such an
$n$
depending only on the number
$r$
of variables and the rank of the module. Around 1997, de Smit conjectured that if
$A\rightarrow B$
is a morphism of Artin local rings with the same embedding dimension, then any
$A$
-flat
$B$
-module is
$B$
-flat (see Corollary 1.2 below). In [Reference Brochard and MézardBM11] we proved de Smit’s conjecture when the embedding dimension
$r$
is
${\leqslant}2$
, and with the additional assumption that
$A\rightarrow B$
was flat. Here we prove the following theorem, which in particular proves the full conjecture, and answers Diamond’s question:
$n=2$
already suffices, for any
$r$
and any module. So, the freeness criterion will be much easier to apply.
Theorem 1.1. Let
$\unicode[STIX]{x1D711}:A\rightarrow B$
be a local morphism of Noetherian local rings. Assume the following:
-
(i)
$\operatorname{edim}(B)\leqslant \operatorname{edim}(A)$
; -
(ii) there is a nonzero
$A$
-flat
$B$
-module
$M$
; -
(iii)
$A$
and
$B$
are Artin or
$M$
is of finite type as a
$B$
-module.
Then:
-
(1) the morphism
$A\rightarrow B$
is flat and
$\operatorname{edim}(B)=\operatorname{edim}(A)$
; -
(2) the ring
$B/\mathfrak{m}_{A}B$
is a complete intersection of dimension zero; -
(3)
$M$
is flat over
$B$
.
Corollary 1.2 (de Smit’s conjecture).
Let
$A\rightarrow B$
be a morphism of Artin local rings with the same embedding dimension. Then any
$A$
-flat
$B$
-module is
$B$
-flat.
Corollary 1.3 (see Theorem 2.5).
Let
$f:X\rightarrow S$
be a morphism of locally Noetherian schemes such that for any
$x\in X$
, the tangent spaces satisfy
$\dim T_{x}\leqslant \dim T_{f(x)}$
. Then any
$S$
-flat coherent
${\mathcal{O}}_{X}$
-module is also flat over
$X$
.
Since its publication, Diamond’s freeness criterion and the related patching method have been used quite a lot. For instance, here is a list of papers (nonexhaustive, in chronological order) that directly use Diamond’s Theorem 2.1: [Reference Conrad, Diamond and TaylorCDT99, Reference DickinsonDic01, Reference Genestier and TilouineGT05, Reference Böckle and KhareBK06, Reference TaylorTay06, Reference Clozel, Harris and TaylorCHT08, Reference DimitrovDim09, Reference PilloniPil12, Reference HarrisHar13, Reference Breuil and DiamondBD14]. A variant of this freeness criterion, due to Kisin (see [Reference KisinKis09c, (3.3.1)]), was also used in several major results, for instance the proof of Serre’s modularity conjecture (see [Reference KisinKis09c, Reference Khare and WintenbergerKW09, Reference KisinKis09b]) or the Fontaine–Mazur conjecture for
$\operatorname{GL}_{2}$
(see [Reference KisinKis09a]). A more functorial approach of the patching method is proposed in [Reference Emerton, Gee and SavittEGS15].
The paper is organized as follows: in § 2 we prove Theorem 1.1. We also give a global version for schemes that are not necessarily local (see Theorem 2.5). In § 3 we briefly explain how this new freeness criterion allows us to simplify Wiles’s proof of Fermat’s last theorem and avoid the use of the patching method.
2 Proof of Theorem 1.1
The following lemma is the heart of the proof.
Lemma 2.1. Let
$B$
be a ring. Let
$(x_{1},\ldots ,x_{n})$
and
$(u_{1},\ldots ,u_{n})$
be sequences of elements of
$B$
and let us denote by
$J_{x}$
and
$J_{u}$
the ideals they generate. Let
$M$
be a
$B$
-module. Assume that:
-
(i) we have the inclusion of ideals
$J_{x}\subset J_{u}$
, in other words, if
$x$
and
$u$
denote the column matrices
$(x_{1},\ldots ,x_{n})^{T}$
and
$(u_{1},\ldots ,u_{n})^{T}$
, there is a square
$n\times n$
matrix
$W=(c_{ij})$
with entries in
$B$
such that
$x=Wu$
. Let
$\unicode[STIX]{x1D6E5}=\det W$
; -
(ii) for any
$m_{1},\ldots ,m_{n}\in M$
, if we have the relation
$\sum _{i=1}^{n}x_{i}m_{i}=0$
, then
$m_{i}\in J_{x}M$
for all
$i$
.
Then, for any
$m\in M$
, if
$\unicode[STIX]{x1D6E5}m\in J_{x}M$
, then
$m\in J_{u}M$
.
Proof. We will need some notations for the minors of
$W$
. For any integer
$\ell$
, let
$E_{\ell }$
be the set
$\{1,\ldots ,\ell \}$
and let
${\mathcal{P}}_{\ell }$
be the set of subsets
$I\subset E_{n}$
such that
$|I|=\ell$
. For
$I,J\in {\mathcal{P}}_{\ell }$
, let
$\unicode[STIX]{x1D6E5}_{J}^{I}$
denote the minor of
$W$
obtained by deleting the rows (respectively the columns) whose index is in
$I$
(respectively
$J$
). In other words,
$\unicode[STIX]{x1D6E5}_{J}^{I}=\det (c_{ij})_{\substack{ i\in E_{n}\smallsetminus I \\ j\in E_{n}\smallsetminus J}}$
. In particular,
$\unicode[STIX]{x1D6E5}_{\varnothing }^{\varnothing }=\unicode[STIX]{x1D6E5}$
and
$\unicode[STIX]{x1D6E5}_{E_{n}}^{E_{n}}=1$
. The comatrix is
$\operatorname{Com}(W)=((-1)^{i+j}\unicode[STIX]{x1D6E5}_{j}^{i})$
. If
$I\subset E_{n}$
and
$i\in E_{n}$
, we write
$I-i$
for
$I\smallsetminus \{i\}$
. For
$i\neq j\in E_{n}$
, let
$\overline{\unicode[STIX]{x1D700}}(i,j)=1$
if
$i<j$
and
$\overline{\unicode[STIX]{x1D700}}(i,j)=-1$
if
$i>j$
. For
$I\subset E_{n}$
and
$i\in I$
, let
$\unicode[STIX]{x1D700}(i,I)=(-1)^{p}$
, where
$p$
is the position of
$i$
in the ordered set
$E_{n}\smallsetminus (I-i)$
. Note that
$\unicode[STIX]{x1D700}(i,I)=(-1)^{i}\prod _{j\in I-i}\overline{\unicode[STIX]{x1D700}}(i,j)$
. For any
$i,j\in I$
with
$i\neq j$
, we have the relation
$$\begin{eqnarray}\unicode[STIX]{x1D700}(i,I)\unicode[STIX]{x1D700}(i,I-j)=\overline{\unicode[STIX]{x1D700}}(i,j).\end{eqnarray}$$
Now, for any
$0\leqslant \ell \leqslant n-1$
, if
$I\in {\mathcal{P}}_{\ell +1}$
and
$i\in I$
, the expansion of the minor
$\unicode[STIX]{x1D6E5}_{I-i}^{E_{\ell }}$
along the column
$i$
is
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{I-i}^{E_{\ell }}=(-1)^{\ell }\unicode[STIX]{x1D700}(i,I)\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}c_{ki}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}.\end{eqnarray}$$
If
$i\notin I$
, pick an element
$j\in I$
and consider the expansion along the column
$j$
of the minor
$\unicode[STIX]{x1D6E5}_{I-j}^{E_{\ell }}$
in which we have replaced the column
$j$
by the column
$i$
. Since the latter minor has two identical columns, it is zero and we see that for any
$i\notin I$
,
$$\begin{eqnarray}\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}c_{ki}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}=0.\end{eqnarray}$$
Now let us come back to our module
$M$
. Let
$m\in M$
be such that
$\unicode[STIX]{x1D6E5}m\in J_{x}M$
. For
$0\leqslant \ell \leqslant n$
, let
$(A_{\ell })$
denote the following statement.
-
$(A_{\ell })$
-
There is a family
$(a_{I}^{\ell })_{I\in {\mathcal{P}}_{\ell -1}}$
of elements of
$M$
such that for any
$I\in {\mathcal{P}}_{\ell }$
, the element
$$\begin{eqnarray}g_{I}=\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }}m+\mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}a_{I-i}^{\ell }\end{eqnarray}$$
belongs to
$J_{x}M$
.
We will prove that
$(A_{\ell })$
holds for any
$0\leqslant \ell \leqslant n$
by induction on
$\ell$
. The statement
$(A_{0})$
means that
$\unicode[STIX]{x1D6E5}m\in J_{x}M$
and holds by assumption. Assume that
$(A_{\ell })$
holds for some
$0\leqslant \ell \leqslant n-1$
and let us prove the statement
$(A_{\ell +1})$
. For any
$I\in {\mathcal{P}}_{\ell }$
, since
$g_{I}\in J_{x}M$
, we can write
$g_{I}=\sum _{k\in E_{n}}x_{k}a_{I}^{k}$
for some elements
$a_{I}^{k}\in M$
. Let
$I\in {\mathcal{P}}_{\ell +1}$
. We will compute
$m^{\prime }=\sum _{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}g_{I-i}$
. For this, we first compute
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}(g_{I-i}-\unicode[STIX]{x1D6E5}_{I-i}^{E_{\ell }}m) & = & \displaystyle \mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}\mathop{\sum }_{j\in I-i}\unicode[STIX]{x1D700}(j,I-i)u_{j}a_{I\smallsetminus \{i,j\}}^{\ell }\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\substack{ i,j\in I \\ i\neq j}}u_{i}u_{j}a_{I\smallsetminus \{i,j\}}^{\ell }S(i,j),\nonumber\end{eqnarray}$$
where
$S(i,j)=\unicode[STIX]{x1D700}(i,I)\unicode[STIX]{x1D700}(j,I-i)$
. Now the sum vanishes because
$S(i,j)=-S(j,i)$
. Indeed,
$S(i,j)S(j,i)=\overline{\unicode[STIX]{x1D700}}(i,j)\overline{\unicode[STIX]{x1D700}}(j,i)$
by (1) above. Hence,
$$\begin{eqnarray}m^{\prime }=\mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}\unicode[STIX]{x1D6E5}_{I-i}^{E_{\ell }}m.\end{eqnarray}$$
We expand
$\unicode[STIX]{x1D6E5}_{I-i}^{E_{\ell }}$
along the column
$i$
:
$$\begin{eqnarray}\displaystyle m^{\prime } & = & \displaystyle \mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}(-1)^{\ell }\unicode[STIX]{x1D700}(i,I)\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}c_{ki}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}m\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\ell }\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}\biggl(\mathop{\sum }_{i\in I}c_{ki}u_{i}\biggr)m\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\ell }\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}\biggl(x_{k}-\mathop{\sum }_{i\notin I}c_{ki}u_{i}\biggr)m\quad (\text{because}~x=Wu)\nonumber\\ \displaystyle & = & \displaystyle (-1)^{\ell }\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}x_{k}m\quad (\text{using}~(3)~\text{for each}~i\notin I).\nonumber\end{eqnarray}$$
On the other hand, by definition
$$\begin{eqnarray}m^{\prime }=\mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}g_{I-i}=\mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}\mathop{\sum }_{k\in E_{n}}x_{k}a_{I-i}^{k}.\end{eqnarray}$$
Hence,
$$\begin{eqnarray}\mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}\mathop{\sum }_{k\in E_{n}}x_{k}a_{I-i}^{k}-(-1)^{\ell }\mathop{\sum }_{k=\ell +1}^{n}(-1)^{k}\unicode[STIX]{x1D6E5}_{I}^{E_{\ell }\cup \{k\}}x_{k}m=0.\end{eqnarray}$$
By our assumption (ii), the coefficient of
$x_{\ell +1}$
in the above equation belongs to
$J_{x}M$
. But this coefficient is
$$\begin{eqnarray}\mathop{\sum }_{i\in I}\unicode[STIX]{x1D700}(i,I)u_{i}a_{I-i}^{\ell +1}+\unicode[STIX]{x1D6E5}_{I}^{E_{\ell +1}}m.\end{eqnarray}$$
This proves the statement
$(A_{\ell +1})$
. In particular,
$(A_{n})$
holds and hence there are elements
$a_{I}^{n}\in M$
for
$I\in {\mathcal{P}}_{n-1}$
such that the element
$$\begin{eqnarray}g_{E_{n}}=\unicode[STIX]{x1D6E5}_{E_{n}}^{E_{n}}m+\mathop{\sum }_{i\in E_{n}}\unicode[STIX]{x1D700}(i,E_{n})u_{i}a_{E_{n}-i}^{n}\end{eqnarray}$$
belongs to
$J_{x}M$
. Since
$\unicode[STIX]{x1D6E5}_{E_{n}}^{E_{n}}=1$
, this proves that
$m\in J_{u}M$
.◻
Before proceeding to the proof of Theorem 1.1, let us recall a result from [Reference Brochard and MézardBM11]. It will provide a useful characterization for the flatness of
$M$
over
$B$
.
Definition 2.2 [Reference Brochard and MézardBM11, 3.1].
Let
$R$
be a local ring and
$M$
be an
$R$
-module. We say that
$M$
is weakly torsion-free if, for every
$\unicode[STIX]{x1D706}\in R$
and every
$m\in M$
, the relation
$\unicode[STIX]{x1D706}m=0$
implies that
$\unicode[STIX]{x1D706}=0$
or
$m\in \mathfrak{m}_{R}M$
.
Proposition 2.3 [Reference Brochard and MézardBM11, 3.7].
Let
$R$
be an Artin local ring. Assume that
$R$
is Gorenstein and contains a field. Then an
$R$
-module
$M$
is flat over
$R$
if and only if it is weakly torsion-free.
Proof of Theorem 1.1.
Let
$M$
be a nonzero
$A$
-flat
$B$
-module. We apply Lemma 2.1 with
$(x_{1},\ldots ,x_{n})$
the image in
$B$
of a minimal system of generators of
$\mathfrak{m}_{A}$
, and
$(u_{1},\ldots ,u_{n})$
a system of generators of
$\mathfrak{m}_{B}$
, so that
$J_{x}=\mathfrak{m}_{A}B$
and
$J_{u}=\mathfrak{m}_{B}$
. The assumption (i) holds because the morphism
$A\rightarrow B$
is local, and the assumption (ii) holds by [Reference Brochard and MézardBM11, 4.2 and 4.3] because
$M$
is flat over
$A$
. Then
$\unicode[STIX]{x1D6E5}\notin \mathfrak{m}_{A}B$
, otherwise we would have
$\unicode[STIX]{x1D6E5}M\subset \mathfrak{m}_{A}M$
, which would imply that
$M=\mathfrak{m}_{B}M$
by Lemma 2.1; hence,
$M=0$
, which is a contradiction. In particular, for any choice of the matrix
$W$
and the generators
$u_{1},\ldots ,u_{n}$
of
$\mathfrak{m}_{B}$
such that
$x=Wu$
, we have
$\det W\neq 0$
. This proves that
$\operatorname{edim}(B)=\operatorname{edim}(A)$
, because if
$\operatorname{edim}(B)<\operatorname{edim}(A)$
we can choose
$W$
with a zero column. Moreover, in the ring
$B/\mathfrak{m}_{A}B$
, the matrix
$\overline{W}$
satisfies
$\overline{W}u=0$
and
$\det \overline{W}\neq 0$
. In the language of [Reference Simon and StrookerSS06, Definition 2.6], this means that
$\overline{W}$
is (the transpose of) a
$u$
-Wiebe matrix for the ring
$B/\mathfrak{m}_{A}B$
. By [Reference Simon and StrookerSS06, 2.7], this implies that the ring
$B/\mathfrak{m}_{A}B$
is a complete intersection of dimension zero, and proves (2).
Let us prove that
$M$
is
$B$
-flat. By [Reference Brochard and MézardBM11, 2.3], it suffices to prove that
$M/\mathfrak{m}_{A}M$
is flat over
$B/\mathfrak{m}_{A}B$
. We have seen that
$B/\mathfrak{m}_{A}B$
is a complete intersection of dimension zero and hence a Gorenstein Artin local ring. Moreover, it contains the field
$\unicode[STIX]{x1D705}(A)$
. Hence, by Proposition 2.3, it suffices to prove that
$M/\mathfrak{m}_{A}M$
is weakly torsion-free over
$B/\mathfrak{m}_{A}B$
, i.e. that for any
$\unicode[STIX]{x1D706}\in B$
and any
$m\in M$
, the relation
$\unicode[STIX]{x1D706}m\in \mathfrak{m}_{A}M$
implies that
$\unicode[STIX]{x1D706}\in \mathfrak{m}_{A}B$
or
$m\in \mathfrak{m}_{B}M$
. So, let
$\unicode[STIX]{x1D706}\in B$
and
$m\in M$
be such that
$\unicode[STIX]{x1D706}m\in \mathfrak{m}_{A}M$
and
$\unicode[STIX]{x1D706}\notin \mathfrak{m}_{A}B$
; let us prove that
$m\in \mathfrak{m}_{B}M$
. By [Reference Simon and StrookerSS06, 2.7], we know that the image
$\overline{\unicode[STIX]{x1D6E5}}$
of
$\unicode[STIX]{x1D6E5}$
is a generator of the socle of the Gorenstein ring
$B/\mathfrak{m}_{A}B$
. Hence,
$(\overline{\unicode[STIX]{x1D6E5}})\subset (\overline{\unicode[STIX]{x1D706}})$
in
$B/\mathfrak{m}_{A}B$
. Since
$\unicode[STIX]{x1D706}m\in \mathfrak{m}_{A}M$
, this implies that
$\unicode[STIX]{x1D6E5}m\in \mathfrak{m}_{A}M$
. By Lemma 2.1, we get that
$m\in \mathfrak{m}_{B}M$
, as required.
Lastly let us prove that
$A\rightarrow B$
is flat. Let
$E\rightarrow F$
be an injection of
$A$
-modules. Let
$K$
be the kernel of
$E\otimes _{A}B\rightarrow F\otimes _{A}B$
. Since
$M$
is
$B$
-flat,
$K\otimes _{B}M$
is the kernel of
$E\otimes _{A}M\rightarrow F\otimes _{A}M$
, which is zero because
$M$
is
$A$
-flat. But
$M$
is faithfully flat over
$B$
(because it is free and nonzero) and hence
$K=0$
.
Remark 2.4. If we replace the assumption (iii) of Theorem 1.1 with ‘
$A$
and
$B$
are Artin or
$M$
is of finite type over
$A$
’, then we do not need to assume that the morphism
$\unicode[STIX]{x1D711}:A\rightarrow B$
is local: it is then a consequence of the other hypotheses. Indeed, if there is an element
$a\in \mathfrak{m}_{A}$
such that
$\unicode[STIX]{x1D711}(a)\in B^{\times }$
, then
$M=\unicode[STIX]{x1D711}(a)M$
and hence
$M=\mathfrak{m}_{A}M$
. Then
$M=0$
by Nakayama’s lemma (or because
$\mathfrak{m}_{A}$
is nilpotent if
$A$
is Artin), which is a contradiction. On the other hand, if
$A$
is Artin, I am not sure that we really need the assumption that
$B$
is Artin too.
The following is a global version of Theorem 1.1.
Theorem 2.5. Let
$f:X\rightarrow S$
be a morphism of locally Noetherian schemes. Assume that for any
$x\in X$
, the dimensions of the tangent spaces
$T_{x}$
and
$T_{f(x)}$
satisfy
$$\begin{eqnarray}\dim T_{x}\leqslant \dim T_{f(x)}.\end{eqnarray}$$
Let
${\mathcal{M}}$
be a coherent
${\mathcal{O}}_{X}$
-module, flat over
$S$
. Then:
-
(1)
${\mathcal{M}}$
is flat over
$X$
; -
(2) for each point
$x\in \operatorname{Supp}({\mathcal{M}})$
,
$f$
is flat at
$x$
, the fiber
$f^{-1}(f(x))$
is a complete intersection of dimension zero at
$x$
(i.e. its local ring at
$x$
is a complete intersection of dimension zero) and
$\dim T_{x}=\dim T_{f(x)}$
.
In particular, if there exists a coherent
${\mathcal{O}}_{X}$
-module
${\mathcal{M}}$
flat over
$S$
whose support is
$X$
, then
$f$
is a complete intersection morphism of relative dimension zero (i.e.
$f$
is flat and its fibers are zero-dimensional complete intersections).
Proof. Note that the local ring of
$X$
at a point
$x$
is unaltered through the base change
$\operatorname{Spec}{\mathcal{O}}_{S,f(x)}\rightarrow S$
. By [Reference BourbakiBou06, ch. II, § 3, no. 4, Proposition 14], the module
${\mathcal{M}}_{x}$
is flat over
${\mathcal{O}}_{S,f(x)}$
. Since
$\dim T_{x}=\operatorname{edim}({\mathcal{O}}_{X,x})$
and
$\dim (T_{f(x)})=\operatorname{edim}({\mathcal{O}}_{S,f(x)})$
, we can apply Theorem 1.1 and
${\mathcal{M}}_{x}$
is flat over
${\mathcal{O}}_{X,x}$
. This proves (1). If
$x\in \operatorname{Supp}({\mathcal{M}})$
, then
${\mathcal{M}}_{x}\neq 0$
and by Theorem 1.1 we deduce that
${\mathcal{O}}_{X,x}$
is flat over
${\mathcal{O}}_{S,f(x)}$
, that these rings have the same embedding dimension and that
${\mathcal{O}}_{X,x}/\mathfrak{m}{\mathcal{O}}_{X,x}$
is a zero-dimensional complete intersection (where
$\mathfrak{m}$
is the maximal ideal of
${\mathcal{O}}_{S,f(x)}$
). Since the latter ring
${\mathcal{O}}_{X,x}/\mathfrak{m}{\mathcal{O}}_{X,x}$
identifies with the local ring at
$x$
of the fiber
$X_{f(x)}$
, this proves (2).◻
3 Application to the proof of Fermat’s last theorem
To conclude his proof, Wiles had to prove that a certain morphism of
${\mathcal{O}}$
-algebras
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6F4}}:R_{\unicode[STIX]{x1D6F4}}\rightarrow T_{\unicode[STIX]{x1D6F4}}$
is an isomorphism and that
$T_{\unicode[STIX]{x1D6F4}}$
is a complete intersection over
${\mathcal{O}}$
. Here
${\mathcal{O}}$
is the ring of integers of a finite extension of
$\mathbb{Q}_{\ell }$
,
$R_{\unicode[STIX]{x1D6F4}}$
is the universal deformation ring for a Galois representation
$\overline{\unicode[STIX]{x1D70C}}:\operatorname{Gal}(\overline{\mathbb{Q}}/\mathbb{Q})\rightarrow \operatorname{GL}_{2}(k)$
(where
$k$
is the residue field of
${\mathcal{O}}$
) and
$T_{\unicode[STIX]{x1D6F4}}$
is a certain Hecke algebra. The proof proceeds in two steps: first it is proved for
$\unicode[STIX]{x1D6F4}=\varnothing$
(the ‘minimal case’), then the general case is deduced from this one using some numerical criterion for complete intersections. To handle the minimal case, Wiles constructs a system of sets
$Q_{n}$
,
$n\geqslant 1$
, where
$Q_{n}$
is a set of primes congruent to 1 mod
$\ell ^{n}$
with some other ad hoc properties. Then, by considering a kind of ‘patching’ of the morphisms
$\unicode[STIX]{x1D6F7}_{Q_{n}}:R_{Q_{n}}\rightarrow T_{Q_{n}}$
, Wiles manages to prove the desired result for
$\unicode[STIX]{x1D6F4}=\varnothing$
. Among other things, the proof relied on the fact (due to Mazur and Ribet) that the homology of the modular curve is a free module of rank 2 over
$T_{\varnothing }$
(known as a ‘multiplicity one’ result). Diamond improved the method in [Reference DiamondDia97]: by patching the modules as well as the algebras, he managed to remove multiplicity one as an ingredient of the proof of Fermat’s last theorem. His proof relies on his freeness criterion [Reference DiamondDia97, 2.1]. Since we only want to illustrate how our Theorem 1.1 can be used to avoid the patching method and the use of Taylor–Wiles systems, we will work in the rather restrictive setting of [Reference Darmon, Diamond and TaylorDDT97] and [Reference DiamondDia97]. We use their notations and statements in the sequel.
Let us prove that
$\unicode[STIX]{x1D6F7}_{\varnothing }$
is an isomorphism. Let
$\unicode[STIX]{x1D706}$
be a uniformizer of
${\mathcal{O}}$
. By [Reference Darmon, Diamond and TaylorDDT97, 2.49] (note that we only use it for
$n=1$
, so here also the proof can be simplified), there exists a finite set of prime numbers
$Q$
such that:
-
–
$\operatorname{edim}(\overline{R_{Q}})\leqslant \#Q=:r$
, where
$\overline{R_{Q}}=R_{Q}\otimes _{{\mathcal{O}}}k=R_{Q}/\unicode[STIX]{x1D706}R_{Q}$
; -
– for any
$q\in Q$
,
$q\equiv 1~(\ell )$
,
$\overline{\unicode[STIX]{x1D70C}}$
is unramified at
$q$
and
$\overline{\unicode[STIX]{x1D70C}}(\operatorname{Frob}_{q})$
has distinct eigenvalues.
Let
$G$
be the
$\ell$
-Sylow subgroup of
$\prod _{q\in Q}(\mathbb{Z}/q\mathbb{Z})^{\times }$
. We endow
$R_{Q}$
with the structure of an
${\mathcal{O}}[G]$
-algebra as in [Reference Darmon, Diamond and TaylorDDT97, § 2.8]. Let
$N$
be the integer
$N_{\varnothing }$
of [Reference Darmon, Diamond and TaylorDDT97, (4.2.1)] and
$M=p^{2}\prod _{q\in Q}q$
, where
$p$
is a well-chosen auxiliary prime (see [Reference Darmon, Diamond and TaylorDDT97, § 4.3]). Consider the group
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{0}(N)\cap \unicode[STIX]{x1D6E4}_{1}(M)\end{eqnarray}$$
and let
$X_{\unicode[STIX]{x1D6E4}}$
be the associated modular curve. By [Reference Darmon, Diamond and TaylorDDT97, 4.10], there is an isomorphism
$T_{Q}\rightarrow T_{\mathfrak{m}}^{\prime }$
, where
$T^{\prime }$
is the algebra of Hecke operators acting on
$H^{1}(X_{\unicode[STIX]{x1D6E4}},{\mathcal{O}})$
and
$\mathfrak{m}$
is a certain maximal ideal of
$T^{\prime }$
. Consider the
$T_{\mathfrak{m}}^{\prime }$
-module
$$\begin{eqnarray}H:=H^{1}(X_{\unicode[STIX]{x1D6E4}},{\mathcal{O}})_{\mathfrak{ m}}^{-}\end{eqnarray}$$
of elements on which complex conjugation acts by
$-1$
. We can view
$H$
as a module over
${\mathcal{O}}[G]$
,
$R_{Q}$
, or
$T_{Q}$
via the
${\mathcal{O}}$
-algebra morphisms
$$\begin{eqnarray}{\mathcal{O}}[G]\rightarrow R_{Q}\rightarrow T_{Q}\rightarrow T_{\mathfrak{m}}^{\prime }.\end{eqnarray}$$
Theorem 3.1. With the above notation:
-
(i)
$H$
is free over
$T_{Q}$
; -
(ii)
$T_{Q}$
is free over
${\mathcal{O}}[G]$
; -
(iii)
$T_{Q}$
is a relative complete intersection over
${\mathcal{O}}[G]$
(hence also over
${\mathcal{O}}$
); -
(iv)
$\unicode[STIX]{x1D6F7}_{Q}:R_{Q}\rightarrow T_{Q}$
is an isomorphism.
Proof. By [Reference DiamondDia97, Lemma 3.2],
$\overline{H}=H/\unicode[STIX]{x1D706}H$
is free over
$k[G]$
. Note that there is an isomorphism
${\mathcal{O}}[G]\simeq {\mathcal{O}}[[S_{1},\ldots ,S_{r}]]/((1+S_{1})^{\unicode[STIX]{x1D6FC}_{1}}-1,\ldots ,(1+S_{r})^{\unicode[STIX]{x1D6FC}_{r}}-1)$
, where the
$\unicode[STIX]{x1D6FC}_{i}$
are the cardinalities of the
$l$
-Sylow subgroups of the
$(\mathbb{Z}/q\mathbb{Z})^{\times }$
for
$q\in Q$
. In particular,
$\unicode[STIX]{x1D6FC}_{i}\geqslant \ell \geqslant 2$
and it follows that
$\operatorname{edim}(k[G])=r$
. We can apply Theorem 1.1 to the morphism
$k[G]\rightarrow \overline{R_{Q}}$
and the module
$\overline{H}$
. We get that
$\overline{H}$
is free over
$\overline{R_{Q}}$
, and that
$\overline{R_{Q}}$
is free and is a relative complete intersection over
$k[G]$
. In particular,
$\overline{R_{Q}}\rightarrow \overline{T_{Q}}$
must be injective (otherwise
$\overline{H}$
would have torsion over
$\overline{R_{Q}}$
). Since it is already known to be surjective, it is an isomorphism. We have proved all the statements after
$\otimes _{{\mathcal{O}}}k$
. Since
$T_{Q}$
is free over
${\mathcal{O}}$
, the theorem now follows from Lemma 3.2 below.◻
Lemma 3.2. Let
${\mathcal{O}}$
be a Noetherian local ring with maximal ideal
$\mathfrak{m}$
and residue field
$k$
.
-
(i) Let
$f:M\rightarrow N$
be a morphism of finite-type
${\mathcal{O}}$
-modules. Assume that
$N$
is free over
${\mathcal{O}}$
and that
$f\otimes _{{\mathcal{O}}}k$
is an isomorphism. Then
$f$
is an isomorphism. -
(ii) Let
$A$
be a finite
${\mathcal{O}}$
-algebra and
$M$
be an
$A$
-module which is free of finite rank over
${\mathcal{O}}$
. If
$M\otimes _{{\mathcal{O}}}k$
is free over
$A\otimes _{{\mathcal{O}}}k$
, then
$M$
is free over
$A$
. -
(iii) Assume that
${\mathcal{O}}$
is complete. Let
$A\rightarrow B$
be a morphism of finite local
${\mathcal{O}}$
-algebras, with
$B$
free over
${\mathcal{O}}$
. If
$B\otimes _{{\mathcal{O}}}k$
is a relative complete intersection over
$A\otimes _{{\mathcal{O}}}k$
, then
$B$
is a relative complete intersection over
$A$
(i.e. the ring
$B/\mathfrak{m}_{A}B$
is a complete intersection).
Proof. These are standard consequences of Nakayama’s lemma. ◻
Remark 3.3. By [Reference Darmon, Diamond and TaylorDDT97, Corollaries 2.45 and 3.32], the canonical morphisms
$R_{Q}\rightarrow R_{\varnothing }$
and
$T_{Q}\rightarrow T_{\varnothing }$
induce isomorphisms
$R_{Q}/\mathfrak{a}_{Q}R_{Q}\simeq R_{\varnothing }$
and
$T_{Q}/\mathfrak{a}_{Q}T_{Q}\simeq T_{\varnothing }$
, where
$\mathfrak{a}_{Q}$
is the augmentation ideal of
${\mathcal{O}}[G]$
(i.e. the ideal generated by
$S_{1},\ldots ,S_{R}$
). Hence, from Theorem 3.1, it follows immediately that
$\unicode[STIX]{x1D6F7}_{\varnothing }:R_{\varnothing }\rightarrow T_{\varnothing }$
is an isomorphism and
$T_{\varnothing }$
is a complete intersection over
${\mathcal{O}}$
.
Acknowledgements
I warmly thank Bart de Smit for raising his conjecture and for pointing out to me the freeness criterion [Reference DiamondDia97, Theorem 2.1]. I also thank Michel Raynaud and Stefano Morra for interesting conversations, and the anonymous referee for valuable comments that helped to clarify the exposition.
