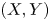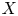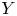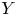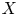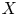1. Introduction
Gini mean difference, which was first introduced by Gini [Reference Gini12] as an alternative measure of variability, has been known for over a century. The Gini mean difference and its related parameters which are derived from it (such as the Gini coefficient, Gini covariance and extended Gini) have been used in various application areas, such as economics and statistics. The focus of this article is on tail Gini-type variability measures, which are the evolution of the Gini mean difference in the form of covariance (see Section 2.1.3 of [Reference Yitzhaki and Schechtman21]):
\begin{equation} \mathrm{Gini}(X) = 4 \mathrm{Cov} (X, F_{1}(X)), \end{equation}where 
$F_{1}$ is the distribution function of 
$X$. Eq. (1) is a quantity related to the covariance of the variable and its distribution so that can be used to measure association. In order to reflect tail variability, Furman et al. [Reference Furman, Wang and Zitikis11] introduced the tail-Gini functional for a univariate random variable which can be written in the form of a conditional covariance: 
$\mathrm {TGini}_{p} (X) = {4}/{p} \cdot \mathrm {Cov} (X, F_{1}(X)\,|\, F_{1}(X) > 1-p)$, where 
$F_{1}$ is the distribution of a continuous random variable 
$X$ and 
$p$ is a small probability. When it comes to the case of bivariate random vector 
$(X, Y)$, where 
$X$ is the objective variable and 
$Y$ is a benchmark variable, the tail-Gini functional in a bivariate setup was introduced by Hou and Wang [Reference Hou and Wang13], that is
\begin{equation} \mathrm{TGini}_{p}(X; Y) = \frac{4}{p} \,\mathrm{Cov} (X,F_{2}(Y)\,|\,F_{2}(Y) > 1-p), \end{equation}where 
$F_{2}$ is the marginal distribution of 
$Y$. The motivation of Eq. (2) is to define a good tail variability measure incorporating both the marginal risk severity of 
$X$ and the tail structure of 
$(X, Y)$ to reflect the tail variability of 
$X$ under the tail scenarios of the benchmark variable 
$Y$. Under the assumption that 
$X$ is in the Fréchet domain of attraction, Hou and Wang [Reference Hou and Wang13] studied the asymptotic behavior of the tail-Gini functional when the two random variables are asymptotic dependent. This result can help us better understand this variability measure. However, with the increasing attention on the study of risk measures for an asymptotical independent pair (see [Reference Cai and Musta5,Reference Das and Fasen-Hartmann7,Reference Kulik and Soulier16], etc.), it is necessary to extend the idea to variability measures. Therefore, it is our first goal to explore the asymptotic behavior of the tail-Gini functional under asymptotic independence.
Under the basic setting of 
$(X, Y)$ mentioned above, the benchmark variable 
$Y$ can take the form of a function of 
$X$, such as a sum or product of random variables including 
$X$ or the maximum (minimum) of 
$n$ random variables including 
$X$ (see [Reference Asimit and Li1,Reference Cai and Li4], etc.). However, one of the problems that may arise is that the tail information of 
$Y$ does not fully reflect the tail behavior of 
$X$, especially in the case when 
$X$ and 
$Y$ are tail independent. Mathematically speaking, one promising way is to add the tail event of 
$X$ into the modeling, that is, to consider a joint tail event involved with both 
$X$ and 
$Y$ in the part of the condition which has been developed in recent literature. Specifically, Ji et al. [Reference Ji, Tan and Yang15] proposed a risk measure called joint expected shortfall which can be viewed as a consolidation of both expected shortfall and marginal expected shortfall. It is natural to extend the variability measure to a context with the joint tail event. In order to realize this idea and incorporate various dependence structures in the study of extreme risk variability, this paper proposes a new variability measure for a random pair 
$(X, Y)$ called joint tail-Gini functional, which is defined as follows:
\begin{equation} \mathrm{JTGini}_{p}(X;Y) := \frac{4}{p} \,\mathrm{Cov} (X, F_{2}(Y)\,|\,X > Q_{1}(1-p), Y > Q_{2}(1-p)), \end{equation}where 
$F_{2}$ is the marginal distribution of 
$Y$, 
$Q_{1}$ and 
$Q_{2}$ are quantile functions of 
$X$ and 
$Y$, respectively.
In practice, 
$X$ may be some interesting variable, say, loss of an individual asset or portfolio; while 
$Y$ could be a benchmark variable, say, loss of a financial system or benchmark portfolio. For the tail-Gini functional of 
$(X, Y)$, we consider extreme scenarios of the systemic variable 
$Y$ by calling the extreme event 
$Y > t$, where 
$t$ is a high threshold such that 
$\mathbb {P}(Y > t)$ is extremely small. Hence, we set 
$t = Q_{2}(1-p)$, that is, the 
$(1-p)$th quantile of the distribution of 
$Y$. Obviously, the extreme region of 
$\mathrm {TGini}_{p}(X; Y)$ as 
$p \downarrow 0$ is only related to the benchmark variable 
$Y$ and it is attained only when 
$Y$ is large. However, observing Eq. (3), 
$\mathrm {JTGini}_{p}(X; Y)$ defines a new variability measure where the extreme region is related to both the benchmark variable 
$Y$ and the loss variable 
$X$ itself and it is attained when both 
$X$ and 
$Y$ exceed their corresponding 
$(1-p)$th quantile. Compared with the tail-Gini functional, the joint tail-Gini functional can be viewed as a novel variability measure by adding the tail information of 
$X$ itself based on it.
The tail Gini-type variability measures play an important role in tail risk and variability theory which has been presented in the recent literature, see Furman et al. [Reference Furman, Wang and Zitikis11], Berkhouch et al. [Reference Berkhouch, Lakhnati and Righi2] and Hou and Wang [Reference Hou and Wang13]. The joint tail-Gini functional as a new variability measure also belongs to the family of tail Gini-type variability measures. In view of these existing papers, our contribution can be summarized in two main aspects. First, the asymptotic property of the tail-Gini functional is obtained by using the tail order property of copula to model the tail dependence. In this way, the asymptotic result implies that the rate of increase of the variability measure is determined by the tail behavior of 
$X$, the tail behavior of 
$Y$ has no apparent influence. Second, we proposed a new variability measure called the joint tail-Gini functional, which considers not only the tail event of benchmark variable 
$Y$, but also the tail information of 
$X$ itself. Its asymptotic property is explored and a generalization of joint tail-Gini functional is introduced.
We organize the paper as follows. In Section 2, we recall some basic concepts in extreme value theory and characterize the tail dependence structure by tail order property. The main results concerning the asymptotic expansions of tail Gini-type variability measures are presented in Sections 3 and 4. Relevant examples are discussed in Section 5. Section 6 contains some concluding remarks and discussions.
2. Preliminaries
In this section, we discuss the necessary tools and definitions that are used in the subsequent sections. First, this section reviews some concepts in extreme value theory and introduces the definition of regular variation. Then, the tail dependence characterized by the tail order property of the copula is presented.
Throughout this article, we restrict our attention to the bivariate copulas. For two positive functions 
$f(\cdot )$ and 
$g(\cdot )$, the notation 
$f(\cdot ) \sim g(\cdot )$ means that the functions 
$f(\cdot )$ and 
$g(\cdot )$ are asymptotically equivalent, that is, 
$\lim _{t\rightarrow t_{0}} f(t)/g(t) =1$ with 
$t_{0}$ being the corresponding limiting point that is usually 
$0$ or 
$\infty$.
2.1. Extreme value theory
Before introducing regular variation, it is useful to review some basic concepts in extreme value theory. Let 
$\{X_{i}\}_{i \geq 1}$ be a sequence of independent and identically distributed random variables with a common distribution 
$F$. Extreme value theory assumes that there exist sequences of normalizing constants 
$a_{n} >0$ and 
$b_{n} \in \mathbb {R}$ such that
$$\lim_{n \rightarrow \infty} \mathbb{P} \left( \frac{\max \{X_{1},X_{2},\ldots,X_{n}\} - b_{n}}{a_{n}} \leq x \right) = G(x),\quad x \in \mathbb{R}.$$Then, the distribution function 
$F$ is said to belong to the max-domain of attraction of 
$G$, denoted by 
$F \in \mathrm {MDA}(G)$. The classical Fisher–Tippett theorem [Reference Fisher and Tippett10] states that 
$G$ is the generalized extreme value distribution, which has the following standard version:
$$G_{\gamma}(x) = \exp \{-(1+\gamma x)^{{-}1/\gamma}\}, \quad 1+\gamma x >0,$$with 
$\gamma \in \mathbb {R}$ and where for 
$\gamma =0$ the right-hand side is interpreted as 
$\exp (-e^{-x})$. Moreover, the regions 
$\gamma >0, \gamma =0$ and 
$\gamma <0$ correspond to the Fréchet, Gumbel and Weibull cases, respectively. In this article, we restrict our attention to the risk variables with heavy tails. Hence, the Fréchet case, that is, 
$\gamma >0$ is only taken into consideration.
A distribution function 
$F$ belongs to the domain of Fréchet distribution if and only if its upper endpoint is infinite and
$$\lim_{t \rightarrow \infty} \frac{\bar{F}(tx)}{\bar{F}(t)} = x^{{-}1/\gamma},\quad x>0$$holds. This means that the function 
$\bar {F}$ is regularly varying at 
$\infty$ with index 
$-1/\gamma$. We refer to Bingham et al. [Reference Bingham, Goldie and Teugels3] for a standard reference on regular variation. The specific definition of regular variation is as follows.
Definition 2.1 (Regular variation)
A measurable function 
$f: (0,\infty ) \mapsto (0,\infty )$ is regularly varying at 
$t_{0} = \infty$ or 
$0$ with an index 
$\alpha \in \mathbb {R}_{+}$ if for any 
$x >0$,
\begin{equation} \lim_{t \rightarrow t_{0}} \frac{f(tx)}{f(t)} = x ^{\alpha} \end{equation}and we write 
$f \in \mathrm {RV}_{\alpha }(t_{0})$. If Eq. (4) holds with 
$\alpha =0$ for any 
$x>0$, then 
$f$ is said to be slowly varying at 
$t_{0}$ and written as 
$f \in \mathrm {RV}_{0}(t_{0})$. When 
$t_{0} = \infty$, for simplicity we use the notation 
$f \in RV_{\alpha }$.
A random variable 
$X$ with its survival function 
$\bar {F}$ has a regularly varying tail if 
$\bar {F} \in \mathrm {RV}_{-\alpha }$ for some 
$\alpha > 0$. Actually, when we say that a random variable is regularly varying, it means that the survival function of the random variable is regularly varying. The theory of regular variation, which provides a tractable mathematical approach to understand more subtle tail behavior, plays an important role in the analysis of tail risk and tail variability measures.
2.2. Tail dependence
To introduce tail dependence, we first recall the conception of copula, which is commonly used to characterize the dependence structure. See Nelsen [Reference Nelsen19] for the details about copula. A bivariate copula is a joint distribution function defined on 
$[0,1]^{2}$ with uniform marginals. Assume that 
$(X,Y)$ is a pair of random loss variables with marginal distributions 
$F_{1} = 1- \bar {F}_{1}$ and 
$F_{2} = 1 - \bar {F}_{2}$, respectively. By Sklar's Theorem [Reference Sklar20], if 
$F_{1}$ and 
$F_{2}$ are continuous, then there exists a unique copula 
$C$ such that 
$\mathbb {P}(X \leq x, Y \leq y) = C(F_{1}(x), F_{2}(y))$. In this paper, we concentrate our interest on the tail independence which is related to the survival copula 
$\hat {C}$. Let 
$C$ be a two-dimensional copula and 
$\hat {C}$ be the corresponding survival copula, then the survival copula satisfies 
$\hat {C} (u, v) = u + v - 1 + C(1-u,1-v)$ for 
$(u,v) \in [0,1]^{2}$. We say 
$(X,Y)$ follows a survival copula 
$\hat {C}$, if for any 
$x$ and 
$y$, it holds that
$$\mathbb{P}(X>x, Y>y) = \hat{C} (\bar{F}_{1}(x), \bar{F}_{2}(y)).$$ In order to characterize a wide dependence structure that covers both tail dependent and tail independent cases, we make use of the so-called tail order property of the copula [Reference Hua and Joe14] to capture the degree of dependence. Hua and Joe [Reference Hua and Joe14] proposed the concept of tail order by indicating that tail order “
$\kappa$” corresponds to “
$1/\eta$” of Ledford and Tawn's representation in Ledford and Tawn [Reference Ledford and Tawn17]. In fact, the tail order includes lower tail order and upper tail order, and the upper tail order is our focus since our work involves only the upper tail. For convenience, we use the tail order to refer to the upper tail order.
Definition 2.2 (Tail order)
Suppose 
${C}$ is a bivariate copula with corresponding survival copula 
$\hat {C}$. If there exist some 
$\kappa >0$ and 
$\ell \in \mathrm {RV}_{0}(0^{+})$ such that
$$\hat{C}(u,u) \sim u^{\kappa} \ell(u), \quad u\downarrow 0,$$then we refer to 
$\kappa$ as the tail order of 
$C$.
As for the tail order 
$\kappa$, it can be seen that 
$\kappa \geq 1$ due to the fact 
$\hat {C}(u,u) \leq u$. Moreover, we only focus on the case under the positive dependence assumption:
$$\mathbb{P}(X>x,Y>y) \geq \mathbb{P}(X>x) \mathbb{P}(Y>y)\quad \text{for any}\ (x,y) \in \mathbb{R}^{2},$$that is, the joint events of 
$(X, Y)$ happen more often than those of a distribution with independent components of 
$X$ and 
$Y$. Therefore, the scenario for tail order 
$\kappa$ that we need to pay attention to is 
$1 \leq \kappa \leq 2$, which covers both tail dependent and tail independent cases. Specifically, if 
$\kappa =1$, then 
$X$ and 
$Y$ are tail dependent; if 
$1<\kappa \leq 2$, then they are tail independent. For more details on tail order, such as how to identify or estimate it, refer to Chapter 15 in Li and Li [Reference Li and Li18] and Draisma et al. [Reference Draisma, Drees, Ferreira and de Haan9], the latter provided the estimation of 
$\eta$.
The tail order property indeed is the regular variation property of the copula. It is often more convenient to use the following regular variation version of the tail order property for survival copulas.
Assumption 2.1 There exists a non-degenerate and continuous tail function 
$\tau (x, y):[0, \infty )^{2} \mapsto \mathbb {R}_{+}$ and some 
$\kappa \in [1,2]$ such that
\begin{equation} \lim_{u \downarrow 0} \frac{\hat{C}(ux,uy)}{u^{\kappa}} = \tau(x,y). \end{equation} Eq. (5) describes the flexible and elaborate dependence structure. As a consequence, 
$\tau$ is a homogeneous function of order 
$\kappa$, that is, 
$\tau (ax,ay) = a^{\kappa } \tau (x,y)$ for all 
$a,x,y >0$. It is natural to obtain 
$\tau (x,0) = \tau (0,y) = \tau (0,0) =0$ since 
$\hat {C}(x,0) = \hat {C}(0,y) = \hat {C}(0,0) =0$. Note that, when 
$\kappa =1$, the 
$\tau (x,y)$ corresponds to the 
$R$-function 
$R(x,y)$, which is defined in Section 6.1 of de Haan and Ferreira [Reference de Haan and Ferreira8] and frequently used in recent literature (see [Reference Asimit and Li1,Reference Cai, Einmahl, Haan and Zhou6,Reference Das and Fasen-Hartmann7]).
Next, we derive the asymptotic behaviors of tail Gini-type variability measures, including tail-Gini functional, joint tail-Gini functional and a generalization of joint tail-Gini functional. For ease of presentation, we assume in this article 
$X$ is a non-negative random variable, although the result of tail Gini-type variability measures can be extended to 
$X$ takes values in 
$\mathbb {R}$ with some modifications on the conditions; see further discussion on the case of 
$X \in \mathbb {R}$ in Section 6.
3. Tail-Gini functional
Let 
$(X,Y)$ be a bivariate risk vector with a survival copula 
$\hat {C}$. Under the assumption that the survival function 
$\bar {F}_{1}$ of 
$X$ is regularly varying with index 
$-1/\gamma _{1}$ and 
$\gamma _{1}$ is the extreme value index, define
$$R(x,y) := \lim_{u \downarrow 0} u^{{-}1} \hat{C}(ux,uy),\quad (x,y) \in [0,\infty)^{2},$$if the limit exists. Hou and Wang [Reference Hou and Wang13] have established the following asymptotic behavior, for 
$Q_{1}$, the quantile function of 
$X$,
\begin{equation} \lim_{p \downarrow 0} \frac{\mathrm{TGini}_{p}(X;Y)}{Q_{1}(1-p)} = \frac{2\gamma_{1}}{2 - \gamma_{1}} \int_{0}^{\infty} R(x^{{-}1/\gamma_{1}}, 1) \,dx . \end{equation}Thus, we obtain that as 
$p \downarrow 0$,
$$\mathrm{TGini}_{p}(X;Y) \sim \mathrm{const.}\quad Q_{1}(1-p).$$Unfortunately, if 
$X$ and 
$Y$ are tail independent the 
$R(x,y) \equiv 0$ which implies that the limit in Eq. (6) is 
$0$ and hence, is not very useful. We aim to provide a closed-form result for the tail-Gini functional in both tail dependent and tail independent cases.
In addition to Assumption 2.1 proposed in Section 2, we need the further assumption as follows with defining
$$\tau_{p} (x,y) = \frac{\hat{C}(px,py)}{p^{\kappa}},\quad (x,y) \in [0,\infty)^{2},\ p >0.$$Assumption 3.1
(a) Assume that
$\bar {F}_{1} \in \mathrm {RV}_{-{1}/{\gamma _{1}}}, \gamma _{1} >0$, and there exists $d \in (0,\infty )$ such that
$$\lim_{t \rightarrow \infty} \frac{\bar{F}(t)}{t^{-{1}/{\gamma_{1}}}} =d.$$(b) There exists
$\beta _{1} > \gamma _{1}$ such that $\lim _{p \downarrow 0} \sup _{0 < x \leq 1, 0< y \leq 1} |\tau _{p}(x,y) - \tau (x,y)| x^{-\beta _{1}} =0$.(c) There exists
$0<\beta _{2}<\gamma _{1}$ such that $\lim _{p \downarrow 0} \sup _{1 < x < \infty,0< y \leq 1} |\tau _{p}(x,y) - \tau (x,y)| x^{-\beta _{2}} =0$.
In Assumption 3.1, (a) is a second-order strengthening condition based on the regular variation of 
$\bar {F}_{1}$. Since 
$\mathrm {TGini}_{p}(X;Y)$ can be written as a double integral, Assumption 3.1 guarantees the generalized dominated convergence condition for obtaining the integrability.
Theorem 3.1 Let 
$(X,Y)$ be a bivariate random vector with survival copula 
$\hat {C}$ and 
$X$ is non-negative with the survival distribution 
$\bar {F}_{1}$. Suppose Assumptions 2.1 and 3.1 hold with 
$\gamma _{1} \in (0,1)$. If 
$1 + \gamma _{1} - \kappa >0$, 
$\int _{0}^{\infty } \tau (x^{-{1}/{\gamma _{1}}} , 1)\, dx < \infty$, then we have
\begin{equation} \lim_{p \downarrow 0} \frac{\mathrm{TGini}_{p}(X;Y)}{p^{\kappa -1} Q_{1}(1-p)} = \frac{2(1 + \gamma_{1}- \kappa)}{ 1 - \gamma_{1} + \kappa } \int_{0}^{\infty} \tau(x^{{-}1/\gamma_{1}},1) \,dx. \end{equation}Proof. For any two non-negative random variables 
$U, V$ with finite variances, we can simply write
\begin{align*} \mathrm{Cov}(U,V) & = \int_{0}^{\infty} \int_{0}^{\infty} (F(u,v) - F_{U}(u)F_{V}(v)) \,du\,dv\\ & = \int_{0}^{\infty} \int_{0}^{\infty} (\bar{F}(u,v) - \bar{F}_{U}(u) \bar{F}_{V}(v)) \,du\,dv, \end{align*}where 
$F, F_{U}, F_{V}$ are the joint and marginal distributions of 
$U,V$, respectively, and 
$\bar {F}, \bar {F}_{1}, \bar {F}_{2}$ are survival ones (we denote 
$\bar {F}(u,v) = \mathbb {P}(U >u, V>v)$). Thus, for 
$(X,Y)$ with survival copula 
$\hat {C}$ and marginal distribution 
$F_{i}, i = 1,2,$ we have
\begin{align*} \mathrm{TGini}_{p}(X ; Y)& = \frac{4}{p} \,{\rm Cov}(X, F_{2}(Y) \mid F_{2}(Y)>1-p) \\ & = \frac{4}{p} \int_{0}^{\infty} \int_{0}^{1}(\mathbb{P}(X>x, F_{2}(Y)>y \mid F_{2}(Y)>1-p )\\ & \quad -\mathbb{P}(X>x \mid F_{2}(Y)>1-p ) \mathbb{P}(F_{2}(Y)>y \mid F_{2}(Y)>1-p )) \,d y \,d x\\ & = \frac{4}{p} \int_{0}^{\infty} \int_{1-p}^{1}(\mathbb{P}(X>x, F_{2}(Y)>y \mid F_{2}(Y)>1-p )\\ & \quad -\mathbb{P}(X>x \mid F_{2}(Y)>1-p ) \mathbb{P}(F_{2}(Y)>y \mid F_{2}(Y)>1-p ))\,d y \,d x\\ & = 4 \int_{0}^{\infty} \int_{1-p}^{1}\left(\frac{ \hat{C} (\bar{F}_{1}(x), 1-y)}{p}-\frac{\hat{C} (\bar{F}_{1}(x), p )}{p} \times \frac{1-y}{p}\right) d\left(\frac{y}{p}\right) d x\\ & = 4 \int_{0}^{\infty} \int_{0}^{1}\left(\frac{\hat{C} (\bar{F}_{1}(x), py)}{p}-\frac{\hat{C} (\bar{F}_{1}(x), p)}{p} y\right) d y \,d x, \end{align*}where the last step is due to a change in variables. Thus, we only need to show that
\begin{align*} & \lim_{p \downarrow 0} \frac{1}{p^{\kappa - 1} Q_{1}(1 - p)} \int_{0}^{\infty} \int_{0}^{1}\left(\frac{\hat{C} (\bar{F}_{1}(x), py)}{p}-\frac{\hat{C}(\bar{F}_{1}(x), p)}{p} y\right)d y \,d x\\ & \quad = \frac{1 +\gamma_{1}- \kappa}{2 (1 - \gamma_{1}+ \kappa)} \int_{0}^{\infty} \tau (x^{{-}1/\gamma_{1}},1) \,dx . \end{align*}Let 
$s_{p}(x) := \bar {F}_{1} (Q_{1}(1-p) x)/p, x \in (0.\infty )$. Note that
\begin{align*} & \frac{1}{p^{\kappa - 1} Q_{1}(1 - p)} \int_{0}^{\infty} \int_{0}^{1}\left(\frac{\hat{C}(\bar{F}_{1}(x), p y)}{p}-\frac{\hat{C} (\bar{F}_{1}(x),p )}{p} y\right) d y \,d x\\ & \quad = \int_{0}^{\infty} \int_{0}^{1} \left( \frac{\hat{C} (p s_{p}(x), p y)}{p^{\kappa}} - \frac{\hat{C} (p s_{p}(x), p )}{p^{\kappa}} y\right) d y \,d x. \end{align*}Then, by Lemma A.1 in Appendix A and the 
$\kappa$-order homogeneous property of 
$\tau$, we have
\begin{align*} \lim_{p \downarrow 0} \frac{\mathrm{TGini}_{p}(X;Y)}{4p^{\kappa - 1} Q_{1}(1-p)} & = \int_{0}^{\infty}\int_{0}^{1} \tau(x^{-{1}/{\gamma_{1}}},y) \,dy\,dx - \int_{0}^{\infty} \int_{0}^{1} \tau(x^{-{1}/{\gamma_{1}}},1) y \,dy\,dx \\ & = \int_{0}^{\infty}\int_{0}^{1} y^{\kappa} \tau(x^{-{1}/{\gamma_{1}}}/y,1) \,dy\,dx - \frac{1}{2} \int_{0}^{\infty} \tau(x^{-{1}/{\gamma_{1}}},1) \,dx\\ & = \int_{0}^{\infty}\int_{0}^{1} y^{\kappa - \gamma_{1}} \tau(x^{-{1}/{\gamma_{1}}},1) \,dy\,dx - \frac{1}{2} \int_{0}^{\infty} \tau(x^{-{1}/{\gamma_{1}}},1) \,dx\\ & = \frac{1 + \gamma_{1}- \kappa }{2 (1 - \gamma_{1}+ \kappa )} \int_{0}^{\infty} \tau(x^{{-}1/\gamma_{1}},1)\,dx, \end{align*}which completes the proof.
Remark 3.1. As 
$\mathrm {TGini}_{p}(X; Y)$ can be written as a double integral, the main challenge is to validate the interchangeability of the limit and the integral by dominated convergence theorem, and Assumption 3.1 is imposed to serve this purpose. Note that if 
$\kappa =1$, then the result of Eq. (7) coincides with the result of Theorem 1 in Hou and Wang [Reference Hou and Wang13]. The condition of 
$1 + \gamma _{1} -\kappa > 0$ implies that 
$p^{\kappa -1}Q_{1}(1-p) \rightarrow \infty$; thus, 
$\mathrm {TGini}_{p}(X;Y) \rightarrow \infty$ as 
$p \downarrow 0$.
4. Joint tail-Gini functional
In this section, the asymptotic limit result is derived first. Then, a generalization of joint tail-Gini functional is introduced and a similar asymptotic result is presented.
4.1. Asymptotic analysis
To obtain the asymptotic results like Theorem 3.1, we need to impose some regularity to the limit function 
$\tau (\cdot,\cdot )$, as stated in the following assumptions:
Assumption 4.1. Assume that 
$\tau (\cdot, 1) \in \mathrm {RV}_{\beta }(0)$ for some 
$\beta >0$ and for any 
$\delta >0$, there exists 
$c>0$ and 
$u_{0} \in (0,1)$ such that for all 
$u \in (0,u_{0})$ and all 
$x \in [0,1]$,
\begin{equation} \frac{\hat{C}(ux,u)}{\hat{C}(u,u)} \leq cx^{\beta - \delta}. \end{equation} The inequality (8) provides the uniform bound on the survival copula 
$\hat {C}$ to guarantee the integrability, which plays a similar role with Assumption 3.1.
Many widely used copulas including the extreme value survival copulas and Archimedean survival copulas with regularly varying generator, satisfy Assumption 4.1.
Theorem 4.1. Let 
$(X,Y)$ be a bivariate random vector with survival copula 
$\hat {C}$ satisfying Assumptions 2.1 and 4.1. Suppose that 
$X$ is non-negative and its survival function 
$\bar {F} \in \mathrm {RV}_{-1/\gamma _{1}}$ with 
$0<\gamma _{1} < 1 \wedge \beta$. 
$Y$ follows a distribution function 
$F_{2}$. Then, we have
$$\lim_{p \downarrow 0} \frac{\mathrm{JTGini}_{p}(X;Y)}{Q_{1}(1 - p)} = 4 \int_{1}^{\infty}\int_{0}^{1} \tau'(x^{{-}1/\gamma_{1}},y) -\tau'(x^{{-}1/\gamma_{1}},1) \tau'(1,y) \,dy\,dx,$$where 
$\tau '(x,y) = \tau (x,y)/\tau (1,1)$.
Proof. For 
$(X,Y)$ with a survival copula 
$\hat {C}$ and marginal distributions 
$F_{1}$ and 
$F_{2}$, we have
\begin{align*} & \mathrm{JTGini}_{p}(X:Y)\\ & \quad = \frac{4}{p} \,\mathrm{Cov} (X, F_{2}(Y) \,|\, X > Q_{1}(1-p), Y > Q_{2}(1-p)) \\ & \quad = \frac{4}{p} \int_{0}^{\infty} \int_{0}^{1} \mathbb{P} (X > x, F_{2}(Y) > y\,|\, X > Q_{1}(1-p), Y > Q_{2}(1-p) ) \\ & \qquad - \mathbb{P} (X > x \,|\, X > Q_{1}(1-p), Y > Q_{2}(1-p))\\ &\qquad \times \mathbb{P} ( F_{2}(Y) > y \,| X > Q_{1}(1-p), Y > Q_{2}(1-p) ) \,dy\,dx \\ & \quad =\frac{4}{p} \int_{Q_{1}(1 - p)}^{\infty} \int_{1-p}^{1} \mathbb{P} (X > x, F_{2}(Y) > y\,|\, X >Q_{1}(1-p), Y > Q_{2}(1-p) ) \\ & \qquad - \mathbb{P} (X > x \,|\, X > Q_{1}(1-p), Y > Q_{2}(1-p) )\\ &\qquad \times \mathbb{P} (F_{2}(Y) >y \,|\, X > Q_{1}(1-p), Y > Q_{2}(1-p) )\, dy\,dx\\ & \quad =\frac{4}{p} \int_{Q_{1}(1 - p)}^{\infty} \int_{1-p}^{1} \frac{\hat{C}(\bar{F}_{1}(x), 1-y)}{\hat{C}(p,p)} - \frac{\hat{C}(\bar{F}_{1}(x), p)}{\hat{C}(p,p)} \frac{\hat{C}(p,1-y)}{\hat{C}(p,p)} \,dy\,dx\\ & \quad = 4 \int_{Q_{1}(1-p)}^{\infty} \int_{0}^{1} \frac{\hat{C}(\bar{F}_{1}(x), py)}{\hat{C}(p,p)} - \frac{\hat{C}(\bar{F}_{1}(x), p)}{\hat{C}(p,p)}\frac{\hat{C}(p,py)}{\hat{C}(p,p)} \,dy\,dx. \end{align*}Define 
$t_{p}(x) := \bar {F}_{1}(Q_{1}(1 - p) x^{-\gamma _{1}})/p, x \in (0,1)$. Note that
\begin{align*} & \frac{1}{Q_{1}(1-p)} \int_{Q_{1}(1-p)}^{\infty} \int_{0}^{1} \frac{\hat{C}(\bar{F}_{1}(x), py)}{\hat{C}(p,p)} - \frac{\hat{C}(\bar{F}_{1}(x), p)}{\hat{C}(p,p)}\frac{\hat{C}(p,py)}{\hat{C}(p,p)} \,dy\,dx\\ & \quad ={-} \int_{0}^{1} \int_{0}^{1} \frac{\hat{C}((p t_{p}(x), py)}{\hat{C}(p,p)} - \frac{\hat{C}(p t_{p}(x),p)}{\hat{C}(p,p)} \frac{\hat{C}(p, py)}{\hat{C}(p,p)} \,dy\,dx^{-\gamma_{1}}. \end{align*}Define 
$\tau '(x,y) = \tau (x,y)/\tau (1,1)$, then by Lemma A.2 in Appendix A we have
\begin{align*} & \lim_{p \downarrow 0} - \int_{0}^{1} \int_{0}^{1} \frac{\hat{C}((p t_{p}(x), py)}{\hat{C}(p,p)} - \frac{\hat{C}(p t_{p}(x),p)}{\hat{C}(p,p)} \frac{\hat{C}(p, py)}{\hat{C}(p,p)} \,dy\,dx^{-\gamma_{1}}\\ & \quad ={-}\int_{0}^{1} \int_{0}^{1} \tau'(x,y) - \tau'(x,1)\tau'(1,y) \,dy\,dx^{-\gamma_{1}} \\ & \quad = \int_{1}^{\infty}\int_{0}^{1} \tau'(x^{{-}1/\gamma_{1}},y) -\tau'(x^{{-}1/\gamma_{1}},1) \tau'(1,y) \,dy\,dx, \end{align*}which completes the proof.
Remark 4.1. The above results are derived under Assumption 2.1 so that both tail dependent and tail independent cases are covered.
4.2. A generalization
We conclude this section by considering a further generalization of joint tail-Gini functional, that is,
\begin{equation} \frac{4}{p} \mathrm{Cov}(X, F_{2}(Y)\, |\, X > \zeta Q_{1}(1 - p), Y > Q_{2}(1 - p)), \end{equation}where 
$\zeta$ is a constant between 
$0$ and 
$1$. When 
$\zeta$ approaches 
$1$, then Eq. (9) recovers the original definition of joint tail-Gini functional. When 
$\zeta$ is close to 
$0$, then it becomes more like tail-Gini functional of 
$(X, Y)$ as Eq. (2). Hence, we refer Eq. (9) as the general joint tail-Gini functional. The asymptotic expansion of the general joint tail-Gini functional is shown in the theorem below.
Theorem 4.2. Let 
$(X,Y)$ be a bivariate random vector with survival copula 
$\hat {C}$ satisfying Assumptions 2.1 and 4.1. Suppose that 
$X$ is non-negative and its survival function 
$\bar {F} \in \mathrm {RV}_{-1/\gamma _{1}}$ with 
$0<\gamma _{1} < 1 \wedge \beta$. 
$Y$ follows a distribution function 
$F_{2}$. Then, we have for 
$0 < \zeta \leq 1$,
\begin{align} \lim_{p \downarrow 0} \frac{\mathrm{JTGini}_{p}(X;Y)}{Q_{1}(1-p)}& = \frac{4}{\tau(\zeta^{-{1}/{\gamma_{1}}}, 1)} \int_{\zeta }^{\infty} \int_{0}^{1} \tau(x^{-{1}/{\gamma_{1}}},y) \,dy\,dx \nonumber\\ & \quad - \frac{4}{(\tau(\zeta^{-{1}/{\gamma_{1}}}, 1))^{2}} \int_{\zeta }^{\infty} \int_{0}^{1} \tau(x^{-{1}/{\gamma_{1}}},1) \tau(\zeta^{-{1}/{\gamma_{1}}},y)\,dy\,dx. \end{align}Proof. Follow the same setup as in the proof of Theorem 2. Define 
$t_{p}(x) := \bar {F}_{1}(Q_{1}(1 - p) x^{-\gamma _{1}})/p, x \in (0,1)$. Then, we get
\begin{align*} & \frac{\mathrm{JTGini}_{p}(X:Y)}{4Q_{1}(1-p)}\\ & \quad = \frac{1}{pQ_{1}(1-p)} \,\mathrm{Cov}(X, F_{2}(Y)\,|\,X > \zeta Q_{1}(1 - p), Y > Q_{2}(1 - p))\\ & \quad = \frac{1}{Q_{1}(1-p)} \int_{\zeta Q_{1}(1 - p)}^{\infty} \int_{0}^{1} \frac{\hat{C}(\bar{F}_{1}(x), py)}{\hat{C}(\bar{F}_{1}(\zeta Q_{1}(1-p)),p)}\notag\\ &\qquad - \frac{\hat{C}(\bar{F}_{1}(x), p)}{\hat{C}(\bar{F}_{1}(\zeta Q_{1}(1 - p)),p)} \frac{\hat{C}(\bar{F}_{1}(\zeta Q_{1}(1 - p)),py)} {\hat{C}(\bar{F}_{1}(\zeta Q_{1}(1 - p)),p)} \,dy\,dx\\ & \quad = \int_{\zeta}^{\infty} \int_{0}^{1} \frac{\hat{C}(\bar{F}_{1}( Q_{1}(1-p)x), py)}{\hat{C}(\bar{F}_{1}(\zeta Q_{1}(1-p)x),p)} - \frac{\hat{C}(\bar{F}_{1}( Q_{1}(1-p)x), p)}{\hat{C}(\bar{F}_{1}(\zeta Q_{1}(1 - p)),p)} \frac{\hat{C}(\bar{F}(\zeta Q_{1}(1 - p)),py)} {\hat{C}(\bar{F}(\zeta Q_{1}(1 - p)),p)} \,dy\,dx\\ & \quad = \int_{0}^{\zeta^{{-}1/\gamma_{1}}} \int_{0}^{1} \left(\frac{\hat{C}(p,p)}{\hat{C}(pt_{p}(\zeta^{{-}1/\gamma_{1}}), p)}\right)^{2} \frac{\hat{C}(p t_{p}(x), p)}{\hat{C}(p, p)} \frac{\hat{C}((pt_{p}(\zeta^{{-}1/\gamma_{1}}),py)} {\hat{C}(p,p)} \,dy\,dx^{-\gamma_{1}}\\ & \qquad - \int_{0}^{\zeta^{{-}1/\gamma_{1}}} \int_{0}^{1} \frac{\hat{C}(p,p)}{\hat{C}(p t_{p}(\zeta^{{-}1/\gamma_{1}}), p)} \frac{\hat{C}(p t_{p}(x), py)}{\hat{C}(p, p)} \,dy\,dx^{-\gamma_{1}}. \end{align*}Define 
$\tau '(x,y) = \tau (x,y)/\tau (1,1)$. By Lemma A.2 in Appendix A, we have that
\begin{align*} & \lim_{p \downarrow 0} \frac{\mathrm{JTGini}_{p}(X:Y)}{Q_{1}(1-p)}\\ & \quad =\frac{4}{(\tau'(\zeta^{-{1}/{\gamma_{1}}}, 1))^{2}} \int_{0}^{\zeta^{{-}1/\gamma_{1}}} \int_{0}^{1} \tau'(x,1) \tau'(1,y) \,dy\,dx^{-\gamma_{1}}\\ &\qquad - \frac{4}{\tau'(\zeta^{-{1}/{\gamma_{1}}}, 1)} \int_{0}^{\zeta^{{-}1/\gamma_{1}}} \int_{0}^{1} \tau'(x,y) \,dy\,dx^{-\gamma_{1}}\\ & \quad=\frac{4}{\tau'(\zeta^{-{1}/{\gamma_{1}}}, 1)} \int_{\zeta }^{\infty} \int_{0}^{1} \tau'(x^{-{1}/{\gamma_{1}}},y) \,dy\,dx\\ &\qquad - \frac{4}{(\tau'(\zeta^{-{1}/{\gamma_{1}}}, 1))^{2}} \int_{\zeta }^{\infty} \int_{0}^{1} \tau'(x^{-{1}/{\gamma_{1}}},1) \tau'(\zeta^{-{1}/{\gamma_{1}}},y)\,dy\,dx\\ & \quad= \frac{4}{\tau(\zeta^{-{1}/{\gamma_{1}}}, 1)} \int_{\zeta }^{\infty} \int_{0}^{1} \tau(x^{-{1}/{\gamma_{1}}},y) \,dy\,dx - \frac{4}{(\tau(\zeta^{-{1}/{\gamma_{1}}}, 1))^{2}} \int_{\zeta }^{\infty} \int_{0}^{1} \tau(x^{-{1}/{\gamma_{1}}},1) \tau(\zeta^{-{1}/{\gamma_{1}}},y)\,dy\,dx. \end{align*}Thus, we complete this proof.
Remark 4.2. When 
$\zeta =1$, Eq. (10) reduces to the same result of Theorem 4.1 with 
$\tau (\zeta ^{-{1}/{\gamma _{1}}}, 1)=\tau (1,1)$. When 
$\zeta =0$, our method of proof is not directly applicable in general. But for the special case considered in Hou and Wang [Reference Hou and Wang13] with 
$\kappa = 1$ in Eq. (5), that is, 
$\hat {C}(ux,uy) \sim u\tau (x,y)$ as 
$u \downarrow 0$, our result Eq. (10) leads to the asymptotic expansion of 
$\mathrm {TGini}_{p}(X,Y)$ as
\begin{align*} & \frac{\mathrm{TGini}_{p}(X;Y)}{Q_{1}(1-p)} \rightarrow 4\int_{0}^{\infty} \int_{0}^{1} \tau(x^{-{1}/{\gamma_{1}}},y) - \tau(x^{-{1}/{\gamma_{1}}},1)\cdot y\,dy\,dx \\ & \quad = \frac{2\gamma_{1}}{2-\gamma_{1}} \int_{0}^{\infty} \tau(x^{{-}1/\gamma_{1}},1), \quad p \downarrow 0, \end{align*}which coincides with Theorem 1 of Hou and Wang [Reference Hou and Wang13] due to the fact that 
$\tau (\infty,1)= 1$ and the function 
$\tau$ corresponds to 
$R$-function.
5. Examples
In this section, some typical copula examples satisfying Assumptions 2.1, 3.1 and 4.1 are given. For the marginal distribution of 
$X$, we focus on heavy-tailed distribution and uniformly choose Pareto distribution for each case, that is, for some 
$\gamma _{1}>0$,
$$F_{1}(x) = 1- \left(\frac{1}{x+1}\right)^{1/\gamma_{1}},\quad x>0,$$which satisfies Assumption 3.1 (a) with 
$d=1$ and 
$\gamma _{1}$ can take any positive value that satisfies Assumptions and the conditions in Theorems. Then, by Theorems 3.1 and 4.1, we calculate the asymptotic expansions of tail-Gini functional and joint tail-Gini functional for these copulas.
Case I: Independence survival copula
The independence survival copula is 
$\hat {C}(u,v) = uv$. Straightforwardly, we have 
$\hat {C}(u,u) \sim u^{2}$ and
$$\frac{\hat{C} (ux,uy)}{u^{2}} = \frac{uxuy}{u^{2}} = xy := \tau(x,y) \equiv \tau'(x,y),$$so that Assumption 2.1 is satisfied. Also by the definition 2, the tail order 
$\kappa$ is 2, and 
$\ell (t) =1$. Unfortunately, the conditions 
$\gamma _{1} \in (0,1)$ and 
$1+\gamma _{1} - \kappa >0$ cannot hold at the same time, and 
$\int _{0}^{\infty } \tau (x^{-1/\gamma _{1}},1) dx < \infty$ is not satisfied so that Theorem 3.1 may not be appropriate for this case. Next, we verify Assumption 4.1. Obviously, 
$\tau (x,1) =x$ for all 
$0 \leq x \leq 1$, which implies 
$\beta = 1$, and for any 
$u>0$ and 
$0 \leq x \leq 1$,
$$\frac{\hat{C}(ux,u)}{\hat{C}(u,u)} = \frac{u^{2}x}{u^{2}} = x.$$By Theorem 4.1, for 
$X$ with a distribution function 
$F$ and a survival function 
$\bar {F} \in \mathrm {RV}_{-1/\gamma _{1}}$ with 
$0 < \gamma _{1} <1$. We can show the expansions:
$$\lim_{p \downarrow 0} \frac{\mathrm{JTGini}_{p}(X;Y)}{Q_{1}(1 - p)} = 4 \int_{1}^{\infty}\int_{0}^{1} x^{-{1}/{\gamma_{1}}}y -x^{-{1}/{\gamma_{1}}} \cdot y \,dy\,dx =0.$$Remark 5.1. Under the independence survival copula, according to the definitions of the two tail Gini-type variability measures, we can obtain that
$$\mathrm{TGini}_{p}(X;Y) = \mathrm{JTGini}_{p}(X;Y) =0$$by the property of covariance that 
$\mathrm {Cov}(U,V) =0$ if 
$U$ and 
$V$ are independent.
Case II: Fréchet–Hoeffding upper bound survival copula
The Fréchet–Hoeffding upper bound survival copula in the form of 
$\hat {C}(u,v) =\min \{u,v\}$ satisfies Assumption 2.1 with 
$\kappa =1$ and
$$\frac{\hat{C}(ux,uy)}{u} = \frac{\min\{ux,uy\}}{u}=\min\{x,y\} := \tau(x,y) \equiv \tau'(x,y).$$Assumptions 3.1 (a) and (b) hold with the fact 
$\tau _{p}(x,y) = \tau (x,y), ~x,y \geq 0$. By Theorem 3.1, we can get
$$\lim_{p \downarrow 0} \frac{\mathrm{TGini}_{p}(X;Y)}{Q_{1}(1-p)} = \frac{2\gamma_{1}}{2-\gamma_{1}} \int_{0}^{\infty} \min\{x^{{-}1/\gamma_{1}},1\} \,dx = \frac{2\gamma_{1}}{(2-\gamma_{1})(1-\gamma_{1})}.$$As for Assumption 4.1, 
$\tau '(x,1) = x$ for all 
$0 < x <1$, which implies 
$\beta =1$. For any 
$u >0$ and 
$o < x < 1$,
$$\frac{\hat{C}(ux,u)}{\hat{C}(u,u)} = \frac{u\min\{x,1\}}{u} = x.$$Then, Theorem 4.1 implies that
\begin{align*} \lim_{p \downarrow 0} \frac{\mathrm{JTGini}_{p}(X;Y)}{Q_{1}(1 - p)} & = 4 \int_{1}^{\infty} \int_{0}^{1} \min\{x^{-{1}/{\gamma_{1}}},y\} - \min\{x^{-{1}/{\gamma_{1}}}, 1\} \cdot \min\{1,y\} \,dy\,dx\\ & = \frac{2\gamma_{1}}{(2-\gamma_{1})(1-\gamma_{1})}. \end{align*}Remark 5.2. Under the Fréchet–Hoeffding upper bound survival copula, the asymptotic limit of the 
$\mathrm {JTGini}_{p}(X;Y)$ is the same with that of the 
$\mathrm {TGini}_{p}(X;Y)$. Note that if 
$X=Y, \ {\rm a.s.}$, the survival copula of 
$(X,Y)$ is in the form of Fréchet–Hoeffding upper bound survival copula. Then, it is intuitively reasonable since 
$\mathrm {JTGini}_{p}(X;Y)$ reduces to 
$\mathrm {TGini}_{p}(X;Y)$ when 
$X=Y, \ {\rm a.s.}$
Case III: Clayton survival copula
As a special case of Archimedean copula, the Clayton survival copula takes the form of
$$\hat{C}(u,v) = \psi(\psi^{{-}1}(u) + \psi^{{-}1}(v)),$$with the generator function 
$\psi (t) = (1+t)^{-a}$. In our example, we take 
$a=1$, that is, 
$\hat {C}(u,v) = (u^{-1} + v^{-1} -1)^{-1}$, then 
$\hat {C}(u,u) \sim u/2$. One can check that this Clayton survival copula satisfies Assumption 2.1 with 
$\kappa =1$ and
$$\tau(x,y) = (x^{{-}1} + y^{{-}1})^{{-}1}.$$Assomption 3.1 holds with 
$\tau _{p}(x,y) = (x^{-1} + y^{-1} -p)^{-1}$. Then, we make the following result
$$\lim_{p \downarrow 0} \frac{\mathrm{TGini}_{p}(X;Y)}{Q_{1}(1-p)} = \frac{2\gamma_{1}}{2-\gamma_{1}} \int_{0}^{\infty} (x^{{1}/{\gamma_{1}}} + 1 )^{{-}1} \,dx.$$Moreover, 
$\tau (x,1) = (x^{-1} + 1)^{-1}$ so that 
$\tau (\cdot, 1) \in \mathrm {RV}_{1}(0)$, that is, 
$\beta =1$. For the uniform bound, first note that if 
$x=0$, then
$$\frac{\hat{C}(ux,u)}{\hat{C}(u,u)} = 0.$$Next consider 
$x\in (0,1]$. By potter's bounds, for any 
$0<\varepsilon, \delta <1$, there exist 
$c>0$ and 
$u_{0}>0$ such that for all 
$u< u_{0}$ and 
$x \in (0,1]$ that
\begin{align*} \frac{\hat{C}(ux,u)}{\hat{C}(u,u)} & = \frac{((ux)^{{-}1} + u^{{-}1} -1)^{{-}1}}{(2u^{{-}1} -1)^{{-}1}} \\ & \leq \frac{(((1-\epsilon)x^{{-}1+\delta} +1)(u^{{-}1}-1))^{{-}1}}{(2u^{{-}1} -1)^{{-}1}}\\ & \leq (1+\epsilon) \left(\frac{(1-\epsilon)x^{{-}1+\delta} +1}{2}\right)^{{-}1+\delta}\\ & \leq cx^{1-\delta}. \end{align*}Thus, Assumption 4.1 is satisfied. Combining Theorem 4.1 with 
$\tau '(x,y) = \tau (x,y)/\tau (1,1) = 2(x^{-1} +y^{-1})^{-1}$, we have
$$\lim_{p \downarrow 0} \frac{\mathrm{JTGini}_{p}(X;Y)}{Q_{1}(1-p)} = 8 \int_{1}^{\infty} \int_{0}^{1} (x^{{1}/{\gamma_{1}}} + y^{{-}1})^{{-}1} - 2(x^{{1}/{\gamma_{1}}}+1 )^{{-}1} (1+y^{{-}1})^{{-}1}\, dy\,dx.$$6. Concluding remarks and discussions
In this article, the tail order property of the copula provides a tractable theoretical approach for studying the asymptotic behaviors of the tail Gini-type variability measures under wide dependence structures. From the viewpoint of risk management, the asymptotic limit of tail-Gini functional provides a closed-form result that extends the study of Hou and Wang [Reference Hou and Wang13]. Moreover, the joint tail-Gini functional is proposed to measure multivariate risk variability. Compared with the tail-Gini functional, the joint tail-Gini functional takes more of the factor of heavy tailedness into consideration by adding the tail information of 
$X$ itself. Hence, the advantage of joint tail-Gini functional is reflecting the variability of 
$X$ under the tail scenarios more realistically and accurately. Among future research perspectives, there is a series of interesting open questions, such as:
• The extension to the case of a real-valued
$X$. In our approach, the tail Gini-type variability measures are investigated under the setting that $p \downarrow 0$ and $X$ is non-negative. The development can be extended to the case where $X$ is real in principle, although some assumptions may need to be imposed to accommodate $X \in \mathbb {R}$. Denote $X^{+} = \max (X,0)$ and $X^{-} = \min (X,0)$, then $X=X^{+} + X^{-}$. For tail-Gini functional in the case of a real-valued $X$ with $\mathbb {E}|X^{-}|^{1/\gamma _{1}} < \infty$, if some conditions are strengthened, then
(11)Refer to Hou and Wang [Reference Hou and Wang13] for more details. When it comes to joint tail-Gini functional, we can obtain a result similar to Eq. (11) under some assumptions by following a similar way as done in Hou and Wang [Reference Hou and Wang13]. In fact, both tail-Gini functional and joint tail-Gini functional of a general loss variable\begin{equation} \lim_{p \downarrow 0} \frac{\mathrm{TGini}_{p}(X;Y)}{\mathrm{TGini}_{p}(X^{+};Y)} =1. \end{equation}$X$ is dominated by its positive component. From an intuitive perspective, we focus on the right tail variability of $X$, so that the contribution to the tail variability from the negative component will eventually disappear as the level $p$ goes to zero.• The estimation of joint tail-Gini functional. Similar to tail-Gini functional, joint tail-Gini functional can be formulated as the conditional covariance. Following Hou and Wang [Reference Hou and Wang13], based on the random sample
$\{(X_{i},Y_{i})\}_{i=1}^{n}$ and intermediate sequence $k$, we can construct a nonparametric estimator of $\mathrm {JTGini}_{k/n}(X;Y)$ :
where$$\frac{4n}{km} \sum_{i< j} (X_{i} -X_{j})(F_{n2}(Y_{i}) - F_{n2}(Y_{j})) I(X_{i} > X_{(n-k)}, X_{j}> X_{(n-k)}, Y_{i} > Y_{(n-k)},Y_{j} > Y_{(n-k)}),$$$X_{(1)} \leq X_{(2)} \leq \cdots \leq X_{(n)}, Y_{(1)} \leq Y_{(2)} \leq \cdots \leq Y_{(n)}$ are the order statistics of $X_{i}$ and $Y_{i}$ in their respective samples, $m\,=\,\sum _{i< j}I(X_{i} \,>\, X_{(n-k)}, X_{j}> X_{(n-k)}, Y_{i} > Y_{(n-k)},Y_{j} > Y_{(n-k)})$ and $F_{n2}(y) = ({1}/{n})\sum _{i} I(Y_{i} \leq y)$. However, it is a complicated research project to explore the asymptotic properties such as the consistency and asymptotic normality of the estimator which we defer to future work.
Acknowledgments
The authors would like to thank the anonymous referees and the Editor for their constructive comments that improved the quality of this paper. This work was supported in part by the National Natural Science Foundation of China (No. 71771203) and the Natural Science Foundation of Anhui Province (No. 2208085MA05).
Appendix
Lemma A.1. Assume that 
$\hat {C}$ is a survival copula and 
$\bar {F}_{1}$ is a survival function satisfying Assumptions 2.1 and 3.1 with 
$\gamma _{1} \in (0,1)$. If 
$1+\gamma _{1}-\kappa >0, \int _{0}^{\infty } \tau (x^{-1/\gamma _{1}},1) \,dx <\infty$, then we have
\begin{equation} \lim_{p \downarrow 0} \int_{0}^{\infty} \int_{0}^{1} \frac{\hat{C}(ps_{p}(x), py)}{p^{\kappa}} \,dy\,dx = \int_{0}^{\infty} \int_{0}^{1} \tau(x^{-{1}/{\gamma_{1}}},y) \,dy\,dx, \end{equation}where 
$s_{p}(x) = \bar {F}(Q_{1}(1-p)x)/p, x \in (0,\infty )$.
Proof. Define 
$f_{p} (x,y) := p^{-\kappa }\hat {C}(ps_{p}(x), py)$. Recall that 
$\tau (x,y): [0, \infty )^{2} \mapsto \mathbb {R}_{+}$ is a non-degenerate continuous function. Then, the limit relationship (5) in Assumption 2.1 and the regular variation property 
$\bar {F}_{1} \in \mathrm {RV}_{-{1}/ {\gamma _{1}}}$ imply that for any positive and finite 
$T$
$$\lim_{p \downarrow 0} f_{p}(x,y) = \lim_{p \downarrow 0} \frac{\hat{C}(ps_{p}(x), py)}{p^{\kappa}} = \tau(x^{-{1}/{\gamma_{1}}},y),\quad (x,y) \in (0,\infty) \times (0,T].$$Then, we use the generalized dominated convergence theorem to validate that
$$\lim_{p \downarrow 0} \int_{0}^{\infty} \int_{0}^{1} f_{p} (x,y) \,dy\,dx = \int_{0}^{\infty}\int_{0}^{1} \lim_{p \downarrow 0} f_{p} (x,y) \,dy\,dx = \int_{0}^{\infty} \int_{0}^{1} \tau(x^{-{1}/{\gamma_{1}}},y) \,dy\,dx .$$By Assumption 3.1 , for any 
$\epsilon$, there exists 
$t_{0}$ such that
$$\left|\frac{\bar{F}_{1}(t)}{t^{-{1}/{\gamma_{1}}}} - d\right| < \epsilon, \quad \text{for all}\ t > t_{0}.$$Hence, for 
$c_{1} =((d-\epsilon )/(d+\epsilon ))^{-\gamma _{1}}$ and 
$0 < x \leq c_{1}(p/p_{0})$, we get
$$\frac{\bar{F}_{1}(Q_{1}(1-p) x)}{p(x/c_{1})^{-{1}/{\gamma_{1}}}} = \frac{\bar{F}_{1} (Q_{1}(1-p)x)/(Q_{1}(1-p)x)^{-{1}/{\gamma_{1}}}}{\bar{F}_{1} (Q_{1}(1-p))/(Q_{1}(1-p)^{-{1}/{\gamma_{1}}})} \cdot c_{1}^{-{1}/{\gamma_{1}}} < \frac{d + \epsilon}{d - \epsilon} (c_{1}^{-{1}/{\gamma_{1}}}) =1.$$Consequently, for 
$x > c_{1}(p/p_{0})^{\gamma _{1}}$,
$$f_{p}(x,y) \leq {p^{-\kappa}}{\hat{C}\left(p\left(\frac{x}{c_{1}}\right)^{-{1}/{\gamma_{1}}},py\right)}.$$On the other hand, for 
$0 < x < c_{1}(p/p_{0})^{\gamma _{1}}$, 
$f_{p}(x,y) \leq py/{p^{\kappa }} = p^{1-\kappa }y.$ Define
$$g_{p}(x,y) := \begin{cases} p^{-\kappa}{\hat{C}\left(p\left(\dfrac{x}{c_{1}}\right)^{-{1}/{\gamma_{1}}},py\right)}, & \text{if}\ x > c_{1}(p/p_{0})^{\gamma_{1}} \\ p^{1-\kappa}y, & \text{otherwise}. \end{cases}$$then, 
$f_{p}(x,y) \leq g_{p}(x,y)$. By generalized dominated convergence theorem, it is then sufficient to prove that
$$\lim_{p \downarrow 0} \int_{0}^{\infty} \int_{0}^{1} g_{p}(x,y) \,dy\,dx = \int_{0}^{\infty} \int_{0}^{1} \lim_{p \downarrow 0} g_{p}(x,y) \,dy\,dx = \int_{0}^{\infty} \int_{0}^{1} \tau(x^{-{1}/{\gamma_{1}}},y) \,dy\,dx.$$Observe that
\begin{align*} \int_{0}^{\infty} \int_{0}^{1} g_{p}(x,y) \,dy\,dx & = \int_{0}^{c_{1}(p/p_{0})^{\gamma_{1}}} \int_{0}^{1} p^{1-\kappa}y\,dy\,dx + \int_{c_{1}(p/p_{0})^{\gamma_{1}}}^{\infty} \int_{0}^{1} p^{-\kappa}{\hat{C}\left(p\left(\frac{x}{c_{1}}\right)^{-{1}/{\gamma_{1}}},py\right)} dy\,dx\\ & =\frac{1}{2} \int_{0}^{c_{1}(p/p_{0})^{\gamma_{1}}} p^{1-\kappa} \,dx + c_{1} \int_{(p/p_{0})^{\gamma_{1}}}^{\infty} \int_{0}^{1} p^{-\kappa} \hat{C}(px^{-{1}/{\gamma_{1}}},py) \,dy\,dx\\ & = \frac{1}{2}c_{1} p_{0}^{-\gamma_{1}} p^{1+\gamma_{1}-\kappa} + c_{1}\int_{(p/p_{0})^{\gamma_{1}}}^{\infty} \int_{0}^{1} p^{-\kappa} \hat{C}(px^{-{1}/{\gamma_{1}}},py) \,dy\,dx\\ & \rightarrow 0 + \int_{0}^{\infty} \int_{0}^{1} \tau (x^{-{1}/{\gamma_{1}}}, y) \,dy \,dx \end{align*}as 
$p \downarrow 0$. The last convergence follows from 
$1+\gamma _{1}-\kappa >0, c_{1} \rightarrow 1, (p/p_{0})^{\gamma _{1}} \rightarrow 0$ and the fact that
\begin{align*} & \left|\int_{0}^{\infty} \int_{0}^{1} p^{-\kappa} \hat{C} (px^{-{1}/{\gamma_{1}}}, py) \,dy\,dx - \int_{0}^{\infty} \int_{0}^{1} \tau(x^{{-}1/\gamma_{1}}, 1) \,dy\,dx \right|\\ & \quad \leq \int_{0}^{\infty} \int_{0}^{1} \left|\tau_{p}(x^{-{1}/{\gamma_{1}}},y) - \tau(x^{-{1}/{\gamma_{1}}},y)\right| \,dy\,dx\\ & \quad= o(1) \int_{0}^{1} x^{-\beta_{2}/\gamma_{1}}\,dx + o(1) \int_{1}^{\infty} x^{-\beta_{1}/\gamma_{1}} \,dx \rightarrow 0. \end{align*}Lemma A.2. Assume that 
$\hat {C}$ is a survival copula satisfying Assumptions 2.1 and 4.1. Suppose that a survival function 
$\bar {F}_{1} \in \mathrm {RV}_{-1/\gamma _{1}}$ with 
$\gamma _{1} < 1 \wedge \beta$. Then, we have
$$\lim_{p \downarrow 0} \int_{0}^{1}\int_{0}^{1} \frac{\hat{C}(p t_{p}(x),py)}{\hat{C}(p,p)} \,dy\,dx^{-\gamma_{1}} = \int_{0}^{1}\int_{0}^{1} \tau'(x,y) \,dy\,dx^{-\gamma_{1}}$$where 
$t_{p}(x) := \bar {F}_{1}(Q_{1}(1-p)x^{-{\gamma _{1}}})/p, x \in (0,1)$, 
$\tau '(x,y) = \tau (x,y)/\tau (1,1)$.
Proof. Assumptions 2.1 and 
$\bar {F}_{1} \in \mathrm {RV}_{-1/\gamma _{1}}$ imply that
$$\lim_{p \downarrow 0} \frac{\hat{C}(p t_{p}(x),py)}{\hat{C}(p,p)} = \frac{\tau(x, y)}{\tau(1,1)} =: \tau'(x, y),\quad (x,y) \in (0, 1)^{2}.$$Then, we need to prove that the limit and the integral are interchangeable. As 
$\beta - \delta > \gamma _{1}$, take 
$0 < \varepsilon < 1- {\gamma _{1}}/{(\beta - \delta )}$, by Potter's inequality, there exists 
$p_{0} \in (0,1)$ such that for any 
$0 < p < p_{0}$ and 
$0 < x < 1$,
$$t_{p}(x) \leq 2x^{1-\varepsilon}.$$For 
$(x,y) \in (0,1)^{2}$, we have
$$0 \leq \frac{\hat{C}(p t_{p}(x),py)}{\hat{C}(p,p)} \leq \frac{\hat{C}(p t_{p}(x),p)}{\hat{C}(p,p)} \leq \frac{\hat{C}(2p x^{1-\varepsilon},p)}{\hat{C}(p,p)}.$$Note that Assumption 4.1 directly implies that
$$\frac{\hat{C}(2p x^{1-\varepsilon},p)}{\hat{C}(p,p)} \leq cx^{(1-\varepsilon)(\beta - \delta)}.$$It is straightforward to see that 
$\int _{0}^{1} cx^{(1-\varepsilon )(\beta - \delta )} \,dx^{-\gamma _{1}} < \infty$. By the dominated convergence theorem, we have that
$$\lim_{p \downarrow 0} \int_{0}^{1}\int_{0}^{1} \frac{\hat{C}(p t_{p}(x),py)}{\hat{C}(p,p)} \,dy\,dx^{-\gamma_{1}} = \int_{0}^{1}\int_{0}^{1} \tau'(x,y) \, dy\,dx^{-\gamma_{1}}$$which completes the proof.
