Introduction

It is widely recognized that sea ice controls atmosphere/ ocean heat exchange in the polar regions, and hence plays a very important role in the Earth’s climate system. The melt/ freeze cycle of sea ice also has a critical impact on the density structure and circulation of the world ocean through brine rejection and freshwater release. In addition, the role of sea ice in ocean biogeochemistry has drawn increasing attention recently. For example, sea ice can effectively transport trace elements by entraining sediments during freezing and releasing them when and where melting takes place (Reference Eicken, Kolatschek, Freitag, Lindemann, Kassens and DmitrenkoEicken and others, 2000, Reference Eicken2005). Nevertheless, the mechanism of new ice formation, the most important stage for processes listed above, is not yet sufficiently understood. In the case of a calm ocean surface, cooling by cold air leads to formation of a solid thin ice cover termed nilas. In contrast, with a turbulent ocean surface a large number of fine crystals (called frazil) are formed in supercooled sea water at first, then they gradually concentrate near the surface due to buoyancy and constitute grease ice, a mixture of solid ice crystals and sea water (Reference Martin and KauffmanMartin, 1981; Reference Martin and KauffmanMartin and Kauffman, 1981). Therefore, the state of newly formed sea ice depends significantly on local and temporal conditions at the ocean surface. The sea-ice state has a great impact on the heat budget between the atmosphere and the ocean (Reference Doble and WadhamsDoble and others, 2003; Reference WeeksWeeks, 2010). While a solid ice cover reduces the atmosphere/ocean heat flux due to its low thermal conductivity, underwater frazil ice does not reduce the flux. The higher surface heat loss results in more sea-ice production and greater buoyancy forcing on the ocean surface. In spite of its substantial importance, even present-day numerical sea-ice models developed to study ocean circulation and the climate system do not take sufficient account of such differences in the sea-ice state (Reference HiblerHibler, 1979; Reference HunkeHunke and Dukowicz, 1997).

The basic physical aspects of frazil crystals are comprehensively reviewed by Reference DalyDaly (1994). Laboratory experiments using a 0.6 m deep tank (Reference Ushio and WakatsuchiUshio and Wakatsuchi, 1993) showed thermal convection driven by supercooled sea water at ∽10^–1 K and subsequent underwater frazil-ice formation. Some mooring observations in coastal polynyas have detected evidence of underwater frazil ice down to 20 m and coincident supercooling of ∽10^–2 K down to depths of 20-40 m (Reference Drucker, Martin and MoritzDrucker and others, 2003; Reference DmitrenkoDmitrenko and others, 2010; Reference ItoIto and others, 2015). Nonetheless, how and to what extent supercooling of sea water and underwater frazil-ice formation are realized in the ocean is not yet well understood, because direct observations have been limited. Reference Omstedt and SvenssonOmstedt and Svensson (1984) derived a one-dimensional (1-D) theoretical model for supercooling and frazil-ice mass conservation using empirical parameters. Reference Skyllingstad and DenboSkyllingstad and Denbo (2001) introduced this concept into a three-dimensional (3-D) large-eddy simulation, and performed numerical experiments on an ocean mixed layer under sea ice with active ice formation in a lead. To our knowledge, their work is the first study to consider the effect of underwater frazil ice and its convective transport in a full 3-D non-hydrostatic ocean simulation. However, because their main focus is the quantification of turbulent activity induced by a drifting sea-ice cover, representation of frazil ice is simplified by cell-averaged concentration in the Eulerian form, where all crystals are assumed to be the same size.

Recently several modelling studies of frazil ice have been conducted that focus on ice-shelf cavities, where cooling by the ice-shelf base effectively produces supercooled sea water and underwater frazil crystals (Reference Jenkins and BomboschJenkins and Bombosch, 1995; Reference Smedsrud and JenkinsSmedsrud and Jenkins, 2004; Reference HollandHolland and Feltham, 2005; Reference Galton-Fenzi, Hunter and ColemanGalton-Fenzi and others, 2012). However, formation of frazil ice due to surface atmospheric cooling, its transport by wind stirring, and its accumulation and transition to a grease-ice cover in the open ocean have not yet been explicitly modelled. In the present study we introduce a new modelling framework for simulation of underwater frazil ice, implemented by a Lagrangian particle-tracking method, to explicitly deal with thermodynamic growth of frazil particles and their transition to grease ice. Using this model, we investigate the detailed behaviour of frazil ice and its impacts on the atmosphere/ocean heat budget through an idealized numerical experiment.

Model Description

The numerical model used in the present study is a 3-D incompressible non-hydrostatic ocean model with the Boussinesq approximation, developed by Reference Matsumura and HasumiMatsumura and Hasumi (2008). This ocean model is coupled to a newly developed frazil-ice model represented by an online Lagrangian particle-tracking method. The governing equations for a continuous water phase are

where u = (u, v, w), 6 and S are velocity vector, potential temperature and salinity, respectively, and k is the unit vector pointing upward. Density, p, is obtained from 6, S and depth, by an approximated equation of state for sea water following Reference MellorMellor (1991), and pressure, p, is solved at each time step, so that incompressibility (Eqn(2)) is satisfied. The term bk represents the buoyancy force caused by underwater frazil ice, discussed below and given by Eqn (17). The source/sink terms qθ and qS reflect latent heat absorption/release and brine rejection/freshwater release, both caused by freezing/melting of sea ice. Constants f, g and p₀ are the Coriolis parameter, the gravity acceleration and the reference density of sea water, respectively. The last term on the right-hand side of Eqn (1) specifically represents eddy viscosity, including the effects of the concentration of frazil ice. Since the grid resolution (defined below) seems to be sufficiently fine and subgrid-scale motions can be considered as isotropic turbulence, we adopt a Smagorinsky-type shear-dependent large-eddy simulation scheme (Reference SmagorinskySmagorinsky, 1963; Lesieur, 2008). That is, eddy viscosity, v, and eddy diffusivity, k, are parameterized as

where

is the strain-rate tensor for gridscale resolved velocity, CS is a non-dimensional model constant, A is the length scale of grid spacing and Pr is the eddy Prandtl number. The sub-grid-scale stress tensor r is represented as

where is the effective kinematic viscosity of molecular origin. Note that the molecular kinematic viscosity in the present study is not a constant but is enhanced by the concentration of frazil particles as described below. The values of all physical constants and parameters used in the present study are listed in Table 1.

Since these equations for a continuous water phase are formulated following a finite-volume methodology, predicted velocity field and water properties at each discretized gridcell represent the cell-averaged values. However, a Lagrangian particle-tracking method allows each individual particle to be associated with subgrid location and other accompanying properties (mass, age and rise/fall of velocity, etc.), and we can trace their history. Tracking the Lagrangian particles is performed in each time step at the same time as the integration for the continuous water-phase progresses, so frazil ice introduced by this method is not a mere passive tracer but can dynamically and thermodynamically affect the ocean currents and water-mass properties. In this sense, the method is referred to as ‘online’ particle tracking. However, actual frazil crystals in the real ocean are so tiny and numerous that it is impossible to simulate them all. Thus, we treat a modelled Lagrangian particle as a crowded group, or a cluster, of a large number of frazil crystals advected as a bulk, and each particle has information about the total mass of all the crystals constituting that cluster (denoted by M; see below). Hereafter the term ‘frazil particle’ is used to specify this cluster of frazil crystals represented by a Lagrangian particle in the model, and is distinguished from an individual frazil crystal which is not explicitly modelled.

The present Lagrangian frazil-ice model performs the following procedure at each time step. First, all existing frazil particles are individually advected by the fourth-order Runge-Kutta method using the summation of the gridscale ocean velocity, buoyant rise velocity (denoted w _r), and velocity reflecting subgrid-scale turbulent eddy transport (denoted wt). In reality, the buoyant rise velocity of frazil crystals in a static water column is determined by the balance between buoyancy force and drag force, and hence it depends on the size and shape of each individual crystal (Reference GosinkGosink and Osterkamp, 1983), but we cannot obtain this quantity because we do not consider the shape and size of individual crystals. In general, the buoyancy force is proportional to the volume of the object, whereas drag force is proportional to the length scale of the projected area on a horizontal plane. Therefore, the rise velocity increases as frazil crystals grow. To include this factor we simply parameterize the buoyant rise velocity of the modelled frazil particle, w _r, proportional to the ice mass of the particle, M:

where w ₀ is the reference rise velocity and M ₀ is a normalizing constant. One of the major improvements of the present model (by Reference Skyllingstad and DenboSkyllingstad and Denbo, 2001) is the representation of the non-uniform rise velocity of frazil ice, which reflects thermodynamic growth of individual particles, but the actual rise velocity of each particle fully depends on the choices for w ₀ and M0_. We use w 0 = 1.0 x 1 0 ³ m s ¹ following previous studies (Reference Omstedt and SvenssonOmstedt and Svensson, 1984; Reference Skyllingstad and DenboSkyllingstad and Denbo, 2001), and the typical ice mass of particle M0 is set to 1.0 kg because the probability density of M in the model simulation is highest at ∽1.0 kg during active underwater frazil formation.

The turbulent eddy transport of each frazil particle is evaluated as follows. Since frazil ice is less dense than ambient sea water, its vertical motion increases or decreases the potential energy (PE). The buoyancy force acting on a frazil particle of ice mass M is

where g ^' = (p₀ P _i )=p _i is the buoyancy force per unit mass of underwater frazil ice. Therefore, the rate of PE gain due to turbulent eddy transport of frazil particles in a specific cell is P _cell Mg'wt, where the summation is taken for all particles in the corresponding cell, and wt is the vertical velocity representing subgrid-scale turbulent transport. This PE gain/ loss due to subgrid-scale eddy transport should be consistent with the budget of subgrid-scale turbulent kinetic energy (TKE). The production of TKE is realized by the energy cascading from gridscale velocity to subgrid-scale turbulence through eddy viscosity dissipation. The TKE production rate integrated over a specific cell volume can be written as 2v€ij_€ijp _0&V, where v is the eddy viscosity coefficient defined in Eqn (5), eij is the gridscale strain-rate tensor and AV is the cell volume. While the major part of TKE is dissipated as heat, some of it is used to transport frazil crystals against buoyancy. The ratio of the buoyant PE gain to the shear production of TKE is knows as the flux Richardson number (Kantha and Clayson, 2000), in the present case

Osborn (1980) estimates the critical value of the flux Richardson number for sustainable oceanic turbulence as ∽0.15, i.e. if Rf>0.15 the TKE production rate is not sufficient to maintain turbulent mixing against buoyancy. In other words, up to 15% of TKE produced by the shear of gridscale velocity could be used to do work against buoyancy instead of being dissipated as heat. Although the estimation of this critical value for Rf (Reference OsbornOsborn, 1980) is derived for different circumstances (turbulence in an equatorial ocean surface mixed layer) than those of the present study, we adopt this value of critical Rf. Therefore, the available TKE for the turbulent transport of frazil particles in a specific cell per unit time is estimated as 0.15 x 2p0veij_eijAV. This available TKE is uniformly distributed to all particles existing in the cell. Accordingly, the turbulent transport of each particle is evaluated as

where n is the number of particles in each cell. The estimated downward turbulent transport velocity, wt, is proportional to M–1, and hence smaller particles tend to be transported longer distances by turbulence. Note that we omit lateral turbulent transport because it does not affect the energy balance between PE and TKE.

After being advected, frazil particles will decay by melting or grow by freezing, depending on the in situ temperature relative to the freezing point, T _f, at the location of each particle. The rate of melting/freezing is likely to be proportional to the product of the total surface area of crystals, A, and the heat transfer coefficient, 7. If all crystals constituting a frazil cluster are disc-shaped with thickness d, the total surface area can be approximated as A = 2M=(pid), if we assume the disc radius is much greater than the thickness, where pi is reference density of sea ice. The heat transfer coefficient for frazil freezing and melting can be parameterized by the Nusselt number, Nu, molecular thermal diffusivity, KT, and crystal size (Reference Jenkins and BomboschJenkins and Bombosch, 1995; Reference HollandHolland and Feltham, 2005). In the present study we define 7 as

where r is the effective radius of the frazil crystals. Accordingly, the ice mass of each frazil particle progresses in time as

where Cp and L are the specific heat of sea water and the latent heat of freezing, respectively. Although A and 7 should depend on the size of individual crystals, the crystal size distribution is not simulated in the present model; we substitute a constant effective thickness, d = 0.05 mm, and effective radius, r = 1.0 mm. These typical crystal sizes and the ratio of disc radius to thickness, r=d = 20, are adopted from Reference GosinkGosink and Osterkamp (1983) and Reference DalyDaly (1994), but the sensitivity of the model to these values needs to be investigated in future work.

The conversion between predicted potential temperature, 6, and in situ temperature, T, follows Reference BrydenBryden (1973). The local freezing point, Tf, is a function of salinity and pressure (relative to 1 atm), approximated by Reference MilleroMillero (1978) as

where units for Tf, S and p are °C, psu and dB, respectively. If M becomes less than a threshold, Mmin (defined below), we force the particle to melt entirely and then delete it. The influence of latent heat and freshwater exchange caused by melting/freezing of frazil particles on water properties at a specific gridcell is written as

where S ₀ and Si are reference salinity of sea water and sea ice, respectively. In the present study we set S _i = 0psu, since newly formed frazil crystals should be purely fresh. The summation on the right-hand side is taken for all particles inside the corresponding cell.

If in situ temperature at a specific cell becomes less than the local freezing point after these procedures, we generate new frazil particles so that the supercooling state is cancelled by release of corresponding latent heat. To avoid creating too many frazil particles of infinitesimal mass we set the lower limit for the mass of a single particle to Mmin=2.5x 1 0 ² kg. New frazil particles are generated only if the in situ temperature falls below M _mi_n L=(∆VCpp0) ∽ 2 x 1 0 ³ K with respect to the local freezing point. In other words, the model allows in situ supercooling up to 2 x 1 0 ³ K, and the supercooling state will be immediately relaxed by generating frazil particles when it exceeds this threshold. The initial location of newly generated particles within the cell is horizontally random, whereas the initial depth is set to the middle of the cell. Note that the limit of in situ supercooling allowed in the model is one order of magnitude smaller than the observed record (Reference Skogseth and NilsenSkogseth and others, 2009; see the Discussion section).

Here we evaluate the upward buoyancy force, bk, appearing in the prediction equation of ocean velocity (Eqn (1)). The origin of this term is the reaction of the drag force acting on each frazil crystal. The magnitude of the drag force depends on the shape and orientation of each crystal, as well as its velocity relative to the surrounding sea water. However, in the present study we assume that each particle is in an equilibrium state, such that the downward drag force is balanced by the upward buoyancy force, i.e. all particles are rising at terminal velocity. Since the buoyancy force acting on a frazil particle of ice mass M is Mg', the total upward force acting on sea water per unit mass in a specific cell is

The model domain is 64 m x 64 m x 64 m, with horizontally periodic boundaries in both x- and y-directions, and the grid spacing is 1 m in each direction. The initial and surface boundary conditions are designed to idealize the wintertime Arctic Ocean, where active sea-ice formation is taking place. The initial salinity is uniformly 30psu and the initial potential temperature is uniformly set to the surface freezing point, 6= 1.6378°C, over the whole domain. Following Reference HaneyHaney (1971), surface heat flux induced by the cold atmosphere in regions of open water is simplified as

where QT, T _a and T _s are the heat relaxation coefficient, air temperature and sea surface temperature, respectively. In the present study we set QT = 40 W m ₂ K ¹ and T _a = –20 ° C, yielding a surface heat flux, Q, of ∽730 W m ² when the sea surface is at the freezing point.

The surface wind stress forcing is given by the bulk formula using the velocity difference between the wind and the ocean surface:

where ρa = 1.3 kg m ³ is air density, CD = 1.1 x 1 0 ³ is the drag coefficient and U – u is wind speed relative to the ocean surface. In the present study we apply a constant wind speed of 10 m s ¹ in the x-direction, so the wind stress τx ≈ 0.14 kg m ¹ s ² . The condition of the present study – that open water is suddenly exposed to severe atmospheric cooling and strong wind stress – is typical at coastal polynyas or sea-ice leads in the coldest period.

Frazil particles are sustained underwater by wind stirring and/or ocean convection in the early stages, but after some degree of growth, their buoyant rise velocity becomes high enough to overcome these. Thereby, ice masses gradually condense near the surface and then constitute grease ice, a slurry mixture of sea water and solid ice particles. In the present study the kinetic effect of grease ice is represented by enhancing the molecular viscosity depending on frazil concentration. Following an empirical formula derived for colloidal fluids by Reference ThomasThomas (1965), the effective molecular kinematic viscosity coefficient, v*m, is parameterized as

where

is the solid volume fraction in each cell and vm is the reference molecular kinematic viscosity coefficient of water, with a value of 1.0 x 1 0 ⁶ m² s ¹ .

In addition, when the solid volume fraction in the grease-ice cover becomes sufficiently high near the surface, it should have an insulating effect and reduce surface heat flux. In the case of an ocean surface covered by a solid ice sheet of thickness h _i, upward heat flux at the ice/ocean interface can be written as

assuming the heat capacity of sea ice is ignored (Reference SemtnerSemtner, 1976), where re_i is the thermal conductivity of solid sea ice, Tf is the surface freezing temperature and QT is the same thermal relaxation coefficient as in Eqn (18). In the present study we replace the ice thickness, hi, in Eqn (22) with an effective ice thickness, h*, defined as an integration of frazil-ice volume per unit area weighted by the distance from the ocean surface,

where ∆A is the horizontal area of each cell and S is the scale height of surface layer in which frazil particles have an insulating effect. In the present study we set S = 0.10 m, but the sensitivity to this parameter is not significant because large frazil particles (which account for the majority of the total ice mass) tend to exist very close to the surface, due to their buoyancy.

The model is integrated for 120 hours from a state of rest with no frazil particles initially. To make a comparison, we also perform an experiment in which surface heat loss directly leads to columnar growth of a solid ice sheet covering the entire domain instead of generating frazil particles. The standard experiment with frazil ice is referred to as CTRL, and the experiment with a solid ice cover but without frazil ice is referred to as NOFRAZIL. Unless specified, results in the following section are from the CTRL experiment.

Results

First, we qualitatively investigate results using 3-D volume rendering images of frazil mass distribution (Fig. 1) and maps of effective ice thickness, h* (Fig. 2). Since the initial ocean temperature is at the freezing point, surface cooling immediately results in frazil-ice formation. After 3 hours of model integration, generated frazil particles are distributed throughout the ∽10m thick layer below the surface by turbulent eddy transport. The energy source for this downward transport of frazil ice near the surface originates from the shear of gridscale velocity provided by the surface wind stress forcing. Since frazil particles are so small at this stage that their buoyant rise velocity is not significant, few frazil particles exist at the surface. After 6 hours, this frazil-rich layer extends to ∽20m thick, due to continuous wind stirring, while some frazil particles rise to the surface and accumulate locally at nodes of convective cells where surface currents converge. At 12 hours, a substantial portion of frazil particles are suspended near the surface, forming a streak structure aligned in the wind direction. These suspended particles move as a group and behave like grease, i.e. a viscous fluid suspended on the ocean surface. The percentage of surface area covered by grease ice (defined as h* > 0.1 m) at this stage is ∽20%. Only a small fraction of frazil particles begins to penetrate into the subsurface by brine-driven convection. After 24 hours the percentage of area covered by grease ice increases to 54%, and the clear contrast between the open water and the grease-ice-covered region has disappeared, but the convective motion at the subsurface is still active. By hour 48, the grease-ice-covered area increases to 84%. As the volume fraction of frazil ice at the surface increases, wind stirring becomes less active, due to the damping effect from enhanced viscosity, and hence the occurrence of frazil particles suspended in the ocean interior begins to decrease. After 72 hours, the ocean surface has been completely covered by grease ice and underwater frazil particles are almost eliminated from the ocean interior.

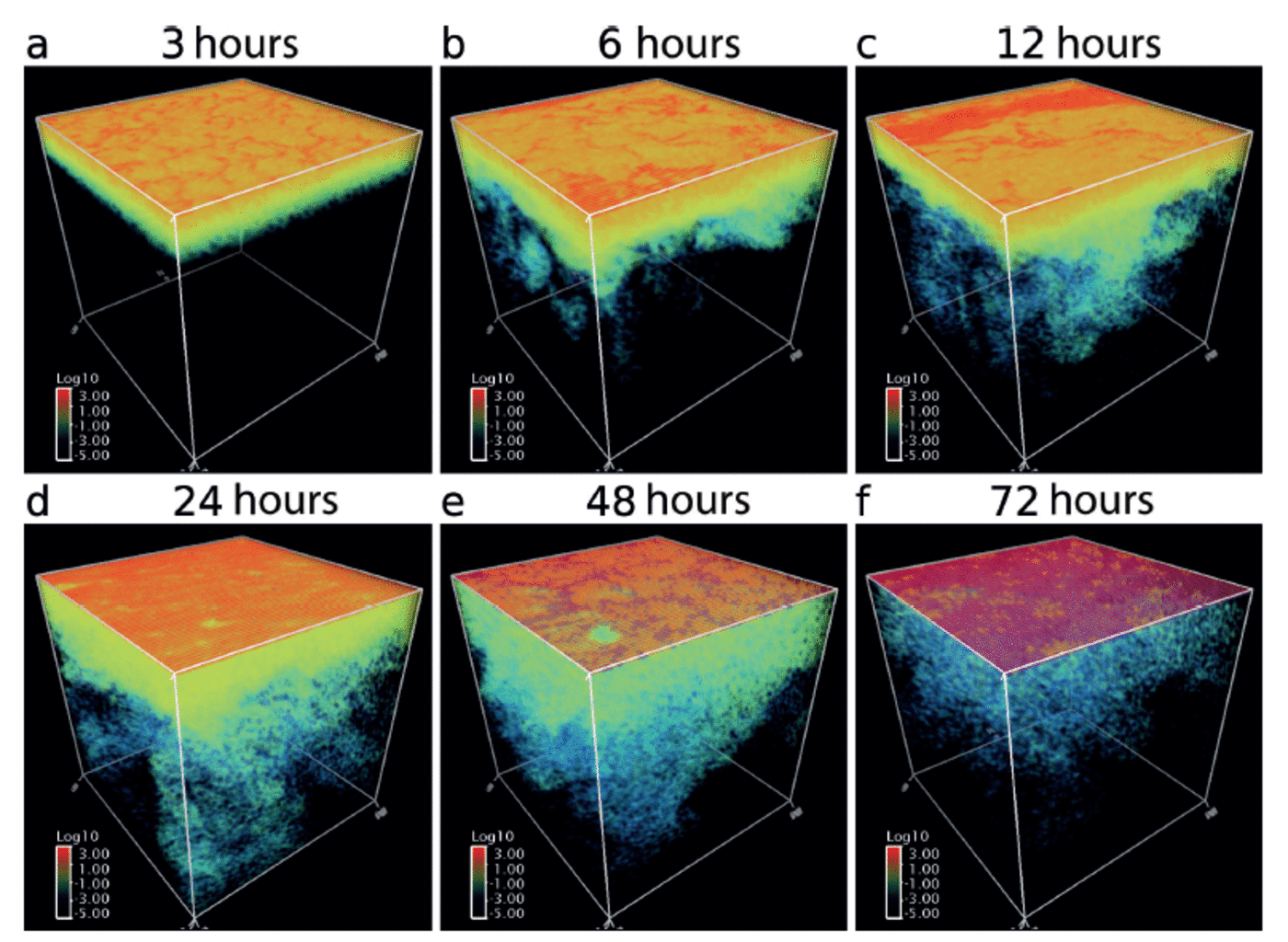
Fig. 1. Three-dimensional volume rendering images of frazil-ice mass concentration of the entire model domain (64 m x 64 m x 64 m) at 3, 6, 12, 24, 48 and 72 hours. Colours indicate the magnitude on a log scale, where blue, green and red correspond to approximately < 1 0 ², 10¹ – 1 0 and >10² kg m ³, respectively.

Fig. 2. Horizontal distribution of the effective ice thickness, hf, at 3, 6, 12, 24, 48 and 72 hours.

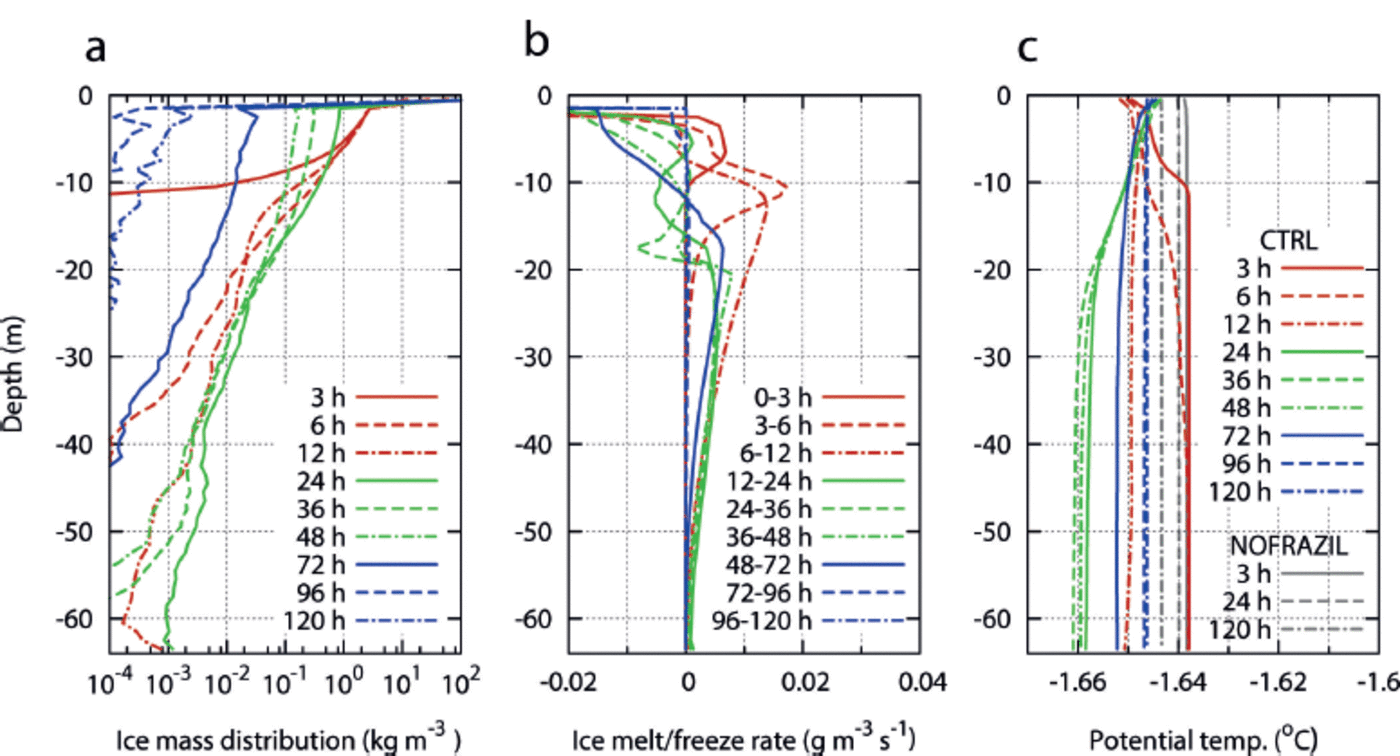
Fig. 3. Horizontally averaged vertical profile of (a) frazil-ice mass concentration, (b) melt/freeze rate of frazil ice (positive indicates melting) and (c) potential temperature, at specific times. The potential temperature profiles of NOFRAZIL are also plotted in (c) as grey curves. (a) and (c) plot snapshots while (b) plots the temporal mean of specific periods. Note that curves for the uppermost layer in (b) are out of range, due to the greater freeze rate at the surface.

Next we analyse the detailed behaviour of frazil particles and their effects on the ocean interior based on horizontally averaged vertical profiles of several properties. Figure 3a shows the vertical profile of the concentration of frazil-ice mass in sea water. While the majority of frazil particles are located near the surface due to their buoyancy, some fraction of these are transported down to 10–20 m by wind stirring at an early stage. The vertical profile of potential temperature (Fig. 3c) exhibits a characteristic depression at >10 m depth at hour 3 and >20m depth at hour 6, which seems to be correlated with the underwater frazil concentration. This potential temperature decline near the surface in the early stages is caused by the freezing point decline due to salinity increase by brine rejection. Because the relatively high concentration of underwater frazil ice in the near-surface layer reduces the effective density of sea water, brine rejection does not immediately lead to convection, and hence the surface salinity increases. However, by hour 12 sufficient brine has been supplied to make the water column unstable, then brine-driven convection takes place and the potential temperature profile becomes almost vertically uniform, with the value of the surface freezing point. This brine-driven convection transports frazil particles to the subsurface from below depths achievable by active wind stirring alone. Although the horizontally averaged concentration of underwater frazil ice is very small at the lower levels, it locally exhibits large values up to 0.13 kg m ³ even at 50 m depth.

Figure 3b shows the vertical profile of the frazil melt/freeze rate (positive when melting). Because the freezing point declines with depth, frazil ice tends to melt at deeper levels, even though the potential temperature is vertically uniform. In the first few hours, all the frazil particles are generated in the uppermost layer and entirely melt in the upper 20 m. However, as time progresses, the depth of highest melt rate shifts to deeper levels, and during hours 24-72 melting mainly takes place at 20-40 m depths. A key role of underwater frazil ice is to absorb latent heat from surrounding sea water at the depth of melting. Therefore, downward transport of frazil ice induces upward latent heat flux. If sufficient frazil ice is continually supplied from above, the water column can be cooled to the local freezing point. The vertical profile of potential temperature >20m deep at hours 24-48 agrees with the gradient of freezing point decline with respect to depth (∽7.5 x 10^–4 K m ¹ ) . The supply of frazil ice below 20 m is not enough to cool the water column down to the local freezing point, and the potential temperature at depths <25 m is uniformly -1.66°C at this time, which is 0.018 K below the surface freezing point. The state of the water column such that the potential temperature is less than the surface freezing point is referred to as potential supercooling. After hour 48, the entire surface is covered by grease ice. Consequently, the frazil-ice supply to the lower levels and corresponding upward latent heat flux are rapidly reduced. In this stage downward sensible heatflux by residual convection induces heating of the lower levels, thereby gradually relaxing the underwater potential supercooling state. After 72 hours of integration, almost all frazil particles have risen to the surface, due to increasing buoyancy and decreasing wind stirring. Note that underwater potential supercooling is never realized in the NOFRAZIL experiment, in which all surface heat loss is directly used for columnar growth of a solid ice cover and hence there is no underwater latent heat flux. Obviously, the potential temperature profile in NOFRAZIL is equal to the surface freezing point for the entire domain (grey curves in Fig. 3c).

Finally, we estimate the impact of frazil ice on the atmosphere/ocean heat budget and net sea-ice production, by comparing CTRL with NOFRAZIL. Net sea-ice production can be estimated using the equivalent ice thickness, which is defined as the total ice mass in the whole water column per unit area. Note that this equivalent ice thickness is different from the effective ice thickness defined in Eqn (23): the former is an index for total ice mass, whereas the latter is an index for ice mass existing near the surface which disturbs the atmosphere/ocean heat exchange. The solid black and grey curves in Figure 4 are the time series of mean surface heat flux in CTRL and NOFRAZIL, respectively, and the dashed black and dashed grey curves are the time series of mean equivalent ice thickness in CTRL and mean ice cover thickness in NOFRAZIL, respectively. In both cases the surface heat flux is ∽730 W m ² initially, but in NOFRAZIL it rapidly decreases as the ice cover thickens. It decreases to 320 W m ² at 12 hours, when the ice cover is 0.06m thick, and to <240 W m ² at 24 hours, when the ice cover is 0.10 m thick. In contrast, the surface heat flux remains at relatively high values for a longer time in CTRL, even though the equivalent ice thickness is greater than the thickness of solid ice cover in NOFRAZIL. It remains >520 W m ² for 16 hours, because newly generated frazil particles are held underwater by active wind stirring and hence do not insulate the surface heat flux during this period. However, the surface heat flux in CTRL suddenly decreases at between 18 and 24 hours and becomes similar to the level in NOFRAZIL thereafter. This is because the majority of frazil particles have thermodynamically grown large in this period, and their buoyant rise velocity begins to overcome wind stirring. The entire ocean surface has been covered by grease ice of high solid mass fraction and hence the surface heat exchange is restricted afterwards. The total heat loss per unit area during the first 24 hours in CTRL is 44.8 x 10⁶ J m^–2, which is 4 1 % higher than the 31.7 x 1 0 ⁶ J m ² for NOFRAZIL. The net sea-ice production of CTRL is 3 1 % greater than that of NOFRAZIL over the same time.

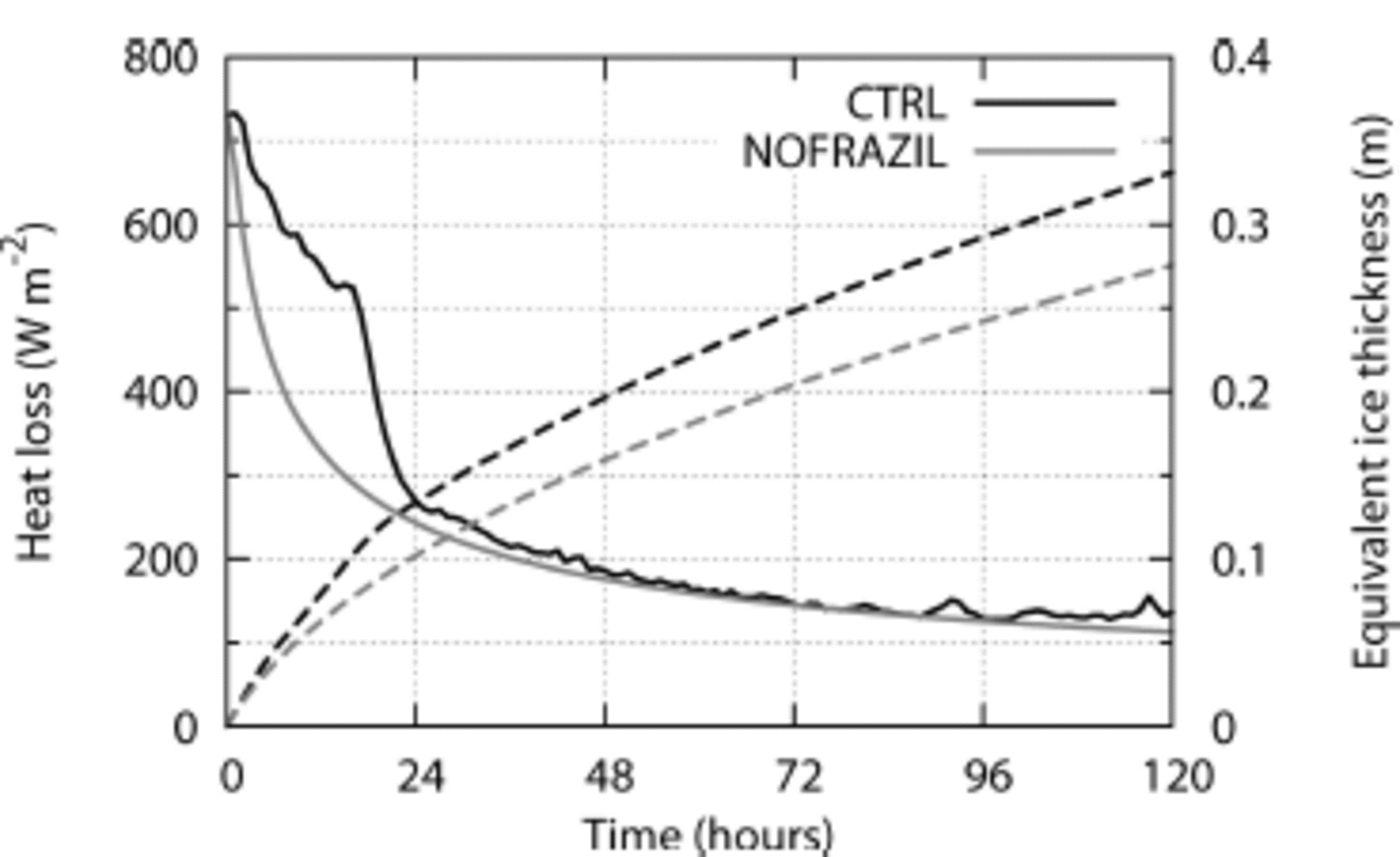
Fig. 4. Time series of the surface heat flux (solid) and the equivalent ice thickness (dashed). Black and grey curves are for CTRL and NOFRAZIL, respectively.

Discussion

Reference Skogseth and NilsenSkogseth and others (2009) detected in situ supercooling of up to 0.037 K at 5 m depth during times of strong winds and low air temperatures at an Arctic coastal polynya, and several observations (Reference Drucker, Martin and MoritzDrucker and others, 2003; Reference ShcherbinaShcherbina and others, 2004; Reference FukamachiFukamachi and others, 2009; Reference DmitrenkoDmitrenko and others, 2010; Reference ItoIto and others, 2015) have detected potential supercooling of ∽0.010-0.040 K at depths of ∽20- 100 m in various polynyas. A simple scenario for forming underwater potential supercooling is as follows. First, sea water is supercooled near the ocean surface by severe atmospheric cooling, then it adiabatically descends to the observed depths by thermal convection or some other process without freezing. Results of laboratory experiments by Reference Ushio and WakatsuchiUshio and Wakatsuchi (1993) support this scenario, but the experiments were performed in a clean shallow tank, which might not be representative of the real ocean, where seeding nuclei, physical disturbances and turbulent diabatic mixing are ubiquitous.

In the present study we have successfully reproduced underwater potential supercooling of ∽0.018K below 60 m depth, even though the model does not allow sustainable in situ supercooling. The potential supercooling state of the water column in the present simulation is realized by downward turbulent transport of underwater frazil ice, supported by active wind stirring. Newly generated frazil particles near the surface tend to be transported downward against buoyancy by strong wind stirring, then they melt in the ocean interior and absorb latent heat. In this way, potential temperature could drop to the local freezing point if sufficient frazil ice is continuously supplied from above, and the vertical profile of temperature in the frazil-rich layer becomes the same gradient as the freezing temperature decline (green curves for hours 24-48 in Fig. 3c). Since the effective density of sea water in the frazil-rich layer is much lower than in the water below, the stratification at the interface with the frazil-rich layer is stable. The depth of such a frazil-rich layer is determined by the rate of TKE input by surface wind forcing. In the present study we apply a constant wind speed of 1 0 m s ¹, the frazil-rich layer develops up to 25 m thick and the maximum temperature decline relative to the surface freezing point is 0.018 K. Figure 3a and c suggests that an underwater frazil-ice fraction of ∽10^–2 kg m ³ is required to cause the potential temperature to fall to the local freezing point. The frazil-ice fraction is much less than this threshold in the subsurface, where the effects of surface wind forcing hardly reach. In the subsurface, however, stratification becomes unstable due to the brine leaked from above, and active brine-driven convection mixes the potential temperature over the whole water column. Consequently, the potential supercooling state of 0.018K is realized down to the ocean floor (64 m depth). The degree of potential supercooling realized by this process is determined by the thickness of the surface frazil-rich layer, which should be extended deeper as the wind stress forcing becomes stronger. This scenario seems to be consistent with direct field measurements where the detection of underwater potential supercooling coincides with the periods of strong winds (cf. Reference ItoIto and others, 2015).

The subsurface brine-driven convection induces the upwelling of potentially supercooled water, which results in in situ supercooling and underwater freezing. This is the reason why melt rate turns negative, i.e. freezing overcomes melting, at 10–20m depth at hours 24–36 (Fig. 3b). This mechanism is clearly demonstrated by the scatter plot of frazil melt/freeze rate against local vertical velocity (Fig. 5), where upwelling and downwelling coincide with freezing and melting, respectively. The present simulation suggests that underwater in situ supercooling could be realized by upwelling of potentially supercooled water in the real ocean. This hypothesis is in contrast to the previous thought: in situ supercooling in the ocean interior is realized by direct downwelling of significantly supercooled water driven by severe surface cooling. The underwater freezing releases latent heat, and hence the potential supercooling state will be relaxed unless continuous upward latent heat transport by wind stirring exists. In the later periods of the present simulation, the majority of frazil particles have grown so large that their buoyant rise velocity overcomes wind stirring. In addition, once frazil particles have accumulated at the surface and constitute a grease-ice cover, wind stirring is effectively damped by enhanced viscosity, and frazil-ice supply to the ocean interior is further reduced. Therefore, potential supercooling of the water column cannot be sustained after 72 hours, and the potential temperature profile of the water column settles down to the surface freezing point (blue curves in Fig. 3c).

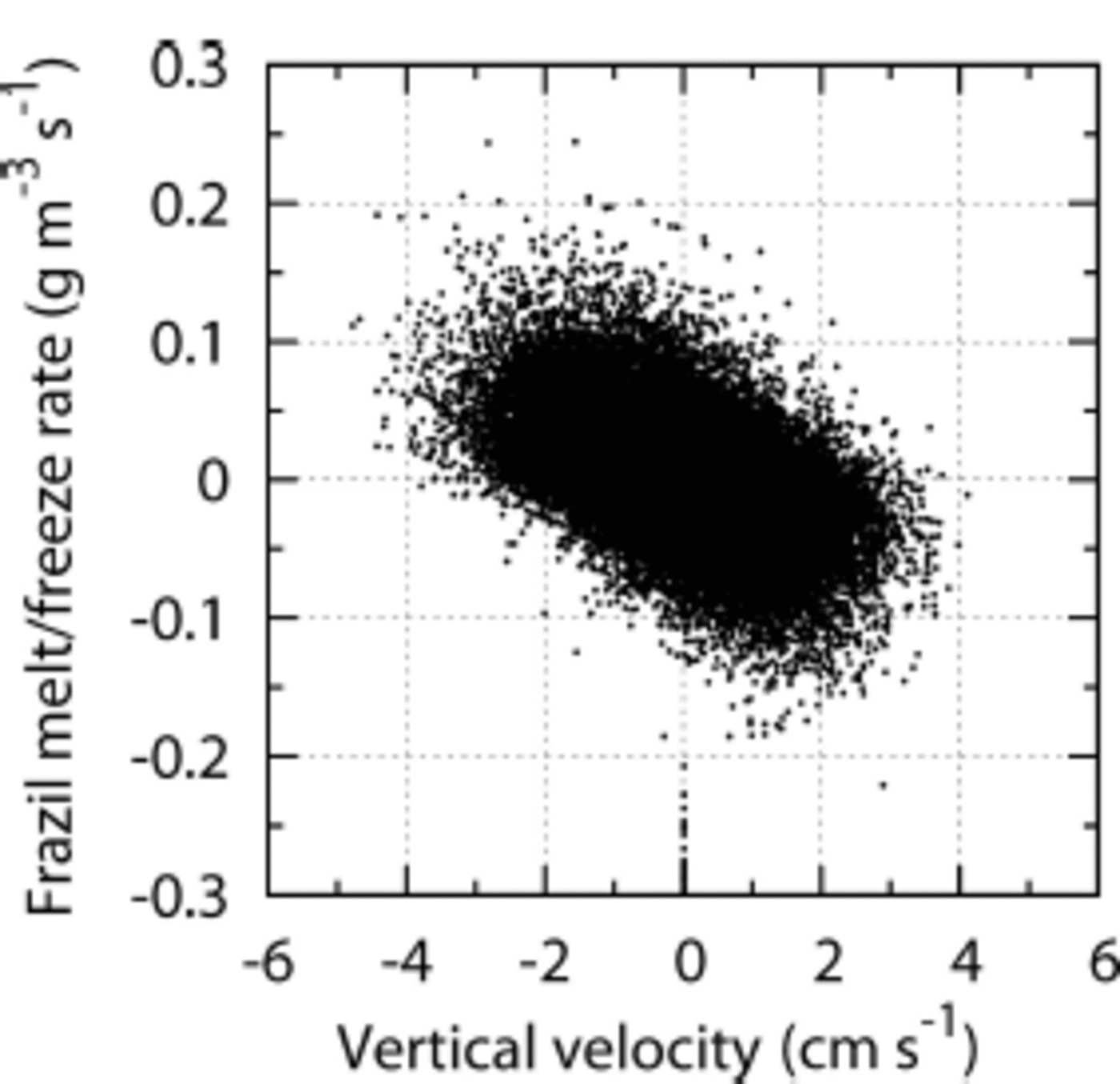
Fig. 5. Scatter plot of the local frazil melt/freeze rate against the vertical velocity sampled at 5-25 m depths at hour 24.

The model results are quantitatively consistent with observations in terms of the degree of potential supercooling, observed depths and the periods with intense surface cooling. This implies that the processes of formation and turbulent transport of underwater frazil ice simulated in the present numerical experiment may be taking place in the real ocean. However, it should be noted that the results of the present simulation do not exclude the possibility of a contribution of sensible heat transport by direct descent of supercooled water to the observed underwater potential supercooling. Detailed analysis of the relative importance of the sensible heat flux by direct descent of supercooled water and the latent heat flux by the turbulent eddy transport of underwater frazil ice should be conducted in the future in both modelling and observational studies.

Conclusion and Future Work

We have developed a new framework for modelling frazil ice using a Lagrangian particle-tracking method coupled with a 3-D non-hydrostatic ocean model. The present Lagrangian frazil-ice model includes thermodynamic growth of individual frazil particles and corresponding latent heat and brine release/absorption, buoyancy effects which reduce effective density of sea water, turbulent eddy transport of frazil particles (which reflects strong wind stirring) and an enhancement of viscosity as a function of frazil volume fraction. Although the modelled particles do not correspond to individual frazil crystals but are treated as clusters of crystals, the present study successfully reproduces formation of underwater frazil ice and its transition to grease ice at the surface. The upward latent heat transport associated with downward transport of frazil particles due to wind stirring realizes potential supercooling of ∽0.018K at the lower levels after a few days of model integration. The degree of potential supercooling in the present model quantitatively agrees with observations.

Because the rise velocity of frazil particles increases with their thermodynamic growth, they gradually accumulate at the surface and transit to a viscous grease-ice cover, which reduces both the atmosphere/ocean heat exchange and turbulent kinetic energy input. The total heat loss and the net sea-ice production during the first 24 hours in the present simulation are, respectively, 4 1 % and 3 1 % greater than those of the experiment with no frazil-ice formation. This suggests that widely used sea-ice models which do not take account of the effects of frazil and grease ice underestimate the atmosphere/ocean heat exchange, particularly during periods of active new ice formation. Relatively higher atmosphere/ocean heat flux over grease ice compared with that over a solid ice cover has effects not only on the ocean but also on the atmosphere. Because the horizontal scale of variation of frazil and grease ice is much smaller than the resolution of climate models, such effects of grease ice should be parameterized in large-scale climate models (e.g. Reference Smedsrud and MartinSmedsrud and Martin, 2015). The present results of a high-resolution 3-D simulation support this approach and provide quantitative information to improve such parameterizations.

To the best of our knowledge, this is the first modelling study that explicitly deals with dynamic and thermodynamic effects of underwater frazil-ice formation and its transition to a grease-ice cover using a Lagrangian particle-tracking method. However, the present model does not take account of the consolidation process of grease ice. Reference Maus and RosaMaus and De la Rosa (2012) showed that the limit of solid volume fraction of grease ice is ∽0.3, and when it exceeds this threshold, grease ice will freeze into a solid ice cover. The water phase treatment in the present model ignores the volume occupied by the frazil particles. This approximation is valid for small solid ice volume fractions, but this factor needs to be taken into account when dealing with the consolidation process from grease ice to a solid ice sheet. Although the present study includes wind stress forcing and corresponding turbulent mixing, the effect of wind is not sufficiently modelled because of the narrow domain with periodic boundaries. In reality, wind forcing plays a great role on the atmosphere/ocean heat budget by blowing frazil and grease ice downwind and keeping the ocean surface open. The combined processes of wind forcing and grease-ice consolidation are essential for refreezing of sea-ice leads (Reference Bauer and MartinBauer and Martin, 1983) or opening and closing of coastal polynyas (Reference PeasePease, 1987). While the present experimental design is quite idealized with a limited domain, owing to present-day computing resources, it is possible to perform simulations using larger domains and longer time spans with more-realistic settings. In addition, the new model framework with online particle tracking developed in the present study has the potential to comprehensively handle both frazil-ice accumulation and bottom sediment suspension at the same time. Simulating the entrainment processes of sediments into newly formed sea ice, as suggested by Reference SmedsrudSmedsrud (1998, Reference Smedsrud2001, Reference Smedsrud2002, Reference Smedsrud2003), Reference SherwoodSherwood (2000), Reference DethleffDethleff (2005) and Reference DethleffDethleff and Kempema (2007), is another challenging step following the present study.