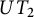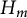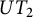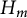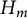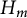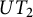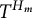1 Introduction
One of the most interesting problems in the theory of algebras with polynomial identities (PI-algebras) is the so-called Specht problem. We outline briefly what the Specht problem is: given a variety of algebras (associative, Lie, Jordan, graded, etc.), one can ask whether or not any subvariety is finitely generated. In the languages of T-ideals (the ideals of polynomial identities of a given algebra), the Specht problem can be formulated as follows: given any algebra A is it true that any T-ideal containing the T-ideal of A is finitely generated (or based) as a T-ideal? If we restrict our attention to the associative environment, the Specht problem was solved positively in [Reference Kemer29, Reference Kemer30] by Kemer provided the ground field of the algebras therein is of characteristic 0. Further generalizations of Kemer’s result are due to Sviridova [Reference Sviridova40] (PI-algebras graded by a finite abelian group), Aljadeff and Kanel-Belov [Reference Aljadeff and Kanel-Belov1] (PI-algebras graded by a finite group), Karasik [Reference Karasik27] (PI-algebras that are module algebras under the action of a finite dimensional semisimple Hopf algebra), and Centrone, Estrada, and Ioppolo [Reference Centrone, Estrada and Ioppolo12] (PI-algebras that are superalgebras with superinvolution).
In this paper, we study the Specht property for the variety of
$H_m$
-module algebras generated by the algebra
$UT_2$
of
$2\times 2$
upper triangular matrices over a field of characteristic 0 containing a primitive mth root of unit where
$H_m$
denotes a Taft’s Hopf algebra of dimension
$m^2$
. We want to point out although
$H_m$
is finite dimensional, it is not semisimple. Hence, we are not allowed to use Karasik’s result in order to establish whether or not our variety satisfies the Specht property. Anyway, the main result of the paper is the next (see Theorem 16).
Theorem 1 Let
$m\geq 2$
be an integer, and let us consider the Taft’s Hopf algebra
$H_m$
over a field of characteristic 0 containing a primitive mth root of unit. Then the variety of
$H_m$
-module algebras generated by
$UT_2$
satisfies the Specht property.
As far as we know, this is the first result in the literature toward Specht property of varieties of algebras under the action of a Taft’s Hopf algebra.
Hereby, we would like to highlight the role of
$UT_2$
in the theory of PI-algebras. In [Reference Regev38], Regev proved that the codimension sequence of any associative PI-algebra is exponentially bounded. Later Kemer in [Reference Kemer31] showed that such codimensions are either polynomially bounded or grow exponentially. Moreover, Giambruno and Zaicev in a famous couple of paper (see [Reference Giambruno and Zaicev21, Reference Giambruno and Zaicev22]) computed the exponential rate of growth of a PI-algebra and proved that it is a nonnegative integer. By a well-known Kemer’s result [Reference Kemer28], we get the variety of algebras generated by
$UT_2$
is a variety of almost polynomial growth, i.e., it has exponential growth, but every proper subvariety has polynomial growth. An analogous result was found by Valenti in [Reference Valenti42] for varieties of algebras graded by a finite group and by Mishchenko and Valenti in [Reference Mishchenko and Valenti35] for varieties of algebras with involution. Notice that, in the latter paper, the authors constructed out of
$UT_2$
a suitable algebra generating a variety of almost polynomial growth. We would also like to cite the paper [Reference Giambruno and Rizzo20] by Giambruno and Rizzo toward differential identities: here, the authors prove that
$UT_2$
under the action of its algebra of derivation does not generate a variety of almost polynomial growth and they construct a subvariety of almost polynomial growth. Notice that the variety of
$H_m$
-module algebras generated by
$UT_2$
is not of almost polynomial growth too as showed by one of the authors and Yasumura in [Reference Centrone and Yasumura14].
In the present paper, we also get
$$\begin{align*} \textit{the}\ H_m\textit{-cocharacter}\ \textit{sequence of}\ \textit{UT}_2\ \textit{and its colength},\end{align*}$$
$$\begin{align*}\textit{the relatively free}\ H_m\textit{-algebra of}\ \textit{UT}_2\ \textit{is automata},\end{align*}$$
$$\begin{align*}\textit{the Gelfand--Kirillov dimension of the relatively free}\ H_m\textit{-algebra of}\ \textit{UT}_2,\end{align*}$$
confirming, in the case of Taft’s Hopf algebra, a result obtained by one of the authors in [Reference Centrone11].
2 Preliminaries
2.1 Gradings
We start off with the classical notion of grading by a group. Let
$G=\{g_1,\ldots ,g_s\}$
be any group of finite order s, and let F be a field. If A is an F-algebra, we say that A is a G-graded algebra if there are subspaces
$A_{g}$
for each
$g\in G$
such that
$$\begin{align*}A=\bigoplus_{g\in G}A_{g} \ \textrm{and} \ A_{g}A_{h}\subseteq A_{gh}.\end{align*}$$
If
$0\neq a\in A_{g}$
, we say that a is homogeneous of G-degree g or G-graded homogeneous of G-degree g, and we write
$\deg (a)=g$
.
Assume that the characteristic of F does not divide m and F contains primitive mth roots of the unit. Let
$\alpha $
be an automorphism of A of order m (i.e.,
$\alpha $
has order m as an element of the group Aut
$(A)$
of the automorphisms of A). It is well known that
$\alpha $
induces a
$\mathbb {Z}_m$
-grading on A, that is,
$$ \begin{align*}A = A_0 \oplus A_1 \oplus \cdots \oplus A_{m-1},\end{align*} $$
where, for a fixed primitive m-root of unit
$\gamma $
,
$$ \begin{align*}A_k = \{ a \in A \mid \alpha(a) = \gamma^k a \}.\end{align*} $$
Moreover, there is a one-to-one correspondence (duality) between gradings by a group and the action of a group of automorphisms under some restrictions (see [Reference Giambruno and Zaicev23, Theorem 3.2.1]).
2.2 Taft’s algebras
Let F be a field containing an mth root of the unit
$\gamma $
for some positive integer m. Let
$H_{m^2}(\gamma )$
be the bialgebra defined by generators c and d with relations
$$ \begin{align*}c^m=1, \quad d^m = 0, \quad dc = \gamma cd.\end{align*} $$
The coalgebra structure is given by
$$ \begin{align*}\Delta(c) = c \otimes c, \quad \Delta(d) = c \otimes d + d \otimes 1,\end{align*} $$
$$ \begin{align*}\varepsilon(c) = 1, \quad \varepsilon(d) = 0.\end{align*} $$
As an F-vector space,
$H_{m^2}(\gamma )$
has dimension
$m^2$
with basis
$ \{ c^ix^j \mid 0 \leq i, j, \leq m-1 \} $
. The bialgebra
$H_{m^2}(\gamma )$
becomes a Hopf algebra if we define the antipode as
$S(c) = c^{-1}$
and
$S(d) = -c^{-1}d$
. This Hopf algebra is known as the mth Taft’s Hopf algebra
2.3 H-module algebras
Let F be a field of characteristic zero, and let H be a Hopf algebra over F. We remand to the books [Reference Dăscălescu, Năstăsescu and Raianu16, Reference Montgomery36, Reference Radford37, Reference Sweedler41] for basic definitions, examples, and further information about Hopf algebras. An algebra A is an H-module algebra if A is endowed with a left H-action
$h \otimes a \mapsto ha$
or, equivalently, with a homomorphism
$H \to \text {End}_F(A)$
such that:
-
1.
$h(ab) = (h_{(1)}a)(h_{(2)}b)$
. -
2.
$h(1_A) = \varepsilon (h) 1_A$
, for all
$ h \in H, a, b \in A$
.
Here, we use Sweedler’s notation
$\Delta (h) = h_{(1)} \otimes h_{(2)}$
, where
$\Delta $
and
$\varepsilon $
are the comultiplication and the counit in H, respectively.
Let A be a finite dimensional algebra over a field F; assume that the characteristic of F does not divide m. Since
$c^m = 1$
, then c acts as an automorphism of A of order m, d acts as a c-derivation, that is, it satisfies
$d(ab) = d(a)b + c(a)d(b)$
, for all
$a,b \in A$
, and the actions of c and d are related by
$dc = \gamma cd$
. Thus, an action of
$H_m$
on A is completely determined by a choice of:
-
(1) an automorphism
$\alpha $
of A of order m and -
(2) an
$\alpha $
-derivation d of A such that
$d^m=0$
and
$d\alpha = \gamma \alpha d$
,
or equivalently (see [Reference Centrone and Yasumura14, Proposition 4]), a choice of:
-
(1) a
$\mathbb {Z}_m$
-grading
$A = \bigoplus _{i \in \mathbb {Z}_m} A_i$
and -
(2) an
$\alpha $
-derivation d (where
$\alpha $
defines the
$\mathbb {Z}_m$
-grading) such that
$d(A_i) \subseteq A_{i-1}$
and
$d^m =0$
.
The proof of [Reference Giambruno and Zaicev23, Proposition 3.3.6] gives us a linear basis
$\mathcal {B}_1 = \{ \chi _1, \dots , \chi _m \}$
of the subalgebra
$\langle c \rangle $
of
$H_m$
generated by c, such that each
$\chi _i$
corresponds to a projection
$\phi _i \colon A \to A_i$
with respect to the decomposition
$A = \bigoplus _{i \in \mathbb {Z}_m} A_i$
. Then
$\{ d^j\chi _i \mid i,j = 0, 1, \dots , m-1 \}$
turns out to be a basis of
$H_m$
. Let
$D_m = \textrm{span}_F\{ 1, d, d^2, \dots , d^{m-1} \}$
, then by [Reference Bahturin and Yasumura3] we have that the variables
$d^j\chi _i \cdot x$
correspond to graded variables under the action of
$d^j$
. Then
$H_m$
-polynomials correspond to
$\mathbb {Z}_m$
-graded polynomials with the action of
$D_m$
and their polynomial identities coincide, that is,
$\operatorname {\mathrm {Id}}^{H_m}(A) = \operatorname {\mathrm {Id}}^{\mathbb{Z}_m,Dm} (A)$
(see [Reference Centrone and Yasumura14, Proposition 14]).
2.4 Free H-module algebras
Let
$F \langle X \rangle $
be the free F-algebra on the set of countable noncommutative variables
$X = \{x_1, x_2, \ldots \}$
and consider the vector space
$V = F \langle X \rangle \otimes _F H $
. The free H-module algebra over X, denoted by
$F^H \langle X \rangle $
, is the tensor algebra over V. Any element of
$F^H \langle X \rangle $
will be called H-polynomial. In what follows, we shall use the notation
Now, let H be finite dimensional, and let
$\{b_1, \dots , b_m \}$
be a basis (as a vector space) of H. It follows that
$F^H \langle X \rangle $
is isomorphic to the free algebra over F with free formal (noncommutative) generators
$x^{b_j}$
,
$ j \in \{1, \ldots , m \}$
,
$x \in X$
. Notice that
$F^H \langle X \rangle $
has a structure of left H-module algebra by defining the next H-action
$$ \begin{align*}h (x_{i_1}^{h_1} x_{i_2}^{h_2} \cdots x_{i_n}^{h_n}) = x_{i_1}^{h_{(1)}h_1} x_{i_2}^{h_{(2)}h_2} \cdots x_{i_n}^{h_{(n)}h_n},\end{align*} $$
where
$h_{(1)} \otimes h_{(2)} \otimes \cdots \otimes h_{(n)}$
is the image of
$h\in H$
under the comultiplication
$\Delta $
of H applied
$(n-1)$
times. Thus,
$F^H \langle X \rangle $
is the free H-module algebra on X. This means that, for any H-module algebra
$ W$
and for every function
$ \alpha \colon X \to W$
, there exists a unique homomorphism of algebras and H-modules (we call these kinds of homomorphisms simply H-homomorphisms)
$\beta \colon F^H \langle X \rangle \to W$
extending
$\alpha $
. In what follows, we shall identify X with the set
$\{ x^{1_H} | x \in X \} \subset F^H \langle X \rangle $
.
Given any H-module algebra W, we say that an H-polynomial
$f \in F^H \langle X \rangle $
is an H-identity for W if, for every H-homomorphism
$ \varphi \colon F^H \langle X \rangle \to W$
, the polynomial f is in the kernel of
$\varphi $
. In other words,
$f(x_1, \ldots , x_n) \in F^H \langle X \rangle $
is an H-identity of W if and only if
$f(w_1, \ldots , w_n) = 0$
, for all
$w_1 \ldots , w_n \in W$
. The set
$\operatorname {\mathrm {Id}}^H(W)$
of all identities satisfied by W is an ideal of
$F^H \langle X \rangle $
, and it is invariant under all H-endomorphisms of
$F^H \langle X \rangle $
. The ideals having such a property are called
$T^H$
-ideals. Moreover, all
$T^H$
-ideals are of this form: in fact, it is not difficult to see that, given a
$T^H$
-ideal I of
$F^H \langle X \rangle $
, then
$\operatorname {\mathrm {Id}}^H(F^H \langle X \rangle / I )= I$
.
Two H-module algebras
$W_1$
and
$W_2$
are said to be
$T^H$
-equivalent, and we write
$W_1 \sim _{T^H} W_2$
, if
$\operatorname {\mathrm {Id}}^H(W_1) = \operatorname {\mathrm {Id}}^H(W_2)$
.
Given a nonempty set
$S \subseteq F^H\langle X \rangle $
, the class var
$^H(S)$
of all H-module algebras W such that f is an H-identity for W for all
$f \in S$
is called the variety determined (or generated) by S. Similarly, given an H-module algebra W, the variety of H-module algebras generated by W, denoted by var
$^H(W)$
, is the class of all H-module algebras satisfying the H-identities of W. Hence, we say that
$A \in $
var
$^H(W)$
if and only if
$\operatorname {\mathrm {Id}}^H(W) \subseteq \operatorname {\mathrm {Id}}^H(A)$
.
Let
$f(x_1, \dots , x_n, Y) \in F^H \langle X \rangle $
be a multilinear H-polynomial, where Y is a set of variables disjoint from
$x_1, \dots , x_n$
. We say f is alternating on
$\{ x_1, \ldots , x_n \}$
if there exists a multilinear H-polynomial
$h(x_1, \ldots , x_n, Y) $
such that
$$ \begin{align*}f(X) = \sum_{\sigma \in S_n} (-1)^\sigma h(x_{\sigma(1)}, \ldots, x_{\sigma(n)}, Y).\end{align*} $$
Equivalently, f is alternating on
$\{ x_1, \ldots , x_n \}$
if substituting in
$f\ x_i$
by
$x_j$
(for every i and j) and vice versa, and we get
$-f$
.
2.5 H-cocharacters and H-PI-exponent
From now on, any Hopf algebra is supposed to be finite dimensional over F. Let A be an H-module algebra. Denote by
$P_n^H$
the space (of dimension (
$\dim _F H$
)
$^n \cdot n!$
) of all multilinear H-polynomials in
$x_1, \dots , x_n$
,
$n \in \mathbb {N}$
, i.e.,
where
$S_n$
is the symmetric group on n elements. The space
$P_n^H$
has a natural structure of left
$S_n$
-module induced by
$\sigma \cdot x_1^{h_1} x_2^{h_2} \cdots x_n^{h_n} = x_{\sigma (1)}^{h_1} x_{\sigma (2)}^{h_2} \cdots x_{\sigma (n)}^{h_n} $
, if
$\sigma \in S_n$
. Since
$P_n^H \cap \operatorname {\mathrm {Id}}^H(A)$
is a subspace invariant under the above action,
is a left
$S_n$
-module. This leads us to consider the
$S_n$
-character of
$P_n^H(A)$
, namely
$\chi _n^H(A)$
, which is called nth H-cocharacter of A. The nonnegative integer
is called nth H-codimension of A. Moreover, the sequences
$\{ \chi _n^H(A)\}_{n \geq 0} $
and
$\{ c_n^H(A) \}_{n \geq 0} $
are called the H-cocharacter sequence of A and the H-codimension sequence of A, respectively.
Given an H-module algebra A, if the limit
$$ \begin{align*}\limsup_{n \to \infty} \sqrt[n]{c_n^H(A)}\end{align*} $$
exists, we shall call it H PI-exponent of A and we shall denote it by exp
$^H(A)$
(see [Reference Centrone, Estrada and Ioppolo12, Section 9]).
The existence of the exponent for H-module algebras was studied in [Reference Karasik27] in the case H is finite dimensional and semisimple acting on an associative algebra over a field of characteristic 0. In particular, in [Reference Karasik27], the author proved that the H-exponent exists and is an integer. It is easy to see that Taft’s algebras are not semisimple algebras. In [Reference Gordienko24], the author proved the existence of the exponent for finite dimensional algebras over an algebraically closed field of characteristic 0 that are simple under the action of a Taft’s algebra. We recall Taft’s algebras are noncommutative, noncocommutative, and not semisimple Hopf algebras.
Let
$n \geq 1$
be an integer. A partition
$\lambda $
of n is a finite sequence of integers
$\lambda = (\lambda _1, \dots , \lambda _k)$
such that
$\lambda _1 \geq \cdots \geq \lambda _k> 0$
and
$\sum _{i=1}^{r}\lambda _i = n$
. In this case, we write
$\lambda \vdash n$
or
$\left | \lambda \right | = n $
. By representation theory of
$S_n$
in characteristic zero, there is a one-to-one correspondence between irreducible
$S_n$
-characters and partitions of n see [Reference Curtis and Reiner15] or Sagan’s book [Reference Sagan39]. If
$\chi _\lambda $
denotes the irreducible
$S_n$
-character corresponding to the partition
$\lambda \vdash n$
, then we can write
$$\begin{align*}\chi_n^H(A) = \sum_{\lambda \vdash n} m_\lambda^H \chi_\lambda, \end{align*}$$
where
$m_\lambda ^H \geq 0$
are the corresponding multiplicities. The irreducible
$S_n$
-submodules of
$P_n^H(A)$
can be written as
$FS_n e_{T_\lambda }\cdot f$
, where f is some H-polynomial in
$P_n^H(A)$
,
$T_\lambda $
is some Young tableau of the partition
$\lambda \vdash n$
and
$$ \begin{align*}e_{T_\lambda} = \sum_{\sigma \in \mathcal{R}_{T_\lambda}, \tau \in \mathcal{C}_{T_\lambda} } (-1)^\tau \sigma \tau,\end{align*} $$
where
$\mathcal {R}_{T_\lambda }$
and
$\mathcal {C}_{T_\lambda }$
are the rows and columns stabilizers, respectively. For more details towardH-cocharacters, we remand the reader to Berele’s seminal paper [Reference Berele6].
2.6 Gradings on
$UT_2$
Let
$UT_2$
be the algebra of
$2 \times 2$
upper triangular matrices over the field F. A detailed description of the G-graded identities satisfied by the algebra
$UT_2$
when the characteristic of F is 0 is given in [Reference Valenti42]. In particular, in [Reference Valenti42], the author shows that, up to isomorphism, there is only one nontrivial grading. So any G-grading on
$UT_2$
is actually a
$\mathbb {Z}_2$
-grading. The algebras with
$\mathbb {Z}_2$
-grading are called superalgebras.
2.7
$H_m$
actions on
$UT_2$
From now on, F is a field of characteristic zero containing a primitive mth root of the unit;
$H_m$
is an mth Taft’s Hopf algebra over F.
Consider the
$H_m$
-action on
$UT_2$
. Then, by a result of Centrone and Yasumura (see page 738 of [Reference Centrone and Yasumura14]), there exist three structures of
$H_m$
-module algebra on
$UT_2$
:
-
(i) the trivial grading and d acts trivially: in this case,
$\operatorname {\mathrm {Id}}^{H_m}(UT2)$
is merely the ideal of ordinary polynomial identities of
$UT_2$
; -
(ii) the canonical
$\mathbb {Z}_2$
-grading and d acts trivially: in this case,
$\operatorname {\mathrm {Id}}^{H_m}(UT2)$
coincides with the ideal of
$\mathbb {Z}_2$
-graded polynomial identities of
$UT_2$
which was originally calculated by Valenti in [Reference Valenti42]; and -
(iii) the canonical
$\mathbb {Z}_2$
-grading and d acts nontrivially: in this case, necessarily
$d =\,{}$
ad
$_{\alpha } (a e_{12})$
, for some
$0 \neq a \in F$
, that is, if
$A = \begin {pmatrix} x_{11} & x_{12} \\ 0 & x_{22} \end {pmatrix} \in UT_2 $
, then (1)
$$ \begin{align} A^d = \textrm{ad}_{\alpha} (a e_{12}) \left(\begin{pmatrix} x_{11} & x_{12} \\ 0 & x_{22} \end{pmatrix} \right) = \begin{pmatrix} 0 & a(x_{22} - x_{11}) \\ 0 & 0 \end{pmatrix}. \end{align} $$
The Specht properties for (i) and (ii) are particular cases of the Specht property for ordinary PI-algebras [Reference Kemer30] and G-graded PI-algebras [Reference Aljadeff and Kanel-Belov1], respectively. Therefore, we will study the case (iii). Thus, from now on, an
$H_m$
-action on
$UT_2$
means the canonical
$\mathbb {Z}_2$
-grading on
$UT_2$
with a nontrivial action of d on
$UT_2$
. This forces us to see an action of
$H_m$
on the algebra
$UT_2$
as an action of
$H_2$
on
$UT_2$
. It is worth recalling that, in [Reference Gordienko25], the author gives an explicit description of the simple algebras that are module algebra under the action of a Sweedler’s algebra that is a Taft’s algebra of dimension 4.
2.8 The
$H_m$
-identities of
$UT_2$
Let
$F \langle X \rangle $
be the free associative algebra over the countable set
$X = \{ x_1, x_2, \dots \}$
. If we write
$X = Y \cup Z$
where
$Y = \{ y_1, y_2, \dots \}$
is the countable set of variables of degree zero and
$Z = \{ z_1, z_2, \dots \}$
is the countable set of variables of degree one, and
$Y \cap Z = \emptyset $
, then
$F\langle Y\cup Z \rangle $
has a natural structure of free superalgebra on
$Y \cup Z$
. The elements of
$F\langle Y\cup Z \rangle $
are called graded polynomials.
A graded polynomial
$f(y_1,\ldots ,y_t, z_1,\ldots ,z_s) \in F\langle Y\cup Z \rangle $
is a graded identity of the superalgebra
$A = A_0 \oplus A_1$
, and we write
$f\equiv 0,$
if, for all
$a_1, \ldots , a_t \in A_0, b_1, \ldots , b_s \in A_1$
, we have
$f(a_1, \ldots , a_t, b_1, \ldots , b_s) = 0.$
We denote by
$\operatorname {\mathrm {Id}}^{gr}(A)=\{f\in F\langle Y\cup Z \rangle \mid f\equiv 0 \textrm{ on } A\}$
the ideal of graded identities of A. Notice that
$\operatorname {\mathrm {Id}}^{gr}(A)$
is a
$T_2$
-ideal of
$F\langle Y\cup Z \rangle $
, i.e., an ideal that is invariant under all
$\mathbb {Z}_2$
-graded endomorphisms of the free superalgebra
$F\langle Y\cup Z \rangle $
. Since the characteristic of F is zero, it is well known that
$\operatorname {\mathrm {Id}}^{gr}(A)$
is completely determined by its multilinear graded polynomials.
Now, we construct
$F\langle Y\cup Z \mid D_2 \rangle $
the free superalgebra on
$X = Y \cup Z$
with action of
$D_2 = F \langle d \mid d^2=0 \rangle $
as follows. The algebra
$F\langle Y\cup Z \mid D_2 \rangle $
is the algebra freely generated by the set
$\{ x^{d_1} = d_1(x) \mid x\in Y $
or
$x \in Z, d_1 \in D_2 \} $
. We let
$D_2$
act on
$F\langle Y\cup Z \mid D_2 \rangle $
by requiring that if
$d_1, d_2 \in D_2$
, then
$(x^{d_1})^{d_2} = x^{d_1d_2}$
, and then by extending this action on all of
$F\langle Y\cup Z \mid D_2 \rangle $
as follows: if
$v, w$
are monomials, then define
$(vw)^d = v^d w + (-1)^{\deg (v)} v w^d$
and then extend this action by linearity to all of
$F\langle Y\cup Z \mid D_2 \rangle $
. The elements of
$F\langle Y\cup Z \mid D_2 \rangle $
are called
$\mathbb {Z}_2$
–
$D_2$
-polynomials.
The algebra
$F\langle Y\cup Z \mid D_2 \rangle $
has the following universal property: given any superalgebra
$A = A_0 \oplus A_1$
with
$D_2$
-action, any set-theoretic map
$\varphi \colon Y \cup Z \to A$
such that
$\varphi (Y) \subseteq A_0$
and
$\varphi (Z) \subseteq A_1$
can be extended to a unique homomorphism of superalgebras
$\bar {\varphi } \colon F\langle Y\cup Z \mid D_2 \rangle \to A$
such that
$\bar {\varphi }(f^d_1) = \bar {\varphi }(f)^d_1$
, for any
$f \in F\langle Y\cup Z \mid D_2 \rangle $
,
$d_1 \in D_2$
.
If we let
$\Phi $
be the set of all such homomorphisms, then
$\operatorname {\mathrm {Id}}^{\mathbb {Z}_2,D_2}(A) = \cap _{\bar {\phi } \in \Phi } \ker \bar {\phi }$
is the ideal of
$\mathbb {Z}_2$
–
$D_2$
-polynomials identities of A. This means that a
$\mathbb {Z}_2$
–
$D_2$
-polynomial
$f(y_1, \dots , y_s, z_1, \dots , z_t) \in F\langle Y\cup Z \mid D_2 \rangle $
is a
$\mathbb {Z}_2$
–
$D_2$
-identity for A if
$f(a_1, \dots , a_s, b_1, \dots , b_t) = 0$
for all
$a_1, \dots , a_s \in A_0$
and
$b_1 , \dots , b_t \in A_1$
. We write
$f \equiv 0$
on A, in this case.
Assume
$\mathbb {Z}_2 = \{ 1, c \}$
.
Definition 2
$\operatorname {\mathrm {Id}}^{\mathbb {Z}_2,D_2}(A) = \{ f \in F\langle Y\cup Z \mid D_2 \rangle \mid f\equiv 0$
on A} is the ideal of
$\mathbb {Z}_2$
–
$D_2$
-polynomial identities of A.
Proposition 3 [Reference Centrone and Yasumura14, Proposition 14]
$$\begin{align*}\operatorname{\mathrm{Id}}^{H_2}(A) = \operatorname{\mathrm{Id}}^{\mathbb{Z}_2,D_2}(A), \end{align*}$$
and
$$\begin{align*}F^{H_2}\langle X \rangle \cong F\langle Y\cup Z \mid D_2 \rangle. \end{align*}$$
Theorem 4 [Reference Centrone and Yasumura14, Theorem 17]
For each
$j = 0,1, \dots , m-1$
, let
$\beta _j = \sum _{l=0}^{m-1} \gamma ^{jl} c^l$
,
$y_i = x_i^{\beta _0}$
, and
$z_i = x_i^{\beta _1}$
. Then the
$T^{H_m}$
-ideal of
$UT_2$
is generated by the following polynomials:
$$\begin{align*}[y_1, y_2], \, z_1x^hz_2, \, z^d, \, x^{d^2}, \, y_1^d x^h y_2^d, \, x^{\beta_j}, \end{align*}$$
where
$h \in H_m$
and
$j = 2, \dots , m-1$
.
3 The space of multilinear
$H_m$
Let
$P^{\mathbb {Z}_2, D_2}_n$
the vector space of multilinear
$\mathbb {Z}_2$
–
$D_2$
-polynomials of degree n in
$x_1, \dots , x_n$
, i.e.,
$$ \begin{align*}P^{\mathbb{Z}_2, D_2}_n &= \textrm{span}_F \{ x_{\sigma(1)}^{d_1} \cdots x_{\sigma(n)}^{d_n} \mid \sigma \in S_n, d_i \in D_2, x_i = y_i \ \textrm{or} \ x_i = z_i, i = 1, \dots , n \}\\ & \quad \subset F\langle Y\cup Z \mid D_2 \rangle.\end{align*} $$
Recall that the wreath product of
$\mathbb {Z}_2$
and
$S_n$
(called the hyperoctahedral group) is the group defined by
$$ \begin{align*}\mathbb{Z}_2 \wr S_n = \{ (g_1, \dots, g_n; \sigma) \mid g_1, \dots, g_n \in \mathbb{Z}_2, \sigma \in S_n, \}\end{align*} $$
with multiplication given by
$$ \begin{align*}(g_1, \dots , g_n; \sigma) (h_1, \dots , h_n; \tau ) = (g_1 h_{\sigma^{-1}(1)}, \dots , g_n h_{\sigma^{-1}(n)}; \sigma \tau ).\end{align*} $$
Let
$\mathbb {Z}_2 = \{ 1,c\}$
. Then the space
$P^{\mathbb {Z}_2, D_2}_n$
has a structure of left
$\mathbb {Z}_2 \wr S_n$
-module induced by defining for
$ (g_1, \dots , g_n; \sigma ) \in \mathbb {Z}_2 \wr S_n$
and
$ f(x_1, \dots , x_n ) \in P^{\mathbb {Z}_2, D_2}_n$
(see [Reference Giambruno and Zaicev23, Lemma 10.1.5]),
$$ \begin{align*}(g_1, \dots , g_n; \sigma) f(x_1, \dots , x_n ) = f ( x_{\sigma(1)}^{g_{\sigma(1)}^{-1}}, \dots , x_{\sigma(n)}^{g_{\sigma(n)}^{-1}}),\end{align*} $$
where
$y^c_{\sigma (i)} = y_{\sigma (i)}$
and
$z^c_{\sigma (i)} = -z_{\sigma (i)}. $
Notice that the vector space
$P^{\mathbb {Z}_2, D_2}_n \cap \operatorname {\mathrm {Id}}^{\mathbb {Z}_2,D_2}(A)$
is invariant under this action, and hence
is a left
$\mathbb {Z}_2 \wr S_n$
-module. Let
$\chi ^{\mathbb {Z}_2, D_2}_n (A)$
be its character. It is known (see, for instance, Section 10.4 of [Reference Giambruno and Zaicev23]) that there is a one-to-one correspondence between irreducible
$\mathbb {Z}_2 \wr S_n$
-character and pairs of partitions
$(\lambda , \mu )$
, where
$\lambda \vdash r$
,
$\mu \vdash n-r$
, for all
$r = 0,1, \dots , n$
. If
$\chi _{\lambda , \mu }$
denotes the irreducible
$\mathbb {Z}_2 \wr S_n$
-character corresponding to
$(\lambda , \mu )$
, then we can write
$$ \begin{align*}\chi^{\mathbb{Z}_2, D_2}_n (A) = \sum_{r=0}^n \sum_{\substack{\lambda \vdash r \\ \mu \vdash n-r}} m_{\lambda, \mu} \chi_{\lambda, \mu},\end{align*} $$
where
$m_{\lambda , \mu } \geq 0 $
are the corresponding multiplicities.
For fixed
$r \in \{ 0, \dots , n \}$
, let
$$ \begin{align*} P_{r, n-r} = \textrm{span}_F & \{ x_{\sigma(1)}^{d_1} \cdots x_{\sigma(n)}^{d_n} \mid \sigma \in S_n, d_i \in D_2, x_i = y_i \textrm{ for } i = 1, \dots , r, \\ & \textrm{ and } x_i = z_i \textrm{ for } i = r+1, \dots , n \} \end{align*} $$
be the subspace of multilinear
$\mathbb {Z}_2$
–
$D_2$
-polynomials in the variables
$y_1, \dots , y_r, z_{r+1}, \dots , z_n$
. In order to study
$P^{\mathbb {Z}_2, D_2}_n(A)$
, it is enough to study
$$ \begin{align*}P_{r,n-r}(A) = \frac{P_{r,n-r}}{P_{r,n-r} \cap \operatorname{\mathrm{Id}}^{\mathbb{Z}_2,D_2}(A)}\end{align*} $$
for all
$r = 0, \dots , n$
. If we let
$S_r$
acting on the variables
$y_1, \dots , y_r$
and
$S_{n-r}$
acting on the variables
$z_{r+1}, \dots , z_n$
, we obtain an action of
$S_r \times S_{n-r}$
on
$P_{r,n-r}$
and
$P_{r,n-r}(A)$
becomes a left
$S_r \times S_{n-r}$
-module. Let
$\chi _{r,n-r} (A)$
be its character. It is well known that the irreducible
$S_r \times S_{n-r}$
-characters are obtained by taking the outer tensor product of
$S_r$
and
$S_{n-r}$
irreducible characters, respectively. Then, we can write
$$ \begin{align*}\chi_{r,n-r} (A) = \sum_{\substack{\lambda \vdash r \\ \mu \vdash n-r}} m_{\lambda, \mu}(\chi_\lambda \otimes \chi_\mu ),\end{align*} $$
where
$\chi _\lambda $
(respectively,
$\chi _\mu $
) denotes the irreducible
$S_r$
-character (respectively,
$S_{n-r}$
-character) and
$m_{\lambda , \mu } \geq 0 $
are the corresponding multiplicities.
The relation between the character
$\chi ^H_n(A)$
and the character
$\chi _{r,n-r} (A)$
for any
$H_m$
-module algebra A is given by
$$\begin{align*}\chi^{\mathbb{Z}_2,D_2}_n (A) = \sum_{r=0}^n \sum_{\substack{\lambda \vdash r \\ \mu \vdash n-r}} m_{\lambda, \mu} \chi_{\lambda, \mu} \quad \textrm{ and } \quad \chi_{r,n-r} (A) = \sum_{\substack{\lambda \vdash r \\ \mu \vdash n-r}} m_{\lambda, \mu}(\chi_\lambda \otimes \chi_\mu ) \end{align*}$$
for all
$r \leq n$
. Moreover,
$$ \begin{align*}c_n^H(A) = \sum_{r=0}^{n} \binom{n}{r} \dim_F P_{r,n-r}(A).\end{align*} $$
Remark that since
$[y_1, y_2]^d$
is an
$H_m$
-identity of
$UT_2$
, then we have the following equality modulo
$\operatorname {\mathrm {Id}}^{H_m}(UT_2)$
:
$$ \begin{align} y_1^dy_2 -y_2^dy_1 = y_2y_1^d - y_1 y_2^d. \end{align} $$
Moreover, for every
$n \geq 0$
, a linear basis for the space
$P_{n,0}(UT_2)$
is given by the following set of polynomials:
-
•
$y_1 \cdots y_n$
and -
•
,
where S denotes the ordered k-tuple
$(i_1, \dots , i_k)$
,
$i_j \in \{1, \dots ,n\}$
, and all the other indexes are ordered. This implies that the space
$P_{n,0}(UT_2)$
has dimension
$\sum _{k=0}^{n}\binom {n}{k} = 2^n$
.
A linear basis for the space
$P_{n-1,1}(UT_2)$
is given by the following set of polynomials:
-
•
,
where S denotes the ordered k-tuple
$(i_1, \dots , i_k)$
,
$i_j \in \{1, \dots ,n\}$
, and all the other indexes are ordered. Since the number of polynomials
$u_S$
is given by
$\sum _{k=0}^{n-1}\binom {n-1}{k}$
, then the space
$P_{n-1,1}(UT_2)$
has dimension
$ 2^{n-1}$
. The spaces
$P_{r,n-r}(UT_2)$
vanishes for
$r = 0, 1, \dots , n-2$
. Therefore, we obtain the following.
Proposition 5 The nth
$H_m$
-codimension of
$UT_2$
is
$$ \begin{align*}c_n^{H_m}(UT_2) = \sum_{r=0}^{n} \binom{n}{r} \dim_F P_{r,n-r}(UT_2) = n2^{n-1} + 2^n = (n+2)2^{n-1},\end{align*} $$
and the
$H_m$
PI-exponent of
$UT_2$
is
$$\begin{align*}\mathrm{exp}^{H_m}(UT_2) = \limsup_{n \to \infty} \sqrt[n]{c_n^{H_m}(UT_2)} = 2. \end{align*}$$
4
$H_m$
-Cocharacters of
$UT_2$
The goal of this section is giving a complete description of the
$H_m$
-cocharacter sequence of
$UT_2$
, where
$H_m$
is an mth Taft’s Hopf algebra.
Let
$\lambda \vdash r$
,
$\mu \vdash n-r$
, and let
$W_{\lambda ,\mu }$
be a left irreducible
$S_r \times S_{n-r}$
-module. It is well known that if
$T_\lambda $
is a tableau of shape
$\lambda $
and
$T_\mu $
is a tableau of shape
$\mu $
, then
$W_{\lambda , \mu } \cong F(S_r \times S_{n-r})e_{T_\lambda }e_{T_\mu }$
where
$S_r$
and
$S_{n-r}$
act on disjoint sets of integers.
For a partition
$\lambda \vdash n$
, we denote by
$h(\lambda )$
the height of the diagram associated to
$\lambda $
, that is, if
$\lambda = (\lambda _1, \dots , \lambda _k)$
, then
$h(\lambda ) = k$
.
We can now write the explicit decomposition of the nth
$H_m$
-cocharacter of
$UT_2$
into irreducibles.
Theorem 6 Let
$$\begin{align*}\chi^{\mathbb{Z}_2,D_2}_n (UT_2) = \sum_{r=0}^n \sum_{\substack{\lambda \vdash r \\ \mu \vdash n-r}} m_{\lambda, \mu} \chi_{\lambda, \mu} \end{align*}$$
be the nth
$H_m$
-cocharacter of the H-module algebra
$UT_2$
. Then:
-
(i)
$m_{\lambda , \emptyset } = l+1 $
if
$\lambda = (k+l, k)$
; -
(ii)
$m_{\lambda , \mu } = l+1 $
if
$\lambda = (k+l, k)$
,
$\mu = (1)$
; and -
(iii)
$m_{\lambda , \mu } = 0$
in all other cases.
Proof Let
$A = UT_2$
, and consider the canonical grading
$A = A_0 \oplus A_1$
, where
$A_0 = \textrm{span}\{ e_{11}, e_{22} \}$
and
$A_1 = \textrm{span}\{ e_{12}\}$
. Since
$ \dim A_0 = 2 $
and
$\dim A_1 = 1$
, any
$H_m$
-polynomial alternating on three even variables or in two odd variables vanishes on A; it follows that
$m_{\lambda , \mu } = 0$
if either
$h(\lambda ) \geq 3$
or
$h(\mu ) \geq 2$
, and this proves the case
$(iii)$
. By Proposition 4,
$z_1 x z_2 \in \operatorname {\mathrm {Id}}^{H_m}(A)$
, then
$m_{\lambda , \mu } = 0$
whenever
$\left | \mu \right | \geq 2$
. So we have two cases left to study, namely
$\mu = \emptyset $
or
$\mu = (1)$
.
First, we consider the case
$\mu = \emptyset $
. Let
$\lambda = (k+l,k)$
, with
$k \geq 0$
,
$l \geq 0$
, and
${2k+l = n}$
. For each
$i=0, \dots , l$
, let us consider the following tableau:
We associate to
$T_\lambda ^{(i)}$
the
$H_m$
-polynomial
$$\begin{align*}b_{k,l}^{(i)}(y_1, y_2) = y_1^i \underbrace{\overline{y_1} \cdots \widehat{y_1} (\widetilde{y_1})^d }_k \underbrace{\overline{y_2} \cdots \widehat{y_2} \widetilde{y_2} }_k y_1^{l-i}, \end{align*}$$
where
$ -, ^\wedge , \thicksim $
mean alternation on the corresponding elements. It is not hard to see
$$\begin{align*}b_{k,l}^{(i)}(y_1, y_2)=\sum_{\sigma_1,\ldots,\sigma_k\in S_2}(-1)^{\sigma_1}\cdots (-1)^{\sigma_k}y_1^iy_{\sigma_1(1)}\cdots y_{\sigma_k(1)}^dy_{\sigma_1(2)}\cdots y_{\sigma_k(2)}y_1^{l-i}.\end{align*}$$
We shall prove the
$l+1\ H_m$
-polynomials
$b_{k,l}^{(i)}(y_1, y_2)$
,
$i = 0, \dots , l$
, are linearly independent over F modulo
$\operatorname {\mathrm {Id}}^{H_m}(A)$
. Suppose by absurd
$\sum _{i=0}^l \beta _i b_{k,l}^{(i)}(y_1, y_2) = 0$
(mod
$\operatorname {\mathrm {Id}}^{H_m}(A)$
), and let
$t = $
max
$\{i \mid \beta _i \neq 0 \} $
. Then
$\beta _t b_{k,l}^{(t)}(y_1, y_2) + \sum _{i < t} \beta _i b_{k,l}^{(i)}(y_1, y_2) = 0 $
(mod
$\operatorname {\mathrm {Id}}^{H_m}(A)$
). If we consider the substitution
$y_1 =y_1 + y_3$
, we get
$$ \begin{align} & \beta_t(y_1 + y_3)^t \overline{(y_1 + y_3)} \cdots \widehat{(y_1 + y_3)} \widetilde{(y_1 + y_3)}^d \overline{y_2} \cdots \widehat{y_2} \widetilde{y_2}(y_1 + y_3)^{l-t} \nonumber\\ &\qquad\qquad + \sum_{i < t} \beta_i (y_1 + y_3)^i \overline{(y_1 + y_3)} \cdots \widehat{(y_1 + y_3)} \widetilde{(y_1 + y_3)}^d \overline{y_2} \cdots \widehat{y_2} \widetilde{y_2}(y_1 + y_3)^{l-i} \nonumber\\ &\qquad\qquad=0 ( \textrm{mod } \operatorname{\mathrm{Id}}^{H_m}(A)). \end{align} $$
Let us consider the homogeneous component of degree
$t+k$
in
$y_1$
and of degree
$l-t$
in
$y_3$
. Considering the substitution
$y_1 = e_{11}$
and
$y_2 = y_3 = e_{22}$
, then, by equation (1), we get
$y_1^d = -ae_{12}$
, and we obtain
$(-\beta _t a) e_{12} = 0$
, which implies
$\beta _t =0$
, a contradiction. Hence, the
$H_m$
-polynomials
$b_{k,l}^{(i)}(y_1, y_2)$
,
$i = 0, \dots , l$
, are linearly independent (mod
$\operatorname {\mathrm {Id}}^{H_m}(A)$
).
Notice that, for all i,
$e_{T_{\lambda }^{(i)}}(y_1, \dots , y_n)$
is the complete linearization of the
$H_m$
-polynomial
$b_{k,l}^{(i)}(y_1, y_2)$
. It follows that the
$H_m$
-polynomials
$e_{T_{\lambda }^{(i)}}$
,
$i = 0, \dots , l$
, are linearly independent (mod
$\operatorname {\mathrm {Id}}^{H_m}(A)$
) and this implies that
$m_{\lambda ,\mu } \geq l+1$
.
We want to prove the multiplicities are exactly
$l+1$
. For, let
$T_\lambda $
be any tableau and
$e_{T_\lambda }(y_1, \dots , y_n)$
the corresponding
$H_m$
-polynomial. If
$e_{T_\lambda } \notin \operatorname {\mathrm {Id}}^{H_m}(A) $
, then any two alternating variables in
$e_{T_\lambda }$
must lie on different sides of the elements of type
$y_i^d$
. Since
$e_{T_\lambda }$
is a linear combination (mod
$\operatorname {\mathrm {Id}}^{H_m}(A)$
) of
$H_m$
-polynomials alternating on k pairs of
$y_i$
’s, we get
$e_{T_\lambda }$
is a linear combination of the
$H_m$
-polynomials
$e_{T_{\lambda }^{(i)}}$
,
$i = 0, \dots , l$
. Hence,
$m_{\lambda ,\mu } = l+1$
, and this proves item
$(i)$
of the sentence.
We only need to study the case
$\mu = (1)$
. Let
$\lambda = (k+l,k)$
, with
$k \geq 0$
,
$l \geq 0$
, and
$2k+l = n-1$
. This case can be proved following word by word the last part of the proof of Theorem 3 of [Reference Valenti42], where the
$H_m$
-polynomials
$$\begin{align*}a_{k,l}^{(i)}(y_1, y_2,z) = y_1^i \underbrace{\overline{y_1} \cdots \widetilde{y_1} }_k z \underbrace{\overline{y_2} \cdots \widetilde{y_2} }_k y_1^{l-i}, \qquad i = 0, 1, \dots , l, \end{align*}$$
are the highest weight vectors corresponding to
$\lambda $
. As above,
$$\begin{align*}a_{k,l}^{(i)}(y_1, y_2,z)=\sum_{\sigma_1,\ldots,\sigma_k\in S_2}(-1)^{\sigma_1}\cdots (-1)^{\sigma_k}y_1^iy_{\sigma_1(1)}\cdots y_{\sigma_k(1)}zy_{\sigma_1(2)}\cdots y_{\sigma_k(2)}y_1^{l-i}.\end{align*}$$
This proves
$(ii)$
, and the proof is complete.▪
Recall that in characteristic zero, any result on multilinear polynomial identities obtained in the language of representations of the symmetric group is equivalent to a corresponding result on homogeneous polynomial identities obtained in the language of representations of the general linear group.
Notice that the
$H_m$
-polynomial
$b_{k,l}^{(i)}$
is obtained from the essential idempotent corresponding to the tableau
$T_\lambda ^{(i)}$
by identifying all the elements in each row of
$\lambda $
. Therefore, the
$H_m$
-polynomial
$b_{k,l}^{(i)}$
is a highest weight vector, according to the representation theory of
$GL_n$
(see [Reference Drensky18, Chapter 12] for more details). We recall that the complete linearization of a highest weight vector associated to an irreducible
$GL_n$
-module generates an irreducible
$S_n$
-module.
Corollary 7 The highest weight vectors whose characters appear with nonzero multiplicity in the decomposition of
$\chi _n^{\mathbb {Z}_2, D_2} (UT_2)$
are linear combinations of
$H_m$
-polynomials of the form:
-
(1)
where
$$ \begin{align*}b_{k,l}^{(i)}(y_1, y_2) = y_1^i \underbrace{\overline{y_1} \cdots \widehat{y_1} (\widetilde{y_1})^d }_k \underbrace{\overline{y_2} \cdots \widehat{y_2} \widetilde{y_2} }_k y_1^{l-i}, \qquad i = 0, 1, \dots , l,\end{align*} $$
$2k + l = n$
; and
-
(2)
where
$$ \begin{align*}a_{k,l}^{(i)}(y_1, y_2,z) = y_1^i \underbrace{\overline{y_1} \cdots \widetilde{y_1} }_k z \underbrace{\overline{y_2} \dots \widetilde{y_2} }_k y_1^{l-i}, \qquad i = 0, 1, \dots , l,\end{align*} $$
$2k+l+1 = n$
.
If
$ \chi ^{\mathbb {Z}_2, D_2}_n (A) = \sum _{r=0}^n \sum _{\substack {\lambda \vdash r \\ \mu \vdash n-r}} m_{\lambda , \mu } \chi _{\lambda , \mu } $
is the decomposition of the
$\mathbb {Z}_2 \wr S_n$
-character of A, then one defines the nth
$\mathbb {Z}_2 \wr S_n$
-colength of A as
$$ \begin{align*}l^{\mathbb{Z}_2, D_2}_n (A) = \sum_{r=0}^n \sum_{\substack{\lambda \vdash r \\ \mu \vdash n-r}} m_{\lambda, \mu}.\end{align*} $$
By Theorem 6, we immediately get the following.
Corollary 8 For all
$n \geq 1$
,
$$ \begin{align*}l^{\mathbb{Z}_2, D_2}_n (UT_2) = \sum_{r=0}^n \sum_{\substack{\lambda \vdash r \\ \mu \vdash n-r}} m_{\lambda, \mu} = \frac{n^2 + 3n +2}{2}.\end{align*} $$
5 Specht property for the
$H_m$
-module algebra
$UT_2$
In this section, we prove that the variety of
$H_m$
-module algebras generated by the
$H_m$
-module algebra
$UT_2$
has the Specht property.
Definition 9 Let W be an H-module algebra. We say that
$\operatorname {\mathrm {Id}}^H(W)$
has the Specht property if any
$T^H$
-ideal I such that
$I \supseteq \operatorname {\mathrm {Id}}^H(W)$
, has a finite basis, that is, I is finitely generated as a
$T^H$
-ideal. We say that the variety
$\mathcal {V}$
has the Specht property if the corresponding
$T^H$
-ideal has the Specht property.
We recall that a binary relation
$\leq $
on a set A is a quasi-order if
$\leq $
is reflexive and transitive, i.e., (i)
$a \leq a$
for all
$a \in A$
, and (ii)
$a \leq b$
and
$b \leq c$
imply
$a \leq c$
, with
${a,b,c \in A}$
. If B is a subset of a quasi-ordered set A, the closure of B, written
$\overline {B}$
, is defined as
$$ \begin{align*}\overline{B} = \{ a \in A \mid \text{ exists } b \in B \text{ such that } b \leq a \}.\end{align*} $$
We say that the quasi-ordered set A has the finite basis property (f.b.p.) if for any subset B of A, there exists a finite subset
$B_0$
of A such that
$B_0 \subseteq B \subseteq \overline {B_0} $
. Every well-ordered set has f.b.p. In particular, the set
$\mathbb {N}$
of natural numbers with standard ordering has f.b.p. The following theorem gives an equivalent definition for f.b.p.
Theorem 10 [Reference Higman26, Theorem 2.1]
The following conditions on a quasi-ordered set A are equivalent.
-
(1) If B is any subset of A, there is a finite set
$B_0$
such that
$B_0 \subseteq B \subseteq \overline {B_0} $
. -
(2) There exists neither an infinite strictly descending sequence in A nor an infinite one of mutually incomparable elements of A.
Let
$A_1, A_2, \dots , A_n$
be quasi-ordered sets. The Cartesian product
$A_1 \times A_2 \times \cdots \times A_n$
ordered by
$(a_1, a_2, \ldots , a_n ) \leq (b_1, b_2, \dots , b_n)$
if and only if
$a_i \leq b_i$
for all
$i \in \{1,2, \dots , n \} $
is a quasi-ordered set.
The following theorems are useful.
Theorem 11 [Reference Higman26, Theorem 2.3]
Let
$A_1, A_2, \dots , A_n$
be quasi-ordered sets satisfying f.b.p. so their Cartesian product satisfies f.b.p.
Theorem 12 Let
$A_1, A_2, \dots , A_n$
be quasi-ordered sets satisfying f.b.p., so the disjoint union
$A_1 \sqcup A_2 \sqcup \cdots \sqcup A_n $
endowed with the quasi-order
$a \leq b$
if and only if
$a, b \in A_i$
and
$a \leq _{A_i} b$
for some
$i \in \{ 1 , \dots , n\} $
satisfies f.b.p.
The free H-module algebra
$F^H\langle X \rangle $
is a quasi-ordered set if we define for
$f,g \in F^H\langle X \rangle $
,
$$ \begin{align*}f \leq g \text{ if and only if } g \in \langle f \rangle_{T^H},\end{align*} $$
where
$\langle f \rangle _{T^H} $
denotes the
$T^H$
-ideal generated by f.
If I is a
$T^H$
-ideal of
$F^H\langle X \rangle $
, the quasi-order on
$F^H\langle X \rangle $
is inherited by
$\frac {F^H\langle X \rangle }{I}$
. Here, we shall consider
$\frac {F^{H_m}\langle X \rangle }{\operatorname {\mathrm {Id}}^{H_m}(UT_2)}$
as a quasi-ordered set. Hence, if
$f, g \in F^{H_m}\langle X \rangle $
, we define
$$ \begin{align*}f \leq g \text{ if and only if } g \in \langle \{f\} \cup \operatorname{\mathrm{Id}}^{H_m}(UT_2) \rangle_{T^{H_m}}.\end{align*} $$
In this case, we way that g is a consequence of f modulo
$\operatorname {\mathrm {Id}}^{H_m}(UT_2)$
or simply that g is a consequence of f.
Remark 13 Let M be a subset of
$F^H\langle X \rangle $
. Then
$\overline {M} \subseteq \langle M \rangle _{T^{H}}$
by definition. On the other hand, since
$M \subseteq \overline {M}$
, we have that
$\langle \overline {M} \rangle _{T^{H}} = \langle M \rangle _{T^{H}}$
.
Let M be the set of all the highest weight vectors corresponding to the cocharacters appearing with nonzero multiplicities in
$\chi _n^{\mathbb {Z}_2, D_2} (UT_2) $
. By Corollary 7, the highest weight vectors lying in M are a linear combination of
$H_m$
-polynomials of the form:
-
(1)
$y_1^i \underbrace {\overline {y_1} \cdots \widetilde {y_1} }_k z \underbrace {\overline {y_2} \dots \widetilde {y_2} }_k y_1^{l-i}$
and -
(2)
$y_1^i \underbrace {\overline {y_1} \cdots \widehat {y_1} (\widetilde {y_1})^d }_k \underbrace {\overline {y_2} \cdots \widehat {y_2} \widetilde {y_2} }_k y_1^{l-i}$
.
Let us denote by
$\mathcal {B}_1$
the set of
$H_m$
-polynomials of the form (1) and
$\mathcal {B}_2$
the set of
$H_m$
-polynomials of the form (2). For
$i = 1,2$
, we define the quasi-order
$\leq $
in
$\mathcal {B}_i $
by
$f \leq g $
if and only if g is a consequence of f, where
$f,g \in \mathcal {B}_i$
. We consider the following sets which are in one-to-one correspondence with the highest weight vectors of
$\mathcal {B}_1$
and
$\mathcal {B}_2$
, respectively:
$$ \begin{align*} B_1 &= \{ (i, l-i, k) \mid 0 \leq i \leq l\} \\ & = \{ (i, j, k) \} = \mathbb{N}^3; \\ B_2 &= \{ (i, l-i, k) \mid 0 \leq i \leq l \} \\ & = \{ (i, j, k) \} = \mathbb{N}^3. \end{align*} $$
By Theorem 11,
$B_1$
and
$B_2$
have f.b.p. with the natural quasi-order of
$\mathbb {N}^3$
. We shall show that the quasi-order
$\leq $
in
$B_1$
and
$B_2$
induces the quasi-order
$\leq $
in
$\mathcal {B}_1$
and
$\mathcal {B}_2$
, respectively.
Lemma 14
$(i,j,k) \leq (i',j',k')$
implies
-
(1)
$y_1^i \underbrace {\overline {y_1} \cdots \widetilde {y_1} }_k z \underbrace {\overline {y_2} \dots \widetilde {y_2} }_k y_1^{j} \leq y_1^{i'} \underbrace {\overline {y_1} \cdots \widetilde {y_1} }_{k'} z \underbrace {\overline {y_2} \dots \widetilde {y_2} }_{k'} y_1^{j'}$
, and -
(2)
$y_1^i \underbrace {\overline {y_1} \cdots \widehat {y_1} \widetilde {y_1}^d }_k \underbrace {\overline {y_2} \cdots \widehat {y_2} \widetilde {y_2} }_k y_1^{j} \leq y_1^{i'} \underbrace {\overline {y_1} \cdots \widehat {y_1} \widetilde {y_1}^d }_{k'} \underbrace {\overline {y_2} \cdots \widehat {y_2} \widetilde {y_2} }_{k'} y_1^{j'}$
.
Proof By transitivity of the quasi-order, in order to prove (1), we prove that:
-
(i)
$(i,j,k) \leq (i',j,k)$
implies
$a_{i,j,k} \leq a_{i',j,k}$
, -
(ii)
$(i,j,k) \leq (i,j',k)$
implies
$a_{i,j,k} \leq a_{i,j',k}$
, and -
(iii)
$(i,j,k) \leq (i,j,k')$
implies
$a_{i,j,k} \leq a_{i,j,k'}$
,
where
$i,i',j,j',k,k'$
are integers and
$$ \begin{align} a_{i,j,k} = a_{i,j,k}(y_1,y_2,z) = y_1^i \underbrace{\overline{y_1} \cdots \widetilde{y_1} }_k z \underbrace{\overline{y_2} \dots \widetilde{y_2} }_k y_1^{j}. \end{align} $$
The statements (i) and (ii) follow from the fact that
$a_{i,j,k} \equiv y_1^{i'-i} a_{i,j,k} \mod (\operatorname {\mathrm {Id}}^H (UT_2)) $
and
$a_{i,j,k} \equiv a_{i,j,k} y_1^{j'-j} \mod (\operatorname {\mathrm {Id}}^H (UT_2)), $
respectively. In order to prove the statement (iii), without loss of generality, we may suppose
$k'=k+1$
. The general statement will follow by a standard induction argument.
Notice that
$a_{i,j,k}$
is a linear combination (mod
$(\operatorname {\mathrm {Id}}^H (UT_2))$
) of the polynomials:
$$ \begin{align*}y_1^{i+t} y_2^{k-t} z y_1^{k-t} y_2^t y_1^j, \qquad t = 0,1, \dots , k.\end{align*} $$
Thus, if we multiply by appropriate variables y’s to the right or to the left of these polynomials, we obtain that for all
$ t = 0,1, \dots , k$
,
$$ \begin{align*}y_1^{i+t} y_2^{k-t} z y_1^{k-t} y_2^t y_1^j \leq y_1^{i+t} y_2^{(k+1)-t} z y_1^{(k+1)-t} y_2^t y_1^j,\end{align*} $$
and therefore
$a_{i,j,k} \leq a_{i,j,k'}$
.
The proof of
$(2)$
is analogous.▪
Lemma 15 The sets
$\mathcal {B}_1$
and
$\mathcal {B}_2$
with the quasi-order given above satisfy the f.b.p.
Proof Let
$\mathcal {B}_1'$
be a subset of
$\mathcal {B}_1 $
and
$B_1'$
a subset of
$B_1 = \{ (i, l-i,k) \mid a_{k,l}^{(i)} \in \mathcal {B}_1 \}$
corresponding to
$\mathcal {B}_1'$
, i.e.,
$B_1' = \{ (i, l-i,k) \mid a_{k,l}^{(i)} \in \mathcal {B}_1' \} $
. Since
$B_1' \subseteq B_1 \subseteq \mathbb {N}^3$
, and, by Theorem 11,
$\mathbb {N}^3$
has f.b.p., we have that there is a finite set
$B_1^0 \subseteq B_1'$
such that
$B_1^0 \subseteq B_1' \subseteq \overline {B_1^0}$
. Consider
$\mathcal {B}_1^{0} = \{a_{k,l}^{(i)} \mid (i, l-i,k) \in B_1^0 \} \subseteq \mathcal {B}_1'$
and
$a_{k,l}^{(i)} \in \mathcal {B}_1'$
. This implies
$(i,l-i,k) \in B_1' \subseteq \overline {B_1^0} $
; therefore, there is
$(i_0, l_0 - i_0, k_0) \in B_1^0$
, where
$(i_0, l_0 - i_0, k_0) \leq (i, l - i, k)$
. By the previous lemma,
$a_{k_0,l_0}^{(i_0)} \leq a_{k,l}^{(i)}$
, where
$a_{k_0,l_0}^{(i_0)} \in \mathcal {B}_1^0$
. Thus,
$a_{k,l}^{(i)} \in \overline {\mathcal {B}_1^0}$
, and consequently
$\mathcal {B}_1^0 \subseteq \mathcal {B}_1' \subseteq \overline {\mathcal {B}_1^0}$
, where
$\mathcal {B}_1^0$
is a finite set. This shows
$(\mathcal {B}_1, \leq )$
satisfies f.b.p.
The proof for the set
$(\mathcal {B}_2, \leq )$
is analogous and we are done.▪
We already have the key ingredients to prove the main result of this section. We want to highlight that we are going to use the algorithm described in full details in the paper [Reference Centrone, Martino and Souza13].
Theorem 16 var
$^{H_m}(UT_2)$
has the Specht property.
Proof If
$I=\operatorname {\mathrm {Id}}^{H_m}(UT_2)$
, then Theorem 4 ensures us that I is finitely generated. So let us suppose
$I \supsetneq \operatorname {\mathrm {Id}}^{H_m}(UT_2) $
. Let M be the set of highest weight vectors corresponding to cocharacters appearing with nonzero multiplicities in
$\chi _n^{\mathbb {Z}_2, D_2} (UT_2) $
,
$n\geq 0$
; hence,
$F^{H_m}\langle X \rangle $
is generated by M modulo
$\operatorname {\mathrm {Id}}^{H_m}(UT_2)$
. Since
$F^{H_m}\langle X \rangle \supseteq I \supsetneq \operatorname {\mathrm {Id}}^{H_m}(UT_2)$
, there exists
$M' \subseteq M$
such that I is generated by
$M'$
modulo
$\operatorname {\mathrm {Id}}^{H_m}(UT_2)$
. We will show that
$(M, \leq )$
satisfies f.b.p., where
$\leq $
is the quasi-order given by the consequence, i.e.,
$f \leq g$
if and only if g is a consequence of f in
$F^{H_m}\langle X \rangle / \operatorname {\mathrm {Id}}^{H_m}(UT_2)$
.
A highest weight vector of degree n in M is a linear combination of
$H_m$
-polynomials of the form
$a_{k,l}^{(i)}$
,
$i = 0, \dots , l$
and
$k,l$
fixed such that
$2k +l+1=n$
, or
$H_m$
-polynomials of the form
$b_{k,l}^{(i)}$
,
$i = 0, \dots , l$
, and
$k,l$
fixed such that
$2k +l=n$
because they correspond to different modules. Thus,
$M = \mathcal {S}_1 \sqcup \mathcal {S}_2$
, where
$\mathcal {S}_1$
is the set of highest weight vectors associated to
$\mathcal {B}_1$
and
$\mathcal {S}_2$
is the set of highest weight vectors associated to
$\mathcal {B}_2$
. Then, by Theorem 12, it suffices to show that the sets
$\mathcal { S}_i$
satisfy f.b.p., where
$f \leq g $
if and only if g is a consequence of f, where
$f,g \in \mathcal {S}_i$
for
$i = 1,2$
.
Consider the set
$\mathcal {S}_1$
. A highest weight vector of degree n in
$\mathcal {S}_1$
is of the form
$\sum _{i=0}^{l} \alpha _i a_{k,l}^{(i)}$
. Define the leading term of this highest weight vector as the element
$a_{k,l}^{(i_0)}$
, where
$i_0 = $
min
$\{i \mid \alpha _i \neq 0\}$
. Notice that
$\mathcal {B}_1$
can be seen as the set of all the leading terms of the set
$\mathcal {S}$
, and, by Lemma 15,
$(\mathcal {B}_1, \leq )$
satisfies f.b.p. Hence,
$\mathcal {B}_1$
has a finite subset
$\mathcal {B}_1^0$
such that every element in
$\mathcal {B}_1$
is bigger than some element of
$\mathcal {B}_1^0$
. Let
$\mathcal {S}_1^0 \subseteq \mathcal {S}_1$
be the finite subset with leading terms in
$\mathcal {B}_1^0$
.
Let
$$ \begin{align*}h_1 = \sum_{i=0}^{l} \alpha_i a_{k,l}^{(i)} \in \mathcal{S}_1^0 \quad \text{ and } \quad h_2 = \sum_{j=0}^{l'} \beta_j a_{k',l'}^{(j)} \in \mathcal{S}_1\end{align*} $$
be two highest weight vectors with leading terms
$a_{k,l}^{(i_0)}, a_{k',l'}^{(j_0)}$
, respectively, and such that
$a_{k,l}^{(i_0)} \leq a_{k',l'}^{(j_0)}$
. Then,
$$ \begin{align*}a_{k',l'}^{(j_0)} \equiv y_1^{j_0 - i_0} \underbrace{\overline{y_1} \cdots \widetilde{y_1} }_{k'-k} a_{k,l}^{(i_0)} \underbrace{\overline{y_2} \cdots \widetilde{y_2} }_{k'-k} y_1^{l'-j_0-l+i_0} \quad (\textrm{mod }\operatorname{\mathrm{Id}}^{H_m}(UT_2)).\end{align*} $$
At light of this, we consider the highest weight vector
which is a consequence of
$h_1$
and its leading term is exactly
$a_{k' ,l' }^{ (j_0)}$
. Therefore, the leading term of
$$ \begin{align*}h_2 - \frac{\beta_{j_0}}{\alpha_{i_0}} h\end{align*} $$
is smaller than the leading term of
$h_2$
and by inductive arguments is a consequence of
$\mathcal {S}_1^0$
. This shows that
$\mathcal {S}_1$
satisfies f.b.p.
Similarly,
$\mathcal {S}_2$
satisfies f.b.p. too.
Finally, since I is generated by
$M'$
modulo
$\operatorname {\mathrm {Id}}^{H_m}(UT_2)$
and
$(M, \leq )$
satisfies f.b.p., then there exists a finite set
$M_0 \subseteq M' \subseteq M$
such that
$M_0 \subseteq M' \subseteq \overline {M_0}$
. By Remark 13,
$$ \begin{align*}I = \langle M' \rangle_{T^{H_m}} = \langle \overline{M_0} \rangle_{T^{H_m}} = \langle M_0 \rangle_{T^{H_m}},\end{align*} $$
and we are done.▪
6 Final remarks: Gelfand–Kirillov dimension and automata structure
In this section, we would like to add more details in the depicted description of the relatively free
$H_m$
-algebra of
$UT_2$
. We add some information regarding the asymptotic of its growth function and a note toward the regularity of the language it represents. For more details about the Gelfand–Kirillov dimension (GK dimension) of an algebra, we remand to the books [Reference Krause and Lenagan33] by Krause and Lenagan and [Reference McConnell and Robson34] by McConnell and Robson.
6.1 Gelfand–Kirillov dimension
In what follows, we shall introduce an H-module algebra version of the GK dimension of the relatively free H-module algebra. Let A be an finitely generated H-module algebra over F, where H is a finite dimensional Hopf algebra over F with F-basis
$\{b_1, \dots , b_m \}$
. We shall denote with the symbol
$F_k^H(A)$
the relatively free H-module algebra of A in k variables, that is,
$$ \begin{align*} F_k^H(A) := F^H \left \langle x_1, \dots , x_k \right \rangle / ( F^H \left \langle x_1, \dots , x_k \right \rangle \cap T^H(A)). \end{align*} $$
Recall that
$F^H \left \langle x_1, \dots , x_k \right \rangle $
is isomorphic to the free algebra over F with free formal generators
$x_i^{b_j}$
, where
$i \in \{1, \cdots , k \}$
and
$j \in \{1, \cdots , m \}$
. Thus,
$$ \begin{align*} F_k^H(A) = \frac{F^H \left \langle x_1^{b_1}, \dots , x_1^{b_m}, \dots , x_k^{b_1}, \dots , x_k^{b_m} \right \rangle}{ F^H \left \langle x_1^{b_1}, \dots , x_1^{b_m}, \dots , x_k^{b_1}, \dots , x_k^{b_m} \right \rangle \cap T^H(A)}. \end{align*} $$
Definition 17 (H-Gelfand–Kirillov dimension in k variables)
Let H be a finite dimensional Hopf algebra over a field F with F-basis
$\{b_1, \dots , b_m \}$
, and let A be a finitely generated H-module algebra over F. The H-Gelfand–Kirillov dimension of A in k variables is
In [Reference Belov4], the author studies several properties of
$\text {GKdim}_r(A)$
(that is, when H is the trivial Hopf algebra). In particular, it can be proved that
$\text {GKdim}_r(A)$
is defined by the complexity type of the algebra A or by a set of semidirect products of matrix algebras over the ring of polynomials from the variety generated by A. See also the paper [Reference Berele7] by Berele for explicit computations of the GK dimension of some remarkable PI-algebras, the paper [Reference Aljadeff and Kanel-Belov2] by Aljadeff and Kanel-Belov the papers [Reference Centrone8, Reference Centrone9] by Centrone, or the surveys [Reference Drensky17] by Drensky and [Reference Centrone10] by Centrone.
Here, we have the next result based on direct computations.
Theorem 18 Let
$m,k\geq 2$
integers, and let us consider
$H_m$
. Then,
$$\begin{align*}\mathrm{GKdim}_k^{H_m}(UT_2)=2k.\end{align*}$$
Proof From the results showed in Section 2.8, it turns out the monomials
$$\begin{align*}y_1^{a_1}\cdots y_k^{a_k}, y_1^{b_1}\cdots y_k^{b_k}y^dy_1^{c_1}\cdots y_k^{c_k},y_1^{b_1}\cdots y_k^{b_k}zy_1^{c_1}\cdots y_k^{c_k}\end{align*}$$
constitute a linear basis of
$F_k^{H_m}(UT_2)$
. Then the growth function of
$F_k^{H_m}(UT_2)$
, for sufficiently large n, is
$$\begin{align*}g_V(n):=2\binom{n-1+2k}{2k} +\binom{n+k}{k}+k+2,\end{align*}$$
which grows as a polynomial in n of degree
$2k$
, and we are done at light of the definition of GK dimension of an algebra.▪
Because the
$H_m$
-exponent of
$UT_2$
is 2, the previous result is an experimental confirmation of the following result obtained by one of the authors in [Reference Centrone11] in the environment of graded algebras.
Theorem 19 Let A be a finite dimensional G-graded algebra. Then,
$$\begin{align*}\mathrm{GKdim}_k^{G}(A)=\mathrm{exp}^G(A)k+\alpha,\end{align*}$$
where
$\alpha $
is integer and
$\mathrm {exp}^G(A)$
denotes the G-graded exponent of A.
We can formulate the next conjecture.
Conjecture 20 Let A be a finite dimensional
$H_m$
-module algebra. Then,
$$\begin{align*}\mathrm{GKdim}_k^{H_m}(A)=\mathrm{exp}^{H_m}(A)k+\alpha,\end{align*}$$
where
$\alpha $
is integer and
$\mathrm {exp}^{H_m}(A)$
denotes the
$H_m$
-exponent of A.
6.2 Automata algebras and regular languages
Given a (possibly infinite) set of variables X, we consider the set of monomials
$M(X)$
in the free algebra
$F\langle X\rangle $
. We define formal language any subset L of
$M(X)$
.
Definition 21 Given two languages
$L,L'\subseteq M(X)$
, we consider the set-theoretic union
$L\cup L'$
and the product
$L\cdot L'=\{w\cdot w'|w\in L,w'\in L'\}$
. Moreover, one defines the star operation
$L^*=\bigcup _{d\geq 0} L_d$
, where
$L_0 = \{1\}$
and
$L_d = LL_{d-1}$
, for any
$d \geq 1$
. The union, the product, and the star operation are called the regular operations over the languages. One also considers the set-theoretic intersection
$L\cap L'$
and the complement
$L^c = \{w\in M(X)| w \notin L\}$
.
A language is said to be regular if it can be generated by a regular grammar. We remand to the book of [Reference Eilenberg19] for a general overview toward grammars, languages, and formal computer science. Notice that regular languages can be obtained from finite languages by means of regular operations. We have the following, well-known, result due to Kleene (see [Reference Kleene32]).
Theorem 22 A language
$L\subseteq M(X)$
is regular if and only if it can be obtained from finite languages by applying a finite number of regular operations.
We recall that a monomial algebra over a field F is an algebra that is isomorphic to
$F\langle X\rangle /I$
, where I is generated by elements of
$M(X)$
. Moreover, a monomial algebra is said to be automata if I is a regular language. We advise the reader to read the book by [Reference Belov, Borisenko and Latyshev5] for a compendium about monomial algebras. With a slight modification of the original definition of automata algebra, we have the notion of automata algebra on relatively free algebra.
Definition 23 Let A be a PI-algebra, and let
$R_A:=F\langle X\rangle /I$
be its relatively free algebra, where
$I=T(A)$
. We say
$R_A$
is automata if
$\hat {I}$
is a regular language, where
$\hat {I}$
denotes the ideal of leading terms of I.
Of course, the previous definition can be adapted trivially to graded algebras, module algebras, and so on. It is also convenient to recall a sort of duality between regularity of a monomial ideal and regularity of its quotient algebra.
Proposition 24 Let I be a monomial ideal of
$F\langle X\rangle $
, and let
$\mathcal {B}$
be a basis of
$F\langle X\rangle /I$
as a vector space. Then I is regular if and only if
$\mathcal {B}$
is regular.
By the proof of Theorem 18, we get a basis of the relatively free
$H_m$
-algebra of
$UT_2$
in k variables is monomial and can be written in terms of regular operation as
$$\begin{align*}\{y_1\}^*\cdots \{y_k\}^*\cup\{y_1\}^*\cdots \{y_k\}^*\{y^d\}\{y_1\}^*\cdots \{y_k\}^*\cup\{y_1\}^*\cdots \{y_k\}^*\{z\}\{y_1\}^*\cdots \{y_k\}^*,\end{align*}$$
i.e., in the light of Proposition 24 and Theorem 22,
$\hat {I}$
is regular. This is the content of the following.
Theorem 25 Let
$k\geq 2$
be an integer. Then the relatively free
$H_m$
-algebra of
$UT_2$
in k variables is an automata algebra.
