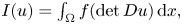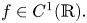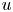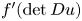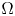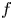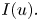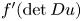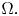1. Introduction
Let $n\ge 2$![]() be an integer. We denote by $\mathbb {M}^{n\times n}$
be an integer. We denote by $\mathbb {M}^{n\times n}$![]() the standard space of real $n\times n$
the standard space of real $n\times n$![]() matrices with inner product
matrices with inner product

Also denote by $A^T$![]() , $\det A$
, $\det A$![]() and $\operatorname {cof} A$
and $\operatorname {cof} A$![]() the transpose, determinant, and the cofactor matrix of $A\in \mathbb {M}^{n\times n},$
the transpose, determinant, and the cofactor matrix of $A\in \mathbb {M}^{n\times n},$![]() respectively, so that the identity $A^T\operatorname {cof} A=(\operatorname {cof} A)A^T=(\det A)I$
respectively, so that the identity $A^T\operatorname {cof} A=(\operatorname {cof} A)A^T=(\det A)I$![]() holds for all $A\in \mathbb {M}^{n\times n}.$
holds for all $A\in \mathbb {M}^{n\times n}.$![]()
Let $f\colon \mathbb {R}\to \mathbb {R}$![]() be a $C^1$
be a $C^1$![]() function; i.e., $f\in C^1(\mathbb {R}),$
function; i.e., $f\in C^1(\mathbb {R}),$![]() and $\Omega$
and $\Omega$![]() be a bounded domain in $\mathbb {R}^n.$
be a bounded domain in $\mathbb {R}^n.$![]() We study the special energy functional
We study the special energy functional
for functions $u\colon \Omega \to \mathbb {R}^n,$![]() where $Du$
where $Du$![]() is the Jacobian matrix of $u$
is the Jacobian matrix of $u$![]() ; that is, $(Du)^i_j=\partial u^i/\partial x_j$
; that is, $(Du)^i_j=\partial u^i/\partial x_j$![]() if $u =(u^1,\, \dots,\,u^n)$
if $u =(u^1,\, \dots,\,u^n)$![]() and $x=(x_1,\, \dots,\,x_n)\in \Omega.$
and $x=(x_1,\, \dots,\,x_n)\in \Omega.$![]() Such a functional $I_\Omega$
Such a functional $I_\Omega$![]() and its Euler–Lagrange equations have been studied in [Reference Dacorogna3, Reference Evans, Savin and Gangbo5, Reference Kirchheim, Müller and Šverák8, Reference Taheri17] concerning the energy minimizers, weak solutions and the gradient flows. Our motivation to further study the functional $I_\Omega$
and its Euler–Lagrange equations have been studied in [Reference Dacorogna3, Reference Evans, Savin and Gangbo5, Reference Kirchheim, Müller and Šverák8, Reference Taheri17] concerning the energy minimizers, weak solutions and the gradient flows. Our motivation to further study the functional $I_\Omega$![]() is closely related to the counterexamples on existence and regularity given in [Reference Müller and Šverák13, Reference Székelyhidi16, Reference Yan20]. From the identity
is closely related to the counterexamples on existence and regularity given in [Reference Müller and Šverák13, Reference Székelyhidi16, Reference Yan20]. From the identity
it follows that the Euler–Lagrange equation of $I_\Omega$![]() is given by
is given by
By a weak solution of equation (1.2) we mean a function $u\in W^{1,1}_{loc}(\Omega ;\mathbb {R}^n)$![]() such that $f'(\det Du)\operatorname {cof} Du\in L^1_{loc}(\Omega ;\mathbb {M}^{n\times n})$
such that $f'(\det Du)\operatorname {cof} Du\in L^1_{loc}(\Omega ;\mathbb {M}^{n\times n})$![]() and
and
This is a very weak sense of solutions. Usually, under suitable growth conditions on $f,$![]() the weak solutions are studied in the space $u\in W^{1,p}_{loc}(\Omega ;\mathbb {R}^n)$
the weak solutions are studied in the space $u\in W^{1,p}_{loc}(\Omega ;\mathbb {R}^n)$![]() for some $1\le p\le \infty$
for some $1\le p\le \infty$![]() with $f'(\det Du)\operatorname {cof} Du\in L^{p'}_{loc}(\Omega ;\mathbb {M}^{n\times n})$
with $f'(\det Du)\operatorname {cof} Du\in L^{p'}_{loc}(\Omega ;\mathbb {M}^{n\times n})$![]() , where $p'= {p}/{(p-1)}$
, where $p'= {p}/{(p-1)}$![]() is the Hölder conjugate of $p.$
is the Hölder conjugate of $p.$![]() However, in this paper, we will not specify the growth conditions on $f,$
However, in this paper, we will not specify the growth conditions on $f,$![]() but may assume some higher integrability of $f'(\det Du)\operatorname {cof} Du.$
but may assume some higher integrability of $f'(\det Du)\operatorname {cof} Du.$![]() For example, if a weak solution $u$
For example, if a weak solution $u$![]() satisfies, in addition, $f'(\det Du)\operatorname {cof} Du\in L^q(\Omega ;\mathbb {M}^{n\times n})$
satisfies, in addition, $f'(\det Du)\operatorname {cof} Du\in L^q(\Omega ;\mathbb {M}^{n\times n})$![]() for some $q\ge 1$
for some $q\ge 1$![]() , then (1.3) holds for all $\zeta \in W^{1,q'}_0(\Omega ;\mathbb {R}^n).$
, then (1.3) holds for all $\zeta \in W^{1,q'}_0(\Omega ;\mathbb {R}^n).$![]()
It is well-known that $\operatorname {div}(\operatorname {cof} Du)=0$![]() for all $u\in C^2(\Omega ;\mathbb {R}^n)$
for all $u\in C^2(\Omega ;\mathbb {R}^n)$![]() and thus by approximation it holds that
and thus by approximation it holds that
Consequently, any functions $u\in W^{1,n-1}_{loc}(\Omega ;\mathbb {R}^n)$![]() with $f'(\det Du)$
with $f'(\det Du)$![]() being constant almost everywhere on $\Omega$
being constant almost everywhere on $\Omega$![]() are automatically a weak solution of equation (1.2); however, the converse is false, at least when $n=2$
are automatically a weak solution of equation (1.2); however, the converse is false, at least when $n=2$![]() (see example 3.4). Some formal calculations based on the identity $\operatorname {div}(\operatorname {cof} Du)=0$
(see example 3.4). Some formal calculations based on the identity $\operatorname {div}(\operatorname {cof} Du)=0$![]() show that $f'(\det Du)$
show that $f'(\det Du)$![]() must be constant on $\Omega$
must be constant on $\Omega$![]() if $u\in C^2(\Omega ;\mathbb {R}^n)$
if $u\in C^2(\Omega ;\mathbb {R}^n)$![]() is a classical solution of (1.2) (see [Reference Evans, Savin and Gangbo5, Reference Taheri17]). We prove that the same result holds for all weak solutions $u\in C^1(\Omega ;\mathbb {R}^n)$
is a classical solution of (1.2) (see [Reference Evans, Savin and Gangbo5, Reference Taheri17]). We prove that the same result holds for all weak solutions $u\in C^1(\Omega ;\mathbb {R}^n)$![]() (see also [Reference Kirchheim, Müller and Šverák8]) or $u\in W^{1,p}_{loc}(\Omega ;\mathbb {R}^n)$
(see also [Reference Kirchheim, Müller and Šverák8]) or $u\in W^{1,p}_{loc}(\Omega ;\mathbb {R}^n)$![]() with $f'(\det Du)\in W_{loc}^{1,\bar p}(\Omega )$
with $f'(\det Du)\in W_{loc}^{1,\bar p}(\Omega )$![]() for some $p\ge n-1$
for some $p\ge n-1$![]() and $\bar p=p/(p+1-n).$
and $\bar p=p/(p+1-n).$![]() If, in addition, $f$
If, in addition, $f$![]() is convex, then all weak solutions $u\in W^{1,n}_{loc}(\Omega ;\mathbb {R}^n)$
is convex, then all weak solutions $u\in W^{1,n}_{loc}(\Omega ;\mathbb {R}^n)$![]() of (1.2) with $f'(\det Du)$
of (1.2) with $f'(\det Du)$![]() being constant almost everywhere on $\Omega$
being constant almost everywhere on $\Omega$![]() must be an energy minimizer of the energy $I_G$
must be an energy minimizer of the energy $I_G$![]() among all $W^{1,n}(G;\mathbb {R}^n)$
among all $W^{1,n}(G;\mathbb {R}^n)$![]() functions having the same boundary value as $u$
functions having the same boundary value as $u$![]() on $\partial G$
on $\partial G$![]() for all subdomains $G$
for all subdomains $G$![]() of $\Omega.$
of $\Omega.$![]()
We study further conditions under which a weak solution $u$![]() of (1.2) must have constant $f'(\det Du)$
of (1.2) must have constant $f'(\det Du)$![]() almost everywhere on $\Omega.$
almost everywhere on $\Omega.$![]() In addition, we prove that $f'(\det Du)$
In addition, we prove that $f'(\det Du)$![]() must be constant in the case of homeomorphism weak solutions $u\in W^{1,p}(\Omega ;\mathbb {R}^n)$
must be constant in the case of homeomorphism weak solutions $u\in W^{1,p}(\Omega ;\mathbb {R}^n)$![]() for $p>n$
for $p>n$![]() (see theorem 2.8). When the domain $\Omega$
(see theorem 2.8). When the domain $\Omega$![]() is a ball, we study the radially symmetric weak solutions and establish a specific characterization about certain weak solutions (see § 3). Finally, in the 2-Dimensional cases, equation (1.2) is reformulated as a first-order partial differential relation [Reference Kirchheim, Müller and Šverák8, Reference Müller and Šverák13] and we prove some stability results for certain approximate solutions of this relation (see § 4).
is a ball, we study the radially symmetric weak solutions and establish a specific characterization about certain weak solutions (see § 3). Finally, in the 2-Dimensional cases, equation (1.2) is reformulated as a first-order partial differential relation [Reference Kirchheim, Müller and Šverák8, Reference Müller and Šverák13] and we prove some stability results for certain approximate solutions of this relation (see § 4).
2. Some general results for all dimensions
In what follows, unless otherwise specified, we assume $h\in C(\mathbb {R})$![]() is a given function. Recall that $u\in W^{1,1}_{loc}(\Omega ;\mathbb {R}^n)$
is a given function. Recall that $u\in W^{1,1}_{loc}(\Omega ;\mathbb {R}^n)$![]() is a weak solution of equation
is a weak solution of equation
provided that $h(\det Du)\operatorname {cof} Du\in L^1_{loc}(\Omega ;\mathbb {M}^{n\times n})$![]() and
and
If, in addition, $h(\det Du)\operatorname {cof} Du\in L_{loc}^q(\Omega ;\mathbb {M}^{n\times n})$![]() for some $q\ge 1,$
for some $q\ge 1,$![]() then equation (2.2) holds for all $\zeta \in W^{1,q'}(\Omega ;\mathbb {R}^n)$
then equation (2.2) holds for all $\zeta \in W^{1,q'}(\Omega ;\mathbb {R}^n)$![]() with compact support in $\Omega,$
with compact support in $\Omega,$![]() where $q'={q}/({q-1}).$
where $q'={q}/({q-1}).$![]() Since equation (2.1) and the related energy functional highly lack the ellipticity and coercivity, there is no feasible theory of existence and regularity for (2.1)
Since equation (2.1) and the related energy functional highly lack the ellipticity and coercivity, there is no feasible theory of existence and regularity for (2.1)
2.1. Formal calculations and some implications
It is well-known that $\operatorname {div}(\operatorname {cof} Dw)=0$![]() holds in $\Omega$
holds in $\Omega$![]() for all $w\in C^2(\Omega ;\mathbb {R}^n).$
for all $w\in C^2(\Omega ;\mathbb {R}^n).$![]() From this, we easily have the following point-wise identity:
From this, we easily have the following point-wise identity:
Thus, for all $a\in C^1(\Omega ),\,\;w\in C^2(\Omega ;\mathbb {R}^n)$![]() and $\zeta \in C^1_c(\Omega ;\mathbb {R}^n),$
and $\zeta \in C^1_c(\Omega ;\mathbb {R}^n),$![]() it follows that
it follows that
Lemma 2.1 Identity (2.3) holds for all functions
where $n-1\le p\le \infty$![]() and $\bar p={p}/({p+1-n})$
and $\bar p={p}/({p+1-n})$![]() are given numbers.
are given numbers.
Proof. Note that if $w\in W^{1, p}_{loc}(\Omega ;\mathbb {R}^n)$![]() then $\operatorname {cof} Dw\in L^{{p}/({n-1})}_{loc}(\Omega ;\mathbb {M}^{n\times n}).$
then $\operatorname {cof} Dw\in L^{{p}/({n-1})}_{loc}(\Omega ;\mathbb {M}^{n\times n}).$![]() Since $\bar p$
Since $\bar p$![]() and ${p}/({n-1})$
and ${p}/({n-1})$![]() are Hölder conjugate numbers, it follows, by the standard approximation arguments, that identity (2.3) holds for the given functions.
are Hölder conjugate numbers, it follows, by the standard approximation arguments, that identity (2.3) holds for the given functions.
Lemma 2.2 Let $H(t)=th(t)-\int _0^t h(s)\,{\rm d}s.$![]() Then
Then
holds for all $w\in C^2(\Omega ;\mathbb {R}^n)$![]() and $\phi \in C_c^1(\Omega ;\mathbb {R}^n).$
and $\phi \in C_c^1(\Omega ;\mathbb {R}^n).$![]()
Proof. First we assume $h\in C^1(\mathbb {R})$![]() and let $a (x)=h(\det Dw(x)).$
and let $a (x)=h(\det Dw(x)).$![]() Then $a\in C^1(\Omega )$
Then $a\in C^1(\Omega )$![]() and $Da=h'(\det Dw ) D(\det Dw ).$
and $Da=h'(\det Dw ) D(\det Dw ).$![]() Take $\zeta =(Dw)\phi \in C_c^1(\Omega ;\mathbb {R}^n)$
Take $\zeta =(Dw)\phi \in C_c^1(\Omega ;\mathbb {R}^n)$![]() in (2.3) and, from $Dw^T \operatorname {cof} Dw=(\det Dw)I$
in (2.3) and, from $Dw^T \operatorname {cof} Dw=(\det Dw)I$![]() and $H'(t)=th'(t),$
and $H'(t)=th'(t),$![]() we have
we have

This proves identity (2.4) for $h\in C^1(\mathbb {R}).$![]() The proof of (2.4) for $h\in C(\mathbb {R})$
The proof of (2.4) for $h\in C(\mathbb {R})$![]() follows by approximating $h$
follows by approximating $h$![]() by $C^1$
by $C^1$![]() functions.
functions.
Proposition 2.3 Let $u\in C^2(\Omega ;\mathbb {R}^n)$![]() be a weak solution of (2.1). Then $h(\det Du)$
be a weak solution of (2.1). Then $h(\det Du)$![]() is constant on $\Omega.$
is constant on $\Omega.$![]()
Proof. Let $d(x)=\det Du(x);$![]() then $d\in C^1(\Omega ).$
then $d\in C^1(\Omega ).$![]() By (2.2) and (2.4), it follows that $\int _\Omega H(d(x))\operatorname {div}\phi \,{\rm d}x=0$
By (2.2) and (2.4), it follows that $\int _\Omega H(d(x))\operatorname {div}\phi \,{\rm d}x=0$![]() for all $\phi \in C_c^1(\Omega ;\mathbb {R}^n);$
for all $\phi \in C_c^1(\Omega ;\mathbb {R}^n);$![]() hence $H(d(x))=C$
hence $H(d(x))=C$![]() is a constant on $\Omega.$
is a constant on $\Omega.$![]() Suppose, on the contrary, that $h(d(x_1))\ne h(d(x_2))$
Suppose, on the contrary, that $h(d(x_1))\ne h(d(x_2))$![]() for some $x_1,\,x_2\in \Omega.$
for some $x_1,\,x_2\in \Omega.$![]() Then $d_1=d(x_1)\ne d_2=d(x_2),$
Then $d_1=d(x_1)\ne d_2=d(x_2),$![]() say $d_1< d_2.$
say $d_1< d_2.$![]() Since $d(x)$
Since $d(x)$![]() is continuous, by the intermediate value theorem, it follows that $H(t)=C$
is continuous, by the intermediate value theorem, it follows that $H(t)=C$![]() for all $t\in [d_1,\,d_2].$
for all $t\in [d_1,\,d_2].$![]() Solving for $h(t)$
Solving for $h(t)$![]() from the integral equation $th(t)-\int _0^t h(s)\,{\rm d}s=C$
from the integral equation $th(t)-\int _0^t h(s)\,{\rm d}s=C$![]() on $(d_1,\,d_2)$
on $(d_1,\,d_2)$![]() , we obtain that $h(t)$
, we obtain that $h(t)$![]() is constant on $(d_1,\,d_2),$
is constant on $(d_1,\,d_2),$![]() contradicting $h(d_1)\ne h(d_2).$
contradicting $h(d_1)\ne h(d_2).$![]()
Proposition 2.4 Let $p\ge n-1$![]() , $\bar p={p}/({p+1-n}),$
, $\bar p={p}/({p+1-n}),$![]() and $u\in W^{1, p}_{loc}(\Omega ;\mathbb {R}^n)$
and $u\in W^{1, p}_{loc}(\Omega ;\mathbb {R}^n)$![]() be a weak solution of (2.1) such that $h(\det Du)\in W^{1,\bar p}_{loc}(\Omega ).$
be a weak solution of (2.1) such that $h(\det Du)\in W^{1,\bar p}_{loc}(\Omega ).$![]() Then $h(\det Du)$
Then $h(\det Du)$![]() is constant almost everywhere on $\Omega.$
is constant almost everywhere on $\Omega.$![]()
Proof. With $a=h(\det Du)\in W^{1,\bar p}_{loc}(\Omega )$![]() and $w=u\in W^{1, p}_{loc}(\Omega ;\mathbb {R}^n)$
and $w=u\in W^{1, p}_{loc}(\Omega ;\mathbb {R}^n)$![]() in lemma 2.1 and by (2.2), we have
in lemma 2.1 and by (2.2), we have
for all $\zeta \in C_c^1(\Omega ;\mathbb {R}^n).$![]() As a result, we have $(\operatorname {cof} Du)D(h(\det Du ))=0$
As a result, we have $(\operatorname {cof} Du)D(h(\det Du ))=0$![]() a.e. on $\Omega.$
a.e. on $\Omega.$![]() Thus $D(h(\det Du ))=0$
Thus $D(h(\det Du ))=0$![]() a.e. on the set $\Omega _0=\{x\in \Omega :\det Du(x)\ne 0\}.$
a.e. on the set $\Omega _0=\{x\in \Omega :\det Du(x)\ne 0\}.$![]() Clearly, $D(h(\det Du ))=0$
Clearly, $D(h(\det Du ))=0$![]() a.e. on the set $E=\{x\in \Omega :\det Du(x) = 0\}$
a.e. on the set $E=\{x\in \Omega :\det Du(x) = 0\}$![]() because $h(\det Du)=h(0)$
because $h(\det Du)=h(0)$![]() a.e. on $E.$
a.e. on $E.$![]() Therefore, $D(h(\det Du ))=0$
Therefore, $D(h(\det Du ))=0$![]() a.e. on the whole domain $\Omega ;$
a.e. on the whole domain $\Omega ;$![]() this proves that $h(\det Du)$
this proves that $h(\det Du)$![]() is constant a.e. on $\Omega.$
is constant a.e. on $\Omega.$![]()
2.2. The change of variables
The formal calculations leading to proposition 2.3 do not work for the $C^1$![]() weak solutions of equation (2.1); however, the same conclusion still holds, as has been discussed in [Reference Kirchheim, Müller and Šverák8] without proof. We give a proof by choosing suitable test functions based on change of variables.
weak solutions of equation (2.1); however, the same conclusion still holds, as has been discussed in [Reference Kirchheim, Müller and Šverák8] without proof. We give a proof by choosing suitable test functions based on change of variables.
Let us first recall the change of variables for general Sobolev functions; see, e.g., [Reference Marcus and Mizel14]. Let $p>n$![]() and $w\in W^{1,p}(\Omega ;\mathbb {R}^n);$
and $w\in W^{1,p}(\Omega ;\mathbb {R}^n);$![]() then $w\in C_{loc}^\alpha (\Omega ;\mathbb {R}^n)$
then $w\in C_{loc}^\alpha (\Omega ;\mathbb {R}^n)$![]() with $\alpha =1-({n}/{p}).$
with $\alpha =1-({n}/{p}).$![]() Let $E$
Let $E$![]() be a measurable subset of $\Omega.$
be a measurable subset of $\Omega.$![]() Denote by $N(w|E;y)$
Denote by $N(w|E;y)$![]() the cardinality of the set $\{x\in E: w(x)=y\}.$
the cardinality of the set $\{x\in E: w(x)=y\}.$![]() Then, for all measurable functions $g\colon w(\Omega )\to \mathbb {R},$
Then, for all measurable functions $g\colon w(\Omega )\to \mathbb {R},$![]() the change of variable formula:
the change of variable formula:
is valid, whenever one of the two sides is meaningful (see [Reference Marcus and Mizel14, Theorem 2]).
Theorem 2.5 Let $u\in C^1(\Omega ;\mathbb {R}^2)$![]() be a weak solution of equation (2.1). Then $h(\det Du)$
be a weak solution of equation (2.1). Then $h(\det Du)$![]() is constant on $\Omega.$
is constant on $\Omega.$![]()
Proof. Let $E=\{x\in \Omega :\det Du(x)=0\},$![]() which is relatively closed in $\Omega.$
which is relatively closed in $\Omega.$![]() There is nothing to prove if $E=\Omega ;$
There is nothing to prove if $E=\Omega ;$![]() thus we assume $\Omega _0=\Omega \setminus E\ne \emptyset.$
thus we assume $\Omega _0=\Omega \setminus E\ne \emptyset.$![]() Let $C$
Let $C$![]() be a component of the open set $\Omega _0.$
be a component of the open set $\Omega _0.$![]() Without loss of generality, we assume $\det Du>0$
Without loss of generality, we assume $\det Du>0$![]() on $C.$
on $C.$![]() Let $x_0\in C$
Let $x_0\in C$![]() and $y_0=u(x_0).$
and $y_0=u(x_0).$![]() Since $y_0$
Since $y_0$![]() is a regular value of $u$
is a regular value of $u$![]() , by the inverse function theorem, there exists an open disc $D=B_\epsilon (y_0)$
, by the inverse function theorem, there exists an open disc $D=B_\epsilon (y_0)$![]() such that
such that

Given any $\phi \in C^1_c(D;\mathbb {R}^n),$![]() the function $\zeta (x)=\phi (u(x))\in C^1_c(U;\mathbb {R}^n)$
the function $\zeta (x)=\phi (u(x))\in C^1_c(U;\mathbb {R}^n)$![]() is a test function for (2.2) with $D\zeta (x)=D\phi (u(x))Du(x);$
is a test function for (2.2) with $D\zeta (x)=D\phi (u(x))Du(x);$![]() thus, by the change of variables, we obtain that
thus, by the change of variables, we obtain that

This holding for all $\phi \in C^1_c(D;\mathbb {R}^n)$![]() proves that $h(\det Du(v(y))$
proves that $h(\det Du(v(y))$![]() is constant on $D;$
is constant on $D;$![]() hence $h(\det Du)$
hence $h(\det Du)$![]() is constant on $U.$
is constant on $U.$![]() Since $C$
Since $C$![]() is connected and $h$
is connected and $h$![]() is continuous, it follows that $h(\det Du)$
is continuous, it follows that $h(\det Du)$![]() is constant on the relative closure $\bar C$
is constant on the relative closure $\bar C$![]() of $C$
of $C$![]() in $\Omega.$
in $\Omega.$![]() If $E=\emptyset,$
If $E=\emptyset,$![]() we have $C=\Omega ;$
we have $C=\Omega ;$![]() hence, $h(\det Du)$
hence, $h(\det Du)$![]() is constant on $\Omega.$
is constant on $\Omega.$![]() If $E\ne \emptyset,$
If $E\ne \emptyset,$![]() we have $\bar C\cap E\ne \emptyset$
we have $\bar C\cap E\ne \emptyset$![]() and thus $h(\det Du)=h(0)$
and thus $h(\det Du)=h(0)$![]() on $\bar C,$
on $\bar C,$![]() which proves that $h(\det Du) =h(0)$
which proves that $h(\det Du) =h(0)$![]() on $\Omega _0;$
on $\Omega _0;$![]() hence $h(\det Du) =h(0)$
hence $h(\det Du) =h(0)$![]() on the whole $\Omega.$
on the whole $\Omega.$![]()
Corollary 2.6 Let $u$![]() be a weak solution of equation (2.1). Then $\det Du$
be a weak solution of equation (2.1). Then $\det Du$![]() is constant almost everywhere on $\Omega$
is constant almost everywhere on $\Omega$![]() if one of the following assumptions holds:
if one of the following assumptions holds:
(a) $u \in C^1(\Omega ;\mathbb {R}^n)$
 and $h$
and $h$ is not constant on any intervals.
is not constant on any intervals.(b) $u\in W^{1,p}_{loc}(\Omega ;\mathbb {R}^n)$
 , $h(\det Du)\in W^{1,\bar p}_{loc}(\Omega )$
, $h(\det Du)\in W^{1,\bar p}_{loc}(\Omega )$ , where $n-1\le p\le \infty$
, where $n-1\le p\le \infty$ and $\bar p={p}/({p+1-n})$
and $\bar p={p}/({p+1-n})$ are given numbers, and $h$
are given numbers, and $h$ is one-to-one.
is one-to-one.
Proof. Assuming (a), by theorem 2.5, we have that $h(\det Du)=c$![]() is constant in $\Omega$
is constant in $\Omega$![]() and thus $\det Du(x)\in h^{-1}(c).$
and thus $\det Du(x)\in h^{-1}(c).$![]() Since $\Omega$
Since $\Omega$![]() is connected, $\det Du$
is connected, $\det Du$![]() is continuous in $\Omega$
is continuous in $\Omega$![]() and $h^{-1}(c)$
and $h^{-1}(c)$![]() contains no intervals, it follows that $\det Du$
contains no intervals, it follows that $\det Du$![]() is constant in $\Omega.$
is constant in $\Omega.$![]() Assuming (b), by proposition 2.4, we have that $h(\det Du)$
Assuming (b), by proposition 2.4, we have that $h(\det Du)$![]() is constant a.e. on $\Omega.$
is constant a.e. on $\Omega.$![]() Since $h$
Since $h$![]() is one-to-one, it follows that $\det Du$
is one-to-one, it follows that $\det Du$![]() is constant a.e. on $\Omega.$
is constant a.e. on $\Omega.$![]()
The following result applies to the weak solutions $u$![]() of (2.1) such that $u\in C^1(\Omega ;\mathbb {R}^n)$
of (2.1) such that $u\in C^1(\Omega ;\mathbb {R}^n)$![]() or $u\in W^{1,p}_{loc}(\Omega ;\mathbb {R}^n)$
or $u\in W^{1,p}_{loc}(\Omega ;\mathbb {R}^n)$![]() with $h(\det Du)\in W^{1,\bar p}_{loc}(\Omega )$
with $h(\det Du)\in W^{1,\bar p}_{loc}(\Omega )$![]() for some $p\ge n$
for some $p\ge n$![]() and $\bar p={p}/({p+1-n}).$
and $\bar p={p}/({p+1-n}).$![]()
Proposition 2.7 Assume $h$![]() is nondecreasing and let $f(t)=\int _0^t h(s)\,{\rm d}s.$
is nondecreasing and let $f(t)=\int _0^t h(s)\,{\rm d}s.$![]() Suppose that $u\in W^{1,n}_{loc}(\Omega ;\mathbb {R}^n)$
Suppose that $u\in W^{1,n}_{loc}(\Omega ;\mathbb {R}^n)$![]() is a weak solution of (2.1) such that $h(\det Du)$
is a weak solution of (2.1) such that $h(\det Du)$![]() is constant a.e. on $\Omega.$
is constant a.e. on $\Omega.$![]() Then for all subdomains $G\subset \subset \Omega,$
Then for all subdomains $G\subset \subset \Omega,$![]() the inequality
the inequality
holds for all $v\in W^{1,n}(G;\mathbb {R}^n)$![]() satisfying $v-u\in W^{1,n}_0(G;\mathbb {R}^n).$
satisfying $v-u\in W^{1,n}_0(G;\mathbb {R}^n).$![]()
Proof. Let $h(\det Du)=\mu$![]() be a constant a.e. on $\Omega.$
be a constant a.e. on $\Omega.$![]() Since $f'=h$
Since $f'=h$![]() is nondecreasing, it follows that $f$
is nondecreasing, it follows that $f$![]() is convex and thus $f(t)\ge f(t_0)+h(t_0)(t-t_0)$
is convex and thus $f(t)\ge f(t_0)+h(t_0)(t-t_0)$![]() for all $t,\, t_0\in \mathbb {R}.$
for all $t,\, t_0\in \mathbb {R}.$![]() Let $v\in W^{1,n}(G;\mathbb {R}^n)$
Let $v\in W^{1,n}(G;\mathbb {R}^n)$![]() satisfy $v-u\in W^{1,n}_0(G;\mathbb {R}^n).$
satisfy $v-u\in W^{1,n}_0(G;\mathbb {R}^n).$![]() Then
Then
Integrating over $G,$![]() since $\int _G \det Dv=\int _G \det Du$
since $\int _G \det Dv=\int _G \det Du$![]() , we have
, we have
2.3. Weak solutions in $W^{1,p}(\Omega ;\mathbb {R}^n)$ for $p\ge n$
for $p\ge n$
It remains open that whether weak solutions $u\in W^{1,n}_{loc}(\Omega ;\mathbb {R}^n)$![]() of equation (2.1) must have a constant $h(\det Du)$
of equation (2.1) must have a constant $h(\det Du)$![]() a.e. on $\Omega$
a.e. on $\Omega$![]() without assuming $h(\det Du)\in W^{1,1}_{loc}(\Omega ).$
without assuming $h(\det Du)\in W^{1,1}_{loc}(\Omega ).$![]() In fact, despite the example of very weak solutions in example 3.4, we do not know whether a weak solution $u\in W^{1,n}_{loc}(\Omega ;\mathbb {R}^n)$
In fact, despite the example of very weak solutions in example 3.4, we do not know whether a weak solution $u\in W^{1,n}_{loc}(\Omega ;\mathbb {R}^n)$![]() of (2.1) satisfying $h(\det Du)\in L^q_{loc}(\Omega )$
of (2.1) satisfying $h(\det Du)\in L^q_{loc}(\Omega )$![]() for some $q>1$
for some $q>1$![]() will have a constant $h(\det Du)$
will have a constant $h(\det Du)$![]() a.e. on $\Omega.$
a.e. on $\Omega.$![]()
However, we have some partial results. The following result concerns certain homeomorphism weak solutions of equation (2.1).
Theorem 2.8 Assume $h$![]() is nondecreasing. Let $p>n$
is nondecreasing. Let $p>n$![]() , $\tilde p={p}/({p-n}),$
, $\tilde p={p}/({p-n}),$![]() and let $u\in W^{1,p}(\Omega ;\mathbb {R}^n)$
and let $u\in W^{1,p}(\Omega ;\mathbb {R}^n)$![]() be a weak solution of (2.1) with $h(\det Du)\in L^{\tilde p}(\Omega )$
be a weak solution of (2.1) with $h(\det Du)\in L^{\tilde p}(\Omega )$![]() such that
such that

Then $h(\det Du)$![]() is a constant a.e. on $\Omega.$
is a constant a.e. on $\Omega.$![]()
Proof. Recall that $\operatorname {div}(\operatorname {cof} (Du))=0.$![]() Without loss of generality, we assume ${h(0)=0};$
Without loss of generality, we assume ${h(0)=0};$![]() thus $h(t)t=|h(t)t|\ge 0$
thus $h(t)t=|h(t)t|\ge 0$![]() for all $t\in \mathbb {R}.$
for all $t\in \mathbb {R}.$![]() From the assumption, we have
From the assumption, we have
Let $\phi \in C^1_c(u(\Omega );\mathbb {R}^n).$![]() Then $\zeta (x)=\phi (u(x))\in W^{1,p}_0(\Omega ;\mathbb {R}^n)$
Then $\zeta (x)=\phi (u(x))\in W^{1,p}_0(\Omega ;\mathbb {R}^n)$![]() is a legitimate test function for (2.2). Since $u$
is a legitimate test function for (2.2). Since $u$![]() is one-to-one on $\Omega,$
is one-to-one on $\Omega,$![]() we have $N(u|\Omega ;y) =1$
we have $N(u|\Omega ;y) =1$![]() for all $y\in u(\Omega );$
for all $y\in u(\Omega );$![]() thus, by the change of variable formula (2.5), we obtain
thus, by the change of variable formula (2.5), we obtain

This holding for all $\phi \in C^1_c(u(\Omega );\mathbb {R}^n)$![]() proves that $|h(\det Du(v(y))|$
proves that $|h(\det Du(v(y))|$![]() is constant a.e. on $u(\Omega );$
is constant a.e. on $u(\Omega );$![]() hence $|h(\det Du)|=\lambda$
hence $|h(\det Du)|=\lambda$![]() is a constant a.e. on $\Omega.$
is a constant a.e. on $\Omega.$![]() If $\lambda =0$
If $\lambda =0$![]() then $h(\det Du)=0$
then $h(\det Du)=0$![]() a.e. on $\Omega.$
a.e. on $\Omega.$![]() We now assume $\lambda >0.$
We now assume $\lambda >0.$![]() Let
Let
Then $|\Omega _+|+|\Omega _-|=|\Omega |.$![]() Since $\lambda >0$
Since $\lambda >0$![]() and $h$
and $h$![]() is nondecreasing, we have $\det Du\ge 0$
is nondecreasing, we have $\det Du\ge 0$![]() a.e. on $\Omega _+$
a.e. on $\Omega _+$![]() and $\det Du\le 0$
and $\det Du\le 0$![]() a.e. on $\Omega _-.$
a.e. on $\Omega _-.$![]() We claim that either $|\Omega _+|=0$
We claim that either $|\Omega _+|=0$![]() or $|\Omega _+|=|\Omega |,$
or $|\Omega _+|=|\Omega |,$![]() which proves the theorem. To prove the claim, we observe that, for all $\zeta \in C^1_c(\Omega ;\mathbb {R}^n),$
which proves the theorem. To prove the claim, we observe that, for all $\zeta \in C^1_c(\Omega ;\mathbb {R}^n),$![]()
moreover,
and hence,
As above, we take $\zeta (x)=\phi (u(x))$![]() with arbitrary $\phi \in C^1_c(u(\Omega );\mathbb {R}^n)$
with arbitrary $\phi \in C^1_c(u(\Omega );\mathbb {R}^n)$![]() to obtain
to obtain
Again, this holding for all $\phi \in C^1_c(u(\Omega );\mathbb {R}^n)$![]() proves that $\chi _{u(\Omega _+)}$
proves that $\chi _{u(\Omega _+)}$![]() is constant a.e. on $u(\Omega );$
is constant a.e. on $u(\Omega );$![]() hence, either $|u(\Omega _+)|=0$
hence, either $|u(\Omega _+)|=0$![]() or $|u(\Omega _+)|=|u(\Omega )|.$
or $|u(\Omega _+)|=|u(\Omega )|.$![]() If $|u(\Omega _+)|=0,$
If $|u(\Omega _+)|=0,$![]() then $\int _{\Omega _+} \det Du \,{\rm d}x= |u(\Omega _+)| =0;$
then $\int _{\Omega _+} \det Du \,{\rm d}x= |u(\Omega _+)| =0;$![]() thus $\det Du=0$
thus $\det Du=0$![]() a.e. on $\Omega _+,$
a.e. on $\Omega _+,$![]() which proves $|\Omega _+|=0$
which proves $|\Omega _+|=0$![]() because, otherwise, we would have $\lambda =h(0)=0.$
because, otherwise, we would have $\lambda =h(0)=0.$![]() Similarly, if $|u(\Omega _+)|=|u(\Omega )|$
Similarly, if $|u(\Omega _+)|=|u(\Omega )|$![]() then $|\Omega _+|=|\Omega |.$
then $|\Omega _+|=|\Omega |.$![]() This completes the proof.
This completes the proof.
Remark 2.9 A sufficient condition for the invertibility of Sobolev functions has been given in [Reference Ball1]. For example, suppose that $\Omega$![]() is a bounded Lipschitz domain and $u_0\in C(\bar \Omega ;\mathbb {R}^n)$
is a bounded Lipschitz domain and $u_0\in C(\bar \Omega ;\mathbb {R}^n)$![]() is such that $u_0$
is such that $u_0$![]() is one-to-one on $\bar \Omega$
is one-to-one on $\bar \Omega$![]() and $u_0(\Omega )$
and $u_0(\Omega )$![]() satisfies the cone condition. Then, condition (2.6) is satisfied provided that
satisfies the cone condition. Then, condition (2.6) is satisfied provided that

See [Reference Krömer9] for recent studies and more references in this direction.
The following result concerns the weak solutions with certain linear Dirichlet boundary conditions.
Proposition 2.10 Let $h(0)=0$![]() , $p\ge n$
, $p\ge n$![]() , $\tilde p={p}/({p-n}),$
, $\tilde p={p}/({p-n}),$![]() and $u\in W^{1,p}(\Omega ;\mathbb {R}^n)$
and $u\in W^{1,p}(\Omega ;\mathbb {R}^n)$![]() with $h(\det Du)\in L^{\tilde p}(\Omega )$
with $h(\det Du)\in L^{\tilde p}(\Omega )$![]() be a weak solution of (2.1) satisfying the Dirichlet boundary condition $u|_{\partial \Omega }=Ax,$
be a weak solution of (2.1) satisfying the Dirichlet boundary condition $u|_{\partial \Omega }=Ax,$![]() where $A\in \mathbb {M}^{n\times n}$
where $A\in \mathbb {M}^{n\times n}$![]() is given. Let
is given. Let
Then $BA^T=\lambda I.$![]() Moreover, if $\det A=0$
Moreover, if $\det A=0$![]() and $h$
and $h$![]() is one-to-one, then $\det Du=0$
is one-to-one, then $\det Du=0$![]() a.e. on $\Omega,$
a.e. on $\Omega,$![]() and thus $B=0.$
and thus $B=0.$![]()
Proof. For $P\in \mathbb {M}^{n\times n},$![]() the function $\zeta (x)=P(u(x)-Ax)\in W^{1,p}_0(\Omega ;\mathbb {R}^n)$
the function $\zeta (x)=P(u(x)-Ax)\in W^{1,p}_0(\Omega ;\mathbb {R}^n)$![]() is a legitimate test function for (2.2), which, from $D\zeta =PDu-PA$
is a legitimate test function for (2.2), which, from $D\zeta =PDu-PA$![]() and $\operatorname {cof} Du: PDu =( \operatorname {tr} P )\det Du,$
and $\operatorname {cof} Du: PDu =( \operatorname {tr} P )\det Du,$![]() yields that
yields that
This is simply $(\lambda I-BA^T):P=0.$![]() Since $P\in \mathbb {M}^{n\times n}$
Since $P\in \mathbb {M}^{n\times n}$![]() is arbitrary, we have $BA^T=\lambda I.$
is arbitrary, we have $BA^T=\lambda I.$![]() If $\det A=0,$
If $\det A=0,$![]() then $\lambda =0.$
then $\lambda =0.$![]() Furthermore, if $h$
Furthermore, if $h$![]() is one-to-one, then $\lambda =0$
is one-to-one, then $\lambda =0$![]() implies $\det Du=0$
implies $\det Du=0$![]() a.e. on $\Omega$
a.e. on $\Omega$![]() and thus $B=0.$
and thus $B=0.$![]()
Remark 2.11
(i) Assume $h(0)=0$
 and $h$
and $h$ is one-to-one. If $\det A\ne 0$
is one-to-one. If $\det A\ne 0$ , then $B=\mu h(\det A)\operatorname {cof} A,$
, then $B=\mu h(\det A)\operatorname {cof} A,$ where $\mu ={\lambda }/{h(\det A)\det A}>0.$
where $\mu ={\lambda }/{h(\det A)\det A}>0.$ It remains open whether $\mu =1.$
It remains open whether $\mu =1.$ Note that if $\mu \ne 1$
Note that if $\mu \ne 1$ then $\det Du$
then $\det Du$ cannot be a constant a.e. on $\Omega.$
cannot be a constant a.e. on $\Omega.$
(ii) There are many (very) weak solutions $u\in W^{1,p}(\Omega ;\mathbb {R}^n)$
 of equation (2.1) satisfying $u|_{\partial \Omega }=Ax$
of equation (2.1) satisfying $u|_{\partial \Omega }=Ax$ for some $p< n$
for some $p< n$ such that $\det Du$
such that $\det Du$ is not constant a.e. on $\Omega.$
is not constant a.e. on $\Omega.$ See example 3.4.
See example 3.4.
3. Radially symmetric solutions
Let $B=B_1(0)$![]() be the open unit ball in $\mathbb {R}^n.$
be the open unit ball in $\mathbb {R}^n.$![]() We consider the radially symmetric or radial functions
We consider the radially symmetric or radial functions
where $\phi \colon (0,\,1)\to \mathbb {R}$![]() is weakly differentiable. With $r=|x|$
is weakly differentiable. With $r=|x|$![]() and $\omega ={x}/{|x|}$
and $\omega ={x}/{|x|}$![]() , we have
, we have

for a.e. $x\in B,$![]() where $\alpha (r)=\phi ^{n-1}+r\phi ^{n-2}\phi '$
where $\alpha (r)=\phi ^{n-1}+r\phi ^{n-2}\phi '$![]() and $\beta (r)=-r\phi ^{n-2}\phi '.$
and $\beta (r)=-r\phi ^{n-2}\phi '.$![]()
3.1. Some properties of radial functions
We study some properties of radial functions pertaining to equation (2.1).
Lemma 3.1 Let $p\ge 1$![]() and $v\in L^p_{loc}(B\setminus \{0\}).$
and $v\in L^p_{loc}(B\setminus \{0\}).$![]() Define $\tilde v=M(v)\colon (0,\,1)\to \mathbb {R}$
Define $\tilde v=M(v)\colon (0,\,1)\to \mathbb {R}$![]() by setting
by setting
where $S_r=\partial B_r(0)$![]() , ${\rm d}\sigma _r= {\rm d} \mathcal {H}^{n-1}$
, ${\rm d}\sigma _r= {\rm d} \mathcal {H}^{n-1}$![]() denotes the $(n-1)$
denotes the $(n-1)$![]() -Hausdorff measure on $S_r,$
-Hausdorff measure on $S_r,$![]() and $\omega _n=\mathcal {H}^{n-1}(S_1).$
and $\omega _n=\mathcal {H}^{n-1}(S_1).$![]() Then $\tilde v\in L^p_{loc}(0,\,1).$
Then $\tilde v\in L^p_{loc}(0,\,1).$![]() Furthermore, if $v\in W^{1,p}_{loc}(B\setminus \{0\}),$
Furthermore, if $v\in W^{1,p}_{loc}(B\setminus \{0\}),$![]() then $\tilde v\in W^{1,p}_{loc}(0,\,1)$
then $\tilde v\in W^{1,p}_{loc}(0,\,1)$![]() with
with
Since $W^{1,p}_{loc}(0,\,1)\subset C(0,\,1)$![]() , $\tilde v$
, $\tilde v$![]() can be identified as a continuous function in $(0,\,1)$
can be identified as a continuous function in $(0,\,1)$![]() if $v\in W^{1,p}_{loc}(B\setminus \{0\}).$
if $v\in W^{1,p}_{loc}(B\setminus \{0\}).$![]()
Proof. Note that

Thus, for all $0< a< b<1$![]() ,
,

This proves $\tilde v\in L^p_{loc}(0,\,1).$![]() Now assume $v\in W^{1,p}_{loc}(B\setminus \{0\})$
Now assume $v\in W^{1,p}_{loc}(B\setminus \{0\})$![]() and let
and let
Let $0< a< b<1$![]() and $\eta \in C^\infty _c(a,\,b).$
and $\eta \in C^\infty _c(a,\,b).$![]() Then
Then

This proves $g=\tilde v'.$![]()
Proposition 3.2 Assume $\phi \in W_{loc}^{1,1}(0,\,1)$![]() and $u(x)=\phi (|x|)x.$
and $u(x)=\phi (|x|)x.$![]() Let $p\ge 1$
Let $p\ge 1$![]() and $p'={p}/({p-1}).$
and $p'={p}/({p-1}).$![]() Suppose that $q(r)$
Suppose that $q(r)$![]() is a measurable function on $(0,\,1)$
is a measurable function on $(0,\,1)$![]() such that
such that
Then, for all $0< a< b<1$![]() and $v\in W_{loc}^{1,p'}(B;\mathbb {R}^n),$
and $v\in W_{loc}^{1,p'}(B;\mathbb {R}^n),$![]() it follows that
it follows that

where $\psi (r)=M(v\cdot x)(r)={r}/{\omega _n} \int _{S_1}v(r\omega )\cdot \omega \,{\rm d}\sigma _1.$![]()
Proof. Note that $q(|x|)\operatorname {cof} Du:Dv\in L^1_{loc}(B\setminus \{0\}).$![]() Since $\operatorname {cof} Du: Dv =\alpha (r)\operatorname {div} v + \beta (r) Dv:(\omega \otimes \omega ),$
Since $\operatorname {cof} Du: Dv =\alpha (r)\operatorname {div} v + \beta (r) Dv:(\omega \otimes \omega ),$![]() we have
we have

We now compute the two spherical integrals. First, for all $a< t<1,$![]() by the divergence theorem,
by the divergence theorem,

Hence
Second, since $D(v\cdot x) \cdot x =Dv : (x\otimes x) +v\cdot x,$![]() we have
we have
Thus $M(Dv : (x\otimes x)) =r \psi ' - \psi$![]() and hence
and hence

Since $\alpha +\beta =\phi ^{n-1}$![]() and $\beta =-r\phi ^{n-2}\phi '$
and $\beta =-r\phi ^{n-2}\phi '$![]() , elementary computations lead to
, elementary computations lead to

Theorem 3.3 Assume $h\in C(\mathbb {R})$![]() is one-to-one, $p\ge {n}/({n-1})$
is one-to-one, $p\ge {n}/({n-1})$![]() and $\phi \in W^{1,p}_{loc}(0,\,1).$
and $\phi \in W^{1,p}_{loc}(0,\,1).$![]() Let $u(x)=\phi (|x|)x$
Let $u(x)=\phi (|x|)x$![]() be a weak solution of (2.1) such that
be a weak solution of (2.1) such that
Then either $\phi \equiv 0,$![]() or
or
where $\lambda$![]() and $c$
and $c$![]() are constants. (When $n$
are constants. (When $n$![]() is even, we need $\lambda + {c}/({r^n})> 0$
is even, we need $\lambda + {c}/({r^n})> 0$![]() in $(0,\,1)$
in $(0,\,1)$![]() and there are two nonzero branches of the $n$
and there are two nonzero branches of the $n$![]() th roots.)
th roots.)
Proof. Let $S=\{r\in (0,\,1):\phi (r)\ne 0\};$![]() then $S$
then $S$![]() is open. If $S=\emptyset,$
is open. If $S=\emptyset,$![]() then $\phi \equiv 0.$
then $\phi \equiv 0.$![]() Assume $S$
Assume $S$![]() is nonempty. Let $(a,\,b)$
is nonempty. Let $(a,\,b)$![]() be a component of $S.$
be a component of $S.$![]() Let $\eta (r)\in C_c^\infty (0,\,1)$
Let $\eta (r)\in C_c^\infty (0,\,1)$![]() be any function with compact support contained in $(a,\,b).$
be any function with compact support contained in $(a,\,b).$![]() Define the radial function
Define the radial function

Then $\zeta \in W^{1,p}(B;\mathbb {R}^n)$![]() with $\operatorname {supp} \zeta \subset \{a<|x|< b\}.$
with $\operatorname {supp} \zeta \subset \{a<|x|< b\}.$![]() Let $\psi =M(\zeta \cdot x);$
Let $\psi =M(\zeta \cdot x);$![]() then $r^{n-2}\phi ^{n-1}\psi =\eta.$
then $r^{n-2}\phi ^{n-1}\psi =\eta.$![]() Let $\det Du=\phi ^n +r\phi ' \phi ^{n-1}=:d(r).$
Let $\det Du=\phi ^n +r\phi ' \phi ^{n-1}=:d(r).$![]() By assumption (3.7), $\zeta$
By assumption (3.7), $\zeta$![]() is a legitimate test function for equation (2.1); thus, by (3.5), we obtain that
is a legitimate test function for equation (2.1); thus, by (3.5), we obtain that

This holds for all $\eta \in C^\infty _c(a,\,b);$![]() thus $h(d(r))$
thus $h(d(r))$![]() is constant a.e. in $(a,\,b)$
is constant a.e. in $(a,\,b)$![]() . As $h$
. As $h$![]() is one-to-one, we have that $d(r)$
is one-to-one, we have that $d(r)$![]() is constant a.e. in $(a,\,b).$
is constant a.e. in $(a,\,b).$![]() Assume $d(r) =\phi ^n +r\phi ' \phi ^{n-1}= \lambda$
Assume $d(r) =\phi ^n +r\phi ' \phi ^{n-1}= \lambda$![]() in $(a,\,b).$
in $(a,\,b).$![]() Solving the differential equation we obtain that
Solving the differential equation we obtain that
If one of $a$![]() and $b$
and $b$![]() is inside $(0,\,1),$
is inside $(0,\,1),$![]() then $\phi =0$
then $\phi =0$![]() at this point; but in this case, $\phi \notin W^{1,q}_{loc}(0,\,1)$
at this point; but in this case, $\phi \notin W^{1,q}_{loc}(0,\,1)$![]() for any $q\ge {n}/{n-1}.$
for any $q\ge {n}/{n-1}.$![]() So $(a,\,b)=(0,\,1);$
So $(a,\,b)=(0,\,1);$![]() this completes the proof.
this completes the proof.
3.2. Very weak solutions
We consider some examples of (very) weak solutions of (2.1) in $W^{1,p}(B;\mathbb {R}^n)$![]() with $p<{n}/{n-1}.$
with $p<{n}/{n-1}.$![]()
Example 3.4 Let $n\ge 2$![]() , $0< a\le b<1$
, $0< a\le b<1$![]() and $\lambda _1\ne \lambda _2.$
and $\lambda _1\ne \lambda _2.$![]() Let $u=\phi (|x|)x$
Let $u=\phi (|x|)x$![]() , where
, where

Then $u \in W^{1,p}(B;\mathbb {R}^n)$![]() for all $1\le p< {n}/({n-1})$
for all $1\le p< {n}/({n-1})$![]() and $u$
and $u$![]() is a weak solution of equation (2.1) in $B$
is a weak solution of equation (2.1) in $B$![]() satisfying the Dirichlet boundary condition
satisfying the Dirichlet boundary condition
but $\det Du$![]() is not a constant on $B.$
is not a constant on $B.$![]() Moreover, if $\lambda _2=0$
Moreover, if $\lambda _2=0$![]() , then $u\chi _B$
, then $u\chi _B$![]() is a weak solution of (2.1) on the whole $\mathbb {R}^n$
is a weak solution of (2.1) on the whole $\mathbb {R}^n$![]() ; namely,
; namely,
Proof. If $\lambda _1=0$![]() , then only $Du$
, then only $Du$![]() blows up at $r=|x|=b,$
blows up at $r=|x|=b,$![]() with $|Du(x)|\approx |\phi '(r)|\approx |r-b|^{{1}/({n})-1}$
with $|Du(x)|\approx |\phi '(r)|\approx |r-b|^{{1}/({n})-1}$![]() and $|\operatorname {cof} Du(x)|\approx |\phi (r)|^{n-2}|\phi '(r)|\approx |r-b|^{-{1}/{n}}$
and $|\operatorname {cof} Du(x)|\approx |\phi (r)|^{n-2}|\phi '(r)|\approx |r-b|^{-{1}/{n}}$![]() near $r=b.$
near $r=b.$![]() Hence, in this case, $u \in W^{1,p}(B;\mathbb {R}^n)$
Hence, in this case, $u \in W^{1,p}(B;\mathbb {R}^n)$![]() for $1\le p< {n}/({n-1})$
for $1\le p< {n}/({n-1})$![]() and $\operatorname {cof} Du\in L^q(B;\mathbb {M}^{n\times n})$
and $\operatorname {cof} Du\in L^q(B;\mathbb {M}^{n\times n})$![]() for all $1\le q< n.$
for all $1\le q< n.$![]()
If $\lambda _1\ne 0$![]() , then $u$
, then $u$![]() and $Du$
and $Du$![]() also blow up at $x=0$
also blow up at $x=0$![]() and $Du$
and $Du$![]() blows up at $r=a$
blows up at $r=a$![]() and $r=b.$
and $r=b.$![]() In this case, the similar blow-up estimates show that $u \in W^{1,p}(B;\mathbb {R}^n)$
In this case, the similar blow-up estimates show that $u \in W^{1,p}(B;\mathbb {R}^n)$![]() and $\operatorname {cof} Du\in L^p(B;\mathbb {M}^{n\times n})$
and $\operatorname {cof} Du\in L^p(B;\mathbb {M}^{n\times n})$![]() for $1\le p< {n}/({n-1}).$
for $1\le p< {n}/({n-1}).$![]()
Hence, in all cases, $u \in W^{1,p}(B;\mathbb {R}^n)$![]() and $h(\det Du) \operatorname {cof} Du \in L^p(B;\mathbb {M}^{n\times n})$
and $h(\det Du) \operatorname {cof} Du \in L^p(B;\mathbb {M}^{n\times n})$![]() for all $1\le p< {n}/({n-1}).$
for all $1\le p< {n}/({n-1}).$![]() Given any $\zeta \in C^1(\mathbb {R}^n;\mathbb {R}^n),$
Given any $\zeta \in C^1(\mathbb {R}^n;\mathbb {R}^n),$![]() let $\psi (t)= M(\zeta \cdot x)(t)={t}/{\omega _n} \int _{S_1}\zeta (t\omega )\cdot \omega \,{\rm d}\sigma _1.$
let $\psi (t)= M(\zeta \cdot x)(t)={t}/{\omega _n} \int _{S_1}\zeta (t\omega )\cdot \omega \,{\rm d}\sigma _1.$![]() Then
Then
By proposition 3.2, we have

If $\zeta \in C^1_c(B;\mathbb {R}^n)$![]() , then $\psi (1)=0$
, then $\psi (1)=0$![]() ; this proves that $u$
; this proves that $u$![]() is a weak solution of (2.1). Moreover, if $\lambda _2=0$
is a weak solution of (2.1). Moreover, if $\lambda _2=0$![]() then $\phi (1)=0;$
then $\phi (1)=0;$![]() in this case, we obtain (3.9).
in this case, we obtain (3.9).
Example 3.5 Let $\Omega$![]() be any bounded domain in $\mathbb {R}^n$
be any bounded domain in $\mathbb {R}^n$![]() , $\{\bar B_{r_i}(c_i)\}_{i=1}^\infty$
, $\{\bar B_{r_i}(c_i)\}_{i=1}^\infty$![]() be a family of disjoint-closed balls in $\Omega,$
be a family of disjoint-closed balls in $\Omega,$![]() and $u_i(x)= \phi _i(|x|)x$
and $u_i(x)= \phi _i(|x|)x$![]() be the radial function on $B=B_1(0),$
be the radial function on $B=B_1(0),$![]() where $\phi _i(r)$
where $\phi _i(r)$![]() is defined by (3.8) with $\lambda _1=t_i\ne 0$
is defined by (3.8) with $\lambda _1=t_i\ne 0$![]() , $a=a_i\in (0,\,1)$
, $a=a_i\in (0,\,1)$![]() and $\lambda _2=0.$
and $\lambda _2=0.$![]() By choosing suitable $t_i$
By choosing suitable $t_i$![]() and $a_i$
and $a_i$![]() , we assume
, we assume
for some constants $M>0$![]() and $1\le p< {n}/({n-1}).$
and $1\le p< {n}/({n-1}).$![]() Define
Define

Then $u \in W^{1,p}(\Omega ;\mathbb {R}^n)$![]() , $\operatorname {cof} Du\in L^p(\Omega ;\mathbb {M}^{n\times n})$
, $\operatorname {cof} Du\in L^p(\Omega ;\mathbb {M}^{n\times n})$![]() and $|\{x\in \Omega : \det Du(x)=t_i\}|\ge a_i^n |B_i|$
and $|\{x\in \Omega : \det Du(x)=t_i\}|\ge a_i^n |B_i|$![]() (with equality holding if $t_i\ne t_j$
(with equality holding if $t_i\ne t_j$![]() for all $i\ne j$
for all $i\ne j$![]() ).
).
Moreover, $u$![]() is a weak solution of (2.1) on $\Omega ;$
is a weak solution of (2.1) on $\Omega ;$![]() in fact, $u\chi _\Omega$
in fact, $u\chi _\Omega$![]() is a weak solution of (2.1) on $\mathbb {R}^n.$
is a weak solution of (2.1) on $\mathbb {R}^n.$![]() To see this, given any $\zeta \in C^1(\mathbb {R}^n;\mathbb {R}^n),$
To see this, given any $\zeta \in C^1(\mathbb {R}^n;\mathbb {R}^n),$![]() we observe that
we observe that

where $\zeta _i(z) =r_i^{n-1} \zeta (c_i+r_iz)\in C^1(\mathbb {R}^n;\mathbb {R}^n).$![]() By (3.9), we have
By (3.9), we have
Hence $\int _\Omega h(\det Du) \operatorname {cof} Du:D\zeta \,{\rm d}x=0$![]() for all $\zeta \in C^1(\mathbb {R}^n;\mathbb {R}^n).$
for all $\zeta \in C^1(\mathbb {R}^n;\mathbb {R}^n).$![]()
3.3. Non-quasimonotonicity
Quasimonotonicity is an important condition related to the existence and regularity of weak solutions of certain systems of partial differential equations; see [Reference Chabrowski and Zhang2, Reference Fuchs6, Reference Hamburger7, Reference Kristensen and Mingione10, Reference Landes11, Reference Zhang21].
Definition 3.6 A function $\sigma \colon \mathbb {M}^{n\times n}\to \mathbb {M}^{n\times n}$![]() is said to be quasimonotone at $A\in \mathbb {M}^{n\times n}$
is said to be quasimonotone at $A\in \mathbb {M}^{n\times n}$![]() provided that
provided that
(This condition is independent of the domain $\Omega.$![]() )
)
We have the following result, which holds for the model case $h(t)=t;$![]() the result also holds for a more general class of functions including $h(t)=e^t$
the result also holds for a more general class of functions including $h(t)=e^t$![]() , but we do not intend to dwell on the generality. There are other examples of quasiconvex functions whose gradient map is not quasimonotone; see [Reference Chabrowski and Zhang2, Reference Hamburger7].
, but we do not intend to dwell on the generality. There are other examples of quasiconvex functions whose gradient map is not quasimonotone; see [Reference Chabrowski and Zhang2, Reference Hamburger7].
Theorem 3.7 Let $n\ge 2$![]() and $h\in C^1(\mathbb {R})$
and $h\in C^1(\mathbb {R})$![]() be such that
be such that
where $\Lambda >\lambda >0$![]() , $k_1$
, $k_1$![]() and $k_2$
and $k_2$![]() are constants such that $0\le k_1\le k_2< k_1+1.$
are constants such that $0\le k_1\le k_2< k_1+1.$![]() Then $\sigma (A)=h(\det A)\operatorname {cof} A$
Then $\sigma (A)=h(\det A)\operatorname {cof} A$![]() is not quasimonotone at $I\in \mathbb {M}^{n\times n}.$
is not quasimonotone at $I\in \mathbb {M}^{n\times n}.$![]()
Proof. Let $\Omega$![]() be the unit ball in $\mathbb {R}^n.$
be the unit ball in $\mathbb {R}^n.$![]() We show that there exists a radial function $\phi (x)=\rho (|x|)x,\,$
We show that there exists a radial function $\phi (x)=\rho (|x|)x,\,$![]() where $\rho \in W^{1,\infty }(0,\,1)$
where $\rho \in W^{1,\infty }(0,\,1)$![]() with $\rho (1)=0,$
with $\rho (1)=0,$![]() such that
such that
Using the spherical coordinates, we compute that
where

with $A =(1+\rho )^n,\, B =(1+\rho )^{n-1}\rho ' r,\, C =n\rho (1+\rho )^{n-1}r^{n-1}$![]() and $D =(1+n\rho) (1+\rho )^{n-2}\rho 'r^n.$
and $D =(1+n\rho) (1+\rho )^{n-2}\rho 'r^n.$![]() We write $h(A+B)=h(A+B)-h(A)+h(A)=EB+h(A),$
We write $h(A+B)=h(A+B)-h(A)+h(A)=EB+h(A),$![]() where
where
Thus $P=EBC+EBD+h(A)C+h(A)D.$![]()
Let $0< a<1$![]() be fixed and $b=a-\epsilon$
be fixed and $b=a-\epsilon$![]() with $0<\epsilon < a$
with $0<\epsilon < a$![]() sufficiently small. Define
sufficiently small. Define

(See Fig. 1.) Then, with $P(r)=P_\epsilon (r)$![]() , we have
, we have
where $M_1$![]() (likewise, each of the $M_k$
(likewise, each of the $M_k$![]() 's below) is a positive constant independent of $\epsilon.$
's below) is a positive constant independent of $\epsilon.$![]() For all $b< r< a$
For all $b< r< a$![]() we have $\rho '=({n-1})/{n\epsilon }$
we have $\rho '=({n-1})/{n\epsilon }$![]() , $n\rho +1=({n-1})/{ \epsilon } (r-a)$
, $n\rho +1=({n-1})/{ \epsilon } (r-a)$![]() and $\rho +1 =({n-1}/{n\epsilon } (r-b).$
and $\rho +1 =({n-1}/{n\epsilon } (r-b).$![]() Hence $0< A<1$
Hence $0< A<1$![]() and $B> 0$
and $B> 0$![]() on $(b,\,a)$
on $(b,\,a)$![]() ; moreover,
; moreover,

Figure 1. The graph of $\rho =\rho _\epsilon (r),$![]() where $0< a<1$
where $0< a<1$![]() is fixed and $b=a-\epsilon$
is fixed and $b=a-\epsilon$![]() with $\epsilon \in (0,\,a)$
with $\epsilon \in (0,\,a)$![]() sufficiently small.
sufficiently small.
Moreover,
Since
it follows that for all $k\ge 0$![]()
Thus
Since $BD\le 0$![]() on $(b,\,a)$
on $(b,\,a)$![]() , we have
, we have

This, combined with (3.13)–(3.15), proves that
Consequently, $\int _0^1 P_\epsilon (r)\,{\rm d}r<0$![]() if $\epsilon \in (0,\,a)$
if $\epsilon \in (0,\,a)$![]() is sufficiently small; this establishes (3.11).
is sufficiently small; this establishes (3.11).
4. The two-dimensional case
The rest of the paper is devoted to the study of certain exact and certain approximate Lipschitz solutions of Euler–Lagrange equation (2.1) in the 2-D case. Throughout this section, upon replacing $h(t)$![]() by $h(t)-h(0)$
by $h(t)-h(0)$![]() , we shall always assume $h\in C(\mathbb {R})$
, we shall always assume $h\in C(\mathbb {R})$![]() and $h(0)=0.$
and $h(0)=0.$![]()
It is well-known [Reference Kirchheim, Müller and Šverák8, Reference Müller and Šverák13] that $u\in W^{1,\infty }_{loc}(\Omega ;\mathbb {R}^2)$![]() is a Lipschitz weak solution of equation (2.1) if and only if there exists a function $v\in W^{1,\infty }_{loc}(\Omega ;\mathbb {R}^2)$
is a Lipschitz weak solution of equation (2.1) if and only if there exists a function $v\in W^{1,\infty }_{loc}(\Omega ;\mathbb {R}^2)$![]() such that the function $U=(u,\,v)\colon \Omega \to \mathbb {R}^4$
such that the function $U=(u,\,v)\colon \Omega \to \mathbb {R}^4$![]() is a solution of the first-order partial differential relation:
is a solution of the first-order partial differential relation:
where $J=\begin{bmatrix}0 & -1\\1 & 0\end{bmatrix};$![]() note that $\operatorname {cof} A=-JAJ$
note that $\operatorname {cof} A=-JAJ$![]() for all $A\in \mathbb {M}^{2\times 2}.$
for all $A\in \mathbb {M}^{2\times 2}.$![]() In general, if $U=(u,\,v)\in W^{1,1}_{loc}(\Omega ;\mathbb {R}^4)$
In general, if $U=(u,\,v)\in W^{1,1}_{loc}(\Omega ;\mathbb {R}^4)$![]() is a solution of relation (4.1), then we have $h(\det Du)\operatorname {cof} Du=-Dv J$
is a solution of relation (4.1), then we have $h(\det Du)\operatorname {cof} Du=-Dv J$![]() a.e. on $\Omega$
a.e. on $\Omega$![]() and thus $u$
and thus $u$![]() is a weak solution of (2.1). Let $W=(u,\,-Jv)$
is a weak solution of (2.1). Let $W=(u,\,-Jv)$![]() for $U=(u,\,v)\colon \Omega \to \mathbb {R}^4.$
for $U=(u,\,v)\colon \Omega \to \mathbb {R}^4.$![]() Then relation (4.1) is equivalent to the relation:
Then relation (4.1) is equivalent to the relation:
We focus on certain exact and approximate Lipschitz solutions to relation (4.2). Recall that in studying a general partial differential relation of the form
where $\Omega \subset \mathbb {R}^n$![]() , $\phi \colon \Omega \to \mathbb {R}^m$
, $\phi \colon \Omega \to \mathbb {R}^m$![]() and $\mathcal {S}\subset \mathbb {M}^{m\times n},$
and $\mathcal {S}\subset \mathbb {M}^{m\times n},$![]() various semi-convex hulls of the set $\mathcal {S}$
various semi-convex hulls of the set $\mathcal {S}$![]() play an important role; we refer to [Reference Dacorogna4, Reference Kirchheim, Müller and Šverák8] for the definitions and further properties of these semi-convex hulls. In particular, the quasiconvex hull $\mathcal {S}^{qc}$
play an important role; we refer to [Reference Dacorogna4, Reference Kirchheim, Müller and Šverák8] for the definitions and further properties of these semi-convex hulls. In particular, the quasiconvex hull $\mathcal {S}^{qc}$![]() of $\mathcal {S}$
of $\mathcal {S}$![]() can be equivalently defined as follows.
can be equivalently defined as follows.
Definition 4.1 A matrix $\xi \in \mathbb {M}^{m\times n}$![]() belongs to $\mathcal {S}^{qc}$
belongs to $\mathcal {S}^{qc}$![]() if and only if there exists a uniformly bounded sequence $\{\phi _j\}$
if and only if there exists a uniformly bounded sequence $\{\phi _j\}$![]() in $W^{1,\infty }(\Omega ;\mathbb {R}^m)$
in $W^{1,\infty }(\Omega ;\mathbb {R}^m)$![]() such that $\phi _j|_{\partial \Omega }=\xi x$
such that $\phi _j|_{\partial \Omega }=\xi x$![]() and
and
where $\Omega$![]() is any fixed bounded Lipschitz domain in $\mathbb {R}^n$
is any fixed bounded Lipschitz domain in $\mathbb {R}^n$![]() and $\operatorname {dist}(\eta,\,\mathcal {S})$
and $\operatorname {dist}(\eta,\,\mathcal {S})$![]() is the distance from $\eta \in \mathbb {M}^{m\times n}$
is the distance from $\eta \in \mathbb {M}^{m\times n}$![]() to the set $\mathcal {S}.$
to the set $\mathcal {S}.$![]()
Remark 4.2
(i) If $\{\phi _j\}$
 is uniformly bounded in $W^{1,\infty }(\Omega ;\mathbb {R}^m)$
is uniformly bounded in $W^{1,\infty }(\Omega ;\mathbb {R}^m)$ and satisfies (4.4), then it is easily shown that $\int _\Omega H(D\phi _j)\,{\rm d}x\to 0$
and satisfies (4.4), then it is easily shown that $\int _\Omega H(D\phi _j)\,{\rm d}x\to 0$ as $j\to \infty$
as $j\to \infty$ for all nonnegative continuous functions $H$
for all nonnegative continuous functions $H$ on $\mathbb {M}^{m\times n}$
on $\mathbb {M}^{m\times n}$ that vanish on $\mathcal {S}.$
that vanish on $\mathcal {S}.$
(ii) Any sequence $\{\phi _j\}$
 in $W^{1,1}(\Omega ;\mathbb {R}^m)$
in $W^{1,1}(\Omega ;\mathbb {R}^m)$ satisfying (4.4) is called an approximate sequence of relation (4.3). We say that relation (4.3) is stable if the limit of every weakly* convergent approximate sequence in $W^{1,\infty }(\Omega ;\mathbb {R}^m)$
satisfying (4.4) is called an approximate sequence of relation (4.3). We say that relation (4.3) is stable if the limit of every weakly* convergent approximate sequence in $W^{1,\infty }(\Omega ;\mathbb {R}^m)$ is a solution of the relation. We say that (4.3) is rigid if every weakly* convergent approximate sequence in $W^{1,\infty }(\Omega ;\mathbb {R}^m)$
is a solution of the relation. We say that (4.3) is rigid if every weakly* convergent approximate sequence in $W^{1,\infty }(\Omega ;\mathbb {R}^m)$ converges strongly in $W_{loc}^{1,p}(\Omega ;\mathbb {R}^m)$
converges strongly in $W_{loc}^{1,p}(\Omega ;\mathbb {R}^m)$ for all $1\le p<\infty.$
for all $1\le p<\infty.$
(iii) It is known that the stability of (4.3) is equivalent to the equality $\mathcal {S}^{qc}=\mathcal {S},$
 while the rigidity involves much stronger conditions on the set $\mathcal {S}$
while the rigidity involves much stronger conditions on the set $\mathcal {S}$ that cannot be generally given but can only be studied individually for a given problem.
that cannot be generally given but can only be studied individually for a given problem.
4.1. Some algebraic restrictions on $\mathcal {K}^{qc}$
Let $\mathcal {K}$![]() be the set defined in (4.2). In the model case when $h(t)=t$
be the set defined in (4.2). In the model case when $h(t)=t$![]() , it has been proved in [Reference Kirchheim, Müller and Šverák8] that the rank-one convex hull $\mathcal {K}^{rc}=\mathcal {K}$
, it has been proved in [Reference Kirchheim, Müller and Šverák8] that the rank-one convex hull $\mathcal {K}^{rc}=\mathcal {K}$![]() ; therefore, the set $\mathcal {K}$
; therefore, the set $\mathcal {K}$![]() does not support any open structures of $T_N$
does not support any open structures of $T_N$![]() -configurations [Reference Kirchheim, Müller and Šverák8, Reference Tartar18], which makes the construction of counterexamples in [Reference Müller and Šverák13, Reference Székelyhidi16, Reference Yan20] impossible by using such a set $\mathcal {K}.$
-configurations [Reference Kirchheim, Müller and Šverák8, Reference Tartar18], which makes the construction of counterexamples in [Reference Müller and Šverák13, Reference Székelyhidi16, Reference Yan20] impossible by using such a set $\mathcal {K}.$![]()
The following result gives some algebraic restrictions on $\mathcal {K}^{qc}$![]() for the set $\mathcal {K}.$
for the set $\mathcal {K}.$![]()
Proposition 4.3 Assume $h$![]() is one-to-one. Let $\begin{bmatrix}A\\ {B}\end{bmatrix}\in \mathcal {K}^{qc}.$
is one-to-one. Let $\begin{bmatrix}A\\ {B}\end{bmatrix}\in \mathcal {K}^{qc}.$![]() Then ${B=\mu h(\det A) A}$
Then ${B=\mu h(\det A) A}$![]() for some $\mu >0;$
for some $\mu >0;$![]() in particular, $B=0$
in particular, $B=0$![]() if $\det A=0.$
if $\det A=0.$![]()
Proof. Let $\{u_n\}$![]() and $\{v_n\}$
and $\{v_n\}$![]() be uniformly bounded in $W^{1,\infty }(\Omega ;\mathbb {R}^2)$
be uniformly bounded in $W^{1,\infty }(\Omega ;\mathbb {R}^2)$![]() such that
such that
In what follows, for any two vectors $\chi ^1$![]() and $\chi ^2$
and $\chi ^2$![]() in $\mathbb {R}^2$
in $\mathbb {R}^2$![]() , we define $\chi ^1\wedge \chi ^2=\det X,$
, we define $\chi ^1\wedge \chi ^2=\det X,$![]() where $X$
where $X$![]() is the matrix in $\mathbb {M}^{2\times 2}$
is the matrix in $\mathbb {M}^{2\times 2}$![]() having $\chi ^1$
having $\chi ^1$![]() and $\chi ^2$
and $\chi ^2$![]() as its first and second rows. For $\eta \in \mathbb {M}^{4\times 2},$
as its first and second rows. For $\eta \in \mathbb {M}^{4\times 2},$![]() let $\eta ^i\in \mathbb {R}^2$
let $\eta ^i\in \mathbb {R}^2$![]() be its $i$
be its $i$![]() th row vector for $1\le i\le 4.$
th row vector for $1\le i\le 4.$![]() Consider functions: $H_1(\eta )=|h(\eta ^1\wedge \eta ^2) (\eta ^1\wedge \eta ^2) -(\eta ^1\wedge \eta ^4)|$
Consider functions: $H_1(\eta )=|h(\eta ^1\wedge \eta ^2) (\eta ^1\wedge \eta ^2) -(\eta ^1\wedge \eta ^4)|$![]() , $H_2(\eta )=|h(\eta ^1\wedge \eta ^2) (\eta ^1\wedge \eta ^2) -(\eta ^3\wedge \eta ^2)|$
, $H_2(\eta )=|h(\eta ^1\wedge \eta ^2) (\eta ^1\wedge \eta ^2) -(\eta ^3\wedge \eta ^2)|$![]() , and $H_3(\eta )=|\eta ^1\wedge \eta ^3|+| \eta ^2\wedge \eta ^4|;$
, and $H_3(\eta )=|\eta ^1\wedge \eta ^3|+| \eta ^2\wedge \eta ^4|;$![]() they are all nonnegative continuous and vanish on the set $\mathcal {K}.$
they are all nonnegative continuous and vanish on the set $\mathcal {K}.$![]() By (4.5) and remark 4.2(i), we have
By (4.5) and remark 4.2(i), we have

where $\alpha _n^i$![]() and $\beta _n^i$
and $\beta _n^i$![]() are the $i$
are the $i$![]() th row of $Du_n$
th row of $Du_n$![]() and $Dv_n,$
and $Dv_n,$![]() respectively, for $i=1,\,2.$
respectively, for $i=1,\,2.$![]() Let $\alpha ^i$
Let $\alpha ^i$![]() and $\beta ^i$
and $\beta ^i$![]() be the $i$
be the $i$![]() th row of $A$
th row of $A$![]() and $B,$
and $B,$![]() respectively, for $i=1,\,2.$
respectively, for $i=1,\,2.$![]() Then, by the boundary conditions in (4.5) and the null-Lagrangian property of $2\times 2$
Then, by the boundary conditions in (4.5) and the null-Lagrangian property of $2\times 2$![]() minors, we have $\int _\Omega \alpha _n^i\wedge \beta _n^k \,{\rm d}x = (\alpha ^i\wedge \beta ^k) |\Omega |$
minors, we have $\int _\Omega \alpha _n^i\wedge \beta _n^k \,{\rm d}x = (\alpha ^i\wedge \beta ^k) |\Omega |$![]() for $i,\,k=1,\,2.$
for $i,\,k=1,\,2.$![]() Thus, it follows from (4.6) that
Thus, it follows from (4.6) that
where
Case 1: $\lambda =0.$![]() Since $h(0)=0$
Since $h(0)=0$![]() and $h$
and $h$![]() is one-to-one, we have that either $h(t)t >0$
is one-to-one, we have that either $h(t)t >0$![]() for all $t\ne 0$
for all $t\ne 0$![]() or $h(t)t <0$
or $h(t)t <0$![]() for all $t\ne 0.$
for all $t\ne 0.$![]() In this case,
In this case,
Via a subsequence of $n\to \infty,$![]() we have $h(\alpha _n^1\wedge \alpha _n^2)(\alpha _n^1\wedge \alpha _n^2)\to 0;$
we have $h(\alpha _n^1\wedge \alpha _n^2)(\alpha _n^1\wedge \alpha _n^2)\to 0;$![]() thus $\alpha _n^1\wedge \alpha _n^2=\det Du_n \to 0$
thus $\alpha _n^1\wedge \alpha _n^2=\det Du_n \to 0$![]() a.e. on $\Omega.$
a.e. on $\Omega.$![]() Hence $\det A={1}/{|\Omega |}\int _\Omega \det Du_n \to 0$
Hence $\det A={1}/{|\Omega |}\int _\Omega \det Du_n \to 0$![]() and $\det A=0.$
and $\det A=0.$![]() Moreover, since $h(\det Du_n)\to 0$
Moreover, since $h(\det Du_n)\to 0$![]() a.e. on $\Omega,$
a.e. on $\Omega,$![]() we have
we have
So, in this case, we have $\det A=0$![]() , $B=0,$
, $B=0,$![]() and thus $B=\mu h(\det A) A$
and thus $B=\mu h(\det A) A$![]() for all $\mu >0.$
for all $\mu >0.$![]()
Case 2: $\lambda \ne 0.$![]() In this case, by (4.7), both $\alpha ^1$
In this case, by (4.7), both $\alpha ^1$![]() and $\alpha ^2$
and $\alpha ^2$![]() are nonzero, and we have $\beta ^1=t\alpha ^1$
are nonzero, and we have $\beta ^1=t\alpha ^1$![]() and $\beta ^2=s\alpha ^2$
and $\beta ^2=s\alpha ^2$![]() for some constants $t,\,s\in \mathbb {R};$
for some constants $t,\,s\in \mathbb {R};$![]() thus $\alpha ^1\wedge \beta ^2=\beta ^1\wedge \alpha ^2=t\alpha ^1\wedge \alpha ^2=s\alpha ^1\wedge \alpha ^2= \lambda \ne 0.$
thus $\alpha ^1\wedge \beta ^2=\beta ^1\wedge \alpha ^2=t\alpha ^1\wedge \alpha ^2=s\alpha ^1\wedge \alpha ^2= \lambda \ne 0.$![]() It follows that $\det A=\alpha ^1\wedge \alpha ^2\ne 0$
It follows that $\det A=\alpha ^1\wedge \alpha ^2\ne 0$![]() and $t=s= {\lambda }/{\det A}.$
and $t=s= {\lambda }/{\det A}.$![]() Therefore, in this case, we have $B=tA=\mu h(\det A) A,$
Therefore, in this case, we have $B=tA=\mu h(\det A) A,$![]() where $\mu = {\lambda }/{h(\det A)\det A}>0,\,$
where $\mu = {\lambda }/{h(\det A)\det A}>0,\,$![]() because the signs of $h(t)t$
because the signs of $h(t)t$![]() and $\lambda$
and $\lambda$![]() are the same for all $t\ne 0.$
are the same for all $t\ne 0.$![]()
Finally, from the two cases above, we see that $\det A=0$![]() if and only if $\lambda =0.$
if and only if $\lambda =0.$![]() Thus $B=0$
Thus $B=0$![]() if $\det A=0.$
if $\det A=0.$![]()
The quasiconvex hull $\mathcal {K}^{qc}$![]() would be completely determined if, for given $\det A\ne 0$
would be completely determined if, for given $\det A\ne 0$![]() and positive $\mu \ne 1$
and positive $\mu \ne 1$![]() , we know whether there exist sequences $\{ u_n\}$
, we know whether there exist sequences $\{ u_n\}$![]() and $\{ v_n\}$
and $\{ v_n\}$![]() uniformly bounded in $W^{1,\infty }(\Omega ;\mathbb {R}^2)$
uniformly bounded in $W^{1,\infty }(\Omega ;\mathbb {R}^2)$![]() such that
such that

However, a complete answer to this question is at present out of reach. In the final two remaining subsections, we discuss some related partial results.
4.2. A related Dirichlet problem
Assume $h$![]() is one-to-one. Let $\det A\ne 0$
is one-to-one. Let $\det A\ne 0$![]() and $\mu >0.$
and $\mu >0.$![]() Closely related to the approximation problem (4.8), we study the exact Dirichlet problem:
Closely related to the approximation problem (4.8), we study the exact Dirichlet problem:

The main question is whether (4.9) has a Lipschitz solution for positive $\mu \ne 1.$![]()
Remark 4.4 Let $\Omega$![]() be the unit open disc in $\mathbb {R}^2.$
be the unit open disc in $\mathbb {R}^2.$![]() Given any $\mu >1,$
Given any $\mu >1,$![]() let $\lambda >1$
let $\lambda >1$![]() be the unique number such that $h(\lambda )=\mu h(1).$
be the unique number such that $h(\lambda )=\mu h(1).$![]() Define the radial functions $u(x)= \phi (|x|) x$
Define the radial functions $u(x)= \phi (|x|) x$![]() and $v(x)= h(\lambda ) u (x),$
and $v(x)= h(\lambda ) u (x),$![]() where
where

It follows from example 3.4 that $(u,\,v)\in C(\bar \Omega ;\mathbb {R}^4)\cap W^{1,p}(\Omega ;\mathbb {R}^4)$![]() for all $1\le p<2$
for all $1\le p<2$![]() and is a solution of (4.9) with $A=I,$
and is a solution of (4.9) with $A=I,$![]() but $(u,\,v)\notin W^{1,p}(\Omega ;\mathbb {R}^4)$
but $(u,\,v)\notin W^{1,p}(\Omega ;\mathbb {R}^4)$![]() for any $p\ge 2.$
for any $p\ge 2.$![]()
However, it remains open whether problem (4.9) has a Lipschitz or even a $W^{1,2}(\Omega ;\mathbb {R}^4)$![]() solution $(u,\,v)$
solution $(u,\,v)$![]() for some positive $\mu \ne 1.$
for some positive $\mu \ne 1.$![]()
We have the following partial result.
Theorem 4.5 Assume $h$![]() is one-to-one and $\det A \ne 0.$
is one-to-one and $\det A \ne 0.$![]() Let $\mu >0$
Let $\mu >0$![]() and suppose that $(u,\,v)\colon \bar \Omega \to \mathbb {R}^4$
and suppose that $(u,\,v)\colon \bar \Omega \to \mathbb {R}^4$![]() is a Lipschitz solution to problem (4.9) such that $(\det A) {\det Du} \ge 0$
is a Lipschitz solution to problem (4.9) such that $(\det A) {\det Du} \ge 0$![]() a.e. in $\Omega.$
a.e. in $\Omega.$![]() Then, $\det Du=\det A$
Then, $\det Du=\det A$![]() a.e. on $\Omega$
a.e. on $\Omega$![]() , $\mu =1$
, $\mu =1$![]() , and $v=h(\det A) u$
, and $v=h(\det A) u$![]() on $\bar \Omega.$
on $\bar \Omega.$![]()
Proof. Write $g=h(\det Du).$![]() Since $gDu=Dv$
Since $gDu=Dv$![]() , we have
, we have
Integrating over $\Omega$![]() and using the null-Lagrangian property of $2\times 2$
and using the null-Lagrangian property of $2\times 2$![]() minors, we have
minors, we have

and thus

Since $(\det A) {\det Du} \ge 0$![]() a.e. in $\Omega,$
a.e. in $\Omega,$![]() it follows that $g =h(\det Du)=\mu h(\det A)$
it follows that $g =h(\det Du)=\mu h(\det A)$![]() a.e. on the set $E=\{x\in \Omega : (\det A) \det Du(x)> 0\}.$
a.e. on the set $E=\{x\in \Omega : (\det A) \det Du(x)> 0\}.$![]() As $h$
As $h$![]() is one-to-one, we have $\det Du=\lambda \chi _E$
is one-to-one, we have $\det Du=\lambda \chi _E$![]() , where $\lambda \ne 0$
, where $\lambda \ne 0$![]() is the unique number such that $h(\lambda )=\mu h(\det A).$
is the unique number such that $h(\lambda )=\mu h(\det A).$![]() Thus $Dv = h(\lambda ) (Du) \chi _E$
Thus $Dv = h(\lambda ) (Du) \chi _E$![]() and $\det Dv=(h(\lambda ))^2\lambda \chi _E.$
and $\det Dv=(h(\lambda ))^2\lambda \chi _E.$![]() Let $\tilde v (x)=Pv(x),$
Let $\tilde v (x)=Pv(x),$![]() where $P=\mbox {diag}(1,\,{1}/{(h(\lambda ))^2\lambda })$
where $P=\mbox {diag}(1,\,{1}/{(h(\lambda ))^2\lambda })$![]() is a diagonal matrix. Then $\tilde v$
is a diagonal matrix. Then $\tilde v$![]() is Lipschitz on $\Omega$
is Lipschitz on $\Omega$![]() , $D\tilde v = h(\lambda ) P(Du) \chi _E$
, $D\tilde v = h(\lambda ) P(Du) \chi _E$![]() , and $\det D\tilde v= \chi _E;$
, and $\det D\tilde v= \chi _E;$![]() thus,
thus,
where $L= \|D\tilde v\|^2_{L^\infty (\Omega )}$![]() . Since $\det Du=\lambda \chi _E$
. Since $\det Du=\lambda \chi _E$![]() , we have $\lambda |E| = \int _\Omega \det Du =|\Omega |\det A \ne 0;$
, we have $\lambda |E| = \int _\Omega \det Du =|\Omega |\det A \ne 0;$![]() thus $|E|>0.$
thus $|E|>0.$![]() Hence $\tilde v$
Hence $\tilde v$![]() is not constant on $\Omega.$
is not constant on $\Omega.$![]() This proves that $\tilde v$
This proves that $\tilde v$![]() is a non-constant $L$
is a non-constant $L$![]() -quasiregular map on $\Omega.$
-quasiregular map on $\Omega.$![]() It is well-known (see [Reference Lehto and Virtanen12, Reference Reshetnyak15]) that any non-constant $L$
It is well-known (see [Reference Lehto and Virtanen12, Reference Reshetnyak15]) that any non-constant $L$![]() -quasiregular mapping cannot have its Jacobian determinant equal to zero on a set of positive measure; hence $|\Omega \setminus E|=0,$
-quasiregular mapping cannot have its Jacobian determinant equal to zero on a set of positive measure; hence $|\Omega \setminus E|=0,$![]() which implies that $\det Du=\lambda,$
which implies that $\det Du=\lambda,$![]() $h(\lambda ) Du=Dv$
$h(\lambda ) Du=Dv$![]() a.e. on $\Omega,$
a.e. on $\Omega,$![]() and $\lambda ={1}/{|\Omega |}\int _\Omega \det Du =\det A.$
and $\lambda ={1}/{|\Omega |}\int _\Omega \det Du =\det A.$![]() Thus, from $h(\lambda )=\mu h(\det A),$
Thus, from $h(\lambda )=\mu h(\det A),$![]() we have $\mu = 1.$
we have $\mu = 1.$![]() Finally, since $Dv=h(\lambda ) Du$
Finally, since $Dv=h(\lambda ) Du$![]() a.e. on $\Omega$
a.e. on $\Omega$![]() and $v= h(\lambda )u$
and $v= h(\lambda )u$![]() on $\partial \Omega,$
on $\partial \Omega,$![]() it follows that $v=h(\lambda )u$
it follows that $v=h(\lambda )u$![]() on $\bar \Omega.$
on $\bar \Omega.$![]()
4.3. Stability of certain restricted subsets of $\mathcal {K}$
We now study some restricted subsets of $\mathcal {K}$![]() that are more suitable for problems in nonlinear elasticity. For each $\epsilon >0,$
that are more suitable for problems in nonlinear elasticity. For each $\epsilon >0,$![]() let
let
Theorem 4.6 Let $h$![]() be one-to-one. Then $\mathcal {K}_\epsilon ^{qc}=\mathcal {K}_\epsilon$
be one-to-one. Then $\mathcal {K}_\epsilon ^{qc}=\mathcal {K}_\epsilon$![]() for all $\epsilon >0.$
for all $\epsilon >0.$![]()
Proof. Let $\begin{bmatrix} A\\ {B}\end{bmatrix} \in \mathcal {K}_\epsilon ^{qc}.$![]() Then there exist sequences $\{u_n\}$
Then there exist sequences $\{u_n\}$![]() and $\{v_n\}$
and $\{v_n\}$![]() uniformly bounded in $W^{1,\infty }(\Omega ;\mathbb {R}^2)$
uniformly bounded in $W^{1,\infty }(\Omega ;\mathbb {R}^2)$![]() such that
such that
Since $\mathcal {K}_\epsilon$![]() is closed, it follows that there exist measurable functions $A_n\colon \Omega \to \mathbb {M}^{2\times 2}$
is closed, it follows that there exist measurable functions $A_n\colon \Omega \to \mathbb {M}^{2\times 2}$![]() with $\det A_n(x)\ge \epsilon$
with $\det A_n(x)\ge \epsilon$![]() a.e. $x\in \Omega$
a.e. $x\in \Omega$![]() such that
such that
It is easily seen that $\{A_n\}$![]() is uniformly bounded in $L^\infty (\Omega ; \mathbb {M}^{2\times 2}).$
is uniformly bounded in $L^\infty (\Omega ; \mathbb {M}^{2\times 2}).$![]() Thus, we have
Thus, we have

By proposition 4.3, we have $B=tA$![]() for some number $t.$
for some number $t.$![]() Note that ${1}/{|\Omega |}\int _\Omega \det Du_n =\det A$
Note that ${1}/{|\Omega |}\int _\Omega \det Du_n =\det A$![]() and, as in the proof of proposition 4.3,
and, as in the proof of proposition 4.3,
furthermore,
Hence
Since $\det A_n\ge \epsilon,$![]() we obtain
we obtain
Via a subsequence $n_j\to \infty$![]() , we have $h(\det Du_{n_j}(x))\to t$
, we have $h(\det Du_{n_j}(x))\to t$![]() for a.e. $x\in \Omega.$
for a.e. $x\in \Omega.$![]() Since $h$
Since $h$![]() is continuous and one-to-one, this implies $\det Du_{n_j}(x)\to h^{-1}(t)$
is continuous and one-to-one, this implies $\det Du_{n_j}(x)\to h^{-1}(t)$![]() for a.e. $x\in \Omega.$
for a.e. $x\in \Omega.$![]() Thus,
Thus,
and $t=h(\det A).$![]() This proves $B=h(\det A)A;$
This proves $B=h(\det A)A;$![]() thus $\begin{bmatrix} A\\ {B}\end{bmatrix} \in \mathcal {K}_\epsilon,$
thus $\begin{bmatrix} A\\ {B}\end{bmatrix} \in \mathcal {K}_\epsilon,$![]() as $\det A\ge \epsilon.$
as $\det A\ge \epsilon.$![]()
Proposition 4.7 Let $h$![]() be one-to-one. Suppose that sequences $\{u_n\}$
be one-to-one. Suppose that sequences $\{u_n\}$![]() and $\{v_n\}$
and $\{v_n\}$![]() converge weakly* to $\bar u$
converge weakly* to $\bar u$![]() and $\bar v$
and $\bar v$![]() in $W^{1,\infty }(\Omega ;\mathbb {R}^2)$
in $W^{1,\infty }(\Omega ;\mathbb {R}^2)$![]() as $n\to \infty,$
as $n\to \infty,$![]() respectively, and satisfy
respectively, and satisfy
Then $\begin{bmatrix} D\bar u (x) \\ D\bar v(x)\end{bmatrix} \in \mathcal {K}_\epsilon$![]() for a.e. $x\in \Omega ;$
for a.e. $x\in \Omega ;$![]() moreover, $\det Du_n \to \det D\bar u$
moreover, $\det Du_n \to \det D\bar u$![]() strongly in $L^p(\Omega )$
strongly in $L^p(\Omega )$![]() for all $1\le p<\infty.$
for all $1\le p<\infty.$![]()
Proof. Note that the stated inclusion follows from theorem 4.6 by a general theorem on quasiconvex hulls; however, we give a direct proof without using such a result. As in the proof of theorem 4.6, let $\{A_n\}$![]() be a uniformly bounded sequence in $L^\infty (\Omega ; \mathbb {M}^{2\times 2})$
be a uniformly bounded sequence in $L^\infty (\Omega ; \mathbb {M}^{2\times 2})$![]() with $\det A_n(x)\ge \epsilon$
with $\det A_n(x)\ge \epsilon$![]() for a.e. $x\in \Omega$
for a.e. $x\in \Omega$![]() such that
such that
Thus, for all measurable sets $E\subset \Omega,$![]()
From this it follows that
As before, let $\alpha ^i$![]() and $\beta ^i$
and $\beta ^i$![]() be the $i$
be the $i$![]() th row of $D\bar u$
th row of $D\bar u$![]() and $D\bar v,$
and $D\bar v,$![]() respectively, and let $\alpha _n^i$
respectively, and let $\alpha _n^i$![]() and $\beta _n^i$
and $\beta _n^i$![]() be the $i$
be the $i$![]() th row of $Du_n$
th row of $Du_n$![]() and $Dv_n,$
and $Dv_n,$![]() respectively, for $i=1,\,2.$
respectively, for $i=1,\,2.$![]() Then all the limits listed in (4.6) above still hold. By the weak* convergence of minors, for all measurable sets $E\subset \Omega,$
Then all the limits listed in (4.6) above still hold. By the weak* convergence of minors, for all measurable sets $E\subset \Omega,$![]() we have
we have
and similarly,

So $\alpha ^1\wedge \beta ^1=\alpha ^2\wedge \beta ^2=0$![]() and $\alpha ^1\wedge \beta ^2=\beta ^1\wedge \alpha ^2$
and $\alpha ^1\wedge \beta ^2=\beta ^1\wedge \alpha ^2$![]() a.e. on $\Omega.$
a.e. on $\Omega.$![]() Since $\alpha ^1\wedge \alpha ^2=\det D\bar u \ge \epsilon,$
Since $\alpha ^1\wedge \alpha ^2=\det D\bar u \ge \epsilon,$![]() it follows that $\beta ^1=g\alpha ^1$
it follows that $\beta ^1=g\alpha ^1$![]() and $\beta ^2=g\alpha ^2,$
and $\beta ^2=g\alpha ^2,$![]() where $g={\alpha ^1\wedge \beta ^2}/{\alpha ^1\wedge \alpha ^2}\in L^\infty (\Omega ).$
where $g={\alpha ^1\wedge \beta ^2}/{\alpha ^1\wedge \alpha ^2}\in L^\infty (\Omega ).$![]() Again by (4.6) and the weak* convergence of $2\times 2$
Again by (4.6) and the weak* convergence of $2\times 2$![]() minors, we have
minors, we have

Therefore,
Since $\det A_n\ge \epsilon$![]() , it follows that $h(\det Du_n) \to g$
, it follows that $h(\det Du_n) \to g$![]() strongly in $L^2(\Omega ).$
strongly in $L^2(\Omega ).$![]() We assume, along a subsequence $n_j\to \infty,$
We assume, along a subsequence $n_j\to \infty,$![]() that $h(\det Du_{n_j}(x))\to g(x)$
that $h(\det Du_{n_j}(x))\to g(x)$![]() for a.e. $x\in \Omega.$
for a.e. $x\in \Omega.$![]() Since $h$
Since $h$![]() is continuous and one-to-one, we have $\det Du_{n_j}(x)\to h^{-1}(g(x))$
is continuous and one-to-one, we have $\det Du_{n_j}(x)\to h^{-1}(g(x))$![]() for a.e. $x\in \Omega.$
for a.e. $x\in \Omega.$![]() But, since $\det Du_n\rightharpoonup \det D\bar u$
But, since $\det Du_n\rightharpoonup \det D\bar u$![]() weakly* in $L^\infty (\Omega ),$
weakly* in $L^\infty (\Omega ),$![]() it follows that $h^{-1}(g(x))=\det D\bar u(x)$
it follows that $h^{-1}(g(x))=\det D\bar u(x)$![]() a.e. $x\in \Omega,$
a.e. $x\in \Omega,$![]() which proves $g=h(\det D\bar u)$
which proves $g=h(\det D\bar u)$![]() and hence $D\bar v= h(\det D\bar u)D\bar u.$
and hence $D\bar v= h(\det D\bar u)D\bar u.$![]() Finally, the strong convergence of $h(\det Du_n) \to h(\det D\bar u)$
Finally, the strong convergence of $h(\det Du_n) \to h(\det D\bar u)$![]() in $L^2(\Omega )$
in $L^2(\Omega )$![]() and the weak* convergence of $\{u_n\}$
and the weak* convergence of $\{u_n\}$![]() and $\{v_n\}$
and $\{v_n\}$![]() in $W^{1,\infty }(\Omega ;\mathbb {R}^2)$
in $W^{1,\infty }(\Omega ;\mathbb {R}^2)$![]() establish the strong convergence of $\det Du_n\to \det D\bar u$
establish the strong convergence of $\det Du_n\to \det D\bar u$![]() in $L^p(\Omega )$
in $L^p(\Omega )$![]() for all $1\le p<\infty.$
for all $1\le p<\infty.$![]()
Acknowledgements
The author is greatly thankful to the referee for making many helpful suggestions that improve the presentation of the paper.
Note added in proof
After the completion of this work, the author has gratefully received from Dr. Riccardo Tione the work [Reference Tione19] which studies the same problem but with different focuses.