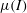1 Introduction
Self-channelisation and levee formation can occur in a wide range of geophysical mass flows that take place in volcanic and mountainous regions throughout the world. These include highly mobile and destructive pyroclastic flows (Rowley, Kuntz & MacLeod Reference Rowley, Kuntz, MacLeod, Lipman and Mullineaux1981; Wilson & Head Reference Wilson, Head, Lipman and Mullineaux1981; Branney & Kokelaar Reference Branney and Kokelaar1992; Calder, Sparks & Gardeweg Reference Calder, Sparks and Gardeweg2000; Jessop et al. Reference Jessop, Kelfoun, Labazuy, Mangeney, Roche, Tillier, Trouillet and Thibault2012), water-saturated lahars (Vallance Reference Vallance and Sigurdsson2000; Vallance & Iverson Reference Vallance, Iverson and Sigurdsson2015) and debris flows (Sharp & Nobles Reference Sharp and Nobles1953; Costa & Williams Reference Costa and Williams1984; Pierson Reference Pierson and Abrahams1986; Iverson Reference Iverson1997; Major Reference Major1997) as well as wet snow avalanches (Jomelli & Bertran Reference Jomelli and Bertran2001; Ancey Reference Ancey2012; Bartelt et al. Reference Bartelt, Glover, Feistl, Bühler and Buser2012; Schweizer, Bartelt & van Herwijnen Reference Schweizer, Bartelt, van Herwijnen, Haeberli and Whiteman2014). Although these flows vary greatly in composition, a unifying feature is that, on shallow slopes, they spontaneously form static parallel-sided levees that bound a central flowing channel. The static levees prevent lateral spreading, allowing deeper flows to be sustained for longer than a spreading flow, and thereby increase the flow’s mobility and its eventual run-out distance.
Although the mobility of grains is important for both industrial and geophysical applications, modelling the self-channelisation process still presents a significant theoretical challenge. This is firstly because it is a particularly subtle test of the granular rheology, since the flow spontaneously selects its own width, rather than being laterally unconfined or having the width imposed by side walls. Secondly, it also raises fundamental questions about how static and flowing regions can coexist, which is a longstanding issue in modelling granular materials. Although this paper is motivated by complex geophysical granular flows, it is focussed on determining the simplest possible formulation that will capture the levee formation process in quasi-monodisperse dry granular flows (Félix & Thomas Reference Félix and Thomas2004; Deboeuf et al. Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006; Takagi, McElwaine & Huppert Reference Takagi, McElwaine and Huppert2011).
In order to narrow down the physical mechanisms required for levee formation, Félix & Thomas (Reference Félix and Thomas2004) performed small-scale experiments with 300–
![]() $400~\unicode[STIX]{x03BC}\text{m}$
spherical dry glass beads that were steadily released from a point source onto an inclined plane roughened with a glued layer of 425–
$400~\unicode[STIX]{x03BC}\text{m}$
spherical dry glass beads that were steadily released from a point source onto an inclined plane roughened with a glued layer of 425–
![]() $600~\unicode[STIX]{x03BC}\text{m}$
glass beads, to ensure that there was no slip at the base. For illustration, a similar experiment using 160–
$600~\unicode[STIX]{x03BC}\text{m}$
glass beads, to ensure that there was no slip at the base. For illustration, a similar experiment using 160–
![]() $200~\unicode[STIX]{x03BC}\text{m}$
red sand on a bed of turquoise ballotini (750–
$200~\unicode[STIX]{x03BC}\text{m}$
red sand on a bed of turquoise ballotini (750–
![]() $1000~\unicode[STIX]{x03BC}\text{m}$
) is shown in figures 1 and 2 as well as supplementary movie 1 (online) available at https://doi.org/10.1017/jfm.2019.518. Both of these sets of experiments are dry and have a very narrow range of particle sizes, but, as Félix & Thomas (Reference Félix and Thomas2004) showed, static levees still form. This suggests that neither interstitial fluid nor particle-size segregation are essential to the self-channelisation process, although they may strongly enhance its effects (Pouliquen, Delour & Savage Reference Pouliquen, Delour and Savage1997; Pouliquen & Vallance Reference Pouliquen and Vallance1999; Félix & Thomas Reference Félix and Thomas2004; Goujon, Dalloz-Dubrujeaud & Thomas Reference Goujon, Dalloz-Dubrujeaud and Thomas2007; Iverson et al.
Reference Iverson, Logan, LaHusen and Berti2010; Woodhouse et al.
Reference Woodhouse, Thornton, Johnson, Kokelaar and Gray2012; Kokelaar et al.
Reference Kokelaar, Graham, Gray and Vallance2014; Baker, Johnson & Gray Reference Baker, Johnson and Gray2016b
).
$1000~\unicode[STIX]{x03BC}\text{m}$
) is shown in figures 1 and 2 as well as supplementary movie 1 (online) available at https://doi.org/10.1017/jfm.2019.518. Both of these sets of experiments are dry and have a very narrow range of particle sizes, but, as Félix & Thomas (Reference Félix and Thomas2004) showed, static levees still form. This suggests that neither interstitial fluid nor particle-size segregation are essential to the self-channelisation process, although they may strongly enhance its effects (Pouliquen, Delour & Savage Reference Pouliquen, Delour and Savage1997; Pouliquen & Vallance Reference Pouliquen and Vallance1999; Félix & Thomas Reference Félix and Thomas2004; Goujon, Dalloz-Dubrujeaud & Thomas Reference Goujon, Dalloz-Dubrujeaud and Thomas2007; Iverson et al.
Reference Iverson, Logan, LaHusen and Berti2010; Woodhouse et al.
Reference Woodhouse, Thornton, Johnson, Kokelaar and Gray2012; Kokelaar et al.
Reference Kokelaar, Graham, Gray and Vallance2014; Baker, Johnson & Gray Reference Baker, Johnson and Gray2016b
).

Figure 1. An oblique view of a self-channelised leveed flow of 160–
![]() $200~\unicode[STIX]{x03BC}\text{m}$
red sand on a plane roughened with a layer of 750–
$200~\unicode[STIX]{x03BC}\text{m}$
red sand on a plane roughened with a layer of 750–
![]() $1000~\unicode[STIX]{x03BC}\text{m}$
turquoise spherical ballotini and inclined at
$1000~\unicode[STIX]{x03BC}\text{m}$
turquoise spherical ballotini and inclined at
![]() $\unicode[STIX]{x1D701}=34^{\circ }\pm 0.1^{\circ }$
. The granular material is released from a funnel at the top of the chute, and a self-channelised flow rapidly develops, which moves down the plane at constant speed. The grains spontaneously select a flowing channel width
$\unicode[STIX]{x1D701}=34^{\circ }\pm 0.1^{\circ }$
. The granular material is released from a funnel at the top of the chute, and a self-channelised flow rapidly develops, which moves down the plane at constant speed. The grains spontaneously select a flowing channel width
![]() $W=3.60\pm 0.05$
cm and the total width of the levees and the channel is
$W=3.60\pm 0.05$
cm and the total width of the levees and the channel is
![]() $W_{total}=5.00\pm 0.05$
cm. A long shutter time is used to blur the moving grains and thus highlight the parallel-sided static levees where the grains are in sharp focus. The steady-state mass flux
$W_{total}=5.00\pm 0.05$
cm. A long shutter time is used to blur the moving grains and thus highlight the parallel-sided static levees where the grains are in sharp focus. The steady-state mass flux
![]() $Q_{M}=8.6\pm 0.1~\text{g}~\text{s}^{-1}$
is measured as the grains flow off the end of the chute. A movie showing the time-dependent evolution is available in the online supplementary material (movie 1).
$Q_{M}=8.6\pm 0.1~\text{g}~\text{s}^{-1}$
is measured as the grains flow off the end of the chute. A movie showing the time-dependent evolution is available in the online supplementary material (movie 1).

Figure 2. Photographs of a self-channelised leveed flow of 160–
![]() $200~\unicode[STIX]{x03BC}\text{m}$
red sand on a rough plane inclined at
$200~\unicode[STIX]{x03BC}\text{m}$
red sand on a rough plane inclined at
![]() $\unicode[STIX]{x1D701}=34^{\circ }\pm 0.1^{\circ }$
. They show (a) the flow front propagating down the plane and forming static parallel-sided levees just behind the head, (b) the steady-state fully developed levee–channel morphology and (c) the static partially drained channel, which forms when the inflow ceases. Grains are supplied from a funnel near the top of the plane (a,b) with a mass flux
$\unicode[STIX]{x1D701}=34^{\circ }\pm 0.1^{\circ }$
. They show (a) the flow front propagating down the plane and forming static parallel-sided levees just behind the head, (b) the steady-state fully developed levee–channel morphology and (c) the static partially drained channel, which forms when the inflow ceases. Grains are supplied from a funnel near the top of the plane (a,b) with a mass flux
![]() $Q_{M}=8.6\pm 0.1~\text{g}~\text{s}^{-1}$
. The central flowing channel very rapidly selects its own width
$Q_{M}=8.6\pm 0.1~\text{g}~\text{s}^{-1}$
. The central flowing channel very rapidly selects its own width
![]() $W=3.60\pm 0.05$
cm and the total width of the channel and the static levees is
$W=3.60\pm 0.05$
cm and the total width of the channel and the static levees is
![]() $W_{total}=5.00\pm 0.05$
cm. A movie showing the time-dependent evolution is available in the online supplementary material (movie 1).
$W_{total}=5.00\pm 0.05$
cm. A movie showing the time-dependent evolution is available in the online supplementary material (movie 1).
A self-channelised leveed flow has three distinct phases of motion (Félix & Thomas Reference Félix and Thomas2004) as illustrated in figure 2(a–c) respectively and supplementary movie 1. As grains flow down the incline they form a fully mobilised head at the front of the flow, which propagates at a constant speed and lies downslope of the levees. The downslope velocity is greatest in the surface layers in the centre of the channel (Jop, Forterre & Pouliquen Reference Jop, Forterre and Pouliquen2005; Kokelaar et al. Reference Kokelaar, Graham, Gray and Vallance2014; Baker, Barker & Gray Reference Baker, Barker and Gray2016a ). This region therefore transports grains towards the flow head, but when the grains reach the front they lose their confinement and spread out. Some of the grains are overrun by the flow itself, while others are advected to the sides and come to rest, extending the static levees (Johnson et al. Reference Johnson, Kokelaar, Iverson, Logan, LaHusen and Gray2012), which advance downslope at the back of the head (figures 1 and 2 a).
The flow within the head is slightly deeper than that in the channel (Félix & Thomas Reference Félix and Thomas2004), so as the head passes by there is a small decrease in flow thickness and the levees stabilise, selecting a width for the channel (figure 2 b). For sufficiently wide flows the central channel is of almost constant thickness (Félix & Thomas Reference Félix and Thomas2004), but in narrower channels the flow may have a pronounced cross-slope gradient in the free surface (Félix & Thomas Reference Félix and Thomas2004; Takagi et al. Reference Takagi, McElwaine and Huppert2011), with the deepest flow in the centre of the channel. This gradient may be an indication that normal stress differences are an important component of the underlying granular rheology (McElwaine, Takagi & Huppert Reference McElwaine, Takagi and Huppert2012). Once the parallel-sided levee–channel morphology has been established, it persists until the inflow ceases and the channel then partially drains to leave pronounced levee walls on either side of a thinner deposit within the channel (figure 2 c). The thickness of these levees is similar to the thickness of the flow that generated them, especially for wide channels.

Figure 3. (a–f) A series of overhead images at
![]() $t=3$
, 5, 7, 9, 10 and 11 s showing (a–c) the initial formation of the static levees and (d–f) their subsequent reworking by levee-bank overtopping. The mass flux
$t=3$
, 5, 7, 9, 10 and 11 s showing (a–c) the initial formation of the static levees and (d–f) their subsequent reworking by levee-bank overtopping. The mass flux
![]() $Q_{M}=8.6\pm 0.1~\text{g}~\text{s}^{-1}$
,
$Q_{M}=8.6\pm 0.1~\text{g}~\text{s}^{-1}$
,
![]() $\unicode[STIX]{x1D701}=34^{\circ }\pm 0.1^{\circ }$
and the final width of the flow (moving channel plus levees) is
$\unicode[STIX]{x1D701}=34^{\circ }\pm 0.1^{\circ }$
and the final width of the flow (moving channel plus levees) is
![]() $W_{total}=5.00\pm 0.05$
cm. Note that at 9 s a wave begins to propagate down the channel and continuously overtops the levee bank on one side, forming a new levee that is slightly further out. This allows the flowing channel width to readjust to its steady-state value
$W_{total}=5.00\pm 0.05$
cm. Note that at 9 s a wave begins to propagate down the channel and continuously overtops the levee bank on one side, forming a new levee that is slightly further out. This allows the flowing channel width to readjust to its steady-state value
![]() $W=3.60\pm 0.05$
cm. The downslope flow direction is from left to right. A movie showing the time-dependent evolution is available in the online supplementary material (movie 1).
$W=3.60\pm 0.05$
cm. The downslope flow direction is from left to right. A movie showing the time-dependent evolution is available in the online supplementary material (movie 1).
The width of the flowing channel is not necessarily set at the point where the levees are emplaced immediately behind the head. Figure 3(a–c) shows an overhead view of the flow front advancing from left to right down the slope and depositing levees behind the flow head. A subsequent internal surge in the flow (figure 3 d–f) then pushes material over the top of one of the levee walls and re-mobilises it. This allows the central channel to become slightly wider and a new levee is formed, further out, which maintains the self-channelisation of the flow. This process of levee-bank overtopping allows the channel to adjust to its final steady-state width after the initial passage of the flow head. For the angular red sand particles used in this paper, the final steady-state levee width is achieved within a few tens of seconds. Smaller fluctuations around the steady state constantly erode and deposit small amounts of material on the inside of the levee walls (see movie 2) without remobilising the entire levee. The levees are therefore in active equilibrium with the flow, constantly undergoing minor readjustments that ensure that the width of the channel reflects its current inflow mass flux.
Particle shape strongly influences the formation of self-channelised leveed flows. In flows of spherical glass ballotini, the levees are considerably less stable (resistant to erosion) than they are for sand, and the levees creep outwards over a time scale that is much longer than that of their initial emplacement. Deboeuf et al. (Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006) found that for flows of 300–
![]() $400~\unicode[STIX]{x03BC}\text{m}$
spherical glass beads on a rough plane made of
$400~\unicode[STIX]{x03BC}\text{m}$
spherical glass beads on a rough plane made of
![]() $200~\unicode[STIX]{x03BC}\text{m}$
sandpaper, the channel widened and the flow thickness decreased very slowly until an asymptotic state was approached after very long times (
$200~\unicode[STIX]{x03BC}\text{m}$
sandpaper, the channel widened and the flow thickness decreased very slowly until an asymptotic state was approached after very long times (
![]() ${>}1$
h). Similar experiments for even longer times (Takagi et al.
Reference Takagi, McElwaine and Huppert2011) indicated that the flow widened and eventually became intermittent, with waves further widening the levees, implying that a steady-state width was never attained.
${>}1$
h). Similar experiments for even longer times (Takagi et al.
Reference Takagi, McElwaine and Huppert2011) indicated that the flow widened and eventually became intermittent, with waves further widening the levees, implying that a steady-state width was never attained.
In contrast, Takagi et al. (Reference Takagi, McElwaine and Huppert2011) showed that flows of 300–
![]() $600~\unicode[STIX]{x03BC}\text{m}$
angular sand particles, on a bed made of the same sand, rapidly established a steady-state leveed channel for sufficiently high mass fluxes. The flow had a fixed channel width and thickness, as well as a well-defined downslope surface velocity profile across the channel. As the mass flux was increased, Takagi et al. (Reference Takagi, McElwaine and Huppert2011) found that the flow thickness stayed approximately constant, but the width of the channel increased. If the mass flux was decreased below a critical threshold, however, an unsteady regime developed in which regular pulses of material flowed down the static channel as a series of erosion–deposition waves (Daerr Reference Daerr2001; Börzsönyi, Halsey & Ecke Reference Börzsönyi, Halsey and Ecke2005; Clément et al.
Reference Clément, Malloggi, Andreotti and Aranson2007; Börzsönyi, Halsey & Ecke Reference Börzsönyi, Halsey and Ecke2008; Takagi et al.
Reference Takagi, McElwaine and Huppert2011; Edwards & Gray Reference Edwards and Gray2015; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017).
$600~\unicode[STIX]{x03BC}\text{m}$
angular sand particles, on a bed made of the same sand, rapidly established a steady-state leveed channel for sufficiently high mass fluxes. The flow had a fixed channel width and thickness, as well as a well-defined downslope surface velocity profile across the channel. As the mass flux was increased, Takagi et al. (Reference Takagi, McElwaine and Huppert2011) found that the flow thickness stayed approximately constant, but the width of the channel increased. If the mass flux was decreased below a critical threshold, however, an unsteady regime developed in which regular pulses of material flowed down the static channel as a series of erosion–deposition waves (Daerr Reference Daerr2001; Börzsönyi, Halsey & Ecke Reference Börzsönyi, Halsey and Ecke2005; Clément et al.
Reference Clément, Malloggi, Andreotti and Aranson2007; Börzsönyi, Halsey & Ecke Reference Börzsönyi, Halsey and Ecke2008; Takagi et al.
Reference Takagi, McElwaine and Huppert2011; Edwards & Gray Reference Edwards and Gray2015; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017).

Figure 4. Sequence of overhead images of a self-channelised flow of 160–
![]() $200~\unicode[STIX]{x03BC}\text{m}$
red sand on a rough plane inclined at
$200~\unicode[STIX]{x03BC}\text{m}$
red sand on a rough plane inclined at
![]() $\unicode[STIX]{x1D701}=34^{\circ }\pm 0.1^{\circ }$
. The aperture of the funnel supplying the grains to the top of the chute is changed in order to reduce the mass flux from (a) its initial value of
$\unicode[STIX]{x1D701}=34^{\circ }\pm 0.1^{\circ }$
. The aperture of the funnel supplying the grains to the top of the chute is changed in order to reduce the mass flux from (a) its initial value of
![]() $Q_{M}=17.0\pm 0.1~\text{g}~\text{s}^{-1}$
to (b)
$Q_{M}=17.0\pm 0.1~\text{g}~\text{s}^{-1}$
to (b)
![]() $7.7\pm 0.1~\text{g}~\text{s}^{-1}$
and then (c) back up to
$7.7\pm 0.1~\text{g}~\text{s}^{-1}$
and then (c) back up to
![]() $27.0\pm 0.1~\text{g}~\text{s}^{-1}$
. As the mass flux is reduced, the flowing channel width narrows from (a)
$27.0\pm 0.1~\text{g}~\text{s}^{-1}$
. As the mass flux is reduced, the flowing channel width narrows from (a)
![]() $W=4.40\pm 0.05$
cm to (b)
$W=4.40\pm 0.05$
cm to (b)
![]() $W=2.70\pm 0.05$
cm by mass accretion to the inside of the levee walls. The old levees are left in situ and record the fact that a higher flux once propagated down the channel. When (c) the mass flux is subsequently increased again the levee walls are pushed out by levee-bank overtopping and the old levees are fully remobilised to form a new channel of width
$W=2.70\pm 0.05$
cm by mass accretion to the inside of the levee walls. The old levees are left in situ and record the fact that a higher flux once propagated down the channel. When (c) the mass flux is subsequently increased again the levee walls are pushed out by levee-bank overtopping and the old levees are fully remobilised to form a new channel of width
![]() $W=5.70\pm 0.05$
cm. The downslope flow direction is from left to right. A movie showing the narrowing and widening of the channel is available in the online supplementary material (movie 3).
$W=5.70\pm 0.05$
cm. The downslope flow direction is from left to right. A movie showing the narrowing and widening of the channel is available in the online supplementary material (movie 3).
A less well studied aspect of self-channelised leveed flow is the changing shape of the static levees as the inflow mass flux is altered (figure 4). For an inflow mass flux of
![]() $Q_{M}=17.0\pm 0.1~\text{g}~\text{s}^{-1}$
a stable central channel forms with a width
$Q_{M}=17.0\pm 0.1~\text{g}~\text{s}^{-1}$
a stable central channel forms with a width
![]() $W=4.40\pm 0.05$
cm (figure 4
a). When the flux is reduced to
$W=4.40\pm 0.05$
cm (figure 4
a). When the flux is reduced to
![]() $Q_{M}=7.7\pm 0.1~\text{g}~\text{s}^{-1}$
the channel narrows to a new steady-state width
$Q_{M}=7.7\pm 0.1~\text{g}~\text{s}^{-1}$
the channel narrows to a new steady-state width
![]() $W=2.70\pm 0.05$
cm (figure 4
b). The old levee is left in situ and, as the flowing region retreats into the centre of the channel, very small leveed structures are left on the inside of the old levee walls. For these small-scale experiments these features are barely one grain-diameter thick, but they can be still be seen in figure 4(b) due to the oblique lighting. An immediate consequence of this observation is that the shape of the material outside of the central flowing channel is not unique and at least partially records the history of the flow. If, on the other hand, the inflow mass flux is increased to
$W=2.70\pm 0.05$
cm (figure 4
b). The old levee is left in situ and, as the flowing region retreats into the centre of the channel, very small leveed structures are left on the inside of the old levee walls. For these small-scale experiments these features are barely one grain-diameter thick, but they can be still be seen in figure 4(b) due to the oblique lighting. An immediate consequence of this observation is that the shape of the material outside of the central flowing channel is not unique and at least partially records the history of the flow. If, on the other hand, the inflow mass flux is increased to
![]() $Q_{M}=27.0\pm 0.1~\text{g}~\text{s}^{-1}$
a new stable width
$Q_{M}=27.0\pm 0.1~\text{g}~\text{s}^{-1}$
a new stable width
![]() $W=5.70\pm 0.05$
cm rapidly develops by levee-bank overtopping (figure 4
c) and the history, preserved in the old stacked levees, is erased. The significance of this process is that it may allow information about the time history of natural geophysical flows to be inferred from the deposit, for example from sequences of subtly stacked levees that occur in pyroclastic deposits (Rowley et al.
Reference Rowley, Kuntz, MacLeod, Lipman and Mullineaux1981; Wilson & Head Reference Wilson, Head, Lipman and Mullineaux1981; Branney & Kokelaar Reference Branney and Kokelaar1992; Calder et al.
Reference Calder, Sparks and Gardeweg2000).
$W=5.70\pm 0.05$
cm rapidly develops by levee-bank overtopping (figure 4
c) and the history, preserved in the old stacked levees, is erased. The significance of this process is that it may allow information about the time history of natural geophysical flows to be inferred from the deposit, for example from sequences of subtly stacked levees that occur in pyroclastic deposits (Rowley et al.
Reference Rowley, Kuntz, MacLeod, Lipman and Mullineaux1981; Wilson & Head Reference Wilson, Head, Lipman and Mullineaux1981; Branney & Kokelaar Reference Branney and Kokelaar1992; Calder et al.
Reference Calder, Sparks and Gardeweg2000).
The fact that static levees are deposited on an inclined plane alongside flowing grains led Félix & Thomas (Reference Félix and Thomas2004) to suggest that levee formation is related to frictional hysteresis (Daerr & Douady Reference Daerr and Douady1999; Pouliquen Reference Pouliquen1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002; Edwards & Gray Reference Edwards and Gray2015; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017). A simple example of this hysteresis is when a steady uniform flow is brought to rest on a slope of angle
![]() $\unicode[STIX]{x1D701}$
, it leaves a deposit of thickness
$\unicode[STIX]{x1D701}$
, it leaves a deposit of thickness
![]() $h=h_{stop}(\unicode[STIX]{x1D701})$
, but a layer of this thickness will not start to flow again until the inclination angle is increased to
$h=h_{stop}(\unicode[STIX]{x1D701})$
, but a layer of this thickness will not start to flow again until the inclination angle is increased to
![]() $\unicode[STIX]{x1D701}=\unicode[STIX]{x1D701}_{start}(h)$
. Since the inverse function
$\unicode[STIX]{x1D701}=\unicode[STIX]{x1D701}_{start}(h)$
. Since the inverse function
![]() $h_{start}(\unicode[STIX]{x1D701})$
is greater than
$h_{start}(\unicode[STIX]{x1D701})$
is greater than
![]() $h_{stop}(\unicode[STIX]{x1D701})$
, there are a range of thicknesses over which static and flowing layers can coexist. The underlying cause of this behaviour is a non-monotonic relationship between the flow velocity and the basal friction coefficient, as expressed by the friction law of Pouliquen & Forterre (Reference Pouliquen and Forterre2002). This phenomenological law is applicable to spherical grains and combines a flow rule for steady uniform flows (Pouliquen Reference Pouliquen1999) with measurements of
$h_{stop}(\unicode[STIX]{x1D701})$
, there are a range of thicknesses over which static and flowing layers can coexist. The underlying cause of this behaviour is a non-monotonic relationship between the flow velocity and the basal friction coefficient, as expressed by the friction law of Pouliquen & Forterre (Reference Pouliquen and Forterre2002). This phenomenological law is applicable to spherical grains and combines a flow rule for steady uniform flows (Pouliquen Reference Pouliquen1999) with measurements of
![]() $\unicode[STIX]{x1D701}_{start}(h)$
to describe the friction of both static and flowing layers.
$\unicode[STIX]{x1D701}_{start}(h)$
to describe the friction of both static and flowing layers.
Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) used Pouliquen & Forterre’s (Reference Pouliquen and Forterre2002) non-monotonic empirical friction law to model the self-channelisation process within the framework of classical depth-averaged avalanche equations (e.g. Grigorian, Eglit & Iakimov Reference Grigorian, Eglit and Iakimov1967; Savage & Hutter Reference Savage and Hutter1989; Gray, Wieland & Hutter Reference Gray, Wieland and Hutter1999; Heinrich, Piatanesi & Hebert Reference Heinrich, Piatanesi and Hebert2001; Gray, Tai & Noelle Reference Gray, Tai and Noelle2003; Mangeney-Castelnau et al.
Reference Mangeney-Castelnau, Vilotte, Bristeau, Perthame, Bouchut, Simeoni and Yerneni2003; Pitman et al.
Reference Pitman, Nichita, Patra, Bauer, Sheridan and Bursik2003). Mangeney et al.’s (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) numerical simulations exhibited both a central flowing channel and parallel-sided static/very-slowly creeping margins that were similar to those seen in experiments. The computations explicitly demonstrated how the material flowing down the central channel spread out laterally at the flow front, slowed down and then deposited to form static lateral margins behind the head. These simulations therefore implied that a heterogenous rheology, due to interstitial fluid and/or size segregation, was not essential for modelling levee formation. Despite the ground-breaking nature of this work, the computed flow thickness in the fully developed flowing channel was only very slightly greater than
![]() $h_{stop}$
, the minimum thickness for steady uniform flow in the friction law of Pouliquen & Forterre (Reference Pouliquen and Forterre2002). The channel was therefore significantly thinner and wider than those observed experimentally (Félix & Thomas Reference Félix and Thomas2004) as Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) acknowledged themselves. Moreover, the downslope velocity in Mangeney et al.’s (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) simulations was plug-like across the channel, which contradicted the experimental observation that the downslope velocity decreases smoothly to zero at the levee–channel interfaces across a shear band (Félix & Thomas Reference Félix and Thomas2004; Deboeuf et al.
Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006; Takagi et al.
Reference Takagi, McElwaine and Huppert2011).
$h_{stop}$
, the minimum thickness for steady uniform flow in the friction law of Pouliquen & Forterre (Reference Pouliquen and Forterre2002). The channel was therefore significantly thinner and wider than those observed experimentally (Félix & Thomas Reference Félix and Thomas2004) as Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) acknowledged themselves. Moreover, the downslope velocity in Mangeney et al.’s (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) simulations was plug-like across the channel, which contradicted the experimental observation that the downslope velocity decreases smoothly to zero at the levee–channel interfaces across a shear band (Félix & Thomas Reference Félix and Thomas2004; Deboeuf et al.
Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006; Takagi et al.
Reference Takagi, McElwaine and Huppert2011).
In this paper a depth-integrated model for self-channelised flows is developed, taking into account contributions of the in-plane deviatoric stress, which lead to depth-averaged viscous-like terms (Gray & Edwards Reference Gray and Edwards2014; Baker et al. Reference Baker, Barker and Gray2016a ). This model is referred to as the viscous depth-averaged model in this paper to distinguish it from classical inviscid shallow-water-like depth-averaged avalanche models, which do not have viscous second-order gradient terms in their depth-averaged momentum balances. A steady-state equation of motion is derived, which describes the balance of stresses that cause shear bands (e.g. Pouliquen & Gutfraind Reference Pouliquen and Gutfraind1996; Schall & van Hecke Reference Schall and van Hecke2010) to form, and shows that these stresses provides the vital missing physics that sets the steady-state thickness and width of the whole channel. This stress balance results from the interaction of two physical mechanisms, namely frictional hysteresis (Daerr & Douady Reference Daerr and Douady1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002; Mangeney et al. Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007; Edwards et al. Reference Edwards, Viroulet, Kokelaar and Gray2017, Reference Edwards, Russell, Johnson and Gray2019) and lateral viscous stresses (Baker et al. Reference Baker, Barker and Gray2016a ). Steady-state theoretical predictions of the width, thickness and velocity profile across the channel (as functions of mass flux and slope angle) are in good quantitative agreement with laboratory experiments performed with spherical glass beads (Félix & Thomas Reference Félix and Thomas2004), and also sand (Takagi et al. Reference Takagi, McElwaine and Huppert2011). Importantly, this paper clearly demonstrates that the inviscid theory is a singular limit of the viscous case, with degenerate non-unique steady longitudinally uniform states that have a range of channel thicknesses and widths for the same mass flux. In addition, two-dimensional time-dependent numerical solutions of this viscous avalanche model are able to explicitly compute how channels with the correct steady-state thickness and width are established dynamically, as well as allowing more complex unsteady flows to be investigated.
2 Governing equations
The depth-averaged theory of Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) for erosion–deposition waves is used here to model the formation of self-channelised leveed flows on non-erodible slopes.
2.1 Depth-averaged model

Figure 5. A schematic diagram of the coordinate system
![]() $Oxyz$
inclined at an angle
$Oxyz$
inclined at an angle
![]() $\unicode[STIX]{x1D701}$
to the horizontal, where the
$\unicode[STIX]{x1D701}$
to the horizontal, where the
![]() $x$
-axis points downslope, the
$x$
-axis points downslope, the
![]() $y$
-axis is the cross-slope direction and the
$y$
-axis is the cross-slope direction and the
![]() $z$
-axis is the upward normal to the chute. For a steady uniform self-channelised flow, the cross-slope thickness profile is
$z$
-axis is the upward normal to the chute. For a steady uniform self-channelised flow, the cross-slope thickness profile is
![]() $h(y)$
, whilst the velocity field is given by
$h(y)$
, whilst the velocity field is given by
![]() $\boldsymbol{u}(y,z)$
. The moving central channel has width
$\boldsymbol{u}(y,z)$
. The moving central channel has width
![]() $W$
and is bounded on either side by parallel static levees.
$W$
and is bounded on either side by parallel static levees.
Granular material is supplied with constant mass flux from a funnel onto a rough plane inclined at an angle
![]() $\unicode[STIX]{x1D701}$
to the horizontal. A rectangular Cartesian coordinate system
$\unicode[STIX]{x1D701}$
to the horizontal. A rectangular Cartesian coordinate system
![]() $Oxyz$
is defined with the
$Oxyz$
is defined with the
![]() $x$
-axis pointing downslope, the
$x$
-axis pointing downslope, the
![]() $y$
-axis in the cross-slope direction and
$y$
-axis in the cross-slope direction and
![]() $z$
the upward perpendicular to the plane (figure 5). The granular material is assumed to be incompressible with constant bulk density
$z$
the upward perpendicular to the plane (figure 5). The granular material is assumed to be incompressible with constant bulk density
![]() $\unicode[STIX]{x1D70C}$
and velocity components
$\unicode[STIX]{x1D70C}$
and velocity components
![]() $\boldsymbol{u}=(u,v,w)$
in the downslope, cross-slope and normal directions, respectively. The depth-averaged velocity field
$\boldsymbol{u}=(u,v,w)$
in the downslope, cross-slope and normal directions, respectively. The depth-averaged velocity field
![]() $\bar{\boldsymbol{u}}=(\bar{u},\bar{v})$
in the downslope and cross-slope directions is then defined as
$\bar{\boldsymbol{u}}=(\bar{u},\bar{v})$
in the downslope and cross-slope directions is then defined as
where
![]() $h$
is the avalanche thickness. Depth averaging the incompressibility condition and applying kinematic boundary conditions (Savage & Hutter Reference Savage and Hutter1989) yields the depth-averaged mass balance
$h$
is the avalanche thickness. Depth averaging the incompressibility condition and applying kinematic boundary conditions (Savage & Hutter Reference Savage and Hutter1989) yields the depth-averaged mass balance
A similar procedure (Gray & Edwards Reference Gray and Edwards2014; Baker et al. Reference Baker, Barker and Gray2016a ) for the momentum balance equation implies that the depth-averaged momentum balances in the downslope and cross-slope directions are
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(h\bar{u})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(h\bar{u}^{2})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}(h\bar{u}\bar{v})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\frac{1}{2}gh^{2}\cos \unicode[STIX]{x1D701}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =ghS_{1}\cos \unicode[STIX]{x1D701}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\unicode[STIX]{x1D708}h^{3/2}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}x}\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(\frac{1}{2}\unicode[STIX]{x1D708}h^{3/2}\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}x}\right)\right),\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(h\bar{u})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(h\bar{u}^{2})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}(h\bar{u}\bar{v})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\frac{1}{2}gh^{2}\cos \unicode[STIX]{x1D701}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =ghS_{1}\cos \unicode[STIX]{x1D701}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\unicode[STIX]{x1D708}h^{3/2}\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}x}\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(\frac{1}{2}\unicode[STIX]{x1D708}h^{3/2}\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}x}\right)\right),\qquad\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(h\bar{v})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(h\bar{u}\bar{v})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}(h\bar{v}^{2})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(\frac{1}{2}gh^{2}\cos \unicode[STIX]{x1D701}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =ghS_{2}\cos \unicode[STIX]{x1D701}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\frac{1}{2}\unicode[STIX]{x1D708}h^{3/2}\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}x}\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(\unicode[STIX]{x1D708}h^{3/2}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}y}\right),\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}(h\bar{v})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}(h\bar{u}\bar{v})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}(h\bar{v}^{2})+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(\frac{1}{2}gh^{2}\cos \unicode[STIX]{x1D701}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =ghS_{2}\cos \unicode[STIX]{x1D701}+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}x}\left(\frac{1}{2}\unicode[STIX]{x1D708}h^{3/2}\left(\frac{\unicode[STIX]{x2202}\bar{u}}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}x}\right)\right)+\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}y}\left(\unicode[STIX]{x1D708}h^{3/2}\frac{\unicode[STIX]{x2202}\bar{v}}{\unicode[STIX]{x2202}y}\right),\qquad\end{eqnarray}$$
where
![]() $g$
is the constant of gravitational acceleration and
$g$
is the constant of gravitational acceleration and
![]() $\unicode[STIX]{x1D708}$
is a coefficient in the depth-averaged kinematic viscosity
$\unicode[STIX]{x1D708}$
is a coefficient in the depth-averaged kinematic viscosity
![]() $\unicode[STIX]{x1D708}h^{1/2}/2$
, discussed in § 2.3. Implicit in the momentum transport terms of these equations is the assumption that the shape factor
$\unicode[STIX]{x1D708}h^{1/2}/2$
, discussed in § 2.3. Implicit in the momentum transport terms of these equations is the assumption that the shape factor
![]() $(\overline{u^{2}}/\bar{u}^{2})$
is unity (Pouliquen Reference Pouliquen1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002; Hogg & Pritchard Reference Hogg and Pritchard2004; Gray & Edwards Reference Gray and Edwards2014; Saingier, Deboeuf & Lagrée Reference Saingier, Deboeuf and Lagrée2016; Viroulet et al.
Reference Viroulet, Baker, Edwards, Johnson, Gjaltema, Clavel and Gray2017). The source term has components
$(\overline{u^{2}}/\bar{u}^{2})$
is unity (Pouliquen Reference Pouliquen1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002; Hogg & Pritchard Reference Hogg and Pritchard2004; Gray & Edwards Reference Gray and Edwards2014; Saingier, Deboeuf & Lagrée Reference Saingier, Deboeuf and Lagrée2016; Viroulet et al.
Reference Viroulet, Baker, Edwards, Johnson, Gjaltema, Clavel and Gray2017). The source term has components
which arise from the gravitational force that pulls the grains downslope and the effective basal friction. The direction of the frictional force is determined by the vector
 $$\begin{eqnarray}\boldsymbol{e}=(e_{1},e_{2})=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{\bar{\boldsymbol{u}}}{|\bar{\boldsymbol{u}}|},\quad & |\bar{\boldsymbol{u}}|>0,\\ \displaystyle \frac{\tan \unicode[STIX]{x1D701}\boldsymbol{i}-\unicode[STIX]{x1D735}h}{|\text{tan}\,\unicode[STIX]{x1D701}\boldsymbol{i}-\unicode[STIX]{x1D735}h|},\quad & |\bar{\boldsymbol{u}}|=0,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{e}=(e_{1},e_{2})=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{\bar{\boldsymbol{u}}}{|\bar{\boldsymbol{u}}|},\quad & |\bar{\boldsymbol{u}}|>0,\\ \displaystyle \frac{\tan \unicode[STIX]{x1D701}\boldsymbol{i}-\unicode[STIX]{x1D735}h}{|\text{tan}\,\unicode[STIX]{x1D701}\boldsymbol{i}-\unicode[STIX]{x1D735}h|},\quad & |\bar{\boldsymbol{u}}|=0,\end{array}\right.\end{eqnarray}$$
where
![]() $\boldsymbol{i}$
is the unit vector in the downslope direction and
$\boldsymbol{i}$
is the unit vector in the downslope direction and
![]() $\unicode[STIX]{x1D735}$
is the two-dimensional gradient operator. This ensures that the friction opposes the motion when
$\unicode[STIX]{x1D735}$
is the two-dimensional gradient operator. This ensures that the friction opposes the motion when
![]() $\bar{\boldsymbol{u}}$
is non-zero, and opposes the resultant force due to gravity and the depth-averaged pressure gradient when the material is stationary.
$\bar{\boldsymbol{u}}$
is non-zero, and opposes the resultant force due to gravity and the depth-averaged pressure gradient when the material is stationary.
Equations (2.2)–(2.4) were originally derived by assuming that the flow was shallow and depth averaging the mass and momentum balance equations, assuming the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology (GDR-MiDi 2004; Jop, Forterre & Pouliquen Reference Jop, Forterre and Pouliquen2006) and a no-slip condition at the base (Gray & Edwards Reference Gray and Edwards2014; Baker et al.
Reference Baker, Barker and Gray2016a
). To leading and first order in the aspect ratio, this process yielded the classical inviscid depth-averaged avalanche equations (given by setting
$\unicode[STIX]{x1D707}(I)$
-rheology (GDR-MiDi 2004; Jop, Forterre & Pouliquen Reference Jop, Forterre and Pouliquen2006) and a no-slip condition at the base (Gray & Edwards Reference Gray and Edwards2014; Baker et al.
Reference Baker, Barker and Gray2016a
). To leading and first order in the aspect ratio, this process yielded the classical inviscid depth-averaged avalanche equations (given by setting
![]() $\unicode[STIX]{x1D708}=0$
), with an effective basal friction law corresponding to that measured empirically by Pouliquen & Forterre (Reference Pouliquen and Forterre2002) for steady uniform flows (which is referred to as the dynamic frictional regime in § 2.2). The depth-averaged viscous terms (i.e. those terms multiplied by
$\unicode[STIX]{x1D708}=0$
), with an effective basal friction law corresponding to that measured empirically by Pouliquen & Forterre (Reference Pouliquen and Forterre2002) for steady uniform flows (which is referred to as the dynamic frictional regime in § 2.2). The depth-averaged viscous terms (i.e. those terms multiplied by
![]() $\unicode[STIX]{x1D708}$
) emerge at second order, by retaining the in-plane normal and shear stresses and approximating them using the leading-order lithostatic pressure distribution and Bagnold velocity profile through the flow depth. This explicitly determines the coefficient
$\unicode[STIX]{x1D708}$
) emerge at second order, by retaining the in-plane normal and shear stresses and approximating them using the leading-order lithostatic pressure distribution and Bagnold velocity profile through the flow depth. This explicitly determines the coefficient
![]() $\unicode[STIX]{x1D708}$
in terms of known frictional parameters, see § 2.3, rather than it being a fitting parameter. The viscous terms are usually very small, but the fact that they are the highest gradient terms makes their inclusion a singular perturbation of the equations. As a result there are some problems where they play a crucial role. These include (i) obtaining the correct cutoff frequency of roll waves (Forterre Reference Forterre2006; Gray & Edwards Reference Gray and Edwards2014), (ii) generating cross-stream velocity profiles in channels (Baker et al.
Reference Baker, Barker and Gray2016a
) and (iii) producing well-posed models of segregation-induced fingering (Baker et al.
Reference Baker, Johnson and Gray2016b
). It shall be shown in this paper that they are also play a vital role in the selection of the height, width and velocity profile across a monodisperse leveed channel.
$\unicode[STIX]{x1D708}$
in terms of known frictional parameters, see § 2.3, rather than it being a fitting parameter. The viscous terms are usually very small, but the fact that they are the highest gradient terms makes their inclusion a singular perturbation of the equations. As a result there are some problems where they play a crucial role. These include (i) obtaining the correct cutoff frequency of roll waves (Forterre Reference Forterre2006; Gray & Edwards Reference Gray and Edwards2014), (ii) generating cross-stream velocity profiles in channels (Baker et al.
Reference Baker, Barker and Gray2016a
) and (iii) producing well-posed models of segregation-induced fingering (Baker et al.
Reference Baker, Johnson and Gray2016b
). It shall be shown in this paper that they are also play a vital role in the selection of the height, width and velocity profile across a monodisperse leveed channel.
2.2 The effective basal friction law
The effective coefficient of basal friction
![]() $\unicode[STIX]{x1D707}_{b}$
encodes information about the
$\unicode[STIX]{x1D707}_{b}$
encodes information about the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology (GDR-MiDi 2004; Jop et al.
Reference Jop, Forterre and Pouliquen2006) as well as the hysteretic behaviour of the granular material (Daerr & Douady Reference Daerr and Douady1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002; Mangeney et al.
Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017, Reference Edwards, Russell, Johnson and Gray2019). This hysteretic behaviour is described by a non-monotonic friction law (Pouliquen & Forterre Reference Pouliquen and Forterre2002; Forterre & Pouliquen Reference Forterre and Pouliquen2003; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017, Reference Edwards, Russell, Johnson and Gray2019)
$\unicode[STIX]{x1D707}(I)$
-rheology (GDR-MiDi 2004; Jop et al.
Reference Jop, Forterre and Pouliquen2006) as well as the hysteretic behaviour of the granular material (Daerr & Douady Reference Daerr and Douady1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002; Mangeney et al.
Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017, Reference Edwards, Russell, Johnson and Gray2019). This hysteretic behaviour is described by a non-monotonic friction law (Pouliquen & Forterre Reference Pouliquen and Forterre2002; Forterre & Pouliquen Reference Forterre and Pouliquen2003; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017, Reference Edwards, Russell, Johnson and Gray2019)
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{b}(h,Fr)=\left\{\begin{array}{@{}lrcl@{}}\unicode[STIX]{x1D707}_{D}, & Fr\hspace{2.5pt} & {\geqslant}\hspace{2.5pt} & \unicode[STIX]{x1D6FD}_{\ast },\\ \unicode[STIX]{x1D707}_{I}, & 0<Fr\hspace{2.5pt} & {<}\hspace{2.5pt} & \unicode[STIX]{x1D6FD}_{\ast },\\ \unicode[STIX]{x1D707}_{S}, & Fr\hspace{2.5pt} & =\hspace{2.5pt} & 0,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{b}(h,Fr)=\left\{\begin{array}{@{}lrcl@{}}\unicode[STIX]{x1D707}_{D}, & Fr\hspace{2.5pt} & {\geqslant}\hspace{2.5pt} & \unicode[STIX]{x1D6FD}_{\ast },\\ \unicode[STIX]{x1D707}_{I}, & 0<Fr\hspace{2.5pt} & {<}\hspace{2.5pt} & \unicode[STIX]{x1D6FD}_{\ast },\\ \unicode[STIX]{x1D707}_{S}, & Fr\hspace{2.5pt} & =\hspace{2.5pt} & 0,\end{array}\right.\end{eqnarray}$$
which is split into dynamic,
![]() $\unicode[STIX]{x1D707}_{D}$
, intermediate,
$\unicode[STIX]{x1D707}_{D}$
, intermediate,
![]() $\unicode[STIX]{x1D707}_{I}$
, and static,
$\unicode[STIX]{x1D707}_{I}$
, and static,
![]() $\unicode[STIX]{x1D707}_{S}$
, regimes, depending on the local Froude number
$\unicode[STIX]{x1D707}_{S}$
, regimes, depending on the local Froude number
and the threshold
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
between the dynamic and intermediate regimes.
$\unicode[STIX]{x1D6FD}_{\ast }$
between the dynamic and intermediate regimes.
In Pouliquen & Forterre (Reference Pouliquen and Forterre2002) the dynamic friction
![]() $\unicode[STIX]{x1D707}_{D}$
is based on the empirical flow rule for glass beads
$\unicode[STIX]{x1D707}_{D}$
is based on the empirical flow rule for glass beads
![]() $Fr=\unicode[STIX]{x1D6FD}h/h_{stop}$
(Pouliquen Reference Pouliquen1999), where
$Fr=\unicode[STIX]{x1D6FD}h/h_{stop}$
(Pouliquen Reference Pouliquen1999), where
![]() $\unicode[STIX]{x1D6FD}$
is a constant obtained experimentally. By combining this with measurements of
$\unicode[STIX]{x1D6FD}$
is a constant obtained experimentally. By combining this with measurements of
![]() $h_{stop}$
, Pouliquen (Reference Pouliquen1999) derived a dynamic friction law that was an increasing function of
$h_{stop}$
, Pouliquen (Reference Pouliquen1999) derived a dynamic friction law that was an increasing function of
![]() $Fr/h$
and was valid for
$Fr/h$
and was valid for
![]() $Fr\geqslant \unicode[STIX]{x1D6FD}$
. Angular sand grains obey a more general flow rule (Forterre & Pouliquen Reference Forterre and Pouliquen2003)
$Fr\geqslant \unicode[STIX]{x1D6FD}$
. Angular sand grains obey a more general flow rule (Forterre & Pouliquen Reference Forterre and Pouliquen2003)
where
![]() $\unicode[STIX]{x1D6E4}=0.84$
, and
$\unicode[STIX]{x1D6E4}=0.84$
, and
![]() $\unicode[STIX]{x1D6FD}=0.71$
is considerably higher than the value
$\unicode[STIX]{x1D6FD}=0.71$
is considerably higher than the value
![]() $\unicode[STIX]{x1D6FD}=0.15$
for glass beads (Forterre & Pouliquen Reference Forterre and Pouliquen2003). Note that these values have been corrected from the previously published values to account for the factor
$\unicode[STIX]{x1D6FD}=0.15$
for glass beads (Forterre & Pouliquen Reference Forterre and Pouliquen2003). Note that these values have been corrected from the previously published values to account for the factor
![]() $\sqrt{\cos \unicode[STIX]{x1D701}}$
in the Froude number (2.8). The flow rule (2.9) implies that a steady uniform flow at
$\sqrt{\cos \unicode[STIX]{x1D701}}$
in the Froude number (2.8). The flow rule (2.9) implies that a steady uniform flow at
![]() $h=h_{stop}$
has a Froude number
$h=h_{stop}$
has a Froude number
![]() $Fr=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
that is negative for the parameters for sand, a contradiction since
$Fr=\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
that is negative for the parameters for sand, a contradiction since
![]() $Fr\geqslant 0$
from (2.8). This led Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) to suggest that (2.9) is valid only for
$Fr\geqslant 0$
from (2.8). This led Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) to suggest that (2.9) is valid only for
![]() $Fr\geqslant \unicode[STIX]{x1D6FD}_{\ast }$
, where
$Fr\geqslant \unicode[STIX]{x1D6FD}_{\ast }$
, where
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
is both strictly positive and greater than
$\unicode[STIX]{x1D6FD}_{\ast }$
is both strictly positive and greater than
![]() $\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6FD}-\unicode[STIX]{x1D6E4}$
.
The flow rule (2.9) can be used to eliminate
![]() $h_{stop}$
in the reciprocal form of the empirical
$h_{stop}$
in the reciprocal form of the empirical
![]() $h_{stop}$
curve (Pouliquen & Forterre Reference Pouliquen and Forterre2002) to derive the dynamic friction law
$h_{stop}$
curve (Pouliquen & Forterre Reference Pouliquen and Forterre2002) to derive the dynamic friction law
where
![]() $Fr\geqslant \unicode[STIX]{x1D6FD}_{\ast }$
and the parameters
$Fr\geqslant \unicode[STIX]{x1D6FD}_{\ast }$
and the parameters
![]() $\unicode[STIX]{x1D707}_{1}=\tan \unicode[STIX]{x1D701}_{1}$
,
$\unicode[STIX]{x1D707}_{1}=\tan \unicode[STIX]{x1D701}_{1}$
,
![]() $\unicode[STIX]{x1D707}_{2}=\tan \unicode[STIX]{x1D701}_{2}$
and
$\unicode[STIX]{x1D707}_{2}=\tan \unicode[STIX]{x1D701}_{2}$
and
![]() $\mathscr{L}$
are fitted to measurements of the
$\mathscr{L}$
are fitted to measurements of the
![]() $h_{stop}(\unicode[STIX]{x1D701})$
curve (Pouliquen Reference Pouliquen1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002; Forterre & Pouliquen Reference Forterre and Pouliquen2003). The angles
$h_{stop}(\unicode[STIX]{x1D701})$
curve (Pouliquen Reference Pouliquen1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002; Forterre & Pouliquen Reference Forterre and Pouliquen2003). The angles
![]() $\unicode[STIX]{x1D701}_{1}$
and
$\unicode[STIX]{x1D701}_{1}$
and
![]() $\unicode[STIX]{x1D701}_{2}$
are the minimum and maximum angles, respectively, at which steady uniform flow is observed.
$\unicode[STIX]{x1D701}_{2}$
are the minimum and maximum angles, respectively, at which steady uniform flow is observed.
The friction force for static material (
![]() $Fr=0$
) is exactly that which is required to keep the material stationary, up to a maximum static friction coefficient. This coefficient therefore takes the form
$Fr=0$
) is exactly that which is required to keep the material stationary, up to a maximum static friction coefficient. This coefficient therefore takes the form
where the first argument to the
![]() $\min$
function is the friction required to balance the other forces acting on the static layer and the second argument is the maximum static friction. The maximum static friction is obtained by fitting measurements of
$\min$
function is the friction required to balance the other forces acting on the static layer and the second argument is the maximum static friction. The maximum static friction is obtained by fitting measurements of
![]() $h_{start}(\unicode[STIX]{x1D701})$
, and introduces a further friction-law parameter
$h_{start}(\unicode[STIX]{x1D701})$
, and introduces a further friction-law parameter
![]() $\unicode[STIX]{x1D707}_{3}=\tan \unicode[STIX]{x1D701}_{3}$
, where
$\unicode[STIX]{x1D707}_{3}=\tan \unicode[STIX]{x1D701}_{3}$
, where
![]() $\unicode[STIX]{x1D701}_{3}$
is the minimum angle at which an infinitely deep static layer will start to flow spontaneously (Daerr & Douady Reference Daerr and Douady1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002).
$\unicode[STIX]{x1D701}_{3}$
is the minimum angle at which an infinitely deep static layer will start to flow spontaneously (Daerr & Douady Reference Daerr and Douady1999; Pouliquen & Forterre Reference Pouliquen and Forterre2002).
The friction in the intermediate regime
![]() $0<Fr<\unicode[STIX]{x1D6FD}_{\ast }$
is a power-law interpolation between the maximum static friction and the minimum dynamic friction at
$0<Fr<\unicode[STIX]{x1D6FD}_{\ast }$
is a power-law interpolation between the maximum static friction and the minimum dynamic friction at
![]() $Fr=\unicode[STIX]{x1D6FD}_{\ast }$
and takes a much more complicated form for angular particles than for spherical ballotini (Pouliquen & Forterre Reference Pouliquen and Forterre2002). The general form that accounts for spherical and irregular particles is given by Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) as
$Fr=\unicode[STIX]{x1D6FD}_{\ast }$
and takes a much more complicated form for angular particles than for spherical ballotini (Pouliquen & Forterre Reference Pouliquen and Forterre2002). The general form that accounts for spherical and irregular particles is given by Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) as
where
![]() $\unicode[STIX]{x1D705}$
is a constant interpolation power. In the absence of experimental measurements for slow flows
$\unicode[STIX]{x1D705}$
is a constant interpolation power. In the absence of experimental measurements for slow flows
![]() $0<Fr<\unicode[STIX]{x1D6FD}_{\ast }$
, Pouliquen & Forterre (Reference Pouliquen and Forterre2002) suggested that
$0<Fr<\unicode[STIX]{x1D6FD}_{\ast }$
, Pouliquen & Forterre (Reference Pouliquen and Forterre2002) suggested that
![]() $\unicode[STIX]{x1D705}=10^{-3}$
. However, this value produces an extremely rapid decrease in the friction as the Froude number is increased from zero, so sharp that it cannot be resolved numerically using standard double-precision floating-point numbers (Edwards et al.
Reference Edwards, Russell, Johnson and Gray2019). Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) instead suggest that
$\unicode[STIX]{x1D705}=10^{-3}$
. However, this value produces an extremely rapid decrease in the friction as the Froude number is increased from zero, so sharp that it cannot be resolved numerically using standard double-precision floating-point numbers (Edwards et al.
Reference Edwards, Russell, Johnson and Gray2019). Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) instead suggest that
![]() $\unicode[STIX]{x1D705}$
needs to be at least
$\unicode[STIX]{x1D705}$
needs to be at least
![]() $10^{-1}$
to create a robust metastable state, in which a static layer, just slightly thinner than
$10^{-1}$
to create a robust metastable state, in which a static layer, just slightly thinner than
![]() $h_{start}$
(i.e. within the hysteretic region), remains stationary unless it is perturbed. In this paper it is assumed for simplicity, as in Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017, Reference Edwards, Russell, Johnson and Gray2019), that
$h_{start}$
(i.e. within the hysteretic region), remains stationary unless it is perturbed. In this paper it is assumed for simplicity, as in Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017, Reference Edwards, Russell, Johnson and Gray2019), that
![]() $\unicode[STIX]{x1D705}=1$
, which is consistent with the experimental results of Russell et al. (Reference Russell, Johnson, Edwards, Viroulet, Rocha and Gray2019) on retrogressive failures.
$\unicode[STIX]{x1D705}=1$
, which is consistent with the experimental results of Russell et al. (Reference Russell, Johnson, Edwards, Viroulet, Rocha and Gray2019) on retrogressive failures.
The parameter
![]() $\unicode[STIX]{x1D6FD}_{\ast }$
sets the Froude number of the transition between the dynamic and intermediate regimes. It also defines the thickness
$\unicode[STIX]{x1D6FD}_{\ast }$
sets the Froude number of the transition between the dynamic and intermediate regimes. It also defines the thickness
![]() $h_{\ast }$
of the minimum steady uniform flow, which lies between
$h_{\ast }$
of the minimum steady uniform flow, which lies between
![]() $h_{stop}(\unicode[STIX]{x1D701})$
and
$h_{stop}(\unicode[STIX]{x1D701})$
and
![]() $h_{start}(\unicode[STIX]{x1D701})$
. In Pouliquen & Forterre (Reference Pouliquen and Forterre2002)
$h_{start}(\unicode[STIX]{x1D701})$
. In Pouliquen & Forterre (Reference Pouliquen and Forterre2002)
![]() $\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}$
(and thus
$\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}$
(and thus
![]() $h_{\ast }=h_{stop}$
), while Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) assumed that
$h_{\ast }=h_{stop}$
), while Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) assumed that
![]() $h_{\ast }$
was half-way between
$h_{\ast }$
was half-way between
![]() $h_{stop}$
and
$h_{stop}$
and
![]() $h_{start}$
. This paper follows Edwards et al. (Reference Edwards, Russell, Johnson and Gray2019) who suggested that
$h_{start}$
. This paper follows Edwards et al. (Reference Edwards, Russell, Johnson and Gray2019) who suggested that
![]() $h_{\ast }$
was a multiple of
$h_{\ast }$
was a multiple of
![]() $h_{stop}$
$h_{stop}$
where
![]() $\unicode[STIX]{x1D6EC}$
is a constant for all slope angles. Since steady uniform flows satisfy the empirical flow rule (2.9) it follows that the transition Froude number is constant
$\unicode[STIX]{x1D6EC}$
is a constant for all slope angles. Since steady uniform flows satisfy the empirical flow rule (2.9) it follows that the transition Froude number is constant
In general,
![]() $\unicode[STIX]{x1D6EC}$
must be greater than unity and chosen so that
$\unicode[STIX]{x1D6EC}$
must be greater than unity and chosen so that
![]() $h_{\ast }<h_{start}$
, to ensure that there is hysteresis in flows of thickness
$h_{\ast }<h_{start}$
, to ensure that there is hysteresis in flows of thickness
![]() $h\in [h_{\ast },h_{start}]$
. The new approach (Edwards et al.
Reference Edwards, Russell, Johnson and Gray2019) has the advantage that it defines
$h\in [h_{\ast },h_{start}]$
. The new approach (Edwards et al.
Reference Edwards, Russell, Johnson and Gray2019) has the advantage that it defines
![]() $h_{\ast }$
over the complete range of steady uniform flow angles
$h_{\ast }$
over the complete range of steady uniform flow angles
![]() $\unicode[STIX]{x1D701}\in [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}]$
, rather than just in the range
$\unicode[STIX]{x1D701}\in [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}]$
, rather than just in the range
![]() $[\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{2}]$
, as in Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017). It also allows the intermediate friction to be accessed even for materials, such as sand, for which
$[\unicode[STIX]{x1D701}_{3},\unicode[STIX]{x1D701}_{2}]$
, as in Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017). It also allows the intermediate friction to be accessed even for materials, such as sand, for which
![]() $\unicode[STIX]{x1D6E4}>\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6E4}>\unicode[STIX]{x1D6FD}$
.
It is important to note that the extended law proposed by Edwards et al. (Reference Edwards, Russell, Johnson and Gray2019) preserves exactly the same structure as that of Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017), it just changes the functional dependence of the transition point
![]() $\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}_{\ast }(\unicode[STIX]{x1D701})$
on the inclination angle
$\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}_{\ast }(\unicode[STIX]{x1D701})$
on the inclination angle
![]() $\unicode[STIX]{x1D701}$
. Both approaches makes a clear distinction between the thickness of a deposit left by a steady uniform flow,
$\unicode[STIX]{x1D701}$
. Both approaches makes a clear distinction between the thickness of a deposit left by a steady uniform flow,
![]() $h_{stop}$
, and the thickness of the slowest possible steady uniform flow
$h_{stop}$
, and the thickness of the slowest possible steady uniform flow
![]() $h_{\ast }$
. In the original formulation of Pouliquen & Forterre (Reference Pouliquen and Forterre2002) this distinction was not made and hence
$h_{\ast }$
. In the original formulation of Pouliquen & Forterre (Reference Pouliquen and Forterre2002) this distinction was not made and hence
![]() $h_{\ast }=h_{stop}$
. Evidence that
$h_{\ast }=h_{stop}$
. Evidence that
![]() $h_{\ast }$
and
$h_{\ast }$
and
![]() $h_{stop}$
are indeed different is provided by a wide range of existing experimental measurements (see, for example, figure 4 Pouliquen Reference Pouliquen1999; figure 8 Forterre & Pouliquen Reference Forterre and Pouliquen2003; figure 3 Deboeuf et al.
Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006; figure 11 Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017), which all show that the minimum steady uniform flow thickness is in the range
$h_{stop}$
are indeed different is provided by a wide range of existing experimental measurements (see, for example, figure 4 Pouliquen Reference Pouliquen1999; figure 8 Forterre & Pouliquen Reference Forterre and Pouliquen2003; figure 3 Deboeuf et al.
Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006; figure 11 Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017), which all show that the minimum steady uniform flow thickness is in the range
![]() $[h_{stop},2h_{stop}]$
. As a result the value of
$[h_{stop},2h_{stop}]$
. As a result the value of
![]() $\unicode[STIX]{x1D6EC}=1.34\in [1,2]$
is used in this paper to best match experimental results. This is very close to the value
$\unicode[STIX]{x1D6EC}=1.34\in [1,2]$
is used in this paper to best match experimental results. This is very close to the value
![]() $h_{\ast }/h_{stop}=1.33$
measured in flows of glass beads by Russell et al. (Reference Russell, Johnson, Edwards, Viroulet, Rocha and Gray2019).
$h_{\ast }/h_{stop}=1.33$
measured in flows of glass beads by Russell et al. (Reference Russell, Johnson, Edwards, Viroulet, Rocha and Gray2019).

Figure 6. (a) Experimental measurements of
![]() $h_{stop}(\unicode[STIX]{x1D701})$
for sand (Takagi et al.
Reference Takagi, McElwaine and Huppert2011, blue markers) and glass beads (Félix & Thomas Reference Félix and Thomas2004, red markers), with best-fit
$h_{stop}(\unicode[STIX]{x1D701})$
for sand (Takagi et al.
Reference Takagi, McElwaine and Huppert2011, blue markers) and glass beads (Félix & Thomas Reference Félix and Thomas2004, red markers), with best-fit
![]() $h_{stop}$
curves using the friction-law parameters calibrated from these experiments (table 1). (b) The two friction laws for sand (blue curve) and glass beads (red curve) as a function of the Froude number
$h_{stop}$
curves using the friction-law parameters calibrated from these experiments (table 1). (b) The two friction laws for sand (blue curve) and glass beads (red curve) as a function of the Froude number
![]() $Fr$
at fixed thickness and inclination angle. Parameters
$Fr$
at fixed thickness and inclination angle. Parameters
![]() $h=8$
mm and
$h=8$
mm and
![]() $\unicode[STIX]{x1D701}=32^{\circ }$
for sand and
$\unicode[STIX]{x1D701}=32^{\circ }$
for sand and
![]() $h=3.2$
mm and
$h=3.2$
mm and
![]() $\unicode[STIX]{x1D701}=25^{\circ }$
for glass beads are chosen to match those in the respective experiments.
$\unicode[STIX]{x1D701}=25^{\circ }$
for glass beads are chosen to match those in the respective experiments.
Table 1. Physical parameters used for all steady-state and time-dependent solutions obtained throughout the paper. The parameters for sand are obtained, where possible, from the
![]() $h_{stop}$
curve of Takagi et al. (Reference Takagi, McElwaine and Huppert2011). The parameters for glass beads are those used by Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) to model the experiments of Félix & Thomas (Reference Félix and Thomas2004), but with a smaller
$h_{stop}$
curve of Takagi et al. (Reference Takagi, McElwaine and Huppert2011). The parameters for glass beads are those used by Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) to model the experiments of Félix & Thomas (Reference Félix and Thomas2004), but with a smaller
![]() $\mathscr{L}$
to quantitatively fit the
$\mathscr{L}$
to quantitatively fit the
![]() $h_{stop}$
measurements of Félix & Thomas (Reference Félix and Thomas2004). Note that the values for
$h_{stop}$
measurements of Félix & Thomas (Reference Félix and Thomas2004). Note that the values for
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D6E4}$
differ from those in Pouliquen & Forterre (Reference Pouliquen and Forterre2002) and Forterre & Pouliquen (Reference Forterre and Pouliquen2003) to account for the factor
$\unicode[STIX]{x1D6E4}$
differ from those in Pouliquen & Forterre (Reference Pouliquen and Forterre2002) and Forterre & Pouliquen (Reference Forterre and Pouliquen2003) to account for the factor
![]() $\sqrt{\cos \unicode[STIX]{x1D701}}$
in the definition of the Froude number (2.8).
$\sqrt{\cos \unicode[STIX]{x1D701}}$
in the definition of the Froude number (2.8).

To enable quantitative comparison between theory and experiment, the material parameters used throughout the paper (table 1) correspond as closely as possible to the sand used by Takagi et al. (Reference Takagi, McElwaine and Huppert2011) and the glass beads used by Félix & Thomas (Reference Félix and Thomas2004). For the experiments with sand, the angles in the friction law,
![]() $\unicode[STIX]{x1D701}_{1}$
and
$\unicode[STIX]{x1D701}_{1}$
and
![]() $\unicode[STIX]{x1D701}_{2}$
, are obtained by fitting
$\unicode[STIX]{x1D701}_{2}$
, are obtained by fitting
![]() $h_{stop}(\unicode[STIX]{x1D701})$
to the experimental data of Takagi et al. (Reference Takagi, McElwaine and Huppert2011) using the functional form proposed by Pouliquen & Forterre (Reference Pouliquen and Forterre2002) (figure 6
a), which leads to friction coefficients in the form of (2.10)–(2.12). The characteristic length scale
$h_{stop}(\unicode[STIX]{x1D701})$
to the experimental data of Takagi et al. (Reference Takagi, McElwaine and Huppert2011) using the functional form proposed by Pouliquen & Forterre (Reference Pouliquen and Forterre2002) (figure 6
a), which leads to friction coefficients in the form of (2.10)–(2.12). The characteristic length scale
![]() $\mathscr{L}$
and the parameters
$\mathscr{L}$
and the parameters
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $\unicode[STIX]{x1D6E4}$
are taken from measurements of Forterre & Pouliquen (Reference Forterre and Pouliquen2003) for a similar flow of sand on a rough bed of the same material. The angle
$\unicode[STIX]{x1D6E4}$
are taken from measurements of Forterre & Pouliquen (Reference Forterre and Pouliquen2003) for a similar flow of sand on a rough bed of the same material. The angle
![]() $\unicode[STIX]{x1D701}_{3}$
is determined from measurements of
$\unicode[STIX]{x1D701}_{3}$
is determined from measurements of
![]() $h_{start}(\unicode[STIX]{x1D701})$
, but these measurements are not reported by Takagi et al. (Reference Takagi, McElwaine and Huppert2011). Instead,
$h_{start}(\unicode[STIX]{x1D701})$
, but these measurements are not reported by Takagi et al. (Reference Takagi, McElwaine and Huppert2011). Instead,
![]() $\unicode[STIX]{x1D701}_{3}=\unicode[STIX]{x1D701}_{1}+2^{\circ }$
is chosen, based on measurements of similar flows of sand over a rough bed. For the experiments with glass beads performed by Félix & Thomas (Reference Félix and Thomas2004), the parameters are chosen to be the same as the ones used by Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) to simulate these flows, although here a value of
$\unicode[STIX]{x1D701}_{3}=\unicode[STIX]{x1D701}_{1}+2^{\circ }$
is chosen, based on measurements of similar flows of sand over a rough bed. For the experiments with glass beads performed by Félix & Thomas (Reference Félix and Thomas2004), the parameters are chosen to be the same as the ones used by Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) to simulate these flows, although here a value of
![]() $\mathscr{L}$
smaller than that of Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) is used to quantitatively match the experimental
$\mathscr{L}$
smaller than that of Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) is used to quantitatively match the experimental
![]() $h_{stop}$
curve (figure 6
a). The resultant friction laws are plotted in figure 6(b) as a function of the Froude number. The frictional hysteresis of the angular sand particles (
$h_{stop}$
curve (figure 6
a). The resultant friction laws are plotted in figure 6(b) as a function of the Froude number. The frictional hysteresis of the angular sand particles (
![]() $\unicode[STIX]{x1D707}(Fr=0)-\unicode[STIX]{x1D707}(Fr=\unicode[STIX]{x1D6FD}^{\star })$
) is much greater than that of glass beads, which makes the sand levees significantly stronger.
$\unicode[STIX]{x1D707}(Fr=0)-\unicode[STIX]{x1D707}(Fr=\unicode[STIX]{x1D6FD}^{\star })$
) is much greater than that of glass beads, which makes the sand levees significantly stronger.
2.3 Depth-averaged kinematic viscosity
The second-order depth-averaged viscous-like terms in the momentum balances (2.3)–(2.4) contain a parameter
![]() $\unicode[STIX]{x1D708}$
in the depth-averaged kinematic viscosity
$\unicode[STIX]{x1D708}$
in the depth-averaged kinematic viscosity
![]() $\unicode[STIX]{x1D708}h^{1/2}/2$
, for which Gray & Edwards (Reference Gray and Edwards2014) derived the formula
$\unicode[STIX]{x1D708}h^{1/2}/2$
, for which Gray & Edwards (Reference Gray and Edwards2014) derived the formula
This is a function of the slope angle
![]() $\unicode[STIX]{x1D701}$
and parameters that are already known from the effective basal friction law, so no new parameters are introduced into the theory. It is well-defined provided
$\unicode[STIX]{x1D701}$
and parameters that are already known from the effective basal friction law, so no new parameters are introduced into the theory. It is well-defined provided
![]() $\unicode[STIX]{x1D701}\in [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}]$
, i.e. in the range of angles where steady uniform flows develop. Outside this range, some form of regularisation is required to ensure that it does not become negative. In this paper, the two-dimensional viscous terms derived by Baker et al. (Reference Baker, Barker and Gray2016a
) are used for flows in all three frictional regimes, even though their original derivation (Gray & Edwards Reference Gray and Edwards2014) implicitly assumed the flow was in the dynamic frictional regime.
$\unicode[STIX]{x1D701}\in [\unicode[STIX]{x1D701}_{1},\unicode[STIX]{x1D701}_{2}]$
, i.e. in the range of angles where steady uniform flows develop. Outside this range, some form of regularisation is required to ensure that it does not become negative. In this paper, the two-dimensional viscous terms derived by Baker et al. (Reference Baker, Barker and Gray2016a
) are used for flows in all three frictional regimes, even though their original derivation (Gray & Edwards Reference Gray and Edwards2014) implicitly assumed the flow was in the dynamic frictional regime.
3 Fully developed self-channelised flow
This section presents exact steady-state solutions for the height, width and downslope velocity profile across the central flowing channel. The depth-averaged granular viscosity provides the vital mechanism for producing a smoothly varying velocity profile across the channel, allowing appropriate boundary conditions to be imposed at the levee–channel interfaces. These boundary conditions together with an integral mass flux constraint are then able to determine a unique equilibrium channel thickness and width, completely independently of the flow head dynamics. In the absence of viscosity the equations are not closed, so there is no unique solution and inviscid theories therefore lack a crucial thickness and width selection mechanism.
Outside of this region, in the levees, there are multiple static states (as demonstrated experimentally in figure 4) because the static friction encoded in (2.11) can take any value between zero and its maximum value. While there is not a unique solution for the width of the levees, the minimum levee width necessary to support a central flowing channel of a given thickness, can be determined by assuming all the static grains are at the maximum static friction.
3.1 Steady-state depth-averaged equations in the flowing channel
Consider a fully developed steady-state parallel-sided leveed flow that has a central flowing channel of width
![]() $W$
and is supplied by a mass flux
$W$
and is supplied by a mass flux
![]() $Q_{M}$
. It follows that the flow is independent of time
$Q_{M}$
. It follows that the flow is independent of time
![]() $t$
and the downstream coordinate
$t$
and the downstream coordinate
![]() $x$
. In the central channel the depth-averaged mass balance (2.2) then reduces to
$x$
. In the central channel the depth-averaged mass balance (2.2) then reduces to
which is subject to a condition of no flow across the levee–channel interfaces,
Integrating (3.1) directly, it follows that for non-trivial solutions, in which
![]() $h\neq 0$
, the depth-averaged lateral velocity is zero everywhere, i.e.
$h\neq 0$
, the depth-averaged lateral velocity is zero everywhere, i.e.
![]() $\bar{v}=0$
for all
$\bar{v}=0$
for all
![]() $y$
. In flowing regions (
$y$
. In flowing regions (
![]() $\bar{u}\neq 0$
), the cross-slope component of the momentum balance (2.4) then implies that the depth-averaged pressure is constant across the channel
$\bar{u}\neq 0$
), the cross-slope component of the momentum balance (2.4) then implies that the depth-averaged pressure is constant across the channel
This can be integrated to show that the flow thickness is constant
where the constant
![]() $H$
is, as yet, unknown. The downslope component of the depth-averaged momentum balance (2.3) then reduces to
$H$
is, as yet, unknown. The downslope component of the depth-averaged momentum balance (2.3) then reduces to
where
![]() $\bar{u}$
is assumed to be strictly positive. This is a second order autonomous ordinary differential equation (ODE) for the downslope velocity profile
$\bar{u}$
is assumed to be strictly positive. This is a second order autonomous ordinary differential equation (ODE) for the downslope velocity profile
![]() $\bar{u}(y)$
across the central flowing channel. Motivated by experimental observations of Félix & Thomas (Reference Félix and Thomas2004) (see their inset image in figure 4), Deboeuf et al. (Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006) (see their figure 2) and Takagi et al. (Reference Takagi, McElwaine and Huppert2011) (see their figure 5), it is assumed that there is no slip
$\bar{u}(y)$
across the central flowing channel. Motivated by experimental observations of Félix & Thomas (Reference Félix and Thomas2004) (see their inset image in figure 4), Deboeuf et al. (Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006) (see their figure 2) and Takagi et al. (Reference Takagi, McElwaine and Huppert2011) (see their figure 5), it is assumed that there is no slip
and no lateral shear stress
at both channel–levee interfaces. In the fully developed steady state, the mass flux of grains entering the chute is equal to the mass flux flowing down the central channel at any downstream location. Hence,
![]() $\bar{u}(y)$
is subject to the integral constraint
$\bar{u}(y)$
is subject to the integral constraint
The thickness
![]() $H$
, width
$H$
, width
![]() $W$
and the depth-averaged downslope velocity
$W$
and the depth-averaged downslope velocity
![]() $\bar{u}(y)$
across the flowing channel, are direct predictions of the model (3.5)–(3.8). To visualise the solution for the entire flow including the levees, two additional assumptions can be made, which are described in appendices A and B. The first assumption is of a constant velocity profile through the depth of the flow, which allows the downslope velocity
$\bar{u}(y)$
across the flowing channel, are direct predictions of the model (3.5)–(3.8). To visualise the solution for the entire flow including the levees, two additional assumptions can be made, which are described in appendices A and B. The first assumption is of a constant velocity profile through the depth of the flow, which allows the downslope velocity
![]() $u(y,z)$
to be reconstructed from the depth averaged downslope velocity
$u(y,z)$
to be reconstructed from the depth averaged downslope velocity
![]() $\bar{u}(y)$
. The second assumption is that the static levees are everywhere on the brink of yield (Hulme Reference Hulme1974; Balmforth, Burbidge & Craster Reference Balmforth, Burbidge and Craster2001), which allows the thickness profile of the static levee to be computed. These assumptions are not intrinsic to the model, but extend its predictions to allow comparison with experimental measurements of the surface velocity and the combined width of the flow and levees, respectively.
$\bar{u}(y)$
. The second assumption is that the static levees are everywhere on the brink of yield (Hulme Reference Hulme1974; Balmforth, Burbidge & Craster Reference Balmforth, Burbidge and Craster2001), which allows the thickness profile of the static levee to be computed. These assumptions are not intrinsic to the model, but extend its predictions to allow comparison with experimental measurements of the surface velocity and the combined width of the flow and levees, respectively.
3.2 Inviscid solutions
In the inviscid case, the coefficient
![]() $\unicode[STIX]{x1D708}=0$
and the steady-state equation of motion (3.5) reduces from a second-order ODE to an algebraic balance between friction and gravity only,
$\unicode[STIX]{x1D708}=0$
and the steady-state equation of motion (3.5) reduces from a second-order ODE to an algebraic balance between friction and gravity only,
![]() $\unicode[STIX]{x1D707}_{b}=\tan \unicode[STIX]{x1D701}$
. This reduction in order is indicative of a singular perturbation problem in which, as is the case here, the inviscid
$\unicode[STIX]{x1D707}_{b}=\tan \unicode[STIX]{x1D701}$
. This reduction in order is indicative of a singular perturbation problem in which, as is the case here, the inviscid
![]() $\unicode[STIX]{x1D708}=0$
model differs qualitatively from the model with any non-zero viscosity
$\unicode[STIX]{x1D708}=0$
model differs qualitatively from the model with any non-zero viscosity
![]() $\unicode[STIX]{x1D708}>0$
. Since the thickness
$\unicode[STIX]{x1D708}>0$
. Since the thickness
![]() $H$
is constant across the channel, solving
$H$
is constant across the channel, solving
![]() $\unicode[STIX]{x1D707}_{b}(H,\bar{u})=\tan \unicode[STIX]{x1D701}$
with
$\unicode[STIX]{x1D707}_{b}(H,\bar{u})=\tan \unicode[STIX]{x1D701}$
with
![]() $\unicode[STIX]{x1D707}_{b}$
in the dynamic regime (3.4) gives a constant velocity
$\unicode[STIX]{x1D707}_{b}$
in the dynamic regime (3.4) gives a constant velocity
across the channel, where
and the thickness
![]() $H$
is still a free parameter. The reduction of order in the inviscid system means that both tangential velocity boundary conditions (3.6) and (3.7) must be relaxed. Instead, since the material in the central channel moves at constant speed
$H$
is still a free parameter. The reduction of order in the inviscid system means that both tangential velocity boundary conditions (3.6) and (3.7) must be relaxed. Instead, since the material in the central channel moves at constant speed
![]() $\bar{u}_{steady}$
and the grains in the levee are static, there will be contact discontinuities at the levee–channel boundaries
$\bar{u}_{steady}$
and the grains in the levee are static, there will be contact discontinuities at the levee–channel boundaries
![]() $y=\pm W/2$
(i.e. jumps in the downslope velocity parallel to the margins, see e.g. Chadwick Reference Chadwick1976) as shown in figure 7. This is not what is observed in experiment (Félix & Thomas Reference Félix and Thomas2004; Deboeuf et al.
Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006; Takagi et al.
Reference Takagi, McElwaine and Huppert2011), where there are smoothly varying velocity profiles across the channel, rather than frictionless surfaces sliding past one another.
$y=\pm W/2$
(i.e. jumps in the downslope velocity parallel to the margins, see e.g. Chadwick Reference Chadwick1976) as shown in figure 7. This is not what is observed in experiment (Félix & Thomas Reference Félix and Thomas2004; Deboeuf et al.
Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006; Takagi et al.
Reference Takagi, McElwaine and Huppert2011), where there are smoothly varying velocity profiles across the channel, rather than frictionless surfaces sliding past one another.

Figure 7. Steady-state downstream inviscid velocity profile
![]() $u(y,z)$
for a self-channelised flow of glass beads at an angle
$u(y,z)$
for a self-channelised flow of glass beads at an angle
![]() $\unicode[STIX]{x1D701}=25^{\circ }$
, mass flux
$\unicode[STIX]{x1D701}=25^{\circ }$
, mass flux
![]() $Q_{M}=12~\text{g}~\text{s}^{-1}$
and the parameters for glass beads in table 1. The velocity is reconstructed using an exponential velocity profile defined in (A 2) with
$Q_{M}=12~\text{g}~\text{s}^{-1}$
and the parameters for glass beads in table 1. The velocity is reconstructed using an exponential velocity profile defined in (A 2) with
![]() $\unicode[STIX]{x1D706}=2.05$
. This is appropriate for thin flows close to
$\unicode[STIX]{x1D706}=2.05$
. This is appropriate for thin flows close to
![]() $h_{\ast }$
, which feel the non-local effect of the base. There are an infinite number of solutions for
$h_{\ast }$
, which feel the non-local effect of the base. There are an infinite number of solutions for
![]() $H\in [h_{\ast },h_{start}]$
. The thinnest and widest flowing channel is obtained when (a)
$H\in [h_{\ast },h_{start}]$
. The thinnest and widest flowing channel is obtained when (a)
![]() $H=h_{\ast }$
, whilst the deepest and narrowest is recovered for (c)
$H=h_{\ast }$
, whilst the deepest and narrowest is recovered for (c)
![]() $H=h_{start}$
. The minimal static levees required to hold up the central channel are also shown (see appendix B). The narrowest levees occur at
$H=h_{start}$
. The minimal static levees required to hold up the central channel are also shown (see appendix B). The narrowest levees occur at
![]() $H=h_{\ast }$
, while the widest levees occur at
$H=h_{\ast }$
, while the widest levees occur at
![]() $H=h_{start}$
. As a result, the total width of the channel is not a monotonically increasing function of the channel height
$H=h_{start}$
. As a result, the total width of the channel is not a monotonically increasing function of the channel height
![]() $H$
, i.e. the total channel width in panel (b) is narrower than the end members in panels (a,c).
$H$
, i.e. the total channel width in panel (b) is narrower than the end members in panels (a,c).
Assuming that there is a single channel, the integral constraint (3.8) together with the velocity field (3.9) provide one equation expressing the flowing channel width
![]() $W$
as a function of the thickness
$W$
as a function of the thickness
![]() $H$
,
$H$
,
With no further boundary conditions imposed in the inviscid model, there is no equation to determine the thickness
![]() $H$
. The only additional constraint on the inviscid solution is that the depth-averaged pressure across the contact discontinuities must be equal (Chadwick Reference Chadwick1976), i.e. the depth-averaged pressure in the levee is just sufficient to balance the depth-averaged pressure in the central channel at
$H$
. The only additional constraint on the inviscid solution is that the depth-averaged pressure across the contact discontinuities must be equal (Chadwick Reference Chadwick1976), i.e. the depth-averaged pressure in the levee is just sufficient to balance the depth-averaged pressure in the central channel at
![]() $y=\pm W/2$
. This is equivalent to the condition that the thickness must be continuous across the contact discontinuities. Since static and moving grains must coexist for the same thickness, it follows that
$y=\pm W/2$
. This is equivalent to the condition that the thickness must be continuous across the contact discontinuities. Since static and moving grains must coexist for the same thickness, it follows that
![]() $H$
must lie in the metastable range
$H$
must lie in the metastable range
![]() $h_{\ast }\leqslant H\leqslant h_{start}$
. These inequalities are not sufficient, however, to determine
$h_{\ast }\leqslant H\leqslant h_{start}$
. These inequalities are not sufficient, however, to determine
![]() $H$
uniquely, and hence (3.9) and (3.11) do not determine
$H$
uniquely, and hence (3.9) and (3.11) do not determine
![]() $\bar{u}(H)$
and
$\bar{u}(H)$
and
![]() $W(H)$
uniquely either.
$W(H)$
uniquely either.
For a given mass flux
![]() $Q_{M}$
, the inviscid avalanche model has an infinite set of solutions that are parameterised by the
$Q_{M}$
, the inviscid avalanche model has an infinite set of solutions that are parameterised by the
![]() $H\in [h_{\ast },h_{start}]$
. Figure 7 shows three cases for
$H\in [h_{\ast },h_{start}]$
. Figure 7 shows three cases for
![]() $Q_{M}=12~\text{g}~\text{s}^{-1}$
and a slope angle
$Q_{M}=12~\text{g}~\text{s}^{-1}$
and a slope angle
![]() $\unicode[STIX]{x1D701}=25^{\circ }$
using the parameters for glass beads from table 1. The widest and slowest moving central channel (
$\unicode[STIX]{x1D701}=25^{\circ }$
using the parameters for glass beads from table 1. The widest and slowest moving central channel (
![]() $W=9.42$
cm,
$W=9.42$
cm,
![]() $\bar{u}_{steady}=2.93~\text{cm}~\text{s}^{-1}$
) occurs when
$\bar{u}_{steady}=2.93~\text{cm}~\text{s}^{-1}$
) occurs when
![]() $H=h_{\ast }=2.9$
mm, while the narrowest and fastest moving flow (
$H=h_{\ast }=2.9$
mm, while the narrowest and fastest moving flow (
![]() $W=5.73$
cm,
$W=5.73$
cm,
![]() $\bar{u}_{steady}=3.94~\text{cm}~\text{s}^{-1}$
) is obtained when
$\bar{u}_{steady}=3.94~\text{cm}~\text{s}^{-1}$
) is obtained when
![]() $h=h_{start}=3.54$
mm. It follows, that even a relatively modest range of thicknesses (
$h=h_{start}=3.54$
mm. It follows, that even a relatively modest range of thicknesses (
![]() $H\in [2.9,3.54]$
mm) can lead to a substantial range of channel widths. In this case the widest flowing channel is 1.64 times wider than the narrowest. Interestingly, the total width, including the minimal static levees on either side of the central flowing channel, is almost the same for both cases (i.e.
$H\in [2.9,3.54]$
mm) can lead to a substantial range of channel widths. In this case the widest flowing channel is 1.64 times wider than the narrowest. Interestingly, the total width, including the minimal static levees on either side of the central flowing channel, is almost the same for both cases (i.e.
![]() $W_{total}(h_{\ast })=12.61$
cm,
$W_{total}(h_{\ast })=12.61$
cm,
![]() $W_{total}(h_{start})=12.14$
cm) as shown in figure 7(a,c). The relative insensitivity of the total channel width arises because the static levees need to be much wider to support the central flowing channel as its thickness approaches
$W_{total}(h_{start})=12.14$
cm) as shown in figure 7(a,c). The relative insensitivity of the total channel width arises because the static levees need to be much wider to support the central flowing channel as its thickness approaches
![]() $h_{start}$
. This is due to the fact that
$h_{start}$
. This is due to the fact that
![]() $\text{d}h/\text{d}y\rightarrow 0$
in (B 4) as
$\text{d}h/\text{d}y\rightarrow 0$
in (B 4) as
![]() $h\rightarrow h_{start}$
, i.e. the levee becomes less stable (in the sense that it finds it harder to support thickness gradients) as the thickness approaches
$h\rightarrow h_{start}$
, i.e. the levee becomes less stable (in the sense that it finds it harder to support thickness gradients) as the thickness approaches
![]() $h_{start}$
. Note that the total width of the channel is a non-monotonic function of
$h_{start}$
. Note that the total width of the channel is a non-monotonic function of
![]() $H$
, since
$H$
, since
![]() $W_{total}=11.27$
cm when
$W_{total}=11.27$
cm when
![]() $H=0.5(h_{\ast }+h_{start})$
as shown in figure 7(b).
$H=0.5(h_{\ast }+h_{start})$
as shown in figure 7(b).
A prime example of a physical system that has an infinite number of steady states are the static levees. As shown in figure 4, these can have arbitrary free-surface shapes that are dependent on the history of the flow that emplaced them. Having an infinite number of steady states for the inviscid flowing channel is not, however, physically realistic, because there is strong experimental evidence (Félix & Thomas Reference Félix and Thomas2004; Deboeuf et al.
Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006; Takagi et al.
Reference Takagi, McElwaine and Huppert2011) that the thickness
![]() $H$
and width
$H$
and width
![]() $W$
are functions of the imposed mass flux
$W$
are functions of the imposed mass flux
![]() $Q_{M}$
. Since the model is not able to uniquely determine the central channel thickness
$Q_{M}$
. Since the model is not able to uniquely determine the central channel thickness
![]() $H$
, and therefore (3.9) and (3.11) cannot be used to calculate
$H$
, and therefore (3.9) and (3.11) cannot be used to calculate
![]() $W(H)$
and
$W(H)$
and
![]() $\bar{u}(H)$
uniquely either, the inviscid theory is missing an important physical mechanism for selecting the channel thickness, width and velocity profile.
$\bar{u}(H)$
uniquely either, the inviscid theory is missing an important physical mechanism for selecting the channel thickness, width and velocity profile.
3.3 Viscous solutions for the central flowing channel
A solution to the steady-state equation of motion (3.5) will now be constructed that includes the effects of lateral viscous stresses. The system to be solved comprises of the second-order ODE (3.5) with two unknown parameters
![]() $H$
and
$H$
and
![]() $W$
. Four boundary conditions are therefore required to close the system. These are provided by the boundary conditions at the levee–channel interface (3.6) and (3.7) (which, due to the symmetry of the solutions as
$W$
. Four boundary conditions are therefore required to close the system. These are provided by the boundary conditions at the levee–channel interface (3.6) and (3.7) (which, due to the symmetry of the solutions as
![]() $y\rightarrow -y$
, provide three independent conditions) and by the integral mass flux condition (3.8). The boundary value problem, associated boundary conditions and the flux constraint therefore provide a closed system of equations, which determines the thickness, width, and velocity profile of a self-channelised flow.
$y\rightarrow -y$
, provide three independent conditions) and by the integral mass flux condition (3.8). The boundary value problem, associated boundary conditions and the flux constraint therefore provide a closed system of equations, which determines the thickness, width, and velocity profile of a self-channelised flow.
Much of the solution can be obtained algebraically if the problem is written in terms of the flow thickness
![]() $H$
, and the mass flux
$H$
, and the mass flux
![]() $Q_{M}$
is obtained as a function of
$Q_{M}$
is obtained as a function of
![]() $H$
using (3.8). This relationship
$H$
using (3.8). This relationship
![]() $Q_{M}(H)$
can then be inverted to numerically solve for the thickness at a specified mass flux. The symmetry implies that it is sufficient to solve the problem in the half-domain
$Q_{M}(H)$
can then be inverted to numerically solve for the thickness at a specified mass flux. The symmetry implies that it is sufficient to solve the problem in the half-domain
![]() $y\in [-W/2,0]$
and it is therefore convenient to define a new coordinate system that is centred at the levee–channel interface
$y\in [-W/2,0]$
and it is therefore convenient to define a new coordinate system that is centred at the levee–channel interface
Immediately adjacent to the levees there is a slowly moving region that lies in the intermediate frictional regime. Recalling that
![]() $\unicode[STIX]{x1D705}=1$
, the transformed ODE (3.5) with the intermediate friction law (2.12) takes a particularly simple form,
$\unicode[STIX]{x1D705}=1$
, the transformed ODE (3.5) with the intermediate friction law (2.12) takes a particularly simple form,
where the coefficients are thickness dependent,
Solving (3.13) subject to the boundary conditions (3.6) and (3.7) it follows that
in the slowly moving layer adjacent to the levee. If the Froude number
![]() $Fr<\unicode[STIX]{x1D6FD}_{\ast }$
everywhere in the channel, the solution (3.16) is valid everywhere and the channel width is equal to one period of the cosine function, i.e.
$Fr<\unicode[STIX]{x1D6FD}_{\ast }$
everywhere in the channel, the solution (3.16) is valid everywhere and the channel width is equal to one period of the cosine function, i.e.
![]() $W=2\unicode[STIX]{x03C0}/\sqrt{a}$
. These solutions are, however, not the ones that are observed physically.
$W=2\unicode[STIX]{x03C0}/\sqrt{a}$
. These solutions are, however, not the ones that are observed physically.
Instead, the velocity increases until
![]() $Fr=\unicode[STIX]{x1D6FD}_{\ast }$
and then the flow transitions across to the dynamic frictional regime. From the definition of the friction law (2.7) and the Froude number (2.8), it follows that this occurs when
$Fr=\unicode[STIX]{x1D6FD}_{\ast }$
and then the flow transitions across to the dynamic frictional regime. From the definition of the friction law (2.7) and the Froude number (2.8), it follows that this occurs when
![]() $\bar{u}$
is equal to a transition velocity
$\bar{u}$
is equal to a transition velocity
From (3.16) this transition occurs when
and, from (3.16)–(3.18), the velocity gradient at this point is
These transition points are shown with yellow filled circles in the phase plane and physical space in figure 8 and lie at a local minimum in the friction. Equations (3.17)–(3.19) determine the interfacial boundary conditions for the dynamic problem in the centre of the channel for
![]() ${\hat{y}}\geqslant {\hat{y}}_{transition}$
. The green circular markers in figure 8 show where the magnitude of the shear rate is maximum and the curvature of the solutions in physical space changes sign. This lies in the intermediate friction regime, so the solution (3.16) is vital to smoothly connect the interior solution with zero velocity gradient at the levee–channel interfaces.
${\hat{y}}\geqslant {\hat{y}}_{transition}$
. The green circular markers in figure 8 show where the magnitude of the shear rate is maximum and the curvature of the solutions in physical space changes sign. This lies in the intermediate friction regime, so the solution (3.16) is vital to smoothly connect the interior solution with zero velocity gradient at the levee–channel interfaces.

Figure 8. Schematic diagram of the velocity solutions in (a) the phase plane, and (b) physical space using the parameters for sand in table 1. A typical solution is shown by the blue curve for
![]() $H=8.2$
mm (
$H=8.2$
mm (
![]() $Q_{M}=9.6~\text{g}~\text{s}^{-1}$
) which forms a closed orbit in phase space. The yellow circular markers on this line indicate the transition between the intermediate and dynamic frictional regimes. The green markers, which lie in the intermediate frictional regime, show where the velocity gradient is a maximum/minimum and the curvature of the velocity profile changes sign. The red marker lies in the dynamic regime and is where the maximum velocity is reached in the centre of the channel. Solutions only exist for
$Q_{M}=9.6~\text{g}~\text{s}^{-1}$
) which forms a closed orbit in phase space. The yellow circular markers on this line indicate the transition between the intermediate and dynamic frictional regimes. The green markers, which lie in the intermediate frictional regime, show where the velocity gradient is a maximum/minimum and the curvature of the velocity profile changes sign. The red marker lies in the dynamic regime and is where the maximum velocity is reached in the centre of the channel. Solutions only exist for
![]() $H\in [H_{min},H_{max}]$
and these limiting cases are shown with the green and black dashed lines, respectively. The light blue point corresponds to where the velocity in the centre of the flow is equal to the steady uniform value
$H\in [H_{min},H_{max}]$
and these limiting cases are shown with the green and black dashed lines, respectively. The light blue point corresponds to where the velocity in the centre of the flow is equal to the steady uniform value
![]() $\bar{u}_{steady}$
and the channel is infinitely wide, while the yellow marker on the dashed black curve shows the case when
$\bar{u}_{steady}$
and the channel is infinitely wide, while the yellow marker on the dashed black curve shows the case when
![]() $\bar{u}_{centre}=\bar{u}_{transition}$
. The purple curve shows another solution for
$\bar{u}_{centre}=\bar{u}_{transition}$
. The purple curve shows another solution for
![]() $H=7.92$
mm (
$H=7.92$
mm (
![]() $Q_{M}=28.4~\text{g}~\text{s}^{-1}$
), which produces a wider flow with higher velocities even though it is thinner than the blue solution. The blue dotted line shows the maximum attainable steady uniform velocity
$Q_{M}=28.4~\text{g}~\text{s}^{-1}$
), which produces a wider flow with higher velocities even though it is thinner than the blue solution. The blue dotted line shows the maximum attainable steady uniform velocity
![]() $\bar{u}_{steady}(H_{min})$
.
$\bar{u}_{steady}(H_{min})$
.
The ODE for the dynamic regime is determined by substituting (2.10) into (3.5) and applying the coordinate transformation (3.12) to give
where
![]() $\bar{u}_{steady}$
is the steady uniform flow velocity defined in (3.9),
$\bar{u}_{steady}$
is the steady uniform flow velocity defined in (3.9),
Since
![]() $H$
is constant,
$H$
is constant,
![]() $\bar{u}_{steady}$
,
$\bar{u}_{steady}$
,
![]() $c$
and
$c$
and
![]() $d$
are constant, and hence (3.20) is an autonomous second-order ODE that can be solved by making the substitution
$d$
are constant, and hence (3.20) is an autonomous second-order ODE that can be solved by making the substitution
![]() $p=\text{d}\bar{u}/\text{d}{\hat{y}}$
and using the chain rule to give
$p=\text{d}\bar{u}/\text{d}{\hat{y}}$
and using the chain rule to give
Integrating (3.22) subject to the boundary conditions that
![]() $\bar{u}=\bar{u}_{centre}$
and
$\bar{u}=\bar{u}_{centre}$
and
![]() $p=\text{d}\bar{u}/\text{d}{\hat{y}}=0$
on the symmetry line, and taking the positive root, implies that
$p=\text{d}\bar{u}/\text{d}{\hat{y}}=0$
on the symmetry line, and taking the positive root, implies that
Evaluating (3.23) at the transition
![]() ${\hat{y}}={\hat{y}}_{transition}$
yields an implicit equation for the centreline velocity
${\hat{y}}={\hat{y}}_{transition}$
yields an implicit equation for the centreline velocity
![]() $\bar{u}_{centre}$
,
$\bar{u}_{centre}$
,
where
![]() $a$
,
$a$
,
![]() $b$
,
$b$
,
![]() $c$
,
$c$
,
![]() $d$
,
$d$
,
![]() $\bar{u}_{transition}$
,
$\bar{u}_{transition}$
,
![]() $\text{d}\bar{u}/\text{d}{\hat{y}}|_{{\hat{y}}_{transition}}$
and
$\text{d}\bar{u}/\text{d}{\hat{y}}|_{{\hat{y}}_{transition}}$
and
![]() $\bar{u}_{steady}$
are all functions of
$\bar{u}_{steady}$
are all functions of
![]() $H$
, given by (3.14), (3.15), (3.21), (3.17), (3.19) and (3.9).
$H$
, given by (3.14), (3.15), (3.21), (3.17), (3.19) and (3.9).
Valid solutions are only found for certain values of
![]() $\bar{u}_{centre}$
, and since the centreline velocity is a function of the thickness, there should be a range of possible values for
$\bar{u}_{centre}$
, and since the centreline velocity is a function of the thickness, there should be a range of possible values for
![]() $H$
. In fact, it is observed that in order to obtain a self-channelised solution the thickness is limited to a finite interval, i.e.
$H$
. In fact, it is observed that in order to obtain a self-channelised solution the thickness is limited to a finite interval, i.e.
![]() $H\in [H_{min},H_{max}]$
. The first boundary can be found by assuming that the central steady flow is at the transition between dynamic and intermediate friction, i.e. that the centreline velocity
$H\in [H_{min},H_{max}]$
. The first boundary can be found by assuming that the central steady flow is at the transition between dynamic and intermediate friction, i.e. that the centreline velocity
![]() $\bar{u}_{centre}=\bar{u}_{transition}$
. In this case, the right-hand side of (3.24) is zero, so
$\bar{u}_{centre}=\bar{u}_{transition}$
. In this case, the right-hand side of (3.24) is zero, so
![]() $\text{d}\bar{u}/\text{d}{\hat{y}}|_{{\hat{y}}_{transition}}=0$
. Using (3.19) it follows that
$\text{d}\bar{u}/\text{d}{\hat{y}}|_{{\hat{y}}_{transition}}=0$
. Using (3.19) it follows that
![]() $\bar{u}_{transition}(H)=2b(H)/a(H)$
, which can be solved to determine an upper bound for
$\bar{u}_{transition}(H)=2b(H)/a(H)$
, which can be solved to determine an upper bound for
![]() $H\leqslant H_{max}(\unicode[STIX]{x1D701})$
. The second limit,
$H\leqslant H_{max}(\unicode[STIX]{x1D701})$
. The second limit,
![]() $H_{min}$
, is found by noticing that
$H_{min}$
, is found by noticing that
![]() $\bar{u}_{centre}$
is a decreasing function of
$\bar{u}_{centre}$
is a decreasing function of
![]() $H$
, and that there is a value of the thickness, for which the self-channelised orbit in the phase space becomes homoclinic. For this value of
$H$
, and that there is a value of the thickness, for which the self-channelised orbit in the phase space becomes homoclinic. For this value of
![]() $H$
trajectories starting at the origin of the phase plane go directly to the saddle point given by the equilibrium point between dynamic friction and gravity (dashed green line in figure 8
a). Hence, the lower boundary
$H$
trajectories starting at the origin of the phase plane go directly to the saddle point given by the equilibrium point between dynamic friction and gravity (dashed green line in figure 8
a). Hence, the lower boundary
![]() $H_{min}(\unicode[STIX]{x1D701})$
is determined by setting
$H_{min}(\unicode[STIX]{x1D701})$
is determined by setting
![]() $\bar{u}_{centre}=\bar{u}_{steady}$
in (3.24). For the friction-law parameters and slope angle calibrated to the experiments of Takagi et al. (Reference Takagi, McElwaine and Huppert2011) (table 1),
$\bar{u}_{centre}=\bar{u}_{steady}$
in (3.24). For the friction-law parameters and slope angle calibrated to the experiments of Takagi et al. (Reference Takagi, McElwaine and Huppert2011) (table 1),
![]() $H_{min}\approx 7.9$
mm and
$H_{min}\approx 7.9$
mm and
![]() $H_{max}\approx 9.2$
mm, which are significantly deeper than both
$H_{max}\approx 9.2$
mm, which are significantly deeper than both
![]() $h_{stop}\approx 5$
mm and
$h_{stop}\approx 5$
mm and
![]() $h_{\ast }\approx 6.7$
mm. On the other hand, for the glass beads parameters (Félix & Thomas Reference Félix and Thomas2004; Mangeney et al.
Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) (table 1) the range is much narrower,
$h_{\ast }\approx 6.7$
mm. On the other hand, for the glass beads parameters (Félix & Thomas Reference Félix and Thomas2004; Mangeney et al.
Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) (table 1) the range is much narrower,
![]() $H_{min}\approx 3.152$
mm and
$H_{min}\approx 3.152$
mm and
![]() $H_{max}\approx 3.166$
mm, but, nonetheless, is still deeper than
$H_{max}\approx 3.166$
mm, but, nonetheless, is still deeper than
![]() $h_{stop}\approx 2.16$
mm and
$h_{stop}\approx 2.16$
mm and
![]() $h_{\ast }\approx 2.9$
mm.
$h_{\ast }\approx 2.9$
mm.
By choosing
![]() $H\in [H_{min},H_{max}]$
a solution to (3.24) for the centreline velocity
$H\in [H_{min},H_{max}]$
a solution to (3.24) for the centreline velocity
![]() $\bar{u}_{centre}$
is guaranteed to exist and can be found by numerical root finding techniques. Once this is given, the separable ODE (3.23) can then be solved by quadrature, i.e.
$\bar{u}_{centre}$
is guaranteed to exist and can be found by numerical root finding techniques. Once this is given, the separable ODE (3.23) can then be solved by quadrature, i.e.
 $$\begin{eqnarray}{\hat{y}}={\hat{y}}_{transition}+\int _{\bar{u}_{transition}}^{\bar{u}}\frac{c}{\sqrt{2(c\bar{u}_{steady}+d)\ln \left(\displaystyle \frac{c\bar{u}_{centre}+d}{c\bar{u}^{\prime }+d}\right)-2c(\bar{u}_{centre}-\bar{u}^{\prime })}}\,\text{d}\bar{u}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}{\hat{y}}={\hat{y}}_{transition}+\int _{\bar{u}_{transition}}^{\bar{u}}\frac{c}{\sqrt{2(c\bar{u}_{steady}+d)\ln \left(\displaystyle \frac{c\bar{u}_{centre}+d}{c\bar{u}^{\prime }+d}\right)-2c(\bar{u}_{centre}-\bar{u}^{\prime })}}\,\text{d}\bar{u}^{\prime }.\end{eqnarray}$$
By construction the velocity gradient in (3.23) is zero when
![]() $\bar{u}=\bar{u}_{centre}$
, so it follows that the integrand in (3.25) is singular as
$\bar{u}=\bar{u}_{centre}$
, so it follows that the integrand in (3.25) is singular as
![]() $\bar{u}\rightarrow \bar{u}_{centre}$
. However, as
$\bar{u}\rightarrow \bar{u}_{centre}$
. However, as
![]() $\bar{u}_{centre}\rightarrow \bar{u}_{steady}$
there is a large central region of the flow where the downslope velocity profile is flat and the integral (3.25) is difficult to evaluate. It is therefore useful to linearise the right-hand side of (3.23) about
$\bar{u}_{centre}\rightarrow \bar{u}_{steady}$
there is a large central region of the flow where the downslope velocity profile is flat and the integral (3.25) is difficult to evaluate. It is therefore useful to linearise the right-hand side of (3.23) about
![]() $\bar{u}=\bar{u}_{steady}$
and then solve to obtain the approximate solution
$\bar{u}=\bar{u}_{steady}$
and then solve to obtain the approximate solution
By integrating (3.25) to
![]() $\bar{u}=\bar{u}_{centre}(1-\unicode[STIX]{x1D700})$
, where
$\bar{u}=\bar{u}_{centre}(1-\unicode[STIX]{x1D700})$
, where
![]() $\unicode[STIX]{x1D700}\ll 1$
, and then using the approximation (3.26) it is possible to accurately determine the solution close to
$\unicode[STIX]{x1D700}\ll 1$
, and then using the approximation (3.26) it is possible to accurately determine the solution close to
![]() $\bar{u}_{steady}$
and hence the half-width of the channel
$\bar{u}_{steady}$
and hence the half-width of the channel
![]() ${\hat{y}}_{centre}=W/2$
. The solutions for the velocity profile and channel width
${\hat{y}}_{centre}=W/2$
. The solutions for the velocity profile and channel width
![]() $W$
are shown in figure 8(b) for a range of flow thicknesses
$W$
are shown in figure 8(b) for a range of flow thicknesses
![]() $H$
. This relationship is inverted numerically to find the solution corresponding to a given mass flux
$H$
. This relationship is inverted numerically to find the solution corresponding to a given mass flux
![]() $Q_{M}$
. For a fixed slope angle, flows with larger mass flux are wider and faster moving (but, somewhat counter-intuitively, are thinner) than those with a smaller mass flux.
$Q_{M}$
. For a fixed slope angle, flows with larger mass flux are wider and faster moving (but, somewhat counter-intuitively, are thinner) than those with a smaller mass flux.
3.4 Shear-band structure adjacent to the levees
The physical mechanism that prevents erosion of the levees is the granular viscosity, since it allows steady-state solutions to be constructed that do not exert any shear stress on the inside of the levee walls, even though material is flowing down the central channel. It is therefore of interest to understand the boundary layer structure that allows this.

Figure 9. (a) Phase space (b) downslope velocity profiles across the central flowing channel, and (c) downslope velocity profiles centred on the levee–channel interface for mass fluxes
![]() $Q_{M}=50$
, 100, 150, 200 and
$Q_{M}=50$
, 100, 150, 200 and
![]() $250~\text{g}~\text{s}^{-1}$
. In (a) the filled blue circle is the position of the centre and the open blue circle is the saddle point for the case of
$250~\text{g}~\text{s}^{-1}$
. In (a) the filled blue circle is the position of the centre and the open blue circle is the saddle point for the case of
![]() $Q_{M}=250~\text{g}~\text{s}^{-1}$
, although these points are almost the same for all the fluxes. The inset graph shows a close up of the solutions close to the saddle. The pink shaded region in panel (c) is the width of the inner boundary layer
$Q_{M}=250~\text{g}~\text{s}^{-1}$
, although these points are almost the same for all the fluxes. The inset graph shows a close up of the solutions close to the saddle. The pink shaded region in panel (c) is the width of the inner boundary layer
![]() $W_{inner}$
and the green shaded region is the width of the outer boundary layer
$W_{inner}$
and the green shaded region is the width of the outer boundary layer
![]() $W_{outer}$
. (d) Non-dimensional forces are plotted as a function of the levee-centred cross-slope direction for
$W_{outer}$
. (d) Non-dimensional forces are plotted as a function of the levee-centred cross-slope direction for
![]() $Q_{M}=150~\text{g}~\text{s}^{-1}$
. All the forces are rescaled by the downslope component of the gravitational force
$Q_{M}=150~\text{g}~\text{s}^{-1}$
. All the forces are rescaled by the downslope component of the gravitational force
![]() $\unicode[STIX]{x1D70C}gH\sin \unicode[STIX]{x1D701}$
. The magenta solid line represents the net force due to gravity and friction, whilst the blue line is the non-dimensional viscous force. Dot-dashed lines represent the maximum static friction.
$\unicode[STIX]{x1D70C}gH\sin \unicode[STIX]{x1D701}$
. The magenta solid line represents the net force due to gravity and friction, whilst the blue line is the non-dimensional viscous force. Dot-dashed lines represent the maximum static friction.
For sufficiently large mass flux the thickness
![]() $H$
is almost equal to
$H$
is almost equal to
![]() $H_{min}$
and hence the constants
$H_{min}$
and hence the constants
![]() $a(H)$
,
$a(H)$
,
![]() $b(H)$
,
$b(H)$
,
![]() $c(H)$
,
$c(H)$
,
![]() $d(H)$
and
$d(H)$
and
![]() $\bar{u}_{steady}(H)$
barely change in the ODEs (3.13) and (3.20). As a result, the position of the centre at
$\bar{u}_{steady}(H)$
barely change in the ODEs (3.13) and (3.20). As a result, the position of the centre at
![]() $\bar{u}=b/a$
and the saddle point at
$\bar{u}=b/a$
and the saddle point at
![]() $\bar{u}=\bar{u}_{steady}$
(see e.g. Strogatz Reference Strogatz1994) are almost independent of mass flux and the orbits in the phase plane lie almost on top of each other (figure 9
a), with a slight difference visible only close to the saddle point (figure 9
a inset). These small variations in phase space are more significant in physical space (figure 9
b). At
$\bar{u}=\bar{u}_{steady}$
(see e.g. Strogatz Reference Strogatz1994) are almost independent of mass flux and the orbits in the phase plane lie almost on top of each other (figure 9
a), with a slight difference visible only close to the saddle point (figure 9
a inset). These small variations in phase space are more significant in physical space (figure 9
b). At
![]() $Q_{M}=50~\text{g}~\text{s}^{-1}$
the solution has a rounded profile with the fastest velocity occurring in the centre of the channel. As the mass flux is increased, the centreline velocity approaches the steady uniform flow solution
$Q_{M}=50~\text{g}~\text{s}^{-1}$
the solution has a rounded profile with the fastest velocity occurring in the centre of the channel. As the mass flux is increased, the centreline velocity approaches the steady uniform flow solution
![]() $\bar{u}_{steady}$
and the velocity profile flattens, forming a central region of material of uniform thickness and approximately uniform depth-averaged velocity. As
$\bar{u}_{steady}$
and the velocity profile flattens, forming a central region of material of uniform thickness and approximately uniform depth-averaged velocity. As
![]() $H\rightarrow H_{min}$
the orbit becomes homoclinic, directly connecting the origin and the saddle point, and the period of the orbit, channel width
$H\rightarrow H_{min}$
the orbit becomes homoclinic, directly connecting the origin and the saddle point, and the period of the orbit, channel width
![]() $W$
and mass flux
$W$
and mass flux
![]() $Q_{M}$
all diverge. The centreline velocity
$Q_{M}$
all diverge. The centreline velocity
![]() $\bar{u}_{centre}$
tends to the steady uniform flow velocity
$\bar{u}_{centre}$
tends to the steady uniform flow velocity
![]() $\bar{u}_{steady}$
, given by (3.9). Equation (3.9) therefore defines an upper bound for the velocity in a self-channelised flow, as observed experimentally (Takagi et al.
Reference Takagi, McElwaine and Huppert2011). Close to this limit, an increase in mass flux primarily increases the channel width, with little effect on the flow thickness or speed. At constant mass flux, an increase in slope angle decreases the flow thickness (since
$\bar{u}_{steady}$
, given by (3.9). Equation (3.9) therefore defines an upper bound for the velocity in a self-channelised flow, as observed experimentally (Takagi et al.
Reference Takagi, McElwaine and Huppert2011). Close to this limit, an increase in mass flux primarily increases the channel width, with little effect on the flow thickness or speed. At constant mass flux, an increase in slope angle decreases the flow thickness (since
![]() $H_{min}(\unicode[STIX]{x1D701})$
is decreasing in
$H_{min}(\unicode[STIX]{x1D701})$
is decreasing in
![]() $\unicode[STIX]{x1D701}$
), which, counter-intuitively, decreases the flow velocity.
$\unicode[STIX]{x1D701}$
), which, counter-intuitively, decreases the flow velocity.
Away from the saddle point the orbits are almost identical, so the boundary layers at the sides of the flow collapse on top of one another when plotted in the levee-centred coordinate
![]() ${\hat{y}}$
(figure 9
c). These boundary layers have a shear-band structure (Pouliquen & Gutfraind Reference Pouliquen and Gutfraind1996; Fenistein & van Hecke Reference Fenistein and van Hecke2003; Schall & van Hecke Reference Schall and van Hecke2010) that seamlessly connects the static material in the levee with the central region. The boundary layer has two length scales associated with it: an inner boundary layer where the intermediate friction is active, and an outer layer that is in the dynamic friction regime. The exact intermediate solution (3.16) implies that the inner boundary layer is of width
${\hat{y}}$
(figure 9
c). These boundary layers have a shear-band structure (Pouliquen & Gutfraind Reference Pouliquen and Gutfraind1996; Fenistein & van Hecke Reference Fenistein and van Hecke2003; Schall & van Hecke Reference Schall and van Hecke2010) that seamlessly connects the static material in the levee with the central region. The boundary layer has two length scales associated with it: an inner boundary layer where the intermediate friction is active, and an outer layer that is in the dynamic friction regime. The exact intermediate solution (3.16) implies that the inner boundary layer is of width
while the approximate solution (3.26) suggests that the outer boundary layer has a typical width
For the parameters given in table 1 for sand, the inner boundary layer width
![]() $W_{inner}\approx y_{transition}(H_{min})=7.16$
mm, whilst the outer dynamic boundary layer is approximately 8.52 mm wide. These are shown by the pink and light green shaded regions in figure 9(c) and provide a good order of magnitude estimate for the boundary layer width.
$W_{inner}\approx y_{transition}(H_{min})=7.16$
mm, whilst the outer dynamic boundary layer is approximately 8.52 mm wide. These are shown by the pink and light green shaded regions in figure 9(c) and provide a good order of magnitude estimate for the boundary layer width.
The governing ODE (3.5) describes a balance between its three terms, the forces due to the slope-tangential component of gravity, basal friction and lateral viscous stress. Hysteresis in the basal friction results in two distinct force balances, depending on the local flow velocity. In figure 9(d) forces are plotted as a function of the levee-centred cross slope direction
![]() ${\hat{y}}$
. The magenta solid line represents the resultant force of gravity and friction, whilst the blue curve shows how viscous forces vary across the channel for
${\hat{y}}$
. The magenta solid line represents the resultant force of gravity and friction, whilst the blue curve shows how viscous forces vary across the channel for
![]() $Q_{M}=150~\text{g}~\text{s}^{-1}$
. All the forces are non-dimensionalised. Right next to the levees, where the flow is slow, the basal friction is greater than the downslope component of gravity, leading to an upslope resistive force. In this region, viscous stresses act in the downslope direction, balancing the friction and sustaining motion. As the velocity increases towards the centre, friction decreases and eventually is balanced by gravity at the intermediate equilibrium (the green circle in figure 9
c,d). Since this is an inflection point
$Q_{M}=150~\text{g}~\text{s}^{-1}$
. All the forces are non-dimensionalised. Right next to the levees, where the flow is slow, the basal friction is greater than the downslope component of gravity, leading to an upslope resistive force. In this region, viscous stresses act in the downslope direction, balancing the friction and sustaining motion. As the velocity increases towards the centre, friction decreases and eventually is balanced by gravity at the intermediate equilibrium (the green circle in figure 9
c,d). Since this is an inflection point
![]() $\text{d}^{2}\bar{u}/\text{d}y^{2}=0$
and viscous forces also vanish. In the faster flow away from the levee wall,
$\text{d}^{2}\bar{u}/\text{d}y^{2}=0$
and viscous forces also vanish. In the faster flow away from the levee wall,
![]() $\text{d}^{2}\bar{u}/\text{d}y^{2}<0$
and the viscous stress instead acts in the upslope direction, slowing the flow. In the absence of viscous stresses the flow in this region would accelerate to the steady uniform flow velocity
$\text{d}^{2}\bar{u}/\text{d}y^{2}<0$
and the viscous stress instead acts in the upslope direction, slowing the flow. In the absence of viscous stresses the flow in this region would accelerate to the steady uniform flow velocity
![]() $\bar{u}_{steady}$
(3.9). In the central region, where the profile flattens (
$\bar{u}_{steady}$
(3.9). In the central region, where the profile flattens (
![]() ${\hat{y}}>5$
cm), viscous contributions are extremely small and the flow is basically governed by the balance between gravity and friction explaining why the velocity approaches
${\hat{y}}>5$
cm), viscous contributions are extremely small and the flow is basically governed by the balance between gravity and friction explaining why the velocity approaches
![]() $\bar{u}_{steady}$
. Therefore, lateral viscous stresses provide the mechanism that connects the flow in these two regions and allow the interface between static and flowing granular layers to be modelled.
$\bar{u}_{steady}$
. Therefore, lateral viscous stresses provide the mechanism that connects the flow in these two regions and allow the interface between static and flowing granular layers to be modelled.
3.5 Comparison with experiments
The steady-state viscous theory is now compared with the experimental results of Takagi et al. (Reference Takagi, McElwaine and Huppert2011), for sand, and Félix & Thomas (Reference Félix and Thomas2004) for glass beads. The width
![]() $W$
and thickness
$W$
and thickness
![]() $H$
of the central flowing channel are direct results from the depth-averaged theory and provide the strongest comparisons with the experiments. The theory also solves for the depth-averaged velocity profile across the channel
$H$
of the central flowing channel are direct results from the depth-averaged theory and provide the strongest comparisons with the experiments. The theory also solves for the depth-averaged velocity profile across the channel
![]() $\bar{u}(y)$
, but this is not directly comparable with the surface velocities
$\bar{u}(y)$
, but this is not directly comparable with the surface velocities
![]() $u_{s}(y)$
measured in Takagi et al.’s (Reference Takagi, McElwaine and Huppert2011) experiments, because there is shear through the depth of the avalanche. The additional assumptions necessary to make a comparison are summarised in appendix A. Similarly Félix & Thomas (Reference Félix and Thomas2004) report the total width of the flow
$u_{s}(y)$
measured in Takagi et al.’s (Reference Takagi, McElwaine and Huppert2011) experiments, because there is shear through the depth of the avalanche. The additional assumptions necessary to make a comparison are summarised in appendix A. Similarly Félix & Thomas (Reference Félix and Thomas2004) report the total width of the flow
![]() $W_{total}$
, rather than the width of the flowing channel
$W_{total}$
, rather than the width of the flowing channel
![]() $W$
, so a comparison requires additional assumptions about the minimal width of the levees as detailed in appendix B.
$W$
, so a comparison requires additional assumptions about the minimal width of the levees as detailed in appendix B.
3.5.1 Takagi et al.’s (Reference Takagi, McElwaine and Huppert2011) experiments with sand
The predicted flow thickness
![]() $H$
is plotted in figure 10(a) as a function of the mass flux
$H$
is plotted in figure 10(a) as a function of the mass flux
![]() $Q_{M}$
for the slope angle
$Q_{M}$
for the slope angle
![]() $32^{\circ }$
used by Takagi et al. (Reference Takagi, McElwaine and Huppert2011). The solution consists of two regimes. At low mass fluxes, only the intermediate friction is active and the solution is given by (3.16), while above a critical threshold (
$32^{\circ }$
used by Takagi et al. (Reference Takagi, McElwaine and Huppert2011). The solution consists of two regimes. At low mass fluxes, only the intermediate friction is active and the solution is given by (3.16), while above a critical threshold (
![]() $Q_{min}=5.045~\text{g}~\text{s}^{-1}$
) the solutions also have a region of dynamic friction. These will be referred to as the intermediate and dynamic regimes. In the intermediate regime, the thickness
$Q_{min}=5.045~\text{g}~\text{s}^{-1}$
) the solutions also have a region of dynamic friction. These will be referred to as the intermediate and dynamic regimes. In the intermediate regime, the thickness
![]() $H\in [H_{max},h_{start}]$
is a rapidly decreasing function of the mass flux
$H\in [H_{max},h_{start}]$
is a rapidly decreasing function of the mass flux
![]() $Q_{M}$
and is not physically realised. In the dynamic regime, the thickness
$Q_{M}$
and is not physically realised. In the dynamic regime, the thickness
![]() $H\in [H_{min},H_{max}]\approx [7.9,9.2]$
mm is almost constant and asymptotes to
$H\in [H_{min},H_{max}]\approx [7.9,9.2]$
mm is almost constant and asymptotes to
![]() $H_{min}$
as
$H_{min}$
as
![]() $Q_{M}\rightarrow \infty$
. This is significantly above
$Q_{M}\rightarrow \infty$
. This is significantly above
![]() $h_{stop}=5$
mm and
$h_{stop}=5$
mm and
![]() $h_{\ast }=6.7$
mm. These observations are consistent with the experiments of Takagi et al. (Reference Takagi, McElwaine and Huppert2011) with 300–
$h_{\ast }=6.7$
mm. These observations are consistent with the experiments of Takagi et al. (Reference Takagi, McElwaine and Huppert2011) with 300–
![]() $600~\unicode[STIX]{x03BC}\text{m}$
angular sand particles on a
$600~\unicode[STIX]{x03BC}\text{m}$
angular sand particles on a
![]() $32^{\circ }$
slope who found that maximum flow thickness stayed approximately constant at a value of
$32^{\circ }$
slope who found that maximum flow thickness stayed approximately constant at a value of
![]() $H=8.3\pm 0.4$
mm as the mass flux was increased as shown in figure 10(a). Notably, if
$H=8.3\pm 0.4$
mm as the mass flux was increased as shown in figure 10(a). Notably, if
![]() $\unicode[STIX]{x1D705}=10^{-3}$
is chosen, as in Pouliquen & Forterre (Reference Pouliquen and Forterre2002), instead of
$\unicode[STIX]{x1D705}=10^{-3}$
is chosen, as in Pouliquen & Forterre (Reference Pouliquen and Forterre2002), instead of
![]() $\unicode[STIX]{x1D705}=1$
, both
$\unicode[STIX]{x1D705}=1$
, both
![]() $H_{min}$
and
$H_{min}$
and
![]() $H_{max}$
are only slightly (
$H_{max}$
are only slightly (
![]() ${\sim}0.1\,\%$
) greater than
${\sim}0.1\,\%$
) greater than
![]() $h_{\ast }=6.7$
mm, in contradiction with the experimental measurements.
$h_{\ast }=6.7$
mm, in contradiction with the experimental measurements.

Figure 10. The solutions for (a) the thickness
![]() $H$
and (b) the channel width
$H$
and (b) the channel width
![]() $W$
as a function of the mass flux
$W$
as a function of the mass flux
![]() $Q_{M}$
. The markers and error bars correspond to the data of Takagi et al. (Reference Takagi, McElwaine and Huppert2011). Blue solid lines correspond to solutions that have active zones of dynamic and intermediate friction, while the red dashed lines are purely in the intermediate regime. The magenta dashed line in (b) shows an approximate solution for the width.
$Q_{M}$
. The markers and error bars correspond to the data of Takagi et al. (Reference Takagi, McElwaine and Huppert2011). Blue solid lines correspond to solutions that have active zones of dynamic and intermediate friction, while the red dashed lines are purely in the intermediate regime. The magenta dashed line in (b) shows an approximate solution for the width.
For
![]() $\unicode[STIX]{x1D705}=1$
, the intermediate and dynamic regimes for the flowing channel width
$\unicode[STIX]{x1D705}=1$
, the intermediate and dynamic regimes for the flowing channel width
![]() $W$
, as a function of
$W$
, as a function of
![]() $Q_{M}$
, are compared to the experimental data of Takagi et al. (Reference Takagi, McElwaine and Huppert2011) in figure 10(b). The width in the dynamic regime rises approximately linearly as a function of the mass flux. This is in very good agreement with the Takagi et al.’s (Reference Takagi, McElwaine and Huppert2011) experimental data. An approximate solution for the width can be found by substituting
$Q_{M}$
, are compared to the experimental data of Takagi et al. (Reference Takagi, McElwaine and Huppert2011) in figure 10(b). The width in the dynamic regime rises approximately linearly as a function of the mass flux. This is in very good agreement with the Takagi et al.’s (Reference Takagi, McElwaine and Huppert2011) experimental data. An approximate solution for the width can be found by substituting
![]() $\bar{u}=0$
at
$\bar{u}=0$
at
![]() ${\hat{y}}=0$
in (3.26) to show that
${\hat{y}}=0$
in (3.26) to show that
where the velocities
![]() $\bar{u}_{steady}$
and
$\bar{u}_{steady}$
and
![]() $\bar{u}_{centre}$
are given by (3.9) and by solving (3.24), respectively. The approximate solution is shown by the magenta line in figure 10(b) and lies very close to the experimental data, as well as the physical solution. The approximation (3.29) therefore provides a useful formula for the channel width.
$\bar{u}_{centre}$
are given by (3.9) and by solving (3.24), respectively. The approximate solution is shown by the magenta line in figure 10(b) and lies very close to the experimental data, as well as the physical solution. The approximation (3.29) therefore provides a useful formula for the channel width.

Figure 11. (a) Solutions for the maximum surface velocity as a function of the mass flux
![]() $Q_{M}$
. The solid blue line is the maximum depth-averaged downslope velocity, whilst the green line is the best fit to the data, which suggests that the surface velocity
$Q_{M}$
. The solid blue line is the maximum depth-averaged downslope velocity, whilst the green line is the best fit to the data, which suggests that the surface velocity
![]() $u_{s}=2.35\bar{u}$
. (b) A comparison between surface velocity profile across the channel (assuming that
$u_{s}=2.35\bar{u}$
. (b) A comparison between surface velocity profile across the channel (assuming that
![]() $u_{s}=2.35\bar{u}$
) with Takagi et al.’s (Reference Takagi, McElwaine and Huppert2011) data for
$u_{s}=2.35\bar{u}$
) with Takagi et al.’s (Reference Takagi, McElwaine and Huppert2011) data for
![]() $Q_{M}=50~\text{g}~\text{s}^{-1}$
on a
$Q_{M}=50~\text{g}~\text{s}^{-1}$
on a
![]() $32^{\circ }$
slope.
$32^{\circ }$
slope.
The maximum depth-averaged velocity increases initially with the mass flux and then saturates above
![]() $Q_{M}=50~\text{g}~\text{s}^{-1}$
. This trend is broadly in line with what Takagi et al. (Reference Takagi, McElwaine and Huppert2011) observed for the maximal surface velocity (figure 11
a). The near-constant ratio of the surface velocity to the depth-averaged velocity provides information about shear through the depth of the avalanche. The best fit for the data implies
$Q_{M}=50~\text{g}~\text{s}^{-1}$
. This trend is broadly in line with what Takagi et al. (Reference Takagi, McElwaine and Huppert2011) observed for the maximal surface velocity (figure 11
a). The near-constant ratio of the surface velocity to the depth-averaged velocity provides information about shear through the depth of the avalanche. The best fit for the data implies
![]() $u_{s}/\bar{u}=2.35$
, which lies significantly above the ratio
$u_{s}/\bar{u}=2.35$
, which lies significantly above the ratio
![]() $u_{s}/\bar{u}=1.67$
for Bagnold flow. This is consistent with the discrete element method (DEM) simulations of Silbert, Landry & Grest (Reference Silbert, Landry and Grest2003) and non-local theory of Kamrin & Henann (Reference Kamrin and Henann2015), which predict a transition from Bagnold flow to exponential-like velocity profiles with depth, as the flow gets close to
$u_{s}/\bar{u}=1.67$
for Bagnold flow. This is consistent with the discrete element method (DEM) simulations of Silbert, Landry & Grest (Reference Silbert, Landry and Grest2003) and non-local theory of Kamrin & Henann (Reference Kamrin and Henann2015), which predict a transition from Bagnold flow to exponential-like velocity profiles with depth, as the flow gets close to
![]() $h_{\ast }$
, even in the complete absence of side walls. The ratio of the surface velocity to depth-averaged velocity in figure 11 strongly motivates the use of a concave exponential velocity profile with
$h_{\ast }$
, even in the complete absence of side walls. The ratio of the surface velocity to depth-averaged velocity in figure 11 strongly motivates the use of a concave exponential velocity profile with
![]() $u_{s}/\bar{u}=2.35$
to reconstruct the non-depth-averaged velocity in this paper, which is discussed in more detail in appendix A.
$u_{s}/\bar{u}=2.35$
to reconstruct the non-depth-averaged velocity in this paper, which is discussed in more detail in appendix A.
Figure 11(b) shows a comparison between the predicted surface velocity across the channel, assuming
![]() $u_{s}=2.35\bar{u}$
, and that derived from particle image velocimetry (PIV) measurements of Takagi et al. (Reference Takagi, McElwaine and Huppert2011) for a flow of sand on a
$u_{s}=2.35\bar{u}$
, and that derived from particle image velocimetry (PIV) measurements of Takagi et al. (Reference Takagi, McElwaine and Huppert2011) for a flow of sand on a
![]() $32^{\circ }$
slope 2 m down from the source. The steady-state theory predicts a slightly narrower channel with a slightly faster maximum surface velocity than that observed in the experiments. This may be an indication that the depth-averaged viscosity
$32^{\circ }$
slope 2 m down from the source. The steady-state theory predicts a slightly narrower channel with a slightly faster maximum surface velocity than that observed in the experiments. This may be an indication that the depth-averaged viscosity
![]() $\unicode[STIX]{x1D708}h^{1/2}$
is slightly larger than that assumed in the theory, which is derived for thicker flows that have well-developed Bagnold profiles.
$\unicode[STIX]{x1D708}h^{1/2}$
is slightly larger than that assumed in the theory, which is derived for thicker flows that have well-developed Bagnold profiles.
Takagi et al. (Reference Takagi, McElwaine and Huppert2011) observed that there was a minimum mass flux below which the steadily flowing leveed channel was replaced by an unsteady sequence of avalanches triggered at equal time intervals as the grains piled up near the source and failed periodically. An illustrative movie showing the equivalent experiment with the red sand used in this paper is available online (movie 4). This will be investigated further in § 4.4.

Figure 12. The solutions for (a) the channel thickness
![]() $H$
and (b) the width
$H$
and (b) the width
![]() $W$
for glass beads as a function of the mass flux
$W$
for glass beads as a function of the mass flux
![]() $Q_{M}$
. The blue solid lines correspond to solutions that have active zones of dynamic friction, while the red dashed lines are purely in the intermediate regime. In addition the dot-dash line in (b) shows an approximation for the total width of the channel (see appendix B). The solutions are compared to Félix & Thomas’s (Reference Félix and Thomas2004) experimental data for (a) the thickness and (b) the total width (markers). Solid lines in (c) represent exact steady-state solutions for the thickness profile of the whole flow, including the minimal levees, when
$Q_{M}$
. The blue solid lines correspond to solutions that have active zones of dynamic friction, while the red dashed lines are purely in the intermediate regime. In addition the dot-dash line in (b) shows an approximation for the total width of the channel (see appendix B). The solutions are compared to Félix & Thomas’s (Reference Félix and Thomas2004) experimental data for (a) the thickness and (b) the total width (markers). Solid lines in (c) represent exact steady-state solutions for the thickness profile of the whole flow, including the minimal levees, when
![]() $Q_{M}=3.7$
, 8.0, 17.5,
$Q_{M}=3.7$
, 8.0, 17.5,
![]() $38~\text{g}~\text{s}^{-1}$
, whereas the dots are experimental laser profiles from Félix & Thomas (Reference Félix and Thomas2004). The theoretical levee profiles assume a perfect balance between gravity, pressure gradient and maximum static friction as described in appendix B.
$38~\text{g}~\text{s}^{-1}$
, whereas the dots are experimental laser profiles from Félix & Thomas (Reference Félix and Thomas2004). The theoretical levee profiles assume a perfect balance between gravity, pressure gradient and maximum static friction as described in appendix B.
3.5.2 Félix & Thomas’s (Reference Félix and Thomas2004) experiments with glass beads
The solution for glass beads has the same structure as that for sand, consisting of an unphysical intermediate regime for low fluxes and a physically realised dynamic regime above
![]() $Q_{min}=3.6~\text{g}~\text{s}^{-1}$
. The small range of
$Q_{min}=3.6~\text{g}~\text{s}^{-1}$
. The small range of
![]() $H\in [H_{min},H_{max}]\approx [3.152,3.166]$
mm implies that the predicted channel thickness is almost independent of the mass flux
$H\in [H_{min},H_{max}]\approx [3.152,3.166]$
mm implies that the predicted channel thickness is almost independent of the mass flux
![]() $Q_{M}$
and is also significantly larger than both
$Q_{M}$
and is also significantly larger than both
![]() $h_{stop}\approx 2.16$
mm and
$h_{stop}\approx 2.16$
mm and
![]() $h_{\ast }\approx 2.9$
mm. The agreement between
$h_{\ast }\approx 2.9$
mm. The agreement between
![]() $H$
and the experimental thickness data of Félix & Thomas (Reference Félix and Thomas2004) is very good, as shown in figure 12(a). As with sand, the channel thickness
$H$
and the experimental thickness data of Félix & Thomas (Reference Félix and Thomas2004) is very good, as shown in figure 12(a). As with sand, the channel thickness
![]() $H$
is in agreement with experiments when
$H$
is in agreement with experiments when
![]() $\unicode[STIX]{x1D705}=1$
, but if
$\unicode[STIX]{x1D705}=1$
, but if
![]() $\unicode[STIX]{x1D705}=10^{-3}$
is chosen the thickness is under-predicted, with both
$\unicode[STIX]{x1D705}=10^{-3}$
is chosen the thickness is under-predicted, with both
![]() $H_{min}$
and
$H_{min}$
and
![]() $H_{max}$
extremely close to
$H_{max}$
extremely close to
![]() $h_{\ast }\approx 2.9$
mm.
$h_{\ast }\approx 2.9$
mm.
Félix & Thomas (Reference Félix and Thomas2004) also reported the total width of the flow as a function of the mass flux. This makes direct comparison with experiments more difficult, not least because frictional hysteresis implies that the levee widths are not unique. However, by assuming that all points in the levee are on the brink of yield (Hulme Reference Hulme1974; Balmforth et al.
Reference Balmforth, Burbidge and Craster2001) a unique solution for the minimal levee width can be obtained, as described in detail in appendix B. Adding two minimal levees widths to the flowing channel width
![]() $W$
then gives a good approximation for the minimum total width
$W$
then gives a good approximation for the minimum total width
![]() $W_{total}$
of the channel.
$W_{total}$
of the channel.
Figure 12(b) shows a comparison of both
![]() $W_{total}$
and
$W_{total}$
and
![]() $W$
to the total width measured by Félix & Thomas (Reference Félix and Thomas2004) as a function of the mass flux
$W$
to the total width measured by Félix & Thomas (Reference Félix and Thomas2004) as a function of the mass flux
![]() $Q_{M}$
. For relatively low mass fluxes most of the experimental data lie close to the minimum total width
$Q_{M}$
. For relatively low mass fluxes most of the experimental data lie close to the minimum total width
![]() $W_{total}$
predicted by the solutions in which the dynamic friction is active. However, for larger values of
$W_{total}$
predicted by the solutions in which the dynamic friction is active. However, for larger values of
![]() $Q_{M}$
the width appears to be over predicted by the steady-state theory. Félix & Thomas (Reference Félix and Thomas2004) do not report the time or position at which their steady-state data were collected, but their chute was relatively short (2 m) and they only collected data for 80 s. The most likely explanation for the apparent discrepancy at high mass fluxes is therefore not that the steady-state predictions are wrong, but that the experimental data were not collected far enough downstream or after long enough times. For instance, Deboeuf et al. (Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006) performed experiments at
$Q_{M}$
the width appears to be over predicted by the steady-state theory. Félix & Thomas (Reference Félix and Thomas2004) do not report the time or position at which their steady-state data were collected, but their chute was relatively short (2 m) and they only collected data for 80 s. The most likely explanation for the apparent discrepancy at high mass fluxes is therefore not that the steady-state predictions are wrong, but that the experimental data were not collected far enough downstream or after long enough times. For instance, Deboeuf et al. (Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006) performed experiments at
![]() $Q_{M}=25~\text{g}~\text{s}^{-1}$
on a 3 m chute and found that although the thickness was close to steady state within 100 s the width of the channel adjusted on a much longer time scale and was still slowly widening at 3500 s (see their figure 2). Even longer experiments by Takagi et al. (Reference Takagi, McElwaine and Huppert2011) found that the levee margins for glass beads eventually became unstable after 70–90 min.
$Q_{M}=25~\text{g}~\text{s}^{-1}$
on a 3 m chute and found that although the thickness was close to steady state within 100 s the width of the channel adjusted on a much longer time scale and was still slowly widening at 3500 s (see their figure 2). Even longer experiments by Takagi et al. (Reference Takagi, McElwaine and Huppert2011) found that the levee margins for glass beads eventually became unstable after 70–90 min.
Deboeuf et al.’s (Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006) and Takagi et al.’s (Reference Takagi, McElwaine and Huppert2011) observations suggests that for weakly hysteretic materials, such as glass beads, it can take a long time and/or distance for the width of the flow to reach steady state and that steady state may itself be unstable. This is borne out by a comparison between the experiments of Félix & Thomas (Reference Félix and Thomas2004) and the full steady-state thickness profiles (including the levees and the central channel) in figure 12(c). All of the experimental flows have thicknesses that are close to their steady-state value and the widths also agree for low mass fluxes
![]() $Q_{M}=3.7$
and
$Q_{M}=3.7$
and
![]() $8.0~\text{g}~\text{s}^{-1}$
. However, as the mass flux is increased to
$8.0~\text{g}~\text{s}^{-1}$
. However, as the mass flux is increased to
![]() $Q_{M}=17.5$
and
$Q_{M}=17.5$
and
![]() $38~\text{g}~\text{s}^{-1}$
the width of the channel is seen to be far from steady state. As stated above, this apparent lack of agreement at high mass fluxes is most likely due to the experiments having not been run for long enough and/or the measurement position not being far enough downstream.
$38~\text{g}~\text{s}^{-1}$
the width of the channel is seen to be far from steady state. As stated above, this apparent lack of agreement at high mass fluxes is most likely due to the experiments having not been run for long enough and/or the measurement position not being far enough downstream.
3.6 Reconstruction of the smoothly varying velocity field
Figure 13 shows a reconstruction of the steady-state downslope velocity for glass beads in a cross-section through the channel for
![]() $Q_{M}=3.7$
, 8.0, 17.5,
$Q_{M}=3.7$
, 8.0, 17.5,
![]() $38~\text{g}~\text{s}^{-1}$
. These solutions assume an exponential velocity profile through the avalanche depth, which is appropriate for thin flows close to
$38~\text{g}~\text{s}^{-1}$
. These solutions assume an exponential velocity profile through the avalanche depth, which is appropriate for thin flows close to
![]() $h_{\ast }$
(see appendix A). It is striking that the velocity varies smoothly across the whole channel, with a maximum at the surface and centre of the flow, as well as boundary layers adjacent to the levee–channel interfaces providing a seamless connection to the static levees. This is in stark contrast to the inviscid model, which has a uniform velocity profile across the channel with contact discontinuities (velocity jumps) at the levee–channel margins as shown in figure 7. These plots also highlight that for a given mass flux
$h_{\ast }$
(see appendix A). It is striking that the velocity varies smoothly across the whole channel, with a maximum at the surface and centre of the flow, as well as boundary layers adjacent to the levee–channel interfaces providing a seamless connection to the static levees. This is in stark contrast to the inviscid model, which has a uniform velocity profile across the channel with contact discontinuities (velocity jumps) at the levee–channel margins as shown in figure 7. These plots also highlight that for a given mass flux
![]() $Q_{M}$
and inclination angle
$Q_{M}$
and inclination angle
![]() $\unicode[STIX]{x1D701}$
, the viscous model has a unique solution for the height, width and velocity, rather than an infinite number of steady states, parameterised by
$\unicode[STIX]{x1D701}$
, the viscous model has a unique solution for the height, width and velocity, rather than an infinite number of steady states, parameterised by
![]() $H\in [h_{\ast },h_{start}]$
, in the inviscid case. Moreover the height of the flows is approximately the same and the minimal levees are therefore closely similar. It should be noted that in the bottom left and right corners of the central channel the flow is moving very slowly. This is consistent with Deboeuf et al.’s (Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006) and Kokelaar et al.’s (Reference Kokelaar, Graham, Gray and Vallance2014) colour change observations, which demonstrated that the material in these regions was either static or very slowly moving. Such linings of the channel do not occur in the inviscid model as shown in figure 7.
$H\in [h_{\ast },h_{start}]$
, in the inviscid case. Moreover the height of the flows is approximately the same and the minimal levees are therefore closely similar. It should be noted that in the bottom left and right corners of the central channel the flow is moving very slowly. This is consistent with Deboeuf et al.’s (Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006) and Kokelaar et al.’s (Reference Kokelaar, Graham, Gray and Vallance2014) colour change observations, which demonstrated that the material in these regions was either static or very slowly moving. Such linings of the channel do not occur in the inviscid model as shown in figure 7.

Figure 13. Steady-state downstream velocity profile
![]() $u(y,z)$
for a self-channelised flow of glass beads at an angle
$u(y,z)$
for a self-channelised flow of glass beads at an angle
![]() $\unicode[STIX]{x1D701}=25^{\circ }$
, and mass fluxes
$\unicode[STIX]{x1D701}=25^{\circ }$
, and mass fluxes
![]() $Q_{M}=3.7$
, 8.0, 17.5,
$Q_{M}=3.7$
, 8.0, 17.5,
![]() $38~\text{g}~\text{s}^{-1}$
. The velocity is reconstructed using an exponential profile with
$38~\text{g}~\text{s}^{-1}$
. The velocity is reconstructed using an exponential profile with
![]() $\unicode[STIX]{x1D706}=2.05$
as discussed in appendix A. The viscous formulation predicts a unique solution for each mass flux and slope angle. This contrasts with the inviscid case, where there is an infinite set of solutions parameterised by
$\unicode[STIX]{x1D706}=2.05$
as discussed in appendix A. The viscous formulation predicts a unique solution for each mass flux and slope angle. This contrasts with the inviscid case, where there is an infinite set of solutions parameterised by
![]() $H\in [h_{\ast },h_{start}]$
as shown in figure 7. In the viscous case, the thickness of the central channel is almost independent of the mass flux and hence the shape of the minimum levees required to support the flowing central channel are almost the same for all fluxes.
$H\in [h_{\ast },h_{start}]$
as shown in figure 7. In the viscous case, the thickness of the central channel is almost independent of the mass flux and hence the shape of the minimum levees required to support the flowing central channel are almost the same for all fluxes.
4 Time-dependent numerical simulations
To investigate the evolution towards the steady state, fully time and spatially dependent numerical solutions to the system of conservation laws (2.2)–(2.4) are now computed.
4.1 Numerical method
Numerical solutions are calculated using a high-resolution semi-discrete non-oscillatory central (NOC) scheme for convection–diffusion equations (Kurganov & Tadmor Reference Kurganov and Tadmor2000). This method has proved its ability to solve similar systems of conservation laws for erosion–deposition waves (Edwards & Gray Reference Edwards and Gray2015; Edwards et al. Reference Edwards, Viroulet, Kokelaar and Gray2017), segregation-induced finger formation (Baker et al. Reference Baker, Johnson and Gray2016b ) and bi-disperse roll waves (Viroulet et al. Reference Viroulet, Baker, Rocha, Johnson, Kokelaar and Gray2018). The equations are solved in conservative form,
where
![]() $\boldsymbol{U}=(h,h\bar{u},h\bar{v})^{\text{T}}$
is the vector of conserved fields, with
$\boldsymbol{U}=(h,h\bar{u},h\bar{v})^{\text{T}}$
is the vector of conserved fields, with
![]() $\boldsymbol{U}_{x}$
and
$\boldsymbol{U}_{x}$
and
![]() $\boldsymbol{U}_{y}$
being the derivatives of
$\boldsymbol{U}_{y}$
being the derivatives of
![]() $\boldsymbol{U}$
with respect to
$\boldsymbol{U}$
with respect to
![]() $x$
and
$x$
and
![]() $y$
, respectively. Comparing the governing equations (2.2)–(2.4) with (4.1) yields convective fluxes
$y$
, respectively. Comparing the governing equations (2.2)–(2.4) with (4.1) yields convective fluxes
 $$\begin{eqnarray}\boldsymbol{c}_{1}=\left(\begin{array}{@{}c@{}}m\\ \displaystyle \frac{m^{2}}{h}+\frac{h^{2}}{2}g\cos \unicode[STIX]{x1D701}\\ \displaystyle \frac{mn}{h}\end{array}\right),\quad \boldsymbol{c}_{2}=\left(\begin{array}{@{}c@{}}n\\ \displaystyle \frac{mn}{h}\\ \displaystyle \frac{n^{2}}{h}+\frac{h^{2}}{2}g\cos \unicode[STIX]{x1D701}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{c}_{1}=\left(\begin{array}{@{}c@{}}m\\ \displaystyle \frac{m^{2}}{h}+\frac{h^{2}}{2}g\cos \unicode[STIX]{x1D701}\\ \displaystyle \frac{mn}{h}\end{array}\right),\quad \boldsymbol{c}_{2}=\left(\begin{array}{@{}c@{}}n\\ \displaystyle \frac{mn}{h}\\ \displaystyle \frac{n^{2}}{h}+\frac{h^{2}}{2}g\cos \unicode[STIX]{x1D701}\end{array}\right),\end{eqnarray}$$
and diffusive fluxes
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{D}_{1}=\unicode[STIX]{x1D708}h^{1/2}\left(\begin{array}{@{}c@{}}0\\ \displaystyle \frac{\unicode[STIX]{x2202}m}{\unicode[STIX]{x2202}x}-\frac{m}{h}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}\\ \displaystyle \frac{1}{2}\left(\frac{\unicode[STIX]{x2202}m}{\unicode[STIX]{x2202}y}-\frac{m}{h}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}x}-\frac{n}{h}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}\right)\end{array}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{D}_{1}=\unicode[STIX]{x1D708}h^{1/2}\left(\begin{array}{@{}c@{}}0\\ \displaystyle \frac{\unicode[STIX]{x2202}m}{\unicode[STIX]{x2202}x}-\frac{m}{h}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}\\ \displaystyle \frac{1}{2}\left(\frac{\unicode[STIX]{x2202}m}{\unicode[STIX]{x2202}y}-\frac{m}{h}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}y}+\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}x}-\frac{n}{h}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}\right)\end{array}\right), & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{D}_{2}=\unicode[STIX]{x1D708}h^{1/2}\left(\begin{array}{@{}c@{}}0\\ \displaystyle \frac{1}{2}\left(\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}x}-\frac{n}{h}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}m}{\unicode[STIX]{x2202}y}-\frac{m}{h}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}y}\right)\\ \displaystyle \frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}y}-\frac{n}{h}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}y}\end{array}\right), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \boldsymbol{D}_{2}=\unicode[STIX]{x1D708}h^{1/2}\left(\begin{array}{@{}c@{}}0\\ \displaystyle \frac{1}{2}\left(\frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}x}-\frac{n}{h}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}x}+\frac{\unicode[STIX]{x2202}m}{\unicode[STIX]{x2202}y}-\frac{m}{h}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}y}\right)\\ \displaystyle \frac{\unicode[STIX]{x2202}n}{\unicode[STIX]{x2202}y}-\frac{n}{h}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}y}\end{array}\right), & \displaystyle\end{eqnarray}$$
where
![]() $\boldsymbol{m}=(m,n)^{\text{T}}=(h\bar{u},h\bar{v})^{\text{T}}$
. The source term vector is
$\boldsymbol{m}=(m,n)^{\text{T}}=(h\bar{u},h\bar{v})^{\text{T}}$
. The source term vector is
 $$\begin{eqnarray}\boldsymbol{S}=\left(\begin{array}{@{}c@{}}\displaystyle S_{inflow}(x,y)\\ \displaystyle hg\sin \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}_{b}e_{1}hg\cos \unicode[STIX]{x1D701}\\ \displaystyle -\unicode[STIX]{x1D707}_{b}e_{2}hg\cos \unicode[STIX]{x1D701}\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{S}=\left(\begin{array}{@{}c@{}}\displaystyle S_{inflow}(x,y)\\ \displaystyle hg\sin \unicode[STIX]{x1D701}-\unicode[STIX]{x1D707}_{b}e_{1}hg\cos \unicode[STIX]{x1D701}\\ \displaystyle -\unicode[STIX]{x1D707}_{b}e_{2}hg\cos \unicode[STIX]{x1D701}\end{array}\right),\end{eqnarray}$$
where an additional volume source term
![]() $S_{inflow}(x,y)$
has been added to the right-hand side of the depth-averaged mass balance equation (2.2). This provides a simple way of modelling the experimental supply of grains onto the chute from a funnel (see § 1). Grains are added to the domain in a small circular region, described by
$S_{inflow}(x,y)$
has been added to the right-hand side of the depth-averaged mass balance equation (2.2). This provides a simple way of modelling the experimental supply of grains onto the chute from a funnel (see § 1). Grains are added to the domain in a small circular region, described by
where
![]() $\tilde{S}$
is a normalisation constant,
$\tilde{S}$
is a normalisation constant,
![]() $R=2.5$
cm is the radius of the circular inflow and
$R=2.5$
cm is the radius of the circular inflow and
![]() $x_{0}=15$
cm is the downstream position of its centre. Defining polar coordinates with an origin at the centre of the circle by
$x_{0}=15$
cm is the downstream position of its centre. Defining polar coordinates with an origin at the centre of the circle by
![]() $x=x_{0}+r\cos \unicode[STIX]{x1D703}$
and
$x=x_{0}+r\cos \unicode[STIX]{x1D703}$
and
![]() $y=r\sin \unicode[STIX]{x1D703}$
, the total volume flux of material entering the chute is
$y=r\sin \unicode[STIX]{x1D703}$
, the total volume flux of material entering the chute is
Since the total mass flux is
the normalisation factor in (4.6) is
The numerical solutions start with initial conditions of an empty chute,
![]() $h=0$
,
$h=0$
,
![]() $\boldsymbol{m}=\mathbf{0}$
at
$\boldsymbol{m}=\mathbf{0}$
at
![]() $t=0$
. An outflow boundary condition is implemented at the bottom of the chute by extrapolating the solution to a row of ghost cells beyond the computational domain (LeVeque Reference LeVeque2002). The flow does not reach the top (
$t=0$
. An outflow boundary condition is implemented at the bottom of the chute by extrapolating the solution to a row of ghost cells beyond the computational domain (LeVeque Reference LeVeque2002). The flow does not reach the top (
![]() $x=0$
) or sides (
$x=0$
) or sides (
![]() $y=\pm L_{y}/2$
) of the domain and so a boundary condition
$y=\pm L_{y}/2$
) of the domain and so a boundary condition
![]() $h=0$
is trivially satisfied here.
$h=0$
is trivially satisfied here.
The two-dimensional numerical domain
![]() $(L_{x},L_{y})=(2.5,0.3)$
m is discretised into a rectangular grid with
$(L_{x},L_{y})=(2.5,0.3)$
m is discretised into a rectangular grid with
![]() $(n_{x},n_{y})=(1000,300)$
grid points, respectively. Numerical fluxes are computed by a generalised minmod limiter with
$(n_{x},n_{y})=(1000,300)$
grid points, respectively. Numerical fluxes are computed by a generalised minmod limiter with
![]() $\unicode[STIX]{x1D703}=2$
(Kurganov & Tadmor Reference Kurganov and Tadmor2000) and the spatially discretised equations are integrated in time using a second-order Runge–Kutta method, with time steps determined by a CFL (Courant–Friedrichs–Lewy) number of 0.225, and a maximum step size
$\unicode[STIX]{x1D703}=2$
(Kurganov & Tadmor Reference Kurganov and Tadmor2000) and the spatially discretised equations are integrated in time using a second-order Runge–Kutta method, with time steps determined by a CFL (Courant–Friedrichs–Lewy) number of 0.225, and a maximum step size
![]() $\unicode[STIX]{x0394}t=10^{-4}$
s (LeVeque Reference LeVeque2002), which is required to minimise creep of the levees. Numerical errors caused by the degeneracy in the conservative form of the equations when
$\unicode[STIX]{x0394}t=10^{-4}$
s (LeVeque Reference LeVeque2002), which is required to minimise creep of the levees. Numerical errors caused by the degeneracy in the conservative form of the equations when
![]() $h=0$
are mitigated by introducing a minimum thickness threshold (set to
$h=0$
are mitigated by introducing a minimum thickness threshold (set to
![]() $10^{-5}$
m or approximately one tenth of a grain diameter), below which the thickness and momentum are set to zero.
$10^{-5}$
m or approximately one tenth of a grain diameter), below which the thickness and momentum are set to zero.

Figure 14. Fully time and spatially dependent numerical solutions for the downslope velocity of sand at (a)
![]() $t=20$
s, (b)
$t=20$
s, (b)
![]() $t=80$
s and (c)
$t=80$
s and (c)
![]() $t=105$
s for an inflow mass flux
$t=105$
s for an inflow mass flux
![]() $Q_{M}=85~\text{g}~\text{s}^{-1}$
and inclination
$Q_{M}=85~\text{g}~\text{s}^{-1}$
and inclination
![]() $\unicode[STIX]{x1D701}=32^{\circ }$
. (a) Shows the flow front propagating steadily down the plane and forming the levee–channel morphology behind it, (b) shows the steady-state fully developed self-channelised flow and (c) the channel in the process of draining out to leave behind a static deposit with parallel-sided levees and a partially drained central channel. The final panel (d) shows the downslope velocity profile across the channel
$\unicode[STIX]{x1D701}=32^{\circ }$
. (a) Shows the flow front propagating steadily down the plane and forming the levee–channel morphology behind it, (b) shows the steady-state fully developed self-channelised flow and (c) the channel in the process of draining out to leave behind a static deposit with parallel-sided levees and a partially drained central channel. The final panel (d) shows the downslope velocity profile across the channel
![]() $\bar{u}(y)$
at
$\bar{u}(y)$
at
![]() $x=1.75$
m at
$x=1.75$
m at
![]() $t=31$
to 91 s in intervals of 10 s. Markers indicate fully time-dependent simulations, whereas the solid black line represents the exact steady-state solution. A movie showing the time and spatially evolving flow is available in the online supplementary material (movie 5).
$t=31$
to 91 s in intervals of 10 s. Markers indicate fully time-dependent simulations, whereas the solid black line represents the exact steady-state solution. A movie showing the time and spatially evolving flow is available in the online supplementary material (movie 5).

Figure 15. Fully time and spatially dependent numerical solutions for the thickness of sand at (a)
![]() $t=20$
s, (b)
$t=20$
s, (b)
![]() $t=80$
s and (c)
$t=80$
s and (c)
![]() $t=105$
s for an inflow mass flux
$t=105$
s for an inflow mass flux
![]() $Q_{M}=85~\text{g}~\text{s}^{-1}$
and inclination
$Q_{M}=85~\text{g}~\text{s}^{-1}$
and inclination
![]() $\unicode[STIX]{x1D701}=32^{\circ }$
as in figure 14. (a) Shows the flow front propagating steadily down the plane and forming the levee–channel morphology behind it, (b) shows the steady-state fully developed self-channelised flow and (c) the channel in the process of draining out to leave behind a static deposit with parallel-sided levees and a partially drained central channel. The final panel (d) shows numerical solutions for the thickness profile at
$\unicode[STIX]{x1D701}=32^{\circ }$
as in figure 14. (a) Shows the flow front propagating steadily down the plane and forming the levee–channel morphology behind it, (b) shows the steady-state fully developed self-channelised flow and (c) the channel in the process of draining out to leave behind a static deposit with parallel-sided levees and a partially drained central channel. The final panel (d) shows numerical solutions for the thickness profile at
![]() $x=1.75$
m at three different times. A movie showing the time and spatially evolving flow is available in the online supplementary material (movie 6).
$x=1.75$
m at three different times. A movie showing the time and spatially evolving flow is available in the online supplementary material (movie 6).
4.2 Formation and partial drainage of a self-channelised flow
The downslope velocity
![]() $\bar{u}$
and thickness
$\bar{u}$
and thickness
![]() $h$
of a typical numerical solution are shown in figures 14(a) and 15(a) respectively (supplementary movies 5 and 6). For the parameters of sand at a slope angle
$h$
of a typical numerical solution are shown in figures 14(a) and 15(a) respectively (supplementary movies 5 and 6). For the parameters of sand at a slope angle
![]() $\unicode[STIX]{x1D701}=32^{\circ }$
, the mass flux
$\unicode[STIX]{x1D701}=32^{\circ }$
, the mass flux
![]() $Q_{M}=85~\text{g}~\text{s}^{-1}$
is large enough for a self-channelised avalanche to form. After an initial adjustment from the source condition in the uppermost
$Q_{M}=85~\text{g}~\text{s}^{-1}$
is large enough for a self-channelised avalanche to form. After an initial adjustment from the source condition in the uppermost
![]() ${\sim}1$
m, the simulated flow spontaneously selects its own steady-state channel thickness, width and cross-slope velocity profile. A flow head is rapidly established and propagates down the plane at constant speed (figure 14
a), laying down a steady-state levee–channel morphology behind it once some initial transients have dissipated. Figure 14(d) shows the downslope velocity at
${\sim}1$
m, the simulated flow spontaneously selects its own steady-state channel thickness, width and cross-slope velocity profile. A flow head is rapidly established and propagates down the plane at constant speed (figure 14
a), laying down a steady-state levee–channel morphology behind it once some initial transients have dissipated. Figure 14(d) shows the downslope velocity at
![]() $x=1.75$
m. At
$x=1.75$
m. At
![]() $t=32$
s the whole width of the flow is mobile at
$t=32$
s the whole width of the flow is mobile at
![]() $x=1.75$
m, but, as the front passes by, the sides of the flow rapidly solidify and by
$x=1.75$
m, but, as the front passes by, the sides of the flow rapidly solidify and by
![]() $t\geqslant 60$
s the velocity profile across the channel is rapidly tending to the steady-state solution computed directly from (3.5). The velocity therefore is almost constant in the centre of the channel and smoothly connects to the levee–channel interfaces on either side across two boundary layers. The thickness in this flowing section is constant, as shown in figure 15(b) and by the thickness profile lines across the channel at
$t\geqslant 60$
s the velocity profile across the channel is rapidly tending to the steady-state solution computed directly from (3.5). The velocity therefore is almost constant in the centre of the channel and smoothly connects to the levee–channel interfaces on either side across two boundary layers. The thickness in this flowing section is constant, as shown in figure 15(b) and by the thickness profile lines across the channel at
![]() $x=0.5$
, 1, 1.5 and 2 m in figures 14 and 15.
$x=0.5$
, 1, 1.5 and 2 m in figures 14 and 15.
By
![]() $t=60$
s (figures 14
b and 15
b) the velocity profile and constant channel thickness
$t=60$
s (figures 14
b and 15
b) the velocity profile and constant channel thickness
![]() $H=7.9$
mm are in good agreement with the steady-state predictions in § 3.3 (figures 14
d and 15
d). Once established the width of the flowing channel remains constant in the numerical simulations. The outer edges of the levees have some residual creep, which is less than 1 % of the flow velocity in the channel, for the time step of
$H=7.9$
mm are in good agreement with the steady-state predictions in § 3.3 (figures 14
d and 15
d). Once established the width of the flowing channel remains constant in the numerical simulations. The outer edges of the levees have some residual creep, which is less than 1 % of the flow velocity in the channel, for the time step of
![]() $10^{-4}$
s used here. Importantly this creep velocity scales with the time step and so the levees converge to a static state under time step refinement.
$10^{-4}$
s used here. Importantly this creep velocity scales with the time step and so the levees converge to a static state under time step refinement.
The time scale for establishment of the steady state is comparable to that in the experiments with 160–
![]() $200~\unicode[STIX]{x03BC}\text{m}$
red sand (see supplementary movie 1), but is much quicker than Takagi et al.’s (Reference Takagi, McElwaine and Huppert2011) experiments which took up to 20 min. This discrepancy may be due to a difference in bed roughness: whereas Takagi et al. (Reference Takagi, McElwaine and Huppert2011) used a base roughened by grains of the same size as the grains in the flow, the experiments in this paper use larger particles in the bed than in the flow, which reduces slip between the levee and base.
$200~\unicode[STIX]{x03BC}\text{m}$
red sand (see supplementary movie 1), but is much quicker than Takagi et al.’s (Reference Takagi, McElwaine and Huppert2011) experiments which took up to 20 min. This discrepancy may be due to a difference in bed roughness: whereas Takagi et al. (Reference Takagi, McElwaine and Huppert2011) used a base roughened by grains of the same size as the grains in the flow, the experiments in this paper use larger particles in the bed than in the flow, which reduces slip between the levee and base.
The steady fully developed state is maintained until
![]() $t=100$
s when the inflow is shut off (supplementary movies 5 and 6). The flow then thins near the top of the chute and a deposition wave moves rapidly downslope, thinning and then depositing material that was previously flowing in the central channel (figures 14
c and 15
c). This process is illustrated by cross-slope thickness profiles at
$t=100$
s when the inflow is shut off (supplementary movies 5 and 6). The flow then thins near the top of the chute and a deposition wave moves rapidly downslope, thinning and then depositing material that was previously flowing in the central channel (figures 14
c and 15
c). This process is illustrated by cross-slope thickness profiles at
![]() $x=1.75$
for
$x=1.75$
for
![]() $t=100$
, 105.3, 110 s in figure 15(d). At
$t=100$
, 105.3, 110 s in figure 15(d). At
![]() $t=100$
s the channel thickness is still equal to the theoretically predicted steady-state value
$t=100$
s the channel thickness is still equal to the theoretically predicted steady-state value
![]() $H=7.9$
mm and the surface gradient of the levee walls is below the maximum static friction, so they are stable and support the central channel. At
$H=7.9$
mm and the surface gradient of the levee walls is below the maximum static friction, so they are stable and support the central channel. At
![]() $t=105.3$
s, in the middle of the deposition wave, the flow wanes and only a region near the centre of the channel remains flowing. This deposition wave leaves behind a static deposit with super-elevated levee walls that have a maximum thickness close to the original flow thickness
$t=105.3$
s, in the middle of the deposition wave, the flow wanes and only a region near the centre of the channel remains flowing. This deposition wave leaves behind a static deposit with super-elevated levee walls that have a maximum thickness close to the original flow thickness
![]() $H$
and a deposit in the central channel that lies just above
$H$
and a deposit in the central channel that lies just above
![]() $h_{stop}$
(figure 15
d,
$h_{stop}$
(figure 15
d,
![]() $t=110$
s). As noted by Félix & Thomas (Reference Félix and Thomas2004) and Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007), the flow thickness
$t=110$
s). As noted by Félix & Thomas (Reference Félix and Thomas2004) and Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007), the flow thickness
![]() $H$
and channel width
$H$
and channel width
![]() $W$
are preserved in the deposit, allowing field observations to be used to estimate the inflow mass flux required to sustain the channel during flow. This provides an important constraint on the time evolution of the geophysical processes that created the levees, even when the flow event was not observed directly.
$W$
are preserved in the deposit, allowing field observations to be used to estimate the inflow mass flux required to sustain the channel during flow. This provides an important constraint on the time evolution of the geophysical processes that created the levees, even when the flow event was not observed directly.

Figure 16. Spatial contours of (a,c) the depth-averaged downslope velocity and (b,d) the thickness at (a,b) time
![]() $t=105.5$
s and (c,d) 155 s using the same contour scales as in figures 14 and 15. Panels (a,b) show the mass flux being reduced from
$t=105.5$
s and (c,d) 155 s using the same contour scales as in figures 14 and 15. Panels (a,b) show the mass flux being reduced from
![]() $Q_{M}=85~\text{g}~\text{s}^{-1}$
to
$Q_{M}=85~\text{g}~\text{s}^{-1}$
to
![]() $Q_{M}=70~\text{g}~\text{s}^{-1}$
, while (c,d) show the flux being increased from
$Q_{M}=70~\text{g}~\text{s}^{-1}$
, while (c,d) show the flux being increased from
![]() $Q_{M}=70~\text{g}~\text{s}^{-1}$
and
$Q_{M}=70~\text{g}~\text{s}^{-1}$
and
![]() $Q_{M}=100~\text{g}~\text{s}^{-1}$
on a slope inclined at
$Q_{M}=100~\text{g}~\text{s}^{-1}$
on a slope inclined at
![]() $\unicode[STIX]{x1D701}=32^{\circ }$
. (e) Shows the computed thickness at
$\unicode[STIX]{x1D701}=32^{\circ }$
. (e) Shows the computed thickness at
![]() $x=1.75$
m at
$x=1.75$
m at
![]() $t=100$
, 150 and 200 s and (f) shows the computed downslope velocity across the channel at the same location and times and a comparison with the steady-state solution in § 3.1. In (f) the steady-state theory is shown with red, blue and black solid lines and the computed solutions are shown with markers. Two movies showing the evolving velocity and thickness are available online (movies 7 and 8).
$t=100$
, 150 and 200 s and (f) shows the computed downslope velocity across the channel at the same location and times and a comparison with the steady-state solution in § 3.1. In (f) the steady-state theory is shown with red, blue and black solid lines and the computed solutions are shown with markers. Two movies showing the evolving velocity and thickness are available online (movies 7 and 8).
4.3 Narrowing and widening of the central flowing channel
The response of the steady fully developed solution to changes in the inflow mass flux is now investigated. The initial state is chosen to be the same as in figures 14(b) and 15(b) for an inflow mass flux
![]() $Q_{M}=85~\text{g}~\text{s}^{-1}$
and slope angle
$Q_{M}=85~\text{g}~\text{s}^{-1}$
and slope angle
![]() $\unicode[STIX]{x1D701}=32^{\circ }$
. The mass flux is then reduced to
$\unicode[STIX]{x1D701}=32^{\circ }$
. The mass flux is then reduced to
![]() $Q_{M}=70~\text{g}~\text{s}^{-1}$
at
$Q_{M}=70~\text{g}~\text{s}^{-1}$
at
![]() $t=100$
s as shown in movies 7 and 8. The channel does not narrow uniformly as shown in figure 16(a,b). An expanding wave travels rapidly downslope, which separates a downstream region, where the channel is still at the steady state for
$t=100$
s as shown in movies 7 and 8. The channel does not narrow uniformly as shown in figure 16(a,b). An expanding wave travels rapidly downslope, which separates a downstream region, where the channel is still at the steady state for
![]() $Q_{M}=85~\text{g}~\text{s}^{-1}$
, and an upstream region where the flow attains the new steady state for
$Q_{M}=85~\text{g}~\text{s}^{-1}$
, and an upstream region where the flow attains the new steady state for
![]() $Q_{M}=70~\text{g}~\text{s}^{-1}$
. The front section of this wave travels slightly faster than the rear, so the flowing regions pinch off and separate from one another. As a result there is a brief period where the grains come to rest in the channel, before they are remobilised by the second half of the wave as shown in figure 16(a,b). This behaviour is also observed in the experiments with red sand as shown in movie 3. The wave eventually propagates out of the domain to leave a parallel-sided leveed channel with a width
$Q_{M}=70~\text{g}~\text{s}^{-1}$
. The front section of this wave travels slightly faster than the rear, so the flowing regions pinch off and separate from one another. As a result there is a brief period where the grains come to rest in the channel, before they are remobilised by the second half of the wave as shown in figure 16(a,b). This behaviour is also observed in the experiments with red sand as shown in movie 3. The wave eventually propagates out of the domain to leave a parallel-sided leveed channel with a width
![]() $W=10.3$
cm that is narrower than the original width
$W=10.3$
cm that is narrower than the original width
![]() $W=12.1$
cm for
$W=12.1$
cm for
![]() $Q_{M}=85~\text{g}~\text{s}^{-1}$
. The thickness of the channel before and after the change in flux are
$Q_{M}=85~\text{g}~\text{s}^{-1}$
. The thickness of the channel before and after the change in flux are
![]() $H_{before}=7.9145$
mm and
$H_{before}=7.9145$
mm and
![]() $H_{after}=7.904$
mm, respectively, which are virtually the same as shown in figure 16(e). Once the channel has established itself the computed downslope velocities at
$H_{after}=7.904$
mm, respectively, which are virtually the same as shown in figure 16(e). Once the channel has established itself the computed downslope velocities at
![]() $x=1.75$
m are almost identical to the steady-state theory in § 3.3 as shown in figure 16(f). During the process of channel narrowing, grains are deposited on the inside of the pre-existing levee walls, but there is no change to the existing levees, so the total width of the channel does not change, as shown in figure 16(b).
$x=1.75$
m are almost identical to the steady-state theory in § 3.3 as shown in figure 16(f). During the process of channel narrowing, grains are deposited on the inside of the pre-existing levee walls, but there is no change to the existing levees, so the total width of the channel does not change, as shown in figure 16(b).
Once the new fully developed steady state for
![]() $Q_{M}=70~\text{g}~\text{s}^{-1}$
has been established the inflow flux is increased to
$Q_{M}=70~\text{g}~\text{s}^{-1}$
has been established the inflow flux is increased to
![]() $Q_{M}=100~\text{g}~\text{s}^{-1}$
at
$Q_{M}=100~\text{g}~\text{s}^{-1}$
at
![]() $t=150$
s as shown in movies 7 and 8. A wave again propagates down the channel, which adjusts its width. This time the wave remobilises the levees on both sides, broadening the central channel and then re-solidifying to form levees that are slightly further out as shown in figure 16(c,d). This process is inherently unsteady and so the outer margins of the new levees are no longer perfectly parallel. The initial wavefront, associated with the change in mass flux, grows in size as it erodes the static material in the pre-existing wide levees and deposits a narrower levee behind it. As a result it moves faster than the steady uniform flow behind it and therefore detaches from it, producing a brief period where the grains come to rest before the new steady-state flow establishes itself. The computed steady-state thickness and velocity profiles across the channel are shown in figures 16(e) and 16(f), respectively. These show that, as the mass flux is increased, the width increases to
$t=150$
s as shown in movies 7 and 8. A wave again propagates down the channel, which adjusts its width. This time the wave remobilises the levees on both sides, broadening the central channel and then re-solidifying to form levees that are slightly further out as shown in figure 16(c,d). This process is inherently unsteady and so the outer margins of the new levees are no longer perfectly parallel. The initial wavefront, associated with the change in mass flux, grows in size as it erodes the static material in the pre-existing wide levees and deposits a narrower levee behind it. As a result it moves faster than the steady uniform flow behind it and therefore detaches from it, producing a brief period where the grains come to rest before the new steady-state flow establishes itself. The computed steady-state thickness and velocity profiles across the channel are shown in figures 16(e) and 16(f), respectively. These show that, as the mass flux is increased, the width increases to
![]() $W=13.7$
cm, the thickness barely changes and the velocity profile lies very close to the steady-state value in § 3. All traces of the previous history of the flow that was recorded in the earlier levees are therefore destroyed, which is consistent with the experiments in figure 4.
$W=13.7$
cm, the thickness barely changes and the velocity profile lies very close to the steady-state value in § 3. All traces of the previous history of the flow that was recorded in the earlier levees are therefore destroyed, which is consistent with the experiments in figure 4.
4.4 Unsteady periodic avalanching regime
When the mass flux is reduced to
![]() $Q_{M}=16~\text{g}~\text{s}^{-1}$
grains pile up near the source, fail periodically and then come to rest again by upslope propagating stopping waves. The initial phases of this solution are very complicated with a sequence of pile collapses that produce two avalanches that propagate down either side of a central ridge, as shown in the online supplementary movies 9 and 10. However, after approximately 95 s the collapses become more structured, producing a single erosion–deposition wave that propagates downslope over a thin deposit that has been laid down by previous flows, as shown in figures 17 and 18. Erosion–deposition waves continuously erode material at their leading edge and deposit material at the rear as they propagate downslope (Edwards & Gray Reference Edwards and Gray2015; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017). The waves therefore do not represent a single body of material that is released from the collapse, but a constantly changing body of grains. From
$Q_{M}=16~\text{g}~\text{s}^{-1}$
grains pile up near the source, fail periodically and then come to rest again by upslope propagating stopping waves. The initial phases of this solution are very complicated with a sequence of pile collapses that produce two avalanches that propagate down either side of a central ridge, as shown in the online supplementary movies 9 and 10. However, after approximately 95 s the collapses become more structured, producing a single erosion–deposition wave that propagates downslope over a thin deposit that has been laid down by previous flows, as shown in figures 17 and 18. Erosion–deposition waves continuously erode material at their leading edge and deposit material at the rear as they propagate downslope (Edwards & Gray Reference Edwards and Gray2015; Edwards et al.
Reference Edwards, Viroulet, Kokelaar and Gray2017). The waves therefore do not represent a single body of material that is released from the collapse, but a constantly changing body of grains. From
![]() $t=95$
–300 s the static deposit has an approximately elliptical shape that becomes progressively elongated with increasing time, with the source centred at the upstream focus point. The erosion–deposition waves are able to propagate easily on top of this deposit and grow in size in the first half of the ellipse expanding laterally to span its width. However, as the width of the elliptical deposit narrows, the avalanche overtops the sides and the material on the static bed travels a short distance before it stops. As a result, as the avalanche continues to propagate downslope, it is progressively deposited at the sides and decreases in size, before it eventually overtops the deposit front and then rapidly comes to rest. The front and sides of the deposit are therefore progressively advanced in a sequence of steps as each avalanche passes by.
$t=95$
–300 s the static deposit has an approximately elliptical shape that becomes progressively elongated with increasing time, with the source centred at the upstream focus point. The erosion–deposition waves are able to propagate easily on top of this deposit and grow in size in the first half of the ellipse expanding laterally to span its width. However, as the width of the elliptical deposit narrows, the avalanche overtops the sides and the material on the static bed travels a short distance before it stops. As a result, as the avalanche continues to propagate downslope, it is progressively deposited at the sides and decreases in size, before it eventually overtops the deposit front and then rapidly comes to rest. The front and sides of the deposit are therefore progressively advanced in a sequence of steps as each avalanche passes by.

Figure 17. Fully time and spatially dependent numerical solutions for the downslope velocity of sand at (a)
![]() $t=125.5$
s, (b)
$t=125.5$
s, (b)
![]() $t=127.3$
s and (c)
$t=127.3$
s and (c)
![]() $t=250$
s for an inflow mass flux
$t=250$
s for an inflow mass flux
![]() $Q_{M}=16~\text{g}~\text{s}^{-1}$
and inclination
$Q_{M}=16~\text{g}~\text{s}^{-1}$
and inclination
![]() $\unicode[STIX]{x1D701}=32^{\circ }$
. In the unsteady flow regime a series of erosion–deposition waves flow over the previously deposited grains until they overrun the front and rapidly stop. The flow front therefore advances intermittently downslope. A thicker layer of material forms at the centre line, as well as at the sides of the source. A movie showing the time and spatially evolving velocity is available in the online supplementary material (movie 9).
$\unicode[STIX]{x1D701}=32^{\circ }$
. In the unsteady flow regime a series of erosion–deposition waves flow over the previously deposited grains until they overrun the front and rapidly stop. The flow front therefore advances intermittently downslope. A thicker layer of material forms at the centre line, as well as at the sides of the source. A movie showing the time and spatially evolving velocity is available in the online supplementary material (movie 9).

Figure 18. Fully time and spatially dependent numerical solutions for the thickness of sand at (a)
![]() $t=125.5$
s, (b)
$t=125.5$
s, (b)
![]() $t=127.3$
s and (c)
$t=127.3$
s and (c)
![]() $t=250$
s for an inflow mass flux
$t=250$
s for an inflow mass flux
![]() $Q_{M}=16~\text{g}~\text{s}^{-1}$
and inclination
$Q_{M}=16~\text{g}~\text{s}^{-1}$
and inclination
![]() $\unicode[STIX]{x1D701}=32^{\circ }$
as in figure 17. In the unsteady flow regime a series of erosion–deposition waves flow over the previously deposited grains until they overrun the front and rapidly stop. The flow front therefore advances intermittently downslope. A thicker layer of material forms at the centreline, as well as at the sides of the source. A movie showing the time and spatially evolving thickness is available in the online supplementary material (movie 10).
$\unicode[STIX]{x1D701}=32^{\circ }$
as in figure 17. In the unsteady flow regime a series of erosion–deposition waves flow over the previously deposited grains until they overrun the front and rapidly stop. The flow front therefore advances intermittently downslope. A thicker layer of material forms at the centreline, as well as at the sides of the source. A movie showing the time and spatially evolving thickness is available in the online supplementary material (movie 10).

Figure 19. Computed thickness
![]() $h$
for sand as a function of time at
$h$
for sand as a function of time at
![]() $x=1.25$
m and
$x=1.25$
m and
![]() $y=0$
m for a mass flux
$y=0$
m for a mass flux
![]() $Q_{M}=16~\text{g}~\text{s}^{-1}$
and inclination
$Q_{M}=16~\text{g}~\text{s}^{-1}$
and inclination
![]() $\unicode[STIX]{x1D701}=32^{\circ }$
. The flow front first reaches this point at
$\unicode[STIX]{x1D701}=32^{\circ }$
. The flow front first reaches this point at
![]() $t=78$
s, the flow thickness then builds up above
$t=78$
s, the flow thickness then builds up above
![]() $h_{stop}$
, and the waves rapidly develop a constant period
$h_{stop}$
, and the waves rapidly develop a constant period
![]() $T_{\infty }\approx 4$
s as shown in the inset space–time plot.
$T_{\infty }\approx 4$
s as shown in the inset space–time plot.
The movies also show that as the erosion–deposition wave propagates downslope it detaches from the flowing material at the source and a retrogressive (upslope propagating) stopping wave forms that travels up to the source and brings the grains to rest. As material then builds up at the source it eventually overcomes the static friction and collapses to form the next erosion–deposition wave. In this way a quasi-periodic sequence of avalanches is formed that transport the grains downslope in a series of steps. This process is visualised in figure 19, which shows the thickness at a fixed position
![]() $x=1.25$
m as a function of time. The front first reaches this position at approximately 90 s. During the passage of the first five or six waves the deposit thickness builds up to just over 6 mm, which lies between
$x=1.25$
m as a function of time. The front first reaches this position at approximately 90 s. During the passage of the first five or six waves the deposit thickness builds up to just over 6 mm, which lies between
![]() $h_{stop}=5$
mm and
$h_{stop}=5$
mm and
![]() $h_{\ast }=6.7$
mm. The presence of this erodible layer allows the avalanches to propagate easily downslope with a total thickness of approximately 8 mm. The erodible layer reduces the apparent friction experienced by the grains, in the sense that an avalanche of the same volume released on the same slope, but without the erodible layer, would rapidly come to rest. Each of the individual waves have the same shape as the one-dimensional erosion–deposition waves modelled by Edwards & Gray (Reference Edwards and Gray2015) and develop into a periodic wave train with a period of approximately 4 s. Qualitatively, the simulated thickness as a function of time (figure 19) is very similar to that observed experimentally (figure 17 of Takagi et al.
Reference Takagi, McElwaine and Huppert2011); indeed, the trough thickness and the final amplitude of the waves are in close quantitative agreement. However, Takagi et al. (Reference Takagi, McElwaine and Huppert2011) observed experimental waves of period approximately 11.5 s, which is significantly longer than the 4 s period that emerges from the simulations. This is probably because the depth-averaged theory is not able to accurately model the complicated failure processes that occur during the build-up and collapse of the pile near the source. The model can nevertheless predict the onset of unstable flow at low mass fluxes, which was observed experimentally by Takagi et al. (Reference Takagi, McElwaine and Huppert2011) as well as for the red sand in movie 4. Periodic waves propagating over previously deposited material have been observed in debris flows at Illgraben, Switzerland (McArdell Reference McArdell2016) and the Jiangjia Valley, China (Yong et al.
Reference Yong, Jingjing, Kaiheng and Pengcheng2012).
$h_{\ast }=6.7$
mm. The presence of this erodible layer allows the avalanches to propagate easily downslope with a total thickness of approximately 8 mm. The erodible layer reduces the apparent friction experienced by the grains, in the sense that an avalanche of the same volume released on the same slope, but without the erodible layer, would rapidly come to rest. Each of the individual waves have the same shape as the one-dimensional erosion–deposition waves modelled by Edwards & Gray (Reference Edwards and Gray2015) and develop into a periodic wave train with a period of approximately 4 s. Qualitatively, the simulated thickness as a function of time (figure 19) is very similar to that observed experimentally (figure 17 of Takagi et al.
Reference Takagi, McElwaine and Huppert2011); indeed, the trough thickness and the final amplitude of the waves are in close quantitative agreement. However, Takagi et al. (Reference Takagi, McElwaine and Huppert2011) observed experimental waves of period approximately 11.5 s, which is significantly longer than the 4 s period that emerges from the simulations. This is probably because the depth-averaged theory is not able to accurately model the complicated failure processes that occur during the build-up and collapse of the pile near the source. The model can nevertheless predict the onset of unstable flow at low mass fluxes, which was observed experimentally by Takagi et al. (Reference Takagi, McElwaine and Huppert2011) as well as for the red sand in movie 4. Periodic waves propagating over previously deposited material have been observed in debris flows at Illgraben, Switzerland (McArdell Reference McArdell2016) and the Jiangjia Valley, China (Yong et al.
Reference Yong, Jingjing, Kaiheng and Pengcheng2012).
4.5 Comparison with Mangeney et al.’s (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) inviscid numerical simulations
Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) developed a depth-averaged inviscid model for levee formation using the conservation laws (2.2)–(2.4) with
![]() $\unicode[STIX]{x1D708}=0$
(no viscous terms) and the non-monotonic friction law of Pouliquen & Forterre (Reference Pouliquen and Forterre2002) for glass beads (obtained by setting
$\unicode[STIX]{x1D708}=0$
(no viscous terms) and the non-monotonic friction law of Pouliquen & Forterre (Reference Pouliquen and Forterre2002) for glass beads (obtained by setting
![]() $\unicode[STIX]{x1D6E4}=0$
,
$\unicode[STIX]{x1D6E4}=0$
,
![]() $\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FD}_{\ast }=\unicode[STIX]{x1D6FD}$
,
![]() $\unicode[STIX]{x1D705}=10^{-3}$
and introducing
$\unicode[STIX]{x1D705}=10^{-3}$
and introducing
![]() $\unicode[STIX]{x1D6FF}_{4}$
, the maximum slope angle at which a static layer exists). Using a shock-capturing numerical method to solve the time-dependent equations, Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) qualitatively captured the process of self-channelisation, with grains spreading laterally at the flow front, slowing and then depositing to form parallel-sided very slowly moving levees behind the head, that supported the flow in the central channel. The thickness and downslope velocity were approximately constant in the central moving channel with a rapid decrease in downstream velocity at the levee–channel boundary as shown in their figures 12 and 15, for a mass flux
$\unicode[STIX]{x1D6FF}_{4}$
, the maximum slope angle at which a static layer exists). Using a shock-capturing numerical method to solve the time-dependent equations, Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) qualitatively captured the process of self-channelisation, with grains spreading laterally at the flow front, slowing and then depositing to form parallel-sided very slowly moving levees behind the head, that supported the flow in the central channel. The thickness and downslope velocity were approximately constant in the central moving channel with a rapid decrease in downstream velocity at the levee–channel boundary as shown in their figures 12 and 15, for a mass flux
![]() $Q_{M}=12~\text{g}~\text{s}^{-1}$
of glass beads on a slope of
$Q_{M}=12~\text{g}~\text{s}^{-1}$
of glass beads on a slope of
![]() $25^{\circ }$
. At
$25^{\circ }$
. At
![]() $t=145$
s (just prior to their inflow being stopped) the width of the shear layer that connected the central flow to the static levees was
$t=145$
s (just prior to their inflow being stopped) the width of the shear layer that connected the central flow to the static levees was
![]() $W_{boundary}\approx 0.0022$
m. Since their numerical experiments were performed on a rectangular domain
$W_{boundary}\approx 0.0022$
m. Since their numerical experiments were performed on a rectangular domain
![]() $(L_{x},L_{y})=(2.2,0.2)$
m that was divided into
$(L_{x},L_{y})=(2.2,0.2)$
m that was divided into
![]() $(n_{x},n_{y})=(400,300)$
grid points, this implies that the downslope velocity dropped from the steady uniform value to zero over
$(n_{x},n_{y})=(400,300)$
grid points, this implies that the downslope velocity dropped from the steady uniform value to zero over
![]() $(n_{y}/L_{y})W_{boundary}\approx 3.3$
grid cells.
$(n_{y}/L_{y})W_{boundary}\approx 3.3$
grid cells.
Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) used friction parameters corresponding to those in the experiments of Félix & Thomas’s (Reference Félix and Thomas2004), but with a thickness length scale
![]() $\mathscr{L}=0.8$
mm that was larger than the experimental best fit of
$\mathscr{L}=0.8$
mm that was larger than the experimental best fit of
![]() $\mathscr{L}=0.65$
mm, leading to a numerical
$\mathscr{L}=0.65$
mm, leading to a numerical
![]() $h_{stop}$
about 25 % larger than that in experiments. Despite this, their simulated flow thickness of
$h_{stop}$
about 25 % larger than that in experiments. Despite this, their simulated flow thickness of
![]() $H\approx 1.03h_{stop}=2.754$
mm was still considerably thinner than the 3.12 mm and 3.37 mm measured experimentally by Félix & Thomas (Reference Félix and Thomas2004) for
$H\approx 1.03h_{stop}=2.754$
mm was still considerably thinner than the 3.12 mm and 3.37 mm measured experimentally by Félix & Thomas (Reference Félix and Thomas2004) for
![]() $Q_{M}=8~\text{g}~\text{s}^{-1}$
and
$Q_{M}=8~\text{g}~\text{s}^{-1}$
and
![]() $Q_{M}=17.5~\text{g}~\text{s}^{-1}$
, respectively. Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) acknowledged this discrepancy, and concluded that ‘[in] particular, the absence of lateral dissipation between the flowing mass and the quasi-static shoulders likely leads to underestimation of the flowing thickness and the thickness of the deposit in the central channel’.
$Q_{M}=17.5~\text{g}~\text{s}^{-1}$
, respectively. Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) acknowledged this discrepancy, and concluded that ‘[in] particular, the absence of lateral dissipation between the flowing mass and the quasi-static shoulders likely leads to underestimation of the flowing thickness and the thickness of the deposit in the central channel’.
As shown in this paper, lateral dissipation (viscosity) is required to produce a unique steady channel thickness, but a hysteretic friction law with
![]() $\unicode[STIX]{x1D705}=1$
(a gradual transition from static to dynamic friction coefficient) is also required, in order for this unique thickness to be significantly greater than both
$\unicode[STIX]{x1D705}=1$
(a gradual transition from static to dynamic friction coefficient) is also required, in order for this unique thickness to be significantly greater than both
![]() $h_{stop}$
and
$h_{stop}$
and
![]() $h_{\ast }$
, as observed in experiments.
$h_{\ast }$
, as observed in experiments.
As has been seen in § 3, the depth-averaged viscous terms in (2.3)–(2.4) are a singular perturbation of the model that produces qualitatively different solutions. Rather than the unique solution found when the viscous terms are present, in the inviscid case (
![]() $\unicode[STIX]{x1D708}=0$
) there are an infinite family of steady-state solutions with constant channel thicknesses in the metastable range
$\unicode[STIX]{x1D708}=0$
) there are an infinite family of steady-state solutions with constant channel thicknesses in the metastable range
![]() $[h_{stop},h_{start}]$
, plug-like downslope velocity profiles across the slope and contact discontinuities at the channel edge (§ 3.2). Mangeney et al.’s (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) numerical simulations are consistent with a flow that is approaching one of these steady-state inviscid solutions. Indeed, Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) derived equations for the velocity and width of the flow (their equations (24) and (25)), which are directly equivalent to the steady-state equations (3.9) and (3.11) for glass beads (
$[h_{stop},h_{start}]$
, plug-like downslope velocity profiles across the slope and contact discontinuities at the channel edge (§ 3.2). Mangeney et al.’s (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) numerical simulations are consistent with a flow that is approaching one of these steady-state inviscid solutions. Indeed, Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) derived equations for the velocity and width of the flow (their equations (24) and (25)), which are directly equivalent to the steady-state equations (3.9) and (3.11) for glass beads (
![]() $\unicode[STIX]{x1D6E4}=0$
). However, they did not draw out the fact that the steady-state inviscid system of equations is not uniquely determined, nor why the observed thickness
$\unicode[STIX]{x1D6E4}=0$
). However, they did not draw out the fact that the steady-state inviscid system of equations is not uniquely determined, nor why the observed thickness
![]() $H\approx 1.03h_{stop}$
is so close to the thinnest possible steady-state solution.
$H\approx 1.03h_{stop}$
is so close to the thinnest possible steady-state solution.
In the absence of any numerical viscosity, the initial conditions and time-dependent evolution of the inviscid equations could, in principle, select the observed channel width from the many possible steady-state solutions. In reality, this time dependence does not appear to be the mechanism setting the channel width, since Deboeuf et al. (Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006) found that the width was independent of past changes in flux and Takagi et al. (Reference Takagi, McElwaine and Huppert2011) showed that an initial layer of erodible particles covering the chute did not influence the equilibrium flowing channel width.
Based on solutions of Mangeney et al.’s (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) inviscid equations and quantitative reproduction of their observations made using the numerical scheme of this paper, there appear to be two reasons why the numerical solutions of Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) select a flow thickness very close to
![]() $h_{stop}$
. These relate to the Mangeney et al.’s (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) use of an extremely rapid transition from static to flowing friction (
$h_{stop}$
. These relate to the Mangeney et al.’s (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) use of an extremely rapid transition from static to flowing friction (
![]() $\unicode[STIX]{x1D705}=10^{-3}$
) and the interaction of this with small but unavoidable errors in numerical schemes.
$\unicode[STIX]{x1D705}=10^{-3}$
) and the interaction of this with small but unavoidable errors in numerical schemes.
Firstly, as pointed out by Edwards et al. (Reference Edwards, Russell, Johnson and Gray2019), the initial sharp decrease in the friction as
![]() $Fr$
increases from zero, when
$Fr$
increases from zero, when
![]() $\unicode[STIX]{x1D705}=10^{-3}$
, is extremely difficult to represent in standard floating-point numerical computations. For instance, at the smallest non-zero value the Froude number (
$\unicode[STIX]{x1D705}=10^{-3}$
, is extremely difficult to represent in standard floating-point numerical computations. For instance, at the smallest non-zero value the Froude number (
![]() ${\sim}10^{-16}$
, based on IEEE-754 double precision round-off error of
${\sim}10^{-16}$
, based on IEEE-754 double precision round-off error of
![]() $O(1)$
numerical quantities in the finite-volume scheme) the friction coefficient drops to a value that is well below the maximum static friction and is insufficient to bring to rest any flowing material thicker than
$O(1)$
numerical quantities in the finite-volume scheme) the friction coefficient drops to a value that is well below the maximum static friction and is insufficient to bring to rest any flowing material thicker than
![]() $1.02h_{stop}=2.727$
mm. This suggests that when Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) stopped their numerical simulations (when
$1.02h_{stop}=2.727$
mm. This suggests that when Mangeney et al. (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) stopped their numerical simulations (when
![]() $H\sim 1.03h_{stop}$
) the flow was still slowly spreading, but that it was very close to the range of thicknesses where inviscid steady-state solutions could exist.
$H\sim 1.03h_{stop}$
) the flow was still slowly spreading, but that it was very close to the range of thicknesses where inviscid steady-state solutions could exist.
Secondly, the singular nature of the viscous terms in the governing equations means that even a small amount of numerical viscosity results in the solution of the viscous equations, with the viscosity coefficient in this case determined artificially by the grid resolution and details of the numerical scheme. As noted previously, when
![]() $\unicode[STIX]{x1D705}=10^{-3}$
the unique steady viscous solution for a given flux lies in a very narrow range of thicknesses
$\unicode[STIX]{x1D705}=10^{-3}$
the unique steady viscous solution for a given flux lies in a very narrow range of thicknesses
![]() $[H_{min},H_{max}]$
that is slightly (
$[H_{min},H_{max}]$
that is slightly (
![]() ${\sim}0.1\,\%$
) greater than the thinnest steady uniform flow (i.e.
${\sim}0.1\,\%$
) greater than the thinnest steady uniform flow (i.e.
![]() $h_{stop}$
, for the friction law used by Mangeney et al.
Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007). It is therefore possible that Mangeney et al.’s (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) inviscid solutions are approaching a steady state of the viscous equations, but this relies entirely on the mesh-size dependent and numerical scheme dependent viscosity.
$h_{stop}$
, for the friction law used by Mangeney et al.
Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007). It is therefore possible that Mangeney et al.’s (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) inviscid solutions are approaching a steady state of the viscous equations, but this relies entirely on the mesh-size dependent and numerical scheme dependent viscosity.
In contrast, the combination in this paper of physically derived viscous terms and the friction law of Edwards et al. (Reference Edwards, Russell, Johnson and Gray2019) (with
![]() $\unicode[STIX]{x1D705}=1$
) provides (i) a unique steady channel thickness and width in good agreement with experiments, and (ii) a time-dependent model that unambiguously approaches this unique steady state at late times.
$\unicode[STIX]{x1D705}=1$
) provides (i) a unique steady channel thickness and width in good agreement with experiments, and (ii) a time-dependent model that unambiguously approaches this unique steady state at late times.
5 Discussion and conclusions
5.1 Summary of results
This paper shows that two physical processes are needed to quantitatively predict self-channelisation and levee formation in monodisperse granular flows using depth-averaged avalanche models. These are (i) a non-monotonic effective basal friction law (Pouliquen & Forterre Reference Pouliquen and Forterre2002; Félix & Thomas Reference Félix and Thomas2004; Deboeuf et al. Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006; Mangeney et al. Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007; Edwards & Gray Reference Edwards and Gray2015; Edwards et al. Reference Edwards, Viroulet, Kokelaar and Gray2017, Reference Edwards, Russell, Johnson and Gray2019) and (ii) depth-averaged lateral viscous stresses (Gray & Edwards Reference Gray and Edwards2014; Baker et al. Reference Baker, Barker and Gray2016a ). The non-monotonic friction models the hysteretic behaviour that allows static and flowing regions to coexist, while the viscous terms are vital to close the system of equations and produce smooth transitions between the static and flowing regions that do not exert shear stresses on the levee walls.
The two-dimensional time-dependent simulations in figures 14 and 15 show that the resultant equations (2.2)–(2.15) model the formation of a central flowing channel bounded by parallel-sided static levees. When material flowing down the channel reaches the front, it loses its lateral confinement, spreads out and slows down. The grains that are still in the centre of the flow are then overrun, while the particles that migrate to the sides come to rest and build a new section of the levee wall, advancing it downslope (Félix & Thomas Reference Félix and Thomas2004; Johnson et al. Reference Johnson, Kokelaar, Iverson, Logan, LaHusen and Gray2012). In this way the flow front is able to propagate downslope as a steadily travelling wave, continuously laying down a pair of levees at the back of the flow head. The final width of the channel is not always set immediately behind the head; an equilibrium width of the central channel is established when the flow thickness and depth-averaged velocity profile are such that there is no net erosion or deposition at the levee–channel boundaries. Once the channel has formed, the levees prevent the flow spreading laterally and thereby maintain the flow’s thickness, and hence mobility, leading to enhanced run-out. The flow can widen by levee-bank overtopping in response to an increase in mass flux, and retreat into the centre of the channel if the flux is reduced, as shown experimentally (figure 4, movie 3) and in the numerical simulations (figure 16, movies 7 and 8).
To understand the force balance leading to the leveed channel, a steady-state problem is formulated in § 3.1, which shows that across the width
![]() $W$
of a parallel-sided flowing channel, the thickness
$W$
of a parallel-sided flowing channel, the thickness
![]() $h$
is equal to a constant
$h$
is equal to a constant
![]() $H$
and the downslope velocity profile
$H$
and the downslope velocity profile
![]() $\bar{u}(y)$
satisfies the second-order ODE (3.5). For a given mass flux
$\bar{u}(y)$
satisfies the second-order ODE (3.5). For a given mass flux
![]() $Q_{M}$
, this can be solved as a boundary value problem for
$Q_{M}$
, this can be solved as a boundary value problem for
![]() $W$
,
$W$
,
![]() $H$
and
$H$
and
![]() $\bar{u}(y)$
, subject to zero velocity (3.6) and zero shear stress (3.7) boundary conditions at the levee–channel interfaces, as well as the integral constraint (3.8) on the mass flux. The viscous terms allow the static shear-stress-free levees to be connected to the central flow, where steady uniform flow dominates, across a viscous boundary layer or shear band (see figure 9
c). There is a unique solution to the problem for all values of the mass flux
$\bar{u}(y)$
, subject to zero velocity (3.6) and zero shear stress (3.7) boundary conditions at the levee–channel interfaces, as well as the integral constraint (3.8) on the mass flux. The viscous terms allow the static shear-stress-free levees to be connected to the central flow, where steady uniform flow dominates, across a viscous boundary layer or shear band (see figure 9
c). There is a unique solution to the problem for all values of the mass flux
![]() $Q_{M}$
although the character of the solution changes at
$Q_{M}$
although the character of the solution changes at
![]() $Q=Q_{min}$
. For
$Q=Q_{min}$
. For
![]() $Q_{M}<Q_{min}$
the solutions are purely in the intermediate frictional regime (2.12), whilst for
$Q_{M}<Q_{min}$
the solutions are purely in the intermediate frictional regime (2.12), whilst for
![]() $Q_{M}>Q_{min}$
, the solutions also have regions of dynamic friction (2.10). It is these latter solutions that are physically realised.
$Q_{M}>Q_{min}$
, the solutions also have regions of dynamic friction (2.10). It is these latter solutions that are physically realised.
The solutions to the boundary value problem (see figures 8–9) are in excellent quantitative agreement with the experimental measurements of the height and width of the central flowing channel (Takagi et al.
Reference Takagi, McElwaine and Huppert2011) as shown in figure 10 for sand. These solutions show that, as the mass flux
![]() $Q_{M}$
is increased, the thickness of the central flowing channel remains nearly constant and its width increases approximately linearly. The constant thickness
$Q_{M}$
is increased, the thickness of the central flowing channel remains nearly constant and its width increases approximately linearly. The constant thickness
![]() $H$
in the channel is significantly above both
$H$
in the channel is significantly above both
![]() $h_{stop}$
and
$h_{stop}$
and
![]() $h_{\ast }$
. Takagi et al. (Reference Takagi, McElwaine and Huppert2011) also made measurements of the surface velocity profile across the channel. These are harder to compare, because the velocity shear through the depth of the avalanche necessarily implies that the surface velocity is not equal to the depth-averaged velocity calculated by the theory. Figure 11 shows that the depth-averaged velocity
$h_{\ast }$
. Takagi et al. (Reference Takagi, McElwaine and Huppert2011) also made measurements of the surface velocity profile across the channel. These are harder to compare, because the velocity shear through the depth of the avalanche necessarily implies that the surface velocity is not equal to the depth-averaged velocity calculated by the theory. Figure 11 shows that the depth-averaged velocity
![]() $\bar{u}$
and the surface velocity measurements
$\bar{u}$
and the surface velocity measurements
![]() $u_{s}$
have the same functional behaviour with the mass flux
$u_{s}$
have the same functional behaviour with the mass flux
![]() $Q_{M}$
, and that
$Q_{M}$
, and that
![]() $u_{s}/\bar{u}\approx 2.35$
. This large ratio of surface velocity to depth-averaged velocity is consistent with the discrete element method simulations of Silbert et al. (Reference Silbert, Landry and Grest2003) and non-local theory of Kamrin & Henann (Reference Kamrin and Henann2015), which predict a transition from Bagnold flow to exponential-like velocity profiles as the flow gets close to
$u_{s}/\bar{u}\approx 2.35$
. This large ratio of surface velocity to depth-averaged velocity is consistent with the discrete element method simulations of Silbert et al. (Reference Silbert, Landry and Grest2003) and non-local theory of Kamrin & Henann (Reference Kamrin and Henann2015), which predict a transition from Bagnold flow to exponential-like velocity profiles as the flow gets close to
![]() $h_{\ast }$
.
$h_{\ast }$
.
The model is also in very good agreement with the thickness measurements of Félix & Thomas (Reference Félix and Thomas2004) for glass beads as shown in figure 12 for a wide range of mass fluxes. However, the predictions of the steady-state minimal total width of the channel (see § 3.5.2 and appendix B) do not agree with those measured by Félix & Thomas (Reference Félix and Thomas2004) at high mass fluxes. The most likely explanation for this discrepancy is that either Félix & Thomas’s (Reference Félix and Thomas2004) experimental chute was not long enough, or the flow was not observed for a sufficiently long time, to measure a true steady state. This is certainly consistent with the observations of Deboeuf et al. (Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006) and Takagi et al. (Reference Takagi, McElwaine and Huppert2011) who found that for weakly hysteretic materials, such as glass beads, the width of the flow adjusted on very long time scales (
![]() ${\sim}70$
–90 min).
${\sim}70$
–90 min).
Below a critical mass flux the steady-state solutions go unstable in experiments (Félix & Thomas Reference Félix and Thomas2004; Takagi et al. Reference Takagi, McElwaine and Huppert2011) as shown for red sand in movie 4. This also occurs in the numerical solutions (figures 17, 18 and 19), which produce a series of finite pulses of flowing material separated by intervals during which the grains are completely static. These are another example of erosion–deposition waves, which have previously been observed on erodible beds (Daerr & Douady Reference Daerr and Douady1999; Börzsönyi et al. Reference Börzsönyi, Halsey and Ecke2005; Clément et al. Reference Clément, Malloggi, Andreotti and Aranson2007; Edwards & Gray Reference Edwards and Gray2015; Edwards et al. Reference Edwards, Viroulet, Kokelaar and Gray2017) and have been simulated numerically by Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) using the same system of equations used in this paper. The governing equations (2.2)–(2.15) are therefore extremely versatile and have the potential to explain many flows with qualitatively very different behaviour.
The viscous terms play a critical role in setting the velocity profile and hence the thickness and width of the self-channelised flow. In the absence of viscosity, the system of equations (2.2)–(2.5) reduce to the classical avalanche equations, which are hyperbolic in character (see e.g. Grigorian et al.
Reference Grigorian, Eglit and Iakimov1967; Savage & Hutter Reference Savage and Hutter1989; Gray et al.
Reference Gray, Wieland and Hutter1999, Reference Gray, Tai and Noelle2003; Mangeney et al.
Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007). As shown in § 3.2, in this inviscid model the constant channel thickness
![]() $H$
implies that the velocity is equal to the steady-uniform value (3.9) across the whole channel, with contact discontinuities at the levee–channel interfaces where the downslope velocity jumps from the steady-uniform value
$H$
implies that the velocity is equal to the steady-uniform value (3.9) across the whole channel, with contact discontinuities at the levee–channel interfaces where the downslope velocity jumps from the steady-uniform value
![]() $\bar{u}_{steady}$
to zero. The thickness of the flow
$\bar{u}_{steady}$
to zero. The thickness of the flow
![]() $H$
is not determined, and may lie anywhere in the range
$H$
is not determined, and may lie anywhere in the range
![]() $[h_{\ast },h_{start}]$
, where
$[h_{\ast },h_{start}]$
, where
![]() $h_{\ast }>h_{stop}$
is the minimum observable thickness of a steady uniform flow (Edwards et al.
Reference Edwards, Russell, Johnson and Gray2019). As a result, even for the same mass flux
$h_{\ast }>h_{stop}$
is the minimum observable thickness of a steady uniform flow (Edwards et al.
Reference Edwards, Russell, Johnson and Gray2019). As a result, even for the same mass flux
![]() $Q_{M}$
, there are a corresponding range of possible widths (see figure 7), which implies that inviscid theories lack the physical mechanism to set the steady-state thickness and width of the flow.
$Q_{M}$
, there are a corresponding range of possible widths (see figure 7), which implies that inviscid theories lack the physical mechanism to set the steady-state thickness and width of the flow.
In practical numerical computations there is usually some mesh-size-dependent numerical diffusion. It follows that numerical computations with Mangeney et al.’s (Reference Mangeney, Bouchut, Thomas, Vilotte and Bristeau2007) inviscid model will appear to behave somewhat like the theory presented in this paper (see 4.5). The important distinction is that it is the mesh-size-dependent numerical diffusion that selects the solution, rather than the physically based depth-averaged viscosity (Gray & Edwards Reference Gray and Edwards2014; Baker et al.
Reference Baker, Barker and Gray2016a
) derived from the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology (GDR-MiDi 2004; Jop et al.
Reference Jop, Forterre and Pouliquen2006). The viscous depth-averaged theory presented in this paper is therefore a significant advance over previous models.
$\unicode[STIX]{x1D707}(I)$
-rheology (GDR-MiDi 2004; Jop et al.
Reference Jop, Forterre and Pouliquen2006). The viscous depth-averaged theory presented in this paper is therefore a significant advance over previous models.
Despite the theory’s clear success in simulating many features of the flow, one subtle aspect that is not captured correctly is the shape of the free surface. Experimental measurements of self-channelised flows (Félix & Thomas Reference Félix and Thomas2004; Deboeuf et al.
Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006; Takagi et al.
Reference Takagi, McElwaine and Huppert2011) show that, instead of having a constant depth across the channel, the maximum thickness occurs in the centre, where the material moves faster. The curvature in the free surface appears to coincide with regions of high shear, i.e. for narrow channels, with a parabolic-like velocity profile, experiments suggest that the free surface is curved across the whole channel. For wider channels, the free surface is almost flat in the central steady uniform region, with curvature observed only at the boundary layers at the sides (Félix & Thomas Reference Félix and Thomas2004). This observation may be important in the development of new constitutive equations for granular flows that go beyond the
![]() $\unicode[STIX]{x1D707}(I)$
-rheology (see e.g. Kamrin & Koval Reference Kamrin and Koval2012; Bouzid et al.
Reference Bouzid, Trulsson, Claudin, Clément and Andreotti2013; Henann & Kamrin Reference Henann and Kamrin2013; Kamrin & Henann Reference Kamrin and Henann2015; Lee & Yang Reference Lee and Yang2017). For example, second normal stress differences can result in variations in free surface height as a function of the downstream velocity (McElwaine et al.
Reference McElwaine, Takagi and Huppert2012). Another possible explanation is that the low velocity regions, on the inside walls at the base levees, jam and become quasi-static rather than inertial (Deboeuf et al.
Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006; Kokelaar et al.
Reference Kokelaar, Graham, Gray and Vallance2014). This would change the height of the effective topography that the avalanche was flowing over and potentially allow cross-slope variations in thickness. Understanding how to model this quantitatively would probably require a compressible granular theory (see e.g. Barker et al.
Reference Barker, Schaeffer, Shearer and Gray2017; Heyman et al.
Reference Heyman, Delannay, Tabuteau and Valance2017; Schaeffer et al.
Reference Schaeffer, Barker, Tsuji, Gremaud, Shearer and Gray2019) that could span the quasi-static and inertial regimes (Chialvo, Sun & Sundaresan Reference Chialvo, Sun and Sundaresan2012). There is, however, a long way to go before either of these effects can be included in depth-averaged avalanche models, and the existing theory appears to be able to make accurate predictions without them.
$\unicode[STIX]{x1D707}(I)$
-rheology (see e.g. Kamrin & Koval Reference Kamrin and Koval2012; Bouzid et al.
Reference Bouzid, Trulsson, Claudin, Clément and Andreotti2013; Henann & Kamrin Reference Henann and Kamrin2013; Kamrin & Henann Reference Kamrin and Henann2015; Lee & Yang Reference Lee and Yang2017). For example, second normal stress differences can result in variations in free surface height as a function of the downstream velocity (McElwaine et al.
Reference McElwaine, Takagi and Huppert2012). Another possible explanation is that the low velocity regions, on the inside walls at the base levees, jam and become quasi-static rather than inertial (Deboeuf et al.
Reference Deboeuf, Lajeunesse, Dauchot and Andreotti2006; Kokelaar et al.
Reference Kokelaar, Graham, Gray and Vallance2014). This would change the height of the effective topography that the avalanche was flowing over and potentially allow cross-slope variations in thickness. Understanding how to model this quantitatively would probably require a compressible granular theory (see e.g. Barker et al.
Reference Barker, Schaeffer, Shearer and Gray2017; Heyman et al.
Reference Heyman, Delannay, Tabuteau and Valance2017; Schaeffer et al.
Reference Schaeffer, Barker, Tsuji, Gremaud, Shearer and Gray2019) that could span the quasi-static and inertial regimes (Chialvo, Sun & Sundaresan Reference Chialvo, Sun and Sundaresan2012). There is, however, a long way to go before either of these effects can be included in depth-averaged avalanche models, and the existing theory appears to be able to make accurate predictions without them.
5.2 Implications for the interpretation of levee–channel deposits
The results of this paper provide a theoretical framework for the interpretation of leveed deposits from geophysical mass flows such as debris flows and pyroclastic density currents. Specifically, the predictions of the thickness and width of a self-channelised leveed flow in § 3.3 may be inverted to infer information about the mass flux or rheology of the original flow from measurements of the deposit. A key observation is that the thickness of a levee is similar to the thickness of the flow that created it, and is nearly independent of the mass flux of that flow (figures 10 a and 12 a). A difference in thickness between levees in successive flows therefore suggests a change in flow composition and rheology, not simply mass flux. The width of the static channel between the levees is roughly proportional to the mass flux of the originating flow (figures 10 b and 12 b). Very wide levees, with a sequence of nested parallel levees inside the main channel, are strongly indicative of a decrease in mass flux prior to deposition (figure 4 b). However, an increase in flux with time may not be reflected in the deposit, due to erosion of the existing levees (figure 4 c).
Interpretation of deposits with levee–channel morphology is complicated by the existence of other levee-forming flows. A disturbance to an erodible layer of grains on an inclined plane may lead to a localised erosion–deposition wave, in which the static layer is continuously eroded at the flow front and deposited a short time later at the back of the avalanche (Edwards et al. Reference Edwards, Viroulet, Kokelaar and Gray2017). This flow leaves behind a pair of static parallel-sided levees that are raised above the surface of the original erodible layer, located either side of a depression or trough. The leveed deposit resulting from this erosion–deposition wave therefore looks similar to that produced by a continuous flux of grains (figure 2 c), which might make the two cases difficult to distinguish in geophysical flow deposits. A key difference between these flows is the origin of the material that forms the levees. The levees described in this paper are composed of grains provided by a continuous source upslope, whereas those generated by the erosion–deposition waves of Edwards et al. (Reference Edwards, Viroulet, Kokelaar and Gray2017) are composed of grains that are continuously eroded at the front of the avalanche.
Field observations (Wilson & Head Reference Wilson, Head, Lipman and Mullineaux1981; Bartelt et al. Reference Bartelt, Glover, Feistl, Bühler and Buser2012) suggest that the margins of the flow may be differentially fluidised during emplacement of levees, which implies that the rheology is inhomogeneous (Iverson & Vallance Reference Iverson and Vallance2001; Iverson Reference Iverson, Rickenmann and Chen2003). In debris flows, the evolving pore fluid pressure (Iverson Reference Iverson1997; Iverson & Denlinger Reference Iverson and Denlinger2001) and particle-size distribution due to segregation (Gray Reference Gray2018) significantly alter the bulk flow by generating drier bouldery margins that resist the motion and form pronounced levees (Johnson et al. Reference Johnson, Kokelaar, Iverson, Logan, LaHusen and Gray2012). Although these effects present additional modelling challenges, the heterogeneous particle-size distribution of a deposit also potentially provides considerably more information about the flow that created it than the deposit geometry alone. The incorporation of such heterogeneity into the model for levee formation presented here is, therefore, a promising avenue for future research.
Acknowledgements
This research was supported by NERC grants NE/E003206/1 and NE/K003011/1 as well as EPSRC grants EP/I019189/1, EP/K00428X/1 and EP/M022447/1. F.M.R. acknowledges financial support from CNPq, Conselho Nacional de Desenvolvimento Científico e Tecnológico – Brazil. J.M.N.T.G. is a Royal Society Wolfson Research Merit Award holder (WM150058) and an EPSRC Established Career Fellow (EP/M022447/1).
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/jfm.2019.518.
Appendix A. Velocity reconstruction
The full downslope velocity profile
![]() $u(y,z)$
can be reconstructed from the depth-averaged value
$u(y,z)$
can be reconstructed from the depth-averaged value
![]() $\bar{u}(y)$
by assuming a velocity profile
$\bar{u}(y)$
by assuming a velocity profile
![]() $f(z)$
through the avalanche depth
$f(z)$
through the avalanche depth
Steady uniform granular flows usually develop a convex Bagnold velocity profile (Silbert et al.
Reference Silbert, Ertaş, Grest, Halsey, Levine and Plimpton2001; GDR-MiDi 2004), but this can become concave when the flow is confined between lateral side walls (e.g. Komatsu et al.
Reference Komatsu, Inagaki, Nakagawa and Nasuno2001; Jop et al.
Reference Jop, Forterre and Pouliquen2005; Wiederseiner et al.
Reference Wiederseiner, Andreini, Epely-Chauvin, Moser, Monnereau, Gray and Ancey2011; Baker et al.
Reference Baker, Barker and Gray2016a
). Even in the absence of side walls, the DEM simulations of Silbert et al. (Reference Silbert, Landry and Grest2003) and the non-local theory of Kamrin & Henann (Reference Kamrin and Henann2015) predict a transition from Bagnold to concave velocity profiles as the flow thickness approaches
![]() $h_{\ast }$
, which for steady uniform flow lies at the transition between dynamic and intermediate frictional regimes. The exponential profile of Wiederseiner et al. (Reference Wiederseiner, Andreini, Epely-Chauvin, Moser, Monnereau, Gray and Ancey2011)
$h_{\ast }$
, which for steady uniform flow lies at the transition between dynamic and intermediate frictional regimes. The exponential profile of Wiederseiner et al. (Reference Wiederseiner, Andreini, Epely-Chauvin, Moser, Monnereau, Gray and Ancey2011)
provides a good fit to the observations in this paper, where
![]() $\unicode[STIX]{x1D706}$
is an adjustable parameter. Evaluating this at the free surface implies that the surface velocity
$\unicode[STIX]{x1D706}$
is an adjustable parameter. Evaluating this at the free surface implies that the surface velocity
![]() $u_{s}$
is related to the depth-averaged velocity
$u_{s}$
is related to the depth-averaged velocity
![]() $\bar{u}$
by the relation
$\bar{u}$
by the relation
The surface velocity data for sand (Takagi et al.
Reference Takagi, McElwaine and Huppert2011) shown in figure 11 suggest that
![]() $u_{s}=2.35\bar{u}$
, which implies
$u_{s}=2.35\bar{u}$
, which implies
![]() $\unicode[STIX]{x1D706}=2.05$
. This is within 15 % of the value
$\unicode[STIX]{x1D706}=2.05$
. This is within 15 % of the value
![]() $u_{s}=2.7\bar{u}$
(corresponding to
$u_{s}=2.7\bar{u}$
(corresponding to
![]() $\unicode[STIX]{x1D706}=2.45$
) measured experimentally in a thin unconfined flow of glass beads (Russell et al.
Reference Russell, Johnson, Edwards, Viroulet, Rocha and Gray2019).
$\unicode[STIX]{x1D706}=2.45$
) measured experimentally in a thin unconfined flow of glass beads (Russell et al.
Reference Russell, Johnson, Edwards, Viroulet, Rocha and Gray2019).
Appendix B. Shape of the minimal levees
Outside the flowing channel, the shape of the static levees is constrained, but not determined uniquely, by the static friction. Assuming that these static levees are uniform in the
![]() $x$
-direction, the cross-slope component of the depth-averaged momentum balance (2.4) reduces not to (3.3), but to a balance between surface gradients and friction
$x$
-direction, the cross-slope component of the depth-averaged momentum balance (2.4) reduces not to (3.3), but to a balance between surface gradients and friction
where the second component of the friction direction (2.6) is
The static friction law (2.11) implies that
![]() $\unicode[STIX]{x1D707}_{b}=\unicode[STIX]{x1D707}_{S}$
, which can take any value between zero and the maximum static friction. This implies that in general there are infinitely many solutions for the levee shape. It is, however, possible to calculate a unique minimal solution for the levee by assuming that the granular material is on the brink of yield (Hulme Reference Hulme1974; Balmforth et al.
Reference Balmforth, Burbidge and Craster2001), i.e. that the basal friction
$\unicode[STIX]{x1D707}_{b}=\unicode[STIX]{x1D707}_{S}$
, which can take any value between zero and the maximum static friction. This implies that in general there are infinitely many solutions for the levee shape. It is, however, possible to calculate a unique minimal solution for the levee by assuming that the granular material is on the brink of yield (Hulme Reference Hulme1974; Balmforth et al.
Reference Balmforth, Burbidge and Craster2001), i.e. that the basal friction
![]() $\unicode[STIX]{x1D707}_{b}$
is at its maximum static value everywhere
$\unicode[STIX]{x1D707}_{b}$
is at its maximum static value everywhere
With the basal friction determined by (B 3), equations (B 1) and (B 2) can be rearranged to determine a first-order ODE for the minimal levee wall shape
In this equation the
![]() $\pm$
sign allows decreasing solutions to be calculated on either side of the central channel starting from where
$\pm$
sign allows decreasing solutions to be calculated on either side of the central channel starting from where
![]() $h=H$
at
$h=H$
at
![]() $y=\pm W/2$
. Integrating the ODE (B 4) backwards and forwards, respectively, from
$y=\pm W/2$
. Integrating the ODE (B 4) backwards and forwards, respectively, from
![]() $y=-W/2$
and
$y=-W/2$
and
![]() $y=W/2$
, until the height is equal to zero at
$y=W/2$
, until the height is equal to zero at
![]() $y=\pm W_{total}/2$
, determines the minimum total width
$y=\pm W_{total}/2$
, determines the minimum total width
![]() $W_{total}$
that is capable of sustaining a flow of thickness
$W_{total}$
that is capable of sustaining a flow of thickness
![]() $H$
.
$H$
.