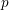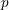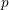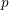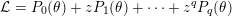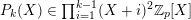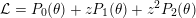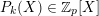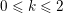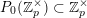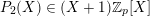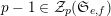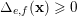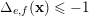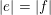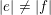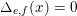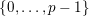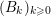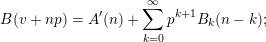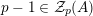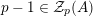1 Introduction
1.1 Classical results of Lucas and Kummer
It is a well-known result of Lucas [Reference LucasLuc78] that, for all nonnegative integers
![]() $m,n$
and all primes
$m,n$
and all primes
![]() $p$
, we have
$p$
, we have
 $$\begin{eqnarray}\binom{m}{n}\equiv \mathop{\prod }_{i=0}^{k}\binom{m_{i}}{n_{i}}\hspace{0.6em}{\rm mod}\hspace{0.2em}p,\end{eqnarray}$$
$$\begin{eqnarray}\binom{m}{n}\equiv \mathop{\prod }_{i=0}^{k}\binom{m_{i}}{n_{i}}\hspace{0.6em}{\rm mod}\hspace{0.2em}p,\end{eqnarray}$$
where
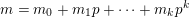 $m=m_{0}+m_{1}p+\cdots +m_{k}p^{k}$
and
$m=m_{0}+m_{1}p+\cdots +m_{k}p^{k}$
and
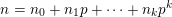 $n=n_{0}+n_{1}p+\cdots +n_{k}p^{k}$
are the base-
$n=n_{0}+n_{1}p+\cdots +n_{k}p^{k}$
are the base-
![]() $p$
expansions of
$p$
expansions of
![]() $m$
and
$m$
and
![]() $n$
.
$n$
.
In particular, a prime
![]() $p$
divides the binomial
$p$
divides the binomial
![]() $\binom{m}{n}$
if and only if there is
$\binom{m}{n}$
if and only if there is
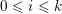 $0\leqslant i\leqslant k$
such that
$0\leqslant i\leqslant k$
such that
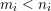 $m_{i}<n_{i}$
. Precisely, Kummer proved in [Reference KummerKum52] that, for all nonnegative integers
$m_{i}<n_{i}$
. Precisely, Kummer proved in [Reference KummerKum52] that, for all nonnegative integers
![]() $m\geqslant n$
, the
$m\geqslant n$
, the
![]() $p$
-adic valuationFootnote
1
of the binomial
$p$
-adic valuationFootnote
1
of the binomial
![]() $\binom{m}{n}$
is the number of carries which occur when
$\binom{m}{n}$
is the number of carries which occur when
![]() $n$
is added to
$n$
is added to
![]() $m-n$
in base
$m-n$
in base
![]() $p$
. As a consequence, we have
$p$
. As a consequence, we have
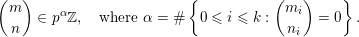 $$\begin{eqnarray}\binom{m}{n}\in p^{\unicode[STIX]{x1D6FC}}\mathbb{Z},\quad \text{where }\unicode[STIX]{x1D6FC}=\#\left\{0\leqslant i\leqslant k:\binom{m_{i}}{n_{i}}=0\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\binom{m}{n}\in p^{\unicode[STIX]{x1D6FC}}\mathbb{Z},\quad \text{where }\unicode[STIX]{x1D6FC}=\#\left\{0\leqslant i\leqslant k:\binom{m_{i}}{n_{i}}=0\right\}.\end{eqnarray}$$
In this article, we show that many sequences
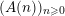 $(A(n))_{n\geqslant 0}$
of Apéry-like numbers satisfy congruences similar to (1.1), that is, for all nonnegative integers
$(A(n))_{n\geqslant 0}$
of Apéry-like numbers satisfy congruences similar to (1.1), that is, for all nonnegative integers
![]() $n$
and all primes
$n$
and all primes
![]() $p$
, we have
$p$
, we have
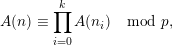 $$\begin{eqnarray}A(n)\equiv \mathop{\prod }_{i=0}^{k}A(n_{i})\hspace{0.6em}{\rm mod}\hspace{0.2em}p,\end{eqnarray}$$
$$\begin{eqnarray}A(n)\equiv \mathop{\prod }_{i=0}^{k}A(n_{i})\hspace{0.6em}{\rm mod}\hspace{0.2em}p,\end{eqnarray}$$
where
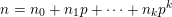 $n=n_{0}+n_{1}p+\cdots +n_{k}p^{k}$
is the base-
$n=n_{0}+n_{1}p+\cdots +n_{k}p^{k}$
is the base-
![]() $p$
expansion of
$p$
expansion of
![]() $n$
. Furthermore, we prove that an analogue of (1.2) holds for those numbers, that is,
$n$
. Furthermore, we prove that an analogue of (1.2) holds for those numbers, that is,
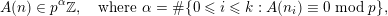 $$\begin{eqnarray}A(n)\in p^{\unicode[STIX]{x1D6FC}}\mathbb{Z},\quad \text{where }\unicode[STIX]{x1D6FC}=\#\{0\leqslant i\leqslant k:A(n_{i})\equiv 0\;\text{mod}\;p\},\end{eqnarray}$$
$$\begin{eqnarray}A(n)\in p^{\unicode[STIX]{x1D6FC}}\mathbb{Z},\quad \text{where }\unicode[STIX]{x1D6FC}=\#\{0\leqslant i\leqslant k:A(n_{i})\equiv 0\;\text{mod}\;p\},\end{eqnarray}$$
which proves Beukers’ conjectures on the
![]() $p$
-adic valuation of Apéry numbers.
$p$
-adic valuation of Apéry numbers.
1.2 Beukers’ conjectures on Apéry numbers
For all nonnegative integers
![]() $n$
, we set
$n$
, we set
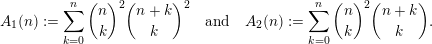 $$\begin{eqnarray}A_{1}(n):=\mathop{\sum }_{k=0}^{n}\binom{n}{k}^{2}\binom{n+k}{k}^{2}\quad \text{and}\quad A_{2}(n):=\mathop{\sum }_{k=0}^{n}\binom{n}{k}^{2}\binom{n+k}{k}.\end{eqnarray}$$
$$\begin{eqnarray}A_{1}(n):=\mathop{\sum }_{k=0}^{n}\binom{n}{k}^{2}\binom{n+k}{k}^{2}\quad \text{and}\quad A_{2}(n):=\mathop{\sum }_{k=0}^{n}\binom{n}{k}^{2}\binom{n+k}{k}.\end{eqnarray}$$
These sequences were used in
![]() $1979$
by Apéry in his proofs of the irrationality of
$1979$
by Apéry in his proofs of the irrationality of
![]() $\unicode[STIX]{x1D701}(3)$
and
$\unicode[STIX]{x1D701}(3)$
and
![]() $\unicode[STIX]{x1D701}(2)$
(see [Reference ApéryApé79]). In the
$\unicode[STIX]{x1D701}(2)$
(see [Reference ApéryApé79]). In the
![]() $1980$
s, several congruences satisfied by these sequences were proved (see, for example, [Reference BeukersBeu85, Reference BeukersBeu87, Reference Chowla, Cowles and CowlesCCC80, Reference GesselGes82, Reference MimuraMim83]). In particular, Gessel proved in [Reference GesselGes82] that
$1980$
s, several congruences satisfied by these sequences were proved (see, for example, [Reference BeukersBeu85, Reference BeukersBeu87, Reference Chowla, Cowles and CowlesCCC80, Reference GesselGes82, Reference MimuraMim83]). In particular, Gessel proved in [Reference GesselGes82] that
![]() $A_{1}$
satisfies the
$A_{1}$
satisfies the
![]() $p$
-Lucas property for all prime numbers
$p$
-Lucas property for all prime numbers
![]() $p$
, that is, for any prime
$p$
, that is, for any prime
![]() $p$
, all
$p$
, all
![]() $v$
in
$v$
in
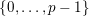 $\{0,\ldots ,p-1\}$
and all nonnegative integers
$\{0,\ldots ,p-1\}$
and all nonnegative integers
![]() $n$
, we have
$n$
, we have
 $$\begin{eqnarray}A_{1}(v+np)\equiv A_{1}(v)A_{1}(n)\hspace{0.6em}{\rm mod}\hspace{0.2em}p.\end{eqnarray}$$
$$\begin{eqnarray}A_{1}(v+np)\equiv A_{1}(v)A_{1}(n)\hspace{0.6em}{\rm mod}\hspace{0.2em}p.\end{eqnarray}$$
Thereby, if
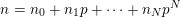 $n=n_{0}+n_{1}p+\cdots +n_{N}p^{N}$
is the base-
$n=n_{0}+n_{1}p+\cdots +n_{N}p^{N}$
is the base-
![]() $p$
expansion of
$p$
expansion of
![]() $n$
, then we obtain
$n$
, then we obtain
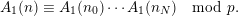 $$\begin{eqnarray}A_{1}(n)\equiv A_{1}(n_{0})\cdots A_{1}(n_{N})\hspace{0.6em}{\rm mod}\hspace{0.2em}p.\end{eqnarray}$$
$$\begin{eqnarray}A_{1}(n)\equiv A_{1}(n_{0})\cdots A_{1}(n_{N})\hspace{0.6em}{\rm mod}\hspace{0.2em}p.\end{eqnarray}$$
In particular,
![]() $p$
divides
$p$
divides
![]() $A_{1}(n)$
if and only if there exists
$A_{1}(n)$
if and only if there exists
![]() $k$
in
$k$
in
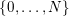 $\{0,\ldots ,N\}$
such that
$\{0,\ldots ,N\}$
such that
![]() $p$
divides
$p$
divides
![]() $A_{1}(n_{k})$
. Beukers stated in [Reference BeukersBeu86] two conjectures, when
$A_{1}(n_{k})$
. Beukers stated in [Reference BeukersBeu86] two conjectures, when
![]() $p=5$
or
$p=5$
or
![]() $11$
, which generalize this property.Footnote
2
Before stating these conjectures, we observe that the set of all
$11$
, which generalize this property.Footnote
2
Before stating these conjectures, we observe that the set of all
![]() $v$
in
$v$
in
 $\{0,\ldots ,4\}$
(respectively
$\{0,\ldots ,4\}$
(respectively
![]() $v$
in
$v$
in
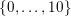 $\{0,\ldots ,10\}$
) satisfying
$\{0,\ldots ,10\}$
) satisfying
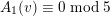 $A_{1}(v)\equiv 0\;\text{mod}\;5$
(respectively
$A_{1}(v)\equiv 0\;\text{mod}\;5$
(respectively
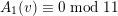 $A_{1}(v)\equiv 0\;\text{mod}\;11$
) is
$A_{1}(v)\equiv 0\;\text{mod}\;11$
) is
![]() $\{1,3\}$
(respectively
$\{1,3\}$
(respectively
![]() $\{5\}$
).
$\{5\}$
).
Conjecture A (Beukers [Reference BeukersBeu86]).
Let
![]() $n$
be a nonnegative integer whose base-
$n$
be a nonnegative integer whose base-
![]() $5$
expansion is
$5$
expansion is
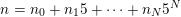 $n=n_{0}+n_{1}5+\cdots +n_{N}5^{N}$
. Let
$n=n_{0}+n_{1}5+\cdots +n_{N}5^{N}$
. Let
![]() $\unicode[STIX]{x1D6FC}$
be the number of
$\unicode[STIX]{x1D6FC}$
be the number of
![]() $k$
in
$k$
in
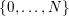 $\{0,\ldots ,N\}$
such that
$\{0,\ldots ,N\}$
such that
![]() $n_{k}=1$
or
$n_{k}=1$
or
![]() $3$
. Then
$3$
. Then
![]() $5^{\unicode[STIX]{x1D6FC}}$
divides
$5^{\unicode[STIX]{x1D6FC}}$
divides
![]() $A_{1}(n)$
.
$A_{1}(n)$
.
Conjecture B (Beukers [Reference BeukersBeu86]).
Let
![]() $n$
be a nonnegative integer whose base-
$n$
be a nonnegative integer whose base-
![]() $11$
expansion is
$11$
expansion is
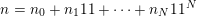 $n=n_{0}+n_{1}11+\cdots +n_{N}11^{N}$
. Let
$n=n_{0}+n_{1}11+\cdots +n_{N}11^{N}$
. Let
![]() $\unicode[STIX]{x1D6FC}$
be the number of
$\unicode[STIX]{x1D6FC}$
be the number of
![]() $k$
in
$k$
in
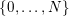 $\{0,\ldots ,N\}$
such that
$\{0,\ldots ,N\}$
such that
![]() $n_{k}=5$
. Then
$n_{k}=5$
. Then
![]() $11^{\unicode[STIX]{x1D6FC}}$
divides
$11^{\unicode[STIX]{x1D6FC}}$
divides
![]() $A_{1}(n)$
.
$A_{1}(n)$
.
Similarly, Sequence
![]() $A_{2}$
satisfies the
$A_{2}$
satisfies the
![]() $p$
-Lucas property for all primes
$p$
-Lucas property for all primes
![]() $p$
. Furthermore, Beukers and Stienstra proved in [Reference Beukers and StienstraBS85] that, if
$p$
. Furthermore, Beukers and Stienstra proved in [Reference Beukers and StienstraBS85] that, if
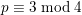 $p\equiv 3\;\text{mod}\;4$
, then
$p\equiv 3\;\text{mod}\;4$
, then
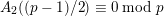 $A_{2}((p-1)/2)\equiv 0\;\text{mod}\;p$
, and Beukers stated in [Reference BeukersBeu86] the following conjecture.
$A_{2}((p-1)/2)\equiv 0\;\text{mod}\;p$
, and Beukers stated in [Reference BeukersBeu86] the following conjecture.
Conjecture C. Let
![]() $p$
be a prime number satisfying
$p$
be a prime number satisfying
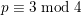 $p\equiv 3\;\text{mod}\;4$
. Let
$p\equiv 3\;\text{mod}\;4$
. Let
![]() $n$
be a nonnegative integer whose base-
$n$
be a nonnegative integer whose base-
![]() $p$
expansion is
$p$
expansion is
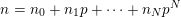 $n=n_{0}+n_{1}p+\cdots +n_{N}p^{N}$
. Let
$n=n_{0}+n_{1}p+\cdots +n_{N}p^{N}$
. Let
![]() $\unicode[STIX]{x1D6FC}$
be the number of
$\unicode[STIX]{x1D6FC}$
be the number of
![]() $k$
in
$k$
in
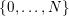 $\{0,\ldots ,N\}$
such that
$\{0,\ldots ,N\}$
such that
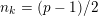 $n_{k}=(p-1)/2$
. Then
$n_{k}=(p-1)/2$
. Then
![]() $p^{\unicode[STIX]{x1D6FC}}$
divides
$p^{\unicode[STIX]{x1D6FC}}$
divides
![]() $A_{2}(n)$
.
$A_{2}(n)$
.
Conjectures A–C have been extended to generalized Apéry numbers and any prime
![]() $p$
by Deutsch and Sagan in [Reference Deutsch and SaganDS06, Conjecture 5.13] but this extension is false for at least one generalization of Apéry numbers. Indeed, a counterexample is given by
$p$
by Deutsch and Sagan in [Reference Deutsch and SaganDS06, Conjecture 5.13] but this extension is false for at least one generalization of Apéry numbers. Indeed, a counterexample is given by
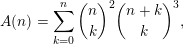 $$\begin{eqnarray}A(n)=\mathop{\sum }_{k=0}^{n}\binom{n}{k}^{2}\binom{n+k}{k}^{3},\end{eqnarray}$$
$$\begin{eqnarray}A(n)=\mathop{\sum }_{k=0}^{n}\binom{n}{k}^{2}\binom{n+k}{k}^{3},\end{eqnarray}$$
since
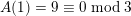 $A(1)=9\equiv 0\;\text{mod}\;3$
but
$A(1)=9\equiv 0\;\text{mod}\;3$
but
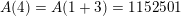 $A(4)=A(1+3)=1152501$
is not divisible by
$A(4)=A(1+3)=1152501$
is not divisible by
![]() $3^{2}$
.
$3^{2}$
.
The main aim of this article is to prove Theorem 1, stated in § 1.4, which confirms and generalizes Conjectures A–C. First, we introduce some notations which we use throughout this article.
1.3 Notations
In order to study arithmetic properties of sums of products of binomial coefficients, such as Apéry numbers, we first study families, indexed by
![]() $\mathbb{N}^{d}$
, of ratios of factorials of linear forms with integer coefficients. For example, we will obtain congruences for
$\mathbb{N}^{d}$
, of ratios of factorials of linear forms with integer coefficients. For example, we will obtain congruences for
![]() $A_{1}(n)$
by studying the factorial ratios
$A_{1}(n)$
by studying the factorial ratios
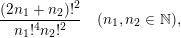 $$\begin{eqnarray}\frac{(2n_{1}+n_{2})!^{2}}{n_{1}!^{4}n_{2}!^{2}}\quad (n_{1},n_{2}\in \mathbb{N}),\end{eqnarray}$$
$$\begin{eqnarray}\frac{(2n_{1}+n_{2})!^{2}}{n_{1}!^{4}n_{2}!^{2}}\quad (n_{1},n_{2}\in \mathbb{N}),\end{eqnarray}$$
as we have the useful formula
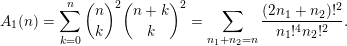 $$\begin{eqnarray}A_{1}(n)=\mathop{\sum }_{k=0}^{n}\binom{n}{k}^{2}\binom{n+k}{k}^{2}=\mathop{\sum }_{n_{1}+n_{2}=n}\frac{(2n_{1}+n_{2})!^{2}}{n_{1}!^{4}n_{2}!^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}A_{1}(n)=\mathop{\sum }_{k=0}^{n}\binom{n}{k}^{2}\binom{n+k}{k}^{2}=\mathop{\sum }_{n_{1}+n_{2}=n}\frac{(2n_{1}+n_{2})!^{2}}{n_{1}!^{4}n_{2}!^{2}}.\end{eqnarray}$$
Let
![]() $d$
be a positive integer. Given tuples of vectors in
$d$
be a positive integer. Given tuples of vectors in
![]() $\mathbb{N}^{d}$
,
$\mathbb{N}^{d}$
,
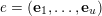 $e=(\mathbf{e}_{1},\ldots ,\mathbf{e}_{u})$
and
$e=(\mathbf{e}_{1},\ldots ,\mathbf{e}_{u})$
and
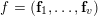 $f=(\mathbf{f}_{1},\ldots ,\mathbf{f}_{v})$
, we shall prove congruences for the factorial ratios
$f=(\mathbf{f}_{1},\ldots ,\mathbf{f}_{v})$
, we shall prove congruences for the factorial ratios
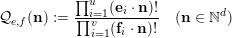 $$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{n}):=\frac{\mathop{\prod }_{i=1}^{u}(\mathbf{e}_{i}\cdot \mathbf{n})!}{\mathop{\prod }_{i=1}^{v}(\mathbf{f}_{i}\cdot \mathbf{n})!}\quad (\mathbf{n}\in \mathbb{N}^{d})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{n}):=\frac{\mathop{\prod }_{i=1}^{u}(\mathbf{e}_{i}\cdot \mathbf{n})!}{\mathop{\prod }_{i=1}^{v}(\mathbf{f}_{i}\cdot \mathbf{n})!}\quad (\mathbf{n}\in \mathbb{N}^{d})\end{eqnarray}$$
to deduce arithmetic properties of the numbersFootnote 3
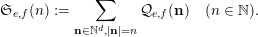 $$\begin{eqnarray}\mathfrak{S}_{e,f}(n):=\mathop{\sum }_{\mathbf{n}\in \mathbb{N}^{d},|\mathbf{n}|=n}{\mathcal{Q}}_{e,f}(\mathbf{n})\quad (n\in \mathbb{N}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}_{e,f}(n):=\mathop{\sum }_{\mathbf{n}\in \mathbb{N}^{d},|\mathbf{n}|=n}{\mathcal{Q}}_{e,f}(\mathbf{n})\quad (n\in \mathbb{N}).\end{eqnarray}$$
Here
![]() $\cdot$
denotes the standard scalar product on
$\cdot$
denotes the standard scalar product on
![]() $\mathbb{R}^{d}$
and
$\mathbb{R}^{d}$
and
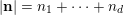 $|\mathbf{n}|=n_{1}+\cdots +n_{d}$
if
$|\mathbf{n}|=n_{1}+\cdots +n_{d}$
if
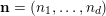 $\mathbf{n}=(n_{1},\ldots ,n_{d})$
. For example, we obtain that
$\mathbf{n}=(n_{1},\ldots ,n_{d})$
. For example, we obtain that
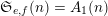 $\mathfrak{S}_{e,f}(n)=A_{1}(n)$
with the tuples
$\mathfrak{S}_{e,f}(n)=A_{1}(n)$
with the tuples
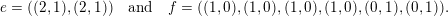 $$\begin{eqnarray}e=((2,1),(2,1))\quad \text{and}\quad f=((1,0),(1,0),(1,0),(1,0),(0,1),(0,1)).\end{eqnarray}$$
$$\begin{eqnarray}e=((2,1),(2,1))\quad \text{and}\quad f=((1,0),(1,0),(1,0),(1,0),(0,1),(0,1)).\end{eqnarray}$$
Because of the summation in (1.4), it is usually difficult to study arithmetic properties of
![]() $\mathfrak{S}_{e,f}(n)$
; however, we will show that, in many interesting cases, we can transfer the
$\mathfrak{S}_{e,f}(n)$
; however, we will show that, in many interesting cases, we can transfer the
![]() $p$
-Lucas property from
$p$
-Lucas property from
![]() ${\mathcal{Q}}_{e,f}(\mathbf{n})$
to
${\mathcal{Q}}_{e,f}(\mathbf{n})$
to
![]() $\mathfrak{S}_{e,f}(n)$
. To that purpose, we define the
$\mathfrak{S}_{e,f}(n)$
. To that purpose, we define the
![]() $p$
-Lucas property for families of
$p$
-Lucas property for families of
![]() $p$
-adic integers indexed by
$p$
-adic integers indexed by
![]() $\mathbb{N}^{d}$
. For all primes
$\mathbb{N}^{d}$
. For all primes
![]() $p$
, we write
$p$
, we write
![]() $\mathbb{Z}_{p}$
for the ring of
$\mathbb{Z}_{p}$
for the ring of
![]() $p$
-adic integers.
$p$
-adic integers.
If
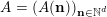 $A=(A(\mathbf{n}))_{\mathbf{n}\in \mathbb{N}^{d}}$
is a
$A=(A(\mathbf{n}))_{\mathbf{n}\in \mathbb{N}^{d}}$
is a
![]() $\mathbb{Z}_{p}$
-valued family, then we say that
$\mathbb{Z}_{p}$
-valued family, then we say that
![]() $A$
satisfies the
$A$
satisfies the
![]() $p$
-Lucas property if, for all vectors
$p$
-Lucas property if, for all vectors
![]() $\mathbf{v}$
in
$\mathbf{v}$
in
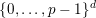 $\{0,\ldots ,p-1\}^{d}$
and
$\{0,\ldots ,p-1\}^{d}$
and
![]() $\mathbf{n}$
in
$\mathbf{n}$
in
![]() $\mathbb{N}^{d}$
, we have
$\mathbb{N}^{d}$
, we have
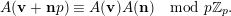 $$\begin{eqnarray}A(\mathbf{v}+\mathbf{n}p)\equiv A(\mathbf{v})A(\mathbf{n})\hspace{0.6em}{\rm mod}\hspace{0.2em}p\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}A(\mathbf{v}+\mathbf{n}p)\equiv A(\mathbf{v})A(\mathbf{n})\hspace{0.6em}{\rm mod}\hspace{0.2em}p\mathbb{Z}_{p}.\end{eqnarray}$$
If
![]() $\mathbf{n}$
is nonzero, then we say that
$\mathbf{n}$
is nonzero, then we say that
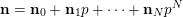 $\mathbf{n}=\mathbf{n}_{0}+\mathbf{n}_{1}p+\cdots +\mathbf{n}_{N}p^{N}$
is the base-
$\mathbf{n}=\mathbf{n}_{0}+\mathbf{n}_{1}p+\cdots +\mathbf{n}_{N}p^{N}$
is the base-
![]() $p$
expansion of
$p$
expansion of
![]() $\mathbf{n}$
if, for all
$\mathbf{n}$
if, for all
![]() $i$
in
$i$
in
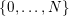 $\{0,\ldots ,N\}$
, we have
$\{0,\ldots ,N\}$
, we have
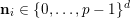 $\mathbf{n}_{i}\in \{0,\ldots ,p-1\}^{d}$
and
$\mathbf{n}_{i}\in \{0,\ldots ,p-1\}^{d}$
and
![]() $\mathbf{n}_{N}\neq \mathbf{0}$
, where
$\mathbf{n}_{N}\neq \mathbf{0}$
, where
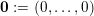 $\mathbf{0}:=(0,\ldots ,0)$
. Hence, if
$\mathbf{0}:=(0,\ldots ,0)$
. Hence, if
![]() $A$
satisfies the
$A$
satisfies the
![]() $p$
-Lucas property, then we have
$p$
-Lucas property, then we have
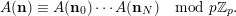 $$\begin{eqnarray}A(\mathbf{n})\equiv A(\mathbf{n}_{0})\cdots A(\mathbf{n}_{N})\hspace{0.6em}{\rm mod}\hspace{0.2em}p\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}A(\mathbf{n})\equiv A(\mathbf{n}_{0})\cdots A(\mathbf{n}_{N})\hspace{0.6em}{\rm mod}\hspace{0.2em}p\mathbb{Z}_{p}.\end{eqnarray}$$
We write
![]() ${\mathcal{Z}}_{p}(A)$
for the set of all vectors
${\mathcal{Z}}_{p}(A)$
for the set of all vectors
![]() $\mathbf{v}$
in
$\mathbf{v}$
in
 $\{0,\ldots ,p-1\}^{d}$
such that
$\{0,\ldots ,p-1\}^{d}$
such that
![]() $A(\mathbf{v})$
belongs to
$A(\mathbf{v})$
belongs to
![]() $p\mathbb{Z}_{p}$
. Hence,
$p\mathbb{Z}_{p}$
. Hence,
![]() $A(\mathbf{n})$
is in
$A(\mathbf{n})$
is in
![]() $p\mathbb{Z}_{p}$
if and only if at least one
$p\mathbb{Z}_{p}$
if and only if at least one
![]() $\mathbf{n}_{i}$
,
$\mathbf{n}_{i}$
,
 $0\leqslant i\leqslant N$
, belongs to
$0\leqslant i\leqslant N$
, belongs to
![]() ${\mathcal{Z}}_{p}(A)$
. To state our generalization of Conjectures A–C, we define the following counting function. For every nonzero vector
${\mathcal{Z}}_{p}(A)$
. To state our generalization of Conjectures A–C, we define the following counting function. For every nonzero vector
![]() $\mathbf{n}$
in
$\mathbf{n}$
in
![]() $\mathbb{N}^{d}$
whose base-
$\mathbb{N}^{d}$
whose base-
![]() $p$
expansion is
$p$
expansion is
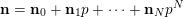 $\mathbf{n}=\mathbf{n}_{0}+\mathbf{n}_{1}p+\cdots +\mathbf{n}_{N}p^{N}$
, we write
$\mathbf{n}=\mathbf{n}_{0}+\mathbf{n}_{1}p+\cdots +\mathbf{n}_{N}p^{N}$
, we write
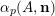 $\unicode[STIX]{x1D6FC}_{p}(A,\mathbf{n})$
for the number of
$\unicode[STIX]{x1D6FC}_{p}(A,\mathbf{n})$
for the number of
![]() $i$
in
$i$
in
 $\{0,\ldots ,N\}$
such that
$\{0,\ldots ,N\}$
such that
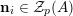 $\mathbf{n}_{i}\in {\mathcal{Z}}_{p}(A)$
, and we set
$\mathbf{n}_{i}\in {\mathcal{Z}}_{p}(A)$
, and we set
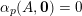 $\unicode[STIX]{x1D6FC}_{p}(A,\mathbf{0})=0$
. Thereby, to prove Conjectures A–C, it is enough to show that
$\unicode[STIX]{x1D6FC}_{p}(A,\mathbf{0})=0$
. Thereby, to prove Conjectures A–C, it is enough to show that
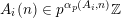 $A_{i}(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(A_{i},n)}\mathbb{Z}$
with
$A_{i}(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(A_{i},n)}\mathbb{Z}$
with
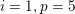 $i=1,p=5$
or
$i=1,p=5$
or
![]() $11$
and
$11$
and
![]() $i=2$
,
$i=2$
,
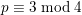 $p\equiv 3\;\text{mod}\;4$
.
$p\equiv 3\;\text{mod}\;4$
.
Our generalization of Beukers’ conjectures will apply to sequences
![]() $\mathfrak{S}_{e,f}$
restricted to the following two conditions.
$\mathfrak{S}_{e,f}$
restricted to the following two conditions.
The first condition (the
![]() $r$
-admissibility) ensures that we can transfer the
$r$
-admissibility) ensures that we can transfer the
![]() $p$
-Lucas property from
$p$
-Lucas property from
![]() ${\mathcal{Q}}_{e,f}(\mathbf{n})$
to
${\mathcal{Q}}_{e,f}(\mathbf{n})$
to
![]() $\mathfrak{S}_{e,f}(n)$
. If
$\mathfrak{S}_{e,f}(n)$
. If
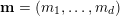 $\mathbf{m}=(m_{1},\ldots ,m_{d})$
and
$\mathbf{m}=(m_{1},\ldots ,m_{d})$
and
 $\mathbf{n}=(n_{1},\ldots ,n_{d})$
belong to
$\mathbf{n}=(n_{1},\ldots ,n_{d})$
belong to
![]() $\mathbb{R}^{d}$
, then we write
$\mathbb{R}^{d}$
, then we write
![]() $\mathbf{m}\geqslant \mathbf{n}$
if, for all
$\mathbf{m}\geqslant \mathbf{n}$
if, for all
![]() $i$
in
$i$
in
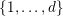 $\{1,\ldots ,d\}$
, we have
$\{1,\ldots ,d\}$
, we have
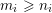 $m_{i}\geqslant n_{i}$
. Furthermore, we set
$m_{i}\geqslant n_{i}$
. Furthermore, we set
 $\mathbf{1}:=(1,\ldots ,1)\in \mathbb{N}^{d}$
and we write
$\mathbf{1}:=(1,\ldots ,1)\in \mathbb{N}^{d}$
and we write
![]() $\mathbf{1}_{k}$
for the vector in
$\mathbf{1}_{k}$
for the vector in
![]() $\mathbb{N}^{d}$
, all of whose coordinates equal zero except the
$\mathbb{N}^{d}$
, all of whose coordinates equal zero except the
![]() $k$
th, which is
$k$
th, which is
![]() $1$
. Let
$1$
. Let
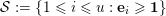 ${\mathcal{S}}:=\{1\leqslant i\leqslant u:\mathbf{e}_{i}\geqslant \mathbf{1}\}$
. For every positive integer
${\mathcal{S}}:=\{1\leqslant i\leqslant u:\mathbf{e}_{i}\geqslant \mathbf{1}\}$
. For every positive integer
![]() $r$
, we say that
$r$
, we say that
![]() $e$
is
$e$
is
![]() $r$
-admissible if
$r$
-admissible if
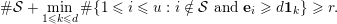 $$\begin{eqnarray}\#{\mathcal{S}}+\min _{1\leqslant k\leqslant d}\#\{1\leqslant i\leqslant u:i\notin {\mathcal{S}}\text{ and }\mathbf{e}_{i}\geqslant d\mathbf{1}_{k}\}\geqslant r.\end{eqnarray}$$
$$\begin{eqnarray}\#{\mathcal{S}}+\min _{1\leqslant k\leqslant d}\#\{1\leqslant i\leqslant u:i\notin {\mathcal{S}}\text{ and }\mathbf{e}_{i}\geqslant d\mathbf{1}_{k}\}\geqslant r.\end{eqnarray}$$
We will use this definition with
![]() $r=1$
or
$r=1$
or
![]() $2$
. In the case of the Apéry numbers
$2$
. In the case of the Apéry numbers
![]() $A_{1}(n)$
, we study the family
$A_{1}(n)$
, we study the family
![]() ${\mathcal{Q}}_{e,f}$
with the tuple
${\mathcal{Q}}_{e,f}$
with the tuple
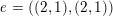 $e=((2,1),(2,1))$
, so that
$e=((2,1),(2,1))$
, so that
 $\#{\mathcal{S}}=2$
and
$\#{\mathcal{S}}=2$
and
![]() $e$
is
$e$
is
![]() $2$
-admissible. As another example, we will also prove a result similar to Beukers’ conjectures for the sequence
$2$
-admissible. As another example, we will also prove a result similar to Beukers’ conjectures for the sequence
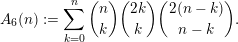 $$\begin{eqnarray}A_{6}(n):=\mathop{\sum }_{k=0}^{n}\binom{n}{k}\binom{2k}{k}\binom{2(n-k)}{n-k}.\end{eqnarray}$$
$$\begin{eqnarray}A_{6}(n):=\mathop{\sum }_{k=0}^{n}\binom{n}{k}\binom{2k}{k}\binom{2(n-k)}{n-k}.\end{eqnarray}$$
We can write
 $$\begin{eqnarray}A_{6}(n)=\mathop{\sum }_{n_{1}+n_{2}=n}\frac{(n_{1}+n_{2})!(2n_{1})!(2n_{2})!}{n_{1}!^{3}n_{2}!^{3}},\end{eqnarray}$$
$$\begin{eqnarray}A_{6}(n)=\mathop{\sum }_{n_{1}+n_{2}=n}\frac{(n_{1}+n_{2})!(2n_{1})!(2n_{2})!}{n_{1}!^{3}n_{2}!^{3}},\end{eqnarray}$$
so that
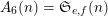 $A_{6}(n)=\mathfrak{S}_{e,f}(n)$
with
$A_{6}(n)=\mathfrak{S}_{e,f}(n)$
with
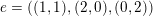 $e=((1,1),(2,0),(0,2))$
. In this case, we have
$e=((1,1),(2,0),(0,2))$
. In this case, we have
![]() $d=2$
,
$d=2$
,
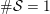 $\#{\mathcal{S}}=1$
but
$\#{\mathcal{S}}=1$
but
![]() $e$
is also
$e$
is also
![]() $2$
-admissible because for
$2$
-admissible because for
![]() $k=1$
or
$k=1$
or
![]() $2$
we have
$2$
we have
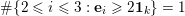 $\#\{2\leqslant i\leqslant 3:\mathbf{e}_{i}\geqslant 2\mathbf{1}_{k}\}=1$
.
$\#\{2\leqslant i\leqslant 3:\mathbf{e}_{i}\geqslant 2\mathbf{1}_{k}\}=1$
.
The second condition is of differential type. To apply our main result, we need the generating series of
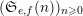 $(\mathfrak{S}_{e,f}(n))_{n\geqslant 0}$
to be annihilated by a differential operator of a special form that we describe below. We set
$(\mathfrak{S}_{e,f}(n))_{n\geqslant 0}$
to be annihilated by a differential operator of a special form that we describe below. We set
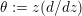 $\unicode[STIX]{x1D703}:=z(d/dz)$
and we say that a differential operator
$\unicode[STIX]{x1D703}:=z(d/dz)$
and we say that a differential operator
![]() ${\mathcal{L}}$
in
${\mathcal{L}}$
in
![]() $\mathbb{Z}_{p}[z,\unicode[STIX]{x1D703}]$
is of type I if there is a nonnegative integer
$\mathbb{Z}_{p}[z,\unicode[STIX]{x1D703}]$
is of type I if there is a nonnegative integer
![]() $q$
such that:
$q$
such that:
-
–
 ${\mathcal{L}}=P_{0}(\unicode[STIX]{x1D703})+zP_{1}(\unicode[STIX]{x1D703})+\cdots +z^{q}P_{q}(\unicode[STIX]{x1D703})$
with
${\mathcal{L}}=P_{0}(\unicode[STIX]{x1D703})+zP_{1}(\unicode[STIX]{x1D703})+\cdots +z^{q}P_{q}(\unicode[STIX]{x1D703})$
with
 $P_{k}(X)\in \mathbb{Z}_{p}[X]$
for
$P_{k}(X)\in \mathbb{Z}_{p}[X]$
for
 $0\leqslant k\leqslant q$
;
$0\leqslant k\leqslant q$
; -
–
 $P_{0}(\mathbb{Z}_{p}^{\times })\subset \mathbb{Z}_{p}^{\times }$
;
$P_{0}(\mathbb{Z}_{p}^{\times })\subset \mathbb{Z}_{p}^{\times }$
; -
– for all
 $k$
in
$k$
in
 $\{2,\ldots ,q\}$
, we have
$\{2,\ldots ,q\}$
, we have
 $P_{k}(X)\in \prod _{i=1}^{k-1}(X+i)^{2}\mathbb{Z}_{p}[X]$
.
$P_{k}(X)\in \prod _{i=1}^{k-1}(X+i)^{2}\mathbb{Z}_{p}[X]$
.
We say that a differential operator
![]() ${\mathcal{L}}$
in
${\mathcal{L}}$
in
![]() $\mathbb{Z}_{p}[z,\unicode[STIX]{x1D703}]$
is of type II if:
$\mathbb{Z}_{p}[z,\unicode[STIX]{x1D703}]$
is of type II if:
-
–
 ${\mathcal{L}}=P_{0}(\unicode[STIX]{x1D703})+zP_{1}(\unicode[STIX]{x1D703})+z^{2}P_{2}(\unicode[STIX]{x1D703})$
with
${\mathcal{L}}=P_{0}(\unicode[STIX]{x1D703})+zP_{1}(\unicode[STIX]{x1D703})+z^{2}P_{2}(\unicode[STIX]{x1D703})$
with
 $P_{k}(X)\in \mathbb{Z}_{p}[X]$
for
$P_{k}(X)\in \mathbb{Z}_{p}[X]$
for
 $0\leqslant k\leqslant 2$
;
$0\leqslant k\leqslant 2$
; -
–
 $P_{0}(\mathbb{Z}_{p}^{\times })\subset \mathbb{Z}_{p}^{\times }$
;
$P_{0}(\mathbb{Z}_{p}^{\times })\subset \mathbb{Z}_{p}^{\times }$
; -
–
 $P_{2}(X)\in (X+1)\mathbb{Z}_{p}[X]$
.
$P_{2}(X)\in (X+1)\mathbb{Z}_{p}[X]$
.
For example, the generating series of
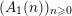 $(A_{1}(n))_{n\geqslant 0}$
is annihilated by the differential operator
$(A_{1}(n))_{n\geqslant 0}$
is annihilated by the differential operator
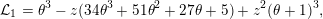 $$\begin{eqnarray}{\mathcal{L}}_{1}=\unicode[STIX]{x1D703}^{3}-z(34\unicode[STIX]{x1D703}^{3}+51\unicode[STIX]{x1D703}^{2}+27\unicode[STIX]{x1D703}+5)+z^{2}(\unicode[STIX]{x1D703}+1)^{3},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}_{1}=\unicode[STIX]{x1D703}^{3}-z(34\unicode[STIX]{x1D703}^{3}+51\unicode[STIX]{x1D703}^{2}+27\unicode[STIX]{x1D703}+5)+z^{2}(\unicode[STIX]{x1D703}+1)^{3},\end{eqnarray}$$
which is of type I for every prime
![]() $p$
. We will also prove a result similar to Beukers’ conjectures for the numbers
$p$
. We will also prove a result similar to Beukers’ conjectures for the numbers
 $$\begin{eqnarray}A_{5}(n)=\mathop{\sum }_{k=0}^{n}\binom{n}{k}^{4}.\end{eqnarray}$$
$$\begin{eqnarray}A_{5}(n)=\mathop{\sum }_{k=0}^{n}\binom{n}{k}^{4}.\end{eqnarray}$$
The generating series of
![]() $A_{5}$
is annihilated by the differential operator
$A_{5}$
is annihilated by the differential operator
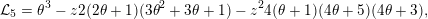 $$\begin{eqnarray}{\mathcal{L}}_{5}=\unicode[STIX]{x1D703}^{3}-z2(2\unicode[STIX]{x1D703}+1)(3\unicode[STIX]{x1D703}^{2}+3\unicode[STIX]{x1D703}+1)-z^{2}4(\unicode[STIX]{x1D703}+1)(4\unicode[STIX]{x1D703}+5)(4\unicode[STIX]{x1D703}+3),\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}_{5}=\unicode[STIX]{x1D703}^{3}-z2(2\unicode[STIX]{x1D703}+1)(3\unicode[STIX]{x1D703}^{2}+3\unicode[STIX]{x1D703}+1)-z^{2}4(\unicode[STIX]{x1D703}+1)(4\unicode[STIX]{x1D703}+5)(4\unicode[STIX]{x1D703}+3),\end{eqnarray}$$
which is of type II for every prime
![]() $p$
.
$p$
.
Our main result confirms Conjectures A–C, and also provides surprising similar properties for some deformations of Apéry-like numbers. For example, while proving that, for every prime
![]() $p$
and all nonnegative integers
$p$
and all nonnegative integers
![]() $n$
, we have
$n$
, we have
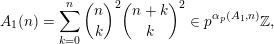 $$\begin{eqnarray}A_{1}(n)=\mathop{\sum }_{k=0}^{n}\binom{n}{k}^{2}\binom{n+k}{k}^{2}\in p^{\unicode[STIX]{x1D6FC}_{p}(A_{1},n)}\mathbb{Z},\end{eqnarray}$$
$$\begin{eqnarray}A_{1}(n)=\mathop{\sum }_{k=0}^{n}\binom{n}{k}^{2}\binom{n+k}{k}^{2}\in p^{\unicode[STIX]{x1D6FC}_{p}(A_{1},n)}\mathbb{Z},\end{eqnarray}$$
we will also show that, for every nonnegative integer
![]() $a$
, we have
$a$
, we have
 $$\begin{eqnarray}\mathop{\sum }_{k=0}^{n}k^{a}\binom{n}{k}^{2}\binom{n+k}{k}^{2}\in p^{\unicode[STIX]{x1D6FC}_{p}(A_{1},n)-1}\mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k=0}^{n}k^{a}\binom{n}{k}^{2}\binom{n+k}{k}^{2}\in p^{\unicode[STIX]{x1D6FC}_{p}(A_{1},n)-1}\mathbb{Z}.\end{eqnarray}$$
More generally, we will obtain congruences for deformations
![]() $\mathfrak{S}_{e,f}^{g}$
of the sequences
$\mathfrak{S}_{e,f}^{g}$
of the sequences
![]() $\mathfrak{S}_{e,f}$
defined as follows. For any prime
$\mathfrak{S}_{e,f}$
defined as follows. For any prime
![]() $p$
, we write
$p$
, we write
![]() $\mathfrak{F}_{p}^{d}$
for the set of all functions
$\mathfrak{F}_{p}^{d}$
for the set of all functions
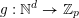 $g:\mathbb{N}^{d}\rightarrow \mathbb{Z}_{p}$
such that, for all nonnegative integers
$g:\mathbb{N}^{d}\rightarrow \mathbb{Z}_{p}$
such that, for all nonnegative integers
![]() $K$
, there exists a sequence
$K$
, there exists a sequence
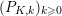 $(P_{K,k})_{k\geqslant 0}$
of polynomial functions with coefficients in
$(P_{K,k})_{k\geqslant 0}$
of polynomial functions with coefficients in
![]() $\mathbb{Z}_{p}$
which converges pointwise to
$\mathbb{Z}_{p}$
which converges pointwise to
![]() $g$
on
$g$
on
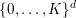 $\{0,\ldots ,K\}^{d}$
. For all tuples
$\{0,\ldots ,K\}^{d}$
. For all tuples
![]() $e$
and
$e$
and
![]() $f$
of vectors in
$f$
of vectors in
![]() $\mathbb{N}^{d}$
, all
$\mathbb{N}^{d}$
, all
![]() $g\in \mathfrak{F}_{p}^{d}$
and all nonnegative integers
$g\in \mathfrak{F}_{p}^{d}$
and all nonnegative integers
![]() $m$
, we set
$m$
, we set
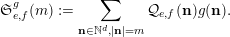 $$\begin{eqnarray}\mathfrak{S}_{e,f}^{g}(m):=\mathop{\sum }_{\mathbf{n}\in \mathbb{N}^{d},|\mathbf{n}|=m}{\mathcal{Q}}_{e,f}(\mathbf{n})g(\mathbf{n}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}_{e,f}^{g}(m):=\mathop{\sum }_{\mathbf{n}\in \mathbb{N}^{d},|\mathbf{n}|=m}{\mathcal{Q}}_{e,f}(\mathbf{n})g(\mathbf{n}).\end{eqnarray}$$
1.4 Main results
In the rest of the article, if
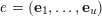 $e=(\mathbf{e}_{1},\ldots ,\mathbf{e}_{u})$
is a tuple of vectors in
$e=(\mathbf{e}_{1},\ldots ,\mathbf{e}_{u})$
is a tuple of vectors in
![]() $\mathbb{N}^{d}$
, then we set
$\mathbb{N}^{d}$
, then we set
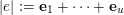 $|e|:=\mathbf{e}_{1}+\cdots +\mathbf{e}_{u}$
. The main result of this article is the following.
$|e|:=\mathbf{e}_{1}+\cdots +\mathbf{e}_{u}$
. The main result of this article is the following.
Theorem 1. Let
![]() $e$
and
$e$
and
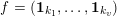 $f=(\mathbf{1}_{k_{1}},\ldots ,\mathbf{1}_{k_{v}})$
be two disjoint tuples of vectors in
$f=(\mathbf{1}_{k_{1}},\ldots ,\mathbf{1}_{k_{v}})$
be two disjoint tuples of vectors in
![]() $\mathbb{N}^{d}$
such that
$\mathbb{N}^{d}$
such that
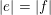 $|e|=|f|$
, for all
$|e|=|f|$
, for all
![]() $i$
in
$i$
in
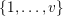 $\{1,\ldots ,v\}$
,
$\{1,\ldots ,v\}$
,
![]() $k_{i}$
is in
$k_{i}$
is in
 $\{1,\ldots ,d\}$
, and
$\{1,\ldots ,d\}$
, and
![]() $e$
is
$e$
is
![]() $2$
-admissible. Let
$2$
-admissible. Let
![]() $p$
be a fixed prime. Assume that the generating series of
$p$
be a fixed prime. Assume that the generating series of
![]() $\mathfrak{S}_{e,f}$
is annihilated by a differential operator
$\mathfrak{S}_{e,f}$
is annihilated by a differential operator
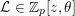 ${\mathcal{L}}\in \mathbb{Z}_{p}[z,\unicode[STIX]{x1D703}]$
such that at least one of the following conditions holds:
${\mathcal{L}}\in \mathbb{Z}_{p}[z,\unicode[STIX]{x1D703}]$
such that at least one of the following conditions holds:
-
–
 ${\mathcal{L}}$
is of type I;
${\mathcal{L}}$
is of type I; -
–
 ${\mathcal{L}}$
is of type II and
${\mathcal{L}}$
is of type II and
 $p-1\in {\mathcal{Z}}_{p}(\mathfrak{S}_{e,f})$
.
$p-1\in {\mathcal{Z}}_{p}(\mathfrak{S}_{e,f})$
.
Then, for all nonnegative integers
![]() $n$
and all functions
$n$
and all functions
![]() $g$
in
$g$
in
![]() $\mathfrak{F}_{p}^{d}$
, we have
$\mathfrak{F}_{p}^{d}$
, we have
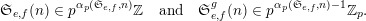 $$\begin{eqnarray}\mathfrak{S}_{e,f}(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(\mathfrak{S}_{e,f},n)}\mathbb{Z}\quad \text{and}\quad \mathfrak{S}_{e,f}^{g}(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(\mathfrak{S}_{e,f},n)-1}\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}_{e,f}(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(\mathfrak{S}_{e,f},n)}\mathbb{Z}\quad \text{and}\quad \mathfrak{S}_{e,f}^{g}(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(\mathfrak{S}_{e,f},n)-1}\mathbb{Z}_{p}.\end{eqnarray}$$
In § 1.6, we show that Theorem 1 applies to many classical sequences. In particular, Theorem 1 implies Conjectures A–C. Indeed, we have
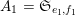 $A_{1}=\mathfrak{S}_{e_{1},f_{1}}$
and
$A_{1}=\mathfrak{S}_{e_{1},f_{1}}$
and
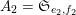 $A_{2}=\mathfrak{S}_{e_{2},f_{2}}$
with
$A_{2}=\mathfrak{S}_{e_{2},f_{2}}$
with
![]() $d=2$
,
$d=2$
,
 $$\begin{eqnarray}e_{1}=((2,1),(2,1))\quad \text{and}\quad f_{1}=((1,0),(1,0),(1,0),(1,0),(0,1),(0,1))\end{eqnarray}$$
$$\begin{eqnarray}e_{1}=((2,1),(2,1))\quad \text{and}\quad f_{1}=((1,0),(1,0),(1,0),(1,0),(0,1),(0,1))\end{eqnarray}$$
and
 $$\begin{eqnarray}e_{2}=((2,1),(1,1))\quad \text{and}\quad f_{2}=((1,0),(1,0),(1,0),(0,1),(0,1)).\end{eqnarray}$$
$$\begin{eqnarray}e_{2}=((2,1),(1,1))\quad \text{and}\quad f_{2}=((1,0),(1,0),(1,0),(0,1),(0,1)).\end{eqnarray}$$
Furthermore, it is well known that
![]() $f_{A_{1}}$
, respectively
$f_{A_{1}}$
, respectively
![]() $f_{A_{2}}$
, is annihilated by the differential operator
$f_{A_{2}}$
, is annihilated by the differential operator
![]() ${\mathcal{L}}_{1}$
, respectively
${\mathcal{L}}_{1}$
, respectively
![]() ${\mathcal{L}}_{2}$
, defined by
${\mathcal{L}}_{2}$
, defined by
 $$\begin{eqnarray}{\mathcal{L}}_{1}=\unicode[STIX]{x1D703}^{3}-z(34\unicode[STIX]{x1D703}^{3}+51\unicode[STIX]{x1D703}^{2}+27\unicode[STIX]{x1D703}+5)+z^{2}(\unicode[STIX]{x1D703}+1)^{3}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}_{1}=\unicode[STIX]{x1D703}^{3}-z(34\unicode[STIX]{x1D703}^{3}+51\unicode[STIX]{x1D703}^{2}+27\unicode[STIX]{x1D703}+5)+z^{2}(\unicode[STIX]{x1D703}+1)^{3}\end{eqnarray}$$
and
 $$\begin{eqnarray}{\mathcal{L}}_{2}=\unicode[STIX]{x1D703}^{2}-z(11\unicode[STIX]{x1D703}^{2}+11\unicode[STIX]{x1D703}+3)-z^{2}(\unicode[STIX]{x1D703}+1)^{2}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}_{2}=\unicode[STIX]{x1D703}^{2}-z(11\unicode[STIX]{x1D703}^{2}+11\unicode[STIX]{x1D703}+3)-z^{2}(\unicode[STIX]{x1D703}+1)^{2}.\end{eqnarray}$$
Since
![]() ${\mathcal{L}}_{1}$
and
${\mathcal{L}}_{1}$
and
![]() ${\mathcal{L}}_{2}$
are of type I for all primes
${\mathcal{L}}_{2}$
are of type I for all primes
![]() $p$
, the conditions of Theorem 1 are satisfied by
$p$
, the conditions of Theorem 1 are satisfied by
![]() $A_{1}$
and
$A_{1}$
and
![]() $A_{2}$
, and Conjectures A–C hold. In addition, for all primes
$A_{2}$
, and Conjectures A–C hold. In addition, for all primes
![]() $p$
and all nonnegative integers
$p$
and all nonnegative integers
![]() $n$
and
$n$
and
![]() $a$
, we obtain that
$a$
, we obtain that
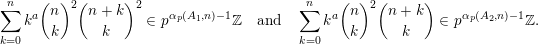 $$\begin{eqnarray}\mathop{\sum }_{k=0}^{n}k^{a}\binom{n}{k}^{2}\binom{n+k}{k}^{2}\in p^{\unicode[STIX]{x1D6FC}_{p}(A_{1},n)-1}\mathbb{Z}\quad \text{and}\quad \mathop{\sum }_{k=0}^{n}k^{a}\binom{n}{k}^{2}\binom{n+k}{k}\in p^{\unicode[STIX]{x1D6FC}_{p}(A_{2},n)-1}\mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k=0}^{n}k^{a}\binom{n}{k}^{2}\binom{n+k}{k}^{2}\in p^{\unicode[STIX]{x1D6FC}_{p}(A_{1},n)-1}\mathbb{Z}\quad \text{and}\quad \mathop{\sum }_{k=0}^{n}k^{a}\binom{n}{k}^{2}\binom{n+k}{k}\in p^{\unicode[STIX]{x1D6FC}_{p}(A_{2},n)-1}\mathbb{Z}.\end{eqnarray}$$
We provide a similar result which applies to the constant terms of powers of certain Laurent polynomials. Consider a Laurent polynomial
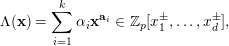 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\mathbf{x})=\mathop{\sum }_{i=1}^{k}\unicode[STIX]{x1D6FC}_{i}\mathbf{x}^{\mathbf{a}_{i}}\in \mathbb{Z}_{p}[x_{1}^{\pm },\ldots ,x_{d}^{\pm }],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\mathbf{x})=\mathop{\sum }_{i=1}^{k}\unicode[STIX]{x1D6FC}_{i}\mathbf{x}^{\mathbf{a}_{i}}\in \mathbb{Z}_{p}[x_{1}^{\pm },\ldots ,x_{d}^{\pm }],\end{eqnarray}$$
where
![]() $\mathbf{a}_{i}\in \mathbb{Z}^{d}$
and
$\mathbf{a}_{i}\in \mathbb{Z}^{d}$
and
![]() $\unicode[STIX]{x1D6FC}_{i}\neq 0$
for
$\unicode[STIX]{x1D6FC}_{i}\neq 0$
for
![]() $i$
in
$i$
in
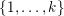 $\{1,\ldots ,k\}$
. Recall that the Newton polyhedron of
$\{1,\ldots ,k\}$
. Recall that the Newton polyhedron of
![]() $\unicode[STIX]{x1D6EC}$
is the convex hull of
$\unicode[STIX]{x1D6EC}$
is the convex hull of
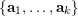 $\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{k}\}$
in
$\{\mathbf{a}_{1},\ldots ,\mathbf{a}_{k}\}$
in
![]() $\mathbb{R}^{d}$
. Hence, we have the following result.
$\mathbb{R}^{d}$
. Hence, we have the following result.
Theorem 2. Let
![]() $p$
be a fixed prime. Let
$p$
be a fixed prime. Let
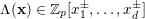 $\unicode[STIX]{x1D6EC}(\mathbf{x})\in \mathbb{Z}_{p}[x_{1}^{\pm },\ldots ,x_{d}^{\pm }]$
be a Laurent polynomial and consider the sequence of the constant terms of powers of
$\unicode[STIX]{x1D6EC}(\mathbf{x})\in \mathbb{Z}_{p}[x_{1}^{\pm },\ldots ,x_{d}^{\pm }]$
be a Laurent polynomial and consider the sequence of the constant terms of powers of
![]() $\unicode[STIX]{x1D6EC}$
defined, for all nonnegative integers
$\unicode[STIX]{x1D6EC}$
defined, for all nonnegative integers
![]() $n$
, by
$n$
, by
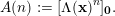 $$\begin{eqnarray}A(n):=[\unicode[STIX]{x1D6EC}(\mathbf{x})^{n}]_{\boldsymbol{ 0}}.\end{eqnarray}$$
$$\begin{eqnarray}A(n):=[\unicode[STIX]{x1D6EC}(\mathbf{x})^{n}]_{\boldsymbol{ 0}}.\end{eqnarray}$$
Assume that the Newton polyhedron of
![]() $\unicode[STIX]{x1D6EC}$
contains the origin as its only interior integral point, and that
$\unicode[STIX]{x1D6EC}$
contains the origin as its only interior integral point, and that
![]() $f_{A}$
is annihilated by a differential operator
$f_{A}$
is annihilated by a differential operator
![]() ${\mathcal{L}}$
in
${\mathcal{L}}$
in
![]() $\mathbb{Z}_{p}[z,\unicode[STIX]{x1D703}]$
such that at least one of the following conditions holds:
$\mathbb{Z}_{p}[z,\unicode[STIX]{x1D703}]$
such that at least one of the following conditions holds:
-
–
 ${\mathcal{L}}$
is of type I;
${\mathcal{L}}$
is of type I; -
–
 ${\mathcal{L}}$
is of type II and
${\mathcal{L}}$
is of type II and
 $p-1\in {\mathcal{Z}}_{p}(A)$
.
$p-1\in {\mathcal{Z}}_{p}(A)$
.
Then, for all nonnegative integers
![]() $n$
, we have
$n$
, we have
 $$\begin{eqnarray}A(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(A,n)}\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}A(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(A,n)}\mathbb{Z}_{p}.\end{eqnarray}$$
For example, Theorem 2 applies to Apéry numbers
![]() $A_{1}$
thanks to the following formula of Lairez (personal communication, 2013):
$A_{1}$
thanks to the following formula of Lairez (personal communication, 2013):
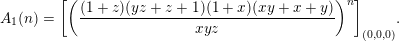 $$\begin{eqnarray}A_{1}(n)=\biggl[\biggl(\frac{(1+z)(yz+z+1)(1+x)(xy+x+y)}{xyz}\biggr)^{n}\biggr]_{(0,0,0)}.\end{eqnarray}$$
$$\begin{eqnarray}A_{1}(n)=\biggl[\biggl(\frac{(1+z)(yz+z+1)(1+x)(xy+x+y)}{xyz}\biggr)^{n}\biggr]_{(0,0,0)}.\end{eqnarray}$$
By a result of Samol and van Straten [Reference Samol and van StratenSvS15], if
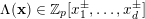 $\unicode[STIX]{x1D6EC}(\mathbf{x})\in \mathbb{Z}_{p}[x_{1}^{\pm },\ldots ,x_{d}^{\pm }]$
contains the origin as its only interior integral point, then
$\unicode[STIX]{x1D6EC}(\mathbf{x})\in \mathbb{Z}_{p}[x_{1}^{\pm },\ldots ,x_{d}^{\pm }]$
contains the origin as its only interior integral point, then
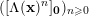 $([\unicode[STIX]{x1D6EC}(\mathbf{x})^{n}]_{\mathbf{0}})_{n\geqslant 0}$
satisfies the
$([\unicode[STIX]{x1D6EC}(\mathbf{x})^{n}]_{\mathbf{0}})_{n\geqslant 0}$
satisfies the
![]() $p$
-Lucas property, which is essential for the proof of Theorem 2. Likewise, the proof of Theorem 1 rests on the fact that
$p$
-Lucas property, which is essential for the proof of Theorem 2. Likewise, the proof of Theorem 1 rests on the fact that
![]() $\mathfrak{S}_{e,f}$
satisfies the
$\mathfrak{S}_{e,f}$
satisfies the
![]() $p$
-Lucas property when
$p$
-Lucas property when
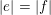 $|e|=|f|$
,
$|e|=|f|$
,
![]() $e$
is
$e$
is
![]() $2$
-admissible and
$2$
-admissible and
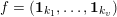 $f=(\mathbf{1}_{k_{1}},\ldots ,\mathbf{1}_{k_{v}})$
. Since those results deal with multisums of factorial ratios, it seems natural to study similar arithmetic properties for simpler numbers such as families of factorial ratios. To that purpose, we prove Theorem 3 below, which gives an effective criterion for
$f=(\mathbf{1}_{k_{1}},\ldots ,\mathbf{1}_{k_{v}})$
. Since those results deal with multisums of factorial ratios, it seems natural to study similar arithmetic properties for simpler numbers such as families of factorial ratios. To that purpose, we prove Theorem 3 below, which gives an effective criterion for
![]() ${\mathcal{Q}}_{e,f}$
to satisfy the
${\mathcal{Q}}_{e,f}$
to satisfy the
![]() $p$
-Lucas property for almost all primes
$p$
-Lucas property for almost all primes
![]() $p$
.Footnote
4
Furthermore, Theorem 3 shows that if
$p$
.Footnote
4
Furthermore, Theorem 3 shows that if
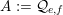 $A:={\mathcal{Q}}_{e,f}$
satisfies the
$A:={\mathcal{Q}}_{e,f}$
satisfies the
![]() $p$
-Lucas property for almost all primes
$p$
-Lucas property for almost all primes
![]() $p$
, then, for all nonnegative integers
$p$
, then, for all nonnegative integers
![]() $n$
and all primes
$n$
and all primes
![]() $p$
, we have
$p$
, we have
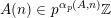 $A(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(A,n)}\mathbb{Z}$
.
$A(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(A,n)}\mathbb{Z}$
.
To state this result, we introduce some additional notations. For all tuples
![]() $e$
and
$e$
and
![]() $f$
of vectors in
$f$
of vectors in
![]() $\mathbb{N}^{d}$
, we write
$\mathbb{N}^{d}$
, we write
![]() $\unicode[STIX]{x1D6E5}_{e,f}$
for Landau’s function defined, for all
$\unicode[STIX]{x1D6E5}_{e,f}$
for Landau’s function defined, for all
![]() $\mathbf{x}$
in
$\mathbf{x}$
in
![]() $\mathbb{R}^{d}$
, by
$\mathbb{R}^{d}$
, by
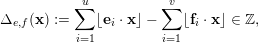 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x}):=\mathop{\sum }_{i=1}^{u}\lfloor \mathbf{e}_{i}\cdot \mathbf{x}\rfloor -\mathop{\sum }_{i=1}^{v}\lfloor \mathbf{f}_{i}\cdot \mathbf{x}\rfloor \in \mathbb{Z},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x}):=\mathop{\sum }_{i=1}^{u}\lfloor \mathbf{e}_{i}\cdot \mathbf{x}\rfloor -\mathop{\sum }_{i=1}^{v}\lfloor \mathbf{f}_{i}\cdot \mathbf{x}\rfloor \in \mathbb{Z},\end{eqnarray}$$
where
![]() $\lfloor \cdot \rfloor$
denotes the floor function. Therefore, according to Landau’s criterion [Reference LandauLan00] and a result of the author [Reference DelaygueDel13], we have the following dichotomy.
$\lfloor \cdot \rfloor$
denotes the floor function. Therefore, according to Landau’s criterion [Reference LandauLan00] and a result of the author [Reference DelaygueDel13], we have the following dichotomy.
-
– If, for all
 $\mathbf{x}$
in
$\mathbf{x}$
in
 $[0,1]^{d}$
, we have
$[0,1]^{d}$
, we have
 $\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})\geqslant 0$
, then
$\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})\geqslant 0$
, then
 ${\mathcal{Q}}_{e,f}$
is a family of integers.
${\mathcal{Q}}_{e,f}$
is a family of integers. -
– If there exists
 $\mathbf{x}$
in
$\mathbf{x}$
in
 $[0,1]^{d}$
such that
$[0,1]^{d}$
such that
 $\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})\leqslant -1$
, then there are only finitely many primes
$\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})\leqslant -1$
, then there are only finitely many primes
 $p$
such that
$p$
such that
 ${\mathcal{Q}}_{e,f}$
is a family of
${\mathcal{Q}}_{e,f}$
is a family of
 $p$
-adic integers.
$p$
-adic integers.
In the rest of the article, we write
![]() ${\mathcal{D}}_{e,f}$
for the semi-algebraic set of all
${\mathcal{D}}_{e,f}$
for the semi-algebraic set of all
![]() $\mathbf{x}$
in
$\mathbf{x}$
in
![]() $[\!0,1\!)^{d}$
such that there exists a component
$[\!0,1\!)^{d}$
such that there exists a component
![]() $\mathbf{d}$
of
$\mathbf{d}$
of
![]() $e$
or
$e$
or
![]() $f$
satisfying
$f$
satisfying
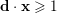 $\mathbf{d}\cdot \mathbf{x}\geqslant 1$
. Observe that
$\mathbf{d}\cdot \mathbf{x}\geqslant 1$
. Observe that
![]() $\unicode[STIX]{x1D6E5}_{e,f}$
vanishes on the nonempty set
$\unicode[STIX]{x1D6E5}_{e,f}$
vanishes on the nonempty set
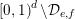 $[\!0,1\!)^{d}\setminus {\mathcal{D}}_{e,f}$
.
$[\!0,1\!)^{d}\setminus {\mathcal{D}}_{e,f}$
.
Theorem 3. Let
![]() $e$
and
$e$
and
![]() $f$
be disjoint tuples of vectors in
$f$
be disjoint tuples of vectors in
![]() $\mathbb{N}^{d}$
such that
$\mathbb{N}^{d}$
such that
![]() ${\mathcal{Q}}_{e,f}$
is a family of integers. Then we have the following dichotomy.
${\mathcal{Q}}_{e,f}$
is a family of integers. Then we have the following dichotomy.
-
(i) If
 $|e|=|f|$
and if, for all
$|e|=|f|$
and if, for all
 $\mathbf{x}$
in
$\mathbf{x}$
in
 ${\mathcal{D}}_{e,f}$
, we have
${\mathcal{D}}_{e,f}$
, we have
 $\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})\geqslant 1$
, then, for all primes
$\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})\geqslant 1$
, then, for all primes
 $p$
,
$p$
,
 ${\mathcal{Q}}_{e,f}$
satisfies the
${\mathcal{Q}}_{e,f}$
satisfies the
 $p$
-Lucas property.
$p$
-Lucas property. -
(ii) If
 $|e|\neq |f|$
or if there exists
$|e|\neq |f|$
or if there exists
 $\mathbf{x}$
in
$\mathbf{x}$
in
 ${\mathcal{D}}_{e,f}$
such that
${\mathcal{D}}_{e,f}$
such that
 $\unicode[STIX]{x1D6E5}_{e,f}(x)=0$
, then there are only finitely many primes
$\unicode[STIX]{x1D6E5}_{e,f}(x)=0$
, then there are only finitely many primes
 $p$
such that
$p$
such that
 ${\mathcal{Q}}_{e,f}$
satisfies the
${\mathcal{Q}}_{e,f}$
satisfies the
 $p$
-Lucas property.
$p$
-Lucas property.
Furthermore, if
![]() ${\mathcal{Q}}_{e,f}$
satisfies the
${\mathcal{Q}}_{e,f}$
satisfies the
![]() $p$
-Lucas property for all primes
$p$
-Lucas property for all primes
![]() $p$
, then, for all
$p$
, then, for all
![]() $\mathbf{n}$
in
$\mathbf{n}$
in
![]() $\mathbb{N}^{d}$
and every prime
$\mathbb{N}^{d}$
and every prime
![]() $p$
, we have
$p$
, we have
 $$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{n})\in p^{\unicode[STIX]{x1D6FC}_{p}({\mathcal{Q}}_{e,f},\mathbf{n})}\mathbb{Z}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{n})\in p^{\unicode[STIX]{x1D6FC}_{p}({\mathcal{Q}}_{e,f},\mathbf{n})}\mathbb{Z}.\end{eqnarray}$$
Remark.
Theorem 3 implies that
![]() ${\mathcal{Q}}_{e,f}$
satisfies the
${\mathcal{Q}}_{e,f}$
satisfies the
![]() $p$
-Lucas property for all primes
$p$
-Lucas property for all primes
![]() $p$
if and only if all Taylor coefficients at the origin of the associated mirror maps
$p$
if and only if all Taylor coefficients at the origin of the associated mirror maps
![]() $z_{e,f,k}$
,
$z_{e,f,k}$
,
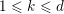 $1\leqslant k\leqslant d$
, are integers (see [Reference DelaygueDel13, Theorems 1 and 3]). Indeed, if
$1\leqslant k\leqslant d$
, are integers (see [Reference DelaygueDel13, Theorems 1 and 3]). Indeed, if
![]() $\unicode[STIX]{x1D6E5}_{e,f}$
is nonnegative on
$\unicode[STIX]{x1D6E5}_{e,f}$
is nonnegative on
![]() $[0,1]^{d}$
and if
$[0,1]^{d}$
and if
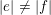 $|e|\neq |f|$
, then there exists
$|e|\neq |f|$
, then there exists
![]() $k$
in
$k$
in
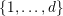 $\{1,\ldots ,d\}$
such that the
$\{1,\ldots ,d\}$
such that the
![]() $k$
th component of
$k$
th component of
![]() $|e|$
is greater than the
$|e|$
is greater than the
![]() $k$
th component of
$k$
th component of
![]() $|f|$
.
$|f|$
.
Coster proved in [Reference CosterCos88] results similar to Theorems 1–3 for the coefficients of certain algebraic power series. Namely, given a prime
![]() $p\geqslant 3$
, integers
$p\geqslant 3$
, integers
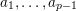 $a_{1},\ldots ,a_{p-1}$
and a sequence
$a_{1},\ldots ,a_{p-1}$
and a sequence
![]() $A$
such that
$A$
such that
 $$\begin{eqnarray}f_{A}(z)=(1+a_{1}z+\cdots +a_{p-1}z^{p-1})^{1/(1-p)},\end{eqnarray}$$
$$\begin{eqnarray}f_{A}(z)=(1+a_{1}z+\cdots +a_{p-1}z^{p-1})^{1/(1-p)},\end{eqnarray}$$
Coster proved that, for all nonnegative integers
![]() $n$
, we have
$n$
, we have
 $$\begin{eqnarray}v_{p}(A(n))\geqslant \biggl\lfloor\frac{\unicode[STIX]{x1D6FC}_{p}(A,n)+1}{2}\biggr\rfloor.\end{eqnarray}$$
$$\begin{eqnarray}v_{p}(A(n))\geqslant \biggl\lfloor\frac{\unicode[STIX]{x1D6FC}_{p}(A,n)+1}{2}\biggr\rfloor.\end{eqnarray}$$
1.5 Auxiliary results
The proof of Theorem 1 rests on three important results. The first one is stated rather formally but we believe that it may be useful to study results similar to Beukers’ conjectures for other sequences. Throughout this article, if
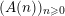 $(A(n))_{n\geqslant 0}$
is a sequence taking its values in
$(A(n))_{n\geqslant 0}$
is a sequence taking its values in
![]() $\mathbb{Z}$
or
$\mathbb{Z}$
or
![]() $\mathbb{Z}_{p}$
, then, for all negative integers
$\mathbb{Z}_{p}$
, then, for all negative integers
![]() $n$
, we set
$n$
, we set
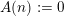 $A(n):=0$
.
$A(n):=0$
.
Proposition 1. Let
![]() $p$
be a fixed prime and
$p$
be a fixed prime and
![]() $A$
a
$A$
a
![]() $\mathbb{Z}_{p}$
-valued sequence satisfying the
$\mathbb{Z}_{p}$
-valued sequence satisfying the
![]() $p$
-Lucas property with
$p$
-Lucas property with
![]() $A(0)$
in
$A(0)$
in
![]() $\mathbb{Z}_{p}^{\times }$
. Let
$\mathbb{Z}_{p}^{\times }$
. Let
![]() $\mathfrak{A}$
be the
$\mathfrak{A}$
be the
![]() $\mathbb{Z}_{p}$
-module spanned by
$\mathbb{Z}_{p}$
-module spanned by
![]() $A$
. Assume that:
$A$
. Assume that:
-
(a) there exists a set
 $\mathfrak{B}$
of
$\mathfrak{B}$
of
 $\mathbb{Z}_{p}$
-valued sequences with
$\mathbb{Z}_{p}$
-valued sequences with
 $\mathfrak{A}\subset \mathfrak{B}$
such that, for all
$\mathfrak{A}\subset \mathfrak{B}$
such that, for all
 $B$
in
$B$
in
 $\mathfrak{B}$
, all
$\mathfrak{B}$
, all
 $v$
in
$v$
in
 $\{0,\ldots ,p-1\}$
and all positive integers
$\{0,\ldots ,p-1\}$
and all positive integers
 $n$
, there exist
$n$
, there exist
 $A^{\prime }$
in
$A^{\prime }$
in
 $\mathfrak{A}$
and a sequence
$\mathfrak{A}$
and a sequence
 $(B_{k})_{k\geqslant 0}$
,
$(B_{k})_{k\geqslant 0}$
,
 $B_{k}$
in
$B_{k}$
in
 $\mathfrak{B}$
, such that
$\mathfrak{B}$
, such that  $$\begin{eqnarray}B(v+np)=A^{\prime }(n)+\mathop{\sum }_{k=0}^{\infty }p^{k+1}B_{k}(n-k);\end{eqnarray}$$
$$\begin{eqnarray}B(v+np)=A^{\prime }(n)+\mathop{\sum }_{k=0}^{\infty }p^{k+1}B_{k}(n-k);\end{eqnarray}$$
-
(b)
 $f_{A}(z)$
is annihilated by a differential operator
$f_{A}(z)$
is annihilated by a differential operator
 ${\mathcal{L}}$
in
${\mathcal{L}}$
in
 $\mathbb{Z}_{p}[z,\unicode[STIX]{x1D703}]$
such that at least one of the following conditions holds:
$\mathbb{Z}_{p}[z,\unicode[STIX]{x1D703}]$
such that at least one of the following conditions holds:-
∗
 ${\mathcal{L}}$
is of type I;
${\mathcal{L}}$
is of type I; -
∗
 ${\mathcal{L}}$
is of type II and
${\mathcal{L}}$
is of type II and
 $p-1\in {\mathcal{Z}}_{p}(A)$
.
$p-1\in {\mathcal{Z}}_{p}(A)$
.
-
Then, for all
![]() $B$
in
$B$
in
![]() $\mathfrak{B}$
and all nonnegative integers
$\mathfrak{B}$
and all nonnegative integers
![]() $n$
, we have
$n$
, we have
 $$\begin{eqnarray}A(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(A,n)}\mathbb{Z}_{p}\quad \text{and}\quad B(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(A,n)-1}\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}A(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(A,n)}\mathbb{Z}_{p}\quad \text{and}\quad B(n)\in p^{\unicode[STIX]{x1D6FC}_{p}(A,n)-1}\mathbb{Z}_{p}.\end{eqnarray}$$
We will apply Proposition 1 with
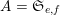 $A=\mathfrak{S}_{e,f}$
for some tuples
$A=\mathfrak{S}_{e,f}$
for some tuples
![]() $e$
and
$e$
and
![]() $f$
satisfying the conditions of Theorem 1 for a fixed prime
$f$
satisfying the conditions of Theorem 1 for a fixed prime
![]() $p$
. Then we will choose the set
$p$
. Then we will choose the set
![]() $\mathfrak{B}$
to be the set of the deformations
$\mathfrak{B}$
to be the set of the deformations
![]() $\mathfrak{S}_{e,f}^{g}$
for
$\mathfrak{S}_{e,f}^{g}$
for
![]() $g$
in
$g$
in
![]() $\mathfrak{F}_{p}^{d}$
. Taking
$\mathfrak{F}_{p}^{d}$
. Taking
![]() $g$
to be a constant in
$g$
to be a constant in
![]() $\mathbb{Z}_{p}$
shows that the set
$\mathbb{Z}_{p}$
shows that the set
![]() $\mathfrak{B}$
contains the
$\mathfrak{B}$
contains the
![]() $\mathbb{Z}_{p}$
-module
$\mathbb{Z}_{p}$
-module
![]() $\mathfrak{A}$
spanned by
$\mathfrak{A}$
spanned by
![]() $A$
. The main difficulty in this article is to show, by
$A$
. The main difficulty in this article is to show, by
![]() $p$
-adic techniques, that Assertion (a) in Proposition 1 holds with these choices. In particular, we shall prove and use several times the following result.
$p$
-adic techniques, that Assertion (a) in Proposition 1 holds with these choices. In particular, we shall prove and use several times the following result.
Proposition 2. Let
![]() $p$
be a fixed prime. We write
$p$
be a fixed prime. We write
![]() $\unicode[STIX]{x1D6E4}_{p}$
for the
$\unicode[STIX]{x1D6E4}_{p}$
for the
![]() $p$
-adic Gamma function. Then there exists a function
$p$
-adic Gamma function. Then there exists a function
![]() $g$
in
$g$
in
![]() $\mathfrak{F}_{p}^{2}$
such that, for all nonnegative integers
$\mathfrak{F}_{p}^{2}$
such that, for all nonnegative integers
![]() $n$
and
$n$
and
![]() $m$
, we have
$m$
, we have
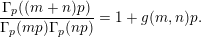 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D6E4}_{p}((m+n)p)}{\unicode[STIX]{x1D6E4}_{p}(mp)\unicode[STIX]{x1D6E4}_{p}(np)}=1+g(m,n)p.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6E4}_{p}((m+n)p)}{\unicode[STIX]{x1D6E4}_{p}(mp)\unicode[STIX]{x1D6E4}_{p}(np)}=1+g(m,n)p.\end{eqnarray}$$
Our proof of Theorem 2 does not use Proposition 1 but rests on the beautiful result of Mellit and Vlasenko [Reference Mellit and VlasenkoMV16, Lemma 1], which gives useful congruences modulo powers of
![]() $p$
for some constant terms of powers of Laurent polynomials. In this case, the
$p$
for some constant terms of powers of Laurent polynomials. In this case, the
![]() $p$
-adic difficulties are hidden in the result of Mellit and Vlasenko.
$p$
-adic difficulties are hidden in the result of Mellit and Vlasenko.
Finally, we give a general result to prove the
![]() $p$
-Lucas property for many sums of products of binomial coefficients. We recall that a tuple
$p$
-Lucas property for many sums of products of binomial coefficients. We recall that a tuple
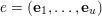 $e=(\mathbf{e}_{1},\ldots ,\mathbf{e}_{u})$
of vectors in
$e=(\mathbf{e}_{1},\ldots ,\mathbf{e}_{u})$
of vectors in
![]() $\mathbb{N}^{d}$
is
$\mathbb{N}^{d}$
is
![]() $1$
-admissible if either
$1$
-admissible if either
![]() $\mathbf{e}_{i}\geqslant \mathbf{1}$
for some
$\mathbf{e}_{i}\geqslant \mathbf{1}$
for some
![]() $i$
or if, for every
$i$
or if, for every
![]() $k$
in
$k$
in
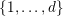 $\{1,\ldots ,d\}$
, we have
$\{1,\ldots ,d\}$
, we have
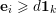 $\mathbf{e}_{i}\geqslant d\mathbf{1}_{k}$
for some
$\mathbf{e}_{i}\geqslant d\mathbf{1}_{k}$
for some
![]() $i$
.
$i$
.
Proposition 3. Let
![]() $e$
and
$e$
and
![]() $f$
be disjoint tuples of vectors in
$f$
be disjoint tuples of vectors in
![]() $\mathbb{N}^{d}$
such that
$\mathbb{N}^{d}$
such that
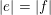 $|e|=|f|$
and, for all
$|e|=|f|$
and, for all
![]() $\mathbf{x}$
in
$\mathbf{x}$
in
![]() ${\mathcal{D}}_{e,f}$
,
${\mathcal{D}}_{e,f}$
,
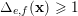 $\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})\geqslant 1$
. Assume that
$\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})\geqslant 1$
. Assume that
![]() $e$
is
$e$
is
![]() $1$
-admissible. Then
$1$
-admissible. Then
![]() $\mathfrak{S}_{e,f}$
is integer-valued and satisfies the
$\mathfrak{S}_{e,f}$
is integer-valued and satisfies the
![]() $p$
-Lucas property for all primes
$p$
-Lucas property for all primes
![]() $p$
.
$p$
.
1.6 Application of Theorem 1
By applying Theorem 1, we obtain results similar to Conjectures A–C for numbers satisfying Apéry-like recurrence relations, which we list below. Characters in brackets in the last column of the following table form the sequence number in the On-line Encyclopedia of Integer Sequences [OEIS13].

All differential operators listed in the above table are of type I for all primes
![]() $p$
, except the one associated with
$p$
, except the one associated with
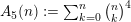 $A_{5}(n):=\sum _{k=0}^{n}\binom{n}{k}^{4}$
, which reads
$A_{5}(n):=\sum _{k=0}^{n}\binom{n}{k}^{4}$
, which reads
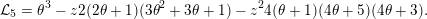 $$\begin{eqnarray}{\mathcal{L}}_{5}=\unicode[STIX]{x1D703}^{3}-z2(2\unicode[STIX]{x1D703}+1)(3\unicode[STIX]{x1D703}^{2}+3\unicode[STIX]{x1D703}+1)-z^{2}4(\unicode[STIX]{x1D703}+1)(4\unicode[STIX]{x1D703}+5)(4\unicode[STIX]{x1D703}+3).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}_{5}=\unicode[STIX]{x1D703}^{3}-z2(2\unicode[STIX]{x1D703}+1)(3\unicode[STIX]{x1D703}^{2}+3\unicode[STIX]{x1D703}+1)-z^{2}4(\unicode[STIX]{x1D703}+1)(4\unicode[STIX]{x1D703}+5)(4\unicode[STIX]{x1D703}+3).\end{eqnarray}$$
Hence,
![]() ${\mathcal{L}}_{5}$
is of type II for all primes
${\mathcal{L}}_{5}$
is of type II for all primes
![]() $p$
. By a result of Calkin [Reference CalkinCal98, Proposition 3], for all primes
$p$
. By a result of Calkin [Reference CalkinCal98, Proposition 3], for all primes
![]() $p$
, we have
$p$
, we have
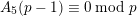 $A_{5}(p-1)\equiv 0\;\text{mod}\;p$
, i.e.
$A_{5}(p-1)\equiv 0\;\text{mod}\;p$
, i.e.
![]() $p-1$
is in
$p-1$
is in
![]() ${\mathcal{Z}}_{p}(A_{5})$
. Thus, we can apply Theorem 1 to
${\mathcal{Z}}_{p}(A_{5})$
. Thus, we can apply Theorem 1 to
![]() $A_{5}$
.
$A_{5}$
.
Observe that the generating function of the central binomial coefficients is annihilated by the differential operator
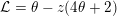 ${\mathcal{L}}=\unicode[STIX]{x1D703}-z(4\unicode[STIX]{x1D703}+2)$
, which is of type I for all primes
${\mathcal{L}}=\unicode[STIX]{x1D703}-z(4\unicode[STIX]{x1D703}+2)$
, which is of type I for all primes
![]() $p$
.
$p$
.
We set
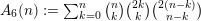 $A_{6}(n):=\sum _{k=0}^{n}\binom{n}{k}\binom{2k}{k}\binom{2(n-k)}{n-k}$
. In 1885, Catalan gave in [Reference CatalanCat85] a recurrence relation for the Catalan–Larcombe–French sequence
$A_{6}(n):=\sum _{k=0}^{n}\binom{n}{k}\binom{2k}{k}\binom{2(n-k)}{n-k}$
. In 1885, Catalan gave in [Reference CatalanCat85] a recurrence relation for the Catalan–Larcombe–French sequence
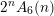 $2^{n}A_{6}(n)$
from which we deduce a recurrence relation for
$2^{n}A_{6}(n)$
from which we deduce a recurrence relation for
![]() $A_{6}(n)$
(see also Case (d) in [Reference Almkvist and ZudilinAZ06]). According to this relation,
$A_{6}(n)$
(see also Case (d) in [Reference Almkvist and ZudilinAZ06]). According to this relation,
![]() $A_{6}(n)$
is also Sequence E in Zagier’s list [Reference ZagierZag09], that is,
$A_{6}(n)$
is also Sequence E in Zagier’s list [Reference ZagierZag09], that is,
 $$\begin{eqnarray}A_{6}(n)=\mathop{\sum }_{k=0}^{\lfloor n/2\rfloor }4^{n-2k}\binom{n}{2k}\binom{2k}{k}^{2}.\end{eqnarray}$$
$$\begin{eqnarray}A_{6}(n)=\mathop{\sum }_{k=0}^{\lfloor n/2\rfloor }4^{n-2k}\binom{n}{2k}\binom{2k}{k}^{2}.\end{eqnarray}$$
Furthermore, according to [Reference Richmond and ShallitRS09], Domb numbers
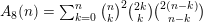 $A_{8}(n)=\sum _{k=0}^{n}\binom{n}{k}^{2}\binom{2k}{k}\binom{2(n-k)}{n-k}$
are also the numbers of abelian squares of length
$A_{8}(n)=\sum _{k=0}^{n}\binom{n}{k}^{2}\binom{2k}{k}\binom{2(n-k)}{n-k}$
are also the numbers of abelian squares of length
![]() $2n$
over an alphabet with four letters.
$2n$
over an alphabet with four letters.
Now we consider the numbers
![]() $C_{i}(n)$
of abelian squares of length
$C_{i}(n)$
of abelian squares of length
![]() $2n$
over an alphabet with
$2n$
over an alphabet with
![]() $i$
letters, which, for all positive integers
$i$
letters, which, for all positive integers
![]() $i\geqslant 2$
, satisfy (see [Reference Richmond and ShallitRS09])
$i\geqslant 2$
, satisfy (see [Reference Richmond and ShallitRS09])
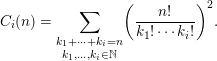 $$\begin{eqnarray}C_{i}(n)=\underset{k_{1},\ldots ,k_{i}\in \mathbb{N}}{\mathop{\sum }_{k_{1}+\cdots +k_{i}=n}}\biggl(\frac{n!}{k_{1}!\cdots k_{i}!}\biggr)^{2}.\end{eqnarray}$$
$$\begin{eqnarray}C_{i}(n)=\underset{k_{1},\ldots ,k_{i}\in \mathbb{N}}{\mathop{\sum }_{k_{1}+\cdots +k_{i}=n}}\biggl(\frac{n!}{k_{1}!\cdots k_{i}!}\biggr)^{2}.\end{eqnarray}$$
According to [Reference Borwein, Nuyens, Straub and WanBNSW11],
![]() $C_{i}(n)$
is also the
$C_{i}(n)$
is also the
![]() $(2n)$
th moment of the distance to the origin after
$(2n)$
th moment of the distance to the origin after
![]() $i$
steps travelled by a walk in the plane with unit steps in random directions.
$i$
steps travelled by a walk in the plane with unit steps in random directions.
To apply Theorem 1 to
![]() $C_{i}$
, it suffices to show that its generating series
$C_{i}$
, it suffices to show that its generating series
![]() $f_{C_{i}}$
is annihilated by a differential operator of type I for all primes
$f_{C_{i}}$
is annihilated by a differential operator of type I for all primes
![]() $p$
. Indeed, by [Reference Borwein, Nuyens, Straub and WanBNSW11, Proposition 1 and Theorem 2], for all
$p$
. Indeed, by [Reference Borwein, Nuyens, Straub and WanBNSW11, Proposition 1 and Theorem 2], for all
![]() $j\geqslant 2$
,
$j\geqslant 2$
,
![]() $C_{j}(n)$
satisfies the recurrence relation of order
$C_{j}(n)$
satisfies the recurrence relation of order
![]() $\lceil j/2\rceil$
with polynomial coefficients of degree
$\lceil j/2\rceil$
with polynomial coefficients of degree
![]() $j-1$
:
$j-1$
:
 $$\begin{eqnarray}n^{j-1}C_{j}(n)+\mathop{\sum }_{i\geqslant 1}\biggl(n^{j-1}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{i}}\mathop{\prod }_{k=1}^{i}(-\unicode[STIX]{x1D6FC}_{k})(j+1-\unicode[STIX]{x1D6FC}_{k})\biggl(\frac{n-k}{n-k+1}\biggr)^{\unicode[STIX]{x1D6FC}_{k}-1}\biggr)C_{j}(n-i)=0,\end{eqnarray}$$
$$\begin{eqnarray}n^{j-1}C_{j}(n)+\mathop{\sum }_{i\geqslant 1}\biggl(n^{j-1}\mathop{\sum }_{\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{i}}\mathop{\prod }_{k=1}^{i}(-\unicode[STIX]{x1D6FC}_{k})(j+1-\unicode[STIX]{x1D6FC}_{k})\biggl(\frac{n-k}{n-k+1}\biggr)^{\unicode[STIX]{x1D6FC}_{k}-1}\biggr)C_{j}(n-i)=0,\end{eqnarray}$$
where the sum is over all sequences of positive integers
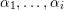 $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{i}$
satisfying
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{i}$
satisfying
![]() $\unicode[STIX]{x1D6FC}_{k}\leqslant j$
and
$\unicode[STIX]{x1D6FC}_{k}\leqslant j$
and
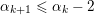 $\unicode[STIX]{x1D6FC}_{k+1}\leqslant \unicode[STIX]{x1D6FC}_{k}-2$
. We consider
$\unicode[STIX]{x1D6FC}_{k+1}\leqslant \unicode[STIX]{x1D6FC}_{k}-2$
. We consider
![]() $i\geqslant 2$
and
$i\geqslant 2$
and
![]() $i$
positive integers
$i$
positive integers
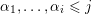 $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{i}\leqslant j$
satisfying
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{i}\leqslant j$
satisfying
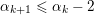 $\unicode[STIX]{x1D6FC}_{k+1}\leqslant \unicode[STIX]{x1D6FC}_{k}-2$
. We have
$\unicode[STIX]{x1D6FC}_{k+1}\leqslant \unicode[STIX]{x1D6FC}_{k}-2$
. We have
 $$\begin{eqnarray}n^{j-1}\mathop{\prod }_{k=1}^{i}\biggl(\frac{n-k}{n-k+1}\biggr)^{\unicode[STIX]{x1D6FC}_{k}-1}=\frac{n^{j-1}}{n^{\unicode[STIX]{x1D6FC}_{1}-1}}\biggl(\mathop{\prod }_{k=1}^{i-1}(n-k)^{\unicode[STIX]{x1D6FC}_{k}-\unicode[STIX]{x1D6FC}_{k+1}}\biggr)(n-i)^{\unicode[STIX]{x1D6FC}_{i}-1}\end{eqnarray}$$
$$\begin{eqnarray}n^{j-1}\mathop{\prod }_{k=1}^{i}\biggl(\frac{n-k}{n-k+1}\biggr)^{\unicode[STIX]{x1D6FC}_{k}-1}=\frac{n^{j-1}}{n^{\unicode[STIX]{x1D6FC}_{1}-1}}\biggl(\mathop{\prod }_{k=1}^{i-1}(n-k)^{\unicode[STIX]{x1D6FC}_{k}-\unicode[STIX]{x1D6FC}_{k+1}}\biggr)(n-i)^{\unicode[STIX]{x1D6FC}_{i}-1}\end{eqnarray}$$
with
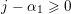 $j-\unicode[STIX]{x1D6FC}_{1}\geqslant 0$
,
$j-\unicode[STIX]{x1D6FC}_{1}\geqslant 0$
,
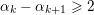 $\unicode[STIX]{x1D6FC}_{k}-\unicode[STIX]{x1D6FC}_{k+1}\geqslant 2$
and
$\unicode[STIX]{x1D6FC}_{k}-\unicode[STIX]{x1D6FC}_{k+1}\geqslant 2$
and
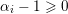 $\unicode[STIX]{x1D6FC}_{i}-1\geqslant 0$
. Then
$\unicode[STIX]{x1D6FC}_{i}-1\geqslant 0$
. Then
![]() $f_{C_{j}}(z)$
is annihilated by a differential operator
$f_{C_{j}}(z)$
is annihilated by a differential operator
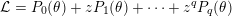 ${\mathcal{L}}=P_{0}(\unicode[STIX]{x1D703})+zP_{1}(\unicode[STIX]{x1D703})+\cdots +z^{q}P_{q}(\unicode[STIX]{x1D703})$
with
${\mathcal{L}}=P_{0}(\unicode[STIX]{x1D703})+zP_{1}(\unicode[STIX]{x1D703})+\cdots +z^{q}P_{q}(\unicode[STIX]{x1D703})$
with
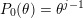 $P_{0}(\unicode[STIX]{x1D703})=\unicode[STIX]{x1D703}^{j-1}$
and, for all
$P_{0}(\unicode[STIX]{x1D703})=\unicode[STIX]{x1D703}^{j-1}$
and, for all
![]() $i\geqslant 2$
,
$i\geqslant 2$
,
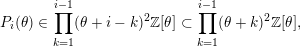 $$\begin{eqnarray}P_{i}(\unicode[STIX]{x1D703})\in \mathop{\prod }_{k=1}^{i-1}(\unicode[STIX]{x1D703}+i-k)^{2}\mathbb{Z}[\unicode[STIX]{x1D703}]\subset \mathop{\prod }_{k=1}^{i-1}(\unicode[STIX]{x1D703}+k)^{2}\mathbb{Z}[\unicode[STIX]{x1D703}],\end{eqnarray}$$
$$\begin{eqnarray}P_{i}(\unicode[STIX]{x1D703})\in \mathop{\prod }_{k=1}^{i-1}(\unicode[STIX]{x1D703}+i-k)^{2}\mathbb{Z}[\unicode[STIX]{x1D703}]\subset \mathop{\prod }_{k=1}^{i-1}(\unicode[STIX]{x1D703}+k)^{2}\mathbb{Z}[\unicode[STIX]{x1D703}],\end{eqnarray}$$
so that
![]() ${\mathcal{L}}$
is of type I for all primes
${\mathcal{L}}$
is of type I for all primes
![]() $p$
, as expected.
$p$
, as expected.
1.7 Structure of the article
In § 2, we use several results of [Reference DelaygueDel13] to prove Theorem 3. Section 3 is devoted to the proofs of Theorem 2 and Proposition 1. In particular, we prove Lemma 1, which points out the role played by differential operators in our proofs. In § 4, we prove Theorem 1 by applying Proposition 1 to
![]() $\mathfrak{S}_{e,f}$
. It is the most technical part of this article.
$\mathfrak{S}_{e,f}$
. It is the most technical part of this article.
2 Proof of Theorem 3
First, we prove that if
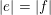 $|e|=|f|$
, then, for all primes
$|e|=|f|$
, then, for all primes
![]() $p$
, all
$p$
, all
![]() $\mathbf{a}$
in
$\mathbf{a}$
in
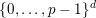 $\{0,\ldots ,p-1\}^{d}$
and all
$\{0,\ldots ,p-1\}^{d}$
and all
![]() $\mathbf{n}$
in
$\mathbf{n}$
in
![]() $\mathbb{N}^{d}$
, we have
$\mathbb{N}^{d}$
, we have
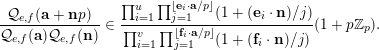 $$\begin{eqnarray}\frac{{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p)}{{\mathcal{Q}}_{e,f}(\mathbf{a}){\mathcal{Q}}_{e,f}(\mathbf{n})}\in \frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{j=1}^{\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor }(1+(\mathbf{e}_{i}\cdot \mathbf{n})/j)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{j=1}^{\lfloor \mathbf{f}_{i}\cdot \mathbf{a}/p\rfloor }(1+(\mathbf{f}_{i}\cdot \mathbf{n})/j)}(1+p\mathbb{Z}_{p}).\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p)}{{\mathcal{Q}}_{e,f}(\mathbf{a}){\mathcal{Q}}_{e,f}(\mathbf{n})}\in \frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{j=1}^{\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor }(1+(\mathbf{e}_{i}\cdot \mathbf{n})/j)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{j=1}^{\lfloor \mathbf{f}_{i}\cdot \mathbf{a}/p\rfloor }(1+(\mathbf{f}_{i}\cdot \mathbf{n})/j)}(1+p\mathbb{Z}_{p}).\end{eqnarray}$$
Indeed, we have
 $$\begin{eqnarray}\frac{{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p)}{{\mathcal{Q}}_{e,f}(\mathbf{a}){\mathcal{Q}}_{e,f}(\mathbf{n})}=\frac{{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p)}{{\mathcal{Q}}_{e,f}(\mathbf{a}){\mathcal{Q}}_{e,f}(\mathbf{n}p)}\cdot \frac{{\mathcal{Q}}_{e,f}(\mathbf{n}p)}{{\mathcal{Q}}_{e,f}(\mathbf{n})}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p)}{{\mathcal{Q}}_{e,f}(\mathbf{a}){\mathcal{Q}}_{e,f}(\mathbf{n})}=\frac{{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p)}{{\mathcal{Q}}_{e,f}(\mathbf{a}){\mathcal{Q}}_{e,f}(\mathbf{n}p)}\cdot \frac{{\mathcal{Q}}_{e,f}(\mathbf{n}p)}{{\mathcal{Q}}_{e,f}(\mathbf{n})}.\end{eqnarray}$$
Since
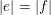 $|e|=|f|$
, we can apply [Reference DelaygueDel13, Lemma 7]Footnote
5
with
$|e|=|f|$
, we can apply [Reference DelaygueDel13, Lemma 7]Footnote
5
with
![]() $\mathbf{c}=\mathbf{0}$
,
$\mathbf{c}=\mathbf{0}$
,
![]() $\mathbf{m}=\mathbf{n}$
and
$\mathbf{m}=\mathbf{n}$
and
![]() $s=0$
, which yields
$s=0$
, which yields
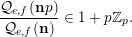 $$\begin{eqnarray}\frac{{\mathcal{Q}}_{e,f}(\mathbf{n}p)}{{\mathcal{Q}}_{e,f}(\mathbf{n})}\in 1+p\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{{\mathcal{Q}}_{e,f}(\mathbf{n}p)}{{\mathcal{Q}}_{e,f}(\mathbf{n})}\in 1+p\mathbb{Z}_{p}.\end{eqnarray}$$
Furthermore, we have
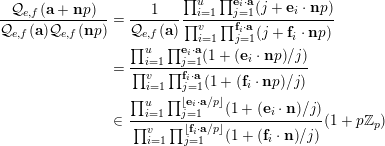 $$\begin{eqnarray}\displaystyle \frac{{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p)}{{\mathcal{Q}}_{e,f}(\mathbf{a}){\mathcal{Q}}_{e,f}(\mathbf{n}p)} & = & \displaystyle \frac{1}{{\mathcal{Q}}_{e,f}(\mathbf{a})}\frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{j=1}^{\mathbf{e}_{i}\cdot \mathbf{a}}(j+\mathbf{e}_{i}\cdot \mathbf{n}p)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{j=1}^{\mathbf{f}_{i}\cdot \mathbf{a}}(j+\mathbf{f}_{i}\cdot \mathbf{n}p)}\nonumber\\ \displaystyle & = & \displaystyle \frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{j=1}^{\mathbf{e}_{i}\cdot \mathbf{a}}(1+(\mathbf{e}_{i}\cdot \mathbf{n}p)/j)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{j=1}^{\mathbf{f}_{i}\cdot \mathbf{a}}(1+(\mathbf{f}_{i}\cdot \mathbf{n}p)/j)}\nonumber\\ \displaystyle & \in & \displaystyle \frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{j=1}^{\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor }(1+(\mathbf{e}_{i}\cdot \mathbf{n})/j)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{j=1}^{\lfloor \mathbf{f}_{i}\cdot \mathbf{a}/p\rfloor }(1+(\mathbf{f}_{i}\cdot \mathbf{n})/j)}(1+p\mathbb{Z}_{p})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p)}{{\mathcal{Q}}_{e,f}(\mathbf{a}){\mathcal{Q}}_{e,f}(\mathbf{n}p)} & = & \displaystyle \frac{1}{{\mathcal{Q}}_{e,f}(\mathbf{a})}\frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{j=1}^{\mathbf{e}_{i}\cdot \mathbf{a}}(j+\mathbf{e}_{i}\cdot \mathbf{n}p)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{j=1}^{\mathbf{f}_{i}\cdot \mathbf{a}}(j+\mathbf{f}_{i}\cdot \mathbf{n}p)}\nonumber\\ \displaystyle & = & \displaystyle \frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{j=1}^{\mathbf{e}_{i}\cdot \mathbf{a}}(1+(\mathbf{e}_{i}\cdot \mathbf{n}p)/j)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{j=1}^{\mathbf{f}_{i}\cdot \mathbf{a}}(1+(\mathbf{f}_{i}\cdot \mathbf{n}p)/j)}\nonumber\\ \displaystyle & \in & \displaystyle \frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{j=1}^{\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor }(1+(\mathbf{e}_{i}\cdot \mathbf{n})/j)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{j=1}^{\lfloor \mathbf{f}_{i}\cdot \mathbf{a}/p\rfloor }(1+(\mathbf{f}_{i}\cdot \mathbf{n})/j)}(1+p\mathbb{Z}_{p})\nonumber\end{eqnarray}$$
because, if
![]() $p$
does not divide
$p$
does not divide
![]() $j$
, then
$j$
, then
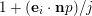 $1+(\mathbf{e}_{i}\cdot \mathbf{n}p)/j$
belongs to
$1+(\mathbf{e}_{i}\cdot \mathbf{n}p)/j$
belongs to
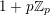 $1+p\mathbb{Z}_{p}$
. This finishes the proof of (2.1).
$1+p\mathbb{Z}_{p}$
. This finishes the proof of (2.1).
Now we prove Assertion (i) in Theorem 3. Let
![]() $p$
be a fixed prime number. It is well known that, for all nonnegative integers
$p$
be a fixed prime number. It is well known that, for all nonnegative integers
![]() $n$
, we have
$n$
, we have
 $$\begin{eqnarray}v_{p}(n!)=\mathop{\sum }_{\ell =1}^{\infty }\biggl\lfloor\frac{n}{p^{\ell }}\biggr\rfloor.\end{eqnarray}$$
$$\begin{eqnarray}v_{p}(n!)=\mathop{\sum }_{\ell =1}^{\infty }\biggl\lfloor\frac{n}{p^{\ell }}\biggr\rfloor.\end{eqnarray}$$
We remind the reader that the Landau function
![]() $\unicode[STIX]{x1D6E5}_{e,f}$
is defined by
$\unicode[STIX]{x1D6E5}_{e,f}$
is defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})=\mathop{\sum }_{i=1}^{u}\lfloor \mathbf{e}_{i}\cdot \mathbf{x}\rfloor -\mathop{\sum }_{j=1}^{v}\lfloor \mathbf{f}_{j}\cdot \mathbf{x}\rfloor \quad (\mathbf{x}\in \mathbb{R}^{d}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})=\mathop{\sum }_{i=1}^{u}\lfloor \mathbf{e}_{i}\cdot \mathbf{x}\rfloor -\mathop{\sum }_{j=1}^{v}\lfloor \mathbf{f}_{j}\cdot \mathbf{x}\rfloor \quad (\mathbf{x}\in \mathbb{R}^{d}).\end{eqnarray}$$
Thus, for all vectors
![]() $\mathbf{n}$
in
$\mathbf{n}$
in
![]() $\mathbb{N}^{d}$
, we have
$\mathbb{N}^{d}$
, we have
 $$\begin{eqnarray}v_{p}({\mathcal{Q}}_{e,f}(\mathbf{n}))=\mathop{\sum }_{\ell =1}^{\infty }\unicode[STIX]{x1D6E5}_{e,f}\biggl(\frac{\mathbf{n}}{p^{\ell }}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}v_{p}({\mathcal{Q}}_{e,f}(\mathbf{n}))=\mathop{\sum }_{\ell =1}^{\infty }\unicode[STIX]{x1D6E5}_{e,f}\biggl(\frac{\mathbf{n}}{p^{\ell }}\biggr).\end{eqnarray}$$
Fix
![]() $\mathbf{n}$
in
$\mathbf{n}$
in
![]() $\mathbb{N}^{d}$
and
$\mathbb{N}^{d}$
and
![]() $\mathbf{a}$
in
$\mathbf{a}$
in
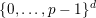 $\{0,\ldots ,p-1\}^{d}$
. Let
$\{0,\ldots ,p-1\}^{d}$
. Let
![]() $\{\cdot \}$
denote the fractional part function. For any vector of real numbers
$\{\cdot \}$
denote the fractional part function. For any vector of real numbers
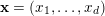 $\mathbf{x}=(x_{1},\ldots ,x_{d})$
, we set
$\mathbf{x}=(x_{1},\ldots ,x_{d})$
, we set
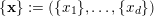 $\{\mathbf{x}\}:=(\{x_{1}\},\ldots ,\{x_{d}\})$
. Since
$\{\mathbf{x}\}:=(\{x_{1}\},\ldots ,\{x_{d}\})$
. Since
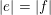 $|e|=|f|$
, we have
$|e|=|f|$
, we have
 $$\begin{eqnarray}v_{p}({\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p))=\mathop{\sum }_{\ell =1}^{\infty }\unicode[STIX]{x1D6E5}_{e,f}\biggl(\biggl\{\frac{\mathbf{a}+\mathbf{n}p}{p^{\ell }}\biggr\}\biggr)\geqslant \unicode[STIX]{x1D6E5}_{e,f}\biggl(\frac{\mathbf{a}}{p}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}v_{p}({\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p))=\mathop{\sum }_{\ell =1}^{\infty }\unicode[STIX]{x1D6E5}_{e,f}\biggl(\biggl\{\frac{\mathbf{a}+\mathbf{n}p}{p^{\ell }}\biggr\}\biggr)\geqslant \unicode[STIX]{x1D6E5}_{e,f}\biggl(\frac{\mathbf{a}}{p}\biggr)\end{eqnarray}$$
because
![]() $\unicode[STIX]{x1D6E5}_{e,f}$
is nonnegative on
$\unicode[STIX]{x1D6E5}_{e,f}$
is nonnegative on
![]() $[0,1]^{d}$
. By assumption, if
$[0,1]^{d}$
. By assumption, if
![]() $\mathbf{x}$
belongs to
$\mathbf{x}$
belongs to
![]() ${\mathcal{D}}_{e,f}$
, then
${\mathcal{D}}_{e,f}$
, then
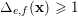 $\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})\geqslant 1$
. On the one hand, if
$\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})\geqslant 1$
. On the one hand, if
![]() $\mathbf{a}/p$
is in
$\mathbf{a}/p$
is in
![]() ${\mathcal{D}}_{e,f}$
, then both
${\mathcal{D}}_{e,f}$
, then both
 ${\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p)$
and
${\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p)$
and
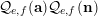 ${\mathcal{Q}}_{e,f}(\mathbf{a}){\mathcal{Q}}_{e,f}(\mathbf{n})$
are congruent to
${\mathcal{Q}}_{e,f}(\mathbf{a}){\mathcal{Q}}_{e,f}(\mathbf{n})$
are congruent to
![]() $0$
modulo
$0$
modulo
![]() $p$
. On the other hand, if
$p$
. On the other hand, if
![]() $\mathbf{a}/p$
is not in
$\mathbf{a}/p$
is not in
![]() ${\mathcal{D}}_{e,f}$
, then, by definition, for all
${\mathcal{D}}_{e,f}$
, then, by definition, for all
![]() $\mathbf{d}$
in
$\mathbf{d}$
in
![]() $e$
or
$e$
or
![]() $f$
, we have
$f$
, we have
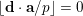 $\lfloor \mathbf{d}\cdot \mathbf{a}/p\rfloor =0$
, so that (2.1) yields
$\lfloor \mathbf{d}\cdot \mathbf{a}/p\rfloor =0$
, so that (2.1) yields
 $$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p)\equiv {\mathcal{Q}}_{e,f}(\mathbf{a}){\mathcal{Q}}_{e,f}(\mathbf{n})\hspace{0.6em}{\rm mod}\hspace{0.2em}p\mathbb{Z}_{p},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{n}p)\equiv {\mathcal{Q}}_{e,f}(\mathbf{a}){\mathcal{Q}}_{e,f}(\mathbf{n})\hspace{0.6em}{\rm mod}\hspace{0.2em}p\mathbb{Z}_{p},\end{eqnarray}$$
as expected. This proves Assertion (i) in Theorem 3.
Now we prove Assertion (ii) in Theorem 3. If
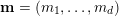 $\mathbf{m}=(m_{1},\ldots ,m_{d})$
is a vector in
$\mathbf{m}=(m_{1},\ldots ,m_{d})$
is a vector in
![]() $\mathbb{R}^{d}$
and
$\mathbb{R}^{d}$
and
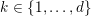 $k\in \{1,\ldots ,d\}$
, then we set
$k\in \{1,\ldots ,d\}$
, then we set
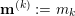 $\mathbf{m}^{(k)}:=m_{k}$
. If
$\mathbf{m}^{(k)}:=m_{k}$
. If
 $|e|\neq |f|$
, then, since
$|e|\neq |f|$
, then, since
![]() $\unicode[STIX]{x1D6E5}_{e,f}$
is nonnegative on
$\unicode[STIX]{x1D6E5}_{e,f}$
is nonnegative on
![]() $[0,1]^{d}$
, there exists
$[0,1]^{d}$
, there exists
![]() $k$
in
$k$
in
 $\{1,\ldots ,d\}$
such that
$\{1,\ldots ,d\}$
such that
 $|e|^{(k)}-|f|^{(k)}=\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{1}_{k})\geqslant 1$
. Thereby, for almost all primes
$|e|^{(k)}-|f|^{(k)}=\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{1}_{k})\geqslant 1$
. Thereby, for almost all primes
![]() $p$
, we have
$p$
, we have
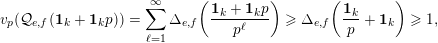 $$\begin{eqnarray}v_{p}({\mathcal{Q}}_{e,f}(\mathbf{1}_{k}+\mathbf{1}_{k}p))=\mathop{\sum }_{\ell =1}^{\infty }\unicode[STIX]{x1D6E5}_{e,f}\biggl(\frac{\mathbf{1}_{k}+\mathbf{1}_{k}p}{p^{\ell }}\biggr)\geqslant \unicode[STIX]{x1D6E5}_{e,f}\biggl(\frac{\mathbf{1}_{k}}{p}+\mathbf{1}_{k}\biggr)\geqslant 1,\end{eqnarray}$$
$$\begin{eqnarray}v_{p}({\mathcal{Q}}_{e,f}(\mathbf{1}_{k}+\mathbf{1}_{k}p))=\mathop{\sum }_{\ell =1}^{\infty }\unicode[STIX]{x1D6E5}_{e,f}\biggl(\frac{\mathbf{1}_{k}+\mathbf{1}_{k}p}{p^{\ell }}\biggr)\geqslant \unicode[STIX]{x1D6E5}_{e,f}\biggl(\frac{\mathbf{1}_{k}}{p}+\mathbf{1}_{k}\biggr)\geqslant 1,\end{eqnarray}$$
but
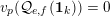 $v_{p}({\mathcal{Q}}_{e,f}(\mathbf{1}_{k}))=0$
, so that
$v_{p}({\mathcal{Q}}_{e,f}(\mathbf{1}_{k}))=0$
, so that
![]() ${\mathcal{Q}}_{e,f}$
does not satisfy the
${\mathcal{Q}}_{e,f}$
does not satisfy the
![]() $p$
-Lucas property.
$p$
-Lucas property.
Throughout the rest of this proof, we assume that
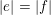 $|e|=|f|$
. According to [Reference DelaygueDel13, § 7.3.2], there exist
$|e|=|f|$
. According to [Reference DelaygueDel13, § 7.3.2], there exist
![]() $k$
in
$k$
in
 $\{1,\ldots ,d\}$
and a rational fraction
$\{1,\ldots ,d\}$
and a rational fraction
![]() $R(X)$
in
$R(X)$
in
![]() $\mathbb{Q}(X)$
,
$\mathbb{Q}(X)$
,
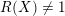 $R(X)\neq 1$
, such that, for all large enough prime numbers
$R(X)\neq 1$
, such that, for all large enough prime numbers
![]() $p$
, we can choose
$p$
, we can choose
![]() $\mathbf{a}_{p}$
in
$\mathbf{a}_{p}$
in
 $\{0,\ldots ,p-1\}^{d}$
satisfying
$\{0,\ldots ,p-1\}^{d}$
satisfying
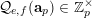 ${\mathcal{Q}}_{e,f}(\mathbf{a}_{p})\in \mathbb{Z}_{p}^{\times }$
and such that, for all nonnegative integers
${\mathcal{Q}}_{e,f}(\mathbf{a}_{p})\in \mathbb{Z}_{p}^{\times }$
and such that, for all nonnegative integers
![]() $n$
, we have (see [Reference DelaygueDel13, (7.10)])
$n$
, we have (see [Reference DelaygueDel13, (7.10)])
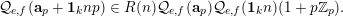 $$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{a}_{p}+\mathbf{1}_{k}np)\in R(n){\mathcal{Q}}_{e,f}(\mathbf{a}_{p}){\mathcal{Q}}_{e,f}(\mathbf{1}_{k}n)(1+p\mathbb{Z}_{p}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{a}_{p}+\mathbf{1}_{k}np)\in R(n){\mathcal{Q}}_{e,f}(\mathbf{a}_{p}){\mathcal{Q}}_{e,f}(\mathbf{1}_{k}n)(1+p\mathbb{Z}_{p}).\end{eqnarray}$$
We fix a nonnegative integer
![]() $n$
satisfying
$n$
satisfying
 $R(n)\neq 1$
. For almost all primes
$R(n)\neq 1$
. For almost all primes
![]() $p$
, the numbers
$p$
, the numbers
![]() $R(n)$
,
$R(n)$
,
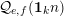 ${\mathcal{Q}}_{e,f}(\mathbf{1}_{k}n)$
and
${\mathcal{Q}}_{e,f}(\mathbf{1}_{k}n)$
and
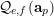 ${\mathcal{Q}}_{e,f}(\mathbf{a}_{p})$
are invertible in
${\mathcal{Q}}_{e,f}(\mathbf{a}_{p})$
are invertible in
![]() $\mathbb{Z}_{p}$
, and
$\mathbb{Z}_{p}$
, and
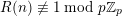 $R(n)\not \equiv 1\;\text{mod}\;p\mathbb{Z}_{p}$
. Thus, we obtain
$R(n)\not \equiv 1\;\text{mod}\;p\mathbb{Z}_{p}$
. Thus, we obtain
 $$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{a}_{p}+\mathbf{1}_{k}np)\not \equiv {\mathcal{Q}}_{e,f}(\mathbf{a}_{p}){\mathcal{Q}}_{e,f}(\mathbf{1}_{k}n)\hspace{0.6em}{\rm mod}\hspace{0.2em}p\mathbb{Z}_{p},\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{a}_{p}+\mathbf{1}_{k}np)\not \equiv {\mathcal{Q}}_{e,f}(\mathbf{a}_{p}){\mathcal{Q}}_{e,f}(\mathbf{1}_{k}n)\hspace{0.6em}{\rm mod}\hspace{0.2em}p\mathbb{Z}_{p},\end{eqnarray}$$
which finishes the proof of Assertion (ii) in Theorem 3.
Now we assume that
 $|e|=|f|$
and that, for all
$|e|=|f|$
and that, for all
![]() $\mathbf{x}$
in
$\mathbf{x}$
in
![]() ${\mathcal{D}}_{e,f}$
, we have
${\mathcal{D}}_{e,f}$
, we have
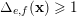 $\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})\geqslant 1$
. Hence, for every prime
$\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})\geqslant 1$
. Hence, for every prime
![]() $p$
, we have
$p$
, we have
 $$\begin{eqnarray}{\mathcal{Z}}_{p}({\mathcal{Q}}_{e,f})=\{\mathbf{v}\in \{0,\ldots ,p-1\}^{d}:\mathbf{v}/p\in {\mathcal{D}}_{e,f}\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}_{p}({\mathcal{Q}}_{e,f})=\{\mathbf{v}\in \{0,\ldots ,p-1\}^{d}:\mathbf{v}/p\in {\mathcal{D}}_{e,f}\}.\end{eqnarray}$$
Furthermore, if
![]() $\mathbf{v}/p$
belongs to
$\mathbf{v}/p$
belongs to
![]() ${\mathcal{D}}_{e,f}$
, then, for all positive integers
${\mathcal{D}}_{e,f}$
, then, for all positive integers
![]() $N$
and all vectors
$N$
and all vectors
 $\mathbf{a}_{0},\ldots ,\mathbf{a}_{N-1}$
in
$\mathbf{a}_{0},\ldots ,\mathbf{a}_{N-1}$
in
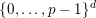 $\{0,\ldots ,p-1\}^{d}$
, we have
$\{0,\ldots ,p-1\}^{d}$
, we have
 $$\begin{eqnarray}\biggl\{\frac{\mathbf{a}_{0}+\mathbf{a}_{1}p+\cdots +\mathbf{a}_{N-1}p^{N-1}+\mathbf{v}p^{N}}{p^{N+1}}\biggr\}=\frac{\mathbf{a}_{0}+\mathbf{a}_{1}p+\cdots +\mathbf{a}_{N-1}p^{N-1}+\mathbf{v}p^{N}}{p^{N+1}}\geqslant \frac{\mathbf{v}}{p},\end{eqnarray}$$
$$\begin{eqnarray}\biggl\{\frac{\mathbf{a}_{0}+\mathbf{a}_{1}p+\cdots +\mathbf{a}_{N-1}p^{N-1}+\mathbf{v}p^{N}}{p^{N+1}}\biggr\}=\frac{\mathbf{a}_{0}+\mathbf{a}_{1}p+\cdots +\mathbf{a}_{N-1}p^{N-1}+\mathbf{v}p^{N}}{p^{N+1}}\geqslant \frac{\mathbf{v}}{p},\end{eqnarray}$$
so that
 $$\begin{eqnarray}\biggl\{\frac{\mathbf{a}_{0}+\mathbf{a}_{1}p+\cdots +\mathbf{a}_{N-1}p^{N-1}+\mathbf{v}p^{N}}{p^{N+1}}\biggr\}\in {\mathcal{D}}_{e,f}.\end{eqnarray}$$
$$\begin{eqnarray}\biggl\{\frac{\mathbf{a}_{0}+\mathbf{a}_{1}p+\cdots +\mathbf{a}_{N-1}p^{N-1}+\mathbf{v}p^{N}}{p^{N+1}}\biggr\}\in {\mathcal{D}}_{e,f}.\end{eqnarray}$$
Hence, for every
![]() $\mathbf{n}$
in
$\mathbf{n}$
in
![]() $\mathbb{N}^{d}$
,
$\mathbb{N}^{d}$
,
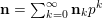 $\mathbf{n}=\sum _{k=0}^{\infty }\mathbf{n}_{k}p^{k}$
with
$\mathbf{n}=\sum _{k=0}^{\infty }\mathbf{n}_{k}p^{k}$
with
 $\mathbf{n}_{k}\in \{0,\ldots ,p-1\}^{d}$
, we have
$\mathbf{n}_{k}\in \{0,\ldots ,p-1\}^{d}$
, we have
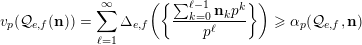 $$\begin{eqnarray}v_{p}({\mathcal{Q}}_{e,f}(\mathbf{n}))=\mathop{\sum }_{\ell =1}^{\infty }\unicode[STIX]{x1D6E5}_{e,f}\biggl(\biggl\{\frac{\mathop{\sum }_{k=0}^{\ell -1}\mathbf{n}_{k}p^{k}}{p^{\ell }}\biggr\}\biggr)\geqslant \unicode[STIX]{x1D6FC}_{p}({\mathcal{Q}}_{e,f},\mathbf{n})\end{eqnarray}$$
$$\begin{eqnarray}v_{p}({\mathcal{Q}}_{e,f}(\mathbf{n}))=\mathop{\sum }_{\ell =1}^{\infty }\unicode[STIX]{x1D6E5}_{e,f}\biggl(\biggl\{\frac{\mathop{\sum }_{k=0}^{\ell -1}\mathbf{n}_{k}p^{k}}{p^{\ell }}\biggr\}\biggr)\geqslant \unicode[STIX]{x1D6FC}_{p}({\mathcal{Q}}_{e,f},\mathbf{n})\end{eqnarray}$$
and Theorem 3 is proved.
3 Proofs of Theorem 2 and Proposition 1
3.1 Induction via Apéry-like recurrence relations
In this section, we fix a prime
![]() $p$
. We remind the reader that if
$p$
. We remind the reader that if
![]() $A$
is a
$A$
is a
![]() $\mathbb{Z}_{p}$
-valued sequence, then
$\mathbb{Z}_{p}$
-valued sequence, then
![]() ${\mathcal{Z}}_{p}(A)$
is the set of the digits
${\mathcal{Z}}_{p}(A)$
is the set of the digits
 $v\in \{0,\ldots ,p-1\}$
such that
$v\in \{0,\ldots ,p-1\}$
such that
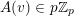 $A(v)\in p\mathbb{Z}_{p}$
. If
$A(v)\in p\mathbb{Z}_{p}$
. If
![]() $n$
is a nonnegative integer whose base-
$n$
is a nonnegative integer whose base-
![]() $p$
expansion is
$p$
expansion is
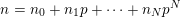 $n=n_{0}+n_{1}p+\cdots +n_{N}p^{N}$
, then
$n=n_{0}+n_{1}p+\cdots +n_{N}p^{N}$
, then
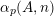 $\unicode[STIX]{x1D6FC}_{p}(A,n)$
is the number of
$\unicode[STIX]{x1D6FC}_{p}(A,n)$
is the number of
![]() $i$
in
$i$
in
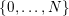 $\{0,\ldots ,N\}$
such that
$\{0,\ldots ,N\}$
such that
![]() $n_{i}$
belongs to
$n_{i}$
belongs to
![]() ${\mathcal{Z}}_{p}(A)$
.
${\mathcal{Z}}_{p}(A)$
.
If
![]() $A$
is a
$A$
is a
![]() $\mathbb{Z}_{p}$
-valued sequence, then, for all nonnegative integers
$\mathbb{Z}_{p}$
-valued sequence, then, for all nonnegative integers
![]() $r$
, we write
$r$
, we write
![]() ${\mathcal{U}}_{A}(r)$
for the assertion ‘For all
${\mathcal{U}}_{A}(r)$
for the assertion ‘For all
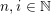 $n,i\in \mathbb{N}$
,
$n,i\in \mathbb{N}$
,
![]() $i\leqslant r$
, if
$i\leqslant r$
, if
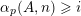 $\unicode[STIX]{x1D6FC}_{p}(A,n)\geqslant i$
, then
$\unicode[STIX]{x1D6FC}_{p}(A,n)\geqslant i$
, then
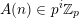 $A(n)\in p^{i}\mathbb{Z}_{p}$
.’. As a first step, we shall prove the following result.
$A(n)\in p^{i}\mathbb{Z}_{p}$
.’. As a first step, we shall prove the following result.
Lemma 1. Let
![]() $A$
be a
$A$
be a
![]() $\mathbb{Z}_{p}$
-valued sequence satisfying the
$\mathbb{Z}_{p}$
-valued sequence satisfying the
![]() $p$
-Lucas property with
$p$
-Lucas property with
![]() $A(0)$
in
$A(0)$
in
![]() $\mathbb{Z}_{p}^{\times }$
. Assume that the generating series of
$\mathbb{Z}_{p}^{\times }$
. Assume that the generating series of
![]() $A$
is annihilated by a differential operator
$A$
is annihilated by a differential operator
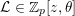 ${\mathcal{L}}\in \mathbb{Z}_{p}[z,\unicode[STIX]{x1D703}]$
such that at least one of the following conditions holds:
${\mathcal{L}}\in \mathbb{Z}_{p}[z,\unicode[STIX]{x1D703}]$
such that at least one of the following conditions holds:
-
–
 ${\mathcal{L}}$
is of type I;
${\mathcal{L}}$
is of type I; -
–
 ${\mathcal{L}}$
is of type II and
${\mathcal{L}}$
is of type II and
 $p-1\in {\mathcal{Z}}_{p}(A)$
.
$p-1\in {\mathcal{Z}}_{p}(A)$
.
Let
![]() $r$
be a nonnegative integer such that
$r$
be a nonnegative integer such that
![]() ${\mathcal{U}}_{A}(r)$
holds. Then, for all
${\mathcal{U}}_{A}(r)$
holds. Then, for all
![]() $n_{0}$
in
$n_{0}$
in
![]() ${\mathcal{Z}}_{p}(A)$
and all nonnegative integers
${\mathcal{Z}}_{p}(A)$
and all nonnegative integers
![]() $m$
satisfying
$m$
satisfying
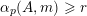 $\unicode[STIX]{x1D6FC}_{p}(A,m)\geqslant r$
, we have
$\unicode[STIX]{x1D6FC}_{p}(A,m)\geqslant r$
, we have
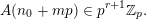 $$\begin{eqnarray}A(n_{0}+mp)\in p^{r+1}\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}A(n_{0}+mp)\in p^{r+1}\mathbb{Z}_{p}.\end{eqnarray}$$
Proof. Since
![]() $A$
satisfies the
$A$
satisfies the
![]() $p$
-Lucas property, we can assume that
$p$
-Lucas property, we can assume that
![]() $r$
is nonzero. The generating series of
$r$
is nonzero. The generating series of
![]() $A$
is annihilated by a differential operator
$A$
is annihilated by a differential operator
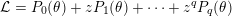 ${\mathcal{L}}=P_{0}(\unicode[STIX]{x1D703})+zP_{1}(\unicode[STIX]{x1D703})+\cdots +z^{q}P_{q}(\unicode[STIX]{x1D703})$
with
${\mathcal{L}}=P_{0}(\unicode[STIX]{x1D703})+zP_{1}(\unicode[STIX]{x1D703})+\cdots +z^{q}P_{q}(\unicode[STIX]{x1D703})$
with
![]() $P_{k}(X)$
in
$P_{k}(X)$
in
![]() $\mathbb{Z}_{p}[X]$
and
$\mathbb{Z}_{p}[X]$
and
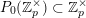 $P_{0}(\mathbb{Z}_{p}^{\times })\subset \mathbb{Z}_{p}^{\times }$
. Thus, for every nonnegative integer
$P_{0}(\mathbb{Z}_{p}^{\times })\subset \mathbb{Z}_{p}^{\times }$
. Thus, for every nonnegative integer
![]() $n$
, we have
$n$
, we have
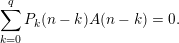 $$\begin{eqnarray}\mathop{\sum }_{k=0}^{q}P_{k}(n-k)A(n-k)=0.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k=0}^{q}P_{k}(n-k)A(n-k)=0.\end{eqnarray}$$
We fix a nonnegative integer
![]() $m$
satisfying
$m$
satisfying
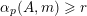 $\unicode[STIX]{x1D6FC}_{p}(A,m)\geqslant r$
. In particular, since
$\unicode[STIX]{x1D6FC}_{p}(A,m)\geqslant r$
. In particular, since
![]() $r$
is nonzero and
$r$
is nonzero and
![]() $A(0)$
is invertible in
$A(0)$
is invertible in
![]() $\mathbb{Z}_{p}$
, we have
$\mathbb{Z}_{p}$
, we have
![]() $m\geqslant 1$
. Furthermore, for all
$m\geqslant 1$
. Furthermore, for all
![]() $v$
in
$v$
in
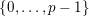 $\{0,\ldots ,p-1\}$
, we also have
$\{0,\ldots ,p-1\}$
, we also have
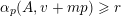 $\unicode[STIX]{x1D6FC}_{p}(A,v+mp)\geqslant r$
. According to
$\unicode[STIX]{x1D6FC}_{p}(A,v+mp)\geqslant r$
. According to
![]() ${\mathcal{U}}_{A}(r)$
, we obtain that, for all
${\mathcal{U}}_{A}(r)$
, we obtain that, for all
![]() $v$
in
$v$
in
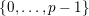 $\{0,\ldots ,p-1\}$
,
$\{0,\ldots ,p-1\}$
,
 $A(v+mp)$
belongs to
$A(v+mp)$
belongs to
![]() $p^{r}\mathbb{Z}_{p}$
, so that
$p^{r}\mathbb{Z}_{p}$
, so that
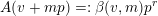 $A(v+mp)=:\unicode[STIX]{x1D6FD}(v,m)p^{r}$
with
$A(v+mp)=:\unicode[STIX]{x1D6FD}(v,m)p^{r}$
with
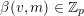 $\unicode[STIX]{x1D6FD}(v,m)\in \mathbb{Z}_{p}$
.
$\unicode[STIX]{x1D6FD}(v,m)\in \mathbb{Z}_{p}$
.
By (3.1), for all
![]() $v$
in
$v$
in
 $\{q,\ldots ,p-1\}$
, we have
$\{q,\ldots ,p-1\}$
, we have
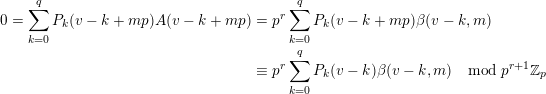 $$\begin{eqnarray}\displaystyle 0=\mathop{\sum }_{k=0}^{q}P_{k}(v-k+mp)A(v-k+mp) & = & \displaystyle p^{r}\mathop{\sum }_{k=0}^{q}P_{k}(v-k+mp)\unicode[STIX]{x1D6FD}(v-k,m)\nonumber\\ \displaystyle & \equiv & \displaystyle p^{r}\mathop{\sum }_{k=0}^{q}P_{k}(v-k)\unicode[STIX]{x1D6FD}(v-k,m)\quad \text{mod}\;p^{r+1}\mathbb{Z}_{p}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0=\mathop{\sum }_{k=0}^{q}P_{k}(v-k+mp)A(v-k+mp) & = & \displaystyle p^{r}\mathop{\sum }_{k=0}^{q}P_{k}(v-k+mp)\unicode[STIX]{x1D6FD}(v-k,m)\nonumber\\ \displaystyle & \equiv & \displaystyle p^{r}\mathop{\sum }_{k=0}^{q}P_{k}(v-k)\unicode[STIX]{x1D6FD}(v-k,m)\quad \text{mod}\;p^{r+1}\mathbb{Z}_{p}\nonumber\end{eqnarray}$$
because, for all polynomials
![]() $P$
in
$P$
in
![]() $\mathbb{Z}_{p}[X]$
and all integers
$\mathbb{Z}_{p}[X]$
and all integers
![]() $a$
and
$a$
and
![]() $c$
, we have
$c$
, we have
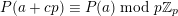 $P(a+cp)\equiv P(a)\;\text{mod}\;p\mathbb{Z}_{p}$
. Thus, for all
$P(a+cp)\equiv P(a)\;\text{mod}\;p\mathbb{Z}_{p}$
. Thus, for all
![]() $v$
in
$v$
in
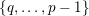 $\{q,\ldots ,p-1\}$
, we obtain
$\{q,\ldots ,p-1\}$
, we obtain
 $$\begin{eqnarray}\mathop{\sum }_{k=0}^{q}P_{k}(v-k)\unicode[STIX]{x1D6FD}(v-k,m)\equiv 0\quad \text{mod}\;p\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k=0}^{q}P_{k}(v-k)\unicode[STIX]{x1D6FD}(v-k,m)\equiv 0\quad \text{mod}\;p\mathbb{Z}_{p}.\end{eqnarray}$$
We claim that if
![]() $v$
is in
$v$
is in
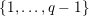 $\{1,\ldots ,q-1\}$
, then, for all
$\{1,\ldots ,q-1\}$
, then, for all
![]() $k$
in
$k$
in
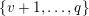 $\{v+1,\ldots ,q\}$
, we have
$\{v+1,\ldots ,q\}$
, we have
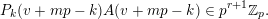 $$\begin{eqnarray}P_{k}(v+mp-k)A(v+mp-k)\in p^{r+1}\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}P_{k}(v+mp-k)A(v+mp-k)\in p^{r+1}\mathbb{Z}_{p}.\end{eqnarray}$$
Indeed, on the one hand, if
![]() ${\mathcal{L}}$
is of type II, then we have
${\mathcal{L}}$
is of type II, then we have
![]() $q=2$
and
$q=2$
and
![]() $P_{2}(X)$
belongs to
$P_{2}(X)$
belongs to
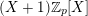 $(X+1)\mathbb{Z}_{p}[X]$
, which yields
$(X+1)\mathbb{Z}_{p}[X]$
, which yields
 $$\begin{eqnarray}P_{2}(-1+mp)A(-1+mp)\in pA(p-1+(m-1)p)\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}P_{2}(-1+mp)A(-1+mp)\in pA(p-1+(m-1)p)\mathbb{Z}_{p}.\end{eqnarray}$$
Since
![]() $0$
is not in
$0$
is not in
![]() ${\mathcal{Z}}_{p}(A)$
, we have
${\mathcal{Z}}_{p}(A)$
, we have
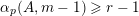 $\unicode[STIX]{x1D6FC}_{p}(A,m-1)\geqslant r-1$
, which, together with
$\unicode[STIX]{x1D6FC}_{p}(A,m-1)\geqslant r-1$
, which, together with
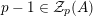 $p-1\in {\mathcal{Z}}_{p}(A)$
, leads to
$p-1\in {\mathcal{Z}}_{p}(A)$
, leads to
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{p}(A,p-1+(m-1)p)\geqslant r.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{p}(A,p-1+(m-1)p)\geqslant r.\end{eqnarray}$$
According to
![]() ${\mathcal{U}}_{A}(r)$
, we obtain that
${\mathcal{U}}_{A}(r)$
, we obtain that
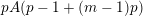 $pA(p-1+(m-1)p)$
is in
$pA(p-1+(m-1)p)$
is in
![]() $p^{r+1}\mathbb{Z}_{p}$
, as expected. On the other hand, if
$p^{r+1}\mathbb{Z}_{p}$
, as expected. On the other hand, if
![]() ${\mathcal{L}}$
is of type I, then, for all
${\mathcal{L}}$
is of type I, then, for all
![]() $v$
in
$v$
in
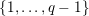 $\{1,\ldots ,q-1\}$
and all
$\{1,\ldots ,q-1\}$
and all
![]() $k$
in
$k$
in
 $\{v+1,\ldots ,q\}$
, we have
$\{v+1,\ldots ,q\}$
, we have
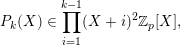 $$\begin{eqnarray}P_{k}(X)\in \mathop{\prod }_{i=1}^{k-1}(X+i)^{2}\mathbb{Z}_{p}[X],\end{eqnarray}$$
$$\begin{eqnarray}P_{k}(X)\in \mathop{\prod }_{i=1}^{k-1}(X+i)^{2}\mathbb{Z}_{p}[X],\end{eqnarray}$$
so that
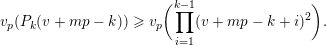 $$\begin{eqnarray}v_{p}(P_{k}(v+mp-k))\geqslant v_{p}\biggl(\mathop{\prod }_{i=1}^{k-1}(v+mp-k+i)^{2}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}v_{p}(P_{k}(v+mp-k))\geqslant v_{p}\biggl(\mathop{\prod }_{i=1}^{k-1}(v+mp-k+i)^{2}\biggr).\end{eqnarray}$$
Writing
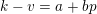 $k-v=a+bp$
with
$k-v=a+bp$
with
![]() $a$
in
$a$
in
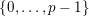 $\{0,\ldots ,p-1\}$
and
$\{0,\ldots ,p-1\}$
and
![]() $b$
in
$b$
in
![]() $\mathbb{N}$
, we obtain
$\mathbb{N}$
, we obtain
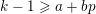 $k-1\geqslant a+bp$
, so that
$k-1\geqslant a+bp$
, so that
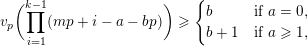 $$\begin{eqnarray}v_{p}\biggl(\mathop{\prod }_{i=1}^{k-1}(mp+i-a-bp)\biggr)\geqslant \left\{\begin{array}{@{}ll@{}}b\quad & \text{if }a=0,\\ b+1\quad & \text{if }a\geqslant 1,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}v_{p}\biggl(\mathop{\prod }_{i=1}^{k-1}(mp+i-a-bp)\biggr)\geqslant \left\{\begin{array}{@{}ll@{}}b\quad & \text{if }a=0,\\ b+1\quad & \text{if }a\geqslant 1,\end{array}\right.\end{eqnarray}$$
which yields
 $$\begin{eqnarray}v_{p}(P_{k}(v+mp-k))\geqslant \left\{\begin{array}{@{}ll@{}}2b\quad & \text{if }a=0,\\ 2b+2\quad & \text{if }a\geqslant 1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}v_{p}(P_{k}(v+mp-k))\geqslant \left\{\begin{array}{@{}ll@{}}2b\quad & \text{if }a=0,\\ 2b+2\quad & \text{if }a\geqslant 1.\end{array}\right.\end{eqnarray}$$
Thus, to prove (3.3), it is enough to show that
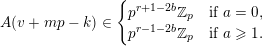 $$\begin{eqnarray}A(v+mp-k)\in \left\{\begin{array}{@{}ll@{}}p^{r+1-2b}\mathbb{Z}_{p}\quad & \text{if }a=0,\\ p^{r-1-2b}\mathbb{Z}_{p}\quad & \text{if }a\geqslant 1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}A(v+mp-k)\in \left\{\begin{array}{@{}ll@{}}p^{r+1-2b}\mathbb{Z}_{p}\quad & \text{if }a=0,\\ p^{r-1-2b}\mathbb{Z}_{p}\quad & \text{if }a\geqslant 1.\end{array}\right.\end{eqnarray}$$
By definition of
![]() $a$
and
$a$
and
![]() $b$
, we have
$b$
, we have
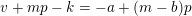 $v+mp-k=-a+(m-b)p$
with
$v+mp-k=-a+(m-b)p$
with
![]() $a$
in
$a$
in
 $\{0,\ldots ,p-1\}$
. If
$\{0,\ldots ,p-1\}$
. If
 $-a+(m-b)p$
is negative, then
$-a+(m-b)p$
is negative, then
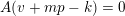 $A(v+mp-k)=0$
and (3.4) holds. By assumption, we have
$A(v+mp-k)=0$
and (3.4) holds. By assumption, we have
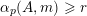 $\unicode[STIX]{x1D6FC}_{p}(A,m)\geqslant r$
and
$\unicode[STIX]{x1D6FC}_{p}(A,m)\geqslant r$
and
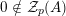 $0\notin {\mathcal{Z}}_{p}(A)$
. Hence, if
$0\notin {\mathcal{Z}}_{p}(A)$
. Hence, if
![]() $m-b$
is nonnegative, then we have
$m-b$
is nonnegative, then we have
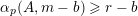 $\unicode[STIX]{x1D6FC}_{p}(A,m-b)\geqslant r-b$
. Thus, we have either
$\unicode[STIX]{x1D6FC}_{p}(A,m-b)\geqslant r-b$
. Thus, we have either
![]() $a=0$
and
$a=0$
and
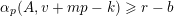 $\unicode[STIX]{x1D6FC}_{p}(A,v+mp-k)\geqslant r-b$
, or
$\unicode[STIX]{x1D6FC}_{p}(A,v+mp-k)\geqslant r-b$
, or
 $a,m-b\geqslant 1$
and
$a,m-b\geqslant 1$
and
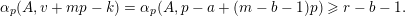 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{p}(A,v+mp-k)=\unicode[STIX]{x1D6FC}_{p}(A,p-a+(m-b-1)p)\geqslant r-b-1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{p}(A,v+mp-k)=\unicode[STIX]{x1D6FC}_{p}(A,p-a+(m-b-1)p)\geqslant r-b-1.\end{eqnarray}$$
Hence, Assertion
![]() ${\mathcal{U}}_{A}(r)$
yields
${\mathcal{U}}_{A}(r)$
yields
 $$\begin{eqnarray}A(v+mp-k)\in \left\{\begin{array}{@{}ll@{}}p^{r-b}\mathbb{Z}_{p}\quad & \text{if }a=0,\\ p^{r-1-b}\mathbb{Z}_{p}\quad & \text{if }a\geqslant 1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}A(v+mp-k)\in \left\{\begin{array}{@{}ll@{}}p^{r-b}\mathbb{Z}_{p}\quad & \text{if }a=0,\\ p^{r-1-b}\mathbb{Z}_{p}\quad & \text{if }a\geqslant 1.\end{array}\right.\end{eqnarray}$$
If
![]() $a=0$
, then
$a=0$
, then
![]() $b\geqslant 1$
and
$b\geqslant 1$
and
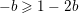 $-b\geqslant 1-2b$
, so that (3.4) holds and (3.3) is proved.
$-b\geqslant 1-2b$
, so that (3.4) holds and (3.3) is proved.
By (3.3), for all nonnegative integers
![]() $v$
satisfying
$v$
satisfying
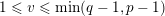 $1\leqslant v\leqslant \min (q-1,p-1)$
, we have
$1\leqslant v\leqslant \min (q-1,p-1)$
, we have
 $$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \mathop{\sum }_{k=0}^{q}P_{k}(v-k+mp)A(v-k+mp)\nonumber\\ \displaystyle & \equiv & \displaystyle \mathop{\sum }_{k=0}^{v}P_{k}(v-k+mp)A(v-k+mp)\quad \text{mod}\;p^{r+1}\mathbb{Z}_{p}\nonumber\\ \displaystyle & \equiv & \displaystyle p^{r}\mathop{\sum }_{k=0}^{v}P_{k}(v-k+mp)\unicode[STIX]{x1D6FD}(v-k,m)\quad \text{mod}\;p^{r+1}\mathbb{Z}_{p}\nonumber\\ \displaystyle & \equiv & \displaystyle p^{r}\mathop{\sum }_{k=0}^{v}P_{k}(v-k)\unicode[STIX]{x1D6FD}(v-k,m)\quad \text{mod}\;p^{r+1}\mathbb{Z}_{p}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & = & \displaystyle \mathop{\sum }_{k=0}^{q}P_{k}(v-k+mp)A(v-k+mp)\nonumber\\ \displaystyle & \equiv & \displaystyle \mathop{\sum }_{k=0}^{v}P_{k}(v-k+mp)A(v-k+mp)\quad \text{mod}\;p^{r+1}\mathbb{Z}_{p}\nonumber\\ \displaystyle & \equiv & \displaystyle p^{r}\mathop{\sum }_{k=0}^{v}P_{k}(v-k+mp)\unicode[STIX]{x1D6FD}(v-k,m)\quad \text{mod}\;p^{r+1}\mathbb{Z}_{p}\nonumber\\ \displaystyle & \equiv & \displaystyle p^{r}\mathop{\sum }_{k=0}^{v}P_{k}(v-k)\unicode[STIX]{x1D6FD}(v-k,m)\quad \text{mod}\;p^{r+1}\mathbb{Z}_{p}.\nonumber\end{eqnarray}$$
Thus, for all nonnegative integers
![]() $v$
satisfying
$v$
satisfying
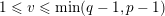 $1\leqslant v\leqslant \min (q-1,p-1)$
, we have
$1\leqslant v\leqslant \min (q-1,p-1)$
, we have
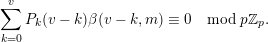 $$\begin{eqnarray}\mathop{\sum }_{k=0}^{v}P_{k}(v-k)\unicode[STIX]{x1D6FD}(v-k,m)\equiv 0\quad \text{mod}\;p\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{k=0}^{v}P_{k}(v-k)\unicode[STIX]{x1D6FD}(v-k,m)\equiv 0\quad \text{mod}\;p\mathbb{Z}_{p}.\end{eqnarray}$$
Both sequences
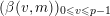 $(\unicode[STIX]{x1D6FD}(v,m))_{0\leqslant v\leqslant p-1}$
and
$(\unicode[STIX]{x1D6FD}(v,m))_{0\leqslant v\leqslant p-1}$
and
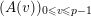 $(A(v))_{0\leqslant v\leqslant p-1}$
satisfy (3.2) and (3.5). Furthermore, for all
$(A(v))_{0\leqslant v\leqslant p-1}$
satisfy (3.2) and (3.5). Furthermore, for all
![]() $v$
in
$v$
in
 $\{1,\ldots ,p-1\}$
,
$\{1,\ldots ,p-1\}$
,
![]() $P_{0}(v)$
and
$P_{0}(v)$
and
![]() $A(0)$
are invertible in
$A(0)$
are invertible in
![]() $\mathbb{Z}_{p}$
. Hence, there exists
$\mathbb{Z}_{p}$
. Hence, there exists
![]() $\unicode[STIX]{x1D6FE}(m)$
in
$\unicode[STIX]{x1D6FE}(m)$
in
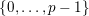 $\{0,\ldots ,p-1\}$
such that, for all
$\{0,\ldots ,p-1\}$
such that, for all
![]() $v$
in
$v$
in
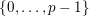 $\{0,\ldots ,p-1\}$
, we have
$\{0,\ldots ,p-1\}$
, we have
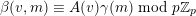 $\unicode[STIX]{x1D6FD}(v,m)\equiv A(v)\unicode[STIX]{x1D6FE}(m)\;\text{mod}\;p\mathbb{Z}_{p}$
, so that
$\unicode[STIX]{x1D6FD}(v,m)\equiv A(v)\unicode[STIX]{x1D6FE}(m)\;\text{mod}\;p\mathbb{Z}_{p}$
, so that
 $$\begin{eqnarray}A(v+mp)\equiv A(v)\unicode[STIX]{x1D6FE}(m)p^{r}\quad \text{mod}\;p^{r+1}\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}A(v+mp)\equiv A(v)\unicode[STIX]{x1D6FE}(m)p^{r}\quad \text{mod}\;p^{r+1}\mathbb{Z}_{p}.\end{eqnarray}$$
Since
![]() $n_{0}$
is in
$n_{0}$
is in
![]() ${\mathcal{Z}}_{p}(A)$
, we have
${\mathcal{Z}}_{p}(A)$
, we have
 $A(n_{0})\in p\mathbb{Z}_{p}$
, so that
$A(n_{0})\in p\mathbb{Z}_{p}$
, so that
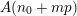 $A(n_{0}+mp)$
belongs to
$A(n_{0}+mp)$
belongs to
![]() $p^{r+1}\mathbb{Z}_{p}$
and Lemma 1 is proved.◻
$p^{r+1}\mathbb{Z}_{p}$
and Lemma 1 is proved.◻
3.2 Proof of Theorem 2
Let
![]() $p$
be a fixed prime number. For every positive integer
$p$
be a fixed prime number. For every positive integer
![]() $n$
, we set
$n$
, we set
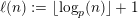 $\ell (n):=\lfloor \log _{p}(n)\rfloor +1$
, the length of the expansion of
$\ell (n):=\lfloor \log _{p}(n)\rfloor +1$
, the length of the expansion of
![]() $n$
to the base
$n$
to the base
![]() $p$
, and
$p$
, and
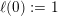 $\ell (0):=1$
. For all nonnegative integers
$\ell (0):=1$
. For all nonnegative integers
 $n_{1},\ldots ,n_{r}$
, we set
$n_{1},\ldots ,n_{r}$
, we set
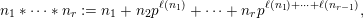 $$\begin{eqnarray}n_{1}\ast \cdots \ast n_{r}:=n_{1}+n_{2}p^{\ell (n_{1})}+\cdots +n_{r}p^{\ell (n_{1})+\cdots +\ell (n_{r-1})},\end{eqnarray}$$
$$\begin{eqnarray}n_{1}\ast \cdots \ast n_{r}:=n_{1}+n_{2}p^{\ell (n_{1})}+\cdots +n_{r}p^{\ell (n_{1})+\cdots +\ell (n_{r-1})},\end{eqnarray}$$
so that the expansion of
 $n_{1}\ast \cdots \ast n_{r}$
to the base
$n_{1}\ast \cdots \ast n_{r}$
to the base
![]() $p$
is the concatenation of the respective expansions of
$p$
is the concatenation of the respective expansions of
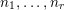 $n_{1},\ldots ,n_{r}$
. Then, by a result of Mellit and Vlasenko [Reference Mellit and VlasenkoMV16, Lemma 1], there exists a
$n_{1},\ldots ,n_{r}$
. Then, by a result of Mellit and Vlasenko [Reference Mellit and VlasenkoMV16, Lemma 1], there exists a
![]() $\mathbb{Z}_{p}$
-valued sequence
$\mathbb{Z}_{p}$
-valued sequence
![]() $(c_{n})_{n\geqslant 0}$
such that, for all positive integers
$(c_{n})_{n\geqslant 0}$
such that, for all positive integers
![]() $n$
, we have
$n$
, we have
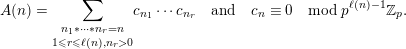 $$\begin{eqnarray}A(n)=\underset{1\leqslant r\leqslant \ell (n),n_{r}>0}{\mathop{\sum }_{n_{1}\ast \cdots \ast n_{r}=n}}c_{n_{1}}\cdots c_{n_{r}}\quad \text{and}\quad c_{n}\equiv 0\quad \text{mod}\;p^{\ell (n)-1}\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}A(n)=\underset{1\leqslant r\leqslant \ell (n),n_{r}>0}{\mathop{\sum }_{n_{1}\ast \cdots \ast n_{r}=n}}c_{n_{1}}\cdots c_{n_{r}}\quad \text{and}\quad c_{n}\equiv 0\quad \text{mod}\;p^{\ell (n)-1}\mathbb{Z}_{p}.\end{eqnarray}$$
For every nonnegative integer
![]() $r$
, we write
$r$
, we write
![]() ${\mathcal{U}}(r)$
for the assertion: ‘For all
${\mathcal{U}}(r)$
for the assertion: ‘For all
 $n,i\in \mathbb{N}$
,
$n,i\in \mathbb{N}$
,
![]() $i\leqslant r$
, if
$i\leqslant r$
, if
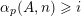 $\unicode[STIX]{x1D6FC}_{p}(A,n)\geqslant i$
, then
$\unicode[STIX]{x1D6FC}_{p}(A,n)\geqslant i$
, then
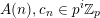 $A(n),c_{n}\in p^{i}\mathbb{Z}_{p}$
.’. To prove Theorem 2, it suffices to show that, for all nonnegative integers
$A(n),c_{n}\in p^{i}\mathbb{Z}_{p}$
.’. To prove Theorem 2, it suffices to show that, for all nonnegative integers
![]() $r$
, Assertion
$r$
, Assertion
![]() ${\mathcal{U}}(r)$
holds.
${\mathcal{U}}(r)$
holds.
First, we prove
![]() ${\mathcal{U}}(1)$
. By [Reference Mellit and VlasenkoMV16, Theorem 1],
${\mathcal{U}}(1)$
. By [Reference Mellit and VlasenkoMV16, Theorem 1],
![]() $A$
satisfies the
$A$
satisfies the
![]() $p$
-Lucas property. In addition, if
$p$
-Lucas property. In addition, if
![]() $v$
is in
$v$
is in
![]() ${\mathcal{Z}}_{p}(A)$
, then
${\mathcal{Z}}_{p}(A)$
, then
![]() $v$
is nonzero because
$v$
is nonzero because
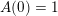 $A(0)=1$
and, by (3.6), we have
$A(0)=1$
and, by (3.6), we have
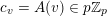 $c_{v}=A(v)\in p\mathbb{Z}_{p}$
. Now, if a nonnegative integer
$c_{v}=A(v)\in p\mathbb{Z}_{p}$
. Now, if a nonnegative integer
![]() $n$
satisfies
$n$
satisfies
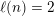 $\ell (n)=2$
and
$\ell (n)=2$
and
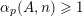 $\unicode[STIX]{x1D6FC}_{p}(A,n)\geqslant 1$
, then (3.6) yields
$\unicode[STIX]{x1D6FC}_{p}(A,n)\geqslant 1$
, then (3.6) yields
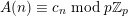 $A(n)\equiv c_{n}\;\text{mod}\;p\mathbb{Z}_{p}$
, so that
$A(n)\equiv c_{n}\;\text{mod}\;p\mathbb{Z}_{p}$
, so that
![]() $c_{n}$
is in
$c_{n}$
is in
![]() $p\mathbb{Z}_{p}$
. Hence, by induction on
$p\mathbb{Z}_{p}$
. Hence, by induction on
![]() $\ell (n)$
, we obtain that, for all nonnegative integers
$\ell (n)$
, we obtain that, for all nonnegative integers
![]() $n$
satisfying
$n$
satisfying
 $\unicode[STIX]{x1D6FC}_{p}(A,n)\geqslant 1$
,
$\unicode[STIX]{x1D6FC}_{p}(A,n)\geqslant 1$
,
![]() $c_{n}$
belongs to
$c_{n}$
belongs to
![]() $p\mathbb{Z}_{p}$
, so that
$p\mathbb{Z}_{p}$
, so that
![]() ${\mathcal{U}}(1)$
holds.
${\mathcal{U}}(1)$
holds.
Let
![]() $r$
be a positive integer such that
$r$
be a positive integer such that
![]() ${\mathcal{U}}(r)$
holds. We shall prove that
${\mathcal{U}}(r)$
holds. We shall prove that
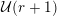 ${\mathcal{U}}(r+1)$
is true. For all positive integers
${\mathcal{U}}(r+1)$
is true. For all positive integers
![]() $M$
, we write
$M$
, we write
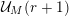 ${\mathcal{U}}_{M}(r+1)$
for the assertion:
${\mathcal{U}}_{M}(r+1)$
for the assertion:
 $$\begin{eqnarray}\text{`For all }n,i\in \mathbb{N},n\leqslant M,i\leqslant r+1,\text{ if }\unicode[STIX]{x1D6FC}_{p}(A,n)\geqslant i,\text{ then }A(n),c_{n}\in p^{i}\mathbb{Z}_{p}.\text{'}\end{eqnarray}$$
$$\begin{eqnarray}\text{`For all }n,i\in \mathbb{N},n\leqslant M,i\leqslant r+1,\text{ if }\unicode[STIX]{x1D6FC}_{p}(A,n)\geqslant i,\text{ then }A(n),c_{n}\in p^{i}\mathbb{Z}_{p}.\text{'}\end{eqnarray}$$
Hence,
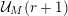 ${\mathcal{U}}_{M}(r+1)$
is true if
${\mathcal{U}}_{M}(r+1)$
is true if
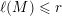 $\ell (M)\leqslant r$
. Let
$\ell (M)\leqslant r$
. Let
![]() $M$
be a positive integer such that
$M$
be a positive integer such that
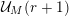 ${\mathcal{U}}_{M}(r+1)$
holds. We shall prove
${\mathcal{U}}_{M}(r+1)$
holds. We shall prove
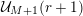 ${\mathcal{U}}_{M+1}(r+1)$
. By Assertions
${\mathcal{U}}_{M+1}(r+1)$
. By Assertions
![]() ${\mathcal{U}}(r)$
and
${\mathcal{U}}(r)$
and
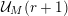 ${\mathcal{U}}_{M}(r+1)$
, it suffices to prove that if
${\mathcal{U}}_{M}(r+1)$
, it suffices to prove that if
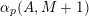 $\unicode[STIX]{x1D6FC}_{p}(A,M+1)$
is greater than
$\unicode[STIX]{x1D6FC}_{p}(A,M+1)$
is greater than
![]() $r$
, then
$r$
, then
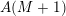 $A(M+1)$
and
$A(M+1)$
and
![]() $c_{M+1}$
belong to
$c_{M+1}$
belong to
![]() $p^{r+1}\mathbb{Z}_{p}$
. In the rest of the proof, we assume that
$p^{r+1}\mathbb{Z}_{p}$
. In the rest of the proof, we assume that
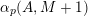 $\unicode[STIX]{x1D6FC}_{p}(A,M+1)$
is greater than
$\unicode[STIX]{x1D6FC}_{p}(A,M+1)$
is greater than
![]() $r$
.
$r$
.
If
![]() $u$
and
$u$
and
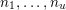 $n_{1},\ldots ,n_{u}$
are nonnegative integers satisfying
$n_{1},\ldots ,n_{u}$
are nonnegative integers satisfying
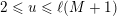 $2\leqslant u\leqslant \ell (M+1)$
and
$2\leqslant u\leqslant \ell (M+1)$
and
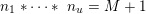 $n_{1}\ast \cdots \ast ~n_{u}=M+1$
with
$n_{1}\ast \cdots \ast ~n_{u}=M+1$
with
![]() $n_{u}>0$
, then, for all
$n_{u}>0$
, then, for all
![]() $i$
in
$i$
in
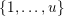 $\{1,\ldots ,u\}$
, we have
$\{1,\ldots ,u\}$
, we have
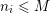 $n_{i}\leqslant M$
and
$n_{i}\leqslant M$
and
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{p}(A,n_{1})+\cdots +\unicode[STIX]{x1D6FC}_{p}(A,n_{u})=\unicode[STIX]{x1D6FC}_{p}(A,M+1)\geqslant r+1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{p}(A,n_{1})+\cdots +\unicode[STIX]{x1D6FC}_{p}(A,n_{u})=\unicode[STIX]{x1D6FC}_{p}(A,M+1)\geqslant r+1.\end{eqnarray}$$
Then there exist a positive integer
![]() $k$
and integers
$k$
and integers
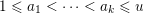 $1\leqslant a_{1}<\cdots <a_{k}\leqslant u$
and
$1\leqslant a_{1}<\cdots <a_{k}\leqslant u$
and
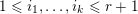 $1\leqslant i_{1},\ldots ,i_{k}\leqslant r+1$
such that
$1\leqslant i_{1},\ldots ,i_{k}\leqslant r+1$
such that
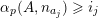 $\unicode[STIX]{x1D6FC}_{p}(A,n_{a_{j}})\geqslant i_{j}$
and
$\unicode[STIX]{x1D6FC}_{p}(A,n_{a_{j}})\geqslant i_{j}$
and
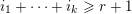 $i_{1}+\cdots +i_{k}\geqslant r+1$
. Thereby, Assertion
$i_{1}+\cdots +i_{k}\geqslant r+1$
. Thereby, Assertion
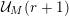 ${\mathcal{U}}_{M}(r+1)$
yields
${\mathcal{U}}_{M}(r+1)$
yields
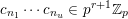 $c_{n_{1}}\cdots c_{n_{u}}\in p^{r+1}\mathbb{Z}_{p}$
, so that
$c_{n_{1}}\cdots c_{n_{u}}\in p^{r+1}\mathbb{Z}_{p}$
, so that
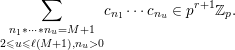 $$\begin{eqnarray}\underset{2\leqslant u\leqslant \ell (M+1),n_{u}>0}{\mathop{\sum }_{n_{1}\ast \cdots \ast n_{u}=M+1}}c_{n_{1}}\cdots c_{n_{u}}\in p^{r+1}\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}\underset{2\leqslant u\leqslant \ell (M+1),n_{u}>0}{\mathop{\sum }_{n_{1}\ast \cdots \ast n_{u}=M+1}}c_{n_{1}}\cdots c_{n_{u}}\in p^{r+1}\mathbb{Z}_{p}.\end{eqnarray}$$
By (3.6), we obtain
 $$\begin{eqnarray}A(M+1)\equiv c_{M+1}\quad \text{mod}\;p^{r+1}\mathbb{Z}_{p}\quad \text{and}\quad c_{M+1}\equiv 0\quad \text{mod}\;p^{\ell (M+1)-1}\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}A(M+1)\equiv c_{M+1}\quad \text{mod}\;p^{r+1}\mathbb{Z}_{p}\quad \text{and}\quad c_{M+1}\equiv 0\quad \text{mod}\;p^{\ell (M+1)-1}\mathbb{Z}_{p}.\end{eqnarray}$$
Hence, it suffices to consider the case
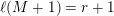 $\ell (M+1)=r+1$
. In particular, we have
$\ell (M+1)=r+1$
. In particular, we have
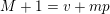 $M+1=v+mp$
, where
$M+1=v+mp$
, where
![]() $v$
is in
$v$
is in
![]() ${\mathcal{Z}}_{p}(A)$
and
${\mathcal{Z}}_{p}(A)$
and
![]() $m$
is a nonnegative integer satisfying
$m$
is a nonnegative integer satisfying
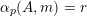 $\unicode[STIX]{x1D6FC}_{p}(A,m)=r$
. Since
$\unicode[STIX]{x1D6FC}_{p}(A,m)=r$
. Since
![]() ${\mathcal{U}}(r)$
holds, Lemma 1 yields
${\mathcal{U}}(r)$
holds, Lemma 1 yields
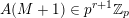 $A(M+1)\in p^{r+1}\mathbb{Z}_{p}$
. Thus, we also have
$A(M+1)\in p^{r+1}\mathbb{Z}_{p}$
. Thus, we also have
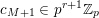 $c_{M+1}\in p^{r+1}\mathbb{Z}_{p}$
and Assertion
$c_{M+1}\in p^{r+1}\mathbb{Z}_{p}$
and Assertion
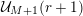 ${\mathcal{U}}_{M+1}(r+1)$
holds. This finishes the proof of
${\mathcal{U}}_{M+1}(r+1)$
holds. This finishes the proof of
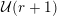 ${\mathcal{U}}(r+1)$
and so that of Theorem 2.◻
${\mathcal{U}}(r+1)$
and so that of Theorem 2.◻
3.3 Proof of Proposition 1
Let
![]() $p$
be a prime and
$p$
be a prime and
![]() $A$
a
$A$
a
![]() $\mathbb{Z}_{p}$
-valued sequence satisfying the hypotheses of Proposition 1. For every nonnegative integer
$\mathbb{Z}_{p}$
-valued sequence satisfying the hypotheses of Proposition 1. For every nonnegative integer
![]() $n$
, we write
$n$
, we write
![]() $\unicode[STIX]{x1D6FC}(n)$
, respectively
$\unicode[STIX]{x1D6FC}(n)$
, respectively
![]() ${\mathcal{Z}}$
, as a shorthand for
${\mathcal{Z}}$
, as a shorthand for
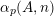 $\unicode[STIX]{x1D6FC}_{p}(A,n)$
, respectively for
$\unicode[STIX]{x1D6FC}_{p}(A,n)$
, respectively for
![]() ${\mathcal{Z}}_{p}(A)$
. For every nonnegative integer
${\mathcal{Z}}_{p}(A)$
. For every nonnegative integer
![]() $r$
, we define Assertions
$r$
, we define Assertions
 $$\begin{eqnarray}{\mathcal{U}}(r):\text{`For all }n,i\in \mathbb{N},i\leqslant r,\text{if }\unicode[STIX]{x1D6FC}(n)\geqslant i,\text{then }A(n)\in p^{i}\mathbb{Z}_{p}.\text{'}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{U}}(r):\text{`For all }n,i\in \mathbb{N},i\leqslant r,\text{if }\unicode[STIX]{x1D6FC}(n)\geqslant i,\text{then }A(n)\in p^{i}\mathbb{Z}_{p}.\text{'}\end{eqnarray}$$
and
 $$\begin{eqnarray}{\mathcal{V}}(r):\text{`For all }n,i\in \mathbb{N},i\leqslant r,\text{and all }B\in \mathfrak{B},\text{if }\unicode[STIX]{x1D6FC}(n)\geqslant i,\text{then }B(n)\in p^{i-1}\mathbb{Z}_{p}.\text{'}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{V}}(r):\text{`For all }n,i\in \mathbb{N},i\leqslant r,\text{and all }B\in \mathfrak{B},\text{if }\unicode[STIX]{x1D6FC}(n)\geqslant i,\text{then }B(n)\in p^{i-1}\mathbb{Z}_{p}.\text{'}\end{eqnarray}$$
To prove Proposition 1, we have to show that, for all nonnegative integers
![]() $r$
, Assertions
$r$
, Assertions
![]() ${\mathcal{U}}(r)$
and
${\mathcal{U}}(r)$
and
![]() ${\mathcal{V}}(r)$
are true. We shall prove those assertions by induction on
${\mathcal{V}}(r)$
are true. We shall prove those assertions by induction on
![]() $r$
.
$r$
.
Observe that Assertions
![]() ${\mathcal{U}}(0)$
,
${\mathcal{U}}(0)$
,
![]() ${\mathcal{V}}(0)$
and
${\mathcal{V}}(0)$
and
![]() ${\mathcal{V}}(1)$
are trivial. Furthermore, since
${\mathcal{V}}(1)$
are trivial. Furthermore, since
![]() $A$
satisfies the
$A$
satisfies the
![]() $p$
-Lucas property, Assertion
$p$
-Lucas property, Assertion
![]() ${\mathcal{U}}(1)$
holds. Let
${\mathcal{U}}(1)$
holds. Let
![]() $r_{0}$
be a fixed positive integer,
$r_{0}$
be a fixed positive integer,
![]() $r_{0}\geqslant 2$
, such that Assertions
$r_{0}\geqslant 2$
, such that Assertions
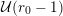 ${\mathcal{U}}(r_{0}-1)$
and
${\mathcal{U}}(r_{0}-1)$
and
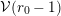 ${\mathcal{V}}(r_{0}-1)$
are true. First, we prove Assertion
${\mathcal{V}}(r_{0}-1)$
are true. First, we prove Assertion
![]() ${\mathcal{V}}(r_{0})$
.
${\mathcal{V}}(r_{0})$
.
Let
![]() $B$
in
$B$
in
![]() $\mathfrak{B}$
and
$\mathfrak{B}$
and
![]() $m$
in
$m$
in
![]() $\mathbb{N}$
be such that
$\mathbb{N}$
be such that
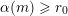 $\unicode[STIX]{x1D6FC}(m)\geqslant r_{0}$
. We write
$\unicode[STIX]{x1D6FC}(m)\geqslant r_{0}$
. We write
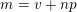 $m=v+np$
with
$m=v+np$
with
![]() $v$
in
$v$
in
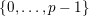 $\{0,\ldots ,p-1\}$
. Since
$\{0,\ldots ,p-1\}$
. Since
![]() $r_{0}\geqslant 2$
and
$r_{0}\geqslant 2$
and
![]() $0$
does not belong to
$0$
does not belong to
![]() ${\mathcal{Z}}$
, we have
${\mathcal{Z}}$
, we have
![]() $n\geqslant 1$
and, by Assertion (a) in Proposition 1, there exist
$n\geqslant 1$
and, by Assertion (a) in Proposition 1, there exist
![]() $A^{\prime }$
in
$A^{\prime }$
in
![]() $\mathfrak{A}$
and a sequence
$\mathfrak{A}$
and a sequence
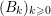 $(B_{k})_{k\geqslant 0}$
, with
$(B_{k})_{k\geqslant 0}$
, with
![]() $B_{k}$
in
$B_{k}$
in
![]() $\mathfrak{B}$
, such that
$\mathfrak{B}$
, such that
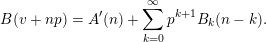 $$\begin{eqnarray}B(v+np)=A^{\prime }(n)+\mathop{\sum }_{k=0}^{\infty }p^{k+1}B_{k}(n-k).\end{eqnarray}$$
$$\begin{eqnarray}B(v+np)=A^{\prime }(n)+\mathop{\sum }_{k=0}^{\infty }p^{k+1}B_{k}(n-k).\end{eqnarray}$$
In addition, we have
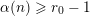 $\unicode[STIX]{x1D6FC}(n)\geqslant r_{0}-1$
and, since
$\unicode[STIX]{x1D6FC}(n)\geqslant r_{0}-1$
and, since
![]() $0$
is not in
$0$
is not in
![]() ${\mathcal{Z}}$
, we have
${\mathcal{Z}}$
, we have
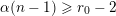 $\unicode[STIX]{x1D6FC}(n-1)\geqslant r_{0}-2$
. By induction, for all nonnegative integers
$\unicode[STIX]{x1D6FC}(n-1)\geqslant r_{0}-2$
. By induction, for all nonnegative integers
![]() $k$
satisfying
$k$
satisfying
![]() $k\leqslant n$
, we have
$k\leqslant n$
, we have
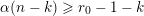 $\unicode[STIX]{x1D6FC}(n-k)\geqslant r_{0}-1-k$
. Thus, by (3.7) in combination with
$\unicode[STIX]{x1D6FC}(n-k)\geqslant r_{0}-1-k$
. Thus, by (3.7) in combination with
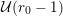 ${\mathcal{U}}(r_{0}-1)$
and
${\mathcal{U}}(r_{0}-1)$
and
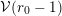 ${\mathcal{V}}(r_{0}-1)$
, we obtain
${\mathcal{V}}(r_{0}-1)$
, we obtain
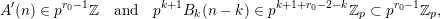 $$\begin{eqnarray}A^{\prime }(n)\in p^{r_{0}-1}\mathbb{Z}\quad \text{and}\quad p^{k+1}B_{k}(n-k)\in p^{k+1+r_{0}-2-k}\mathbb{Z}_{p}\subset p^{r_{0}-1}\mathbb{Z}_{p},\end{eqnarray}$$
$$\begin{eqnarray}A^{\prime }(n)\in p^{r_{0}-1}\mathbb{Z}\quad \text{and}\quad p^{k+1}B_{k}(n-k)\in p^{k+1+r_{0}-2-k}\mathbb{Z}_{p}\subset p^{r_{0}-1}\mathbb{Z}_{p},\end{eqnarray}$$
so that
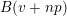 $B(v+np)$
belongs to
$B(v+np)$
belongs to
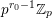 $p^{r_{0}-1}\mathbb{Z}_{p}$
and
$p^{r_{0}-1}\mathbb{Z}_{p}$
and
![]() ${\mathcal{V}}(r_{0})$
is true.
${\mathcal{V}}(r_{0})$
is true.
Now we prove Assertion
![]() ${\mathcal{U}}(r_{0})$
. We write
${\mathcal{U}}(r_{0})$
. We write
![]() ${\mathcal{U}}_{N}(r_{0})$
for the assertion:
${\mathcal{U}}_{N}(r_{0})$
for the assertion:
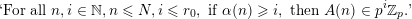 $$\begin{eqnarray}\text{`For all }n,i\in \mathbb{N},n\leqslant N,i\leqslant r_{0},\text{ if }\unicode[STIX]{x1D6FC}(n)\geqslant i,\text{ then }A(n)\in p^{i}\mathbb{Z}_{p}.\text{'}\end{eqnarray}$$
$$\begin{eqnarray}\text{`For all }n,i\in \mathbb{N},n\leqslant N,i\leqslant r_{0},\text{ if }\unicode[STIX]{x1D6FC}(n)\geqslant i,\text{ then }A(n)\in p^{i}\mathbb{Z}_{p}.\text{'}\end{eqnarray}$$
We shall prove
![]() ${\mathcal{U}}_{N}(r_{0})$
by induction on
${\mathcal{U}}_{N}(r_{0})$
by induction on
![]() $N$
. Assertion
$N$
. Assertion
![]() ${\mathcal{U}}_{1}(r_{0})$
holds. Let
${\mathcal{U}}_{1}(r_{0})$
holds. Let
![]() $N$
be a positive integer such that
$N$
be a positive integer such that
![]() ${\mathcal{U}}_{N}(r_{0})$
is true. Let
${\mathcal{U}}_{N}(r_{0})$
is true. Let
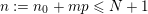 $n:=n_{0}+mp\leqslant N+1$
with
$n:=n_{0}+mp\leqslant N+1$
with
![]() $n_{0}$
in
$n_{0}$
in
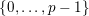 $\{0,\ldots ,p-1\}$
and
$\{0,\ldots ,p-1\}$
and
![]() $m$
in
$m$
in
![]() $\mathbb{N}$
. We can assume that
$\mathbb{N}$
. We can assume that
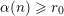 $\unicode[STIX]{x1D6FC}(n)\geqslant r_{0}$
.
$\unicode[STIX]{x1D6FC}(n)\geqslant r_{0}$
.
If
![]() $n_{0}$
is in
$n_{0}$
is in
![]() ${\mathcal{Z}}$
, then we have
${\mathcal{Z}}$
, then we have
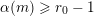 $\unicode[STIX]{x1D6FC}(m)\geqslant r_{0}-1$
and, by Lemma 1, we obtain that
$\unicode[STIX]{x1D6FC}(m)\geqslant r_{0}-1$
and, by Lemma 1, we obtain that
![]() $A(n)$
belongs to
$A(n)$
belongs to
![]() $p^{r_{0}}\mathbb{Z}_{p}$
, as expected. If
$p^{r_{0}}\mathbb{Z}_{p}$
, as expected. If
![]() $n_{0}$
is not in
$n_{0}$
is not in
![]() ${\mathcal{Z}}$
, then we have
${\mathcal{Z}}$
, then we have
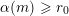 $\unicode[STIX]{x1D6FC}(m)\geqslant r_{0}$
. By Assertion (a) in Proposition 1, there exist
$\unicode[STIX]{x1D6FC}(m)\geqslant r_{0}$
. By Assertion (a) in Proposition 1, there exist
![]() $A^{\prime }$
in
$A^{\prime }$
in
![]() $\mathfrak{A}$
and a sequence
$\mathfrak{A}$
and a sequence
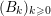 $(B_{k})_{k\geqslant 0}$
with
$(B_{k})_{k\geqslant 0}$
with
![]() $B_{k}$
in
$B_{k}$
in
![]() $\mathfrak{B}$
such that
$\mathfrak{B}$
such that
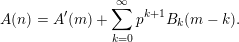 $$\begin{eqnarray}A(n)=A^{\prime }(m)+\mathop{\sum }_{k=0}^{\infty }p^{k+1}B_{k}(m-k).\end{eqnarray}$$
$$\begin{eqnarray}A(n)=A^{\prime }(m)+\mathop{\sum }_{k=0}^{\infty }p^{k+1}B_{k}(m-k).\end{eqnarray}$$
We have
![]() $m\leqslant N$
,
$m\leqslant N$
,
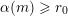 $\unicode[STIX]{x1D6FC}(m)\geqslant r_{0}$
and
$\unicode[STIX]{x1D6FC}(m)\geqslant r_{0}$
and
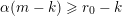 $\unicode[STIX]{x1D6FC}(m-k)\geqslant r_{0}-k$
; hence, by Assertions
$\unicode[STIX]{x1D6FC}(m-k)\geqslant r_{0}-k$
; hence, by Assertions
![]() ${\mathcal{U}}_{N}(r_{0})$
and
${\mathcal{U}}_{N}(r_{0})$
and
![]() ${\mathcal{V}}(r_{0})$
, we obtain that
${\mathcal{V}}(r_{0})$
, we obtain that
![]() $A(n)$
belongs to
$A(n)$
belongs to
![]() $p^{r_{0}}\mathbb{Z}_{p}$
. This finishes the induction on
$p^{r_{0}}\mathbb{Z}_{p}$
. This finishes the induction on
![]() $N$
and proves
$N$
and proves
![]() ${\mathcal{U}}(r_{0})$
. Therefore, by induction on
${\mathcal{U}}(r_{0})$
. Therefore, by induction on
![]() $r_{0}$
, Proposition 1 is proved.◻
$r_{0}$
, Proposition 1 is proved.◻
4 Proof of Theorem 1
To prove Theorem 1, we shall apply Proposition 1 to
![]() $\mathfrak{S}_{e,f}$
. As a first step, we prove that this sequence satisfies the
$\mathfrak{S}_{e,f}$
. As a first step, we prove that this sequence satisfies the
![]() $p$
-Lucas property.
$p$
-Lucas property.
Proof of Proposition 3.
For all
![]() $\mathbf{x}$
in
$\mathbf{x}$
in
![]() $[0,1]^{d}$
, we have
$[0,1]^{d}$
, we have
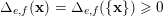 $\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})=\unicode[STIX]{x1D6E5}_{e,f}(\{\mathbf{x}\})\geqslant 0$
, so that, by Landau’s criterion,
$\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})=\unicode[STIX]{x1D6E5}_{e,f}(\{\mathbf{x}\})\geqslant 0$
, so that, by Landau’s criterion,
![]() ${\mathcal{Q}}_{e,f}$
is integer-valued. Let
${\mathcal{Q}}_{e,f}$
is integer-valued. Let
![]() $p$
be a fixed prime,
$p$
be a fixed prime,
![]() $v$
in
$v$
in
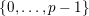 $\{0,\ldots ,p-1\}$
and
$\{0,\ldots ,p-1\}$
and
![]() $n$
a nonnegative integer. We have
$n$
a nonnegative integer. We have
 $$\begin{eqnarray}\mathfrak{S}_{e,f}(v+np)=\underset{k_{i}\in \mathbb{N}}{\mathop{\sum }_{k_{1}+\cdots +k_{d}=v+np}}{\mathcal{Q}}_{e,f}(k_{1},\ldots ,k_{d}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}_{e,f}(v+np)=\underset{k_{i}\in \mathbb{N}}{\mathop{\sum }_{k_{1}+\cdots +k_{d}=v+np}}{\mathcal{Q}}_{e,f}(k_{1},\ldots ,k_{d}).\end{eqnarray}$$
Write
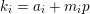 $k_{i}=a_{i}+m_{i}p$
with
$k_{i}=a_{i}+m_{i}p$
with
![]() $a_{i}$
in
$a_{i}$
in
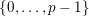 $\{0,\ldots ,p-1\}$
and
$\{0,\ldots ,p-1\}$
and
![]() $m_{i}$
in
$m_{i}$
in
![]() $\mathbb{N}$
. If
$\mathbb{N}$
. If
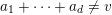 $a_{1}+\cdots +a_{d}\neq v$
, then we have
$a_{1}+\cdots +a_{d}\neq v$
, then we have
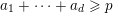 $a_{1}+\cdots +a_{d}\geqslant p$
and there exists
$a_{1}+\cdots +a_{d}\geqslant p$
and there exists
![]() $i$
in
$i$
in
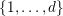 $\{1,\ldots ,d\}$
such that
$\{1,\ldots ,d\}$
such that
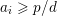 $a_{i}\geqslant p/d$
. Write
$a_{i}\geqslant p/d$
. Write
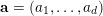 $\mathbf{a}=(a_{1},\ldots ,a_{d})$
, so that
$\mathbf{a}=(a_{1},\ldots ,a_{d})$
, so that
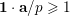 $\mathbf{1}\cdot \mathbf{a}/p\geqslant 1$
and
$\mathbf{1}\cdot \mathbf{a}/p\geqslant 1$
and
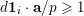 $d\mathbf{1}_{i}\cdot \mathbf{a}/p\geqslant 1$
. Since
$d\mathbf{1}_{i}\cdot \mathbf{a}/p\geqslant 1$
. Since
 $e=(\mathbf{e}_{1},\ldots ,\mathbf{e}_{u})$
is
$e=(\mathbf{e}_{1},\ldots ,\mathbf{e}_{u})$
is
![]() $1$
-admissible, there exists a
$1$
-admissible, there exists a
![]() $j$
in
$j$
in
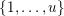 $\{1,\ldots ,u\}$
such that either
$\{1,\ldots ,u\}$
such that either
![]() $\mathbf{e}_{j}\geqslant \mathbf{1}$
or
$\mathbf{e}_{j}\geqslant \mathbf{1}$
or
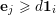 $\mathbf{e}_{j}\geqslant d\mathbf{1}_{i}$
. Hence,
$\mathbf{e}_{j}\geqslant d\mathbf{1}_{i}$
. Hence,
 $\mathbf{e}_{j}\cdot \mathbf{a}/p\geqslant 1$
and
$\mathbf{e}_{j}\cdot \mathbf{a}/p\geqslant 1$
and
![]() $\mathbf{a}/p$
belongs to
$\mathbf{a}/p$
belongs to
![]() ${\mathcal{D}}_{e,f}$
, so that
${\mathcal{D}}_{e,f}$
, so that
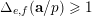 $\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)\geqslant 1$
and
$\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)\geqslant 1$
and
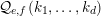 ${\mathcal{Q}}_{e,f}(k_{1},\ldots ,k_{d})$
is in
${\mathcal{Q}}_{e,f}(k_{1},\ldots ,k_{d})$
is in
![]() $p\mathbb{Z}_{p}$
. In addition, by Theorem 3,
$p\mathbb{Z}_{p}$
. In addition, by Theorem 3,
![]() ${\mathcal{Q}}_{e,f}$
satisfies the
${\mathcal{Q}}_{e,f}$
satisfies the
![]() $p$
-Lucas property for all primes
$p$
-Lucas property for all primes
![]() $p$
. Hence, we obtain
$p$
. Hence, we obtain
 $$\begin{eqnarray}\displaystyle \mathfrak{S}_{e,f}(v+np) & \equiv & \displaystyle \underset{0\leqslant a_{i}\leqslant p-1}{\mathop{\sum }_{a_{1}+\cdots +a_{d}=v}}\;\underset{m_{i}\in \mathbb{N}}{\mathop{\sum }_{m_{1}+\cdots +m_{d}=n}}{\mathcal{Q}}_{e,f}(a_{1}+m_{1}p,\ldots ,a_{d}+m_{d}p)\quad \text{mod}\;p\mathbb{Z}_{p}\nonumber\\ \displaystyle & \equiv & \displaystyle \underset{0\leqslant a_{i}\leqslant p-1}{\mathop{\sum }_{a_{1}+\cdots +a_{d}=v}}\;\underset{m_{i}\in \mathbb{N}}{\mathop{\sum }_{m_{1}+\cdots +m_{d}=n}}{\mathcal{Q}}_{e,f}(a_{1},\ldots ,a_{d}){\mathcal{Q}}_{e,f}(m_{1},\ldots ,m_{d})\quad \text{mod}\;p\mathbb{Z}_{p}\nonumber\\ \displaystyle & \equiv & \displaystyle \mathfrak{S}_{e,f}(v)\mathfrak{S}_{e,f}(n)\quad \text{mod}\;p\mathbb{Z}_{p}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{S}_{e,f}(v+np) & \equiv & \displaystyle \underset{0\leqslant a_{i}\leqslant p-1}{\mathop{\sum }_{a_{1}+\cdots +a_{d}=v}}\;\underset{m_{i}\in \mathbb{N}}{\mathop{\sum }_{m_{1}+\cdots +m_{d}=n}}{\mathcal{Q}}_{e,f}(a_{1}+m_{1}p,\ldots ,a_{d}+m_{d}p)\quad \text{mod}\;p\mathbb{Z}_{p}\nonumber\\ \displaystyle & \equiv & \displaystyle \underset{0\leqslant a_{i}\leqslant p-1}{\mathop{\sum }_{a_{1}+\cdots +a_{d}=v}}\;\underset{m_{i}\in \mathbb{N}}{\mathop{\sum }_{m_{1}+\cdots +m_{d}=n}}{\mathcal{Q}}_{e,f}(a_{1},\ldots ,a_{d}){\mathcal{Q}}_{e,f}(m_{1},\ldots ,m_{d})\quad \text{mod}\;p\mathbb{Z}_{p}\nonumber\\ \displaystyle & \equiv & \displaystyle \mathfrak{S}_{e,f}(v)\mathfrak{S}_{e,f}(n)\quad \text{mod}\;p\mathbb{Z}_{p}.\nonumber\end{eqnarray}$$
This finishes the proof of Proposition 3. ◻
If
![]() $e$
is
$e$
is
![]() $2$
-admissible, then
$2$
-admissible, then
![]() $e$
is also
$e$
is also
![]() $1$
-admissible. Furthermore, if
$1$
-admissible. Furthermore, if
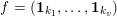 $f=(\mathbf{1}_{k_{1}},\ldots ,\mathbf{1}_{k_{v}})$
, then, for all
$f=(\mathbf{1}_{k_{1}},\ldots ,\mathbf{1}_{k_{v}})$
, then, for all
![]() $\mathbf{x}$
in
$\mathbf{x}$
in
![]() ${\mathcal{D}}_{e,f}$
, we have
${\mathcal{D}}_{e,f}$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})=\mathop{\sum }_{i=1}^{u}\lfloor \mathbf{e}_{i}\cdot \mathbf{x}\rfloor \geqslant 1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{x})=\mathop{\sum }_{i=1}^{u}\lfloor \mathbf{e}_{i}\cdot \mathbf{x}\rfloor \geqslant 1.\end{eqnarray}$$
Hence, if
![]() $e$
and
$e$
and
![]() $f$
satisfy the conditions of Theorem 1, then Proposition 3 implies that, for all primes
$f$
satisfy the conditions of Theorem 1, then Proposition 3 implies that, for all primes
![]() $p$
,
$p$
,
![]() $\mathfrak{S}_{e,f}$
has the
$\mathfrak{S}_{e,f}$
has the
![]() $p$
-Lucas property and
$p$
-Lucas property and
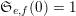 $\mathfrak{S}_{e,f}(0)=1$
is invertible in
$\mathfrak{S}_{e,f}(0)=1$
is invertible in
![]() $\mathbb{Z}_{p}$
. Thereby, to prove Theorem 1, it remains to prove that
$\mathbb{Z}_{p}$
. Thereby, to prove Theorem 1, it remains to prove that
![]() $\mathfrak{S}_{e,f}$
satisfies Condition (a) in Proposition 1 with the set
$\mathfrak{S}_{e,f}$
satisfies Condition (a) in Proposition 1 with the set
 $$\begin{eqnarray}\mathfrak{B}=\{\mathfrak{S}_{e,f}^{g}:g\in \mathfrak{F}_{p}^{d}\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{B}=\{\mathfrak{S}_{e,f}^{g}:g\in \mathfrak{F}_{p}^{d}\}.\end{eqnarray}$$
First, we prove that some special functions belong to
![]() $\mathfrak{F}_{p}^{1}$
.
$\mathfrak{F}_{p}^{1}$
.
4.1 Special functions in
 $\mathfrak{F}_{p}^{1}$
$\mathfrak{F}_{p}^{1}$
For all primes
![]() $p$
, we write
$p$
, we write
![]() $|\cdot |_{p}$
for the ultrametric norm on
$|\cdot |_{p}$
for the ultrametric norm on
![]() $\mathbb{Q}_{p}$
(the field of
$\mathbb{Q}_{p}$
(the field of
![]() $p$
-adic numbers) defined by
$p$
-adic numbers) defined by
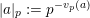 $|a|_{p}:=p^{-v_{p}(a)}$
. Note that
$|a|_{p}:=p^{-v_{p}(a)}$
. Note that
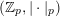 $(\mathbb{Z}_{p},|\cdot |_{p})$
is a compact space. Furthermore, if
$(\mathbb{Z}_{p},|\cdot |_{p})$
is a compact space. Furthermore, if
![]() $(c_{n})_{n\geqslant 0}$
is a
$(c_{n})_{n\geqslant 0}$
is a
![]() $\mathbb{Z}_{p}$
-valued sequence, then
$\mathbb{Z}_{p}$
-valued sequence, then
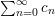 $\sum _{n=0}^{\infty }c_{n}$
is convergent in
$\sum _{n=0}^{\infty }c_{n}$
is convergent in
 $(\mathbb{Z}_{p},|\cdot |_{p})$
if and only if
$(\mathbb{Z}_{p},|\cdot |_{p})$
if and only if
![]() $|c_{n}|_{p}$
tends to
$|c_{n}|_{p}$
tends to
![]() $0$
as
$0$
as
![]() $n$
tends to infinity. In addition, if
$n$
tends to infinity. In addition, if
 $\sum _{n=0}^{\infty }c_{n}$
converges, then
$\sum _{n=0}^{\infty }c_{n}$
converges, then
![]() $(c_{n})_{n\in \mathbb{N}}$
is a summable family in
$(c_{n})_{n\in \mathbb{N}}$
is a summable family in
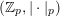 $(\mathbb{Z}_{p},|\cdot |_{p})$
.
$(\mathbb{Z}_{p},|\cdot |_{p})$
.
In the rest of the article, for all primes
![]() $p$
and all positive integers
$p$
and all positive integers
![]() $k$
, we set
$k$
, we set
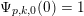 $\unicode[STIX]{x1D6F9}_{p,k,0}(0)=1$
,
$\unicode[STIX]{x1D6F9}_{p,k,0}(0)=1$
,
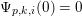 $\unicode[STIX]{x1D6F9}_{p,k,i}(0)=0$
for
$\unicode[STIX]{x1D6F9}_{p,k,i}(0)=0$
for
![]() $i\geqslant 1$
and, for all nonnegative integers
$i\geqslant 1$
and, for all nonnegative integers
![]() $i$
and
$i$
and
![]() $m$
,
$m$
,
![]() $m\geqslant 1$
, we set
$m\geqslant 1$
, we set
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{p,k,i}(m):=(-1)^{i}\unicode[STIX]{x1D70E}_{m,i}\biggl(\frac{1}{k},\frac{1}{k+p},\ldots ,\frac{1}{k+(m-1)p}\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{p,k,i}(m):=(-1)^{i}\unicode[STIX]{x1D70E}_{m,i}\biggl(\frac{1}{k},\frac{1}{k+p},\ldots ,\frac{1}{k+(m-1)p}\biggr),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D70E}_{m,i}$
is the
$\unicode[STIX]{x1D70E}_{m,i}$
is the
![]() $i$
th elementary symmetric polynomial of
$i$
th elementary symmetric polynomial of
![]() $m$
variables. Let us remind the reader that, for all nonnegative integers
$m$
variables. Let us remind the reader that, for all nonnegative integers
![]() $m$
and
$m$
and
![]() $i$
satisfying
$i$
satisfying
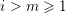 $i>m\geqslant 1$
, we have
$i>m\geqslant 1$
, we have
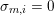 $\unicode[STIX]{x1D70E}_{m,i}=0$
.
$\unicode[STIX]{x1D70E}_{m,i}=0$
.
The aim of this section is to prove that, for all primes
![]() $p$
, all
$p$
, all
![]() $k$
in
$k$
in
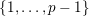 $\{1,\ldots ,p-1\}$
and all nonnegative integers
$\{1,\ldots ,p-1\}$
and all nonnegative integers
![]() $i$
, we have
$i$
, we have
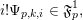 $$\begin{eqnarray}i!\unicode[STIX]{x1D6F9}_{p,k,i}\in \mathfrak{F}_{p}^{1},\end{eqnarray}$$
$$\begin{eqnarray}i!\unicode[STIX]{x1D6F9}_{p,k,i}\in \mathfrak{F}_{p}^{1},\end{eqnarray}$$
that is, for every nonnegative integer
![]() $M$
, there exists a sequence of polynomial functions with coefficients in
$M$
, there exists a sequence of polynomial functions with coefficients in
![]() $\mathbb{Z}_{p}$
which converges pointwise to
$\mathbb{Z}_{p}$
which converges pointwise to
![]() $i!\unicode[STIX]{x1D6F9}_{p,k,i}$
on
$i!\unicode[STIX]{x1D6F9}_{p,k,i}$
on
 $\{0,\ldots ,M\}$
.
$\{0,\ldots ,M\}$
.
Proof of (4.1).
Throughout this proof, we fix a prime number
![]() $p$
and an integer
$p$
and an integer
![]() $k$
in
$k$
in
 $\{1,\ldots ,p-1\}$
. Furthermore, for all nonnegative integers
$\{1,\ldots ,p-1\}$
. Furthermore, for all nonnegative integers
![]() $i$
, we use
$i$
, we use
![]() $\unicode[STIX]{x1D6F9}_{i}$
as a shorthand for
$\unicode[STIX]{x1D6F9}_{i}$
as a shorthand for
![]() $\unicode[STIX]{x1D6F9}_{p,k,i}$
and
$\unicode[STIX]{x1D6F9}_{p,k,i}$
and
![]() $\mathbb{N}_{{\geqslant}i}$
as a shorthand for the set of integers larger than or equal to
$\mathbb{N}_{{\geqslant}i}$
as a shorthand for the set of integers larger than or equal to
![]() $i$
. We shall prove (4.1) by induction on
$i$
. We shall prove (4.1) by induction on
![]() $i$
. To that end, for all nonnegative integers
$i$
. To that end, for all nonnegative integers
![]() $i$
, we write
$i$
, we write
![]() ${\mathcal{A}}_{i}$
for the following assertion:
${\mathcal{A}}_{i}$
for the following assertion:
‘There exists a sequence
 $(T_{i,r})_{r\geqslant 0}$
of polynomial functions with coefficients in
$(T_{i,r})_{r\geqslant 0}$
of polynomial functions with coefficients in
![]() $\mathbb{Z}_{p}$
which converges uniformly to
$\mathbb{Z}_{p}$
which converges uniformly to
![]() $i!\unicode[STIX]{x1D6F9}_{i}$
on
$i!\unicode[STIX]{x1D6F9}_{i}$
on
![]() $\mathbb{N}.$
’
$\mathbb{N}.$
’
First, observe that, for all nonnegative integers
![]() $m$
, we have
$m$
, we have
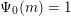 $\unicode[STIX]{x1D6F9}_{0}(m)=1$
, so that Assertion
$\unicode[STIX]{x1D6F9}_{0}(m)=1$
, so that Assertion
![]() ${\mathcal{A}}_{0}$
is true. Let
${\mathcal{A}}_{0}$
is true. Let
![]() $i$
be a fixed positive integer such that Assertions
$i$
be a fixed positive integer such that Assertions
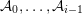 ${\mathcal{A}}_{0},\ldots ,{\mathcal{A}}_{i-1}$
are true. According to the Newton–Girard formulas, for all integers
${\mathcal{A}}_{0},\ldots ,{\mathcal{A}}_{i-1}$
are true. According to the Newton–Girard formulas, for all integers
![]() $m\geqslant i$
, we have
$m\geqslant i$
, we have
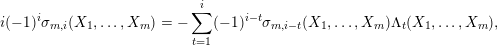 $$\begin{eqnarray}i(-1)^{i}\unicode[STIX]{x1D70E}_{m,i}(X_{1},\ldots ,X_{m})=-\mathop{\sum }_{t=1}^{i}(-1)^{i-t}\unicode[STIX]{x1D70E}_{m,i-t}(X_{1},\ldots ,X_{m})\unicode[STIX]{x1D6EC}_{t}(X_{1},\ldots ,X_{m}),\end{eqnarray}$$
$$\begin{eqnarray}i(-1)^{i}\unicode[STIX]{x1D70E}_{m,i}(X_{1},\ldots ,X_{m})=-\mathop{\sum }_{t=1}^{i}(-1)^{i-t}\unicode[STIX]{x1D70E}_{m,i-t}(X_{1},\ldots ,X_{m})\unicode[STIX]{x1D6EC}_{t}(X_{1},\ldots ,X_{m}),\end{eqnarray}$$
where
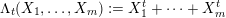 $\unicode[STIX]{x1D6EC}_{t}(X_{1},\ldots ,X_{m}):=X_{1}^{t}+\cdots +X_{m}^{t}$
. Thereby, for all integers
$\unicode[STIX]{x1D6EC}_{t}(X_{1},\ldots ,X_{m}):=X_{1}^{t}+\cdots +X_{m}^{t}$
. Thereby, for all integers
![]() $m\geqslant i$
, we have
$m\geqslant i$
, we have
 $$\begin{eqnarray}i\unicode[STIX]{x1D6F9}_{i}(m)=-\mathop{\sum }_{t=1}^{i}\unicode[STIX]{x1D6F9}_{i-t}(m)\unicode[STIX]{x1D6EC}_{t}\biggl(\frac{1}{k},\ldots ,\frac{1}{k+(m-1)p}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}i\unicode[STIX]{x1D6F9}_{i}(m)=-\mathop{\sum }_{t=1}^{i}\unicode[STIX]{x1D6F9}_{i-t}(m)\unicode[STIX]{x1D6EC}_{t}\biggl(\frac{1}{k},\ldots ,\frac{1}{k+(m-1)p}\biggr).\end{eqnarray}$$
For all nonnegative integers
![]() $j$
and
$j$
and
![]() $t$
, we have
$t$
, we have
 $$\begin{eqnarray}\frac{1}{(k+jp)^{t}}=\frac{1}{k^{t}}\frac{1}{(1+(j/k)p)^{t}}=\frac{1}{k^{t}}+\mathop{\sum }_{s=1}^{\infty }\frac{(-1)^{s}}{k^{t}}\binom{t-1+s}{s}\biggl(\frac{j}{k}\biggr)^{s}p^{s},\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{(k+jp)^{t}}=\frac{1}{k^{t}}\frac{1}{(1+(j/k)p)^{t}}=\frac{1}{k^{t}}+\mathop{\sum }_{s=1}^{\infty }\frac{(-1)^{s}}{k^{t}}\binom{t-1+s}{s}\biggl(\frac{j}{k}\biggr)^{s}p^{s},\end{eqnarray}$$
where the right-hand side of (4.3) is a convergent series in
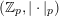 $(\mathbb{Z}_{p},|\cdot |_{p})$
because
$(\mathbb{Z}_{p},|\cdot |_{p})$
because
![]() $k$
is invertible in
$k$
is invertible in
![]() $\mathbb{Z}_{p}$
. Therefore, we obtain that
$\mathbb{Z}_{p}$
. Therefore, we obtain that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}_{t}\biggl(\frac{1}{k},\ldots ,\frac{1}{k+(m-1)p}\biggr) & = & \displaystyle \frac{m}{k^{t}}+\mathop{\sum }_{j=0}^{m-1}\mathop{\sum }_{s=1}^{\infty }\frac{(-1)^{s}}{k^{t}}\binom{t-1+s}{s}\biggl(\frac{j}{k}\biggr)^{s}p^{s}\nonumber\\ \displaystyle & = & \displaystyle \frac{m}{k^{t}}+\mathop{\sum }_{s=1}^{\infty }\frac{(-1)^{s}}{k^{t+s}}\binom{t-1+s}{s}p^{s}\biggl(\mathop{\sum }_{j=0}^{m-1}j^{s}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EC}_{t}\biggl(\frac{1}{k},\ldots ,\frac{1}{k+(m-1)p}\biggr) & = & \displaystyle \frac{m}{k^{t}}+\mathop{\sum }_{j=0}^{m-1}\mathop{\sum }_{s=1}^{\infty }\frac{(-1)^{s}}{k^{t}}\binom{t-1+s}{s}\biggl(\frac{j}{k}\biggr)^{s}p^{s}\nonumber\\ \displaystyle & = & \displaystyle \frac{m}{k^{t}}+\mathop{\sum }_{s=1}^{\infty }\frac{(-1)^{s}}{k^{t+s}}\binom{t-1+s}{s}p^{s}\biggl(\mathop{\sum }_{j=0}^{m-1}j^{s}\biggr).\end{eqnarray}$$
According to Faulhaber’s formula (see [Reference Conway and GuyCG96]), for all positive integers
![]() $s$
, we have
$s$
, we have
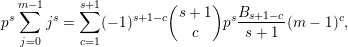 $$\begin{eqnarray}p^{s}\mathop{\sum }_{j=0}^{m-1}j^{s}=\mathop{\sum }_{c=1}^{s+1}(-1)^{s+1-c}\binom{s+1}{c}p^{s}\frac{B_{s+1-c}}{s+1}(m-1)^{c},\end{eqnarray}$$
$$\begin{eqnarray}p^{s}\mathop{\sum }_{j=0}^{m-1}j^{s}=\mathop{\sum }_{c=1}^{s+1}(-1)^{s+1-c}\binom{s+1}{c}p^{s}\frac{B_{s+1-c}}{s+1}(m-1)^{c},\end{eqnarray}$$
where
![]() $B_{k}$
is the
$B_{k}$
is the
![]() $k$
th first Bernoulli number. For all positive integers
$k$
th first Bernoulli number. For all positive integers
![]() $s$
and
$s$
and
![]() $t$
, we set
$t$
, we set
 $R_{0,t}(X):=X/k^{t}$
and
$R_{0,t}(X):=X/k^{t}$
and
 $$\begin{eqnarray}R_{s,t}(X):=\frac{1}{k^{t+s}}\binom{t-1+s}{s}\mathop{\sum }_{c=1}^{s+1}(-1)^{1-c}\binom{s+1}{c}p^{s}\frac{B_{s+1-c}}{s+1}(X-1)^{c},\end{eqnarray}$$
$$\begin{eqnarray}R_{s,t}(X):=\frac{1}{k^{t+s}}\binom{t-1+s}{s}\mathop{\sum }_{c=1}^{s+1}(-1)^{1-c}\binom{s+1}{c}p^{s}\frac{B_{s+1-c}}{s+1}(X-1)^{c},\end{eqnarray}$$
so that
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{t}\biggl(\frac{1}{k},\ldots ,\frac{1}{k+(m-1)p}\biggr)=\mathop{\sum }_{s=0}^{\infty }R_{s,t}(m).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{t}\biggl(\frac{1}{k},\ldots ,\frac{1}{k+(m-1)p}\biggr)=\mathop{\sum }_{s=0}^{\infty }R_{s,t}(m).\end{eqnarray}$$
In the rest of this article, for all polynomials
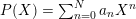 $P(X)=\sum _{n=0}^{N}a_{n}X^{n}$
in
$P(X)=\sum _{n=0}^{N}a_{n}X^{n}$
in
![]() $\mathbb{Z}_{p}[X]$
, we set
$\mathbb{Z}_{p}[X]$
, we set
 $$\begin{eqnarray}\Vert P\Vert _{p}:=\max \{|a_{n}|_{p}:0\leqslant n\leqslant N\}.\end{eqnarray}$$
$$\begin{eqnarray}\Vert P\Vert _{p}:=\max \{|a_{n}|_{p}:0\leqslant n\leqslant N\}.\end{eqnarray}$$
We claim that, for all nonnegative integers
![]() $s$
and
$s$
and
![]() $t$
,
$t$
,
![]() $t\geqslant 1$
, we have
$t\geqslant 1$
, we have
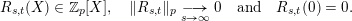 $$\begin{eqnarray}R_{s,t}(X)\in \mathbb{Z}_{p}[X],\quad \Vert R_{s,t}\Vert _{p}\underset{s\rightarrow \infty }{\longrightarrow }0\quad \text{and}\quad R_{s,t}(0)=0.\end{eqnarray}$$
$$\begin{eqnarray}R_{s,t}(X)\in \mathbb{Z}_{p}[X],\quad \Vert R_{s,t}\Vert _{p}\underset{s\rightarrow \infty }{\longrightarrow }0\quad \text{and}\quad R_{s,t}(0)=0.\end{eqnarray}$$
Indeed, on the one hand, if
![]() $p=2$
and
$p=2$
and
![]() $s=1$
, then we have
$s=1$
, then we have
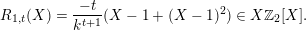 $$\begin{eqnarray}R_{1,t}(X)=\frac{-t}{k^{t+1}}(X-1+(X-1)^{2})\in X\mathbb{Z}_{2}[X].\end{eqnarray}$$
$$\begin{eqnarray}R_{1,t}(X)=\frac{-t}{k^{t+1}}(X-1+(X-1)^{2})\in X\mathbb{Z}_{2}[X].\end{eqnarray}$$
On the other hand, if
![]() $p\geqslant 3$
or
$p\geqslant 3$
or
![]() $s\geqslant 2$
, then we have
$s\geqslant 2$
, then we have
 $p^{s}>s+1$
, so that
$p^{s}>s+1$
, so that
 $v_{p}(s+1)\leqslant s-1$
. Furthermore, according to the von Staudt–Clausen theorem, we have
$v_{p}(s+1)\leqslant s-1$
. Furthermore, according to the von Staudt–Clausen theorem, we have
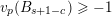 $v_{p}(B_{s+1-c})\geqslant -1$
. Thus, the coefficients of
$v_{p}(B_{s+1-c})\geqslant -1$
. Thus, the coefficients of
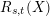 $R_{s,t}(X)$
belong to
$R_{s,t}(X)$
belong to
![]() $\mathbb{Z}_{p}$
. To be more precise, we have
$\mathbb{Z}_{p}$
. To be more precise, we have
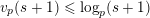 $v_{p}(s+1)\leqslant \log _{p}(s+1)$
, so that
$v_{p}(s+1)\leqslant \log _{p}(s+1)$
, so that
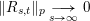 $\Vert R_{s,t}\Vert _{p}\underset{s\rightarrow \infty }{\longrightarrow }0$
, as expected. In addition, we have
$\Vert R_{s,t}\Vert _{p}\underset{s\rightarrow \infty }{\longrightarrow }0$
, as expected. In addition, we have
 $$\begin{eqnarray}\displaystyle R_{s,t}(0) & = & \displaystyle -\frac{p^{s}}{(s+1)k^{t+s}}\binom{t-1+s}{s}\mathop{\sum }_{c=1}^{s+1}\binom{s+1}{c}B_{s+1-c}\nonumber\\ \displaystyle & = & \displaystyle -\frac{p^{s}}{(s+1)k^{t+s}}\binom{t-1+s}{s}\mathop{\sum }_{d=0}^{s}\binom{s+1}{d}B_{d}=0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R_{s,t}(0) & = & \displaystyle -\frac{p^{s}}{(s+1)k^{t+s}}\binom{t-1+s}{s}\mathop{\sum }_{c=1}^{s+1}\binom{s+1}{c}B_{s+1-c}\nonumber\\ \displaystyle & = & \displaystyle -\frac{p^{s}}{(s+1)k^{t+s}}\binom{t-1+s}{s}\mathop{\sum }_{d=0}^{s}\binom{s+1}{d}B_{d}=0,\nonumber\end{eqnarray}$$
where we used the well-known relation satisfied by the Bernoulli numbers
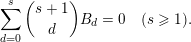 $$\begin{eqnarray}\mathop{\sum }_{d=0}^{s}\binom{s+1}{d}B_{d}=0\quad (s\geqslant 1).\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{d=0}^{s}\binom{s+1}{d}B_{d}=0\quad (s\geqslant 1).\end{eqnarray}$$
According to
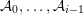 ${\mathcal{A}}_{0},\ldots ,{\mathcal{A}}_{i-1}$
, for all
${\mathcal{A}}_{0},\ldots ,{\mathcal{A}}_{i-1}$
, for all
![]() $j$
in
$j$
in
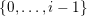 $\{0,\ldots ,i-1\}$
, there exists a sequence
$\{0,\ldots ,i-1\}$
, there exists a sequence
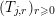 $(T_{j,r})_{r\geqslant 0}$
of polynomial functions with coefficients in
$(T_{j,r})_{r\geqslant 0}$
of polynomial functions with coefficients in
![]() $\mathbb{Z}_{p}$
which converges uniformly to
$\mathbb{Z}_{p}$
which converges uniformly to
![]() $j!\unicode[STIX]{x1D6F9}_{j}$
on
$j!\unicode[STIX]{x1D6F9}_{j}$
on
![]() $\mathbb{N}$
. According to (4.2) and (4.5), for all nonnegative integers
$\mathbb{N}$
. According to (4.2) and (4.5), for all nonnegative integers
![]() $N$
, there exists
$N$
, there exists
![]() $S_{N}$
in
$S_{N}$
in
![]() $\mathbb{N}$
such that, for all
$\mathbb{N}$
such that, for all
![]() $r\geqslant S_{N}$
and all
$r\geqslant S_{N}$
and all
![]() $m\geqslant i$
, we have
$m\geqslant i$
, we have
 $$\begin{eqnarray}i!\unicode[STIX]{x1D6F9}_{i}(m)\equiv -\mathop{\sum }_{t=1}^{i}\frac{(i-1)!}{(i-t)!}T_{i-t,r}(m)\mathop{\sum }_{s=0}^{r}R_{s,t}(m)\quad \text{mod}\;p^{N}\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}i!\unicode[STIX]{x1D6F9}_{i}(m)\equiv -\mathop{\sum }_{t=1}^{i}\frac{(i-1)!}{(i-t)!}T_{i-t,r}(m)\mathop{\sum }_{s=0}^{r}R_{s,t}(m)\quad \text{mod}\;p^{N}\mathbb{Z}_{p}.\end{eqnarray}$$
Thus, the sequence
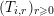 $(T_{i,r})_{r\geqslant 0}$
of polynomial functions with coefficients in
$(T_{i,r})_{r\geqslant 0}$
of polynomial functions with coefficients in
![]() $\mathbb{Z}_{p}$
, defined by
$\mathbb{Z}_{p}$
, defined by
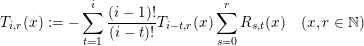 $$\begin{eqnarray}T_{i,r}(x):=-\mathop{\sum }_{t=1}^{i}\frac{(i-1)!}{(i-t)!}T_{i-t,r}(x)\mathop{\sum }_{s=0}^{r}R_{s,t}(x)\quad (x,r\in \mathbb{N})\end{eqnarray}$$
$$\begin{eqnarray}T_{i,r}(x):=-\mathop{\sum }_{t=1}^{i}\frac{(i-1)!}{(i-t)!}T_{i-t,r}(x)\mathop{\sum }_{s=0}^{r}R_{s,t}(x)\quad (x,r\in \mathbb{N})\end{eqnarray}$$
converges uniformly to
![]() $i!\unicode[STIX]{x1D6F9}_{i}$
on
$i!\unicode[STIX]{x1D6F9}_{i}$
on
![]() $\mathbb{N}_{{\geqslant}i}$
. To prove
$\mathbb{N}_{{\geqslant}i}$
. To prove
![]() ${\mathcal{A}}_{i}$
, it suffices to show that, for all
${\mathcal{A}}_{i}$
, it suffices to show that, for all
![]() $m$
in
$m$
in
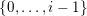 $\{0,\ldots ,i-1\}$
, we have
$\{0,\ldots ,i-1\}$
, we have
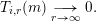 $$\begin{eqnarray}T_{i,r}(m)\underset{r\rightarrow \infty }{\longrightarrow }0.\end{eqnarray}$$
$$\begin{eqnarray}T_{i,r}(m)\underset{r\rightarrow \infty }{\longrightarrow }0.\end{eqnarray}$$
Observe that (4.6) and (4.5) lead to
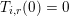 $T_{i,r}(0)=0$
. In particular, if
$T_{i,r}(0)=0$
. In particular, if
![]() $i=1$
, then (4.7) holds. Now we assume that
$i=1$
, then (4.7) holds. Now we assume that
![]() $i\geqslant 2$
. For all
$i\geqslant 2$
. For all
![]() $m\geqslant 2$
, we have
$m\geqslant 2$
, we have
 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{j=0}^{m}\unicode[STIX]{x1D6F9}_{j}(m)X^{j} & = & \displaystyle \mathop{\prod }_{w=0}^{m-1}\biggl(1-\frac{X}{k+wp}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \biggl(1-\frac{X}{k+(m-1)p}\biggr)\mathop{\prod }_{w=0}^{m-2}\biggl(1-\frac{X}{k+wp}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \biggl(1-\frac{X}{k+(m-1)p}\biggr)\mathop{\sum }_{j=0}^{m-1}\unicode[STIX]{x1D6F9}_{j}(m-1)X^{j}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{j=0}^{m}\unicode[STIX]{x1D6F9}_{j}(m)X^{j} & = & \displaystyle \mathop{\prod }_{w=0}^{m-1}\biggl(1-\frac{X}{k+wp}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \biggl(1-\frac{X}{k+(m-1)p}\biggr)\mathop{\prod }_{w=0}^{m-2}\biggl(1-\frac{X}{k+wp}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \biggl(1-\frac{X}{k+(m-1)p}\biggr)\mathop{\sum }_{j=0}^{m-1}\unicode[STIX]{x1D6F9}_{j}(m-1)X^{j}.\nonumber\end{eqnarray}$$
Thereby, for all
![]() $j$
in
$j$
in
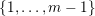 $\{1,\ldots ,m-1\}$
, we obtain that
$\{1,\ldots ,m-1\}$
, we obtain that
 $$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{j}(m)=\unicode[STIX]{x1D6F9}_{j}(m-1)-\frac{\unicode[STIX]{x1D6F9}_{j-1}(m-1)}{k+(m-1)p}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F9}_{j}(m)=\unicode[STIX]{x1D6F9}_{j}(m-1)-\frac{\unicode[STIX]{x1D6F9}_{j-1}(m-1)}{k+(m-1)p}\end{eqnarray}$$
with
 $$\begin{eqnarray}\frac{1}{k+(m-1)p}=\mathop{\sum }_{s=0}^{\infty }\frac{(-1)^{s}}{k^{s+1}}p^{s}(m-1)^{s}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{k+(m-1)p}=\mathop{\sum }_{s=0}^{\infty }\frac{(-1)^{s}}{k^{s+1}}p^{s}(m-1)^{s}.\end{eqnarray}$$
Thus, there exists a sequence
![]() $(U_{r})_{r\geqslant 0}$
of polynomials with coefficients in
$(U_{r})_{r\geqslant 0}$
of polynomials with coefficients in
![]() $\mathbb{Z}_{p}$
such that, for all positive integers
$\mathbb{Z}_{p}$
such that, for all positive integers
![]() $N$
, there exists a nonnegative integer
$N$
, there exists a nonnegative integer
![]() $S_{N}$
such that, for all
$S_{N}$
such that, for all
![]() $r\geqslant S_{N}$
and all
$r\geqslant S_{N}$
and all
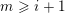 $m\geqslant i+1$
, we have
$m\geqslant i+1$
, we have
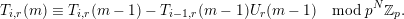 $$\begin{eqnarray}T_{i,r}(m)\equiv T_{i,r}(m-1)-T_{i-1,r}(m-1)U_{r}(m-1)\quad \text{mod}\;p^{N}\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}T_{i,r}(m)\equiv T_{i,r}(m-1)-T_{i-1,r}(m-1)U_{r}(m-1)\quad \text{mod}\;p^{N}\mathbb{Z}_{p}.\end{eqnarray}$$
But, if
![]() $V_{1}(X)$
and
$V_{1}(X)$
and
![]() $V_{2}(X)$
are polynomials with coefficients in
$V_{2}(X)$
are polynomials with coefficients in
![]() $\mathbb{Z}_{p}$
and if there exists a nonnegative integer
$\mathbb{Z}_{p}$
and if there exists a nonnegative integer
![]() $a$
such that, for all
$a$
such that, for all
![]() $m\geqslant a$
, we have
$m\geqslant a$
, we have
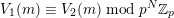 $V_{1}(m)\equiv V_{2}(m)\;\text{mod}\;p^{N}\mathbb{Z}_{p}$
, then, for all integers
$V_{1}(m)\equiv V_{2}(m)\;\text{mod}\;p^{N}\mathbb{Z}_{p}$
, then, for all integers
![]() $n$
, we have
$n$
, we have
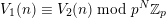 $V_{1}(n)\equiv V_{2}(n)\;\text{mod}\;p^{N}\mathbb{Z}_{p}$
. Indeed, let
$V_{1}(n)\equiv V_{2}(n)\;\text{mod}\;p^{N}\mathbb{Z}_{p}$
. Indeed, let
![]() $n$
be an integer; there exists a nonnegative integer
$n$
be an integer; there exists a nonnegative integer
![]() $v$
such that
$v$
such that
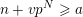 $n+vp^{N}\geqslant a$
. Thus, we obtain that
$n+vp^{N}\geqslant a$
. Thus, we obtain that
 $$\begin{eqnarray}V_{1}(n)\equiv V_{1}(n+vp^{N})\equiv V_{2}(n+vp^{N})\equiv V_{2}(n)\quad \text{mod}\;p^{N}\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}V_{1}(n)\equiv V_{1}(n+vp^{N})\equiv V_{2}(n+vp^{N})\equiv V_{2}(n)\quad \text{mod}\;p^{N}\mathbb{Z}_{p}.\end{eqnarray}$$
In particular, (4.8) also holds for all positive integers
![]() $m$
.
$m$
.
Furthermore, according to
![]() ${\mathcal{A}}_{i-1}$
, for all
${\mathcal{A}}_{i-1}$
, for all
![]() $m$
in
$m$
in
 $\{0,\ldots ,i-2\}$
,
$\{0,\ldots ,i-2\}$
,
 $T_{i-1,r}(m)$
tends to zero as
$T_{i-1,r}(m)$
tends to zero as
![]() $r$
tends to infinity. Thus, for all positive integers
$r$
tends to infinity. Thus, for all positive integers
![]() $N$
, there exists a nonnegative integer
$N$
, there exists a nonnegative integer
![]() $S_{N}$
such that, for all
$S_{N}$
such that, for all
![]() $r\geqslant S_{N}$
and all
$r\geqslant S_{N}$
and all
![]() $m$
in
$m$
in
 $\{1,\ldots ,i-1\}$
, we have
$\{1,\ldots ,i-1\}$
, we have
 $$\begin{eqnarray}T_{i,r}(m)\equiv T_{i,r}(m-1)\quad \text{mod}\;p^{N}\mathbb{Z}_{p}.\end{eqnarray}$$
$$\begin{eqnarray}T_{i,r}(m)\equiv T_{i,r}(m-1)\quad \text{mod}\;p^{N}\mathbb{Z}_{p}.\end{eqnarray}$$
Since
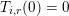 $T_{i,r}(0)=0$
, we obtain that
$T_{i,r}(0)=0$
, we obtain that
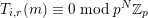 $T_{i,r}(m)\equiv 0\;\text{mod}\;p^{N}\mathbb{Z}_{p}$
for all
$T_{i,r}(m)\equiv 0\;\text{mod}\;p^{N}\mathbb{Z}_{p}$
for all
![]() $m$
in
$m$
in
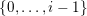 $\{0,\ldots ,i-1\}$
and
$\{0,\ldots ,i-1\}$
and
![]() $r\geqslant S_{N}$
, so that (4.7) holds. This finishes the induction on
$r\geqslant S_{N}$
, so that (4.7) holds. This finishes the induction on
![]() $i$
and proves (4.1).◻
$i$
and proves (4.1).◻
4.2 On the
 $p$
-adic Gamma function
$p$
-adic Gamma function
For every prime
![]() $p$
, we write
$p$
, we write
![]() $\unicode[STIX]{x1D6E4}_{p}$
for the
$\unicode[STIX]{x1D6E4}_{p}$
for the
![]() $p$
-adic Gamma function, so that, for all nonnegative integers
$p$
-adic Gamma function, so that, for all nonnegative integers
![]() $n$
, we have
$n$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{p}(n)=(-1)^{n}\underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{n-1}}\unicode[STIX]{x1D706}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{p}(n)=(-1)^{n}\underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{n-1}}\unicode[STIX]{x1D706}.\end{eqnarray}$$
The aim of this section is to prove Proposition 2.
Proof of Proposition 2.
Let
![]() $p$
be a fixed prime number. For all nonnegative integers
$p$
be a fixed prime number. For all nonnegative integers
![]() $n$
and
$n$
and
![]() $m$
, we have
$m$
, we have
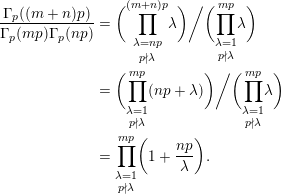 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6E4}_{p}((m+n)p)}{\unicode[STIX]{x1D6E4}_{p}(mp)\unicode[STIX]{x1D6E4}_{p}(np)} & = & \displaystyle \biggl(\underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=np}^{(m+n)p}}\unicode[STIX]{x1D706}\biggr)\bigg/\biggl(\underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{mp}}\unicode[STIX]{x1D706}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \biggl(\underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{mp}}(np+\unicode[STIX]{x1D706})\biggr)\bigg/\biggl(\underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{mp}}\unicode[STIX]{x1D706}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{mp}}\biggl(1+\frac{np}{\unicode[STIX]{x1D706}}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D6E4}_{p}((m+n)p)}{\unicode[STIX]{x1D6E4}_{p}(mp)\unicode[STIX]{x1D6E4}_{p}(np)} & = & \displaystyle \biggl(\underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=np}^{(m+n)p}}\unicode[STIX]{x1D706}\biggr)\bigg/\biggl(\underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{mp}}\unicode[STIX]{x1D706}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \biggl(\underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{mp}}(np+\unicode[STIX]{x1D706})\biggr)\bigg/\biggl(\underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{mp}}\unicode[STIX]{x1D706}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{mp}}\biggl(1+\frac{np}{\unicode[STIX]{x1D706}}\biggr).\end{eqnarray}$$
Let
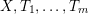 $X,T_{1},\ldots ,T_{m}$
be
$X,T_{1},\ldots ,T_{m}$
be
![]() $m+1$
variables. Then we have
$m+1$
variables. Then we have
 $$\begin{eqnarray}\mathop{\prod }_{j=1}^{m}(X-T_{j})=X^{m}+\mathop{\sum }_{i=1}^{\infty }(-1)^{i}\unicode[STIX]{x1D70E}_{m,i}(T_{1},\ldots ,T_{m})X^{m-i}.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{j=1}^{m}(X-T_{j})=X^{m}+\mathop{\sum }_{i=1}^{\infty }(-1)^{i}\unicode[STIX]{x1D70E}_{m,i}(T_{1},\ldots ,T_{m})X^{m-i}.\end{eqnarray}$$
Therefore, we obtain that
 $$\begin{eqnarray}\displaystyle \underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{mp}}\biggl(1+\frac{np}{\unicode[STIX]{x1D706}}\biggr) & = & \displaystyle \mathop{\prod }_{k=1}^{p-1}\mathop{\prod }_{\unicode[STIX]{x1D714}=0}^{m-1}\biggl(1+\frac{np}{k+\unicode[STIX]{x1D714}p}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{k=1}^{p-1}\biggl(1+\mathop{\sum }_{i=1}^{\infty }(-1)^{i}\unicode[STIX]{x1D70E}_{m,i}\biggl(\frac{-np}{k},\ldots ,\frac{-np}{k+(m-1)p}\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{k=1}^{p-1}\biggl(1+\mathop{\sum }_{i=1}^{\infty }(-1)^{i}n^{i}p^{i}\unicode[STIX]{x1D6F9}_{p,k,i}(m)\biggr).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{mp}}\biggl(1+\frac{np}{\unicode[STIX]{x1D706}}\biggr) & = & \displaystyle \mathop{\prod }_{k=1}^{p-1}\mathop{\prod }_{\unicode[STIX]{x1D714}=0}^{m-1}\biggl(1+\frac{np}{k+\unicode[STIX]{x1D714}p}\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{k=1}^{p-1}\biggl(1+\mathop{\sum }_{i=1}^{\infty }(-1)^{i}\unicode[STIX]{x1D70E}_{m,i}\biggl(\frac{-np}{k},\ldots ,\frac{-np}{k+(m-1)p}\biggr)\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{k=1}^{p-1}\biggl(1+\mathop{\sum }_{i=1}^{\infty }(-1)^{i}n^{i}p^{i}\unicode[STIX]{x1D6F9}_{p,k,i}(m)\biggr).\end{eqnarray}$$
Let
![]() $k$
in
$k$
in
 $\{1,\ldots ,p-1\}$
be fixed. By (4.1), for all positive integers
$\{1,\ldots ,p-1\}$
be fixed. By (4.1), for all positive integers
![]() $i$
, there exists a sequence
$i$
, there exists a sequence
 $(P_{i,\ell })_{\ell \geqslant 0}$
of polynomial functions with coefficients in
$(P_{i,\ell })_{\ell \geqslant 0}$
of polynomial functions with coefficients in
![]() $\mathbb{Z}_{p}$
which converges pointwise to
$\mathbb{Z}_{p}$
which converges pointwise to
![]() $i!\unicode[STIX]{x1D6F9}_{p,k,i}$
. We fix a nonnegative integer
$i!\unicode[STIX]{x1D6F9}_{p,k,i}$
. We fix a nonnegative integer
![]() $K$
. For all positive integers
$K$
. For all positive integers
![]() $N$
, we set
$N$
, we set
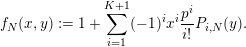 $$\begin{eqnarray}f_{N}(x,y):=1+\mathop{\sum }_{i=1}^{K+1}(-1)^{i}x^{i}\frac{p^{i}}{i!}P_{i,N}(y).\end{eqnarray}$$
$$\begin{eqnarray}f_{N}(x,y):=1+\mathop{\sum }_{i=1}^{K+1}(-1)^{i}x^{i}\frac{p^{i}}{i!}P_{i,N}(y).\end{eqnarray}$$
If
![]() $n$
and
$n$
and
![]() $m$
belong to
$m$
belong to
 $\{0,\ldots ,K\}$
, then we have
$\{0,\ldots ,K\}$
, then we have
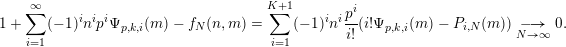 $$\begin{eqnarray}1+\mathop{\sum }_{i=1}^{\infty }(-1)^{i}n^{i}p^{i}\unicode[STIX]{x1D6F9}_{p,k,i}(m)-f_{N}(n,m)=\mathop{\sum }_{i=1}^{K+1}(-1)^{i}n^{i}\frac{p^{i}}{i!}(i!\unicode[STIX]{x1D6F9}_{p,k,i}(m)-P_{i,N}(m))\underset{N\rightarrow \infty }{\longrightarrow }0.\end{eqnarray}$$
$$\begin{eqnarray}1+\mathop{\sum }_{i=1}^{\infty }(-1)^{i}n^{i}p^{i}\unicode[STIX]{x1D6F9}_{p,k,i}(m)-f_{N}(n,m)=\mathop{\sum }_{i=1}^{K+1}(-1)^{i}n^{i}\frac{p^{i}}{i!}(i!\unicode[STIX]{x1D6F9}_{p,k,i}(m)-P_{i,N}(m))\underset{N\rightarrow \infty }{\longrightarrow }0.\end{eqnarray}$$
Furthermore, we have
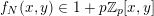 $f_{N}(x,y)\in 1+p\mathbb{Z}_{p}[x,y]$
. Indeed, if
$f_{N}(x,y)\in 1+p\mathbb{Z}_{p}[x,y]$
. Indeed, if
 $i=i_{0}+i_{1}p+\cdots +i_{a}p^{a}$
with
$i=i_{0}+i_{1}p+\cdots +i_{a}p^{a}$
with
![]() $i_{j}$
in
$i_{j}$
in
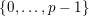 $\{0,\ldots ,p-1\}$
, then we set
$\{0,\ldots ,p-1\}$
, then we set
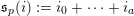 $\mathfrak{s}_{p}(i):=i_{0}+\cdots +i_{a}$
, so that, for all positive integers
$\mathfrak{s}_{p}(i):=i_{0}+\cdots +i_{a}$
, so that, for all positive integers
![]() $i$
, we have
$i$
, we have
 $$\begin{eqnarray}i-v_{p}(i!)=i-\frac{i-\mathfrak{s}_{p}(i)}{p-1}=\frac{i(p-2)+\mathfrak{s}_{p}(i)}{p-1}>0.\end{eqnarray}$$
$$\begin{eqnarray}i-v_{p}(i!)=i-\frac{i-\mathfrak{s}_{p}(i)}{p-1}=\frac{i(p-2)+\mathfrak{s}_{p}(i)}{p-1}>0.\end{eqnarray}$$
Hence, by (4.10), we obtain that there exists a function
![]() $g$
in
$g$
in
![]() $\mathfrak{F}_{p}^{2}$
such that, for all nonnegative integers
$\mathfrak{F}_{p}^{2}$
such that, for all nonnegative integers
![]() $n$
and
$n$
and
![]() $m$
, we have
$m$
, we have
 $$\begin{eqnarray}\underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{mp}}\biggl(1+\frac{np}{\unicode[STIX]{x1D706}}\biggr)=1+g(n,m)p,\end{eqnarray}$$
$$\begin{eqnarray}\underset{p\nmid \unicode[STIX]{x1D706}}{\mathop{\prod }_{\unicode[STIX]{x1D706}=1}^{mp}}\biggl(1+\frac{np}{\unicode[STIX]{x1D706}}\biggr)=1+g(n,m)p,\end{eqnarray}$$
which, together with (4.9), finishes the proof of Proposition 2. ◻
4.3 Last step in the proof of Theorem 1
Let
![]() $e$
and
$e$
and
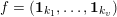 $f=(\mathbf{1}_{k_{1}},\ldots ,\mathbf{1}_{k_{v}})$
be two disjoint tuples of vectors in
$f=(\mathbf{1}_{k_{1}},\ldots ,\mathbf{1}_{k_{v}})$
be two disjoint tuples of vectors in
![]() $\mathbb{N}^{d}$
such that
$\mathbb{N}^{d}$
such that
 $|e|=|f|$
, for all
$|e|=|f|$
, for all
![]() $i$
in
$i$
in
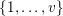 $\{1,\ldots ,v\}$
,
$\{1,\ldots ,v\}$
,
![]() $k_{i}$
is in
$k_{i}$
is in
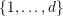 $\{1,\ldots ,d\}$
, and
$\{1,\ldots ,d\}$
, and
![]() $e$
is
$e$
is
![]() $2$
-admissible. Let
$2$
-admissible. Let
![]() $p$
be a fixed prime and
$p$
be a fixed prime and
![]() $\mathfrak{A}$
the
$\mathfrak{A}$
the
![]() $\mathbb{Z}_{p}$
-module spanned by
$\mathbb{Z}_{p}$
-module spanned by
![]() $\mathfrak{S}_{e,f}$
. We set
$\mathfrak{S}_{e,f}$
. We set
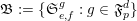 $\mathfrak{B}:=\{\mathfrak{S}_{e,f}^{g}:g\in \mathfrak{F}_{p}^{d}\}$
, which is obviously constituted of
$\mathfrak{B}:=\{\mathfrak{S}_{e,f}^{g}:g\in \mathfrak{F}_{p}^{d}\}$
, which is obviously constituted of
![]() $\mathbb{Z}_{p}$
-valued sequences and contains
$\mathbb{Z}_{p}$
-valued sequences and contains
![]() $\mathfrak{A}$
. To finish the proof of Theorem 1, we shall prove that
$\mathfrak{A}$
. To finish the proof of Theorem 1, we shall prove that
![]() $\mathfrak{S}_{e,f}$
and
$\mathfrak{S}_{e,f}$
and
![]() $\mathfrak{B}$
satisfy Condition (a) in Proposition 1. Hence, we have to show that, for all
$\mathfrak{B}$
satisfy Condition (a) in Proposition 1. Hence, we have to show that, for all
![]() $B$
in
$B$
in
![]() $\mathfrak{B}$
, all
$\mathfrak{B}$
, all
![]() $v$
in
$v$
in
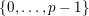 $\{0,\ldots ,p-1\}$
and all positive integers
$\{0,\ldots ,p-1\}$
and all positive integers
![]() $n$
, there exist
$n$
, there exist
![]() $A^{\prime }$
in
$A^{\prime }$
in
![]() $\mathfrak{A}$
and a sequence
$\mathfrak{A}$
and a sequence
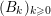 $(B_{k})_{k\geqslant 0}$
,
$(B_{k})_{k\geqslant 0}$
,
![]() $B_{k}$
in
$B_{k}$
in
![]() $\mathfrak{B}$
, such that
$\mathfrak{B}$
, such that
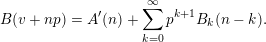 $$\begin{eqnarray}B(v+np)=A^{\prime }(n)+\mathop{\sum }_{k=0}^{\infty }p^{k+1}B_{k}(n-k).\end{eqnarray}$$
$$\begin{eqnarray}B(v+np)=A^{\prime }(n)+\mathop{\sum }_{k=0}^{\infty }p^{k+1}B_{k}(n-k).\end{eqnarray}$$
Let
![]() $g$
be a fixed function in
$g$
be a fixed function in
![]() $\mathfrak{F}_{p}^{d}$
that is a function
$\mathfrak{F}_{p}^{d}$
that is a function
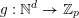 $g:\mathbb{N}^{d}\rightarrow \mathbb{Z}_{p}$
such that, for all nonnegative integers
$g:\mathbb{N}^{d}\rightarrow \mathbb{Z}_{p}$
such that, for all nonnegative integers
![]() $K$
, there exists a sequence of polynomial functions with coefficients in
$K$
, there exists a sequence of polynomial functions with coefficients in
![]() $\mathbb{Z}_{p}$
which converges pointwise to
$\mathbb{Z}_{p}$
which converges pointwise to
![]() $g$
on
$g$
on
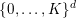 $\{0,\ldots ,K\}^{d}$
. In the rest of the proof, we write
$\{0,\ldots ,K\}^{d}$
. In the rest of the proof, we write
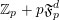 $\mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
for the set of functions of the form
$\mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
for the set of functions of the form
![]() $\unicode[STIX]{x1D6FC}+ph$
, where
$\unicode[STIX]{x1D6FC}+ph$
, where
![]() $\unicode[STIX]{x1D6FC}$
is a constant in
$\unicode[STIX]{x1D6FC}$
is a constant in
![]() $\mathbb{Z}_{p}$
and
$\mathbb{Z}_{p}$
and
![]() $h$
belongs to
$h$
belongs to
![]() $\mathfrak{F}_{p}^{d}$
. Observe that
$\mathfrak{F}_{p}^{d}$
. Observe that
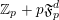 $\mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
is a ring. We consider the sequence
$\mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
is a ring. We consider the sequence
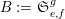 $B:=\mathfrak{S}_{e,f}^{g}$
. Let
$B:=\mathfrak{S}_{e,f}^{g}$
. Let
![]() $\mathbf{a}$
be in
$\mathbf{a}$
be in
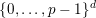 $\{0,\ldots ,p-1\}^{d}$
and
$\{0,\ldots ,p-1\}^{d}$
and
![]() $\mathbf{m}$
in
$\mathbf{m}$
in
![]() $\mathbb{N}^{d}$
. First, we shall prove that, for every
$\mathbb{N}^{d}$
. First, we shall prove that, for every
![]() $\mathbf{a}$
in
$\mathbf{a}$
in
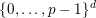 $\{0,\ldots ,p-1\}^{d}$
, there exists a function
$\{0,\ldots ,p-1\}^{d}$
, there exists a function
![]() $\unicode[STIX]{x1D70F}_{\mathbf{a}}$
in
$\unicode[STIX]{x1D70F}_{\mathbf{a}}$
in
 $\mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
such that, for all
$\mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
such that, for all
![]() $v$
in
$v$
in
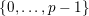 $\{0,\ldots ,p-1\}$
and
$\{0,\ldots ,p-1\}$
and
![]() $n$
in
$n$
in
![]() $\mathbb{N}$
, we have
$\mathbb{N}$
, we have
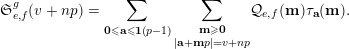 $$\begin{eqnarray}\mathfrak{S}_{e,f}^{g}(v+np)=\mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}\underset{|\mathbf{a}+\mathbf{m}p|=v+np}{\mathop{\sum }_{\mathbf{m}\geqslant \mathbf{0}}}{\mathcal{Q}}_{e,f}(\mathbf{m})\unicode[STIX]{x1D70F}_{\mathbf{a}}(\mathbf{m}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}_{e,f}^{g}(v+np)=\mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}\underset{|\mathbf{a}+\mathbf{m}p|=v+np}{\mathop{\sum }_{\mathbf{m}\geqslant \mathbf{0}}}{\mathcal{Q}}_{e,f}(\mathbf{m})\unicode[STIX]{x1D70F}_{\mathbf{a}}(\mathbf{m}).\end{eqnarray}$$
To that end, we express
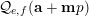 ${\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{m}p)$
as a product of
${\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{m}p)$
as a product of
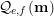 ${\mathcal{Q}}_{e,f}(\mathbf{m})$
and elements of
${\mathcal{Q}}_{e,f}(\mathbf{m})$
and elements of
 $\mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
. We have
$\mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
. We have
 $$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{m}p)=\frac{\mathop{\prod }_{i=1}^{u}(\mathbf{e}_{i}\cdot \mathbf{m}p)!\mathop{\prod }_{k=1}^{\mathbf{e}_{i}\cdot \mathbf{a}}(\mathbf{e}_{i}\cdot \mathbf{m}p+k)}{\mathop{\prod }_{i=1}^{v}(\mathbf{f}_{i}\cdot \mathbf{m}p)!\mathop{\prod }_{k=1}^{\mathbf{f}_{i}\cdot \mathbf{a}}(\mathbf{f}_{i}\cdot \mathbf{m}p+k)}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{m}p)=\frac{\mathop{\prod }_{i=1}^{u}(\mathbf{e}_{i}\cdot \mathbf{m}p)!\mathop{\prod }_{k=1}^{\mathbf{e}_{i}\cdot \mathbf{a}}(\mathbf{e}_{i}\cdot \mathbf{m}p+k)}{\mathop{\prod }_{i=1}^{v}(\mathbf{f}_{i}\cdot \mathbf{m}p)!\mathop{\prod }_{k=1}^{\mathbf{f}_{i}\cdot \mathbf{a}}(\mathbf{f}_{i}\cdot \mathbf{m}p+k)}.\end{eqnarray}$$
For every nonnegative integer
![]() $n$
, we have
$n$
, we have
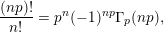 $$\begin{eqnarray}\frac{(np)!}{n!}=p^{n}(-1)^{np}\unicode[STIX]{x1D6E4}_{p}(np),\end{eqnarray}$$
$$\begin{eqnarray}\frac{(np)!}{n!}=p^{n}(-1)^{np}\unicode[STIX]{x1D6E4}_{p}(np),\end{eqnarray}$$
so that we have
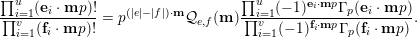 $$\begin{eqnarray}\frac{\mathop{\prod }_{i=1}^{u}(\mathbf{e}_{i}\cdot \mathbf{m}p)!}{\mathop{\prod }_{i=1}^{v}(\mathbf{f}_{i}\cdot \mathbf{m}p)!}=p^{(|e|-|f|)\cdot \mathbf{m}}{\mathcal{Q}}_{e,f}(\mathbf{m})\frac{\mathop{\prod }_{i=1}^{u}(-1)^{\mathbf{e}_{i}\cdot \mathbf{m}p}\unicode[STIX]{x1D6E4}_{p}(\mathbf{e}_{i}\cdot \mathbf{m}p)}{\mathop{\prod }_{i=1}^{v}(-1)^{\mathbf{f}_{i}\cdot \mathbf{m}p}\unicode[STIX]{x1D6E4}_{p}(\mathbf{f}_{i}\cdot \mathbf{m}p)}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathop{\prod }_{i=1}^{u}(\mathbf{e}_{i}\cdot \mathbf{m}p)!}{\mathop{\prod }_{i=1}^{v}(\mathbf{f}_{i}\cdot \mathbf{m}p)!}=p^{(|e|-|f|)\cdot \mathbf{m}}{\mathcal{Q}}_{e,f}(\mathbf{m})\frac{\mathop{\prod }_{i=1}^{u}(-1)^{\mathbf{e}_{i}\cdot \mathbf{m}p}\unicode[STIX]{x1D6E4}_{p}(\mathbf{e}_{i}\cdot \mathbf{m}p)}{\mathop{\prod }_{i=1}^{v}(-1)^{\mathbf{f}_{i}\cdot \mathbf{m}p}\unicode[STIX]{x1D6E4}_{p}(\mathbf{f}_{i}\cdot \mathbf{m}p)}.\end{eqnarray}$$
Furthermore, we have
 $$\begin{eqnarray}\frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1}^{\mathbf{e}_{i}\cdot \mathbf{a}}(\mathbf{e}_{i}\cdot \mathbf{m}p+k)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{k=1}^{\mathbf{f}_{i}\cdot \mathbf{a}}(\mathbf{f}_{i}\cdot \mathbf{m}p+k)}=\frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1,p\nmid k}^{\mathbf{e}_{i}\cdot \mathbf{a}}(\mathbf{e}_{i}\cdot \mathbf{m}p+k)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{k=1,p\nmid k}^{\mathbf{f}_{i}\cdot \mathbf{a}}(\mathbf{f}_{i}\cdot \mathbf{m}p+k)}\cdot p^{\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)}\frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1}^{\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor }(\mathbf{e}_{i}\cdot \mathbf{m}+k)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{k=1}^{\lfloor \mathbf{f}_{i}\cdot \mathbf{a}/p\rfloor }(\mathbf{f}_{i}\cdot \mathbf{m}+k)}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1}^{\mathbf{e}_{i}\cdot \mathbf{a}}(\mathbf{e}_{i}\cdot \mathbf{m}p+k)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{k=1}^{\mathbf{f}_{i}\cdot \mathbf{a}}(\mathbf{f}_{i}\cdot \mathbf{m}p+k)}=\frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1,p\nmid k}^{\mathbf{e}_{i}\cdot \mathbf{a}}(\mathbf{e}_{i}\cdot \mathbf{m}p+k)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{k=1,p\nmid k}^{\mathbf{f}_{i}\cdot \mathbf{a}}(\mathbf{f}_{i}\cdot \mathbf{m}p+k)}\cdot p^{\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)}\frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1}^{\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor }(\mathbf{e}_{i}\cdot \mathbf{m}+k)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{k=1}^{\lfloor \mathbf{f}_{i}\cdot \mathbf{a}/p\rfloor }(\mathbf{f}_{i}\cdot \mathbf{m}+k)}.\end{eqnarray}$$
Since
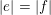 $|e|=|f|$
, we obtain that
$|e|=|f|$
, we obtain that
 $$\begin{eqnarray}\frac{\mathop{\prod }_{i=1}^{u}(-1)^{\mathbf{e}_{i}\cdot \mathbf{m}p}\unicode[STIX]{x1D6E4}_{p}(\mathbf{e}_{i}\cdot \mathbf{m}p)}{\mathop{\prod }_{i=1}^{v}(-1)^{\mathbf{f}_{i}\cdot \mathbf{m}p}\unicode[STIX]{x1D6E4}_{p}(\mathbf{f}_{i}\cdot \mathbf{m}p)}=\frac{\mathop{\prod }_{i=1}^{u}\unicode[STIX]{x1D6E4}_{p}(\mathbf{e}_{i}\cdot \mathbf{m}p)}{\mathop{\prod }_{i=1}^{v}\unicode[STIX]{x1D6E4}_{p}(\mathbf{f}_{i}\cdot \mathbf{m}p)}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathop{\prod }_{i=1}^{u}(-1)^{\mathbf{e}_{i}\cdot \mathbf{m}p}\unicode[STIX]{x1D6E4}_{p}(\mathbf{e}_{i}\cdot \mathbf{m}p)}{\mathop{\prod }_{i=1}^{v}(-1)^{\mathbf{f}_{i}\cdot \mathbf{m}p}\unicode[STIX]{x1D6E4}_{p}(\mathbf{f}_{i}\cdot \mathbf{m}p)}=\frac{\mathop{\prod }_{i=1}^{u}\unicode[STIX]{x1D6E4}_{p}(\mathbf{e}_{i}\cdot \mathbf{m}p)}{\mathop{\prod }_{i=1}^{v}\unicode[STIX]{x1D6E4}_{p}(\mathbf{f}_{i}\cdot \mathbf{m}p)}.\end{eqnarray}$$
Let
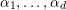 $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{d}$
be nonnegative integers with
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{d}$
be nonnegative integers with
![]() $\unicode[STIX]{x1D6FC}_{i_{0}}\geqslant 1$
for some
$\unicode[STIX]{x1D6FC}_{i_{0}}\geqslant 1$
for some
![]() $i_{0}$
in
$i_{0}$
in
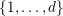 $\{1,\ldots ,d\}$
. By Proposition 2, there exists a function
$\{1,\ldots ,d\}$
. By Proposition 2, there exists a function
![]() $h$
in
$h$
in
![]() $\mathfrak{F}_{p}^{d}$
such that, for all nonnegative integers
$\mathfrak{F}_{p}^{d}$
such that, for all nonnegative integers
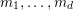 $m_{1},\ldots ,m_{d}$
, we have
$m_{1},\ldots ,m_{d}$
, we have
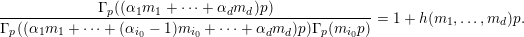 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D6E4}_{p}((\unicode[STIX]{x1D6FC}_{1}m_{1}+\cdots +\unicode[STIX]{x1D6FC}_{d}m_{d})p)}{\unicode[STIX]{x1D6E4}_{p}((\unicode[STIX]{x1D6FC}_{1}m_{1}+\cdots +(\unicode[STIX]{x1D6FC}_{i_{0}}-1)m_{i_{0}}+\cdots +\unicode[STIX]{x1D6FC}_{d}m_{d})p)\unicode[STIX]{x1D6E4}_{p}(m_{i_{0}}p)}=1+h(m_{1},\ldots ,m_{d})p.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6E4}_{p}((\unicode[STIX]{x1D6FC}_{1}m_{1}+\cdots +\unicode[STIX]{x1D6FC}_{d}m_{d})p)}{\unicode[STIX]{x1D6E4}_{p}((\unicode[STIX]{x1D6FC}_{1}m_{1}+\cdots +(\unicode[STIX]{x1D6FC}_{i_{0}}-1)m_{i_{0}}+\cdots +\unicode[STIX]{x1D6FC}_{d}m_{d})p)\unicode[STIX]{x1D6E4}_{p}(m_{i_{0}}p)}=1+h(m_{1},\ldots ,m_{d})p.\end{eqnarray}$$
Hence, there exists a function
![]() $h^{\prime }$
in
$h^{\prime }$
in
![]() $\mathfrak{F}_{p}^{d}$
such that, for all nonnegative integers
$\mathfrak{F}_{p}^{d}$
such that, for all nonnegative integers
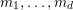 $m_{1},\ldots ,m_{d}$
, we have
$m_{1},\ldots ,m_{d}$
, we have
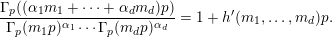 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D6E4}_{p}((\unicode[STIX]{x1D6FC}_{1}m_{1}+\cdots +\unicode[STIX]{x1D6FC}_{d}m_{d})p)}{\unicode[STIX]{x1D6E4}_{p}(m_{1}p)^{\unicode[STIX]{x1D6FC}_{1}}\cdots \unicode[STIX]{x1D6E4}_{p}(m_{d}p)^{\unicode[STIX]{x1D6FC}_{d}}}=1+h^{\prime }(m_{1},\ldots ,m_{d})p.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D6E4}_{p}((\unicode[STIX]{x1D6FC}_{1}m_{1}+\cdots +\unicode[STIX]{x1D6FC}_{d}m_{d})p)}{\unicode[STIX]{x1D6E4}_{p}(m_{1}p)^{\unicode[STIX]{x1D6FC}_{1}}\cdots \unicode[STIX]{x1D6E4}_{p}(m_{d}p)^{\unicode[STIX]{x1D6FC}_{d}}}=1+h^{\prime }(m_{1},\ldots ,m_{d})p.\end{eqnarray}$$
Since
![]() $f$
is only constituted by vectors
$f$
is only constituted by vectors
![]() $\mathbf{1}_{k}$
, there exists
$\mathbf{1}_{k}$
, there exists
![]() $g^{\prime }$
in
$g^{\prime }$
in
![]() $\mathfrak{F}_{p}^{d}$
such that, for all
$\mathfrak{F}_{p}^{d}$
such that, for all
![]() $\mathbf{m}$
in
$\mathbf{m}$
in
![]() $\mathbb{N}^{d}$
, we have
$\mathbb{N}^{d}$
, we have
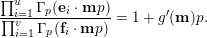 $$\begin{eqnarray}\frac{\mathop{\prod }_{i=1}^{u}\unicode[STIX]{x1D6E4}_{p}(\mathbf{e}_{i}\cdot \mathbf{m}p)}{\mathop{\prod }_{i=1}^{v}\unicode[STIX]{x1D6E4}_{p}(\mathbf{f}_{i}\cdot \mathbf{m}p)}=1+g^{\prime }(\mathbf{m})p.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathop{\prod }_{i=1}^{u}\unicode[STIX]{x1D6E4}_{p}(\mathbf{e}_{i}\cdot \mathbf{m}p)}{\mathop{\prod }_{i=1}^{v}\unicode[STIX]{x1D6E4}_{p}(\mathbf{f}_{i}\cdot \mathbf{m}p)}=1+g^{\prime }(\mathbf{m})p.\end{eqnarray}$$
Furthermore, if
![]() $k$
is an integer coprime to
$k$
is an integer coprime to
![]() $p$
and
$p$
and
![]() $\mathbf{d}$
a vector in
$\mathbf{d}$
a vector in
![]() $\mathbb{N}^{d}$
, then, for every
$\mathbb{N}^{d}$
, then, for every
![]() $\mathbf{m}$
in
$\mathbf{m}$
in
![]() $\mathbb{N}^{d}$
, we have
$\mathbb{N}^{d}$
, we have
 $$\begin{eqnarray}\frac{1}{\mathbf{d}\cdot \mathbf{m}p+k}=\mathop{\sum }_{s=0}^{\infty }(-1)^{s}\frac{(\mathbf{d}\cdot \mathbf{m})^{s}}{k^{s+1}}p^{s},\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{\mathbf{d}\cdot \mathbf{m}p+k}=\mathop{\sum }_{s=0}^{\infty }(-1)^{s}\frac{(\mathbf{d}\cdot \mathbf{m})^{s}}{k^{s+1}}p^{s},\end{eqnarray}$$
so that there is a function
![]() $g^{\prime \prime }$
in
$g^{\prime \prime }$
in
![]() $\mathfrak{F}_{p}^{d}$
such that, for all
$\mathfrak{F}_{p}^{d}$
such that, for all
![]() $\mathbf{m}$
in
$\mathbf{m}$
in
![]() $\mathbb{N}^{d}$
, we have
$\mathbb{N}^{d}$
, we have
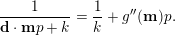 $$\begin{eqnarray}\frac{1}{\mathbf{d}\cdot \mathbf{m}p+k}=\frac{1}{k}+g^{\prime \prime }(\mathbf{m})p.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{\mathbf{d}\cdot \mathbf{m}p+k}=\frac{1}{k}+g^{\prime \prime }(\mathbf{m})p.\end{eqnarray}$$
Hence, for all
![]() $\mathbf{a}$
in
$\mathbf{a}$
in
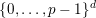 $\{0,\ldots ,p-1\}^{d}$
, there exist a
$\{0,\ldots ,p-1\}^{d}$
, there exist a
![]() $p$
-adic integer
$p$
-adic integer
![]() $\unicode[STIX]{x1D706}_{\mathbf{a}}$
and a function
$\unicode[STIX]{x1D706}_{\mathbf{a}}$
and a function
![]() $g_{\mathbf{a}}$
in
$g_{\mathbf{a}}$
in
![]() $\mathfrak{F}_{p}^{d}$
such that, for all
$\mathfrak{F}_{p}^{d}$
such that, for all
![]() $\mathbf{m}$
in
$\mathbf{m}$
in
![]() $\mathbb{N}^{d}$
, we have
$\mathbb{N}^{d}$
, we have
 $$\begin{eqnarray}\frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1,p\nmid k}^{\mathbf{e}_{i}\cdot \mathbf{a}}(\mathbf{e}_{i}\cdot \mathbf{m}p+k)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{k=1,p\nmid k}^{\mathbf{f}_{i}\cdot \mathbf{a}}(\mathbf{f}_{i}\cdot \mathbf{m}p+k)}=\unicode[STIX]{x1D706}_{\mathbf{a}}+g_{\mathbf{a}}(\mathbf{m})p.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1,p\nmid k}^{\mathbf{e}_{i}\cdot \mathbf{a}}(\mathbf{e}_{i}\cdot \mathbf{m}p+k)}{\mathop{\prod }_{i=1}^{v}\mathop{\prod }_{k=1,p\nmid k}^{\mathbf{f}_{i}\cdot \mathbf{a}}(\mathbf{f}_{i}\cdot \mathbf{m}p+k)}=\unicode[STIX]{x1D706}_{\mathbf{a}}+g_{\mathbf{a}}(\mathbf{m})p.\end{eqnarray}$$
Since
![]() $f$
is only constituted by vectors
$f$
is only constituted by vectors
![]() $\mathbf{1}_{k}$
, for all
$\mathbf{1}_{k}$
, for all
![]() $i$
in
$i$
in
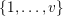 $\{1,\ldots ,v\}$
, we have
$\{1,\ldots ,v\}$
, we have
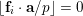 $\lfloor \mathbf{f}_{i}\cdot \mathbf{a}/p\rfloor =0$
. Thereby, for all
$\lfloor \mathbf{f}_{i}\cdot \mathbf{a}/p\rfloor =0$
. Thereby, for all
![]() $\mathbf{a}$
in
$\mathbf{a}$
in
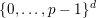 $\{0,\ldots ,p-1\}^{d}$
, there exists a function
$\{0,\ldots ,p-1\}^{d}$
, there exists a function
![]() $h_{\mathbf{a}}$
in
$h_{\mathbf{a}}$
in
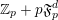 $\mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
such that, for all
$\mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
such that, for all
![]() $\mathbf{m}$
in
$\mathbf{m}$
in
![]() $\mathbb{N}^{d}$
, we have
$\mathbb{N}^{d}$
, we have
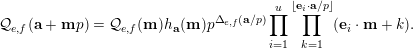 $$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{m}p)={\mathcal{Q}}_{e,f}(\mathbf{m})h_{\mathbf{a}}(\mathbf{m})p^{\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)}\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1}^{\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor }(\mathbf{e}_{i}\cdot \mathbf{m}+k).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{m}p)={\mathcal{Q}}_{e,f}(\mathbf{m})h_{\mathbf{a}}(\mathbf{m})p^{\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)}\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1}^{\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor }(\mathbf{e}_{i}\cdot \mathbf{m}+k).\end{eqnarray}$$
Furthermore, we have either
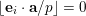 $\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor =0$
for all
$\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor =0$
for all
![]() $i$
, or
$i$
, or
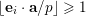 $\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor \geqslant 1$
for some
$\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor \geqslant 1$
for some
![]() $i$
and so
$i$
and so
 $\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)\geqslant 1$
. In both cases, we obtain that
$\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)\geqslant 1$
. In both cases, we obtain that
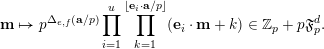 $$\begin{eqnarray}\mathbf{m}\mapsto p^{\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)}\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1}^{\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor }(\mathbf{e}_{i}\cdot \mathbf{m}+k)\in \mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{m}\mapsto p^{\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)}\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1}^{\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor }(\mathbf{e}_{i}\cdot \mathbf{m}+k)\in \mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}.\end{eqnarray}$$
Let
![]() $g$
be a function in
$g$
be a function in
![]() $\mathfrak{F}_{p}^{d}$
. For all
$\mathfrak{F}_{p}^{d}$
. For all
![]() $\mathbf{a}$
in
$\mathbf{a}$
in
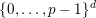 $\{0,\ldots ,p-1\}^{d}$
, the function
$\{0,\ldots ,p-1\}^{d}$
, the function
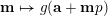 $\mathbf{m}\mapsto g(\mathbf{a}+\mathbf{m}p)$
belongs to
$\mathbf{m}\mapsto g(\mathbf{a}+\mathbf{m}p)$
belongs to
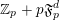 $\mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
. For all
$\mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
. For all
![]() $\mathbf{m}$
in
$\mathbf{m}$
in
![]() $\mathbb{N}^{d}$
, we set
$\mathbb{N}^{d}$
, we set
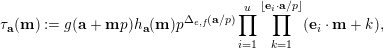 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{\mathbf{a}}(\mathbf{m}):=g(\mathbf{a}+\mathbf{m}p)h_{\mathbf{a}}(\mathbf{m})p^{\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)}\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1}^{\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor }(\mathbf{e}_{i}\cdot \mathbf{m}+k),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{\mathbf{a}}(\mathbf{m}):=g(\mathbf{a}+\mathbf{m}p)h_{\mathbf{a}}(\mathbf{m})p^{\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)}\mathop{\prod }_{i=1}^{u}\mathop{\prod }_{k=1}^{\lfloor \mathbf{e}_{i}\cdot \mathbf{a}/p\rfloor }(\mathbf{e}_{i}\cdot \mathbf{m}+k),\end{eqnarray}$$
so that
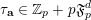 $\unicode[STIX]{x1D70F}_{\mathbf{a}}\in \mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
. Therefore, for all
$\unicode[STIX]{x1D70F}_{\mathbf{a}}\in \mathbb{Z}_{p}+p\mathfrak{F}_{p}^{d}$
. Therefore, for all
![]() $v$
in
$v$
in
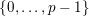 $\{0,\ldots ,p-1\}$
and
$\{0,\ldots ,p-1\}$
and
![]() $n$
in
$n$
in
![]() $\mathbb{N}$
, we have
$\mathbb{N}$
, we have
 $$\begin{eqnarray}\displaystyle \mathfrak{S}_{e,f}^{g}(v+np) & = & \displaystyle \mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}\underset{|\mathbf{a}+\mathbf{m}p|=v+np}{\mathop{\sum }_{\mathbf{m}\geqslant \mathbf{0}}}g(\mathbf{a}+\mathbf{m}p){\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{m}p)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}\underset{|\mathbf{a}+\mathbf{m}p|=v+np}{\mathop{\sum }_{\mathbf{m}\geqslant \mathbf{0}}}{\mathcal{Q}}_{e,f}(\mathbf{m})\unicode[STIX]{x1D70F}_{\mathbf{a}}(\mathbf{m}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{S}_{e,f}^{g}(v+np) & = & \displaystyle \mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}\underset{|\mathbf{a}+\mathbf{m}p|=v+np}{\mathop{\sum }_{\mathbf{m}\geqslant \mathbf{0}}}g(\mathbf{a}+\mathbf{m}p){\mathcal{Q}}_{e,f}(\mathbf{a}+\mathbf{m}p)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}\underset{|\mathbf{a}+\mathbf{m}p|=v+np}{\mathop{\sum }_{\mathbf{m}\geqslant \mathbf{0}}}{\mathcal{Q}}_{e,f}(\mathbf{m})\unicode[STIX]{x1D70F}_{\mathbf{a}}(\mathbf{m}),\nonumber\end{eqnarray}$$
which proves (4.12).
Now, if
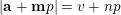 $|\mathbf{a}+\mathbf{m}p|=v+np$
, then we have
$|\mathbf{a}+\mathbf{m}p|=v+np$
, then we have
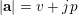 $|\mathbf{a}|=v+jp$
with
$|\mathbf{a}|=v+jp$
with
 $$\begin{eqnarray}0\leqslant j\leqslant \min \biggl(n,\biggl\lfloor\frac{d(p-1)-v}{p}\biggr\rfloor\biggr)=:M.\end{eqnarray}$$
$$\begin{eqnarray}0\leqslant j\leqslant \min \biggl(n,\biggl\lfloor\frac{d(p-1)-v}{p}\biggr\rfloor\biggr)=:M.\end{eqnarray}$$
Furthermore, we have
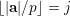 $\lfloor |\mathbf{a}|/p\rfloor =j$
and there is
$\lfloor |\mathbf{a}|/p\rfloor =j$
and there is
![]() $k$
in
$k$
in
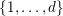 $\{1,\ldots ,d\}$
such that
$\{1,\ldots ,d\}$
such that
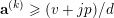 $\mathbf{a}^{(k)}\geqslant (v+jp)/d$
. Since
$\mathbf{a}^{(k)}\geqslant (v+jp)/d$
. Since
![]() $e$
is
$e$
is
![]() $2$
-admissible, there are
$2$
-admissible, there are
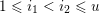 $1\leqslant i_{1}<i_{2}\leqslant u$
such that
$1\leqslant i_{1}<i_{2}\leqslant u$
such that
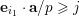 $\mathbf{e}_{i_{1}}\cdot \mathbf{a}/p\geqslant j$
and
$\mathbf{e}_{i_{1}}\cdot \mathbf{a}/p\geqslant j$
and
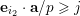 $\mathbf{e}_{i_{2}}\cdot \mathbf{a}/p\geqslant j$
. Hence, we obtain that
$\mathbf{e}_{i_{2}}\cdot \mathbf{a}/p\geqslant j$
. Hence, we obtain that
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)=\mathop{\sum }_{i=1}^{u}\biggl\lfloor\frac{\mathbf{e}_{i}\cdot \mathbf{a}}{p}\biggr\rfloor\geqslant 2j\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{e,f}(\mathbf{a}/p)=\mathop{\sum }_{i=1}^{u}\biggl\lfloor\frac{\mathbf{e}_{i}\cdot \mathbf{a}}{p}\biggr\rfloor\geqslant 2j\end{eqnarray}$$
because
![]() $f$
is constituted by vectors
$f$
is constituted by vectors
![]() $\mathbf{1}_{k}$
. In particular, there is
$\mathbf{1}_{k}$
. In particular, there is
![]() $\unicode[STIX]{x1D70F}_{\mathbf{a}}^{\prime }$
in
$\unicode[STIX]{x1D70F}_{\mathbf{a}}^{\prime }$
in
![]() $\mathfrak{F}_{p}^{d}$
such that
$\mathfrak{F}_{p}^{d}$
such that
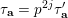 $\unicode[STIX]{x1D70F}_{\mathbf{a}}=p^{2j}\unicode[STIX]{x1D70F}_{\mathbf{a}}^{\prime }$
. Hence, we have
$\unicode[STIX]{x1D70F}_{\mathbf{a}}=p^{2j}\unicode[STIX]{x1D70F}_{\mathbf{a}}^{\prime }$
. Hence, we have
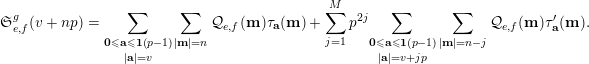 $$\begin{eqnarray}\mathfrak{S}_{e,f}^{g}(v+np)=\underset{|\mathbf{a}|=v}{\mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}}\mathop{\sum }_{|\mathbf{m}|=n}{\mathcal{Q}}_{e,f}(\mathbf{m})\unicode[STIX]{x1D70F}_{\mathbf{a}}(\mathbf{m})+\mathop{\sum }_{j=1}^{M}p^{2j}\underset{|\mathbf{a}|=v+jp}{\mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}}\mathop{\sum }_{|\mathbf{m}|=n-j}{\mathcal{Q}}_{e,f}(\mathbf{m})\unicode[STIX]{x1D70F}_{\mathbf{a}}^{\prime }(\mathbf{m}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}_{e,f}^{g}(v+np)=\underset{|\mathbf{a}|=v}{\mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}}\mathop{\sum }_{|\mathbf{m}|=n}{\mathcal{Q}}_{e,f}(\mathbf{m})\unicode[STIX]{x1D70F}_{\mathbf{a}}(\mathbf{m})+\mathop{\sum }_{j=1}^{M}p^{2j}\underset{|\mathbf{a}|=v+jp}{\mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}}\mathop{\sum }_{|\mathbf{m}|=n-j}{\mathcal{Q}}_{e,f}(\mathbf{m})\unicode[STIX]{x1D70F}_{\mathbf{a}}^{\prime }(\mathbf{m}).\end{eqnarray}$$
For every
![]() $\mathbf{a}$
in
$\mathbf{a}$
in
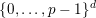 $\{0,\ldots ,p-1\}^{d}$
, we write
$\{0,\ldots ,p-1\}^{d}$
, we write
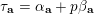 $\unicode[STIX]{x1D70F}_{\mathbf{a}}=\unicode[STIX]{x1D6FC}_{\mathbf{a}}+p\unicode[STIX]{x1D6FD}_{\mathbf{a}}$
, where
$\unicode[STIX]{x1D70F}_{\mathbf{a}}=\unicode[STIX]{x1D6FC}_{\mathbf{a}}+p\unicode[STIX]{x1D6FD}_{\mathbf{a}}$
, where
![]() $\unicode[STIX]{x1D6FC}_{\mathbf{a}}$
is a constant in
$\unicode[STIX]{x1D6FC}_{\mathbf{a}}$
is a constant in
![]() $\mathbb{Z}_{p}$
and
$\mathbb{Z}_{p}$
and
![]() $\unicode[STIX]{x1D6FD}_{\mathbf{a}}$
is a function in
$\unicode[STIX]{x1D6FD}_{\mathbf{a}}$
is a function in
![]() $\mathfrak{F}_{p}^{d}$
. We set
$\mathfrak{F}_{p}^{d}$
. We set
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}:=\underset{|\mathbf{a}|=v}{\mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}}\unicode[STIX]{x1D6FC}_{\mathbf{a}}\in \mathbb{Z}_{p}\quad \text{and}\quad \unicode[STIX]{x1D6FD}:=\underset{|\mathbf{a}|=v}{\mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}}\unicode[STIX]{x1D6FD}_{\mathbf{a}}\in \mathfrak{F}_{p}^{d}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}:=\underset{|\mathbf{a}|=v}{\mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}}\unicode[STIX]{x1D6FC}_{\mathbf{a}}\in \mathbb{Z}_{p}\quad \text{and}\quad \unicode[STIX]{x1D6FD}:=\underset{|\mathbf{a}|=v}{\mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}}\unicode[STIX]{x1D6FD}_{\mathbf{a}}\in \mathfrak{F}_{p}^{d}.\end{eqnarray}$$
Finally, for every
![]() $j$
in
$j$
in
 $\{1,\ldots ,M\}$
, we set
$\{1,\ldots ,M\}$
, we set
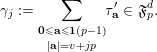 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{j}:=\underset{|\mathbf{a}|=v+jp}{\mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}}\unicode[STIX]{x1D70F}_{\mathbf{a}}^{\prime }\in \mathfrak{F}_{p}^{d}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{j}:=\underset{|\mathbf{a}|=v+jp}{\mathop{\sum }_{\mathbf{0}\leqslant \mathbf{a}\leqslant \mathbf{1}(p-1)}}\unicode[STIX]{x1D70F}_{\mathbf{a}}^{\prime }\in \mathfrak{F}_{p}^{d}.\end{eqnarray}$$
Hence, we obtain that
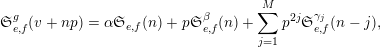 $$\begin{eqnarray}\mathfrak{S}_{e,f}^{g}(v+np)=\unicode[STIX]{x1D6FC}\mathfrak{S}_{e,f}(n)+p\mathfrak{S}_{e,f}^{\unicode[STIX]{x1D6FD}}(n)+\mathop{\sum }_{j=1}^{M}p^{2j}\mathfrak{S}_{e,f}^{\unicode[STIX]{x1D6FE}_{j}}(n-j),\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}_{e,f}^{g}(v+np)=\unicode[STIX]{x1D6FC}\mathfrak{S}_{e,f}(n)+p\mathfrak{S}_{e,f}^{\unicode[STIX]{x1D6FD}}(n)+\mathop{\sum }_{j=1}^{M}p^{2j}\mathfrak{S}_{e,f}^{\unicode[STIX]{x1D6FE}_{j}}(n-j),\end{eqnarray}$$
where
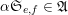 $\unicode[STIX]{x1D6FC}\mathfrak{S}_{e,f}\in \mathfrak{A}$
,
$\unicode[STIX]{x1D6FC}\mathfrak{S}_{e,f}\in \mathfrak{A}$
,
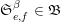 $\mathfrak{S}_{e,f}^{\unicode[STIX]{x1D6FD}}\in \mathfrak{B}$
and
$\mathfrak{S}_{e,f}^{\unicode[STIX]{x1D6FD}}\in \mathfrak{B}$
and
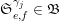 $\mathfrak{S}_{e,f}^{\unicode[STIX]{x1D6FE}_{j}}\in \mathfrak{B}$
. For every
$\mathfrak{S}_{e,f}^{\unicode[STIX]{x1D6FE}_{j}}\in \mathfrak{B}$
. For every
![]() $j$
,
$j$
,
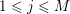 $1\leqslant j\leqslant M$
, we have
$1\leqslant j\leqslant M$
, we have
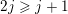 $2j\geqslant j+1$
, so that there exist
$2j\geqslant j+1$
, so that there exist
![]() $A^{\prime }$
in
$A^{\prime }$
in
![]() $\mathfrak{A}$
and a sequence
$\mathfrak{A}$
and a sequence
![]() $(B_{j})_{j\geqslant 0}$
, with
$(B_{j})_{j\geqslant 0}$
, with
![]() $B_{j}$
in
$B_{j}$
in
![]() $\mathfrak{B}$
, such that
$\mathfrak{B}$
, such that
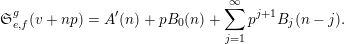 $$\begin{eqnarray}\mathfrak{S}_{e,f}^{g}(v+np)=A^{\prime }(n)+pB_{0}(n)+\mathop{\sum }_{j=1}^{\infty }p^{j+1}B_{j}(n-j).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{S}_{e,f}^{g}(v+np)=A^{\prime }(n)+pB_{0}(n)+\mathop{\sum }_{j=1}^{\infty }p^{j+1}B_{j}(n-j).\end{eqnarray}$$
This shows that
![]() $\mathfrak{S}_{e,f}$
and
$\mathfrak{S}_{e,f}$
and
![]() $\mathfrak{B}$
satisfy Condition (a) in Proposition 1, so that Theorem 1 is proved.◻
$\mathfrak{B}$
satisfy Condition (a) in Proposition 1, so that Theorem 1 is proved.◻