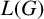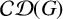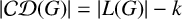1 Introduction
Let G be a finite group and
![]() $L(G)$
be the subgroup lattice of G. The Chermak–Delgado measure of a subgroup H of G is defined by
$L(G)$
be the subgroup lattice of G. The Chermak–Delgado measure of a subgroup H of G is defined by
Let
Then the set
![]() ${\cal CD}(G)$
forms a modular, self-dual sublattice of
${\cal CD}(G)$
forms a modular, self-dual sublattice of
![]() $L(G)$
, which is called the Chermak–Delgado lattice of G. It was first introduced by Chermak and Delgado [Reference Chermak and Delgado4] and revisited by Isaacs [Reference Isaacs5]. In the last few years, there has been a growing interest in understanding this lattice (see [Reference An, Brennan, Qu and Wilcox1–Reference Brewster and Wilcox3, Reference McCulloch6–Reference McCulloch and Tărnăuceanu8, Reference Tărnăuceanu11–Reference Zuccari, Russo and Scoppola14]). We recall several important properties of the Chermak–Delgado measure:
$L(G)$
, which is called the Chermak–Delgado lattice of G. It was first introduced by Chermak and Delgado [Reference Chermak and Delgado4] and revisited by Isaacs [Reference Isaacs5]. In the last few years, there has been a growing interest in understanding this lattice (see [Reference An, Brennan, Qu and Wilcox1–Reference Brewster and Wilcox3, Reference McCulloch6–Reference McCulloch and Tărnăuceanu8, Reference Tărnăuceanu11–Reference Zuccari, Russo and Scoppola14]). We recall several important properties of the Chermak–Delgado measure:
-
• if
 $H\leq G$
, then
$H\leq G$
, then
 $m_G(H)\leq m_G(C_G(H))$
, and if the measures are equal, then
$m_G(H)\leq m_G(C_G(H))$
, and if the measures are equal, then
 $C_G(C_G(H))=H$
;
$C_G(C_G(H))=H$
; -
• if
 $H\in {\cal CD}(G)$
, then
$H\in {\cal CD}(G)$
, then
 $C_G(H)\in {\cal CD}(G)$
and
$C_G(H)\in {\cal CD}(G)$
and
 $C_G(C_G(H))=H$
;
$C_G(C_G(H))=H$
; -
• the maximal member M of
 ${\cal CD}(G)$
is characteristic and
${\cal CD}(G)$
is characteristic and
 ${\cal CD}(M)={\cal CD}(G)$
;
${\cal CD}(M)={\cal CD}(G)$
; -
• the minimal member
 $M(G)$
of
$M(G)$
of
 ${\cal CD}(G)$
(called the Chermak–Delgado subgroup of G) is characteristic, abelian and contains
${\cal CD}(G)$
(called the Chermak–Delgado subgroup of G) is characteristic, abelian and contains
 $Z(G)$
.
$Z(G)$
.
In [Reference Tărnăuceanu12], the Chermak–Delgado measure of G has been seen as a function:
If G is nontrivial, then
![]() $m_G$
has at least two distinct values, or equivalently
$m_G$
has at least two distinct values, or equivalently
![]() ${\cal CD}(G)\neq L(G)$
(see [Reference Tărnăuceanu11, Corollary 3]). This leads to the following natural question.
${\cal CD}(G)\neq L(G)$
(see [Reference Tărnăuceanu11, Corollary 3]). This leads to the following natural question.
Question 1.1. How large can the lattice
![]() ${\cal CD}(G)$
be?
${\cal CD}(G)$
be?
The dual problem of finding finite groups with small Chermak–Delgado lattices has been studied in [Reference McCulloch6, Reference McCulloch and Tărnăuceanu7].
Our main result is stated as follows.
Theorem 1.2. Let G be a finite group. Then:
-
(a)
 $|{\cal CD}(G)|=|L(G)|-1$
if and only if
$|{\cal CD}(G)|=|L(G)|-1$
if and only if
 $G\cong \mathbb {Z}_p$
or
$G\cong \mathbb {Z}_p$
or
 $G\cong Q_8$
;
$G\cong Q_8$
; -
(b)
 $|{\cal CD}(G)|=|L(G)|-2$
if and only if
$|{\cal CD}(G)|=|L(G)|-2$
if and only if
 $G\cong \mathbb {Z}_{p^2}$
.
$G\cong \mathbb {Z}_{p^2}$
.
For the proof of the above theorem, we need the following well-known result (see, for example, [Reference Suzuki10, Volume II, (4.4)]).
Theorem 1.3. A finite p-group has a unique subgroup of order p if and only if it is either cyclic or a generalised quaternion
![]() $2$
-group.
$2$
-group.
We recall that a generalised quaternion
![]() $2$
-group is a group of order
$2$
-group is a group of order
![]() $2^n$
for some positive integer
$2^n$
for some positive integer
![]() $n\geq 3$
, defined by
$n\geq 3$
, defined by
We also need the following theorem taken from [Reference Tărnăuceanu12].
Theorem 1.4. Let G be a finite group. For each prime p dividing the order of G and
![]() $P\in \mathrm {Syl}_p(G)$
, let
$P\in \mathrm {Syl}_p(G)$
, let
![]() $|Z(P)|=p^{n_p}$
. Then
$|Z(P)|=p^{n_p}$
. Then
 $$ \begin{align} |\mathrm{Im}(m_G)|\geq 1+\sum_{p}n_p. \end{align} $$
$$ \begin{align} |\mathrm{Im}(m_G)|\geq 1+\sum_{p}n_p. \end{align} $$
Finally, we indicate a natural open problem concerning the above study.
Open problem. Determine the finite groups G such that
![]() $|{\cal CD}(G)|=|L(G)|-k$
, where
$|{\cal CD}(G)|=|L(G)|-k$
, where
![]() $k\geq 3$
.
$k\geq 3$
.
Most of our notation is standard and will usually not be repeated here. Elementary notions and results on groups can be found in [Reference Isaacs5]. For subgroup lattice concepts, we refer to [Reference Schmidt9].
2 Proof of the main result
First of all, we solve the problem for generalised quaternion
![]() $2$
-groups.
$2$
-groups.
Lemma 2.1. With the above notation:
-
(a)
 $|{\cal CD}(Q_{2^n})|=|L(Q_{2^n})|-1$
if and only if
$|{\cal CD}(Q_{2^n})|=|L(Q_{2^n})|-1$
if and only if
 $n=3$
, that is,
$n=3$
, that is,
 $G\cong Q_8$
;
$G\cong Q_8$
; -
(b)
 $|{\cal CD}(Q_{2^n})|\neq |L(Q_{2^n})|-2$
for all
$|{\cal CD}(Q_{2^n})|\neq |L(Q_{2^n})|-2$
for all
 $n\geq 3$
.
$n\geq 3$
.
Proof. We easily obtain
and
 $$ \begin{align*} {\cal CD}(Q_{2^n})=\begin{cases} \{Q_8, \langle a\rangle, \langle b\rangle, \langle ab\rangle, \langle a^2\rangle\}&\hbox{if } n=3\\ \{\langle a\rangle\}&\hbox{if } n\geq 4.\end{cases} \end{align*} $$
$$ \begin{align*} {\cal CD}(Q_{2^n})=\begin{cases} \{Q_8, \langle a\rangle, \langle b\rangle, \langle ab\rangle, \langle a^2\rangle\}&\hbox{if } n=3\\ \{\langle a\rangle\}&\hbox{if } n\geq 4.\end{cases} \end{align*} $$
These lead immediately to the desired conclusions.
We are now able to prove our main result.
Proof of Theorem 1.2
We divide the proof into two parts corresponding to the two parts of the theorem.
Part (a). Since
![]() $|{\cal CD}(G)|=|L(G)|-1$
, we have
$|{\cal CD}(G)|=|L(G)|-1$
, we have
![]() ${\cal CD}(G)=L(G)\setminus \{H_0\}$
, where
${\cal CD}(G)=L(G)\setminus \{H_0\}$
, where
![]() $H_0\leq G$
. We infer that
$H_0\leq G$
. We infer that
![]() $|\mathrm { Im}(m_G)|=2$
and so G is a p-group with
$|\mathrm { Im}(m_G)|=2$
and so G is a p-group with
![]() $|Z(G)|=p$
by Theorem 1.4. Then
$|Z(G)|=p$
by Theorem 1.4. Then
![]() $m_G(1)<m_G(Z(G))$
, implying that
$m_G(1)<m_G(Z(G))$
, implying that
where
![]() $|G|=p^n$
.
$|G|=p^n$
.
Assume that there exists
![]() $H\leq G$
with
$H\leq G$
with
![]() $|H|=p$
and
$|H|=p$
and
![]() $H\neq Z(G)$
. Then
$H\neq Z(G)$
. Then
![]() $H\notin {\cal CD}(G)$
, which shows that
$H\notin {\cal CD}(G)$
, which shows that
![]() $H=1$
and this contradicts the hypothesis. Thus, G has a unique subgroup of order p and Theorem 1.3 leads to
$H=1$
and this contradicts the hypothesis. Thus, G has a unique subgroup of order p and Theorem 1.3 leads to
In the first case, we easily get
![]() $n=1$
, that is,
$n=1$
, that is,
![]() $G\cong \mathbb {Z}_p$
, while in the second one, we get
$G\cong \mathbb {Z}_p$
, while in the second one, we get
![]() $G\cong Q_8$
by Lemma 2.1(a).
$G\cong Q_8$
by Lemma 2.1(a).
Part (b). The condition
![]() $|{\cal CD}(G)|=|L(G)|-2$
means
$|{\cal CD}(G)|=|L(G)|-2$
means
![]() ${\cal CD}(G)=L(G)\setminus \{H_1,H_2\}$
, where
${\cal CD}(G)=L(G)\setminus \{H_1,H_2\}$
, where
![]() $H_1,H_2\leq G$
. Then
$H_1,H_2\leq G$
. Then
![]() $|\mathrm {Im}(m_G)|\leq 3$
. Recall that we cannot have
$|\mathrm {Im}(m_G)|\leq 3$
. Recall that we cannot have
![]() $|\mathrm {Im}(m_G)|=1$
.
$|\mathrm {Im}(m_G)|=1$
.
If
![]() $|\mathrm {Im}(m_G)|=2$
, then
$|\mathrm {Im}(m_G)|=2$
, then
and again G is a p-group with
![]() $|Z(G)|=p$
. It is clear that one of the two subgroups
$|Z(G)|=p$
. It is clear that one of the two subgroups
![]() $H_1$
and
$H_1$
and
![]() $H_2$
must be trivial, say
$H_2$
must be trivial, say
![]() $H_1=1$
. Then G has at most two subgroups of order p, namely
$H_1=1$
. Then G has at most two subgroups of order p, namely
![]() $Z(G)$
and possibly
$Z(G)$
and possibly
![]() $H_2$
. This implies that it has exactly one subgroup of order p because the number of subgroups of order p in a finite p-group is congruent to
$H_2$
. This implies that it has exactly one subgroup of order p because the number of subgroups of order p in a finite p-group is congruent to
![]() $1 \ (\mathrm {mod}\, p)$
. Consequently, one obtains again (2.1). For
$1 \ (\mathrm {mod}\, p)$
. Consequently, one obtains again (2.1). For
![]() $G\cong \mathbb {Z}_{p^n}$
, we easily get
$G\cong \mathbb {Z}_{p^n}$
, we easily get
![]() $n=2$
, that is,
$n=2$
, that is,
![]() $G\cong \mathbb {Z}_{p^2}$
, while for
$G\cong \mathbb {Z}_{p^2}$
, while for
![]() $G\cong Q_{2^n}$
, we get no solution by Lemma 2.1(b).
$G\cong Q_{2^n}$
, we get no solution by Lemma 2.1(b).
If
![]() $|\mathrm {Im}(m_G)|=3$
, then
$|\mathrm {Im}(m_G)|=3$
, then
![]() $m_G(H_1)$
,
$m_G(H_1)$
,
![]() $m_G(H_2)$
and
$m_G(H_2)$
and
![]() $m^*(G)$
are distinct. Also, (1.1) becomes
$m^*(G)$
are distinct. Also, (1.1) becomes
 $$ \begin{align*} 3\geq 1+\sum_{p}n_p. \end{align*} $$
$$ \begin{align*} 3\geq 1+\sum_{p}n_p. \end{align*} $$
Since
![]() $n_p\geq 1$
for all p, we have the two possibilities described in Cases 1 and 2.
$n_p\geq 1$
for all p, we have the two possibilities described in Cases 1 and 2.
Case 1:
![]() $|G|=p^n$
and
$|G|=p^n$
and
![]() $|Z(G)|\in \{p,p^2\}$
.
$|Z(G)|\in \{p,p^2\}$
.
Obviously, if G is abelian, we get
![]() $G\cong \mathbb {Z}_{p^2}$
. Assume that G is not abelian. Since
$G\cong \mathbb {Z}_{p^2}$
. Assume that G is not abelian. Since
![]() $m_G(1)<m_G(Z(G))=m_G(G)$
, we infer that one of the two subgroups
$m_G(1)<m_G(Z(G))=m_G(G)$
, we infer that one of the two subgroups
![]() $H_1$
and
$H_1$
and
![]() $H_2$
is trivial and that
$H_2$
is trivial and that
If
![]() $|Z(G)|=p$
, then G has a unique subgroup of order p and so it is a generalised quaternion
$|Z(G)|=p$
, then G has a unique subgroup of order p and so it is a generalised quaternion
![]() $2$
-group, contradicting Lemma 2.1(b). The same can also be said when
$2$
-group, contradicting Lemma 2.1(b). The same can also be said when
![]() $|Z(G)|=p^2$
because all subgroups of order p of G are outside of
$|Z(G)|=p^2$
because all subgroups of order p of G are outside of
![]() ${\cal CD}(G)$
.
${\cal CD}(G)$
.
Case 2:
![]() $|G|=p^nq^m$
and the Sylow p-subgroups and q-subgroups of G have centres of orders p and q, respectively.
$|G|=p^nq^m$
and the Sylow p-subgroups and q-subgroups of G have centres of orders p and q, respectively.
Let P be a Sylow p-subgroup and Q be a Sylow q-subgroup of G. Since
![]() $P\subseteq C_G(Z(P))$
, we have
$P\subseteq C_G(Z(P))$
, we have
and similarly,
Also,
We observe that the measures
![]() $m_G(Z(P))$
,
$m_G(Z(P))$
,
![]() $m_G(Z(Q))$
and
$m_G(Z(Q))$
and
![]() $m_G(1)$
are distinct and consequently they are all possible measures of the subgroups of G. We distinguish two subcases.
$m_G(1)$
are distinct and consequently they are all possible measures of the subgroups of G. We distinguish two subcases.
Subcase 2.1:
![]() $Z(G)=1$
.
$Z(G)=1$
.
Then
![]() $m^*(G)=m_G(1)=m_G(G)$
. Indeed, if
$m^*(G)=m_G(1)=m_G(G)$
. Indeed, if
![]() $m^*(G)=m_G(Z(P))$
, then
$m^*(G)=m_G(Z(P))$
, then
![]() $1$
, G and
$1$
, G and
![]() $Z(Q)$
will be outside of
$Z(Q)$
will be outside of
![]() ${\cal CD}(G)$
, and this contradicts the hypothesis. In the same way, we cannot have
${\cal CD}(G)$
, and this contradicts the hypothesis. In the same way, we cannot have
![]() $m^*(G)=m_G(Z(Q))$
. Since
$m^*(G)=m_G(Z(Q))$
. Since
![]() $m_G(P)$
is divisible by
$m_G(P)$
is divisible by
![]() $p^{n+1}$
and
$p^{n+1}$
and
![]() $m_G(Q)$
is divisible by
$m_G(Q)$
is divisible by
![]() $q^{m+1}$
, we infer that
$q^{m+1}$
, we infer that
![]() $m_G(P)=m_G(Z(P))$
and
$m_G(P)=m_G(Z(P))$
and
![]() $m_G(Q)=m_G(Z(Q))$
. Thus,
$m_G(Q)=m_G(Z(Q))$
. Thus,
![]() $P,Z(P),Q,Z(Q)\notin {\cal CD}(G)$
and our hypothesis implies that
$P,Z(P),Q,Z(Q)\notin {\cal CD}(G)$
and our hypothesis implies that
![]() $P=Z(P)$
and
$P=Z(P)$
and
![]() $Q=Z(Q)$
, that is, G is a nonabelian group of order
$Q=Z(Q)$
, that is, G is a nonabelian group of order
![]() $pq$
. Assume that
$pq$
. Assume that
![]() $p<q$
. Then
$p<q$
. Then
![]() ${\cal CD}(G)$
consists of the unique subgroup of order q of G and therefore we obtain
${\cal CD}(G)$
consists of the unique subgroup of order q of G and therefore we obtain
![]() $|L(G)|=3$
, and this contradicts the hypothesis.
$|L(G)|=3$
, and this contradicts the hypothesis.
Subcase 2.2:
![]() $Z(G)\neq 1$
.
$Z(G)\neq 1$
.
Then
![]() $m_G(1)<m_G(G)$
, which shows that
$m_G(1)<m_G(G)$
, which shows that
![]() $m_G(G)$
equals either
$m_G(G)$
equals either
![]() $m_G(Z(P))$
or
$m_G(Z(P))$
or
![]() $m_G(Z(Q))$
. Assume that
$m_G(Z(Q))$
. Assume that
![]() $m_G(G)=m_G(Z(P))$
. Then
$m_G(G)=m_G(Z(P))$
. Then
![]() $x=m$
and
$x=m$
and
![]() $|Z(G)|=p$
, implying that
$|Z(G)|=p$
, implying that
Note that we cannot have
![]() $m^*(G)=m_G(Z(Q))$
because in this case,
$m^*(G)=m_G(Z(Q))$
because in this case,
![]() $1$
,
$1$
,
![]() $Z(G)$
and G will be outside of
$Z(G)$
and G will be outside of
![]() ${\cal CD}(G)$
, and this contradicts the hypothesis. Consequently,
${\cal CD}(G)$
, and this contradicts the hypothesis. Consequently,
It follows that
![]() $1$
,
$1$
,
![]() $Z(Q)$
and Q are not contained in
$Z(Q)$
and Q are not contained in
![]() ${\cal CD}(G)$
, which leads to
${\cal CD}(G)$
, which leads to
![]() $Q=Z(Q)$
. In other words,
$Q=Z(Q)$
. In other words,
![]() ${\cal CD}(G)=L(G)\setminus \{1,Q\}$
. Thus,
${\cal CD}(G)=L(G)\setminus \{1,Q\}$
. Thus,
![]() ${\cal CD}(G)$
is the lattice interval
${\cal CD}(G)$
is the lattice interval
and [Reference Tărnăuceanu11, Corollary 2] shows that G is nilpotent. Then
![]() $G=P\times Q$
and it follows that
$G=P\times Q$
and it follows that
![]() $Z(G)=Z(P)\times Q$
, which contradicts (2.2).
$Z(G)=Z(P)\times Q$
, which contradicts (2.2).
This completes the proof.