Published online by Cambridge University Press: 14 December 2021
Let
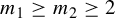 $m_1 \geq m_2 \geq 2$
be integers. We consider subsets of the product symbolic sequence space
$m_1 \geq m_2 \geq 2$
be integers. We consider subsets of the product symbolic sequence space
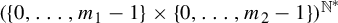 $(\{0,\ldots ,m_1-1\} \times \{0,\ldots ,m_2-1\})^{\mathbb {N}^*}$
that are invariant under the action of the semigroup of multiplicative integers. These sets are defined following Kenyon, Peres, and Solomyak and using a fixed integer
$(\{0,\ldots ,m_1-1\} \times \{0,\ldots ,m_2-1\})^{\mathbb {N}^*}$
that are invariant under the action of the semigroup of multiplicative integers. These sets are defined following Kenyon, Peres, and Solomyak and using a fixed integer
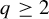 $q \geq 2$
. We compute the Hausdorff and Minkowski dimensions of the projection of these sets onto an affine grid of the unit square. The proof of our Hausdorff dimension formula proceeds via a variational principle over some class of Borel probability measures on the studied sets. This extends well-known results on self-affine Sierpiński carpets. However, the combinatoric arguments we use in our proofs are more elaborate than in the self-similar case and involve a new parameter, namely
$q \geq 2$
. We compute the Hausdorff and Minkowski dimensions of the projection of these sets onto an affine grid of the unit square. The proof of our Hausdorff dimension formula proceeds via a variational principle over some class of Borel probability measures on the studied sets. This extends well-known results on self-affine Sierpiński carpets. However, the combinatoric arguments we use in our proofs are more elaborate than in the self-similar case and involve a new parameter, namely
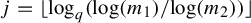 $j = \lfloor \log _q ( {\log (m_1)}/{\log (m_2)} ) \rfloor $
. We then generalize our results to the same subsets defined in dimension
$j = \lfloor \log _q ( {\log (m_1)}/{\log (m_2)} ) \rfloor $
. We then generalize our results to the same subsets defined in dimension
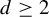 $d \geq 2$
. There, the situation is even more delicate and our formulas involve a collection of
$d \geq 2$
. There, the situation is even more delicate and our formulas involve a collection of
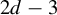 $2d-3$
parameters.
$2d-3$
parameters.