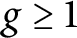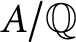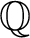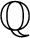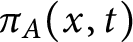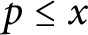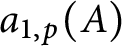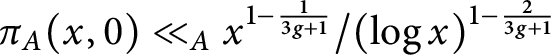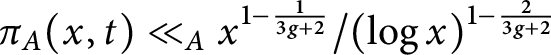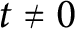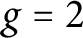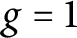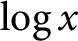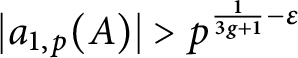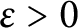1 Introduction
A prominent open problem in arithmetic geometry, formulated by Lang and Trotter in the 1970s [Reference Lang and TrotterLaTr76, Part I], concerns the distribution of the Frobenius traces associated to the reductions modulo primes of an elliptic curve defined over
$\mathbb Q$
and without complex multiplication. In recent years, this problem has been formulated in broader settings, such as that of abelian varieties (e.g., [Reference Cojocaru, Davis, Silverberg and StangeCoDaSiSt17, Reference Chen, Jones and SerbanChJoSe20, Reference KatzKa09]). The goal of the present article is to provide upper bounds related to the distribution of the Frobenius traces defined by the product of non-isogenous elliptic curves defined over
$\mathbb Q$
and having no complex multiplication, as explained below.
Let
$g \geq 1$
be an integer and let
$A/\mathbb Q$
be an abelian variety that is isogenous over
$\mathbb Q$
to a product of g elliptic curves defined over
$\mathbb Q$
, pairwise non-isogenous over
$\overline {\mathbb Q}$
and each without complex multiplication. Denote by
$N_A$
the conductor of A. For a prime
$p \nmid N_A$
, we write the characteristic polynomial of the Frobenius endomorphism acting on the reduction of A modulo p as
$$ \begin{align*}P_{A, p}(X) = X^{2g} + a_{1, p}(A) X^{2g-1} + \cdots + a_{2g-1, p}(A) X + a_{2g, p}(A) \in \mathbb Z[X]. \end{align*} $$
Then, for a fixed integer t, we study the counting function
$$ \begin{align*}\pi_A(x, t) := \#\left\{p \leq x: p \nmid N_A, a_{1, p}(A) = t\right\}. \end{align*} $$
When
$g = 1$
, the asymptotic behavior of
$\pi _A(x, t)$
is predicted by the Lang–Trotter Conjecture on Frobenius traces (see [Reference Lang and TrotterLaTr76, Part I, p. 33] for the original and [Reference Baier and JonesBaJo09, Conjectures 2 and 3, p. 435] for refined versions). Specifically, in [Reference Lang and TrotterLaTr76], it is conjectured that there exists an explicit non-negative constant
$C(A, t)$
, which depends on the arithmetic of A and t, such that, as
$x \rightarrow \infty $
,
$$ \begin{align*}\pi_A(x, t) \sim C(A, t) \frac{\sqrt{x}}{\operatorname{log} x}. \end{align*} $$
When
$g = 2$
and
$t \neq 0$
, a similar asymptotic formula is predicted by a conjecture of Chen, Jones, and Serban, formulated in [Reference Chen, Jones and SerbanChJoSe20, Conjecture 1.0.5, p. 3]. An analogous asymptotic behavior is expected to hold for arbitrary t and g in our given setting.
When
$g =1$
, in [Reference Murty, Murty and SaradhaMuMuSa88, Theorem, p. 254], Murty, Murty, and Saradhabuilt on the work of Serre [Reference SerreSe81, Section 8, pp. 188–191] and proved that, under the assumption of a Generalized Riemann Hypothesis (GRH),
$\pi _{A}(x, 0) \ll _{A} x^{\frac {3}{4}}$
and
$\displaystyle \pi _{A}(x, t) \ll _{A} \frac {x^{\frac {4}{5}}}{(\operatorname {log} x)^{\frac {1}{5}}}$
if
$t \neq 0$
. More recently, Zywina [Reference ZywinaZy15, Theorem 1.2, p. 236] obtained the improvements
$\displaystyle \pi _A(x, 0) \ll _{A} \frac {x^{\frac {3}{4}}}{(\operatorname {log} x)^{\frac {1}{2}}}$
and
$\displaystyle \pi _A(x, t) \ll _{A} \frac {x^{\frac {4}{5}}}{(\operatorname {log} x)^{\frac {3}{5}}}$
if
$t \neq 0$
. The bound
$\pi _A(x, 0) \ll _{A} x^{\frac {3}{4}}$
was also proven unconditionally using the interpretation of the condition
$a_{1, p}(A) = 0$
as p being a supersingular prime for the elliptic curve A (see [Reference ElkiesEl91, Theorem B, p. 131]). When
$t \neq 0$
, only the bound
$\displaystyle \pi _A(x, t) \ll _{A} \frac {x (\operatorname {log} \operatorname {log} x)^2}{(\operatorname {log} x)^2}$
is known unconditionally, thanks to the work of Thorner and Zaman [Reference Thorner and ZamanThZa17, Theorem 1.4, p. 4997], who built on prior results of Serre [Reference SerreSe81, Section 8, pp. 188–191], Wan [Reference WanWan90, Theorem 1.3, p. 250], and Murty [Reference MurtyMu97, Theorem 5.1, p. 302].
When
$g = 2$
and
$t \neq 0$
, in [Reference Chen, Jones and SerbanChJoSe20, Theorem 2.4.1, p. 14], Chen, Jones, and Serbanproved that, under the assumption of a GRH, we have
$\displaystyle \pi _A(x, t) \ll _{A} \frac {x^{\frac {13}{14}}}{(\operatorname {log} x)^{\frac {5}{7}}}$
; unconditionally, they proved that
$\displaystyle \pi _A(x, t) \ll _{A} \frac {x (\operatorname {log} \operatorname {log} x)^{\frac {2}{7}} (\operatorname {log} \operatorname {log} \operatorname {log} x)^{\frac {1}{7}} }{(\operatorname {log} x)^{\frac {8}{7}}}$
.
In this paper, we prove conditional upper bounds for
$\pi _A(x, t)$
that largely improve upon the conditional bound of Chen, Jones, and Serban when
$g = 2$
, and recover the conditional bound of Murty, Murty, Saradha, and Zywina when
$g=1$
.
Theorem 1 Let
$t \in \mathbb Z$
and let
$A/\mathbb Q$
be an abelian variety that is isogenous over
$\mathbb Q$
to a product of g elliptic curves defined over
$\mathbb Q$
, pairwise non-isogenous over
$\overline {\mathbb Q}$
and each without complex multiplication. Under the assumption of GRH for Dedekind zeta functions, we have that, for any sufficiently large x,
$$ \begin{align*}\pi_A(x, t) \ll_{A} \left\{ \begin{array}{cl} \displaystyle\frac{x^{1 - \frac{1}{3 g+1}}}{(\operatorname{log} x)^{1 - \frac{2}{3 g+1}}}, & \text{if }t = 0, \\[-5pt] \displaystyle\frac{x^{1 - \frac{1}{3 g + 2}}}{ (\operatorname{log} x)^{1 - \frac{2}{3 g + 2}} }, & \text{if }t \neq 0. \end{array} \right. \end{align*} $$
As an immediate application of Theorem 1, we obtain a result about the non-lacunarity of the sequence
$(a_{1, p}(A))_{p}$
, that is, about the non-zero values of
$a_{1, p}(A)$
. In fact, we obtain a result about any fixed value of
$a_{1, p}(A)$
.
Corollary 2 In the setting and under the assumptions of Theorem 1, we have that, as
$x \rightarrow \infty $
,
$$ \begin{align} \#\left\{p \leq x: p \nmid N_A, a_{1, p}(A) \neq t \right\} \sim \pi(x). \end{align} $$
As another quick application of Theorem 1, we obtain the existence of a density one set of primes p with large Frobenius traces
$a_{1, p}(A)$
. Namely, in the setting and under the assumptions of Theorem 1, we have that, for any
$\varepsilon> 0$
and as
$x \rightarrow \infty $
,
$$ \begin{align} \#\left\{p \leq x: p \nmid N_A, |a_{1, p}(A)|> p^{\frac{1}{3 g + 2} - \varepsilon} \right\} \sim \pi(x). \end{align} $$
Without applying Theorem 1 directly, but instead using a proof strategy similar to that of the proof of Theorem 1, we can improve upon (2) to show the following.
Theorem 3 Let
$A/\mathbb Q$
be an abelian variety that is isogenous over
$\mathbb Q$
to a product of g elliptic curves defined over
$\mathbb Q$
, pairwise non-isogenous over
$\overline {\mathbb Q}$
and each without complex multiplication. Under the assumption of GRH for Dedekind zeta functions, we have that, for any
$\varepsilon> 0$
and as
$x \rightarrow \infty $
,
$$ \begin{align*}\#\left\{p \leq x: p \nmid N_A, |a_{1, p}(A)|> p^{\frac{1}{3 g + 1} - \varepsilon} \right\} \sim \pi(x). \end{align*} $$
The above results may be re-written solely in terms of a g-tuple of elliptic curves
$E_1/\mathbb Q, \ldots , E_g/\mathbb Q$
, assumed to be pairwise non-isogenous over
$\overline {\mathbb Q}$
and each without complex multiplication, as follows. Denote by
$N_{E_1}, \ldots , N_{E_g}$
the conductors of
$E_1, \ldots , E_g$
, respectively. For each integer
$1 \leq i \leq g$
and for each prime
$p \nmid N_{E_i}$
, denote by
$a_p(E_i)$
the integer defined by
$|\overline {E}_i(\mathbb F_p)| =p + 1 - a_p(E_i)$
, where
$\overline {E}_i$
is the reduction of
$E_i$
modulo p. Taking
$A := E_1 \times \cdots \times E_g$
, we have that
$a_{1, p}(A) = - (a_p(E_1) + \cdots + a_p(E_g))$
for any prime
$p \nmid N_{E_1} \cdots N_{E_g}$
(to be explained in Section 6). Letting
$t \in \mathbb Z$
, equivalent formulations of Theorem 1, Corollary 2, and Theorem 3 are that, under the assumption of GRH, for any sufficiently large x, we have
$$ \begin{align*}&\#\left\{ p \leq x: p \kern1.5pt{\nmid}\kern1.5pt N_{E_1} \cdots N_{E_g}, a_p(E_1) + \cdots + a_p(E_g) \kern1pt{=}\kern1pt t \right\} \ll_{E_1, \ldots, E_g} \!\!\left\{\!\!\! \begin{array}{cl} \displaystyle\frac{x^{1 - \frac{1}{3 g+1}}}{(\operatorname{log} x)^{1 - \frac{2}{3 g+1}}}, & \textit{if}\ t \kern1.5pt{=}\kern1.5pt 0, \\ \\ \displaystyle\frac{x^{1 - \frac{1}{3 g + 2}}}{ (\operatorname{log} x)^{1 - \frac{2}{3 g + 2}} }, & \textit{if}\ t \kern1.5pt{\neq}\kern1.5pt 0, \end{array} \right. \end{align*} $$
and, for any
$\varepsilon> 0$
and as
$x \rightarrow \infty $
, we have
$$ \begin{align*} \#\left\{ p \leq x: p \nmid N_{E_1} \cdots N_{E_g}, a_p(E_1) + \cdots + a_p(E_g) \neq t \right\} \sim \pi(x), \end{align*} $$
$$ \begin{align*} \#\left\{ p \leq x: p \nmid N_{E_1} \cdots N_{E_g}, \left|a_p(E_1) + \cdots + a_p(E_g)\right|> p^{\frac{1}{3 g + 1} - \varepsilon} \right\} \sim \pi(x). \end{align*} $$
The general strategy of proving an upper bound for
$\pi _A(x, t)$
is to relax the equality
$a_{1, p}(A) = t$
to a congruence
$\operatorname {tr} \bar {\rho }_{A, m} \left (\left (\frac {\mathbb Q(A[m])/\mathbb Q}{p}\right )\right ) \equiv - t (\operatorname {mod} m)$
, where m is an arbitrary integer coprime to p,
$\bar {\rho }_{A, m}$
is the Galois representation associated to the m-division field
$\mathbb Q(A[m])$
of A, and
$\left (\frac {\mathbb Q(A[m])/\mathbb Q}{p}\right )$
is the Artin symbol at p in the Galois group
$\operatorname {Gal}(\mathbb Q(A[m])/\mathbb Q)$
. An upper bound for
$\pi _A(x, t)$
may be derived by interpreting this congruence as a Chebotarev condition in the finite Galois extension
$\mathbb Q(A[m])/\mathbb Q$
and by invoking an effective version of the Chebotarev Density Theorem.
Inspired by [Reference Murty, Murty and SaradhaMuMuSa88], we pursue a refinement of this general strategy and relax the equality
$a_{1, p}(A) = t$
to a Chebotarev condition that holds in a suitably chosen proper subextension of
$\mathbb Q(A[m])/\mathbb Q$
in which Artin’s Holomorphy Conjecture is known to hold. When
$g \geq 2$
, we unravel a few such possible subextensions and carry out the refined strategy in the subextension that leads to the best result, in particular, the subextension that leads to a generalization of the best upper bounds known for
$g=1$
.
When studying the Frobenius traces of an elliptic curve, it is natural to place a special focus on elliptic curves
$A/\mathbb Q$
having the property that
$\operatorname {End}_{\overline {\mathbb Q}}(A) \simeq \mathbb Z$
, since this case is regarded as generic. When studying the Frobenius traces of an abelian variety A of higher dimension, it is then natural to place an initial focus on the following two cases: that of an abelian variety
$A/\mathbb Q$
with
$\operatorname {End}_{\overline {\mathbb Q}}(A) \simeq \mathbb Z$
, as pursued in [Reference Cojocaru, Davis, Silverberg and StangeCoDaSiSt17] and in an upcoming paper by the present authors, and that of an abelian variety that is
$\mathbb Q$
-isogenous to a product of g elliptic curves defined over
$\mathbb Q$
, pairwise non-isogenous over
$\overline {\mathbb Q}$
and each without complex multiplication, as pursued in the present paper.
Note that, when
$A/\mathbb Q$
is
$\mathbb Q$
-isogenous to a product of g elliptic curves defined over
$\mathbb Q$
that are pairwise isogenous over
$\overline {\mathbb Q}$
, the study of
$\pi _A(x, t)$
for
$g \geq 2$
reduces to the study of
$\pi _A(x, t)$
for
$g = 1$
. Other cases remain to be pursued separately.
Finally, let us note that different variations of questions inspired by the Lang–Trotter Conjecture have been investigated in the setting of pairs of elliptic curves in works such as [Reference Akbari, David and JuricevicAkDaJu04, Reference Akbary and ParkAkPa19, Reference Fouvry and MurtyFoMu95].
General notation. Throughout the paper, we use the following notation.
$\bullet $
For a set S, we denote its cardinality by
$|S|$
or
$\# S$
.
$\bullet{\kern-4pt} $
Given suitably defined real functions
$h_1, h_2$
, we say that
$h_1 = \operatorname {o}(h_2)$
if
$\displaystyle \lim _{x \rightarrow \infty } \frac {h_1(x)}{h_2(x)} = 0$
; we say that
$h_1 = \operatorname {O}(h_2)$
or, equivalently, that
$h_1 \ll h_2$
or
$h_2 \gg h_1$
, if
$h_2$
is positive valued and there exists a positive constant c such that
$|h_1(x)| \leq c \ h_2(x)$
for all x in the domain of
$h_1$
and
$h_2$
; we say that
$h_1 \asymp h_2$
if
$h_1$
,
$h_2$
are positive valued and
$h_1 \ll h_2 \ll h_1$
; we say that
$h_1 = \operatorname {O}_D(h_2)$
or, equivalently, that
$h_1 \ll _D h_2$
or
$h_2 \gg _D h_1$
, if
$h_1 = \operatorname {O}(h_2)$
and the implied
$\operatorname {O}$
-constant c depends on priorly given data D; we say that
$h_1 \asymp _D h_2$
if the implied constant c in at least one of the
$\ll $
-bounds
$h_1 \ll h_2 \ll h_1$
depends on priorly given data D; finally, we say that
$h_1 \sim h_2$
if
$\displaystyle \lim _{x \rightarrow \infty } \frac {h_1(x)}{h_2(x)} = 1$
.
$\bullet $
We use the letters p and
$\ell $
to denote rational primes. We use
$\pi (x)$
to denote the number of primes
$p \leq x$
, and
$\operatorname {li} x$
to denote the logarithmic integral
$\displaystyle \int _{2}^x \frac {1}{\operatorname {log} t} \ d t$
. Note that
$\displaystyle \operatorname {li} x \sim \frac {x}{\operatorname {log} x}$
and recall that the Prime Number Theorem asserts that
$\pi (x) \sim \operatorname {li} x$
.
$\bullet $
Given a number field K, we denote by
${{\cal O}}_K$
its ring of integers; we denote by
$\overline {K}$
a fixed algebraic closure of K; we denote by
$\operatorname {Gal}(\overline {K}/K)$
the absolute Galois group of K; we denote by
${\sum }_K$
the set of non-zero prime ideals of K; we denote by
$[K:\mathbb Q]$
the degree of K over
$\mathbb Q$
; we denote by
$d_K \in \mathbb Z$
the discriminant of an integral basis of
${{\cal O}}_K$
and by
$\operatorname {disc}(K/\mathbb Q) = \mathbb Z d_K \unlhd \mathbb Z$
the discriminant ideal of
$K/\mathbb Q$
. For a prime ideal
$\mathfrak {p} \in {\sum }_K$
, we denote by
$N_{K/\mathbb Q}(\mathfrak {p})$
its norm in
$K/\mathbb Q$
and by
$\operatorname {Frob}_{\mathfrak {p}} \in \operatorname {Gal}(\overline {K}/K)$
its Frobenius class. We say that K satisfies the GRH if the Dedekind zeta function
$\zeta _K$
of K has the property that, for any
$\rho \in \mathbb C$
with
$0 \leq \operatorname {Re} \rho \leq 1$
and
$\zeta _K(\rho ) = 0$
, we have
$\operatorname {Re}(\rho ) = \frac {1}{2}$
. When
$K=\mathbb Q$
, the Dedekind zeta function is the Riemann zeta function, in which case GRH is typically referred to as RH.
$\bullet $
For a non-zero unitary commutative ring R, we denote by
$R^{\times }$
its group of multiplicative units. For an integer
$n \geq 1$
, we denote by
$I_n$
the identity
$n \times n$
matrix with entries in R. For an arbitrary
$n \times n$
matrix M with entries in R, we denote by
$\operatorname {tr} M$
and
$\operatorname {det} M$
its trace and determinant. We define the general linear group
$\operatorname {GL}_{n}(R)$
as the collection of
$n \times n$
matrices M with entries in R and with
$\operatorname {det} M \in R^{\times }$
.
$\bullet $
For a positive integer m, we denote by
$\mathbb Z/m \mathbb Z$
the ring of integers modulo m. For an arbitrary prime
$\ell $
, we denote by
$\mathbb Z_{\ell }$
the ring of
$\ell $
-adic integers. We set
$\hat {\mathbb Z} := \displaystyle \lim _{\leftarrow \atop m} \mathbb Z/m \mathbb Z$
and note that there is a ring isomorphism
$\hat {\mathbb Z} \simeq \displaystyle \prod _{\ell } \mathbb Z_{\ell }$
.
2 The Chebotarev Density Theorem
The proofs of Theorems 1 and 3 are based on multi-step applications of different effective versions of the Chebotarev Density Theorem, which we now recall.
Let
$L/K$
be a Galois extension of number fields, with
$G:= \operatorname {Gal}(L/K)$
, and let
${{\cal C}} \subseteq G$
be a union of conjugacy classes of G; throughout the paper, we will assume
${{\cal C}}\neq \emptyset $
. We denote by
$[L:K]$
the degree of L over K and by
$\operatorname {disc}(L/K) \unlhd {{\cal O}}_K$
the discriminant ideal of
$L/K$
. For each
$\mathfrak {p} \in {\sum }_K$
, we denote by
$\wp \in {\sum }_L$
an arbitrary prime ideal with
$\wp \mid \mathfrak {p}$
, by
${{\cal D}}_{\wp }$
the decomposition group of
$\wp $
in
$L/K$
, and by
${{\cal I}}_{\wp }$
the inertia group of
$\wp $
in
$L/K$
. We denote by
$ \left (\frac {L/K}{\wp }\right ) \in {{\cal D}}_{\wp }/{{\cal I}}_{\wp }$
the Artin symbol associated to
$\wp $
, and by
$\left (\frac {L/K}{\mathfrak {p}}\right ) := \left \{\gamma \in G: \exists \wp \mid \mathfrak {p} \text { such that } \gamma \in {{\cal D}}_{\wp } \ \text {and} \ \gamma {{\cal I}}_{\wp } =\left (\frac {L/K}{\wp }\right ) \right \}$
the Artin symbol associated to
$\mathfrak {p}$
in the extension
$L/K$
. Notice that, for any integer
$m \geq 1$
, the set
$\left (\frac {L/K}{\mathfrak {p}}\right )^m := \left \{ \gamma ^m: \gamma \in \left (\frac {L/K}{\mathfrak {p}}\right )\right \} \subseteq G$
is invariant under conjugation by elements of G. We set
$$ \begin{align*}{{\cal P}}(L/K) := \{p: \: \ \exists \ \mathfrak{p} \in {\sum}_{K} \ \text{such that} \ \mathfrak{p} \mid p \ \text{and} \ \mathfrak{p} \mid \operatorname{disc}(L/K)\}, \end{align*} $$
$$ \begin{align*}M(L/K) := 2 [L:K] |d_K|^{\frac{1}{[K:\mathbb Q]}} \displaystyle\prod_{p \in {{\cal P}}(L/K)} p, \end{align*} $$
and recall that
$$ \begin{align} \operatorname{log} \left|N_{K/\mathbb Q} (\operatorname{disc} (L/K))\right| &\leq ([L : \mathbb Q] - [K : \mathbb Q]) \left( \displaystyle\sum_{p \in {{\cal P}}(L/K)} \operatorname{log} p \right) + [L : \mathbb Q] \operatorname{log} [L : K] \end{align} $$
(see [Reference SerreSe81, Proposition 5, p. 129]).
The extension
$L/K$
is said to satisfy the Artin Holomorphy Conjecture (AHC) if, for any irreducible character
$\chi : G \longrightarrow \mathbb C$
, the Artin L-function
$L(s, \chi )$
extends to a function that is analytic on
$\mathbb C$
when
$\chi \neq 1$
and that is analytic on
$\mathbb C \backslash \{1\}$
when
$\chi = 1$
. It is known that AHC holds if
$\operatorname {Gal}(L/K)$
is abelian [Reference ArtinAr37].
We denote by
$\delta _{{\cal C}} : G \longrightarrow \{0, 1\}$
the characteristic function on
${{\cal C}}$
. For any prime ideal
$\mathfrak {p} \in {\sum }_K$
, we choose an arbitrary prime ideal
$\wp \in {\sum }_L$
with
$\wp \mid \mathfrak {p}$
, and then, for any integer
$m \geq 1$
, we define
$$ \begin{align*}\delta_{{\cal C}}\left(\left(\frac{L/K}{\mathfrak{p}}\right)^m\right) := \frac{1}{|{{\cal I}}_{\wp}|} \displaystyle\sum_{ \gamma \in {{\cal D}}_{\wp} \atop{ \gamma {{\cal I}}_{\wp} = \left(\frac{L/K}{\wp}\right)^m } } \delta_{{\cal C}}(\gamma). \end{align*} $$
Note that this definition is independent of the choice of
$\wp $
. For an arbitrary real number
$x> 0$
, we define
$$ \begin{align*} \pi_{{\cal C}}(x, L/K) &:= \displaystyle\sum_{ \mathfrak{p} \in {\sum}_K \atop{ \mathfrak{p} \nmid \operatorname{disc}(L/K) \atop{ N_{K/\mathbb Q}(\mathfrak{p})\leq x } } } \delta_{{\cal C}}\left( \left(\frac{L/K}{\mathfrak{p}}\right) \right), \\ \widetilde{\pi}_{{\cal C}}(x, L/K) &:= \displaystyle\sum_{m \geq 1} \frac{1}{m} \displaystyle\sum_{ \mathfrak{p} \in {\sum}_K \atop{ N_{K/\mathbb Q}(\mathfrak{p}^m) \leq x } } \delta_{{\cal C}}\left( \left(\frac{L/K}{\mathfrak{p}}\right)^m \right). \end{align*} $$
For simplicity of notation, we use
$\pi _1(x, L/K)$
and
$\widetilde {\pi }_1(x, L/K)$
to denote
$\pi _{\{\operatorname {id}_L\}}(x, L/K)$
and
$\widetilde {\pi }_{\{\operatorname {id}_L\}}(x, L/K)$
, respectively.
The Chebotarev Density Theorem states that, as
$x \rightarrow \infty $
,
$$ \begin{align} \pi_{{\cal C}}(x, L/K) \sim \frac{|{{\cal C}}|}{|G|} \operatorname{li} x. \end{align} $$
Since the growth in x of the counting function
$\widetilde {\pi }_{{\cal C}}(x, L/K)$
is closely related to that of
$\pi _{{\cal C}}(x, L/K)$
thanks to the bound
$$ \begin{align} \left| \widetilde{\pi}_{{\cal C}}(x, L/K) - \pi_{{\cal C}}(x, L/K) \right| \ll [K:\mathbb Q] \left( \frac{x^{\frac{1}{2}}}{\operatorname{log} x} + \operatorname{log} M(L/K) \right) \end{align} $$
(see [Reference SerreSe81, Proposition 7, p. 138]), asymptotic (4) is equivalent to
$$ \begin{align} \widetilde{\pi}_{{\cal C}}(x, L/K) \sim \frac{|{{\cal C}}|}{|G|} \operatorname{li} x. \end{align} $$
The advantage of considering
$\widetilde {\pi }_{{\cal C}}(x, L/K)$
over
$\pi _{{\cal C}}(x, L/K)$
is that the former satisfies the following two functorial properties.
Proposition 4 Let
$L/K$
be a Galois extension of number fields with
$G:= \operatorname {Gal}(L/K)$
and let
${{\cal C}} \subseteq G$
be a union of conjugacy classes of G.
-
(i) Let
$H \leq G$
be a subgroup of G such that every element of
${{\cal C}}$
is conjugate to some element of H. Denote by
$L^H$
the subfield of L fixed by H. Then, for any
$x> 0$
,
$$ \begin{align*}\widetilde{\pi}_{{\cal C}}(x, L/K) \leq \widetilde{\pi}_{{{\cal C}} \cap H}(x, L/L^H). \end{align*} $$
-
(ii) Let
$N \unlhd G$
be a normal subgroup of G such that
$N {{\cal C}} \subseteq {{\cal C}}$
. Denote by
$L^N$
the subfield of L fixed by N. Denote by
$\widehat {{\cal C}} $
the image of
${{\cal C}}$
in the quotient group
$G/N$
, viewed as
$\operatorname {Gal}(L^N/K)$
. Then, for any
$x> 0$
,
$$ \begin{align*}\widetilde{\pi}_{{\cal C}}(x, L/K) = \widetilde{\pi}_{\widehat{{\cal C}}}(x, L^N/K). \end{align*} $$
Proof See [Reference SerreSe81, Proposition 8, pp. 139–140].▪
Corollary 5 Let
$L/K$
be a Galois extension of number fields with
$G:= \operatorname {Gal}(L/K)$
, and let
${{\cal C}} \subseteq G$
be a union of conjugacy classes of G. Let
$H \leq G$
be a subgroup of G such that every element of
${{\cal C}}$
is conjugate to some element of H. Let
$N \unlhd H$
be a normal subgroup of H such that
$N ({{\cal C}} \cap H)\subseteq {{\cal C}} \cap H$
. Denote by
$\widehat {{\cal C} \cap H} $
the image of
${{\cal C}} \cap H$
in the quotient group
$H/N$
, viewed as
$\operatorname {Gal}(L^N/L^H)$
. Then, for any
$x> 0$
,
$$ \begin{align*}\widetilde{\pi}_{{\cal C}}(x, L/K) \leq \widetilde{\pi}_{\widehat{{\cal C} \cap H}}\left(x, L^N/L^H\right). \end{align*} $$
Consequently, for any sufficiently large x,
$$ \begin{align} \pi_{{\cal C}}(x, L/K) &\ll \pi_{\widehat{{\cal C} \cap H}}\left(x, L^N/L^H\right)\nonumber \\ & + [K:\mathbb Q] \left( \frac{x^{\frac{1}{2}}}{\operatorname{log} x} + \operatorname{log} M(L/K) \right) + [L^H:\mathbb Q] \left( \frac{x^{\frac{1}{2}}}{\operatorname{log} x} + \operatorname{log} M(L^N/L^H) \right). \end{align} $$
In spite of its strength, asymptotic formula (4) for
$\pi _{{{\cal C}}}(x, L/K)$
does not suffice for our purposes. Instead, the proofs of our main results will require an effective version with an explicit error term, such as the following conditional result.
Theorem 6 Let
$L/K$
be a Galois extension of number fields, with
$G:= \operatorname {Gal}(L/K)$
, and let
${{\cal C}} \subseteq G$
be a union of conjugacy classes of G. Assume that GRH holds for the number field L. Then there exists an absolute constant
$c> 0$
such that, for any
$x>2$
,
$$ \begin{align*} \left| \pi_{{\cal C}}(x, L/K) - \frac{|{\cal C}|}{|G|} \pi(x) \right| \leq c \frac{|{\cal C}|}{|G|} x^{\frac{1}{2}} \left( \operatorname{log} |d_L| + [L : \mathbb Q] \operatorname{log} x \right). \end{align*} $$
Proof The original reference is [Reference Lagarias, Odlyzko and FröhlichLaOd77]. For this variation, see [Reference SerreSe81, Théorème 4, p. 133].▪
The proofs of our main results will also use the following conditional upper bound for
$\pi _{{\cal C}}(x, L/K)$
.
Theorem 7 Let
$L/K$
be a Galois extension of number fields with
$G:= \operatorname {Gal}(L/K)$
, and let
${{\cal C}} \subseteq G$
be a union of conjugacy classes of G. Assume that GRH holds for the number field L and that AHC holds for the number field extension
$L/K$
. Then, for any sufficiently large x,
$$ \begin{align*}\pi_{{\cal C}}(x, L/K) \ll \frac{|{\cal C}|}{|G|}\cdot \frac{x}{\operatorname{log} x} + |{\cal C}|^{\frac{1}{2}} [K:\mathbb Q] \left(\operatorname{log} M(L/K)\right) { \cdot } \frac{x^{\frac{1}{2}}}{\operatorname{log} x}. \end{align*} $$
Proof See [Reference ZywinaZy15, Theorem 2.3, p. 240].▪
Corollary 8 Let
$L/K$
be a Galois extension of number fields with
$G:= \operatorname {Gal}(L/K)$
, and let
${{\cal C}} \subseteq G$
be a union of conjugacy classes of G. Let
$H \leq G$
be a subgroup of G such that every element of
${{\cal C}}$
is conjugate to some element of H. Let
$N \unlhd H$
be a normal subgroup of H such that
$N ({{\cal C}} \cap H)\subseteq {{\cal C}} \cap H$
. Denote by
$\widehat {{\cal C} \cap H} $
the image of
${{\cal C}} \cap H$
in the quotient group
$H/N$
, viewed as
$\operatorname {Gal}(L^N/L^H)$
. Assume that the group
$H/N$
is abelian and that GRH holds for
$L^N$
. Then, for any sufficiently large x,
$$ \begin{align*} \pi_{{\cal C}}(x, L/K) &\ll \frac{\left|\widehat{{\cal C} \cap H}\right| \cdot |N|}{|H|} \cdot \frac{x}{\operatorname{log} x} \\ &+ \left|\widehat{{{\cal C}} \cap H}\right|{}^{\frac{1}{2}} [L^H :\mathbb Q] \frac{x^{\frac{1}{2}}}{\operatorname{log} x} \operatorname{log} M(L^N/L^H) \\ &+ [K:\mathbb Q] \left(\frac{x^{\frac{1}{2}}}{\operatorname{log} x} + \operatorname{log} M(L/K)\right) + [L^H:\mathbb Q] \left(\frac{x^{\frac{1}{2}}}{\operatorname{log} x} + \operatorname{log} M(L^N/L^H)\right). \end{align*} $$
3 An application of the effective version of the Chebotarev Density Theorem
The proofs of Theorems 1 and 3 will make use of the following application of Theorem 6.
Lemma 9 Let
${{\cal S}}$
be a non-empty set of rational primes, let
$(K_p)_{p \in {{\cal S}}}$
be a family of finite Galois extensions of
$\mathbb Q$
, and let
$({\mathcal {C}}_p)_{p\in {\cal S}}$
be a family of non-empty sets such that each
${\mathcal {C}}_p$
is a union of conjugacy classes of
$\operatorname {Gal}(K_p/\mathbb Q)$
. Assume that there exist an absolute constant
$c_1> 0$
and a function
$f: \mathbb R \to (0, \infty )$
such that
$$ \begin{align} \displaystyle [K_p:\mathbb Q] \leq c_1 \quad \text{for any sufficiently large} \ p, \end{align} $$
$$ \begin{align} \displaystyle \operatorname{log} |d_{K_p}| \leq f(z) \quad \text{for any sufficiently large } z \text{ and all } p\leq z. \end{align} $$
For each
$x>2$
, let
$y = y(x)> 2$
,
$u =u(x)> 2$
be such that
$$ \begin{align} u \leq y, \end{align} $$
and assume that, for any
$\varepsilon> 0$
,
$$ \begin{align} u \geq c_2(\varepsilon) y^{\frac{1}{2}} (\operatorname{log} y)^{2 + \varepsilon} \ \text{for some constant} \ c_2(\varepsilon)> 0 \end{align} $$
and
$$ \begin{align} \displaystyle\lim_{x \rightarrow \infty} \frac{f(x)}{(\operatorname{log} y)^{1 + \varepsilon}} = 0. \end{align} $$
Assume GRH for Dedekind zeta functions. Then, for any
$\varepsilon> 0$
, there exists a constant
$c(\varepsilon )> 0$
such that, for any sufficiently large x,
$$ \begin{align} & \#\left\{p \leq x: p \in {{\cal S}}\right\} \leq c(\varepsilon) \displaystyle\max_{ y \leq \ell \leq y + u } \#\left\{p \leq x: p \in {{\cal S}}, \ell \nmid d_{K_p}, \left(\frac{K_p/\mathbb Q}{\ell} \right)\subseteq {\mathcal{C}}_p \right\}. \end{align} $$
Proof The proof follows the strategy of [Reference Murty, Murty and SaradhaMuMuSa88, Lemma 4.4, p. 269], adapted to our general setting. We start by fixing
$x> 2$
,
$y = y(x)> 2$
,
$u = u(x)> 2$
, and
$\varepsilon> 0$
such that (10)–(12) hold. Then, we observe that
$$ \begin{align} & (\pi(y + u) - \pi(y)) \displaystyle\max_{y \leq \ell \leq y + u} \#\left\{p \leq x: p \in {{\cal S}}, \ell \nmid d_{K_p}, \left(\frac{K_p/\mathbb Q}{\ell} \right)\subseteq {\mathcal{C}}_p \right\} \\ &\geq \displaystyle\sum_{y \leq \ell \leq y + u} \#\left\{p \leq x: p \in {{\cal S}}, \ell \nmid d_{K_p}, \left(\frac{K_p/\mathbb Q}{\ell} \right)\subseteq {\mathcal{C}}_p \right\} \nonumber \\ &= \displaystyle\sum_{ p \leq x \atop{ p \in {{\cal S}} } } \#\left\{y \leq \ell \leq y + u: \ell \nmid d_{K_p}, \left(\frac{K_p/\mathbb Q}{\ell} \right)\subseteq {\mathcal{C}}_p \right\} \nonumber \\ &= \displaystyle\sum_{ p \leq x \atop{ p \in {{\cal S}} } } \left(\pi_{{\mathcal{C}}_p}(y+u, K_p/\mathbb Q) - \pi_{{\mathcal{C}}_p}(y, K_p/\mathbb Q)\right). \nonumber \end{align} $$
To estimate the above difference, we apply Theorem 6 under GRH and deduce that
$$ \begin{align} &\displaystyle\sum_{ p \leq x \atop{ p \in {{\cal S}} } } \left(\pi_{{\mathcal{C}}_p}(y+u, K_p/\mathbb Q) - \pi_{{\mathcal{C}}_p}(y, K_p/\mathbb Q)\right) \\ =& \displaystyle\sum_{ p \leq x \atop{p \in {{\cal S}}} } \frac{|{\mathcal{C}}_p|}{[K_p:\mathbb Q]} (\pi(y + u) - \pi(y)) + \displaystyle\sum_{ p \leq x \atop{p \in {{\cal S}}} } \left( E_1(y, u, {\mathcal{C}}_p, K_p) + E_2(y, u, {\mathcal{C}}_p, K_p) \right) \nonumber \end{align} $$
for some real-valued functions
$E_1(y, u, {\mathcal {C}}_p, K_p)$
,
$E_2(y, u,{\mathcal {C}}_p, K_p)$
, which depend on y, u,
${\mathcal {C}}_p$
, and
$K_p$
, and for which there exist absolute constants
$c_3> 0$
and
$c_4> 0$
such that
$$ \begin{align*} |E_1(y, u,{\mathcal{C}}_p, K_p)| \leq c_3 (y + u)^{\frac{1}{2}} \left( \frac{|{\mathcal{C}}_p| \operatorname{log} |d_{K_p}|}{[K_p : \mathbb Q]} + |{\mathcal{C}}_p| \operatorname{log} (y + u) \right), \end{align*} $$
$$ \begin{align*} |E_2(y, u, {\mathcal{C}}_p, K_p)| \leq c_4 y^{\frac{1}{2}} \left( \frac{|{\mathcal{C}}_p| \operatorname{log} |d_{K_p}|}{[K_p : \mathbb Q]} + |{\mathcal{C}}_p| \operatorname{log} y \right). \end{align*} $$
Recalling assumptions (8) and (9), we obtain the upper bound
$$ \begin{align} &\left| \displaystyle\sum_{ p \leq x \atop{p \in {{\cal S}}} } \left( E_1(y, u, {\mathcal{C}}_p, K_p) + E_2(y, u, {\mathcal{C}}_p, K_p) \right) \right| \nonumber\\&\quad\leq c_5 (y + u)^{\frac{1}{2}}(f(x) + \operatorname{log}(y+u)) \ \#\left\{p \leq x: p \in {{\cal S}}\right\} \end{align} $$
for some absolute constant
$c_5> 0$
.
Thanks to (11) and the assumption of GRH (specifically, RH in this case), there exists some constant
$c_6(\varepsilon )> 0$
such that
$$ \begin{align} \pi(y + u) - \pi(y) \geq c_6(\varepsilon) \frac{u}{\operatorname{log} u}. \end{align} $$
In particular,
$\pi (y + u) - \pi (y)> 0$
.
Putting together (14)–(17) and dividing the resulting inequality by
$\pi (y + u) - \pi (y)$
, we obtain that
$$ \begin{align} & \qquad\displaystyle\max_{y \leq \ell \leq y + u} \#\left\{p \leq x: p \in {{\cal S}}, \ell \nmid d_{K_p}, \left(\frac{K_p/\mathbb Q}{\ell} \right)\subseteq {\mathcal{C}}_p\right\} \nonumber \\ & \qquad\quad \geq\displaystyle\sum_{ p \leq x \atop{p \in {{\cal S}}} } \frac{|{\mathcal{C}}_p|}{[K_p:\mathbb Q]} + \operatorname{O}_{\varepsilon} \left( \frac{\operatorname{log} u}{u} (y + u)^{\frac{1}{2}} (f(x) + \operatorname{log} (y + u)) \ \#\{p \leq x: p \in {{\cal S}}\} \right). \end{align} $$
Invoking assumptions (10) and (11), we deduce that the above
$\operatorname {O}_{\varepsilon }$
-term becomes
$$ \begin{align*}\operatorname{O}_{\varepsilon} \left( \frac{f(x) + \operatorname{log} y}{(\operatorname{log} y)^{1 + \varepsilon}} \ \#\{p \leq x: p \in {{\cal S}}\} \right). \end{align*} $$
Invoking assumption (12), we deduce that the latter
$\operatorname {O}_{\varepsilon }$
-term is
$\operatorname {o}(\#\{p \leq x: p \in {{\cal S}}\})$
. Finally, recalling (8) and that each
${\mathcal {C}}_p$
is non-empty, we deduce that
$$ \begin{align*} \displaystyle\sum_{ p \leq x \atop{p \in {{\cal S}}} } \frac{|{\mathcal{C}}_p|}{[K_p:\mathbb Q]} \geq \frac{1}{c_1} \ \#\{p \leq x: p \in {{\cal S}}\}. \end{align*} $$
Then (18) gives
$$ \begin{align*} \displaystyle\max_{y \leq \ell \leq y + u} \#\left\{p \leq x: p \in {{\cal S}}, \ell \nmid d_{K_p}, \left(\frac{K_p/\mathbb Q}{\ell} \right)\subseteq {\mathcal{C}}_p\right\} \gg_{\varepsilon} \#\{p \leq x: p \in {{\cal S}}\}, \end{align*} $$
as desired.▪
Remark 10 In the proof of Lemma 9, instead of assumptions (8) and (9), it suffices to make the weaker assumptions that there exist absolute constants
$c^{\prime }_1, c^{\prime }_2, c^{\prime }_3> 0$
such that, for any sufficiently large z,
$$ \begin{align*} \displaystyle\sum_{p \leq z \atop{ p \in {{\cal S}}}} \frac{\left| {\mathcal{C}}_p \right|}{[K_p : \mathbb Q]} \geq c^{\prime}_1 \ \#\{p \leq z: p \in {{\cal S}}\}, \end{align*} $$
$$ \begin{align*} \displaystyle\sum_{p \leq z \atop{ p \in {{\cal S}}}} \frac{\left| {\mathcal{C}}_p \right| \operatorname{log} |d_{K_p}|}{[K_p : \mathbb Q]} \leq c^{\prime}_2 f(z) \ \#\{p \leq z: p \in {{\cal S}}\}, \end{align*} $$
$$ \begin{align*} \displaystyle\sum_{p \leq z \atop{ p \in {{\cal S}}}} \left|{\mathcal{C}}_p\right| \leq c^{\prime}_3 \ \#\{p \leq z: p \in {{\cal S}}\}. \end{align*} $$
4 Subgroups of
$\operatorname {GL}_{2}(\mathbb Z/\ell \mathbb Z)^g$
Our main contribution to generalizing the method of Murty, Murty, and Saradha, used in [Reference Murty, Murty and SaradhaMuMuSa88], to the case of a product of g non-isogenous elliptic curves without complex multiplication consists of unravelling suitable Galois extensions
$L/K$
of number fields with
$\operatorname {Gal}(L/K) \leq \operatorname {GL}_{2}(\mathbb Z/\ell \mathbb Z)^g$
for some well-chosen prime
$\ell $
, together with suitable conjugacy classes
${\cal C} \subseteq \operatorname {Gal}(L/K)$
, so that we can invoke Corollary 8. With this goal in mind, we devote Section 4 to investigations of particular subgroups of
$\operatorname {GL}_{2}(\mathbb Z/\ell \mathbb Z)^g$
.
For a fixed rational prime
$\ell $
, our main focus will be on the subgroup
$$ \begin{align} G(\ell) := \{(M_1, \ldots, M_g)\in \mathbb G(\ell): \operatorname{det} M_1 = \cdots = \operatorname{det} M_g\} \end{align} $$
of the product group
$$ \begin{align*}\mathbb G(\ell) :=\operatorname{GL}_2(\ell)^g, \end{align*} $$
where
$$ \begin{align*}\operatorname{GL}_2(\ell) := \operatorname{GL}_2(\mathbb Z/\ell\mathbb Z).\end{align*} $$
Denoting by
${{\cal G}}_m(\ell )$
the multiplicative group
$(\mathbb Z/\ell \mathbb Z)^{\times }$
and by
${{\cal G}}_a(\ell )$
the additive group
$\mathbb Z/\ell \mathbb Z$
, we set
$ \mathcal {B}_{\operatorname {GL}_2}(\ell ) := \left \{ \begin {pmatrix} a_1 & b_1\\ 0 & a_2 \end {pmatrix} \in \operatorname {GL}_2(\ell ) : a_1, a_2 \in \mathcal {G}_m(\ell ), b_1\in \mathcal {G}_a(\ell ) \right \}, $
$ \mathcal {U}_{\operatorname {GL}_2}(\ell ) := \left \{ \begin {pmatrix} 1 & b\\ 0 & 1 \end {pmatrix} \in \operatorname {GL}_2(\ell ) : b\in \mathcal {G}_a(\ell ) \right \}, $
$ \mathcal {T}_{\operatorname {GL}_2}(\ell ) := \left \{ \begin {pmatrix} a_1 & 0\\ 0 & a_2 \end {pmatrix} \in \operatorname {GL}_2(\ell ) : a_1, a_2 \in \mathcal {G}_m(\ell ) \right \}, $
$ B(\ell ) := \{(M_1, \ldots , M_g)\in \mathcal {B}_{\operatorname {GL}_2}(\ell )^g: \operatorname {det} M_1 = \cdots = \operatorname {det} M_g\}, $
$ U(\ell ) := \mathcal {U}_{\operatorname {GL}_2}(\ell )^g, $
$ U'(\ell ) := (\mathbb Z/\ell \mathbb Z)^{\times }\cdot U(\ell ), $
$ T(\ell ) := \{(M_1, \ldots , M_g)\in \mathcal {T}_{\operatorname {GL}_2}(\ell )^g: \operatorname {det} M_1 = \cdots = \operatorname {det} M_g\}. $
The following lemmas will be crucial in the proof of our main theorems.
Lemma 11 For any prime
$\ell $
, we have that
$U(\ell )$
and
$U'(\ell )$
are normal subgroups of
$B(\ell )$
, and that
$B(\ell )/U(\ell )$
are
$B(\ell )/U'(\ell )$
are abelian groups.
Proof Observe that the subgroup
$\mathcal {U}_{\operatorname {GL}_2}(\ell )$
is normal in
$\mathcal {B}_{\operatorname {GL}_2}(\ell )$
. The quotient
$\mathcal {B}_{\operatorname {GL}_2}(\ell )/\mathcal {U}_{\operatorname {GL}_2}(\ell )$
is abelian, since it satisfies a group isomorphism
$\mathcal {B}_{\operatorname {GL}_2}(\ell )/\mathcal {U}_{\operatorname {GL}_2}(\ell ) \simeq \mathcal {T}_{\operatorname {GL}_2}(\ell )$
. Consequently, the subgroup
$U(\ell )$
is normal in
$\mathcal {B}_{\operatorname {GL}_2}(\ell )^g$
, with
$ \mathcal {B}_{\operatorname {GL}_2}(\ell )^g/U(\ell ) $
an abelian group. By the inclusion of subgroups
$ U(\ell ) \subseteq U'(\ell ) \subseteq B(\ell ) \subseteq \mathcal {B}_{\operatorname {GL}_2}(\ell )^g, $
we deduce that both
$U(\ell )$
and
$U'(\ell )$
are normal subgroups in
$B(\ell )$
and that both
$B(\ell )/U(\ell )$
and
$B(\ell )/U'(\ell )$
are abelian.▪
Lemma 12 For any prime
$\ell $
, we have
$$ \begin{align*} |\operatorname{GL}_2(\ell)| &= (\ell - 1) \ell (\ell^2 - 1), \\ |\mathbb G(\ell)| &= (\ell - 1)^g \ell^g (\ell^2 - 1)^g, \\ |\mathcal{B}_{\operatorname{GL}_2}(\ell)^g| &= (\ell - 1)^{2 g} \ell^{ g}, \\ |G(\ell)| &= (\ell - 1) \ell^{g} (\ell^2 - 1)^{g}, \\ |B(\ell)| &= (\ell-1)^{g + 1} \ell^g, \\ |U(\ell)| &= \ell^{g}, \\ \left|U'(\ell)\right| &= (\ell - 1) \ell^g, \\ |T(\ell)| &= (\ell-1)^{g + 1}. \end{align*} $$
Proof The formula for the order of
$\operatorname {GL}_2(\ell )$
is well known and easy to derive. The formulae for the orders of
$\mathbb G(\ell )$
,
$\mathcal {B}_{\operatorname {GL}_2}(\ell )^g$
,
$U(\ell )$
,
$U'(\ell )$
, and
$T(\ell )$
are clear from the definitions of the groups. To find the orders of
$G(\ell )$
and
$B(\ell )$
, observe that there are short exact sequences of finite groups
$$ \begin{align*}1 \to G(\ell) \to \mathbb G(\ell) \xrightarrow{\operatorname{det}_{1, \ldots, g-1}} \mathcal{G}_m(\ell)^{g-1} \to 1, \end{align*} $$
$$ \begin{align*}1 \to B(\ell) \to \mathcal{B}_{\operatorname{GL}_2}(\ell)^g \xrightarrow{\operatorname{det}_{1, \ldots, g-1}} \mathcal{G}_m(\ell)^{g-1} \to 1, \end{align*} $$
where
$\operatorname {det}_{1, \ldots , g-1}(M_1, \ldots , M_g) := ((\operatorname {det} M_1) (\operatorname {det} M_2)^{-1}, \ldots , (\operatorname {det} M_1) (\operatorname {det} M_g)^{-1})$
. We deduce that
$$ \begin{align*}|G(\ell)| = |\mathbb G(\ell)|/|\mathcal{G}_m(\ell)|^{g-1} = (\ell-1) \ell^g (\ell^2 -1)^g,\end{align*} $$
$$ \begin{align*}|B(\ell)| = |\mathcal{B}_{\operatorname{GL}_2}(\ell)^g|/|\mathcal{G}_m(\ell)|^{g-1} = (\ell-1)^{g+1} \ell^g.\\[-38pt] \end{align*} $$
▪
Lemma 13 For any prime
$\ell $
, we have a group isomorphism
$B(\ell )/U(\ell ) \simeq T(\ell )$
.
Proof Consider the group homomorphisms
$ T(\ell ) \hookrightarrow B(\ell ) \twoheadrightarrow B(\ell )/U(\ell ). $
The composition has kernel
$T(\ell )\cap U(\ell )= 1$
, hence it is injective. Since, by Lemma 12, each of the groups
$B(\ell )/U(\ell )$
and
$T(\ell )$
has size
$(\ell -1)^{g+1}$
, the composition must be an isomorphism.▪
5 Conjugacy classes of subgroups of
$G(\ell )$
Let
$\ell \nmid 2 g$
be a fixed prime and let
$t \in \mathbb Z$
be a fixed integer. We devote Section 5 to investigations of particular unions of conjugacy classes of the groups
$G(\ell )$
,
$B(\ell )$
, and
$T(\ell )$
introduced in Section 4. As usual, when we regard
$\mathbb Z/\ell \mathbb Z$
as a field, we use the notation
$\mathbb F_{\ell }$
. In this case, we denote by
$\overline {\mathbb F}_{\ell }$
a fixed algebraic closure of
$\mathbb F_{\ell }$
.
Before introducing the unions of conjugacy classes we are interested in investigating, let us observe that if
$M = (M_1, \ldots , M_g) \in G(\ell )$
, then the characteristic polynomial of M relates to the characteristic polynomials of
$M_1, \ldots , M_g \in \operatorname {GL}_2(\ell )$
through the equation
$$ \begin{align} \operatorname{char}_M(X)=\operatorname{char}_{M_1}(X) \ldots \operatorname{char}_{M_g}(X) \in \mathbb F_{\ell}[X]. \end{align} $$
When working over the algebraic closure
$\overline {\mathbb F}_{\ell }$
of the field
$\mathbb F_{\ell }$
, for each
$1 \leq i \leq g$
we may write the linear factorization of
$\operatorname {char}_{M_i}(X)$
as
$$ \begin{align} \operatorname{char}_{M_i}(X) = (X - \lambda_1(M_i)) (X - \lambda_2(M_i)) \in \overline{\mathbb F}_{\ell}[X]. \end{align} $$
Then, by putting together (20) and (21), we see that the linear factorization of
$\operatorname {char}_{M}(X)$
over
$\overline {\mathbb F}_{\ell }$
is
$$ \begin{align} \operatorname{char}_{M}(X) = \displaystyle\prod_{1 \leq i \leq g} (X - \lambda_1(M_i)) (X - \lambda_2(M_i)) \in \overline{\mathbb F}_{\ell}[X]. \end{align} $$
Using the above notation and fixing
$z> 0$
, we now introduce the sets to be investigated in this section:
$$ \begin{align*} &{\cal C}(\ell, t) :=\\ &\!\quad\left\{\! (M_1, \ldots, M_g) \kern1.5pt{\in}\kern1.5pt G(\ell): \lambda_1(M_i), \lambda_2(M_i) \kern1.5pt{\in}\kern1.5pt \mathbb F_{\ell}^{\times} \ \forall 1 \kern1.5pt{\leq}\kern1.5pt i \kern1.5pt{\leq}\kern1.5pt g, \displaystyle\sum_{ 1 \leq i \leq g }\! \operatorname{tr} M_i \kern1.5pt{\equiv}\kern1.5pt - t (\operatorname{mod} \ell) \!\right\}\!, \end{align*} $$
$$ \begin{align*} {\mathcal{C}}_{\text{Borel}}(\ell, t) &:= {{\cal C}}(\ell, t) \cap B(\ell), \\ \widehat{{\cal C}}_{\text{Borel}}(\ell, t) &:= \; \text{the image of }{\mathcal{C}}_{\text{Borel}}(\ell, t)\text{ in }B(\ell)/U(\ell), \\ \widehat{{\cal C}}^{\prime}_{\text{Borel}}(\ell, t) &:= \; \text{the image of }{\mathcal{C}}_{\text{Borel}}(\ell, t)\text{ in }B(\ell)/U'(\ell), \\ {{\cal C}}_{\text{Torus}}(\ell, t) &:= {{\cal C}}(\ell, t) \cap T(\ell), \\ {\cal C}(\ell, |t|\leq z) &:= \bigcup_{\substack{t\in \mathbb Z\\|t|\leq z}}{\cal C}(\ell, t), \\ {\mathcal{C}}_{\text{Borel}}(\ell, |t|\leq z) & := {\cal C}(\ell, |t|\leq z) \cap B(\ell), \\ \widehat{{\cal C}}_{\text{Borel}}(\ell, |t|\leq z) & := \text{the image of } {\mathcal{C}}_{\text{Borel}}(\ell, |t| \leq z) \text{ in } B(\ell)/U(\ell). \end{align*} $$
Lemma 14
-
(i)
$\emptyset \neq {\mathcal {C}}_{\text {Torus}}(\ell , t) \subseteq {{\cal C}}_{\text {Borel}}(\ell , t) \subseteq {{\cal C}}(\ell , t)$
and
${\mathcal {C}}_{\text {Borel}}(\ell , |t|\leq z)\neq \emptyset $
. -
(ii)
${\cal C}(\ell , t)$
is a union of conjugacy classes of
$G(\ell )$
. -
(iii)
${\mathcal {C}}_{\text {Borel}}(\ell , t)$
is a union of conjugacy classes of
$B(\ell )$
, and
${\mathcal {C}}_{\text {Borel}}(\ell , |t|\leq z)$
is a union of conjugacy classes of
$B(\ell )$
. -
(iv)
${\mathcal {C}}_{\text {Torus}}(\ell , t)$
is a union of conjugacy classes of
$T(\ell )$
. -
(v)
$U(\ell ) \ {{\cal C}}_{\text {Borel}}(\ell , t) \subseteq {{\cal C}}_{\text {Borel}} (\ell , t)$
and
$U(\ell ) \ {\mathcal {C}}_{\text {Borel}}(\ell , |t|\leq z)\subseteq {\mathcal {C}}_{\text {Borel}}(\ell , |t|\leq z)$
. -
(vi)
$U'(\ell ) \ {\mathcal {C}}_{\text {Borel}}(\ell , 0) \subseteq {\mathcal {C}}_{\text {Borel}} (\ell , 0)$
.
Proof (i) Since
$\ell $
is a prime such that
$\ell \nmid 2 g$
, we know that
$(2 g)^{-1} (\operatorname {mod} \ell )$
exists. Now, we consider the cases
$t \neq 0$
and
$t = 0$
separately. When
$t \neq 0$
, for each
$1\leq i\leq g$
, we take
$$ \begin{align*}M_i := \begin{pmatrix} - t (2 g)^{-1} (\operatorname{mod} \ell) & 0 \\ 0 & - t (2 g)^{-1} (\operatorname{mod} \ell) \\ \end{pmatrix}. \end{align*} $$
Then
$$ \begin{align*} \lambda_{1}(M_i) \equiv \lambda_2(M_i)\equiv - t (2 g)^{-1} (\operatorname{mod} \ell) \in \mathbb F_{\ell}^{\times} \ \forall 1\leq i\leq g, \quad \sum_{ 1 \leq i \leq g } \operatorname{tr} M_i \equiv - t (\operatorname{mod} \ell), \end{align*} $$
and so
$(M_1, \ldots , M_g) \in {\mathcal {C}}_{\text {Torus}}(\ell , t)$
. When
$t = 0$
, for each
$1\leq i\leq g$
, we take
$$ \begin{align*}M_i := \begin{pmatrix} (2 g)^{-1} (\operatorname{mod} \ell) & 0 \\ 0 & -(2 g)^{-1} (\operatorname{mod} \ell) \end{pmatrix}. \end{align*} $$
Then,
$$ \begin{align*} \lambda_{1}(M_i)&\equiv (2 g)^{-1} (\operatorname{mod} \ell) \ \text{and} \ \lambda_2(M_i)\equiv-(2 g)^{-1}(\operatorname{mod} \ell) \in \mathbb F_{\ell}^{\times} \ \forall 1\leq i\leq g,\\ &\qquad\qquad\qquad\quad\sum_{ 1 \leq i \leq g } \operatorname{tr} M_i \equiv 0 (\operatorname{mod} \ell), \end{align*} $$
and so
$(M_1, \ldots , M_g) \in {\mathcal {C}}_{\text {Torus}}(\ell , 0)$
. We conclude that
${\mathcal {C}}_{\text {Torus}}(\ell , t) \neq \emptyset $
.
The inclusions
${\mathcal {C}}_{\text {Torus}}(\ell , t) \subseteq {{\cal C}}_{\text {Borel}}(\ell , t) \subseteq {{\cal C}}(\ell , t)$
are clear from the definitions of the sets.
Finally, observing that
$\displaystyle {\mathcal {C}}_{\text {Borel}}(\ell , |t|\leq z) = \bigcup _{\substack {t\in \mathbb Z\\|t|\leq z}}{\mathcal {C}}_{\text {Borel}}(\ell , t)$
, the claim that
${\mathcal {C}}_{\text {Borel}}(\ell , |t|\leq z)\neq \emptyset $
follows from the previous inclusions and the non-emptiness of
${\mathcal {C}}_{\text {Borel}}(\ell , t)$
.
(ii)
${\cal C}(\ell , t)$
is a subset of
$G(\ell )$
characterized by some condition on the eigenvalues of g invertible
$2\times 2$
matrices. Since eigenvalues are invariant under conjugation,
${\cal C}(\ell , t)$
is a union of conjugacy classes of
$G(\ell ).$
(iii) By (ii),
${\cal C}(\ell , t)$
is invariant under conjugation by
$B(\ell )$
. Since
$B(\ell )$
is invariant under conjugation by
$B(\ell )$
, so is the intersection
${{\cal C}}(\ell , t) \cap B(\ell )$
. This implies that
${\mathcal {C}}_{\text {Borel}}(\ell , t)$
is a union of conjugacy classes of
$B(\ell )$
. Similarly,
${\mathcal {C}}_{\text {Borel}}(\ell , |t|\leq z)$
is a union of conjugacy classes of
$B(\ell )$
.
(iv) Since
${{\cal C}}(\ell , t) $
and
$T(\ell )$
are invariant under conjugation by
$T(\ell )$
, the set
${\mathcal {C}}_{\text {Torus}}(\ell , t)$
is a union of conjugacy classes of
$T(\ell )$
.
(v) Let
$M' \in U(\ell )$
,
$M \in {{\cal C}}_{\text {Borel}}(\ell , t)$
. Then
$M' M \in B(\ell )$
, with
$M' M$
having the same diagonal entries as M. Since
$\operatorname {tr} M = - t$
, we obtain that
$\operatorname {tr} (M' M) = - t$
. Thus
$U(\ell ) \ {{\cal C}}_{\text {Borel}}(\ell , t) \subseteq {{\cal C}}_{\text {Borel}} (\ell , t)$
. Upon recalling that
$\displaystyle {\mathcal {C}}_{\text {Borel}}(\ell , |t|\leq z) =\bigcup _{\substack {t\in \mathbb Z\\|t|\leq z}}{\mathcal {C}}_{\text {Borel}}(\ell , t)$
, it also follows that
$U(\ell )\ {\mathcal {C}}_{\text {Borel}}(\ell , |t|\leq z)\subseteq {\mathcal {C}}_{\text {Borel}}(\ell , |t|\leq z)$
.
(vi) Let
$M' \in U'(\ell )$
be such that its diagonal elements are all equal to some
$a\in (\mathbb Z/\ell \mathbb Z)^{\times }$
. Let
$M\in {{\cal C}}_{\text {Borel}}(\ell , 0)$
. Then
$M' M\in B(\ell )$
and
$\operatorname {tr} (M' M)=a \operatorname {tr} M=0$
, which implies that
$U'(\ell ) \ {\mathcal {C}}_{\text {Borel}}(\ell , 0) \subseteq {\mathcal {C}}_{\text {Borel}} (\ell , 0)$
.▪
Lemma 15 Any element of
$\operatorname {GL}_2(\ell )$
with a split characteristic polynomial in
$\mathbb F_{\ell }[X]$
is conjugate to an element of
$\mathcal {B}_{\operatorname {GL}_2}(\ell )$
by an element of
$\operatorname {SL}_2(\ell ) := \{M \in \operatorname {GL}_2(\ell ): \operatorname {det} M = 1\}$
.
Proof Let
$M \in \operatorname {GL}_2(\ell )$
. Observe that
$\lambda _1(M), \lambda _2(M)\in \mathbb F_{\ell }^{\times }$
. This means that there exists
$N \in \operatorname {GL}_2(\ell )$
such that
$$ \begin{align*}N M N^{-1} = \begin{pmatrix} \lambda_1(M) & \ast \\ 0 & \lambda_2(M) \end{pmatrix}\in \mathcal{B}_{\operatorname{GL}_2}(\ell). \end{align*} $$
If
$\operatorname {det} N=1$
, we are done. Otherwise, by taking
$$ \begin{align*}N' := \begin{pmatrix} (\operatorname{det} N)^{-1} & 0 \\ 0 & 1 \end{pmatrix} N, \end{align*} $$
we have that
$N' M N^{\prime -1}\in \mathcal {B}_{\operatorname {GL}_2}(\ell )$
, as well as that
$\operatorname {det} N'=1$
, and again we are done.▪
Lemma 16 Every conjugacy class in
${\cal C}(\ell , t)$
or
${\cal C}(\ell , |t|\leq z)$
contains an element of
$B(\ell )$
.
Proof Let
$M = (M_1, \ldots , M_g) \in {{\cal C}}(\ell , t)$
. Upon fixing
$1 \leq i \leq g$
, we observe that, by Lemma 15, there exists
$N_i\in \operatorname {SL}_2(\ell )$
such that
$N_i M_i N_i^{-1}\in \mathcal {B}_{\operatorname {GL}_2}(\ell )$
. Let
$N:= (N_1, \ldots , N_g)$
. Then
$N\in G(\ell )$
and
$N M N^{-1}\in \mathcal {B}_{\operatorname {GL}_2}(\ell )^g \cap G(\ell ) =B(\ell )$
. We deduce that M is conjugate to an element of
$B(\ell )$
. Thus, every conjugacy class in
${\cal C}(\ell , t)$
contains an element of
$B(\ell )$
. The similar statement about
${\cal C}(\ell , |t|\leq z)$
follows upon noting that every conjugacy class in this set is a conjugacy class in
${\cal C}(\ell , t)$
for some integer t with
$|t| \leq z$
.▪
Lemma 17
-
(i)
$|{{\cal C}}_{\text {Torus}}(\ell , t)| \leq 2 (\ell -1)^g$
. -
(ii)
$|{{\cal C}}_{\text {Borel}}(\ell , t)| = \ell ^g |{{\cal C}}_{\text {Torus}}(\ell , t)|\leq 2 (\ell -1)^g\ell ^g.$
-
(iii)
$|\widehat {{\cal C}}_{\text {Borel}}(\ell , t)| = |{{\cal C}}_{\text {Torus}}(\ell , t)| \leq 2 (\ell -1)^g.$
-
(iv)
$|\widehat {{\cal C}}^{\prime }_{\text {Borel}}(\ell , 0)|= \displaystyle \frac {|\widehat {{\cal C}}_{\text {Borel}}(\ell , 0)| }{\ell -1}\leq 2 (\ell -1)^{g-1}.$
-
(v)
$|\widehat {{\cal C}}_{\text {Borel}}(\ell , |t|\leq z) |< 5 (\ell -1)^g z$
.
Proof (i) Observe that
$$ \begin{align*} {{\cal C}}_{\text{Torus}}(\ell, t) = \{(M_1, \ldots, M_g)\in T(\ell): \sum_{1\leq i\leq g} \operatorname{tr} M_i \equiv -t (\operatorname{mod} \ell)\}. \end{align*} $$
Then,
$$ \begin{align*} |{{\cal C}}_{\text{Torus}}(\ell, t)| & = \displaystyle\sum_{ d \in (\mathbb Z/\ell \mathbb Z)^{\times}} \quad \displaystyle\sum_{ M_1 , \ldots, M_{g-1} \in \mathcal{T}_{\operatorname{GL}_2}(\ell) \atop{ \operatorname{det} M_1 = \cdots = \operatorname{det} M_g = d } } \# \{ M_g\in \mathcal{T}_{\operatorname{GL}_2}(\ell): \operatorname{det} M_g=d, \\\operatorname{tr} M_g&\equiv -t-\sum_{1\leq i\leq g-1} \operatorname{tr} M_i (\operatorname{mod} \ell) \} \\ & \leq \displaystyle\sum_{ d \in (\mathbb Z/\ell \mathbb Z)^{\times}} \quad \displaystyle\sum_{ M_1 , \ldots, M_{g-1} \in \mathcal{T}_{\operatorname{GL}_2}(\ell) \atop{ \operatorname{det} M_1 = \cdots = \operatorname{det} M_g = d } } 2\\ & = 2 (\ell-1)^{g}. \end{align*} $$
(ii) Observe that
$$ \begin{align*} {{\cal C}}_{\text{Borel}}(\ell, t) = \{(M_1, \ldots, M_g)\in B(\ell): \sum_{1\leq i\leq g} \operatorname{tr} M_i \equiv -t (\operatorname{mod} \ell)\}. \end{align*} $$
Then,
$$ \begin{align*} |{{\cal C}}_{\text{Borel}}(\ell, t)| & = \displaystyle\sum_{ d \in (\mathbb Z/\ell \mathbb Z)^{\times}} \quad \displaystyle\sum_{ M_1 , \ldots, M_{g-1} \in \mathcal{T}_{\operatorname{GL}_2}(\ell) \atop{ \operatorname{det} M_1 = \cdots = \operatorname{det} M_g = d } } \# \{ M_g\in \mathcal{B}_{\operatorname{GL}_2}(\ell): \operatorname{det} M_g=d, \\\operatorname{tr} M_g&\equiv -t-\sum_{1\leq i\leq g-1} \operatorname{tr} M_i (\operatorname{mod} \ell) \}. \end{align*} $$
Since we have the equality
$$ \begin{align*} & \# \{ M_g\in \mathcal{B}_{\operatorname{GL}_2}(\ell): \operatorname{det} M_g=d, \operatorname{tr} M_g\equiv -t-\sum_{1\leq i\leq g-1} \operatorname{tr} M_i (\operatorname{mod} \ell) \} \\ = & \ \ell^g \ \# \{ M_g\in \mathcal{T}_{\operatorname{GL}_2}(\ell): \operatorname{det} M_g=d, \operatorname{tr} M_g\equiv -t-\sum_{1\leq i\leq g-1} \operatorname{tr} M_i (\operatorname{mod} \ell) \} , \end{align*} $$
we obtain that
$|{{\cal C}}_{\text {Borel}}(\ell , t)| =\ell ^g |{{\cal C}}_{\text {Torus}}(\ell , t)|$
.
(iii) Observe that, upon identifying
$B(\ell )/U(\ell )$
with
$T(\ell )$
via Lemma 13, there is a bijection between the sets
$\widehat {{\cal C}}_{\text {Borel}}(\ell , t)$
and
${\mathcal {C}}_{\text {Torus}}(\ell , t)$
. Thus
$|\widehat {{\cal C}}_{\text {Borel}}(\ell , t)| = |{{\cal C}}_{\text {Torus}}(\ell , t)|.$
(iv) Since
$U(\ell )\leq U'(\ell )$
and
$U'(\ell )/U(\ell ) \simeq (\mathbb Z/\ell \mathbb Z)^{\times }$
, there is a natural surjection
$ B(\ell )/U(\ell )\to B(\ell )/U'(\ell ) $
whose kernel
$U'(\ell )/U(\ell )$
has cardinality
$\ell - 1$
. We deduce that
$\widehat {{\cal C}}^{\prime }_{\text {Borel}}(\ell , 0)$
is the image of
$\widehat {{\cal C}}_{\text {Borel}}(\ell , 0)$
in
$B(\ell )/U'(\ell )$
.
By a similar argument as that in the proof of part (vi) of Lemma 14, we obtain that
$U'(\ell )\widehat {{\cal C}}_{\text {Borel}}(\ell , 0)=\widehat {{\cal C}}_{\text {Borel}}(\ell , 0)$
. Thus
$\widehat {{\cal C}}_{\text {Borel}}(\ell , 0)$
is the full inverse image of
$\widehat {{\cal C}}^{\prime }_{\text {Borel}}(\ell , 0)$
in
$B(\ell )/U(\ell )$
.
From the above, we infer that
$|\widehat {{\cal C}}^{\prime }_{\text {Borel}}(\ell , 0)| = \displaystyle \frac {|\widehat {{\cal C}}_{\text {Borel}}(\ell , 0)| }{\ell -1}\leq 2 (\ell -1)^{g-1}\ell ^g$
, as claimed.
(v) Recall that
$$ \begin{align*}\displaystyle{\mathcal{C}}_{\text{Borel}}(\ell, |t|\leq z) =\bigcup_{\substack{t\in \mathbb Z\\|t|\leq z}}{\mathcal{C}}_{\text{Borel}}(\ell, t).\end{align*} $$
Then, by part (v) of Lemma 14, we deduce that
$$ \begin{align*} \widehat{{\cal C}}_{\text{Borel}}(\ell, |t|\leq z) =\bigcup_{\substack{t\in \mathbb Z\\|t|\leq z}}\widehat{{\cal C}}_{\text{Borel}}(\ell, t). \end{align*} $$
Using part (iii) of the present lemma, we deduce further that
$$ \begin{align*} |\widehat{{\cal C}}_{\text{Borel}}(\ell, |t|\leq z)|\leq 2 \ \#\{t\in \mathbb Z: |t|\leq z\}(\ell-1)^g < 5z(\ell-1)^g. \\[-38pt] \end{align*} $$
▪
6 Proof of Theorem 1
6.1 Setting and basic properties
Let A be an abelian variety defined over
$\mathbb Q$
that is isogenous over
$\mathbb Q$
to a product of g elliptic curves defined over
$\mathbb Q$
, pairwise non-isogenous over
$\overline {\mathbb Q}$
and each without complex multiplication. In what follows, we record a few properties of A that we will need in the proofs of our main results. We keep all the associated notation introduced in the prior sections, some of which we recall below. For background on abelian varieties, we refer the reader to [Reference FaltingsFa83, Reference HondaHo68, Reference LangLa83, Reference OortOo08, Reference Serre and TateSeTa68, Reference WaterhouseWat69].
We fix a g-tuple of elliptic curves,
$E_1/\mathbb Q$
,
$\ldots $
,
$E_g/\mathbb Q$
, equipped with a
$\mathbb Q$
-isogeny between A and
$E_1 \times \cdots \times E_g$
of minimal degree, denoted
$d_A$
, among all such choices. We denote by
$N_{E_1}, \ldots , N_{E_g}$
the conductors of
$E_1, \ldots , E_g$
, respectively.
We denote by
$$ \begin{align*}\rho_A : \operatorname{Gal}\left(\overline{\mathbb Q}/\mathbb Q\right) \longrightarrow \operatorname{GL}_{2g}(\widehat{\mathbb Z})\end{align*} $$
the adelic Galois representation of A, defined by the inverse limit of the residual representations
$$ \begin{align*}\bar{\rho}_{A, m} : \operatorname{Gal}(\overline{\mathbb Q}/\mathbb Q) \longrightarrow \operatorname{GL}_{2g}(\mathbb Z/m \mathbb Z)\end{align*} $$
of the absolute Galois group
$\operatorname {Gal}(\overline {\mathbb Q}/\mathbb Q)$
acting on the m-torsion group
$A[m] := \{P \in A(\overline {\mathbb Q}): m P = 0_A\}$
, with m a positive integer. For any prime
$\ell $
, we denote by
$$ \begin{align*}\rho_{A, \ell} : \operatorname{Gal}\left(\overline{\mathbb Q}/\mathbb Q\right) \longrightarrow \operatorname{GL}_{2g}(\mathbb Z_{\ell})\end{align*} $$
the
$\ell $
-adic representation of
$\operatorname {Gal}(\overline {\mathbb Q}/\mathbb Q)$
on the
$\ell $
-adic Tate module
${\displaystyle \lim _{\leftarrow \atop {n}} A[\ell ^n}]$
.
Similarly to notation (19) introduced in Section 4, we set
$$ \begin{align*}G(\widehat{\mathbb Z}) := \{(M_1, \ldots, M_g)\in \operatorname{GL}_2(\widehat{\mathbb Z})^g: \operatorname{det} M_1 = \ldots = \operatorname{det} M_g\}, \end{align*} $$
$$ \begin{align*}G(m) := \{(M_1, \ldots, M_g)\in \operatorname{GL}_2(\mathbb Z/m \mathbb Z)^g: \operatorname{det} M_1 = \ldots = \operatorname{det} M_g\}, \end{align*} $$
and recall that
$$ \begin{align*} \operatorname{Im} \rho_A \subseteq G(\widehat{\mathbb Z}), \end{align*} $$
$$ \begin{align*} \operatorname{Im} \bar{\rho}_{A, m} \subseteq G(m), \end{align*} $$
where m is an arbitrary positive integer.
For any prime
$p \nmid N_A$
, we denote by
$\operatorname {Frob}_p$
the Frobenius at p in
$\operatorname {Gal}(\overline {\mathbb Q}/\mathbb Q)$
, and for any prime
$\ell \neq p$
, we denote by
$$ \begin{align*}P_{A, p}(X) := \operatorname{det} (X I_{2g} - \rho_{A, \ell}(\operatorname{Frob}_p))\end{align*} $$
the characteristic polynomial of
$\rho _{A, \ell }(\operatorname {Frob}_p)$
in
$\operatorname {GL}_{2g}(\mathbb Z_{\ell })$
.
We recall that
$P_{A, p}(X)$
is the characteristic polynomial of the Frobenius endomorphism acting on the reduction of A modulo p. We also recall that
$P_{A, p}(X)$
is a p-Weil polynomial, has integer coefficients independent of
$\ell $
, and satisfies the congruence
$$ \begin{align} P_{A, p}(X) \equiv \operatorname{det} \left(X I_{2g} - \bar{\rho}_{A, m} \left(\left(\frac{\mathbb Q(A[m])/\mathbb Q}{p}\right)\right) \right) (\operatorname{mod} m) \end{align} $$
for any integer m coprime to p.
In analogy with the discussion and notation for A, for each
$1 \leq i \leq g$
we denote by
$\rho _{E_i}$
,
$\overline {\rho }_{E_i, m}$
, and
$\rho _{E_i, \ell }$
the adelic, residual, and
$\ell $
-adic Galois representations of
$E_i$
, and for each prime
$p \nmid N_{E_i}$
we denote by
$P_{E_i, p}(X)$
the associated p-Weil polynomial. We recall the congruence relation
$$ \begin{align} P_{E_i, p}(X) \equiv \operatorname{det} \left(X I_{2} - \bar{\rho}_{E_i, m} \left(\frac{\mathbb Q(E_i[m])/\mathbb Q}{p}\right) \right)(\operatorname{mod} m), \end{align} $$
which holds for any integer m coprime to p.
Now let us fix a prime
$p \nmid N_A d_A$
. We write the polynomials
$P_{A, p}(X)$
,
$P_{E_i, p}(X)$
explicitly as
$$ \begin{align*} P_{A, p}(X) &= X^{2g} + a_{1, p}(A) X^{2g-1} + \ldots + a_{2g-1, p}(A) X + a_{2g, p}(A) \in \mathbb Z[X], \\ P_{E_i, p}(X) &= X^2 - a_p(E_i) X + p \in \mathbb Z[X]. \end{align*} $$
On one hand, we have the polynomial relation
$$ \begin{align} P_{A, p}(X) = P_{E_1, p}(X) \ldots P_{E_g, p}(X), \end{align} $$
from which we obtain that
$$ \begin{align} a_{1, p}(A) = - (a_p(E_1) + \ldots + a_p(E_g)). \end{align} $$
On the other hand, by restricting the residual representations
$\overline {\rho }_{A, m}$
,
$\overline {\rho }_{E_i, m}$
to the division fields
$\mathbb Q(A[m])$
,
$\mathbb Q(E_i[m])$
, respectively, we deduce from (23) to (24) that, for any integer m coprime to p, we have
$$ \begin{align} \operatorname{tr} \bar{\rho}_{A, m} \left( \left(\frac{\mathbb Q(A[m])/\mathbb Q}{p}\right) \right) &\equiv - a_{1, p}(A) (\operatorname{mod} m), \end{align} $$
$$ \begin{align} \operatorname{tr} \bar{\rho}_{E_i, m} \left( \left(\frac{\mathbb Q(E_i[m])/\mathbb Q}{p}\right) \right) &\equiv a_{p}(E_i) (\operatorname{mod} m). \end{align} $$
From (26) to (28), we deduce that, for any integer m coprime to p, we have
$$ \begin{align} \qquad\operatorname{tr} \bar{\rho}_{A, m} \left( \left(\frac{\mathbb Q(A[m])/\mathbb Q}{p}\right) \right) \equiv - \displaystyle\sum_{1 \leq i \leq g} \operatorname{tr} \bar{\rho}_{E_i, m} \left( \left(\frac{\mathbb Q(E_i[m])/\mathbb Q}{p}\right) \right) (\operatorname{mod} m). \end{align} $$
6.2 A conditional reduction step
For an abelian variety
$A/\mathbb Q$
, a prime
$p \nmid N_A$
, and an integer t, we remark that congruence (27) already allows us to relax the equality
$a_{1, p}(A) = t$
to the congruence
$\operatorname {tr} \bar {\rho }_{A, \ell } \left ( \left (\frac {\mathbb Q(A[\ell ])/\mathbb Q}{p}\right ) \right ) \equiv - t (\operatorname {mod} \ell )$
for some prime
$\ell $
and then to apply an effective version of the Chebotarev Density Theorem in the extension
$\mathbb Q(A[\ell ])/\mathbb Q$
. However, we can obtain better results by relaxing the equality
$a_{1, p}(A) = t$
to a Chebotarev condition that takes place in the extension
$\mathbb Q(A[\ell ])^{U(\ell )}/\mathbb Q(A[\ell ])^{B(\ell )}$
. The key ingredient is as follows.
Lemma 18 Let
$t \in \mathbb Z$
. Let
$A/\mathbb Q$
be an abelian variety defined over
$\mathbb Q$
that is isogenous over
$\mathbb Q$
to a product
$E_1 \times \cdots \times E_g$
of elliptic curves
$E_1/\mathbb Q$
,
$\ldots $
,
$E_g/\mathbb Q$
, pairwise non-isogenous over
$\overline {\mathbb Q}$
and each without complex multiplication. For each
$x>2$
, let
$y = y(x)> 2$
,
$u =u(x)> 2$
be such that
$$ \begin{align} u \leq y. \end{align} $$
Assume that, for any
$\varepsilon> 0$
,
$$ \begin{align} u \geq c'(\varepsilon) y^{\frac{1}{2}} (\operatorname{log} y)^{2 + \varepsilon} \ \text{for some} \ c'(\varepsilon)> 0 \end{align} $$
and
$$ \begin{align} \displaystyle\lim_{x \rightarrow \infty} \frac{\operatorname{log} x}{(\operatorname{log} y)^{1 + \varepsilon}} = 0. \end{align} $$
Assume GRH for Dedekind zeta functions. Then, for any
$\varepsilon> 0$
, there exists a constant
$c(\varepsilon )> 0$
such that, for any positive real number z and for any sufficiently large x, we have
$$ \begin{align} \pi_A(x, t) \leq c(\varepsilon) \displaystyle\max_{y \leq \ell \leq y + u} \pi_A(x, \ell, t) \end{align} $$
and
$$ \begin{align} \sum_{\substack{t\in \mathbb Z\\|t|\leq z}}\ \pi_A(x, t) \leq c(\varepsilon) \displaystyle\max_{y \leq \ell \leq y + u} \sum_{\substack{t\in \mathbb Z\\|t|\leq z}}\ \pi_A(x, \ell, t), \end{align} $$
where, as before,
$$ \begin{align*} \pi_A(x, t) = \#\{p \leq x: p \nmid N_A, a_{1, p}(A) = t\}, \end{align*} $$
and where
$$ \begin{align*}\pi_A(x, \ell, t)&:=\#\left\{p \leq x: p \nmid \ell N_A, a_{1, p}(A) = t,\right.\nonumber\\&\left.\ell \ \text{splits completely in each of the fields} \ {\mathbb Q}({\pi}_p(E_1)), \ldots, {\mathbb Q}({\pi}_p(E_g))\right\}. \end{align*} $$
Proof We apply Lemma 9 to the set
${{\cal S}} = \left \{p: p \nmid N_A, a_{1, p}(A) = t \right \}$
, the field
$K_p = $
the compositum of the fields
$\mathbb Q(\pi _p(E_1)), \ldots , \mathbb Q(\pi _p(E_g))$
, the conjugacy class
${{\cal C}}_p = \left \{\operatorname {id}_{K_p}\right \}$
, and the function
$f(v) = \operatorname {log} v$
.
Note that
$K_p/\mathbb Q$
is Galois and that
$1 \neq [K_p:\mathbb Q] \mid 2^g$
. Also note that if a prime
$\ell $
is ramified in
$K_p$
, then
$\ell \mid \left (4p - a_p(E_1)^2\right ) \cdots \left (4p - a_p(E_g)^2\right )$
(see [Reference ToyamaTo55, Theorem, p. 43]). Therefore, upon recalling (3), we have that
$\displaystyle \operatorname {log} |d_{K_p}| \ll _{E_1, \ldots , E_g} \operatorname {log} p$
. Since all hypotheses of Lemma 9 are satisfied, bound (33) follows. Bound (34) follows from a similar argument, except for taking
${{\cal S}} = \left \{p: p \nmid N_A, |a_{1, p}(A)| \leq z\right \}$
, while keeping
$K_p$
,
${{\cal C}}_p$
, and f as before.▪
6.3 Proof of Theorem 1 for arbitrary t
Let A be an abelian variety defined over
$\mathbb Q$
that is isogenous over
$\mathbb Q$
to a product of g elliptic curves defined over
$\mathbb Q$
, pairwise non-isogenous over
$\overline {\mathbb Q}$
and each without complex multiplication. As in Section 6.1, we fix a g-tuple of elliptic curves,
$E_1/\mathbb Q$
,
$\ldots $
,
$E_g/\mathbb Q$
, equipped with a
$\mathbb Q$
-isogeny between A and
$E_1 \times \cdots \times E_g$
of minimal degree
$d_A$
among all such choices. We keep all the associated notation introduced so far.
Let
$t \in \mathbb Z$
and
$x> 2$
. By Lemma 18, we can bound
$\pi _A(x, t)$
from above if we succeed in bounding
$\pi _A(x, \ell , t)$
from above for some suitably chosen prime
$\ell = \ell (x)$
.
For now, we fix a prime
$\ell \nmid 2 g$
such that
$$ \begin{align} \operatorname{Im} \overline{\rho}_{A, \ell} = G(\ell). \end{align} $$
The existence of infinitely many such primes
$\ell $
is ensured by [Reference SerreSe72, Théorème 6, p. 324] and [Reference LombardoLo16, Theorem 1.1, p. 387] under our hypotheses that
$E_1/\mathbb Q, \ldots , E_g/\mathbb Q$
are without complex multiplication and pairwise non-isogenous over
$\overline {\mathbb Q}$
. Indeed, from [Reference LombardoLo16, Theorem 1.1, p. 387], we infer that there exists a least positive integer
$m_A$
such that
$\operatorname {Im} \rho _A$
equals the inverse image under the canonical projection
$G (\widehat {\mathbb Z}) \longrightarrow G(m_A)$
of
$\operatorname {Im} \overline {\rho }_{A, m_A}$
. In particular, this means that
$\operatorname {Im} \bar {\rho }_{A, \ell } = G(\ell )$
for any prime
$\ell \nmid m_A$
. Later on, we will choose
$\ell $
in an explicit interval that depends on x.
The choice of a prime
$\ell $
such that (35) holds allows us to consider the subextensions of
$\mathbb Q(A[\ell ])$
fixed by the groups
$U(\ell )$
and
$B(\ell )$
, namely
$$ \begin{align*}\mathbb Q \subseteq \mathbb Q(A[\ell])^{B(\ell)} \subseteq \mathbb Q(A[\ell])^{U(\ell)} \subseteq \mathbb Q(A[\ell]), \end{align*} $$
for which we immediately obtain the following Galois group structures:
$$ \begin{align*} \operatorname{Gal}(\mathbb Q(A[\ell])/\mathbb Q) &\simeq G(\ell), \\ \operatorname{Gal}\left(\mathbb Q(A[\ell])/\mathbb Q(A[\ell])^{B(\ell)}\right) &\simeq B(\ell), \\ \operatorname{Gal}\left(\mathbb Q(A[\ell])/\mathbb Q(A[\ell])^{U(\ell)}\right) &\simeq U(\ell), \\ \operatorname{Gal}\left(\mathbb Q(A[\ell])^{U(\ell)}/\mathbb Q(A[\ell])^{B(\ell)}\right) &\simeq B(\ell)/U(\ell). \end{align*} $$
In relation to these Galois groups, we recall from part (v) of Lemma 11 that
$U(\ell ) \unlhd B(\ell )$
and that
$B(\ell )/U(\ell )$
is abelian.
Using (25), (29), and (35), we deduce that every prime
$p \nmid d_A$
counted by
$\pi _A(x, \ell , t)$
is also counted by
$\pi _{{\cal C}(\ell , t)}(x, \mathbb Q(A[\ell ])/\mathbb Q)$
, where
${\cal C}(\ell , t)$
is the union of conjugacy classes of
$G(\ell )$
studied in Lemma 14 of Section 5. Thus
$$ \begin{align} \pi_A(x, \ell, t) \ll_A \pi_{{\cal C}(\ell, t)}(x, \mathbb Q(A[\ell])/\mathbb Q). \end{align} $$
To estimate
$\pi _{{\cal C}(\ell , t)}(x, \mathbb Q(A[\ell ])/\mathbb Q)$
, we invoke part (ii) of Corollary 8 of Section 2 with
$K = \mathbb Q$
,
$L = \mathbb Q(A[\ell ])$
,
$G = G(\ell )$
,
$H = B(\ell )$
,
$N = U(\ell )$
, and
${{\cal C}} = {{\cal C}}(\ell , t)$
. The hypotheses of this corollary hold thanks to our assumption of GRH and to part (v) of Lemma 11, part (v) of Lemma 14, and Lemma 16. We deduce that
$$ \begin{align*} &\pi_{{\cal C}(\ell, t)}(x, \mathbb Q(A[\ell])/\mathbb Q) \ll \frac{\left|\widehat{{\cal C}}_{\text{Borel}}(\ell, t)\right| \cdot |U(\ell)|}{|B(\ell)|} \cdot \frac{x}{\operatorname{log} x} \\ &\quad+ \left|\widehat{{{\cal C}}}_{\text{Borel}}(\ell, t)\right|{}^{\frac{1}{2}} [\mathbb Q(A[\ell])^{B(\ell)} :\mathbb Q] \frac{x^{\frac{1}{2}}}{\operatorname{log} x} \operatorname{log} M\left(\mathbb Q(A[\ell])^{U(\ell)}/\mathbb Q(A[\ell])^{B(\ell)}\right) \\ &\quad+ \left(\frac{x^{\frac{1}{2}}}{\operatorname{log} x} + \operatorname{log} M \left( \mathbb Q(A[\ell])/\mathbb Q\right) \right) \\ &\quad+ [\mathbb Q(A[\ell])^{B(\ell)}:\mathbb Q] \left(\frac{x^{\frac{1}{2}}}{\operatorname{log} x} + \operatorname{log} M\left(\mathbb Q(A[\ell])^{U(\ell)}/\mathbb Q(A[\ell])^{B(\ell)}\right)\right). \end{align*} $$
Using Lemmas 12 and 17, we deduce from the above that
$$ \begin{align} &\pi_{{\cal C}(\ell, t)}(x, \mathbb Q(A[\ell])/\mathbb Q) \nonumber\\&\quad\ll \frac{x}{\ell \operatorname{log} x} + (\ell-1)^{\frac{g}{2}} (\ell + 1)^g \frac{x^{\frac{1}{2}}}{\operatorname{log} x} \operatorname{log} M\left(\mathbb Q(A[\ell])^{U(\ell)}/\mathbb Q(A[\ell])^{B(\ell)}\right). \end{align} $$
We estimate
$ \operatorname {log} M\left (\mathbb Q(A[\ell ])^{U(\ell )}/\mathbb Q(A[\ell ])^{B(\ell )}\right )$
by putting together (3), Lemma 12, and the Néron–Ogg–Shafarevich criterion for
$A/\mathbb Q$
, which states that the extension
$\mathbb Q(A[\ell ])/\mathbb Q$
is unramified outside of
$\ell N_A$
(see [Reference Serre and TateSeTa68, Theorem 1, p. 493]). We obtain that
$$ \begin{align} &\operatorname{log} M\left(\mathbb Q(A[\ell])^{U(\ell)}/\mathbb Q(A[\ell])^{B(\ell)}\right)\nonumber\\&\quad \leq 2 \operatorname{log} |B(\ell)/U(\ell)| + 2\operatorname{log} (\ell N_A) + \operatorname{log} 2 \ll g \operatorname{log} (\ell N_A). \end{align} $$
Using this bound in the upper-estimate (37) for
$\pi _{{\cal C}(\ell , t)}(x, \mathbb Q(A[\ell ])/\mathbb Q)$
, we deduce that
$$ \begin{align} \pi_{{\cal C}(\ell, t)}(x, \mathbb Q(A[\ell])/\mathbb Q) \ll \frac{x}{\ell \operatorname{log} x} + g\ \ell^{\frac{3g}{2}} \frac{x^{\frac{1}{2}}}{\operatorname{log} x} \operatorname{log} (\ell N_A). \end{align} $$
Finally, we apply Lemma 18 with
$$ \begin{align*}y \asymp \frac{x^{\frac{1}{3 g + 2}}}{(\operatorname{log} x)^{\frac{2}{3 g + 2}}}\end{align*} $$
and
$$ \begin{align*}u \asymp y^{\frac{1}{2}} (\operatorname{log} y)^{2 + \varepsilon}\end{align*} $$
for an arbitrarily chosen
$\varepsilon> 0$
, and conclude that
$$ \begin{align*}\pi_A(x, t) \leq c(\varepsilon) \displaystyle\max_{y \leq \ell \leq y + u} \pi_A(x, \ell, t) \ll_{\varepsilon, A} \frac{ x^{1 - \frac{1}{3g+2} } }{ (\operatorname{log} x)^{1 - \frac{2}{3 g + 2} }}. \end{align*} $$
6.4 Proof of Theorem 1 for
$t = 0$
We keep the setting of Section 6.3. Let
$x> 2$
. As before, we take
$\ell \nmid 2 g$
to be a sufficiently large prime such that (35) holds. Then taking
$t = 0$
in (36), we have that
$$ \begin{align} \pi_A(x, \ell, 0) \ll_A \pi_{{\cal C}(\ell, 0)}(x, \mathbb Q(A[\ell])/\mathbb Q). \end{align} $$
To estimate
$\pi _{{\cal C}(\ell , 0)}(x, \mathbb Q(A[\ell ])/\mathbb Q)$
, we follow the strategy of the previous subsection, the main difference being that we will now work with the subextensions of
$\mathbb Q(A[\ell ])$
fixed by the groups
$U'(\ell )$
and
$B(\ell )$
, instead of by
$U(\ell )$
and
$B(\ell )$
. More precisely, we will work with the extensions
$$ \begin{align*}\mathbb Q \subseteq \mathbb Q(A[\ell])^{B(\ell)} \subseteq \mathbb Q(A[\ell])^{U'(\ell)} \subseteq \mathbb Q(A[\ell]). \end{align*} $$
Observe that
$\operatorname {Gal}\left (\mathbb Q(A[\ell ])/\mathbb Q(A[\ell ])^{U'(\ell )}\right ) \simeq U'(\ell )$
and
$\operatorname {Gal}(\mathbb Q(A[\ell ])^{U(\ell )}/\mathbb Q(A[\ell ])^{B(\ell )}) \simeq B(\ell )/U'(\ell )$
. Recall from part (vi) of Lemma 11 that
$U'(\ell ) \unlhd B(\ell )$
and that
$B(\ell )/U'(\ell )$
is abelian. Upon also recalling part (vi) of Lemmas 14 and 16, we apply part (ii) of Corollary 8 of Section 2 with
$K = \mathbb Q$
,
$L = \mathbb Q(A[\ell ])$
,
$G = G(\ell )$
,
$H = B(\ell )$
,
$N = U'(\ell )$
, and
${{\cal C}} = {{\cal C}}(\ell , 0)$
, and deduce that
$$ \begin{align*} &\pi_{{\cal C}(\ell, 0)}(x, \mathbb Q(A[\ell])/\mathbb Q) \ll\frac{\left|\widehat{{\cal C}}^{\prime}_{\text{Borel}}(\ell, 0)\right| \cdot |U'(\ell)|}{|B(\ell)|} \cdot \frac{x}{\operatorname{log} x} \\ &\quad+ \left|\widehat{{{\cal C}}}^{\prime}_{\text{Borel}}(\ell, 0)\right|{}^{\frac{1}{2}} [\mathbb Q(A[\ell])^{B(\ell)} :\mathbb Q] \frac{x^{\frac{1}{2}}}{\operatorname{log} x} \operatorname{log} M\left(\mathbb Q(A[\ell])^{U'(\ell)}/\mathbb Q(A[\ell])^{B(\ell)}\right) \\ &\quad+ \left(\frac{x^{\frac{1}{2}}}{\operatorname{log} x} + \operatorname{log} M\left(\mathbb Q(A[\ell])/\mathbb Q\right)\right) \\ &\quad+ [\mathbb Q(A[\ell])^{B(\ell)}:\mathbb Q] \left(\frac{x^{\frac{1}{2}}}{\operatorname{log} x} + \operatorname{log} M\left(\mathbb Q(A[\ell])^{U'(\ell)}/\mathbb Q(A[\ell])^{B(\ell)}\right)\right). \end{align*} $$
Using Lemmas 12 and 17, we infer from the above that
$$ \begin{align*} &\pi_{{\cal C}(\ell, 0)}(x, \mathbb Q(A[\ell])/\mathbb Q) \\&\quad\ll \frac{x}{\ell \operatorname{log} x} + \ell^{\frac{g-1}{2}} (\ell + 1)^g \frac{x^{\frac{1}{2}}}{\operatorname{log} x} \operatorname{log} M(\mathbb Q(A[\ell])^{U'(\ell)}/\mathbb Q(A[\ell])^{B(\ell)}). \end{align*} $$
Similarly to how we deduced (38), we obtain that
$$ \begin{align} &\operatorname{log} M\left(\mathbb Q(A[\ell])^{U'(\ell)}/\mathbb Q(A[\ell])^{B(\ell)}\right)\nonumber\\&\quad \leq 2 \operatorname{log} |B(\ell)/U'(\ell)| +2 \operatorname{log} (\ell N_A) + \operatorname{log} 2 \ll g \operatorname{log} (\ell N_A). \end{align} $$
Thus
$$ \begin{align*} \pi_{{\cal C}(\ell, t)}(x, \mathbb Q(A[\ell])/\mathbb Q) &\ll \frac{x}{\ell \operatorname{log} x} + g\ \ell^{\frac{3g-1}{2}} \frac{x^{\frac{1}{2}}}{\operatorname{log} x} \operatorname{log} (\ell N_A). \end{align*} $$
Now we apply Lemma 18 with
$$ \begin{align*}y \asymp \frac{x^{\frac{1}{3 g + 1}}}{(\operatorname{log} x)^{\frac{2}{3 g + 1}}}\end{align*} $$
and
$$ \begin{align*}u \asymp y^{\frac{1}{2}} (\operatorname{log} y)^{2 + \varepsilon}\end{align*} $$
for an arbitrarily chosen
$\varepsilon> 0$
. We conclude that
$$ \begin{align*}\pi_A(x, 0) \leq c(\varepsilon) \displaystyle\max_{y \leq \ell \leq y + u} \pi_A(x, \ell, 0) \ll_{\varepsilon, A} \frac{ x^{1 - \frac{1}{3g+1} } }{ (\operatorname{log} x)^{1 - \frac{2}{3 g + 1} }}. \end{align*} $$
This completes the proof of Theorem 1.
6.5 Proof of applications (1) and (2)
We keep the setting of Section 6.3. Let
$t \in \mathbb Z$
and
$x> 2$
. By applying Theorem 1, we deduce right away that
$$ \begin{align*} &\#\left\{p \leq x: p \nmid N_A, a_{1, p}(A) \neq t \right\} \\&\quad= \pi(x) - \#\left\{p \leq x: p \nmid N_A, a_{1, p}(A) = t\right\} - \#\left\{p \leq x: p \mid N_A\right\} \sim \pi(x), \end{align*} $$
which confirms (1). To confirm (2), we fix
$\varepsilon> 0$
and make the following observations, the third of which uses Theorem 1:
$$ \begin{align*} \pi(x) &= \#\left\{p \leq x: p \nmid N_A, |a_{1, p}(A)|> p^{\frac{1}{3g+2} - \varepsilon} \right\} \\&\quad+ \#\left\{p \leq x: p \nmid N_A, |a_{1, p}(A)| \leq p^{\frac{1}{3g+2} - \varepsilon} \right\} + \#\left\{p \leq x: p \mid N_A\right\} \\ &= \#\left\{p \leq x: p \nmid N_A, |a_{1, p}(A)| > p^{\frac{1}{3g+2} - \varepsilon} \right\} + \operatorname{O}\left( \displaystyle\sum_{t \in \mathbb Z \atop{|t| \leq x^{\frac{1}{3g+2} - \varepsilon} }} \pi_A(x, t) \right) + \operatorname{O}_{A}(1) \\ &= \#\left\{p \leq x: p \nmid N_A, |a_{1, p}(A)| > p^{\frac{1}{3g+2} - \varepsilon} \right\} + \operatorname{O}_{A, \varepsilon}\left( x^{\frac{1}{3g+2} - \varepsilon} \cdot \displaystyle\frac{x^{1 - \frac{1}{3 g + 2}}}{ (\operatorname{log} x)^{1 - \frac{2}{3 g + 2}} } \right) \\ &= \#\left\{p \leq x: p \nmid N_A, |a_{1, p}(A)| > p^{\frac{1}{3g+2} - \varepsilon} \right\} + \operatorname{O}_{A, \varepsilon}\left( \displaystyle\frac{x^{1 - \varepsilon} }{ (\operatorname{log} x)^{1 - \frac{2}{3 g + 2}} } \right) \\ &= \#\left\{p \leq x: p \nmid N_A, |a_{1, p}(A)| > p^{\frac{1}{3g+2} - \varepsilon} \right\} + \operatorname{o}\left(\pi(x)\right). \end{align*} $$
6.6 Proof of Theorem 3
We keep the setting of Section 6.3. Let
$x> 2$
and
$z = z(x)> 1$
. Note that, for any prime
$\ell $
, we have
$$ \begin{align} \sum_{\substack{t\in \mathbb Z \\|t|\leq z}}\ \pi_A(x, \ell, t) &:= \#\left\{p \leq x: p \nmid \ell N_A, |a_{1, p}(A)| \leq z, \right. \nonumber \\ & \left. \ell \ \text{splits completely in each of the fields} \ \mathbb Q(\pi_p(E_1)), \ldots, \mathbb Q(\pi_p(E_g)) \right\}. \end{align} $$
As before, observe that every prime
$p \nmid d_A$
which is counted on the right-hand side of (42) is also counted by
$\pi _{{\cal C}(\ell , |t|\leq z) }(x, \mathbb Q(A[\ell ])/\mathbb Q)$
. Thus
$$ \begin{align*} \displaystyle\sum_{\substack{t\in \mathbb Z\\|t|\leq z}} \pi_A(x, \ell, t) \ll_A \pi_{{\cal C}(\ell, |t|\leq z) }(x, \mathbb Q(A[\ell])/\mathbb Q). \end{align*} $$
We take
$\ell \nmid 2 g$
to be a sufficiently large prime such that (35) holds. Recalling part (vi) of Lemma 14 and Lemma 16, we apply part (ii) of Corollary 8 of Section 2 with
$K = \mathbb Q$
,
$L = \mathbb Q(A[\ell ])$
,
$G = G(\ell )$
,
$H = B(\ell )$
,
$N = U(\ell )$
, and
${{\cal C}} = {{\cal C}}(\ell , |t|\leq z)$
, and obtain
$$ \begin{align*} &\pi_{{\cal C}(\ell, |t|\leq z) }(x, \mathbb Q(A[\ell])/\mathbb Q) \ll \frac{\left|\widehat{{\cal C}}_{\text{Borel}}(\ell, |t|\leq z) \right| }{\left|B(\ell)/U(\ell)\right| } \cdot \frac{x}{\operatorname{log} x} \\ &\quad\!\!+ \left|\widehat{{\cal C}}_{\text{Borel}}(\ell, |t|\leq z) \right|{}^{\frac{1}{2}}\kern-1pt \left[\mathbb Q(A[\ell])^{B(\ell)} \kern1.2pt{:}\kern1.2pt \mathbb Q\right] \frac{x^{\frac{1}{2}}}{\operatorname{log} x}\kern-1pt \left(\operatorname{log} M\left(\mathbb Q(A[\ell])^{U(\ell)}/\mathbb Q(A[\ell])^{B(\ell)}\kern-1pt\right)\kern-1pt\right)\kern-1.5pt. \nonumber \end{align*} $$
Using Proposition 12 and Lemma 17, we infer from the above that
$$ \begin{align*} \pi_{{\cal C}(\ell, |t|\leq z) }(x, \mathbb Q(A[\ell])/\mathbb Q)\ll \frac{z}{\ell}\cdot \frac{x}{\operatorname{log} x} + g \ z^{\frac{1}{2}}\ell^{\frac{3g}{2}} \frac{x^{\frac{1}{2}}}{\operatorname{log} x}\operatorname{log} (\ell N_A). \end{align*} $$
Applying (34) in Lemma 18 with
$y \asymp z(\operatorname {log} x)^{\eta }$
for some fixed arbitrary
$\eta>0$
, we obtain that
$$ \begin{align*} \sum_{\substack{t\in \mathbb Z\\|t|\leq z}}\pi_A(x, t)& \ll_{A} \frac{x}{(\operatorname{log} x)^{1+\eta}}+x^{\frac{1}{2}} (\operatorname{log} x)^{\frac{3g\eta}{2}-1}z^{\frac{3g+1}{2}}(\operatorname{log} z+\operatorname{log}\operatorname{log} x). \end{align*} $$
Now fix an arbitrary
$\varepsilon>0$
and set
$ z := x^{\frac {1}{3g+1}-\varepsilon }. $
Then
$$ \begin{align*} \sum_{\substack{t\in \mathbb Z\\ |t|\leq x^{\frac{1}{3g+1}-\varepsilon}}}\pi_A(x, t) \ll_{A, \varepsilon} \frac{x}{(\operatorname{log} x)^{1+\eta}} = \operatorname{o}(\pi(x)). \end{align*} $$
Theorem 3 follows from the above upper bound and the following observations:
$$ \begin{align*}\pi(x)&=\#\left\{p \leq x: p \nmid N_A, |a_{1, p}(A)|> p^{\frac{1}{3g+1} - \varepsilon} \right\}\\&\quad+\#\left\{p \leq x: p \nmid N_A, |a_{1, p}(A)| \leq p^{\frac{1}{3g+1} - \varepsilon} \right\}+\#\left\{p \leq x: p \mid N_A\right\}\\ &=\#\left\{p \leq x: p \nmid N_A, |a_{1, p}(A)| > p^{\frac{1}{3g+1} - \varepsilon} \right\}+\displaystyle\sum_{t \in \mathbb Z \atop{|t| \leq x^{\frac{1}{3g+1} - \varepsilon} }}\pi_A(x, t)+\operatorname{O}_A(1)\\ &=\#\left\{p \leq x: p \nmid N_A, |a_{1, p}(A)| > p^{\frac{1}{3g+1} - \varepsilon} \right\}+\operatorname{o}\left(\pi(x)\right).\end{align*} $$
7 Final remarks
It is a natural question to ask whether one can find subgroups and conjugacy classes other than those chosen in Sections 4 and 5 and use them, following a strategy similar to the one of Theorem 1, to obtain a better upper bound for
$\pi _A(x, t)$
. We relegate this question to future research. Below are candidates of subgroups and conjugacy classes which, used mutatis mutandis in our proof, do not improve on Theorem 1.
We keep the setting of Section 6.3. We could replace
$B(\ell )$
with
$T(\ell )$
,
$U(\ell )$
with
$\{I_{2g}\}$
, and
${\widehat {{{\cal C}}}}_{\text {Borel}}(\ell , t)$
with
${\mathcal {C}}_{\text {Torus}}(\ell , t)$
. For every
$t\in {\mathbb Z}$
, this would lead to the upper bound
$$ \begin{align} {\pi}_A(x, t){\ll}_A {\frac{x^{1-\frac{1}{5g+2}}}{(\text{log } x)^{1-\frac{2}{5g+2}}}}. \end{align} $$
Alternatively, we could replace
$B(\ell )$
with
$C^{ns}_{\xi }(\ell )^g\cap G(\ell )$
,
$U(\ell )$
with
$\{I_{2g}\}$
, and
$\widehat {{{\cal C}}}_{\text {Borel}}(\ell , t)$
with
${\mathcal {C}}_{ns}(\ell , \xi , t)$
, where
$C^{ns}_{\xi }(\ell )$
is the nonsplit Cartan subgroup of
$\operatorname {GL}_2(\ell )$
defined by
$$ \begin{align*}C^{ns}_{\xi}(\ell) := \left\{ \begin{pmatrix} a & \xi b\\ b & a \end{pmatrix}: a, b\in {\mathbb F}_{\ell}, (a, b)\neq (0, 0) \right\} \end{align*} $$
for some nonsquare element
$\xi $
of
$\mathbb F_{\ell }^{\times }$
, and where
$$ \begin{align*} &{\mathcal{C}}_{ns}(\ell, \xi, t) :=\left\{\! (M_1, \ldots, M_g) \in C^{ns}_{\xi}(\ell)^g\cap G(\ell) : \displaystyle\sum_{ 1 \leq i \leq g } \operatorname{tr} M_i \equiv - t (\operatorname{mod} \ell) \!\right\}\!. \end{align*} $$
Note that
$C^{ns}_{\xi }(\ell )^g\simeq ( \mathbb F_{\ell ^2}^{\times })^g$
, where
$\mathbb F_{\ell ^2}$
denotes the finite field with
$\ell ^2$
elements. Hence
$C^{ns}_{\xi }(\ell )^g$
is an abelian group. With the above choices, instead of considering the counting function
$\pi _{A}(x, \ell , t)$
, we would consider
$$ \begin{align*} &\pi^{ns}_{A}(x, \ell, t) := \#\{p\leq x: p\nmid N_A, a_{1, p}(A)=t,\\&\quad\ell \ \text{inert in each of the fields} \ \mathbb Q(\pi_p(E_1)), \ldots, \mathbb Q(\pi_p(E_g))\} \end{align*} $$
and prove an upper bound similar to that of Lemma 18. Then, applying Corollary 8, we would obtain the previous bound (43), which is weaker than that of Theorem 1.
Acknowledgment
We thank Jacob Mayle for a careful reading of the manuscript and for useful remarks. We are deeply grateful to the referees for their detailed comments and suggestions.
