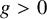1 Introduction
Building on the work of many people [Reference Mori and MukaiMM83, Reference ChenChe99, Reference Bogomolov and TschinkelBT00, Reference Bogomolov, Hassett and TschinkelBHT11, Reference Li and LiedtkeLL11], it was recently proved in [Reference Chen, Gounelas and LiedtkeCGL19] that, for any integer
![]() $g\geq 0$
and any complex projective K3 surface X, there is an infinite sequence of integral curves
$g\geq 0$
and any complex projective K3 surface X, there is an infinite sequence of integral curves
![]() $C_n\subset X$
of geometric genus
$C_n\subset X$
of geometric genus
![]() $g\ge 0$
such that for any ample divisor H
$g\ge 0$
such that for any ample divisor H
The aim of this paper is to strengthen and give a new proof of this result for curves of genus
![]() $g>0$
, assuming only the case
$g>0$
, assuming only the case
![]() $g=0$
, and then to derive a number of applications to the geometry of K3 surfaces. In particular, we prove the following.
$g=0$
, and then to derive a number of applications to the geometry of K3 surfaces. In particular, we prove the following.
Theorem A. Let X be a K3 surface over an algebraically closed field of characteristic zero and
![]() $g>0$
an integer. There exists a sequence of integral curves
$g>0$
an integer. There exists a sequence of integral curves
![]() $C_n\subset X$
of geometric genus g such that
$C_n\subset X$
of geometric genus g such that
and the normalisation morphism of each
![]() $C_n$
deforms in a family of morphisms from smooth genus g curves to X with maximal variation in moduli.
$C_n$
deforms in a family of morphisms from smooth genus g curves to X with maximal variation in moduli.
More precisely, for each such
![]() $C_n\subset X$
there exists a diagram
$C_n\subset X$
there exists a diagram

where
![]() $f_n$
is a smooth family of curves over an irreducible variety
$f_n$
is a smooth family of curves over an irreducible variety
![]() $T_n$
so that there exists a point
$T_n$
so that there exists a point
![]() $t\in T_n$
so that
$t\in T_n$
so that
![]() $F_{n,t}:\mathcal {C}_{n,t}\to X$
is the normalisation morphism of
$F_{n,t}:\mathcal {C}_{n,t}\to X$
is the normalisation morphism of
![]() $C_n$
composed with the inclusion, and
$C_n$
composed with the inclusion, and
![]() $\dim T_n = \dim \phi (T_n) = g$
, where
$\dim T_n = \dim \phi (T_n) = g$
, where
![]() $\phi _n$
is the moduli map to the moduli space of curves.
$\phi _n$
is the moduli map to the moduli space of curves.
We give first an idea of the proof of this theorem. As mentioned, its proof relies on the existence of infinitely many rational curves on a K3 surface and not on the full statement of [Reference Chen, Gounelas and LiedtkeCGL19, Theorem A] so provides a new proof and a strengthening of the higher genus case of loc. cit., both in that
![]() $C_n^2 \to \infty $
implies
$C_n^2 \to \infty $
implies
![]() $HC_n \to \infty $
by the Hodge index theorem but also that the curves produced vary in moduli.
$HC_n \to \infty $
by the Hodge index theorem but also that the curves produced vary in moduli.
The second key ingredient in proving the above theorem is the logarithmic Bogomolov–Miyaoka–Yau inequality, which allows us, using local analysis of Orevkov–Zaidenberg, which we expand on in Section 3, to control the singularities of rational curves in X as their self-intersection increases. In particular, we show first in Proposition 3.4 that if
for C is a rational curve on a K3 surface, then C must have a locally reducible singularity (i.e., one with at least two branches). As it is not known whether such a rational curve always exists on a K3 surface, we also show in Proposition 3.5 that if
![]() $C_1, C_2$
are two rational curves so that
$C_1, C_2$
are two rational curves so that
![]() $C_1C_2$
is large enough with respect to
$C_1C_2$
is large enough with respect to
![]() $C_1^2, C_2^2$
, then they must meet in at least two distinct points (e.g., if
$C_1^2, C_2^2$
, then they must meet in at least two distinct points (e.g., if
![]() $C^2\leq 4690$
for all rational curves in the K3, then
$C^2\leq 4690$
for all rational curves in the K3, then
![]() $C_1C_2> 1,299,546$
suffices). As a consequence, a partial normalisation of such a C or of such a union
$C_1C_2> 1,299,546$
suffices). As a consequence, a partial normalisation of such a C or of such a union
![]() $C_1\cup C_2$
may now be deformed in
$C_1\cup C_2$
may now be deformed in
![]() $\overline {\mathscr {M}}_1(X,\beta )$
to produce a genus one curve which necessarily deforms with maximal moduli. The argument then proceeds by induction on the genus.
$\overline {\mathscr {M}}_1(X,\beta )$
to produce a genus one curve which necessarily deforms with maximal moduli. The argument then proceeds by induction on the genus.
By results of Mukai, the general curve of genus g is contained in a K3 surface if and only if
![]() $2\leq g\leq 9$
or
$2\leq g\leq 9$
or
![]() $g=11$
. Our result above, however, says that, for any fixed K3 surface X and any
$g=11$
. Our result above, however, says that, for any fixed K3 surface X and any
![]() $g\geq 0$
, there exist g-dimensional subvarieties of
$g\geq 0$
, there exist g-dimensional subvarieties of
![]() $\mathscr {M}_g$
whose general member parametrises a curve which admits a morphism to X birational onto its image. In the opposite direction, it is worth noting that it is expected yet not known that a very general K3 surface cannot be dominated by the product of two curves, which would imply that curves of constant moduli should not exist on most K3 surfaces.
$\mathscr {M}_g$
whose general member parametrises a curve which admits a morphism to X birational onto its image. In the opposite direction, it is worth noting that it is expected yet not known that a very general K3 surface cannot be dominated by the product of two curves, which would imply that curves of constant moduli should not exist on most K3 surfaces.
As far as applications are concerned, although the existence of rational curves is satisfying to know, they do not provide much to work with. It turns out that the existence of one single genus 1 curve produced by Theorem 1 has numerous applications, so we begin by stating it as a separate corollary.
Corollary. A K3 surface in characteristic zero contains a nonisotrivial family of integral curves of geometric genus 1.
It is well-known that any K3 surface contains a family of genus 1 curves, so what is new in the above is the variation in moduli. As an application, combined with a result of Voisin [Reference HuybrechtsHuy14, Theorem 11.1] (where the existence of curves produced by the corollary is implicitly asked), the above immediately implies a conjecture of Huybrechts [Reference HuybrechtsHuy14, Conjecture 2.3].
Corollary. There are infinitely many constant cycle curves of bounded order on every complex K3 surface X, and their union is dense in the strong topology.
In a different direction, even though
![]() $\mathrm {H}^0(X,\Omega ^1_X)=0$
is easy to see for a complex K3 surface X via Hodge theory, Kobayashi [Reference KobayashiKob80, Corollary 8] also proved that a simply connected Calabi–Yau manifold has no symmetric differentials or, in other words, that
$\mathrm {H}^0(X,\Omega ^1_X)=0$
is easy to see for a complex K3 surface X via Hodge theory, Kobayashi [Reference KobayashiKob80, Corollary 8] also proved that a simply connected Calabi–Yau manifold has no symmetric differentials or, in other words, that
His proof is also analytic in nature and relies on the resolution of the Calabi conjecture by Yau. We give an algebraic proof of this fact for K3 surfaces, using only the existence of one nonisotrivial family of genus 1 curves, which follows from the corollary above.
Theorem B Kobayashi
The cotangent bundle of a complex K3 surface is not
![]() ${\mathbb {Q}}$
-effective.
${\mathbb {Q}}$
-effective.
Based on his generalised Zariski decomposition, Nakayama in [Reference NakayamaNak04] proved that this implies that the divisor
![]() ${\mathcal O}_{{\mathbb {P}}(\Omega ^1_X)}(1)$
is not even pseudoeffective (see Theorem 5.6 for a proof).
${\mathcal O}_{{\mathbb {P}}(\Omega ^1_X)}(1)$
is not even pseudoeffective (see Theorem 5.6 for a proof).
Even though we do not provide a proof of Kobayashi’s theorem or Theorem A in positive characteristic, we state as many results as possible in that direction, and in the final Section 5, we prove a conditional vanishing of global 1-forms (known by theorems of Rudakov–Shafarevich or Nygaard) and stability of the cotangent bundle (which holds if X is not uniruled but is known to fail otherwise).
Notation. Throughout this paper a K3 surface will always be a smooth projective simply connected surface with trivial canonical divisor over an algebraically closed field.
2 Deformations and singular curves
Let A be an effective divisor on a complex K3 surface. We consider the moduli map
where
![]() $\overline {\mathscr {M}}_g$
is the moduli space of stable curves of genus g and
$\overline {\mathscr {M}}_g$
is the moduli space of stable curves of genus g and
![]() $V_{A,g}$
is the Severi variety parametrising integral curves in
$V_{A,g}$
is the Severi variety parametrising integral curves in
![]() $|A|$
of geometric genus g. It is expected that this map is generically finite over its image for ‘most’ divisors
$|A|$
of geometric genus g. It is expected that this map is generically finite over its image for ‘most’ divisors
![]() $A\in \mathrm {Pic\ }(X)$
, and we call such variation in moduli maximal (see Definition 2.3 for a more rigorous definition). The problem of existence of curves moving with maximal moduli has been studied by various authors for generic complex K3 surfaces (cf. [Reference Flamini, Knutsen, Pacienza and SernesiFKPS08, Reference KemenyKem15, Reference Ciliberto, Flamini, Galati and KnutsenCFGK17]).
$A\in \mathrm {Pic\ }(X)$
, and we call such variation in moduli maximal (see Definition 2.3 for a more rigorous definition). The problem of existence of curves moving with maximal moduli has been studied by various authors for generic complex K3 surfaces (cf. [Reference Flamini, Knutsen, Pacienza and SernesiFKPS08, Reference KemenyKem15, Reference Ciliberto, Flamini, Galati and KnutsenCFGK17]).
Definition 2.1. Let
![]() $\mathbf {k}$
be an algebraically closed field and C an integral curve over
$\mathbf {k}$
be an algebraically closed field and C an integral curve over
![]() $\mathbf {k}$
. We say that a point
$\mathbf {k}$
. We say that a point
![]() $p\in C$
is a locally reducible singularity of C if the formal completion
$p\in C$
is a locally reducible singularity of C if the formal completion
![]() $\widehat {{\mathcal O}}_{C,p}$
of the stalk of C at p is not an integral domain. Equivalently,
$\widehat {{\mathcal O}}_{C,p}$
of the stalk of C at p is not an integral domain. Equivalently,
![]() $\nu ^{-1}(p)$
consists of at least two distinct points under the normalisation
$\nu ^{-1}(p)$
consists of at least two distinct points under the normalisation
![]() $\nu : C^\nu \to C$
of C. Otherwise, we say that C is locally irreducible at p. The number of local branches of C at p is the number of points in
$\nu : C^\nu \to C$
of C. Otherwise, we say that C is locally irreducible at p. The number of local branches of C at p is the number of points in
![]() $\nu ^{-1}(p)$
.
$\nu ^{-1}(p)$
.
The following is standard and is the main reason we are interested in such singularities.
Lemma 2.2. Let
![]() $p\in C$
be a locally reducible singularity of an integral curve. Then the normalisation
$p\in C$
be a locally reducible singularity of an integral curve. Then the normalisation
![]() $\nu :C^\nu \to C$
factors through a curve
$\nu :C^\nu \to C$
factors through a curve
![]() $C'$
which has one node and is smooth otherwise.
$C'$
which has one node and is smooth otherwise.
Proof. Choose a sufficiently ample line bundle L on C. For
![]() $q_1\neq q_2\in \nu ^{-1}(p)$
, consider the subspace
$q_1\neq q_2\in \nu ^{-1}(p)$
, consider the subspace
Then
![]() $s_1(q_1) = s_2(q_2)$
for all
$s_1(q_1) = s_2(q_2)$
for all
![]() $s_1,s_2\in V$
. Let
$s_1,s_2\in V$
. Let
![]() $f: C^\nu \to G \subset {\mathbb {P}} V^*$
be the morphism given by the linear series V. Clearly,
$f: C^\nu \to G \subset {\mathbb {P}} V^*$
be the morphism given by the linear series V. Clearly,
![]() $\nu $
factors through f. For L sufficiently ample, G has a node
$\nu $
factors through f. For L sufficiently ample, G has a node
![]() $q = f(q_1) = f(q_2)$
over p as the only singularity.
$q = f(q_1) = f(q_2)$
over p as the only singularity.
For
![]() $C\subset X$
a curve on a K3 surface, we denote by
$C\subset X$
a curve on a K3 surface, we denote by
the Kontsevich moduli space of stable maps of arithmetic genus g to X with image of class
![]() ${\mathcal O}(C)$
. For
${\mathcal O}(C)$
. For
![]() $f:D\to X$
such a morphism, we denote by
$f:D\to X$
such a morphism, we denote by
![]() $[f]$
the induced point in moduli.
$[f]$
the induced point in moduli.
Definition 2.3. Let
![]() $f:C\to X$
be a stable map of arithmetic genus g to a K3 surface over an algebraically closed field. We say that f deforms
$f:C\to X$
be a stable map of arithmetic genus g to a K3 surface over an algebraically closed field. We say that f deforms
-
1. in the expected dimension if
 $\dim M=g$
for every irreducible component
$\dim M=g$
for every irreducible component
 $[f]\in M\subset \overline {\mathscr {M}}_g(X,{\mathcal O}(C))$
and
$[f]\in M\subset \overline {\mathscr {M}}_g(X,{\mathcal O}(C))$
and -
2. with maximal moduli if the induced moduli map
 $\phi _M:M\to \overline {\mathscr {M}}_g$
satisfies
$\phi _M:M\to \overline {\mathscr {M}}_g$
satisfies
 $\dim ( \operatorname {im}\phi _M) \geq g$
for at least one irreducible component
$\dim ( \operatorname {im}\phi _M) \geq g$
for at least one irreducible component
 $[f]\in M\subset \overline {\mathscr {M}}_g(X,{\mathcal O}(C))$
.
$[f]\in M\subset \overline {\mathscr {M}}_g(X,{\mathcal O}(C))$
.
We say that an integral curve
![]() $C\subset X$
satisfies one of the above properties if its normalisation morphism
$C\subset X$
satisfies one of the above properties if its normalisation morphism
![]() $\nu :C^\nu \to C\subset X$
composed with the embedding into X does so.
$\nu :C^\nu \to C\subset X$
composed with the embedding into X does so.
Remark 2.4. From [Reference Chen, Gounelas and LiedtkeCGL19, Theorem 2.11], for any
![]() $C\subset X$
integral with normalisation morphism contained in some irreducible component
$C\subset X$
integral with normalisation morphism contained in some irreducible component
![]() $[\nu :C^\nu \to X]\in M\subset \overline {\mathscr {M}}_g(X,{\mathcal O}(C))$
, we have
$[\nu :C^\nu \to X]\in M\subset \overline {\mathscr {M}}_g(X,{\mathcal O}(C))$
, we have
![]() $\dim M\geq g$
. Moreover, in characteristic zero any such C deforms in the expected dimension (from Proposition 2.5 below), but it is not necessarily the case that C deforms with maximal moduli, as seen, for example, by the existence of isotrivial elliptic fibrations. In positive characteristic, the situation is more complicated, as on a uniruled K3 there exist genus 0 curves which deform too much. Nodal rational curves on a K3 surface are always rigid though, and on a nonuniruled K3 surface, every curve of geometric genus 1 deforms in the expected dimension (see [Reference Chen, Gounelas and LiedtkeCGL19, Proposition 2.9]). We do not know any examples of curves that do not deform in the expected dimension on a nonuniruled K3 surface.
$\dim M\geq g$
. Moreover, in characteristic zero any such C deforms in the expected dimension (from Proposition 2.5 below), but it is not necessarily the case that C deforms with maximal moduli, as seen, for example, by the existence of isotrivial elliptic fibrations. In positive characteristic, the situation is more complicated, as on a uniruled K3 there exist genus 0 curves which deform too much. Nodal rational curves on a K3 surface are always rigid though, and on a nonuniruled K3 surface, every curve of geometric genus 1 deforms in the expected dimension (see [Reference Chen, Gounelas and LiedtkeCGL19, Proposition 2.9]). We do not know any examples of curves that do not deform in the expected dimension on a nonuniruled K3 surface.
The following is basically the Arbarello–Cornalba lemma (see [Reference Arbarello and CornalbaAC81, Lemma 1.4] or [Reference Arbarello, Cornalba and GriffithsACG11, §XXI.9] for a more thorough reference) in the case of K3 surfaces.
Proposition 2.5. Let X be a K3 surface over an algebraically closed field of characteristic zero, and
![]() $C\subset X$
an integral curve of geometric genus
$C\subset X$
an integral curve of geometric genus
![]() $g\geq 1$
. Then if
$g\geq 1$
. Then if
![]() $[\nu ]\in M\subset \overline {\mathscr {M}}_g(X, {\mathcal O}(C))$
is an irreducible component containing the normalisation
$[\nu ]\in M\subset \overline {\mathscr {M}}_g(X, {\mathcal O}(C))$
is an irreducible component containing the normalisation
![]() $\nu :C^\nu \to C$
, we have:
$\nu :C^\nu \to C$
, we have:
-
1. A general element
 $[f:D\to X]\in M$
corresponds to an unramified morphism.
$[f:D\to X]\in M$
corresponds to an unramified morphism. -
2.
 $\dim M = g$
.
$\dim M = g$
. -
3. If
 $D'\subset X$
an integral curve and
$D'\subset X$
an integral curve and
 $[f:D\to X]\in M$
general, then the support of
$[f:D\to X]\in M$
general, then the support of
 $f^*{\mathcal O}_X(D')$
consists of
$f^*{\mathcal O}_X(D')$
consists of
 $D'f(D)$
distinct points.
$D'f(D)$
distinct points.
Proof. The first claim is an application of the usual Arbarello–Cornalba lemma in the case of K3 surfaces (see, e.g., [Reference Dedieu and SernesiDS17]), whereas the second and third follow essentially from the first (see [Reference Chen, Gounelas and LiedtkeCGL19, §2] and the proof of [Reference Chen, Gounelas and LiedtkeCGL19, Lemma 6.3]).
Remark 2.6. In positive characteristic, it is not the case that (1) in the above is true (e.g., in a quasi-elliptic fibration the general fibre has ramified normalisation as it is a cusp), but we expect it to be true in most cases (see Question 4.6). It is, however, true that (1) implies (2) and (3).
We recall the following argument, essentially due to Bogomolov–Mumford, cf. [Reference HuybrechtsHuy16, §13.2.1].
Proposition 2.7. Let X be a K3 surface over an algebraically closed field and
![]() $C\subset X$
be an integral curve of geometric genus g. Assume further that C
$C\subset X$
be an integral curve of geometric genus g. Assume further that C
-
1. deforms in the expected dimension,
-
2. deforms with maximal moduli and
-
3. has a locally reducible singularity at a point p.
Then C deforms to an integral curve D of geometric genus
![]() $g+1$
which deforms in the expected dimension and with maximal moduli.
$g+1$
which deforms in the expected dimension and with maximal moduli.
Proof. As the singularity at p is locally reducible, from Lemma 2.2 we may take
![]() $f:\widetilde {C}\to X$
to be a partial normalisation of C which has one node over the point p and is smooth otherwise. In particular,
$f:\widetilde {C}\to X$
to be a partial normalisation of C which has one node over the point p and is smooth otherwise. In particular,
![]() $[f]\in \overline {\mathscr {M}}_{g+1}(X, {\mathcal O}(C))$
. Let M be an irreducible component of
$[f]\in \overline {\mathscr {M}}_{g+1}(X, {\mathcal O}(C))$
. Let M be an irreducible component of
![]() $\overline {\mathscr {M}}_{g+1}(X,{\mathcal O}(C))$
containing
$\overline {\mathscr {M}}_{g+1}(X,{\mathcal O}(C))$
containing
![]() $[f]$
. From [Reference Chen, Gounelas and LiedtkeCGL19, Theorem 2.11],
$[f]$
. From [Reference Chen, Gounelas and LiedtkeCGL19, Theorem 2.11],
![]() $\dim M\geq g+1$
. Consider now the moduli map
$\dim M\geq g+1$
. Consider now the moduli map
Let
![]() $D_M$
be an irreducible component of
$D_M$
be an irreducible component of
![]() $M\cap \phi ^{-1}(\partial \overline {\mathscr {M}}_{g+1})$
containing
$M\cap \phi ^{-1}(\partial \overline {\mathscr {M}}_{g+1})$
containing
![]() $[f]$
, where
$[f]$
, where
![]() $\partial \overline {\mathscr {M}}_{g+1} = \overline {\mathscr {M}}_{g+1} - \mathscr {M}_{g+1}$
is the boundary divisor of
$\partial \overline {\mathscr {M}}_{g+1} = \overline {\mathscr {M}}_{g+1} - \mathscr {M}_{g+1}$
is the boundary divisor of
![]() $\overline {\mathscr {M}}_{g+1}$
.
$\overline {\mathscr {M}}_{g+1}$
.
For a general point,
![]() $[h]\in D_M$
,
$[h]\in D_M$
,
![]() $h: \Gamma \to X$
is a stable map such that
$h: \Gamma \to X$
is a stable map such that
![]() $\Gamma $
is an integral curve of geometric genus g with a node and
$\Gamma $
is an integral curve of geometric genus g with a node and
![]() $h(\Gamma )$
and C lie on the same component of
$h(\Gamma )$
and C lie on the same component of
![]() $V_{C,g}$
. Since C deforms in the expected dimension,
$V_{C,g}$
. Since C deforms in the expected dimension,
![]() $\dim D_M \le g$
, and hence,
$\dim D_M \le g$
, and hence,
![]() $D_M \subsetneq M$
. On the other hand, since
$D_M \subsetneq M$
. On the other hand, since
![]() $\partial \overline {\mathscr {M}}_{g+1}$
is a
$\partial \overline {\mathscr {M}}_{g+1}$
is a
![]() ${\mathbb {Q}}$
-Cartier divisor,
${\mathbb {Q}}$
-Cartier divisor,
![]() $D_M$
has codimension one in M. We must have
$D_M$
has codimension one in M. We must have
and hence,
![]() $\dim M = g+1$
. This proves that for a general point
$\dim M = g+1$
. This proves that for a general point
![]() $h:\Gamma \to X$
of M,
$h:\Gamma \to X$
of M,
![]() $D = h(\Gamma )$
is an integral curve of geometric genus
$D = h(\Gamma )$
is an integral curve of geometric genus
![]() $g+1$
that deforms in the expected dimension.
$g+1$
that deforms in the expected dimension.
Since C deforms with maximal moduli, there exists an irreducible component D of
![]() $ \phi ^{-1}(\partial \overline {\mathscr {M}}_{g+1})$
containing
$ \phi ^{-1}(\partial \overline {\mathscr {M}}_{g+1})$
containing
![]() $[f]$
such that
$[f]$
such that
![]() $\dim \phi (D) = g$
. Let
$\dim \phi (D) = g$
. Let
![]() $M'$
be an irreducible component of
$M'$
be an irreducible component of
![]() $\overline {\mathscr {M}}_{g+1}(X,{\mathcal O}(C))$
containing D. Since
$\overline {\mathscr {M}}_{g+1}(X,{\mathcal O}(C))$
containing D. Since
![]() $\phi (M')$
is not contained in
$\phi (M')$
is not contained in
![]() $\partial \overline {\mathscr {M}}_{g+1}$
, we conclude
$\partial \overline {\mathscr {M}}_{g+1}$
, we conclude
and hence,
![]() $\dim \phi (M') = g+1$
. Therefore, for a general point
$\dim \phi (M') = g+1$
. Therefore, for a general point
![]() $h:\Gamma \to X$
of
$h:\Gamma \to X$
of
![]() $M'$
,
$M'$
,
![]() $D = h(\Gamma )$
is an integral curve of geometric genus
$D = h(\Gamma )$
is an integral curve of geometric genus
![]() $g+1$
that deforms with maximal moduli.
$g+1$
that deforms with maximal moduli.
Although we will not be using it in this paper, we include the following immediate corollary, which is well-known to experts, as an application.
Corollary 2.8. Let X be a K3 surface over an algebraically closed field and
![]() $R\subset X$
be a nodal rational curve of arithmetic genus
$R\subset X$
be a nodal rational curve of arithmetic genus
![]() $g\geq 1$
. For any
$g\geq 1$
. For any
![]() $1\leq d\leq g$
, R deforms to a nodal integral curve C of geometric genus d which deforms in the expected dimension and with maximal moduli.
$1\leq d\leq g$
, R deforms to a nodal integral curve C of geometric genus d which deforms in the expected dimension and with maximal moduli.
Proof. The result follows by induction, Proposition 2.7 and the fact that a general deformation of a nodal curve will be nodal and as such has unramified normalisation morphism, hence deforms in the expected dimension from [Reference Chen, Gounelas and LiedtkeCGL19, Proposition 2.9].
One similarly obtains the following.
Proposition 2.9. Let X be a K3 surface over an algebraically closed field and
![]() $C_1,C_2\subset X$
be two integral curves of geometric genus
$C_1,C_2\subset X$
be two integral curves of geometric genus
![]() $g_1, g_2$
, respectively. Assume further that
$g_1, g_2$
, respectively. Assume further that
-
1.
 $C_i$
deforms in the expected dimension for
$C_i$
deforms in the expected dimension for
 $i=1,2$
,
$i=1,2$
, -
2.
 $C_i$
deforms with maximal moduli for
$C_i$
deforms with maximal moduli for
 $i=1,2$
,
$i=1,2$
, -
3.
 $|C_1\cap C_2|$
contains at least two distinct points.
$|C_1\cap C_2|$
contains at least two distinct points.
Then
![]() $C_1\cup C_2$
deforms to an integral curve D of geometric genus
$C_1\cup C_2$
deforms to an integral curve D of geometric genus
![]() $g_1+g_2+1$
which deforms in the expected dimension and with maximal moduli.
$g_1+g_2+1$
which deforms in the expected dimension and with maximal moduli.
3 Families of curves of maximal moduli
There are two main ingredients in the proof of Theorem A
-
○ the existence of infinitely many rational curves on every complex K3 surface [Reference Chen, Gounelas and LiedtkeCGL19],
-
○ the logarithmic Bogomolov–Miyaoka–Yau (BMY) inequality [Reference MiyaokaMiy84].
Let us first review the basics of the latter. For the applications that we have in mind, we start with a reduced but possibly reducible curve D on a smooth projective surface X over
![]() ${\mathbb {C}}$
. Take now a log resolution
${\mathbb {C}}$
. Take now a log resolution
i.e., a birational projective morphism
![]() $f: \widehat {X}\to X$
such that the total transform
$f: \widehat {X}\to X$
such that the total transform
![]() $\widehat {D} = f^{-1}(D)= \sum _{i=1}^n \Gamma _i$
of D has simple normal crossings, with irreducible components
$\widehat {D} = f^{-1}(D)= \sum _{i=1}^n \Gamma _i$
of D has simple normal crossings, with irreducible components
![]() $\Gamma _i$
and
$\Gamma _i$
and
![]() $X\backslash D \cong \widehat {X}\backslash \widehat {D}$
. We usually choose
$X\backslash D \cong \widehat {X}\backslash \widehat {D}$
. We usually choose
![]() $(\widehat {X}, \widehat {D})$
to be the minimal resolution of
$(\widehat {X}, \widehat {D})$
to be the minimal resolution of
![]() $(X,D)$
.
$(X,D)$
.
Now, for such a pair
![]() $(\widehat {X}, \widehat {D})$
of a smooth projective surface and a SNC divisor, the log BMY inequality says that if
$(\widehat {X}, \widehat {D})$
of a smooth projective surface and a SNC divisor, the log BMY inequality says that if
![]() $K_{\widehat {X}} + \widehat {D}$
is
$K_{\widehat {X}} + \widehat {D}$
is
![]() ${\mathbb {Q}}$
-effective, then
${\mathbb {Q}}$
-effective, then
We recall that
![]() $\Omega ^1_{\widehat {X}}(\log \widehat {D})$
is the locally free sheaf which sits in the following short exact sequence
$\Omega ^1_{\widehat {X}}(\log \widehat {D})$
is the locally free sheaf which sits in the following short exact sequence

and we refer, for example, to [Reference Esnault and ViehwegEV92, §2] for further details.
Remark 3.1. Note that there is a version of the log BMY inequality over fields of positive characteristic, proven recently by Langer [Reference LangerLan16]. The conclusion is essentially the same inequality; however, one requires that the pair
![]() $(\widehat {X},\widehat {D})$
lifts in a compatible way to
$(\widehat {X},\widehat {D})$
lifts in a compatible way to
![]() $W_2(k)$
.
$W_2(k)$
.
Over the complex numbers, we have
where
![]() $e(\bullet )$
is the topological Euler characteristic.
$e(\bullet )$
is the topological Euler characteristic.
For the applications we have in mind, X will be a K3 surface, and hence,
![]() $K_{\widehat {X}} + \widehat {D}$
will always be effective.
$K_{\widehat {X}} + \widehat {D}$
will always be effective.
Although
![]() $c_2(\Omega ^1_{\widehat {X}}(\log \widehat {D}))$
can be computed topologically by equation (3.2) over
$c_2(\Omega ^1_{\widehat {X}}(\log \widehat {D}))$
can be computed topologically by equation (3.2) over
![]() ${\mathbb {C}}$
, we want to give a purely algebraic formula for it in terms of
${\mathbb {C}}$
, we want to give a purely algebraic formula for it in terms of
![]() $c_2(X)$
,
$c_2(X)$
,
![]() $p_a(D)$
and the invariants of the singularities of D (we refer to [Reference de Jong and PfisterdJP00, §5] for the basics of curve singularities). As the proof of this works in arbitrary characteristic, we state it in this generality.
$p_a(D)$
and the invariants of the singularities of D (we refer to [Reference de Jong and PfisterdJP00, §5] for the basics of curve singularities). As the proof of this works in arbitrary characteristic, we state it in this generality.
Lemma 3.2. Let X be a smooth projective surface over an algebraically closed field and D be a reduced curve on X. Let
![]() $(\widehat {X}, \widehat {D})$
be the minimal log resolution of
$(\widehat {X}, \widehat {D})$
be the minimal log resolution of
![]() $(X,D)$
. Then
$(X,D)$
. Then
where
![]() $\delta _p$
and
$\delta _p$
and
![]() $\gamma _p$
are the
$\gamma _p$
are the
![]() $\delta $
-invariant and the number of local branches of D at p, respectively.
$\delta $
-invariant and the number of local branches of D at p, respectively.
Proof. Let
![]() $\widehat {D} = \sum _{i=1}^n \Gamma _i$
, where
$\widehat {D} = \sum _{i=1}^n \Gamma _i$
, where
![]() $\Gamma _i$
are the irreducible components of
$\Gamma _i$
are the irreducible components of
![]() $\widehat {D}$
. From the exact sequences
$\widehat {D}$
. From the exact sequences

for
![]() $m=1,\ldots ,n$
, we obtain
$m=1,\ldots ,n$
, we obtain
 $$\begin{align*}\begin{aligned} \mathop{\mathrm{ch}}\nolimits(\Omega^1_{\widehat{X}}(\log \widehat{D})) &= \mathop{\mathrm{ch}}\nolimits(\Omega^1_{\widehat{X}}) + \sum_{m=1}^n \mathop{\mathrm{ch}}\nolimits({\mathcal O}_{\Gamma_m})\\ &= \mathop{\mathrm{ch}}\nolimits(\Omega^1_{\widehat{X}}) + \sum_{m=1}^n (\mathop{\mathrm{ch}}\nolimits({\mathcal O}_{\widehat{X}})-\mathop{\mathrm{ch}}\nolimits({\mathcal O}_{\widehat{X}}(-\Gamma_m)))\\ &= K_{\widehat{X}} + \widehat{D} + \frac{1}2(K_{\widehat{X}}^2 - 2c_2(\widehat{X}) - \sum_{m=1}^n \Gamma_m^2), \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \mathop{\mathrm{ch}}\nolimits(\Omega^1_{\widehat{X}}(\log \widehat{D})) &= \mathop{\mathrm{ch}}\nolimits(\Omega^1_{\widehat{X}}) + \sum_{m=1}^n \mathop{\mathrm{ch}}\nolimits({\mathcal O}_{\Gamma_m})\\ &= \mathop{\mathrm{ch}}\nolimits(\Omega^1_{\widehat{X}}) + \sum_{m=1}^n (\mathop{\mathrm{ch}}\nolimits({\mathcal O}_{\widehat{X}})-\mathop{\mathrm{ch}}\nolimits({\mathcal O}_{\widehat{X}}(-\Gamma_m)))\\ &= K_{\widehat{X}} + \widehat{D} + \frac{1}2(K_{\widehat{X}}^2 - 2c_2(\widehat{X}) - \sum_{m=1}^n \Gamma_m^2), \end{aligned} \end{align*}$$
where
![]() $\mathop {\mathrm {ch}}\nolimits (\bullet )$
is the Chern character. It follows that
$\mathop {\mathrm {ch}}\nolimits (\bullet )$
is the Chern character. It follows that
 $$\begin{align*}\begin{aligned} c_2(\Omega^1_{\widehat{X}}(\log \widehat{D})) &= c_2(\widehat{X}) + \frac{1}2(K_{\widehat{X}} + \widehat{D})^2 - \frac{1}2 K_{\widehat{X}}^2 + \frac{1}2\sum_{m=1}^n \Gamma_m^2\\ &= c_2(\widehat{X}) + (K_{\widehat{X}} + \widehat{D}) \widehat{D} - \sum_{1\le i<j\le n} \Gamma_i \Gamma_j. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} c_2(\Omega^1_{\widehat{X}}(\log \widehat{D})) &= c_2(\widehat{X}) + \frac{1}2(K_{\widehat{X}} + \widehat{D})^2 - \frac{1}2 K_{\widehat{X}}^2 + \frac{1}2\sum_{m=1}^n \Gamma_m^2\\ &= c_2(\widehat{X}) + (K_{\widehat{X}} + \widehat{D}) \widehat{D} - \sum_{1\le i<j\le n} \Gamma_i \Gamma_j. \end{aligned} \end{align*}$$
Note that further blowing up
![]() $\widehat {X}$
at a singularity of
$\widehat {X}$
at a singularity of
![]() $\widehat {D}$
does not change
$\widehat {D}$
does not change
![]() $c_2(\Omega ^1_{\widehat {X}}(\log \widehat {D}))$
. The minimal log resolution of
$c_2(\Omega ^1_{\widehat {X}}(\log \widehat {D}))$
. The minimal log resolution of
![]() $(X,D)$
does not blow up all singularities of D in case that D is reducible: If D has an ordinary double point at p where two components of D meet transversely, we do not need to blow up X at p. On the other hand, we can choose to blow up X at such p since it does not change
$(X,D)$
does not blow up all singularities of D in case that D is reducible: If D has an ordinary double point at p where two components of D meet transversely, we do not need to blow up X at p. On the other hand, we can choose to blow up X at such p since it does not change
![]() $c_2(\Omega ^1_{\widehat {X}}(\log \widehat {D}))$
. This has the advantage of streamlining our argument. Hence, we choose a log resolution
$c_2(\Omega ^1_{\widehat {X}}(\log \widehat {D}))$
. This has the advantage of streamlining our argument. Hence, we choose a log resolution
![]() $(\widehat {X}, \widehat {D})$
of
$(\widehat {X}, \widehat {D})$
of
![]() $(X,D)$
which is minimal with the properties that
$(X,D)$
which is minimal with the properties that
![]() $\widehat {D}$
has simple normal crossings and the proper transforms of the components of D are disjoint from each other.
$\widehat {D}$
has simple normal crossings and the proper transforms of the components of D are disjoint from each other.
Let us write
 $$\begin{align*}\widehat{D} = \sum_{i=1}^n \Gamma_i = \Delta + \sum_{p\in D_s} E_p, \end{align*}$$
$$\begin{align*}\widehat{D} = \sum_{i=1}^n \Gamma_i = \Delta + \sum_{p\in D_s} E_p, \end{align*}$$
where
![]() $\Delta $
is the proper transform of D under
$\Delta $
is the proper transform of D under
![]() $\pi : \widehat {X}\to X$
and
$\pi : \widehat {X}\to X$
and
![]() $E_p = \pi ^{-1}(p)$
for
$E_p = \pi ^{-1}(p)$
for
![]() $p\in D_s$
, where
$p\in D_s$
, where
![]() $D_s$
is the set of singularities of D. Clearly,
$D_s$
is the set of singularities of D. Clearly,
![]() $E_p$
is a tree of smooth rational curves for all
$E_p$
is a tree of smooth rational curves for all
![]() $p\in D_s$
. Then the above equality takes the form
$p\in D_s$
. Then the above equality takes the form
 $$\begin{align*}\begin{aligned} c_2(\Omega^1_{\widehat{X}}(\log \widehat{D})) &= c_2(\widehat{X}) + (K_{\widehat{X}} + \Delta) \Delta + \sum_{p\in D_s} (K_{\widehat{X}} + E_p) E_p + \sum_{p\in D_s} \Delta E_p\\ &\quad - \sum_{p\in D_s} \sum_{\substack{1\le i<j\le n\\ \Gamma_i\cup \Gamma_j\subset E_p}} \Gamma_i \Gamma_j. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} c_2(\Omega^1_{\widehat{X}}(\log \widehat{D})) &= c_2(\widehat{X}) + (K_{\widehat{X}} + \Delta) \Delta + \sum_{p\in D_s} (K_{\widehat{X}} + E_p) E_p + \sum_{p\in D_s} \Delta E_p\\ &\quad - \sum_{p\in D_s} \sum_{\substack{1\le i<j\le n\\ \Gamma_i\cup \Gamma_j\subset E_p}} \Gamma_i \Gamma_j. \end{aligned} \end{align*}$$
Since
![]() $\Delta $
is the normalisation of D,
$\Delta $
is the normalisation of D,
 $$\begin{align*}\begin{aligned} (K_{\widehat{X}} + \Delta) \Delta &= 2p_a(\Delta) - 2 = 2p_a(D) - 2 - 2 \sum_{p\in D} \delta_p\\ &= (K_X + D) D - 2 \sum_{p\in D} \delta_p. \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} (K_{\widehat{X}} + \Delta) \Delta &= 2p_a(\Delta) - 2 = 2p_a(D) - 2 - 2 \sum_{p\in D} \delta_p\\ &= (K_X + D) D - 2 \sum_{p\in D} \delta_p. \end{aligned} \end{align*}$$
For every
![]() $p\in D_s$
,
$p\in D_s$
,
![]() $p_a(E_p) = 0$
, and hence,
$p_a(E_p) = 0$
, and hence,
It is also clear that
![]() $\Delta E_p$
equals the number of local branches of D at
$\Delta E_p$
equals the number of local branches of D at
![]() $p\in D_s$
. Therefore,
$p\in D_s$
. Therefore,
Since
![]() $E_p$
is a tree of smooth rational curves,
$E_p$
is a tree of smooth rational curves,
 $$\begin{align*}\sum_{\substack{1\le i<j\le n\\ \Gamma_i\cup \Gamma_j\subset E_p}} \Gamma_i \Gamma_j = |E_p| - 1 \end{align*}$$
$$\begin{align*}\sum_{\substack{1\le i<j\le n\\ \Gamma_i\cup \Gamma_j\subset E_p}} \Gamma_i \Gamma_j = |E_p| - 1 \end{align*}$$
for
![]() $p\in D_s$
, where
$p\in D_s$
, where
![]() $|E_p|$
is the number of irreducible components of
$|E_p|$
is the number of irreducible components of
![]() $E_p$
. Finally,
$E_p$
. Finally,
Combining all the above, we obtain equation (3.3).
For convenience, we write
Over the complex numbers,
![]() $\mu _p$
agrees with the Milnor number of D at p (see [Reference MilnorMil68, Theorem 10.5]). However, this can fail in positive characteristic, so we will call
$\mu _p$
agrees with the Milnor number of D at p (see [Reference MilnorMil68, Theorem 10.5]). However, this can fail in positive characteristic, so we will call
![]() $\mu _p$
the pseudo-Milnor number of D at p.
$\mu _p$
the pseudo-Milnor number of D at p.
We now work towards constructing a lower bound for
![]() $(K_{\widehat {X}} + \widehat {D})^2$
in terms of
$(K_{\widehat {X}} + \widehat {D})^2$
in terms of
![]() $(K_X+D)^2$
and the local contribution of the singularities of D. The following lemma is basically due to Orevkov–Zaidenberg [Reference Orevkov and ZaidenbergOZ95, §4], but we give here a simple proof that works in all characteristics.
$(K_X+D)^2$
and the local contribution of the singularities of D. The following lemma is basically due to Orevkov–Zaidenberg [Reference Orevkov and ZaidenbergOZ95, §4], but we give here a simple proof that works in all characteristics.
Lemma 3.3. Let X be a smooth projective surface over an algebraically closed field and D be a reduced curve on X. Let
![]() $(\widehat {X}, \widehat {D})$
be the minimal log resolution of
$(\widehat {X}, \widehat {D})$
be the minimal log resolution of
![]() $(X,D)$
. Then
$(X,D)$
. Then
 $$ \begin{align} (K_{\widehat{X}} + \widehat{D})^2 \ge (K_X+D)^2 - \sum_{p\in D} \left(1 - \frac{1}{m_p}\right)\mu_p, \end{align} $$
$$ \begin{align} (K_{\widehat{X}} + \widehat{D})^2 \ge (K_X+D)^2 - \sum_{p\in D} \left(1 - \frac{1}{m_p}\right)\mu_p, \end{align} $$
where
![]() $m_p$
and
$m_p$
and
![]() $\mu _p$
are the multiplicity and pseudo-Milnor number of D at p, respectively.
$\mu _p$
are the multiplicity and pseudo-Milnor number of D at p, respectively.
Proof. As in the proof of Lemma 3.2, further blowing up
![]() $\widehat {X}$
at a singularity of
$\widehat {X}$
at a singularity of
![]() $\widehat {D}$
does not change
$\widehat {D}$
does not change
![]() $(K_{\widehat {X}} + \widehat {D})^2$
. So we choose a log resolution
$(K_{\widehat {X}} + \widehat {D})^2$
. So we choose a log resolution
![]() $(\widehat {X}, \widehat {D})$
of
$(\widehat {X}, \widehat {D})$
of
![]() $(X,D)$
which is minimal with the properties that
$(X,D)$
which is minimal with the properties that
![]() $\widehat {D}$
has simple normal crossings and the proper transforms of the components of D are disjoint from each other.
$\widehat {D}$
has simple normal crossings and the proper transforms of the components of D are disjoint from each other.
The proof of Lemma 3.2 already gives
From now on, we denote
![]() $K_{\widehat {X}/X}=K_{\widehat {X}}-\pi ^*K_X$
. Then, equation (3.5) and the fact that
$K_{\widehat {X}/X}=K_{\widehat {X}}-\pi ^*K_X$
. Then, equation (3.5) and the fact that
![]() $K_{\widehat {X}/X}.\pi ^*F=0$
for any divisor F on X yield
$K_{\widehat {X}/X}.\pi ^*F=0$
for any divisor F on X yield
 $$\begin{align*}\begin{aligned} (K_{\widehat{X}} + \widehat{D})^2 - (K_X + D)^2 &= - \sum_{p\in D_s} \mu_p + \sum_{p\in D_s} (\gamma_p - 1) + (K_{\widehat{X}}^2 - K_X^2)\\ &\quad + \sum_{p\in D_s} K_{\widehat{X}} E_p + (K_{\widehat{X}} \Delta - K_X D)\\ &= - \sum_{p\in D_s} \mu_p + \sum_{p\in D_s} (\gamma_p - 1) + K_{\widehat{X}/X}^2\\ &\quad + \sum_{p\in D_s} K_{\widehat{X}} E_p + K_{\widehat{X}} (\Delta - \pi^* D). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} (K_{\widehat{X}} + \widehat{D})^2 - (K_X + D)^2 &= - \sum_{p\in D_s} \mu_p + \sum_{p\in D_s} (\gamma_p - 1) + (K_{\widehat{X}}^2 - K_X^2)\\ &\quad + \sum_{p\in D_s} K_{\widehat{X}} E_p + (K_{\widehat{X}} \Delta - K_X D)\\ &= - \sum_{p\in D_s} \mu_p + \sum_{p\in D_s} (\gamma_p - 1) + K_{\widehat{X}/X}^2\\ &\quad + \sum_{p\in D_s} K_{\widehat{X}} E_p + K_{\widehat{X}} (\Delta - \pi^* D). \end{aligned} \end{align*}$$
Thus, equation (3.4) holds as long as we can prove
for all
![]() $p\in D_s$
. The problem is local, so we work in a formal neighbourhood of a point
$p\in D_s$
. The problem is local, so we work in a formal neighbourhood of a point
![]() $p\in D_s$
in X. For simplicity, we drop the subscript p in all notation so that
$p\in D_s$
in X. For simplicity, we drop the subscript p in all notation so that
![]() $m = m_p$
,
$m = m_p$
,
![]() $\mu = \mu _p$
,
$\mu = \mu _p$
,
![]() $\gamma = \gamma _p$
and
$\gamma = \gamma _p$
and
![]() $E = E_p$
.
$E = E_p$
.
We can factor
![]() $\pi : \widehat {X}\to X$
into a sequence of blowups:
$\pi : \widehat {X}\to X$
into a sequence of blowups:
where each
![]() $\pi _{i,i-1}: X_i\to X_{i-1}$
is the blowup of
$\pi _{i,i-1}: X_i\to X_{i-1}$
is the blowup of
![]() $X_{i-1}$
at one point for
$X_{i-1}$
at one point for
![]() $i=1,2,\ldots ,a$
. Let
$i=1,2,\ldots ,a$
. Let
![]() $\pi _{i,j} = \pi _{j+1,j} \circ \pi _{j+2,j+1} \circ \ldots \circ \pi _{i,i-1}$
be the birational map
$\pi _{i,j} = \pi _{j+1,j} \circ \pi _{j+2,j+1} \circ \ldots \circ \pi _{i,i-1}$
be the birational map
![]() $X_i\to X_j$
for
$X_i\to X_j$
for
![]() $0\le j < i\le a$
, and let
$0\le j < i\le a$
, and let
![]() $F_i$
be the exceptional divisor of
$F_i$
be the exceptional divisor of
![]() $\pi _{i,i-1}: X_i\to X_{i-1}$
for
$\pi _{i,i-1}: X_i\to X_{i-1}$
for
![]() $i=1,2,\ldots ,a$
. Then
$i=1,2,\ldots ,a$
. Then
 $$\begin{align*}\begin{aligned} K_{\widehat{X}/X} &= \pi_{a,1}^* F_1 + \pi_{a,2}^* F_2 + \ldots + \pi_{a,a-1}^* F_{a-1} + F_a\\ \Delta &= \pi^* D - m_1 \pi_{a,1}^* F_1 - m_2 \pi_{a,2}^* F_2 - \ldots - m_{a-1}\pi_{a,a-1}^* F_{a-1} - m_a F_a \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} K_{\widehat{X}/X} &= \pi_{a,1}^* F_1 + \pi_{a,2}^* F_2 + \ldots + \pi_{a,a-1}^* F_{a-1} + F_a\\ \Delta &= \pi^* D - m_1 \pi_{a,1}^* F_1 - m_2 \pi_{a,2}^* F_2 - \ldots - m_{a-1}\pi_{a,a-1}^* F_{a-1} - m_a F_a \end{aligned} \end{align*}$$
for some
![]() $m_i\in {\mathbb {Z}}_+$
satisfying that
$m_i\in {\mathbb {Z}}_+$
satisfying that
It follows (see, e.g., [Reference de Jong and PfisterdJP00, Theorem 5.4.13]) that
 $$\begin{align*}\begin{aligned} \mu + \gamma - 1 = 2\delta &= \sum_{i=1}^a m_i(m_i - 1)\\ K_{\widehat{X}/X}^2 + K_{\widehat{X}} (\Delta - \pi^* D) &= \sum_{i=1}^a (m_i - 1). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} \mu + \gamma - 1 = 2\delta &= \sum_{i=1}^a m_i(m_i - 1)\\ K_{\widehat{X}/X}^2 + K_{\widehat{X}} (\Delta - \pi^* D) &= \sum_{i=1}^a (m_i - 1). \end{aligned} \end{align*}$$
Therefore, equation (3.6) holds provided that we can prove
We recall that
![]() $E = \pi ^{-1}(p)$
is a tree of smooth rational curves. Thus, from the adjunction formula,
$E = \pi ^{-1}(p)$
is a tree of smooth rational curves. Thus, from the adjunction formula,
where
![]() $E^2\le -1$
because the components of E have negative definite intersection matrix. So we have equation (3.7) if
$E^2\le -1$
because the components of E have negative definite intersection matrix. So we have equation (3.7) if
![]() $\gamma \ge 2$
. Otherwise,
$\gamma \ge 2$
. Otherwise,
![]() $\gamma = 1$
, i.e., D has a locally irreducible or unibranch singularity at p. We claim that
$\gamma = 1$
, i.e., D has a locally irreducible or unibranch singularity at p. We claim that
![]() $K_{\widehat {X}} E \ge 0$
in this case.
$K_{\widehat {X}} E \ge 0$
in this case.
Let
![]() $E_i = \pi _{i,0}^{-1}(p)$
for
$E_i = \pi _{i,0}^{-1}(p)$
for
![]() $i=1,2,\ldots ,a$
. Then
$i=1,2,\ldots ,a$
. Then
![]() $E_1 = F_1$
and
$E_1 = F_1$
and
![]() $K_{X_1} E_1 = -1$
. If
$K_{X_1} E_1 = -1$
. If
![]() $\pi _{i,i-1}: X_i \to X_{i-1}$
is the blowup of
$\pi _{i,i-1}: X_i \to X_{i-1}$
is the blowup of
![]() $X_{i-1}$
at a smooth point of
$X_{i-1}$
at a smooth point of
![]() $E_{i-1}$
, then
$E_{i-1}$
, then
Otherwise, if
![]() $\pi _{i,i-1}: X_i \to X_{i-1}$
is the blowup of
$\pi _{i,i-1}: X_i \to X_{i-1}$
is the blowup of
![]() $X_{i-1}$
at a singular point of
$X_{i-1}$
at a singular point of
![]() $E_{i-1}$
, then
$E_{i-1}$
, then
In conclusion, we have
 $$\begin{align*}K_{X_1} E_1 = -1 \text{ and } K_{X_i} E_i = \begin{cases} K_{X_{i-1}} E_{i-1} & \text{if } \pi_{i,i-1}(F_i) \not\in (E_{i-1})_{\text{sing}}\\ K_{X_{i-1}} E_{i-1} + 1 & \text{if } \pi_{i,i-1}(F_i) \in (E_{i-1})_{\text{sing}} \end{cases} \end{align*}$$
$$\begin{align*}K_{X_1} E_1 = -1 \text{ and } K_{X_i} E_i = \begin{cases} K_{X_{i-1}} E_{i-1} & \text{if } \pi_{i,i-1}(F_i) \not\in (E_{i-1})_{\text{sing}}\\ K_{X_{i-1}} E_{i-1} + 1 & \text{if } \pi_{i,i-1}(F_i) \in (E_{i-1})_{\text{sing}} \end{cases} \end{align*}$$
for
![]() $2\le i\le a$
. Therefore,
$2\le i\le a$
. Therefore,
![]() $K_{\widehat {X}} E = K_{X_a} E_a \ge 0$
as long as one of
$K_{\widehat {X}} E = K_{X_a} E_a \ge 0$
as long as one of
![]() $\pi _{i,i-1}$
is the blowup of
$\pi _{i,i-1}$
is the blowup of
![]() $X_{i-1}$
at a singular point of
$X_{i-1}$
at a singular point of
![]() $E_{i-1}$
. For a locally irreducible singularity
$E_{i-1}$
. For a locally irreducible singularity
![]() $p\in D_s$
, it is easy to see that
$p\in D_s$
, it is easy to see that
![]() $\pi _{a,a-1}: X_a \to X_{a-1}$
blows up
$\pi _{a,a-1}: X_a \to X_{a-1}$
blows up
![]() $X_{a-1}$
at a singular point of
$X_{a-1}$
at a singular point of
![]() $E_{a-1}$
. Consequently,
$E_{a-1}$
. Consequently,
![]() $K_{\widehat {X}} E \ge 0$
when
$K_{\widehat {X}} E \ge 0$
when
![]() $\gamma = 1$
. This proves equation (3.7) and hence equation (3.6), giving equation (3.4).
$\gamma = 1$
. This proves equation (3.7) and hence equation (3.6), giving equation (3.4).
Combining equations (3.1), (3.3) and (3.4), we obtain
 $$ \begin{align} (K_X+D)^2 - \sum_{p\in D} \left(1 - \frac{1}{m_p}\right)\mu_p \le 3 \left(c_2(X) + (K_X + D) D - \sum_{p\in D} \mu_p\right). \end{align} $$
$$ \begin{align} (K_X+D)^2 - \sum_{p\in D} \left(1 - \frac{1}{m_p}\right)\mu_p \le 3 \left(c_2(X) + (K_X + D) D - \sum_{p\in D} \mu_p\right). \end{align} $$
We are now in a position to put all the above together for K3 surfaces in the characteristic zero case, where the BMY inequality holds.
Proposition 3.4. Let
![]() $D\subset X$
be an integral curve of geometric genus g in a K3 surface over an algebraically closed field of characteristic zero. If
$D\subset X$
be an integral curve of geometric genus g in a K3 surface over an algebraically closed field of characteristic zero. If
then D has at least one locally reducible singularity.
Proof. Suppose that D only has locally irreducible singularities. Then
By equation (3.8) and
![]() $\mathrm {c}_2(X)=24$
, we have
$\mathrm {c}_2(X)=24$
, we have
 $$ \begin{align} D^2 - \sum_{p\in D} \left(1 - \frac{1}{m_p}\right) \mu_p \le 66 + 6g. \end{align} $$
$$ \begin{align} D^2 - \sum_{p\in D} \left(1 - \frac{1}{m_p}\right) \mu_p \le 66 + 6g. \end{align} $$
Combining equations (3.9) and (3.10), we have
 $$ \begin{align} \sum_{p\in D} \frac{\mu_p}{m_p}\le 68 + 4g. \end{align} $$
$$ \begin{align} \sum_{p\in D} \frac{\mu_p}{m_p}\le 68 + 4g. \end{align} $$
On the other hand,
for all
![]() $p\in D$
. Putting equations 3.9–3.12 together gives
$p\in D$
. Putting equations 3.9–3.12 together gives
 $$\begin{align*}\begin{aligned} 68 + 4g\ge \sum_{p\in D} \frac{\mu_p}{m_p} \ge \sum_{p\in D} \left( \sqrt{\mu_p + \frac{1}4} - \frac{1}2 \right) \ge \sqrt{D^2 + \frac{9}4 - 2g} - \frac{1}2, \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} 68 + 4g\ge \sum_{p\in D} \frac{\mu_p}{m_p} \ge \sum_{p\in D} \left( \sqrt{\mu_p + \frac{1}4} - \frac{1}2 \right) \ge \sqrt{D^2 + \frac{9}4 - 2g} - \frac{1}2, \end{aligned} \end{align*}$$
where we note that we have used that the function
![]() $f(x)=\sqrt {x+\frac 14}-\frac 12$
vanishes at 0 and has everywhere negative second derivative, hence is concave and
$f(x)=\sqrt {x+\frac 14}-\frac 12$
vanishes at 0 and has everywhere negative second derivative, hence is concave and
![]() $\sum f(x_i) \geq f(\sum x_i)$
for positive real
$\sum f(x_i) \geq f(\sum x_i)$
for positive real
![]() $x_i$
. It follows that
$x_i$
. It follows that
![]() $D^2 \le 4690 + 550g + 16g^2$
. Therefore, D has at least one locally reducible singularity if
$D^2 \le 4690 + 550g + 16g^2$
. Therefore, D has at least one locally reducible singularity if
![]() $D^2> 4690 + 550g + 16g^2$
.
$D^2> 4690 + 550g + 16g^2$
.
Proposition 3.5. Let
![]() $D_1, D_2\subset X$
be two distinct integral curves in a K3 surface X over an algebraically closed field of characteristic 0. If
$D_1, D_2\subset X$
be two distinct integral curves in a K3 surface X over an algebraically closed field of characteristic 0. If
 $$\begin{align*}2 D_1D_2> \left(\sqrt{4D_1^2 + 9} + \sqrt{4D_2^2 + 9} + 2\right)(37 + D_1^2 + D_2^2) + 1, \end{align*}$$
$$\begin{align*}2 D_1D_2> \left(\sqrt{4D_1^2 + 9} + \sqrt{4D_2^2 + 9} + 2\right)(37 + D_1^2 + D_2^2) + 1, \end{align*}$$
then
![]() $D_1$
and
$D_1$
and
![]() $D_2$
meet at (at least) two distinct points.
$D_2$
meet at (at least) two distinct points.
Proof. Suppose that
![]() $D_1$
and
$D_1$
and
![]() $D_2$
meet at a unique point q. Applying equation (3.8) to
$D_2$
meet at a unique point q. Applying equation (3.8) to
![]() $(X, D = D_1 + D_2)$
, we have
$(X, D = D_1 + D_2)$
, we have
 $$ \begin{align} D^2 - \sum_{p\in D} \left(1 - \frac{1}{m_{D,p}}\right)\mu_{D,p}\le 72 + 3(D^2 - \sum_{p\in D} \mu_{D,p}), \end{align} $$
$$ \begin{align} D^2 - \sum_{p\in D} \left(1 - \frac{1}{m_{D,p}}\right)\mu_{D,p}\le 72 + 3(D^2 - \sum_{p\in D} \mu_{D,p}), \end{align} $$
where we use
![]() $\mu _{C,p}$
and
$\mu _{C,p}$
and
![]() $m_{C,p}$
to denote the pseudo-Milnor number and multiplicity of a reduced curve C at p, respectively.
$m_{C,p}$
to denote the pseudo-Milnor number and multiplicity of a reduced curve C at p, respectively.
Note the following simple facts for
![]() $i=1,2$
,
$i=1,2$
,
![]() $p\in D$
and
$p\in D$
and
![]() $D_1\cap D_2=\{q\}$
as above
$D_1\cap D_2=\{q\}$
as above
 $$ \begin{align} \begin{aligned} \mu_{D,p} &= \mu_{D_1,p} + \mu_{D_2,p} + 2 (D_1.D_2)_p - 1 \\ &= \mu_{D_1,p} + \mu_{D_2,p} -1 \text{ if }p\neq q\\ \mu_{D,q} &= \mu_{D_1,q} + \mu_{D_2,q} + 2D_1D_2 - 1\\ m_{D,p} &= m_{D_1,p} + m_{D_2,p} \le M:= \sqrt{D_1^2 + \frac{9}4} + \sqrt{D_2^2 + \frac94} + 1. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mu_{D,p} &= \mu_{D_1,p} + \mu_{D_2,p} + 2 (D_1.D_2)_p - 1 \\ &= \mu_{D_1,p} + \mu_{D_2,p} -1 \text{ if }p\neq q\\ \mu_{D,q} &= \mu_{D_1,q} + \mu_{D_2,q} + 2D_1D_2 - 1\\ m_{D,p} &= m_{D_1,p} + m_{D_2,p} \le M:= \sqrt{D_1^2 + \frac{9}4} + \sqrt{D_2^2 + \frac94} + 1. \end{aligned} \end{align} $$
Combining equations (3.13) and (3.14), we obtain
 $$\begin{align*}\begin{aligned} 75 - 3\sum_{i=1}^2 \sum_{p\in D_i} \mu_{D_i,p} =&\ 72 + 3 (D^2 - \sum_{p\in D} \mu_p) - 3(D_1^2 + D_2^2)\\ \ge&\ D^2 - \sum_{p\in D} \left(1 - \frac{1}{m_{D,p}}\right)\mu_{D,p} - 3(D_1^2 + D_2^2)\\ \ge&\ 2(D_1D_2 - D_1^2 - D_2^2) - \sum_{p\in D} \left(1 - \frac{1}M\right)\mu_{D,p}\\ =&\ \frac{2}M D_1D_2 - 2(D_1^2 + D_2^2) + \frac{M-1}{M}\left(1-\sum_{i=1}^2 \sum_{p\in D_i} \mu_{D_i,p}\right). \end{aligned} \end{align*}$$
$$\begin{align*}\begin{aligned} 75 - 3\sum_{i=1}^2 \sum_{p\in D_i} \mu_{D_i,p} =&\ 72 + 3 (D^2 - \sum_{p\in D} \mu_p) - 3(D_1^2 + D_2^2)\\ \ge&\ D^2 - \sum_{p\in D} \left(1 - \frac{1}{m_{D,p}}\right)\mu_{D,p} - 3(D_1^2 + D_2^2)\\ \ge&\ 2(D_1D_2 - D_1^2 - D_2^2) - \sum_{p\in D} \left(1 - \frac{1}M\right)\mu_{D,p}\\ =&\ \frac{2}M D_1D_2 - 2(D_1^2 + D_2^2) + \frac{M-1}{M}\left(1-\sum_{i=1}^2 \sum_{p\in D_i} \mu_{D_i,p}\right). \end{aligned} \end{align*}$$
Hence,
and the proposition follows.
The lower bounds in the above propositions are almost certainly not optimal. Better results can be achieved with improvement to equation (3.4) (cf. [Reference MoeMoe15]).
We are now ready to prove Theorem A.
Proof of Theorem A
Let us first prove it for
![]() $g = 1$
.
$g = 1$
.
By [Reference Chen, Gounelas and LiedtkeCGL19, Theorem A], there are infinitely many integral rational curves
![]() $C_n$
on X. Suppose that
$C_n$
on X. Suppose that
![]() $C_n^2$
is unbounded. Then
$C_n^2$
is unbounded. Then
![]() $C_n$
has a locally reducible singularity by Proposition 3.4 for
$C_n$
has a locally reducible singularity by Proposition 3.4 for
![]() $C_n^2$
sufficiently large. Such
$C_n^2$
sufficiently large. Such
![]() $C_n$
can be deformed to a nonisotrivial family of curves of geometric genus 1 by Proposition 2.7.
$C_n$
can be deformed to a nonisotrivial family of curves of geometric genus 1 by Proposition 2.7.
Suppose that
![]() $C_n^2\le c$
for all n. We claim that
$C_n^2\le c$
for all n. We claim that
Fixing
![]() $N\in {\mathbb {Z}}_+$
, since
$N\in {\mathbb {Z}}_+$
, since
![]() $\mathop {\mathrm {rank}}\nolimits _{\mathbb {Z}}\mathrm {Pic\ }(X)\le 20$
,
$\mathop {\mathrm {rank}}\nolimits _{\mathbb {Z}}\mathrm {Pic\ }(X)\le 20$
,
![]() $C_N,C_{N+1},\ldots ,C_{N+20}$
are linearly dependent in
$C_N,C_{N+1},\ldots ,C_{N+20}$
are linearly dependent in
![]() $\mathrm {Pic\ }(X)_{\mathbb {Q}}$
. Suppose that
$\mathrm {Pic\ }(X)_{\mathbb {Q}}$
. Suppose that
in
![]() $\mathrm {Pic\ }(X)$
for some integers
$\mathrm {Pic\ }(X)$
for some integers
![]() $a_i$
, not all zero. Since
$a_i$
, not all zero. Since
![]() $C_i$
are effective,
$C_i$
are effective,
![]() $a_i$
cannot be all positive or negative. Let us rewrite equation (3.16) as
$a_i$
cannot be all positive or negative. Let us rewrite equation (3.16) as
 $$\begin{align*}F = \sum_{a_i>0} a_i C_{N+i} = - \sum_{a_j < 0} a_j C_{N+j}. \end{align*}$$
$$\begin{align*}F = \sum_{a_i>0} a_i C_{N+i} = - \sum_{a_j < 0} a_j C_{N+j}. \end{align*}$$
Since
![]() $C_N, C_{N+1}, \ldots , C_{N+20}$
are distinct integral curves, it is easy to see that F is nef. This implies that there are only finitely many integral rational curves R such that
$C_N, C_{N+1}, \ldots , C_{N+20}$
are distinct integral curves, it is easy to see that F is nef. This implies that there are only finitely many integral rational curves R such that
![]() $FR = 0$
, since if
$FR = 0$
, since if
![]() $F^2=0$
, then F can only be zero on the (up to 24) singular fibres of the elliptic fibration induced by F, and if
$F^2=0$
, then F can only be zero on the (up to 24) singular fibres of the elliptic fibration induced by F, and if
![]() $F^2>0$
, then from the Hodge index theorem the orthogonal space
$F^2>0$
, then from the Hodge index theorem the orthogonal space
![]() $F^\perp $
in the effective cone is negative definite and spanned by finitely many
$F^\perp $
in the effective cone is negative definite and spanned by finitely many
![]() $-2$
-curves. Hence, there exists
$-2$
-curves. Hence, there exists
![]() $m\ge N$
such that
$m\ge N$
such that
![]() $FC_m \ge 1$
. Then
$FC_m \ge 1$
. Then
![]() $C_m + 2F$
is nef and big, and hence,
$C_m + 2F$
is nef and big, and hence,
Thus, there exists
![]() $C\in \{C_N,C_{N+1},\ldots ,C_{N+20}, C_m\}$
such that
$C\in \{C_N,C_{N+1},\ldots ,C_{N+20}, C_m\}$
such that
![]() $C C_n$
is unbounded. This proves equation (3.15).
$C C_n$
is unbounded. This proves equation (3.15).
By Proposition 3.5,
![]() $C_m$
and
$C_m$
and
![]() $C_n$
meet at (at least) two distinct points for
$C_n$
meet at (at least) two distinct points for
![]() $C_m C_n$
sufficiently large since
$C_m C_n$
sufficiently large since
![]() $C_m^2\le c$
and
$C_m^2\le c$
and
![]() $C_n^2 \le c$
. There are infinitely many such pairs
$C_n^2 \le c$
. There are infinitely many such pairs
![]() $C_m$
and
$C_m$
and
![]() $C_n$
by equation (3.15), and
$C_n$
by equation (3.15), and
Such
![]() $C_m\cup C_n$
can be deformed to a nonisotrivial family of curves of geometric genus 1 by Proposition 2.9, which as pointed out above will have unbounded self-intersection. This proves the theorem for
$C_m\cup C_n$
can be deformed to a nonisotrivial family of curves of geometric genus 1 by Proposition 2.9, which as pointed out above will have unbounded self-intersection. This proves the theorem for
![]() $g=1$
. The remaining cases follow from Propositions 2.7 and 3.4 by induction.
$g=1$
. The remaining cases follow from Propositions 2.7 and 3.4 by induction.
4 An algebraic proof of Kobayashi’s theorem
We say that a vector bundle E on a quasi-projective variety X is
![]() ${\mathbb {Q}}$
-effective if
${\mathbb {Q}}$
-effective if
for some positive integer m, where
![]() $\operatorname {Sym}^m E$
is the m-th symmetric product of E. We call E pseudoeffective if, for every
$\operatorname {Sym}^m E$
is the m-th symmetric product of E. We call E pseudoeffective if, for every
![]() $n\in {\mathbb {Z}}_+$
, there exists
$n\in {\mathbb {Z}}_+$
, there exists
![]() $m\in {\mathbb {Z}}_+$
such that
$m\in {\mathbb {Z}}_+$
such that
where A is a fixed ample divisor on X. Alternatively, let
be the projectivisation of
![]() $E^\vee $
, and let
$E^\vee $
, and let
![]() ${\mathcal O}_Y(1)$
be the tautological bundle of Y over X. By the Leray spectral sequence, the
${\mathcal O}_Y(1)$
be the tautological bundle of Y over X. By the Leray spectral sequence, the
![]() ${\mathbb {Q}}$
-effectivity (resp. pseudoeffectivity) of E coincides with that of
${\mathbb {Q}}$
-effectivity (resp. pseudoeffectivity) of E coincides with that of
![]() ${\mathcal O}_Y(1)$
.
${\mathcal O}_Y(1)$
.
Let now X be a K3 surface, and let
![]() $Y = \mathrm {Proj}\:(S^\bullet \Omega ^1_X)$
with
$Y = \mathrm {Proj}\:(S^\bullet \Omega ^1_X)$
with
![]() $L = {\mathcal O}_Y(1)$
being the tautological bundle of
$L = {\mathcal O}_Y(1)$
being the tautological bundle of
![]() $\pi : Y\to X$
. The following follows easily from Hodge theory over the complex numbers, whereas in positive characteristic is a theorem of Rudakov–Shafarevich [Reference Rudakov and ŠafarevičRS76] (see also Nygaard [Reference NygaardNyg79]).
$\pi : Y\to X$
. The following follows easily from Hodge theory over the complex numbers, whereas in positive characteristic is a theorem of Rudakov–Shafarevich [Reference Rudakov and ŠafarevičRS76] (see also Nygaard [Reference NygaardNyg79]).
Theorem 4.1. Let X be a K3 surface over an algebraically closed field. Then
![]() $\mathrm {H}^0(X, \Omega ^1_X)=0$
.
$\mathrm {H}^0(X, \Omega ^1_X)=0$
.
See Proposition 5.1 for a simple, conditional algebraic proof of the above. In what follows, we will give an algebraic proof of Kobayashi’s theorem (i.e., Theorem B of the introduction) by reducing it to the above. The proof in fact works in arbitrary characteristic under the following, minimal assumption.
Hypothesis 4.2. There exists an unramified morphism
![]() $f:E\to X$
from a smooth genus 1 curve which deforms in the expected dimension and with maximal moduli.
$f:E\to X$
from a smooth genus 1 curve which deforms in the expected dimension and with maximal moduli.
In characteristic zero, Theorem A (in combination with Proposition 2.5) produces infinitely many such curves, whereas in positive characteristic we are not able to produce such a curve, although in remarks after the proof we will give various cases in which such a curve does exist.
Theorem 4.3. Let X be a K3 surface over an algebraically closed field. If we assume Hypothesis (4.2), then
Proof. We maintain the notation for
![]() $Y,L$
from the beginning of this section. Suppose for a contradiction that L is
$Y,L$
from the beginning of this section. Suppose for a contradiction that L is
![]() ${\mathbb {Q}}$
-effective. Let m be the smallest positive integer such that
${\mathbb {Q}}$
-effective. Let m be the smallest positive integer such that
![]() $mL$
is effective, and let
$mL$
is effective, and let
![]() $G\in |mL|$
. We write
$G\in |mL|$
. We write
where
![]() $D_i \in |a_i L + \pi ^* F_i|$
are the irreducible components of G for some
$D_i \in |a_i L + \pi ^* F_i|$
are the irreducible components of G for some
![]() $a_i \in {\mathbb {N}}$
and some divisors
$a_i \in {\mathbb {N}}$
and some divisors
![]() $F_i\in \mathrm {Pic\ }(X)$
, and
$F_i\in \mathrm {Pic\ }(X)$
, and
![]() $b_i\in {\mathbb {Z}}_+$
is the multiplicity of
$b_i\in {\mathbb {Z}}_+$
is the multiplicity of
![]() $D_i$
in G. Since
$D_i$
in G. Since
![]() $mL=\sum a_i b_i L + \sum b_i \pi ^*F_i$
, we obtain that
$mL=\sum a_i b_i L + \sum b_i \pi ^*F_i$
, we obtain that
Let
![]() $C\subset X$
be an integral curve of geometric genus 1 as given by Hypothesis 4.2. From the assumption, there exists an irreducible curve
$C\subset X$
be an integral curve of geometric genus 1 as given by Hypothesis 4.2. From the assumption, there exists an irreducible curve
![]() $B\subset |C|$
with C as member and such that every curve
$B\subset |C|$
with C as member and such that every curve
![]() $\Gamma \in B$
is of geometric genus 1.
$\Gamma \in B$
is of geometric genus 1.
When
![]() $a_i = 0$
,
$a_i = 0$
,
![]() $F_i$
is necessarily effective and
$F_i$
is necessarily effective and
![]() $CF_i \ge 0$
. Note also that there exists at least one i such that
$CF_i \ge 0$
. Note also that there exists at least one i such that
![]() $CF_i\le 0$
and
$CF_i\le 0$
and
![]() $a_i> 0$
since otherwise,
$a_i> 0$
since otherwise,
![]() $CF_i> 0$
for all
$CF_i> 0$
for all
![]() $a_i> 0$
and so
$a_i> 0$
and so
![]() $\sum CF_i> 0$
, contradicting equation (4.1).
$\sum CF_i> 0$
, contradicting equation (4.1).
From now on, we denote by
![]() $a=a_i$
,
$a=a_i$
,
![]() $D = D_i$
and
$D = D_i$
and
![]() $F = F_i$
so that
$F = F_i$
so that
![]() $a_i> 0$
and
$a_i> 0$
and
![]() $CF_i \le 0$
.
$CF_i \le 0$
.
From the assumption, the general deformation of the normalisation of C is an immersion. We henceforth replace C by a general member of B and let
![]() $\nu : E = C^\nu \to X$
be its normalisation, i.e., we have that
$\nu : E = C^\nu \to X$
be its normalisation, i.e., we have that
![]() $\nu ^* \Omega ^1_X \to \Omega ^1_E$
is a surjection. As the kernel is torsion-free on a smooth curve, it is a line bundle, and by taking determinants we see that it must be isomorphic to
$\nu ^* \Omega ^1_X \to \Omega ^1_E$
is a surjection. As the kernel is torsion-free on a smooth curve, it is a line bundle, and by taking determinants we see that it must be isomorphic to
![]() $(\Omega ^1_E)^\vee \cong {\mathcal O}_E$
. This leads to the exact sequence
$(\Omega ^1_E)^\vee \cong {\mathcal O}_E$
. This leads to the exact sequence

where
![]() ${\mathscr N}_\nu $
is the normal bundle of
${\mathscr N}_\nu $
is the normal bundle of
![]() $\nu $
. From our assumption and the following lemma, the above sequence does not split.
$\nu $
. From our assumption and the following lemma, the above sequence does not split.
Lemma 4.4. Sequence (4.2) splits if and only if B parametrises an isotrivial family of elliptic curves.
Proof. If
![]() $f:\mathcal {C}\to B$
the family with B a smooth projective curve and E the generic fibre of f, then a section
$f:\mathcal {C}\to B$
the family with B a smooth projective curve and E the generic fibre of f, then a section
![]() $\Omega ^1_E\to \nu ^*\Omega ^1_X$
also induces a splitting of
$\Omega ^1_E\to \nu ^*\Omega ^1_X$
also induces a splitting of
on some open subset
![]() $U\subset B$
. Dualising this sequence and pushing forward to U, we get a split sequence whose first coboundary map in cohomology is the Kodaira–Spencer map. Hence, this map is necessarily zero so the family over U is isotrivial.
$U\subset B$
. Dualising this sequence and pushing forward to U, we get a split sequence whose first coboundary map in cohomology is the Kodaira–Spencer map. Hence, this map is necessarily zero so the family over U is isotrivial.
Since
![]() $aL+F$
is effective,
$aL+F$
is effective,
![]() $\mathrm {H}^0(S^a \Omega ^1_X \otimes {\mathcal O}_X(F)) \ne 0$
and as C is a general member of a covering family of curves on X, we see that
$\mathrm {H}^0(S^a \Omega ^1_X \otimes {\mathcal O}_X(F)) \ne 0$
and as C is a general member of a covering family of curves on X, we see that
as otherwise a global section of
![]() $S^a \Omega ^1_X \otimes {\mathcal O}_X(F)$
would vanish everywhere. By equation (4.2),
$S^a \Omega ^1_X \otimes {\mathcal O}_X(F)$
would vanish everywhere. By equation (4.2),
![]() $S^a \nu ^* \Omega ^1_X \otimes {\mathcal O}_E(\nu ^* F)$
has a filtration
$S^a \nu ^* \Omega ^1_X \otimes {\mathcal O}_E(\nu ^* F)$
has a filtration
with graded pieces all isomorphic to
![]() ${\mathcal O}_E(\nu ^* F)$
. If the global section
${\mathcal O}_E(\nu ^* F)$
. If the global section
![]() ${\mathcal O}_E\to E_{a+1}$
from above vanishes when mapped to
${\mathcal O}_E\to E_{a+1}$
from above vanishes when mapped to
![]() $E_{a+1}/E_a={\mathcal O}_E(\nu ^* F)$
, then it must induce a nonzero global section of
$E_{a+1}/E_a={\mathcal O}_E(\nu ^* F)$
, then it must induce a nonzero global section of
![]() $E_a$
. By induction, one of the quotients
$E_a$
. By induction, one of the quotients
![]() $E_i/E_{i-1}$
must have a nonzero global section, and hence,
$E_i/E_{i-1}$
must have a nonzero global section, and hence,
![]() $\mathrm {H}^0({\mathcal O}_E(\nu ^* F)) \ne 0$
. On the other hand,
$\mathrm {H}^0({\mathcal O}_E(\nu ^* F)) \ne 0$
. On the other hand,
![]() $CF \le 0$
and
$CF \le 0$
and
![]() $\deg \nu ^* F \le 0$
. So we necessarily have
$\deg \nu ^* F \le 0$
. So we necessarily have
![]() ${\mathcal O}_E(\nu ^* F) = {\mathcal O}_E$
.
${\mathcal O}_E(\nu ^* F) = {\mathcal O}_E$
.
This proves that for all i satisfying
![]() $a_i> 0$
and
$a_i> 0$
and
![]() $C F_i \le 0$
we have
$C F_i \le 0$
we have
![]() ${\mathcal O}_E (\nu ^* F_i) = {\mathcal O}_E$
, and hence,
${\mathcal O}_E (\nu ^* F_i) = {\mathcal O}_E$
, and hence,
![]() $CF_i = 0$
. For the remaining i, we clearly have
$CF_i = 0$
. For the remaining i, we clearly have
![]() $CF_i \ge 0$
. Therefore, we conclude that
$CF_i \ge 0$
. Therefore, we conclude that
![]() $C F_i = 0$
for all i from equation (4.1). In summary, we have
$C F_i = 0$
for all i from equation (4.1). In summary, we have
-
○ if
 $a_i> 0$
,
$a_i> 0$
,
 ${\mathcal O}_E (\nu ^* F_i) = {\mathcal O}_E$
,
${\mathcal O}_E (\nu ^* F_i) = {\mathcal O}_E$
, -
○ if
 $a_i = 0$
,
$a_i = 0$
,
 $F_i$
is effective and
$F_i$
is effective and
 $CF_i = 0$
.
$CF_i = 0$
.
As exact sequence (4.2) does not split,
for all
![]() $n\in {\mathbb {Z}}_+$
.
$n\in {\mathbb {Z}}_+$
.
Work now again with a fixed i so that
![]() $a_i>0$
as above, keeping the notation
$a_i>0$
as above, keeping the notation
![]() $D,F,a$
. Since D is reduced,
$D,F,a$
. Since D is reduced,
![]() $Y_p = \pi ^{-1}(p)$
meets D transversely for
$Y_p = \pi ^{-1}(p)$
meets D transversely for
![]() $p\in X$
general, and as C is a general member of a covering family of curves on X, also
$p\in X$
general, and as C is a general member of a covering family of curves on X, also
![]() $Y_p = \pi ^{-1}(p)$
meets D transversely for
$Y_p = \pi ^{-1}(p)$
meets D transversely for
![]() $p\in C$
general. Let now
$p\in C$
general. Let now
![]() $R = E\times _X Y \cong \mathrm {Proj}\:(S^\bullet (\nu ^* \Omega ^1_X))$
with diagram
$R = E\times _X Y \cong \mathrm {Proj}\:(S^\bullet (\nu ^* \Omega ^1_X))$
with diagram

Since
![]() $Y_p$
and D meet transversely for
$Y_p$
and D meet transversely for
![]() $p\in C$
general,
$p\in C$
general,
![]() $R_q$
and
$R_q$
and
![]() $\rho ^* D$
meet transversely for
$\rho ^* D$
meet transversely for
![]() $q\in E$
general, where
$q\in E$
general, where
![]() $R_q$
is the fibre of R over q.
$R_q$
is the fibre of R over q.
Note that
![]() $\rho ^* D$
is a section of
$\rho ^* D$
is a section of
![]() $a \rho ^* L$
. From equation (4.3),
$a \rho ^* L$
. From equation (4.3),
![]() $h^0(R, n \rho ^* L) = 1$
for all
$h^0(R, n \rho ^* L) = 1$
for all
![]() $n\geq 0$
, and so we must have
$n\geq 0$
, and so we must have
![]() $\rho ^* D = a \Gamma $
, where
$\rho ^* D = a \Gamma $
, where
![]() $\Gamma $
is the unique section of
$\Gamma $
is the unique section of
![]() $\rho ^* L$
. Then we must have
$\rho ^* L$
. Then we must have
![]() $a = 1$
because
$a = 1$
because
![]() $R_q$
and
$R_q$
and
![]() $\rho ^* D$
meet transversely for
$\rho ^* D$
meet transversely for
![]() $q\in E$
general.
$q\in E$
general.
Hence, we have concluded that
![]() $a_i = 0$
or
$a_i = 0$
or
![]() $1$
for all i. If there are two distinct components
$1$
for all i. If there are two distinct components
![]() $D_i$
and
$D_i$
and
![]() $D_j$
of G such that
$D_j$
of G such that
![]() $a_i = a_j = 1$
, then
$a_i = a_j = 1$
, then
![]() $\rho ^* D_i = \rho ^* D_j = \Gamma $
. Therefore,
$\rho ^* D_i = \rho ^* D_j = \Gamma $
. Therefore,
for
![]() $C\in B$
general, and hence,
$C\in B$
general, and hence,
![]() $D_i = D_j$
. Consequently, G has only one component
$D_i = D_j$
. Consequently, G has only one component
![]() $D_i$
with
$D_i$
with
![]() $a_i = 1$
, and so we have
$a_i = 1$
, and so we have
![]() $\mathrm {H}^0(\Omega ^1_X \otimes {\mathcal O}_X(F)) \ne 0$
for some
$\mathrm {H}^0(\Omega ^1_X \otimes {\mathcal O}_X(F)) \ne 0$
for some
![]() $F\in \mathrm {Pic\ }(X)$
such that
$F\in \mathrm {Pic\ }(X)$
such that
![]() $-F=\sum F_i$
is effective. As
$-F=\sum F_i$
is effective. As
![]() $\mathrm {H}^0(\Omega ^1_X \otimes {\mathcal O}_X(F))\subset \mathrm {H}^0(\Omega ^1_X)$
, we obtain a contradiction from the case
$\mathrm {H}^0(\Omega ^1_X \otimes {\mathcal O}_X(F))\subset \mathrm {H}^0(\Omega ^1_X)$
, we obtain a contradiction from the case
![]() $m=1$
, namely Theorem 4.1.
$m=1$
, namely Theorem 4.1.
In conclusion, we have proved that
![]() $\Omega ^1_X$
is not
$\Omega ^1_X$
is not
![]() ${\mathbb {Q}}$
-effective if Hypothesis (4.2) holds. This of course is a consequence of Theorem A in characteristic zero, but in the following remark, we outline various cases where this is true in characteristic zero under far weaker assumptions than the existence of infinitely many rational curves on X.
${\mathbb {Q}}$
-effective if Hypothesis (4.2) holds. This of course is a consequence of Theorem A in characteristic zero, but in the following remark, we outline various cases where this is true in characteristic zero under far weaker assumptions than the existence of infinitely many rational curves on X.
Remark 4.5.
-
1. Recall that from Propositions 2.7 and 2.9, the existence of either one rational curve
 $C\subset X$
with a locally reducible singularity or two distinct rational curves meeting in at least two distinct points guarantee the existence of a nonisotrivial family of genus 1 curves in X.
$C\subset X$
with a locally reducible singularity or two distinct rational curves meeting in at least two distinct points guarantee the existence of a nonisotrivial family of genus 1 curves in X. -
2. More generally, we can produce a nonisotrivial family of genus 1 curves on X if there are distinct rational curves
 $C_1,\ldots ,C_n \subset X$
and points
$C_1,\ldots ,C_n \subset X$
and points
 $p_i\ne q_i\in C_i^\nu $
on their normalisations such that for all
$p_i\ne q_i\in C_i^\nu $
on their normalisations such that for all
 $1\leq i<n$
where
$1\leq i<n$
where $$\begin{align*}\nu(p_{i}) = \nu(q_{i+1}) \text{ and } \nu(p_n) = \nu(q_1), \end{align*}$$
$$\begin{align*}\nu(p_{i}) = \nu(q_{i+1}) \text{ and } \nu(p_n) = \nu(q_1), \end{align*}$$
 $\nu : \sqcup C_i^\nu \to X$
is the normalisation of
$\nu : \sqcup C_i^\nu \to X$
is the normalisation of
 $\cup C_i$
. In this case, we can find a stable map
$\cup C_i$
. In this case, we can find a stable map
 $f: \Gamma \to X$
such that
$f: \Gamma \to X$
such that
 $\Gamma = \cup \Gamma _i$
,
$\Gamma = \cup \Gamma _i$
,
 $\Gamma _i \cong C_i^\nu $
,
$\Gamma _i \cong C_i^\nu $
,
 $f(\Gamma _i) = C_i$
,
$f(\Gamma _i) = C_i$
,  $$\begin{align*}|\Gamma_1\cap \Gamma_2| = \ldots = |\Gamma_n \cap \Gamma_1| = 1 \text{ and } \Gamma_i \cap \Gamma_j = \emptyset \text{ otherwise}. \end{align*}$$
$$\begin{align*}|\Gamma_1\cap \Gamma_2| = \ldots = |\Gamma_n \cap \Gamma_1| = 1 \text{ and } \Gamma_i \cap \Gamma_j = \emptyset \text{ otherwise}. \end{align*}$$
In positive characteristic, even though there exist rational curves which deform too much and without unramified deformations (e.g., a quasi-elliptic fibration on a supersingular K3 surface), a version of the Arbarello–Cornalba lemma (Proposition 2.5) eludes us for the time being. One could ask the following.
Question 4.6. Let
![]() $f:C\to X$
be a morphism from a smooth projective curve of genus
$f:C\to X$
be a morphism from a smooth projective curve of genus
![]() $g\geq 1$
to a K3 surface over an algebraically closed field. If f deforms in the expected dimension, is a general deformation of f unramified?
$g\geq 1$
to a K3 surface over an algebraically closed field. If f deforms in the expected dimension, is a general deformation of f unramified?
Assuming the above and that all rational curves in Remark 4.5 are rigid, Propositions 2.7 and 2.9 imply that the cases listed in Remark 4.5 also provide a genus 1 curve satisfying the properties of Hypothesis 4.2, and hence, Kobayashi’s theorem holds.
5 Global 1-forms and stability
As mentioned in the introduction and in the previous section (see Theorem 4.1), the proof that a K3 surface does not have any global 1-forms uses analytic techniques in characteristic zero (Hodge theory) and is rather nontrivial in positive characteristic. In this section, we gather some auxiliary results and questions, giving simple, conditional algebraic proofs of the fact that for a K3 surface X we have that
![]() $\mathrm {H}^0(X, \Omega ^1_X)=0$
and that
$\mathrm {H}^0(X, \Omega ^1_X)=0$
and that
![]() $\Omega ^1_X$
is slope-stable (with respect to any ample divisor), using only the existence of special curves in X.
$\Omega ^1_X$
is slope-stable (with respect to any ample divisor), using only the existence of special curves in X.
Proposition 5.1. Let X be a smooth projective variety of dimension n over an algebraically closed field and
![]() $f:C\to X$
an unramified morphism from a smooth curve of genus
$f:C\to X$
an unramified morphism from a smooth curve of genus
![]() $g> 1$
so that f deforms in a family which dominates X and varies with maximal moduli. Then
$g> 1$
so that f deforms in a family which dominates X and varies with maximal moduli. Then
![]() $\mathrm {H}^0(X, T_X)=0$
.
$\mathrm {H}^0(X, T_X)=0$
.
Proof. Taking cohomology of the sequence
the Kodaira–Spencer map
![]() $\mathrm {H}^0(C,N_f)\to \mathrm {H}^1(C, T_C)$
must be injective, as it is the induced differential to the moduli map and C deforms with maximal moduli. This implies that
$\mathrm {H}^0(C,N_f)\to \mathrm {H}^1(C, T_C)$
must be injective, as it is the induced differential to the moduli map and C deforms with maximal moduli. This implies that
![]() $\mathrm {H}^0(C, f^*T_X)=0$
, but as C deforms to cover X, we obtain the result.
$\mathrm {H}^0(C, f^*T_X)=0$
, but as C deforms to cover X, we obtain the result.
In the case of K3 surfaces, the existence of such curves in characteristic zero is guaranteed by Theorem A, but the current proof relies on the existence of infinitely many rational curves, whose proof in fact uses the vanishing of 1-forms in a number of ways. The assumptions of the above do hold unconditionally for K3 surfaces in the cases listed in Remark 4.5.
We move now to the question of stability of the (co)tangent bundle. We recall that for an ample divisor
![]() $A\in \mathrm {Pic\ }(X)$
on a projective variety X we say that a vector bundle E on X is
$A\in \mathrm {Pic\ }(X)$
on a projective variety X we say that a vector bundle E on X is
![]() $\mu _A$
-(semi)stable (often just
$\mu _A$
-(semi)stable (often just
![]() $\mu $
) if
$\mu $
) if
 $$\begin{align*}\mu_A(F):=\frac{\det(F)A^{\dim X-1}}{\operatorname{rk}(F)} {< \atop (\leq)} \frac{\det(E)A^{\dim X-1}}{\operatorname{rk(E)}} \end{align*}$$
$$\begin{align*}\mu_A(F):=\frac{\det(F)A^{\dim X-1}}{\operatorname{rk}(F)} {< \atop (\leq)} \frac{\det(E)A^{\dim X-1}}{\operatorname{rk(E)}} \end{align*}$$
for all torsion-free subsheaves
![]() $F\subsetneq E$
. In fact, if F does not satisfy the above inequality, then we say that F destabilises E, and we may assume that F is a subvector bundle with torsion-free quotient. In particular, if, for a K3 surface X,
$F\subsetneq E$
. In fact, if F does not satisfy the above inequality, then we say that F destabilises E, and we may assume that F is a subvector bundle with torsion-free quotient. In particular, if, for a K3 surface X,
![]() $E=\Omega ^1_X$
is not semistable, then there exists a destabilising line bundle
$E=\Omega ^1_X$
is not semistable, then there exists a destabilising line bundle
![]() $L\subset \Omega ^1_X$
, i.e.,
$L\subset \Omega ^1_X$
, i.e.,
![]() $LA\geq 0$
.
$LA\geq 0$
.
The assumption we will be making to give a quick proof of stability of the tangent bundle will be the following.
Question 5.2. Let X be a K3 surface over an algebraically closed field. Is it true that for any ample divisor
![]() $D\in \mathrm {Pic\ }(X)_{\mathbb {Q}}$
there exist integral curves
$D\in \mathrm {Pic\ }(X)_{\mathbb {Q}}$
there exist integral curves
![]() $E_1,\ldots , E_n\subset X$
of geometric genus 1 so that
$E_1,\ldots , E_n\subset X$
of geometric genus 1 so that
![]() $D=\sum _{i=1}^n a_i E_i$
for
$D=\sum _{i=1}^n a_i E_i$
for
![]() $a_i\in {\mathbb {Q}}_{\geq 0}$
?
$a_i\in {\mathbb {Q}}_{\geq 0}$
?
Remark 5.3. We note that the above is known to be true in the following cases
-
1. The Picard rank of X is
 $\leq 2$
[Reference Chen, Gounelas and LiedtkeCGL19, Corollary 7.3, Theorem 8.4].
$\leq 2$
[Reference Chen, Gounelas and LiedtkeCGL19, Corollary 7.3, Theorem 8.4]. -
2. X contains no smooth rational curves: In many such cases, the effective cone is generated by smooth genus 1 curves even (see [Reference KovácsKov94]). For the rest (in particular the case where the cone is not polyhedral), one can use the fact that every nef divisor can be written as a sum of minimal nef divisors and that each such divisor is linearly equivalent to an integral curve of geometric genus 1 (see [Reference Chen, Gounelas and LiedtkeCGL19, §3] for the definition and for this result).
We claim that the stability of
![]() $\Omega _X^1$
follows from a positive answer to Question 5.2 for K3 surfaces X. In fact, we can prove a more general statement. For that purpose, let us recall some basic facts about Harder–Narasimhan filtrations and the cone of curves.
$\Omega _X^1$
follows from a positive answer to Question 5.2 for K3 surfaces X. In fact, we can prove a more general statement. For that purpose, let us recall some basic facts about Harder–Narasimhan filtrations and the cone of curves.
Let E be a vector bundle on a smooth projective variety X. We use the notation
![]() $\mu _{A,\max }(E)$
to denote that the maximum of the slopes
$\mu _{A,\max }(E)$
to denote that the maximum of the slopes
![]() $\mu _A(F)$
for all subsheaves
$\mu _A(F)$
for all subsheaves
![]() $F\subset E$
and some ample A, which we from now on suppress in the notation. This number is given by the Harder–Narasimhan filtration
$F\subset E$
and some ample A, which we from now on suppress in the notation. This number is given by the Harder–Narasimhan filtration
of E, where
![]() $F_i = E_i/E_{i+1}$
are torsion-free and semistable sheaves satisfying
$F_i = E_i/E_{i+1}$
are torsion-free and semistable sheaves satisfying
and
![]() $\mu _{\max }(E)$
is given by
$\mu _{\max }(E)$
is given by
![]() $\mu (F_m) = \mu (E_m)$
. Using Harder–Narasimhan filtrations, we have
$\mu (F_m) = \mu (E_m)$
. Using Harder–Narasimhan filtrations, we have
for all
![]() $1\le r\le \mathop {\mathrm {rank}}\nolimits (E)$
.
$1\le r\le \mathop {\mathrm {rank}}\nolimits (E)$
.
For a smooth projective variety X, we let
![]() $N_1(X)$
denote the group of
$N_1(X)$
denote the group of
![]() $1$
-cycles modulo numerical equivalence and let
$1$
-cycles modulo numerical equivalence and let
![]() $N_1(X)_{\mathbb {Q}}$
and
$N_1(X)_{\mathbb {Q}}$
and
![]() $N_1(X)_{\mathbb {R}}$
denote
$N_1(X)_{\mathbb {R}}$
denote
![]() $N_1(X)\otimes {\mathbb {Q}}$
and
$N_1(X)\otimes {\mathbb {Q}}$
and
![]() $N_1(X)\otimes {\mathbb {R}}$
, respectively. For X over
$N_1(X)\otimes {\mathbb {R}}$
, respectively. For X over
![]() ${\mathbb {C}}$
, we have
${\mathbb {C}}$
, we have
For lack of a better term, we call the classes
![]() $A_1A_2\ldots A_{n-1}\in N_1(X)$
for ample
$A_1A_2\ldots A_{n-1}\in N_1(X)$
for ample
![]() $A_1,A_2,\ldots ,A_{n-1}\in \mathrm {Pic\ }(X)$
ample complete intersection classes. We call the cone
$A_1,A_2,\ldots ,A_{n-1}\in \mathrm {Pic\ }(X)$
ample complete intersection classes. We call the cone
![]() $\mathrm {Amp}_1(X)_{\mathbb {R}}\subset N_1(X)_{\mathbb {R}}$
generated by these classes the cone of ample complete intersection curves.
$\mathrm {Amp}_1(X)_{\mathbb {R}}\subset N_1(X)_{\mathbb {R}}$
generated by these classes the cone of ample complete intersection curves.
Theorem 5.4. Let X be a smoooth projective variety of dimension n over an algebraically closed field of characteristic
![]() $0$
, and let
$0$
, and let
![]() $G\subset N_1(X)_{\mathbb {R}}$
be the set consisting of numerical classes
$G\subset N_1(X)_{\mathbb {R}}$
be the set consisting of numerical classes
![]() $\xi $
with the following property: There exists a sequence
$\xi $
with the following property: There exists a sequence
![]() $f_m: C_m\to X$
of morphisms from smooth projective curves
$f_m: C_m\to X$
of morphisms from smooth projective curves
![]() $C_m$
to X such that
$C_m$
to X such that
-
○
 $f_m(C_m)$
passes through a general point of X, i.e., the deformation of
$f_m(C_m)$
passes through a general point of X, i.e., the deformation of
 $f_m$
dominates X for each m,
$f_m$
dominates X for each m, -
○ the numerical classes
 $[(f_m)_* C_m]$
of
$[(f_m)_* C_m]$
of
 $(f_m)_* C_m$
satisfy
$(f_m)_* C_m$
satisfy  $$ \begin{align*}\lim_{m\to\infty} \frac{[(f_m)_* C_m]}{\deg (f_m)_* C_m} = \xi \end{align*} $$
$$ \begin{align*}\lim_{m\to\infty} \frac{[(f_m)_* C_m]}{\deg (f_m)_* C_m} = \xi \end{align*} $$
-
○ and the conormal bundles
of $$ \begin{align*}M_{f_m} = \ker(f_m^*\Omega^1_X \xrightarrow{} \Omega^1_{C_m}) \end{align*} $$
$$ \begin{align*}M_{f_m} = \ker(f_m^*\Omega^1_X \xrightarrow{} \Omega^1_{C_m}) \end{align*} $$
 $f_m$
satisfy
$f_m$
satisfy  $$ \begin{align*}\varlimsup_{m\to\infty} \frac{n\max (\mu_{\max}(M_{f_m}), \deg K_{C_m}) - \deg f_m^* K_X}{n \deg (f_m)_* C_m} \le 0, \end{align*} $$
$$ \begin{align*}\varlimsup_{m\to\infty} \frac{n\max (\mu_{\max}(M_{f_m}), \deg K_{C_m}) - \deg f_m^* K_X}{n \deg (f_m)_* C_m} \le 0, \end{align*} $$
where
![]() $\deg (f_m)_* C_m$
is the degree of
$\deg (f_m)_* C_m$
is the degree of
![]() $(f_m)_* C_m$
with respect to a fixed ample line bundle on X.
$(f_m)_* C_m$
with respect to a fixed ample line bundle on X.
If
![]() $\mathrm {Amp}_1(X)_{\mathbb {R}}$
is asymptotically generated by G, i.e.,
$\mathrm {Amp}_1(X)_{\mathbb {R}}$
is asymptotically generated by G, i.e.,
![]() $\mathrm {Amp}_1(X)_{\mathbb {R}}$
is contained in the closure of the cone generated by G, then
$\mathrm {Amp}_1(X)_{\mathbb {R}}$
is contained in the closure of the cone generated by G, then
![]() $\Omega ^1_X$
is
$\Omega ^1_X$
is
![]() $\mu $
-semistable for all ample divisors A on X. More precisely, if
$\mu $
-semistable for all ample divisors A on X. More precisely, if
![]() $\Omega ^1_X$
contains a locally free subsheaf E of rank r such that
$\Omega ^1_X$
contains a locally free subsheaf E of rank r such that
![]() $\mu (E) \ge \mu (\Omega ^1_X)$
, then
$\mu (E) \ge \mu (\Omega ^1_X)$
, then
![]() $n c_1(E) - r K_X$
is numerically trivial.
$n c_1(E) - r K_X$
is numerically trivial.
In particular, if X is a complex K3 surface, A is an ample divisor on X and there is a positive answer to Question 5.2, then
![]() $\Omega ^1_X$
is
$\Omega ^1_X$
is
![]() $\mu _A$
-stable.
$\mu _A$
-stable.
Proof. Suppose that there exists a locally free subsheaf
![]() $E\subset \Omega ^1_X$
of rank r such that
$E\subset \Omega ^1_X$
of rank r such that
![]() $\mu (E) \ge \mu (\Omega ^1_X)$
. Then
$\mu (E) \ge \mu (\Omega ^1_X)$
. Then
![]() $L = \wedge ^r E$
is a subsheaf of
$L = \wedge ^r E$
is a subsheaf of
![]() $\Omega _X^r$
, and hence,
$\Omega _X^r$
, and hence,
![]() $H^0(\Omega _X^r(-L)) \ne 0$
.
$H^0(\Omega _X^r(-L)) \ne 0$
.
Let
![]() $\xi \in G$
and
$\xi \in G$
and
![]() $f_m: C_m\to X$
be the sequence of morphisms associated to
$f_m: C_m\to X$
be the sequence of morphisms associated to
![]() $\xi $
. Since
$\xi $
. Since
![]() $f_m(C_m)$
passes through a general point of X, we see that
$f_m(C_m)$
passes through a general point of X, we see that
Then we have
by the left exact sequence
where
![]() $M_{f_m}^a = \wedge ^a M_{f_m}$
. On the other hand, we know that
$M_{f_m}^a = \wedge ^a M_{f_m}$
. On the other hand, we know that
for a vector bundle V and a divisor B on a smooth projective curve. It follows that
 $$ \begin{align*}\begin{aligned} L. (f_m)_* C_m = \deg f_m^* L &\le \max\big(\mu_{max}(M_{f_m}^r), \mu_{\max}(M_{f_m}^{r-1}) + \deg K_{C_m}\big) \\ &\le \max\big(r \mu_{\max}(M_{f_m}), (r-1)\mu_{\max}(M_{f_m}) + \deg K_{C_m}\big)\\ &\le r \max(\mu_{\max}(M_{f_m}), \deg K_{C_m}). \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} L. (f_m)_* C_m = \deg f_m^* L &\le \max\big(\mu_{max}(M_{f_m}^r), \mu_{\max}(M_{f_m}^{r-1}) + \deg K_{C_m}\big) \\ &\le \max\big(r \mu_{\max}(M_{f_m}), (r-1)\mu_{\max}(M_{f_m}) + \deg K_{C_m}\big)\\ &\le r \max(\mu_{\max}(M_{f_m}), \deg K_{C_m}). \end{aligned} \end{align*} $$
Therefore,
 $$ \begin{align*}\left(\frac{L}r - \frac{K_X}{n}\right) \frac{(f_m)_* C_m}{\deg (f_m)_* C_m} \le \frac{n\max (\mu_{\max}(M_{f_m}), \deg K_{C_m}) - \deg f_m^* K_X}{n \deg (f_m)_* C_m}. \end{align*} $$
$$ \begin{align*}\left(\frac{L}r - \frac{K_X}{n}\right) \frac{(f_m)_* C_m}{\deg (f_m)_* C_m} \le \frac{n\max (\mu_{\max}(M_{f_m}), \deg K_{C_m}) - \deg f_m^* K_X}{n \deg (f_m)_* C_m}. \end{align*} $$
By our definition of G, we conclude that
 $$ \begin{align*}\left(\frac{L}r - \frac{K_X}{n}\right) \xi \le 0 \end{align*} $$
$$ \begin{align*}\left(\frac{L}r - \frac{K_X}{n}\right) \xi \le 0 \end{align*} $$
for all
![]() $\xi \in G$
. On the other hand, since
$\xi \in G$
. On the other hand, since
![]() $\mu (E)\ge \mu (\Omega ^1_X)$
,
$\mu (E)\ge \mu (\Omega ^1_X)$
,
 $$ \begin{align*}\left(\frac{L}r - \frac{K_X}{n}\right) A^{n-1} \ge 0. \end{align*} $$
$$ \begin{align*}\left(\frac{L}r - \frac{K_X}{n}\right) A^{n-1} \ge 0. \end{align*} $$
Fixing
![]() $\xi \in G$
, since
$\xi \in G$
, since
![]() $\mathrm {Amp}_1(X)_{\mathbb {R}}$
is open in
$\mathrm {Amp}_1(X)_{\mathbb {R}}$
is open in
![]() $N_1(X)_{\mathbb {R}}$
,
$N_1(X)_{\mathbb {R}}$
,
for some
![]() $t>0$
sufficiently small. Since
$t>0$
sufficiently small. Since
![]() $\mathrm {Amp}_1(X)_{\mathbb {R}}$
is asymptotically generated by G,
$\mathrm {Amp}_1(X)_{\mathbb {R}}$
is asymptotically generated by G,
 $$ \begin{align*}A^{n-1} - t\xi = \sum_{m=1}^\infty t_m \xi_m \end{align*} $$
$$ \begin{align*}A^{n-1} - t\xi = \sum_{m=1}^\infty t_m \xi_m \end{align*} $$
for some
![]() $t_m> 0$
and
$t_m> 0$
and
![]() $\xi _m\in G$
. Finally, from
$\xi _m\in G$
. Finally, from
we conclude that
![]() $(nL - rK_X)\xi = 0$
. Therefore,
$(nL - rK_X)\xi = 0$
. Therefore,
for all
![]() $\xi \in G$
. This implies that
$\xi \in G$
. This implies that
![]() $nL - rK_X$
is numerically trivial since G also generates
$nL - rK_X$
is numerically trivial since G also generates
![]() $N_1(X)_{\mathbb {R}}$
.
$N_1(X)_{\mathbb {R}}$
.
For a complex K3 surface X, it is easy to see that
![]() $E/\deg E\in G$
for every elliptic curve E on X. Since by hypothesis the elliptic curves generate the ample cone
$E/\deg E\in G$
for every elliptic curve E on X. Since by hypothesis the elliptic curves generate the ample cone
![]() $\mathrm {Amp}(X)$
of X,
$\mathrm {Amp}(X)$
of X,
![]() $\mathrm {Amp}(X)$
is generated by G. If
$\mathrm {Amp}(X)$
is generated by G. If
![]() $\Omega _X^1$
is destabilised by a line bundle L, then L is numerically trivial. For K3 surfaces, this implies that
$\Omega _X^1$
is destabilised by a line bundle L, then L is numerically trivial. For K3 surfaces, this implies that
![]() $L = {\mathcal O}_X$
so that
$L = {\mathcal O}_X$
so that
![]() $H^0(\Omega _X^1(-L)) = H^0(\Omega _X^1) \ne 0$
which is a contradiction.
$H^0(\Omega _X^1(-L)) = H^0(\Omega _X^1) \ne 0$
which is a contradiction.
Remark 5.5. In positive characteristic, Langer [Reference LangerLan15, §4] proves that K3 surfaces not dominated by
![]() ${\mathbb {P}}^2$
have strongly semistable cotangent bundle and that K3 surfaces admitting a quasi-elliptic fibration (e.g., unirational K3 surfaces in characteristic 2) do not have semistable cotangent bundle. If semistable, then
${\mathbb {P}}^2$
have strongly semistable cotangent bundle and that K3 surfaces admitting a quasi-elliptic fibration (e.g., unirational K3 surfaces in characteristic 2) do not have semistable cotangent bundle. If semistable, then
![]() $\Omega ^1_X$
must also be stable as
$\Omega ^1_X$
must also be stable as
![]() $\mathrm {H}^0(X, \Omega ^1_X)=0$
is known for an arbitrary K3. We expect Question 5.2 to still have a positive answer here though. In fact if one could furthermore assume that all the genus
$\mathrm {H}^0(X, \Omega ^1_X)=0$
is known for an arbitrary K3. We expect Question 5.2 to still have a positive answer here though. In fact if one could furthermore assume that all the genus
![]() $1$
curves generating the nef cone admit normalisations which deform to unramified morphisms (something which does not occur for fibres of a quasi-elliptic fibrations), the above proof goes through.
$1$
curves generating the nef cone admit normalisations which deform to unramified morphisms (something which does not occur for fibres of a quasi-elliptic fibrations), the above proof goes through.
We conclude this section by giving the proof of Nakayama’s theorem in arbitrary characteristic. This proof is essentially the same as in [Reference Boucksom, Demailly, Păun and PeternellBDPP13, Theorem 7.8] (which draws from Nakayama’s original proof from [Reference NakayamaNak04]) with the necessary adjustments for positive characteristic in place.
Theorem 5.6 Nakayama in characteristic
 $p\geq 0$
$p\geq 0$
Let X be a K3 surface over an algebraically closed field k. Assume further that
![]() $\Omega ^1_X$
is
$\Omega ^1_X$
is
![]() $\mu $
-stable and that
$\mu $
-stable and that
Then
![]() $\Omega ^1_X$
is not pseudoeffective.
$\Omega ^1_X$
is not pseudoeffective.
Proof. Since stability persists if we pass to a larger algebraically closed field, we may assume k is uncountable. Let
![]() $Y={\mathbb {P}}(\Omega ^1_X)$
, and suppose for a contradiction that
$Y={\mathbb {P}}(\Omega ^1_X)$
, and suppose for a contradiction that
![]() $L={\mathcal O}_Y(1)$
is pseudoeffective. Then there is a Nakayama–Zariski decomposition of
$L={\mathcal O}_Y(1)$
is pseudoeffective. Then there is a Nakayama–Zariski decomposition of
![]() $L=E+N$
, where E is an effective
$L=E+N$
, where E is an effective
![]() ${\mathbb {R}}$
-divisor and N is nef in codimension 1 (due to [Reference NakayamaNak04] in characteristic 0 and [Reference MustaţăMus13, Reference Fulger and LehmannFL17] otherwise).
${\mathbb {R}}$
-divisor and N is nef in codimension 1 (due to [Reference NakayamaNak04] in characteristic 0 and [Reference MustaţăMus13, Reference Fulger and LehmannFL17] otherwise).
From [Reference LangerLan10, Theorem 4.1] (or Flenner or Mehta–Ramanathan’s theorem in characteristic zero), we may pick a very ample smooth curve C on X so that
![]() $\Omega ^1_X|_C$
is strongly semistable (or just semistable in characteristic zero). Then on the ruled surface
$\Omega ^1_X|_C$
is strongly semistable (or just semistable in characteristic zero). Then on the ruled surface
![]() $R={\mathbb {P}}(\Omega ^1_X|_C)$
every pseudoeffective line bundle is nef (in fact for the projectivisation of a degree zero strongly semistable bundle on a curve, these cones agree). On the other hand,
$R={\mathbb {P}}(\Omega ^1_X|_C)$
every pseudoeffective line bundle is nef (in fact for the projectivisation of a degree zero strongly semistable bundle on a curve, these cones agree). On the other hand,
![]() $L|_R$
is not ample, since
$L|_R$
is not ample, since
![]() $L^2|_R=c_1(\Omega ^1_X)\cdot C=0$
. Hence,
$L^2|_R=c_1(\Omega ^1_X)\cdot C=0$
. Hence,
![]() $L|_R$
is on the boundary of the nef cone of R. Write
$L|_R$
is on the boundary of the nef cone of R. Write
![]() $E=aL+\pi ^*E'$
. As the Picard number of R is two and
$E=aL+\pi ^*E'$
. As the Picard number of R is two and
![]() $E|_R$
is also
$E|_R$
is also
![]() ${\mathbb {R}}$
-effective, it must be that
${\mathbb {R}}$
-effective, it must be that
![]() $E'.C\geq 0$
. If
$E'.C\geq 0$
. If
![]() $E'.C>0$
, then
$E'.C>0$
, then
![]() $E'$
is effective on X (as C can vary), so in particular,
$E'$
is effective on X (as C can vary), so in particular,
![]() $E|_R$
is big and hence ample. This contradicts
$E|_R$
is big and hence ample. This contradicts
![]() $L|_R=E|_R+N|_R$
being boundary on the nef cone though. In other words,
$L|_R=E|_R+N|_R$
being boundary on the nef cone though. In other words,
![]() $CE'=0$
and as C can vary,
$CE'=0$
and as C can vary,
![]() $E'=0$
, forcing
$E'=0$
, forcing
![]() $E=aL$
. Then
$E=aL$
. Then
![]() $a=0$
since from the assumption L has no effective multiple. It follows that
$a=0$
since from the assumption L has no effective multiple. It follows that
![]() $E=0$
and L is nef in codimension 1. In particular, it fails to be nef on at most countably many curves
$E=0$
and L is nef in codimension 1. In particular, it fails to be nef on at most countably many curves
![]() $C_i$
. Taking a hyperplane section H of Y, we see then that
$C_i$
. Taking a hyperplane section H of Y, we see then that
![]() $L|_H$
is nef. In particular,
$L|_H$
is nef. In particular,
![]() $L^2\cdot H\ge 0$
. In terms of Chern classes, this means that
$L^2\cdot H\ge 0$
. In terms of Chern classes, this means that
which contradicts
![]() $c_2(T_X)=24$
.
$c_2(T_X)=24$
.
Acknowledgements
The idea to use rational curves to prove Nakayama’s theorem had been suggested to the second author by Claire Voisin during a talk on the subject, and we would like to thank her for this insight. We would like to thank Adrian Langer for pointing out and filling in some missing steps in the proof of Theorem 5.6. The first named author is partially supported by the NSERC Discovery Grant 262265, whereas the second is supported by the ERC Consolidator Grant 681838 “K3CRYSTAL”.
Funding statement
This research was supported by grants from the NSERC Discovery Grant (262265); ERC Consolidator Grant (681838). We acknowledge support by the Open Access Publication Funds of the Göttingen University.
Conflicts of Interest
None.