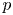Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T19:09:48.836Z Has data issue: false hasContentIssue false
  • English
  • Français

Harnack inequality for the nonlocal equations with general growth

Part of: Representations of solutions Partial differential equations Miscellaneous topics - Partial differential equations Linear function spaces and their duals Integral, integro-differential, and pseudodifferential operators

Published online by Cambridge University Press:  23 August 2022

Yuzhou Fang  and
Chao Zhang Open the ORCID record for Chao Zhang [Opens in a new window]
Yuzhou Fang
Affiliation:
School of Mathematics, Harbin Institute of Technology, Harbin 150001, China ([email protected])
Chao Zhang
Affiliation:
School of Mathematics and Institute for Advanced Study in Mathematics, Harbin Institute of Technology, Harbin 150001, China ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

We consider a class of generalized nonlocal $p$-Laplacian equations. We find some proper structural conditions to establish a version of nonlocal Harnack inequalities of weak solutions to such nonlocal problems by using the expansion of positivity and energy estimates.

Keywords

Expansion of positivityfractional Orlicz–Sobolev spacegeneral growthHarnack inequalitynonlocal equations

MSC classification

Primary: 35R11: Fractional partial differential equations
Secondary: 47G20: Integro-differential operators 35B65: Smoothness and regularity of solutions 35D30: Weak solutions 46E30: Spaces of measurable functions ($L^p$-spaces, Orlicz spaces, Köthe function spaces, Lorentz spaces, rearrangement invariant spaces, ideal spaces, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 5 , October 2023 , pp. 1479 - 1502
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

1. Introduction

Let $\Omega \subset \mathbb {R}^{n} \,(n\geq 2)$ be a bounded domain. In this paper, we are interested in the following class of integro-differential equations with general growth

(1.1)\begin{equation} \mathcal{L}u=0 \quad\text{in } \Omega \end{equation}

with

\[\mathcal{L}u(x):=\mathrm{P.V.}\int_{\mathbb{R}^{n}}g\left(\frac{|u(x)-u(y)|}{|x-y|^{s}}\right)\frac{u(x)-u(y)}{|u(x)-u(y)|} \frac{K(x,y)}{|x-y|^{s}}\,{\rm d}y,\]

where the symbol $\mathrm {P.V.}$ represents ‘in the principal value sense’, $s\in (0,\,1)$ and the function $K(x,\,y):\mathbb {R}^{n}\times \mathbb {R}^{n}\rightarrow (0,\,\infty ]$ is a symmetric measurable kernel such that

(1.2)\begin{equation} \frac{\Lambda^{{-}1}}{|x-y|^{n}}\leq K(x,y)\leq \frac{\Lambda}{|x-y|^{n}}, \quad \Lambda\geq 1. \end{equation}

Particularly when $\Lambda =1$, Eq. (1.1) is called $s$-fractional $G$-Laplace equation. The function $g:[0,\,\infty )\rightarrow [0,\,\infty )$ is continuous and strictly increasing fulfilling $g(0)=0$, $\lim _{t\rightarrow \infty }g(t)=\infty$ and

(1.3)\begin{equation} 1< p\leq\frac{tg(t)}{G(t)}\leq q<\infty \quad \text{ with } G(t)=\int_0^{t}g(\tau)\,{\rm d}\tau, \end{equation}

where $G(\cdot )$ is an $N$-function possessing the $\Delta _2$ and $\nabla _2$ conditions (see § 2).

In recent years, a great attention has been concentrated on the nonlocal $p$-Laplacian problems, which is the special case that $g(t)=t^{p-1}$. For the regularity theory on this kind of problems, Kassmann [Reference Kassmann28] proved the nonlocal Harnack inequality with tail-term for the fractional Laplacian. Di Castro-Kuusi-Palatucci [Reference Di Castro, Kuusi and Palatucci13] further investigated the local behaviour of weak solutions incorporating boundedness and Hölder continuity in the spirit of De Giorgi-Nash-Moser iteration; see also [Reference Di Castro, Kuusi and Palatucci12] for the nonlocal Harnack inequalities. The Hölder regularity up to the boundary was whereafter showed by Iannizzotto–Mosconi–Squassina [Reference Iannizzotto, Mosconi and Squassina27]. We also refer the readers to [Reference Brasco and Lindgren1] for higher Sobolev regularity, [Reference Kuusi, Mingione and Sire33] for self-improving properties [Reference Korvenpää, Kuusi and Lindgren30, Reference Korvenpää, Kuusi and Palatucci32], for the viscosity and potential theory [Reference Brasco and Parini3, Reference Franzina and Palatucci20], for fractional $p$-eigenvalue problems. When it comes to the parabolic counterpart, several features of solutions have already been studied, such as the local regularity [Reference Brasco, Lindgren and Strömqvist2, Reference Ding, Zhang and Zhou15, Reference Strömqvist45] and the well-posedness [Reference Mazón, Rossi and Toledo37, Reference Vázquez46]. For more results on the nonlocal nonlinear problems of the $p$-Laplacian type, one can see for instance [Reference Caffarelli, Chan and Vasseur7, Reference Felsinger and Kassmann17, Reference Korvenpää, Kuusi and Palatucci31, Reference Kuusi, Mingione and Sire34, Reference Palatucci40, Reference Vázquez47].

When $g(\cdot )$ carries a more general structure, Eq. (1.1) can be viewed naturally as the nonlocal analogue of the $G$-Laplace equation whose classical model is

(1.4)\begin{equation} -\operatorname{div}\left(g(|\nabla u|)\frac{\nabla u}{|\nabla u|} \right)=0 \quad\text{with } g(t)=G'(t). \end{equation}

The so-called $G$-Laplace equations have been extensively studied over the past years. The regularity theory, especially for the scenario that $g(t)\approx t^{p-1}+t^{q-1}$, is initially explored by the celebrated papers of Marcellini [Reference Marcellini35, Reference Marcellini36]. More results on the generalized $p$-Laplace equations can be found in [Reference Buryachenko and Skrypnik4, Reference De Filippis and Mingione10, Reference Diening, Stroffolini and Verde14, Reference Harjulehto, Hästö and Lee26, Reference Salort41, Reference Skrypnik and Voitovych44]. On the other hand, Fernández Bonder–Salort–Vivas [Reference Fernández Bonder, Salort and Vivas18] established the Hölder continuity for weak solutions to the fractional $g$-Laplacian with Dirichlet boundary values; see also [Reference Fernández Bonder, Salort and Vivas19] for the global regularity of eigenfunctions. Chaker–Kim–Weidner [Reference Chaker, Kim and Weidner9] proved, via De Giorgi classes, the interior regularity properties for the nonlocal functionals with $(p,\,q)$-growth and related equations. More recently, the weak solutions to (1.1) were proved to be locally bounded and Hölder continuous in [Reference Byun, Kim and Ok5] under the assumption (1.3). Regarding further studies of the nonlocal problems possessing non-standard growth, including also double phase equations and equations with variable exponents, one can refer to [Reference Byun, Ok and Song6, Reference Chaker and Kim8, Reference De Filippis and Palatucci11, Reference Fang and Zhang16, Reference Giacomoni, Kumar and Sreenadh21, Reference Giacomoni, Kumar and Sreenadh22, Reference Goel, Kumar and Sreenadh25, Reference Ok39, Reference Salort42, Reference Salort and Vivas43] and references therein.

Although pretty abundant research results have been obtained for the nonlocal problems with non-standard growth, to the best of our knowledge, there are few results regarding the pointwise estimates such as the Harnack inequalities. To this end, our aim of this manuscript is to investigate Harnack estimate for Eq. (1.1), which can be regarded as a natural outgrowth of the result in [Reference Di Castro, Kuusi and Palatucci12]. Due to the possibly inhomogeneous growth of the function $G$, we have to explore the suitable conditions on $G$ in order to infer the desired result. Additionally, we require that the function $G$ satisfies the following condition:

(1.5)\begin{equation} G(t\tau)\leq c_0G(t)G(\tau) \end{equation}

for any $t,\,\tau \geq 0$ and $c_0$ being a positive constant. Examples of $G$ satisfying the requirements (1.3) and (1.5) include

  • • $G(t)=t^{p}$, $t\ge 0$, $p>1$;

  • • $G(t)=\max \{t^{p},\,t^{q}\}$, $t\ge 0$, $1< p\le q<\infty$;

  • • $G(t)=t^{p}+a_0t^{q} \text { with } a_0>0$, $t\ge 0$, $1< p\le q<\infty$;

  • • $G(t)=t^{p}\log (e+t)$, $t\ge 0$, $p>1$.

Before giving our main result, we introduce the so-called ‘tail space’,

\[L^{g}_s(\mathbb{R}^{n})=\left\{u \text{ is measurable function in } \mathbb{R}^{n}: \int_{\mathbb{R}^{n}} g\left(\frac{|u(x)|}{(1+|x|)^{s}}\right)\,\frac{{\rm d}x}{(1+|x|)^{n+s}}<\infty\right\}.\]

The corresponding nonlocal tail of $u$ is given by

(1.6)\begin{equation} \mathrm{Tail}(u;x_0,R)=\int_{\mathbb{R}^{n}\setminus B_R(x_0)}g\left(\frac{|u(x)|}{|x-x_0|^{s}}\right)\,\frac{{\rm d}x}{|x-x_0|^{n+s}}. \end{equation}

Notice that $u\in L^{g}_s(\mathbb {R}^{n})$ if and only if $\mathrm {Tail}(u;x_0,\,R)$ is finite for any $x_0\in \mathbb {R}^{n}$ and $R>0$. The details can be found in [Reference Byun, Kim and Ok5, subsection 2.3].

Now we are in a position to state the main result as follows.

Theorem 1.1 Suppose that $s\in (0,\,1)$ and the assumptions (1.3) and (1.5) are in force. Let $u\in \mathbb {W}^{s,G}(\Omega )\cap L^{g}_s(\mathbb {R}^{n})$ be a weak solution of Eq. (1.1) such that $u\geq 0$ in $B_R:=B_R(x_0)\subset \Omega$. Then, for every $B_r:=B_r(x_0)\subset B_\frac {R}{2}(x_0),$ we have the following nonlocal Harnack inequality

\begin{align*} \sup_{B_r}u& \leq Cr^{s(1-\frac{q}{p})\frac{q}{\epsilon}}\max_{\iota\in\{1,\frac{q}{p},\frac{p}{q}\}}\left\{\left(\inf_{B_r}u+r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R))\right)^{\iota}\right\}\\ & \quad+Cr^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R)), \end{align*}

where Tail $(\cdot )$ is defined in (1.6), $u_-:=\max \{-u,\,0\}$, the positive constant $C$ depends on $n,\,p,\,q,\,s,\,\Lambda$ as well as the structural constant $c_0$ given by (1.5), and the absolute constant $\epsilon \in (0,\,1)$, coming from lemma 3.3 below, is a priori determined by $n,\,p,\,q,\,s,\,\Lambda$.

Remark 1.2 Let us point out that the extra hypothesis (1.5) is only exploited in the proof of theorem 1.1 below. The reason why we impose the additional strong condition on $G$ is that we need to split the term $G(u)$ into $G(u^{1-\varepsilon })G(u^{\varepsilon })$ with $\varepsilon$ being an arbitrary number in $(0,\,1)$, and then get the integral of $u^{\varepsilon '}$ $(\varepsilon '\in (0,\,1))$ as the integrand, which enables us to apply lemma 3.3. Observe that, if $g(t)=t^{p-1}$, then $q=p$ and

\begin{align*} r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R))& =r^{s}\left(r^{s}\int_{\mathbb{R}^{n}\setminus B_R(x_0)}\frac{u_-^{p-1}(x)}{|x-x_0|^{s(p-1)}}\frac{{\rm d}x}{|x-x_0|^{n+s}}\right)^{\frac{1}{p-1}}\\ & =\left(\frac{r}{R}\right)^{\frac{sp}{p-1}}\left(R^{sp}\int_{\mathbb{R}^{n}\setminus B_R(x_0)}\frac{u_-^{p-1}(x)}{|x-x_0|^{n+sp}}\,{\rm d}x\right)^{\frac{1}{p-1}}. \end{align*}

Hence, our result is reduced to the Harnack inequality obtained in [Reference Di Castro, Kuusi and Palatucci12, theorem 1.1].

Remark 1.3 The result obtained in theorem 1.1 can be extended to the nonhomogeneous equation $\mathcal {L}u=f$ with $f$ being bounded locally. In fact, we just need to consider the additional integral involving $f$, $\int _\Omega f\phi \,{\rm d}x$, in proposition 3.1, lemmas 3.2, 4.1 and 4.2, where $\phi$ is a test function varying in different contexts. For the nonhomogeneous counterpart, we could deduce the following Harnack inequality

\begin{align*} \sup_{B_r}u& \leq Cr^{s(1-\frac{q}{p})\frac{q}{\epsilon}}\max_{\iota\in\{1,\frac{q}{p},\frac{p}{q}\}}\left\{\left(\inf_{B_r}u+r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R)+r^{s}\|f\|_{L^{\infty}(B_R)})\right)^{\iota}\right\}\\ & \quad+Cr^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R)+r^{s}\|f\|_{L^{\infty}(B_R)}). \end{align*}

The paper is organized as follows. In § 2, we give the definition of weak solutions to Eq. (1.1), and collect some notations and auxiliary inequalities to be used later. Section 3 is devoted to deducing infimum estimates for weak supersolutions by employing the expansion of positivity. Finally, we prove the Harnack inequality in § 4.

2. Preliminaries

In this section, we shall give some basic inequalities, state the notions of some functional spaces and weak solutions, and then provide a covering lemma.

In what follows, we denote by $C$ a generic positive constant which may change from line to line. Relevant dependencies on parameters will be illustrated utilizing parentheses, i.e., $C\equiv C(n,\,p,\,q)$ means that $C$ depends on $n,\,p,\,q$. Let $B_r(x_0):=\{x\in \mathbb {R}^{n}:|x-x_0|< r\}$ stand for the open ball with centre $x_0$ and radius $r>0$. If not important, or clear from the context, we do not denote the centre as follows: $B_r:=B_r(x_0)$. If $f\in L^{1}(A)$ and $A\subset \mathbb {R}^{n}$ is a measurable subset with positive measure $0<|A|<\infty$, we denote its integral average by

\[(f)_A:={{\int\hspace{-0.38cm}-}}_Af(x)\,{\rm d}x=\frac{1}{|A|}\int_Af(x)\,{\rm d}x.\]

The function $G:[0,\,\infty )\rightarrow [0,\,\infty )$ is an $N$-function which means that it is convex and increasing, and satisfies that

\[G(0)=0, \quad \lim_{t\rightarrow 0+}\frac{G(t)}{t}=0 \quad\text{and} \quad \lim_{t\rightarrow\infty}\frac{G(t)}{t}=\infty.\]

The conjugate function of $N$-function $G$ is denoted by

\[G^{*}(t)=\sup_{\tau\geq 0}\{\tau t-G(\tau)\}.\]

From the relation (1.3), we now give several inequalities to be utilized later:

  1. (a) for $t\in [0,\,\infty )$,

    (2.1)\begin{equation} \begin{cases} a^{q}G(t)\leq G(at)\leq a^{p}G(t) & \text{if } a\in(0,1),\\ a^{p}G(t)\leq G(at)\leq a^{q}G(t) & \text{if } a\in(1,\infty) \end{cases} \end{equation}
    and
    (2.2)\begin{equation} \begin{cases} a^{p'}G^{*}(t)\leq G^{*}(at)\leq a^{q'}G^{*}(t) & \text{if} a\in(0,1),\\ a^{q'}G^{*}(t)\leq G^{*}(at)\leq a^{p'}G^{*}(t) & \text{if} a\in(1,\infty), \end{cases} \end{equation}
    where $p',\,q'$ are the Hölder conjugates of $p,\,q$.

  2. (b) Young's inequality with $\epsilon \in (0,\,1]$

    (2.3)\begin{equation} t\tau\leq \epsilon^{1-q}G(t)+\epsilon G^{*}(\tau), \quad t,\tau\geq 0. \end{equation}

  3. (c) for $t,\,\tau \geq 0$,

    (2.4)\begin{equation} G^{*}(g(t))\leq (q-1)G(t), \end{equation}
    and
    (2.5)\begin{equation} 2^{{-}1}(G(t)+G(\tau))\leq G(t+\tau)\leq 2^{q-1}(G(t)+G(\tau)). \end{equation}

Moreover, the function $G$ fulfills the following $\Delta _2$ and $\nabla _2$ conditions (see [Reference Mihăilescu and Rădulescu38, proposition 2.3]):

  1. (Δ2) there is a constant $\mu >1$ such that $G(2t)\leq \mu G(t)$ for $t\geq 0$;

  2. (∇2) there is a constant $\nu >1$ such that $G(t)\leq \frac {1}{2\nu }G(\nu t)$ for $t\geq 0$,

where $\mu,\,\nu$ depend on $p,\,q$. As a matter of fact, the condition $\nabla _2$ is just $\Delta _2$ applied to $G^{*}$.

We next introduce the notion of Orlicz–Sobolev spaces. For an $N$-function $G$ with the $\Delta _2$ and $\nabla _2$ conditions, the Orlicz space $L^{G}(\Omega )$ is defined as

\[L^{G}(\Omega)=\left\{u \text{ is measurable function in } \Omega: \int_\Omega G(|u(x)|)\,{\rm d}x<\infty\right\}\]

equipped with the Luxemburg norm

\[\|u\|_{L^{G}(\Omega)}=\inf\left\{\lambda>0: \int_\Omega G\left(\frac{|u(x)|}{\lambda}\right)\,{\rm d}x\leq 1\right\}.\]

The fractional Orlicz–Sobolev space $W^{s,G}(\Omega )$ ($s\in (0,\,1$)) is given by

\[W^{s,G}(\Omega)=\left\{u\in L^{G}(\Omega):\int_\Omega\int_\Omega G\left(\frac{|u(x)-u(y)|}{|x-y|^{s}}\right)\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n}}<\infty\right\}\]

endowed with the norm

\[\|u\|_{W^{s,G}(\Omega)}=\|u\|_{L^{G}(\Omega)}+[u]_{s,G,\Omega},\]

where $[u]_{s,G,\Omega }$ is the Gagliardo semi-norm defined as

\[[u]_{s,G,\Omega}=\inf\left\{\lambda>0:\int_\Omega\int_\Omega G\left(\frac{|u(x)-u(y)|}{\lambda|x-y|^{s}}\right)\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n}}\leq 1\right\}.\]

Let $C_{\Omega }\equiv (\Omega \times \mathbb {R}^{n})\cup (\mathbb {R}^{n}\times \Omega )$. For measurable function $u$ in $\mathbb {R}^{n}$, we define

\[\mathbb{W}^{s,G}(\Omega)=\left\{u\big |_{\Omega}\in L^{G}(\Omega) : \iint_{C_{\Omega}}G\left(\frac{|u(x)-u(y)|}{|x-y|^{s}}\right)\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n}}<\infty\right\},\]

which is the space weak solutions of (1.1) belong to.

Now we give the definition of weak solutions to (1.1).

Definition 2.1 We call $u\in \mathbb {W}^{s,G}(\Omega )$ a weak supersolution of Eq. (1.1) if

(2.6)\begin{equation} \iint_{C_{\Omega}}g\left(\frac{|u(x)-u(y)|}{|x-y|^{s}}\right)\frac{u(x)-u(y)}{|u(x)-u(y)|} (\psi(x)-\psi(y))\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\geq 0 \end{equation}

for each nonnegative function $\psi \in \mathbb {W}^{s,G}(\Omega )$ with compact support in $\Omega$. For weak subsolution, the above inequality is reversed. $u\in \mathbb {W}^{s,G}(\Omega )$ is a weak solution to (1.1) if and only if it is both a weak supersolution and a weak subsolution.

We conclude this section by presenting the Krylov–Sofonov covering lemma (see for instance [Reference Kinnunen and Shanmugalingam29]) playing an important role in proving lemma 3.3 below.

Lemma 2.2 Let $\overline {\delta }\in (0,\,1)$ and $E\subset B_r(x_0)$ be a measurable set. Denote

\[[E]_{\overline{\delta}}=\bigcup_{\rho>0}\left\{B_{3\rho}(x)\cap B_r(x_0), x\in B_r(x_0): |E\cap B_{3\rho}(x)|>\overline{\delta}|B_\rho(x)|\right\}.\]

Then one of the following must hold:

  1. (i) $|[E]_{\overline {\delta }}|\geq \frac {c(n)}{\overline {\delta }}|E|;$

  2. (ii) $[E]_{\overline {\delta }}=B_r(x_0).$

3. Expansion of positivity

This section is devoted to deriving the infimum estimates on the weak supersolutions of (1.1) by expansion of positivity. The following proposition exhibits the spread of pointwise positivity in space.

Proposition 3.1 Let $k\geq 0$ and $u\in \mathbb {W}^{s,G}(\Omega )$ be a weak supersolution to Eq. (1.1) such that $u\geq 0$ in $B_R(x_0)\subset \Omega$. If

\[|B_r\cap\{u\geq k\}|\geq \sigma|B_r|\]

for some $\sigma \in (0,\,1]$ and $r$ fulfilling $0< r<\frac {R}{16}\leq 1$, then there is $\delta \in (0,\,\frac {1}{2})$, which depends on $n,\,p,\,q,\,s,\,\Lambda,\,\sigma$, such that

\[u(x)\geq \frac{1}{2}\delta k-r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R)) \quad \text{in } B_{4r}.\]

Before proving this proposition, we first need the propagation of positivity in measure, that is the forthcoming lemma.

Lemma 3.2 Let $k\geq 0$ and $u\in \mathbb {W}^{s,G}(\Omega )$ be a weak supersolution to Eq. (1.1) such that $u\geq 0$ in $B_R(x_0)\subset \Omega$. If there is a $\sigma \in (0,\,1]$ satisfying

\[|B_r\cap\{u\geq k\}|\geq \sigma|B_r|\]

with $0< r<\frac {R}{16}\leq 1$, then we infer that, for any $\delta \in (0,\,\frac {1}{2})$,

\[|B_{6r}\cap\{u\leq 2\delta k-r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R))\}|\leq \frac{C}{\sigma \log\frac{1}{2\delta}}|B_{6r}|\]

with the constant $C>0$ depending only on $n,\,p,\,q,\,s,\,\Lambda$.

Proof. Let $v(x):=u(x)+d$ with $d=r^{s}g^{-1}(r^{s}\mathrm {Tail}(u_-;x_0,\,R))$. Now take a cut-off function $\varphi \in C^{\infty }_0(B_{7r})$ such that

\[0\leq \varphi\leq 1,\quad \varphi\equiv 1 \text{ in } B_{6r} \quad \text{and} \quad |\nabla\varphi|\leq\frac{c}{r}.\]

We select $\eta :=\varphi ^{q}\frac {v}{G(v/r^{s})}$ as a test function in the weak formulation (2.6), and then slightly modify the expression to have

(3.1)\begin{align} 0& \leq \int_{B_{8r}}\int_{B_{8r}}g\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\frac{v(x)-v(y)}{|v(x)-v(y)|}\left(\frac{v(x)\varphi^{q}(x)}{G(v(x)/r^{s})} -\frac{v(y)\varphi^{q}(y)}{G(v(y)/r^{s})}\right)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y \nonumber\\ & \quad+2\int_{\mathbb{R}^{n}\setminus B_{8r}}\int_{B_{8r}}g\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\frac{v(x)-v(y)}{|v(x)-v(y)|}\frac{v(x)\varphi^{q}(x)}{G(v(x)/r^{s})} \frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y \nonumber\\ & =:I_1+2I_2. \end{align}

Following the arguments of steps 1–3 in [Reference Byun, Kim and Ok5, proposition 3.4], we get

(3.2)\begin{equation} I_1\leq{-}\frac{1}{C}\int_{B_{6r}}\int_{B_{6r}}\left|\log\frac{v(x)}{v(y)}\right|\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n}}+Cr^{n}. \end{equation}

For the integral $I_2$,

\begin{align*} I_2& =\int_{\mathbb{R}^{n}\setminus B_{8r}\cap\{v(y)<0\}}\int_{B_{8r}}g\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\frac{v(x)-v(y)}{|v(x)-v(y)|}\frac{v(x)\varphi^{q}(x)}{G(v(x)/r^{s})}\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \quad+\int_{\mathbb{R}^{n}\setminus B_{8r}\cap\{v(y)\geq 0\}}\int_{B_{8r}}g\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\frac{v(x)-v(y)}{|v(x)-v(y)|}\frac{v(x)\varphi^{q}(x)}{G(v(x)/r^{s})}\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & =:I_{21}+I_{22}. \end{align*}

We first evaluate $I_{21}$. Note that, by (1.3), (2.1) and (2.5),

\begin{align*} g\left(\frac{v(x)+v_-(y)}{|x-y|^{s}}\right)& \leq q2^{q-1}\frac{G\left(\frac{v(x)}{|x-y|^{s}}\right)+G\left(\frac{v_-(y)}{|x-y|^{s}}\right)}{\frac{v(x)+v_-(y)}{|x-y|^{s}}}\\ & \leq\frac{q2^{q-1}}{p}\left(g\left(\frac{v(x)}{|x-y|^{s}}\right)+g\left(\frac{v_-(y)}{|x-y|^{s}}\right)\right). \end{align*}

Then,

\begin{align*} I_{21}& =\int_{\mathbb{R}^{n}\setminus B_{8r}\cap\{v(y)<0\}}\int_{B_{8r}}g\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\frac{v(x)\varphi^{q}(x)}{G(v(x)/r^{s})}\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \leq C\int_{\mathbb{R}^{n}\setminus B_{8r}}\int_{B_{8r}}\left(g\left(\frac{v(x)}{|x-y|^{s}}\right)+g\left(\frac{v_-(y)}{|x-y|^{s}}\right)\right)\frac{\varphi^{q}(x)r^{s}}{g(v(x)/r^{s})}\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \leq C\int_{\mathbb{R}^{n}\setminus B_{8r}}\int_{B_{7r}}\left(g\left(\frac{v(x)}{r^{s}}\right)+g\left(\frac{v_-(y)}{|x-y|^{s}}\right)\right)\frac{r^{s}}{g(v(x)/r^{s})|x-y|^{n+s}} \,{\rm d}x{\rm d}y. \end{align*}

When $x\in B_{7r}$ and $y\in \mathbb {R}^{n}\setminus B_{8r}$,

\[|y-x_0|\leq \left(1+\frac{|x-x_0|}{|y-x|}\right)|y-x|\leq 8|y-x|,\]

we further get

\begin{align*} I_{21}& \leq Cr^{s}\int_{\mathbb{R}^{n}\setminus B_{8r}}\int_{B_{7r}}\,\frac{{\rm d}x{\rm d}y}{|y-x_0|^{n+s}}+C\frac{r^{s}}{g(d/r^{s})}\int_{\mathbb{R}^{n}\setminus B_{8r}}\int_{B_{7r}}g\left(\frac{u_-(y)}{|x_0-y|^{s}}\right)\,\frac{{\rm d}x{\rm d}y}{|y-x_0|^{n+s}}\\ & \leq Cr^{n}+C\frac{r^{n+s}}{g(d/r^{s})}\mathrm{Tail}(u_-;x_0,R), \end{align*}

where we utilized the fact $u(y)\geq 0$ in $B_R\supset B_{8r}$ and the constant $C$ depends on $n,\,p,\,q,\,s,\,\Lambda$. We next estimate $I_{22}$ as

\begin{align*} I_{22}& \leq\Lambda\int_{\mathbb{R}^{n}\setminus B_{8r}\cap\{v(y)\geq 0\}}\int_{B_{8r}\cap\{v(x)>v(y)\}}g\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\frac{v(x)\varphi^{q}(x)}{G(v(x)/r^{s})}\frac{1}{|x-y|^{n+s}}\,{\rm d}x{\rm d}y\\ & \leq \Lambda\int_{\mathbb{R}^{n}\setminus B_{8r}}\int_{B_{8r}}g\left(\frac{v(x)}{|x-y|^{s}}\right)\frac{r^{s}\varphi^{q}(x)v(x)/r^{s}}{G(v(x)/r^{s})}\frac{1}{|x-y|^{n+s}}\,{\rm d}x{\rm d}y\\ & \leq C\int_{\mathbb{R}^{n}\setminus B_{8r}}\int_{B_{7r}}\frac{r^{s}}{|x-y|^{n+s}}\,{\rm d}x{\rm d}y\\ & \leq Cr^{n}. \end{align*}

Recalling the definition of $d$, we arrive at

(3.3)\begin{equation} I_2\leq Cr^{n} \end{equation}

with $C$ depending on $n,\,p,\,q,\,s,\,\Lambda$.

Merging (3.2), (3.3) with (3.1) yields that

\[\int_{B_{6r}}\int_{B_{6r}}\left|\log\frac{v(x)}{v(y)}\right|\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n}}\leq Cr^{n}.\]

For all $\delta \in (0,\,\frac {1}{2})$, set

\[w:=\left[\min\left\{\log\frac{1}{2\delta},\log\frac{k+d}{v}\right\}\right]_+.\]

Owing to $w$ being a truncation of $\log (k+d)-\log v$, there holds that

\[\int_{B_{6r}}\int_{B_{6r}}\frac{|w(x)-w(y)|}{|x-y|^{n}}\,{\rm d}x{\rm d}y\leq\int_{B_{6r}}\int_{B_{6r}}\left|\log\frac{v(x)}{v(y)}\right|\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n}}\leq Cr^{n}.\]

Observe that

\[\int_{B_{6r}}|w(x)-(w)_{B_{6r}}|\,{\rm d}x\leq C(n)\int_{B_{6r}}\int_{B_{6r}}\frac{|w(x)-w(y)|}{|x-y|^{n}}\,{\rm d}x{\rm d}y.\]

Hence,

\[\int_{B_{6r}}|w(x)-(w)_{B_{6r}}|\,{\rm d}x\leq Cr^{n}=C|B_{6r}|.\]

In the same way as the computations in [Reference Di Castro, Kuusi and Palatucci12, page 1819], we finally deduce that

\[|\{u\leq 2\delta k-d\}\cap B_{6r}|\leq |\{v\leq 2\delta k+2\delta d\}\cap B_{6r}|\leq \frac{C}{\sigma \log\frac{1}{2\delta}}|B_{6r}|.\]

We now have finished the proof.

Based on the above lemma, we can conclude the proof of proposition 3.1.

Proof of proposition 3.1. We may suppose, with no loss of generality, that

\[\frac{1}{2}\delta k>r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R)).\]

We now choose a cut-off function $\varphi \in C^{\infty }_0(B_\rho )$ with $4r\leq \rho \leq 6r$ and take the test function $\eta =v_-\varphi ^{q}:=(l-u)_+\varphi ^{q}$ for $l\in (\frac {1}{2}\delta k,\,2\delta k)$ in the weak formulation (2.6). Then we have

(3.4)\begin{align} 0& \leq \int_{B_\rho}\int_{B_\rho}g\left(\frac{|u(x)-u(y)|}{|x-y|^{s}}\right)\frac{u(x)-u(y)}{|u(x)-u(y)|}(v_-(x)\varphi^{q}(x) -v_-(y)\varphi^{q}(y))\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y \nonumber\\ & \quad+2\int_{\mathbb{R}^{n}\setminus B_\rho}\int_{B_\rho}g\left(\frac{|u(x)-u(y)|}{|x-y|^{s}}\right)\frac{u(x)-u(y)}{|u(x)-u(y)|}v_-(x)\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y \nonumber\\ & =:I_1+2I_2. \end{align}

We first evaluate $I_2$,

\begin{align*} I_2& \leq \int_{\mathbb{R}^{n}{\setminus} B_\rho\cap\{u(y)<0\}}\int_{B_\rho}g\left(\frac{u(x)-u(y)}{|x-y|^{s}}\right)(l-u(x))_+\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \quad +\int_{\mathbb{R}^{n}{\setminus} B_\rho\cap\{u(y)\geq 0\}}\int_{B_\rho}g\left(\frac{|u(x)-u(y)|}{|x-y|^{s}}\right)\\ & \quad \times\frac{u(x)-u(y)}{|u(x)-u(y)|}(l-u(x))_+\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \leq 2l\int_{\mathbb{R}^{n}{\setminus} B_\rho}\int_{B_\rho}g\left(\frac{l+u_-(y)}{|x-y|^{s}}\right)\chi_{\{u< l\}}(x)\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \leq Cl|B_\rho\cap\{u< l\}|\sup_{x\in\mathrm{supp}\,\varphi}\int_{\mathbb{R}^{n}{\setminus} B_\rho}g\left(\frac{l+u_-(y)}{|x-y|^{s}}\right) \frac{K(x,y)}{|x-y|^{s}}\,{\rm d}y. \end{align*}

We proceed with treating the integral $I_1$. This procedure is similar to the estimate on $I$ in [Reference Byun, Kim and Ok5, proposition 3.1], but for the sake of readability we give a sketched proof. Assume $u(x)\geq u(y)$. Then

\begin{align*} & \quad g\left(\frac{|u(x)-u(y)|}{|x-y|^{s}}\right)\frac{u(x)-u(y)}{|u(x)-u(y)|}(v_-(x)\varphi^{q}(x) -v_-(y)\varphi^{q}(y))\\ & \leq{-}g\left(\frac{|v_-(x)-v_-(y)|}{|x-y|^{s}}\right)\frac{v_-(x)-v_-(y)}{|v_-(x)-v_-(y)|}(v_-(x)\varphi^{q}(x) -v_-(y)\varphi^{q}(y)), \end{align*}

by distinguishing three cases that $l\geq u(x)\geq u(y)$, $u(x)\geq l>u(y)$ and $u(x)\geq u(y)\geq l$. Exchanging the roles of $x$ and $y$, we in general case also have the previous inequality. We next consider two cases:

\[\begin{cases} \textbf{Case 1: }v_-(x)>v_-(y) & \text{and} \quad \varphi(x)\leq\varphi(y),\\ \textbf{Case 2: }v_-(x)>v_-(y) & \text{and} \quad \varphi(x)>\varphi(y). \end{cases}\]

The case that $v_-(x)\leq v_-(y)$ is symmetric. In case 1, from (1.3) and (2.2)–(2.4), we have

\begin{align*} & -g\left(\frac{|v_-(x)-v_-(y)|}{|x-y|^{s}}\right)\frac{v_-(x)-v_-(y)}{|v_-(x)-v_-(y)|}\frac{(v_-(x)\varphi^{q}(x) -v_-(y)\varphi^{q}(y))}{|x-y|^{s}}\\ & \quad={-}g\left(\frac{v_-(x)-v_-(y)}{|x-y|^{s}}\right)\frac{v_-(x)-v_-(y)}{|x-y|^{s}}\varphi^{q}(y)\\ & \qquad + g\left(\frac{v_-(x)-v_-(y)}{|x-y|^{s}}\right)\frac{\varphi^{q}(y)-\varphi^{q}(x)}{|x-y|^{s}}v_-(x)\\ & \quad\leq{-}pG\left(\frac{v_-(x)\!-\!v_-(y)}{|x-y|^{s}}\right)\varphi^{q}(y)\!+\!q g\left(\frac{v_-(x)\!-\!v_-(y)}{|x-y|^{s}}\right)\varphi^{q-1}(y)\frac{\varphi(y)-\varphi(x)}{|x-y|^{s}}v_-(x)\\ & \quad\leq{-}pG\left(\frac{v_-(x)-v_-(y)}{|x-y|^{s}}\right)\varphi^{q}(y)+\epsilon q(q-1)G\left(\frac{v_-(x)-v_-(y)}{|x-y|^{s}}\right)\varphi^{q}(y) \\ & \qquad+C(\epsilon)qG\left(\frac{\varphi(y)-\varphi(x)}{|x-y|^{s}}v_-(x)\right)\\ & \quad\leq{-}\frac{p}{2}G\left(\frac{v_-(x)-v_-(y)}{|x-y|^{s}}\right)\varphi^{q}(y)+C(p,q)G\left(\frac{\varphi(y)-\varphi(x)}{|x-y|^{s}}v_-(x)\right), \end{align*}

where we take $\epsilon =\frac {p}{2q(q-1)}$. In the other case,

\begin{align*} & -g\left(\frac{|v_-(x)-v_-(y)|}{|x-y|^{s}}\right)\frac{v_-(x)-v_-(y)}{|v_-(x)-v_-(y)|}\frac{(v_-(x)\varphi^{q}(x) -v_-(y)\varphi^{q}(y))}{|x-y|^{s}}\\ & \quad\leq{-}g\left(\frac{v_-(x)-v_-(y)}{|x-y|^{s}}\right)\frac{v_-(x)-v_-(y)}{|x-y|^{s}}\varphi^{q}(x)\\ & \quad + g\left(\frac{v_-(x)-v_-(y)}{|x-y|^{s}}\right)\frac{\varphi^{q}(y)-\varphi^{q}(x)}{|x-y|^{s}}v_-(y)\\ & \quad\leq{-}pG\left(\frac{v_-(x)-v_-(y)}{|x-y|^{s}}\right)\varphi^{q}(x). \end{align*}

In summary, we derive

\begin{align*} & -g\left(\frac{|v_-(x)-v_-(y)|}{|x-y|^{s}}\right)\frac{v_-(x)-v_-(y)}{|v_-(x)-v_-(y)|}\frac{(v_-(x)\varphi^{q}(x) -v_-(y)\varphi^{q}(y))}{|x-y|^{s}}\\ & \quad\leq{-}C(p)G\left(\frac{|v_-(x)-v_-(y)|}{|x-y|^{s}}\right)\min\{\varphi^{q}(x),\varphi^{q}(y)\}\\ & \qquad+C(p,q)G\left(\frac{|\varphi(y)-\varphi(x)|}{|x-y|^{s}}\max\{v_-(x),v_-(y)\}\right). \end{align*}

Therefore,

\begin{align*} I_1& \leq{-}C\int_{B_\rho}\int_{B_\rho}G\left(\frac{|v_-(x)-v_-(y)|}{|x-y|^{s}}\right)\min\{\varphi^{q}(x),\varphi^{q}(y)\}K(x,y)\,{\rm d}x{\rm d}y\\ & \quad+C\int_{B_\rho}\int_{B_\rho}G\left(\frac{|\varphi(x)-\varphi(y)|}{|x-y|^{s}}\max\{v_-(x),v_-(y)\}\right)K(x,y)\,{\rm d}x{\rm d}y. \end{align*}

Combining the estimates on $I_1$ and $I_2$ with (3.4), we know that

(3.5)\begin{align} & \int_{B_\rho}\int_{B_\rho}G\left(\frac{|v_-(x)-v_-(y)|}{|x-y|^{s}}\right)\min\{\varphi^{q}(x),\varphi^{q}(y)\}K(x,y)\,{\rm d}x{\rm d}y \nonumber\\ & \quad\leq C\int_{B_\rho}\int_{B_\rho}G\left(\frac{|\varphi(x)-\varphi(y)|}{|x-y|^{s}}\max\{v_-(x),v_-(y)\}\right)K(x,y)\,{\rm d}x{\rm d}y \nonumber\\ & \qquad+Cl|B_\rho\cap\{u< l\}|\sup_{x\in\mathrm{supp}\,\varphi}\int_{\mathbb{R}^{n}\setminus B_\rho}g\left(\frac{l+u_-(y)}{|x-y|^{s}}\right)\frac{1}{|x-y|^{n+s}}\,{\rm d}y. \end{align}

Next, we will perform an iteration process. Set

\begin{align*} & l_j=\left(\frac{1}{2}+\frac{1}{2^{j+1}}\right)\delta k, \quad \rho_j=4r+\frac{1}{2^{j-1}}r,\\ & B_j:=B_{\rho_j}(x_0), \quad \tilde{\rho}_j=\frac{\rho_j+\rho_{j+1}}{2}, \quad v_j=(l_j-u)_+ \end{align*}

for $j=0,\,1,\,2,\,\cdots$. We can find that

\[4r\leq\rho_j,\tilde{\rho}_j\leq 6r, \quad l_j-l_{j+1}=\frac{1}{2^{j+2}}\delta k\geq \frac{1}{2^{j+2}}l_j\]

and

(3.6)\begin{equation} v_j\geq(l_j-l_{j+1})\chi_{\{u< l_{j+1}\}}\geq 2^{{-}j-2}l_j\chi_{\{u< l_{j+1}\}}. \end{equation}

Take cut-off functions $\varphi _j\in C^{\infty }_0(B_{\tilde {\rho }_j}(x_0))$ ($j=0,\,1,\,2,\,\cdots$) such that

\[0\leq \varphi_j\leq 1, \quad \varphi_j\equiv 1 \text{ in } B_{j+1} \quad\text{and}\quad |\nabla\varphi_j|\leq c\frac{2^{j}}{r}.\]

With $v_-,\,\varphi,\,l,\,\rho$ being replaced by $v_j,\,\varphi _j,\,l_j,\,\rho _j$ respectively, (3.5) turns into

\begin{align*} & \int_{B_j}\int_{B_j}G\left(\frac{|v_j(x)-v_j(y)|}{|x-y|^{s}}\right)\min\{\varphi_j^{q}(x),\varphi_j^{q}(y)\}K(x,y)\,{\rm d}x{\rm d}y\\ & \quad\leq C\int_{B_j}\int_{B_j}G\left(\frac{|\varphi_j(x)-\varphi_j(y)|}{|x-y|^{s}}\max\{v_j(x),v_j(y)\}\right)K(x,y)\,{\rm d}x{\rm d}y \nonumber\\ & \qquad+Cl_j|B_j\cap\{u< l_j\}|\sup_{x\in\mathrm{supp}\,\varphi_j}\int_{\mathbb{R}^{n}\setminus B_j}g\left(\frac{l_j+u_-(y)}{|x-y|^{s}}\right)\frac{1}{|x-y|^{n+s}}\,{\rm d}y\\ & \quad\leq C2^{qj}\int_{B_j}\int_{B_j}\left(\frac{|x-y|}{r}\right)^{(1-s)p}G\left(\frac{\max\{v_j(x),v_j(y)\}}{r^{s}}\right)\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n}}\\ & \qquad+C2^{j(n+qs)}l_j|B_j\cap\{u< l_j\}|\int_{\mathbb{R}^{n}\setminus B_j}g\left(\frac{l_j+u_-(y)}{|x_0-y|^{s}}\right)\frac{1}{|x_0-y|^{n+s}}\,{\rm d}y\\ & =:J_1+J_2, \end{align*}

where we have employed (2.1) and the facts that

\[|\varphi_j(x)-\varphi_j(y)|\leq C\frac{2^{j}}{r}|x-y|\]

and for $x\in \mathrm {supp}\,\varphi _j\subset B_{\tilde {\rho }_j}$ and $y\in \mathbb {R}^{n}\setminus B_j$,

\[|y-x_0|\leq\left(1+\frac{\tilde{\rho}_j}{\rho_j-\tilde{\rho}_j}\right)|y-x|\leq 2^{j+4}|y-x|.\]

Observe that, by (1.3) and (2.5),

\[g\left(\frac{l_j+u_-(y)}{|x_0-y|^{s}}\right)\leq q\frac{G\left(\frac{l_j+u_-(y)}{|x_0-y|^{s}}\right)}{\frac{l_j+u_-(y)}{|x_0-y|^{s}}}\leq \frac{q2^{q-1}}{p}\left(g\left(\frac{l_j}{|x_0-y|^{s}}\right)+g\left(\frac{u_-(y)}{|x_0-y|^{s}}\right)\right).\]

Since $u(y)\geq 0$ in $B_R$, for the integral in $J_2$ there holds that

\begin{align*} & \int_{\mathbb{R}^{n}\setminus B_j}g\left(\frac{l_j+u_-(y)}{|x_0-y|^{s}}\right) \frac{1}{|x_0-y|^{n+s}}\,{\rm d}y\\ & \quad\leq C\int_{\mathbb{R}^{n}\setminus B_j}g\left(\frac{l_j}{\rho_j^{s}}\right)+g\left(\frac{u_-(y)}{|x_0-y|^{s}}\right)\,\frac{{\rm d}y}{|x_0-y|^{n+s}}\\ & \quad\leq Cr^{{-}s}g(l_j/r^{s})+C\mathrm{Tail}(u_-;x_0,R)\\ & \quad\leq Cr^{{-}s}g(l_j/r^{s}), \end{align*}

where in the last inequality we note that

\[l_j>\frac{1}{2}\delta k\geq r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R)),\]

namely,

\[\mathrm{Tail}(u_-;x_0,R)\leq r^{{-}s}g(l_j/r^{s}).\]

As for $J_1$, it follows from (2.5) that

\begin{align*} J_1& \leq C2^{qj}\int_{B_j}\int_{B_j}\left(\frac{|x-y|}{r}\right)^{(1-s)p}G\left(\frac{v_j(x)}{r^{s}}\right)\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n}}\\ & \leq C2^{qj}r^{-(1-s)p}\int_{B_j}G(v_j(x)/r^{s})\,{\rm d}x\int_{B_{2\rho_j}(x)}\,\frac{{\rm d}y}{|x-y|^{n-(1-s)p}}\\ & \leq C2^{qj}\int_{B_j}G(v_j(x)/r^{s})\,{\rm d}x\\ & \leq C2^{qj}G(l_j/r^{s})|B_j\cap\{u< l_j\}|. \end{align*}

Putting together these preceding estimates yields that

\begin{align*} & \quad \int_{B_{j+1}}\int_{B_{j+1}}G\left(\frac{|v_j(x)-v_j(y)|}{|x-y|^{s}}\right)K(x,y)\,{\rm d}x{\rm d}y\\ & \leq C2^{j(n+sq+q)}G(l_j/r^{s})|B_j\cap\{u< l_j\}|. \end{align*}

According to lemma 4.1 in [Reference Byun, Kim and Ok5], we obtain

(3.7)\begin{align} & \left({{\int\hspace{-0.38cm}-}}_{B_{j+1}}G^{\theta}\left(\frac{|v_j-(v_j)_{B_{j+1}}|}{\rho_{j+1}^{s}}\right)\,{\rm d}x\right)^{\frac{1}{\theta}} \nonumber\\ & \quad\leq C{{\int\hspace{-0.38cm}-}}_{B_{j+1}}\int_{B_{j+1}}G\left(\frac{|v_j(x)-v_j(y)|}{|x-y|^{s}}\right)\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n}} \nonumber\\ & \quad\leq C2^{j(n+sq+q)}G(l_j/r^{s})\frac{|B_j\cap\{u< l_j\}|}{|B_j|}, \end{align}

with $\theta >1$ depending only on $n,\,s$.

On the other hand, by means of (2.5) and Jensen's inequality, the following display

(3.8)\begin{equation} \begin{aligned} \left({{\int\hspace{-0.38cm}-}}_{B_{j+1}}G^{\theta}\left(\frac{v_j}{\rho_{j+1}^{s}}\right)\,{\rm d}x\right)^{\frac{1}{\theta}} & \leq C\left({{\int\hspace{-0.38cm}-}}_{B_{j+1}}G^{\theta}\left(\frac{|v_j-(v_j)_{B_{j+1}}|}{\rho_{j+1}^{s}}\right)\,{\rm d}x\right)^{\frac{1}{\theta}}\\ & \quad+C{{\int\hspace{-0.38cm}-}}_{B_{j+1}}G\left(\frac{v_j}{\rho_{j+1}^{s}}\right)\,{\rm d}x \end{aligned} \end{equation}

is valid. Moreover, via (3.6) and $4r\leq \rho _{j+1}\leq 6r$,

(3.9)\begin{equation} G^{\theta}(v_j/\rho_{j+1}^{s})\geq G^{\theta}(2^{{-}j-2}l_j/\rho_{j+1}^{s})\chi_{\{u< l_{j+1}\}}\geq C2^{{-}jq\theta}G(l_j/r^{s})\chi_{\{u< l_{j+1}\}}. \end{equation}

It then follows from (3.7)–(3.9) that

\begin{align*} & C2^{{-}jq}G(l_j/r^{s})\left({{\int\hspace{-0.38cm}-}}_{B_{j+1}}\chi_{\{u< l_{j+1}\}}\,{\rm d}x\right)^{\frac{1}{\theta}}\\ & \quad\leq C2^{j(n+sq+q)}G(l_j/r^{s})\frac{|B_j\cap\{u< l_j\}|}{|B_j|}+C{{\int\hspace{-0.38cm}-}}_{B_{j+1}}G(l_j/r^{s})\chi_{\{u< l_{j}\}}\,{\rm d}x\\ & \quad\leq C2^{j(n+sq+q)}G(l_j/r^{s})\frac{|B_j\cap\{u< l_j\}|}{|B_j|}, \end{align*}

that is,

\[\left(\frac{|B_{j+1}\cap\{u< l_{j+1}\}|}{|B_{j+1}|}\right)^{\frac{1}{\theta}}\leq C2^{j(n+sq+2q)}\frac{|B_j\cap\{u< l_j\}|}{|B_j|}.\]

Denote

\[A_j=\frac{|B_j\cap\{u< l_j\}|}{|B_j|}.\]

Then

\[A_{j+1}\leq C2^{j(n+sq+2q)\theta}A_j^{\theta}.\]

We can apply the iteration lemma (see, e.g., [Reference Giusti24, lemma 7.1]) to deduce that if

\[A_0\leq C^{\frac{-1}{\theta-1}}2^{-(n+sq+2q)\frac{\theta}{(\theta-1)^{2}}}=:\beta,\]

then $A_j\rightarrow 0$ as $j\rightarrow \infty$. Now from lemma 3.2 we examine

\begin{align*} A_0& =\frac{|B_{6r}\cap\{u<\delta k\}|}{|B_{6r}|}\\ & \leq \frac{|B_{6r}\cap\{u\leq 2\delta k-r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R))\}|}{|B_{6r}|}\\ & \leq \frac{C}{\sigma \log\frac{1}{2\delta}}. \end{align*}

As long as we choose such small $\delta$ that

\[\frac{C}{\sigma \log\frac{1}{2\delta}}\leq \beta \quad\Rightarrow\quad \delta\leq \frac{1}{2}e^{-\frac{C}{\sigma\beta}}<\frac{1}{2},\]

the desired result $\lim _{j\rightarrow \infty }A_j=0$ can be justified. In other words, we draw a conclusion that there exists $\delta$, determined by $n,\,p,\,q,\,s,\,\Lambda$ and $\sigma$, such that

\[u(x)\geq \frac{1}{2}\delta k\]

in $B_{4r}$. We now complete the proof.

At the end of this section, as a consequence of proposition 3.1 and the Krylov–Sofonov covering lemma, we derive the following result.

Lemma 3.3 Suppose that $u\in \mathbb {W}^{s,G}(\Omega ),$ satisfying $u\geq 0$ in $B_R(x_0)\subset \Omega,$ is a weak supersolution to Eq. (1.1). Then we can find two constants $\epsilon \in (0,\,1)$ and $C\geq 1,$ both of which depend only upon $n,\,p,\,q,\,s,\,\Lambda,$ such that, when $B_r(x_0)\subset B_R(x_0),$

\[\left({{\int\hspace{-0.38cm}-}}_{B_r}u^{\epsilon}\,{\rm d}x\right)^{\frac{1}{\epsilon}}\leq C\inf_{B_r}u+Cr^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R))\]

is valid.

Proof. Define for any $t>0$

\[A^{i}_t=\left\{x\in B_r: u(x)>t\left(\frac{1}{2}\delta\right)^{i}-\frac{T}{1-\delta/2}\right\}, \quad i=0,1,2,\cdots,\]

where $\delta$ is identical to that of proposition 3.1, and $T$ stands for

\[T=r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R)).\]

Recalling lemma 2.2 and proposition 3.1, we could follow the proof of [Reference Di Castro, Kuusi and Palatucci12, lemma 4.1] verbatim, except substituting $\delta$ in [Reference Di Castro, Kuusi and Palatucci12, lemma 4.1] with $\frac {1}{2}\delta$ here, to arrive at

\[{{\int\hspace{-0.38cm}-}}_{B_r}u^{\epsilon}\,{\rm d}x\leq C\left(\inf_{B_r}u+\frac{T}{1-\delta/2}\right)^{\epsilon}.\]

This directly implies the desired result.

4. Nonlocal Harnack inequality

In this section, we are going to show the nonlocal Harnack inequality by merging the local boundedness on subsolutions (lemma 4.2) along with the infimum estimate of supersolution (lemma 3.3), and taking into account the tail estimate for solutions (lemma 4.1) in a suitable way.

Lemma 4.1 Assume that $u\in \mathbb {W}^{s,G}(\Omega )\cap L^{g}_s(\mathbb {R}^{n})$ is a weak solution to Eq. (1.1) such that $u\geq 0$ in $B_R(x_0)\subset \Omega$. Then the tail estimate

\[r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_+;x_0,r))\leq C\sup_{B_r}u+Cr^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R))\]

holds true for all $0< r< R,$ where $C>0$ depends only on $n,\,p,\,q,\,s,\,\Lambda$.

Proof. Let $l=\sup _{B_r}u$. We take the test function

\[\eta:=(u-2l)\varphi^{q}\]

in the weak formulation (2.6), where $\varphi \in C^{\infty }_0(B_r)$ satisfies that

\[0\leq\varphi\leq 1, \quad \varphi\equiv 1 \text{ in } B_\frac{r}{2}, \quad \varphi\equiv 0 \text{ on } \mathbb{R}^{n}\setminus B_\frac{3r}{4} \quad \text{and} \quad |\nabla \varphi|\leq \frac{c}{r},\]

to derive

(4.1)\begin{align} 0& = \int_{B_r}\int_{B_r}g\left(\frac{|u(x)-u(y)|}{|x-y|^{s}}\right)\frac{u(x)-u(y)}{|u(x)-u(y)|}(\eta(x) -\eta(y))\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y \nonumber\\ & \quad+2\int_{\mathbb{R}^{n}\setminus B_r}\int_{B_r}g\left(\frac{|u(x)-u(y)|}{|x-y|^{s}}\right)\frac{u(x)-u(y)}{|u(x)-u(y)|}\eta(x) \frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y \nonumber\\ & =:I_1+2I_2. \end{align}

For $I_2$, we can see that

\begin{align*} I_2& \geq \int_{\mathbb{R}^{n}\setminus B_r\cap\{u(y)\geq l\}}\int_{B_r}g\left(\frac{u(y)-u(x)}{|x-y|^{s}}\right)(2l-u(x))\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \quad-\int_{\mathbb{R}^{n}\setminus B_r\cap\{u(y)< l\}}\int_{B_r}2lg\left(\frac{|u(y)-u(x)|}{|x-y|^{s}}\right)\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \geq \int_{\mathbb{R}^{n}\setminus B_r}\int_{B_r}lg\left(\frac{(u(y)-l)_+}{|x-y|^{s}}\right)\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \quad-\int_{\mathbb{R}^{n}\setminus B_r}\int_{B_r}2lg\left(\frac{|u(y)-u(x)|}{|x-y|^{s}}\right)\chi_{\{u(y)< l\}}\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & =:I_{21}-I_{22}. \end{align*}

We know from (1.3) and (2.5) that

\begin{align*} g\left(\frac{u_+(y)}{|x-y|^{s}}\right)& \leq g\left(\frac{(u(y)-l)_+{+}l}{|x-y|^{s}}\right)\\ & \leq C\left(g\left(\frac{(u(y)-l)_+}{|x-y|^{s}}\right)+g\left(\frac{l}{|x-y|^{s}}\right)\right). \end{align*}

Thereby,

\begin{align*} I_{21} & \geq Cl\int_{\mathbb{R}^{n}\setminus B_r}\int_{B_r}g\left(\frac{u_+(y)}{|x-y|^{s}}\right)\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \quad-l\int_{\mathbb{R}^{n}\setminus B_r}\int_{B_r}g\left(\frac{l}{|x-y|^{s}}\right)\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \geq Cl\int_{\mathbb{R}^{n}\setminus B_r}\int_{B_\frac{r}{2}}g\left(\frac{u_+(y)}{|x-y|^{s}}\right)\frac{1}{|x-y|^{n+s}}\,{\rm d}x{\rm d}y\\ & \quad-Cl\int_{\mathbb{R}^{n}\setminus B_r}\int_{B_\frac{3r}{4}}g\left(\frac{l}{|x-y|^{s}}\right)\frac{1}{|x-y|^{n+s}}\,{\rm d}x{\rm d}y\\ & \geq Cl\int_{\mathbb{R}^{n}\setminus B_r}\int_{B_\frac{r}{2}}g\left(\frac{u_+(y)}{|x_0-y|^{s}}\right)\frac{1}{|x_0-y|^{n+s}}\,{\rm d}x{\rm d}y\\ & \quad-Cl\int_{\mathbb{R}^{n}\setminus B_r}\int_{B_\frac{3r}{4}}g\left(\frac{l}{r^{s}}\right)\frac{1}{|x_0-y|^{n+s}}\,{\rm d}x{\rm d}y\\ & =Cl|B_r|\mathrm{Tail}(u_+;x_0,r)-Clr^{{-}s}g(l/r^{s})|B_r|, \end{align*}

where we have used (1.3) and the facts that, for $x\in B_\frac {r}{2}$ and $y\in \mathbb {R}^{n}\setminus B_r$

\[|x-y|\leq \left(1+\frac{|x-x_0|}{|y-x_0|}\right)|y-x_0|\leq 2|y-x_0|,\]

and for $x\in B_\frac {3r}{4}$ and $y\in \mathbb {R}^{n}\setminus B_r$

\[|y-x_0|\leq \left(1+\frac{|x-x_0|}{|y-x|}\right)|y-x|\leq 4|y-x|.\]

On the other hand, with the help of (1.3) and (2.5), we get

\begin{align*} I_{22} & =2l\int_{B_R{\setminus} B_r}\int_{B_r}g\left(\frac{|u(y)-u(x)|}{|x-y|^{s}}\right)\chi_{\{u(y)< l\}}\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \quad+2l\int_{\mathbb{R}^{n}{\setminus} B_R}\int_{B_r}g\left(\frac{|u(y)-u(x)|}{|x-y|^{s}}\right)\chi_{\{u(y)< l\}}\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \leq 2l\int_{B_R{\setminus} B_r}\int_{B_r}g\left(\frac{l}{|x-y|^{s}}\right)\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \quad+2l\int_{\mathbb{R}^{n}{\setminus} B_R}\int_{B_r}g\left(\frac{l+u_-(y)}{|x-y|^{s}}\right)\varphi^{q}(x)\frac{K(x,y)}{|x-y|^{s}}\,{\rm d}x{\rm d}y\\ & \leq Cl\int_{\mathbb{R}^{n}{\setminus} B_r}\int_{B_\frac{3r}{4}}g\left(\frac{l}{|x-y|^{s}}\right)\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n+s}}\\ & \qquad +Cl\int_{\mathbb{R}^{n}{\setminus} B_R}\int_{B_r}g\left(\frac{u_-(y)}{|x-y|^{s}}\right)\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n+s}}\\ & \leq Clr^{{-}s}g(l/r^{s})|B_r|+Cl|B_r|\mathrm{Tail}(u_-;x_0,R). \end{align*}

As a result,

(4.2)\begin{equation} I_2\geq Cl|B_r|\mathrm{Tail}(u_+;x_0,r)-Clr^{{-}s}g(l/r^{s})|B_r|-Cl|B_r|\mathrm{Tail}(u_-;x_0,R). \end{equation}

Next it remains to deal with the integral $I_1$. Set $v:=u-2\,l$. Suppose, without loss of generality, that $\varphi (x)\geq \varphi (y)$. Then $\varphi ^{q}(x)-\varphi ^{q}(y)\leq q\varphi ^{q-1}(x)(\varphi (x)-\varphi (y))$. For $(x,\,y)\in B_r\times B_r$, we in turn employ the inequalities (1.3), (2.2)–(2.4) to arrive at

\begin{align*} & g\left(\frac{|u(x)-u(y)|}{|x-y|^{s}}\right)\frac{u(x)-u(y)}{|u(x)-u(y)|}(v(x)\varphi^{q}(x) -v(y)\varphi^{q}(y))\frac{1}{|x-y|^{s}}\\ & \quad=g\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\frac{|v(x)-v(y)|}{|x-y|^{s}}\varphi^{q}(x)\\ & \qquad+ g\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\frac{u(x)-u(y)}{|u(x)-u(y)|}\frac{\varphi^{q}(x) -\varphi^{q}(y)}{|x-y|^{s}}v(y)\\ & \quad\geq pG\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\varphi^{q}(x)-qg\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\varphi^{q-1}(x)\frac{|\varphi(x)-\varphi(y)|}{|x-y|^{s}}|v(y)|\\ & \quad\geq pG\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\varphi^{q}(x)-\epsilon qG^{*}\left(g\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\varphi^{q-1}(x)\right)\\ & \qquad-\epsilon^{q-1}qG\left(\frac{|\varphi(x)-\varphi(y)|}{|x-y|^{s}}|v(y)|\right)\\ & \quad\geq pG\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\varphi^{q}(x)-\epsilon qG\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\varphi^{q}(x)\\ & \qquad-\epsilon^{q-1}qG\left(\frac{|\varphi(x)-\varphi(y)|}{|x-y|^{s}}|v(y)|\right)\\ & \quad=\frac{p}{2}G\left(\frac{|v(x)-v(y)|}{|x-y|^{s}}\right)\varphi^{q}(x)-CG\left(\frac{|\varphi(x)-\varphi(y)|}{|x-y|^{s}}|v(y)|\right)\\ & \quad\geq{-}CG\left(l\frac{|\varphi(x)-\varphi(y)|}{|x-y|^{s}}\right). \end{align*}

Here we need note $\varphi ^{q-1}(x)\leq 1$ and take $\epsilon =\frac {p}{2q}$. From this, we find that

(4.3)\begin{align} I_1& \geq{-}C\int_{B_r}\int_{B_r}G\left(l\frac{|\varphi(x)-\varphi(y)|}{|x-y|^{s}}\right)\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n}} \nonumber\\ & \geq{-}C\int_{B_r}\int_{B_r}G\left(\frac{l}{r^{s}}\left(\frac{|x-y|}{r}\right)^{1-s}\right)\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n}} \nonumber\\ & \geq{-}C\int_{B_r}\int_{B_r}r^{(s-1)p}G(l/r^{s})\,\frac{{\rm d}x{\rm d}y}{|x-y|^{n-(1-s)p}} \nonumber\\ & \geq{-}CG(l/r^{s})|B_r|. \end{align}

Consequently, it holds, by combing (4.2), (4.3) with (4.1), that

\begin{align*} \mathrm{Tail}(u_+;x_0,r)& \leq C\mathrm{Tail}(u_-;x_0,R)+C\frac{1}{l}G(l/r^{s})\\ & \leq Cr^{{-}s}g(l/r^{s})+C\mathrm{Tail}(u_-;x_0,R). \end{align*}

Finally, observe that for $a,\,b\geq 0$ and $c\geq 1$,

\begin{align*} & a+b=g(g^{{-}1}(a))+g(g^{{-}1}(b))\leq 2g(g^{{-}1}(a)+g^{{-}1}(b))\\ & \quad\Rightarrow g^{{-}1}\left(\frac{a+b}{2}\right)\leq g^{{-}1}(a)+g^{{-}1}(b) \end{align*}

and

(4.4)\begin{equation} g^{{-}1}(c^{{-}1}a)\geq (qc/p)^{-\frac{1}{p-1}}g^{{-}1}(a). \end{equation}

Otherwise, by (1.3), (2.1) and the strictly increasing property of $g$,

\begin{align*} c^{{-}1}a& < g\left((qc/p)^{-\frac{1}{p-1}}g^{{-}1}(a)\right)\\ & \leq q\frac{G\left((qc/p)^{-\frac{1}{p-1}}g^{{-}1}(a)\right)}{(qc/p)^{-\frac{1}{p-1}}g^{{-}1}(a)}\\ & \leq q(qc/p)^{{-}1}\frac{G(g^{{-}1}(a))}{g^{{-}1}(a)}\leq c^{{-}1}a, \end{align*}

which is a contradiction. Then we have

\begin{align*} g^{{-}1}((2C)^{{-}1}r^{s}\mathrm{Tail}(u_+;x_0,r))& \leq g^{{-}1}\left(\frac{g(l/r^{s})+r^{s}\mathrm{Tail}(u_-;x_0,R)}{2}\right)\\ & \leq\frac{l}{r^{s}}+g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R)) \end{align*}

and

\[g^{{-}1}((2C)^{{-}1}r^{s}\mathrm{Tail}(u_+;x_0,r))\geq \frac{1}{C}g^{{-}1}(r^{s}\mathrm{Tail}(u_+;x_0,r)),\]

which means the desired result.

In order to infer Harnack inequality for Eq. (1.1), we need the following local boundedness result on weak subsolutions that is a slightly modified version of [Reference Byun, Kim and Ok5, theorem 4.4].

Lemma 4.2 Let $B_r(x_0)\subset \subset \Omega$. Assume that $u\in \mathbb {W}^{s,G}(\Omega )\cap L^{g}_s(\mathbb {R}^{n})$ is a weak subsolution to Eq. (1.1). Then there holds that

(4.5)\begin{equation} \sup_{B_\frac{r}{2}}u\leq Cr^{s}G^{{-}1}\left(\delta^{\frac{\theta}{1-\theta}}{{\int\hspace{-0.38cm}-}}_{B_r}G\left(\frac{u_+}{r^{s}}\right)\,{\rm d}x\right) +\left(\frac{r}{2}\right)^{s}g^{{-}1}\left(\delta \left(\frac{r}{2}\right)^{s}\mathrm{Tail}\left(u_+;x_0,\frac{r}{2}\right)\right), \end{equation}

where $C$ depends on $n,\,p,\,q,\,s,\,\Lambda$.

Proof. The process is the same as that of [Reference Byun, Kim and Ok5, theorem 4.4]. Let us point out that the notations below adopt identically those in [Reference Byun, Kim and Ok5, theorem 4.4]. We just need to notice that, after the inequality (4.14) in [Reference Byun, Kim and Ok5], the parameter $k$ is first chosen so large that

\[k\geq \left(\frac{r}{2}\right)^{s}g^{{-}1}\left(\delta \left(\frac{r}{2}\right)^{s}\mathrm{Tail}\left(u_+;x_0,\frac{r}{2}\right)\right)\]

with $\delta \in (0,\,1]$, instead of the value of $k$ there. Then the inequality (4.14) in [Reference Byun, Kim and Ok5] becomes

\[a_{j+1}\leq C2^{j(n+sq+2q)\theta}\left(1+\frac{1}{\delta}\right)^{\theta} a^{\theta}_j\leq 2^{\theta} C2^{j(n+sq+2q)\theta}\delta^{-\theta} a^{\theta}_j.\]

Let $C_0=2^{\theta } C$ and $B=2^{(n+sq+2q)\theta }$. Then

\[a_{j+1}\leq(\delta^{-\theta}C_0)B^{j}a^{\theta}_j.\]

By the iteration lemma (see, e.g. [Reference Giusti24, lemma 7.1]), we need

\[a_0\leq (\delta^{-\theta}C_0)^{-\frac{1}{\theta-1}}B^{-\frac{1}{(\theta-1)^{2}}},\]

namely,

\[\frac{{{\int\hspace{-0.38cm}-}}_{B_r}G\left(\frac{u_+}{r^{s}}\right)\,{\rm d}x}{G(k/r^{s})}\leq (\delta^{-\theta}C_0)^{-\frac{1}{\theta-1}}B^{-\frac{1}{(\theta-1)^{2}}},\]

so that $a_j\rightarrow 0$ as $j\rightarrow \infty$. Now we pick

\begin{align*} k& =r^{s}G^{{-}1}\left(\delta^{\frac{\theta}{1-\theta}}C_0^{\frac{1}{\theta-1}}B^{\frac{1}{(\theta-1)^{2}}}{{\int\hspace{-0.38cm}-}}_{B_r}G\left(\frac{u_+}{r^{s}}\right)\,{\rm d}x\right)\\ & \quad +\left(\frac{r}{2}\right)^{s}g^{{-}1}\left(\delta \left(\frac{r}{2}\right)^{s}\mathrm{Tail}\left(u_+;x_0,\frac{r}{2}\right)\right). \end{align*}

Terminally, the limit $\lim _{j\rightarrow \infty }a_j=0$ leads to (4.5).

Finally, we implement the proof of the nonlocal Harnack inequality stated in theorem 1.1. From this procedure, one can apparently understand the reason why we impose the condition (1.5).

Proof of theorem 1.1. For simplicity, let $\lambda =\frac {\theta }{1-\theta }$. Putting together the local boundedness estimate (lemma 4.2) and the tail estimate (lemma 4.1), we derive that, for $B_\rho \subset \subset \Omega$,

\begin{align*} k& =r^{s}G^{{-}1}\left(\delta^{\frac{\theta}{1-\theta}}C_0^{\frac{1}{\theta-1}}B^{\frac{1}{(\theta-1)^{2}}}{{\int\hspace{-0.38cm}-}}_{B_r}G\left(\frac{u_+}{r^{s}}\right)\,{\rm d}x\right)\\ & \quad +\left(\frac{r}{2}\right)^{s}g^{{-}1}\left(\delta \left(\frac{r}{2}\right)^{s}\mathrm{Tail}\left(u_+;x_0,\frac{r}{2}\right)\right). \end{align*}

Here we have utilized

\[\begin{cases}g^{{-}1}(at)\leq (q/p)^{\frac{1}{p-1}}a^{\frac{1}{q-1}}g^{{-}1}(t) & \text{for} 0< a<1, t\geq 0,\\ g^{{-}1}(at)\leq (q/p)^{\frac{1}{p-1}}a^{\frac{1}{p-1}}g^{{-}1}(t) & \text{for} a\geq 1, t\geq 0, \end{cases}\]

which can be justified in a similar way to (4.4).

We next would like to apply the iteration [Reference Giaquinta and Giusti23, lemma 1] (see also [Reference Di Castro, Kuusi and Palatucci12, lemma 2.7]). Denote $\rho =(\gamma -\gamma ')r$ with $\frac {1}{2}\leq \gamma '<\gamma \leq 1$. By a covering argument, we obtain

(4.6)\begin{align} \sup_{B_{\gamma'r}}u& \leq \frac{Cr^{s(1-\frac{q}{p})}}{(\gamma-\gamma')^{\frac{n}{p}+s(\frac{q}{p}-1)}}G^{{-}1}\left(\delta^{\lambda}{{\int\hspace{-0.38cm}-}}_{B_{\gamma r}}G(u)\,{\rm d}x\right) \nonumber\\ & \quad+C\delta^{\frac{1}{q-1}}r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R))+C\delta^{\frac{1}{q-1}}\sup_{B_{\gamma r}}u, \end{align}

where we note the positivity of $u$ in $B_R(x_0)$. Observe that from (1.3) we can get an important inequality $\min \{t^{p},\,t^{q}\}\leq G(t)\leq c\max \{t^{p},\,t^{q}\}$. Now making use of this inequality and the assumption (1.5), we evaluate, for any $\varepsilon \in (0,\,1)$,

(4.7)\begin{align} & G^{{-}1}\left(\delta^{\lambda}{{\int\hspace{-0.38cm}-}}_{B_{\gamma r}}G(u)\,{\rm d}x\right) \nonumber\\ & \quad\leq G^{{-}1}\left(c_0\delta^{\lambda}{{\int\hspace{-0.38cm}-}}_{B_{\gamma r}}G(u^{1-\varepsilon})G(u^{\varepsilon})\,{\rm d}x\right) \nonumber\\ & \quad\leq CG^{{-}1}\left(\delta^{\lambda}{{\int\hspace{-0.38cm}-}}_{B_{\gamma r}}G\left(\left(\sup_{B_{\gamma r}}u\right)^{1-\varepsilon}\right)G(u^{\varepsilon})\,{\rm d}x\right) \nonumber\\ & \quad\leq C(\delta)\left(\sup_{B_{\gamma r}}u\right)^{1-\varepsilon}\max\left\{\left({{\int\hspace{-0.38cm}-}}_{B_{\gamma r}}G(u^{\varepsilon})\,{\rm d}x\right)^{\frac{1}{p}},\left({{\int\hspace{-0.38cm}-}}_{B_{\gamma r}}G(u^{\varepsilon})\,{\rm d}x\right)^{\frac{1}{q}}\right\}. \end{align}

Via selecting $\delta =(\frac {1}{4C})^{q-1}$, merging the displays (4.6), (4.7) and an application of Young's inequality, we have

\begin{align*} \sup_{B_{\gamma'r}}u& \leq \left(\sup_{B_{\gamma r}}u\right)^{1-\varepsilon}\frac{Cr^{s(1-\frac{q}{p})}}{(\gamma-\gamma')^{\frac{n}{p}+s(\frac{q}{p}-1)}}\max\left\{\left({{\int\hspace{-0.38cm}-}}_{B_{\gamma r}}G(u^{\varepsilon})\,{\rm d}x\right)^{\frac{1}{p}},\left({{\int\hspace{-0.38cm}-}}_{B_{\gamma r}}G(u^{\varepsilon})\,{\rm d}x\right)^{\frac{1}{q}}\right\}\\ & \quad+\frac{1}{4}\sup_{B_{\gamma r}}u+Cr^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R))\\ & \leq \frac{1}{2}\sup_{B_{\gamma r}}u+\frac{Cr^{s(1-\frac{q}{p})\frac{1}{\varepsilon}}}{(\gamma-\gamma')^{[\frac{n}{p}+s(\frac{q}{p}-1)]\frac{1}{\varepsilon}}} \left[\max\left\{\left({{\int\hspace{-0.38cm}-}}_{B_r}G(u^{\varepsilon})\,{\rm d}x\right)^{\frac{1}{p}},\left({{\int\hspace{-0.38cm}-}}_{B_{r}}G(u^{\varepsilon})\,{\rm d}x\right)^{\frac{1}{q}}\right\}\right]^{\frac{1}{\varepsilon}}\\ & \quad+Cr^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R)). \end{align*}

We can apply [Reference Giaquinta and Giusti23, lemma 1] to infer that

\begin{align*} \sup_{B_r}u& \leq Cr^{s(1-\frac{q}{p})\frac{1}{\varepsilon}} \left[\max\left\{\left({{\int\hspace{-0.38cm}-}}_{B_r}G(u^{\varepsilon})\,{\rm d}x\right)^{\frac{1}{p}},\left({{\int\hspace{-0.38cm}-}}_{B_{r}}G(u^{\varepsilon})\,{\rm d}x\right)^{\frac{1}{q}}\right\}\right]^{\frac{1}{\varepsilon}}\\ & \quad+Cr^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R)). \end{align*}

In order to make use of lemma 3.3, we need to invoke the relation that $G(t)\leq c\max \{t^{p},\,t^{q}\}$.

We proceed by considering the integral term in the above display,

\begin{align*} {{\int\hspace{-0.38cm}-}}_{B_r}G(u^{\varepsilon})\,{\rm d}x& =\frac{1}{|B_r|}\left(\int_{B_r\cap\{u<1\}}G(u^{\varepsilon})\,{\rm d}x+\int_{B_r\cap\{u\geq 1\}}G(u^{\varepsilon})\,{\rm d}x\right)\\ & \leq \frac{c_1}{|B_r|}\left(\int_{B_r}u^{p\varepsilon}\,{\rm d}x+\int_{B_r}u^{q\varepsilon}\,{\rm d}x\right)\\ & \leq c_1\left({{\int\hspace{-0.38cm}-}}_{B_r}u^{q\varepsilon}\,{\rm d}x\right)^{\frac{p}{q}}+c_1{{\int\hspace{-0.38cm}-}}_{B_r}u^{q\varepsilon}\,{\rm d}x. \end{align*}

Combining the last two displays and choosing $\varepsilon =\frac {\epsilon }{q}$ with $\epsilon$ given by lemma 3.3, we finally arrive at

\begin{align*} \sup_{B_r}u & \leq Cr^{s(1-\frac{q}{p})\frac{q}{\epsilon}}\max_{i\in\{\frac{1}{\epsilon},\frac{q}{p\epsilon}\}} \Bigg\{\left(\inf_{B_r}u+r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R))\right)^{\frac{ip\epsilon}{q}}\\ & \quad+\left(\inf_{B_r}u+r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R))\right)^{i\epsilon}\Bigg\}\\ & \quad+Cr^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R))\\ & \leq Cr^{s(1-\frac{q}{p})\frac{q}{\epsilon}}\max_{\iota\in\{1,\frac{q}{p},\frac{p}{q}\}}\left\{\left(\inf_{B_r}u+r^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R))\right)^{\iota}\right\}\\ & \quad+Cr^{s}g^{{-}1}(r^{s}\mathrm{Tail}(u_-;x_0,R)). \end{align*}

The proof is complete now.

Acknowledgments

The authors wish to thank the anonymous reviewer for valuable comments and suggestions to improve the manuscript. This work was supported by the National Natural Science Foundation of China (No. 12071098) and the National Postdoctoral Program for Innovative Talents of China (No. BX20220381).

References

Brasco, L. and Lindgren, E.. Higher Sobolev regularity for the fractional $p$-Laplace equation in the superquadratic case. Adv. Math. 304 (2017), 300–354.10.1016/j.aim.2016.03.039CrossRefGoogle Scholar
Brasco, L., Lindgren, E. and Strömqvist, M.. Continuity of solutions to a nonlinear fractional diffusion equation. J. Evol. Equ. 21 (2021), 4319–4381.10.1007/s00028-021-00721-2CrossRefGoogle Scholar
Brasco, L. and Parini, E.. The second eigenvalue of the fractional $p$-Laplacian. Adv. Calc. Var. 9 (2016), 323–355.10.1515/acv-2015-0007CrossRefGoogle Scholar
Buryachenko, K. O. and Skrypnik, I. I.. Local continuity and Harnack's inequality for double-phase parabolic equations. Potential Anal. 56 (2022), 137–164.CrossRefGoogle Scholar
Byun, S. S., Kim, H. and Ok, J.. Local Hölder continuity for fractional nonlocal equations with general growth, eprint arXiv:2112.13958.Google Scholar
Byun, S. S., Ok, J. and Song, K.. Hölder regularity for weak solutions to nonlocal double phase problems, eprint arXiv:2108.09623.Google Scholar
Caffarelli, L., Chan, C. and Vasseur, A.. Regularity theory for parabolic nonlinear integral operators. J. Am. Math. Soc. 24 (2011), 849–869.10.1090/S0894-0347-2011-00698-XCrossRefGoogle Scholar
Chaker, J. and Kim, M.. Local regularity for nonlocal equations with variable exponents eprint, arXiv:2107.06043.Google Scholar
Chaker, J., Kim, M. and Weidner, M.. Regularity for nonlocal problems with non-standard growth, eprint arXiv:2111.09182.Google Scholar
De Filippis, C. and Mingione, G.. Nonuniformly elliptic Schauder theory, eprint arXiv:2201.07369.Google Scholar
De Filippis, C. and Palatucci, G.. Hölder regularity for nonlocal double phase equations. J. Differ. Equ. 267 (2019), 547–586.10.1016/j.jde.2019.01.017CrossRefGoogle Scholar
Di Castro, A., Kuusi, T. and Palatucci, G.. Nonlocal Harnack inequalities. J. Funct. Anal. 267 (2014), 1807–1836.10.1016/j.jfa.2014.05.023CrossRefGoogle Scholar
Di Castro, A., Kuusi, T. and Palatucci, G.. Local behavior of fractional $p$-minimizers. Ann. Inst. H. Poincaré Anal. Non Linéaire 33 (2016), 1279–1299.10.1016/j.anihpc.2015.04.003CrossRefGoogle Scholar
Diening, L., Stroffolini, B. and Verde, A.. Everywhere regularity of functionals with $\varphi$-growth. Manuscripta Math. 129 (2009), 449–481.10.1007/s00229-009-0277-0CrossRefGoogle Scholar
Ding, M., Zhang, C. and Zhou, S.. Local boundedness and Hölder continuity for the parabolic fractional $p$-Laplace equations. Calc. Var. Partial Differ. Equ. 60 (2021), 38.10.1007/s00526-020-01870-xCrossRefGoogle Scholar
Fang, Y. and Zhang, C.. On weak and viscosity solutions of nonlocal double phase equations. Int. Math. Res. Not. IMRN (2021). doi:10.1093/imrn/rnab351Google Scholar
Felsinger, M. and Kassmann, M.. Local regularity for parabolic nonlocal operators. Comm. Partial Differ. Equ. 38 (2013), 1539–1573.CrossRefGoogle Scholar
Fernández Bonder, J., Salort, A. and Vivas, H.. Interior and up to the boundary regularity for the fractional $g$-Laplacian: the convex case. Nonlinear Anal. 223 (2022), 113060.10.1016/j.na.2022.113060CrossRefGoogle Scholar
Fernández Bonder, J., Salort, A. and Vivas, H.. Global Hölder regularity for eigenfunctions of the fractional $g$-Laplacian, eprint arXiv:2112.00830.Google Scholar
Franzina, G. and Palatucci, G.. Fractional $p$-eigenvalues. Riv. Mat. Univ. Parma 5 (2014), 315–328.Google Scholar
Giacomoni, J., Kumar, D. and Sreenadh, K.. Interior and boundary regularity results for strongly nonhomogeneous $p,\, q$-fractional problems eprint arXiv:2102.06080.Google Scholar
Giacomoni, J., Kumar, D. and Sreenadh, K.. Global regularity results for nonhomogeneous growth fractional problems. J. Geom. Anal. 32 (2022), 36.10.1007/s12220-021-00837-4CrossRefGoogle Scholar
Giaquinta, M. and Giusti, E.. On the regularity of the minima of variational integrals. Acta Math. 148 (1982), 31–46.10.1007/BF02392725CrossRefGoogle Scholar
Giusti, E.. Direct Methods in the Calculus of Variations (River Edge: World Scientific Publishing Co Inc., 2003).CrossRefGoogle Scholar
Goel, D., Kumar, D. and Sreenadh, K.. Regularity and multiplicity results for fractional $(p,\, q)$-Laplacian equations. Commun. Contemp. Math. 22 (2020), 1950065.10.1142/S0219199719500652CrossRefGoogle Scholar
Harjulehto, P., Hästö, P. and Lee, M.. Hölder continuity of quasiminimizers and $\omega$-minimizers of functionals with generalized Orlicz growth. Ann. Sc. Norm. Super. Pisa Cl. Sci. 2 (2021), 549–582.Google Scholar
Iannizzotto, A., Mosconi, S. and Squassina, M.. Global Hölder regularity for the fractional $p$-Laplacian. Rev. Mat. Iberoam. 32 (2016), 1353–1392.10.4171/RMI/921CrossRefGoogle Scholar
Kassmann, M.. A new formulation of Harnack's inequality for nonlocal operators. C. R. Math. Acad. Sci. Paris 349 (2011), 637–640.CrossRefGoogle Scholar
Kinnunen, J. and Shanmugalingam, N.. Regularity of quasi-minimizers of metric spaces. Manuscripta Math. 105 (2001), 401–423.CrossRefGoogle Scholar
Korvenpää, J., Kuusi, T. and Lindgren, E.. Equivalence of solutions to fractional $p$-Laplace type equations. J. Math. Pures Appl. 132 (2019), 1–26.10.1016/j.matpur.2017.10.004CrossRefGoogle Scholar
Korvenpää, J., Kuusi, T. and Palatucci, G.. The obstacle problem for nonlinear integro-differential operators. Calc. Var. Partial Differ. Equ. 55 (2016), 63.CrossRefGoogle Scholar
Korvenpää, J., Kuusi, T. and Palatucci, G.. Fractional superharmonic functions and the Perron method for nonlinear integro-differential equations. Math. Ann. 369 (2017), 1443–1489.10.1007/s00208-016-1495-xCrossRefGoogle Scholar
Kuusi, T., Mingione, G. and Sire, Y.. Nonlocal self-improving properties. Anal. PDE 8 (2015), 57–114.CrossRefGoogle Scholar
Kuusi, T., Mingione, G. and Sire, Y.. Nonlocal equations with measure data. Commun. Math. Phys. 337 (2015), 1317–1368.CrossRefGoogle Scholar
Marcellini, P.. Regularity of minimizers of integrals of the calculus of variations with non standard growth conditions. Arch. Ration. Mech. Anal. 105 (1989), 267–284.CrossRefGoogle Scholar
Marcellini, P.. Regularity and existence of solutions of elliptic equations with $p,\, q$-growth conditions. J. Differ. Equ. 90 (1991), 1–30.10.1016/0022-0396(91)90158-6CrossRefGoogle Scholar
Mazón, J. M., Rossi, J. D. and Toledo, J.. Fractional $p$-Laplacian evolution equations. J. Math. Pures Appl. 105 (2016), 810–844.CrossRefGoogle Scholar
Mihăilescu, M. and Rădulescu, V.. Neumann problems associated to nonhomogeneous differential operators in Orlicz-Sobolev spaces. Ann. Inst. Fourier (Grenoble) 58 (2008), 2087–2111.CrossRefGoogle Scholar
Ok, J., Local Hölder regularity for nonlocal equations with variable powers, eprint arXiv:2107.06611.Google Scholar
Palatucci, G.. The Dirichlet problem for the fractional $p$-Laplace equation. Nonlinear Anal. 177 (2018), 699–732.10.1016/j.na.2018.05.004CrossRefGoogle Scholar
Salort, A.. Lower bounds for Orlicz eigenvalues. Discrete Contin. Dyn. Syst. 42 (2022), 1415–1434.CrossRefGoogle Scholar
Salort, A.. Eigenvalues and minimizers for a non-standard growth non-local operator. J. Differ. Equ. 268 (2020), 5413–5439.10.1016/j.jde.2019.11.027CrossRefGoogle Scholar
Salort, A. and Vivas, H.. Fractional eigenvalues in Orlicz spaces with no $\Delta _2$ condition. J. Differ. Equ. 327 (2022), 166–188.10.1016/j.jde.2022.04.029CrossRefGoogle Scholar
Skrypnik, I. I. and Voitovych, M. V.. On the continuity of solutions of quasilinear parabolic equations with generalized Orlicz growth under non-logarithmic conditions. Ann. Mat. Pura Appl. 201 (2022), 1381–1416.10.1007/s10231-021-01161-yCrossRefGoogle Scholar
Strömqvist, M.. Local boundedness of solutions to nonlocal parabolic equations modeled on the fractional $p$-Laplacian. J. Differ. Equ. 266 (2019), 7948–7979.10.1016/j.jde.2018.12.021CrossRefGoogle Scholar
Vázquez, J. L.. The Dirichlet problem for the fractional $p$-Laplacian evolution equation. J. Differ. Equ. 260 (2016), 6038–6056.10.1016/j.jde.2015.12.033CrossRefGoogle Scholar
Vázquez, J. L.. The fractional $p$-Laplacian evolution equation in $\mathbb {R}^{N}$ in the sublinear case. Calc. Var. Partial Differ. Eq. 60 (2021), 140.10.1007/s00526-021-02005-6CrossRefGoogle Scholar