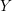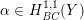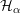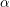Introduction
Let
![]() $Y$
be a compact Kähler manifold and
$Y$
be a compact Kähler manifold and
![]() $\unicode[STIX]{x1D6FC}_{Y}\in H^{1,1}(Y,\mathbb{R})$
a Kähler class. The space
$\unicode[STIX]{x1D6FC}_{Y}\in H^{1,1}(Y,\mathbb{R})$
a Kähler class. The space
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
of Kähler metrics
${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
of Kähler metrics
![]() $\unicode[STIX]{x1D714}_{Y}$
in
$\unicode[STIX]{x1D714}_{Y}$
in
![]() $\unicode[STIX]{x1D6FC}_{Y}$
can be seen as an infinite dimensional Riemannian manifold, whose tangent spaces
$\unicode[STIX]{x1D6FC}_{Y}$
can be seen as an infinite dimensional Riemannian manifold, whose tangent spaces
![]() $T_{\unicode[STIX]{x1D714}_{Y}}{\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
can all be identified with
$T_{\unicode[STIX]{x1D714}_{Y}}{\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
can all be identified with
![]() ${\mathcal{C}}^{\infty }(Y,\mathbb{R})$
. Mabuchi has introduced in [Reference MabuchiMab87] an
${\mathcal{C}}^{\infty }(Y,\mathbb{R})$
. Mabuchi has introduced in [Reference MabuchiMab87] an
![]() $L^{2}$
-metric on
$L^{2}$
-metric on
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
, by setting
${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
, by setting
where
![]() $n=\dim _{\mathbb{C}}Y$
and
$n=\dim _{\mathbb{C}}Y$
and
![]() $V_{\unicode[STIX]{x1D6FC}_{Y}}=\int _{Y}{\unicode[STIX]{x1D714}_{Y}}^{n}=\unicode[STIX]{x1D6FC}_{Y}^{n}$
denotes the volume of
$V_{\unicode[STIX]{x1D6FC}_{Y}}=\int _{Y}{\unicode[STIX]{x1D714}_{Y}}^{n}=\unicode[STIX]{x1D6FC}_{Y}^{n}$
denotes the volume of
![]() $\unicode[STIX]{x1D6FC}_{Y}$
.
$\unicode[STIX]{x1D6FC}_{Y}$
.
Mabuchi studied the corresponding geometry of
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
, showing, in particular, that it can formally be seen as a locally symmetric space of non-positive curvature. Semmes [Reference SemmesSem92] re-interpreted the geodesic equation as a complex homogeneous equation, while Donaldson [Reference DonaldsonDon99] strongly motivated the search for smooth geodesics through its connection with the uniqueness of constant scalar curvature Kähler metrics.
${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
, showing, in particular, that it can formally be seen as a locally symmetric space of non-positive curvature. Semmes [Reference SemmesSem92] re-interpreted the geodesic equation as a complex homogeneous equation, while Donaldson [Reference DonaldsonDon99] strongly motivated the search for smooth geodesics through its connection with the uniqueness of constant scalar curvature Kähler metrics.
In a series of remarkable works [Reference ChenChe00, Reference Calabi and ChenCC02, Reference Chen and TianCT08, Reference ChenChe09, Reference Chen and SunCS12], Chen and his collaborators have studied the metric and geometric properties of the space
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
, showing in particular that it is a path metric space (a non-trivial assertion in this infinite-dimensional setting). A key step from [Reference ChenChe00] has been the production of
${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
, showing in particular that it is a path metric space (a non-trivial assertion in this infinite-dimensional setting). A key step from [Reference ChenChe00] has been the production of
![]() ${\mathcal{C}}^{1,\overline{1}}$
-geodesics, which turn out to minimize the intrinsic distance
${\mathcal{C}}^{1,\overline{1}}$
-geodesics, which turn out to minimize the intrinsic distance
![]() $d$
. Very recently, such a regularity result was improved by Chu et al. [Reference Chu, Tosatti and WeinkoveCTW17]: they showed that geodesics are
$d$
. Very recently, such a regularity result was improved by Chu et al. [Reference Chu, Tosatti and WeinkoveCTW17]: they showed that geodesics are
![]() $C^{1,1}$
. It follows from the work of Lempert and Vivas [Reference Lempert and VivasLV13], Darvas and Lempert [Reference Darvas and LempertDL12], and Ross and Witt-Nyström [Reference Ross and Witt-NyströmRW15] that one cannot expect better regularity, but for the toric setting.
$C^{1,1}$
. It follows from the work of Lempert and Vivas [Reference Lempert and VivasLV13], Darvas and Lempert [Reference Darvas and LempertDL12], and Ross and Witt-Nyström [Reference Ross and Witt-NyströmRW15] that one cannot expect better regularity, but for the toric setting.
The metric study of the space
![]() $({\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}},d)$
has been recently pushed further by Darvas [Reference DarvasDar17b, Reference DarvasDar17c, Reference DarvasDar15]. He characterized there the metric completion of
$({\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}},d)$
has been recently pushed further by Darvas [Reference DarvasDar17b, Reference DarvasDar17c, Reference DarvasDar15]. He characterized there the metric completion of
![]() $({\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}},d)$
and showed that such a completion is non-positively curved in the sense of Alexandrov. He also introduced several Finsler-type metrics on
$({\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}},d)$
and showed that such a completion is non-positively curved in the sense of Alexandrov. He also introduced several Finsler-type metrics on
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
, which turn out to be quite useful (see [Reference Darvas and RubinsteinDR17, Reference Berman, Boucksom and JonssonBBJ15]). For each
${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
, which turn out to be quite useful (see [Reference Darvas and RubinsteinDR17, Reference Berman, Boucksom and JonssonBBJ15]). For each
![]() $p\geqslant 1$
, we set
$p\geqslant 1$
, we set
where
and
![]() $\operatorname{MA}(\unicode[STIX]{x1D719}_{t}):=(\unicode[STIX]{x1D714}_{Y}+dd^{c}\unicode[STIX]{x1D719}_{t})^{n}/V_{\unicode[STIX]{x1D6FC}_{Y}}$
. The goal of this article is to extend these studies to the case when the underlying space has singularities.
$\operatorname{MA}(\unicode[STIX]{x1D719}_{t}):=(\unicode[STIX]{x1D714}_{Y}+dd^{c}\unicode[STIX]{x1D719}_{t})^{n}/V_{\unicode[STIX]{x1D6FC}_{Y}}$
. The goal of this article is to extend these studies to the case when the underlying space has singularities.
From now on, let
![]() $Y$
be a compact Kähler normal space and
$Y$
be a compact Kähler normal space and
![]() $\unicode[STIX]{x1D6FC}_{Y}\in H_{\mathit{BC}}^{1,1}(Y)$
a Kähler class, where
$\unicode[STIX]{x1D6FC}_{Y}\in H_{\mathit{BC}}^{1,1}(Y)$
a Kähler class, where
![]() $H_{\mathit{BC}}^{1,1}(Y)$
denotes the Bott–Chern cohomology space. We fix a base point
$H_{\mathit{BC}}^{1,1}(Y)$
denotes the Bott–Chern cohomology space. We fix a base point
![]() $\unicode[STIX]{x1D714}_{Y}$
representing
$\unicode[STIX]{x1D714}_{Y}$
representing
![]() $\unicode[STIX]{x1D6FC}_{Y}$
and work with the space of Kähler potentials
$\unicode[STIX]{x1D6FC}_{Y}$
and work with the space of Kähler potentials
Our first main result extends the main results of [Reference ChenChe00] and [Reference DarvasDar15, Theorem 1], as follows.
Theorem A.
(i)
 $({\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}},d_{p})$
is a metric space.
$({\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}},d_{p})$
is a metric space.(ii)
 $d_{p}(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1})=(\int _{Y}|\dot{\unicode[STIX]{x1D719}}_{0}|^{p}\operatorname{MA}(\unicode[STIX]{x1D719}_{0}))^{1/p}=(\int _{Y}|\dot{\unicode[STIX]{x1D719}}_{1}|^{p}\operatorname{MA}(\unicode[STIX]{x1D719}_{1}))^{1/p}$
,
$d_{p}(\unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1})=(\int _{Y}|\dot{\unicode[STIX]{x1D719}}_{0}|^{p}\operatorname{MA}(\unicode[STIX]{x1D719}_{0}))^{1/p}=(\int _{Y}|\dot{\unicode[STIX]{x1D719}}_{1}|^{p}\operatorname{MA}(\unicode[STIX]{x1D719}_{1}))^{1/p}$
,
 $\forall \unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
.
$\forall \unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
.
As we are going to discuss, in Remark 1.11, the singularities of
![]() $Y$
prevent us from defining the distance
$Y$
prevent us from defining the distance
![]() $d_{p}$
as in (1). We instead work on a resolution of
$d_{p}$
as in (1). We instead work on a resolution of
![]() $Y$
and there define
$Y$
and there define
![]() $d_{p}$
as a limit of path length metrics. We refer to Definition 1.10 and Remark 1.14 for the precise definition of
$d_{p}$
as a limit of path length metrics. We refer to Definition 1.10 and Remark 1.14 for the precise definition of
![]() $d_{p}$
.
$d_{p}$
.
Following [Reference DarvasDar17c, Reference DarvasDar15] we then study the metric completion of the space
![]() $({\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}},d_{p})$
and establish the following generalization of [Reference DarvasDar15, Theorem 2].
$({\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}},d_{p})$
and establish the following generalization of [Reference DarvasDar15, Theorem 2].
Theorem B. Let
![]() $Y$
be a projective normal variety and assume that
$Y$
be a projective normal variety and assume that
![]() $\unicode[STIX]{x1D714}_{Y}$
is a Hodge form. The metric completion of
$\unicode[STIX]{x1D714}_{Y}$
is a Hodge form. The metric completion of
![]() $({\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}},d_{p})$
is a geodesic metric space, which can be identified with the finite-energy class
$({\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}},d_{p})$
is a geodesic metric space, which can be identified with the finite-energy class
![]() $({\mathcal{E}}^{p}(Y,\unicode[STIX]{x1D714}_{Y}),I_{p})$
.
$({\mathcal{E}}^{p}(Y,\unicode[STIX]{x1D714}_{Y}),I_{p})$
.
Finite-energy classes have been introduced in [Reference Guedj and ZeriahiGZ07] and further studied in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13]; we recall their definition in § 2. The Mabuchi geodesics can be extended to finite-energy geodesics, which are still metric geodesics. A key technical tool here is Theorem 3.6, which compares
![]() $d_{p}$
and
$d_{p}$
and
![]() $I_{p}$
, where
$I_{p}$
, where
This is a natural quantity which allows one to define the ‘strong topology’ on
![]() ${\mathcal{E}}^{p}(Y,\unicode[STIX]{x1D714}_{Y})$
.
${\mathcal{E}}^{p}(Y,\unicode[STIX]{x1D714}_{Y})$
.
The metric completion of
![]() $({\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}},d)$
has been considered by Streets in his study of the Calabi flow [Reference StreetsStr16] and also plays an important role in recent works by Berman et al. [Reference Berman, Boucksom and JonssonBBJ15] and Berman et al. [Reference Berman, Darvas and LuBDL16]. There is no doubt that the extension to the singular setting will play a leading role in subsequent applications. We illustrate this here by generalizing Tian’s analytic criterion [Reference TianTia97, Reference Phong, Song, Sturm and WeinkovePSSW08], using results in [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ] and an idea in [Reference Darvas and RubinsteinDR17].
$({\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}},d)$
has been considered by Streets in his study of the Calabi flow [Reference StreetsStr16] and also plays an important role in recent works by Berman et al. [Reference Berman, Boucksom and JonssonBBJ15] and Berman et al. [Reference Berman, Darvas and LuBDL16]. There is no doubt that the extension to the singular setting will play a leading role in subsequent applications. We illustrate this here by generalizing Tian’s analytic criterion [Reference TianTia97, Reference Phong, Song, Sturm and WeinkovePSSW08], using results in [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ] and an idea in [Reference Darvas and RubinsteinDR17].
Theorem C. Let
![]() $(Y,D)$
be a log Fano pair. It admits a unique Kähler–Einstein metric if and only if there exists
$(Y,D)$
be a log Fano pair. It admits a unique Kähler–Einstein metric if and only if there exists
![]() $\unicode[STIX]{x1D700},M>0$
, such that, for all
$\unicode[STIX]{x1D700},M>0$
, such that, for all
![]() $\unicode[STIX]{x1D719}\in {\mathcal{H}}_{\text{norm}}$
,
$\unicode[STIX]{x1D719}\in {\mathcal{H}}_{\text{norm}}$
,
Here,
![]() ${\mathcal{F}}$
is a functional whose critical points are Kähler–Einstein potentials (§ 5) and
${\mathcal{F}}$
is a functional whose critical points are Kähler–Einstein potentials (§ 5) and
![]() ${\mathcal{H}}_{\text{norm}}$
is the set of potentials in
${\mathcal{H}}_{\text{norm}}$
is the set of potentials in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
normalized such that the supremum is 0. This result has been independently obtained by Darvas [Reference DarvasDar17a] using a different approach.
${\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
normalized such that the supremum is 0. This result has been independently obtained by Darvas [Reference DarvasDar17a] using a different approach.
Our results should also be useful in analyzing more generally constant scalar curvature Kähler (cscK) metrics on mildly singular varieties (see, for example, the recent construction by Arezzo and Spotti of cscK metrics on crepant resolutions of Calabi–Yau varieties with non-orbifold singularities [Reference Arezzo and SpottiAS16]).
A way to establish these results is to consider a resolution of singularities
![]() $\unicode[STIX]{x1D70B}:X\rightarrow Y$
and to work with the space
$\unicode[STIX]{x1D70B}:X\rightarrow Y$
and to work with the space
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
of potentials associated with the form
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
of potentials associated with the form
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{Y}$
. All these results actually hold in the more general setting when
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{Y}$
. All these results actually hold in the more general setting when
![]() $\unicode[STIX]{x1D714}$
is merely a semi-positive and big form (i.e.
$\unicode[STIX]{x1D714}$
is merely a semi-positive and big form (i.e.
![]() $\int _{X}\unicode[STIX]{x1D714}^{n}>0$
). We approximate
$\int _{X}\unicode[STIX]{x1D714}^{n}>0$
). We approximate
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
by spaces of Kähler potentials
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
by spaces of Kähler potentials
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}}$
and show that the most important metric properties of
${\mathcal{H}}_{\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}}$
and show that the most important metric properties of
![]() $({\mathcal{H}}_{\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}},d_{\unicode[STIX]{x1D700}})$
pass to the limit.
$({\mathcal{H}}_{\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}},d_{\unicode[STIX]{x1D700}})$
pass to the limit.
The organization of the paper is as follows. Section 1 starts with a recap of Mabuchi geodesics and metrics. Theorem A is proved in § 1.2, where we develop a low-regularity approach for understanding geodesics by approximation. We introduce in § 2 classes of finite-energy currents and compare their natural topologies with the one induced by the Mabuchi distances in § 3. We study finite-energy geodesics in § 4 and prove Theorem B. We finally prove Theorem C in § 5.
1 The space of Kähler currents
Let
![]() $(Y,\unicode[STIX]{x1D714}_{Y})$
be a compact Kähler normal space of dimension
$(Y,\unicode[STIX]{x1D714}_{Y})$
be a compact Kähler normal space of dimension
![]() $n$
. It follows from the definition of
$n$
. It follows from the definition of
![]() $H_{\mathit{BC}}^{1,1}(Y)$
(see, for example, [Reference Boucksom, Eyssidieux and GuedjBEG13, Definition 4.6.2]) that any other Kähler metric on
$H_{\mathit{BC}}^{1,1}(Y)$
(see, for example, [Reference Boucksom, Eyssidieux and GuedjBEG13, Definition 4.6.2]) that any other Kähler metric on
![]() $Y$
in the same Bott–Chern cohomology class of
$Y$
in the same Bott–Chern cohomology class of
![]() $\unicode[STIX]{x1D714}_{Y}$
can be written as
$\unicode[STIX]{x1D714}_{Y}$
can be written as
where
![]() $d=\unicode[STIX]{x2202}+\overline{\unicode[STIX]{x2202}}$
and
$d=\unicode[STIX]{x2202}+\overline{\unicode[STIX]{x2202}}$
and
![]() $d^{c}=(1/2i\unicode[STIX]{x1D70B})(\unicode[STIX]{x2202}-\overline{\unicode[STIX]{x2202}})$
. Let
$d^{c}=(1/2i\unicode[STIX]{x1D70B})(\unicode[STIX]{x2202}-\overline{\unicode[STIX]{x2202}})$
. Let
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
be the space of Kähler potentials
${\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
be the space of Kähler potentials
This is a convex open subset of the Fréchet vector space
![]() $C^{\infty }(Y):=C^{\infty }(Y,\mathbb{R})$
and thus itself a Fréchet manifold, which is, moreover, parallelizable:
$C^{\infty }(Y):=C^{\infty }(Y,\mathbb{R})$
and thus itself a Fréchet manifold, which is, moreover, parallelizable:
For any
![]() $\unicode[STIX]{x1D719}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
, each tangent space
$\unicode[STIX]{x1D719}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
, each tangent space
![]() $T_{\unicode[STIX]{x1D719}}{\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
is identified with
$T_{\unicode[STIX]{x1D719}}{\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
is identified with
![]() $C^{\infty }(Y)$
.
$C^{\infty }(Y)$
.
As two Kähler potentials define the same metric when (and only when) they differ by an additive constant, we set
where
![]() $\mathbb{R}$
acts on
$\mathbb{R}$
acts on
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
by addition. The set
${\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
by addition. The set
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
is therefore the space of Kähler metrics on
${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{Y}}$
is therefore the space of Kähler metrics on
![]() $Y$
in the cohomology class
$Y$
in the cohomology class
![]() $\unicode[STIX]{x1D6FC}_{Y}:=\{\unicode[STIX]{x1D714}_{Y}\}\in H_{\mathit{BC}}^{1,1}(Y)$
.
$\unicode[STIX]{x1D6FC}_{Y}:=\{\unicode[STIX]{x1D714}_{Y}\}\in H_{\mathit{BC}}^{1,1}(Y)$
.
In the whole article we fix
![]() $\unicode[STIX]{x1D70B}:X\rightarrow Y$
a resolution of singularities and set
$\unicode[STIX]{x1D70B}:X\rightarrow Y$
a resolution of singularities and set
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{Y}$
,
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{Y}$
,
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6FC}_{Y}$
. Since
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6FC}_{Y}$
. Since
![]() $\unicode[STIX]{x1D6FC}$
is no longer Kähler, we fix
$\unicode[STIX]{x1D6FC}$
is no longer Kähler, we fix
![]() $\unicode[STIX]{x1D714}_{X}$
a Kähler form on
$\unicode[STIX]{x1D714}_{X}$
a Kähler form on
![]() $X$
and set
$X$
and set
for
![]() $\unicode[STIX]{x1D700}>0$
. We will study the geometry and the topology of the spaces
$\unicode[STIX]{x1D700}>0$
. We will study the geometry and the topology of the spaces
by approximating them by the spaces
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}},{\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
, where
${\mathcal{H}}_{\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D700}}},{\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
, where
All the properties that we are going to establish actually hold for cohomology classes
![]() $\unicode[STIX]{x1D6FC}$
that are merely semi-positive and big (not necessarily the pull-back of a Kähler class under a desingularization).
$\unicode[STIX]{x1D6FC}$
that are merely semi-positive and big (not necessarily the pull-back of a Kähler class under a desingularization).
Our analysis will focus on the ample locus of
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
Definition 1.1. The ample locus
![]() $\operatorname{Amp}(\unicode[STIX]{x1D6FC})$
of
$\operatorname{Amp}(\unicode[STIX]{x1D6FC})$
of
![]() $\unicode[STIX]{x1D6FC}$
is the Zariski open set of those points
$\unicode[STIX]{x1D6FC}$
is the Zariski open set of those points
![]() $x\in X$
, such that
$x\in X$
, such that
![]() $\unicode[STIX]{x1D6FC}$
can be represented by a positive closed
$\unicode[STIX]{x1D6FC}$
can be represented by a positive closed
![]() $(1,1)$
-current that is a smooth positive form near
$(1,1)$
-current that is a smooth positive form near
![]() $x$
.
$x$
.
We then let
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
denote the space of potentials
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
denote the space of potentials
![]() $\unicode[STIX]{x1D711}\in C^{\infty }(X,\mathbb{R})$
such that
$\unicode[STIX]{x1D711}\in C^{\infty }(X,\mathbb{R})$
such that
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}$
is a Kähler form in
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}$
is a Kähler form in
![]() $\operatorname{Amp}(\unicode[STIX]{x1D6FC})$
. In our main case of interest, i.e. when
$\operatorname{Amp}(\unicode[STIX]{x1D6FC})$
. In our main case of interest, i.e. when
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6FC}_{Y}$
for some Kähler class
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D6FC}_{Y}$
for some Kähler class
![]() $\unicode[STIX]{x1D6FC}_{Y}$
on a normal space
$\unicode[STIX]{x1D6FC}_{Y}$
on a normal space
![]() $Y$
, the ample locus
$Y$
, the ample locus
is the preimage of the set of regular points of
![]() $Y$
.
$Y$
.
1.1 The Riemannian structure
1.1.1 Mabuchi geodesics
Definition 1.2 [Reference MabuchiMab87].
The Mabuchi metric is the
![]() $L^{2}$
Riemannian metric on
$L^{2}$
Riemannian metric on
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
. It is defined by
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
. It is defined by
where
![]() $\unicode[STIX]{x1D711}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
,
$\unicode[STIX]{x1D711}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
,
![]() $\unicode[STIX]{x1D713}_{1},\unicode[STIX]{x1D713}_{2}\in C^{\infty }(X)$
, and
$\unicode[STIX]{x1D713}_{1},\unicode[STIX]{x1D713}_{2}\in C^{\infty }(X)$
, and
![]() $(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711})^{n}/V_{\unicode[STIX]{x1D6FC}}$
is the volume element, normalized so that it is a probability measure. Here,
$(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711})^{n}/V_{\unicode[STIX]{x1D6FC}}$
is the volume element, normalized so that it is a probability measure. Here,
![]() $V_{\unicode[STIX]{x1D6FC}}:=\unicode[STIX]{x1D6FC}^{n}=\int _{X}\unicode[STIX]{x1D714}^{n}$
.
$V_{\unicode[STIX]{x1D6FC}}:=\unicode[STIX]{x1D6FC}^{n}=\int _{X}\unicode[STIX]{x1D714}^{n}$
.
In the following, we shall also use the notation
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}:=\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}:=\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}$
and
Geodesics between two points
![]() $\unicode[STIX]{x1D711}_{0}$
,
$\unicode[STIX]{x1D711}_{0}$
,
![]() $\unicode[STIX]{x1D711}_{1}$
in
$\unicode[STIX]{x1D711}_{1}$
in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
correspond to the extremals of the energy functional
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
correspond to the extremals of the energy functional
where
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{t}$
is a smooth path in
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{t}$
is a smooth path in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
joining
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
joining
![]() $\unicode[STIX]{x1D711}_{0}$
and
$\unicode[STIX]{x1D711}_{0}$
and
![]() $\unicode[STIX]{x1D711}_{1}$
. The geodesic equation is formally obtained by computing the Euler–Lagrange equation for this energy functional (with fixed end points). It is given by
$\unicode[STIX]{x1D711}_{1}$
. The geodesic equation is formally obtained by computing the Euler–Lagrange equation for this energy functional (with fixed end points). It is given by
We are interested in the boundary value problem for the geodesic equation: given
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
, two distinct points in
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
, two distinct points in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
, can one find a path
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
, can one find a path
![]() $(\unicode[STIX]{x1D711}(t))_{0\leqslant t\leqslant 1}$
in
$(\unicode[STIX]{x1D711}(t))_{0\leqslant t\leqslant 1}$
in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
which is a solution of (2) with end points
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
which is a solution of (2) with end points
![]() $\unicode[STIX]{x1D711}(0)=\unicode[STIX]{x1D711}_{0}$
and
$\unicode[STIX]{x1D711}(0)=\unicode[STIX]{x1D711}_{0}$
and
![]() $\unicode[STIX]{x1D711}(1)=\unicode[STIX]{x1D711}_{1}$
?
$\unicode[STIX]{x1D711}(1)=\unicode[STIX]{x1D711}_{1}$
?
For each path
![]() $(\unicode[STIX]{x1D711}_{t})_{t\in [0,1]}$
in
$(\unicode[STIX]{x1D711}_{t})_{t\in [0,1]}$
in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
, we set
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
, we set
i.e. we associate with each path
![]() $(\unicode[STIX]{x1D711}_{t})$
a function
$(\unicode[STIX]{x1D711}_{t})$
a function
![]() $\unicode[STIX]{x1D711}$
on the complex manifold
$\unicode[STIX]{x1D711}$
on the complex manifold
![]() $M=X\times S$
, which only depends on the real part of the strip coordinate: we consider
$M=X\times S$
, which only depends on the real part of the strip coordinate: we consider
![]() $S$
as a Riemann surface with boundary and use the complex coordinate
$S$
as a Riemann surface with boundary and use the complex coordinate
![]() $z=t+is$
to parametrize the strip
$z=t+is$
to parametrize the strip
![]() $S$
. Set
$S$
. Set
![]() $\unicode[STIX]{x1D714}(x,z):=\unicode[STIX]{x1D714}(x)$
.
$\unicode[STIX]{x1D714}(x,z):=\unicode[STIX]{x1D714}(x)$
.
Semmes observed [Reference SemmesSem92] that the path
![]() $\unicode[STIX]{x1D711}_{t}$
is a geodesic in
$\unicode[STIX]{x1D711}_{t}$
is a geodesic in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
if and only if the associated function
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
if and only if the associated function
![]() $\unicode[STIX]{x1D711}$
on
$\unicode[STIX]{x1D711}$
on
![]() $X\times S$
is a
$X\times S$
is a
![]() $\unicode[STIX]{x1D714}$
-psh solution of the homogeneous complex Monge–Ampère equation
$\unicode[STIX]{x1D714}$
-psh solution of the homogeneous complex Monge–Ampère equation
This motivates the following.
Definition 1.3. The function
is the Mabuchi geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
.
$\unicode[STIX]{x1D711}_{1}$
.
Here
![]() $\text{PSH}(M,\unicode[STIX]{x1D714})$
denotes the set of
$\text{PSH}(M,\unicode[STIX]{x1D714})$
denotes the set of
![]() $\unicode[STIX]{x1D714}$
-psh functions on
$\unicode[STIX]{x1D714}$
-psh functions on
![]() $M$
: these are functions
$M$
: these are functions
![]() $u:M\rightarrow \mathbb{R}\cap \{-\infty \}$
that are locally the sum of a plurisubharmonic and a smooth function, such that
$u:M\rightarrow \mathbb{R}\cap \{-\infty \}$
that are locally the sum of a plurisubharmonic and a smooth function, such that
![]() $\unicode[STIX]{x1D714}+dd_{x,z}^{c}u\geqslant 0$
in the sense of currents (see § 2.1.1 for more details).
$\unicode[STIX]{x1D714}+dd_{x,z}^{c}u\geqslant 0$
in the sense of currents (see § 2.1.1 for more details).
Proposition 1.4. Let
![]() $(\unicode[STIX]{x1D711}_{t})_{0\leqslant t\leqslant 1}$
be the Mabuchi geodesic joining
$(\unicode[STIX]{x1D711}_{t})_{0\leqslant t\leqslant 1}$
be the Mabuchi geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
. Then:
$\unicode[STIX]{x1D711}_{1}$
. Then:
(i)
 $\unicode[STIX]{x1D711}\in \text{PSH}(M,\unicode[STIX]{x1D714})$
is uniformly bounded on
$\unicode[STIX]{x1D711}\in \text{PSH}(M,\unicode[STIX]{x1D714})$
is uniformly bounded on
 $M$
and continuous on
$M$
and continuous on
 $\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})\times \bar{S}$
;
$\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})\times \bar{S}$
;(ii)
 $|\unicode[STIX]{x1D711}(x,z)-\unicode[STIX]{x1D711}(x,z^{\prime })|\leqslant A|\Re (z)-\Re (z^{\prime })|$
with
$|\unicode[STIX]{x1D711}(x,z)-\unicode[STIX]{x1D711}(x,z^{\prime })|\leqslant A|\Re (z)-\Re (z^{\prime })|$
with
 $A=\Vert \unicode[STIX]{x1D711}_{0}-\unicode[STIX]{x1D711}_{1}\Vert _{L^{\infty }(X)}$
;
$A=\Vert \unicode[STIX]{x1D711}_{0}-\unicode[STIX]{x1D711}_{1}\Vert _{L^{\infty }(X)}$
;(iii)
 $\unicode[STIX]{x1D711}_{|\{\Re (z)=0\}}=\unicode[STIX]{x1D711}_{0}$
,
$\unicode[STIX]{x1D711}_{|\{\Re (z)=0\}}=\unicode[STIX]{x1D711}_{0}$
,
 $\unicode[STIX]{x1D711}_{|\{\Re (z)=1\}}=\unicode[STIX]{x1D711}_{1}$
and
$\unicode[STIX]{x1D711}_{|\{\Re (z)=1\}}=\unicode[STIX]{x1D711}_{1}$
and
 $(\unicode[STIX]{x1D714}+dd_{x,z}^{c}\unicode[STIX]{x1D711})^{n+1}=0$
.
$(\unicode[STIX]{x1D714}+dd_{x,z}^{c}\unicode[STIX]{x1D711})^{n+1}=0$
.
It is, moreover, the unique bounded
![]() $\unicode[STIX]{x1D714}$
-psh solution to this Dirichlet problem.
$\unicode[STIX]{x1D714}$
-psh solution to this Dirichlet problem.
We thank Hoang Chinh Lu for sharing his ideas on the continuity of
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
Proof. The proof follows from a classical balayage technique together with a barrier argument, as noted by Berndtsson [Reference BerndtssonBer15]. Set
![]() $A=\Vert \unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\Vert _{L^{\infty }(X)}$
.
$A=\Vert \unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\Vert _{L^{\infty }(X)}$
.
Observe that the function
![]() $\unicode[STIX]{x1D711}_{0}-At$
, with
$\unicode[STIX]{x1D711}_{0}-At$
, with
![]() $t=\Re (z)$
, is
$t=\Re (z)$
, is
![]() $\unicode[STIX]{x1D714}$
-psh on
$\unicode[STIX]{x1D714}$
-psh on
![]() $M$
and
$M$
and
![]() $\unicode[STIX]{x1D711}_{0}-At|_{\unicode[STIX]{x2202}M}\leqslant \unicode[STIX]{x1D711}_{0,1}$
. Hence, it belongs to the family
$\unicode[STIX]{x1D711}_{0}-At|_{\unicode[STIX]{x2202}M}\leqslant \unicode[STIX]{x1D711}_{0,1}$
. Hence, it belongs to the family
![]() ${\mathcal{F}}$
defining the upper envelope
${\mathcal{F}}$
defining the upper envelope
![]() $\unicode[STIX]{x1D711}$
, so
$\unicode[STIX]{x1D711}$
, so
![]() $\unicode[STIX]{x1D711}_{0}-At\leqslant \unicode[STIX]{x1D711}_{t}$
.
$\unicode[STIX]{x1D711}_{0}-At\leqslant \unicode[STIX]{x1D711}_{t}$
.
Similarly,
![]() $\unicode[STIX]{x1D711}_{0}+At$
is a
$\unicode[STIX]{x1D711}_{0}+At$
is a
![]() $\unicode[STIX]{x1D714}$
-psh function on
$\unicode[STIX]{x1D714}$
-psh function on
![]() $M$
and
$M$
and
![]() $\unicode[STIX]{x1D711}_{0}+At|_{\unicode[STIX]{x2202}M}\geqslant \unicode[STIX]{x1D711}_{0,1}$
. Since
$\unicode[STIX]{x1D711}_{0}+At|_{\unicode[STIX]{x2202}M}\geqslant \unicode[STIX]{x1D711}_{0,1}$
. Since
![]() $(\unicode[STIX]{x1D714}+dd_{x,z}^{c}(\unicode[STIX]{x1D711}_{0}+At))^{n+1}=0$
, it follows from the maximum principle that
$(\unicode[STIX]{x1D714}+dd_{x,z}^{c}(\unicode[STIX]{x1D711}_{0}+At))^{n+1}=0$
, it follows from the maximum principle that
![]() $u\leqslant \unicode[STIX]{x1D711}_{0}+At$
, for any
$u\leqslant \unicode[STIX]{x1D711}_{0}+At$
, for any
![]() $u\in {\mathcal{F}}$
in the family. Therefore,
$u\in {\mathcal{F}}$
in the family. Therefore,
Similar arguments show that
The upper semi-continuous regularization
![]() $\unicode[STIX]{x1D711}^{\ast }$
of
$\unicode[STIX]{x1D711}^{\ast }$
of
![]() $\unicode[STIX]{x1D711}$
satisfies the same estimates, showing, in particular, that
$\unicode[STIX]{x1D711}$
satisfies the same estimates, showing, in particular, that
![]() $\unicode[STIX]{x1D711}^{\ast }|_{\unicode[STIX]{x2202}M}=\unicode[STIX]{x1D711}_{0,1}$
. Since
$\unicode[STIX]{x1D711}^{\ast }|_{\unicode[STIX]{x2202}M}=\unicode[STIX]{x1D711}_{0,1}$
. Since
![]() $\unicode[STIX]{x1D711}^{\ast }$
is
$\unicode[STIX]{x1D711}^{\ast }$
is
![]() $\unicode[STIX]{x1D714}$
-psh, we infer
$\unicode[STIX]{x1D714}$
-psh, we infer
![]() $\unicode[STIX]{x1D711}^{\ast }\in {\mathcal{F}}$
; hence,
$\unicode[STIX]{x1D711}^{\ast }\in {\mathcal{F}}$
; hence,
![]() $\unicode[STIX]{x1D711}^{\ast }=\unicode[STIX]{x1D711}$
. Thus
$\unicode[STIX]{x1D711}^{\ast }=\unicode[STIX]{x1D711}$
. Thus
![]() $\unicode[STIX]{x1D711}$
is
$\unicode[STIX]{x1D711}$
is
![]() $\unicode[STIX]{x1D714}$
-psh and uniformly bounded, proving the first statement in part (i). Classical balayage arguments show that
$\unicode[STIX]{x1D714}$
-psh and uniformly bounded, proving the first statement in part (i). Classical balayage arguments show that
![]() $(\unicode[STIX]{x1D714}+dd_{x,z}^{c}\unicode[STIX]{x1D711})^{n+1}=0$
, proving part (iii).
$(\unicode[STIX]{x1D714}+dd_{x,z}^{c}\unicode[STIX]{x1D711})^{n+1}=0$
, proving part (iii).
We now prove part (ii). Consider the function
and note that it belongs to
![]() ${\mathcal{F}}$
and has the right boundary values.
${\mathcal{F}}$
and has the right boundary values.
Since
![]() $\unicode[STIX]{x1D712}_{-}=\unicode[STIX]{x1D711}_{0}(x)-At\leqslant \unicode[STIX]{x1D711}$
with equality at
$\unicode[STIX]{x1D712}_{-}=\unicode[STIX]{x1D711}_{0}(x)-At\leqslant \unicode[STIX]{x1D711}$
with equality at
![]() $t=0$
, we infer, for all
$t=0$
, we infer, for all
![]() $x$
,
$x$
,
Similarly
![]() $\unicode[STIX]{x1D712}_{+}=\unicode[STIX]{x1D711}_{1}(x)+A(t-1)\leqslant \unicode[STIX]{x1D711}$
with equality at
$\unicode[STIX]{x1D712}_{+}=\unicode[STIX]{x1D711}_{1}(x)+A(t-1)\leqslant \unicode[STIX]{x1D711}$
with equality at
![]() $t=1$
yields, for all
$t=1$
yields, for all
![]() $x$
,
$x$
,
![]() $\dot{\unicode[STIX]{x1D711}}_{1}(x)\leqslant +A=(\unicode[STIX]{x2202}\unicode[STIX]{x1D712}_{+}/\unicode[STIX]{x2202}t)_{|t=1}$
. Since
$\dot{\unicode[STIX]{x1D711}}_{1}(x)\leqslant +A=(\unicode[STIX]{x2202}\unicode[STIX]{x1D712}_{+}/\unicode[STIX]{x2202}t)_{|t=1}$
. Since
![]() $t\mapsto \unicode[STIX]{x1D711}_{t}(x)$
is convex (by subharmonicity in
$t\mapsto \unicode[STIX]{x1D711}_{t}(x)$
is convex (by subharmonicity in
![]() $z$
), we infer that for a.e.
$z$
), we infer that for a.e.
![]() $t,x$
,
$t,x$
,
![]() $-A\leqslant \dot{\unicode[STIX]{x1D711}}_{0}(x)\leqslant \dot{\unicode[STIX]{x1D711}}_{t}(x)\leqslant \dot{\unicode[STIX]{x1D711}}_{1}(x)\leqslant +A$
.
$-A\leqslant \dot{\unicode[STIX]{x1D711}}_{0}(x)\leqslant \dot{\unicode[STIX]{x1D711}}_{t}(x)\leqslant \dot{\unicode[STIX]{x1D711}}_{1}(x)\leqslant +A$
.
It remains to show that
![]() $\unicode[STIX]{x1D711}$
is continuous on
$\unicode[STIX]{x1D711}$
is continuous on
![]() $\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})\times \bar{S}$
. We can assume, without loss of generality, that
$\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})\times \bar{S}$
. We can assume, without loss of generality, that
![]() $\unicode[STIX]{x1D711}_{0}<\unicode[STIX]{x1D711}_{1}$
. Indeed, given any
$\unicode[STIX]{x1D711}_{0}<\unicode[STIX]{x1D711}_{1}$
. Indeed, given any
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
, there exists
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
, there exists
![]() $C>0$
, such that
$C>0$
, such that
![]() $\unicode[STIX]{x1D711}_{0}<\unicode[STIX]{x1D711}_{1}+C$
. By Lemma 1.8, the Mabuchi geodesic joining
$\unicode[STIX]{x1D711}_{0}<\unicode[STIX]{x1D711}_{1}+C$
. By Lemma 1.8, the Mabuchi geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
and
$\unicode[STIX]{x1D711}_{0}$
and
![]() $\unicode[STIX]{x1D711}_{1}+C$
is
$\unicode[STIX]{x1D711}_{1}+C$
is
![]() $\unicode[STIX]{x1D713}_{t}=\unicode[STIX]{x1D711}_{t}+Ct$
,
$\unicode[STIX]{x1D713}_{t}=\unicode[STIX]{x1D711}_{t}+Ct$
,
![]() $t\in [0,1]$
. The continuity of
$t\in [0,1]$
. The continuity of
![]() $(x,t)\rightarrow \unicode[STIX]{x1D713}_{t}(x)$
will then imply the continuity of
$(x,t)\rightarrow \unicode[STIX]{x1D713}_{t}(x)$
will then imply the continuity of
![]() $(x,t)\rightarrow \unicode[STIX]{x1D711}_{t}(x)$
.
$(x,t)\rightarrow \unicode[STIX]{x1D711}_{t}(x)$
.
We change notation slightly, replacing the strip
![]() $S$
by the annulus
$S$
by the annulus
![]() $D:=\{z=e^{t+is}\in \mathbb{C}:1\leqslant |w|\leqslant e\}$
. We are going to express the function
$D:=\{z=e^{t+is}\in \mathbb{C}:1\leqslant |w|\leqslant e\}$
. We are going to express the function
![]() $\unicode[STIX]{x1D711}$
as a global
$\unicode[STIX]{x1D711}$
as a global
![]() $\unicode[STIX]{x1D6E9}$
-psh envelope on the compact manifold
$\unicode[STIX]{x1D6E9}$
-psh envelope on the compact manifold
![]() $X\times \mathbb{P}^{1}$
, where we view the annulus
$X\times \mathbb{P}^{1}$
, where we view the annulus
![]() $D$
as a subset of the Riemann sphere,
$D$
as a subset of the Riemann sphere,
![]() $\mathbb{C}\subset \mathbb{P}^{1}=\mathbb{C}\cup \{\infty \}$
. The form
$\mathbb{C}\subset \mathbb{P}^{1}=\mathbb{C}\cup \{\infty \}$
. The form
![]() $\unicode[STIX]{x1D6E9}(x,z)=\unicode[STIX]{x1D714}(x)+A\unicode[STIX]{x1D714}_{\text{FS}}(z)$
is a semi-positive and big form on the compact Kähler manifold
$\unicode[STIX]{x1D6E9}(x,z)=\unicode[STIX]{x1D714}(x)+A\unicode[STIX]{x1D714}_{\text{FS}}(z)$
is a semi-positive and big form on the compact Kähler manifold
![]() $\widetilde{M}:=X\times \mathbb{P}^{1}$
, so the viscosity approach of [Reference Eyssidieux, Guedj and ZeriahiEGZ17] can be applied, showing that the envelope
$\widetilde{M}:=X\times \mathbb{P}^{1}$
, so the viscosity approach of [Reference Eyssidieux, Guedj and ZeriahiEGZ17] can be applied, showing that the envelope
![]() $\unicode[STIX]{x1D711}$
is continuous on
$\unicode[STIX]{x1D711}$
is continuous on
![]() $\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})\times \bar{S}$
. Here,
$\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})\times \bar{S}$
. Here,
![]() $\unicode[STIX]{x1D714}_{\text{FS}}$
denotes the Fubini–Study metric on
$\unicode[STIX]{x1D714}_{\text{FS}}$
denotes the Fubini–Study metric on
![]() $\mathbb{P}^{1}$
and
$\mathbb{P}^{1}$
and
![]() $A>0$
is a constant to be chosen next.
$A>0$
is a constant to be chosen next.
Consider
![]() $U=\max (U_{0},U_{1})$
, where
$U=\max (U_{0},U_{1})$
, where
![]() $U_{0}(x,z):=\unicode[STIX]{x1D711}_{0}(x)$
and
$U_{0}(x,z):=\unicode[STIX]{x1D711}_{0}(x)$
and
We choose
![]() $A>0$
so large that
$A>0$
so large that
![]() $U(x,1)\equiv \unicode[STIX]{x1D711}_{0}(x)$
. Note that
$U(x,1)\equiv \unicode[STIX]{x1D711}_{0}(x)$
. Note that
![]() $U(x,e)\equiv \unicode[STIX]{x1D711}_{1}(x)$
since
$U(x,e)\equiv \unicode[STIX]{x1D711}_{1}(x)$
since
![]() $\unicode[STIX]{x1D711}_{0}<\unicode[STIX]{x1D711}_{1}$
. Both
$\unicode[STIX]{x1D711}_{0}<\unicode[STIX]{x1D711}_{1}$
. Both
![]() $U_{0}$
and
$U_{0}$
and
![]() $U_{1}$
are
$U_{1}$
are
![]() $\unicode[STIX]{x1D6E9}$
-psh on
$\unicode[STIX]{x1D6E9}$
-psh on
![]() $\widetilde{M}$
, hence so is
$\widetilde{M}$
, hence so is
![]() $U$
.
$U$
.
Fix
![]() $\unicode[STIX]{x1D70C}$
a local potential of
$\unicode[STIX]{x1D70C}$
a local potential of
![]() $A\unicode[STIX]{x1D714}_{\text{FS}}$
in
$A\unicode[STIX]{x1D714}_{\text{FS}}$
in
![]() $D$
, such that
$D$
, such that
![]() $\unicode[STIX]{x1D70C}|_{\unicode[STIX]{x2202}D}=0$
and let
$\unicode[STIX]{x1D70C}|_{\unicode[STIX]{x2202}D}=0$
and let
![]() $F$
be a continuous
$F$
be a continuous
![]() $S^{1}$
-invariant function on
$S^{1}$
-invariant function on
![]() $\widetilde{M}$
, such that:
$\widetilde{M}$
, such that:
(a)
 $F=\unicode[STIX]{x1D711}_{0,1}$
on
$F=\unicode[STIX]{x1D711}_{0,1}$
on
 $X\times \unicode[STIX]{x2202}D$
;
$X\times \unicode[STIX]{x2202}D$
;(b)
 $F(x,z)\geqslant U(x,z)\geqslant \unicode[STIX]{x1D711}_{0}(x)$
;
$F(x,z)\geqslant U(x,z)\geqslant \unicode[STIX]{x1D711}_{0}(x)$
;(c)
 $F(x,z)+\unicode[STIX]{x1D70C}(z)>\unicode[STIX]{x1D711}_{t}(x)$
in
$F(x,z)+\unicode[STIX]{x1D70C}(z)>\unicode[STIX]{x1D711}_{t}(x)$
in
 $X\times D$
, with
$X\times D$
, with
 $t=\log |z|$
.
$t=\log |z|$
.
We let the reader check that the function
![]() $F=U$
in
$F=U$
in
![]() $\widetilde{M}\setminus X\times D$
and
$\widetilde{M}\setminus X\times D$
and
for
![]() $(x,z)\in X\times D$
, does the job.
$(x,z)\in X\times D$
, does the job.
We claim that for all
![]() $(x,z)\in X\times D$
,
$(x,z)\in X\times D$
,
where
Indeed
![]() $P_{\unicode[STIX]{x1D6E9}}(F)+\unicode[STIX]{x1D70C}$
is
$P_{\unicode[STIX]{x1D6E9}}(F)+\unicode[STIX]{x1D70C}$
is
![]() $\unicode[STIX]{x1D714}$
-psh in
$\unicode[STIX]{x1D714}$
-psh in
![]() $X\times D$
and has boundary values
$X\times D$
and has boundary values
![]() ${\leqslant}\unicode[STIX]{x1D711}_{0,1}$
. It follows from the definition of the geodesic that
${\leqslant}\unicode[STIX]{x1D711}_{0,1}$
. It follows from the definition of the geodesic that
![]() $P_{\unicode[STIX]{x1D6E9}}(F)+\unicode[STIX]{x1D70C}\leqslant \unicode[STIX]{x1D711}_{t}$
. Conversely,
$P_{\unicode[STIX]{x1D6E9}}(F)+\unicode[STIX]{x1D70C}\leqslant \unicode[STIX]{x1D711}_{t}$
. Conversely,
![]() $F+\unicode[STIX]{x1D70C}\geqslant U+\unicode[STIX]{x1D70C}\in \operatorname{PSH}(X\times D,\unicode[STIX]{x1D714})$
and
$F+\unicode[STIX]{x1D70C}\geqslant U+\unicode[STIX]{x1D70C}\in \operatorname{PSH}(X\times D,\unicode[STIX]{x1D714})$
and
![]() $U=\unicode[STIX]{x1D711}_{0,1}$
on
$U=\unicode[STIX]{x1D711}_{0,1}$
on
![]() $\unicode[STIX]{x2202}M$
, thus
$\unicode[STIX]{x2202}M$
, thus
![]() $P_{\unicode[STIX]{x1D6E9}}(F)+\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D711}_{0,1}$
on
$P_{\unicode[STIX]{x1D6E9}}(F)+\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D711}_{0,1}$
on
![]() $\unicode[STIX]{x2202}M$
. Condition (c) ensures that
$\unicode[STIX]{x2202}M$
. Condition (c) ensures that
![]() $M=X\times D$
does not meet the contact set
$M=X\times D$
does not meet the contact set
![]() $\{P_{\unicode[STIX]{x1D6E9}}(F)=F\}$
, since
$\{P_{\unicode[STIX]{x1D6E9}}(F)=F\}$
, since
![]() $F+\unicode[STIX]{x1D70C}>\unicode[STIX]{x1D711}_{t}\geqslant P_{\unicode[STIX]{x1D6E9}}(F)+\unicode[STIX]{x1D70C}$
. It thus follows from a balayage argument [Reference Bedford and TaylorBT82] that
$F+\unicode[STIX]{x1D70C}>\unicode[STIX]{x1D711}_{t}\geqslant P_{\unicode[STIX]{x1D6E9}}(F)+\unicode[STIX]{x1D70C}$
. It thus follows from a balayage argument [Reference Bedford and TaylorBT82] that
![]() $(\unicode[STIX]{x1D6E9}+dd^{c}P_{\unicode[STIX]{x1D6E9}}(F))^{n+1}=0$
in
$(\unicode[STIX]{x1D6E9}+dd^{c}P_{\unicode[STIX]{x1D6E9}}(F))^{n+1}=0$
in
![]() $M$
, and the maximum principle yields
$M$
, and the maximum principle yields
The continuity of
![]() $\unicode[STIX]{x1D711}$
on
$\unicode[STIX]{x1D711}$
on
![]() $\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})\times \bar{S}$
now follows from [Reference Eyssidieux, Guedj and ZeriahiEGZ17], together with the following easy observation: the arguments in [Reference Eyssidieux, Guedj and ZeriahiEGZ17, § 2.2] ensure that if
$\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})\times \bar{S}$
now follows from [Reference Eyssidieux, Guedj and ZeriahiEGZ17], together with the following easy observation: the arguments in [Reference Eyssidieux, Guedj and ZeriahiEGZ17, § 2.2] ensure that if
![]() $F$
is a smooth function on
$F$
is a smooth function on
![]() $\widetilde{M}$
,
$\widetilde{M}$
,
![]() $P_{\unicode[STIX]{x1D6E9}}(F)$
is a
$P_{\unicode[STIX]{x1D6E9}}(F)$
is a
![]() $\unicode[STIX]{x1D6E9}$
-psh function, continuous on
$\unicode[STIX]{x1D6E9}$
-psh function, continuous on
![]() $\operatorname{Amp}(\{\unicode[STIX]{x1D6E9}\})$
. The same result holds if
$\operatorname{Amp}(\{\unicode[STIX]{x1D6E9}\})$
. The same result holds if
![]() $F$
is merely continuous. Indeed, let
$F$
is merely continuous. Indeed, let
![]() $F_{j}$
be a sequence of smooth functions on
$F_{j}$
be a sequence of smooth functions on
![]() $\widetilde{M}$
converging uniformly to
$\widetilde{M}$
converging uniformly to
![]() $F$
. Taking the envelope at both sides of the inequality
$F$
. Taking the envelope at both sides of the inequality
![]() $F_{j}\leqslant F+\Vert F_{j}-F\Vert _{L^{\infty }(X)}$
, we get
$F_{j}\leqslant F+\Vert F_{j}-F\Vert _{L^{\infty }(X)}$
, we get
![]() $P_{\unicode[STIX]{x1D6E9}}(F_{j})\leqslant P_{\unicode[STIX]{x1D6E9}}(F)+\Vert F_{j}-F\Vert _{L^{\infty }(X)}$
. Hence,
$P_{\unicode[STIX]{x1D6E9}}(F_{j})\leqslant P_{\unicode[STIX]{x1D6E9}}(F)+\Vert F_{j}-F\Vert _{L^{\infty }(X)}$
. Hence,
![]() $\Vert P_{\unicode[STIX]{x1D6E9}}(F_{j})-P_{\unicode[STIX]{x1D6E9}}(F)\Vert _{L^{\infty }(X)}\leqslant \Vert F_{j}-F\Vert _{L^{\infty }(X)}$
. Thus,
$\Vert P_{\unicode[STIX]{x1D6E9}}(F_{j})-P_{\unicode[STIX]{x1D6E9}}(F)\Vert _{L^{\infty }(X)}\leqslant \Vert F_{j}-F\Vert _{L^{\infty }(X)}$
. Thus,
![]() $P_{\unicode[STIX]{x1D6E9}}(F_{j})$
converges uniformly to
$P_{\unicode[STIX]{x1D6E9}}(F_{j})$
converges uniformly to
![]() $P_{\unicode[STIX]{x1D6E9}}(F)$
, and so
$P_{\unicode[STIX]{x1D6E9}}(F)$
, and so
![]() $P_{\unicode[STIX]{x1D6E9}}(F)$
is a
$P_{\unicode[STIX]{x1D6E9}}(F)$
is a
![]() $\unicode[STIX]{x1D6E9}$
-psh function that is continuous on
$\unicode[STIX]{x1D6E9}$
-psh function that is continuous on
![]() $\operatorname{Amp}(\{\unicode[STIX]{x1D6E9}\})=\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})\times \bar{S}$
.◻
$\operatorname{Amp}(\{\unicode[STIX]{x1D6E9}\})=\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})\times \bar{S}$
.◻
Remark 1.5. If one could choose
![]() $F$
smooth in this proof, it would follow from [Reference Berman and DemaillyBD12] (or [Reference BermanBer13, Theorem 1.2]) that
$F$
smooth in this proof, it would follow from [Reference Berman and DemaillyBD12] (or [Reference BermanBer13, Theorem 1.2]) that
![]() $\unicode[STIX]{x1D711}\in {\mathcal{C}}^{1,\bar{1}}(\operatorname{Amp}(\unicode[STIX]{x1D6FC})\times S)$
. This would also provide a compact proof of Chen’s regularity result.
$\unicode[STIX]{x1D711}\in {\mathcal{C}}^{1,\bar{1}}(\operatorname{Amp}(\unicode[STIX]{x1D6FC})\times S)$
. This would also provide a compact proof of Chen’s regularity result.
We now observe that geodesics in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
are projections of those in
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
are projections of those in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
,
${\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
,
Proposition 1.6. Let
![]() $\unicode[STIX]{x1D711}$
denote the geodesic joining
$\unicode[STIX]{x1D711}$
denote the geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
in
$\unicode[STIX]{x1D711}_{1}$
in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
and let
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
and let
![]() $\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}$
denote the corresponding geodesic in the space
$\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}$
denote the corresponding geodesic in the space
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
. The map
${\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
. The map
![]() $\unicode[STIX]{x1D700}\mapsto \unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}$
is increasing and
$\unicode[STIX]{x1D700}\mapsto \unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}$
is increasing and
![]() $\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}$
decreases to
$\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}$
decreases to
![]() $\unicode[STIX]{x1D711}$
as
$\unicode[STIX]{x1D711}$
as
![]() $\unicode[STIX]{x1D700}$
decreases to zero. Moreover,
$\unicode[STIX]{x1D700}$
decreases to zero. Moreover,
where
![]() $P$
denotes the projection operator onto the space
$P$
denotes the projection operator onto the space
![]() $\text{PSH}(M,\unicode[STIX]{x1D714})$
.
$\text{PSH}(M,\unicode[STIX]{x1D714})$
.
Recall that, for an upper semi-continuous function
![]() $u:M\rightarrow \mathbb{R}$
, its projection
$u:M\rightarrow \mathbb{R}$
, its projection
![]() $P(u)$
is defined by
$P(u)$
is defined by
The function
![]() $P(u)$
is either identical to
$P(u)$
is either identical to
![]() $-\infty$
or belongs to
$-\infty$
or belongs to
![]() $\text{PSH}(M,\unicode[STIX]{x1D714})$
. It is the greatest
$\text{PSH}(M,\unicode[STIX]{x1D714})$
. It is the greatest
![]() $\unicode[STIX]{x1D714}$
-psh function on
$\unicode[STIX]{x1D714}$
-psh function on
![]() $M$
that lies below
$M$
that lies below
![]() $u$
.
$u$
.
Proof. Set
![]() $\unicode[STIX]{x1D713}:=P(\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}})$
. Since
$\unicode[STIX]{x1D713}:=P(\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}})$
. Since
![]() $\unicode[STIX]{x1D714}\leqslant \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
, it follows from the envelope point of view that
$\unicode[STIX]{x1D714}\leqslant \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
, it follows from the envelope point of view that
![]() $\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}$
. Thus,
$\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}$
. Thus,
![]() $\unicode[STIX]{x1D711}=P(\unicode[STIX]{x1D711})\leqslant P(\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}})=\unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D711}=P(\unicode[STIX]{x1D711})\leqslant P(\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}})=\unicode[STIX]{x1D713}$
and
![]() $\unicode[STIX]{x1D713}\in \text{PSH}(M,\unicode[STIX]{x1D714})$
. Now
$\unicode[STIX]{x1D713}\in \text{PSH}(M,\unicode[STIX]{x1D714})$
. Now
![]() $\unicode[STIX]{x1D713}\leqslant \unicode[STIX]{x1D711}$
, since
$\unicode[STIX]{x1D713}\leqslant \unicode[STIX]{x1D711}$
, since
![]() $\unicode[STIX]{x1D713}\leqslant \unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
on
$\unicode[STIX]{x1D713}\leqslant \unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
on
![]() $\unicode[STIX]{x2202}M$
and
$\unicode[STIX]{x2202}M$
and
![]() $\unicode[STIX]{x1D713}\in \text{PSH}(M,\unicode[STIX]{x1D714})$
. Thus,
$\unicode[STIX]{x1D713}\in \text{PSH}(M,\unicode[STIX]{x1D714})$
. Thus,
![]() $\unicode[STIX]{x1D713}=P(\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}})=\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D713}=P(\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}})=\unicode[STIX]{x1D711}$
.
Fix
![]() $\unicode[STIX]{x1D700}^{\prime }\leqslant \unicode[STIX]{x1D700}$
. The inclusion
$\unicode[STIX]{x1D700}^{\prime }\leqslant \unicode[STIX]{x1D700}$
. The inclusion
![]() $\text{PSH}(M,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}^{\prime }})\subset \text{PSH}(M,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})$
implies similarly that
$\text{PSH}(M,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}^{\prime }})\subset \text{PSH}(M,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})$
implies similarly that
![]() $\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}^{\prime }}\leqslant \unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}$
. The decreasing limit
$\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}^{\prime }}\leqslant \unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}$
. The decreasing limit
![]() $v$
of
$v$
of
![]() $\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}$
, as
$\unicode[STIX]{x1D711}^{\unicode[STIX]{x1D700}}$
, as
![]() $\unicode[STIX]{x1D700}$
decreases to zero, satisfies both
$\unicode[STIX]{x1D700}$
decreases to zero, satisfies both
![]() $\unicode[STIX]{x1D711}\leqslant v$
and
$\unicode[STIX]{x1D711}\leqslant v$
and
![]() $v\in \text{PSH}(M,\unicode[STIX]{x1D714})$
with boundary values
$v\in \text{PSH}(M,\unicode[STIX]{x1D714})$
with boundary values
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
, thus
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
, thus
![]() $v=\unicode[STIX]{x1D711}$
.◻
$v=\unicode[STIX]{x1D711}$
.◻
It will also be interesting to consider subgeodesics.
Definition 1.7. A subgeodesic is a path
![]() $(\unicode[STIX]{x1D711}_{t})$
of functions in
$(\unicode[STIX]{x1D711}_{t})$
of functions in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
(or in larger classes of
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
(or in larger classes of
![]() $\unicode[STIX]{x1D714}$
-psh functions) such that the associated function is a
$\unicode[STIX]{x1D714}$
-psh functions) such that the associated function is a
![]() $\unicode[STIX]{x1D714}$
-psh function on
$\unicode[STIX]{x1D714}$
-psh function on
![]() $X\times S$
.
$X\times S$
.
We shall soon need the following simple observation.
Lemma 1.8. Fix
![]() $c\in \mathbb{R}$
,
$c\in \mathbb{R}$
,
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
and let
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
and let
![]() $(\unicode[STIX]{x1D711}_{t})_{0\leqslant t\leqslant 1}$
denote the Mabuchi geodesic joining
$(\unicode[STIX]{x1D711}_{t})_{0\leqslant t\leqslant 1}$
denote the Mabuchi geodesic joining
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D713}$
. Then
$\unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D713}$
. Then
![]() $\unicode[STIX]{x1D713}_{t}(x):=\unicode[STIX]{x1D711}_{t}(x)-ct,0\leqslant t\leqslant 1,x\in X,$
is the Mabuchi geodesic joining
$\unicode[STIX]{x1D713}_{t}(x):=\unicode[STIX]{x1D711}_{t}(x)-ct,0\leqslant t\leqslant 1,x\in X,$
is the Mabuchi geodesic joining
![]() $\unicode[STIX]{x1D711}$
to
$\unicode[STIX]{x1D711}$
to
![]() $\unicode[STIX]{x1D713}-c$
.
$\unicode[STIX]{x1D713}-c$
.
Proof. The proof follows from Definition 1.3 and the definition of envelopes, since
![]() $\sup \{v;v\in \text{PSH}(M,\unicode[STIX]{x1D714})~\text{and}~v\leqslant \unicode[STIX]{x1D711},v\leqslant \unicode[STIX]{x1D713}-c~\text{on}~\unicode[STIX]{x2202}M\}=\unicode[STIX]{x1D711}_{t}-ct$
.◻
$\sup \{v;v\in \text{PSH}(M,\unicode[STIX]{x1D714})~\text{and}~v\leqslant \unicode[STIX]{x1D711},v\leqslant \unicode[STIX]{x1D713}-c~\text{on}~\unicode[STIX]{x2202}M\}=\unicode[STIX]{x1D711}_{t}-ct$
.◻
1.1.2 Mabuchi and other Finsler distances
When
![]() $\unicode[STIX]{x1D714}$
is Kähler, the length of a smooth path
$\unicode[STIX]{x1D714}$
is Kähler, the length of a smooth path
![]() $(\unicode[STIX]{x1D711}_{t})_{t\in [0,1]}$
in
$(\unicode[STIX]{x1D711}_{t})_{t\in [0,1]}$
in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
is defined in a standard way,
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
is defined in a standard way,
The distance between two points in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
is then
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
is then
It is easy to verify that
![]() $d$
defines a semi-distance (i.e. non-negative, symmetric, and satisfying the triangle inequality). It is, however, non-trivial to check that
$d$
defines a semi-distance (i.e. non-negative, symmetric, and satisfying the triangle inequality). It is, however, non-trivial to check that
![]() $d$
is non-degenerate (see [Reference Michor and MumfordMM05] for a striking example).
$d$
is non-degenerate (see [Reference Michor and MumfordMM05] for a striking example).
Observe that
![]() $d$
induces a distance on
$d$
induces a distance on
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D6FC}}$
(that we abusively still denote
${\mathcal{H}}_{\unicode[STIX]{x1D6FC}}$
(that we abusively still denote
![]() $d$
) compatible with the Riemannian splitting
$d$
) compatible with the Riemannian splitting
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}={\mathcal{H}}_{\unicode[STIX]{x1D6FC}}\times \mathbb{R}$
, by setting
${\mathcal{H}}_{\unicode[STIX]{x1D714}}={\mathcal{H}}_{\unicode[STIX]{x1D6FC}}\times \mathbb{R}$
, by setting
whenever the potentials
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
of
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
of
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}$
are normalized by
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}},\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}$
are normalized by
![]() $E(\unicode[STIX]{x1D711})=E(\unicode[STIX]{x1D713})=0$
(see § 2.2.1 for the definition of the functional
$E(\unicode[STIX]{x1D711})=E(\unicode[STIX]{x1D713})=0$
(see § 2.2.1 for the definition of the functional
![]() $E$
).
$E$
).
It is rather easy to check that
![]() $({\mathcal{H}}_{\unicode[STIX]{x1D6FC}},d)$
is not a complete metric space. We shall describe the metric completion
$({\mathcal{H}}_{\unicode[STIX]{x1D6FC}},d)$
is not a complete metric space. We shall describe the metric completion
![]() $(\overline{{\mathcal{H}}}_{\unicode[STIX]{x1D6FC}},d)$
in § 4. Following Darvas [Reference DarvasDar15], we introduce a family of distances that generalize
$(\overline{{\mathcal{H}}}_{\unicode[STIX]{x1D6FC}},d)$
in § 4. Following Darvas [Reference DarvasDar15], we introduce a family of distances that generalize
![]() $d$
:
$d$
:
Definition 1.9. For
![]() $p\geqslant 1$
and
$p\geqslant 1$
and
![]() $\unicode[STIX]{x1D714}$
Kähler, we set
$\unicode[STIX]{x1D714}$
Kähler, we set
where
![]() $\ell _{p}(\unicode[STIX]{x1D711}):=\int _{0}^{1}|\dot{\unicode[STIX]{x1D711}_{t}}|_{p}\,dt=\int _{0}^{1}(\int _{X}|\dot{\unicode[STIX]{x1D711}}_{t}|^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{t}))^{1/p}\,dt$
.
$\ell _{p}(\unicode[STIX]{x1D711}):=\int _{0}^{1}|\dot{\unicode[STIX]{x1D711}_{t}}|_{p}\,dt=\int _{0}^{1}(\int _{X}|\dot{\unicode[STIX]{x1D711}}_{t}|^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{t}))^{1/p}\,dt$
.
Note that
![]() $d_{2}=d$
is the Mabuchi distance. Mabuchi geodesics have constant speed with respect to all the Finsler structures
$d_{2}=d$
is the Mabuchi distance. Mabuchi geodesics have constant speed with respect to all the Finsler structures
![]() $\ell _{p}$
, as was observed by Berndtsson [Reference BerndtssonBer09, Lemma 2.1]: for any
$\ell _{p}$
, as was observed by Berndtsson [Reference BerndtssonBer09, Lemma 2.1]: for any
![]() ${\mathcal{C}}^{1}$
-function
${\mathcal{C}}^{1}$
-function
![]() $\unicode[STIX]{x1D712}$
,
$\unicode[STIX]{x1D712}$
,
is constant along a geodesic. Indeed
 $$\begin{eqnarray}\displaystyle \frac{d}{dt}\int _{X}\unicode[STIX]{x1D712}(\dot{\unicode[STIX]{x1D711}}_{t})\operatorname{MA}(\unicode[STIX]{x1D711}_{t}) & = & \displaystyle \int _{X}\unicode[STIX]{x1D712}^{\prime }(\dot{\unicode[STIX]{x1D711}}_{t})\ddot{\unicode[STIX]{x1D711}}_{t}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})+\frac{n}{V_{\unicode[STIX]{x1D6FC}}}\int _{X}\unicode[STIX]{x1D712}(\dot{\unicode[STIX]{x1D711}}_{t})\,dd^{c}\dot{\unicode[STIX]{x1D711}}_{t}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}_{t}}^{n-1}\nonumber\\ \displaystyle & = & \displaystyle \int _{X}\unicode[STIX]{x1D712}^{\prime }(\dot{\unicode[STIX]{x1D711}}_{t})\biggl\{\ddot{\unicode[STIX]{x1D711}}_{t}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})-\frac{n}{V_{\unicode[STIX]{x1D6FC}}}d\dot{\unicode[STIX]{x1D711}}_{t}\wedge d^{c}\dot{\unicode[STIX]{x1D711}}_{t}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}_{t}}^{n-1}\biggr\}=0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{d}{dt}\int _{X}\unicode[STIX]{x1D712}(\dot{\unicode[STIX]{x1D711}}_{t})\operatorname{MA}(\unicode[STIX]{x1D711}_{t}) & = & \displaystyle \int _{X}\unicode[STIX]{x1D712}^{\prime }(\dot{\unicode[STIX]{x1D711}}_{t})\ddot{\unicode[STIX]{x1D711}}_{t}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})+\frac{n}{V_{\unicode[STIX]{x1D6FC}}}\int _{X}\unicode[STIX]{x1D712}(\dot{\unicode[STIX]{x1D711}}_{t})\,dd^{c}\dot{\unicode[STIX]{x1D711}}_{t}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}_{t}}^{n-1}\nonumber\\ \displaystyle & = & \displaystyle \int _{X}\unicode[STIX]{x1D712}^{\prime }(\dot{\unicode[STIX]{x1D711}}_{t})\biggl\{\ddot{\unicode[STIX]{x1D711}}_{t}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})-\frac{n}{V_{\unicode[STIX]{x1D6FC}}}d\dot{\unicode[STIX]{x1D711}}_{t}\wedge d^{c}\dot{\unicode[STIX]{x1D711}}_{t}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}_{t}}^{n-1}\biggr\}=0\nonumber\end{eqnarray}$$
since
![]() $\ddot{\unicode[STIX]{x1D711}}_{t}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})-(n/V_{\unicode[STIX]{x1D6FC}})\,d\dot{\unicode[STIX]{x1D711}}_{t}\wedge d^{c}\dot{\unicode[STIX]{x1D711}}_{t}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}_{t}}^{n-1}=0$
. Applying this observation to
$\ddot{\unicode[STIX]{x1D711}}_{t}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})-(n/V_{\unicode[STIX]{x1D6FC}})\,d\dot{\unicode[STIX]{x1D711}}_{t}\wedge d^{c}\dot{\unicode[STIX]{x1D711}}_{t}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}_{t}}^{n-1}=0$
. Applying this observation to
![]() $\unicode[STIX]{x1D712}(t)=t^{p}$
shows that Mabuchi geodesics have constant
$\unicode[STIX]{x1D712}(t)=t^{p}$
shows that Mabuchi geodesics have constant
![]() $\ell _{p}$
-speed.
$\ell _{p}$
-speed.
When
![]() $\unicode[STIX]{x1D714}$
is merely semi-positive, there are fewer smooth paths within
$\unicode[STIX]{x1D714}$
is merely semi-positive, there are fewer smooth paths within
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
. It is natural to consider smooth paths in
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
. It is natural to consider smooth paths in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
and pass to the limit in the previous definitions.
${\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
and pass to the limit in the previous definitions.
Definition 1.10. Assume
![]() $\unicode[STIX]{x1D714}$
is semi-positive and big. Let
$\unicode[STIX]{x1D714}$
is semi-positive and big. Let
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
. We define the Mabuchi distance between
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
. We define the Mabuchi distance between
![]() $\unicode[STIX]{x1D711}_{0}$
and
$\unicode[STIX]{x1D711}_{0}$
and
![]() $\unicode[STIX]{x1D711}_{1}$
as
$\unicode[STIX]{x1D711}_{1}$
as
where
![]() $d_{p,\unicode[STIX]{x1D700}}$
is the distance with respect to the Kähler form
$d_{p,\unicode[STIX]{x1D700}}$
is the distance with respect to the Kähler form
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}:=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}$
.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}:=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}$
.
We will show in Theorem 1.13 that it is a distance, which moreover does not depend on the way we approximate
![]() $\unicode[STIX]{x1D714}$
by Kähler classes.
$\unicode[STIX]{x1D714}$
by Kähler classes.
Remark 1.11. For any smooth path
![]() $\unicode[STIX]{x1D713}:[0,1]\rightarrow {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
, we can still define
$\unicode[STIX]{x1D713}:[0,1]\rightarrow {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
, we can still define
when
![]() $\unicode[STIX]{x1D714}$
is merely semi-positive. Since
$\unicode[STIX]{x1D714}$
is merely semi-positive. Since
![]() $\text{PSH}(M,\unicode[STIX]{x1D714})\subset \text{PSH}(M,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})$
,
$\text{PSH}(M,\unicode[STIX]{x1D714})\subset \text{PSH}(M,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})$
,
![]() $\unicode[STIX]{x1D713}_{t}$
is both in
$\unicode[STIX]{x1D713}_{t}$
is both in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
and
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
and
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
. Observe that
${\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
. Observe that
 $$\begin{eqnarray}\displaystyle V_{\unicode[STIX]{x1D700}}^{-1}\int _{X}|\dot{\unicode[STIX]{x1D713}}_{t}|^{p}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D713}_{t})^{n} & = & \displaystyle V_{\unicode[STIX]{x1D700}}^{-1}\int _{X}|\dot{\unicode[STIX]{x1D713}}_{t}|^{p}(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D713}_{t}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X})^{n}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle V^{-1}\int _{X}|\dot{\unicode[STIX]{x1D713}}_{t}|^{p}(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D713}_{t})^{n}+A\unicode[STIX]{x1D700},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle V_{\unicode[STIX]{x1D700}}^{-1}\int _{X}|\dot{\unicode[STIX]{x1D713}}_{t}|^{p}(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D713}_{t})^{n} & = & \displaystyle V_{\unicode[STIX]{x1D700}}^{-1}\int _{X}|\dot{\unicode[STIX]{x1D713}}_{t}|^{p}(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D713}_{t}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X})^{n}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle V^{-1}\int _{X}|\dot{\unicode[STIX]{x1D713}}_{t}|^{p}(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D713}_{t})^{n}+A\unicode[STIX]{x1D700},\nonumber\end{eqnarray}$$
hence
where
![]() $\ell _{p,\unicode[STIX]{x1D700}}$
denotes the length in
$\ell _{p,\unicode[STIX]{x1D700}}$
denotes the length in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
. We infer
${\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
. We infer
The converse inequality is, however, unclear, owing to the lack of positivity of
![]() $\unicode[STIX]{x1D714}$
: it is difficult to smooth out
$\unicode[STIX]{x1D714}$
: it is difficult to smooth out
![]() $\unicode[STIX]{x1D714}$
-psh functions if
$\unicode[STIX]{x1D714}$
-psh functions if
![]() $\unicode[STIX]{x1D714}$
is not Kähler. This partially explains Definition 1.10.
$\unicode[STIX]{x1D714}$
is not Kähler. This partially explains Definition 1.10.
1.2 Approximation by Kähler classes
Fix
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
. We let
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
. We let
![]() $(\unicode[STIX]{x1D711}_{t})_{0\leqslant t\leqslant 1}$
denote the Mabuchi geodesic in
$(\unicode[STIX]{x1D711}_{t})_{0\leqslant t\leqslant 1}$
denote the Mabuchi geodesic in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
joining
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
.
$\unicode[STIX]{x1D711}_{1}$
.
Definition 1.12. For
![]() $t=0,1$
we set
$t=0,1$
we set
Theorem 1.13. Set
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}$
,
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}$
,
![]() $\unicode[STIX]{x1D700}>0$
. Then
$\unicode[STIX]{x1D700}>0$
. Then
![]() $\lim _{\unicode[STIX]{x1D700}\rightarrow 0}d_{p,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
exists and is independent of
$\lim _{\unicode[STIX]{x1D700}\rightarrow 0}d_{p,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
exists and is independent of
![]() $\unicode[STIX]{x1D714}_{X}$
. More precisely,
$\unicode[STIX]{x1D714}_{X}$
. More precisely,
In particular,
![]() $d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})=I(0)^{1/p}=I(1)^{1/p}$
defines a distance on
$d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})=I(0)^{1/p}=I(1)^{1/p}$
defines a distance on
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
.
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
.
In the definition of
![]() $I(0),I(1)$
, the time derivatives
$I(0),I(1)$
, the time derivatives
![]() $\dot{\unicode[STIX]{x1D711}}_{0}=\dot{\unicode[STIX]{x1D711}}_{0}^{+}$
,
$\dot{\unicode[STIX]{x1D711}}_{0}=\dot{\unicode[STIX]{x1D711}}_{0}^{+}$
,
![]() $\dot{\unicode[STIX]{x1D711}}_{1}=\dot{\unicode[STIX]{x1D711}}_{1}^{-}$
denote the right and left derivatives, respectively.
$\dot{\unicode[STIX]{x1D711}}_{1}=\dot{\unicode[STIX]{x1D711}}_{1}^{-}$
denote the right and left derivatives, respectively.
Remark 1.14. When
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{Y}$
, for some Kähler form
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{Y}$
, for some Kähler form
![]() $\unicode[STIX]{x1D714}_{Y}$
on a compact normal space
$\unicode[STIX]{x1D714}_{Y}$
on a compact normal space
![]() $Y$
, for each
$Y$
, for each
![]() $p\geqslant 1$
and
$p\geqslant 1$
and
![]() $\forall \unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
, we define
$\forall \unicode[STIX]{x1D719}_{0},\unicode[STIX]{x1D719}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}_{Y}}$
, we define
This definition does not depend on the choice of resolution. Indeed, let
![]() $\unicode[STIX]{x1D70B}^{\prime }:X^{\prime }\rightarrow Y$
be another resolution of
$\unicode[STIX]{x1D70B}^{\prime }:X^{\prime }\rightarrow Y$
be another resolution of
![]() $Y$
that dominates
$Y$
that dominates
![]() $X$
, i.e. there exists a holomorphic and bimeromorphic map
$X$
, i.e. there exists a holomorphic and bimeromorphic map
![]() $f:X^{\prime }\rightarrow X$
, such that
$f:X^{\prime }\rightarrow X$
, such that
![]() $\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}\circ f$
. Set
$\unicode[STIX]{x1D70B}^{\prime }=\unicode[STIX]{x1D70B}\circ f$
. Set
![]() $\unicode[STIX]{x1D714}^{\prime }:={\unicode[STIX]{x1D70B}^{\prime }}^{\ast }\unicode[STIX]{x1D714}_{Y}=f^{\ast }\unicode[STIX]{x1D714}$
. We need to show that
$\unicode[STIX]{x1D714}^{\prime }:={\unicode[STIX]{x1D70B}^{\prime }}^{\ast }\unicode[STIX]{x1D714}_{Y}=f^{\ast }\unicode[STIX]{x1D714}$
. We need to show that
Denote by
![]() $\unicode[STIX]{x1D713}_{t}$
the
$\unicode[STIX]{x1D713}_{t}$
the
![]() $f^{\ast }\unicode[STIX]{x1D714}$
-geodesic joining
$f^{\ast }\unicode[STIX]{x1D714}$
-geodesic joining
![]() $f^{\ast }\unicode[STIX]{x1D711}_{0}$
and
$f^{\ast }\unicode[STIX]{x1D711}_{0}$
and
![]() $f^{\ast }\unicode[STIX]{x1D711}_{1}$
. We claim that
$f^{\ast }\unicode[STIX]{x1D711}_{1}$
. We claim that
![]() $\unicode[STIX]{x1D713}_{t}=f^{\ast }\unicode[STIX]{x1D711}_{t}$
. We first observe that, since
$\unicode[STIX]{x1D713}_{t}=f^{\ast }\unicode[STIX]{x1D711}_{t}$
. We first observe that, since
![]() $\unicode[STIX]{x1D713}_{t}$
is a
$\unicode[STIX]{x1D713}_{t}$
is a
![]() $f^{\ast }\unicode[STIX]{x1D714}$
-psh function for each fixed
$f^{\ast }\unicode[STIX]{x1D714}$
-psh function for each fixed
![]() $t$
,
$t$
,
![]() $\unicode[STIX]{x1D713}_{t}=f^{\ast }\unicode[STIX]{x1D6FE}_{t}$
, where
$\unicode[STIX]{x1D713}_{t}=f^{\ast }\unicode[STIX]{x1D6FE}_{t}$
, where
![]() $\unicode[STIX]{x1D6FE}_{t}$
is a
$\unicode[STIX]{x1D6FE}_{t}$
is a
![]() $\unicode[STIX]{x1D714}$
-psh function on
$\unicode[STIX]{x1D714}$
-psh function on
![]() $X$
. Set
$X$
. Set
![]() $M^{\prime }:=X^{\prime }\times S$
,
$M^{\prime }:=X^{\prime }\times S$
,
![]() $\unicode[STIX]{x1D713}(x^{\prime },t):=\unicode[STIX]{x1D713}_{t}(x^{\prime })$
, and
$\unicode[STIX]{x1D713}(x^{\prime },t):=\unicode[STIX]{x1D713}_{t}(x^{\prime })$
, and
![]() $\unicode[STIX]{x1D6FE}(x^{\prime },t):=\unicode[STIX]{x1D6FE}_{t}(x^{\prime })$
for each
$\unicode[STIX]{x1D6FE}(x^{\prime },t):=\unicode[STIX]{x1D6FE}_{t}(x^{\prime })$
for each
![]() $(x^{\prime },t)\in M^{\prime }$
. By construction, we have that
$(x^{\prime },t)\in M^{\prime }$
. By construction, we have that
The claim follows from the uniqueness of the solution of the Dirichlet problem in Proposition 1.4. The invariance of the non-pluripolar Monge–Ampère measure under bimeromorphic maps [Reference Di NezzaDiN15], together with the fact that
![]() $V:=\int _{X}\unicode[STIX]{x1D714}^{n}=\int _{X^{\prime }}f^{\ast }\unicode[STIX]{x1D714}$
, give
$V:=\int _{X}\unicode[STIX]{x1D714}^{n}=\int _{X^{\prime }}f^{\ast }\unicode[STIX]{x1D714}$
, give
The conclusion then follows from Theorem 1.13.
Proof. Observe that
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
and let
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
and let
![]() $\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}}$
be the corresponding geodesic. It follows from [Reference DarvasDar15, Theorem 3.5] that
$\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}}$
be the corresponding geodesic. It follows from [Reference DarvasDar15, Theorem 3.5] that
Now observe that
where the first inequality follows from the fact that
![]() $\unicode[STIX]{x1D700}\rightarrow \unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}}$
is decreasing (Proposition 1.6), while the second uses the convexity of
$\unicode[STIX]{x1D700}\rightarrow \unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}}$
is decreasing (Proposition 1.6), while the second uses the convexity of
![]() $t\mapsto \unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}}$
. Thus,
$t\mapsto \unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}}$
. Thus,
Letting
![]() $\unicode[STIX]{x1D700}{\searrow}0$
and then
$\unicode[STIX]{x1D700}{\searrow}0$
and then
![]() $t\rightarrow 0$
shows that
$t\rightarrow 0$
shows that
![]() $|\dot{\unicode[STIX]{x1D711}}_{0}^{\unicode[STIX]{x1D700}}-\dot{\unicode[STIX]{x1D711}}_{0}^{+}|$
converges pointwise to zero. Moreover,
$|\dot{\unicode[STIX]{x1D711}}_{0}^{\unicode[STIX]{x1D700}}-\dot{\unicode[STIX]{x1D711}}_{0}^{+}|$
converges pointwise to zero. Moreover,
![]() $(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D711}_{0})^{n}=f_{\unicode[STIX]{x1D700}}\,dV$
where
$(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D711}_{0})^{n}=f_{\unicode[STIX]{x1D700}}\,dV$
where
![]() $dV$
is the Lebesgue measure and
$dV$
is the Lebesgue measure and
![]() $f_{\unicode[STIX]{x1D700}}>0$
are smooth densities, which converge locally uniformly to
$f_{\unicode[STIX]{x1D700}}>0$
are smooth densities, which converge locally uniformly to
![]() $f\geqslant 0$
with
$f\geqslant 0$
with
![]() $(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}_{0})^{n}=f\,dV$
. The dominated convergence theorem thus yields
$(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}_{0})^{n}=f\,dV$
. The dominated convergence theorem thus yields
The argument for
![]() $I(1)$
is similar.
$I(1)$
is similar.
This shows, in particular, that
![]() $d_{p}$
is a distance on
$d_{p}$
is a distance on
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
: if
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
: if
![]() $d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})=0$
, then
$d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})=0$
, then
![]() $I(0)=I(1)=0$
, hence,
$I(0)=I(1)=0$
, hence,
![]() $\dot{\unicode[STIX]{x1D711}}_{0}(x)=\dot{\unicode[STIX]{x1D711}}_{1}(x)=0$
for a.e.
$\dot{\unicode[STIX]{x1D711}}_{0}(x)=\dot{\unicode[STIX]{x1D711}}_{1}(x)=0$
for a.e.
![]() $x\in X$
, which implies
$x\in X$
, which implies
![]() $\dot{\unicode[STIX]{x1D711}}_{t}(x)=0$
for a.e.
$\dot{\unicode[STIX]{x1D711}}_{t}(x)=0$
for a.e.
![]() $x\in X$
, by convexity of
$x\in X$
, by convexity of
![]() $t\mapsto \unicode[STIX]{x1D711}_{t}(x)$
. Thus,
$t\mapsto \unicode[STIX]{x1D711}_{t}(x)$
. Thus,
![]() $\unicode[STIX]{x1D711}_{0}(x)=\unicode[STIX]{x1D711}_{1}(x)$
for a.e.
$\unicode[STIX]{x1D711}_{0}(x)=\unicode[STIX]{x1D711}_{1}(x)$
for a.e.
![]() $x\in X$
.◻
$x\in X$
.◻
We now extend the definition of the distance
![]() $d_{p}$
for bounded
$d_{p}$
for bounded
![]() $\unicode[STIX]{x1D714}$
-psh potentials.
$\unicode[STIX]{x1D714}$
-psh potentials.
Definition 1.15. Let
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in \operatorname{PSH}(X,\unicode[STIX]{x1D714})\cap L^{\infty }(X)$
; then
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in \operatorname{PSH}(X,\unicode[STIX]{x1D714})\cap L^{\infty }(X)$
; then
where
![]() $\unicode[STIX]{x1D711}_{0}^{j},\unicode[STIX]{x1D711}_{1}^{k}$
are smooth sequences of
$\unicode[STIX]{x1D711}_{0}^{j},\unicode[STIX]{x1D711}_{1}^{k}$
are smooth sequences of
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
-psh functions decreasing to
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
-psh functions decreasing to
![]() $\unicode[STIX]{x1D711}_{0}$
and
$\unicode[STIX]{x1D711}_{0}$
and
![]() $\unicode[STIX]{x1D711}_{1}$
, respectively.
$\unicode[STIX]{x1D711}_{1}$
, respectively.
Observe that
![]() $d_{p,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
is well defined for potentials in
$d_{p,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
is well defined for potentials in
![]() ${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})$
[Reference DarvasDar15], and so, in particular, for bounded
${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})$
[Reference DarvasDar15], and so, in particular, for bounded
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
-psh functions.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
-psh functions.
Proposition 1.16. Let
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in \operatorname{PSH}(X,\unicode[STIX]{x1D714})\cap L^{\infty }(X)$
. The limit of
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in \operatorname{PSH}(X,\unicode[STIX]{x1D714})\cap L^{\infty }(X)$
. The limit of
![]() $d_{p,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
as
$d_{p,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
as
![]() $\unicode[STIX]{x1D700}$
goes to zero exists and does not depend on the choice of
$\unicode[STIX]{x1D700}$
goes to zero exists and does not depend on the choice of
![]() $\unicode[STIX]{x1D714}_{X}$
.
$\unicode[STIX]{x1D714}_{X}$
.
Proof. First, observe that since
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
are bounded, they belong to
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
are bounded, they belong to
![]() ${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})$
for any
${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})$
for any
![]() $0\leqslant \unicode[STIX]{x1D700}\leqslant 1$
. By [Reference DarvasDar15, Corollary 4.14] we know that the Pythagorean formula holds true, i.e.
$0\leqslant \unicode[STIX]{x1D700}\leqslant 1$
. By [Reference DarvasDar15, Corollary 4.14] we know that the Pythagorean formula holds true, i.e.
where
![]() $\unicode[STIX]{x1D713}:=\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}$
is the greatest
$\unicode[STIX]{x1D713}:=\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}$
is the greatest
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
-psh function that lies below
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
-psh function that lies below
![]() $\min (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
. Fix
$\min (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
. Fix
![]() $\unicode[STIX]{x1D700}\leqslant \unicode[STIX]{x1D700}^{\prime }$
. We claim that
$\unicode[STIX]{x1D700}\leqslant \unicode[STIX]{x1D700}^{\prime }$
. We claim that
Let
![]() $\unicode[STIX]{x1D713}_{t}^{\unicode[STIX]{x1D700}}$
,
$\unicode[STIX]{x1D713}_{t}^{\unicode[STIX]{x1D700}}$
,
![]() $\unicode[STIX]{x1D713}_{t}^{\unicode[STIX]{x1D700}^{\prime }}$
denote the
$\unicode[STIX]{x1D713}_{t}^{\unicode[STIX]{x1D700}^{\prime }}$
denote the
![]() $\unicode[STIX]{x1D700}$
-geodesic and the
$\unicode[STIX]{x1D700}$
-geodesic and the
![]() $\unicode[STIX]{x1D700}^{\prime }$
-geodesic, both joining
$\unicode[STIX]{x1D700}^{\prime }$
-geodesic, both joining
![]() $\unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D713}$
and
![]() $\unicode[STIX]{x1D711}_{0}$
. Since
$\unicode[STIX]{x1D711}_{0}$
. Since
![]() $\unicode[STIX]{x1D700}\rightarrow \unicode[STIX]{x1D713}_{t}^{\unicode[STIX]{x1D700}}$
is increasing (Proposition 1.6), we have that, for any
$\unicode[STIX]{x1D700}\rightarrow \unicode[STIX]{x1D713}_{t}^{\unicode[STIX]{x1D700}}$
is increasing (Proposition 1.6), we have that, for any
![]() $t\in (0,1)$
$t\in (0,1)$
which implies
![]() $\dot{\unicode[STIX]{x1D713}}_{0}^{\unicode[STIX]{x1D700}}\leqslant \dot{\unicode[STIX]{x1D713}}_{0}^{\unicode[STIX]{x1D700}^{\prime }}$
. Moreover, observe that, since
$\dot{\unicode[STIX]{x1D713}}_{0}^{\unicode[STIX]{x1D700}}\leqslant \dot{\unicode[STIX]{x1D713}}_{0}^{\unicode[STIX]{x1D700}^{\prime }}$
. Moreover, observe that, since
![]() $\unicode[STIX]{x1D711}_{0}(x)\geqslant \unicode[STIX]{x1D713}(x)$
for all
$\unicode[STIX]{x1D711}_{0}(x)\geqslant \unicode[STIX]{x1D713}(x)$
for all
![]() $x\in X$
, Lemma 3.3 yields
$x\in X$
, Lemma 3.3 yields
![]() $\dot{\unicode[STIX]{x1D713}}_{0}^{\unicode[STIX]{x1D700}}(x)\geqslant 0$
for all
$\dot{\unicode[STIX]{x1D713}}_{0}^{\unicode[STIX]{x1D700}}(x)\geqslant 0$
for all
![]() $x\in X$
. It then follows that
$x\in X$
. It then follows that
hence the claim. The same type of arguments give
![]() $V_{\unicode[STIX]{x1D700}}d_{p,\unicode[STIX]{x1D700}}^{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D711}_{1})\leqslant V_{\unicode[STIX]{x1D700}^{\prime }}d_{p,\unicode[STIX]{x1D700}^{\prime }}^{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D711}_{1})$
. Hence,
$V_{\unicode[STIX]{x1D700}}d_{p,\unicode[STIX]{x1D700}}^{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D711}_{1})\leqslant V_{\unicode[STIX]{x1D700}^{\prime }}d_{p,\unicode[STIX]{x1D700}^{\prime }}^{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D711}_{1})$
. Hence,
Using again [Reference DarvasDar15, Corollary 4.14] and the triangle inequality we get
Moreover, since
![]() $\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}^{\prime }}\unicode[STIX]{x1D711}_{1}\geqslant \unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}$
, [Reference DarvasDar15, Lemma 5.1] yields
$\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}^{\prime }}\unicode[STIX]{x1D711}_{1}\geqslant \unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}$
, [Reference DarvasDar15, Lemma 5.1] yields
 $$\begin{eqnarray}\displaystyle d_{p,\unicode[STIX]{x1D700}^{\prime }}^{p}(\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}^{\prime }}\unicode[STIX]{x1D711}_{1}) & {\leqslant} & \displaystyle \frac{1}{V_{\unicode[STIX]{x1D700}^{\prime }}}\int _{X}(\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}^{\prime }}\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1})^{p}\,(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}^{\prime }}+dd^{c}(\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}))^{n}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{V_{\unicode[STIX]{x1D700}^{\prime }}}\int _{X}(\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}^{\prime }}\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1})^{p}\,(\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{X}+dd^{c}(\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}))^{n}\nonumber\\ \displaystyle & := & \displaystyle V_{\unicode[STIX]{x1D700}^{\prime }}^{-1}\unicode[STIX]{x1D702}(\unicode[STIX]{x1D700},\unicode[STIX]{x1D700}^{\prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{p,\unicode[STIX]{x1D700}^{\prime }}^{p}(\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}^{\prime }}\unicode[STIX]{x1D711}_{1}) & {\leqslant} & \displaystyle \frac{1}{V_{\unicode[STIX]{x1D700}^{\prime }}}\int _{X}(\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}^{\prime }}\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1})^{p}\,(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}^{\prime }}+dd^{c}(\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}))^{n}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{V_{\unicode[STIX]{x1D700}^{\prime }}}\int _{X}(\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}^{\prime }}\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1})^{p}\,(\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{X}+dd^{c}(\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}))^{n}\nonumber\\ \displaystyle & := & \displaystyle V_{\unicode[STIX]{x1D700}^{\prime }}^{-1}\unicode[STIX]{x1D702}(\unicode[STIX]{x1D700},\unicode[STIX]{x1D700}^{\prime }).\nonumber\end{eqnarray}$$
Observe that
![]() $\unicode[STIX]{x1D702}(\unicode[STIX]{x1D700},\unicode[STIX]{x1D700}^{\prime })$
converges to 0 as
$\unicode[STIX]{x1D702}(\unicode[STIX]{x1D700},\unicode[STIX]{x1D700}^{\prime })$
converges to 0 as
![]() $\unicode[STIX]{x1D700}^{\prime }$
goes to 0. From above, we have
$\unicode[STIX]{x1D700}^{\prime }$
goes to 0. From above, we have
Hence, the limit exists.
Now, let
![]() $\unicode[STIX]{x1D714}_{X},\widetilde{\unicode[STIX]{x1D714}}_{X}$
be two Kähler metrics on
$\unicode[STIX]{x1D714}_{X},\widetilde{\unicode[STIX]{x1D714}}_{X}$
be two Kähler metrics on
![]() $X$
, such that
$X$
, such that
for some
![]() $C>0$
. Assume first
$C>0$
. Assume first
![]() $\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
. Set
$\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
. Set
![]() $\widetilde{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D700}}:=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\widetilde{\unicode[STIX]{x1D714}}_{X}$
and observe that
$\widetilde{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D700}}:=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\widetilde{\unicode[STIX]{x1D714}}_{X}$
and observe that
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}\leqslant \widetilde{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D700}}\leqslant \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}^{\prime }}$
, where
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}\leqslant \widetilde{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D700}}\leqslant \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}^{\prime }}$
, where
![]() $\unicode[STIX]{x1D700}^{\prime }=\unicode[STIX]{x1D700}C$
. Let
$\unicode[STIX]{x1D700}^{\prime }=\unicode[STIX]{x1D700}C$
. Let
![]() $\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D711}}_{t}^{\unicode[STIX]{x1D700}}$
be the geodesic with respect to
$\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}},\tilde{\unicode[STIX]{x1D711}}_{t}^{\unicode[STIX]{x1D700}}$
be the geodesic with respect to
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
and
![]() $\widetilde{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D700}}$
, respectively, and observe that
$\widetilde{\unicode[STIX]{x1D714}}_{\unicode[STIX]{x1D700}}$
, respectively, and observe that
![]() $\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}}\leqslant \tilde{\unicode[STIX]{x1D711}}_{t}^{\unicode[STIX]{x1D700}}\leqslant \unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}^{\prime }}$
. The same arguments as before give
$\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}}\leqslant \tilde{\unicode[STIX]{x1D711}}_{t}^{\unicode[STIX]{x1D700}}\leqslant \unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}^{\prime }}$
. The same arguments as before give
hence
The latter tells us that the limit does not depend on
![]() $\unicode[STIX]{x1D714}_{X}$
. To get rid of the assumption
$\unicode[STIX]{x1D714}_{X}$
. To get rid of the assumption
![]() $\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
, one can use the Pythagorean formula, as before.◻
$\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
, one can use the Pythagorean formula, as before.◻
An adaptation of the classical Perron envelope technique yields the following result of Berndtsson [Reference BerndtssonBer15].
Proposition 1.17. Assume that
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
are bounded
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
are bounded
![]() $\unicode[STIX]{x1D714}$
-psh functions. Then
$\unicode[STIX]{x1D714}$
-psh functions. Then
is the unique bounded
![]() $\unicode[STIX]{x1D714}$
-psh function on
$\unicode[STIX]{x1D714}$
-psh function on
![]() $X\times S$
, which is the solution of the Dirichlet problem
$X\times S$
, which is the solution of the Dirichlet problem
![]() $\unicode[STIX]{x1D711}_{|X\times \unicode[STIX]{x2202}S}=\unicode[STIX]{x1D711}_{0,1}$
, with
$\unicode[STIX]{x1D711}_{|X\times \unicode[STIX]{x2202}S}=\unicode[STIX]{x1D711}_{0,1}$
, with
Moreover
![]() $\unicode[STIX]{x1D711}(x,z)=\unicode[STIX]{x1D711}(x,t)$
only depends on
$\unicode[STIX]{x1D711}(x,z)=\unicode[STIX]{x1D711}(x,t)$
only depends on
![]() $\Re (z)$
and
$\Re (z)$
and
![]() $|\dot{\unicode[STIX]{x1D711}}|\leqslant \Vert \unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\Vert _{L^{\infty }(X)}$
.
$|\dot{\unicode[STIX]{x1D711}}|\leqslant \Vert \unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\Vert _{L^{\infty }(X)}$
.
The proof goes exactly as that of Proposition 1.4. The function
![]() $\unicode[STIX]{x1D711}$
(or rather the path
$\unicode[STIX]{x1D711}$
(or rather the path
![]() $\unicode[STIX]{x1D711}_{t}\subset \text{PSH}(X,\unicode[STIX]{x1D714})\cap L^{\infty }(X)$
) is called a bounded geodesic in [Reference BerndtssonBer15]. We use the same terminology here, as it turns out that bounded geodesics are geodesics in the metric sense.
$\unicode[STIX]{x1D711}_{t}\subset \text{PSH}(X,\unicode[STIX]{x1D714})\cap L^{\infty }(X)$
) is called a bounded geodesic in [Reference BerndtssonBer15]. We use the same terminology here, as it turns out that bounded geodesics are geodesics in the metric sense.
Proposition 1.18. Bounded geodesics are metric geodesics. More precisely, if
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
are bounded
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
are bounded
![]() $\unicode[STIX]{x1D714}$
-psh functions and
$\unicode[STIX]{x1D714}$
-psh functions and
![]() $\unicode[STIX]{x1D711}(x,z)=\unicode[STIX]{x1D711}_{t}(x)$
is the bounded geodesic joining
$\unicode[STIX]{x1D711}(x,z)=\unicode[STIX]{x1D711}_{t}(x)$
is the bounded geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
, then for all
$\unicode[STIX]{x1D711}_{1}$
, then for all
![]() $t,s\in [0,1]$
,
$t,s\in [0,1]$
,
Proof. Let
![]() $\unicode[STIX]{x1D711}_{0}^{j},\unicode[STIX]{x1D711}_{1}^{k}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
be sequences decreasing, respectively, to
$\unicode[STIX]{x1D711}_{0}^{j},\unicode[STIX]{x1D711}_{1}^{k}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
be sequences decreasing, respectively, to
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
. It follows from the comparison principle and the uniqueness in Proposition 1.17 that
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
. It follows from the comparison principle and the uniqueness in Proposition 1.17 that
![]() $\unicode[STIX]{x1D711}_{t,j}$
decreases to
$\unicode[STIX]{x1D711}_{t,j}$
decreases to
![]() $\unicode[STIX]{x1D711}_{t}$
as
$\unicode[STIX]{x1D711}_{t}$
as
![]() $j$
increases to
$j$
increases to
![]() $+\infty$
. From Definition 1.15, Proposition 1.16 and the fact that the identity in the statement holds in the Kähler setting for
$+\infty$
. From Definition 1.15, Proposition 1.16 and the fact that the identity in the statement holds in the Kähler setting for
![]() $d_{\unicode[STIX]{x1D700}}$
we obtain
$d_{\unicode[STIX]{x1D700}}$
we obtain
 $$\begin{eqnarray}\displaystyle d_{p}(\unicode[STIX]{x1D711}_{t},\unicode[STIX]{x1D711}_{s}) & = & \displaystyle \liminf _{\unicode[STIX]{x1D700}\rightarrow 0}\liminf _{j,k\rightarrow +\infty }d_{p,\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D711}_{t,j},\unicode[STIX]{x1D711}_{s,k})\nonumber\\ \displaystyle & = & \displaystyle |t-s|\liminf _{\unicode[STIX]{x1D700}\rightarrow 0}\liminf _{j,k\rightarrow +\infty }d_{p,\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D711}_{0}^{j},\unicode[STIX]{x1D711}_{1}^{k})=|t-s|d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}).\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{p}(\unicode[STIX]{x1D711}_{t},\unicode[STIX]{x1D711}_{s}) & = & \displaystyle \liminf _{\unicode[STIX]{x1D700}\rightarrow 0}\liminf _{j,k\rightarrow +\infty }d_{p,\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D711}_{t,j},\unicode[STIX]{x1D711}_{s,k})\nonumber\\ \displaystyle & = & \displaystyle |t-s|\liminf _{\unicode[STIX]{x1D700}\rightarrow 0}\liminf _{j,k\rightarrow +\infty }d_{p,\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D711}_{0}^{j},\unicode[STIX]{x1D711}_{1}^{k})=|t-s|d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}).\Box \nonumber\end{eqnarray}$$
Remark 1.19. One can no longer expect that
![]() $d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})^{p}=\int _{X}|\dot{\unicode[STIX]{x1D711}}_{t}|^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})$
for a.e.
$d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})^{p}=\int _{X}|\dot{\unicode[STIX]{x1D711}}_{t}|^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})$
for a.e.
![]() $t\in [0,1]$
, as simple examples show. One can, e.g., take
$t\in [0,1]$
, as simple examples show. One can, e.g., take
![]() $\unicode[STIX]{x1D711}_{0}\equiv 0$
and
$\unicode[STIX]{x1D711}_{0}\equiv 0$
and
![]() $\unicode[STIX]{x1D711}_{1}=\max (u,0)$
, where
$\unicode[STIX]{x1D711}_{1}=\max (u,0)$
, where
![]() $u$
takes positive values, has isolated singularities, and solves
$u$
takes positive values, has isolated singularities, and solves
![]() $\operatorname{MA}(u)=\text{Dirac mass}$
at some point: in this case
$\operatorname{MA}(u)=\text{Dirac mass}$
at some point: in this case
![]() $\operatorname{MA}(\unicode[STIX]{x1D711}_{1})$
is concentrated on the contact set
$\operatorname{MA}(\unicode[STIX]{x1D711}_{1})$
is concentrated on the contact set
![]() $(u=0)$
while
$(u=0)$
while
![]() $\dot{\unicode[STIX]{x1D711}}_{1}\equiv 0$
on this set, hence
$\dot{\unicode[STIX]{x1D711}}_{1}\equiv 0$
on this set, hence
![]() $\int _{X}|\dot{\unicode[STIX]{x1D711}}_{1}|^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{1})=0$
. We thank Darvas for pointing this out to us.
$\int _{X}|\dot{\unicode[STIX]{x1D711}}_{1}|^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{1})=0$
. We thank Darvas for pointing this out to us.
As this remark points out, we do not have that
![]() $d_{p}^{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})=I(0)=I(1)$
when
$d_{p}^{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})=I(0)=I(1)$
when
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
are just bounded
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
are just bounded
![]() $\unicode[STIX]{x1D714}$
-psh functions. Nevertheless, we can still recover the formula in some special cases.
$\unicode[STIX]{x1D714}$
-psh functions. Nevertheless, we can still recover the formula in some special cases.
We start by recalling the following.
Theorem 1.20. Let
![]() $f$
be a continuous function, such that
$f$
be a continuous function, such that
![]() $dd^{c}f\leqslant C\unicode[STIX]{x1D714}_{X}$
on
$dd^{c}f\leqslant C\unicode[STIX]{x1D714}_{X}$
on
![]() $X$
, for some
$X$
, for some
![]() $C>0$
. Then
$C>0$
. Then
![]() $P(f)$
has bounded Laplacian on
$P(f)$
has bounded Laplacian on
![]() $\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})$
and
$\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})$
and
The fact that
![]() $P(f)$
has a locally bounded Laplacian in
$P(f)$
has a locally bounded Laplacian in
![]() $\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})$
is essentially [Reference BermanBer13, Theorem 1.2]. We do not assume here that
$\operatorname{Amp}(\{\unicode[STIX]{x1D714}\})$
is essentially [Reference BermanBer13, Theorem 1.2]. We do not assume here that
![]() $f$
is smooth but one can check that the upper bound on
$f$
is smooth but one can check that the upper bound on
![]() $dd^{c}f$
is the only estimate needed to pursue Berman’s approach. One can then argue as in [Reference Guedj and ZeriahiGZ17, Theorem 9.25] to get (4).
$dd^{c}f$
is the only estimate needed to pursue Berman’s approach. One can then argue as in [Reference Guedj and ZeriahiGZ17, Theorem 9.25] to get (4).
Set
Theorem 1.21. Assume that
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
. Let
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
. Let
![]() $\unicode[STIX]{x1D711}_{t}$
be the Mabuchi geodesic joining
$\unicode[STIX]{x1D711}_{t}$
be the Mabuchi geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
and
$\unicode[STIX]{x1D711}_{0}$
and
![]() $\unicode[STIX]{x1D711}_{1}$
. Then
$\unicode[STIX]{x1D711}_{1}$
. Then
Proof. Set
![]() $\unicode[STIX]{x1D711}_{0,\unicode[STIX]{x1D700}}:=P_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(f_{0})$
and
$\unicode[STIX]{x1D711}_{0,\unicode[STIX]{x1D700}}:=P_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(f_{0})$
and
![]() $\unicode[STIX]{x1D711}_{1,\unicode[STIX]{x1D700}}:=P_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(f_{1})$
. Clearly,
$\unicode[STIX]{x1D711}_{1,\unicode[STIX]{x1D700}}:=P_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(f_{1})$
. Clearly,
![]() $\unicode[STIX]{x1D711}_{i,\unicode[STIX]{x1D700}}$
decreases pointwise to
$\unicode[STIX]{x1D711}_{i,\unicode[STIX]{x1D700}}$
decreases pointwise to
![]() $\unicode[STIX]{x1D711}_{i}$
,
$\unicode[STIX]{x1D711}_{i}$
,
![]() $i=1,2$
. Let
$i=1,2$
. Let
![]() $\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}}$
be the
$\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}}$
be the
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
-geodesic joining
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
-geodesic joining
![]() $\unicode[STIX]{x1D711}_{0,\unicode[STIX]{x1D700}}$
and
$\unicode[STIX]{x1D711}_{0,\unicode[STIX]{x1D700}}$
and
![]() $\unicode[STIX]{x1D711}_{1,\unicode[STIX]{x1D700}}$
. Combining [Reference DarvasDar15, Theorem 3.5] with (4), we get
$\unicode[STIX]{x1D711}_{1,\unicode[STIX]{x1D700}}$
. Combining [Reference DarvasDar15, Theorem 3.5] with (4), we get
Set
![]() $D_{\unicode[STIX]{x1D700}}:=\{\unicode[STIX]{x1D711}_{0,\unicode[STIX]{x1D700}}=f_{0}\}$
,
$D_{\unicode[STIX]{x1D700}}:=\{\unicode[STIX]{x1D711}_{0,\unicode[STIX]{x1D700}}=f_{0}\}$
,
![]() $D_{0}:=\{\unicode[STIX]{x1D711}_{0}=f_{0}\}$
, and observe that
$D_{0}:=\{\unicode[STIX]{x1D711}_{0}=f_{0}\}$
, and observe that
![]() $D_{0}\subseteq D_{\unicode[STIX]{x1D700}}$
. Since
$D_{0}\subseteq D_{\unicode[STIX]{x1D700}}$
. Since
![]() $\unicode[STIX]{x1D711}_{0,\unicode[STIX]{x1D700}}=P_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(f)$
and
$\unicode[STIX]{x1D711}_{0,\unicode[STIX]{x1D700}}=P_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(f)$
and
![]() $\unicode[STIX]{x1D711}_{0}=P_{\unicode[STIX]{x1D714}}(f)$
, Theorem 1.20 ensures that
$\unicode[STIX]{x1D711}_{0}=P_{\unicode[STIX]{x1D714}}(f)$
, Theorem 1.20 ensures that
![]() $(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D711}_{0,\unicode[STIX]{x1D700}})^{n}=g_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}_{X}^{n}$
and
$(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D711}_{0,\unicode[STIX]{x1D700}})^{n}=g_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}_{X}^{n}$
and
![]() $(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}_{0})^{n}=g_{0}\unicode[STIX]{x1D714}_{X}^{n}$
where
$(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}_{0})^{n}=g_{0}\unicode[STIX]{x1D714}_{X}^{n}$
where
![]() $g_{\unicode[STIX]{x1D700}},g_{0}$
are defined as
$g_{\unicode[STIX]{x1D700}},g_{0}$
are defined as
 $$\begin{eqnarray}g_{\unicode[STIX]{x1D700}}:=\left\{\begin{array}{@{}ll@{}}0,\quad & x\notin D_{\unicode[STIX]{x1D700}},\\ \displaystyle \frac{(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}f_{0})^{n}}{\unicode[STIX]{x1D714}_{X}^{n}},\quad & x\in D_{\unicode[STIX]{x1D700}},\end{array}\right.\quad g_{0}:=\left\{\begin{array}{@{}ll@{}}0,\quad & x\notin D_{0},\\ \displaystyle \frac{(\unicode[STIX]{x1D714}+dd^{c}f_{0})^{n}}{\unicode[STIX]{x1D714}_{X}^{n}},\quad & x\in D_{0}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}g_{\unicode[STIX]{x1D700}}:=\left\{\begin{array}{@{}ll@{}}0,\quad & x\notin D_{\unicode[STIX]{x1D700}},\\ \displaystyle \frac{(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}f_{0})^{n}}{\unicode[STIX]{x1D714}_{X}^{n}},\quad & x\in D_{\unicode[STIX]{x1D700}},\end{array}\right.\quad g_{0}:=\left\{\begin{array}{@{}ll@{}}0,\quad & x\notin D_{0},\\ \displaystyle \frac{(\unicode[STIX]{x1D714}+dd^{c}f_{0})^{n}}{\unicode[STIX]{x1D714}_{X}^{n}},\quad & x\in D_{0}.\end{array}\right.\end{eqnarray}$$
We claim that
![]() $g_{\unicode[STIX]{x1D700}}$
converges pointwise to
$g_{\unicode[STIX]{x1D700}}$
converges pointwise to
![]() $g_{0}$
. Indeed, when
$g_{0}$
. Indeed, when
![]() $x\in D_{0}\subseteq D_{\unicode[STIX]{x1D700}}$
, then
$x\in D_{0}\subseteq D_{\unicode[STIX]{x1D700}}$
, then
![]() $g_{\unicode[STIX]{x1D700}}(x)=((\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}f_{0})^{n}/\unicode[STIX]{x1D714}_{X}^{n})(x)$
converges to
$g_{\unicode[STIX]{x1D700}}(x)=((\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}f_{0})^{n}/\unicode[STIX]{x1D714}_{X}^{n})(x)$
converges to
![]() $((\unicode[STIX]{x1D714}+dd^{c}f_{0})^{n}/\unicode[STIX]{x1D714}_{X}^{n})(x)=g_{0}(x)$
as
$((\unicode[STIX]{x1D714}+dd^{c}f_{0})^{n}/\unicode[STIX]{x1D714}_{X}^{n})(x)=g_{0}(x)$
as
![]() $\unicode[STIX]{x1D700}$
goes to 0. In the case when
$\unicode[STIX]{x1D700}$
goes to 0. In the case when
![]() $x\notin D_{0}$
, i.e.
$x\notin D_{0}$
, i.e.
![]() $\unicode[STIX]{x1D711}_{0}(x)<f_{0}(x)$
, since
$\unicode[STIX]{x1D711}_{0}(x)<f_{0}(x)$
, since
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}(x)$
decreases to
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}(x)$
decreases to
![]() $\unicode[STIX]{x1D711}_{0}(x)$
as
$\unicode[STIX]{x1D711}_{0}(x)$
as
![]() $\unicode[STIX]{x1D700}$
goes to zero, we can infer that, for
$\unicode[STIX]{x1D700}$
goes to zero, we can infer that, for
![]() $\unicode[STIX]{x1D700}$
sufficiently small, we still have
$\unicode[STIX]{x1D700}$
sufficiently small, we still have
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}(x)<f_{0}(x)$
, which means
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700}}(x)<f_{0}(x)$
, which means
![]() $x\notin D_{\unicode[STIX]{x1D700}}$
. Hence,
$x\notin D_{\unicode[STIX]{x1D700}}$
. Hence,
![]() $g_{\unicode[STIX]{x1D700}}(x)=0=g_{0}(x)$
. The claim is then proved.
$g_{\unicode[STIX]{x1D700}}(x)=0=g_{0}(x)$
. The claim is then proved.
Since
![]() $\unicode[STIX]{x1D7D9}_{D_{\unicode[STIX]{x1D700}}}\unicode[STIX]{x1D711}_{0}^{\unicode[STIX]{x1D700}}=f_{0}=\unicode[STIX]{x1D7D9}_{D_{0}}\unicode[STIX]{x1D711}_{0}$
, the same arguments in Theorem 1.13 show that
$\unicode[STIX]{x1D7D9}_{D_{\unicode[STIX]{x1D700}}}\unicode[STIX]{x1D711}_{0}^{\unicode[STIX]{x1D700}}=f_{0}=\unicode[STIX]{x1D7D9}_{D_{0}}\unicode[STIX]{x1D711}_{0}$
, the same arguments in Theorem 1.13 show that
![]() $|\unicode[STIX]{x1D7D9}_{D_{\unicode[STIX]{x1D700}}}\dot{\unicode[STIX]{x1D711}}_{0}^{\unicode[STIX]{x1D700}}-\unicode[STIX]{x1D7D9}_{D_{0}}\dot{\unicode[STIX]{x1D711}}_{0}|$
converges pointwise to 0 as
$|\unicode[STIX]{x1D7D9}_{D_{\unicode[STIX]{x1D700}}}\dot{\unicode[STIX]{x1D711}}_{0}^{\unicode[STIX]{x1D700}}-\unicode[STIX]{x1D7D9}_{D_{0}}\dot{\unicode[STIX]{x1D711}}_{0}|$
converges pointwise to 0 as
![]() $\unicode[STIX]{x1D700}$
goes to zero.
$\unicode[STIX]{x1D700}$
goes to zero.
We thus infer that
![]() $\unicode[STIX]{x1D7D9}_{D_{\unicode[STIX]{x1D700}}}|\dot{\unicode[STIX]{x1D711}_{0}^{\unicode[STIX]{x1D700}}}|^{p}g_{\unicode[STIX]{x1D700}}$
converges pointwise to
$\unicode[STIX]{x1D7D9}_{D_{\unicode[STIX]{x1D700}}}|\dot{\unicode[STIX]{x1D711}_{0}^{\unicode[STIX]{x1D700}}}|^{p}g_{\unicode[STIX]{x1D700}}$
converges pointwise to
![]() $\unicode[STIX]{x1D7D9}_{D_{0}}|\dot{\unicode[STIX]{x1D711}_{0}}|^{p}g_{0}$
as
$\unicode[STIX]{x1D7D9}_{D_{0}}|\dot{\unicode[STIX]{x1D711}_{0}}|^{p}g_{0}$
as
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
. The dominated convergence theorem yields
$\unicode[STIX]{x1D700}\rightarrow 0$
. The dominated convergence theorem yields
hence the conclusion. ◻
Observe that if
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
, then
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
, then
![]() $\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
. Indeed, since
$\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
. Indeed, since
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
are smooth, the functions
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
are smooth, the functions
![]() $-\unicode[STIX]{x1D711}_{0},-\unicode[STIX]{x1D711}_{1}$
are quasi-plurisubharmonic, i.e. there exists
$-\unicode[STIX]{x1D711}_{0},-\unicode[STIX]{x1D711}_{1}$
are quasi-plurisubharmonic, i.e. there exists
![]() $C>0$
such that
$C>0$
such that
![]() $dd^{c}(-\unicode[STIX]{x1D711}_{i})\geqslant -C\unicode[STIX]{x1D714}_{X}$
for any
$dd^{c}(-\unicode[STIX]{x1D711}_{i})\geqslant -C\unicode[STIX]{x1D714}_{X}$
for any
![]() $i=1,2$
. Thus,
$i=1,2$
. Thus,
![]() $\min (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})=-\text{max}(-\unicode[STIX]{x1D711}_{0},-\unicode[STIX]{x1D711}_{1})$
is such that
$\min (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})=-\text{max}(-\unicode[STIX]{x1D711}_{0},-\unicode[STIX]{x1D711}_{1})$
is such that
In particular, (5) holds for
![]() $d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1})$
and
$d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1})$
and
![]() $d_{p}(\unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1})$
.
$d_{p}(\unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1})$
.
2 Finite-energy classes
We define in this section the set
![]() ${\mathcal{E}}(\unicode[STIX]{x1D6FC})$
(respectively
${\mathcal{E}}(\unicode[STIX]{x1D6FC})$
(respectively
![]() ${\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC})$
) of positive closed currents
${\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC})$
) of positive closed currents
![]() $T=\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}$
with full Monge–Ampère mass (respectively finite weighted energy) in
$T=\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}$
with full Monge–Ampère mass (respectively finite weighted energy) in
![]() $\unicode[STIX]{x1D6FC}$
, by defining the corresponding class
$\unicode[STIX]{x1D6FC}$
, by defining the corresponding class
![]() ${\mathcal{E}}(X,\unicode[STIX]{x1D714})$
(respectively
${\mathcal{E}}(X,\unicode[STIX]{x1D714})$
(respectively
![]() ${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
) of finite-energy potentials
${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
) of finite-energy potentials
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
2.1 The space
 ${\mathcal{E}}(\unicode[STIX]{x1D6FC})$
${\mathcal{E}}(\unicode[STIX]{x1D6FC})$
2.1.1 Quasi-plurisubharmonic functions
Recall that a function is quasi-plurisubharmonic if it is locally given as the sum of a smooth and a psh function. In particular quasi-psh (qpsh for short) functions are upper semi-continuous and integrable.
Definition 2.1. We let
![]() $\text{PSH}(X,\unicode[STIX]{x1D714})$
denote the set of all
$\text{PSH}(X,\unicode[STIX]{x1D714})$
denote the set of all
![]() $\unicode[STIX]{x1D714}$
-plurisubharmonic functions. These are quasi-psh functions
$\unicode[STIX]{x1D714}$
-plurisubharmonic functions. These are quasi-psh functions
![]() $\unicode[STIX]{x1D711}:X\rightarrow \mathbb{R}\cup \{-\infty \}$
such that
$\unicode[STIX]{x1D711}:X\rightarrow \mathbb{R}\cup \{-\infty \}$
such that
in the weak sense of currents.
The set
![]() $\text{PSH}(X,\unicode[STIX]{x1D714})$
is a closed subset of
$\text{PSH}(X,\unicode[STIX]{x1D714})$
is a closed subset of
![]() $L^{1}(X)$
, for the
$L^{1}(X)$
, for the
![]() $L^{1}$
-topology.
$L^{1}$
-topology.
2.1.2 The class
 ${\mathcal{E}}(X,\unicode[STIX]{x1D714})$
${\mathcal{E}}(X,\unicode[STIX]{x1D714})$
Given
![]() $\unicode[STIX]{x1D711}\in \text{PSH}(X,\unicode[STIX]{x1D714})$
, we consider
$\unicode[STIX]{x1D711}\in \text{PSH}(X,\unicode[STIX]{x1D714})$
, we consider
It follows from the Bedford–Taylor theory [Reference Bedford and TaylorBT82] that the
![]() $\operatorname{MA}(\unicode[STIX]{x1D711}_{j})$
are well-defined probability measures. Moreover, the sequence
$\operatorname{MA}(\unicode[STIX]{x1D711}_{j})$
are well-defined probability measures. Moreover, the sequence
![]() $\unicode[STIX]{x1D707}_{j}:=\unicode[STIX]{x1D7D9}_{\{\unicode[STIX]{x1D711}>-j\}}\operatorname{MA}(\unicode[STIX]{x1D711}_{j})$
is increasing [Reference Guedj and ZeriahiGZ07, p. 445]. Since the
$\unicode[STIX]{x1D707}_{j}:=\unicode[STIX]{x1D7D9}_{\{\unicode[STIX]{x1D711}>-j\}}\operatorname{MA}(\unicode[STIX]{x1D711}_{j})$
is increasing [Reference Guedj and ZeriahiGZ07, p. 445]. Since the
![]() $\unicode[STIX]{x1D707}_{j}$
all have total mass bounded from above by
$\unicode[STIX]{x1D707}_{j}$
all have total mass bounded from above by
![]() $1$
, we consider
$1$
, we consider
which is a positive Borel measure on
![]() $X$
, with total mass
$X$
, with total mass
![]() ${\leqslant}1$
.
${\leqslant}1$
.
Definition 2.2. We set
For
![]() $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D714})$
, we set
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D714})$
, we set
![]() $\operatorname{MA}(\unicode[STIX]{x1D711}):=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D711}}$
.
$\operatorname{MA}(\unicode[STIX]{x1D711}):=\unicode[STIX]{x1D707}_{\unicode[STIX]{x1D711}}$
.
The latter can be characterized as the largest class for which the complex Monge–Ampère mass is well defined and the maximum principle holds [Reference Guedj and ZeriahiGZ07, Theorem 1.5]. We further note that the domination principle holds ([Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Corollary 2.5], [Reference Darvas, Di Nezza and LuDDL18, Proposition 2.4]).
Proposition 2.3. If
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D714})$
are such that
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D714})$
are such that
then
![]() $\unicode[STIX]{x1D711}(x)\leqslant \unicode[STIX]{x1D713}(x)$
for all
$\unicode[STIX]{x1D711}(x)\leqslant \unicode[STIX]{x1D713}(x)$
for all
![]() $x\in X$
.
$x\in X$
.
It follows from the
![]() $\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma that any positive closed current
$\unicode[STIX]{x2202}\overline{\unicode[STIX]{x2202}}$
-lemma that any positive closed current
![]() $T\in \unicode[STIX]{x1D6FC}$
can be written
$T\in \unicode[STIX]{x1D6FC}$
can be written
![]() $T=\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}$
for some function
$T=\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}$
for some function
![]() $\unicode[STIX]{x1D711}\in \text{PSH}(X,\unicode[STIX]{x1D714})$
that is unique up to an additive constant.
$\unicode[STIX]{x1D711}\in \text{PSH}(X,\unicode[STIX]{x1D714})$
that is unique up to an additive constant.
Definition 2.4. We let
![]() ${\mathcal{E}}(\unicode[STIX]{x1D6FC})$
denote the set of all positive currents in
${\mathcal{E}}(\unicode[STIX]{x1D6FC})$
denote the set of all positive currents in
![]() $\unicode[STIX]{x1D6FC}$
,
$\unicode[STIX]{x1D6FC}$
,
![]() $T=\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}$
, with
$T=\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}$
, with
![]() $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D714})$
.
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D714})$
.
Note that this definition does not depend on the choice of
![]() $\unicode[STIX]{x1D714}$
, nor does it depend on the choice of
$\unicode[STIX]{x1D714}$
, nor does it depend on the choice of
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
2.2 The class
 ${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
2.2.1 The Aubin–Mabuchi functional
Each tangent space
![]() $T_{\unicode[STIX]{x1D711}}{\mathcal{H}}_{\unicode[STIX]{x1D714}}$
admits the following orthogonal decomposition
$T_{\unicode[STIX]{x1D711}}{\mathcal{H}}_{\unicode[STIX]{x1D714}}$
admits the following orthogonal decomposition
where
![]() $\unicode[STIX]{x1D6FD}=\operatorname{MA}$
is the 1-form defined on
$\unicode[STIX]{x1D6FD}=\operatorname{MA}$
is the 1-form defined on
![]() ${\mathcal{H}}$
by
${\mathcal{H}}$
by
It is a classical observation of Mabuchi that the 1-form
![]() $\unicode[STIX]{x1D6FD}$
is closed. Therefore, there exists a unique function
$\unicode[STIX]{x1D6FD}$
is closed. Therefore, there exists a unique function
![]() $E$
defined on the convex open set
$E$
defined on the convex open set
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
, such that
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
, such that
![]() $\unicode[STIX]{x1D6FD}=dE$
and
$\unicode[STIX]{x1D6FD}=dE$
and
![]() $E(0)=0$
. It is often called the Aubin–Mabuchi functional and can be expressed (after integration along affine paths) by
$E(0)=0$
. It is often called the Aubin–Mabuchi functional and can be expressed (after integration along affine paths) by
Lemma 2.5. The Aubin–Mabuchi functional
![]() $E$
is concave along Euclidean segments, non-decreasing, and satisfies the cocycle condition
$E$
is concave along Euclidean segments, non-decreasing, and satisfies the cocycle condition
It is affine along geodesics and convex along subgeodesics in
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
.
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
.
Proof. These properties are well known when
![]() $\unicode[STIX]{x1D714}$
is in a Kähler class.
$\unicode[STIX]{x1D714}$
is in a Kähler class.
The monotonicity property follows from the definition since the first derivative of
![]() $E$
is
$E$
is
![]() $dE=\unicode[STIX]{x1D6FD}=\operatorname{MA}\geqslant 0$
, a probability measure: if
$dE=\unicode[STIX]{x1D6FD}=\operatorname{MA}\geqslant 0$
, a probability measure: if
![]() $\unicode[STIX]{x1D711}_{t}$
is an arbitrary path, then
$\unicode[STIX]{x1D711}_{t}$
is an arbitrary path, then
It follows from Stokes theorem that
 $$\begin{eqnarray}\displaystyle \frac{d^{2}}{dt^{2}}E(\unicode[STIX]{x1D711}_{t}) & = & \displaystyle \int _{X}\ddot{\unicode[STIX]{x1D711}_{t}}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})+\frac{n}{V_{\unicode[STIX]{x1D6FC}}}\int _{X}\dot{\unicode[STIX]{x1D711}_{t}}\,dd^{c}\dot{\unicode[STIX]{x1D711}_{t}}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}^{n-1}\nonumber\\ \displaystyle & = & \displaystyle \int _{X}\biggl\{\ddot{\unicode[STIX]{x1D711}_{t}}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})-\frac{n}{V_{\unicode[STIX]{x1D6FC}}}\,d\dot{\unicode[STIX]{x1D711}_{t}}\wedge d^{c}\dot{\unicode[STIX]{x1D711}_{t}}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}_{t}}^{n-1}\biggr\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{d^{2}}{dt^{2}}E(\unicode[STIX]{x1D711}_{t}) & = & \displaystyle \int _{X}\ddot{\unicode[STIX]{x1D711}_{t}}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})+\frac{n}{V_{\unicode[STIX]{x1D6FC}}}\int _{X}\dot{\unicode[STIX]{x1D711}_{t}}\,dd^{c}\dot{\unicode[STIX]{x1D711}_{t}}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}^{n-1}\nonumber\\ \displaystyle & = & \displaystyle \int _{X}\biggl\{\ddot{\unicode[STIX]{x1D711}_{t}}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})-\frac{n}{V_{\unicode[STIX]{x1D6FC}}}\,d\dot{\unicode[STIX]{x1D711}_{t}}\wedge d^{c}\dot{\unicode[STIX]{x1D711}_{t}}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}_{t}}^{n-1}\biggr\}.\nonumber\end{eqnarray}$$
Thus,
![]() $E$
is concave along Euclidean segments (
$E$
is concave along Euclidean segments (
![]() $\ddot{\unicode[STIX]{x1D711}}_{t}=0$
), affine along Mabuchi geodesics, and convex along Mabuchi subgeodesics. The cocycle condition follows by differentiating
$\ddot{\unicode[STIX]{x1D711}}_{t}=0$
), affine along Mabuchi geodesics, and convex along Mabuchi subgeodesics. The cocycle condition follows by differentiating
![]() $E(t\unicode[STIX]{x1D711}+(1-t)\unicode[STIX]{x1D713})$
.
$E(t\unicode[STIX]{x1D711}+(1-t)\unicode[STIX]{x1D713})$
.
These computations are merely heuristic as
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}(x)$
is poorly regular when
$t\rightarrow \unicode[STIX]{x1D711}_{t}(x)$
is poorly regular when
![]() $\unicode[STIX]{x1D711}_{t}$
is a geodesic or subgeodesic. We can, however, approximate
$\unicode[STIX]{x1D711}_{t}$
is a geodesic or subgeodesic. We can, however, approximate
![]() $\unicode[STIX]{x1D714}$
by
$\unicode[STIX]{x1D714}$
by
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}$
; consider
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}$
; consider
![]() $(\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}})$
the corresponding geodesic
$(\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}})$
the corresponding geodesic
It follows from Proposition 1.6 that
![]() $\unicode[STIX]{x1D700}\mapsto \unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}}$
decreases to
$\unicode[STIX]{x1D700}\mapsto \unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}}$
decreases to
![]() $\unicode[STIX]{x1D711}_{t}$
; hence,
$\unicode[STIX]{x1D711}_{t}$
; hence,
![]() $t\mapsto E(\unicode[STIX]{x1D711}_{t})$
is affine, where the limit of the affine maps
$t\mapsto E(\unicode[STIX]{x1D711}_{t})$
is affine, where the limit of the affine maps
![]() $t\mapsto E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}})$
.
$t\mapsto E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711}_{t}^{\unicode[STIX]{x1D700}})$
.
For subgeodesics, we again approximate
![]() $\unicode[STIX]{x1D714}$
by
$\unicode[STIX]{x1D714}$
by
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
and we proceed as in the Kähler case.◻
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
and we proceed as in the Kähler case.◻
Observe that
![]() $E(\unicode[STIX]{x1D711}+t)=E(\unicode[STIX]{x1D711})+t$
. Given
$E(\unicode[STIX]{x1D711}+t)=E(\unicode[STIX]{x1D711})+t$
. Given
![]() $\unicode[STIX]{x1D711}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
there exists a unique
$\unicode[STIX]{x1D711}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
there exists a unique
![]() $c\in \mathbb{R}$
such that
$c\in \mathbb{R}$
such that
![]() $E(\unicode[STIX]{x1D711}+c)=0$
. The restriction of the Mabuchi metric to the fiber
$E(\unicode[STIX]{x1D711}+c)=0$
. The restriction of the Mabuchi metric to the fiber
![]() $E^{-1}(0)$
induces a Riemannian structure on the quotient space
$E^{-1}(0)$
induces a Riemannian structure on the quotient space
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D6FC}}={\mathcal{H}}_{\unicode[STIX]{x1D714}}/\mathbb{R}$
and allows decomposition of
${\mathcal{H}}_{\unicode[STIX]{x1D6FC}}={\mathcal{H}}_{\unicode[STIX]{x1D714}}/\mathbb{R}$
and allows decomposition of
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}={\mathcal{H}}_{\unicode[STIX]{x1D6FC}}\times \mathbb{R}$
as a product of Riemannian manifolds.
${\mathcal{H}}_{\unicode[STIX]{x1D714}}={\mathcal{H}}_{\unicode[STIX]{x1D6FC}}\times \mathbb{R}$
as a product of Riemannian manifolds.
Definition 2.6. For
![]() $\unicode[STIX]{x1D711}\in \text{PSH}(X,\unicode[STIX]{x1D714})$
, we set
$\unicode[STIX]{x1D711}\in \text{PSH}(X,\unicode[STIX]{x1D714})$
, we set
and
![]() ${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714}):=\{\unicode[STIX]{x1D711}\in \text{PSH}(X,\unicode[STIX]{x1D714});E(\unicode[STIX]{x1D711})>-\infty \}$
.
${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714}):=\{\unicode[STIX]{x1D711}\in \text{PSH}(X,\unicode[STIX]{x1D714});E(\unicode[STIX]{x1D711})>-\infty \}$
.
2.2.2 Strong topology on
 ${\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC})$
${\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC})$
Set
It has been shown in [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ] that
![]() $I$
defines a complete metrizable uniform structure on
$I$
defines a complete metrizable uniform structure on
![]() ${\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC})$
. More precisely, we identify
${\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC})$
. More precisely, we identify
![]() ${\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC})$
with the set
${\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC})$
with the set
of normalized potentials. Then:
(a)
 $I$
is symmetric and positive on
$I$
is symmetric and positive on
 ${\mathcal{E}}_{\text{norm}}^{1}(X,\unicode[STIX]{x1D714})^{2}\setminus \{\text{diagonal}\}$
;
${\mathcal{E}}_{\text{norm}}^{1}(X,\unicode[STIX]{x1D714})^{2}\setminus \{\text{diagonal}\}$
;(b)
 $I$
satisfies a quasi-triangle inequality [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Theorem 1.8];
$I$
satisfies a quasi-triangle inequality [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Theorem 1.8];(c)
 $I$
induces a uniform structure that is metrizable [Reference BourbakiBou07];
$I$
induces a uniform structure that is metrizable [Reference BourbakiBou07];(d) the metric space
 $({\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC}),d_{I})$
is complete [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Proposition 2.4], where
$({\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC}),d_{I})$
is complete [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Proposition 2.4], where
 $d_{I}$
denotes one of the distances induced by the uniform structure
$d_{I}$
denotes one of the distances induced by the uniform structure
 $I$
.
$I$
.
Definition 2.7. The strong topology on
![]() ${\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC})$
is the metrizable topology defined by
${\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC})$
is the metrizable topology defined by
![]() $I$
.
$I$
.
The corresponding notion of convergence is the convergence in energy previously introduced in [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13] (see [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Proposition 2.3]). It is the coarsest refinement of the weak topology such that
![]() $E$
becomes continuous. In particular, if
$E$
becomes continuous. In particular, if
![]() $T_{j}\longrightarrow T$
in
$T_{j}\longrightarrow T$
in
![]() $({\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC}),d_{I})$
, then
$({\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC}),d_{I})$
, then
in the weak sense of Radon measures, while the Monge–Ampère operator is usually discontinuous for the weak topology of currents.
2.2.3 Yet another distance
To fit in with the notation of the next section, we introduce yet another notion of convergence in
![]() ${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
. We set
${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
. We set
This symmetric quantity is non-negative. It follows from Proposition 2.3 that it only vanishes on the diagonal of
![]() ${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})^{2}$
, while Theorem 3.6 will insure that it satisfies a quasi-triangle inequality. Hence,
${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})^{2}$
, while Theorem 3.6 will insure that it satisfies a quasi-triangle inequality. Hence,
![]() $I_{1}$
induces a uniform structure, which is metrizable [Reference BourbakiBou07].
$I_{1}$
induces a uniform structure, which is metrizable [Reference BourbakiBou07].
For
![]() $C>0$
, we set
$C>0$
, we set
It follows from Hartogs’ lemma, the upper semi-continuity, and the concavity of
![]() $E$
along Euclidean segments (Lemma 2.5) that this set is a compact and convex subset of
$E$
along Euclidean segments (Lemma 2.5) that this set is a compact and convex subset of
![]() $\text{PSH}(X,\unicode[STIX]{x1D714})$
, when endowed with the
$\text{PSH}(X,\unicode[STIX]{x1D714})$
, when endowed with the
![]() $L^{1}$
-topology (see [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Lemma 2.6]).
$L^{1}$
-topology (see [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Lemma 2.6]).
Proposition 2.8. For all
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
,
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
,
![]() $I(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\leqslant 2I_{1}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
. Conversely, for each
$I(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\leqslant 2I_{1}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
. Conversely, for each
![]() $C>0$
, there exists
$C>0$
, there exists
![]() $A>0$
such that, for all
$A>0$
such that, for all
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}_{C}^{1}(X,\unicode[STIX]{x1D714})$
,
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}_{C}^{1}(X,\unicode[STIX]{x1D714})$
,
In particular, the topologies induced by
![]() $I,I_{1}$
on
$I,I_{1}$
on
![]() ${\mathcal{E}}_{\text{norm}}^{1}(X,\unicode[STIX]{x1D714})$
are the same.
${\mathcal{E}}_{\text{norm}}^{1}(X,\unicode[STIX]{x1D714})$
are the same.
Observe that
![]() $I_{1}$
induces a distance on
$I_{1}$
induces a distance on
![]() ${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
, but
${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
, but
![]() $I$
is merely defined on
$I$
is merely defined on
![]() ${\mathcal{E}}_{\text{norm}}^{1}(X,\unicode[STIX]{x1D714})$
, as
${\mathcal{E}}_{\text{norm}}^{1}(X,\unicode[STIX]{x1D714})$
, as
![]() $I(\unicode[STIX]{x1D711}+c,\unicode[STIX]{x1D713}+c^{\prime })=I(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
, for any
$I(\unicode[STIX]{x1D711}+c,\unicode[STIX]{x1D713}+c^{\prime })=I(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
, for any
![]() $c,c^{\prime }\in \mathbb{R}$
.
$c,c^{\prime }\in \mathbb{R}$
.
Proof. The first inequality is obvious, as
It follows from Proposition 2.13 that
hence it suffices to establish the second inequality when
![]() $\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D713}$
. In this case
$\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D713}$
. In this case
by Lemma 2.12, while the Cauchy–Schwarz inequality yields
 $$\begin{eqnarray}\displaystyle \int _{X}(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D711})\operatorname{MA}(\unicode[STIX]{x1D711}) & = & \displaystyle \int _{X}(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D711})\operatorname{MA}(0)+\int _{X}d(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D713})\wedge d^{c}\unicode[STIX]{x1D711}\wedge S_{\unicode[STIX]{x1D711}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \int _{X}(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D711})\operatorname{MA}(0)+I(\unicode[STIX]{x1D711},0)^{1/2}\biggl(\int _{X}d(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D713})\wedge d^{c}(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D713})\wedge S_{\unicode[STIX]{x1D711}}\biggr)^{1/2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{X}(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D711})\operatorname{MA}(\unicode[STIX]{x1D711}) & = & \displaystyle \int _{X}(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D711})\operatorname{MA}(0)+\int _{X}d(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D713})\wedge d^{c}\unicode[STIX]{x1D711}\wedge S_{\unicode[STIX]{x1D711}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \int _{X}(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D711})\operatorname{MA}(0)+I(\unicode[STIX]{x1D711},0)^{1/2}\biggl(\int _{X}d(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D713})\wedge d^{c}(\unicode[STIX]{x1D711}-\unicode[STIX]{x1D713})\wedge S_{\unicode[STIX]{x1D711}}\biggr)^{1/2},\nonumber\end{eqnarray}$$
where we have set
![]() $S_{\unicode[STIX]{x1D711}}:=\sum _{j=0}^{n-1}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}^{j}\wedge \unicode[STIX]{x1D714}^{n-1-j}$
. Observing that
$S_{\unicode[STIX]{x1D711}}:=\sum _{j=0}^{n-1}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}^{j}\wedge \unicode[STIX]{x1D714}^{n-1-j}$
. Observing that
![]() $S_{\unicode[STIX]{x1D711}}\leqslant 2^{n-1}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}/2}^{n-1}$
, we can invoke [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Lemma 1.9] to obtain
$S_{\unicode[STIX]{x1D711}}\leqslant 2^{n-1}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}/2}^{n-1}$
, we can invoke [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Lemma 1.9] to obtain
Now
![]() $I(\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}/2)\leqslant a_{n}I(\unicode[STIX]{x1D711},0)\leqslant C^{\prime }$
and [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Theorem 1.3] yields
$I(\unicode[STIX]{x1D711},\unicode[STIX]{x1D711}/2)\leqslant a_{n}I(\unicode[STIX]{x1D711},0)\leqslant C^{\prime }$
and [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Theorem 1.3] yields
We thus get (7).
To prove the last statement, we need to show that, given a sequence
![]() $\unicode[STIX]{x1D711}_{j}\in {\mathcal{E}}_{\text{norm}}^{1}(X,\unicode[STIX]{x1D714})$
converging to
$\unicode[STIX]{x1D711}_{j}\in {\mathcal{E}}_{\text{norm}}^{1}(X,\unicode[STIX]{x1D714})$
converging to
![]() $\unicode[STIX]{x1D713}$
with respect to
$\unicode[STIX]{x1D713}$
with respect to
![]() $I$
, then it also converges to
$I$
, then it also converges to
![]() $\unicode[STIX]{x1D713}$
with respect to
$\unicode[STIX]{x1D713}$
with respect to
![]() $I_{1}$
, and vice versa. We first note that the
$I_{1}$
, and vice versa. We first note that the
![]() $I$
-convergence implies the
$I$
-convergence implies the
![]() $L^{1}$
-convergence of the potentials [Reference Guedj and ZeriahiGZ17, Theorem 10.37]. This ensures that
$L^{1}$
-convergence of the potentials [Reference Guedj and ZeriahiGZ17, Theorem 10.37]. This ensures that
and moreover we have that
![]() $\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}\in {\mathcal{E}}_{C}^{1}(X,\unicode[STIX]{x1D714})$
for some
$\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}\in {\mathcal{E}}_{C}^{1}(X,\unicode[STIX]{x1D714})$
for some
![]() $C>0$
[Reference Guedj and ZeriahiGZ17, Lemma 10.33 and Definition 10.34]. The
$C>0$
[Reference Guedj and ZeriahiGZ17, Lemma 10.33 and Definition 10.34]. The
![]() $I_{1}$
-convergence would then follow from (7). Moreover, since
$I_{1}$
-convergence would then follow from (7). Moreover, since
![]() $I(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713})\leqslant 2I_{1}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713})$
, we conclude that the
$I(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713})\leqslant 2I_{1}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713})$
, we conclude that the
![]() $I_{1}$
-convergence implies the
$I_{1}$
-convergence implies the
![]() $I$
-convergence.◻
$I$
-convergence.◻
2.3 The complete metric spaces
 ${\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC})$
${\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC})$
Fix
![]() $p\geqslant 1$
. Following [Reference Guedj and ZeriahiGZ07, Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10], we consider the following finite-energy classes.
$p\geqslant 1$
. Following [Reference Guedj and ZeriahiGZ07, Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10], we consider the following finite-energy classes.
Definition 2.9. We set
and let
![]() ${\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC})=\{T=\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}\mid \unicode[STIX]{x1D711}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})\}$
denote the corresponding sets of finite-energy currents.
${\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC})=\{T=\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}\mid \unicode[STIX]{x1D711}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})\}$
denote the corresponding sets of finite-energy currents.
On the class
![]() ${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
,
${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
,
![]() $p\geqslant 1$
, we define
$p\geqslant 1$
, we define
This quantity is well defined by [Reference Guedj and ZeriahiGZ07, Proposition 3.6]. It is obviously non-negative and symmetric. It follows from the domination principle (Proposition 2.3) that
Moreover, it will follow from Theorem 3.6 (which shows in particular that
![]() $I_{p}$
satisfies a quasi-triangle inequality) that
$I_{p}$
satisfies a quasi-triangle inequality) that
![]() $I_{p}$
induces a uniform structure. We can then define the following:
$I_{p}$
induces a uniform structure. We can then define the following:
Definition 2.10. The strong topology on
![]() ${\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC})$
is the one induced by
${\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC})$
is the one induced by
![]() $I_{p}$
.
$I_{p}$
.
By [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem 2.17], a decreasing sequence converges strongly. We also have good convergence properties if we approximate by slightly larger finite-energy classes
![]() ${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})$
.
${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})$
.
Proposition 2.11. Fix
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}$
,
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}$
,
![]() $\unicode[STIX]{x1D700}>0$
. If
$\unicode[STIX]{x1D700}>0$
. If
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})\cap L^{\infty }(X)$
, then
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})\cap L^{\infty }(X)$
, then
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})\cap L^{\infty }(X)$
and
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})\cap L^{\infty }(X)$
and
![]() $I_{p,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\rightarrow I_{p,\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
as
$I_{p,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\rightarrow I_{p,\unicode[STIX]{x1D714}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
as
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
.
$\unicode[STIX]{x1D700}\rightarrow 0$
.
Moreover, if
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
and
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
and
![]() $\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{j}$
are sequences of smooth
$\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{j}$
are sequences of smooth
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}_{j}}$
-psh functions decreasing to
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}_{j}}$
-psh functions decreasing to
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
with
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
with
![]() $\unicode[STIX]{x1D700}_{j}\rightarrow 0$
, then
$\unicode[STIX]{x1D700}_{j}\rightarrow 0$
, then
as
![]() $j$
goes to
$j$
goes to
![]() $+\infty$
.
$+\infty$
.
Proof. Note that
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
belong to any energy class with respect to any Kähler form since they are bounded. In particular,
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
belong to any energy class with respect to any Kähler form since they are bounded. In particular,
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})$
. The first assertion follows from the fact that
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}})$
. The first assertion follows from the fact that
![]() $(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D711})^{n}$
and
$(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D711})^{n}$
and
![]() $(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D713})^{n}$
converge weakly to
$(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D713})^{n}$
converge weakly to
![]() $(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711})^{n}$
and
$(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711})^{n}$
and
![]() $(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D713})^{n}$
as
$(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D713})^{n}$
as
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
, respectively. For the second statement, we observe that, by symmetry, it suffices to prove that
$\unicode[STIX]{x1D700}\rightarrow 0$
, respectively. For the second statement, we observe that, by symmetry, it suffices to prove that
Given a bounded function
![]() $f$
on
$f$
on
![]() $X$
, we set
$X$
, we set
The triangle inequality yields
and similarly
Since
![]() $\unicode[STIX]{x1D711}-\unicode[STIX]{x1D713}$
is a positive quasi-continuous uniformly bounded function on
$\unicode[STIX]{x1D711}-\unicode[STIX]{x1D713}$
is a positive quasi-continuous uniformly bounded function on
![]() $X$
, it follows from [Reference Guedj and ZeriahiGZ17, Theorem 4.26] that
$X$
, it follows from [Reference Guedj and ZeriahiGZ17, Theorem 4.26] that
as
![]() $j\rightarrow +\infty$
. Moreover, we claim that the terms
$j\rightarrow +\infty$
. Moreover, we claim that the terms
![]() $|(\unicode[STIX]{x1D711}_{j}-\unicode[STIX]{x1D711})|_{p}$
and
$|(\unicode[STIX]{x1D711}_{j}-\unicode[STIX]{x1D711})|_{p}$
and
![]() $|(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D713}_{j})|_{p}$
go to 0 as
$|(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D713}_{j})|_{p}$
go to 0 as
![]() $j\rightarrow +\infty$
. Lemma 2.12, together with the fact that
$j\rightarrow +\infty$
. Lemma 2.12, together with the fact that
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}_{j}}\leqslant \unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{X}$
, yields
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}_{j}}\leqslant \unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{X}$
, yields
Note that
![]() $\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D711}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{X})$
(since they are bounded). Hence [Reference Guedj and ZeriahiGZ07, Theorem 3.8] ensures that the integral at the right-hand side of this inequality is finite.
$\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D711}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{X})$
(since they are bounded). Hence [Reference Guedj and ZeriahiGZ07, Theorem 3.8] ensures that the integral at the right-hand side of this inequality is finite.
Since
![]() $\unicode[STIX]{x1D711}_{j}$
is decreasing to
$\unicode[STIX]{x1D711}_{j}$
is decreasing to
![]() $\unicode[STIX]{x1D711}$
, it then follows from the dominated convergence theorem that
$\unicode[STIX]{x1D711}$
, it then follows from the dominated convergence theorem that
![]() $|(\unicode[STIX]{x1D711}_{j}-\unicode[STIX]{x1D711})|_{p}^{p}\rightarrow 0$
as
$|(\unicode[STIX]{x1D711}_{j}-\unicode[STIX]{x1D711})|_{p}^{p}\rightarrow 0$
as
![]() $j\rightarrow +\infty$
. Fix
$j\rightarrow +\infty$
. Fix
![]() $j_{0}<j$
. Then
$j_{0}<j$
. Then
It follows again from the continuity of the Monge–Ampère operator along the decreasing sequence, [Reference KolodziejKol05, Corollary 1.14], and the dominated convergence theorem that letting
![]() $j\rightarrow +\infty$
and then
$j\rightarrow +\infty$
and then
![]() $j_{0}\rightarrow +\infty$
we get
$j_{0}\rightarrow +\infty$
we get
Thus,
![]() $|(\unicode[STIX]{x1D713}_{j}-\unicode[STIX]{x1D713})|_{p}^{p}\rightarrow 0$
as
$|(\unicode[STIX]{x1D713}_{j}-\unicode[STIX]{x1D713})|_{p}^{p}\rightarrow 0$
as
![]() $j\rightarrow +\infty$
. Hence the conclusion.◻
$j\rightarrow +\infty$
. Hence the conclusion.◻
It follows from Hölder’s inequality that the strong topology on
![]() ${\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC})$
is stronger than the one on
${\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC})$
is stronger than the one on
![]() ${\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC})$
: if a sequence
${\mathcal{E}}^{1}(\unicode[STIX]{x1D6FC})$
: if a sequence
![]() $(\unicode[STIX]{x1D711}_{j})\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
is a Cauchy sequence for
$(\unicode[STIX]{x1D711}_{j})\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
is a Cauchy sequence for
![]() $I_{p}$
, then it is a Cauchy sequence in
$I_{p}$
, then it is a Cauchy sequence in
![]() $({\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714}),d_{I})$
, since
$({\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714}),d_{I})$
, since
Since
![]() $({\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714}),d_{I})$
is complete, there is
$({\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714}),d_{I})$
is complete, there is
![]() $\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
such that
$\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
such that
![]() $d_{I}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D711})\rightarrow 0$
. Now
$d_{I}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D711})\rightarrow 0$
. Now
![]() $I_{p}(\unicode[STIX]{x1D711}_{j},0)$
is bounded and
$I_{p}(\unicode[STIX]{x1D711}_{j},0)$
is bounded and
![]() $\operatorname{MA}(\unicode[STIX]{x1D711}_{j})$
converges to
$\operatorname{MA}(\unicode[STIX]{x1D711}_{j})$
converges to
![]() $\operatorname{MA}(\unicode[STIX]{x1D711})$
(by [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Proposition 5.6]). Thus,
$\operatorname{MA}(\unicode[STIX]{x1D711})$
(by [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Proposition 5.6]). Thus,
![]() $\unicode[STIX]{x1D711}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
by Fatou’s and Hartogs’ lemmas.
$\unicode[STIX]{x1D711}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
by Fatou’s and Hartogs’ lemmas.
One would now like to prove that
![]() $I_{p}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D711})\rightarrow 0$
and conclude that the space
$I_{p}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D711})\rightarrow 0$
and conclude that the space
![]() $({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),I_{p})$
is complete, arguing as in [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Proposition 2.4]. We refer the reader to Theorem 4.2 for a neat treatment.
$({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),I_{p})$
is complete, arguing as in [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Proposition 2.4]. We refer the reader to Theorem 4.2 for a neat treatment.
Lemma 2.12. Let
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
be bounded
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
be bounded
![]() $\unicode[STIX]{x1D714}$
-psh functions and
$\unicode[STIX]{x1D714}$
-psh functions and
![]() $S$
be a positive closed current of bidimension
$S$
be a positive closed current of bidimension
![]() $(1,1)$
on
$(1,1)$
on
![]() $X$
. If
$X$
. If
![]() $\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D713}$
, then
$\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D713}$
, then
In particular,
![]() $V_{\unicode[STIX]{x1D6FC}}^{-1}\int _{X}(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D711})^{p}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}^{j}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}^{n-j}\leqslant \int _{X}(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D711})^{p}\operatorname{MA}(\unicode[STIX]{x1D711})$
.
$V_{\unicode[STIX]{x1D6FC}}^{-1}\int _{X}(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D711})^{p}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}^{j}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}^{n-j}\leqslant \int _{X}(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D711})^{p}\operatorname{MA}(\unicode[STIX]{x1D711})$
.
Proof. By Stokes’ theorem,
is non-negative if
![]() $(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D711})\geqslant 0$
.
$(\unicode[STIX]{x1D713}-\unicode[STIX]{x1D711})\geqslant 0$
.
The second assertion follows by applying the first one inductively. ◻
We now establish a few useful properties of
![]() $I_{p}$
that will notably allow us to compare
$I_{p}$
that will notably allow us to compare
![]() $I_{p}$
with
$I_{p}$
with
![]() $d_{p}$
in the next section.
$d_{p}$
in the next section.
Proposition 2.13. For
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
,
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
,
Proof. Recall that the maximum principle ensures that
while
![]() $(\unicode[STIX]{x1D711}-\text{max}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}))^{p}=0$
on
$(\unicode[STIX]{x1D711}-\text{max}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}))^{p}=0$
on
![]() $(\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D713})$
; thus,
$(\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D713})$
; thus,
Similarly,
![]() $2I_{p}(\unicode[STIX]{x1D713},\max (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}))^{p}=\int _{\{\unicode[STIX]{x1D711}>\unicode[STIX]{x1D713}\}}|\unicode[STIX]{x1D711}-\unicode[STIX]{x1D713}|^{p}[\operatorname{MA}(\unicode[STIX]{x1D711})+\operatorname{MA}(\unicode[STIX]{x1D713})]$
and the result follows, since
$2I_{p}(\unicode[STIX]{x1D713},\max (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}))^{p}=\int _{\{\unicode[STIX]{x1D711}>\unicode[STIX]{x1D713}\}}|\unicode[STIX]{x1D711}-\unicode[STIX]{x1D713}|^{p}[\operatorname{MA}(\unicode[STIX]{x1D711})+\operatorname{MA}(\unicode[STIX]{x1D713})]$
and the result follows, since
Corollary 2.14. For all
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
,
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
,
Proof. By approximating
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
from the above by a decreasing sequence, it suffices to treat the case when
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
from the above by a decreasing sequence, it suffices to treat the case when
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
. Changing
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
. Changing
![]() $\unicode[STIX]{x1D714}$
in
$\unicode[STIX]{x1D714}$
in
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}$
, we can further assume that
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}}$
, we can further assume that
![]() $\unicode[STIX]{x1D713}=0$
. It follows from Proposition 2.13 that
$\unicode[STIX]{x1D713}=0$
. It follows from Proposition 2.13 that
It follows from Lemma 2.12 that
 $$\begin{eqnarray}\displaystyle I_{p}(0,\max (0,\unicode[STIX]{x1D711}/2))^{p} & {\leqslant} & \displaystyle \int _{X}\max (0,\unicode[STIX]{x1D711}/2)^{p}\operatorname{MA}(0)\nonumber\\ \displaystyle & = & \displaystyle 2^{-p}\int _{X}\max (0,\unicode[STIX]{x1D711})^{p}\operatorname{MA}(0)\leqslant I_{p}(0,\max (0,\unicode[STIX]{x1D711}))^{p}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{p}(0,\max (0,\unicode[STIX]{x1D711}/2))^{p} & {\leqslant} & \displaystyle \int _{X}\max (0,\unicode[STIX]{x1D711}/2)^{p}\operatorname{MA}(0)\nonumber\\ \displaystyle & = & \displaystyle 2^{-p}\int _{X}\max (0,\unicode[STIX]{x1D711})^{p}\operatorname{MA}(0)\leqslant I_{p}(0,\max (0,\unicode[STIX]{x1D711}))^{p}.\nonumber\end{eqnarray}$$
We claim that, for all
![]() $0\leqslant j\leqslant n$
,
$0\leqslant j\leqslant n$
,
Assuming this for the moment, it follows again from Lemma 2.12 that
 $$\begin{eqnarray}\displaystyle I_{p}(\max (0,\unicode[STIX]{x1D711}/2),\unicode[STIX]{x1D711}/2)^{p} & {\leqslant} & \displaystyle \int _{X}(\max (0,\unicode[STIX]{x1D711}/2)-\unicode[STIX]{x1D711}/2)^{p}\operatorname{MA}(\unicode[STIX]{x1D711}/2)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2^{n+p}V_{\unicode[STIX]{x1D6FC}}}\mathop{\sum }_{j=0}^{n}C_{n}^{j}\int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}^{j}\wedge \unicode[STIX]{x1D714}^{n-j}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{2}\int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\operatorname{MA}(\unicode[STIX]{x1D711})\leqslant I_{p}(\unicode[STIX]{x1D711},\max (0,\unicode[STIX]{x1D711}))^{p}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I_{p}(\max (0,\unicode[STIX]{x1D711}/2),\unicode[STIX]{x1D711}/2)^{p} & {\leqslant} & \displaystyle \int _{X}(\max (0,\unicode[STIX]{x1D711}/2)-\unicode[STIX]{x1D711}/2)^{p}\operatorname{MA}(\unicode[STIX]{x1D711}/2)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{2^{n+p}V_{\unicode[STIX]{x1D6FC}}}\mathop{\sum }_{j=0}^{n}C_{n}^{j}\int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}^{j}\wedge \unicode[STIX]{x1D714}^{n-j}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{1}{2}\int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\operatorname{MA}(\unicode[STIX]{x1D711})\leqslant I_{p}(\unicode[STIX]{x1D711},\max (0,\unicode[STIX]{x1D711}))^{p}.\nonumber\end{eqnarray}$$
We infer
by using Proposition 2.13 again.
It remains to justify our claim. Set
![]() $S=\unicode[STIX]{x1D714}^{j-1}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}^{n-j}$
. It suffices, by induction, to establish the following inequality:
$S=\unicode[STIX]{x1D714}^{j-1}\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}^{n-j}$
. It suffices, by induction, to establish the following inequality:
 $$\begin{eqnarray}\displaystyle \int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\unicode[STIX]{x1D714}\wedge S & = & \displaystyle \int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}\wedge S-\int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\,dd^{c}\unicode[STIX]{x1D711}\wedge S\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}\wedge S.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\unicode[STIX]{x1D714}\wedge S & = & \displaystyle \int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}\wedge S-\int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\,dd^{c}\unicode[STIX]{x1D711}\wedge S\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D711}}\wedge S.\nonumber\end{eqnarray}$$
This follows by observing that
 $$\begin{eqnarray}\displaystyle -\int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\,dd^{c}\unicode[STIX]{x1D711}\wedge S & = & \displaystyle p\int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p-1}\,d(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})\wedge d^{c}\unicode[STIX]{x1D711}\wedge S\nonumber\\ \displaystyle & = & \displaystyle -p\int _{\{\unicode[STIX]{x1D711}<0\}}(-\unicode[STIX]{x1D711})^{p-1}\,d\unicode[STIX]{x1D711}\wedge d^{c}\unicode[STIX]{x1D711}\wedge S\leqslant 0.\Box \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p}\,dd^{c}\unicode[STIX]{x1D711}\wedge S & = & \displaystyle p\int _{X}(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})^{p-1}\,d(\max (0,\unicode[STIX]{x1D711})-\unicode[STIX]{x1D711})\wedge d^{c}\unicode[STIX]{x1D711}\wedge S\nonumber\\ \displaystyle & = & \displaystyle -p\int _{\{\unicode[STIX]{x1D711}<0\}}(-\unicode[STIX]{x1D711})^{p-1}\,d\unicode[STIX]{x1D711}\wedge d^{c}\unicode[STIX]{x1D711}\wedge S\leqslant 0.\Box \nonumber\end{eqnarray}$$
3 Comparing distances
In this section, we show that
![]() $I_{p}$
is equivalent to
$I_{p}$
is equivalent to
![]() $d_{p}$
(Theorem 3.6). Recall that
$d_{p}$
(Theorem 3.6). Recall that
In the following, we are going to use several times and in a crucial way the fact that Theorem 1.21 ensures
3.1 Kiselman transform and geodesics
Let
![]() $(\unicode[STIX]{x1D711}_{t})_{0\leqslant t\leqslant 1}$
be the Mabuchi geodesic. For all
$(\unicode[STIX]{x1D711}_{t})_{0\leqslant t\leqslant 1}$
be the Mabuchi geodesic. For all
![]() $x\in X$
,
$x\in X$
,
![]() $t\in [0,1]\mapsto \unicode[STIX]{x1D711}_{t}(x)\in \mathbb{R}$
is convex. It is natural to consider its Legendre transform,
$t\in [0,1]\mapsto \unicode[STIX]{x1D711}_{t}(x)\in \mathbb{R}$
is convex. It is natural to consider its Legendre transform,
![]() $u_{s}(x):s\mapsto \sup _{t\in [0,1]}\{st-\unicode[STIX]{x1D711}_{t}(x)\}$
. This function is convex in
$u_{s}(x):s\mapsto \sup _{t\in [0,1]}\{st-\unicode[STIX]{x1D711}_{t}(x)\}$
. This function is convex in
![]() $s$
, but the dependence in
$s$
, but the dependence in
![]() $x$
is
$x$
is
![]() $-\unicode[STIX]{x1D714}$
-psh, so we rather consider
$-\unicode[STIX]{x1D714}$
-psh, so we rather consider
![]() $-u_{s}$
. We finally change
$-u_{s}$
. We finally change
![]() $s$
in
$s$
in
![]() $-s$
to obtain a more elegant formula,
$-s$
to obtain a more elegant formula,
Proposition 3.1. The functions
![]() $x\mapsto \unicode[STIX]{x1D713}_{s}(x)$
are
$x\mapsto \unicode[STIX]{x1D713}_{s}(x)$
are
![]() $\unicode[STIX]{x1D714}$
-plurisubharmonic. In particular,
$\unicode[STIX]{x1D714}$
-plurisubharmonic. In particular,
![]() $x\mapsto \unicode[STIX]{x1D713}_{0}(x)=\inf _{0\leqslant t\leqslant 1}\unicode[STIX]{x1D711}_{t}(x)$
is
$x\mapsto \unicode[STIX]{x1D713}_{0}(x)=\inf _{0\leqslant t\leqslant 1}\unicode[STIX]{x1D711}_{t}(x)$
is
![]() $\unicode[STIX]{x1D714}$
-psh.
$\unicode[STIX]{x1D714}$
-psh.
This is the minimum principle of Kiselman [Reference KiselmanKis78]. For
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
, we let
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
, we let
![]() $\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
denote the greatest
$\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
denote the greatest
![]() $\unicode[STIX]{x1D714}$
-psh function that lies below
$\unicode[STIX]{x1D714}$
-psh function that lies below
![]() $\unicode[STIX]{x1D711}_{0}$
and
$\unicode[STIX]{x1D711}_{0}$
and
![]() $\unicode[STIX]{x1D711}_{1}$
. In the notation of Berman and Demailly [Reference Berman and DemaillyBD12]
$\unicode[STIX]{x1D711}_{1}$
. In the notation of Berman and Demailly [Reference Berman and DemaillyBD12]
while
![]() $\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
is denoted
$\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
is denoted
![]() $P(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
in [Reference DarvasDar17c].
$P(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
in [Reference DarvasDar17c].
An important consequence of Kiselman’s minimum principle [Reference KiselmanKis78] is the following observation of Darvas and Rubinstein [Reference Darvas and RubinsteinDR16].
Proposition 3.2. The function
![]() $\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
is a bounded
$\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
is a bounded
![]() $\unicode[STIX]{x1D714}$
-psh, which has a locally bounded Laplacian on the ample locus of
$\unicode[STIX]{x1D714}$
-psh, which has a locally bounded Laplacian on the ample locus of
![]() $\unicode[STIX]{x1D6FC}=\{\unicode[STIX]{x1D714}\}$
, and its Monge–Ampère measure
$\unicode[STIX]{x1D6FC}=\{\unicode[STIX]{x1D714}\}$
, and its Monge–Ampère measure
![]() $\operatorname{MA}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1})$
is supported on the coincidence set
$\operatorname{MA}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1})$
is supported on the coincidence set
Moreover,
![]() $\operatorname{MA}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1})=\unicode[STIX]{x1D7D9}_{\{\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{0}\}}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})+\unicode[STIX]{x1D7D9}_{\{\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{1}<\unicode[STIX]{x1D711}_{0}\}}\operatorname{MA}(\unicode[STIX]{x1D711}_{1})$
.
$\operatorname{MA}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1})=\unicode[STIX]{x1D7D9}_{\{\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{0}\}}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})+\unicode[STIX]{x1D7D9}_{\{\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{1}<\unicode[STIX]{x1D711}_{0}\}}\operatorname{MA}(\unicode[STIX]{x1D711}_{1})$
.
Let
![]() $(\unicode[STIX]{x1D711}_{t})$
be the Mabuchi geodesic joining
$(\unicode[STIX]{x1D711}_{t})$
be the Mabuchi geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
and
$\unicode[STIX]{x1D711}_{0}$
and
![]() $\unicode[STIX]{x1D711}_{1}$
. Then, for all
$\unicode[STIX]{x1D711}_{1}$
. Then, for all
![]() $x\in X$
,
$x\in X$
,
Proof. It follows from a classical balayage procedure that goes back to Bedford and Taylor [Reference Bedford and TaylorBT82] that
![]() $\operatorname{MA}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1})$
is supported on the coincidence set
$\operatorname{MA}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1})$
is supported on the coincidence set
![]() $\{x\in X\mid \unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}(x)=\min (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})(x)\}$
. This holds true more generally for the Monge–Ampère measure of any envelope, namely
$\{x\in X\mid \unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}(x)=\min (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})(x)\}$
. This holds true more generally for the Monge–Ampère measure of any envelope, namely
where
![]() $h$
is a bounded lower semi-continuous function.
$h$
is a bounded lower semi-continuous function.
We have observed in Proposition 3.1 that
![]() $x\mapsto \inf _{t\in [0,1]}\unicode[STIX]{x1D711}_{t}(x)$
is a
$x\mapsto \inf _{t\in [0,1]}\unicode[STIX]{x1D711}_{t}(x)$
is a
![]() $\unicode[STIX]{x1D714}$
-psh function. Since it lies both below
$\unicode[STIX]{x1D714}$
-psh function. Since it lies both below
![]() $\unicode[STIX]{x1D711}_{0}$
and
$\unicode[STIX]{x1D711}_{0}$
and
![]() $\unicode[STIX]{x1D711}_{1}$
, we infer
$\unicode[STIX]{x1D711}_{1}$
, we infer
Conversely,
![]() $(t,x)\mapsto \unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}(x)$
is a subgeodesic (independent of
$(t,x)\mapsto \unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}(x)$
is a subgeodesic (independent of
![]() $t$
); hence, for all
$t$
); hence, for all
![]() $t,x$
,
$t,x$
,
![]() $\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}(x)\leqslant \unicode[STIX]{x1D711}_{t}(x)$
. Thus,
$\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}(x)\leqslant \unicode[STIX]{x1D711}_{t}(x)$
. Thus,
![]() $\unicode[STIX]{x1D713}:=\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}=\inf _{t\in [0,1]}\unicode[STIX]{x1D711}_{t}$
; hence,
$\unicode[STIX]{x1D713}:=\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}=\inf _{t\in [0,1]}\unicode[STIX]{x1D711}_{t}$
; hence,
![]() $\unicode[STIX]{x1D713}$
is bounded, thanks to Proposition 1.4.
$\unicode[STIX]{x1D713}$
is bounded, thanks to Proposition 1.4.
By Proposition 3.1,
![]() $\unicode[STIX]{x1D713}$
is
$\unicode[STIX]{x1D713}$
is
![]() $\unicode[STIX]{x1D714}$
-psh, hence
$\unicode[STIX]{x1D714}$
-psh, hence
![]() $A\unicode[STIX]{x1D714}_{X}$
-psh for some Kähler form
$A\unicode[STIX]{x1D714}_{X}$
-psh for some Kähler form
![]() $\unicode[STIX]{x1D714}_{X}$
and
$\unicode[STIX]{x1D714}_{X}$
and
![]() $A>0$
. Thus,
$A>0$
. Thus,
![]() $\sup _{X}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D714}_{X}}\unicode[STIX]{x1D713}\geqslant -C$
for some
$\sup _{X}\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D714}_{X}}\unicode[STIX]{x1D713}\geqslant -C$
for some
![]() $C>0$
.
$C>0$
.
It follows from the work of Berman and Demailly [Reference Berman and DemaillyBD12] (see also [Reference BermanBer13, Theorem 1.2]) that for any compact subset
![]() $K\subset \operatorname{Amp}(\unicode[STIX]{x1D6FC})$
, there exists
$K\subset \operatorname{Amp}(\unicode[STIX]{x1D6FC})$
, there exists
![]() $C_{K}>0$
, such that, for all
$C_{K}>0$
, such that, for all
![]() $t\in [0,1]$
,
$t\in [0,1]$
,
Thus
![]() $(-\unicode[STIX]{x1D711}_{t})$
is a family of
$(-\unicode[STIX]{x1D711}_{t})$
is a family of
![]() $C_{K}\unicode[STIX]{x1D714}_{X}$
-psh functions in a neighborhood of
$C_{K}\unicode[STIX]{x1D714}_{X}$
-psh functions in a neighborhood of
![]() $K$
, which are uniformly bounded from above. Thus,
$K$
, which are uniformly bounded from above. Thus,
is
![]() $C_{K}\unicode[STIX]{x1D714}_{X}$
-psh near
$C_{K}\unicode[STIX]{x1D714}_{X}$
-psh near
![]() $K$
, in particular
$K$
, in particular
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D714}_{X}}\unicode[STIX]{x1D713}<C_{K}n$
. This means that
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D714}_{X}}\unicode[STIX]{x1D713}<C_{K}n$
. This means that
![]() $\unicode[STIX]{x1D713}$
has a locally bounded Laplacian on
$\unicode[STIX]{x1D713}$
has a locally bounded Laplacian on
![]() $\operatorname{Amp}(\unicode[STIX]{x1D6FC})$
.
$\operatorname{Amp}(\unicode[STIX]{x1D6FC})$
.
It follows then from classical arguments that the measure
![]() $\operatorname{MA}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1})$
is absolutely continuous with respect to the Lebesgue measure. Since
$\operatorname{MA}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1})$
is absolutely continuous with respect to the Lebesgue measure. Since
![]() $\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}$
(respectively
$\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}$
(respectively
![]() $\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{1}$
) have locally bounded Laplacians in
$\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{1}$
) have locally bounded Laplacians in
![]() $\operatorname{Amp}(\unicode[STIX]{x1D6FC})$
, it follows from [Reference Gilbarg and TrudingerGT83, Lemma 7.7] that their second partial derivatives agree on
$\operatorname{Amp}(\unicode[STIX]{x1D6FC})$
, it follows from [Reference Gilbarg and TrudingerGT83, Lemma 7.7] that their second partial derivatives agree on
![]() $\{\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{0}\}$
(respectively on
$\{\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{0}\}$
(respectively on
![]() $\{\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{1}\}$
), hence
$\{\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D711}_{1}\}$
), hence
We have used here the fact that none of the measures
![]() $\operatorname{MA}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}),\operatorname{MA}(\unicode[STIX]{x1D711}_{0})$
,
$\operatorname{MA}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}),\operatorname{MA}(\unicode[STIX]{x1D711}_{0})$
,
![]() $\operatorname{MA}(\unicode[STIX]{x1D711}_{1})$
charges the pluripolar set
$\operatorname{MA}(\unicode[STIX]{x1D711}_{1})$
charges the pluripolar set
![]() $X\setminus \operatorname{Amp}(\unicode[STIX]{x1D6FC})$
.◻
$X\setminus \operatorname{Amp}(\unicode[STIX]{x1D6FC})$
.◻
A basic observation that we shall use on several occasions is the following.
Lemma 3.3. Assume
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
and let
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
and let
![]() $(\unicode[STIX]{x1D711}_{t})_{0\leqslant t\leqslant 1}$
be the Mabuchi geodesic joining
$(\unicode[STIX]{x1D711}_{t})_{0\leqslant t\leqslant 1}$
be the Mabuchi geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
. Then
$\unicode[STIX]{x1D711}_{1}$
. Then
Moreover,
(i) if
 $\unicode[STIX]{x1D711}_{0}(x)\leqslant \unicode[STIX]{x1D711}_{1}(x)$
for some
$\unicode[STIX]{x1D711}_{0}(x)\leqslant \unicode[STIX]{x1D711}_{1}(x)$
for some
 $x\in X$
, then
$x\in X$
, then
 $\dot{\unicode[STIX]{x1D711}}_{1}(x)\geqslant 0$
;
$\dot{\unicode[STIX]{x1D711}}_{1}(x)\geqslant 0$
;(ii) if
 $\unicode[STIX]{x1D711}_{0}(x)\leqslant \unicode[STIX]{x1D711}_{1}(x)$
for all
$\unicode[STIX]{x1D711}_{0}(x)\leqslant \unicode[STIX]{x1D711}_{1}(x)$
for all
 $x\in X$
then
$x\in X$
then
 $\dot{\unicode[STIX]{x1D711}}_{t}(x)\geqslant 0$
for all
$\dot{\unicode[STIX]{x1D711}}_{t}(x)\geqslant 0$
for all
 $x\in X$
and a.e.
$x\in X$
and a.e.
 $t\in [0,1]$
.
$t\in [0,1]$
.
By symmetry, if
![]() $\unicode[STIX]{x1D711}_{1}(x)\leqslant \unicode[STIX]{x1D711}_{0}(x)$
, it follows that
$\unicode[STIX]{x1D711}_{1}(x)\leqslant \unicode[STIX]{x1D711}_{0}(x)$
, it follows that
![]() $\dot{\unicode[STIX]{x1D711}}_{0}(x)\leqslant 0$
. Moreover, if
$\dot{\unicode[STIX]{x1D711}}_{0}(x)\leqslant 0$
. Moreover, if
![]() $\unicode[STIX]{x1D711}_{1}(x)\leqslant \unicode[STIX]{x1D711}_{0}(x)$
for all
$\unicode[STIX]{x1D711}_{1}(x)\leqslant \unicode[STIX]{x1D711}_{0}(x)$
for all
![]() $x\in X$
then
$x\in X$
then
![]() $\dot{\unicode[STIX]{x1D711}}_{t}(x)\leqslant 0$
for a.e.
$\dot{\unicode[STIX]{x1D711}}_{t}(x)\leqslant 0$
for a.e.
![]() $x,t$
. Here, and in the following,
$x,t$
. Here, and in the following,
![]() $\dot{\unicode[STIX]{x1D711}_{0}}$
,
$\dot{\unicode[STIX]{x1D711}_{0}}$
,
![]() $\dot{\unicode[STIX]{x1D711}_{1}}$
denote the right and left derivatives, respectively, while we recall that
$\dot{\unicode[STIX]{x1D711}_{1}}$
denote the right and left derivatives, respectively, while we recall that
![]() $\dot{\unicode[STIX]{x1D711}}_{t}(x)$
is well defined for a.e.
$\dot{\unicode[STIX]{x1D711}}_{t}(x)$
is well defined for a.e.
![]() $(x,t)$
.
$(x,t)$
.
Proof. From Theorem 1.21 we know that
![]() $d_{p}^{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})\,=\,\int _{X}|\dot{\unicode[STIX]{x1D711}}_{0}|^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})$
. Moreover, Proposition 1.4 ensures that
$d_{p}^{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})\,=\,\int _{X}|\dot{\unicode[STIX]{x1D711}}_{0}|^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})$
. Moreover, Proposition 1.4 ensures that
![]() $|\dot{\unicode[STIX]{x1D711}}_{0}|\leqslant \Vert \unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\Vert _{L^{\infty }(X)}$
. Hence, the first statement.
$|\dot{\unicode[STIX]{x1D711}}_{0}|\leqslant \Vert \unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\Vert _{L^{\infty }(X)}$
. Hence, the first statement.
Assume
![]() $\dot{\unicode[STIX]{x1D711}}_{1}(x)<0$
. Since
$\dot{\unicode[STIX]{x1D711}}_{1}(x)<0$
. Since
![]() $t\mapsto \unicode[STIX]{x1D711}_{t}(x)$
is convex, we infer
$t\mapsto \unicode[STIX]{x1D711}_{t}(x)$
is convex, we infer
![]() $\dot{\unicode[STIX]{x1D711}_{t}}(x)\leqslant \dot{\unicode[STIX]{x1D711}_{1}}(x)<0$
. Thus,
$\dot{\unicode[STIX]{x1D711}_{t}}(x)\leqslant \dot{\unicode[STIX]{x1D711}_{1}}(x)<0$
. Thus,
![]() $t\mapsto \unicode[STIX]{x1D711}_{t}(x)$
is decreasing, hence
$t\mapsto \unicode[STIX]{x1D711}_{t}(x)$
is decreasing, hence
![]() $\unicode[STIX]{x1D711}_{1}(x)<\unicode[STIX]{x1D711}_{0}(x)$
, a contradiction. This proves part (i).
$\unicode[STIX]{x1D711}_{1}(x)<\unicode[STIX]{x1D711}_{0}(x)$
, a contradiction. This proves part (i).
Assume now that
![]() $\unicode[STIX]{x1D711}_{0}(x)\leqslant \unicode[STIX]{x1D711}_{1}(x)$
for all
$\unicode[STIX]{x1D711}_{0}(x)\leqslant \unicode[STIX]{x1D711}_{1}(x)$
for all
![]() $x\in X$
. Then
$x\in X$
. Then
The first of these inequalities follows from the fact that, by Proposition 1.4,
with
![]() $\unicode[STIX]{x1D711}(x,t+is)=\unicode[STIX]{x1D711}_{t}(x)$
, and that
$\unicode[STIX]{x1D711}(x,t+is)=\unicode[STIX]{x1D711}_{t}(x)$
, and that
![]() $\unicode[STIX]{x1D711}_{0}(x,t+is)=\unicode[STIX]{x1D711}_{0}(x)$
is a subsolution (i.e. a candidate in the envelope). The other inequality follows from the fact that
$\unicode[STIX]{x1D711}_{0}(x,t+is)=\unicode[STIX]{x1D711}_{0}(x)$
is a subsolution (i.e. a candidate in the envelope). The other inequality follows from the fact that
![]() $\unicode[STIX]{x1D711}_{1}(x,t+is)=\unicode[STIX]{x1D711}_{1}(x)$
is a supersolution of (3) since
$\unicode[STIX]{x1D711}_{1}(x,t+is)=\unicode[STIX]{x1D711}_{1}(x)$
is a supersolution of (3) since
![]() $(\unicode[STIX]{x1D714}+dd_{x,z}^{c}\unicode[STIX]{x1D711}_{1})^{n+1}=0$
and
$(\unicode[STIX]{x1D714}+dd_{x,z}^{c}\unicode[STIX]{x1D711}_{1})^{n+1}=0$
and
![]() $\unicode[STIX]{x1D711}_{1}\geqslant \unicode[STIX]{x1D711}_{0,1}$
. The same argument shows that
$\unicode[STIX]{x1D711}_{1}\geqslant \unicode[STIX]{x1D711}_{0,1}$
. The same argument shows that
![]() $\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{s}\leqslant \unicode[STIX]{x1D711}_{t}$
for all
$\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{s}\leqslant \unicode[STIX]{x1D711}_{t}$
for all
![]() $0<s<t$
and
$0<s<t$
and
![]() $x\in X$
, hence
$x\in X$
, hence
![]() $\dot{\unicode[STIX]{x1D711}}_{t}(x)\geqslant 0$
for all
$\dot{\unicode[STIX]{x1D711}}_{t}(x)\geqslant 0$
for all
![]() $x\in X$
and a.e.
$x\in X$
and a.e.
![]() $t\in [0,1]$
, since the derivative in time of
$t\in [0,1]$
, since the derivative in time of
![]() $\unicode[STIX]{x1D711}_{t}$
is well defined for a.e.
$\unicode[STIX]{x1D711}_{t}$
is well defined for a.e.
![]() $t$
.◻
$t$
.◻
We now establish a very useful relation established by Darvas [Reference DarvasDar17c, Proposition 8.1] when
![]() $\unicode[STIX]{x1D714}$
is Kähler (see also [Reference DarvasDar15, Corollary 4.14]).
$\unicode[STIX]{x1D714}$
is Kähler (see also [Reference DarvasDar15, Corollary 4.14]).
Proposition 3.4. Assume
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
. Then, for all
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
. Then, for all
![]() $p\geqslant 1$
,
$p\geqslant 1$
,
Proof. We proceed by approximation, so as to reduce to the Kähler case. The identity is known to hold for
![]() $d_{p,\unicode[STIX]{x1D700}}$
and
$d_{p,\unicode[STIX]{x1D700}}$
and
![]() $\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}$
, where
$\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}$
, where
![]() $d_{p,\unicode[STIX]{x1D700}}$
denotes the distance associated with the Kähler form
$d_{p,\unicode[STIX]{x1D700}}$
denotes the distance associated with the Kähler form
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}$
and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}$
and
![]() $\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}$
is the greatest
$\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}$
is the greatest
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
-psh function that lies below
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
-psh function that lies below
![]() $\min (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
.
$\min (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
.
Using Theorem 1.21 and the triangle inequality, the proof boils down to checking that
![]() $d_{p,\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1})\rightarrow 0$
as
$d_{p,\unicode[STIX]{x1D700}}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1})\rightarrow 0$
as
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
. The same arguments used in the proof of Proposition 1.16 yield
$\unicode[STIX]{x1D700}\rightarrow 0$
. The same arguments used in the proof of Proposition 1.16 yield
We claim that
![]() $d_{p,\unicode[STIX]{x1D700}^{\prime }}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1})$
goes to zero as
$d_{p,\unicode[STIX]{x1D700}^{\prime }}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1})$
goes to zero as
![]() $\unicode[STIX]{x1D700}$
goes to zero, since
$\unicode[STIX]{x1D700}$
goes to zero, since
![]() $\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}$
decreases to
$\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}$
decreases to
![]() $\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
as
$\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
as
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
. Indeed, observe that
$\unicode[STIX]{x1D700}\rightarrow 0$
. Indeed, observe that
![]() $\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}^{\prime })\cap L^{\infty }(X)$
and that by Proposition 3.8 we know that
$\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}^{\prime })\cap L^{\infty }(X)$
and that by Proposition 3.8 we know that
The same arguments in the proof of Proposition 2.11 then show that
![]() $I_{p,\unicode[STIX]{x1D700}^{\prime }}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1})\rightarrow 0$
as
$I_{p,\unicode[STIX]{x1D700}^{\prime }}(\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{0}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{1})\rightarrow 0$
as
![]() $\unicode[STIX]{x1D700}$
goes to zero. The conclusion then follows.◻
$\unicode[STIX]{x1D700}$
goes to zero. The conclusion then follows.◻
We note for later use the following consequence.
Corollary 3.5. If
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
, then
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
, then
3.2 Comparing
 $d_{p}$
and
$d_{p}$
and
 $I_{p}$
$I_{p}$
The goal of this section is to establish that
![]() $d_{p}$
and
$d_{p}$
and
![]() $I_{p}$
are equivalent, extending [Reference DarvasDar15, Theorem 5.5].
$I_{p}$
are equivalent, extending [Reference DarvasDar15, Theorem 5.5].
Theorem 3.6. For all
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
,
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
,
It follows from Definition 1.10 and Proposition 2.11 that
so it suffices to establish these inequalities when
![]() $\unicode[STIX]{x1D714}$
is a Kähler form.
$\unicode[STIX]{x1D714}$
is a Kähler form.
We nevertheless give a direct proof, valid when
![]() $\unicode[STIX]{x1D714}$
is merely semi-positive, with several intermediate results of independent interest. Several of these results have been obtained by Darvas [Reference DarvasDar17b, Reference DarvasDar17c, Reference DarvasDar15] when
$\unicode[STIX]{x1D714}$
is merely semi-positive, with several intermediate results of independent interest. Several of these results have been obtained by Darvas [Reference DarvasDar17b, Reference DarvasDar17c, Reference DarvasDar15] when
![]() $\unicode[STIX]{x1D714}$
is Kähler.
$\unicode[STIX]{x1D714}$
is Kähler.
Lemma 3.7. Assume that
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
satisfy
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
satisfy
![]() $\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
.
$\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
.
(i)
 $d_{p}(\unicode[STIX]{x1D711}_{1},(\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1})/2)\leqslant d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
.
$d_{p}(\unicode[STIX]{x1D711}_{1},(\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1})/2)\leqslant d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
.(ii)
 $d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})\leqslant 2^{1+n/p}d_{p}(\unicode[STIX]{x1D711}_{0}/2,\unicode[STIX]{x1D711}_{1}/2)$
.
$d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})\leqslant 2^{1+n/p}d_{p}(\unicode[STIX]{x1D711}_{0}/2,\unicode[STIX]{x1D711}_{1}/2)$
.(iii) If
 $\unicode[STIX]{x1D711}_{1}=0$
then
$\unicode[STIX]{x1D711}_{1}=0$
then
 $d_{p}(\unicode[STIX]{x1D711}_{0},0)\geqslant 2d_{p}(\unicode[STIX]{x1D711}_{0}/2,0)$
.
$d_{p}(\unicode[STIX]{x1D711}_{0},0)\geqslant 2d_{p}(\unicode[STIX]{x1D711}_{0}/2,0)$
.(iv) If
 $\unicode[STIX]{x1D713}\in {\mathcal{H}}_{bd}$
is such that
$\unicode[STIX]{x1D713}\in {\mathcal{H}}_{bd}$
is such that
 $\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D713}\leqslant \unicode[STIX]{x1D711}_{1}$
, then
$\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D713}\leqslant \unicode[STIX]{x1D711}_{1}$
, then  $$\begin{eqnarray}\max \{d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D713});d_{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D711}_{1})\}\leqslant d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}).\end{eqnarray}$$
$$\begin{eqnarray}\max \{d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D713});d_{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D711}_{1})\}\leqslant d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}).\end{eqnarray}$$
Proof. Let
![]() $\unicode[STIX]{x1D711}_{t}$
(respectively
$\unicode[STIX]{x1D711}_{t}$
(respectively
![]() $\unicode[STIX]{x1D713}_{t}$
) denote the Mabuchi geodesic joining
$\unicode[STIX]{x1D713}_{t}$
) denote the Mabuchi geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
(respectively
$\unicode[STIX]{x1D711}_{0}$
(respectively
![]() $(\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1})/2$
) to
$(\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1})/2$
) to
![]() $\unicode[STIX]{x1D711}_{1}$
. Since
$\unicode[STIX]{x1D711}_{1}$
. Since
![]() $\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
, it follows from Lemma 3.3(ii) that
$\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
, it follows from Lemma 3.3(ii) that
![]() $t\mapsto \unicode[STIX]{x1D711}_{t}$
,
$t\mapsto \unicode[STIX]{x1D711}_{t}$
,
![]() $t\mapsto \unicode[STIX]{x1D713}_{t}$
are increasing and
$t\mapsto \unicode[STIX]{x1D713}_{t}$
are increasing and
![]() $\unicode[STIX]{x1D711}_{t}\leqslant \unicode[STIX]{x1D713}_{t}$
, hence
$\unicode[STIX]{x1D711}_{t}\leqslant \unicode[STIX]{x1D713}_{t}$
, hence
since
![]() $\unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D713}_{1}$
. Therefore,
$\unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D713}_{1}$
. Therefore,
![]() $\dot{\unicode[STIX]{x1D711}}_{1}\geqslant \dot{\unicode[STIX]{x1D713}}_{1}\geqslant 0$
and we infer
$\dot{\unicode[STIX]{x1D711}}_{1}\geqslant \dot{\unicode[STIX]{x1D713}}_{1}\geqslant 0$
and we infer
This, together with Theorem 1.21, proves part (i).
Now let
![]() $(\unicode[STIX]{x1D711}_{t})$
(respectively
$(\unicode[STIX]{x1D711}_{t})$
(respectively
![]() $(\unicode[STIX]{x1D713}_{t})$
) denote the geodesic joining
$(\unicode[STIX]{x1D713}_{t})$
) denote the geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
(respectively
$\unicode[STIX]{x1D711}_{1}$
(respectively
![]() $\unicode[STIX]{x1D711}_{0}/2$
to
$\unicode[STIX]{x1D711}_{0}/2$
to
![]() $\unicode[STIX]{x1D711}_{1}/2$
). Observe that
$\unicode[STIX]{x1D711}_{1}/2$
). Observe that
![]() $t\mapsto \unicode[STIX]{x1D711}_{t},\unicode[STIX]{x1D713}_{t}$
are increasing, hence
$t\mapsto \unicode[STIX]{x1D711}_{t},\unicode[STIX]{x1D713}_{t}$
are increasing, hence
![]() $\dot{\unicode[STIX]{x1D711}}_{0}\geqslant 0$
. The family
$\dot{\unicode[STIX]{x1D711}}_{0}\geqslant 0$
. The family
![]() $(\unicode[STIX]{x1D711}_{t}/2)$
is a subgeodesic joining
$(\unicode[STIX]{x1D711}_{t}/2)$
is a subgeodesic joining
![]() $\unicode[STIX]{x1D711}_{0}/2$
to
$\unicode[STIX]{x1D711}_{0}/2$
to
![]() $\unicode[STIX]{x1D711}_{1}/2$
, hence
$\unicode[STIX]{x1D711}_{1}/2$
, hence
![]() $\unicode[STIX]{x1D711}_{t}/2\leqslant \unicode[STIX]{x1D713}_{t}$
and
$\unicode[STIX]{x1D711}_{t}/2\leqslant \unicode[STIX]{x1D713}_{t}$
and
Moreover,
![]() $\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\leqslant 2^{n}\operatorname{MA}(\unicode[STIX]{x1D711}_{0}/2)$
, so we infer
$\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\leqslant 2^{n}\operatorname{MA}(\unicode[STIX]{x1D711}_{0}/2)$
, so we infer
which proves part (ii). A similar argument shows that
Now
![]() $\operatorname{MA}(\unicode[STIX]{x1D711}_{1}/2)=\operatorname{MA}(\unicode[STIX]{x1D711}_{1})=\operatorname{MA}(0)$
when
$\operatorname{MA}(\unicode[STIX]{x1D711}_{1}/2)=\operatorname{MA}(\unicode[STIX]{x1D711}_{1})=\operatorname{MA}(0)$
when
![]() $\unicode[STIX]{x1D711}_{1}=0$
, hence
$\unicode[STIX]{x1D711}_{1}=0$
, hence
which yields part (iii).
It remains to prove part (iv). Let
![]() $(\unicode[STIX]{x1D711}_{t})_{0\leqslant t\leqslant 1}$
(respectively
$(\unicode[STIX]{x1D711}_{t})_{0\leqslant t\leqslant 1}$
(respectively
![]() $(\unicode[STIX]{x1D713}_{t})_{0\leqslant t\leqslant 1}$
) be the geodesic joining
$(\unicode[STIX]{x1D713}_{t})_{0\leqslant t\leqslant 1}$
) be the geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
(respectively
$\unicode[STIX]{x1D711}_{1}$
(respectively
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D713}$
). Observe that
$\unicode[STIX]{x1D713}$
). Observe that
![]() $\unicode[STIX]{x1D711}_{0}=\unicode[STIX]{x1D713}_{0}$
and
$\unicode[STIX]{x1D711}_{0}=\unicode[STIX]{x1D713}_{0}$
and
![]() $\unicode[STIX]{x1D713}_{t}\leqslant \unicode[STIX]{x1D711}_{t}$
, hence
$\unicode[STIX]{x1D713}_{t}\leqslant \unicode[STIX]{x1D711}_{t}$
, hence
![]() $\dot{\unicode[STIX]{x1D713}}_{0}\leqslant \dot{\unicode[STIX]{x1D711}}_{0}$
. Moreover,
$\dot{\unicode[STIX]{x1D713}}_{0}\leqslant \dot{\unicode[STIX]{x1D711}}_{0}$
. Moreover,
![]() $0\leqslant \dot{\unicode[STIX]{x1D713}}_{0}$
since
$0\leqslant \dot{\unicode[STIX]{x1D713}}_{0}$
since
![]() $t\mapsto \unicode[STIX]{x1D713}_{t}(x)$
is increasing. We infer
$t\mapsto \unicode[STIX]{x1D713}_{t}(x)$
is increasing. We infer
The other inequality is proved similarly. ◻
Proposition 3.8. For all
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
,
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
,
Moreover, if
![]() $\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
then
$\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
then
![]() $I_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})\leqslant (\int _{X}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0}))^{1/p}$
and
$I_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})\leqslant (\int _{X}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0}))^{1/p}$
and
Proof. We first assume that
![]() $\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
. The inequality
$\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
. The inequality
follows from Lemma 2.12. Let
![]() $(\unicode[STIX]{x1D711}_{t})$
be the geodesic joining
$(\unicode[STIX]{x1D711}_{t})$
be the geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
. It follows from Lemma 3.3 that
$\unicode[STIX]{x1D711}_{1}$
. It follows from Lemma 3.3 that
![]() $0\leqslant \dot{\unicode[STIX]{x1D711}}_{0}\leqslant \unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\leqslant \dot{\unicode[STIX]{x1D711}}_{1}$
, hence
$0\leqslant \dot{\unicode[STIX]{x1D711}}_{0}\leqslant \unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\leqslant \dot{\unicode[STIX]{x1D711}}_{1}$
, hence
and, similarly,
![]() $d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})^{p}\leqslant \int _{X}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})$
.
$d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})^{p}\leqslant \int _{X}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})$
.
We now show that
![]() $\int _{X}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\leqslant 2^{n+p}d(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})^{p}$
. Observe that
$\int _{X}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\leqslant 2^{n+p}d(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})^{p}$
. Observe that
![]() $(\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1})/2\in {\mathcal{H}}_{bd}$
with
$(\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1})/2\in {\mathcal{H}}_{bd}$
with
![]() $\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\leqslant 2^{n}\,\operatorname{MA}((\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1})/2)$
, hence
$\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\leqslant 2^{n}\,\operatorname{MA}((\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1})/2)$
, hence
 $$\begin{eqnarray}\displaystyle \int _{X}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0}) & = & \displaystyle 2^{p}\int _{X}\biggl(\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}-\unicode[STIX]{x1D711}_{0}\biggr)^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2^{n+p}\int _{X}\biggl(\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}-\unicode[STIX]{x1D711}_{0}\biggr)^{p}\operatorname{MA}\biggl(\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2^{n+p}d_{p}\biggl(\unicode[STIX]{x1D711}_{0},\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\biggr)^{p},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{X}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0}) & = & \displaystyle 2^{p}\int _{X}\biggl(\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}-\unicode[STIX]{x1D711}_{0}\biggr)^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2^{n+p}\int _{X}\biggl(\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}-\unicode[STIX]{x1D711}_{0}\biggr)^{p}\operatorname{MA}\biggl(\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\biggr)\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2^{n+p}d_{p}\biggl(\unicode[STIX]{x1D711}_{0},\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\biggr)^{p},\nonumber\end{eqnarray}$$
as follows from the first step of the proof, since
![]() $\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
. Lemma 3.7(iv) yields
$\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
. Lemma 3.7(iv) yields
hence
![]() $\int _{X}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\leqslant 2^{n+p}d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})^{p}$
.
$\int _{X}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\leqslant 2^{n+p}d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})^{p}$
.
We finally treat the first upper bound of the proposition, which does not require
![]() $\unicode[STIX]{x1D711}_{0}$
to lie below
$\unicode[STIX]{x1D711}_{0}$
to lie below
![]() $\unicode[STIX]{x1D711}_{1}$
. It follows from the triangle inequality that
$\unicode[STIX]{x1D711}_{1}$
. It follows from the triangle inequality that
 $$\begin{eqnarray}\displaystyle d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}) & {\leqslant} & \displaystyle d_{p}(\unicode[STIX]{x1D711}_{0},\max (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}))+d_{p}(\max (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}),\unicode[STIX]{x1D711}_{1})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl(\int _{\{\unicode[STIX]{x1D711}_{0}<\unicode[STIX]{x1D711}_{1}\}}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\biggr)^{1/p}+\biggl(\int _{\{\unicode[STIX]{x1D711}_{0}>\unicode[STIX]{x1D711}_{1}\}}(\unicode[STIX]{x1D711}_{0}-\unicode[STIX]{x1D711}_{1})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{1})\biggr)^{1/p}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2^{1-1/p}\biggl(\int _{X}|\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}|^{p}[\operatorname{MA}(\unicode[STIX]{x1D711}_{0})+\operatorname{MA}(\unicode[STIX]{x1D711}_{1})]\biggr)^{1/p}\nonumber\\ \displaystyle & = & \displaystyle 2\biggl(\int _{X}|\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}|^{p}\frac{[\operatorname{MA}(\unicode[STIX]{x1D711}_{0})+\operatorname{MA}(\unicode[STIX]{x1D711}_{1})]}{2}\biggr)^{1/p}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}) & {\leqslant} & \displaystyle d_{p}(\unicode[STIX]{x1D711}_{0},\max (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}))+d_{p}(\max (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}),\unicode[STIX]{x1D711}_{1})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \biggl(\int _{\{\unicode[STIX]{x1D711}_{0}<\unicode[STIX]{x1D711}_{1}\}}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\biggr)^{1/p}+\biggl(\int _{\{\unicode[STIX]{x1D711}_{0}>\unicode[STIX]{x1D711}_{1}\}}(\unicode[STIX]{x1D711}_{0}-\unicode[STIX]{x1D711}_{1})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{1})\biggr)^{1/p}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2^{1-1/p}\biggl(\int _{X}|\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}|^{p}[\operatorname{MA}(\unicode[STIX]{x1D711}_{0})+\operatorname{MA}(\unicode[STIX]{x1D711}_{1})]\biggr)^{1/p}\nonumber\\ \displaystyle & = & \displaystyle 2\biggl(\int _{X}|\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}|^{p}\frac{[\operatorname{MA}(\unicode[STIX]{x1D711}_{0})+\operatorname{MA}(\unicode[STIX]{x1D711}_{1})]}{2}\biggr)^{1/p}\nonumber\end{eqnarray}$$
by using the elementary inequality
![]() $a^{1/p}+b^{1/p}\leqslant 2^{1-1/p}(a+b)^{1/p}$
.◻
$a^{1/p}+b^{1/p}\leqslant 2^{1-1/p}(a+b)^{1/p}$
.◻
Remark 3.9. Working with
![]() $\unicode[STIX]{x1D713}=t\unicode[STIX]{x1D711}_{0}+(1-t)\unicode[STIX]{x1D711}_{1}$
,
$\unicode[STIX]{x1D713}=t\unicode[STIX]{x1D711}_{0}+(1-t)\unicode[STIX]{x1D711}_{1}$
,
![]() $0<t<1$
, instead of
$0<t<1$
, instead of
![]() $(\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1})/2$
, one can improve this inequality and obtain
$(\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1})/2$
, one can improve this inequality and obtain
We now extend Lemma 3.7(i), following [Reference DarvasDar15, Lemma 5.3].
Lemma 3.10. For all
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
,
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
,
Proof. When
![]() $\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
, this follows from Lemma 3.7(i). Replacing
$\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
, this follows from Lemma 3.7(i). Replacing
![]() $\unicode[STIX]{x1D714}$
with
$\unicode[STIX]{x1D714}$
with
![]() $\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}_{0}$
, we can assume, without loss of generality, that
$\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}_{0}$
, we can assume, without loss of generality, that
![]() $\unicode[STIX]{x1D711}_{0}=0$
. The triangle inequality yields
$\unicode[STIX]{x1D711}_{0}=0$
. The triangle inequality yields
Observe that
![]() $0\vee \unicode[STIX]{x1D711}_{1}\leqslant 0\vee \unicode[STIX]{x1D711}_{1}/2\leqslant \min (0,\unicode[STIX]{x1D711}_{1}/2)$
. It follows, therefore, from Lemma 3.7(iv) that
$0\vee \unicode[STIX]{x1D711}_{1}\leqslant 0\vee \unicode[STIX]{x1D711}_{1}/2\leqslant \min (0,\unicode[STIX]{x1D711}_{1}/2)$
. It follows, therefore, from Lemma 3.7(iv) that
Since
![]() $0\vee \unicode[STIX]{x1D711}_{1}\leqslant 0$
and
$0\vee \unicode[STIX]{x1D711}_{1}\leqslant 0$
and
![]() $0\vee \unicode[STIX]{x1D711}_{1}\leqslant \unicode[STIX]{x1D711}_{1}/2$
, we can invoke Proposition 3.8 to obtain
$0\vee \unicode[STIX]{x1D711}_{1}\leqslant \unicode[STIX]{x1D711}_{1}/2$
, we can invoke Proposition 3.8 to obtain
 $$\begin{eqnarray}\displaystyle d_{p}(0,0\vee \unicode[STIX]{x1D711}_{1})+d_{p}\biggl(0\vee \unicode[STIX]{x1D711}_{1},\frac{\unicode[STIX]{x1D711}_{1}}{2}\biggr) & {\leqslant} & \displaystyle \biggl(\int _{X}|0\vee \unicode[STIX]{x1D711}_{1}|^{p}\operatorname{MA}(0\vee \unicode[STIX]{x1D711}_{1})\biggr)^{1/p}\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(\int _{X}\biggl|0\vee \unicode[STIX]{x1D711}_{1}-\frac{\unicode[STIX]{x1D711}_{1}}{2}\biggr|^{p}\operatorname{MA}(0\vee \unicode[STIX]{x1D711}_{1})\biggr)^{1/p}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2^{1-1/p}\biggl(\int _{X}\biggl[|0\vee \unicode[STIX]{x1D711}_{1}|^{p}+\biggl|0\vee \unicode[STIX]{x1D711}_{1}-\frac{\unicode[STIX]{x1D711}_{1}}{2}\biggr|^{p}\biggr]\operatorname{MA}(0\vee \unicode[STIX]{x1D711}_{1})\biggr)^{1/p}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{p}(0,0\vee \unicode[STIX]{x1D711}_{1})+d_{p}\biggl(0\vee \unicode[STIX]{x1D711}_{1},\frac{\unicode[STIX]{x1D711}_{1}}{2}\biggr) & {\leqslant} & \displaystyle \biggl(\int _{X}|0\vee \unicode[STIX]{x1D711}_{1}|^{p}\operatorname{MA}(0\vee \unicode[STIX]{x1D711}_{1})\biggr)^{1/p}\nonumber\\ \displaystyle & & \displaystyle +\,\biggl(\int _{X}\biggl|0\vee \unicode[STIX]{x1D711}_{1}-\frac{\unicode[STIX]{x1D711}_{1}}{2}\biggr|^{p}\operatorname{MA}(0\vee \unicode[STIX]{x1D711}_{1})\biggr)^{1/p}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 2^{1-1/p}\biggl(\int _{X}\biggl[|0\vee \unicode[STIX]{x1D711}_{1}|^{p}+\biggl|0\vee \unicode[STIX]{x1D711}_{1}-\frac{\unicode[STIX]{x1D711}_{1}}{2}\biggr|^{p}\biggr]\operatorname{MA}(0\vee \unicode[STIX]{x1D711}_{1})\biggr)^{1/p}.\nonumber\end{eqnarray}$$
Recall now that the measure
![]() $\operatorname{MA}(0\vee \unicode[STIX]{x1D711}_{1})$
is supported on the contact set
$\operatorname{MA}(0\vee \unicode[STIX]{x1D711}_{1})$
is supported on the contact set
![]() $S:=\{x\in X;0\vee \unicode[STIX]{x1D711}_{1}(x)=\min (0,\unicode[STIX]{x1D711}_{1})(x)\}$
. On this set, we have
$S:=\{x\in X;0\vee \unicode[STIX]{x1D711}_{1}(x)=\min (0,\unicode[STIX]{x1D711}_{1})(x)\}$
. On this set, we have
while Proposition 3.8 yields
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X}[|0\vee \unicode[STIX]{x1D711}_{1}|^{p}+|0\vee \unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{1}|^{p}]\operatorname{MA}(0\vee \unicode[STIX]{x1D711}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2^{p+n}[d_{p}(0,0\vee \unicode[STIX]{x1D711}_{1})^{p}+d_{p}(0\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{1})^{p}]=2^{p+n}d_{p}(0,\unicode[STIX]{x1D711}_{1})^{p},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{X}[|0\vee \unicode[STIX]{x1D711}_{1}|^{p}+|0\vee \unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{1}|^{p}]\operatorname{MA}(0\vee \unicode[STIX]{x1D711}_{1})\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant 2^{p+n}[d_{p}(0,0\vee \unicode[STIX]{x1D711}_{1})^{p}+d_{p}(0\vee \unicode[STIX]{x1D711}_{1},\unicode[STIX]{x1D711}_{1})^{p}]=2^{p+n}d_{p}(0,\unicode[STIX]{x1D711}_{1})^{p},\nonumber\end{eqnarray}$$
where the last equality follows from Proposition 3.4. Altogether, this yields
![]() $d_{p}(0,\unicode[STIX]{x1D711}_{1}/2)\leqslant 2^{2+n/p}d_{p}(0,\unicode[STIX]{x1D711}_{1})$
, as claimed.◻
$d_{p}(0,\unicode[STIX]{x1D711}_{1}/2)\leqslant 2^{2+n/p}d_{p}(0,\unicode[STIX]{x1D711}_{1})$
, as claimed.◻
We are now ready to prove Theorem 3.6.
Proof. We have already observed that
![]() $d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})\leqslant 2I_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
in Proposition 3.8, so we focus on the reverse control. Lemma 3.10 and Proposition 3.4 yield
$d_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})\leqslant 2I_{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
in Proposition 3.8, so we focus on the reverse control. Lemma 3.10 and Proposition 3.4 yield
 $$\begin{eqnarray}\displaystyle 2^{2p+n}d_{p}^{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}) & {\geqslant} & \displaystyle d_{p}^{p}\biggl(\unicode[STIX]{x1D711}_{0},\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\biggr)\nonumber\\ \displaystyle & = & \displaystyle d_{p}^{p}\biggl(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{0}\vee \frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\biggr)+d_{p}^{p}\biggl(\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2},\unicode[STIX]{x1D711}_{0}\vee \frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2^{2p+n}d_{p}^{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}) & {\geqslant} & \displaystyle d_{p}^{p}\biggl(\unicode[STIX]{x1D711}_{0},\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\biggr)\nonumber\\ \displaystyle & = & \displaystyle d_{p}^{p}\biggl(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{0}\vee \frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\biggr)+d_{p}^{p}\biggl(\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2},\unicode[STIX]{x1D711}_{0}\vee \frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\biggr).\nonumber\end{eqnarray}$$
It follows from (8) together with the fact that
![]() $2^{n}\operatorname{MA}((\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1})/2)\geqslant \operatorname{MA}(\unicode[STIX]{x1D711}_{0})$
that
$2^{n}\operatorname{MA}((\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1})/2)\geqslant \operatorname{MA}(\unicode[STIX]{x1D711}_{0})$
that
and
Hence
 $$\begin{eqnarray}\displaystyle d_{p}^{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}) & {\geqslant} & \displaystyle 2^{-2(p+n)}\int _{X}\biggl[\biggl(\unicode[STIX]{x1D711}_{0}-\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\vee \unicode[STIX]{x1D711}_{0}\biggr)^{p}+\biggl(\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}-\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\vee \unicode[STIX]{x1D711}_{0}\biggr)^{p}\biggr]\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 2^{1-3p-2n}\int _{X}\biggl|\unicode[STIX]{x1D711}_{0}-\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\biggr|^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\nonumber\\ \displaystyle & = & \displaystyle 2^{1-4p-2n}\int _{X}|\unicode[STIX]{x1D711}_{0}-\unicode[STIX]{x1D711}_{1}|^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{p}^{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}) & {\geqslant} & \displaystyle 2^{-2(p+n)}\int _{X}\biggl[\biggl(\unicode[STIX]{x1D711}_{0}-\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\vee \unicode[STIX]{x1D711}_{0}\biggr)^{p}+\biggl(\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}-\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\vee \unicode[STIX]{x1D711}_{0}\biggr)^{p}\biggr]\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle 2^{1-3p-2n}\int _{X}\biggl|\unicode[STIX]{x1D711}_{0}-\frac{\unicode[STIX]{x1D711}_{0}+\unicode[STIX]{x1D711}_{1}}{2}\biggr|^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0})\nonumber\\ \displaystyle & = & \displaystyle 2^{1-4p-2n}\int _{X}|\unicode[STIX]{x1D711}_{0}-\unicode[STIX]{x1D711}_{1}|^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{0}),\nonumber\end{eqnarray}$$
where in the last inequality we used the fact that
![]() $|a-b|^{p}\leqslant 2^{p-1}(a^{p}+b^{p})$
, for any
$|a-b|^{p}\leqslant 2^{p-1}(a^{p}+b^{p})$
, for any
![]() $a,b\in \mathbb{R}^{+}$
.
$a,b\in \mathbb{R}^{+}$
.
Reversing the roles of
![]() $\unicode[STIX]{x1D711}_{0}$
and
$\unicode[STIX]{x1D711}_{0}$
and
![]() $\unicode[STIX]{x1D711}_{1}$
, we get
$\unicode[STIX]{x1D711}_{1}$
, we get
from which it follows that
![]() $d_{p}^{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})\geqslant 2^{1-4p-2n}I_{p}^{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
.◻
$d_{p}^{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})\geqslant 2^{1-4p-2n}I_{p}^{p}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
.◻
3.3 Controlling the supremum
It follows from previous results that the supremum of a bounded potential with locally bounded Laplacian in
![]() $\operatorname{Amp}(\unicode[STIX]{x1D6FC})$
is controlled by the distance to the base point.
$\operatorname{Amp}(\unicode[STIX]{x1D6FC})$
is controlled by the distance to the base point.
Lemma 3.11. There exists
![]() $C>0$
, such that for all
$C>0$
, such that for all
![]() $\unicode[STIX]{x1D711}\in {\mathcal{H}}_{bd}$
,
$\unicode[STIX]{x1D711}\in {\mathcal{H}}_{bd}$
,
Proof. If
![]() $\sup _{X}\unicode[STIX]{x1D711}\leqslant 0$
, then
$\sup _{X}\unicode[STIX]{x1D711}\leqslant 0$
, then
![]() $\sup _{X}\unicode[STIX]{x1D711}\leqslant 0\leqslant (n+1)d_{1}(0,\unicode[STIX]{x1D711})+C$
, while
$\sup _{X}\unicode[STIX]{x1D711}\leqslant 0\leqslant (n+1)d_{1}(0,\unicode[STIX]{x1D711})+C$
, while
as follows from Proposition 3.12. We therefore assume in what follows that
![]() $\sup _{X}\unicode[STIX]{x1D711}\geqslant 0$
. If
$\sup _{X}\unicode[STIX]{x1D711}\geqslant 0$
. If
![]() $\unicode[STIX]{x1D711}\geqslant 0$
, Proposition 3.12 yields
$\unicode[STIX]{x1D711}\geqslant 0$
, Proposition 3.12 yields
It is a classical consequence of the
![]() $\unicode[STIX]{x1D714}$
-plurisubharmonicity [Reference Guedj and ZeriahiGZ05, Proposition 2.7] that there exists
$\unicode[STIX]{x1D714}$
-plurisubharmonicity [Reference Guedj and ZeriahiGZ05, Proposition 2.7] that there exists
![]() $C>0$
such that, for all
$C>0$
such that, for all
![]() $\unicode[STIX]{x1D711}\in \text{PSH}(X,\unicode[STIX]{x1D714})$
,
$\unicode[STIX]{x1D711}\in \text{PSH}(X,\unicode[STIX]{x1D714})$
,
Thus,
![]() $\sup _{X}\unicode[STIX]{x1D711}\leqslant (n+1)d_{1}(0,\unicode[STIX]{x1D711})+C$
.
$\sup _{X}\unicode[STIX]{x1D711}\leqslant (n+1)d_{1}(0,\unicode[STIX]{x1D711})+C$
.
When
![]() $\sup _{X}\unicode[STIX]{x1D711}\geqslant 0$
but
$\sup _{X}\unicode[STIX]{x1D711}\geqslant 0$
but
![]() $\unicode[STIX]{x1D711}$
takes both positive and negative values, we set
$\unicode[STIX]{x1D711}$
takes both positive and negative values, we set
![]() $\unicode[STIX]{x1D713}=\max (0,\unicode[STIX]{x1D711})$
and observe that
$\unicode[STIX]{x1D713}=\max (0,\unicode[STIX]{x1D711})$
and observe that
![]() $\sup _{X}\unicode[STIX]{x1D713}=\sup _{X}\unicode[STIX]{x1D711}$
. Using Propositions 2.13 and 3.8 and Theorem 3.6, we obtain
$\sup _{X}\unicode[STIX]{x1D713}=\sup _{X}\unicode[STIX]{x1D711}$
. Using Propositions 2.13 and 3.8 and Theorem 3.6, we obtain
The conclusion, therefore, follows from the previous case. ◻
Proposition 3.12. Assume
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{H}}_{bd}$
. Then
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{H}}_{bd}$
. Then
Proof. We proceed by approximation, so as to reduce to the Kähler case. By [Reference DarvasDar15, Corollary 4.14], we know that
where
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}:=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}$
,
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}:=\unicode[STIX]{x1D714}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}_{X}$
,
![]() $\unicode[STIX]{x1D711}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D713}$
is the greatest
$\unicode[STIX]{x1D711}\vee _{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D713}$
is the greatest
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
-psh function that lies below
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}$
-psh function that lies below
![]() $\min (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
, and
$\min (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
, and
![]() $E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
is as in (6). Since
$E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
is as in (6). Since
![]() $(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D711})^{n}$
converges weakly to
$(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D711})^{n}$
converges weakly to
![]() $(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711})^{n}$
, we have that
$(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711})^{n}$
, we have that
![]() $E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711})$
converges to
$E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711})$
converges to
![]() $E(\unicode[STIX]{x1D711})$
as
$E(\unicode[STIX]{x1D711})$
as
![]() $\unicode[STIX]{x1D700}$
goes to
$\unicode[STIX]{x1D700}$
goes to
![]() $0$
. The same holds for
$0$
. The same holds for
![]() $E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D713})$
. We then need to ensure that
$E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D713})$
. We then need to ensure that
![]() $E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711}\vee _{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}\unicode[STIX]{x1D713})$
converges to
$E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D711}\vee _{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}\unicode[STIX]{x1D713})$
converges to
![]() $E(\unicode[STIX]{x1D711}\vee \unicode[STIX]{x1D713})$
. Denote
$E(\unicode[STIX]{x1D711}\vee \unicode[STIX]{x1D713})$
. Denote
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}}:=\unicode[STIX]{x1D711}\vee _{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}\unicode[STIX]{x1D713}$
and
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}}:=\unicode[STIX]{x1D711}\vee _{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}\unicode[STIX]{x1D713}$
and
![]() $\unicode[STIX]{x1D719}:=\unicode[STIX]{x1D711}\vee \unicode[STIX]{x1D713}$
. Fix
$\unicode[STIX]{x1D719}:=\unicode[STIX]{x1D711}\vee \unicode[STIX]{x1D713}$
. Fix
![]() $\unicode[STIX]{x1D700}^{\prime }>\unicode[STIX]{x1D700}$
. Using Lemma 2.5 and the fact that
$\unicode[STIX]{x1D700}^{\prime }>\unicode[STIX]{x1D700}$
. Using Lemma 2.5 and the fact that
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}}$
is decreasing to
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}}$
is decreasing to
![]() $\unicode[STIX]{x1D719}$
, we get
$\unicode[STIX]{x1D719}$
, we get
 $$\begin{eqnarray}\displaystyle 0\geqslant E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}})-E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D719}) & = & \displaystyle \frac{1}{(n+1)V_{\unicode[STIX]{x1D700}}}\mathop{\sum }_{j=0}^{n}\int _{X}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}}-\unicode[STIX]{x1D719})(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}})^{j}\wedge (\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D719})^{n-j}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{(n+1)V_{\unicode[STIX]{x1D700}}}\mathop{\sum }_{j=0}^{n}\int _{X}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}^{\prime }}-\unicode[STIX]{x1D719})(\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{X}+dd^{c}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}})^{j}\wedge (\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{X}+dd^{c}\unicode[STIX]{x1D719})^{n-j}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0\geqslant E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}})-E_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}(\unicode[STIX]{x1D719}) & = & \displaystyle \frac{1}{(n+1)V_{\unicode[STIX]{x1D700}}}\mathop{\sum }_{j=0}^{n}\int _{X}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}}-\unicode[STIX]{x1D719})(\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}})^{j}\wedge (\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D719})^{n-j}\nonumber\\ \displaystyle & {\geqslant} & \displaystyle \frac{1}{(n+1)V_{\unicode[STIX]{x1D700}}}\mathop{\sum }_{j=0}^{n}\int _{X}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}^{\prime }}-\unicode[STIX]{x1D719})(\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{X}+dd^{c}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D700}})^{j}\wedge (\unicode[STIX]{x1D714}+\unicode[STIX]{x1D714}_{X}+dd^{c}\unicode[STIX]{x1D719})^{n-j}.\nonumber\end{eqnarray}$$
Letting first
![]() $\unicode[STIX]{x1D700}$
to zero and the
$\unicode[STIX]{x1D700}$
to zero and the
![]() $\unicode[STIX]{x1D700}^{\prime }$
, we get the result. The conclusion then follows from the previous arguments and Proposition 1.16.◻
$\unicode[STIX]{x1D700}^{\prime }$
, we get the result. The conclusion then follows from the previous arguments and Proposition 1.16.◻
4 The complete geodesic space
 $({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
$({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
4.1 Metric completion
For
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
, we let
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
, we let
![]() $\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{k}$
denote sequences of elements in
$\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{k}$
denote sequences of elements in
![]() ${\mathcal{H}}_{bd}$
decreasing to
${\mathcal{H}}_{bd}$
decreasing to
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
, respectively, and set
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
, respectively, and set
We list in the following proposition various properties of this extension.
Proposition 4.1.
(i)
 $D_{p}$
is a distance on
$D_{p}$
is a distance on
 ${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
, which coincides with
${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
, which coincides with
 $d_{p}$
on
$d_{p}$
on
 ${\mathcal{H}}_{bd}$
.
${\mathcal{H}}_{bd}$
.(ii) The definition of
 $D_{p}$
is independent of the choice of the approximants.
$D_{p}$
is independent of the choice of the approximants.(iii)
 $D_{p}$
is continuous along decreasing sequences in
$D_{p}$
is continuous along decreasing sequences in
 ${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
.
${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
.
Moreover all previous inequalities comparing
![]() $d_{p}$
and
$d_{p}$
and
![]() $I_{p}$
on
$I_{p}$
on
![]() ${\mathcal{H}}_{bd}$
extend to inequalities between
${\mathcal{H}}_{bd}$
extend to inequalities between
![]() $D_{p}$
and
$D_{p}$
and
![]() $I_{p}$
on
$I_{p}$
on
![]() ${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
.
${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
.
In the following, therefore, we will denote
![]() $D_{p}$
by
$D_{p}$
by
![]() $d_{p}$
.
$d_{p}$
.
Proof. It is a tedious exercise to verify that
![]() $D_{p}$
defines a ‘semi-distance’, i.e. satisfies all properties of a distance but for the separation property. It follows from the definition of
$D_{p}$
defines a ‘semi-distance’, i.e. satisfies all properties of a distance but for the separation property. It follows from the definition of
![]() $D_{p}$
and Proposition 2.11 that Theorem 3.6 extends in a natural way to potentials in
$D_{p}$
and Proposition 2.11 that Theorem 3.6 extends in a natural way to potentials in
![]() ${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
. If
${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
. If
![]() $D_{p}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})=0$
, it therefore follows that
$D_{p}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})=0$
, it therefore follows that
![]() $I_{p}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})=0$
, hence
$I_{p}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})=0$
, hence
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D713}$
by the domination principle.
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D713}$
by the domination principle.
One can check that
![]() $D_{p}$
coincides with
$D_{p}$
coincides with
![]() $d_{p}$
on
$d_{p}$
on
![]() ${\mathcal{H}}_{bd}$
as follows: using part (ii), one can use the constant sequences
${\mathcal{H}}_{bd}$
as follows: using part (ii), one can use the constant sequences
![]() $\unicode[STIX]{x1D711}_{j}\equiv \unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}_{j}\equiv \unicode[STIX]{x1D711}$
and
![]() $\unicode[STIX]{x1D713}_{k}\equiv \unicode[STIX]{x1D713}$
to obtain this equality.
$\unicode[STIX]{x1D713}_{k}\equiv \unicode[STIX]{x1D713}$
to obtain this equality.
We now prove part (ii). Let
![]() $\unicode[STIX]{x1D711}_{j},u_{j}$
(respectively
$\unicode[STIX]{x1D711}_{j},u_{j}$
(respectively
![]() $\unicode[STIX]{x1D713}_{k},v_{k}$
) denote two sequences of elements of
$\unicode[STIX]{x1D713}_{k},v_{k}$
) denote two sequences of elements of
![]() ${\mathcal{H}}_{bd}$
decreasing to
${\mathcal{H}}_{bd}$
decreasing to
![]() $\unicode[STIX]{x1D711}$
(respectively
$\unicode[STIX]{x1D711}$
(respectively
![]() $\unicode[STIX]{x1D713}$
). We can assume without loss of generality that these sequences are intertwining, i.e. for all
$\unicode[STIX]{x1D713}$
). We can assume without loss of generality that these sequences are intertwining, i.e. for all
![]() $j,k\in \mathbb{N}$
, there exists
$j,k\in \mathbb{N}$
, there exists
![]() $\ell ,q\in \mathbb{N}$
, such that
$\ell ,q\in \mathbb{N}$
, such that
![]() $\unicode[STIX]{x1D711}_{j}\leqslant u_{\ell }$
and
$\unicode[STIX]{x1D711}_{j}\leqslant u_{\ell }$
and
![]() $\unicode[STIX]{x1D713}_{k}\leqslant v_{q}$
, with similar reverse inequalities. It follows from Proposition 3.8 and the triangle inequality that
$\unicode[STIX]{x1D713}_{k}\leqslant v_{q}$
, with similar reverse inequalities. It follows from Proposition 3.8 and the triangle inequality that
Now, again by Proposition 3.8, we get
where the last inequality follows from [Reference Guedj and ZeriahiGZ07, Lemma 3.5]. The monotone convergence theorem, therefore, yields
![]() $I_{p}(\unicode[STIX]{x1D711}_{j},u_{\ell })+I_{p}(\unicode[STIX]{x1D713}_{k},v_{q})\rightarrow 0$
as
$I_{p}(\unicode[STIX]{x1D711}_{j},u_{\ell })+I_{p}(\unicode[STIX]{x1D713}_{k},v_{q})\rightarrow 0$
as
![]() $\ell ,q\rightarrow +\infty$
, proving part (ii).
$\ell ,q\rightarrow +\infty$
, proving part (ii).
One shows part (iii) with similar arguments. The extension of the inequalities comparing
![]() $d_{p}$
and
$d_{p}$
and
![]() $I_{p}$
follows from [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem 2.17].◻
$I_{p}$
follows from [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem 2.17].◻
Proposition 4.2. The metric spaces
![]() $({\mathcal{E}}_{\text{norm}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
and
$({\mathcal{E}}_{\text{norm}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
and
![]() $({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
are complete. The Mabuchi topology
$({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
are complete. The Mabuchi topology
![]() $d_{p}$
dominates the topology induced by
$d_{p}$
dominates the topology induced by
![]() $I$
: if a sequence converges for
$I$
: if a sequence converges for
![]() $d_{p}$
, it converges in energy.
$d_{p}$
, it converges in energy.
Proof. Let
![]() $(\unicode[STIX]{x1D711}_{j})\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})^{\mathbb{N}}$
be a Cauchy sequence for
$(\unicode[STIX]{x1D711}_{j})\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})^{\mathbb{N}}$
be a Cauchy sequence for
![]() $d_{p}$
. We claim that there exists
$d_{p}$
. We claim that there exists
![]() $\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
, such that
$\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
, such that
Extracting and relabelling, we can assume that
Set
![]() $\unicode[STIX]{x1D711}_{-1}\equiv 0$
and for
$\unicode[STIX]{x1D711}_{-1}\equiv 0$
and for
![]() $k\geqslant j$
,
$k\geqslant j$
,
![]() $\unicode[STIX]{x1D713}_{j,k}:=\unicode[STIX]{x1D711}_{j}\vee \unicode[STIX]{x1D711}_{j+1}\vee \cdots \vee \unicode[STIX]{x1D711}_{k}$
, and observe that
$\unicode[STIX]{x1D713}_{j,k}:=\unicode[STIX]{x1D711}_{j}\vee \unicode[STIX]{x1D711}_{j+1}\vee \cdots \vee \unicode[STIX]{x1D711}_{k}$
, and observe that
![]() $\unicode[STIX]{x1D713}_{j,k}:=\unicode[STIX]{x1D711}_{j}\vee \unicode[STIX]{x1D713}_{j,k+1}$
. Hence, the Pythagorean formula gives
$\unicode[STIX]{x1D713}_{j,k}:=\unicode[STIX]{x1D711}_{j}\vee \unicode[STIX]{x1D713}_{j,k+1}$
. Hence, the Pythagorean formula gives
Repeating this argument, we get
![]() $d_{p}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{j,k})\leqslant 2^{-j+1}$
. We then have
$d_{p}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{j,k})\leqslant 2^{-j+1}$
. We then have
 $$\begin{eqnarray}\displaystyle d_{p}(0,\unicode[STIX]{x1D713}_{j,k}) & {\leqslant} & \displaystyle \mathop{\sum }_{\ell =-1}^{j-1}d_{p}(\unicode[STIX]{x1D711}_{\ell },\unicode[STIX]{x1D711}_{\ell +1})+d_{p}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{j,k})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{\ell =-1}^{j}d_{p}(\unicode[STIX]{x1D711}_{\ell },\unicode[STIX]{x1D711}_{\ell +1})+d_{p}(\unicode[STIX]{x1D711}_{j+1},\unicode[STIX]{x1D713}_{j+1,k})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle d_{p}(0,\unicode[STIX]{x1D711}_{1})+2+2^{-j+1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{p}(0,\unicode[STIX]{x1D713}_{j,k}) & {\leqslant} & \displaystyle \mathop{\sum }_{\ell =-1}^{j-1}d_{p}(\unicode[STIX]{x1D711}_{\ell },\unicode[STIX]{x1D711}_{\ell +1})+d_{p}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{j,k})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \mathop{\sum }_{\ell =-1}^{j}d_{p}(\unicode[STIX]{x1D711}_{\ell },\unicode[STIX]{x1D711}_{\ell +1})+d_{p}(\unicode[STIX]{x1D711}_{j+1},\unicode[STIX]{x1D713}_{j+1,k})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle d_{p}(0,\unicode[STIX]{x1D711}_{1})+2+2^{-j+1}.\nonumber\end{eqnarray}$$
It follows from Theorem 3.6 that
![]() $I_{p}(0,\unicode[STIX]{x1D713}_{j,k})$
is uniformly bounded, hence its decreasing limit
$I_{p}(0,\unicode[STIX]{x1D713}_{j,k})$
is uniformly bounded, hence its decreasing limit
![]() $\unicode[STIX]{x1D713}_{j}:=\lim _{k\rightarrow +\infty }\unicode[STIX]{x1D713}_{j,k}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
[Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.19]. From the above, we also have
$\unicode[STIX]{x1D713}_{j}:=\lim _{k\rightarrow +\infty }\unicode[STIX]{x1D713}_{j,k}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
[Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.19]. From the above, we also have
Lemma 3.11 then ensures that
![]() $(\sup _{X}\unicode[STIX]{x1D713}_{j})_{j}$
is uniformly bounded, hence
$(\sup _{X}\unicode[STIX]{x1D713}_{j})_{j}$
is uniformly bounded, hence
![]() $\unicode[STIX]{x1D713}_{j}$
increases a.e. towards
$\unicode[STIX]{x1D713}_{j}$
increases a.e. towards
![]() $\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D714})$
. Also,
$\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D714})$
. Also,
![]() $\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
thanks to [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.4]. Moreover, [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem 2.17] yields
$\unicode[STIX]{x1D713}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
thanks to [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.4]. Moreover, [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem 2.17] yields
It follows, therefore, from Proposition 3.8 that
![]() $d_{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D713}_{j})\rightarrow 0$
and
$d_{p}(\unicode[STIX]{x1D713},\unicode[STIX]{x1D713}_{j})\rightarrow 0$
and
Recalling that
![]() $\unicode[STIX]{x1D713}_{j}\leqslant \unicode[STIX]{x1D711}_{j}$
, it follows from the quasi-triangle inequality, Proposition 2.8, and Theorem 3.6 that
$\unicode[STIX]{x1D713}_{j}\leqslant \unicode[STIX]{x1D711}_{j}$
, it follows from the quasi-triangle inequality, Proposition 2.8, and Theorem 3.6 that
Recall that the precompletion of a metric space
![]() $(X,d)$
is the set of all Cauchy sequences
$(X,d)$
is the set of all Cauchy sequences
![]() $C_{X}$
of
$C_{X}$
of
![]() $X$
, together with the semi-distance
$X$
, together with the semi-distance
The metric completion
![]() $(\overline{X},d)$
of
$(\overline{X},d)$
of
![]() $(X,d)$
is the quotient space
$(X,d)$
is the quotient space
![]() $C_{X}/\sim$
, where
$C_{X}/\sim$
, where
equipped with the induced distance, which we still denote
![]() $d$
.
$d$
.
We are now taking advantage of the fact that
![]() ${\mathcal{H}}_{bd}$
lives inside the complete metric space
${\mathcal{H}}_{bd}$
lives inside the complete metric space
![]() $({\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC}),d_{p})$
to conclude the following.
$({\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC}),d_{p})$
to conclude the following.
Theorem 4.3. The metric completion of
![]() $({\mathcal{H}}_{bd},d_{p})$
is isometric to
$({\mathcal{H}}_{bd},d_{p})$
is isometric to
![]() $({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
.
$({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
.
Thanks to Theorem 3.6, an equivalent formulation of this statement is that the metric completion of
![]() $({\mathcal{H}}_{bd},d_{p})$
is bi-Lipschitz equivalent to
$({\mathcal{H}}_{bd},d_{p})$
is bi-Lipschitz equivalent to
![]() $({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),I_{p})$
.
$({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),I_{p})$
.
Proof. We work at the level of normalized potentials,
and
![]() ${\mathcal{H}}_{0}:=\{\unicode[STIX]{x1D711}\in {\mathcal{H}}_{bd}\mid \unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}\geqslant 0~\text{and}~E(\unicode[STIX]{x1D711})=0\}$
.
${\mathcal{H}}_{0}:=\{\unicode[STIX]{x1D711}\in {\mathcal{H}}_{bd}\mid \unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711}\geqslant 0~\text{and}~E(\unicode[STIX]{x1D711})=0\}$
.
Since
![]() $({\mathcal{E}}_{0}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
is a complete metric space that contains
$({\mathcal{E}}_{0}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
is a complete metric space that contains
![]() ${\mathcal{H}}_{0}$
, it suffices to show that the latter is dense in
${\mathcal{H}}_{0}$
, it suffices to show that the latter is dense in
![]() ${\mathcal{E}}_{0}^{p}(X,\unicode[STIX]{x1D714})$
. Fix
${\mathcal{E}}_{0}^{p}(X,\unicode[STIX]{x1D714})$
. Fix
![]() $\unicode[STIX]{x1D711}\in {\mathcal{E}}_{0}^{p}(X,\unicode[STIX]{x1D714})$
and let
$\unicode[STIX]{x1D711}\in {\mathcal{E}}_{0}^{p}(X,\unicode[STIX]{x1D714})$
and let
![]() $(\unicode[STIX]{x1D711}_{j})\in {\mathcal{H}}_{0}^{\mathbb{N}}$
be a sequence quasi-decreasing to
$(\unicode[STIX]{x1D711}_{j})\in {\mathcal{H}}_{0}^{\mathbb{N}}$
be a sequence quasi-decreasing to
![]() $\unicode[STIX]{x1D711}$
: the normalization condition
$\unicode[STIX]{x1D711}$
: the normalization condition
![]() $E(\unicode[STIX]{x1D711}_{j})=0$
prevents us from getting a truly decreasing sequence; however,
$E(\unicode[STIX]{x1D711}_{j})=0$
prevents us from getting a truly decreasing sequence; however,
![]() $\unicode[STIX]{x1D711}_{j}+\unicode[STIX]{x1D700}_{j}$
is decreasing where
$\unicode[STIX]{x1D711}_{j}+\unicode[STIX]{x1D700}_{j}$
is decreasing where
![]() $\unicode[STIX]{x1D700}_{j}$
is a sequence of real numbers decreasing to zero. It follows from Proposition 3.8 that
$\unicode[STIX]{x1D700}_{j}$
is a sequence of real numbers decreasing to zero. It follows from Proposition 3.8 that
Now [Reference Guedj and ZeriahiGZ07, Lemma 3.5] shows that the latter is bounded from above by
which converges to zero as
![]() $j\rightarrow +\infty$
, as follows from the monotone convergence theorem. Therefore
$j\rightarrow +\infty$
, as follows from the monotone convergence theorem. Therefore
![]() $(\unicode[STIX]{x1D711}_{j})$
is a Cauchy sequence in
$(\unicode[STIX]{x1D711}_{j})$
is a Cauchy sequence in
![]() $({\mathcal{H}}_{0},d_{p})$
that converges to
$({\mathcal{H}}_{0},d_{p})$
that converges to
![]() $\unicode[STIX]{x1D711}$
, since
$\unicode[STIX]{x1D711}$
, since
by Proposition 3.8 and [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem 2.17].
We note the following alternative approach of independent interest. One first shows that
![]() ${\mathcal{H}}_{0}$
is dense in the set of all bounded
${\mathcal{H}}_{0}$
is dense in the set of all bounded
![]() $\unicode[STIX]{x1D714}$
-psh functions. Given
$\unicode[STIX]{x1D714}$
-psh functions. Given
![]() $\unicode[STIX]{x1D711}\in {\mathcal{E}}_{0}^{p}(X,\unicode[STIX]{x1D714})$
, one then considers its ‘canonical approximants’,
$\unicode[STIX]{x1D711}\in {\mathcal{E}}_{0}^{p}(X,\unicode[STIX]{x1D714})$
, one then considers its ‘canonical approximants’,
which decrease towards
![]() $\unicode[STIX]{x1D711}\in {\mathcal{E}}_{0}^{p}(X,\unicode[STIX]{x1D714})$
. It follows from Proposition 3.8 that
$\unicode[STIX]{x1D711}\in {\mathcal{E}}_{0}^{p}(X,\unicode[STIX]{x1D714})$
. It follows from Proposition 3.8 that
 $$\begin{eqnarray}\displaystyle d_{p}(\unicode[STIX]{x1D711}_{j+\ell },\unicode[STIX]{x1D711}_{j})^{p} & {\leqslant} & \displaystyle o(1)+\int _{X}(\unicode[STIX]{x1D711}_{j}-\unicode[STIX]{x1D711}_{j+\ell })^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{j+\ell })\nonumber\\ \displaystyle & = & \displaystyle o(1)+\int _{(\unicode[STIX]{x1D711}\leqslant -j-\ell )}\ell ^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{j+\ell })+\int _{(-j-\ell <\unicode[STIX]{x1D711}<-j)}(\unicode[STIX]{x1D711}_{j}-\unicode[STIX]{x1D711}_{j+\ell })^{p}\operatorname{MA}(\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & = & \displaystyle o(1)+\int _{(\unicode[STIX]{x1D711}\leqslant -j-\ell )}\ell ^{p}\operatorname{MA}(\unicode[STIX]{x1D711})+\int _{(-j-\ell <\unicode[STIX]{x1D711}<-j)}(\unicode[STIX]{x1D711}_{j}-\unicode[STIX]{x1D711}_{j+\ell })^{p}\operatorname{MA}(\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle o(1)+\int _{(\unicode[STIX]{x1D711}<-j)}\unicode[STIX]{x1D711}^{p}\operatorname{MA}(\unicode[STIX]{x1D711}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle d_{p}(\unicode[STIX]{x1D711}_{j+\ell },\unicode[STIX]{x1D711}_{j})^{p} & {\leqslant} & \displaystyle o(1)+\int _{X}(\unicode[STIX]{x1D711}_{j}-\unicode[STIX]{x1D711}_{j+\ell })^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{j+\ell })\nonumber\\ \displaystyle & = & \displaystyle o(1)+\int _{(\unicode[STIX]{x1D711}\leqslant -j-\ell )}\ell ^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{j+\ell })+\int _{(-j-\ell <\unicode[STIX]{x1D711}<-j)}(\unicode[STIX]{x1D711}_{j}-\unicode[STIX]{x1D711}_{j+\ell })^{p}\operatorname{MA}(\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & = & \displaystyle o(1)+\int _{(\unicode[STIX]{x1D711}\leqslant -j-\ell )}\ell ^{p}\operatorname{MA}(\unicode[STIX]{x1D711})+\int _{(-j-\ell <\unicode[STIX]{x1D711}<-j)}(\unicode[STIX]{x1D711}_{j}-\unicode[STIX]{x1D711}_{j+\ell })^{p}\operatorname{MA}(\unicode[STIX]{x1D711})\nonumber\\ \displaystyle & {\leqslant} & \displaystyle o(1)+\int _{(\unicode[STIX]{x1D711}<-j)}\unicode[STIX]{x1D711}^{p}\operatorname{MA}(\unicode[STIX]{x1D711}),\nonumber\end{eqnarray}$$
where we have used the maximum principle, together with the fact that
since
![]() $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D714})$
, as follows again from the maximum principle. We infer that
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D714})$
, as follows again from the maximum principle. We infer that
![]() $(\unicode[STIX]{x1D711}_{j})$
is a Cauchy sequence, which converges to
$(\unicode[STIX]{x1D711}_{j})$
is a Cauchy sequence, which converges to
![]() $\unicode[STIX]{x1D711}$
.◻
$\unicode[STIX]{x1D711}$
.◻
We are now in a position to prove Theorem B of the introduction.
Corollary 4.4. Assume
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{Y}$
, where
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{Y}$
, where
![]() $\unicode[STIX]{x1D714}_{Y}$
is a Hodge form. Then the metric completion
$\unicode[STIX]{x1D714}_{Y}$
is a Hodge form. Then the metric completion
![]() $(\overline{{\mathcal{H}}}_{\unicode[STIX]{x1D6FC}},d_{p})$
is isometric to
$(\overline{{\mathcal{H}}}_{\unicode[STIX]{x1D6FC}},d_{p})$
is isometric to
![]() $({\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC}),d_{p})$
. Similarly, the metric completion
$({\mathcal{E}}^{p}(\unicode[STIX]{x1D6FC}),d_{p})$
. Similarly, the metric completion
![]() $(\overline{{\mathcal{H}}}_{\unicode[STIX]{x1D714}},d_{p})$
is isometric to
$(\overline{{\mathcal{H}}}_{\unicode[STIX]{x1D714}},d_{p})$
is isometric to
![]() $({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
.
$({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
.
Proof. Thanks to [Reference Coman, Guedj and ZeriahiCGZ13, Corollary C] we can ensure that the space
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
is dense in
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
is dense in
![]() ${\mathcal{H}}_{bd}$
. The result then follows from Theorem 4.3.◻
${\mathcal{H}}_{bd}$
. The result then follows from Theorem 4.3.◻
4.2 Weak geodesics
4.2.1 Finite-energy geodesics
We now define finite-energy geodesics joining two finite-energy endpoints
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
. Fix
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
. Fix
![]() $j\in \mathbb{N}$
and consider
$j\in \mathbb{N}$
and consider
![]() $\unicode[STIX]{x1D711}_{0}^{j},\unicode[STIX]{x1D711}_{1}^{j}$
bounded
$\unicode[STIX]{x1D711}_{0}^{j},\unicode[STIX]{x1D711}_{1}^{j}$
bounded
![]() $\unicode[STIX]{x1D714}$
-psh functions decreasing to
$\unicode[STIX]{x1D714}$
-psh functions decreasing to
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
. We let
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
. We let
![]() $\unicode[STIX]{x1D711}_{t,j}$
denote the bounded geodesic joining
$\unicode[STIX]{x1D711}_{t,j}$
denote the bounded geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}^{j}$
to
$\unicode[STIX]{x1D711}_{0}^{j}$
to
![]() $\unicode[STIX]{x1D711}_{1}^{j}$
. It follows from the maximum principle that
$\unicode[STIX]{x1D711}_{1}^{j}$
. It follows from the maximum principle that
![]() $j\mapsto \unicode[STIX]{x1D711}_{t,j}$
is non-increasing. We can thus set
$j\mapsto \unicode[STIX]{x1D711}_{t,j}$
is non-increasing. We can thus set
Definition 4.5. The map
![]() $(t,x)\mapsto \unicode[STIX]{x1D711}_{t}(x)$
is the (finite-energy) Mabuchi geodesic joining
$(t,x)\mapsto \unicode[STIX]{x1D711}_{t}(x)$
is the (finite-energy) Mabuchi geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
.
$\unicode[STIX]{x1D711}_{1}$
.
The
![]() $\unicode[STIX]{x1D711}_{t}$
indeed form a family of finite-energy functions: since
$\unicode[STIX]{x1D711}_{t}$
indeed form a family of finite-energy functions: since
![]() $t\mapsto E(\unicode[STIX]{x1D711}_{t,j})$
is affine (Lemma 2.5), we infer, for all
$t\mapsto E(\unicode[STIX]{x1D711}_{t,j})$
is affine (Lemma 2.5), we infer, for all
![]() $j\in \mathbb{N}$
,
$j\in \mathbb{N}$
,
hence
![]() $\unicode[STIX]{x1D711}_{t}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
with
$\unicode[STIX]{x1D711}_{t}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
with
![]() $(1-t)E(\unicode[STIX]{x1D711}_{0})+tE(\unicode[STIX]{x1D711}_{1})=E(\unicode[STIX]{x1D711}_{t})$
.
$(1-t)E(\unicode[STIX]{x1D711}_{0})+tE(\unicode[STIX]{x1D711}_{1})=E(\unicode[STIX]{x1D711}_{t})$
.
It follows from the maximum principle that
![]() $\unicode[STIX]{x1D711}_{t}$
is independent of the choice of the approximants
$\unicode[STIX]{x1D711}_{t}$
is independent of the choice of the approximants
![]() $\unicode[STIX]{x1D711}_{0}^{j},\unicode[STIX]{x1D711}_{1}^{j}$
: if we set
$\unicode[STIX]{x1D711}_{0}^{j},\unicode[STIX]{x1D711}_{1}^{j}$
: if we set
![]() $\unicode[STIX]{x1D711}(x,z):=\unicode[STIX]{x1D711}_{t}(x)$
,
$\unicode[STIX]{x1D711}(x,z):=\unicode[STIX]{x1D711}_{t}(x)$
,
![]() $z=t+is$
, then
$z=t+is$
, then
![]() $\unicode[STIX]{x1D711}$
is a maximal
$\unicode[STIX]{x1D711}$
is a maximal
![]() $\unicode[STIX]{x1D714}$
-psh function in
$\unicode[STIX]{x1D714}$
-psh function in
![]() $X\times S$
, as a decreasing limit of maximal
$X\times S$
, as a decreasing limit of maximal
![]() $\unicode[STIX]{x1D714}$
-psh functions. It is thus the unique maximal
$\unicode[STIX]{x1D714}$
-psh functions. It is thus the unique maximal
![]() $\unicode[STIX]{x1D714}$
-psh function in
$\unicode[STIX]{x1D714}$
-psh function in
![]() $X\times S$
with boundary values
$X\times S$
with boundary values
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
.
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
.
When
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
belong to
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
belong to
![]() ${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
, these weak geodesics are again metric geodesics in the complete metric space
${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
, these weak geodesics are again metric geodesics in the complete metric space
![]() $({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
.
$({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
.
Proposition 4.6. Given
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
, the Mabuchi geodesic
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
, the Mabuchi geodesic
![]() $\unicode[STIX]{x1D711}$
joining
$\unicode[STIX]{x1D711}$
joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
lies in
$\unicode[STIX]{x1D711}_{1}$
lies in
![]() ${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
and satisfies, for all
${\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
and satisfies, for all
![]() $t,s\in [0,1]$
,
$t,s\in [0,1]$
,
Thus,
![]() $({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
is a geodesic space.
$({\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714}),d_{p})$
is a geodesic space.
Proof. We can assume, without loss of generality, that
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\leqslant 0$
. Fix
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\leqslant 0$
. Fix
![]() $j\in \mathbb{N}$
and consider
$j\in \mathbb{N}$
and consider
![]() $\unicode[STIX]{x1D711}_{0}^{j},\unicode[STIX]{x1D711}_{1}^{j}$
bounded
$\unicode[STIX]{x1D711}_{0}^{j},\unicode[STIX]{x1D711}_{1}^{j}$
bounded
![]() $\unicode[STIX]{x1D714}$
-psh functions decreasing to
$\unicode[STIX]{x1D714}$
-psh functions decreasing to
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
. We let
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
. We let
![]() $\unicode[STIX]{x1D711}_{t,j}$
denote the bounded geodesic joining
$\unicode[STIX]{x1D711}_{t,j}$
denote the bounded geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}^{j}$
to
$\unicode[STIX]{x1D711}_{0}^{j}$
to
![]() $\unicode[STIX]{x1D711}_{1}^{j}$
, which decreases towards
$\unicode[STIX]{x1D711}_{1}^{j}$
, which decreases towards
![]() $\unicode[STIX]{x1D711}_{t}$
as
$\unicode[STIX]{x1D711}_{t}$
as
![]() $j$
increases to
$j$
increases to
![]() $+\infty$
. Observe that
$+\infty$
. Observe that
It therefore follows from [Reference Guedj and ZeriahiGZ07, Lemma 3.5] and Lemma 4.7 that
hence the monotone convergence theorem yields
![]() $\int _{X}(-\unicode[STIX]{x1D711}_{t})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})<+\infty$
, for all
$\int _{X}(-\unicode[STIX]{x1D711}_{t})^{p}\operatorname{MA}(\unicode[STIX]{x1D711}_{t})<+\infty$
, for all
![]() $t$
, i.e.
$t$
, i.e.
![]() $\unicode[STIX]{x1D711}_{t}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
.
$\unicode[STIX]{x1D711}_{t}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
.
The remaining assertion is proved as in the case of bounded geodesics (Proposition 1.18). ◻
Lemma 4.7. Assume
![]() $0\geqslant \unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
. Then
$0\geqslant \unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
. Then
![]() $\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
and
$\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}^{p}(X,\unicode[STIX]{x1D714})$
and
Proof. It suffices to establish the claimed inequality when
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
and then proceed by approximation. It follows from Proposition 3.2 that
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
and then proceed by approximation. It follows from Proposition 3.2 that
The inequality follows, since
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\leqslant 0$
.◻
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\leqslant 0$
.◻
4.2.2 (Non-)uniqueness of geodesics
Fix
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
. If the sets
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
. If the sets
![]() $(\unicode[STIX]{x1D711}_{0}<\unicode[STIX]{x1D711}_{1})$
and
$(\unicode[STIX]{x1D711}_{0}<\unicode[STIX]{x1D711}_{1})$
and
![]() $(\unicode[STIX]{x1D711}_{0}>\unicode[STIX]{x1D711}_{1})$
are both non-empty, the function
$(\unicode[STIX]{x1D711}_{0}>\unicode[STIX]{x1D711}_{1})$
are both non-empty, the function
![]() $\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
differs from
$\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
differs from
![]() $\unicode[STIX]{x1D711}_{0}$
and
$\unicode[STIX]{x1D711}_{0}$
and
![]() $\unicode[STIX]{x1D711}_{1}$
and it follows from Proposition 3.4 that
$\unicode[STIX]{x1D711}_{1}$
and it follows from Proposition 3.4 that
thus the concatenation of the geodesic joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
and of that joining
$\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
and of that joining
![]() $\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
to
$\unicode[STIX]{x1D711}_{0}\vee \unicode[STIX]{x1D711}_{1}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
gives another minimizing path joining
$\unicode[STIX]{x1D711}_{1}$
gives another minimizing path joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
.
$\unicode[STIX]{x1D711}_{1}$
.
When
![]() $\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
, this argument no longer works, but there are nevertheless very many minimizing paths, as shown by the following result.
$\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
, this argument no longer works, but there are nevertheless very many minimizing paths, as shown by the following result.
Lemma 4.8. Assume
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
are such that
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in {\mathcal{H}}_{bd}$
are such that
![]() $\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
. Let
$\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}$
. Let
![]() $(\unicode[STIX]{x1D713}_{t})_{0\leqslant t\leqslant 1}$
be a path joining
$(\unicode[STIX]{x1D713}_{t})_{0\leqslant t\leqslant 1}$
be a path joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
. Then
$\unicode[STIX]{x1D711}_{1}$
. Then
In particular,
![]() $t\mapsto t\unicode[STIX]{x1D711}_{1}(x)+(1-t)\unicode[STIX]{x1D711}_{0}$
is a minimizing path for
$t\mapsto t\unicode[STIX]{x1D711}_{1}(x)+(1-t)\unicode[STIX]{x1D711}_{0}$
is a minimizing path for
![]() $d_{1}$
, which is not a Mabuchi geodesic, unless
$d_{1}$
, which is not a Mabuchi geodesic, unless
![]() $\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}$
is constant.
$\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}$
is constant.
Proof. Observe that
 $$\begin{eqnarray}\displaystyle \ell _{1}(\unicode[STIX]{x1D713}) & = & \displaystyle \int _{0}^{1}\int _{X}|\dot{\unicode[STIX]{x1D713}}_{t}(x)|\operatorname{MA}(\unicode[STIX]{x1D713}_{t})\,dt\geqslant \biggl|\int _{0}^{1}\int _{X}\dot{\unicode[STIX]{x1D713}}_{t}(x)\operatorname{MA}(\unicode[STIX]{x1D713}_{t})\,dt\biggr|\nonumber\\ \displaystyle & = & \displaystyle \biggl|\int _{0}^{1}\frac{d}{dt}E(\unicode[STIX]{x1D713}_{t})\,dt\biggr|=|E(\unicode[STIX]{x1D711}_{1})-E(\unicode[STIX]{x1D711}_{0})|=d_{1}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \ell _{1}(\unicode[STIX]{x1D713}) & = & \displaystyle \int _{0}^{1}\int _{X}|\dot{\unicode[STIX]{x1D713}}_{t}(x)|\operatorname{MA}(\unicode[STIX]{x1D713}_{t})\,dt\geqslant \biggl|\int _{0}^{1}\int _{X}\dot{\unicode[STIX]{x1D713}}_{t}(x)\operatorname{MA}(\unicode[STIX]{x1D713}_{t})\,dt\biggr|\nonumber\\ \displaystyle & = & \displaystyle \biggl|\int _{0}^{1}\frac{d}{dt}E(\unicode[STIX]{x1D713}_{t})\,dt\biggr|=|E(\unicode[STIX]{x1D711}_{1})-E(\unicode[STIX]{x1D711}_{0})|=d_{1}(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}),\nonumber\end{eqnarray}$$
where the last identity follows from Proposition 3.12. There is equality if and only if
![]() $|\dot{\unicode[STIX]{x1D713}}_{t}(x)|=\dot{\unicode[STIX]{x1D713}}_{t}(x)\geqslant 0$
for a.e.
$|\dot{\unicode[STIX]{x1D713}}_{t}(x)|=\dot{\unicode[STIX]{x1D713}}_{t}(x)\geqslant 0$
for a.e.
![]() $(t,x)$
(the sign has to be positive because
$(t,x)$
(the sign has to be positive because
![]() $\unicode[STIX]{x1D713}_{0}=\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D713}_{1}$
).
$\unicode[STIX]{x1D713}_{0}=\unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}=\unicode[STIX]{x1D713}_{1}$
).
In particular,
![]() $t\mapsto \unicode[STIX]{x1D713}_{t}=t\unicode[STIX]{x1D711}_{1}(x)+(1-t)\unicode[STIX]{x1D711}_{0}$
has this property, since
$t\mapsto \unicode[STIX]{x1D713}_{t}=t\unicode[STIX]{x1D711}_{1}(x)+(1-t)\unicode[STIX]{x1D711}_{0}$
has this property, since
![]() $\dot{\unicode[STIX]{x1D713}}_{t}=\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\geqslant 0$
. We recall that, since
$\dot{\unicode[STIX]{x1D713}}_{t}=\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}\geqslant 0$
. We recall that, since
![]() $\unicode[STIX]{x1D713}_{t}$
is a smooth path, the geodesic equation can be written as
$\unicode[STIX]{x1D713}_{t}$
is a smooth path, the geodesic equation can be written as
(see § 1.1.1). Now
![]() $\ddot{\unicode[STIX]{x1D713}}_{t}=0$
, hence
$\ddot{\unicode[STIX]{x1D713}}_{t}=0$
, hence
![]() $t\mapsto \unicode[STIX]{x1D713}_{t}$
is not a Mabuchi geodesic, unless
$t\mapsto \unicode[STIX]{x1D713}_{t}$
is not a Mabuchi geodesic, unless
![]() $d(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})\wedge d^{c}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{t}}^{n-1}=0$
for all
$d(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})\wedge d^{c}(\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0})\wedge \unicode[STIX]{x1D714}_{\unicode[STIX]{x1D713}_{t}}^{n-1}=0$
for all
![]() $t$
, i.e.
$t$
, i.e.
![]() $\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}$
is constant.◻
$\unicode[STIX]{x1D711}_{1}-\unicode[STIX]{x1D711}_{0}$
is constant.◻
Conversely, it follows from the work of Darvas [Reference DarvasDar17c, Lemma 6.12] (based on [Reference Calabi and ChenCC02, § 2.4]) that geodesics are unique in
![]() ${\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714})$
.
${\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714})$
.
Theorem 4.9. Assume
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{Y}$
, where
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{Y}$
, where
![]() $\unicode[STIX]{x1D714}_{Y}$
is a Hodge form. Then the space
$\unicode[STIX]{x1D714}_{Y}$
is a Hodge form. Then the space
![]() $({\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714}),d_{2})$
is a
$({\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714}),d_{2})$
is a
![]() $\text{CAT}(0)$
space.
$\text{CAT}(0)$
space.
Complete CAT(0) spaces are also called Hadamard spaces. Recall that a CAT(0) space is a geodesic space that has non-positive curvature in the sense of Alexandrov. Hadamard spaces enjoy many interesting properties (uniqueness of geodesics, contractibility, convexity properties, etc., see [Reference Bridson and HaefligerBH99]).
Proof. By Corollary 4.4 we know that
![]() $({\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714}),d_{2})$
is the completion of
$({\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714}),d_{2})$
is the completion of
![]() $({\mathcal{H}}_{\unicode[STIX]{x1D714}},d_{2})$
and by Proposition 4.6 that it is a geodesic metric space. [Reference Bridson and HaefligerBH99, Exercise 1.9.1.c (p. 163)] ensures that
$({\mathcal{H}}_{\unicode[STIX]{x1D714}},d_{2})$
and by Proposition 4.6 that it is a geodesic metric space. [Reference Bridson and HaefligerBH99, Exercise 1.9.1.c (p. 163)] ensures that
![]() $({\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714}),d_{2})$
is a CAT(0) space if and only if the CN inequality of Bruhat and Tits [Reference Bruhat and TitsBT72] holds, i.e.
$({\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714}),d_{2})$
is a CAT(0) space if and only if the CN inequality of Bruhat and Tits [Reference Bruhat and TitsBT72] holds, i.e.
![]() $\forall P,Q,R\in {\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714})$
and, for any
$\forall P,Q,R\in {\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714})$
and, for any
![]() $M\in {\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714})$
such that
$M\in {\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714})$
such that
![]() $d_{2}(Q,M)=d_{2}(R,M)=d_{2}(Q,R)/2$
(in other words
$d_{2}(Q,M)=d_{2}(R,M)=d_{2}(Q,R)/2$
(in other words
![]() $M=\unicode[STIX]{x1D711}_{t}^{QR}|_{t=1/2}$
where
$M=\unicode[STIX]{x1D711}_{t}^{QR}|_{t=1/2}$
where
![]() $\unicode[STIX]{x1D711}_{t}^{QR}$
is the geodesic joining
$\unicode[STIX]{x1D711}_{t}^{QR}$
is the geodesic joining
![]() $Q,R$
), one has
$Q,R$
), one has
Assume first that
![]() $P,Q,R\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}\subset {\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
. Then by [Reference Calabi and ChenCC02, § 2.4] (see also [Reference DarvasDar17c, Lemma 6.12]), we have that
$P,Q,R\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}\subset {\mathcal{H}}_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D700}}}$
. Then by [Reference Calabi and ChenCC02, § 2.4] (see also [Reference DarvasDar17c, Lemma 6.12]), we have that
where
![]() $M_{\unicode[STIX]{x1D700}}$
is the point of
$M_{\unicode[STIX]{x1D700}}$
is the point of
![]() $\unicode[STIX]{x1D700}$
-geodesic joining
$\unicode[STIX]{x1D700}$
-geodesic joining
![]() $Q,R$
such that
$Q,R$
such that
![]() $d_{2,\unicode[STIX]{x1D700}}(Q,M)=d_{2,\unicode[STIX]{x1D700}}(R,M)=d_{2,\unicode[STIX]{x1D700}}(Q,R)/2$
. Thanks to Theorem 1.13, the right-hand side in the inequality converges to the right-hand side of (9) as
$d_{2,\unicode[STIX]{x1D700}}(Q,M)=d_{2,\unicode[STIX]{x1D700}}(R,M)=d_{2,\unicode[STIX]{x1D700}}(Q,R)/2$
. Thanks to Theorem 1.13, the right-hand side in the inequality converges to the right-hand side of (9) as
![]() $\unicode[STIX]{x1D700}$
goes to zero. We claim that
$\unicode[STIX]{x1D700}$
goes to zero. We claim that
![]() $d_{2,\unicode[STIX]{x1D700}}(P,M_{\unicode[STIX]{x1D700}})$
converges to
$d_{2,\unicode[STIX]{x1D700}}(P,M_{\unicode[STIX]{x1D700}})$
converges to
![]() $d(P,M)$
. Observe first that
$d(P,M)$
. Observe first that
![]() $M_{\unicode[STIX]{x1D700}}$
decreases to
$M_{\unicode[STIX]{x1D700}}$
decreases to
![]() $M$
, since
$M$
, since
![]() $\unicode[STIX]{x1D700}$
-geodesics decreases as
$\unicode[STIX]{x1D700}$
-geodesics decreases as
![]() $\unicode[STIX]{x1D700}$
decrease to zero (Proposition 1.6). Moreover, the triangle inequality yields
$\unicode[STIX]{x1D700}$
decrease to zero (Proposition 1.6). Moreover, the triangle inequality yields
![]() $|d_{2,\unicode[STIX]{x1D700}}(P,M_{\unicode[STIX]{x1D700}})-d_{2,\unicode[STIX]{x1D700}}(P,M)|\leqslant d_{2,\unicode[STIX]{x1D700}}(M,M_{\unicode[STIX]{x1D700}})$
. Since
$|d_{2,\unicode[STIX]{x1D700}}(P,M_{\unicode[STIX]{x1D700}})-d_{2,\unicode[STIX]{x1D700}}(P,M)|\leqslant d_{2,\unicode[STIX]{x1D700}}(M,M_{\unicode[STIX]{x1D700}})$
. Since
![]() $M,M_{\unicode[STIX]{x1D700}}$
are both bounded, it follows from Theorem 3.6 and Proposition 2.11 that
$M,M_{\unicode[STIX]{x1D700}}$
are both bounded, it follows from Theorem 3.6 and Proposition 2.11 that
![]() $d_{2,\unicode[STIX]{x1D700}^{\prime }}(M,M_{\unicode[STIX]{x1D700}})\rightarrow 0$
as
$d_{2,\unicode[STIX]{x1D700}^{\prime }}(M,M_{\unicode[STIX]{x1D700}})\rightarrow 0$
as
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
. This proves the claim.
$\unicode[STIX]{x1D700}\rightarrow 0$
. This proves the claim.
If
![]() $P,Q,R\in {\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714})$
, we choose smooth approximants
$P,Q,R\in {\mathcal{E}}^{2}(X,\unicode[STIX]{x1D714})$
, we choose smooth approximants
![]() $P_{k},Q_{k},R_{k}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
decreasing to
$P_{k},Q_{k},R_{k}\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}$
decreasing to
![]() $P,Q,R$
. The above arguments ensure that
$P,Q,R$
. The above arguments ensure that
The comparison principle implies that
![]() $M_{k}$
decreases to
$M_{k}$
decreases to
![]() $M$
as
$M$
as
![]() $k$
goes to
$k$
goes to
![]() $+\infty$
. It then follows from Propositions 3.8 and 4.1 that
$+\infty$
. It then follows from Propositions 3.8 and 4.1 that
![]() $d_{2}(M,M_{k})\rightarrow 0$
as
$d_{2}(M,M_{k})\rightarrow 0$
as
![]() $k$
goes to
$k$
goes to
![]() $+\infty$
. This, together with Proposition 4.1, gives (9) when letting
$+\infty$
. This, together with Proposition 4.1, gives (9) when letting
![]() $k\rightarrow +\infty$
.◻
$k\rightarrow +\infty$
.◻
5 Singular Kähler–Einstein metrics of positive curvature
The existence of singular Kähler–Einstein metrics of non-positive curvature has been established in [Reference Eyssidieux, Guedj and ZeriahiEGZ09], generalizing the fundamental work of Aubin [Reference AubinAub78] and Yau [Reference YauYau78]. They always exist, provided the underlying variety has mild singularities and the first Chern class is non-positive.
Singular Kähler–Einstein metrics of positive curvature are more difficult to construct. It is already so in the smooth case [Reference Chen, Donaldson and SunCDS15]. Their first properties have been obtained in [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ]. In § 5.3, pushing further these works, we provide a necessary and sufficient analytic condition for their existence, generalizing a result of Tian [Reference TianTia97] and Phong et al. [Reference Phong, Song, Sturm and WeinkovePSSW08].
5.1 Log terminal singularities
A pair
![]() $(Y,D)$
is the data of a connected normal compact complex variety
$(Y,D)$
is the data of a connected normal compact complex variety
![]() $Y$
and an effective
$Y$
and an effective
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $D$
, such that
$D$
, such that
![]() $K_{Y}+D$
is
$K_{Y}+D$
is
![]() $\mathbb{Q}$
-Cartier. We write
$\mathbb{Q}$
-Cartier. We write
Given a log resolution
![]() $\unicode[STIX]{x1D70B}:X\rightarrow Y$
of
$\unicode[STIX]{x1D70B}:X\rightarrow Y$
of
![]() $(Y,D)$
(which may be chosen to be an isomorphism over
$(Y,D)$
(which may be chosen to be an isomorphism over
![]() $Y_{0}$
), there exists a unique
$Y_{0}$
), there exists a unique
![]() $\mathbb{Q}$
-divisor
$\mathbb{Q}$
-divisor
![]() $\sum _{i}a_{i}E_{i}$
, whose push-forward to
$\sum _{i}a_{i}E_{i}$
, whose push-forward to
![]() $Y$
is
$Y$
is
![]() $-D$
, such that
$-D$
, such that
Definition 5.1. The pair
![]() $(Y,D)$
is klt if
$(Y,D)$
is klt if
![]() $a_{j}>-1$
for all
$a_{j}>-1$
for all
![]() $j$
.
$j$
.
The same condition will then hold for all log resolutions of
![]() $Y$
. When
$Y$
. When
![]() $D=0$
, one says that
$D=0$
, one says that
![]() $Y$
is log terminal when the pair
$Y$
is log terminal when the pair
![]() $(Y,0)$
is klt. We have the following analytic interpretation. Fix
$(Y,0)$
is klt. We have the following analytic interpretation. Fix
![]() $r\in \mathbb{N}^{\ast }$
such that
$r\in \mathbb{N}^{\ast }$
such that
![]() $r(K_{Y}+D)$
is Cartier. If
$r(K_{Y}+D)$
is Cartier. If
![]() $\unicode[STIX]{x1D70E}$
is a nowhere-vanishing section of the corresponding line bundle over a small open set
$\unicode[STIX]{x1D70E}$
is a nowhere-vanishing section of the corresponding line bundle over a small open set
![]() $U$
of
$U$
of
![]() $Y$
, then
$Y$
, then
defines a smooth, positive volume form on
![]() $U_{0}:=U\cap Y_{0}$
. If
$U_{0}:=U\cap Y_{0}$
. If
![]() $f_{j}$
is a local equation of
$f_{j}$
is a local equation of
![]() $E_{j}$
around a point of
$E_{j}$
around a point of
![]() $\unicode[STIX]{x1D70B}^{-1}(U)$
, then
$\unicode[STIX]{x1D70B}^{-1}(U)$
, then
locally on
![]() $\unicode[STIX]{x1D70B}^{-1}(U)$
for some local volume form
$\unicode[STIX]{x1D70B}^{-1}(U)$
for some local volume form
![]() $dV$
. Since
$dV$
. Since
![]() $\sum _{i}E_{i}$
has normal crossings, this shows that
$\sum _{i}E_{i}$
has normal crossings, this shows that
![]() $(Y,D)$
is klt if and only if each volume form of the form of (11) has locally finite mass near singular points of
$(Y,D)$
is klt if and only if each volume form of the form of (11) has locally finite mass near singular points of
![]() $Y$
.
$Y$
.
The previous construction globalizes as follows.
Definition 5.2. Let
![]() $(Y,D)$
be a pair and let
$(Y,D)$
be a pair and let
![]() $\unicode[STIX]{x1D719}$
be a smooth Hermitian metric on the
$\unicode[STIX]{x1D719}$
be a smooth Hermitian metric on the
![]() $\mathbb{Q}$
-line bundle
$\mathbb{Q}$
-line bundle
![]() $-(K_{Y}+D)$
. The corresponding adapted measure
$-(K_{Y}+D)$
. The corresponding adapted measure
![]() $\text{mes}_{\unicode[STIX]{x1D719}}$
on
$\text{mes}_{\unicode[STIX]{x1D719}}$
on
![]() $Y_{\text{reg}}$
is locally defined by choosing a nowhere-zero section
$Y_{\text{reg}}$
is locally defined by choosing a nowhere-zero section
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $r(K_{Y}+D)$
over a small open set
$r(K_{Y}+D)$
over a small open set
![]() $U$
and setting
$U$
and setting
The point is that the measure
![]() $\text{mes}_{\unicode[STIX]{x1D719}}$
does not depend on the choice of
$\text{mes}_{\unicode[STIX]{x1D719}}$
does not depend on the choice of
![]() $\unicode[STIX]{x1D70E}$
; hence, it is globally defined. This discussion shows that
$\unicode[STIX]{x1D70E}$
; hence, it is globally defined. This discussion shows that
in which case we view it as a Radon measure on the whole of
![]() $Y$
.
$Y$
.
5.2 Kähler–Einstein metrics on log Fano pairs
Definition 5.3. A log Fano pair is a klt pair
![]() $(Y,D)$
such that
$(Y,D)$
such that
![]() $Y$
is projective and
$Y$
is projective and
![]() $-(K_{Y}+D)$
is ample.
$-(K_{Y}+D)$
is ample.
Let
![]() $(Y,D)$
be a log Fano pair. Fix a reference smooth strictly psh metric
$(Y,D)$
be a log Fano pair. Fix a reference smooth strictly psh metric
![]() $\unicode[STIX]{x1D719}_{0}$
on
$\unicode[STIX]{x1D719}_{0}$
on
![]() $-(K_{Y}+D)$
, with curvature
$-(K_{Y}+D)$
, with curvature
![]() $\unicode[STIX]{x1D714}_{0}$
and adapted measure
$\unicode[STIX]{x1D714}_{0}$
and adapted measure
![]() $\unicode[STIX]{x1D707}_{0}=\text{mes}_{\unicode[STIX]{x1D719}_{0}}$
. We normalize
$\unicode[STIX]{x1D707}_{0}=\text{mes}_{\unicode[STIX]{x1D719}_{0}}$
. We normalize
![]() $\unicode[STIX]{x1D719}_{0}$
so that
$\unicode[STIX]{x1D719}_{0}$
so that
![]() $\unicode[STIX]{x1D707}_{0}$
is a probability measure. The volume of
$\unicode[STIX]{x1D707}_{0}$
is a probability measure. The volume of
![]() $(Y,D)$
is
$(Y,D)$
is
Definition 5.4. A Kähler–Einstein metric
![]() $T$
for the log Fano pair
$T$
for the log Fano pair
![]() $(Y,D)$
is a finite-energy current
$(Y,D)$
is a finite-energy current
![]() $T\in c_{1}(Y,D)$
. such that
$T\in c_{1}(Y,D)$
. such that
![]() $T^{n}=V\cdot \unicode[STIX]{x1D707}_{T}$
.
$T^{n}=V\cdot \unicode[STIX]{x1D707}_{T}$
.
We now list some important properties of these objects, established in [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Reference BerndtssonBer15, Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ].
(i) A Kähler–Einstein metric
 $\unicode[STIX]{x1D714}$
is automatically smooth on
$\unicode[STIX]{x1D714}$
is automatically smooth on
 $Y_{0}$
, with continuous potentials on
$Y_{0}$
, with continuous potentials on
 $Y$
, and it satisfies
$Y$
, and it satisfies  $$\begin{eqnarray}\operatorname{Ric}(\unicode[STIX]{x1D714}_{\mathit{KE}})=\unicode[STIX]{x1D714}_{\mathit{KE}}+[D]\quad \text{on}~Y_{\text{reg}}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ric}(\unicode[STIX]{x1D714}_{\mathit{KE}})=\unicode[STIX]{x1D714}_{\mathit{KE}}+[D]\quad \text{on}~Y_{\text{reg}}.\end{eqnarray}$$
(ii) The definition of a log Fano pair requires the singularities to be klt. This condition is, in fact, necessary to obtain K–E metrics on
 $Y_{\text{reg}}$
.
$Y_{\text{reg}}$
.(iii) The Kähler–Einstein equation reads
 $(\unicode[STIX]{x1D714}_{0}+dd^{c}\unicode[STIX]{x1D719})^{n}=e^{-\unicode[STIX]{x1D719}+c}\unicode[STIX]{x1D707}_{0}$
for some constant
$(\unicode[STIX]{x1D714}_{0}+dd^{c}\unicode[STIX]{x1D719})^{n}=e^{-\unicode[STIX]{x1D719}+c}\unicode[STIX]{x1D707}_{0}$
for some constant
 $c\in \mathbb{R}$
. If we choose a log resolution, the equation becomes
$c\in \mathbb{R}$
. If we choose a log resolution, the equation becomes
 $(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711})^{n}=e^{-\unicode[STIX]{x1D711}+c}\widetilde{\unicode[STIX]{x1D707}}_{0}$
, where
$(\unicode[STIX]{x1D714}+dd^{c}\unicode[STIX]{x1D711})^{n}=e^{-\unicode[STIX]{x1D711}+c}\widetilde{\unicode[STIX]{x1D707}}_{0}$
, where
 $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{0}$
is semi-positive and big and
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D714}_{0}$
is semi-positive and big and
 $\widetilde{\unicode[STIX]{x1D707}}_{0}=\prod _{i}|f_{i}|^{2a_{i}}\,dV$
.
$\widetilde{\unicode[STIX]{x1D707}}_{0}=\prod _{i}|f_{i}|^{2a_{i}}\,dV$
.(iv) The potential
 $\unicode[STIX]{x1D711}$
belongs to
$\unicode[STIX]{x1D711}$
belongs to
 ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
and maximizes the functional Conversely, any maximizer of
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
and maximizes the functional Conversely, any maximizer of $$\begin{eqnarray}{\mathcal{F}}(\unicode[STIX]{x1D711}):=E(\unicode[STIX]{x1D711})+\log \biggl[\int _{\tilde{X}}e^{-\unicode[STIX]{x1D711}}d\widetilde{\unicode[STIX]{x1D707}}_{0}\biggr].\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{F}}(\unicode[STIX]{x1D711}):=E(\unicode[STIX]{x1D711})+\log \biggl[\int _{\tilde{X}}e^{-\unicode[STIX]{x1D711}}d\widetilde{\unicode[STIX]{x1D707}}_{0}\biggr].\end{eqnarray}$$
 ${\mathcal{F}}$
is a Kähler–Einstein metric.
${\mathcal{F}}$
is a Kähler–Einstein metric.(v) Two Kähler–Einstein metrics are connected by the flow of a holomorphic vector field that leaves
 $D$
invariant.
$D$
invariant.(vi) If the functional
 ${\mathcal{F}}$
is proper (i.e. if
${\mathcal{F}}$
is proper (i.e. if
 $E(\unicode[STIX]{x1D711}_{j})\rightarrow -\infty \Rightarrow {\mathcal{F}}(\unicode[STIX]{x1D711}_{j})\rightarrow -\infty$
), then there exists a unique Kähler–Einstein metric.
$E(\unicode[STIX]{x1D711}_{j})\rightarrow -\infty \Rightarrow {\mathcal{F}}(\unicode[STIX]{x1D711}_{j})\rightarrow -\infty$
), then there exists a unique Kähler–Einstein metric.
Here,
![]() $[D]$
is the integration current on
$[D]$
is the integration current on
![]() $D|_{Y_{\text{reg}}}$
. Writing
$D|_{Y_{\text{reg}}}$
. Writing
![]() $\operatorname{Ric}(\unicode[STIX]{x1D714}_{\mathit{KE}})$
on
$\operatorname{Ric}(\unicode[STIX]{x1D714}_{\mathit{KE}})$
on
![]() $Y_{\text{reg}}$
implicitly means that the positive measure
$Y_{\text{reg}}$
implicitly means that the positive measure
![]() $\unicode[STIX]{x1D714}_{\mathit{KE}}^{n}|_{Y_{\text{reg}}}$
corresponds to a singular metric on
$\unicode[STIX]{x1D714}_{\mathit{KE}}^{n}|_{Y_{\text{reg}}}$
corresponds to a singular metric on
![]() $-K_{Y_{\text{reg}}}$
, whose curvature is then
$-K_{Y_{\text{reg}}}$
, whose curvature is then
![]() $\operatorname{Ric}(\unicode[STIX]{x1D714}_{KE})$
by definition.
$\operatorname{Ric}(\unicode[STIX]{x1D714}_{KE})$
by definition.
5.3 The analytic criterion
Following an idea of Darvas and Rubinstein [Reference Darvas and RubinsteinDR17], we now extend [Reference TianTia97, Theorem 1.6] and [Reference Phong, Song, Sturm and WeinkovePSSW08] by proving the following.
Theorem 5.5. Let
![]() $(Y,D)$
be a log Fano pair. It admits a unique Kähler–Einstein metric if and only if there exists
$(Y,D)$
be a log Fano pair. It admits a unique Kähler–Einstein metric if and only if there exists
![]() $\unicode[STIX]{x1D700},M>0$
such that, for all
$\unicode[STIX]{x1D700},M>0$
such that, for all
![]() $\unicode[STIX]{x1D711}\in {\mathcal{H}}_{\text{norm}}$
,
$\unicode[STIX]{x1D711}\in {\mathcal{H}}_{\text{norm}}$
,
This is Theorem D of the introduction.
Proof. We are going to use Theorem B. Note that
![]() $\unicode[STIX]{x1D714}_{Y}\in c_{1}(-K_{X}-D)$
is a Hodge form. One implication is given by [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Theorems 4.8 and 5.4]: if
$\unicode[STIX]{x1D714}_{Y}\in c_{1}(-K_{X}-D)$
is a Hodge form. One implication is given by [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Theorems 4.8 and 5.4]: if
then
![]() ${\mathcal{F}}$
is proper, hence there exists a unique Kähler–Einstein metric.
${\mathcal{F}}$
is proper, hence there exists a unique Kähler–Einstein metric.
So we assume now that there exists
![]() $\unicode[STIX]{x1D714}$
, a unique Kähler–Einstein metric, which we take as our base point of
$\unicode[STIX]{x1D714}$
, a unique Kähler–Einstein metric, which we take as our base point of
![]() ${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
. It is the unique maximizer of
${\mathcal{H}}_{\unicode[STIX]{x1D714}}$
. It is the unique maximizer of
![]() ${\mathcal{F}}$
on
${\mathcal{F}}$
on
![]() ${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
,
${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
,
as follows from [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Theorem 6.6], [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Theorems 4.8 and 5.3].
Note that
![]() ${\mathcal{F}}$
is invariant by translations, so we actually consider the restriction of
${\mathcal{F}}$
is invariant by translations, so we actually consider the restriction of
![]() ${\mathcal{F}}$
on
${\mathcal{F}}$
on
![]() ${\mathcal{E}}_{\text{norm}}^{1}(X,\unicode[STIX]{x1D714})=\{\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714}),\sup _{X}\unicode[STIX]{x1D711}=0\}$
. Assume for contradiction that there is no
${\mathcal{E}}_{\text{norm}}^{1}(X,\unicode[STIX]{x1D714})=\{\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714}),\sup _{X}\unicode[STIX]{x1D711}=0\}$
. Assume for contradiction that there is no
![]() $\unicode[STIX]{x1D700}>0$
such that
$\unicode[STIX]{x1D700}>0$
such that
![]() ${\mathcal{F}}(\unicode[STIX]{x1D711})\leqslant -\unicode[STIX]{x1D700}d_{1}(0,\unicode[STIX]{x1D711})+M$
for all
${\mathcal{F}}(\unicode[STIX]{x1D711})\leqslant -\unicode[STIX]{x1D700}d_{1}(0,\unicode[STIX]{x1D711})+M$
for all
![]() $\unicode[STIX]{x1D711}\in {\mathcal{H}}_{\text{norm}}$
, where we set
$\unicode[STIX]{x1D711}\in {\mathcal{H}}_{\text{norm}}$
, where we set
![]() $M:={\mathcal{F}}(0)+1$
. Then we can find a sequence
$M:={\mathcal{F}}(0)+1$
. Then we can find a sequence
![]() $(\unicode[STIX]{x1D711}_{j})\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}^{\mathbb{N}}$
such that
$(\unicode[STIX]{x1D711}_{j})\in {\mathcal{H}}_{\unicode[STIX]{x1D714}}^{\mathbb{N}}$
such that
![]() $\sup _{X}\unicode[STIX]{x1D711}_{j}=0$
and
$\sup _{X}\unicode[STIX]{x1D711}_{j}=0$
and
If
![]() $E(\unicode[STIX]{x1D711}_{j})$
does not blow up to
$E(\unicode[STIX]{x1D711}_{j})$
does not blow up to
![]() $-\infty$
, we reach a contradiction: up to extracting and relabelling, we can assume that
$-\infty$
, we reach a contradiction: up to extracting and relabelling, we can assume that
![]() $E(\unicode[STIX]{x1D711}_{j})$
is bounded and
$E(\unicode[STIX]{x1D711}_{j})$
is bounded and
![]() $\unicode[STIX]{x1D711}_{j}$
converges to some
$\unicode[STIX]{x1D711}_{j}$
converges to some
![]() $\unicode[STIX]{x1D713}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
. Since
$\unicode[STIX]{x1D713}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714})$
. Since
![]() ${\mathcal{F}}$
is upper semi-continuous, we infer
${\mathcal{F}}$
is upper semi-continuous, we infer
![]() ${\mathcal{F}}(\unicode[STIX]{x1D713})\geqslant {\mathcal{F}}(0)+1$
, a contradiction.
${\mathcal{F}}(\unicode[STIX]{x1D713})\geqslant {\mathcal{F}}(0)+1$
, a contradiction.
So we assume now that
![]() $E(\unicode[STIX]{x1D711}_{j})\rightarrow -\infty$
. It follows from Lemma 3.12 that
$E(\unicode[STIX]{x1D711}_{j})\rightarrow -\infty$
. It follows from Lemma 3.12 that
![]() $d_{j}:=d_{1}(0,\unicode[STIX]{x1D711}_{j})=-E(\unicode[STIX]{x1D711}_{j})\rightarrow +\infty$
. We let
$d_{j}:=d_{1}(0,\unicode[STIX]{x1D711}_{j})=-E(\unicode[STIX]{x1D711}_{j})\rightarrow +\infty$
. We let
![]() $(\unicode[STIX]{x1D711}_{t,j})_{0\leqslant t\leqslant d_{j}}$
denote the Mabuchi geodesic with unit speed joining
$(\unicode[STIX]{x1D711}_{t,j})_{0\leqslant t\leqslant d_{j}}$
denote the Mabuchi geodesic with unit speed joining
![]() $0$
to
$0$
to
![]() $\unicode[STIX]{x1D711}_{j}$
and set
$\unicode[STIX]{x1D711}_{j}$
and set
![]() $\unicode[STIX]{x1D713}_{j}:=\unicode[STIX]{x1D711}_{1,j}$
. Note that the arguments in Lemma 3.3 show that
$\unicode[STIX]{x1D713}_{j}:=\unicode[STIX]{x1D711}_{1,j}$
. Note that the arguments in Lemma 3.3 show that
![]() $t\mapsto \unicode[STIX]{x1D711}_{t,j}$
is decreasing, hence
$t\mapsto \unicode[STIX]{x1D711}_{t,j}$
is decreasing, hence
![]() $\unicode[STIX]{x1D711}_{j}\leqslant \unicode[STIX]{x1D713}_{j}\leqslant 0$
. In particular,
$\unicode[STIX]{x1D711}_{j}\leqslant \unicode[STIX]{x1D713}_{j}\leqslant 0$
. In particular,
![]() $\sup _{X}\unicode[STIX]{x1D713}_{j}=0$
, while, by definition,
$\sup _{X}\unicode[STIX]{x1D713}_{j}=0$
, while, by definition,
![]() $d_{1}(0,\unicode[STIX]{x1D713}_{j})=1=-E(\unicode[STIX]{x1D713}_{j})$
.
$d_{1}(0,\unicode[STIX]{x1D713}_{j})=1=-E(\unicode[STIX]{x1D713}_{j})$
.
It now follows from Berndtsson’s convexity result [Reference BerndtssonBer15, § 6.2] and its generalization to the singular context [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Theorem 11.1] that the map
![]() $t\mapsto {\mathcal{F}}(\unicode[STIX]{x1D711}_{t,j})$
is concave. We infer
$t\mapsto {\mathcal{F}}(\unicode[STIX]{x1D711}_{t,j})$
is concave. We infer
thus
![]() ${\mathcal{F}}(\unicode[STIX]{x1D713}_{j})\rightarrow {\mathcal{F}}(0)$
. This shows that
${\mathcal{F}}(\unicode[STIX]{x1D713}_{j})\rightarrow {\mathcal{F}}(0)$
. This shows that
![]() $(\unicode[STIX]{x1D713}_{j})$
is a maximizing sequence for
$(\unicode[STIX]{x1D713}_{j})$
is a maximizing sequence for
![]() ${\mathcal{F}}$
, which therefore strongly converges to
${\mathcal{F}}$
, which therefore strongly converges to
![]() $0$
, by [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Theorem 5.3.3]. This yields a contradiction, since
$0$
, by [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ, Theorem 5.3.3]. This yields a contradiction, since
![]() $d_{1}(0,\unicode[STIX]{x1D713}_{j})=1$
.◻
$d_{1}(0,\unicode[STIX]{x1D713}_{j})=1$
.◻
Acknowledgements
We thank Darvas, Lu and Zeriahi for useful conversations.
E.D.N. was supported by a Marie Sklodowska Curie individual fellowship 660940KRFCY (MSCAIF). V.G. was partially supported by the ANR project GRACK.
This paper is based on work supported also by the NSF Grant DMS-1440140, while E.D.N. was in residence at the MSRI, during the Spring 2016 semester. It is partially based on lecture notes of V.G. [Reference GuedjGue14], after a series of lectures he gave at KIAS in April 2013. The authors thank J.-M. Hwang and M. Paun for their invitation and the staff of KIAS and MSRI for providing excellent conditions of work.