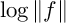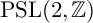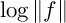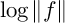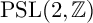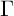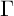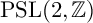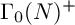1 Introduction and statement of results
1.1 The Poisson–Jensen formula
Let
![]() $D_{R} = \{z =x+iy\in {\mathbb C} : \vert z \vert < R\}$
be the disk of radius R centered at the origin in the complex plane
$D_{R} = \{z =x+iy\in {\mathbb C} : \vert z \vert < R\}$
be the disk of radius R centered at the origin in the complex plane
![]() ${\mathbb C}$
. Let F be a nonconstant meromorphic function on the closure
${\mathbb C}$
. Let F be a nonconstant meromorphic function on the closure
![]() $\overline {D_{R}}$
of
$\overline {D_{R}}$
of
![]() $D_{R}$
. Denote by
$D_{R}$
. Denote by
![]() $c_{F}$
the leading nonzero coefficient of F at zero, meaning that for some integer m, we have that
$c_{F}$
the leading nonzero coefficient of F at zero, meaning that for some integer m, we have that
![]() $F(z) = c_{F}z^{m} + O(z^{m+1})$
as z approaches zero. For any
$F(z) = c_{F}z^{m} + O(z^{m+1})$
as z approaches zero. For any
![]() $a \in D_{R}$
, let
$a \in D_{R}$
, let
![]() $n_{F}(a)$
denote the order of F at a; there are a finite number of points a for which
$n_{F}(a)$
denote the order of F at a; there are a finite number of points a for which
![]() $n_{F}(a) \neq 0$
; in this notation,
$n_{F}(a) \neq 0$
; in this notation,
![]() $n_{F}(0) = m$
. Jensen’s formula, as stated on page 341 of [Reference Lang18], asserts that
$n_{F}(0) = m$
. Jensen’s formula, as stated on page 341 of [Reference Lang18], asserts that
 $$ \begin{align} \frac{1}{2\pi}\int\limits_{0}^{2\pi}\log\vert F(Re^{i\theta})\vert d\theta + \sum\limits_{a \in D_{R}} n_{F}(a) \log (\vert a \vert/R) + n_{F}(0) \log (1/R) = \log \vert c_{F}\vert. \end{align} $$
$$ \begin{align} \frac{1}{2\pi}\int\limits_{0}^{2\pi}\log\vert F(Re^{i\theta})\vert d\theta + \sum\limits_{a \in D_{R}} n_{F}(a) \log (\vert a \vert/R) + n_{F}(0) \log (1/R) = \log \vert c_{F}\vert. \end{align} $$
One can consider the action of a Möbius transformation which preserves
![]() $D_{R}$
and seek to compute the resulting expression from (1). Such a consideration leads to the Poisson–Jensen formula, and we refer the reader to page 161 of [Reference Lang17] for a statement and proof.
$D_{R}$
and seek to compute the resulting expression from (1). Such a consideration leads to the Poisson–Jensen formula, and we refer the reader to page 161 of [Reference Lang17] for a statement and proof.
On their own, the Jensen formula and the Poisson–Jensen formula paved the way toward Nevanlinna theory, which in its most elementary interpretation establishes subtle growth estimates for meromorphic functions (see Chapter VI of [Reference Lang18]). Going further, Nevanlinna theory provided motivation for Vojta’s conjectures whose insight into arithmetic algebraic geometry is profound. In particular, page 34 of [Reference Vojta23] contains a type of “dictionary” which translates between Nevalinna theory and number theory where Vojta proposes that Jensen’s formula should be viewed as analogous to the Artin–Whaples product formula from class field theory.
1.2 A modular generalization
In [Reference Rohrlich20], Rohrlich proved what he aptly called a modular version of Jensen’s formula. We now shall describe Rohrlich’s result.
Let f be a meromorphic function on the upper half plane
![]() ${\mathbb H}$
which is invariant with respect to the action of the full modular group
${\mathbb H}$
which is invariant with respect to the action of the full modular group
![]() $\mathrm {PSL}(2,\mathbb {Z})$
. Set
$\mathrm {PSL}(2,\mathbb {Z})$
. Set
![]() $\mathcal {F}$
to be the “usual” fundamental domain of the quotient
$\mathcal {F}$
to be the “usual” fundamental domain of the quotient
![]() $\mathrm {PSL}(2,\mathbb {Z})\backslash {\mathbb H}$
, and let
$\mathrm {PSL}(2,\mathbb {Z})\backslash {\mathbb H}$
, and let
![]() $d\mu $
denote the area form of the hyperbolic metric. Assume that f does not have a pole at the cusp
$d\mu $
denote the area form of the hyperbolic metric. Assume that f does not have a pole at the cusp
![]() $\infty $
of
$\infty $
of
![]() $\mathcal {F}$
, and assume further that the Fourier expansion of f at
$\mathcal {F}$
, and assume further that the Fourier expansion of f at
![]() $\infty $
has its constant term equal to one. Let
$\infty $
has its constant term equal to one. Let
![]() $P(w)$
be the Kronecker limit function associated with the parabolic Eisenstein series associated with
$P(w)$
be the Kronecker limit function associated with the parabolic Eisenstein series associated with
![]() $\mathrm {PSL}(2,\mathbb {Z})$
; below we will write
$\mathrm {PSL}(2,\mathbb {Z})$
; below we will write
![]() $P(w)$
in terms of the Dedekind Delta function, but for now, we want to keep the concept of a Kronecker limit function in the conversation. With all this, the Rohrlich–Jensen formula is the statement that
$P(w)$
in terms of the Dedekind Delta function, but for now, we want to keep the concept of a Kronecker limit function in the conversation. With all this, the Rohrlich–Jensen formula is the statement that
 $$ \begin{align} \frac{1}{2\pi}\int\limits_{\mathrm{PSL}(2,\mathbb{Z})\backslash \mathbb{H}} \log|f(z)|d\mu(z) + \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)}P(w) =0. \end{align} $$
$$ \begin{align} \frac{1}{2\pi}\int\limits_{\mathrm{PSL}(2,\mathbb{Z})\backslash \mathbb{H}} \log|f(z)|d\mu(z) + \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)}P(w) =0. \end{align} $$
In this expression,
![]() $\mathrm {ord}_w(f)$
denotes the order of f at w as a meromorphic function, and
$\mathrm {ord}_w(f)$
denotes the order of f at w as a meromorphic function, and
![]() $\mathrm {ord}(w)$
denotes the order of the action of
$\mathrm {ord}(w)$
denotes the order of the action of
![]() $\mathrm {PSL}(2,\mathbb {Z})$
on
$\mathrm {PSL}(2,\mathbb {Z})$
on
![]() ${\mathbb H}$
. As a means by which one can see beyond the above setting, one can view (2) as evaluating the inner product
${\mathbb H}$
. As a means by which one can see beyond the above setting, one can view (2) as evaluating the inner product
 $$ \begin{align*}\langle 1,\log|f(z)| \rangle=\int\limits_{\mathrm{PSL}(2,\mathbb{Z})\backslash \mathbb{H}} 1\cdot \log|f(z)|d\mu(z) \end{align*} $$
$$ \begin{align*}\langle 1,\log|f(z)| \rangle=\int\limits_{\mathrm{PSL}(2,\mathbb{Z})\backslash \mathbb{H}} 1\cdot \log|f(z)|d\mu(z) \end{align*} $$
within the Hilbert space of
![]() $L^{2}$
functions on
$L^{2}$
functions on
![]() $\mathrm {PSL}(2,\mathbb {Z})\backslash {\mathbb H}$
.
$\mathrm {PSL}(2,\mathbb {Z})\backslash {\mathbb H}$
.
There are various directions in which (2) has been extended. In [Reference Rohrlich20], Rohrlich described the analog of (2) for general Fuchsian groups of the first kind and for meromorphic modular forms f of nonzero weight (see page 19 of [Reference Rohrlich20]). In [Reference Herrero, Imamoğlu, von Pippich and Tóth10], the authors studied the quotient of hyperbolic three space when acted upon by the discrete group
![]() $\mathrm {PSL}(2,\mathcal {O}_K)$
, where
$\mathrm {PSL}(2,\mathcal {O}_K)$
, where
![]() $\mathcal {O}_K$
denotes the ring of integers of an imaginary quadratic field K. In that setting, the function
$\mathcal {O}_K$
denotes the ring of integers of an imaginary quadratic field K. In that setting, the function
![]() $\log \vert f \vert $
is replaced by a function which is harmonic at all but a finite number of points and at those points the function has prescribed singularities. As in [Reference Rohrlich20], the analog of (2) involves a function P which is constructed from a type of Kronecker limit formula.
$\log \vert f \vert $
is replaced by a function which is harmonic at all but a finite number of points and at those points the function has prescribed singularities. As in [Reference Rohrlich20], the analog of (2) involves a function P which is constructed from a type of Kronecker limit formula.
In [Reference Bringmann and Kane2], the authors returned to the setting of
![]() $\mathrm {PSL}(2,\mathbb {Z})$
acting on
$\mathrm {PSL}(2,\mathbb {Z})$
acting on
![]() ${\mathbb H}$
. Let
${\mathbb H}$
. Let
![]() $q_{z}=e^{2\pi i z}$
be the standard local coordinate near
$q_{z}=e^{2\pi i z}$
be the standard local coordinate near
![]() $\infty $
of
$\infty $
of
![]() $\mathrm {PSL}(2,\mathbb {Z})\backslash {\mathbb H}$
. The Hauptmodul
$\mathrm {PSL}(2,\mathbb {Z})\backslash {\mathbb H}$
. The Hauptmodul
![]() $j(z)$
is the unique
$j(z)$
is the unique
![]() $\mathrm {PSL}(2,\mathbb {Z})$
invariant holomorphic function on
$\mathrm {PSL}(2,\mathbb {Z})$
invariant holomorphic function on
![]() ${\mathbb H}$
whose expansion near
${\mathbb H}$
whose expansion near
![]() $\infty $
is
$\infty $
is
![]() $j(z) = q_{z}^{-1} +744+ O(q_{z})$
as z approaches
$j(z) = q_{z}^{-1} +744+ O(q_{z})$
as z approaches
![]() $\infty $
. Define
$\infty $
. Define
![]() $j_1(z)=j(z)-744$
. For integers
$j_1(z)=j(z)-744$
. For integers
![]() $n\geq 2$
, let
$n\geq 2$
, let
![]() $T_{n}$
denote the nth Hecke operator, and set
$T_{n}$
denote the nth Hecke operator, and set
![]() $j_{n}(z) = j|T_n (z)$
. The main results of [Reference Bringmann and Kane2] are the derivation of formulas for the regularized scalar product
$j_{n}(z) = j|T_n (z)$
. The main results of [Reference Bringmann and Kane2] are the derivation of formulas for the regularized scalar product
![]() $\langle j_n(z),\log (({\mathrm {Im}} (z))^k|f(z)|) \rangle $
, where f is a weight
$\langle j_n(z),\log (({\mathrm {Im}} (z))^k|f(z)|) \rangle $
, where f is a weight
![]() $2k$
meromorphic modular form with respect to
$2k$
meromorphic modular form with respect to
![]() $\mathrm {PSL}(2,\mathbb {Z})$
. Below, we will discuss further the formulas from [Reference Bringmann and Kane2] and describe the way in which their results are natural extensions of (2).
$\mathrm {PSL}(2,\mathbb {Z})$
. Below, we will discuss further the formulas from [Reference Bringmann and Kane2] and describe the way in which their results are natural extensions of (2).
1.3 Revisiting Rohrlich’s theorem
The purpose of this article is to extend the point of view that the Rohlrich–Jensen formula is the evaluation of a particular type of inner product and to prove the extension of this formula in the setting of an arbitrary, not necessarily arithmetic, Fuchsian group of the first kind with one cusp. To do so, we shall revisit the role of each of the two terms
![]() $j|T_n (z)$
and
$j|T_n (z)$
and
![]() $\log (({\mathrm {Im}} (z))^k|f(z)|)$
.
$\log (({\mathrm {Im}} (z))^k|f(z)|)$
.
The function
![]() $j|T_n (z)$
can be characterized as the unique holomorphic function, up to an additive constant, which is
$j|T_n (z)$
can be characterized as the unique holomorphic function, up to an additive constant, which is
![]() $\mathrm {PSL}(2,\mathbb {Z})$
invariant on
$\mathrm {PSL}(2,\mathbb {Z})$
invariant on
![]() ${\mathbb H}$
and whose expansion near
${\mathbb H}$
and whose expansion near
![]() $\infty $
is
$\infty $
is
![]() $q_{z}^{-n} + o(q_{z}^{-1})$
. These properties hold for the special value
$q_{z}^{-n} + o(q_{z}^{-1})$
. These properties hold for the special value
![]() $s=1$
of the Niebur–Poincaré series
$s=1$
of the Niebur–Poincaré series
![]() $F_{-n}^{\Gamma }(z,s)$
, which is defined in [Reference Niebur19] for any Fuchsian group
$F_{-n}^{\Gamma }(z,s)$
, which is defined in [Reference Niebur19] for any Fuchsian group
![]() $\Gamma $
of the first kind with one cusp (see §3.1). As proved in [Reference Niebur19], for any
$\Gamma $
of the first kind with one cusp (see §3.1). As proved in [Reference Niebur19], for any
![]() $m\in \mathbb {Z} \setminus \{0\}$
, the Niebur–Poincaré series
$m\in \mathbb {Z} \setminus \{0\}$
, the Niebur–Poincaré series
![]() $F_{m}^{\Gamma }(z,s)$
is an eigenfunction of the hyperbolic Laplacian
$F_{m}^{\Gamma }(z,s)$
is an eigenfunction of the hyperbolic Laplacian
![]() $\Delta _{\operatorname {\mathrm {hyp}}}$
; specifically, we have that
$\Delta _{\operatorname {\mathrm {hyp}}}$
; specifically, we have that
Also,
![]() $F_{m}^{\Gamma }(z,s)$
is orthogonal to constant functions. Furthermore, if
$F_{m}^{\Gamma }(z,s)$
is orthogonal to constant functions. Furthermore, if
![]() $\Gamma = \mathrm {PSL}(2,\mathbb {Z})$
, then for any positive integer n there is an explicitly computable constant
$\Gamma = \mathrm {PSL}(2,\mathbb {Z})$
, then for any positive integer n there is an explicitly computable constant
![]() $c_{n}$
such that
$c_{n}$
such that
 $$ \begin{align} F_{-n}^{\mathrm{PSL}(2,\mathbb{Z})}(z,1) = \frac{1}{2\pi\sqrt{n}}j_{n}(z) + c_{n}. \end{align} $$
$$ \begin{align} F_{-n}^{\mathrm{PSL}(2,\mathbb{Z})}(z,1) = \frac{1}{2\pi\sqrt{n}}j_{n}(z) + c_{n}. \end{align} $$
As a result, the Rohrlich–Jensen formula proved in [Reference Bringmann and Kane2], when combined with Rohrlich’s formula from [Reference Rohrlich20], reduces to computing the regularized inner product of
![]() $F_{-n}^{\mathrm {PSL}(2,\mathbb {Z})}(z,1)$
with
$F_{-n}^{\mathrm {PSL}(2,\mathbb {Z})}(z,1)$
with
![]() $\log (({\mathrm {Im}} (z))^k|f(z)|)$
.
$\log (({\mathrm {Im}} (z))^k|f(z)|)$
.
As for the term
![]() $\log (({\mathrm {Im}} (z))^k|f(z)|)$
, we begin by recalling Proposition 12 from [Reference Jorgenson, von Pippich and Smajlović16]. Let
$\log (({\mathrm {Im}} (z))^k|f(z)|)$
, we begin by recalling Proposition 12 from [Reference Jorgenson, von Pippich and Smajlović16]. Let
![]() $\Gamma $
be a cofinite Fuchsian group with one cusp; the cusp is assumed to be at
$\Gamma $
be a cofinite Fuchsian group with one cusp; the cusp is assumed to be at
![]() $\infty $
with the identity as its scaling matrix. Let
$\infty $
with the identity as its scaling matrix. Let
![]() $2k\geq 2$
be any even positive integer, and let f be a weight
$2k\geq 2$
be any even positive integer, and let f be a weight
![]() $2k$
holomorphic form which is
$2k$
holomorphic form which is
![]() $\Gamma $
invariant and with q-expansion at
$\Gamma $
invariant and with q-expansion at
![]() $\infty $
that is normalized so its constant term is equal to one. Set
$\infty $
that is normalized so its constant term is equal to one. Set
![]() $\Vert f\Vert (z) = y^{k}\vert f(z) \vert $
, where
$\Vert f\Vert (z) = y^{k}\vert f(z) \vert $
, where
![]() $z=x+iy$
. Let
$z=x+iy$
. Let
![]() $\mathcal {E}^{\mathrm {ell}}_{\Gamma ,w}(z,s)$
be the elliptic Eisenstein series associated with the aforementioned data; a summary of the relevant properties of
$\mathcal {E}^{\mathrm {ell}}_{\Gamma ,w}(z,s)$
be the elliptic Eisenstein series associated with the aforementioned data; a summary of the relevant properties of
![]() $\mathcal {E}^{\mathrm {ell}}_{\Gamma ,w}(z,s)$
is given in §4.3. Then, in [Reference Jorgenson, von Pippich and Smajlović16], it is proved that one has the asymptotic relation
$\mathcal {E}^{\mathrm {ell}}_{\Gamma ,w}(z,s)$
is given in §4.3. Then, in [Reference Jorgenson, von Pippich and Smajlović16], it is proved that one has the asymptotic relation
 $$ \begin{align} \sum_{w\in \mathcal{F}_\Gamma} \mathrm{ord}_w(f) \mathcal{E}^{\mathrm{ell}}_{\Gamma,w}(z,s)= -s\log\left( |f(z)| |\eta_{\Gamma,\infty}^4(z)|^{-k}\right) + O(s^2) \,\,\,\,\, \mathrm{as }s \to 0, \end{align} $$
$$ \begin{align} \sum_{w\in \mathcal{F}_\Gamma} \mathrm{ord}_w(f) \mathcal{E}^{\mathrm{ell}}_{\Gamma,w}(z,s)= -s\log\left( |f(z)| |\eta_{\Gamma,\infty}^4(z)|^{-k}\right) + O(s^2) \,\,\,\,\, \mathrm{as }s \to 0, \end{align} $$
where
![]() $\mathcal {F}_\Gamma $
is the fundamental domain for the action of
$\mathcal {F}_\Gamma $
is the fundamental domain for the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\mathbb {H}$
and
$\mathbb {H}$
and
![]() $\eta _{\Gamma ,\infty }(z)$
is the analog of the classical eta function for the modular group (see (28) for the Kronecker limit formula for the non-holomorphic parabolic Eisenstein series). With this, formula (4) can be written as
$\eta _{\Gamma ,\infty }(z)$
is the analog of the classical eta function for the modular group (see (28) for the Kronecker limit formula for the non-holomorphic parabolic Eisenstein series). With this, formula (4) can be written as
 $$ \begin{align} \log\left( \Vert f\Vert (z) \right) = kP_{\Gamma}(z) - \sum_{w\in \mathcal{F}_\Gamma} \mathrm{ord}_w(f) \lim_{s\to 0} \frac{1}{s} \mathcal{E}^{\mathrm{ell}}_{\Gamma,w}(z,s),\end{align} $$
$$ \begin{align} \log\left( \Vert f\Vert (z) \right) = kP_{\Gamma}(z) - \sum_{w\in \mathcal{F}_\Gamma} \mathrm{ord}_w(f) \lim_{s\to 0} \frac{1}{s} \mathcal{E}^{\mathrm{ell}}_{\Gamma,w}(z,s),\end{align} $$
where
![]() $P_{\Gamma }(z)=\log (|\eta _{\Gamma ,\infty }^4(z)|{\mathrm {Im}} (z))$
is the Kronecker limit function associated with the non-holomorphic parabolic Eisenstein series
$P_{\Gamma }(z)=\log (|\eta _{\Gamma ,\infty }^4(z)|{\mathrm {Im}} (z))$
is the Kronecker limit function associated with the non-holomorphic parabolic Eisenstein series
![]() $\mathcal {E}^{\mathrm {par}}_{\Gamma ,\infty }(z,s)$
; the precise normalizations and expressions which define
$\mathcal {E}^{\mathrm {par}}_{\Gamma ,\infty }(z,s)$
; the precise normalizations and expressions which define
![]() $\mathcal {E}^{\mathrm {par}}_{\Gamma ,\infty }(z,s)$
will be clarified below.
$\mathcal {E}^{\mathrm {par}}_{\Gamma ,\infty }(z,s)$
will be clarified below.
Following [Reference Cogdell, Jorgenson and Smajlović3], one can recast (5) in terms of the resolvent kernel, which we now shall undertake.
The resolvent kernel, also called the automorphic Green’s function,
![]() $G_s^{\Gamma }(z,w)$
is the integral kernel which for almost all
$G_s^{\Gamma }(z,w)$
is the integral kernel which for almost all
![]() $s \in {\mathbb C}$
inverts the operator
$s \in {\mathbb C}$
inverts the operator
![]() $\Delta _{\operatorname {\mathrm {hyp}}} + s(s-1)$
, meaning that for each
$\Delta _{\operatorname {\mathrm {hyp}}} + s(s-1)$
, meaning that for each
![]() $s\in {\mathbb C}$
for which
$s\in {\mathbb C}$
for which
![]() $s(1-s)$
is not the eigenvalue of
$s(1-s)$
is not the eigenvalue of
![]() $\Delta _{\operatorname {\mathrm {hyp}}}$
, function
$\Delta _{\operatorname {\mathrm {hyp}}}$
, function
![]() $G_s^{\Gamma }(z,w)$
it is the integral kernel of the operator
$G_s^{\Gamma }(z,w)$
it is the integral kernel of the operator
![]() $(\Delta _{\operatorname {\mathrm {hyp}}} + s(s-1))^{-1}$
. Moreover,
$(\Delta _{\operatorname {\mathrm {hyp}}} + s(s-1))^{-1}$
. Moreover,
The resolvent kernel is closely related to the elliptic Eisenstein series (see [Reference von Pippich25] as well as [Reference Cogdell, Jorgenson and Smajlović3]). Specifically, from Corollary 7.4 of [Reference von Pippich25], after taking into account a sign difference in our normalization, we have that
 $$ \begin{align} \mathrm{ord}(w) \mathcal{E}^{\mathrm{ell}}_{\Gamma,w}(z,s) = -\frac{2^{s+1}\sqrt{\pi} \Gamma(s+1/2)}{\Gamma(s)}G_s^{\Gamma}(z,w) +O(s^2) \,\,\,\,\, \mathrm{as}\ s \to 0 \end{align} $$
$$ \begin{align} \mathrm{ord}(w) \mathcal{E}^{\mathrm{ell}}_{\Gamma,w}(z,s) = -\frac{2^{s+1}\sqrt{\pi} \Gamma(s+1/2)}{\Gamma(s)}G_s^{\Gamma}(z,w) +O(s^2) \,\,\,\,\, \mathrm{as}\ s \to 0 \end{align} $$
for all
![]() $z,w \in \mathbb {H}$
with
$z,w \in \mathbb {H}$
with
![]() $z\neq \gamma w$
when
$z\neq \gamma w$
when
![]() $\gamma \in \Gamma $
. It is now evident that one can express
$\gamma \in \Gamma $
. It is now evident that one can express
![]() $\log \left ( \Vert f \Vert (z) \right )$
as a type of Kronecker limit function. Indeed, upon using the functional equation for the Green’s function, we will prove below (§5.2) the following result.
$\log \left ( \Vert f \Vert (z) \right )$
as a type of Kronecker limit function. Indeed, upon using the functional equation for the Green’s function, we will prove below (§5.2) the following result.
Proposition 1. Let
![]() $\Gamma $
be a cofinite Fuchsian group with one cusp at
$\Gamma $
be a cofinite Fuchsian group with one cusp at
![]() $\infty $
with identity as its scaling matrix. Let
$\infty $
with identity as its scaling matrix. Let
![]() $2k\geq 0$
be an even integer, and let f be a weight
$2k\geq 0$
be an even integer, and let f be a weight
![]() $2k$
meromorphic form which is
$2k$
meromorphic form which is
![]() $\Gamma $
invariant and with q-expansion at
$\Gamma $
invariant and with q-expansion at
![]() $\infty $
normalized so its constant term is equal to one. Then,
$\infty $
normalized so its constant term is equal to one. Then,
 $$ \begin{align} \log\left( \Vert f\Vert (z) \right)&=-2k + 2\pi \sum_{w\in \mathcal{F}_{\Gamma}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \lim_{s\to 1}\left(G_s^{\Gamma}(z,w) + \mathcal{E}_{\Gamma,\infty}^{\mathrm{par}}(z,s)\right)\notag \\ &= 2\pi \sum_{w\in \mathcal{F}_\Gamma} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \left[ \lim_{s\to 1}\left(G_s^{\Gamma}(z,w) + \mathcal{E}_{\Gamma,\infty}^{\mathrm{par}}(z,s)\right) - \frac{2}{\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(\Gamma \backslash {\mathbb H})} \right]. \end{align} $$
$$ \begin{align} \log\left( \Vert f\Vert (z) \right)&=-2k + 2\pi \sum_{w\in \mathcal{F}_{\Gamma}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \lim_{s\to 1}\left(G_s^{\Gamma}(z,w) + \mathcal{E}_{\Gamma,\infty}^{\mathrm{par}}(z,s)\right)\notag \\ &= 2\pi \sum_{w\in \mathcal{F}_\Gamma} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \left[ \lim_{s\to 1}\left(G_s^{\Gamma}(z,w) + \mathcal{E}_{\Gamma,\infty}^{\mathrm{par}}(z,s)\right) - \frac{2}{\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(\Gamma \backslash {\mathbb H})} \right]. \end{align} $$
With all this, it is evident that one can view the inner product realization of the Rohrlich–Jensen formula as a special value of the inner product of the Niebur–Poincaré series
![]() $F_{m}^\Gamma (z,s)$
for
$F_{m}^\Gamma (z,s)$
for
![]() $m\in \mathbb {Z}_{<0}$
and the resolvent kernel
$m\in \mathbb {Z}_{<0}$
and the resolvent kernel
![]() $G_{s}^{\Gamma }(z,w)$
plus the parabolic Eisenstein series
$G_{s}^{\Gamma }(z,w)$
plus the parabolic Eisenstein series
![]() $\mathcal {E}_{\Gamma ,\infty }^{\mathrm {par}}(z,s)$
.
$\mathcal {E}_{\Gamma ,\infty }^{\mathrm {par}}(z,s)$
.
Furthermore, because all terms are eigenfunctions of the Laplacian, one can seek to compute the inner product in hand in a manner similar to that which yields the Maass–Selberg formula.
1.4 Our main results
Unless otherwise explicitly stated, we will assume for the remainder of this article that
![]() $\Gamma $
is any Fuchsian group of the first kind with one cusp. By conjugating
$\Gamma $
is any Fuchsian group of the first kind with one cusp. By conjugating
![]() $\Gamma $
, if necessary, we may assume that the cusp is at
$\Gamma $
, if necessary, we may assume that the cusp is at
![]() $\infty $
, with the cuspidal width equal to one. The group
$\infty $
, with the cuspidal width equal to one. The group
![]() $\Gamma $
will be arbitrary, but fixed, throughout this article, so, for the sake of brevity, in the sequel, we will suppress the index
$\Gamma $
will be arbitrary, but fixed, throughout this article, so, for the sake of brevity, in the sequel, we will suppress the index
![]() $\Gamma $
in the notation for Eisenstein series, the Niebur–Poincaré series, the Kronecker limit function, the fundamental domain, and the resolvent kernel. When
$\Gamma $
in the notation for Eisenstein series, the Niebur–Poincaré series, the Kronecker limit function, the fundamental domain, and the resolvent kernel. When
![]() $\Gamma $
is taken to be the modular group or the Atkin–Lehner group, that will be indicated in the notation.
$\Gamma $
is taken to be the modular group or the Atkin–Lehner group, that will be indicated in the notation.
With the above discussion, we have established that one manner in which the Rohrlich–Jensen formula can be understood is through the study of the regularized inner product
which is defined as follows. Since
![]() $\Gamma $
has one cusp at
$\Gamma $
has one cusp at
![]() $\infty $
, one can construct a (Ford) fundamental domain
$\infty $
, one can construct a (Ford) fundamental domain
![]() $\mathcal {F}$
of the action of
$\mathcal {F}$
of the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() ${\mathbb H}$
. Let
${\mathbb H}$
. Let
![]() $M = \Gamma \backslash {\mathbb H}$
. A cuspidal neighborhood
$M = \Gamma \backslash {\mathbb H}$
. A cuspidal neighborhood
![]() $\mathcal {F}_\infty (Y)$
of
$\mathcal {F}_\infty (Y)$
of
![]() $\infty $
is given by
$\infty $
is given by
![]() $0 < x \leq 1$
and
$0 < x \leq 1$
and
![]() $y \geq Y$
, where
$y \geq Y$
, where
![]() $z=x+iy$
and some
$z=x+iy$
and some
![]() $Y \in {\mathbb R}$
sufficiently large. (We recall that we have normalized the cusp to be of width one.) Let
$Y \in {\mathbb R}$
sufficiently large. (We recall that we have normalized the cusp to be of width one.) Let
![]() $\mathcal {F}(Y) = \mathcal {F}\setminus \mathcal {F}_\infty (Y)$
. Then, we define (8) to be
$\mathcal {F}(Y) = \mathcal {F}\setminus \mathcal {F}_\infty (Y)$
. Then, we define (8) to be
 $$ \begin{align*}\lim_{Y\to \infty} \int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(z,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z), \end{align*} $$
$$ \begin{align*}\lim_{Y\to \infty} \int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(z,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z), \end{align*} $$
where
![]() $d\mu _{\operatorname {\mathrm {hyp}}}(z)$
denotes the hyperbolic volume element. The function
$d\mu _{\operatorname {\mathrm {hyp}}}(z)$
denotes the hyperbolic volume element. The function
![]() $G_s(z,w) + \mathcal {E}_\infty ^{\mathrm {par}}(z,s)$
is unbounded as
$G_s(z,w) + \mathcal {E}_\infty ^{\mathrm {par}}(z,s)$
is unbounded as
![]() $z \to w$
. However, the asymptotic growth of the function is logarithmic, thus integrable; hence, it is not necessary to regularize the integral in (8) in a neighborhood containing w. The need to regularize the inner product (8) stems solely from the exponential growth behavior of the factor
$z \to w$
. However, the asymptotic growth of the function is logarithmic, thus integrable; hence, it is not necessary to regularize the integral in (8) in a neighborhood containing w. The need to regularize the inner product (8) stems solely from the exponential growth behavior of the factor
![]() $F_{-n}(z,1)$
as
$F_{-n}(z,1)$
as
![]() $z\to \infty $
.
$z\to \infty $
.
Our first main result of this article is the following theorem.
Theorem 1. For any positive integer n and any point
![]() $w\in \mathcal {F}$
,
$w\in \mathcal {F}$
,
We can combine Theorem 1 with the factorization formula (7) together with properties of
![]() $F_{-n}(z,1)$
, as proved in [Reference Niebur19], in order to obtain the following extension of the Rohrlich–Jensen formula.
$F_{-n}(z,1)$
, as proved in [Reference Niebur19], in order to obtain the following extension of the Rohrlich–Jensen formula.
Corollary 1. In addition to the notation above, assume that the even weight
![]() $2k\geq 0$
meromorphic form f has been normalized so its q-expansion at
$2k\geq 0$
meromorphic form f has been normalized so its q-expansion at
![]() $\infty $
has constant term equal to
$\infty $
has constant term equal to
![]() $1$
. Then we have that
$1$
. Then we have that
 $$ \begin{align} \langle F_{-n}(\cdot ,1), \log\Vert f\Vert \rangle = - 2\pi \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)}\frac{\partial}{\partial s} F_{-n}(w,s) \Big|_{s=1}. \end{align} $$
$$ \begin{align} \langle F_{-n}(\cdot ,1), \log\Vert f\Vert \rangle = - 2\pi \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)}\frac{\partial}{\partial s} F_{-n}(w,s) \Big|_{s=1}. \end{align} $$
Let g be a
![]() $\Gamma $
invariant analytic function which has a pole at
$\Gamma $
invariant analytic function which has a pole at
![]() $\infty $
. As such, there is a positive integer K and set of complex numbers
$\infty $
. As such, there is a positive integer K and set of complex numbers
![]() $\{a_{n}\}_{n=1}^{K}$
such that
$\{a_{n}\}_{n=1}^{K}$
such that
 $$ \begin{align*}g(z) = \sum_{n=1}^K a_n q_z^{-n} + O(1) \,\,\,\,\, \mathrm{as }z \rightarrow \infty. \end{align*} $$
$$ \begin{align*}g(z) = \sum_{n=1}^K a_n q_z^{-n} + O(1) \,\,\,\,\, \mathrm{as }z \rightarrow \infty. \end{align*} $$
It is proved in [Reference Niebur19] that
 $$ \begin{align} g(z) = \sum_{n=1}^K 2\pi \sqrt{n}a_n F_{-n}(z,1) + c(g) \end{align} $$
$$ \begin{align} g(z) = \sum_{n=1}^K 2\pi \sqrt{n}a_n F_{-n}(z,1) + c(g) \end{align} $$
for some constant depending only upon g. With this, we can combine Corollary 1 and the theorem on page 19 of [Reference Rohrlich20] to obtain the following result.
Corollary 2. With notation as above, there is a constant
![]() $\beta $
, defined by the Laurent expansion of
$\beta $
, defined by the Laurent expansion of
![]() $\mathcal {E}_\infty ^{\mathrm {par}}(z,s)$
near
$\mathcal {E}_\infty ^{\mathrm {par}}(z,s)$
near
![]() $s=1$
, such that
$s=1$
, such that
 $$ \begin{align}\nonumber \langle g, \log\Vert f\Vert \rangle = - 2\pi \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} &\Bigg(2\pi \sum_{n=1}^K \sqrt{n}a_n\frac{\partial}{\partial s} F_{-n}(w,s) \Big|_{s=1} \\& \quad + c(g)(P(w) - \beta \operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M) +2) \Bigg). \end{align} $$
$$ \begin{align}\nonumber \langle g, \log\Vert f\Vert \rangle = - 2\pi \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} &\Bigg(2\pi \sum_{n=1}^K \sqrt{n}a_n\frac{\partial}{\partial s} F_{-n}(w,s) \Big|_{s=1} \\& \quad + c(g)(P(w) - \beta \operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M) +2) \Bigg). \end{align} $$
The constant
![]() $\beta $
is given in (28). We refer the reader to equation (28) for further details regarding the normalizations which define
$\beta $
is given in (28). We refer the reader to equation (28) for further details regarding the normalizations which define
![]() $\beta $
and the parabolic Kronecker limit function P.
$\beta $
and the parabolic Kronecker limit function P.
Finally, we will consider the generating function of the normalized series constructed from the right-hand side of (9). Specifically, we will prove the following result.
Theorem 2. With notation as above, the generating series
 $$ \begin{align*}\sum_{n\geq 1}2\pi \sqrt{n} \frac{\partial}{\partial s} F_{-n}(w,s) \Big|_{s=1}q_z^n \end{align*} $$
$$ \begin{align*}\sum_{n\geq 1}2\pi \sqrt{n} \frac{\partial}{\partial s} F_{-n}(w,s) \Big|_{s=1}q_z^n \end{align*} $$
is, in the z variable, the holomorphic part of the weight two biharmonic Maass form
 $$ \begin{align*}\mathcal{G}_w(z):=i\frac{\partial}{\partial z} \left( \frac{\partial}{\partial s} \left( G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right) \Big|_{s=1} \right). \end{align*} $$
$$ \begin{align*}\mathcal{G}_w(z):=i\frac{\partial}{\partial z} \left( \frac{\partial}{\partial s} \left( G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right) \Big|_{s=1} \right). \end{align*} $$
Note that a weight two biharmonic Maass form is a function which satisfies the weight two modularity in z and which is annihilated by
![]() $\Delta _2^2=(\xi _0\circ \xi _2)^2$
, where, classically
$\Delta _2^2=(\xi _0\circ \xi _2)^2$
, where, classically
![]() $\xi _\kappa := 2iy^\kappa \overline {\frac {\partial }{\partial \overline {z}}}$
. It is clear from the definition that
$\xi _\kappa := 2iy^\kappa \overline {\frac {\partial }{\partial \overline {z}}}$
. It is clear from the definition that
![]() $\mathcal {G}_w(z)$
satisfies the weight two modularity in the z variable. In §5.4, we will prove that
$\mathcal {G}_w(z)$
satisfies the weight two modularity in the z variable. In §5.4, we will prove that
![]() $(\xi _0\circ \xi _2)^2\mathcal {G}_w(z)=0$
.
$(\xi _0\circ \xi _2)^2\mathcal {G}_w(z)=0$
.
In the case
![]() $\Gamma = {\mathrm {PSL}}(2,{\mathbb {Z}})$
, our results yield the main theorems from [Reference Bringmann and Kane2], as we will discuss below.
$\Gamma = {\mathrm {PSL}}(2,{\mathbb {Z}})$
, our results yield the main theorems from [Reference Bringmann and Kane2], as we will discuss below.
1.5 Outline of the paper
In §2, we will establish notation and recall certain results from the literature. There are two specific examples of Poincaré series which are particularly important for our study, the Niebur–Poincaré series and the resolvent kernel. Both series are defined, and basic properties are summarized in §3. In §4, we state the Kronecker limit formulas associated with parabolic and elliptic Eisenstein series, and then prove Proposition 1. The proofs of the main results listed above will be given in §5.
To illustrate our results, various examples are given in §6. Our first example is when
![]() $\Gamma = {\mathrm {PSL}}(2,{\mathbb {Z}})$
, where, as claimed above, our results yield the main theorems of [Reference Bringmann and Kane2]. We then turn to the case when
$\Gamma = {\mathrm {PSL}}(2,{\mathbb {Z}})$
, where, as claimed above, our results yield the main theorems of [Reference Bringmann and Kane2]. We then turn to the case when
![]() $\Gamma $
is an Atkin–Lehner group
$\Gamma $
is an Atkin–Lehner group
![]() $\Gamma _0(N)^+$
for square-free level N. The first examples are when the genus of the quotient spaces
$\Gamma _0(N)^+$
for square-free level N. The first examples are when the genus of the quotient spaces
![]() $\overline {\Gamma _0(N)^+}\backslash {\mathbb H}$
are zero and when the function g in Corollary 2 is the Hauptmodul
$\overline {\Gamma _0(N)^+}\backslash {\mathbb H}$
are zero and when the function g in Corollary 2 is the Hauptmodul
![]() $j_N^+(z)$
. In somewhat common notation, we write
$j_N^+(z)$
. In somewhat common notation, we write
![]() $\overline {\Gamma _0(N)^+}$
to denote the projection of
$\overline {\Gamma _0(N)^+}$
to denote the projection of
![]() $\Gamma _0(N)^+$
onto
$\Gamma _0(N)^+$
onto
![]() $\mathrm {PSL}(2,\mathbb {R})$
. The next two examples we present are for levels
$\mathrm {PSL}(2,\mathbb {R})$
. The next two examples we present are for levels
![]() $N=37$
and
$N=37$
and
![]() $N=103$
. For these levels, the genus of the quotients of
$N=103$
. For these levels, the genus of the quotients of
![]() ${\mathbb H}$
by
${\mathbb H}$
by
![]() $\overline {\Gamma _0(N)^+}$
are one and two, respectively. In these cases, certain generators of the corresponding function fields were constructed in [Reference Jorgenson, Smajlović and Then13]. Consequently, we are able to employ the results from [Reference Jorgenson, Smajlović and Then13] and fully develop Corollary 2.
$\overline {\Gamma _0(N)^+}$
are one and two, respectively. In these cases, certain generators of the corresponding function fields were constructed in [Reference Jorgenson, Smajlović and Then13]. Consequently, we are able to employ the results from [Reference Jorgenson, Smajlović and Then13] and fully develop Corollary 2.
2 Background material
2.1 Basic notation
Let
![]() $\Gamma \subset {\mathrm {PSL}}(2,\mathbb {R})$
denote a Fuchsian group of the first kind acting by fractional linear transformations on the hyperbolic upper half-plane
$\Gamma \subset {\mathrm {PSL}}(2,\mathbb {R})$
denote a Fuchsian group of the first kind acting by fractional linear transformations on the hyperbolic upper half-plane
![]() $\mathbb {H}:=\{z=x+iy\in \mathbb {C}\, |\,x,y\in \mathbb {R};\,y>0\}$
. We let
$\mathbb {H}:=\{z=x+iy\in \mathbb {C}\, |\,x,y\in \mathbb {R};\,y>0\}$
. We let
![]() $M:=\Gamma \backslash \mathbb {H}$
, which is a finite volume hyperbolic Riemann surface, and denote by
$M:=\Gamma \backslash \mathbb {H}$
, which is a finite volume hyperbolic Riemann surface, and denote by
![]() $p:\mathbb {H}\longrightarrow M$
the natural projection. We assume that M has
$p:\mathbb {H}\longrightarrow M$
the natural projection. We assume that M has
![]() $e_{\Gamma }$
elliptic fixed points and one cusp at
$e_{\Gamma }$
elliptic fixed points and one cusp at
![]() $\infty $
of width one. By an abuse of notation, we also say that
$\infty $
of width one. By an abuse of notation, we also say that
![]() $\Gamma $
has a cusp at
$\Gamma $
has a cusp at
![]() $\infty $
of width one, meaning that the stabilizer
$\infty $
of width one, meaning that the stabilizer
![]() $\Gamma _\infty $
of
$\Gamma _\infty $
of
![]() $\infty $
is generated by the matrix
$\infty $
is generated by the matrix
![]() $\bigl (\begin {smallmatrix} 1&1\\0&1\end {smallmatrix}\bigr )$
. We identify M locally with its universal cover
$\bigl (\begin {smallmatrix} 1&1\\0&1\end {smallmatrix}\bigr )$
. We identify M locally with its universal cover
![]() $\mathbb {H}$
. By
$\mathbb {H}$
. By
![]() $\mathcal {F}$
we denote the “usual” (Ford) fundamental domain for
$\mathcal {F}$
we denote the “usual” (Ford) fundamental domain for
![]() $\Gamma $
acting on
$\Gamma $
acting on
![]() $\mathbb H$
.
$\mathbb H$
.
We let
![]() $\mu _{\mathrm {hyp}}$
denote the hyperbolic metric on M which is compatible with the complex structure of M and has constant negative curvature equal to minus one. The hyperbolic line element
$\mu _{\mathrm {hyp}}$
denote the hyperbolic metric on M which is compatible with the complex structure of M and has constant negative curvature equal to minus one. The hyperbolic line element
![]() $ds^{2}_{\operatorname {\mathrm {hyp}}}$
, respectively, the hyperbolic Laplacian
$ds^{2}_{\operatorname {\mathrm {hyp}}}$
, respectively, the hyperbolic Laplacian
![]() $\Delta _{\operatorname {\mathrm {hyp}}}$
acting on functions, are given in the coordinate
$\Delta _{\operatorname {\mathrm {hyp}}}$
acting on functions, are given in the coordinate
![]() $z=x+iy$
on
$z=x+iy$
on
![]() $\mathbb {H}$
by
$\mathbb {H}$
by
 $$ \begin{align*} ds^{2}_{\operatorname{\mathrm{hyp}}}:=\frac{dx^{2}+dy^{2}}{y^{2}},\quad\mathrm{respectively,} \quad\Delta_{\operatorname{\mathrm{hyp}}}:=-y^{2}\left(\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}\right). \end{align*} $$
$$ \begin{align*} ds^{2}_{\operatorname{\mathrm{hyp}}}:=\frac{dx^{2}+dy^{2}}{y^{2}},\quad\mathrm{respectively,} \quad\Delta_{\operatorname{\mathrm{hyp}}}:=-y^{2}\left(\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}\right). \end{align*} $$
By
![]() $d_{\mathrm {hyp}}(z,w)$
, we denote the hyperbolic distance between the two points
$d_{\mathrm {hyp}}(z,w)$
, we denote the hyperbolic distance between the two points
![]() $z\in \mathbb {H}$
and
$z\in \mathbb {H}$
and
![]() $w\in \mathbb {H}$
. Our normalization of the hyperbolic Laplacian is different from the one considered in [Reference Hejhal9] and [Reference Niebur19] where the Laplacian is taken with the plus sign.
$w\in \mathbb {H}$
. Our normalization of the hyperbolic Laplacian is different from the one considered in [Reference Hejhal9] and [Reference Niebur19] where the Laplacian is taken with the plus sign.
2.2 Modular forms
Following [Reference Serre21], we define a weakly modular form f of even weight
![]() $2k$
for
$2k$
for
![]() $k \geq 0$
associated with
$k \geq 0$
associated with
![]() $\Gamma $
to be a function f which is meromorphic on
$\Gamma $
to be a function f which is meromorphic on
![]() $\mathbb H$
, and at the cusps of
$\mathbb H$
, and at the cusps of
![]() $\Gamma $
, and satisfies the transformation property
$\Gamma $
, and satisfies the transformation property
 $$ \begin{align} f\left(\frac{az+b}{cz+d}\right) = (cz+d)^{2k}f(z), \quad\mathrm{for any }\begin{pmatrix}a&b\\c&d\end{pmatrix} \in \Gamma. \end{align} $$
$$ \begin{align} f\left(\frac{az+b}{cz+d}\right) = (cz+d)^{2k}f(z), \quad\mathrm{for any }\begin{pmatrix}a&b\\c&d\end{pmatrix} \in \Gamma. \end{align} $$
In the setting of this paper, any weakly modular form f will satisfy the relation
![]() $f(z+1)=f(z)$
, so that for some positive integer N, we can write
$f(z+1)=f(z)$
, so that for some positive integer N, we can write
 $$ \begin{align*}f(z) = \sum\limits_{n=-N}^{\infty}a_{n}q_z^{n}, \quad\text{ where } q_z =e(z)= e^{2\pi iz}. \end{align*} $$
$$ \begin{align*}f(z) = \sum\limits_{n=-N}^{\infty}a_{n}q_z^{n}, \quad\text{ where } q_z =e(z)= e^{2\pi iz}. \end{align*} $$
If
![]() $a_{n} = 0$
, for all
$a_{n} = 0$
, for all
![]() $n < 0$
, then f is said to be holomorphic at the cusp at
$n < 0$
, then f is said to be holomorphic at the cusp at
![]() $\infty $
. A holomorphic modular form with respect to
$\infty $
. A holomorphic modular form with respect to
![]() $\Gamma $
is a weakly modular form which is holomorphic on
$\Gamma $
is a weakly modular form which is holomorphic on
![]() $\mathbb H$
and at all the cusps of
$\mathbb H$
and at all the cusps of
![]() $\Gamma $
.
$\Gamma $
.
When the weight k is zero, the transformation property (13) indicates that the function f is invariant with respect to the action of elements of the group
![]() $\Gamma $
, so it may be viewed as a meromorphic function on the surface
$\Gamma $
, so it may be viewed as a meromorphic function on the surface
![]() $M=\Gamma \backslash \mathbb {H}$
. In other words, a meromorphic function on M is a weakly modular form of weight
$M=\Gamma \backslash \mathbb {H}$
. In other words, a meromorphic function on M is a weakly modular form of weight
![]() $0$
.
$0$
.
For any two weight
![]() $2k$
weakly modular forms f and g associated with
$2k$
weakly modular forms f and g associated with
![]() $\Gamma $
, with integrable singularities at finitely many points in
$\Gamma $
, with integrable singularities at finitely many points in
![]() $\mathcal {F}$
, the generalized inner product
$\mathcal {F}$
, the generalized inner product
![]() $\langle \cdot ,\, \cdot \rangle $
is defined as
$\langle \cdot ,\, \cdot \rangle $
is defined as
 $$ \begin{align} \langle f,g\rangle = \lim_{Y\to \infty} \int\limits_{\mathcal{F}(Y)}f(z) \overline{g(z)}(\mathrm{Im}(z))^{2k}d\mu_{\operatorname{\mathrm{hyp}}}(z), \end{align} $$
$$ \begin{align} \langle f,g\rangle = \lim_{Y\to \infty} \int\limits_{\mathcal{F}(Y)}f(z) \overline{g(z)}(\mathrm{Im}(z))^{2k}d\mu_{\operatorname{\mathrm{hyp}}}(z), \end{align} $$
where the integration is taken over the portion
![]() $\mathcal {F}(Y)$
of the fundamental domain
$\mathcal {F}(Y)$
of the fundamental domain
![]() $\mathcal {F}$
equal to
$\mathcal {F}$
equal to
![]() $\mathcal {F}\setminus \mathcal {F}_\infty (Y)$
.
$\mathcal {F}\setminus \mathcal {F}_\infty (Y)$
.
2.3 Atkin–Lehner groups
Let
![]() $N=p_1\ldots p_r$
be a square-free, nonnegative integer including the case
$N=p_1\ldots p_r$
be a square-free, nonnegative integer including the case
![]() $N=1$
. The subset of
$N=1$
. The subset of
![]() $\mathrm {SL}(2,\mathbb {R})$
, defined by
$\mathrm {SL}(2,\mathbb {R})$
, defined by
 $$ \begin{align*} \Gamma_0(N)^+: =\Big\{ \frac{1}{\sqrt{e}}\begin{pmatrix}a&b\\c&d\end{pmatrix}\in \mathrm{SL}(2,\mathbb{R}): & \, ad-bc=e, \, a,b,c,d,e\in\mathbb{Z}, \,e>0, \\& e\mid N,\ e\mid a, \ e\mid d,\ N\mid c \Big\} \end{align*} $$
$$ \begin{align*} \Gamma_0(N)^+: =\Big\{ \frac{1}{\sqrt{e}}\begin{pmatrix}a&b\\c&d\end{pmatrix}\in \mathrm{SL}(2,\mathbb{R}): & \, ad-bc=e, \, a,b,c,d,e\in\mathbb{Z}, \,e>0, \\& e\mid N,\ e\mid a, \ e\mid d,\ N\mid c \Big\} \end{align*} $$
is an arithmetic subgroup of
![]() $\mathrm {SL}(2,\mathbb {R})$
. We use the terminology Atkin–Lehner group of level N to describe
$\mathrm {SL}(2,\mathbb {R})$
. We use the terminology Atkin–Lehner group of level N to describe
![]() $\Gamma _0(N)^+$
in part because the group is obtained by adding all Atkin–Lehner involutions to the congruence group
$\Gamma _0(N)^+$
in part because the group is obtained by adding all Atkin–Lehner involutions to the congruence group
![]() $\Gamma _0(N)$
(see [Reference Atkin and Lehner1]). Let
$\Gamma _0(N)$
(see [Reference Atkin and Lehner1]). Let
![]() $\{\pm \mathrm {Id}\}$
denote the set of two elements, where
$\{\pm \mathrm {Id}\}$
denote the set of two elements, where
![]() $\mathrm {Id}$
is the identity matrix. In general, if
$\mathrm {Id}$
is the identity matrix. In general, if
![]() $\Gamma $
is a subgroup of
$\Gamma $
is a subgroup of
![]() $\mathrm {SL}(2,\mathbb {R})$
, we let
$\mathrm {SL}(2,\mathbb {R})$
, we let
![]() $\overline {\Gamma } := \Gamma /\{\pm \mathrm {Id}\}$
denote its projection into
$\overline {\Gamma } := \Gamma /\{\pm \mathrm {Id}\}$
denote its projection into
![]() $\mathrm {PSL}(2,\mathbb {R})$
.
$\mathrm {PSL}(2,\mathbb {R})$
.
Set
![]() $Y_N^{+}:=\overline {\Gamma _0(N)^+} \backslash \mathbb {H}$
. According to [Reference Cummins5], for any square-free N, the quotient space
$Y_N^{+}:=\overline {\Gamma _0(N)^+} \backslash \mathbb {H}$
. According to [Reference Cummins5], for any square-free N, the quotient space
![]() $Y_{N}^{+}$
has one cusp at
$Y_{N}^{+}$
has one cusp at
![]() $\infty $
with the cusp width equal to one. The spaces
$\infty $
with the cusp width equal to one. The spaces
![]() $Y_{N}^{+}$
will be used in the last section where we give examples of our results for generators of function fields of meromorphic functions on
$Y_{N}^{+}$
will be used in the last section where we give examples of our results for generators of function fields of meromorphic functions on
![]() $Y_N^{+}$
.
$Y_N^{+}$
.
2.4 Generators of function fields of Atkin–Lehner groups of small genus
An explicit construction of generators of function fields of all meromorphic functions on
![]() $Y_N^{+}$
with genus
$Y_N^{+}$
with genus
![]() $g_{N,+}\leq 3$
was given in [Reference Jorgenson, Smajlović and Then13].
$g_{N,+}\leq 3$
was given in [Reference Jorgenson, Smajlović and Then13].
When
![]() $g_{N,+}=0$
, the function field of meromorphic functions on
$g_{N,+}=0$
, the function field of meromorphic functions on
![]() $Y_N^+$
is generated by a single function, the Hauptmodul
$Y_N^+$
is generated by a single function, the Hauptmodul
![]() $j_N^+(z)$
, which is normalized so that its q-expansion is of the form
$j_N^+(z)$
, which is normalized so that its q-expansion is of the form
![]() $q_z^{-1}+O(q_z)$
. The Hauptmodul
$q_z^{-1}+O(q_z)$
. The Hauptmodul
![]() $j_N^+(z)$
appears in the “Monstrous Moonshine” and was investigated in many papers, starting with Conway and Norton [Reference Conway and Norton4]. The action of the mth Hecke operator
$j_N^+(z)$
appears in the “Monstrous Moonshine” and was investigated in many papers, starting with Conway and Norton [Reference Conway and Norton4]. The action of the mth Hecke operator
![]() $T_m$
on
$T_m$
on
![]() $j_N^+(z)$
produces a meromorphic function on
$j_N^+(z)$
produces a meromorphic function on
![]() $Y_N^{+}$
with the q-expansion
$Y_N^{+}$
with the q-expansion
![]() $j_N^+|T_{m}(z)= q_z^{-m} + O(q_z)$
.
$j_N^+|T_{m}(z)= q_z^{-m} + O(q_z)$
.
When
![]() $g_{N,+}\geq 1$
, the function field of meromorphic functions on
$g_{N,+}\geq 1$
, the function field of meromorphic functions on
![]() $Y_N^+$
is generated by two functions. For
$Y_N^+$
is generated by two functions. For
![]() $g_{N,+}\leq 3$
, the results in [Reference Jorgenson, Smajlović and Then13] provided the explicit construction of certain generators
$g_{N,+}\leq 3$
, the results in [Reference Jorgenson, Smajlović and Then13] provided the explicit construction of certain generators
![]() $x_N^+(z)$
and
$x_N^+(z)$
and
![]() $y_N^+(z)$
. Furthermore, it is shown that the q-expansions of these generators are of the form
$y_N^+(z)$
. Furthermore, it is shown that the q-expansions of these generators are of the form
 $$ \begin{align*}x_N^+(z)=q_z^{-a}+\sum_{j=1}^{a-1}a_jq_z^{-j}+O(q_z) \quad \text{and} \quad y_N^+(z)=q_z^{-b}+\sum_{j=1}^{b-1}b_jq_z^{-j}+O(q_z), \end{align*} $$
$$ \begin{align*}x_N^+(z)=q_z^{-a}+\sum_{j=1}^{a-1}a_jq_z^{-j}+O(q_z) \quad \text{and} \quad y_N^+(z)=q_z^{-b}+\sum_{j=1}^{b-1}b_jq_z^{-j}+O(q_z), \end{align*} $$
where
![]() $a,b$
are positive integers with
$a,b$
are positive integers with
![]() $a\leq 1+g_{N,+}$
, and
$a\leq 1+g_{N,+}$
, and
![]() $b\leq 2+g_{N,+}$
. Furthermore, for
$b\leq 2+g_{N,+}$
. Furthermore, for
![]() $g_{N,+} \leq 3$
, it is shown in [Reference Jorgenson, Smajlović and Then13] that all coefficients in the q-expansion for
$g_{N,+} \leq 3$
, it is shown in [Reference Jorgenson, Smajlović and Then13] that all coefficients in the q-expansion for
![]() $x_N^+(z)$
and
$x_N^+(z)$
and
![]() $y_N^+(z)$
are integers. For all such N, the precise values of these coefficients out to large order were computed, and the results are available at [Reference Jorgenson, Smajlović and Then15].
$y_N^+(z)$
are integers. For all such N, the precise values of these coefficients out to large order were computed, and the results are available at [Reference Jorgenson, Smajlović and Then15].
3 Two Poincaré series
In this section, we will define the Niebur–Poincaré series
![]() $F_{m}(z,s)$
and the resolvent kernel
$F_{m}(z,s)$
and the resolvent kernel
![]() $G_s(z,w)$
; one also refers to
$G_s(z,w)$
; one also refers to
![]() $G_s(z,w)$
as the automorphic Green’s function. We refer the reader to [Reference Niebur19] for additional information regarding
$G_s(z,w)$
as the automorphic Green’s function. We refer the reader to [Reference Niebur19] for additional information regarding
![]() $F_{m}(z,s)$
and to [Reference Hejhal9] and [Reference Iwaniec11] and references therein for further details regarding
$F_{m}(z,s)$
and to [Reference Hejhal9] and [Reference Iwaniec11] and references therein for further details regarding
![]() $G_s(z,w)$
. As said above, we will suppress the group
$G_s(z,w)$
. As said above, we will suppress the group
![]() $\Gamma $
from the notation.
$\Gamma $
from the notation.
3.1 Niebur–Poincaré series
We start with the definition and properties of the Niebur–Poincaré series
![]() $F_{m}(z,s)$
associated with a co-finite Fuchsian group with one cusp. We then will specialize results to the setting of Atkin–Lehner groups.
$F_{m}(z,s)$
associated with a co-finite Fuchsian group with one cusp. We then will specialize results to the setting of Atkin–Lehner groups.
3.1.1 Niebur–Poincaré series associated with a co-finite Fuchsian group with one cusp
Let m be a nonzero integer,
![]() $z=x+iy\in \mathbb {H}$
, and
$z=x+iy\in \mathbb {H}$
, and
![]() $s\in \mathbb {C}$
with
$s\in \mathbb {C}$
with
![]() ${\mathrm {Re}}(s)>1$
. Recall the notation
${\mathrm {Re}}(s)>1$
. Recall the notation
![]() $e(x):=\exp (2\pi i x)$
, and let
$e(x):=\exp (2\pi i x)$
, and let
![]() $I_{s-1/2}$
denote the modified I-Bessel function of the first kind (see (A.2)). The Niebur–Poincaré series
$I_{s-1/2}$
denote the modified I-Bessel function of the first kind (see (A.2)). The Niebur–Poincaré series
![]() $F_{m}(z,s)$
is defined formally by the series
$F_{m}(z,s)$
is defined formally by the series
 $$ \begin{align} F_m(z,s)=F_m^\Gamma(z,s):= \sum_{\gamma\in\Gamma_\infty \backslash \Gamma} e(m{\mathrm{Re}}(\gamma z))({\mathrm{Im}}(\gamma z))^{1/2}I_{s-1/2}(2\pi |m| {\mathrm{Im}}(\gamma z)). \end{align} $$
$$ \begin{align} F_m(z,s)=F_m^\Gamma(z,s):= \sum_{\gamma\in\Gamma_\infty \backslash \Gamma} e(m{\mathrm{Re}}(\gamma z))({\mathrm{Im}}(\gamma z))^{1/2}I_{s-1/2}(2\pi |m| {\mathrm{Im}}(\gamma z)). \end{align} $$
For fixed m and z, the series (15) converges absolutely and uniformly on any compact subset of the half plane
![]() ${\mathrm {Re}}(s)>1$
. Moreover,
${\mathrm {Re}}(s)>1$
. Moreover,
![]() $\Delta _{\operatorname {\mathrm {hyp}}}F_m(z,s) = s(1-s) F_m(z,s)$
for all
$\Delta _{\operatorname {\mathrm {hyp}}}F_m(z,s) = s(1-s) F_m(z,s)$
for all
![]() $s\in \mathbb {C}$
in the half plane
$s\in \mathbb {C}$
in the half plane
![]() ${\mathrm {Re}}(s)>1$
. From Theorem 5 of [Reference Niebur19], we have that for any nonzero integer m, the function
${\mathrm {Re}}(s)>1$
. From Theorem 5 of [Reference Niebur19], we have that for any nonzero integer m, the function
![]() $F_m(z,s)$
admits a meromorphic continuation to the whole complex plane
$F_m(z,s)$
admits a meromorphic continuation to the whole complex plane
![]() $s\in {\mathbb C}$
. Moreover,
$s\in {\mathbb C}$
. Moreover,
![]() $F_m(z,s)$
is holomorphic at
$F_m(z,s)$
is holomorphic at
![]() $s=1$
and, according to the spectral expansion given in Theorem 5 of [Reference Niebur19],
$s=1$
and, according to the spectral expansion given in Theorem 5 of [Reference Niebur19],
![]() $F_m(z,1)$
is orthogonal to constant functions, meaning that
$F_m(z,1)$
is orthogonal to constant functions, meaning that
For our purposes, it is necessary to employ the Fourier expansion of
![]() $F_{m}(z,s)$
in the cusp
$F_{m}(z,s)$
in the cusp
![]() $\infty $
. The Fourier expansion is proved in [Reference Niebur19] and involves the Kloosterman sums
$\infty $
. The Fourier expansion is proved in [Reference Niebur19] and involves the Kloosterman sums
![]() $S(m,n;c)$
, which we now define. For any integers m and n, and real number
$S(m,n;c)$
, which we now define. For any integers m and n, and real number
![]() $c\neq 0$
, define
$c\neq 0$
, define
 $$ \begin{align*}S(m,n;c):= \sum_{\bigl(\begin{smallmatrix} a&\ast\\c&d\end{smallmatrix}\bigr)\in \Gamma_\infty \diagdown \Gamma \diagup \Gamma_\infty } e\left( \frac{ma + nd}{c}\right). \end{align*} $$
$$ \begin{align*}S(m,n;c):= \sum_{\bigl(\begin{smallmatrix} a&\ast\\c&d\end{smallmatrix}\bigr)\in \Gamma_\infty \diagdown \Gamma \diagup \Gamma_\infty } e\left( \frac{ma + nd}{c}\right). \end{align*} $$
For
![]() ${\mathrm {Re}}(s)>1$
and
${\mathrm {Re}}(s)>1$
and
![]() $z=x+iy\in \mathbb {H}$
, the Fourier expansion of
$z=x+iy\in \mathbb {H}$
, the Fourier expansion of
![]() $F_m(z,s)$
is given by
$F_m(z,s)$
is given by
 $$ \begin{align} F_m(z,s)=e(mx)y^{1/2}I_{s-1/2}(2\pi |m|y) + \sum_{k=-\infty}^{\infty}b_k(y,s;m)e(kx), \end{align} $$
$$ \begin{align} F_m(z,s)=e(mx)y^{1/2}I_{s-1/2}(2\pi |m|y) + \sum_{k=-\infty}^{\infty}b_k(y,s;m)e(kx), \end{align} $$
where
 $$ \begin{align*}b_0(y,s;m) = \frac{y^{1-s}}{(2s-1)\Gamma(s)}2\pi^s |m|^{s-1/2} \sum_{c>0} S(m,0;c)c^{-2s}=\frac{y^{1-s}}{(2s-1)}B_0(s;m). \end{align*} $$
$$ \begin{align*}b_0(y,s;m) = \frac{y^{1-s}}{(2s-1)\Gamma(s)}2\pi^s |m|^{s-1/2} \sum_{c>0} S(m,0;c)c^{-2s}=\frac{y^{1-s}}{(2s-1)}B_0(s;m). \end{align*} $$
The function
![]() $B_0(s;m)$
is denoted by
$B_0(s;m)$
is denoted by
![]() $a_m(s)$
in [Reference Niebur19]. For
$a_m(s)$
in [Reference Niebur19]. For
![]() $k\neq 0$
, we have that
$k\neq 0$
, we have that
with
 $$ \begin{align*}B_k(s;m)= 2 \sum_{c>0}S(m,k;c)c^{-1}\cdot \left\{ \begin{array}{ll} J_{2s-1}\left(\frac{4\pi}{c} \sqrt{mk}\right), & \mathrm{if \,}mk>0, \\ I_{2s-1}\left(\frac{4\pi}{c} \sqrt{|mk|}\right), & \mathrm{if \,} mk<0, \end{array} \right. \end{align*} $$
$$ \begin{align*}B_k(s;m)= 2 \sum_{c>0}S(m,k;c)c^{-1}\cdot \left\{ \begin{array}{ll} J_{2s-1}\left(\frac{4\pi}{c} \sqrt{mk}\right), & \mathrm{if \,}mk>0, \\ I_{2s-1}\left(\frac{4\pi}{c} \sqrt{|mk|}\right), & \mathrm{if \,} mk<0, \end{array} \right. \end{align*} $$
where we corrected certain typos in Theorem 1 of [Reference Niebur19]. In the above expression,
![]() $J_{2s-1}$
denotes the J-Bessel function and
$J_{2s-1}$
denotes the J-Bessel function and
![]() $K_{s-1/2}$
is the modified Bessel function (see formulas (A.1) and (A.3)). According to the proof of Theorem 6 from [Reference Niebur19], the Fourier expansion (16) extends by the principle of analytic continuation to the case when
$K_{s-1/2}$
is the modified Bessel function (see formulas (A.1) and (A.3)). According to the proof of Theorem 6 from [Reference Niebur19], the Fourier expansion (16) extends by the principle of analytic continuation to the case when
![]() $s=1$
. Hence, by putting
$s=1$
. Hence, by putting
![]() $B_k(1;m):= \lim _{s\downarrow 1} B_k(s;m)$
, and using the special values (A.5) of I-Bessel and K-Bessel functions of order
$B_k(1;m):= \lim _{s\downarrow 1} B_k(s;m)$
, and using the special values (A.5) of I-Bessel and K-Bessel functions of order
![]() $1/2$
, we have that
$1/2$
, we have that
 $$ \begin{align} F_m(z,1)=\frac{\sinh(2\pi|m|y)}{\pi \sqrt{|m|}}e(mx) + B_0(1;m)+ \sum_{k\in\mathbb{Z}\setminus\{0\}}\frac{1}{2 \sqrt{|k|}} e^{-2\pi|k|y}B_k(1;m)e(kx). \end{align} $$
$$ \begin{align} F_m(z,1)=\frac{\sinh(2\pi|m|y)}{\pi \sqrt{|m|}}e(mx) + B_0(1;m)+ \sum_{k\in\mathbb{Z}\setminus\{0\}}\frac{1}{2 \sqrt{|k|}} e^{-2\pi|k|y}B_k(1;m)e(kx). \end{align} $$
From page 75 of [Reference Iwaniec11], one has the trivial bounds
![]() $I_1(y)\ll \min \{y,y^{-1/2}\}e^y$
and
$I_1(y)\ll \min \{y,y^{-1/2}\}e^y$
and
![]() $J_1(y)\ll \min \{y,y^{-1/2}\}$
, which hold for any positive real number y. From this, we obtain the bound that
$J_1(y)\ll \min \{y,y^{-1/2}\}$
, which hold for any positive real number y. From this, we obtain the bound that
The constant
![]() $c_{\Gamma }>0$
is equal to the smallest left-lower entry
$c_{\Gamma }>0$
is equal to the smallest left-lower entry
![]() $c>0$
of
$c>0$
of
![]() $\Gamma $
, and the implied constant is independent of
$\Gamma $
, and the implied constant is independent of
![]() $k,m$
.
$k,m$
.
It is clear from (17) that for
![]() $n>0$
one has that
$n>0$
one has that
 $$ \begin{align*} F_{-n}(z,1) = \frac{1}{2\pi\sqrt{n}}q_{z}^{-n} + O(1) \,\,\,\,\,\mathrm{as }z \rightarrow \infty \end{align*} $$
$$ \begin{align*} F_{-n}(z,1) = \frac{1}{2\pi\sqrt{n}}q_{z}^{-n} + O(1) \,\,\,\,\,\mathrm{as }z \rightarrow \infty \end{align*} $$
(see also [Reference Niebur19, Th. 6]). The Fourier expansion (17) combined with (18) also suffices to show that
for any nonzero integer n.
A similar bound holds true for the derivative of
![]() $F_{n}(z,s)$
in s, at
$F_{n}(z,s)$
in s, at
![]() $s=1$
. More precisely, we have the following lemma.
$s=1$
. More precisely, we have the following lemma.
Lemma 3. Let n be a nonzero integer. Then
 $$ \begin{align} \left.\frac{\partial}{\partial s} F_{n}(z,s)\right|_{s=1} \ll \exp\left( 2\pi |n| {\mathrm{Im}}(z)\right) \,\,\,\,\, \mathrm{as Im}(z) \to \infty. \end{align} $$
$$ \begin{align} \left.\frac{\partial}{\partial s} F_{n}(z,s)\right|_{s=1} \ll \exp\left( 2\pi |n| {\mathrm{Im}}(z)\right) \,\,\,\,\, \mathrm{as Im}(z) \to \infty. \end{align} $$
Proof. The proof is similar to that of Lemma 4.3(1), page 19 of [Reference Bringmann and Kane2]. We begin by applying
![]() $\frac {\partial }{\partial s}$
to the Fourier expansion (16) and then take
$\frac {\partial }{\partial s}$
to the Fourier expansion (16) and then take
![]() $s=1$
. Recall that the series in (16) converges uniformly in compact subsets of the half plane
$s=1$
. Recall that the series in (16) converges uniformly in compact subsets of the half plane
![]() ${\mathrm {Re}}(s)>1$
. Also,
${\mathrm {Re}}(s)>1$
. Also,
![]() $ F_{n}(z,s)$
is holomorphic at
$ F_{n}(z,s)$
is holomorphic at
![]() $s=1$
. Therefore, we can differentiate the series (16) termwise at
$s=1$
. Therefore, we can differentiate the series (16) termwise at
![]() $s=1$
to get that
$s=1$
to get that
 $$ \begin{align} \left.\frac{\partial}{\partial s} F_{n}(z,s)\right|_{s=1}= e(nx)y^{1/2} \left.\frac{\partial }{\partial \nu} I_{\nu}(2\pi |n|y)\right|_{\nu=1/2}+ \sum_{k=-\infty}^{\infty} \left.\frac{\partial}{\partial s} b_k(y,s;n)\right|_{s=1} e(kx). \end{align} $$
$$ \begin{align} \left.\frac{\partial}{\partial s} F_{n}(z,s)\right|_{s=1}= e(nx)y^{1/2} \left.\frac{\partial }{\partial \nu} I_{\nu}(2\pi |n|y)\right|_{\nu=1/2}+ \sum_{k=-\infty}^{\infty} \left.\frac{\partial}{\partial s} b_k(y,s;n)\right|_{s=1} e(kx). \end{align} $$
The bound (A.15) ensures that the first term on the right-hand side of (21) is of order
![]() $O(\exp \left ( 2\pi |n| y \right ))$
as
$O(\exp \left ( 2\pi |n| y \right ))$
as
![]() $y={\mathrm {Im}}(z) \to \infty $
.
$y={\mathrm {Im}}(z) \to \infty $
.
Next, we estimate
![]() $\left .\frac {\partial }{\partial s} b_k(y,s;n)\right |_{s=1}$
as
$\left .\frac {\partial }{\partial s} b_k(y,s;n)\right |_{s=1}$
as
![]() $y \to \infty $
. When
$y \to \infty $
. When
![]() $k=0$
, it is immediate that
$k=0$
, it is immediate that
 $$ \begin{align*}\left.\frac{\partial }{\partial s} b_0(y,s;n)\right|_{s=1}=O(\log (y)) \,\,\,\,\, \text{as } y \to \infty.\end{align*} $$
$$ \begin{align*}\left.\frac{\partial }{\partial s} b_0(y,s;n)\right|_{s=1}=O(\log (y)) \,\,\,\,\, \text{as } y \to \infty.\end{align*} $$
For
![]() $k\neq 0$
,
$k\neq 0$
,
 $$ \begin{align} \left.\frac{\partial }{\partial s} b_k(y,s;n)\right|_{s=1}= \sqrt{y}\left(\left.\frac{\partial }{\partial s} B_k(s;n)\right|_{s=1} K_{1/2}(2\pi |k|y) + B_k(1;n) \left.\frac{\partial }{\partial \nu} K_{\nu}(2\pi |k|y)\right|_{\nu=1/2} \right). \end{align} $$
$$ \begin{align} \left.\frac{\partial }{\partial s} b_k(y,s;n)\right|_{s=1}= \sqrt{y}\left(\left.\frac{\partial }{\partial s} B_k(s;n)\right|_{s=1} K_{1/2}(2\pi |k|y) + B_k(1;n) \left.\frac{\partial }{\partial \nu} K_{\nu}(2\pi |k|y)\right|_{\nu=1/2} \right). \end{align} $$
The first term on the right-hand side of (22) can be estimated using the identity (A.5) combined with bounds (A.18) to deduce
 $$ \begin{align*}\sqrt{y}\left.\frac{\partial }{\partial s} B_k(s;n)\right|_{s=1} K_{1/2}(2\pi |k|y)\ll \frac{e^{-2\pi |k|y}}{2\sqrt{k}}\cdot\frac{e^{4\pi\sqrt{|kn|}/c_{\Gamma}}}{\sqrt{|kn|}}. \end{align*} $$
$$ \begin{align*}\sqrt{y}\left.\frac{\partial }{\partial s} B_k(s;n)\right|_{s=1} K_{1/2}(2\pi |k|y)\ll \frac{e^{-2\pi |k|y}}{2\sqrt{k}}\cdot\frac{e^{4\pi\sqrt{|kn|}/c_{\Gamma}}}{\sqrt{|kn|}}. \end{align*} $$
Combining (18) with (A.15) yields that the second term on the right-hand side of (22) is
![]() $O\left (\exp \left (-2\pi |k|y + \frac {4\pi }{c_{\Gamma }}\sqrt {|nk|}\right )\right )$
as
$O\left (\exp \left (-2\pi |k|y + \frac {4\pi }{c_{\Gamma }}\sqrt {|nk|}\right )\right )$
as
![]() $y\to \infty $
.
$y\to \infty $
.
This shows that the series on the right-hand side of (21) converges uniformly for y large enough and tends to zero as
![]() $y\to \infty $
. Since the first term is
$y\to \infty $
. Since the first term is
![]() $O(\exp \left ( 2\pi |n| y \right ))$
as
$O(\exp \left ( 2\pi |n| y \right ))$
as
![]() $y={\mathrm {Im}}(z) \to \infty $
, the proof is complete.
$y={\mathrm {Im}}(z) \to \infty $
, the proof is complete.
We note that the value of the derivative of the Niebur–Poincaré series at
![]() $s=1$
satisfies a differential equation, namely that
$s=1$
satisfies a differential equation, namely that
 $$ \begin{align} \notag \Delta_{\operatorname{\mathrm{hyp}}}\left(\frac{\partial}{\partial s}\left. F_{-n}(z,s) \right|_{s=1} \right) &=\lim_{s\to 1} \Delta_{\operatorname{\mathrm{hyp}}} \left(\frac{F_{-n}(z,s) - F_{-n}(z,1)}{(s-1)}\right)\\&=\lim_{s\to 1} \left(\frac{s(1-s)F_{-n}(z,s) -0}{(s-1)}\right) = -F_{-n}(z,1) \end{align} $$
$$ \begin{align} \notag \Delta_{\operatorname{\mathrm{hyp}}}\left(\frac{\partial}{\partial s}\left. F_{-n}(z,s) \right|_{s=1} \right) &=\lim_{s\to 1} \Delta_{\operatorname{\mathrm{hyp}}} \left(\frac{F_{-n}(z,s) - F_{-n}(z,1)}{(s-1)}\right)\\&=\lim_{s\to 1} \left(\frac{s(1-s)F_{-n}(z,s) -0}{(s-1)}\right) = -F_{-n}(z,1) \end{align} $$
for positive integers n.
3.1.2 Fourier expansion when
 $\Gamma $
is an Atkin–Lehner group
$\Gamma $
is an Atkin–Lehner group
One can explicitly evaluate
![]() $B_0(1;m)$
for
$B_0(1;m)$
for
![]() $m> 0$
when
$m> 0$
when
![]() $\Gamma $
is an Atkin–Lehner group. Set
$\Gamma $
is an Atkin–Lehner group. Set
![]() $\Gamma =\overline {\Gamma _0(N)^+}$
where N is squarefree, which we express as
$\Gamma =\overline {\Gamma _0(N)^+}$
where N is squarefree, which we express as
![]() $N=\prod \limits _{\nu =1}^r p_\nu $
. Let
$N=\prod \limits _{\nu =1}^r p_\nu $
. Let
![]() $B_{0,N}^+(1;m)$
denote the coefficient
$B_{0,N}^+(1;m)$
denote the coefficient
![]() $B_0(1;m)$
for
$B_0(1;m)$
for
![]() $\overline {\Gamma _0(N)^+}$
.
$\overline {\Gamma _0(N)^+}$
.
From Theorem 8 and Proposition 9 of [Reference Jorgenson, Smajlović and Then13], we get that
 $$ \begin{align} B_{0,N}^+(1;m)= \frac{12\sigma(m)}{\pi\sqrt{m}}\prod\limits_{\nu=1}^r \left(1- \frac{p_\nu^{\alpha_{p_\nu}(m)+1}(p_\nu -1) }{\left(p_\nu^{\alpha_{p_\nu}(m)+1} - 1\right)(p_\nu+1)}\right) , \end{align} $$
$$ \begin{align} B_{0,N}^+(1;m)= \frac{12\sigma(m)}{\pi\sqrt{m}}\prod\limits_{\nu=1}^r \left(1- \frac{p_\nu^{\alpha_{p_\nu}(m)+1}(p_\nu -1) }{\left(p_\nu^{\alpha_{p_\nu}(m)+1} - 1\right)(p_\nu+1)}\right) , \end{align} $$
where
![]() $\sigma (m)$
denotes the sum of divisors of a positive integer m and
$\sigma (m)$
denotes the sum of divisors of a positive integer m and
![]() $\alpha _p(m)$
is the largest integer such that
$\alpha _p(m)$
is the largest integer such that
![]() $p^{\alpha _p(m)}$
divides m. These expressions will be used in our explicit examples in §6.
$p^{\alpha _p(m)}$
divides m. These expressions will be used in our explicit examples in §6.
3.2 Automorphic Green’s function
The automorphic Green’s function, or resolvent kernel,
![]() $G_s(z,w)$
for the Laplacian on M is defined on page 31 of [Reference Hejhal9]. In the notation of [Reference Hejhal9], let
$G_s(z,w)$
for the Laplacian on M is defined on page 31 of [Reference Hejhal9]. In the notation of [Reference Hejhal9], let
![]() $\chi $
be the identity character,
$\chi $
be the identity character,
![]() $z,w\in \mathbb {H}$
with
$z,w\in \mathbb {H}$
with
![]() $w\neq \gamma z$
, for
$w\neq \gamma z$
, for
![]() $\gamma \in \Gamma $
, and
$\gamma \in \Gamma $
, and
![]() $s\in \mathbb {C}$
with
$s\in \mathbb {C}$
with
![]() ${\mathrm {Re}}(s)>1$
. Consider the series
${\mathrm {Re}}(s)>1$
. Consider the series
 $$ \begin{align*}G_s(z,w)= \sum_{\gamma\in\Gamma} k_s(\gamma z,w), \end{align*} $$
$$ \begin{align*}G_s(z,w)= \sum_{\gamma\in\Gamma} k_s(\gamma z,w), \end{align*} $$
where
 $$ \begin{align*}k_s(z,w):=-\frac{\Gamma(s)^2}{4\pi \Gamma(2s)}\left[1-\left| \frac{z-w}{z-\overline{w}}\right|{}^2\right]^s F\left(s,s;2s;1-\left| \frac{z-w}{z-\overline{w}}\right|{}^2\right) \end{align*} $$
$$ \begin{align*}k_s(z,w):=-\frac{\Gamma(s)^2}{4\pi \Gamma(2s)}\left[1-\left| \frac{z-w}{z-\overline{w}}\right|{}^2\right]^s F\left(s,s;2s;1-\left| \frac{z-w}{z-\overline{w}}\right|{}^2\right) \end{align*} $$
with
![]() $F(\alpha ,\beta ;\gamma ;u)$
denoting the classical hypergeometric function. We should point out that the normalization we are using, which follows [Reference Hejhal9], differs from the normalization for the Green’s function in Chapter 5 of [Reference Iwaniec11]; the two normalizations differ by a minus sign. With this said, it is proved in [Reference Hejhal9], Proposition 6.5 on page 33 that the series which defines
$F(\alpha ,\beta ;\gamma ;u)$
denoting the classical hypergeometric function. We should point out that the normalization we are using, which follows [Reference Hejhal9], differs from the normalization for the Green’s function in Chapter 5 of [Reference Iwaniec11]; the two normalizations differ by a minus sign. With this said, it is proved in [Reference Hejhal9], Proposition 6.5 on page 33 that the series which defines
![]() $G_{s}(z,w)$
converges uniformly and absolutely on compact subsets of
$G_{s}(z,w)$
converges uniformly and absolutely on compact subsets of
![]() $(z,w,s) \in (\mathcal {F} \times \mathcal {F})'\times \{s\in \mathbb {C} :{\mathrm {Re}}(s)>1\}$
, where
$(z,w,s) \in (\mathcal {F} \times \mathcal {F})'\times \{s\in \mathbb {C} :{\mathrm {Re}}(s)>1\}$
, where
![]() $(\mathcal {F} \times \mathcal {F})'= (\mathcal {F} \times \mathcal {F})\setminus \{(z,w)\in \mathcal {F}: z=w\}$
.
$(\mathcal {F} \times \mathcal {F})'= (\mathcal {F} \times \mathcal {F})\setminus \{(z,w)\in \mathcal {F}: z=w\}$
.
Furthermore, for all
![]() $s\in \mathbb {C}$
with
$s\in \mathbb {C}$
with
![]() ${\mathrm {Re}}(s)>1$
, and all
${\mathrm {Re}}(s)>1$
, and all
![]() $z,w \in \mathbb {H}$
with
$z,w \in \mathbb {H}$
with
![]() $z\neq \gamma w$
for
$z\neq \gamma w$
for
![]() $\gamma \in \Gamma $
, the function
$\gamma \in \Gamma $
, the function
![]() $G_s(z,w)$
is the eigenfunction of
$G_s(z,w)$
is the eigenfunction of
![]() $\Delta _{\operatorname {\mathrm {hyp}}}$
associated with the eigenvalue
$\Delta _{\operatorname {\mathrm {hyp}}}$
associated with the eigenvalue
![]() $s(1-s)$
.
$s(1-s)$
.
Combining formulas 9.134.1 and 8.703 from [Reference Gradshteyn and Ryzhik8] and applying the identity
 $$ \begin{align*}\cosh(d_{\operatorname{\mathrm{hyp}}}(z,w))=\left(2-\left[1-\left| \frac{z-w}{z-\overline{w}}\right|{}^2\right]\right)\left(1-\left| \frac{z-w}{z-\overline{w}}\right|{}^2\right)^{-1}, \end{align*} $$
$$ \begin{align*}\cosh(d_{\operatorname{\mathrm{hyp}}}(z,w))=\left(2-\left[1-\left| \frac{z-w}{z-\overline{w}}\right|{}^2\right]\right)\left(1-\left| \frac{z-w}{z-\overline{w}}\right|{}^2\right)^{-1}, \end{align*} $$
we get that
where
![]() $Q_\nu ^{\mu }$
is the associated Legendre function, as defined by formula 8.703 in [Reference Gradshteyn and Ryzhik8], with
$Q_\nu ^{\mu }$
is the associated Legendre function, as defined by formula 8.703 in [Reference Gradshteyn and Ryzhik8], with
![]() $\nu =s-1$
and
$\nu =s-1$
and
![]() $\mu =0$
.
$\mu =0$
.
Now, we can combine Theorem 4 of [Reference Niebur19] with Theorem 5.3 of [Reference Iwaniec11] to obtain the Fourier expansion of the automorphic Green’s function in terms of the Niebur–Poincaré series. Specifically, let
![]() $w\in \mathcal {F}$
be fixed. Assume
$w\in \mathcal {F}$
be fixed. Assume
![]() $z \in \mathcal {F}$
with
$z \in \mathcal {F}$
with
![]() $y={\mathrm {Im}}(z)> \max \{{\mathrm {Im}}(\gamma w): \gamma \in \Gamma \}$
, and assume
$y={\mathrm {Im}}(z)> \max \{{\mathrm {Im}}(\gamma w): \gamma \in \Gamma \}$
, and assume
![]() $s\in \mathbb {C}$
with
$s\in \mathbb {C}$
with
![]() ${\mathrm {Re}}(s)> 1$
. Then
${\mathrm {Re}}(s)> 1$
. Then
![]() $G_{s}(z,w)$
admits the expansion
$G_{s}(z,w)$
admits the expansion
 $$ \begin{align} G_s(z,w)=-\frac{y^{1-s}}{2s-1}\mathcal{E}_\infty^{\mathrm{par}}(w,s)-\sum_{k\in\mathbb{Z}\smallsetminus \{0\}} y^{1/2}K_{s-1/2}(2\pi |k| y) F_{-k}(w,s)e(kx), \end{align} $$
$$ \begin{align} G_s(z,w)=-\frac{y^{1-s}}{2s-1}\mathcal{E}_\infty^{\mathrm{par}}(w,s)-\sum_{k\in\mathbb{Z}\smallsetminus \{0\}} y^{1/2}K_{s-1/2}(2\pi |k| y) F_{-k}(w,s)e(kx), \end{align} $$
where
![]() $\mathcal {E}_\infty ^{\mathrm {par}}(w,s)$
is the parabolic Eisenstein series associated with the cusp at
$\mathcal {E}_\infty ^{\mathrm {par}}(w,s)$
is the parabolic Eisenstein series associated with the cusp at
![]() $\infty $
of
$\infty $
of
![]() $\Gamma $
(see the next section for its full description).
$\Gamma $
(see the next section for its full description).
The function
![]() $G_s(z,w)$
is unbounded as
$G_s(z,w)$
is unbounded as
![]() $z\to w$
and, according to Proposition 6.5 from [Reference Hejhal9], we have the asymptotic formula
$z\to w$
and, according to Proposition 6.5 from [Reference Hejhal9], we have the asymptotic formula
4 Eisenstein series and their Kronecker limit formulas
The purpose of this section is twofold. First, we state the definitions of parabolic and elliptic Eisenstein series as well as their associated Kronecker limit formulas. Specific examples of the parabolic Kronecker limit formulas are recalled from [Reference Jorgenson, Smajlović and Then13]. Second, we prove the factorization theorem for meromorphic forms in terms of elliptic Kronecker limit functions, as stated in (5).
4.1 Parabolic Kronecker limit functions
Associated with the cusp at
![]() $\infty $
of
$\infty $
of
![]() $\Gamma $
one has a parabolic Eisenstein series
$\Gamma $
one has a parabolic Eisenstein series
![]() ${\cal E}^{\mathrm {par}}_{\infty }(z,s)$
. Let
${\cal E}^{\mathrm {par}}_{\infty }(z,s)$
. Let
![]() $\Gamma _{\infty }$
denote the stabilizer subgroup within
$\Gamma _{\infty }$
denote the stabilizer subgroup within
![]() $\Gamma $
of
$\Gamma $
of
![]() $\infty $
. For
$\infty $
. For
![]() $z\in \mathbb {H}$
and
$z\in \mathbb {H}$
and
![]() $s \in \mathbb {C}$
with
$s \in \mathbb {C}$
with
![]() $\mathrm {Re}(s)> 1$
,
$\mathrm {Re}(s)> 1$
,
![]() ${\cal E}^{\mathrm {par}}_{\infty }(z,s)$
is defined by the series
${\cal E}^{\mathrm {par}}_{\infty }(z,s)$
is defined by the series
 $$ \begin{align*} {\cal E}^{\mathrm{par}}_{\infty}(z,s) = \sum\limits_{\gamma \in \Gamma_{\infty}\backslash \Gamma}\mathrm{Im}(\gamma z)^{s}. \end{align*} $$
$$ \begin{align*} {\cal E}^{\mathrm{par}}_{\infty}(z,s) = \sum\limits_{\gamma \in \Gamma_{\infty}\backslash \Gamma}\mathrm{Im}(\gamma z)^{s}. \end{align*} $$
It is well known that
![]() ${\cal E}^{\mathrm {par}}_{\infty }(z,s)$
admits a meromorphic continuation to all
${\cal E}^{\mathrm {par}}_{\infty }(z,s)$
admits a meromorphic continuation to all
![]() $s\in {\mathbb C}$
and a functional equation in s.
$s\in {\mathbb C}$
and a functional equation in s.
For us, the Kronecker limit formula means the determination of the constant term in the Laurent expansion of
![]() ${\cal E}^{\mathrm {par}}_{\infty }(z,s)$
at
${\cal E}^{\mathrm {par}}_{\infty }(z,s)$
at
![]() $s=1$
. Classically, Kronecker’s limit formula is the assertion that for
$s=1$
. Classically, Kronecker’s limit formula is the assertion that for
![]() $\Gamma = \mathrm {PSL}(2,\mathbb {Z})$
one has that
$\Gamma = \mathrm {PSL}(2,\mathbb {Z})$
one has that
 $$ \begin{align} \mathcal{E}^{\mathrm{par}}_{\infty}(z,s)= \frac{3}{\pi(s-1)} -\frac{1}{2\pi}\log\bigl(|\Delta(z)|{\mathrm{Im}}(z)^{6}\bigr)+C+O(s-1) \,\,\,\mathrm{as} \,\,\, s \rightarrow 1, \end{align} $$
$$ \begin{align} \mathcal{E}^{\mathrm{par}}_{\infty}(z,s)= \frac{3}{\pi(s-1)} -\frac{1}{2\pi}\log\bigl(|\Delta(z)|{\mathrm{Im}}(z)^{6}\bigr)+C+O(s-1) \,\,\,\mathrm{as} \,\,\, s \rightarrow 1, \end{align} $$
where
![]() $C=6(1-12\,\zeta '(-1)-\log (4\pi ))/\pi $
and
$C=6(1-12\,\zeta '(-1)-\log (4\pi ))/\pi $
and
![]() $\Delta (z)$
is Dedekind’s Delta function which is defined by
$\Delta (z)$
is Dedekind’s Delta function which is defined by
 $$ \begin{align} \Delta(z) = \left[q_{z}^{1/24}\prod\limits_{n=1}^{\infty}\left(1 - q_{z}^{n}\right)\right]^{24} = \eta(z)^{24}. \end{align} $$
$$ \begin{align} \Delta(z) = \left[q_{z}^{1/24}\prod\limits_{n=1}^{\infty}\left(1 - q_{z}^{n}\right)\right]^{24} = \eta(z)^{24}. \end{align} $$
We refer to [Reference Siegel22] for a proof of (26), though the above formulation follows the normalization from [Reference Jorgenson, Smajlović and Then13].
For general Fuchsian groups of the first kind, Goldstein [Reference Goldstein7] studied analogs of the Kronecker’s limit formula associated with parabolic Eisenstein series. After a slight renormalization and trivial generalization, Theorem 3-1 from [Reference Goldstein7] asserts that the parabolic Eisenstein series
![]() $\mathcal {E}^{\mathrm {par}}_{\infty }(z,s)$
admits the Laurent expansion
$\mathcal {E}^{\mathrm {par}}_{\infty }(z,s)$
admits the Laurent expansion
 $$ \begin{align} \mathcal{E}^{\mathrm{par}}_{\infty}(z,s)= \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M) (s-1)} + \beta- \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)} \log (\vert\eta_{\infty}^4(z)\vert {\mathrm{Im}}(z)) + O(s-1), \end{align} $$
$$ \begin{align} \mathcal{E}^{\mathrm{par}}_{\infty}(z,s)= \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M) (s-1)} + \beta- \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)} \log (\vert\eta_{\infty}^4(z)\vert {\mathrm{Im}}(z)) + O(s-1), \end{align} $$
as
![]() $s \to 1$
and where
$s \to 1$
and where
![]() $\beta =\beta _{\Gamma }$
is a certain real constant depending only on the group
$\beta =\beta _{\Gamma }$
is a certain real constant depending only on the group
![]() $\Gamma $
. As the notation suggests, the function
$\Gamma $
. As the notation suggests, the function
![]() $\eta _{\infty }(z)$
is a holomorphic form for
$\eta _{\infty }(z)$
is a holomorphic form for
![]() $\Gamma $
and can be viewed as a generalization of the eta function
$\Gamma $
and can be viewed as a generalization of the eta function
![]() $\eta (z)$
which is defined in (27) for the full modular group.
$\eta (z)$
which is defined in (27) for the full modular group.
By employing the functional equation for the parabolic Eisenstein series, as stated in Theorem 6.5 of [Reference Iwaniec11], one can re-write the Kronecker limit formula as stating that
(see [Reference Jorgenson, von Pippich and Smajlović16, Cor. 3]). In this formulation, we will call the function
the parabolic Kronecker limit function of
![]() $\Gamma $
.
$\Gamma $
.
4.2 Atkin–Lehner groups
Let
![]() $N=p_1\ldots p_r$
be a positive square-free number, which includes the possibility that
$N=p_1\ldots p_r$
be a positive square-free number, which includes the possibility that
![]() $N=1$
and set
$N=1$
and set
 $$ \begin{align*}\ell_N = 2^{1-r}\mathrm{lcm}\Big(4,\ 2^{r-1}\frac{24}{\mathrm{gcd}(24,\sigma(N))}\Big), \end{align*} $$
$$ \begin{align*}\ell_N = 2^{1-r}\mathrm{lcm}\Big(4,\ 2^{r-1}\frac{24}{\mathrm{gcd}(24,\sigma(N))}\Big), \end{align*} $$
where
![]() $\mathrm {lcm}$
stands for the least common multiple of its argument and
$\mathrm {lcm}$
stands for the least common multiple of its argument and
![]() $\mathrm {gcd}$
denotes the greatest common divisor of its argument. In [Reference Jorgenson, Smajlović and Then13, Th. 16], it is proved that
$\mathrm {gcd}$
denotes the greatest common divisor of its argument. In [Reference Jorgenson, Smajlović and Then13, Th. 16], it is proved that
 $$ \begin{align} \Delta_N(z):=\left( \prod_{v \mid N} \eta(v z) \right)^{\ell_N} \end{align} $$
$$ \begin{align} \Delta_N(z):=\left( \prod_{v \mid N} \eta(v z) \right)^{\ell_N} \end{align} $$
is a weight
![]() $k_N=2^{r-1} \ell _N$
holomorphic form for
$k_N=2^{r-1} \ell _N$
holomorphic form for
![]() $\Gamma _0(N)^+$
vanishing only at the cusp. By the valence formula, the order of vanishing of
$\Gamma _0(N)^+$
vanishing only at the cusp. By the valence formula, the order of vanishing of
![]() $\Delta _N(z)$
at the cusp is
$\Delta _N(z)$
at the cusp is
![]() $\nu _N:=k_N \operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_N^{+})/(4\pi )$
, where
$\nu _N:=k_N \operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_N^{+})/(4\pi )$
, where
![]() $\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_N^{+})=\pi \sigma (N)/(3\cdot 2^r)$
is the hyperbolic volume of the surface
$\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_N^{+})=\pi \sigma (N)/(3\cdot 2^r)$
is the hyperbolic volume of the surface
![]() $Y_N^{+}$
.
$Y_N^{+}$
.
The Kronecker limit formula (28) for the parabolic Eisenstein series
![]() $\mathcal {E}^{\mathrm {par},N}_{\infty }(z,s)$
associated with
$\mathcal {E}^{\mathrm {par},N}_{\infty }(z,s)$
associated with
![]() $Y_N^{+}$
reads as
$Y_N^{+}$
reads as
 $$ \begin{align} \mathcal{E}^{\mathrm{par},N}_{\infty}(z,s)= \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(Y_N^{+}) (s-1)} + \beta_N - \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(Y_N^{+})}P_N(z) + O((s-1)) \end{align} $$
$$ \begin{align} \mathcal{E}^{\mathrm{par},N}_{\infty}(z,s)= \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(Y_N^{+}) (s-1)} + \beta_N - \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(Y_N^{+})}P_N(z) + O((s-1)) \end{align} $$
as
![]() $s \to 1$
. From Examples 4 and 7 of [Reference Jorgenson, von Pippich and Smajlović16], we have the explicit evaluations of
$s \to 1$
. From Examples 4 and 7 of [Reference Jorgenson, von Pippich and Smajlović16], we have the explicit evaluations of
![]() $\beta _{N}$
and
$\beta _{N}$
and
![]() $P_{N}(z)$
. Namely,
$P_{N}(z)$
. Namely,
 $$ \begin{align} \beta_N=- \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}} (Y_N^{+}) }\left( \sum_{j=1}^{r} \frac{(p_j -1)\log p_j}{2(p_j+1)}- \log N + 2\log (4\pi) + 24\zeta'(-1) - 2\right) \end{align} $$
$$ \begin{align} \beta_N=- \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}} (Y_N^{+}) }\left( \sum_{j=1}^{r} \frac{(p_j -1)\log p_j}{2(p_j+1)}- \log N + 2\log (4\pi) + 24\zeta'(-1) - 2\right) \end{align} $$
and the parabolic Kronecker limit function
![]() $P_N(z)$
is given by
$P_N(z)$
is given by
 $$ \begin{align*}P_N(z)= \log\left( \sqrt[2^r]{\prod_{v \mid N} \vert \eta(vz)\vert ^4} \cdot {\mathrm{Im}}(z) \right). \end{align*} $$
$$ \begin{align*}P_N(z)= \log\left( \sqrt[2^r]{\prod_{v \mid N} \vert \eta(vz)\vert ^4} \cdot {\mathrm{Im}}(z) \right). \end{align*} $$
4.3 Elliptic Kronecker limit functions
Elliptic subgroups of
![]() $\Gamma $
have finite order and a unique fixed point within
$\Gamma $
have finite order and a unique fixed point within
![]() $\mathbb H$
. For all but a finite number of
$\mathbb H$
. For all but a finite number of
![]() $w \in \mathcal {F}$
, the order
$w \in \mathcal {F}$
, the order
![]() $\mathrm {ord}(w)$
of the elliptic subgroup
$\mathrm {ord}(w)$
of the elliptic subgroup
![]() $\Gamma _{w}$
which fixes w is one. For
$\Gamma _{w}$
which fixes w is one. For
![]() $z\in \mathbb {H}$
with
$z\in \mathbb {H}$
with
![]() $z\not =\gamma w$
, for
$z\not =\gamma w$
, for
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $s \in \mathbb {C}$
with
$s \in \mathbb {C}$
with
![]() $\mathrm {Re}(s)> 1$
, the elliptic Eisenstein series
$\mathrm {Re}(s)> 1$
, the elliptic Eisenstein series
![]() ${\cal E}^{\mathrm {ell}}_{w}(z,s)$
is defined by the series
${\cal E}^{\mathrm {ell}}_{w}(z,s)$
is defined by the series
 $$ \begin{align} {\cal E}^{\mathrm{ell}}_{w}(z,s) =\sum\limits_{\gamma \in \Gamma_{w}\backslash \Gamma} \sinh(d_{\mathrm{hyp}}(\gamma z, w))^{-s} = \sum\limits_{\gamma \in \Gamma_{w}\backslash \Gamma} \left( \frac{2\,\mathrm{Im}(w)\mathrm{Im}(\gamma z)}{|\gamma z-w|\,|\gamma z-\overline{w}|} \right)^s. \end{align} $$
$$ \begin{align} {\cal E}^{\mathrm{ell}}_{w}(z,s) =\sum\limits_{\gamma \in \Gamma_{w}\backslash \Gamma} \sinh(d_{\mathrm{hyp}}(\gamma z, w))^{-s} = \sum\limits_{\gamma \in \Gamma_{w}\backslash \Gamma} \left( \frac{2\,\mathrm{Im}(w)\mathrm{Im}(\gamma z)}{|\gamma z-w|\,|\gamma z-\overline{w}|} \right)^s. \end{align} $$
It was first shown in [Reference von Pippich24] that (33) admits a meromorphic continuation to all
![]() $s \in {\mathbb C}$
.
$s \in {\mathbb C}$
.
The analog of the Kronecker limit formula for
![]() ${\cal E}^{\mathrm {ell}}_{w}(z,s)$
was first proved in [Reference von Pippich24] (see also [Reference Jorgenson, von Pippich and Smajlović16, (4)], [Reference von Pippich25, Th. 5.2]). In the setting of this paper, it is shown in [Reference von Pippich24] that for any
${\cal E}^{\mathrm {ell}}_{w}(z,s)$
was first proved in [Reference von Pippich24] (see also [Reference Jorgenson, von Pippich and Smajlović16, (4)], [Reference von Pippich25, Th. 5.2]). In the setting of this paper, it is shown in [Reference von Pippich24] that for any
![]() $w\in \mathcal {F}$
and
$w\in \mathcal {F}$
and
![]() $z\in \mathbb {H}$
with
$z\in \mathbb {H}$
with
![]() $z\not =\gamma w$
, the series (33) admits the Laurent expansion
$z\not =\gamma w$
, the series (33) admits the Laurent expansion
 $$ \begin{align}\nonumber \mathcal{E}^{\mathrm{ell}}_{w}(z,s) &- \frac{2^{s}\sqrt{\pi}\,\Gamma(s-\frac{1}{2})}{\mathrm{ord}(w)\Gamma(s)}\mathcal{E}^{\mathrm{par}}_{\infty}(w,1-s) \,\mathcal{E}^{\mathrm{par}}_{\infty}(z,s) \\ & = -c_w -\log\bigl(|H_{\Gamma}(z,w)|{\mathrm{Im}}(z)^{c_w}\bigr)\cdot s+O(s^2)\quad\mathrm{as}\ s \rightarrow 0, \end{align} $$
$$ \begin{align}\nonumber \mathcal{E}^{\mathrm{ell}}_{w}(z,s) &- \frac{2^{s}\sqrt{\pi}\,\Gamma(s-\frac{1}{2})}{\mathrm{ord}(w)\Gamma(s)}\mathcal{E}^{\mathrm{par}}_{\infty}(w,1-s) \,\mathcal{E}^{\mathrm{par}}_{\infty}(z,s) \\ & = -c_w -\log\bigl(|H_{\Gamma}(z,w)|{\mathrm{Im}}(z)^{c_w}\bigr)\cdot s+O(s^2)\quad\mathrm{as}\ s \rightarrow 0, \end{align} $$
where
 $$ \begin{align*}c_w= \frac{2\pi}{\mathrm{ord}(w)\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}. \end{align*} $$
$$ \begin{align*}c_w= \frac{2\pi}{\mathrm{ord}(w)\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}. \end{align*} $$
In the notation of [Reference von Pippich25], we are writing that
![]() $|H_{\Gamma }(z,w)|=|H_w(z)| {\mathrm {Im}}(w)^{c_w}$
.
$|H_{\Gamma }(z,w)|=|H_w(z)| {\mathrm {Im}}(w)^{c_w}$
.
Moreover, von Pippich proved that when viewed as a function of z,
![]() $H(z,w):=H_{\Gamma }(z,w)$
is holomorphic on
$H(z,w):=H_{\Gamma }(z,w)$
is holomorphic on
![]() $\mathbb {H}$
and uniquely determined up to multiplication by a complex constant of absolute value one. Additionally,
$\mathbb {H}$
and uniquely determined up to multiplication by a complex constant of absolute value one. Additionally,
![]() $H(z,w)$
is an automorphic form with a nontrivial multiplier system with respect to
$H(z,w)$
is an automorphic form with a nontrivial multiplier system with respect to
![]() $\Gamma $
acting on z and which depends on w.
$\Gamma $
acting on z and which depends on w.
In order to deduce behavior of
![]() $H(z,w)$
as
$H(z,w)$
as
![]() $z\to \gamma w$
for
$z\to \gamma w$
for
![]() $\gamma \in \Gamma $
, we apply Proposition 5.1 of [Reference von Pippich25]. In doing so, one gets that
$\gamma \in \Gamma $
, we apply Proposition 5.1 of [Reference von Pippich25]. In doing so, one gets that
 $$ \begin{align*}\mathcal{E}^{\mathrm{ell}}_{w}(z,s)- \frac{2^{s}\sqrt{\pi}\,\Gamma(s-\frac{1}{2})}{\mathrm{ord}(w)\Gamma(s)}\mathcal{E}^{\mathrm{par}}_{\infty}(w,1-s) \,\mathcal{E}^{\mathrm{par}}_{\infty}(z,s)= -c_w+ \mathcal{K}_w(z)\cdot s +O(s^2) \,\,\, \mathrm{as} s \rightarrow 0, \end{align*} $$
$$ \begin{align*}\mathcal{E}^{\mathrm{ell}}_{w}(z,s)- \frac{2^{s}\sqrt{\pi}\,\Gamma(s-\frac{1}{2})}{\mathrm{ord}(w)\Gamma(s)}\mathcal{E}^{\mathrm{par}}_{\infty}(w,1-s) \,\mathcal{E}^{\mathrm{par}}_{\infty}(z,s)= -c_w+ \mathcal{K}_w(z)\cdot s +O(s^2) \,\,\, \mathrm{as} s \rightarrow 0, \end{align*} $$
and with
![]() $\mathcal {K}_w(z)=-\log |z-\gamma w| + O(1)$
as
$\mathcal {K}_w(z)=-\log |z-\gamma w| + O(1)$
as
![]() $z\to \gamma w$
for some
$z\to \gamma w$
for some
![]() $\gamma \in \Gamma $
. Combining this statement with (34), we immediately deduce that
$\gamma \in \Gamma $
. Combining this statement with (34), we immediately deduce that
![]() $H(z,w)$
, viewed as a function of variable
$H(z,w)$
, viewed as a function of variable
![]() $z\in \mathbb {H}$
, vanishes if and only if
$z\in \mathbb {H}$
, vanishes if and only if
![]() $z= \gamma w$
for some
$z= \gamma w$
for some
![]() $\gamma \in \Gamma $
. Furthermore, the order of vanishing of
$\gamma \in \Gamma $
. Furthermore, the order of vanishing of
![]() $H(z,w)$
equals one.
$H(z,w)$
equals one.
4.4 A factorization theorem
In this section, we prove that equation (5) holds for meromorphic forms on
![]() $\Gamma $
of even weight
$\Gamma $
of even weight
![]() $2k$
, suitably normalized at the cusp at
$2k$
, suitably normalized at the cusp at
![]() $\infty $
. For meromorphic forms, we let
$\infty $
. For meromorphic forms, we let
![]() $\mathrm {ord}_w(f)$
denote the order of f at w which is positive if w is a zero of f and negative if w is a pole of f. Let us start by proving that the factorization theorem holds for meromorphic forms.
$\mathrm {ord}_w(f)$
denote the order of f at w which is positive if w is a zero of f and negative if w is a pole of f. Let us start by proving that the factorization theorem holds for meromorphic forms.
Proposition 2. With notation as above, let f be an even weight
![]() $2k\geq 0$
meromorphic form on
$2k\geq 0$
meromorphic form on
![]() $\mathbb {H}$
with q-expansion at
$\mathbb {H}$
with q-expansion at
![]() $\infty $
given by
$\infty $
given by
 $$ \begin{align} f(z)= 1+ \sum_{n=1}^{\infty} b_{f}(n)q_z^n. \end{align} $$
$$ \begin{align} f(z)= 1+ \sum_{n=1}^{\infty} b_{f}(n)q_z^n. \end{align} $$
Let
![]() $\mathrm {ord}_w(f)$
denote the order f at w and define the function
$\mathrm {ord}_w(f)$
denote the order f at w and define the function
 $$ \begin{align*}H_{f}(z):= \prod_{w \in \mathcal{F}} H(z,w)^{\mathrm{ord}_w(f)}, \end{align*} $$
$$ \begin{align*}H_{f}(z):= \prod_{w \in \mathcal{F}} H(z,w)^{\mathrm{ord}_w(f)}, \end{align*} $$
where
![]() $H(z,w)=H_{\Gamma }(z,w)$
is given in (34). Then there exists a complex constant
$H(z,w)=H_{\Gamma }(z,w)$
is given in (34). Then there exists a complex constant
![]() $c_{f}$
such that
$c_{f}$
such that
Furthermore,
 $$ \begin{align*}\left\vert c_{f}\right\vert = \exp \left(-\frac{2\pi}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)} \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \left( 2-\log 2 + P(w)- \beta\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)\right) \right ), \end{align*} $$
$$ \begin{align*}\left\vert c_{f}\right\vert = \exp \left(-\frac{2\pi}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)} \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \left( 2-\log 2 + P(w)- \beta\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)\right) \right ), \end{align*} $$
where
![]() $P(w)$
and
$P(w)$
and
![]() $\beta $
are defined through the parabolic Kronecker limit function (28).
$\beta $
are defined through the parabolic Kronecker limit function (28).
Proof. The proof closely follows the proof of Theorem 9 from [Reference Jorgenson, von Pippich and Smajlović16]. Specifically, following the first part of the proof almost verbatim, we conclude that the quotient
 $$ \begin{align*}F_f(z):=\frac{H_f(z)}{f(z)} \end{align*} $$
$$ \begin{align*}F_f(z):=\frac{H_f(z)}{f(z)} \end{align*} $$
is a nonvanishing holomorphic function on M which is bounded and nonzero at the cusp at
![]() $\infty $
. The argument for this assertion is as follows. When viewed as a (multi-valued) function of
$\infty $
. The argument for this assertion is as follows. When viewed as a (multi-valued) function of
![]() $z\in M$
,
$z\in M$
,
![]() $H(z,w)$
vanishes if and only if
$H(z,w)$
vanishes if and only if
![]() $z=w$
, and the order of vanishing is one. Therefore, we conclude that
$z=w$
, and the order of vanishing is one. Therefore, we conclude that
![]() $F_f(z)$
is a quotient of two multi-valued meromorphic functions on M with the same divisors. By applying the Riemann–Roch theorem as in the proof of Theorem 9 from [Reference Jorgenson, von Pippich and Smajlović16], we conclude that yields that
$F_f(z)$
is a quotient of two multi-valued meromorphic functions on M with the same divisors. By applying the Riemann–Roch theorem as in the proof of Theorem 9 from [Reference Jorgenson, von Pippich and Smajlović16], we conclude that yields that
![]() $H_f(z)$
is a weight
$H_f(z)$
is a weight
![]() $2k$
meromorphic form on M, possibly twisted by a unitary character. Therefore,
$2k$
meromorphic form on M, possibly twisted by a unitary character. Therefore,
![]() $F_f(z)$
is holomorphic on M.
$F_f(z)$
is holomorphic on M.
From [Reference Jorgenson, von Pippich and Smajlović16, Prop. 6], we have the asymptotic expansion in the cusp of
![]() $H(z,w)$
, namely that
$H(z,w)$
, namely that
where
![]() $a_{w,\infty }$
is a constant of modulus one and
$a_{w,\infty }$
is a constant of modulus one and
 $$ \begin{align*}B_{w,\infty}= - \frac{2\pi}{\mathrm{ord}(w)\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}\left( 2-\log 2 + P(w)- \beta\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)\right). \end{align*} $$
$$ \begin{align*}B_{w,\infty}= - \frac{2\pi}{\mathrm{ord}(w)\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}\left( 2-\log 2 + P(w)- \beta\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)\right). \end{align*} $$
When combining (37) with the q-expansion of f, as stated in (35), we obtain that
![]() $F_f(z)$
is bounded and nonzero at the cusp
$F_f(z)$
is bounded and nonzero at the cusp
![]() $\infty $
.
$\infty $
.
Since
![]() $F_{f}$
is holomorphic, nonvanishing and nonzero in the cusp, then the function
$F_{f}$
is holomorphic, nonvanishing and nonzero in the cusp, then the function
![]() $\log \vert F_{f}(z)\vert $
is
$\log \vert F_{f}(z)\vert $
is
![]() $L^{2}$
and bounded on M. From its spectral expansion and the fact that
$L^{2}$
and bounded on M. From its spectral expansion and the fact that
![]() $\log \vert F_{f}(z)\vert $
is harmonic, one concludes
$\log \vert F_{f}(z)\vert $
is harmonic, one concludes
![]() $\log \vert F_{f}(z)\vert $
is constant, hence so is
$\log \vert F_{f}(z)\vert $
is constant, hence so is
![]() $F_{f}(z)$
. The evaluation of the constant is obtained by considering the limiting behavior (37) as z approaches
$F_{f}(z)$
. The evaluation of the constant is obtained by considering the limiting behavior (37) as z approaches
![]() $\infty $
.
$\infty $
.
In summary, by following the proof of Proposition 12 from [Reference Jorgenson, von Pippich and Smajlović16] verbatim, we obtain (4), and hence (5), for meromorphic forms f on
![]() $\mathbb {H}$
with q-expansion (35).
$\mathbb {H}$
with q-expansion (35).
5 Proofs of main results
5.1 Proof of Theorem 1
Let
![]() $Y>1$
be sufficiently large so that the cuspidal neighborhood
$Y>1$
be sufficiently large so that the cuspidal neighborhood
![]() $\mathcal {F}_{\infty }(Y)$
of the cusp
$\mathcal {F}_{\infty }(Y)$
of the cusp
![]() $\infty $
in
$\infty $
in
![]() $\mathcal {F}$
is of the form
$\mathcal {F}$
is of the form
![]() $\{z \in {\mathbb H} : 0 < x \leq 1, y> Y\}$
. For
$\{z \in {\mathbb H} : 0 < x \leq 1, y> Y\}$
. For
![]() $s\in \mathbb {C}$
with
$s\in \mathbb {C}$
with
![]() ${\mathrm {Re}}(s)>1$
, and arbitrary, but fixed
${\mathrm {Re}}(s)>1$
, and arbitrary, but fixed
![]() $w\in \mathcal {F}$
, we then have that
$w\in \mathcal {F}$
, we then have that
 $$ \begin{align*} \int\limits_{\mathcal{F}(Y)}\Delta_{\operatorname{\mathrm{hyp}}}(F_{-n}(z,1))&\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \\ & -\int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\Delta_{\operatorname{\mathrm{hyp}}} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \\ &= -s(1-s)\int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z). \end{align*} $$
$$ \begin{align*} \int\limits_{\mathcal{F}(Y)}\Delta_{\operatorname{\mathrm{hyp}}}(F_{-n}(z,1))&\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \\ & -\int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\Delta_{\operatorname{\mathrm{hyp}}} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \\ &= -s(1-s)\int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z). \end{align*} $$
Actually, the first summand on the left-hand side is zero since
![]() $F_{-n}(z,1)$
is holomorphic; however, this judicious form of the number zero is significant since we will use the method behind the Maass–Selberg theorem to study the left-hand side of the above equation. Before this, note that the integrand on the right-hand side of the above equation is holomorphic at
$F_{-n}(z,1)$
is holomorphic; however, this judicious form of the number zero is significant since we will use the method behind the Maass–Selberg theorem to study the left-hand side of the above equation. Before this, note that the integrand on the right-hand side of the above equation is holomorphic at
![]() $s=1$
. As a result, we can write
$s=1$
. As a result, we can write
 $$ \begin{align*} \frac{\partial}{\partial s}&\left.\left(-s(1-s)\int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z)\right)\right|_{s=1}\\&= \int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\lim_{s\to 1}\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z). \end{align*} $$
$$ \begin{align*} \frac{\partial}{\partial s}&\left.\left(-s(1-s)\int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z)\right)\right|_{s=1}\\&= \int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\lim_{s\to 1}\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z). \end{align*} $$
When reversing the order of the above steps, we get that
 $$ \begin{align} \langle F_{-n}(z,1), &\overline{\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)} \rangle \notag \\&=\lim_{Y\to \infty} \int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(z,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \notag \\&= \lim_{Y\to \infty} \left[\frac{\partial}{\partial s}\left( \int\limits_{\mathcal{F}(Y)}\Delta_{\operatorname{\mathrm{hyp}}}(F_{-n}(z,1))\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \right. \right.\notag \\&- \left.\left. \left. \int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\Delta_{\operatorname{\mathrm{hyp}}} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \right) \right|_{s=1}\right]. \end{align} $$
$$ \begin{align} \langle F_{-n}(z,1), &\overline{\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)} \rangle \notag \\&=\lim_{Y\to \infty} \int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(z,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \notag \\&= \lim_{Y\to \infty} \left[\frac{\partial}{\partial s}\left( \int\limits_{\mathcal{F}(Y)}\Delta_{\operatorname{\mathrm{hyp}}}(F_{-n}(z,1))\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \right. \right.\notag \\&- \left.\left. \left. \int\limits_{\mathcal{F}(Y)}F_{-n}(z,1)\Delta_{\operatorname{\mathrm{hyp}}} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)d\mu_{\operatorname{\mathrm{hyp}}}(z) \right) \right|_{s=1}\right]. \end{align} $$
The quantity on the right-hand side of (38) is setup for an application of Green’s theorem as in the proof of the Maass–Selberg relations for the Eisenstein series. As described on page 89 of [Reference Iwaniec11], when applying Green’s theorem to each term on the right-side of (38) for fixed Y, the resulting boundary terms on the sides of the fundamental domain, which are identified by
![]() $\Gamma $
, will sum to zero. Therefore, we get that
$\Gamma $
, will sum to zero. Therefore, we get that
 $$ \begin{align} \langle F_{-n}(z,1),& \overline{\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)} \rangle \notag \\&= \lim_{Y\to \infty} \left[\frac{\partial}{\partial s}\left( \int\limits_{0}^{1}\frac{\partial}{\partial y}F_{-n}(z,1)\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)dx \right. \right. \notag\\ &- \left.\left. \left. \int\limits_{0}^{1}F_{-n}(z,1)\frac{\partial}{\partial y} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)dx \right) \right|_{s=1}\right], \end{align} $$
$$ \begin{align} \langle F_{-n}(z,1),& \overline{\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)} \rangle \notag \\&= \lim_{Y\to \infty} \left[\frac{\partial}{\partial s}\left( \int\limits_{0}^{1}\frac{\partial}{\partial y}F_{-n}(z,1)\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)dx \right. \right. \notag\\ &- \left.\left. \left. \int\limits_{0}^{1}F_{-n}(z,1)\frac{\partial}{\partial y} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)dx \right) \right|_{s=1}\right], \end{align} $$
where the functions of z and their derivatives with respect to
![]() $y={\mathrm {Im}}(z)$
are evaluated at
$y={\mathrm {Im}}(z)$
are evaluated at
![]() $z=x+iY$
.
$z=x+iY$
.
In order to compute the difference of the two integrals of the right-hand side of (39), we will use the Fourier expansions (17) and (25) of the series
![]() $F_{-n}(z,1)$
and
$F_{-n}(z,1)$
and
![]() $G_s(z,w)$
, respectively. It will be more convenient to write the first coefficient in the expansion (17) as
$G_s(z,w)$
, respectively. It will be more convenient to write the first coefficient in the expansion (17) as
![]() $e(-nx)\sqrt {y}I_{\tfrac {1}{2}}(2\pi n y)$
, as in (16). As is well known, the various exponential functions
$e(-nx)\sqrt {y}I_{\tfrac {1}{2}}(2\pi n y)$
, as in (16). As is well known, the various exponential functions
![]() $e(-nx)$
when integrated with respect to x are orthogonal to each other for different values of n. Using this observation, we can write the difference of two integrals on the right-hand side of (39) when evaluated at
$e(-nx)$
when integrated with respect to x are orthogonal to each other for different values of n. Using this observation, we can write the difference of two integrals on the right-hand side of (39) when evaluated at
![]() $z=x+iY$
as
$z=x+iY$
as
 $$ \begin{align*} &\quad -F_{-n}(w,s)\sqrt{Y} \bigg(\frac{\partial}{\partial y}\left(\sqrt{y}I_{\tfrac{1}{2}}(2\pi n y)\right)\bigg|_{y=Y}\cdot K_{s-\tfrac{1}{2}}(2\pi n Y) \\&\quad - I_{\tfrac{1}{2}}(2\pi n Y)\cdot \frac{\partial}{\partial y}\left(\sqrt{y}K_{s- \tfrac{1}{2}}(2\pi n y) \right)\bigg|_{y=Y}\bigg)\\&\quad + B_0(1;-n)(1-s)\frac{Y^{-s}}{2s-1}\mathcal{E}_\infty^{\mathrm{par}}(w,s) \\&\quad + \sum_{k\in\mathbb{Z}\smallsetminus\{0\}}F_k(w,s) \bigg( b_k(Y,1;-n)\cdot \frac{\partial}{\partial y}\left(\sqrt{y}K_{s- \tfrac{1}{2}}(2\pi |k| y) \right)\bigg|_{y=Y} \\&\quad -\frac{\partial}{\partial y}b_k(y,1;-n)\bigg|_{y=Y}\cdot \sqrt{Y} K_{s-\tfrac{1}{2}}(2\pi |k| Y) \bigg)\\& =T_1(Y,s;w) + T_2(Y,s;w)+T_3(Y,s;w), \end{align*} $$
$$ \begin{align*} &\quad -F_{-n}(w,s)\sqrt{Y} \bigg(\frac{\partial}{\partial y}\left(\sqrt{y}I_{\tfrac{1}{2}}(2\pi n y)\right)\bigg|_{y=Y}\cdot K_{s-\tfrac{1}{2}}(2\pi n Y) \\&\quad - I_{\tfrac{1}{2}}(2\pi n Y)\cdot \frac{\partial}{\partial y}\left(\sqrt{y}K_{s- \tfrac{1}{2}}(2\pi n y) \right)\bigg|_{y=Y}\bigg)\\&\quad + B_0(1;-n)(1-s)\frac{Y^{-s}}{2s-1}\mathcal{E}_\infty^{\mathrm{par}}(w,s) \\&\quad + \sum_{k\in\mathbb{Z}\smallsetminus\{0\}}F_k(w,s) \bigg( b_k(Y,1;-n)\cdot \frac{\partial}{\partial y}\left(\sqrt{y}K_{s- \tfrac{1}{2}}(2\pi |k| y) \right)\bigg|_{y=Y} \\&\quad -\frac{\partial}{\partial y}b_k(y,1;-n)\bigg|_{y=Y}\cdot \sqrt{Y} K_{s-\tfrac{1}{2}}(2\pi |k| Y) \bigg)\\& =T_1(Y,s;w) + T_2(Y,s;w)+T_3(Y,s;w), \end{align*} $$
where the last equality above provides the definitions of the functions
![]() $T_{1}$
,
$T_{1}$
,
![]() $T_{2}$
, and
$T_{2}$
, and
![]() $T_{3}$
. Therefore, from (39), we have that
$T_{3}$
. Therefore, from (39), we have that
 $$ \begin{align} &\langle F_{-n}(z,1), \overline{\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)} \rangle \nonumber\\ & \quad = \lim_{Y\to \infty} \left[\left.\frac{\partial}{\partial s}\left( T_1(Y,s;w) + T_2(Y,s;w)+T_3(Y,s;w) \right)\right|_{s=1}\right]. \end{align} $$
$$ \begin{align} &\langle F_{-n}(z,1), \overline{\lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)} \rangle \nonumber\\ & \quad = \lim_{Y\to \infty} \left[\left.\frac{\partial}{\partial s}\left( T_1(Y,s;w) + T_2(Y,s;w)+T_3(Y,s;w) \right)\right|_{s=1}\right]. \end{align} $$
We will study each of the three terms on the right-hand side of (40) separately.
To evaluate the term
![]() $T_{1}$
in (40), we apply formulas (A.19) and (A.20) in order to compute the derivatives of the Bessel functions in hand. In doing so, we conclude that
$T_{1}$
in (40), we apply formulas (A.19) and (A.20) in order to compute the derivatives of the Bessel functions in hand. In doing so, we conclude that
 $$ \begin{align*} T_1(Y,s;w) &=-\frac{X}{2}F_{-n}(w,s)\bigg[K_{s-\tfrac{1}{2}}(X)(I_{-\tfrac{1}{2}}(X) \\& \qquad\qquad\qquad\qquad + I_{\tfrac{3}{2}}(X)) + I_{\tfrac{1}{2}}(X)(K_{s-\tfrac{3}{2}}(X) + K_{s+\tfrac{1}{2}}(X)) \bigg], \end{align*} $$
$$ \begin{align*} T_1(Y,s;w) &=-\frac{X}{2}F_{-n}(w,s)\bigg[K_{s-\tfrac{1}{2}}(X)(I_{-\tfrac{1}{2}}(X) \\& \qquad\qquad\qquad\qquad + I_{\tfrac{3}{2}}(X)) + I_{\tfrac{1}{2}}(X)(K_{s-\tfrac{3}{2}}(X) + K_{s+\tfrac{1}{2}}(X)) \bigg], \end{align*} $$
where we set
![]() $X=2\pi n Y$
. Next, we can express
$X=2\pi n Y$
. Next, we can express
![]() $K_{s+\tfrac {1}{2}} (X)$
in terms of
$K_{s+\tfrac {1}{2}} (X)$
in terms of
![]() $K_{s-\tfrac {1}{2}} (X)$
and
$K_{s-\tfrac {1}{2}} (X)$
and
![]() $K_{s-\tfrac {3}{2}}(X)$
by using formula (A.6) with
$K_{s-\tfrac {3}{2}}(X)$
by using formula (A.6) with
![]() $\nu =s-1/2$
, which gives that
$\nu =s-1/2$
, which gives that
 $$ \begin{align} K_{s+\tfrac{1}{2}} (X)= K_{s-\tfrac{3}{2}} (X) + \frac{2s-1}{X}K_{s-\tfrac{1}{2}} (X). \end{align} $$
$$ \begin{align} K_{s+\tfrac{1}{2}} (X)= K_{s-\tfrac{3}{2}} (X) + \frac{2s-1}{X}K_{s-\tfrac{1}{2}} (X). \end{align} $$
Therefore,
 $$ \begin{align*} T_1(Y,s;w) &=-\frac{X}{2}F_{-n}(w,s)\bigg[K_{s-\tfrac{1}{2}}(X)\bigg(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X) + \frac{2s-1}{X}I_{\tfrac{1}{2}}(X)\bigg) \\& \qquad\qquad\qquad\qquad + 2 I_{\tfrac{1}{2}}(X)K_{s-\tfrac{3}{2}}(X) \bigg]. \end{align*} $$
$$ \begin{align*} T_1(Y,s;w) &=-\frac{X}{2}F_{-n}(w,s)\bigg[K_{s-\tfrac{1}{2}}(X)\bigg(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X) + \frac{2s-1}{X}I_{\tfrac{1}{2}}(X)\bigg) \\& \qquad\qquad\qquad\qquad + 2 I_{\tfrac{1}{2}}(X)K_{s-\tfrac{3}{2}}(X) \bigg]. \end{align*} $$
Now, let us use formula (A.14) in order to differentiate
![]() $K_{s-\tfrac {1}{2}}(X)$
and
$K_{s-\tfrac {1}{2}}(X)$
and
![]() $K_{s-\tfrac {3}{2}}(X)$
with respect to s at
$K_{s-\tfrac {3}{2}}(X)$
with respect to s at
![]() $s=1$
. When combined with the expression (A.5), for
$s=1$
. When combined with the expression (A.5), for
![]() $I_{\tfrac {1}{2}}(X)$
, we deduce that
$I_{\tfrac {1}{2}}(X)$
, we deduce that
 $$ \begin{align*} &\frac{\partial}{\partial s}\left.\left[K_{s-\tfrac{1}{2}}(X)\left(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X) + \frac{2s-1}{X}I_{\tfrac{1}{2}}(X)\right) +2 I_{\tfrac{1}{2}}(X)K_{s-\tfrac{3}{2}}(X) \right]\right|_{s=1}\\& \quad = \sqrt{\frac{\pi}{2X}}e^X\mathrm{Ei}(-2X)\left[ -(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X)) + \sqrt{\frac{2}{\pi X}} (2-1/X) \sinh (X) \right]\\& \qquad +\frac{2}{X^2}e^{-X}\sinh (X), \end{align*} $$
$$ \begin{align*} &\frac{\partial}{\partial s}\left.\left[K_{s-\tfrac{1}{2}}(X)\left(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X) + \frac{2s-1}{X}I_{\tfrac{1}{2}}(X)\right) +2 I_{\tfrac{1}{2}}(X)K_{s-\tfrac{3}{2}}(X) \right]\right|_{s=1}\\& \quad = \sqrt{\frac{\pi}{2X}}e^X\mathrm{Ei}(-2X)\left[ -(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X)) + \sqrt{\frac{2}{\pi X}} (2-1/X) \sinh (X) \right]\\& \qquad +\frac{2}{X^2}e^{-X}\sinh (X), \end{align*} $$
where
![]() $\mathrm {Ei}(x)$
denotes the exponential integral (see (A.7)).
$\mathrm {Ei}(x)$
denotes the exponential integral (see (A.7)).
Continuing, we now employ the bound (A.11) with
![]() $\nu =-1/2$
and when
$\nu =-1/2$
and when
![]() $\nu =3/2$
. This result, together with the bound (A.8) for the exponential integral yields that
$\nu =3/2$
. This result, together with the bound (A.8) for the exponential integral yields that
 $$ \begin{align*}\lim_{X\to\infty}\frac{X}{2}\frac{\partial}{\partial s}\left.\left[K_{s-\tfrac{1}{2}}(X)\left(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X) + \frac{2s-1}{X}I_{\tfrac{1}{2}}(X)\right) +2 I_{\tfrac{1}{2}}(X)K_{s-\tfrac{3}{2}}(X) \right]\right|_{s=1} =0. \end{align*} $$
$$ \begin{align*}\lim_{X\to\infty}\frac{X}{2}\frac{\partial}{\partial s}\left.\left[K_{s-\tfrac{1}{2}}(X)\left(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X) + \frac{2s-1}{X}I_{\tfrac{1}{2}}(X)\right) +2 I_{\tfrac{1}{2}}(X)K_{s-\tfrac{3}{2}}(X) \right]\right|_{s=1} =0. \end{align*} $$
Therefore,
 $$ \begin{align*} &\lim_{Y\to \infty}\frac{\partial}{\partial s}\left. T_1(Y,s;w)\right|_{s=1}= - \frac{\partial}{\partial s}\left. F_{-n}(w,s)\right|_{s=1}\cdot \\& \quad \cdot\lim_{X\to \infty}\frac{X}{2}\left[K_{\tfrac{1}{2}}(X)(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X)) + I_{\tfrac{1}{2}}(X)(K_{-\tfrac{1}{2}}(X) + K_{\tfrac{3}{2}}(X)) \right]. \end{align*} $$
$$ \begin{align*} &\lim_{Y\to \infty}\frac{\partial}{\partial s}\left. T_1(Y,s;w)\right|_{s=1}= - \frac{\partial}{\partial s}\left. F_{-n}(w,s)\right|_{s=1}\cdot \\& \quad \cdot\lim_{X\to \infty}\frac{X}{2}\left[K_{\tfrac{1}{2}}(X)(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X)) + I_{\tfrac{1}{2}}(X)(K_{-\tfrac{1}{2}}(X) + K_{\tfrac{3}{2}}(X)) \right]. \end{align*} $$
Finally, by applying (A.11) and (A.12) with
![]() $\nu =\pm 1/2$
and
$\nu =\pm 1/2$
and
![]() $\nu =3/2$
, we deduce that
$\nu =3/2$
, we deduce that
 $$ \begin{align*}\lim_{X\to \infty}\frac{X}{2}\left[K_{\tfrac{1}{2}}(X)(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X)) + I_{\tfrac{1}{2}}(X)(K_{-\tfrac{1}{2}}(X) + K_{\tfrac{3}{2}}(X)) \right]=1. \end{align*} $$
$$ \begin{align*}\lim_{X\to \infty}\frac{X}{2}\left[K_{\tfrac{1}{2}}(X)(I_{-\tfrac{1}{2}}(X) + I_{\tfrac{3}{2}}(X)) + I_{\tfrac{1}{2}}(X)(K_{-\tfrac{1}{2}}(X) + K_{\tfrac{3}{2}}(X)) \right]=1. \end{align*} $$
Therefore, we have proved that
As for the term
![]() $T_{2}$
in (40), let us use the Laurent series expansion (28) of
$T_{2}$
in (40), let us use the Laurent series expansion (28) of
![]() $\mathcal {E}_\infty ^{\mathrm {par}}(w,s)$
, from which one easily deduces that
$\mathcal {E}_\infty ^{\mathrm {par}}(w,s)$
, from which one easily deduces that
 $$ \begin{align*}\frac{\partial}{\partial s}\left.(s-1)\frac{Y^{-s}}{2s-1}\mathcal{E}_\infty^{\mathrm{par}}(w,s)\right|_{s=1} = \frac{1}{Y}\left( \beta - \frac{P(w)+2+\log Y}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}\right). \end{align*} $$
$$ \begin{align*}\frac{\partial}{\partial s}\left.(s-1)\frac{Y^{-s}}{2s-1}\mathcal{E}_\infty^{\mathrm{par}}(w,s)\right|_{s=1} = \frac{1}{Y}\left( \beta - \frac{P(w)+2+\log Y}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}\right). \end{align*} $$
Therefore,
It remains to study the term
![]() $T_{3}$
in (40). Let us set
$T_{3}$
in (40). Let us set
![]() $g(s,y,\ell ):=\sqrt {y}K_{s-\tfrac {1}{2}}(2\pi \ell y)$
for some positive integer
$g(s,y,\ell ):=\sqrt {y}K_{s-\tfrac {1}{2}}(2\pi \ell y)$
for some positive integer
![]() $\ell $
. Then
$\ell $
. Then
![]() $b_k(y,1;-n)=B_k(1;-n)g(1,y,|n|)$
and
$b_k(y,1;-n)=B_k(1;-n)g(1,y,|n|)$
and
 $$ \begin{align} T_3(Y,s;w)&=\sum_{k\in\mathbb{Z}\smallsetminus\{0\}} B_k(1;-n) F_k(w,s) \left( g(1,Y,|n|) \frac{\partial}{\partial y}\left.g(s,y,|k|)\right|_{y=Y} \right. \nonumber\\& \qquad\qquad\qquad\qquad\qquad\qquad\qquad - \left. g(s,Y,|k|)\frac{\partial}{\partial y}\left.g(1,y,|n|)\right|_{y=Y} \right). \end{align} $$
$$ \begin{align} T_3(Y,s;w)&=\sum_{k\in\mathbb{Z}\smallsetminus\{0\}} B_k(1;-n) F_k(w,s) \left( g(1,Y,|n|) \frac{\partial}{\partial y}\left.g(s,y,|k|)\right|_{y=Y} \right. \nonumber\\& \qquad\qquad\qquad\qquad\qquad\qquad\qquad - \left. g(s,Y,|k|)\frac{\partial}{\partial y}\left.g(1,y,|n|)\right|_{y=Y} \right). \end{align} $$
For positive integers m and
![]() $\ell $
, let us define, for notational convenience,
$\ell $
, let us define, for notational convenience,
 $$ \begin{align*}G(s,Y,m,\ell):=g(1,Y,m) \frac{\partial}{\partial y}\left.g(s,y,\ell)\right|_{y=Y}- g(s,Y,\ell)\frac{\partial}{\partial y}\left.g(1,y,m)\right|_{y=Y}; \end{align*} $$
$$ \begin{align*}G(s,Y,m,\ell):=g(1,Y,m) \frac{\partial}{\partial y}\left.g(s,y,\ell)\right|_{y=Y}- g(s,Y,\ell)\frac{\partial}{\partial y}\left.g(1,y,m)\right|_{y=Y}; \end{align*} $$
observe that, according to (A.5),
 $$ \begin{align*}g(1,y,m)=\frac{1}{2\sqrt{m}} e^{-2\pi my}. \end{align*} $$
$$ \begin{align*}g(1,y,m)=\frac{1}{2\sqrt{m}} e^{-2\pi my}. \end{align*} $$
In order to compute the derivative of the K-Bessel function with respect to the argument, we will use formula (A.20). When combining with equation (41), for
![]() $K_{s+\tfrac {1}{2}}(2\pi \ell Y)$
, we get that
$K_{s+\tfrac {1}{2}}(2\pi \ell Y)$
, we get that
 $$ \begin{align} G(s,Y,m,\ell) =\frac{e^{-2\pi m Y}}{2\sqrt{mY}}\left(( (1-s)+2\pi mY) K_{s-\tfrac{1}{2}}(2\pi \ell Y)-2\pi \ell Y K_{s-\tfrac{3}{2}}(2\pi\ell Y)\right). \end{align} $$
$$ \begin{align} G(s,Y,m,\ell) =\frac{e^{-2\pi m Y}}{2\sqrt{mY}}\left(( (1-s)+2\pi mY) K_{s-\tfrac{1}{2}}(2\pi \ell Y)-2\pi \ell Y K_{s-\tfrac{3}{2}}(2\pi\ell Y)\right). \end{align} $$
When
![]() $s=1$
, the bound (A.12) for the K-Bessel function immediately yields that
$s=1$
, the bound (A.12) for the K-Bessel function immediately yields that
and for any two positive integers
![]() $m,\ell $
. Also, the implied constant is independent of
$m,\ell $
. Also, the implied constant is independent of
![]() $m, \ell , Y$
.
$m, \ell , Y$
.
Observe that when differentiating the expression (45) for
![]() $G(s,Y,m,\ell )$
with respect to s and taking
$G(s,Y,m,\ell )$
with respect to s and taking
![]() $s=1$
, the computations amount to computing various derivatives of the K-Bessel functions
$s=1$
, the computations amount to computing various derivatives of the K-Bessel functions
![]() $K_\nu (z)$
with respect to the order
$K_\nu (z)$
with respect to the order
![]() $\nu $
at
$\nu $
at
![]() $\nu =\pm \frac {1}{2}$
which is easily done by applying formula (A.14). In doing so, and when combined with the bound (A.8) for the exponential integral, one immediately gets the bound that
$\nu =\pm \frac {1}{2}$
which is easily done by applying formula (A.14). In doing so, and when combined with the bound (A.8) for the exponential integral, one immediately gets the bound that
 $$ \begin{align} \max\left\{G(s,Y,m,\ell), \left.\frac{\partial }{\partial s} G(s,Y,m,\ell)\right|_{s=1}\right\}\ll (m + \ell)\exp(-2\pi Y (m+\ell)) \,\,\, \mathrm{as} Y\to +\infty. \end{align} $$
$$ \begin{align} \max\left\{G(s,Y,m,\ell), \left.\frac{\partial }{\partial s} G(s,Y,m,\ell)\right|_{s=1}\right\}\ll (m + \ell)\exp(-2\pi Y (m+\ell)) \,\,\, \mathrm{as} Y\to +\infty. \end{align} $$
As above, the implied constant is independent of
![]() $Y,m,\ell $
.
$Y,m,\ell $
.
Notice that
![]() $G(s,Y,m,\ell )$
with
$G(s,Y,m,\ell )$
with
![]() $m=|n|$
and
$m=|n|$
and
![]() $\ell =|k|$
equals the expression inside the parenthesis in the sum (44) which defines
$\ell =|k|$
equals the expression inside the parenthesis in the sum (44) which defines
![]() $T_3(Y,s;w)$
. Therefore, in order to estimate
$T_3(Y,s;w)$
. Therefore, in order to estimate
![]() $\left .\frac {\partial }{\partial s} T_3(Y,s;w)\right |_{s=1}$
as
$\left .\frac {\partial }{\partial s} T_3(Y,s;w)\right |_{s=1}$
as
![]() $Y\to \infty $
it suffices to combine the bound (46), with
$Y\to \infty $
it suffices to combine the bound (46), with
![]() $m=|n|$
and
$m=|n|$
and
![]() $\ell =|k|$
, with the bounds (19) and (20) for
$\ell =|k|$
, with the bounds (19) and (20) for
![]() $F_{k}(w,s)$
and
$F_{k}(w,s)$
and
![]() $\frac {\partial }{\partial s} F_{k}(w,s)$
at
$\frac {\partial }{\partial s} F_{k}(w,s)$
at
![]() $s=1$
. In doing so, we get that
$s=1$
. In doing so, we get that
 $$ \begin{align*}\frac{\partial}{\partial s} T_3(Y,s;w)\Big|_{s=1}\ll \sum_{k\in\mathbb{Z}\smallsetminus\{0\}}(|n| + |k|) | B_k(1;-n)| \exp\left( -2\pi Y (|k|+|n|) + 2\pi|k| {\mathrm{Im}}(w)\right). \end{align*} $$
$$ \begin{align*}\frac{\partial}{\partial s} T_3(Y,s;w)\Big|_{s=1}\ll \sum_{k\in\mathbb{Z}\smallsetminus\{0\}}(|n| + |k|) | B_k(1;-n)| \exp\left( -2\pi Y (|k|+|n|) + 2\pi|k| {\mathrm{Im}}(w)\right). \end{align*} $$
It remains to estimate the sum on the right-hand side of the above equation as
![]() $Y\to \infty $
. The bound (18) gives that
$Y\to \infty $
. The bound (18) gives that
 $$ \begin{align*} \frac{\partial}{\partial s}&\left. T_3(Y,s;w)\right|_{s=1} \\& \ll \sum_{k\in\mathbb{Z}\smallsetminus\{0\}} (|n| + |k| )\sqrt{|kn|}\exp\left( -2\pi \left( (|k|+|n|)Y - 2\sqrt{|kn|}/c_\Gamma -|k| {\mathrm{Im}}(w) \right) \right). \end{align*} $$
$$ \begin{align*} \frac{\partial}{\partial s}&\left. T_3(Y,s;w)\right|_{s=1} \\& \ll \sum_{k\in\mathbb{Z}\smallsetminus\{0\}} (|n| + |k| )\sqrt{|kn|}\exp\left( -2\pi \left( (|k|+|n|)Y - 2\sqrt{|kn|}/c_\Gamma -|k| {\mathrm{Im}}(w) \right) \right). \end{align*} $$
For
![]() $Y> 2{\mathrm {Im}}(w) + 2\sqrt {n}/c_\Gamma $
, this series over j is uniformly convergent and is
$Y> 2{\mathrm {Im}}(w) + 2\sqrt {n}/c_\Gamma $
, this series over j is uniformly convergent and is
![]() $o(1)$
as
$o(1)$
as
![]() $Y\to \infty $
. In other words,
$Y\to \infty $
. In other words,
With all this, when combining (47) with (40), (42), and (43), we have that
which completes the proof of (9).
5.2 Proof of Corollary 1
The proof of Corollary 1 is a combination of Theorem 1 and the factorization theorem as stated in Proposition 1. The details are as follows.
To begin, we shall prove Proposition 1. Starting with (5), which is written as
 $$ \begin{align*}\log\left( y^k |f(z)| \right) = kP(z) - \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \lim_{s\to 0} \frac{1}{s} \mathrm{ord}(w)\mathcal{E}^{\mathrm{ell}}_{w}(z,s), \end{align*} $$
$$ \begin{align*}\log\left( y^k |f(z)| \right) = kP(z) - \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \lim_{s\to 0} \frac{1}{s} \mathrm{ord}(w)\mathcal{E}^{\mathrm{ell}}_{w}(z,s), \end{align*} $$
we can express
![]() $\lim _{s\to 0} \frac {1}{s}\mathrm {ord}(w) \mathcal {E}^{\mathrm {ell}}_{w}(z,s)$
in terms of the resolvent kernel. Specifically, using (6), we have that
$\lim _{s\to 0} \frac {1}{s}\mathrm {ord}(w) \mathcal {E}^{\mathrm {ell}}_{w}(z,s)$
in terms of the resolvent kernel. Specifically, using (6), we have that
 $$ \begin{align} \log\left( y^k |f(z)| \right)=kP(z) + \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \lim_{s\to 0} \left(\frac{2^{s}\sqrt{\pi} \Gamma(s-1/2)}{\Gamma(s+1)}(2s-1)G_s(z,w)\right). \end{align} $$
$$ \begin{align} \log\left( y^k |f(z)| \right)=kP(z) + \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)} \lim_{s\to 0} \left(\frac{2^{s}\sqrt{\pi} \Gamma(s-1/2)}{\Gamma(s+1)}(2s-1)G_s(z,w)\right). \end{align} $$
By applying the functional equation for the Green’s function, see Theorem 3.5 of [Reference Hejhal9] on pages 250–251, we get
 $$ \begin{align*} \lim_{s\to 0}\frac{2^{s}\sqrt{\pi} \Gamma(s-1/2)}{\Gamma(s+1)}(2s-1)G_s(z,w) = \lim_{s\to 1} \frac{2^{1-s}\sqrt{\pi} \Gamma(1/2-s)}{\Gamma(2-s)}(1-2s)G_{1-s}(z,w)\\ =\lim_{s\to 1}\left(\frac{2^{1-s}\sqrt{\pi} \Gamma(1/2-s)}{\Gamma(2-s)}\left((1-2s)G_s(z,w)- \frac{}{}\mathcal{E}_\infty^{\mathrm{par}}(z,1-s)\mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)\right). \end{align*} $$
$$ \begin{align*} \lim_{s\to 0}\frac{2^{s}\sqrt{\pi} \Gamma(s-1/2)}{\Gamma(s+1)}(2s-1)G_s(z,w) = \lim_{s\to 1} \frac{2^{1-s}\sqrt{\pi} \Gamma(1/2-s)}{\Gamma(2-s)}(1-2s)G_{1-s}(z,w)\\ =\lim_{s\to 1}\left(\frac{2^{1-s}\sqrt{\pi} \Gamma(1/2-s)}{\Gamma(2-s)}\left((1-2s)G_s(z,w)- \frac{}{}\mathcal{E}_\infty^{\mathrm{par}}(z,1-s)\mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)\right). \end{align*} $$
From the Kronecker limit formula (29), we know that
When combined with the standard Taylor series expansion of the gamma function, we get that
 $$ \begin{align*} \lim_{s\to 0}&\frac{2^{s}\sqrt{\pi} \Gamma(s-1/2)}{\Gamma(s+1)}(2s-1)G_s(z,w)= \lim_{s\to 1}\Big((2\pi (-1+(s-1)(2-\log 2))\cdot \\& \cdot \left[2(1-s)G_s(z,w) - (G_s(z,w)+\mathcal{E}_\infty^{\mathrm{par}}(w,s)) - P(z)(1-s)\mathcal{E}_\infty^{\mathrm{par}}(w,s)\right]\Big). \end{align*} $$
$$ \begin{align*} \lim_{s\to 0}&\frac{2^{s}\sqrt{\pi} \Gamma(s-1/2)}{\Gamma(s+1)}(2s-1)G_s(z,w)= \lim_{s\to 1}\Big((2\pi (-1+(s-1)(2-\log 2))\cdot \\& \cdot \left[2(1-s)G_s(z,w) - (G_s(z,w)+\mathcal{E}_\infty^{\mathrm{par}}(w,s)) - P(z)(1-s)\mathcal{E}_\infty^{\mathrm{par}}(w,s)\right]\Big). \end{align*} $$
According to [Reference Iwaniec11, p. 106], the point
![]() $s=1$
is the simple pole of
$s=1$
is the simple pole of
![]() $G_s(z,w)$
with the residue
$G_s(z,w)$
with the residue
![]() $-1/\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(M)$
. (Note: Our
$-1/\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(M)$
. (Note: Our
![]() $G_s(z,w)$
differs from the automorphic Green’s function from [Reference Iwaniec11] by a factor of
$G_s(z,w)$
differs from the automorphic Green’s function from [Reference Iwaniec11] by a factor of
![]() $-1$
.) Therefore, the Kronecker limit formula (28) gives that
$-1$
.) Therefore, the Kronecker limit formula (28) gives that
 $$ \begin{align} \lim_{s\to 0}\frac{2^{s}\sqrt{\pi} \Gamma(s-1/2)}{\Gamma(s+1)}(2s-1)G_s(z,w)&= -\frac{2\pi}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}P(z)- \frac{4\pi}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)} \\&\quad + 2\pi\lim_{s\to 1}\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right).\notag \end{align} $$
$$ \begin{align} \lim_{s\to 0}\frac{2^{s}\sqrt{\pi} \Gamma(s-1/2)}{\Gamma(s+1)}(2s-1)G_s(z,w)&= -\frac{2\pi}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}P(z)- \frac{4\pi}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)} \\&\quad + 2\pi\lim_{s\to 1}\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right).\notag \end{align} $$
Recall that the classical the Riemann–Roch theorem implies that
 $$ \begin{align*}k\frac{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}{2\pi}=\sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)}; \end{align*} $$
$$ \begin{align*}k\frac{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}{2\pi}=\sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)}; \end{align*} $$
hence, after multiplying (49) by
![]() $\frac {\mathrm {ord}_w(f)}{\mathrm {ord}(w)} $
and taking the sum over all
$\frac {\mathrm {ord}_w(f)}{\mathrm {ord}(w)} $
and taking the sum over all
![]() $w\in \mathcal {F}$
from (48), we arrive at (7), as claimed.
$w\in \mathcal {F}$
from (48), we arrive at (7), as claimed.
Having proved Proposition 1, observe that the left-hand side of (7) is real-valued. As proved in [Reference Niebur19],
![]() $F_{-n}(z,1)$
is orthogonal to constant functions. Therefore, in order to prove (10) one simply applies (9), which was established above.
$F_{-n}(z,1)$
is orthogonal to constant functions. Therefore, in order to prove (10) one simply applies (9), which was established above.
5.3 Proof of Corollary 2
In order to prove (12), it suffices to compute
![]() $\langle 1, \overline {\lim _{s\to 1}(G_s(z,w) + \mathcal {E}_{\infty }^{\mathrm {par}}(w,s))} \rangle $
, which we will write as
$\langle 1, \overline {\lim _{s\to 1}(G_s(z,w) + \mathcal {E}_{\infty }^{\mathrm {par}}(w,s))} \rangle $
, which we will write as
 $$ \begin{align*}\int\limits_{\mathcal{F}}\lim_{s\to 1}\left(G_s(z,w) + \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)(s-1)}+ \mathcal{E}_{\infty}^{\mathrm{par}}(w,s)-\frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)(s-1)}\right)d\mu_{\operatorname{\mathrm{hyp}}}(z). \end{align*} $$
$$ \begin{align*}\int\limits_{\mathcal{F}}\lim_{s\to 1}\left(G_s(z,w) + \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)(s-1)}+ \mathcal{E}_{\infty}^{\mathrm{par}}(w,s)-\frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)(s-1)}\right)d\mu_{\operatorname{\mathrm{hyp}}}(z). \end{align*} $$
From its spectral expansion, the function
![]() $\lim _{s\to 1}\left (G_s(z,w) + \frac {1}{\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(M)(s-1)}\right )$
is
$\lim _{s\to 1}\left (G_s(z,w) + \frac {1}{\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(M)(s-1)}\right )$
is
![]() $L^2$
on
$L^2$
on
![]() $\mathcal {F}$
and orthogonal to constant functions. Therefore, by using the Laurent series expansion (28), we get that
$\mathcal {F}$
and orthogonal to constant functions. Therefore, by using the Laurent series expansion (28), we get that
 $$ \begin{align*}\langle 1, \overline{\lim_{s\to 1}(G_s(z,w) + \mathcal{E}_{\infty}^{\mathrm{par}}(w,s))} \rangle =\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)\left(\beta - \frac{P(w)}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}\right), \end{align*} $$
$$ \begin{align*}\langle 1, \overline{\lim_{s\to 1}(G_s(z,w) + \mathcal{E}_{\infty}^{\mathrm{par}}(w,s))} \rangle =\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)\left(\beta - \frac{P(w)}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}\right), \end{align*} $$
which completes the proof.
5.4 Proof of Theorem 2
Our starting point is the Fourier expansion of the sum
![]() $G_s(z,w) + \mathcal {E}_\infty ^{\mathrm {par}}(w,s)$
. Namely, for
$G_s(z,w) + \mathcal {E}_\infty ^{\mathrm {par}}(w,s)$
. Namely, for
![]() ${\mathrm {Re}}(s)>1$
and
${\mathrm {Re}}(s)>1$
and
![]() ${\mathrm {Im}}(w)$
sufficiently large, we have that
${\mathrm {Im}}(w)$
sufficiently large, we have that
 $$ \begin{align} G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)&=\left(1-\frac{y^{1-s}}{2s-1}\right)\mathcal{E}_\infty^{\mathrm{par}}(w,s) \notag \\& \quad -\sum_{k\in\mathbb{Z}\setminus\{0\}} \sqrt{y}K_{s-\tfrac{1}{2}}(2\pi |k| y)F_{-k}(w,s)e(kx). \end{align} $$
$$ \begin{align} G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)&=\left(1-\frac{y^{1-s}}{2s-1}\right)\mathcal{E}_\infty^{\mathrm{par}}(w,s) \notag \\& \quad -\sum_{k\in\mathbb{Z}\setminus\{0\}} \sqrt{y}K_{s-\tfrac{1}{2}}(2\pi |k| y)F_{-k}(w,s)e(kx). \end{align} $$
If
![]() ${\mathrm {Im}}(z)$
is sufficiently large, the exponential decay of
${\mathrm {Im}}(z)$
is sufficiently large, the exponential decay of
![]() $K_{s-\tfrac {1}{2}}(2\pi |k| y)$
is sufficient to ensure that the right-hand side of (50) is holomorphic at
$K_{s-\tfrac {1}{2}}(2\pi |k| y)$
is sufficient to ensure that the right-hand side of (50) is holomorphic at
![]() $s=1$
. The Laurent series expansion of
$s=1$
. The Laurent series expansion of
![]() $\mathcal {E}_\infty ^{\mathrm {par}}(w,s)$
, when combined with the expansions
$\mathcal {E}_\infty ^{\mathrm {par}}(w,s)$
, when combined with the expansions
and
yields that
 $$ \begin{align*} \frac{\partial}{\partial s}\bigg(1-\frac{y^{1-s}}{2s-1}\bigg)\mathcal{E}_\infty^{\mathrm{par}}(w,s) \bigg|_{s=1} &=\frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}\bigg[ -4+2\beta\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)-2P(w) \\& \quad + \log y \bigg(\beta\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M) - P(w)-2\bigg) - \tfrac{1}{2}\log^2y \bigg]. \end{align*} $$
$$ \begin{align*} \frac{\partial}{\partial s}\bigg(1-\frac{y^{1-s}}{2s-1}\bigg)\mathcal{E}_\infty^{\mathrm{par}}(w,s) \bigg|_{s=1} &=\frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)}\bigg[ -4+2\beta\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)-2P(w) \\& \quad + \log y \bigg(\beta\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M) - P(w)-2\bigg) - \tfrac{1}{2}\log^2y \bigg]. \end{align*} $$
Additionally, for
![]() ${\mathrm {Im}}(z)$
sufficiently large, the series on the right-hand side of (50) is a uniformly convergent series of functions which are holomorphic at
${\mathrm {Im}}(z)$
sufficiently large, the series on the right-hand side of (50) is a uniformly convergent series of functions which are holomorphic at
![]() $s=1$
. As such, we may differentiate the series term by term. By employing (A.5) and (A.14), we deduce, for
$s=1$
. As such, we may differentiate the series term by term. By employing (A.5) and (A.14), we deduce, for
![]() $k\neq 0$
, that
$k\neq 0$
, that
 $$ \begin{align*} &\frac{\partial}{\partial s}\left. \left(\sqrt{y}K_{s-\tfrac{1}{2}}(2\pi |k| y)F_{-k}(w,s) \right) \right|_{s=1}=\frac{e^{-2\pi|k|y}}{2\sqrt{|k|}}\cdot \\& \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \cdot\left[ \frac{\partial}{\partial s}\left. F_{-k}(w,s) \right|_{s=1}- F_{-k}(w,1)e^{4\pi|k|y} \mathrm{Ei}(-4\pi |k|y)\right], \end{align*} $$
$$ \begin{align*} &\frac{\partial}{\partial s}\left. \left(\sqrt{y}K_{s-\tfrac{1}{2}}(2\pi |k| y)F_{-k}(w,s) \right) \right|_{s=1}=\frac{e^{-2\pi|k|y}}{2\sqrt{|k|}}\cdot \\& \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad \cdot\left[ \frac{\partial}{\partial s}\left. F_{-k}(w,s) \right|_{s=1}- F_{-k}(w,1)e^{4\pi|k|y} \mathrm{Ei}(-4\pi |k|y)\right], \end{align*} $$
where
![]() $\mathrm {Ei}(x)$
denotes the exponential integral function. From this, we get the expression that
$\mathrm {Ei}(x)$
denotes the exponential integral function. From this, we get the expression that
 $$ \begin{align*} &\frac{\partial}{\partial s}\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)\Big|_{s=1} = (\log y+2) \left(\beta - \frac{P(w)+2} {\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M)}\right) - \frac{\log^2 y}{2\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M)} \\& \quad - \sum_{k\in\mathbb{Z}\setminus\{0\}}\frac{1}{2\sqrt{|k|}}\left[ \frac{\partial}{\partial s} \left. F_{-k}(w,s) \right|_{s=1}- F_{-k}(w,1)e^{4\pi|k|y} \mathrm{Ei}(-4\pi |k|y)\right]e^{2\pi i kx - 2\pi|k|y}. \end{align*} $$
$$ \begin{align*} &\frac{\partial}{\partial s}\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)\Big|_{s=1} = (\log y+2) \left(\beta - \frac{P(w)+2} {\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M)}\right) - \frac{\log^2 y}{2\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M)} \\& \quad - \sum_{k\in\mathbb{Z}\setminus\{0\}}\frac{1}{2\sqrt{|k|}}\left[ \frac{\partial}{\partial s} \left. F_{-k}(w,s) \right|_{s=1}- F_{-k}(w,1)e^{4\pi|k|y} \mathrm{Ei}(-4\pi |k|y)\right]e^{2\pi i kx - 2\pi|k|y}. \end{align*} $$
Let us now compute the derivative
![]() $\frac {\partial }{\partial z}$
of the above expression. After multiplying by
$\frac {\partial }{\partial z}$
of the above expression. After multiplying by
![]() $i=\sqrt {-1}$
, we get that
$i=\sqrt {-1}$
, we get that
 $$ \begin{align*} &\mathcal{G}_w(z)=\frac{1}{y}\left(\beta - \frac{P(w)+2}{\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M)}\right) - \frac{\log y}{y \mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M)} +\sum_{k\geq 1} 2\pi \sqrt{k} \frac{\partial}{\partial s}\left. F_{-k}(w,s) \right|_{s=1}q_z^k \\& \quad +\sum_{k\geq 1}\frac{F_{-k}(w,1)}{2\sqrt{k}y}q_z^k -\sum_{k\leq -1} 2\pi \sqrt{|k|} F_{-k}(w,1) \mathrm{Ei}(4\pi ky) q_z^k + \sum_{k\leq -1}\frac{F_{-k}(w,1)}{2\sqrt{|k|}y}e^{2\pi i k(x-iy)}. \end{align*} $$
$$ \begin{align*} &\mathcal{G}_w(z)=\frac{1}{y}\left(\beta - \frac{P(w)+2}{\mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M)}\right) - \frac{\log y}{y \mathrm{vol}_{\operatorname{\mathrm{hyp}}}(M)} +\sum_{k\geq 1} 2\pi \sqrt{k} \frac{\partial}{\partial s}\left. F_{-k}(w,s) \right|_{s=1}q_z^k \\& \quad +\sum_{k\geq 1}\frac{F_{-k}(w,1)}{2\sqrt{k}y}q_z^k -\sum_{k\leq -1} 2\pi \sqrt{|k|} F_{-k}(w,1) \mathrm{Ei}(4\pi ky) q_z^k + \sum_{k\leq -1}\frac{F_{-k}(w,1)}{2\sqrt{|k|}y}e^{2\pi i k(x-iy)}. \end{align*} $$
The proof of the assertion that
![]() $\sum _{k\geq 1} 2\pi \sqrt {k} \frac {\partial }{\partial s}\left. F_{-k}(w,s) \right |_{s=1}q_z^k$
is the holomorphic part of
$\sum _{k\geq 1} 2\pi \sqrt {k} \frac {\partial }{\partial s}\left. F_{-k}(w,s) \right |_{s=1}q_z^k$
is the holomorphic part of
![]() $\mathcal {G}_w(z)$
follows by citing the uniqueness of the analytic continuation in z.
$\mathcal {G}_w(z)$
follows by citing the uniqueness of the analytic continuation in z.
It is left to prove that
![]() $\mathcal {G}_w(z)$
is weight two biharmonic Maass form. Since
$\mathcal {G}_w(z)$
is weight two biharmonic Maass form. Since
![]() $\mathcal {G}_w(z)$
is obtained by taking the derivative
$\mathcal {G}_w(z)$
is obtained by taking the derivative
![]() $\frac {\partial }{\partial z}$
of a
$\frac {\partial }{\partial z}$
of a
![]() $\Gamma $
-invariant function, it is obvious that
$\Gamma $
-invariant function, it is obvious that
![]() $\mathcal {G}_w(z)$
is weight two in z. Moreover, the straightforward computation that
$\mathcal {G}_w(z)$
is weight two in z. Moreover, the straightforward computation that
 $$ \begin{align*}iy^2 \frac{\partial}{\partial \bar z}\mathcal{G}_w(z)=\Delta_{\operatorname{\mathrm{hyp}}}\left(\frac{\partial}{\partial s}\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)\Big|_{s=1}\right)=- \lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right), \end{align*} $$
$$ \begin{align*}iy^2 \frac{\partial}{\partial \bar z}\mathcal{G}_w(z)=\Delta_{\operatorname{\mathrm{hyp}}}\left(\frac{\partial}{\partial s}\left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right)\Big|_{s=1}\right)=- \lim_{s\to 1} \left(G_s(z,w) + \mathcal{E}_\infty^{\mathrm{par}}(w,s)\right), \end{align*} $$
when combined with the fact that
![]() $\Delta _{\operatorname {\mathrm {hyp}}}\left ( \lim _{s\to 1} \left (G_s(z,w) + \mathcal {E}_\infty ^{\mathrm {par}}(w,s)\right )\right )=0$
, proves that
$\Delta _{\operatorname {\mathrm {hyp}}}\left ( \lim _{s\to 1} \left (G_s(z,w) + \mathcal {E}_\infty ^{\mathrm {par}}(w,s)\right )\right )=0$
, proves that
![]() $\mathcal {G}_w(z)$
is biharmonic.
$\mathcal {G}_w(z)$
is biharmonic.
6 Examples
6.1 The full modular group
Throughout this subsection, let
![]() $\Gamma =\mathrm {PSL}(2,\mathbb {Z})$
, in which case the parabolic Kronecker limit function,
$\Gamma =\mathrm {PSL}(2,\mathbb {Z})$
, in which case the parabolic Kronecker limit function,
![]() $P(w)$
can be expressed, in the notation of [Reference Bringmann and Kane2], as
$P(w)$
can be expressed, in the notation of [Reference Bringmann and Kane2], as
where
![]() $\eta (w)$
is Dedekind’s eta function and the last equality follows from the definition of
$\eta (w)$
is Dedekind’s eta function and the last equality follows from the definition of
given on page 1 of [Reference Bringmann and Kane2].
In this setting, Corollary 1, when combined with (3) and Rohrlich’s theorem (2) yields that
 $$ \begin{align} \langle j_n,\log||f||\rangle =2\pi\sqrt{n}\left( - 2\pi \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)}\left(\frac{\partial}{\partial s} F_{-n}(w,s) \bigg|_{s=1} -c_nP(w)\right)\right). \end{align} $$
$$ \begin{align} \langle j_n,\log||f||\rangle =2\pi\sqrt{n}\left( - 2\pi \sum_{w\in \mathcal{F}} \frac{\mathrm{ord}_w(f)}{\mathrm{ord}(w)}\left(\frac{\partial}{\partial s} F_{-n}(w,s) \bigg|_{s=1} -c_nP(w)\right)\right). \end{align} $$
Moreover, equating the constant terms in the Fourier series expansions for
![]() $F_{-n}(z,1)$
and
$F_{-n}(z,1)$
and
![]() $j_n(z)$
, one easily deduces that
$j_n(z)$
, one easily deduces that
![]() $2\pi \sqrt {n}c_n=24\sigma (n)$
. This proves Theorem 1.2 of [Reference Bringmann and Kane2]. Furthermore, we have shown, in the notation of [Reference Bringmann and Kane2] one has that
$2\pi \sqrt {n}c_n=24\sigma (n)$
. This proves Theorem 1.2 of [Reference Bringmann and Kane2]. Furthermore, we have shown, in the notation of [Reference Bringmann and Kane2] one has that
This identity provides a description of
, for
![]() $n\geq 1$
different from the one given by formula (3.10) of [Reference Bringmann and Kane2]. Finally, from the identity (23), when combined with the fact that
$n\geq 1$
different from the one given by formula (3.10) of [Reference Bringmann and Kane2]. Finally, from the identity (23), when combined with the fact that
![]() $ \Delta _{\operatorname {\mathrm {hyp}}}P(w)=1$
, which is a straightforward implication of the Kronecker limit formula (28), it follows that
$ \Delta _{\operatorname {\mathrm {hyp}}}P(w)=1$
, which is a straightforward implication of the Kronecker limit formula (28), it follows that
which agrees with formula (3.10) of [Reference Bringmann and Kane2].
By reasoning as above, we easily see that Theorem 1.3 of [Reference Bringmann and Kane2] follows from Corollary 2 with
![]() $g(z)=j_n(z)$
.
$g(z)=j_n(z)$
.
Finally, in view of (51), Theorem 2 is closely related to the first part of Theorem 1.4 of [Reference Bringmann and Kane2]. Namely, for large enough
![]() ${\mathrm {Im}}(z)$
, in the notation of [Reference Bringmann and Kane2], we can write
${\mathrm {Im}}(z)$
, in the notation of [Reference Bringmann and Kane2], we can write

Theorem 2 implies that the function
![]() $\mathbb {H}_w(z)$
is the holomorphic part of the weight two biharmonic Maass form
$\mathbb {H}_w(z)$
is the holomorphic part of the weight two biharmonic Maass form
where
 $$ \begin{align*}\widehat{E}_2(z)=1-24\sum_{n\geq 1}\sigma(n)q_z^n - \frac{3}{\pi y} \end{align*} $$
$$ \begin{align*}\widehat{E}_2(z)=1-24\sum_{n\geq 1}\sigma(n)q_z^n - \frac{3}{\pi y} \end{align*} $$
is the weight two completed Eisenstein series for the full modular group.
Remark 4. The identity (52) also appears on page 99 of [Reference Jeon, Kang and Kim12]. Furthermore, it is observed in [Reference Jeon, Kang and Kim12] that
![]() $h^\ast _n(w)=\xi _0\left (\frac {\partial }{\partial s}\left. F_{-n}(w,s) \right |_{s=1} \right )$
is a harmonic weak Maass form of weight
$h^\ast _n(w)=\xi _0\left (\frac {\partial }{\partial s}\left. F_{-n}(w,s) \right |_{s=1} \right )$
is a harmonic weak Maass form of weight
![]() $2$
for which
$2$
for which
![]() $\xi _2(h^\ast _n(w))=j_n(w)+24\sigma (n)$
and where
$\xi _2(h^\ast _n(w))=j_n(w)+24\sigma (n)$
and where
![]() $\xi _\kappa := 2iy^\kappa \overline {\frac {\partial }{\partial \overline {z}}}$
. Moreover, in Section 4 of [Reference Jeon, Kang and Kim12], it is proved that each
$\xi _\kappa := 2iy^\kappa \overline {\frac {\partial }{\partial \overline {z}}}$
. Moreover, in Section 4 of [Reference Jeon, Kang and Kim12], it is proved that each
![]() $h_n(w)$
is a harmonic Maass forms with bounded holomorphic parts. Additionally, it is shown in [Reference Jeon, Kang and Kim12] that for each
$h_n(w)$
is a harmonic Maass forms with bounded holomorphic parts. Additionally, it is shown in [Reference Jeon, Kang and Kim12] that for each
![]() $n>0$
one has that
$n>0$
one has that
![]() $h^\ast _n(w)=4\pi h_n(w)$
, where the set
$h^\ast _n(w)=4\pi h_n(w)$
, where the set
![]() $\{h_m(w)\}_{m\in \mathbb {Z}}$
is a basis for the space
$\{h_m(w)\}_{m\in \mathbb {Z}}$
is a basis for the space
![]() $\mathcal {V}$
of weight
$\mathcal {V}$
of weight
![]() $2$
harmonic weak Maass forms; the basis was constructed in [Reference Duke, Imamoğlu and Tóth6].
$2$
harmonic weak Maass forms; the basis was constructed in [Reference Duke, Imamoğlu and Tóth6].
6.2 Genus zero Atkin–Lehner groups
Let
![]() $N=\prod _{\nu =1}^r p_\nu $
be a positive square-free integer which is one of the
$N=\prod _{\nu =1}^r p_\nu $
be a positive square-free integer which is one of the
![]() $44$
possible values for which the quotient space
$44$
possible values for which the quotient space
![]() $Y_{N}^{+} =\overline { \Gamma _{0}^{+}(N)}\backslash {\mathbb H}$
has genus zero (see [Reference Cummins5] for a list of such N as well as [Reference Jorgenson, Smajlović and Then14]). Let
$Y_{N}^{+} =\overline { \Gamma _{0}^{+}(N)}\backslash {\mathbb H}$
has genus zero (see [Reference Cummins5] for a list of such N as well as [Reference Jorgenson, Smajlović and Then14]). Let
![]() $\Delta _{N}(z)$
be the Kronecker limit function on
$\Delta _{N}(z)$
be the Kronecker limit function on
![]() $Y_{N}^{+}$
associated with the parabolic Eisenstein series; it is given by formula (30) above.
$Y_{N}^{+}$
associated with the parabolic Eisenstein series; it is given by formula (30) above.
In the notation of §4.2, the function
![]() $\Delta _N(z)(j_N^+(z)-j_N^+(w))^{\nu _N}$
, is the weight
$\Delta _N(z)(j_N^+(z)-j_N^+(w))^{\nu _N}$
, is the weight
![]() $k_N=2^{r-1}\ell _N$
holomorphic modular form which possesses the constant term
$k_N=2^{r-1}\ell _N$
holomorphic modular form which possesses the constant term
![]() $1$
in its q-expansion. Furthermore, this function vanishes only at the point
$1$
in its q-expansion. Furthermore, this function vanishes only at the point
![]() $z=w$
, and, by the Riemann–Roch formula, its order of vanishing is equal to
$z=w$
, and, by the Riemann–Roch formula, its order of vanishing is equal to
![]() $k_N \operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_N^{+})\cdot \mathrm {ord}(w)/(4\pi )$
.
$k_N \operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_N^{+})\cdot \mathrm {ord}(w)/(4\pi )$
.
When
![]() $N=1$
, one has
$N=1$
, one has
![]() $k_1=12$
,
$k_1=12$
,
![]() $\ell _1=24$
,
$\ell _1=24$
,
![]() $\nu _1=1$
and
$\nu _1=1$
and
![]() $\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_N^{+})=\pi /3$
, hence
$\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_N^{+})=\pi /3$
, hence
![]() $\Delta _1(z)(j_1^+(z)-j_1^+(w))^{\nu _1}$
equals the prime form
$\Delta _1(z)(j_1^+(z)-j_1^+(w))^{\nu _1}$
equals the prime form
![]() $(\Delta (z)(j(z)-j(w)))^{1/\mathrm {ord}(w)}$
taken to the power
$(\Delta (z)(j(z)-j(w)))^{1/\mathrm {ord}(w)}$
taken to the power
![]() $\mathrm {ord}(w)$
(see page 3 of [Reference Bringmann and Kane2]).
$\mathrm {ord}(w)$
(see page 3 of [Reference Bringmann and Kane2]).
For any integer
![]() $m>1$
, the q-expansion of the form
$m>1$
, the q-expansion of the form
![]() $j_N^+|T_{m}(z)$
is
$j_N^+|T_{m}(z)$
is
![]() $q_z^{-m}+O(q_z)$
; hence there exists a constant
$q_z^{-m}+O(q_z)$
; hence there exists a constant
![]() $C_{m,N}$
such that
$C_{m,N}$
such that
![]() $j_N^+|T_{m}(z)=2\pi \sqrt {m} F_{-m}(z,1) + C_{m,N}$
. The constant
$j_N^+|T_{m}(z)=2\pi \sqrt {m} F_{-m}(z,1) + C_{m,N}$
. The constant
![]() $C_{m,N}$
can be explicitly evaluated in terms of m and N by equating the constant terms in the q-expansions. Upon doing so, one obtains, using equation (24), that
$C_{m,N}$
can be explicitly evaluated in terms of m and N by equating the constant terms in the q-expansions. Upon doing so, one obtains, using equation (24), that
 $$ \begin{align*} C_{m,N}=-2\pi \sqrt{m} B_{0,N}^+(1;-m)&=-24\sigma(m)\prod\limits_{\nu=1}^r \left(1- \frac{p_\nu^{\alpha_{p_\nu}(m)+1}(p_\nu -1) }{\left(p_\nu^{\alpha_{p_\nu}(m)+1} - 1\right)(p_\nu+1)}\right)\\&=-24\sigma(m) \prod\limits_{\nu=1}^r \left(1- \kappa_{m}(p_\nu)\right), \end{align*} $$
$$ \begin{align*} C_{m,N}=-2\pi \sqrt{m} B_{0,N}^+(1;-m)&=-24\sigma(m)\prod\limits_{\nu=1}^r \left(1- \frac{p_\nu^{\alpha_{p_\nu}(m)+1}(p_\nu -1) }{\left(p_\nu^{\alpha_{p_\nu}(m)+1} - 1\right)(p_\nu+1)}\right)\\&=-24\sigma(m) \prod\limits_{\nu=1}^r \left(1- \kappa_{m}(p_\nu)\right), \end{align*} $$
where we simplified the notation by denoting the second term in the product over
![]() $\nu $
by
$\nu $
by
![]() $\kappa _m(p_\nu )$
. We now can apply Corollary 2 with
$\kappa _m(p_\nu )$
. We now can apply Corollary 2 with
 $$ \begin{align*}g(z)= j_N^+|T_{m}(z)=2\pi \sqrt{m} F_{-m}(z,1)-24\sigma(m)\prod\limits_{\nu=1}^r \left(1- \kappa_{m}(p_\nu)\right) \end{align*} $$
$$ \begin{align*}g(z)= j_N^+|T_{m}(z)=2\pi \sqrt{m} F_{-m}(z,1)-24\sigma(m)\prod\limits_{\nu=1}^r \left(1- \kappa_{m}(p_\nu)\right) \end{align*} $$
and
![]() $f(z)=\Delta _N(z)(j_N^+(z)-j_N^+(w))^{\nu _N}$
. Corollary 2 becomes the statement that
$f(z)=\Delta _N(z)(j_N^+(z)-j_N^+(w))^{\nu _N}$
. Corollary 2 becomes the statement that
 $$ \begin{align*} &\langle j_N^+|T_{m}(z), \log(y^{\tfrac{k_N}{2}} |\Delta_N(z)(j_N^+(z)-j_N^+(w))^{\nu_N}|) \rangle \\& \quad = -k_N \operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(Y_N^{+})\bigg[\pi\sqrt{m}\frac{\partial}{\partial s}F_{-m}(w,s)\bigg|_{s=1} \\& \qquad +12\sigma(m)\prod\limits_{\nu=1}^r \left(1- \kappa_{m}(p_\nu)\right) \left(\beta_N\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(Y_N^{+})-\log\left( |\Delta_N(w)|^{2/k_N} \cdot {\mathrm{Im}} (w)\right) -2\right)\bigg], \end{align*} $$
$$ \begin{align*} &\langle j_N^+|T_{m}(z), \log(y^{\tfrac{k_N}{2}} |\Delta_N(z)(j_N^+(z)-j_N^+(w))^{\nu_N}|) \rangle \\& \quad = -k_N \operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(Y_N^{+})\bigg[\pi\sqrt{m}\frac{\partial}{\partial s}F_{-m}(w,s)\bigg|_{s=1} \\& \qquad +12\sigma(m)\prod\limits_{\nu=1}^r \left(1- \kappa_{m}(p_\nu)\right) \left(\beta_N\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(Y_N^{+})-\log\left( |\Delta_N(w)|^{2/k_N} \cdot {\mathrm{Im}} (w)\right) -2\right)\bigg], \end{align*} $$
where
![]() $\beta _N$
is given by (32).
$\beta _N$
is given by (32).
In this form, we have obtained an alternate proof and generalization of formula (1.2) from [Reference Bringmann and Kane2], which is the special case
![]() $N=1$
.
$N=1$
.
6.3 A genus one example
Let us consider the case when
![]() $\Gamma = \overline {\Gamma _{0}(37)^{+}}$
. The choice of
$\Gamma = \overline {\Gamma _{0}(37)^{+}}$
. The choice of
![]() $N=37$
is significant since this level corresponds to the smallest square-free integer N such that
$N=37$
is significant since this level corresponds to the smallest square-free integer N such that
![]() $Y_{N}^{+}$
is genus one. From Proposition 11 of [Reference Jorgenson, Smajlović and Then13], we have that
$Y_{N}^{+}$
is genus one. From Proposition 11 of [Reference Jorgenson, Smajlović and Then13], we have that
![]() $\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_{37}^{+})= 19\pi /3$
and
$\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_{37}^{+})= 19\pi /3$
and
 $$ \begin{align*}\beta_{37}=\frac{3}{19\pi}\left(\frac{10}{19}\log37+2-2\log(4\pi)-24\zeta'(-1)\right). \end{align*} $$
$$ \begin{align*}\beta_{37}=\frac{3}{19\pi}\left(\frac{10}{19}\log37+2-2\log(4\pi)-24\zeta'(-1)\right). \end{align*} $$
The function field generators are
![]() $x_{37}^+(z)=q_z^{-2} + 2q_z^{-1}+ O(q_z)$
and
$x_{37}^+(z)=q_z^{-2} + 2q_z^{-1}+ O(q_z)$
and
![]() $y_{37}^+(z)=q_z^{-3} + 3q_z^{-1}+ O(q_z)$
, as displayed in Table 5 of [Reference Jorgenson, Smajlović and Then13]. The generators
$y_{37}^+(z)=q_z^{-3} + 3q_z^{-1}+ O(q_z)$
, as displayed in Table 5 of [Reference Jorgenson, Smajlović and Then13]. The generators
![]() $x_{37}^+(z)$
and
$x_{37}^+(z)$
and
![]() $y_{37}^+(z)$
satisfy the cubic relation
$y_{37}^+(z)$
satisfy the cubic relation
![]() $y^2 - x^3 + 6xy - 6x^2 + 41y + 49x + 300 = 0$
.
$y^2 - x^3 + 6xy - 6x^2 + 41y + 49x + 300 = 0$
.
The functions
![]() $x_{37}^+(z)$
and
$x_{37}^+(z)$
and
![]() $y_{37}^+(z)$
can be expressed in in terms of the Niebur–Poincaré series by comparing their q-expansions. The resulting expressions are that
$y_{37}^+(z)$
can be expressed in in terms of the Niebur–Poincaré series by comparing their q-expansions. The resulting expressions are that
 $$ \begin{align*} x_{37}^+(z)&=2\pi[\sqrt{2}F_{-2}(z,1)+ 2F_{-1}(z,1)]-2\pi(\sqrt{2}B_{0,37}^+(1;-2)+2B_{0,37}^+(1;-1))\\&=2\pi[\sqrt{2}F_{-2}(z,1)+ 2F_{-1}(z,1)]-\frac{60}{19} \end{align*} $$
$$ \begin{align*} x_{37}^+(z)&=2\pi[\sqrt{2}F_{-2}(z,1)+ 2F_{-1}(z,1)]-2\pi(\sqrt{2}B_{0,37}^+(1;-2)+2B_{0,37}^+(1;-1))\\&=2\pi[\sqrt{2}F_{-2}(z,1)+ 2F_{-1}(z,1)]-\frac{60}{19} \end{align*} $$
and
 $$ \begin{align*} y_{37}^+(z)&=2\pi[\sqrt{3}F_{-3}(z,1)+ 3F_{-1}(z,1)]-2\pi(\sqrt{3}B_{0,37}^+(1;-3)+3B_{0,37}^+(1;-1))\\&=2\pi[\sqrt{3}F_{-3}(z,1)+ +3F_{-1}(z,1)]-\frac{84}{19}. \end{align*} $$
$$ \begin{align*} y_{37}^+(z)&=2\pi[\sqrt{3}F_{-3}(z,1)+ 3F_{-1}(z,1)]-2\pi(\sqrt{3}B_{0,37}^+(1;-3)+3B_{0,37}^+(1;-1))\\&=2\pi[\sqrt{3}F_{-3}(z,1)+ +3F_{-1}(z,1)]-\frac{84}{19}. \end{align*} $$
It is important to note that
![]() $x_{37}^+(z)$
has a pole of order two at
$x_{37}^+(z)$
has a pole of order two at
![]() $z=\infty $
, that is, its q-expansion begins with
$z=\infty $
, that is, its q-expansion begins with
![]() $q_z^{-2}$
. As such,
$q_z^{-2}$
. As such,
![]() $x_{37}^+(z)$
is a linear transformation of the Weierstrass
$x_{37}^+(z)$
is a linear transformation of the Weierstrass
![]() $\wp $
-function, in the coordinates of the upper half plane, associated with the elliptic curve obtained by compactifying the space
$\wp $
-function, in the coordinates of the upper half plane, associated with the elliptic curve obtained by compactifying the space
![]() $Y_{37}^{+}$
. Hence, there are three distinct points
$Y_{37}^{+}$
. Hence, there are three distinct points
![]() $\{w\}$
on
$\{w\}$
on
![]() $Y_{37}^{+}$
, corresponding to the two torsion points under the group law, such that
$Y_{37}^{+}$
, corresponding to the two torsion points under the group law, such that
![]() $x_{37}^+(z)-x_{37}^+(w)$
vanishes as a function of z only when
$x_{37}^+(z)-x_{37}^+(w)$
vanishes as a function of z only when
![]() $z=w$
. The order of vanishing necessarily is equal to two. The cusp form
$z=w$
. The order of vanishing necessarily is equal to two. The cusp form
![]() $\Delta _{37}(z)$
vanishes at
$\Delta _{37}(z)$
vanishes at
![]() $\infty $
to order
$\infty $
to order
![]() $19$
. Therefore, for such w, the form
$19$
. Therefore, for such w, the form
is a weight
![]() $2k_{37}=24$
holomorphic form. The constant term in its q-expansion is equal to
$2k_{37}=24$
holomorphic form. The constant term in its q-expansion is equal to
![]() $1$
, and
$1$
, and
![]() $f_{37,w}(z)$
vanishes for points
$f_{37,w}(z)$
vanishes for points
![]() $z \in \mathcal {F}$
only when
$z \in \mathcal {F}$
only when
![]() $z=w$
. The order of vanishing of
$z=w$
. The order of vanishing of
![]() $f_{37,w}(z)$
at
$f_{37,w}(z)$
at
![]() $z=w$
is
$z=w$
is
![]() $38\cdot \mathrm {ord}(w)$
.
$38\cdot \mathrm {ord}(w)$
.
With all this, we can apply Corollary 2. The resulting formulas are that
 $$ \begin{align*} \langle x_{37}^+, \log(\Vert f_{37,w}\Vert ) \rangle &= -152\pi^2 \left(\frac{\partial}{\partial s} (\sqrt{2}F_{-2}(w,s) + 2F_{-1}(w,s))\bigg|_{s=1}\right)\\& \quad +240\pi\left(\log\left(|\eta(w)\eta(37w)|^2\cdot{\mathrm{Im}} (w)\right) -\frac{10}{19}\log37+2\log(4\pi) +24\zeta'(-1)\right) \end{align*} $$
$$ \begin{align*} \langle x_{37}^+, \log(\Vert f_{37,w}\Vert ) \rangle &= -152\pi^2 \left(\frac{\partial}{\partial s} (\sqrt{2}F_{-2}(w,s) + 2F_{-1}(w,s))\bigg|_{s=1}\right)\\& \quad +240\pi\left(\log\left(|\eta(w)\eta(37w)|^2\cdot{\mathrm{Im}} (w)\right) -\frac{10}{19}\log37+2\log(4\pi) +24\zeta'(-1)\right) \end{align*} $$
and
 $$ \begin{align*} \langle y_{37}^+, \log (\Vert f_{37,w}\Vert ) \rangle &= - 152\pi^2 \left(\frac{\partial}{\partial s} (\sqrt{3}F_{-3}(w,s) +3F_{-1}(w,s))\bigg|_{s=1}\right)\\& \quad + 336\pi\left(\!\log\left(|\eta(w)\eta(37w)|^2\cdot{\mathrm{Im}} (w)\right) -\frac{10}{19}\log37+2\log(4\pi) +24\zeta'(-1)\!\right). \end{align*} $$
$$ \begin{align*} \langle y_{37}^+, \log (\Vert f_{37,w}\Vert ) \rangle &= - 152\pi^2 \left(\frac{\partial}{\partial s} (\sqrt{3}F_{-3}(w,s) +3F_{-1}(w,s))\bigg|_{s=1}\right)\\& \quad + 336\pi\left(\!\log\left(|\eta(w)\eta(37w)|^2\cdot{\mathrm{Im}} (w)\right) -\frac{10}{19}\log37+2\log(4\pi) +24\zeta'(-1)\!\right). \end{align*} $$
Of course, one does not need to assume that w corresponds to a two torsion point. In general, Corollary 2 yields an expression where the right-hand side is a sum of two terms, and the corresponding factor in front would be one-half of the factors above.
6.4 A genus two example
Consider the level
![]() $N=103$
. In this case,
$N=103$
. In this case,
![]() $\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_{103}^{+})= 52\pi /3$
and the function field generators are
$\operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(Y_{103}^{+})= 52\pi /3$
and the function field generators are
![]() $x_{103}^+(z)=q_z^{-3} + q_z^{-1} + O(q_z)$
and
$x_{103}^+(z)=q_z^{-3} + q_z^{-1} + O(q_z)$
and
![]() $y_{103}^+(z)=q_z^{-4} + 3q_z^{-2} + 3q_z^{-1} + O(q_z)$
, as displayed in Table 7 of [Reference Jorgenson, Smajlović and Then13]. The generators
$y_{103}^+(z)=q_z^{-4} + 3q_z^{-2} + 3q_z^{-1} + O(q_z)$
, as displayed in Table 7 of [Reference Jorgenson, Smajlović and Then13]. The generators
![]() $x_{103}^+(z)$
and
$x_{103}^+(z)$
and
![]() $y_{103}^+(z)$
satisfy the polynomial relation
$y_{103}^+(z)$
satisfy the polynomial relation
![]() $y^3 - x^4 - 5yx^2 - 9x^3 + 16y^2 - 21yx - 60x^2 + 65y - 164x + 18 = 0$
. The surface
$y^3 - x^4 - 5yx^2 - 9x^3 + 16y^2 - 21yx - 60x^2 + 65y - 164x + 18 = 0$
. The surface
![]() $Y_{103}^{+}$
has genus two.
$Y_{103}^{+}$
has genus two.
From Theorem 6 of [Reference Niebur19], we can write
![]() $x_{103}^+(z)$
and
$x_{103}^+(z)$
and
![]() $y_{103}^+(z)$
in terms of the Niebur–Poincaré series. Explicitly, we have that
$y_{103}^+(z)$
in terms of the Niebur–Poincaré series. Explicitly, we have that
 $$ \begin{align*} x_{103}^+(z)&=2\pi[\sqrt{3}F_{-3}(z,1)+ F_{-1}(z,1)]-2\pi(\sqrt{3}B_{0,103}^+(1;-3)+B_{0,103}^+(1;-1))\\&=2\pi[\sqrt{3}F_{-3}(z,1)+ F_{-1}(z,1)]-\frac{15}{13} \end{align*} $$
$$ \begin{align*} x_{103}^+(z)&=2\pi[\sqrt{3}F_{-3}(z,1)+ F_{-1}(z,1)]-2\pi(\sqrt{3}B_{0,103}^+(1;-3)+B_{0,103}^+(1;-1))\\&=2\pi[\sqrt{3}F_{-3}(z,1)+ F_{-1}(z,1)]-\frac{15}{13} \end{align*} $$
and
 $$ \begin{align*} y_{103}^+(z)&=2\pi[\sqrt{4}F_{-4}(z,1)+ 3\sqrt{2}F_{-2}(z,1) +3F_{-1}(z,1)]\\& \quad -2\pi(\sqrt{4}B_{0,103}^+(1;-4)+3\sqrt{2}B_{0,103}^+(1;-2)+3B_{0,103}^+(1;-1))\\&=2\pi[2F_{-4}(z,1)+ 3\sqrt{2}F_{-2}(z,1) +3F_{-1}(z,1)]-\frac{57}{13}. \end{align*} $$
$$ \begin{align*} y_{103}^+(z)&=2\pi[\sqrt{4}F_{-4}(z,1)+ 3\sqrt{2}F_{-2}(z,1) +3F_{-1}(z,1)]\\& \quad -2\pi(\sqrt{4}B_{0,103}^+(1;-4)+3\sqrt{2}B_{0,103}^+(1;-2)+3B_{0,103}^+(1;-1))\\&=2\pi[2F_{-4}(z,1)+ 3\sqrt{2}F_{-2}(z,1) +3F_{-1}(z,1)]-\frac{57}{13}. \end{align*} $$
The order of vanishing of
![]() $\Delta _{103}(z)$
at the cusp is
$\Delta _{103}(z)$
at the cusp is
![]() $\nu _{103}=(12\cdot 52\pi /3)/(4\pi )=52$
. Therefore, for an arbitrary, fixed
$\nu _{103}=(12\cdot 52\pi /3)/(4\pi )=52$
. Therefore, for an arbitrary, fixed
![]() $w\in {\mathbb H}$
, the form
$w\in {\mathbb H}$
, the form
is the weight
![]() $3k_{103}=36$
holomorphic form which has constant term in the q-expansion equal to
$3k_{103}=36$
holomorphic form which has constant term in the q-expansion equal to
![]() $1$
. Let
$1$
. Let
![]() $\{w_{1}, w_{2}, w_{3}\}$
be the three, not necessarily distinct, points in the fundamental domain
$\{w_{1}, w_{2}, w_{3}\}$
be the three, not necessarily distinct, points in the fundamental domain
![]() $\mathcal {F}$
where
$\mathcal {F}$
where
![]() $(x_{103}^+(z)-x_{103}^+(w))$
vanishes. One of the points
$(x_{103}^+(z)-x_{103}^+(w))$
vanishes. One of the points
![]() $w_{j}$
is equal to w. The form
$w_{j}$
is equal to w. The form
![]() $f_{103,w_j}(z)$
vanishes at
$f_{103,w_j}(z)$
vanishes at
![]() $z=w_{j}$
to order
$z=w_{j}$
to order
![]() $52 \cdot \mathrm {ord}(w_j)$
,
$52 \cdot \mathrm {ord}(w_j)$
,
![]() $j=1,2,3$
.
$j=1,2,3$
.
From §4.2, we have that
 $$ \begin{align*}\beta_{103}=\frac{3}{52\pi}\left(\frac{53}{104}\log103+2-2\log(4\pi)-24\zeta'(-1)\right) \end{align*} $$
$$ \begin{align*}\beta_{103}=\frac{3}{52\pi}\left(\frac{53}{104}\log103+2-2\log(4\pi)-24\zeta'(-1)\right) \end{align*} $$
and
![]() $P_{103}(z)=\log \left (|\eta (z)\eta (103z)|^2\cdot {\mathrm {Im}} (z)\right )$
. Let us now apply Corollary 2 with
$P_{103}(z)=\log \left (|\eta (z)\eta (103z)|^2\cdot {\mathrm {Im}} (z)\right )$
. Let us now apply Corollary 2 with
![]() $g(z)= x_{103}^+(z)$
, in which case
$g(z)= x_{103}^+(z)$
, in which case
![]() $c(g)=-15/13$
. In doing so, we get that
$c(g)=-15/13$
. In doing so, we get that
 $$ \begin{align*} \langle x_{103}^+, \log (\Vert f_{103,w}\Vert ) \rangle &= - 208\pi^2 \sum\limits_{j=1}^{3}\left(\frac{\partial}{\partial s}\left. (\sqrt{3}F_{-3}(w_j,s) +F_{-1}(w_j,s))\right|_{s=1}\right) \\& \quad +120\pi\sum\limits_{j=1}^{3}\left(\log\left(|\eta(w_j)\eta(103w_j)|^2\cdot{\mathrm{Im}} (w_{j})\right)\right) \\& \quad -360\pi\left(\frac{53}{104}\log103-2\log(4\pi) -24\zeta'(-1)\right). \end{align*} $$
$$ \begin{align*} \langle x_{103}^+, \log (\Vert f_{103,w}\Vert ) \rangle &= - 208\pi^2 \sum\limits_{j=1}^{3}\left(\frac{\partial}{\partial s}\left. (\sqrt{3}F_{-3}(w_j,s) +F_{-1}(w_j,s))\right|_{s=1}\right) \\& \quad +120\pi\sum\limits_{j=1}^{3}\left(\log\left(|\eta(w_j)\eta(103w_j)|^2\cdot{\mathrm{Im}} (w_{j})\right)\right) \\& \quad -360\pi\left(\frac{53}{104}\log103-2\log(4\pi) -24\zeta'(-1)\right). \end{align*} $$
Similarly, we can take
![]() $g(z)= y_{103}^+(z)$
, in which case
$g(z)= y_{103}^+(z)$
, in which case
![]() $c(g)=-57/13$
and we get that
$c(g)=-57/13$
and we get that
 $$ \begin{align*} \langle y_{103}^+, \log (\Vert f_{103,w}\Vert ) \rangle &= - 208\pi^2 \sum\limits_{j=1}^{3} \left(\frac{\partial}{\partial s}\left. (2F_{-4}(w_{j},s)+ 3\sqrt{2}F_{-2}(w_{j},s) +3F_{-1}(w_{j},s))\right|_{s=1}\right) \\& \quad +456\pi\sum\limits_{j=1}^{3}\left(\log\left(|\eta(w_{j})\eta(103w_{j})|^2\cdot{\mathrm{Im}} (w_{j})\right)\right) \\& \quad -1368\pi\left(\frac{53}{104}\log103-2\log(4\pi) -24\zeta'(-1)\right). \end{align*} $$
$$ \begin{align*} \langle y_{103}^+, \log (\Vert f_{103,w}\Vert ) \rangle &= - 208\pi^2 \sum\limits_{j=1}^{3} \left(\frac{\partial}{\partial s}\left. (2F_{-4}(w_{j},s)+ 3\sqrt{2}F_{-2}(w_{j},s) +3F_{-1}(w_{j},s))\right|_{s=1}\right) \\& \quad +456\pi\sum\limits_{j=1}^{3}\left(\log\left(|\eta(w_{j})\eta(103w_{j})|^2\cdot{\mathrm{Im}} (w_{j})\right)\right) \\& \quad -1368\pi\left(\frac{53}{104}\log103-2\log(4\pi) -24\zeta'(-1)\right). \end{align*} $$
6.5 An alternative formulation
In the above discussion, we have written the constant
![]() $\beta $
and the Kronecker limit function P separately. However, it should be pointed out that in all instances the appearance of these terms are in the combination
$\beta $
and the Kronecker limit function P separately. However, it should be pointed out that in all instances the appearance of these terms are in the combination
![]() $\beta \operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(M)- P(z)$
. From (28), we can write
$\beta \operatorname {\mathrm {vol}}_{\operatorname {\mathrm {hyp}}}(M)- P(z)$
. From (28), we can write
 $$ \begin{align*}\beta \operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)- P(z) = \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)} \mathrm{CT}_{s=1} \mathcal{E}^{\mathrm{par}}_{\infty}(z,s), \end{align*} $$
$$ \begin{align*}\beta \operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)- P(z) = \frac{1}{\operatorname{\mathrm{vol}}_{\operatorname{\mathrm{hyp}}}(M)} \mathrm{CT}_{s=1} \mathcal{E}^{\mathrm{par}}_{\infty}(z,s), \end{align*} $$
where
![]() $\mathrm {CT}_{s=1}$
denotes the constant term in the Laurent expansion at
$\mathrm {CT}_{s=1}$
denotes the constant term in the Laurent expansion at
![]() $s=1$
. It may be possible that such notational change can provide additional insight concerning the formulas presented above.
$s=1$
. It may be possible that such notational change can provide additional insight concerning the formulas presented above.
A Appendix: Special functions
For the sake of clarity, we define the special functions used throughout the paper and list some of their properties, such as asymptotic expansions, bounds, special values, and various relations.
A.1 The Bessel functions: Definitions and special values
The Bessel functions are solutions to a certain second-order differential equations. For a complex parameter
![]() $\nu $
, the J-Bessel function of order
$\nu $
, the J-Bessel function of order
![]() $\nu $
is given by the absolutely convergent power series
$\nu $
is given by the absolutely convergent power series
 $$ \begin{align} J_{\nu}(z)= \sum_{k=0}^{\infty}\frac{(-1)^k}{k! \Gamma(k+1+\nu)}\left(\frac{z}{2}\right)^{\nu + 2k}. \end{align} $$
$$ \begin{align} J_{\nu}(z)= \sum_{k=0}^{\infty}\frac{(-1)^k}{k! \Gamma(k+1+\nu)}\left(\frac{z}{2}\right)^{\nu + 2k}. \end{align} $$
The variable z is complex valued and lies in the cut complex plane
![]() $\mathbb {C}\setminus (-\infty ,0]$
. Also,
$\mathbb {C}\setminus (-\infty ,0]$
. Also,
![]() $\Gamma $
denotes the classical gamma function. The I-Bessel function is given for the same range of variables
$\Gamma $
denotes the classical gamma function. The I-Bessel function is given for the same range of variables
![]() $\nu $
and z by the absolutely convergent power series
$\nu $
and z by the absolutely convergent power series
 $$ \begin{align} I_{\nu}(z)= \sum_{k=0}^{\infty}\frac{1}{k! \Gamma(k+1+\nu)}\left(\frac{z}{2}\right)^{\nu + 2k}. \end{align} $$
$$ \begin{align} I_{\nu}(z)= \sum_{k=0}^{\infty}\frac{1}{k! \Gamma(k+1+\nu)}\left(\frac{z}{2}\right)^{\nu + 2k}. \end{align} $$
For
![]() $\nu \in \mathbb {C}\setminus \mathbb {Z}$
and
$\nu \in \mathbb {C}\setminus \mathbb {Z}$
and
![]() $z\in \mathbb {C}\setminus (-\infty ,0]$
, the K-Bessel function is defined as
$z\in \mathbb {C}\setminus (-\infty ,0]$
, the K-Bessel function is defined as
while Y-Bessel is defined by
 $$ \begin{align} Y_{\nu}(z) = \frac{1}{\sin(\pi \nu)}\left( \cos(\pi \nu)J_{\nu}(z) - J_{-\nu}(z)\right). \end{align} $$
$$ \begin{align} Y_{\nu}(z) = \frac{1}{\sin(\pi \nu)}\left( \cos(\pi \nu)J_{\nu}(z) - J_{-\nu}(z)\right). \end{align} $$
To define
![]() $ K_{n}(z)$
and
$ K_{n}(z)$
and
![]() $Y_n(z)$
, for
$Y_n(z)$
, for
![]() $n \in \mathbb {Z}$
, one simply takes the limit as
$n \in \mathbb {Z}$
, one simply takes the limit as
![]() $\nu \to n$
in (A.3) and (A.4).
$\nu \to n$
in (A.3) and (A.4).
For
![]() $\nu =1/2$
, the I-Bessel and K-Bessel functions reduce to hyperbolic and exponential function, respectively; from page 204 of [Reference Iwaniec11], we quote the identities that
$\nu =1/2$
, the I-Bessel and K-Bessel functions reduce to hyperbolic and exponential function, respectively; from page 204 of [Reference Iwaniec11], we quote the identities that
 $$ \begin{align} I_{1/2} (z) = \sqrt{\frac{2}{\pi z}}\sinh z \quad \text{and} \quad K_{1/2}(z) = \sqrt{\frac{\pi}{2 z}} e^{-z}, \end{align} $$
$$ \begin{align} I_{1/2} (z) = \sqrt{\frac{2}{\pi z}}\sinh z \quad \text{and} \quad K_{1/2}(z) = \sqrt{\frac{\pi}{2 z}} e^{-z}, \end{align} $$
for
![]() $z\in \mathbb {C}\setminus (-\infty ,0]$
, where the square root is defined using the principal branch of the logarithm.
$z\in \mathbb {C}\setminus (-\infty ,0]$
, where the square root is defined using the principal branch of the logarithm.
The I-Bessel and K-Bessel functions also satisfy recursion formulas. Quoting from [Reference Gradshteyn and Ryzhik8], equations 8.486.1 and 8.486.10, we have that
A.2 Exponential integral
The exponential integral function is defined for a negative real number x as
 $$ \begin{align*}\mathrm{Ei}(x)=\int\limits_{-\infty}^x \frac{e^t}{t}dt=\mathrm{li}(e^x) \end{align*} $$
$$ \begin{align*}\mathrm{Ei}(x)=\int\limits_{-\infty}^x \frac{e^t}{t}dt=\mathrm{li}(e^x) \end{align*} $$
(see [Reference Gradshteyn and Ryzhik8, (8.211)]). For our purposes, we will use the following two representations of
![]() $\mathrm {Ei}(x)$
which we quote from [Reference Gradshteyn and Ryzhik8], formulas 8.212.2 and 8.212.3. First, for
$\mathrm {Ei}(x)$
which we quote from [Reference Gradshteyn and Ryzhik8], formulas 8.212.2 and 8.212.3. First, for
![]() $x>0$
, we have that
$x>0$
, we have that
 $$ \begin{align} \mathrm{Ei}(\pm x)=e^{\pm x}\left(\pm \frac{ 1}{x} + \int\limits_{0}^{\infty}\frac{e^{-t}}{(\pm x-t)^2}\right). \end{align} $$
$$ \begin{align} \mathrm{Ei}(\pm x)=e^{\pm x}\left(\pm \frac{ 1}{x} + \int\limits_{0}^{\infty}\frac{e^{-t}}{(\pm x-t)^2}\right). \end{align} $$
Second,
![]() $x>0$
, we have the series expansion
$x>0$
, we have the series expansion
 $$ \begin{align*}\mathrm{Ei}(x)=\gamma + \log x + \sum_{k=1}^{\infty}\frac{x^k}{k\cdot k!} \end{align*} $$
$$ \begin{align*}\mathrm{Ei}(x)=\gamma + \log x + \sum_{k=1}^{\infty}\frac{x^k}{k\cdot k!} \end{align*} $$
stated in [Reference Gradshteyn and Ryzhik8], formula 8.214.2, where
![]() $\gamma $
denotes the Euler constant. The series expansion yields the coarse bound that
$\gamma $
denotes the Euler constant. The series expansion yields the coarse bound that
![]() $\mathrm {Ei}(x) \ll e^x$
as
$\mathrm {Ei}(x) \ll e^x$
as
![]() $x\to \infty $
. A bound for
$x\to \infty $
. A bound for
![]() $\mathrm {Ei}(-x)$
as
$\mathrm {Ei}(-x)$
as
![]() $x\to \infty $
can be obtained from the equation
$x\to \infty $
can be obtained from the equation
 $$ \begin{align*}\mathrm{Ei}(-x)=-e^{-x}\int\limits_{1}^{\infty}\frac{1}{x+\log t}\frac{dt}{t^2} \,\,\,\,\, \mathrm{for} x>0, \end{align*} $$
$$ \begin{align*}\mathrm{Ei}(-x)=-e^{-x}\int\limits_{1}^{\infty}\frac{1}{x+\log t}\frac{dt}{t^2} \,\,\,\,\, \mathrm{for} x>0, \end{align*} $$
which we quote from [Reference Gradshteyn and Ryzhik8], formula 8.212.10. From this expression, we get that
 $$ \begin{align*}\left|\mathrm{Ei}(-x)\right|\leq e^{-x}\int\limits_{1}^{\infty}\frac{1}{x}\frac{dt}{t^2}=\frac{e^{-x}}{x} \,\,\,\,\, \mathrm{for} x>0. \end{align*} $$
$$ \begin{align*}\left|\mathrm{Ei}(-x)\right|\leq e^{-x}\int\limits_{1}^{\infty}\frac{1}{x}\frac{dt}{t^2}=\frac{e^{-x}}{x} \,\,\,\,\, \mathrm{for} x>0. \end{align*} $$
In summary, we have the following bounds for
![]() $\mathrm {Ei}(\pm x)$
, as
$\mathrm {Ei}(\pm x)$
, as
![]() $x\to \infty $
:
$x\to \infty $
:
A.3 Asymptotic behavior
We quote from [Reference Iwaniec11], formulas (B.35) and (B.36), the asymptotic behavior of Bessel functions in the real positive variable y and for a fixed order
![]() $\nu $
. Namely, for
$\nu $
. Namely, for
![]() $y>1+|\nu |^2$
, we have the following estimates:
$y>1+|\nu |^2$
, we have the following estimates:
 $$ \begin{align} J_{\nu}(y) = \sqrt{\frac{2}{\pi y}}\left( \cos\left(y-\frac{\pi}{2}\nu -\frac{\pi}{4}\right) + O\left(\frac{1+|\nu|^2}{y}\right)\right), \end{align} $$
$$ \begin{align} J_{\nu}(y) = \sqrt{\frac{2}{\pi y}}\left( \cos\left(y-\frac{\pi}{2}\nu -\frac{\pi}{4}\right) + O\left(\frac{1+|\nu|^2}{y}\right)\right), \end{align} $$
 $$ \begin{align} Y_{\nu}(y) = \sqrt{\frac{2}{\pi y}}\left( \sin\left(y-\frac{\pi}{2}\nu -\frac{\pi}{4}\right) + O\left(\frac{1+|\nu|^2}{y}\right)\right), \end{align} $$
$$ \begin{align} Y_{\nu}(y) = \sqrt{\frac{2}{\pi y}}\left( \sin\left(y-\frac{\pi}{2}\nu -\frac{\pi}{4}\right) + O\left(\frac{1+|\nu|^2}{y}\right)\right), \end{align} $$
 $$ \begin{align} I_{\nu}(y) = \sqrt{\frac{1}{2\pi y}}e^y \left( 1 + O\left(\frac{1+|\nu|^2}{y}\right)\right), \end{align} $$
$$ \begin{align} I_{\nu}(y) = \sqrt{\frac{1}{2\pi y}}e^y \left( 1 + O\left(\frac{1+|\nu|^2}{y}\right)\right), \end{align} $$
and
 $$ \begin{align} K_{\nu}(y) = \sqrt{\frac{\pi}{2 y}}e^{-y} \left( 1 + O\left(\frac{1+|\nu|^2}{y}\right)\right). \end{align} $$
$$ \begin{align} K_{\nu}(y) = \sqrt{\frac{\pi}{2 y}}e^{-y} \left( 1 + O\left(\frac{1+|\nu|^2}{y}\right)\right). \end{align} $$
For each of the stated bounds, the implied constant is absolute.
A.4 Bessel functions: Derivatives with respect to order and to argument
In this section, we quote results from [Reference Gradshteyn and Ryzhik8] related to special values of derivatives of I-Bessel and K-Bessel functions with respect both to order and argument.
A.4.1 Derivatives with respect to the order
First, we quote formulas 8.486(1).20 and 8.486(1).21 for the derivative with respect to the order
![]() $\nu $
at
$\nu $
at
![]() $\nu =\pm 1/2$
:
$\nu =\pm 1/2$
:
 $$ \begin{align} \left.\frac{\partial}{\partial\nu} I_{\nu}(x)\right|_{\nu=\pm1/2} = \frac{1}{\sqrt{2\pi x}}\left(e^x \mathrm{Ei}(-2x) \mp e^{-x} \mathrm{Ei}(2x)\right) \,\,\,\,\, \mathrm{for} x>0 \end{align} $$
$$ \begin{align} \left.\frac{\partial}{\partial\nu} I_{\nu}(x)\right|_{\nu=\pm1/2} = \frac{1}{\sqrt{2\pi x}}\left(e^x \mathrm{Ei}(-2x) \mp e^{-x} \mathrm{Ei}(2x)\right) \,\,\,\,\, \mathrm{for} x>0 \end{align} $$
and
 $$ \begin{align} \left.\frac{\partial}{\partial\nu} K_{\nu}(x)\right|_{\nu=\pm 1/2} =\mp\sqrt{\frac{\pi}{2x}}e^x \mathrm{Ei}(-2x) \,\,\,\,\, \mathrm{for} x>0. \end{align} $$
$$ \begin{align} \left.\frac{\partial}{\partial\nu} K_{\nu}(x)\right|_{\nu=\pm 1/2} =\mp\sqrt{\frac{\pi}{2x}}e^x \mathrm{Ei}(-2x) \,\,\,\,\, \mathrm{for} x>0. \end{align} $$
Combining (A.13) and (A.14) with the bound (A.8) shows that for
![]() $x\to \infty $
, we have that
$x\to \infty $
, we have that
 $$ \begin{align} \left|\left.\frac{\partial}{\partial\nu} I_{\nu}(x)\right|_{\nu=\pm 1/2}\right|\ll\frac{e^x} {\sqrt{2\pi x}} \quad \text{and} \quad \left|\left.\frac{\partial}{\partial\nu}K_{\nu}(x)\right|_{\nu=\pm 1/2}\right|\ll \sqrt{\frac{\pi}{2x}}\frac{e^{-x}}{x}. \end{align} $$
$$ \begin{align} \left|\left.\frac{\partial}{\partial\nu} I_{\nu}(x)\right|_{\nu=\pm 1/2}\right|\ll\frac{e^x} {\sqrt{2\pi x}} \quad \text{and} \quad \left|\left.\frac{\partial}{\partial\nu}K_{\nu}(x)\right|_{\nu=\pm 1/2}\right|\ll \sqrt{\frac{\pi}{2x}}\frac{e^{-x}}{x}. \end{align} $$
Second, we quote formulas 8.486(1).8 and 8.486(1).6 with
![]() $n=1$
for the derivative with respect to the order
$n=1$
for the derivative with respect to the order
![]() $\nu $
at
$\nu $
at
![]() $\nu =1$
:
$\nu =1$
:
 $$ \begin{align} \left.\frac{\partial}{\partial\nu} I_{\nu}(x)\right|_{\nu=1} = K_1(x)-\frac{1}{x}I_0(x) \,\,\,\,\, \mathrm{for} x>0 \end{align} $$
$$ \begin{align} \left.\frac{\partial}{\partial\nu} I_{\nu}(x)\right|_{\nu=1} = K_1(x)-\frac{1}{x}I_0(x) \,\,\,\,\, \mathrm{for} x>0 \end{align} $$
and
 $$ \begin{align} \left.\frac{\partial}{\partial\nu} J_{\nu}(x)\right|_{\nu=1} = \frac{\pi}{2}Y_1(x) +\frac{1}{x} J_0(x) \,\,\,\,\, \mathrm{for} x>0. \end{align} $$
$$ \begin{align} \left.\frac{\partial}{\partial\nu} J_{\nu}(x)\right|_{\nu=1} = \frac{\pi}{2}Y_1(x) +\frac{1}{x} J_0(x) \,\,\,\,\, \mathrm{for} x>0. \end{align} $$
By combining the bounds (A.9)–(A.12), we immediately deduce the following bounds as
![]() $x\to \infty $
:
$x\to \infty $
:
 $$ \begin{align} \left|\left.\frac{\partial}{\partial\nu} I_{\nu}(x)\right|_{\nu=1}\right|\ll\frac{e^x} {x\sqrt{2\pi x}} \quad \text{and} \quad \left|\left.\frac{\partial}{\partial\nu}J_{\nu}(x)\right|_{\nu=1}\right|\ll \sqrt{\frac{\pi}{2x}}. \end{align} $$
$$ \begin{align} \left|\left.\frac{\partial}{\partial\nu} I_{\nu}(x)\right|_{\nu=1}\right|\ll\frac{e^x} {x\sqrt{2\pi x}} \quad \text{and} \quad \left|\left.\frac{\partial}{\partial\nu}J_{\nu}(x)\right|_{\nu=1}\right|\ll \sqrt{\frac{\pi}{2x}}. \end{align} $$
A.4.2 Derivatives with respect to the argument
We will quote formulas 8.486.2 and 8.486.11 of [Reference Gradshteyn and Ryzhik8] expressing derivative of the I-Bessel and K-Bessel functions with respect to the argument in terms of a linear combination of the I-Bessel and K-Bessel functions with shifted orders:
and
Acknowledgment
We thank the anonymous referee for many valuable suggestions which helped us improve the clarity of the exposition.