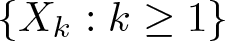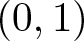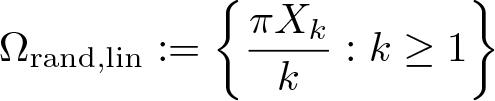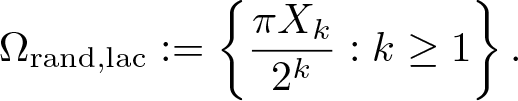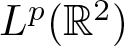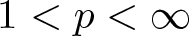We denote by ![]() $\mathcal{R}$ the collection of all rectangles in the plane; if R belongs to
$\mathcal{R}$ the collection of all rectangles in the plane; if R belongs to ![]() $\mathcal{R}$, we denote by
$\mathcal{R}$, we denote by ![]() $\omega_R \in (0,\pi)$ the angle that its longest side makes with the Oy-axis. Without loss of generality, we will always suppose that we have actually
$\omega_R \in (0,\pi)$ the angle that its longest side makes with the Oy-axis. Without loss of generality, we will always suppose that we have actually ![]() $0 \leq \omega_R \leq \frac{\pi}{2}$.
$0 \leq \omega_R \leq \frac{\pi}{2}$.
1. Introduction
Given any set of directions ![]() $\Omega \subset \mathbb{S}^1$, one can define the directional family of rectangle
$\Omega \subset \mathbb{S}^1$, one can define the directional family of rectangle ![]() $\mathcal{R}_\Omega$ as
$\mathcal{R}_\Omega$ as
and then consider the directional maximal operator ![]() $M_\Omega$ defined for
$M_\Omega$ defined for ![]() $f : \mathbb{R}^2 \rightarrow \mathbb{R}$ locally integrable and
$f : \mathbb{R}^2 \rightarrow \mathbb{R}$ locally integrable and ![]() $x \in \mathbb{R}^2$ as
$x \in \mathbb{R}^2$ as
 \begin{equation*}M_\Omega f(x) := \sup_{x \in R \in \mathcal{R}_\Omega} \frac{1}{\left| R\right|}\int_R \left| f\right|.\end{equation*}
\begin{equation*}M_\Omega f(x) := \sup_{x \in R \in \mathcal{R}_\Omega} \frac{1}{\left| R\right|}\int_R \left| f\right|.\end{equation*} The boundedness property of the operator ![]() $M_\Omega$ is deeply related to the geometric structure of the set of directions Ω. For example, in the case where
$M_\Omega$ is deeply related to the geometric structure of the set of directions Ω. For example, in the case where ![]() $\Omega = \mathbb{S}^1$, the following obstruction of the Euclidean plane (which is also true in higher dimension) allows us to completely describe the boundedness property of the operator
$\Omega = \mathbb{S}^1$, the following obstruction of the Euclidean plane (which is also true in higher dimension) allows us to completely describe the boundedness property of the operator ![]() $M_{\mathbb{S}^1}$.
$M_{\mathbb{S}^1}$.
Theorem 1. (Kakeya blow with  $\mathcal{R}$)
$\mathcal{R}$)
Given any large constant ![]() $A \gg 1$, there exists a finite family of rectangles
$A \gg 1$, there exists a finite family of rectangles ![]() $\left\{R_i : i \in I \right\} \subset {\mathcal{R}}$ such that we have
$\left\{R_i : i \in I \right\} \subset {\mathcal{R}}$ such that we have
 \begin{equation*}\left| \bigcup_{i \in I} TR_i \right| \geq A\left| \bigcup_{i \in I} R_i \right|.\end{equation*}
\begin{equation*}\left| \bigcup_{i \in I} TR_i \right| \geq A\left| \bigcup_{i \in I} R_i \right|.\end{equation*}Here, we have denoted by TR the rectangle R translated along its longest side by its own length
The reader can find a proof of this Theorem in [Reference Fefferman4]: it follows that given any large constant ![]() $A \gg 1$, there exists a bounded set E satisfying the following estimate
$A \gg 1$, there exists a bounded set E satisfying the following estimate
 \begin{equation*} \left| \left\{M_{\mathbb{S}^1} \mathbb{1}_E \geq \frac{1}{2} \right\} \right| \geq A\left|E \right|.\end{equation*}
\begin{equation*} \left| \left\{M_{\mathbb{S}^1} \mathbb{1}_E \geq \frac{1}{2} \right\} \right| \geq A\left|E \right|.\end{equation*} It suffices to set ![]() $E = \cup_{i \in I} R_i$ and to observe that we have the following inclusion:
$E = \cup_{i \in I} R_i$ and to observe that we have the following inclusion:
 \begin{equation*}\bigcup_{i \in I} TR_i \subset \left\{M_{\mathbb{S}^1} \mathbb{1}_E \geq \frac{1}{2} \right\}.\end{equation*}
\begin{equation*}\bigcup_{i \in I} TR_i \subset \left\{M_{\mathbb{S}^1} \mathbb{1}_E \geq \frac{1}{2} \right\}.\end{equation*}The previous estimate easily implies the following.
Theorem 2. The operator ![]() $M_{\mathbb{S}^1}$ is not bounded on L p for any
$M_{\mathbb{S}^1}$ is not bounded on L p for any ![]() $p \lt \infty$.
$p \lt \infty$.
Far from being exotic, Theorem 1 has deep implications in harmonic analysis: for example, it is a central part of Fefferman’s work in [Reference Fefferman4] where he disproves the famous Ball multiplier conjecture. A natural question is the following: given a set of directions Ω, is it possible to make a Kakeya blow only with the directional family ![]() $\mathcal{R}_\Omega$? This question has been investigated by different analyst among which are [Reference D’Aniello and Moonens2, Reference Gauvan5–Reference Katz7, Reference Nagel, Stein and Wainger9] to cite a few. In [Reference Bateman1], Bateman answered this question as he classified the
$\mathcal{R}_\Omega$? This question has been investigated by different analyst among which are [Reference D’Aniello and Moonens2, Reference Gauvan5–Reference Katz7, Reference Nagel, Stein and Wainger9] to cite a few. In [Reference Bateman1], Bateman answered this question as he classified the ![]() $L^p(\mathbb{R}^2)$ behaviour of those operators according to the geometry of the set Ω. Precisely, he proved that the notion of finitely lacunary for a set of directions were the correct one to consider.
$L^p(\mathbb{R}^2)$ behaviour of those operators according to the geometry of the set Ω. Precisely, he proved that the notion of finitely lacunary for a set of directions were the correct one to consider.
Theorem 3. (Bateman)
We have the following alternative:
• If Ω is finitely lacunary, then
 $M_\Omega$ is bounded on L p for any p > 1.
$M_\Omega$ is bounded on L p for any p > 1.• If Ω is not finitely lacunary, then it is possible to make a Kakeya blow with the family
 $\mathcal{R}_\Omega$. In particular, the operator
$\mathcal{R}_\Omega$. In particular, the operator  $M_\Omega$ is not bounded on L p for any
$M_\Omega$ is not bounded on L p for any  $p \lt \infty$.
$p \lt \infty$.
Let us define the notion of finite lacunarity following a nice presentation made by Kroc and Pramanik [Reference Kroc and Pramanik8]: we start by defining the notion of lacunary sequence and then the notion of lacunary set of finite order. We say that a sequence of real numbers ![]() $L=\left\{\ell_k : k \geq 1\right\}$ is a lacunary sequence converging to
$L=\left\{\ell_k : k \geq 1\right\}$ is a lacunary sequence converging to ![]() $\ell \in \mathbb{R}$ when there exists
$\ell \in \mathbb{R}$ when there exists ![]() $0 \lt \lambda \lt 1$ such that
$0 \lt \lambda \lt 1$ such that
for any k. For example, the sequences  $\left\{\frac{1}{2^k} : k \geq 2\right\}$ and
$\left\{\frac{1}{2^k} : k \geq 2\right\}$ and  $\left\{\frac{1}{k!} : k\geq 4\right\}$ are lacunary. We define now by induction the notion of lacunary set of finite order.
$\left\{\frac{1}{k!} : k\geq 4\right\}$ are lacunary. We define now by induction the notion of lacunary set of finite order.
Definition 4. (Lacunary set of finite order)
A lacunary set of order 0 in ![]() $\mathbb{R}$ is a set which is either empty or a singleton. Recursively, for
$\mathbb{R}$ is a set which is either empty or a singleton. Recursively, for ![]() $N \in \mathbb{N}^*$, we say that a set Ω included in
$N \in \mathbb{N}^*$, we say that a set Ω included in ![]() $\mathbb{R}$ is a lacunary set of order at most N + 1 – and write
$\mathbb{R}$ is a lacunary set of order at most N + 1 – and write ![]() $\Omega \in \Lambda(N+1)$ – wether there exists a lacunary sequence L with the following properties: for any
$\Omega \in \Lambda(N+1)$ – wether there exists a lacunary sequence L with the following properties: for any ![]() $a,b \in L$ such that a < b and
$a,b \in L$ such that a < b and ![]() $(a,b) \cap L = \emptyset$, the set
$(a,b) \cap L = \emptyset$, the set ![]() $\Omega \cap (a,b)$ is a lacunary set of order at most N, that is,
$\Omega \cap (a,b)$ is a lacunary set of order at most N, that is, ![]() $\Omega \cap (a,b) \in \Lambda(N)$.
$\Omega \cap (a,b) \in \Lambda(N)$.
For example, the set
 \begin{equation*}\Omega := \left\{\frac{\pi}{2^k} + \frac{\pi}{4^l} : k,l \in \mathbb{N}, l \leq k \right\} \end{equation*}
\begin{equation*}\Omega := \left\{\frac{\pi}{2^k} + \frac{\pi}{4^l} : k,l \in \mathbb{N}, l \leq k \right\} \end{equation*}is a lacunary set of order 2. In this case, observe that the set Ω cannot be re-written as a monotone sequence, since it has several points of accumulation. We can finally give a definition of a finitely lacunary set.
Definition 5. (Finitely lacunary set)
A set Ω in ![]() $[0,\pi)$ is said to be finitely lacunary if there exists a finite number of set
$[0,\pi)$ is said to be finitely lacunary if there exists a finite number of set ![]() $\Omega_1, \dots, \Omega_M$, which are lacunary of finite order such that
$\Omega_1, \dots, \Omega_M$, which are lacunary of finite order such that
 \begin{equation*} \Omega \subset \bigcup_{k \leq M } \Omega_k.\end{equation*}
\begin{equation*} \Omega \subset \bigcup_{k \leq M } \Omega_k.\end{equation*}2. Can we apply Bateman’s Theorem?
A classic example of set which is known to be not finitely lacunary is the set
 \begin{equation*}\Omega_{\text{lin}} = \left\{\frac{\pi}{n} : n \in \mathbb{N}^* \right\}.\end{equation*}
\begin{equation*}\Omega_{\text{lin}} = \left\{\frac{\pi}{n} : n \in \mathbb{N}^* \right\}.\end{equation*} Indeed, the classic construction of Perron trees shows that it is possible to make a Kakeya blow with the family ![]() $\mathcal{R}_{\Omega_{\text{lin}}}$: hence, an application of Bateman’s Theorem implies that
$\mathcal{R}_{\Omega_{\text{lin}}}$: hence, an application of Bateman’s Theorem implies that ![]() $\Omega_{\text{lin}}$ is not finitely lacunary. The second classic example of set which is known to be finitely lacunary is the set
$\Omega_{\text{lin}}$ is not finitely lacunary. The second classic example of set which is known to be finitely lacunary is the set
 \begin{equation*}\Omega_{\text{lac}} = \left\{\frac{\pi}{2^n} : n \in \mathbb{N}^* \right\}.\end{equation*}
\begin{equation*}\Omega_{\text{lac}} = \left\{\frac{\pi}{2^n} : n \in \mathbb{N}^* \right\}.\end{equation*} One can see that the set ![]() $\Omega_{\text{lac}}$ is finitely lacunary by definition, and it was in [Reference Nagel, Stein and Wainger9] that Nagel, Stein and Waigner proved that the maximal operator
$\Omega_{\text{lac}}$ is finitely lacunary by definition, and it was in [Reference Nagel, Stein and Wainger9] that Nagel, Stein and Waigner proved that the maximal operator ![]() $M_{\Omega_{\text{lac}}}$ is bounded on
$M_{\Omega_{\text{lac}}}$ is bounded on ![]() $L^p(\mathbb{R}^2)$ for any
$L^p(\mathbb{R}^2)$ for any ![]() $1 \lt p \lt \infty$; their proof relies on Fourier analysis. Also, let us say that the comprehension of the sets
$1 \lt p \lt \infty$; their proof relies on Fourier analysis. Also, let us say that the comprehension of the sets ![]() $\Omega_{\text{lin}}$ and
$\Omega_{\text{lin}}$ and ![]() $\Omega_{\text{lac}}$ is important because they are the most simple (and smallest) cases of infinite sets which yield maximal operator having different boundedness properties.
$\Omega_{\text{lac}}$ is important because they are the most simple (and smallest) cases of infinite sets which yield maximal operator having different boundedness properties.
However, even if Bateman’s Theorem is extremely satisfying, it appears to be difficult to decide if a given set Ω is finitely lacunary or not. The most striking example was raised by Stokolos: at the present time, it is not known if the set
 \begin{equation*} \Omega_{\sin,{lac}} := \left\{\frac{\pi\, \sin(n)}{2^n} : n \in \mathbb{N}^* \right\}\end{equation*}
\begin{equation*} \Omega_{\sin,{lac}} := \left\{\frac{\pi\, \sin(n)}{2^n} : n \in \mathbb{N}^* \right\}\end{equation*}is finitely lacunary or not. The main problem of this set of directions is that we have a very poor control on the deterministic sequence ![]() $\left\{\sin(n) : n \geq 1 \right\}$ and that initially, the set
$\left\{\sin(n) : n \geq 1 \right\}$ and that initially, the set ![]() $\Omega_{\text{lac}} $ is finitely lacunary; hence, the perturbations are quite difficult to handle. In [Reference D’Aniello, Gauvan and Moonens3], with D’Aniello and Moonens, we were able to show that the following set
$\Omega_{\text{lac}} $ is finitely lacunary; hence, the perturbations are quite difficult to handle. In [Reference D’Aniello, Gauvan and Moonens3], with D’Aniello and Moonens, we were able to show that the following set
 \begin{equation*} \Omega_{\sin,{lin}} := \left\{\frac{\pi\, \sin(n)}{n} : n \in \mathbb{N}^* \right\}\end{equation*}
\begin{equation*} \Omega_{\sin,{lin}} := \left\{\frac{\pi\, \sin(n)}{n} : n \in \mathbb{N}^* \right\}\end{equation*}is not finitely lacunary (this was also a set considered by Stokolos). More precisely, we studied the maximal operator  $M_{\Omega_{\sin,\text{lin}}}$ associated, and improving on concrete techniques, we proved that this operator is not bounded on
$M_{\Omega_{\sin,\text{lin}}}$ associated, and improving on concrete techniques, we proved that this operator is not bounded on ![]() $L^p(\mathbb{R}^2)$ for any
$L^p(\mathbb{R}^2)$ for any ![]() $1 \lt p \lt \infty$: the heart of the method relied on the introduction of the Perron’s capacity of a set of directions. We need some notations to recall our results: given an infinite set of directions
$1 \lt p \lt \infty$: the heart of the method relied on the introduction of the Perron’s capacity of a set of directions. We need some notations to recall our results: given an infinite set of directions ![]() $\Omega \subset \mathbb{S}^1$ whose only point of accumulation is 0 and we denote, for notational convenience, by Ω−1, the set
$\Omega \subset \mathbb{S}^1$ whose only point of accumulation is 0 and we denote, for notational convenience, by Ω−1, the set  $\left\{\frac{\pi}{u} : u \in \Omega \right\}$, that is
$\left\{\frac{\pi}{u} : u \in \Omega \right\}$, that is
 \begin{equation*} \Omega^{-1} := \frac{\pi}{\Omega},\end{equation*}
\begin{equation*} \Omega^{-1} := \frac{\pi}{\Omega},\end{equation*}and we order Ω−1 as a strictly increasing sequence ![]() $\left\{ u_k:k\in{\mathbb{N}}^* \right\}$. With those notations, we define the Perron’s factor of Ω as
$\left\{ u_k:k\in{\mathbb{N}}^* \right\}$. With those notations, we define the Perron’s factor of Ω as
 \begin{equation*}G(\Omega) := \sup_{\begin{subarray}{c}k \geq 1\\ l \leq k\end{subarray}} \left( \frac{u_{k+2l} - u_{k+l}}{u_{k+l} - u_{k}} + \frac{u_{k+l} - u_{k}}{u_{k+2l} - u_{k+l}} \right).\end{equation*}
\begin{equation*}G(\Omega) := \sup_{\begin{subarray}{c}k \geq 1\\ l \leq k\end{subarray}} \left( \frac{u_{k+2l} - u_{k+l}}{u_{k+l} - u_{k}} + \frac{u_{k+l} - u_{k}}{u_{k+2l} - u_{k+l}} \right).\end{equation*}In [Reference Hare and Rönning6], Hare and Ronning proved the following Theorem.
Theorem 6 (Hare and Ronning)
If we have ![]() $G(\Omega) \lt \infty$, then it is possible to make a Kakeya blow with the family
$G(\Omega) \lt \infty$, then it is possible to make a Kakeya blow with the family ![]() $\mathcal{R}_\Omega$.
$\mathcal{R}_\Omega$.
It turns out that it is difficult to compute the Perron factor of the set
 \begin{equation*}\Omega_{\sin,{lin}} = \left\{\frac{\pi\, \sin(n)}{n} : n \geq 1 \right\}\end{equation*}
\begin{equation*}\Omega_{\sin,{lin}} = \left\{\frac{\pi\, \sin(n)}{n} : n \geq 1 \right\}\end{equation*}since the oscillation of the cosinus prevent us to obtain a good description of the increasing sequence ![]() $\left\{ u_k:k\in\mathbb{N}^* \right\}$ associated to
$\left\{ u_k:k\in\mathbb{N}^* \right\}$ associated to ![]() $\Omega_{\sin,\text{lin}}$. Based on a careful reading of the proof of Theorem 6, for an arbitrary set of directions Ω included in
$\Omega_{\sin,\text{lin}}$. Based on a careful reading of the proof of Theorem 6, for an arbitrary set of directions Ω included in ![]() $\mathbb{S}^1$, we define its Perron’s capacity as
$\mathbb{S}^1$, we define its Perron’s capacity as
 \begin{equation*}P(\Omega) :=\liminf_{N \to\infty} \inf_{\begin{subarray}{c}U \subset \Omega^{-1} \\ \#U = 2^N \end{subarray}} G(\Omega) \in [2,\infty],\end{equation*}
\begin{equation*}P(\Omega) :=\liminf_{N \to\infty} \inf_{\begin{subarray}{c}U \subset \Omega^{-1} \\ \#U = 2^N \end{subarray}} G(\Omega) \in [2,\infty],\end{equation*}where as before
 \begin{equation*}G(\Omega) = \sup_{\begin{subarray}{c}k,l \geq 1\\ k+2l \leq 2^N\end{subarray}} \left( \frac{u_{k+2l} - u_{k+l}}{u_{k+l} - u_{k}} + \frac{u_{k+l} - u_{k}}{u_{k+2l} - u_{k+l}} \right)\end{equation*}
\begin{equation*}G(\Omega) = \sup_{\begin{subarray}{c}k,l \geq 1\\ k+2l \leq 2^N\end{subarray}} \left( \frac{u_{k+2l} - u_{k+l}}{u_{k+l} - u_{k}} + \frac{u_{k+l} - u_{k}}{u_{k+2l} - u_{k+l}} \right)\end{equation*}if ![]() $U = \{u_1 \lt \cdots \lt u_{2^N} \}$. In [Reference D’Aniello, Gauvan and Moonens3], we proved the following (in contrast with Hare and Ronning Theorem, we do not assume that the set Ω is ordered).
$U = \{u_1 \lt \cdots \lt u_{2^N} \}$. In [Reference D’Aniello, Gauvan and Moonens3], we proved the following (in contrast with Hare and Ronning Theorem, we do not assume that the set Ω is ordered).
Theorem 7. (D’Aniello, G. and Moonens)
For any set of directions Ω, if we have
then it is possible to make a Kakeya blow with the family ![]() $\mathcal{R}_\Omega$. In particular, for any
$\mathcal{R}_\Omega$. In particular, for any ![]() $p \lt \infty$, one has
$p \lt \infty$, one has  $ \left\|M_\Omega \right\|_p = \infty$.
$ \left\|M_\Omega \right\|_p = \infty$.
Loosely speaking, if ![]() $P(\Omega) \lt \infty$, then the set Ω contains arbitrary large set which are (more or less) uniformly distributed, and this geometric pattern prevents the set Ω to be finitely lacunary. The advantage of Theorem 7 is that it allows us to make effective computation. However, as mentioned earlier, the following case is still unsettled.
$P(\Omega) \lt \infty$, then the set Ω contains arbitrary large set which are (more or less) uniformly distributed, and this geometric pattern prevents the set Ω to be finitely lacunary. The advantage of Theorem 7 is that it allows us to make effective computation. However, as mentioned earlier, the following case is still unsettled.
Question 1.
Is the following set of direction
 \begin{equation*} \Omega_{\sin,{lac}} := \left\{\frac{\pi\,\sin(n)}{2^n} : n \in \mathbb{N}^* \right\}\end{equation*}
\begin{equation*} \Omega_{\sin,{lac}} := \left\{\frac{\pi\,\sin(n)}{2^n} : n \in \mathbb{N}^* \right\}\end{equation*}finitely lacunary or not?
3. Results
Our result concerns random sets of directions which are meant to give a generic comprehension of the two classic examples ![]() $\Omega_{\text{lin}}$ and
$\Omega_{\text{lin}}$ and ![]() $\Omega_{\text{lac}}$ when they are randomly perturbated. Precisely, we consider the following random sets of slopes
$\Omega_{\text{lac}}$ when they are randomly perturbated. Precisely, we consider the following random sets of slopes
 \begin{equation*}\Omega_{\text{rand},\text{lin}} := \left\{\frac{\pi X_k}{k} : k \geq 1 \right\} \end{equation*}
\begin{equation*}\Omega_{\text{rand},\text{lin}} := \left\{\frac{\pi X_k}{k} : k \geq 1 \right\} \end{equation*}and
 \begin{equation*}\Omega_{\text{rand},\text{lac}} := \left\{\frac{\pi X_k}{2^k} : k \geq 1 \right\}, \end{equation*}
\begin{equation*}\Omega_{\text{rand},\text{lac}} := \left\{\frac{\pi X_k}{2^k} : k \geq 1 \right\}, \end{equation*}where ![]() $\left\{X_k : k \geq 1 \right\}$ are random variables uniformly distributed in
$\left\{X_k : k \geq 1 \right\}$ are random variables uniformly distributed in ![]() $(0,1)$ and independent. To begin with, we prove the following Theorem.
$(0,1)$ and independent. To begin with, we prove the following Theorem.
Theorem 8. The Perron’s capacities of ![]() $\Omega_{\text{rand},\text{lin}}$ is finite almost surely, that is, we have almost surely
$\Omega_{\text{rand},\text{lin}}$ is finite almost surely, that is, we have almost surely
In some sense, Theorem 8 means that if a set Ω presents structured patterns – like large uniformly distributed sequence – then a small perturbation of Ω will still exhibit those patterns. The second result reads as follow.
Theorem 9. The Perron’s capacities of ![]() $\Omega_{\text{rand},\text{lac}}$ is finite almost surely, that is, we have almost surely
$\Omega_{\text{rand},\text{lac}}$ is finite almost surely, that is, we have almost surely
The proof of Theorems 8 and 9 relies on the possibility to compute effectively the Perron’s capacity of the random sets ![]() $\Omega_{\text{rand},\text{lin}}$ and
$\Omega_{\text{rand},\text{lin}}$ and ![]() $\Omega_{\text{rand},\text{lac}}$.
$\Omega_{\text{rand},\text{lac}}$.
4. Proof of Theorem 8
We wish to prove that the Perron’s capacity of ![]() $\Omega_{\text{rand},\text{lin}}$ is finite almost surely. We are simply going to prove that the set
$\Omega_{\text{rand},\text{lin}}$ is finite almost surely. We are simply going to prove that the set  $\Omega^{-1}_{\text{rand},\text{lin}}$ contains small perturbation of arbitrarily long homogeneous sets. We say that a set H of the form
$\Omega^{-1}_{\text{rand},\text{lin}}$ contains small perturbation of arbitrarily long homogeneous sets. We say that a set H of the form
 \begin{equation*}H := H_{a,N} = \{ka :1 \leq k \leq 2^N \}\end{equation*}
\begin{equation*}H := H_{a,N} = \{ka :1 \leq k \leq 2^N \}\end{equation*}for some integer ![]() $a \in \mathbb{N}^*$ is a homogeneous set. The following claim is easy.
$a \in \mathbb{N}^*$ is a homogeneous set. The following claim is easy.
Claim 1.
For any ![]() $a,N \in \mathbb{N}$, one has
$a,N \in \mathbb{N}$, one has ![]() $G(H_{a,N}) = 2$.
$G(H_{a,N}) = 2$.
We wish to perturb a little a homogeneous set H into a set Hʹ such that the Perron’s factor of Hʹ is still controlled. Precisely, fix any ![]() $a,N\in \mathbb{N}^*$ and let ϵ be an arbitrary function
$a,N\in \mathbb{N}^*$ and let ϵ be an arbitrary function
Define then the set ![]() $H_{a,N}(\epsilon)$ as
$H_{a,N}(\epsilon)$ as
If the perturbation ϵ is small enough compared to the integer N, one can control uniformly ![]() $G(H^{\prime})$.
$G(H^{\prime})$.
Proposition 1. With the previous notations, if we have
 \begin{equation*}2^N\|\epsilon\|_\infty \leq \frac{1}{2},\end{equation*}
\begin{equation*}2^N\|\epsilon\|_\infty \leq \frac{1}{2},\end{equation*}then we have ![]() $G(H_{a,N}(\epsilon)) \lt 6$.
$G(H_{a,N}(\epsilon)) \lt 6$.
We are now ready to prove Theorem 8. We fix a large integer ![]() $N \in \mathbb{N}$ and consider the following set of indices
$N \in \mathbb{N}$ and consider the following set of indices
 \begin{equation*}E_N := \left\{k \in \mathbb{N} : |X_k-1| \leq 2^{-N} \right\}.\end{equation*}
\begin{equation*}E_N := \left\{k \in \mathbb{N} : |X_k-1| \leq 2^{-N} \right\}.\end{equation*} In other words, an integer k belongs to EN when Xk is close to 1 with precision ![]() $2^{-N}$. We claim that this random set EN contains almost surely large (with at least 2N points) homogeneous sequences.
$2^{-N}$. We claim that this random set EN contains almost surely large (with at least 2N points) homogeneous sequences.
Claim 2.
For any ![]() $N \geq 1$, the set EN contains a homogeneous set of cardinal 2N almost surely.
$N \geq 1$, the set EN contains a homogeneous set of cardinal 2N almost surely.
Proof. Observe that for any ![]() $a \in \mathbb{N}^*$, the following probability
$a \in \mathbb{N}^*$, the following probability ![]() $\mathbb{P}( H_{a,N} \subset E_N)$ is independent of a: indeed since the random variables
$\mathbb{P}( H_{a,N} \subset E_N)$ is independent of a: indeed since the random variables ![]() $\left\{X_k : k \geq 1 \right\}$ are independent and uniformly distributed, we have
$\left\{X_k : k \geq 1 \right\}$ are independent and uniformly distributed, we have
 \begin{equation*}\mathbb{P}( H_{a,N} \subset E_N) = \prod_{k \in H_{a,N}}\mathbb{P}\left(|X_k-1| \leq 2^{-N}\right) = \frac{1}{2^{N2^N}} .\end{equation*}
\begin{equation*}\mathbb{P}( H_{a,N} \subset E_N) = \prod_{k \in H_{a,N}}\mathbb{P}\left(|X_k-1| \leq 2^{-N}\right) = \frac{1}{2^{N2^N}} .\end{equation*} Hence, we fix a sequence  $\left\{a_i \right\}_{i \geq 1}$ satisfying for any i ≠ j
$\left\{a_i \right\}_{i \geq 1}$ satisfying for any i ≠ j
 \begin{equation*}H_{a_i,N} \cap H_{a_j,N} = \emptyset.\end{equation*}
\begin{equation*}H_{a_i,N} \cap H_{a_j,N} = \emptyset.\end{equation*} For example, setting ![]() $a_i = 2^{2N(i+1)}$ works since we have
$a_i = 2^{2N(i+1)}$ works since we have ![]() $a_i 2^N \lt a_{i+1}$ for any
$a_i 2^N \lt a_{i+1}$ for any ![]() $i \geq 1$. In particular, this means that the events
$i \geq 1$. In particular, this means that the events
 \begin{equation*}\{\left(H_{a_i,N} \subset E_N\right) : i \geq 1 \}\end{equation*}
\begin{equation*}\{\left(H_{a_i,N} \subset E_N\right) : i \geq 1 \}\end{equation*}are independent, and since we have
 \begin{equation*}\sum_{i \geq 1} \mathbb{P}( H_{a_i,N} \subset E_N) = \infty, \end{equation*}
\begin{equation*}\sum_{i \geq 1} \mathbb{P}( H_{a_i,N} \subset E_N) = \infty, \end{equation*}an application of Borel–Cantelli lemma yields the conclusion.
We can now conclude the proof: we define a perturbation ϵ for any ![]() $n \geq 1$ as
$n \geq 1$ as
We fix a large integer ![]() $N \gg 1$, and we know that almost surely there exists an integer
$N \gg 1$, and we know that almost surely there exists an integer ![]() $a \in \mathbb{N}^*$ such that
$a \in \mathbb{N}^*$ such that ![]() $H_{a,N} \subset E_N$. Observe now that by definition one has the following inclusion
$H_{a,N} \subset E_N$. Observe now that by definition one has the following inclusion
 \begin{equation*}H_{a,N}(\epsilon) \subset \Omega^{-1}_{\text{rand},\text{lin}}.\end{equation*}
\begin{equation*}H_{a,N}(\epsilon) \subset \Omega^{-1}_{\text{rand},\text{lin}}.\end{equation*} However, since ![]() $H_{a,N} \subset E_N $ and that it is not difficult to see that we have
$H_{a,N} \subset E_N $ and that it is not difficult to see that we have
 \begin{equation*} \|\epsilon_{|H_{a,N}} \|_\infty \lesssim 2^{-N}.\end{equation*}
\begin{equation*} \|\epsilon_{|H_{a,N}} \|_\infty \lesssim 2^{-N}.\end{equation*} Indeed, for ![]() $k \in H_{a,N} \subset E_N$, we have
$k \in H_{a,N} \subset E_N$, we have
 \begin{equation*}\left|1 + \epsilon(k) \right| = \left| \frac{1}{1 +(X_k-1)} \right| \lesssim 1 + 2\left|X_k-1\right| \lesssim 1 + 2^{-N}.\end{equation*}
\begin{equation*}\left|1 + \epsilon(k) \right| = \left| \frac{1}{1 +(X_k-1)} \right| \lesssim 1 + 2\left|X_k-1\right| \lesssim 1 + 2^{-N}.\end{equation*} It follows that we have ![]() $P(\Omega_{\text{rand},\text{lin}}) \lt 6$ almost surely applying Proposition 1.
$P(\Omega_{\text{rand},\text{lin}}) \lt 6$ almost surely applying Proposition 1.
5. Proof of Theorem 9
We wish to prove that the Perron’s capacity of ![]() $\Omega_{\text{rand},\text{lac}}$ is finite almost surely. Observe that if U is a set in
$\Omega_{\text{rand},\text{lac}}$ is finite almost surely. Observe that if U is a set in ![]() $\mathbb{R}$ who is well distributed, then one can control its Perron’s capacity.
$\mathbb{R}$ who is well distributed, then one can control its Perron’s capacity.
Claim 3.
If we have δ > 0 and a set
 \begin{equation*}U = \left\{u_1 \lt \cdots \lt u_{2^N} \right\} \end{equation*}
\begin{equation*}U = \left\{u_1 \lt \cdots \lt u_{2^N} \right\} \end{equation*}such that for any ![]() $1 \leq i \leq 2^N-1$, we have
$1 \leq i \leq 2^N-1$, we have
then one has ![]() $G(U) \lesssim 1$.
$G(U) \lesssim 1$.
Proof. For any ![]() $i,j$ such that
$i,j$ such that ![]() $i+j \leq 2^N-1$, one has
$i+j \leq 2^N-1$, one has ![]() $u_{i+j} - u_i \simeq j\delta$. Hence,
$u_{i+j} - u_i \simeq j\delta$. Hence, ![]() $i,j$ such that
$i,j$ such that ![]() $i+2j \leq 2^{N-1}$, we have
$i+2j \leq 2^{N-1}$, we have
 \begin{equation*}\frac{u_{i+2j} - u_{i+j}}{u_{i+j} - u_{i}} + \frac{u_{i+j} - u_{i}}{u_{i+2j} - u_{i+j}} \simeq \frac{2j\delta}{j\delta} + \frac{j\delta}{2j\delta} \simeq 1.\end{equation*}
\begin{equation*}\frac{u_{i+2j} - u_{i+j}}{u_{i+j} - u_{i}} + \frac{u_{i+j} - u_{i}}{u_{i+2j} - u_{i+j}} \simeq \frac{2j\delta}{j\delta} + \frac{j\delta}{2j\delta} \simeq 1.\end{equation*} Hence, we obtain ![]() $G(U) \lesssim 1$ as claimed
$G(U) \lesssim 1$ as claimed
We are going to prove the following proposition.
Proposition 2. For any ![]() $N \geq 1$, there exists almost surely a scale δ > 0 and a set
$N \geq 1$, there exists almost surely a scale δ > 0 and a set  $U \subset \Omega^{-1}_{\text{rand},\text{lac}}$ such that
$U \subset \Omega^{-1}_{\text{rand},\text{lac}}$ such that
 \begin{equation*}U := \left\{u_1 \lt \cdots \lt u_{2^{N-1}} \right\} \end{equation*}
\begin{equation*}U := \left\{u_1 \lt \cdots \lt u_{2^{N-1}} \right\} \end{equation*}and for any ![]() $i \leq 2^{N-1}$, one has
$i \leq 2^{N-1}$, one has
Theorem 9 is a consequence of Claim 3 and Proposition 2: for any N, we can exhibit almost surely a set  $U \subset \Omega^{-1}_{\text{rand},\text{lac}}$ of cardinal 2N such that
$U \subset \Omega^{-1}_{\text{rand},\text{lac}}$ of cardinal 2N such that ![]() $G(U) \lesssim 1,$ and so we obtain
$G(U) \lesssim 1,$ and so we obtain
as expected. The rest of the section is devoted to the proof of Proposition 2.
Proof of Proposition 2
We consider the following dyadic intervals for ![]() $d \in \mathbb{N}$
$d \in \mathbb{N}$
 \begin{equation*}I_d := \left[2^d ,2^{d+1}\right].\end{equation*}
\begin{equation*}I_d := \left[2^d ,2^{d+1}\right].\end{equation*} We wish to obtain information on the distribution of the points of the set ![]() $\Omega_{\text{rand},\text{lac}}$ that may be in the interval Id. We fix a large integer
$\Omega_{\text{rand},\text{lac}}$ that may be in the interval Id. We fix a large integer ![]() $N \gg 1$, and we divide each dyadic interval Id into 2N intervals of same length, that is, for any
$N \gg 1$, and we divide each dyadic interval Id into 2N intervals of same length, that is, for any ![]() $1 \leq l \leq 2^N$, we set
$1 \leq l \leq 2^N$, we set
 \begin{equation*}I_{d,l} = \left[2^d\left(1 + \frac{l-1}{2^N} \right), 2^d\left(1 + \frac{l}{2^N} \right) \right].\end{equation*}
\begin{equation*}I_{d,l} = \left[2^d\left(1 + \frac{l-1}{2^N} \right), 2^d\left(1 + \frac{l}{2^N} \right) \right].\end{equation*}Claim 4.
For any ![]() $d \geq 2^N+1$ and any
$d \geq 2^N+1$ and any ![]() $1 \leq l \leq 2^N$, the probability
$1 \leq l \leq 2^N$, the probability
 \begin{equation*}\mathbb{P}\left( \frac{2^{d-l}}{X_{d-l}} \in I_{d,l} \right) := p_{N,l}\end{equation*}
\begin{equation*}\mathbb{P}\left( \frac{2^{d-l}}{X_{d-l}} \in I_{d,l} \right) := p_{N,l}\end{equation*}is independent of d.
Proof. By definition of ![]() $I_{d,l}$, one has
$I_{d,l}$, one has  $2^{d-l}X_{d-l}^{-1} \in I_{d,l}$ if and only if
$2^{d-l}X_{d-l}^{-1} \in I_{d,l}$ if and only if
 \begin{equation*} 2^{-l}\left(1 + \frac{l}{2^N} \right)^{-1} \leq X_{d-l} \leq 2^{-l}\left(1 + \frac{l-1}{2^N} \right)^{-1}.\end{equation*}
\begin{equation*} 2^{-l}\left(1 + \frac{l}{2^N} \right)^{-1} \leq X_{d-l} \leq 2^{-l}\left(1 + \frac{l-1}{2^N} \right)^{-1}.\end{equation*}One has
 \begin{equation*}\mathbb{P}\left( 2^{d-l}X_{d-l}^{-1} \in I_{d,l} \right) = 2^{-l}\left( \left( 1 + \frac{l-1}{2^N} \right)^{-1} - \left(1 + \frac{l}{2^N} \right)^{-1} \right) := p_{l,N}\end{equation*}
\begin{equation*}\mathbb{P}\left( 2^{d-l}X_{d-l}^{-1} \in I_{d,l} \right) = 2^{-l}\left( \left( 1 + \frac{l-1}{2^N} \right)^{-1} - \left(1 + \frac{l}{2^N} \right)^{-1} \right) := p_{l,N}\end{equation*}since the variable ![]() $X_{d-l}$ is uniformly distributed in
$X_{d-l}$ is uniformly distributed in ![]() $(0,1)$.
$(0,1)$.
We fix an extraction ![]() $\{d_s : s \geq 1 \}$ satisfying the following property
$\{d_s : s \geq 1 \}$ satisfying the following property
for any ![]() $s \geq 1$; this growth condition will assure that the events we will consider are independent and we will be able to apply Borel–Cantelli lemma when needed. Thanks to Claim 4 and independence, one can see that for any
$s \geq 1$; this growth condition will assure that the events we will consider are independent and we will be able to apply Borel–Cantelli lemma when needed. Thanks to Claim 4 and independence, one can see that for any ![]() $s \geq 1$, the following probability is independent of s
$s \geq 1$, the following probability is independent of s
 \begin{equation*} \mathbb{P}\left( \bigcap_{l \leq 2^N} \left(\frac{2^{d_s-l}}{X_{d_s-l}} \in I_{d_s,l}\right) \right) = \prod_{l \leq 2^N} p_{N,l} := \eta_N. \end{equation*}
\begin{equation*} \mathbb{P}\left( \bigcap_{l \leq 2^N} \left(\frac{2^{d_s-l}}{X_{d_s-l}} \in I_{d_s,l}\right) \right) = \prod_{l \leq 2^N} p_{N,l} := \eta_N. \end{equation*} Now for any ![]() $d \geq 1$, we consider the following event
$d \geq 1$, we consider the following event ![]() $A_{d,N}$ defined as
$A_{d,N}$ defined as
 \begin{equation*}A_{d,N} := \bigcap_{l \leq 2^N} \left\{\Omega^{-1}_{\text{rand},\text{lac}} \cap I_{d,l} \neq \emptyset \right\}.\end{equation*}
\begin{equation*}A_{d,N} := \bigcap_{l \leq 2^N} \left\{\Omega^{-1}_{\text{rand},\text{lac}} \cap I_{d,l} \neq \emptyset \right\}.\end{equation*} In other words, the event ![]() $A_{d,N}$ occurs when the random set
$A_{d,N}$ occurs when the random set  $\Omega^{-1}_{\text{rand},\text{lac}}$ fills each subintervals
$\Omega^{-1}_{\text{rand},\text{lac}}$ fills each subintervals ![]() $\left\{I_{d,l} : 1 \leq l\leq 2^N \right\}$ with at least one point. In particular, observe that we have
$\left\{I_{d,l} : 1 \leq l\leq 2^N \right\}$ with at least one point. In particular, observe that we have
 \begin{equation*} \bigcap_{l \leq 2^N} \left(\frac{2^{d-l}}{X_{d-l}} \in I_{d,l}\right) \subset A_{d,N}.\end{equation*}
\begin{equation*} \bigcap_{l \leq 2^N} \left(\frac{2^{d-l}}{X_{d-l}} \in I_{d,l}\right) \subset A_{d,N}.\end{equation*}We claim that the union of those events
 \begin{equation*}B_N := \bigcup_{d \geq 1} A_{d,N}\end{equation*}
\begin{equation*}B_N := \bigcup_{d \geq 1} A_{d,N}\end{equation*}occurs almost surely.
Claim 5.
One has ![]() $\mathbb{P}\left(B_N\right) = 1$.
$\mathbb{P}\left(B_N\right) = 1$.
Proof. Indeed, we have
 \begin{equation*}\sum_s \mathbb{P}\left( \bigcap_{l \leq 2^N} \left(\frac{2^{d_s-l}}{X_{d_s-l}} \in I_{d_s,l}\right) \right) = \sum_s \eta_N = \infty.\end{equation*}
\begin{equation*}\sum_s \mathbb{P}\left( \bigcap_{l \leq 2^N} \left(\frac{2^{d_s-l}}{X_{d_s-l}} \in I_{d_s,l}\right) \right) = \sum_s \eta_N = \infty.\end{equation*}Using Borel–Cantelli lemma, one obtains
 \begin{equation*}\mathbb{P}\left( \bigcup_{s \geq 1} A_{N,d_s} \right) = 1.\end{equation*}
\begin{equation*}\mathbb{P}\left( \bigcup_{s \geq 1} A_{N,d_s} \right) = 1.\end{equation*} In particular, one has ![]() $\mathbb{P}(B_N) = 1$.
$\mathbb{P}(B_N) = 1$.
We can now prove Proposition 2 since we have
 \begin{equation*}\mathbb{P}\left( \bigcap_{N \geq 1} B_N \right) = 1.\end{equation*}
\begin{equation*}\mathbb{P}\left( \bigcap_{N \geq 1} B_N \right) = 1.\end{equation*} Precisely, for any ![]() $N \geq 1$, the event BN occurs almost surely, and this means that there exists a (for each N, we just need one) dyadic interval Id such that
$N \geq 1$, the event BN occurs almost surely, and this means that there exists a (for each N, we just need one) dyadic interval Id such that
 \begin{equation*} \Omega^{-1}_{\text{rand},\text{lac}} \cap I_{d,l} \neq \emptyset \end{equation*}
\begin{equation*} \Omega^{-1}_{\text{rand},\text{lac}} \cap I_{d,l} \neq \emptyset \end{equation*}for any ![]() $1 \leq l \leq 2^N$. We let ul be one point in
$1 \leq l \leq 2^N$. We let ul be one point in  $\Omega^{-1}_{\text{rand},\text{lac}} \cap I_{d,l}$, and we claim that the set
$\Omega^{-1}_{\text{rand},\text{lac}} \cap I_{d,l}$, and we claim that the set
 \begin{equation*}U := \left\{u_{2l} : 1 \leq l \leq 2^{N-1} \right\}\end{equation*}
\begin{equation*}U := \left\{u_{2l} : 1 \leq l \leq 2^{N-1} \right\}\end{equation*}satisfy the condition of Proposition 2 with ![]() $\delta \simeq 2^{d-N}$. In particular, we have
$\delta \simeq 2^{d-N}$. In particular, we have ![]() $G(U) \lesssim 1 $ for
$G(U) \lesssim 1 $ for  $U \subset \Omega^{-1}_{\text{rand},\text{lac}} $ with arbitrary large cardinal. This yields almost surely
$U \subset \Omega^{-1}_{\text{rand},\text{lac}} $ with arbitrary large cardinal. This yields almost surely
which concludes the proof.