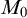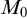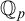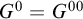1 Introduction
In this paper we study abelian groups definable in p-adically closed fields. Our first main result is a decomposition of these groups into fsg and dfg components. Recall that a definable group G has finitely satisfiable generics (fsg) if there is a global type on G, finitely satisfiable in a small model, with boundedly many left translates. Similarly, G has definable f-generics (dfg) if there is a definable global type on G with boundedly many left translates. If G is definable in an o-minimal expansion of RCF or a p-adically closed field, then G has fsg iff it is definably compact [Reference Hrushovski and Pillay7, Reference Johnson12, Reference Onshuus and Pillay15], and G has dfg iff it is totally non-compact [Reference Conversano and Pillay4, Reference Pillay and Yao19].
The central theorem of this paper is the following decomposition of abelian definable groups in p-adically closed fields into dfg and fsg components.
Theorem 1.1. Suppose that M is a p-adically closed field and G is an abelian group definable in M. Then there is a short exact sequence of definable groups
$$ \begin{align*} 1 \to H \to G \to C \to 1, \end{align*} $$
where H has dfg and C is definably compact and has fsg.
The proof, and several examples of the decomposition, appear in Section 3.
Remark 1.2. An analogous decomposition for abelian groups in o-minimal structures was proved by Conversano and Pillay [Reference Conversano and Pillay4, Propositions 4.6–7]. In fact, they give the decomposition in the more general setting of definably amenable groups. Recall from [Reference Hrushovski and Pillay7, Section 5] that a definable group G is definably amenable if there is a finitely additive probability measure on definable subsets of G, invariant under left translation. Solvable definable groups are definably amenable, because they are amenable in the classical sense from analysis. Definable groups in stable theories are also known to be definably amenable. In NIP theories, a definable group G is definably amenable iff there is a global type on G with boundedly many left translates [Reference Cubides-Kovacsics, Darnière and Leenknegt3]. In particular, dfg and fsg groups are definably amenable.
As mentioned above, Conversano and Pillay proved a decomposition analogous to Theorem 1.1 for definably amenable groups in o-minimal structures [Reference Conversano and Pillay4, Propositions 4.6–7] (see also the discussion around [Reference Pillay and Yao18, Fact 1.18]). Pillay and the second author asked whether such a decomposition exists for any definably amenable group in a distal theory [Reference Pillay and Yao18, Question 1.19]. Theorem 1.1 can be seen as evidence towards a positive answer.
When
$M = \mathbb {Q}_p$
, we obtain two useful consequences from Theorem 1.1:
Theorem 1.3. Suppose that G is an abelian group definable in
$\mathbb {Q}_p$
.
-
(i)
$G^{00} = G^0$
(in a monster model extending
$\mathbb {Q}_p$
). -
(ii) There is a finite index definable subgroup
$E \subseteq G$
and a finite subgroup
$F \subseteq E$
such that
$E/F$
is isomorphic to an open subgroup of an algebraic group.
The proof appears in Section 4. We will generalize Theorem 1.3(i) to non-abelian groups (over
$\mathbb {Q}_p$
) in a future paper. Note that Theorem 1.3(i) needn’t be true when the group is definable over a non-standard model. In fact, Onshuus and Pillay show that
$E^0 \ne E^{00}$
for “nonstandard Tate [elliptic] curves” over monster models of pCF [Reference Onshuus and Pillay15, Proposition 3.7].
Theorem 1.3(ii) yields a loose “classification” of abelian definable groups in
$\mathbb {Q}_p$
—up to finite factors, they are exactly the open subgroups of commutative algebraic groups.Footnote
1
For the case of one-dimensional definable groups in arbitrary p-adically closed fields, a similar classification up to finite factors was obtained by Acosta López [Reference Andújar Guerrero and Johnson1]. It seems possible that his methods could be used to give another proof of Theorem 1.3 or generalize it beyond the specific field
$\mathbb {Q}_p$
.
1.1 Outline
In Section 2, we review some tools needed in the proof. In Section 3 we prove the decomposition in Theorem 1.1 and give some examples. In Section 4 we obtain the consequences for
$\mathbb {Q}_p$
-definable groups listed in Theorem 1.3. In Section 5 we discuss our original strategy for Theorem 1.1, which suggests a generalization of Theorem 1.1 to interpretable groups (Conjecture 5.14).
There are also two appendices. Appendix A proves a technical statement about topological properties of ict patterns in interpretable groups, needed in Lemma 5.8. Appendix B is on dfg in short exact sequences, and generalizes some facts in Section 2.1 beyond the context of
$p\mathrm {CF}$
.
1.2 Notation and conventions
“Definable” means “definable with parameters.” We work in a monster model
$\mathbb {M}$
, which will usually be NIP. We say that a set A is “small” or “bounded” if it is smaller than the degree of saturation of
$\mathbb {M}$
. If X is definable over a small model M, then
$X(M)$
denotes the set of M-points of X, i.e., the corresponding definable set in M.
A “type” is a complete type, and a “partial type” is a partial type. Every type over a small subset is realized in
$\mathbb {M}$
. A set in
$\mathbb {M}$
is “type-definable” if it is a small intersection of definable sets, or equivalently, it is defined by a type over a small subset. Tuples are finite by default. We usually write tuples as
$a, b, x, y$
rather than
$\bar a, \bar b, \bar x, \bar y$
. We distinguish between “real” elements or tuples (in
$\mathbb {M}$
) and “imaginaries” (in
$\mathbb {M}^{\mathrm {eq}}$
), and we distinguish between “definable” (in
$\mathbb {M}$
) and “interpretable” (in
$\mathbb {M}^{\mathrm {eq}}$
). The exception is Appendix B, where we work in
$\mathbb {M}^{\mathrm {eq}}$
. If D is a definable set, then
$\ulcorner D \urcorner $
denotes its code, a tuple in
$\mathbb {M}^{\mathrm {eq}}$
. If p is a definable type, then
$\ulcorner p \urcorner $
denotes its code, an infinite tuple in
$\mathbb {M}^{\mathrm {eq}}$
.
Throughout,
$p\mathrm {CF}$
means the complete theory of
$\mathbb {Q}_p$
, and a “p-adically closed field” is a model of this theory, or equivalently, a field elementarily equivalent to
$\mathbb {Q}_p$
. We do not consider “p-adically closed fields” in the broader sense (fields elementarily equivalent to finite extensions of
$\mathbb {Q}_p$
), though we strongly suspect that all the results generalize to these theories. We write the language of
$p\mathrm {CF}$
as
$\mathcal {L}$
. The language
$\mathcal {L}$
should be one-sorted; the choice of
$\mathcal {L}$
is otherwise irrelevant. We write the valuation as
$v(x)$
and the value group as
$\Gamma $
.
2 Tools
In this section, we review a few tools that will be needed in the proof of the main theorems. In Section 2.1 we show that certain properties (
$G^0 = G^{00}$
, dfg) behave well in short exact sequences. In Section 2.2 we show that we can take quotients by certain dfg groups without leaving the definable category. Throughout this section, work in a monster model
$\mathbb {M}$
of some complete theory.
2.1 Extensions
Let G be a group definable in
$\mathbb {M}$
. Following standard terminology, we say that “
$G^0$
exists” if the family of definable subgroups of finite index is small, in which case
$G^0$
is defined to be the intersection of this family. Similarly, we say that
$G^{00}$
exists if the family of type-definable subgroups of bounded index is small, in which case
$G^{00}$
is defined to be the intersection of this family. When they exist,
$G^{00}$
and
$G^0$
are type-definable normal subgroups of bounded index, and
$G^{00} \subseteq G^0 \subseteq G$
. In NIP theories,
$G^0$
and
$G^{00}$
always exist [Reference Hrushovski and Pillay7, Proposition 6.1].
Recall that if X is a type-definable set and E a type-definable equivalence relation on X with
$X/E$
bounded, then we can define a topology on
$X/E$
called the logic topology. Let
$\pi :X\to X/E$
be the natural projection. Then
$Z \subseteq X/E$
is closed in the logic topology iff
$\pi ^{-1}(Z)\subseteq X$
is type-definable. This makes
$X/E$
into a compact Hausdorff space. See [Reference Peterzil and Starchenko17, Section 2] for more about the logic topology.
When
$G^0$
or
$G^{00}$
exists, the logic topology makes the quotient
$G/G^0$
or
$G/G^{00}$
into a compact Hausdorff topological group, and
$G/G^0$
is even profinite. When
$G^{00}$
exists,
$G/G^0$
is the largest profinite quotient of
$G/G^{00}$
. Consequently,
$G^0 = G^{00}$
if and only if
$G/G^{00}$
is profinite.
Lemma 2.1 (Assuming NIP)
Let
$\pi : G \to X$
be a surjective homomorphism of definable groups. Then
$\pi (G^{00}) = X^{00}$
.
Proof There is a surjection
$G/G^{00} \to X/\pi (G^{00})$
, so
$X/\pi (G^{00})$
is bounded and
$\pi (G^{00}) \supseteq X^{00}$
. There is a bijection
$G/\pi ^{-1}(X^{00}) \to X/X^{00}$
, so
$G/\pi ^{-1}(X^{00})$
is bounded and
$G^{00} \subseteq \pi ^{-1}(X^{00})$
. This implies
$\pi (G^{00}) \subseteq X^{00}$
.
Lemma 2.2 (Assuming NIP)
Let
$1 \to H \to G \overset {\pi }{\to } X \to 1$
be a short exact sequence of definable groups. If
$H^0 = H^{00}$
and
$X^0 = X^{00}$
, then
$G^0 = G^{00}$
.
Proof The fact that
$H^0 = H^{00}$
and
$X^0 = X^{00}$
means that
$H/H^{00}$
and
$X/X^{00}$
are profinite. The short exact sequence
$$ \begin{align} 1 \to H/(H \cap G^{00}) \to G/G^{00} \to X/X^{00} \to 1 \end{align} $$
shows that
$H/(H \cap G^{00})$
is bounded, and then (
$\ast $
) is continuous in the logic topology. As
$H/(H \cap G^{00})$
is bounded, it must be a quotient of
$H/H^{00}$
which is profinite. Therefore
$H/(H \cap G^{00})$
is profinite. In the category of compact Hausdorff groups, an extension of a profinite group by a profinite group is profinite. Therefore
$G/G^{00}$
is profinite, which implies
$G^0 = G^{00}$
.
Recall that
$p\mathrm {CF}$
has definable Skolem functions.
Lemma 2.3. Suppose that
$\mathbb {M}$
is a saturated model of
$p\mathrm {CF}$
. Let
$$ \begin{align*} 1\longrightarrow A\overset{i}{\longrightarrow}B\overset{\pi}{\longrightarrow} C \longrightarrow 1 \end{align*} $$
be a short exact sequence of definable groups. Then B has dfg iff A and C do.
Proof We prove the following:
-
1. If B has dfg, then C has dfg.
-
2. If B has dfg, then A has dfg.
-
3. If A and C have dfg, then B has dfg.
By definable Skolem functions, there is a definable function
$f : C \to B$
which is a set-theoretic section of
$\pi $
, in the sense that
$\pi (f(c)) = c$
for
$c \in C$
. Now we proceed with the proofs:
-
1. If
$\operatorname {tp}(b/\mathbb {M})$
is a definable f-generic type in B, then
$\operatorname {tp}(\pi (b)/\mathbb {M})$
is a definable f-generic type in C. -
2. The proof is nearly identical to [Reference Pillay and Yao19, Lemmas 2.24 and 2.25]. In an elementary extension
$\mathbb {M}' \succeq \mathbb {M}$
, take
$b_0 \in B(\mathbb {M}')$
realizing a definable f-generic type in B. Write
$b_0$
as
$a_0 \cdot f(\pi (b_0))$
for some
$a_0 \in A(\mathbb {M}')$
. Then
$a_0 \in \operatorname {dcl}(\mathbb {M} b_0)$
, so
$\operatorname {tp}(a_0/\mathbb {M})$
is definable. We claim that
$\operatorname {tp}(a_0/\mathbb {M})$
has boundedly many left translates, and is therefore a definable f-generic type in A. Note that
$A^{00} \subseteq B^{00}$
because
$A/(A \cap B^{00}) \cong AB^{00}/B^{00}$
is bounded. If
$\delta \in A^{00}(\mathbb {M})$
, then
$\operatorname {tp}(\delta \cdot b_0 / \mathbb {M}) = \operatorname {tp}(b_0 / \mathbb {M})$
, and therefore But
$$ \begin{align*} \operatorname{tp}(\delta \cdot b_0 \cdot f(\pi(\delta \cdot b_0))^{-1} / \mathbb{M}) = \operatorname{tp}(b_0 \cdot f(\pi(b_0))^{-1}/\mathbb{M}) = \operatorname{tp}(a_0/\mathbb{M}). \end{align*} $$
$\pi (\delta \cdot b_0) = \pi (b_0)$
, and so Therefore
$$ \begin{align*} \operatorname{tp}(\delta \cdot b_0 \cdot f(\pi(\delta \cdot b_0))^{-1} / \mathbb{M}) = \operatorname{tp}(\delta \cdot b_0 \cdot f(\pi(b_0))^{-1} / \mathbb{M}) = \operatorname{tp}(\delta \cdot a_0 / \mathbb{M}). \end{align*} $$
$\operatorname {tp}(a_0/\mathbb {M})$
is invariant under left translation by any
$\delta \in A^{00}$
, and it has boundedly many left translates.
-
3. Let
$p(x)\in S_A(\mathbb {M})$
and
$q(y)\in S_C(\mathbb {M})$
be dfg types of A and C respectively. Let
$M_0$
be a small model defining the section f, the short exact sequence, and all the left translates of p and q.In some elementary extension
$\mathbb {M}' \succeq \mathbb {M}$
, take
$c_0 \models q$
and
$a_0 \models p|\mathbb {M} c_0$
. Then
$\operatorname {tp}(a_0,c_0/\mathbb {M})$
is
$M_0$
-definable—it is the Morley product of p and q. Let
$b_0 = f(c_0) \cdot a_0$
. Then
$\operatorname {tp}(b_0/\mathbb {M})$
is again
$M_0$
-definable. We claim that every left translate of
$\operatorname {tp}(b_0/\mathbb {M})$
is
$M_0$
-definable.Fix some
$\delta \in B(\mathbb {M})$
. Let
$b_1 = \delta \cdot b_0$
. Let
$c_1 = \pi (\delta ) \cdot c_0$
. Let
$\delta ' = f(c_1)^{-1} \cdot \delta \cdot f(c_0)$
. Note so
$$ \begin{align*} \pi(\delta') = \pi(f(c_1))^{-1} \cdot \pi(\delta) \cdot \pi(f(c_0)) = c_1^{-1} \cdot \pi(\delta) \cdot c_0 = 1, \end{align*} $$
$\delta ' \in A(\mathbb {M}')$
. Let
$a_1 = \delta ' \cdot a_0$
. Then Now
$$ \begin{align*} b_1 = \delta \cdot b_0 = \delta \cdot f(c_0) \cdot a_0 = f(c_1) \cdot \delta' \cdot a_0 = f(c_1) \cdot a_1. \end{align*} $$
$\operatorname {tp}(c_1/\mathbb {M}) = \operatorname {tp}(\pi (\delta ) \cdot c_0 / \mathbb {M})$
is a left-translate of the dfg type
$\operatorname {tp}(c_0/\mathbb {M}) = q$
, and so
$\operatorname {tp}(c_1/\mathbb {M})$
is
$M_0$
-definable. If U is
$\operatorname {dcl}(\mathbb {M} c_0) = \operatorname {dcl}(\mathbb {M} c_1)$
, then
$\operatorname {tp}(a_1 / U) = \operatorname {tp}(\delta ' \cdot a_0 / U)$
is a left translate of the dfg type
$\operatorname {tp}(a_0 / U) = p | U$
(because
$\delta ' \in U$
). Therefore
$\operatorname {tp}(a_1 / U)$
is again
$M_0$
-definable. As
$b_1 = f(c_1) \cdot a_1$
, we see that
$\operatorname {tp}(\delta \cdot b_0 / \mathbb {M}) = \operatorname {tp}(b_1/\mathbb {M})$
is
$M_0$
-definable for the same reason that
$\operatorname {tp}(b_0/\mathbb {M})$
is
$M_0$
-definable, essentially because
$\operatorname {tp}(c_1/\mathbb {M})$
and
$\operatorname {tp}(a_1/\mathbb {M} c_1)$
are
$M_0$
-definable.
See Theorem B.6 in Appendix B for an alternate proof of (3) not using definable Skolem functions.
2.2 Codes and quotients
Let G be a definable group and let H be a normal subgroup. A priori, the quotient group
$G/H$
is interpretable, not definable.
Example 2.4. If X is the multiplicative group
$\mathbb {M}^\times $
and G is the subgroup
$\{x \in X : v(x) = 0\}$
, then
$X/G$
is the value group
$\Gamma $
, which is interpretable but not definable, since
$\dim (\Gamma ) = 0 \ne \operatorname {dp-rk}(\Gamma ) = 1$
, for example. On definable sets, dp-rank agrees with dimension.
In this section, we show that for certain dfg groups H in pCF, the quotient
$G/H$
is automatically definable (Corollary 2.10). The key is to show that certain definable types are coded by real tuples (Theorem 2.8). Both of these results are proved in greater generality in a later paper with Andújar Guerrero [Reference Acosta López2, Theorems 3.4 and 4.1].
If D is a definable set in a model M, let
$\ulcorner D \urcorner $
denote “the” code of D in
$M^{\mathrm {eq}}$
, which is well-defined up to interdefinability. If
$\sigma \in \operatorname {Aut}(M)$
, then
$$ \begin{align*} \sigma(D) = D \iff \sigma(\ulcorner D \urcorner) = \ulcorner D \urcorner, \end{align*} $$
and this property characterizes
$\ulcorner D \urcorner $
when M is sufficiently saturated and homogeneous.
Lemma 2.5. Let K be a field and let
$V \subseteq K^n$
be Zariski closed. Then the definable set V is coded by a tuple in K (rather than
$K^{\mathrm {eq}}$
). In particular, finite subsets of
$K^n$
are coded by tuples in K.
Proof Passing to an elementary extension, we may assume K is
$\aleph _1$
-saturated and strongly
$\aleph _1$
-homogeneous. Let
$M = K^{alg}$
. Let
$\overline {V}$
be the Zariski closure of V in
$M^n$
. Note
$V = \overline {V} \cap K^n$
. By elimination of imaginaries in ACF, there is a tuple
$b \in M$
which codes
$\overline {V}$
in the structure
$M^n$
. If
$\sigma \in \operatorname {Aut}(M/K)$
then
$\sigma $
fixes V setwise, so it also fixes the Zariski closure
$\overline {V}$
. Therefore
$\sigma (b) = b$
, for any
$\sigma \in \operatorname {Aut}(M/K)$
. By Galois theory, b is in the perfect closure of K. Replacing b with
$b^{p^n}$
if necessary, we may assume b is a tuple in K.
We claim that b codes V in the structure K. Suppose
$\sigma _0 \in \operatorname {Aut}(K)$
. Extend
$\sigma _0$
to an automorphism
$\sigma \in \operatorname {Aut}(M)$
arbitrarily. Then b codes V because
$$ \begin{align*} \sigma_0(V) = V \iff \sigma(V) = V \overset{\ast}{\iff} \sigma(\overline{V}) = \overline{V} \iff \sigma(b) = b \iff \sigma_0(b) = b. \end{align*} $$
The starred
$\overset {\ast }{\iff }$
requires some explanation. The direction
$\Rightarrow $
holds because the formation of Zariski closures is automorphism invariant. The direction
$\Leftarrow $
holds because
$\sigma $
fixes K setwise and
$V = \overline {V} \cap K^n$
.
Lemma 2.6. Work in a monster model
$\mathbb {M}$
of
$p\mathrm {CF}$
.
-
1. If an imaginary tuple a is algebraic over a real tuple b, then a is definable over b.
-
2. If an imaginary tuple a is interalgebraic with a real tuple b, then a is interdefinable with some real tuple
$b'$
.
More generally, both statements hold if we work over a set of real parameters
$C \subseteq \mathbb {M}$
.
Proof
-
1. Note that
$\operatorname {dcl}(b) \preceq \mathbb {M}$
by definable Skolem functions, and so
$\operatorname {dcl}^{\mathrm {eq}}(b) \preceq \mathbb {M}^{\mathrm {eq}}$
. Submodels are algebraically closed, so
$\operatorname {acl}^{\mathrm {eq}}(b) = \operatorname {dcl}^{\mathrm {eq}}(b)$
and
$a \in \operatorname {dcl}^{\mathrm {eq}}(b)$
. -
2. By part (1),
$a \in \operatorname {dcl}^{\mathrm {eq}}(b)$
. Write a as
$f(b)$
for some
$\varnothing $
-definable function f. Let
$S \subseteq \mathbb {M}^n$
be the set of realizations of
$\operatorname {tp}(b/a)$
. Then S is finite as
$b \in \operatorname {acl}^{\mathrm {eq}}(a)$
. Moreover, S is a-definable, and so the code
$\ulcorner S \urcorner $
is in
$\operatorname {dcl}^{\mathrm {eq}}(a)$
. By Lemma 2.5, we can take the code
$\ulcorner S \urcorner $
to be a real tuple. For any
$c \in S$
, we have
$f(c) = a$
, which implies
$a \in \operatorname {dcl}^{\mathrm {eq}}(\ulcorner S \urcorner )$
. Then a is interdefinable with the real tuple
$\ulcorner S \urcorner $
.
The “more general” statements follow by the same proofs. Indeed, we can name the elements of C as constants without losing definable Skolem functions or codes for finite sets.
If p is a definable n-type over M, let
$\ulcorner p \urcorner $
denote the infinite tuple
$(\ulcorner D_\varphi \urcorner : \varphi \in L)$
, where
$$ \begin{align*} D_\varphi = \{b \in M^m : \varphi(x,b) \in p(x)\}. \end{align*} $$
For
$\sigma \in \operatorname {Aut}(M)$
, we have
$$ \begin{align*} \sigma(p) = p \iff \sigma(\ulcorner p \urcorner) = \ulcorner p \urcorner, \end{align*} $$
and this property determines
$\ulcorner p \urcorner $
up to interdefinability when M is sufficiently saturated and homogeneous.
Lemma 2.7. If
$q \in S_1(\mathbb {M})$
is definable, then
$\ulcorner q \urcorner $
is interdefinable with a
$($
finite
$)$
real tuple.
Proof By [Reference Johnson and Yao13, Proposition 2.24], the type q must accumulate at some point c in the projective line
$\mathbb {P}^1(\mathbb {M})$
, because
$\mathbb {P}^1(\mathbb {M})$
is definably compact. If necessary, we can push q forward along the map
$x \mapsto 1/x$
to ensure
$c \ne \infty $
. Then
$c \in \mathbb {M}$
. Note
$c \in \operatorname {dcl}^{\mathrm {eq}}(\ulcorner q \urcorner )$
. There are only boundedly many types concentrating at c by [Reference Johnson9, Corollary 7.5] or [Reference Johnson and Yao13, Fact 2.20], so
$\ulcorner q \urcorner $
has a small orbit under
$\operatorname {Aut}(\mathbb {M}/c)$
. Then
$\ulcorner q \urcorner \in \operatorname {acl}^{\mathrm {eq}}(c)$
. As in the proof of Lemma 2.6(1),
$\ulcorner q \urcorner \in \operatorname {dcl}^{\mathrm {eq}}(c)$
, so
$\ulcorner q \urcorner $
is interdefinable with c.
Theorem 2.8. Suppose
$q \in S_n(\mathbb {M})$
is a definable type, and
$\dim (q) = 1$
. Then
$\ulcorner q \urcorner $
is interdefinable with a real tuple.
Proof Take an elementary extension
$\mathbb {M}' \succeq \mathbb {M}$
containing a realization
$\bar {a}$
of q. Then
$\operatorname {tr.deg}(\bar {a}/\mathbb {M}) = \dim (q) = 1$
, so there is some i such that
$a_i$
is a transcendence basis of
$\bar {a}$
over
$\mathbb {M}$
, implying that
$\bar {a}$
is field-theoretically algebraic over
$\mathbb {M}$
and
$a_i$
. Then there is a Zariski-closed set
$V_0 \subseteq \mathbb {M}^n$
such that there are only finitely many
$\bar {b} \in V_0(\mathbb {M}')$
with
$b_i = a_i$
.
Let
$V \subseteq \mathbb {M}^n$
be the smallest Zariski-closed set such that
$\bar {a} \in V(\mathbb {M}')$
, or equivalently, the smallest Zariski-closed set on which q concentrates. Any automorphism of
$\mathbb {M}$
which fixes q fixes V, and so
$$ \begin{align} \ulcorner V \urcorner \in \operatorname{dcl}^{\mathrm{eq}}(\ulcorner q \urcorner). \end{align} $$
As
$V \subseteq V_0$
, there are only finitely many
$\bar {b} \in V(\mathbb {M}')$
with
$b_i = a_i$
. Therefore
$\bar {a} \in \operatorname {acl}^{\mathrm {eq}}(\ulcorner V \urcorner a_i)$
. By Lemma 2.5, we may assume
$\ulcorner V \urcorner $
is a real tuple in
$\mathbb {M}$
, and then
$\bar {a} \in \operatorname {dcl}^{\mathrm {eq}}(\ulcorner V \urcorner a_i)$
by Lemma 2.6(1). Therefore
$\bar {a}$
and
$a_i$
are interdefinable over
$\ulcorner V \urcorner $
.
Take a bijection f defined over
$\ulcorner V \urcorner $
such that
$\bar {a} = f(a_i)$
. Then
$q = \operatorname {tp}(\bar {a}/\mathbb {M})$
is the pushforward of the definable type
$r := \operatorname {tp}(a_i/\mathbb {M})$
along the
$\ulcorner V \urcorner $
-definable bijection f. Therefore
$$ \begin{align} \ulcorner q \urcorner \in \operatorname{dcl}^{\mathrm{eq}}(\ulcorner V \urcorner \ulcorner r \urcorner). \end{align} $$
Likewise, r is the pushforward of q along the 0-definable coordinate projection
$\pi (\bar {x}) = x_i$
, so
$$ \begin{align} \ulcorner r \urcorner \in \operatorname{dcl}^{\mathrm{eq}}(\ulcorner q \urcorner). \end{align} $$
Combining equations (1)–(3), we see that
$\ulcorner q \urcorner $
is interdefinable with
$\ulcorner V \urcorner \ulcorner r \urcorner $
. But
$\ulcorner V \urcorner $
is a real tuple by Lemma 2.5 as noted above, and
$\ulcorner r \urcorner $
is a real tuple by Lemma 2.7.
Using a different argument, one can show that Theorem 2.8 holds for any definable n-type, without the assumption
$\dim (q) = 1$
[Reference Acosta López2, Theorem 3.4]. However, the real tuple may need to be infinite [Reference Acosta López2, Proposition 3.7].
Proposition 2.9. If a one-dimensional dfg group G acts on a definable set X, then the quotient space
$X/G$
is definable
$($
not just interpretable
$)$
.
Proof Take a global definable type p on G with boundedly many right translates. Take a small model
$M_0$
over which everything is defined, including the boundedly many right translates of p. It suffices to show that every element of the interpretable set
$X/G$
is interdefinable over
$M_0$
with a real tuple. By Lemma 2.6(2), it suffices to show that every element of
$X/G$
is interalgebraic over
$M_0$
with a real tuple. Fix some element
$e = G \cdot a \in X/G$
, where
$a \in X$
. Let
$p \cdot a$
denote the pushforward of p along the map
$x \mapsto x \cdot a$
. Note that the global types p and
$p \cdot a$
both have dimension 1 (or less). By Theorem 2.8, the code
$\ulcorner p \cdot a \urcorner $
can be taken to be a real tuple. We claim that
$\ulcorner p \cdot a \urcorner $
is interalgebraic with e over
$M_0$
.
In one direction,
$p \cdot a$
is contained in the collection
$$ \begin{align*} \mathfrak{S} &= \{p \cdot a' : a' \in G \cdot a\} \\ &= \{p \cdot (g \cdot a) : g \in G\} = \{(p \cdot g) \cdot a : g \in G\}, \end{align*} $$
which is
$\operatorname {Aut}(\mathbb {M}/M_0e)$
-invariant by the first line, and small by the second line. It follows that
$p \cdot a$
has a small number of conjugates over
$M_0 e$
, and so
$\ulcorner p \cdot a \urcorner \in \operatorname {acl}^{\mathrm {eq}}(M_0 e)$
.
In the other direction, the type
$p \cdot a$
concentrates on
$G \cdot a$
, so its pushforward along the
$M_0$
-definable map
$X \to X/G$
is the constant type
$x = e$
. Therefore
$e \in \operatorname {dcl}^{\mathrm {eq}}(M_0 \ulcorner p \cdot a \urcorner )$
. This completes the proof that e is interalgebraic with
$\ulcorner p \cdot a \urcorner $
over
$M_0$
.
Again, this holds without the assumption
$\dim (G) = 1$
. See [Reference Acosta López2, Theorem 4.1].
Corollary 2.10. Let G be a definable group and let H be a one-dimensional definable normal subgroup. If H has dfg, then
$G/H$
is definable and
$\dim (G/H) = \dim (G) - 1$
.
3 Proof of Theorem 1.1
Work in a model
$M \models p\mathrm {CF}$
.
Theorem 1.1. Suppose that M is a p-adically closed field and G is an abelian group definable in M. Then there is a short exact sequence of definable groups
$$ \begin{align*} 1 \to H \to G \to C \to 1, \end{align*} $$
where H has dfg and C is definably compact and has fsg.
Proof For definable groups, fsg is equivalent to definable compactness [Reference Johnson12, Theorem 1.2]. Say a definable subgroup
$H \subseteq G$
is “good” if
$G/H$
is definable and H has dfg. For example,
$H = \{1\}$
is good. Take a good subgroup H maximizing
$\dim (H)$
. If
$G/H$
is definably compact then we are done. Otherwise,
$G/H$
is not definably compact. By [Reference Johnson and Yao13, Corollary 6.11], there is a one-dimensional definable dfg subgroup of
$G/H$
. This subgroup has the form
$H'/H$
for some definable subgroup
$H'$
of G. The short exact sequence
$$ \begin{align*} 1 \to H \to H' \to H'/H \to 1 \end{align*} $$
shows that
$H'$
has dfg by Lemma 2.3, and that
$$ \begin{align*} \dim(H') = \dim(H) + \dim(H'/H) = \dim(H) + 1> \dim(H). \end{align*} $$
The quotient
$ G/H' = (G/H)/(H'/H)$
is definable by Corollary 2.10, and so
$H'$
is a good subgroup, contradicting the choice of H.
Here are some examples of this decomposition.
Example 3.1. Suppose
$p = 2$
or
$p \equiv 3 \pmod {4}$
. Then
${-}1$
is not a square in
$\mathbb {Q}_p$
. Let G be the multiplicative group of the quadratic extension
$\mathbb {Q}_p(\sqrt {-1})$
, regarded as a definable group in
$\mathbb {Q}_p$
. Explicitly, G is the set
$\mathbb {Q}_p^2 \setminus \{(0,0)\}$
with the group operation given by
$$ \begin{align*} (x,y) \cdot (x',y') := (xx' - yy', xy' + x'y). \end{align*} $$
The decomposition of G into dfg and fsg groups is
$$ \begin{align*} 1 \to \mathbb{Q}_p^\times \to G \to C \to 1, \end{align*} $$
where C is the subgroup
$\{(x,y) \in G : x^2 + y^2 = 1\} \subseteq G$
, and the two maps are
$$ \begin{align*} \mathbb{Q}_p^\times &\to G, & G &\to C, \\ x &\mapsto (x,0), & (x,y) &\mapsto \left(\frac{x^2 - y^2}{x^2 + y^2},\frac{2xy}{x^2+y^2}\right). \end{align*} $$
We leave the verification of these details as an exercise to the reader.
Example 3.2. Let M be a p-adically closed field, and let a be an element of positive valuation. Let G be the set of pairs
$(x,y) \in M^\times \times M^\times $
such that
$0 \le v(y) < v(a)$
. The operation
$$ \begin{align*} (x,y) \star (x',y') = \begin{cases} (xx',yy'), & \text{ if } v(yy') < v(a) \\ \left(\frac{xx'}{p},\frac{yy'}{a}\right), & \text{ if } v(yy') \ge v(a) \end{cases} \end{align*} $$
makes G into a group. The decomposition of G into dfg and fsg components looks like
$$ \begin{align*} 1 \to M^\times \to G \to C \to 1, \end{align*} $$
where C is
$\{y \in M^\times : 0 \le v(y) < v(a)\}$
with the group operation
$$ \begin{align*} y \star y' = \begin{cases} yy', & \text{ if } v(yy') < v(a), \\ \frac{yy'}{a}, & \text{ if } v(yy') \ge v(a). \end{cases} \end{align*} $$
The inclusion
$M^\times \to G$
is
$x \mapsto (x,1)$
, while the projection
$G \to C$
is
$(x,y) \mapsto y$
. Again, we leave the verification as an exercise.
Example 3.3. If we understand correctly, abelian varieties can have extensions by powers of the additive group or the multiplicative group. More precisely, there are non-trivial short exact sequences of abelian algebraic groups of the forms
$$ \begin{gather*} 0 \to (\mathbb{G}_m)^n \to G \to A \to 0, \\ 0 \to (\mathbb{G}_a)^n \to G \to A \to 0, \end{gather*} $$
where
$\mathbb {G}_m$
is the multiplicative group,
$\mathbb {G}_a$
is the additive group, and A is an abelian variety. Extensions by the multiplicative group are semiabelian varieties. For extensions by the additive group, see [Reference Rosenlicht21].
We can find such sequences over p-adic fields, because of the well-known fact that any finitely generated field of characteristic zero embeds into at least one p-adic field.
These sequences of algebraic groups yield sequences of definable groups:Footnote 2
$$ \begin{gather*} 0 \to (\mathbb{Q}_p^\times)^n \to G(\mathbb{Q}_p) \to A(\mathbb{Q}_p) \to 0, \\ 0 \to \mathbb{Q}_p^n \to G(\mathbb{Q}_p) \to A(\mathbb{Q}_p) \to 0. \end{gather*} $$
In each case, this is a decomposition as in Theorem 1.1. The group
$A(\mathbb {Q}_p)$
has fsg because it is definably compact, while the additive and multiplicative groups have dfg.
Remark 3.4. The sequence in Theorem 1.1 need not split. That is, there are non-split short exact sequences of definable groups
$$ \begin{align} 1 \to H \to G \to C \to 1, \end{align} $$
where H has dfg and C has fsg. A simple example is
$$ \begin{align*} 0 \to \mathbb{Z}/2 \to \mathbb{Z}/4 \to \mathbb{Z}/2 \to 0. \end{align*} $$
(Finite groups have both dfg and fsg.)
Nevertheless, one could ask whether the sequence splits “up to finite factors” in some sense. This does not happen either. Let M be a moderately saturated elementary extension of
$\mathbb {Q}_p$
, and take an element
$a \in M$
with positive valuation, such that a is an nth power for every n. Using this value of a in Example 3.2, we get groups G and C and a short exact sequence of definable groups
$$ \begin{align*} 1 \to M^\times \to G \to C \to 1. \end{align*} $$
This sequence does not split, even non-definably (as a sequence of abstract groups), even “up to finite factors.” More precisely, the following is true:
Claim 3.5. There is no injective homomorphism from C to G. More generally, let
$\sim $
be the smallest equivalence relation on abelian groups such that
$A \sim B$
whenever there is a homomorphism
$f : A \to B$
with finite kernel and cokernel. If
$G' \sim G$
and
$C' \sim C$
, then there is no injective homomorphism from
$C'$
to
$G'$
.
Proof sketch
Say that an abelian group A is “spacious” if it has a subgroup isomorphic to
$\mathbb {Q}/\mathbb {Z}$
. If
$g : A \to B$
is an injective homomorphism and A is spacious, then B is spacious. It is an exercise in homological algebra to show that if
$f : A \to B$
is a homomorphism with finite kernel and cokernel, then A is spacious if and only if B is spacious. Therefore, it suffices to show that C is spacious and G is not.
Using saturation of M and divisibility of the element a in
$M^\times $
, extend the homomorphism
$$ \begin{align*} \mathbb{Z} &\to M^\times \\ n &\mapsto a^n \end{align*} $$
to a homomorphism
$$ \begin{align*} \mathbb{Q} &\to M^\times \\ q &\mapsto \text{"}a^q\text{"}. \end{align*} $$
Then there is an injective group homomorphism
$$ \begin{align*} \mathbb{Q}/\mathbb{Z} &\to C \\ q &\mapsto a^q. \end{align*} $$
This homomorphism shows that C is spacious.
Next, consider G. Suppose that
$(x,y) \in G$
and
$(x,y)^n = (1,1)$
for some
$n> 0$
. Then
$$ \begin{align*} (1,1) = (x,y)^n = \left(\frac{x^n}{p^m},\frac{y^n}{a^m}\right) \end{align*} $$
for some integer
$m \ge 0$
. Then
$y^n = a^m$
and
$x^n = p^m$
. The fact that
$0 \le v(y) < v(a)$
implies that
$$ \begin{align*} v(a^m) = v(y^n) < v(a^n), \end{align*} $$
so that
$m < n$
. On the other hand,
$n \cdot v(x) = v(x^n) = v(p^m) = m$
, so m is a multiple of n. This forces
$m = 0$
, so that
$x^n = y^n = 1$
. In other words, we have shown
$$ \begin{align*} (x,y)^n = (1,1) \implies x^n = y^n = 1. \end{align*} $$
Therefore, the torsion subgroup of G is isomorphic to the torsion subgroup of
$M^\times \times M^\times $
. But the torsion subgroup of
$M^\times $
is finite, owing to the isomorphisms
$$ \begin{align*} \mathbb{Z}_2^\times &\cong \mathbb{Z} \times \mathbb{Z}/2 \times \mathbb{Z}_2 \\ \mathbb{Z}_p^\times &\cong \mathbb{Z} \times \mathbb{Z}/(p-1) \times \mathbb{Z}_p \text{ for } p> 2. \end{align*} $$
Therefore the groups
$M^\times $
,
$M^\times \times M^\times $
, and G have finite torsion, and G is not spacious.
Remark 3.6. As a different example, we suspect that the exact sequences of Example 3.3 do not split definably, even up to finite factors, provided that the underlying sequence of algebraic groups doesn’t split. But at least in the additive case, the sequence
$$ \begin{align*} 0 \to \mathbb{Q}_p^n \to G(\mathbb{Q}_p) \to A(\mathbb{Q}_p) \to 0 \end{align*} $$
splits non-definably, because the group
$\mathbb {Q}_p^n$
is divisible, hence injective as a
$\mathbb {Z}$
-module. We don’t know whether the sequence splits non-definably in the semiabelian case.
4 Abelian groups over
$\mathbb {Q}_p$
Fact 4.1. Let G be a definably amenable group definable over
$\mathbb {Q}_p$
. There is an algebraic group H over
$\mathbb {Q}_p$
and a definable finite-to-one group homomorphism from
$G^{00}$
to H.
Proof This follows from [Reference Montenegro, Onshuus and Simon14, Theorem 2.19] via the proof of [Reference Montenegro, Onshuus and Simon14, Corollary 2.22].
Theorem 1.3. Suppose that G is an abelian group definable in
$\mathbb {Q}_p$
.
-
(i)
$G^{00} = G^0$
(in a monster model extending
$\mathbb {Q}_p$
). -
(ii) There is a finite index definable subgroup
$E \subseteq G$
and a finite subgroup
$F \subseteq E$
such that
$E/F$
is isomorphic to an open subgroup of an algebraic group.
Proof For part (i), Theorem 1.1 gives a short exact sequence
$$ \begin{align*} 1 \to H \to G \to C \to 1, \end{align*} $$
where H has dfg and C is definably compact. Then
$C^0 = C^{00}$
because C is definably compact and defined over
$\mathbb {Q}_p$
[Reference Onshuus and Pillay15, Corollary 2.4], and
$H^0 = H^{00}$
because H is dfg [Reference Pillay and Yao18, Proof of Lemma 1.15]. Then
$G^0 = G^{00}$
by Lemma 2.2.
By (i), we have
$G^0 = G^{00}$
. Since G is an abelian group, it is amenable as an abstract group, so it is also definably amenable. By Fact 4.1, there is an algebraic group H and a finite-to-one definable homomorphism
$f : G^0 \to H$
. Now
$G^0$
is the intersection of all
$\mathbb {Q}_p$
-definable finite-index subgroups of G. By compactness there is a
$\mathbb {Q}_p$
-definable finite-index subgroup
$E \subseteq G$
such that f extends to a finite-to-one definable homomorphism
$f' : E \to H$
. Changing
$f'$
, we may assume
$f'$
is
$\mathbb {Q}_p$
-definable, in case this wasn’t provided by Fact 4.1. Replacing H with the Zariski closure of the image of
$f'$
, we may assume the image is an open subgroup of H.
5 Interpretable groups
In this section, we discuss our original approach to Theorem 1.1, which yielded a weaker result, only giving an interpretable group. However, this approach is more general in one way—one can start with an interpretable group. Unfortunately, in the interpretable case we don’t know how to prove the termination of the recursive process implicit in the proof of Theorem 1.1.
Proposition 5.1. Let G be an abelian definable group, let H be a definable subgroup, and let
$X = G/H$
be the interpretable quotient group. Consider the canonical definable manifold topology on G, and the quotient topology on X.
-
1. The quotient map
$\pi : G \to X$
is an open map. -
2. The quotient topology on X is definable.
-
3. The quotient topology on X is a group topology.
-
4. The quotient topology on X is Hausdorff.
Proof
-
1. If
$U \subseteq G$
is open, then
$\pi ^{-1}(\pi (U)) = U \cdot H = \bigcup _{h \in H} (U \cdot h)$
which is open. By definition of the quotient topology,
$\pi (U)$
is open. -
2. If
$\mathcal {B}$
is a definable basis of opens on G, then
$\{\pi (U) : U \in \mathcal {B}\}$
is a definable basis of opens on X, because
$\pi $
is an open map. -
3. We claim
$(x,y) \mapsto x \cdot y^{-1}$
is continuous on X. Fix
$a, b \in X$
. Let
$U \subseteq X$
be an open neighborhood of
$a \cdot b^{-1}$
. Take
$\tilde {a}, \tilde {b} \in G$
lifting a and b. Then
$\tilde {a} \cdot \tilde {b}^{-1} \in \pi ^{-1}(U)$
, which is open. By continuity of the group operations on G, there are open neighborhoods
$V \ni \tilde {a}$
and
$W \ni \tilde {b}$
such that
$x \in V, ~ y \in W \implies x \cdot y^{-1} \in \pi ^{-1}(U)$
. Because
$\pi $
is an open map,
$\pi (V)$
and
$\pi (W)$
are open neighborhoods of a and b, respectively. If
$x \in \pi (V)$
and
$y \in \pi (W)$
, then
$x \cdot y^{-1} \in U$
, because we can write
$x = \pi (\tilde {x}), ~ y = \pi (\tilde {y})$
for
$\tilde {x} \in V, ~ \tilde {y} \in W$
, and then
$x \cdot y^{-1} = \pi (\tilde {x} \cdot \tilde {y}^{-1}) \in \pi (\pi ^{-1}(U)) = U$
. This proves continuity of
$x \cdot y^{-1}$
at
$(a,b)$
. -
4. Because the quotient topology is a group topology, it suffices to show that
$\{1_X\}$
is closed. By definition of the quotient topology, it suffices to show that H is closed in G. On definable manifolds, the frontier of a set is lower-dimensional than the set itself [Reference Chernikov and Simon5, Theorem 3.5]: But
$$ \begin{align*} \dim(\overline{H} \setminus H) < \dim(H). \end{align*} $$
$\overline {H} \setminus H$
is a union of cosets of H, and each coset has dimension
$\dim (H)$
. Therefore
$\overline {H} \setminus H$
must be empty, and H is closed.
Definition 5.2. A manifold-dominated group is an interpretable group X with a Hausdorff definable group topology such that there is a definable manifold
$\tilde {X}$
and an interpretable surjective continuous open map
$f : \tilde {X} \to X$
.
In the setting of Proposition 5.1, X is manifold dominated via the map
$G \to X$
.
Remark 5.3. If X is any interpretable group, then there is a definable group topology
$\tau $
on X making
$(X,\tau )$
be manifold-dominated [Reference Johnson11, Theorem 5.10]. Moreover,
$\tau $
is uniquely determined, though the manifold
$\tilde {X}$
is not. This motivates working in the more general context of manifold-dominated abelian groups, rather than the special case of quotient groups
$G/H$
.
Theorem 5.4. Let X be a manifold-dominated interpretable abelian group. Suppose X is not definably compact. Then there is an interpretable subgroup
$X' \subseteq X$
with the following properties
$:$
-
1.
$X'$
is not definably compact. -
2.
$\operatorname {dp-rk}(X') = 1$
. -
3.
$X'$
has dfg.
Theorem 5.4 is an analogue of [Reference Johnson and Yao13, Theorem 6.8 and Corollary 6.11], and the proof is similar. Nevertheless, we sketch the proof for completeness.
For the rest of the section, work in a monster model
$\mathbb {M}$
. Fix a definable manifold
$\tilde {X}$
, an interpretable abelian group X with a Hausdorff definable group topology, and an interpretable continuous surjective open map
$\pi : \tilde {X} \to X$
. Also fix a small model K over which everything is defined.
Definition 5.5. If S is an interpretable topological space (in
$p\mathrm {CF}$
) and
$x_0 \in S$
, then a good neighborhood basis of
$x_0$
is an interpretable family
$\{O_t\}_{t \in \Gamma }$
with the following properties:
-
1.
$\{O_t\}_{t \in \Gamma }$
is a neighborhood basis of
$x_0$
. -
2.
$t \le t' \implies O_t \subseteq O_{t'}$
. -
3. Each set
$O_t$
is clopen and definably compact. -
4.
$\bigcup _t O_t = S$
.
This is more general than the definition in [Reference Johnson and Yao13, Definition 2.27], since we are considering topological spaces rather than topological groups. The definition here is slightly weaker, since we do not require
$O_t^{-1} = O_t$
when S is a group.
Fix some element
$\tilde {1} \in \tilde {X}$
lifting
$1 \in X$
. By the proof of [Reference Johnson and Yao13, Proposition 2.28], there is a good neighborhood basis
$\{O_t\}_{t \in \Gamma }$
of
$\tilde {1}$
in
$\tilde {X}$
. Let
$V_t = \pi (O_t)$
. Then
$\{V_t\}_{t \in \Gamma }$
is a good neighborhood basis of
$1$
in X. The analogue of [Reference Johnson and Yao13, Proposition 2.29] holds, via the same proof:
-
1. For any
$t \in \Gamma $
, there is
$t' \in \Gamma $
such that
$V_{t'} \cdot V_{t'}^{-1} \subseteq V_t$
. -
2. For any
$t \in \Gamma $
, there is
$t" \in \Gamma $
such that
$V_t \cdot V_t^{-1} \subseteq V_{t"}$
.
Say that a set
$S \subseteq X$
, not necessarily interpretable, is bounded if
$S \subseteq V_t$
for some
$t \in \Gamma $
. As in [Reference Johnson and Yao13, Proposition 2.10], S is bounded if and only if S is contained in a definably compact subset of X. If
$A, B \subseteq X$
, let
$A \diamond B$
denote the set
$$ \begin{align*} \{g \in A : gB \cap A = \varnothing\}, \end{align*} $$
as in [Reference Johnson and Yao13, Section 4.1]. Let
$A \diamond B \setminus C$
mean
$A \diamond (B \setminus C)$
.
Lemma 5.6. Let
$I \subseteq X$
be an unbounded interpretable set. Let
$A \subseteq X$
be bounded, but not necessarily interpretable. Then there is
$t \in \Gamma _{\mathbb {M}}$
such that
$I \diamond V_t \setminus A$
is bounded.
Proof The proofs of Lemmas 4.9–4.11 in [Reference Johnson and Yao13] work here, after making a couple trivial changes. The interpretable group X has finite dp-rank because
$\operatorname {dp-rk}(X) \le \operatorname {dp-rk}(\tilde {X}) = \dim (\tilde {X}) < \infty $
.
Recall our assumption that
$\pi : \tilde {X} \to X$
is K-interpretable for some small model K. Fix
$|K|^+$
-saturated L with
$K \preceq L \preceq \mathbb {M}$
. If
$\Sigma $
is a definable type or definable partial type over K, then
$\Sigma ^L$
denotes its canonical extension over L. (See [Reference Pillay16, Definition 2.12] for definability of partial types. When
$\Sigma $
is complete,
$\Sigma ^L$
is the heir of
$\Sigma $
.)
Lemma 5.7. There is a one-dimensional definable type
$p \in S_{\tilde {X}}(K)$
whose pushforward
$q = \pi _* p$
has the following properties:
-
1. q is “unbounded” over K, in the sense that q does not concentrate on any K-interpretable bounded set, or equivalently, q does not concentrate on
$V_t$
for any
$t \in \Gamma _K$
. -
2. Similarly, the heir
$q^L$
is unbounded over L. -
3. If
$b \in X$
realizes q and
$b \notin V_t$
for any
$t \in \Gamma _L$
, then b realizes
$q^L$
.
Proof Take
$u \in \mathbb {M}$
with
$v(u)> \Gamma _K$
. In other words, u is infinitesimally close to 0 over K. Then
$\operatorname {tp}(u/K)$
is definable. Let
$\gamma = v(u)$
. As X is not definably compact,
$V_\gamma \ne X$
. The set
$\pi ^{-1}(X \setminus V_\gamma )$
is a non-empty
$Ku$
-definable subset of
$\tilde {X}$
. By definable Skolem functions, there is
$\beta _0 \in \pi ^{-1}(X \setminus V_\gamma )$
with
$\beta _0 \in \operatorname {dcl}(Ku)$
. Then
$\beta _0 = f(u)$
for some K-definable function f. Let
$p = \operatorname {tp}(\beta _0/K)$
. Then
$p = f_*(\operatorname {tp}(u/K))$
, so p is definable. Let
$b_0 = \pi (\beta _0)$
and let
$q = \pi _* p = \operatorname {tp}(b_0/K)$
. By choice of
$\beta _0$
,
$b_0 = \pi (\beta _0) \notin V_\gamma $
, which implies
$b_0 \notin V_t \subseteq V_\gamma $
for any
$t \in \Gamma _K$
. Thus q is unbounded over K. As
$q^L$
is the heir, it is similarly unbounded over L.
Finally, suppose that b satisfies the assumptions of (3). Then
$\operatorname {tp}(b/K) = q = \operatorname {tp}(b_0/K)$
, so there is
$\sigma \in \operatorname {Aut}(\mathbb {M}/K)$
with
$\sigma (b_0) = b$
. Let
$\beta = \sigma (\beta _0)$
. Then
$(b,\beta ) \equiv _K (b_0,\beta _0)$
, and in particular
$\beta $
realizes p and
$\pi (\beta ) = b$
. Recall the sets
$O_t$
used to define
$V_t$
. If
$\beta \in O_t$
for some
$t \in \Gamma _L$
, then
$b = \pi (\beta ) \in \pi (O_t) = V_t$
, contradicting the assumptions. Therefore,
$\beta \notin O_t$
for any
$t \in \Gamma _L$
. By [Reference Johnson and Yao13, Lemma 2.25],
$\beta $
realizes
$p^L$
. Then
$b = \pi (\beta )$
realizes
$\pi _* (p^L) = q^L$
.
Fix
$p, q$
as in Lemma 5.7. Fix
$\beta \in \tilde {X}$
realizing
$p^L$
and let
$b = \pi (\beta ) \in X$
. Then b realizes
$q^L$
.
We will make use of the notation and facts from [Reference Johnson and Yao13, Section 5], applied to the group X and the definable type q. In particular,
$\mu $
is the infinitesimal partial type of X over K,
$\mu ^L$
is the infinitesimal partial type of X over L, and
$\mathrm {st}^{\mathbb {M}}_L$
is the standard part map, a partial map from X to
$X(L)$
. The domain of
$\mathrm {st}^{\mathbb {M}}_L$
is the subgroup
$\mu ^L(\mathbb {M}) \cdot X(L)$
of points in X infinitesimally close to points in
$X(L)$
. If
$Y \subseteq X$
, then
$\mathrm {st}^{\mathbb {M}}_L(Y)$
denotes the image of
$Y \cap (\mu ^L(\mathbb {M}) \cdot X(L))$
under
$\mathrm {st}^{\mathbb {M}}_L$
.
The following lemma takes the place of [Reference Johnson and Yao13, Fact 6.3].
Lemma 5.8. Suppose
$Y \subseteq X$
is
$\beta $
-interpretable.
-
1. The set
$\mathrm {st}^{\mathbb {M}}_L(Y) \subseteq X(L)$
is interpretable (in the structure L). -
2.
$\operatorname {dp-rk}(\mathrm {st}^{\mathbb {M}}_L(Y)) \le \operatorname {dp-rk}(Y)$
.
See Remark A.1 for the definition of ict pattern and dp-rank.
Proof
-
1. Fix some interpretable basis of opens for X. Let
$\mathcal {F}$
be the collection of L-interpretable basic open sets which intersect Y. Then
$\mathcal {F}$
is interpretable in the structure L, because
$\mathcal {F}$
is defined externally using
$\beta $
, but
$\operatorname {tp}(\beta /L)$
is definable. Now if
$a \in X(L)$
, the following are equivalent:-
(a)
$a \in \mathrm {st}^{\mathbb {M}}_L(Y)$
. -
(b) There is
$a' \in Y$
such that for every L-interpretable basic open neighborhood
$U \ni a$
, we have
$a' \in U$
. -
(c) For every L-interpretable basic open neighborhood
$U \ni a$
, there is
$a' \in Y$
such that
$a' \in U$
. -
(d) Every L-interpretable basic open neighborhood of a is in
$\mathcal {F}$
.
Indeed, (a)
$\iff $
(b) by definition, (b)
$\iff $
(c) by saturation of
$\mathbb {M}$
, and (c)
$\iff $
(d) by definition of
$\mathcal {F}$
. Condition (d) is definable because
$\mathcal {F}$
is. -
-
2. Let r be the dp-rank of the interpretable set
$D := \mathrm {st}^{\mathbb {M}}_L(Y)$
. It is finite, bounded by
$\operatorname {dp-rk}(X)$
. There is an ict-pattern of depth r in D. That is, there are uniformly interpretable sets
$S_{i,j} \subseteq D$
for
$i < r$
and
$j < \omega $
, and points
$b_\eta \in D$
for
$\eta \in \omega ^r$
, such that
$b_\eta \in S_{i,j} \iff j = \eta (i)$
. By Theorem A.6 in Appendix A, we can also ensure that
$S_{i,j}$
is open and
$j \ne \eta (i) \implies b_\eta \notin \overline {S_{i,j}}$
. As L is
$\aleph _1$
-saturated, we can arrange for all the data to be L-interpretable. Then each
$b_\eta $
is
$\mathrm {st}^{\mathbb {M}}_L(b^{\prime }_\eta )$
for some
$b^{\prime }_\eta \in Y$
. Since
$S_{i,j}$
is open and L-interpretable, we have
$b^{\prime }_\eta \in S_{i,j}$
for
$j = \eta (i)$
. Since
$\overline {S_{i,j}}$
is closed and L-interpretable, we have
$b^{\prime }_\eta \notin \overline {S_{i,j}}$
for
$j \ne \eta (i)$
. Then the sets
$S_{i,j}$
and elements
$b^{\prime }_\eta $
are an ict-pattern of depth r in Y, showing
$\operatorname {dp-rk}(Y) \ge r = \operatorname {dp-rk}(D)$
.
Lemma 5.9. The following subsets of
$X(L)$
are equal
$:$
-
1.
$\operatorname {\mathrm {stab}}(\mu ^L \cdot q^L)$
. -
2.
$\bigcap _{\varphi \in \mathcal {L}} \operatorname {\mathrm {stab}}_\varphi (\mu \cdot q)(L)$
. -
3.
$\mathrm {st}^{\mathbb {M}}_L(q^L(\mathbb {M}) b^{-1})$
. -
4.
$\bigcap _{\psi \in q^L} \mathrm {st}^{\mathbb {M}}_L(\psi (\mathbb {M}) b^{-1})$
. -
5.
$\bigcap _{\psi \in q} \mathrm {st}^{\mathbb {M}}_L(\psi (\mathbb {M}) b^{-1})$
.
See [Reference Johnson and Yao13, Definition 5.3] for the definition of
$\operatorname {\mathrm {stab}}_\varphi (-)$
.
Proof The equivalence of (1)–(4) is Remark 5.12 and Lemma 5.13 in [Reference Johnson and Yao13]. The equivalence of (4) and (5) follows by a similar argument to the proof of [Reference Johnson and Yao13, Lemma 6.2], using Lemma 5.7(3) instead of [Reference Johnson and Yao13, Lemma 2.25].
Lemma 5.10. If
$I \subseteq X$
is L-interpretable and contains b, then
$\mathrm {st}^{\mathbb {M}}_L(Ib^{-1})$
is unbounded in
$X(L)$
.
Proof If not, take
$t \in \Gamma _L$
such that
$\mathrm {st}^{\mathbb {M}}_L(Ib^{-1}) \subseteq V_t$
. By Lemma 5.7(2), b is not in any L-interpretable bounded sets. Therefore I is unbounded. By Lemma 5.6, we can find
$t' \in \Gamma _L$
such that
$I \diamond V_{t'} \setminus V_t$
is bounded. Then
$b \notin I \diamond V_{t'} \setminus V_t$
. This means that
$$ \begin{align*} b \cdot (V_{t'} \setminus V_t) \cap I \ne \varnothing. \end{align*} $$
Therefore there is
$a \in V_{t'} \setminus V_t$
such that
$ba \in I$
. Then there is
$\alpha \in O_{t'}$
with
$\pi (\alpha ) = a$
. The conditions on
$\alpha $
and a are definable over
$\operatorname {dcl}(Lb) \subseteq \operatorname {dcl}(L\beta )$
(where
$\beta $
is the realization of
$p^L$
). By definable Skolem functions, we can assume
$\alpha \in \operatorname {dcl}(L\beta )$
. Then
$\operatorname {tp}(\alpha /L)$
is a pushforward of
$\operatorname {tp}(\beta /L)$
, so
$\operatorname {tp}(\alpha /L)$
is a one-dimensional definable type on
$\tilde {X}$
. This type
$\operatorname {tp}(\alpha /L)$
concentrates on the definably compact set
$O_{t'} \subseteq \tilde {X}$
, and therefore
$\operatorname {tp}(\alpha /L)$
specializes to some point
$\gamma \in G(L)$
by [Reference Johnson and Yao13, Lemma 2.23]. As the map
$\pi : \tilde {X} \to X$
is continuous,
$\operatorname {tp}(a/L)$
specializes to
$c := \pi (\gamma ) \in X(L)$
. Thus
$\mathrm {st}^{\mathbb {M}}_L(a)$
exists and equals c. Since
$V_{t'} \setminus V_t$
is closed,
$\mathrm {st}^{\mathbb {M}}_L(a) \in V_{t'} \setminus V_t$
. But
$a \in b^{-1}I = Ib^{-1}$
, and
$$ \begin{align*} \mathrm{st}^{\mathbb{M}}_L(a) \in \mathrm{st}^{\mathbb{M}}_L(Ib^{-1}) \subseteq V_t, \end{align*} $$
a contradiction.
We can now complete the proof of Theorem 5.4. By Lemma 5.9,
$$ \begin{align} \bigcap_{\varphi \in \mathcal{L}} \operatorname{\mathrm{stab}}_\varphi(\mu \cdot q)(L) = \bigcap_{\psi \in q} \mathrm{st}^{\mathbb{M}}_L(\psi(\mathbb{M}) b^{-1}). \end{align} $$
The groups
$\operatorname {\mathrm {stab}}_\varphi (\mu \cdot q)$
are K-interpretable because
$\mu \cdot q$
is a K-definable partial type. The sets
$\mathrm {st}^{\mathbb {M}}_L(\psi (\mathbb {M}) b^{-1})$
are interpretable by Lemma 5.8(1). Both intersections involve at most
$|K|$
terms, and both intersections are filtered.
If some
$\operatorname {\mathrm {stab}}_\varphi (\mu \cdot q)(L)$
is bounded, then by
$|K|^+$
-saturation of L we have
$\mathrm {st}^{\mathbb {M}}_L(\psi (\mathbb {M}) b^{-1}) \subseteq \operatorname {\mathrm {stab}}_\varphi (\mu \cdot q)(L)$
for some
$\psi (x) \in q(x)$
, contradicting Lemma 5.10. Therefore, every group
$\operatorname {\mathrm {stab}}_\varphi (\mu \cdot q)(L)$
is unbounded. Consequently, no
$\operatorname {\mathrm {stab}}_\varphi (\mu \cdot q)$
is definably compact.
Since
$\operatorname {tp}(\beta /K)$
has dimension 1, there is some K-definable set
$D \ni \beta $
of dimension 1. Then
$\operatorname {dp-rk}(\pi (D)) \le \operatorname {dp-rk}(D) = \dim (D) = 1$
. If
$\psi (x)$
defines
$\pi (D)$
, then
$\psi (x) \in q = \operatorname {tp}(b/K)$
, and
$\mathrm {st}^{\mathbb {M}}_L(\psi (\mathbb {M}) b^{-1})$
has dp-rank at most 1 by Lemma 5.8(2). By
$|K|^+$
-saturation, (
$\ast $
) gives some
$\varphi $
such that
$\operatorname {\mathrm {stab}}_\varphi (\mu \cdot q)(L) \subseteq \mathrm {st}^{\mathbb {M}}_L(\psi (\mathbb {M}) b^{-1})$
. Then
$\operatorname {\mathrm {stab}}_\varphi (\mu \cdot q)$
has dp-rank at most 1. On the other hand,
$\operatorname {\mathrm {stab}}_\varphi (\mu \cdot q)$
is infinite, since it is not definably compact. Therefore
$X' := \operatorname {\mathrm {stab}}_\varphi (\mu \cdot q)$
has dp-rank at least 1.
It remains to show that the interpretable subgroup
$X' \subseteq X$
has dfg. The proof of [Reference Johnson and Yao13, Lemma 6.10] works with minor changes. For completeness, we give the details. For abelian groups of dp-rank 1, “not fsg” implies dfg as in the proof of [Reference Pillay and Yao19, Lemma 2.9]. It suffices to show that
$X'$
does not have fsg. Assume for the sake of contradiction that
$X'$
has fsg. By [Reference Hrushovski and Pillay7, Proposition 4.2], non-generic sets form an ideal, and there is a small model
$M_0$
such that every generic set contains an
$M_0$
-point. Take t large enough that
$V_t$
contains every point in
$X(M_0)$
. Then
$X' \setminus V_t$
is not generic in
$X'$
, so
$X' \cap V_t$
is generic, meaning that finitely many translates of
$X' \cap V_t$
cover
$X'$
. But
$X' \cap V_t$
and its translates are bounded (as subsets of X), so then
$X'$
is bounded, a contradiction. This completes the proof of Theorem 5.4.
Corollary 5.11. Let X be an abelian interpretable group. Then there is
$\alpha \le \omega $
and an increasing chain of dfg subgroups
$(Y_i : i < \alpha )$
with
$Y_0 = 0$
such that the quotients
$Y_i/Y_{i+1}$
have dp-rank 1. In the case when
$\alpha < \omega $
, the quotient
$X/Y_{\alpha -1}$
is definably compact and has fsg.
Proof Any interpretable group is manifold-dominated [Reference Johnson11, Theorem 5.10], so we can apply Theorem 5.4 to any interpretable group. The first application gives
$Y_1$
; applying the theorem to
$X/Y_1$
gives
$Y_2$
, and so on. The process terminates if any quotient
$X/Y_i$
is definably compact. Definably compact groups have fsg [Reference Johnson11, Theorem 7.1]. To prove that the groups
$Y_i$
have dfg, we can no longer use Lemma 2.3, as
$p\mathrm {CF}^{\mathrm {eq}}$
lacks definable Skolem functions. But Theorem B.6 in Appendix B works.
Remark 5.12. If we start with a quotient group
$G/H$
, we can replace the use of [Reference Johnson11, Theorem 5.10] with Proposition 5.1.
Remark 5.13. If X is definable, then the quotients
$Y_i/Y_j$
are definable by induction on
$i-j$
, using Corollary 2.10. Then
$\dim (Y_{i+1}/Y_i) = \operatorname {dp-rk}(Y_{i+1}/Y_i) = 1$
, which implies
$\dim (Y_{i+1})> \dim (Y_i)$
. Therefore, the sequence must terminate, as we saw in the proof of Theorem 1.1. In the general interpretable case, it’s unclear whether this works, so we make a conjecture:
Conjecture 5.14. In Corollary 5.11,
$\alpha $
is finite. Therefore, any abelian interpretable group X sits in a short exact sequence
$1 \to Y_{\alpha -1} \to X \to X/Y_{\alpha -1} \to 1$
where
$Y_{\alpha -1}$
has dfg and
$X/Y_{\alpha -1}$
has fsg and is definably compact.
Pillay and Yao asked whether any definably amenable group G in a distal theory sits in a short exact sequence
$1 \to H \to G \to C \to 1$
with C having fsg and H having dfg [Reference Pillay and Yao18, Question 1.19]. If Conjecture 5.14 is true, it would provide further evidence for this.
A Nice ict patterns
Remark A.1. Following [Reference Simon22, Definition 4.21], an ict-pattern of depth
$\kappa $
in a partial type
$\Sigma (x)$
is a sequence of formulas
$\varphi _i(x;y_i)$
and an array
$(b_{i,j} : i <\kappa , ~ j < \omega )$
with
$|b_{i,j}| = |y_i|$
such that for any function
$\eta : \kappa \to \omega $
, the following partial type is consistent:
$$\begin{align*}\Sigma(x) \cup \{\varphi_{i,\eta(i)}(x,b_{i,\eta(i)}) : i < \kappa\} \cup \{\neg \varphi_{i,j}(x,b_{i,j}):i < \kappa, ~ j \ne \eta(i)\}.\end{align*}$$
Abusing notation, we say that
$(\varphi _i(x;b_{i,j}) : i < \kappa , ~ j < \omega )$
is an ict-pattern to mean that the pair
$((\varphi _i : i < \kappa ),(b_{i,j} : i <\kappa , ~ j <\omega ))$
is an ict-pattern. Sometimes we consider ict-patterns where the columns are indexed by an infinite linear order I other than
$\omega $
. The definition is analogous, and ict-patterns of this sort can be converted to ict-patterns indexed by
$\omega $
via a compactness argument.
Finally, the dp-rank of
$\Sigma (x)$
is the supremum of cardinals
$\kappa $
such that there is an ict-pattern of depth
$\kappa $
in
$\Sigma (x)$
, possibly in an elementary extension.
Work in
$\mathbb {M}^{\mathrm {eq}}$
for some monster model
$\mathbb {M} \models p\mathrm {CF}$
. There is a well-behaved notion of dimension on
$\mathbb {M}^{\mathrm {eq}}$
[Reference Gagelman6], which gives rise to a notion of independence:
This notion satisfies many of the usual properties [Reference Johnson11, Section 2.1].Footnote
3
Say that a sequence
$\{a_i : i \in I\}$
is dimensionally independent over a set B if
for
$i \in I$
, where
$a_{<i} = \{a_j : j < i\}$
. As usual, this is independent of the order on I.
Lemma A.2. If
$\operatorname {tp}(a/Cb)$
is finitely satisfiable in C, then
.
Proof Suppose not. Let
$n = \dim (b/Ca) < \dim (b/C)$
. By [Reference Gagelman6, Proposition 3.7], there is a
$Ca$
-interpretable set X containing b with
$\dim (X) = n$
. Write X as
$\varphi (a,\mathbb {M})$
for some
$\mathcal {L}^{\mathrm {eq}}_C$
-formula
$\varphi (x,y)$
. By [Reference Johnson11, Proposition 2.12], the set
$\{a' \in \mathbb {M} : \dim (\varphi (a',\mathbb {M})) = n\}$
is definable, defined by some
$\mathcal {L}^{\mathrm {eq}}_C$
-formula
$\psi (x)$
. Then
$\mathbb {M} \models \varphi (a,b) \wedge \psi (a)$
. As
$\operatorname {tp}(a/Cb)$
is finitely satisfiable in C, there is some
$a' \in C$
such that
$\mathbb {M} \models \varphi (a',b) \wedge \psi (a')$
. Then b is in the C-interpretable set
$\varphi (a',\mathbb {M})$
which has dimension n as
$\mathbb {M} \models \psi (a')$
. Therefore
$\dim (b/C) \le n$
, a contradiction.
Corollary A.3. Suppose
$\ldots , b_{-1}, b_0, b_1, \ldots , \ldots , c_{-1}, c_0, c_1, \ldots $
is
$C_0$
-indiscernible. Then the sequence
$\ldots , b_{-1}, b_0, b_1, \ldots $
is dimensionally independent over
$C = C_0 \cup \{c_i : i \in \mathbb {Z}\}$
.
Proof For example,
$p = \operatorname {tp}(b_n/Cb_1 b_2 \cdots b_{n-1})$
is finitely satisfiable in C; any formula in p is satisfied by
$c_i$
for
$i \ll 0$
. This argument shows that any finite subsequence of
$\{b_i\}_{i \in \mathbb {Z}}$
is dimensionally independent over C. This implies the full sequence is dimensionally independent, by finite character of
.
Lemma A.4. If
$\{b_i : i \in I\}$
is dimensionally independent over C, and
$\dim (a/C) = n$
, then
for all but at most n values of i.
The proof is standard, but we include it for completeness.
Proof Otherwise, passing to a subsequence, we could arrange for
$b_1,\ldots ,b_{n+1}$
to be dimensionally independent over C, but
for each i. The sequence
$(\dim (a/Cb_1,\ldots ,b_i) : 0 \le i \le n+1)$
cannot decrease
$n+1$
times, so there is some
$0 \le i \le n$
such that
$\dim (a/Cb_1,\ldots ,b_i) = \dim (a/Cb_1,\ldots ,b_{i+1})$
, i.e.,
As
, left transitivity gives
, a contradiction.
Lemma A.5. Let X be a C-interpretable set of parameters, with dp-rank r. Then there is
$C' \supseteq C$
and an ict pattern of depth r in X of the form
$(\varphi _i(x;b_{i,j}) : i < r, j \in \mathbb {Z})$
, such that the array
$(b_{i,j} : i < r, ~ j \in \mathbb {Z})$
is mutually
$C'$
-indiscernible, and for each i, the sequence
$(b_{i,j} : j \in \mathbb {Z})$
is dimensionally independent over
$C'$
.
Proof Let
$\mathbb {Z} + \mathbb {Z}'$
denote two copies of
$\mathbb {Z}$
laid end to end, with the second copy denoted
$\mathbb {Z}'$
. Take an ict pattern
$(\varphi _i(x;b^0_{i,j}) : i < r, ~ j < \omega )$
in X. Let
$(b_{i,j} : i < r, ~ j \in \mathbb {Z} + \mathbb {Z}')$
be a mutually C-indiscernible array extracted from
$(b^0_{i,j} : i < r, ~ j < \omega )$
. Then
$(\varphi _i(x;b_{i,j}) : i < r, ~ j \in \mathbb {Z} + \mathbb {Z}')$
is an ict pattern in X. Let
$C' = C \cup \{b_{i,j}, i < r, ~ j \in \mathbb {Z}'\}$
. Then
$(b_{i,j} : i < r, ~ j \in \mathbb {Z})$
is mutually
$C'$
-indiscernible, and each row is dimensionally independent over
$C'$
by Corollary A.3.
Theorem A.6. Let G be a manifold-dominated interpretable group of dp-rank r. There is an ict-pattern
$(\varphi _i(x;b_{i,j}) : i < r, ~ j < \omega )$
in G such that if
$S_{i,j} = \varphi _i(\mathbb {M};b_{i,j})$
, then the following properties hold
$:$
-
1. Each set
$S_{i,j}$
is open. -
2. For each function
$\eta : r \to \omega $
, there is an element
$a_\eta \in G$
such that
$$ \begin{gather*} j = \eta(i) \implies a_\eta \in S_{i,j}, \\ j \ne \eta(i) \implies a_\eta \notin \overline{S_{i,j}}. \end{gather*} $$
Proof By [Reference Johnson11, Theorem 5.10], the topology on G is “admissible,” and so
$$ \begin{align} \dim(\overline{D} \setminus D) < \dim(D) \end{align} $$
for any interpretable subset
$D \subseteq G$
, by [Reference Johnson11, Proposition 4.34]. By Lemma A.5, there is an ict-pattern
$(\psi _i(x;b_{i,j}) : i < r, ~ j \in \mathbb {Z})$
and a set of parameters C (over which G is interpretable) such that the
$b_{i,j}$
are mutually indiscernible over C, and each row is dimensionally independent over C. Take some a such that
$\mathbb {M} \models \psi _i(a;b_{i,j}) \Leftrightarrow j = 0$
for all
$i < r$
and
$j \in \mathbb {Z}$
. By [Reference Gagelman6, Proposition 3.7] there is a formula
$\theta _i(x;b_{i,0},c_i)$
in
$\operatorname {tp}(a/Cb_{i,0})$
such that
$\dim (\theta _i(x;b_{i,0},c_i)) = \dim (a/Cb_{i,0})$
. Replacing
$b_{i,j}$
with
$b_{i,j}c_i$
and replacing
$\psi _i(x;b_{i,j})$
with
$\psi _i(x;b_{i,j}) \wedge \theta _i(x;b_{i,j},c_i)$
, we may assume that
$\dim (\psi _i(x;b_{i,0})) = \dim (a/Cb_{i,0}) =: k_i$
. Let
$V_{i,j} = \psi _i(\mathbb {M};b_{i,j})$
. Then
$\dim (V_{i,j}) = \dim (V_{i,0}) = k_i$
by indiscernibility.
For each i, we have
for all but finitely many j, by Lemma A.4. Throwing away the finitely many bad values of
$b_{i,j}$
in each row, we may assume
for all
$j \ne 0$
. Thus
$\dim (a/Cb_{i,j}) = \dim (a/C)$
for
$j \ne 0$
. By the Small Boundaries Property,
$$ \begin{align*} \dim(\overline{V_{i,j}} \setminus V_{i,j}) &< \dim(V_{i,j}) = \dim(V_{i,0}) = k_i = \dim(a/Cb_{i,0})\\ &\le \dim(a/C) = \dim(a/Cb_{i,j}), \end{align*} $$
for
$j \ne 0$
. Then a cannot be in the
$Cb_{i,j}$
-interpretable set
$\overline {V_{i,j}} \setminus V_{i,j}$
. By choice of a, we also have
$a \notin V_{i,j}$
. So
$a \notin \overline {V_{i,j}}$
for any
$j \ne 0$
. Thus
$$ \begin{gather*} j = 0 \implies a \in V_{i,j}, \\ j \ne 0 \implies a \notin \overline{V_{i,j}}. \end{gather*} $$
By mutual indiscernibility, we can find
$a_\eta $
for any
$\eta : r \to \mathbb {Z}$
such that
$$ \begin{gather*} j = \eta(i) \implies a_\eta \in V_{i,j}, \\ j \ne \eta(i) \implies a_\eta \notin \overline{V_{i,j}}. \end{gather*} $$
Recall that the topology on G is a group topology, so every open neighborhood of
$a_\eta $
has the form
$a_\eta \cdot N$
for some open neighborhood N of
$1$
. For each
$i,j,\eta $
with
$j \ne \eta (i)$
, we can find an open neighborhood
$N_{i,j,\eta } \ni 1$
such that
$(a_\eta \cdot N_{i,j,\eta }) \cap V_{i,j} = \varnothing $
. By saturation, there is an interpretable open neighborhood
$N_0 \ni 1$
with
$N_0 \subseteq N_{i,j,\eta }$
for all
$i,j,\eta $
. Because the topology is a group topology, there is a smaller interpretable open neighborhood
$N \ni 1$
such that
$N = N^{-1}$
and
$N \cdot N \subseteq N_0$
.
Let
$U_{i,j} = V_{i,j} \cdot N = \{x \cdot y : x \in V_{i,j}, ~ y \in N\}$
. Note that
$U_{i,j}$
is open. If
$j \ne \eta (i)$
, then
$$ \begin{align*} (a_\eta \cdot N \cdot N) \cap V_{i,j} \subseteq a_\eta \cdot N_{i,j,\eta} \cap V_{i,j} = \varnothing. \end{align*} $$
The fact that
$(a_\eta \cdot N \cdot N) \cap V_{i,j} = \varnothing $
implies that
$$\begin{align*}(a_\eta \cdot N) \cap U_{i,j} = (a_\eta \cdot N) \cap (V_{i,j} \cdot N) = \varnothing.\end{align*}$$
The neighborhood
$a_\eta \cdot N$
then shows that
$a_\eta \notin \overline {U_{i,j}}$
. On the other hand,
$1 \in N$
, so
$V_{i,j} \subseteq U_{i,j}$
. Therefore, if
$j = \eta (i)$
, then
$a_\eta \in V_{i,j} \subseteq U_{i,j}$
. Putting everything together, we get
$$ \begin{gather*} j = \eta(i) \implies a_\eta \in U_{i,j}, \\ j \ne \eta(i) \implies a_\eta \notin \overline{U_{i,j}}. \end{gather*} $$
The sets
$U_{i,j}$
are uniformly interpretable, so we can find some formula
$\varphi (x;y)$
such that each
$U_{i,j}$
has the form
$\varphi (\mathbb {M};b_{i,j})$
for some
$b_{i,j}$
(not the original ones). Then
$(\varphi (\mathbb {M};b_{i,j}) : i < r, ~ j < \omega )$
is the desired ict pattern.
B Extensions and dfg
Work in a highly resplendent monster model
$\mathbb {M}$
.
$\operatorname {acl}(-)$
always means
$\operatorname {acl}^{\mathrm {eq}}$
. All sets and parameters can come from
$\mathbb {M}^{\mathrm {eq}}$
by default. “Definable” means “interpretable.”
Definition B.1. A definable set D is almost A-definable if it is
$\operatorname {acl}(A)$
-definable, or equivalently,
$\{\sigma (D) : \sigma \in \operatorname {Aut}(\mathbb {M}/A)\}$
is finite. A global definable type p is almost A-definable if it is
$\operatorname {acl}(A)$
-definable, or equivalently,
$\{\sigma (p) : \sigma \in \operatorname {Aut}(\mathbb {M}/A)\}$
is small.
The following is folklore; see [Reference Johnson10, Lemma 3.13] for a proof.
Fact B.2. Suppose b realizes
$p | A$
for some almost A-definable global type p. Suppose c realizes
$q | (Ab)$
for some almost
$Ab$
-definable global type q. Then c realizes
$r | A$
for some almost A-definable global type r.
Definition B.3. Let G be an A-definable group. Say that G has dfg over A if there is a global definable type p on G such that p and all its left-translates are almost A-definable.
Lemma B.4. Let G be a definable dfg group and let S be a definable set with a regular right action of G. Suppose everything is A-definable, and G has dfg over A. Then there is a global type on S that is almost A-definable.
Proof For
$b \in S$
, let
$b \cdot p$
denote the pushforward of the A-definable type p along the map
$x \mapsto b \cdot x$
from G to S. Note that
$b \cdot p$
is a definable type on S.
The set
$\mathfrak {S} = \{b \cdot p : b \in S\}$
is small, because it is
$\{b_0 \cdot g \cdot p : g \in G\}$
for any fixed
$b_0 \in S$
. If
$\sigma \in \operatorname {Aut}(\mathbb {M}/\operatorname {acl}(A))$
, then
$\sigma $
fixes p and
$\sigma $
fixes
$\mathfrak {S}$
setwise, since
$\mathfrak {S}$
was defined in an invariant way. Therefore any
$b \cdot p$
has small orbit under
$\operatorname {Aut}(\mathbb {M}/\operatorname {acl}(A))$
, implying that
$b \cdot p$
is almost A-definable.
If G is a
$\varnothing $
-definable group, let
$\mathbb {M} \ltimes G$
be the new structure obtained by adding a copy of G as a new sort S, and putting no structure on S other than the regular right action of G. For any
$g \in G$
, there is an automorphism of
$\mathbb {M} \ltimes G$
fixing
$\mathbb {M}$
and acting as left translation by g on the new sort S. In fact,
$\operatorname {Aut}(\mathbb {M} \ltimes G) \cong \operatorname {Aut}(\mathbb {M}) \ltimes G$
.
This construction is called “Construction C” in [Reference Hrushovski, Peterzil and Pillay8, Section 1], where it is attributed to Hrushovski’s thesis. It also appears in [Reference Simon22] above Lemma 8.19. As mentioned in [Reference Simon22],
$\mathbb {M} \ltimes G$
is a conservative extension of
$\mathbb {M}$
, in the sense that it introduces no new
$\varnothing $
-definable or definable sets on
$\mathbb {M}$
. After naming the element
$1 \in S$
, the two structures are bi-interpretable. Since we assumed
$\mathbb {M}$
was very resplendent,
$\mathbb {M} \ltimes G$
will be too.
Lemma B.5. Let
$A \subseteq \mathbb {M}$
be a small set of parameters. Suppose that in
$\mathbb {M} \ltimes G$
, there is a global type p on S that is almost A-definable. Then G has dfg over A.
Proof For
$b, s \in S$
, let
$b^{-1} \cdot s$
denote the unique
$x \in G$
such that
$s = b \cdot x$
. Let
$b^{-1} \cdot p$
denote the pushforward of p along the map
$x \mapsto b^{-1} \cdot x$
from S to G. Then
$b^{-1} \cdot p$
is a definable type on G. If
$\sigma \in \operatorname {Aut}(\mathbb {M}/A)$
, we can extend
$\sigma $
to
$\hat {\sigma } \in \operatorname {Aut}((\mathbb {M} \ltimes G) / A)$
fixing b. Then
$$ \begin{align*} \sigma(b^{-1} \cdot p) = \hat{\sigma}(b^{-1} \cdot p) = b^{-1} \cdot \hat{\sigma}(p). \end{align*} $$
There are only a small number of possibilities for
$\hat {\sigma }(p)$
, and so
$b^{-1} \cdot p =: q$
is almost A-definable.
If
$g \in G$
, then
$g \cdot b^{-1} \cdot x = (b \cdot g^{-1})^{-1} \cdot x$
for
$x \in S$
, and so
$$ \begin{align*} g \cdot q = g \cdot b^{-1} \cdot p = (b \cdot g^{-1})^{-1} \cdot p = (b')^{-1} \cdot p \end{align*} $$
for
$b' = b \cdot g^{-1}$
. Replacing b with
$b'$
in the argument above, we see that
$(b')^{-1} \cdot p = g \cdot q$
is almost A-definable. In other words, every translate
$g \cdot q$
of q is almost A-definable, showing G has dfg over A.
Lemmas B.4 and B.5 are formally analogous to [Reference Simon22, Lemma 8.19], replacing “non-forking over A” with “almost A-definable.”
Theorem B.6. If
$1 \to N \to G \to H \to 1$
is a short exact sequence of definable groups, and
$N, H$
have dfg, then G has dfg.
Proof Naming parameters, we may assume the whole sequence is
$\varnothing $
-definable, and that N and H have dfg over
$\varnothing $
. Construct
$\mathbb {M} \ltimes G$
. Let S be the new sort with a regular right action of G. Let
$S'$
be the quotient
$S/N$
. Then
$S'$
has a regular right action by H. By Lemma B.4, there is an almost
$\varnothing $
-definable global type p on
$S'$
. Take b realizing
$p | \varnothing $
. Let
$S"$
be the fiber of
$S \to S'$
over
$b \in S'$
. Then
$S"$
is a b-definable set with a b-definable regular right action by N. By Lemma B.4, there is an almost b-definable global type q on
$S"$
. Let c realize
$q | b$
. Note
$c \in S$
. By Fact B.2, there is an almost
$\varnothing $
-definable global type r on S such that c realizes
$r | \varnothing $
. By Lemma B.5, G has dfg.
Theorem B.6 generalizes one direction of Lemma 2.3. We cannot expect the reverse direction to hold (if G has dfg, then N and H have dfg). For example, in
$p\mathrm {CF}^{\mathrm {eq}}$
, the short exact sequence
$$ \begin{align*} 0 \to \mathbb{Z}_p \to \mathbb{Q}_p \to \mathbb{Q}_p/\mathbb{Z}_p \to 0 \end{align*} $$
is a counterexample:
$\mathbb {Q}_p$
has dfg but
$\mathbb {Z}_p$
does not. So the use of definable Skolem functions in Lemma 2.3 is essential.
Acknowledgments
Section 5 was partially based on joint work with Zhentao Zhang, who declined to be an author on this paper. We would like to thank the referee, who provided many helpful comments and suggested adding examples in Section 3.
Funding
The first author was supported by the National Natural Science Foundation of China (Grant No. 12101131). The second author was supported by the National Social Fund of China (Grant No. 20CZX050).
