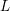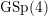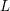1 Introduction
The analytic class number formula of Dedekind and Dirichlet, proved in the middle of the nineteenth century, is a mysterious relationship between an analytic invariant and an arithmetic invariant of a number field
![]() $K$
. It relates the leading Taylor coefficient at zero of the zeta function of
$K$
. It relates the leading Taylor coefficient at zero of the zeta function of
![]() $K$
to the units
$K$
to the units
![]() ${\mathcal{O}}_{K}^{\times }$
of
${\mathcal{O}}_{K}^{\times }$
of
![]() $K$
through the regulator map
$K$
through the regulator map

where
![]() $r_{1}$
and
$r_{1}$
and
![]() $r_{2}$
denote the number of real and complex places of
$r_{2}$
denote the number of real and complex places of
![]() $K$
, respectively. According to Beilinson’s conjectures on special values of motivic
$K$
, respectively. According to Beilinson’s conjectures on special values of motivic
![]() $L$
-functions [Reference BeilinsonBei85], such relationships should exist in great generality. To generalize the analytic class number formula, Beilinson replaces units by motivic cohomology classes and the classical regulator by the higher regulator
$L$
-functions [Reference BeilinsonBei85], such relationships should exist in great generality. To generalize the analytic class number formula, Beilinson replaces units by motivic cohomology classes and the classical regulator by the higher regulator

from motivic cohomology to absolute Hodge cohomology. Here
![]() $X$
denotes a smooth projective scheme over
$X$
denotes a smooth projective scheme over
![]() $\mathbb{Q}$
. For an introduction to Beilinson’s conjectures, to the motivic formalism underlying them, and for a survey of known results, the interested reader might consult the article [Reference NekovarNek94]. In this paper, we establish a connection between elements in the motivic cohomology of the Siegel threefold and special values of the degree-four
$\mathbb{Q}$
. For an introduction to Beilinson’s conjectures, to the motivic formalism underlying them, and for a survey of known results, the interested reader might consult the article [Reference NekovarNek94]. In this paper, we establish a connection between elements in the motivic cohomology of the Siegel threefold and special values of the degree-four
![]() $L$
-function of some cuspidal automorphic representations of the symplectic group
$L$
-function of some cuspidal automorphic representations of the symplectic group
![]() $\text{GSp}(4)$
. The author hopes that the present work may not be useless to discover more general phenomena explaining the connection between special values of automorphic
$\text{GSp}(4)$
. The author hopes that the present work may not be useless to discover more general phenomena explaining the connection between special values of automorphic
![]() $L$
-functions and mixed motives.
$L$
-functions and mixed motives.
Like in the previous approaches, the motivic cohomology classes that we work with are constructed using Beilinson’s Eisenstein symbol and the functorial properties of motivic cohomology. For any non-negative integer
![]() $n$
and level
$n$
and level
![]() $K$
, the Eisenstein symbol [Reference BeilinsonBei88, §3] is a
$K$
, the Eisenstein symbol [Reference BeilinsonBei88, §3] is a
![]() $\mathbb{Q}$
-linear map
$\mathbb{Q}$
-linear map

whose target is the motivic cohomology of the Shimura variety
![]() $M_{K}$
of
$M_{K}$
of
![]() $\text{GL}(2)$
, or modular curve, of level
$\text{GL}(2)$
, or modular curve, of level
![]() $K$
, with coefficients in the
$K$
, with coefficients in the
![]() $n$
th symmetric power of the motivic sheaf
$n$
th symmetric power of the motivic sheaf
![]() $V_{2}$
associated to the standard representation of
$V_{2}$
associated to the standard representation of
![]() $\text{GL}(2)$
. The definition of
$\text{GL}(2)$
. The definition of
![]() ${\mathcal{B}}_{n}$
will be given later, but we would like to mention that for
${\mathcal{B}}_{n}$
will be given later, but we would like to mention that for
 $\unicode[STIX]{x1D719}_{f}\in {\mathcal{B}}_{n}$
, the image of
$\unicode[STIX]{x1D719}_{f}\in {\mathcal{B}}_{n}$
, the image of
 $\operatorname{Eis}_{{\mathcal{M}}}^{n}(\unicode[STIX]{x1D719}_{f})$
under the regulator
$\operatorname{Eis}_{{\mathcal{M}}}^{n}(\unicode[STIX]{x1D719}_{f})$
under the regulator

in Deligne–Beilinson cohomology can be explicitly described by real analytic Eisenstein series. At present, most of the results relating special values of
![]() $L$
-functions to regulators rely on the Eisenstein symbol (see, for example, [Reference BeilinsonBei88, Reference DeningerDen89, Reference DeningerDen90, Reference KingsKin98, Reference KatoKat04]).
$L$
-functions to regulators rely on the Eisenstein symbol (see, for example, [Reference BeilinsonBei88, Reference DeningerDen89, Reference DeningerDen90, Reference KingsKin98, Reference KatoKat04]).
To explain the construction of the motivic cohomology classes that we shall study, let us introduce some notation. Let
![]() $I_{2}$
be the identity matrix of size two and let
$I_{2}$
be the identity matrix of size two and let
![]() $\unicode[STIX]{x1D713}$
be the symplectic form whose matrix is
$\unicode[STIX]{x1D713}$
be the symplectic form whose matrix is
 $$\begin{eqnarray}\unicode[STIX]{x1D713}=\left(\begin{array}{@{}cc@{}} & I_{2}\\ -I_{2} & \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}=\left(\begin{array}{@{}cc@{}} & I_{2}\\ -I_{2} & \end{array}\right).\end{eqnarray}$$
The symplectic group
![]() $\text{GSp}(4)$
is defined as
$\text{GSp}(4)$
is defined as
 $$\begin{eqnarray}\text{GSp}(4)=\{g\in \text{GL}_{4/\mathbb{Q}}\mid \text{}^{t}\!g\unicode[STIX]{x1D713}g=\unicode[STIX]{x1D708}(g)\unicode[STIX]{x1D713},\unicode[STIX]{x1D708}(g)\in \mathbb{G}_{m}\}.\end{eqnarray}$$
$$\begin{eqnarray}\text{GSp}(4)=\{g\in \text{GL}_{4/\mathbb{Q}}\mid \text{}^{t}\!g\unicode[STIX]{x1D713}g=\unicode[STIX]{x1D708}(g)\unicode[STIX]{x1D713},\unicode[STIX]{x1D708}(g)\in \mathbb{G}_{m}\}.\end{eqnarray}$$
It is a reductive linear algebraic group over
![]() $\mathbb{Q}$
and contains the group
$\mathbb{Q}$
and contains the group
 $\text{GL}(2)\times _{\mathbb{G}_{m}}\text{GL}(2)$
, where the fiber product is over the determinant, via the embedding
$\text{GL}(2)\times _{\mathbb{G}_{m}}\text{GL}(2)$
, where the fiber product is over the determinant, via the embedding

defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D704}\left(\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right),\left(\begin{array}{@{}cc@{}}a^{\prime } & b^{\prime }\\ c^{\prime } & d^{\prime }\end{array}\right)\right)=\left(\begin{array}{@{}cccc@{}}a & & b & \\ & a^{\prime } & & b^{\prime }\\ c & & d & \\ & c^{\prime } & & d^{\prime }\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}\left(\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right),\left(\begin{array}{@{}cc@{}}a^{\prime } & b^{\prime }\\ c^{\prime } & d^{\prime }\end{array}\right)\right)=\left(\begin{array}{@{}cccc@{}}a & & b & \\ & a^{\prime } & & b^{\prime }\\ c & & d & \\ & c^{\prime } & & d^{\prime }\end{array}\right).\end{eqnarray}$$
For a fixed level
![]() $L$
, the Shimura variety
$L$
, the Shimura variety
![]() $S_{L}$
associated to
$S_{L}$
associated to
![]() $\text{GSp}(4)$
is a smooth quasi-projective threefold defined over
$\text{GSp}(4)$
is a smooth quasi-projective threefold defined over
![]() $\mathbb{Q}$
. Moreover, for any level
$\mathbb{Q}$
. Moreover, for any level
![]() $K$
, the morphism
$K$
, the morphism
![]() $\unicode[STIX]{x1D704}$
induces a closed embedding
$\unicode[STIX]{x1D704}$
induces a closed embedding

for some
![]() $L$
. The basic idea is to map the external cup-product
$L$
. The basic idea is to map the external cup-product
 $\operatorname{Eis}_{{\mathcal{M}}}^{p}\sqcup \operatorname{Eis}_{{\mathcal{M}}}^{q}$
to the motivic cohomology of
$\operatorname{Eis}_{{\mathcal{M}}}^{p}\sqcup \operatorname{Eis}_{{\mathcal{M}}}^{q}$
to the motivic cohomology of
![]() $S_{L}$
via this embedding. To be more precise, let
$S_{L}$
via this embedding. To be more precise, let
![]() $p$
and
$p$
and
![]() $q$
be non-negative integers, and let
$q$
be non-negative integers, and let
 $(\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2})(3)$
denote the irreducible algebraic representation
$(\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2})(3)$
denote the irreducible algebraic representation
 $(\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2})\otimes \text{det}^{\otimes 3}$
of
$(\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2})\otimes \text{det}^{\otimes 3}$
of
 $\text{GL}(2)\times _{\mathbb{G}_{m}}\text{GL}(2)$
, where
$\text{GL}(2)\times _{\mathbb{G}_{m}}\text{GL}(2)$
, where
![]() $\text{det}$
is the determinant character. Let
$\text{det}$
is the determinant character. Let
![]() $W$
be an irreducible representation of
$W$
be an irreducible representation of
![]() $\text{GSp}(4)$
such that, as representations of
$\text{GSp}(4)$
such that, as representations of
 $\text{GL}(2)\times _{\mathbb{G}_{m}}\text{GL}(2)$
, we have
$\text{GL}(2)\times _{\mathbb{G}_{m}}\text{GL}(2)$
, we have
 $$\begin{eqnarray}(\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2})(3)\subset \unicode[STIX]{x1D704}^{\ast }W.\end{eqnarray}$$
$$\begin{eqnarray}(\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2})(3)\subset \unicode[STIX]{x1D704}^{\ast }W.\end{eqnarray}$$
In what follows, we shall take the liberty to denote by the same symbol
![]() $W$
the motivic sheaf on
$W$
the motivic sheaf on
![]() $S_{L}$
corresponding to
$S_{L}$
corresponding to
![]() $W$
(see § 4.1). Taking the external cup-product of
$W$
(see § 4.1). Taking the external cup-product of
![]() $\operatorname{Eis}_{{\mathcal{M}}}^{p}$
and
$\operatorname{Eis}_{{\mathcal{M}}}^{p}$
and
![]() $\operatorname{Eis}_{{\mathcal{M}}}^{q}$
, we obtain the map
$\operatorname{Eis}_{{\mathcal{M}}}^{q}$
, we obtain the map

Composing with the map induced by the inclusion
 $(\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2})(2)\subset \unicode[STIX]{x1D704}^{\ast }W(-1)$
and with the Gysin morphism corresponding to
$(\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2})(2)\subset \unicode[STIX]{x1D704}^{\ast }W(-1)$
and with the Gysin morphism corresponding to
![]() $\unicode[STIX]{x1D704}$
, we obtain the map
$\unicode[STIX]{x1D704}$
, we obtain the map

To go further, let us recall the main result of [Reference LemmaLem15], which will be crucial for us. Irreducible algebraic representations of
![]() $\text{GSp}(4)$
are classified by their highest weight, i.e. by two integers
$\text{GSp}(4)$
are classified by their highest weight, i.e. by two integers
 $k\geqslant k^{\prime }\geqslant 0$
. Let
$k\geqslant k^{\prime }\geqslant 0$
. Let
![]() $k$
and
$k$
and
![]() $k^{\prime }$
be two such integers. Assume that
$k^{\prime }$
be two such integers. Assume that
 $k+k^{\prime }\equiv p+q~(\text{mod}~2)$
and let
$k+k^{\prime }\equiv p+q~(\text{mod}~2)$
and let
![]() $W$
be an irreducible algebraic representation of
$W$
be an irreducible algebraic representation of
![]() $\text{GSp}(4)$
with highest weight
$\text{GSp}(4)$
with highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },c)$
, with the notation of § 2, where
$\unicode[STIX]{x1D706}(k,k^{\prime },c)$
, with the notation of § 2, where
 $c=p+q+6$
. Then, condition (2) above is equivalent to the following inequalities:
$c=p+q+6$
. Then, condition (2) above is equivalent to the following inequalities:
-
(i) we have
 $p\leqslant k$
;
$p\leqslant k$
; -
(ii) if
 $0\leqslant p<k^{\prime }$
and
$0\leqslant p<k^{\prime }$
and
 $p<k-k^{\prime }$
, then
$p<k-k^{\prime }$
, then
 $k-k^{\prime }-p\leqslant q\leqslant k-k^{\prime }+p$
;
$k-k^{\prime }-p\leqslant q\leqslant k-k^{\prime }+p$
; -
(iii) if
 $0\leqslant p<k^{\prime }$
and
$0\leqslant p<k^{\prime }$
and
 $k-k^{\prime }\leqslant p$
, then
$k-k^{\prime }\leqslant p$
, then
 $p-k+k^{\prime }\leqslant q\leqslant p+k-k^{\prime }$
;
$p-k+k^{\prime }\leqslant q\leqslant p+k-k^{\prime }$
; -
(iv) if
 $k^{\prime }\leqslant p\leqslant k$
and
$k^{\prime }\leqslant p\leqslant k$
and
 $k^{\prime }<k-p$
, then
$k^{\prime }<k-p$
, then
 $k-k^{\prime }-p\leqslant q\leqslant k+k^{\prime }-p$
;
$k-k^{\prime }-p\leqslant q\leqslant k+k^{\prime }-p$
; -
(v) if
 $k^{\prime }\leqslant p\leqslant k$
and
$k^{\prime }\leqslant p\leqslant k$
and
 $k-p\leqslant k^{\prime }$
, then
$k-p\leqslant k^{\prime }$
, then
 $p-k+k^{\prime }\leqslant q\leqslant k+k^{\prime }-p$
.
$p-k+k^{\prime }\leqslant q\leqslant k+k^{\prime }-p$
.
Let
 $H_{B,!}^{3}(S_{L},W)$
be the image of the Betti cohomology with compact support in the cohomology without support, in the middle degree. By the theory of mixed Hodge modules, there is a pure real
$H_{B,!}^{3}(S_{L},W)$
be the image of the Betti cohomology with compact support in the cohomology without support, in the middle degree. By the theory of mixed Hodge modules, there is a pure real
![]() $\mathbb{Q}$
-Hodge structure of weight
$\mathbb{Q}$
-Hodge structure of weight
 $3-c=-p-q-3$
on
$3-c=-p-q-3$
on
 $H_{B,!}^{3}(S_{L},W)$
. ‘Real’ means that the vector space
$H_{B,!}^{3}(S_{L},W)$
. ‘Real’ means that the vector space
 $H_{B,!}^{3}(S_{L},W)$
is endowed with an involution whose
$H_{B,!}^{3}(S_{L},W)$
is endowed with an involution whose
![]() $\mathbb{C}$
-antilinear complexification stabilizes the Hodge filtration. For
$\mathbb{C}$
-antilinear complexification stabilizes the Hodge filtration. For
 $H_{B,!}^{3}(S_{L},W)$
, this involution is just the map induced by complex conjugation on the complex points of
$H_{B,!}^{3}(S_{L},W)$
, this involution is just the map induced by complex conjugation on the complex points of
![]() $S$
and on
$S$
and on
![]() $W$
. Let us also denote by
$W$
. Let us also denote by
 $\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}$
the composite of
$\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}$
the composite of
 $\operatorname{Eis}_{{\mathcal{M}}}^{p,q,W}$
and of the regulator
$\operatorname{Eis}_{{\mathcal{M}}}^{p,q,W}$
and of the regulator

in absolute Hodge cohomology.
Theorem 1.1 [Reference LemmaLem15, Theorem 6.8].
Assume
 $k>k^{\prime }>0$
,
$k>k^{\prime }>0$
,
 $k+k^{\prime }\neq p+q$
,
$k+k^{\prime }\neq p+q$
,
 $k-p-q-1\neq 0$
,
$k-p-q-1\neq 0$
,
 $k-k^{\prime }-p-q-2\neq 0$
and
$k-k^{\prime }-p-q-2\neq 0$
and
 $k-p-q-2\neq 0$
. Assume that
$k-p-q-2\neq 0$
. Assume that
 $(k-k^{\prime }-p-q-2)/2$
and
$(k-k^{\prime }-p-q-2)/2$
and
 $(k-k^{\prime }+p+q)/2$
are even and that the cusps in the boundary of the Baily–Borel compactifications of
$(k-k^{\prime }+p+q)/2$
are even and that the cusps in the boundary of the Baily–Borel compactifications of
 $M_{K}\times M_{K}$
and of
$M_{K}\times M_{K}$
and of
![]() $S_{L}$
are totally real. Then
$S_{L}$
are totally real. Then
 $\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}$
factors through the inclusion
$\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}$
factors through the inclusion
 $$\begin{eqnarray}\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),H_{B,!}^{3}(S_{L},W)_{\mathbb{R}})\subset H_{{\mathcal{H}}}^{4}(S_{L}/\mathbb{R},W)\end{eqnarray}$$
$$\begin{eqnarray}\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),H_{B,!}^{3}(S_{L},W)_{\mathbb{R}})\subset H_{{\mathcal{H}}}^{4}(S_{L}/\mathbb{R},W)\end{eqnarray}$$
where
![]() $\text{MHS}_{\mathbb{R}}^{+}$
denotes the abelian category of mixed real
$\text{MHS}_{\mathbb{R}}^{+}$
denotes the abelian category of mixed real
![]() $\mathbb{R}$
-Hodge structures and
$\mathbb{R}$
-Hodge structures and
 $H_{B,!}^{3}(S_{L},W)_{\mathbb{R}}$
denotes
$H_{B,!}^{3}(S_{L},W)_{\mathbb{R}}$
denotes
 $H_{B,!}^{3}(S_{L},W)\otimes _{\mathbb{Q}}\mathbb{R}$
.
$H_{B,!}^{3}(S_{L},W)\otimes _{\mathbb{Q}}\mathbb{R}$
.
Let
 $\unicode[STIX]{x1D70B}=\bigotimes _{v}^{\prime }\unicode[STIX]{x1D70B}_{v}$
be a cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}=\bigotimes _{v}^{\prime }\unicode[STIX]{x1D70B}_{v}$
be a cuspidal automorphic representation of
![]() $\text{GSp}(4)$
. As
$\text{GSp}(4)$
. As
![]() $\text{GSp}(4)$
is its own Langlands dual group, we can associate to
$\text{GSp}(4)$
is its own Langlands dual group, we can associate to
![]() $\unicode[STIX]{x1D70B}$
the partial Euler product
$\unicode[STIX]{x1D70B}$
the partial Euler product
 $$\begin{eqnarray}L_{V}(s,\unicode[STIX]{x1D70B},r)=\mathop{\prod }_{v\notin V}L(s,\unicode[STIX]{x1D70B}_{v},r)\end{eqnarray}$$
$$\begin{eqnarray}L_{V}(s,\unicode[STIX]{x1D70B},r)=\mathop{\prod }_{v\notin V}L(s,\unicode[STIX]{x1D70B}_{v},r)\end{eqnarray}$$
where
![]() $V$
denotes the set of places of
$V$
denotes the set of places of
![]() $\mathbb{Q}$
where
$\mathbb{Q}$
where
![]() $\unicode[STIX]{x1D70B}$
is ramified together with the archimedean place and where
$\unicode[STIX]{x1D70B}$
is ramified together with the archimedean place and where
 $r:\text{GSp}(4)\longrightarrow \text{GL}(4)$
is the natural inclusion. This
$r:\text{GSp}(4)\longrightarrow \text{GL}(4)$
is the natural inclusion. This
![]() $L$
-function is called the spinor, or degree-four,
$L$
-function is called the spinor, or degree-four,
![]() $L$
-function in the literature. Assume that
$L$
-function in the literature. Assume that
 $p=k-1$
,
$p=k-1$
,
 $q=k^{\prime }-1$
and that the non-archimedean component of
$q=k^{\prime }-1$
and that the non-archimedean component of
![]() $\unicode[STIX]{x1D70B}$
occurs in the middle degree cohomology of
$\unicode[STIX]{x1D70B}$
occurs in the middle degree cohomology of
![]() $S$
, with coefficients in
$S$
, with coefficients in
![]() $W$
. This means that the central character of
$W$
. This means that the central character of
![]() $\unicode[STIX]{x1D70B}$
has infinity type
$\unicode[STIX]{x1D70B}$
has infinity type
 $-k-k^{\prime }-4$
and that the archimedean component of
$-k-k^{\prime }-4$
and that the archimedean component of
![]() $\unicode[STIX]{x1D70B}$
is a discrete series of Harish-Chandra parameter
$\unicode[STIX]{x1D70B}$
is a discrete series of Harish-Chandra parameter
 $(k+2,k^{\prime }+1)$
. Then, the non-archimedean part
$(k+2,k^{\prime }+1)$
. Then, the non-archimedean part
![]() $\unicode[STIX]{x1D70B}_{f}$
of
$\unicode[STIX]{x1D70B}_{f}$
of
![]() $\unicode[STIX]{x1D70B}$
is defined over its rationality field, which is a number field
$\unicode[STIX]{x1D70B}$
is defined over its rationality field, which is a number field
![]() $E(\unicode[STIX]{x1D70B}_{f})$
(see [Reference Blasius, Harris and RamakrishnanBHR94]) and that will be enlarged if necessary. As a consequence, we can look at the
$E(\unicode[STIX]{x1D70B}_{f})$
(see [Reference Blasius, Harris and RamakrishnanBHR94]) and that will be enlarged if necessary. As a consequence, we can look at the
![]() $L$
-function
$L$
-function
 $L_{V}(s,\unicode[STIX]{x1D70B},r)$
as an
$L_{V}(s,\unicode[STIX]{x1D70B},r)$
as an
 $E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{C}$
-valued function. In general, the automorphic representation
$E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{C}$
-valued function. In general, the automorphic representation
![]() $\unicode[STIX]{x1D70B}$
will be stable at infinity (Definition 4.16 and Remark 4.18) and we assume here that it is the case. Then, the
$\unicode[STIX]{x1D70B}$
will be stable at infinity (Definition 4.16 and Remark 4.18) and we assume here that it is the case. Then, the
![]() $\mathbb{Q}$
-vector space
$\mathbb{Q}$
-vector space
 $$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)=\text{Hom}_{\mathbb{Q}[G(\mathbb{A}_{f})]}(\operatorname{Res}_{E(\unicode[STIX]{x1D70B}_{f})/\mathbb{Q}}\unicode[STIX]{x1D70B}_{f},H_{B,!}^{3}(S,W))\end{eqnarray}$$
$$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)=\text{Hom}_{\mathbb{Q}[G(\mathbb{A}_{f})]}(\operatorname{Res}_{E(\unicode[STIX]{x1D70B}_{f})/\mathbb{Q}}\unicode[STIX]{x1D70B}_{f},H_{B,!}^{3}(S,W))\end{eqnarray}$$
underlies a pure real
![]() $\mathbb{Q}$
-Hodge structure with coefficients in
$\mathbb{Q}$
-Hodge structure with coefficients in
![]() $E(\unicode[STIX]{x1D70B}_{f})$
, which is of rank four and weight
$E(\unicode[STIX]{x1D70B}_{f})$
, which is of rank four and weight
 $-k-k^{\prime }-1$
. Let
$-k-k^{\prime }-1$
. Let
![]() $\mathbb{A}_{f}$
be the finite adeles of
$\mathbb{A}_{f}$
be the finite adeles of
![]() $\mathbb{Q}$
and let
$\mathbb{Q}$
and let
 $$\begin{eqnarray}\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),H_{B,!}^{3}(S,W)_{\mathbb{ R}})=\mathop{\varinjlim }\nolimits_{L}\text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),H_{B,!}^{3}(S_{L},W)_{\mathbb{R}})\end{eqnarray}$$
$$\begin{eqnarray}\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),H_{B,!}^{3}(S,W)_{\mathbb{ R}})=\mathop{\varinjlim }\nolimits_{L}\text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),H_{B,!}^{3}(S_{L},W)_{\mathbb{R}})\end{eqnarray}$$
where the limit is taken over all levels
 $L\subset \text{GSp}(4)(\mathbb{A}_{f})$
, which is a
$L\subset \text{GSp}(4)(\mathbb{A}_{f})$
, which is a
 $\mathbb{R}[\text{GSp}(4)(\mathbb{A}_{f})]$
-module. The sub-
$\mathbb{R}[\text{GSp}(4)(\mathbb{A}_{f})]$
-module. The sub-
 $\mathbb{Q}[\text{GSp}(4)(\mathbb{A}_{f})]$
-module generated by the images of the
$\mathbb{Q}[\text{GSp}(4)(\mathbb{A}_{f})]$
-module generated by the images of the
 $\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}$
for varying levels will be denoted by
$\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}$
for varying levels will be denoted by
 ${\mathcal{K}}(p,q,W)$
. As
${\mathcal{K}}(p,q,W)$
. As
![]() $\unicode[STIX]{x1D70B}$
is assumed to be stable, the
$\unicode[STIX]{x1D70B}$
is assumed to be stable, the
![]() $\unicode[STIX]{x1D70B}_{f}$
-isotypical component
$\unicode[STIX]{x1D70B}_{f}$
-isotypical component
 $\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})$
of
$\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})$
of
 $\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),H_{B,!}^{3}(S,W)_{\mathbb{ R}})$
is a rank-one
$\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),H_{B,!}^{3}(S,W)_{\mathbb{ R}})$
is a rank-one
 $E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{R}$
-module and is endowed with its Deligne
$E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{R}$
-module and is endowed with its Deligne
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-structure
$E(\unicode[STIX]{x1D70B}_{f})$
-structure
 ${\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)$
. Let
${\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)$
. Let
 ${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
denote the projection of
${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
denote the projection of
 ${\mathcal{K}}(p,q,W)$
on
${\mathcal{K}}(p,q,W)$
on
 $\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})$
. To state our main result, we need to consider the Deligne period
$\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})$
. To state our main result, we need to consider the Deligne period
 $c^{-}(\unicode[STIX]{x1D70B}_{f},W)$
associated to
$c^{-}(\unicode[STIX]{x1D70B}_{f},W)$
associated to
![]() $\unicode[STIX]{x1D70B}_{f}$
and
$\unicode[STIX]{x1D70B}_{f}$
and
![]() $W$
and Harris’ occult period invariant
$W$
and Harris’ occult period invariant
 $a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
, first introduced in [Reference HarrisHar04]. Roughly speaking, the invariant
$a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
, first introduced in [Reference HarrisHar04]. Roughly speaking, the invariant
 $a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
measures the difference between the rational structure on
$a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
measures the difference between the rational structure on
![]() $\unicode[STIX]{x1D70B}_{f}$
coming from de Rham cohomology and that coming from the Fourier expansion of cusp forms along the Siegel parabolic. A precise definition will be given in the body of the paper but note that the notation
$\unicode[STIX]{x1D70B}_{f}$
coming from de Rham cohomology and that coming from the Fourier expansion of cusp forms along the Siegel parabolic. A precise definition will be given in the body of the paper but note that the notation
 $a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
is slightly abusive as the occult period invariant cannot be defined merely by reference to the abstract representation
$a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
is slightly abusive as the occult period invariant cannot be defined merely by reference to the abstract representation
![]() $\unicode[STIX]{x1D70B}$
but depends on its realization in cohomology. The following theorem is our main result.
$\unicode[STIX]{x1D70B}$
but depends on its realization in cohomology. The following theorem is our main result.
Theorem 1.2. Let
![]() $\unicode[STIX]{x1D70B}$
be as above and let
$\unicode[STIX]{x1D70B}$
be as above and let
![]() $\check{\unicode[STIX]{x1D70B}}$
be the contragredient representation. Let
$\check{\unicode[STIX]{x1D70B}}$
be the contragredient representation. Let
![]() $\unicode[STIX]{x1D708}_{1}^{0}$
, respectively
$\unicode[STIX]{x1D708}_{1}^{0}$
, respectively
![]() $\unicode[STIX]{x1D708}_{2}^{0}$
, be a finite order Hecke character of
$\unicode[STIX]{x1D708}_{2}^{0}$
, be a finite order Hecke character of
 $\operatorname{sign}(-1)^{k-1}$
, respectively of
$\operatorname{sign}(-1)^{k-1}$
, respectively of
 $\operatorname{sign}(-1)^{k^{\prime }-1}$
, and let
$\operatorname{sign}(-1)^{k^{\prime }-1}$
, and let
 $\unicode[STIX]{x1D708}_{1}=|\;|^{1-k^{\prime }}\unicode[STIX]{x1D708}_{1}^{0}$
, respectively
$\unicode[STIX]{x1D708}_{1}=|\;|^{1-k^{\prime }}\unicode[STIX]{x1D708}_{1}^{0}$
, respectively
 $\unicode[STIX]{x1D708}_{2}=|\;|^{1-k}\unicode[STIX]{x1D708}_{2}^{0}$
. Let
$\unicode[STIX]{x1D708}_{2}=|\;|^{1-k}\unicode[STIX]{x1D708}_{2}^{0}$
. Let
![]() $V$
be the finite set of places where
$V$
be the finite set of places where
![]() $\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1}$
or
$\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1}$
or
![]() $\unicode[STIX]{x1D708}_{2}$
is ramified together with the archimedean place. Assume that:
$\unicode[STIX]{x1D708}_{2}$
is ramified together with the archimedean place. Assume that:
-
(a) we have
 $k>k^{\prime }>0$
;
$k>k^{\prime }>0$
; -
(b) we have
 $k+1\equiv k^{\prime }\equiv 0~(\text{mod}~2)$
;
$k+1\equiv k^{\prime }\equiv 0~(\text{mod}~2)$
; -
(c) we have
 $k\neq 3,k^{\prime }\neq 2$
;
$k\neq 3,k^{\prime }\neq 2$
; -
(d) the automorphic representation
 $\unicode[STIX]{x1D70B}$
is stable at infinity.
$\unicode[STIX]{x1D70B}$
is stable at infinity.
Then
 $$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\unicode[STIX]{x1D70B}^{-2}a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)L_{V}(k+k^{\prime }-1/2,\check{\unicode[STIX]{x1D70B}}){\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\unicode[STIX]{x1D70B}^{-2}a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)L_{V}(k+k^{\prime }-1/2,\check{\unicode[STIX]{x1D70B}}){\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
Three remarks are in order.
(i) The author announced a similar result some time ago [Reference LemmaLem08, Theorem 4], but the proof he thought he had found contained an error. The present work shows that a slight variant of [Reference LemmaLem08, Theorem 4] is true and goes significantly further (see Corollary 1.3 below).
(ii) The hypothesis
 $k+1\equiv k^{\prime }\equiv 0~(\text{mod}~2)$
implies that we can apply Theorem 1.1 to
$k+1\equiv k^{\prime }\equiv 0~(\text{mod}~2)$
implies that we can apply Theorem 1.1 to
 $p=k-1$
and
$p=k-1$
and
 $q=k^{\prime }-1$
. This limitation on
$q=k^{\prime }-1$
. This limitation on
![]() $p$
and
$p$
and
![]() $q$
can be called technical and we would be able to get a similar result for arbitrary
$q$
can be called technical and we would be able to get a similar result for arbitrary
![]() $p$
and
$p$
and
![]() $q$
satisfying the assumption of Theorem 1.1 at the cost of very long (but elementary) calculations. See Remark 4.31 for more details.
$q$
satisfying the assumption of Theorem 1.1 at the cost of very long (but elementary) calculations. See Remark 4.31 for more details.
(iii) The term
 $\unicode[STIX]{x1D70B}^{-2}a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)$
is expected to be an algebraic number according to Beilinson’s conjecture. This expectation is coherent with the main result of the paper [Reference HarrisHar04], where the transcendental part of critical values of the spinor
$\unicode[STIX]{x1D70B}^{-2}a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)$
is expected to be an algebraic number according to Beilinson’s conjecture. This expectation is coherent with the main result of the paper [Reference HarrisHar04], where the transcendental part of critical values of the spinor
![]() $L$
-function are computed in terms of
$L$
-function are computed in terms of
 $a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
. By looking closely at the arguments of [Reference HarrisHar04], it is not too difficult to see that the transcendental part of the uncomputed constants appearing in the main result of [Reference HarrisHar04] are powers of
$a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
. By looking closely at the arguments of [Reference HarrisHar04], it is not too difficult to see that the transcendental part of the uncomputed constants appearing in the main result of [Reference HarrisHar04] are powers of
![]() $\unicode[STIX]{x1D70B}$
. As a consequence, according to the Deligne conjecture on critical values [Reference DeligneDel79], as stated for example in [Reference HarrisHar04, 2.6], we should have
$\unicode[STIX]{x1D70B}$
. As a consequence, according to the Deligne conjecture on critical values [Reference DeligneDel79], as stated for example in [Reference HarrisHar04, 2.6], we should have
 $a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)\in \unicode[STIX]{x1D70B}^{\mathbb{Z}}\overline{\mathbb{Q}}^{\times }$
. The explicit computation of these constants and of the archimedean integrals in [Reference HarrisHar04] should give
$a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)\in \unicode[STIX]{x1D70B}^{\mathbb{Z}}\overline{\mathbb{Q}}^{\times }$
. The explicit computation of these constants and of the archimedean integrals in [Reference HarrisHar04] should give
 $a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)\in \unicode[STIX]{x1D70B}^{2}\overline{\mathbb{Q}}^{\times }$
. For more details on the compatibility between the main result of [Reference HarrisHar04] and Deligne conjecture see [Reference HarrisHar04, Remarks following Theorem 3.5.5].
$a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)\in \unicode[STIX]{x1D70B}^{2}\overline{\mathbb{Q}}^{\times }$
. For more details on the compatibility between the main result of [Reference HarrisHar04] and Deligne conjecture see [Reference HarrisHar04, Remarks following Theorem 3.5.5].
Corollary 1.3. Let
![]() $n\geqslant 0$
be an integer. Let
$n\geqslant 0$
be an integer. Let
 $A\longrightarrow S$
be the universal abelian surface of infinite level over the Siegel threefold and let
$A\longrightarrow S$
be the universal abelian surface of infinite level over the Siegel threefold and let
![]() $A^{n}$
be the
$A^{n}$
be the
![]() $n$
th-fold fiber product over
$n$
th-fold fiber product over
![]() $S$
. If
$S$
. If
![]() $n$
is odd and
$n$
is odd and
![]() $n\geqslant 7$
, then the motivic cohomology space
$n\geqslant 7$
, then the motivic cohomology space
 $H_{{\mathcal{M}}}^{n+4}(A^{n},\mathbb{Q}(n+2))$
is non-zero.
$H_{{\mathcal{M}}}^{n+4}(A^{n},\mathbb{Q}(n+2))$
is non-zero.
The proof of Theorem 1.2 relies on three main ingredients. The first is Theorem 1.1. The second is the analytic description of the composite
 $\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}=r_{{\mathcal{D}}}\circ \operatorname{Eis}_{{\mathcal{M}}}^{p,q,W}$
where
$\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}=r_{{\mathcal{D}}}\circ \operatorname{Eis}_{{\mathcal{M}}}^{p,q,W}$
where

is the regulator in real Deligne–Beilinson cohomology. This follows from Beilinson’s explicit description of the image of the Eisenstein symbol in Deligne–Beilinson cohomology, the functoriality of the regulator and the explicit description of the cup-product and the Gysin morphism in Deligne–Beilinson cohomology. The third ingredient is an integral representation of the spinor
![]() $L$
-function whose study was initiated in [Reference Piatetski-ShapiroPia97] and carried on in [Reference Bump, Friedberg and FurusawaBFF97, Reference MoriyamaMor11, Reference Takloo-BighashTak00]. The contribution of the present work is to explain why these three ingredients, which might seem of quite different natures, are in fact closely related.
$L$
-function whose study was initiated in [Reference Piatetski-ShapiroPia97] and carried on in [Reference Bump, Friedberg and FurusawaBFF97, Reference MoriyamaMor11, Reference Takloo-BighashTak00]. The contribution of the present work is to explain why these three ingredients, which might seem of quite different natures, are in fact closely related.
Let us give an overview of the different sections of the article. In § 2 we collect conventions and notation that will be important in the following. We would like to draw the reader’s attention to § 2.4 where the normalizations of the measures on adelic groups are explained and to § 2.5 where the convention on the weight of variation of Hodge structures is adopted, as this last point differs from one author to the other. Section 3 recalls the connection between discrete series
![]() $L$
-packets for
$L$
-packets for
![]() $\text{GSp}(4)$
and the Hodge decomposition of
$\text{GSp}(4)$
and the Hodge decomposition of
![]() $H_{!}^{3}$
. In § 4, we provide the basis for the computation of the regulator. First, the explicit description of the map
$H_{!}^{3}$
. In § 4, we provide the basis for the computation of the regulator. First, the explicit description of the map
 $\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}$
is given (Proposition 4.10). Then, we adapt to our setting an idea of Beilinson which permits the reduction of the computation of the regulator to the computation of a Poincaré duality pairing (Lemma 4.21). Finally, in a series of lemmas, the computation of the pairing, hence of the regulator, is reduced to the computation of an adelic integral, where the integrand is the product of a cusp form by an Eisenstein series (Corollary 4.29). Section 5 is devoted to the computation of this integral. First, we need to compare very precisely the Eisenstein series appearing in our integral with that defined by Piatetski-Shapiro in [Reference Piatetski-ShapiroPia97]. This is done in Proposition 5.3. Then, we have to study an integral as defined by Piatetski-Shapiro. The constructions of [Reference Piatetski-ShapiroPia97] are based on the Fourier expansion of cusp forms along the Siegel parabolic and more precisely, on the existence of Bessel models for automorphic representations of
$\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}$
is given (Proposition 4.10). Then, we adapt to our setting an idea of Beilinson which permits the reduction of the computation of the regulator to the computation of a Poincaré duality pairing (Lemma 4.21). Finally, in a series of lemmas, the computation of the pairing, hence of the regulator, is reduced to the computation of an adelic integral, where the integrand is the product of a cusp form by an Eisenstein series (Corollary 4.29). Section 5 is devoted to the computation of this integral. First, we need to compare very precisely the Eisenstein series appearing in our integral with that defined by Piatetski-Shapiro in [Reference Piatetski-ShapiroPia97]. This is done in Proposition 5.3. Then, we have to study an integral as defined by Piatetski-Shapiro. The constructions of [Reference Piatetski-ShapiroPia97] are based on the Fourier expansion of cusp forms along the Siegel parabolic and more precisely, on the existence of Bessel models for automorphic representations of
![]() $\text{GSp}(4)$
. The integrals of [Reference Piatetski-ShapiroPia97] expand into Euler products, whose factors need to be computed. In the case we are interested in, the unramified non-archimedean local integrals are computed in Proposition 5.9. The ramified non-archimedean integrals and the archimedean integral are analyzed in Propositions 5.11 and 5.12, respectively. In § 6, we introduce Deligne periods, Harris’ occult period invariant and perform a period computation which explains the contribution of
$\text{GSp}(4)$
. The integrals of [Reference Piatetski-ShapiroPia97] expand into Euler products, whose factors need to be computed. In the case we are interested in, the unramified non-archimedean local integrals are computed in Proposition 5.9. The ramified non-archimedean integrals and the archimedean integral are analyzed in Propositions 5.11 and 5.12, respectively. In § 6, we introduce Deligne periods, Harris’ occult period invariant and perform a period computation which explains the contribution of
 ${\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)$
to Theorem 1.2. In § 7, we explain how to deduce the existence of split Bessel models from results of Moriyama [Reference MoriyamaMor04] and Takloo-Bighash [Reference Takloo-BighashTak00]. We finally prove Theorem 1.2 and Corollary 1.3 as an easy consequence of the previous results.
${\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)$
to Theorem 1.2. In § 7, we explain how to deduce the existence of split Bessel models from results of Moriyama [Reference MoriyamaMor04] and Takloo-Bighash [Reference Takloo-BighashTak00]. We finally prove Theorem 1.2 and Corollary 1.3 as an easy consequence of the previous results.
2 Notation and conventions
In this section, we collect some notation, conventions and basic results that will be used in the rest of the article. The reader might prefer to look at this section only according to their needs, following the references given in the paper.
2.1
Given a ring
![]() $A$
, an
$A$
, an
![]() $A$
-algebra
$A$
-algebra
 $A\longrightarrow B$
and an
$A\longrightarrow B$
and an
![]() $A$
-module
$A$
-module
![]() $M$
, we will denote by
$M$
, we will denote by
![]() $M_{B}$
the
$M_{B}$
the
![]() $B$
-module
$B$
-module
 $B\otimes _{A}M$
when the base ring
$B\otimes _{A}M$
when the base ring
![]() $A$
is clear from the context. Similarly for any
$A$
is clear from the context. Similarly for any
![]() $A$
-scheme
$A$
-scheme
![]() $X$
, we will denote by
$X$
, we will denote by
![]() $X_{B}$
the
$X_{B}$
the
![]() $B$
-scheme obtained by extension of scalars to
$B$
-scheme obtained by extension of scalars to
![]() $B$
.
$B$
.
2.2
Let
 $\mathbb{A}_{f}=\mathbb{Q}\otimes _{\mathbb{Z}}\widehat{\mathbb{Z}}$
, respectively
$\mathbb{A}_{f}=\mathbb{Q}\otimes _{\mathbb{Z}}\widehat{\mathbb{Z}}$
, respectively
 $\mathbb{A}=\mathbb{R}\times \mathbb{A}_{f}$
, denote the topological rings of finite adeles, respectively of adeles, of
$\mathbb{A}=\mathbb{R}\times \mathbb{A}_{f}$
, denote the topological rings of finite adeles, respectively of adeles, of
![]() $\mathbb{Q}$
. The field
$\mathbb{Q}$
. The field
![]() $\mathbb{R}$
is endowed with its usual absolute value. For every prime number
$\mathbb{R}$
is endowed with its usual absolute value. For every prime number
![]() $p$
, we normalize the non-archimedean absolute value on
$p$
, we normalize the non-archimedean absolute value on
![]() $\mathbb{Q}_{p}$
by
$\mathbb{Q}_{p}$
by
 $|p|=p^{-1}$
as usual. Hence, the map
$|p|=p^{-1}$
as usual. Hence, the map
 $\mathbb{A}^{\times }\longrightarrow \mathbb{C}^{\times }$
defined by
$\mathbb{A}^{\times }\longrightarrow \mathbb{C}^{\times }$
defined by
 $(x_{v})_{v}\longmapsto \prod _{v}|x_{v}|$
induces a continuous character
$(x_{v})_{v}\longmapsto \prod _{v}|x_{v}|$
induces a continuous character
 $|\;|:\mathbb{Q}^{\times }\backslash \mathbb{A}^{\times }\longrightarrow \mathbb{C}^{\times }$
. Every continuous character
$|\;|:\mathbb{Q}^{\times }\backslash \mathbb{A}^{\times }\longrightarrow \mathbb{C}^{\times }$
. Every continuous character
 $\unicode[STIX]{x1D708}=\bigotimes _{v}^{\prime }\unicode[STIX]{x1D708}_{v}:\mathbb{Q}^{\times }\backslash \mathbb{A}^{\times }\longrightarrow \mathbb{C}^{\times }$
can be written uniquely
$\unicode[STIX]{x1D708}=\bigotimes _{v}^{\prime }\unicode[STIX]{x1D708}_{v}:\mathbb{Q}^{\times }\backslash \mathbb{A}^{\times }\longrightarrow \mathbb{C}^{\times }$
can be written uniquely
 $\unicode[STIX]{x1D708}=|\;|^{s}\unicode[STIX]{x1D708}^{0}$
for some complex number
$\unicode[STIX]{x1D708}=|\;|^{s}\unicode[STIX]{x1D708}^{0}$
for some complex number
![]() $s$
and some finite-order character
$s$
and some finite-order character
![]() $\unicode[STIX]{x1D708}^{0}$
(see [Reference BumpBum97, Proposition 3.1.2(ii)]). The infinity type of
$\unicode[STIX]{x1D708}^{0}$
(see [Reference BumpBum97, Proposition 3.1.2(ii)]). The infinity type of
![]() $\unicode[STIX]{x1D708}$
is by definition the complex number
$\unicode[STIX]{x1D708}$
is by definition the complex number
![]() $s$
and the sign of
$s$
and the sign of
![]() $\unicode[STIX]{x1D708}$
, is by definition
$\unicode[STIX]{x1D708}$
, is by definition
 $\unicode[STIX]{x1D708}_{\infty }(-1)$
.
$\unicode[STIX]{x1D708}_{\infty }(-1)$
.
2.3
Let
![]() $I_{2}$
be the identity matrix of size two and let
$I_{2}$
be the identity matrix of size two and let
 $$\begin{eqnarray}\unicode[STIX]{x1D713}=\left(\begin{array}{@{}cc@{}} & I_{2}\\ -I_{2} & \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}=\left(\begin{array}{@{}cc@{}} & I_{2}\\ -I_{2} & \end{array}\right).\end{eqnarray}$$
The symplectic group
 $G=\text{GSp}(4)$
is the reductive linear algebraic group over
$G=\text{GSp}(4)$
is the reductive linear algebraic group over
![]() $\mathbb{Q}$
defined as
$\mathbb{Q}$
defined as
 $$\begin{eqnarray}G=\{g\in \text{GL}_{4/\mathbb{Q}}\mid \text{}^{t}\!g\unicode[STIX]{x1D713}g=\unicode[STIX]{x1D708}(g)\unicode[STIX]{x1D713},\unicode[STIX]{x1D708}(g)\in \mathbb{G}_{m}\}.\end{eqnarray}$$
$$\begin{eqnarray}G=\{g\in \text{GL}_{4/\mathbb{Q}}\mid \text{}^{t}\!g\unicode[STIX]{x1D713}g=\unicode[STIX]{x1D708}(g)\unicode[STIX]{x1D713},\unicode[STIX]{x1D708}(g)\in \mathbb{G}_{m}\}.\end{eqnarray}$$
Then
 $\unicode[STIX]{x1D708}:G\longrightarrow \mathbb{G}_{m}$
is a character and the derived group of
$\unicode[STIX]{x1D708}:G\longrightarrow \mathbb{G}_{m}$
is a character and the derived group of
![]() $G$
is
$G$
is
 $\text{Sp}(4)=\text{Ker}\,\unicode[STIX]{x1D708}$
. We denote by
$\text{Sp}(4)=\text{Ker}\,\unicode[STIX]{x1D708}$
. We denote by
![]() $T\subset G$
the diagonal maximal torus defined as
$T\subset G$
the diagonal maximal torus defined as
 $$\begin{eqnarray}T=\{\text{diag}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}^{-1}\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}^{-1}\unicode[STIX]{x1D708})\mid \unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D708}\in \mathbb{G}_{m}\}\end{eqnarray}$$
$$\begin{eqnarray}T=\{\text{diag}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}^{-1}\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}^{-1}\unicode[STIX]{x1D708})\mid \unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D708}\in \mathbb{G}_{m}\}\end{eqnarray}$$
and by
 $B=TU$
the standard Borel subgroup of upper triangular matrices in
$B=TU$
the standard Borel subgroup of upper triangular matrices in
![]() $G$
. We identify the group
$G$
. We identify the group
![]() $X^{\ast }(T)$
of algebraic characters (we will also, as usual, say ‘weights’) of
$X^{\ast }(T)$
of algebraic characters (we will also, as usual, say ‘weights’) of
![]() $T$
to the subgroup of
$T$
to the subgroup of
![]() $\mathbb{Z}^{2}\oplus \mathbb{Z}$
of triples
$\mathbb{Z}^{2}\oplus \mathbb{Z}$
of triples
 $(k,k^{\prime },c)$
such that
$(k,k^{\prime },c)$
such that
 $k+k^{\prime }\equiv c~(\text{mod}~2)$
via
$k+k^{\prime }\equiv c~(\text{mod}~2)$
via
 $$\begin{eqnarray}\unicode[STIX]{x1D706}(k,k^{\prime },c):\text{diag}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}^{-1}\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}^{-1}\unicode[STIX]{x1D708})\longmapsto \unicode[STIX]{x1D6FC}_{1}^{k}\unicode[STIX]{x1D6FC}_{2}^{k^{\prime }}\unicode[STIX]{x1D708}^{(c-k-k^{\prime })/2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}(k,k^{\prime },c):\text{diag}(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FC}_{1}^{-1}\unicode[STIX]{x1D708},\unicode[STIX]{x1D6FC}_{2}^{-1}\unicode[STIX]{x1D708})\longmapsto \unicode[STIX]{x1D6FC}_{1}^{k}\unicode[STIX]{x1D6FC}_{2}^{k^{\prime }}\unicode[STIX]{x1D708}^{(c-k-k^{\prime })/2}.\end{eqnarray}$$
Let
 $\unicode[STIX]{x1D70C}_{1}=\unicode[STIX]{x1D706}(1,-1,0)$
be the short simple root and
$\unicode[STIX]{x1D70C}_{1}=\unicode[STIX]{x1D706}(1,-1,0)$
be the short simple root and
 $\unicode[STIX]{x1D70C}_{2}=\unicode[STIX]{x1D706}(0,2,0)$
be the long simple root. Then the set
$\unicode[STIX]{x1D70C}_{2}=\unicode[STIX]{x1D706}(0,2,0)$
be the long simple root. Then the set
 $R\subset X^{\ast }(T)$
of roots of
$R\subset X^{\ast }(T)$
of roots of
![]() $T$
in
$T$
in
![]() $G$
is
$G$
is
 $$\begin{eqnarray}R=\{\pm \unicode[STIX]{x1D70C}_{1},\pm \unicode[STIX]{x1D70C}_{2},\pm (\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2}),\pm (2\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})\}\end{eqnarray}$$
$$\begin{eqnarray}R=\{\pm \unicode[STIX]{x1D70C}_{1},\pm \unicode[STIX]{x1D70C}_{2},\pm (\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2}),\pm (2\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})\}\end{eqnarray}$$
and the subset
 $R^{+}\subset R$
of positive roots with respect to
$R^{+}\subset R$
of positive roots with respect to
![]() $B$
is
$B$
is
 $$\begin{eqnarray}R^{+}=\{\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2},2\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2}\}.\end{eqnarray}$$
$$\begin{eqnarray}R^{+}=\{\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2},\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2},2\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2}\}.\end{eqnarray}$$
Then, the set of dominant weights is the set of
 $\unicode[STIX]{x1D706}(k,k^{\prime },c)$
such that
$\unicode[STIX]{x1D706}(k,k^{\prime },c)$
such that
 $k\geqslant k^{\prime }\geqslant 0$
. For any dominant weight
$k\geqslant k^{\prime }\geqslant 0$
. For any dominant weight
![]() $\unicode[STIX]{x1D706}$
, there is an irreducible algebraic representation
$\unicode[STIX]{x1D706}$
, there is an irreducible algebraic representation
![]() $V_{\unicode[STIX]{x1D706}}$
of
$V_{\unicode[STIX]{x1D706}}$
of
![]() $G$
of highest weight
$G$
of highest weight
![]() $\unicode[STIX]{x1D706}$
, unique up to isomorphism, and all isomorphism classes of irreducible algebraic representations of
$\unicode[STIX]{x1D706}$
, unique up to isomorphism, and all isomorphism classes of irreducible algebraic representations of
![]() $G$
are obtained in this way. If
$G$
are obtained in this way. If
![]() $V_{\unicode[STIX]{x1D706}}$
is irreducible with highest weight
$V_{\unicode[STIX]{x1D706}}$
is irreducible with highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },c)$
, the contragredient of
$\unicode[STIX]{x1D706}(k,k^{\prime },c)$
, the contragredient of
![]() $V_{\unicode[STIX]{x1D706}}$
has highest weight
$V_{\unicode[STIX]{x1D706}}$
has highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },-c)$
.
$\unicode[STIX]{x1D706}(k,k^{\prime },-c)$
.
The Weyl group
![]() $W$
of
$W$
of
![]() $(G,T)$
is defined as the normalizer of
$(G,T)$
is defined as the normalizer of
![]() $T$
in
$T$
in
![]() $G$
modulo its centralizer. It is a group of order eight such that the images in
$G$
modulo its centralizer. It is a group of order eight such that the images in
![]() $W$
of the elements
$W$
of the elements
 $$\begin{eqnarray}s_{1}=\left(\begin{array}{@{}cccc@{}} & 1 & & \\ 1 & & & \\ & & & 1\\ & & 1 & \end{array}\right),\quad s_{2}=\left(\begin{array}{@{}cccc@{}}1 & & & \\ & & & 1\\ & & 1 & \\ & -1 & & \end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}s_{1}=\left(\begin{array}{@{}cccc@{}} & 1 & & \\ 1 & & & \\ & & & 1\\ & & 1 & \end{array}\right),\quad s_{2}=\left(\begin{array}{@{}cccc@{}}1 & & & \\ & & & 1\\ & & 1 & \\ & -1 & & \end{array}\right)\end{eqnarray}$$
generate
![]() $W$
. Then
$W$
. Then
![]() $W$
acts on
$W$
acts on
![]() $X^{\ast }(T)$
according to the rule
$X^{\ast }(T)$
according to the rule
 $$\begin{eqnarray}(w.\unicode[STIX]{x1D706})(t)=\unicode[STIX]{x1D706}(w^{-1}tw)\end{eqnarray}$$
$$\begin{eqnarray}(w.\unicode[STIX]{x1D706})(t)=\unicode[STIX]{x1D706}(w^{-1}tw)\end{eqnarray}$$
and we have
 $s_{1}.\unicode[STIX]{x1D706}(k,k^{\prime },c)=\unicode[STIX]{x1D706}(k^{\prime },k,c)$
and
$s_{1}.\unicode[STIX]{x1D706}(k,k^{\prime },c)=\unicode[STIX]{x1D706}(k^{\prime },k,c)$
and
 $s_{2}.\unicode[STIX]{x1D706}(k,k^{\prime },c)=\unicode[STIX]{x1D706}(k,-k^{\prime },c)$
which means that
$s_{2}.\unicode[STIX]{x1D706}(k,k^{\prime },c)=\unicode[STIX]{x1D706}(k,-k^{\prime },c)$
which means that
![]() $s_{1}$
corresponds to the reflection associated to the short simple root
$s_{1}$
corresponds to the reflection associated to the short simple root
![]() $\unicode[STIX]{x1D70C}_{1}$
and
$\unicode[STIX]{x1D70C}_{1}$
and
![]() $s_{2}$
to that associated to the long simple root
$s_{2}$
to that associated to the long simple root
![]() $\unicode[STIX]{x1D70C}_{2}$
.
$\unicode[STIX]{x1D70C}_{2}$
.
We shall also denote by
![]() $G^{\prime }$
the reductive linear algebraic group
$G^{\prime }$
the reductive linear algebraic group
 $\text{GL}_{2}\times _{\mathbb{G}_{m}}\text{GL}_{2}$
over
$\text{GL}_{2}\times _{\mathbb{G}_{m}}\text{GL}_{2}$
over
![]() $\mathbb{Q}$
, where the fiber product is over the determinant. As mentioned in the introduction, we have the embedding
$\mathbb{Q}$
, where the fiber product is over the determinant. As mentioned in the introduction, we have the embedding
 $\unicode[STIX]{x1D704}:G^{\prime }\longrightarrow G$
defined by
$\unicode[STIX]{x1D704}:G^{\prime }\longrightarrow G$
defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D704}\left(\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right),\left(\begin{array}{@{}cc@{}}a^{\prime } & b^{\prime }\\ c^{\prime } & d^{\prime }\end{array}\right)\right)=\left(\begin{array}{@{}cccc@{}}a & & b & \\ & a^{\prime } & & b^{\prime }\\ c & & d & \\ & c^{\prime } & & d^{\prime }\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}\left(\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right),\left(\begin{array}{@{}cc@{}}a^{\prime } & b^{\prime }\\ c^{\prime } & d^{\prime }\end{array}\right)\right)=\left(\begin{array}{@{}cccc@{}}a & & b & \\ & a^{\prime } & & b^{\prime }\\ c & & d & \\ & c^{\prime } & & d^{\prime }\end{array}\right).\end{eqnarray}$$
The subgroup of upper triangular matrices in
![]() $G^{\prime }$
is denoted by
$G^{\prime }$
is denoted by
![]() $B^{\prime }$
.
$B^{\prime }$
.
2.4
Let us explain our normalizations of the Haar measures on adeles groups, in the case of
![]() $G(\mathbb{A})$
. A similar discussion can be done for
$G(\mathbb{A})$
. A similar discussion can be done for
![]() $G^{\prime }(\mathbb{A})$
. Consider the unitary group
$G^{\prime }(\mathbb{A})$
. Consider the unitary group
 $\text{U}(2)=\{g\in \text{GL}(2,\mathbb{C})\mid \text{}^{t}\!\,\overline{g}g=I_{2}\}$
where
$\text{U}(2)=\{g\in \text{GL}(2,\mathbb{C})\mid \text{}^{t}\!\,\overline{g}g=I_{2}\}$
where
![]() $\overline{g}$
denotes the complex conjugate of
$\overline{g}$
denotes the complex conjugate of
![]() $g$
. The map
$g$
. The map
 $\unicode[STIX]{x1D705}:\text{U}(2)\longrightarrow \text{Sp}(4,\mathbb{R})$
defined by
$\unicode[STIX]{x1D705}:\text{U}(2)\longrightarrow \text{Sp}(4,\mathbb{R})$
defined by
 $$\begin{eqnarray}g=A+iB\longmapsto \left(\begin{array}{@{}cc@{}}A & B\\ -B & A\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}g=A+iB\longmapsto \left(\begin{array}{@{}cc@{}}A & B\\ -B & A\end{array}\right),\end{eqnarray}$$
where
![]() $A$
and
$A$
and
![]() $B$
denote the real and imaginary parts of
$B$
denote the real and imaginary parts of
![]() $g$
, identifies
$g$
, identifies
![]() $\text{U}(2)$
with a maximal compact subgroup
$\text{U}(2)$
with a maximal compact subgroup
![]() $K$
of
$K$
of
 $\text{Sp}(4,\mathbb{R})$
. Let
$\text{Sp}(4,\mathbb{R})$
. Let
 $A_{G}=\mathbb{R}_{+}^{\times }$
be the identity component of the center of
$A_{G}=\mathbb{R}_{+}^{\times }$
be the identity component of the center of
![]() $G$
, write
$G$
, write
![]() $K_{G}$
for the subgroup
$K_{G}$
for the subgroup
![]() $A_{G}K$
of
$A_{G}K$
of
![]() $G(\mathbb{R})$
, which is maximal compact modulo the center, and let
$G(\mathbb{R})$
, which is maximal compact modulo the center, and let
 $\unicode[STIX]{x1D709}:A_{G}\longrightarrow \mathbb{C}^{\times }$
be a continuous character. Denote again by
$\unicode[STIX]{x1D709}:A_{G}\longrightarrow \mathbb{C}^{\times }$
be a continuous character. Denote again by
 $\unicode[STIX]{x1D709}:G(\mathbb{A})\longrightarrow \mathbb{C}^{\times }$
the extension of
$\unicode[STIX]{x1D709}:G(\mathbb{A})\longrightarrow \mathbb{C}^{\times }$
the extension of
![]() $\unicode[STIX]{x1D709}$
to
$\unicode[STIX]{x1D709}$
to
![]() $G(\mathbb{A})$
given by
$G(\mathbb{A})$
given by
 $\unicode[STIX]{x1D709}((g_{v})_{v})=|\unicode[STIX]{x1D708}(g_{\infty })|^{1/2}$
. The choice of a generator
$\unicode[STIX]{x1D709}((g_{v})_{v})=|\unicode[STIX]{x1D708}(g_{\infty })|^{1/2}$
. The choice of a generator
![]() $\mathbf{1}_{G}$
of the highest exterior power of
$\mathbf{1}_{G}$
of the highest exterior power of
 $\text{Lie}\,G_{\mathbb{R}}/\text{Lie}(A_{G}K)$
determines a left translation invariant measure on
$\text{Lie}\,G_{\mathbb{R}}/\text{Lie}(A_{G}K)$
determines a left translation invariant measure on
 $G(\mathbb{R})/(A_{G}K)$
. Together with the Haar measure on
$G(\mathbb{R})/(A_{G}K)$
. Together with the Haar measure on
![]() $K$
whose total mass is one, this datum determines a left translation invariant measure
$K$
whose total mass is one, this datum determines a left translation invariant measure
![]() $dg_{\infty }$
on
$dg_{\infty }$
on
 $G(\mathbb{R})/A_{G}$
. For every prime number
$G(\mathbb{R})/A_{G}$
. For every prime number
![]() $p$
, we endow
$p$
, we endow
![]() $G(\mathbb{Q}_{p})$
with the Haar measure
$G(\mathbb{Q}_{p})$
with the Haar measure
![]() $dg_{p}$
for which
$dg_{p}$
for which
![]() $G(\mathbb{Z}_{p})$
has volume one. Then, we have the translation invariant measure
$G(\mathbb{Z}_{p})$
has volume one. Then, we have the translation invariant measure
 $dg=\prod _{v\leqslant \infty }dg_{v}$
on
$dg=\prod _{v\leqslant \infty }dg_{v}$
on
![]() $G(\mathbb{A})$
. To introduce automorphic representations, let
$G(\mathbb{A})$
. To introduce automorphic representations, let
 $L^{2}(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
be the space of functions
$L^{2}(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
be the space of functions
 $f:G(\mathbb{Q})\backslash G(\mathbb{A})\longrightarrow \mathbb{C}$
such that:
$f:G(\mathbb{Q})\backslash G(\mathbb{A})\longrightarrow \mathbb{C}$
such that:
-
(i) for all
 $z\in A_{G}$
, for all
$z\in A_{G}$
, for all
 $g\in G(\mathbb{A})$
,
$g\in G(\mathbb{A})$
,
 $f(zg)=\unicode[STIX]{x1D709}(z)f(g)$
;
$f(zg)=\unicode[STIX]{x1D709}(z)f(g)$
; -
(ii) the function
 $\unicode[STIX]{x1D709}^{-1}f$
is square-integrable on
$\unicode[STIX]{x1D709}^{-1}f$
is square-integrable on
 $A_{G}G(\mathbb{Q})\backslash G(\mathbb{A})$
.
$A_{G}G(\mathbb{Q})\backslash G(\mathbb{A})$
.
The subspace
 $^{0}L^{2}(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
of admissible cuspidal functions is a discrete sum with finite multiplicities of closed irreducible
$^{0}L^{2}(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
of admissible cuspidal functions is a discrete sum with finite multiplicities of closed irreducible
 $((\mathfrak{g},K_{G})\times G(\mathbb{A}_{f}))$
-invariant subspaces, which are cuspidal automorphic representations of
$((\mathfrak{g},K_{G})\times G(\mathbb{A}_{f}))$
-invariant subspaces, which are cuspidal automorphic representations of
![]() $G$
by definition. Here, we denote by
$G$
by definition. Here, we denote by
![]() $\mathfrak{g}$
the Lie algebra of
$\mathfrak{g}$
the Lie algebra of
![]() $G(\mathbb{R})$
. Let
$G(\mathbb{R})$
. Let
 ${\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
, respectively
${\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
, respectively
 ${\mathcal{C}}_{c}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
, be the space of functions
${\mathcal{C}}_{c}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
, be the space of functions
 $f:G(\mathbb{Q})\backslash G(\mathbb{A})\longrightarrow \mathbb{C}$
such that:
$f:G(\mathbb{Q})\backslash G(\mathbb{A})\longrightarrow \mathbb{C}$
such that:
-
(i) for all
 $z\in A_{G}$
, for all
$z\in A_{G}$
, for all
 $g\in G(\mathbb{A})$
,
$g\in G(\mathbb{A})$
,
 $f(zg)=\unicode[STIX]{x1D709}(z)f(g)$
;
$f(zg)=\unicode[STIX]{x1D709}(z)f(g)$
; -
(ii) the restriction of
 $f$
to
$f$
to
 $G(\mathbb{R})$
is
$G(\mathbb{R})$
is
 ${\mathcal{C}}^{\infty }$
, respectively
${\mathcal{C}}^{\infty }$
, respectively
 ${\mathcal{C}}^{\infty }$
and compactly supported modulo
${\mathcal{C}}^{\infty }$
and compactly supported modulo
 $A_{G}$
;
$A_{G}$
; -
(iii) the restriction of
 $f$
to
$f$
to
 $G(\mathbb{A}_{f})$
is locally constant and compactly supported.
$G(\mathbb{A}_{f})$
is locally constant and compactly supported.
Let
 ${\mathcal{C}}_{(2)}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
denote the space
${\mathcal{C}}_{(2)}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
denote the space
 $L^{2}(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})\cap {\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
. We have natural inclusions of
$L^{2}(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})\cap {\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
. We have natural inclusions of
 $((\mathfrak{g},K_{G})\times G(\mathbb{A}_{f}))$
-modules
$((\mathfrak{g},K_{G})\times G(\mathbb{A}_{f}))$
-modules
 $$\begin{eqnarray}{\mathcal{C}}_{c}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})\subset {\mathcal{C}}_{(2)}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})\subset {\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}_{c}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})\subset {\mathcal{C}}_{(2)}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})\subset {\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709}).\end{eqnarray}$$
Finally, let
 ${\mathcal{C}}_{\text{cusp}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
denote
${\mathcal{C}}_{\text{cusp}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
denote
 $^{0}L^{2}(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})\cap {\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
. Smooth truncation to a large compact modulo the center subset induces a map
$^{0}L^{2}(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})\cap {\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
. Smooth truncation to a large compact modulo the center subset induces a map
 $$\begin{eqnarray}{\mathcal{C}}_{\text{cusp}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})\longrightarrow {\mathcal{C}}_{c}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}_{\text{cusp}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})\longrightarrow {\mathcal{C}}_{c}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709}).\end{eqnarray}$$
2.5
Let
 $\mathbb{S}=\operatorname{Res}_{\mathbb{C}/\mathbb{R}}\mathbb{G}_{m,\mathbb{C}}$
be the Deligne torus. Following Deligne and Pink, our convention for the equivalence of categories between algebraic representations of
$\mathbb{S}=\operatorname{Res}_{\mathbb{C}/\mathbb{R}}\mathbb{G}_{m,\mathbb{C}}$
be the Deligne torus. Following Deligne and Pink, our convention for the equivalence of categories between algebraic representations of
![]() $\mathbb{S}$
in finite-dimensional
$\mathbb{S}$
in finite-dimensional
![]() $\mathbb{R}$
-vector spaces and (semisimple) mixed
$\mathbb{R}$
-vector spaces and (semisimple) mixed
![]() $\mathbb{R}$
-Hodge structures is as follows. Let
$\mathbb{R}$
-Hodge structures is as follows. Let
![]() $(\unicode[STIX]{x1D70C},V)$
be such a representation of
$(\unicode[STIX]{x1D70C},V)$
be such a representation of
![]() $\mathbb{S}$
. Then the summand
$\mathbb{S}$
. Then the summand
![]() $V^{p,q}$
of
$V^{p,q}$
of
![]() $V_{\mathbb{C}}$
of type
$V_{\mathbb{C}}$
of type
![]() $(p,q)$
is the summand on which
$(p,q)$
is the summand on which
 $\unicode[STIX]{x1D70C}(z_{1},z_{2})$
acts by multiplication by
$\unicode[STIX]{x1D70C}(z_{1},z_{2})$
acts by multiplication by
![]() $z_{1}^{-p}z_{2}^{-q}$
for any
$z_{1}^{-p}z_{2}^{-q}$
for any
 $(z_{1},z_{2})\in \mathbb{S}(\mathbb{C})$
. In particular, any algebraic representation
$(z_{1},z_{2})\in \mathbb{S}(\mathbb{C})$
. In particular, any algebraic representation
![]() $V$
of
$V$
of
![]() $\mathbb{S}$
with central character
$\mathbb{S}$
with central character
![]() $c$
corresponds to a pure Hodge structure of weight
$c$
corresponds to a pure Hodge structure of weight
![]() $-c$
. This convention disagrees with that adopted in [Reference HarrisHar04, Reference TaylorTay93] and [Reference WeissauerWei05] but agrees with that adopted in [Reference KingsKin98, Reference LemmaLem08] and [Reference PinkPin90].
$-c$
. This convention disagrees with that adopted in [Reference HarrisHar04, Reference TaylorTay93] and [Reference WeissauerWei05] but agrees with that adopted in [Reference KingsKin98, Reference LemmaLem08] and [Reference PinkPin90].
3 Motives for
 $\text{GSp}(4)$
$\text{GSp}(4)$
In this section, we are mainly interested in reviewing the connection between the Hodge decomposition of the middle degree cohomology of Siegel threefolds and the discrete series
![]() $L$
-packets for
$L$
-packets for
![]() $G$
. Let us start by recalling the classification of discrete series for
$G$
. Let us start by recalling the classification of discrete series for
![]() $G$
.
$G$
.
3.1 Discrete series
 $L$
-packets
$L$
-packets
In this section and in several other places of the present article, the reader will have to be familiar with the representation theory of compact Lie groups as exposed, for example, in [Reference KnappKna86, ch. IV].
In § 2.4, we identified the unitary group
![]() $\text{U}(2)$
to a maximal compact subgroup
$\text{U}(2)$
to a maximal compact subgroup
![]() $K$
of
$K$
of
 $\text{Sp}(4,\mathbb{R})$
via the isomorphism
$\text{Sp}(4,\mathbb{R})$
via the isomorphism
 $\unicode[STIX]{x1D705}:\text{U}(2)\simeq K$
. Let
$\unicode[STIX]{x1D705}:\text{U}(2)\simeq K$
. Let
![]() $\mathfrak{k}$
denote the Lie algebra of
$\mathfrak{k}$
denote the Lie algebra of
![]() $K$
and by
$K$
and by
![]() $\mathfrak{k}_{\mathbb{C}}$
its complexification. The differential of
$\mathfrak{k}_{\mathbb{C}}$
its complexification. The differential of
![]() $\unicode[STIX]{x1D705}$
induces an isomorphism of Lie algebras
$\unicode[STIX]{x1D705}$
induces an isomorphism of Lie algebras
 $d\unicode[STIX]{x1D705}:\mathfrak{gl}_{2,\mathbb{C}}\simeq \mathfrak{k}_{\mathbb{C}}$
. Let
$d\unicode[STIX]{x1D705}:\mathfrak{gl}_{2,\mathbb{C}}\simeq \mathfrak{k}_{\mathbb{C}}$
. Let
![]() $\mathfrak{sp}_{4}$
denote the Lie algebra of
$\mathfrak{sp}_{4}$
denote the Lie algebra of
 $\text{Sp}(4,\mathbb{R})$
and by
$\text{Sp}(4,\mathbb{R})$
and by
![]() $\mathfrak{sp}_{4,\mathbb{C}}$
its complexification. A compact Cartan subalgebra of
$\mathfrak{sp}_{4,\mathbb{C}}$
its complexification. A compact Cartan subalgebra of
![]() $\mathfrak{sp}_{4}$
is defined as
$\mathfrak{sp}_{4}$
is defined as
 $\mathfrak{h}=\mathbb{R}T_{1}\oplus \mathbb{R}T_{2}$
where
$\mathfrak{h}=\mathbb{R}T_{1}\oplus \mathbb{R}T_{2}$
where
 $$\begin{eqnarray}\displaystyle T_{1} & = & \displaystyle d\unicode[STIX]{x1D705}\left(\left(\begin{array}{@{}cc@{}}i & \\ & \end{array}\right)\right)=\left(\begin{array}{@{}cccc@{}} & & 1 & \\ & & & \\ -1 & & & \\ & & & \end{array}\right),\nonumber\\ \displaystyle T_{2} & = & \displaystyle d\unicode[STIX]{x1D705}\left(\left(\begin{array}{@{}cc@{}} & \\ & i\end{array}\right)\right)=\left(\begin{array}{@{}cccc@{}} & & & \\ & & & 1\\ & & & \\ & -1 & & \end{array}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{1} & = & \displaystyle d\unicode[STIX]{x1D705}\left(\left(\begin{array}{@{}cc@{}}i & \\ & \end{array}\right)\right)=\left(\begin{array}{@{}cccc@{}} & & 1 & \\ & & & \\ -1 & & & \\ & & & \end{array}\right),\nonumber\\ \displaystyle T_{2} & = & \displaystyle d\unicode[STIX]{x1D705}\left(\left(\begin{array}{@{}cc@{}} & \\ & i\end{array}\right)\right)=\left(\begin{array}{@{}cccc@{}} & & & \\ & & & 1\\ & & & \\ & -1 & & \end{array}\right).\nonumber\end{eqnarray}$$
Define a
![]() $\mathbb{C}$
-basis of
$\mathbb{C}$
-basis of
![]() $\mathfrak{h}_{\mathbb{C}}^{\ast }$
by
$\mathfrak{h}_{\mathbb{C}}^{\ast }$
by
 $e_{1}(T_{1})=i,e_{1}(T_{2})=0,e_{2}(T_{1})=0,e_{2}(T_{2})=i$
. The root system
$e_{1}(T_{1})=i,e_{1}(T_{2})=0,e_{2}(T_{1})=0,e_{2}(T_{2})=i$
. The root system
![]() $\unicode[STIX]{x1D6E5}$
of the pair
$\unicode[STIX]{x1D6E5}$
of the pair
 $(\mathfrak{sp}_{4,\mathbb{C}},\mathfrak{h}_{\mathbb{C}})$
is
$(\mathfrak{sp}_{4,\mathbb{C}},\mathfrak{h}_{\mathbb{C}})$
is
 $\unicode[STIX]{x1D6E5}=\{\pm 2e_{1},\pm 2e_{2},\pm (e_{1}\pm e_{2})\}$
. We denote by
$\unicode[STIX]{x1D6E5}=\{\pm 2e_{1},\pm 2e_{2},\pm (e_{1}\pm e_{2})\}$
. We denote by
![]() $\unicode[STIX]{x1D6E5}_{c}$
, respectively
$\unicode[STIX]{x1D6E5}_{c}$
, respectively
![]() $\unicode[STIX]{x1D6E5}_{nc}$
, the set of compact, respectively non-compact, roots in
$\unicode[STIX]{x1D6E5}_{nc}$
, the set of compact, respectively non-compact, roots in
![]() $\unicode[STIX]{x1D6E5}$
. We have
$\unicode[STIX]{x1D6E5}$
. We have
 $\unicode[STIX]{x1D6E5}_{c}=\{\pm (e_{1}-e_{2})\}$
and
$\unicode[STIX]{x1D6E5}_{c}=\{\pm (e_{1}-e_{2})\}$
and
 $\unicode[STIX]{x1D6E5}_{nc}=\unicode[STIX]{x1D6E5}-\unicode[STIX]{x1D6E5}_{c}$
. We choose the set of positive roots as
$\unicode[STIX]{x1D6E5}_{nc}=\unicode[STIX]{x1D6E5}-\unicode[STIX]{x1D6E5}_{c}$
. We choose the set of positive roots as
 $\unicode[STIX]{x1D6E5}^{+}=\{e_{1}-e_{2},2e_{1},e_{1}+e_{2},2e_{2}\}$
. Then, the set of compact, respectively non-compact, positive roots is
$\unicode[STIX]{x1D6E5}^{+}=\{e_{1}-e_{2},2e_{1},e_{1}+e_{2},2e_{2}\}$
. Then, the set of compact, respectively non-compact, positive roots is
 $\unicode[STIX]{x1D6E5}_{c}^{+}=\unicode[STIX]{x1D6E5}_{c}\cap \unicode[STIX]{x1D6E5}^{+}$
, respectively
$\unicode[STIX]{x1D6E5}_{c}^{+}=\unicode[STIX]{x1D6E5}_{c}\cap \unicode[STIX]{x1D6E5}^{+}$
, respectively
 $\unicode[STIX]{x1D6E5}_{nc}^{+}=\unicode[STIX]{x1D6E5}_{nc}\cap \unicode[STIX]{x1D6E5}^{+}$
. For each symmetric matrix
$\unicode[STIX]{x1D6E5}_{nc}^{+}=\unicode[STIX]{x1D6E5}_{nc}\cap \unicode[STIX]{x1D6E5}^{+}$
. For each symmetric matrix
 $Z\in \mathfrak{gl}_{2,\mathbb{C}}$
, define the element
$Z\in \mathfrak{gl}_{2,\mathbb{C}}$
, define the element
![]() $p_{\pm }(Z)$
of
$p_{\pm }(Z)$
of
![]() $\mathfrak{sp}_{4,\mathbb{C}}$
by
$\mathfrak{sp}_{4,\mathbb{C}}$
by
 $$\begin{eqnarray}p_{\pm }(Z)=\left(\begin{array}{@{}cc@{}}Z & \pm iZ\\ \pm iZ & -Z\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}p_{\pm }(Z)=\left(\begin{array}{@{}cc@{}}Z & \pm iZ\\ \pm iZ & -Z\end{array}\right).\end{eqnarray}$$
Let
 $X_{(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})}\in \mathfrak{sp}_{4,\mathbb{C}}$
be defined as
$X_{(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})}\in \mathfrak{sp}_{4,\mathbb{C}}$
be defined as
 $$\begin{eqnarray}X_{\pm (2,0)}=p_{\pm }\left(\left(\begin{array}{@{}cc@{}}1 & \\ & \end{array}\right)\right),\quad X_{\pm (1,1)}=p_{\pm }\left(\left(\begin{array}{@{}cc@{}} & 1\\ 1 & \end{array}\right)\right),\quad X_{\pm (0,2)}=p_{\pm }\left(\left(\begin{array}{@{}cc@{}} & \\ & 1\end{array}\right)\right).\end{eqnarray}$$
$$\begin{eqnarray}X_{\pm (2,0)}=p_{\pm }\left(\left(\begin{array}{@{}cc@{}}1 & \\ & \end{array}\right)\right),\quad X_{\pm (1,1)}=p_{\pm }\left(\left(\begin{array}{@{}cc@{}} & 1\\ 1 & \end{array}\right)\right),\quad X_{\pm (0,2)}=p_{\pm }\left(\left(\begin{array}{@{}cc@{}} & \\ & 1\end{array}\right)\right).\end{eqnarray}$$
It follows from an easy computation that
 $X_{(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})}$
is a root vector corresponding to the non-compact root
$X_{(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})}$
is a root vector corresponding to the non-compact root
 $(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})=\unicode[STIX]{x1D6FC}_{1}e_{1}+\unicode[STIX]{x1D6FC}_{2}e_{2}$
. If we set
$(\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2})=\unicode[STIX]{x1D6FC}_{1}e_{1}+\unicode[STIX]{x1D6FC}_{2}e_{2}$
. If we set
 $$\begin{eqnarray}\mathfrak{p}^{\pm }=\bigoplus _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{nc}^{+}}\mathbb{C}X_{\pm \unicode[STIX]{x1D6FC}},\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{p}^{\pm }=\bigoplus _{\unicode[STIX]{x1D6FC}\in \unicode[STIX]{x1D6E5}_{nc}^{+}}\mathbb{C}X_{\pm \unicode[STIX]{x1D6FC}},\end{eqnarray}$$
we have the Cartan decomposition
 $\mathfrak{sp}_{4,\mathbb{C}}=\mathfrak{k}_{\mathbb{C}}\oplus \mathfrak{p}^{+}\oplus \mathfrak{p}^{-}$
.
$\mathfrak{sp}_{4,\mathbb{C}}=\mathfrak{k}_{\mathbb{C}}\oplus \mathfrak{p}^{+}\oplus \mathfrak{p}^{-}$
.
Integral weights are defined as
 $(k,k^{\prime })=ke_{1}+k^{\prime }e_{2}\in \mathfrak{h}_{\mathbb{C}}^{\ast }$
with
$(k,k^{\prime })=ke_{1}+k^{\prime }e_{2}\in \mathfrak{h}_{\mathbb{C}}^{\ast }$
with
 $k,k^{\prime }\in \mathbb{Z}$
and an integral weight is dominant for
$k,k^{\prime }\in \mathbb{Z}$
and an integral weight is dominant for
![]() $\unicode[STIX]{x1D6E5}_{c}^{+}$
if
$\unicode[STIX]{x1D6E5}_{c}^{+}$
if
![]() $k\geqslant k^{\prime }$
. Assigning its highest weight to a finite-dimensional irreducible complex representation
$k\geqslant k^{\prime }$
. Assigning its highest weight to a finite-dimensional irreducible complex representation
![]() $\unicode[STIX]{x1D70F}$
of
$\unicode[STIX]{x1D70F}$
of
![]() $K$
, we define a bijection between isomorphism classes of finite-dimensional irreducible complex representations of
$K$
, we define a bijection between isomorphism classes of finite-dimensional irreducible complex representations of
![]() $K$
and dominant integral weights, whose inverse will be denoted by
$K$
and dominant integral weights, whose inverse will be denoted by
 $(k,k^{\prime })\longmapsto \unicode[STIX]{x1D70F}_{(k,k^{\prime })}$
. Let
$(k,k^{\prime })\longmapsto \unicode[STIX]{x1D70F}_{(k,k^{\prime })}$
. Let
![]() $(k,k^{\prime })$
be a dominant integral weight and let
$(k,k^{\prime })$
be a dominant integral weight and let
 $d=k-k^{\prime }$
. Then
$d=k-k^{\prime }$
. Then
 $\dim _{\mathbb{C}}\unicode[STIX]{x1D70F}_{(k,k^{\prime })}=d+1$
. More precisely, there exists a basis
$\dim _{\mathbb{C}}\unicode[STIX]{x1D70F}_{(k,k^{\prime })}=d+1$
. More precisely, there exists a basis
 $(v_{s})_{0\leqslant s\leqslant d}$
of
$(v_{s})_{0\leqslant s\leqslant d}$
of
![]() $\unicode[STIX]{x1D70F}_{(k,k^{\prime })}$
, such that
$\unicode[STIX]{x1D70F}_{(k,k^{\prime })}$
, such that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{(k,k^{\prime })}\left(d\unicode[STIX]{x1D705}\left(\begin{array}{@{}cc@{}}1 & \\ & \end{array}\right)\right)v_{s} & = & \displaystyle (s+k^{\prime })v_{s},\nonumber\\ \displaystyle \unicode[STIX]{x1D70F}_{(k,k^{\prime })}\left(d\unicode[STIX]{x1D705}\left(\begin{array}{@{}cc@{}} & \\ & 1\end{array}\right)\right)v_{s} & = & \displaystyle (-s+k)v_{s},\nonumber\\ \displaystyle \unicode[STIX]{x1D70F}_{(k,k^{\prime })}\left(d\unicode[STIX]{x1D705}\left(\begin{array}{@{}cc@{}} & 1\\ & \end{array}\right)\right)v_{s} & = & \displaystyle (s+1)v_{s+1},\nonumber\\ \displaystyle \unicode[STIX]{x1D70F}_{(k,k^{\prime })}\left(d\unicode[STIX]{x1D705}\left(\begin{array}{@{}cc@{}} & \\ 1 & \end{array}\right)\right)v_{s} & = & \displaystyle (d-s+1)v_{s-1}\nonumber\\ \displaystyle & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{(k,k^{\prime })}\left(d\unicode[STIX]{x1D705}\left(\begin{array}{@{}cc@{}}1 & \\ & \end{array}\right)\right)v_{s} & = & \displaystyle (s+k^{\prime })v_{s},\nonumber\\ \displaystyle \unicode[STIX]{x1D70F}_{(k,k^{\prime })}\left(d\unicode[STIX]{x1D705}\left(\begin{array}{@{}cc@{}} & \\ & 1\end{array}\right)\right)v_{s} & = & \displaystyle (-s+k)v_{s},\nonumber\\ \displaystyle \unicode[STIX]{x1D70F}_{(k,k^{\prime })}\left(d\unicode[STIX]{x1D705}\left(\begin{array}{@{}cc@{}} & 1\\ & \end{array}\right)\right)v_{s} & = & \displaystyle (s+1)v_{s+1},\nonumber\\ \displaystyle \unicode[STIX]{x1D70F}_{(k,k^{\prime })}\left(d\unicode[STIX]{x1D705}\left(\begin{array}{@{}cc@{}} & \\ 1 & \end{array}\right)\right)v_{s} & = & \displaystyle (d-s+1)v_{s-1}\nonumber\\ \displaystyle & & \displaystyle \nonumber\end{eqnarray}$$
which we call a standard basis of
![]() $\unicode[STIX]{x1D70F}_{(k,k^{\prime })}$
. In the identities above, we agree to use the convention
$\unicode[STIX]{x1D70F}_{(k,k^{\prime })}$
. In the identities above, we agree to use the convention
 $v_{-1}=v_{d+1}=0$
. We will denote by
$v_{-1}=v_{d+1}=0$
. We will denote by
![]() $W_{K}$
the Weyl group of
$W_{K}$
the Weyl group of
![]() $(\mathfrak{k}_{\mathbb{C}},\mathfrak{h}_{\mathbb{C}})$
. According to the classification theorem [Reference KnappKna86, Theorem 9.20], we have the following result.
$(\mathfrak{k}_{\mathbb{C}},\mathfrak{h}_{\mathbb{C}})$
. According to the classification theorem [Reference KnappKna86, Theorem 9.20], we have the following result.
Proposition 3.1. Let
![]() $G(\mathbb{R})^{+}$
be the identity component of
$G(\mathbb{R})^{+}$
be the identity component of
![]() $G(\mathbb{R})$
, let
$G(\mathbb{R})$
, let
![]() $\unicode[STIX]{x1D709}$
be a character of
$\unicode[STIX]{x1D709}$
be a character of
![]() $A_{G}$
and let
$A_{G}$
and let
 $(k,k^{\prime })\in \mathfrak{h}_{\mathbb{C}}^{\ast }$
be an integral weight. Assume
$(k,k^{\prime })\in \mathfrak{h}_{\mathbb{C}}^{\ast }$
be an integral weight. Assume
 $k\geqslant k^{\prime }\geqslant 0$
. Then, there exist four isomorphism classes
$k\geqslant k^{\prime }\geqslant 0$
. Then, there exist four isomorphism classes
![]() $\unicode[STIX]{x1D70B}_{\infty }^{H}$
,
$\unicode[STIX]{x1D70B}_{\infty }^{H}$
,
![]() $\unicode[STIX]{x1D70B}_{\infty }^{W}$
,
$\unicode[STIX]{x1D70B}_{\infty }^{W}$
,
![]() $\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}$
,
$\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}$
,
![]() $\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}$
of irreducible discrete series representations of
$\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}$
of irreducible discrete series representations of
![]() $G(\mathbb{R})^{+}$
with Harish-Chandra parameter
$G(\mathbb{R})^{+}$
with Harish-Chandra parameter
 $(k+2,k^{\prime }+1)$
and central character
$(k+2,k^{\prime }+1)$
and central character
![]() $\unicode[STIX]{x1D709}$
. Furthermore, the restrictions of these representations to
$\unicode[STIX]{x1D709}$
. Furthermore, the restrictions of these representations to
![]() $K$
contain as minimal
$K$
contain as minimal
![]() $K$
-types the representations
$K$
-types the representations
 $\unicode[STIX]{x1D70F}_{(k+3,k^{\prime }+3)}$
,
$\unicode[STIX]{x1D70F}_{(k+3,k^{\prime }+3)}$
,
 $\unicode[STIX]{x1D70F}_{(k+3,-k^{\prime }-1)}$
,
$\unicode[STIX]{x1D70F}_{(k+3,-k^{\prime }-1)}$
,
 $\unicode[STIX]{x1D70F}_{(k^{\prime }+1,-k-3)}$
and
$\unicode[STIX]{x1D70F}_{(k^{\prime }+1,-k-3)}$
and
 $\unicode[STIX]{x1D70F}_{(-k^{\prime }-3,-k-3)}$
, respectively.
$\unicode[STIX]{x1D70F}_{(-k^{\prime }-3,-k-3)}$
, respectively.
Remark 3.2. For the cohomological considerations that follow, we need to be more precise and explain the specific representatives of the isomorphism classes of discrete series that we choose. Let
![]() $N$
be the element of
$N$
be the element of
![]() $G(\mathbb{R})$
defined as
$G(\mathbb{R})$
defined as
 $$\begin{eqnarray}\displaystyle N & = & \displaystyle \left(\begin{array}{@{}cccc@{}} & -1 & & \\ -1 & & & \\ & & & 1\\ & & 1 & \end{array}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle N & = & \displaystyle \left(\begin{array}{@{}cccc@{}} & -1 & & \\ -1 & & & \\ & & & 1\\ & & 1 & \end{array}\right).\nonumber\end{eqnarray}$$
We shall see that
![]() $N$
is related to the action of complex conjugation on the set of complex points of Siegel threefolds (Proposition 3.13). For the adjoint action
$N$
is related to the action of complex conjugation on the set of complex points of Siegel threefolds (Proposition 3.13). For the adjoint action
 $\operatorname{Ad}:G(\mathbb{R})\longrightarrow \text{GL}(\mathfrak{h})$
, we have
$\operatorname{Ad}:G(\mathbb{R})\longrightarrow \text{GL}(\mathfrak{h})$
, we have
 $$\begin{eqnarray}\displaystyle \operatorname{Ad}_{N}(T_{1}) & = & \displaystyle -T_{2},\nonumber\\ \displaystyle \operatorname{Ad}_{N}(T_{2}) & = & \displaystyle -T_{1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Ad}_{N}(T_{1}) & = & \displaystyle -T_{2},\nonumber\\ \displaystyle \operatorname{Ad}_{N}(T_{2}) & = & \displaystyle -T_{1}.\nonumber\end{eqnarray}$$
Furthermore, as
 $\unicode[STIX]{x1D708}(N)=-1$
, the matrix
$\unicode[STIX]{x1D708}(N)=-1$
, the matrix
![]() $N$
normalizes
$N$
normalizes
![]() $G(\mathbb{R})^{+}$
. It follows from the identities above and from [Reference KnappKna86, Theorem 9.20] that the representation of
$G(\mathbb{R})^{+}$
. It follows from the identities above and from [Reference KnappKna86, Theorem 9.20] that the representation of
![]() $G(\mathbb{R})^{+}$
obtained by conjugating
$G(\mathbb{R})^{+}$
obtained by conjugating
![]() $\unicode[STIX]{x1D70B}_{\infty }^{H}$
, respectively
$\unicode[STIX]{x1D70B}_{\infty }^{H}$
, respectively
![]() $\unicode[STIX]{x1D70B}_{\infty }^{W}$
, by
$\unicode[STIX]{x1D70B}_{\infty }^{W}$
, by
![]() $N$
is isomorphic to
$N$
is isomorphic to
![]() $\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}$
, respectively
$\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}$
, respectively
![]() $\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}$
. If we fix such isomorphisms, given a vector
$\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}$
. If we fix such isomorphisms, given a vector
![]() $\unicode[STIX]{x1D6F9}_{\infty }$
belonging to the space underlying
$\unicode[STIX]{x1D6F9}_{\infty }$
belonging to the space underlying
![]() $\unicode[STIX]{x1D70B}_{\infty }^{W}$
, of weight
$\unicode[STIX]{x1D70B}_{\infty }^{W}$
, of weight
![]() $(u,v)$
, we will denote by
$(u,v)$
, we will denote by
![]() $\overline{\unicode[STIX]{x1D6F9}}_{\infty }$
the same vector regarded as a vector of the space underlying
$\overline{\unicode[STIX]{x1D6F9}}_{\infty }$
the same vector regarded as a vector of the space underlying
![]() $\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}$
. It has weight
$\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}$
. It has weight
 $(-v,-u)$
.
$(-v,-u)$
.
For the arithmetic applications we aim at, we will need the following result.
Proposition 3.3 [Reference Blasius, Harris and RamakrishnanBHR94, Theorem 3.2.2].
Let
 $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}$
be a cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}$
be a cuspidal automorphic representation of
![]() $G$
such that
$G$
such that
 $\unicode[STIX]{x1D70B}_{\infty }|_{G(\mathbb{R})^{+}}$
is a discrete series. Then
$\unicode[STIX]{x1D70B}_{\infty }|_{G(\mathbb{R})^{+}}$
is a discrete series. Then
![]() $\unicode[STIX]{x1D70B}_{f}$
is defined over its rationality field, which is a number field
$\unicode[STIX]{x1D70B}_{f}$
is defined over its rationality field, which is a number field
![]() $E(\unicode[STIX]{x1D70B}_{f})$
.
$E(\unicode[STIX]{x1D70B}_{f})$
.
3.2 Cohomology of Siegel threefolds
Siegel threefolds are the Shimura varieties associated to the group
![]() $G$
. Let us briefly recall their definition. Let
$G$
. Let us briefly recall their definition. Let
 $\mathbb{S}=\operatorname{Res}_{\mathbb{C}/\mathbb{R}}\mathbb{G}_{m,\mathbb{C}}$
be the Deligne torus and let
$\mathbb{S}=\operatorname{Res}_{\mathbb{C}/\mathbb{R}}\mathbb{G}_{m,\mathbb{C}}$
be the Deligne torus and let
![]() ${\mathcal{H}}$
be the
${\mathcal{H}}$
be the
![]() $G(\mathbb{R})$
-conjugacy class of the morphism
$G(\mathbb{R})$
-conjugacy class of the morphism
 $h:\mathbb{S}\longrightarrow G_{\mathbb{R}}$
given on
$h:\mathbb{S}\longrightarrow G_{\mathbb{R}}$
given on
![]() $\mathbb{R}$
-points by
$\mathbb{R}$
-points by
 $$\begin{eqnarray}x+iy\longmapsto \left(\begin{array}{@{}cccc@{}}x & & y & \\ & x & & y\\ -y & & x & \\ & -y & & x\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}x+iy\longmapsto \left(\begin{array}{@{}cccc@{}}x & & y & \\ & x & & y\\ -y & & x & \\ & -y & & x\end{array}\right).\end{eqnarray}$$
The pair
![]() $(G,{\mathcal{H}})$
is a pure Shimura datum in the sense of [Reference PinkPin90, 2.1]. The cocharacter
$(G,{\mathcal{H}})$
is a pure Shimura datum in the sense of [Reference PinkPin90, 2.1]. The cocharacter
![]() $\unicode[STIX]{x1D707}$
of
$\unicode[STIX]{x1D707}$
of
![]() $G_{\mathbb{C}}$
associated to the morphism
$G_{\mathbb{C}}$
associated to the morphism
![]() $h$
as in [Reference PinkPin90, 1.3] induces
$h$
as in [Reference PinkPin90, 1.3] induces
 $$\begin{eqnarray}z\longmapsto \left(\begin{array}{@{}cccc@{}}z & & & \\ & z & & \\ & & 1 & \\ & & & 1\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}z\longmapsto \left(\begin{array}{@{}cccc@{}}z & & & \\ & z & & \\ & & 1 & \\ & & & 1\end{array}\right)\end{eqnarray}$$
on complex points, hence it is defined over
![]() $\mathbb{Q}$
. In other terms, the reflex field of
$\mathbb{Q}$
. In other terms, the reflex field of
![]() $(G,{\mathcal{H}})$
is
$(G,{\mathcal{H}})$
is
![]() $\mathbb{Q}$
. For any neat compact open subgroup
$\mathbb{Q}$
. For any neat compact open subgroup
![]() $L$
of
$L$
of
![]() $G(\mathbb{A}_{f})$
, we denote by
$G(\mathbb{A}_{f})$
, we denote by
![]() $S_{L}$
the Siegel threefold of level
$S_{L}$
the Siegel threefold of level
![]() $L$
. This is a smooth quasi-projective
$L$
. This is a smooth quasi-projective
![]() $\mathbb{Q}$
-scheme such that, as complex analytic varieties, we have
$\mathbb{Q}$
-scheme such that, as complex analytic varieties, we have
 $$\begin{eqnarray}S_{L,\mathbb{C}}^{\text{an}}=G(\mathbb{Q})\backslash ({\mathcal{H}}\times G(\mathbb{A}_{f})/L),\end{eqnarray}$$
$$\begin{eqnarray}S_{L,\mathbb{C}}^{\text{an}}=G(\mathbb{Q})\backslash ({\mathcal{H}}\times G(\mathbb{A}_{f})/L),\end{eqnarray}$$
where
![]() $S_{L,\mathbb{C}}^{\text{an}}$
denotes the analytification of the base change of
$S_{L,\mathbb{C}}^{\text{an}}$
denotes the analytification of the base change of
![]() $S_{L}$
to
$S_{L}$
to
![]() $\mathbb{C}$
. For
$\mathbb{C}$
. For
 $g\in G(\mathbb{A}_{f})$
and
$g\in G(\mathbb{A}_{f})$
and
![]() $L$
,
$L$
,
![]() $L^{\prime }$
two neat compact open subgroups of
$L^{\prime }$
two neat compact open subgroups of
![]() $G(\mathbb{A}_{f})$
such that
$G(\mathbb{A}_{f})$
such that
 $g^{-1}L^{\prime }g\subset L$
, right multiplication by
$g^{-1}L^{\prime }g\subset L$
, right multiplication by
![]() $g$
on
$g$
on
![]() $S_{L,\mathbb{C}}^{\text{an}}$
descends to a morphism
$S_{L,\mathbb{C}}^{\text{an}}$
descends to a morphism
 $[g]:S_{L^{\prime }}\longrightarrow S_{L}$
of
$[g]:S_{L^{\prime }}\longrightarrow S_{L}$
of
![]() $\mathbb{Q}$
-schemes, which is finite étale. This implies that there is an action of
$\mathbb{Q}$
-schemes, which is finite étale. This implies that there is an action of
![]() $G(\mathbb{A}_{f})$
on the projective system
$G(\mathbb{A}_{f})$
on the projective system
![]() $(S_{L})_{L}$
indexed by neat compact open subgroups of
$(S_{L})_{L}$
indexed by neat compact open subgroups of
![]() $G(\mathbb{A}_{f})$
. In what follows, all compact open subgroups of
$G(\mathbb{A}_{f})$
. In what follows, all compact open subgroups of
![]() $G(\mathbb{A}_{f})$
will be assumed to be neat and we will not mention it again. Because the
$G(\mathbb{A}_{f})$
will be assumed to be neat and we will not mention it again. Because the
![]() $S_{L}$
are Shimura varieties associated to
$S_{L}$
are Shimura varieties associated to
![]() $(G,{\mathcal{H}})$
, for any algebraic representation
$(G,{\mathcal{H}})$
, for any algebraic representation
![]() $E$
of
$E$
of
![]() $G$
in a finite-dimensional
$G$
in a finite-dimensional
![]() $\mathbb{Q}$
-vector space, we have a polarizable variation of
$\mathbb{Q}$
-vector space, we have a polarizable variation of
![]() $\mathbb{Q}$
-Hodge structure, abusively denoted again by
$\mathbb{Q}$
-Hodge structure, abusively denoted again by
![]() $E$
, on
$E$
, on
![]() $S_{L}$
. We take the liberty not to mention the level
$S_{L}$
. We take the liberty not to mention the level
![]() $L$
in the notation because these variation of Hodge structures are compatible under the pull-back maps induced by the above morphisms
$L$
in the notation because these variation of Hodge structures are compatible under the pull-back maps induced by the above morphisms
![]() $[g]$
. We will also denote by
$[g]$
. We will also denote by
![]() $E$
the local system underlying the variation of Hodge structure
$E$
the local system underlying the variation of Hodge structure
![]() $E$
. This should not lead to confusion.
$E$
. This should not lead to confusion.
Let
![]() $E$
an irreducible algebraic representation of
$E$
an irreducible algebraic representation of
![]() $G$
in a finite-dimensional
$G$
in a finite-dimensional
![]() $\mathbb{C}$
-vector space, let
$\mathbb{C}$
-vector space, let
![]() $\unicode[STIX]{x1D709}$
be the inverse of its central character and let
$\unicode[STIX]{x1D709}$
be the inverse of its central character and let
![]() $L$
be a compact open subgroup of
$L$
be a compact open subgroup of
![]() $G(\mathbb{A}_{f})$
. Let
$G(\mathbb{A}_{f})$
. Let
 ${\mathcal{A}}_{c}^{\ast }(S_{L},E)$
be the de Rham complex of
${\mathcal{A}}_{c}^{\ast }(S_{L},E)$
be the de Rham complex of
![]() ${\mathcal{C}}^{\infty }$
differential forms with compact support on
${\mathcal{C}}^{\infty }$
differential forms with compact support on
![]() $S_{L,\mathbb{C}}^{\text{an}}$
with values in the local system
$S_{L,\mathbb{C}}^{\text{an}}$
with values in the local system
![]() $E$
, let
$E$
, let
 ${\mathcal{A}}_{(2)}^{\ast }(S_{L},E)$
be the complex of square integrable differential forms and let
${\mathcal{A}}_{(2)}^{\ast }(S_{L},E)$
be the complex of square integrable differential forms and let
 ${\mathcal{A}}^{\ast }(S_{L},E)$
be the complex of usual differential forms. If
${\mathcal{A}}^{\ast }(S_{L},E)$
be the complex of usual differential forms. If
![]() $\circ$
is the symbol
$\circ$
is the symbol
![]() $c,(2)$
or the empty symbol define
$c,(2)$
or the empty symbol define
 $$\begin{eqnarray}{\mathcal{A}}_{\circ }^{\ast }(S,E)=\mathop{\varinjlim }\nolimits_{L}{\mathcal{A}}_{\circ }^{\ast }(S_{L},E).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}_{\circ }^{\ast }(S,E)=\mathop{\varinjlim }\nolimits_{L}{\mathcal{A}}_{\circ }^{\ast }(S_{L},E).\end{eqnarray}$$
When
![]() $\circ$
is
$\circ$
is
![]() $c$
or
$c$
or
![]() $(2)$
, this definition is legitimate because the transition morphisms
$(2)$
, this definition is legitimate because the transition morphisms
![]() $[g]$
are finite étale. Moreover, these complexes carry an action of
$[g]$
are finite étale. Moreover, these complexes carry an action of
![]() $G(\mathbb{A}_{f})$
induced by the action on
$G(\mathbb{A}_{f})$
induced by the action on
![]() $(S_{L})_{L}$
described above. In § 2.4, we introduced the Lie algebra
$(S_{L})_{L}$
described above. In § 2.4, we introduced the Lie algebra
![]() $\mathfrak{g}$
of
$\mathfrak{g}$
of
![]() $G(\mathbb{R})$
and the subgroup
$G(\mathbb{R})$
and the subgroup
 $K_{G}=A_{G}K$
of
$K_{G}=A_{G}K$
of
![]() $G(\mathbb{R})$
, which is maximal compact modulo the center. For any
$G(\mathbb{R})$
, which is maximal compact modulo the center. For any
 $(\mathfrak{g}_{\mathbb{C}},K_{G})$
-module
$(\mathfrak{g}_{\mathbb{C}},K_{G})$
-module
![]() $V$
, let
$V$
, let
 $C^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},V)$
be the
$C^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},V)$
be the
 $(\mathfrak{g}_{\mathbb{C}},K_{G})$
-complex of
$(\mathfrak{g}_{\mathbb{C}},K_{G})$
-complex of
![]() $V$
as defined in [Reference Borel and WallachBW80, I]. According to [Reference Borel and WallachBW80, VII §2], we have
$V$
as defined in [Reference Borel and WallachBW80, I]. According to [Reference Borel and WallachBW80, VII §2], we have
![]() $G(\mathbb{A}_{f})$
-equivariant isomorphisms of complexes
$G(\mathbb{A}_{f})$
-equivariant isomorphisms of complexes
 $$\begin{eqnarray}\displaystyle {\mathcal{A}}_{c}^{\ast }(S,E) & \simeq & \displaystyle C^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}_{c}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})),\nonumber\\ \displaystyle {\mathcal{A}}^{\ast }(S,E) & \simeq & \displaystyle C^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709}))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{A}}_{c}^{\ast }(S,E) & \simeq & \displaystyle C^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}_{c}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})),\nonumber\\ \displaystyle {\mathcal{A}}^{\ast }(S,E) & \simeq & \displaystyle C^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709}))\nonumber\end{eqnarray}$$
which are compatible with the inclusions
 ${\mathcal{A}}_{c}^{\ast }(S,E)\subset {\mathcal{A}}^{\ast }(S,E)$
and
${\mathcal{A}}_{c}^{\ast }(S,E)\subset {\mathcal{A}}^{\ast }(S,E)$
and
 $$\begin{eqnarray}C^{\ast }(\mathfrak{g}_{\mathbb{ C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}_{c}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709}))\subset C^{\ast }(\mathfrak{g}_{\mathbb{ C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})).\end{eqnarray}$$
$$\begin{eqnarray}C^{\ast }(\mathfrak{g}_{\mathbb{ C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}_{c}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709}))\subset C^{\ast }(\mathfrak{g}_{\mathbb{ C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})).\end{eqnarray}$$
Taking cohomology, we obtain
![]() $G(\mathbb{A}_{f})$
-equivariant isomorphisms
$G(\mathbb{A}_{f})$
-equivariant isomorphisms
 $$\begin{eqnarray}\displaystyle H_{dR,c}^{\ast }(S,E) & \simeq & \displaystyle H^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}_{c}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})),\nonumber\\ \displaystyle H_{dR}^{\ast }(S,E) & \simeq & \displaystyle H^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709}))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{dR,c}^{\ast }(S,E) & \simeq & \displaystyle H^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}_{c}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})),\nonumber\\ \displaystyle H_{dR}^{\ast }(S,E) & \simeq & \displaystyle H^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709}))\nonumber\end{eqnarray}$$
which are compatible with the maps from cohomology with compact support to cohomology without support. Let
 $H_{(2)}^{\ast }(S,E)$
denote the
$H_{(2)}^{\ast }(S,E)$
denote the
![]() $L^{2}$
cohomology of
$L^{2}$
cohomology of
![]() $S$
with coefficients in
$S$
with coefficients in
![]() $E$
, i.e. the cohomology of the complex
$E$
, i.e. the cohomology of the complex
 ${\mathcal{A}}_{(2)}^{\ast }(S,E)$
. According to [Reference BorelBor83], we have a
${\mathcal{A}}_{(2)}^{\ast }(S,E)$
. According to [Reference BorelBor83], we have a
![]() $G(\mathbb{A}_{f})$
-equivariant isomorphism
$G(\mathbb{A}_{f})$
-equivariant isomorphism
 $$\begin{eqnarray}H_{(2)}^{\ast }(S,E)=H^{\ast }(\mathfrak{g}_{\mathbb{ C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}_{(2)}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})).\end{eqnarray}$$
$$\begin{eqnarray}H_{(2)}^{\ast }(S,E)=H^{\ast }(\mathfrak{g}_{\mathbb{ C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}_{(2)}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})).\end{eqnarray}$$
Applying the
 $(\mathfrak{g}_{\mathbb{C}},K_{G})$
-cohomology functor to the maps appearing in (4) and (5) of § 2.3, we obtain the maps
$(\mathfrak{g}_{\mathbb{C}},K_{G})$
-cohomology functor to the maps appearing in (4) and (5) of § 2.3, we obtain the maps
 $$\begin{eqnarray}H_{\text{cusp}}^{\ast }(S,E)\rightarrow H_{dR,c}^{\ast }(S,E)\rightarrow H_{(2)}^{\ast }(S,E)\rightarrow H_{dR}^{\ast }(S,E)\end{eqnarray}$$
$$\begin{eqnarray}H_{\text{cusp}}^{\ast }(S,E)\rightarrow H_{dR,c}^{\ast }(S,E)\rightarrow H_{(2)}^{\ast }(S,E)\rightarrow H_{dR}^{\ast }(S,E)\end{eqnarray}$$
where
 $H_{\text{cusp}}^{\ast }(S,E)$
denotes
$H_{\text{cusp}}^{\ast }(S,E)$
denotes
 $H^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}_{\text{cusp}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709}))$
. Let
$H^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}_{\text{cusp}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709}))$
. Let
 $$\begin{eqnarray}H_{dR,!}^{\ast }(S,E)=\text{Im}(H_{dR,c}^{\ast }(S,E)\longrightarrow H_{dR}^{\ast }(S,E)).\end{eqnarray}$$
$$\begin{eqnarray}H_{dR,!}^{\ast }(S,E)=\text{Im}(H_{dR,c}^{\ast }(S,E)\longrightarrow H_{dR}^{\ast }(S,E)).\end{eqnarray}$$
Proposition 3.4 [Reference Mokrane and TilouineMT02, Proposition 1].
The maps (7) induce
![]() $G(\mathbb{A}_{f})$
-equivariant isomorphisms
$G(\mathbb{A}_{f})$
-equivariant isomorphisms
 $$\begin{eqnarray}H_{\text{cusp}}^{\ast }(S,E)=H_{(2)}^{\ast }(S,E)=H_{dR,!}^{\ast }(S,E)=H_{dR,!}^{3}(S,E).\end{eqnarray}$$
$$\begin{eqnarray}H_{\text{cusp}}^{\ast }(S,E)=H_{(2)}^{\ast }(S,E)=H_{dR,!}^{\ast }(S,E)=H_{dR,!}^{3}(S,E).\end{eqnarray}$$
The
 $((\mathfrak{g}_{\mathbb{C}},K_{G})\times G(\mathbb{A}_{f}))$
-module
$((\mathfrak{g}_{\mathbb{C}},K_{G})\times G(\mathbb{A}_{f}))$
-module
 ${\mathcal{C}}_{\text{cusp}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
decomposes into a direct sum
${\mathcal{C}}_{\text{cusp}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})$
decomposes into a direct sum
 $$\begin{eqnarray}{\mathcal{C}}_{\text{cusp}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})=\bigoplus _{\unicode[STIX]{x1D70B}}m(\unicode[STIX]{x1D70B})\unicode[STIX]{x1D70B}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{C}}_{\text{cusp}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}),\unicode[STIX]{x1D709})=\bigoplus _{\unicode[STIX]{x1D70B}}m(\unicode[STIX]{x1D70B})\unicode[STIX]{x1D70B}\end{eqnarray}$$
indexed by irreducible cuspidal automorphic representations of
![]() $G$
, with finite multiplicities. This induces a decomposition
$G$
, with finite multiplicities. This induces a decomposition
 $$\begin{eqnarray}H_{dR,!}^{3}(S,E)=\bigoplus _{\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}}m(\unicode[STIX]{x1D70B})H^{3}(\mathfrak{g}_{\mathbb{ C}},K_{G},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty })\otimes \unicode[STIX]{x1D70B}_{f}\end{eqnarray}$$
$$\begin{eqnarray}H_{dR,!}^{3}(S,E)=\bigoplus _{\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}}m(\unicode[STIX]{x1D70B})H^{3}(\mathfrak{g}_{\mathbb{ C}},K_{G},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty })\otimes \unicode[STIX]{x1D70B}_{f}\end{eqnarray}$$
into irreducible
 $\mathbb{C}[G(\mathbb{A}_{f})]$
-modules.
$\mathbb{C}[G(\mathbb{A}_{f})]$
-modules.
Definition 3.5. Let
![]() $E$
be an irreducible algebraic representation of
$E$
be an irreducible algebraic representation of
![]() $G$
. The discrete series
$G$
. The discrete series
![]() $L$
-packet
$L$
-packet
![]() $P(E)$
associated to
$P(E)$
associated to
![]() $E$
is the set of isomorphism classes of discrete series of
$E$
is the set of isomorphism classes of discrete series of
![]() $G(\mathbb{R})^{+}$
whose Harish-Chandra parameter and central character are opposed to those of
$G(\mathbb{R})^{+}$
whose Harish-Chandra parameter and central character are opposed to those of
![]() $E$
.
$E$
.
Lemma 3.6. Assume that
![]() $E$
has highest weight
$E$
has highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },c)$
. Then,
$\unicode[STIX]{x1D706}(k,k^{\prime },c)$
. Then,
 $$\begin{eqnarray}P(E)=\{\unicode[STIX]{x1D70B}_{\infty }^{H},\unicode[STIX]{x1D70B}_{\infty }^{W},\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W},\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\}\end{eqnarray}$$
$$\begin{eqnarray}P(E)=\{\unicode[STIX]{x1D70B}_{\infty }^{H},\unicode[STIX]{x1D70B}_{\infty }^{W},\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W},\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\}\end{eqnarray}$$
and the restrictions of
 $\unicode[STIX]{x1D70B}_{\infty }^{H},\unicode[STIX]{x1D70B}_{\infty }^{W},\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}$
and
$\unicode[STIX]{x1D70B}_{\infty }^{H},\unicode[STIX]{x1D70B}_{\infty }^{W},\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}$
and
![]() $\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}$
to
$\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}$
to
![]() $K$
contain as minimal
$K$
contain as minimal
![]() $K$
types the representations
$K$
types the representations
 $\unicode[STIX]{x1D70F}_{(k+3,k^{\prime }+3)}$
,
$\unicode[STIX]{x1D70F}_{(k+3,k^{\prime }+3)}$
,
 $\unicode[STIX]{x1D70F}_{(k+3,-k^{\prime }-1)}$
,
$\unicode[STIX]{x1D70F}_{(k+3,-k^{\prime }-1)}$
,
 $\unicode[STIX]{x1D70F}_{(k^{\prime }+1,-k-3)}$
and
$\unicode[STIX]{x1D70F}_{(k^{\prime }+1,-k-3)}$
and
 $\unicode[STIX]{x1D70F}_{(-k^{\prime }-3,-k-3)}$
, respectively.
$\unicode[STIX]{x1D70F}_{(-k^{\prime }-3,-k-3)}$
, respectively.
Proof. If
![]() $E$
is irreducible, with highest weight
$E$
is irreducible, with highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },c)$
, then it has infinitesimal character
$\unicode[STIX]{x1D706}(k,k^{\prime },c)$
, then it has infinitesimal character
 $(k+2,k^{\prime }+1)$
. So, the statement is a direct consequence of Proposition 3.1.◻
$(k+2,k^{\prime }+1)$
. So, the statement is a direct consequence of Proposition 3.1.◻
The main result of [Reference Vogan and ZuckermannVZ84] implies that the
![]() $\unicode[STIX]{x1D70B}$
contributing to the above sum, i.e. those for which
$\unicode[STIX]{x1D70B}$
contributing to the above sum, i.e. those for which
 $H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},\unicode[STIX]{x1D70B}_{\infty }\otimes _{\mathbb{C}}E)$
is non-zero, are those such that
$H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},\unicode[STIX]{x1D70B}_{\infty }\otimes _{\mathbb{C}}E)$
is non-zero, are those such that
 $\unicode[STIX]{x1D70B}_{\infty }|_{G(\mathbb{R})^{+}}\in P(E)$
(see the proof of [Reference Mokrane and TilouineMT02, Proposition 1] for more details). As a consequence, we have
$\unicode[STIX]{x1D70B}_{\infty }|_{G(\mathbb{R})^{+}}\in P(E)$
(see the proof of [Reference Mokrane and TilouineMT02, Proposition 1] for more details). As a consequence, we have
 $$\begin{eqnarray}H_{dR,!}^{3}(S,E)=\bigoplus _{\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}\mid \unicode[STIX]{x1D70B}_{\infty }\in P(E)}H_{dR,!}^{3}(S,E)(\unicode[STIX]{x1D70B}_{f})\otimes \unicode[STIX]{x1D70B}_{f}\end{eqnarray}$$
$$\begin{eqnarray}H_{dR,!}^{3}(S,E)=\bigoplus _{\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}\mid \unicode[STIX]{x1D70B}_{\infty }\in P(E)}H_{dR,!}^{3}(S,E)(\unicode[STIX]{x1D70B}_{f})\otimes \unicode[STIX]{x1D70B}_{f}\end{eqnarray}$$
where the sum is indexed by irreducible cuspidal automorphic representations of
![]() $G$
whose archimedean component belongs to
$G$
whose archimedean component belongs to
![]() $P(E)$
and where
$P(E)$
and where
 $$\begin{eqnarray}H_{dR,!}^{3}(S,E)(\unicode[STIX]{x1D70B}_{f})=\bigoplus _{\unicode[STIX]{x1D70B}_{\infty }\in P(E)}m(\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{ C}},K_{G},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }).\end{eqnarray}$$
$$\begin{eqnarray}H_{dR,!}^{3}(S,E)(\unicode[STIX]{x1D70B}_{f})=\bigoplus _{\unicode[STIX]{x1D70B}_{\infty }\in P(E)}m(\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{ C}},K_{G},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }).\end{eqnarray}$$
According to [Reference Borel and WallachBW80, II. §3, Proposition 3.1], for any
 $\unicode[STIX]{x1D70B}_{\infty }\in P(E)$
, the
$\unicode[STIX]{x1D70B}_{\infty }\in P(E)$
, the
 $(\mathfrak{g}_{\mathbb{C}},K_{G})$
-complex of
$(\mathfrak{g}_{\mathbb{C}},K_{G})$
-complex of
 $\unicode[STIX]{x1D70B}_{\infty }\otimes _{\mathbb{C}}E$
has zero differential. Hence, we have
$\unicode[STIX]{x1D70B}_{\infty }\otimes _{\mathbb{C}}E$
has zero differential. Hence, we have
 $$\begin{eqnarray}H^{3}(\mathfrak{g}_{\mathbb{ C}},K_{G},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty })=\text{Hom}_{K_{G}}\biggl(\bigwedge ^{3}\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }\biggr).\end{eqnarray}$$
$$\begin{eqnarray}H^{3}(\mathfrak{g}_{\mathbb{ C}},K_{G},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty })=\text{Hom}_{K_{G}}\biggl(\bigwedge ^{3}\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }\biggr).\end{eqnarray}$$
In this last equality, we are using the fact that the inclusion
 $\mathfrak{sp}_{4,\mathbb{C}}\subset \mathfrak{g}_{\mathbb{C}}$
induces an isomorphism
$\mathfrak{sp}_{4,\mathbb{C}}\subset \mathfrak{g}_{\mathbb{C}}$
induces an isomorphism
 $\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}}\simeq \mathfrak{g}_{\mathbb{C}}/(\text{Lie}K_{G})_{\mathbb{C}}$
. By the Cartan decomposition
$\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}}\simeq \mathfrak{g}_{\mathbb{C}}/(\text{Lie}K_{G})_{\mathbb{C}}$
. By the Cartan decomposition
 $\mathfrak{sp}_{4,\mathbb{C}}=\mathfrak{k}_{\mathbb{C}}\oplus \mathfrak{p}^{+}\oplus \mathfrak{p}^{-}$
, where
$\mathfrak{sp}_{4,\mathbb{C}}=\mathfrak{k}_{\mathbb{C}}\oplus \mathfrak{p}^{+}\oplus \mathfrak{p}^{-}$
, where
![]() $\mathfrak{p}^{\pm }$
are defined by (6), we have
$\mathfrak{p}^{\pm }$
are defined by (6), we have
 $\bigwedge ^{3}\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}}=\bigoplus _{p+q=3}\bigwedge ^{p}\mathfrak{p}^{+}\otimes _{\mathbb{C}}\bigwedge ^{q}\mathfrak{p}^{-}$
. As the weights for the adjoint representation of
$\bigwedge ^{3}\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}}=\bigoplus _{p+q=3}\bigwedge ^{p}\mathfrak{p}^{+}\otimes _{\mathbb{C}}\bigwedge ^{q}\mathfrak{p}^{-}$
. As the weights for the adjoint representation of
![]() $\mathfrak{h}_{\mathbb{C}}$
on
$\mathfrak{h}_{\mathbb{C}}$
on
 $\bigwedge ^{p}\mathfrak{p}^{+}\otimes _{\mathbb{C}}\bigwedge ^{q}\mathfrak{p}^{-}$
are the sums of
$\bigwedge ^{p}\mathfrak{p}^{+}\otimes _{\mathbb{C}}\bigwedge ^{q}\mathfrak{p}^{-}$
are the sums of
![]() $p$
distinct weights of
$p$
distinct weights of
![]() $\mathfrak{p}^{+}$
and of
$\mathfrak{p}^{+}$
and of
![]() $q$
distinct weights of
$q$
distinct weights of
![]() $\mathfrak{p}^{-}$
, the reader will easily deduce the following decompositions
$\mathfrak{p}^{-}$
, the reader will easily deduce the following decompositions
 $$\begin{eqnarray}\displaystyle \bigwedge ^{3}\mathfrak{p}^{+} & = & \displaystyle \unicode[STIX]{x1D70F}_{(3,3)},\nonumber\\ \displaystyle \bigwedge ^{2}\mathfrak{p}^{+}\otimes _{\mathbb{C}}\mathfrak{p}^{-} & = & \displaystyle \unicode[STIX]{x1D70F}_{(3,-1)}\oplus \unicode[STIX]{x1D70F}_{(2,0)}\oplus \unicode[STIX]{x1D70F}_{(1,1)},\nonumber\\ \displaystyle \mathfrak{p}^{+}\otimes _{\mathbb{C}}\bigwedge ^{2}\mathfrak{p}^{-} & = & \displaystyle \unicode[STIX]{x1D70F}_{(1,-3)}\oplus \unicode[STIX]{x1D70F}_{(0,-2)}\oplus \unicode[STIX]{x1D70F}_{(-1,-1)},\nonumber\\ \displaystyle \bigwedge ^{3}\mathfrak{p}^{-} & = & \displaystyle \unicode[STIX]{x1D70F}_{(-3,-3)}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \bigwedge ^{3}\mathfrak{p}^{+} & = & \displaystyle \unicode[STIX]{x1D70F}_{(3,3)},\nonumber\\ \displaystyle \bigwedge ^{2}\mathfrak{p}^{+}\otimes _{\mathbb{C}}\mathfrak{p}^{-} & = & \displaystyle \unicode[STIX]{x1D70F}_{(3,-1)}\oplus \unicode[STIX]{x1D70F}_{(2,0)}\oplus \unicode[STIX]{x1D70F}_{(1,1)},\nonumber\\ \displaystyle \mathfrak{p}^{+}\otimes _{\mathbb{C}}\bigwedge ^{2}\mathfrak{p}^{-} & = & \displaystyle \unicode[STIX]{x1D70F}_{(1,-3)}\oplus \unicode[STIX]{x1D70F}_{(0,-2)}\oplus \unicode[STIX]{x1D70F}_{(-1,-1)},\nonumber\\ \displaystyle \bigwedge ^{3}\mathfrak{p}^{-} & = & \displaystyle \unicode[STIX]{x1D70F}_{(-3,-3)}\nonumber\end{eqnarray}$$
into irreducible
![]() $\mathbb{C}[K]$
-modules from the basic facts on irreducible representations of
$\mathbb{C}[K]$
-modules from the basic facts on irreducible representations of
![]() $K$
reviewed in § 3.1. If
$K$
reviewed in § 3.1. If
![]() $E$
has highest weight
$E$
has highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },c)$
, its infinitesimal character is
$\unicode[STIX]{x1D706}(k,k^{\prime },c)$
, its infinitesimal character is
 $(k+2,k^{\prime }+1)$
.
$(k+2,k^{\prime }+1)$
.
Proposition 3.7. The
![]() $\mathbb{C}$
-vector spaces
$\mathbb{C}$
-vector spaces
 $$\begin{eqnarray}\displaystyle H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},\unicode[STIX]{x1D70B}_{\infty }^{H}\otimes _{\mathbb{C}}E) & = & \displaystyle \text{Hom}_{K_{G}}\biggl(\bigwedge ^{3}\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{H}\biggr),\nonumber\\ \displaystyle H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},\unicode[STIX]{x1D70B}_{\infty }^{W}\otimes _{\mathbb{C}}E) & = & \displaystyle \text{Hom}_{K_{G}}\biggl(\bigwedge ^{3}\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{W}\biggr),\nonumber\\ \displaystyle H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\otimes _{\mathbb{C}}E) & = & \displaystyle \text{Hom}_{K_{G}}\biggl(\bigwedge ^{3}\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}},E\otimes _{\mathbb{C}}\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\biggr),\nonumber\\ \displaystyle H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\otimes _{\mathbb{C}}E) & = & \displaystyle \text{Hom}_{K_{G}}\biggl(\bigwedge ^{3}\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}},E\otimes _{\mathbb{C}}\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\biggr)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},\unicode[STIX]{x1D70B}_{\infty }^{H}\otimes _{\mathbb{C}}E) & = & \displaystyle \text{Hom}_{K_{G}}\biggl(\bigwedge ^{3}\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{H}\biggr),\nonumber\\ \displaystyle H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},\unicode[STIX]{x1D70B}_{\infty }^{W}\otimes _{\mathbb{C}}E) & = & \displaystyle \text{Hom}_{K_{G}}\biggl(\bigwedge ^{3}\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{W}\biggr),\nonumber\\ \displaystyle H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\otimes _{\mathbb{C}}E) & = & \displaystyle \text{Hom}_{K_{G}}\biggl(\bigwedge ^{3}\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}},E\otimes _{\mathbb{C}}\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\biggr),\nonumber\\ \displaystyle H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\otimes _{\mathbb{C}}E) & = & \displaystyle \text{Hom}_{K_{G}}\biggl(\bigwedge ^{3}\mathfrak{sp}_{4,\mathbb{C}}/\mathfrak{k}_{\mathbb{C}},E\otimes _{\mathbb{C}}\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\biggr)\nonumber\end{eqnarray}$$
have dimension one.
Proof. This is a particular case of [Reference Borel and WallachBW80, II. Proposition 3.1 and Theorem 5.3]. ◻
From now on, let us assume that the irreducible algebraic representation
![]() $E$
takes values in a finite-dimensional
$E$
takes values in a finite-dimensional
![]() $\mathbb{Q}$
-vector space. In particular, the results explained above can be applied to the complexification
$\mathbb{Q}$
-vector space. In particular, the results explained above can be applied to the complexification
![]() $E_{\mathbb{C}}$
of
$E_{\mathbb{C}}$
of
![]() $E$
. For any cuspidal automorphic representation
$E$
. For any cuspidal automorphic representation
 $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}$
of
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}$
of
![]() $G$
such that
$G$
such that
 $\unicode[STIX]{x1D70B}_{\infty }\in P(E)$
, denote again by
$\unicode[STIX]{x1D70B}_{\infty }\in P(E)$
, denote again by
![]() $\unicode[STIX]{x1D70B}_{f}$
the model of
$\unicode[STIX]{x1D70B}_{f}$
the model of
![]() $\unicode[STIX]{x1D70B}_{f}$
defined over its rationality field, which is the number field
$\unicode[STIX]{x1D70B}_{f}$
defined over its rationality field, which is the number field
![]() $E(\unicode[STIX]{x1D70B}_{f})$
(see Proposition 3.3). Following [Reference HarrisHar97, 2.6.2 and 2.6.3], define
$E(\unicode[STIX]{x1D70B}_{f})$
(see Proposition 3.3). Following [Reference HarrisHar97, 2.6.2 and 2.6.3], define
 $$\begin{eqnarray}M_{dR}(\unicode[STIX]{x1D70B}_{f},E)=\text{Hom}_{\mathbb{Q}[G(\mathbb{A}_{f})]}(\operatorname{Res}_{E(\unicode[STIX]{x1D70B}_{f})/\mathbb{Q}}\unicode[STIX]{x1D70B}_{f},H_{dR,!}^{3}(S,E))\end{eqnarray}$$
$$\begin{eqnarray}M_{dR}(\unicode[STIX]{x1D70B}_{f},E)=\text{Hom}_{\mathbb{Q}[G(\mathbb{A}_{f})]}(\operatorname{Res}_{E(\unicode[STIX]{x1D70B}_{f})/\mathbb{Q}}\unicode[STIX]{x1D70B}_{f},H_{dR,!}^{3}(S,E))\end{eqnarray}$$
and similarly
 $$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},E)=\text{Hom}_{\mathbb{Q}[G(\mathbb{A}_{f})]}(\operatorname{Res}_{E(\unicode[STIX]{x1D70B}_{f})/\mathbb{Q}}\unicode[STIX]{x1D70B}_{f},H_{B,!}^{3}(S,E))\end{eqnarray}$$
$$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},E)=\text{Hom}_{\mathbb{Q}[G(\mathbb{A}_{f})]}(\operatorname{Res}_{E(\unicode[STIX]{x1D70B}_{f})/\mathbb{Q}}\unicode[STIX]{x1D70B}_{f},H_{B,!}^{3}(S,E))\end{eqnarray}$$
where
 $H_{B,!}^{3}(S,E)$
denotes the Betti cohomology with coefficients in
$H_{B,!}^{3}(S,E)$
denotes the Betti cohomology with coefficients in
![]() $E$
. These are
$E$
. These are
![]() $\mathbb{Q}$
-vector spaces endowed with a
$\mathbb{Q}$
-vector spaces endowed with a
![]() $\mathbb{Q}$
-linear action of
$\mathbb{Q}$
-linear action of
![]() $E(\unicode[STIX]{x1D70B}_{f})$
. Extending scalars from
$E(\unicode[STIX]{x1D70B}_{f})$
. Extending scalars from
![]() $\mathbb{Q}$
to
$\mathbb{Q}$
to
![]() $\mathbb{C}$
, according to the identities (8) and (9), we have
$\mathbb{C}$
, according to the identities (8) and (9), we have
 $$\begin{eqnarray}M_{dR}(\unicode[STIX]{x1D70B}_{f},E)_{\mathbb{C}}=\bigoplus _{\unicode[STIX]{x1D70E}:E(\unicode[STIX]{x1D70B}_{f})\rightarrow \mathbb{C}}\bigoplus _{\unicode[STIX]{x1D70B}_{\infty }\in P(E)}m(\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{ C}},K_{G},E_{\mathbb{C}}\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }).\end{eqnarray}$$
$$\begin{eqnarray}M_{dR}(\unicode[STIX]{x1D70B}_{f},E)_{\mathbb{C}}=\bigoplus _{\unicode[STIX]{x1D70E}:E(\unicode[STIX]{x1D70B}_{f})\rightarrow \mathbb{C}}\bigoplus _{\unicode[STIX]{x1D70B}_{\infty }\in P(E)}m(\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{ C}},K_{G},E_{\mathbb{C}}\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }).\end{eqnarray}$$
For any
![]() $\unicode[STIX]{x1D70B}_{f}$
, the
$\unicode[STIX]{x1D70B}_{f}$
, the
![]() $\mathbb{C}$
-vector space
$\mathbb{C}$
-vector space
 $$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D70B}_{\infty }\in P(E)}m(\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{ C}},K_{G},E_{\mathbb{C}}\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }),\end{eqnarray}$$
$$\begin{eqnarray}\bigoplus _{\unicode[STIX]{x1D70B}_{\infty }\in P(E)}m(\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{ C}},K_{G},E_{\mathbb{C}}\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }),\end{eqnarray}$$
has finite dimension
 $$\begin{eqnarray}m(\unicode[STIX]{x1D70B}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})+m(\unicode[STIX]{x1D70B}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})+m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})+m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})\end{eqnarray}$$
$$\begin{eqnarray}m(\unicode[STIX]{x1D70B}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})+m(\unicode[STIX]{x1D70B}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})+m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})+m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})\end{eqnarray}$$
according to Proposition 3.7. As a consequence, the dimension of
 $M_{dR}(\unicode[STIX]{x1D70B}_{f},E)$
as an
$M_{dR}(\unicode[STIX]{x1D70B}_{f},E)$
as an
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-vector space is
$E(\unicode[STIX]{x1D70B}_{f})$
-vector space is
 $$\begin{eqnarray}m(\unicode[STIX]{x1D70B}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})+m(\unicode[STIX]{x1D70B}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})+m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})+m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f}).\end{eqnarray}$$
$$\begin{eqnarray}m(\unicode[STIX]{x1D70B}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})+m(\unicode[STIX]{x1D70B}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})+m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})+m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f}).\end{eqnarray}$$
The same holds for
 $M_{B}(\unicode[STIX]{x1D70B}_{f},E)$
because of the comparison isomorphism
$M_{B}(\unicode[STIX]{x1D70B}_{f},E)$
because of the comparison isomorphism

It follows from Saito’s formalism of mixed Hodge modules that for any open compact subgroup
![]() $L$
of
$L$
of
![]() $G(\mathbb{A}_{f})$
, the interior cohomology
$G(\mathbb{A}_{f})$
, the interior cohomology
 $H_{!}^{3}(S_{L},E)$
underlies a
$H_{!}^{3}(S_{L},E)$
underlies a
![]() $\mathbb{Q}$
-Hodge structure. With the convention adopted here, and explained in § 2.4, this
$\mathbb{Q}$
-Hodge structure. With the convention adopted here, and explained in § 2.4, this
![]() $\mathbb{Q}$
-Hodge structure is in fact pure of weight
$\mathbb{Q}$
-Hodge structure is in fact pure of weight
![]() $3-c$
, where
$3-c$
, where
 $x\longmapsto x^{c}$
is the central character of
$x\longmapsto x^{c}$
is the central character of
![]() $E$
. Hence, we obtain a pure
$E$
. Hence, we obtain a pure
![]() $\mathbb{Q}$
-Hodge structure on
$\mathbb{Q}$
-Hodge structure on
 $M_{B}(\unicode[STIX]{x1D70B}_{f},E)$
:
$M_{B}(\unicode[STIX]{x1D70B}_{f},E)$
:
Proposition 3.8. Let
 $t=(c-k-k^{\prime })/2$
. The Hodge decomposition of
$t=(c-k-k^{\prime })/2$
. The Hodge decomposition of
 $M_{B}(\unicode[STIX]{x1D70B}_{f},E)$
is
$M_{B}(\unicode[STIX]{x1D70B}_{f},E)$
is
 $$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},E)_{\mathbb{C}}=M_{B}^{3-t,-k-k^{\prime }-t}\oplus M_{B}^{2-k^{\prime }-t,1-k-t}\oplus M_{B}^{1-k-t,2-k^{\prime }-t}\oplus M_{B}^{-k-k^{\prime }-t,3-t}\end{eqnarray}$$
$$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},E)_{\mathbb{C}}=M_{B}^{3-t,-k-k^{\prime }-t}\oplus M_{B}^{2-k^{\prime }-t,1-k-t}\oplus M_{B}^{1-k-t,2-k^{\prime }-t}\oplus M_{B}^{-k-k^{\prime }-t,3-t}\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle M_{B}^{3-t,-k-k^{\prime }-t} & = & \displaystyle \bigoplus _{\unicode[STIX]{x1D70E}:E(\unicode[STIX]{x1D70B}_{f})\rightarrow \mathbb{C}}m(\unicode[STIX]{x1D70B}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{H}),\nonumber\\ \displaystyle M_{B}^{2-k^{\prime }-t,1-k-t} & = & \displaystyle \bigoplus _{\unicode[STIX]{x1D70E}:E(\unicode[STIX]{x1D70B}_{f})\rightarrow \mathbb{C}}m(\unicode[STIX]{x1D70B}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{W}),\nonumber\\ \displaystyle M_{B}^{1-k-t,2-k^{\prime }-t} & = & \displaystyle \bigoplus _{\unicode[STIX]{x1D70E}:E(\unicode[STIX]{x1D70B}_{f})\rightarrow \mathbb{C}}m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}),\nonumber\\ \displaystyle M_{B}^{-k-k^{\prime }-t,3-t} & = & \displaystyle \bigoplus _{\unicode[STIX]{x1D70E}:E(\unicode[STIX]{x1D70B}_{f})\rightarrow \mathbb{C}}m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle M_{B}^{3-t,-k-k^{\prime }-t} & = & \displaystyle \bigoplus _{\unicode[STIX]{x1D70E}:E(\unicode[STIX]{x1D70B}_{f})\rightarrow \mathbb{C}}m(\unicode[STIX]{x1D70B}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{H}),\nonumber\\ \displaystyle M_{B}^{2-k^{\prime }-t,1-k-t} & = & \displaystyle \bigoplus _{\unicode[STIX]{x1D70E}:E(\unicode[STIX]{x1D70B}_{f})\rightarrow \mathbb{C}}m(\unicode[STIX]{x1D70B}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{W}),\nonumber\\ \displaystyle M_{B}^{1-k-t,2-k^{\prime }-t} & = & \displaystyle \bigoplus _{\unicode[STIX]{x1D70E}:E(\unicode[STIX]{x1D70B}_{f})\rightarrow \mathbb{C}}m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}),\nonumber\\ \displaystyle M_{B}^{-k-k^{\prime }-t,3-t} & = & \displaystyle \bigoplus _{\unicode[STIX]{x1D70E}:E(\unicode[STIX]{x1D70B}_{f})\rightarrow \mathbb{C}}m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})H^{3}(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}).\nonumber\end{eqnarray}$$
Proof. A reference for the statement on Hodge types is [Reference HarrisHar04, (1.4)]. However, let us remark that [Reference HarrisHar04] uses the sign convention opposite to ours (see § 2.4). The result then follows from the fact that the Hodge decomposition of
![]() $L^{2}$
cohomology given by harmonic forms coincides with the Hodge decomposition given by the theory of mixed Hodge modules (Proposition 3.4 and [Reference Harris and ZuckerHZ99, Theorem 5.4]).◻
$L^{2}$
cohomology given by harmonic forms coincides with the Hodge decomposition given by the theory of mixed Hodge modules (Proposition 3.4 and [Reference Harris and ZuckerHZ99, Theorem 5.4]).◻
The following definition is taken from [Reference BeilinsonBei86, §7].
Definition 3.9. Let
![]() $A$
be a subfield of
$A$
be a subfield of
![]() $\mathbb{R}$
. A real mixed
$\mathbb{R}$
. A real mixed
![]() $A$
-Hodge structure is a mixed
$A$
-Hodge structure is a mixed
![]() $A$
-Hodge structure whose underlying
$A$
-Hodge structure whose underlying
![]() $A$
-vector space is endowed with an involution
$A$
-vector space is endowed with an involution
![]() $F_{\infty }$
stabilizing the weight filtration and whose
$F_{\infty }$
stabilizing the weight filtration and whose
![]() $\mathbb{C}$
-antilinear complexification
$\mathbb{C}$
-antilinear complexification
![]() $F_{\infty }\otimes \unicode[STIX]{x1D70F}$
, where
$F_{\infty }\otimes \unicode[STIX]{x1D70F}$
, where
![]() $\unicode[STIX]{x1D70F}$
denotes the complex conjugation, stabilizes the Hodge filtration. We call
$\unicode[STIX]{x1D70F}$
denotes the complex conjugation, stabilizes the Hodge filtration. We call
![]() $F_{\infty }\otimes \unicode[STIX]{x1D70F}$
the de Rham involution.
$F_{\infty }\otimes \unicode[STIX]{x1D70F}$
the de Rham involution.
Let
![]() $\text{MHS}_{A}^{+}$
denote the abelian category of real mixed
$\text{MHS}_{A}^{+}$
denote the abelian category of real mixed
![]() $A$
-Hodge structures.
$A$
-Hodge structures.
Definition 3.10. Let
![]() $F$
be a number field. A real mixed
$F$
be a number field. A real mixed
![]() $A$
-Hodge structure with coefficients in
$A$
-Hodge structure with coefficients in
![]() $F$
is a pair
$F$
is a pair
![]() $(M,s)$
where
$(M,s)$
where
![]() $M$
is an object of
$M$
is an object of
![]() $\text{MHS}_{A}^{+}$
and
$\text{MHS}_{A}^{+}$
and
 $s:F\longrightarrow \text{End}_{\text{MHS}_{A}^{+}}(M)$
is a ring homomorphism.
$s:F\longrightarrow \text{End}_{\text{MHS}_{A}^{+}}(M)$
is a ring homomorphism.
Let
 $\text{MHS}_{A,F}^{+}$
denote the abelian category of real mixed
$\text{MHS}_{A,F}^{+}$
denote the abelian category of real mixed
![]() $A$
-Hodge structures with coefficients in
$A$
-Hodge structures with coefficients in
![]() $F$
.
$F$
.
Proposition 3.11. Let
![]() $F_{\infty }$
be the involution on
$F_{\infty }$
be the involution on
 $M_{B}(\unicode[STIX]{x1D70B}_{f},E)$
induced by the complex conjugation on
$M_{B}(\unicode[STIX]{x1D70B}_{f},E)$
induced by the complex conjugation on
![]() $S(\mathbb{C})$
and on
$S(\mathbb{C})$
and on
![]() $E$
. Then
$E$
. Then
 $(M_{B}(\unicode[STIX]{x1D70B}_{f},E),F_{\infty })$
is an object of
$(M_{B}(\unicode[STIX]{x1D70B}_{f},E),F_{\infty })$
is an object of
 $\text{MHS}_{\mathbb{Q},E(\unicode[STIX]{x1D70B}_{f})}^{+}$
.
$\text{MHS}_{\mathbb{Q},E(\unicode[STIX]{x1D70B}_{f})}^{+}$
.
Proposition 3.12 [Reference HarrisHar94, Corollary 2.3.1].
The Hodge filtration
 $F^{\ast }M_{B}(\unicode[STIX]{x1D70B}_{f},E)_{\mathbb{C}}$
, which is defined by
$F^{\ast }M_{B}(\unicode[STIX]{x1D70B}_{f},E)_{\mathbb{C}}$
, which is defined by
 $$\begin{eqnarray}F^{p}M_{B}(\unicode[STIX]{x1D70B}_{f},E)_{\mathbb{C}}=\bigoplus _{p^{\prime }\geqslant p}M_{B}^{p^{\prime },q},\end{eqnarray}$$
$$\begin{eqnarray}F^{p}M_{B}(\unicode[STIX]{x1D70B}_{f},E)_{\mathbb{C}}=\bigoplus _{p^{\prime }\geqslant p}M_{B}^{p^{\prime },q},\end{eqnarray}$$
is the image of the complexification of a filtration
 $F^{\ast }M_{dR}(\unicode[STIX]{x1D70B}_{f},E)$
of
$F^{\ast }M_{dR}(\unicode[STIX]{x1D70B}_{f},E)$
of
 $M_{dR}(\unicode[STIX]{x1D70B}_{f},E)$
under the comparison isomorphism
$M_{dR}(\unicode[STIX]{x1D70B}_{f},E)$
under the comparison isomorphism
![]() $I_{\infty }^{-1}$
.
$I_{\infty }^{-1}$
.
Proposition 3.13. Let
 $N\in G(\mathbb{R})$
be as in Remark 3.2. Then, the involution
$N\in G(\mathbb{R})$
be as in Remark 3.2. Then, the involution
![]() $F_{\infty }$
of
$F_{\infty }$
of
 $M_{B}(\unicode[STIX]{x1D70B}_{f},E)_{\mathbb{C}}$
is induced by the action of
$M_{B}(\unicode[STIX]{x1D70B}_{f},E)_{\mathbb{C}}$
is induced by the action of
![]() $N$
on
$N$
on
 $C^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A})))$
defined by
$C^{\ast }(\mathfrak{g}_{\mathbb{C}},K_{G},E\otimes _{\mathbb{C}}{\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A})))$
defined by
 $$\begin{eqnarray}f\in \text{Hom}_{K}\biggl(\bigwedge ^{\ast }\mathfrak{g}_{\mathbb{ C}}/\mathfrak{k}_{\mathbb{C}},E\otimes _{\mathbb{C}}{\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}))\biggr)\longmapsto (X\longmapsto Nf(\operatorname{Ad}_{N}(X))).\end{eqnarray}$$
$$\begin{eqnarray}f\in \text{Hom}_{K}\biggl(\bigwedge ^{\ast }\mathfrak{g}_{\mathbb{ C}}/\mathfrak{k}_{\mathbb{C}},E\otimes _{\mathbb{C}}{\mathcal{C}}^{\infty }(G(\mathbb{Q})\backslash G(\mathbb{A}))\biggr)\longmapsto (X\longmapsto Nf(\operatorname{Ad}_{N}(X))).\end{eqnarray}$$
Proof. Note that
 $$\begin{eqnarray}N=\left(\begin{array}{@{}cccc@{}} & 1 & & \\ 1 & & & \\ & & & 1\\ & & 1 & \end{array}\right)\left(\begin{array}{@{}cccc@{}}-1 & & & \\ & -1 & & \\ & & 1 & \\ & & & 1\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}N=\left(\begin{array}{@{}cccc@{}} & 1 & & \\ 1 & & & \\ & & & 1\\ & & 1 & \end{array}\right)\left(\begin{array}{@{}cccc@{}}-1 & & & \\ & -1 & & \\ & & 1 & \\ & & & 1\end{array}\right).\end{eqnarray}$$
As the cocharacter
 $\unicode[STIX]{x1D707}:\mathbb{G}_{m,\mathbb{C}}\longrightarrow G_{\mathbb{C}}$
associated to the morphism
$\unicode[STIX]{x1D707}:\mathbb{G}_{m,\mathbb{C}}\longrightarrow G_{\mathbb{C}}$
associated to the morphism
 $h:\mathbb{S}\longrightarrow G_{\mathbb{R}}$
defined above induces
$h:\mathbb{S}\longrightarrow G_{\mathbb{R}}$
defined above induces
 $$\begin{eqnarray}z\longmapsto \left(\begin{array}{@{}cccc@{}}z & & & \\ & z & & \\ & & 1 & \\ & & & 1\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}z\longmapsto \left(\begin{array}{@{}cccc@{}}z & & & \\ & z & & \\ & & 1 & \\ & & & 1\end{array}\right)\end{eqnarray}$$
on complex points, the matrix
![]() $N$
satisfies the assumptions of [Reference Milne and ShihMS81, Lemma 3.2]. So the statement follows from the proof of Langlands conjecture on the action of complex conjugation on the set of complex points of a Shimura varieties which, in the case of Siegel varieties, is explained in [Reference Milne and ShihMS81, Remark 3.3(c)]. ◻
$N$
satisfies the assumptions of [Reference Milne and ShihMS81, Lemma 3.2]. So the statement follows from the proof of Langlands conjecture on the action of complex conjugation on the set of complex points of a Shimura varieties which, in the case of Siegel varieties, is explained in [Reference Milne and ShihMS81, Remark 3.3(c)]. ◻
4 Computation of the regulator
Let
![]() $p,q,k$
and
$p,q,k$
and
![]() $k^{\prime }$
be integers as in the introduction and let
$k^{\prime }$
be integers as in the introduction and let
![]() ${\mathcal{B}}_{p}$
, respectively
${\mathcal{B}}_{p}$
, respectively
![]() ${\mathcal{B}}_{q}$
, be the source of Beilinson’s Eisenstein symbol (1) of weight
${\mathcal{B}}_{q}$
, be the source of Beilinson’s Eisenstein symbol (1) of weight
![]() $p$
, respectively
$p$
, respectively
![]() $q$
. Assume that
$q$
. Assume that
![]() $p,q,k$
and
$p,q,k$
and
![]() $k^{\prime }$
satisfy the assumptions of Theorem 1.1. Then, we have the extension class
$k^{\prime }$
satisfy the assumptions of Theorem 1.1. Then, we have the extension class
 $$\begin{eqnarray}\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\in \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),H_{!}^{3}(S,W)_{\mathbb{ R}})\subset H_{{\mathcal{H}}}^{4}(S/\mathbb{R},W)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\in \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),H_{!}^{3}(S,W)_{\mathbb{ R}})\subset H_{{\mathcal{H}}}^{4}(S/\mathbb{R},W)\end{eqnarray}$$
for any
 $\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }\in {\mathcal{B}}_{p}\otimes _{\mathbb{Q}}{\mathcal{B}}_{q}$
. Let
$\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }\in {\mathcal{B}}_{p}\otimes _{\mathbb{Q}}{\mathcal{B}}_{q}$
. Let
 $\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
denote the image of
$\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
denote the image of
 $\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
by the natural map
$\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
by the natural map

from absolute Hodge to Deligne–Beilinson cohomology (see [Reference BeilinsonBei86, 5.7] and [Reference JannsenJan88, §2]). Thanks to the work of Jannsen [Reference JannsenJan88], the Deligne–Beilinson cohomology groups can be explicitly described by pairs of currents
![]() $(S,T)$
(Proposition 4.8) and this will permit us to give an explicit description of
$(S,T)$
(Proposition 4.8) and this will permit us to give an explicit description of
 $\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
(Proposition 4.10). In § 4.3, we introduce Deligne rational structure
$\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
(Proposition 4.10). In § 4.3, we introduce Deligne rational structure
![]() ${\mathcal{D}}$
on
${\mathcal{D}}$
on
![]() $\text{Ext}^{1}$
and explain how the image
$\text{Ext}^{1}$
and explain how the image
![]() ${\mathcal{K}}$
of
${\mathcal{K}}$
of
 $\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}$
can be compared with
$\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}$
can be compared with
![]() ${\mathcal{D}}$
via the computation of a Poincaré duality pairing related to
${\mathcal{D}}$
via the computation of a Poincaré duality pairing related to
![]() ${\mathcal{K}}$
and another related to
${\mathcal{K}}$
and another related to
![]() ${\mathcal{D}}$
(Lemma 4.21). This idea goes back to Beilinson [Reference BeilinsonBei88] (see also [Reference KingsKin98, 6.1]). In § 4.4, the pairing related to
${\mathcal{D}}$
(Lemma 4.21). This idea goes back to Beilinson [Reference BeilinsonBei88] (see also [Reference KingsKin98, 6.1]). In § 4.4, the pairing related to
![]() ${\mathcal{K}}$
is shown to be equal to an explicit adelic integral. Before this, let us introduce some relative motives.
${\mathcal{K}}$
is shown to be equal to an explicit adelic integral. Before this, let us introduce some relative motives.
4.1 The relative motives
In this section, we give a definition of motivic cohomology of the Shimura varieties we are interested in, with coefficients in sheaves such as
 $\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2}$
or
$\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2}$
or
![]() $W$
. This relies on the work of Ancona [Reference AnconaAnc15] and Cisinski and Déglise [Reference Cisinski and DégliseCD09], whose ideas were initiated by Voevodsky et al. [Reference Voevodsky, Suslin and FriedlanderVSF00]. Ideally, motivic cohomology should be defined as a space of extensions in categories of mixed motivic sheaves, but these categories have not been discovered yet.
$W$
. This relies on the work of Ancona [Reference AnconaAnc15] and Cisinski and Déglise [Reference Cisinski and DégliseCD09], whose ideas were initiated by Voevodsky et al. [Reference Voevodsky, Suslin and FriedlanderVSF00]. Ideally, motivic cohomology should be defined as a space of extensions in categories of mixed motivic sheaves, but these categories have not been discovered yet.
For the necessary background on relative motives of abelian schemes and relative Weil cohomologies, see [Reference AnconaAnc15, §§2 and 3], respectively. Let
![]() $A/S$
be the universal abelian surface over the Siegel threefold and let
$A/S$
be the universal abelian surface over the Siegel threefold and let
![]() $A^{k+k^{\prime }}$
be the
$A^{k+k^{\prime }}$
be the
![]() $(k+k^{\prime })$
th-fold fiber product over
$(k+k^{\prime })$
th-fold fiber product over
![]() $S$
. Let
$S$
. Let
 $R(A^{k+k^{\prime }})$
denote the relative motive over
$R(A^{k+k^{\prime }})$
denote the relative motive over
![]() $S$
associated to
$S$
associated to
![]() $A^{k+k^{\prime }}$
.
$A^{k+k^{\prime }}$
.
Proposition 4.1. Let
![]() $k,k^{\prime }$
and
$k,k^{\prime }$
and
![]() $c$
be such that
$c$
be such that
 $k\geqslant k^{\prime }\geqslant 0$
and
$k\geqslant k^{\prime }\geqslant 0$
and
 $c\equiv k+k^{\prime }~(\text{mod}~2)$
. Let
$c\equiv k+k^{\prime }~(\text{mod}~2)$
. Let
![]() $t$
denote the integer
$t$
denote the integer
 $(k+k^{\prime }+c)/2$
. Let
$(k+k^{\prime }+c)/2$
. Let
![]() $W$
be an irreducible algebraic representation of
$W$
be an irreducible algebraic representation of
![]() $G$
of highest weight
$G$
of highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },c)$
. Then, there exists a relative Chow motive over the Siegel threefold which is a direct factor of
$\unicode[STIX]{x1D706}(k,k^{\prime },c)$
. Then, there exists a relative Chow motive over the Siegel threefold which is a direct factor of
 $R(A^{k+k^{\prime }})(t)$
and whose Betti realization is the variation of Hodge structure
$R(A^{k+k^{\prime }})(t)$
and whose Betti realization is the variation of Hodge structure
![]() $W$
.
$W$
.
Proof. Let
 $r:G\longrightarrow \text{GL}(4)$
be the standard representation of
$r:G\longrightarrow \text{GL}(4)$
be the standard representation of
![]() $G$
. It follows from Weyl’s invariants theory that
$G$
. It follows from Weyl’s invariants theory that
![]() $W$
is a direct factor, defined by a certain explicit Schur projector, of the representation
$W$
is a direct factor, defined by a certain explicit Schur projector, of the representation
 $r^{\otimes (k+k^{\prime })}\otimes \unicode[STIX]{x1D708}^{\otimes t}$
(see [Reference Fulton and HarrisFH91, §17.3]). Hence, the statement is a direct consequence of [Reference AnconaAnc15, Theorem 1.3].◻
$r^{\otimes (k+k^{\prime })}\otimes \unicode[STIX]{x1D708}^{\otimes t}$
(see [Reference Fulton and HarrisFH91, §17.3]). Hence, the statement is a direct consequence of [Reference AnconaAnc15, Theorem 1.3].◻
Let
 $\text{DM}_{B,c}(S)$
is the triangulated category of constructible Beilinson motives over
$\text{DM}_{B,c}(S)$
is the triangulated category of constructible Beilinson motives over
![]() $S$
with
$S$
with
![]() $\mathbb{Q}$
-coefficients as defined in [Reference Cisinski and DégliseCD09, Definition 15.1.1]. Then
$\mathbb{Q}$
-coefficients as defined in [Reference Cisinski and DégliseCD09, Definition 15.1.1]. Then
![]() $W$
is an object of
$W$
is an object of
 $\text{DM}_{B,c}(S)$
. Let
$\text{DM}_{B,c}(S)$
. Let
![]() $\mathbf{1}_{S}$
be the unit object of
$\mathbf{1}_{S}$
be the unit object of
 $\text{DM}_{B,c}(S)$
. Motivic cohomology with coefficients in
$\text{DM}_{B,c}(S)$
. Motivic cohomology with coefficients in
![]() $W$
is the
$W$
is the
![]() $\mathbb{Q}$
-vector space defined by
$\mathbb{Q}$
-vector space defined by
 $$\begin{eqnarray}H_{{\mathcal{M}}}^{\ast }(S,W)=\text{Hom}_{\text{DM}_{B,c}(S)}(\mathbf{1}_{S},W[\ast ]).\end{eqnarray}$$
$$\begin{eqnarray}H_{{\mathcal{M}}}^{\ast }(S,W)=\text{Hom}_{\text{DM}_{B,c}(S)}(\mathbf{1}_{S},W[\ast ]).\end{eqnarray}$$
The compatibility of this definition with the
![]() $K$
-theoretical one follows from [Reference Cisinski and DégliseCD09, Corollary 14.2.14]. For integers
$K$
-theoretical one follows from [Reference Cisinski and DégliseCD09, Corollary 14.2.14]. For integers
![]() $p\geqslant 0$
and
$p\geqslant 0$
and
![]() $q\geqslant 0$
, we can define
$q\geqslant 0$
, we can define
 $H_{{\mathcal{M}}}^{\ast }(M\times M,(\operatorname{Sym}^{p}V_{2}\,\boxtimes \,\operatorname{Sym}^{q}V_{2})(2))$
similarly. Here
$H_{{\mathcal{M}}}^{\ast }(M\times M,(\operatorname{Sym}^{p}V_{2}\,\boxtimes \,\operatorname{Sym}^{q}V_{2})(2))$
similarly. Here
![]() $M$
denotes a modular curve. Moreover, if
$M$
denotes a modular curve. Moreover, if
![]() $p,q,k$
and
$p,q,k$
and
![]() $k^{\prime }$
verify the conditions stated in the introduction, the relative motive
$k^{\prime }$
verify the conditions stated in the introduction, the relative motive
 $(\operatorname{Sym}^{p}V_{2}\,\boxtimes \,\operatorname{Sym}^{q}V_{2})(2)$
over
$(\operatorname{Sym}^{p}V_{2}\,\boxtimes \,\operatorname{Sym}^{q}V_{2})(2)$
over
 $M\times M$
is naturally a direct factor of
$M\times M$
is naturally a direct factor of
![]() $\unicode[STIX]{x1D704}^{\ast }W$
, as Ancona’s construction is functorial. As a consequence, the motivic cohomology space
$\unicode[STIX]{x1D704}^{\ast }W$
, as Ancona’s construction is functorial. As a consequence, the motivic cohomology space
 $H_{{\mathcal{M}}}^{\ast }(M\times M,(\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2})(2))$
is a naturally a direct factor of
$H_{{\mathcal{M}}}^{\ast }(M\times M,(\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2})(2))$
is a naturally a direct factor of
 $H_{{\mathcal{M}}}^{\ast }(M\times M,\unicode[STIX]{x1D704}^{\ast }W(-1))$
. As the triangulated category of constructible Beilinson motives has the formalism of Grothendieck six functors, duality [Reference Cisinski and DégliseCD09, Theorem 15.2.4] and the absolute purity isomorphism [Reference Pépin LehalleurPép15, Proposition 1.7], we have the Gysin morphism
$H_{{\mathcal{M}}}^{\ast }(M\times M,\unicode[STIX]{x1D704}^{\ast }W(-1))$
. As the triangulated category of constructible Beilinson motives has the formalism of Grothendieck six functors, duality [Reference Cisinski and DégliseCD09, Theorem 15.2.4] and the absolute purity isomorphism [Reference Pépin LehalleurPép15, Proposition 1.7], we have the Gysin morphism

In this setting, the definition of the regulator in Deligne–Beilinson cohomology and the compatibility with the previous one has been explained in [Reference ScholbachSch15].
4.2 Explicit description of the cohomology classes
Let us start by reviewing basic facts about Deligne–Beilinson cohomology. In what follows, we shall consider Deligne–Beilinson cohomology with coefficients in algebraic representations of the group underlying a given Shimura variety. This means that, like in [Reference KingsKin98, 2.3], we consider Deligne–Beilinson cohomology of the corresponding relative motives.
Let
![]() $\operatorname{Sch}(\mathbb{Q})$
be the category of smooth quasi-projective
$\operatorname{Sch}(\mathbb{Q})$
be the category of smooth quasi-projective
![]() $\mathbb{Q}$
-schemes. Let
$\mathbb{Q}$
-schemes. Let
![]() $X$
be an object of
$X$
be an object of
![]() $\operatorname{Sch}(\mathbb{Q})$
and let
$\operatorname{Sch}(\mathbb{Q})$
and let
![]() $n$
be an integer. For a definition of the real Deligne–Beilinson cohomology
$n$
be an integer. For a definition of the real Deligne–Beilinson cohomology
 $H_{{\mathcal{D}}}^{\ast }(X/\mathbb{R},\mathbb{R}(n))$
, the reader is referred to [Reference NekovarNek94, 7]. We also have the real absolute Hodge cohomology
$H_{{\mathcal{D}}}^{\ast }(X/\mathbb{R},\mathbb{R}(n))$
, the reader is referred to [Reference NekovarNek94, 7]. We also have the real absolute Hodge cohomology
 $H_{{\mathcal{H}}}^{\ast }(X/\mathbb{R},\mathbb{R}(n))$
of
$H_{{\mathcal{H}}}^{\ast }(X/\mathbb{R},\mathbb{R}(n))$
of
![]() $X$
with coefficients in
$X$
with coefficients in
 $\mathbb{R}(n)=(2\unicode[STIX]{x1D70B}i)^{n}\mathbb{R}$
as defined in [Reference Huber and WildeshausHW98a, Definition A.2.6] and there is a canonical map
$\mathbb{R}(n)=(2\unicode[STIX]{x1D70B}i)^{n}\mathbb{R}$
as defined in [Reference Huber and WildeshausHW98a, Definition A.2.6] and there is a canonical map

Let
 ${\mathcal{S}}^{m}(X/\mathbb{R},\mathbb{R}(n))$
be the vector space of
${\mathcal{S}}^{m}(X/\mathbb{R},\mathbb{R}(n))$
be the vector space of
![]() ${\mathcal{C}}^{\infty }$
differential forms on
${\mathcal{C}}^{\infty }$
differential forms on
![]() $X(\mathbb{C})$
on which the map
$X(\mathbb{C})$
on which the map
![]() $F_{\infty }$
induced by complex conjugation on
$F_{\infty }$
induced by complex conjugation on
![]() $X(\mathbb{C})$
acts by multiplication by
$X(\mathbb{C})$
acts by multiplication by
![]() $(-1)^{n}$
. Let
$(-1)^{n}$
. Let
 ${\mathcal{S}}_{c}^{m}(X/\mathbb{R},\mathbb{R}(n))$
be the compactly supported differential forms belonging to
${\mathcal{S}}_{c}^{m}(X/\mathbb{R},\mathbb{R}(n))$
be the compactly supported differential forms belonging to
 ${\mathcal{S}}^{m}(X/\mathbb{R},\mathbb{R}(n))$
. Let us consider a smooth projective compactification
${\mathcal{S}}^{m}(X/\mathbb{R},\mathbb{R}(n))$
. Let us consider a smooth projective compactification
 $j:X\longrightarrow X^{\ast }$
and let
$j:X\longrightarrow X^{\ast }$
and let
 $i:Y\longrightarrow X^{\ast }$
be the complementary reduced closed embedding. Assume that
$i:Y\longrightarrow X^{\ast }$
be the complementary reduced closed embedding. Assume that
![]() $Y$
is a normal crossing divisor and let
$Y$
is a normal crossing divisor and let
![]() $\unicode[STIX]{x1D6FA}_{X}^{m}\langle Y\rangle$
be the
$\unicode[STIX]{x1D6FA}_{X}^{m}\langle Y\rangle$
be the
![]() $\mathbb{C}$
-vector space of holomorphic differentials of degree
$\mathbb{C}$
-vector space of holomorphic differentials of degree
![]() $m$
on
$m$
on
![]() $X$
with logarithmic singularities along
$X$
with logarithmic singularities along
![]() $Y$
, endowed with its Hodge filtration (see [Reference DeligneDel74, 3.1 and 3.2.2]). For any integer
$Y$
, endowed with its Hodge filtration (see [Reference DeligneDel74, 3.1 and 3.2.2]). For any integer
![]() $n$
, let
$n$
, let
 $\unicode[STIX]{x1D70B}_{n}:\mathbb{C}\longrightarrow \mathbb{R}(n)$
denote the map
$\unicode[STIX]{x1D70B}_{n}:\mathbb{C}\longrightarrow \mathbb{R}(n)$
denote the map
 $z\longmapsto {\textstyle \frac{1}{2}}(z+(-1)^{n}\overline{z})$
.
$z\longmapsto {\textstyle \frac{1}{2}}(z+(-1)^{n}\overline{z})$
.
Proposition 4.2 [Reference NekovarNek94, 7.3].
For any integer
![]() $m$
, we have a canonical isomorphism of
$m$
, we have a canonical isomorphism of
![]() $\mathbb{R}$
-vector spaces
$\mathbb{R}$
-vector spaces
 $$\begin{eqnarray}H_{{\mathcal{D}}}^{m}(X/\mathbb{R},\mathbb{R}(m))=\frac{\{(\unicode[STIX]{x1D719},\unicode[STIX]{x1D714})\in {\mathcal{S}}^{m-1}(X/\mathbb{R},\mathbb{R}(m))\times \unicode[STIX]{x1D6FA}_{X}^{m}\langle Y\rangle \mid d\unicode[STIX]{x1D719}=\unicode[STIX]{x1D70B}_{m}(\unicode[STIX]{x1D714})\}}{d{\mathcal{S}}^{m-2}(X/\mathbb{R},\mathbb{R}(m))}.\end{eqnarray}$$
$$\begin{eqnarray}H_{{\mathcal{D}}}^{m}(X/\mathbb{R},\mathbb{R}(m))=\frac{\{(\unicode[STIX]{x1D719},\unicode[STIX]{x1D714})\in {\mathcal{S}}^{m-1}(X/\mathbb{R},\mathbb{R}(m))\times \unicode[STIX]{x1D6FA}_{X}^{m}\langle Y\rangle \mid d\unicode[STIX]{x1D719}=\unicode[STIX]{x1D70B}_{m}(\unicode[STIX]{x1D714})\}}{d{\mathcal{S}}^{m-2}(X/\mathbb{R},\mathbb{R}(m))}.\end{eqnarray}$$
The Eisenstein symbol [Reference BeilinsonBei88, §3] is a
![]() $\mathbb{Q}$
-linear map
$\mathbb{Q}$
-linear map

where we denote by
 $H_{{\mathcal{M}}}^{n+1}(E^{n},\mathbb{Q}(n+1))$
the inductive limit over compact open subgroups
$H_{{\mathcal{M}}}^{n+1}(E^{n},\mathbb{Q}(n+1))$
the inductive limit over compact open subgroups
![]() $K$
of
$K$
of
 $\text{GL}_{2}(\mathbb{A}_{f})$
of the motivic cohomology
$\text{GL}_{2}(\mathbb{A}_{f})$
of the motivic cohomology
 $H_{{\mathcal{M}}}^{n+1}(E_{K}^{n},\mathbb{Q}(n+1))$
of the
$H_{{\mathcal{M}}}^{n+1}(E_{K}^{n},\mathbb{Q}(n+1))$
of the
![]() $n$
th-fold fiber product of the universal elliptic curve
$n$
th-fold fiber product of the universal elliptic curve
 $E_{K}/M_{K}$
over the modular curve of level
$E_{K}/M_{K}$
over the modular curve of level
![]() $K$
. The notation
$K$
. The notation
![]() ${\mathcal{B}}_{n}$
stands for the space of locally constant
${\mathcal{B}}_{n}$
stands for the space of locally constant
![]() $\mathbb{Q}$
-valued functions
$\mathbb{Q}$
-valued functions
![]() $\unicode[STIX]{x1D719}_{f}$
on
$\unicode[STIX]{x1D719}_{f}$
on
 $\text{GL}_{2}(\mathbb{A}_{f})$
such that for any
$\text{GL}_{2}(\mathbb{A}_{f})$
such that for any
![]() $b\in \mathbb{A}_{f}$
, any
$b\in \mathbb{A}_{f}$
, any
 $a,d\in \mathbb{Q}$
such that
$a,d\in \mathbb{Q}$
such that
![]() $ad>0$
and any
$ad>0$
and any
 $g\in \text{GL}_{2}(\mathbb{A}_{f})$
, we have
$g\in \text{GL}_{2}(\mathbb{A}_{f})$
, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{f}\left(\left(\begin{array}{@{}cc@{}}a & b\\ & d\end{array}\right)g\right) & = & \displaystyle a^{-(n+1)}\,d\unicode[STIX]{x1D719}_{f}(g),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{f}\left(\left(\begin{array}{@{}cc@{}}a & b\\ & d\end{array}\right)g\right) & = & \displaystyle a^{-(n+1)}\,d\unicode[STIX]{x1D719}_{f}(g),\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{f}\left(\left(\begin{array}{@{}cc@{}}-1 & \\ & 1\end{array}\right)g\right) & = & \displaystyle \unicode[STIX]{x1D719}_{f}(g)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}_{f}\left(\left(\begin{array}{@{}cc@{}}-1 & \\ & 1\end{array}\right)g\right) & = & \displaystyle \unicode[STIX]{x1D719}_{f}(g)\end{eqnarray}$$
and which are invariant by right translation under
![]() $(\!\begin{smallmatrix}\widehat{\mathbb{Z}}^{\times } & \\ & 1\end{smallmatrix}\!)$
. The source of the Eisenstein symbol is indentified to a space of
$(\!\begin{smallmatrix}\widehat{\mathbb{Z}}^{\times } & \\ & 1\end{smallmatrix}\!)$
. The source of the Eisenstein symbol is indentified to a space of
![]() $\mathbb{Q}$
-valued functions
$\mathbb{Q}$
-valued functions
![]() ${\mathcal{F}}^{n}$
on
${\mathcal{F}}^{n}$
on
 $\text{GL}_{2}(\mathbb{A}_{f})$
in [Reference BeilinsonBei88, p. 7]. Note that the map
$\text{GL}_{2}(\mathbb{A}_{f})$
in [Reference BeilinsonBei88, p. 7]. Note that the map
 $\unicode[STIX]{x1D713}_{f}\mapsto (\unicode[STIX]{x1D719}_{f}:g\mapsto \unicode[STIX]{x1D719}_{f}(g)=\unicode[STIX]{x1D713}_{f}(\text{det}(g)^{-1}~\text{}^{t}\!g))$
defines a
$\unicode[STIX]{x1D713}_{f}\mapsto (\unicode[STIX]{x1D719}_{f}:g\mapsto \unicode[STIX]{x1D719}_{f}(g)=\unicode[STIX]{x1D713}_{f}(\text{det}(g)^{-1}~\text{}^{t}\!g))$
defines a
 $\text{GL}_{2}(\mathbb{A}_{f})$
-equivariant isomorphism
$\text{GL}_{2}(\mathbb{A}_{f})$
-equivariant isomorphism
 ${\mathcal{F}}^{n}\simeq {\mathcal{B}}_{n}$
when
${\mathcal{F}}^{n}\simeq {\mathcal{B}}_{n}$
when
 $\text{GL}_{2}(\mathbb{A}_{f})$
acts on
$\text{GL}_{2}(\mathbb{A}_{f})$
acts on
![]() ${\mathcal{F}}^{n}$
, respectively
${\mathcal{F}}^{n}$
, respectively
![]() ${\mathcal{B}}_{n}$
, by left, respectively right, translation. By definition of the motivic sheaf
${\mathcal{B}}_{n}$
, by left, respectively right, translation. By definition of the motivic sheaf
 $\operatorname{Sym}^{n}V_{2}(1)$
, the motivic cohomology
$\operatorname{Sym}^{n}V_{2}(1)$
, the motivic cohomology
 $H_{{\mathcal{M}}}^{1}(M,\operatorname{Sym}^{n}V_{2}(1))$
is a direct factor of
$H_{{\mathcal{M}}}^{1}(M,\operatorname{Sym}^{n}V_{2}(1))$
is a direct factor of
 $H_{{\mathcal{M}}}^{n+1}(E^{n},\mathbb{Q}(n+1))$
. Furthermore, the Eisenstein symbol factors through the natural inclusion
$H_{{\mathcal{M}}}^{n+1}(E^{n},\mathbb{Q}(n+1))$
. Furthermore, the Eisenstein symbol factors through the natural inclusion
 $H_{{\mathcal{M}}}^{1}(M,\operatorname{Sym}^{n}V_{2}(1))\subset H_{{\mathcal{M}}}^{n+1}(E^{n},\mathbb{Q}(n+1))$
and we denote again by
$H_{{\mathcal{M}}}^{1}(M,\operatorname{Sym}^{n}V_{2}(1))\subset H_{{\mathcal{M}}}^{n+1}(E^{n},\mathbb{Q}(n+1))$
and we denote again by
![]() $\operatorname{Eis}_{{\mathcal{M}}}^{n}$
the induced map
$\operatorname{Eis}_{{\mathcal{M}}}^{n}$
the induced map
 ${\mathcal{B}}_{n}\longrightarrow H_{{\mathcal{M}}}^{1}(M,\operatorname{Sym}^{n}V_{2}(1))$
. The following lemma will be very useful later.
${\mathcal{B}}_{n}\longrightarrow H_{{\mathcal{M}}}^{1}(M,\operatorname{Sym}^{n}V_{2}(1))$
. The following lemma will be very useful later.
Lemma 4.3. Let
![]() ${\mathcal{B}}_{n,\overline{\mathbb{Q}}}$
be the vector space
${\mathcal{B}}_{n,\overline{\mathbb{Q}}}$
be the vector space
 ${\mathcal{B}}_{n}\otimes _{\mathbb{Q}}\overline{\mathbb{Q}}$
with the action of
${\mathcal{B}}_{n}\otimes _{\mathbb{Q}}\overline{\mathbb{Q}}$
with the action of
 $\text{GL}_{2}(\mathbb{A}_{f})$
by right translation. For any finite-order Hecke character
$\text{GL}_{2}(\mathbb{A}_{f})$
by right translation. For any finite-order Hecke character
![]() $\unicode[STIX]{x1D708}$
let
$\unicode[STIX]{x1D708}$
let
![]() ${\mathcal{I}}_{n}(\unicode[STIX]{x1D708})$
denote the space of locally constant functions
${\mathcal{I}}_{n}(\unicode[STIX]{x1D708})$
denote the space of locally constant functions
 $f:\text{GL}_{2}(\mathbb{A}_{f})\longrightarrow \overline{\mathbb{Q}}$
such that for all
$f:\text{GL}_{2}(\mathbb{A}_{f})\longrightarrow \overline{\mathbb{Q}}$
such that for all
 $a,d\in \mathbb{Q}_{+}^{\times }$
, for all
$a,d\in \mathbb{Q}_{+}^{\times }$
, for all
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FF}\in \widehat{\mathbb{Z}}^{\times }$
, for all
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FF}\in \widehat{\mathbb{Z}}^{\times }$
, for all
![]() $b\in \mathbb{A}_{f}$
and for all
$b\in \mathbb{A}_{f}$
and for all
 $g\in \text{GL}_{2}(\mathbb{A}_{f})$
,
$g\in \text{GL}_{2}(\mathbb{A}_{f})$
,
 $$\begin{eqnarray}f\left(\left(\begin{array}{@{}cc@{}}a\unicode[STIX]{x1D6FC} & b\\ & d\unicode[STIX]{x1D6FF}\end{array}\right)g\right)=a^{-(n+1)}\,d\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})f(g)\end{eqnarray}$$
$$\begin{eqnarray}f\left(\left(\begin{array}{@{}cc@{}}a\unicode[STIX]{x1D6FC} & b\\ & d\unicode[STIX]{x1D6FF}\end{array}\right)g\right)=a^{-(n+1)}\,d\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})f(g)\end{eqnarray}$$
and which are invariant by
![]() $(\!\begin{smallmatrix}\widehat{\mathbb{Z}}^{\times } & \\ & 1\end{smallmatrix}\!)$
when
$(\!\begin{smallmatrix}\widehat{\mathbb{Z}}^{\times } & \\ & 1\end{smallmatrix}\!)$
when
![]() ${\mathcal{I}}_{n}(\unicode[STIX]{x1D708})$
is endowed with the action of
${\mathcal{I}}_{n}(\unicode[STIX]{x1D708})$
is endowed with the action of
 $\text{GL}_{2}(\mathbb{A}_{f})$
by right translation. Then, there is a
$\text{GL}_{2}(\mathbb{A}_{f})$
by right translation. Then, there is a
 $\text{GL}_{2}(\mathbb{A}_{f})$
-equivariant decomposition
$\text{GL}_{2}(\mathbb{A}_{f})$
-equivariant decomposition
 $$\begin{eqnarray}{\mathcal{B}}_{n,\overline{\mathbb{Q}}}=\bigoplus _{\text{sgn}(\unicode[STIX]{x1D708})=(-1)^{n}}{\mathcal{I}}_{n}(\unicode[STIX]{x1D708})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}_{n,\overline{\mathbb{Q}}}=\bigoplus _{\text{sgn}(\unicode[STIX]{x1D708})=(-1)^{n}}{\mathcal{I}}_{n}(\unicode[STIX]{x1D708})\end{eqnarray}$$
where the sum is indexed by all finite-order Hecke characters
![]() $\unicode[STIX]{x1D708}$
of
$\unicode[STIX]{x1D708}$
of
 $\operatorname{sign}(-1)^{n}$
.
$\operatorname{sign}(-1)^{n}$
.
Proof. Let
![]() $\text{T}_{2}$
denote the diagonal maximal torus of
$\text{T}_{2}$
denote the diagonal maximal torus of
![]() $\text{GL}_{2}$
. We are interested in the action of
$\text{GL}_{2}$
. We are interested in the action of
![]() $\text{T}_{2}(\mathbb{A}_{f})$
on the space
$\text{T}_{2}(\mathbb{A}_{f})$
on the space
![]() ${\mathcal{B}}_{n,\overline{\mathbb{Q}}}$
by left translation. Because of the decomposition
${\mathcal{B}}_{n,\overline{\mathbb{Q}}}$
by left translation. Because of the decomposition
 $\mathbb{A}_{f}^{\times }=\mathbb{Q}_{+}^{\times }\widehat{\mathbb{Z}}^{\times }$
, we are reduced to study the action of
$\mathbb{A}_{f}^{\times }=\mathbb{Q}_{+}^{\times }\widehat{\mathbb{Z}}^{\times }$
, we are reduced to study the action of
![]() $\text{T}_{2}(\widehat{\mathbb{Z}})$
thanks to the equality (11). The Iwasawa decomposition
$\text{T}_{2}(\widehat{\mathbb{Z}})$
thanks to the equality (11). The Iwasawa decomposition
 $\text{GL}_{2}(\mathbb{A}_{f})=\text{B}_{2}(\mathbb{A}_{f})\text{GL}_{2}(\widehat{\mathbb{Z}})$
and the fact that functions in
$\text{GL}_{2}(\mathbb{A}_{f})=\text{B}_{2}(\mathbb{A}_{f})\text{GL}_{2}(\widehat{\mathbb{Z}})$
and the fact that functions in
![]() ${\mathcal{B}}_{n,\overline{\mathbb{Q}}}$
are locally constant implies that
${\mathcal{B}}_{n,\overline{\mathbb{Q}}}$
are locally constant implies that
![]() ${\mathcal{B}}_{n,\overline{\mathbb{Q}}}$
is a union of finite-dimensional
${\mathcal{B}}_{n,\overline{\mathbb{Q}}}$
is a union of finite-dimensional
![]() $\overline{\mathbb{Q}}$
-vector spaces
$\overline{\mathbb{Q}}$
-vector spaces
![]() $V$
which are stable under
$V$
which are stable under
![]() $\text{T}_{2}(\widehat{\mathbb{Z}})$
. By continuity, the action is trivial on an open subgroup of
$\text{T}_{2}(\widehat{\mathbb{Z}})$
. By continuity, the action is trivial on an open subgroup of
![]() $\text{T}_{2}(\widehat{\mathbb{Z}})$
and so
$\text{T}_{2}(\widehat{\mathbb{Z}})$
and so
![]() $V$
is a sum of finite-order characters
$V$
is a sum of finite-order characters
 $$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \\ & \unicode[STIX]{x1D6FF}\end{array}\right)\longmapsto \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \\ & \unicode[STIX]{x1D6FF}\end{array}\right)\longmapsto \unicode[STIX]{x1D712}(\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}).\end{eqnarray}$$
By
![]() $(\!\begin{smallmatrix}\widehat{\mathbb{Z}}^{\times } & \\ & 1\end{smallmatrix}\!)$
-invariance, the character
$(\!\begin{smallmatrix}\widehat{\mathbb{Z}}^{\times } & \\ & 1\end{smallmatrix}\!)$
-invariance, the character
![]() $\unicode[STIX]{x1D712}$
has to be trivial and by condition (11), the character
$\unicode[STIX]{x1D712}$
has to be trivial and by condition (11), the character
![]() $\unicode[STIX]{x1D708}$
has to be of
$\unicode[STIX]{x1D708}$
has to be of
 $\operatorname{sign}(-1)^{n}$
.◻
$\operatorname{sign}(-1)^{n}$
.◻
Let us recall now the explicit description of the image of the Eisenstein symbol in Deligne–Beilinson cohomology, via the isomorphism of Proposition 4.2. Here, we follow [Reference KingsKin98, 6.3] very closely.
Let us regard the circle
![]() $\text{U}(1)$
as a maximal compact subgroup of
$\text{U}(1)$
as a maximal compact subgroup of
![]() $\text{SL}_{2}(\mathbb{R})$
in the usual way. We will also sometimes consider the maximal torus
$\text{SL}_{2}(\mathbb{R})$
in the usual way. We will also sometimes consider the maximal torus
 $Z_{2}(\mathbb{R})^{+}\text{U}(1)$
, where
$Z_{2}(\mathbb{R})^{+}\text{U}(1)$
, where
![]() $Z_{2}(\mathbb{R})^{+}$
denotes the identity component of the center of
$Z_{2}(\mathbb{R})^{+}$
denotes the identity component of the center of
 $\text{GL}_{2}(\mathbb{R})$
. In what follows, we shall implicitly use the isomorphism between the de Rham complex on modular curves and a
$\text{GL}_{2}(\mathbb{R})$
. In what follows, we shall implicitly use the isomorphism between the de Rham complex on modular curves and a
 $(\mathfrak{gl}_{2,\mathbb{C}},Z_{2}(\mathbb{R})^{+}\text{U}(1))$
-complex which is analogous to that stated in § 3.2 for Siegel threefolds. If
$(\mathfrak{gl}_{2,\mathbb{C}},Z_{2}(\mathbb{R})^{+}\text{U}(1))$
-complex which is analogous to that stated in § 3.2 for Siegel threefolds. If
![]() $\mathfrak{k}_{2}$
denotes the Lie algebra of
$\mathfrak{k}_{2}$
denotes the Lie algebra of
![]() $\text{U}(1)$
, we have the Cartan decomposition
$\text{U}(1)$
, we have the Cartan decomposition
 $\mathfrak{sl}_{2,\mathbb{C}}=\mathfrak{k}_{2,\mathbb{C}}\oplus \mathfrak{p}^{\prime +}\oplus \mathfrak{p}^{\prime -}$
where
$\mathfrak{sl}_{2,\mathbb{C}}=\mathfrak{k}_{2,\mathbb{C}}\oplus \mathfrak{p}^{\prime +}\oplus \mathfrak{p}^{\prime -}$
where
 $$\begin{eqnarray}\mathfrak{p}^{\prime \pm }=\left\{\left(\begin{array}{@{}cc@{}}z & \pm iz\\ \pm iz & -z\end{array}\right)\in \mathfrak{sl}_{2,\mathbb{C}}\mid z\in \mathbb{C}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{p}^{\prime \pm }=\left\{\left(\begin{array}{@{}cc@{}}z & \pm iz\\ \pm iz & -z\end{array}\right)\in \mathfrak{sl}_{2,\mathbb{C}}\mid z\in \mathbb{C}\right\}.\end{eqnarray}$$
Let
 $v^{\pm }\in \mathfrak{p}^{\prime \pm }$
denote the vector
$v^{\pm }\in \mathfrak{p}^{\prime \pm }$
denote the vector
 $v^{\pm }={\textstyle \frac{1}{2}}(\!\begin{smallmatrix}1 & \pm i\\ \pm i & -1\end{smallmatrix}\!)\in \mathfrak{p}^{\prime \pm }$
. Let
$v^{\pm }={\textstyle \frac{1}{2}}(\!\begin{smallmatrix}1 & \pm i\\ \pm i & -1\end{smallmatrix}\!)\in \mathfrak{p}^{\prime \pm }$
. Let
![]() $(X,Y)$
be a basis of the standard representation
$(X,Y)$
be a basis of the standard representation
![]() $V_{2}$
of
$V_{2}$
of
![]() $\text{GL}(2)$
such that
$\text{GL}(2)$
such that
 $(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \text{GL}_{2}(\mathbb{Q})$
acts by
$(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \text{GL}_{2}(\mathbb{Q})$
acts by
 $$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)X=aX+cY, & & \displaystyle \nonumber\\ \displaystyle \left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)Y=bX+dY. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)X=aX+cY, & & \displaystyle \nonumber\\ \displaystyle \left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)Y=bX+dY. & & \displaystyle \nonumber\end{eqnarray}$$
We regard
 $\operatorname{Sym}^{n}V_{2,\mathbb{C}}$
as the space of homogeneous polynomials of degree
$\operatorname{Sym}^{n}V_{2,\mathbb{C}}$
as the space of homogeneous polynomials of degree
![]() $n$
in the variables
$n$
in the variables
![]() $X$
and
$X$
and
![]() $Y$
, with coefficients in
$Y$
, with coefficients in
![]() $\mathbb{C}$
. For any integer
$\mathbb{C}$
. For any integer
 $0\leqslant j\leqslant n$
, let
$0\leqslant j\leqslant n$
, let
 $b_{j}^{(n)}\in \operatorname{Sym}^{n}V_{2,\mathbb{C}}$
be the vector
$b_{j}^{(n)}\in \operatorname{Sym}^{n}V_{2,\mathbb{C}}$
be the vector
 $b_{j}^{(n)}=(iX-Y)^{j}(iX+Y)^{n-j}$
. The family
$b_{j}^{(n)}=(iX-Y)^{j}(iX+Y)^{n-j}$
. The family
 $(b_{j}^{(n)})_{0\leqslant j\leqslant n}$
is a basis of
$(b_{j}^{(n)})_{0\leqslant j\leqslant n}$
is a basis of
 $\operatorname{Sym}^{n}V_{2,\mathbb{C}}$
and we will denote by
$\operatorname{Sym}^{n}V_{2,\mathbb{C}}$
and we will denote by
 $(a_{j}^{(n)})_{0\leqslant j\leqslant n}$
the dual basis.
$(a_{j}^{(n)})_{0\leqslant j\leqslant n}$
the dual basis.
Lemma 4.4. Let
![]() $n,c$
be two integers such that
$n,c$
be two integers such that
 $n\equiv c~(\text{mod}~2)$
. Let
$n\equiv c~(\text{mod}~2)$
. Let
![]() $\unicode[STIX]{x1D706}^{\prime }(n,c)$
be the character of the torus
$\unicode[STIX]{x1D706}^{\prime }(n,c)$
be the character of the torus
 $Z_{2}(\mathbb{R})^{+}\text{U}(1)$
defined by
$Z_{2}(\mathbb{R})^{+}\text{U}(1)$
defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D706}^{\prime }(n,c):\left(\begin{array}{@{}cc@{}}x & y\\ -y & x\end{array}\right)\longmapsto (x+iy)^{n}(x^{2}+y^{2})^{(c-n)/2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}^{\prime }(n,c):\left(\begin{array}{@{}cc@{}}x & y\\ -y & x\end{array}\right)\longmapsto (x+iy)^{n}(x^{2}+y^{2})^{(c-n)/2}.\end{eqnarray}$$
Then, the vector
![]() $a_{j}^{(n)}$
has weight
$a_{j}^{(n)}$
has weight
 $\unicode[STIX]{x1D706}^{\prime }(n-2j,-n)$
.
$\unicode[STIX]{x1D706}^{\prime }(n-2j,-n)$
.
Proof. This follows from a trivial computation. ◻
Let
![]() $\text{B}_{2}$
denote the standard Borel of
$\text{B}_{2}$
denote the standard Borel of
![]() $\text{GL}_{2}$
, and by
$\text{GL}_{2}$
, and by
 $\text{GL}_{2}(\mathbb{R})^{+}$
, respectively
$\text{GL}_{2}(\mathbb{R})^{+}$
, respectively
![]() $\text{B}_{2}(\mathbb{R})^{+}$
, the identity component of
$\text{B}_{2}(\mathbb{R})^{+}$
, the identity component of
 $\text{GL}_{2}(\mathbb{R})$
, respectively
$\text{GL}_{2}(\mathbb{R})$
, respectively
![]() $\text{B}_{2}(\mathbb{R})$
. Given
$\text{B}_{2}(\mathbb{R})$
. Given
![]() $n,c$
as above, we denote by
$n,c$
as above, we denote by
![]() $\unicode[STIX]{x1D706}(n,c)$
the algebraic character of the diagonal maximal torus of
$\unicode[STIX]{x1D706}(n,c)$
the algebraic character of the diagonal maximal torus of
![]() $\text{GL}_{2}$
defined by
$\text{GL}_{2}$
defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D706}(d,c):\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \\ & \unicode[STIX]{x1D6FC}^{-1}\unicode[STIX]{x1D708}\end{array}\right)\longmapsto \unicode[STIX]{x1D6FC}^{n}\unicode[STIX]{x1D708}^{(c-n)/2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}(d,c):\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \\ & \unicode[STIX]{x1D6FC}^{-1}\unicode[STIX]{x1D708}\end{array}\right)\longmapsto \unicode[STIX]{x1D6FC}^{n}\unicode[STIX]{x1D708}^{(c-n)/2}.\end{eqnarray}$$
For any integer
![]() $r$
such that
$r$
such that
 $r\equiv n~(\text{mod}~2)$
, the function
$r\equiv n~(\text{mod}~2)$
, the function
 $\unicode[STIX]{x1D719}_{r}^{n}\in \operatorname{ind}_{\text{B}_{2}(\mathbb{R})^{+}}^{\text{GL}_{2}(\mathbb{R})^{+}}\unicode[STIX]{x1D706}(n+2,n)$
is defined as
$\unicode[STIX]{x1D719}_{r}^{n}\in \operatorname{ind}_{\text{B}_{2}(\mathbb{R})^{+}}^{\text{GL}_{2}(\mathbb{R})^{+}}\unicode[STIX]{x1D706}(n+2,n)$
is defined as
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{r}^{n}=(z_{2}-\overline{z}_{2})^{n+1}w_{2}^{(n-r)/2}\overline{w}_{2}^{(n+r)/2}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{r}^{n}=(z_{2}-\overline{z}_{2})^{n+1}w_{2}^{(n-r)/2}\overline{w}_{2}^{(n+r)/2}\end{eqnarray}$$
where
 $$\begin{eqnarray}z_{2}\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)=\frac{ai+b}{ci+d},\quad w_{2}\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)=ci+d.\end{eqnarray}$$
$$\begin{eqnarray}z_{2}\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)=\frac{ai+b}{ci+d},\quad w_{2}\left(\begin{array}{@{}cc@{}}a & b\\ c & d\end{array}\right)=ci+d.\end{eqnarray}$$
Consider
 $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{n}=\frac{(2\unicode[STIX]{x1D70B}i)^{n+1}}{2(n+1)}\mathop{\sum }_{j=0}^{n}a_{j}^{(n)}\otimes \unicode[STIX]{x1D719}_{2j-n}^{n}\in \operatorname{Sym}^{n}V_{2,\mathbb{C}}^{\vee }\otimes \operatorname{ind}_{\text{B}_{2}(\mathbb{R})^{+}}^{\text{GL}_{2}(\mathbb{R})^{+}}\unicode[STIX]{x1D706}(n+2,n).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{n}=\frac{(2\unicode[STIX]{x1D70B}i)^{n+1}}{2(n+1)}\mathop{\sum }_{j=0}^{n}a_{j}^{(n)}\otimes \unicode[STIX]{x1D719}_{2j-n}^{n}\in \operatorname{Sym}^{n}V_{2,\mathbb{C}}^{\vee }\otimes \operatorname{ind}_{\text{B}_{2}(\mathbb{R})^{+}}^{\text{GL}_{2}(\mathbb{R})^{+}}\unicode[STIX]{x1D706}(n+2,n).\end{eqnarray}$$
Given
 $\unicode[STIX]{x1D719}_{f}\in {\mathcal{B}}_{n}$
, we can consider the vector valued series of functions
$\unicode[STIX]{x1D719}_{f}\in {\mathcal{B}}_{n}$
, we can consider the vector valued series of functions
 $$\begin{eqnarray}\operatorname{Eis}_{{\mathcal{H}}}^{n}(\unicode[STIX]{x1D719}_{f})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \text{B}_{2}(\mathbb{Q})\backslash \text{GL}_{2}(\mathbb{Q})}\unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D6E9}_{n}\otimes \unicode[STIX]{x1D719}_{f}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Eis}_{{\mathcal{H}}}^{n}(\unicode[STIX]{x1D719}_{f})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \text{B}_{2}(\mathbb{Q})\backslash \text{GL}_{2}(\mathbb{Q})}\unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D6E9}_{n}\otimes \unicode[STIX]{x1D719}_{f}),\end{eqnarray}$$
which is absolutely convergent provided
![]() $n\geqslant 1$
. Because of the limitations given by the hypothesis of Theorem 1.1, we only need to work with the Eisenstein symbol
$n\geqslant 1$
. Because of the limitations given by the hypothesis of Theorem 1.1, we only need to work with the Eisenstein symbol
![]() $\operatorname{Eis}_{{\mathcal{M}}}^{n}$
for
$\operatorname{Eis}_{{\mathcal{M}}}^{n}$
for
![]() $n\geqslant 1$
in this work.
$n\geqslant 1$
in this work.
Lemma 4.5. Let
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{n}^{\pm }\in \text{Hom}_{\text{U}(1)}(\mathfrak{p}^{\prime +}\oplus \mathfrak{p}^{\prime -},\operatorname{Sym}^{n}V_{2,\mathbb{C}}^{\vee }\otimes \operatorname{ind}_{\text{B}_{2}(\mathbb{R})^{+}}^{\text{GL}_{2}(\mathbb{R})^{+}}\unicode[STIX]{x1D706}(n+2,n))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{n}^{\pm }\in \text{Hom}_{\text{U}(1)}(\mathfrak{p}^{\prime +}\oplus \mathfrak{p}^{\prime -},\operatorname{Sym}^{n}V_{2,\mathbb{C}}^{\vee }\otimes \operatorname{ind}_{\text{B}_{2}(\mathbb{R})^{+}}^{\text{GL}_{2}(\mathbb{R})^{+}}\unicode[STIX]{x1D706}(n+2,n))\end{eqnarray}$$
be the differential form defined by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{n}^{+}(v^{+}) & = & \displaystyle (2\unicode[STIX]{x1D70B}i)^{n+1}a_{n}^{(n)}\otimes \unicode[STIX]{x1D719}_{n+2}^{n},\nonumber\\ \displaystyle \unicode[STIX]{x1D714}_{n}^{+}(v^{-}) & = & \displaystyle 0,\nonumber\\ \displaystyle \unicode[STIX]{x1D714}_{n}^{-}(v^{+}) & = & \displaystyle 0,\nonumber\\ \displaystyle \unicode[STIX]{x1D714}_{n}^{-}(v^{-}) & = & \displaystyle (2\unicode[STIX]{x1D70B}i)^{n+1}a_{0}^{(n)}\otimes \unicode[STIX]{x1D719}_{-n-2}^{n}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D714}_{n}^{+}(v^{+}) & = & \displaystyle (2\unicode[STIX]{x1D70B}i)^{n+1}a_{n}^{(n)}\otimes \unicode[STIX]{x1D719}_{n+2}^{n},\nonumber\\ \displaystyle \unicode[STIX]{x1D714}_{n}^{+}(v^{-}) & = & \displaystyle 0,\nonumber\\ \displaystyle \unicode[STIX]{x1D714}_{n}^{-}(v^{+}) & = & \displaystyle 0,\nonumber\\ \displaystyle \unicode[STIX]{x1D714}_{n}^{-}(v^{-}) & = & \displaystyle (2\unicode[STIX]{x1D70B}i)^{n+1}a_{0}^{(n)}\otimes \unicode[STIX]{x1D719}_{-n-2}^{n}.\nonumber\end{eqnarray}$$
Let
![]() $\overline{\unicode[STIX]{x1D714}}_{n}^{\pm }$
be the differential form deduced from
$\overline{\unicode[STIX]{x1D714}}_{n}^{\pm }$
be the differential form deduced from
![]() $\unicode[STIX]{x1D714}_{n}^{\pm }$
by applying the complex conjugation on
$\unicode[STIX]{x1D714}_{n}^{\pm }$
by applying the complex conjugation on
 $\operatorname{Sym}^{n}V_{2,\mathbb{C}}^{\vee }\otimes \operatorname{ind}_{\text{B}_{2}(\mathbb{R})^{+}}^{\text{GL}_{2}(\mathbb{R})^{+}}\unicode[STIX]{x1D706}(n+2,n)$
. Then
$\operatorname{Sym}^{n}V_{2,\mathbb{C}}^{\vee }\otimes \operatorname{ind}_{\text{B}_{2}(\mathbb{R})^{+}}^{\text{GL}_{2}(\mathbb{R})^{+}}\unicode[STIX]{x1D706}(n+2,n)$
. Then
 $\overline{\unicode[STIX]{x1D714}}_{n}^{\pm }=(-1)^{n}\unicode[STIX]{x1D714}_{n}^{\mp }$
.
$\overline{\unicode[STIX]{x1D714}}_{n}^{\pm }=(-1)^{n}\unicode[STIX]{x1D714}_{n}^{\mp }$
.
Proof. This follows from the identities
 $\overline{\unicode[STIX]{x1D719}}_{n+2}^{n}=(-1)^{n+1}\unicode[STIX]{x1D719}_{-n-2}^{n}$
and
$\overline{\unicode[STIX]{x1D719}}_{n+2}^{n}=(-1)^{n+1}\unicode[STIX]{x1D719}_{-n-2}^{n}$
and
 $\overline{a_{j}^{(n)}}=(-1)^{n}a_{j}^{(n)}$
.◻
$\overline{a_{j}^{(n)}}=(-1)^{n}a_{j}^{(n)}$
.◻
For any
 $\unicode[STIX]{x1D719}_{f}\in {\mathcal{B}}_{n}$
, the infinite series
$\unicode[STIX]{x1D719}_{f}\in {\mathcal{B}}_{n}$
, the infinite series
 $$\begin{eqnarray}\operatorname{Eis}_{B}^{n}(\unicode[STIX]{x1D719}_{f})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \text{B}_{2}(\mathbb{Q})\backslash \text{GL}_{2}(\mathbb{Q})}\unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D714}_{n}^{+}\otimes \unicode[STIX]{x1D719}_{f})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Eis}_{B}^{n}(\unicode[STIX]{x1D719}_{f})=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \text{B}_{2}(\mathbb{Q})\backslash \text{GL}_{2}(\mathbb{Q})}\unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D714}_{n}^{+}\otimes \unicode[STIX]{x1D719}_{f})\end{eqnarray}$$
is absolutely convergent and defines a vector valued closed holomorphic differential one-form on
![]() $M$
, i.e. an element of
$M$
, i.e. an element of
 $$\begin{eqnarray}\text{Hom}_{\text{U}(1)}\biggl(\bigwedge ^{1}(\mathfrak{p}^{\prime +}\oplus \mathfrak{p}^{\prime -}),\operatorname{Sym}^{n}V_{2,\mathbb{C}}^{\vee }\otimes {\mathcal{C}}^{\infty }(\text{GL}_{2}(\mathbb{Q})\backslash \text{GL}_{2}(\mathbb{A}_{f}))\biggr),\end{eqnarray}$$
$$\begin{eqnarray}\text{Hom}_{\text{U}(1)}\biggl(\bigwedge ^{1}(\mathfrak{p}^{\prime +}\oplus \mathfrak{p}^{\prime -}),\operatorname{Sym}^{n}V_{2,\mathbb{C}}^{\vee }\otimes {\mathcal{C}}^{\infty }(\text{GL}_{2}(\mathbb{Q})\backslash \text{GL}_{2}(\mathbb{A}_{f}))\biggr),\end{eqnarray}$$
as explained in [Reference KingsKin98, 6.3]. Let
 $E\longrightarrow M$
denote the universal elliptic curve over
$E\longrightarrow M$
denote the universal elliptic curve over
![]() $M$
. By definition of the relative motive associated to the standard representation
$M$
. By definition of the relative motive associated to the standard representation
![]() $V_{2}$
of
$V_{2}$
of
![]() $\text{GL}(2)$
, the cohomology
$\text{GL}(2)$
, the cohomology
 $H_{{\mathcal{D}}}^{1}(M/\mathbb{R},\operatorname{Sym}^{n}V_{2}(1))$
is a direct factor of
$H_{{\mathcal{D}}}^{1}(M/\mathbb{R},\operatorname{Sym}^{n}V_{2}(1))$
is a direct factor of
 $H_{{\mathcal{D}}}^{n+1}(E^{n}/\mathbb{R},\mathbb{R}(n+1))$
, where
$H_{{\mathcal{D}}}^{n+1}(E^{n}/\mathbb{R},\mathbb{R}(n+1))$
, where
![]() $E^{n}$
denotes the
$E^{n}$
denotes the
![]() $n$
th-fold fiber product over
$n$
th-fold fiber product over
![]() $M$
.
$M$
.
Proposition 4.6 [Reference KingsKin98, (6.3.5)].
Let
 $\operatorname{Eis}_{{\mathcal{D}}}^{n}:{\mathcal{B}}_{n}\longrightarrow H_{{\mathcal{D}}}^{1}(M/\mathbb{R},\operatorname{Sym}^{n}V_{2}(1))$
be the composite of
$\operatorname{Eis}_{{\mathcal{D}}}^{n}:{\mathcal{B}}_{n}\longrightarrow H_{{\mathcal{D}}}^{1}(M/\mathbb{R},\operatorname{Sym}^{n}V_{2}(1))$
be the composite of
![]() $\operatorname{Eis}_{{\mathcal{M}}}^{n}$
and of the regulator
$\operatorname{Eis}_{{\mathcal{M}}}^{n}$
and of the regulator

If
![]() $n\geqslant 1$
, then for any
$n\geqslant 1$
, then for any
 $\unicode[STIX]{x1D719}_{f}\in {\mathcal{B}}_{n}$
, the class of
$\unicode[STIX]{x1D719}_{f}\in {\mathcal{B}}_{n}$
, the class of
 $\operatorname{Eis}_{{\mathcal{D}}}^{n}(\unicode[STIX]{x1D719}_{f})$
is represented by
$\operatorname{Eis}_{{\mathcal{D}}}^{n}(\unicode[STIX]{x1D719}_{f})$
is represented by
 $(\operatorname{Eis}_{{\mathcal{H}}}^{n}(\unicode[STIX]{x1D719}_{f}),\operatorname{Eis}_{B}^{n}(\unicode[STIX]{x1D719}_{f}))$
via the isomorphism of Proposition 4.2.
$(\operatorname{Eis}_{{\mathcal{H}}}^{n}(\unicode[STIX]{x1D719}_{f}),\operatorname{Eis}_{B}^{n}(\unicode[STIX]{x1D719}_{f}))$
via the isomorphism of Proposition 4.2.
By functoriality of the natural map between absolute Hodge and Deligne–Beilinson cohomology, the Deligne-Beilisnon cohomology classes
 $\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
we are interested in are the image under the Gysin morphism associated to the closed embedding
$\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
we are interested in are the image under the Gysin morphism associated to the closed embedding

of cup-products of Eisenstein classes
 $\operatorname{Eis}_{{\mathcal{D}}}^{p}(\unicode[STIX]{x1D719}_{f})\sqcup \operatorname{Eis}_{{\mathcal{D}}}^{q}(\unicode[STIX]{x1D719}_{f}^{\prime })$
. Hence, to get an explicit description of the classes
$\operatorname{Eis}_{{\mathcal{D}}}^{p}(\unicode[STIX]{x1D719}_{f})\sqcup \operatorname{Eis}_{{\mathcal{D}}}^{q}(\unicode[STIX]{x1D719}_{f}^{\prime })$
. Hence, to get an explicit description of the classes
 $\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
, we need an explicit description of the cup-product and of the Gysin morphism.
$\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
, we need an explicit description of the cup-product and of the Gysin morphism.
Proposition 4.7. Let
![]() $X$
and
$X$
and
![]() $Y$
be two objects of
$Y$
be two objects of
![]() $\operatorname{Sch}(\mathbb{Q})$
. Let
$\operatorname{Sch}(\mathbb{Q})$
. Let
 $p_{X}:X\times Y\longrightarrow X$
and
$p_{X}:X\times Y\longrightarrow X$
and
 $p_{Y}:X\times Y\longrightarrow Y$
be the canonical projections. Then, via the isomorphism of Proposition 4.2, the external cup-product
$p_{Y}:X\times Y\longrightarrow Y$
be the canonical projections. Then, via the isomorphism of Proposition 4.2, the external cup-product
 $$\begin{eqnarray}\sqcup :H_{{\mathcal{D}}}^{m}(X/\mathbb{R},\mathbb{R}(m))\otimes H_{{\mathcal{D}}}^{m^{\prime }}(X/\mathbb{R},\mathbb{R}(m^{\prime }))\longrightarrow H_{{\mathcal{D}}}^{m+m^{\prime }}(X/\mathbb{R},\mathbb{R}(m+m^{\prime }))\end{eqnarray}$$
$$\begin{eqnarray}\sqcup :H_{{\mathcal{D}}}^{m}(X/\mathbb{R},\mathbb{R}(m))\otimes H_{{\mathcal{D}}}^{m^{\prime }}(X/\mathbb{R},\mathbb{R}(m^{\prime }))\longrightarrow H_{{\mathcal{D}}}^{m+m^{\prime }}(X/\mathbb{R},\mathbb{R}(m+m^{\prime }))\end{eqnarray}$$
is
 $$\begin{eqnarray}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D714})\sqcup (\unicode[STIX]{x1D719}^{\prime },\unicode[STIX]{x1D714}^{\prime })=(p_{X}^{\ast }\unicode[STIX]{x1D719}\wedge p_{Y}^{\ast }(\unicode[STIX]{x1D70B}_{m^{\prime }}\unicode[STIX]{x1D714}^{\prime })+(-1)^{m}p_{X}^{\ast }(\unicode[STIX]{x1D70B}_{m}\unicode[STIX]{x1D714})\wedge p_{Y}^{\ast }\unicode[STIX]{x1D719}^{\prime },p_{X}^{\ast }\unicode[STIX]{x1D714}\wedge p_{Y}^{\ast }\unicode[STIX]{x1D714}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D719},\unicode[STIX]{x1D714})\sqcup (\unicode[STIX]{x1D719}^{\prime },\unicode[STIX]{x1D714}^{\prime })=(p_{X}^{\ast }\unicode[STIX]{x1D719}\wedge p_{Y}^{\ast }(\unicode[STIX]{x1D70B}_{m^{\prime }}\unicode[STIX]{x1D714}^{\prime })+(-1)^{m}p_{X}^{\ast }(\unicode[STIX]{x1D70B}_{m}\unicode[STIX]{x1D714})\wedge p_{Y}^{\ast }\unicode[STIX]{x1D719}^{\prime },p_{X}^{\ast }\unicode[STIX]{x1D714}\wedge p_{Y}^{\ast }\unicode[STIX]{x1D714}^{\prime })\end{eqnarray}$$
for any
![]() $m,m^{\prime }$
.
$m,m^{\prime }$
.
Proof. The external cup-product is by definition
 $x\,\sqcup \,y=p_{X}^{\ast }(x)\,\cup \,p_{Y}^{\ast }(y)$
, where
$x\,\sqcup \,y=p_{X}^{\ast }(x)\,\cup \,p_{Y}^{\ast }(y)$
, where
![]() $\cup$
denotes the usual cup-product. Hence, the statement follows from the explicit formulas for the usual cup-product given in [Reference Deninger and SchollDS91, 2.5] (see also [Reference Esnault and ViehwegEV88, 3.10]).◻
$\cup$
denotes the usual cup-product. Hence, the statement follows from the explicit formulas for the usual cup-product given in [Reference Deninger and SchollDS91, 2.5] (see also [Reference Esnault and ViehwegEV88, 3.10]).◻
To give an explicit description of the Gysin morphism, we need to introduce currents and Deligne–Beilinson homology. For
 $X\in \operatorname{Sch}(\mathbb{Q})$
and any integer
$X\in \operatorname{Sch}(\mathbb{Q})$
and any integer
![]() $m$
, let
$m$
, let
 ${\mathcal{T}}^{\circ }(X/\mathbb{R},\mathbb{R}(m))$
be the complex of
${\mathcal{T}}^{\circ }(X/\mathbb{R},\mathbb{R}(m))$
be the complex of
![]() $\mathbb{R}(m)$
-valued currents on which the map
$\mathbb{R}(m)$
-valued currents on which the map
![]() $F_{\infty }$
, induced by complex conjugation on
$F_{\infty }$
, induced by complex conjugation on
![]() $X(\mathbb{C})$
, acts by multiplication by
$X(\mathbb{C})$
, acts by multiplication by
![]() $(-1)^{m}$
. Let us consider as above a smooth projective compactification
$(-1)^{m}$
. Let us consider as above a smooth projective compactification
 $j:X\longrightarrow X^{\ast }$
and let
$j:X\longrightarrow X^{\ast }$
and let
 $i:Y\longrightarrow X^{\ast }$
be the complementary reduced closed embedding. Assume
$i:Y\longrightarrow X^{\ast }$
be the complementary reduced closed embedding. Assume
![]() $Y$
is a normal crossing divisor. Let
$Y$
is a normal crossing divisor. Let
 ${\mathcal{T}}_{\log }^{\circ }(X/\mathbb{R},\mathbb{C})$
be the complex of currents with logarithmic singularities along
${\mathcal{T}}_{\log }^{\circ }(X/\mathbb{R},\mathbb{C})$
be the complex of currents with logarithmic singularities along
![]() $Y$
, endowed with the Hodge filtration
$Y$
, endowed with the Hodge filtration
 $(F^{r}{\mathcal{T}}_{\log }^{\circ }(X/\mathbb{R},\mathbb{C}))_{r}$
. Details on these notions are given in [Reference JannsenJan88, 1.4].
$(F^{r}{\mathcal{T}}_{\log }^{\circ }(X/\mathbb{R},\mathbb{C}))_{r}$
. Details on these notions are given in [Reference JannsenJan88, 1.4].
Proposition 4.8 [Reference KingsKin98, Lemma 6.3.9].
Let
![]() $i$
and
$i$
and
![]() $j$
be two integers. The real Deligne–Beilinson homology
$j$
be two integers. The real Deligne–Beilinson homology
 $H_{i}^{{\mathcal{D}}}(X/\mathbb{R},\mathbb{R}(j))$
is the
$H_{i}^{{\mathcal{D}}}(X/\mathbb{R},\mathbb{R}(j))$
is the
![]() $\mathbb{R}$
-vector space
$\mathbb{R}$
-vector space
 $$\begin{eqnarray}H_{i}^{{\mathcal{D}}}(X/\mathbb{R},\mathbb{R}(j))=\frac{\{(S,T)\mid dS=\unicode[STIX]{x1D70B}_{j-1}T\}}{\{d(\widetilde{S},\widetilde{T})\}}\end{eqnarray}$$
$$\begin{eqnarray}H_{i}^{{\mathcal{D}}}(X/\mathbb{R},\mathbb{R}(j))=\frac{\{(S,T)\mid dS=\unicode[STIX]{x1D70B}_{j-1}T\}}{\{d(\widetilde{S},\widetilde{T})\}}\end{eqnarray}$$
where
 $$\begin{eqnarray}(S,T)\in {\mathcal{T}}^{-i-1}(X/\mathbb{R},\mathbb{R}(j-1))\oplus F^{j}{\mathcal{T}}_{\log }^{-i}(X/\mathbb{R},\mathbb{C})\end{eqnarray}$$
$$\begin{eqnarray}(S,T)\in {\mathcal{T}}^{-i-1}(X/\mathbb{R},\mathbb{R}(j-1))\oplus F^{j}{\mathcal{T}}_{\log }^{-i}(X/\mathbb{R},\mathbb{C})\end{eqnarray}$$
and
 $$\begin{eqnarray}(\widetilde{S},\widetilde{T})\in {\mathcal{T}}^{-i-2}(X/\mathbb{R},\mathbb{R}(j-1))\oplus F^{j}{\mathcal{T}}_{\log }^{-i-1}(X/\mathbb{R},\mathbb{C}).\end{eqnarray}$$
$$\begin{eqnarray}(\widetilde{S},\widetilde{T})\in {\mathcal{T}}^{-i-2}(X/\mathbb{R},\mathbb{R}(j-1))\oplus F^{j}{\mathcal{T}}_{\log }^{-i-1}(X/\mathbb{R},\mathbb{C}).\end{eqnarray}$$
As currents are covariant for proper maps, the proposition above gives an explicit description of the Gysin morphism in Deligne–Beilinson cohomology.
Proposition 4.9. The following statements hold.
![]() $(\text{i})$
See [Reference JannsenJan88, Theorem 1.15]. Let
$(\text{i})$
See [Reference JannsenJan88, Theorem 1.15]. Let
![]() $X$
be an object of
$X$
be an object of
![]() $\operatorname{Sch}(\mathbb{Q})$
of pure dimension
$\operatorname{Sch}(\mathbb{Q})$
of pure dimension
![]() $d_{X}$
. There is a canonical isomorphism between Deligne–Beilinson homology and cohomology
$d_{X}$
. There is a canonical isomorphism between Deligne–Beilinson homology and cohomology
 $$\begin{eqnarray}H_{i}^{{\mathcal{D}}}(X/\mathbb{R},\mathbb{R}(j))\simeq H_{{\mathcal{D}}}^{2d_{X}+i}(X/\mathbb{R},\mathbb{R}(d_{X}+j)).\end{eqnarray}$$
$$\begin{eqnarray}H_{i}^{{\mathcal{D}}}(X/\mathbb{R},\mathbb{R}(j))\simeq H_{{\mathcal{D}}}^{2d_{X}+i}(X/\mathbb{R},\mathbb{R}(d_{X}+j)).\end{eqnarray}$$
![]() $(\text{ii})$
See [Reference KingsKin98, Lemma 6.3.10]. Let
$(\text{ii})$
See [Reference KingsKin98, Lemma 6.3.10]. Let
![]() $Y$
be an object of
$Y$
be an object of
![]() $\operatorname{Sch}(\mathbb{Q})$
of pure dimension
$\operatorname{Sch}(\mathbb{Q})$
of pure dimension
![]() $d_{Y}$
and let
$d_{Y}$
and let
 $i:Y\longrightarrow X$
be a closed embedding of codimension
$i:Y\longrightarrow X$
be a closed embedding of codimension
 $c=d_{X}-d_{Y}$
. Then, via the isomorphism above and the explicit description of Deligne–Beilinson homology classes given in Proposition 4.8, the Gysin morphism
$c=d_{X}-d_{Y}$
. Then, via the isomorphism above and the explicit description of Deligne–Beilinson homology classes given in Proposition 4.8, the Gysin morphism
 $$\begin{eqnarray}i_{\ast }:H_{{\mathcal{D}}}^{m}(Y/\mathbb{R},\mathbb{R}(n))\longrightarrow H_{{\mathcal{D}}}^{m+2c}(X/\mathbb{R},\mathbb{R}(n+c))\end{eqnarray}$$
$$\begin{eqnarray}i_{\ast }:H_{{\mathcal{D}}}^{m}(Y/\mathbb{R},\mathbb{R}(n))\longrightarrow H_{{\mathcal{D}}}^{m+2c}(X/\mathbb{R},\mathbb{R}(n+c))\end{eqnarray}$$
is induced by the map
 $(S,T)\longmapsto (i_{\ast }S,i_{\ast }T)$
.
$(S,T)\longmapsto (i_{\ast }S,i_{\ast }T)$
.
Let us fix an orientation on the complex manifold
![]() $X(\mathbb{C})$
and let
$X(\mathbb{C})$
and let
 $\unicode[STIX]{x1D719}\in {\mathcal{S}}^{i}(X/\mathbb{R},\mathbb{R}(j))$
. Following [Reference JannsenJan88, §1], let
$\unicode[STIX]{x1D719}\in {\mathcal{S}}^{i}(X/\mathbb{R},\mathbb{R}(j))$
. Following [Reference JannsenJan88, §1], let
 $T_{\unicode[STIX]{x1D719}}\in {\mathcal{T}}^{i-2d_{X}}(X/\mathbb{R},\mathbb{R}(j-d_{X}))$
denote the current defined by
$T_{\unicode[STIX]{x1D719}}\in {\mathcal{T}}^{i-2d_{X}}(X/\mathbb{R},\mathbb{R}(j-d_{X}))$
denote the current defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D714}\in {\mathcal{S}}_{c}^{i}(X/\mathbb{R},\mathbb{R}(d_{X}-j))\longmapsto T_{\unicode[STIX]{x1D719}}(\unicode[STIX]{x1D714})=\frac{1}{(2\unicode[STIX]{x1D70B}i)^{d_{X}}}\int _{X(\mathbb{C})}\unicode[STIX]{x1D714}\wedge \unicode[STIX]{x1D719}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}\in {\mathcal{S}}_{c}^{i}(X/\mathbb{R},\mathbb{R}(d_{X}-j))\longmapsto T_{\unicode[STIX]{x1D719}}(\unicode[STIX]{x1D714})=\frac{1}{(2\unicode[STIX]{x1D70B}i)^{d_{X}}}\int _{X(\mathbb{C})}\unicode[STIX]{x1D714}\wedge \unicode[STIX]{x1D719}.\end{eqnarray}$$
Proposition 4.10. Let

be the composite of the map (3) and of the regulator

in Deligne–Beilinson cohomology. For
 $j=1,2$
let
$j=1,2$
let
 $p_{j}:M\times M\longrightarrow M$
denote the
$p_{j}:M\times M\longrightarrow M$
denote the
![]() $j$
th projection. Then
$j$
th projection. Then
 $$\begin{eqnarray}\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })=(\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })},\unicode[STIX]{x1D704}_{\ast }T_{P_{B}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })=(\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })},\unicode[STIX]{x1D704}_{\ast }T_{P_{B}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })})\end{eqnarray}$$
where
 $P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
is defined by
$P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
is defined by
 $$\begin{eqnarray}P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })=p_{1}^{\ast }\operatorname{Eis}_{{\mathcal{H}}}^{p}(\unicode[STIX]{x1D719}_{f})\wedge p_{2}^{\ast }(\unicode[STIX]{x1D70B}_{q}\operatorname{Eis}_{B}^{q}(\unicode[STIX]{x1D719}_{f}^{\prime }))+(-1)^{p}p_{1}^{\ast }(\unicode[STIX]{x1D70B}_{p}\operatorname{Eis}_{B}^{p}(\unicode[STIX]{x1D719}_{f}))\wedge p_{2}^{\ast }\operatorname{Eis}_{{\mathcal{H}}}^{q}(\unicode[STIX]{x1D719}_{f}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })=p_{1}^{\ast }\operatorname{Eis}_{{\mathcal{H}}}^{p}(\unicode[STIX]{x1D719}_{f})\wedge p_{2}^{\ast }(\unicode[STIX]{x1D70B}_{q}\operatorname{Eis}_{B}^{q}(\unicode[STIX]{x1D719}_{f}^{\prime }))+(-1)^{p}p_{1}^{\ast }(\unicode[STIX]{x1D70B}_{p}\operatorname{Eis}_{B}^{p}(\unicode[STIX]{x1D719}_{f}))\wedge p_{2}^{\ast }\operatorname{Eis}_{{\mathcal{H}}}^{q}(\unicode[STIX]{x1D719}_{f}^{\prime })\end{eqnarray}$$
and
 $P_{B}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
is defined by
$P_{B}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
is defined by
 $$\begin{eqnarray}P_{B}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })=p_{1}^{\ast }\operatorname{Eis}_{B}^{p}(\unicode[STIX]{x1D719}_{f})\wedge p_{2}^{\ast }\operatorname{Eis}_{B}^{q}(\unicode[STIX]{x1D719}_{f}).\end{eqnarray}$$
$$\begin{eqnarray}P_{B}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })=p_{1}^{\ast }\operatorname{Eis}_{B}^{p}(\unicode[STIX]{x1D719}_{f})\wedge p_{2}^{\ast }\operatorname{Eis}_{B}^{q}(\unicode[STIX]{x1D719}_{f}).\end{eqnarray}$$
4.3 The use of Poincaré duality
This section explains how the Poincaré duality pairing can be used to compute the regulator. This idea is due to Beilinson [Reference BeilinsonBei88] (see also [Reference KingsKin98, 6.1]). Let us start with a general result.
Lemma 4.11. Let
![]() $E$
be a number field and let
$E$
be a number field and let
![]() $M$
be an object of
$M$
be an object of
 $\text{MHS}_{\mathbb{R},E}^{+}$
(Definition 3.10) which is pure weight
$\text{MHS}_{\mathbb{R},E}^{+}$
(Definition 3.10) which is pure weight
![]() $w<0$
. Let
$w<0$
. Let
![]() $M_{dR}$
be the sub-
$M_{dR}$
be the sub-
 $E\otimes _{\mathbb{Q}}\mathbb{R}$
-module of
$E\otimes _{\mathbb{Q}}\mathbb{R}$
-module of
![]() $M_{\mathbb{C}}$
where the de Rham involution acts trivially and let
$M_{\mathbb{C}}$
where the de Rham involution acts trivially and let
![]() $M^{-}$
be the submodule of
$M^{-}$
be the submodule of
![]() $M$
where
$M$
where
![]() $F_{\infty }$
acts by multiplication by
$F_{\infty }$
acts by multiplication by
![]() $-1$
. Let
$-1$
. Let
 $M^{-}(-1)=1/(2\unicode[STIX]{x1D70B}i)M^{-}$
. Then, there is an exact sequence of
$M^{-}(-1)=1/(2\unicode[STIX]{x1D70B}i)M^{-}$
. Then, there is an exact sequence of
 $E\otimes _{\mathbb{Q}}\mathbb{R}$
-modules
$E\otimes _{\mathbb{Q}}\mathbb{R}$
-modules
 $$\begin{eqnarray}0\longrightarrow F^{0}M_{dR}\longrightarrow M^{-}(-1)\longrightarrow \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),M)\longrightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow F^{0}M_{dR}\longrightarrow M^{-}(-1)\longrightarrow \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),M)\longrightarrow 0\end{eqnarray}$$
where the second map is the composite of the natural inclusions
 $$\begin{eqnarray}F^{0}M_{dR}\longrightarrow M_{dR}\longrightarrow M_{\mathbb{C}}\end{eqnarray}$$
$$\begin{eqnarray}F^{0}M_{dR}\longrightarrow M_{dR}\longrightarrow M_{\mathbb{C}}\end{eqnarray}$$
and of the projections
 $$\begin{eqnarray}M_{\mathbb{C}}\longrightarrow M(-1)\longrightarrow M^{-}(-1)\end{eqnarray}$$
$$\begin{eqnarray}M_{\mathbb{C}}\longrightarrow M(-1)\longrightarrow M^{-}(-1)\end{eqnarray}$$
defined by
 $v\longmapsto {\textstyle \frac{1}{2}}(v-\overline{v})$
and
$v\longmapsto {\textstyle \frac{1}{2}}(v-\overline{v})$
and
 $v\longmapsto {\textstyle \frac{1}{2}}(v-F_{\infty }(v))$
, respectively.
$v\longmapsto {\textstyle \frac{1}{2}}(v-F_{\infty }(v))$
, respectively.
Proof. Immediate consequence of [Reference NekovarNek94, (2.1) and (2.5)]. ◻
Corollary 4.12. Let
![]() $W$
be an irreducible algebraic representation of
$W$
be an irreducible algebraic representation of
![]() $G$
of highest weight
$G$
of highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },c)$
, with
$\unicode[STIX]{x1D706}(k,k^{\prime },c)$
, with
 $w=3-c<0$
. Let
$w=3-c<0$
. Let
![]() $\unicode[STIX]{x1D70B}_{f}$
be the non-archimedean part of an irreducible cuspidal automorphic representation
$\unicode[STIX]{x1D70B}_{f}$
be the non-archimedean part of an irreducible cuspidal automorphic representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $G$
whose archimedean component
$G$
whose archimedean component
![]() $\unicode[STIX]{x1D70B}_{\infty }$
belongs to the discrete series
$\unicode[STIX]{x1D70B}_{\infty }$
belongs to the discrete series
![]() $L$
-packet
$L$
-packet
![]() $P(W)$
. Then, there is an exact sequence
$P(W)$
. Then, there is an exact sequence
 $$\begin{eqnarray}0\longrightarrow F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}\longrightarrow M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\longrightarrow \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})\longrightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}\longrightarrow M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\longrightarrow \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})\longrightarrow 0,\end{eqnarray}$$
where the second map is as above.
Proof. For any compact open subgroup
![]() $L$
of
$L$
of
![]() $G(\mathbb{A}_{f})$
, let
$G(\mathbb{A}_{f})$
, let
 $F^{0}H_{dR,!}^{3}(S_{L},W)_{\mathbb{R}}$
denote the
$F^{0}H_{dR,!}^{3}(S_{L},W)_{\mathbb{R}}$
denote the
![]() $\mathbb{R}$
-subspace of
$\mathbb{R}$
-subspace of
 $F^{0}H_{B,!}^{3}(S_{L},W)_{\mathbb{C}}$
of vectors which are fixed by the de Rham involution and by
$F^{0}H_{B,!}^{3}(S_{L},W)_{\mathbb{C}}$
of vectors which are fixed by the de Rham involution and by
 $F^{0}H_{dR,!}^{3}(S,W)_{\mathbb{R}}$
the colimit of the
$F^{0}H_{dR,!}^{3}(S,W)_{\mathbb{R}}$
the colimit of the
 $F^{0}H_{dR,!}^{3}(S_{L},W)_{\mathbb{R}}$
over all compact open subgroups
$F^{0}H_{dR,!}^{3}(S_{L},W)_{\mathbb{R}}$
over all compact open subgroups
![]() $L$
of
$L$
of
![]() $G(\mathbb{A}_{f})$
. As filtered colimits of vector spaces preserve exact sequences, the lemma above implies that we have a
$G(\mathbb{A}_{f})$
. As filtered colimits of vector spaces preserve exact sequences, the lemma above implies that we have a
![]() $G(\mathbb{A}_{f})$
-equivariant exact sequence
$G(\mathbb{A}_{f})$
-equivariant exact sequence
 $$\begin{eqnarray}0\longrightarrow F^{0}H_{dR,!}^{3}(S,W)_{\mathbb{ R}}\longrightarrow H_{B,!}^{3}(S,W)_{\mathbb{ R}}^{-}(-1)\longrightarrow \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),H_{B,!}^{3}(S,W)_{\mathbb{ R}})\longrightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow F^{0}H_{dR,!}^{3}(S,W)_{\mathbb{ R}}\longrightarrow H_{B,!}^{3}(S,W)_{\mathbb{ R}}^{-}(-1)\longrightarrow \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),H_{B,!}^{3}(S,W)_{\mathbb{ R}})\longrightarrow 0\end{eqnarray}$$
of
![]() $\mathbb{R}$
-vector spaces. As
$\mathbb{R}$
-vector spaces. As
![]() $\unicode[STIX]{x1D70B}_{f}$
is irreducible, applying the functor
$\unicode[STIX]{x1D70B}_{f}$
is irreducible, applying the functor
 $$\begin{eqnarray}X\longmapsto \text{Hom}_{\mathbb{Q}[G(\mathbb{A}_{f})]}(\operatorname{Res}_{E(\unicode[STIX]{x1D70B}_{f})/\mathbb{Q}}\unicode[STIX]{x1D70B}_{f},X)\end{eqnarray}$$
$$\begin{eqnarray}X\longmapsto \text{Hom}_{\mathbb{Q}[G(\mathbb{A}_{f})]}(\operatorname{Res}_{E(\unicode[STIX]{x1D70B}_{f})/\mathbb{Q}}\unicode[STIX]{x1D70B}_{f},X)\end{eqnarray}$$
to the above exact sequence, we still get an exact sequence, which is that of the statement of the corollary. ◻
The first term, respectively the second term, of the exact sequence above is obtained applying
![]() $\otimes _{\mathbb{Q}}\mathbb{R}$
to the finite-dimensional
$\otimes _{\mathbb{Q}}\mathbb{R}$
to the finite-dimensional
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-vector space
$E(\unicode[STIX]{x1D70B}_{f})$
-vector space
 $F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)$
, respectively
$F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)$
, respectively
 $M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{-}(-1)$
(see Propositions 3.11 and 3.12). Let
$M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{-}(-1)$
(see Propositions 3.11 and 3.12). Let
 $F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)^{\ast }$
be the dual of
$F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)^{\ast }$
be the dual of
 $F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)$
. As a consequence, the one-dimensional
$F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)$
. As a consequence, the one-dimensional
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-vector space
$E(\unicode[STIX]{x1D70B}_{f})$
-vector space
 $$\begin{eqnarray}{\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)=\text{det}_{E(\unicode[STIX]{x1D70B}_{f})}F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)^{\ast }\otimes _{E(\unicode[STIX]{x1D70B}_{f})}\text{det}_{E(\unicode[STIX]{x1D70B}_{f})}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)=\text{det}_{E(\unicode[STIX]{x1D70B}_{f})}F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)^{\ast }\otimes _{E(\unicode[STIX]{x1D70B}_{f})}\text{det}_{E(\unicode[STIX]{x1D70B}_{f})}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\end{eqnarray}$$
is an
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-structure of the
$E(\unicode[STIX]{x1D70B}_{f})$
-structure of the
 $E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{R}$
-module
$E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{R}$
-module
 $$\begin{eqnarray}\text{det}_{E(\unicode[STIX]{x1D70B}_{f})\,\otimes _{\mathbb{Q}}\mathbb{R}}\,\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}).\end{eqnarray}$$
$$\begin{eqnarray}\text{det}_{E(\unicode[STIX]{x1D70B}_{f})\,\otimes _{\mathbb{Q}}\mathbb{R}}\,\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}).\end{eqnarray}$$
By definition
 ${\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)$
is the Beilinson
${\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)$
is the Beilinson
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-structure, which occurs in one of the two equivalent formulations of Beilinson’s conjecture (see [Reference NekovarNek94, 6.1]). Because we are dealing with a partial
$E(\unicode[STIX]{x1D70B}_{f})$
-structure, which occurs in one of the two equivalent formulations of Beilinson’s conjecture (see [Reference NekovarNek94, 6.1]). Because we are dealing with a partial
![]() $L$
-function, we do not want to use the functional equation in this work. As a consequence, we prefer to work with the Deligne
$L$
-function, we do not want to use the functional equation in this work. As a consequence, we prefer to work with the Deligne
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-structure.
$E(\unicode[STIX]{x1D70B}_{f})$
-structure.
Definition 4.13. Let
 $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{f},W)\in (E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{C})^{\times }$
be the determinant of the comparison isomorphism
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{f},W)\in (E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{C})^{\times }$
be the determinant of the comparison isomorphism
 $M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}\longrightarrow M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}$
computed in basis defined over
$M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}\longrightarrow M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}$
computed in basis defined over
![]() $E(\unicode[STIX]{x1D70B}_{f})$
on both sides. The Deligne
$E(\unicode[STIX]{x1D70B}_{f})$
on both sides. The Deligne
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-structure of
$E(\unicode[STIX]{x1D70B}_{f})$
-structure of
 $\text{det}_{E(\unicode[STIX]{x1D70B}_{f})\,\otimes _{\mathbb{Q}}\,\mathbb{R}}\,\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})$
is
$\text{det}_{E(\unicode[STIX]{x1D70B}_{f})\,\otimes _{\mathbb{Q}}\,\mathbb{R}}\,\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})$
is
 $$\begin{eqnarray}{\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)=(2\unicode[STIX]{x1D70B}i)^{\dim _{E(\unicode[STIX]{x1D70B}_{f})}M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{-}}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{f},W)^{-1}{\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)=(2\unicode[STIX]{x1D70B}i)^{\dim _{E(\unicode[STIX]{x1D70B}_{f})}M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{-}}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{f},W)^{-1}{\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
Remark 4.14. Of course, this definition does not depend on the choice of the basis.
The ranks of the
 $E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{R}$
-modules of the exact sequence of Corollary 4.12 are related to multiplicities of automorphic representations in the discrete series
$E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{R}$
-modules of the exact sequence of Corollary 4.12 are related to multiplicities of automorphic representations in the discrete series
![]() $L$
-packet
$L$
-packet
![]() $P(W)$
.
$P(W)$
.
Lemma 4.15. The following equalities hold:
-
(a) we have
 $rk_{E(\unicode[STIX]{x1D70B}_{f})\,\otimes _{\mathbb{Q}}\,\mathbb{R}}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)=m(\unicode[STIX]{x1D70B}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})+m(\unicode[STIX]{x1D70B}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})$
;
$rk_{E(\unicode[STIX]{x1D70B}_{f})\,\otimes _{\mathbb{Q}}\,\mathbb{R}}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)=m(\unicode[STIX]{x1D70B}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})+m(\unicode[STIX]{x1D70B}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})$
; -
(b) we have
 $rk_{E(\unicode[STIX]{x1D70B}_{f})\,\otimes _{\mathbb{Q}}\,\mathbb{R}}F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}=m(\unicode[STIX]{x1D70B}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})$
;
$rk_{E(\unicode[STIX]{x1D70B}_{f})\,\otimes _{\mathbb{Q}}\,\mathbb{R}}F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}=m(\unicode[STIX]{x1D70B}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})$
; -
(c) we have
 $rk_{E(\unicode[STIX]{x1D70B}_{f})\,\otimes _{\mathbb{Q}}\,\mathbb{R}}\,\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})=m(\unicode[STIX]{x1D70B}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})$
.
$rk_{E(\unicode[STIX]{x1D70B}_{f})\,\otimes _{\mathbb{Q}}\,\mathbb{R}}\,\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})=m(\unicode[STIX]{x1D70B}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})$
.
Proof. Thanks to the exact sequence of Corollary 4.12, it is enough to prove the first two statements. Write
 $t=(p+q+6-k-k^{\prime })/2$
. Then, the first statement easily follows from the Hodge decomposition
$t=(p+q+6-k-k^{\prime })/2$
. Then, the first statement easily follows from the Hodge decomposition
 $$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}=M_{B}^{3-t,-k-k^{\prime }-t}\oplus M_{B}^{2-k^{\prime }-t,1-k-t}\oplus M_{B}^{1-k-t,2-k^{\prime }-t}\oplus M_{B}^{-k-k^{\prime }-t,3-t},\end{eqnarray}$$
$$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}=M_{B}^{3-t,-k-k^{\prime }-t}\oplus M_{B}^{2-k^{\prime }-t,1-k-t}\oplus M_{B}^{1-k-t,2-k^{\prime }-t}\oplus M_{B}^{-k-k^{\prime }-t,3-t},\end{eqnarray}$$
where
 $M_{B}^{3-t,-k-k^{\prime }-t},M_{B}^{2-k^{\prime }-t,1-k-t},M_{B}^{1-k-t,2-k^{\prime }-t}$
and
$M_{B}^{3-t,-k-k^{\prime }-t},M_{B}^{2-k^{\prime }-t,1-k-t},M_{B}^{1-k-t,2-k^{\prime }-t}$
and
 $M_{B}^{-k-k^{\prime }-t,3-t}$
are
$M_{B}^{-k-k^{\prime }-t,3-t}$
are
 $E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{C}$
-modules of respective ranks
$E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{C}$
-modules of respective ranks
 $m(\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}),m(\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}),m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})$
and
$m(\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}),m(\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}),m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\otimes \unicode[STIX]{x1D70B}_{f})$
and
 $m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})$
(Propositions 3.7 and 3.8), and from the fact that
$m(\overline{\unicode[STIX]{x1D70B}}_{\infty }^{H}\otimes \unicode[STIX]{x1D70B}_{f})$
(Propositions 3.7 and 3.8), and from the fact that
![]() $F_{\infty }$
exchanges
$F_{\infty }$
exchanges
![]() $M_{B}^{r,s}$
and
$M_{B}^{r,s}$
and
![]() $M_{B}^{s,r}$
. The proof of the second statement follows from the fact that the conditions on
$M_{B}^{s,r}$
. The proof of the second statement follows from the fact that the conditions on
![]() $p,q,k$
and
$p,q,k$
and
![]() $k^{\prime }$
stated in the introduction imply that
$k^{\prime }$
stated in the introduction imply that
 $2-k^{\prime }-t<0$
, hence that
$2-k^{\prime }-t<0$
, hence that
 $$\begin{eqnarray}F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}=M_{B}^{3-t,-k-k^{\prime }-t}.\square\end{eqnarray}$$
$$\begin{eqnarray}F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}=M_{B}^{3-t,-k-k^{\prime }-t}.\square\end{eqnarray}$$
Definition 4.16. Let
![]() $E$
be an irreducible algebraic representation
$E$
be an irreducible algebraic representation
![]() $E$
of
$E$
of
![]() $G$
. Let
$G$
. Let
 $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}$
be an irreducible cuspidal automorphic representation such that
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}$
be an irreducible cuspidal automorphic representation such that
![]() $\unicode[STIX]{x1D70B}_{\infty }$
belongs to the discrete series
$\unicode[STIX]{x1D70B}_{\infty }$
belongs to the discrete series
![]() $L$
-packet
$L$
-packet
![]() $P(E)$
(Definition 3.5). The automorphic representation
$P(E)$
(Definition 3.5). The automorphic representation
![]() $\unicode[STIX]{x1D70B}$
is stable at infinity if
$\unicode[STIX]{x1D70B}$
is stable at infinity if
 $m(\unicode[STIX]{x1D70B}_{\infty }^{\prime }\otimes \unicode[STIX]{x1D70B}_{f})=1$
for any
$m(\unicode[STIX]{x1D70B}_{\infty }^{\prime }\otimes \unicode[STIX]{x1D70B}_{f})=1$
for any
 $\unicode[STIX]{x1D70B}_{\infty }^{\prime }\in P(E)$
.
$\unicode[STIX]{x1D70B}_{\infty }^{\prime }\in P(E)$
.
Hypothesis 4.17. In the rest of the paper, we assume that the considered cuspidal automorphic representation
![]() $\unicode[STIX]{x1D70B}$
is stable at infinity.
$\unicode[STIX]{x1D70B}$
is stable at infinity.
Remark 4.18. It follows from Arthur’s classification [Reference ArthurArt04] that, for most of
![]() $\unicode[STIX]{x1D70B}$
whose
$\unicode[STIX]{x1D70B}$
whose
![]() $\unicode[STIX]{x1D70B}_{\infty }$
is a discrete series,
$\unicode[STIX]{x1D70B}_{\infty }$
is a discrete series,
![]() $\unicode[STIX]{x1D70B}$
is stable. Specific examples constructed via theta lifts of Hilbert modular forms over real quadratic fields are discussed in [Reference Mokrane and TilouineMT02, 7.3].
$\unicode[STIX]{x1D70B}$
is stable. Specific examples constructed via theta lifts of Hilbert modular forms over real quadratic fields are discussed in [Reference Mokrane and TilouineMT02, 7.3].
Note that Hypothesis 4.17 and Lemma 4.15 imply that
 $\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})$
is a rank-one
$\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})$
is a rank-one
 $E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{R}$
-module. From now on, we consider integers
$E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{R}$
-module. From now on, we consider integers
 $p,q,k,k^{\prime }$
and a coefficient system
$p,q,k,k^{\prime }$
and a coefficient system
![]() $W$
of highest weight
$W$
of highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },p+q+6)$
as in the statement of Theorem 1.1. Let
$\unicode[STIX]{x1D706}(k,k^{\prime },p+q+6)$
as in the statement of Theorem 1.1. Let
 ${\mathcal{K}}(p,q,W)$
denote the sub-
${\mathcal{K}}(p,q,W)$
denote the sub-
 $\mathbb{Q}[G(\mathbb{A}_{f})]$
-module of
$\mathbb{Q}[G(\mathbb{A}_{f})]$
-module of
 $$\begin{eqnarray}\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),H_{!}^{3}(S,W)_{\mathbb{ R}})=\mathop{\varinjlim }\nolimits_{L}\text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),H_{!}^{3}(S_{L},W)_{\mathbb{R}})\end{eqnarray}$$
$$\begin{eqnarray}\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),H_{!}^{3}(S,W)_{\mathbb{ R}})=\mathop{\varinjlim }\nolimits_{L}\text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),H_{!}^{3}(S_{L},W)_{\mathbb{R}})\end{eqnarray}$$
generated by the image of
 $\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}$
and let
$\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}$
and let
 ${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
be defined as
${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
be defined as
 $$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\text{Hom}_{\mathbb{Q}[G(\mathbb{A}_{f})]}(\operatorname{Res}_{E(\unicode[STIX]{x1D70B}_{f})/\mathbb{Q}}\unicode[STIX]{x1D70B}_{f},{\mathcal{K}}(p,q,W)).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\text{Hom}_{\mathbb{Q}[G(\mathbb{A}_{f})]}(\operatorname{Res}_{E(\unicode[STIX]{x1D70B}_{f})/\mathbb{Q}}\unicode[STIX]{x1D70B}_{f},{\mathcal{K}}(p,q,W)).\end{eqnarray}$$
This is an
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-submodule of
$E(\unicode[STIX]{x1D70B}_{f})$
-submodule of
 $\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})$
. We have two
$\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})$
. We have two
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-submodules of
$E(\unicode[STIX]{x1D70B}_{f})$
-submodules of
 $\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})$
‘geometrically defined’. The elementary one, namely
$\text{Ext}_{\text{MHS}_{\mathbb{ R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})$
‘geometrically defined’. The elementary one, namely
 ${\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)$
, is defined in terms of the de Rham and Betti cohomology. The sophisticated one, namely
${\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)$
, is defined in terms of the de Rham and Betti cohomology. The sophisticated one, namely
 ${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
, is defined in terms of the regulator. Of course, whereas
${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
, is defined in terms of the regulator. Of course, whereas
 ${\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)$
is non-zero by definition, we do not know at this point whether
${\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)$
is non-zero by definition, we do not know at this point whether
 ${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
is zero or not.
${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
is zero or not.
Definition 4.19. If
![]() $\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D707}$
and
![]() $\unicode[STIX]{x1D707}^{\prime }$
are two elements of
$\unicode[STIX]{x1D707}^{\prime }$
are two elements of
 $E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{C}$
, denote
$E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{C}$
, denote
![]() $\unicode[STIX]{x1D707}\sim \unicode[STIX]{x1D707}^{\prime }$
if there exists
$\unicode[STIX]{x1D707}\sim \unicode[STIX]{x1D707}^{\prime }$
if there exists
 $\unicode[STIX]{x1D706}\in E(\unicode[STIX]{x1D70B}_{f})^{\times }$
such that
$\unicode[STIX]{x1D706}\in E(\unicode[STIX]{x1D70B}_{f})^{\times }$
such that
 $\unicode[STIX]{x1D707}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}^{\prime }$
.
$\unicode[STIX]{x1D707}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D707}^{\prime }$
.
Lemma 4.20. Let
![]() $v_{{\mathcal{D}}}$
be a non-zero vector of
$v_{{\mathcal{D}}}$
be a non-zero vector of
 ${\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)$
and
${\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)$
and
![]() $v_{{\mathcal{K}}}$
be a vector of
$v_{{\mathcal{K}}}$
be a vector of
 ${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
. Let
${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
. Let
 $\widetilde{v_{{\mathcal{D}}}}\in M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)$
, respectively
$\widetilde{v_{{\mathcal{D}}}}\in M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)$
, respectively
![]() $\widetilde{v_{{\mathcal{K}}}}$
, be an element mapped to
$\widetilde{v_{{\mathcal{K}}}}$
, be an element mapped to
![]() $v_{{\mathcal{D}}}$
, respectively
$v_{{\mathcal{D}}}$
, respectively
![]() $v_{{\mathcal{K}}}$
, by the third map of the exact sequence of Corollary 4.12. Then
$v_{{\mathcal{K}}}$
, by the third map of the exact sequence of Corollary 4.12. Then
 $$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\frac{\unicode[STIX]{x1D713}(\widetilde{v_{{\mathcal{K}}}})}{\unicode[STIX]{x1D713}(\widetilde{v_{{\mathcal{D}}}})}{\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\frac{\unicode[STIX]{x1D713}(\widetilde{v_{{\mathcal{K}}}})}{\unicode[STIX]{x1D713}(\widetilde{v_{{\mathcal{D}}}})}{\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)\end{eqnarray}$$
for any
 $E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{R}$
-linear map
$E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{R}$
-linear map
 $\unicode[STIX]{x1D713}:M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\longrightarrow E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{C}$
whose kernel contains
$\unicode[STIX]{x1D713}:M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\longrightarrow E(\unicode[STIX]{x1D70B}_{f})\otimes _{\mathbb{Q}}\mathbb{C}$
whose kernel contains
 $F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}$
.
$F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}$
.
Proof. Trivial. ◻
Our goal is now to compute
![]() $\unicode[STIX]{x1D713}(\widetilde{v_{{\mathcal{K}}}})$
and
$\unicode[STIX]{x1D713}(\widetilde{v_{{\mathcal{K}}}})$
and
![]() $\unicode[STIX]{x1D713}(\widetilde{v_{{\mathcal{D}}}})$
for a well-chosen
$\unicode[STIX]{x1D713}(\widetilde{v_{{\mathcal{D}}}})$
for a well-chosen
![]() $\unicode[STIX]{x1D713}$
as above. To this end, let us recall the properties of the Poincaré duality pairing for Siegel threefolds. As the representation
$\unicode[STIX]{x1D713}$
as above. To this end, let us recall the properties of the Poincaré duality pairing for Siegel threefolds. As the representation
![]() $W$
has highest weight
$W$
has highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },p+q+6)$
, its contragredient has highest weight
$\unicode[STIX]{x1D706}(k,k^{\prime },p+q+6)$
, its contragredient has highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },-p-q-6)$
. In other words, we have a perfect bilinear pairing
$\unicode[STIX]{x1D706}(k,k^{\prime },-p-q-6)$
. In other words, we have a perfect bilinear pairing
 $W\otimes W\longrightarrow \mathbb{Q}(p+q+6)$
where
$W\otimes W\longrightarrow \mathbb{Q}(p+q+6)$
where
 $\mathbb{Q}(p+q+6)$
denotes the one-dimensional
$\mathbb{Q}(p+q+6)$
denotes the one-dimensional
![]() $\mathbb{Q}$
-vector space on which
$\mathbb{Q}$
-vector space on which
![]() $G$
acts by the
$G$
acts by the
 $(p+q+6)$
th power of the multiplier character
$(p+q+6)$
th power of the multiplier character
![]() $\unicode[STIX]{x1D708}$
. This pairing induces a
$\unicode[STIX]{x1D708}$
. This pairing induces a
![]() $G(\mathbb{A}_{f})$
-equivariant pairing
$G(\mathbb{A}_{f})$
-equivariant pairing

which becomes perfect after restriction to the vectors which are invariant by a compact open subgroup of
![]() $G(\mathbb{A}_{f})$
, when
$G(\mathbb{A}_{f})$
, when
![]() $\mathbb{Q}(0)$
is given the action of
$\mathbb{Q}(0)$
is given the action of
![]() $G(\mathbb{A}_{f})$
by
$G(\mathbb{A}_{f})$
by
![]() $|\unicode[STIX]{x1D708}|^{-3}$
(see [Reference TaylorTay93, p. 295]). This induces a morphism of Hodge structures
$|\unicode[STIX]{x1D708}|^{-3}$
(see [Reference TaylorTay93, p. 295]). This induces a morphism of Hodge structures

Recall that according to Proposition 3.8, we have the Hodge decomposition
 $$\begin{eqnarray}\displaystyle & & \displaystyle M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}\nonumber\\ \displaystyle & & \displaystyle \quad =M_{B}^{3-t^{\prime },-k-k^{\prime }-t^{\prime }}\oplus M_{B}^{2-k^{\prime }-t^{\prime },1-k-t^{\prime }}\oplus M_{B}^{1-k-t^{\prime },2-k^{\prime }-t^{\prime }}\oplus M_{B}^{-k-k^{\prime }-t^{\prime },3-t^{\prime }}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}\nonumber\\ \displaystyle & & \displaystyle \quad =M_{B}^{3-t^{\prime },-k-k^{\prime }-t^{\prime }}\oplus M_{B}^{2-k^{\prime }-t^{\prime },1-k-t^{\prime }}\oplus M_{B}^{1-k-t^{\prime },2-k^{\prime }-t^{\prime }}\oplus M_{B}^{-k-k^{\prime }-t^{\prime },3-t^{\prime }}\nonumber\end{eqnarray}$$
where
 $t^{\prime }=-(k+k^{\prime }+p+q)/2$
.
$t^{\prime }=-(k+k^{\prime }+p+q)/2$
.
Lemma 4.21. Let
 $\unicode[STIX]{x1D714}\in M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}$
. Let
$\unicode[STIX]{x1D714}\in M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}$
. Let

be defined as the composition of the natural inclusion
 $M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\rightarrow M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}$
and of the pairing with
$M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\rightarrow M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}$
and of the pairing with
![]() $\unicode[STIX]{x1D714}$
. Assume that
$\unicode[STIX]{x1D714}$
. Assume that
![]() $\unicode[STIX]{x1D714}$
belongs to
$\unicode[STIX]{x1D714}$
belongs to
 $M_{B}^{2-k^{\prime }-t^{\prime },1-k-t^{\prime }}\oplus M_{B}^{1-k-t^{\prime },2-k^{\prime }-t^{\prime }}$
. Then, with the notation of Lemma 4.20, we have
$M_{B}^{2-k^{\prime }-t^{\prime },1-k-t^{\prime }}\oplus M_{B}^{1-k-t^{\prime },2-k^{\prime }-t^{\prime }}$
. Then, with the notation of Lemma 4.20, we have
 $$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\frac{\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{K}}}\rangle _{B}}{\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}}{\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\frac{\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{K}}}\rangle _{B}}{\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}}{\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
Proof. According to Lemma 4.20, it is enough to know that the kernel of
 $x\longmapsto \langle \unicode[STIX]{x1D714},x\rangle _{B}$
contains
$x\longmapsto \langle \unicode[STIX]{x1D714},x\rangle _{B}$
contains
 $F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}$
. Write
$F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}$
. Write
 $t=(p+q+6-k-k^{\prime })/2$
. We have the Hodge decomposition
$t=(p+q+6-k-k^{\prime })/2$
. We have the Hodge decomposition
 $$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}=M_{B}^{3-t,-k-k^{\prime }-t}\oplus M_{B}^{2-k^{\prime }-t,1-k-t}\oplus M_{B}^{1-k-t,2-k^{\prime }-t}\oplus M_{B}^{-k-k^{\prime }-t,3-t}\end{eqnarray}$$
$$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}=M_{B}^{3-t,-k-k^{\prime }-t}\oplus M_{B}^{2-k^{\prime }-t,1-k-t}\oplus M_{B}^{1-k-t,2-k^{\prime }-t}\oplus M_{B}^{-k-k^{\prime }-t,3-t}\end{eqnarray}$$
where
 $3-t=(k+k^{\prime }-p-q)/2\geqslant 0$
and
$3-t=(k+k^{\prime }-p-q)/2\geqslant 0$
and
 $2-k^{\prime }-t=(k-k^{\prime }-p-q-2)/2<0$
according to the inequalities relating
$2-k^{\prime }-t=(k-k^{\prime }-p-q-2)/2<0$
according to the inequalities relating
![]() $p,q,k$
and
$p,q,k$
and
![]() $k^{\prime }$
stated in the introduction. As a consequence, we have
$k^{\prime }$
stated in the introduction. As a consequence, we have
 $F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}=\bigoplus _{p\geqslant 0}M_{B}^{p,q}=M_{B}^{3-t,-k-k^{\prime }-t}$
. This implies that the image of the inclusion
$F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}=\bigoplus _{p\geqslant 0}M_{B}^{p,q}=M_{B}^{3-t,-k-k^{\prime }-t}$
. This implies that the image of the inclusion

of the exact sequence of Corollary 4.12 is included in
 $$\begin{eqnarray}M_{B}^{3-t,-k-k^{\prime }-t}\oplus \overline{M_{B}^{3-t,-k-k^{\prime }-t}}=M_{B}^{3-t,-k-k^{\prime }-t}\oplus M_{B}^{-k-k^{\prime }-t,3-t}.\end{eqnarray}$$
$$\begin{eqnarray}M_{B}^{3-t,-k-k^{\prime }-t}\oplus \overline{M_{B}^{3-t,-k-k^{\prime }-t}}=M_{B}^{3-t,-k-k^{\prime }-t}\oplus M_{B}^{-k-k^{\prime }-t,3-t}.\end{eqnarray}$$
Hence, the statement follows from the assumption on the Hodge types of
![]() $\unicode[STIX]{x1D714}$
and fact that
$\unicode[STIX]{x1D714}$
and fact that
![]() $\langle \,,\rangle _{B}$
is a morphism of Hodge structures.◻
$\langle \,,\rangle _{B}$
is a morphism of Hodge structures.◻
4.4 From the regulator to a global integral
In this section, we shall explain how to associate a class
![]() $\unicode[STIX]{x1D714}$
whose Hodge types are as in Lemma 4.21 to some cusp forms
$\unicode[STIX]{x1D714}$
whose Hodge types are as in Lemma 4.21 to some cusp forms
![]() $\unicode[STIX]{x1D6F9}$
on
$\unicode[STIX]{x1D6F9}$
on
![]() $G$
. When
$G$
. When
![]() $\unicode[STIX]{x1D714}$
is associated to
$\unicode[STIX]{x1D714}$
is associated to
![]() $\unicode[STIX]{x1D6F9}$
, we shall see that the pairing
$\unicode[STIX]{x1D6F9}$
, we shall see that the pairing
 $\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{K}}}\rangle _{B}$
is an integral on
$\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{K}}}\rangle _{B}$
is an integral on
 $G^{\prime }(\mathbb{Q})Z^{\prime }(\mathbb{A})\backslash G^{\prime }(\mathbb{A})$
of a function of the shape
$G^{\prime }(\mathbb{Q})Z^{\prime }(\mathbb{A})\backslash G^{\prime }(\mathbb{A})$
of a function of the shape
![]() $\unicode[STIX]{x1D6F9}E_{{\mathcal{H}}}$
, where
$\unicode[STIX]{x1D6F9}E_{{\mathcal{H}}}$
, where
![]() $E_{{\mathcal{H}}}$
is an Eisenstein series on
$E_{{\mathcal{H}}}$
is an Eisenstein series on
![]() $G^{\prime }$
related to the Deligne–Beilinson realization
$G^{\prime }$
related to the Deligne–Beilinson realization
 $\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
of the motivic classes
$\operatorname{Eis}_{{\mathcal{D}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
of the motivic classes
 $\operatorname{Eis}_{{\mathcal{M}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
.
$\operatorname{Eis}_{{\mathcal{M}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
.
Remark 4.22. At several places in this article, we consider a
![]() $G(\mathbb{A}_{f})$
-module
$G(\mathbb{A}_{f})$
-module
![]() ${\mathcal{V}}$
and its
${\mathcal{V}}$
and its
![]() $\unicode[STIX]{x1D70B}_{f}$
-isotypical component
$\unicode[STIX]{x1D70B}_{f}$
-isotypical component
 ${\mathcal{V}}(\unicode[STIX]{x1D70B}_{f})=\text{Hom}_{G(\mathbb{A}_{f})}(\unicode[STIX]{x1D70B}_{f},{\mathcal{V}})$
. Let us choose a vector
${\mathcal{V}}(\unicode[STIX]{x1D70B}_{f})=\text{Hom}_{G(\mathbb{A}_{f})}(\unicode[STIX]{x1D70B}_{f},{\mathcal{V}})$
. Let us choose a vector
![]() $x\in \unicode[STIX]{x1D70B}_{f}$
, that will be fixed until the end. Then, the linear map
$x\in \unicode[STIX]{x1D70B}_{f}$
, that will be fixed until the end. Then, the linear map
 ${\mathcal{V}}(\unicode[STIX]{x1D70B}_{f})\longrightarrow {\mathcal{V}},\unicode[STIX]{x1D719}\longmapsto \unicode[STIX]{x1D719}(x)$
is injective because
${\mathcal{V}}(\unicode[STIX]{x1D70B}_{f})\longrightarrow {\mathcal{V}},\unicode[STIX]{x1D719}\longmapsto \unicode[STIX]{x1D719}(x)$
is injective because
![]() $\unicode[STIX]{x1D70B}_{f}$
is irreducible. In what follows, we will often regard
$\unicode[STIX]{x1D70B}_{f}$
is irreducible. In what follows, we will often regard
![]() ${\mathcal{V}}(\unicode[STIX]{x1D70B}_{f})$
as a subspace of
${\mathcal{V}}(\unicode[STIX]{x1D70B}_{f})$
as a subspace of
![]() ${\mathcal{V}}$
, via the choice of
${\mathcal{V}}$
, via the choice of
![]() $x$
.
$x$
.
According to Theorem 1.1, for any
 $\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }\in {\mathcal{B}}_{p}\otimes _{\mathbb{Q}}{\mathcal{B}}_{q}$
, we have the extension class
$\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }\in {\mathcal{B}}_{p}\otimes _{\mathbb{Q}}{\mathcal{B}}_{q}$
, we have the extension class
 $$\begin{eqnarray}\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\in \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),H_{B,!}^{3}(S,W)_{\mathbb{ R}})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\in \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),H_{B,!}^{3}(S,W)_{\mathbb{ R}})\end{eqnarray}$$
whose image in the Deligne–Beilinson cohomology
 $H_{{\mathcal{D}}}^{4}(S/\mathbb{R},W)$
coincides with the class of the pair of currents
$H_{{\mathcal{D}}}^{4}(S/\mathbb{R},W)$
coincides with the class of the pair of currents
 $(\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })},\unicode[STIX]{x1D704}_{\ast }T_{P_{B}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })})$
(Proposition 4.10). Due to the above remark and Lemma 4.21, we need to compute a pairing of the shape
$(\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })},\unicode[STIX]{x1D704}_{\ast }T_{P_{B}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })})$
(Proposition 4.10). Due to the above remark and Lemma 4.21, we need to compute a pairing of the shape
 $\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{K}}}\rangle _{B}$
where
$\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{K}}}\rangle _{B}$
where
![]() $\widetilde{v}_{{\mathcal{K}}}$
is a class in
$\widetilde{v}_{{\mathcal{K}}}$
is a class in
 $H_{B,!}^{3}(S,W)_{\mathbb{R}}^{-}(-1)$
which is mapped to
$H_{B,!}^{3}(S,W)_{\mathbb{R}}^{-}(-1)$
which is mapped to
 $\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
by the surjection
$\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
by the surjection

In the following lemma, whose aim is to describe as explicitly as necessary such a lifting
![]() $\widetilde{v}_{{\mathcal{K}}}$
, we use two standard facts. The first is that Betti cohomology can be computed by closed currents. The second is the so-called Liebermann’s trick: let
$\widetilde{v}_{{\mathcal{K}}}$
, we use two standard facts. The first is that Betti cohomology can be computed by closed currents. The second is the so-called Liebermann’s trick: let
 $p:A\longrightarrow S$
be an abelian scheme and let
$p:A\longrightarrow S$
be an abelian scheme and let
![]() $W$
be a sheaf on
$W$
be a sheaf on
![]() $S$
which is a direct factor of
$S$
which is a direct factor of
 $(R^{1}p_{\ast }\mathbb{Q}(0))^{\otimes n}(m)$
, for some integers
$(R^{1}p_{\ast }\mathbb{Q}(0))^{\otimes n}(m)$
, for some integers
![]() $m$
and
$m$
and
![]() $n$
. Then, the cohomology
$n$
. Then, the cohomology
 $H^{i}(S,W)$
is a direct factor of
$H^{i}(S,W)$
is a direct factor of
 $H^{i+n}(A^{n},\mathbb{Q}(t))$
, for some
$H^{i+n}(A^{n},\mathbb{Q}(t))$
, for some
![]() $t$
, where
$t$
, where
![]() $A^{n}$
denotes the
$A^{n}$
denotes the
![]() $n$
th fiber product of
$n$
th fiber product of
![]() $A$
over
$A$
over
![]() $S$
. Let
$S$
. Let
 $r:G\longrightarrow \text{GL}(4)$
be the standard representation of
$r:G\longrightarrow \text{GL}(4)$
be the standard representation of
![]() $G$
. It follows from Weyl’s invariants theory that any irreducible algebraic representation
$G$
. It follows from Weyl’s invariants theory that any irreducible algebraic representation
![]() $W$
of
$W$
of
![]() $G$
of highest weight
$G$
of highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },c)$
is a direct factor, defined by a certain explicit Schur projector, of the representation
$\unicode[STIX]{x1D706}(k,k^{\prime },c)$
is a direct factor, defined by a certain explicit Schur projector, of the representation
 $r^{\otimes (k+k^{\prime })}$
twisted by a power of
$r^{\otimes (k+k^{\prime })}$
twisted by a power of
![]() $\unicode[STIX]{x1D708}$
(see [Reference Fulton and HarrisFH91, §17.3]). As the variation of Hodge structure associated to
$\unicode[STIX]{x1D708}$
(see [Reference Fulton and HarrisFH91, §17.3]). As the variation of Hodge structure associated to
![]() $r$
is
$r$
is
 $R^{1}p_{\ast }\mathbb{Q}(1)$
, the variation of Hodge structure associated to such a
$R^{1}p_{\ast }\mathbb{Q}(1)$
, the variation of Hodge structure associated to such a
![]() $W$
is a direct factor of a Tate twist of
$W$
is a direct factor of a Tate twist of
 $(R^{1}\unicode[STIX]{x1D70B}_{\ast }\mathbb{Q}(0))^{\otimes (k+k^{\prime })}$
where
$(R^{1}\unicode[STIX]{x1D70B}_{\ast }\mathbb{Q}(0))^{\otimes (k+k^{\prime })}$
where
 $p:A\longrightarrow S$
is the universal abelian surface over the Siegel threefold. It is not necessary for us to be more precise. However, the reader might consult [Reference AnconaAnc15] for much more precise and general statements and their proofs.
$p:A\longrightarrow S$
is the universal abelian surface over the Siegel threefold. It is not necessary for us to be more precise. However, the reader might consult [Reference AnconaAnc15] for much more precise and general statements and their proofs.
Lemma 4.23. Let
 $\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }\in {\mathcal{B}}_{p}\otimes _{\mathbb{Q}}{\mathcal{B}}_{q}$
. Let
$\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }\in {\mathcal{B}}_{p}\otimes _{\mathbb{Q}}{\mathcal{B}}_{q}$
. Let
![]() $A$
be the universal abelian surface over
$A$
be the universal abelian surface over
![]() $S$
, of infinite level, and let
$S$
, of infinite level, and let
![]() $A^{k+k^{\prime }}$
be the
$A^{k+k^{\prime }}$
be the
![]() $(k+k^{\prime })$
th-fold fiber product over
$(k+k^{\prime })$
th-fold fiber product over
![]() $S$
. Let
$S$
. Let
![]() $\widetilde{A}^{k+k^{\prime }}$
be a smooth projective toroidal compactification of
$\widetilde{A}^{k+k^{\prime }}$
be a smooth projective toroidal compactification of
![]() $A^{k+k^{\prime }}$
such that the complement
$A^{k+k^{\prime }}$
such that the complement
 $\widetilde{A}^{k+k^{\prime }}-A^{k+k^{\prime }}$
is a normal crossing divisor. Then, there exists a closed current
$\widetilde{A}^{k+k^{\prime }}-A^{k+k^{\prime }}$
is a normal crossing divisor. Then, there exists a closed current
 $\unicode[STIX]{x1D70C}\in {\mathcal{T}}(\widetilde{A}^{k+k^{\prime }}/\mathbb{R},\mathbb{R}(\circ ))$
, for some integer
$\unicode[STIX]{x1D70C}\in {\mathcal{T}}(\widetilde{A}^{k+k^{\prime }}/\mathbb{R},\mathbb{R}(\circ ))$
, for some integer
![]() $\circ$
, such that:
$\circ$
, such that:
-
(i) the restriction of the cohomology class
 $[\unicode[STIX]{x1D70C}]$
of
$[\unicode[STIX]{x1D70C}]$
of
 $\unicode[STIX]{x1D70C}$
to
$\unicode[STIX]{x1D70C}$
to
 $A^{k+k^{\prime }}$
belongs to
$A^{k+k^{\prime }}$
belongs to
 $H_{B,!}^{3}(S,W)_{\mathbb{R}}^{-}(-1)$
;
$H_{B,!}^{3}(S,W)_{\mathbb{R}}^{-}(-1)$
; -
(ii) the class
 $[\unicode[STIX]{x1D70C}]$
is mapped to the extension class
$[\unicode[STIX]{x1D70C}]$
is mapped to the extension class
 $\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
by the third mapof the exact sequence of the proof of Corollary 4.12;
$\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
by the third mapof the exact sequence of the proof of Corollary 4.12;
-
(iii) the pairs of currents
 $(\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })},\unicode[STIX]{x1D704}_{\ast }T_{P_{B}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })})$
and
$(\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })},\unicode[STIX]{x1D704}_{\ast }T_{P_{B}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })})$
and
 $(\unicode[STIX]{x1D70C},0)$
represent the same cohomology class in
$(\unicode[STIX]{x1D70C},0)$
represent the same cohomology class in
 $H_{{\mathcal{D}}}^{4}(S/\mathbb{R},W)$
(see Proposition 4.10).
$H_{{\mathcal{D}}}^{4}(S/\mathbb{R},W)$
(see Proposition 4.10).
Proof. The natural map
 $H_{c}^{\ast }(A^{k+k^{\prime }})\longrightarrow H^{\ast }(A^{k+k^{\prime }})$
factors through
$H_{c}^{\ast }(A^{k+k^{\prime }})\longrightarrow H^{\ast }(A^{k+k^{\prime }})$
factors through
 $H^{\ast }(\widetilde{A}^{k+k^{\prime }})\longrightarrow H^{\ast }(A^{k+k^{\prime }})$
. Hence, for the first and the second statement, we can take
$H^{\ast }(\widetilde{A}^{k+k^{\prime }})\longrightarrow H^{\ast }(A^{k+k^{\prime }})$
. Hence, for the first and the second statement, we can take
![]() $\unicode[STIX]{x1D70C}$
to be any closed current on
$\unicode[STIX]{x1D70C}$
to be any closed current on
![]() $\widetilde{A}^{k+k^{\prime }}$
representing a lifting of
$\widetilde{A}^{k+k^{\prime }}$
representing a lifting of
 $\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
by the map
$\operatorname{Eis}_{{\mathcal{H}}}^{p,q,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
by the map

Note that a current on
![]() $\widetilde{A}^{k+k^{\prime }}$
can be regarded as a current on
$\widetilde{A}^{k+k^{\prime }}$
can be regarded as a current on
![]() $A^{k+k^{\prime }}$
, so that the third statement is meaningful. As
$A^{k+k^{\prime }}$
, so that the third statement is meaningful. As
![]() $\widetilde{A}^{k+k^{\prime }}$
is smooth and projective, it follows from [Reference JannsenJan88, 4.5.1] that there exists a natural map
$\widetilde{A}^{k+k^{\prime }}$
is smooth and projective, it follows from [Reference JannsenJan88, 4.5.1] that there exists a natural map
 $H_{B}^{\ast }(\widetilde{A}^{k+k^{\prime }},\mathbb{R}(\circ ))^{-}\longrightarrow H_{{\mathcal{D}}}^{\ast +1}(\widetilde{A}^{k+k^{\prime }}/\mathbb{R},\mathbb{R}(\circ +1))$
. This map is induced by the map sending a closed current
$H_{B}^{\ast }(\widetilde{A}^{k+k^{\prime }},\mathbb{R}(\circ ))^{-}\longrightarrow H_{{\mathcal{D}}}^{\ast +1}(\widetilde{A}^{k+k^{\prime }}/\mathbb{R},\mathbb{R}(\circ +1))$
. This map is induced by the map sending a closed current
![]() $\unicode[STIX]{x1D70F}$
to the pair
$\unicode[STIX]{x1D70F}$
to the pair
![]() $(\unicode[STIX]{x1D70F},0)$
via the description of Deligne–Beilinson homology classes by pairs of currents (Proposition 4.8) and the isomorphism of the Deligne–Beilinson cohomology and homology (Proposition 4.9). Composing with the restriction map
$(\unicode[STIX]{x1D70F},0)$
via the description of Deligne–Beilinson homology classes by pairs of currents (Proposition 4.8) and the isomorphism of the Deligne–Beilinson cohomology and homology (Proposition 4.9). Composing with the restriction map
 $$\begin{eqnarray}H_{{\mathcal{D}}}(\widetilde{A}^{k+k^{\prime }}/\mathbb{R},\mathbb{R}(\circ +1))\longrightarrow H_{{\mathcal{D}}}(A^{k+k^{\prime }}/\mathbb{R},\mathbb{R}(\circ +1)),\end{eqnarray}$$
$$\begin{eqnarray}H_{{\mathcal{D}}}(\widetilde{A}^{k+k^{\prime }}/\mathbb{R},\mathbb{R}(\circ +1))\longrightarrow H_{{\mathcal{D}}}(A^{k+k^{\prime }}/\mathbb{R},\mathbb{R}(\circ +1)),\end{eqnarray}$$
we obtain the upper map of a commutative diagram

where the vertical maps are induced by the Schur projectors defining
![]() $W$
. Hence, the third statement follows from the second.◻
$W$
. Hence, the third statement follows from the second.◻
To compute the pairing
 $\langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B}$
, we shall use the notion of rapidly decreasing and slowly increasing differential form and the fact that the Poincaré duality pairing can be represented by a pairing between rapidly decreasing and slowly increasing differential forms. For definitions, we refer the reader to [Reference HarrisHar90, 1.3] (see also [Reference BorelBor81, 3.2]) and for the statement about the Poincaré duality pairing, we refer the reader to [Reference HarrisHar90, Proposition 1.4.4(c)].
$\langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B}$
, we shall use the notion of rapidly decreasing and slowly increasing differential form and the fact that the Poincaré duality pairing can be represented by a pairing between rapidly decreasing and slowly increasing differential forms. For definitions, we refer the reader to [Reference HarrisHar90, 1.3] (see also [Reference BorelBor81, 3.2]) and for the statement about the Poincaré duality pairing, we refer the reader to [Reference HarrisHar90, Proposition 1.4.4(c)].
The differential forms
 $\operatorname{Eis}_{B}^{p}(\unicode[STIX]{x1D719}_{f})$
and
$\operatorname{Eis}_{B}^{p}(\unicode[STIX]{x1D719}_{f})$
and
 $\operatorname{Eis}_{B}^{q}(\unicode[STIX]{x1D719}_{f}^{\prime })$
are slowly increasing as explained in [Reference KingsKin98, (6.3.1)] and [Reference KingsKin98, p. 120]. Moreover, according to Proposition 4.10, we have
$\operatorname{Eis}_{B}^{q}(\unicode[STIX]{x1D719}_{f}^{\prime })$
are slowly increasing as explained in [Reference KingsKin98, (6.3.1)] and [Reference KingsKin98, p. 120]. Moreover, according to Proposition 4.10, we have
 $$\begin{eqnarray}P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })=p_{1}^{\ast }\operatorname{Eis}_{{\mathcal{H}}}^{p}(\unicode[STIX]{x1D719}_{f})\wedge p_{2}^{\ast }(\unicode[STIX]{x1D70B}_{q}\operatorname{Eis}_{B}^{q}(\unicode[STIX]{x1D719}_{f}^{\prime }))+(-1)^{p}p_{1}^{\ast }(\unicode[STIX]{x1D70B}_{p}\operatorname{Eis}_{B}^{p}(\unicode[STIX]{x1D719}_{f}))\wedge p_{2}^{\ast }\operatorname{Eis}_{{\mathcal{H}}}^{q}(\unicode[STIX]{x1D719}_{f}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })=p_{1}^{\ast }\operatorname{Eis}_{{\mathcal{H}}}^{p}(\unicode[STIX]{x1D719}_{f})\wedge p_{2}^{\ast }(\unicode[STIX]{x1D70B}_{q}\operatorname{Eis}_{B}^{q}(\unicode[STIX]{x1D719}_{f}^{\prime }))+(-1)^{p}p_{1}^{\ast }(\unicode[STIX]{x1D70B}_{p}\operatorname{Eis}_{B}^{p}(\unicode[STIX]{x1D719}_{f}))\wedge p_{2}^{\ast }\operatorname{Eis}_{{\mathcal{H}}}^{q}(\unicode[STIX]{x1D719}_{f}^{\prime }).\end{eqnarray}$$
Hence,
 $P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
is slowly increasing. On the other hand, according to Proposition 3.4, the cohomology class
$P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
is slowly increasing. On the other hand, according to Proposition 3.4, the cohomology class
![]() $\unicode[STIX]{x1D714}$
can be computed by cuspidal cohomology. So, let
$\unicode[STIX]{x1D714}$
can be computed by cuspidal cohomology. So, let
![]() $\unicode[STIX]{x1D6FA}$
be a cuspidal differential form representing
$\unicode[STIX]{x1D6FA}$
be a cuspidal differential form representing
![]() $\unicode[STIX]{x1D714}$
. As
$\unicode[STIX]{x1D714}$
. As
![]() $\unicode[STIX]{x1D6FA}$
is rapidly decreasing by definition, the differential form
$\unicode[STIX]{x1D6FA}$
is rapidly decreasing by definition, the differential form
 $\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
, where
$\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
, where
![]() $\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}$
denotes the restriction of
$\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}$
denotes the restriction of
![]() $\unicode[STIX]{x1D6FA}$
to
$\unicode[STIX]{x1D6FA}$
to
 $M\times M$
, is rapidly decreasing. This differential form has values in the vector space underlying the algebraic representation
$M\times M$
, is rapidly decreasing. This differential form has values in the vector space underlying the algebraic representation
 $$\begin{eqnarray}\unicode[STIX]{x1D704}^{\ast }W(-p-q-3)_{\mathbb{ C}}\otimes (\operatorname{Sym}^{p}V_{2,\mathbb{C}}^{\vee }\boxtimes \operatorname{Sym}^{q}V_{2,\mathbb{C}}^{\vee })\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}^{\ast }W(-p-q-3)_{\mathbb{ C}}\otimes (\operatorname{Sym}^{p}V_{2,\mathbb{C}}^{\vee }\boxtimes \operatorname{Sym}^{q}V_{2,\mathbb{C}}^{\vee })\end{eqnarray}$$
of
![]() $G^{\prime }$
. Recall that the irreducible representation
$G^{\prime }$
. Recall that the irreducible representation
 $\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2}$
occurs in the isotypical decomposition of
$\operatorname{Sym}^{p}V_{2}\boxtimes \operatorname{Sym}^{q}V_{2}$
occurs in the isotypical decomposition of
 $\unicode[STIX]{x1D704}^{\ast }W(-3)$
by our choice of
$\unicode[STIX]{x1D704}^{\ast }W(-3)$
by our choice of
![]() $p,q,k$
and
$p,q,k$
and
![]() $k^{\prime }$
. Hence, we have the
$k^{\prime }$
. Hence, we have the
![]() $G^{\prime }$
-equivariant pairing
$G^{\prime }$
-equivariant pairing

defined as the composite of the natural projection
 $$\begin{eqnarray}\unicode[STIX]{x1D704}^{\ast }W(-p-q-3)\longrightarrow (\operatorname{Sym}^{p}V_{2,\mathbb{C}}^{\vee }\boxtimes \operatorname{Sym}^{q}V_{2,\mathbb{C}}^{\vee })\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}^{\ast }W(-p-q-3)\longrightarrow (\operatorname{Sym}^{p}V_{2,\mathbb{C}}^{\vee }\boxtimes \operatorname{Sym}^{q}V_{2,\mathbb{C}}^{\vee })\end{eqnarray}$$
and of the natural pairing

which is given by
 $$\begin{eqnarray}\langle a_{r}^{p}\boxtimes a_{s}^{q},a_{r^{\prime }}^{p}\boxtimes a_{s^{\prime }}^{q}\rangle =\left\{\begin{array}{@{}ll@{}}0\quad & \text{if }r+r^{\prime }\neq p\text{ or }s+s^{\prime }\neq q,\\ \displaystyle (-1)^{r+s}(2i)^{-p-q}\binom{p}{r}\binom{q}{s}\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\langle a_{r}^{p}\boxtimes a_{s}^{q},a_{r^{\prime }}^{p}\boxtimes a_{s^{\prime }}^{q}\rangle =\left\{\begin{array}{@{}ll@{}}0\quad & \text{if }r+r^{\prime }\neq p\text{ or }s+s^{\prime }\neq q,\\ \displaystyle (-1)^{r+s}(2i)^{-p-q}\binom{p}{r}\binom{q}{s}\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
Let
 $A_{G^{\prime }}=\mathbb{R}_{+}^{\times }$
be the identity component of the center of
$A_{G^{\prime }}=\mathbb{R}_{+}^{\times }$
be the identity component of the center of
![]() $G^{\prime }(\mathbb{R})$
and let
$G^{\prime }(\mathbb{R})$
and let
![]() $\mathfrak{g}^{\prime }$
, respectively
$\mathfrak{g}^{\prime }$
, respectively
![]() $\mathfrak{k}^{\prime }$
, be the Lie algebra of
$\mathfrak{k}^{\prime }$
, be the Lie algebra of
![]() $G^{\prime }(\mathbb{R})$
, respectively of its subgroup
$G^{\prime }(\mathbb{R})$
, respectively of its subgroup
 $A_{G^{\prime }}(\text{U}(1)\times _{\mathbb{R}^{\times }}\text{U}(1))$
. Then, with the notation of the beginning of § 4.2, we have
$A_{G^{\prime }}(\text{U}(1)\times _{\mathbb{R}^{\times }}\text{U}(1))$
. Then, with the notation of the beginning of § 4.2, we have
 $$\begin{eqnarray}\mathfrak{g}_{\mathbb{C}}^{\prime }/\mathfrak{k}_{\mathbb{ C}}^{\prime }=(\mathfrak{p}^{\prime +}\oplus \mathfrak{p}^{\prime -})\oplus (\mathfrak{p}^{\prime +}\oplus \mathfrak{p}^{\prime -}).\end{eqnarray}$$
$$\begin{eqnarray}\mathfrak{g}_{\mathbb{C}}^{\prime }/\mathfrak{k}_{\mathbb{ C}}^{\prime }=(\mathfrak{p}^{\prime +}\oplus \mathfrak{p}^{\prime -})\oplus (\mathfrak{p}^{\prime +}\oplus \mathfrak{p}^{\prime -}).\end{eqnarray}$$
Let
![]() $\mathbf{1}$
be the generator of the highest exterior power
$\mathbf{1}$
be the generator of the highest exterior power
 $\bigwedge ^{4}\mathfrak{g}_{\mathbb{C}}^{\prime }/\mathfrak{k}_{\mathbb{C}}^{\prime }$
defined by
$\bigwedge ^{4}\mathfrak{g}_{\mathbb{C}}^{\prime }/\mathfrak{k}_{\mathbb{C}}^{\prime }$
defined by
 $$\begin{eqnarray}\mathbf{1}=(v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0)\wedge (0,v^{-})\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{1}=(v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0)\wedge (0,v^{-})\end{eqnarray}$$
where
 $v^{\pm }={\textstyle \frac{1}{2}}(\!\begin{smallmatrix}1 & \pm i\\ \pm i & -1\end{smallmatrix}\!)\in \mathfrak{p}^{\prime \pm }$
. Evaluating the differential form
$v^{\pm }={\textstyle \frac{1}{2}}(\!\begin{smallmatrix}1 & \pm i\\ \pm i & -1\end{smallmatrix}\!)\in \mathfrak{p}^{\prime \pm }$
. Evaluating the differential form
 $\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
at the tangent vector
$\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
at the tangent vector
![]() $\mathbf{1}$
, we get the rapidly decreasing vector valued function
$\mathbf{1}$
, we get the rapidly decreasing vector valued function
 $$\begin{eqnarray}(\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})\in \unicode[STIX]{x1D704}^{\ast }W(-p-q-3)_{\mathbb{ C}}\otimes (\operatorname{Sym}^{p}V_{2,\mathbb{C}}^{\vee }\boxtimes \operatorname{Sym}^{q}V_{2,\mathbb{C}}^{\vee })\otimes {\mathcal{C}}_{\text{rd}}^{\infty }(G^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{A})).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})\in \unicode[STIX]{x1D704}^{\ast }W(-p-q-3)_{\mathbb{ C}}\otimes (\operatorname{Sym}^{p}V_{2,\mathbb{C}}^{\vee }\boxtimes \operatorname{Sym}^{q}V_{2,\mathbb{C}}^{\vee })\otimes {\mathcal{C}}_{\text{rd}}^{\infty }(G^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{A})).\end{eqnarray}$$
Here
 ${\mathcal{C}}_{\text{rd}}^{\infty }(G^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{A}))$
denotes the space of rapidly decreasing functions defined in [Reference HarrisHar90, p. 48]. Composing with the pairing defined above, finally, we get the rapidly decreasing function
${\mathcal{C}}_{\text{rd}}^{\infty }(G^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{A}))$
denotes the space of rapidly decreasing functions defined in [Reference HarrisHar90, p. 48]. Composing with the pairing defined above, finally, we get the rapidly decreasing function
 $$\begin{eqnarray}\langle (\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})\rangle \in {\mathcal{C}}_{\text{rd}}^{\infty }(G^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{A})).\end{eqnarray}$$
$$\begin{eqnarray}\langle (\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})\rangle \in {\mathcal{C}}_{\text{rd}}^{\infty }(G^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{A})).\end{eqnarray}$$
Proposition 4.24. Let
![]() $\unicode[STIX]{x1D714}$
be a vector of
$\unicode[STIX]{x1D714}$
be a vector of
 $M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}$
satisfying the condition on Hodge types of Lemma 4.21. Let
$M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}$
satisfying the condition on Hodge types of Lemma 4.21. Let
![]() $\unicode[STIX]{x1D6FA}$
be a cuspidal differential form representing
$\unicode[STIX]{x1D6FA}$
be a cuspidal differential form representing
![]() $\unicode[STIX]{x1D714}$
, let
$\unicode[STIX]{x1D714}$
, let
![]() $\unicode[STIX]{x1D70C}$
be a closed current as in the statement of Lemma 4.23 and let
$\unicode[STIX]{x1D70C}$
be a closed current as in the statement of Lemma 4.23 and let
![]() $[\unicode[STIX]{x1D70C}]$
be its cohomology class. Let
$[\unicode[STIX]{x1D70C}]$
be its cohomology class. Let
![]() $dg$
be the measure on
$dg$
be the measure on
 $G^{\prime }(\mathbb{Q})Z^{\prime }(\mathbb{A})\backslash G^{\prime }(\mathbb{A})$
associated to
$G^{\prime }(\mathbb{Q})Z^{\prime }(\mathbb{A})\backslash G^{\prime }(\mathbb{A})$
associated to
![]() $\mathbf{1}$
(see § 2.4). Then,
$\mathbf{1}$
(see § 2.4). Then,
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B}=\frac{1}{(2\unicode[STIX]{x1D70B}i)^{p+q+2}}\int _{G^{\prime }(\mathbb{Q})Z^{\prime }(\mathbb{A})\backslash G^{\prime }(\mathbb{A})}\langle (\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})\rangle (g)|\text{det}\,g|^{3}\,dg.\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B}=\frac{1}{(2\unicode[STIX]{x1D70B}i)^{p+q+2}}\int _{G^{\prime }(\mathbb{Q})Z^{\prime }(\mathbb{A})\backslash G^{\prime }(\mathbb{A})}\langle (\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})\rangle (g)|\text{det}\,g|^{3}\,dg.\end{eqnarray}$$
Proof. There exists a rapidly decreasing differential form
![]() $\unicode[STIX]{x1D702}$
such that
$\unicode[STIX]{x1D702}$
such that
 $\unicode[STIX]{x1D6FA}^{\prime }=\unicode[STIX]{x1D6FA}-d\unicode[STIX]{x1D702}$
is compactly supported [Reference BorelBor81, Corollary 5.5]. We claim that the pairing
$\unicode[STIX]{x1D6FA}^{\prime }=\unicode[STIX]{x1D6FA}-d\unicode[STIX]{x1D702}$
is compactly supported [Reference BorelBor81, Corollary 5.5]. We claim that the pairing
 $\langle \unicode[STIX]{x1D704}^{\ast }d\unicode[STIX]{x1D702},P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle$
is zero. To prove this, recall that according to the third statement of Lemma 4.23, the classes of the pairs of currents
$\langle \unicode[STIX]{x1D704}^{\ast }d\unicode[STIX]{x1D702},P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle$
is zero. To prove this, recall that according to the third statement of Lemma 4.23, the classes of the pairs of currents
 $(\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })},\unicode[STIX]{x1D704}_{\ast }T_{P_{B}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })})$
and
$(\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })},\unicode[STIX]{x1D704}_{\ast }T_{P_{B}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })})$
and
![]() $(\unicode[STIX]{x1D70C},0)$
coincide in
$(\unicode[STIX]{x1D70C},0)$
coincide in
 $H_{{\mathcal{D}}}^{4}(S/\mathbb{R},W)$
. According to Proposition 4.8, this implies the existence of a current
$H_{{\mathcal{D}}}^{4}(S/\mathbb{R},W)$
. According to Proposition 4.8, this implies the existence of a current
![]() $\unicode[STIX]{x1D70C}^{\prime }$
on the open part
$\unicode[STIX]{x1D70C}^{\prime }$
on the open part
![]() $A^{k+k^{\prime }}$
such that
$A^{k+k^{\prime }}$
such that
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })}+d\unicode[STIX]{x1D70C}^{\prime }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })}+d\unicode[STIX]{x1D70C}^{\prime }.\end{eqnarray}$$
As
![]() $d\unicode[STIX]{x1D70C}=0$
, for any compactly supported differential form
$d\unicode[STIX]{x1D70C}=0$
, for any compactly supported differential form
![]() $\unicode[STIX]{x1D702}_{c}$
of suitable degree on
$\unicode[STIX]{x1D702}_{c}$
of suitable degree on
![]() $S$
, we have
$S$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })}(d\unicode[STIX]{x1D702}_{c})=(\unicode[STIX]{x1D70C}-d\unicode[STIX]{x1D70C}^{\prime })(d\unicode[STIX]{x1D702}_{c})=0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })}(d\unicode[STIX]{x1D702}_{c})=(\unicode[STIX]{x1D70C}-d\unicode[STIX]{x1D70C}^{\prime })(d\unicode[STIX]{x1D702}_{c})=0.\end{eqnarray}$$
The differential form
 $\unicode[STIX]{x1D704}^{\ast }d\unicode[STIX]{x1D702}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
on
$\unicode[STIX]{x1D704}^{\ast }d\unicode[STIX]{x1D702}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
on
 $M\times M$
is rapidly decreasing, hence it extends to a differential form on a smooth compactification
$M\times M$
is rapidly decreasing, hence it extends to a differential form on a smooth compactification
 $\widetilde{M\times M}$
, which is zero on the boundary. As a consequence, we can see the pairing
$\widetilde{M\times M}$
, which is zero on the boundary. As a consequence, we can see the pairing
 $\langle \unicode[STIX]{x1D704}^{\ast }d\unicode[STIX]{x1D702},P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle$
as an integral
$\langle \unicode[STIX]{x1D704}^{\ast }d\unicode[STIX]{x1D702},P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle$
as an integral
 $$\begin{eqnarray}\int _{\widetilde{M\times M}}\unicode[STIX]{x1D704}^{\ast }\,d\unicode[STIX]{x1D702}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}\int _{\widetilde{M\times M}}\unicode[STIX]{x1D704}^{\ast }\,d\unicode[STIX]{x1D702}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\end{eqnarray}$$
over the compactification. To prove that this integral is zero, approximate
![]() $\unicode[STIX]{x1D702}$
by a form
$\unicode[STIX]{x1D702}$
by a form
![]() $\unicode[STIX]{x1D702}_{c}$
whose support is compact in
$\unicode[STIX]{x1D702}_{c}$
whose support is compact in
![]() $S$
. We have
$S$
. We have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\widetilde{M\times M}}\unicode[STIX]{x1D704}^{\ast }\,d\unicode[STIX]{x1D702}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\widetilde{M\times M}}\unicode[STIX]{x1D704}^{\ast }\,d\unicode[STIX]{x1D702}_{c}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })+\int _{\widetilde{M\times M}}\unicode[STIX]{x1D704}^{\ast }\,d(\unicode[STIX]{x1D702}-\unicode[STIX]{x1D702}_{c})\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \int _{\widetilde{M\times M}}\unicode[STIX]{x1D704}^{\ast }\,d\unicode[STIX]{x1D702}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{\widetilde{M\times M}}\unicode[STIX]{x1D704}^{\ast }\,d\unicode[STIX]{x1D702}_{c}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })+\int _{\widetilde{M\times M}}\unicode[STIX]{x1D704}^{\ast }\,d(\unicode[STIX]{x1D702}-\unicode[STIX]{x1D702}_{c})\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }).\nonumber\end{eqnarray}$$
On the one hand, the first integral coincides with
 $\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })}(d\unicode[STIX]{x1D702}_{c})$
, hence is equal to zero. On the other hand, as the manifold
$\unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })}(d\unicode[STIX]{x1D702}_{c})$
, hence is equal to zero. On the other hand, as the manifold
 $\widetilde{M\times M}$
is compact, the second integral can be made arbitrarily small if the support of
$\widetilde{M\times M}$
is compact, the second integral can be made arbitrarily small if the support of
![]() $\unicode[STIX]{x1D702}_{c}$
is sufficiently close to the support of
$\unicode[STIX]{x1D702}_{c}$
is sufficiently close to the support of
![]() $\unicode[STIX]{x1D702}$
. Hence,
$\unicode[STIX]{x1D702}$
. Hence,
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D704}^{\ast }d\unicode[STIX]{x1D702},P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle =0.\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D704}^{\ast }d\unicode[STIX]{x1D702},P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle =0.\end{eqnarray}$$
As a consequence,
 $$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B} & = & \displaystyle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FA}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })}(\unicode[STIX]{x1D6FA}^{\prime })+d\unicode[STIX]{x1D70C}^{\prime }(\unicode[STIX]{x1D6FA}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })}(\unicode[STIX]{x1D6FA}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \langle \unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}^{\prime },P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle \nonumber\\ \displaystyle & = & \displaystyle \langle \unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA},P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B} & = & \displaystyle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FA}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })}(\unicode[STIX]{x1D6FA}^{\prime })+d\unicode[STIX]{x1D70C}^{\prime }(\unicode[STIX]{x1D6FA}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D704}_{\ast }T_{P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })}(\unicode[STIX]{x1D6FA}^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \langle \unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}^{\prime },P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle \nonumber\\ \displaystyle & = & \displaystyle \langle \unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA},P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle .\nonumber\end{eqnarray}$$
The second equality follows from the definition of
![]() $\unicode[STIX]{x1D70C}^{\prime }$
, the third from the fact that
$\unicode[STIX]{x1D70C}^{\prime }$
, the third from the fact that
![]() $\unicode[STIX]{x1D6FA}^{\prime }$
is closed, the fourth from the definition of the current associated to a differential form (13), and the last from the vanishing of
$\unicode[STIX]{x1D6FA}^{\prime }$
is closed, the fourth from the definition of the current associated to a differential form (13), and the last from the vanishing of
 $\langle \unicode[STIX]{x1D704}^{\ast }d\unicode[STIX]{x1D702},P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle$
. The fact that
$\langle \unicode[STIX]{x1D704}^{\ast }d\unicode[STIX]{x1D702},P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle$
. The fact that
 $\langle \unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA},P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle$
is computed by the integral given in the statement of the proposition follows from [Reference HarrisHar90, Proposition 1.4.4(c)]. This completes the proof.◻
$\langle \unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA},P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\rangle$
is computed by the integral given in the statement of the proposition follows from [Reference HarrisHar90, Proposition 1.4.4(c)]. This completes the proof.◻
Our goal is now to give an explicit formula for the integrand in the above integral. The first step is to explain precisely how to associate differential forms on
![]() $S$
to cusp forms on
$S$
to cusp forms on
![]() $G$
. Once we have the results of § 3 at our disposal, this association relies on rather elementary representation theoretic considerations.
$G$
. Once we have the results of § 3 at our disposal, this association relies on rather elementary representation theoretic considerations.
Let
![]() $T^{\prime }$
be the maximal compact subtorus of
$T^{\prime }$
be the maximal compact subtorus of
 $\text{Sp}(4,\mathbb{R})$
defined by
$\text{Sp}(4,\mathbb{R})$
defined by
 $$\begin{eqnarray}T^{\prime }=\left.\left\{\left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)\,\right|\,x^{2}+y^{2}={x^{\prime }}^{2}+{y^{\prime }}^{2}=1\right\}.\end{eqnarray}$$
$$\begin{eqnarray}T^{\prime }=\left.\left\{\left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)\,\right|\,x^{2}+y^{2}={x^{\prime }}^{2}+{y^{\prime }}^{2}=1\right\}.\end{eqnarray}$$
The Lie algebra of
![]() $T^{\prime }$
is the compact Cartan subalgebra of
$T^{\prime }$
is the compact Cartan subalgebra of
![]() $\mathfrak{sp}_{4}$
that we denoted by
$\mathfrak{sp}_{4}$
that we denoted by
![]() $\mathfrak{h}$
in § 3.1. Let
$\mathfrak{h}$
in § 3.1. Let
 $A_{G}=\mathbb{R}_{+}^{\times }$
be the identity component of the center of
$A_{G}=\mathbb{R}_{+}^{\times }$
be the identity component of the center of
![]() $G(\mathbb{R})$
. For integers
$G(\mathbb{R})$
. For integers
![]() $n,n^{\prime },c$
such that
$n,n^{\prime },c$
such that
 $n+n^{\prime }\equiv c~(\text{mod}~2)$
, let
$n+n^{\prime }\equiv c~(\text{mod}~2)$
, let
 $\unicode[STIX]{x1D706}^{\prime }(n,n^{\prime },c):A_{G}T^{\prime }\longrightarrow \mathbb{C}^{\times }$
denote the character defined by
$\unicode[STIX]{x1D706}^{\prime }(n,n^{\prime },c):A_{G}T^{\prime }\longrightarrow \mathbb{C}^{\times }$
denote the character defined by
 $$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)\longmapsto (x+iy)^{n}(x^{\prime }+iy^{\prime })^{n^{\prime }}(x^{2}+y^{2})^{(c-n-n^{\prime })/2},\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)\longmapsto (x+iy)^{n}(x^{\prime }+iy^{\prime })^{n^{\prime }}(x^{2}+y^{2})^{(c-n-n^{\prime })/2},\end{eqnarray}$$
and by
 $\unicode[STIX]{x1D706}^{\prime }(n,n^{\prime })$
the restriction of
$\unicode[STIX]{x1D706}^{\prime }(n,n^{\prime })$
the restriction of
 $\unicode[STIX]{x1D706}^{\prime }(n,n^{\prime },c)$
to
$\unicode[STIX]{x1D706}^{\prime }(n,n^{\prime },c)$
to
![]() $T^{\prime }$
. Note that the simple root
$T^{\prime }$
. Note that the simple root
![]() $e_{1}-e_{2}$
, respectively
$e_{1}-e_{2}$
, respectively
![]() $2e_{2}$
, defined in § 3.1, coincides with the differential at the identity matrix of the restriction to
$2e_{2}$
, defined in § 3.1, coincides with the differential at the identity matrix of the restriction to
![]() $T^{\prime }$
of the character
$T^{\prime }$
of the character
 $\unicode[STIX]{x1D706}^{\prime }(1,-1,0)$
, respectively
$\unicode[STIX]{x1D706}^{\prime }(1,-1,0)$
, respectively
 $\unicode[STIX]{x1D706}(0,2,0)$
.
$\unicode[STIX]{x1D706}(0,2,0)$
.
Lemma 4.25. Let
![]() $E$
be an irreducible algebraic representation of
$E$
be an irreducible algebraic representation of
![]() $G$
in a finite dimensional
$G$
in a finite dimensional
![]() $\mathbb{Q}$
-vector space and let
$\mathbb{Q}$
-vector space and let
![]() $w\in E$
be a vector of weight
$w\in E$
be a vector of weight
 $\unicode[STIX]{x1D706}(u,u^{\prime },c)$
. Let
$\unicode[STIX]{x1D706}(u,u^{\prime },c)$
. Let
 $$\begin{eqnarray}J=\frac{1}{\sqrt{2}}\left(\begin{array}{@{}cccc@{}}1 & & i & \\ & 1 & & i\\ i & & 1 & \\ & i & & 1\end{array}\right)\in \text{Sp}(4,\mathbb{C}).\end{eqnarray}$$
$$\begin{eqnarray}J=\frac{1}{\sqrt{2}}\left(\begin{array}{@{}cccc@{}}1 & & i & \\ & 1 & & i\\ i & & 1 & \\ & i & & 1\end{array}\right)\in \text{Sp}(4,\mathbb{C}).\end{eqnarray}$$
Let
 $v=Jw\in E_{\mathbb{C}}$
and let
$v=Jw\in E_{\mathbb{C}}$
and let
 $\overline{v}=Nv$
, where
$\overline{v}=Nv$
, where
 $N\in G(\mathbb{R})$
is defined in Remark 3.2. Then, for the action of the torus
$N\in G(\mathbb{R})$
is defined in Remark 3.2. Then, for the action of the torus
 $A_{G}T^{\prime }\subset G(\mathbb{R})$
, the vector
$A_{G}T^{\prime }\subset G(\mathbb{R})$
, the vector
![]() $v$
, respectively
$v$
, respectively
![]() $\overline{v}$
, has weight
$\overline{v}$
, has weight
 $\unicode[STIX]{x1D706}^{\prime }(u,u^{\prime },c)$
, respectively
$\unicode[STIX]{x1D706}^{\prime }(u,u^{\prime },c)$
, respectively
 $\unicode[STIX]{x1D706}^{\prime }(-u^{\prime },-u,c)$
.
$\unicode[STIX]{x1D706}^{\prime }(-u^{\prime },-u,c)$
.
Proof. The statement on the weight of
![]() $v$
is a straightforward consequence of the fact that for any
$v$
is a straightforward consequence of the fact that for any
 $x,x^{\prime },y,y^{\prime }\in \mathbb{R}$
, we have
$x,x^{\prime },y,y^{\prime }\in \mathbb{R}$
, we have
 $$\begin{eqnarray}\displaystyle J^{-1}\left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)J & = & \displaystyle \overline{J}\left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)J\nonumber\\ \displaystyle & = & \displaystyle \left(\begin{array}{@{}cccc@{}}x+iy & & & \\ & x^{\prime }+iy^{\prime } & & \\ & & x-iy & \\ & & & x^{\prime }-iy^{\prime }\end{array}\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J^{-1}\left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)J & = & \displaystyle \overline{J}\left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)J\nonumber\\ \displaystyle & = & \displaystyle \left(\begin{array}{@{}cccc@{}}x+iy & & & \\ & x^{\prime }+iy^{\prime } & & \\ & & x-iy & \\ & & & x^{\prime }-iy^{\prime }\end{array}\right).\nonumber\end{eqnarray}$$
Hence, the statement on the weight of
![]() $\overline{v}$
follows from the identities
$\overline{v}$
follows from the identities
 $$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)\overline{v} & = & \displaystyle NN^{-1}\left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)Nv\nonumber\\ \displaystyle & = & \displaystyle N\left(\begin{array}{@{}cccc@{}}x^{\prime } & & -y^{\prime } & \\ & x & & -y\\ y^{\prime } & & x^{\prime } & \\ & y & & x\end{array}\right)v\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D706}(-u^{\prime },-u,c)\left(\left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)\right)\overline{v}.\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)\overline{v} & = & \displaystyle NN^{-1}\left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)Nv\nonumber\\ \displaystyle & = & \displaystyle N\left(\begin{array}{@{}cccc@{}}x^{\prime } & & -y^{\prime } & \\ & x & & -y\\ y^{\prime } & & x^{\prime } & \\ & y & & x\end{array}\right)v\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D706}(-u^{\prime },-u,c)\left(\left(\begin{array}{@{}cccc@{}}x & & y & \\ & x^{\prime } & & y^{\prime }\\ -y & & x & \\ & -y^{\prime } & & x^{\prime }\end{array}\right)\right)\overline{v}.\square\nonumber\end{eqnarray}$$
Lemma 4.26. Let
 $X_{(1,-1)}\in \mathfrak{k}_{\mathbb{C}}$
be defined by
$X_{(1,-1)}\in \mathfrak{k}_{\mathbb{C}}$
be defined by
 $$\begin{eqnarray}X_{(1,-1)}=d\unicode[STIX]{x1D705}\left(\left(\begin{array}{@{}cc@{}} & 1\\ & \end{array}\right)\right)=\left(\begin{array}{@{}cccc@{}} & 1 & & -i\\ -1 & & -i & \\ & i & & 1\\ i & & -1 & \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}X_{(1,-1)}=d\unicode[STIX]{x1D705}\left(\left(\begin{array}{@{}cc@{}} & 1\\ & \end{array}\right)\right)=\left(\begin{array}{@{}cccc@{}} & 1 & & -i\\ -1 & & -i & \\ & i & & 1\\ i & & -1 & \end{array}\right).\end{eqnarray}$$
Let
![]() $\unicode[STIX]{x1D70B}_{\infty }^{W}$
and
$\unicode[STIX]{x1D70B}_{\infty }^{W}$
and
 $\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\in P(W(-p-q-3))$
be as in Lemma 3.6. Let
$\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\in P(W(-p-q-3))$
be as in Lemma 3.6. Let
 $\unicode[STIX]{x1D6F9}_{\infty }\in \unicode[STIX]{x1D70B}_{\infty }^{W}$
be a lowest weight vector of the minimal
$\unicode[STIX]{x1D6F9}_{\infty }\in \unicode[STIX]{x1D70B}_{\infty }^{W}$
be a lowest weight vector of the minimal
![]() $K$
-type
$K$
-type
 $\unicode[STIX]{x1D70F}_{(k+3,-k^{\prime }-1)}$
of
$\unicode[STIX]{x1D70F}_{(k+3,-k^{\prime }-1)}$
of
![]() $\unicode[STIX]{x1D70B}_{\infty }^{W}$
and let
$\unicode[STIX]{x1D70B}_{\infty }^{W}$
and let
 $\overline{\unicode[STIX]{x1D6F9}}_{\infty }\in \overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}$
be the vector associated to
$\overline{\unicode[STIX]{x1D6F9}}_{\infty }\in \overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}$
be the vector associated to
![]() $\unicode[STIX]{x1D6F9}_{\infty }$
as in Remark 3.2. Let
$\unicode[STIX]{x1D6F9}_{\infty }$
as in Remark 3.2. Let
 $w\in W(-p-q-3)$
be a vector of weight
$w\in W(-p-q-3)$
be a vector of weight
 $\unicode[STIX]{x1D706}(-k,k^{\prime },-p-q)$
and let
$\unicode[STIX]{x1D706}(-k,k^{\prime },-p-q)$
and let
 $v,\overline{v}\in W(-p-q-3)_{\mathbb{C}}$
be the vectors associated to
$v,\overline{v}\in W(-p-q-3)_{\mathbb{C}}$
be the vectors associated to
![]() $w$
as in Lemma 4.25. Let
$w$
as in Lemma 4.25. Let
 $$\begin{eqnarray}\displaystyle X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)} & \in & \displaystyle \bigwedge ^{2}\mathfrak{p}^{+}\otimes \mathfrak{p}^{-},\nonumber\\ \displaystyle X_{(0,-2)}\wedge X_{(-1,-1)}\otimes X_{(2,0)} & \in & \displaystyle \bigwedge ^{2}\mathfrak{p}^{-}\otimes _{\mathbb{C}}\mathfrak{p}^{+},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)} & \in & \displaystyle \bigwedge ^{2}\mathfrak{p}^{+}\otimes \mathfrak{p}^{-},\nonumber\\ \displaystyle X_{(0,-2)}\wedge X_{(-1,-1)}\otimes X_{(2,0)} & \in & \displaystyle \bigwedge ^{2}\mathfrak{p}^{-}\otimes _{\mathbb{C}}\mathfrak{p}^{+},\nonumber\end{eqnarray}$$
where the
![]() $X_{(u,u^{\prime })}$
are the root vectors defined in § 3.1. Then:
$X_{(u,u^{\prime })}$
are the root vectors defined in § 3.1. Then:
-
(i) there exists a unique non-zero map
such that $$\begin{eqnarray}\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })\in \text{Hom}_{K_{G}}\biggl(\bigwedge ^{2}\mathfrak{p}^{+}\otimes _{\mathbb{ C}}\mathfrak{p}^{-},W(-p-q-3)\otimes _{\mathbb{ C}}\unicode[STIX]{x1D70B}_{\infty }^{W}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })\in \text{Hom}_{K_{G}}\biggl(\bigwedge ^{2}\mathfrak{p}^{+}\otimes _{\mathbb{ C}}\mathfrak{p}^{-},W(-p-q-3)\otimes _{\mathbb{ C}}\unicode[STIX]{x1D70B}_{\infty }^{W}\biggr)\end{eqnarray}$$
 $$\begin{eqnarray}\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)})=\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty };\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)})=\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty };\end{eqnarray}$$
-
(ii) for the action of
 $N$
on the de Rham complex defined in Proposition 3.13, we have and
$N$
on the de Rham complex defined in Proposition 3.13, we have and $$\begin{eqnarray}N\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })\in \text{Hom}_{K_{G}}\biggl(\bigwedge ^{2}\mathfrak{p}^{-}\otimes _{\mathbb{ C}}\mathfrak{p}^{+},W(-p-q-3)\otimes _{\mathbb{ C}}\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}N\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })\in \text{Hom}_{K_{G}}\biggl(\bigwedge ^{2}\mathfrak{p}^{-}\otimes _{\mathbb{ C}}\mathfrak{p}^{+},W(-p-q-3)\otimes _{\mathbb{ C}}\overline{\unicode[STIX]{x1D70B}}_{\infty }^{W}\biggr)\end{eqnarray}$$
 $$\begin{eqnarray}(N\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty }))(X_{(0,-2)}\wedge X_{(-1,-1)}\otimes X_{(2,0)})=\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}\overline{v}\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\overline{\unicode[STIX]{x1D6F9}}_{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}(N\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty }))(X_{(0,-2)}\wedge X_{(-1,-1)}\otimes X_{(2,0)})=\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}\overline{v}\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\overline{\unicode[STIX]{x1D6F9}}_{\infty }.\end{eqnarray}$$
Proof. Note that
![]() $X_{(1,-1)}$
is a root vector corresponding to the positive compact root and recall that we have the isotypical decomposition
$X_{(1,-1)}$
is a root vector corresponding to the positive compact root and recall that we have the isotypical decomposition
 $$\begin{eqnarray}\bigwedge ^{2}\mathfrak{p}^{+}\otimes _{\mathbb{ C}}\mathfrak{p}^{-}=\unicode[STIX]{x1D70F}_{(3,-1)}\oplus \unicode[STIX]{x1D70F}_{(2,0)}\oplus \unicode[STIX]{x1D70F}_{(1,1)}.\end{eqnarray}$$
$$\begin{eqnarray}\bigwedge ^{2}\mathfrak{p}^{+}\otimes _{\mathbb{ C}}\mathfrak{p}^{-}=\unicode[STIX]{x1D70F}_{(3,-1)}\oplus \unicode[STIX]{x1D70F}_{(2,0)}\oplus \unicode[STIX]{x1D70F}_{(1,1)}.\end{eqnarray}$$
Hence, the vector
 $X_{(2,0)}\,\wedge \,X_{(1,1)}\,\otimes \,X_{(0,-2)}$
is a highest weight vector. As a consequence, to define the restriction of a
$X_{(2,0)}\,\wedge \,X_{(1,1)}\,\otimes \,X_{(0,-2)}$
is a highest weight vector. As a consequence, to define the restriction of a
![]() $K_{G}$
-equivariant map
$K_{G}$
-equivariant map
 $\unicode[STIX]{x1D6FA}:\bigwedge ^{2}\mathfrak{p}^{+}\otimes _{\mathbb{C}}\mathfrak{p}^{-}\longrightarrow W(-p-q-3)\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{W}$
to
$\unicode[STIX]{x1D6FA}:\bigwedge ^{2}\mathfrak{p}^{+}\otimes _{\mathbb{C}}\mathfrak{p}^{-}\longrightarrow W(-p-q-3)\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{W}$
to
![]() $\unicode[STIX]{x1D70F}_{(3,-1)}$
amounts to give the image of
$\unicode[STIX]{x1D70F}_{(3,-1)}$
amounts to give the image of
 $X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}$
, under the condition that
$X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}$
, under the condition that
 $\unicode[STIX]{x1D6FA}(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)})$
must have the same highest weight as
$\unicode[STIX]{x1D6FA}(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)})$
must have the same highest weight as
 $X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}$
. For every
$X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}$
. For every
 $0\leqslant i\leqslant k+k^{\prime }+4$
, the vector
$0\leqslant i\leqslant k+k^{\prime }+4$
, the vector
 $X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty }$
has weight
$X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty }$
has weight
 $\unicode[STIX]{x1D706}^{\prime }(k+3,-k^{\prime }-1,c)-i\unicode[STIX]{x1D706}^{\prime }(1,-1,0)$
where
$\unicode[STIX]{x1D706}^{\prime }(k+3,-k^{\prime }-1,c)-i\unicode[STIX]{x1D706}^{\prime }(1,-1,0)$
where
 $c=p+q+6$
. Similarly, the vector
$c=p+q+6$
. Similarly, the vector
 $X_{(1,-1)}^{i}v$
has weight
$X_{(1,-1)}^{i}v$
has weight
 $\unicode[STIX]{x1D706}^{\prime }(-k,k^{\prime },-c)+i\unicode[STIX]{x1D706}^{\prime }(1,-1,0)$
. As a consequence, the vector
$\unicode[STIX]{x1D706}^{\prime }(-k,k^{\prime },-c)+i\unicode[STIX]{x1D706}^{\prime }(1,-1,0)$
. As a consequence, the vector
 $\sum _{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty }$
has weight
$\sum _{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty }$
has weight
 $\unicode[STIX]{x1D706}^{\prime }(3,-1,0)$
, which is the weight of
$\unicode[STIX]{x1D706}^{\prime }(3,-1,0)$
, which is the weight of
 $X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}$
. Furthermore,
$X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}$
. Furthermore,
 $$\begin{eqnarray}\displaystyle X_{(1,-1)}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D713}_{\infty } & = & \displaystyle \mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i+1}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty }\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i+1}\unicode[STIX]{x1D6F9}_{\infty }\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=0}^{k+k^{\prime }-2}(-1)^{i}X_{(1,-1)}^{i+1}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty }\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i=1}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i+1}\unicode[STIX]{x1D6F9}_{\infty }\nonumber\\ \displaystyle & = & \displaystyle 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{(1,-1)}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D713}_{\infty } & = & \displaystyle \mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i+1}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty }\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i+1}\unicode[STIX]{x1D6F9}_{\infty }\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=0}^{k+k^{\prime }-2}(-1)^{i}X_{(1,-1)}^{i+1}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty }\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{i=1}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i+1}\unicode[STIX]{x1D6F9}_{\infty }\nonumber\\ \displaystyle & = & \displaystyle 0.\nonumber\end{eqnarray}$$
In other terms,
 $\sum _{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty }$
is a highest weight vector of the
$\sum _{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty }$
is a highest weight vector of the
![]() $K_{G}$
-module
$K_{G}$
-module
 $W(-p-q-3)\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{W}$
. As a consequence, there exists a unique non-zero
$W(-p-q-3)\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{W}$
. As a consequence, there exists a unique non-zero
![]() $K_{G}$
-equivariant map
$K_{G}$
-equivariant map
 $\unicode[STIX]{x1D70F}_{(3,-1)}\longrightarrow W(-p-q-3)\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{W}$
sending
$\unicode[STIX]{x1D70F}_{(3,-1)}\longrightarrow W(-p-q-3)\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{W}$
sending
 $X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}$
to
$X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}$
to
 $\sum _{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty }$
. Thanks to Proposition 3.7, this proves the first statement. Let us prove the second: by definition of the action of
$\sum _{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}_{\infty }$
. Thanks to Proposition 3.7, this proves the first statement. Let us prove the second: by definition of the action of
![]() $N$
on the de Rham complex (Proposition 3.13), we have
$N$
on the de Rham complex (Proposition 3.13), we have
 $$\begin{eqnarray}\displaystyle (N\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty }))(X_{(0,-2)}\wedge X_{(-1,-1)}\otimes X_{(2,0)})=N(\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })(\operatorname{Ad}_{N^{-1}}(X_{(0,-2)}\wedge X_{(-1,-1)}\otimes X_{(2,0)}))). & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (N\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty }))(X_{(0,-2)}\wedge X_{(-1,-1)}\otimes X_{(2,0)})=N(\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })(\operatorname{Ad}_{N^{-1}}(X_{(0,-2)}\wedge X_{(-1,-1)}\otimes X_{(2,0)}))). & & \displaystyle \nonumber\end{eqnarray}$$
An easy computation shows that
 $$\begin{eqnarray}\operatorname{Ad}_{N^{-1}}(X_{(0,-2)}\wedge X_{(-1,-1)}\otimes X_{(2,0)})=X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ad}_{N^{-1}}(X_{(0,-2)}\wedge X_{(-1,-1)}\otimes X_{(2,0)})=X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}.\end{eqnarray}$$
Hence,
 $$\begin{eqnarray}\displaystyle (N\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty }))(X_{(0,-2)}\wedge X_{(-1,-1)}\otimes X_{(2,0)}) & = & \displaystyle N(\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}))\nonumber\\ \displaystyle & = & \displaystyle N\biggl(\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i},\unicode[STIX]{x1D6F9}_{\infty }\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}\overline{v}\otimes X_{(1,-1)}^{k+k^{\prime }+4-i},\overline{\unicode[STIX]{x1D6F9}}_{\infty }.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle (N\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty }))(X_{(0,-2)}\wedge X_{(-1,-1)}\otimes X_{(2,0)}) & = & \displaystyle N(\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}))\nonumber\\ \displaystyle & = & \displaystyle N\biggl(\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}v\otimes X_{(1,-1)}^{k+k^{\prime }+4-i},\unicode[STIX]{x1D6F9}_{\infty }\biggr)\nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{i}\overline{v}\otimes X_{(1,-1)}^{k+k^{\prime }+4-i},\overline{\unicode[STIX]{x1D6F9}}_{\infty }.\nonumber\end{eqnarray}$$
The last identity follows from the fact that, by definition of a
![]() $(\mathfrak{g},K)$
-module
$(\mathfrak{g},K)$
-module
![]() ${\mathcal{V}}$
, we have
${\mathcal{V}}$
, we have
 $$\begin{eqnarray}kXv=\operatorname{Ad}_{k}(X)kv\end{eqnarray}$$
$$\begin{eqnarray}kXv=\operatorname{Ad}_{k}(X)kv\end{eqnarray}$$
for any
 $k\in K,X\in \mathfrak{g}$
and
$k\in K,X\in \mathfrak{g}$
and
![]() $v\in {\mathcal{V}}$
and from the equality
$v\in {\mathcal{V}}$
and from the equality
 $\operatorname{Ad}_{N}(X_{(1,-1)})=X_{(1,-1)}$
.◻
$\operatorname{Ad}_{N}(X_{(1,-1)})=X_{(1,-1)}$
.◻
Lemma 4.27. Let
 $\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }\in {\mathcal{B}}_{p}\otimes _{\mathbb{Q}}{\mathcal{B}}_{q}$
. Let
$\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }\in {\mathcal{B}}_{p}\otimes _{\mathbb{Q}}{\mathcal{B}}_{q}$
. Let
 $\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F9}_{\infty }\otimes \unicode[STIX]{x1D6F9}_{f}$
be a factorizable cusp form on
$\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F9}_{\infty }\otimes \unicode[STIX]{x1D6F9}_{f}$
be a factorizable cusp form on
![]() $G$
. Assume that
$G$
. Assume that
![]() $\unicode[STIX]{x1D6F9}_{\infty }$
satisfies the conditions of Lemma 4.26. Let
$\unicode[STIX]{x1D6F9}_{\infty }$
satisfies the conditions of Lemma 4.26. Let
 $A_{k,k^{\prime },i,j},B_{k,k^{\prime },i}$
and
$A_{k,k^{\prime },i,j},B_{k,k^{\prime },i}$
and
![]() $C_{k,k^{\prime },i}$
denote the integers
$C_{k,k^{\prime },i}$
denote the integers
 $$\begin{eqnarray}\displaystyle A_{k,k^{\prime },i,j} & = & \displaystyle \frac{(k+k^{\prime }+4-i)!}{(k+k^{\prime }+4-(i+j))!}\frac{(i+j)!}{(i-j)!}\frac{(k+k^{\prime }-i+j)!}{(k+k^{\prime }-i)!},\nonumber\\ \displaystyle B_{k,k^{\prime },i} & = & \displaystyle (i+1)(k+k^{\prime }+4-i),\nonumber\\ \displaystyle C_{k,k^{\prime },i} & = & \displaystyle i(k+k^{\prime }-i+1).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle A_{k,k^{\prime },i,j} & = & \displaystyle \frac{(k+k^{\prime }+4-i)!}{(k+k^{\prime }+4-(i+j))!}\frac{(i+j)!}{(i-j)!}\frac{(k+k^{\prime }-i+j)!}{(k+k^{\prime }-i)!},\nonumber\\ \displaystyle B_{k,k^{\prime },i} & = & \displaystyle (i+1)(k+k^{\prime }+4-i),\nonumber\\ \displaystyle C_{k,k^{\prime },i} & = & \displaystyle i(k+k^{\prime }-i+1).\nonumber\end{eqnarray}$$
Then,
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D704}^{\ast }(\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })\otimes \unicode[STIX]{x1D6F9}_{f})\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3}{160}\frac{(2\unicode[STIX]{x1D70B}i)^{p+q+2}}{(p+1)}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}\mathop{\sum }_{j=0}^{3}(-1)^{i}\binom{3}{j}A_{k,k^{\prime },i,j}X_{(1,-1)}^{k+k^{\prime }+4-(i+j)}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i-j}v\nonumber\\ \displaystyle & & \displaystyle \qquad \otimes \,\mathop{\sum }_{r=0}^{p}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{r}^{(p)}\otimes a_{0}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{2r-p}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{-q-2}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{(-1)^{p}(2\unicode[STIX]{x1D70B}i)^{p+q+2}}{8(q+1)}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}B_{k,k^{\prime },i}X_{(1,-1)}^{k+k^{\prime }+4-(i+1)}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i}v\nonumber\\ \displaystyle & & \displaystyle \qquad \otimes \,\mathop{\sum }_{s=0}^{q}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{0}^{(p)}\otimes a_{s}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{-p-2}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{2s-q}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{(-1)^{p}(2\unicode[STIX]{x1D70B}i)^{p+q+2}}{8(q+1)}\mathop{\sum }_{i=1}^{k+k^{\prime }-1}(-1)^{i}C_{k,k^{\prime },i}X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i-1}v\nonumber\\ \displaystyle & & \displaystyle \qquad \otimes \,\mathop{\sum }_{s=0}^{q}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{0}^{(p)}\otimes a_{s}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{-p-2}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{2s-q}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D704}^{\ast }(\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })\otimes \unicode[STIX]{x1D6F9}_{f})\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3}{160}\frac{(2\unicode[STIX]{x1D70B}i)^{p+q+2}}{(p+1)}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}\mathop{\sum }_{j=0}^{3}(-1)^{i}\binom{3}{j}A_{k,k^{\prime },i,j}X_{(1,-1)}^{k+k^{\prime }+4-(i+j)}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i-j}v\nonumber\\ \displaystyle & & \displaystyle \qquad \otimes \,\mathop{\sum }_{r=0}^{p}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{r}^{(p)}\otimes a_{0}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{2r-p}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{-q-2}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{(-1)^{p}(2\unicode[STIX]{x1D70B}i)^{p+q+2}}{8(q+1)}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}B_{k,k^{\prime },i}X_{(1,-1)}^{k+k^{\prime }+4-(i+1)}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i}v\nonumber\\ \displaystyle & & \displaystyle \qquad \otimes \,\mathop{\sum }_{s=0}^{q}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{0}^{(p)}\otimes a_{s}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{-p-2}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{2s-q}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{(-1)^{p}(2\unicode[STIX]{x1D70B}i)^{p+q+2}}{8(q+1)}\mathop{\sum }_{i=1}^{k+k^{\prime }-1}(-1)^{i}C_{k,k^{\prime },i}X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i-1}v\nonumber\\ \displaystyle & & \displaystyle \qquad \otimes \,\mathop{\sum }_{s=0}^{q}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{0}^{(p)}\otimes a_{s}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{-p-2}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{2s-q}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }),\nonumber\end{eqnarray}$$
and
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D704}^{\ast }F_{\infty }(\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })\otimes \unicode[STIX]{x1D6F9}_{f})\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3}{160}\frac{(-1)^{p}(2\unicode[STIX]{x1D70B}i)^{p+q+2}}{(q+1)}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}\mathop{\sum }_{j=0}^{3}(-1)^{i}\binom{3}{j}A_{k,k^{\prime },i,j}X_{(1,-1)}^{k+k^{\prime }+4-(i+j)}\overline{\unicode[STIX]{x1D6F9}}\otimes X_{(1,-1)}^{i-j}\overline{v}\nonumber\\ \displaystyle & & \displaystyle \qquad \otimes \,\mathop{\sum }_{s=0}^{q}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{p}^{(p)}\otimes a_{s}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{p+2}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{2s-q}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{(2\unicode[STIX]{x1D70B}i)^{p+q+2}}{8(q+1)}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}B_{k,k^{\prime },i}X_{(1,-1)}^{k+k^{\prime }+4-(i+1)}\overline{\unicode[STIX]{x1D6F9}}\otimes X_{(1,-1)}^{i}\overline{v}\nonumber\\ \displaystyle & & \displaystyle \qquad \otimes \,\mathop{\sum }_{r=0}^{p}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{r}^{(p)}\otimes a_{q}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{2r-p}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{q+2}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{(2\unicode[STIX]{x1D70B}i)^{p+q+2}}{8(q+1)}\mathop{\sum }_{i=1}^{k+k^{\prime }-1}(-1)^{i}C_{k,k^{\prime },i}X_{(1,-1)}^{k+k^{\prime }+4-i}\overline{\unicode[STIX]{x1D6F9}}\otimes X_{(1,-1)}^{i-1}\overline{v}\nonumber\\ \displaystyle & & \displaystyle \qquad \otimes \,\mathop{\sum }_{r=0}^{p}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{r}^{(p)}\otimes a_{q}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{2r-p}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{q+2}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D704}^{\ast }F_{\infty }(\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })\otimes \unicode[STIX]{x1D6F9}_{f})\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{3}{160}\frac{(-1)^{p}(2\unicode[STIX]{x1D70B}i)^{p+q+2}}{(q+1)}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}\mathop{\sum }_{j=0}^{3}(-1)^{i}\binom{3}{j}A_{k,k^{\prime },i,j}X_{(1,-1)}^{k+k^{\prime }+4-(i+j)}\overline{\unicode[STIX]{x1D6F9}}\otimes X_{(1,-1)}^{i-j}\overline{v}\nonumber\\ \displaystyle & & \displaystyle \qquad \otimes \,\mathop{\sum }_{s=0}^{q}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{p}^{(p)}\otimes a_{s}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{p+2}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{2s-q}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{(2\unicode[STIX]{x1D70B}i)^{p+q+2}}{8(q+1)}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}B_{k,k^{\prime },i}X_{(1,-1)}^{k+k^{\prime }+4-(i+1)}\overline{\unicode[STIX]{x1D6F9}}\otimes X_{(1,-1)}^{i}\overline{v}\nonumber\\ \displaystyle & & \displaystyle \qquad \otimes \,\mathop{\sum }_{r=0}^{p}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{r}^{(p)}\otimes a_{q}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{2r-p}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{q+2}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \qquad -\,\frac{(2\unicode[STIX]{x1D70B}i)^{p+q+2}}{8(q+1)}\mathop{\sum }_{i=1}^{k+k^{\prime }-1}(-1)^{i}C_{k,k^{\prime },i}X_{(1,-1)}^{k+k^{\prime }+4-i}\overline{\unicode[STIX]{x1D6F9}}\otimes X_{(1,-1)}^{i-1}\overline{v}\nonumber\\ \displaystyle & & \displaystyle \qquad \otimes \,\mathop{\sum }_{r=0}^{p}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{r}^{(p)}\otimes a_{q}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{2r-p}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{q+2}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }).\nonumber\end{eqnarray}$$
Proof. Let
![]() $\unicode[STIX]{x1D6FA}$
denote
$\unicode[STIX]{x1D6FA}$
denote
 $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })\otimes \unicode[STIX]{x1D6F9}_{f}$
and
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })\otimes \unicode[STIX]{x1D6F9}_{f}$
and
 $$\begin{eqnarray}\displaystyle e_{1} & = & \displaystyle (v^{+},0),\nonumber\\ \displaystyle e_{2} & = & \displaystyle (0,v^{+}),\nonumber\\ \displaystyle e_{3} & = & \displaystyle (v^{-},0),\nonumber\\ \displaystyle e_{4} & = & \displaystyle (0,v^{-}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle e_{1} & = & \displaystyle (v^{+},0),\nonumber\\ \displaystyle e_{2} & = & \displaystyle (0,v^{+}),\nonumber\\ \displaystyle e_{3} & = & \displaystyle (v^{-},0),\nonumber\\ \displaystyle e_{4} & = & \displaystyle (0,v^{-}),\nonumber\end{eqnarray}$$
which are vectors of
 $\mathfrak{g}_{\mathbb{C}}^{\prime }/\mathfrak{k}_{\mathbb{C}}^{\prime }=(\mathfrak{p}^{\prime +}\oplus \mathfrak{p}^{\prime -})^{2}$
. Let
$\mathfrak{g}_{\mathbb{C}}^{\prime }/\mathfrak{k}_{\mathbb{C}}^{\prime }=(\mathfrak{p}^{\prime +}\oplus \mathfrak{p}^{\prime -})^{2}$
. Let
![]() ${\mathcal{S}}_{4}$
be the symmetric group on four elements. For
${\mathcal{S}}_{4}$
be the symmetric group on four elements. For
![]() $\unicode[STIX]{x1D70E}\in {\mathcal{S}}_{4}$
, let
$\unicode[STIX]{x1D70E}\in {\mathcal{S}}_{4}$
, let
![]() $\unicode[STIX]{x1D716}(\unicode[STIX]{x1D70E})$
denote the signature of
$\unicode[STIX]{x1D716}(\unicode[STIX]{x1D70E})$
denote the signature of
![]() $\unicode[STIX]{x1D70E}$
. Then,
$\unicode[STIX]{x1D70E}$
. Then,
 $$\begin{eqnarray}(\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})=\mathop{\sum }_{\unicode[STIX]{x1D70E}\in {\mathcal{S}}_{4}}\unicode[STIX]{x1D716}(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(e_{\unicode[STIX]{x1D70E}(1)}\wedge e_{\unicode[STIX]{x1D70E}(2)}\wedge e_{\unicode[STIX]{x1D70E}(3)}))\otimes P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(e_{\unicode[STIX]{x1D70E}(4)}).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6FA}\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})=\mathop{\sum }_{\unicode[STIX]{x1D70E}\in {\mathcal{S}}_{4}}\unicode[STIX]{x1D716}(\unicode[STIX]{x1D70E})\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(e_{\unicode[STIX]{x1D70E}(1)}\wedge e_{\unicode[STIX]{x1D70E}(2)}\wedge e_{\unicode[STIX]{x1D70E}(3)}))\otimes P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(e_{\unicode[STIX]{x1D70E}(4)}).\end{eqnarray}$$
By definition, we have
 $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(e_{\unicode[STIX]{x1D70E}(1)}\,\wedge \,e_{\unicode[STIX]{x1D70E}(2)}\,\wedge \,e_{\unicode[STIX]{x1D70E}(3)}))=0$
whenever
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(e_{\unicode[STIX]{x1D70E}(1)}\,\wedge \,e_{\unicode[STIX]{x1D70E}(2)}\,\wedge \,e_{\unicode[STIX]{x1D70E}(3)}))=0$
whenever
 $e_{\unicode[STIX]{x1D70E}(1)}\,\wedge \,e_{\unicode[STIX]{x1D70E}(2)}\,\wedge \,e_{\unicode[STIX]{x1D70E}(3)}$
is not
$e_{\unicode[STIX]{x1D70E}(1)}\,\wedge \,e_{\unicode[STIX]{x1D70E}(2)}\,\wedge \,e_{\unicode[STIX]{x1D70E}(3)}$
is not
 $\pm (v^{+},0)$
$\pm (v^{+},0)$
 $\,\wedge \,(0,v^{+})\wedge (0,v^{-})$
or
$\,\wedge \,(0,v^{+})\wedge (0,v^{-})$
or
 $\pm (v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0)$
. So we have to compute
$\pm (v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0)$
. So we have to compute
 $\unicode[STIX]{x1D6FA}\!(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})$
$\unicode[STIX]{x1D6FA}\!(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})$
 $\,\wedge \,(0,v^{-})\!)$
and
$\,\wedge \,(0,v^{-})\!)$
and
 $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0))$
. Recall the decomposition
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0))$
. Recall the decomposition
 $$\begin{eqnarray}\bigwedge ^{2}\mathfrak{p}^{+}\otimes \mathfrak{p}^{-}=\unicode[STIX]{x1D70F}_{(3,-1)}\oplus \unicode[STIX]{x1D70F}_{(2,0)}\oplus \unicode[STIX]{x1D70F}_{(1,1)}\end{eqnarray}$$
$$\begin{eqnarray}\bigwedge ^{2}\mathfrak{p}^{+}\otimes \mathfrak{p}^{-}=\unicode[STIX]{x1D70F}_{(3,-1)}\oplus \unicode[STIX]{x1D70F}_{(2,0)}\oplus \unicode[STIX]{x1D70F}_{(1,1)}\end{eqnarray}$$
into irreducible
![]() $\mathbb{C}[K]$
-modules. By construction (Lemma 4.26),
$\mathbb{C}[K]$
-modules. By construction (Lemma 4.26),
![]() $\unicode[STIX]{x1D6FA}$
factors through the projection
$\unicode[STIX]{x1D6FA}$
factors through the projection
 $\bigwedge ^{2}\mathfrak{p}^{+}\otimes \mathfrak{p}^{-}\longrightarrow \unicode[STIX]{x1D70F}_{(3,-1)}$
and sends the highest weight vector
$\bigwedge ^{2}\mathfrak{p}^{+}\otimes \mathfrak{p}^{-}\longrightarrow \unicode[STIX]{x1D70F}_{(3,-1)}$
and sends the highest weight vector
 $X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}$
of
$X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}$
of
![]() $\unicode[STIX]{x1D70F}_{(3,-1)}$
to
$\unicode[STIX]{x1D70F}_{(3,-1)}$
to
 $$\begin{eqnarray}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i}v.\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i}v.\end{eqnarray}$$
Hence, we need to compute the image of
 $\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (0,v^{-})$
by the projection above. The identities
$\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (0,v^{-})$
by the projection above. The identities
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D704}_{\ast }(v^{\pm },0) & = & \displaystyle X_{\pm (2,0)},\nonumber\\ \displaystyle \unicode[STIX]{x1D704}_{\ast }(0,v^{\pm }) & = & \displaystyle X_{\pm (0,2)}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D704}_{\ast }(v^{\pm },0) & = & \displaystyle X_{\pm (2,0)},\nonumber\\ \displaystyle \unicode[STIX]{x1D704}_{\ast }(0,v^{\pm }) & = & \displaystyle X_{\pm (0,2)}\nonumber\end{eqnarray}$$
imply
 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (0,v^{-})=X_{(2,0)}\wedge X_{(0,2)}\otimes X_{(0,-2)},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (0,v^{-})=X_{(2,0)}\wedge X_{(0,2)}\otimes X_{(0,-2)},\end{eqnarray}$$
which has weight
 $(2,0)=(3,-1)+(-1,1)$
. Let us write
$(2,0)=(3,-1)+(-1,1)$
. Let us write
 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (0,v^{-})=\unicode[STIX]{x1D6FC}x_{(3,-1)}+\unicode[STIX]{x1D6FD}x_{(2,0)}+\unicode[STIX]{x1D6FE}x_{(1,1)}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (0,v^{-})=\unicode[STIX]{x1D6FC}x_{(3,-1)}+\unicode[STIX]{x1D6FD}x_{(2,0)}+\unicode[STIX]{x1D6FE}x_{(1,1)}\end{eqnarray}$$
where
 $x_{(3,-1)}\in \unicode[STIX]{x1D70F}_{(3,-1)}$
,
$x_{(3,-1)}\in \unicode[STIX]{x1D70F}_{(3,-1)}$
,
 $x_{(2,0)}\in \unicode[STIX]{x1D70F}_{(2,0)},x_{(1,1)}\in \unicode[STIX]{x1D70F}_{(1,1)}$
are weight vectors and
$x_{(2,0)}\in \unicode[STIX]{x1D70F}_{(2,0)},x_{(1,1)}\in \unicode[STIX]{x1D70F}_{(1,1)}$
are weight vectors and
 $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in \mathbb{C}$
. Because weights of
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE}\in \mathbb{C}$
. Because weights of
![]() $T^{\prime }$
in irreducible representations of
$T^{\prime }$
in irreducible representations of
![]() $K$
are multiplicity free, we can assume that
$K$
are multiplicity free, we can assume that
 $x_{(3,-1)}=\operatorname{ad}_{X_{(-1,1)}}(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)})$
where
$x_{(3,-1)}=\operatorname{ad}_{X_{(-1,1)}}(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)})$
where
![]() $\operatorname{ad}$
denotes the adjoint representation
$\operatorname{ad}$
denotes the adjoint representation
 $\mathfrak{g}_{\mathbb{C}}\longrightarrow \text{End}(\mathfrak{g}_{\mathbb{C}})$
. As
$\mathfrak{g}_{\mathbb{C}}\longrightarrow \text{End}(\mathfrak{g}_{\mathbb{C}})$
. As
![]() $\unicode[STIX]{x1D70F}_{(1,1)}$
does not contain vectors of weight
$\unicode[STIX]{x1D70F}_{(1,1)}$
does not contain vectors of weight
![]() $(2,0)$
, we have
$(2,0)$
, we have
![]() $\unicode[STIX]{x1D6FE}=0$
. Furthermore, as
$\unicode[STIX]{x1D6FE}=0$
. Furthermore, as
![]() $\unicode[STIX]{x1D70F}_{(2,0)}$
has highest weight
$\unicode[STIX]{x1D70F}_{(2,0)}$
has highest weight
![]() $(2,0)$
, we have
$(2,0)$
, we have
 $$\begin{eqnarray}\operatorname{ad}_{X_{(1,-1)}}(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (0,v^{-}))=\unicode[STIX]{x1D6FC}\operatorname{ad}_{X_{(1,-1)}}(x_{(3,-1)}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{ad}_{X_{(1,-1)}}(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (0,v^{-}))=\unicode[STIX]{x1D6FC}\operatorname{ad}_{X_{(1,-1)}}(x_{(3,-1)}),\end{eqnarray}$$
that is,
 $$\begin{eqnarray}\operatorname{ad}_{X_{(1,-1)}}(X_{(2,0)}\wedge X_{(0,2)}\otimes X_{(0,-2)})=\unicode[STIX]{x1D6FC}\operatorname{ad}_{X_{(1,-1)}}(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{ad}_{X_{(1,-1)}}(X_{(2,0)}\wedge X_{(0,2)}\otimes X_{(0,-2)})=\unicode[STIX]{x1D6FC}\operatorname{ad}_{X_{(1,-1)}}(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)}).\end{eqnarray}$$
An easy computation shows that
![]() $\unicode[STIX]{x1D6FC}={\textstyle \frac{1}{4}}$
. As a consequence, we have
$\unicode[STIX]{x1D6FC}={\textstyle \frac{1}{4}}$
. As a consequence, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (0,v^{-})) & = & \displaystyle \unicode[STIX]{x1D6FA}\biggl(\frac{1}{4}\operatorname{ad}_{X_{(-1,1)}}(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)})\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{4}X_{(-1,1)}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i}v.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (0,v^{-})) & = & \displaystyle \unicode[STIX]{x1D6FA}\biggl(\frac{1}{4}\operatorname{ad}_{X_{(-1,1)}}(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)})\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{1}{4}X_{(-1,1)}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i}v.\nonumber\end{eqnarray}$$
It follows from the definition of standard basis (§ 3.1) that
 $$\begin{eqnarray}\displaystyle X_{(-1,1)}^{m}X_{(1,-1)}^{n}\unicode[STIX]{x1D6F9}_{\infty } & = & \displaystyle \frac{n!}{(n-m)!}\frac{(k+k^{\prime }+4-n+m)!}{(k+k^{\prime }+4-n)!}X_{(1,-1)}^{n-m}\unicode[STIX]{x1D6F9}_{\infty },\nonumber\\ \displaystyle X_{(-1,1)}^{m}X_{(1,-1)}^{n}v & = & \displaystyle \frac{n!}{(n-m)!}\frac{(k+k^{\prime }-n+m)!}{(k+k^{\prime }-n)!}X_{(1,-1)}^{n-m}v.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle X_{(-1,1)}^{m}X_{(1,-1)}^{n}\unicode[STIX]{x1D6F9}_{\infty } & = & \displaystyle \frac{n!}{(n-m)!}\frac{(k+k^{\prime }+4-n+m)!}{(k+k^{\prime }+4-n)!}X_{(1,-1)}^{n-m}\unicode[STIX]{x1D6F9}_{\infty },\nonumber\\ \displaystyle X_{(-1,1)}^{m}X_{(1,-1)}^{n}v & = & \displaystyle \frac{n!}{(n-m)!}\frac{(k+k^{\prime }-n+m)!}{(k+k^{\prime }-n)!}X_{(1,-1)}^{n-m}v.\nonumber\end{eqnarray}$$
Hence,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (0,v^{-}))\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{4}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}(k+k^{\prime }+4-i)(i+1)X_{(1,-1)}^{k+k^{\prime }+4-(i+1)}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i}v\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{4}\mathop{\sum }_{i=1}^{k+k^{\prime }-1}(-1)^{i}i(k+k^{\prime }-i+1)X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i-1}v.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (0,v^{-}))\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{1}{4}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}(-1)^{i}(k+k^{\prime }+4-i)(i+1)X_{(1,-1)}^{k+k^{\prime }+4-(i+1)}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i}v\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{1}{4}\mathop{\sum }_{i=1}^{k+k^{\prime }-1}(-1)^{i}i(k+k^{\prime }-i+1)X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i-1}v.\nonumber\end{eqnarray}$$
To compute
 $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0))$
, note that the vector
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0))$
, note that the vector
 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0)=X_{(2,0)}\wedge X_{(0,2)}\otimes X_{(-2,0)}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0)=X_{(2,0)}\wedge X_{(0,2)}\otimes X_{(-2,0)}\end{eqnarray}$$
has weight
 $(0,2)=(3,-1)+3(-1,1)$
. A computation as above shows that the image of the vector
$(0,2)=(3,-1)+3(-1,1)$
. A computation as above shows that the image of the vector
 $\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0)$
by the natural projection
$\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0)$
by the natural projection
 $\bigwedge ^{2}\mathfrak{p}^{+}\otimes \mathfrak{p}^{-}\longrightarrow \unicode[STIX]{x1D70F}_{(3,-1)}$
is equal to
$\bigwedge ^{2}\mathfrak{p}^{+}\otimes \mathfrak{p}^{-}\longrightarrow \unicode[STIX]{x1D70F}_{(3,-1)}$
is equal to
 ${\textstyle \frac{3}{80}}\operatorname{ad}_{X_{(-1,1)}}^{3}(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)})$
. Hence,
${\textstyle \frac{3}{80}}\operatorname{ad}_{X_{(-1,1)}}^{3}(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)})$
. Hence,
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0)) & = & \displaystyle \unicode[STIX]{x1D6FA}\biggl(\frac{3}{80}\operatorname{ad}_{X_{(-1,1)}}^{3}(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)})\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{3}{80}X_{(-1,1)}^{3}\mathop{\sum }_{i\geqslant 0}(-1)^{i}X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i}v\nonumber\\ \displaystyle & = & \displaystyle \frac{3}{80}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}\mathop{\sum }_{j=0}^{3}(-1)^{i}\binom{3}{j}A_{k,k^{\prime },i,j}X_{(1,-1)}^{k+k^{\prime }+4-(i+j)}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i-j}v.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D704}_{\ast }(v^{+},0)\wedge (0,v^{+})\wedge (v^{-},0)) & = & \displaystyle \unicode[STIX]{x1D6FA}\biggl(\frac{3}{80}\operatorname{ad}_{X_{(-1,1)}}^{3}(X_{(2,0)}\wedge X_{(1,1)}\otimes X_{(0,-2)})\biggr)\nonumber\\ \displaystyle & = & \displaystyle \frac{3}{80}X_{(-1,1)}^{3}\mathop{\sum }_{i\geqslant 0}(-1)^{i}X_{(1,-1)}^{k+k^{\prime }+4-i}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i}v\nonumber\\ \displaystyle & = & \displaystyle \frac{3}{80}\mathop{\sum }_{i=0}^{k+k^{\prime }-1}\mathop{\sum }_{j=0}^{3}(-1)^{i}\binom{3}{j}A_{k,k^{\prime },i,j}X_{(1,-1)}^{k+k^{\prime }+4-(i+j)}\unicode[STIX]{x1D6F9}\otimes X_{(1,-1)}^{i-j}v.\nonumber\end{eqnarray}$$
To finish the proof, we have to compute
 $P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(v^{-},0)$
and
$P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(v^{-},0)$
and
 $P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(0,v^{-})$
. The differential form
$P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(0,v^{-})$
. The differential form
 $P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
is defined in Proposition 4.10. Unraveling the definitions, we get
$P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
is defined in Proposition 4.10. Unraveling the definitions, we get
 $$\begin{eqnarray}\displaystyle P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(v^{-},0) & = & \displaystyle (-1)^{p}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}\unicode[STIX]{x1D6FE}^{\ast }\unicode[STIX]{x1D70B}_{p}(\unicode[STIX]{x1D714}_{p}^{+}\otimes \unicode[STIX]{x1D719}_{f})(v^{-}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D6E9}_{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(v^{-},0) & = & \displaystyle (-1)^{p}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}\unicode[STIX]{x1D6FE}^{\ast }\unicode[STIX]{x1D70B}_{p}(\unicode[STIX]{x1D714}_{p}^{+}\otimes \unicode[STIX]{x1D719}_{f})(v^{-}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D6E9}_{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }).\nonumber\end{eqnarray}$$
According to Lemma 4.5, we have
 $\unicode[STIX]{x1D70B}_{p}(\unicode[STIX]{x1D714}_{p}^{+}\otimes \unicode[STIX]{x1D719}_{f})={\textstyle \frac{1}{2}}(\unicode[STIX]{x1D714}_{p}^{+}+\unicode[STIX]{x1D714}_{p}^{-})\otimes \unicode[STIX]{x1D719}_{f}$
. Hence,
$\unicode[STIX]{x1D70B}_{p}(\unicode[STIX]{x1D714}_{p}^{+}\otimes \unicode[STIX]{x1D719}_{f})={\textstyle \frac{1}{2}}(\unicode[STIX]{x1D714}_{p}^{+}+\unicode[STIX]{x1D714}_{p}^{-})\otimes \unicode[STIX]{x1D719}_{f}$
. Hence,
 $$\begin{eqnarray}\displaystyle & & \displaystyle P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(v^{-},0)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(-1)^{p}(2\unicode[STIX]{x1D70B}i)^{p+1}(2\unicode[STIX]{x1D70B}i)^{q+1}}{4(q+1)}\mathop{\sum }_{s=0}^{q}\,\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{0}^{(p)}\otimes a_{s}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{-p-2}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{2s-q}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(v^{-},0)\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(-1)^{p}(2\unicode[STIX]{x1D70B}i)^{p+1}(2\unicode[STIX]{x1D70B}i)^{q+1}}{4(q+1)}\mathop{\sum }_{s=0}^{q}\,\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{0}^{(p)}\otimes a_{s}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{-p-2}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{2s-q}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }).\nonumber\end{eqnarray}$$
Similarly,
 $$\begin{eqnarray}\displaystyle & & \displaystyle P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(0,v^{-})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(2\unicode[STIX]{x1D70B}i)^{p+1}(2\unicode[STIX]{x1D70B}i)^{q+1}}{4(p+1)}\mathop{\sum }_{r=0}^{p}\,\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{r}^{(p)}\otimes a_{0}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{2r-p}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{-q-2}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(0,v^{-})\nonumber\\ \displaystyle & & \displaystyle \quad =\frac{(2\unicode[STIX]{x1D70B}i)^{p+1}(2\unicode[STIX]{x1D70B}i)^{q+1}}{4(p+1)}\mathop{\sum }_{r=0}^{p}\,\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}a_{r}^{(p)}\otimes a_{0}^{(q)}\otimes \unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{2r-p}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{-q-2}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }).\nonumber\end{eqnarray}$$
The proof of the first statement follows by putting the previous computations together. The proof of the second statement is a direct consequence of the first, of the identities
 $$\begin{eqnarray}\displaystyle \operatorname{Ad}_{N^{-1}}(v^{\pm },0) & = & \displaystyle (0,v^{\mp }),\nonumber\\ \displaystyle \operatorname{Ad}_{N^{-1}}(0,v^{\pm }) & = & \displaystyle (v^{\mp },0)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Ad}_{N^{-1}}(v^{\pm },0) & = & \displaystyle (0,v^{\mp }),\nonumber\\ \displaystyle \operatorname{Ad}_{N^{-1}}(0,v^{\pm }) & = & \displaystyle (v^{\mp },0)\nonumber\end{eqnarray}$$
and of the formula for
 $P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(v^{+},0)$
and
$P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(v^{+},0)$
and
 $P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(0,v^{+})$
deduced as above from Proposition 4.9.◻
$P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(0,v^{+})$
deduced as above from Proposition 4.9.◻
According to Lemma 4.27, to compute the integral
 $$\begin{eqnarray}\int _{G^{\prime }(\mathbb{Q})Z^{\prime }(\mathbb{A})\backslash G^{\prime }(\mathbb{A})}\langle (\unicode[STIX]{x1D704}^{\ast }(\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })\otimes \unicode[STIX]{x1D713}_{f})\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})\rangle (g)|\text{det}\,g|^{3}\,dg,\end{eqnarray}$$
$$\begin{eqnarray}\int _{G^{\prime }(\mathbb{Q})Z^{\prime }(\mathbb{A})\backslash G^{\prime }(\mathbb{A})}\langle (\unicode[STIX]{x1D704}^{\ast }(\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })\otimes \unicode[STIX]{x1D713}_{f})\wedge P_{{\mathcal{H}}}^{p,q}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }))(\mathbf{1})\rangle (g)|\text{det}\,g|^{3}\,dg,\end{eqnarray}$$
we need to compute pairings of the shape
 $\langle X_{(1,-1)}^{i}v,a_{r}^{(p)}\otimes a_{0}^{(q)}\rangle ,\langle X_{(1,-1)}^{i}v,a_{0}^{(p)}\otimes a_{s}^{(q)}\rangle$
and of the shape
$\langle X_{(1,-1)}^{i}v,a_{r}^{(p)}\otimes a_{0}^{(q)}\rangle ,\langle X_{(1,-1)}^{i}v,a_{0}^{(p)}\otimes a_{s}^{(q)}\rangle$
and of the shape
 $\langle X_{(1,-1)}^{i}\overline{v},a_{p}^{(p)}\otimes a_{s}^{(q)}\rangle ,\langle X_{(1,-1)}^{i}v,a_{r}^{(p)}\otimes a_{q}^{(q)}\rangle$
. In fact, a lot of these pairings vanish for weight reasons.
$\langle X_{(1,-1)}^{i}\overline{v},a_{p}^{(p)}\otimes a_{s}^{(q)}\rangle ,\langle X_{(1,-1)}^{i}v,a_{r}^{(p)}\otimes a_{q}^{(q)}\rangle$
. In fact, a lot of these pairings vanish for weight reasons.
Lemma 4.28. Let
![]() $i,r,s$
be integers such that
$i,r,s$
be integers such that
 $i\geqslant 0,p\geqslant r\geqslant 0,q\geqslant s\geqslant 0$
. Then, the following statements hold
$i\geqslant 0,p\geqslant r\geqslant 0,q\geqslant s\geqslant 0$
. Then, the following statements hold
-
(i) if
 $\langle X_{(1,-1)}^{i}v,a_{r}^{(p)}\otimes a_{0}^{(q)}\rangle \neq 0$
, then
$\langle X_{(1,-1)}^{i}v,a_{r}^{(p)}\otimes a_{0}^{(q)}\rangle \neq 0$
, then
 $i=k^{\prime }+q$
,
$i=k^{\prime }+q$
,
 $r=(-k+k^{\prime }+p+q)/2$
;
$r=(-k+k^{\prime }+p+q)/2$
; -
(ii) if
 $\langle X_{(1,-1)}^{i}v,a_{0}^{(p)}\otimes a_{s}^{(q)}\rangle \neq 0$
, then
$\langle X_{(1,-1)}^{i}v,a_{0}^{(p)}\otimes a_{s}^{(q)}\rangle \neq 0$
, then
 $i=k-p$
,
$i=k-p$
,
 $s=(-k+k^{\prime }+p+q)/2$
;
$s=(-k+k^{\prime }+p+q)/2$
; -
(iii) if
 $\langle X_{(1,-1)}^{i}\overline{v},a_{p}^{(p)}\otimes a_{s}^{(q)}\rangle \neq 0$
, then
$\langle X_{(1,-1)}^{i}\overline{v},a_{p}^{(p)}\otimes a_{s}^{(q)}\rangle \neq 0$
, then
 $i=k^{\prime }+p$
,
$i=k^{\prime }+p$
,
 $s=(-k+k^{\prime }+p+q)/2$
;
$s=(-k+k^{\prime }+p+q)/2$
; -
(iv) if
 $\langle X_{(1,-1)}^{i}\overline{v},a_{r}^{(p)}\otimes a_{q}^{(q)}\rangle \neq 0$
, then
$\langle X_{(1,-1)}^{i}\overline{v},a_{r}^{(p)}\otimes a_{q}^{(q)}\rangle \neq 0$
, then
 $i=k+q$
,
$i=k+q$
,
 $r=(-k+k^{\prime }+p-q)/2$
.
$r=(-k+k^{\prime }+p-q)/2$
.
Proof. The vector
 $a_{r}^{(p)}\,\boxtimes \,a_{s}^{(q)}$
has weight
$a_{r}^{(p)}\,\boxtimes \,a_{s}^{(q)}$
has weight
 $\unicode[STIX]{x1D706}^{\prime }(p-2r,q-2s)$
for the action of
$\unicode[STIX]{x1D706}^{\prime }(p-2r,q-2s)$
for the action of
 $\text{U}(1)^{2}=T^{\prime }$
(Lemma 4.4), the vector
$\text{U}(1)^{2}=T^{\prime }$
(Lemma 4.4), the vector
 $X_{(1,-1)}^{i}v$
, respectively
$X_{(1,-1)}^{i}v$
, respectively
 $X_{(1,-1)}^{i}\overline{v}$
, has weight
$X_{(1,-1)}^{i}\overline{v}$
, has weight
 $\unicode[STIX]{x1D706}^{\prime }(-k,k^{\prime })+i\unicode[STIX]{x1D706}^{\prime }(1,-1)$
, respectively
$\unicode[STIX]{x1D706}^{\prime }(-k,k^{\prime })+i\unicode[STIX]{x1D706}^{\prime }(1,-1)$
, respectively
 $\unicode[STIX]{x1D706}^{\prime }(-k^{\prime },k)+i\unicode[STIX]{x1D706}^{\prime }(1,-1)$
. Hence, the statement follows from the fact that, if two weight vectors pair non-trivially, they have opposite weights.◻
$\unicode[STIX]{x1D706}^{\prime }(-k^{\prime },k)+i\unicode[STIX]{x1D706}^{\prime }(1,-1)$
. Hence, the statement follows from the fact that, if two weight vectors pair non-trivially, they have opposite weights.◻
Corollary 4.29. Let
 $\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F9}_{\infty }\otimes \unicode[STIX]{x1D6F9}_{f}$
be as above, let
$\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F9}_{\infty }\otimes \unicode[STIX]{x1D6F9}_{f}$
be as above, let
 $w\in W(-p-q-3)$
be a vector of weight
$w\in W(-p-q-3)$
be a vector of weight
 $\unicode[STIX]{x1D706}(-k,k^{\prime },-p-q)$
and let
$\unicode[STIX]{x1D706}(-k,k^{\prime },-p-q)$
and let
![]() $\unicode[STIX]{x1D714}$
be the vector in
$\unicode[STIX]{x1D714}$
be the vector in
 $M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}$
associated to
$M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}$
associated to
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $w$
by Lemma 4.26. Let
$w$
by Lemma 4.26. Let
 $\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }\in {\mathcal{B}}_{p}\otimes _{\mathbb{Q}}{\mathcal{B}}_{q}$
and let
$\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }\in {\mathcal{B}}_{p}\otimes _{\mathbb{Q}}{\mathcal{B}}_{q}$
and let
![]() $\unicode[STIX]{x1D70C}$
be a closed current lifting the extension class
$\unicode[STIX]{x1D70C}$
be a closed current lifting the extension class
 $\operatorname{Eis}_{{\mathcal{H}}}^{p,q,k,k^{\prime }}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
as in Lemma 4.23. Let
$\operatorname{Eis}_{{\mathcal{H}}}^{p,q,k,k^{\prime }}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
as in Lemma 4.23. Let
 $\unicode[STIX]{x1D6EF}_{n,r,s}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })$
and
$\unicode[STIX]{x1D6EF}_{n,r,s}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })$
and
 $\overline{\unicode[STIX]{x1D6EF}}_{n,r,s}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })$
denote the functions on
$\overline{\unicode[STIX]{x1D6EF}}_{n,r,s}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })$
denote the functions on
![]() $G^{\prime }(\mathbb{A})$
defined by
$G^{\prime }(\mathbb{A})$
defined by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}_{n,r,s}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime }) & = & \displaystyle X_{(1,-1)}^{n}\unicode[STIX]{x1D6F9}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })}\unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{r}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{s}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }),\nonumber\\ \displaystyle \overline{\unicode[STIX]{x1D6EF}}_{n,r,s}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime }) & = & \displaystyle X_{(1,-1)}^{n}\overline{\unicode[STIX]{x1D6F9}}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })}\unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{r}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{s}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6EF}_{n,r,s}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime }) & = & \displaystyle X_{(1,-1)}^{n}\unicode[STIX]{x1D6F9}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })}\unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{r}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{s}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime }),\nonumber\\ \displaystyle \overline{\unicode[STIX]{x1D6EF}}_{n,r,s}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime }) & = & \displaystyle X_{(1,-1)}^{n}\overline{\unicode[STIX]{x1D6F9}}\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })}\unicode[STIX]{x1D6FE}^{\ast }(\unicode[STIX]{x1D719}_{r}^{p}\otimes \unicode[STIX]{x1D719}_{f}){\unicode[STIX]{x1D6FE}^{\prime }}^{\ast }(\unicode[STIX]{x1D719}_{s}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\end{eqnarray}$$
where the sums are indexed by all
 $(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})$
. Let
$(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})$
. Let
 $$\begin{eqnarray}\displaystyle C_{1} & = & \displaystyle \langle X_{(1,-1)}^{k^{\prime }+q}v,a_{r}^{(p)}\otimes a_{0}^{(q)}\rangle ,\nonumber\\ \displaystyle C_{2} & = & \displaystyle \langle X_{(1,-1)}^{k-p}v,a_{r}^{(p)}\otimes a_{0}^{(q)}\rangle ,\nonumber\\ \displaystyle C_{3} & = & \displaystyle \langle X_{(1,-1)}^{k^{\prime }+p}\overline{v},a_{p}^{(p)}\otimes a_{s}^{(q)}\rangle ,\nonumber\\ \displaystyle C_{4} & = & \displaystyle \langle X_{(1,-1)}^{k+q}\overline{v},a_{p}^{(p)}\otimes a_{s}^{(q)}\rangle .\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle C_{1} & = & \displaystyle \langle X_{(1,-1)}^{k^{\prime }+q}v,a_{r}^{(p)}\otimes a_{0}^{(q)}\rangle ,\nonumber\\ \displaystyle C_{2} & = & \displaystyle \langle X_{(1,-1)}^{k-p}v,a_{r}^{(p)}\otimes a_{0}^{(q)}\rangle ,\nonumber\\ \displaystyle C_{3} & = & \displaystyle \langle X_{(1,-1)}^{k^{\prime }+p}\overline{v},a_{p}^{(p)}\otimes a_{s}^{(q)}\rangle ,\nonumber\\ \displaystyle C_{4} & = & \displaystyle \langle X_{(1,-1)}^{k+q}\overline{v},a_{p}^{(p)}\otimes a_{s}^{(q)}\rangle .\nonumber\end{eqnarray}$$
Then, the pairing
 $\langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B}$
equals
$\langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B}$
equals
 $$\begin{eqnarray}\displaystyle & & \displaystyle C_{1}\frac{3}{160(p+1)}\mathop{\sum }_{j=0}^{3}(-1)^{k^{\prime }+q+j}\binom{3}{j}A_{k,k^{\prime },k^{\prime }+q+j,j}\int \unicode[STIX]{x1D6EF}_{k-q-2j+4,-k+k^{\prime }+q,-q-2}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad -\,C_{2}\frac{(-1)^{k}}{8(q+1)}(B_{k,k^{\prime },k-p}-C_{k,k^{\prime },k-p+1})\int \unicode[STIX]{x1D6EF}_{k^{\prime }+p+3,-p-2,-k+k^{\prime }+p}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad +\,C_{3}\frac{3}{160(q+1)}\mathop{\sum }_{j=0}^{3}(-1)^{k^{\prime }+j}\binom{3}{j}A_{k,k^{\prime },k^{\prime }+p+j,j}\int \overline{\unicode[STIX]{x1D6EF}}_{k-p-2j+4,p+2,-k+k^{\prime }+p}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad -\,C_{4}\frac{(-1)^{k^{\prime }+p+1}}{8(q+1)}(B_{k,k^{\prime },k^{\prime }+p}-C_{k,k^{\prime },k^{\prime }-p+1})\int \overline{\unicode[STIX]{x1D6EF}}_{k-p+3,-k+k^{\prime }-q,q+2}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime }),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle C_{1}\frac{3}{160(p+1)}\mathop{\sum }_{j=0}^{3}(-1)^{k^{\prime }+q+j}\binom{3}{j}A_{k,k^{\prime },k^{\prime }+q+j,j}\int \unicode[STIX]{x1D6EF}_{k-q-2j+4,-k+k^{\prime }+q,-q-2}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad -\,C_{2}\frac{(-1)^{k}}{8(q+1)}(B_{k,k^{\prime },k-p}-C_{k,k^{\prime },k-p+1})\int \unicode[STIX]{x1D6EF}_{k^{\prime }+p+3,-p-2,-k+k^{\prime }+p}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad +\,C_{3}\frac{3}{160(q+1)}\mathop{\sum }_{j=0}^{3}(-1)^{k^{\prime }+j}\binom{3}{j}A_{k,k^{\prime },k^{\prime }+p+j,j}\int \overline{\unicode[STIX]{x1D6EF}}_{k-p-2j+4,p+2,-k+k^{\prime }+p}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad -\,C_{4}\frac{(-1)^{k^{\prime }+p+1}}{8(q+1)}(B_{k,k^{\prime },k^{\prime }+p}-C_{k,k^{\prime },k^{\prime }-p+1})\int \overline{\unicode[STIX]{x1D6EF}}_{k-p+3,-k+k^{\prime }-q,q+2}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime }),\nonumber\end{eqnarray}$$
where the numbers
 $A_{k,k^{\prime },i,j},B_{k,k^{\prime },i}$
and
$A_{k,k^{\prime },i,j},B_{k,k^{\prime },i}$
and
![]() $C_{k,k^{\prime },i}$
are defined in Lemma 4.27 and where the integrals are over
$C_{k,k^{\prime },i}$
are defined in Lemma 4.27 and where the integrals are over
 $G^{\prime }(\mathbb{Q})Z^{\prime }(\mathbb{A})\backslash G^{\prime }(\mathbb{A})$
.
$G^{\prime }(\mathbb{Q})Z^{\prime }(\mathbb{A})\backslash G^{\prime }(\mathbb{A})$
.
To compute the constants
 $C_{1},C_{2},C_{3}$
and
$C_{1},C_{2},C_{3}$
and
![]() $C_{4}$
, let us start with a trivial remark. The family
$C_{4}$
, let us start with a trivial remark. The family
 $(a_{r}^{(p)}\boxtimes a_{s}^{(q)})_{0\leqslant r\leqslant p,0\leqslant s\leqslant q}$
is a weight basis of
$(a_{r}^{(p)}\boxtimes a_{s}^{(q)})_{0\leqslant r\leqslant p,0\leqslant s\leqslant q}$
is a weight basis of
 $\operatorname{Sym}^{p}V_{2,\mathbb{C}}^{\vee }\,\boxtimes \,\operatorname{Sym}^{q}V_{2,\mathbb{C}}^{\vee }$
for the action of
$\operatorname{Sym}^{p}V_{2,\mathbb{C}}^{\vee }\,\boxtimes \,\operatorname{Sym}^{q}V_{2,\mathbb{C}}^{\vee }$
for the action of
![]() $\text{U}(1)^{2}$
and, by definition, the vector
$\text{U}(1)^{2}$
and, by definition, the vector
![]() $v$
is a weight vector for the maximal compact torus
$v$
is a weight vector for the maximal compact torus
 $T^{\prime }\subset G(\mathbb{R})$
. Hence, the vector
$T^{\prime }\subset G(\mathbb{R})$
. Hence, the vector
 $X_{(1,-1)}^{i}v\in W(-p-q-3)$
is again a weight vector and, because
$X_{(1,-1)}^{i}v\in W(-p-q-3)$
is again a weight vector and, because
 $\text{U}(1)^{2}=T^{\prime }$
, its image under the
$\text{U}(1)^{2}=T^{\prime }$
, its image under the
![]() $\text{U}(1)^{2}$
-equivariant projection
$\text{U}(1)^{2}$
-equivariant projection
 $$\begin{eqnarray}\unicode[STIX]{x1D71A}:\unicode[STIX]{x1D704}^{\ast }W(-p-q-3)\longrightarrow \operatorname{Sym}^{p}V_{2,\mathbb{C}}^{\vee }\boxtimes \operatorname{Sym}^{q}V_{2,\mathbb{C}}^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D71A}:\unicode[STIX]{x1D704}^{\ast }W(-p-q-3)\longrightarrow \operatorname{Sym}^{p}V_{2,\mathbb{C}}^{\vee }\boxtimes \operatorname{Sym}^{q}V_{2,\mathbb{C}}^{\vee }\end{eqnarray}$$
is equal to
 $\unicode[STIX]{x1D706}_{i}(v)a_{r_{i}}^{(p)}\boxtimes a_{s_{i}}^{(q)}$
for some complex number
$\unicode[STIX]{x1D706}_{i}(v)a_{r_{i}}^{(p)}\boxtimes a_{s_{i}}^{(q)}$
for some complex number
![]() $\unicode[STIX]{x1D706}_{i}(v)$
and some integers
$\unicode[STIX]{x1D706}_{i}(v)$
and some integers
![]() $r_{i},s_{i}$
.
$r_{i},s_{i}$
.
Given
![]() $i$
, is
$i$
, is
![]() $\unicode[STIX]{x1D706}_{i}(v)$
zero or not? Note that we have the liberty to multiply the vector
$\unicode[STIX]{x1D706}_{i}(v)$
zero or not? Note that we have the liberty to multiply the vector
![]() $w$
which enters the definition of the cohomology class
$w$
which enters the definition of the cohomology class
![]() $\unicode[STIX]{x1D714}$
associated to the cusp form
$\unicode[STIX]{x1D714}$
associated to the cusp form
![]() $\unicode[STIX]{x1D6F9}$
(Lemma 4.26) by any non-zero complex number. Of course, this has the effect to multiply
$\unicode[STIX]{x1D6F9}$
(Lemma 4.26) by any non-zero complex number. Of course, this has the effect to multiply
![]() $\unicode[STIX]{x1D714}$
by a scalar, but does not change the ratio
$\unicode[STIX]{x1D714}$
by a scalar, but does not change the ratio
 $\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{K}}}\rangle _{B}/\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}$
that has to be computed (see Lemma 4.21). If
$\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{K}}}\rangle _{B}/\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}$
that has to be computed (see Lemma 4.21). If
 $\unicode[STIX]{x1D706}_{i}(v)\neq 0$
, we can replace the vector
$\unicode[STIX]{x1D706}_{i}(v)\neq 0$
, we can replace the vector
![]() $w$
by
$w$
by
 $\unicode[STIX]{x1D706}_{i}(v)^{-1}w$
. This has the effect of replacing the vector
$\unicode[STIX]{x1D706}_{i}(v)^{-1}w$
. This has the effect of replacing the vector
![]() $v=Jw$
by
$v=Jw$
by
 $\unicode[STIX]{x1D706}_{i}(v)^{-1}v$
. For this choice,
$\unicode[STIX]{x1D706}_{i}(v)^{-1}v$
. For this choice,
 $\unicode[STIX]{x1D71A}(X_{(1,-1)}^{i}v)=a_{r_{i}}^{(p)}\boxtimes a_{s_{i}}^{(q)}$
and so the computation of the pairing follows (see (14)).
$\unicode[STIX]{x1D71A}(X_{(1,-1)}^{i}v)=a_{r_{i}}^{(p)}\boxtimes a_{s_{i}}^{(q)}$
and so the computation of the pairing follows (see (14)).
Lemma 4.30. Let
 $p=k-1$
and
$p=k-1$
and
 $q=k^{\prime }-1$
. Then, for any non-zero vector
$q=k^{\prime }-1$
. Then, for any non-zero vector
 $v\in W(-p-q-3)$
of weight
$v\in W(-p-q-3)$
of weight
 $\unicode[STIX]{x1D706}^{\prime }(-k,k^{\prime },-p-q)$
, the image of
$\unicode[STIX]{x1D706}^{\prime }(-k,k^{\prime },-p-q)$
, the image of
 $X_{(1,-1)}v$
under the
$X_{(1,-1)}v$
under the
![]() $G^{\prime }$
-equivariant projection
$G^{\prime }$
-equivariant projection
 $$\begin{eqnarray}\unicode[STIX]{x1D71A}:\unicode[STIX]{x1D704}^{\ast }W(-p-q-3)\longrightarrow \operatorname{Sym}^{p}V_{2,\mathbb{C}}^{\vee }\boxtimes \operatorname{Sym}^{q}V_{2,\mathbb{C}}^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D71A}:\unicode[STIX]{x1D704}^{\ast }W(-p-q-3)\longrightarrow \operatorname{Sym}^{p}V_{2,\mathbb{C}}^{\vee }\boxtimes \operatorname{Sym}^{q}V_{2,\mathbb{C}}^{\vee }\end{eqnarray}$$
is non-zero.
Proof. Thanks to the explanations preceding Lemma 4.26 and by symmetry under the Weyl group, we are reduced to prove the following statement. If
 $X_{-(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})}\in \mathfrak{g}$
is a root vector associated to
$X_{-(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})}\in \mathfrak{g}$
is a root vector associated to
 $-(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})$
and if
$-(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})$
and if
 $v\in W(-p-q-3)$
is a highest weight vector for the action of the diagonal maximal torus
$v\in W(-p-q-3)$
is a highest weight vector for the action of the diagonal maximal torus
![]() $T$
, then
$T$
, then
 $\unicode[STIX]{x1D70C}(X_{-(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})}v)\neq 0$
. Let
$\unicode[STIX]{x1D70C}(X_{-(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})}v)\neq 0$
. Let
 $X_{-\unicode[STIX]{x1D70C}_{1}},X_{-\unicode[STIX]{x1D70C}_{2}}\in \mathfrak{g}$
be root vectors associated to the simple negative roots. We can assume that
$X_{-\unicode[STIX]{x1D70C}_{1}},X_{-\unicode[STIX]{x1D70C}_{2}}\in \mathfrak{g}$
be root vectors associated to the simple negative roots. We can assume that
 $X_{-\unicode[STIX]{x1D70C}_{2}}\in \mathfrak{g}^{\prime }$
and that
$X_{-\unicode[STIX]{x1D70C}_{2}}\in \mathfrak{g}^{\prime }$
and that
 $X_{-(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})}=[X_{-\unicode[STIX]{x1D70C}_{1}},X_{-\unicode[STIX]{x1D70C}_{2}}]$
. The vector
$X_{-(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})}=[X_{-\unicode[STIX]{x1D70C}_{1}},X_{-\unicode[STIX]{x1D70C}_{2}}]$
. The vector
![]() $X_{-\unicode[STIX]{x1D70C}_{1}}v$
is a highest weight vector of the representation
$X_{-\unicode[STIX]{x1D70C}_{1}}v$
is a highest weight vector of the representation
 $\operatorname{Sym}^{k-1}V_{2,\mathbb{C}}^{\vee }\boxtimes \operatorname{Sym}^{k^{\prime }-1}V_{2,\mathbb{C}}^{\vee }$
which is a subrepresentation of
$\operatorname{Sym}^{k-1}V_{2,\mathbb{C}}^{\vee }\boxtimes \operatorname{Sym}^{k^{\prime }-1}V_{2,\mathbb{C}}^{\vee }$
which is a subrepresentation of
 $\unicode[STIX]{x1D704}^{\ast }W(-k-k^{\prime }-1)$
. Hence, we have
$\unicode[STIX]{x1D704}^{\ast }W(-k-k^{\prime }-1)$
. Hence, we have
 $\unicode[STIX]{x1D71A}(X_{-\unicode[STIX]{x1D70C}_{2}}X_{-\unicode[STIX]{x1D70C}_{1}}v)=0$
. It is well known that
$\unicode[STIX]{x1D71A}(X_{-\unicode[STIX]{x1D70C}_{2}}X_{-\unicode[STIX]{x1D70C}_{1}}v)=0$
. It is well known that
 $W(-k-k^{\prime }-1)$
is generated by applying monomials in the variables
$W(-k-k^{\prime }-1)$
is generated by applying monomials in the variables
![]() $X_{-\unicode[STIX]{x1D70C}_{1}}$
and
$X_{-\unicode[STIX]{x1D70C}_{1}}$
and
![]() $X_{-\unicode[STIX]{x1D70C}_{2}}$
to
$X_{-\unicode[STIX]{x1D70C}_{2}}$
to
![]() $v$
. Furthermore,
$v$
. Furthermore,
 $X_{-\unicode[STIX]{x1D70C}_{2}}X_{-\unicode[STIX]{x1D70C}_{1}}$
and
$X_{-\unicode[STIX]{x1D70C}_{2}}X_{-\unicode[STIX]{x1D70C}_{1}}$
and
 $X_{-\unicode[STIX]{x1D70C}_{1}}X_{-\unicode[STIX]{x1D70C}_{2}}$
are the only two such monomials whose application to
$X_{-\unicode[STIX]{x1D70C}_{1}}X_{-\unicode[STIX]{x1D70C}_{2}}$
are the only two such monomials whose application to
![]() $v$
gives weight
$v$
gives weight
 $\unicode[STIX]{x1D706}(k-1,k^{\prime }-1,-k-k^{\prime }-2)$
, which is the highest weight of the representation
$\unicode[STIX]{x1D706}(k-1,k^{\prime }-1,-k-k^{\prime }-2)$
, which is the highest weight of the representation
 $\operatorname{Sym}^{k-1}V_{2,\mathbb{C}}^{\vee }\,\boxtimes \,\operatorname{Sym}^{k^{\prime }-1}V_{2,\mathbb{C}}^{\vee }$
. So, the fact that
$\operatorname{Sym}^{k-1}V_{2,\mathbb{C}}^{\vee }\,\boxtimes \,\operatorname{Sym}^{k^{\prime }-1}V_{2,\mathbb{C}}^{\vee }$
. So, the fact that
 $\unicode[STIX]{x1D71A}(X_{-\unicode[STIX]{x1D70C}_{2}}X_{-\unicode[STIX]{x1D70C}_{1}}v)=0$
implies that
$\unicode[STIX]{x1D71A}(X_{-\unicode[STIX]{x1D70C}_{2}}X_{-\unicode[STIX]{x1D70C}_{1}}v)=0$
implies that
 $\unicode[STIX]{x1D71A}(X_{-\unicode[STIX]{x1D70C}_{1}}X_{-\unicode[STIX]{x1D70C}_{2}}v)\neq 0$
which implies
$\unicode[STIX]{x1D71A}(X_{-\unicode[STIX]{x1D70C}_{1}}X_{-\unicode[STIX]{x1D70C}_{2}}v)\neq 0$
which implies
 $\unicode[STIX]{x1D71A}(X_{-(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})}v)\neq 0$
.◻
$\unicode[STIX]{x1D71A}(X_{-(\unicode[STIX]{x1D70C}_{1}+\unicode[STIX]{x1D70C}_{2})}v)\neq 0$
.◻
Remark 4.31. In [Reference MolevMol07, Theorem 9.6.2], Molev constructs a basis of irreducible representations
![]() $W$
of
$W$
of
![]() $G$
and is able to derive explicit formulas for the action of generators of the Lie algebra of
$G$
and is able to derive explicit formulas for the action of generators of the Lie algebra of
![]() $G$
on the vectors of the basis. The non-vanishing of
$G$
on the vectors of the basis. The non-vanishing of
![]() $\unicode[STIX]{x1D706}_{i}(v)$
can be derived from his result at the price of a very lengthy (but elementary) calculation. Thanks to a program implementing Molev’s result and written in Python by Molin, the author verified numerically the non-vanishing of
$\unicode[STIX]{x1D706}_{i}(v)$
can be derived from his result at the price of a very lengthy (but elementary) calculation. Thanks to a program implementing Molev’s result and written in Python by Molin, the author verified numerically the non-vanishing of
![]() $\unicode[STIX]{x1D706}_{i}(v)$
for some small values of
$\unicode[STIX]{x1D706}_{i}(v)$
for some small values of
![]() $p,q,k$
and
$p,q,k$
and
![]() $k^{\prime }$
.
$k^{\prime }$
.
Corollary 4.32. Assume
 $p=k-1$
and
$p=k-1$
and
 $q=k^{\prime }-1$
. There exists
$q=k^{\prime }-1$
. There exists
 $v\in W(-p-q-3)$
of weight
$v\in W(-p-q-3)$
of weight
 $\unicode[STIX]{x1D706}^{\prime }(-k,k^{\prime },-p-q)$
such that
$\unicode[STIX]{x1D706}^{\prime }(-k,k^{\prime },-p-q)$
such that
 $\langle X_{(1,-1)}v,a_{0}^{(p)}\boxtimes a_{q}^{(q)}\rangle =(-1)^{p}(2i)^{-k-k^{\prime }-2}$
.
$\langle X_{(1,-1)}v,a_{0}^{(p)}\boxtimes a_{q}^{(q)}\rangle =(-1)^{p}(2i)^{-k-k^{\prime }-2}$
.
5 Computation of the integral
Given a cuspidal automorphic representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $G$
, the spinor
$G$
, the spinor
![]() $L$
-function is defined as the partial Euler product
$L$
-function is defined as the partial Euler product
 $$\begin{eqnarray}L_{V}(s,\unicode[STIX]{x1D70B},r)=\mathop{\prod }_{v\notin V}L(s,\unicode[STIX]{x1D70B}_{v},r)\end{eqnarray}$$
$$\begin{eqnarray}L_{V}(s,\unicode[STIX]{x1D70B},r)=\mathop{\prod }_{v\notin V}L(s,\unicode[STIX]{x1D70B}_{v},r)\end{eqnarray}$$
where
![]() $V$
denotes the set of places where
$V$
denotes the set of places where
![]() $\unicode[STIX]{x1D70B}$
is ramified and where
$\unicode[STIX]{x1D70B}$
is ramified and where
 $r:\text{}^{L}G^{0}\simeq G\longrightarrow \text{GL}(4)$
is the natural inclusion. This Euler product is absolutely convergent for
$r:\text{}^{L}G^{0}\simeq G\longrightarrow \text{GL}(4)$
is the natural inclusion. This Euler product is absolutely convergent for
![]() $\text{Re}\,s$
big enough. In [Reference Piatetski-ShapiroPia97], the analytic continuation and a functional equation of
$\text{Re}\,s$
big enough. In [Reference Piatetski-ShapiroPia97], the analytic continuation and a functional equation of
 $L_{V}(s,\unicode[STIX]{x1D70B},r)$
are deduced from the analytic continuation and a functional equation of a family of Eisenstein series
$L_{V}(s,\unicode[STIX]{x1D70B},r)$
are deduced from the analytic continuation and a functional equation of a family of Eisenstein series
![]() $E^{\unicode[STIX]{x1D6F7}}$
, via an integral representation. In this section, as a direct consequence of Proposition 5.3, we show that for suitable choice of data, the integrals that appear in the statement of Corollary 4.29 coincide with a special value of such an integral representation. Via Bessel models, the integrals of [Reference Piatetski-ShapiroPia97] expand into Euler products and we perform the relevant local unramified computation in Proposition 5.9. The ramified non-archimedean integrals are considered in Proposition 5.11. The archimedean integral is computed in Proposition 5.12.
$E^{\unicode[STIX]{x1D6F7}}$
, via an integral representation. In this section, as a direct consequence of Proposition 5.3, we show that for suitable choice of data, the integrals that appear in the statement of Corollary 4.29 coincide with a special value of such an integral representation. Via Bessel models, the integrals of [Reference Piatetski-ShapiroPia97] expand into Euler products and we perform the relevant local unramified computation in Proposition 5.9. The ramified non-archimedean integrals are considered in Proposition 5.11. The archimedean integral is computed in Proposition 5.12.
5.1 Comparison with Piatetski-Shapiro’s integral
Let
![]() $dt_{\infty }$
be the Lebesgue measure on the additive group
$dt_{\infty }$
be the Lebesgue measure on the additive group
![]() $\mathbb{R}$
. If
$\mathbb{R}$
. If
![]() $v$
is a non-archimedean place of
$v$
is a non-archimedean place of
![]() $\mathbb{Q}$
, let
$\mathbb{Q}$
, let
![]() $dt_{v}$
be the measure for which
$dt_{v}$
be the measure for which
![]() $\mathbb{Z}_{v}$
has volume one. Following [Reference Tate, Cassels and FrölichTat67], let
$\mathbb{Z}_{v}$
has volume one. Following [Reference Tate, Cassels and FrölichTat67], let
![]() $d^{\times }t_{v}$
be the Haar measure on
$d^{\times }t_{v}$
be the Haar measure on
![]() $\mathbb{Q}_{v}^{\times }$
defined by
$\mathbb{Q}_{v}^{\times }$
defined by
 $$\begin{eqnarray}d^{\times }t_{v}=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{dt_{v}}{|t_{v}|}\quad & \text{if }v\text{ is archimedean},\\ \displaystyle \frac{p}{p-1}\frac{dt_{v}}{|t_{v}|}\quad & \text{if }v\text{ is }p\text{-adic}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}d^{\times }t_{v}=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{dt_{v}}{|t_{v}|}\quad & \text{if }v\text{ is archimedean},\\ \displaystyle \frac{p}{p-1}\frac{dt_{v}}{|t_{v}|}\quad & \text{if }v\text{ is }p\text{-adic}.\end{array}\right.\end{eqnarray}$$
Let
![]() $dt$
, respectively
$dt$
, respectively
![]() $d^{\times }t$
, denote the product measure
$d^{\times }t$
, denote the product measure
![]() $\prod _{v}dt_{v}$
on
$\prod _{v}dt_{v}$
on
![]() $\mathbb{A}$
, respectively the product measure
$\mathbb{A}$
, respectively the product measure
 $\prod _{v}d^{\times }t_{v}$
on
$\prod _{v}d^{\times }t_{v}$
on
![]() $\mathbb{A}^{\times }$
.
$\mathbb{A}^{\times }$
.
Proposition 5.1. Let
 $\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2}:\mathbb{Q}^{\times }\backslash \mathbb{A}^{\times }\longrightarrow \mathbb{C}^{\times }$
be continuous characters and let
$\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2}:\mathbb{Q}^{\times }\backslash \mathbb{A}^{\times }\longrightarrow \mathbb{C}^{\times }$
be continuous characters and let
![]() $s\in \mathbb{C}$
. Let
$s\in \mathbb{C}$
. Let
 $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s}$
be the character of
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s}$
be the character of
![]() $B^{\prime }(\mathbb{A})$
defined by
$B^{\prime }(\mathbb{A})$
defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s}\left(\left(\begin{array}{@{}cc@{}}a_{1} & b_{1}\\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & b_{2}\\ & d_{2}\end{array}\right)\right)=\unicode[STIX]{x1D707}(a_{1}/d_{2})|a_{1}/d_{2}|^{s+1/2}\unicode[STIX]{x1D708}_{1}^{-1}(d_{1})\unicode[STIX]{x1D708}_{2}^{-1}(d_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s}\left(\left(\begin{array}{@{}cc@{}}a_{1} & b_{1}\\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & b_{2}\\ & d_{2}\end{array}\right)\right)=\unicode[STIX]{x1D707}(a_{1}/d_{2})|a_{1}/d_{2}|^{s+1/2}\unicode[STIX]{x1D708}_{1}^{-1}(d_{1})\unicode[STIX]{x1D708}_{2}^{-1}(d_{2}).\end{eqnarray}$$
Then, for any Schwartz–Bruhat function
![]() $\unicode[STIX]{x1D6F7}$
on
$\unicode[STIX]{x1D6F7}$
on
![]() $\mathbb{A}^{4}$
, the following statements hold:
$\mathbb{A}^{4}$
, the following statements hold:
-
(i) the function on
 $G^{\prime }(\mathbb{A})$
defined by belongs to
$G^{\prime }(\mathbb{A})$
defined by belongs to $$\begin{eqnarray}\displaystyle & & \displaystyle (g_{1},g_{2})\longmapsto f^{\unicode[STIX]{x1D6F7}}(g_{1},g_{2},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D707}(\text{det}\,g_{1})|\text{det}\,g_{1}|^{s+1/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\mathbb{A}^{\times }}\int _{\mathbb{A}^{\times }}\unicode[STIX]{x1D6F7}((0,t_{1})g_{1},(0,t_{2})g_{2})|t_{1}t_{2}|^{s+1/2}\unicode[STIX]{x1D707}(t_{1}t_{2})\unicode[STIX]{x1D708}_{1}(t_{1})\unicode[STIX]{x1D708}_{2}(t_{2})\,d^{\times }t_{1}\,d^{\times }t_{2}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (g_{1},g_{2})\longmapsto f^{\unicode[STIX]{x1D6F7}}(g_{1},g_{2},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D707}(\text{det}\,g_{1})|\text{det}\,g_{1}|^{s+1/2}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\int _{\mathbb{A}^{\times }}\int _{\mathbb{A}^{\times }}\unicode[STIX]{x1D6F7}((0,t_{1})g_{1},(0,t_{2})g_{2})|t_{1}t_{2}|^{s+1/2}\unicode[STIX]{x1D707}(t_{1}t_{2})\unicode[STIX]{x1D708}_{1}(t_{1})\unicode[STIX]{x1D708}_{2}(t_{2})\,d^{\times }t_{1}\,d^{\times }t_{2}\nonumber\end{eqnarray}$$
 $\operatorname{ind}_{B^{\prime }(\mathbb{A})}^{G^{\prime }(\mathbb{A})}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s}$
;
$\operatorname{ind}_{B^{\prime }(\mathbb{A})}^{G^{\prime }(\mathbb{A})}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s}$
;
-
(ii) the Eisenstein series
is absolutely convergent for $$\begin{eqnarray}E^{\unicode[STIX]{x1D6F7}}(g_{1},g_{2},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)=\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}f^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FE}g_{1},\unicode[STIX]{x1D6FE}^{\prime }g_{2},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)\end{eqnarray}$$
$$\begin{eqnarray}E^{\unicode[STIX]{x1D6F7}}(g_{1},g_{2},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)=\mathop{\sum }_{(\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime })\in B^{\prime }(\mathbb{Q})\backslash G^{\prime }(\mathbb{Q})}f^{\unicode[STIX]{x1D6F7}}(\unicode[STIX]{x1D6FE}g_{1},\unicode[STIX]{x1D6FE}^{\prime }g_{2},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)\end{eqnarray}$$
 $\text{Re}\,s$
big enough and satisfies a functional equation.
$\text{Re}\,s$
big enough and satisfies a functional equation.
Proof. The first statement follows from a trivial computation and the second from [Reference Piatetski-ShapiroPia97, Theorem 5.1]. ◻
When
![]() $\unicode[STIX]{x1D707}$
is the trivial character, we denote
$\unicode[STIX]{x1D707}$
is the trivial character, we denote
 $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s}$
by
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s}$
by
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s}$
for simplicity.
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s}$
for simplicity.
Let us recall that for
 $d\equiv c~(\text{mod}~2)$
, the algebraic character
$d\equiv c~(\text{mod}~2)$
, the algebraic character
![]() $\unicode[STIX]{x1D706}(d,c)$
of the diagonal maximal torus of
$\unicode[STIX]{x1D706}(d,c)$
of the diagonal maximal torus of
![]() $\text{GL}_{2}$
is defined by
$\text{GL}_{2}$
is defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D706}(d,c):\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \\ & \unicode[STIX]{x1D6FC}^{-1}\unicode[STIX]{x1D708}\end{array}\right)\longmapsto \unicode[STIX]{x1D6FC}^{d}\unicode[STIX]{x1D708}^{(c-d)/2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}(d,c):\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC} & \\ & \unicode[STIX]{x1D6FC}^{-1}\unicode[STIX]{x1D708}\end{array}\right)\longmapsto \unicode[STIX]{x1D6FC}^{d}\unicode[STIX]{x1D708}^{(c-d)/2}.\end{eqnarray}$$
Lemma 5.2. Let
![]() $\unicode[STIX]{x1D708}_{1}^{0}$
and
$\unicode[STIX]{x1D708}_{1}^{0}$
and
![]() $\unicode[STIX]{x1D708}_{2}^{0}$
be two finite-order Hecke characters of respective signs
$\unicode[STIX]{x1D708}_{2}^{0}$
be two finite-order Hecke characters of respective signs
![]() $(-1)^{p}$
and
$(-1)^{p}$
and
![]() $(-1)^{q}$
. Let
$(-1)^{q}$
. Let
![]() $\unicode[STIX]{x1D708}_{1}$
denote the Hecke character
$\unicode[STIX]{x1D708}_{1}$
denote the Hecke character
![]() $|\,|^{-q}\unicode[STIX]{x1D708}_{1}^{0}$
and
$|\,|^{-q}\unicode[STIX]{x1D708}_{1}^{0}$
and
![]() $\unicode[STIX]{x1D708}_{2}$
denote the Hecke character
$\unicode[STIX]{x1D708}_{2}$
denote the Hecke character
![]() $|\,|^{-p}\unicode[STIX]{x1D708}_{2}^{0}$
. Then, the following statements are satisfied:
$|\,|^{-p}\unicode[STIX]{x1D708}_{2}^{0}$
. Then, the following statements are satisfied:
-
(i) the restriction of the archimedean part of
 $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2}$
to the identity component of the diagonal maximal torus of
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2}$
to the identity component of the diagonal maximal torus of
 $G^{\prime }(\mathbb{R})$
is
$G^{\prime }(\mathbb{R})$
is
 $\unicode[STIX]{x1D706}(p+2,p)\boxtimes \unicode[STIX]{x1D706}(q+2,q)$
;
$\unicode[STIX]{x1D706}(p+2,p)\boxtimes \unicode[STIX]{x1D706}(q+2,q)$
; -
(ii) the non-archimedean part
 $\unicode[STIX]{x1D712}_{f}$
of
$\unicode[STIX]{x1D712}_{f}$
of
 $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2}$
verifies for any
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2}$
verifies for any $$\begin{eqnarray}\unicode[STIX]{x1D712}_{f}\left(\left(\begin{array}{@{}cc@{}}a_{1}\unicode[STIX]{x1D6FC}_{1} & b_{1}\\ & d_{1}\unicode[STIX]{x1D6FF}_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2}\unicode[STIX]{x1D6FC}_{2} & b_{2}\\ & d_{2}\unicode[STIX]{x1D6FF}_{2}\end{array}\right)\right)=a_{1}^{-(p+1)}d_{1}a_{2}^{-(q+1)}d_{2}\unicode[STIX]{x1D708}_{1}^{0}(\unicode[STIX]{x1D6FF}_{1})^{-1}\unicode[STIX]{x1D708}_{2}^{0}(\unicode[STIX]{x1D6FF}_{2})^{-1}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{f}\left(\left(\begin{array}{@{}cc@{}}a_{1}\unicode[STIX]{x1D6FC}_{1} & b_{1}\\ & d_{1}\unicode[STIX]{x1D6FF}_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2}\unicode[STIX]{x1D6FC}_{2} & b_{2}\\ & d_{2}\unicode[STIX]{x1D6FF}_{2}\end{array}\right)\right)=a_{1}^{-(p+1)}d_{1}a_{2}^{-(q+1)}d_{2}\unicode[STIX]{x1D708}_{1}^{0}(\unicode[STIX]{x1D6FF}_{1})^{-1}\unicode[STIX]{x1D708}_{2}^{0}(\unicode[STIX]{x1D6FF}_{2})^{-1}\end{eqnarray}$$
 $a_{1},d_{1},a_{2},d_{2}\in \mathbb{Q}^{+},\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FF}_{2}\in \widehat{\mathbb{Z}}^{\times }$
such that
$a_{1},d_{1},a_{2},d_{2}\in \mathbb{Q}^{+},\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FF}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FF}_{2}\in \widehat{\mathbb{Z}}^{\times }$
such that
 $a_{1}d_{1}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FF}_{1}=a_{2}d_{2}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FF}_{2}$
and any
$a_{1}d_{1}\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FF}_{1}=a_{2}d_{2}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FF}_{2}$
and any
 $b_{1},b_{2}\in \mathbb{A}_{f}$
.
$b_{1},b_{2}\in \mathbb{A}_{f}$
.
Proof. Let
 $$\begin{eqnarray}\left(\left(\begin{array}{@{}cc@{}}a_{1} & b_{1}\\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & b_{2}\\ & d_{2}\end{array}\right)\right)\in G^{\prime }(\mathbb{A}).\end{eqnarray}$$
$$\begin{eqnarray}\left(\left(\begin{array}{@{}cc@{}}a_{1} & b_{1}\\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & b_{2}\\ & d_{2}\end{array}\right)\right)\in G^{\prime }(\mathbb{A}).\end{eqnarray}$$
Because
 $a_{1}d_{1}=a_{2}d_{2}$
, we have the identities
$a_{1}d_{1}=a_{2}d_{2}$
, we have the identities
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2}\left(\left(\begin{array}{@{}cc@{}}a_{1} & b_{1}\\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & b_{2}\\ & d_{2}\end{array}\right)\right) & = & \displaystyle |a_{1}/d_{2}|^{p+q+2}|d_{1}|^{q}|d_{2}|^{p}\unicode[STIX]{x1D708}_{1}^{0}(d_{1})^{-1}\unicode[STIX]{x1D708}_{2}^{0}(d_{2})^{-1}\nonumber\\ \displaystyle & = & \displaystyle |a_{1}|^{p+2}|a_{1}d_{1}|^{-1}\unicode[STIX]{x1D708}_{1}^{0}(d_{1})^{-1}|a_{2}|^{q+2}|a_{2}d_{2}|^{-1}\unicode[STIX]{x1D708}_{2}^{0}(d_{2})^{-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2}\left(\left(\begin{array}{@{}cc@{}}a_{1} & b_{1}\\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & b_{2}\\ & d_{2}\end{array}\right)\right) & = & \displaystyle |a_{1}/d_{2}|^{p+q+2}|d_{1}|^{q}|d_{2}|^{p}\unicode[STIX]{x1D708}_{1}^{0}(d_{1})^{-1}\unicode[STIX]{x1D708}_{2}^{0}(d_{2})^{-1}\nonumber\\ \displaystyle & = & \displaystyle |a_{1}|^{p+2}|a_{1}d_{1}|^{-1}\unicode[STIX]{x1D708}_{1}^{0}(d_{1})^{-1}|a_{2}|^{q+2}|a_{2}d_{2}|^{-1}\unicode[STIX]{x1D708}_{2}^{0}(d_{2})^{-1}.\nonumber\end{eqnarray}$$
For a diagonal element
 $$\begin{eqnarray}\left(\left(\begin{array}{@{}cc@{}}a_{1} & \\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & \\ & d_{2}\end{array}\right)\right)\in G^{\prime }(\mathbb{R})^{+},\end{eqnarray}$$
$$\begin{eqnarray}\left(\left(\begin{array}{@{}cc@{}}a_{1} & \\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & \\ & d_{2}\end{array}\right)\right)\in G^{\prime }(\mathbb{R})^{+},\end{eqnarray}$$
we have
 $a_{1}d_{1}=a_{2}d_{2}>0$
, hence
$a_{1}d_{1}=a_{2}d_{2}>0$
, hence
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2}\left(\left(\begin{array}{@{}cc@{}}a_{1} & \\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & \\ & d_{2}\end{array}\right)\right) & = & \displaystyle |a_{1}|^{p+2}|a_{1}d_{1}|^{-1}\operatorname{sgn}(d_{1})^{p}|a_{2}|^{q+2}|a_{2}d_{2}|^{-1}\operatorname{sgn}(d_{2})^{q}\nonumber\\ \displaystyle & = & \displaystyle |a_{1}|^{p+2}(a_{1}d_{1})^{-1}\operatorname{sgn}(a_{1})^{p}|a_{2}|^{q+2}(a_{2}d_{2})^{-1}\operatorname{sgn}(a_{2})^{q}\nonumber\\ \displaystyle & = & \displaystyle a_{1}^{p+2}(a_{1}d_{1})^{-1}a_{2}^{q+2}(a_{2}d_{2})^{-1}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D706}(p+2,p)\boxtimes \unicode[STIX]{x1D706}(q+2,q))\left(\left(\begin{array}{@{}cc@{}}a_{1} & \\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & \\ & d_{2}\end{array}\right)\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2}\left(\left(\begin{array}{@{}cc@{}}a_{1} & \\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & \\ & d_{2}\end{array}\right)\right) & = & \displaystyle |a_{1}|^{p+2}|a_{1}d_{1}|^{-1}\operatorname{sgn}(d_{1})^{p}|a_{2}|^{q+2}|a_{2}d_{2}|^{-1}\operatorname{sgn}(d_{2})^{q}\nonumber\\ \displaystyle & = & \displaystyle |a_{1}|^{p+2}(a_{1}d_{1})^{-1}\operatorname{sgn}(a_{1})^{p}|a_{2}|^{q+2}(a_{2}d_{2})^{-1}\operatorname{sgn}(a_{2})^{q}\nonumber\\ \displaystyle & = & \displaystyle a_{1}^{p+2}(a_{1}d_{1})^{-1}a_{2}^{q+2}(a_{2}d_{2})^{-1}\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D706}(p+2,p)\boxtimes \unicode[STIX]{x1D706}(q+2,q))\left(\left(\begin{array}{@{}cc@{}}a_{1} & \\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & \\ & d_{2}\end{array}\right)\right).\nonumber\end{eqnarray}$$
This proves the first statement. Let
![]() $\unicode[STIX]{x1D712}_{\infty }$
denote the archimedean part of
$\unicode[STIX]{x1D712}_{\infty }$
denote the archimedean part of
 $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2}$
. Then, the second statement follows from the equalities
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2}$
. Then, the second statement follows from the equalities
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D712}_{f}\left(\left(\begin{array}{@{}cc@{}}a_{1}\unicode[STIX]{x1D6FC}_{1} & b_{1}\\ & d_{1}\unicode[STIX]{x1D6FF}_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2}\unicode[STIX]{x1D6FC}_{2} & b_{2}\\ & d_{2}\unicode[STIX]{x1D6FF}_{2}\end{array}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D712}_{f}\left(\left(\begin{array}{@{}cc@{}}a_{1} & \\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & \\ & d_{2}\end{array}\right)\right)\unicode[STIX]{x1D712}_{f}\left(\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{1} & b_{1}/a_{1}\\ & \unicode[STIX]{x1D6FF}_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{2} & b_{2}/a_{2}\\ & \unicode[STIX]{x1D6FF}_{2}\end{array}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D712}_{\infty }\left(\left(\begin{array}{@{}cc@{}}a_{1} & \\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & \\ & d_{2}\end{array}\right)\right)^{-1}\unicode[STIX]{x1D712}_{f}\left(\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{1} & b_{1}/a_{1}\\ & \unicode[STIX]{x1D6FF}_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{2} & b_{2}/a_{2}\\ & \unicode[STIX]{x1D6FF}_{2}\end{array}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =(a_{1}^{p+2}(a_{1}d_{1})^{-1}a_{2}^{q+2}(a_{2}d_{2})^{-1})^{-1}\unicode[STIX]{x1D708}_{1}^{0}(\unicode[STIX]{x1D6FF}_{1})^{-1}\unicode[STIX]{x1D708}_{2}^{0}(\unicode[STIX]{x1D6FF}_{2})^{-1}.\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D712}_{f}\left(\left(\begin{array}{@{}cc@{}}a_{1}\unicode[STIX]{x1D6FC}_{1} & b_{1}\\ & d_{1}\unicode[STIX]{x1D6FF}_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2}\unicode[STIX]{x1D6FC}_{2} & b_{2}\\ & d_{2}\unicode[STIX]{x1D6FF}_{2}\end{array}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D712}_{f}\left(\left(\begin{array}{@{}cc@{}}a_{1} & \\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & \\ & d_{2}\end{array}\right)\right)\unicode[STIX]{x1D712}_{f}\left(\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{1} & b_{1}/a_{1}\\ & \unicode[STIX]{x1D6FF}_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{2} & b_{2}/a_{2}\\ & \unicode[STIX]{x1D6FF}_{2}\end{array}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D712}_{\infty }\left(\left(\begin{array}{@{}cc@{}}a_{1} & \\ & d_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}a_{2} & \\ & d_{2}\end{array}\right)\right)^{-1}\unicode[STIX]{x1D712}_{f}\left(\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{1} & b_{1}/a_{1}\\ & \unicode[STIX]{x1D6FF}_{1}\end{array}\right),\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}_{2} & b_{2}/a_{2}\\ & \unicode[STIX]{x1D6FF}_{2}\end{array}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \quad =(a_{1}^{p+2}(a_{1}d_{1})^{-1}a_{2}^{q+2}(a_{2}d_{2})^{-1})^{-1}\unicode[STIX]{x1D708}_{1}^{0}(\unicode[STIX]{x1D6FF}_{1})^{-1}\unicode[STIX]{x1D708}_{2}^{0}(\unicode[STIX]{x1D6FF}_{2})^{-1}.\square\nonumber\end{eqnarray}$$
The following result obviously implies that, for a suitable choice of data, the Eisenstein series appearing in the integrals of Corollary 4.29 coincide with a special value of that defined above.
Proposition 5.3. Let
![]() $\unicode[STIX]{x1D708}_{1}^{0}$
and
$\unicode[STIX]{x1D708}_{1}^{0}$
and
![]() $\unicode[STIX]{x1D708}_{2}^{0}$
be two finite-order Hecke characters of respective signs
$\unicode[STIX]{x1D708}_{2}^{0}$
be two finite-order Hecke characters of respective signs
![]() $(-1)^{p}$
and
$(-1)^{p}$
and
![]() $(-1)^{q}$
. Let
$(-1)^{q}$
. Let
![]() $\unicode[STIX]{x1D708}_{1}$
denote the Hecke character
$\unicode[STIX]{x1D708}_{1}$
denote the Hecke character
![]() $|\,|^{-q}\unicode[STIX]{x1D708}_{1}^{0}$
and
$|\,|^{-q}\unicode[STIX]{x1D708}_{1}^{0}$
and
![]() $\unicode[STIX]{x1D708}_{2}$
denote the Hecke character
$\unicode[STIX]{x1D708}_{2}$
denote the Hecke character
![]() $|\,|^{-p}\unicode[STIX]{x1D708}_{2}^{0}$
. Let
$|\,|^{-p}\unicode[STIX]{x1D708}_{2}^{0}$
. Let
 $\unicode[STIX]{x1D6F7}_{1,f}=\prod _{v<\infty }\unicode[STIX]{x1D6F7}_{1,v}$
and
$\unicode[STIX]{x1D6F7}_{1,f}=\prod _{v<\infty }\unicode[STIX]{x1D6F7}_{1,v}$
and
 $\unicode[STIX]{x1D6F7}_{2,f}=\prod _{v<\infty }\unicode[STIX]{x1D6F7}_{2,v}$
be factorizable Schwartz–Bruhat functions on
$\unicode[STIX]{x1D6F7}_{2,f}=\prod _{v<\infty }\unicode[STIX]{x1D6F7}_{2,v}$
be factorizable Schwartz–Bruhat functions on
![]() $\mathbb{A}_{f}^{2}$
such that for
$\mathbb{A}_{f}^{2}$
such that for
 $j=1,2$
and any
$j=1,2$
and any
![]() $v$
, the function
$v$
, the function
![]() $\unicode[STIX]{x1D6F7}_{j,v}$
is
$\unicode[STIX]{x1D6F7}_{j,v}$
is
![]() $\overline{\mathbb{Q}}$
-valued. Let
$\overline{\mathbb{Q}}$
-valued. Let
![]() $S_{j}$
be the set of places where
$S_{j}$
be the set of places where
![]() $\unicode[STIX]{x1D708}_{j}$
and
$\unicode[STIX]{x1D708}_{j}$
and
![]() $\unicode[STIX]{x1D6F7}_{j,f}$
are ramified. Then, there exist
$\unicode[STIX]{x1D6F7}_{j,f}$
are ramified. Then, there exist
 $\unicode[STIX]{x1D719}_{f}\in {\mathcal{B}}_{p,\overline{\mathbb{Q}}}$
and
$\unicode[STIX]{x1D719}_{f}\in {\mathcal{B}}_{p,\overline{\mathbb{Q}}}$
and
 $\unicode[STIX]{x1D719}_{f}^{\prime }\in {\mathcal{B}}_{q,\overline{\mathbb{Q}}}$
such that the following statement is verified. For any integers
$\unicode[STIX]{x1D719}_{f}^{\prime }\in {\mathcal{B}}_{q,\overline{\mathbb{Q}}}$
such that the following statement is verified. For any integers
 $r\equiv p~(\text{mod}~2)$
and
$r\equiv p~(\text{mod}~2)$
and
 $s\equiv q~(\text{mod}~2)$
, let
$s\equiv q~(\text{mod}~2)$
, let
![]() $\unicode[STIX]{x1D6F7}$
be the Schwartz–Bruhat function on
$\unicode[STIX]{x1D6F7}$
be the Schwartz–Bruhat function on
![]() $\mathbb{A}^{4}$
defined by
$\mathbb{A}^{4}$
defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}(x_{1},y_{1},x_{2},y_{2})=\frac{(-1)^{p+q+r+s}(2i)^{p+q+2}\unicode[STIX]{x1D70B}^{2(p+q)}}{((p+q-1)!)^{2}L_{S_{1}}(p+q+2,\unicode[STIX]{x1D708}_{1})L_{S_{2}}(p+q+2,\unicode[STIX]{x1D708}_{2})}\unicode[STIX]{x1D6F7}_{1}(x_{1},y_{1})\unicode[STIX]{x1D6F7}_{2}(x_{2},y_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}(x_{1},y_{1},x_{2},y_{2})=\frac{(-1)^{p+q+r+s}(2i)^{p+q+2}\unicode[STIX]{x1D70B}^{2(p+q)}}{((p+q-1)!)^{2}L_{S_{1}}(p+q+2,\unicode[STIX]{x1D708}_{1})L_{S_{2}}(p+q+2,\unicode[STIX]{x1D708}_{2})}\unicode[STIX]{x1D6F7}_{1}(x_{1},y_{1})\unicode[STIX]{x1D6F7}_{2}(x_{2},y_{2}).\end{eqnarray}$$
Here, we denote by
![]() $\unicode[STIX]{x1D6F7}_{1}$
and
$\unicode[STIX]{x1D6F7}_{1}$
and
![]() $\unicode[STIX]{x1D6F7}_{2}$
the factorizable Schwartz–Bruhat functions
$\unicode[STIX]{x1D6F7}_{2}$
the factorizable Schwartz–Bruhat functions
 $\unicode[STIX]{x1D6F7}_{1}=\prod _{v}\unicode[STIX]{x1D6F7}_{1,v}$
and
$\unicode[STIX]{x1D6F7}_{1}=\prod _{v}\unicode[STIX]{x1D6F7}_{1,v}$
and
 $\unicode[STIX]{x1D6F7}_{2}=\prod _{v}\unicode[STIX]{x1D6F7}_{2,v}$
on
$\unicode[STIX]{x1D6F7}_{2}=\prod _{v}\unicode[STIX]{x1D6F7}_{2,v}$
on
![]() $\mathbb{A}^{2}$
where
$\mathbb{A}^{2}$
where
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{1,\infty }(x_{1},y_{1}) & = & \displaystyle (ix_{1}+y_{1})^{(p-r)/2}(ix_{1}-y_{1})^{(p+r)/2}e^{-\unicode[STIX]{x1D70B}(x_{1}^{2}+y_{1}^{2})},\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}_{2,\infty }(x_{2},y_{2}) & = & \displaystyle (ix_{2}+y_{2})^{(q-s)/2}(ix_{2}-y_{2})^{(q+s)/2}e^{-\unicode[STIX]{x1D70B}(x_{2}^{2}+y_{2}^{2})}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{1,\infty }(x_{1},y_{1}) & = & \displaystyle (ix_{1}+y_{1})^{(p-r)/2}(ix_{1}-y_{1})^{(p+r)/2}e^{-\unicode[STIX]{x1D70B}(x_{1}^{2}+y_{1}^{2})},\nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}_{2,\infty }(x_{2},y_{2}) & = & \displaystyle (ix_{2}+y_{2})^{(q-s)/2}(ix_{2}-y_{2})^{(q+s)/2}e^{-\unicode[STIX]{x1D70B}(x_{2}^{2}+y_{2}^{2})}.\nonumber\end{eqnarray}$$
Then, for any
 $(g_{1},g_{2})\in G^{\prime }(\mathbb{A})$
, we have
$(g_{1},g_{2})\in G^{\prime }(\mathbb{A})$
, we have
 $$\begin{eqnarray}(\unicode[STIX]{x1D719}_{r}^{p}\otimes \unicode[STIX]{x1D719}_{f})(g_{1})(\unicode[STIX]{x1D719}_{s}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(g_{2})=f^{\unicode[STIX]{x1D6F7}}((g_{1},g_{2}),1,\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D719}_{r}^{p}\otimes \unicode[STIX]{x1D719}_{f})(g_{1})(\unicode[STIX]{x1D719}_{s}^{q}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })(g_{2})=f^{\unicode[STIX]{x1D6F7}}((g_{1},g_{2}),1,\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2).\end{eqnarray}$$
Proof. For any place
![]() $v$
and any
$v$
and any
 $g_{v}\in \text{GL}_{2}(\mathbb{Q}_{v})$
let
$g_{v}\in \text{GL}_{2}(\mathbb{Q}_{v})$
let
 $$\begin{eqnarray}Z_{v}^{\unicode[STIX]{x1D6F7}_{j,v}}(g_{v},\unicode[STIX]{x1D708}_{j,v},s)=\int _{\mathbb{Q}_{v}^{\times }}\unicode[STIX]{x1D6F7}_{j,v}((0,t)g_{v})|t|^{s+1/2}\unicode[STIX]{x1D708}_{j,v}(t)\,d^{\times }t.\end{eqnarray}$$
$$\begin{eqnarray}Z_{v}^{\unicode[STIX]{x1D6F7}_{j,v}}(g_{v},\unicode[STIX]{x1D708}_{j,v},s)=\int _{\mathbb{Q}_{v}^{\times }}\unicode[STIX]{x1D6F7}_{j,v}((0,t)g_{v})|t|^{s+1/2}\unicode[STIX]{x1D708}_{j,v}(t)\,d^{\times }t.\end{eqnarray}$$
Then, we have the following factorization into an Euler product of local Tate integrals
 $$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(\frac{(-1)^{p+q+r+s}(2i)^{p+q+2}\unicode[STIX]{x1D70B}^{2(p+q)}}{((p+q-1)!)^{2}L_{S_{1}}(p+q+2,\unicode[STIX]{x1D708}_{1})L_{S_{2}}(p+q+2,\unicode[STIX]{x1D708}_{2})}\biggr)^{-1}f^{\unicode[STIX]{x1D6F7}}(g_{1},g_{2},1,\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2)\nonumber\\ \displaystyle & & \displaystyle \quad =|\text{det}\,g_{1}|^{p+q+2}\mathop{\prod }_{j=1}^{2}\biggl(\mathop{\prod }_{v}Z_{v}^{\unicode[STIX]{x1D6F7}_{j,v}}(g_{j,v},\unicode[STIX]{x1D708}_{j,v},p+q+3/2)\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \biggl(\frac{(-1)^{p+q+r+s}(2i)^{p+q+2}\unicode[STIX]{x1D70B}^{2(p+q)}}{((p+q-1)!)^{2}L_{S_{1}}(p+q+2,\unicode[STIX]{x1D708}_{1})L_{S_{2}}(p+q+2,\unicode[STIX]{x1D708}_{2})}\biggr)^{-1}f^{\unicode[STIX]{x1D6F7}}(g_{1},g_{2},1,\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},p+q+3/2)\nonumber\\ \displaystyle & & \displaystyle \quad =|\text{det}\,g_{1}|^{p+q+2}\mathop{\prod }_{j=1}^{2}\biggl(\mathop{\prod }_{v}Z_{v}^{\unicode[STIX]{x1D6F7}_{j,v}}(g_{j,v},\unicode[STIX]{x1D708}_{j,v},p+q+3/2)\biggr).\nonumber\end{eqnarray}$$
At the archimedean place, we have
 $$\begin{eqnarray}Z_{\infty }^{\unicode[STIX]{x1D6F7}_{1,\infty }}(1,\unicode[STIX]{x1D708}_{1,\infty },p+q+3/2)Z_{\infty }^{\unicode[STIX]{x1D6F7}_{2,\infty }}(1,\unicode[STIX]{x1D708}_{2,\infty },p+q+3/2)=(-1)^{(p+q+r+s)/2}\unicode[STIX]{x1D70B}^{-2(p+q)}\unicode[STIX]{x1D6E4}(p+q)^{2}\end{eqnarray}$$
$$\begin{eqnarray}Z_{\infty }^{\unicode[STIX]{x1D6F7}_{1,\infty }}(1,\unicode[STIX]{x1D708}_{1,\infty },p+q+3/2)Z_{\infty }^{\unicode[STIX]{x1D6F7}_{2,\infty }}(1,\unicode[STIX]{x1D708}_{2,\infty },p+q+3/2)=(-1)^{(p+q+r+s)/2}\unicode[STIX]{x1D70B}^{-2(p+q)}\unicode[STIX]{x1D6E4}(p+q)^{2}\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6E4}$
is the gamma function. The function
$\unicode[STIX]{x1D6E4}$
is the gamma function. The function
![]() $\unicode[STIX]{x1D6F7}_{\infty }$
has weight
$\unicode[STIX]{x1D6F7}_{\infty }$
has weight
![]() $\unicode[STIX]{x1D706}^{\prime }(r,s)$
for the action of
$\unicode[STIX]{x1D706}^{\prime }(r,s)$
for the action of
![]() $\text{U}(1)^{2}$
, which is the same weight as
$\text{U}(1)^{2}$
, which is the same weight as
![]() $\unicode[STIX]{x1D719}_{r}^{p}\unicode[STIX]{x1D719}_{s}^{q}$
. The Iwasawa decomposition for
$\unicode[STIX]{x1D719}_{r}^{p}\unicode[STIX]{x1D719}_{s}^{q}$
. The Iwasawa decomposition for
![]() $G^{\prime }(\mathbb{R})$
implies that the weights for
$G^{\prime }(\mathbb{R})$
implies that the weights for
![]() $\text{U}(1)^{2}$
in
$\text{U}(1)^{2}$
in
 $\operatorname{ind}_{B^{\prime }(\mathbb{R})}^{G^{\prime }(\mathbb{R})}(\unicode[STIX]{x1D706}(p+2,p)\boxtimes \unicode[STIX]{x1D706}(q+2,q))$
are multiplicity free. Hence, it follows from the first statement of Proposition 5.1 and from Lemma 5.2 that the archimedean part
$\operatorname{ind}_{B^{\prime }(\mathbb{R})}^{G^{\prime }(\mathbb{R})}(\unicode[STIX]{x1D706}(p+2,p)\boxtimes \unicode[STIX]{x1D706}(q+2,q))$
are multiplicity free. Hence, it follows from the first statement of Proposition 5.1 and from Lemma 5.2 that the archimedean part
 $$\begin{eqnarray}\frac{(-1)^{p+q+r+s}(2i)^{p+q+2}\unicode[STIX]{x1D70B}^{2(p+q)}}{((p+q-1)!)^{2}}Z_{\infty }^{\unicode[STIX]{x1D6F7}_{1,\infty }}(g_{1,\infty },\unicode[STIX]{x1D708}_{1,\infty },p+q+3/2)Z_{\infty }^{\unicode[STIX]{x1D6F7}_{2,\infty }}(g_{2,\infty },\unicode[STIX]{x1D708}_{2,\infty },p+q+3/2)\end{eqnarray}$$
$$\begin{eqnarray}\frac{(-1)^{p+q+r+s}(2i)^{p+q+2}\unicode[STIX]{x1D70B}^{2(p+q)}}{((p+q-1)!)^{2}}Z_{\infty }^{\unicode[STIX]{x1D6F7}_{1,\infty }}(g_{1,\infty },\unicode[STIX]{x1D708}_{1,\infty },p+q+3/2)Z_{\infty }^{\unicode[STIX]{x1D6F7}_{2,\infty }}(g_{2,\infty },\unicode[STIX]{x1D708}_{2,\infty },p+q+3/2)\end{eqnarray}$$
of
![]() $f^{\unicode[STIX]{x1D6F7}}$
is proportional to
$f^{\unicode[STIX]{x1D6F7}}$
is proportional to
![]() $\unicode[STIX]{x1D719}_{r}^{p}\unicode[STIX]{x1D719}_{s}^{q}$
. By the choice of our normalization factor, the two are in fact equal. We claim that the non-archimedean part
$\unicode[STIX]{x1D719}_{r}^{p}\unicode[STIX]{x1D719}_{s}^{q}$
. By the choice of our normalization factor, the two are in fact equal. We claim that the non-archimedean part
![]() $f^{\unicode[STIX]{x1D6F7}_{f}}$
belongs to
$f^{\unicode[STIX]{x1D6F7}_{f}}$
belongs to
 ${\mathcal{B}}_{p,\overline{\mathbb{Q}}}\otimes {\mathcal{B}}_{q,\overline{\mathbb{Q}}}$
. To prove this, let
${\mathcal{B}}_{p,\overline{\mathbb{Q}}}\otimes {\mathcal{B}}_{q,\overline{\mathbb{Q}}}$
. To prove this, let
![]() $v$
be a non-archimedean place. By the first statement of Proposition 5.1 and the Iwasawa decomposition
$v$
be a non-archimedean place. By the first statement of Proposition 5.1 and the Iwasawa decomposition
 $\text{GL}_{2}(\mathbb{Q}_{v})=\text{B}_{2}(\mathbb{Q}_{v})\text{GL}_{2}(\mathbb{Z}_{v})$
, the function
$\text{GL}_{2}(\mathbb{Q}_{v})=\text{B}_{2}(\mathbb{Q}_{v})\text{GL}_{2}(\mathbb{Z}_{v})$
, the function
 $$\begin{eqnarray}g\longmapsto Z_{v}^{\unicode[STIX]{x1D6F7}_{j,v}}(g,\unicode[STIX]{x1D708}_{j,v},p+q+3/2)\end{eqnarray}$$
$$\begin{eqnarray}g\longmapsto Z_{v}^{\unicode[STIX]{x1D6F7}_{j,v}}(g,\unicode[STIX]{x1D708}_{j,v},p+q+3/2)\end{eqnarray}$$
is determined by its restriction to
 $\text{GL}_{2}(\mathbb{Z}_{v})$
. Assume that
$\text{GL}_{2}(\mathbb{Z}_{v})$
. Assume that
![]() $v$
does not belong to
$v$
does not belong to
![]() $S_{1}\cup S_{2}$
, in other words, for
$S_{1}\cup S_{2}$
, in other words, for
 $j=1,2$
, the character
$j=1,2$
, the character
![]() $\unicode[STIX]{x1D708}_{j}$
is unramified at
$\unicode[STIX]{x1D708}_{j}$
is unramified at
![]() $v$
and
$v$
and
![]() $\unicode[STIX]{x1D6F7}_{j,v}$
is the indicator function of
$\unicode[STIX]{x1D6F7}_{j,v}$
is the indicator function of
![]() $\mathbb{Z}_{v}^{2}$
. Let us show that
$\mathbb{Z}_{v}^{2}$
. Let us show that
 $g\mapsto Z_{v}^{\unicode[STIX]{x1D6F7}_{j,v}}(g,\unicode[STIX]{x1D708}_{j,v},p+q+3/2)$
is constant on
$g\mapsto Z_{v}^{\unicode[STIX]{x1D6F7}_{j,v}}(g,\unicode[STIX]{x1D708}_{j,v},p+q+3/2)$
is constant on
 $\text{GL}_{2}(\mathbb{Z}_{v})$
and let us compute its value. Let
$\text{GL}_{2}(\mathbb{Z}_{v})$
and let us compute its value. Let
 $g=(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \text{GL}_{2}(\mathbb{Z}_{v})$
. As
$g=(\!\begin{smallmatrix}a & b\\ c & d\end{smallmatrix}\!)\in \text{GL}_{2}(\mathbb{Z}_{v})$
. As
![]() $c$
is coprime to
$c$
is coprime to
![]() $d$
, for any non-negative integer
$d$
, for any non-negative integer
![]() $n$
and any
$n$
and any
![]() $t\in \mathbb{Q}_{v}^{\times }$
, we have
$t\in \mathbb{Q}_{v}^{\times }$
, we have
 $$\begin{eqnarray}(0,t)\in \mathbb{Z}_{v}^{2}\;\Longleftrightarrow \;(tc_{v},td_{v})\in \mathbb{Z}_{v}^{2}\end{eqnarray}$$
$$\begin{eqnarray}(0,t)\in \mathbb{Z}_{v}^{2}\;\Longleftrightarrow \;(tc_{v},td_{v})\in \mathbb{Z}_{v}^{2}\end{eqnarray}$$
and this implies
 $\unicode[STIX]{x1D6F7}_{j,v}((0,t)g)=\unicode[STIX]{x1D6F7}_{j,v}(tc,td)=\unicode[STIX]{x1D6F7}_{j,v}(0,t)$
. Hence, by a standard computation, for any
$\unicode[STIX]{x1D6F7}_{j,v}((0,t)g)=\unicode[STIX]{x1D6F7}_{j,v}(tc,td)=\unicode[STIX]{x1D6F7}_{j,v}(0,t)$
. Hence, by a standard computation, for any
 $j=1,2$
, any non-archimedean
$j=1,2$
, any non-archimedean
 $v\notin S_{1}\cup S_{2}$
and any
$v\notin S_{1}\cup S_{2}$
and any
 $g\in \text{GL}_{2}(\mathbb{Z}_{v})$
, we have
$g\in \text{GL}_{2}(\mathbb{Z}_{v})$
, we have
 $$\begin{eqnarray}Z_{v}^{\unicode[STIX]{x1D6F7}_{j,v}}(g,\unicode[STIX]{x1D708}_{j,v},p+q+3/2)=L_{v}(p+q+2,\unicode[STIX]{x1D708}_{j})\end{eqnarray}$$
$$\begin{eqnarray}Z_{v}^{\unicode[STIX]{x1D6F7}_{j,v}}(g,\unicode[STIX]{x1D708}_{j,v},p+q+3/2)=L_{v}(p+q+2,\unicode[STIX]{x1D708}_{j})\end{eqnarray}$$
where
 $L_{v}(s,\unicode[STIX]{x1D708}_{j})$
is the local
$L_{v}(s,\unicode[STIX]{x1D708}_{j})$
is the local
![]() $L$
-factor (see [Reference Tate, Cassels and FrölichTat67, 2.5, p. 320]). Moreover, it follows from the computations of [Reference Tate, Cassels and FrölichTat67, 2.5, p. 321] that, for any non-archimedean
$L$
-factor (see [Reference Tate, Cassels and FrölichTat67, 2.5, p. 320]). Moreover, it follows from the computations of [Reference Tate, Cassels and FrölichTat67, 2.5, p. 321] that, for any non-archimedean
 $v\in S_{1}\cup S_{2}$
and any
$v\in S_{1}\cup S_{2}$
and any
 $g\in \text{GL}_{2}(\mathbb{Z}_{v})$
, we have
$g\in \text{GL}_{2}(\mathbb{Z}_{v})$
, we have
 $$\begin{eqnarray}Z_{v}^{\unicode[STIX]{x1D6F7}_{j,v}}(g,\unicode[STIX]{x1D708}_{j,v},p+q+3/2)\in \overline{\mathbb{Q}}.\end{eqnarray}$$
$$\begin{eqnarray}Z_{v}^{\unicode[STIX]{x1D6F7}_{j,v}}(g,\unicode[STIX]{x1D708}_{j,v},p+q+3/2)\in \overline{\mathbb{Q}}.\end{eqnarray}$$
Hence, by our choice of the normalization factor
 $1/(L_{S_{1}}(p+q+2,\unicode[STIX]{x1D708}_{1})L_{S_{2}}(p+q+2,\unicode[STIX]{x1D708}_{2}))$
, the non-archimedean part
$1/(L_{S_{1}}(p+q+2,\unicode[STIX]{x1D708}_{1})L_{S_{2}}(p+q+2,\unicode[STIX]{x1D708}_{2}))$
, the non-archimedean part
![]() $f^{\unicode[STIX]{x1D6F7}_{f}}$
of
$f^{\unicode[STIX]{x1D6F7}_{f}}$
of
![]() $f^{\unicode[STIX]{x1D6F7}}$
is
$f^{\unicode[STIX]{x1D6F7}}$
is
![]() $\overline{\mathbb{Q}}$
-valued. Furthermore, it is obviously invariant by right translation by the subgroup
$\overline{\mathbb{Q}}$
-valued. Furthermore, it is obviously invariant by right translation by the subgroup
![]() $(\!\begin{smallmatrix}\widehat{\mathbb{Z}}^{\times } & \\ & 1\end{smallmatrix}\!)$
of
$(\!\begin{smallmatrix}\widehat{\mathbb{Z}}^{\times } & \\ & 1\end{smallmatrix}\!)$
of
![]() $\text{GL}_{2}(\widehat{\mathbb{Z}})$
. As a consequence, it follows from Lemma 4.3 and from the second statement of Lemma 5.2 that
$\text{GL}_{2}(\widehat{\mathbb{Z}})$
. As a consequence, it follows from Lemma 4.3 and from the second statement of Lemma 5.2 that
![]() $f^{\unicode[STIX]{x1D6F7}_{f}}$
belongs to
$f^{\unicode[STIX]{x1D6F7}_{f}}$
belongs to
 ${\mathcal{B}}_{p,\overline{\mathbb{Q}}}\otimes {\mathcal{B}}_{q,\overline{\mathbb{Q}}}$
. The conclusion follows.◻
${\mathcal{B}}_{p,\overline{\mathbb{Q}}}\otimes {\mathcal{B}}_{q,\overline{\mathbb{Q}}}$
. The conclusion follows.◻
5.2 Bessel models and local computations
The previous result shows that the integrals of Corollary 4.29, which compute the regulator, coincide with special values of integrals of the shape
 $$\begin{eqnarray}\int _{G^{\prime }(\mathbb{Q})Z^{\prime }(\mathbb{A})\backslash G^{\prime }(\mathbb{A})}\unicode[STIX]{x1D6F9}(g)E^{\unicode[STIX]{x1D6F7}}(g,\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)\,dg\end{eqnarray}$$
$$\begin{eqnarray}\int _{G^{\prime }(\mathbb{Q})Z^{\prime }(\mathbb{A})\backslash G^{\prime }(\mathbb{A})}\unicode[STIX]{x1D6F9}(g)E^{\unicode[STIX]{x1D6F7}}(g,\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)\,dg\end{eqnarray}$$
for some specific choices of
![]() $\unicode[STIX]{x1D6F9}$
and
$\unicode[STIX]{x1D6F9}$
and
![]() $\unicode[STIX]{x1D6F7}$
. The properties of these integrals rely on the Fourier expansion of the cusp form
$\unicode[STIX]{x1D6F7}$
. The properties of these integrals rely on the Fourier expansion of the cusp form
![]() $\unicode[STIX]{x1D6F9}$
along the Siegel parabolic subgroup
$\unicode[STIX]{x1D6F9}$
along the Siegel parabolic subgroup
 $$\begin{eqnarray}P=\left\{\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}A & AS\\ & \text{}^{t}\!\!A^{-1}\end{array}\right),\unicode[STIX]{x1D6FC}\in \mathbb{G}_{m},A\in \text{GL}_{2},\text{}^{t}\!S=S\right\}\end{eqnarray}$$
$$\begin{eqnarray}P=\left\{\left(\begin{array}{@{}cc@{}}\unicode[STIX]{x1D6FC}A & AS\\ & \text{}^{t}\!\!A^{-1}\end{array}\right),\unicode[STIX]{x1D6FC}\in \mathbb{G}_{m},A\in \text{GL}_{2},\text{}^{t}\!S=S\right\}\end{eqnarray}$$
of
![]() $G$
. More precisely, they rely on the existence of Bessel models for cuspidal automorphic representations of
$G$
. More precisely, they rely on the existence of Bessel models for cuspidal automorphic representations of
![]() $G$
. Let us remark that some authors use the terminology ‘generalized Whittaker model’ rather than ‘Bessel model’. As a motivation for the study of such objects, the reader might find the first section of [Reference MoriyamaMor11] very interesting. To introduce Bessel models, let
$G$
. Let us remark that some authors use the terminology ‘generalized Whittaker model’ rather than ‘Bessel model’. As a motivation for the study of such objects, the reader might find the first section of [Reference MoriyamaMor11] very interesting. To introduce Bessel models, let
 $\unicode[STIX]{x1D702}:\mathbb{Q}\backslash \mathbb{A}\longrightarrow \mathbb{C}^{\times }$
be a fixed additive character, let
$\unicode[STIX]{x1D702}:\mathbb{Q}\backslash \mathbb{A}\longrightarrow \mathbb{C}^{\times }$
be a fixed additive character, let
![]() $U$
denote the unipotent radical of
$U$
denote the unipotent radical of
![]() $P$
and let
$P$
and let
 $\unicode[STIX]{x1D6EC}:U(\mathbb{Q})\backslash U(\mathbb{A})\longrightarrow \mathbb{C}^{\times }$
denote the character defined by
$\unicode[STIX]{x1D6EC}:U(\mathbb{Q})\backslash U(\mathbb{A})\longrightarrow \mathbb{C}^{\times }$
denote the character defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}\left(\left(\begin{array}{@{}cccc@{}}1 & & r & t\\ & 1 & t & s\\ & & 1 & \\ & & & 1\end{array}\right)\right)=\unicode[STIX]{x1D702}(t).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}\left(\left(\begin{array}{@{}cccc@{}}1 & & r & t\\ & 1 & t & s\\ & & 1 & \\ & & & 1\end{array}\right)\right)=\unicode[STIX]{x1D702}(t).\end{eqnarray}$$
Introduce the following subgroups of
![]() $G$
:
$G$
:
 $$\begin{eqnarray}\displaystyle D & = & \displaystyle \left\{d=\left(\begin{array}{@{}cccc@{}}d_{1} & & & \\ & d_{2} & & \\ & & d_{2} & \\ & & & d_{1}\end{array}\right),d_{1},d_{2}\in \mathbb{G}_{m}\right\},\nonumber\\ \displaystyle N & = & \displaystyle \left\{n=\left(\begin{array}{@{}cccc@{}}1 & & r & \\ & 1 & & s\\ & & 1 & \\ & & & 1\end{array}\right),u,w\in \mathbb{G}_{a}\right\},\nonumber\\ \displaystyle R & = & \displaystyle DU.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D & = & \displaystyle \left\{d=\left(\begin{array}{@{}cccc@{}}d_{1} & & & \\ & d_{2} & & \\ & & d_{2} & \\ & & & d_{1}\end{array}\right),d_{1},d_{2}\in \mathbb{G}_{m}\right\},\nonumber\\ \displaystyle N & = & \displaystyle \left\{n=\left(\begin{array}{@{}cccc@{}}1 & & r & \\ & 1 & & s\\ & & 1 & \\ & & & 1\end{array}\right),u,w\in \mathbb{G}_{a}\right\},\nonumber\\ \displaystyle R & = & \displaystyle DU.\nonumber\end{eqnarray}$$
Definition 5.4. Let
 $\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2}:\mathbb{Q}^{\times }\backslash \mathbb{A}^{\times }\longrightarrow \mathbb{C}^{\times }$
be continuous characters. Let
$\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2}:\mathbb{Q}^{\times }\backslash \mathbb{A}^{\times }\longrightarrow \mathbb{C}^{\times }$
be continuous characters. Let
![]() $\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D708}}$
be the character of
$\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D708}}$
be the character of
![]() $R(\mathbb{A})$
defined by
$R(\mathbb{A})$
defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D708}}(du)=\unicode[STIX]{x1D708}_{1}(d_{1})\unicode[STIX]{x1D708}_{2}(d_{2})\unicode[STIX]{x1D6EC}(u).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D708}}(du)=\unicode[STIX]{x1D708}_{1}(d_{1})\unicode[STIX]{x1D708}_{2}(d_{2})\unicode[STIX]{x1D6EC}(u).\end{eqnarray}$$
A cuspidal automorphic representation
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $G$
has a split Bessel model associated to
$G$
has a split Bessel model associated to
![]() $(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
if its central character
$(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
if its central character
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
coincides with
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D70B}}$
coincides with
![]() $\unicode[STIX]{x1D708}_{1}\unicode[STIX]{x1D708}_{2}$
and if there exists
$\unicode[STIX]{x1D708}_{1}\unicode[STIX]{x1D708}_{2}$
and if there exists
![]() $\unicode[STIX]{x1D6F9}\in \unicode[STIX]{x1D70B}$
such that the function on
$\unicode[STIX]{x1D6F9}\in \unicode[STIX]{x1D70B}$
such that the function on
![]() $G(\mathbb{A})$
defined by
$G(\mathbb{A})$
defined by
 $$\begin{eqnarray}g\longmapsto W_{\unicode[STIX]{x1D6F9}}(g)=\int _{(Z(\mathbb{A})R(\mathbb{Q}))\backslash R(\mathbb{A})}\unicode[STIX]{x1D6F9}(rg)\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D708}}(r)^{-1}\,dr\end{eqnarray}$$
$$\begin{eqnarray}g\longmapsto W_{\unicode[STIX]{x1D6F9}}(g)=\int _{(Z(\mathbb{A})R(\mathbb{Q}))\backslash R(\mathbb{A})}\unicode[STIX]{x1D6F9}(rg)\unicode[STIX]{x1D6FC}_{\unicode[STIX]{x1D708}}(r)^{-1}\,dr\end{eqnarray}$$
is not identically zero.
Remark 5.5. Obviously,
![]() $\unicode[STIX]{x1D70B}$
has a split Bessel model associated to
$\unicode[STIX]{x1D70B}$
has a split Bessel model associated to
![]() $(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
if and only if the function
$(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
if and only if the function
 $g\longmapsto W_{\unicode[STIX]{x1D6F9}}(g)$
is non-zero for any non-zero
$g\longmapsto W_{\unicode[STIX]{x1D6F9}}(g)$
is non-zero for any non-zero
![]() $\unicode[STIX]{x1D6F9}\in \unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D6F9}\in \unicode[STIX]{x1D70B}$
.
The connection between the integral we are interested in and split Bessel models is given by the following result.
Lemma 5.6. Let
![]() $\unicode[STIX]{x1D70B}$
be a cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}$
be a cuspidal automorphic representation of
![]() $G$
and let
$G$
and let
![]() $\unicode[STIX]{x1D6F9}\in \unicode[STIX]{x1D70B}$
. Let
$\unicode[STIX]{x1D6F9}\in \unicode[STIX]{x1D70B}$
. Let
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D6F9},\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)=\int _{(Z(\mathbb{A})G^{\prime }(\mathbb{Q}))\backslash G^{\prime }(\mathbb{A})}\unicode[STIX]{x1D6F9}(g)E^{\unicode[STIX]{x1D6F7}}(g,\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)\,dg.\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D6F9},\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)=\int _{(Z(\mathbb{A})G^{\prime }(\mathbb{Q}))\backslash G^{\prime }(\mathbb{A})}\unicode[STIX]{x1D6F9}(g)E^{\unicode[STIX]{x1D6F7}}(g,\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)\,dg.\end{eqnarray}$$
Then
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D6F9},\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)=\int _{(D(\mathbb{A})N(\mathbb{A})\backslash G^{\prime }(\mathbb{A}))}W_{\unicode[STIX]{x1D6F9}}(g)f^{\unicode[STIX]{x1D6F7}}(g,\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)\,dg\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D6F9},\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)=\int _{(D(\mathbb{A})N(\mathbb{A})\backslash G^{\prime }(\mathbb{A}))}W_{\unicode[STIX]{x1D6F9}}(g)f^{\unicode[STIX]{x1D6F7}}(g,\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)\,dg\end{eqnarray}$$
for
![]() $\text{Re}\,s$
big enough.
$\text{Re}\,s$
big enough.
Proof. Note that we are in the setting of [Reference Piatetski-ShapiroPia97, 2], for the choice
 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}=\left(\begin{array}{@{}cc@{}} & 1/2\\ 1/2 & \end{array}\right)\in U(\mathbb{Q}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}=\left(\begin{array}{@{}cc@{}} & 1/2\\ 1/2 & \end{array}\right)\in U(\mathbb{Q}).\end{eqnarray}$$
Hence, the statement follows from the proof of [Reference Piatetski-ShapiroPia97, Theorem 5.2]. ◻
Remark 5.7. The lemma shows that if
![]() $\unicode[STIX]{x1D70B}$
does not have a split Bessel model associated to
$\unicode[STIX]{x1D70B}$
does not have a split Bessel model associated to
![]() $(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
, then the integrals
$(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
, then the integrals
 $Z(\unicode[STIX]{x1D6F9},\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)$
are identically zero.
$Z(\unicode[STIX]{x1D6F9},\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)$
are identically zero.
The global definition above has a local analog. Roughly speaking, given an irreducible representation
 $(\unicode[STIX]{x1D70B}_{v},V_{\unicode[STIX]{x1D70B}_{v}})$
of
$(\unicode[STIX]{x1D70B}_{v},V_{\unicode[STIX]{x1D70B}_{v}})$
of
![]() $G(\mathbb{Q}_{v})$
, a local Bessel model of
$G(\mathbb{Q}_{v})$
, a local Bessel model of
![]() $\unicode[STIX]{x1D70B}_{v}$
is a
$\unicode[STIX]{x1D70B}_{v}$
is a
![]() $G(\mathbb{Q}_{v})$
equivariant map from
$G(\mathbb{Q}_{v})$
equivariant map from
![]() $V_{\unicode[STIX]{x1D70B}_{v}}$
to a space of functions
$V_{\unicode[STIX]{x1D70B}_{v}}$
to a space of functions
 $W:G(\mathbb{Q}_{v})\longrightarrow \mathbb{C}$
such that
$W:G(\mathbb{Q}_{v})\longrightarrow \mathbb{C}$
such that
 $W(rg)=\unicode[STIX]{x1D6FC}(r)W(g)$
, for some character
$W(rg)=\unicode[STIX]{x1D6FC}(r)W(g)$
, for some character
![]() $\unicode[STIX]{x1D6FC}$
of
$\unicode[STIX]{x1D6FC}$
of
![]() $R(\mathbb{Q}_{v})$
. For a precise definition, in particular at the archimedean place, we refer the reader to [Reference MoriyamaMor11, 1.5]. Assume that
$R(\mathbb{Q}_{v})$
. For a precise definition, in particular at the archimedean place, we refer the reader to [Reference MoriyamaMor11, 1.5]. Assume that
![]() $\unicode[STIX]{x1D70B}$
has split Bessel model associated to
$\unicode[STIX]{x1D70B}$
has split Bessel model associated to
![]() $(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
. If
$(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
. If
 $\unicode[STIX]{x1D6F9}=\bigotimes _{v}^{\prime }\unicode[STIX]{x1D6F9}_{v}$
is factorizable, it follows from the unicity of local Bessel models [Reference Piatetski-ShapiroPia97, Theorem 3.1] that the function
$\unicode[STIX]{x1D6F9}=\bigotimes _{v}^{\prime }\unicode[STIX]{x1D6F9}_{v}$
is factorizable, it follows from the unicity of local Bessel models [Reference Piatetski-ShapiroPia97, Theorem 3.1] that the function
![]() $W_{\unicode[STIX]{x1D6F9}}$
factors into a restricted product
$W_{\unicode[STIX]{x1D6F9}}$
factors into a restricted product
 $W_{\unicode[STIX]{x1D6F9}}=\prod _{v}^{\prime }W_{\unicode[STIX]{x1D6F9}_{v}}$
of local Bessel functions.
$W_{\unicode[STIX]{x1D6F9}}=\prod _{v}^{\prime }W_{\unicode[STIX]{x1D6F9}_{v}}$
of local Bessel functions.
Corollary 5.8. Assume that
 $\unicode[STIX]{x1D6F7}=\prod _{v}^{\prime }\unicode[STIX]{x1D6F7}_{v}$
and
$\unicode[STIX]{x1D6F7}=\prod _{v}^{\prime }\unicode[STIX]{x1D6F7}_{v}$
and
 $\unicode[STIX]{x1D6F9}=\bigotimes _{v}^{\prime }\unicode[STIX]{x1D6F9}_{v}$
are factorizable. Then, for
$\unicode[STIX]{x1D6F9}=\bigotimes _{v}^{\prime }\unicode[STIX]{x1D6F9}_{v}$
are factorizable. Then, for
![]() $\text{Re}\,s$
big enough, we have the Euler product expansion
$\text{Re}\,s$
big enough, we have the Euler product expansion
 $$\begin{eqnarray}Z(\unicode[STIX]{x1D6F9},\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)=\mathop{\prod }_{v}Z_{v}(W_{\unicode[STIX]{x1D6F9}_{v}},\unicode[STIX]{x1D6F7}_{v},\unicode[STIX]{x1D707}_{v},\unicode[STIX]{x1D708}_{1,v},\unicode[STIX]{x1D708}_{2,v},s)\end{eqnarray}$$
$$\begin{eqnarray}Z(\unicode[STIX]{x1D6F9},\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D707},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2},s)=\mathop{\prod }_{v}Z_{v}(W_{\unicode[STIX]{x1D6F9}_{v}},\unicode[STIX]{x1D6F7}_{v},\unicode[STIX]{x1D707}_{v},\unicode[STIX]{x1D708}_{1,v},\unicode[STIX]{x1D708}_{2,v},s)\end{eqnarray}$$
where
 $$\begin{eqnarray}Z_{v}(W_{\unicode[STIX]{x1D6F9}_{v}},\unicode[STIX]{x1D6F7}_{v},\unicode[STIX]{x1D707}_{v},\unicode[STIX]{x1D708}_{1,v},\unicode[STIX]{x1D708}_{2,v},s)=\int _{(D(\mathbb{Q}_{v})N(\mathbb{Q}_{v})\backslash G^{\prime }(\mathbb{Q}_{v}))}W_{\unicode[STIX]{x1D6F9}_{v}}(g_{v})f^{\unicode[STIX]{x1D6F7}_{v}}(g_{v},\unicode[STIX]{x1D707}_{v},\unicode[STIX]{x1D708}_{1,v},\unicode[STIX]{x1D708}_{2,v},s)\,dg_{v}\end{eqnarray}$$
$$\begin{eqnarray}Z_{v}(W_{\unicode[STIX]{x1D6F9}_{v}},\unicode[STIX]{x1D6F7}_{v},\unicode[STIX]{x1D707}_{v},\unicode[STIX]{x1D708}_{1,v},\unicode[STIX]{x1D708}_{2,v},s)=\int _{(D(\mathbb{Q}_{v})N(\mathbb{Q}_{v})\backslash G^{\prime }(\mathbb{Q}_{v}))}W_{\unicode[STIX]{x1D6F9}_{v}}(g_{v})f^{\unicode[STIX]{x1D6F7}_{v}}(g_{v},\unicode[STIX]{x1D707}_{v},\unicode[STIX]{x1D708}_{1,v},\unicode[STIX]{x1D708}_{2,v},s)\,dg_{v}\end{eqnarray}$$
for all places
![]() $v$
.
$v$
.
The end of § 5 is devoted to the computation of some of the local integrals above, under the assumption that
![]() $\unicode[STIX]{x1D70B}$
has a split Bessel model associated to
$\unicode[STIX]{x1D70B}$
has a split Bessel model associated to
![]() $(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
.
$(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
.
Proposition 5.9. Let
![]() $p$
be a non-archimedean place where
$p$
be a non-archimedean place where
![]() $\unicode[STIX]{x1D70B}$
,
$\unicode[STIX]{x1D70B}$
,
![]() $\unicode[STIX]{x1D708}_{1}$
and
$\unicode[STIX]{x1D708}_{1}$
and
![]() $\unicode[STIX]{x1D708}_{2}$
are unramified. Let
$\unicode[STIX]{x1D708}_{2}$
are unramified. Let
![]() $\unicode[STIX]{x1D6F9}_{p}$
be the standard unramified vector of
$\unicode[STIX]{x1D6F9}_{p}$
be the standard unramified vector of
![]() $\unicode[STIX]{x1D70B}_{p}$
and let
$\unicode[STIX]{x1D70B}_{p}$
and let
![]() $\unicode[STIX]{x1D6F7}_{p}$
be the indicator function of
$\unicode[STIX]{x1D6F7}_{p}$
be the indicator function of
![]() $\mathbb{Z}_{p}^{4}$
. Normalize
$\mathbb{Z}_{p}^{4}$
. Normalize
![]() $W_{\unicode[STIX]{x1D6F9}_{p}}$
in such a way that
$W_{\unicode[STIX]{x1D6F9}_{p}}$
in such a way that
 $W_{\unicode[STIX]{x1D6F9}_{p}}(1)=1$
. Then,
$W_{\unicode[STIX]{x1D6F9}_{p}}(1)=1$
. Then,
 $$\begin{eqnarray}Z_{p}(W_{\unicode[STIX]{x1D6F9}_{p}},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s)=L(s+1/2,\unicode[STIX]{x1D708}_{1,p})L(s+1/2,\unicode[STIX]{x1D708}_{2,p})L(s+2,\unicode[STIX]{x1D70B}_{p},r)\end{eqnarray}$$
$$\begin{eqnarray}Z_{p}(W_{\unicode[STIX]{x1D6F9}_{p}},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s)=L(s+1/2,\unicode[STIX]{x1D708}_{1,p})L(s+1/2,\unicode[STIX]{x1D708}_{2,p})L(s+2,\unicode[STIX]{x1D70B}_{p},r)\end{eqnarray}$$
for
![]() $\text{Re}\,s$
big enough.
$\text{Re}\,s$
big enough.
Proof. The representation
![]() $\unicode[STIX]{x1D70B}_{p}$
is a subquotient of an unramified principal series representation
$\unicode[STIX]{x1D70B}_{p}$
is a subquotient of an unramified principal series representation
 $\operatorname{ind}_{B(\mathbb{Q}_{p})}^{G(\mathbb{Q}_{p})}\unicode[STIX]{x1D712}_{p}$
(see [Reference CasselmanCas80, Proposition 2.6]), where
$\operatorname{ind}_{B(\mathbb{Q}_{p})}^{G(\mathbb{Q}_{p})}\unicode[STIX]{x1D712}_{p}$
(see [Reference CasselmanCas80, Proposition 2.6]), where
![]() $\unicode[STIX]{x1D712}_{p}$
is an unramified character of
$\unicode[STIX]{x1D712}_{p}$
is an unramified character of
![]() $T(\mathbb{Q}_{p})$
and where
$T(\mathbb{Q}_{p})$
and where
![]() $\text{ind}$
denotes normalized induction. As explained in [Reference Asgari and SchmidtAS01, 3.2], the Satake parameters are
$\text{ind}$
denotes normalized induction. As explained in [Reference Asgari and SchmidtAS01, 3.2], the Satake parameters are
 $$\begin{eqnarray}\displaystyle b_{0} & = & \displaystyle \unicode[STIX]{x1D712}_{p}\left(\left(\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & & \\ & & p & \\ & & & p\end{array}\right)\right),\nonumber\\ \displaystyle b_{1} & = & \displaystyle \unicode[STIX]{x1D712}_{p}\left(\left(\begin{array}{@{}cccc@{}}p & & & \\ & 1 & & \\ & & p^{-1} & \\ & & & 1\end{array}\right)\right),\nonumber\\ \displaystyle b_{2} & = & \displaystyle \unicode[STIX]{x1D712}_{p}\left(\left(\begin{array}{@{}cccc@{}}1 & & & \\ & p & & \\ & & 1 & \\ & & & p^{-1}\end{array}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle b_{0} & = & \displaystyle \unicode[STIX]{x1D712}_{p}\left(\left(\begin{array}{@{}cccc@{}}1 & & & \\ & 1 & & \\ & & p & \\ & & & p\end{array}\right)\right),\nonumber\\ \displaystyle b_{1} & = & \displaystyle \unicode[STIX]{x1D712}_{p}\left(\left(\begin{array}{@{}cccc@{}}p & & & \\ & 1 & & \\ & & p^{-1} & \\ & & & 1\end{array}\right)\right),\nonumber\\ \displaystyle b_{2} & = & \displaystyle \unicode[STIX]{x1D712}_{p}\left(\left(\begin{array}{@{}cccc@{}}1 & & & \\ & p & & \\ & & 1 & \\ & & & p^{-1}\end{array}\right)\right)\nonumber\\ \displaystyle & & \displaystyle \nonumber\end{eqnarray}$$
and the Langlands Euler factor is
 $$\begin{eqnarray}\displaystyle L(s,\unicode[STIX]{x1D70B}_{p},r) & = & \displaystyle \frac{1}{(1-\unicode[STIX]{x1D6FC}_{1}p^{-s})(1-\unicode[STIX]{x1D6FC}_{2}p^{-s})(1-\unicode[STIX]{x1D6FC}_{3}p^{-s})(1-\unicode[STIX]{x1D6FC}_{4}p^{-s})}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle L(s,\unicode[STIX]{x1D70B}_{p},r) & = & \displaystyle \frac{1}{(1-\unicode[STIX]{x1D6FC}_{1}p^{-s})(1-\unicode[STIX]{x1D6FC}_{2}p^{-s})(1-\unicode[STIX]{x1D6FC}_{3}p^{-s})(1-\unicode[STIX]{x1D6FC}_{4}p^{-s})}\nonumber\end{eqnarray}$$
where we introduced the convenient notation
 $\unicode[STIX]{x1D6FC}_{1}=b_{0}b_{1}b_{2}$
,
$\unicode[STIX]{x1D6FC}_{1}=b_{0}b_{1}b_{2}$
,
 $\unicode[STIX]{x1D6FC}_{2}=b_{0}b_{1}$
,
$\unicode[STIX]{x1D6FC}_{2}=b_{0}b_{1}$
,
![]() $\unicode[STIX]{x1D6FC}_{3}=b_{0}$
and
$\unicode[STIX]{x1D6FC}_{3}=b_{0}$
and
 $\unicode[STIX]{x1D6FC}_{4}=b_{0}b_{2}$
. It follows from the first statement of Proposition 5.1 that the function
$\unicode[STIX]{x1D6FC}_{4}=b_{0}b_{2}$
. It follows from the first statement of Proposition 5.1 that the function
 $g\longmapsto f^{\unicode[STIX]{x1D6F7}_{p}}(g,1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s)$
belongs to
$g\longmapsto f^{\unicode[STIX]{x1D6F7}_{p}}(g,1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s)$
belongs to
 $\operatorname{ind}_{B^{\prime }(\mathbb{Q}_{p})}^{G^{\prime }(\mathbb{Q}_{p})}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s}$
. Furthermore, it is easy to see that with our choice of
$\operatorname{ind}_{B^{\prime }(\mathbb{Q}_{p})}^{G^{\prime }(\mathbb{Q}_{p})}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s}$
. Furthermore, it is easy to see that with our choice of
![]() $\unicode[STIX]{x1D6F7}_{p}$
,
$\unicode[STIX]{x1D6F7}_{p}$
,
![]() $f^{\unicode[STIX]{x1D6F7}_{p}}$
is constant on
$f^{\unicode[STIX]{x1D6F7}_{p}}$
is constant on
![]() $G^{\prime }(\mathbb{Z}_{p})$
. As a consequence, according to the Iwasawa decomposition
$G^{\prime }(\mathbb{Z}_{p})$
. As a consequence, according to the Iwasawa decomposition
 $G^{\prime }(\mathbb{Q}_{p})=B^{\prime }(\mathbb{Q}_{p})G^{\prime }(\mathbb{Z}_{p})$
, the local integral
$G^{\prime }(\mathbb{Q}_{p})=B^{\prime }(\mathbb{Q}_{p})G^{\prime }(\mathbb{Z}_{p})$
, the local integral
 $Z_{p}(W_{\unicode[STIX]{x1D6F9}_{p}},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s)$
equals
$Z_{p}(W_{\unicode[STIX]{x1D6F9}_{p}},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s)$
equals
 $$\begin{eqnarray}\displaystyle & & \displaystyle f^{\unicode[STIX]{x1D6F7}_{p}}(1,1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s)\int _{\mathbb{Q}_{p}^{\times }}|x|^{s+1/2}W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)\right)d^{\times }x\nonumber\\ \displaystyle & & \displaystyle \quad =L(s+1/2,\unicode[STIX]{x1D708}_{1,p})L(s+1/2,\unicode[STIX]{x1D708}_{2,p})\int _{\mathbb{Q}_{p}^{\times }}|x|^{s+1/2}W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)\right)d^{\times }x.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle f^{\unicode[STIX]{x1D6F7}_{p}}(1,1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s)\int _{\mathbb{Q}_{p}^{\times }}|x|^{s+1/2}W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)\right)d^{\times }x\nonumber\\ \displaystyle & & \displaystyle \quad =L(s+1/2,\unicode[STIX]{x1D708}_{1,p})L(s+1/2,\unicode[STIX]{x1D708}_{2,p})\int _{\mathbb{Q}_{p}^{\times }}|x|^{s+1/2}W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)\right)d^{\times }x.\nonumber\end{eqnarray}$$
As the Bessel function
![]() $W_{\unicode[STIX]{x1D6F9}_{p}}$
satisfies
$W_{\unicode[STIX]{x1D6F9}_{p}}$
satisfies
 $W_{\unicode[STIX]{x1D6F9}_{p}}(ugk)=\unicode[STIX]{x1D6EC}_{p}(u)W_{\unicode[STIX]{x1D713}_{p}}(g)$
for any
$W_{\unicode[STIX]{x1D6F9}_{p}}(ugk)=\unicode[STIX]{x1D6EC}_{p}(u)W_{\unicode[STIX]{x1D713}_{p}}(g)$
for any
 $u\in U(\mathbb{Q}_{p})$
, any
$u\in U(\mathbb{Q}_{p})$
, any
 $g\in G(\mathbb{Q}_{p})$
and
$g\in G(\mathbb{Q}_{p})$
and
 $k\in G(\mathbb{Z}_{p})$
, we have
$k\in G(\mathbb{Z}_{p})$
, we have
 $$\begin{eqnarray}\displaystyle W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}p^{-m} & & & \\ & p^{-m} & & \\ & & 1 & \\ & & & 1\end{array}\right)\right) & = & \displaystyle W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}p^{-m} & & & \\ & p^{-m} & & \\ & & 1 & \\ & & & 1\end{array}\right)\left(\begin{array}{@{}cccc@{}}1 & & & 1\\ & 1 & 1 & \\ & & 1 & \\ & & & 1\end{array}\right)\right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D702}(p^{-m})W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}p^{-m} & & & \\ & p^{-m} & & \\ & & 1 & \\ & & & 1\end{array}\right)\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}p^{-m} & & & \\ & p^{-m} & & \\ & & 1 & \\ & & & 1\end{array}\right)\right) & = & \displaystyle W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}p^{-m} & & & \\ & p^{-m} & & \\ & & 1 & \\ & & & 1\end{array}\right)\left(\begin{array}{@{}cccc@{}}1 & & & 1\\ & 1 & 1 & \\ & & 1 & \\ & & & 1\end{array}\right)\right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D702}(p^{-m})W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}p^{-m} & & & \\ & p^{-m} & & \\ & & 1 & \\ & & & 1\end{array}\right)\right).\nonumber\end{eqnarray}$$
For any integer
![]() $m>0,$
we have
$m>0,$
we have
 $\unicode[STIX]{x1D702}(p^{-m})\neq 1$
. Hence,
$\unicode[STIX]{x1D702}(p^{-m})\neq 1$
. Hence,
 $$\begin{eqnarray}W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}p^{-m} & & & \\ & p^{-m} & & \\ & & 1 & \\ & & & 1\end{array}\right)\right)=0.\end{eqnarray}$$
$$\begin{eqnarray}W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}p^{-m} & & & \\ & p^{-m} & & \\ & & 1 & \\ & & & 1\end{array}\right)\right)=0.\end{eqnarray}$$
As a consequence,
 $$\begin{eqnarray}\displaystyle & & \displaystyle Z_{p}(\unicode[STIX]{x1D6F9}_{p},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s)\nonumber\\ \displaystyle & & \displaystyle \quad =L(s+1/2,\unicode[STIX]{x1D708}_{1,p})L(s+1/2,\unicode[STIX]{x1D708}_{2,p})\mathop{\sum }_{m=0}^{+\infty }p^{-m(s+1/2)}W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}p^{m} & & & \\ & p^{m} & & \\ & & 1 & \\ & & & 1\end{array}\right)\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle Z_{p}(\unicode[STIX]{x1D6F9}_{p},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s)\nonumber\\ \displaystyle & & \displaystyle \quad =L(s+1/2,\unicode[STIX]{x1D708}_{1,p})L(s+1/2,\unicode[STIX]{x1D708}_{2,p})\mathop{\sum }_{m=0}^{+\infty }p^{-m(s+1/2)}W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}p^{m} & & & \\ & p^{m} & & \\ & & 1 & \\ & & & 1\end{array}\right)\right).\nonumber\end{eqnarray}$$
Let
 $\unicode[STIX]{x1D6FD}_{1}=\unicode[STIX]{x1D708}_{1,p}(p)$
and
$\unicode[STIX]{x1D6FD}_{1}=\unicode[STIX]{x1D708}_{1,p}(p)$
and
 $\unicode[STIX]{x1D6FD}_{2}=\unicode[STIX]{x1D708}_{2,p}(p)$
. Because we assume that
$\unicode[STIX]{x1D6FD}_{2}=\unicode[STIX]{x1D708}_{2,p}(p)$
. Because we assume that
![]() $\unicode[STIX]{x1D70B}$
has a split Bessel model associated to
$\unicode[STIX]{x1D70B}$
has a split Bessel model associated to
![]() $(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
,
$(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
,
![]() $\unicode[STIX]{x1D708}_{1}\unicode[STIX]{x1D708}_{2}$
coincides with the central character of
$\unicode[STIX]{x1D708}_{1}\unicode[STIX]{x1D708}_{2}$
coincides with the central character of
![]() $\unicode[STIX]{x1D70B}$
, hence we have
$\unicode[STIX]{x1D70B}$
, hence we have
 $\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{3}=\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{4}=\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}$
. The Weyl group
$\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{3}=\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{4}=\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D6FD}_{2}$
. The Weyl group
![]() $W$
acts on the
$W$
acts on the
![]() $\unicode[STIX]{x1D6FC}_{i}$
through all permutations which preserve the relation
$\unicode[STIX]{x1D6FC}_{i}$
through all permutations which preserve the relation
 $\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{3}=\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{4}$
. More precisely, with the notation of § 2.3, we have
$\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{3}=\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{4}$
. More precisely, with the notation of § 2.3, we have
 $s_{1}\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D6FC}_{2}$
,
$s_{1}\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D6FC}_{2}$
,
 $s_{1}\unicode[STIX]{x1D6FC}_{2}=\unicode[STIX]{x1D6FC}_{1}$
,
$s_{1}\unicode[STIX]{x1D6FC}_{2}=\unicode[STIX]{x1D6FC}_{1}$
,
 $s_{1}\unicode[STIX]{x1D6FC}_{3}=\unicode[STIX]{x1D6FC}_{4}$
,
$s_{1}\unicode[STIX]{x1D6FC}_{3}=\unicode[STIX]{x1D6FC}_{4}$
,
 $s_{1}\unicode[STIX]{x1D6FC}_{4}=\unicode[STIX]{x1D6FC}_{3}$
and
$s_{1}\unicode[STIX]{x1D6FC}_{4}=\unicode[STIX]{x1D6FC}_{3}$
and
 $s_{2}\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D6FC}_{1}$
,
$s_{2}\unicode[STIX]{x1D6FC}_{1}=\unicode[STIX]{x1D6FC}_{1}$
,
 $s_{2}\unicode[STIX]{x1D6FC}_{2}=\unicode[STIX]{x1D6FC}_{4}$
,
$s_{2}\unicode[STIX]{x1D6FC}_{2}=\unicode[STIX]{x1D6FC}_{4}$
,
 $s_{2}\unicode[STIX]{x1D6FC}_{3}=\unicode[STIX]{x1D6FC}_{3}$
,
$s_{2}\unicode[STIX]{x1D6FC}_{3}=\unicode[STIX]{x1D6FC}_{3}$
,
 $s_{2}\unicode[STIX]{x1D6FC}_{4}=\unicode[STIX]{x1D6FC}_{2}$
. Let
$s_{2}\unicode[STIX]{x1D6FC}_{4}=\unicode[STIX]{x1D6FC}_{2}$
. Let
![]() ${\mathcal{A}}$
denote
${\mathcal{A}}$
denote
 $\sum _{w\in W}(-1)^{l(w)}w$
, seen as an element of the group algebra
$\sum _{w\in W}(-1)^{l(w)}w$
, seen as an element of the group algebra
![]() $\mathbb{C}[W]$
, where
$\mathbb{C}[W]$
, where
![]() $l(w)$
denotes the length of
$l(w)$
denotes the length of
![]() $w$
. According to [Reference Bump, Friedberg and FurusawaBFF97, Theorem 1.6 and Corollary 1.9(2)], the following explicit formula
$w$
. According to [Reference Bump, Friedberg and FurusawaBFF97, Theorem 1.6 and Corollary 1.9(2)], the following explicit formula
 $$\begin{eqnarray}W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}p^{m} & & & \\ & p^{m} & & \\ & & 1 & \\ & & & 1\end{array}\right)\right)W_{\unicode[STIX]{x1D6F9}_{p}}(1)^{-1}=p^{-3m/2}\frac{{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{m+2}\unicode[STIX]{x1D6FC}_{4}^{-1})}{{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1})}\end{eqnarray}$$
$$\begin{eqnarray}W_{\unicode[STIX]{x1D6F9}_{p}}\left(\left(\begin{array}{@{}cccc@{}}p^{m} & & & \\ & p^{m} & & \\ & & 1 & \\ & & & 1\end{array}\right)\right)W_{\unicode[STIX]{x1D6F9}_{p}}(1)^{-1}=p^{-3m/2}\frac{{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{m+2}\unicode[STIX]{x1D6FC}_{4}^{-1})}{{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1})}\end{eqnarray}$$
is true for any integer
![]() $m\geqslant 0$
. As a consequence, using
$m\geqslant 0$
. As a consequence, using
 $W_{\unicode[STIX]{x1D6F9}_{p}}(1)=1$
, we have
$W_{\unicode[STIX]{x1D6F9}_{p}}(1)=1$
, we have
 $$\begin{eqnarray}\displaystyle Z_{p}(W_{\unicode[STIX]{x1D6F9}_{p}},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s) & = & \displaystyle L(s+1/2,\unicode[STIX]{x1D708}_{1,p})L(s+1/2,\unicode[STIX]{x1D708}_{2,p})\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4})^{-1}{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}(1-\unicode[STIX]{x1D6FC}_{3}p^{-(s+2)})^{-1})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Z_{p}(W_{\unicode[STIX]{x1D6F9}_{p}},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s) & = & \displaystyle L(s+1/2,\unicode[STIX]{x1D708}_{1,p})L(s+1/2,\unicode[STIX]{x1D708}_{2,p})\nonumber\\ \displaystyle & & \displaystyle \times \,{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4})^{-1}{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}(1-\unicode[STIX]{x1D6FC}_{3}p^{-(s+2)})^{-1})\nonumber\end{eqnarray}$$
which can be rewritten as
 $$\begin{eqnarray}\displaystyle & & \displaystyle L(s+1/2,\unicode[STIX]{x1D708}_{1,p})L(s+1/2,\unicode[STIX]{x1D708}_{2,p})L(s+2,\unicode[STIX]{x1D70B}_{p},r)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4})^{-1}{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}(1-\unicode[STIX]{x1D6FC}_{1}p^{-(s+2)})(1-\unicode[STIX]{x1D6FC}_{2}p^{-(s+2)})(1-\unicode[STIX]{x1D6FC}_{4}p^{-(s+2)}))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle L(s+1/2,\unicode[STIX]{x1D708}_{1,p})L(s+1/2,\unicode[STIX]{x1D708}_{2,p})L(s+2,\unicode[STIX]{x1D70B}_{p},r)\nonumber\\ \displaystyle & & \displaystyle \quad \times \,{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4})^{-1}{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}(1-\unicode[STIX]{x1D6FC}_{1}p^{-(s+2)})(1-\unicode[STIX]{x1D6FC}_{2}p^{-(s+2)})(1-\unicode[STIX]{x1D6FC}_{4}p^{-(s+2)}))\nonumber\end{eqnarray}$$
because the local
![]() $L$
-factor
$L$
-factor
 $L(s+2,\unicode[STIX]{x1D70B}_{p},r)$
is invariant under
$L(s+2,\unicode[STIX]{x1D70B}_{p},r)$
is invariant under
![]() $W$
. We claim that
$W$
. We claim that
 $$\begin{eqnarray}{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}(1-\unicode[STIX]{x1D6FC}_{1}p^{-(s+2)})(1-\unicode[STIX]{x1D6FC}_{2}p^{-(s+2)})(1-\unicode[STIX]{x1D6FC}_{4}p^{-(s+2)}))={\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}(1-\unicode[STIX]{x1D6FC}_{1}p^{-(s+2)})(1-\unicode[STIX]{x1D6FC}_{2}p^{-(s+2)})(1-\unicode[STIX]{x1D6FC}_{4}p^{-(s+2)}))={\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}).\end{eqnarray}$$
Indeed, using the relation,
 $\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{3}=\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{4}$
, we find
$\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{3}=\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{4}$
, we find
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}(1-\unicode[STIX]{x1D6FC}_{1}p^{-(s+2)})(1-\unicode[STIX]{x1D6FC}_{2}p^{-(s+2)})(1-\unicode[STIX]{x1D6FC}_{4}p^{-(s+2)})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}-(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}+\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}+\unicode[STIX]{x1D6FC}_{3}^{2})p^{-(s+2)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{3}^{2}+\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}+\unicode[STIX]{x1D6FC}_{2}^{2}\unicode[STIX]{x1D6FC}_{3})p^{-2(s+2)}-\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}p^{-3(s+2)}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}(1-\unicode[STIX]{x1D6FC}_{1}p^{-(s+2)})(1-\unicode[STIX]{x1D6FC}_{2}p^{-(s+2)})(1-\unicode[STIX]{x1D6FC}_{4}p^{-(s+2)})\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}-(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}+\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}+\unicode[STIX]{x1D6FC}_{3}^{2})p^{-(s+2)}\nonumber\\ \displaystyle & & \displaystyle \qquad +\,(\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{3}^{2}+\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}+\unicode[STIX]{x1D6FC}_{2}^{2}\unicode[STIX]{x1D6FC}_{3})p^{-2(s+2)}-\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}p^{-3(s+2)}.\nonumber\end{eqnarray}$$
But, as
![]() $\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}$
is fixed by
$\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}$
is fixed by
 $s_{2}s_{1}s_{2}\in W$
, which has odd length, we have
$s_{2}s_{1}s_{2}\in W$
, which has odd length, we have
 ${\mathcal{A}}(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}p^{-(s+2)})=0$
. Similarly, note that
${\mathcal{A}}(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}p^{-(s+2)})=0$
. Similarly, note that
 $\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}$
is fixed by
$\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}$
is fixed by
![]() $s_{2}s_{1}s_{2}$
because of the relation
$s_{2}s_{1}s_{2}$
because of the relation
 $\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{3}=\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{4}$
. So
$\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{3}=\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{4}$
. So
 ${\mathcal{A}}(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}p^{-(s+2)})=0$
. Similarly we find that
${\mathcal{A}}(\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{4}^{-1}p^{-(s+2)})=0$
. Similarly we find that
 $$\begin{eqnarray}{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}p^{-(s+2)})={\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{1}p^{-2(s+2)})={\mathcal{A}}(\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}p^{-3(s+2)})=0.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}p^{-(s+2)})={\mathcal{A}}(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{1}p^{-2(s+2)})={\mathcal{A}}(\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}p^{-3(s+2)})=0.\end{eqnarray}$$
As
 $(s_{2}s_{1}s_{2})(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{2})=\unicode[STIX]{x1D6FC}_{2}^{2}\unicode[STIX]{x1D6FC}_{3}$
, we have
$(s_{2}s_{1}s_{2})(\unicode[STIX]{x1D6FC}_{3}^{2}\unicode[STIX]{x1D6FC}_{2})=\unicode[STIX]{x1D6FC}_{2}^{2}\unicode[STIX]{x1D6FC}_{3}$
, we have
 ${\mathcal{A}}((\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}+\unicode[STIX]{x1D6FC}_{2}^{2}\unicode[STIX]{x1D6FC}_{3})p^{-2(s+2)})=0$
. This proves our claim. As a consequence, we have the equality
${\mathcal{A}}((\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FC}_{3}^{2}+\unicode[STIX]{x1D6FC}_{2}^{2}\unicode[STIX]{x1D6FC}_{3})p^{-2(s+2)})=0$
. This proves our claim. As a consequence, we have the equality
 $$\begin{eqnarray}Z_{p}(W_{\unicode[STIX]{x1D6F9}_{p}},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s)=L(s+1/2,\unicode[STIX]{x1D708}_{1,p})L(s+1/2,\unicode[STIX]{x1D708}_{2,p})L(s+2,\unicode[STIX]{x1D70B}_{p},r).\square\end{eqnarray}$$
$$\begin{eqnarray}Z_{p}(W_{\unicode[STIX]{x1D6F9}_{p}},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},s)=L(s+1/2,\unicode[STIX]{x1D708}_{1,p})L(s+1/2,\unicode[STIX]{x1D708}_{2,p})L(s+2,\unicode[STIX]{x1D70B}_{p},r).\square\end{eqnarray}$$
Remark 5.10. A similar result is stated without proof in [Reference Piatetski-ShapiroPia97, Theorem 4.4].
Let us consider the ramified non-archimedean integrals.
Proposition 5.11 [Reference HarrisHar04, Lemma 3.5.4].
Let
![]() $p$
be a non-archimedean place. Then, if the Schwartz function
$p$
be a non-archimedean place. Then, if the Schwartz function
![]() $\unicode[STIX]{x1D6F7}_{p}$
and the Bessel function
$\unicode[STIX]{x1D6F7}_{p}$
and the Bessel function
![]() $W_{\unicode[STIX]{x1D6F9}_{p}}$
are
$W_{\unicode[STIX]{x1D6F9}_{p}}$
are
![]() $\overline{\mathbb{Q}}$
-valued, we have
$\overline{\mathbb{Q}}$
-valued, we have
 $$\begin{eqnarray}Z_{p}(W_{\unicode[STIX]{x1D6F9}_{p}},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},p+q+2)\in \overline{\mathbb{Q}}.\end{eqnarray}$$
$$\begin{eqnarray}Z_{p}(W_{\unicode[STIX]{x1D6F9}_{p}},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},p+q+2)\in \overline{\mathbb{Q}}.\end{eqnarray}$$
Furthermore, if
![]() $\unicode[STIX]{x1D6F9}_{p}$
has a split Bessel model associated to
$\unicode[STIX]{x1D6F9}_{p}$
has a split Bessel model associated to
 $(\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p})$
, then there exists a
$(\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p})$
, then there exists a
![]() $\overline{\mathbb{Q}}$
-valued function
$\overline{\mathbb{Q}}$
-valued function
![]() $\unicode[STIX]{x1D6F7}_{p}$
such that
$\unicode[STIX]{x1D6F7}_{p}$
such that
 $$\begin{eqnarray}Z_{p}(W_{\unicode[STIX]{x1D6F9}_{p}},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},p+q+2)\in \overline{\mathbb{Q}}^{\times }.\end{eqnarray}$$
$$\begin{eqnarray}Z_{p}(W_{\unicode[STIX]{x1D6F9}_{p}},\unicode[STIX]{x1D6F7}_{p},1,\unicode[STIX]{x1D708}_{1,p},\unicode[STIX]{x1D708}_{2,p},p+q+2)\in \overline{\mathbb{Q}}^{\times }.\end{eqnarray}$$
The archimedean computation below is a direct application of [Reference MoriyamaMor11, Theorem 7.1] and of the Mellin inversion formula.
Proposition 5.12. Let
![]() $\unicode[STIX]{x1D70B}_{\infty }$
be a discrete series representation of
$\unicode[STIX]{x1D70B}_{\infty }$
be a discrete series representation of
![]() $G(\mathbb{R})^{+}$
with minimal
$G(\mathbb{R})^{+}$
with minimal
![]() $K$
-type
$K$
-type
![]() $\unicode[STIX]{x1D70F}_{(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2})}$
. Let
$\unicode[STIX]{x1D70F}_{(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2})}$
. Let
 $\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty }:\mathbb{R}^{\times }\longrightarrow \mathbb{C}^{\times }$
be the characters defined by
$\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty }:\mathbb{R}^{\times }\longrightarrow \mathbb{C}^{\times }$
be the characters defined by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{1,\infty }(x)=|x|^{q}\operatorname{sgn}(x)^{p}, & & \displaystyle \nonumber\\ \displaystyle \unicode[STIX]{x1D708}_{2,\infty }(x)=|x|^{p}\operatorname{sgn}(x)^{q}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{1,\infty }(x)=|x|^{q}\operatorname{sgn}(x)^{p}, & & \displaystyle \nonumber\\ \displaystyle \unicode[STIX]{x1D708}_{2,\infty }(x)=|x|^{p}\operatorname{sgn}(x)^{q}. & & \displaystyle \nonumber\end{eqnarray}$$
Let
 $(v_{t})_{0\leqslant t\leqslant \unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}}$
be a standard basis of
$(v_{t})_{0\leqslant t\leqslant \unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}}$
be a standard basis of
![]() $\unicode[STIX]{x1D70F}_{(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2})}$
and for any integer
$\unicode[STIX]{x1D70F}_{(\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2})}$
and for any integer
 $0\leqslant t\leqslant \unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}$
, let
$0\leqslant t\leqslant \unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}$
, let
 $W_{\infty ,t}:G(\mathbb{R})^{+}\longrightarrow \mathbb{C}$
denote a Bessel function corresponding to
$W_{\infty ,t}:G(\mathbb{R})^{+}\longrightarrow \mathbb{C}$
denote a Bessel function corresponding to
![]() $v_{t}$
in the sense of [Reference MoriyamaMor11, 3.1]. Let
$v_{t}$
in the sense of [Reference MoriyamaMor11, 3.1]. Let
 $r\equiv p~(\text{mod}~2)$
and
$r\equiv p~(\text{mod}~2)$
and
 $s\equiv q~(\text{mod}~2)$
be two integers. Assume that
$s\equiv q~(\text{mod}~2)$
be two integers. Assume that
![]() $\unicode[STIX]{x1D6F7}_{\infty }$
is of the shape
$\unicode[STIX]{x1D6F7}_{\infty }$
is of the shape
 $$\begin{eqnarray}(x_{1},y_{1},x_{2},y_{2})\longmapsto \unicode[STIX]{x1D6F7}_{\infty }(x_{1},y_{1},x_{2},y_{2})=\unicode[STIX]{x1D6F7}_{\infty ,1}(x_{1},y_{1})\unicode[STIX]{x1D6F7}_{\infty ,2}(x_{2},y_{2})\end{eqnarray}$$
$$\begin{eqnarray}(x_{1},y_{1},x_{2},y_{2})\longmapsto \unicode[STIX]{x1D6F7}_{\infty }(x_{1},y_{1},x_{2},y_{2})=\unicode[STIX]{x1D6F7}_{\infty ,1}(x_{1},y_{1})\unicode[STIX]{x1D6F7}_{\infty ,2}(x_{2},y_{2})\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{\infty ,1}(x_{1},y_{1})=(ix_{1}+y_{1})^{(p-r)/2}(ix_{1}-y_{1})^{(p+r)/2}e^{-\unicode[STIX]{x1D70B}(x_{1}^{2}+y_{1}^{2})}, & & \displaystyle \nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}_{\infty ,2}(x_{2},y_{2})=(ix_{2}+y_{2})^{(q-s)/2}(ix_{2}-y_{2})^{(q+s)/2}e^{-\unicode[STIX]{x1D70B}(x_{2}^{2}+y_{2}^{2})}. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{\infty ,1}(x_{1},y_{1})=(ix_{1}+y_{1})^{(p-r)/2}(ix_{1}-y_{1})^{(p+r)/2}e^{-\unicode[STIX]{x1D70B}(x_{1}^{2}+y_{1}^{2})}, & & \displaystyle \nonumber\\ \displaystyle \unicode[STIX]{x1D6F7}_{\infty ,2}(x_{2},y_{2})=(ix_{2}+y_{2})^{(q-s)/2}(ix_{2}-y_{2})^{(q+s)/2}e^{-\unicode[STIX]{x1D70B}(x_{2}^{2}+y_{2}^{2})}. & & \displaystyle \nonumber\end{eqnarray}$$
Then, the following statements are satisfied.
![]() $(\text{i})$
If
$(\text{i})$
If
 $t+\unicode[STIX]{x1D706}_{2}+r\neq 0$
or
$t+\unicode[STIX]{x1D706}_{2}+r\neq 0$
or
 $-t+\unicode[STIX]{x1D706}_{1}+s\neq 0$
, then
$-t+\unicode[STIX]{x1D706}_{1}+s\neq 0$
, then
 $$\begin{eqnarray}Z_{\infty }(W_{\infty ,t},\unicode[STIX]{x1D6F7}_{\infty },1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },p+q+3/2)=0.\end{eqnarray}$$
$$\begin{eqnarray}Z_{\infty }(W_{\infty ,t},\unicode[STIX]{x1D6F7}_{\infty },1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },p+q+3/2)=0.\end{eqnarray}$$
![]() $(\text{ii})$
Otherwise, let
$(\text{ii})$
Otherwise, let
 $$\begin{eqnarray}\displaystyle a_{1} & = & \displaystyle \frac{t-\unicode[STIX]{x1D706}_{2}-(q-p)/2+2}{2},\nonumber\\ \displaystyle a_{2} & = & \displaystyle \frac{2\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}-t+(q-p)/2+2}{2},\nonumber\\ \displaystyle c_{1} & = & \displaystyle \frac{\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}+4}{4},\nonumber\\ \displaystyle c_{2} & = & \displaystyle \frac{\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}+4}{4},\nonumber\\ \displaystyle c_{3} & = & \displaystyle \frac{\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}+2}{4},\nonumber\\ \displaystyle c_{4} & = & \displaystyle \frac{\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}+2}{4}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{1} & = & \displaystyle \frac{t-\unicode[STIX]{x1D706}_{2}-(q-p)/2+2}{2},\nonumber\\ \displaystyle a_{2} & = & \displaystyle \frac{2\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}-t+(q-p)/2+2}{2},\nonumber\\ \displaystyle c_{1} & = & \displaystyle \frac{\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}+4}{4},\nonumber\\ \displaystyle c_{2} & = & \displaystyle \frac{\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}+4}{4},\nonumber\\ \displaystyle c_{3} & = & \displaystyle \frac{\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}+2}{4},\nonumber\\ \displaystyle c_{4} & = & \displaystyle \frac{\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}+2}{4}.\nonumber\end{eqnarray}$$
Then,
 $$\begin{eqnarray}\displaystyle & & \displaystyle Z_{\infty }(W_{\infty ,t},\unicode[STIX]{x1D6F7}_{\infty },1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },p+q+3/2)\nonumber\\ \displaystyle & & \displaystyle \quad =W_{\infty ,t}(1)\biggl(2\unicode[STIX]{x1D70B}^{(3(p+q)+6)/2}\int _{L}\frac{\unicode[STIX]{x1D6E4}(c_{1}-s)\unicode[STIX]{x1D6E4}(c_{2}-s)\unicode[STIX]{x1D6E4}(c_{3}-s)\unicode[STIX]{x1D6E4}(c_{4}-s)}{\unicode[STIX]{x1D6E4}(a_{1}-s)\unicode[STIX]{x1D6E4}(a_{2}-s)}\unicode[STIX]{x1D70B}^{2s}\,\frac{ds}{2\unicode[STIX]{x1D70B}i}\biggr)^{-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{\unicode[STIX]{x1D6E4}(c_{1}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(c_{2}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(c_{3}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(c_{4}+{\textstyle \frac{3(p+q)+6}{4}})}{\unicode[STIX]{x1D6E4}(a_{1}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(a_{2}+{\textstyle \frac{3(p+q)+6}{4}})}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle Z_{\infty }(W_{\infty ,t},\unicode[STIX]{x1D6F7}_{\infty },1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },p+q+3/2)\nonumber\\ \displaystyle & & \displaystyle \quad =W_{\infty ,t}(1)\biggl(2\unicode[STIX]{x1D70B}^{(3(p+q)+6)/2}\int _{L}\frac{\unicode[STIX]{x1D6E4}(c_{1}-s)\unicode[STIX]{x1D6E4}(c_{2}-s)\unicode[STIX]{x1D6E4}(c_{3}-s)\unicode[STIX]{x1D6E4}(c_{4}-s)}{\unicode[STIX]{x1D6E4}(a_{1}-s)\unicode[STIX]{x1D6E4}(a_{2}-s)}\unicode[STIX]{x1D70B}^{2s}\,\frac{ds}{2\unicode[STIX]{x1D70B}i}\biggr)^{-1}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \,\frac{\unicode[STIX]{x1D6E4}(c_{1}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(c_{2}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(c_{3}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(c_{4}+{\textstyle \frac{3(p+q)+6}{4}})}{\unicode[STIX]{x1D6E4}(a_{1}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(a_{2}+{\textstyle \frac{3(p+q)+6}{4}})}\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6E4}$
denotes the gamma function and where the path
$\unicode[STIX]{x1D6E4}$
denotes the gamma function and where the path
![]() $L$
is a loop starting and ending at
$L$
is a loop starting and ending at
![]() $+\infty$
and encircling all the poles of
$+\infty$
and encircling all the poles of
 $\unicode[STIX]{x1D6E4}(c_{j}-s)$
for
$\unicode[STIX]{x1D6E4}(c_{j}-s)$
for
 $1\leqslant j\leqslant 4$
once, in the negative direction.
$1\leqslant j\leqslant 4$
once, in the negative direction.
Proof. The vector
![]() $v_{t}$
has weight
$v_{t}$
has weight
 $\unicode[STIX]{x1D706}^{\prime }(t+\unicode[STIX]{x1D706}_{2},-t+\unicode[STIX]{x1D706}_{1})$
and the function
$\unicode[STIX]{x1D706}^{\prime }(t+\unicode[STIX]{x1D706}_{2},-t+\unicode[STIX]{x1D706}_{1})$
and the function
![]() $\unicode[STIX]{x1D6F7}_{\infty }$
has weight
$\unicode[STIX]{x1D6F7}_{\infty }$
has weight
![]() $\unicode[STIX]{x1D706}^{\prime }(r,s)$
for
$\unicode[STIX]{x1D706}^{\prime }(r,s)$
for
 $T^{\prime }=\text{U}(1)^{2}$
. Hence,
$T^{\prime }=\text{U}(1)^{2}$
. Hence,
![]() $W_{\infty ,t}$
has weight
$W_{\infty ,t}$
has weight
 $\unicode[STIX]{x1D706}^{\prime }(t+\unicode[STIX]{x1D706}_{2},-t+\unicode[STIX]{x1D706}_{1})$
and
$\unicode[STIX]{x1D706}^{\prime }(t+\unicode[STIX]{x1D706}_{2},-t+\unicode[STIX]{x1D706}_{1})$
and
![]() $f^{\unicode[STIX]{x1D6F7}_{\infty }}$
has weight
$f^{\unicode[STIX]{x1D6F7}_{\infty }}$
has weight
![]() $\unicode[STIX]{x1D706}^{\prime }(r,s)$
. The Iwasawa decomposition
$\unicode[STIX]{x1D706}^{\prime }(r,s)$
. The Iwasawa decomposition
 $G^{\prime }(\mathbb{R})=B^{\prime }(\mathbb{R})\text{U}(1)^{2}$
implies that
$G^{\prime }(\mathbb{R})=B^{\prime }(\mathbb{R})\text{U}(1)^{2}$
implies that
 $Z_{\infty }(W_{\infty ,t},\unicode[STIX]{x1D6F7}_{\infty },1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },s)$
equals
$Z_{\infty }(W_{\infty ,t},\unicode[STIX]{x1D6F7}_{\infty },1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },s)$
equals
 $$\begin{eqnarray}\displaystyle \int _{\mathbb{R}_{+}^{\times }}\int _{\text{U}(1)^{2}}W_{\infty ,t}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)k\right)f^{\unicode[STIX]{x1D6F7}_{\infty }}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)k,1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },s\right)d^{\times }x\,dk. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\mathbb{R}_{+}^{\times }}\int _{\text{U}(1)^{2}}W_{\infty ,t}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)k\right)f^{\unicode[STIX]{x1D6F7}_{\infty }}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)k,1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },s\right)d^{\times }x\,dk. & & \displaystyle \nonumber\end{eqnarray}$$
So, if
 $t+\unicode[STIX]{x1D706}_{2}+r\neq 0$
or
$t+\unicode[STIX]{x1D706}_{2}+r\neq 0$
or
 $-t+\unicode[STIX]{x1D706}_{1}+s\neq 0$
, we have
$-t+\unicode[STIX]{x1D706}_{1}+s\neq 0$
, we have
 $$\begin{eqnarray}\int _{\text{U}(1)^{2}}W_{\infty ,t}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)k\right)f^{\unicode[STIX]{x1D6F7}_{\infty }}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)k,1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },s\right)\,dk=0\end{eqnarray}$$
$$\begin{eqnarray}\int _{\text{U}(1)^{2}}W_{\infty ,t}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)k\right)f^{\unicode[STIX]{x1D6F7}_{\infty }}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)k,1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },s\right)\,dk=0\end{eqnarray}$$
for all
![]() $x$
because the integral of a non-trivial character on a group is zero. In the case where
$x$
because the integral of a non-trivial character on a group is zero. In the case where
 $t+\unicode[STIX]{x1D706}_{2}+r=-t+\unicode[STIX]{x1D706}_{1}+s=0$
, the integral equals
$t+\unicode[STIX]{x1D706}_{2}+r=-t+\unicode[STIX]{x1D706}_{1}+s=0$
, the integral equals
 $$\begin{eqnarray}\displaystyle \int _{\mathbb{R}_{+}^{\times }}W_{\infty ,t}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)\right)f^{\unicode[STIX]{x1D6F7}_{\infty }}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right),1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },s\right)d^{\times }x. & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\mathbb{R}_{+}^{\times }}W_{\infty ,t}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)\right)f^{\unicode[STIX]{x1D6F7}_{\infty }}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right),1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },s\right)d^{\times }x. & & \displaystyle \nonumber\end{eqnarray}$$
The Meijer
![]() $G$
-function
$G$
-function
 $G_{2,4}^{4,0}(z,a_{1},a_{2},c_{1},c_{2},c_{3},c_{4})$
is defined for any non-zero complex number
$G_{2,4}^{4,0}(z,a_{1},a_{2},c_{1},c_{2},c_{3},c_{4})$
is defined for any non-zero complex number
![]() $z$
by
$z$
by
 $$\begin{eqnarray}G_{2,4}^{4,0}(z,a_{1},a_{2},c_{1},c_{2},c_{3},c_{4})=\int _{L}\frac{\unicode[STIX]{x1D6E4}(c_{1}-s)\unicode[STIX]{x1D6E4}(c_{2}-s)\unicode[STIX]{x1D6E4}(c_{3}-s)\unicode[STIX]{x1D6E4}(c_{4}-s)}{\unicode[STIX]{x1D6E4}(a_{1}-s)\unicode[STIX]{x1D6E4}(a_{2}-s)}z^{s}\,\frac{ds}{2\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$
$$\begin{eqnarray}G_{2,4}^{4,0}(z,a_{1},a_{2},c_{1},c_{2},c_{3},c_{4})=\int _{L}\frac{\unicode[STIX]{x1D6E4}(c_{1}-s)\unicode[STIX]{x1D6E4}(c_{2}-s)\unicode[STIX]{x1D6E4}(c_{3}-s)\unicode[STIX]{x1D6E4}(c_{4}-s)}{\unicode[STIX]{x1D6E4}(a_{1}-s)\unicode[STIX]{x1D6E4}(a_{2}-s)}z^{s}\,\frac{ds}{2\unicode[STIX]{x1D70B}i}.\end{eqnarray}$$
It follows from [Reference MoriyamaMor11, Theorem 7.1(ii)] that for any positive real number
![]() $x$
, we have
$x$
, we have
 $$\begin{eqnarray}W_{\infty ,t}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)\right)=W_{\infty ,t}(1)x^{(p+q)/2}\frac{G_{2,4}^{4,0}((\unicode[STIX]{x1D70B}x)^{2},a_{1},a_{2},c_{1},c_{2},c_{3},c_{4})}{G_{2,4}^{4,0}(\unicode[STIX]{x1D70B}^{2},a_{1},a_{2},c_{1},c_{2},c_{3},c_{4})}.\end{eqnarray}$$
$$\begin{eqnarray}W_{\infty ,t}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right)\right)=W_{\infty ,t}(1)x^{(p+q)/2}\frac{G_{2,4}^{4,0}((\unicode[STIX]{x1D70B}x)^{2},a_{1},a_{2},c_{1},c_{2},c_{3},c_{4})}{G_{2,4}^{4,0}(\unicode[STIX]{x1D70B}^{2},a_{1},a_{2},c_{1},c_{2},c_{3},c_{4})}.\end{eqnarray}$$
It is well known and explained in [Reference Beals and SzmigielskiBS13, p. 870], for example, that the contour
![]() $L$
can be replaced by a path
$L$
can be replaced by a path
![]() $L^{\prime }$
from
$L^{\prime }$
from
![]() $-i\infty$
to
$-i\infty$
to
![]() $+i\infty$
such that for
$+i\infty$
such that for
 $1\leqslant j\leqslant 4$
, the poles of
$1\leqslant j\leqslant 4$
, the poles of
 $\unicode[STIX]{x1D6E4}(c_{j}-s)$
are on the right of
$\unicode[STIX]{x1D6E4}(c_{j}-s)$
are on the right of
![]() $L^{\prime }$
. Furthermore, we have
$L^{\prime }$
. Furthermore, we have
 $$\begin{eqnarray}f^{\unicode[STIX]{x1D6F7}_{\infty }}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right),1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },s\right)=(-1)^{(p+q+r+s)/2}\unicode[STIX]{x1D70B}^{-2(p+q)}((p+q-1)!)^{2}x^{p+q+2}\end{eqnarray}$$
$$\begin{eqnarray}f^{\unicode[STIX]{x1D6F7}_{\infty }}\left(\left(\begin{array}{@{}cccc@{}}x & & & \\ & x & & \\ & & 1 & \\ & & & 1\end{array}\right),1,\unicode[STIX]{x1D708}_{1,\infty },\unicode[STIX]{x1D708}_{2,\infty },s\right)=(-1)^{(p+q+r+s)/2}\unicode[STIX]{x1D70B}^{-2(p+q)}((p+q-1)!)^{2}x^{p+q+2}\end{eqnarray}$$
for any
![]() $x\in \mathbb{R}_{+}^{\times }$
. Hence, we need to compute
$x\in \mathbb{R}_{+}^{\times }$
. Hence, we need to compute
 $$\begin{eqnarray}\int _{\mathbb{R}_{+}^{\times }}x^{(3(p+q)/2)+2}\int _{L^{\prime }}\frac{\unicode[STIX]{x1D6E4}(c_{1}-s)\unicode[STIX]{x1D6E4}(c_{2}-s)\unicode[STIX]{x1D6E4}(c_{3}-s)\unicode[STIX]{x1D6E4}(c_{4}-s)}{\unicode[STIX]{x1D6E4}(a_{1}-s)\unicode[STIX]{x1D6E4}(a_{2}-s)}(\unicode[STIX]{x1D70B}x)^{2s}\,\frac{ds}{2\unicode[STIX]{x1D70B}i}\,\frac{dx}{x}\end{eqnarray}$$
$$\begin{eqnarray}\int _{\mathbb{R}_{+}^{\times }}x^{(3(p+q)/2)+2}\int _{L^{\prime }}\frac{\unicode[STIX]{x1D6E4}(c_{1}-s)\unicode[STIX]{x1D6E4}(c_{2}-s)\unicode[STIX]{x1D6E4}(c_{3}-s)\unicode[STIX]{x1D6E4}(c_{4}-s)}{\unicode[STIX]{x1D6E4}(a_{1}-s)\unicode[STIX]{x1D6E4}(a_{2}-s)}(\unicode[STIX]{x1D70B}x)^{2s}\,\frac{ds}{2\unicode[STIX]{x1D70B}i}\,\frac{dx}{x}\end{eqnarray}$$
which equals
 $$\begin{eqnarray}\frac{1}{2}\unicode[STIX]{x1D70B}^{-(3(p+q)+6)/2}\frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}+3(p+q)+10}{4}})\unicode[STIX]{x1D6E4}({\textstyle \frac{\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}+3(p+q)+10}{4}})\unicode[STIX]{x1D6E4}({\textstyle \frac{\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}+3(p+q)+8}{4}})\unicode[STIX]{x1D6E4}({\textstyle \frac{\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}+3(p+q)+8}{4}})}{\unicode[STIX]{x1D6E4}({\textstyle \frac{2(t-\unicode[STIX]{x1D706}_{2})+4p+2q+10}{4}})\unicode[STIX]{x1D6E4}({\textstyle \frac{2(2\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}-t)+4q+2p+10}{4}})}\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{2}\unicode[STIX]{x1D70B}^{-(3(p+q)+6)/2}\frac{\unicode[STIX]{x1D6E4}({\textstyle \frac{\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}+3(p+q)+10}{4}})\unicode[STIX]{x1D6E4}({\textstyle \frac{\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}+3(p+q)+10}{4}})\unicode[STIX]{x1D6E4}({\textstyle \frac{\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}+3(p+q)+8}{4}})\unicode[STIX]{x1D6E4}({\textstyle \frac{\unicode[STIX]{x1D706}_{1}-\unicode[STIX]{x1D706}_{2}+3(p+q)+8}{4}})}{\unicode[STIX]{x1D6E4}({\textstyle \frac{2(t-\unicode[STIX]{x1D706}_{2})+4p+2q+10}{4}})\unicode[STIX]{x1D6E4}({\textstyle \frac{2(2\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D706}_{2}-t)+4q+2p+10}{4}})}\end{eqnarray}$$
by the Mellin inversion formula. This completes the proof. ◻
6 Periods
In this section, we compute the pairing
 $\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}$
(see Lemma 4.21) and we introduce Harris’ occult period invariant, which plays a crucial role in the present work.
$\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}$
(see Lemma 4.21) and we introduce Harris’ occult period invariant, which plays a crucial role in the present work.
The
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-module
$E(\unicode[STIX]{x1D70B}_{f})$
-module
 $M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{-}(-1)$
has rank two and the
$M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{-}(-1)$
has rank two and the
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-module
$E(\unicode[STIX]{x1D70B}_{f})$
-module
 $F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)$
has rank one (Lemma 4.15 and Hypothesis 4.17). Let us fix a basis
$F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)$
has rank one (Lemma 4.15 and Hypothesis 4.17). Let us fix a basis
![]() $(v_{1},v_{2})$
of
$(v_{1},v_{2})$
of
 $M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{-}(-1)$
and let
$M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{-}(-1)$
and let
![]() $\unicode[STIX]{x1D703}$
be a non-zero vector of
$\unicode[STIX]{x1D703}$
be a non-zero vector of
 $F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)$
. This vector can be regarded as a vector of
$F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)$
. This vector can be regarded as a vector of
 $M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)$
via the second arrow of the exact sequence of Lemma 4.12. Let
$M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)$
via the second arrow of the exact sequence of Lemma 4.12. Let
 $\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\in E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{R}$
be its coordinates in the basis
$\unicode[STIX]{x1D706}_{1},\unicode[STIX]{x1D706}_{2}\in E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{R}$
be its coordinates in the basis
![]() $(v_{1},v_{2})$
.
$(v_{1},v_{2})$
.
Lemma 6.1. Let
 $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{R}$
. Then
$\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{R}$
. Then
 $\unicode[STIX]{x1D707}_{1}v_{1}+\unicode[STIX]{x1D707}_{2}v_{2}$
is mapped to a generator of
$\unicode[STIX]{x1D707}_{1}v_{1}+\unicode[STIX]{x1D707}_{2}v_{2}$
is mapped to a generator of
 ${\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)$
by the surjection
${\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)$
by the surjection

of Corollary 4.12 if and only if
 $\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D707}_{1}\in E(\unicode[STIX]{x1D70B}_{f})^{\times }$
.
$\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D707}_{1}\in E(\unicode[STIX]{x1D70B}_{f})^{\times }$
.
Proof. The map
 $$\begin{eqnarray}\unicode[STIX]{x1D703}\wedge :M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\longrightarrow \text{det}_{E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{R}}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}\wedge :M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\longrightarrow \text{det}_{E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{R}}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\end{eqnarray}$$
is part of the following commutative diagram with exact lines

Moreover, via the isomorphism
 ${\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)\simeq \text{det}_{E(\unicode[STIX]{x1D70B}_{f})}M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{-}(-1)$
induced by the choice of
${\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)\simeq \text{det}_{E(\unicode[STIX]{x1D70B}_{f})}M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{-}(-1)$
induced by the choice of
![]() $\unicode[STIX]{x1D703}$
, the vector
$\unicode[STIX]{x1D703}$
, the vector
 $\unicode[STIX]{x1D707}_{1}v_{1}+\unicode[STIX]{x1D707}_{2}v_{2}$
is mapped to a generator of
$\unicode[STIX]{x1D707}_{1}v_{1}+\unicode[STIX]{x1D707}_{2}v_{2}$
is mapped to a generator of
 ${\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)$
if and only if
${\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)$
if and only if
 $\unicode[STIX]{x1D703}\wedge (\unicode[STIX]{x1D707}_{1}v_{1}+\unicode[STIX]{x1D707}_{2}v_{2})=\unicode[STIX]{x1D70C}v_{1}\wedge v_{2}$
for some
$\unicode[STIX]{x1D703}\wedge (\unicode[STIX]{x1D707}_{1}v_{1}+\unicode[STIX]{x1D707}_{2}v_{2})=\unicode[STIX]{x1D70C}v_{1}\wedge v_{2}$
for some
 $\unicode[STIX]{x1D70C}\in E(\unicode[STIX]{x1D70B}_{f})^{\times }$
. As
$\unicode[STIX]{x1D70C}\in E(\unicode[STIX]{x1D70B}_{f})^{\times }$
. As
 $\unicode[STIX]{x1D703}\wedge (\unicode[STIX]{x1D707}_{1}v_{1}+\unicode[STIX]{x1D707}_{2}v_{2})=(\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D707}_{1})v_{1}\wedge v_{2}$
, the statement is proven.◻
$\unicode[STIX]{x1D703}\wedge (\unicode[STIX]{x1D707}_{1}v_{1}+\unicode[STIX]{x1D707}_{2}v_{2})=(\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D707}_{1})v_{1}\wedge v_{2}$
, the statement is proven.◻
We need to recall the definition of the Deligne periods
 $c^{\pm }(\unicode[STIX]{x1D70B}_{f},W)$
of the ‘motive’
$c^{\pm }(\unicode[STIX]{x1D70B}_{f},W)$
of the ‘motive’
 $M(\unicode[STIX]{x1D70B}_{f},W)$
from [Reference DeligneDel79, 1.7]. Let
$M(\unicode[STIX]{x1D70B}_{f},W)$
from [Reference DeligneDel79, 1.7]. Let
![]() $t$
denote the integer
$t$
denote the integer
 $t=(p+q+6-k-k^{\prime })/2$
. We have the Hodge decomposition
$t=(p+q+6-k-k^{\prime })/2$
. We have the Hodge decomposition
 $$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}=M_{B}^{3-t,-k-k^{\prime }-t}\oplus M_{B}^{2-k^{\prime }-t,1-k-t}\oplus M_{B}^{1-k-t,2-k^{\prime }-t}\oplus M_{B}^{-k-k^{\prime }-t,3-t}\end{eqnarray}$$
$$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}=M_{B}^{3-t,-k-k^{\prime }-t}\oplus M_{B}^{2-k^{\prime }-t,1-k-t}\oplus M_{B}^{1-k-t,2-k^{\prime }-t}\oplus M_{B}^{-k-k^{\prime }-t,3-t}\end{eqnarray}$$
where each
![]() $M_{B}^{r,s}$
is an
$M_{B}^{r,s}$
is an
 $E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{C}$
-module of rank one (Propositions 3.7 and 3.8 and Hypothesis 4.16). Furthermore, the involution
$E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{C}$
-module of rank one (Propositions 3.7 and 3.8 and Hypothesis 4.16). Furthermore, the involution
![]() $F_{\infty }$
exchanges
$F_{\infty }$
exchanges
![]() $M_{B}^{r,s}$
and
$M_{B}^{r,s}$
and
![]() $M_{B}^{s,r}$
. This implies that the
$M_{B}^{s,r}$
. This implies that the
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-subspaces
$E(\unicode[STIX]{x1D70B}_{f})$
-subspaces
 $M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{\pm }$
of
$M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{\pm }$
of
 $M_{B}(\unicode[STIX]{x1D70B}_{f},W)$
where
$M_{B}(\unicode[STIX]{x1D70B}_{f},W)$
where
![]() $F_{\infty }$
acts by multiplication by
$F_{\infty }$
acts by multiplication by
![]() $\pm 1$
both have dimension two. Let
$\pm 1$
both have dimension two. Let
 $I_{\infty }:M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}\longrightarrow M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}$
denote the comparison isomorphism. The subspaces
$I_{\infty }:M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}\longrightarrow M_{dR}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}$
denote the comparison isomorphism. The subspaces
 $F^{\pm }(\unicode[STIX]{x1D70B}_{f},W)$
of the de Rham filtration of
$F^{\pm }(\unicode[STIX]{x1D70B}_{f},W)$
of the de Rham filtration of
 $M_{dR}(\unicode[STIX]{x1D70B}_{f},W)$
defined in [Reference DeligneDel79, 1.7] are equal and characterized by the fact that their complexification is mapped isomorphically to
$M_{dR}(\unicode[STIX]{x1D70B}_{f},W)$
defined in [Reference DeligneDel79, 1.7] are equal and characterized by the fact that their complexification is mapped isomorphically to
 $M_{B}^{3-t,-k-k^{\prime }-t}\oplus M_{B}^{2-k^{\prime }-t,1-k-t}$
by
$M_{B}^{3-t,-k-k^{\prime }-t}\oplus M_{B}^{2-k^{\prime }-t,1-k-t}$
by
![]() $I_{\infty }^{-1}$
. The determinant of the isomorphism
$I_{\infty }^{-1}$
. The determinant of the isomorphism
 $$\begin{eqnarray}I_{\infty }^{\pm }:M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}^{\pm }\longrightarrow (M_{dR}(\unicode[STIX]{x1D70B}_{f},W)/F^{\pm }(\unicode[STIX]{x1D70B}_{f},W))_{\mathbb{C}},\end{eqnarray}$$
$$\begin{eqnarray}I_{\infty }^{\pm }:M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{C}}^{\pm }\longrightarrow (M_{dR}(\unicode[STIX]{x1D70B}_{f},W)/F^{\pm }(\unicode[STIX]{x1D70B}_{f},W))_{\mathbb{C}},\end{eqnarray}$$
computed in basis defined over
![]() $E(\unicode[STIX]{x1D70B}_{f})$
, is by definition the Deligne period
$E(\unicode[STIX]{x1D70B}_{f})$
, is by definition the Deligne period
 $c^{\pm }(\unicode[STIX]{x1D70B}_{f},W)$
. Its equivalence class modulo the relation
$c^{\pm }(\unicode[STIX]{x1D70B}_{f},W)$
. Its equivalence class modulo the relation
![]() ${\sim}$
of Definition 4.19 does not depend on the chosen basis. The Deligne periods
${\sim}$
of Definition 4.19 does not depend on the chosen basis. The Deligne periods
 $c^{\pm }(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))$
are defined similarly.
$c^{\pm }(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))$
are defined similarly.
Proposition 6.2. Let
 $\unicode[STIX]{x1D714}\in M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}$
satisfying the condition of Lemma 4.21. Assume that
$\unicode[STIX]{x1D714}\in M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}$
satisfying the condition of Lemma 4.21. Assume that
![]() $\unicode[STIX]{x1D714}$
belongs to
$\unicode[STIX]{x1D714}$
belongs to
 $M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}^{+}$
and that the image of
$M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}^{+}$
and that the image of
![]() $\unicode[STIX]{x1D714}$
by the comparison isomorphism
$\unicode[STIX]{x1D714}$
by the comparison isomorphism
 $$\begin{eqnarray}I_{\infty }^{+}:M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{ C}}^{+}\longrightarrow (M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{+})_{\mathbb{ C}}\end{eqnarray}$$
$$\begin{eqnarray}I_{\infty }^{+}:M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{ C}}^{+}\longrightarrow (M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{+})_{\mathbb{ C}}\end{eqnarray}$$
belongs to the
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-structure
$E(\unicode[STIX]{x1D70B}_{f})$
-structure
 $M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{+}$
. Let
$M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{+}$
. Let
![]() $\widetilde{v}_{{\mathcal{D}}}$
be a lift of a generator of
$\widetilde{v}_{{\mathcal{D}}}$
be a lift of a generator of
 ${\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)$
by the surjection
${\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)$
by the surjection
 $$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\longrightarrow \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})\end{eqnarray}$$
$$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\longrightarrow \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})\end{eqnarray}$$
of Corollary 4.12. Then,
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}\sim (2\unicode[STIX]{x1D70B}i)^{2}c^{-}(\unicode[STIX]{x1D70B}_{f},W)^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}\sim (2\unicode[STIX]{x1D70B}i)^{2}c^{-}(\unicode[STIX]{x1D70B}_{f},W)^{-1}.\end{eqnarray}$$
Proof. Recall that the Deligne and Beilinson
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-structures are related by the identity
$E(\unicode[STIX]{x1D70B}_{f})$
-structures are related by the identity
 $$\begin{eqnarray}{\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)=(2\unicode[STIX]{x1D70B}i)^{2}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{f},W)^{-1}{\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W)=(2\unicode[STIX]{x1D70B}i)^{2}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{f},W)^{-1}{\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
Let
 $\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{R}$
such that
$\unicode[STIX]{x1D707}_{1},\unicode[STIX]{x1D707}_{2}\in E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{R}$
such that
 $\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D707}_{1}=1$
. Then, according to Lemma 6.1, the vector
$\unicode[STIX]{x1D706}_{1}\unicode[STIX]{x1D707}_{2}-\unicode[STIX]{x1D706}_{2}\unicode[STIX]{x1D707}_{1}=1$
. Then, according to Lemma 6.1, the vector
 $v=\unicode[STIX]{x1D707}_{1}v_{1}+\unicode[STIX]{x1D707}_{2}v_{2}$
is a lift of a generator of
$v=\unicode[STIX]{x1D707}_{1}v_{1}+\unicode[STIX]{x1D707}_{2}v_{2}$
is a lift of a generator of
 ${\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)$
by the surjection
${\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)$
by the surjection
 $$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\longrightarrow \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}).\end{eqnarray}$$
$$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\longrightarrow \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}).\end{eqnarray}$$
For any other lift
![]() $w$
of any other generator of
$w$
of any other generator of
 ${\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)$
, we have
${\mathcal{B}}(\unicode[STIX]{x1D70B}_{f},W)$
, we have
 $\langle \unicode[STIX]{x1D714},v\rangle _{B}\sim \langle \unicode[STIX]{x1D714},w\rangle _{B}$
. Hence, we need to compute
$\langle \unicode[STIX]{x1D714},v\rangle _{B}\sim \langle \unicode[STIX]{x1D714},w\rangle _{B}$
. Hence, we need to compute
 $\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}=(2\unicode[STIX]{x1D70B}i)^{2}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{f},W)^{-1}\langle \unicode[STIX]{x1D714},v\rangle _{B}$
. Let
$\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}=(2\unicode[STIX]{x1D70B}i)^{2}\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{f},W)^{-1}\langle \unicode[STIX]{x1D714},v\rangle _{B}$
. Let
![]() $\langle \,,\rangle _{dR}$
denote the Poincaré duality pairing in de Rham cohomology. Its complexification is part of the following commutative diagram
$\langle \,,\rangle _{dR}$
denote the Poincaré duality pairing in de Rham cohomology. Its complexification is part of the following commutative diagram

where the vertical maps are the comparison isomorphisms. Let
![]() $1_{B}$
and
$1_{B}$
and
![]() $1_{dR}$
be generators of
$1_{dR}$
be generators of
 $E(\unicode[STIX]{x1D70B}_{f})(0)_{B}$
and
$E(\unicode[STIX]{x1D70B}_{f})(0)_{B}$
and
 $E(\unicode[STIX]{x1D70B}_{f})(0)_{dR}$
, respectively. We can assume that
$E(\unicode[STIX]{x1D70B}_{f})(0)_{dR}$
, respectively. We can assume that
 $J_{\infty }(1_{B})=1_{dR}$
. Let
$J_{\infty }(1_{B})=1_{dR}$
. Let
![]() $\unicode[STIX]{x1D703}^{\prime }$
be an element of
$\unicode[STIX]{x1D703}^{\prime }$
be an element of
 $M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))$
such that
$M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))$
such that
 $\langle \unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }\rangle =1_{dR}$
, where
$\langle \unicode[STIX]{x1D703},\unicode[STIX]{x1D703}^{\prime }\rangle =1_{dR}$
, where
 $\unicode[STIX]{x1D703}\in F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)$
is as above. Let
$\unicode[STIX]{x1D703}\in F^{0}M_{dR}(\unicode[STIX]{x1D70B}_{f},W)$
is as above. Let
![]() $\unicode[STIX]{x1D714}^{\prime }$
denote
$\unicode[STIX]{x1D714}^{\prime }$
denote
![]() $I_{\infty }^{+}(\unicode[STIX]{x1D714})$
. It follows easily from the consideration of Hodge types that
$I_{\infty }^{+}(\unicode[STIX]{x1D714})$
. It follows easily from the consideration of Hodge types that
![]() $(\unicode[STIX]{x1D714}^{\prime },\unicode[STIX]{x1D703}^{\prime })$
is a basis of
$(\unicode[STIX]{x1D714}^{\prime },\unicode[STIX]{x1D703}^{\prime })$
is a basis of
 $M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{\pm }$
. By definition
$M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{\pm }$
. By definition
![]() $(v_{1},v_{2})$
is a basis of the
$(v_{1},v_{2})$
is a basis of the
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-vector space
$E(\unicode[STIX]{x1D70B}_{f})$
-vector space
 $M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{-}(-1)$
. As a consequence,
$M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{-}(-1)$
. As a consequence,
 $(2\unicode[STIX]{x1D70B}iv_{1},2\unicode[STIX]{x1D70B}iv_{2})$
is a basis of
$(2\unicode[STIX]{x1D70B}iv_{1},2\unicode[STIX]{x1D70B}iv_{2})$
is a basis of
 $M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{+}$
. Let
$M_{B}(\unicode[STIX]{x1D70B}_{f},W)^{+}$
. Let
![]() $w_{1},w_{2}$
be vectors of
$w_{1},w_{2}$
be vectors of
 $M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))^{+}$
such that
$M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))^{+}$
such that
 $\langle 2\unicode[STIX]{x1D70B}iv_{1},w_{1}\rangle _{B}=\langle 2\unicode[STIX]{x1D70B}iv_{2},w_{2}\rangle _{B}=1_{B}$
and
$\langle 2\unicode[STIX]{x1D70B}iv_{1},w_{1}\rangle _{B}=\langle 2\unicode[STIX]{x1D70B}iv_{2},w_{2}\rangle _{B}=1_{B}$
and
 $\langle 2\unicode[STIX]{x1D70B}iv_{1},w_{2}\rangle _{B}=\langle 2\unicode[STIX]{x1D70B}iv_{2},w_{1}\rangle _{B}=0$
. Hence,
$\langle 2\unicode[STIX]{x1D70B}iv_{1},w_{2}\rangle _{B}=\langle 2\unicode[STIX]{x1D70B}iv_{2},w_{1}\rangle _{B}=0$
. Hence,
 $(w_{1},w_{2})$
is a basis of
$(w_{1},w_{2})$
is a basis of
 $M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))^{+}$
. Let
$M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))^{+}$
. Let
 $\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}\in E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{C}$
be such that
$\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2},\unicode[STIX]{x1D6FD}_{1},\unicode[STIX]{x1D6FD}_{2}\in E(\unicode[STIX]{x1D70B}_{f})\otimes \mathbb{C}$
be such that
 $I_{\infty }^{+}(w_{1})=\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D714}^{\prime }+\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D703}^{\prime }$
and
$I_{\infty }^{+}(w_{1})=\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D714}^{\prime }+\unicode[STIX]{x1D6FD}_{1}\unicode[STIX]{x1D703}^{\prime }$
and
 $I_{\infty }^{+}(w_{2})=\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D714}^{\prime }+\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D703}^{\prime }$
. By definition, we have
$I_{\infty }^{+}(w_{2})=\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D714}^{\prime }+\unicode[STIX]{x1D6FD}_{2}\unicode[STIX]{x1D703}^{\prime }$
. By definition, we have
 $$\begin{eqnarray}c^{+}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))=\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}\end{eqnarray}$$
$$\begin{eqnarray}c^{+}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))=\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D6FC}_{2}\unicode[STIX]{x1D6FD}_{1}\end{eqnarray}$$
and this implies the identity
 $$\begin{eqnarray}\unicode[STIX]{x1D714}=c^{+}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))^{-1}(\unicode[STIX]{x1D6FD}_{2}w_{1}-\unicode[STIX]{x1D6FD}_{1}w_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}=c^{+}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))^{-1}(\unicode[STIX]{x1D6FD}_{2}w_{1}-\unicode[STIX]{x1D6FD}_{1}w_{2}).\end{eqnarray}$$
Hence,
 $$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D714},v\rangle _{B} & = & \displaystyle c^{+}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))^{-1}\langle \unicode[STIX]{x1D6FD}_{2}w_{1}-\unicode[STIX]{x1D6FD}_{1}w_{2},\unicode[STIX]{x1D707}_{1}v_{1}+\unicode[STIX]{x1D707}_{2}v_{2}\rangle \nonumber\\ \displaystyle & = & \displaystyle c^{+}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))^{-1}(\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D707}_{2}\unicode[STIX]{x1D6FD}_{1}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D714},v\rangle _{B} & = & \displaystyle c^{+}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))^{-1}\langle \unicode[STIX]{x1D6FD}_{2}w_{1}-\unicode[STIX]{x1D6FD}_{1}w_{2},\unicode[STIX]{x1D707}_{1}v_{1}+\unicode[STIX]{x1D707}_{2}v_{2}\rangle \nonumber\\ \displaystyle & = & \displaystyle c^{+}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))^{-1}(\unicode[STIX]{x1D707}_{1}\unicode[STIX]{x1D6FD}_{2}-\unicode[STIX]{x1D707}_{2}\unicode[STIX]{x1D6FD}_{1}).\nonumber\end{eqnarray}$$
To finish the proof, note that the pairing
![]() $\langle \unicode[STIX]{x1D703},\,\rangle _{dR}$
vanishes on
$\langle \unicode[STIX]{x1D703},\,\rangle _{dR}$
vanishes on
![]() $F^{\pm }$
because the Hodge types do not match. So
$F^{\pm }$
because the Hodge types do not match. So
 $\langle \unicode[STIX]{x1D703},\unicode[STIX]{x1D714}^{\prime }\rangle _{dR}$
is meaningful, and in fact equal to zero, again because of the Hodge types. As a consequence, we have
$\langle \unicode[STIX]{x1D703},\unicode[STIX]{x1D714}^{\prime }\rangle _{dR}$
is meaningful, and in fact equal to zero, again because of the Hodge types. As a consequence, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{1}1_{dR}=\langle \unicode[STIX]{x1D703},I_{\infty }^{+}(w_{1})\rangle _{dR}=J_{\infty }(\langle \unicode[STIX]{x1D706}_{1}v_{1}+\unicode[STIX]{x1D706}_{2}v_{2},w_{1}\rangle _{B})=\unicode[STIX]{x1D706}_{1}1_{dR}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FD}_{1}1_{dR}=\langle \unicode[STIX]{x1D703},I_{\infty }^{+}(w_{1})\rangle _{dR}=J_{\infty }(\langle \unicode[STIX]{x1D706}_{1}v_{1}+\unicode[STIX]{x1D706}_{2}v_{2},w_{1}\rangle _{B})=\unicode[STIX]{x1D706}_{1}1_{dR}.\end{eqnarray}$$
Hence,
 $\unicode[STIX]{x1D6FD}_{1}=\unicode[STIX]{x1D706}_{1}$
. Similarly
$\unicode[STIX]{x1D6FD}_{1}=\unicode[STIX]{x1D706}_{1}$
. Similarly
 $\unicode[STIX]{x1D6FD}_{2}=\unicode[STIX]{x1D706}_{2}$
. Hence,
$\unicode[STIX]{x1D6FD}_{2}=\unicode[STIX]{x1D706}_{2}$
. Hence,
 $\langle \unicode[STIX]{x1D714},v\rangle _{B}=-c^{+}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))^{-1}$
. It follows from [Reference DeligneDel79, (5.1.7) and (5.1.1)] that
$\langle \unicode[STIX]{x1D714},v\rangle _{B}=-c^{+}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))^{-1}$
. It follows from [Reference DeligneDel79, (5.1.7) and (5.1.1)] that
 $c^{+}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))\sim \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{f},W)^{-1}c^{-}(\unicode[STIX]{x1D70B}_{f},W)$
. As a consequence,
$c^{+}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))\sim \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{f},W)^{-1}c^{-}(\unicode[STIX]{x1D70B}_{f},W)$
. As a consequence,
 $\langle \unicode[STIX]{x1D714},v\rangle _{B}\sim \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{f},W)c^{-}(\unicode[STIX]{x1D70B}_{f},W)^{-1}$
. This completes the proof.◻
$\langle \unicode[STIX]{x1D714},v\rangle _{B}\sim \unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{f},W)c^{-}(\unicode[STIX]{x1D70B}_{f},W)^{-1}$
. This completes the proof.◻
In the paper [Reference HarrisHar04], Harris defines the occult period invariant and relates it to critical values of the spinor
![]() $L$
-function. Roughly speaking, the occult period invariant measures the difference between the rational structure on
$L$
-function. Roughly speaking, the occult period invariant measures the difference between the rational structure on
![]() $\unicode[STIX]{x1D70B}_{f}$
defined in terms of de Rham cohomology with that defined in terms of the Bessel model. To give a precise definition, let us fix
$\unicode[STIX]{x1D70B}_{f}$
defined in terms of de Rham cohomology with that defined in terms of the Bessel model. To give a precise definition, let us fix
 $\unicode[STIX]{x1D6F9}=\bigotimes _{v}\unicode[STIX]{x1D6F9}_{v}\in \unicode[STIX]{x1D70B}^{\prime }=\check{\unicode[STIX]{x1D70B}}|\unicode[STIX]{x1D708}|^{-3}$
a factorizable vector whose archimedean component
$\unicode[STIX]{x1D6F9}=\bigotimes _{v}\unicode[STIX]{x1D6F9}_{v}\in \unicode[STIX]{x1D70B}^{\prime }=\check{\unicode[STIX]{x1D70B}}|\unicode[STIX]{x1D708}|^{-3}$
a factorizable vector whose archimedean component
![]() $\unicode[STIX]{x1D6F9}_{\infty }$
is a lowest weight vector of the minimal
$\unicode[STIX]{x1D6F9}_{\infty }$
is a lowest weight vector of the minimal
![]() $K$
-type of the discrete series
$K$
-type of the discrete series
 $\unicode[STIX]{x1D70B}_{\infty }^{W}\in P(W(-p-q-3))$
(see Definition 3.5). This defines a cuspidal differential form
$\unicode[STIX]{x1D70B}_{\infty }^{W}\in P(W(-p-q-3))$
(see Definition 3.5). This defines a cuspidal differential form
![]() $\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })$
belonging to
$\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty })$
belonging to
 $\text{Hom}_{K_{G}}(\bigwedge ^{2}\mathfrak{p}^{+}\otimes _{\mathbb{C}}\mathfrak{p}^{-},W(-p-q-3)\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{W})$
(Lemma 4.26) and hence an element
$\text{Hom}_{K_{G}}(\bigwedge ^{2}\mathfrak{p}^{+}\otimes _{\mathbb{C}}\mathfrak{p}^{-},W(-p-q-3)\otimes _{\mathbb{C}}\unicode[STIX]{x1D70B}_{\infty }^{W})$
(Lemma 4.26) and hence an element
 $(\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty }))_{\unicode[STIX]{x1D70E}:E(\unicode[STIX]{x1D70B}_{f})\rightarrow \mathbb{C}}\in M_{B}^{2-k^{\prime }-t^{\prime },1-k-t^{\prime }}$
(Propositions 3.7 and 3.8). As
$(\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty }))_{\unicode[STIX]{x1D70E}:E(\unicode[STIX]{x1D70B}_{f})\rightarrow \mathbb{C}}\in M_{B}^{2-k^{\prime }-t^{\prime },1-k-t^{\prime }}$
(Propositions 3.7 and 3.8). As
![]() $F_{\infty }$
exchanges
$F_{\infty }$
exchanges
 $M_{B}^{2-k^{\prime }-t^{\prime },1-k-t^{\prime }}$
and
$M_{B}^{2-k^{\prime }-t^{\prime },1-k-t^{\prime }}$
and
 $M_{B}^{1-k-t^{\prime },2-k^{\prime }-t^{\prime }}$
, the class
$M_{B}^{1-k-t^{\prime },2-k^{\prime }-t^{\prime }}$
, the class
 $\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6F9}_{\infty })={\textstyle \frac{1}{2}}((\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty }))_{\unicode[STIX]{x1D70E}}+F_{\infty }((\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty }))_{\unicode[STIX]{x1D70E}}))$
satisfies the conditions of Lemma 4.21 and belongs to
$\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6F9}_{\infty })={\textstyle \frac{1}{2}}((\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty }))_{\unicode[STIX]{x1D70E}}+F_{\infty }((\unicode[STIX]{x1D6FA}(\unicode[STIX]{x1D6F9}_{\infty }))_{\unicode[STIX]{x1D70E}}))$
satisfies the conditions of Lemma 4.21 and belongs to
 $M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}^{+}$
.
$M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}^{+}$
.
Definition 6.3. A vector
 $\unicode[STIX]{x1D6F9}_{f}\in \unicode[STIX]{x1D70B}_{f}^{\prime }$
is arithmetic if it is the non-archimedean component of a factorizable cusp form
$\unicode[STIX]{x1D6F9}_{f}\in \unicode[STIX]{x1D70B}_{f}^{\prime }$
is arithmetic if it is the non-archimedean component of a factorizable cusp form
 $\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F9}_{\infty }\otimes \unicode[STIX]{x1D6F9}_{f}\in \unicode[STIX]{x1D70B}^{\prime }$
such that the image of
$\unicode[STIX]{x1D6F9}=\unicode[STIX]{x1D6F9}_{\infty }\otimes \unicode[STIX]{x1D6F9}_{f}\in \unicode[STIX]{x1D70B}^{\prime }$
such that the image of
![]() $\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6F9}_{\infty })$
by the comparison isomorphism
$\unicode[STIX]{x1D714}(\unicode[STIX]{x1D6F9}_{\infty })$
by the comparison isomorphism
 $$\begin{eqnarray}I_{\infty }^{+}:M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{ C}}^{+}\longrightarrow (M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{+})_{\mathbb{ C}}\end{eqnarray}$$
$$\begin{eqnarray}I_{\infty }^{+}:M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{ C}}^{+}\longrightarrow (M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{+})_{\mathbb{ C}}\end{eqnarray}$$
belongs to the
![]() $E(\unicode[STIX]{x1D70B}_{f})$
-structure
$E(\unicode[STIX]{x1D70B}_{f})$
-structure
 $M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{+}$
.
$M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{+}$
.
The following proposition is a reformulation of [Reference HarrisHar04, Proposition 3.5.2].
Proposition 6.4. Assume that
![]() $\unicode[STIX]{x1D70B}$
has a split Bessel model associated to
$\unicode[STIX]{x1D70B}$
has a split Bessel model associated to
![]() $(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
. Then, there exists
$(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
. Then, there exists
 $a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})\in \mathbb{C}^{\times }$
such that the functional
$a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})\in \mathbb{C}^{\times }$
such that the functional
 $\unicode[STIX]{x1D6F9}_{f}\longmapsto a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})W_{\unicode[STIX]{x1D6F9}_{f}}$
sends the
$\unicode[STIX]{x1D6F9}_{f}\longmapsto a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})W_{\unicode[STIX]{x1D6F9}_{f}}$
sends the
![]() $\unicode[STIX]{x1D6F9}_{f}$
which are arithmetic to functions
$\unicode[STIX]{x1D6F9}_{f}$
which are arithmetic to functions
![]() $W_{\unicode[STIX]{x1D713}_{f}}$
which are
$W_{\unicode[STIX]{x1D713}_{f}}$
which are
![]() $\overline{\mathbb{Q}}$
-valued.
$\overline{\mathbb{Q}}$
-valued.
7 The main result
Theorem 7.1. Let
 $k\geqslant k^{\prime }\geqslant 0$
be two integers. Let
$k\geqslant k^{\prime }\geqslant 0$
be two integers. Let
![]() $W$
be an irreducible algebraic representation of
$W$
be an irreducible algebraic representation of
![]() $G$
of highest weight
$G$
of highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },k+k^{\prime }+4)$
. Let
$\unicode[STIX]{x1D706}(k,k^{\prime },k+k^{\prime }+4)$
. Let
 $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}$
be a cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\otimes \unicode[STIX]{x1D70B}_{f}$
be a cuspidal automorphic representation of
![]() $G$
whose central character has infinity type
$G$
whose central character has infinity type
 $-k-k^{\prime }-4$
and whose archimedean component
$-k-k^{\prime }-4$
and whose archimedean component
![]() $\unicode[STIX]{x1D70B}_{\infty }$
is a discrete series of Harish-Chandra parameter
$\unicode[STIX]{x1D70B}_{\infty }$
is a discrete series of Harish-Chandra parameter
 $(k+2,k^{\prime }+1)$
. Let
$(k+2,k^{\prime }+1)$
. Let
![]() $\unicode[STIX]{x1D708}_{1}^{0}$
be a finite-order Hecke character of
$\unicode[STIX]{x1D708}_{1}^{0}$
be a finite-order Hecke character of
 $\operatorname{sign}(-1)^{k-1}$
and let
$\operatorname{sign}(-1)^{k-1}$
and let
![]() $\unicode[STIX]{x1D708}_{1}$
denote the Hecke character
$\unicode[STIX]{x1D708}_{1}$
denote the Hecke character
 $|\;|^{1-k^{\prime }}\unicode[STIX]{x1D708}_{1}^{0}$
. Let
$|\;|^{1-k^{\prime }}\unicode[STIX]{x1D708}_{1}^{0}$
. Let
![]() $\unicode[STIX]{x1D708}_{2}^{0}$
be a finite-order Hecke character of
$\unicode[STIX]{x1D708}_{2}^{0}$
be a finite-order Hecke character of
 $\operatorname{sign}(-1)^{k^{\prime }-1}$
and let
$\operatorname{sign}(-1)^{k^{\prime }-1}$
and let
![]() $\unicode[STIX]{x1D708}_{2}$
denote the Hecke character
$\unicode[STIX]{x1D708}_{2}$
denote the Hecke character
![]() $|\;|^{1-k}\unicode[STIX]{x1D708}_{2}^{0}$
. Let
$|\;|^{1-k}\unicode[STIX]{x1D708}_{2}^{0}$
. Let
![]() $V$
be the finite set of places where
$V$
be the finite set of places where
![]() $\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1}$
or
$\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1}$
or
![]() $\unicode[STIX]{x1D708}_{2}$
is ramified, together with the archimedean place. Assume that:
$\unicode[STIX]{x1D708}_{2}$
is ramified, together with the archimedean place. Assume that:
-
(i) we have
 $k>k^{\prime }>0$
;
$k>k^{\prime }>0$
; -
(ii) we have
 $k+1\equiv k^{\prime }\equiv 0~(\text{mod}~2)$
;
$k+1\equiv k^{\prime }\equiv 0~(\text{mod}~2)$
; -
(iii) the automorphic representation
 $\unicode[STIX]{x1D70B}$
is stable at infinity;
$\unicode[STIX]{x1D70B}$
is stable at infinity; -
(iv) the automorphic representation
 $\unicode[STIX]{x1D70B}^{\prime }=\check{\unicode[STIX]{x1D70B}}|\unicode[STIX]{x1D708}|^{-3}$
has a split Bessel model associated to
$\unicode[STIX]{x1D70B}^{\prime }=\check{\unicode[STIX]{x1D70B}}|\unicode[STIX]{x1D708}|^{-3}$
has a split Bessel model associated to
 $(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
.
$(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
.
Then,
 $$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\unicode[STIX]{x1D70B}^{-2}a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)L_{V}(k+k^{\prime }-1/2,\check{\unicode[STIX]{x1D70B}}){\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\unicode[STIX]{x1D70B}^{-2}a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)L_{V}(k+k^{\prime }-1/2,\check{\unicode[STIX]{x1D70B}}){\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
Proof. The assumptions on
![]() $k$
and
$k$
and
![]() $k^{\prime }$
imply that if we take
$k^{\prime }$
imply that if we take
 $p=k-1$
and
$p=k-1$
and
 $q=k^{\prime }-1$
, then
$q=k^{\prime }-1$
, then
 $p,q,k,k^{\prime }$
satisfy the assumptions of Theorem 1.1. Let
$p,q,k,k^{\prime }$
satisfy the assumptions of Theorem 1.1. Let
 $\unicode[STIX]{x1D6F9}=\bigotimes _{v}\unicode[STIX]{x1D6F9}_{v}\in \unicode[STIX]{x1D70B}^{\prime }=\check{\unicode[STIX]{x1D70B}}|\unicode[STIX]{x1D708}|^{-3}$
be a factorizable cusp form whose archimedean component
$\unicode[STIX]{x1D6F9}=\bigotimes _{v}\unicode[STIX]{x1D6F9}_{v}\in \unicode[STIX]{x1D70B}^{\prime }=\check{\unicode[STIX]{x1D70B}}|\unicode[STIX]{x1D708}|^{-3}$
be a factorizable cusp form whose archimedean component
![]() $\unicode[STIX]{x1D6F9}_{\infty }$
is a lowest weight vector of the minimal
$\unicode[STIX]{x1D6F9}_{\infty }$
is a lowest weight vector of the minimal
![]() $K$
-type
$K$
-type
 $\unicode[STIX]{x1D70F}_{(k+3,-k^{\prime }-1)}$
of the element
$\unicode[STIX]{x1D70F}_{(k+3,-k^{\prime }-1)}$
of the element
![]() $\unicode[STIX]{x1D70B}_{\infty }^{W}$
of
$\unicode[STIX]{x1D70B}_{\infty }^{W}$
of
 $P(W(-p-q-3))$
. Via a vector
$P(W(-p-q-3))$
. Via a vector
![]() $v$
given by Corollary 4.32, and as explained above the statement of Definition 6.3, we associate to
$v$
given by Corollary 4.32, and as explained above the statement of Definition 6.3, we associate to
![]() $\unicode[STIX]{x1D6F9}$
the Betti cohomology class
$\unicode[STIX]{x1D6F9}$
the Betti cohomology class
 $\unicode[STIX]{x1D714}\in M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}^{+}$
satisfying the Hodge types conditions of Lemma 4.21. Note that multiplying
$\unicode[STIX]{x1D714}\in M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{C}}^{+}$
satisfying the Hodge types conditions of Lemma 4.21. Note that multiplying
![]() $\unicode[STIX]{x1D714}$
by a scalar, we can assume that the image of
$\unicode[STIX]{x1D714}$
by a scalar, we can assume that the image of
![]() $\unicode[STIX]{x1D714}$
by the comparison isomorphism
$\unicode[STIX]{x1D714}$
by the comparison isomorphism
 $$\begin{eqnarray}I_{\infty }^{+}:M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{ C}}^{+}\longrightarrow (M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{+})_{\mathbb{ C}}\end{eqnarray}$$
$$\begin{eqnarray}I_{\infty }^{+}:M_{B}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))_{\mathbb{ C}}^{+}\longrightarrow (M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{+})_{\mathbb{ C}}\end{eqnarray}$$
belongs to
 $M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{+}$
. Let
$M_{dR}(\check{\unicode[STIX]{x1D70B}}_{f}|\unicode[STIX]{x1D708}|^{-3},W(-p-q-3))/F^{+}$
. Let
 $\operatorname{Eis}_{{\mathcal{H}}}^{k-1,k^{\prime }-1,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\in {\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
. Let
$\operatorname{Eis}_{{\mathcal{H}}}^{k-1,k^{\prime }-1,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })\in {\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
. Let
![]() $\unicode[STIX]{x1D70C}$
be a current given by Lemma 4.23. According to the first statement of Lemma 4.23, the Betti cohomology class
$\unicode[STIX]{x1D70C}$
be a current given by Lemma 4.23. According to the first statement of Lemma 4.23, the Betti cohomology class
![]() $[\unicode[STIX]{x1D70C}]$
of
$[\unicode[STIX]{x1D70C}]$
of
![]() $\unicode[STIX]{x1D70C}$
is a lift of
$\unicode[STIX]{x1D70C}$
is a lift of
 $\operatorname{Eis}_{{\mathcal{H}}}^{k-1,k^{\prime }-1,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
by the natural surjection
$\operatorname{Eis}_{{\mathcal{H}}}^{k-1,k^{\prime }-1,W}(\unicode[STIX]{x1D719}_{f}\otimes \unicode[STIX]{x1D719}_{f}^{\prime })$
by the natural surjection
 $$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\longrightarrow \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})\end{eqnarray}$$
$$\begin{eqnarray}M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}}^{-}(-1)\longrightarrow \text{Ext}_{\text{MHS}_{\mathbb{R}}^{+}}^{1}(\mathbb{R}(0),M_{B}(\unicode[STIX]{x1D70B}_{f},W)_{\mathbb{R}})\end{eqnarray}$$
of Lemma 4.12. Hence, Lemma 4.21 implies that
 $$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\frac{\langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B}}{\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}}{\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\frac{\langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B}}{\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}}{\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
According to Proposition 6.2, we have
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}\sim (2\unicode[STIX]{x1D70B}i)^{2}c^{-}(\unicode[STIX]{x1D70B}_{f},W)^{-1}.\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}\sim (2\unicode[STIX]{x1D70B}i)^{2}c^{-}(\unicode[STIX]{x1D70B}_{f},W)^{-1}.\end{eqnarray}$$
With the notation of Corollary 4.29, the pairing
 $\langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B}$
is equal to
$\langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B}$
is equal to
 $$\begin{eqnarray}\displaystyle & & \displaystyle C_{1}\frac{3}{160(p+1)}\mathop{\sum }_{j=0}^{3}(-1)^{k^{\prime }+q+j}\binom{3}{j}A_{k,k^{\prime },k^{\prime }+q+j,j}\int \unicode[STIX]{x1D6EF}_{k-q-2j+4,-k+k^{\prime }+q,-q-2}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad -\,C_{2}\frac{(-1)^{k}}{8(q+1)}(B_{k,k^{\prime },k-p}-C_{k,k^{\prime },k-p+1})\int \unicode[STIX]{x1D6EF}_{k^{\prime }+p+3,-p-2,-k+k^{\prime }+p}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad +\,C_{3}\frac{3}{160(q+1)}\mathop{\sum }_{j=0}^{3}(-1)^{k^{\prime }+j}\binom{3}{j}A_{k,k^{\prime },k^{\prime }+p+j,j}\int \overline{\unicode[STIX]{x1D6EF}}_{k-p-2j+4,p+2,-k+k^{\prime }+p}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad -\,C_{4}\frac{(-1)^{k^{\prime }+p+1}}{8(q+1)}(B_{k,k^{\prime },k^{\prime }+p}-C_{k,k^{\prime },k^{\prime }-p+1})\int \overline{\unicode[STIX]{x1D6EF}}_{k-p+3,-k+k^{\prime }-q,q+2}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime }).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle C_{1}\frac{3}{160(p+1)}\mathop{\sum }_{j=0}^{3}(-1)^{k^{\prime }+q+j}\binom{3}{j}A_{k,k^{\prime },k^{\prime }+q+j,j}\int \unicode[STIX]{x1D6EF}_{k-q-2j+4,-k+k^{\prime }+q,-q-2}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad -\,C_{2}\frac{(-1)^{k}}{8(q+1)}(B_{k,k^{\prime },k-p}-C_{k,k^{\prime },k-p+1})\int \unicode[STIX]{x1D6EF}_{k^{\prime }+p+3,-p-2,-k+k^{\prime }+p}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad +\,C_{3}\frac{3}{160(q+1)}\mathop{\sum }_{j=0}^{3}(-1)^{k^{\prime }+j}\binom{3}{j}A_{k,k^{\prime },k^{\prime }+p+j,j}\int \overline{\unicode[STIX]{x1D6EF}}_{k-p-2j+4,p+2,-k+k^{\prime }+p}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & & \displaystyle \quad -\,C_{4}\frac{(-1)^{k^{\prime }+p+1}}{8(q+1)}(B_{k,k^{\prime },k^{\prime }+p}-C_{k,k^{\prime },k^{\prime }-p+1})\int \overline{\unicode[STIX]{x1D6EF}}_{k-p+3,-k+k^{\prime }-q,q+2}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime }).\nonumber\end{eqnarray}$$
According to Proposition 5.3, if we choose
![]() $\unicode[STIX]{x1D719}_{f}$
and
$\unicode[STIX]{x1D719}_{f}$
and
![]() $\unicode[STIX]{x1D719}_{f}^{\prime }$
properly, we have
$\unicode[STIX]{x1D719}_{f}^{\prime }$
properly, we have
 $$\begin{eqnarray}\displaystyle \int \unicode[STIX]{x1D6EF}_{n,r,s}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime }) & = & \displaystyle \int X_{(1,-1)}^{n}\unicode[STIX]{x1D6F9}E^{\unicode[STIX]{x1D6F7}}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int \unicode[STIX]{x1D6EF}_{n,r,s}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime }) & = & \displaystyle \int X_{(1,-1)}^{n}\unicode[STIX]{x1D6F9}E^{\unicode[STIX]{x1D6F7}}\nonumber\end{eqnarray}$$
where the archimedean component of the Schwartz–Bruhat function
![]() $\unicode[STIX]{x1D6F7}$
is defined by
$\unicode[STIX]{x1D6F7}$
is defined by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{\infty }(x_{1},y_{1},x_{2},y_{2}) & = & \displaystyle (ix_{1}+y_{1})^{(p-r)/2}(ix_{1}-y_{1})^{(p+r)/2}(ix_{2}+y_{2})^{(q-s)/2}\nonumber\\ \displaystyle & & \displaystyle \times \,(ix_{2}-y_{2})^{(q+s)/2}e^{-\unicode[STIX]{x1D70B}(x_{1}^{2}+y_{1}^{2}+x_{2}^{2}+y_{2}^{2})}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}_{\infty }(x_{1},y_{1},x_{2},y_{2}) & = & \displaystyle (ix_{1}+y_{1})^{(p-r)/2}(ix_{1}-y_{1})^{(p+r)/2}(ix_{2}+y_{2})^{(q-s)/2}\nonumber\\ \displaystyle & & \displaystyle \times \,(ix_{2}-y_{2})^{(q+s)/2}e^{-\unicode[STIX]{x1D70B}(x_{1}^{2}+y_{1}^{2}+x_{2}^{2}+y_{2}^{2})}.\nonumber\end{eqnarray}$$
This has weight
![]() $\unicode[STIX]{x1D706}^{\prime }(r,s)$
for the action of
$\unicode[STIX]{x1D706}^{\prime }(r,s)$
for the action of
![]() $\text{U}(1)^{2}$
. Moreover, the archimedean component of
$\text{U}(1)^{2}$
. Moreover, the archimedean component of
![]() $\unicode[STIX]{x1D6F9}$
is chosen to be a lowest weight vector of the minimal
$\unicode[STIX]{x1D6F9}$
is chosen to be a lowest weight vector of the minimal
![]() $K$
-type
$K$
-type
 $\unicode[STIX]{x1D70F}_{(k+3,-k^{\prime }-1)}$
of
$\unicode[STIX]{x1D70F}_{(k+3,-k^{\prime }-1)}$
of
![]() $\unicode[STIX]{x1D70B}_{\infty }^{W}$
. Hence
$\unicode[STIX]{x1D70B}_{\infty }^{W}$
. Hence
 $X_{(1,-1)}^{n}\unicode[STIX]{x1D6F9}$
is the
$X_{(1,-1)}^{n}\unicode[STIX]{x1D6F9}$
is the
![]() $n$
th vector of a standard basis of
$n$
th vector of a standard basis of
 $\unicode[STIX]{x1D70F}_{(k+3,-k^{\prime }-1)}$
. The integrals above expand into Euler products of
$\unicode[STIX]{x1D70F}_{(k+3,-k^{\prime }-1)}$
. The integrals above expand into Euler products of
![]() $v$
-adic integrals (Corollary 5.8) and we have
$v$
-adic integrals (Corollary 5.8) and we have
 $$\begin{eqnarray}\int \unicode[STIX]{x1D6EF}_{k-q-2j+4,-k+k^{\prime }+q,-q-2}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })=0\end{eqnarray}$$
$$\begin{eqnarray}\int \unicode[STIX]{x1D6EF}_{k-q-2j+4,-k+k^{\prime }+q,-q-2}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })=0\end{eqnarray}$$
because the identities
 $$\begin{eqnarray}k-q-2j+4-k^{\prime }-1+(-k+k^{\prime }+q)=-2j+3\neq 0,\end{eqnarray}$$
$$\begin{eqnarray}k-q-2j+4-k^{\prime }-1+(-k+k^{\prime }+q)=-2j+3\neq 0,\end{eqnarray}$$
imply the vanishing of its archimedean factor (see the first statement of Proposition 5.12). Similarly,
 $$\begin{eqnarray}\int \overline{\unicode[STIX]{x1D6EF}}_{k-p-2j+4,p+2,-k+k^{\prime }+p}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })=\int \overline{\unicode[STIX]{x1D6EF}}_{k-p+3,-k+k^{\prime }-q,q+2}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })=0.\end{eqnarray}$$
$$\begin{eqnarray}\int \overline{\unicode[STIX]{x1D6EF}}_{k-p-2j+4,p+2,-k+k^{\prime }+p}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })=\int \overline{\unicode[STIX]{x1D6EF}}_{k-p+3,-k+k^{\prime }-q,q+2}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })=0.\end{eqnarray}$$
As a consequence,
 $$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B} & = & \displaystyle -C_{2}\frac{(-1)^{k}}{8(q+1)}(B_{k,k^{\prime },k-p}-C_{k,k^{\prime },k-p+1})\int \unicode[STIX]{x1D6EF}_{k^{\prime }+p+3,-p-2,-k+k^{\prime }+p}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & {\sim} & \displaystyle C_{2}\int (X_{(1,-1)}^{k^{\prime }+p+3}\unicode[STIX]{x1D6F9})E^{\unicode[STIX]{x1D6F7}}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B} & = & \displaystyle -C_{2}\frac{(-1)^{k}}{8(q+1)}(B_{k,k^{\prime },k-p}-C_{k,k^{\prime },k-p+1})\int \unicode[STIX]{x1D6EF}_{k^{\prime }+p+3,-p-2,-k+k^{\prime }+p}(\unicode[STIX]{x1D719}_{f},\unicode[STIX]{x1D719}_{f}^{\prime })\nonumber\\ \displaystyle & {\sim} & \displaystyle C_{2}\int (X_{(1,-1)}^{k^{\prime }+p+3}\unicode[STIX]{x1D6F9})E^{\unicode[STIX]{x1D6F7}}.\nonumber\end{eqnarray}$$
For this integral, with the notation of Proposition 5.12, we have
 $\unicode[STIX]{x1D706}_{1}=k+3$
,
$\unicode[STIX]{x1D706}_{1}=k+3$
,
 $\unicode[STIX]{x1D706}_{2}=-k^{\prime }-1$
and
$\unicode[STIX]{x1D706}_{2}=-k^{\prime }-1$
and
 $t=n=k^{\prime }+p+3$
hence
$t=n=k^{\prime }+p+3$
hence
 $t+\unicode[STIX]{x1D706}_{2}+r=-t+\unicode[STIX]{x1D706}_{1}+s=0$
, which means that we can apply the second result of Proposition 5.12. Normalize the Bessel functional
$t+\unicode[STIX]{x1D706}_{2}+r=-t+\unicode[STIX]{x1D706}_{1}+s=0$
, which means that we can apply the second result of Proposition 5.12. Normalize the Bessel functional
 $W_{\unicode[STIX]{x1D6F9}}=\prod _{v}^{\prime }W_{\unicode[STIX]{x1D6F9}_{v}}$
in such a way that for any place
$W_{\unicode[STIX]{x1D6F9}}=\prod _{v}^{\prime }W_{\unicode[STIX]{x1D6F9}_{v}}$
in such a way that for any place
![]() $p\notin V$
, we have
$p\notin V$
, we have
 $W_{\unicode[STIX]{x1D6F9}_{p}}(1)=1$
, and that
$W_{\unicode[STIX]{x1D6F9}_{p}}(1)=1$
, and that
 $$\begin{eqnarray}W_{\unicode[STIX]{x1D6F9}_{\infty }}(1)=2\unicode[STIX]{x1D70B}^{(3(p+q)+6)/2}\int _{L}\frac{\unicode[STIX]{x1D6E4}(c_{1}-s)\unicode[STIX]{x1D6E4}(c_{2}-s)\unicode[STIX]{x1D6E4}(c_{3}-s)\unicode[STIX]{x1D6E4}(c_{4}-s)}{\unicode[STIX]{x1D6E4}(a_{1}-s)\unicode[STIX]{x1D6E4}(a_{2}-s)}\unicode[STIX]{x1D70B}^{2s}\,\frac{ds}{2\unicode[STIX]{x1D70B}i}\end{eqnarray}$$
$$\begin{eqnarray}W_{\unicode[STIX]{x1D6F9}_{\infty }}(1)=2\unicode[STIX]{x1D70B}^{(3(p+q)+6)/2}\int _{L}\frac{\unicode[STIX]{x1D6E4}(c_{1}-s)\unicode[STIX]{x1D6E4}(c_{2}-s)\unicode[STIX]{x1D6E4}(c_{3}-s)\unicode[STIX]{x1D6E4}(c_{4}-s)}{\unicode[STIX]{x1D6E4}(a_{1}-s)\unicode[STIX]{x1D6E4}(a_{2}-s)}\unicode[STIX]{x1D70B}^{2s}\,\frac{ds}{2\unicode[STIX]{x1D70B}i}\end{eqnarray}$$
where the notation is the same as in Proposition 5.12. Combining the statements in Corollary 4.32 and Propositions 5.9, 5.11, 5.12 and 6.4, we obtain
 $$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B} & {\sim} & \displaystyle \frac{\unicode[STIX]{x1D6E4}(c_{1}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(c_{2}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(c_{3}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(c_{4}+{\textstyle \frac{3(p+q)+6}{4}})}{\unicode[STIX]{x1D6E4}(a_{1}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(a_{2}+{\textstyle \frac{3(p+q)+6}{4}})}\nonumber\\ \displaystyle & & \displaystyle \times \,a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})L_{V}(p+q+7/2,\check{\unicode[STIX]{x1D70B}},r).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B} & {\sim} & \displaystyle \frac{\unicode[STIX]{x1D6E4}(c_{1}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(c_{2}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(c_{3}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(c_{4}+{\textstyle \frac{3(p+q)+6}{4}})}{\unicode[STIX]{x1D6E4}(a_{1}+{\textstyle \frac{3(p+q)+6}{4}})\unicode[STIX]{x1D6E4}(a_{2}+{\textstyle \frac{3(p+q)+6}{4}})}\nonumber\\ \displaystyle & & \displaystyle \times \,a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})L_{V}(p+q+7/2,\check{\unicode[STIX]{x1D70B}},r).\nonumber\end{eqnarray}$$
We have
 $$\begin{eqnarray}\displaystyle c_{1}+\frac{3(p+q)+6}{4} & = & \displaystyle k+\frac{k^{\prime }}{2}+1,\nonumber\\ \displaystyle c_{2}+\frac{3(p+q)+6}{4} & = & \displaystyle k+k^{\prime }+\frac{4}{2},\nonumber\\ \displaystyle c_{3}+\frac{3(p+q)+6}{4} & = & \displaystyle k-\frac{k^{\prime }}{2}+1,\nonumber\\ \displaystyle c_{4}+\frac{3(p+q)+6}{4} & = & \displaystyle k+k^{\prime }+\frac{3}{2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle c_{1}+\frac{3(p+q)+6}{4} & = & \displaystyle k+\frac{k^{\prime }}{2}+1,\nonumber\\ \displaystyle c_{2}+\frac{3(p+q)+6}{4} & = & \displaystyle k+k^{\prime }+\frac{4}{2},\nonumber\\ \displaystyle c_{3}+\frac{3(p+q)+6}{4} & = & \displaystyle k-\frac{k^{\prime }}{2}+1,\nonumber\\ \displaystyle c_{4}+\frac{3(p+q)+6}{4} & = & \displaystyle k+k^{\prime }+\frac{3}{2}.\nonumber\end{eqnarray}$$
By our assumption
 $k^{\prime }\equiv 0~(\text{mod}~2)$
, the numbers
$k^{\prime }\equiv 0~(\text{mod}~2)$
, the numbers
![]() $c_{1},c_{2}$
and
$c_{1},c_{2}$
and
![]() $c_{3}$
are integers and
$c_{3}$
are integers and
![]() $c_{4}$
is a half-integer. By well-known formulas for the positive integral and half-integral values of the gamma function, for
$c_{4}$
is a half-integer. By well-known formulas for the positive integral and half-integral values of the gamma function, for
 $i=1,2,3$
, we have
$i=1,2,3$
, we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}\biggl(c_{i}+\frac{3(p+q)+6}{4}\biggr) & {\sim} & \displaystyle 1,\nonumber\\ \displaystyle \unicode[STIX]{x1D6E4}\biggl(c_{4}+\frac{3(p+q)+6}{4}\biggr) & {\sim} & \displaystyle \unicode[STIX]{x1D70B}^{1/2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}\biggl(c_{i}+\frac{3(p+q)+6}{4}\biggr) & {\sim} & \displaystyle 1,\nonumber\\ \displaystyle \unicode[STIX]{x1D6E4}\biggl(c_{4}+\frac{3(p+q)+6}{4}\biggr) & {\sim} & \displaystyle \unicode[STIX]{x1D70B}^{1/2}.\nonumber\end{eqnarray}$$
Similarly, using the assumption
 $k+1\equiv k^{\prime }\equiv 0~(\text{mod}~2)$
, we show
$k+1\equiv k^{\prime }\equiv 0~(\text{mod}~2)$
, we show
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}\biggl(a_{1}+\frac{3(p+q)+6}{4}\biggr) & {\sim} & \displaystyle 1\nonumber\\ \displaystyle \unicode[STIX]{x1D6E4}\biggl(a_{2}+\frac{3(p+q)+6}{4}\biggr) & {\sim} & \displaystyle \unicode[STIX]{x1D70B}^{1/2}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}\biggl(a_{1}+\frac{3(p+q)+6}{4}\biggr) & {\sim} & \displaystyle 1\nonumber\\ \displaystyle \unicode[STIX]{x1D6E4}\biggl(a_{2}+\frac{3(p+q)+6}{4}\biggr) & {\sim} & \displaystyle \unicode[STIX]{x1D70B}^{1/2}.\nonumber\end{eqnarray}$$
Then, we obtain
 $$\begin{eqnarray}\frac{\langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B}}{\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}}\sim \unicode[STIX]{x1D70B}^{-2}a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)L_{S}(k+k^{\prime }-1/2,\check{\unicode[STIX]{x1D70B}}).\square\end{eqnarray}$$
$$\begin{eqnarray}\frac{\langle \unicode[STIX]{x1D714},[\unicode[STIX]{x1D70C}]\rangle _{B}}{\langle \unicode[STIX]{x1D714},\widetilde{v}_{{\mathcal{D}}}\rangle _{B}}\sim \unicode[STIX]{x1D70B}^{-2}a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)L_{S}(k+k^{\prime }-1/2,\check{\unicode[STIX]{x1D70B}}).\square\end{eqnarray}$$
In the case we are interested in, the existence of a split Bessel model follows from some results of Moriyama and Takloo-Bighash.
Proposition 7.2. Let
 $k,k^{\prime },\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2}$
be as above. If
$k,k^{\prime },\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2}$
be as above. If
 $k\neq 3,k^{\prime }\neq 2$
and
$k\neq 3,k^{\prime }\neq 2$
and
![]() $\unicode[STIX]{x1D70B}^{\prime }$
is generic, then
$\unicode[STIX]{x1D70B}^{\prime }$
is generic, then
![]() $\unicode[STIX]{x1D70B}^{\prime }$
has a split Bessel model associated to
$\unicode[STIX]{x1D70B}^{\prime }$
has a split Bessel model associated to
![]() $(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
.
$(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
.
Proof. With the notation of Definition 5.4, we see that
 $$\begin{eqnarray}W_{\unicode[STIX]{x1D6F9}}(1)=\int _{\mathbb{Q}^{\times }\backslash \mathbb{A}^{\times }}\int _{(\mathbb{Q}\backslash \mathbb{A})^{3}}\unicode[STIX]{x1D6F9}\left(\left(\begin{array}{@{}cccc@{}}1 & & r & t\\ & 1 & t & s\\ & & 1 & \\ & & & 1\end{array}\right)\left(\begin{array}{@{}cccc@{}}y & & & \\ & 1 & & \\ & & 1 & \\ & & & y\end{array}\right)\right)\unicode[STIX]{x1D708}_{1}(y)^{-1}\unicode[STIX]{x1D702}(t)^{-1}\,dr\,ds\,dt\,d^{\times }y.\end{eqnarray}$$
$$\begin{eqnarray}W_{\unicode[STIX]{x1D6F9}}(1)=\int _{\mathbb{Q}^{\times }\backslash \mathbb{A}^{\times }}\int _{(\mathbb{Q}\backslash \mathbb{A})^{3}}\unicode[STIX]{x1D6F9}\left(\left(\begin{array}{@{}cccc@{}}1 & & r & t\\ & 1 & t & s\\ & & 1 & \\ & & & 1\end{array}\right)\left(\begin{array}{@{}cccc@{}}y & & & \\ & 1 & & \\ & & 1 & \\ & & & y\end{array}\right)\right)\unicode[STIX]{x1D708}_{1}(y)^{-1}\unicode[STIX]{x1D702}(t)^{-1}\,dr\,ds\,dt\,d^{\times }y.\end{eqnarray}$$
This is the central value
 ${\mathcal{Z}}(1/2,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})$
of the integral representation
${\mathcal{Z}}(1/2,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})$
of the integral representation
 ${\mathcal{Z}}(s,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})$
of the spinor
${\mathcal{Z}}(s,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})$
of the spinor
![]() $L$
-function of
$L$
-function of
![]() $\unicode[STIX]{x1D6F9}$
twisted by
$\unicode[STIX]{x1D6F9}$
twisted by
![]() $\unicode[STIX]{x1D708}_{1}^{-1}$
, as defined by Novodvorsky (see [Reference Takloo-BighashTak00]). Let us mention that Novodvorsky’s expression for this integral is obtained from ours after an easy change of variables. To show that this central value is non-zero, it is enough to show that
$\unicode[STIX]{x1D708}_{1}^{-1}$
, as defined by Novodvorsky (see [Reference Takloo-BighashTak00]). Let us mention that Novodvorsky’s expression for this integral is obtained from ours after an easy change of variables. To show that this central value is non-zero, it is enough to show that
 ${\mathcal{Z}}(1/2,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})$
expands into an Euler product where each factor is non-zero. Note that the central character
${\mathcal{Z}}(1/2,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})$
expands into an Euler product where each factor is non-zero. Note that the central character
 $\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1}$
has infinity type
$\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1}$
has infinity type
 $\unicode[STIX]{x1D714}_{\infty }=k+2k^{\prime }-3$
and that, for integers
$\unicode[STIX]{x1D714}_{\infty }=k+2k^{\prime }-3$
and that, for integers
![]() $k,k^{\prime }$
satisfying our assumptions, we have
$k,k^{\prime }$
satisfying our assumptions, we have
 $k+2k^{\prime }\geqslant 7$
. Hence, excluding the case
$k+2k^{\prime }\geqslant 7$
. Hence, excluding the case
![]() $k=3$
and
$k=3$
and
![]() $k^{\prime }=2$
, we have the inequality
$k^{\prime }=2$
, we have the inequality
 $1/2>(5-\unicode[STIX]{x1D714}_{\infty })/2$
, and so it follows from [Reference MoriyamaMor04, Proposition 4], that the above integral expands into an Euler product
$1/2>(5-\unicode[STIX]{x1D714}_{\infty })/2$
, and so it follows from [Reference MoriyamaMor04, Proposition 4], that the above integral expands into an Euler product
 $$\begin{eqnarray}{\mathcal{Z}}(1/2,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})=\mathop{\prod }_{v}{\mathcal{Z}}_{v}(1/2,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}(1/2,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})=\mathop{\prod }_{v}{\mathcal{Z}}_{v}(1/2,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})\end{eqnarray}$$
indexed by all places of
![]() $\mathbb{Q}$
. The archimedean factor is a gamma factor, hence does not vanish. As a consequence, the computations of the local non-archimedean factors
$\mathbb{Q}$
. The archimedean factor is a gamma factor, hence does not vanish. As a consequence, the computations of the local non-archimedean factors
 ${\mathcal{Z}}_{v}(1/2,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})$
performed in [Reference Takloo-BighashTak00] show that
${\mathcal{Z}}_{v}(1/2,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})$
performed in [Reference Takloo-BighashTak00] show that
 $$\begin{eqnarray}{\mathcal{Z}}(1/2,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})\neq 0.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}(1/2,\unicode[STIX]{x1D6F9}\otimes \unicode[STIX]{x1D708}_{1}^{-1})\neq 0.\end{eqnarray}$$
This shows that
![]() $\unicode[STIX]{x1D70B}^{\prime }$
has a split Bessel model associated to
$\unicode[STIX]{x1D70B}^{\prime }$
has a split Bessel model associated to
![]() $(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
.◻
$(\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})$
.◻
As we work with a stable
![]() $L$
-packet, which always contains a generic member, Theorem 7.1 and Proposition 7.2 directly imply the following result.
$L$
-packet, which always contains a generic member, Theorem 7.1 and Proposition 7.2 directly imply the following result.
Theorem 7.3. Let
 $k\geqslant k^{\prime }\geqslant 0$
be two integers. Let
$k\geqslant k^{\prime }\geqslant 0$
be two integers. Let
![]() $W$
be an irreducible algebraic representation of
$W$
be an irreducible algebraic representation of
![]() $G$
of highest weight
$G$
of highest weight
 $\unicode[STIX]{x1D706}(k,k^{\prime },k+k^{\prime }+4)$
. Let
$\unicode[STIX]{x1D706}(k,k^{\prime },k+k^{\prime }+4)$
. Let
 $\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\,\otimes \,\unicode[STIX]{x1D70B}_{f}$
be a cuspidal automorphic representation of
$\unicode[STIX]{x1D70B}=\unicode[STIX]{x1D70B}_{\infty }\,\otimes \,\unicode[STIX]{x1D70B}_{f}$
be a cuspidal automorphic representation of
![]() $G$
whose central character has infinity type
$G$
whose central character has infinity type
 $-k-k^{\prime }-4$
and whose archimedean component
$-k-k^{\prime }-4$
and whose archimedean component
![]() $\unicode[STIX]{x1D70B}_{\infty }$
is a discrete series of Harish-Chandra parameter
$\unicode[STIX]{x1D70B}_{\infty }$
is a discrete series of Harish-Chandra parameter
 $(k+2,k^{\prime }+1)$
. Let
$(k+2,k^{\prime }+1)$
. Let
![]() $\unicode[STIX]{x1D708}_{1}^{0}$
be a finite-order Hecke character of
$\unicode[STIX]{x1D708}_{1}^{0}$
be a finite-order Hecke character of
 $\operatorname{sign}(-1)^{k-1}$
and let
$\operatorname{sign}(-1)^{k-1}$
and let
![]() $\unicode[STIX]{x1D708}_{1}$
denote the Hecke character
$\unicode[STIX]{x1D708}_{1}$
denote the Hecke character
 $|\;|^{1-k^{\prime }}\unicode[STIX]{x1D708}_{1}^{0}$
. Let
$|\;|^{1-k^{\prime }}\unicode[STIX]{x1D708}_{1}^{0}$
. Let
![]() $\unicode[STIX]{x1D708}_{2}^{0}$
be a finite-order Hecke character of
$\unicode[STIX]{x1D708}_{2}^{0}$
be a finite-order Hecke character of
 $\operatorname{sign}(-1)^{k^{\prime }-1}$
and let
$\operatorname{sign}(-1)^{k^{\prime }-1}$
and let
![]() $\unicode[STIX]{x1D708}_{2}$
denote the Hecke character
$\unicode[STIX]{x1D708}_{2}$
denote the Hecke character
![]() $|\;|^{1-k}\unicode[STIX]{x1D708}_{2}^{0}$
. Let
$|\;|^{1-k}\unicode[STIX]{x1D708}_{2}^{0}$
. Let
![]() $V$
be the finite set of places where
$V$
be the finite set of places where
![]() $\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1}$
or
$\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1}$
or
![]() $\unicode[STIX]{x1D708}_{2}$
is ramified, together with the archimedean place. Assume that:
$\unicode[STIX]{x1D708}_{2}$
is ramified, together with the archimedean place. Assume that:
-
(i) we have
 $k>k^{\prime }>0$
;
$k>k^{\prime }>0$
; -
(ii) we have
 $k+1\equiv k^{\prime }\equiv 0~(\text{mod}~2)$
;
$k+1\equiv k^{\prime }\equiv 0~(\text{mod}~2)$
; -
(iii) we have
 $k\neq 3,k^{\prime }\neq 2$
;
$k\neq 3,k^{\prime }\neq 2$
; -
(iv) the automorphic representation
 $\unicode[STIX]{x1D70B}$
is stable at infinity.
$\unicode[STIX]{x1D70B}$
is stable at infinity.
Then,
 $$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\unicode[STIX]{x1D70B}^{-2}a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)L_{V}(k+k^{\prime }-1/2,\check{\unicode[STIX]{x1D70B}}){\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)=\unicode[STIX]{x1D70B}^{-2}a(\unicode[STIX]{x1D70B},\unicode[STIX]{x1D708}_{1},\unicode[STIX]{x1D708}_{2})c^{-}(\unicode[STIX]{x1D70B}_{f},W)L_{V}(k+k^{\prime }-1/2,\check{\unicode[STIX]{x1D70B}}){\mathcal{D}}(\unicode[STIX]{x1D70B}_{f},W).\end{eqnarray}$$
Corollary 7.4. Let
![]() $n$
be an integer. Let
$n$
be an integer. Let
 $A\longrightarrow S$
be the universal abelian surface of infinite level over the Siegel threefold and let
$A\longrightarrow S$
be the universal abelian surface of infinite level over the Siegel threefold and let
![]() $A^{n}$
be the
$A^{n}$
be the
![]() $n$
th-fold fiber product over
$n$
th-fold fiber product over
![]() $S$
. If
$S$
. If
![]() $n$
is odd and
$n$
is odd and
![]() $n\geqslant 7$
, then the motivic cohomology space
$n\geqslant 7$
, then the motivic cohomology space
 $H_{{\mathcal{M}}}^{n+4}(A^{n},\mathbb{Q}(n+2))$
is non-zero.
$H_{{\mathcal{M}}}^{n+4}(A^{n},\mathbb{Q}(n+2))$
is non-zero.
Proof. Let
![]() $k$
and
$k$
and
![]() $k^{\prime }$
be two integers satisfying the assumptions of Theorem 7.3 and such that
$k^{\prime }$
be two integers satisfying the assumptions of Theorem 7.3 and such that
 $n=k+k^{\prime }$
. Let
$n=k+k^{\prime }$
. Let
![]() $t$
denote the integer
$t$
denote the integer
 $(k+k^{\prime }+p+q+6)/2$
. The target of the map
$(k+k^{\prime }+p+q+6)/2$
. The target of the map
 $\operatorname{Eis}_{{\mathcal{M}}}^{p,q,W}$
is the motivic cohomology group
$\operatorname{Eis}_{{\mathcal{M}}}^{p,q,W}$
is the motivic cohomology group
 $H_{{\mathcal{M}}}^{4}(S,W)$
, for
$H_{{\mathcal{M}}}^{4}(S,W)$
, for
![]() $W$
as above, which is a subspace of
$W$
as above, which is a subspace of
 $H_{{\mathcal{M}}}^{k+k^{\prime }+4}(A^{k+k^{\prime }},\mathbb{Q}(t))$
according to Proposition 4.1. Assume that
$H_{{\mathcal{M}}}^{k+k^{\prime }+4}(A^{k+k^{\prime }},\mathbb{Q}(t))$
according to Proposition 4.1. Assume that
 $p=k-1$
and
$p=k-1$
and
 $q=k^{\prime }-1$
. It follows from [Reference MoriyamaMor04, Proposition 4] that the value
$q=k^{\prime }-1$
. It follows from [Reference MoriyamaMor04, Proposition 4] that the value
 $k+k^{\prime }-1/2$
is in the absolute convergence region of the spinor
$k+k^{\prime }-1/2$
is in the absolute convergence region of the spinor
![]() $L$
-function, hence that the special value
$L$
-function, hence that the special value
 $L_{V}(k+k^{\prime }-1/2,\check{\unicode[STIX]{x1D70B}},r)$
is non-zero. As a consequence, Theorem 7.3 implies that the vector space
$L_{V}(k+k^{\prime }-1/2,\check{\unicode[STIX]{x1D70B}},r)$
is non-zero. As a consequence, Theorem 7.3 implies that the vector space
 ${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
is non-zero. Via Beilinson’s regulator, the image of
${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
is non-zero. Via Beilinson’s regulator, the image of
 $\operatorname{Eis}_{{\mathcal{M}}}^{p,q,W}$
surjects on
$\operatorname{Eis}_{{\mathcal{M}}}^{p,q,W}$
surjects on
 ${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
for any
${\mathcal{K}}(\unicode[STIX]{x1D70B}_{f},W)$
for any
![]() $\unicode[STIX]{x1D70B}_{f}$
which is the non-archimedean part of a cuspidal automorphic representation satisfying the conditions of Theorem 7.3. Hence, the motivic cohomology group
$\unicode[STIX]{x1D70B}_{f}$
which is the non-archimedean part of a cuspidal automorphic representation satisfying the conditions of Theorem 7.3. Hence, the motivic cohomology group
 $H_{{\mathcal{M}}}^{n+4}(A^{n},\mathbb{Q}(n+2))$
is non-zero.◻
$H_{{\mathcal{M}}}^{n+4}(A^{n},\mathbb{Q}(n+2))$
is non-zero.◻
Acknowledgements
This article has been written while I benefited from funding from ANR-13-BS01-0012 FERPLAY. I would like to thank Giuseppe Ancona, Jean-Yves Charbonnel, Michael Harris, David Loeffler, Alexander Molev, Brooks Roberts and Jörg Wildeshaus for answering my questions and for useful remarks. Finally, it is a pleasure to thank Pascal Molin for writing a program thanks to which I could perform numerical computations related to this work and the anonymous referee for a careful reading of this article which led to many improvements in the presentation.