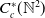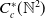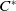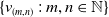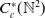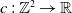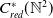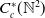1. Introduction
In the recent years, there has been a flurry of activity centred around understanding the inner structure (like
![]() $K$
-theory, KMS states etc.) of
$K$
-theory, KMS states etc.) of
![]() $C^{*}$
-algebras associated to semigroups. The revival of the subject of semigroup
$C^{*}$
-algebras associated to semigroups. The revival of the subject of semigroup
![]() $C^{*}$
-algebras, especially in the last decade, can be attributed to the works of Cuntz and Li on
$C^{*}$
-algebras, especially in the last decade, can be attributed to the works of Cuntz and Li on
![]() $C^{*}$
-algebras associated with rings ([Reference Cuntz6], [Reference Cuntz and Li9], [Reference Cuntz and Li10]). Ring
$C^{*}$
-algebras associated with rings ([Reference Cuntz6], [Reference Cuntz and Li9], [Reference Cuntz and Li10]). Ring
![]() $C^{*}$
-algebras are defined exactly like group
$C^{*}$
-algebras are defined exactly like group
![]() $C^{*}$
-algebras taking into account both the addition and the multiplication rule of the ring, where the ring involved is usually assumed to be an integral domain. Soon, it was realised that it is only appropriate to view these algebras as boundary quotients of semigroup
$C^{*}$
-algebras taking into account both the addition and the multiplication rule of the ring, where the ring involved is usually assumed to be an integral domain. Soon, it was realised that it is only appropriate to view these algebras as boundary quotients of semigroup
![]() $C^{*}$
-algebras.
$C^{*}$
-algebras.
Let
![]() $P$
be a cancellative semigroup. Let the left regular representation of
$P$
be a cancellative semigroup. Let the left regular representation of
![]() $P$
on
$P$
on
![]() $\ell ^{2}(P)$
be denoted by
$\ell ^{2}(P)$
be denoted by
![]() $V\,:\!=\{V_{a}\}_{a \in P}$
. The reduced
$V\,:\!=\{V_{a}\}_{a \in P}$
. The reduced
![]() $C^{*}$
-algebra of the semigroup
$C^{*}$
-algebra of the semigroup
![]() $P$
, denoted
$P$
, denoted
![]() $C_{red}^{*}(P)$
, is the
$C_{red}^{*}(P)$
, is the
![]() $C^{*}$
-algebra generated by
$C^{*}$
-algebra generated by
![]() $\{V_{a}\,:\,a \in P\}$
. Li also defines a universal version, denoted
$\{V_{a}\,:\,a \in P\}$
. Li also defines a universal version, denoted
![]() $C^{*}(P)$
, generated by isometries
$C^{*}(P)$
, generated by isometries
![]() $\{v_{a}\,:\,a \in P\}$
and projections corresponding to ‘certain ideals of
$\{v_{a}\,:\,a \in P\}$
and projections corresponding to ‘certain ideals of
![]() $P$
’ satisfying relations that reflect the relations in the regular representation. The study of
$P$
’ satisfying relations that reflect the relations in the regular representation. The study of
![]() $C_{red}^{*}(P)$
has received much attention in the recent years. Questions concerning its nuclearity,
$C_{red}^{*}(P)$
has received much attention in the recent years. Questions concerning its nuclearity,
![]() $K$
-theory and the structure of KMS states on
$K$
-theory and the structure of KMS states on
![]() $C_{red}^{*}(P)$
were investigated intensively and satisfactory answers were obtained for a large class of semigroups. Some of the notable papers that explore the above mentioned issues are [Reference Cuntz, Echterhoff and Li8], [Reference Li17], [Reference Li16], [Reference Cuntz, Deninger and Laca7], [Reference Laca and Raeburn15], [Reference Laca and Neshveyev14] and [Reference Brownlowe, Larsen, Ramagge and Stammeier4].
$C_{red}^{*}(P)$
were investigated intensively and satisfactory answers were obtained for a large class of semigroups. Some of the notable papers that explore the above mentioned issues are [Reference Cuntz, Echterhoff and Li8], [Reference Li17], [Reference Li16], [Reference Cuntz, Deninger and Laca7], [Reference Laca and Raeburn15], [Reference Laca and Neshveyev14] and [Reference Brownlowe, Larsen, Ramagge and Stammeier4].
However, isometric representations of semigroups other than the regular representation were also considered in the literature, and the associated
![]() $C^{*}$
-algebras were analysed. Let
$C^{*}$
-algebras were analysed. Let
![]() $G$
be a discrete, countable, abelian group, and let
$G$
be a discrete, countable, abelian group, and let
![]() $P \subset G$
be a subsemigroup containing the identity element
$P \subset G$
be a subsemigroup containing the identity element
![]() $0$
. Here is a host of examples of isometric representations of
$0$
. Here is a host of examples of isometric representations of
![]() $P$
. Let
$P$
. Let
![]() $A \subset G$
be a non-empty set such that
$A \subset G$
be a non-empty set such that
![]() $P+A \subset A$
. Consider the Hilbert space
$P+A \subset A$
. Consider the Hilbert space
![]() $\ell ^{2}(A)$
, and let
$\ell ^{2}(A)$
, and let
![]() $\{\delta _{x}\,:\, x \in A\}$
be its standard orthonormal basis. For
$\{\delta _{x}\,:\, x \in A\}$
be its standard orthonormal basis. For
![]() $a \in P$
, let
$a \in P$
, let
![]() $V_a$
be the isometry on
$V_a$
be the isometry on
![]() $\ell ^2(A)$
defined by
$\ell ^2(A)$
defined by
Then,
![]() $V^{A}\,:\!=\{V_{a}\}_{a \in P}$
is an isometric representation of
$V^{A}\,:\!=\{V_{a}\}_{a \in P}$
is an isometric representation of
![]() $P$
, which we call the isometric representation associated to
$P$
, which we call the isometric representation associated to
![]() $A$
. Denote the
$A$
. Denote the
![]() $C^{*}$
-algebra generated by
$C^{*}$
-algebra generated by
![]() $\{V_{a}\,:\, a \in P\}$
by
$\{V_{a}\,:\, a \in P\}$
by
![]() $C^{*}(P,A)$
. The case
$C^{*}(P,A)$
. The case
![]() $A=P$
corresponds to the reduced
$A=P$
corresponds to the reduced
![]() $C^{*}$
-algebra. The
$C^{*}$
-algebra. The
![]() $C^{*}$
-algebras
$C^{*}$
-algebras
![]() $C^{*}(P,A)$
were analysed in great detail in [Reference Salas24] when
$C^{*}(P,A)$
were analysed in great detail in [Reference Salas24] when
![]() $P=\mathbb{N}^{k}$
.
$P=\mathbb{N}^{k}$
.
A common feature that the isometric representations
![]() $V^{A}$
share, when we vary
$V^{A}$
share, when we vary
![]() $A$
, is that the range projections
$A$
, is that the range projections
![]() $\{V_{a}V_{a}^{*}\,:\,a \in P\}$
form a commuting family. Thus, it is natural to consider the following universal
$\{V_{a}V_{a}^{*}\,:\,a \in P\}$
form a commuting family. Thus, it is natural to consider the following universal
![]() $C^{*}$
-algebra. Let
$C^{*}$
-algebra. Let
![]() $C^{*}_{c}(P)$
be the universal
$C^{*}_{c}(P)$
be the universal
![]() $C^{*}$
-algebra generated by isometries
$C^{*}$
-algebra generated by isometries
![]() $\{v_{a}\,:\,a \in P\}$
such that
$\{v_{a}\,:\,a \in P\}$
such that
-
1. for
 $a,b \in P$
,
$a,b \in P$
,
 $v_{a}v_{b}=v_{a+b}$
, and
$v_{a}v_{b}=v_{a+b}$
, and -
2. for
 $a,b \in P$
,
$a,b \in P$
,
 $e_{a}e_{b}=e_{b}e_{a}$
. Here,
$e_{a}e_{b}=e_{b}e_{a}$
. Here,
 $e_{a}\,:\!=\,v_{a}v_{a}^{*}$
and
$e_{a}\,:\!=\,v_{a}v_{a}^{*}$
and
 $e_b\,:\!=\,v_bv_b^{*}$
.
$e_b\,:\!=\,v_bv_b^{*}$
.
The subscript ‘c’ in
![]() $C_{c}^{*}(P)$
stands to indicate that the range projections commute.
$C_{c}^{*}(P)$
stands to indicate that the range projections commute.
The
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $C_{c}^{*}(\mathbb{N}^k)$
was analysed from a groupoid perspective by Salas in [Reference Salas24]. Murphy, in [Reference Murphy19] by independent methods, studied
$C_{c}^{*}(\mathbb{N}^k)$
was analysed from a groupoid perspective by Salas in [Reference Salas24]. Murphy, in [Reference Murphy19] by independent methods, studied
![]() $C_{c}^{*}(\mathbb{N}^2)$
and also the universal one generated by two commuting isometries. He proved that the latter
$C_{c}^{*}(\mathbb{N}^2)$
and also the universal one generated by two commuting isometries. He proved that the latter
![]() $C^{*}$
-algebra is complicated, in particular not nuclear, while the former is nuclear and more manageable. The
$C^{*}$
-algebra is complicated, in particular not nuclear, while the former is nuclear and more manageable. The
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $C_{c}^{*}(P)$
for a numerical semigroup
$C_{c}^{*}(P)$
for a numerical semigroup
![]() $P$
was considered in [Reference Raeburn and Vittadello23] and in [Reference Vittadello26]. The analog of
$P$
was considered in [Reference Raeburn and Vittadello23] and in [Reference Vittadello26]. The analog of
![]() $C_{c}^{*}(P)$
in the topological setting was investigated using groupoid methods by the last author in [Reference Sundar25]. Both [Reference Salas24] and [Reference Sundar25] borrow substantial amount of material from [Reference Muhly and Renault18].
$C_{c}^{*}(P)$
in the topological setting was investigated using groupoid methods by the last author in [Reference Sundar25]. Both [Reference Salas24] and [Reference Sundar25] borrow substantial amount of material from [Reference Muhly and Renault18].
This paper is an attempt to understand the structure of KMS states on
![]() $C_{c}^{*}(P)$
for a natural time evolution. Let
$C_{c}^{*}(P)$
for a natural time evolution. Let
![]() $c\,:\,G \to \mathbb{R}$
be a non-zero homomorphism. By the universal property of
$c\,:\,G \to \mathbb{R}$
be a non-zero homomorphism. By the universal property of
![]() $C_{c}^{*}(P)$
, for every
$C_{c}^{*}(P)$
, for every
![]() $t \in \mathbb{R}$
, there exists a
$t \in \mathbb{R}$
, there exists a
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\sigma _{t}\,:\,C_{c}^{*}(P) \to C_{c}^{*}(P)$
such that
$\sigma _{t}\,:\,C_{c}^{*}(P) \to C_{c}^{*}(P)$
such that
for
![]() $a \in P$
. Then,
$a \in P$
. Then,
![]() $\sigma ^{c}\,:\!=\{\sigma _{t}\}_{t \in \mathbb{R}}$
defines an action of
$\sigma ^{c}\,:\!=\{\sigma _{t}\}_{t \in \mathbb{R}}$
defines an action of
![]() $\mathbb{R}$
on
$\mathbb{R}$
on
![]() $C_{c}^{*}(P)$
. In this paper, we analyse the structure of KMS states for
$C_{c}^{*}(P)$
. In this paper, we analyse the structure of KMS states for
![]() $\sigma ^c$
for a toy model by discussing the case when
$\sigma ^c$
for a toy model by discussing the case when
![]() $P=\mathbb{N}^{2}$
.
$P=\mathbb{N}^{2}$
.
Let
![]() $c\,:\,\mathbb{Z}^2 \to \mathbb{R}$
be a non-zero homomorphism. With no loss of generality, we can assume that
$c\,:\,\mathbb{Z}^2 \to \mathbb{R}$
be a non-zero homomorphism. With no loss of generality, we can assume that
![]() $c(1,0)=1$
and
$c(1,0)=1$
and
![]() $c(0,1)=\theta$
. Let
$c(0,1)=\theta$
. Let
![]() $\Omega \,:\!=\{0,1\}^{\mathbb{Z}}$
be the Cantor space equipped with the product topology. Let
$\Omega \,:\!=\{0,1\}^{\mathbb{Z}}$
be the Cantor space equipped with the product topology. Let
![]() $\tau \,:\,\Omega \to \Omega$
be the Bernoulli shift defined by
$\tau \,:\,\Omega \to \Omega$
be the Bernoulli shift defined by
![]() $ \tau (x)_k=x_{k-1}$
. Define
$ \tau (x)_k=x_{k-1}$
. Define
![]() $\chi \,:\, \Omega \to \mathbb{R}$
by
$\chi \,:\, \Omega \to \mathbb{R}$
by
 \begin{equation*}\chi (x)\,:\!=\,\begin {cases} 1 & \mbox { if } x_{-1} =0,\\ - \theta & \mbox { if } x_{-1}=1. \end {cases} \end{equation*}
\begin{equation*}\chi (x)\,:\!=\,\begin {cases} 1 & \mbox { if } x_{-1} =0,\\ - \theta & \mbox { if } x_{-1}=1. \end {cases} \end{equation*}
Let
![]() $\rho \,:\!=\{\rho _t\}_{t \in \mathbb{R}}$
be the
$\rho \,:\!=\{\rho _t\}_{t \in \mathbb{R}}$
be the
![]() $1$
-parameter group of automorphisms on
$1$
-parameter group of automorphisms on
![]() $C(\Omega )\rtimes \mathbb{Z}$
defined by
$C(\Omega )\rtimes \mathbb{Z}$
defined by
![]() $\rho _t(f)=f$
for
$\rho _t(f)=f$
for
![]() $f \in C(\Omega )$
and
$f \in C(\Omega )$
and
![]() $\rho _t(u)=ue^{it\chi }$
. Here,
$\rho _t(u)=ue^{it\chi }$
. Here,
![]() $u$
is the canonical unitary of the crossed product
$u$
is the canonical unitary of the crossed product
![]() $C(\Omega )\rtimes \mathbb{Z}$
. This kind of flow, given by a continuous potential
$C(\Omega )\rtimes \mathbb{Z}$
. This kind of flow, given by a continuous potential
![]() $F\,:\,X \to \mathbb{R}$
, for a generic dynamical system
$F\,:\,X \to \mathbb{R}$
, for a generic dynamical system
![]() $(X,T)$
, where
$(X,T)$
, where
![]() $X$
is a compact space and
$X$
is a compact space and
![]() $T\,:\,X \to X$
is a homeomorphism, was considered in [Reference Christensen and Thomsen5], and the structure of KMS states on
$T\,:\,X \to X$
is a homeomorphism, was considered in [Reference Christensen and Thomsen5], and the structure of KMS states on
![]() $C(X)\rtimes \mathbb{Z}$
was analysed in depth in [Reference Christensen and Thomsen5].
$C(X)\rtimes \mathbb{Z}$
was analysed in depth in [Reference Christensen and Thomsen5].
We establish a close link between the structure of KMS states on
![]() $C_{c}^{*}(\mathbb{N}^2)$
for
$C_{c}^{*}(\mathbb{N}^2)$
for
![]() $\sigma ^c$
and the structure of KMS states on
$\sigma ^c$
and the structure of KMS states on
![]() $C(\Omega )\rtimes \mathbb{Z}$
for
$C(\Omega )\rtimes \mathbb{Z}$
for
![]() $\rho$
. Strictly speaking, we only establish a bijective correspondence between the conformal measures that appear in the analysis. This brings us to the setup considered in [Reference Christensen and Thomsen5]. We then apply the results of [Reference Christensen and Thomsen5] to deduce the values of
$\rho$
. Strictly speaking, we only establish a bijective correspondence between the conformal measures that appear in the analysis. This brings us to the setup considered in [Reference Christensen and Thomsen5]. We then apply the results of [Reference Christensen and Thomsen5] to deduce the values of
![]() $\theta$
for which there is a KMS state on
$\theta$
for which there is a KMS state on
![]() $C_{c}^{*}(\mathbb{N}^2)$
. Taking inspiration from [Reference Christensen and Thomsen5] and like in [Reference Christensen and Thomsen5], we ask whether extremal KMS states on
$C_{c}^{*}(\mathbb{N}^2)$
. Taking inspiration from [Reference Christensen and Thomsen5] and like in [Reference Christensen and Thomsen5], we ask whether extremal KMS states on
![]() $C_{c}^{*}(\mathbb{N}^2)$
of each type t for
$C_{c}^{*}(\mathbb{N}^2)$
of each type t for
![]() $t \in \{I,II,III\}$
appear or not which we answer in the affirmative by exhibiting uncountably many examples of extremal KMS states of type I, II and III.
$t \in \{I,II,III\}$
appear or not which we answer in the affirmative by exhibiting uncountably many examples of extremal KMS states of type I, II and III.
The results obtained in this paper are summarised below.
-
(1) If either
 $\theta \lt 0$
or
$\theta \lt 0$
or
 $\beta \lt 0$
, there is no
$\beta \lt 0$
, there is no
 $\beta$
-KMS state on
$\beta$
-KMS state on
 $C_{c}^{*}(\mathbb{N}^{2})$
.
$C_{c}^{*}(\mathbb{N}^{2})$
. -
(2) Suppose
 $\theta =0$
and
$\theta =0$
and
 $\beta \gt 0$
. The simplex of
$\beta \gt 0$
. The simplex of
 $\beta$
-KMS states is homeomorphic to the set of probability measures on
$\beta$
-KMS states is homeomorphic to the set of probability measures on
 $\mathbb{T}$
. In this case, the extremal
$\mathbb{T}$
. In this case, the extremal
 $\beta$
-KMS states are of type I.
$\beta$
-KMS states are of type I. -
(3) Suppose
 $\theta$
is irrational, positive and
$\theta$
is irrational, positive and
 $\beta \gt 0$
. The simplex of
$\beta \gt 0$
. The simplex of
 $\beta$
-KMS states is homeomorphic to the set of probability measures
$\beta$
-KMS states is homeomorphic to the set of probability measures
 $m$
on the Cantor space
$m$
on the Cantor space
 $\Omega$
that are
$\Omega$
that are
 $e^{-\beta \chi }$
-conformal, i.e.for every Borel subset
$e^{-\beta \chi }$
-conformal, i.e.for every Borel subset \begin{equation*} m(\tau (B))=\int _B e^{-\beta \chi } dm\end{equation*}
\begin{equation*} m(\tau (B))=\int _B e^{-\beta \chi } dm\end{equation*}
 $B$
of
$B$
of
 $\Omega$
.
$\Omega$
.
-
(4) Suppose
 $\theta \gt 0$
and
$\theta \gt 0$
and
 $\beta \gt 0$
. For each
$\beta \gt 0$
. For each
 $t \in \{I,II,III\}$
, there are uncountably many extremal
$t \in \{I,II,III\}$
, there are uncountably many extremal
 $\beta$
-KMS states of type
$\beta$
-KMS states of type
 $t$
. Moreover, for
$t$
. Moreover, for
 $t \in \{II,III\}$
, the extremal
$t \in \{II,III\}$
, the extremal
 $\beta$
-KMS states of type
$\beta$
-KMS states of type
 $t$
are in bijective correspondence with non-atomic type
$t$
are in bijective correspondence with non-atomic type
 $t$
ergodic, probability measures
$t$
ergodic, probability measures
 $m$
on
$m$
on
 $\Omega$
that are
$\Omega$
that are
 $e^{-\beta \chi }$
-conformal.
$e^{-\beta \chi }$
-conformal. -
(5) The simplex of tracial states of
 $C_{c}^{*}(\mathbb{N}^{2})$
is homeomorphic to the simplex of probability measures on the torus
$C_{c}^{*}(\mathbb{N}^{2})$
is homeomorphic to the simplex of probability measures on the torus
 $\mathbb{T}^{2}$
.
$\mathbb{T}^{2}$
.
We end this introduction by mentioning a result obtained in Section 4, which we believe is worth highlighting. Let
![]() $X$
be a compact metric space, and let
$X$
be a compact metric space, and let
![]() $\phi \,:\,X \to X$
be a homeomorphism. A probability measure
$\phi \,:\,X \to X$
be a homeomorphism. A probability measure
![]() $m$
on
$m$
on
![]() $X$
is said to be a conformal measure with potential
$X$
is said to be a conformal measure with potential
![]() $F$
, where
$F$
, where
![]() $F$
is a measurable function on
$F$
is a measurable function on
![]() $X$
, if
$X$
, if
Up to the authors’ knowledge, the reference in the literature for the proof of the existence of an ergodic type III conformal measure with continuous potential
![]() $F$
is the work of Katznelson ( [Reference Katznelson13]). (The reader is referred to Theorem 3.2, Theorem 3.3 of Part II in [Reference Katznelson13] and is also referred to Theorem 5.2 of [Reference Christensen and Thomsen5]. Also, as we will see in Section 5, Nakada’s examples in [Reference Nakada21] and in [Reference Nakada20] provide such examples). If we demand only the measurability of the potential, then it is well known that odometers provide a rich source of such type III examples (see [Reference Danilenko and Silva11]).
$F$
is the work of Katznelson ( [Reference Katznelson13]). (The reader is referred to Theorem 3.2, Theorem 3.3 of Part II in [Reference Katznelson13] and is also referred to Theorem 5.2 of [Reference Christensen and Thomsen5]. Also, as we will see in Section 5, Nakada’s examples in [Reference Nakada21] and in [Reference Nakada20] provide such examples). If we demand only the measurability of the potential, then it is well known that odometers provide a rich source of such type III examples (see [Reference Danilenko and Silva11]).
Here, by making use of Arnold’s dyadic adding machine, we produce an example of an ergodic type III conformal measure with continuous potential on the Cantor space
![]() $\{0,1\}^{\mathbb{Z}}$
, where the action is the usual shift. This construction is probably simpler, modulo accepting the fact that Arnold’s adding machine is one of the simplest type III examples. But a drawback with our construction is that, unlike the example due to Katznelson, our dynamical system is not minimal. It is not clear to the authors whether this construction can be tweaked to produce an example, based on odometers, which is minimal.
$\{0,1\}^{\mathbb{Z}}$
, where the action is the usual shift. This construction is probably simpler, modulo accepting the fact that Arnold’s adding machine is one of the simplest type III examples. But a drawback with our construction is that, unlike the example due to Katznelson, our dynamical system is not minimal. It is not clear to the authors whether this construction can be tweaked to produce an example, based on odometers, which is minimal.
2. A groupoid model for
 $C_{c}^{*}(P)$
$C_{c}^{*}(P)$
In this section, we review the groupoid model for
![]() $C_{c}^{*}(P)$
described in [Reference Salas24] and in [Reference Sundar25]. We follow the exposition given in [Reference Sundar25]. Let
$C_{c}^{*}(P)$
described in [Reference Salas24] and in [Reference Sundar25]. We follow the exposition given in [Reference Sundar25]. Let
![]() $G$
be a countable, discrete abelian group, and let
$G$
be a countable, discrete abelian group, and let
![]() $P$
be a subsemigroup of
$P$
be a subsemigroup of
![]() $G$
containing the identity element
$G$
containing the identity element
![]() $0$
. We assume that
$0$
. We assume that
![]() $P$
generates
$P$
generates
![]() $G$
, i.e.
$G$
, i.e.
![]() $P-P=G$
.
$P-P=G$
.
Recall that
![]() $C_{c}^{*}(P)$
is the universal unital
$C_{c}^{*}(P)$
is the universal unital
![]() $C^{*}$
-algebra generated by a family of isometries
$C^{*}$
-algebra generated by a family of isometries
![]() $\{v_a\,:\, a \in P\}$
such that
$\{v_a\,:\, a \in P\}$
such that
-
(1) for
 $a,b \in P$
,
$a,b \in P$
,
 $v_av_b=v_{a+b}$
, and
$v_av_b=v_{a+b}$
, and -
(2) for
 $a,b \in P$
,
$a,b \in P$
,
 $e_ae_b=e_be_a$
, where
$e_ae_b=e_be_a$
, where
 $e_a\,:\!=\,v_av_a^{*}$
and
$e_a\,:\!=\,v_av_a^{*}$
and
 $e_b\,:\!=\,v_bv_b^{*}$
.
$e_b\,:\!=\,v_bv_b^{*}$
.
Let
![]() $s \in G$
be given. Choose
$s \in G$
be given. Choose
![]() $a,b\in P$
such that
$a,b\in P$
such that
![]() $s=a-b$
. Set
$s=a-b$
. Set
![]() $w_s\,:\!=\,v_b^{*}v_a$
. Thanks to Proposition 3.4 of [Reference Sundar25],
$w_s\,:\!=\,v_b^{*}v_a$
. Thanks to Proposition 3.4 of [Reference Sundar25],
![]() $w_s$
is well defined, and
$w_s$
is well defined, and
![]() $\{w_s\,:\, s \in G\}$
is a family of partial isometries whose range projections commute. For
$\{w_s\,:\, s \in G\}$
is a family of partial isometries whose range projections commute. For
![]() $s \in G$
, let
$s \in G$
, let
![]() $e_s\,:\!=\,w_sw_s^*$
.
$e_s\,:\!=\,w_sw_s^*$
.
Next, we describe a groupoid whose
![]() $C^{*}$
-algebra is a quotient of
$C^{*}$
-algebra is a quotient of
![]() $C_{c}^{*}(P)$
. Let
$C_{c}^{*}(P)$
. Let
![]() $\mathcal{P}(G)$
be the power set of
$\mathcal{P}(G)$
be the power set of
![]() $G$
which we identify, in the usual way, with
$G$
which we identify, in the usual way, with
![]() $\{0,1\}^{G}$
. Endow
$\{0,1\}^{G}$
. Endow
![]() $\mathcal{P}(G)$
with the product topology inherited via this identification. Then,
$\mathcal{P}(G)$
with the product topology inherited via this identification. Then,
![]() $\mathcal{P}(G)$
is a compact Hausdorff space and is metrisable. The map
$\mathcal{P}(G)$
is a compact Hausdorff space and is metrisable. The map
defines an action of
![]() $G$
on
$G$
on
![]() $\mathcal{P}(G)$
.
$\mathcal{P}(G)$
.
Let
Note that
![]() $\overline{X}_u$
is a closed subset of
$\overline{X}_u$
is a closed subset of
![]() $\mathcal{P}(G)$
and hence a compact subset of
$\mathcal{P}(G)$
and hence a compact subset of
![]() $\mathcal{P}(G)$
. Also,
$\mathcal{P}(G)$
. Also,
![]() $\overline{X}_u$
is
$\overline{X}_u$
is
![]() $P$
-invariant, i.e. if
$P$
-invariant, i.e. if
![]() $A \in \overline{X}_u$
and
$A \in \overline{X}_u$
and
![]() $a \in P$
, then
$a \in P$
, then
![]() $A+a \in \overline{X}_u$
. Let
$A+a \in \overline{X}_u$
. Let
![]() $\mathcal{G}$
be the reduction of the transformation groupoid
$\mathcal{G}$
be the reduction of the transformation groupoid
![]() $\mathcal{P}(G) \rtimes G$
onto
$\mathcal{P}(G) \rtimes G$
onto
![]() $\overline{X}_u$
, i.e.
$\overline{X}_u$
, i.e.
The multiplication and inversion on
![]() $\mathcal{G}$
are given by
$\mathcal{G}$
are given by
The groupoid
![]() $\mathcal{G}$
is étale and is the usual Deaconu-Renault groupoid
$\mathcal{G}$
is étale and is the usual Deaconu-Renault groupoid
![]() $\overline{X}_u \rtimes P$
.
$\overline{X}_u \rtimes P$
.
For
![]() $f \in C(\overline{X}_u)$
, define
$f \in C(\overline{X}_u)$
, define
![]() $\widetilde{f} \in C_{c}(\overline{X}_u \rtimes P)$
by
$\widetilde{f} \in C_{c}(\overline{X}_u \rtimes P)$
by
 \begin{equation} \widetilde{f}(A,s)\,:\!=\,\begin{cases} f(A) & \mbox{ if } s =0, \\ 0 & \mbox{ if $s \neq 0$. } \end{cases} \end{equation}
\begin{equation} \widetilde{f}(A,s)\,:\!=\,\begin{cases} f(A) & \mbox{ if } s =0, \\ 0 & \mbox{ if $s \neq 0$. } \end{cases} \end{equation}
Observe that
![]() $C(\overline{X}_u) \ni f \to \widetilde{f} \in C_{c}(\overline{X}_u \rtimes P)$
is a unital
$C(\overline{X}_u) \ni f \to \widetilde{f} \in C_{c}(\overline{X}_u \rtimes P)$
is a unital
![]() $^*$
-algebra homomorphism which is injective. Via this embedding, we identify
$^*$
-algebra homomorphism which is injective. Via this embedding, we identify
![]() $C(\overline{X}_u)$
as a unital
$C(\overline{X}_u)$
as a unital
![]() $^*$
-subalgebra of
$^*$
-subalgebra of
![]() $C_{c}(\mathcal{G})$
. For
$C_{c}(\mathcal{G})$
. For
![]() $f \in C(\overline{X}_u)$
, we abuse notation and we denote
$f \in C(\overline{X}_u)$
, we abuse notation and we denote
![]() $\widetilde{f}$
by
$\widetilde{f}$
by
![]() $f$
.
$f$
.
For
![]() $s \in G$
, let
$s \in G$
, let
![]() $\overline{w}_s \in C_{c}(\overline{X}_u \rtimes P)$
be defined by
$\overline{w}_s \in C_{c}(\overline{X}_u \rtimes P)$
be defined by
 \begin{equation} \overline{w}_s(A,t)\,:\!=\,\begin{cases} 1 & \mbox{ if } t=-s, \\ 0 & \mbox{ if $t \neq -s$}. \end{cases} \end{equation}
\begin{equation} \overline{w}_s(A,t)\,:\!=\,\begin{cases} 1 & \mbox{ if } t=-s, \\ 0 & \mbox{ if $t \neq -s$}. \end{cases} \end{equation}
For
![]() $a \in P$
, set
$a \in P$
, set
![]() $\overline{v}_a\,:\!=\,\overline{w}_a$
. Observe the following facts. The details involving routine computations are left to the reader.
$\overline{v}_a\,:\!=\,\overline{w}_a$
. Observe the following facts. The details involving routine computations are left to the reader.
-
(1) For
 $a \in P$
,
$a \in P$
,
 $\overline{v}_a$
is an isometry and
$\overline{v}_a$
is an isometry and
 $\overline{v}_a\overline{v}_b=\overline{v}_{a+b}$
.
$\overline{v}_a\overline{v}_b=\overline{v}_{a+b}$
. -
(2) For
 $a,b \in P$
and
$a,b \in P$
and
 $s=a-b$
,
$s=a-b$
,
 $\overline{w}_s=\overline{v}_b^{*}\overline{v}_a$
.
$\overline{w}_s=\overline{v}_b^{*}\overline{v}_a$
. -
(3) For
 $s \in G$
, let
$s \in G$
, let
 $\epsilon _{s} \in C(\overline{X}_u)$
be defined by the equation
$\epsilon _{s} \in C(\overline{X}_u)$
be defined by the equation
 $\epsilon _{s}(A)=1_{A}(s)$
. Then,
$\epsilon _{s}(A)=1_{A}(s)$
. Then,
 $\overline{w}_s\overline{w}_s^{*}=\epsilon _{s}$
for every
$\overline{w}_s\overline{w}_s^{*}=\epsilon _{s}$
for every
 $s \in G$
. Consequently,
$s \in G$
. Consequently,
 $\{\overline{w}_s\overline{w}_s^{*}\,:\,s \in G\}$
generates
$\{\overline{w}_s\overline{w}_s^{*}\,:\,s \in G\}$
generates
 $C(\overline{X}_u)$
. Also, the range projections
$C(\overline{X}_u)$
. Also, the range projections
 $\{\overline{v}_a\overline{v}_a^{*}\,:\,a \in P\}$
form a commuting family.
$\{\overline{v}_a\overline{v}_a^{*}\,:\,a \in P\}$
form a commuting family. -
(4) We claim that the
 $C^{*}$
-algebra generated by
$C^{*}$
-algebra generated by
 $\{\overline{v}_a\,:\,a \in P\}$
is
$\{\overline{v}_a\,:\,a \in P\}$
is
 $C^{*}(\mathcal{G})$
. Let
$C^{*}(\mathcal{G})$
. Let
 $f \in C_{c}(\mathcal{G})=C_c(\overline{X}_u \rtimes P)$
. It suffices to consider the case when
$f \in C_{c}(\mathcal{G})=C_c(\overline{X}_u \rtimes P)$
. It suffices to consider the case when
 $f$
is supported on
$f$
is supported on
 $\overline{X}_u \times \{-s\}$
for some
$\overline{X}_u \times \{-s\}$
for some
 $s \in G$
. Let
$s \in G$
. Let
 $h\,:\,\overline{X}_u \to \mathbb{C}$
be defined byThen,
$h\,:\,\overline{X}_u \to \mathbb{C}$
be defined byThen, \begin{equation*} h(A)\,:\!=\,\begin {cases} f(A,-s) & \mbox { if } (A,-s) \in \overline {X}_u \rtimes P, \\ 0 & \mbox { otherwise}. \end {cases} \end{equation*}
\begin{equation*} h(A)\,:\!=\,\begin {cases} f(A,-s) & \mbox { if } (A,-s) \in \overline {X}_u \rtimes P, \\ 0 & \mbox { otherwise}. \end {cases} \end{equation*}
 $h$
is continuous and
$h$
is continuous and
 $h*\overline{w}_s=f$
. By
$h*\overline{w}_s=f$
. By
 $(3)$
,
$(3)$
,
 $h$
lies in the
$h$
lies in the
 $C^{*}$
-algebra generated by
$C^{*}$
-algebra generated by
 $\{\overline{w}_s\,:\,s \in G\}$
. Therefore,
$\{\overline{w}_s\,:\,s \in G\}$
. Therefore,
 $\{\overline{w}_s\,:\,s \in G\}$
generates
$\{\overline{w}_s\,:\,s \in G\}$
generates
 $C^{*}(\mathcal{G})$
. It follows from
$C^{*}(\mathcal{G})$
. It follows from
 $(2)$
that
$(2)$
that
 $\{\overline{v}_a\,:\, a \in P\}$
generates the
$\{\overline{v}_a\,:\, a \in P\}$
generates the
 $C^{*}$
-algebra
$C^{*}$
-algebra
 $C^{*}(\overline{X}_u \rtimes P)$
.
$C^{*}(\overline{X}_u \rtimes P)$
.
Hence, there exists a unique surjective
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\Phi \,:\,C_{c}^{*}(P) \to C^{*}(\overline{X}_u \rtimes P)$
such that
$\Phi \,:\,C_{c}^{*}(P) \to C^{*}(\overline{X}_u \rtimes P)$
such that
Theorem 7.4 of [Reference Sundar25] asserts that
![]() $\Phi$
is invertible, and
$\Phi$
is invertible, and
![]() $\Phi$
is an isomorphism. Via the map
$\Phi$
is an isomorphism. Via the map
![]() $\Phi$
, we identify
$\Phi$
, we identify
![]() $C_{c}^{*}(P)$
with
$C_{c}^{*}(P)$
with
![]() $C^{*}(\overline{X}_u \rtimes P)$
. Henceforth, we do not distinguish between
$C^{*}(\overline{X}_u \rtimes P)$
. Henceforth, we do not distinguish between
![]() $w_s$
and
$w_s$
and
![]() $\overline{w}_s$
.
$\overline{w}_s$
.
For
![]() $f \in C(\overline{X}_u)$
and
$f \in C(\overline{X}_u)$
and
![]() $s \in G$
, let
$s \in G$
, let
![]() $R_{s}(f) \in C(\overline{X}_u)$
be defined by the equation
$R_{s}(f) \in C(\overline{X}_u)$
be defined by the equation
 \begin{equation*} R_s(f)(A)\,:\!=\,\begin {cases} f(A-s) & \mbox{if} \, A-s \in \overline {X}_u, \\ 0 & \mbox { otherwise}. \end {cases} \end{equation*}
\begin{equation*} R_s(f)(A)\,:\!=\,\begin {cases} f(A-s) & \mbox{if} \, A-s \in \overline {X}_u, \\ 0 & \mbox { otherwise}. \end {cases} \end{equation*}
For
![]() $s \in G$
and
$s \in G$
and
![]() $f \in C(\overline{X}_u) \subset C^{*}(\overline{X}_u \rtimes P)$
, the covariance relation
$f \in C(\overline{X}_u) \subset C^{*}(\overline{X}_u \rtimes P)$
, the covariance relation
is satisfied. A pleasant consequence of the above covariance relation is the fact that the linear span of
![]() $\{fw_s\,:\, f \in C(\overline{X}_u), s \in G\}$
is a unital dense
$\{fw_s\,:\, f \in C(\overline{X}_u), s \in G\}$
is a unital dense
![]() $^*$
-subalgebra of
$^*$
-subalgebra of
![]() $C^{*}(\overline{X}_u \rtimes P)$
.
$C^{*}(\overline{X}_u \rtimes P)$
.
Let
Observe that
![]() $\overline{Y}_u$
is a locally compact Hausdorff space and
$\overline{Y}_u$
is a locally compact Hausdorff space and
![]() $G$
leaves
$G$
leaves
![]() $\overline{Y}_u$
invariant. Also,
$\overline{Y}_u$
invariant. Also,
![]() $\overline{X}_u$
is a clopen set in
$\overline{X}_u$
is a clopen set in
![]() $\overline{Y}_u$
. It is clear that the groupoid
$\overline{Y}_u$
. It is clear that the groupoid
![]() $\overline{X}_u \rtimes P$
is the reduction of the transformation groupoid
$\overline{X}_u \rtimes P$
is the reduction of the transformation groupoid
![]() $\overline{Y}_u \rtimes G$
onto
$\overline{Y}_u \rtimes G$
onto
![]() $\overline{X}_u$
. This has the consequence that
$\overline{X}_u$
. This has the consequence that
![]() $C^{*}(\overline{X}_u \rtimes P)$
is isomorphic to the cut-down
$C^{*}(\overline{X}_u \rtimes P)$
is isomorphic to the cut-down
![]() $p(C_0(\overline{Y}_u) \rtimes G)p$
where
$p(C_0(\overline{Y}_u) \rtimes G)p$
where
![]() $p=1_{\overline{X}_u}$
. Moreover, the union
$p=1_{\overline{X}_u}$
. Moreover, the union
![]() $\displaystyle \bigcup _{a \in P}(\overline{X}_u-a)=\overline{Y}_u$
. Consequently, it follows that
$\displaystyle \bigcup _{a \in P}(\overline{X}_u-a)=\overline{Y}_u$
. Consequently, it follows that
![]() $p$
is a full projection in
$p$
is a full projection in
![]() $C_0(\overline{Y}_u) \rtimes G$
.
$C_0(\overline{Y}_u) \rtimes G$
.
Often, we embed
![]() $C_{c}^{*}(P)$
inside the crossed product
$C_{c}^{*}(P)$
inside the crossed product
![]() $C_0(\overline{Y}_u) \rtimes G$
and view
$C_0(\overline{Y}_u) \rtimes G$
and view
![]() $C_{c}^{*}(P)$
as a full corner of
$C_{c}^{*}(P)$
as a full corner of
![]() $C_{0}(\overline{Y}_u) \rtimes G$
. The embedding
$C_{0}(\overline{Y}_u) \rtimes G$
. The embedding
![]() $C_{c}^{*}(P) \to C_0(\overline{Y}_u) \rtimes G$
is given by the rules
$C_{c}^{*}(P) \to C_0(\overline{Y}_u) \rtimes G$
is given by the rules
Here,
![]() $\{u_s\,:\, s \in G\}$
are the canonical unitaries of the crossed product
$\{u_s\,:\, s \in G\}$
are the canonical unitaries of the crossed product
![]() $C_0(\overline{Y}_u)\rtimes G$
.
$C_0(\overline{Y}_u)\rtimes G$
.
Tracial states on
![]() $C_{c}^{*}(P)$
: We first determine the tracial states on
$C_{c}^{*}(P)$
: We first determine the tracial states on
![]() $C_c^{*}(P)$
. Let
$C_c^{*}(P)$
. Let
![]() $C^*(G)$
be the group
$C^*(G)$
be the group
![]() $C^{*}$
-algebra of
$C^{*}$
-algebra of
![]() $G$
, and let
$G$
, and let
![]() $\{u_s\,:\,s \in G\}$
be the canonical unitaries of
$\{u_s\,:\,s \in G\}$
be the canonical unitaries of
![]() $C^{*}(G)$
. By the universal property, there exists a surjective
$C^{*}(G)$
. By the universal property, there exists a surjective
![]() $^*$
-homomorphism
$^*$
-homomorphism
![]() $\pi \,:\,C_c^{*}(P) \to C^{*}(G)$
such that
$\pi \,:\,C_c^{*}(P) \to C^{*}(G)$
such that
![]() $\pi (v_a)=u_a$
. In the groupoid picture,
$\pi (v_a)=u_a$
. In the groupoid picture,
![]() $\pi$
coincides with the restriction map
$\pi$
coincides with the restriction map
![]() $Res\,:\,C^{*}(\overline{X}_u \rtimes P) \to C^{*}(\overline{X}_u \rtimes P|_{\{G\}}) \cong C^{*}(G)$
. Note that
$Res\,:\,C^{*}(\overline{X}_u \rtimes P) \to C^{*}(\overline{X}_u \rtimes P|_{\{G\}}) \cong C^{*}(G)$
. Note that
![]() $\{G\}$
is an invariant closed subset of the unit space
$\{G\}$
is an invariant closed subset of the unit space
![]() $\overline{X}_u$
of the groupoid
$\overline{X}_u$
of the groupoid
![]() $\mathcal{G}=\overline{X}_u \rtimes P$
.
$\mathcal{G}=\overline{X}_u \rtimes P$
.
Proposition 2.1.
Every tracial state on
![]() $C_{c}^{*}(P)$
factors through
$C_{c}^{*}(P)$
factors through
![]() $C^{*}(G)$
. Thus, tracial states on
$C^{*}(G)$
. Thus, tracial states on
![]() $C_{c}^{*}(P)$
are in bijective correspondence with probability measures on
$C_{c}^{*}(P)$
are in bijective correspondence with probability measures on
![]() $\widehat{G}$
.
$\widehat{G}$
.
Proof. Let
![]() $F\,:\!=\{G\}$
and
$F\,:\!=\{G\}$
and
![]() $X_u\,:\!=\,\overline{X}_u\backslash F$
. Let
$X_u\,:\!=\,\overline{X}_u\backslash F$
. Let
![]() $\omega$
be a tracial state on
$\omega$
be a tracial state on
![]() $C_{c}^{*}(P)$
. Let
$C_{c}^{*}(P)$
. Let
![]() $m$
be the measure on
$m$
be the measure on
![]() $\overline{X}_u$
that corresponds to the state
$\overline{X}_u$
that corresponds to the state
![]() $\omega |_{C(\overline{X}_u)}$
. Let
$\omega |_{C(\overline{X}_u)}$
. Let
![]() $a \in P$
be given. Note that
$a \in P$
be given. Note that
![]() $v_av_a^{*}=1_{\overline{X}_u+a}$
. Since
$v_av_a^{*}=1_{\overline{X}_u+a}$
. Since
![]() $\omega$
is tracial, we have
$\omega$
is tracial, we have
But,
![]() $\overline{X}_u+a \subset \overline{X}_u$
. Hence,
$\overline{X}_u+a \subset \overline{X}_u$
. Hence,
![]() $\overline{X}_u \backslash (\overline{X}_u+a)$
has measure zero. Hence, the set
$\overline{X}_u \backslash (\overline{X}_u+a)$
has measure zero. Hence, the set
![]() $X_u=\bigcup _{a \in P}\overline{X}_u \backslash (\overline{X}_u+a)$
has measure zero. Therefore,
$X_u=\bigcup _{a \in P}\overline{X}_u \backslash (\overline{X}_u+a)$
has measure zero. Therefore,
![]() $m$
is concentrated on
$m$
is concentrated on
![]() $F=\{G\}$
. Now the proof follows from Corollary 1.4 of [Reference Neshveyev22].
$F=\{G\}$
. Now the proof follows from Corollary 1.4 of [Reference Neshveyev22].
We end this section with a few definitions that we need later.
Definition 2.1.
Let
![]() $(Y,\mathcal{B})$
be a standard Borel space on which
$(Y,\mathcal{B})$
be a standard Borel space on which
![]() $G$
acts measurably. Let
$G$
acts measurably. Let
![]() $X$
be a Borel subset of
$X$
be a Borel subset of
![]() $Y$
. We say that
$Y$
. We say that
![]() $(Y,X)$
is a
$(Y,X)$
is a
![]() $(G,P)$
-space if
$(G,P)$
-space if
-
(1) the set
 $X$
is
$X$
is
 $P$
-invariant, i.e.
$P$
-invariant, i.e.
 $X+P \subset X$
, and
$X+P \subset X$
, and
-
(2) the union
 $\displaystyle \bigcup _{a \in P}(X-a)=Y$
.
$\displaystyle \bigcup _{a \in P}(X-a)=Y$
.
Let
![]() $(Y,X)$
be a
$(Y,X)$
be a
![]() $(G,P)$
-space. We say that
$(G,P)$
-space. We say that
![]() $(Y,X)$
is pure if
$(Y,X)$
is pure if
![]() $\displaystyle \bigcap _{a \in P}(X+a)=\emptyset$
.
$\displaystyle \bigcap _{a \in P}(X+a)=\emptyset$
.
Example 2.1.
The pair
![]() $(\overline{Y}_u,\overline{X}_u)$
is a
$(\overline{Y}_u,\overline{X}_u)$
is a
![]() $(G,P)$
-space. Define
$(G,P)$
-space. Define
Then,
![]() $(Y_u,X_u)$
is pure.
$(Y_u,X_u)$
is pure.
Definition 2.2.
Let
![]() $(Y,X)$
be a
$(Y,X)$
be a
![]() $(G,P)$
-space. Let
$(G,P)$
-space. Let
![]() $c\,:\,G \to \mathbb{R}$
be a non-zero homomorphism, and let
$c\,:\,G \to \mathbb{R}$
be a non-zero homomorphism, and let
![]() $\beta$
be a fixed real number. Suppose
$\beta$
be a fixed real number. Suppose
![]() $m$
is a measure on
$m$
is a measure on
![]() $Y$
. We say that
$Y$
. We say that
![]() $m$
is an
$m$
is an
![]() $e^{-\beta c}$
-conformal measure on the
$e^{-\beta c}$
-conformal measure on the
![]() $(G,P)$
-space
$(G,P)$
-space
![]() $(Y,X)$
if
$(Y,X)$
if
-
(i)
 $m(X)=1$
, and
$m(X)=1$
, and
-
(ii) for every Borel set
 $E \subset Y$
and
$E \subset Y$
and
 $s \in G$
,
$s \in G$
, \begin{equation*} m(E+s)=e^{-\beta c(s)}m(E).\end{equation*}
\begin{equation*} m(E+s)=e^{-\beta c(s)}m(E).\end{equation*}
We often abuse terminology and call an
![]() $e^{-\beta c}$
-conformal measure on a
$e^{-\beta c}$
-conformal measure on a
![]() $(G,P)$
-space
$(G,P)$
-space
![]() $(Y,X)$
an
$(Y,X)$
an
![]() $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
![]() $Y$
.
$Y$
.
Definition 2.3.
For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $(Y_i,X_i)$
be a
$(Y_i,X_i)$
be a
![]() $(G,P)$
-space, and suppose that
$(G,P)$
-space, and suppose that
![]() $m_i$
is an
$m_i$
is an
![]() $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
![]() $(Y_i,X_i)$
. We say that
$(Y_i,X_i)$
. We say that
![]() $(Y_1,X_1,m_1)$
and
$(Y_1,X_1,m_1)$
and
![]() $(Y_2,X_2,m_2)$
are metrically isomorphic, or simply isomorphic, if there exist
$(Y_2,X_2,m_2)$
are metrically isomorphic, or simply isomorphic, if there exist
![]() $G$
-invariant null sets
$G$
-invariant null sets
![]() $N_1 \subset Y_1$
,
$N_1 \subset Y_1$
,
![]() $N_2 \subset Y_2$
and an invertible measurable map
$N_2 \subset Y_2$
and an invertible measurable map
![]() $S\,:\,Y_1\backslash N_1 \to Y_2 \backslash N_2$
such that
$S\,:\,Y_1\backslash N_1 \to Y_2 \backslash N_2$
such that
-
(i) the map
 $S$
is
$S$
is
 $G$
-equivariant,
$G$
-equivariant,
 $S(X_1\backslash N_1)=X_2\backslash N_2$
, and
$S(X_1\backslash N_1)=X_2\backslash N_2$
, and
-
(ii) for every Borel subset
 $E \subset Y_2 \backslash N_2$
,
$E \subset Y_2 \backslash N_2$
,
 $m_2(E)=m_1(S^{-1}(E))$
.
$m_2(E)=m_1(S^{-1}(E))$
.
3. KMS states and conformal measures
Let us recall the definition of a
![]() $\beta$
-KMS state. Let
$\beta$
-KMS state. Let
![]() $A$
be a
$A$
be a
![]() $C^*$
-algebra, and suppose
$C^*$
-algebra, and suppose
![]() $\tau \,:\!=\{\tau _t\}_{t \in \mathbb{R}}$
is a
$\tau \,:\!=\{\tau _t\}_{t \in \mathbb{R}}$
is a
![]() $1$
-parameter group of automorphisms of
$1$
-parameter group of automorphisms of
![]() $A$
. Suppose
$A$
. Suppose
![]() $\beta \in \mathbb{R}$
. A state
$\beta \in \mathbb{R}$
. A state
![]() $\omega$
on
$\omega$
on
![]() $A$
is a
$A$
is a
![]() $\beta$
-KMS state for
$\beta$
-KMS state for
![]() $\tau$
if
$\tau$
if
for all
![]() $a, b$
in a norm dense
$a, b$
in a norm dense
![]() $\tau$
-invariant
$\tau$
-invariant
![]() $^*$
-algebra of analytic elements in
$^*$
-algebra of analytic elements in
![]() $A$
.
$A$
.
Let
![]() $\omega$
be a
$\omega$
be a
![]() $\beta$
-KMS state on
$\beta$
-KMS state on
![]() $A$
. Then,
$A$
. Then,
![]() $\omega$
is said to be extremal if it is an extreme point in the simplex of
$\omega$
is said to be extremal if it is an extreme point in the simplex of
![]() $\beta$
-KMS states. It is well known that a
$\beta$
-KMS states. It is well known that a
![]() $\beta$
-KMS state
$\beta$
-KMS state
![]() $\omega$
is extremal if and only if the associated GNS representation
$\omega$
is extremal if and only if the associated GNS representation
![]() $\pi _\omega$
is factorial, i.e.
$\pi _\omega$
is factorial, i.e.
![]() $\pi _\omega (A)^{\prime\prime}$
is a factor. We say an extremal
$\pi _\omega (A)^{\prime\prime}$
is a factor. We say an extremal
![]() $\beta$
-KMS state
$\beta$
-KMS state
![]() $\omega$
is of type
$\omega$
is of type
![]() $t$
if
$t$
if
![]() $\pi _\omega (A)^{\prime\prime}$
is a factor of type
$\pi _\omega (A)^{\prime\prime}$
is a factor of type
![]() $t$
.
$t$
.
Fix a non-zero homomorphism
![]() $c\,:\,G \to \mathbb{R}$
. Recall that the
$c\,:\,G \to \mathbb{R}$
. Recall that the
![]() $1$
-parameter group of automorphisms
$1$
-parameter group of automorphisms
![]() $\sigma ^{c}\,:\!=\{\sigma _{t}\}_{t \in \mathbb{R}}$
on
$\sigma ^{c}\,:\!=\{\sigma _{t}\}_{t \in \mathbb{R}}$
on
![]() $C_{c}^{*}(P)$
is defined by
$C_{c}^{*}(P)$
is defined by
for
![]() $a \in P$
. For
$a \in P$
. For
![]() $t \in G$
, let
$t \in G$
, let
![]() $D(t), R(t)\subset \overline{X}_u$
be defined by
$D(t), R(t)\subset \overline{X}_u$
be defined by
For
![]() $t \in G$
, denote the map
$t \in G$
, denote the map
![]() $D(t) \ni A\to A+t \in R(t)$
by
$D(t) \ni A\to A+t \in R(t)$
by
![]() $T_t$
.
$T_t$
.
Let
![]() $\beta$
be a real number. As we have already described the tracial states on
$\beta$
be a real number. As we have already described the tracial states on
![]() $C_c^{*}(P)$
in Proposition 2.1, we assume for the rest of this section that
$C_c^{*}(P)$
in Proposition 2.1, we assume for the rest of this section that
![]() $\beta$
is an arbitrary, but a fixed non-zero real number. Let
$\beta$
is an arbitrary, but a fixed non-zero real number. Let
![]() $\omega$
be a
$\omega$
be a
![]() $\beta$
-KMS state on the
$\beta$
-KMS state on the
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $C_c^{*}(P)=C^*(\overline{X}_u \rtimes P)$
for
$C_c^{*}(P)=C^*(\overline{X}_u \rtimes P)$
for
![]() $\sigma ^c$
. Restriction of
$\sigma ^c$
. Restriction of
![]() $\omega$
to
$\omega$
to
![]() $C(\overline{X}_u)$
defines a probability measure
$C(\overline{X}_u)$
defines a probability measure
![]() $m$
on
$m$
on
![]() $\overline{X}_u$
. It can be checked from the covariance relation and the KMS condition that
$\overline{X}_u$
. It can be checked from the covariance relation and the KMS condition that
for every
![]() $f \in C(R(t))$
, or equivalently
$f \in C(R(t))$
, or equivalently
![]() $m(E+t)=e^{-\beta c(t)}m(E)$
for every Borel subset
$m(E+t)=e^{-\beta c(t)}m(E)$
for every Borel subset
![]() $E$
of
$E$
of
![]() $ D(t)$
.
$ D(t)$
.
For
![]() $s,t \in G$
, we say
$s,t \in G$
, we say
![]() $s \leq t$
if
$s \leq t$
if
![]() $t-s \in P$
. Then,
$t-s \in P$
. Then,
![]() $G$
with the preorder
$G$
with the preorder
![]() $\leq$
is a directed set. Note that
$\leq$
is a directed set. Note that
![]() $P$
is a cofinal subset of
$P$
is a cofinal subset of
![]() $G$
. Moreover, if
$G$
. Moreover, if
![]() $s \leq t$
, then
$s \leq t$
, then
![]() $\overline{X}_u-s\subseteq \overline{X}_u-t$
. Let
$\overline{X}_u-s\subseteq \overline{X}_u-t$
. Let
![]() $s \in G$
. Define a measure
$s \in G$
. Define a measure
![]() $m_s$
on
$m_s$
on
![]() $\overline{X}_u-s$
by
$\overline{X}_u-s$
by
Thanks to the fact that
![]() $m$
is conformal, it is clear that
$m$
is conformal, it is clear that
![]() $m_t|_{\overline{X}_u-s}=m_s$
for
$m_t|_{\overline{X}_u-s}=m_s$
for
![]() $s\leq t$
. Define a
$s\leq t$
. Define a
![]() $\sigma$
-finite measure
$\sigma$
-finite measure
![]() $m_\omega$
on
$m_\omega$
on
![]() $\overline{Y}_u$
by setting
$\overline{Y}_u$
by setting
Proposition 3.1.
The measure
![]() $m_\omega$
on
$m_\omega$
on
![]() $\overline{Y}_u$
defined as in Equation
3.4
is an
$\overline{Y}_u$
defined as in Equation
3.4
is an
![]() $e^{-\beta c}$
-conformal measure on the
$e^{-\beta c}$
-conformal measure on the
![]() $(G,P)$
-space
$(G,P)$
-space
![]() $(\overline{Y}_u,\overline{X}_u)$
.
$(\overline{Y}_u,\overline{X}_u)$
.
Proof. It is clear that
![]() $m_\omega |_{\overline{X}_u}=m$
and so
$m_\omega |_{\overline{X}_u}=m$
and so
![]() $m_\omega (\overline{X}_u)=1$
. For
$m_\omega (\overline{X}_u)=1$
. For
![]() $t\in G$
and a Borel subset
$t\in G$
and a Borel subset
![]() $E\subset \overline{Y}_u$
,
$E\subset \overline{Y}_u$
,
 \begin{eqnarray*} m_\omega (E+t)&=&\lim _sm_s((E+t)\cap (\overline{X}_u-s))\\ &=&\lim _s e^{\beta c(s)}m(((E+t)\cap (\overline{X}_u-s))+s)\\ &=& \lim _s e^{\beta c(s)}m((E\cap ( \overline{X}_u-(s+t)))+s+t)\\ &=& e^{-\beta c(t)}\lim _r e^{\beta c(r)} m((E\cap (\overline{X}_u-r))+r)\,\,(\textrm{by a change of variable} r=s+t)\\ &=& e^{-\beta c(t)}\lim _r m_r(E\cap (\overline{X}_u-r))\\ &=& e^{-\beta c(t)}m_\omega (E). \end{eqnarray*}
\begin{eqnarray*} m_\omega (E+t)&=&\lim _sm_s((E+t)\cap (\overline{X}_u-s))\\ &=&\lim _s e^{\beta c(s)}m(((E+t)\cap (\overline{X}_u-s))+s)\\ &=& \lim _s e^{\beta c(s)}m((E\cap ( \overline{X}_u-(s+t)))+s+t)\\ &=& e^{-\beta c(t)}\lim _r e^{\beta c(r)} m((E\cap (\overline{X}_u-r))+r)\,\,(\textrm{by a change of variable} r=s+t)\\ &=& e^{-\beta c(t)}\lim _r m_r(E\cap (\overline{X}_u-r))\\ &=& e^{-\beta c(t)}m_\omega (E). \end{eqnarray*}
Hence the proof.
Recall that for an étale groupoid
![]() $\mathcal{G}$
, the map
$\mathcal{G}$
, the map
![]() $f \mapsto f|_{\mathcal{G}^{(0)}}$
from
$f \mapsto f|_{\mathcal{G}^{(0)}}$
from
![]() $C_c(\mathcal{G})$
to
$C_c(\mathcal{G})$
to
![]() $C_0(\mathcal{G}^{(0)})$
defines a conditional expectation
$C_0(\mathcal{G}^{(0)})$
defines a conditional expectation
![]() $E\,:\,C^*(\mathcal{G}) \to C_0(\mathcal{G}^{(0)})$
. For
$E\,:\,C^*(\mathcal{G}) \to C_0(\mathcal{G}^{(0)})$
. For
![]() $\mathcal{G}\,:\!=\,\overline{X}_u \rtimes P$
, the conditional expectation
$\mathcal{G}\,:\!=\,\overline{X}_u \rtimes P$
, the conditional expectation
![]() $E$
has the following form
$E$
has the following form
 \begin{equation*} E(fw_s)\,:\!=\,\begin {cases} f & \mbox{if} \,\, s=0,\\ 0 & \mbox { otherwise}. \end {cases} \end{equation*}
\begin{equation*} E(fw_s)\,:\!=\,\begin {cases} f & \mbox{if} \,\, s=0,\\ 0 & \mbox { otherwise}. \end {cases} \end{equation*}
The next proposition is a direct consequence of Theorem 1.3 of [Reference Neshveyev22]. Hence, we omit the proof.
Proposition 3.2.
The map
![]() $\omega \mapsto m_{\omega }$
from the set of
$\omega \mapsto m_{\omega }$
from the set of
![]() $\beta$
-KMS states for
$\beta$
-KMS states for
![]() $\sigma =\sigma ^c$
to the set of
$\sigma =\sigma ^c$
to the set of
![]() $e^{-\beta c}$
-conformal measures on
$e^{-\beta c}$
-conformal measures on
![]() $\overline{Y}_u$
is surjective. More specifically, for an
$\overline{Y}_u$
is surjective. More specifically, for an
![]() $e^{-\beta c}$
-conformal
$e^{-\beta c}$
-conformal
![]() $m$
on
$m$
on
![]() $\overline{Y}_u$
, the state
$\overline{Y}_u$
, the state
![]() $\omega _m$
on
$\omega _m$
on
![]() $C^{*}(\overline{X}_u \rtimes P)$
defined by
$C^{*}(\overline{X}_u \rtimes P)$
defined by
is a
![]() $\beta$
-KMS state such that
$\beta$
-KMS state such that
![]() $m_{\omega _{m}}=m$
.
$m_{\omega _{m}}=m$
.
Remark 3.1.
In general, the map
![]() $\omega \to m_\omega$
of Proposition 3.1 need not be injective. The structure of a generic KMS state is determined by Neshveyev’s result (Theorem 1.3 of Reference Neshveyev[22]
). Let
$\omega \to m_\omega$
of Proposition 3.1 need not be injective. The structure of a generic KMS state is determined by Neshveyev’s result (Theorem 1.3 of Reference Neshveyev[22]
). Let
![]() $\mathcal{G}$
be an étale groupoid, and let
$\mathcal{G}$
be an étale groupoid, and let
![]() $\overline{c}\,:\,\mathcal{G} \to \mathbb{R}$
be a continuous homomorphism. For
$\overline{c}\,:\,\mathcal{G} \to \mathbb{R}$
be a continuous homomorphism. For
![]() $t \in \mathbb{R}$
, let
$t \in \mathbb{R}$
, let
![]() $\sigma _t$
be the automorphism of
$\sigma _t$
be the automorphism of
![]() $C^{*}(\mathcal{G})$
defined by
$C^{*}(\mathcal{G})$
defined by
for
![]() $f \in C_{c}(\mathcal{G})$
. Then,
$f \in C_{c}(\mathcal{G})$
. Then,
![]() $\sigma ^{\overline{c}}\,:\!=\{\sigma _t\}_{t \in \mathbb{R}}$
defines a
$\sigma ^{\overline{c}}\,:\!=\{\sigma _t\}_{t \in \mathbb{R}}$
defines a
![]() $1$
-parameter group of automorphisms on
$1$
-parameter group of automorphisms on
![]() $C^{*}(\mathcal{G})$
. Theorem 1.3 of Reference Neshveyev[22] describes the set of
$C^{*}(\mathcal{G})$
. Theorem 1.3 of Reference Neshveyev[22] describes the set of
![]() $\beta$
-KMS states for
$\beta$
-KMS states for
![]() $\sigma ^{\overline{c}}$
.
$\sigma ^{\overline{c}}$
.
In our situation, the groupoid
![]() $\mathcal{G}$
is the Deaconu-Renault groupoid
$\mathcal{G}$
is the Deaconu-Renault groupoid
![]() $\overline{X}_u \rtimes P$
, and the homomorphism
$\overline{X}_u \rtimes P$
, and the homomorphism
![]() $\overline{c}\,:\,\mathcal{G} \to \mathbb{R}$
is given by
$\overline{c}\,:\,\mathcal{G} \to \mathbb{R}$
is given by
One immediate corollary of Theorem 1.3 of Reference Neshveyev[22] is that, if the homomorphism
![]() $c\,:\,G \to \mathbb{R}$
is injective, then the map
$c\,:\,G \to \mathbb{R}$
is injective, then the map
![]() $\omega \to m_{\omega }$
of Proposition
3.1
is a bijection.
$\omega \to m_{\omega }$
of Proposition
3.1
is a bijection.
Proposition 3.3.
Let
![]() $\beta \neq 0$
, and let
$\beta \neq 0$
, and let
![]() $\omega$
be an extremal
$\omega$
be an extremal
![]() $\beta$
-KMS state for
$\beta$
-KMS state for
![]() $\sigma =\sigma ^{c}$
on the
$\sigma =\sigma ^{c}$
on the
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $C^*(\overline{X}_u \rtimes P)$
. Then, the
$C^*(\overline{X}_u \rtimes P)$
. Then, the
![]() $e^{-\beta c}$
-conformal measure
$e^{-\beta c}$
-conformal measure
![]() $m_\omega$
on
$m_\omega$
on
![]() $\overline{Y}_u$
defined as in Proposition
3.1
is ergodic for the
$\overline{Y}_u$
defined as in Proposition
3.1
is ergodic for the
![]() $G$
-action on
$G$
-action on
![]() $\overline{Y}_u$
.
$\overline{Y}_u$
.
Proof. The proof is an adaptation of the proof of Lemma 3.6 in [Reference Christensen and Thomsen5] with appropriate modifications. Assume that
![]() $m_\omega$
is not ergodic. Then, there exists a
$m_\omega$
is not ergodic. Then, there exists a
![]() $G$
-invariant Borel subset
$G$
-invariant Borel subset
![]() $A\subset \overline{Y}_u$
such that neither
$A\subset \overline{Y}_u$
such that neither
![]() $A$
nor
$A$
nor
![]() $A^c$
has measure zero. We claim that
$A^c$
has measure zero. We claim that
![]() $0\lt m_\omega (A\cap \overline{X}_u)\lt 1$
and
$0\lt m_\omega (A\cap \overline{X}_u)\lt 1$
and
![]() $0\lt m_\omega (A^c\cap \overline{X}_u)\lt 1$
.
$0\lt m_\omega (A^c\cap \overline{X}_u)\lt 1$
.
Suppose that
![]() $m_\omega (A\cap \overline{X}_u)=0$
. By conformality,
$m_\omega (A\cap \overline{X}_u)=0$
. By conformality,
![]() $m_\omega ((A\cap \overline{X}_u)-t)=0$
for every
$m_\omega ((A\cap \overline{X}_u)-t)=0$
for every
![]() $t \in G$
. Hence,
$t \in G$
. Hence,
![]() $\bigcup _{t \in G}(A\cap \overline{X}_u)-t$
is a null set. The fact that
$\bigcup _{t \in G}(A\cap \overline{X}_u)-t$
is a null set. The fact that
![]() $A$
is
$A$
is
![]() $G$
-invariant implies that
$G$
-invariant implies that
Therefore,
![]() $m_\omega (A)=0$
which is a contradiction. This proves that
$m_\omega (A)=0$
which is a contradiction. This proves that
![]() $m_\omega (A\cap \overline{X}_u)\neq 0$
. Similarly, we can prove that
$m_\omega (A\cap \overline{X}_u)\neq 0$
. Similarly, we can prove that
![]() $m_\omega (A^c \cap \overline{X}_u) \neq 0$
. Consequently,
$m_\omega (A^c \cap \overline{X}_u) \neq 0$
. Consequently,
![]() $0 \lt m_\omega (A \cap \overline{X}_u)\lt 1$
and
$0 \lt m_\omega (A \cap \overline{X}_u)\lt 1$
and
![]() $0 \lt m_\omega (A^c \cap \overline{X}_u)\lt 1$
. This proves the claim.
$0 \lt m_\omega (A^c \cap \overline{X}_u)\lt 1$
. This proves the claim.
Let
![]() $(H_\omega,\pi _\omega, \Omega _\omega )$
be the GNS representation of
$(H_\omega,\pi _\omega, \Omega _\omega )$
be the GNS representation of
![]() $\omega$
. Extend the homomorphism
$\omega$
. Extend the homomorphism
![]() $\pi _\omega |_{C(\overline{X}_u)}$
to a
$\pi _\omega |_{C(\overline{X}_u)}$
to a
![]() $^*$
- homomorphism
$^*$
- homomorphism
![]() $\overline{\pi }_\omega \,:\, L^{\infty }(\overline{X}_u,m_\omega ) \to \pi _\omega (C^*(\overline{X}_u \rtimes P))^{\prime\prime}$
by defining
$\overline{\pi }_\omega \,:\, L^{\infty }(\overline{X}_u,m_\omega ) \to \pi _\omega (C^*(\overline{X}_u \rtimes P))^{\prime\prime}$
by defining
Here, the limit is taken in the SOT sense and
![]() $\{f_n\}$
is any sequence in
$\{f_n\}$
is any sequence in
![]() $C(\overline{X}_u)$
such that for every
$C(\overline{X}_u)$
such that for every
![]() $n$
,
$n$
,
![]() $|f_n| \leq ||h||_\infty$
a.e and the sequence
$|f_n| \leq ||h||_\infty$
a.e and the sequence
![]() $(f_n(x)) \to h(x)$
for almost all
$(f_n(x)) \to h(x)$
for almost all
![]() $x$
.
$x$
.
For
![]() $s \in G$
, set
$s \in G$
, set
![]() $W_s=\pi _\omega (w_s)$
. Then, the following covariance relation is satisfied
$W_s=\pi _\omega (w_s)$
. Then, the following covariance relation is satisfied
for
![]() $s \in G$
and
$s \in G$
and
![]() $f \in L^{\infty }(\overline{X}_u,m_\omega )$
.
$f \in L^{\infty }(\overline{X}_u,m_\omega )$
.
Next, we claim that
![]() $\overline{\pi }_\omega (1_{A \cap \overline{X}_u})$
and
$\overline{\pi }_\omega (1_{A \cap \overline{X}_u})$
and
![]() $\overline{\pi }_\omega (1_{A^c \cap \overline{X}_u})$
are central in
$\overline{\pi }_\omega (1_{A^c \cap \overline{X}_u})$
are central in
![]() $\pi _\omega (C^*(\overline{X}_u \rtimes P))^{\prime\prime}$
. We will give details for
$\pi _\omega (C^*(\overline{X}_u \rtimes P))^{\prime\prime}$
. We will give details for
![]() $\overline{\pi }_\omega (1_{A \cap \overline{X}_u})$
and the centrality of
$\overline{\pi }_\omega (1_{A \cap \overline{X}_u})$
and the centrality of
![]() $\overline{\pi }_\omega (1_{A^c \cap \overline{X}_u})$
follows similarly. Let
$\overline{\pi }_\omega (1_{A^c \cap \overline{X}_u})$
follows similarly. Let
![]() $s \in P$
be given. Note that
$s \in P$
be given. Note that
![]() $R_{-s}(1_{A \cap \overline{X}_u})=1_{(A-s) \cap (\overline{X}_u-s)\cap \overline{X}_u}=1_{A \cap \overline{X}_u}$
and
$R_{-s}(1_{A \cap \overline{X}_u})=1_{(A-s) \cap (\overline{X}_u-s)\cap \overline{X}_u}=1_{A \cap \overline{X}_u}$
and
![]() $\overline{\pi }_\omega (f)$
commutes with
$\overline{\pi }_\omega (f)$
commutes with
![]() $W_sW_s^*$
for every
$W_sW_s^*$
for every
![]() $f \in L^{\infty }(\overline{X}_u,m_\omega )$
.
$f \in L^{\infty }(\overline{X}_u,m_\omega )$
.
Calculate as follows to observe that
 \begin{eqnarray*} \overline{\pi }_\omega (1_{A \cap \overline{X}_u})W_s&=& \overline{\pi }_\omega (1_{A \cap \overline{X}_u})W_sW_s^*W_s\\ &=& W_sW_s^*\overline{\pi }_\omega (1_{A \cap \overline{X}_u})W_s\\ &=&W_s \overline{\pi }_\omega (R_{-s}(1_{A \cap \overline{X}_u}))\\ &=&W_s \overline{\pi }_\omega (1_{A \cap \overline{X}_u}). \end{eqnarray*}
\begin{eqnarray*} \overline{\pi }_\omega (1_{A \cap \overline{X}_u})W_s&=& \overline{\pi }_\omega (1_{A \cap \overline{X}_u})W_sW_s^*W_s\\ &=& W_sW_s^*\overline{\pi }_\omega (1_{A \cap \overline{X}_u})W_s\\ &=&W_s \overline{\pi }_\omega (R_{-s}(1_{A \cap \overline{X}_u}))\\ &=&W_s \overline{\pi }_\omega (1_{A \cap \overline{X}_u}). \end{eqnarray*}
Since
![]() $\{W_s\,:\, s \in P\}$
generates
$\{W_s\,:\, s \in P\}$
generates
![]() $(\pi _\omega (C^*(\overline{X}_u \rtimes P))^{\prime\prime}$
, we can conclude that
$(\pi _\omega (C^*(\overline{X}_u \rtimes P))^{\prime\prime}$
, we can conclude that
![]() $\pi _\omega (1_A \cap \overline{X}_u)$
is central. This proves the claim.
$\pi _\omega (1_A \cap \overline{X}_u)$
is central. This proves the claim.
Define states
![]() $\omega _1$
and
$\omega _1$
and
![]() $\omega _2$
on
$\omega _2$
on
![]() $C^{*}(\overline{X}_u \rtimes P)$
by
$C^{*}(\overline{X}_u \rtimes P)$
by
 \begin{align*} \omega _1(a)&=\frac{1}{m_\omega (A\cap \overline{X}_u)}\langle \overline{\pi }_\omega (1_{A \cap \overline{X}_u})\pi _\omega (a)\Omega _\omega,\Omega _\omega \rangle, \\ \omega _2(a)&=\frac{1}{m_\omega (A^c\cap \overline{X}_u)}\langle \overline{\pi }_\omega (1_{A^c \cap \overline{X}_u})\pi _\omega (a)\Omega _\omega,\Omega _\omega \rangle. \end{align*}
\begin{align*} \omega _1(a)&=\frac{1}{m_\omega (A\cap \overline{X}_u)}\langle \overline{\pi }_\omega (1_{A \cap \overline{X}_u})\pi _\omega (a)\Omega _\omega,\Omega _\omega \rangle, \\ \omega _2(a)&=\frac{1}{m_\omega (A^c\cap \overline{X}_u)}\langle \overline{\pi }_\omega (1_{A^c \cap \overline{X}_u})\pi _\omega (a)\Omega _\omega,\Omega _\omega \rangle. \end{align*}
The centrality of the projections
![]() $\overline{\pi _\omega }(1_{A \cap \overline{X}_u})$
and
$\overline{\pi _\omega }(1_{A \cap \overline{X}_u})$
and
![]() $\overline{\pi _\omega }(1_{A^c \cap \overline{X}_u})$
imply that
$\overline{\pi _\omega }(1_{A^c \cap \overline{X}_u})$
imply that
![]() $\omega _1$
and
$\omega _1$
and
![]() $\omega _2$
are
$\omega _2$
are
![]() $\beta$
-KMS states on
$\beta$
-KMS states on
![]() $C^*(\overline{X}_u \rtimes P)$
. Moreover,
$C^*(\overline{X}_u \rtimes P)$
. Moreover,
![]() $\omega =m_\omega (A\cap \overline{X}_u)\omega _1+m_\omega (A^c\cap \overline{X}_u)\omega _2$
which contradicts the extremality of
$\omega =m_\omega (A\cap \overline{X}_u)\omega _1+m_\omega (A^c\cap \overline{X}_u)\omega _2$
which contradicts the extremality of
![]() $\omega$
. Hence the proof.
$\omega$
. Hence the proof.
Next, we work out the GNS representation of the KMS state
![]() $\omega _m$
given by Proposition 3.2. Suppose
$\omega _m$
given by Proposition 3.2. Suppose
![]() $m$
is an
$m$
is an
![]() $e^{-\beta c}$
conformal measure on
$e^{-\beta c}$
conformal measure on
![]() $\overline{Y}_u$
, and let
$\overline{Y}_u$
, and let
![]() $\omega _m$
be the
$\omega _m$
be the
![]() $\beta$
-KMS state on the
$\beta$
-KMS state on the
![]() $C^*$
-algebra
$C^*$
-algebra
![]() $C_{c}^{*}(P)=C^*(\overline{X}_u \rtimes P)$
obtained via the conditional expectation as in Proposition 3.2. Our goal is to show that if
$C_{c}^{*}(P)=C^*(\overline{X}_u \rtimes P)$
obtained via the conditional expectation as in Proposition 3.2. Our goal is to show that if
![]() $(H_\omega,\pi _\omega, \Omega _\omega )$
is the GNS representation of
$(H_\omega,\pi _\omega, \Omega _\omega )$
is the GNS representation of
![]() $\omega _m$
, then the von Neumann algebra
$\omega _m$
, then the von Neumann algebra
![]() $(\pi _\omega (C^*(\overline{X}_u \rtimes P)))^{\prime\prime}$
is isomorphic to the full corner
$(\pi _\omega (C^*(\overline{X}_u \rtimes P)))^{\prime\prime}$
is isomorphic to the full corner
![]() $1_{\overline{X}_u} (L^\infty (\overline{Y}_u)\rtimes G)1_{\overline{X}_u}$
of
$1_{\overline{X}_u} (L^\infty (\overline{Y}_u)\rtimes G)1_{\overline{X}_u}$
of
![]() $L^\infty (\overline{Y}_u)\rtimes G$
.
$L^\infty (\overline{Y}_u)\rtimes G$
.
Let
![]() $\lambda \,:\!=\{\lambda _s\}_{s \in G}$
be the Koopman representation of
$\lambda \,:\!=\{\lambda _s\}_{s \in G}$
be the Koopman representation of
![]() $G$
on
$G$
on
![]() $L^{2}(\overline{Y}_u,m)$
. Recall that
$L^{2}(\overline{Y}_u,m)$
. Recall that
for
![]() $s \in G$
and
$s \in G$
and
![]() $\xi \in L^{2}(\overline{Y}_u,m)$
.
$\xi \in L^{2}(\overline{Y}_u,m)$
.
Let
![]() $\mathcal{K}=l^2(G,L^2(\overline{Y}_u))$
and
$\mathcal{K}=l^2(G,L^2(\overline{Y}_u))$
and
![]() $\pi _0$
be the representation of
$\pi _0$
be the representation of
![]() $C_0(\overline{Y}_u)\rtimes G$
on
$C_0(\overline{Y}_u)\rtimes G$
on
![]() $\mathcal{K}$
defined by
$\mathcal{K}$
defined by
Then,
![]() $(\pi _0(C_0(\overline{Y}_u) \rtimes G))^{\prime\prime}=L^\infty (\overline{Y}_u)\rtimes G$
. Let
$(\pi _0(C_0(\overline{Y}_u) \rtimes G))^{\prime\prime}=L^\infty (\overline{Y}_u)\rtimes G$
. Let
![]() $\mathcal{H}$
be the Hilbert subspace of
$\mathcal{H}$
be the Hilbert subspace of
![]() $\mathcal{K}$
given by
$\mathcal{K}$
given by
It is clear that
![]() $L^\infty (\overline{Y}_u)\rtimes G$
leaves
$L^\infty (\overline{Y}_u)\rtimes G$
leaves
![]() $\mathcal{H}$
invariant, thus giving a normal representation
$\mathcal{H}$
invariant, thus giving a normal representation
![]() $\overline{\pi }$
of the crossed product
$\overline{\pi }$
of the crossed product
![]() $L^\infty (\overline{Y}_u)\rtimes G$
on
$L^\infty (\overline{Y}_u)\rtimes G$
on
![]() $\mathcal{H}$
. Let
$\mathcal{H}$
. Let
![]() $\pi =\overline{\pi }\circ \pi _0$
.
$\pi =\overline{\pi }\circ \pi _0$
.
Notation: For
![]() $s \in G$
and
$s \in G$
and
![]() $\xi \in L^{2}(\overline{X}_u+s)$
, let
$\xi \in L^{2}(\overline{X}_u+s)$
, let
![]() $\xi \otimes \delta _s \in \mathcal{H}$
be defined by
$\xi \otimes \delta _s \in \mathcal{H}$
be defined by
 \begin{equation*} \xi \otimes \delta _s(t)=\begin {cases} \xi & \mbox{if} \,\, t=s,\\ 0 & \mbox { otherwise}. \end {cases} \end{equation*}
\begin{equation*} \xi \otimes \delta _s(t)=\begin {cases} \xi & \mbox{if} \,\, t=s,\\ 0 & \mbox { otherwise}. \end {cases} \end{equation*}
Lemma 3.1.
The von Neumann algebra
![]() $(\pi (C_0(\overline{Y}_u) \rtimes G))^{\prime\prime}$
is isomorphic to
$(\pi (C_0(\overline{Y}_u) \rtimes G))^{\prime\prime}$
is isomorphic to
![]() $L^\infty (\overline{Y}_u)\rtimes G$
.
$L^\infty (\overline{Y}_u)\rtimes G$
.
Proof. Note that since
![]() $\pi =\overline{\pi }\circ \pi _0$
and the von Neumann algebra generated by
$\pi =\overline{\pi }\circ \pi _0$
and the von Neumann algebra generated by
![]() $\pi _0(C_0(\overline{Y}_u) \rtimes G)$
is
$\pi _0(C_0(\overline{Y}_u) \rtimes G)$
is
![]() $L^\infty (\overline{Y}_u)\rtimes G$
, to complete the proof, it is enough to prove that
$L^\infty (\overline{Y}_u)\rtimes G$
, to complete the proof, it is enough to prove that
![]() $\overline{\pi }$
is injective.
$\overline{\pi }$
is injective.
First, we claim that
![]() $\overline{\pi }$
restricted to
$\overline{\pi }$
restricted to
![]() $L^{\infty }(\overline{Y}_u)$
is injective. Let
$L^{\infty }(\overline{Y}_u)$
is injective. Let
![]() $f \in L^{\infty }(\overline{Y}_u)$
be such that
$f \in L^{\infty }(\overline{Y}_u)$
be such that
![]() $\overline{\pi }(f)=0$
. Suppose
$\overline{\pi }(f)=0$
. Suppose
![]() $s \in G$
. Then, for every
$s \in G$
. Then, for every
![]() $\xi \in L^{2}(\overline{X}_u+s)$
,
$\xi \in L^{2}(\overline{X}_u+s)$
,
Thus,
![]() $f=0$
a.e on
$f=0$
a.e on
![]() $\overline{X}_u+s$
for every
$\overline{X}_u+s$
for every
![]() $s\in G$
. Since
$s\in G$
. Since
![]() $\overline{Y}_u=\bigcup _{s \in G} \overline{X}_u+s$
, it follows that
$\overline{Y}_u=\bigcup _{s \in G} \overline{X}_u+s$
, it follows that
![]() $f=0$
a.e on
$f=0$
a.e on
![]() $\overline{Y}_u$
proving that
$\overline{Y}_u$
proving that
![]() $\overline{\pi }$
is faithful on
$\overline{\pi }$
is faithful on
![]() $L^\infty (\overline{Y}_u)$
.
$L^\infty (\overline{Y}_u)$
.
Let
![]() $E$
be the usual conditional expectation from
$E$
be the usual conditional expectation from
![]() $L^\infty (\overline{Y}_u)\rtimes G\to L^\infty (\overline{Y}_u)$
given by
$L^\infty (\overline{Y}_u)\rtimes G\to L^\infty (\overline{Y}_u)$
given by
![]() $ E(fu_s)=\delta _{s,0}f$
. Here,
$ E(fu_s)=\delta _{s,0}f$
. Here,
![]() $\delta _{s,0}$
is the Kronecker delta. Then, the conditional expectation
$\delta _{s,0}$
is the Kronecker delta. Then, the conditional expectation
![]() $E$
is faithful. Decompose
$E$
is faithful. Decompose
![]() $\mathcal{H}$
as
$\mathcal{H}$
as
![]() $\displaystyle \mathcal{H}=\bigoplus _{t \in G}L^2(\overline{X}_u+t)$
, and for
$\displaystyle \mathcal{H}=\bigoplus _{t \in G}L^2(\overline{X}_u+t)$
, and for
![]() $ t \in G$
, let
$ t \in G$
, let
![]() $P_t$
be the projection onto the subspace
$P_t$
be the projection onto the subspace
![]() $L^2(\overline{X}_u+t)$
. Define a map
$L^2(\overline{X}_u+t)$
. Define a map
![]() $\widetilde{E}\,:\, B(\mathcal{H}) \to B(\mathcal{H})$
by
$\widetilde{E}\,:\, B(\mathcal{H}) \to B(\mathcal{H})$
by
where the convergent sum is w.r.t. the strong operator topology. Clearly,
![]() $\widetilde{E}\circ \overline{\pi }=\overline{\pi }\circ E$
.
$\widetilde{E}\circ \overline{\pi }=\overline{\pi }\circ E$
.
Let
![]() $x \in L^{\infty }(\overline{Y}_u) \rtimes G$
be such that
$x \in L^{\infty }(\overline{Y}_u) \rtimes G$
be such that
![]() $\overline{\pi }(x)=0$
. Then,
$\overline{\pi }(x)=0$
. Then,
![]() $\overline{\pi }(x^*x)=0$
. Therefore,
$\overline{\pi }(x^*x)=0$
. Therefore,
Since
![]() $\overline{\pi }$
is faithful on
$\overline{\pi }$
is faithful on
![]() $L^{\infty }(\overline{Y}_u)$
, we have
$L^{\infty }(\overline{Y}_u)$
, we have
![]() $E(x^*x)=0$
. Since
$E(x^*x)=0$
. Since
![]() $E$
is faithful,
$E$
is faithful,
![]() $x=0$
. This completes the proof.
$x=0$
. This completes the proof.
Recall that
![]() $C^{*}(\overline{X}_u \rtimes P)$
is the full corner
$C^{*}(\overline{X}_u \rtimes P)$
is the full corner
![]() $p(C_0(\overline{Y}_u) \rtimes G)p$
where
$p(C_0(\overline{Y}_u) \rtimes G)p$
where
![]() $p=1_{\overline{X}_u}$
. Consider the Hilbert space
$p=1_{\overline{X}_u}$
. Consider the Hilbert space
where
![]() $P=\pi (p)$
. Define
$P=\pi (p)$
. Define
![]() $\widetilde{\pi }\,:\, C^{*}(\overline{X}_u \rtimes P) \to B(P\mathcal{H})$
by
$\widetilde{\pi }\,:\, C^{*}(\overline{X}_u \rtimes P) \to B(P\mathcal{H})$
by
![]() $\widetilde{\pi }(fw_t)=P\pi (\tilde{f}u_t)P$
where
$\widetilde{\pi }(fw_t)=P\pi (\tilde{f}u_t)P$
where
![]() $\tilde{f}=f1_{\overline{X}_u}$
. Define
$\tilde{f}=f1_{\overline{X}_u}$
. Define
![]() $\xi \in P\mathcal{H}$
by,
$\xi \in P\mathcal{H}$
by,
 \begin{equation*} \xi (t)=\begin {cases} 1_{\overline {X}_u} & \mbox{if} \,\, t=0,\\ 0 & \mbox { otherwise}. \end {cases} \end{equation*}
\begin{equation*} \xi (t)=\begin {cases} 1_{\overline {X}_u} & \mbox{if} \,\, t=0,\\ 0 & \mbox { otherwise}. \end {cases} \end{equation*}
Lemma 3.2.
With the foregoing notation, the triple
![]() $(\widetilde{\pi },P\mathcal{H},\xi )$
is the GNS representation of the
$(\widetilde{\pi },P\mathcal{H},\xi )$
is the GNS representation of the
![]() $\beta$
-KMS state
$\beta$
-KMS state
![]() $\omega _m$
. Moreover, the von Neumann algebra
$\omega _m$
. Moreover, the von Neumann algebra
![]() $\widetilde{\pi }(C^{*}(\overline{X}_u \rtimes P))^{\prime\prime}$
is isomorphic to the full corner
$\widetilde{\pi }(C^{*}(\overline{X}_u \rtimes P))^{\prime\prime}$
is isomorphic to the full corner
![]() $1_{\overline{X}_u}(L^{\infty }(\overline{Y}_u) \rtimes G)1_{\overline{X}_u}$
.
$1_{\overline{X}_u}(L^{\infty }(\overline{Y}_u) \rtimes G)1_{\overline{X}_u}$
.
Proof. Observe that, for
![]() $f \in C(\overline{X_u})$
, and
$f \in C(\overline{X_u})$
, and
![]() $s,t\in G$
,
$s,t\in G$
,
 \begin{align*} \widetilde{\pi}(fw_t)\xi(s)& =P\pi(\tilde f u_t)P\xi(s)\\ & =\pi(1_{\overline{X}_u}\tilde f u_t )\xi(s)\\ & = 1_{\overline{X}_u}\tilde f \lambda_t(\xi(s-t))\\ & = \delta_{s,t}1_{\overline{X}_u}f \lambda_t(\xi(0))\\ & =e^{\frac{\beta c(s)}{2}}\delta_{s,t} 1_{\overline{X}_u}f1_{\overline{X}_u+s}\end{align*}
\begin{align*} \widetilde{\pi}(fw_t)\xi(s)& =P\pi(\tilde f u_t)P\xi(s)\\ & =\pi(1_{\overline{X}_u}\tilde f u_t )\xi(s)\\ & = 1_{\overline{X}_u}\tilde f \lambda_t(\xi(s-t))\\ & = \delta_{s,t}1_{\overline{X}_u}f \lambda_t(\xi(0))\\ & =e^{\frac{\beta c(s)}{2}}\delta_{s,t} 1_{\overline{X}_u}f1_{\overline{X}_u+s}\end{align*}
From the above formula, it is clear that
![]() $\langle \widetilde{\pi }(a)\xi,\xi \rangle =\omega _m(a)$
for every
$\langle \widetilde{\pi }(a)\xi,\xi \rangle =\omega _m(a)$
for every
![]() $a \in C^{*}(\overline{X}_u \rtimes P)$
. Also,
$a \in C^{*}(\overline{X}_u \rtimes P)$
. Also,
![]() $span\{\widetilde{\pi }(fw_t)\xi \,:\, f \in C(\overline{X}_u), t \in G\}=span\{\eta \otimes \delta _s\,:\, \eta \in C(\overline{X}_u \cap (\overline{X}_u+s)), s \in G\}$
, and the latter set is dense in
$span\{\widetilde{\pi }(fw_t)\xi \,:\, f \in C(\overline{X}_u), t \in G\}=span\{\eta \otimes \delta _s\,:\, \eta \in C(\overline{X}_u \cap (\overline{X}_u+s)), s \in G\}$
, and the latter set is dense in
![]() $P\mathcal{H}$
proving that
$P\mathcal{H}$
proving that
![]() $\xi$
is cyclic for
$\xi$
is cyclic for
![]() $\widetilde{\pi }$
. Thus,
$\widetilde{\pi }$
. Thus,
![]() $(\widetilde{\pi },P\mathcal{H},\xi )$
is the GNS representation of the
$(\widetilde{\pi },P\mathcal{H},\xi )$
is the GNS representation of the
![]() $\beta$
-KMS state
$\beta$
-KMS state
![]() $\omega _m$
.
$\omega _m$
.
From the definition of
![]() $\widetilde{\pi }$
, we have
$\widetilde{\pi }$
, we have
The conclusion is now clear from Lemma 3.1.
We have the following main theorem of this section establishing the factor types of extremal
![]() $\beta$
-KMS states
$\beta$
-KMS states
![]() $\omega _m$
.
$\omega _m$
.
Theorem 3.1.
Suppose
![]() $m$
is an
$m$
is an
![]() $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
![]() $\overline{Y}_u$
. Let
$\overline{Y}_u$
. Let
![]() $\omega \,:\!=\,\omega _m$
be the
$\omega \,:\!=\,\omega _m$
be the
![]() $\beta$
-KMS state as in Proposition 3.2
. Denote the GNS representation of
$\beta$
-KMS state as in Proposition 3.2
. Denote the GNS representation of
![]() $\omega$
by
$\omega$
by
![]() $\pi _\omega$
. Suppose
$\pi _\omega$
. Suppose
![]() $t \in \{I_\infty,II_\infty,III\}$
. Then,
$t \in \{I_\infty,II_\infty,III\}$
. Then,
-
(1)
 $(\pi _\omega (C^*(\overline{X}_u \rtimes P)))^{\prime\prime}$
is isomorphic to the full corner
$(\pi _\omega (C^*(\overline{X}_u \rtimes P)))^{\prime\prime}$
is isomorphic to the full corner
 $1_{\overline{X}_u} (L^\infty (\overline{Y}_u)\rtimes G)1_{\overline{X}_u}$
.
$1_{\overline{X}_u} (L^\infty (\overline{Y}_u)\rtimes G)1_{\overline{X}_u}$
. -
(2)
 $\omega _m$
is extremal
$\omega _m$
is extremal
 $\iff L^\infty (\overline{Y}_u)\rtimes G$
is a factor
$\iff L^\infty (\overline{Y}_u)\rtimes G$
is a factor
 $\iff m$
is ergodic and the
$\iff m$
is ergodic and the
 $G$
-action is essentially free. Moreover,
$G$
-action is essentially free. Moreover,
 $\omega _m$
is of type
$\omega _m$
is of type
 $t$
if and only if
$t$
if and only if
 $m$
is of type
$m$
is of type
 $t$
.
$t$
.
Proof. The first equivalence in
![]() $(2)$
follows from Lemma 3.2 and the following facts. It is well known that
$(2)$
follows from Lemma 3.2 and the following facts. It is well known that
-
(i) a
 $\beta$
-KMS state
$\beta$
-KMS state
 $\omega$
is extremal if and only if its GNS representation
$\omega$
is extremal if and only if its GNS representation
 $\pi _\omega$
is factorial, and
$\pi _\omega$
is factorial, and -
(ii) a full corner
 $pMp$
is a factor of type
$pMp$
is a factor of type
 $t$
if and only if
$t$
if and only if
 $M$
is a factor of type
$M$
is a factor of type
 $t$
.
$t$
.
Other conclusions are standard.
A few remarks are in order.
Remark 3.2.
Let
![]() $\beta$
be a non-zero real number.
$\beta$
be a non-zero real number.
-
(1) Let
 $\omega$
be a
$\omega$
be a
 $\beta$
-KMS state. Let
$\beta$
-KMS state. Let
 $m\,:\!=\,m_{\omega }$
be the
$m\,:\!=\,m_{\omega }$
be the
 $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
 $\overline{Y}_u$
associated with
$\overline{Y}_u$
associated with
 $\omega$
as in Proposition
3.1
. Then,
$\omega$
as in Proposition
3.1
. Then,
 $m$
is concentrated on
$m$
is concentrated on
 $Y_u\,:\!=\,\overline{Y}_u \backslash \{G\}$
. Note that, for every
$Y_u\,:\!=\,\overline{Y}_u \backslash \{G\}$
. Note that, for every
 $s \in G$
,Since
$s \in G$
,Since \begin{equation*} m(\{G\})=m(\{G\}+s)=e^{-\beta c(s)}m(\{G\}).\end{equation*}
\begin{equation*} m(\{G\})=m(\{G\}+s)=e^{-\beta c(s)}m(\{G\}).\end{equation*}
 $\{G\}$
is of finite measure (as
$\{G\}$
is of finite measure (as
 $\{G\} \subset \overline{X}_u$
) and
$\{G\} \subset \overline{X}_u$
) and
 $\beta c$
is a non-zero homomorphism, we have
$\beta c$
is a non-zero homomorphism, we have
 $m(\{G\})=0$
.
$m(\{G\})=0$
.
-
(2) Suppose
 $\omega$
is a
$\omega$
is a
 $\beta$
-KMS state on
$\beta$
-KMS state on
 $A\,:\!=\,C_{c}^{*}(P)$
. Assume that
$A\,:\!=\,C_{c}^{*}(P)$
. Assume that
 $\omega$
is extremal, and denote the GNS representation of
$\omega$
is extremal, and denote the GNS representation of
 $A$
associated with
$A$
associated with
 $\omega$
by
$\omega$
by
 $\pi _\omega$
. Denote the associated cyclic vector by
$\pi _\omega$
. Denote the associated cyclic vector by
 $\Omega _\omega$
. Then, the factor
$\Omega _\omega$
. Then, the factor
 $M\,:\!=\,\pi _\omega (A)^{\prime\prime}$
is neither of type
$M\,:\!=\,\pi _\omega (A)^{\prime\prime}$
is neither of type
 $I_n$
for
$I_n$
for
 $n$
finite nor of type
$n$
finite nor of type
 $II_1$
. To see this, let
$II_1$
. To see this, let
 $m$
be the
$m$
be the
 $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
 $\overline{Y}_u$
associated with
$\overline{Y}_u$
associated with
 $\omega$
. Pick
$\omega$
. Pick
 $a \in P$
such that
$a \in P$
such that
 $c(a) \neq 0$
. Note that
$c(a) \neq 0$
. Note that
 $\pi _\omega (e_a)=\pi _\omega (1_{\overline{X}_u+a})$
. Here
$\pi _\omega (e_a)=\pi _\omega (1_{\overline{X}_u+a})$
. Here
 $e_a=v_av_a^*$
. Then,
This implies that
$e_a=v_av_a^*$
. Then,
This implies that \begin{equation*}\langle \pi _\omega (1-e_a)\Omega _\omega |\Omega _\omega \rangle =1-m(\overline {X}_u+a)=1-e^{-\beta c(a)} \neq 0.\end{equation*}
\begin{equation*}\langle \pi _\omega (1-e_a)\Omega _\omega |\Omega _\omega \rangle =1-m(\overline {X}_u+a)=1-e^{-\beta c(a)} \neq 0.\end{equation*}
 $\pi _\omega (1-e_a) \neq 0$
. Thus,
$\pi _\omega (1-e_a) \neq 0$
. Thus,
 $\pi _\omega (e_a)$
is a proper subprojection of
$\pi _\omega (e_a)$
is a proper subprojection of
 $1$
which is Murray von Neumann equivalent to
$1$
which is Murray von Neumann equivalent to
 $1$
in
$1$
in
 $M$
. Hence the conclusion.
$M$
. Hence the conclusion.
In the next proposition, we work out the extremal
![]() $\beta$
-KMS states whose associated measure is supported on an orbit.
$\beta$
-KMS states whose associated measure is supported on an orbit.
Proposition 3.4.
-
(1) Let
 $m$
be an
$m$
be an
 $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
 $Y_u$
supported on an orbit
$Y_u$
supported on an orbit
 $Orb(A)$
for some
$Orb(A)$
for some
 $A$
. Denote the of
$A$
. Denote the of
 $A$
by
$A$
by
 $H$
, i.e.
Let
$H$
, i.e.
Let \begin{equation*}H\,:\!=\{s \in G\,:\, A+s=A\}.\end{equation*}
\begin{equation*}H\,:\!=\{s \in G\,:\, A+s=A\}.\end{equation*}
 $\chi$
be a character of
$\chi$
be a character of
 $H$
. Define a state
$H$
. Define a state
 $\omega _{\chi,m}$
on
$\omega _{\chi,m}$
on
 $C_{c}^{*}(P)$
by
Then,
$C_{c}^{*}(P)$
by
Then, \begin{equation*} \omega _{\chi,m}(f w_s)\,:\!=\,\begin {cases} 0 & \mbox { if } s \notin H \\ \overline {\chi (s)}\displaystyle \int _{X_u} f(A)dm(A) & \mbox { if $s \in H$}. \end {cases} \end{equation*}
\begin{equation*} \omega _{\chi,m}(f w_s)\,:\!=\,\begin {cases} 0 & \mbox { if } s \notin H \\ \overline {\chi (s)}\displaystyle \int _{X_u} f(A)dm(A) & \mbox { if $s \in H$}. \end {cases} \end{equation*}
 $\omega _{\chi,m}$
is an extremal
$\omega _{\chi,m}$
is an extremal
 $\beta$
-KMS state on
$\beta$
-KMS state on
 $C_{c}^{*}(P)$
. Moreover,
$C_{c}^{*}(P)$
. Moreover,
 $\omega _{\chi,m}$
is of type I.
$\omega _{\chi,m}$
is of type I.
-
(2) Let
 $\omega$
be an extremal
$\omega$
be an extremal
 $\beta$
-KMS state on
$\beta$
-KMS state on
 $C_{c}^{*}(P)$
, and let
$C_{c}^{*}(P)$
, and let
 $m$
be the
$m$
be the
 $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
 $Y_u$
associated with
$Y_u$
associated with
 $\omega$
. Suppose that
$\omega$
. Suppose that
 $m$
is atomic and concentrated on
$m$
is atomic and concentrated on
 $Orb(A)$
for some
$Orb(A)$
for some
 $A \in Y_u$
. Let
$A \in Y_u$
. Let
 $H$
be the stabiliser of
$H$
be the stabiliser of
 $A$
. Then,
$A$
. Then,
 $\omega$
is of the form
$\omega$
is of the form
 $\omega _{\chi,m}$
for some character
$\omega _{\chi,m}$
for some character
 $\chi$
of
$\chi$
of
 $H$
.
$H$
.
Proof. The only thing that requires proof is that
![]() $\omega _{\chi,m}$
is of type I. Other assertions follow from Corollary 1.4 of [Reference Neshveyev22]. Let
$\omega _{\chi,m}$
is of type I. Other assertions follow from Corollary 1.4 of [Reference Neshveyev22]. Let
![]() $m$
be an
$m$
be an
![]() $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
![]() $Y_u$
supported on an orbit
$Y_u$
supported on an orbit
![]() $Orb(A)$
for some
$Orb(A)$
for some
![]() $A$
and denote the of
$A$
and denote the of
![]() $A$
by
$A$
by
![]() $H$
. Let
$H$
. Let
![]() $\chi$
be a character of
$\chi$
be a character of
![]() $H$
, and let
$H$
, and let
![]() $\omega \,:\!=\,\omega _{\chi,m}$
. Let
$\omega \,:\!=\,\omega _{\chi,m}$
. Let
![]() $\pi _\omega$
be the GNS representation of
$\pi _\omega$
be the GNS representation of
![]() $\omega _{\chi,m}$
. To prove that
$\omega _{\chi,m}$
. To prove that
![]() $\omega _{\chi,m}$
is extremal of type I, it suffices to show that the von Neumann algebra
$\omega _{\chi,m}$
is extremal of type I, it suffices to show that the von Neumann algebra
![]() $\pi _{\omega }(C^*(\overline{X}_u \rtimes P))^{\prime\prime}$
is a factor of type I. The proof is similar to the proof of Theorem 3.1.
$\pi _{\omega }(C^*(\overline{X}_u \rtimes P))^{\prime\prime}$
is a factor of type I. The proof is similar to the proof of Theorem 3.1.
By the conformality of
![]() $m$
, for a Borel set
$m$
, for a Borel set
![]() $E\subset Orb(A)$
with
$E\subset Orb(A)$
with
![]() $m(E)\gt 0$
and
$m(E)\gt 0$
and
![]() $t \in H$
, we have
$t \in H$
, we have
implying that
![]() $c(t)=0$
. Thus,
$c(t)=0$
. Thus,
![]() $H\subset c^{-1}(0)$
. Let
$H\subset c^{-1}(0)$
. Let
![]() $\lambda =\{\lambda _t\}_{t \in G}$
be the Koopman representation of
$\lambda =\{\lambda _t\}_{t \in G}$
be the Koopman representation of
![]() $G$
on
$G$
on
![]() $L^2(\overline{Y}_u)$
. Note that since
$L^2(\overline{Y}_u)$
. Note that since
![]() $Y_u=Orb(A)$
upto a null set,
$Y_u=Orb(A)$
upto a null set,
![]() $L^2(\overline{Y}_u)=L^2(Orb(A))$
and we can conclude that
$L^2(\overline{Y}_u)=L^2(Orb(A))$
and we can conclude that
![]() $\lambda _t=\lambda _s$
, whenever
$\lambda _t=\lambda _s$
, whenever
![]() $t-s \in H$
. Extend the character
$t-s \in H$
. Extend the character
![]() $\chi$
of
$\chi$
of
![]() $H$
to a character of
$H$
to a character of
![]() $G$
which we denote again by
$G$
which we denote again by
![]() $\chi$
.
$\chi$
.
Let
![]() $\mathcal{K}$
be the Hilbert space defined by
$\mathcal{K}$
be the Hilbert space defined by
![]() $\mathcal{K}=l^2(G/H,L^2(\overline{Y}_u))$
, and let
$\mathcal{K}=l^2(G/H,L^2(\overline{Y}_u))$
, and let
![]() $\pi _0$
be the representation of
$\pi _0$
be the representation of
![]() $C_0(\overline{Y}_u)\rtimes G$
on
$C_0(\overline{Y}_u)\rtimes G$
on
![]() $\mathcal{K}$
given by
$\mathcal{K}$
given by
Clearly,
![]() $\pi _0(C_0(\overline{Y}_u)\rtimes G)^{\prime\prime}=L^\infty (\overline{Y}_u)\rtimes G/H$
. Let
$\pi _0(C_0(\overline{Y}_u)\rtimes G)^{\prime\prime}=L^\infty (\overline{Y}_u)\rtimes G/H$
. Let
![]() $\mathcal{H}$
be the Hilbert subspace of
$\mathcal{H}$
be the Hilbert subspace of
![]() $\mathcal{K}$
given by
$\mathcal{K}$
given by
We have
![]() $\overline{s}=\overline{t}$
implies
$\overline{s}=\overline{t}$
implies
![]() $\overline{X}_u+s=\overline{X}_u+t$
upto a null set, and hence, the definition of
$\overline{X}_u+s=\overline{X}_u+t$
upto a null set, and hence, the definition of
![]() $\mathcal{H}$
makes sense. Since
$\mathcal{H}$
makes sense. Since
![]() $L^\infty (\overline{Y}_u)\rtimes G/H$
leaves
$L^\infty (\overline{Y}_u)\rtimes G/H$
leaves
![]() $\mathcal{H}$
invariant, we get a representation
$\mathcal{H}$
invariant, we get a representation
![]() $\overline{\pi }\,:\, L^\infty (\overline{Y}_u)\rtimes G/H \to B(\mathcal{H})$
. Define
$\overline{\pi }\,:\, L^\infty (\overline{Y}_u)\rtimes G/H \to B(\mathcal{H})$
. Define
![]() $\pi =\overline{\pi }\circ \pi _0$
. Consider the Hilbert space
$\pi =\overline{\pi }\circ \pi _0$
. Consider the Hilbert space
![]() $P\mathcal{H}$
where
$P\mathcal{H}$
where
![]() $P=\pi (1_{\overline{X}_u})$
. Let
$P=\pi (1_{\overline{X}_u})$
. Let
![]() $\xi \in P\mathcal{H}$
be given by,
$\xi \in P\mathcal{H}$
be given by,
 \begin{equation*} \xi (\overline {t})=\begin {cases} 1_{\overline {X}_u} & \mbox{if} \,\, \overline {t}=0,\\ 0 & \mbox { otherwise }. \end {cases} \end{equation*}
\begin{equation*} \xi (\overline {t})=\begin {cases} 1_{\overline {X}_u} & \mbox{if} \,\, \overline {t}=0,\\ 0 & \mbox { otherwise }. \end {cases} \end{equation*}
Let
![]() $\widetilde{\pi }\,:\, C^{*}(\overline{X}_u \rtimes P) \to B(P\mathcal{H})$
be defined by
$\widetilde{\pi }\,:\, C^{*}(\overline{X}_u \rtimes P) \to B(P\mathcal{H})$
be defined by
![]() $\widetilde{\pi }(fw_t)=P\pi (\tilde{f}u_t)P$
where
$\widetilde{\pi }(fw_t)=P\pi (\tilde{f}u_t)P$
where
![]() $\tilde{f}=f1_{\overline{X}_u}$
.
$\tilde{f}=f1_{\overline{X}_u}$
.
Arguing as before, we can conclude the following.
-
1. The map
 $\overline{\pi }$
is injective, and hence, the von Neumann algebra
$\overline{\pi }$
is injective, and hence, the von Neumann algebra
 $\pi (C_0(\overline{Y}_u)\rtimes G)^{\prime\prime}$
is isomorphic to
$\pi (C_0(\overline{Y}_u)\rtimes G)^{\prime\prime}$
is isomorphic to
 $L^\infty (\overline{Y}_u)\rtimes G/H$
.
$L^\infty (\overline{Y}_u)\rtimes G/H$
. -
2. The triple
 $(\widetilde{\pi },P\mathcal{H},\xi )$
is the GNS representation of
$(\widetilde{\pi },P\mathcal{H},\xi )$
is the GNS representation of
 $\omega _{\chi,m}$
.
$\omega _{\chi,m}$
. -
3. The von Neumann algebra generated by
 $\widetilde{\pi }(C^*(\overline{X}_u \rtimes P))$
is isomorphic to the full corner
$\widetilde{\pi }(C^*(\overline{X}_u \rtimes P))$
is isomorphic to the full corner
 $1_{\overline{X}_u} (L^\infty (\overline{Y}_u)\rtimes G/H)1_{\overline{X}_u}$
.
$1_{\overline{X}_u} (L^\infty (\overline{Y}_u)\rtimes G/H)1_{\overline{X}_u}$
.
Thus,
![]() $\pi _{\omega }(C^*(\overline{X}_u \rtimes P))^{\prime\prime}$
is isomorphic to the full corner
$\pi _{\omega }(C^*(\overline{X}_u \rtimes P))^{\prime\prime}$
is isomorphic to the full corner
![]() $1_{\overline{X}_u} (L^\infty (\overline{Y}_u)\rtimes G/H)1_{\overline{X}_u}$
which is clearly a factor of type I (as the measure
$1_{\overline{X}_u} (L^\infty (\overline{Y}_u)\rtimes G/H)1_{\overline{X}_u}$
which is clearly a factor of type I (as the measure
![]() $m$
is atomic). This completes the proof.
$m$
is atomic). This completes the proof.
We end this section with a proposition that allows us to construct conformal measures on the
![]() $(G,P)$
-space
$(G,P)$
-space
![]() $(Y_u,X_u)$
, and consequently, KMS states on
$(Y_u,X_u)$
, and consequently, KMS states on
![]() $C_c^{*}(P)$
of the desired type. Let
$C_c^{*}(P)$
of the desired type. Let
![]() $(Y,X)$
be a pure
$(Y,X)$
be a pure
![]() $(G,P)$
-space. For
$(G,P)$
-space. For
![]() $y \in Y$
, let
$y \in Y$
, let
First, let us check that for
![]() $y \in Y$
,
$y \in Y$
,
![]() $Q_y \in Y_u$
. Fix
$Q_y \in Y_u$
. Fix
![]() $y \in Y$
.
$y \in Y$
.
-
(1) Since,
 $\displaystyle Y=\bigcup _{a \in P}(X-a)$
, it follows that there exists
$\displaystyle Y=\bigcup _{a \in P}(X-a)$
, it follows that there exists
 $a \in P$
such that
$a \in P$
such that
 $y \in X-a$
. Then,
$y \in X-a$
. Then,
 $-a \in Q_y$
. Thus,
$-a \in Q_y$
. Thus,
 $Q_y$
is non-empty.
$Q_y$
is non-empty. -
(2) As the intersection
 $\displaystyle \bigcap _{a \in P}(X+a)=\emptyset$
, it follows that there exists
$\displaystyle \bigcap _{a \in P}(X+a)=\emptyset$
, it follows that there exists
 $a \in P$
such that
$a \in P$
such that
 $y \notin X+a$
. Then,
$y \notin X+a$
. Then,
 $a \notin Q_y$
for such an element
$a \notin Q_y$
for such an element
 $a$
. Hence,
$a$
. Hence,
 $Q_y$
is a proper subset of
$Q_y$
is a proper subset of
 $G$
.
$G$
. -
(3) The fact that
 $X+P \subset X$
implies that
$X+P \subset X$
implies that
 $-P+Q_y \subset Q_y$
.
$-P+Q_y \subset Q_y$
.
Proposition 3.5.
Let
![]() $(Y,X)$
be a pure
$(Y,X)$
be a pure
![]() $(G,P)$
-space, and let
$(G,P)$
-space, and let
![]() $m$
be an
$m$
be an
![]() $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
![]() $Y$
. Denote the map
$Y$
. Denote the map
by
![]() $T$
. Assume that
$T$
. Assume that
![]() $T$
is
$T$
is
![]() $1$
-
$1$
-
![]() $1$
. Then, we have the following.
$1$
. Then, we have the following.
-
(1) The map
 $T$
is
$T$
is
 $G$
-equivariant, measurable, and
$G$
-equivariant, measurable, and
 $T^{-1}(X_u)=X$
.
$T^{-1}(X_u)=X$
. -
(2) The push-forward measure
 $T_*m\,:\!=\,m \circ T^{-1}$
is an
$T_*m\,:\!=\,m \circ T^{-1}$
is an
 $e^{-\beta c}$
-conformal measure on the pure
$e^{-\beta c}$
-conformal measure on the pure
 $(G,P)$
-space
$(G,P)$
-space
 $(Y_u,X_u)$
. Moreover,
$(Y_u,X_u)$
. Moreover,
 $(Y,X,m)$
and
$(Y,X,m)$
and
 $(Y_u,X_u,T_*m)$
are metrically isomorphic.
$(Y_u,X_u,T_*m)$
are metrically isomorphic.
Consequently, for
![]() $t \in \{I,II,III\}$
,
$t \in \{I,II,III\}$
,
![]() $(Y,m,G)$
is essentially free, ergodic and is of type
$(Y,m,G)$
is essentially free, ergodic and is of type
![]() $t$
if and only if
$t$
if and only if
![]() $(Y_u,T_*m,G)$
is essentially free, ergodic and is of type
$(Y_u,T_*m,G)$
is essentially free, ergodic and is of type
![]() $t$
.
$t$
.
Proof. Let
![]() $y \in Y$
and
$y \in Y$
and
![]() $s \in G$
be given. Note that for
$s \in G$
be given. Note that for
![]() $t \in G$
,
$t \in G$
,
![]() $t \in Q_{y+s}$
iff
$t \in Q_{y+s}$
iff
![]() $y+s-t \in X$
iff
$y+s-t \in X$
iff
![]() $y-(t-s) \in X$
iff
$y-(t-s) \in X$
iff
![]() $t-s \in Q_y$
iff
$t-s \in Q_y$
iff
![]() $t \in Q_y+s$
. Thus,
$t \in Q_y+s$
. Thus,
![]() $Q_{y+s}=Q_{y}+s$
. This shows that
$Q_{y+s}=Q_{y}+s$
. This shows that
![]() $T$
is
$T$
is
![]() $G$
-equivariant. To show that
$G$
-equivariant. To show that
![]() $T$
is measurable, it suffices to show that for every
$T$
is measurable, it suffices to show that for every
![]() $s \in G$
, the map
$s \in G$
, the map
is measurable. Fix
![]() $s \in G$
. Clearly, for every
$s \in G$
. Clearly, for every
![]() $y \in Y$
,
$y \in Y$
,
Since
![]() $X+s$
is a measurable subset of
$X+s$
is a measurable subset of
![]() $Y$
, it follows that the map
$Y$
, it follows that the map
is measurable. Hence,
![]() $T$
is a measurable map. Note that for
$T$
is a measurable map. Note that for
![]() $y \in Y$
,
$y \in Y$
,
![]() $y \in T^{-1}(X_u)$
if and only if
$y \in T^{-1}(X_u)$
if and only if
![]() $0 \in Q_y$
if and only if
$0 \in Q_y$
if and only if
![]() $y \in X$
. Thus,
$y \in X$
. Thus,
![]() $T^{-1}(X_u)=X$
. This completes the proof of
$T^{-1}(X_u)=X$
. This completes the proof of
![]() $(1)$
.
$(1)$
.
Since
![]() $T^{-1}(X_u)=X$
, and
$T^{-1}(X_u)=X$
, and
![]() $m(X)=1$
, it follows that
$m(X)=1$
, it follows that
![]() $T_*m(X_u)=1$
. Let
$T_*m(X_u)=1$
. Let
![]() $E$
be a Borel subset of
$E$
be a Borel subset of
![]() $Y_u$
, and let
$Y_u$
, and let
![]() $s \in G$
be given. Thanks to the equivariance of
$s \in G$
be given. Thanks to the equivariance of
![]() $T$
, we have
$T$
, we have
![]() $T^{-1}(E+s)=T^{-1}(E)+s$
. Since
$T^{-1}(E+s)=T^{-1}(E)+s$
. Since
![]() $m$
is
$m$
is
![]() $e^{-\beta c}$
-conformal,
$e^{-\beta c}$
-conformal,
Therefore,
![]() $T_*m$
is an
$T_*m$
is an
![]() $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
![]() $(Y_u,X_u)$
.
$(Y_u,X_u)$
.
Set
![]() $Y^{\prime}_u\,:\!=\,T(Y)$
, and
$Y^{\prime}_u\,:\!=\,T(Y)$
, and
![]() $X^{\prime}_u\,:\!=\,Y^{\prime}_u\cap X_u$
. Since
$X^{\prime}_u\,:\!=\,Y^{\prime}_u\cap X_u$
. Since
![]() $T$
is one-one, and
$T$
is one-one, and
![]() $Y$
and
$Y$
and
![]() $Y_{u}$
are standard Borel spaces,
$Y_{u}$
are standard Borel spaces,
![]() $Y^{\prime}_u$
is a Borel subset of
$Y^{\prime}_u$
is a Borel subset of
![]() $Y_u$
, and the map
$Y_u$
, and the map
![]() $T\,:\,Y \to Y^{\prime}_u$
is a Borel isomorphism. Also,
$T\,:\,Y \to Y^{\prime}_u$
is a Borel isomorphism. Also,
![]() $T(X)=X^{\prime}_u$
. Observe that
$T(X)=X^{\prime}_u$
. Observe that
![]() $T_*m$
is supported on
$T_*m$
is supported on
![]() $Y^{\prime}_u$
. Thus,
$Y^{\prime}_u$
. Thus,
![]() $T$
is an isomorphism between
$T$
is an isomorphism between
![]() $(Y,X,m)$
and
$(Y,X,m)$
and
![]() $(Y^{\prime}_u,X^{\prime}_u,T_*m)$
. Since
$(Y^{\prime}_u,X^{\prime}_u,T_*m)$
. Since
![]() $Y^{\prime}_{u}$
is a co-null
$Y^{\prime}_{u}$
is a co-null
![]() $G$
-invariant subset of
$G$
-invariant subset of
![]() $Y_u$
,
$Y_u$
,
![]() $(Y^{\prime}_{u},X^{\prime}_{u},T_*m)$
and
$(Y^{\prime}_{u},X^{\prime}_{u},T_*m)$
and
![]() $(Y_u,X_u,T_*m)$
are metrically isomorphic. Hence,
$(Y_u,X_u,T_*m)$
are metrically isomorphic. Hence,
![]() $(Y,X,m)$
and
$(Y,X,m)$
and
![]() $(Y_u,X_u,T_*m)$
are metrically isomorphic. This completes the proof of
$(Y_u,X_u,T_*m)$
are metrically isomorphic. This completes the proof of
![]() $(2)$
.
$(2)$
.
The final assertion is clear as metric isomorphism preserves essential freeness, ergodicity and type.
4. The case
 $P=\mathbb{N}^{2}$
$P=\mathbb{N}^{2}$
In this section, we discuss the structure of KMS states on
![]() $C_{c}^{*}(P)$
for
$C_{c}^{*}(P)$
for
![]() $\sigma ^{c}$
when
$\sigma ^{c}$
when
![]() $P=\mathbb{N}^2$
. Let us fix notation. Set
$P=\mathbb{N}^2$
. Let us fix notation. Set
![]() $e_1\,:\!=\,(1,0)$
and
$e_1\,:\!=\,(1,0)$
and
![]() $e_2\,:\!=\,(0,1)$
. Define
$e_2\,:\!=\,(0,1)$
. Define
![]() $v_1\,:\!=\,e_1$
and
$v_1\,:\!=\,e_1$
and
![]() $v_2\,:\!=\,e_1+e_2$
. Let
$v_2\,:\!=\,e_1+e_2$
. Let
![]() $c\,:\,\mathbb{Z}^2 \to \mathbb{R}$
be a non-zero homomorphism. We normalise and assume that
$c\,:\,\mathbb{Z}^2 \to \mathbb{R}$
be a non-zero homomorphism. We normalise and assume that
![]() $c(e_1)=1$
and
$c(e_1)=1$
and
![]() $c(e_2)=\theta$
. This does not lead to any loss of generality. In what follows, the homomorphism
$c(e_2)=\theta$
. This does not lead to any loss of generality. In what follows, the homomorphism
![]() $c$
will be fixed.
$c$
will be fixed.
First, we obtain a reasonable parametrisation of
![]() $Y_u$
. Let
$Y_u$
. Let
![]() $\Omega \,:\!=\{0,1\}^{\mathbb{Z}}$
be the Cantor space. Consider the Bernoulli shift
$\Omega \,:\!=\{0,1\}^{\mathbb{Z}}$
be the Cantor space. Consider the Bernoulli shift
![]() $\tau \,:\,\Omega \to \Omega$
defined by
$\tau \,:\,\Omega \to \Omega$
defined by
Define a
![]() $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
![]() $\Omega \times \mathbb{Z}$
by the following formulae.
$\Omega \times \mathbb{Z}$
by the following formulae.
For
![]() $(x,t)\in \Omega \times \mathbb{Z}$
, define
$(x,t)\in \Omega \times \mathbb{Z}$
, define
![]() $a(x,t)\,:\!=\,a=(a_m)_{m\in \mathbb{Z}}$
as follows.
$a(x,t)\,:\!=\,a=(a_m)_{m\in \mathbb{Z}}$
as follows.
 \begin{equation} a(x,t)_m\,:\!=\,a_m=\begin{cases} t-(x_0+x_1+\cdots +x_{m-1}) & \mbox{if} m\gt 0, \\ t & \mbox{if $m=0$}, \\ t+(x_{-1}+x_{-2}+\cdots +x_{m}) & \mbox{if} m\lt 0. \end{cases} \end{equation}
\begin{equation} a(x,t)_m\,:\!=\,a_m=\begin{cases} t-(x_0+x_1+\cdots +x_{m-1}) & \mbox{if} m\gt 0, \\ t & \mbox{if $m=0$}, \\ t+(x_{-1}+x_{-2}+\cdots +x_{m}) & \mbox{if} m\lt 0. \end{cases} \end{equation}
Note that
![]() $a_m-a_{m+1}=x_m$
. Let
$a_m-a_{m+1}=x_m$
. Let
![]() $A(x,t)$
be defined by
$A(x,t)$
be defined by
It is not difficult to verify that
![]() $-e_1+A(x,t) \subset A(x,t)$
and
$-e_1+A(x,t) \subset A(x,t)$
and
![]() $-e_2+A(x,t) \subset A(x,t)$
. In other words,
$-e_2+A(x,t) \subset A(x,t)$
. In other words,
![]() $A(x,t) \in Y_u$
for every
$A(x,t) \in Y_u$
for every
![]() $(x,t) \in \Omega \times \mathbb{Z}$
.
$(x,t) \in \Omega \times \mathbb{Z}$
.
Lemma 4.1.
Let
![]() $(x^{(k)},t^{(k)})$
be a sequence in
$(x^{(k)},t^{(k)})$
be a sequence in
![]() $\Omega \times \mathbb{Z}$
, and let
$\Omega \times \mathbb{Z}$
, and let
![]() $(x,t) \in \Omega \times \mathbb{Z}$
. For
$(x,t) \in \Omega \times \mathbb{Z}$
. For
![]() $m \in \mathbb{Z}$
and for
$m \in \mathbb{Z}$
and for
![]() $k \in \mathbb{N}$
, set
$k \in \mathbb{N}$
, set
![]() $a^{(k)}_m\,:\!=\,a(x^{(k)},t^{(k)})_m$
and
$a^{(k)}_m\,:\!=\,a(x^{(k)},t^{(k)})_m$
and
![]() $a_m\,:\!=\,a(x,t)_m$
. Let
$a_m\,:\!=\,a(x,t)_m$
. Let
![]() $A_k\,:\!=\,A(x^{(k)},t^{(k)})$
, and
$A_k\,:\!=\,A(x^{(k)},t^{(k)})$
, and
![]() $A\,:\!=\,A(x,t)$
. Then, the following are equivalent.
$A\,:\!=\,A(x,t)$
. Then, the following are equivalent.
-
(1) As
 $k \to \infty$
,
$k \to \infty$
,
 $(x^{(k)},t^{(k)}) \to (x,t)$
.
$(x^{(k)},t^{(k)}) \to (x,t)$
. -
(2) For every
 $m$
,
$m$
,
 $a^{(k)}_m \to a_m$
as
$a^{(k)}_m \to a_m$
as
 $k \to \infty$
.
$k \to \infty$
. -
(3) The sequence
 $(A_k)_k \to A$
.
$(A_k)_k \to A$
.
Proof. It is clear from equation (4.5) that
![]() $(1)$
and
$(1)$
and
![]() $(2)$
are equivalent. Suppose that
$(2)$
are equivalent. Suppose that
![]() $(2)$
holds. Let
$(2)$
holds. Let
![]() $m,n \in \mathbb{Z}$
. Suppose
$m,n \in \mathbb{Z}$
. Suppose
![]() $1_A(mv_1+nv_2)=1$
. Then,
$1_A(mv_1+nv_2)=1$
. Then,
![]() $n \leq a_m$
. Since
$n \leq a_m$
. Since
![]() $a_m^{(k)} \to a_m$
, it follows that eventually
$a_m^{(k)} \to a_m$
, it follows that eventually
![]() $a_{m}^{(k)}=a_m$
. Thus, for large
$a_{m}^{(k)}=a_m$
. Thus, for large
![]() $k$
,
$k$
,
![]() $n \leq a_{m}^{(k)}$
, i.e. for large
$n \leq a_{m}^{(k)}$
, i.e. for large
![]() $k$
,
$k$
,
![]() $1_{A_k}(mv_1+nv_2)=1$
. If
$1_{A_k}(mv_1+nv_2)=1$
. If
![]() $1_{A}(mv_1+nv_2)=0$
. By the same argument, we can conclude that for large
$1_{A}(mv_1+nv_2)=0$
. By the same argument, we can conclude that for large
![]() $k$
,
$k$
,
![]() $1_{A_k}(mv_1+nv_2)=0$
. Thus,
$1_{A_k}(mv_1+nv_2)=0$
. Thus,
![]() $1_{A_k}(mv_1+nv_2) \to 1_{A}(mv_1+nv_2)$
for every
$1_{A_k}(mv_1+nv_2) \to 1_{A}(mv_1+nv_2)$
for every
![]() $m,n \in \mathbb{Z}$
. Hence,
$m,n \in \mathbb{Z}$
. Hence,
![]() $(A_k)_k \to A$
. This completes the proof of the implication
$(A_k)_k \to A$
. This completes the proof of the implication
![]() $(2) \implies (3)$
.
$(2) \implies (3)$
.
Assume that
![]() $(3)$
holds. Let
$(3)$
holds. Let
![]() $m \in \mathbb{Z}$
be given. Note that
$m \in \mathbb{Z}$
be given. Note that
![]() $1_A(mv_1+a_mv_2)=1$
. Since
$1_A(mv_1+a_mv_2)=1$
. Since
![]() $(A_k)_k \to A$
, it follows that for large
$(A_k)_k \to A$
, it follows that for large
![]() $k$
,
$k$
,
![]() $1_{A_k}(mv_1+a_mv_2)=1$
. In other words, for large
$1_{A_k}(mv_1+a_mv_2)=1$
. In other words, for large
![]() $k$
,
$k$
,
![]() $a_m \leq a_{m}^{(k)}$
. Also, note that
$a_m \leq a_{m}^{(k)}$
. Also, note that
![]() $1_{A}(mv_1+(a_m+1)v_2)=0$
. Since
$1_{A}(mv_1+(a_m+1)v_2)=0$
. Since
![]() $(A_k)_k \to A$
, it follows that for large
$(A_k)_k \to A$
, it follows that for large
![]() $k$
,
$k$
,
![]() $1_{A_k}(mv_1+(a_m+1)v_2)=0$
, i.e. for large
$1_{A_k}(mv_1+(a_m+1)v_2)=0$
, i.e. for large
![]() $k$
,
$k$
,
![]() $a_m+1\gt a_{m}^{(k)}$
. Thus, eventually
$a_m+1\gt a_{m}^{(k)}$
. Thus, eventually
![]() $a_m\leq a_{m}^{(k)}\lt a_m+1$
, i.e. eventually
$a_m\leq a_{m}^{(k)}\lt a_m+1$
, i.e. eventually
![]() $a_{m}^{(k)}=a_m$
. Hence, for every
$a_{m}^{(k)}=a_m$
. Hence, for every
![]() $m \in \mathbb{Z}$
,
$m \in \mathbb{Z}$
,
![]() $a_{m}^{(k)} \to a_m$
as
$a_{m}^{(k)} \to a_m$
as
![]() $k \to \infty$
. This completes the proof of the implication
$k \to \infty$
. This completes the proof of the implication
![]() $(3) \implies (2)$
.
$(3) \implies (2)$
.
Proposition 4.1. With the foregoing notation, the map
is a
![]() $\mathbb{Z}^2$
-equivariant homeomorphism.
$\mathbb{Z}^2$
-equivariant homeomorphism.
Proof. First, we check that the prescribed map is
![]() $\mathbb{Z}^2$
-equivariant. Let
$\mathbb{Z}^2$
-equivariant. Let
![]() $(x,t) \in \Omega \times \mathbb{Z}$
be given. By definition, for
$(x,t) \in \Omega \times \mathbb{Z}$
be given. By definition, for
![]() $m,n \in \mathbb{Z}$
,
$m,n \in \mathbb{Z}$
,
![]() $mv_1+nv_2 \in A(x,t)+v_1$
if and only if
$mv_1+nv_2 \in A(x,t)+v_1$
if and only if
![]() $n \leq a(x,t)_{m-1}$
. Thus,
$n \leq a(x,t)_{m-1}$
. Thus,
From equation (4.5), it is clear that
![]() $a(\tau (x),t+x_{-1})_m=a(x,t)_{m-1}$
. Thus,
$a(\tau (x),t+x_{-1})_m=a(x,t)_{m-1}$
. Thus,
![]() $A(x,t)+v_1=A(\tau (x),t+x_{-1})$
.
$A(x,t)+v_1=A(\tau (x),t+x_{-1})$
.
For
![]() $m,n \in \mathbb{Z}$
,
$m,n \in \mathbb{Z}$
,
![]() $mv_1+nv_2 \in A(x,t)+v_2$
if and only if
$mv_1+nv_2 \in A(x,t)+v_2$
if and only if
![]() $n \leq a(x,t)_m+1$
. Thus,
$n \leq a(x,t)_m+1$
. Thus,
From equation (4.5), it is clear that
![]() $a(x,t)_m+1=a(x,t+1)_m$
. Therefore,
$a(x,t)_m+1=a(x,t+1)_m$
. Therefore,
![]() $A(x,t)+v_2=A(x,t+1)$
. As a consequence,
$A(x,t)+v_2=A(x,t+1)$
. As a consequence,
![]() $A(x,t)+v_1=A(\tau (x),t+x_{-1})$
and
$A(x,t)+v_1=A(\tau (x),t+x_{-1})$
and
![]() $A(x,t)+v_2=A(x,t+1)$
. Since
$A(x,t)+v_2=A(x,t+1)$
. Since
![]() $\{v_1,v_2\}$
is a
$\{v_1,v_2\}$
is a
![]() $\mathbb{Z}$
-basis for
$\mathbb{Z}$
-basis for
![]() $\mathbb{Z}^2$
, it follows that the map
$\mathbb{Z}^2$
, it follows that the map
is
![]() $\mathbb{Z}^2$
-equivariant.
$\mathbb{Z}^2$
-equivariant.
Let
![]() $(x,t), (y,s) \in \Omega \times \mathbb{Z}$
be given. Suppose
$(x,t), (y,s) \in \Omega \times \mathbb{Z}$
be given. Suppose
![]() $A(x,t)=A(y,s)$
. Then,
$A(x,t)=A(y,s)$
. Then,
The above equality clearly implies that
![]() $a(x,t)_m=a(y,s)_m$
for every
$a(x,t)_m=a(y,s)_m$
for every
![]() $m$
. It follows from equation (4.5) that
$m$
. It follows from equation (4.5) that
![]() $x=y$
and
$x=y$
and
![]() $t=s$
. Thus, the map
$t=s$
. Thus, the map
![]() $\Omega \times \mathbb{Z} \ni (x,t) \mapsto A(x,t) \in Y_u$
is
$\Omega \times \mathbb{Z} \ni (x,t) \mapsto A(x,t) \in Y_u$
is
![]() $1$
-
$1$
-
![]() $1$
.
$1$
.
We now show that it is onto. Let
![]() $A \in Y_u$
be given. By translating, if necessary, we can assume that
$A \in Y_u$
be given. By translating, if necessary, we can assume that
![]() $0 \in A$
which implies that
$0 \in A$
which implies that
![]() $-\mathbb{N}^2 \subset A$
.
$-\mathbb{N}^2 \subset A$
.
Let
![]() $m \in \mathbb{Z}$
be given. We claim that the set
$m \in \mathbb{Z}$
be given. We claim that the set
![]() $\{k \in \mathbb{Z}\,:\, mv_1+kv_2\in A\}$
is non-empty and bounded above. Choose
$\{k \in \mathbb{Z}\,:\, mv_1+kv_2\in A\}$
is non-empty and bounded above. Choose
![]() $k_0\lt 0$
such that
$k_0\lt 0$
such that
![]() $m+k_0\lt 0$
. Then, we have
$m+k_0\lt 0$
. Then, we have
Hence, the set
![]() $\{k \in \mathbb{Z}\,:\, mv_1+kv_2\in A\}$
is non-empty. Suppose
$\{k \in \mathbb{Z}\,:\, mv_1+kv_2\in A\}$
is non-empty. Suppose
![]() $\{k \in \mathbb{Z}\,:\, mv_1+kv_2\in A\}$
is not bounded above. Then, for every
$\{k \in \mathbb{Z}\,:\, mv_1+kv_2\in A\}$
is not bounded above. Then, for every
![]() $k\in \mathbb{N}$
, there exists a natural number
$k\in \mathbb{N}$
, there exists a natural number
![]() $n_k\geq k$
such that
$n_k\geq k$
such that
![]() $mv_1+n_kv_2\in A$
. Since
$mv_1+n_kv_2\in A$
. Since
![]() $A-\mathbb{N}^2 \subset A$
, we have
$A-\mathbb{N}^2 \subset A$
, we have
![]() $mv_1+(n_k-\ell )v_2\in A$
for every
$mv_1+(n_k-\ell )v_2\in A$
for every
![]() $\ell \in \mathbb{N}$
and for every
$\ell \in \mathbb{N}$
and for every
![]() $k \in \mathbb{N}$
. This means that, for every
$k \in \mathbb{N}$
. This means that, for every
![]() $n \in \mathbb{Z}$
,
$n \in \mathbb{Z}$
,
![]() $mv_1+nv_2\in A$
. Again for any
$mv_1+nv_2\in A$
. Again for any
![]() $k,\ell \in \mathbb{N}$
and
$k,\ell \in \mathbb{N}$
and
![]() $n\in \mathbb{Z}$
, we have
$n\in \mathbb{Z}$
, we have
This implies that
![]() $A=\mathbb{Z}^2$
which contradicts the fact that
$A=\mathbb{Z}^2$
which contradicts the fact that
![]() $A \in Y_u$
. Hence,
$A \in Y_u$
. Hence,
![]() $\{k \in \mathbb{Z}\,:\, mv_1+kv_2\in A\}$
is bounded above. The proof of the claim is now complete.
$\{k \in \mathbb{Z}\,:\, mv_1+kv_2\in A\}$
is bounded above. The proof of the claim is now complete.
For
![]() $m\in \mathbb{Z}$
, define
$m\in \mathbb{Z}$
, define
Then,
![]() $a_m$
is an integer. Let
$a_m$
is an integer. Let
![]() $A_a=\{mv_1+nv_2\,:\, n \leq a_m\}$
. We claim that
$A_a=\{mv_1+nv_2\,:\, n \leq a_m\}$
. We claim that
![]() $A=A_a$
and for every
$A=A_a$
and for every
![]() $m \in \mathbb{Z}$
,
$m \in \mathbb{Z}$
,
![]() $0 \leq a_{m}-a_{m+1} \leq 1$
.
$0 \leq a_{m}-a_{m+1} \leq 1$
.
Clearly,
![]() $A \subset A_a$
. Suppose
$A \subset A_a$
. Suppose
![]() $mv_1+nv_2\in A_a$
. By the definition of
$mv_1+nv_2\in A_a$
. By the definition of
![]() $a_m$
,
$a_m$
,
![]() $mv_1+a_mv_2\in A$
. Note that
$mv_1+a_mv_2\in A$
. Note that
Hence,
![]() $A_a\subseteq A$
. Therefore,
$A_a\subseteq A$
. Therefore,
![]() $A=A_a$
.
$A=A_a$
.
Let
![]() $mv_1+nv_2\in A_a$
be given. Since
$mv_1+nv_2\in A_a$
be given. Since
![]() $A_a-\mathbb{N}^2 \subset A_{a}$
, we have
$A_a-\mathbb{N}^2 \subset A_{a}$
, we have
![]() $mv_1+nv_2-ke_1-\ell e_2\in A_a$
, for every
$mv_1+nv_2-ke_1-\ell e_2\in A_a$
, for every
![]() $k,l\geq 0$
. Therefore, whenever
$k,l\geq 0$
. Therefore, whenever
![]() $mv_1+nv_2\in A_a$
, we have
$mv_1+nv_2\in A_a$
, we have
![]() $a_{m-k+\ell }\geq n-\ell$
. In particular, when
$a_{m-k+\ell }\geq n-\ell$
. In particular, when
![]() $n=a_m,k=1$
and
$n=a_m,k=1$
and
![]() $\ell =0$
, we have
$\ell =0$
, we have
![]() $a_{m-1}\geq a_m$
, and when
$a_{m-1}\geq a_m$
, and when
![]() $n=a_m,k=0$
and
$n=a_m,k=0$
and
![]() $\ell =1$
, we have
$\ell =1$
, we have
![]() $a_{m+1}\geq a_m-1$
. Thus,
$a_{m+1}\geq a_m-1$
. Thus,
![]() $0\leq a_m-a_{m+1}\leq 1$
for every
$0\leq a_m-a_{m+1}\leq 1$
for every
![]() $m\in \mathbb{Z}$
. The proof of the claim is now over.
$m\in \mathbb{Z}$
. The proof of the claim is now over.
Define
![]() $x \in \Omega$
by setting
$x \in \Omega$
by setting
![]() $x_m\,:\!=\,a_{m}-a_{m+1}$
and let
$x_m\,:\!=\,a_{m}-a_{m+1}$
and let
![]() $t\,:\!=\,a_0$
. Clearly, for every
$t\,:\!=\,a_0$
. Clearly, for every
![]() $m$
,
$m$
,
![]() $a_m=a(x,t)_m$
. Therefore,
$a_m=a(x,t)_m$
. Therefore,
![]() $A_a=A(x,t)$
. Consequently,
$A_a=A(x,t)$
. Consequently,
![]() $A=A(x,t)$
. This proves the surjectivity of the map
$A=A(x,t)$
. This proves the surjectivity of the map
The fact that the map
![]() $\Omega \times \mathbb{Z} \ni (x,t) \to A(x,t) \in Y_u$
is a homeomorphism follows from Lemma 4.1. This completes the proof.
$\Omega \times \mathbb{Z} \ni (x,t) \to A(x,t) \in Y_u$
is a homeomorphism follows from Lemma 4.1. This completes the proof.
Remark 4.1.
For
![]() $A \in Y_u$
, let
$A \in Y_u$
, let
![]() $G_A$
be the stabiliser of
$G_A$
be the stabiliser of
![]() $A$
, i.e.
$A$
, i.e.
Let
![]() $(x,t) \in \Omega \times \mathbb{Z}$
, and let
$(x,t) \in \Omega \times \mathbb{Z}$
, and let
![]() $A\,:\!=\,A(x,t) \in Y_u$
be the set defined as in Proposition 4.1
. Then,
$A\,:\!=\,A(x,t) \in Y_u$
be the set defined as in Proposition 4.1
. Then,
![]() $G_A \neq 0$
if and only if
$G_A \neq 0$
if and only if
![]() $x$
is a periodic point, i.e. there exists
$x$
is a periodic point, i.e. there exists
![]() $p\gt 0$
such that
$p\gt 0$
such that
![]() $x_{m+p}=x_m$
for all
$x_{m+p}=x_m$
for all
![]() $m \in \mathbb{Z}$
. Moreover, there are only countably many periodic points in
$m \in \mathbb{Z}$
. Moreover, there are only countably many periodic points in
![]() $\Omega$
. This has the consequence that the groupoid
$\Omega$
. This has the consequence that the groupoid
![]() $\mathcal{G}\,:\!=\,\overline{X}_u \rtimes \mathbb{N}^2$
(and also the transformation groupoid
$\mathcal{G}\,:\!=\,\overline{X}_u \rtimes \mathbb{N}^2$
(and also the transformation groupoid
![]() $\overline{Y}_u \rtimes \mathbb{Z}^2$
) has only countably many points in its unit space whose stabiliser is non-trivial.
$\overline{Y}_u \rtimes \mathbb{Z}^2$
) has only countably many points in its unit space whose stabiliser is non-trivial.
We identify
![]() $Y_u$
with
$Y_u$
with
![]() $\Omega \times \mathbb{Z}$
via the map prescribed in Proposition 4.1. After an abuse of notation, we write
$\Omega \times \mathbb{Z}$
via the map prescribed in Proposition 4.1. After an abuse of notation, we write
![]() $Y_u=\Omega \times \mathbb{Z}$
. Then,
$Y_u=\Omega \times \mathbb{Z}$
. Then,
![]() $X_u=\Omega \times \mathbb{N}$
. Let
$X_u=\Omega \times \mathbb{N}$
. Let
![]() $m$
be a probability measure on
$m$
be a probability measure on
![]() $\Omega$
. Define a measure
$\Omega$
. Define a measure
![]() $\overline{m}$
on
$\overline{m}$
on
![]() $\Omega \times \mathbb{Z}$
by setting
$\Omega \times \mathbb{Z}$
by setting
for a measurable subset
![]() $E \subset \Omega$
.
$E \subset \Omega$
.
Define
![]() $\chi :\Omega \to \mathbb{R}$
by
$\chi :\Omega \to \mathbb{R}$
by
 \begin{equation*} \chi (x)\,:\!=\,\begin {cases} 1 & \mbox { if } x_{-1} =0,\\ - \theta & \mbox { if } x_{-1}=1. \end {cases} \end{equation*}
\begin{equation*} \chi (x)\,:\!=\,\begin {cases} 1 & \mbox { if } x_{-1} =0,\\ - \theta & \mbox { if } x_{-1}=1. \end {cases} \end{equation*}
Let
![]() $\beta$
be a real number, and let
$\beta$
be a real number, and let
![]() $m$
be a probability measure on
$m$
be a probability measure on
![]() $\Omega$
. The probability measure
$\Omega$
. The probability measure
![]() $m$
is said to be
$m$
is said to be
![]() $e^{-\beta \chi }$
-conformal for the Bernoulli shift
$e^{-\beta \chi }$
-conformal for the Bernoulli shift
![]() $\tau$
if for every Borel subset
$\tau$
if for every Borel subset
![]() $E \subset \Omega$
,
$E \subset \Omega$
,
Proposition 4.2.
Suppose
![]() $\beta (\theta +1)\gt 0$
. Then, the map
$\beta (\theta +1)\gt 0$
. Then, the map
![]() $m \to \overline{m}$
defines a bijection between the set of
$m \to \overline{m}$
defines a bijection between the set of
![]() $e^{-\beta \chi }$
-conformal measures on
$e^{-\beta \chi }$
-conformal measures on
![]() $\Omega$
and the set of
$\Omega$
and the set of
![]() $e^{-\beta c}$
-conformal measures on the
$e^{-\beta c}$
-conformal measures on the
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-space
$(\mathbb{Z}^2,\mathbb{N}^2)$
-space
![]() $(Y_u,X_u)=(\Omega \times \mathbb{Z},\Omega \times \mathbb{N})$
.
$(Y_u,X_u)=(\Omega \times \mathbb{Z},\Omega \times \mathbb{N})$
.
Proof. The proof is not difficult. We have included some details for completeness. Suppose that
![]() $m$
is an
$m$
is an
![]() $e^{-\beta \chi }$
-conformal measure on
$e^{-\beta \chi }$
-conformal measure on
![]() $\Omega$
. Clearly,
$\Omega$
. Clearly,
![]() $\overline{m}(X_u)=1$
. Let
$\overline{m}(X_u)=1$
. Let
![]() $F \subset \Omega$
be a Borel subset and let
$F \subset \Omega$
be a Borel subset and let
![]() $n \in \mathbb{Z}$
be given. It suffices to show that
$n \in \mathbb{Z}$
be given. It suffices to show that
Define
![]() $F_0\,:\!=\{x \in F\,:\, x_{-1}=0\}$
and
$F_0\,:\!=\{x \in F\,:\, x_{-1}=0\}$
and
![]() $F_1\,:\!=\{x \in F\,:\, x_{-1}=1\}$
. Calculate as follows to observe that
$F_1\,:\!=\{x \in F\,:\, x_{-1}=1\}$
. Calculate as follows to observe that
 \begin{align*} \frac{1}{1-e^{-\beta (1+\theta )}}\overline{m}((F\times \{n\})+v_1) &=\frac{1}{1-e^{-\beta (1+\theta )}}\Big (\overline{m}(\tau (F_0)\times \{n\})+\overline{m}(\tau (F_1)\times \{n+1\})\Big )\\ &=e^{-\beta n(1+\theta )} m(\tau (F_0))+ e^{-\beta (n+1)(1+\theta )}m(\tau (F_1))\\ &=e^{-\beta n(1+\theta )} e^{-\beta } m(F_0)+ e^{-\beta (n+1)(1+\theta )} e^{\beta \theta }m(F_1)\\ &=e^{-\beta n(1+\theta )} e^{-\beta }\big (m(F_0)+ m(F_1)\big )\\ &=e^{-\beta }\frac{1}{1-e^{-\beta (1+\theta )}}\overline{m}(F\times \{n\}). \end{align*}
\begin{align*} \frac{1}{1-e^{-\beta (1+\theta )}}\overline{m}((F\times \{n\})+v_1) &=\frac{1}{1-e^{-\beta (1+\theta )}}\Big (\overline{m}(\tau (F_0)\times \{n\})+\overline{m}(\tau (F_1)\times \{n+1\})\Big )\\ &=e^{-\beta n(1+\theta )} m(\tau (F_0))+ e^{-\beta (n+1)(1+\theta )}m(\tau (F_1))\\ &=e^{-\beta n(1+\theta )} e^{-\beta } m(F_0)+ e^{-\beta (n+1)(1+\theta )} e^{\beta \theta }m(F_1)\\ &=e^{-\beta n(1+\theta )} e^{-\beta }\big (m(F_0)+ m(F_1)\big )\\ &=e^{-\beta }\frac{1}{1-e^{-\beta (1+\theta )}}\overline{m}(F\times \{n\}). \end{align*}
Similarly, we can prove that
![]() $ \overline{m}((F\times \{n\})+v_2)=e^{-\beta (1+\theta )}\overline{m}(F\times \{n\})$
. Hence,
$ \overline{m}((F\times \{n\})+v_2)=e^{-\beta (1+\theta )}\overline{m}(F\times \{n\})$
. Hence,
![]() $\overline{m}$
is an
$\overline{m}$
is an
![]() $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
![]() $(\Omega \times \mathbb{Z},\Omega \times \mathbb{N})$
.
$(\Omega \times \mathbb{Z},\Omega \times \mathbb{N})$
.
Conversely, suppose
![]() $\mu$
is an
$\mu$
is an
![]() $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
![]() $(Y_u,X_u)$
. Define a measure
$(Y_u,X_u)$
. Define a measure
![]() $m$
on
$m$
on
![]() $\Omega$
by
$\Omega$
by
for a Borel subset
![]() $E \subset \Omega$
. Note that for a Borel set
$E \subset \Omega$
. Note that for a Borel set
![]() $E \subset \Omega$
,
$E \subset \Omega$
,
![]() $E \times \{n\}=(E \times \{0\})+nv_2$
. Using the conformality condition on
$E \times \{n\}=(E \times \{0\})+nv_2$
. Using the conformality condition on
![]() $\mu$
and the fact that
$\mu$
and the fact that
![]() $E \times \{n\}=(E \times \{0\})+nv_2$
, it is routine to see that
$E \times \{n\}=(E \times \{0\})+nv_2$
, it is routine to see that
![]() $\overline{m}=\mu$
.
$\overline{m}=\mu$
.
Let
![]() $F \subset \Omega$
be measurable. Set
$F \subset \Omega$
be measurable. Set
![]() $F_0\,:\!=\{x\in F\,:\, x_{-1}=0\}$
and
$F_0\,:\!=\{x\in F\,:\, x_{-1}=0\}$
and
![]() $F_1\,:\!=\{x\in F\,:\, x_{-1}=1\}$
. Thanks, to the conformality condition on
$F_1\,:\!=\{x\in F\,:\, x_{-1}=1\}$
. Thanks, to the conformality condition on
![]() $\mu$
and the calculation done earlier, it follows that the equality
$\mu$
and the calculation done earlier, it follows that the equality
is equivalent to the equality
In other words, for every Borel subset
![]() $F \subset \Omega$
,
$F \subset \Omega$
,
Hence,
![]() $\frac{d(m\circ \tau )}{dm}=e^{-\beta \chi }$
, i.e.
$\frac{d(m\circ \tau )}{dm}=e^{-\beta \chi }$
, i.e.
![]() $m$
is
$m$
is
![]() $e^{-\beta \chi }$
-conformal. The fact that the map
$e^{-\beta \chi }$
-conformal. The fact that the map
![]() $m \to \overline{m}$
is a bijection is clear.
$m \to \overline{m}$
is a bijection is clear.
Remark 4.2.
Note that for the existence of an
![]() $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
![]() $(Y_u,X_u)$
, it is necessary that
$(Y_u,X_u)$
, it is necessary that
![]() $\beta (1+\theta )\gt 0$
. This is because, if
$\beta (1+\theta )\gt 0$
. This is because, if
![]() $\overline{m}$
is an
$\overline{m}$
is an
![]() $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
![]() $Y_u$
, then
$Y_u$
, then
Hence, the condition
![]() $\beta (1+\theta )\gt 0$
is necessary.
$\beta (1+\theta )\gt 0$
is necessary.
The bijection
![]() $m \to \overline{m}$
of Proposition 4.2 preserves essential freeness, ergodicity and type. Thus,
$m \to \overline{m}$
of Proposition 4.2 preserves essential freeness, ergodicity and type. Thus,
![]() $(\Omega,\tau,m)$
is essentially free if and only if
$(\Omega,\tau,m)$
is essentially free if and only if
![]() $(Y_u,\mathbb{Z}^2,\overline{m})$
is essentially free. Similarly,
$(Y_u,\mathbb{Z}^2,\overline{m})$
is essentially free. Similarly,
![]() $(\Omega,\tau,m)$
is ergodic and is of type
$(\Omega,\tau,m)$
is ergodic and is of type
![]() $t$
if and only if
$t$
if and only if
![]() $(Y_u,\mathbb{Z}^2,\overline{m})$
is ergodic and is of type
$(Y_u,\mathbb{Z}^2,\overline{m})$
is ergodic and is of type
![]() $t$
. Here,
$t$
. Here,
![]() $t \in \{I,II,III\}$
.
$t \in \{I,II,III\}$
.
We are now in a position to determine the values of
![]() $\beta$
and
$\beta$
and
![]() $\theta$
for which there is a
$\theta$
for which there is a
![]() $\beta$
-KMS state on
$\beta$
-KMS state on
![]() $C_{c}^{*}(\mathbb{N}^2)$
for
$C_{c}^{*}(\mathbb{N}^2)$
for
![]() $\sigma ^{c}\,:\!=\{\sigma _t\}_{t \in \mathbb{R}}$
. Recall that the flow
$\sigma ^{c}\,:\!=\{\sigma _t\}_{t \in \mathbb{R}}$
. Recall that the flow
![]() $\sigma ^{c}\,:\!=\{\sigma _t\}_{t \in \mathbb{R}}$
on
$\sigma ^{c}\,:\!=\{\sigma _t\}_{t \in \mathbb{R}}$
on
![]() $C_{c}^{*}(\mathbb{N}^2)$
is defined by
$C_{c}^{*}(\mathbb{N}^2)$
is defined by
Proposition 4.3.
Suppose
![]() $\beta$
is a non-zero real number. The following are equivalent.
$\beta$
is a non-zero real number. The following are equivalent.
-
(1) There is a
 $\beta$
-KMS state on
$\beta$
-KMS state on
 $C_{c}^{*}(\mathbb{N}^2)$
for
$C_{c}^{*}(\mathbb{N}^2)$
for
 $\sigma ^c$
.
$\sigma ^c$
. -
(2) There is an
 $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
 $(Y_u,X_u)$
.
$(Y_u,X_u)$
. -
(3) There is an
 $e^{-\beta \chi }$
-conformal measure on
$e^{-\beta \chi }$
-conformal measure on
 $\Omega$
and
$\Omega$
and
 $\beta (1+\theta )\gt 0$
.
$\beta (1+\theta )\gt 0$
. -
(4)
 $\beta \gt 0$
and
$\beta \gt 0$
and
 $\theta \geq 0$
.
$\theta \geq 0$
.
Proof. The equivalence between
![]() $(1)$
,
$(1)$
,
![]() $(2)$
and
$(2)$
and
![]() $(3)$
follow from Propositions 3.2, 4.2 and Remark 4.2. We prove the equivalence between
$(3)$
follow from Propositions 3.2, 4.2 and Remark 4.2. We prove the equivalence between
![]() $(3)$
and
$(3)$
and
![]() $(4)$
. Assume that
$(4)$
. Assume that
![]() $(3)$
holds. Let
$(3)$
holds. Let
![]() $m$
be an
$m$
be an
![]() $e^{-\beta \chi }$
-conformal measure on
$e^{-\beta \chi }$
-conformal measure on
![]() $\Omega$
. Suppose
$\Omega$
. Suppose
![]() $\theta \lt 0$
. Then, the potential
$\theta \lt 0$
. Then, the potential
![]() $\beta \chi$
is strictly negative or strictly positive. Suppose
$\beta \chi$
is strictly negative or strictly positive. Suppose
![]() $\beta \chi$
is strictly positive. Then, there exists a real number
$\beta \chi$
is strictly positive. Then, there exists a real number
![]() $a\gt 0$
such that
$a\gt 0$
such that
![]() $\beta \chi \gt a$
. Note that
$\beta \chi \gt a$
. Note that
This is a contradiction. A similar contradiction will be met if
![]() $\beta \chi$
is strictly negative. Therefore,
$\beta \chi$
is strictly negative. Therefore,
![]() $\theta \geq 0$
. (A direct application of Theorem 6.2 of [Reference Christensen and Thomsen5] could also have been made instead). The condition
$\theta \geq 0$
. (A direct application of Theorem 6.2 of [Reference Christensen and Thomsen5] could also have been made instead). The condition
![]() $\beta (1+\theta )\gt 0$
implies that
$\beta (1+\theta )\gt 0$
implies that
![]() $\beta \gt 0$
. This completes the proof of
$\beta \gt 0$
. This completes the proof of
![]() $(3) \implies (4)$
.
$(3) \implies (4)$
.
Assume now that
![]() $\beta \gt 0$
and
$\beta \gt 0$
and
![]() $\theta \geq 0$
. Let us fix some notation. For
$\theta \geq 0$
. Let us fix some notation. For
![]() $n \in \mathbb{Z}$
, define
$n \in \mathbb{Z}$
, define
![]() $S_{n}(\chi )$
by setting
$S_{n}(\chi )$
by setting
 \begin{equation*} S_n(\chi )(x)\,:\!=\,\begin {cases} \sum _{j=0}^{n-1} \chi \circ \tau ^{j}(x) & \mbox { if } n \geq 1,\\ 0 & \mbox { if } n=0 \\ - \sum _{j=1}^{|n|}\chi \circ \tau ^{-j}(x) & \mbox { if } n \leq -1. \end {cases} \end{equation*}
\begin{equation*} S_n(\chi )(x)\,:\!=\,\begin {cases} \sum _{j=0}^{n-1} \chi \circ \tau ^{j}(x) & \mbox { if } n \geq 1,\\ 0 & \mbox { if } n=0 \\ - \sum _{j=1}^{|n|}\chi \circ \tau ^{-j}(x) & \mbox { if } n \leq -1. \end {cases} \end{equation*}
Note that if
![]() $n \leq -1$
, then
$n \leq -1$
, then
![]() $S_{n}(\chi )(x)=-|n|+(1+\theta )(x_{0}+x_{1}+\cdots +x_{|n|-1})$
, and if
$S_{n}(\chi )(x)=-|n|+(1+\theta )(x_{0}+x_{1}+\cdots +x_{|n|-1})$
, and if
![]() $n \geq 1$
, we have
$n \geq 1$
, we have
![]() $S_n(\chi )(x)=n-(1+\theta )(x_{-1}+x_{-2}+\cdots +x_{-n})$
.
$S_n(\chi )(x)=n-(1+\theta )(x_{-1}+x_{-2}+\cdots +x_{-n})$
.
We apply Lemma 4.3 of [Reference Christensen and Thomsen5] which states the following. Let
![]() $x\in \Omega$
be given. If
$x\in \Omega$
be given. If
![]() $x$
is periodic of period
$x$
is periodic of period
![]() $p\gt 0$
, then there is an
$p\gt 0$
, then there is an
![]() $e^{-\beta \chi }$
-conformal measure on
$e^{-\beta \chi }$
-conformal measure on
![]() $\Omega$
concentrated on the orbit of
$\Omega$
concentrated on the orbit of
![]() $x$
iff
$x$
iff
![]() $S_p(\chi )(x)=0$
. If
$S_p(\chi )(x)=0$
. If
![]() $x$
is not periodic, then there is an
$x$
is not periodic, then there is an
![]() $e^{-\beta \chi }$
-conformal measure concentrated on the orbit of
$e^{-\beta \chi }$
-conformal measure concentrated on the orbit of
![]() $x$
if and only if
$x$
if and only if
![]() $\displaystyle \sum _{n\in \mathbb{Z}} e^{-\beta S_n(\chi )(x)}\lt \infty$
.
$\displaystyle \sum _{n\in \mathbb{Z}} e^{-\beta S_n(\chi )(x)}\lt \infty$
.
Case 1: Suppose
![]() $\theta =0$
. Let
$\theta =0$
. Let
![]() $x\in \Omega$
be such that
$x\in \Omega$
be such that
![]() $x_m=1$
for every
$x_m=1$
for every
![]() $m \in \mathbb{Z}$
. Clearly,
$m \in \mathbb{Z}$
. Clearly,
![]() $x$
is periodic of period
$x$
is periodic of period
![]() $1$
, and
$1$
, and
![]() $S_{1}(\chi )(x)=0$
. Therefore, there is an
$S_{1}(\chi )(x)=0$
. Therefore, there is an
![]() $e^{-\beta \chi }$
-conformal measure supported on the orbit of
$e^{-\beta \chi }$
-conformal measure supported on the orbit of
![]() $x$
.
$x$
.
Case 2: Suppose
![]() $\theta \gt 0$
. We exhibit uncountably many non-periodic points
$\theta \gt 0$
. We exhibit uncountably many non-periodic points
![]() $x$
for which the series
$x$
for which the series
![]() $\displaystyle \sum _{n \in \mathbb{Z}}e^{-\beta S_n(\chi )(x)}$
converges. Let
$\displaystyle \sum _{n \in \mathbb{Z}}e^{-\beta S_n(\chi )(x)}$
converges. Let
![]() $\ell$
be a positive integer such that
$\ell$
be a positive integer such that
![]() $\ell \gt 1+\theta$
. Suppose
$\ell \gt 1+\theta$
. Suppose
![]() $S \subset \ell \mathbb{N}$
. Denote the indicator function of
$S \subset \ell \mathbb{N}$
. Denote the indicator function of
![]() $S$
by
$S$
by
![]() $1_{S}$
. Define
$1_{S}$
. Define
![]() $x \in \Omega$
by setting
$x \in \Omega$
by setting
 \begin{equation*} x_m\,:\!=\,\begin {cases} 1 & \mbox { if} \, m \geq 0 \\ 1_{S}({-}m) & \,\mbox {if} \, m\lt 0 \end {cases} \end{equation*}
\begin{equation*} x_m\,:\!=\,\begin {cases} 1 & \mbox { if} \, m \geq 0 \\ 1_{S}({-}m) & \,\mbox {if} \, m\lt 0 \end {cases} \end{equation*}
Note that
![]() $S_{n}(\chi )(x)=|n|\theta$
if
$S_{n}(\chi )(x)=|n|\theta$
if
![]() $n \leq -1$
. Therefore, the series
$n \leq -1$
. Therefore, the series
![]() $\sum _{n\leq -1}^{\infty }e^{-\beta S_n(\chi )(x)}$
is convergent.
$\sum _{n\leq -1}^{\infty }e^{-\beta S_n(\chi )(x)}$
is convergent.
For
![]() $n \geq 1$
, observe that since
$n \geq 1$
, observe that since
![]() $x_{-1}+x_{-2}+\cdots +x_{-n} =|S \cap \{1,2,\cdots,n\}| \leq \frac{n}{\ell }$
,
$x_{-1}+x_{-2}+\cdots +x_{-n} =|S \cap \{1,2,\cdots,n\}| \leq \frac{n}{\ell }$
,
Thus,
![]() $ e^{-\beta S_n(\chi )(x)} \leq e^{-\beta n (1-\frac{1+\theta }{\ell })}$
. Consequently, the series
$ e^{-\beta S_n(\chi )(x)} \leq e^{-\beta n (1-\frac{1+\theta }{\ell })}$
. Consequently, the series
![]() $\sum _{n \geq 1}^{\infty }e^{-\beta S_n(\chi )(x)}$
converges. Thanks to Lemma 4.9 of [Reference Christensen and Thomsen5], there is an
$\sum _{n \geq 1}^{\infty }e^{-\beta S_n(\chi )(x)}$
converges. Thanks to Lemma 4.9 of [Reference Christensen and Thomsen5], there is an
![]() $e^{-\beta \chi }$
-conformal measure supported on the orbit of
$e^{-\beta \chi }$
-conformal measure supported on the orbit of
![]() $x$
. The proof is complete.
$x$
. The proof is complete.
We discuss the structure of KMS states in more detail now. Assume hereafter that
![]() $\beta$
is an arbitrary positive real number.
$\beta$
is an arbitrary positive real number.
The case
![]() $\theta =0$
: Assume that
$\theta =0$
: Assume that
![]() $\theta =0$
. Denote the element in
$\theta =0$
. Denote the element in
![]() $\{0,1\}^{\mathbb{Z}}$
whose every entry is 1 by
$\{0,1\}^{\mathbb{Z}}$
whose every entry is 1 by
![]() $\underline{1}$
. Suppose that
$\underline{1}$
. Suppose that
![]() $m$
is an
$m$
is an
![]() $e^{-\beta \chi }$
-conformal measure on
$e^{-\beta \chi }$
-conformal measure on
![]() $\Omega$
. We claim that
$\Omega$
. We claim that
![]() $m$
is concentrated on
$m$
is concentrated on
![]() $\underline{1}$
. We claim that
$\underline{1}$
. We claim that
![]() $m(\{x\,:\,x_{-1}=0\})=0$
. Suppose
$m(\{x\,:\,x_{-1}=0\})=0$
. Suppose
![]() $m(\{x\,:\,x_{-1}=0\})\gt 0$
. Then, by conformality, we have
$m(\{x\,:\,x_{-1}=0\})\gt 0$
. Then, by conformality, we have
 \begin{align*} 1&=m(\tau (\Omega ))\\ &=\int e^{-\beta \chi }dm\\ &=e^{-\beta }m(\{x\,:\,x_{-1}=0\})+m(\{x\,:\,x_{-1}=1\})\\ &\lt m(\{x\,:\,x_{-1}=0\})+m(\{x\,:\,x_{-1}=1\})=1 \end{align*}
\begin{align*} 1&=m(\tau (\Omega ))\\ &=\int e^{-\beta \chi }dm\\ &=e^{-\beta }m(\{x\,:\,x_{-1}=0\})+m(\{x\,:\,x_{-1}=1\})\\ &\lt m(\{x\,:\,x_{-1}=0\})+m(\{x\,:\,x_{-1}=1\})=1 \end{align*}
which is a contradiction.
Therefore, for almost all
![]() $x$
,
$x$
,
![]() $x_{-1}=1$
. Since
$x_{-1}=1$
. Since
![]() $m$
is quasi-invariant for the Bernoulli shift
$m$
is quasi-invariant for the Bernoulli shift
![]() $\tau$
, we have, for every
$\tau$
, we have, for every
![]() $k$
,
$k$
,
![]() $x_k=1$
for almost all
$x_k=1$
for almost all
![]() $x$
. Hence,
$x$
. Hence,
![]() $x=\underline{1}$
for almost all
$x=\underline{1}$
for almost all
![]() $x$
. This proves the claim.
$x$
. This proves the claim.
Let
![]() $\omega$
be a
$\omega$
be a
![]() $\beta$
-KMS state on
$\beta$
-KMS state on
![]() $C_{c}^{*}(\mathbb{N}^2)$
. Thanks to Propositions 4.1 and 4.2 and by what we have proved now, its associated
$C_{c}^{*}(\mathbb{N}^2)$
. Thanks to Propositions 4.1 and 4.2 and by what we have proved now, its associated
![]() $e^{ - \beta c}$
-conformal measure
$e^{ - \beta c}$
-conformal measure
![]() $m_{\omega }$
is supported on
$m_{\omega }$
is supported on
![]() $Orb(A(\underline{1},0))$
. Note that
$Orb(A(\underline{1},0))$
. Note that
whose stabiliser
![]() $G_{A}=\{0\}\times \mathbb{Z}=c^{-1}(\{0\})$
. Appealing to Corollary 1.4 of [Reference Neshveyev22], we see that there exists a state
$G_{A}=\{0\}\times \mathbb{Z}=c^{-1}(\{0\})$
. Appealing to Corollary 1.4 of [Reference Neshveyev22], we see that there exists a state
![]() $\phi$
on
$\phi$
on
![]() $C^{*}(G_A)$
, or equivalently a probability measure
$C^{*}(G_A)$
, or equivalently a probability measure
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{T}$
such that
$\mathbb{T}$
such that
Conversely, given a probability measure
![]() $\mu$
on
$\mu$
on
![]() $\mathbb{T}$
, if we define
$\mathbb{T}$
, if we define
![]() $\omega$
as in equation (4.6), then
$\omega$
as in equation (4.6), then
![]() $\omega$
will be a
$\omega$
will be a
![]() $\beta$
-KMS state. Thus, when
$\beta$
-KMS state. Thus, when
![]() $\theta =0$
, the simplex of
$\theta =0$
, the simplex of
![]() $\beta$
-KMS states for
$\beta$
-KMS states for
![]() $\sigma ^{c}$
is homeomorphic to the simplex of probability measures on the circle.
$\sigma ^{c}$
is homeomorphic to the simplex of probability measures on the circle.
Hereafter, we assume that
![]() $\beta \gt 0$
and
$\beta \gt 0$
and
![]() $\theta \gt 0$
. We summarise the structure of extremal
$\theta \gt 0$
. We summarise the structure of extremal
![]() $\beta$
-KMS states on
$\beta$
-KMS states on
![]() $C_{c}^{*}(\mathbb{N}^2)$
, that result from our discussions so far, as follows.
$C_{c}^{*}(\mathbb{N}^2)$
, that result from our discussions so far, as follows.
-
(1) Suppose
 $\omega$
is an extremal
$\omega$
is an extremal
 $\beta$
-KMS state on
$\beta$
-KMS state on
 $C_{c}^{*}(\mathbb{N}^2)$
. Denote the associated conformal measure on
$C_{c}^{*}(\mathbb{N}^2)$
. Denote the associated conformal measure on
 $Y_u$
by
$Y_u$
by
 $\overline{m}$
, and let
$\overline{m}$
, and let
 $m$
be the corresponding
$m$
be the corresponding
 $e^{-\beta \chi }$
-conformal measure on
$e^{-\beta \chi }$
-conformal measure on
 $\Omega$
obtained via the map in Proposition 4.2. Then, thanks to Proposition 3.3,
$\Omega$
obtained via the map in Proposition 4.2. Then, thanks to Proposition 3.3,
 $m$
is ergodic. Suppose that
$m$
is ergodic. Suppose that
 $m$
is atomic and
$m$
is atomic and
 $m$
is concentrated on
$m$
is concentrated on
 $Orbit(x)$
for some
$Orbit(x)$
for some
 $x \in \{0,1\}^{\mathbb{Z}}$
. Set
$x \in \{0,1\}^{\mathbb{Z}}$
. Set
 $A\,:\!=\,A(x,0)$
. Thanks to Proposition 3.4, if the stabiliser
$A\,:\!=\,A(x,0)$
. Thanks to Proposition 3.4, if the stabiliser
 $G_A=\{0\}$
, then
$G_A=\{0\}$
, then
 $\omega =\omega _{\overline{m}}$
. If
$\omega =\omega _{\overline{m}}$
. If
 $G_A \neq \{0\}$
, then
$G_A \neq \{0\}$
, then
 $\omega$
is as in Proposition 3.4. In both cases,
$\omega$
is as in Proposition 3.4. In both cases,
 $\omega$
is of type I. If
$\omega$
is of type I. If
 $m$
is non-atomic, then
$m$
is non-atomic, then
 $\omega =\omega _{\overline{m}}$
where
$\omega =\omega _{\overline{m}}$
where
 $\omega _{\overline{m}}$
is the state corresponding to
$\omega _{\overline{m}}$
is the state corresponding to
 $\overline{m}$
obtained via the conditional expectation. This follows by applying Corollary 1.2 of [Reference Neshveyev22] and by Remark 4.1. In this case,
$\overline{m}$
obtained via the conditional expectation. This follows by applying Corollary 1.2 of [Reference Neshveyev22] and by Remark 4.1. In this case,
 $\omega$
is of type II or III depending upon whether
$\omega$
is of type II or III depending upon whether
 $m$
(or equivalently
$m$
(or equivalently
 $\overline{m}$
) is of type II or of type III.
$\overline{m}$
) is of type II or of type III. -
(2) Conversely, suppose
 $m$
is an ergodic
$m$
is an ergodic
 $e^{-\beta \chi }$
-conformal measure on
$e^{-\beta \chi }$
-conformal measure on
 $\Omega$
. Let
$\Omega$
. Let
 $\overline{m}$
be the corresponding
$\overline{m}$
be the corresponding
 $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
 $Y_u$
given by Proposition 4.2. If
$Y_u$
given by Proposition 4.2. If
 $m$
is non-atomic, then
$m$
is non-atomic, then
 $\omega _{\overline{m}}$
is an extremal
$\omega _{\overline{m}}$
is an extremal
 $\beta$
-KMS state and its type is the same as that of
$\beta$
-KMS state and its type is the same as that of
 $m$
. To see that
$m$
. To see that
 $\omega _{\overline{m}}$
is extremal, it suffices to show that the GNS representation is factorial. Thanks to Theorem 3.1, it suffices to prove that the
$\omega _{\overline{m}}$
is extremal, it suffices to show that the GNS representation is factorial. Thanks to Theorem 3.1, it suffices to prove that the
 $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
 $Y_u$
is essentially free.
$Y_u$
is essentially free.Let
 $(m,n) \neq (0,0)$
be given. Then, by Remark 4.1, the setis countable. As
$(m,n) \neq (0,0)$
be given. Then, by Remark 4.1, the setis countable. As \begin{equation*}\{A\in Y_u\,:\,A+(m,n)=A\},\end{equation*}
\begin{equation*}\{A\in Y_u\,:\,A+(m,n)=A\},\end{equation*}
 $\overline{m}$
is non-atomic, it follows that
$\overline{m}$
is non-atomic, it follows that
 $\{A \in Y_u\,:\, A+(m,n)=A\}$
, which is countable, is a set of measure zero. Thus, the
$\{A \in Y_u\,:\, A+(m,n)=A\}$
, which is countable, is a set of measure zero. Thus, the
 $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
 $Y_u$
is essentially free.
$Y_u$
is essentially free.
Suppose
 $\overline{m}$
is atomic and
$\overline{m}$
is atomic and
 $\overline{m}$
is concentrated on
$\overline{m}$
is concentrated on
 $Orbit(A)$
for some
$Orbit(A)$
for some
 $A \in Y_u$
. From Proposition 3.4, if the stabiliser
$A \in Y_u$
. From Proposition 3.4, if the stabiliser
 $G_A=\{0\}$
, then
$G_A=\{0\}$
, then
 $\omega _{\overline{m}}$
is an extremal
$\omega _{\overline{m}}$
is an extremal
 $\beta$
-KMS state of type I. If
$\beta$
-KMS state of type I. If
 $G_A\neq \{0\}$
, then
$G_A\neq \{0\}$
, then
 $\omega _{\chi,m}$
, as defined in Proposition 3.4, is an extremal
$\omega _{\chi,m}$
, as defined in Proposition 3.4, is an extremal
 $\beta$
-KMS state of type I.
$\beta$
-KMS state of type I. -
(3) We have exhibited, in the proof of Proposition 4.3, uncountably many atomic probability measures on
 $\Omega$
that are
$\Omega$
that are
 $e^{-\beta \chi }$
-conformal. Thus, there are uncountably many type I
$e^{-\beta \chi }$
-conformal. Thus, there are uncountably many type I
 $\beta$
-KMS states on
$\beta$
-KMS states on
 $C_{c}^{*}(\mathbb{N}^2)$
for
$C_{c}^{*}(\mathbb{N}^2)$
for
 $\sigma ^c$
.
$\sigma ^c$
.
We end this section by exhibiting a type II KMS state when
![]() $\theta$
is irrational and a type III KMS state when
$\theta$
is irrational and a type III KMS state when
![]() $\theta =1$
. We prove this by appealing to Proposition 3.5. Uncountably, many such examples for every
$\theta =1$
. We prove this by appealing to Proposition 3.5. Uncountably, many such examples for every
![]() $\theta \gt 0$
and for every
$\theta \gt 0$
and for every
![]() $\beta \gt 0$
will be constructed in Section 5.
$\beta \gt 0$
will be constructed in Section 5.
A type II example: Assume that
![]() $\theta \in (0,\infty )$
is irrational. Suppose
$\theta \in (0,\infty )$
is irrational. Suppose
![]() $\beta \gt 0$
. Let
$\beta \gt 0$
. Let
![]() $Y\,:\!=\,\mathbb{R}$
and
$Y\,:\!=\,\mathbb{R}$
and
![]() $X\,:\!=\,[0,\infty )$
. Define a
$X\,:\!=\,[0,\infty )$
. Define a
![]() $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
![]() $Y$
by
$Y$
by
Clearly,
![]() $X+\mathbb{N}^2 \subset X$
. Also,
$X+\mathbb{N}^2 \subset X$
. Also,
![]() $(Y,X)$
is a pure
$(Y,X)$
is a pure
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-space. Since
$(\mathbb{Z}^2,\mathbb{N}^2)$
-space. Since
![]() $\theta$
is irrational, the
$\theta$
is irrational, the
![]() $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
![]() $Y$
is free. Let
$Y$
is free. Let
![]() $m$
be the measure on
$m$
be the measure on
![]() $\mathbb{R}$
such that
$\mathbb{R}$
such that
![]() $dm=\beta e^{-\beta t}dt$
. Then,
$dm=\beta e^{-\beta t}dt$
. Then,
![]() $m(X)=1$
and
$m(X)=1$
and
![]() $m$
is
$m$
is
![]() $e^{-\beta c}$
-conformal. As
$e^{-\beta c}$
-conformal. As
![]() $\mathbb{Z}+\mathbb{Z} \theta$
is a dense subgroup of
$\mathbb{Z}+\mathbb{Z} \theta$
is a dense subgroup of
![]() $\mathbb{R}$
, the
$\mathbb{R}$
, the
![]() $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
![]() $Y$
is ergodic. Clearly, it is of type II as
$Y$
is ergodic. Clearly, it is of type II as
![]() $m$
is absolutely continuous w.r.t. the Lebesgue measure.
$m$
is absolutely continuous w.r.t. the Lebesgue measure.
Observe that, for
![]() $t \in \mathbb{R}$
,
$t \in \mathbb{R}$
,
If
![]() $t_1\lt t_2$
, the density of
$t_1\lt t_2$
, the density of
![]() $\mathbb{Z}+\mathbb{Z}\theta$
in
$\mathbb{Z}+\mathbb{Z}\theta$
in
![]() $ \mathbb{R}$
implies that there exists
$ \mathbb{R}$
implies that there exists
![]() $(m,n) \in \mathbb{Z}^2$
such that
$(m,n) \in \mathbb{Z}^2$
such that
![]() $t_1\lt m+n\theta \lt t_2$
. Then,
$t_1\lt m+n\theta \lt t_2$
. Then,
![]() $(m,n) \in Q_{t_2}$
but
$(m,n) \in Q_{t_2}$
but
![]() $(m,n) \notin Q_{t_1}$
. Therefore, the map
$(m,n) \notin Q_{t_1}$
. Therefore, the map
is injective.
Applying Proposition 3.5, we get an extremal
![]() $\beta$
-KMS state of type II when
$\beta$
-KMS state of type II when
![]() $\theta$
is irrational.
$\theta$
is irrational.
A type III example: Assume that
![]() $\theta =1$
. We make use of Arnold’s dyadic adding machine to produce a type III example in this situation. Let us recall the basics on adding machine from [Reference Aaronson1]. Let
$\theta =1$
. We make use of Arnold’s dyadic adding machine to produce a type III example in this situation. Let us recall the basics on adding machine from [Reference Aaronson1]. Let
![]() $\beta \gt 0$
be fixed. Let
$\beta \gt 0$
be fixed. Let
![]() $p \in (0,\frac{1}{2})$
be such that
$p \in (0,\frac{1}{2})$
be such that
![]() $\frac{1-p}{p}=e^{\beta }$
.
$\frac{1-p}{p}=e^{\beta }$
.
Let
be the group of dyadic integers. Let
![]() $\displaystyle \mu \,:\!=\,\otimes _{k=1}^{\infty }\mu _k$
be the product measure where the measure
$\displaystyle \mu \,:\!=\,\otimes _{k=1}^{\infty }\mu _k$
be the product measure where the measure
![]() $\mu _k$
on
$\mu _k$
on
![]() $\{0,1\}$
is given by
$\{0,1\}$
is given by
We remove from
![]() $\mathcal{D}$
the null set of eventually constant sequences, and we denote the resulting set again by
$\mathcal{D}$
the null set of eventually constant sequences, and we denote the resulting set again by
![]() $\mathcal{D}$
.
$\mathcal{D}$
.
Denote the map on
![]() $\mathcal{D}$
that corresponds to addition by
$\mathcal{D}$
that corresponds to addition by
![]() $\underline{1}$
by
$\underline{1}$
by
![]() $\tau$
. Recall that
$\tau$
. Recall that
Define
![]() $\phi \,:\,\mathcal{D} \to \mathbb{Z}$
by
$\phi \,:\,\mathcal{D} \to \mathbb{Z}$
by
![]() $ \phi (x)\,:\!=\,\min \{n \geq 1\,:\, x_n=0\}-2$
. Then,
$ \phi (x)\,:\!=\,\min \{n \geq 1\,:\, x_n=0\}-2$
. Then,
Let
![]() $Y\,:\!=\,\mathcal{D} \times \mathbb{Z}$
and
$Y\,:\!=\,\mathcal{D} \times \mathbb{Z}$
and
![]() $X\,:\!=\,\mathcal{D} \times \{0,1,2,\cdots \}$
. Let
$X\,:\!=\,\mathcal{D} \times \{0,1,2,\cdots \}$
. Let
![]() $\overline{\mu }$
be the measure on
$\overline{\mu }$
be the measure on
![]() $Y$
given by
$Y$
given by
where
![]() $dn$
is the counting measure on
$dn$
is the counting measure on
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
Define a
![]() $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
![]() $Y$
by
$Y$
by
Since
![]() $\phi \geq -1$
, it follows that
$\phi \geq -1$
, it follows that
![]() $X+\mathbb{N}^2 \subset X$
. Also, it is routine to verify that
$X+\mathbb{N}^2 \subset X$
. Also, it is routine to verify that
![]() $(Y,X)$
is a pure
$(Y,X)$
is a pure
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-space and
$(\mathbb{Z}^2,\mathbb{N}^2)$
-space and
![]() $\overline{\mu }$
is an
$\overline{\mu }$
is an
![]() $e^{-\beta c}$
-conformal measure.
$e^{-\beta c}$
-conformal measure.
Lemma 4.2.
Let
![]() $x,y \in \mathcal{D}$
be such that
$x,y \in \mathcal{D}$
be such that
![]() $x \neq y$
. Then, there exists an integer
$x \neq y$
. Then, there exists an integer
![]() $m$
such that
$m$
such that
![]() $\phi (\tau ^{m}(x))\neq \phi (\tau ^{m}(y))$
.
$\phi (\tau ^{m}(x))\neq \phi (\tau ^{m}(y))$
.
Proof. Let
![]() $k$
be the least integer for which
$k$
be the least integer for which
![]() $x_k \neq y_k$
. We can, without loss of generality, assume that
$x_k \neq y_k$
. We can, without loss of generality, assume that
![]() $x_k=0$
and
$x_k=0$
and
![]() $y_k=1$
. Let
$y_k=1$
. Let
![]() $m\,:\!=\,2^{k-1}-1-(x_1+2x_2+\cdots +2^{k-2}x_{k-1})$
. A calculation with ‘binary arithmetic’ shows that
$m\,:\!=\,2^{k-1}-1-(x_1+2x_2+\cdots +2^{k-2}x_{k-1})$
. A calculation with ‘binary arithmetic’ shows that
 \begin{align*} \tau ^{m}(x)&=(\underbrace{1,1,\cdots,1}_{k-1},0,*,*,*,\cdots ) \\ \tau ^{m}(y)&=(\underbrace{1,1,1,\cdots 1}_{k-1},1,*,*,*,\cdots ). \end{align*}
\begin{align*} \tau ^{m}(x)&=(\underbrace{1,1,\cdots,1}_{k-1},0,*,*,*,\cdots ) \\ \tau ^{m}(y)&=(\underbrace{1,1,1,\cdots 1}_{k-1},1,*,*,*,\cdots ). \end{align*}
Thus,
![]() $\phi (\tau ^m(x))=k-2 \lt \phi (\tau ^m(y))$
. The proof is complete.
$\phi (\tau ^m(x))=k-2 \lt \phi (\tau ^m(y))$
. The proof is complete.
Proposition 4.4. With the foregoing notation, we have the following.
-
(1) The
 $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
 $Y$
is essentially free and ergodic.
$Y$
is essentially free and ergodic.
-
(2) The measure
 $\overline{\mu }$
is of type III.
$\overline{\mu }$
is of type III.
-
(3) The map
is injective. \begin{equation*}Y \ni (x,t) \to Q_{(x,t)} \in Y_u,\end{equation*}
\begin{equation*}Y \ni (x,t) \to Q_{(x,t)} \in Y_u,\end{equation*}
Proof. The first two statements are straightforward consequences of Proposition 1.2.8 and Theorem 1.2.9 of [Reference Aaronson1]. We include a brief explanation.
Note that the
![]() $e_2$
-action on
$e_2$
-action on
![]() $Y$
is by translation by
$Y$
is by translation by
![]() $1$
on the second coordinate. This forces that any
$1$
on the second coordinate. This forces that any
![]() $\mathbb{Z}^2$
-invariant subset of
$\mathbb{Z}^2$
-invariant subset of
![]() $Y$
must be of the form
$Y$
must be of the form
![]() $E \times \mathbb{Z}$
for some subset
$E \times \mathbb{Z}$
for some subset
![]() $E$
of
$E$
of
![]() $\mathcal{D}$
. The fact that
$\mathcal{D}$
. The fact that
![]() $E \times \mathbb{Z}$
is invariant under the action of
$E \times \mathbb{Z}$
is invariant under the action of
![]() $e_1$
implies that
$e_1$
implies that
![]() $\tau (E)=E$
. By Proposition 1.2.8 of [Reference Aaronson1], it follows that
$\tau (E)=E$
. By Proposition 1.2.8 of [Reference Aaronson1], it follows that
![]() $E$
is either null or co-null. Hence, the
$E$
is either null or co-null. Hence, the
![]() $\mathbb{Z}^2$
-action is ergodic. Using the fact that the action of
$\mathbb{Z}^2$
-action is ergodic. Using the fact that the action of
![]() $\tau$
on
$\tau$
on
![]() $\mathcal{D}$
is essentially free, it is routine to check that the
$\mathcal{D}$
is essentially free, it is routine to check that the
![]() $\mathbb{Z}^2$
-action is essentially free.
$\mathbb{Z}^2$
-action is essentially free.
Suppose
![]() $\overline{\mu }$
is not of type III. Let
$\overline{\mu }$
is not of type III. Let
![]() $\overline{\nu }$
be a
$\overline{\nu }$
be a
![]() $\sigma$
-finite measure that is absolutely continuous w.r.t.
$\sigma$
-finite measure that is absolutely continuous w.r.t.
![]() $\overline{\mu }$
such that
$\overline{\mu }$
such that
![]() $\overline{\nu }$
is
$\overline{\nu }$
is
![]() $\mathbb{Z}^2$
-invariant. The invariance of
$\mathbb{Z}^2$
-invariant. The invariance of
![]() $\overline{\nu }$
under
$\overline{\nu }$
under
![]() $e_2$
implies that
$e_2$
implies that
![]() $d\overline{\nu }\,:\!=\,d\nu dn$
for some
$d\overline{\nu }\,:\!=\,d\nu dn$
for some
![]() $\sigma$
-finite measure
$\sigma$
-finite measure
![]() $\nu$
on
$\nu$
on
![]() $\mathcal{D}$
which is absolutely w.r.t.
$\mathcal{D}$
which is absolutely w.r.t.
![]() $\mu$
. The invariance of
$\mu$
. The invariance of
![]() $\overline{\nu }$
under
$\overline{\nu }$
under
![]() $e_1$
implies that
$e_1$
implies that
![]() $\nu$
is
$\nu$
is
![]() $\tau$
-invariant which is a contradiction to Theorem 1.2.9 of [Reference Aaronson1]. The proof of
$\tau$
-invariant which is a contradiction to Theorem 1.2.9 of [Reference Aaronson1]. The proof of
![]() $(1)$
and
$(1)$
and
![]() $(2)$
is complete.
$(2)$
is complete.
For
![]() $m \in \mathbb{Z}$
and
$m \in \mathbb{Z}$
and
![]() $x \in \mathcal{D}$
, let
$x \in \mathcal{D}$
, let
![]() $c(m,x) \in \mathbb{Z}$
be defined by
$c(m,x) \in \mathbb{Z}$
be defined by
 \begin{equation} c(m,x)\,:\!=\,\begin{cases} \sum _{k=0}^{m-1}\phi (\tau ^k(x)) & \mbox{if } m \geq 1,\\[3pt] 0 & \mbox{if } m=0, \\[3pt] -\sum _{k=1}^{|m|}\phi (\tau ^{-k}x) & \mbox{if } m \leq -1. \end{cases} \end{equation}
\begin{equation} c(m,x)\,:\!=\,\begin{cases} \sum _{k=0}^{m-1}\phi (\tau ^k(x)) & \mbox{if } m \geq 1,\\[3pt] 0 & \mbox{if } m=0, \\[3pt] -\sum _{k=1}^{|m|}\phi (\tau ^{-k}x) & \mbox{if } m \leq -1. \end{cases} \end{equation}
Let
![]() $(x,s), (y,t) \in Y$
be such that
$(x,s), (y,t) \in Y$
be such that
![]() $Q_{(x,s)}=Q_{(y,t)}$
. Notice that
$Q_{(x,s)}=Q_{(y,t)}$
. Notice that
The equality
![]() $Q_{(x,s)}=Q_{(y,t)}$
implies in particular that for every
$Q_{(x,s)}=Q_{(y,t)}$
implies in particular that for every
![]() $m \in \mathbb{Z}$
,
$m \in \mathbb{Z}$
,
Substituting,
![]() $m=0$
in the above equality, we deduce that
$m=0$
in the above equality, we deduce that
![]() $s=t$
. The fact that
$s=t$
. The fact that
![]() $c({-}m,x)=c({-}m,y)$
for every
$c({-}m,x)=c({-}m,y)$
for every
![]() $m \in \mathbb{Z}$
implies that
$m \in \mathbb{Z}$
implies that
![]() $\phi (\tau ^mx)=\phi (\tau ^my)$
for each
$\phi (\tau ^mx)=\phi (\tau ^my)$
for each
![]() $m \in \mathbb{Z}$
. By Lemma 4.2, we have
$m \in \mathbb{Z}$
. By Lemma 4.2, we have
![]() $x=y$
. This proves
$x=y$
. This proves
![]() $(3)$
and the proof is complete.
$(3)$
and the proof is complete.
Applying Proposition 3.5, we see that when
![]() $\theta =1$
, there is an extremal
$\theta =1$
, there is an extremal
![]() $\beta$
-KMS state of type III.
$\beta$
-KMS state of type III.
5. Examples of type II and type III
In this section, we construct uncountably many extremal
![]() $\beta$
-KMS states of type II and of type III for every
$\beta$
-KMS states of type II and of type III for every
![]() $\beta \gt 0$
and for every
$\beta \gt 0$
and for every
![]() $\theta \gt 0$
. It suffices to exhibit uncountably many non-atomic ergodic
$\theta \gt 0$
. It suffices to exhibit uncountably many non-atomic ergodic
![]() $e^{-\beta c}$
-conformal measures on the
$e^{-\beta c}$
-conformal measures on the
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-space
$(\mathbb{Z}^2,\mathbb{N}^2)$
-space
![]() $(Y_u,X_u)$
of the desired type. We do this by appealing to Proposition 3.5. For the rest of this section, we assume that
$(Y_u,X_u)$
of the desired type. We do this by appealing to Proposition 3.5. For the rest of this section, we assume that
![]() $\beta$
is an arbitrary positive real number. Recall that
$\beta$
is an arbitrary positive real number. Recall that
![]() $e_1=(1,0)$
,
$e_1=(1,0)$
,
![]() $e_2=(0,1)$
,
$e_2=(0,1)$
,
![]() $v_1=e_1$
and
$v_1=e_1$
and
![]() $v_2=e_1+e_2$
.
$v_2=e_1+e_2$
.
Type II examples for an irrational
![]() $\theta$
: Assume that
$\theta$
: Assume that
![]() $\theta \gt 0$
is irrational. Choose
$\theta \gt 0$
is irrational. Choose
![]() $\alpha \in (0,1)$
such that
$\alpha \in (0,1)$
such that
![]() $1,\alpha$
and
$1,\alpha$
and
![]() $\theta$
are rationally independent. For
$\theta$
are rationally independent. For
![]() $\delta \in (0,\theta ]$
, let
$\delta \in (0,\theta ]$
, let
![]() $C^{\delta }$
be the cone in
$C^{\delta }$
be the cone in
![]() $\mathbb{R}^2$
generated by
$\mathbb{R}^2$
generated by
![]() $(0,1)$
and
$(0,1)$
and
![]() $(\alpha,\delta )$
, i.e.
$(\alpha,\delta )$
, i.e.
Let
![]() $\pi \,:\,\mathbb{R}^2 \to \frac{ \mathbb{R}^2}{\mathbb{Z} \times \{0\}}=\mathbb{T} \times \mathbb{R}$
be the quotient map. We denote
$\pi \,:\,\mathbb{R}^2 \to \frac{ \mathbb{R}^2}{\mathbb{Z} \times \{0\}}=\mathbb{T} \times \mathbb{R}$
be the quotient map. We denote
![]() $\pi (x,y)$
by
$\pi (x,y)$
by
![]() $\overline{(x,y)}$
. Denote the subgroup generated by
$\overline{(x,y)}$
. Denote the subgroup generated by
![]() $\overline{(\alpha,\theta )}$
and
$\overline{(\alpha,\theta )}$
and
![]() $\overline{(0,1)}$
by
$\overline{(0,1)}$
by
![]() $\Gamma$
. Let
$\Gamma$
. Let
![]() $\phi \,:\,\mathbb{Z}^2 \to \Gamma$
be the homomorphism defined by
$\phi \,:\,\mathbb{Z}^2 \to \Gamma$
be the homomorphism defined by
Note that
![]() $\phi$
is an isomorphism as
$\phi$
is an isomorphism as
![]() $\alpha$
and
$\alpha$
and
![]() $\theta$
are irrational.
$\theta$
are irrational.
Set
![]() $Y^{\delta }\,:\!=\,\frac{\mathbb{R}^2}{\mathbb{Z} \times \{0\}}=\mathbb{T} \times \mathbb{R}$
and
$Y^{\delta }\,:\!=\,\frac{\mathbb{R}^2}{\mathbb{Z} \times \{0\}}=\mathbb{T} \times \mathbb{R}$
and
![]() $X^{\delta }\,:\!=\,\pi (C^{\delta })$
. It is not difficult to see that
$X^{\delta }\,:\!=\,\pi (C^{\delta })$
. It is not difficult to see that
![]() $X^{\delta }$
is closed. Define a
$X^{\delta }$
is closed. Define a
![]() $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
![]() $Y^{\delta }$
by
$Y^{\delta }$
by
Since,
![]() $\delta \in (0,\theta ]$
, it follows that
$\delta \in (0,\theta ]$
, it follows that
![]() $(\alpha,\theta ) \in C^{\delta }$
. The fact that
$(\alpha,\theta ) \in C^{\delta }$
. The fact that
![]() $C^{\delta }$
is a cone implies that
$C^{\delta }$
is a cone implies that
![]() $X^{\delta }$
is invariant under
$X^{\delta }$
is invariant under
![]() $\mathbb{N}^2$
, i.e.
$\mathbb{N}^2$
, i.e.
![]() $X^{\delta }+\mathbb{N}^2 \subset X^{\delta }$
. Thus,
$X^{\delta }+\mathbb{N}^2 \subset X^{\delta }$
. Thus,
![]() $(Y^{\delta },X^{\delta })$
is a
$(Y^{\delta },X^{\delta })$
is a
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-space. We leave it to the reader to verify that it is pure.
$(\mathbb{Z}^2,\mathbb{N}^2)$
-space. We leave it to the reader to verify that it is pure.
Define a measure
![]() $\mu$
on
$\mu$
on
![]() $Y^{\delta }$
by
$Y^{\delta }$
by
![]() $d\mu \,:\!=\,e^{-\beta y}dx dy$
. Here,
$d\mu \,:\!=\,e^{-\beta y}dx dy$
. Here,
![]() $dx$
is the Haar measure on
$dx$
is the Haar measure on
![]() $\mathbb{T}$
and
$\mathbb{T}$
and
![]() $dy$
is the Lebesgue measure on
$dy$
is the Lebesgue measure on
![]() $\mathbb{R}$
. Note that
$\mathbb{R}$
. Note that
![]() $X^{\delta } \subset \mathbb{T} \times [0,\infty )$
and the latter set has finite
$X^{\delta } \subset \mathbb{T} \times [0,\infty )$
and the latter set has finite
![]() $\mu$
-measure. Thus,
$\mu$
-measure. Thus,
![]() $\mu (X^{\delta })\lt \infty$
. Define a measure
$\mu (X^{\delta })\lt \infty$
. Define a measure
![]() $m$
on
$m$
on
![]() $Y^{\delta }$
by
$Y^{\delta }$
by
![]() $dm\,:\!=\,\frac{1}{\mu (X^{\delta })}d\mu$
. It is clear that
$dm\,:\!=\,\frac{1}{\mu (X^{\delta })}d\mu$
. It is clear that
![]() $m$
is an
$m$
is an
![]() $e^{-\beta c}$
-conformal measure.
$e^{-\beta c}$
-conformal measure.
Remark 5.1. We need the following ‘pictorially’ obvious facts. We omit the rigorous proofs as they are elementary.
-
(1) The interior
 $Int(X^\delta )$
is dense in
$Int(X^\delta )$
is dense in
 $X^{\delta }$
.
$X^{\delta }$
. -
(2) If
 $X^{\delta }+\overline{(x,y)}=X^{\delta }$
for some
$X^{\delta }+\overline{(x,y)}=X^{\delta }$
for some
 $\overline{(x,y)} \in \mathbb{T} \times \mathbb{R}$
, then
$\overline{(x,y)} \in \mathbb{T} \times \mathbb{R}$
, then
 $\overline{(x,y)}=\overline{(0,0)}$
.
$\overline{(x,y)}=\overline{(0,0)}$
. -
(3) Let
 $\delta _1,\delta _2 \in (0,\theta ]$
. Suppose there exists
$\delta _1,\delta _2 \in (0,\theta ]$
. Suppose there exists
 $\overline{(x,y)} \in \mathbb{T} \times \mathbb{R}$
for which
$\overline{(x,y)} \in \mathbb{T} \times \mathbb{R}$
for which
 $X^{\delta _1}+\overline{(x,y)}=X^{\delta _2}$
. Then,
$X^{\delta _1}+\overline{(x,y)}=X^{\delta _2}$
. Then,
 $\delta _1=\delta _2$
.
$\delta _1=\delta _2$
.
Proposition 5.1. Keep the foregoing notation.
-
(1) The
 $\mathbb{Z}^{2}$
-action on
$\mathbb{Z}^{2}$
-action on
 $Y^{\delta }$
is essentially free and ergodic.
$Y^{\delta }$
is essentially free and ergodic.
-
(2) The measure
 $m$
is of type II.
$m$
is of type II.
-
(3) The map, denoted
 $T^{\delta }$
,is injective.
$T^{\delta }$
,is injective. \begin{equation*} Y^{\delta } \ni \overline {(x,y)} \to Q_{\overline {(x,y)}} \in Y_u\end{equation*}
\begin{equation*} Y^{\delta } \ni \overline {(x,y)} \to Q_{\overline {(x,y)}} \in Y_u\end{equation*}
For
![]() $\delta \in (0,\theta ]$
, let
$\delta \in (0,\theta ]$
, let
![]() $\mu ^{\delta }\,:\!=\,T^{\delta }_{*}m$
be the push-forward measure on
$\mu ^{\delta }\,:\!=\,T^{\delta }_{*}m$
be the push-forward measure on
![]() $Y_u$
. If
$Y_u$
. If
![]() $\delta _1 \neq \delta _2$
, then
$\delta _1 \neq \delta _2$
, then
![]() $\mu ^{\delta _1} \neq \mu ^{\delta _2}$
. In particular, there are uncountably many extremal
$\mu ^{\delta _1} \neq \mu ^{\delta _2}$
. In particular, there are uncountably many extremal
![]() $\beta$
-KMS states of type
$\beta$
-KMS states of type
![]() $II$
for every irrational
$II$
for every irrational
![]() $\theta$
.
$\theta$
.
Proof. Note that the measure
![]() $m$
is absolutely continuous with respect to
$m$
is absolutely continuous with respect to
![]() $dxdy$
, which is the Haar measure on the cylinder
$dxdy$
, which is the Haar measure on the cylinder
![]() $\mathbb{T} \times \mathbb{R}$
, and
$\mathbb{T} \times \mathbb{R}$
, and
![]() $dxdy$
is clearly
$dxdy$
is clearly
![]() $\mathbb{Z}^2$
-invariant. As
$\mathbb{Z}^2$
-invariant. As
![]() $1,\alpha$
and
$1,\alpha$
and
![]() $\theta$
are rationally independent, the subgroup
$\theta$
are rationally independent, the subgroup
![]() $\Gamma$
is dense in
$\Gamma$
is dense in
![]() $\mathbb{T} \times \mathbb{R}$
. Hence, the action of
$\mathbb{T} \times \mathbb{R}$
. Hence, the action of
![]() $\mathbb{Z}^2$
on
$\mathbb{Z}^2$
on
![]() $Y^{\delta }$
, which is by translations by
$Y^{\delta }$
, which is by translations by
![]() $\Gamma$
via the isomorphism
$\Gamma$
via the isomorphism
![]() $\phi \,:\,\mathbb{Z}^2 \to \Gamma$
, is ergodic. As the map
$\phi \,:\,\mathbb{Z}^2 \to \Gamma$
, is ergodic. As the map
![]() $\phi$
is an isomorphism, it is also clear that the
$\phi$
is an isomorphism, it is also clear that the
![]() $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
![]() $Y^{\delta }$
is essentially free. The proof of
$Y^{\delta }$
is essentially free. The proof of
![]() $(1)$
and
$(1)$
and
![]() $(2)$
are now complete.
$(2)$
are now complete.
Let
![]() $(x_1,y_1), (x_2,y_2) \in \mathbb{R}^2$
be such that
$(x_1,y_1), (x_2,y_2) \in \mathbb{R}^2$
be such that
![]() $Q_{\overline{(x_1,y_1)}}=Q_{\overline{(x_2,y_2)}}$
. Note that for
$Q_{\overline{(x_1,y_1)}}=Q_{\overline{(x_2,y_2)}}$
. Note that for
![]() $i=1,2$
,
$i=1,2$
,
The above equation, together with the equality
![]() $Q_{(\overline{x_1,y_1})}=Q_{\overline{(x_2,y_2)}}$
implies that
$Q_{(\overline{x_1,y_1})}=Q_{\overline{(x_2,y_2)}}$
implies that
Taking closure in the above equality, and using the fact that
![]() $\overline{Int(X^{\delta })}=X^{\delta }$
and
$\overline{Int(X^{\delta })}=X^{\delta }$
and
![]() $\Gamma$
is dense in
$\Gamma$
is dense in
![]() $Y^{\delta }$
, we deduce that
$Y^{\delta }$
, we deduce that
![]() $-X^{\delta }+\overline{(x_1,y_1)}=-X^{\delta }+\overline{(x_2,y_2)}$
. By
$-X^{\delta }+\overline{(x_1,y_1)}=-X^{\delta }+\overline{(x_2,y_2)}$
. By
![]() $(2)$
of Remark 5.1, we have
$(2)$
of Remark 5.1, we have
![]() $\overline{(x_1,y_1)}=\overline{(x_2,y_2)}$
. This proves
$\overline{(x_1,y_1)}=\overline{(x_2,y_2)}$
. This proves
![]() $(3)$
.
$(3)$
.
Let
![]() $\delta _1,\delta _2 \in (0,\theta ]$
. Suppose
$\delta _1,\delta _2 \in (0,\theta ]$
. Suppose
![]() $\mu ^{\delta _1}=\mu ^{\delta _2}=\mu$
. Note that, for
$\mu ^{\delta _1}=\mu ^{\delta _2}=\mu$
. Note that, for
![]() $i=1,2$
,
$i=1,2$
,
![]() $\mu ^{\delta _i}$
is concentrated on the image of
$\mu ^{\delta _i}$
is concentrated on the image of
![]() $T^{\delta _i}$
. Thus, up to a set of
$T^{\delta _i}$
. Thus, up to a set of
![]() $\mu$
-measure zero,
$\mu$
-measure zero,
![]() $T^{\delta _1}(Y^{\delta _1})=T^{\delta _2}(Y^{\delta _1})$
. Choose
$T^{\delta _1}(Y^{\delta _1})=T^{\delta _2}(Y^{\delta _1})$
. Choose
![]() $(x_1,y_1), (x_2,y_2) \in \mathbb{R}^{2}$
such that
$(x_1,y_1), (x_2,y_2) \in \mathbb{R}^{2}$
such that
![]() $T^{\delta _1}(\overline{(x_1,y_1)})=T^{\delta _2}(\overline{(x_2,y_2)})$
. This implies that
$T^{\delta _1}(\overline{(x_1,y_1)})=T^{\delta _2}(\overline{(x_2,y_2)})$
. This implies that
Taking closure, we deduce
By
![]() $(3)$
of Remark 5.1, we have
$(3)$
of Remark 5.1, we have
![]() $\delta _1=\delta _2$
. This completes the proof.
$\delta _1=\delta _2$
. This completes the proof.
Type II examples for
![]() $\theta =1$
: Assume that
$\theta =1$
: Assume that
![]() $\theta =1$
. Recall that the homomorphism
$\theta =1$
. Recall that the homomorphism
![]() $c\,:\,\mathbb{Z}^2 \to \mathbb{R}$
is defined by
$c\,:\,\mathbb{Z}^2 \to \mathbb{R}$
is defined by
![]() $c(e_1)=1$
and
$c(e_1)=1$
and
![]() $c(e_2)=1$
. For an irrational
$c(e_2)=1$
. For an irrational
![]() $\alpha \in (0,1)$
, let
$\alpha \in (0,1)$
, let
![]() $R_\alpha$
be the rotation by angle
$R_\alpha$
be the rotation by angle
![]() $\alpha$
on
$\alpha$
on
![]() $\mathbb{T}\,:\!=\,[0,1)$
. In additive notation,
$\mathbb{T}\,:\!=\,[0,1)$
. In additive notation,
![]() $R_\alpha (x)=x+\alpha \mod 1$
. For
$R_\alpha (x)=x+\alpha \mod 1$
. For
![]() $\eta \in (0,1)$
, let
$\eta \in (0,1)$
, let
![]() $h_\eta \,:\!=\,1_{[0,\eta )}$
and let
$h_\eta \,:\!=\,1_{[0,\eta )}$
and let
![]() $\phi _{\eta,\alpha }\,:\!=\,h_\eta \circ R_\alpha - h_{\eta }$
.
$\phi _{\eta,\alpha }\,:\!=\,h_\eta \circ R_\alpha - h_{\eta }$
.
Lemma 5.1.
Let
![]() $\alpha \in (0,1)$
be irrational and let
$\alpha \in (0,1)$
be irrational and let
![]() $\eta \in (0,1)$
be given.
$\eta \in (0,1)$
be given.
-
(1) Suppose
 $x,y \in \mathbb{T}$
are distinct points. Then, there exists
$x,y \in \mathbb{T}$
are distinct points. Then, there exists
 $m \in \mathbb{Z}$
such that
$m \in \mathbb{Z}$
such that
 $h_{\eta }(R_{\alpha }^m(x)) \neq h_{\eta }(R_{\alpha }^m(y))$
.
$h_{\eta }(R_{\alpha }^m(x)) \neq h_{\eta }(R_{\alpha }^m(y))$
. -
(2) Suppose
 $\eta \lt \min \{\alpha,1-\alpha \}$
and let
$\eta \lt \min \{\alpha,1-\alpha \}$
and let
 $x,y \in \mathbb{T}$
be distinct points. Then, there exists
$x,y \in \mathbb{T}$
be distinct points. Then, there exists
 $m \in \mathbb{Z}$
such that
$m \in \mathbb{Z}$
such that
 $\phi _{\eta,\alpha }(R_{\alpha }^{m}(x))\neq \phi _{\eta,\alpha }(R_{\alpha }^m(y))$
.
$\phi _{\eta,\alpha }(R_{\alpha }^{m}(x))\neq \phi _{\eta,\alpha }(R_{\alpha }^m(y))$
.
Proof. We denote the map
![]() $h_\eta \,:\,[0,1) \to \mathbb{R}$
simply by
$h_\eta \,:\,[0,1) \to \mathbb{R}$
simply by
![]() $h$
. Denote the periodic extension of
$h$
. Denote the periodic extension of
![]() $h$
to
$h$
to
![]() $\mathbb{R}$
by
$\mathbb{R}$
by
![]() $\widetilde{h}$
. Suppose, for
$\widetilde{h}$
. Suppose, for
![]() $x,y \in \mathbb{T}$
,
$x,y \in \mathbb{T}$
,
![]() $h(R_\alpha ^{m}(x))=h(R_\alpha ^{m}(y))$
for every
$h(R_\alpha ^{m}(x))=h(R_\alpha ^{m}(y))$
for every
![]() $m \in \mathbb{Z}$
. Then,
$m \in \mathbb{Z}$
. Then,
for all
![]() $m,n \in \mathbb{Z}$
. This means that for all
$m,n \in \mathbb{Z}$
. This means that for all
![]() $m,n \in \mathbb{Z}$
,
$m,n \in \mathbb{Z}$
,
![]() $(T_x\widetilde{h})(m\alpha +n)=(T_y\widetilde{h})(m\alpha +n)$
, where
$(T_x\widetilde{h})(m\alpha +n)=(T_y\widetilde{h})(m\alpha +n)$
, where
![]() $T_x\widetilde{h}, T_y\widetilde{h}$
denote the translations of
$T_x\widetilde{h}, T_y\widetilde{h}$
denote the translations of
![]() $\widetilde{h}$
by
$\widetilde{h}$
by
![]() $x,y$
respectively.
$x,y$
respectively.
Since the set
![]() $D=\{m\alpha +n\,:\, m,n \in \mathbb{Z}\}$
is dense in
$D=\{m\alpha +n\,:\, m,n \in \mathbb{Z}\}$
is dense in
![]() $\mathbb{R}$
,
$\mathbb{R}$
,
![]() $T_x\widetilde{h}$
,
$T_x\widetilde{h}$
,
![]() $ T_y\widetilde{h}$
are right continuous and they agree on
$ T_y\widetilde{h}$
are right continuous and they agree on
![]() $D$
, we can conclude that they agree on
$D$
, we can conclude that they agree on
![]() $\mathbb{R}$
. Then,
$\mathbb{R}$
. Then,
![]() $T_z\widetilde{h}=\widetilde{h}$
on
$T_z\widetilde{h}=\widetilde{h}$
on
![]() $\mathbb{R}$
, where
$\mathbb{R}$
, where
![]() $z=x-y$
. This clearly implies that
$z=x-y$
. This clearly implies that
![]() $z$
is an integer. This proves
$z$
is an integer. This proves
![]() $(1)$
.
$(1)$
.
Let
![]() $\eta \lt \min \{\alpha,1-\alpha \}$
be given. Denote
$\eta \lt \min \{\alpha,1-\alpha \}$
be given. Denote
![]() $\phi _{\eta,\alpha }$
by
$\phi _{\eta,\alpha }$
by
![]() $\phi$
. Note that for
$\phi$
. Note that for
![]() $x \in \mathbb{T}$
,
$x \in \mathbb{T}$
,
 \begin{equation} \phi (R_{\alpha }^{-1}x)\,:\!=\,\begin{cases} 1 & \mbox{ if } x \in [0,\eta ),\\ 0 & \mbox{if} x \in [\eta,\alpha ), \\ -1 & \mbox{ if } x \in [\alpha,\alpha +\eta ), \\ 0 & \mbox{if} x \in [\alpha +\eta,1). \end{cases} \end{equation}
\begin{equation} \phi (R_{\alpha }^{-1}x)\,:\!=\,\begin{cases} 1 & \mbox{ if } x \in [0,\eta ),\\ 0 & \mbox{if} x \in [\eta,\alpha ), \\ -1 & \mbox{ if } x \in [\alpha,\alpha +\eta ), \\ 0 & \mbox{if} x \in [\alpha +\eta,1). \end{cases} \end{equation}
Let
![]() $\chi \,:\,\{1,0,-1\} \to \{0,1\}$
be defined by
$\chi \,:\,\{1,0,-1\} \to \{0,1\}$
be defined by
![]() $\chi (1)=1$
and
$\chi (1)=1$
and
![]() $\chi (j)=0$
if
$\chi (j)=0$
if
![]() $j \in \{0,-1\}$
. Then,
$j \in \{0,-1\}$
. Then,
The proof of
![]() $(2)$
follows from the above equality and
$(2)$
follows from the above equality and
![]() $(1)$
. This completes the proof.
$(1)$
. This completes the proof.
Let
![]() $\alpha \in (0,1)$
be irrational, and let
$\alpha \in (0,1)$
be irrational, and let
![]() $\eta \in (0,1)$
be such that
$\eta \in (0,1)$
be such that
![]() $\eta \lt \min \{\alpha,1-\alpha \}$
. Denote
$\eta \lt \min \{\alpha,1-\alpha \}$
. Denote
![]() $h_{\eta }$
by
$h_{\eta }$
by
![]() $h$
and
$h$
and
![]() $\phi _{\eta,\alpha }$
by
$\phi _{\eta,\alpha }$
by
![]() $\phi$
. Let
$\phi$
. Let
![]() $Y_{\alpha,\eta }\,:\!=\,\mathbb{T} \times \mathbb{Z}$
, and let
$Y_{\alpha,\eta }\,:\!=\,\mathbb{T} \times \mathbb{Z}$
, and let
![]() $X_{\alpha,\eta }\,:\!=\,\mathbb{T} \times \mathbb{N}$
. Define a
$X_{\alpha,\eta }\,:\!=\,\mathbb{T} \times \mathbb{N}$
. Define a
![]() $\mathbb{Z}^{2}$
-action on
$\mathbb{Z}^{2}$
-action on
![]() $Y_{\alpha,\eta }$
by
$Y_{\alpha,\eta }$
by
Since
![]() $\phi \geq -1$
, it follows that
$\phi \geq -1$
, it follows that
![]() $X_{\alpha,\eta }+\mathbb{N}^2 \subset X_{\alpha,\eta }$
. Also, it is routine to verify that
$X_{\alpha,\eta }+\mathbb{N}^2 \subset X_{\alpha,\eta }$
. Also, it is routine to verify that
![]() $(Y_{\alpha,\eta },X_{\alpha,\eta })$
is a pure
$(Y_{\alpha,\eta },X_{\alpha,\eta })$
is a pure
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-space.
$(\mathbb{Z}^2,\mathbb{N}^2)$
-space.
Let
![]() $\beta$
be an arbitrary positive real number. Define a probability measure
$\beta$
be an arbitrary positive real number. Define a probability measure
![]() $\nu _{\alpha,\eta }$
on
$\nu _{\alpha,\eta }$
on
![]() $\mathbb{T}$
by
$\mathbb{T}$
by
In the above formula,
![]() $dx$
is the Haar measure on the circle. Clearly,
$dx$
is the Haar measure on the circle. Clearly,
Define a measure
![]() $\mu _{\alpha,\eta }$
on
$\mu _{\alpha,\eta }$
on
![]() $Y_{\alpha,\eta }$
by
$Y_{\alpha,\eta }$
by
It is easily verifiable that
![]() $\mu _{\alpha,\eta }$
is an
$\mu _{\alpha,\eta }$
is an
![]() $e^{-\beta c}$
-conformal measure on the
$e^{-\beta c}$
-conformal measure on the
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-space
$(\mathbb{Z}^2,\mathbb{N}^2)$
-space
![]() $(Y_{\alpha,\eta },X_{\alpha,\eta })$
.
$(Y_{\alpha,\eta },X_{\alpha,\eta })$
.
Proposition 5.2. With the foregoing notation, we have the following.
-
1. The
 $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
 $Y_{\alpha,\eta }$
is essentially free and ergodic.
$Y_{\alpha,\eta }$
is essentially free and ergodic.
-
2. The measure
 $\mu _{\alpha,\eta }$
is of type II.
$\mu _{\alpha,\eta }$
is of type II.
-
3. The map
is injective. \begin{equation*} Y_{\alpha,\eta } \ni {(x,t)} \to Q_{(x,t)} \in Y_u\end{equation*}
\begin{equation*} Y_{\alpha,\eta } \ni {(x,t)} \to Q_{(x,t)} \in Y_u\end{equation*}
-
4. Suppose
 $\alpha _1,\alpha _2 \in (0,\frac{1}{2})$
are distinct irrationals, and let
$\alpha _1,\alpha _2 \in (0,\frac{1}{2})$
are distinct irrationals, and let
 $\eta _1,\eta _2 \in (0,1)$
be such that for
$\eta _1,\eta _2 \in (0,1)$
be such that for
 $i=1,2$
,
$i=1,2$
,
 $\eta _i \lt \min \{\alpha _i,1-\alpha _i\}$
. Then, the
$\eta _i \lt \min \{\alpha _i,1-\alpha _i\}$
. Then, the
 $(\mathbb{Z}^2,\mathbb{N}^2)$
-spaces
$(\mathbb{Z}^2,\mathbb{N}^2)$
-spaces
 $(Y_{\alpha _1,\eta _1}, X_{\alpha _1,\eta _1},\mu _{\alpha _1,\eta _1})$
and
$(Y_{\alpha _1,\eta _1}, X_{\alpha _1,\eta _1},\mu _{\alpha _1,\eta _1})$
and
 $(Y_{\alpha _2,\eta _2}, X_{\alpha _2,\eta _2},\mu _{\alpha _2,\eta _2})$
are not isomorphic. In particular, there are uncountably many type II extremal
$(Y_{\alpha _2,\eta _2}, X_{\alpha _2,\eta _2},\mu _{\alpha _2,\eta _2})$
are not isomorphic. In particular, there are uncountably many type II extremal
 $\beta$
-KMS states for
$\beta$
-KMS states for
 $\theta =1$
.
$\theta =1$
.
Proof. Note that
![]() $\mu _{\alpha,\eta }$
is absolutely continuous w.r.t.
$\mu _{\alpha,\eta }$
is absolutely continuous w.r.t.
![]() $dxdn$
which is a
$dxdn$
which is a
![]() $\mathbb{Z}^2$
-invariant measure. The proofs of
$\mathbb{Z}^2$
-invariant measure. The proofs of
![]() $(1)$
and
$(1)$
and
![]() $(3)$
are very similar to the proof of Proposition 4.4. The proof that the map
$(3)$
are very similar to the proof of Proposition 4.4. The proof that the map
is injective is similar to Proposition 4.4, where instead of Lemma 4.2, we use Part
![]() $(2)$
of Lemma 5.1.
$(2)$
of Lemma 5.1.
We now prove
![]() $(4)$
. Let
$(4)$
. Let
![]() $\alpha _1,\alpha _2 \in (0,\frac{1}{2})$
be irrationals, and let
$\alpha _1,\alpha _2 \in (0,\frac{1}{2})$
be irrationals, and let
![]() $\eta _1,\eta _2 \in (0,1)$
be such that for
$\eta _1,\eta _2 \in (0,1)$
be such that for
![]() $i=1,2$
,
$i=1,2$
,
![]() $\eta _i \lt \min \{\alpha _i,1-\alpha _i\}$
. Suppose
$\eta _i \lt \min \{\alpha _i,1-\alpha _i\}$
. Suppose
![]() $(Y_{\alpha _1,\eta _1},X_{\alpha _1,\eta _1},\mu _{\alpha _1,\eta _1})$
and
$(Y_{\alpha _1,\eta _1},X_{\alpha _1,\eta _1},\mu _{\alpha _1,\eta _1})$
and
![]() $(Y_{\alpha _2,\eta _2},X_{\alpha _2,\eta _2},\mu _{\alpha _2,\eta _2})$
are isomorphic. Then, there exist
$(Y_{\alpha _2,\eta _2},X_{\alpha _2,\eta _2},\mu _{\alpha _2,\eta _2})$
are isomorphic. Then, there exist
![]() $\mathbb{Z}^2$
-invariant null sets
$\mathbb{Z}^2$
-invariant null sets
![]() $N_{\alpha _i} \subset Y_{\alpha _i,\eta _i}$
for
$N_{\alpha _i} \subset Y_{\alpha _i,\eta _i}$
for
![]() $i=1,2$
and an invertible measurable map
$i=1,2$
and an invertible measurable map
![]() $S\,:\,Y_{\alpha _1,\eta _1}\backslash N_{\alpha _1} \to Y_{\alpha _2,\eta _2} \backslash N_{\alpha _2}$
such that
$S\,:\,Y_{\alpha _1,\eta _1}\backslash N_{\alpha _1} \to Y_{\alpha _2,\eta _2} \backslash N_{\alpha _2}$
such that
-
(i) the map
 $S$
is
$S$
is
 $\mathbb{Z}^2$
-equivariant,
$\mathbb{Z}^2$
-equivariant,
 $S(X_{\alpha _1,\eta _1}\backslash N_{\alpha _1})=X_{\alpha _2,\eta _2}\backslash N_{\alpha _2}$
, and
$S(X_{\alpha _1,\eta _1}\backslash N_{\alpha _1})=X_{\alpha _2,\eta _2}\backslash N_{\alpha _2}$
, and -
(ii) for every Borel subset
 $E \subset Y_{\alpha _2,\eta _2} \backslash N_{\alpha _2}$
,
$E \subset Y_{\alpha _2,\eta _2} \backslash N_{\alpha _2}$
,
 $\mu _{\alpha _2,\eta _2}(E)=\mu _{\alpha _1,\eta _1}(S^{-1}(E))$
.
$\mu _{\alpha _2,\eta _2}(E)=\mu _{\alpha _1,\eta _1}(S^{-1}(E))$
.
Since
![]() $\mu _{\alpha _i,\eta _i}$
is absolutely continuous w.r.t.
$\mu _{\alpha _i,\eta _i}$
is absolutely continuous w.r.t.
![]() $dxdn$
, it follows that
$dxdn$
, it follows that
![]() $S$
preserves the measure
$S$
preserves the measure
![]() $dxdn$
. Let
$dxdn$
. Let
![]() $S(x,t)=(S_1(x,t), S_2(x,t))$
, where
$S(x,t)=(S_1(x,t), S_2(x,t))$
, where
![]() $S_1$
and
$S_1$
and
![]() $S_2$
are the coordinate functions. Note that
$S_2$
are the coordinate functions. Note that
![]() $e_2$
acts by translation by 1 on the second coordinate. Hence, for
$e_2$
acts by translation by 1 on the second coordinate. Hence, for
![]() $i=1,2$
,
$i=1,2$
,
![]() $N_{\alpha _i}$
must be of the form
$N_{\alpha _i}$
must be of the form
![]() $N_{\alpha _i}=U_{\alpha _i} \times \mathbb{Z}$
for some
$N_{\alpha _i}=U_{\alpha _i} \times \mathbb{Z}$
for some
![]() $R_{\alpha _i}$
-invariant subset
$R_{\alpha _i}$
-invariant subset
![]() $U_{\alpha _i}\subseteq \mathbb{T}$
. Since the map
$U_{\alpha _i}\subseteq \mathbb{T}$
. Since the map
![]() $S$
is
$S$
is
![]() $\mathbb{Z}^2$
-equivariant, from the action of
$\mathbb{Z}^2$
-equivariant, from the action of
![]() $e_2$
, we notice that,
$e_2$
, we notice that,
In particular, the function
![]() $(x,t) \to S_1(x,t)$
does not depend on
$(x,t) \to S_1(x,t)$
does not depend on
![]() $t$
. As
$t$
. As
![]() $S$
maps
$S$
maps
![]() $X_{\alpha _1,\eta _1}\backslash N_{\alpha _1}$
onto
$X_{\alpha _1,\eta _1}\backslash N_{\alpha _1}$
onto
![]() $X_{\alpha _2,\eta _2}\backslash N_{\alpha _2}$
and
$X_{\alpha _2,\eta _2}\backslash N_{\alpha _2}$
and
![]() $X_{\alpha _i,\eta _i}\backslash (X_{\alpha _i,\eta _i}+e_2)=\mathbb{T} \times \{0\}$
, it follows that
$X_{\alpha _i,\eta _i}\backslash (X_{\alpha _i,\eta _i}+e_2)=\mathbb{T} \times \{0\}$
, it follows that
![]() $S_2(x,0)=0$
for
$S_2(x,0)=0$
for
![]() $x \in \mathbb{T} \backslash U_{\alpha _1}$
. Equation (5.9) implies that
$x \in \mathbb{T} \backslash U_{\alpha _1}$
. Equation (5.9) implies that
![]() $S_2(x,t)=t$
for
$S_2(x,t)=t$
for
![]() $(x,t) \in \mathbb{T}\backslash U_{\alpha _1} \times \mathbb{Z}$
.
$(x,t) \in \mathbb{T}\backslash U_{\alpha _1} \times \mathbb{Z}$
.
Now, from the action of
![]() $e_1$
, and by equation (5.9), we can conclude that
$e_1$
, and by equation (5.9), we can conclude that
Define a map
![]() $\widetilde{S}\,:\,\mathbb{T} \backslash U_{\alpha _1} \to \mathbb{T} \backslash U_{\alpha _2}$
by
$\widetilde{S}\,:\,\mathbb{T} \backslash U_{\alpha _1} \to \mathbb{T} \backslash U_{\alpha _2}$
by
![]() $\widetilde{S}(x)=S_1(x,0)$
. Then,
$\widetilde{S}(x)=S_1(x,0)$
. Then,
![]() $\widetilde{S}$
is an isomorphism between
$\widetilde{S}$
is an isomorphism between
![]() $(\mathbb{T},dx,R_{\alpha _1})$
and
$(\mathbb{T},dx,R_{\alpha _1})$
and
![]() $(\mathbb{T},dx,R_{\alpha _2})$
. This implies that
$(\mathbb{T},dx,R_{\alpha _2})$
. This implies that
![]() $\alpha _1=\alpha _2$
. This completes the proof.
$\alpha _1=\alpha _2$
. This completes the proof.
Type III examples: The uncountably many type III examples that we construct are directly based on the works of Nakada ( [Reference Nakada21] and [Reference Nakada20]) on cylinder flows. We follow the exposition given in [Reference Aaronson, Nakada, Sarig and Solomyak2] and recall a few facts from [Reference Aaronson, Nakada, Sarig and Solomyak2] concerning the ergodicity of cylinder flows. Let
![]() $\beta \gt 0$
be fixed. For an irrational
$\beta \gt 0$
be fixed. For an irrational
![]() $\alpha \in (0,1)$
, let
$\alpha \in (0,1)$
, let
![]() $R_\alpha$
be the rotation on
$R_\alpha$
be the rotation on
![]() $\mathbb{T}$
by angle
$\mathbb{T}$
by angle
![]() $\alpha$
. We use additive notation. Thus,
$\alpha$
. We use additive notation. Thus,
![]() $\mathbb{T}=[0,1)$
and
$\mathbb{T}=[0,1)$
and
![]() $R_\alpha (x)=x+\alpha \mod 1$
. For
$R_\alpha (x)=x+\alpha \mod 1$
. For
![]() $\gamma \gt 0$
, let
$\gamma \gt 0$
, let
![]() $F_{\gamma }\,:\,[0,1) \to \mathbb{C}$
be defined by
$F_{\gamma }\,:\,[0,1) \to \mathbb{C}$
be defined by
 \begin{equation} F_{\gamma }(x)\,:\!=\,\begin{cases} 1 & \mbox{ if } x \in [0,\frac{\gamma }{\gamma +1}),\\ -\gamma & \mbox{ if } x \in [\frac{\gamma }{\gamma +1},1). \end{cases} \end{equation}
\begin{equation} F_{\gamma }(x)\,:\!=\,\begin{cases} 1 & \mbox{ if } x \in [0,\frac{\gamma }{\gamma +1}),\\ -\gamma & \mbox{ if } x \in [\frac{\gamma }{\gamma +1},1). \end{cases} \end{equation}
Remark 5.2 (Nakada). Thanks to Proposition 1.1, Theorem 1.4 and Theorem 1.6 of [2], we have the following.
-
(a) There exists a unique non-atomic probability measure
 $m\,:\!=\,m_{\alpha,\beta,\gamma }$
on
$m\,:\!=\,m_{\alpha,\beta,\gamma }$
on
 $\mathbb{T}$
such that
$\mathbb{T}$
such that
 $\frac{d(m\circ R_\alpha )}{dm}=e^{-\beta F_\gamma }$
. Moreover,
$\frac{d(m\circ R_\alpha )}{dm}=e^{-\beta F_\gamma }$
. Moreover,
 $(R_\alpha,m)$
is ergodic.
$(R_\alpha,m)$
is ergodic.
-
(b) The measure
 $m_{\alpha,\beta,1}$
is of type III.
$m_{\alpha,\beta,1}$
is of type III.
-
(c) Suppose
 $\alpha$
has bounded partial quotients and
$\alpha$
has bounded partial quotients and
 $\frac{\gamma }{\gamma +1} \notin \mathbb{Q}+\mathbb{Q}\alpha$
. Then,
$\frac{\gamma }{\gamma +1} \notin \mathbb{Q}+\mathbb{Q}\alpha$
. Then,
 $m_{\alpha,\beta,\gamma }$
is of type III.
$m_{\alpha,\beta,\gamma }$
is of type III.
We also need the description of the spectrum of
![]() $R_\alpha$
given in [20] (Page 476, Paragraph 1). Let
$R_\alpha$
given in [20] (Page 476, Paragraph 1). Let
![]() $\beta, \gamma \gt 0$
be given. Define
$\beta, \gamma \gt 0$
be given. Define
If
![]() $\alpha$
has bounded partial quotients, then
$\alpha$
has bounded partial quotients, then
![]() $Spec(R_\alpha )=\{e^{2\pi i n\alpha }\,:\,n \in \mathbb{Z}\}$
. In particular, if
$Spec(R_\alpha )=\{e^{2\pi i n\alpha }\,:\,n \in \mathbb{Z}\}$
. In particular, if
![]() $\alpha _1,\alpha _2 \in (0,\frac{1}{2})$
are distinct irrationals having bounded partial quotients, then the dynamical systems
$\alpha _1,\alpha _2 \in (0,\frac{1}{2})$
are distinct irrationals having bounded partial quotients, then the dynamical systems
![]() $(\mathbb{T},m_{\alpha _1,\beta,\gamma }, R_{\alpha _1})$
and
$(\mathbb{T},m_{\alpha _1,\beta,\gamma }, R_{\alpha _1})$
and
![]() $(\mathbb{T},m_{\alpha _2,\beta,\gamma },R_{\alpha _2})$
are not metrically isomorphic.
$(\mathbb{T},m_{\alpha _2,\beta,\gamma },R_{\alpha _2})$
are not metrically isomorphic.
The case
![]() $\theta =1$
: Let
$\theta =1$
: Let
![]() $\alpha \in (0,1)$
be an irrational, and let
$\alpha \in (0,1)$
be an irrational, and let
![]() $R_\alpha$
denote the rotation on
$R_\alpha$
denote the rotation on
![]() $\mathbb{T}$
by angle
$\mathbb{T}$
by angle
![]() $\alpha$
. Take
$\alpha$
. Take
![]() $\gamma =1$
in equation (5.10), and consider
$\gamma =1$
in equation (5.10), and consider
![]() $F_1$
given by,
$F_1$
given by,
 \begin{equation*} F_1(x)=\begin {cases} 1 & \mbox { if} x \in [0,\frac {1}{2}),\\ -1 & \mbox { if } x \in [\frac {1}{2},1). \end {cases} \end{equation*}
\begin{equation*} F_1(x)=\begin {cases} 1 & \mbox { if} x \in [0,\frac {1}{2}),\\ -1 & \mbox { if } x \in [\frac {1}{2},1). \end {cases} \end{equation*}
Then by
![]() $(a)$
and
$(a)$
and
![]() $(b)$
of Remark 5.2, there exists a unique non-atomic type III probability measure
$(b)$
of Remark 5.2, there exists a unique non-atomic type III probability measure
![]() $m\,:\!=\,m_{\alpha,\beta,1}$
such that
$m\,:\!=\,m_{\alpha,\beta,1}$
such that
![]() $\frac{d(m\circ R_\alpha )}{dm}=e^{-\beta F_1}$
.
$\frac{d(m\circ R_\alpha )}{dm}=e^{-\beta F_1}$
.
Recall that the homomorphism
![]() $c\,:\,G \to \mathbb{R}$
is given by
$c\,:\,G \to \mathbb{R}$
is given by
![]() $c(v_1)=1$
and
$c(v_1)=1$
and
![]() $c(v_2)=2$
. Define
$c(v_2)=2$
. Define
![]() $Y_{\alpha }=\mathbb{T} \times \mathbb{Z}$
, and set
$Y_{\alpha }=\mathbb{T} \times \mathbb{Z}$
, and set
![]() $X_{\alpha }=\mathbb{T} \times \{0,1,2,\cdots \}$
. Let
$X_{\alpha }=\mathbb{T} \times \{0,1,2,\cdots \}$
. Let
![]() $\mu _\alpha$
be the measure on
$\mu _\alpha$
be the measure on
![]() $Y_{\alpha }$
defined by,
$Y_{\alpha }$
defined by,
for a measurable subset
![]() $E\subset \mathbb{T}$
. Clearly,
$E\subset \mathbb{T}$
. Clearly,
![]() $\mu _{\alpha }(X_\alpha )=1$
. Define a
$\mu _{\alpha }(X_\alpha )=1$
. Define a
![]() $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
![]() $Y_{\alpha }$
by
$Y_{\alpha }$
by
It is easy to see that
![]() $(Y_{\alpha },X_{\alpha })$
is a pure
$(Y_{\alpha },X_{\alpha })$
is a pure
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-space and
$(\mathbb{Z}^2,\mathbb{N}^2)$
-space and
![]() $\mu _\alpha$
is an
$\mu _\alpha$
is an
![]() $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
![]() $Y_{\alpha }$
.
$Y_{\alpha }$
.
Proposition 5.3. With the foregoing notation, we have the following.
-
1. The
 $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
 $Y_\alpha$
is essentially free and ergodic.
$Y_\alpha$
is essentially free and ergodic.
-
2. The measure
 $\mu _\alpha$
is of type III.
$\mu _\alpha$
is of type III.
-
3. The map
is injective. \begin{equation*} Y_{\alpha } \ni {(x,t)} \to Q_{(x,t)} \in Y_u\end{equation*}
\begin{equation*} Y_{\alpha } \ni {(x,t)} \to Q_{(x,t)} \in Y_u\end{equation*}
-
4. If
 $\alpha _1\neq \alpha _2$
are distinct irrationals in
$\alpha _1\neq \alpha _2$
are distinct irrationals in
 $(0,\frac{1}{2})$
having bounded partial quotients, then the
$(0,\frac{1}{2})$
having bounded partial quotients, then the
 $(\mathbb{Z}^2,\mathbb{N}^2)$
-spaces
$(\mathbb{Z}^2,\mathbb{N}^2)$
-spaces
 $(Y_{\alpha _1}, X_{\alpha _1},\mu _{\alpha _1})$
and
$(Y_{\alpha _1}, X_{\alpha _1},\mu _{\alpha _1})$
and
 $(Y_{\alpha _2}, X_{\alpha _2},\mu _{\alpha _2})$
are not isomorphic. In particular, there are uncountably many type III extremal
$(Y_{\alpha _2}, X_{\alpha _2},\mu _{\alpha _2})$
are not isomorphic. In particular, there are uncountably many type III extremal
 $\beta$
-KMS states for
$\beta$
-KMS states for
 $\theta =1$
.
$\theta =1$
.
Proof. With Remark 5.2 in hand, the proofs of
![]() $(1)$
,
$(1)$
,
![]() $(2)$
and
$(2)$
and
![]() $(3)$
are exactly similar to the proof of Proposition 4.4, and hence, we omit the proof. For example, the proof for the injectivity of the map
$(3)$
are exactly similar to the proof of Proposition 4.4, and hence, we omit the proof. For example, the proof for the injectivity of the map
is similar to that of Proposition 4.4, where we work in the coordinate system determined by
![]() $\{v_1,v_2\}$
, the function
$\{v_1,v_2\}$
, the function
![]() $\phi$
is replaced with
$\phi$
is replaced with
![]() $1_{[\frac{1}{2},1)}$
and in place of Lemma 4.2, we appeal to Lemma 5.1 with
$1_{[\frac{1}{2},1)}$
and in place of Lemma 4.2, we appeal to Lemma 5.1 with
![]() $\eta =\frac{1}{2}$
. With the description of the spectrum alluded to in Remark 5.2, the proof of
$\eta =\frac{1}{2}$
. With the description of the spectrum alluded to in Remark 5.2, the proof of
![]() $(4)$
is very similar to the proof of Part
$(4)$
is very similar to the proof of Part
![]() $(4)$
of Lemma 5.2. We leave the details to the reader.
$(4)$
of Lemma 5.2. We leave the details to the reader.
The case of an irrational
![]() $\theta$
: The construction of type III examples for an irrational
$\theta$
: The construction of type III examples for an irrational
![]() $\theta$
is similar to the case
$\theta$
is similar to the case
![]() $\theta =1$
. Recall that the homomorphism
$\theta =1$
. Recall that the homomorphism
![]() $c\,:\,G \to \mathbb{R}$
is given by
$c\,:\,G \to \mathbb{R}$
is given by
![]() $c(e_1)=1$
and
$c(e_1)=1$
and
![]() $c(e_2)=\theta$
. Take
$c(e_2)=\theta$
. Take
![]() $\gamma =\theta$
in 5.10, and let
$\gamma =\theta$
in 5.10, and let
![]() $F_{\theta }$
be the function defined by
$F_{\theta }$
be the function defined by
 \begin{equation*} F_{\theta }(x)=\begin {cases} 1 & \mbox {if} x \in [0,\frac {\theta }{\theta +1}),\\ -\theta & \mbox { if } x \in [\frac {\theta }{\theta +1},1). \end {cases} \end{equation*}
\begin{equation*} F_{\theta }(x)=\begin {cases} 1 & \mbox {if} x \in [0,\frac {\theta }{\theta +1}),\\ -\theta & \mbox { if } x \in [\frac {\theta }{\theta +1},1). \end {cases} \end{equation*}
Choose
![]() $\alpha \in [0,1)\backslash \mathbb{Q}$
such that
$\alpha \in [0,1)\backslash \mathbb{Q}$
such that
![]() $\alpha$
has bounded partial quotients and
$\alpha$
has bounded partial quotients and
![]() $\frac{\theta }{\theta +1} \notin \mathbb{Q}+\mathbb{Q}\alpha$
. Then, by
$\frac{\theta }{\theta +1} \notin \mathbb{Q}+\mathbb{Q}\alpha$
. Then, by
![]() $(a)$
and
$(a)$
and
![]() $(c)$
of Remark 5.2, there exists a unique non-atomic type III probability measure
$(c)$
of Remark 5.2, there exists a unique non-atomic type III probability measure
![]() $m\,:\!=\,m_{\alpha,\beta,\theta }$
on
$m\,:\!=\,m_{\alpha,\beta,\theta }$
on
![]() $\mathbb{T}$
such that
$\mathbb{T}$
such that
![]() $\frac{d(m\circ R_\alpha )}{dm}=e^{-\beta F_\theta }$
.
$\frac{d(m\circ R_\alpha )}{dm}=e^{-\beta F_\theta }$
.
Define
![]() $Y_{\alpha }=\mathbb{T} \times \mathbb{Z}$
, and set
$Y_{\alpha }=\mathbb{T} \times \mathbb{Z}$
, and set
![]() $X_{\alpha }=\mathbb{T} \times \{0,1,2,\cdots \}$
. Let
$X_{\alpha }=\mathbb{T} \times \{0,1,2,\cdots \}$
. Let
![]() $\mu _\alpha$
be the measure on
$\mu _\alpha$
be the measure on
![]() $Y_{\alpha }$
given by,
$Y_{\alpha }$
given by,
for a measurable subset
![]() $E\subset \mathbb{T}$
. Clearly,
$E\subset \mathbb{T}$
. Clearly,
![]() $\mu _{\alpha }(X_{\alpha })=1$
. Define a
$\mu _{\alpha }(X_{\alpha })=1$
. Define a
![]() $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
![]() $Y_{\alpha }$
by
$Y_{\alpha }$
by
It is easy to see that
![]() $(Y_{\alpha },X_{\alpha })$
is a pure
$(Y_{\alpha },X_{\alpha })$
is a pure
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-space and
$(\mathbb{Z}^2,\mathbb{N}^2)$
-space and
![]() $\mu _\alpha$
is an
$\mu _\alpha$
is an
![]() $e^{-\beta c}$
-conformal measure on
$e^{-\beta c}$
-conformal measure on
![]() $Y_\alpha$
.
$Y_\alpha$
.
If we make use of Remark 5.2, the proof of the following proposition is similar to that of Proposition 5.3, and hence, the proof is omitted.
Proposition 5.4. With the foregoing notation, we have the following.
-
1. The
 $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
 $Y_\alpha$
is essentially free and ergodic.
$Y_\alpha$
is essentially free and ergodic.
-
2. The measure
 $\mu _\alpha$
is of type III.
$\mu _\alpha$
is of type III.
-
3. The map
is injective. \begin{equation*} Y_{\alpha } \ni {(x,t)} \to Q_{(x,t)} \in Y_u\end{equation*}
\begin{equation*} Y_{\alpha } \ni {(x,t)} \to Q_{(x,t)} \in Y_u\end{equation*}
-
4. Suppose
 $\alpha _1\neq \alpha _2$
are distinct irrationals in
$\alpha _1\neq \alpha _2$
are distinct irrationals in
 $(0,\frac{1}{2})$
having bounded partial quotients such that
$(0,\frac{1}{2})$
having bounded partial quotients such that
 $\frac{\theta }{1+\theta } \notin \mathbb{Q}+\mathbb{Q}\alpha _i$
for
$\frac{\theta }{1+\theta } \notin \mathbb{Q}+\mathbb{Q}\alpha _i$
for
 $i=1,2$
. Then, the
$i=1,2$
. Then, the
 $(\mathbb{Z}^2,\mathbb{N}^2)$
-spaces
$(\mathbb{Z}^2,\mathbb{N}^2)$
-spaces
 $(Y_{\alpha _1}, X_{\alpha _1},\mu _{\alpha _1})$
and
$(Y_{\alpha _1}, X_{\alpha _1},\mu _{\alpha _1})$
and
 $(Y_{\alpha _2}, X_{\alpha _2},\mu _{\alpha _2})$
are not isomorphic. In particular, there are uncountably many type III extremal
$(Y_{\alpha _2}, X_{\alpha _2},\mu _{\alpha _2})$
are not isomorphic. In particular, there are uncountably many type III extremal
 $\beta$
-KMS states when
$\beta$
-KMS states when
 $\theta$
is irrational.
$\theta$
is irrational.
The type II and type III examples for other rational values of
![]() $\theta$
can be constructed from the base case
$\theta$
can be constructed from the base case
![]() $\theta =1$
as follows. Let
$\theta =1$
as follows. Let
![]() $\theta \,:\!=\,\frac{p}{q}$
be a positive rational. Assume that
$\theta \,:\!=\,\frac{p}{q}$
be a positive rational. Assume that
![]() $\gcd (p,q)=1$
. Choose a matrix
$\gcd (p,q)=1$
. Choose a matrix
 $\begin{bmatrix} x & \quad y \\[4pt] z & \quad w\\ \end{bmatrix} \in SL_2(\mathbb{Z})$
such that
$\begin{bmatrix} x & \quad y \\[4pt] z & \quad w\\ \end{bmatrix} \in SL_2(\mathbb{Z})$
such that
![]() $x,y,z,w \geq 0$
and
$x,y,z,w \geq 0$
and
To see that this is possible, observe that if
![]() $q=1$
, then the matrix
$q=1$
, then the matrix
 $\begin{bmatrix} 1 & \quad p-1 \\[4pt] 0 & \quad 1 \end{bmatrix}$
will do. Suppose
$\begin{bmatrix} 1 & \quad p-1 \\[4pt] 0 & \quad 1 \end{bmatrix}$
will do. Suppose
![]() $q \geq 2$
. Choose
$q \geq 2$
. Choose
![]() $x \in \{1,2,\cdots,q-1\}$
such that
$x \in \{1,2,\cdots,q-1\}$
such that
![]() $xp \equiv 1 \mod q$
. Write
$xp \equiv 1 \mod q$
. Write
![]() $xp=yq+1$
with
$xp=yq+1$
with
![]() $y \in \mathbb{Z}$
. Set
$y \in \mathbb{Z}$
. Set
![]() $z\,:\!=\,q-x$
and
$z\,:\!=\,q-x$
and
![]() $w\,:\!=\,p-y$
. Then,
$w\,:\!=\,p-y$
. Then,
![]() $x,y,z,w \geq 0$
,
$x,y,z,w \geq 0$
,
 $\begin{bmatrix} x & \quad y \\[4pt] z & \quad w \end{bmatrix} \in SL_2(\mathbb{Z})$
and
$\begin{bmatrix} x & \quad y \\[4pt] z & \quad w \end{bmatrix} \in SL_2(\mathbb{Z})$
and
Let us fix notation. Let
![]() $\phi \,:\,\mathbb{Z}^2 \to \mathbb{Z}^2$
be the isomorphism that corresponds to the matrix
$\phi \,:\,\mathbb{Z}^2 \to \mathbb{Z}^2$
be the isomorphism that corresponds to the matrix
 $\begin{bmatrix} x & \quad y \\[4pt] z & \quad w \end{bmatrix}$
. Note that
$\begin{bmatrix} x & \quad y \\[4pt] z & \quad w \end{bmatrix}$
. Note that
![]() $\phi (\mathbb{N}^2) \subset \mathbb{N}^2$
. We denote the homomorphism
$\phi (\mathbb{N}^2) \subset \mathbb{N}^2$
. We denote the homomorphism
![]() $\mathbb{Z}^2 \to \mathbb{R}$
that sends
$\mathbb{Z}^2 \to \mathbb{R}$
that sends
![]() $e_1 \to 1$
and
$e_1 \to 1$
and
![]() $e_2 \to \theta$
by
$e_2 \to \theta$
by
![]() $c_{\theta }$
. If
$c_{\theta }$
. If
![]() $\theta =1$
, we denote
$\theta =1$
, we denote
![]() $c_\theta$
simply by
$c_\theta$
simply by
![]() $c$
. It is clear that
$c$
. It is clear that
![]() $\frac{1}{q}( c \circ \phi )=c_\theta$
.
$\frac{1}{q}( c \circ \phi )=c_\theta$
.
Fix
![]() $\beta \gt 0$
and let
$\beta \gt 0$
and let
![]() $t \in \{II,III\}$
. Let
$t \in \{II,III\}$
. Let
![]() $(Y,X)$
be a pure
$(Y,X)$
be a pure
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-space together with an
$(\mathbb{Z}^2,\mathbb{N}^2)$
-space together with an
![]() $e^{-\frac{\beta c}{q}}$
-conformal measure
$e^{-\frac{\beta c}{q}}$
-conformal measure
![]() $m$
on
$m$
on
![]() $Y$
such that
$Y$
such that
-
(A1) the map
is injective, and \begin{equation*} Y \ni y \to Q_y\,:\!=\{s \in G\,:\, y-s \in X\} \in Y_u\end{equation*}
\begin{equation*} Y \ni y \to Q_y\,:\!=\{s \in G\,:\, y-s \in X\} \in Y_u\end{equation*}
-
(A2) the dynamical system
 $(Y,m,G)$
is essentially free, ergodic and is of type
$(Y,m,G)$
is essentially free, ergodic and is of type
 $t$
.
$t$
.
Define
Define a new
![]() $\mathbb{Z}^2$
-action on
$\mathbb{Z}^2$
-action on
![]() $Y^{\phi }$
as follows:
$Y^{\phi }$
as follows:
With this new action,
![]() $(Y^{\phi },X^{\phi },m^{\phi })$
is a pure
$(Y^{\phi },X^{\phi },m^{\phi })$
is a pure
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-space and
$(\mathbb{Z}^2,\mathbb{N}^2)$
-space and
![]() $m^{\phi }$
is
$m^{\phi }$
is
![]() $e^{-\beta c_\theta }$
-conformal. Since
$e^{-\beta c_\theta }$
-conformal. Since
![]() $\phi$
is an automorphism of
$\phi$
is an automorphism of
![]() $\mathbb{Z}^2$
, it follows that
$\mathbb{Z}^2$
, it follows that
![]() $(Y^{\phi },m^{\phi },\mathbb{Z}^2)$
inherits the essential freeness, ergodicity and the type from that of
$(Y^{\phi },m^{\phi },\mathbb{Z}^2)$
inherits the essential freeness, ergodicity and the type from that of
![]() $(Y,m,\mathbb{Z}^2)$
. Note that for
$(Y,m,\mathbb{Z}^2)$
. Note that for
![]() $y \in Y^{\phi }$
,
$y \in Y^{\phi }$
,
Since the map
![]() $Y \ni y \to Q_y \in Y_u$
is injective, it follows that
$Y \ni y \to Q_y \in Y_u$
is injective, it follows that
![]() $Y^{\phi } \ni y \to Q_{y}^{\phi } \in Y_u$
is injective. Thus, the
$Y^{\phi } \ni y \to Q_{y}^{\phi } \in Y_u$
is injective. Thus, the
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-space
$(\mathbb{Z}^2,\mathbb{N}^2)$
-space
![]() $(Y^{\phi },X^{\phi })$
together with the
$(Y^{\phi },X^{\phi })$
together with the
![]() $e^{-\beta c_\theta }$
-conformal measure satisfies
$e^{-\beta c_\theta }$
-conformal measure satisfies
![]() $(A1)$
and
$(A1)$
and
![]() $(A2)$
.
$(A2)$
.
Moreover, since
![]() $\phi$
is an automorphism, it is clear that the above construction, i.e.
$\phi$
is an automorphism, it is clear that the above construction, i.e.
maps metrically non-isomorphic spaces to metrically non-isomorphic spaces.
As we have already proved the existence of a continuum of metrically non-isomorphic
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-spaces satisfying
$(\mathbb{Z}^2,\mathbb{N}^2)$
-spaces satisfying
![]() $(A1)$
and
$(A1)$
and
![]() $(A2)$
for
$(A2)$
for
![]() $\theta =1$
and for every
$\theta =1$
and for every
![]() $\beta \gt 0$
, we can conclude that that there is a continuum of metrically non-isomorphic
$\beta \gt 0$
, we can conclude that that there is a continuum of metrically non-isomorphic
![]() $(\mathbb{Z}^2,\mathbb{N}^2)$
-spaces that satisfy
$(\mathbb{Z}^2,\mathbb{N}^2)$
-spaces that satisfy
![]() $(A1)$
and
$(A1)$
and
![]() $(A2)$
for every rational
$(A2)$
for every rational
![]() $\theta \gt 0$
and for every
$\theta \gt 0$
and for every
![]() $\beta \gt 0$
. We can apply Proposition 3.5 to conclude that for a rational
$\beta \gt 0$
. We can apply Proposition 3.5 to conclude that for a rational
![]() $\theta \gt 0$
and for every
$\theta \gt 0$
and for every
![]() $\beta \gt 0$
, there are uncountably many
$\beta \gt 0$
, there are uncountably many
![]() $\beta$
-KMS states of type II and of type III.
$\beta$
-KMS states of type II and of type III.
We have now proved the following theorem.
Theorem 5.1.
Suppose
![]() $\theta \gt 0$
Let
$\theta \gt 0$
Let
![]() $\sigma \,:\!=\{\sigma _t\}_{t \in \mathbb{R}}$
be the
$\sigma \,:\!=\{\sigma _t\}_{t \in \mathbb{R}}$
be the
![]() $1$
-parameter group of automorphisms on
$1$
-parameter group of automorphisms on
![]() $C_{c}^{*}(\mathbb{N}^2)$
given by
$C_{c}^{*}(\mathbb{N}^2)$
given by
Then, for every
![]() $\beta \gt 0$
, there is a continuum of extremal
$\beta \gt 0$
, there is a continuum of extremal
![]() $\beta$
-KMS states on
$\beta$
-KMS states on
![]() $C_{c}^{*}(\mathbb{N}^2)$
for
$C_{c}^{*}(\mathbb{N}^2)$
for
![]() $\sigma$
of both type II and type III.
$\sigma$
of both type II and type III.
We end our paper by posing a problem. Constructing type III product measures for the Bernoulli shift on two symbols have always been a subject of interest. The first such example was due to Hamachi ([Reference Hamachi12]). We refer the reader to [Reference Björklund3] and the references therein for more recent developments. In the recent years, the focus is on constructing product measures of various Krieger types. Given this interest, the following question, we believe, is worth investigating.
Question: Let
![]() $\theta \gt 0$
be irrational, and suppose
$\theta \gt 0$
be irrational, and suppose
![]() $\beta \gt 0$
. Let
$\beta \gt 0$
. Let
![]() $\chi \,:\,\{0,1\}^{\mathbb{Z}} \to \mathbb{R}$
be the potential defined by
$\chi \,:\,\{0,1\}^{\mathbb{Z}} \to \mathbb{R}$
be the potential defined by
 \begin{equation*} \chi (x)=\begin {cases} 1 & \mbox { if} x_{0}=0,\\ -\theta & \mbox { if } x_{0}=1. \end {cases} \end{equation*}
\begin{equation*} \chi (x)=\begin {cases} 1 & \mbox { if} x_{0}=0,\\ -\theta & \mbox { if } x_{0}=1. \end {cases} \end{equation*}
-
(1) Does there exist an ergodic probability measure for the Bernoulli shift of type
 $II_\infty$
that is
$II_\infty$
that is
 $e^{-\beta \chi }$
-conformal?
$e^{-\beta \chi }$
-conformal? -
(2) Let
 $\lambda \in [0,1)$
be given. Does there exist an ergodic probability measure of type
$\lambda \in [0,1)$
be given. Does there exist an ergodic probability measure of type
 $III_\lambda$
that is
$III_\lambda$
that is
 $e^{-\beta \chi }$
-conformal?
$e^{-\beta \chi }$
-conformal?
Nakada’s work shows that type
![]() $III_1$
is possible. Note that the type II examples that we have constructed in this paper are of type
$III_1$
is possible. Note that the type II examples that we have constructed in this paper are of type
![]() $II_1$
.
$II_1$
.
Declaration of competing interest
The authors declare none.