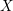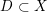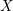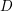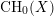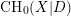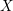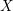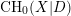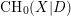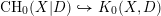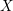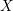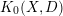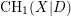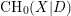1 Introduction
When
![]() $X$
is a smooth quasi-projective scheme over a base field
$X$
is a smooth quasi-projective scheme over a base field
![]() $k$
, the motivic cohomology groups of
$k$
, the motivic cohomology groups of
![]() $X$
admit an explicit description in terms of groups of algebraic cycles, called higher Chow groups, first defined by Bloch [Reference BlochBlo86]. These groups have all the properties that one expects, including Chern classes and a Chern character isomorphism from higher
$X$
admit an explicit description in terms of groups of algebraic cycles, called higher Chow groups, first defined by Bloch [Reference BlochBlo86]. These groups have all the properties that one expects, including Chern classes and a Chern character isomorphism from higher
![]() $K$
-groups, as established in [Reference LevineLev94] and [Reference Friedlander and SuslinFS02], generalizing the well-known relationship between the Chow ring of cycles modulo rational equivalence and the Grothendieck group of vector bundles.
$K$
-groups, as established in [Reference LevineLev94] and [Reference Friedlander and SuslinFS02], generalizing the well-known relationship between the Chow ring of cycles modulo rational equivalence and the Grothendieck group of vector bundles.
Leaving the safe harbor of smooth varieties leads to a different world, where the picture is substantially less clear. One of the simplest examples of singular varieties is the nilpotent thickening
 $X_{m}=X\times _{k}k[t]/(t^{m})$
of a smooth scheme
$X_{m}=X\times _{k}k[t]/(t^{m})$
of a smooth scheme
![]() $X$
. For such a scheme, the beautiful correspondence between motivic cohomology, algebraic cycles and
$X$
. For such a scheme, the beautiful correspondence between motivic cohomology, algebraic cycles and
![]() $K$
-groups is destroyed, since one has
$K$
-groups is destroyed, since one has
 $$\begin{eqnarray}H_{{\mathcal{M}}}^{\ast }(X,\mathbb{Q}(\ast ))=H_{{\mathcal{M}}}^{\ast }(X_{m},\mathbb{Q}(\ast ))\end{eqnarray}$$
$$\begin{eqnarray}H_{{\mathcal{M}}}^{\ast }(X,\mathbb{Q}(\ast ))=H_{{\mathcal{M}}}^{\ast }(X_{m},\mathbb{Q}(\ast ))\end{eqnarray}$$
according to the currently available definitions, preventing the existence of a Grothendieck–Riemann–Roch-type formula relating the motivic cohomology groups of
![]() $X_{m}$
with its higher
$X_{m}$
with its higher
![]() $K$
-groups
$K$
-groups
With the aim of understanding the algebraic
![]() $K$
-theory of the ring
$K$
-theory of the ring
 $k[t]/(t^{2})$
in terms of algebraic cycles, Bloch and Esnault first conceived the idea of algebraic cycles ‘with modulus’, called additive Chow groups at the time, defined by imposing suitable congruence condition at infinity on admissible cycles. This idea subsequently became the starting point of the discovery of the theory of additive cycle complexes and additive higher Chow groups of schemes in the works of Rülling [Reference RüllingRue07], Park [Reference ParkPar09] and Krishna and Levine [Reference Krishna and LevineKL08].
$k[t]/(t^{2})$
in terms of algebraic cycles, Bloch and Esnault first conceived the idea of algebraic cycles ‘with modulus’, called additive Chow groups at the time, defined by imposing suitable congruence condition at infinity on admissible cycles. This idea subsequently became the starting point of the discovery of the theory of additive cycle complexes and additive higher Chow groups of schemes in the works of Rülling [Reference RüllingRue07], Park [Reference ParkPar09] and Krishna and Levine [Reference Krishna and LevineKL08].
The additive higher Chow groups are conjectured to give a cycle-theoretic interpretation of the relative
![]() $K$
-groups
$K$
-groups
 $K_{\ast }(X\times _{k}\mathbb{A}^{1},X_{m})$
for a smooth scheme
$K_{\ast }(X\times _{k}\mathbb{A}^{1},X_{m})$
for a smooth scheme
![]() $X$
. In recent works of Binda and Saito [Reference Binda and SaitoBS16] and Kerz and Saito [Reference Kerz and SaitoKS16], the construction of the additive higher Chow groups was generalized to develop a theory of higher Chow groups with modulus. These groups, denoted
$X$
. In recent works of Binda and Saito [Reference Binda and SaitoBS16] and Kerz and Saito [Reference Kerz and SaitoKS16], the construction of the additive higher Chow groups was generalized to develop a theory of higher Chow groups with modulus. These groups, denoted
 $\text{CH}^{\ast }(X|D,\ast )$
, are designed to study the arithmetic and geometric properties of a smooth variety
$\text{CH}^{\ast }(X|D,\ast )$
, are designed to study the arithmetic and geometric properties of a smooth variety
![]() $X$
with fixed conditions along an effective (possibly non-reduced) Cartier divisor
$X$
with fixed conditions along an effective (possibly non-reduced) Cartier divisor
![]() $D$
on it, and are supposed to give a cycle-theoretic description of the mysterious relative
$D$
on it, and are supposed to give a cycle-theoretic description of the mysterious relative
![]() $K$
-groups
$K$
-groups
 $K_{\ast }(X,D)$
, defined as the homotopy groups of the homotopy fibre of the restriction map
$K_{\ast }(X,D)$
, defined as the homotopy groups of the homotopy fibre of the restriction map
 $K(X)\rightarrow K(D)$
. On the arithmetic side, when
$K(X)\rightarrow K(D)$
. On the arithmetic side, when
![]() $X$
is a smooth variety over a finite field, Kerz and Saito studied the group
$X$
is a smooth variety over a finite field, Kerz and Saito studied the group
 $\text{CH}_{0}(\overline{X}|D)$
for
$\text{CH}_{0}(\overline{X}|D)$
for
![]() $\overline{X}$
an integral compactification of
$\overline{X}$
an integral compactification of
![]() $X$
and
$X$
and
![]() $D$
a non-reduced closed subscheme supported on
$D$
a non-reduced closed subscheme supported on
![]() $\overline{X}\setminus D$
(see [Reference Kerz and SaitoKS16] and 5.1 for the definition), and this has proven to be a fundamental ingredient in the study of wildly ramified class field theory.
$\overline{X}\setminus D$
(see [Reference Kerz and SaitoKS16] and 5.1 for the definition), and this has proven to be a fundamental ingredient in the study of wildly ramified class field theory.
Although recently established results by various authors (see [Reference KaiKai16], [Reference Rülling and SaitoRS16]) have indicated that the Chow groups with modulus (and, more generally, the relative motivic cohomology groups of [Reference Binda and SaitoBS16]) have some of the above expected properties, many questions remain widely open.
In order to provide new evidence that the Chow groups with modulus are the right motivic cohomology groups to compute the relative
![]() $K$
-theory of a smooth scheme with respect to an effective divisor, one would like to know if these groups share enough of the known structural properties of the Chow groups without modulus, and to relate them to some geometric or cohomological invariants of the pair
$K$
-theory of a smooth scheme with respect to an effective divisor, one would like to know if these groups share enough of the known structural properties of the Chow groups without modulus, and to relate them to some geometric or cohomological invariants of the pair
![]() $(X,D)$
. This is the subject of this paper. Our interest is to establish these properties and present (an almost complete) picture for the Chow groups of 0-cycles with modulus.
$(X,D)$
. This is the subject of this paper. Our interest is to establish these properties and present (an almost complete) picture for the Chow groups of 0-cycles with modulus.
We now state our main results. The precise statement of each of these results and the underlying hypothesis and notations will be explained at appropriate places in this text.
1.1 Albanese variety and Roitman torsion theorem with modulus
One of the most important things known about the ordinary Chow group of 0-cycles of a smooth projective variety is that it admits a universal abelian variety quotient (the Albanese variety) which is useful for studying the question of the representability of the Chow group. The celebrated theorem of Roitman [Reference RojtmanRoi80] (see also [Reference MilneMil82] for the case of positive characteristic) says that this quotient map is isomorphism on torsion. This theorem has had profound consequences in the study of the Chow group of 0-cycles. One of the main goals of this paper is to establish these results (under some restrictions in positive characteristic) for the Chow group of 0-cycles with modulus.
Theorem 1.1 (See Theorems 10.3 and 11.3).
Let
![]() $X$
be a smooth projective scheme over an algebraically closed field
$X$
be a smooth projective scheme over an algebraically closed field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then there is a smooth connected algebraic group
$D\subset X$
be an effective Cartier divisor. Then there is a smooth connected algebraic group
 $\text{Alb}(X|D)$
and a group homomorphism
$\text{Alb}(X|D)$
and a group homomorphism
 $\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\text{deg}\,0}\rightarrow \text{Alb}(X|D)$
which is a universal regular quotient of
$\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\text{deg}\,0}\rightarrow \text{Alb}(X|D)$
which is a universal regular quotient of
 $\text{CH}_{0}(X|D)_{\text{deg}\,0}$
.
$\text{CH}_{0}(X|D)_{\text{deg}\,0}$
.
Theorem 1.2 (See Theorems 10.4 and 11.5).
Let
![]() $X$
be a smooth projective scheme over an algebraically closed field
$X$
be a smooth projective scheme over an algebraically closed field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Let
$D\subset X$
be an effective Cartier divisor. Let
![]() $n\in \mathbb{N}$
be an integer prime to the characteristic of
$n\in \mathbb{N}$
be an integer prime to the characteristic of
![]() $k$
. Then
$k$
. Then
![]() $\unicode[STIX]{x1D70C}_{X|D}$
induces an isomorphism
$\unicode[STIX]{x1D70C}_{X|D}$
induces an isomorphism
 $\unicode[STIX]{x1D70C}_{X|D}:\text{}_{n}\text{CH}_{0}(X|D)_{\text{deg}\,0}$
$\unicode[STIX]{x1D70C}_{X|D}:\text{}_{n}\text{CH}_{0}(X|D)_{\text{deg}\,0}$
 $\,\xrightarrow[{}]{\simeq }\,\text{}_{n}\text{Alb}(X|D)$
on the
$\,\xrightarrow[{}]{\simeq }\,\text{}_{n}\text{Alb}(X|D)$
on the
![]() $n$
-torsion subgroups.
$n$
-torsion subgroups.
Note that when
![]() $k=\mathbb{C}$
and
$k=\mathbb{C}$
and
 $D_{\text{red}}\subset X$
is a normal crossing divisor, Theorem 1.1 has been proven, using a completely different approach, in [Reference Binda and SaitoBS16].
$D_{\text{red}}\subset X$
is a normal crossing divisor, Theorem 1.1 has been proven, using a completely different approach, in [Reference Binda and SaitoBS16].
1.2 Bloch’s conjecture for 0-cycles with modulus
Let
![]() $X$
be a smooth projective surface over
$X$
be a smooth projective surface over
![]() $\mathbb{C}$
. Recall that the well-known Bloch conjecture predicts that the Abel–Jacobi map
$\mathbb{C}$
. Recall that the well-known Bloch conjecture predicts that the Abel–Jacobi map
 $\unicode[STIX]{x1D70C}_{X}:\text{CH}_{0}(X)_{\text{deg}~0}\rightarrow \text{Alb}(X)$
is an isomorphism if
$\unicode[STIX]{x1D70C}_{X}:\text{CH}_{0}(X)_{\text{deg}~0}\rightarrow \text{Alb}(X)$
is an isomorphism if
 $H^{2}(X,{\mathcal{O}}_{X})=0$
. Assuming this, we can show that the analogous statement for the Chow group with modulus also holds. In particular, the Bloch conjecture for 0-cycles with modulus is true if
$H^{2}(X,{\mathcal{O}}_{X})=0$
. Assuming this, we can show that the analogous statement for the Chow group with modulus also holds. In particular, the Bloch conjecture for 0-cycles with modulus is true if
![]() $X$
is not of general type. Remarkably, instead of the vanishing of the second cohomology group of the structure sheaf
$X$
is not of general type. Remarkably, instead of the vanishing of the second cohomology group of the structure sheaf
![]() ${\mathcal{O}}_{X}$
, we have to assume the vanishing of the second cohomology group of the ideal sheaf
${\mathcal{O}}_{X}$
, we have to assume the vanishing of the second cohomology group of the ideal sheaf
![]() ${\mathcal{I}}_{D}$
of
${\mathcal{I}}_{D}$
of
![]() $D$
.
$D$
.
Theorem 1.3 (See Theorem 10.8).
Let
![]() $X$
be a smooth projective surface over
$X$
be a smooth projective surface over
![]() $\mathbb{C}$
and let
$\mathbb{C}$
and let
![]() $D\subset X$
be an effective Cartier divisor. Let
$D\subset X$
be an effective Cartier divisor. Let
![]() ${\mathcal{I}}_{D}$
denote the sheaf of ideals defining
${\mathcal{I}}_{D}$
denote the sheaf of ideals defining
![]() $D$
. Assume that the Bloch conjecture is true for
$D$
. Assume that the Bloch conjecture is true for
![]() $X$
. Then the map
$X$
. Then the map
 $\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\text{deg}~0}\rightarrow \text{Alb}(X|D)$
is an isomorphism if
$\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\text{deg}~0}\rightarrow \text{Alb}(X|D)$
is an isomorphism if
 $H^{2}(X,{\mathcal{I}}_{D})=0$
.
$H^{2}(X,{\mathcal{I}}_{D})=0$
.
1.3 Torsion theorem for 0-cycles with modulus on affine schemes
Assume now that
![]() $X$
is a smooth affine variety over an algebraically closed field
$X$
is a smooth affine variety over an algebraically closed field
![]() $k$
. One of the consequences of Roitman’s theorem is that the Chow group of 0-cycles on
$k$
. One of the consequences of Roitman’s theorem is that the Chow group of 0-cycles on
![]() $X$
has no torsion, and this itself has had many applications to projective modules on smooth affine varieties. Here comes the extension of this statement to the 0-cycles with modulus.
$X$
has no torsion, and this itself has had many applications to projective modules on smooth affine varieties. Here comes the extension of this statement to the 0-cycles with modulus.
Theorem 1.4 (See Theorem 14.1).
Let
![]() $X$
be a smooth affine scheme of dimension
$X$
be a smooth affine scheme of dimension
![]() $d\geqslant 2$
over an algebraically closed field
$d\geqslant 2$
over an algebraically closed field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then
$D\subset X$
be an effective Cartier divisor. Then
 $\text{CH}_{0}(X|D)$
is torsion-free.
$\text{CH}_{0}(X|D)$
is torsion-free.
In the presence of a modulus, however, the classical argument to deduce Theorem 1.4 from Roitman’s Theorem does not go through. For example, the localization sequence for the ordinary Chow groups, which is one of the steps of the proof of the classical case, fails in the modulus setting, as explained in [Reference KrishnaKri15a, Theorem 1.5]. Our approach is to deduce Theorem 1.4 directly from Theorem 1.9 below.
1.4 Cycle class map to relative
 $K$
-theory
$K$
-theory
In the direction of understanding the relation between 0-cycles with modulus and relative
![]() $K$
-theory, we have the following results.
$K$
-theory, we have the following results.
Theorem 1.5 (See Theorem 12.4).
Let
![]() $X$
be a smooth quasi-projective scheme of dimension
$X$
be a smooth quasi-projective scheme of dimension
![]() $d\geqslant 1$
over a perfect field
$d\geqslant 1$
over a perfect field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then, there is a cycle class map
$D\subset X$
be an effective Cartier divisor. Then, there is a cycle class map
 $$\begin{eqnarray}\text{cyc}_{X|D}:\text{CH}_{0}(X|D)\rightarrow K_{0}(X,D).\end{eqnarray}$$
$$\begin{eqnarray}\text{cyc}_{X|D}:\text{CH}_{0}(X|D)\rightarrow K_{0}(X,D).\end{eqnarray}$$
This map is injective if
![]() $k$
is algebraically closed and
$k$
is algebraically closed and
![]() $X$
is affine.
$X$
is affine.
When
![]() $X$
has dimension two, we can prove the following stronger statement which completely describes
$X$
has dimension two, we can prove the following stronger statement which completely describes
 $K_{0}(X,D)$
in terms of the Chow groups with modulus.
$K_{0}(X,D)$
in terms of the Chow groups with modulus.
Theorem 1.6 (See Theorems 14.6 and 14.7).
Let
![]() $X$
be a smooth affine surface over an algebraically closed field
$X$
be a smooth affine surface over an algebraically closed field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then, the canonical map
$D\subset X$
be an effective Cartier divisor. Then, the canonical map
 $\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(X|D_{\text{red}})$
is an isomorphism and there is an exact sequence
$\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(X|D_{\text{red}})$
is an isomorphism and there is an exact sequence
 $$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\rightarrow K_{0}(X,D)\rightarrow \text{CH}_{1}(X|D)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\rightarrow K_{0}(X,D)\rightarrow \text{CH}_{1}(X|D)\rightarrow 0.\end{eqnarray}$$
Finally, for arbitrary quasi-projective surfaces, we prove the following structural result, that we may see as an integral version of a Riemann–Roch-type formula for the relative
![]() $K_{0}$
-group of the pair
$K_{0}$
-group of the pair
![]() $(X,D)$
.
$(X,D)$
.
Theorem 1.7 (See Theorem 13.4).
Let
![]() $X$
be a smooth quasi-projective surface over an algebraically closed field
$X$
be a smooth quasi-projective surface over an algebraically closed field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then, there is a cycle class map
$D\subset X$
be an effective Cartier divisor. Then, there is a cycle class map
 $\text{cyc}_{X|D}:\text{CH}_{0}(X|D)\rightarrow K_{0}(X,D)$
and a short exact sequence
$\text{cyc}_{X|D}:\text{CH}_{0}(X|D)\rightarrow K_{0}(X,D)$
and a short exact sequence
 $$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\rightarrow K_{0}(X,D)\rightarrow \operatorname{Pic}(X,D)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\rightarrow K_{0}(X,D)\rightarrow \operatorname{Pic}(X,D)\rightarrow 0.\end{eqnarray}$$
1.5 Bloch’s formula
As an application of Theorem 1.7, we get the following Bloch’s formula for cycles with modulus on surfaces.
Theorem 1.8 (Bloch’s formula).
Let
![]() $X$
be a smooth quasi-projective surface over an algebraically closed field
$X$
be a smooth quasi-projective surface over an algebraically closed field
![]() $k$
. Let
$k$
. Let
![]() $D\subset X$
be an effective Cartier divisor. Then, there are isomorphisms
$D\subset X$
be an effective Cartier divisor. Then, there are isomorphisms
 $$\begin{eqnarray}\text{CH}_{0}(X|D)\xrightarrow[{}]{\simeq }H_{\text{zar}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M})\xrightarrow[{}]{\simeq }H_{\text{nis}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M}).\end{eqnarray}$$
$$\begin{eqnarray}\text{CH}_{0}(X|D)\xrightarrow[{}]{\simeq }H_{\text{zar}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M})\xrightarrow[{}]{\simeq }H_{\text{nis}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M}).\end{eqnarray}$$
1.6 The decomposition theorem
Essentially no case of the above results was previously known, and in order to prove them, we develop a new approach to study the Chow groups with modulus by drawing inspiration from the world of cycles on singular varieties. Given a smooth scheme
![]() $X$
with an effective Cartier divisor
$X$
with an effective Cartier divisor
![]() $D$
, we consider the notion of ‘doubling’
$D$
, we consider the notion of ‘doubling’
![]() $X$
along
$X$
along
![]() $D$
. This idea has previously been used by Milnor [Reference MilnorMil71] to study the patching of projective modules over commutative rings (see [Reference MilnorMil71, ch. 2]), and also by Levine [Reference LevineLev94] to study algebraic cycles in a different context. Doubling
$D$
. This idea has previously been used by Milnor [Reference MilnorMil71] to study the patching of projective modules over commutative rings (see [Reference MilnorMil71, ch. 2]), and also by Levine [Reference LevineLev94] to study algebraic cycles in a different context. Doubling
![]() $X$
along
$X$
along
![]() $D$
gives rise to a new scheme, that we denote by
$D$
gives rise to a new scheme, that we denote by
 $S(X,D)$
, which is, in general, highly singular.
$S(X,D)$
, which is, in general, highly singular.
The novelty of our approach is the observation that the Chow group of 0-cycles with modulus
 $\text{CH}_{0}(X|D)$
can (under some conditions) be suitably realized as a direct summand of the cohomological Chow group of 0-cycles on
$\text{CH}_{0}(X|D)$
can (under some conditions) be suitably realized as a direct summand of the cohomological Chow group of 0-cycles on
 $S(X,D)$
in the sense of Levine and Weibel [Reference Levine and WeibelLW85]. This allows us to transport many of the known statements about the Chow groups of 0-cycles on (possibly singular) schemes to 0-cycles with modulus. The following decomposition theorem can therefore be called the central result of this paper (see Theorem 7.1 for a precise statement).
$S(X,D)$
in the sense of Levine and Weibel [Reference Levine and WeibelLW85]. This allows us to transport many of the known statements about the Chow groups of 0-cycles on (possibly singular) schemes to 0-cycles with modulus. The following decomposition theorem can therefore be called the central result of this paper (see Theorem 7.1 for a precise statement).
Theorem 1.9. Let
![]() $X$
be a smooth quasi-projective scheme over a perfect field
$X$
be a smooth quasi-projective scheme over a perfect field
![]() $k$
. Let
$k$
. Let
![]() $D\subset X$
be an effective Cartier divisor. Then, there is a split short exact sequence
$D\subset X$
be an effective Cartier divisor. Then, there is a split short exact sequence
 $$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(S(X,D))\rightarrow \text{CH}_{0}(X)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(S(X,D))\rightarrow \text{CH}_{0}(X)\rightarrow 0.\end{eqnarray}$$
In fact, it turns out that this approach can be taken forward to study the Chow groups with modulus
 $\text{CH}_{\ast }(X|D)$
in any dimension using the theory of Chow groups of singular schemes developed by Levine [Reference LevineLev85b]. This generalization will be studied in a different project. In this paper, we shall show how this approach works for the relative Picard groups, apart from the above result for 0-cycles.
$\text{CH}_{\ast }(X|D)$
in any dimension using the theory of Chow groups of singular schemes developed by Levine [Reference LevineLev85b]. This generalization will be studied in a different project. In this paper, we shall show how this approach works for the relative Picard groups, apart from the above result for 0-cycles.
We finish this Introduction by remarking that an Albanese variety with modulus has been previously constructed by Kato and Russell in [Reference Kato and RussellKR12] and [Reference RussellRus13]. Their construction uses different techniques and starts from a definition of the Chow group of
![]() $0$
-cycles with modulus that does not agree with the one proposed by Kerz and Saito: as a consequence of this discrepancy, our construction and the Kato–Russell construction are not directly related.
$0$
-cycles with modulus that does not agree with the one proposed by Kerz and Saito: as a consequence of this discrepancy, our construction and the Kato–Russell construction are not directly related.
1.7 Outline of the proofs
This paper is organized as follows. Our principal task is to prove the decomposition Theorem 1.9 for the Chow group of 0-cycles. The proof of this takes up the next five sections of this paper. We describe the double construction in §2 and we prove several properties of it that are used throughout the paper.
The proof of Theorem 1.9 requires a non-trivial Bertini-type argument which allows us to give a new description of the Cartier curves in the definition of the Chow group of 0-cycles on the double. We do this first for surfaces and we then explain how to reduce the general case to this one. This is done in §5. To relate the 0-cycles with modulus with the group of 0-cycles on the double, we define a variant of the Levine–Weibel Chow group of 0-cycles on the double and then show that the two definitions agree in as many cases as possible (see Theorem 3.17). This is done in §3.
We construct the Albanese variety with modulus attached to the pair
![]() $(X,D)$
in § 8 which turns out to be a commutative algebraic group of general type. In characteristic zero, we give an explicit construction of the Albanese variety with modulus using a relative version of Levine’s modified Deligne–Beilinson cohomology. We then use Theorem 1.9 to prove the universality of this Albanese and also the Roitman torsion theorem. We use Theorem 1.9 and the main results of [Reference KrishnaKri09] to deduce the Bloch conjecture for 0-cycles with modulus in §8. Other applications to affine schemes are obtained in §§12–14.
$(X,D)$
in § 8 which turns out to be a commutative algebraic group of general type. In characteristic zero, we give an explicit construction of the Albanese variety with modulus using a relative version of Levine’s modified Deligne–Beilinson cohomology. We then use Theorem 1.9 to prove the universality of this Albanese and also the Roitman torsion theorem. We use Theorem 1.9 and the main results of [Reference KrishnaKri09] to deduce the Bloch conjecture for 0-cycles with modulus in §8. Other applications to affine schemes are obtained in §§12–14.
Notation
Let
![]() $k$
be a field. Since our arguments are geometric in nature, all schemes in this text are assumed to be quasi-projective over
$k$
be a field. Since our arguments are geometric in nature, all schemes in this text are assumed to be quasi-projective over
![]() $k$
and we shall let
$k$
and we shall let
![]() $\mathbf{Sch}_{k}$
denote this category. Let
$\mathbf{Sch}_{k}$
denote this category. Let
![]() $\mathbf{Sm}_{k}$
denote the full subcategory of
$\mathbf{Sm}_{k}$
denote the full subcategory of
![]() $\mathbf{Sch}_{k}$
consisting of smooth schemes over
$\mathbf{Sch}_{k}$
consisting of smooth schemes over
![]() $k$
. We shall let
$k$
. We shall let
![]() $\mathbf{Sch}_{k}^{\text{ess}}$
denote the category of schemes which are essentially of finite type over
$\mathbf{Sch}_{k}^{\text{ess}}$
denote the category of schemes which are essentially of finite type over
![]() $k$
. For a closed subscheme
$k$
. For a closed subscheme
![]() $Z\subset X$
, we shall denote the support of
$Z\subset X$
, we shall denote the support of
![]() $Z$
by
$Z$
by
![]() $|Z|$
. For a scheme
$|Z|$
. For a scheme
![]() $X$
, the notation
$X$
, the notation
![]() $X_{\text{sing}}$
will mean the singular locus of the associated reduced scheme
$X_{\text{sing}}$
will mean the singular locus of the associated reduced scheme
![]() $X_{\text{red}}$
. The nature of the field
$X_{\text{red}}$
. The nature of the field
![]() $k$
will be specified in each section of this paper.
$k$
will be specified in each section of this paper.
2 The double construction
The doubling of a scheme along a closed subscheme is the building block of the proofs of our main results of this paper. In this section, we define this double construction and study its many properties. These properties play crucial roles in the later parts of this paper.
2.1 The definition of the double
Recall that given surjective ring homomorphisms
 $f_{i}:A_{i}\rightarrow A$
for
$f_{i}:A_{i}\rightarrow A$
for
![]() $i=1,2$
, the subring
$i=1,2$
, the subring
 $$\begin{eqnarray}R=\{(a_{1},a_{2})\in A_{1}\times A_{2}\mid f_{1}(a_{1})=f_{2}(a_{2})\}\end{eqnarray}$$
$$\begin{eqnarray}R=\{(a_{1},a_{2})\in A_{1}\times A_{2}\mid f_{1}(a_{1})=f_{2}(a_{2})\}\end{eqnarray}$$
of
 $A_{1}\times A_{2}$
has the property that the diagram
$A_{1}\times A_{2}$
has the property that the diagram

is a Cartesian square in the category of commutative unital rings, where
 $p_{i}:R\rightarrow A_{i}$
is the composite map
$p_{i}:R\rightarrow A_{i}$
is the composite map
 $R{\hookrightarrow}A_{1}\times A_{2}\rightarrow A_{i}$
for
$R{\hookrightarrow}A_{1}\times A_{2}\rightarrow A_{i}$
for
![]() $i=1,2$
. Using the fact that every morphism
$i=1,2$
. Using the fact that every morphism
 $X\rightarrow Y$
in
$X\rightarrow Y$
in
![]() $\mathbf{Sch}_{k}$
, with
$\mathbf{Sch}_{k}$
, with
![]() $Y$
affine, factors through
$Y$
affine, factors through
 $X\rightarrow \operatorname{Spec}({\mathcal{O}}(X))\rightarrow Y$
, one can easily check that the diagram
$X\rightarrow \operatorname{Spec}({\mathcal{O}}(X))\rightarrow Y$
, one can easily check that the diagram

is a Cartesian and co-Cartesian square in
![]() $\mathbf{Sch}_{k}$
.
$\mathbf{Sch}_{k}$
.
Let us now assume that
 $X\in \mathbf{Sch}_{k}$
and let
$X\in \mathbf{Sch}_{k}$
and let
 $\unicode[STIX]{x1D704}:D{\hookrightarrow}X$
be a closed subscheme. If
$\unicode[STIX]{x1D704}:D{\hookrightarrow}X$
be a closed subscheme. If
 $f_{1}=f_{2}=\unicode[STIX]{x1D704}$
, we see that the construction of (2.1) is canonical and so it glues (see [Reference HartshorneHar77, Example II.2.12]) to give us the push-out scheme
$f_{1}=f_{2}=\unicode[STIX]{x1D704}$
, we see that the construction of (2.1) is canonical and so it glues (see [Reference HartshorneHar77, Example II.2.12]) to give us the push-out scheme
 $S(X,D)$
and a commutative diagram.
$S(X,D)$
and a commutative diagram.

One can in fact check, by restricting to affine parts of
![]() $X$
and then by using the gluing construction, that the top square in (2.3) is co-Cartesian in
$X$
and then by using the gluing construction, that the top square in (2.3) is co-Cartesian in
![]() $\mathbf{Sch}_{k}$
. It is also a Cartesian square. The scheme
$\mathbf{Sch}_{k}$
. It is also a Cartesian square. The scheme
 $S(X,D)$
constructed above will be called the double of
$S(X,D)$
constructed above will be called the double of
![]() $X$
along
$X$
along
![]() $D$
. We shall mostly write
$D$
. We shall mostly write
 $S(X,D)$
in short as
$S(X,D)$
in short as
![]() $S_{X}$
if the closed subscheme
$S_{X}$
if the closed subscheme
![]() $D\subset X$
is fixed and remains unchanged in a given context.
$D\subset X$
is fixed and remains unchanged in a given context.
Notice that there is a canonical map
 $\unicode[STIX]{x1D70B}:X\amalg X\xrightarrow[{}]{(\unicode[STIX]{x1D704}_{+},\unicode[STIX]{x1D704}_{-})}S(X,D)$
which is an isomorphism over
$\unicode[STIX]{x1D70B}:X\amalg X\xrightarrow[{}]{(\unicode[STIX]{x1D704}_{+},\unicode[STIX]{x1D704}_{-})}S(X,D)$
which is an isomorphism over
 $S(X,D)\setminus D$
. Given a map
$S(X,D)\setminus D$
. Given a map
 $\unicode[STIX]{x1D708}:C\rightarrow S(X,D)$
, we let
$\unicode[STIX]{x1D708}:C\rightarrow S(X,D)$
, we let
 $C_{+}=C\times _{S(X,D)}X_{+}$
,
$C_{+}=C\times _{S(X,D)}X_{+}$
,
 $C_{-}=C\times _{S(X,D)}X_{-}$
and
$C_{-}=C\times _{S(X,D)}X_{-}$
and
 $E=C\times _{S(X,D)}D$
. Here,
$E=C\times _{S(X,D)}D$
. Here,
![]() $X_{\pm }$
is the component of
$X_{\pm }$
is the component of
![]() $X\amalg X$
where
$X\amalg X$
where
![]() $\unicode[STIX]{x1D70B}$
restricts to
$\unicode[STIX]{x1D70B}$
restricts to
![]() $\unicode[STIX]{x1D704}_{\pm }$
. We then have
$\unicode[STIX]{x1D704}_{\pm }$
. We then have
 $$\begin{eqnarray}E=C\times _{S(X,D)}D=C_{+}\times _{X}D=C_{-}\times _{X}D.\end{eqnarray}$$
$$\begin{eqnarray}E=C\times _{S(X,D)}D=C_{+}\times _{X}D=C_{-}\times _{X}D.\end{eqnarray}$$
More generally, we may often consider the following variant of the double construction.
Definition 2.1. Let
 $j:D{\hookrightarrow}X$
be a closed immersion of quasi-projective schemes over
$j:D{\hookrightarrow}X$
be a closed immersion of quasi-projective schemes over
![]() $k$
and let
$k$
and let
 $f:T\rightarrow X$
be a morphism of quasi-projective schemes. We shall say that
$f:T\rightarrow X$
be a morphism of quasi-projective schemes. We shall say that
![]() $T$
is a join of
$T$
is a join of
![]() $T_{+}$
and
$T_{+}$
and
![]() $T_{-}$
along
$T_{-}$
along
![]() $D$
, if there is a push-out diagram
$D$
, if there is a push-out diagram

such that
![]() $T_{\pm }$
are quasi-projective schemes and
$T_{\pm }$
are quasi-projective schemes and
![]() $j_{\pm }$
are closed immersions.
$j_{\pm }$
are closed immersions.
The following lemma related to the double construction will be often used in this text.
Lemma 2.2. Let
 $\unicode[STIX]{x1D708}:C\rightarrow S(X,D)$
be an affine morphism. Then the push-out
$\unicode[STIX]{x1D708}:C\rightarrow S(X,D)$
be an affine morphism. Then the push-out
 $C_{+}\amalg _{E}C_{-}$
is a closed subscheme of
$C_{+}\amalg _{E}C_{-}$
is a closed subscheme of
![]() $C$
. This closed immersion is an isomorphism if
$C$
. This closed immersion is an isomorphism if
![]() $C$
is reduced.
$C$
is reduced.
Proof. There is clearly a morphism
 $C_{+}\amalg _{E}C_{-}\rightarrow C$
. Showing that this map has the desired properties is a local question on
$C_{+}\amalg _{E}C_{-}\rightarrow C$
. Showing that this map has the desired properties is a local question on
![]() $X$
. So it suffices to verify these properties at the level of rings.
$X$
. So it suffices to verify these properties at the level of rings.
If we set
 $X=\operatorname{Spec}(A)$
,
$X=\operatorname{Spec}(A)$
,
 $S(X,D)=\operatorname{Spec}(R)$
and let
$S(X,D)=\operatorname{Spec}(R)$
and let
![]() $I$
be the defining ideal for
$I$
be the defining ideal for
![]() $D$
, then we have an exact sequence of
$D$
, then we have an exact sequence of
![]() $R$
-modules
$R$
-modules
 $$\begin{eqnarray}0\rightarrow R\xrightarrow[{}]{\unicode[STIX]{x1D719}}A\times A\rightarrow A/I\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow R\xrightarrow[{}]{\unicode[STIX]{x1D719}}A\times A\rightarrow A/I\rightarrow 0.\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D708}$
is affine, we can write
$\unicode[STIX]{x1D708}$
is affine, we can write
 $C=\operatorname{Spec}(B)$
. Let
$C=\operatorname{Spec}(B)$
. Let
![]() $J\subset B$
be the ideal defining the closed subscheme
$J\subset B$
be the ideal defining the closed subscheme
![]() $E$
. Tensoring (2.6) with
$E$
. Tensoring (2.6) with
![]() $B$
, we get an exact sequence
$B$
, we get an exact sequence
 $$\begin{eqnarray}B\xrightarrow[{}]{\unicode[STIX]{x1D719}_{B}}B_{+}\times B_{-}\rightarrow B/J\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}B\xrightarrow[{}]{\unicode[STIX]{x1D719}_{B}}B_{+}\times B_{-}\rightarrow B/J\rightarrow 0\end{eqnarray}$$
and this shows that
 $C_{+}\amalg _{E}C_{-}{\hookrightarrow}C$
is a closed immersion of schemes. It is also clear that this inclusion is an isomorphism in the complement of
$C_{+}\amalg _{E}C_{-}{\hookrightarrow}C$
is a closed immersion of schemes. It is also clear that this inclusion is an isomorphism in the complement of
![]() $E$
. Furthermore, the surjectivity of the map
$E$
. Furthermore, the surjectivity of the map
 $C_{+}\amalg C_{-}\rightarrow C$
shows that the above inclusion is also surjective on points. We conclude from this that the closed immersion
$C_{+}\amalg C_{-}\rightarrow C$
shows that the above inclusion is also surjective on points. We conclude from this that the closed immersion
 $C_{+}\amalg _{E}C_{-}{\hookrightarrow}C$
induces identity on the underlying reduced schemes. In particular, it is an isomorphism if
$C_{+}\amalg _{E}C_{-}{\hookrightarrow}C$
induces identity on the underlying reduced schemes. In particular, it is an isomorphism if
![]() $C$
is reduced. Equivalently,
$C$
is reduced. Equivalently,
![]() $\unicode[STIX]{x1D719}_{B}$
is injective.◻
$\unicode[STIX]{x1D719}_{B}$
is injective.◻
2.2 More properties of the double
We now prove some general properties of the double construction that will be used repeatedly in this text. We shall also show that the double shares many of the nice properties of the given scheme if the underlying closed subscheme is an effective Cartier divisor. This will be our case of interest in the sequel.
For
 $X\in \mathbf{Sch}_{k}$
, let
$X\in \mathbf{Sch}_{k}$
, let
![]() $k(X)$
denote the sheaf of rings of total quotients of
$k(X)$
denote the sheaf of rings of total quotients of
![]() $X$
. For a reduced scheme
$X$
. For a reduced scheme
![]() $X$
, let
$X$
, let
 $k_{\min }(X)$
denote the product of the fields of fractions of the irreducible components of
$k_{\min }(X)$
denote the product of the fields of fractions of the irreducible components of
![]() $X$
. Note that there are maps of sheaves of rings
$X$
. Note that there are maps of sheaves of rings
 ${\mathcal{O}}_{X}{\hookrightarrow}k(X)\rightarrow k_{\min }(X)$
and the latter map is an isomorphism if
${\mathcal{O}}_{X}{\hookrightarrow}k(X)\rightarrow k_{\min }(X)$
and the latter map is an isomorphism if
![]() $X$
is reduced and has no embedded primes.
$X$
is reduced and has no embedded primes.
Proposition 2.3. Let
![]() $X$
be a scheme in
$X$
be a scheme in
![]() $\mathbf{Sch}_{k}^{\text{ess}}$
and let
$\mathbf{Sch}_{k}^{\text{ess}}$
and let
 $\unicode[STIX]{x1D704}:D{\hookrightarrow}X$
be a closed subscheme not containing any irreducible component of
$\unicode[STIX]{x1D704}:D{\hookrightarrow}X$
be a closed subscheme not containing any irreducible component of
![]() $X$
. Then the following hold.
$X$
. Then the following hold.
-
(1) There are finite maps
such that $$\begin{eqnarray}X\amalg X\xrightarrow[{}]{\unicode[STIX]{x1D70B}}S(X,D)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}}X\end{eqnarray}$$
$$\begin{eqnarray}X\amalg X\xrightarrow[{}]{\unicode[STIX]{x1D70B}}S(X,D)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}}X\end{eqnarray}$$
 $(X\setminus D)\amalg (X\setminus D)\xrightarrow[{}]{\unicode[STIX]{x1D70B}}S(X,D)\setminus D=\unicode[STIX]{x1D6E5}^{-1}(X\setminus D)$
is an isomorphism. In particular,
$(X\setminus D)\amalg (X\setminus D)\xrightarrow[{}]{\unicode[STIX]{x1D70B}}S(X,D)\setminus D=\unicode[STIX]{x1D6E5}^{-1}(X\setminus D)$
is an isomorphism. In particular,
 $S$
is affine (projective) if and only if
$S$
is affine (projective) if and only if
 $X$
is so.
$X$
is so.
-
(2) The scheme
 $S(X,D)$
is reduced if
$S(X,D)$
is reduced if
 $X$
is so. In this case, one has If
$X$
is so. In this case, one has If $$\begin{eqnarray}k_{\text{min}}(S(X,D)\setminus D)\simeq k_{\text{min}}(X\setminus D)\times k_{\text{min}}(X\setminus D).\end{eqnarray}$$
$$\begin{eqnarray}k_{\text{min}}(S(X,D)\setminus D)\simeq k_{\text{min}}(X\setminus D)\times k_{\text{min}}(X\setminus D).\end{eqnarray}$$
 $D$
contains no component of
$D$
contains no component of
 $X$
, then
$X$
, then
 $k_{\text{min}}(S(X,D)\setminus D)=k_{\text{min}}(S(X,D))$
.
$k_{\text{min}}(S(X,D)\setminus D)=k_{\text{min}}(S(X,D))$
.
-
(3) The composite map
 $D\stackrel{\unicode[STIX]{x1D704}_{\pm }\circ \unicode[STIX]{x1D704}}{\rightarrow }\unicode[STIX]{x1D6E5}^{\ast }(D)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}}D$
is identity and
$D\stackrel{\unicode[STIX]{x1D704}_{\pm }\circ \unicode[STIX]{x1D704}}{\rightarrow }\unicode[STIX]{x1D6E5}^{\ast }(D)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}}D$
is identity and
 $|\unicode[STIX]{x1D6E5}^{\ast }(D)|=|D|$
.
$|\unicode[STIX]{x1D6E5}^{\ast }(D)|=|D|$
. -
(4) If
 $Y\subseteq X$
is a closed (respectively open) subscheme of
$Y\subseteq X$
is a closed (respectively open) subscheme of
 $X$
and
$X$
and
 $Y\cap D$
is the scheme-theoretic intersection, then
$Y\cap D$
is the scheme-theoretic intersection, then
 $S(Y,Y\cap D)$
is a closed (respectively open) subscheme of
$S(Y,Y\cap D)$
is a closed (respectively open) subscheme of
 $S(X,D)$
. There is an inclusion of subschemes
$S(X,D)$
. There is an inclusion of subschemes
 $S(Y,Y\cap D){\hookrightarrow}\unicode[STIX]{x1D6E5}^{\ast }(Y)$
which is an isomorphism if
$S(Y,Y\cap D){\hookrightarrow}\unicode[STIX]{x1D6E5}^{\ast }(Y)$
which is an isomorphism if
 $Y$
is open.
$Y$
is open. -
(5) Let
 $Y$
be a subscheme of
$Y$
be a subscheme of
 $X$
. Then
$X$
. Then
 $|\unicode[STIX]{x1D6E5}^{\ast }(Y)\cap D|=|Y\cap D|=|S(Y,Y\cap D)\cap D|$
.
$|\unicode[STIX]{x1D6E5}^{\ast }(Y)\cap D|=|Y\cap D|=|S(Y,Y\cap D)\cap D|$
. -
(6) We have
 $S(X,D)_{\text{sing}}=D\cup \unicode[STIX]{x1D6E5}^{-1}(X_{\text{sing}})$
. In particular,
$S(X,D)_{\text{sing}}=D\cup \unicode[STIX]{x1D6E5}^{-1}(X_{\text{sing}})$
. In particular,
 $S(X,D)_{\text{sing}}=D$
if
$S(X,D)_{\text{sing}}=D$
if
 $X$
is non-singular.
$X$
is non-singular. -
(7) If
 $f:Y\rightarrow X$
is a flat morphism, then
$f:Y\rightarrow X$
is a flat morphism, then
 $S(Y,f^{\ast }(D))\simeq S(X,D)\times _{X}Y$
. In particular, the map
$S(Y,f^{\ast }(D))\simeq S(X,D)\times _{X}Y$
. In particular, the map
 $S(f):S(Y,f^{\ast }(D))\rightarrow S(X,D)$
is flat (respectively smooth) if
$S(f):S(Y,f^{\ast }(D))\rightarrow S(X,D)$
is flat (respectively smooth) if
 $f$
is so.
$f$
is so. -
(8) The morphism
 $\unicode[STIX]{x1D70B}$
is the normalization map and
$\unicode[STIX]{x1D70B}$
is the normalization map and
 $D$
is a conducting subscheme, if
$D$
is a conducting subscheme, if
 $X$
is normal.
$X$
is normal.
Proof. To prove the proposition, we can assume that
 $X=\operatorname{Spec}(A)$
is affine. Let
$X=\operatorname{Spec}(A)$
is affine. Let
 $p_{1},p_{2}:A\times A\rightarrow A$
denote the projections and let
$p_{1},p_{2}:A\times A\rightarrow A$
denote the projections and let
 $q:A\rightarrow A/I$
be the quotient map. Set
$q:A\rightarrow A/I$
be the quotient map. Set
 $q_{i}=q\circ p_{i}$
. Set
$q_{i}=q\circ p_{i}$
. Set
 $\unicode[STIX]{x1D713}_{i}=p_{i}\circ \unicode[STIX]{x1D719}$
for
$\unicode[STIX]{x1D713}_{i}=p_{i}\circ \unicode[STIX]{x1D719}$
for
![]() $i=1,2$
. Let
$i=1,2$
. Let
 $\unicode[STIX]{x1D6FF}:A{\hookrightarrow}R{\hookrightarrow}A\times A$
denote the diagonal map. We then have
$\unicode[STIX]{x1D6FF}:A{\hookrightarrow}R{\hookrightarrow}A\times A$
denote the diagonal map. We then have
 $\unicode[STIX]{x1D713}_{i}\circ \unicode[STIX]{x1D6FF}=\text{id}_{A}$
for
$\unicode[STIX]{x1D713}_{i}\circ \unicode[STIX]{x1D6FF}=\text{id}_{A}$
for
![]() $i=1,2$
and this yields
$i=1,2$
and this yields
 $$\begin{eqnarray}A\times A=\unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D6FF}(A)\oplus \text{Ker}(p_{2}),\end{eqnarray}$$
$$\begin{eqnarray}A\times A=\unicode[STIX]{x1D719}\circ \unicode[STIX]{x1D6FF}(A)\oplus \text{Ker}(p_{2}),\end{eqnarray}$$
 $$\begin{eqnarray}R=\unicode[STIX]{x1D6FF}(A)\oplus \text{Ker}(\unicode[STIX]{x1D713}_{2})=\unicode[STIX]{x1D6FF}(A)\oplus I\times \{0\}\simeq A\oplus I.\end{eqnarray}$$
$$\begin{eqnarray}R=\unicode[STIX]{x1D6FF}(A)\oplus \text{Ker}(\unicode[STIX]{x1D713}_{2})=\unicode[STIX]{x1D6FF}(A)\oplus I\times \{0\}\simeq A\oplus I.\end{eqnarray}$$
Since
![]() $A\times A$
is a finite free
$A\times A$
is a finite free
![]() $A$
-module and
$A$
-module and
![]() $R$
is an
$R$
is an
![]() $A$
-submodule, it follows that
$A$
-submodule, it follows that
![]() $R$
is a finite
$R$
is a finite
![]() $A$
-module. This proves (1). The item (2) follows immediately from (2.6).
$A$
-module. This proves (1). The item (2) follows immediately from (2.6).
The ideal of
![]() $D$
inside
$D$
inside
 $S(X,D)$
is
$S(X,D)$
is
 $\text{Ker}(R\xrightarrow[{}]{q\circ \unicode[STIX]{x1D713}_{i}}A/I)$
, which is
$\text{Ker}(R\xrightarrow[{}]{q\circ \unicode[STIX]{x1D713}_{i}}A/I)$
, which is
![]() $I\times I$
. Since
$I\times I$
. Since
 $\unicode[STIX]{x1D6FF}^{\ast }(I)\subseteq I\times I$
, we see that
$\unicode[STIX]{x1D6FF}^{\ast }(I)\subseteq I\times I$
, we see that
 $D\subseteq \unicode[STIX]{x1D6E5}^{\ast }(D)$
and the composite
$D\subseteq \unicode[STIX]{x1D6E5}^{\ast }(D)$
and the composite
 $D{\hookrightarrow}\unicode[STIX]{x1D6E5}^{\ast }(D)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}}D$
is clearly identity. Furthermore, it is clear that
$D{\hookrightarrow}\unicode[STIX]{x1D6E5}^{\ast }(D)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}}D$
is clearly identity. Furthermore, it is clear that
 $R[(a,b)^{-1}]=A[a^{-1}]\times A[b^{-1}]$
and
$R[(a,b)^{-1}]=A[a^{-1}]\times A[b^{-1}]$
and
 $\unicode[STIX]{x1D6FF}^{\ast }(I)[(a,b)^{-1}]=R[(a,b)^{-1}]$
, whenever
$\unicode[STIX]{x1D6FF}^{\ast }(I)[(a,b)^{-1}]=R[(a,b)^{-1}]$
, whenever
 $a,b\in I\setminus \{0\}$
. Hence, we have
$a,b\in I\setminus \{0\}$
. Hence, we have
 $|\unicode[STIX]{x1D6E5}^{\ast }(D)|=|D|$
. This proves (3).
$|\unicode[STIX]{x1D6E5}^{\ast }(D)|=|D|$
. This proves (3).
To prove (4), we only need to consider the closed part. Let
 $A^{\prime }=A/J$
, where
$A^{\prime }=A/J$
, where
![]() $J$
is the ideal defining
$J$
is the ideal defining
![]() $Y$
and let
$Y$
and let
 $R^{\prime }=\{(a^{\prime },b^{\prime })\in A^{\prime }\times A^{\prime }\mid a^{\prime }-b^{\prime }\in (I+J)/J\}$
. Let
$R^{\prime }=\{(a^{\prime },b^{\prime })\in A^{\prime }\times A^{\prime }\mid a^{\prime }-b^{\prime }\in (I+J)/J\}$
. Let
![]() $\overline{a}$
denote the residue class of
$\overline{a}$
denote the residue class of
![]() $a\in A$
modulo
$a\in A$
modulo
![]() $J$
. Suppose there exist
$J$
. Suppose there exist
 $a,b\in A$
such that
$a,b\in A$
such that
 $\overline{a}-\overline{b}\in (I+J)/J$
. This means
$\overline{a}-\overline{b}\in (I+J)/J$
. This means
 $a-b\in I+J$
and so we can write
$a-b\in I+J$
and so we can write
 $a-b=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}$
, where
$a-b=\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D6FD}$
, where
![]() $\unicode[STIX]{x1D6FC}\in I$
and
$\unicode[STIX]{x1D6FC}\in I$
and
![]() $\unicode[STIX]{x1D6FD}\in J$
. We set
$\unicode[STIX]{x1D6FD}\in J$
. We set
 $a^{\prime }=a-\unicode[STIX]{x1D6FD}$
and
$a^{\prime }=a-\unicode[STIX]{x1D6FD}$
and
![]() $b^{\prime }=b$
. This yields
$b^{\prime }=b$
. This yields
 $a^{\prime }-b^{\prime }=a-b-\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FC}\in I$
and
$a^{\prime }-b^{\prime }=a-b-\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FC}\in I$
and
 $a^{\prime }-a=\unicode[STIX]{x1D6FD}\in J,~b^{\prime }-b=0\in J$
. We conclude that
$a^{\prime }-a=\unicode[STIX]{x1D6FD}\in J,~b^{\prime }-b=0\in J$
. We conclude that
 $(a^{\prime },b^{\prime })\in R$
and it maps to
$(a^{\prime },b^{\prime })\in R$
and it maps to
 $(\overline{a},\overline{b})\in R^{\prime }$
. Hence
$(\overline{a},\overline{b})\in R^{\prime }$
. Hence
 $R{\twoheadrightarrow}R^{\prime }$
.
$R{\twoheadrightarrow}R^{\prime }$
.
An element of
![]() $\unicode[STIX]{x1D6FF}^{\ast }(J)$
is of the form
$\unicode[STIX]{x1D6FF}^{\ast }(J)$
is of the form
 $(a\unicode[STIX]{x1D6FC},b\unicode[STIX]{x1D6FC})$
, where
$(a\unicode[STIX]{x1D6FC},b\unicode[STIX]{x1D6FC})$
, where
 $a,b,\in A,\unicode[STIX]{x1D6FC}\in J$
and
$a,b,\in A,\unicode[STIX]{x1D6FC}\in J$
and
 $a-b\in I$
. This element clearly dies in
$a-b\in I$
. This element clearly dies in
![]() $R^{\prime }$
. Hence
$R^{\prime }$
. Hence
 $S(Y,Y\cap D)\subseteq \unicode[STIX]{x1D6E5}^{\ast }(Y)$
.
$S(Y,Y\cap D)\subseteq \unicode[STIX]{x1D6E5}^{\ast }(Y)$
.
To prove (5), let
 $S_{Y}=S(Y,Y\cap D)$
. Then
$S_{Y}=S(Y,Y\cap D)$
. Then
 $$\begin{eqnarray}|\unicode[STIX]{x1D6E5}^{\ast }(Y)\cap D|=|\unicode[STIX]{x1D6E5}^{\ast }(Y)\cap \unicode[STIX]{x1D6E5}^{\ast }(D)|=|\unicode[STIX]{x1D6E5}^{\ast }(Y\cap D)|,\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D6E5}^{\ast }(Y)\cap D|=|\unicode[STIX]{x1D6E5}^{\ast }(Y)\cap \unicode[STIX]{x1D6E5}^{\ast }(D)|=|\unicode[STIX]{x1D6E5}^{\ast }(Y\cap D)|,\end{eqnarray}$$
where the first equality follows from (3). On the other hand, we have
 $$\begin{eqnarray}|S_{Y}\cap D|=|\unicode[STIX]{x1D704}_{1}^{Y}\circ \unicode[STIX]{x1D704}^{Y}(Y\cap D)|=|\unicode[STIX]{x1D6E5}_{Y}^{\ast }(Y\cap D)|=|\unicode[STIX]{x1D6E5}^{\ast }(Y\cap D)|,\end{eqnarray}$$
$$\begin{eqnarray}|S_{Y}\cap D|=|\unicode[STIX]{x1D704}_{1}^{Y}\circ \unicode[STIX]{x1D704}^{Y}(Y\cap D)|=|\unicode[STIX]{x1D6E5}_{Y}^{\ast }(Y\cap D)|=|\unicode[STIX]{x1D6E5}^{\ast }(Y\cap D)|,\end{eqnarray}$$
where the second equality follows from (3) with
![]() $X$
replaced by
$X$
replaced by
![]() $Y$
. The item (5) now follows. The item (6) follows from (1) and the fact that more than one components of
$Y$
. The item (5) now follows. The item (6) follows from (1) and the fact that more than one components of
 $S(X,D)$
meet along
$S(X,D)$
meet along
![]() $D$
.
$D$
.
To prove (7), let
 $Y=\operatorname{Spec}(B)$
and tensor (2.6) with
$Y=\operatorname{Spec}(B)$
and tensor (2.6) with
![]() $B$
. The flatness of
$B$
. The flatness of
![]() $B$
over
$B$
over
![]() $A$
yields the short exact sequence
$A$
yields the short exact sequence
 $$\begin{eqnarray}0\rightarrow R\,\otimes _{A}\,B\xrightarrow[{}]{\unicode[STIX]{x1D719}}B\times B\rightarrow B/IB\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow R\,\otimes _{A}\,B\xrightarrow[{}]{\unicode[STIX]{x1D719}}B\times B\rightarrow B/IB\rightarrow 0\end{eqnarray}$$
and this proves the first part of (7). The second part follows because a base change of a flat (respectively smooth) map is flat (respectively smooth).
The item (8) follows because
![]() $\unicode[STIX]{x1D70B}$
is finite and birational and the ideal of
$\unicode[STIX]{x1D70B}$
is finite and birational and the ideal of
![]() $\unicode[STIX]{x1D70B}^{\ast }(D)$
in
$\unicode[STIX]{x1D70B}^{\ast }(D)$
in
![]() $X\amalg X$
is
$X\amalg X$
is
 $I_{D}\times I_{D}$
which is actually contained in
$I_{D}\times I_{D}$
which is actually contained in
 ${\mathcal{O}}_{S(X,D)}$
. So
${\mathcal{O}}_{S(X,D)}$
. So
![]() $D$
is a conducting subscheme.◻
$D$
is a conducting subscheme.◻
2.3 Double along a Cartier divisor
Recall that a morphism
 $f:X\rightarrow S$
of schemes is called a local complete intersection (l.c.i.) at a point
$f:X\rightarrow S$
of schemes is called a local complete intersection (l.c.i.) at a point
![]() $x\in X$
if it is of finite type and if there is an open neighborhood
$x\in X$
if it is of finite type and if there is an open neighborhood
![]() $U$
of
$U$
of
![]() $x$
and a factorization
$x$
and a factorization

where
![]() $i$
is a regular closed immersion and
$i$
is a regular closed immersion and
![]() $g$
is a smooth morphism. We say that
$g$
is a smooth morphism. We say that
![]() $f$
is a local complete intersection morphism if it is so at every point of
$f$
is a local complete intersection morphism if it is so at every point of
![]() $X$
. We say that
$X$
. We say that
![]() $f$
is l.c.i. along a closed subscheme
$f$
is l.c.i. along a closed subscheme
 $S^{\prime }{\hookrightarrow}S$
if it is l.c.i. at every point in
$S^{\prime }{\hookrightarrow}S$
if it is l.c.i. at every point in
 $f^{-1}(S^{\prime })$
.
$f^{-1}(S^{\prime })$
.
Proposition 2.4. Continuing with the notations of Proposition 2.3, assume further that
![]() $D$
is an effective Cartier divisor on
$D$
is an effective Cartier divisor on
![]() $X$
. Then the following hold.
$X$
. Then the following hold.
-
(1) The morphism
 $\unicode[STIX]{x1D6E5}$
is finite, flat and
$\unicode[STIX]{x1D6E5}$
is finite, flat and
 ${\mathcal{O}}_{S(X,D)}$
is a locally free
${\mathcal{O}}_{S(X,D)}$
is a locally free
 ${\mathcal{O}}_{X}$
-module of rank two via
${\mathcal{O}}_{X}$
-module of rank two via
 $\unicode[STIX]{x1D6E5}$
.
$\unicode[STIX]{x1D6E5}$
. -
(2) The scheme
 $S(X,D)$
is Cohen–Macaulay if
$S(X,D)$
is Cohen–Macaulay if
 $X$
is so.
$X$
is so. -
(3) If
 $f:Y\rightarrow X$
is any morphism, then there is a closed immersion of schemes
$f:Y\rightarrow X$
is any morphism, then there is a closed immersion of schemes
 $S(Y,f^{\ast }(D)){\hookrightarrow}S(X,D)\times _{X}Y$
. This embedding is an isomorphism if
$S(Y,f^{\ast }(D)){\hookrightarrow}S(X,D)\times _{X}Y$
. This embedding is an isomorphism if
 $f$
is transverse to
$f$
is transverse to
 $D{\hookrightarrow}X$
.
$D{\hookrightarrow}X$
. -
(4) If
 $f:Y\rightarrow X$
is any morphism such that
$f:Y\rightarrow X$
is any morphism such that
 $Y$
is Cohen–Macaulay and
$Y$
is Cohen–Macaulay and
 $f^{\ast }(D)$
does not contain any irreducible component of
$f^{\ast }(D)$
does not contain any irreducible component of
 $Y$
, then the embedding
$Y$
, then the embedding
 $S(Y,f^{\ast }(D)){\hookrightarrow}S(X,D)\times _{X}Y$
is an isomorphism. In this case,
$S(Y,f^{\ast }(D)){\hookrightarrow}S(X,D)\times _{X}Y$
is an isomorphism. In this case,
 $f^{\ast }(D)$
is an effective Cartier divisor on
$f^{\ast }(D)$
is an effective Cartier divisor on
 $Y$
.
$Y$
. -
(5) If
 $f:Y\rightarrow X$
is l.c.i. along
$f:Y\rightarrow X$
is l.c.i. along
 $D$
, then
$D$
, then
 $Y\times _{X}S(X,D)\rightarrow S(X,D)$
is l.c.i. along
$Y\times _{X}S(X,D)\rightarrow S(X,D)$
is l.c.i. along
 $D$
.
$D$
.
Proof. We can again assume that
 $X=\operatorname{Spec}(A)$
is affine such that
$X=\operatorname{Spec}(A)$
is affine such that
![]() $I=(a)$
is a principal ideal such that
$I=(a)$
is a principal ideal such that
![]() $a\in A$
is not a zero-divisor. It follows then that
$a\in A$
is not a zero-divisor. It follows then that
![]() $I$
is a free
$I$
is a free
![]() $A$
-module of rank one. We can now apply (2.8) to conclude (1) as the finiteness of
$A$
-module of rank one. We can now apply (2.8) to conclude (1) as the finiteness of
![]() $R$
over
$R$
over
![]() $A$
is already shown in Proposition 2.3.
$A$
is already shown in Proposition 2.3.
To prove (2), let
![]() $\mathfrak{m}\subsetneq R$
be a maximal ideal and let
$\mathfrak{m}\subsetneq R$
be a maximal ideal and let
 $\mathfrak{n}=\unicode[STIX]{x1D6FF}^{-1}(\mathfrak{m})$
. Then
$\mathfrak{n}=\unicode[STIX]{x1D6FF}^{-1}(\mathfrak{m})$
. Then
 $A_{\mathfrak{n}}\rightarrow R_{\mathfrak{n}}$
is a finite and flat map and hence
$A_{\mathfrak{n}}\rightarrow R_{\mathfrak{n}}$
is a finite and flat map and hence
 $A_{\mathfrak{n}}\rightarrow R_{\mathfrak{m}}$
is a faithfully flat local homomorphism of noetherian local rings of same dimension. Since
$A_{\mathfrak{n}}\rightarrow R_{\mathfrak{m}}$
is a faithfully flat local homomorphism of noetherian local rings of same dimension. Since
![]() $A_{\mathfrak{n}}$
is Cohen–Macaulay and since this local homomorphism preserves regular sequences, it follows that
$A_{\mathfrak{n}}$
is Cohen–Macaulay and since this local homomorphism preserves regular sequences, it follows that
 $\text{depth}(R_{\mathfrak{m}})\geqslant \dim (A_{\mathfrak{n}})=\dim (R_{\mathfrak{m}})$
. Hence,
$\text{depth}(R_{\mathfrak{m}})\geqslant \dim (A_{\mathfrak{n}})=\dim (R_{\mathfrak{m}})$
. Hence,
![]() $R_{\mathfrak{m}}$
is Cohen–Macaulay.
$R_{\mathfrak{m}}$
is Cohen–Macaulay.
To prove (3), we let
 $Y=\operatorname{Spec}(B)$
and tensor (2.6) (over
$Y=\operatorname{Spec}(B)$
and tensor (2.6) (over
![]() $A$
) with
$A$
) with
![]() $B$
to get an exact sequence
$B$
to get an exact sequence
 $$\begin{eqnarray}0\rightarrow \text{Tor}_{A}^{1}(A/I,B)\rightarrow R\,\otimes _{A}\,B\xrightarrow[{}]{\unicode[STIX]{x1D719}}B\times B\rightarrow B/IB\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{Tor}_{A}^{1}(A/I,B)\rightarrow R\,\otimes _{A}\,B\xrightarrow[{}]{\unicode[STIX]{x1D719}}B\times B\rightarrow B/IB\rightarrow 0\end{eqnarray}$$
and
 $S(B,IB)$
is (by definition) the kernel of the map
$S(B,IB)$
is (by definition) the kernel of the map
 $B\times B\rightarrow B/IB$
. In particular, we get a surjective map of rings
$B\times B\rightarrow B/IB$
. In particular, we get a surjective map of rings
 $R\otimes _{A}B{\twoheadrightarrow}S(B,IB)$
. This proves the first part of (3). The transversality of
$R\otimes _{A}B{\twoheadrightarrow}S(B,IB)$
. This proves the first part of (3). The transversality of
![]() $B$
with
$B$
with
![]() $A/I$
means precisely that
$A/I$
means precisely that
 $\text{Tor}_{A}^{1}(A/I,B)=0$
and we get that
$\text{Tor}_{A}^{1}(A/I,B)=0$
and we get that
 $R\otimes _{A}B\xrightarrow[{}]{\simeq }S(B,IB)$
. This proves (3).
$R\otimes _{A}B\xrightarrow[{}]{\simeq }S(B,IB)$
. This proves (3).
Suppose next that
![]() $Y$
is Cohen–Macaulay and no irreducible component of
$Y$
is Cohen–Macaulay and no irreducible component of
![]() $Y$
is contained in
$Y$
is contained in
![]() $f^{\ast }(D)$
. It suffices to show in this case that
$f^{\ast }(D)$
. It suffices to show in this case that
 $\text{Tor}_{A}^{1}(A/I,B)=0$
. Let
$\text{Tor}_{A}^{1}(A/I,B)=0$
. Let
 $f:A\rightarrow B$
be the map on the coordinate rings. That no component of
$f:A\rightarrow B$
be the map on the coordinate rings. That no component of
![]() $Y$
is contained in
$Y$
is contained in
![]() $f^{\ast }(D)$
means that
$f^{\ast }(D)$
means that
![]() $f(a)$
does not belong to any minimal prime of
$f(a)$
does not belong to any minimal prime of
![]() $B$
. The Cohen–Macaulay property of
$B$
. The Cohen–Macaulay property of
![]() $B$
implies that it has no embedded associated prime. In particular,
$B$
implies that it has no embedded associated prime. In particular,
![]() $f(a)$
does not belong to any associated prime and hence is not a zero-divisor in
$f(a)$
does not belong to any associated prime and hence is not a zero-divisor in
![]() $B$
.
$B$
.
We have a short exact sequence
 $$\begin{eqnarray}0\rightarrow A\xrightarrow[{}]{a}A\rightarrow A/I\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow A\xrightarrow[{}]{a}A\rightarrow A/I\rightarrow 0\end{eqnarray}$$
which says that
 $\text{Tor}_{A}^{1}(A/I,B)=\text{Ker}(B\xrightarrow[{}]{f(a)}B)$
and we have just shown that the latter group is zero. We have also shown above that
$\text{Tor}_{A}^{1}(A/I,B)=\text{Ker}(B\xrightarrow[{}]{f(a)}B)$
and we have just shown that the latter group is zero. We have also shown above that
![]() $f(a)$
is not a zero-divisor on
$f(a)$
is not a zero-divisor on
![]() $B$
and this implies that
$B$
and this implies that
![]() $f^{\ast }(D)$
is an effective Cartier divisor on
$f^{\ast }(D)$
is an effective Cartier divisor on
![]() $Y$
. This proves (4). The item (5) follows from (1) and an elementary fact that l.c.i. morphisms are preserved under a flat base change.◻
$Y$
. This proves (4). The item (5) follows from (1) and an elementary fact that l.c.i. morphisms are preserved under a flat base change.◻
3 Chow group of
 $0$
-cycles on singular schemes
$0$
-cycles on singular schemes
In this section, we give a definition of the Chow group of
![]() $0$
-cycles on singular schemes that modifies slightly the one given in [Reference Levine and WeibelLW85]. While using the same set of generators, we change the geometric condition imposed on the curves giving the rational equivalence. In many cases, we are able to show that this new definition coincides with the classical one. It turns out that the modified Chow group of 0-cycles has better functorial properties and is more suitable for proving Theorem 1.9.
$0$
-cycles on singular schemes that modifies slightly the one given in [Reference Levine and WeibelLW85]. While using the same set of generators, we change the geometric condition imposed on the curves giving the rational equivalence. In many cases, we are able to show that this new definition coincides with the classical one. It turns out that the modified Chow group of 0-cycles has better functorial properties and is more suitable for proving Theorem 1.9.
3.1 Some properties of l.c.i. and perfect morphisms
Recall that a finite-type morphism
 $f:X\rightarrow S$
of noetherian schemes is called perfect if the local ring
$f:X\rightarrow S$
of noetherian schemes is called perfect if the local ring
![]() ${\mathcal{O}}_{X,x}$
has finite Tor-dimension as a module over the local ring
${\mathcal{O}}_{X,x}$
has finite Tor-dimension as a module over the local ring
![]() ${\mathcal{O}}_{S,f(x)}$
for every point
${\mathcal{O}}_{S,f(x)}$
for every point
![]() $x\in X$
. Equivalently, given any point
$x\in X$
. Equivalently, given any point
![]() $x\in X$
, there are affine neighborhoods
$x\in X$
, there are affine neighborhoods
![]() $U$
of
$U$
of
![]() $x$
and
$x$
and
![]() $V$
of
$V$
of
![]() $f(x)$
such that
$f(x)$
such that
![]() ${\mathcal{O}}(U)$
is an
${\mathcal{O}}(U)$
is an
![]() ${\mathcal{O}}(V)$
-module of finite Tor-dimension. Recall also the following
${\mathcal{O}}(V)$
-module of finite Tor-dimension. Recall also the following
Proposition 3.1 [Reference SrinivasSri08, Proposition 5.12].
Let
 $f:X\rightarrow S$
be a proper and perfect morphism of noetherian schemes. Then there is a well-defined push-forward map
$f:X\rightarrow S$
be a proper and perfect morphism of noetherian schemes. Then there is a well-defined push-forward map
 $K_{0}(X)\xrightarrow[{}]{f_{\ast }}K_{0}(S)$
between the Grothendieck groups of vector bundles.
$K_{0}(X)\xrightarrow[{}]{f_{\ast }}K_{0}(S)$
between the Grothendieck groups of vector bundles.
Some known elementary properties of l.c.i. and perfect morphisms are recalled in the following lemmas.
Lemma 3.2.
-
(1) The l.c.i. and perfect morphisms are preserved under flat base change.
-
(2) A flat morphism of finite type is perfect.
-
(3) An l.c.i. morphism is perfect.
-
(4) l.c.i. and perfect morphisms are closed under composition.
-
(5) l.c.i. and perfect morphisms satisfy faithfully flat (fpqc) descent.
Lemma 3.3. Let
 $f:X\rightarrow S$
be a finite-type morphism of noetherian schemes such that for every
$f:X\rightarrow S$
be a finite-type morphism of noetherian schemes such that for every
 $x\in f^{-1}(S_{\text{sing}})$
, the map
$x\in f^{-1}(S_{\text{sing}})$
, the map
![]() $f$
is l.c.i. at
$f$
is l.c.i. at
![]() $x$
. Then
$x$
. Then
![]() $f$
is perfect.
$f$
is perfect.
Proof. It follows from the definition of a perfect morphism because if
![]() $x\in X$
is such that
$x\in X$
is such that
 $s=f(x)$
is a regular point of
$s=f(x)$
is a regular point of
![]() $S$
, then
$S$
, then
![]() ${\mathcal{O}}_{X,x}$
has finite Tor-dimension over
${\mathcal{O}}_{X,x}$
has finite Tor-dimension over
![]() ${\mathcal{O}}_{S,s}$
. This property for the points over the singular locus of
${\mathcal{O}}_{S,s}$
. This property for the points over the singular locus of
![]() $S$
follows from the hypothesis of the lemma.◻
$S$
follows from the hypothesis of the lemma.◻
3.2 Divisor classes for singular curves
We fix a field
![]() $k$
. For
$k$
. For
![]() $X$
an equidimensional quasi-projective
$X$
an equidimensional quasi-projective
![]() $k$
-scheme and
$k$
-scheme and
![]() $Y\subsetneq X$
a closed subscheme of
$Y\subsetneq X$
a closed subscheme of
![]() $X$
not containing any component of
$X$
not containing any component of
![]() $X$
, write
$X$
, write
 ${\mathcal{Z}}_{0}(X,Y)$
for the free abelian group on the closed points of
${\mathcal{Z}}_{0}(X,Y)$
for the free abelian group on the closed points of
![]() $X$
not in
$X$
not in
![]() $Y$
.
$Y$
.
A curve
![]() $C$
will be in what follows a quasi-projective
$C$
will be in what follows a quasi-projective
![]() $k$
-scheme of pure dimension one. We let
$k$
-scheme of pure dimension one. We let
![]() $k(C)$
denote the ring of total quotients of
$k(C)$
denote the ring of total quotients of
![]() $C$
. Let
$C$
. Let
 $\{\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{r}\}$
denote the set of generic points of
$\{\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{r}\}$
denote the set of generic points of
![]() $C$
with closures
$C$
with closures
 $\{C_{1},\ldots ,C_{r}\}$
. Let
$\{C_{1},\ldots ,C_{r}\}$
. Let
![]() $T$
be a set of closed points of
$T$
be a set of closed points of
![]() $C$
containing
$C$
containing
![]() $C_{\text{sing}}$
and
$C_{\text{sing}}$
and
 $Z=T\cup \{\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{r}\}$
. Write
$Z=T\cup \{\unicode[STIX]{x1D702}_{1},\ldots ,\unicode[STIX]{x1D702}_{r}\}$
. Write
![]() ${\mathcal{O}}_{C,Z}$
for the semi-local ring on the points of
${\mathcal{O}}_{C,Z}$
for the semi-local ring on the points of
![]() $T$
. This yields a sequence of maps
$T$
. This yields a sequence of maps
 $$\begin{eqnarray}{\mathcal{O}}_{C,Z}^{\times }{\hookrightarrow}k(C)^{\times }\rightarrow \mathop{\prod }_{i=1}^{r}k(C_{i})^{\times }.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{C,Z}^{\times }{\hookrightarrow}k(C)^{\times }\rightarrow \mathop{\prod }_{i=1}^{r}k(C_{i})^{\times }.\end{eqnarray}$$
We let
![]() $\unicode[STIX]{x1D703}_{(C,Z)}$
denote the composite map. Letting
$\unicode[STIX]{x1D703}_{(C,Z)}$
denote the composite map. Letting
 $k(C,Z)^{\times }={\mathcal{O}}_{C,Z}^{\times }$
, the localization sequence in
$k(C,Z)^{\times }={\mathcal{O}}_{C,Z}^{\times }$
, the localization sequence in
![]() $K$
-theory yields a natural map
$K$
-theory yields a natural map
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{C,Z}:k(C,Z)^{\times }\rightarrow \amalg _{p\in C\setminus Z}~G_{0}(p)={\mathcal{Z}}_{0}(C,Z).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{C,Z}:k(C,Z)^{\times }\rightarrow \amalg _{p\in C\setminus Z}~G_{0}(p)={\mathcal{Z}}_{0}(C,Z).\end{eqnarray}$$
If
![]() $C$
is a reduced curve, it is a Cohen–Macaulay scheme and hence the second map in (3.1) is an isomorphism. Thus the group
$C$
is a reduced curve, it is a Cohen–Macaulay scheme and hence the second map in (3.1) is an isomorphism. Thus the group
![]() ${\mathcal{O}}_{C,Z}^{\times }$
is the subgroup of
${\mathcal{O}}_{C,Z}^{\times }$
is the subgroup of
![]() $k(C)^{\times }$
consisting of those
$k(C)^{\times }$
consisting of those
![]() $f$
which are regular and invertible in the local rings
$f$
which are regular and invertible in the local rings
![]() ${\mathcal{O}}_{C,x}$
for every
${\mathcal{O}}_{C,x}$
for every
![]() $x\in Z$
. In this case, the boundary
$x\in Z$
. In this case, the boundary
 $\unicode[STIX]{x2202}_{C,Z}(f)$
has a familiar expression: if we let
$\unicode[STIX]{x2202}_{C,Z}(f)$
has a familiar expression: if we let
 $\unicode[STIX]{x1D703}_{(C,Z)}(f)=\{f_{i}\}$
, then
$\unicode[STIX]{x1D703}_{(C,Z)}(f)=\{f_{i}\}$
, then
 $\operatorname{div}(f)=\sum _{i}\operatorname{div}(f_{i})$
, where
$\operatorname{div}(f)=\sum _{i}\operatorname{div}(f_{i})$
, where
![]() $\operatorname{div}(f_{i})$
is the divisor of the rational function
$\operatorname{div}(f_{i})$
is the divisor of the rational function
![]() $f_{i}$
on the integral curve
$f_{i}$
on the integral curve
![]() $C_{i}$
. If
$C_{i}$
. If
![]() $C$
is not reduced,
$C$
is not reduced,
![]() $\unicode[STIX]{x2202}_{C,Z}$
has a more complicated expression which we do not use in this text.
$\unicode[STIX]{x2202}_{C,Z}$
has a more complicated expression which we do not use in this text.
3.3 A Chow group of 0-cycles on singular schemes
Let
![]() $X$
be an equidimensional reduced quasi-projective scheme over
$X$
be an equidimensional reduced quasi-projective scheme over
![]() $k$
of dimension
$k$
of dimension
![]() $d\geqslant 1$
. Let
$d\geqslant 1$
. Let
![]() $X_{\text{sing}}$
and
$X_{\text{sing}}$
and
![]() $X_{\text{reg}}$
denote the singular and regular loci of
$X_{\text{reg}}$
denote the singular and regular loci of
![]() $X$
, respectively. Let
$X$
, respectively. Let
![]() $Y\subsetneq X$
be a closed subset containing
$Y\subsetneq X$
be a closed subset containing
![]() $X_{\text{sing}}$
, but not containing any component of
$X_{\text{sing}}$
, but not containing any component of
![]() $X$
. Write again
$X$
. Write again
 ${\mathcal{Z}}_{0}(X,Y)$
for the free abelian group on closed points of
${\mathcal{Z}}_{0}(X,Y)$
for the free abelian group on closed points of
![]() $X\setminus Y$
. We shall often write
$X\setminus Y$
. We shall often write
 ${\mathcal{Z}}_{0}(X,X_{\text{sing}})$
as
${\mathcal{Z}}_{0}(X,X_{\text{sing}})$
as
![]() ${\mathcal{Z}}_{0}(X)$
.
${\mathcal{Z}}_{0}(X)$
.
Let
 $f:X^{\prime }\rightarrow X$
be a proper morphism from another reduced equidimensional scheme over
$f:X^{\prime }\rightarrow X$
be a proper morphism from another reduced equidimensional scheme over
![]() $k$
. Let
$k$
. Let
 $Y^{\prime }\subsetneq X^{\prime }$
be a closed subset not containing any component of
$Y^{\prime }\subsetneq X^{\prime }$
be a closed subset not containing any component of
![]() $X^{\prime }$
such that
$X^{\prime }$
such that
 $f^{-1}(Y)\cup X_{\text{sing}}^{\prime }\subseteq Y^{\prime }$
. Then there is a push-forward map
$f^{-1}(Y)\cup X_{\text{sing}}^{\prime }\subseteq Y^{\prime }$
. Then there is a push-forward map
 $$\begin{eqnarray}f_{\ast }:{\mathcal{Z}}_{0}(X^{\prime },Y^{\prime })\rightarrow {\mathcal{Z}}_{0}(X,Y).\end{eqnarray}$$
$$\begin{eqnarray}f_{\ast }:{\mathcal{Z}}_{0}(X^{\prime },Y^{\prime })\rightarrow {\mathcal{Z}}_{0}(X,Y).\end{eqnarray}$$
This is defined on a closed point
 $x^{\prime }\in X^{\prime }\setminus Y^{\prime }$
with
$x^{\prime }\in X^{\prime }\setminus Y^{\prime }$
with
 $f(x^{\prime })=x$
by
$f(x^{\prime })=x$
by
 $f_{\ast }([x^{\prime }])=[k(x^{\prime }):k(x)]\cdot [x]$
.
$f_{\ast }([x^{\prime }])=[k(x^{\prime }):k(x)]\cdot [x]$
.
Definition 3.4. Let
![]() $C$
be a reduced curve in
$C$
be a reduced curve in
![]() $\mathbf{Sch}_{k}$
and let
$\mathbf{Sch}_{k}$
and let
 $\unicode[STIX]{x1D708}:C\rightarrow X$
be a finite morphism. We shall say that
$\unicode[STIX]{x1D708}:C\rightarrow X$
be a finite morphism. We shall say that
 $\unicode[STIX]{x1D708}:(C,Z)\rightarrow (X,Y)$
is a good curve relative to
$\unicode[STIX]{x1D708}:(C,Z)\rightarrow (X,Y)$
is a good curve relative to
![]() $(X,Y)$
if there exists a closed proper subscheme
$(X,Y)$
if there exists a closed proper subscheme
![]() $Z\subsetneq C$
such that the following hold:
$Z\subsetneq C$
such that the following hold:
-
(1) no component of
 $C$
is contained in
$C$
is contained in
 $Z$
;
$Z$
; -
(2)
 $\unicode[STIX]{x1D708}^{-1}(Y)\cup C_{\text{sing}}\subseteq Z$
;
$\unicode[STIX]{x1D708}^{-1}(Y)\cup C_{\text{sing}}\subseteq Z$
; -
(3)
 $\unicode[STIX]{x1D708}$
is locally complete intersection morphism at every point
$\unicode[STIX]{x1D708}$
is locally complete intersection morphism at every point
 $x\in C$
such that
$x\in C$
such that
 $\unicode[STIX]{x1D708}(x)\in Y$
.
$\unicode[STIX]{x1D708}(x)\in Y$
.
Given any good curve
![]() $(C,Z)$
relative to
$(C,Z)$
relative to
![]() $(X,Y)$
, we have a push-forward map as in (3.3)
$(X,Y)$
, we have a push-forward map as in (3.3)
 $$\begin{eqnarray}{\mathcal{Z}}_{0}(C,Z)\xrightarrow[{}]{\unicode[STIX]{x1D708}_{\ast }}{\mathcal{Z}}_{0}(X,Y).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}_{0}(C,Z)\xrightarrow[{}]{\unicode[STIX]{x1D708}_{\ast }}{\mathcal{Z}}_{0}(X,Y).\end{eqnarray}$$
We shall write
 ${\mathcal{R}}_{0}(C,Z,X)$
for the subgroup of
${\mathcal{R}}_{0}(C,Z,X)$
for the subgroup of
 ${\mathcal{Z}}_{0}(X,Y)$
generated by the set
${\mathcal{Z}}_{0}(X,Y)$
generated by the set
 $$\begin{eqnarray}\{\unicode[STIX]{x1D708}_{\ast }(\text{div}(f))\mid f\in {\mathcal{O}}_{C,Z}^{\times }\},\end{eqnarray}$$
$$\begin{eqnarray}\{\unicode[STIX]{x1D708}_{\ast }(\text{div}(f))\mid f\in {\mathcal{O}}_{C,Z}^{\times }\},\end{eqnarray}$$
where
![]() $\text{div}(f)$
for a rational function
$\text{div}(f)$
for a rational function
 $f\in {\mathcal{O}}_{C,Z}^{\times }$
is defined as in (3.2) for reduced curves. Let
$f\in {\mathcal{O}}_{C,Z}^{\times }$
is defined as in (3.2) for reduced curves. Let
 ${\mathcal{R}}_{0}(X,Y)$
denote the subgroup of
${\mathcal{R}}_{0}(X,Y)$
denote the subgroup of
 ${\mathcal{Z}}_{0}(X,Y)$
which is the image of the map
${\mathcal{Z}}_{0}(X,Y)$
which is the image of the map
 $$\begin{eqnarray}\underset{\unicode[STIX]{x1D708}:(C,Z)\rightarrow (X,Y)~\text{good}}{\bigoplus }{\mathcal{R}}_{0}(C,Z,X)\rightarrow {\mathcal{Z}}_{0}(X,Y).\end{eqnarray}$$
$$\begin{eqnarray}\underset{\unicode[STIX]{x1D708}:(C,Z)\rightarrow (X,Y)~\text{good}}{\bigoplus }{\mathcal{R}}_{0}(C,Z,X)\rightarrow {\mathcal{Z}}_{0}(X,Y).\end{eqnarray}$$
We define the Chow group of 0-cycles on
![]() $X$
relative to
$X$
relative to
![]() $Y$
to be the quotient
$Y$
to be the quotient
 $$\begin{eqnarray}\text{CH}_{0}(X,Y)=\frac{{\mathcal{Z}}_{0}(X,Y)}{{\mathcal{R}}_{0}(X,Y)}.\end{eqnarray}$$
$$\begin{eqnarray}\text{CH}_{0}(X,Y)=\frac{{\mathcal{Z}}_{0}(X,Y)}{{\mathcal{R}}_{0}(X,Y)}.\end{eqnarray}$$
We write
 $\text{CH}_{0}(X,X_{\text{sing}})$
as
$\text{CH}_{0}(X,X_{\text{sing}})$
as
 $\text{CH}_{0}(X)$
for short and call it the Chow group of
$\text{CH}_{0}(X)$
for short and call it the Chow group of
![]() $0$
-cycles on
$0$
-cycles on
![]() $X$
.
$X$
.
The following result shows that we can always assume that the morphisms
 $\unicode[STIX]{x1D708}:C\rightarrow X$
are l.c.i. in the definition of our rational equivalence.
$\unicode[STIX]{x1D708}:C\rightarrow X$
are l.c.i. in the definition of our rational equivalence.
Lemma 3.5. Let
![]() $(X,Y)$
be as above. Given any good curve
$(X,Y)$
be as above. Given any good curve
 $\unicode[STIX]{x1D708}:(C,Z)\rightarrow (X,Y)$
relative to
$\unicode[STIX]{x1D708}:(C,Z)\rightarrow (X,Y)$
relative to
![]() $(X,Y)$
and any
$(X,Y)$
and any
 $f\in {\mathcal{O}}_{C,Z}^{\times }$
, there exists a good curve
$f\in {\mathcal{O}}_{C,Z}^{\times }$
, there exists a good curve
 $\unicode[STIX]{x1D708}^{\prime }:(C^{\prime },Z^{\prime })\rightarrow (X,Y)$
relative to
$\unicode[STIX]{x1D708}^{\prime }:(C^{\prime },Z^{\prime })\rightarrow (X,Y)$
relative to
![]() $(X,Y)$
and
$(X,Y)$
and
 $f^{\prime }\in {\mathcal{O}}_{C^{\prime },Z^{\prime }}^{\times }$
such that:
$f^{\prime }\in {\mathcal{O}}_{C^{\prime },Z^{\prime }}^{\times }$
such that:
-
(1)
 $\unicode[STIX]{x1D708}_{\ast }(\text{div}(f))=\unicode[STIX]{x1D708}_{\ast }^{\prime }(\text{div}(f^{\prime }))$
;
$\unicode[STIX]{x1D708}_{\ast }(\text{div}(f))=\unicode[STIX]{x1D708}_{\ast }^{\prime }(\text{div}(f^{\prime }))$
; -
(2)
 $\unicode[STIX]{x1D708}^{\prime }:C^{\prime }\rightarrow X$
is an l.c.i. morphism.
$\unicode[STIX]{x1D708}^{\prime }:C^{\prime }\rightarrow X$
is an l.c.i. morphism.
Proof. Let
![]() $U_{1}\subseteq C$
be an open subset of
$U_{1}\subseteq C$
be an open subset of
![]() $C$
containing
$C$
containing
 $S_{1}=\unicode[STIX]{x1D708}^{-1}(X_{\text{sing}})$
such that
$S_{1}=\unicode[STIX]{x1D708}^{-1}(X_{\text{sing}})$
such that
 $(C_{\text{sing}}\setminus S_{1})\cap U_{1}=\emptyset$
. This is possible because
$(C_{\text{sing}}\setminus S_{1})\cap U_{1}=\emptyset$
. This is possible because
![]() $S_{1}$
is a finite set. Let
$S_{1}$
is a finite set. Let
 $\unicode[STIX]{x1D70B}:(C\setminus S_{1})^{N}\rightarrow C\setminus S_{1}$
denote the normalization map. It follows that
$\unicode[STIX]{x1D70B}:(C\setminus S_{1})^{N}\rightarrow C\setminus S_{1}$
denote the normalization map. It follows that
 $\unicode[STIX]{x1D70B}:\unicode[STIX]{x1D70B}^{-1}(U_{1}\setminus S_{1})\rightarrow U_{1}\setminus S_{1}$
is an isomorphism. Setting
$\unicode[STIX]{x1D70B}:\unicode[STIX]{x1D70B}^{-1}(U_{1}\setminus S_{1})\rightarrow U_{1}\setminus S_{1}$
is an isomorphism. Setting
 $U_{2}=(C\setminus S_{1})^{N}$
, we see that
$U_{2}=(C\setminus S_{1})^{N}$
, we see that
![]() $U_{1}$
and
$U_{1}$
and
![]() $U_{2}$
glue along
$U_{2}$
glue along
 $\unicode[STIX]{x1D70B}^{-1}(U_{1}\setminus S_{1})$
to give a unique scheme
$\unicode[STIX]{x1D70B}^{-1}(U_{1}\setminus S_{1})$
to give a unique scheme
![]() $C^{\prime }$
and a unique map
$C^{\prime }$
and a unique map
 $p:C^{\prime }\rightarrow C$
. This scheme has the property that
$p:C^{\prime }\rightarrow C$
. This scheme has the property that
![]() $p$
is finite,
$p$
is finite,
 $p^{-1}(U_{1})\rightarrow U_{1}$
is an isomorphism and
$p^{-1}(U_{1})\rightarrow U_{1}$
is an isomorphism and
 $p^{-1}(C\setminus S_{1})=(C\setminus S_{1})^{N}$
.
$p^{-1}(C\setminus S_{1})=(C\setminus S_{1})^{N}$
.
Setting
 $Z^{\prime }=p^{-1}(Z)$
and
$Z^{\prime }=p^{-1}(Z)$
and
 $f^{\prime }=p^{\ast }(f)\in k(C^{\prime })^{\times }$
, we see that
$f^{\prime }=p^{\ast }(f)\in k(C^{\prime })^{\times }$
, we see that
 $f^{\prime }\in {\mathcal{O}}_{C^{\prime },Z^{\prime }}^{\times }$
and
$f^{\prime }\in {\mathcal{O}}_{C^{\prime },Z^{\prime }}^{\times }$
and
 $\text{div}(f)=p_{\ast }(\text{div}(f^{\prime }))$
. If we let
$\text{div}(f)=p_{\ast }(\text{div}(f^{\prime }))$
. If we let
 $\unicode[STIX]{x1D708}^{\prime }=\unicode[STIX]{x1D708}\circ p$
, we get
$\unicode[STIX]{x1D708}^{\prime }=\unicode[STIX]{x1D708}\circ p$
, we get
 $\unicode[STIX]{x1D708}_{\ast }(\text{div}(f))=\unicode[STIX]{x1D708}_{\ast }^{\prime }(\text{div}(f^{\prime }))$
. Furthermore,
$\unicode[STIX]{x1D708}_{\ast }(\text{div}(f))=\unicode[STIX]{x1D708}_{\ast }^{\prime }(\text{div}(f^{\prime }))$
. Furthermore,
 $\unicode[STIX]{x1D708}^{\prime -1}(X_{\text{reg}})\rightarrow X_{\text{reg}}$
is a finite-type morphism of regular schemes and hence is an l.c.i. morphism. Since
$\unicode[STIX]{x1D708}^{\prime -1}(X_{\text{reg}})\rightarrow X_{\text{reg}}$
is a finite-type morphism of regular schemes and hence is an l.c.i. morphism. Since
![]() $\unicode[STIX]{x1D708}$
is l.c.i. over
$\unicode[STIX]{x1D708}$
is l.c.i. over
![]() $X_{\text{sing}}$
and
$X_{\text{sing}}$
and
![]() $p$
is an isomorphism in a neighborhood of
$p$
is an isomorphism in a neighborhood of
 $\unicode[STIX]{x1D708}^{-1}(X_{\text{sing}})$
, we conclude that
$\unicode[STIX]{x1D708}^{-1}(X_{\text{sing}})$
, we conclude that
![]() $\unicode[STIX]{x1D708}^{\prime }$
is an l.c.i. morphism.◻
$\unicode[STIX]{x1D708}^{\prime }$
is an l.c.i. morphism.◻
3.4 The Levine–Weibel Chow group
We now recall the Levine–Weibel (cohomological) Chow group of 0-cycles for singular schemes as defined in [Reference Levine and WeibelLW85, Definition 1.2]. Let
![]() $X$
be an equidimensional quasi-projective scheme of dimension
$X$
be an equidimensional quasi-projective scheme of dimension
![]() $d\geqslant 1$
over
$d\geqslant 1$
over
![]() $k$
,
$k$
,
 $X\supsetneq Y\supseteq X_{\text{sing}}$
a closed subscheme not containing any component of
$X\supsetneq Y\supseteq X_{\text{sing}}$
a closed subscheme not containing any component of
![]() $X$
.
$X$
.
Definition 3.6. A Cartier curve on
![]() $X$
relative to
$X$
relative to
![]() $Y$
is a purely one-dimensional closed subscheme
$Y$
is a purely one-dimensional closed subscheme
 $C{\hookrightarrow}X$
that has no component contained in
$C{\hookrightarrow}X$
that has no component contained in
![]() $Y$
and is defined by a regular sequence in
$Y$
and is defined by a regular sequence in
![]() $X$
at each point of
$X$
at each point of
![]() $C\cap Y$
.
$C\cap Y$
.
One example of Cartier curves we shall encounter in this text is given by the following.
Lemma 3.7. Let
![]() $X$
be a connected smooth quasi-projective scheme over
$X$
be a connected smooth quasi-projective scheme over
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Let
$D\subset X$
be an effective Cartier divisor. Let
 $\unicode[STIX]{x1D708}:C{\hookrightarrow}X$
be an integral curve which is not contained in
$\unicode[STIX]{x1D708}:C{\hookrightarrow}X$
be an integral curve which is not contained in
![]() $D$
. Assume that
$D$
. Assume that
![]() $C$
is l.c.i. along
$C$
is l.c.i. along
![]() $D$
. Let
$D$
. Let
 $\unicode[STIX]{x1D6E5}:S(X,D)\rightarrow X$
denote the double construction. Then
$\unicode[STIX]{x1D6E5}:S(X,D)\rightarrow X$
denote the double construction. Then
 $S(C,\unicode[STIX]{x1D708}^{\ast }D)$
is a Cartier curve on
$S(C,\unicode[STIX]{x1D708}^{\ast }D)$
is a Cartier curve on
 $S(X,D)$
relative to
$S(X,D)$
relative to
![]() $D$
.
$D$
.
Proof. We write
 $S(X,D)$
and
$S(X,D)$
and
 $S(C,\unicode[STIX]{x1D708}^{\ast }(D))$
as
$S(C,\unicode[STIX]{x1D708}^{\ast }(D))$
as
![]() $S_{X}$
and
$S_{X}$
and
![]() $S_{C}$
, respectively, in this proof. Since the inclusion
$S_{C}$
, respectively, in this proof. Since the inclusion
 $\unicode[STIX]{x1D708}:C{\hookrightarrow}X$
is l.c.i. along
$\unicode[STIX]{x1D708}:C{\hookrightarrow}X$
is l.c.i. along
![]() $D$
, it follows Proposition 2.4 that the square
$D$
, it follows Proposition 2.4 that the square

is Cartesian. It also follows from Proposition 2.4(5) that
 $S_{\unicode[STIX]{x1D708}}:S_{C}{\hookrightarrow}S_{X}$
is l.c.i. along
$S_{\unicode[STIX]{x1D708}}:S_{C}{\hookrightarrow}S_{X}$
is l.c.i. along
![]() $D$
. Moreover, a combination of Proposition 2.4(4) and Proposition 2.3(2) tells us that
$D$
. Moreover, a combination of Proposition 2.4(4) and Proposition 2.3(2) tells us that
![]() $S_{C}$
is reduced with two components, both isomorphic to
$S_{C}$
is reduced with two components, both isomorphic to
![]() $C$
. We conclude that
$C$
. We conclude that
 $S_{C}{\hookrightarrow}S_{X}$
is a (reduced) Cartier curve relative to
$S_{C}{\hookrightarrow}S_{X}$
is a (reduced) Cartier curve relative to
![]() $D$
.◻
$D$
.◻
Given a Cartier curve
 $\unicode[STIX]{x1D704}:C{\hookrightarrow}X$
relative to
$\unicode[STIX]{x1D704}:C{\hookrightarrow}X$
relative to
![]() $Y$
, we let
$Y$
, we let
 ${\mathcal{R}}_{0}^{\text{LW}}(C,Y,X)$
denote the image of the composite map
${\mathcal{R}}_{0}^{\text{LW}}(C,Y,X)$
denote the image of the composite map
 $k(C,C\cap Y)^{\times }\xrightarrow[{}]{\unicode[STIX]{x2202}_{C,C\cap Y}}{\mathcal{Z}}_{0}(C,C\cap Y)\xrightarrow[{}]{\unicode[STIX]{x1D704}_{\ast }}{\mathcal{Z}}_{0}(X,Y)$
. We let
$k(C,C\cap Y)^{\times }\xrightarrow[{}]{\unicode[STIX]{x2202}_{C,C\cap Y}}{\mathcal{Z}}_{0}(C,C\cap Y)\xrightarrow[{}]{\unicode[STIX]{x1D704}_{\ast }}{\mathcal{Z}}_{0}(X,Y)$
. We let
 ${\mathcal{R}}_{0}^{\text{LW}}(X,Y)$
denote the subgroup of
${\mathcal{R}}_{0}^{\text{LW}}(X,Y)$
denote the subgroup of
 ${\mathcal{Z}}_{0}(X,Y)$
generated by
${\mathcal{Z}}_{0}(X,Y)$
generated by
 ${\mathcal{R}}_{0}^{\text{LW}}(C,Z,X)$
, where
${\mathcal{R}}_{0}^{\text{LW}}(C,Z,X)$
, where
![]() $C\subset X$
runs through all Cartier curves relative to
$C\subset X$
runs through all Cartier curves relative to
![]() $Y$
.
$Y$
.
Definition 3.8. The Levine–Weibel Chow group of 0-cycles of
![]() $X$
relative to
$X$
relative to
![]() $Y$
is defined as the quotient
$Y$
is defined as the quotient
 $$\begin{eqnarray}\text{CH}_{0}^{\text{LW}}(X,Y)={\mathcal{Z}}_{0}(X,Y)/{\mathcal{R}}_{0}^{\text{LW}}(X,Y).\end{eqnarray}$$
$$\begin{eqnarray}\text{CH}_{0}^{\text{LW}}(X,Y)={\mathcal{Z}}_{0}(X,Y)/{\mathcal{R}}_{0}^{\text{LW}}(X,Y).\end{eqnarray}$$
The group
 $\text{CH}_{0}^{\text{LW}}(X,X_{\text{sing}})$
is often denoted by
$\text{CH}_{0}^{\text{LW}}(X,X_{\text{sing}})$
is often denoted by
 $\text{CH}_{0}^{\text{LW}}(X)$
.
$\text{CH}_{0}^{\text{LW}}(X)$
.
We recall here the following important moving lemma, due to Levine, that simplifies the set of relations in case
![]() $X$
satisfies additional assumptions.
$X$
satisfies additional assumptions.
Proposition 3.9 (See [Reference LevineLev87, Lemma 1.4] and [Reference Biswas and SrinivasBS99, Lemma 2.1]).
Let
![]() $X$
be an equidimensional quasi-projective
$X$
be an equidimensional quasi-projective
![]() $k$
-scheme and let
$k$
-scheme and let
 $X_{\text{sing}}\subset Y\subsetneq X$
be a closed subset of
$X_{\text{sing}}\subset Y\subsetneq X$
be a closed subset of
![]() $X$
as above. Assume that
$X$
as above. Assume that
![]() $X$
is reduced. Then the subgroup
$X$
is reduced. Then the subgroup
 ${\mathcal{R}}_{0}^{\text{LW}}(X,Y)$
of
${\mathcal{R}}_{0}^{\text{LW}}(X,Y)$
of
 ${\mathcal{Z}}_{0}(X,Y)$
agrees with the subgroup
${\mathcal{Z}}_{0}(X,Y)$
agrees with the subgroup
 ${\mathcal{R}}_{0}^{\text{LW}}(X,Y)_{\text{red}}$
, generated by divisors of rational functions on reduced Cartier curves on
${\mathcal{R}}_{0}^{\text{LW}}(X,Y)_{\text{red}}$
, generated by divisors of rational functions on reduced Cartier curves on
![]() $X$
relative to
$X$
relative to
![]() $Y$
. If
$Y$
. If
![]() $X$
is moreover irreducible, then the Cartier curves generating the rational equivalence can be chosen to be irreducible as well.
$X$
is moreover irreducible, then the Cartier curves generating the rational equivalence can be chosen to be irreducible as well.
Lemma 3.10. Let
![]() $X$
be a reduced quasi-projective
$X$
be a reduced quasi-projective
![]() $k$
-scheme. Then there is a canonical surjection
$k$
-scheme. Then there is a canonical surjection
 $$\begin{eqnarray}\text{CH}_{0}^{\text{LW}}(X,Y){\twoheadrightarrow}\text{CH}_{0}(X,Y).\end{eqnarray}$$
$$\begin{eqnarray}\text{CH}_{0}^{\text{LW}}(X,Y){\twoheadrightarrow}\text{CH}_{0}(X,Y).\end{eqnarray}$$
Proof. The map (3.7) is induced by the identity on the set of generators, so we just have to show that it is well defined. Since
![]() $X$
is reduced, by Proposition 3.9, we can assume that the Cartier curves defining the rational equivalence on the Levine–Weibel Chow group are reduced. Now, we just note that a reduced Cartier curve is a good curve relative to
$X$
is reduced, by Proposition 3.9, we can assume that the Cartier curves defining the rational equivalence on the Levine–Weibel Chow group are reduced. Now, we just note that a reduced Cartier curve is a good curve relative to
![]() $(X,Y)$
.◻
$(X,Y)$
.◻
Lemma 3.11. Let
![]() $X$
be a reduced quasi-projective scheme over
$X$
be a reduced quasi-projective scheme over
![]() $k$
and let
$k$
and let
![]() $Y\subsetneq X$
be a closed subset containing
$Y\subsetneq X$
be a closed subset containing
![]() $X_{\text{sing}}$
and containing no components of
$X_{\text{sing}}$
and containing no components of
![]() $X$
. Let
$X$
. Let
![]() $(C,Z)$
be a good curve relative to
$(C,Z)$
be a good curve relative to
![]() $(X,Y)$
. Then there are cycle class maps
$(X,Y)$
. Then there are cycle class maps
 $\text{cyc}_{C}:{\mathcal{Z}}_{0}(C,Z)\rightarrow K_{0}(C)$
and
$\text{cyc}_{C}:{\mathcal{Z}}_{0}(C,Z)\rightarrow K_{0}(C)$
and
 $\text{cyc}_{X}:{\mathcal{Z}}_{0}(X,Y)\rightarrow K_{0}(X)$
making the diagram
$\text{cyc}_{X}:{\mathcal{Z}}_{0}(X,Y)\rightarrow K_{0}(X)$
making the diagram

commutative.
Proof. Since
 $\unicode[STIX]{x1D708}^{-1}(Y)\cup X_{\text{sing}}^{\prime }\subseteq Y^{\prime }$
, we have a push-forward map
$\unicode[STIX]{x1D708}^{-1}(Y)\cup X_{\text{sing}}^{\prime }\subseteq Y^{\prime }$
, we have a push-forward map
 $\unicode[STIX]{x1D708}_{\ast }:{\mathcal{Z}}_{0}(C,Z)\rightarrow {\mathcal{Z}}_{0}(X,Y)$
, given by
$\unicode[STIX]{x1D708}_{\ast }:{\mathcal{Z}}_{0}(C,Z)\rightarrow {\mathcal{Z}}_{0}(X,Y)$
, given by
 $\unicode[STIX]{x1D708}_{\ast }([x])=[k(x):k(\unicode[STIX]{x1D708}(x))]\cdot [\unicode[STIX]{x1D708}(x)]$
. Since
$\unicode[STIX]{x1D708}_{\ast }([x])=[k(x):k(\unicode[STIX]{x1D708}(x))]\cdot [\unicode[STIX]{x1D708}(x)]$
. Since
![]() $\unicode[STIX]{x1D708}$
is l.c.i. along
$\unicode[STIX]{x1D708}$
is l.c.i. along
![]() $X_{\text{sing}}$
, it follows from Lemma 3.3 that the map
$X_{\text{sing}}$
, it follows from Lemma 3.3 that the map
 $\unicode[STIX]{x1D708}:C\rightarrow X$
is perfect. Hence, there is a push-forward map on
$\unicode[STIX]{x1D708}:C\rightarrow X$
is perfect. Hence, there is a push-forward map on
![]() $K_{0}$
-groups
$K_{0}$
-groups
 $\unicode[STIX]{x1D708}_{\ast }:K_{0}(C)\rightarrow K_{0}(X)$
by Proposition 3.1.
$\unicode[STIX]{x1D708}_{\ast }:K_{0}(C)\rightarrow K_{0}(X)$
by Proposition 3.1.
To construct the cycle class maps and show that the square commutes, let
 $x\in C\setminus Z$
be a closed point and set
$x\in C\setminus Z$
be a closed point and set
 $y=\unicode[STIX]{x1D708}(x)$
. Let
$y=\unicode[STIX]{x1D708}(x)$
. Let
 $\unicode[STIX]{x1D704}_{x}:\operatorname{Spec}(k(x))\rightarrow C$
and
$\unicode[STIX]{x1D704}_{x}:\operatorname{Spec}(k(x))\rightarrow C$
and
 $\unicode[STIX]{x1D704}_{y}:\operatorname{Spec}(k(y))\rightarrow X$
be the closed immersions. Since these maps as well as
$\unicode[STIX]{x1D704}_{y}:\operatorname{Spec}(k(y))\rightarrow X$
be the closed immersions. Since these maps as well as
![]() $\unicode[STIX]{x1D708}$
are perfect (see Lemma 3.3), we have the induced push-forward maps on Grothendieck groups of vector bundles and a commutative diagram by Proposition 3.1.
$\unicode[STIX]{x1D708}$
are perfect (see Lemma 3.3), we have the induced push-forward maps on Grothendieck groups of vector bundles and a commutative diagram by Proposition 3.1.

Setting
 $\text{cyc}_{C}([x])$
to be
$\text{cyc}_{C}([x])$
to be
![]() ${\unicode[STIX]{x1D704}_{x}}_{\ast }(1)$
, we get the cycle class maps
${\unicode[STIX]{x1D704}_{x}}_{\ast }(1)$
, we get the cycle class maps
 $\text{cyc}_{C}:{\mathcal{Z}}_{0}(C)\rightarrow K_{0}(C)$
and
$\text{cyc}_{C}:{\mathcal{Z}}_{0}(C)\rightarrow K_{0}(C)$
and
 $\text{cyc}_{X}:{\mathcal{Z}}_{0}(X)\rightarrow K_{0}(X)$
such that (3.8) commutes.◻
$\text{cyc}_{X}:{\mathcal{Z}}_{0}(X)\rightarrow K_{0}(X)$
such that (3.8) commutes.◻
Lemma 3.12. Suppose that
![]() $X$
is reduced and purely one-dimensional. Then there is a canonical isomorphism
$X$
is reduced and purely one-dimensional. Then there is a canonical isomorphism
 $\text{CH}_{0}(X,Y)\simeq \text{CH}_{0}^{\text{LW}}(X,Y)\simeq \operatorname{Pic}(X)$
.
$\text{CH}_{0}(X,Y)\simeq \text{CH}_{0}^{\text{LW}}(X,Y)\simeq \operatorname{Pic}(X)$
.
Proof. Let
 $\unicode[STIX]{x1D708}:C\rightarrow X$
be a finite map from a reduced curve and let
$\unicode[STIX]{x1D708}:C\rightarrow X$
be a finite map from a reduced curve and let
![]() $Z\subsetneq C$
be a closed subset such that
$Z\subsetneq C$
be a closed subset such that
![]() $(C,Z)$
is good relative to
$(C,Z)$
is good relative to
![]() $(X,Y)$
. By Lemma 3.11, there is a commutative diagram.
$(X,Y)$
. By Lemma 3.11, there is a commutative diagram.

Let
 $f\in {\mathcal{O}}_{C,Z}^{\times }$
. It follows from [Reference Levine and WeibelLW85, Proposition 2.1] that
$f\in {\mathcal{O}}_{C,Z}^{\times }$
. It follows from [Reference Levine and WeibelLW85, Proposition 2.1] that
 $\text{cyc}_{C}(\text{div}(f))=0$
. In particular, we get
$\text{cyc}_{C}(\text{div}(f))=0$
. In particular, we get
 $\text{cyc}_{X}\circ \unicode[STIX]{x1D708}_{\ast }(\text{div}(f))=\unicode[STIX]{x1D708}_{\ast }\circ \text{cyc}_{C}(\text{div}(f))=0$
. It follows again from [Reference Levine and WeibelLW85, Proposition 1.4] that
$\text{cyc}_{X}\circ \unicode[STIX]{x1D708}_{\ast }(\text{div}(f))=\unicode[STIX]{x1D708}_{\ast }\circ \text{cyc}_{C}(\text{div}(f))=0$
. It follows again from [Reference Levine and WeibelLW85, Proposition 1.4] that
 $\unicode[STIX]{x1D708}_{\ast }(\text{div}(f))=0$
in
$\unicode[STIX]{x1D708}_{\ast }(\text{div}(f))=0$
in
 $\text{CH}_{0}^{\text{LW}}(X,Y)\simeq \operatorname{Pic}(X){\hookrightarrow}K_{0}(X)$
. We have thus shown that the surjective map
$\text{CH}_{0}^{\text{LW}}(X,Y)\simeq \operatorname{Pic}(X){\hookrightarrow}K_{0}(X)$
. We have thus shown that the surjective map
 $\text{CH}_{0}^{\text{LW}}(X){\twoheadrightarrow}\text{CH}_{0}(X)$
is also injective, hence an isomorphism.◻
$\text{CH}_{0}^{\text{LW}}(X){\twoheadrightarrow}\text{CH}_{0}(X)$
is also injective, hence an isomorphism.◻
Lemma 3.13. Let
![]() $X$
be a reduced quasi-projective scheme of dimension
$X$
be a reduced quasi-projective scheme of dimension
![]() $d\geqslant 1$
over
$d\geqslant 1$
over
![]() $k$
and let
$k$
and let
![]() $Y\subsetneq X$
be a closed subset containing
$Y\subsetneq X$
be a closed subset containing
![]() $X_{\text{sing}}$
and containing no components of
$X_{\text{sing}}$
and containing no components of
![]() $X$
. Then the cycle class map
$X$
. Then the cycle class map
 $\text{cyc}_{X}:{\mathcal{Z}}_{0}(X,Y)\rightarrow K_{0}(X)$
given by Lemma 3.11 descends to group homomorphisms
$\text{cyc}_{X}:{\mathcal{Z}}_{0}(X,Y)\rightarrow K_{0}(X)$
given by Lemma 3.11 descends to group homomorphisms
 $$\begin{eqnarray}\text{cyc}_{X}:\text{CH}_{0}(X,Y)\rightarrow K_{0}(X);\quad \text{cyc}_{X}^{\text{LW}}:\text{CH}_{0}^{\text{LW}}(X,Y)\rightarrow K_{0}(X)\end{eqnarray}$$
$$\begin{eqnarray}\text{cyc}_{X}:\text{CH}_{0}(X,Y)\rightarrow K_{0}(X);\quad \text{cyc}_{X}^{\text{LW}}:\text{CH}_{0}^{\text{LW}}(X,Y)\rightarrow K_{0}(X)\end{eqnarray}$$
making the diagram

commutative.
Proof. The fact that
![]() $\text{cyc}_{X}$
yields a cycle class map
$\text{cyc}_{X}$
yields a cycle class map
 $\text{cyc}_{X}^{\text{LW}}:\text{CH}_{0}^{\text{LW}}(X,Y)\rightarrow K_{0}(X)$
is proved in [Reference Levine and WeibelLW85, Proposition 2.1]. To show that
$\text{cyc}_{X}^{\text{LW}}:\text{CH}_{0}^{\text{LW}}(X,Y)\rightarrow K_{0}(X)$
is proved in [Reference Levine and WeibelLW85, Proposition 2.1]. To show that
![]() $\text{cyc}_{X}$
descends to a map on our modified version of the Chow group, let
$\text{cyc}_{X}$
descends to a map on our modified version of the Chow group, let
 $\unicode[STIX]{x1D708}:(C,Z)\rightarrow (X,Y)$
be a good curve relative to
$\unicode[STIX]{x1D708}:(C,Z)\rightarrow (X,Y)$
be a good curve relative to
![]() $(X,Y)$
and let
$(X,Y)$
and let
 $f\in {\mathcal{O}}_{C,Z}^{\times }$
. We then have
$f\in {\mathcal{O}}_{C,Z}^{\times }$
. We then have
 $\text{cyc}_{X}\circ \unicode[STIX]{x1D708}_{\ast }(\text{div}(f))=\unicode[STIX]{x1D708}_{\ast }\circ \text{cyc}_{C}(\text{div}(f))$
by Lemma 3.11. On the other hand, it follows from Lemma 3.12 that
$\text{cyc}_{X}\circ \unicode[STIX]{x1D708}_{\ast }(\text{div}(f))=\unicode[STIX]{x1D708}_{\ast }\circ \text{cyc}_{C}(\text{div}(f))$
by Lemma 3.11. On the other hand, it follows from Lemma 3.12 that
 $\text{cyc}_{C}(\text{div}(f))=0$
. This shows that
$\text{cyc}_{C}(\text{div}(f))=0$
. This shows that
![]() $\text{cyc}_{X}$
is defined on the Chow groups. The commutativity of (3.11) is clear from the definitions.◻
$\text{cyc}_{X}$
is defined on the Chow groups. The commutativity of (3.11) is clear from the definitions.◻
3.5 Comparison of two Chow groups in higher dimension
In this section, we prove a comparison theorem for the two Chow groups in higher dimension. More comparison results in positive characteristic will be given in Theorems 7.3 and 9.8.
Suppose that the field
![]() $k$
is algebraically closed and let
$k$
is algebraically closed and let
 $d=\dim (X)$
. Write
$d=\dim (X)$
. Write
 $F^{d}K_{0}(X)$
for the subgroup of
$F^{d}K_{0}(X)$
for the subgroup of
![]() $K_{0}(X)$
generated by the cycle classes of smooth, closed points in
$K_{0}(X)$
generated by the cycle classes of smooth, closed points in
![]() $X$
. In [Reference LevineLev85b, Corollary 5.4] (see also [Reference LevineLev87, Corollary 2.7]), Levine showed the existence of a top Chern class
$X$
. In [Reference LevineLev85b, Corollary 5.4] (see also [Reference LevineLev87, Corollary 2.7]), Levine showed the existence of a top Chern class
 $c_{d}:F^{d}K_{0}(X)\rightarrow \text{CH}_{0}^{\text{LW}}(X)$
such that
$c_{d}:F^{d}K_{0}(X)\rightarrow \text{CH}_{0}^{\text{LW}}(X)$
such that
 $c_{d}\circ \text{cyc}_{X}^{\text{LW}}$
is multiplication by
$c_{d}\circ \text{cyc}_{X}^{\text{LW}}$
is multiplication by
![]() $(d-1)!$
. In particular, the kernel of
$(d-1)!$
. In particular, the kernel of
![]() $\text{cyc}_{X}^{\text{LW}}$
is torsion. An immediate consequence of Lemma 3.13 is then the following.
$\text{cyc}_{X}^{\text{LW}}$
is torsion. An immediate consequence of Lemma 3.13 is then the following.
Corollary 3.14. Let
![]() $X$
be a reduced quasi-projective scheme over an algebraically closed field
$X$
be a reduced quasi-projective scheme over an algebraically closed field
![]() $k$
. Then the canonical map
$k$
. Then the canonical map
 $\text{CH}_{0}^{\text{LW}}(X)_{\mathbb{Q}}\rightarrow \text{CH}_{0}(X)_{\mathbb{Q}}$
is an isomorphism.
$\text{CH}_{0}^{\text{LW}}(X)_{\mathbb{Q}}\rightarrow \text{CH}_{0}(X)_{\mathbb{Q}}$
is an isomorphism.
In order to integrally compare the two Chow groups in dimension larger than or equal to two, we use the following.
Proposition 3.15. Let
![]() $k$
be an algebraically closed field of characteristic zero and let
$k$
be an algebraically closed field of characteristic zero and let
![]() $X$
be a reduced projective scheme of dimension
$X$
be a reduced projective scheme of dimension
![]() $d\geqslant 1$
over
$d\geqslant 1$
over
![]() $k$
. Then
$k$
. Then
![]() $\text{cyc}_{X}^{\text{LW}}$
is injective.
$\text{cyc}_{X}^{\text{LW}}$
is injective.
Proof. Let
 $\unicode[STIX]{x1D6FC}\in \text{CH}_{0}^{\text{LW}}(X)$
be such that
$\unicode[STIX]{x1D6FC}\in \text{CH}_{0}^{\text{LW}}(X)$
be such that
 $\text{cyc}_{X}^{\text{LW}}(\unicode[STIX]{x1D6FC})=0$
. By Levine’s theorem recalled above, we know that
$\text{cyc}_{X}^{\text{LW}}(\unicode[STIX]{x1D6FC})=0$
. By Levine’s theorem recalled above, we know that
![]() $\unicode[STIX]{x1D6FC}$
is a torsion class in
$\unicode[STIX]{x1D6FC}$
is a torsion class in
 $\text{CH}_{0}^{\text{LW}}(X)$
.
$\text{CH}_{0}^{\text{LW}}(X)$
.
To show that
![]() $\unicode[STIX]{x1D6FC}=0$
, we can use the Lefschetz principle argument and rigidity of the Chow group of zero-cycles over algebraically closed fields and assume that
$\unicode[STIX]{x1D6FC}=0$
, we can use the Lefschetz principle argument and rigidity of the Chow group of zero-cycles over algebraically closed fields and assume that
![]() $k=\mathbb{C}$
. Let
$k=\mathbb{C}$
. Let
 $\mathbb{H}_{{\mathcal{D}}^{\ast }}^{2d}(X,\mathbb{Z}(d))$
denote the modified Deligne–Beilinson cohomology of
$\mathbb{H}_{{\mathcal{D}}^{\ast }}^{2d}(X,\mathbb{Z}(d))$
denote the modified Deligne–Beilinson cohomology of
![]() $X$
defined in [Reference LevineLev92, §2] (see also §8 below). There is then a short exact sequence
$X$
defined in [Reference LevineLev92, §2] (see also §8 below). There is then a short exact sequence
 $$\begin{eqnarray}0\rightarrow A^{d}(X)\rightarrow \mathbb{H}_{{\mathcal{D}}^{\ast }}^{2d}(X,\mathbb{Z}(d))\rightarrow H^{2d}(X_{\text{a n}},\mathbb{Z}(d))\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow A^{d}(X)\rightarrow \mathbb{H}_{{\mathcal{D}}^{\ast }}^{2d}(X,\mathbb{Z}(d))\rightarrow H^{2d}(X_{\text{a n}},\mathbb{Z}(d))\rightarrow 0\end{eqnarray}$$
and it was shown in [Reference LevineLev92, § 2] that there is a Chern class map
 $c_{{\mathcal{D}}^{\ast },X}^{d}:K_{0}(X)\,\rightarrow \,\mathbb{H}_{{\mathcal{D}}^{\ast }}^{2d}(X,\mathbb{Z}(d))$
which induces an Abel–Jacobi map
$c_{{\mathcal{D}}^{\ast },X}^{d}:K_{0}(X)\,\rightarrow \,\mathbb{H}_{{\mathcal{D}}^{\ast }}^{2d}(X,\mathbb{Z}(d))$
which induces an Abel–Jacobi map
 $\text{AK}_{X}^{d}:\text{CH}_{0}^{\text{LW}}(X)_{\text{deg}\,0}\rightarrow A^{d}(X)$
given by
$\text{AK}_{X}^{d}:\text{CH}_{0}^{\text{LW}}(X)_{\text{deg}\,0}\rightarrow A^{d}(X)$
given by
 $\text{AK}_{X}^{d}=\,c_{{\mathcal{D}}^{\ast },X}^{d}\circ \text{cyc}_{X}^{\text{LW}}$
, where
$\text{AK}_{X}^{d}=\,c_{{\mathcal{D}}^{\ast },X}^{d}\circ \text{cyc}_{X}^{\text{LW}}$
, where
 $\text{CH}_{0}^{\text{LW}}(X)_{\text{deg}\,0}:=\text{Ker}(\text{CH}_{0}^{\text{LW}}(X)\rightarrow H^{2d}(X_{\text{an}},\mathbb{Z}(d)))$
.
$\text{CH}_{0}^{\text{LW}}(X)_{\text{deg}\,0}:=\text{Ker}(\text{CH}_{0}^{\text{LW}}(X)\rightarrow H^{2d}(X_{\text{an}},\mathbb{Z}(d)))$
.
Since
 $H^{2d}(X_{\text{an}},\mathbb{Z}(d))$
is torsion-free and
$H^{2d}(X_{\text{an}},\mathbb{Z}(d))$
is torsion-free and
![]() $\unicode[STIX]{x1D6FC}$
is torsion, it follows that
$\unicode[STIX]{x1D6FC}$
is torsion, it follows that
 $\unicode[STIX]{x1D6FC}\in \text{CH}_{0}^{\text{LW}}(X)_{\text{deg}\,0}$
. In particular, it is a torsion class in
$\unicode[STIX]{x1D6FC}\in \text{CH}_{0}^{\text{LW}}(X)_{\text{deg}\,0}$
. In particular, it is a torsion class in
 $\text{CH}_{0}^{\text{LW}}(X)_{\text{deg}\,0}$
. A cycle class map
$\text{CH}_{0}^{\text{LW}}(X)_{\text{deg}\,0}$
. A cycle class map
 $$\begin{eqnarray}\widetilde{\text{AK}}_{X}^{d}:\text{CH}_{0}^{\text{LW}}(X)_{\text{deg}\,0}\rightarrow A^{d}(X)\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\text{AK}}_{X}^{d}:\text{CH}_{0}^{\text{LW}}(X)_{\text{deg}\,0}\rightarrow A^{d}(X)\end{eqnarray}$$
is also constructed in [Reference Esnault, Srinivas and ViehwegESV99, § 2] and it is shown in [Reference KrishnaKri09, Lemma 2.2] that
 $\widetilde{\text{AK}}_{X}^{d}=\text{AK}_{X}^{d}$
up to a sign. Now,
$\widetilde{\text{AK}}_{X}^{d}=\text{AK}_{X}^{d}$
up to a sign. Now,
 $\text{cyc}_{X}^{\text{LW}}(\unicode[STIX]{x1D6FC})=0$
implies that
$\text{cyc}_{X}^{\text{LW}}(\unicode[STIX]{x1D6FC})=0$
implies that
 $c_{{\mathcal{D}}^{\ast },X}^{d}\circ \text{cyc}_{X}^{\text{LW}}(\unicode[STIX]{x1D6FC})=0$
in
$c_{{\mathcal{D}}^{\ast },X}^{d}\circ \text{cyc}_{X}^{\text{LW}}(\unicode[STIX]{x1D6FC})=0$
in
![]() $A^{d}(X)$
. We conclude that
$A^{d}(X)$
. We conclude that
![]() $\unicode[STIX]{x1D6FC}$
is a torsion class in
$\unicode[STIX]{x1D6FC}$
is a torsion class in
 $\text{CH}_{0}^{\text{LW}}(X)_{\text{deg}\,0}$
such that
$\text{CH}_{0}^{\text{LW}}(X)_{\text{deg}\,0}$
such that
 $\widetilde{\text{AK}}_{X}^{d}(\unicode[STIX]{x1D6FC})=0$
. We now apply [Reference Biswas and SrinivasBS99, Theorem 1.1] to conclude that
$\widetilde{\text{AK}}_{X}^{d}(\unicode[STIX]{x1D6FC})=0$
. We now apply [Reference Biswas and SrinivasBS99, Theorem 1.1] to conclude that
![]() $\unicode[STIX]{x1D6FC}=0$
. This finishes the proof.◻
$\unicode[STIX]{x1D6FC}=0$
. This finishes the proof.◻
Remark 3.16. Let
![]() $X$
be a projective variety over an algebraically closed field
$X$
be a projective variety over an algebraically closed field
![]() $k$
of exponential characteristic
$k$
of exponential characteristic
![]() $p\geqslant 1$
and let
$p\geqslant 1$
and let
![]() $Y\subsetneq X$
be a closed subset of
$Y\subsetneq X$
be a closed subset of
![]() $X$
containing
$X$
containing
![]() $X_{\text{sing}}$
and containing no components of
$X_{\text{sing}}$
and containing no components of
![]() $X$
. When
$X$
. When
 $\operatorname{codim}_{X}(Y)\geqslant 2$
, the map
$\operatorname{codim}_{X}(Y)\geqslant 2$
, the map
 $\text{cyc}_{X}^{\text{LW}}:\text{CH}_{0}^{\text{LW}}(X)\rightarrow F^{d}K_{0}(X)$
is an isomorphism modulo
$\text{cyc}_{X}^{\text{LW}}:\text{CH}_{0}^{\text{LW}}(X)\rightarrow F^{d}K_{0}(X)$
is an isomorphism modulo
![]() $p$
-torsion by [Reference LevineLev87, Theorem 3.2]. In particular, this shows directly that for such
$p$
-torsion by [Reference LevineLev87, Theorem 3.2]. In particular, this shows directly that for such
![]() $(X,Y)$
the canonical map
$(X,Y)$
the canonical map
 $\text{CH}_{0}^{\text{LW}}(X,Y)\rightarrow \text{CH}_{0}(X,Y)$
is an isomorphism up to
$\text{CH}_{0}^{\text{LW}}(X,Y)\rightarrow \text{CH}_{0}(X,Y)$
is an isomorphism up to
![]() $p$
-torsion. Since in this text we are interested in studying cycles on a double
$p$
-torsion. Since in this text we are interested in studying cycles on a double
 $(S(X,D),D)$
, that is not regular in codimension one, we cannot invoke directly Levine’s result even in the projective case over a field of characteristic
$(S(X,D),D)$
, that is not regular in codimension one, we cannot invoke directly Levine’s result even in the projective case over a field of characteristic
![]() $0$
, and we need the detour of Proposition 3.15.
$0$
, and we need the detour of Proposition 3.15.
We can now deduce our final result comparing the two Chow groups as follows.
Theorem 3.17. Let
![]() $X$
be a reduced quasi-projective scheme of dimension
$X$
be a reduced quasi-projective scheme of dimension
![]() $d\geqslant 1$
over an algebraically closed field
$d\geqslant 1$
over an algebraically closed field
![]() $k$
. Then the canonical map
$k$
. Then the canonical map
 $\text{CH}_{0}^{\text{LW}}(X)\rightarrow \text{CH}_{0}(X)$
is an isomorphism in the following cases:
$\text{CH}_{0}^{\text{LW}}(X)\rightarrow \text{CH}_{0}(X)$
is an isomorphism in the following cases:
-
(1)
 $d\leqslant 2$
;
$d\leqslant 2$
; -
(2)
 $X$
is affine;
$X$
is affine; -
(3)
 $\text{char}(k)=0$
and
$\text{char}(k)=0$
and
 $X$
is projective.
$X$
is projective.
Proof. In each case, it suffices to show using Lemma 3.13 that
![]() $\text{cyc}_{X}^{\text{LW}}$
is injective. The case
$\text{cyc}_{X}^{\text{LW}}$
is injective. The case
![]() $d\leqslant 1$
follows from Lemma 3.12. The
$d\leqslant 1$
follows from Lemma 3.12. The
![]() $d=2$
case follows from [Reference LevineLev85a, Theorem 7], where it is shown that the map
$d=2$
case follows from [Reference LevineLev85a, Theorem 7], where it is shown that the map
 $\text{CH}_{0}^{\text{LW}}(X)\rightarrow F^{2}K_{0}(X)$
is an isomorphism. If
$\text{CH}_{0}^{\text{LW}}(X)\rightarrow F^{2}K_{0}(X)$
is an isomorphism. If
![]() $X$
is affine, this follows from [Reference KrishnaKri15b, Corollary 7.3] and [Reference LevineLev87, Corollary 2.7]. The last case follows from Proposition 3.15.◻
$X$
is affine, this follows from [Reference KrishnaKri15b, Corollary 7.3] and [Reference LevineLev87, Corollary 2.7]. The last case follows from Proposition 3.15.◻
3.6 Some functorial properties of the Chow group of 0-cycles
Recall that any proper map
 $\unicode[STIX]{x1D719}:X^{\prime }\rightarrow X$
admits a push-forward map on the Chow groups of 0-cycles when
$\unicode[STIX]{x1D719}:X^{\prime }\rightarrow X$
admits a push-forward map on the Chow groups of 0-cycles when
![]() $X$
is smooth. This can not be true if
$X$
is smooth. This can not be true if
![]() $X$
is singular. But we expect such a push-forward to exist in the singular case provided
$X$
is singular. But we expect such a push-forward to exist in the singular case provided
![]() $f$
is an l.c.i. morphism. Our next goal is to prove this in special cases. We shall use this result later in this text.
$f$
is an l.c.i. morphism. Our next goal is to prove this in special cases. We shall use this result later in this text.
Proposition 3.18. Let
![]() $X,Y$
be again as in Lemma 3.13. Let
$X,Y$
be again as in Lemma 3.13. Let
 $p:X^{\prime }\rightarrow X$
be a proper morphism which is l.c.i. over
$p:X^{\prime }\rightarrow X$
be a proper morphism which is l.c.i. over
![]() $X_{\text{sing}}$
such that
$X_{\text{sing}}$
such that
![]() $X^{\prime }$
is reduced. Let
$X^{\prime }$
is reduced. Let
 $Y^{\prime }\subsetneq X^{\prime }$
be a closed subset containing
$Y^{\prime }\subsetneq X^{\prime }$
be a closed subset containing
 $p^{-1}(Y)\cup X_{\text{sing}}^{\prime }$
and not containing any component of
$p^{-1}(Y)\cup X_{\text{sing}}^{\prime }$
and not containing any component of
![]() $X^{\prime }$
. Then there are push-forward maps
$X^{\prime }$
. Then there are push-forward maps
 $p_{\ast }:\text{CH}_{0}(X^{\prime },Y^{\prime })\rightarrow \text{CH}_{0}(X,Y)$
and
$p_{\ast }:\text{CH}_{0}(X^{\prime },Y^{\prime })\rightarrow \text{CH}_{0}(X,Y)$
and
 $p_{\ast }:K_{0}(X^{\prime })\rightarrow K_{0}(X)$
and a commutative diagram.
$p_{\ast }:K_{0}(X^{\prime })\rightarrow K_{0}(X)$
and a commutative diagram.

Proof. It follows from our assumption and Lemma 3.3 that
![]() $p$
is perfect and hence there is a push-forward map
$p$
is perfect and hence there is a push-forward map
 $p_{\ast }:K_{0}(X^{\prime })\rightarrow K_{0}(X)$
. We have seen before that there is also a push-forward map
$p_{\ast }:K_{0}(X^{\prime })\rightarrow K_{0}(X)$
. We have seen before that there is also a push-forward map
 $p_{\ast }:{\mathcal{Z}}_{0}(X^{\prime },Y^{\prime })\rightarrow {\mathcal{Z}}_{0}(X,Y)$
.
$p_{\ast }:{\mathcal{Z}}_{0}(X^{\prime },Y^{\prime })\rightarrow {\mathcal{Z}}_{0}(X,Y)$
.
Let us now consider a good curve
 $\unicode[STIX]{x1D708}^{\prime }:(C,Z)\rightarrow (X^{\prime },Y^{\prime })$
relative to
$\unicode[STIX]{x1D708}^{\prime }:(C,Z)\rightarrow (X^{\prime },Y^{\prime })$
relative to
 $(X^{\prime },Y^{\prime })$
. It follows from our assumption that
$(X^{\prime },Y^{\prime })$
. It follows from our assumption that
 $\unicode[STIX]{x1D708}=p\circ \unicode[STIX]{x1D708}^{\prime }:(C,Z)\rightarrow (X,Y)$
is a good curve relative to
$\unicode[STIX]{x1D708}=p\circ \unicode[STIX]{x1D708}^{\prime }:(C,Z)\rightarrow (X,Y)$
is a good curve relative to
![]() $(X,Y)$
. We have the push-forward maps
$(X,Y)$
. We have the push-forward maps
 ${\mathcal{Z}}_{0}(C,Z)\xrightarrow[{}]{\unicode[STIX]{x1D708}_{\ast }^{\prime }}{\mathcal{Z}}_{0}(X^{\prime },Y^{\prime })\xrightarrow[{}]{p_{\ast }}{\mathcal{Z}}_{0}(X,Y)$
such that
${\mathcal{Z}}_{0}(C,Z)\xrightarrow[{}]{\unicode[STIX]{x1D708}_{\ast }^{\prime }}{\mathcal{Z}}_{0}(X^{\prime },Y^{\prime })\xrightarrow[{}]{p_{\ast }}{\mathcal{Z}}_{0}(X,Y)$
such that
 $\unicode[STIX]{x1D708}_{\ast }=p_{\ast }\circ \unicode[STIX]{x1D708}_{\ast }^{\prime }$
. This shows that
$\unicode[STIX]{x1D708}_{\ast }=p_{\ast }\circ \unicode[STIX]{x1D708}_{\ast }^{\prime }$
. This shows that
 $p_{\ast }(\unicode[STIX]{x1D708}_{\ast }^{\prime }(\text{div}(f)))=\unicode[STIX]{x1D708}_{\ast }(\text{div}(f))$
for any
$p_{\ast }(\unicode[STIX]{x1D708}_{\ast }^{\prime }(\text{div}(f)))=\unicode[STIX]{x1D708}_{\ast }(\text{div}(f))$
for any
 $f\in {\mathcal{O}}_{C,Z}^{\times }$
. This implies that
$f\in {\mathcal{O}}_{C,Z}^{\times }$
. This implies that
![]() $p_{\ast }$
descends to a push-forward map on the Chow groups. The commutativity of (3.12) is shown exactly as in the proof of Lemma 3.11.◻
$p_{\ast }$
descends to a push-forward map on the Chow groups. The commutativity of (3.12) is shown exactly as in the proof of Lemma 3.11.◻
Combining this with Theorem 3.17, we have a similar result for the Levine–Weibel Chow group of
![]() $0$
-cycles. Note that this type of functoriality was not previously known.
$0$
-cycles. Note that this type of functoriality was not previously known.
Proposition 3.19. Let
![]() $X$
be as in Theorem 3.17. Let
$X$
be as in Theorem 3.17. Let
 $p:X^{\prime }\rightarrow X$
be a proper morphism between reduced quasi-projective schemes over
$p:X^{\prime }\rightarrow X$
be a proper morphism between reduced quasi-projective schemes over
![]() $k$
. Let
$k$
. Let
![]() $Y$
denote the singular locus of
$Y$
denote the singular locus of
![]() $X$
and let
$X$
and let
 $Y^{\prime }\subset X^{\prime }$
be a closed subscheme containing
$Y^{\prime }\subset X^{\prime }$
be a closed subscheme containing
 $p^{-1}(Y)\cup X_{\text{sing}}^{\prime }$
and not containing any component of
$p^{-1}(Y)\cup X_{\text{sing}}^{\prime }$
and not containing any component of
![]() $X^{\prime }$
. Assume that
$X^{\prime }$
. Assume that
![]() $p$
is l.c.i. along
$p$
is l.c.i. along
![]() $Y$
. Then there is a push-forward map
$Y$
. Then there is a push-forward map
 $p_{\ast }:\text{CH}_{0}^{\text{LW}}(X^{\prime },Y^{\prime })\rightarrow \text{CH}_{0}^{\text{LW}}(X,Y)$
.
$p_{\ast }:\text{CH}_{0}^{\text{LW}}(X^{\prime },Y^{\prime })\rightarrow \text{CH}_{0}^{\text{LW}}(X,Y)$
.
Proof. Proposition 3.18 says that there are maps
 $$\begin{eqnarray}\text{CH}_{0}^{\text{LW}}(X^{\prime },Y^{\prime })\rightarrow \text{CH}_{0}(X^{\prime },Y^{\prime })\xrightarrow[{}]{p_{\ast }}\text{CH}_{0}(X,Y)\leftarrow \text{CH}_{0}^{\text{LW}}(X,Y)\end{eqnarray}$$
$$\begin{eqnarray}\text{CH}_{0}^{\text{LW}}(X^{\prime },Y^{\prime })\rightarrow \text{CH}_{0}(X^{\prime },Y^{\prime })\xrightarrow[{}]{p_{\ast }}\text{CH}_{0}(X,Y)\leftarrow \text{CH}_{0}^{\text{LW}}(X,Y)\end{eqnarray}$$
and Theorem 3.17 says that the last map is an isomorphism. The result follows. ◻
3.7 Cycles in good position
Let
![]() $X$
be a smooth quasi-projective scheme of pure dimension
$X$
be a smooth quasi-projective scheme of pure dimension
![]() $d$
over a field
$d$
over a field
![]() $k$
. For any closed subset
$k$
. For any closed subset
 $W\subsetneq X$
, let
$W\subsetneq X$
, let
 ${\mathcal{Z}}_{0}(X,W)$
denote the free abelian group on the set of closed points in
${\mathcal{Z}}_{0}(X,W)$
denote the free abelian group on the set of closed points in
![]() $X\setminus W$
. Let
$X\setminus W$
. Let
 ${\mathcal{R}}_{0}(X)_{W}$
denote the subgroup of
${\mathcal{R}}_{0}(X)_{W}$
denote the subgroup of
 ${\mathcal{Z}}_{0}(X,W)$
generated by cycles of the form
${\mathcal{Z}}_{0}(X,W)$
generated by cycles of the form
 $\unicode[STIX]{x1D708}_{\ast }\text{div}(f)$
, where
$\unicode[STIX]{x1D708}_{\ast }\text{div}(f)$
, where
![]() $f$
is a rational function on an integral curve
$f$
is a rational function on an integral curve
 $\unicode[STIX]{x1D708}:C{\hookrightarrow}X$
such that
$\unicode[STIX]{x1D708}:C{\hookrightarrow}X$
such that
![]() $C\not \subset W$
and
$C\not \subset W$
and
 $f\in {\mathcal{O}}_{C,C\cap W}^{\times }$
. We denote by
$f\in {\mathcal{O}}_{C,C\cap W}^{\times }$
. We denote by
 $\text{CH}_{0}(X)_{W}$
the quotient
$\text{CH}_{0}(X)_{W}$
the quotient
 ${\mathcal{Z}}_{0}(X,W)/{\mathcal{R}}_{0}(X)_{W}$
. It is the group of
${\mathcal{Z}}_{0}(X,W)/{\mathcal{R}}_{0}(X)_{W}$
. It is the group of
![]() $0$
-cycles that are in good position with respect to
$0$
-cycles that are in good position with respect to
![]() $W$
(i.e.,
$W$
(i.e.,
![]() $0$
-cycles missing
$0$
-cycles missing
![]() $W$
). We have a canonical map
$W$
). We have a canonical map
 $\text{CH}_{0}(X)_{W}\rightarrow \text{CH}_{0}(X)$
. The following result is a consequence of Bloch’s moving lemma.
$\text{CH}_{0}(X)_{W}\rightarrow \text{CH}_{0}(X)$
. The following result is a consequence of Bloch’s moving lemma.
Lemma 3.20. Let
![]() $X$
be a smooth quasi-projective scheme over
$X$
be a smooth quasi-projective scheme over
![]() $k$
. Let
$k$
. Let
 $W\subset X$
be a proper closed subscheme of
$W\subset X$
be a proper closed subscheme of
![]() $X$
. Then the map
$X$
. Then the map
 $\text{CH}_{0}(X)_{W}\rightarrow \text{CH}_{0}(X)$
is an isomorphism.
$\text{CH}_{0}(X)_{W}\rightarrow \text{CH}_{0}(X)$
is an isomorphism.
Proof. We can assume that
![]() $X$
is connected. Let
$X$
is connected. Let
 ${\mathcal{Z}}_{1}(X)_{W}$
denote the free abelian group on integral curves in
${\mathcal{Z}}_{1}(X)_{W}$
denote the free abelian group on integral curves in
![]() $X\times \mathbb{P}_{k}^{1}$
which have the following properties:
$X\times \mathbb{P}_{k}^{1}$
which have the following properties:
-
(1)
 $C\cap (X\times \{0,\infty \})$
is finite;
$C\cap (X\times \{0,\infty \})$
is finite; -
(2)
 $C\cap (W\times \mathbb{P}^{1})$
is finite;
$C\cap (W\times \mathbb{P}^{1})$
is finite; -
(3)
 $C\cap (W\times \{0,\infty \})=\emptyset$
;
$C\cap (W\times \{0,\infty \})=\emptyset$
; -
(4)
 $C\neq \{x\}\times \mathbb{P}^{1}$
for any
$C\neq \{x\}\times \mathbb{P}^{1}$
for any
 $x\in X$
.
$x\in X$
.
Then, the moving lemma of Bloch [Reference BlochBlo86] says that the inclusion of chain complexes
 $$\begin{eqnarray}({\mathcal{Z}}_{1}(X)_{W}\xrightarrow[{}]{\unicode[STIX]{x2202}_{\infty }-\unicode[STIX]{x2202}_{0}}{\mathcal{Z}}_{0}(X,W))\rightarrow ({\mathcal{Z}}_{1}(X)\xrightarrow[{}]{\unicode[STIX]{x2202}_{\infty }-\unicode[STIX]{x2202}_{0}}{\mathcal{Z}}_{0}(X))\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{Z}}_{1}(X)_{W}\xrightarrow[{}]{\unicode[STIX]{x2202}_{\infty }-\unicode[STIX]{x2202}_{0}}{\mathcal{Z}}_{0}(X,W))\rightarrow ({\mathcal{Z}}_{1}(X)\xrightarrow[{}]{\unicode[STIX]{x2202}_{\infty }-\unicode[STIX]{x2202}_{0}}{\mathcal{Z}}_{0}(X))\end{eqnarray}$$
induces isomorphism on
![]() $H^{0}$
. In particular, we get exact sequence
$H^{0}$
. In particular, we get exact sequence
 $$\begin{eqnarray}{\mathcal{Z}}_{1}(X)_{W}\xrightarrow[{}]{\unicode[STIX]{x2202}_{\infty }-\unicode[STIX]{x2202}_{0}}{\mathcal{Z}}_{0}(X,W)\rightarrow \text{CH}_{0}(X)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}_{1}(X)_{W}\xrightarrow[{}]{\unicode[STIX]{x2202}_{\infty }-\unicode[STIX]{x2202}_{0}}{\mathcal{Z}}_{0}(X,W)\rightarrow \text{CH}_{0}(X)\rightarrow 0.\end{eqnarray}$$
On the other hand, there is an isomorphism
 $(\unicode[STIX]{x2202}_{\infty }-\unicode[STIX]{x2202}_{0})({\mathcal{Z}}_{1}(X)_{W})\rightarrow {\mathcal{R}}_{0}(X)_{W}$
given by
$(\unicode[STIX]{x2202}_{\infty }-\unicode[STIX]{x2202}_{0})({\mathcal{Z}}_{1}(X)_{W})\rightarrow {\mathcal{R}}_{0}(X)_{W}$
given by
 $\unicode[STIX]{x2202}([C])\mapsto \text{div}(N(f))$
, where
$\unicode[STIX]{x2202}([C])\mapsto \text{div}(N(f))$
, where
![]() $f$
is the projection map
$f$
is the projection map
 $C\rightarrow \mathbb{P}_{k}^{1}$
,
$C\rightarrow \mathbb{P}_{k}^{1}$
,
![]() $C^{\prime }$
is its image in
$C^{\prime }$
is its image in
![]() $X$
and
$X$
and
![]() $N(f)$
is the norm of
$N(f)$
is the norm of
![]() $f$
under the finite map
$f$
under the finite map
 $k(C^{\prime }){\hookrightarrow}k(C)$
. One checks easily that
$k(C^{\prime }){\hookrightarrow}k(C)$
. One checks easily that
 $N(f)\in {\mathcal{O}}_{C^{\prime },C^{\prime }\cap Y}^{\times }$
.◻
$N(f)\in {\mathcal{O}}_{C^{\prime },C^{\prime }\cap Y}^{\times }$
.◻
4 The pull-back maps
 $\unicode[STIX]{x1D6E5}^{\ast }$
and
$\unicode[STIX]{x1D6E5}^{\ast }$
and
 $\unicode[STIX]{x1D704}_{\pm }^{\ast }$
$\unicode[STIX]{x1D704}_{\pm }^{\ast }$
Let
![]() $k$
be a field. Let
$k$
be a field. Let
![]() $X$
be a smooth and connected quasi-projective scheme of dimension
$X$
be a smooth and connected quasi-projective scheme of dimension
![]() $d\geqslant 1$
over
$d\geqslant 1$
over
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Our goal in this section is to define pull-back maps
$D\subset X$
be an effective Cartier divisor. Our goal in this section is to define pull-back maps
 $\unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)\rightarrow \text{CH}_{0}(S(X,D))$
and
$\unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)\rightarrow \text{CH}_{0}(S(X,D))$
and
 $\unicode[STIX]{x1D704}_{\pm }^{\ast }:\text{CH}_{0}(S(X,D))\rightarrow \text{CH}_{0}(X)$
. As before, we shall write
$\unicode[STIX]{x1D704}_{\pm }^{\ast }:\text{CH}_{0}(S(X,D))\rightarrow \text{CH}_{0}(X)$
. As before, we shall write
 $S(X,D)$
in short as
$S(X,D)$
in short as
![]() $S_{X}$
as long as the divisor
$S_{X}$
as long as the divisor
![]() $D$
is understood. We shall denote the closed subschemes
$D$
is understood. We shall denote the closed subschemes
![]() $\unicode[STIX]{x1D704}_{\pm }(X)$
of
$\unicode[STIX]{x1D704}_{\pm }(X)$
of
![]() $S_{X}$
by
$S_{X}$
by
![]() $X_{\pm }$
, each of which is a copy of
$X_{\pm }$
, each of which is a copy of
![]() $X$
.
$X$
.
4.1 The map
 $\unicode[STIX]{x1D6E5}^{\ast }$
$\unicode[STIX]{x1D6E5}^{\ast }$
We define the map
 $\unicode[STIX]{x1D6E5}^{\ast }:{\mathcal{Z}}_{0}(X,D)\rightarrow {\mathcal{Z}}_{0}(S_{X},D)$
by letting
$\unicode[STIX]{x1D6E5}^{\ast }:{\mathcal{Z}}_{0}(X,D)\rightarrow {\mathcal{Z}}_{0}(S_{X},D)$
by letting
![]() $\unicode[STIX]{x1D6E5}^{\ast }([x])$
be the 0-cycle on
$\unicode[STIX]{x1D6E5}^{\ast }([x])$
be the 0-cycle on
![]() $S_{X}$
associated to the closed subscheme
$S_{X}$
associated to the closed subscheme
 $\{x\}\times _{X}S_{X}$
. It follows from Proposition 2.3(1) that
$\{x\}\times _{X}S_{X}$
. It follows from Proposition 2.3(1) that
 $\unicode[STIX]{x1D6E5}^{\ast }([x])=[x_{+}]+[x_{-}]$
, where
$\unicode[STIX]{x1D6E5}^{\ast }([x])=[x_{+}]+[x_{-}]$
, where
![]() $x_{\pm }$
is the point
$x_{\pm }$
is the point
![]() $x$
in
$x$
in
![]() $X_{\pm }\setminus D$
. Note also that
$X_{\pm }\setminus D$
. Note also that
 $D=(S_{X})_{\text{sing}}$
by Proposition 2.3(6) since
$D=(S_{X})_{\text{sing}}$
by Proposition 2.3(6) since
![]() $X$
is non-singular. We show that
$X$
is non-singular. We show that
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
preserves rational equivalences.
$\unicode[STIX]{x1D6E5}^{\ast }$
preserves rational equivalences.
Theorem 4.1. Let
![]() $X$
be a smooth quasi-projective scheme of dimension
$X$
be a smooth quasi-projective scheme of dimension
![]() $d\geqslant 1$
over
$d\geqslant 1$
over
![]() $k$
and let
$k$
and let
![]() $D\subsetneq X$
be an effective Cartier divisor. Then
$D\subsetneq X$
be an effective Cartier divisor. Then
 $\unicode[STIX]{x1D6E5}^{\ast }:{\mathcal{Z}}_{0}(X,D)\rightarrow {\mathcal{Z}}_{0}(S_{X},D)$
induces a map
$\unicode[STIX]{x1D6E5}^{\ast }:{\mathcal{Z}}_{0}(X,D)\rightarrow {\mathcal{Z}}_{0}(S_{X},D)$
induces a map
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)\rightarrow \text{CH}_{0}(S_{X}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)\rightarrow \text{CH}_{0}(S_{X}).\end{eqnarray}$$
Proof. In view of Lemma 3.20, we need to show that
 $\unicode[STIX]{x1D6E5}^{\ast }((f)_{C})\in {\mathcal{R}}_{0}(S_{X},D)$
for
$\unicode[STIX]{x1D6E5}^{\ast }((f)_{C})\in {\mathcal{R}}_{0}(S_{X},D)$
for
 $C{\hookrightarrow}X$
an integral curve not contained in
$C{\hookrightarrow}X$
an integral curve not contained in
![]() $D$
and
$D$
and
 $f\in {\mathcal{O}}_{C,C\cap D}^{\times }$
. Let
$f\in {\mathcal{O}}_{C,C\cap D}^{\times }$
. Let
 $\unicode[STIX]{x1D708}:C^{N}\rightarrow X$
denote the induced map from the normalization of
$\unicode[STIX]{x1D708}:C^{N}\rightarrow X$
denote the induced map from the normalization of
![]() $C$
and let
$C$
and let
 $E=\unicode[STIX]{x1D708}^{\ast }(D)$
. We then have
$E=\unicode[STIX]{x1D708}^{\ast }(D)$
. We then have
 $f\in {\mathcal{O}}_{C^{N},E}^{\times }$
and
$f\in {\mathcal{O}}_{C^{N},E}^{\times }$
and
 $(f)_{C}=\unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f))$
. We can thus assume that
$(f)_{C}=\unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f))$
. We can thus assume that
![]() $C$
is normal and allow the possibility that
$C$
is normal and allow the possibility that
![]() $\unicode[STIX]{x1D708}$
need not be a closed immersion. With this reduction, we now need to show that
$\unicode[STIX]{x1D708}$
need not be a closed immersion. With this reduction, we now need to show that
 $\unicode[STIX]{x1D6E5}^{\ast }\circ \unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f))\in {\mathcal{R}}_{0}(S_{X},D)$
.
$\unicode[STIX]{x1D6E5}^{\ast }\circ \unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f))\in {\mathcal{R}}_{0}(S_{X},D)$
.
Since
![]() $\unicode[STIX]{x1D6E5}$
is flat, it follows from (3.6) that there is a commutative square (see [Reference FultonFul98, Proposition 1.7])
$\unicode[STIX]{x1D6E5}$
is flat, it follows from (3.6) that there is a commutative square (see [Reference FultonFul98, Proposition 1.7])

where the bottom horizontal arrow is well defined since
 $S_{\unicode[STIX]{x1D708}}^{-1}(D)\subseteq E$
. Note that by Proposition 2.4, the map
$S_{\unicode[STIX]{x1D708}}^{-1}(D)\subseteq E$
. Note that by Proposition 2.4, the map
 $S_{\unicode[STIX]{x1D708}}:S_{C}\rightarrow S_{X}$
is l.c.i. along
$S_{\unicode[STIX]{x1D708}}:S_{C}\rightarrow S_{X}$
is l.c.i. along
![]() $D$
. We also have a commutative square of monomorphisms.
$D$
. We also have a commutative square of monomorphisms.

Setting
 $g=\unicode[STIX]{x1D6E5}_{C}^{\ast }(f)\in {\mathcal{O}}_{S_{C},E}^{\times }$
, it is then clear that
$g=\unicode[STIX]{x1D6E5}_{C}^{\ast }(f)\in {\mathcal{O}}_{S_{C},E}^{\times }$
, it is then clear that
 $\unicode[STIX]{x1D704}_{S_{C}}(g)=(f,f)\in k(C)^{\times }\times k(C)^{\times }=k(S_{C})^{\times }.$
This yields
$\unicode[STIX]{x1D704}_{S_{C}}(g)=(f,f)\in k(C)^{\times }\times k(C)^{\times }=k(S_{C})^{\times }.$
This yields
 $$\begin{eqnarray}\text{div}(\unicode[STIX]{x1D6E5}_{C}^{\ast }(f))=\text{div}(f,f)=\text{div}(f)+\text{div}(f)=\unicode[STIX]{x1D6E5}_{C}^{\ast }(\text{div}(f)).\end{eqnarray}$$
$$\begin{eqnarray}\text{div}(\unicode[STIX]{x1D6E5}_{C}^{\ast }(f))=\text{div}(f,f)=\text{div}(f)+\text{div}(f)=\unicode[STIX]{x1D6E5}_{C}^{\ast }(\text{div}(f)).\end{eqnarray}$$
Combining this with (4.1), we get
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{X}^{\ast }\circ \unicode[STIX]{x1D708}_{\ast }(\text{div}(f))={S_{\unicode[STIX]{x1D708}}}_{\ast }\circ \unicode[STIX]{x1D6E5}_{C}^{\ast }(\text{div}(f))={S_{\unicode[STIX]{x1D708}}}_{\ast }(\text{div}(\unicode[STIX]{x1D6E5}_{C}^{\ast }(f)))={S_{\unicode[STIX]{x1D708}}}_{\ast }(\text{div}(g)).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}_{X}^{\ast }\circ \unicode[STIX]{x1D708}_{\ast }(\text{div}(f))={S_{\unicode[STIX]{x1D708}}}_{\ast }\circ \unicode[STIX]{x1D6E5}_{C}^{\ast }(\text{div}(f))={S_{\unicode[STIX]{x1D708}}}_{\ast }(\text{div}(\unicode[STIX]{x1D6E5}_{C}^{\ast }(f)))={S_{\unicode[STIX]{x1D708}}}_{\ast }(\text{div}(g)).\end{eqnarray}$$
Since
![]() $(S_{C},E)$
is clearly a good curve relative to
$(S_{C},E)$
is clearly a good curve relative to
 $(S_{X},D)$
, the last term lies in
$(S_{X},D)$
, the last term lies in
 ${\mathcal{R}}_{0}(S_{X},D)$
. This finishes the proof.◻
${\mathcal{R}}_{0}(S_{X},D)$
. This finishes the proof.◻
4.2 The maps
 $\unicode[STIX]{x1D704}_{\pm }^{\ast }$
$\unicode[STIX]{x1D704}_{\pm }^{\ast }$
Recall that
 $\unicode[STIX]{x1D704}_{\pm }:X{\hookrightarrow}S_{X}$
denote the two inclusions of
$\unicode[STIX]{x1D704}_{\pm }:X{\hookrightarrow}S_{X}$
denote the two inclusions of
![]() $X$
in
$X$
in
![]() $S_{X}$
via the map
$S_{X}$
via the map
 $\unicode[STIX]{x1D70B}:X\amalg X\rightarrow S_{X}$
. We define two pull-back maps
$\unicode[STIX]{x1D70B}:X\amalg X\rightarrow S_{X}$
. We define two pull-back maps
 $\unicode[STIX]{x1D704}_{\pm }^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X)$
. We do this for
$\unicode[STIX]{x1D704}_{\pm }^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X)$
. We do this for
![]() $\unicode[STIX]{x1D704}_{+}$
as the other case is identical. By Proposition 2.3, we have that
$\unicode[STIX]{x1D704}_{+}$
as the other case is identical. By Proposition 2.3, we have that
 $(S_{X})_{\text{sing}}=D$
and
$(S_{X})_{\text{sing}}=D$
and
 $(S_{X})_{\text{reg}}=(X\setminus D)\amalg (X\setminus D)$
, so that the natural map
$(S_{X})_{\text{reg}}=(X\setminus D)\amalg (X\setminus D)$
, so that the natural map
 $$\begin{eqnarray}{\mathcal{Z}}_{0}(S_{X},D)\rightarrow {\mathcal{Z}}_{0}(X,D)\oplus {\mathcal{Z}}_{0}(X,D)\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}_{0}(S_{X},D)\rightarrow {\mathcal{Z}}_{0}(X,D)\oplus {\mathcal{Z}}_{0}(X,D)\end{eqnarray}$$
is an isomorphism. We define then
 $\unicode[STIX]{x1D704}_{+}^{\ast }:\,{\mathcal{Z}}_{0}(S_{X},D)\,\rightarrow \,{\mathcal{Z}}_{0}(X,D)$
to be the first projection of the direct sum in (4.3). Notice that there are push-forward inclusion maps
$\unicode[STIX]{x1D704}_{+}^{\ast }:\,{\mathcal{Z}}_{0}(S_{X},D)\,\rightarrow \,{\mathcal{Z}}_{0}(X,D)$
to be the first projection of the direct sum in (4.3). Notice that there are push-forward inclusion maps
 ${\unicode[STIX]{x1D704}_{\pm }}_{\ast }:\,{\mathcal{Z}}_{0}(X,D)\,\rightarrow \,{\mathcal{Z}}_{0}(S_{X},D)$
such that
${\unicode[STIX]{x1D704}_{\pm }}_{\ast }:\,{\mathcal{Z}}_{0}(X,D)\,\rightarrow \,{\mathcal{Z}}_{0}(S_{X},D)$
such that
 $\unicode[STIX]{x1D704}_{+}^{\ast }\circ {\unicode[STIX]{x1D704}_{+}}_{\ast }=\text{Id}$
and
$\unicode[STIX]{x1D704}_{+}^{\ast }\circ {\unicode[STIX]{x1D704}_{+}}_{\ast }=\text{Id}$
and
 $\unicode[STIX]{x1D704}_{+}^{\ast }\circ {\unicode[STIX]{x1D704}_{-}}_{\ast }=0$
.
$\unicode[STIX]{x1D704}_{+}^{\ast }\circ {\unicode[STIX]{x1D704}_{-}}_{\ast }=0$
.
Proposition 4.2. The map
 ${\mathcal{Z}}_{0}(S_{X},D)\xrightarrow[{}]{(\unicode[STIX]{x1D704}_{+}^{\ast },\unicode[STIX]{x1D704}_{-}^{\ast })}{\mathcal{Z}}_{0}(X,D)\oplus {\mathcal{Z}}_{0}(X,D)$
descends to the pull-back maps
${\mathcal{Z}}_{0}(S_{X},D)\xrightarrow[{}]{(\unicode[STIX]{x1D704}_{+}^{\ast },\unicode[STIX]{x1D704}_{-}^{\ast })}{\mathcal{Z}}_{0}(X,D)\oplus {\mathcal{Z}}_{0}(X,D)$
descends to the pull-back maps
 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{\pm }^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{\pm }^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X)\end{eqnarray}$$
such that
 $\unicode[STIX]{x1D704}_{\pm }^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}$
.
$\unicode[STIX]{x1D704}_{\pm }^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}$
.
Proof. For the rational equivalence, we argue as follows. Suppose at first that
 $\unicode[STIX]{x1D708}:C{\hookrightarrow}S_{X}$
is an l.c.i. curve relative to
$\unicode[STIX]{x1D708}:C{\hookrightarrow}S_{X}$
is an l.c.i. curve relative to
![]() $D$
and contained in
$D$
and contained in
![]() $S_{X}$
(so, it is in particular a Cartier curve on the double). Set
$S_{X}$
(so, it is in particular a Cartier curve on the double). Set
 $E=\unicode[STIX]{x1D708}^{-1}(D)\cup C_{\text{sing}}$
. Let
$E=\unicode[STIX]{x1D708}^{-1}(D)\cup C_{\text{sing}}$
. Let
![]() $C_{\pm }^{\prime }$
denote the unique reduced closed subscheme of
$C_{\pm }^{\prime }$
denote the unique reduced closed subscheme of
![]() $X_{\pm }$
such that
$X_{\pm }$
such that
 $C_{\pm }^{\prime }\setminus D=(C\setminus D)\cap X_{\pm }$
. Then
$C_{\pm }^{\prime }\setminus D=(C\setminus D)\cap X_{\pm }$
. Then
![]() $C_{+}^{\prime }$
is a closed subscheme of
$C_{+}^{\prime }$
is a closed subscheme of
![]() $C$
with
$C$
with
 $\dim (C_{+}^{\prime })\leqslant 1$
. It is easy to check that
$\dim (C_{+}^{\prime })\leqslant 1$
. It is easy to check that
 $\dim (C_{+}^{\prime })=0$
would violate the condition of
$\dim (C_{+}^{\prime })=0$
would violate the condition of
![]() $C$
being locally defined by a regular sequence at every point of intersection
$C$
being locally defined by a regular sequence at every point of intersection
 $C\cap D\subset S_{X}$
, so that we can assume that
$C\cap D\subset S_{X}$
, so that we can assume that
![]() $C_{+}^{\prime }$
(and similarly
$C_{+}^{\prime }$
(and similarly
![]() $C_{-}^{\prime }$
) is a union of some irreducible components of
$C_{-}^{\prime }$
) is a union of some irreducible components of
![]() $C$
.
$C$
.
Let
 $f\in {\mathcal{O}}_{C,E}^{\times }$
. Let
$f\in {\mathcal{O}}_{C,E}^{\times }$
. Let
 $C=C_{+}^{\prime }\cup C_{-}^{\prime }=(\bigcup _{i=1}^{r_{+}}C_{+}^{i})\cup (\bigcup _{j=1}^{r_{-}}C_{-}^{j})$
. We can clearly assume that we have
$C=C_{+}^{\prime }\cup C_{-}^{\prime }=(\bigcup _{i=1}^{r_{+}}C_{+}^{i})\cup (\bigcup _{j=1}^{r_{-}}C_{-}^{j})$
. We can clearly assume that we have
 $E_{\text{red}}=C_{+}^{\prime }\cap C_{-}^{\prime }$
and a commutative square.
$E_{\text{red}}=C_{+}^{\prime }\cap C_{-}^{\prime }$
and a commutative square.

We can write
 $\unicode[STIX]{x1D703}_{C}(f)=(f_{+},f_{-})$
with
$\unicode[STIX]{x1D703}_{C}(f)=(f_{+},f_{-})$
with
 $f_{\pm }\in k(C_{\pm }^{\prime })^{\times }$
and
$f_{\pm }\in k(C_{\pm }^{\prime })^{\times }$
and
 $\text{div}_{C}(f)~(=(f)_{C})=(f_{+})_{C_{+}}+(f_{-})_{C_{-}}$
, by definition. We now consider the following diagram.
$\text{div}_{C}(f)~(=(f)_{C})=(f_{+})_{C_{+}}+(f_{-})_{C_{-}}$
, by definition. We now consider the following diagram.

This diagram is clearly commutative and yields
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D704}_{+}^{\ast }\circ \unicode[STIX]{x1D708}_{\ast }((f)_{C}) & = & \displaystyle {\unicode[STIX]{x1D708}_{+}}_{\ast }\circ \unicode[STIX]{x1D704}_{+}^{\ast }((f)_{C})\nonumber\\ \displaystyle & = & \displaystyle {\unicode[STIX]{x1D708}_{+}}_{\ast }\circ \unicode[STIX]{x1D704}_{+}^{\ast }[{\unicode[STIX]{x1D704}_{+}}_{\ast }((f_{+})_{C_{+}^{\prime }})+{\unicode[STIX]{x1D704}_{-}}_{\ast }((f_{-})_{C_{-}^{\prime }})]\nonumber\\ \displaystyle & = & \displaystyle {\unicode[STIX]{x1D708}_{+}}_{\ast }((f_{+})_{C_{+}^{\prime }})+0\nonumber\\ \displaystyle & = & \displaystyle {\unicode[STIX]{x1D708}_{+}}_{\ast }((f_{+})_{C_{+}^{\prime }}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D704}_{+}^{\ast }\circ \unicode[STIX]{x1D708}_{\ast }((f)_{C}) & = & \displaystyle {\unicode[STIX]{x1D708}_{+}}_{\ast }\circ \unicode[STIX]{x1D704}_{+}^{\ast }((f)_{C})\nonumber\\ \displaystyle & = & \displaystyle {\unicode[STIX]{x1D708}_{+}}_{\ast }\circ \unicode[STIX]{x1D704}_{+}^{\ast }[{\unicode[STIX]{x1D704}_{+}}_{\ast }((f_{+})_{C_{+}^{\prime }})+{\unicode[STIX]{x1D704}_{-}}_{\ast }((f_{-})_{C_{-}^{\prime }})]\nonumber\\ \displaystyle & = & \displaystyle {\unicode[STIX]{x1D708}_{+}}_{\ast }((f_{+})_{C_{+}^{\prime }})+0\nonumber\\ \displaystyle & = & \displaystyle {\unicode[STIX]{x1D708}_{+}}_{\ast }((f_{+})_{C_{+}^{\prime }}).\end{eqnarray}$$
On the other hand,
 ${\unicode[STIX]{x1D708}_{+}}_{\ast }((f_{+})_{C_{+}^{\prime }})=\sum _{i=1}^{r_{+}}\operatorname{div}(f_{+}^{i})$
by definition, where
${\unicode[STIX]{x1D708}_{+}}_{\ast }((f_{+})_{C_{+}^{\prime }})=\sum _{i=1}^{r_{+}}\operatorname{div}(f_{+}^{i})$
by definition, where
 $$\begin{eqnarray}f_{+}=(f_{+}^{1},\ldots ,f_{+}^{r_{+}})\in k(C_{+}^{\prime })^{\times }=\stackrel{r_{+}}{\underset{i=1}{\prod }}k(C_{+}^{i})^{\times }.\end{eqnarray}$$
$$\begin{eqnarray}f_{+}=(f_{+}^{1},\ldots ,f_{+}^{r_{+}})\in k(C_{+}^{\prime })^{\times }=\stackrel{r_{+}}{\underset{i=1}{\prod }}k(C_{+}^{i})^{\times }.\end{eqnarray}$$
Since each
 $\operatorname{div}(f_{+}^{i})\in {\mathcal{R}}_{0}(X)$
, we conclude that
$\operatorname{div}(f_{+}^{i})\in {\mathcal{R}}_{0}(X)$
, we conclude that
 $\unicode[STIX]{x1D704}_{+}^{\ast }\circ \unicode[STIX]{x1D708}_{\ast }((f)_{C})\in {\mathcal{R}}_{0}(X)$
. In particular, we obtain that the maps
$\unicode[STIX]{x1D704}_{+}^{\ast }\circ \unicode[STIX]{x1D708}_{\ast }((f)_{C})\in {\mathcal{R}}_{0}(X)$
. In particular, we obtain that the maps
![]() $\unicode[STIX]{x1D704}_{\pm }^{\ast }$
descend to group homomorphisms
$\unicode[STIX]{x1D704}_{\pm }^{\ast }$
descend to group homomorphisms
 $\unicode[STIX]{x1D704}_{\pm }^{\ast }:\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X)$
from the Levine–Weibel Chow group.
$\unicode[STIX]{x1D704}_{\pm }^{\ast }:\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X)$
from the Levine–Weibel Chow group.
For the general case of a good curve
 $\unicode[STIX]{x1D708}:C\rightarrow S_{X}$
which is not necessarily an embedding, we can assume by Lemma 3.5 that
$\unicode[STIX]{x1D708}:C\rightarrow S_{X}$
which is not necessarily an embedding, we can assume by Lemma 3.5 that
 $C\rightarrow S_{X}$
is a finite l.c.i. morphism. We now factor
$C\rightarrow S_{X}$
is a finite l.c.i. morphism. We now factor
![]() $\unicode[STIX]{x1D708}$
as
$\unicode[STIX]{x1D708}$
as
 $C{\hookrightarrow}\mathbb{P}_{S_{X}}^{N}\xrightarrow[{}]{\unicode[STIX]{x1D70B}}S_{X}$
, where
$C{\hookrightarrow}\mathbb{P}_{S_{X}}^{N}\xrightarrow[{}]{\unicode[STIX]{x1D70B}}S_{X}$
, where
![]() $\unicode[STIX]{x1D70B}$
is the projection and
$\unicode[STIX]{x1D70B}$
is the projection and
 $\unicode[STIX]{x1D707}:C{\hookrightarrow}\mathbb{P}_{S_{X}}^{N}$
is a regular embedding. By Proposition 2.3, we can identify
$\unicode[STIX]{x1D707}:C{\hookrightarrow}\mathbb{P}_{S_{X}}^{N}$
is a regular embedding. By Proposition 2.3, we can identify
 $\mathbb{P}_{S_{X}}^{N}=\mathbb{P}_{S(X,D)}^{N}$
with
$\mathbb{P}_{S_{X}}^{N}=\mathbb{P}_{S(X,D)}^{N}$
with
 $S(\mathbb{P}_{X}^{N},\mathbb{P}_{D}^{N})$
. We have then a commutative diagram
$S(\mathbb{P}_{X}^{N},\mathbb{P}_{D}^{N})$
. We have then a commutative diagram

by the definition of
![]() $\unicode[STIX]{x1D704}_{\pm }^{\ast }$
. For
$\unicode[STIX]{x1D704}_{\pm }^{\ast }$
. For
 $f\in {\mathcal{O}}_{C,\unicode[STIX]{x1D708}^{\ast }D}^{\times }$
, we have
$f\in {\mathcal{O}}_{C,\unicode[STIX]{x1D708}^{\ast }D}^{\times }$
, we have
 $\unicode[STIX]{x1D704}_{\pm }^{\ast }(\unicode[STIX]{x1D707}_{\ast }((f)_{C}))\in {\mathcal{R}}_{0}(\mathbb{P}_{X}^{N})$
by the embedded case. In particular, we get
$\unicode[STIX]{x1D704}_{\pm }^{\ast }(\unicode[STIX]{x1D707}_{\ast }((f)_{C}))\in {\mathcal{R}}_{0}(\mathbb{P}_{X}^{N})$
by the embedded case. In particular, we get
 $\unicode[STIX]{x1D704}_{\pm }^{\ast }(\unicode[STIX]{x1D708}_{\ast }((f)_{C}))=\unicode[STIX]{x1D704}_{\pm }^{\ast }\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D707}_{\ast }((f)_{C})=\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D704}_{\pm }^{\ast }(\unicode[STIX]{x1D707}_{\ast }((f)_{C}))\in {\mathcal{R}}_{0}(X)$
, completing the proof.◻
$\unicode[STIX]{x1D704}_{\pm }^{\ast }(\unicode[STIX]{x1D708}_{\ast }((f)_{C}))=\unicode[STIX]{x1D704}_{\pm }^{\ast }\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D707}_{\ast }((f)_{C})=\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D704}_{\pm }^{\ast }(\unicode[STIX]{x1D707}_{\ast }((f)_{C}))\in {\mathcal{R}}_{0}(X)$
, completing the proof.◻
5
 $0$
-Cycles on
$0$
-Cycles on
 $S_{X}$
and
$S_{X}$
and
 $0$
-cycles with modulus on
$0$
-cycles with modulus on
 $X$
$X$
5.1 Overture
The goal of this section is to define the difference map
![]() $\unicode[STIX]{x1D70F}_{X}^{\ast }$
from the Chow group of 0-cycles on
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
from the Chow group of 0-cycles on
![]() $S_{X}$
to the Chow group of 0-cycles with modulus
$S_{X}$
to the Chow group of 0-cycles with modulus
![]() $D$
on
$D$
on
![]() $X$
. The heart of this section is the proof that this difference map kills the group of rational equivalences in the Chow group with modulus
$X$
. The heart of this section is the proof that this difference map kills the group of rational equivalences in the Chow group with modulus
 $\text{CH}_{0}(X|D)$
. We start by recalling the definition of the Chow group with modulus, following Kerz and Saito.
$\text{CH}_{0}(X|D)$
. We start by recalling the definition of the Chow group with modulus, following Kerz and Saito.
5.2 0-cycles with modulus
Let
![]() $k$
be any field. Given an integral normal curve
$k$
be any field. Given an integral normal curve
![]() $C$
over
$C$
over
![]() $k$
and an effective divisor
$k$
and an effective divisor
![]() $E\subset C$
, we say that a rational function
$E\subset C$
, we say that a rational function
![]() $f$
on
$f$
on
![]() $C$
has modulus
$C$
has modulus
![]() $E$
if
$E$
if
 $f\in \text{Ker}({\mathcal{O}}_{C,E}^{\times }\rightarrow {\mathcal{O}}_{E}^{\times })$
. Here,
$f\in \text{Ker}({\mathcal{O}}_{C,E}^{\times }\rightarrow {\mathcal{O}}_{E}^{\times })$
. Here,
![]() ${\mathcal{O}}_{C,E}$
is the semi-local ring of
${\mathcal{O}}_{C,E}$
is the semi-local ring of
![]() $C$
at the union of
$C$
at the union of
![]() $E$
and the generic point of
$E$
and the generic point of
![]() $C$
. In particular,
$C$
. In particular,
 $\text{Ker}({\mathcal{O}}_{C,E}^{\times }\rightarrow {\mathcal{O}}_{E}^{\times })$
is just
$\text{Ker}({\mathcal{O}}_{C,E}^{\times }\rightarrow {\mathcal{O}}_{E}^{\times })$
is just
![]() $k(C)^{\times }$
if
$k(C)^{\times }$
if
![]() $|E|=\emptyset$
. Let
$|E|=\emptyset$
. Let
 $G(C,E)$
denote the group of such rational functions.
$G(C,E)$
denote the group of such rational functions.
Let
![]() $X$
be an integral scheme of finite type over
$X$
be an integral scheme of finite type over
![]() $k$
and let
$k$
and let
![]() $D$
be an effective Cartier divisor on
$D$
be an effective Cartier divisor on
![]() $X$
. Let
$X$
. Let
 ${\mathcal{Z}}_{0}(X\setminus D)$
be the free abelian group on the set of closed points of
${\mathcal{Z}}_{0}(X\setminus D)$
be the free abelian group on the set of closed points of
![]() $X\setminus D$
. Let
$X\setminus D$
. Let
![]() $C$
be an integral normal curve over
$C$
be an integral normal curve over
![]() $k$
and let
$k$
and let
 $\unicode[STIX]{x1D711}_{C}:C\rightarrow X$
be a finite morphism such that
$\unicode[STIX]{x1D711}_{C}:C\rightarrow X$
be a finite morphism such that
 $\unicode[STIX]{x1D711}_{C}(C)\not \subset D$
. The push forward of cycles along
$\unicode[STIX]{x1D711}_{C}(C)\not \subset D$
. The push forward of cycles along
![]() $\unicode[STIX]{x1D711}_{C}$
gives a well-defined group homomorphism
$\unicode[STIX]{x1D711}_{C}$
gives a well-defined group homomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{C}:G(C,\unicode[STIX]{x1D711}_{C}^{\ast }(D))\rightarrow {\mathcal{Z}}_{0}(X\setminus D).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{C}:G(C,\unicode[STIX]{x1D711}_{C}^{\ast }(D))\rightarrow {\mathcal{Z}}_{0}(X\setminus D).\end{eqnarray}$$
Recall now the following definition.
Definition 5.1 (Kerz–Saito).
We define the Chow group
 $\text{CH}_{0}(X|D)$
of 0-cycles of
$\text{CH}_{0}(X|D)$
of 0-cycles of
![]() $X$
with modulus
$X$
with modulus
![]() $D$
as the cokernel of the homomorphism
$D$
as the cokernel of the homomorphism
 $$\begin{eqnarray}\operatorname{div}:\bigoplus _{\unicode[STIX]{x1D711}_{C}:C\rightarrow \overline{X}}G(C,\unicode[STIX]{x1D711}_{C}^{\ast }(D))\rightarrow Z_{0}(X\setminus D),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{div}:\bigoplus _{\unicode[STIX]{x1D711}_{C}:C\rightarrow \overline{X}}G(C,\unicode[STIX]{x1D711}_{C}^{\ast }(D))\rightarrow Z_{0}(X\setminus D),\end{eqnarray}$$
where the sum is taken over the set of finite morphisms
 $\unicode[STIX]{x1D711}_{C}:C\rightarrow X$
from an integral normal curve such that
$\unicode[STIX]{x1D711}_{C}:C\rightarrow X$
from an integral normal curve such that
 $\unicode[STIX]{x1D711}_{C}(C)\not \subset D$
.
$\unicode[STIX]{x1D711}_{C}(C)\not \subset D$
.
It is known that the Chow group of 0-cycles with modulus is covariantly functorial for proper maps: if
 $f:X^{\prime }\rightarrow X$
is proper,
$f:X^{\prime }\rightarrow X$
is proper,
![]() $D$
and
$D$
and
![]() $D^{\prime }$
are effective Cartier divisors on
$D^{\prime }$
are effective Cartier divisors on
![]() $X$
and
$X$
and
![]() $X^{\prime }$
respectively such that
$X^{\prime }$
respectively such that
 $f^{\ast }(D)\subset D^{\prime }$
, then there is a push-forward map
$f^{\ast }(D)\subset D^{\prime }$
, then there is a push-forward map
 $f_{\ast }:\text{CH}_{0}(X^{\prime }|D^{\prime })\rightarrow \text{CH}_{0}(X|D)$
(see [Reference Binda and SaitoBS16, Lemma 2.7] or [Reference Krishna and ParkKP14, Proposition 2.10]).
$f_{\ast }:\text{CH}_{0}(X^{\prime }|D^{\prime })\rightarrow \text{CH}_{0}(X|D)$
(see [Reference Binda and SaitoBS16, Lemma 2.7] or [Reference Krishna and ParkKP14, Proposition 2.10]).
5.3 Setting and goals
From now on, we fix a smooth connected quasi-projective scheme
![]() $X$
over
$X$
over
![]() $k$
and an effective Cartier divisor
$k$
and an effective Cartier divisor
![]() $D\subset X$
on it. Let
$D\subset X$
on it. Let
![]() $S_{X}$
be the double of
$S_{X}$
be the double of
![]() $X$
along
$X$
along
![]() $D$
as defined in § 2. Let
$D$
as defined in § 2. Let
 $\unicode[STIX]{x1D704}_{\pm }:X\rightarrow S_{X}$
denote the closed embeddings of the two components
$\unicode[STIX]{x1D704}_{\pm }:X\rightarrow S_{X}$
denote the closed embeddings of the two components
![]() $X_{+}$
and
$X_{+}$
and
![]() $X_{-}$
of the double. We want to construct maps
$X_{-}$
of the double. We want to construct maps
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X|D)\quad \text{and}\quad p_{\pm ,\ast }:\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(S_{X})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X|D)\quad \text{and}\quad p_{\pm ,\ast }:\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(S_{X})\end{eqnarray}$$
and prove that
 $\unicode[STIX]{x1D70F}_{X}^{\ast }\circ p_{\pm ,\ast }=\text{Id}$
. At the level of the free abelian group
$\unicode[STIX]{x1D70F}_{X}^{\ast }\circ p_{\pm ,\ast }=\text{Id}$
. At the level of the free abelian group
 ${\mathcal{Z}}_{0}(S_{X},D)$
, the map
${\mathcal{Z}}_{0}(S_{X},D)$
, the map
![]() $\unicode[STIX]{x1D70F}_{X}^{\ast }$
is simply
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
is simply
![]() $\unicode[STIX]{x1D704}_{+}^{\ast }-\unicode[STIX]{x1D704}_{-}^{\ast }$
:
$\unicode[STIX]{x1D704}_{+}^{\ast }-\unicode[STIX]{x1D704}_{-}^{\ast }$
:
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{Z}}_{0}(S_{X},D)={\mathcal{Z}}_{0}(X\setminus D)\oplus {\mathcal{Z}}_{0}(X\setminus D)\rightarrow {\mathcal{Z}}_{0}(X\setminus D), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}_{+},\unicode[STIX]{x1D6FC}_{-})\mapsto \unicode[STIX]{x1D6FC}_{+}-\unicode[STIX]{x1D6FC}_{-}=\unicode[STIX]{x1D704}_{+}^{\ast }((\unicode[STIX]{x1D6FC}_{+},\unicode[STIX]{x1D6FC}_{-}))-\unicode[STIX]{x1D704}_{-}^{\ast }((\unicode[STIX]{x1D6FC}_{+},\unicode[STIX]{x1D6FC}_{-})). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{Z}}_{0}(S_{X},D)={\mathcal{Z}}_{0}(X\setminus D)\oplus {\mathcal{Z}}_{0}(X\setminus D)\rightarrow {\mathcal{Z}}_{0}(X\setminus D), & \displaystyle \nonumber\\ \displaystyle & \displaystyle (\unicode[STIX]{x1D6FC}_{+},\unicode[STIX]{x1D6FC}_{-})\mapsto \unicode[STIX]{x1D6FC}_{+}-\unicode[STIX]{x1D6FC}_{-}=\unicode[STIX]{x1D704}_{+}^{\ast }((\unicode[STIX]{x1D6FC}_{+},\unicode[STIX]{x1D6FC}_{-}))-\unicode[STIX]{x1D704}_{-}^{\ast }((\unicode[STIX]{x1D6FC}_{+},\unicode[STIX]{x1D6FC}_{-})). & \displaystyle \nonumber\end{eqnarray}$$
We construct the first map in several steps, starting by considering only embedded l.c.i. curves in the definition of the rational equivalence on the double
![]() $S_{X}$
(or, in other words, by proving the existence of the map
$S_{X}$
(or, in other words, by proving the existence of the map
![]() $\unicode[STIX]{x1D70F}_{X}^{\ast }$
for the Levine–Weibel Chow group of zero cycles). The general case is then treated using the same trick as in Proposition 4.2, thanks to the following lemma.
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
for the Levine–Weibel Chow group of zero cycles). The general case is then treated using the same trick as in Proposition 4.2, thanks to the following lemma.
Lemma 5.2. Assume that for every smooth connected quasi-projective scheme
![]() $Y$
over
$Y$
over
![]() $k$
and effective Cartier divisor
$k$
and effective Cartier divisor
![]() $E$
on
$E$
on
![]() $Y$
, the map
$Y$
, the map
![]() $\unicode[STIX]{x1D70F}_{Y}^{\ast }$
given above descends to a well-defined homomorphism
$\unicode[STIX]{x1D70F}_{Y}^{\ast }$
given above descends to a well-defined homomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{Y}^{\ast }:\text{CH}_{0}^{\text{LW}}(S(Y,E))\rightarrow \text{CH}_{0}(Y|E).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{Y}^{\ast }:\text{CH}_{0}^{\text{LW}}(S(Y,E))\rightarrow \text{CH}_{0}(Y|E).\end{eqnarray}$$
Then the map
 $\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
factors through
$\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
factors through
 $\text{CH}_{0}(S_{X})$
, giving a well-defined homomorphism
$\text{CH}_{0}(S_{X})$
, giving a well-defined homomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X|D).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X|D).\end{eqnarray}$$
Proof. Let
 $\unicode[STIX]{x1D6FF}:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow \text{CH}_{0}(X|D)$
be the composition
$\unicode[STIX]{x1D6FF}:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow \text{CH}_{0}(X|D)$
be the composition
 $$\begin{eqnarray}{\mathcal{Z}}_{0}(S_{X},D)\rightarrow \text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{Z}}_{0}(S_{X},D)\rightarrow \text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D).\end{eqnarray}$$
We have to show that
![]() $\unicode[STIX]{x1D6FF}$
factors through
$\unicode[STIX]{x1D6FF}$
factors through
 $\text{CH}_{0}(S_{X})$
, defined using good l.c.i. curves as in Definition 3.4. Using again Lemma 3.5, we have to show more precisely that
$\text{CH}_{0}(S_{X})$
, defined using good l.c.i. curves as in Definition 3.4. Using again Lemma 3.5, we have to show more precisely that
 $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708}_{\ast }(\text{div}_{C}(f)))=0$
for every
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708}_{\ast }(\text{div}_{C}(f)))=0$
for every
 $\unicode[STIX]{x1D708}:C\rightarrow S_{X}$
finite l.c.i. morphism from a reduced curve
$\unicode[STIX]{x1D708}:C\rightarrow S_{X}$
finite l.c.i. morphism from a reduced curve
![]() $C$
that is good relative to
$C$
that is good relative to
 $(S_{X},D)$
and for every rational function
$(S_{X},D)$
and for every rational function
![]() $f$
on
$f$
on
![]() $C$
that is regular and invertible along
$C$
that is regular and invertible along
 $E=(\unicode[STIX]{x1D708}^{-1}(D)\cup C_{\text{sing}})$
. We factor
$E=(\unicode[STIX]{x1D708}^{-1}(D)\cup C_{\text{sing}})$
. We factor
![]() $\unicode[STIX]{x1D708}$
as composition
$\unicode[STIX]{x1D708}$
as composition
 $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D707}$
, where
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D707}$
, where
 $\unicode[STIX]{x1D707}:C{\hookrightarrow}\mathbb{P}_{S_{X}}^{N}=S(\mathbb{P}_{X}^{N},P_{D}^{N})$
(using Proposition 2.3) is a regular embedding and
$\unicode[STIX]{x1D707}:C{\hookrightarrow}\mathbb{P}_{S_{X}}^{N}=S(\mathbb{P}_{X}^{N},P_{D}^{N})$
(using Proposition 2.3) is a regular embedding and
 $\unicode[STIX]{x1D70B}:\mathbb{P}_{S_{X}}^{N}\rightarrow S_{X}$
is the projection. In particular,
$\unicode[STIX]{x1D70B}:\mathbb{P}_{S_{X}}^{N}\rightarrow S_{X}$
is the projection. In particular,
 $\unicode[STIX]{x1D707}(C)=C$
is a Cartier curve on the double
$\unicode[STIX]{x1D707}(C)=C$
is a Cartier curve on the double
 $S(\mathbb{P}_{X}^{N},P_{D}^{N})$
relative to
$S(\mathbb{P}_{X}^{N},P_{D}^{N})$
relative to
![]() $\mathbb{P}_{D}^{N}$
.
$\mathbb{P}_{D}^{N}$
.
It follows from (4.8) and the formula
 $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D704}_{+}^{\ast }-\unicode[STIX]{x1D704}_{-}^{\ast }$
that the square
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D704}_{+}^{\ast }-\unicode[STIX]{x1D704}_{-}^{\ast }$
that the square

commutes, where
![]() $\unicode[STIX]{x1D6FF}_{\mathbb{P}_{S_{X}}^{N}}$
is the composition
$\unicode[STIX]{x1D6FF}_{\mathbb{P}_{S_{X}}^{N}}$
is the composition
 ${\mathcal{Z}}_{0}(\mathbb{P}_{S_{X}}^{N},\mathbb{P}_{D}^{N})\rightarrow \text{CH}_{0}^{\text{LW}}(S(\mathbb{P}_{X}^{N},\mathbb{P}_{D}^{N}))\rightarrow \text{CH}_{0}(\mathbb{P}_{X}^{N}|\mathbb{P}_{D}^{N})$
. That is,
${\mathcal{Z}}_{0}(\mathbb{P}_{S_{X}}^{N},\mathbb{P}_{D}^{N})\rightarrow \text{CH}_{0}^{\text{LW}}(S(\mathbb{P}_{X}^{N},\mathbb{P}_{D}^{N}))\rightarrow \text{CH}_{0}(\mathbb{P}_{X}^{N}|\mathbb{P}_{D}^{N})$
. That is,
 $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708}_{\ast }((f)_{C}))=\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{\ast }(\unicode[STIX]{x1D707}_{\ast }(f)_{C}))=\unicode[STIX]{x1D70B}_{\ast }(\unicode[STIX]{x1D6FF}_{\mathbb{P}_{S_{X}}^{N}}(\unicode[STIX]{x1D707}_{\ast }((f)_{C})))$
.
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D708}_{\ast }((f)_{C}))=\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D70B}_{\ast }(\unicode[STIX]{x1D707}_{\ast }(f)_{C}))=\unicode[STIX]{x1D70B}_{\ast }(\unicode[STIX]{x1D6FF}_{\mathbb{P}_{S_{X}}^{N}}(\unicode[STIX]{x1D707}_{\ast }((f)_{C})))$
.
By assumption, we have
 $\unicode[STIX]{x1D6FF}_{\mathbb{P}_{S_{X}}^{N}}(\unicode[STIX]{x1D707}_{\ast }((f)_{C}))=0\in \text{CH}_{0}(\mathbb{P}_{X}^{N}|\mathbb{P}_{D}^{N})$
. Since the push-forward map
$\unicode[STIX]{x1D6FF}_{\mathbb{P}_{S_{X}}^{N}}(\unicode[STIX]{x1D707}_{\ast }((f)_{C}))=0\in \text{CH}_{0}(\mathbb{P}_{X}^{N}|\mathbb{P}_{D}^{N})$
. Since the push-forward map
 $\unicode[STIX]{x1D70B}_{\ast }:\text{CH}_{0}(\mathbb{P}_{X}^{N}|\mathbb{P}_{D}^{N})\rightarrow \text{CH}_{0}(X|D)$
is well defined, we can finish the proof.◻
$\unicode[STIX]{x1D70B}_{\ast }:\text{CH}_{0}(\mathbb{P}_{X}^{N}|\mathbb{P}_{D}^{N})\rightarrow \text{CH}_{0}(X|D)$
is well defined, we can finish the proof.◻
We have therefore reduced the problem to showing that the map
![]() $\unicode[STIX]{x1D70F}_{X}^{\ast }$
is well defined from the Levine–Weibel Chow group of zero cycles.
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
is well defined from the Levine–Weibel Chow group of zero cycles.
To begin, we need to keep some control over the Cartier curves on the double
![]() $S_{X}$
which generate
$S_{X}$
which generate
 ${\mathcal{R}}_{0}(S_{X},D)^{\text{LW}}$
. We do this in the next few lemmas.
${\mathcal{R}}_{0}(S_{X},D)^{\text{LW}}$
. We do this in the next few lemmas.
5.4 The Cartier curves on the double
 $S_{X}$
$S_{X}$
Our next goal is to use the specific structure of
![]() $S_{X}$
as a join of two smooth schemes to refine the set of Cartier curves used to define
$S_{X}$
as a join of two smooth schemes to refine the set of Cartier curves used to define
 $\text{CH}_{0}^{\text{LW}}(S_{X},D)=\text{CH}_{0}^{\text{LW}}(S_{X})$
. In this section, by Cartier curve on
$\text{CH}_{0}^{\text{LW}}(S_{X},D)=\text{CH}_{0}^{\text{LW}}(S_{X})$
. In this section, by Cartier curve on
![]() $S_{X}$
(respectively
$S_{X}$
(respectively
![]() $X$
) we will always mean curve on
$X$
) we will always mean curve on
![]() $S_{X}$
(respectively
$S_{X}$
(respectively
![]() $X$
) which is Cartier with respect to
$X$
) which is Cartier with respect to
![]() $D$
. For the rest of § 5, we shall assume that the ground field
$D$
. For the rest of § 5, we shall assume that the ground field
![]() $k$
is infinite and perfect.
$k$
is infinite and perfect.
Notation 5.3. Let
![]() $S$
be a quasi-projective
$S$
be a quasi-projective
![]() $k$
-scheme and let
$k$
-scheme and let
![]() ${\mathcal{L}}$
be a line bundle on
${\mathcal{L}}$
be a line bundle on
![]() $S$
. For a global section
$S$
. For a global section
 $t\in H^{0}(S,{\mathcal{L}})$
, we write
$t\in H^{0}(S,{\mathcal{L}})$
, we write
![]() $(t)$
for the divisor of zeros of
$(t)$
for the divisor of zeros of
![]() $s$
, that we consider as a closed subscheme of
$s$
, that we consider as a closed subscheme of
![]() $S$
.
$S$
.
Lemma 5.4. Let
![]() $X$
be a connected smooth quasi-projective scheme of dimension
$X$
be a connected smooth quasi-projective scheme of dimension
![]() $d\geqslant 3$
over
$d\geqslant 3$
over
![]() $k$
. The group of rational equivalences
$k$
. The group of rational equivalences
 ${\mathcal{R}}_{0}^{\text{LW}}(S_{X},D)$
is generated by the divisors of functions on (possibly non-reduced) Cartier curves
${\mathcal{R}}_{0}^{\text{LW}}(S_{X},D)$
is generated by the divisors of functions on (possibly non-reduced) Cartier curves
 $C{\hookrightarrow}S_{X}$
relative to
$C{\hookrightarrow}S_{X}$
relative to
![]() $D$
, where
$D$
, where
![]() $C$
satisfies the following:
$C$
satisfies the following:
-
(1) there is a locally closed embedding
 $S_{X}{\hookrightarrow}\mathbb{P}_{k}^{N}$
and distinct hypersurfaces such that
$S_{X}{\hookrightarrow}\mathbb{P}_{k}^{N}$
and distinct hypersurfaces such that $$\begin{eqnarray}H_{1},\ldots ,H_{d-2}{\hookrightarrow}\mathbb{P}_{k}^{N}\end{eqnarray}$$
$$\begin{eqnarray}H_{1},\ldots ,H_{d-2}{\hookrightarrow}\mathbb{P}_{k}^{N}\end{eqnarray}$$
 $Y=S_{X}\cap H_{1}\cap \cdots \cap H_{d-2}$
is a complete intersection which is geometrically reduced;
$Y=S_{X}\cap H_{1}\cap \cdots \cap H_{d-2}$
is a complete intersection which is geometrically reduced;
-
(2)
 $X_{\pm }\cap Y=X_{\pm }\cap H_{1}\cap \cdots \cap H_{d-2}:=Y_{\pm }$
are integral;
$X_{\pm }\cap Y=X_{\pm }\cap H_{1}\cap \cdots \cap H_{d-2}:=Y_{\pm }$
are integral; -
(3) no component of
 $Y$
is contained in
$Y$
is contained in
 $D$
;
$D$
; -
(4)
 $C\subset Y$
;
$C\subset Y$
; -
(5)
 $C$
is a Cartier divisor on
$C$
is a Cartier divisor on
 $Y$
;
$Y$
; -
(6)
 $Y_{\pm }$
are smooth away from
$Y_{\pm }$
are smooth away from
 $C$
;
$C$
; -
(7)
 $C$
is Cohen–Macaulay.
$C$
is Cohen–Macaulay.
Proof. Let
 $C{\hookrightarrow}S_{X}$
be a reduced Cartier curve relative to
$C{\hookrightarrow}S_{X}$
be a reduced Cartier curve relative to
![]() $D$
and let
$D$
and let
 $f\in {\mathcal{O}}_{C,C\cap D}^{\times }$
. Since
$f\in {\mathcal{O}}_{C,C\cap D}^{\times }$
. Since
![]() $C$
is Cartier along
$C$
is Cartier along
 $D=(S_{X})_{\text{sing}}$
, it follows that it is Cartier in
$D=(S_{X})_{\text{sing}}$
, it follows that it is Cartier in
![]() $S_{X}$
along each of its generic points.
$S_{X}$
along each of its generic points.
We will replace
![]() $C$
by the curves of desired type using a combination of [Reference LevineLev87, Lemma 1.3] and [Reference LevineLev87, Lemma 1.4] as follows. We also refer to [Reference JouanolouJou83, ch. I, § 6] for the Bertini theorem for geometrically reduced schemes and [Reference SeidenbergSei50, Theorem 12] for irreducible schemes.
$C$
by the curves of desired type using a combination of [Reference LevineLev87, Lemma 1.3] and [Reference LevineLev87, Lemma 1.4] as follows. We also refer to [Reference JouanolouJou83, ch. I, § 6] for the Bertini theorem for geometrically reduced schemes and [Reference SeidenbergSei50, Theorem 12] for irreducible schemes.
Since
![]() $S_{X}$
is reduced quasi-projective,
$S_{X}$
is reduced quasi-projective,
![]() $X$
is integral and
$X$
is integral and
 $C{\hookrightarrow}S_{X}$
is Cartier along
$C{\hookrightarrow}S_{X}$
is Cartier along
![]() $D$
, we can apply [Reference LevineLev87, Lemma 1.3] to find a locally closed embedding
$D$
, we can apply [Reference LevineLev87, Lemma 1.3] to find a locally closed embedding
 $S_{X}{\hookrightarrow}\mathbb{P}_{k}^{N}$
and distinct hypersurfaces
$S_{X}{\hookrightarrow}\mathbb{P}_{k}^{N}$
and distinct hypersurfaces
 $H_{1},\ldots ,H_{d-2}{\hookrightarrow}\mathbb{P}_{k}^{N}$
such that the following hold:
$H_{1},\ldots ,H_{d-2}{\hookrightarrow}\mathbb{P}_{k}^{N}$
such that the following hold:
-
(1)
 $Y=S_{X}\cap H_{1}\cap \cdots \cap H_{d-2}$
is a complete intersection which is (geometrically) reduced (note that since
$Y=S_{X}\cap H_{1}\cap \cdots \cap H_{d-2}$
is a complete intersection which is (geometrically) reduced (note that since
 $k$
is perfect,
$k$
is perfect,
 $Y$
is reduced if and only if is geometrically reduced);
$Y$
is reduced if and only if is geometrically reduced); -
(2)
 $X_{\pm }\cap Y=X_{\pm }\cap H_{1}\cap \cdots \cap H_{d-2}:=Y_{\pm }$
are integral;
$X_{\pm }\cap Y=X_{\pm }\cap H_{1}\cap \cdots \cap H_{d-2}:=Y_{\pm }$
are integral; -
(3) no component of
 $Y$
is contained in
$Y$
is contained in
 $D$
;
$D$
; -
(4)
 $C\subset Y$
;
$C\subset Y$
; -
(5)
 $C$
is locally principal in
$C$
is locally principal in
 $Y$
in a neighborhood of the finite set
$Y$
in a neighborhood of the finite set
 $C\cap D$
and at each generic point of
$C\cap D$
and at each generic point of
 $C$
.
$C$
.
Since
 $X_{\pm }=X$
are smooth, we can apply [Reference Kleiman and AltmanKL79, Theorem 1] to further assume that
$X_{\pm }=X$
are smooth, we can apply [Reference Kleiman and AltmanKL79, Theorem 1] to further assume that
![]() $Y_{\pm }$
are smooth away from
$Y_{\pm }$
are smooth away from
![]() $C_{\pm }$
. Here
$C_{\pm }$
. Here
![]() $C_{\pm }$
denotes
$C_{\pm }$
denotes
 $C\cap X_{\pm }=C\times _{S_{X}}X_{\pm }$
.
$C\cap X_{\pm }=C\times _{S_{X}}X_{\pm }$
.
Since
 $Y{\hookrightarrow}S_{X}$
is constructed as a complete intersection of hypersurfaces of arbitrarily large degrees (see [Reference LevineLev87, Lemma 1.4]), we can furthermore find a locally principal closed subscheme
$Y{\hookrightarrow}S_{X}$
is constructed as a complete intersection of hypersurfaces of arbitrarily large degrees (see [Reference LevineLev87, Lemma 1.4]), we can furthermore find a locally principal closed subscheme
![]() $C_{1}$
of
$C_{1}$
of
![]() $Y$
such that:
$Y$
such that:
-
(a)
 $C\subset C_{1}$
;
$C\subset C_{1}$
; -
(b)
 $C_{1}$
equals
$C_{1}$
equals
 $C$
at every generic point of
$C$
at every generic point of
 $C$
;
$C$
; -
(c)
 $\overline{(C_{1}\setminus C)}\cap C\cap D=\emptyset$
.
$\overline{(C_{1}\setminus C)}\cap C\cap D=\emptyset$
.
Since
![]() $Y$
is geometrically reduced, it follows from Lemma 2.2 that
$Y$
is geometrically reduced, it follows from Lemma 2.2 that
![]() $Y$
is the join of
$Y$
is the join of
![]() $Y_{\pm }$
along
$Y_{\pm }$
along
![]() $D$
and there is a short exact sequence
$D$
and there is a short exact sequence
 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{Y}\rightarrow {\mathcal{O}}_{Y_{+}}\times {\mathcal{O}}_{Y_{-}}\rightarrow {\mathcal{O}}_{Y\cap D}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{Y}\rightarrow {\mathcal{O}}_{Y_{+}}\times {\mathcal{O}}_{Y_{-}}\rightarrow {\mathcal{O}}_{Y\cap D}\rightarrow 0.\end{eqnarray}$$
Since
![]() $C_{1}$
is locally principal in
$C_{1}$
is locally principal in
![]() $Y$
, it follows that
$Y$
, it follows that
 $C_{1}\cap X_{\pm }=C_{1}\cap Y_{\pm }$
are locally principal in
$C_{1}\cap X_{\pm }=C_{1}\cap Y_{\pm }$
are locally principal in
![]() $Y_{\pm }$
. Since
$Y_{\pm }$
. Since
![]() $Y_{\pm }$
are integral surfaces, it follows that
$Y_{\pm }$
are integral surfaces, it follows that
 $C_{1}\cap X_{\pm }$
are Cartier divisors in
$C_{1}\cap X_{\pm }$
are Cartier divisors in
![]() $Y_{\pm }$
. It follows from (5.2) that
$Y_{\pm }$
. It follows from (5.2) that
![]() $C_{1}$
is a Cartier divisor in
$C_{1}$
is a Cartier divisor in
![]() $Y$
. Since
$Y$
. Since
![]() $S_{X}$
is Cohen–Macaulay and
$S_{X}$
is Cohen–Macaulay and
 $Y\subset S_{X}$
is a complete intersection, it follows that
$Y\subset S_{X}$
is a complete intersection, it follows that
![]() $Y$
is also Cohen–Macaulay. Since
$Y$
is also Cohen–Macaulay. Since
 $C_{1}\subset Y$
is a Cartier divisor, we conclude that
$C_{1}\subset Y$
is a Cartier divisor, we conclude that
![]() $C_{1}$
is Cohen–Macaulay.
$C_{1}$
is Cohen–Macaulay.
It follows from (c) that
![]() $f$
extends to a function
$f$
extends to a function
 $g\in {\mathcal{O}}_{C_{1},C_{1}\cap D}^{\times }$
by setting
$g\in {\mathcal{O}}_{C_{1},C_{1}\cap D}^{\times }$
by setting
![]() $g=f$
on
$g=f$
on
![]() $C$
and
$C$
and
![]() $g=1$
on
$g=1$
on
![]() $C_{1}\setminus C$
. In particular, we have
$C_{1}\setminus C$
. In particular, we have
 $\operatorname{div}(f)=\operatorname{div}(g)$
. This finishes the proof.◻
$\operatorname{div}(f)=\operatorname{div}(g)$
. This finishes the proof.◻
We now further refine the rational equivalence by specifying the shape of the Cartier curves that generate the group of relations.
Lemma 5.5. Let
![]() $X$
be a connected smooth quasi-projective scheme of dimension
$X$
be a connected smooth quasi-projective scheme of dimension
![]() $d\geqslant 2$
over
$d\geqslant 2$
over
![]() $k$
. Let
$k$
. Let
 $\unicode[STIX]{x1D708}:C\rightarrow S_{X}$
be a (possibly non-reduced) Cartier curve relative to
$\unicode[STIX]{x1D708}:C\rightarrow S_{X}$
be a (possibly non-reduced) Cartier curve relative to
 $D\subset S_{X}$
. Assume that either
$D\subset S_{X}$
. Assume that either
![]() $d=2$
or there are inclusions
$d=2$
or there are inclusions
 $C\subset Y\subset S_{X}$
, where
$C\subset Y\subset S_{X}$
, where
![]() $Y$
is a geometrically reduced complete intersection surface and
$Y$
is a geometrically reduced complete intersection surface and
![]() $C$
is a Cartier divisor on
$C$
is a Cartier divisor on
![]() $Y$
, as in Lemma 5.4. Let
$Y$
, as in Lemma 5.4. Let
 $f\in {\mathcal{O}}_{C,\unicode[STIX]{x1D708}^{\ast }D}^{\times }\subset k(C)^{\times }$
, where
$f\in {\mathcal{O}}_{C,\unicode[STIX]{x1D708}^{\ast }D}^{\times }\subset k(C)^{\times }$
, where
![]() $k(C)$
is the total quotient ring of
$k(C)$
is the total quotient ring of
![]() ${\mathcal{O}}_{C,\unicode[STIX]{x1D708}^{\ast }D}$
.
${\mathcal{O}}_{C,\unicode[STIX]{x1D708}^{\ast }D}$
.
We can then find two Cartier curves
 $\unicode[STIX]{x1D708}^{\prime }:C^{\prime }{\hookrightarrow}S_{X}$
and
$\unicode[STIX]{x1D708}^{\prime }:C^{\prime }{\hookrightarrow}S_{X}$
and
 $\unicode[STIX]{x1D708}^{\prime \prime }:C^{\prime \prime }{\hookrightarrow}S_{X}$
relative to
$\unicode[STIX]{x1D708}^{\prime \prime }:C^{\prime \prime }{\hookrightarrow}S_{X}$
relative to
![]() $D$
satisfying the following:
$D$
satisfying the following:
-
(1) there are very ample line bundles
 ${\mathcal{L}}^{\prime },{\mathcal{L}}^{\prime \prime }$
on
${\mathcal{L}}^{\prime },{\mathcal{L}}^{\prime \prime }$
on
 $S_{X}$
and sections
$S_{X}$
and sections
 $t^{\prime }\in H^{0}(S_{X},{\mathcal{L}}^{\prime }),~t^{\prime \prime }\in H^{0}(S_{X},{\mathcal{L}}^{\prime \prime })$
such that
$t^{\prime }\in H^{0}(S_{X},{\mathcal{L}}^{\prime }),~t^{\prime \prime }\in H^{0}(S_{X},{\mathcal{L}}^{\prime \prime })$
such that
 $C^{\prime }=Y\cap (t^{\prime })$
and
$C^{\prime }=Y\cap (t^{\prime })$
and
 $C^{\prime \prime }=Y\cap (t^{\prime \prime })$
(with the convention
$C^{\prime \prime }=Y\cap (t^{\prime \prime })$
(with the convention
 $Y=S_{X}$
if
$Y=S_{X}$
if
 $d=2$
);
$d=2$
); -
(2)
 $C^{\prime }$
and
$C^{\prime }$
and
 $C^{\prime \prime }$
are geometrically reduced;
$C^{\prime \prime }$
are geometrically reduced; -
(3) the restrictions of both
 $C^{\prime }$
and
$C^{\prime }$
and
 $C^{\prime \prime }$
to
$C^{\prime \prime }$
to
 $X$
via the two closed immersions
$X$
via the two closed immersions
 $\unicode[STIX]{x1D704}_{\pm }$
are integral curves in
$\unicode[STIX]{x1D704}_{\pm }$
are integral curves in
 $X$
, which are Cartier and smooth along
$X$
, which are Cartier and smooth along
 $D$
;
$D$
; -
(4) there are functions
 $f^{\prime }\in {\mathcal{O}}_{C^{\prime },(\unicode[STIX]{x1D708}^{\prime })^{\ast }D}^{\times }$
and
$f^{\prime }\in {\mathcal{O}}_{C^{\prime },(\unicode[STIX]{x1D708}^{\prime })^{\ast }D}^{\times }$
and
 $f^{\prime \prime }\in {\mathcal{O}}_{C^{\prime \prime },(\unicode[STIX]{x1D708}^{\prime \prime })^{\ast }D}^{\times }$
such that
$f^{\prime \prime }\in {\mathcal{O}}_{C^{\prime \prime },(\unicode[STIX]{x1D708}^{\prime \prime })^{\ast }D}^{\times }$
such that
 $\unicode[STIX]{x1D708}_{\ast }^{\prime }(\operatorname{div}(f^{\prime }))+\unicode[STIX]{x1D708}_{\ast }^{\prime \prime }(\operatorname{div}(f^{\prime \prime }))=\unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f))$
in
$\unicode[STIX]{x1D708}_{\ast }^{\prime }(\operatorname{div}(f^{\prime }))+\unicode[STIX]{x1D708}_{\ast }^{\prime \prime }(\operatorname{div}(f^{\prime \prime }))=\unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f))$
in
 ${\mathcal{Z}}_{0}(S_{X},D)$
.
${\mathcal{Z}}_{0}(S_{X},D)$
.
Proof. In this proof, we shall assume that
 $Y=S_{X}$
if
$Y=S_{X}$
if
![]() $d=2$
. In this case, a Cartier curve on
$d=2$
. In this case, a Cartier curve on
![]() $S_{X}$
along
$S_{X}$
along
 $D=(S_{X})_{\operatorname{sing}}$
must be an effective Cartier divisor on
$D=(S_{X})_{\operatorname{sing}}$
must be an effective Cartier divisor on
![]() $S_{X}$
. Hence we can assume that
$S_{X}$
. Hence we can assume that
![]() $C$
is an effective Cartier divisor on
$C$
is an effective Cartier divisor on
![]() $Y$
for any
$Y$
for any
![]() $d\geqslant 2$
. Notice that
$d\geqslant 2$
. Notice that
 $Y=Y_{+}\amalg _{D}Y_{-}$
, again by Lemma 2.2.
$Y=Y_{+}\amalg _{D}Y_{-}$
, again by Lemma 2.2.
Arguing as in Lemma 5.4, since
![]() $S_{X}$
(and hence
$S_{X}$
(and hence
![]() $Y$
) is quasi-projective over
$Y$
) is quasi-projective over
![]() $k$
, we can find an effective Cartier divisor
$k$
, we can find an effective Cartier divisor
![]() $\tilde{C}$
on
$\tilde{C}$
on
![]() $Y$
such that:
$Y$
such that:
-
(1)
 $C\subset \tilde{C}$
;
$C\subset \tilde{C}$
; -
(2)
 $\overline{\tilde{C}\setminus C}\cap (C\cap D)=\emptyset$
;
$\overline{\tilde{C}\setminus C}\cap (C\cap D)=\emptyset$
; -
(3)
 ${\mathcal{O}}_{Y}(\tilde{C})$
is a very ample line bundle on
${\mathcal{O}}_{Y}(\tilde{C})$
is a very ample line bundle on
 $Y$
.
$Y$
.
We can extend the function
![]() $f$
on
$f$
on
![]() $C$
to a function
$C$
to a function
![]() $\tilde{f}$
on
$\tilde{f}$
on
![]() $\tilde{C}$
by setting
$\tilde{C}$
by setting
![]() $\tilde{f}=f$
on
$\tilde{f}=f$
on
![]() $C$
and
$C$
and
![]() $\tilde{f}=1$
on
$\tilde{f}=1$
on
![]() $\tilde{C}\setminus C$
. Condition (2) guarantees that
$\tilde{C}\setminus C$
. Condition (2) guarantees that
![]() $\tilde{f}$
is regular and invertible at each point of
$\tilde{f}$
is regular and invertible at each point of
![]() $\tilde{C}\cap D$
, and it is clear by construction that
$\tilde{C}\cap D$
, and it is clear by construction that
 $\operatorname{div}(\tilde{f})=\operatorname{div}(f)$
. Replacing
$\operatorname{div}(\tilde{f})=\operatorname{div}(f)$
. Replacing
![]() $C$
with
$C$
with
![]() $\tilde{C}$
(and changing the notation for simplicity), we can thus assume that
$\tilde{C}$
(and changing the notation for simplicity), we can thus assume that
![]() $C$
is a Cartier divisor on
$C$
is a Cartier divisor on
![]() $Y$
such that the associated line bundle
$Y$
such that the associated line bundle
![]() ${\mathcal{O}}_{Y}(C)$
is very ample. Choose
${\mathcal{O}}_{Y}(C)$
is very ample. Choose
 $t_{0}\in H^{0}(Y,{\mathcal{O}}_{Y}(C))$
such that
$t_{0}\in H^{0}(Y,{\mathcal{O}}_{Y}(C))$
such that
 $C=(t_{0})$
. Since
$C=(t_{0})$
. Since
![]() $Y$
is geometrically reduced, standard Bertini (see the proof of [Reference LevineLev87, Lemma 1.3]) allows us to choose another divisor
$Y$
is geometrically reduced, standard Bertini (see the proof of [Reference LevineLev87, Lemma 1.3]) allows us to choose another divisor
![]() $C_{\infty }$
in the linear system
$C_{\infty }$
in the linear system
 $H^{0}(Y,{\mathcal{O}}_{Y}(C))$
such that:
$H^{0}(Y,{\mathcal{O}}_{Y}(C))$
such that:
-
(1)
 $C_{\infty }$
is reduced;
$C_{\infty }$
is reduced; -
(2)
 $C_{\infty }\cap C\cap D=\emptyset$
;
$C_{\infty }\cap C\cap D=\emptyset$
; -
(3)
 $C_{\infty }$
contains no component of
$C_{\infty }$
contains no component of
 $C$
;
$C$
; -
(4)
 $D$
contains no component of
$D$
contains no component of
 $C_{\infty }$
.
$C_{\infty }$
.
Denote by
![]() $t_{\infty }$
the section of
$t_{\infty }$
the section of
![]() ${\mathcal{O}}_{Y}(C)$
with
${\mathcal{O}}_{Y}(C)$
with
 $C_{\infty }=(t_{\infty })$
. As before, we extend the function
$C_{\infty }=(t_{\infty })$
. As before, we extend the function
![]() $f$
on
$f$
on
![]() $C$
to a function
$C$
to a function
![]() $h$
on
$h$
on
 $C_{\infty }\cup C$
by setting
$C_{\infty }\cup C$
by setting
![]() $h=f$
on
$h=f$
on
![]() $C$
and
$C$
and
![]() $h=1$
on
$h=1$
on
![]() $C_{\infty }$
. Notice that
$C_{\infty }$
. Notice that
![]() $h$
is meromorphic on
$h$
is meromorphic on
 $C_{\infty }\cup C$
and regular invertible in a neighborhood of
$C_{\infty }\cup C$
and regular invertible in a neighborhood of
 $(C_{\infty }\cup C)\cap D$
by (2). Let
$(C_{\infty }\cup C)\cap D$
by (2). Let
![]() $S$
denote the finite set of points
$S$
denote the finite set of points
 $S=\{\text{poles of }f\}\cup (C\cap C^{\infty })$
. Note that
$S=\{\text{poles of }f\}\cup (C\cap C^{\infty })$
. Note that
 $S\cap D=\emptyset$
.
$S\cap D=\emptyset$
.
Now choose a very ample line bundle
 ${\mathcal{L}}=j^{\ast }({\mathcal{O}}_{\mathbb{P}^{r}}(1))$
on
${\mathcal{L}}=j^{\ast }({\mathcal{O}}_{\mathbb{P}^{r}}(1))$
on
![]() $S_{X}$
, corresponding to an embedding
$S_{X}$
, corresponding to an embedding
 $j:S_{X}\rightarrow \mathbb{P}_{k}^{r}$
for
$j:S_{X}\rightarrow \mathbb{P}_{k}^{r}$
for
![]() $r\gg 0$
of
$r\gg 0$
of
![]() $S_{X}$
as locally closed subscheme. We can assume that
$S_{X}$
as locally closed subscheme. We can assume that
![]() $r$
is sufficiently large so that
$r$
is sufficiently large so that
 ${\mathcal{L}}_{|Y}\otimes _{{\mathcal{O}}_{Y}}{\mathcal{O}}_{Y}(C)$
is also very ample on
${\mathcal{L}}_{|Y}\otimes _{{\mathcal{O}}_{Y}}{\mathcal{O}}_{Y}(C)$
is also very ample on
![]() $Y$
. Since
$Y$
. Since
![]() $k$
is infinite, there is a dense open subset
$k$
is infinite, there is a dense open subset
![]() $V_{X}$
of the dual projective space
$V_{X}$
of the dual projective space
![]() $(\mathbb{P}_{k}^{r})^{\vee }$
such that for
$(\mathbb{P}_{k}^{r})^{\vee }$
such that for
![]() $L\in V_{X}$
, the scheme theoretic intersections
$L\in V_{X}$
, the scheme theoretic intersections
 $L\cdot S_{X}=L\times _{\mathbb{P}_{k}^{r}}S_{X}$
and
$L\cdot S_{X}=L\times _{\mathbb{P}_{k}^{r}}S_{X}$
and
 $L\cdot Y=L\times _{\mathbb{P}_{k}^{r}}Y$
satisfy the following list of properties:
$L\cdot Y=L\times _{\mathbb{P}_{k}^{r}}Y$
satisfy the following list of properties:
-
(a)
 $L\cdot S_{X}$
and
$L\cdot S_{X}$
and
 $L\cdot Y$
are geometrically reduced (since both
$L\cdot Y$
are geometrically reduced (since both
 $S_{X}$
and
$S_{X}$
and
 $Y$
are);
$Y$
are); -
(b)
 $Y\not \subset L\cdot S_{X}$
;
$Y\not \subset L\cdot S_{X}$
; -
(c)
 $L\cdot X_{\pm }=L\times _{\mathbb{P}_{k}^{r}}X_{\pm }$
and
$L\cdot X_{\pm }=L\times _{\mathbb{P}_{k}^{r}}X_{\pm }$
and
 $L\cdot Y_{\pm }=L\times _{\mathbb{P}_{k}^{r}}Y_{\pm }$
are integral (since
$L\cdot Y_{\pm }=L\times _{\mathbb{P}_{k}^{r}}Y_{\pm }$
are integral (since
 $X_{\pm }$
and
$X_{\pm }$
and
 $Y_{\pm }$
are);
$Y_{\pm }$
are); -
(d)
 $L\cdot Y\cap (C\cup C_{\infty })\cap D=\emptyset$
;
$L\cdot Y\cap (C\cup C_{\infty })\cap D=\emptyset$
; -
(e)
 $L\cdot Y\supset S$
;
$L\cdot Y\supset S$
; -
(f)
 $L\cdot Y$
intersects
$L\cdot Y$
intersects
 $C_{\infty }\cup C$
in a finite set of points.
$C_{\infty }\cup C$
in a finite set of points.
The hyperplane
![]() $L$
corresponds to a section
$L$
corresponds to a section
![]() $l$
of the linear system
$l$
of the linear system
 $H^{0}(\mathbb{P}_{k}^{r},{\mathcal{O}}_{\mathbb{P}^{r}}(1))$
. Write
$H^{0}(\mathbb{P}_{k}^{r},{\mathcal{O}}_{\mathbb{P}^{r}}(1))$
. Write
![]() $s_{\infty }$
for the global section of
$s_{\infty }$
for the global section of
![]() ${\mathcal{L}}$
that is the restriction of
${\mathcal{L}}$
that is the restriction of
![]() $l$
to
$l$
to
![]() $S_{X}$
. Then
$S_{X}$
. Then
 $L\cdot S_{X}=(s_{\infty })$
. Note that we can assume that
$L\cdot S_{X}=(s_{\infty })$
. Note that we can assume that
![]() $s_{\infty }$
does not have poles on
$s_{\infty }$
does not have poles on
 $(C\cup C_{\infty })\cap D$
. Let
$(C\cup C_{\infty })\cap D$
. Let
![]() $\overline{S_{X}}$
be the closure of
$\overline{S_{X}}$
be the closure of
![]() $S_{X}$
in
$S_{X}$
in
![]() $\mathbb{P}_{k}^{r}$
and let
$\mathbb{P}_{k}^{r}$
and let
![]() ${\mathcal{I}}$
be the ideal sheaf of
${\mathcal{I}}$
be the ideal sheaf of
![]() $\overline{S_{X}}\setminus S_{X}$
in
$\overline{S_{X}}\setminus S_{X}$
in
![]() $\mathbb{P}_{k}^{r}$
. We can find a section
$\mathbb{P}_{k}^{r}$
. We can find a section
![]() $s_{\infty }^{\prime }$
of the sheaf
$s_{\infty }^{\prime }$
of the sheaf
 ${\mathcal{I}}\otimes {\mathcal{O}}_{\mathbb{P}_{k}^{N}}(m)$
for some
${\mathcal{I}}\otimes {\mathcal{O}}_{\mathbb{P}_{k}^{N}}(m)$
for some
![]() $m\gg 0$
, which restricts to a section
$m\gg 0$
, which restricts to a section
![]() $s_{\infty }$
on
$s_{\infty }$
on
![]() $S_{X}$
satisfying the properties (a)–(f) on
$S_{X}$
satisfying the properties (a)–(f) on
 $S_{X}=\overline{S_{X}}\setminus V({\mathcal{I}})$
. This implies in particular that
$S_{X}=\overline{S_{X}}\setminus V({\mathcal{I}})$
. This implies in particular that
 $S_{X}\setminus (s_{\infty })=\overline{S_{X}}\setminus (s_{\infty }^{\prime })$
is affine. Thus, up to taking a further Veronese embedding of
$S_{X}\setminus (s_{\infty })=\overline{S_{X}}\setminus (s_{\infty }^{\prime })$
is affine. Thus, up to taking a further Veronese embedding of
![]() $\mathbb{P}_{k}^{r}$
(replacing
$\mathbb{P}_{k}^{r}$
(replacing
![]() $s_{\infty }$
with
$s_{\infty }$
with
![]() $s_{\infty }^{\prime }$
) we can assume that (a)–(f) as above as well as the following hold:
$s_{\infty }^{\prime }$
) we can assume that (a)–(f) as above as well as the following hold:
-
(g)
 $S_{X}\setminus (s_{\infty })=S_{X}\setminus L\cdot S_{X}$
is affine.
$S_{X}\setminus (s_{\infty })=S_{X}\setminus L\cdot S_{X}$
is affine.
We now know that
![]() $Y_{\pm }$
is smooth away from
$Y_{\pm }$
is smooth away from
![]() $C$
and (d) tells us that
$C$
and (d) tells us that
![]() $(s_{\infty })$
intersects
$(s_{\infty })$
intersects
![]() $Y_{\pm }$
along
$Y_{\pm }$
along
![]() $D$
at only those points which are away from
$D$
at only those points which are away from
![]() $C$
. It follows that
$C$
. It follows that
 $(s_{\infty })\cap Y_{\pm }\cap D\subset (s_{\infty })\cap (Y_{+})_{\text{reg}}$
. We can then use the Bertini theorem of Altman and Kleiman [Reference Kleiman and AltmanKL79, Theorem 1] to ensure that
$(s_{\infty })\cap Y_{\pm }\cap D\subset (s_{\infty })\cap (Y_{+})_{\text{reg}}$
. We can then use the Bertini theorem of Altman and Kleiman [Reference Kleiman and AltmanKL79, Theorem 1] to ensure that
 $(s_{\infty })\cap (Y_{+})_{\text{reg}}$
is smooth away from the subscheme
$(s_{\infty })\cap (Y_{+})_{\text{reg}}$
is smooth away from the subscheme
 $(C\cup C_{\infty })\cap X_{+}$
where we ask the containment condition. In particular, we can assume that
$(C\cup C_{\infty })\cap X_{+}$
where we ask the containment condition. In particular, we can assume that
 $(s_{\infty })\cap Y_{+}$
is smooth along
$(s_{\infty })\cap Y_{+}$
is smooth along
![]() $D$
. The same holds for
$D$
. The same holds for
![]() $Y_{-}$
as well. We conclude that we can moreover achieve the following property:
$Y_{-}$
as well. We conclude that we can moreover achieve the following property:
-
(h)
 $(s_{\infty })\cap Y_{\pm }$
are smooth along
$(s_{\infty })\cap Y_{\pm }$
are smooth along
 $D$
.
$D$
.
Consider again the function
![]() $h$
on
$h$
on
 $C\cup C_{\infty }$
. By our choice of
$C\cup C_{\infty }$
. By our choice of
![]() $S$
,
$S$
,
![]() $h$
is regular on
$h$
is regular on
 $(C\cup C_{\infty })\setminus S$
. By (g) above,
$(C\cup C_{\infty })\setminus S$
. By (g) above,
![]() $h$
extends to a regular function
$h$
extends to a regular function
![]() $H$
on the affine open
$H$
on the affine open
 $U=S_{X}\setminus (s_{\infty })$
. Since
$U=S_{X}\setminus (s_{\infty })$
. Since
![]() $H$
is a meromorphic function on
$H$
is a meromorphic function on
![]() $S_{X}$
which has poles only along
$S_{X}$
which has poles only along
![]() $(s_{\infty })$
, it follows that for
$(s_{\infty })$
, it follows that for
![]() $N\gg 0$
the section
$N\gg 0$
the section
![]() $Hs_{\infty }^{N}$
is an element of
$Hs_{\infty }^{N}$
is an element of
 $H^{0}(U,{\mathcal{L}}^{\otimes N})$
which extends to a section
$H^{0}(U,{\mathcal{L}}^{\otimes N})$
which extends to a section
![]() $s_{0}$
of
$s_{0}$
of
![]() ${\mathcal{L}}^{\otimes N}$
on all
${\mathcal{L}}^{\otimes N}$
on all
![]() $S_{X}$
. Since
$S_{X}$
. Since
![]() $h$
is regular and invertible at each point of
$h$
is regular and invertible at each point of
 $C\cup C_{\infty }\cap D$
and since
$C\cup C_{\infty }\cap D$
and since
![]() $s_{\infty }$
does not have zeros or poles on
$s_{\infty }$
does not have zeros or poles on
 $C\cup C_{\infty }\cap D$
, it follows that
$C\cup C_{\infty }\cap D$
, it follows that
 $(s_{0})\cap (C\cup C_{\infty })\cap D=\emptyset$
and (using (f) above) that
$(s_{0})\cap (C\cup C_{\infty })\cap D=\emptyset$
and (using (f) above) that
![]() $(s_{0})$
does not contain any component of
$(s_{0})$
does not contain any component of
 $C\cup C_{\infty }$
. Note that up to replacing
$C\cup C_{\infty }$
. Note that up to replacing
![]() $s_{0}$
by
$s_{0}$
by
![]() $s_{0}s_{\infty }^{i}$
, we are free to choose
$s_{0}s_{\infty }^{i}$
, we are free to choose
![]() $N$
as large as needed.
$N$
as large as needed.
Write
![]() ${\mathcal{I}}_{C\cup C_{\infty }}$
for the ideal sheaf of
${\mathcal{I}}_{C\cup C_{\infty }}$
for the ideal sheaf of
 $C\cup C_{\infty }$
in
$C\cup C_{\infty }$
in
![]() $S_{X}$
. We can then find sections
$S_{X}$
. We can then find sections
 $s_{1},\ldots ,s_{m}$
of
$s_{1},\ldots ,s_{m}$
of
 $H^{0}(S_{X},{\mathcal{L}}^{\otimes N}\otimes {\mathcal{I}}_{C\cup C_{\infty }})$
such that the rational map
$H^{0}(S_{X},{\mathcal{L}}^{\otimes N}\otimes {\mathcal{I}}_{C\cup C_{\infty }})$
such that the rational map
 $\unicode[STIX]{x1D719}:S_{X}{\dashrightarrow}\mathbb{P}_{k}^{m-1}$
that they define is a locally closed immersion on
$\unicode[STIX]{x1D719}:S_{X}{\dashrightarrow}\mathbb{P}_{k}^{m-1}$
that they define is a locally closed immersion on
 $S_{X}\setminus (C\cup C_{\infty })$
. In particular, there exists an affine open neighborhood
$S_{X}\setminus (C\cup C_{\infty })$
. In particular, there exists an affine open neighborhood
![]() $U_{x}$
of every
$U_{x}$
of every
 $x\in S_{X}\setminus (C\cup C_{\infty })$
where at least one of the
$x\in S_{X}\setminus (C\cup C_{\infty })$
where at least one of the
![]() $s_{i}$
is not identically zero and where the
$s_{i}$
is not identically zero and where the
![]() $k$
-algebra
$k$
-algebra
 $k[s_{1}/s_{i},\ldots ,s_{m}/s_{i}]$
generated by
$k[s_{1}/s_{i},\ldots ,s_{m}/s_{i}]$
generated by
 $s_{1}/s_{i},\ldots ,s_{m}/s_{i}$
coincides with the coordinate ring of
$s_{1}/s_{i},\ldots ,s_{m}/s_{i}$
coincides with the coordinate ring of
![]() $U_{x}$
. But then the same must be true for the algebra
$U_{x}$
. But then the same must be true for the algebra
 $k[s_{0}/s_{1},s_{1}/s_{i},\ldots ,s_{m}/s_{i}]$
obtained by adding the element
$k[s_{0}/s_{1},s_{1}/s_{i},\ldots ,s_{m}/s_{i}]$
obtained by adding the element
![]() $s_{0}/s_{i}$
. Hence, the rational map
$s_{0}/s_{i}$
. Hence, the rational map
 $\unicode[STIX]{x1D713}:S_{X}{\dashrightarrow}\mathbb{P}_{k}^{m}$
given by the sections
$\unicode[STIX]{x1D713}:S_{X}{\dashrightarrow}\mathbb{P}_{k}^{m}$
given by the sections
 $(s_{0},s_{1},\ldots ,s_{m})$
of
$(s_{0},s_{1},\ldots ,s_{m})$
of
 $H^{0}(S_{X},{\mathcal{L}}^{\otimes }N)$
is also a locally closed immersion on
$H^{0}(S_{X},{\mathcal{L}}^{\otimes }N)$
is also a locally closed immersion on
 $S_{X}\setminus (C\cup C_{\infty })$
, and since the base locus of the linear system associated to
$S_{X}\setminus (C\cup C_{\infty })$
, and since the base locus of the linear system associated to
 $(s_{0},s_{1},\ldots ,s_{m})$
is
$(s_{0},s_{1},\ldots ,s_{m})$
is
 $(s_{0})\cap (C\cup C_{\infty })$
, it is in fact a morphism away from
$(s_{0})\cap (C\cup C_{\infty })$
, it is in fact a morphism away from
 $(s_{0})\cap (C\cup C_{\infty })$
.
$(s_{0})\cap (C\cup C_{\infty })$
.
In particular,
![]() $\unicode[STIX]{x1D713}$
is birational (hence separable) and has image of dimension at least two, so that the linear system
$\unicode[STIX]{x1D713}$
is birational (hence separable) and has image of dimension at least two, so that the linear system
 $V=(s_{0},s_{1},\ldots ,s_{m})$
is not composite with a pencil. By the classical Theorem of Bertini (see, for example, [Reference ZariskiZar58, Theorem I.6.3]), a general divisor
$V=(s_{0},s_{1},\ldots ,s_{m})$
is not composite with a pencil. By the classical Theorem of Bertini (see, for example, [Reference ZariskiZar58, Theorem I.6.3]), a general divisor
![]() $E$
in
$E$
in
![]() $V$
is generically geometrically reduced. Moreover,
$V$
is generically geometrically reduced. Moreover,
![]() $E$
is itself a Cohen–Macaulay scheme (since
$E$
is itself a Cohen–Macaulay scheme (since
![]() $S_{X}$
is Cohen–Macaulay). But a locally noetherian Cohen–Macaulay scheme that is generically reduced is in fact reduced by [Reference Görtz and WedhornGW10, Proposition 14.124]. Hence the general divisor
$S_{X}$
is Cohen–Macaulay). But a locally noetherian Cohen–Macaulay scheme that is generically reduced is in fact reduced by [Reference Görtz and WedhornGW10, Proposition 14.124]. Hence the general divisor
![]() $E$
in
$E$
in
![]() $V$
is indeed geometrically reduced (hence reduced). We can apply the same argument to
$V$
is indeed geometrically reduced (hence reduced). We can apply the same argument to
![]() $E\cdot Y$
, noting that being a complete intersection in
$E\cdot Y$
, noting that being a complete intersection in
![]() $S_{X}$
, the surface
$S_{X}$
, the surface
![]() $Y$
is Cohen–Macaulay.
$Y$
is Cohen–Macaulay.
Since
![]() $Y_{\pm }$
and
$Y_{\pm }$
and
![]() $X_{\pm }$
are all integral, a general divisor
$X_{\pm }$
are all integral, a general divisor
![]() $E$
of
$E$
of
![]() $V$
will be moreover irreducible when restricted to
$V$
will be moreover irreducible when restricted to
![]() $X_{\pm }$
and
$X_{\pm }$
and
![]() $Y_{\pm }$
. We can therefore assume that there is a global section
$Y_{\pm }$
. We can therefore assume that there is a global section
![]() $s_{0}^{\prime }$
of
$s_{0}^{\prime }$
of
 $H^{0}(S_{X},{\mathcal{L}}^{\otimes N})$
of the form
$H^{0}(S_{X},{\mathcal{L}}^{\otimes N})$
of the form
 $s_{0}^{\prime }=s_{0}+\unicode[STIX]{x1D6FC}$
with
$s_{0}^{\prime }=s_{0}+\unicode[STIX]{x1D6FC}$
with
 $\unicode[STIX]{x1D6FC}\in (s_{1},\ldots ,s_{m})$
, that satisfies the following properties:
$\unicode[STIX]{x1D6FC}\in (s_{1},\ldots ,s_{m})$
, that satisfies the following properties:
- (a
 $^{\prime }$
)
$^{\prime }$
) -
 $(s_{0}^{\prime })$
and
$(s_{0}^{\prime })$
and
 $(s_{0}^{\prime })\cap Y$
are (geometrically) reduced;
$(s_{0}^{\prime })\cap Y$
are (geometrically) reduced; - (b
 $^{\prime }$
)
$^{\prime }$
) -
 $Y\not \subset (s_{0}^{\prime })$
;
$Y\not \subset (s_{0}^{\prime })$
; - (c
 $^{\prime }$
)
$^{\prime }$
) -
 $(s_{0}^{\prime })\cap X_{\pm }$
and
$(s_{0}^{\prime })\cap X_{\pm }$
and
 $(s_{0}^{\prime })\cap Y_{\pm }$
are integral;
$(s_{0}^{\prime })\cap Y_{\pm }$
are integral; - (d
 $^{\prime }$
)
$^{\prime }$
) -
 $(s_{0}^{\prime })\cap (C\cup C_{\infty })\cap D=\emptyset$
;
$(s_{0}^{\prime })\cap (C\cup C_{\infty })\cap D=\emptyset$
; - (e
 $^{\prime }$
)
$^{\prime }$
) -
 $C_{\infty }\cup C$
contains no component of
$C_{\infty }\cup C$
contains no component of
 $(s_{0}^{\prime })\cap Y$
;
$(s_{0}^{\prime })\cap Y$
; - (
 $\text{f}^{\prime }$
)
$\text{f}^{\prime }$
) -
 $(s_{0}^{\prime })\cap Y_{\pm }$
are smooth along
$(s_{0}^{\prime })\cap Y_{\pm }$
are smooth along
 $D$
.
$D$
.
The items (a
![]() $^{\prime }$
) and (c
$^{\prime }$
) and (c
![]() $^{\prime }$
) follow from the previous discussion. Properties (b
$^{\prime }$
) follow from the previous discussion. Properties (b
![]() $^{\prime }$
), (d
$^{\prime }$
), (d
![]() $^{\prime }$
) and (e
$^{\prime }$
) and (e
![]() $^{\prime }$
) are clearly open conditions on the space of sections
$^{\prime }$
) are clearly open conditions on the space of sections
![]() $V$
, and are therefore satisfied by the general divisor. As for the last item (
$V$
, and are therefore satisfied by the general divisor. As for the last item (
![]() $\text{f}^{\prime }$
), it follows from the classical Theorem of Bertini on smoothness applied to
$\text{f}^{\prime }$
), it follows from the classical Theorem of Bertini on smoothness applied to
![]() $Y_{\pm }$
, the assumption on
$Y_{\pm }$
, the assumption on
![]() $Y_{\pm }$
and the item (d
$Y_{\pm }$
and the item (d
![]() $^{\prime }$
).
$^{\prime }$
).
We then have
 $$\begin{eqnarray}\frac{s_{0}^{\prime }}{s_{\infty }^{N}}=\frac{Hs_{\infty }^{N}+(\unicode[STIX]{x1D6FC}s_{\infty }^{-N})s_{\infty }^{N}}{s_{\infty }^{N}}=H+\unicode[STIX]{x1D6FC}s_{\infty }^{-N}=H^{\prime },\quad \text{say}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{s_{0}^{\prime }}{s_{\infty }^{N}}=\frac{Hs_{\infty }^{N}+(\unicode[STIX]{x1D6FC}s_{\infty }^{-N})s_{\infty }^{N}}{s_{\infty }^{N}}=H+\unicode[STIX]{x1D6FC}s_{\infty }^{-N}=H^{\prime },\quad \text{say}.\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D6FC}$
vanishes along
$\unicode[STIX]{x1D6FC}$
vanishes along
 $C\cup C_{\infty }$
and
$C\cup C_{\infty }$
and
![]() $s_{\infty }$
does not vanish identically on
$s_{\infty }$
does not vanish identically on
 $U\cap (C\cup C_{\infty })$
by (f), it follows that
$U\cap (C\cup C_{\infty })$
by (f), it follows that
 $H_{|(C\cup C_{\infty })\cap U}^{\prime }=H_{|(C\cup C_{\infty })\cap U}=h_{|U}$
. In other words, we have
$H_{|(C\cup C_{\infty })\cap U}^{\prime }=H_{|(C\cup C_{\infty })\cap U}=h_{|U}$
. In other words, we have
 $s_{0}^{\prime }/s_{\infty }^{N}=h$
as rational functions on
$s_{0}^{\prime }/s_{\infty }^{N}=h$
as rational functions on
 $C\cup C_{\infty }$
. We can now compute
$C\cup C_{\infty }$
. We can now compute
 $$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D708}_{\ast }(\text{div}(f))=(s_{0}^{\prime })\cdot C-N(s_{\infty })\cdot C, & \displaystyle \nonumber\\ \displaystyle & 0=\text{div}(1)=(s_{0}^{\prime })\cdot C_{\infty }-N(s_{\infty })\cdot C_{\infty }. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \unicode[STIX]{x1D708}_{\ast }(\text{div}(f))=(s_{0}^{\prime })\cdot C-N(s_{\infty })\cdot C, & \displaystyle \nonumber\\ \displaystyle & 0=\text{div}(1)=(s_{0}^{\prime })\cdot C_{\infty }-N(s_{\infty })\cdot C_{\infty }. & \displaystyle \nonumber\end{eqnarray}$$
Setting
 $(s_{\infty }^{Y})=(s_{\infty })\cap Y$
and
$(s_{\infty }^{Y})=(s_{\infty })\cap Y$
and
 $(s_{0}^{\prime Y})=(s_{0}^{\prime })\cap Y$
, we get
$(s_{0}^{\prime Y})=(s_{0}^{\prime })\cap Y$
, we get
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f)) & = & \displaystyle (s_{0}^{\prime })\cdot (C-C_{\infty })-N(s_{\infty })(C-C_{\infty })\nonumber\\ \displaystyle & = & \displaystyle (s_{0}^{\prime Y})\cdot (\operatorname{div}(t_{0}/t_{\infty }))-N(s_{\infty }^{Y})\cdot (\operatorname{div}(t_{0}/t_{\infty }))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D704}_{s_{0}^{\prime Y},\ast }(\operatorname{div}(f^{\prime }))-N\unicode[STIX]{x1D704}_{s_{\infty }^{Y},\ast }(\operatorname{div}(f^{\prime \prime })),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f)) & = & \displaystyle (s_{0}^{\prime })\cdot (C-C_{\infty })-N(s_{\infty })(C-C_{\infty })\nonumber\\ \displaystyle & = & \displaystyle (s_{0}^{\prime Y})\cdot (\operatorname{div}(t_{0}/t_{\infty }))-N(s_{\infty }^{Y})\cdot (\operatorname{div}(t_{0}/t_{\infty }))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D704}_{s_{0}^{\prime Y},\ast }(\operatorname{div}(f^{\prime }))-N\unicode[STIX]{x1D704}_{s_{\infty }^{Y},\ast }(\operatorname{div}(f^{\prime \prime })),\nonumber\end{eqnarray}$$
where
 $f^{\prime }=(t_{0}/t_{\infty })|_{(s_{0}^{\prime Y})}\in {\mathcal{O}}_{(s_{0}^{\prime Y}),D\cap (s_{0}^{\prime Y})}^{\times }$
(by (d
$f^{\prime }=(t_{0}/t_{\infty })|_{(s_{0}^{\prime Y})}\in {\mathcal{O}}_{(s_{0}^{\prime Y}),D\cap (s_{0}^{\prime Y})}^{\times }$
(by (d
![]() $^{\prime }$
)) and
$^{\prime }$
)) and
 $f^{\prime \prime }=(t_{0}/t_{\infty })|_{(s_{\infty }^{Y})}\in {\mathcal{O}}_{(s_{\infty }^{Y}),D\cap (s_{\infty }^{Y})}^{\times }$
(by (d)).
$f^{\prime \prime }=(t_{0}/t_{\infty })|_{(s_{\infty }^{Y})}\in {\mathcal{O}}_{(s_{\infty }^{Y}),D\cap (s_{\infty }^{Y})}^{\times }$
(by (d)).
It follows from (h) and (
![]() $\text{f}^{\prime }$
) that
$\text{f}^{\prime }$
) that
 $(s_{0}^{\prime Y})_{|X_{+}},~(s_{0}^{\prime Y})_{|X_{-}},~(s_{\infty }^{Y})_{|X_{+}}$
and
$(s_{0}^{\prime Y})_{|X_{+}},~(s_{0}^{\prime Y})_{|X_{-}},~(s_{\infty }^{Y})_{|X_{+}}$
and
 $(s_{\infty }^{Y})_{|X_{-}}$
are all smooth along
$(s_{\infty }^{Y})_{|X_{-}}$
are all smooth along
![]() $D$
. Setting
$D$
. Setting
 ${\mathcal{L}}^{\prime \prime }=({\mathcal{L}}^{\prime })^{N},~t^{\prime \prime }=(s_{0}^{\prime })$
and
${\mathcal{L}}^{\prime \prime }=({\mathcal{L}}^{\prime })^{N},~t^{\prime \prime }=(s_{0}^{\prime })$
and
 $t^{\prime }=(s_{\infty })$
, the curves
$t^{\prime }=(s_{\infty })$
, the curves
 $C^{\prime }=(t^{\prime })\cap Y$
and
$C^{\prime }=(t^{\prime })\cap Y$
and
 $C^{\prime \prime }=(t^{\prime \prime })\cap Y$
together with the functions
$C^{\prime \prime }=(t^{\prime \prime })\cap Y$
together with the functions
![]() $f^{\prime }$
and
$f^{\prime }$
and
![]() $f^{\prime \prime }$
satisfy the conditions of the lemma.◻
$f^{\prime \prime }$
satisfy the conditions of the lemma.◻
Remark 5.6. It follows from Lemma 2.2 that each of the curves
![]() $C^{\prime }$
and
$C^{\prime }$
and
![]() $C^{\prime \prime }$
constructed in the proof of the lemma is of the form
$C^{\prime \prime }$
constructed in the proof of the lemma is of the form
 $C_{+}\amalg _{E}C_{-}$
for
$C_{+}\amalg _{E}C_{-}$
for
 $E=\unicode[STIX]{x1D708}_{+}^{\ast }(D)=\unicode[STIX]{x1D708}_{-}^{\ast }(D)$
and
$E=\unicode[STIX]{x1D708}_{+}^{\ast }(D)=\unicode[STIX]{x1D708}_{-}^{\ast }(D)$
and
 $\unicode[STIX]{x1D708}_{\pm }:C_{\pm }{\hookrightarrow}X$
are integral Cartier curves in
$\unicode[STIX]{x1D708}_{\pm }:C_{\pm }{\hookrightarrow}X$
are integral Cartier curves in
![]() $X$
, which are smooth along
$X$
, which are smooth along
![]() $D$
. Moreover, by construction,
$D$
. Moreover, by construction,
![]() $C_{\pm }$
are the zero loci of the restrictions
$C_{\pm }$
are the zero loci of the restrictions
![]() $t_{\pm }$
to
$t_{\pm }$
to
![]() $Y_{\pm }$
of a global section of a very ample line bundle
$Y_{\pm }$
of a global section of a very ample line bundle
![]() ${\mathcal{M}}$
on
${\mathcal{M}}$
on
![]() $S_{X}$
. It follows that
$S_{X}$
. It follows that
![]() $(t_{+})_{|D}$
and
$(t_{+})_{|D}$
and
![]() $(t_{-})_{|D}$
agree.
$(t_{-})_{|D}$
agree.
5.5 The map
 $\unicode[STIX]{x1D70F}_{X}^{\ast }$
: the case of curves and surfaces
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
: the case of curves and surfaces
For any smooth quasi-projective scheme
![]() $X$
over
$X$
over
![]() $k$
with effective Cartier divisor
$k$
with effective Cartier divisor
![]() $D\subset X$
, we have defined in 5.3 the map
$D\subset X$
, we have defined in 5.3 the map
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow {\mathcal{Z}}_{0}(X,D)\quad \text{by }\unicode[STIX]{x1D70F}_{X}^{\ast }([x])=\unicode[STIX]{x1D704}_{+}^{\ast }([x])-\unicode[STIX]{x1D704}_{-}^{\ast }([x]),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow {\mathcal{Z}}_{0}(X,D)\quad \text{by }\unicode[STIX]{x1D70F}_{X}^{\ast }([x])=\unicode[STIX]{x1D704}_{+}^{\ast }([x])-\unicode[STIX]{x1D704}_{-}^{\ast }([x]),\end{eqnarray}$$
where
 $x\in S_{X}\setminus D$
is a closed point.
$x\in S_{X}\setminus D$
is a closed point.
Suppose first that
![]() $X$
is a smooth curve. We can clearly assume that
$X$
is a smooth curve. We can clearly assume that
![]() $X$
is connected. If
$X$
is connected. If
 $f\in {\mathcal{O}}_{S_{X},D}^{\times }$
and
$f\in {\mathcal{O}}_{S_{X},D}^{\times }$
and
 $\unicode[STIX]{x1D703}_{X}:{\mathcal{O}}_{S_{X},D}^{\times }\rightarrow k(S_{X})^{\times }=k(X_{+})^{\times }\times k(X_{-})^{\times }$
is the natural map, then
$\unicode[STIX]{x1D703}_{X}:{\mathcal{O}}_{S_{X},D}^{\times }\rightarrow k(S_{X})^{\times }=k(X_{+})^{\times }\times k(X_{-})^{\times }$
is the natural map, then
 $\unicode[STIX]{x1D703}_{X}(f)=(f_{+},f_{-})$
with
$\unicode[STIX]{x1D703}_{X}(f)=(f_{+},f_{-})$
with
 $f_{\pm }\in {\mathcal{O}}_{X_{\pm },D}^{\times }={\mathcal{O}}_{X,D}^{\times }$
. It follows from (2.6) that
$f_{\pm }\in {\mathcal{O}}_{X_{\pm },D}^{\times }={\mathcal{O}}_{X,D}^{\times }$
. It follows from (2.6) that
 $g:=f_{+}f_{-}^{-1}\in \operatorname{Ker}({\mathcal{O}}_{X,D}^{\times }\rightarrow {\mathcal{O}}_{D}^{\times })$
. Moreover,
$g:=f_{+}f_{-}^{-1}\in \operatorname{Ker}({\mathcal{O}}_{X,D}^{\times }\rightarrow {\mathcal{O}}_{D}^{\times })$
. Moreover,
 $\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f))=\unicode[STIX]{x1D704}_{+}^{\ast }(\operatorname{div}(f))-\unicode[STIX]{x1D704}_{-}^{\ast }(\operatorname{div}(f))=\operatorname{div}(f_{+})-\operatorname{div}(f_{-})=\operatorname{div}(g)$
. We conclude that
$\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f))=\unicode[STIX]{x1D704}_{+}^{\ast }(\operatorname{div}(f))-\unicode[STIX]{x1D704}_{-}^{\ast }(\operatorname{div}(f))=\operatorname{div}(f_{+})-\operatorname{div}(f_{-})=\operatorname{div}(g)$
. We conclude that
![]() $\unicode[STIX]{x1D70F}_{X}^{\ast }$
descends to a map
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
descends to a map
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}^{\text{LW}}(S_{X})=\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X|D).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}^{\text{LW}}(S_{X})=\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X|D).\end{eqnarray}$$
Proposition 5.7. Let
![]() $X$
be a smooth connected quasi-projective surface over
$X$
be a smooth connected quasi-projective surface over
![]() $k$
with an effective Cartier divisor
$k$
with an effective Cartier divisor
![]() $D$
. Then the map
$D$
. Then the map
 $\unicode[STIX]{x1D70F}_{X}^{\ast }:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow {\mathcal{Z}}_{0}(X|D)$
of (5.3) descends to a group homomorphism
$\unicode[STIX]{x1D70F}_{X}^{\ast }:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow {\mathcal{Z}}_{0}(X|D)$
of (5.3) descends to a group homomorphism
 $\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
.
$\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
.
Proof. We shall continue to use the notations and various constructions in the proof of Lemma 5.5. We have shown in Lemma 5.5 that in order to prove that
![]() $\unicode[STIX]{x1D70F}_{X}^{\ast }$
preserves the subgroups of rational equivalences, it suffices to show that
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
preserves the subgroups of rational equivalences, it suffices to show that
 $\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f^{\prime }))\in {\mathcal{R}}_{0}(X|D)$
, where
$\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f^{\prime }))\in {\mathcal{R}}_{0}(X|D)$
, where
![]() $f^{\prime }$
is a rational function on a Cartier curve
$f^{\prime }$
is a rational function on a Cartier curve
 $\unicode[STIX]{x1D708}:C^{\prime }{\hookrightarrow}S_{X}$
that we can choose in the following way:
$\unicode[STIX]{x1D708}:C^{\prime }{\hookrightarrow}S_{X}$
that we can choose in the following way:
-
(1) there is a very ample line bundle
 ${\mathcal{L}}$
on
${\mathcal{L}}$
on
 $S_{X}$
and sections
$S_{X}$
and sections
 $t\in H^{0}(S_{X},{\mathcal{L}}),t_{\pm }=\unicode[STIX]{x1D704}_{\pm }^{\ast }(t)\in H^{0}(X,\unicode[STIX]{x1D704}_{\pm }^{\ast }({\mathcal{L}}))$
such that
$t\in H^{0}(S_{X},{\mathcal{L}}),t_{\pm }=\unicode[STIX]{x1D704}_{\pm }^{\ast }(t)\in H^{0}(X,\unicode[STIX]{x1D704}_{\pm }^{\ast }({\mathcal{L}}))$
such that
 $C^{\prime }=(t)$
and
$C^{\prime }=(t)$
and
 $C_{\pm }^{\prime }=(t_{\pm })$
;
$C_{\pm }^{\prime }=(t_{\pm })$
; -
(2)
 $C^{\prime }$
is a (geometrically) reduced Cartier curve of the form
$C^{\prime }$
is a (geometrically) reduced Cartier curve of the form
 $C^{\prime }=C_{+}^{\prime }\amalg _{E}C_{-}^{\prime }$
, where
$C^{\prime }=C_{+}^{\prime }\amalg _{E}C_{-}^{\prime }$
, where
 $E=\unicode[STIX]{x1D708}^{\ast }(D)$
such that
$E=\unicode[STIX]{x1D708}^{\ast }(D)$
such that
 $C_{\pm }^{\prime }$
are integral curves on
$C_{\pm }^{\prime }$
are integral curves on
 $X$
, none of which is contained in
$X$
, none of which is contained in
 $D$
and each of which is smooth along
$D$
and each of which is smooth along
 $D$
(see Remark 5.6).
$D$
(see Remark 5.6).
Let
 $\unicode[STIX]{x1D704}_{D}=\unicode[STIX]{x1D704}_{+}\circ \unicode[STIX]{x1D704}=\unicode[STIX]{x1D704}_{-}\circ \unicode[STIX]{x1D704}:D{\hookrightarrow}S_{X}$
denote the inclusion map. Then, it follows from (1) that
$\unicode[STIX]{x1D704}_{D}=\unicode[STIX]{x1D704}_{+}\circ \unicode[STIX]{x1D704}=\unicode[STIX]{x1D704}_{-}\circ \unicode[STIX]{x1D704}:D{\hookrightarrow}S_{X}$
denote the inclusion map. Then, it follows from (1) that
 $$\begin{eqnarray}(t_{+})_{|D}=\unicode[STIX]{x1D704}_{D}^{\ast }(t)=(t_{-})_{|D}.\end{eqnarray}$$
$$\begin{eqnarray}(t_{+})_{|D}=\unicode[STIX]{x1D704}_{D}^{\ast }(t)=(t_{-})_{|D}.\end{eqnarray}$$
Let
 $(f_{+}^{\prime },f_{-}^{\prime })$
be the image of
$(f_{+}^{\prime },f_{-}^{\prime })$
be the image of
![]() $f^{\prime }$
in
$f^{\prime }$
in
 ${\mathcal{O}}_{C_{+}^{\prime },E}^{\times }\times {\mathcal{O}}_{C_{-}^{\prime },E}^{\times }{\hookrightarrow}k(C_{+}^{\prime })\times k(C_{-}^{\prime })$
. It follows from Lemma 2.2 that there is an exact sequence
${\mathcal{O}}_{C_{+}^{\prime },E}^{\times }\times {\mathcal{O}}_{C_{-}^{\prime },E}^{\times }{\hookrightarrow}k(C_{+}^{\prime })\times k(C_{-}^{\prime })$
. It follows from Lemma 2.2 that there is an exact sequence
 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{C^{\prime },E}\rightarrow {\mathcal{O}}_{C_{+}^{\prime },E}\times {\mathcal{O}}_{C_{-}^{\prime },E}\rightarrow {\mathcal{O}}_{E}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{C^{\prime },E}\rightarrow {\mathcal{O}}_{C_{+}^{\prime },E}\times {\mathcal{O}}_{C_{-}^{\prime },E}\rightarrow {\mathcal{O}}_{E}\rightarrow 0.\end{eqnarray}$$
In particular, we have
 $$\begin{eqnarray}(f_{+}^{\prime })_{|E}=(f_{-}^{\prime })_{|E}\in {\mathcal{O}}_{E}^{\times }.\end{eqnarray}$$
$$\begin{eqnarray}(f_{+}^{\prime })_{|E}=(f_{-}^{\prime })_{|E}\in {\mathcal{O}}_{E}^{\times }.\end{eqnarray}$$
Let us first assume that
 $C_{+}^{\prime }=C_{-}^{\prime }$
as curves on
$C_{+}^{\prime }=C_{-}^{\prime }$
as curves on
![]() $X$
. Let
$X$
. Let
![]() $C$
denote this curve and let
$C$
denote this curve and let
![]() $C^{N}$
denote its normalization. Let
$C^{N}$
denote its normalization. Let
 $\unicode[STIX]{x1D70B}:C^{N}\rightarrow C{\hookrightarrow}X$
denote the composite map. Since
$\unicode[STIX]{x1D70B}:C^{N}\rightarrow C{\hookrightarrow}X$
denote the composite map. Since
![]() $C$
is regular along
$C$
is regular along
![]() $E$
by (2), we get
$E$
by (2), we get
 $f_{+}^{\prime },f_{-}^{\prime }\in {\mathcal{O}}_{C^{N},E}^{\times }$
. Setting
$f_{+}^{\prime },f_{-}^{\prime }\in {\mathcal{O}}_{C^{N},E}^{\times }$
. Setting
 $g:=f_{+}^{\prime }f_{-}^{\prime -1}\in {\mathcal{O}}_{C^{N},E}^{\times }$
, it follows from (5.6) that
$g:=f_{+}^{\prime }f_{-}^{\prime -1}\in {\mathcal{O}}_{C^{N},E}^{\times }$
, it follows from (5.6) that
 $g\in \operatorname{Ker}({\mathcal{O}}_{C^{N},E}^{\times }\rightarrow {\mathcal{O}}_{E}^{\times })$
. Moreover,
$g\in \operatorname{Ker}({\mathcal{O}}_{C^{N},E}^{\times }\rightarrow {\mathcal{O}}_{E}^{\times })$
. Moreover,
 $\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f^{\prime }))=\unicode[STIX]{x1D704}_{+}^{\ast }(\operatorname{div}(f^{\prime }))-\unicode[STIX]{x1D704}_{-}^{\ast }(\operatorname{div}(f^{\prime }))=\operatorname{div}(f_{+}^{\prime })-\operatorname{div}(f_{-})=\unicode[STIX]{x1D70B}_{\ast }(\operatorname{div}(g))$
. We conclude from (5.1) that
$\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f^{\prime }))=\unicode[STIX]{x1D704}_{+}^{\ast }(\operatorname{div}(f^{\prime }))-\unicode[STIX]{x1D704}_{-}^{\ast }(\operatorname{div}(f^{\prime }))=\operatorname{div}(f_{+}^{\prime })-\operatorname{div}(f_{-})=\unicode[STIX]{x1D70B}_{\ast }(\operatorname{div}(g))$
. We conclude from (5.1) that
![]() $\unicode[STIX]{x1D70F}_{X}^{\ast }$
descends to a map
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
descends to a map
 $\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
.
$\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
.
We now assume that
 $C_{+}^{\prime }\neq C_{-}^{\prime }$
. Let
$C_{+}^{\prime }\neq C_{-}^{\prime }$
. Let
![]() $S$
denote the set of closed points on
$S$
denote the set of closed points on
 $C_{+}^{\prime }\cup C_{-}^{\prime }$
, where
$C_{+}^{\prime }\cup C_{-}^{\prime }$
, where
![]() $f_{+}^{\prime }$
or
$f_{+}^{\prime }$
or
![]() $f_{-}^{\prime }$
has a pole. It is clear that
$f_{-}^{\prime }$
has a pole. It is clear that
 $S\cap D=\emptyset$
. We now repeat the constructions in the proof of Lemma 5.5 to find a very ample line bundle
$S\cap D=\emptyset$
. We now repeat the constructions in the proof of Lemma 5.5 to find a very ample line bundle
![]() ${\mathcal{L}}$
on
${\mathcal{L}}$
on
![]() $X$
and a section
$X$
and a section
 $s_{\infty }\in H^{0}(X,{\mathcal{L}})$
such that:
$s_{\infty }\in H^{0}(X,{\mathcal{L}})$
such that:
-
(a)
 $(s_{\infty })$
is integral (because
$(s_{\infty })$
is integral (because
 $X$
is smooth and connected);
$X$
is smooth and connected); -
(b)
 $(s_{\infty })\cap (C_{+}^{\prime }\cup C_{-}^{\prime })\cap D=\emptyset$
;
$(s_{\infty })\cap (C_{+}^{\prime }\cup C_{-}^{\prime })\cap D=\emptyset$
; -
(c)
 $(s_{\infty })\supset S$
;
$(s_{\infty })\supset S$
; -
(d)
 $(s_{\infty })\not \subset C_{+}^{\prime }\cup C_{-}^{\prime }$
;
$(s_{\infty })\not \subset C_{+}^{\prime }\cup C_{-}^{\prime }$
; -
(e)
 $(s_{\infty })$
is smooth away from
$(s_{\infty })$
is smooth away from
 $S$
;
$S$
; -
(f)
 $X\setminus (s_{\infty })$
is affine.
$X\setminus (s_{\infty })$
is affine.
It follows that
![]() $f_{\pm }^{\prime }$
extend to regular functions
$f_{\pm }^{\prime }$
extend to regular functions
![]() $F_{\pm }^{\prime }$
on
$F_{\pm }^{\prime }$
on
 $U=X\setminus (s_{\infty })$
. Since
$U=X\setminus (s_{\infty })$
. Since
![]() $F_{\pm }^{\prime }$
are meromorphic functions on
$F_{\pm }^{\prime }$
are meromorphic functions on
![]() $X$
which have poles only along
$X$
which have poles only along
![]() $(s_{\infty })$
, it follows that
$(s_{\infty })$
, it follows that
![]() $F_{\pm }^{\prime }s_{\infty }^{N}$
are elements of
$F_{\pm }^{\prime }s_{\infty }^{N}$
are elements of
 $H^{0}(U,{\mathcal{L}}^{N})$
which extend to sections
$H^{0}(U,{\mathcal{L}}^{N})$
which extend to sections
![]() $s_{0,\pm }$
of
$s_{0,\pm }$
of
![]() ${\mathcal{L}}^{N}$
on all of
${\mathcal{L}}^{N}$
on all of
![]() $X$
, if we choose
$X$
, if we choose
![]() $N\gg 0$
.
$N\gg 0$
.
Since
 $s_{\infty },~F_{+}^{\prime }$
and
$s_{\infty },~F_{+}^{\prime }$
and
![]() $F_{-}^{\prime }$
are all invertible on
$F_{-}^{\prime }$
are all invertible on
 $C_{+}^{\prime }\cup C_{-}^{\prime }$
along
$C_{+}^{\prime }\cup C_{-}^{\prime }$
along
![]() $D$
, we see that
$D$
, we see that
![]() $(s_{0})_{\pm }$
are invertible on
$(s_{0})_{\pm }$
are invertible on
 $C_{+}^{\prime }\cup C_{-}^{\prime }$
along
$C_{+}^{\prime }\cup C_{-}^{\prime }$
along
![]() $D$
. In particular,
$D$
. In particular,
 $s_{0,\pm }\notin H^{0}(X,{\mathcal{L}}^{\otimes N}\otimes {\mathcal{I}}_{C_{+}\cup C_{-}})$
. As before, we can moreover find
$s_{0,\pm }\notin H^{0}(X,{\mathcal{L}}^{\otimes N}\otimes {\mathcal{I}}_{C_{+}\cup C_{-}})$
. As before, we can moreover find
 $\unicode[STIX]{x1D6FC}_{\pm }\in H^{0}(X,{\mathcal{L}}^{\otimes N}\otimes {\mathcal{I}}_{C_{+}\cup C_{-}})\subset H^{0}(X,{\mathcal{L}}^{N})$
such that
$\unicode[STIX]{x1D6FC}_{\pm }\in H^{0}(X,{\mathcal{L}}^{\otimes N}\otimes {\mathcal{I}}_{C_{+}\cup C_{-}})\subset H^{0}(X,{\mathcal{L}}^{N})$
such that
 $s_{0,\pm }^{\prime }:=s_{0,\pm }+\unicode[STIX]{x1D6FC}_{\pm }$
have the following properties:
$s_{0,\pm }^{\prime }:=s_{0,\pm }+\unicode[STIX]{x1D6FC}_{\pm }$
have the following properties:
- (a
 $^{\prime }$
)
$^{\prime }$
) -
 $(s_{0,\pm }^{\prime })$
are integral;
$(s_{0,\pm }^{\prime })$
are integral; - (b
 $^{\prime }$
)
$^{\prime }$
) -
 $(s_{0,\pm }^{\prime })\not \subset C_{+}^{\prime }\cup C_{-}^{\prime }$
;
$(s_{0,\pm }^{\prime })\not \subset C_{+}^{\prime }\cup C_{-}^{\prime }$
; - (c
 $^{\prime }$
)
$^{\prime }$
) -
 $(s_{0,\pm }^{\prime })\cap (C_{+}^{\prime }\cup C_{-}^{\prime })\cap D=\emptyset$
;
$(s_{0,\pm }^{\prime })\cap (C_{+}^{\prime }\cup C_{-}^{\prime })\cap D=\emptyset$
; - (d
 $^{\prime }$
)
$^{\prime }$
) -
 $(s_{0,\pm }^{\prime })$
are smooth away from
$(s_{0,\pm }^{\prime })$
are smooth away from
 $C_{+}^{\prime }\cup C_{-}^{\prime }$
.
$C_{+}^{\prime }\cup C_{-}^{\prime }$
.
We then have
 $$\begin{eqnarray}\frac{s_{0,\pm }^{\prime }}{s_{\infty }^{N}}=\frac{F_{\pm }^{\prime }s_{\infty }^{N}+(\unicode[STIX]{x1D6FC}_{\pm }s_{\infty }^{-N})s_{\infty }^{N}}{s_{\infty }^{N}}=F_{\pm }^{\prime }+\unicode[STIX]{x1D6FC}_{\pm }s_{\infty }^{-N}=H_{\pm }^{\prime },\quad \text{say}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{s_{0,\pm }^{\prime }}{s_{\infty }^{N}}=\frac{F_{\pm }^{\prime }s_{\infty }^{N}+(\unicode[STIX]{x1D6FC}_{\pm }s_{\infty }^{-N})s_{\infty }^{N}}{s_{\infty }^{N}}=F_{\pm }^{\prime }+\unicode[STIX]{x1D6FC}_{\pm }s_{\infty }^{-N}=H_{\pm }^{\prime },\quad \text{say}.\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D6FC}_{\pm }$
vanish along
$\unicode[STIX]{x1D6FC}_{\pm }$
vanish along
 $C_{+}^{\prime }\cup C_{-}^{\prime }$
and
$C_{+}^{\prime }\cup C_{-}^{\prime }$
and
![]() $s_{\infty }$
does not vanish identically along
$s_{\infty }$
does not vanish identically along
 $U\cap (C_{+}^{\prime }\cup C_{-}^{\prime })$
, it follows that
$U\cap (C_{+}^{\prime }\cup C_{-}^{\prime })$
, it follows that
 $(H_{\pm }^{\prime })_{|(C_{+}^{\prime }\cup C_{-}^{\prime })\cap U}=(F_{\pm }^{\prime })_{|(C_{+}^{\prime }\cup C_{-}^{\prime })\cap U}$
. Since
$(H_{\pm }^{\prime })_{|(C_{+}^{\prime }\cup C_{-}^{\prime })\cap U}=(F_{\pm }^{\prime })_{|(C_{+}^{\prime }\cup C_{-}^{\prime })\cap U}$
. Since
 $(F_{\pm }^{\prime })_{|C_{+}^{\prime }\cup C_{-}^{\prime }}$
are invertible regular functions on
$(F_{\pm }^{\prime })_{|C_{+}^{\prime }\cup C_{-}^{\prime }}$
are invertible regular functions on
 $C_{+}^{\prime }\cup C_{-}^{\prime }$
along
$C_{+}^{\prime }\cup C_{-}^{\prime }$
along
![]() $D$
, it follows that
$D$
, it follows that
 $(H_{+}^{\prime })_{|C_{+}^{\prime }\cup C_{-}^{\prime }}$
and
$(H_{+}^{\prime })_{|C_{+}^{\prime }\cup C_{-}^{\prime }}$
and
 $(H_{-}^{\prime })_{|C_{+}^{\prime }\cup C_{-}^{\prime }}$
are both rational functions on
$(H_{-}^{\prime })_{|C_{+}^{\prime }\cup C_{-}^{\prime }}$
are both rational functions on
 $C_{+}^{\prime }\cup C_{-}^{\prime }$
which are regular and invertible along
$C_{+}^{\prime }\cup C_{-}^{\prime }$
which are regular and invertible along
![]() $D$
. In particular, we have
$D$
. In particular, we have
 $$\begin{eqnarray}(H_{+}^{\prime })_{|E}=(F_{+}^{\prime })_{|E}=(f_{+}^{\prime })_{|E}~=^{\dagger }~(f_{-}^{\prime })_{|E}=(F_{-}^{\prime })_{|E}=(H_{-}^{\prime })_{|E},\end{eqnarray}$$
$$\begin{eqnarray}(H_{+}^{\prime })_{|E}=(F_{+}^{\prime })_{|E}=(f_{+}^{\prime })_{|E}~=^{\dagger }~(f_{-}^{\prime })_{|E}=(F_{-}^{\prime })_{|E}=(H_{-}^{\prime })_{|E},\end{eqnarray}$$
where
![]() $=^{\dagger }$
follows from (5.6).
$=^{\dagger }$
follows from (5.6).
Since
![]() $s_{0,+}^{\prime }$
and
$s_{0,+}^{\prime }$
and
![]() $s_{0,-}^{\prime }$
are both invertible functions on
$s_{0,-}^{\prime }$
are both invertible functions on
![]() $C_{-}^{\prime }$
in a neighborhood of
$C_{-}^{\prime }$
in a neighborhood of
 $C_{-}^{\prime }\cap D$
by (c
$C_{-}^{\prime }\cap D$
by (c
![]() $^{\prime }$
), it follows that the restriction of
$^{\prime }$
), it follows that the restriction of
 $s_{0,-}^{\prime }/s_{0,+}^{\prime }$
on
$s_{0,-}^{\prime }/s_{0,+}^{\prime }$
on
![]() $C_{-}^{\prime }$
is a rational function on
$C_{-}^{\prime }$
is a rational function on
![]() $C_{-}$
, which is regular and invertible in a neighborhood of
$C_{-}$
, which is regular and invertible in a neighborhood of
 $C_{-}^{\prime }\cap D$
. On the other hand, we have
$C_{-}^{\prime }\cap D$
. On the other hand, we have
 $$\begin{eqnarray}\frac{s_{0,-}^{\prime }}{s_{0,+}^{\prime }}=\frac{s_{0,-}^{\prime }/s_{\infty }^{N}}{s_{0,+}^{\prime }/s_{\infty }^{N}}=\frac{H_{-}^{\prime }}{H_{+}^{\prime }},\end{eqnarray}$$
$$\begin{eqnarray}\frac{s_{0,-}^{\prime }}{s_{0,+}^{\prime }}=\frac{s_{0,-}^{\prime }/s_{\infty }^{N}}{s_{0,+}^{\prime }/s_{\infty }^{N}}=\frac{H_{-}^{\prime }}{H_{+}^{\prime }},\end{eqnarray}$$
as rational functions on
![]() $X$
. Since
$X$
. Since
![]() $H_{+}^{\prime }$
and
$H_{+}^{\prime }$
and
![]() $H_{-}^{\prime }$
are also well-defined non-zero rational functions on
$H_{-}^{\prime }$
are also well-defined non-zero rational functions on
![]() $C_{-}^{\prime }$
, we conclude that
$C_{-}^{\prime }$
, we conclude that
 $s_{0,-}^{\prime }/s_{0,+}^{\prime }$
and
$s_{0,-}^{\prime }/s_{0,+}^{\prime }$
and
 $H_{-}^{\prime }/H_{+}^{\prime }$
both restrict to an identical and well-defined rational function on
$H_{-}^{\prime }/H_{+}^{\prime }$
both restrict to an identical and well-defined rational function on
![]() $C_{-}^{\prime }$
, which is invertible along
$C_{-}^{\prime }$
, which is invertible along
![]() $D$
.
$D$
.
We now compute
 $$\begin{eqnarray}\begin{array}{@{}lll@{}}\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f^{\prime }))\ & =\ & \unicode[STIX]{x1D704}_{+}^{\ast }(\operatorname{div}(f^{\prime }))-\unicode[STIX]{x1D704}_{-}^{\ast }(\operatorname{div}(f^{\prime }))\\ \ & =\ & \operatorname{div}(f_{+}^{\prime })-\operatorname{div}(f_{-}^{\prime })\\ \ & =\ & [(s_{0,+}^{\prime })\cdot C_{+}^{\prime }-(s_{\infty }^{N})\cdot C_{+}^{\prime }]-[(s_{0,-}^{\prime })\cdot C_{-}^{\prime }-(s_{\infty }^{N})\cdot C_{-}^{\prime }]\\ \ & =\ & [(s_{0,+}^{\prime })\cdot C_{+}^{\prime }-(s_{0,+}^{\prime })\cdot C_{-}^{\prime }]-[(s_{0,-}^{\prime })\cdot C_{-}^{\prime }-(s_{0,+}^{\prime })\cdot C_{-}^{\prime }]\\ \ & \ & -\,[(s_{\infty }^{N})\cdot C_{+}^{\prime }-(s_{\infty }^{N})\cdot C_{-}^{\prime }]\\ \ & =\ & [(s_{0,+}^{\prime })\cdot (C_{+}^{\prime }-C_{-}^{\prime })]-[C_{-}^{\prime }\cdot (s_{0,-}^{\prime })-(s_{0,+}^{\prime })]-[(s_{\infty }^{N})\cdot (C_{+}^{\prime }-C_{-}^{\prime })]\\ \ & =\ & (s_{0,+}^{\prime })\cdot (\operatorname{div}(t_{+}/t_{-}))-C_{-}^{\prime }\cdot (\operatorname{div}(s_{0,-}^{\prime }/s_{0,+}^{\prime }))-N(s_{\infty })\cdot (\operatorname{div}(t_{+}/t_{-}))\\ \ & =\ & (s_{0,+}^{\prime })\cdot (\operatorname{div}(t_{+}/t_{-}))-C_{-}^{\prime }\cdot (\operatorname{div}(H_{-}^{\prime }/H_{+}^{\prime }))-N(s_{\infty })\cdot (\operatorname{div}(t_{+}/t_{-})).\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}lll@{}}\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f^{\prime }))\ & =\ & \unicode[STIX]{x1D704}_{+}^{\ast }(\operatorname{div}(f^{\prime }))-\unicode[STIX]{x1D704}_{-}^{\ast }(\operatorname{div}(f^{\prime }))\\ \ & =\ & \operatorname{div}(f_{+}^{\prime })-\operatorname{div}(f_{-}^{\prime })\\ \ & =\ & [(s_{0,+}^{\prime })\cdot C_{+}^{\prime }-(s_{\infty }^{N})\cdot C_{+}^{\prime }]-[(s_{0,-}^{\prime })\cdot C_{-}^{\prime }-(s_{\infty }^{N})\cdot C_{-}^{\prime }]\\ \ & =\ & [(s_{0,+}^{\prime })\cdot C_{+}^{\prime }-(s_{0,+}^{\prime })\cdot C_{-}^{\prime }]-[(s_{0,-}^{\prime })\cdot C_{-}^{\prime }-(s_{0,+}^{\prime })\cdot C_{-}^{\prime }]\\ \ & \ & -\,[(s_{\infty }^{N})\cdot C_{+}^{\prime }-(s_{\infty }^{N})\cdot C_{-}^{\prime }]\\ \ & =\ & [(s_{0,+}^{\prime })\cdot (C_{+}^{\prime }-C_{-}^{\prime })]-[C_{-}^{\prime }\cdot (s_{0,-}^{\prime })-(s_{0,+}^{\prime })]-[(s_{\infty }^{N})\cdot (C_{+}^{\prime }-C_{-}^{\prime })]\\ \ & =\ & (s_{0,+}^{\prime })\cdot (\operatorname{div}(t_{+}/t_{-}))-C_{-}^{\prime }\cdot (\operatorname{div}(s_{0,-}^{\prime }/s_{0,+}^{\prime }))-N(s_{\infty })\cdot (\operatorname{div}(t_{+}/t_{-}))\\ \ & =\ & (s_{0,+}^{\prime })\cdot (\operatorname{div}(t_{+}/t_{-}))-C_{-}^{\prime }\cdot (\operatorname{div}(H_{-}^{\prime }/H_{+}^{\prime }))-N(s_{\infty })\cdot (\operatorname{div}(t_{+}/t_{-})).\end{array}\end{eqnarray}$$
It follows from (b) and (c
![]() $^{\prime }$
) that
$^{\prime }$
) that
![]() $t_{\pm }$
restrict to regular invertible functions on
$t_{\pm }$
restrict to regular invertible functions on
![]() $(s_{0,+}^{\prime })$
and
$(s_{0,+}^{\prime })$
and
![]() $(s_{\infty })$
along
$(s_{\infty })$
along
![]() $D$
. We set
$D$
. We set
 $h_{1}=(t_{+}/t_{-})_{|(s_{0,+}^{\prime })},~h_{2}=(H_{-}^{\prime }/H_{+}^{\prime })_{|C_{-}^{\prime }}$
and
$h_{1}=(t_{+}/t_{-})_{|(s_{0,+}^{\prime })},~h_{2}=(H_{-}^{\prime }/H_{+}^{\prime })_{|C_{-}^{\prime }}$
and
 $h_{3}=(t_{+}/t_{-})_{|s_{\infty }}$
. Let
$h_{3}=(t_{+}/t_{-})_{|s_{\infty }}$
. Let
 $(s_{0,+}^{\prime })^{N}\rightarrow (s_{0,+}^{\prime })$
,
$(s_{0,+}^{\prime })^{N}\rightarrow (s_{0,+}^{\prime })$
,
 $(C_{-}^{\prime })^{N}\rightarrow C_{-}^{\prime }$
and
$(C_{-}^{\prime })^{N}\rightarrow C_{-}^{\prime }$
and
 $(s_{\infty })^{N}\rightarrow (s_{\infty })$
denote the normalization maps. Let
$(s_{\infty })^{N}\rightarrow (s_{\infty })$
denote the normalization maps. Let
 $\unicode[STIX]{x1D708}_{1}:(s_{0,+}^{\prime })^{N}\rightarrow X$
,
$\unicode[STIX]{x1D708}_{1}:(s_{0,+}^{\prime })^{N}\rightarrow X$
,
 $\unicode[STIX]{x1D708}_{2}:(C_{-}^{\prime })^{N}\rightarrow X$
and
$\unicode[STIX]{x1D708}_{2}:(C_{-}^{\prime })^{N}\rightarrow X$
and
 $\unicode[STIX]{x1D708}_{3}:(s_{\infty })^{N}\rightarrow X$
denote the composite maps. Since
$\unicode[STIX]{x1D708}_{3}:(s_{\infty })^{N}\rightarrow X$
denote the composite maps. Since
 $(s_{0,+}^{\prime }),~C_{-}^{\prime }$
and
$(s_{0,+}^{\prime }),~C_{-}^{\prime }$
and
![]() $(s_{\infty })$
are all regular along
$(s_{\infty })$
are all regular along
![]() $D$
by (2), (e) and (d
$D$
by (2), (e) and (d
![]() $^{\prime }$
), it follows from (5.5) and (5.7) that
$^{\prime }$
), it follows from (5.5) and (5.7) that
 $h_{1}\in G((s_{0,+}^{\prime }),\unicode[STIX]{x1D708}_{1}^{\ast }(D))$
,
$h_{1}\in G((s_{0,+}^{\prime }),\unicode[STIX]{x1D708}_{1}^{\ast }(D))$
,
 $h_{2}\in G((C_{-}^{\prime })^{N},\unicode[STIX]{x1D708}_{2}^{\ast }(D))$
and
$h_{2}\in G((C_{-}^{\prime })^{N},\unicode[STIX]{x1D708}_{2}^{\ast }(D))$
and
 $h_{3}\in G((s_{\infty })^{N},\unicode[STIX]{x1D708}_{3}^{\ast }(D))$
. We conclude from (5.1) that
$h_{3}\in G((s_{\infty })^{N},\unicode[STIX]{x1D708}_{3}^{\ast }(D))$
. We conclude from (5.1) that
 $\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f^{\prime }))$
dies in
$\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f^{\prime }))$
dies in
 $\text{CH}_{0}(X|D)$
. In particular,
$\text{CH}_{0}(X|D)$
. In particular,
![]() $\unicode[STIX]{x1D70F}_{X}^{\ast }$
descends to a map
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
descends to a map
 $\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
. This finishes the proof.◻
$\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
. This finishes the proof.◻
5.6 The map
 $\unicode[STIX]{x1D70F}_{X}^{\ast }$
: the case of higher dimensions
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
: the case of higher dimensions
We are left to show that the map
 $\unicode[STIX]{x1D70F}_{X}^{\ast }:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow {\mathcal{Z}}_{0}(X|D)$
of (5.3) descends to a group homomorphism
$\unicode[STIX]{x1D70F}_{X}^{\ast }:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow {\mathcal{Z}}_{0}(X|D)$
of (5.3) descends to a group homomorphism
 $\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
when
$\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
when
![]() $X$
has dimension at least three when
$X$
has dimension at least three when
![]() $k$
is infinite and perfect. This is the content of the following.
$k$
is infinite and perfect. This is the content of the following.
Proposition 5.8. Let
![]() $X$
be a smooth connected quasi-projective scheme over
$X$
be a smooth connected quasi-projective scheme over
![]() $k$
of dimension
$k$
of dimension
![]() $d\geqslant 3$
with an effective Cartier divisor
$d\geqslant 3$
with an effective Cartier divisor
![]() $D$
. Then the map
$D$
. Then the map
 $\unicode[STIX]{x1D70F}_{X}^{\ast }:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow {\mathcal{Z}}_{0}(X|D)$
of (5.3) descends to a group homomorphism
$\unicode[STIX]{x1D70F}_{X}^{\ast }:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow {\mathcal{Z}}_{0}(X|D)$
of (5.3) descends to a group homomorphism
 $\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
.
$\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
.
Proof. Let
 $\unicode[STIX]{x1D708}:C{\hookrightarrow}S_{X}$
be a reduced Cartier curve relative to
$\unicode[STIX]{x1D708}:C{\hookrightarrow}S_{X}$
be a reduced Cartier curve relative to
![]() $D$
and let
$D$
and let
 $f\in {\mathcal{O}}_{C,E}^{\times }$
, where
$f\in {\mathcal{O}}_{C,E}^{\times }$
, where
 $E=\unicode[STIX]{x1D708}^{\ast }(D)$
. By Lemma 5.4, we can assume that there are inclusions
$E=\unicode[STIX]{x1D708}^{\ast }(D)$
. By Lemma 5.4, we can assume that there are inclusions
 $C{\hookrightarrow}Y{\hookrightarrow}S_{X}$
satisfying the conditions (1)–(6) of Lemma 5.4. The only price we pay by doing so is that
$C{\hookrightarrow}Y{\hookrightarrow}S_{X}$
satisfying the conditions (1)–(6) of Lemma 5.4. The only price we pay by doing so is that
![]() $C$
may no longer be reduced (but still Cohen–Macaulay). But we solve this by replacing
$C$
may no longer be reduced (but still Cohen–Macaulay). But we solve this by replacing
![]() $C$
with a reduced Cartier curve (which we also denote by
$C$
with a reduced Cartier curve (which we also denote by
![]() $C$
) that is of the form given in Lemma 5.5. We shall now continue with the notations of proof of Lemma 5.5.
$C$
) that is of the form given in Lemma 5.5. We shall now continue with the notations of proof of Lemma 5.5.
We write
 $C=(t)\cap Y$
, where
$C=(t)\cap Y$
, where
 $t\in H^{0}(S_{X},{\mathcal{L}})$
such that
$t\in H^{0}(S_{X},{\mathcal{L}})$
such that
![]() ${\mathcal{L}}$
is a very ample line bundle on
${\mathcal{L}}$
is a very ample line bundle on
![]() $S_{X}$
. Let
$S_{X}$
. Let
 $t_{\pm }=\unicode[STIX]{x1D704}_{\pm }^{\ast }(t)\in H^{0}(X,\unicode[STIX]{x1D704}_{\pm }^{\ast }({\mathcal{L}}))$
and let
$t_{\pm }=\unicode[STIX]{x1D704}_{\pm }^{\ast }(t)\in H^{0}(X,\unicode[STIX]{x1D704}_{\pm }^{\ast }({\mathcal{L}}))$
and let
 $C_{\pm }=(t_{\pm })\cap Y=(t_{\pm })\cap Y_{\pm }$
. Let
$C_{\pm }=(t_{\pm })\cap Y=(t_{\pm })\cap Y_{\pm }$
. Let
 $\unicode[STIX]{x1D708}_{\pm }:C_{\pm }{\hookrightarrow}X$
denote the inclusions. It follows from our choice of the section that
$\unicode[STIX]{x1D708}_{\pm }:C_{\pm }{\hookrightarrow}X$
denote the inclusions. It follows from our choice of the section that
![]() $(t_{\pm })$
are integral. If
$(t_{\pm })$
are integral. If
 $C_{+}=C_{-}$
, exactly the same argument as in the case of surfaces in Proposition 5.7 applies to show that
$C_{+}=C_{-}$
, exactly the same argument as in the case of surfaces in Proposition 5.7 applies to show that
 $\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f))\in {\mathcal{R}}_{0}(X|D)$
. So we assume
$\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f))\in {\mathcal{R}}_{0}(X|D)$
. So we assume
 $C_{+}\neq C_{-}$
.
$C_{+}\neq C_{-}$
.
Let
 $\unicode[STIX]{x1D6E5}(C)=C_{+}\cup C_{-}$
denote the scheme-theoretic image in
$\unicode[STIX]{x1D6E5}(C)=C_{+}\cup C_{-}$
denote the scheme-theoretic image in
![]() $X$
under the finite map
$X$
under the finite map
![]() $\unicode[STIX]{x1D6E5}$
. Since
$\unicode[STIX]{x1D6E5}$
. Since
![]() $X$
is smooth and connected, the Bertini Theorem of Altman and Kleiman [Reference Kleiman and AltmanKL79, Theorem 1] allows us to find once again a complete intersection integral surface
$X$
is smooth and connected, the Bertini Theorem of Altman and Kleiman [Reference Kleiman and AltmanKL79, Theorem 1] allows us to find once again a complete intersection integral surface
![]() $T\subset X$
satisfying:
$T\subset X$
satisfying:
-
(1)
 $T\supset \unicode[STIX]{x1D6E5}(C)$
;
$T\supset \unicode[STIX]{x1D6E5}(C)$
; -
(2)
 $T\cap (t_{\pm })$
are integral curves;
$T\cap (t_{\pm })$
are integral curves; -
(3)
 $T$
is smooth away from
$T$
is smooth away from
 $\unicode[STIX]{x1D6E5}(C)$
.
$\unicode[STIX]{x1D6E5}(C)$
.
Set
 $t_{\pm }^{T}=(t_{\pm })_{|T}$
. Since
$t_{\pm }^{T}=(t_{\pm })_{|T}$
. Since
![]() $C_{\pm }$
are integral and contained in
$C_{\pm }$
are integral and contained in
 $T\cap (t_{\pm })$
, it follows that
$T\cap (t_{\pm })$
, it follows that
 $$\begin{eqnarray}(t_{\pm }^{T})=C_{\pm }.\end{eqnarray}$$
$$\begin{eqnarray}(t_{\pm }^{T})=C_{\pm }.\end{eqnarray}$$
Let
![]() $S$
be the finite set of points of
$S$
be the finite set of points of
![]() $\unicode[STIX]{x1D6E5}(C)$
, where
$\unicode[STIX]{x1D6E5}(C)$
, where
 $f_{+}=\unicode[STIX]{x1D708}_{+}^{\ast }(f)$
or
$f_{+}=\unicode[STIX]{x1D708}_{+}^{\ast }(f)$
or
 $f_{-}=\unicode[STIX]{x1D708}_{-}^{\ast }(f)$
have poles. It is clear that
$f_{-}=\unicode[STIX]{x1D708}_{-}^{\ast }(f)$
have poles. It is clear that
 $S\cap D=\emptyset$
. We now choose another very ample line bundle
$S\cap D=\emptyset$
. We now choose another very ample line bundle
![]() ${\mathcal{M}}$
on
${\mathcal{M}}$
on
![]() $X$
and
$X$
and
 $s_{\infty }\in H^{0}(X,{\mathcal{M}})$
(see the proof of Lemma 5.5) such that:
$s_{\infty }\in H^{0}(X,{\mathcal{M}})$
(see the proof of Lemma 5.5) such that:
-
(i)
 $(s_{\infty })$
is integral;
$(s_{\infty })$
is integral; -
(ii)
 $(s_{\infty })\cap T$
and
$(s_{\infty })\cap T$
and
 $(s_{\infty })\cap (t_{\pm })$
are proper and integral;
$(s_{\infty })\cap (t_{\pm })$
are proper and integral; -
(iii)
 $(s_{\infty })\supset S$
;
$(s_{\infty })\supset S$
; -
(iv)
 $(s_{\infty })\cap \unicode[STIX]{x1D6E5}(C)\cap D=\emptyset$
;
$(s_{\infty })\cap \unicode[STIX]{x1D6E5}(C)\cap D=\emptyset$
; -
(v)
 $X\setminus (s_{\infty })$
is affine;
$X\setminus (s_{\infty })$
is affine; -
(vi)
 $(s_{\infty })$
is smooth away from
$(s_{\infty })$
is smooth away from
 $S$
;
$S$
; -
(vii)
 $(s_{\infty })\cap T$
is smooth away from
$(s_{\infty })\cap T$
is smooth away from
 $\unicode[STIX]{x1D6E5}(C)$
;
$\unicode[STIX]{x1D6E5}(C)$
; -
(viii)
 $(s_{\infty })\cap T\not \subset \unicode[STIX]{x1D6E5}(C)$
.
$(s_{\infty })\cap T\not \subset \unicode[STIX]{x1D6E5}(C)$
.
As shown in the proof of Lemma 5.5, it follows from (3), (iv) and (vii) above that
 $(s_{\infty }^{T}):=(s_{\infty })\cap T$
is smooth along
$(s_{\infty }^{T}):=(s_{\infty })\cap T$
is smooth along
![]() $D$
. Using (v), we can lift
$D$
. Using (v), we can lift
 $f_{\pm }\in k(C_{\pm })^{\times }$
to regular functions
$f_{\pm }\in k(C_{\pm })^{\times }$
to regular functions
![]() $F_{\pm }$
on
$F_{\pm }$
on
 $U=X\setminus (s_{\infty })$
. Using an argument identical to that given in the proof of Proposition 5.7, we can extend the sections
$U=X\setminus (s_{\infty })$
. Using an argument identical to that given in the proof of Proposition 5.7, we can extend the sections
 $s_{0,\pm }=s_{\infty }^{N}F_{\pm }$
(for some
$s_{0,\pm }=s_{\infty }^{N}F_{\pm }$
(for some
![]() $N\gg 0$
) to global sections
$N\gg 0$
) to global sections
![]() $s_{0,\pm }$
of
$s_{0,\pm }$
of
![]() ${\mathcal{M}}^{N}$
on
${\mathcal{M}}^{N}$
on
![]() $X$
so that their zero loci satisfy:
$X$
so that their zero loci satisfy:
-
(a)
 $(s_{0,\pm })$
and
$(s_{0,\pm })$
and
 $(s_{0,\pm })\cap T$
are integral;
$(s_{0,\pm })\cap T$
are integral; -
(b)
 $(s_{0,\pm })\cap T\cap \unicode[STIX]{x1D6E5}(C)\cap D=\emptyset$
;
$(s_{0,\pm })\cap T\cap \unicode[STIX]{x1D6E5}(C)\cap D=\emptyset$
; -
(c)
 $(s_{0,\pm })\cap T\not \subset \unicode[STIX]{x1D6E5}(C)$
;
$(s_{0,\pm })\cap T\not \subset \unicode[STIX]{x1D6E5}(C)$
; -
(d)
 $(s_{0,\pm })\cap T$
are smooth away from
$(s_{0,\pm })\cap T$
are smooth away from
 $\unicode[STIX]{x1D6E5}(C)$
.
$\unicode[STIX]{x1D6E5}(C)$
.
As we argued in the proof of Lemma 5.5, it follows from (iv), (vii), (c) and (d) that
![]() $(s_{\infty }^{T})$
and
$(s_{\infty }^{T})$
and
 $(s_{0,\pm }^{T}):=(s_{0,\pm })\cap T$
are smooth along
$(s_{0,\pm }^{T}):=(s_{0,\pm })\cap T$
are smooth along
![]() $D$
.
$D$
.
Setting
 $H_{\pm }=s_{0,\pm }/s_{\infty }^{N}$
and using the argument of the proof of Proposition 5.7, we get
$H_{\pm }=s_{0,\pm }/s_{\infty }^{N}$
and using the argument of the proof of Proposition 5.7, we get
 $H_{\pm }\in k(X)^{\times }$
and they restrict to rational functions on
$H_{\pm }\in k(X)^{\times }$
and they restrict to rational functions on
![]() $C_{+}$
as well as
$C_{+}$
as well as
![]() $C_{-}$
which are regular and invertible along
$C_{-}$
which are regular and invertible along
![]() $D$
. Moreover, we have
$D$
. Moreover, we have
 $$\begin{eqnarray}(H_{+})_{|E}=(F_{+})_{|E}=(f_{+})_{|E}~=^{\dagger }~(f_{-})_{|E}=(F_{-})_{|E}=(H_{-})_{|E},\end{eqnarray}$$
$$\begin{eqnarray}(H_{+})_{|E}=(F_{+})_{|E}=(f_{+})_{|E}~=^{\dagger }~(f_{-})_{|E}=(F_{-})_{|E}=(H_{-})_{|E},\end{eqnarray}$$
where
![]() $=^{\dagger }$
follows from our assumption that
$=^{\dagger }$
follows from our assumption that
 $f\in {\mathcal{O}}_{C,E}^{\times }$
. It follows that the restriction of the rational function
$f\in {\mathcal{O}}_{C,E}^{\times }$
. It follows that the restriction of the rational function
 $s_{0,-}/s_{0,+}=H_{-}/H_{+}$
to
$s_{0,-}/s_{0,+}=H_{-}/H_{+}$
to
![]() $C_{-}$
is an element of
$C_{-}$
is an element of
 ${\mathcal{O}}_{C_{-},C_{-}\cap D}^{\times }$
such that
${\mathcal{O}}_{C_{-},C_{-}\cap D}^{\times }$
such that
 $(H_{-}/H_{+})_{|E}=1$
.
$(H_{-}/H_{+})_{|E}=1$
.
We now compute
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f)) & = & \displaystyle \,\unicode[STIX]{x1D704}_{+}^{\ast }(\operatorname{div}(f))-\unicode[STIX]{x1D704}_{-}^{\ast }(\operatorname{div}(f))\nonumber\\ \displaystyle & = & \displaystyle \,\operatorname{div}(f_{+})-\operatorname{div}(f_{-})\nonumber\\ \displaystyle & = & \displaystyle \,[(s_{0,+}^{T})\cdot C_{+}-N(s_{\infty }^{T})\cdot C_{+}]-[(s_{0,-}^{T})\cdot C_{-}-N(s_{\infty }^{T})\cdot C_{-}]\nonumber\\ \displaystyle & = & \displaystyle \,[(s_{0,+}^{T})\cdot C_{+}-(s_{0,+}^{T})\cdot C_{-}]-[(s_{0,-}^{T})\cdot C_{-}-(s_{0,+}^{T})\cdot C_{-}]\nonumber\\ \displaystyle & & \displaystyle \,-\,N[(s_{\infty }^{T})\cdot C_{+}-(s_{\infty }^{T})\cdot C_{-}]\nonumber\\ \displaystyle & = & \displaystyle \,[((s_{0}^{T})_{+})\cdot (C_{+}-C_{-})]-[C_{-}\cdot ((s_{0,-}^{T})-(s_{0,+}^{T}))]-N[(s_{\infty }^{T})\cdot (C_{+}-C_{-})]\nonumber\\ \displaystyle & ~=^{\dagger } & \displaystyle \,[(s_{0,+}^{T})\cdot ((t_{+}^{T})-(t_{-}^{T}))]-[C_{-}\cdot ((s_{0,-}^{T})-(s_{0,+}^{T}))]-N[(s_{\infty }^{T})\cdot ((t_{+}^{T})-(t_{-}^{T}))]\nonumber\\ \displaystyle & = & \displaystyle \,(s_{0,+}^{T})\cdot (\operatorname{div}(t_{+}^{T}/t_{-}^{T}))-C_{-}\cdot (\operatorname{div}(s_{0,-}/s_{0,+}))-N(s_{\infty }^{T})\cdot (\operatorname{div}(t_{+}^{T}/t_{-}^{T}))\nonumber\\ \displaystyle & = & \displaystyle \,(s_{0,+}^{T})\cdot (\operatorname{div}(t_{+}^{T}/t_{-}^{T}))-C_{-}\cdot (\operatorname{div}(H_{-}/H_{+}))-N(s_{\infty }^{T})\cdot (\operatorname{div}(t_{+}^{T}/t_{-}^{T})),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f)) & = & \displaystyle \,\unicode[STIX]{x1D704}_{+}^{\ast }(\operatorname{div}(f))-\unicode[STIX]{x1D704}_{-}^{\ast }(\operatorname{div}(f))\nonumber\\ \displaystyle & = & \displaystyle \,\operatorname{div}(f_{+})-\operatorname{div}(f_{-})\nonumber\\ \displaystyle & = & \displaystyle \,[(s_{0,+}^{T})\cdot C_{+}-N(s_{\infty }^{T})\cdot C_{+}]-[(s_{0,-}^{T})\cdot C_{-}-N(s_{\infty }^{T})\cdot C_{-}]\nonumber\\ \displaystyle & = & \displaystyle \,[(s_{0,+}^{T})\cdot C_{+}-(s_{0,+}^{T})\cdot C_{-}]-[(s_{0,-}^{T})\cdot C_{-}-(s_{0,+}^{T})\cdot C_{-}]\nonumber\\ \displaystyle & & \displaystyle \,-\,N[(s_{\infty }^{T})\cdot C_{+}-(s_{\infty }^{T})\cdot C_{-}]\nonumber\\ \displaystyle & = & \displaystyle \,[((s_{0}^{T})_{+})\cdot (C_{+}-C_{-})]-[C_{-}\cdot ((s_{0,-}^{T})-(s_{0,+}^{T}))]-N[(s_{\infty }^{T})\cdot (C_{+}-C_{-})]\nonumber\\ \displaystyle & ~=^{\dagger } & \displaystyle \,[(s_{0,+}^{T})\cdot ((t_{+}^{T})-(t_{-}^{T}))]-[C_{-}\cdot ((s_{0,-}^{T})-(s_{0,+}^{T}))]-N[(s_{\infty }^{T})\cdot ((t_{+}^{T})-(t_{-}^{T}))]\nonumber\\ \displaystyle & = & \displaystyle \,(s_{0,+}^{T})\cdot (\operatorname{div}(t_{+}^{T}/t_{-}^{T}))-C_{-}\cdot (\operatorname{div}(s_{0,-}/s_{0,+}))-N(s_{\infty }^{T})\cdot (\operatorname{div}(t_{+}^{T}/t_{-}^{T}))\nonumber\\ \displaystyle & = & \displaystyle \,(s_{0,+}^{T})\cdot (\operatorname{div}(t_{+}^{T}/t_{-}^{T}))-C_{-}\cdot (\operatorname{div}(H_{-}/H_{+}))-N(s_{\infty }^{T})\cdot (\operatorname{div}(t_{+}^{T}/t_{-}^{T})),\nonumber\end{eqnarray}$$
where
![]() $=^{\dagger }$
follows from (5.9).
$=^{\dagger }$
follows from (5.9).
It follows from (iv) and (b) that
![]() $t_{+}^{T}/t_{-}^{T}$
restricts to regular and invertible functions on
$t_{+}^{T}/t_{-}^{T}$
restricts to regular and invertible functions on
![]() $(s_{0,+}^{T})$
and
$(s_{0,+}^{T})$
and
![]() $(s_{\infty }^{T})$
along
$(s_{\infty }^{T})$
along
![]() $D$
. Since
$D$
. Since
 $t\in H^{0}(S_{X},{\mathcal{L}})$
and
$t\in H^{0}(S_{X},{\mathcal{L}})$
and
 $t_{\pm }=\unicode[STIX]{x1D704}_{\pm }^{\ast }(t)\in H^{0}(X,\unicode[STIX]{x1D704}_{\pm }^{\ast }({\mathcal{L}}))$
, it follows that
$t_{\pm }=\unicode[STIX]{x1D704}_{\pm }^{\ast }(t)\in H^{0}(X,\unicode[STIX]{x1D704}_{\pm }^{\ast }({\mathcal{L}}))$
, it follows that
 $(t_{+})_{|D}=\unicode[STIX]{x1D704}_{D}^{\ast }(t)=(t_{-})_{|D}$
, where
$(t_{+})_{|D}=\unicode[STIX]{x1D704}_{D}^{\ast }(t)=(t_{-})_{|D}$
, where
 $\unicode[STIX]{x1D704}_{D}=\unicode[STIX]{x1D704}_{+}\circ \unicode[STIX]{x1D704}=\unicode[STIX]{x1D704}_{-}\circ \unicode[STIX]{x1D704}:D{\hookrightarrow}S_{X}$
denotes the inclusion map. In particular,
$\unicode[STIX]{x1D704}_{D}=\unicode[STIX]{x1D704}_{+}\circ \unicode[STIX]{x1D704}=\unicode[STIX]{x1D704}_{-}\circ \unicode[STIX]{x1D704}:D{\hookrightarrow}S_{X}$
denotes the inclusion map. In particular,
 $(t_{+}^{T}/t_{-}^{T})_{|E}=1$
. We have seen before that
$(t_{+}^{T}/t_{-}^{T})_{|E}=1$
. We have seen before that
 $(H_{-}/H_{+})_{|C_{-}}$
is a regular and invertible function on
$(H_{-}/H_{+})_{|C_{-}}$
is a regular and invertible function on
![]() $C_{-}$
along
$C_{-}$
along
![]() $D$
and
$D$
and
 $(H_{-}/H_{+})_{|E}=1$
.
$(H_{-}/H_{+})_{|E}=1$
.
We set
 $h_{1}=(t_{+}^{T}/t_{-}^{T})_{|(s_{0,+}^{T})},~h_{2}=(H_{-}/H_{+})_{|C_{-}}$
and
$h_{1}=(t_{+}^{T}/t_{-}^{T})_{|(s_{0,+}^{T})},~h_{2}=(H_{-}/H_{+})_{|C_{-}}$
and
 $h_{3}=(t_{+}^{T}/t_{-}^{T})_{|s_{\infty }^{T}}$
. We finish now using exactly the same argument as in the proof of Proposition 5.7. Let
$h_{3}=(t_{+}^{T}/t_{-}^{T})_{|s_{\infty }^{T}}$
. We finish now using exactly the same argument as in the proof of Proposition 5.7. Let
 $(s_{0,+}^{T})^{N}\rightarrow (s_{0,+}^{T})$
,
$(s_{0,+}^{T})^{N}\rightarrow (s_{0,+}^{T})$
,
 $(C_{-})^{N}\rightarrow C_{-}$
and
$(C_{-})^{N}\rightarrow C_{-}$
and
 $(s_{\infty }^{T})^{N}\rightarrow (s_{\infty }^{T})$
denote the normalization maps. Let
$(s_{\infty }^{T})^{N}\rightarrow (s_{\infty }^{T})$
denote the normalization maps. Let
 $\unicode[STIX]{x1D708}_{1}:(s_{0,+}^{T})^{N}\rightarrow X$
,
$\unicode[STIX]{x1D708}_{1}:(s_{0,+}^{T})^{N}\rightarrow X$
,
 $\unicode[STIX]{x1D708}_{2}:(C_{-})^{N}\rightarrow X$
and
$\unicode[STIX]{x1D708}_{2}:(C_{-})^{N}\rightarrow X$
and
 $\unicode[STIX]{x1D708}_{3}:(s_{\infty }^{T})^{N}\rightarrow X$
denote the composite maps. The curves
$\unicode[STIX]{x1D708}_{3}:(s_{\infty }^{T})^{N}\rightarrow X$
denote the composite maps. The curves
![]() $(s_{0,+}^{T})$
and
$(s_{0,+}^{T})$
and
![]() $(s_{\infty }^{T})$
are all smooth along
$(s_{\infty }^{T})$
are all smooth along
![]() $D$
, and
$D$
, and
![]() $C_{-}$
is smooth along
$C_{-}$
is smooth along
![]() $D$
by Lemma 5.5. It follows that
$D$
by Lemma 5.5. It follows that
 $h_{1}\in G((s_{0,+}^{T})^{N},\unicode[STIX]{x1D708}_{1}^{\ast }(D))$
,
$h_{1}\in G((s_{0,+}^{T})^{N},\unicode[STIX]{x1D708}_{1}^{\ast }(D))$
,
 $h_{2}\in G((C_{-})^{N},\unicode[STIX]{x1D708}_{2}^{\ast }(D))$
and
$h_{2}\in G((C_{-})^{N},\unicode[STIX]{x1D708}_{2}^{\ast }(D))$
and
 $h_{3}\in G((s_{\infty }^{T})^{N},\unicode[STIX]{x1D708}_{3}^{\ast }(D))$
. We conclude from (5.1) that
$h_{3}\in G((s_{\infty }^{T})^{N},\unicode[STIX]{x1D708}_{3}^{\ast }(D))$
. We conclude from (5.1) that
 $\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f))$
dies in
$\unicode[STIX]{x1D70F}_{X}^{\ast }(\operatorname{div}(f))$
dies in
 $\text{CH}_{0}(X|D)$
. In particular,
$\text{CH}_{0}(X|D)$
. In particular,
![]() $\unicode[STIX]{x1D70F}_{X}^{\ast }$
descends to a map
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
descends to a map
 $\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
. This finishes the proof.◻
$\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(X|D)$
. This finishes the proof.◻
5.7 The maps
 $p_{\pm ,\ast }$
$p_{\pm ,\ast }$
Let
![]() $X$
and
$X$
and
![]() $D$
and
$D$
and
![]() $k$
be as above. Now that we have constructed the map
$k$
be as above. Now that we have constructed the map
![]() $\unicode[STIX]{x1D70F}_{X}^{\ast }$
, we build two maps in the opposite direction.
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
, we build two maps in the opposite direction.
 $$\begin{eqnarray}p_{\pm ,\ast }:{\mathcal{Z}}_{0}(X|D)\rightrightarrows {\mathcal{Z}}_{0}(S_{X},D)\end{eqnarray}$$
$$\begin{eqnarray}p_{\pm ,\ast }:{\mathcal{Z}}_{0}(X|D)\rightrightarrows {\mathcal{Z}}_{0}(S_{X},D)\end{eqnarray}$$
by
 $p_{+,\ast }([x])=\unicode[STIX]{x1D704}_{+,\ast }([x])$
(respectively by
$p_{+,\ast }([x])=\unicode[STIX]{x1D704}_{+,\ast }([x])$
(respectively by
 $p_{-,\ast }([x])=\unicode[STIX]{x1D704}_{-,\ast }([x])$
) for a closed point
$p_{-,\ast }([x])=\unicode[STIX]{x1D704}_{-,\ast }([x])$
) for a closed point
 $x\in X\setminus D$
. Concretely, the two maps
$x\in X\setminus D$
. Concretely, the two maps
![]() $p_{+,\ast }$
and
$p_{+,\ast }$
and
![]() $p_{-,\ast }$
copy a cycle
$p_{-,\ast }$
copy a cycle
![]() $\unicode[STIX]{x1D6FC}$
in one of the two components of the double
$\unicode[STIX]{x1D6FC}$
in one of the two components of the double
![]() $S_{X}$
(the
$S_{X}$
(the
![]() $X_{+}$
or the
$X_{+}$
or the
![]() $X_{-}$
copy). Since
$X_{-}$
copy). Since
![]() $\unicode[STIX]{x1D6FC}$
is supported outside
$\unicode[STIX]{x1D6FC}$
is supported outside
![]() $D$
(by definition of
$D$
(by definition of
 ${\mathcal{R}}_{0}(X|D)$
), the cycles
${\mathcal{R}}_{0}(X|D)$
), the cycles
![]() $p_{+,\ast }(\unicode[STIX]{x1D6FC})$
and
$p_{+,\ast }(\unicode[STIX]{x1D6FC})$
and
![]() $p_{-,\ast }(\unicode[STIX]{x1D6FC})$
give classes in
$p_{-,\ast }(\unicode[STIX]{x1D6FC})$
give classes in
 $\text{CH}_{0}(S_{X})$
.
$\text{CH}_{0}(S_{X})$
.
Proposition 5.9. The maps
![]() $p_{\pm ,\ast }$
descend to group homomorphisms
$p_{\pm ,\ast }$
descend to group homomorphisms
 $p_{\pm ,\ast }:\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(S_{X})$
.
$p_{\pm ,\ast }:\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(S_{X})$
.
Proof. Let
 $\unicode[STIX]{x1D708}:C\rightarrow X$
be a finite map from a normal integral curve such that
$\unicode[STIX]{x1D708}:C\rightarrow X$
be a finite map from a normal integral curve such that
 $\unicode[STIX]{x1D708}(C)\not \subset D$
and let
$\unicode[STIX]{x1D708}(C)\not \subset D$
and let
 $E=\unicode[STIX]{x1D708}^{\ast }(D)$
. Since both
$E=\unicode[STIX]{x1D708}^{\ast }(D)$
. Since both
![]() $X$
and
$X$
and
![]() $C$
are smooth, the map
$C$
are smooth, the map
![]() $\unicode[STIX]{x1D708}$
is automatically a local complete intersection. Let
$\unicode[STIX]{x1D708}$
is automatically a local complete intersection. Let
 $f\in k(C)^{\times }$
be a rational function on
$f\in k(C)^{\times }$
be a rational function on
![]() $C$
such that
$C$
such that
 $f\in G(C,E)$
(in the notations of 5.2).
$f\in G(C,E)$
(in the notations of 5.2).
Since
![]() $C$
is smooth, it follows from Proposition 2.3 that
$C$
is smooth, it follows from Proposition 2.3 that
 $S_{C}:=S(C,E)$
is reduced and is smooth away from
$S_{C}:=S(C,E)$
is reduced and is smooth away from
![]() $E$
. If follows from Proposition 2.4 that the double map
$E$
. If follows from Proposition 2.4 that the double map
 $S_{C}\rightarrow S_{X}$
is l.c.i. along
$S_{C}\rightarrow S_{X}$
is l.c.i. along
![]() $D$
. In particular, the pair
$D$
. In particular, the pair
![]() $(S_{C},E)$
is a good curve relative to
$(S_{C},E)$
is a good curve relative to
 $(S_{X},D)$
. We now consider the rational function
$(S_{X},D)$
. We now consider the rational function
 $h=(h_{+},h_{-}):=(f,1)$
on
$h=(h_{+},h_{-}):=(f,1)$
on
![]() $S_{C}$
. The modulus condition satisfied by
$S_{C}$
. The modulus condition satisfied by
![]() $f$
on
$f$
on
![]() $C$
guarantees that
$C$
guarantees that
![]() $h$
is regular and invertible along
$h$
is regular and invertible along
 $E\subset S_{C}$
. It is also easy to see that the divisor of
$E\subset S_{C}$
. It is also easy to see that the divisor of
![]() $h$
trivializes
$h$
trivializes
 $p_{+,\ast }(\unicode[STIX]{x1D708}_{\ast }\text{div}(f))$
. The argument for
$p_{+,\ast }(\unicode[STIX]{x1D708}_{\ast }\text{div}(f))$
. The argument for
![]() $p_{-,\ast }$
is symmetric.◻
$p_{-,\ast }$
is symmetric.◻
To summarize, we have shown the following.
Theorem 5.10. Let
![]() $X$
be a smooth connected quasi-projective scheme of dimension
$X$
be a smooth connected quasi-projective scheme of dimension
![]() $d\geqslant 1$
over an infinite perfect field
$d\geqslant 1$
over an infinite perfect field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then there are maps
$D\subset X$
be an effective Cartier divisor. Then there are maps
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X|D)\quad \text{and}\quad p_{\pm ,\ast }:\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(S_{X})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X|D)\quad \text{and}\quad p_{\pm ,\ast }:\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(S_{X})\end{eqnarray}$$
such that
 $\unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D704}_{+}^{\ast }(\unicode[STIX]{x1D6FC})-\unicode[STIX]{x1D704}_{-}^{\ast }(\unicode[STIX]{x1D6FC})$
and
$\unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D704}_{+}^{\ast }(\unicode[STIX]{x1D6FC})-\unicode[STIX]{x1D704}_{-}^{\ast }(\unicode[STIX]{x1D6FC})$
and
 $p_{\pm ,\ast }(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D704}_{\pm ,\ast }(\unicode[STIX]{x1D6FD})$
on cycles.
$p_{\pm ,\ast }(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D704}_{\pm ,\ast }(\unicode[STIX]{x1D6FD})$
on cycles.
6 Reduction to infinite base field
In the previous section, our results were based on the assumption that the ground field
![]() $k$
is infinite. In order to prove our main theorem for finite fields, we shall use the following descent tricks for cycles on singular varieties and cycles with modulus.
$k$
is infinite. In order to prove our main theorem for finite fields, we shall use the following descent tricks for cycles on singular varieties and cycles with modulus.
Proposition 6.1. Let
![]() $k{\hookrightarrow}k^{\prime }$
be separable algebraic (possibly infinite) extension of fields. Let
$k{\hookrightarrow}k^{\prime }$
be separable algebraic (possibly infinite) extension of fields. Let
![]() $X$
be a reduced quasi-projective scheme over
$X$
be a reduced quasi-projective scheme over
![]() $k$
and let
$k$
and let
 $X^{\prime }=X_{k^{\prime }}:=X\otimes _{k}k^{\prime }$
. Let
$X^{\prime }=X_{k^{\prime }}:=X\otimes _{k}k^{\prime }$
. Let
 $\text{pr}_{k^{\prime }/k}:X^{\prime }\rightarrow X$
be the projection map. Then the following hold.
$\text{pr}_{k^{\prime }/k}:X^{\prime }\rightarrow X$
be the projection map. Then the following hold.
-
(1) There exist pull-back maps
 $\text{pr}_{k^{\prime }/k}^{\ast }:\text{CH}_{0}^{\text{LW}}(X)\rightarrow \text{CH}_{0}^{\text{LW}}(X^{\prime })$
and
$\text{pr}_{k^{\prime }/k}^{\ast }:\text{CH}_{0}^{\text{LW}}(X)\rightarrow \text{CH}_{0}^{\text{LW}}(X^{\prime })$
and
 $\text{pr}_{k^{\prime }/k}^{\ast }:\text{CH}_{0}(X)\rightarrow \text{CH}_{0}(X^{\prime })$
which commute with the canonical map
$\text{pr}_{k^{\prime }/k}^{\ast }:\text{CH}_{0}(X)\rightarrow \text{CH}_{0}(X^{\prime })$
which commute with the canonical map
 $\text{CH}_{0}^{\text{LW}}(X)\rightarrow \text{CH}_{0}(X)$
.
$\text{CH}_{0}^{\text{LW}}(X)\rightarrow \text{CH}_{0}(X)$
. -
(2) If there exists a sequence of separable field extensions
 $k=k_{0}\subset k_{1}\subset \cdots \subset k^{\prime }$
with
$k=k_{0}\subset k_{1}\subset \cdots \subset k^{\prime }$
with
 $k^{\prime }=\bigcup _{i}k_{i}$
such that
$k^{\prime }=\bigcup _{i}k_{i}$
such that
 $X_{i}:=X_{k_{i}}$
for each
$X_{i}:=X_{k_{i}}$
for each
 $i\geqslant 1$
, then we have
$i\geqslant 1$
, then we have
 $\mathop{\varinjlim }\nolimits_{i}\text{CH}_{0}(X_{i})\xrightarrow[{}]{\simeq }\text{CH}_{0}(X^{\prime })$
. The same holds for
$\mathop{\varinjlim }\nolimits_{i}\text{CH}_{0}(X_{i})\xrightarrow[{}]{\simeq }\text{CH}_{0}(X^{\prime })$
. The same holds for
 $\text{CH}_{0}^{\text{LW}}(-)$
as well.
$\text{CH}_{0}^{\text{LW}}(-)$
as well. -
(3) If
 $k{\hookrightarrow}k^{\prime }$
is finite, then there exists a push-forward
$k{\hookrightarrow}k^{\prime }$
is finite, then there exists a push-forward
 $(\text{pr}_{k^{\prime }/k})_{\ast }:\text{CH}_{0}(X^{\prime })\rightarrow \text{CH}_{0}(X)$
such that
$(\text{pr}_{k^{\prime }/k})_{\ast }:\text{CH}_{0}(X^{\prime })\rightarrow \text{CH}_{0}(X)$
such that
 $(\text{pr}_{k^{\prime }/k})_{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }$
is multiplication by
$(\text{pr}_{k^{\prime }/k})_{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }$
is multiplication by
 $[k^{\prime }:k]$
.
$[k^{\prime }:k]$
.
Proof. The proofs of (1) and (2) for
 $\text{CH}_{0}(-)$
and
$\text{CH}_{0}(-)$
and
 $\text{CH}_{0}^{\text{LW}}(-)$
are identical. So we consider only
$\text{CH}_{0}^{\text{LW}}(-)$
are identical. So we consider only
 $\text{CH}_{0}(-)$
in the proof below.
$\text{CH}_{0}(-)$
in the proof below.
We first note that as
![]() $k{\hookrightarrow}k^{\prime }$
or
$k{\hookrightarrow}k^{\prime }$
or
![]() $k{\hookrightarrow}k_{i}$
is a separable algebraic extension, the scheme
$k{\hookrightarrow}k_{i}$
is a separable algebraic extension, the scheme
![]() $X^{\prime }$
is reduced and
$X^{\prime }$
is reduced and
 $X_{\text{sing}}^{\prime }=X_{\text{sing}}\times _{k}k^{\prime }$
. The same holds for each
$X_{\text{sing}}^{\prime }=X_{\text{sing}}\times _{k}k^{\prime }$
. The same holds for each
![]() $X_{i}$
as well.
$X_{i}$
as well.
Let
 $x\in X\setminus X_{\text{sing}}$
be a closed point. Since
$x\in X\setminus X_{\text{sing}}$
be a closed point. Since
![]() $\text{pr}_{k^{\prime }/k}$
is flat, it follows from our hypothesis that
$\text{pr}_{k^{\prime }/k}$
is flat, it follows from our hypothesis that
 $\text{pr}_{k^{\prime }/k}^{\ast }([x])$
is a well-defined 0-cycle in
$\text{pr}_{k^{\prime }/k}^{\ast }([x])$
is a well-defined 0-cycle in
 ${\mathcal{Z}}_{0}(X^{\prime },X_{\text{sing}}^{\prime })$
. We thus have a pull-back map
${\mathcal{Z}}_{0}(X^{\prime },X_{\text{sing}}^{\prime })$
. We thus have a pull-back map
 $\text{pr}_{k^{\prime }/k}^{\ast }:{\mathcal{Z}}_{0}(X,X_{\text{sing}})\rightarrow {\mathcal{Z}}_{0}(X^{\prime },X_{\text{sing}}^{\prime })$
.
$\text{pr}_{k^{\prime }/k}^{\ast }:{\mathcal{Z}}_{0}(X,X_{\text{sing}})\rightarrow {\mathcal{Z}}_{0}(X^{\prime },X_{\text{sing}}^{\prime })$
.
We show that this map preserves rational equivalences. So let
 $\unicode[STIX]{x1D708}:(C,Z)\rightarrow (X,X_{\text{sing}})$
be a good curve and let
$\unicode[STIX]{x1D708}:(C,Z)\rightarrow (X,X_{\text{sing}})$
be a good curve and let
 $f:C{\dashrightarrow}\mathbb{P}_{k}^{1}$
be a rational function which is regular in an open neighborhood
$f:C{\dashrightarrow}\mathbb{P}_{k}^{1}$
be a rational function which is regular in an open neighborhood
 $Z\subsetneq U\subseteq C$
. The base change via
$Z\subsetneq U\subseteq C$
. The base change via
![]() $k{\hookrightarrow}k^{\prime }$
gives a diagram of Cartesian squares.
$k{\hookrightarrow}k^{\prime }$
gives a diagram of Cartesian squares.

Since
![]() $k{\hookrightarrow}k^{\prime }$
is a separable field extension, we see that
$k{\hookrightarrow}k^{\prime }$
is a separable field extension, we see that
![]() $C_{k^{\prime }}$
is reduced and
$C_{k^{\prime }}$
is reduced and
 $C_{k^{\prime }}\setminus Z_{k^{\prime }}=(C\setminus Z)_{k^{\prime }}$
is regular. We also have
$C_{k^{\prime }}\setminus Z_{k^{\prime }}=(C\setminus Z)_{k^{\prime }}$
is regular. We also have
 $\unicode[STIX]{x1D708}_{k^{\prime }}^{-1}(X_{\text{sing}}^{\prime })=\unicode[STIX]{x1D708}_{k^{\prime }}^{-1}(X_{\text{sing}}\times _{k}k^{\prime })\subseteq Z_{k^{\prime }}$
. Moreover, the flatness of
$\unicode[STIX]{x1D708}_{k^{\prime }}^{-1}(X_{\text{sing}}^{\prime })=\unicode[STIX]{x1D708}_{k^{\prime }}^{-1}(X_{\text{sing}}\times _{k}k^{\prime })\subseteq Z_{k^{\prime }}$
. Moreover, the flatness of
![]() $\text{pr}_{k^{\prime }/k}$
ensures that the map
$\text{pr}_{k^{\prime }/k}$
ensures that the map
 $\unicode[STIX]{x1D708}_{k^{\prime }}:C_{k^{\prime }}\rightarrow X^{\prime }$
is l.c.i. over
$\unicode[STIX]{x1D708}_{k^{\prime }}:C_{k^{\prime }}\rightarrow X^{\prime }$
is l.c.i. over
![]() $X_{\text{sing}}^{\prime }$
. It follows that
$X_{\text{sing}}^{\prime }$
. It follows that
 $\unicode[STIX]{x1D708}_{k^{\prime }}:(C_{k^{\prime }},Z_{k^{\prime }})\rightarrow (X^{\prime },X_{\text{sing}}^{\prime })$
is a good curve. Since
$\unicode[STIX]{x1D708}_{k^{\prime }}:(C_{k^{\prime }},Z_{k^{\prime }})\rightarrow (X^{\prime },X_{\text{sing}}^{\prime })$
is a good curve. Since
 $f:C{\dashrightarrow}\mathbb{P}_{k}^{1}$
is regular and invertible along
$f:C{\dashrightarrow}\mathbb{P}_{k}^{1}$
is regular and invertible along
![]() $U$
, it follows that
$U$
, it follows that
 $f^{\prime }:=f_{k^{\prime }}:C_{k^{\prime }}{\dashrightarrow}\mathbb{P}_{k^{\prime }}^{1}$
is a rational function which is regular and invertible along
$f^{\prime }:=f_{k^{\prime }}:C_{k^{\prime }}{\dashrightarrow}\mathbb{P}_{k^{\prime }}^{1}$
is a rational function which is regular and invertible along
![]() $U_{k^{\prime }}$
.
$U_{k^{\prime }}$
.
Let
 $D\subset C\times _{k}\mathbb{P}_{k}^{1}$
denote the closure of the graph of
$D\subset C\times _{k}\mathbb{P}_{k}^{1}$
denote the closure of the graph of
![]() $f$
with the reduced structure. Note that this graph is already reduced over the regular locus of
$f$
with the reduced structure. Note that this graph is already reduced over the regular locus of
![]() $f$
. Let
$f$
. Let
 $p:C\times _{k}\mathbb{P}_{k}^{1}\rightarrow \mathbb{P}_{k}^{1}$
and
$p:C\times _{k}\mathbb{P}_{k}^{1}\rightarrow \mathbb{P}_{k}^{1}$
and
 $q:C\times _{k}\mathbb{P}_{k}^{1}\rightarrow C$
denote the projection maps so that
$q:C\times _{k}\mathbb{P}_{k}^{1}\rightarrow C$
denote the projection maps so that
 $p|_{U}=f|_{U}$
. We thus have a commutative diagram.
$p|_{U}=f|_{U}$
. We thus have a commutative diagram.

We now have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{k^{\prime }\ast }(\operatorname{div}(f^{\prime })) & = & \displaystyle ~\unicode[STIX]{x1D708}_{k^{\prime }\ast }\circ q_{k^{\prime }\ast }([p_{k^{\prime }}^{\ast }(0)]-[p_{k^{\prime }}^{\ast }(\infty )])\nonumber\\ \displaystyle & = & \displaystyle ~\unicode[STIX]{x1D708}_{k^{\prime }\ast }\circ q_{k^{\prime }\ast }([p_{k^{\prime }}^{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }(0)-p_{k^{\prime }}^{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }(\infty )])\nonumber\\ \displaystyle & = & \displaystyle ~\unicode[STIX]{x1D708}_{k^{\prime }~\ast }\circ q_{k^{\prime }\ast }([\text{pr}_{k^{\prime }/k}^{\ast }\circ p^{\ast }(0)-\text{pr}_{k^{\prime }/k}^{\ast }\circ p^{\ast }(\infty )])\nonumber\\ \displaystyle & ~=^{\dagger } & \displaystyle ~\unicode[STIX]{x1D708}_{k^{\prime }\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }\circ q_{\ast }([p^{\ast }(0)-p^{\ast }(\infty )])\nonumber\\ \displaystyle & = & \displaystyle ~\unicode[STIX]{x1D708}_{k^{\prime }~\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }(\operatorname{div}(f))\nonumber\\ \displaystyle & ~~=^{\dagger \dagger } & \displaystyle ~\text{pr}_{k^{\prime }/k}^{\ast }\circ \unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f)),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D708}_{k^{\prime }\ast }(\operatorname{div}(f^{\prime })) & = & \displaystyle ~\unicode[STIX]{x1D708}_{k^{\prime }\ast }\circ q_{k^{\prime }\ast }([p_{k^{\prime }}^{\ast }(0)]-[p_{k^{\prime }}^{\ast }(\infty )])\nonumber\\ \displaystyle & = & \displaystyle ~\unicode[STIX]{x1D708}_{k^{\prime }\ast }\circ q_{k^{\prime }\ast }([p_{k^{\prime }}^{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }(0)-p_{k^{\prime }}^{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }(\infty )])\nonumber\\ \displaystyle & = & \displaystyle ~\unicode[STIX]{x1D708}_{k^{\prime }~\ast }\circ q_{k^{\prime }\ast }([\text{pr}_{k^{\prime }/k}^{\ast }\circ p^{\ast }(0)-\text{pr}_{k^{\prime }/k}^{\ast }\circ p^{\ast }(\infty )])\nonumber\\ \displaystyle & ~=^{\dagger } & \displaystyle ~\unicode[STIX]{x1D708}_{k^{\prime }\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }\circ q_{\ast }([p^{\ast }(0)-p^{\ast }(\infty )])\nonumber\\ \displaystyle & = & \displaystyle ~\unicode[STIX]{x1D708}_{k^{\prime }~\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }(\operatorname{div}(f))\nonumber\\ \displaystyle & ~~=^{\dagger \dagger } & \displaystyle ~\text{pr}_{k^{\prime }/k}^{\ast }\circ \unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f)),\nonumber\end{eqnarray}$$
where
![]() $=^{\dagger }$
and
$=^{\dagger }$
and
![]() $=^{\dagger \dagger }$
follow from [Reference FultonFul98, Proposition 1.7] because all squares in (6.2) are Cartesian, vertical maps are all flat and
$=^{\dagger \dagger }$
follow from [Reference FultonFul98, Proposition 1.7] because all squares in (6.2) are Cartesian, vertical maps are all flat and
![]() $q$
as well as
$q$
as well as
![]() $\unicode[STIX]{x1D708}$
is finite. We conclude that
$\unicode[STIX]{x1D708}$
is finite. We conclude that
 $\text{pr}_{k^{\prime }/k}^{\ast }\circ \unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f))\in {\mathcal{R}}_{0}(X^{\prime },X_{\text{sing}}^{\prime })$
and this proves (1).
$\text{pr}_{k^{\prime }/k}^{\ast }\circ \unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f))\in {\mathcal{R}}_{0}(X^{\prime },X_{\text{sing}}^{\prime })$
and this proves (1).
We now consider (2). It is clear that the map
 $\mathop{\varinjlim }\nolimits_{i}\text{CH}_{0}(X_{i})\rightarrow \text{CH}_{0}(X^{\prime })$
is surjective. To show injectivity, suppose there is some
$\mathop{\varinjlim }\nolimits_{i}\text{CH}_{0}(X_{i})\rightarrow \text{CH}_{0}(X^{\prime })$
is surjective. To show injectivity, suppose there is some
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
 $\unicode[STIX]{x1D6FC}\in {\mathcal{Z}}_{0}(X_{i},(X_{i})_{\text{sing}})$
such that
$\unicode[STIX]{x1D6FC}\in {\mathcal{Z}}_{0}(X_{i},(X_{i})_{\text{sing}})$
such that
 $\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FC})\in {\mathcal{R}}_{0}(X^{\prime },X_{\text{sing}}^{\prime })$
. We can replace
$\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FC})\in {\mathcal{R}}_{0}(X^{\prime },X_{\text{sing}}^{\prime })$
. We can replace
![]() $k$
by
$k$
by
![]() $k_{i}$
and assume
$k_{i}$
and assume
![]() $i=0$
.
$i=0$
.
Let
 $\unicode[STIX]{x1D708}^{j}:(C^{j},Z^{j})\rightarrow (X^{\prime },X_{\text{sing}}^{\prime })$
be good curves and let
$\unicode[STIX]{x1D708}^{j}:(C^{j},Z^{j})\rightarrow (X^{\prime },X_{\text{sing}}^{\prime })$
be good curves and let
 $f^{j}:C^{j}{\dashrightarrow}\mathbb{P}_{k^{\prime }}^{1}$
be a rational function which is regular and invertible in a neighborhood
$f^{j}:C^{j}{\dashrightarrow}\mathbb{P}_{k^{\prime }}^{1}$
be a rational function which is regular and invertible in a neighborhood
![]() $U^{j}$
of
$U^{j}$
of
![]() $Z^{j}$
for
$Z^{j}$
for
 $j=1,\ldots ,r$
such that
$j=1,\ldots ,r$
such that
 $\text{pr}_{k^{\prime }/k}^{\ast }(\unicode[STIX]{x1D6FC})=\sum _{j=1}^{r}\unicode[STIX]{x1D708}_{\ast }^{j}(\operatorname{div}(f^{j}))$
.
$\text{pr}_{k^{\prime }/k}^{\ast }(\unicode[STIX]{x1D6FC})=\sum _{j=1}^{r}\unicode[STIX]{x1D708}_{\ast }^{j}(\operatorname{div}(f^{j}))$
.
Since each
![]() $C^{j}$
has a factorization
$C^{j}$
has a factorization
 $C^{j}{\hookrightarrow}\mathbb{P}_{X^{\prime }}^{N_{j}}\rightarrow X^{\prime }$
, we can find some
$C^{j}{\hookrightarrow}\mathbb{P}_{X^{\prime }}^{N_{j}}\rightarrow X^{\prime }$
, we can find some
![]() $i\gg 0$
and curves
$i\gg 0$
and curves
![]() $W^{j}$
over
$W^{j}$
over
![]() $k_{i}$
, a closed subscheme
$k_{i}$
, a closed subscheme
 $T^{j}\subsetneq W^{j}$
, an open neighborhood
$T^{j}\subsetneq W^{j}$
, an open neighborhood
 $V^{j}\subseteq W^{j}$
of
$V^{j}\subseteq W^{j}$
of
![]() $T^{j}$
and invertible regular function
$T^{j}$
and invertible regular function
 $g^{j}:V^{j}\rightarrow \mathbb{P}_{k_{i}}^{1}$
such that
$g^{j}:V^{j}\rightarrow \mathbb{P}_{k_{i}}^{1}$
such that
 $(C^{j},Z^{j})\simeq (W^{j},T^{j})_{k^{\prime }},~U^{j}=V_{k^{\prime }}^{j}$
and
$(C^{j},Z^{j})\simeq (W^{j},T^{j})_{k^{\prime }},~U^{j}=V_{k^{\prime }}^{j}$
and
 $f^{j}=g_{k^{\prime }}^{j}$
. Furthermore, we can find a finite map
$f^{j}=g_{k^{\prime }}^{j}$
. Furthermore, we can find a finite map
 $\unicode[STIX]{x1D6FF}^{j}:(W^{j},T^{j})\rightarrow (X_{k_{i}},(X_{k_{i}})_{\text{sing}})$
such that
$\unicode[STIX]{x1D6FF}^{j}:(W^{j},T^{j})\rightarrow (X_{k_{i}},(X_{k_{i}})_{\text{sing}})$
such that
 $(C^{j},Z^{j})\simeq (W^{j},T^{j})_{k^{\prime }}$
and
$(C^{j},Z^{j})\simeq (W^{j},T^{j})_{k^{\prime }}$
and
 $\unicode[STIX]{x1D708}^{j}=\unicode[STIX]{x1D6FF}_{k^{\prime }}^{j}$
for each
$\unicode[STIX]{x1D708}^{j}=\unicode[STIX]{x1D6FF}_{k^{\prime }}^{j}$
for each
 $j=1,\ldots ,r$
. Since
$j=1,\ldots ,r$
. Since
 $k_{i}{\hookrightarrow}k^{\prime }$
is separable, it also follows that
$k_{i}{\hookrightarrow}k^{\prime }$
is separable, it also follows that
![]() $W^{j}\setminus T^{j}$
is regular.
$W^{j}\setminus T^{j}$
is regular.
Since the map
 $X^{\prime }\rightarrow X_{i}$
is faithfully flat, it follows from Lemma 3.2 and our hypothesis on
$X^{\prime }\rightarrow X_{i}$
is faithfully flat, it follows from Lemma 3.2 and our hypothesis on
![]() $(X_{i})_{\text{sing}}$
that each
$(X_{i})_{\text{sing}}$
that each
 $W^{j}\rightarrow X_{i}$
is l.c.i. along
$W^{j}\rightarrow X_{i}$
is l.c.i. along
![]() $(X_{i})_{\text{sing}}$
and
$(X_{i})_{\text{sing}}$
and
 $(\unicode[STIX]{x1D6FF}^{j})^{-1}((X_{i})_{\text{sing}})\subseteq T^{j}$
. It follows that each
$(\unicode[STIX]{x1D6FF}^{j})^{-1}((X_{i})_{\text{sing}})\subseteq T^{j}$
. It follows that each
 $(W^{j},T^{j})$
is a good curve relative to
$(W^{j},T^{j})$
is a good curve relative to
 $(X_{k_{i}},(X_{k_{i}})_{\text{sing}})$
. Moreover, we have shown in the proof of (1) (with
$(X_{k_{i}},(X_{k_{i}})_{\text{sing}})$
. Moreover, we have shown in the proof of (1) (with
![]() $k$
replaced by
$k$
replaced by
![]() $k_{i}$
) in this situation that
$k_{i}$
) in this situation that
 $\unicode[STIX]{x1D708}_{\ast }^{j}(\operatorname{div}(f^{j}))=\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FF}_{\ast }^{j}(\operatorname{div}(g^{j})))$
.
$\unicode[STIX]{x1D708}_{\ast }^{j}(\operatorname{div}(f^{j}))=\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FF}_{\ast }^{j}(\operatorname{div}(g^{j})))$
.
We now set
 $\unicode[STIX]{x1D6FC}_{i}=\text{pr}_{k_{i}/k}^{\ast }(\unicode[STIX]{x1D6FC})$
and let
$\unicode[STIX]{x1D6FC}_{i}=\text{pr}_{k_{i}/k}^{\ast }(\unicode[STIX]{x1D6FC})$
and let
 $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FC}_{i}-\sum _{j=1}^{r}\unicode[STIX]{x1D6FF}_{\ast }^{j}(\operatorname{div}(g^{j}))\in {\mathcal{Z}}_{0}(X_{i},(X_{i})_{\text{sing}})$
. It then follows that
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FC}_{i}-\sum _{j=1}^{r}\unicode[STIX]{x1D6FF}_{\ast }^{j}(\operatorname{div}(g^{j}))\in {\mathcal{Z}}_{0}(X_{i},(X_{i})_{\text{sing}})$
. It then follows that
 $\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FD})=\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FC}_{i})-\sum _{j=1}^{r}\unicode[STIX]{x1D708}_{\ast }^{j}(\operatorname{div}(f^{j}))=\text{pr}_{k^{\prime }/k}^{\ast }(\unicode[STIX]{x1D6FC})-\sum _{j=1}^{r}\unicode[STIX]{x1D708}_{\ast }^{j}(\operatorname{div}(f^{j}))=0$
in
$\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FD})=\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FC}_{i})-\sum _{j=1}^{r}\unicode[STIX]{x1D708}_{\ast }^{j}(\operatorname{div}(f^{j}))=\text{pr}_{k^{\prime }/k}^{\ast }(\unicode[STIX]{x1D6FC})-\sum _{j=1}^{r}\unicode[STIX]{x1D708}_{\ast }^{j}(\operatorname{div}(f^{j}))=0$
in
 ${\mathcal{Z}}_{0}(X^{\prime },X_{\text{sing}}^{\prime })$
. Since the map
${\mathcal{Z}}_{0}(X^{\prime },X_{\text{sing}}^{\prime })$
. Since the map
 $\text{pr}_{k^{\prime }/k_{i}}^{\ast }:{\mathcal{Z}}_{0}(X_{i},(X_{i})_{\text{sing}})\rightarrow {\mathcal{Z}}_{0}(X^{\prime },X_{\text{sing}}^{\prime })$
of free abelian groups is clearly injective, we get
$\text{pr}_{k^{\prime }/k_{i}}^{\ast }:{\mathcal{Z}}_{0}(X_{i},(X_{i})_{\text{sing}})\rightarrow {\mathcal{Z}}_{0}(X^{\prime },X_{\text{sing}}^{\prime })$
of free abelian groups is clearly injective, we get
![]() $\unicode[STIX]{x1D6FD}=0$
, which means that
$\unicode[STIX]{x1D6FD}=0$
, which means that
 $\unicode[STIX]{x1D6FC}_{i}\in {\mathcal{R}}_{0}(X_{i},(X_{i})_{\text{sing}})$
. This proves (2).
$\unicode[STIX]{x1D6FC}_{i}\in {\mathcal{R}}_{0}(X_{i},(X_{i})_{\text{sing}})$
. This proves (2).
If
![]() $k{\hookrightarrow}k^{\prime }$
is a finite extension, then
$k{\hookrightarrow}k^{\prime }$
is a finite extension, then
 $\operatorname{Spec}(k^{\prime })\rightarrow \operatorname{Spec}(k)$
is an l.c.i. morphism. In particular, it follows from Lemma 3.2 that
$\operatorname{Spec}(k^{\prime })\rightarrow \operatorname{Spec}(k)$
is an l.c.i. morphism. In particular, it follows from Lemma 3.2 that
 $\text{pr}_{k^{\prime }/k}:X^{\prime }\rightarrow X$
is finite, flat l.c.i. morphism. The push-forward map
$\text{pr}_{k^{\prime }/k}:X^{\prime }\rightarrow X$
is finite, flat l.c.i. morphism. The push-forward map
 $(\text{pr}_{k^{\prime }/k})_{\ast }:\text{CH}_{0}(X^{\prime })\rightarrow \text{CH}_{0}(X)$
now follows from our hypothesis on the singular locus of
$(\text{pr}_{k^{\prime }/k})_{\ast }:\text{CH}_{0}(X^{\prime })\rightarrow \text{CH}_{0}(X)$
now follows from our hypothesis on the singular locus of
![]() $X^{\prime }$
and Proposition 3.18. The property
$X^{\prime }$
and Proposition 3.18. The property
 $(\text{pr}_{k^{\prime }/k})_{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }=[k^{\prime }:k]$
is obvious. This finishes the proof.◻
$(\text{pr}_{k^{\prime }/k})_{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }=[k^{\prime }:k]$
is obvious. This finishes the proof.◻
Proposition 6.2. Let
![]() $k{\hookrightarrow}k^{\prime }$
be a separable algebraic (possibly infinite) extension of fields. Let
$k{\hookrightarrow}k^{\prime }$
be a separable algebraic (possibly infinite) extension of fields. Let
![]() $X$
be a smooth quasi-projective scheme over
$X$
be a smooth quasi-projective scheme over
![]() $k$
with an effective Cartier divisor
$k$
with an effective Cartier divisor
![]() $D$
. Let
$D$
. Let
 $X^{\prime }=X_{k^{\prime }}$
and
$X^{\prime }=X_{k^{\prime }}$
and
 $D^{\prime }=D_{k^{\prime }}$
denote the base change of
$D^{\prime }=D_{k^{\prime }}$
denote the base change of
![]() $X$
and
$X$
and
![]() $D$
, respectively. Let
$D$
, respectively. Let
 $\text{pr}_{k^{\prime }/k}:X^{\prime }\rightarrow X$
be the projection map. Then the following hold.
$\text{pr}_{k^{\prime }/k}:X^{\prime }\rightarrow X$
be the projection map. Then the following hold.
-
(1) There exists a pull-back
 $\text{pr}_{k^{\prime }/k}^{\ast }:\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(X^{\prime }|D^{\prime })$
.
$\text{pr}_{k^{\prime }/k}^{\ast }:\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(X^{\prime }|D^{\prime })$
. -
(2) If there exists a sequence of separable field extensions
 $k=k_{0}\subset k_{1}\subset \cdots \subset k^{\prime }$
with
$k=k_{0}\subset k_{1}\subset \cdots \subset k^{\prime }$
with
 $k^{\prime }=\bigcup _{i}k_{i}$
, then we have
$k^{\prime }=\bigcup _{i}k_{i}$
, then we have
 $\mathop{\varinjlim }\nolimits_{i}\text{CH}_{0}(X_{k_{i}}|D_{k_{i}})\xrightarrow[{}]{\simeq }\text{CH}_{0}(X^{\prime }|D^{\prime })$
.
$\mathop{\varinjlim }\nolimits_{i}\text{CH}_{0}(X_{k_{i}}|D_{k_{i}})\xrightarrow[{}]{\simeq }\text{CH}_{0}(X^{\prime }|D^{\prime })$
. -
(3) If
 $k{\hookrightarrow}k^{\prime }$
is finite, then there exists a push-forward
$k{\hookrightarrow}k^{\prime }$
is finite, then there exists a push-forward
 $\text{pr}_{k^{\prime }/k~\ast }:\text{CH}_{0}(X^{\prime }|D^{\prime })\rightarrow \text{CH}_{0}(X|D)$
such that
$\text{pr}_{k^{\prime }/k~\ast }:\text{CH}_{0}(X^{\prime }|D^{\prime })\rightarrow \text{CH}_{0}(X|D)$
such that
 $(\text{pr}_{k^{\prime }/k})_{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }$
is multiplication by
$(\text{pr}_{k^{\prime }/k})_{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }$
is multiplication by
 $[k^{\prime }:k]$
.
$[k^{\prime }:k]$
.
Proof. Let
 $x\in X\setminus D$
be a closed point. Since
$x\in X\setminus D$
be a closed point. Since
![]() $\text{pr}_{k^{\prime }/k}$
is smooth, it follows from our hypothesis that
$\text{pr}_{k^{\prime }/k}$
is smooth, it follows from our hypothesis that
 $\text{pr}_{k^{\prime }/k}^{\ast }([x])$
is a well-defined 0-cycle in
$\text{pr}_{k^{\prime }/k}^{\ast }([x])$
is a well-defined 0-cycle in
 ${\mathcal{Z}}_{0}(X^{\prime }|D^{\prime })$
. We thus have a pull-back map
${\mathcal{Z}}_{0}(X^{\prime }|D^{\prime })$
. We thus have a pull-back map
 $\text{pr}_{k^{\prime }/k}^{\ast }:{\mathcal{Z}}_{0}(X|D)\rightarrow {\mathcal{Z}}_{0}(X^{\prime }|D^{\prime })$
. To show that this map preserves rational equivalence, we shall use a presentation of
$\text{pr}_{k^{\prime }/k}^{\ast }:{\mathcal{Z}}_{0}(X|D)\rightarrow {\mathcal{Z}}_{0}(X^{\prime }|D^{\prime })$
. To show that this map preserves rational equivalence, we shall use a presentation of
 ${\mathcal{R}}_{0}(X|D)$
which is different from the one given in § 5.2 (see [Reference Binda and SaitoBS16] or [Reference Krishna and ParkKP14]).
${\mathcal{R}}_{0}(X|D)$
which is different from the one given in § 5.2 (see [Reference Binda and SaitoBS16] or [Reference Krishna and ParkKP14]).
Let
 $C{\hookrightarrow}X\times _{k}\mathbb{P}_{k}^{1}$
be an integral curve satisfying the following properties:
$C{\hookrightarrow}X\times _{k}\mathbb{P}_{k}^{1}$
be an integral curve satisfying the following properties:
-
(1)
 $C\cap (D\times _{k}\mathbb{P}_{k}^{1})$
is finite;
$C\cap (D\times _{k}\mathbb{P}_{k}^{1})$
is finite; -
(2)
 $C\cap (D\times _{k}\{0,\infty \})=\emptyset$
;
$C\cap (D\times _{k}\{0,\infty \})=\emptyset$
; -
(3) the Weil divisor
 $\unicode[STIX]{x1D708}^{\ast }(X\times \{1\})-\unicode[STIX]{x1D708}^{\ast }(D\times \mathbb{P}_{k}^{1})$
is effective, where
$\unicode[STIX]{x1D708}^{\ast }(X\times \{1\})-\unicode[STIX]{x1D708}^{\ast }(D\times \mathbb{P}_{k}^{1})$
is effective, where
 $\unicode[STIX]{x1D708}:C^{N}\rightarrow C{\hookrightarrow}X\times _{k}\mathbb{P}_{k}^{1}$
is the composite finite map.
$\unicode[STIX]{x1D708}:C^{N}\rightarrow C{\hookrightarrow}X\times _{k}\mathbb{P}_{k}^{1}$
is the composite finite map.
The group of rational equivalences
 ${\mathcal{R}}_{0}(X|D)$
coincides with the subgroup of
${\mathcal{R}}_{0}(X|D)$
coincides with the subgroup of
 ${\mathcal{Z}}_{0}(X|D)$
generated by
${\mathcal{Z}}_{0}(X|D)$
generated by
 $[C_{0}]-[C_{\infty }]$
, where
$[C_{0}]-[C_{\infty }]$
, where
![]() $C$
runs over all curves as above.
$C$
runs over all curves as above.
Let
 $C\in X\times _{k}\mathbb{P}_{k}^{1}$
be any such curve. It follows again from the smoothness of
$C\in X\times _{k}\mathbb{P}_{k}^{1}$
be any such curve. It follows again from the smoothness of
![]() $\text{pr}_{k^{\prime }/k}$
that
$\text{pr}_{k^{\prime }/k}$
that
 $C^{\prime }=\text{pr}_{k^{\prime }/k}^{\ast }(C)=C_{k^{\prime }}{\hookrightarrow}(X\times _{k}\mathbb{P}_{k}^{1})_{k^{\prime }}=X^{\prime }\times _{k^{\prime }}\mathbb{P}_{k^{\prime }}^{1}$
satisfies conditions (1)–(3) above. In particular,
$C^{\prime }=\text{pr}_{k^{\prime }/k}^{\ast }(C)=C_{k^{\prime }}{\hookrightarrow}(X\times _{k}\mathbb{P}_{k}^{1})_{k^{\prime }}=X^{\prime }\times _{k^{\prime }}\mathbb{P}_{k^{\prime }}^{1}$
satisfies conditions (1)–(3) above. In particular,
 $[C_{0}^{\prime }]-[C_{\infty }^{\prime }]$
dies in
$[C_{0}^{\prime }]-[C_{\infty }^{\prime }]$
dies in
 $\text{CH}_{0}(X^{\prime }|D^{\prime })$
. However, the flatness of
$\text{CH}_{0}(X^{\prime }|D^{\prime })$
. However, the flatness of
![]() $\text{pr}_{k^{\prime }/k}$
again shows that
$\text{pr}_{k^{\prime }/k}$
again shows that
 $[C_{\infty }^{\prime }]=\text{pr}_{k^{\prime }/k}^{\ast }([C_{\infty }])$
and
$[C_{\infty }^{\prime }]=\text{pr}_{k^{\prime }/k}^{\ast }([C_{\infty }])$
and
 $[C_{0}^{\prime }]=\text{pr}_{k^{\prime }/k}^{\ast }([C_{0}])$
so that
$[C_{0}^{\prime }]=\text{pr}_{k^{\prime }/k}^{\ast }([C_{0}])$
so that
 $\text{pr}_{k^{\prime }/k}^{\ast }([C_{0}]-[C_{\infty }])$
dies in
$\text{pr}_{k^{\prime }/k}^{\ast }([C_{0}]-[C_{\infty }])$
dies in
 $\text{CH}_{0}(X^{\prime }|D^{\prime })$
. This proves (1).
$\text{CH}_{0}(X^{\prime }|D^{\prime })$
. This proves (1).
It is clear that the map
 $\mathop{\varinjlim }\nolimits_{i}\text{CH}_{0}(X_{i}|D_{i})\rightarrow \text{CH}_{0}(X^{\prime }|D^{\prime })$
is surjective. To show injectivity, suppose there is some
$\mathop{\varinjlim }\nolimits_{i}\text{CH}_{0}(X_{i}|D_{i})\rightarrow \text{CH}_{0}(X^{\prime }|D^{\prime })$
is surjective. To show injectivity, suppose there is some
![]() $i\geqslant 0$
and
$i\geqslant 0$
and
 $\unicode[STIX]{x1D6FC}\in {\mathcal{Z}}_{0}(X_{i}|D_{i})$
such that
$\unicode[STIX]{x1D6FC}\in {\mathcal{Z}}_{0}(X_{i}|D_{i})$
such that
 $\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FC})\in {\mathcal{R}}_{0}(X^{\prime }|D^{\prime })$
. We can replace
$\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FC})\in {\mathcal{R}}_{0}(X^{\prime }|D^{\prime })$
. We can replace
![]() $k$
by
$k$
by
![]() $k_{i}$
and assume
$k_{i}$
and assume
![]() $i=0$
.
$i=0$
.
Let
 $C^{j}{\hookrightarrow}X^{\prime }\times _{k^{\prime }}\mathbb{P}_{k^{\prime }}^{1}=(X\times _{k}\mathbb{P}_{k}^{1})_{k^{\prime }}$
for
$C^{j}{\hookrightarrow}X^{\prime }\times _{k^{\prime }}\mathbb{P}_{k^{\prime }}^{1}=(X\times _{k}\mathbb{P}_{k}^{1})_{k^{\prime }}$
for
 $j=1,\ldots ,r$
be a collection of curves as in the proof of (1) so that
$j=1,\ldots ,r$
be a collection of curves as in the proof of (1) so that
 $\text{pr}_{k^{\prime }/k}^{\ast }(\unicode[STIX]{x1D6FC})=(\sum _{j=1}^{r}[C_{0}^{j}])-(\sum _{j=1}^{r}[C_{\infty }^{j}])$
. Let
$\text{pr}_{k^{\prime }/k}^{\ast }(\unicode[STIX]{x1D6FC})=(\sum _{j=1}^{r}[C_{0}^{j}])-(\sum _{j=1}^{r}[C_{\infty }^{j}])$
. Let
 $\unicode[STIX]{x1D708}^{j}:C^{j,N}\rightarrow X^{\prime }\times _{k^{\prime }}\mathbb{P}_{k^{\prime }}^{1}$
denote the maps from the normalizations of the above curves.
$\unicode[STIX]{x1D708}^{j}:C^{j,N}\rightarrow X^{\prime }\times _{k^{\prime }}\mathbb{P}_{k^{\prime }}^{1}$
denote the maps from the normalizations of the above curves.
We can then find some
![]() $i\gg 0$
and integral curves
$i\gg 0$
and integral curves
 $W^{j}{\hookrightarrow}X_{i}\times _{k_{i}}\mathbb{P}_{k_{i}}^{1}$
such that
$W^{j}{\hookrightarrow}X_{i}\times _{k_{i}}\mathbb{P}_{k_{i}}^{1}$
such that
 $C^{j}=W^{j}\times _{k_{i}}k^{\prime }$
for each
$C^{j}=W^{j}\times _{k_{i}}k^{\prime }$
for each
 $j=1,\ldots ,r$
. In particular, we have
$j=1,\ldots ,r$
. In particular, we have
 $C_{0}^{j}=\text{pr}_{k^{\prime }/k_{i}}^{\ast }(W_{0}^{j})$
and
$C_{0}^{j}=\text{pr}_{k^{\prime }/k_{i}}^{\ast }(W_{0}^{j})$
and
 $C_{\infty }^{j}=\text{pr}_{k^{\prime }/k_{i}}^{\ast }(W_{\infty }^{j})$
for
$C_{\infty }^{j}=\text{pr}_{k^{\prime }/k_{i}}^{\ast }(W_{\infty }^{j})$
for
 $j=1,\ldots ,r$
. Since
$j=1,\ldots ,r$
. Since
![]() $\text{pr}_{k^{\prime }/k_{i}}$
is smooth, it follows that
$\text{pr}_{k^{\prime }/k_{i}}$
is smooth, it follows that
 $C^{j,N}=W_{k^{\prime }}^{j,N}$
for each
$C^{j,N}=W_{k^{\prime }}^{j,N}$
for each
![]() $j$
. Moreover, it follows from [Reference Krishna and ParkKP14, Lemma 2.2] that condition (3) above holds on each
$j$
. Moreover, it follows from [Reference Krishna and ParkKP14, Lemma 2.2] that condition (3) above holds on each
![]() $W^{j,N}$
. It follows that each
$W^{j,N}$
. It follows that each
![]() $W^{j}$
defines a rational equivalence for 0-cycles with modulus
$W^{j}$
defines a rational equivalence for 0-cycles with modulus
![]() $D_{i}$
on
$D_{i}$
on
![]() $X_{i}$
.
$X_{i}$
.
We now set
 $\unicode[STIX]{x1D6FC}_{i}=\text{pr}_{k_{i}/k}^{\ast }(\unicode[STIX]{x1D6FC})$
and let
$\unicode[STIX]{x1D6FC}_{i}=\text{pr}_{k_{i}/k}^{\ast }(\unicode[STIX]{x1D6FC})$
and let
 $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FC}_{i}-(\sum _{j=1}^{r}([W_{0}^{j}]-[W_{\infty }^{j}]))\in {\mathcal{Z}}_{0}(X_{i}|D_{i})$
. It then follows that
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FC}_{i}-(\sum _{j=1}^{r}([W_{0}^{j}]-[W_{\infty }^{j}]))\in {\mathcal{Z}}_{0}(X_{i}|D_{i})$
. It then follows that
 $\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FD})=\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FC}_{i})-\sum _{j=1}^{r}([C_{0}^{j}]-[C_{\infty }^{j}])=\text{pr}_{k^{\prime }/k}^{\ast }(\unicode[STIX]{x1D6FC})-\sum _{j=1}^{r}([C_{0}^{j}]-[C_{\infty }^{j}])=0$
in
$\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FD})=\text{pr}_{k^{\prime }/k_{i}}^{\ast }(\unicode[STIX]{x1D6FC}_{i})-\sum _{j=1}^{r}([C_{0}^{j}]-[C_{\infty }^{j}])=\text{pr}_{k^{\prime }/k}^{\ast }(\unicode[STIX]{x1D6FC})-\sum _{j=1}^{r}([C_{0}^{j}]-[C_{\infty }^{j}])=0$
in
 ${\mathcal{Z}}_{0}(X^{\prime }|D^{\prime })$
. Since the map
${\mathcal{Z}}_{0}(X^{\prime }|D^{\prime })$
. Since the map
 $\text{pr}_{k^{\prime }/k_{i}}^{\ast }:{\mathcal{Z}}_{0}(X_{i}|D_{i})\rightarrow {\mathcal{Z}}_{0}(X^{\prime }|D^{\prime })$
of free abelian groups is clearly injective, we get
$\text{pr}_{k^{\prime }/k_{i}}^{\ast }:{\mathcal{Z}}_{0}(X_{i}|D_{i})\rightarrow {\mathcal{Z}}_{0}(X^{\prime }|D^{\prime })$
of free abelian groups is clearly injective, we get
![]() $\unicode[STIX]{x1D6FD}=0$
, which means that
$\unicode[STIX]{x1D6FD}=0$
, which means that
 $\unicode[STIX]{x1D6FC}_{i}\in {\mathcal{R}}_{0}(X_{i}|D_{i})$
. This proves (2). The existence of push-forward is already known as remarked above and the formula
$\unicode[STIX]{x1D6FC}_{i}\in {\mathcal{R}}_{0}(X_{i}|D_{i})$
. This proves (2). The existence of push-forward is already known as remarked above and the formula
 $(\text{pr}_{k^{\prime }/k})_{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }=[k^{\prime }:k]$
is obvious from the definitions.◻
$(\text{pr}_{k^{\prime }/k})_{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }=[k^{\prime }:k]$
is obvious from the definitions.◻
7 The main results on the Chow groups of 0-cycles
In this section, we apply the technical results of the previous section to prove our main theorem on the Chow groups of 0-cycles with modulus and the Chow group of 0-cycles on singular varieties. We shall also derive our first set of applications. We shall derive a new presentation of the Chow group of 0-cycles with modulus and prove our main comparison theorem for the two Chow groups of 0-cycles for the double.
Theorem 7.1. Let
![]() $k$
be a field and let
$k$
be a field and let
![]() $X$
be a smooth quasi-projective scheme of dimension
$X$
be a smooth quasi-projective scheme of dimension
![]() $d\geqslant 1$
over
$d\geqslant 1$
over
![]() $k$
with an effective Cartier divisor
$k$
with an effective Cartier divisor
![]() $D\subset X$
.
$D\subset X$
.
Then, there are maps
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)\rightarrow \text{CH}_{0}(S_{X});\quad \unicode[STIX]{x1D704}_{\pm }^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)\rightarrow \text{CH}_{0}(S_{X});\quad \unicode[STIX]{x1D704}_{\pm }^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X)\end{eqnarray}$$
and
 $$\begin{eqnarray}p_{\pm ,\ast }:\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(S_{X})\end{eqnarray}$$
$$\begin{eqnarray}p_{\pm ,\ast }:\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(S_{X})\end{eqnarray}$$
such that
 $\unicode[STIX]{x1D704}_{\pm }^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}$
on
$\unicode[STIX]{x1D704}_{\pm }^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}$
on
 $\text{CH}_{0}(X)$
.
$\text{CH}_{0}(X)$
.
If
![]() $k$
is perfect, then there is also a map
$k$
is perfect, then there is also a map
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X|D)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}(X|D)\end{eqnarray}$$
such that
 $\unicode[STIX]{x1D70F}_{X}^{\ast }\circ p_{\pm ,\ast }=\pm ~\text{Id}$
on
$\unicode[STIX]{x1D70F}_{X}^{\ast }\circ p_{\pm ,\ast }=\pm ~\text{Id}$
on
 $\text{CH}_{0}(X|D)$
. Moreover, the sequences
$\text{CH}_{0}(X|D)$
. Moreover, the sequences
 $$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\xrightarrow[{}]{p_{+,\ast }}\text{CH}_{0}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{-}^{\ast }}\text{CH}_{0}(X)\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\xrightarrow[{}]{p_{+,\ast }}\text{CH}_{0}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{-}^{\ast }}\text{CH}_{0}(X)\rightarrow 0\end{eqnarray}$$
and
 $$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}^{\ast }}\text{CH}_{0}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70F}_{X}^{\ast }}\text{CH}_{0}(X|D)\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}^{\ast }}\text{CH}_{0}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70F}_{X}^{\ast }}\text{CH}_{0}(X|D)\rightarrow 0\end{eqnarray}$$
are split exact.
Proof. We can clearly assume that
![]() $X$
is connected. All the maps (except (7.2)) involved in the theorem are well defined thanks to the results of the previous sections. On the level of cycles, we clearly have
$X$
is connected. All the maps (except (7.2)) involved in the theorem are well defined thanks to the results of the previous sections. On the level of cycles, we clearly have
 $\unicode[STIX]{x1D704}_{\pm }^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}$
on
$\unicode[STIX]{x1D704}_{\pm }^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}$
on
 ${\mathcal{Z}}_{0}(X,D)$
and
${\mathcal{Z}}_{0}(X,D)$
and
 $\unicode[STIX]{x1D70F}_{X}^{\ast }\circ p_{\pm ,\ast }=\pm ~\text{Id}$
on
$\unicode[STIX]{x1D70F}_{X}^{\ast }\circ p_{\pm ,\ast }=\pm ~\text{Id}$
on
 ${\mathcal{Z}}_{0}(X|D)$
. We are only thus left with proving (7.2) when
${\mathcal{Z}}_{0}(X|D)$
. We are only thus left with proving (7.2) when
![]() $k$
is finite and the exactness of the two sequences in general.
$k$
is finite and the exactness of the two sequences in general.
Note that the maps
 $\unicode[STIX]{x1D70F}_{X}^{\ast }:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow {\mathcal{Z}}_{0}(X|D){\twoheadrightarrow}\text{CH}_{0}(X|D)$
are defined over any field and for any field extension
$\unicode[STIX]{x1D70F}_{X}^{\ast }:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow {\mathcal{Z}}_{0}(X|D){\twoheadrightarrow}\text{CH}_{0}(X|D)$
are defined over any field and for any field extension
![]() $k{\hookrightarrow}k^{\prime }$
, the diagram
$k{\hookrightarrow}k^{\prime }$
, the diagram

commutes, where
 $X^{\prime }=X_{k^{\prime }}$
. In particular, we have
$X^{\prime }=X_{k^{\prime }}$
. In particular, we have
 $\unicode[STIX]{x1D70F}_{X^{\prime }}^{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }=\text{pr}_{k^{\prime }/k}^{\ast }\circ \unicode[STIX]{x1D70F}_{X}^{\ast }$
.
$\unicode[STIX]{x1D70F}_{X^{\prime }}^{\ast }\circ \text{pr}_{k^{\prime }/k}^{\ast }=\text{pr}_{k^{\prime }/k}^{\ast }\circ \unicode[STIX]{x1D70F}_{X}^{\ast }$
.
We have to show that the composite map
 $\unicode[STIX]{x1D70F}_{X}^{\ast }:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow \text{CH}_{0}(X|D)$
kills the rational equivalences, assuming
$\unicode[STIX]{x1D70F}_{X}^{\ast }:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow \text{CH}_{0}(X|D)$
kills the rational equivalences, assuming
![]() $k$
is finite. Let us therefore assume that
$k$
is finite. Let us therefore assume that
 $\unicode[STIX]{x1D708}:(C,Z)\rightarrow (S_{X},D)$
is a good curve and that
$\unicode[STIX]{x1D708}:(C,Z)\rightarrow (S_{X},D)$
is a good curve and that
 $f:C{\dashrightarrow}\mathbb{P}_{k}^{1}$
is a rational function which is regular and invertible on a neighborhood of
$f:C{\dashrightarrow}\mathbb{P}_{k}^{1}$
is a rational function which is regular and invertible on a neighborhood of
![]() $Z$
. Let
$Z$
. Let
 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f))$
. We need to show that
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D708}_{\ast }(\operatorname{div}(f))$
. We need to show that
 $\unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=0$
in
$\unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=0$
in
 $\text{CH}_{0}(X|D)$
.
$\text{CH}_{0}(X|D)$
.
We choose two distinct primes
![]() $\ell _{1}$
and
$\ell _{1}$
and
![]() $\ell _{2}$
different from
$\ell _{2}$
different from
![]() $\text{char}(k)$
and let
$\text{char}(k)$
and let
![]() $k_{i}$
denote the pro-
$k_{i}$
denote the pro-
![]() $\ell _{i}$
extension of
$\ell _{i}$
extension of
![]() $k$
for
$k$
for
![]() $i=1,2$
. Since each
$i=1,2$
. Since each
![]() $k_{i}$
is a limit of finite separable extensions of the perfect field
$k_{i}$
is a limit of finite separable extensions of the perfect field
![]() $k$
, the hypotheses of Propositions 6.1 and 6.2 are satisfied.
$k$
, the hypotheses of Propositions 6.1 and 6.2 are satisfied.
It follows from Proposition 6.1 that
 $\text{pr}_{k_{i}/k}^{\ast }(\unicode[STIX]{x1D6FC})\in {\mathcal{R}}_{0}(S_{X_{k_{i}}},D_{k_{i}})$
for
$\text{pr}_{k_{i}/k}^{\ast }(\unicode[STIX]{x1D6FC})\in {\mathcal{R}}_{0}(S_{X_{k_{i}}},D_{k_{i}})$
for
![]() $i=1,2$
. It follows from the case of infinite perfect fields and (7.5) that
$i=1,2$
. It follows from the case of infinite perfect fields and (7.5) that
 $\unicode[STIX]{x1D70F}_{X_{k_{i}}}^{\ast }(\unicode[STIX]{x1D6FC}_{k_{i}})=0$
for
$\unicode[STIX]{x1D70F}_{X_{k_{i}}}^{\ast }(\unicode[STIX]{x1D6FC}_{k_{i}})=0$
for
![]() $i=1,2$
. Equivalently,
$i=1,2$
. Equivalently,
 $\text{pr}_{k_{i}/k}^{\ast }\circ \unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=0$
for
$\text{pr}_{k_{i}/k}^{\ast }\circ \unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=0$
for
![]() $i=1,2$
. Using Proposition 6.2, we can find two finite extensions
$i=1,2$
. Using Proposition 6.2, we can find two finite extensions
![]() $k_{1}^{\prime }$
and
$k_{1}^{\prime }$
and
![]() $k_{2}^{\prime }$
of
$k_{2}^{\prime }$
of
![]() $k$
of relatively prime degrees such that
$k$
of relatively prime degrees such that
 $\text{pr}_{k_{i}^{\prime }/k}^{\ast }\circ \unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=0$
for
$\text{pr}_{k_{i}^{\prime }/k}^{\ast }\circ \unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=0$
for
![]() $i=1,2$
. We finish by applying Proposition 6.2 once again
$i=1,2$
. We finish by applying Proposition 6.2 once again
 $\unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=0$
in
$\unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=0$
in
 $\text{CH}_{0}(X|D)$
. This proves (7.2).
$\text{CH}_{0}(X|D)$
. This proves (7.2).
Now we prove the split exactness of the two sequences in the theorem. Since a cycle
 ${\mathcal{Z}}_{0}(X|D)$
does not meet
${\mathcal{Z}}_{0}(X|D)$
does not meet
![]() $D$
, it is clear that
$D$
, it is clear that
 $\unicode[STIX]{x1D704}_{-}^{\ast }\circ p_{+,\ast }=0$
. Similarly,
$\unicode[STIX]{x1D704}_{-}^{\ast }\circ p_{+,\ast }=0$
. Similarly,
 $\unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=0$
by definitions of these maps and Lemma 3.20. Using the first part of the theorem, we only have to show that both sequences are exact at their middle terms.
$\unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=0$
by definitions of these maps and Lemma 3.20. Using the first part of the theorem, we only have to show that both sequences are exact at their middle terms.
Let
 $\unicode[STIX]{x1D6FE}\in \text{CH}_{0}(S_{X})$
. We can write
$\unicode[STIX]{x1D6FE}\in \text{CH}_{0}(S_{X})$
. We can write
 $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FC}_{+}+\unicode[STIX]{x1D6FD}_{-}$
, where
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D6FC}_{+}+\unicode[STIX]{x1D6FD}_{-}$
, where
![]() $\unicode[STIX]{x1D6FC}_{+}$
is a cycle supported on the component
$\unicode[STIX]{x1D6FC}_{+}$
is a cycle supported on the component
![]() $\unicode[STIX]{x1D704}_{+}(X)$
and
$\unicode[STIX]{x1D704}_{+}(X)$
and
![]() $\unicode[STIX]{x1D6FD}_{-}$
is a cycle supported on the component
$\unicode[STIX]{x1D6FD}_{-}$
is a cycle supported on the component
![]() $\unicode[STIX]{x1D704}_{-}(X)$
. We see then that
$\unicode[STIX]{x1D704}_{-}(X)$
. We see then that
 $\unicode[STIX]{x1D6FE}=p_{+,\ast }(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})+\unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FD})$
, where
$\unicode[STIX]{x1D6FE}=p_{+,\ast }(\unicode[STIX]{x1D6FC}-\unicode[STIX]{x1D6FD})+\unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FD})$
, where
![]() $\unicode[STIX]{x1D6FC}$
and
$\unicode[STIX]{x1D6FC}$
and
![]() $\unicode[STIX]{x1D6FD}$
are the cycles
$\unicode[STIX]{x1D6FD}$
are the cycles
![]() $\unicode[STIX]{x1D6FC}_{+}$
and
$\unicode[STIX]{x1D6FC}_{+}$
and
![]() $\unicode[STIX]{x1D6FD}_{-}$
seen in
$\unicode[STIX]{x1D6FD}_{-}$
seen in
![]() $X\setminus D$
(identifying the two copies of
$X\setminus D$
(identifying the two copies of
![]() $X$
), so that every element in the kernel of
$X$
), so that every element in the kernel of
![]() $\unicode[STIX]{x1D704}_{-}^{\ast }$
is clearly in the image of
$\unicode[STIX]{x1D704}_{-}^{\ast }$
is clearly in the image of
![]() $p_{+,\ast }$
. We have therefore shown that the sequence (7.3) is split exact.
$p_{+,\ast }$
. We have therefore shown that the sequence (7.3) is split exact.
Next, suppose
 $\unicode[STIX]{x1D6FC}\in \text{CH}_{0}(S_{X})$
is such that
$\unicode[STIX]{x1D6FC}\in \text{CH}_{0}(S_{X})$
is such that
 $\unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=0$
. Since (7.3) is split exact, as we just showed, we can write
$\unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=0$
. Since (7.3) is split exact, as we just showed, we can write
 $\unicode[STIX]{x1D6FC}=p_{+,\ast }(\unicode[STIX]{x1D6FC}_{1})+\unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FC}_{2})$
. We then have
$\unicode[STIX]{x1D6FC}=p_{+,\ast }(\unicode[STIX]{x1D6FC}_{1})+\unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FC}_{2})$
. We then have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC}) & = & \displaystyle 0\nonumber\\ \displaystyle & \Leftrightarrow & \displaystyle \unicode[STIX]{x1D70F}_{X}^{\ast }\circ p_{+,\ast }(\unicode[STIX]{x1D6FC}_{1})+\unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FC}_{2})=0\nonumber\\ \displaystyle & \Leftrightarrow & \displaystyle \unicode[STIX]{x1D6FC}_{1}+0=0\nonumber\\ \displaystyle & \Leftrightarrow & \displaystyle \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FC}_{2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC}) & = & \displaystyle 0\nonumber\\ \displaystyle & \Leftrightarrow & \displaystyle \unicode[STIX]{x1D70F}_{X}^{\ast }\circ p_{+,\ast }(\unicode[STIX]{x1D6FC}_{1})+\unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FC}_{2})=0\nonumber\\ \displaystyle & \Leftrightarrow & \displaystyle \unicode[STIX]{x1D6FC}_{1}+0=0\nonumber\\ \displaystyle & \Leftrightarrow & \displaystyle \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FC}_{2}).\nonumber\end{eqnarray}$$
We have therefore shown that the sequence (7.4) is split exact. ◻
7.1 A refinement of the definition of 0-cycles with modulus
As a consequence of Theorem 7.1, we now give the following simplified presentation of the Chow group of 0-cycles with modulus when the ground field is infinite and perfect.
Let
![]() $X$
be a smooth quasi-projective scheme of dimension
$X$
be a smooth quasi-projective scheme of dimension
![]() $d\geqslant 1$
over an infinite perfect field
$d\geqslant 1$
over an infinite perfect field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Let
$D\subset X$
be an effective Cartier divisor. Let
 ${\mathcal{R}}_{0}^{\text{mod}}(X|D)\subset {\mathcal{Z}}_{0}(X|D)$
be the subgroup generated by
${\mathcal{R}}_{0}^{\text{mod}}(X|D)\subset {\mathcal{Z}}_{0}(X|D)$
be the subgroup generated by
 $\operatorname{div}_{C}(f)$
, where
$\operatorname{div}_{C}(f)$
, where
![]() $C\subset X$
is an integral curve not contained in
$C\subset X$
is an integral curve not contained in
![]() $D$
and is smooth along
$D$
and is smooth along
![]() $D$
and
$D$
and
 $f\in \text{Ker}({\mathcal{O}}_{C,D}^{\times }\rightarrow {\mathcal{O}}_{C\cap D}^{\times })$
. Here,
$f\in \text{Ker}({\mathcal{O}}_{C,D}^{\times }\rightarrow {\mathcal{O}}_{C\cap D}^{\times })$
. Here,
![]() ${\mathcal{O}}_{C,D}$
denotes the semi-local ring of
${\mathcal{O}}_{C,D}$
denotes the semi-local ring of
![]() $C$
at
$C$
at
 $(C\cap D)\cup \{\unicode[STIX]{x1D702}\}$
with
$(C\cap D)\cup \{\unicode[STIX]{x1D702}\}$
with
![]() $\unicode[STIX]{x1D702}$
being the generic point of
$\unicode[STIX]{x1D702}$
being the generic point of
![]() $C$
. Set
$C$
. Set
 $\text{CH}_{0}^{\text{mod}}(X|D)={\mathcal{Z}}_{0}(X|D)/{\mathcal{R}}_{0}^{\text{mod}}(X|D)$
. There is an evident surjection
$\text{CH}_{0}^{\text{mod}}(X|D)={\mathcal{Z}}_{0}(X|D)/{\mathcal{R}}_{0}^{\text{mod}}(X|D)$
. There is an evident surjection
 $\text{CH}_{0}^{\text{mod}}(X|D){\twoheadrightarrow}\text{CH}_{0}(X|D)$
.
$\text{CH}_{0}^{\text{mod}}(X|D){\twoheadrightarrow}\text{CH}_{0}(X|D)$
.
Corollary 7.2. Let
![]() $X$
be as above. Then the map
$X$
be as above. Then the map
 $\text{CH}_{0}^{\text{mod}}(X|D){\twoheadrightarrow}\text{CH}_{0}(X|D)$
is an isomorphism.
$\text{CH}_{0}^{\text{mod}}(X|D){\twoheadrightarrow}\text{CH}_{0}(X|D)$
is an isomorphism.
Proof. Under the given assumption, we get maps
 $$\begin{eqnarray}\text{CH}_{0}^{\text{mod}}(X|D)\rightarrow \text{CH}_{0}(X|D)\xrightarrow[{}]{p_{+,\ast }}\text{CH}_{0}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70F}_{X}^{\ast }}\text{CH}_{0}(X|D).\end{eqnarray}$$
$$\begin{eqnarray}\text{CH}_{0}^{\text{mod}}(X|D)\rightarrow \text{CH}_{0}(X|D)\xrightarrow[{}]{p_{+,\ast }}\text{CH}_{0}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70F}_{X}^{\ast }}\text{CH}_{0}(X|D).\end{eqnarray}$$
The proofs of Propositions 5.7 and 5.8 show that
![]() $\unicode[STIX]{x1D70F}_{X}^{\ast }$
actually factors through the map
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
actually factors through the map
 $\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}^{\text{mod}}(X|D)$
. We thus get maps
$\text{CH}_{0}(S_{X})\rightarrow \text{CH}_{0}^{\text{mod}}(X|D)$
. We thus get maps
 $$\begin{eqnarray}\text{CH}_{0}^{\text{mod}}(X|D)\rightarrow \text{CH}_{0}(X|D)\xrightarrow[{}]{p_{+,\ast }}\text{CH}_{0}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70F}_{X}^{\ast }}\text{CH}_{0}^{\text{mod}}(X|D),\end{eqnarray}$$
$$\begin{eqnarray}\text{CH}_{0}^{\text{mod}}(X|D)\rightarrow \text{CH}_{0}(X|D)\xrightarrow[{}]{p_{+,\ast }}\text{CH}_{0}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70F}_{X}^{\ast }}\text{CH}_{0}^{\text{mod}}(X|D),\end{eqnarray}$$
whose composite is clearly the identity. In particular, the map
 $\text{CH}_{0}^{\text{mod}}(X|D)\rightarrow \text{CH}_{0}(X|D)$
is injective. The corollary now follows.◻
$\text{CH}_{0}^{\text{mod}}(X|D)\rightarrow \text{CH}_{0}(X|D)$
is injective. The corollary now follows.◻
7.2 The comparison theorem
Using the modified presentation of
 $\text{CH}_{0}(X|D)$
from Corollary 7.2, we prove the following comparison theorem for the two Chow groups of the double.
$\text{CH}_{0}(X|D)$
from Corollary 7.2, we prove the following comparison theorem for the two Chow groups of the double.
Theorem 7.3. Let
![]() $k$
be an infinite perfect field and let
$k$
be an infinite perfect field and let
![]() $X$
be a smooth quasi-projective scheme of dimension
$X$
be a smooth quasi-projective scheme of dimension
![]() $d\geqslant 1$
over
$d\geqslant 1$
over
![]() $k$
with an effective Cartier divisor
$k$
with an effective Cartier divisor
![]() $D$
. Then the canonical map
$D$
. Then the canonical map
 $\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(S_{X})$
is an isomorphism.
$\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(S_{X})$
is an isomorphism.
Proof. In view of Lemma 3.12, we can assume
![]() $d\geqslant 2$
. Recall from § 5.7 that there are two maps
$d\geqslant 2$
. Recall from § 5.7 that there are two maps
 $p_{\pm ,\ast }:{\mathcal{Z}}_{0}(X|D)\rightrightarrows {\mathcal{Z}}_{0}(S_{X},D)$
. As the first step in the proof of the theorem, we strengthen Proposition 5.9 by showing that these maps descend to group homomorphisms
$p_{\pm ,\ast }:{\mathcal{Z}}_{0}(X|D)\rightrightarrows {\mathcal{Z}}_{0}(S_{X},D)$
. As the first step in the proof of the theorem, we strengthen Proposition 5.9 by showing that these maps descend to group homomorphisms
 $p_{\pm ,\ast }:\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}^{\text{LW}}(S_{X})$
. To show this, we can use Corollary 7.2 and replace
$p_{\pm ,\ast }:\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}^{\text{LW}}(S_{X})$
. To show this, we can use Corollary 7.2 and replace
 $\text{CH}_{0}(X|D)$
by
$\text{CH}_{0}(X|D)$
by
 $\text{CH}_{0}^{\text{mod}}(X|D)$
.
$\text{CH}_{0}^{\text{mod}}(X|D)$
.
So let
 $\unicode[STIX]{x1D708}:C{\hookrightarrow}X$
be an integral curve not contained in
$\unicode[STIX]{x1D708}:C{\hookrightarrow}X$
be an integral curve not contained in
![]() $D$
which is smooth along
$D$
which is smooth along
![]() $D$
and let
$D$
and let
 $f\in \text{Ker}({\mathcal{O}}_{C,D}^{\times }\rightarrow {\mathcal{O}}_{C\cap D}^{\times })$
. Since
$f\in \text{Ker}({\mathcal{O}}_{C,D}^{\times }\rightarrow {\mathcal{O}}_{C\cap D}^{\times })$
. Since
![]() $C$
is smooth along
$C$
is smooth along
![]() $D$
, the inclusion
$D$
, the inclusion
![]() $\unicode[STIX]{x1D708}$
is l.c.i. along
$\unicode[STIX]{x1D708}$
is l.c.i. along
![]() $D$
. Since
$D$
. Since
![]() $C$
is reduced, it follows from Proposition 2.3 that
$C$
is reduced, it follows from Proposition 2.3 that
 $S_{C}:=S(C,E)$
is reduced, where we let
$S_{C}:=S(C,E)$
is reduced, where we let
 $E=\unicode[STIX]{x1D708}^{\ast }(D)$
. It follows from Proposition 2.4 that the double map
$E=\unicode[STIX]{x1D708}^{\ast }(D)$
. It follows from Proposition 2.4 that the double map
 $\unicode[STIX]{x1D708}^{\prime }:S_{C}{\hookrightarrow}S_{X}$
is l.c.i. along
$\unicode[STIX]{x1D708}^{\prime }:S_{C}{\hookrightarrow}S_{X}$
is l.c.i. along
![]() $D$
. In other words,
$D$
. In other words,
 $S_{C}{\hookrightarrow}S_{X}$
is a Cartier curve.
$S_{C}{\hookrightarrow}S_{X}$
is a Cartier curve.
We now consider the rational function
 $h=(h_{+},h_{-}):=(f,1)$
on
$h=(h_{+},h_{-}):=(f,1)$
on
![]() $S_{C}$
. The modulus condition satisfied by
$S_{C}$
. The modulus condition satisfied by
![]() $f$
on
$f$
on
![]() $C$
guarantees that
$C$
guarantees that
![]() $h$
is regular and invertible along
$h$
is regular and invertible along
 $E\subset S_{C}$
. It is clear as in Proposition 5.9 that the divisor of
$E\subset S_{C}$
. It is clear as in Proposition 5.9 that the divisor of
![]() $h$
trivializes
$h$
trivializes
 $p_{+,\ast }(\unicode[STIX]{x1D708}_{\ast }\text{div}(f))$
. The argument for
$p_{+,\ast }(\unicode[STIX]{x1D708}_{\ast }\text{div}(f))$
. The argument for
![]() $p_{-,\ast }$
is symmetric. We denote the maps
$p_{-,\ast }$
is symmetric. We denote the maps
 $\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}^{\text{LW}}(S_{X})$
obtained as above by
$\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}^{\text{LW}}(S_{X})$
obtained as above by
![]() $p_{\pm ,\ast }^{\text{LW}}$
. It is clear that the composite
$p_{\pm ,\ast }^{\text{LW}}$
. It is clear that the composite
 $\text{CH}_{0}(X|D)\xrightarrow[{}]{p_{\pm ,\ast }^{\text{LW}}}\text{CH}_{0}^{\text{LW}}(S_{X}){\twoheadrightarrow}\text{CH}_{0}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70F}_{X}^{\ast }}\text{CH}_{0}(X|D)$
are the identity maps (up to a sign).
$\text{CH}_{0}(X|D)\xrightarrow[{}]{p_{\pm ,\ast }^{\text{LW}}}\text{CH}_{0}^{\text{LW}}(S_{X}){\twoheadrightarrow}\text{CH}_{0}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70F}_{X}^{\ast }}\text{CH}_{0}(X|D)$
are the identity maps (up to a sign).
Recall from Lemma 3.20 that
 $\text{CH}_{0}(X)$
is the quotient of free abelian group on the closed points of
$\text{CH}_{0}(X)$
is the quotient of free abelian group on the closed points of
![]() $X\setminus D$
by the subgroup generated by
$X\setminus D$
by the subgroup generated by
![]() $\operatorname{div}(f)$
, where
$\operatorname{div}(f)$
, where
![]() $f$
is a rational function on an integral curve
$f$
is a rational function on an integral curve
![]() $C$
not contained in
$C$
not contained in
![]() $D$
and
$D$
and
![]() $f$
is regular invertible along
$f$
is regular invertible along
![]() $D$
. Using an easier version of Lemma 5.5, one can now see that the rational equivalences for
$D$
. Using an easier version of Lemma 5.5, one can now see that the rational equivalences for
 $\text{CH}_{0}(X)$
can be defined by further restricting integral curves on
$\text{CH}_{0}(X)$
can be defined by further restricting integral curves on
![]() $X$
which are smooth along
$X$
which are smooth along
![]() $D$
. In particular, they are l.c.i. on
$D$
. In particular, they are l.c.i. on
![]() $X$
along
$X$
along
![]() $D$
. Using such curves, one can check from the proof of Theorem 4.1 that the map
$D$
. Using such curves, one can check from the proof of Theorem 4.1 that the map
 $\unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)\rightarrow \text{CH}_{0}(S_{X})$
can actually be lifted to the pull-back map
$\unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)\rightarrow \text{CH}_{0}(S_{X})$
can actually be lifted to the pull-back map
 $\unicode[STIX]{x1D6E5}^{\text{LW},\ast }:\text{CH}_{0}(X)\rightarrow \text{CH}_{0}^{\text{LW}}(S_{X})$
.
$\unicode[STIX]{x1D6E5}^{\text{LW},\ast }:\text{CH}_{0}(X)\rightarrow \text{CH}_{0}^{\text{LW}}(S_{X})$
.
We next consider the composite maps
 $\text{CH}_{0}^{\text{LW}}(S_{X}){\twoheadrightarrow}\text{CH}_{0}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{\pm }^{\ast }}\text{CH}_{0}(X)$
, which we denote by
$\text{CH}_{0}^{\text{LW}}(S_{X}){\twoheadrightarrow}\text{CH}_{0}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{\pm }^{\ast }}\text{CH}_{0}(X)$
, which we denote by
![]() $\unicode[STIX]{x1D704}_{\pm }^{\text{LW},\ast }$
. It is then clear that
$\unicode[STIX]{x1D704}_{\pm }^{\text{LW},\ast }$
. It is then clear that
 $\unicode[STIX]{x1D704}_{\pm }^{\text{LW},\ast }\circ \unicode[STIX]{x1D6E5}^{\text{LW},\ast }=\text{Id}$
on
$\unicode[STIX]{x1D704}_{\pm }^{\text{LW},\ast }\circ \unicode[STIX]{x1D6E5}^{\text{LW},\ast }=\text{Id}$
on
 $\text{CH}_{0}(X)$
. Now, the proof of (7.3) works in verbatim to give a split exact sequence
$\text{CH}_{0}(X)$
. Now, the proof of (7.3) works in verbatim to give a split exact sequence
 $$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\xrightarrow[{}]{p_{+,\ast }^{\text{LW}}}\text{CH}_{0}^{\text{LW}}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{-}^{\text{LW},\ast }}\text{CH}_{0}(X)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\xrightarrow[{}]{p_{+,\ast }^{\text{LW}}}\text{CH}_{0}^{\text{LW}}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{-}^{\text{LW},\ast }}\text{CH}_{0}(X)\rightarrow 0.\end{eqnarray}$$
We thus have a commutative diagram of split exact sequences.

We conclude from this that the map
 $\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(S_{X})$
is an isomorphism.◻
$\text{CH}_{0}^{\text{LW}}(S_{X})\rightarrow \text{CH}_{0}(S_{X})$
is an isomorphism.◻
8 Albanese with modulus over
 $\mathbb{C}$
$\mathbb{C}$
It is classically known that a smooth projective variety
![]() $X$
over an algebraically closed field has an abelian variety, called the Albanese variety
$X$
over an algebraically closed field has an abelian variety, called the Albanese variety
![]() $\text{Alb}(X)$
of
$\text{Alb}(X)$
of
![]() $X$
, associated to it, which is Cartier dual to the Picard variety
$X$
, associated to it, which is Cartier dual to the Picard variety
 $\operatorname{Pic}^{0}(X)$
. The Albanese comes equipped with a (surjective) Abel–Jacobi map from the Chow group
$\operatorname{Pic}^{0}(X)$
. The Albanese comes equipped with a (surjective) Abel–Jacobi map from the Chow group
 $\text{CH}_{0}(X)_{\deg 0}$
of zero cycles of degree zero on
$\text{CH}_{0}(X)_{\deg 0}$
of zero cycles of degree zero on
![]() $X$
, that is universal among regular maps to abelian varieties. When
$X$
, that is universal among regular maps to abelian varieties. When
![]() $X$
is a smooth projective curve with an effective Cartier divisor
$X$
is a smooth projective curve with an effective Cartier divisor
![]() $D$
on it, a universal regular quotient for what we now call the Chow group of zero cycles with modulus,
$D$
on it, a universal regular quotient for what we now call the Chow group of zero cycles with modulus,
 $\text{CH}_{0}(X|D)_{\deg 0}$
, was already constructed by Serre in [Reference SerreSer88] under the name of the generalized Jacobian variety. Serre showed that this generalized Jacobian is a commutative algebraic group which is an extension of the Jacobian variety of the curve by a linear algebraic group.
$\text{CH}_{0}(X|D)_{\deg 0}$
, was already constructed by Serre in [Reference SerreSer88] under the name of the generalized Jacobian variety. Serre showed that this generalized Jacobian is a commutative algebraic group which is an extension of the Jacobian variety of the curve by a linear algebraic group.
If
![]() $X$
is now a smooth projective variety of arbitrary dimension over the field of complex numbers
$X$
is now a smooth projective variety of arbitrary dimension over the field of complex numbers
![]() $\mathbb{C}$
and
$\mathbb{C}$
and
![]() $D\subset X$
is an effective Cartier divisor such that
$D\subset X$
is an effective Cartier divisor such that
![]() $D_{\text{red}}$
is a strict normal crossing divisor, a universal regular quotient of
$D_{\text{red}}$
is a strict normal crossing divisor, a universal regular quotient of
 $\text{CH}_{0}(X|D)$
was constructed in [Reference Binda and SaitoBS16] as a relative intermediate Jacobian
$\text{CH}_{0}(X|D)$
was constructed in [Reference Binda and SaitoBS16] as a relative intermediate Jacobian
![]() $J_{X|D}^{\dim (X)}$
. However, not many properties of this universal regular quotient are known and the techniques used in the construction are not known to generalize to cover the general case.
$J_{X|D}^{\dim (X)}$
. However, not many properties of this universal regular quotient are known and the techniques used in the construction are not known to generalize to cover the general case.
In this paper, we use our doubling trick to give a direct and explicit construction of the relative Albanese
 $\text{Alb}(X|D)$
and show that it is the universal regular quotient of the Chow group of 0-cycles with modulus. As a result of our construction, we are able to prove the Roitman torsion theorem for the Chow group of 0-cycles with modulus. In this section, we use the modified Deligne cohomology of Levine [Reference LevineLev92] to construct the universal regular quotient when the base field is
$\text{Alb}(X|D)$
and show that it is the universal regular quotient of the Chow group of 0-cycles with modulus. As a result of our construction, we are able to prove the Roitman torsion theorem for the Chow group of 0-cycles with modulus. In this section, we use the modified Deligne cohomology of Levine [Reference LevineLev92] to construct the universal regular quotient when the base field is
![]() $\mathbb{C}$
. By Theorem 3.17, we can identify the Levine–Weibel Chow group of zero cycles with our modified definition 3.3.
$\mathbb{C}$
. By Theorem 3.17, we can identify the Levine–Weibel Chow group of zero cycles with our modified definition 3.3.
8.1 Relative Deligne cohomology
Let
![]() $X$
be a smooth projective connected scheme over
$X$
be a smooth projective connected scheme over
![]() $\mathbb{C}$
. Let
$\mathbb{C}$
. Let
![]() $D$
be any effective Cartier divisor on it. As before, we write
$D$
be any effective Cartier divisor on it. As before, we write
![]() $S_{X}$
for the double construction applied to the pair
$S_{X}$
for the double construction applied to the pair
![]() $(X,D)$
. We shall frequently refer to the following square.
$(X,D)$
. We shall frequently refer to the following square.

Let
![]() $r\geqslant 1$
be an integer. Following Levine [Reference LevineLev92], we denote by
$r\geqslant 1$
be an integer. Following Levine [Reference LevineLev92], we denote by
![]() $\mathbb{Z}(r)_{S_{X}}^{{\mathcal{D}}^{\ast }}$
(respectively
$\mathbb{Z}(r)_{S_{X}}^{{\mathcal{D}}^{\ast }}$
(respectively
![]() $\mathbb{Z}(r)_{D}^{{\mathcal{D}}^{\ast }}$
) the modified Deligne–Beilinson complex on
$\mathbb{Z}(r)_{D}^{{\mathcal{D}}^{\ast }}$
) the modified Deligne–Beilinson complex on
![]() $S_{X}$
(respectively on
$S_{X}$
(respectively on
![]() $D$
). Since
$D$
). Since
![]() $S_{X}$
is projective, both are given by the ‘naive’ Deligne complexes
$S_{X}$
is projective, both are given by the ‘naive’ Deligne complexes
 $$\begin{eqnarray}\mathbb{Z}(r)_{S_{X}}^{{\mathcal{D}}^{\ast }}=\mathbb{Z}(r)_{S_{X}}\rightarrow {\mathcal{O}}_{S_{X}}\xrightarrow[{}]{d}\unicode[STIX]{x1D6FA}_{S_{X}}^{1}\rightarrow \cdots \rightarrow \unicode[STIX]{x1D6FA}_{S_{X}}^{r-1},\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Z}(r)_{S_{X}}^{{\mathcal{D}}^{\ast }}=\mathbb{Z}(r)_{S_{X}}\rightarrow {\mathcal{O}}_{S_{X}}\xrightarrow[{}]{d}\unicode[STIX]{x1D6FA}_{S_{X}}^{1}\rightarrow \cdots \rightarrow \unicode[STIX]{x1D6FA}_{S_{X}}^{r-1},\end{eqnarray}$$
 $$\begin{eqnarray}\mathbb{Z}(r)_{D}^{{\mathcal{D}}^{\ast }}=\mathbb{Z}(r)_{D}\rightarrow {\mathcal{O}}_{D}\xrightarrow[{}]{d}\unicode[STIX]{x1D6FA}_{D}^{1}\rightarrow \cdots \rightarrow \unicode[STIX]{x1D6FA}_{D}^{r-1}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Z}(r)_{D}^{{\mathcal{D}}^{\ast }}=\mathbb{Z}(r)_{D}\rightarrow {\mathcal{O}}_{D}\xrightarrow[{}]{d}\unicode[STIX]{x1D6FA}_{D}^{1}\rightarrow \cdots \rightarrow \unicode[STIX]{x1D6FA}_{D}^{r-1}\end{eqnarray}$$
on
![]() $(S_{X})_{\text{an}}$
(respectively on
$(S_{X})_{\text{an}}$
(respectively on
![]() $D_{\text{an}}$
), the analytic space associated to
$D_{\text{an}}$
), the analytic space associated to
![]() $S_{X}$
(respectively to
$S_{X}$
(respectively to
![]() $D$
).
$D$
).
We can consider the complex
![]() $\mathbb{Z}(r)_{X}^{{\mathcal{D}}^{\ast }}$
on
$\mathbb{Z}(r)_{X}^{{\mathcal{D}}^{\ast }}$
on
![]() $X$
as well. Since
$X$
as well. Since
![]() $X$
is smooth and projective, we have by definition
$X$
is smooth and projective, we have by definition
 $\mathbb{Z}(r)_{X}^{{\mathcal{D}}^{\ast }}=\mathbb{Z}(r)_{X}^{{\mathcal{D}}}$
, where
$\mathbb{Z}(r)_{X}^{{\mathcal{D}}^{\ast }}=\mathbb{Z}(r)_{X}^{{\mathcal{D}}}$
, where
![]() $\mathbb{Z}(r)_{X}^{{\mathcal{D}}}$
is the classical Deligne complex. Let
$\mathbb{Z}(r)_{X}^{{\mathcal{D}}}$
is the classical Deligne complex. Let
 $i_{\pm }:X{\hookrightarrow}S_{X}$
be the inclusions of the two components in the double
$i_{\pm }:X{\hookrightarrow}S_{X}$
be the inclusions of the two components in the double
![]() $S_{X}$
and let
$S_{X}$
and let
 $\unicode[STIX]{x1D6E5}:S_{X}\rightarrow X$
be the natural projection. We denote by
$\unicode[STIX]{x1D6E5}:S_{X}\rightarrow X$
be the natural projection. We denote by
 $\unicode[STIX]{x1D70B}:X\amalg X\rightarrow S_{X}$
the map
$\unicode[STIX]{x1D70B}:X\amalg X\rightarrow S_{X}$
the map
![]() $(i_{+},i_{-})$
from the normalization. Finally, we let
$(i_{+},i_{-})$
from the normalization. Finally, we let
 $j:D{\hookrightarrow}X$
denote the inclusion of
$j:D{\hookrightarrow}X$
denote the inclusion of
![]() $D$
in
$D$
in
![]() $X$
. Recall from Proposition 2.3(8) that
$X$
. Recall from Proposition 2.3(8) that
![]() $D$
is a conducting subscheme for
$D$
is a conducting subscheme for
![]() $\unicode[STIX]{x1D70B}$
.
$\unicode[STIX]{x1D70B}$
.
We define the following objects in the bounded derived category of complexes of sheaves of abelian groups on
![]() $(S_{X})_{\text{an}}$
(respectively on
$(S_{X})_{\text{an}}$
(respectively on
![]() $X_{\text{an}}$
):
$X_{\text{an}}$
):
 $$\begin{eqnarray}\mathbb{Z}(r)_{X|D}^{{\mathcal{D}}^{\ast }}=\text{Cone}(\mathbb{Z}(r)_{S_{X}}^{{\mathcal{D}}^{\ast }}\xrightarrow[{}]{i_{-}^{\ast }}\mathbb{R}i_{-,\ast }\mathbb{Z}(r)_{X}^{{\mathcal{D}}})[-1],\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Z}(r)_{X|D}^{{\mathcal{D}}^{\ast }}=\text{Cone}(\mathbb{Z}(r)_{S_{X}}^{{\mathcal{D}}^{\ast }}\xrightarrow[{}]{i_{-}^{\ast }}\mathbb{R}i_{-,\ast }\mathbb{Z}(r)_{X}^{{\mathcal{D}}})[-1],\end{eqnarray}$$
 $$\begin{eqnarray}\mathbb{Z}(r)_{(X,D)}^{{\mathcal{D}}^{\ast }}=\text{Cone}(\mathbb{Z}(r)_{X}^{{\mathcal{D}}}\xrightarrow[{}]{j^{\ast }}\mathbb{R}j_{\ast }\mathbb{Z}(r)_{D}^{{\mathcal{D}}^{\ast }})[-1].\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{Z}(r)_{(X,D)}^{{\mathcal{D}}^{\ast }}=\text{Cone}(\mathbb{Z}(r)_{X}^{{\mathcal{D}}}\xrightarrow[{}]{j^{\ast }}\mathbb{R}j_{\ast }\mathbb{Z}(r)_{D}^{{\mathcal{D}}^{\ast }})[-1].\end{eqnarray}$$
We define the complexes
 $\mathbb{Z}(r)_{X|D}$
and
$\mathbb{Z}(r)_{X|D}$
and
 $\mathbb{Z}(r)_{(X,D)}$
in a similar fashion.
$\mathbb{Z}(r)_{(X,D)}$
in a similar fashion.
Note that the maps are all finite, so that the derived functors
![]() $\mathbb{R}i_{-,\ast }$
and
$\mathbb{R}i_{-,\ast }$
and
![]() $\mathbb{R}j_{\ast }$
are superfluous. Since all the maps over which we are taking the cones are actually surjective as maps of complexes, the cones can be computed directly as kernels in the category of complexes of sheaves on
$\mathbb{R}j_{\ast }$
are superfluous. Since all the maps over which we are taking the cones are actually surjective as maps of complexes, the cones can be computed directly as kernels in the category of complexes of sheaves on
![]() $S_{X}$
. We have the following commutative diagram relating them.
$S_{X}$
. We have the following commutative diagram relating them.

8.2 Construction of the Albanese varieties
Let
 $r=d=\dim (X)$
. In order to simplify the notation, we denote by
$r=d=\dim (X)$
. In order to simplify the notation, we denote by
 $\overline{S_{X}}\xrightarrow[{}]{\unicode[STIX]{x1D70B}}S_{X}$
the normalization of
$\overline{S_{X}}\xrightarrow[{}]{\unicode[STIX]{x1D70B}}S_{X}$
the normalization of
![]() $S_{X}$
, i.e., the disjoint union of two copies of
$S_{X}$
, i.e., the disjoint union of two copies of
![]() $X$
. This gives an induced map
$X$
. This gives an induced map
 $\unicode[STIX]{x1D70B}_{D}:\overline{D}=D\amalg D\rightarrow D$
. We shall use the relative complexes
$\unicode[STIX]{x1D70B}_{D}:\overline{D}=D\amalg D\rightarrow D$
. We shall use the relative complexes
 $\mathbb{Z}(d)_{X|D}^{{\mathcal{D}}^{\ast }}$
and
$\mathbb{Z}(d)_{X|D}^{{\mathcal{D}}^{\ast }}$
and
 $\mathbb{Z}(d)_{(X,D)}^{{\mathcal{D}}^{\ast }}$
to define in the usual way two natural receptors for the group of algebraic cycles with modulus that are homologically trivial. Coherently with the excision Theorem 7.1 in the projective case over the complex numbers, we will show that the two, a priori different constructions, give rise to the same invariant naturally attached to the pair
$\mathbb{Z}(d)_{(X,D)}^{{\mathcal{D}}^{\ast }}$
to define in the usual way two natural receptors for the group of algebraic cycles with modulus that are homologically trivial. Coherently with the excision Theorem 7.1 in the projective case over the complex numbers, we will show that the two, a priori different constructions, give rise to the same invariant naturally attached to the pair
![]() $(X,D)$
, that we call the Albanese variety with modulus.
$(X,D)$
, that we call the Albanese variety with modulus.
8.2.1 The Albanese with modulus
By construction, the map
 $\unicode[STIX]{x1D6E5}:S_{X}\rightarrow X$
satisfies
$\unicode[STIX]{x1D6E5}:S_{X}\rightarrow X$
satisfies
 $\unicode[STIX]{x1D6E5}\circ i_{\pm }=\text{Id}_{\text{X}}$
, and therefore induces a splitting of the restriction maps
$\unicode[STIX]{x1D6E5}\circ i_{\pm }=\text{Id}_{\text{X}}$
, and therefore induces a splitting of the restriction maps
![]() $i_{\pm }^{\ast }$
from the cohomology of
$i_{\pm }^{\ast }$
from the cohomology of
![]() $S_{X}$
to the cohomology of
$S_{X}$
to the cohomology of
![]() $X$
. This gives the commutative diagram of the analytic cohomology groups
$X$
. This gives the commutative diagram of the analytic cohomology groups

where the vertical maps are induced by the natural projections
 $\mathbb{Z}(d)^{{\mathcal{D}}\ast }\rightarrow \mathbb{Z}(d)$
.
$\mathbb{Z}(d)^{{\mathcal{D}}\ast }\rightarrow \mathbb{Z}(d)$
.
Since
![]() $X$
is smooth projective and connected, we have
$X$
is smooth projective and connected, we have
 $H^{2d}(X,\mathbb{Z}(d)_{X})=\mathbb{Z}$
and
$H^{2d}(X,\mathbb{Z}(d)_{X})=\mathbb{Z}$
and
 $H^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}})=\mathbb{Z}\oplus \mathbb{Z}$
, one copy for each component of
$H^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}})=\mathbb{Z}\oplus \mathbb{Z}$
, one copy for each component of
![]() $S_{X}$
. In particular, the restriction map
$S_{X}$
. In particular, the restriction map
![]() $i_{-}^{\ast }$
sends
$i_{-}^{\ast }$
sends
![]() $(0,1)$
to
$(0,1)$
to
![]() $1$
and we can identify
$1$
and we can identify
 $H^{2d}(S_{X},\mathbb{Z}(d)_{X|D})$
with the other copy of
$H^{2d}(S_{X},\mathbb{Z}(d)_{X|D})$
with the other copy of
![]() $\mathbb{Z}$
. Under this identification, we denote by
$\mathbb{Z}$
. Under this identification, we denote by
 $A^{d}(X|D)$
the kernel of the natural map
$A^{d}(X|D)$
the kernel of the natural map
 $$\begin{eqnarray}0\rightarrow A^{d}(X|D)\rightarrow \mathbb{H}^{2d}(S_{X},\mathbb{Z}(d)_{X|D}^{{\mathcal{D}}^{\ast }})\xrightarrow[{}]{\unicode[STIX]{x1D716}_{X|D}}\mathbb{Z}\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow A^{d}(X|D)\rightarrow \mathbb{H}^{2d}(S_{X},\mathbb{Z}(d)_{X|D}^{{\mathcal{D}}^{\ast }})\xrightarrow[{}]{\unicode[STIX]{x1D716}_{X|D}}\mathbb{Z}\end{eqnarray}$$
and call it the Albanese variety of
![]() $X$
with modulus
$X$
with modulus
![]() $D$
.
$D$
.
By construction, we have an isomorphism
 $$\begin{eqnarray}A^{d}(X|D)=\mathbb{H}^{2d-1}(S_{X},\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{{<}d})/H^{2d-1}(S_{X},\mathbb{Z}(d)_{X|D}),\end{eqnarray}$$
$$\begin{eqnarray}A^{d}(X|D)=\mathbb{H}^{2d-1}(S_{X},\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{{<}d})/H^{2d-1}(S_{X},\mathbb{Z}(d)_{X|D}),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{{<}d}$
denotes
$\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{{<}d}$
denotes
 $\text{Cone}(\unicode[STIX]{x1D6FA}_{S_{X}}^{{<}d}\xrightarrow[{}]{i_{-}^{\ast }}\unicode[STIX]{x1D6FA}_{X}^{{<}d})[-1]$
. Following [Reference Esnault, Srinivas and ViehwegESV99], we define the generalized Albanese variety of
$\text{Cone}(\unicode[STIX]{x1D6FA}_{S_{X}}^{{<}d}\xrightarrow[{}]{i_{-}^{\ast }}\unicode[STIX]{x1D6FA}_{X}^{{<}d})[-1]$
. Following [Reference Esnault, Srinivas and ViehwegESV99], we define the generalized Albanese variety of
![]() $S_{X}$
, denoted
$S_{X}$
, denoted
 $A^{d}(S_{X})$
, as the kernel of the map
$A^{d}(S_{X})$
, as the kernel of the map
 $$\begin{eqnarray}\mathbb{H}^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}^{{\mathcal{D}}^{\ast }}){\twoheadrightarrow}H^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{H}^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}^{{\mathcal{D}}^{\ast }}){\twoheadrightarrow}H^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}).\end{eqnarray}$$
This gives a split short exact sequence

where
 $A^{d}(X)=\text{Alb}(X)$
is the usual Albanese variety of
$A^{d}(X)=\text{Alb}(X)$
is the usual Albanese variety of
![]() $X$
, namely,
$X$
, namely,
 $\mathbb{H}^{2d-1}(X,\unicode[STIX]{x1D6FA}_{X}^{{<}d})/H^{2d-1}(X,\mathbb{Z}(d)_{X})$
. Write
$\mathbb{H}^{2d-1}(X,\unicode[STIX]{x1D6FA}_{X}^{{<}d})/H^{2d-1}(X,\mathbb{Z}(d)_{X})$
. Write
![]() $J^{d}(S_{X})$
for the quotient
$J^{d}(S_{X})$
for the quotient
 $$\begin{eqnarray}J^{d}(S_{X})=\frac{H^{2d-1}(S_{X},\mathbb{C}(d))}{F^{0}H^{2d-1}(S_{X},\mathbb{C}(d))+\text{image}\,H^{2d-1}(S_{X},\mathbb{Z}(d))}.\end{eqnarray}$$
$$\begin{eqnarray}J^{d}(S_{X})=\frac{H^{2d-1}(S_{X},\mathbb{C}(d))}{F^{0}H^{2d-1}(S_{X},\mathbb{C}(d))+\text{image}\,H^{2d-1}(S_{X},\mathbb{Z}(d))}.\end{eqnarray}$$
It is a semi-abelian variety by a result of Deligne. By [Reference Esnault, Srinivas and ViehwegESV99, Lemma 3.1], there is a natural surjection
 $$\begin{eqnarray}\unicode[STIX]{x1D713}:A^{d}(S_{X})\rightarrow J^{d}(S_{X})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}:A^{d}(S_{X})\rightarrow J^{d}(S_{X})\end{eqnarray}$$
whose kernel is a
![]() $\mathbb{C}$
-vector space. Moreover, there is a unique structure of algebraic group on
$\mathbb{C}$
-vector space. Moreover, there is a unique structure of algebraic group on
 $A^{d}(S_{X})$
making
$A^{d}(S_{X})$
making
![]() $\unicode[STIX]{x1D713}$
a morphism of algebraic groups, with unipotent kernel.
$\unicode[STIX]{x1D713}$
a morphism of algebraic groups, with unipotent kernel.
Notice that there is a short exact sequence
 $$\begin{eqnarray}0\rightarrow G\rightarrow A^{d}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\ast }}A^{d}(X)\times A^{d}(X)\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow G\rightarrow A^{d}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70B}^{\ast }}A^{d}(X)\times A^{d}(X)\rightarrow 0,\end{eqnarray}$$
where
![]() $G$
is simply defined as the kernel of the map
$G$
is simply defined as the kernel of the map
![]() $\unicode[STIX]{x1D70B}^{\ast }$
, that is surjective since
$\unicode[STIX]{x1D70B}^{\ast }$
, that is surjective since
 $H^{2d}(S_{X},\mathbb{Z}(d))\simeq H^{2d}(\overline{S_{X}},\mathbb{Z}(d))$
and
$H^{2d}(S_{X},\mathbb{Z}(d))\simeq H^{2d}(\overline{S_{X}},\mathbb{Z}(d))$
and
 $\mathbb{H}^{2d-1}(S_{X},\unicode[STIX]{x1D6FA}_{S_{X}}^{{<}d}){\twoheadrightarrow}\mathbb{H}^{2d-1}(\overline{S_{X}},\unicode[STIX]{x1D6FA}_{\overline{S_{X}}}^{{<}d})$
because of GAGA and the fact that
$\mathbb{H}^{2d-1}(S_{X},\unicode[STIX]{x1D6FA}_{S_{X}}^{{<}d}){\twoheadrightarrow}\mathbb{H}^{2d-1}(\overline{S_{X}},\unicode[STIX]{x1D6FA}_{\overline{S_{X}}}^{{<}d})$
because of GAGA and the fact that
![]() $\unicode[STIX]{x1D70B}$
is finite and birational. A combination of (8.3) and (8.4) gives then the short exact sequence
$\unicode[STIX]{x1D70B}$
is finite and birational. A combination of (8.3) and (8.4) gives then the short exact sequence
 $$\begin{eqnarray}0\rightarrow G\rightarrow A^{d}(X|D)\xrightarrow[{}]{\unicode[STIX]{x1D719}}A^{d}(X)\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow G\rightarrow A^{d}(X|D)\xrightarrow[{}]{\unicode[STIX]{x1D719}}A^{d}(X)\rightarrow 0,\end{eqnarray}$$
where the (surjective) forgetful map
![]() $\unicode[STIX]{x1D719}$
is same as the map
$\unicode[STIX]{x1D719}$
is same as the map
 $i_{+}^{\ast }\circ p_{_{+},\ast }:A^{d}(X|D)\rightarrow A^{d}(X)$
.
$i_{+}^{\ast }\circ p_{_{+},\ast }:A^{d}(X|D)\rightarrow A^{d}(X)$
.
8.2.2 The relative Albanese
Taking cohomology of the bottom exact sequence in (8.2), we get exact sequence
 $$\begin{eqnarray}\mathbb{H}^{2d-1}(D,\mathbb{Z}(d)_{D}^{{\mathcal{D}}^{\ast }})\rightarrow \mathbb{H}^{2d}(X,\mathbb{Z}(d)_{(X,D)}^{{\mathcal{D}}^{\ast }})\rightarrow \mathbb{H}^{2d}(X,\mathbb{Z}(d)_{X}^{{\mathcal{D}}})\rightarrow 0,\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{H}^{2d-1}(D,\mathbb{Z}(d)_{D}^{{\mathcal{D}}^{\ast }})\rightarrow \mathbb{H}^{2d}(X,\mathbb{Z}(d)_{(X,D)}^{{\mathcal{D}}^{\ast }})\rightarrow \mathbb{H}^{2d}(X,\mathbb{Z}(d)_{X}^{{\mathcal{D}}})\rightarrow 0,\end{eqnarray}$$
where the term
 $\mathbb{H}^{2d}(D,\mathbb{Z}(d)_{D}^{{\mathcal{D}}^{\ast }})=0$
for dimension reasons.
$\mathbb{H}^{2d}(D,\mathbb{Z}(d)_{D}^{{\mathcal{D}}^{\ast }})=0$
for dimension reasons.
We denote by
 $A^{d}(X,D)$
the kernel of the natural map
$A^{d}(X,D)$
the kernel of the natural map
 $$\begin{eqnarray}\mathbb{H}^{2d}(X,\mathbb{Z}(d)_{(X,D)}^{{\mathcal{D}}^{\ast }})\rightarrow \mathbb{H}^{2d}(X,\mathbb{Z}(d)_{(X,D)})\simeq H^{2d}(X,\mathbb{Z}(d)_{X})=\mathbb{Z},\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{H}^{2d}(X,\mathbb{Z}(d)_{(X,D)}^{{\mathcal{D}}^{\ast }})\rightarrow \mathbb{H}^{2d}(X,\mathbb{Z}(d)_{(X,D)})\simeq H^{2d}(X,\mathbb{Z}(d)_{X})=\mathbb{Z},\end{eqnarray}$$
and call it the relative Albanese variety of the pair
![]() $(X,D)$
. It fits in a short exact sequence
$(X,D)$
. It fits in a short exact sequence
 $$\begin{eqnarray}0\rightarrow \frac{\mathbb{H}^{2d-1}(D,\mathbb{Z}(d)_{D}^{{\mathcal{D}}^{\ast }})}{\mathbb{H}^{2d-1}(X,\mathbb{Z}(d)_{X}^{{\mathcal{D}}})}\rightarrow A^{d}(X,D)\rightarrow A^{d}(X)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \frac{\mathbb{H}^{2d-1}(D,\mathbb{Z}(d)_{D}^{{\mathcal{D}}^{\ast }})}{\mathbb{H}^{2d-1}(X,\mathbb{Z}(d)_{X}^{{\mathcal{D}}})}\rightarrow A^{d}(X,D)\rightarrow A^{d}(X)\rightarrow 0.\end{eqnarray}$$
The vertical maps in (8.2) induce then the following diagram.

Proposition 8.1. Let
![]() $X$
be a smooth projective
$X$
be a smooth projective
![]() $\mathbb{C}$
-scheme of dimension
$\mathbb{C}$
-scheme of dimension
![]() $d\geqslant 1$
. Then the natural map
$d\geqslant 1$
. Then the natural map
 $\unicode[STIX]{x1D719}_{X|D}^{d}:A^{d}(X|D)\rightarrow A^{d}(X,D)$
of (8.6) is an isomorphism.
$\unicode[STIX]{x1D719}_{X|D}^{d}:A^{d}(X|D)\rightarrow A^{d}(X,D)$
of (8.6) is an isomorphism.
Proof. If
![]() $d=1$
, it follows from [Reference Levine and WeibelLW85, Proposition 1.4] and Proposition 12.2 that
$d=1$
, it follows from [Reference Levine and WeibelLW85, Proposition 1.4] and Proposition 12.2 that
 $A^{1}(X|D)\simeq \operatorname{Pic}(X,D)$
. On the other hand, we have
$A^{1}(X|D)\simeq \operatorname{Pic}(X,D)$
. On the other hand, we have
 $$\begin{eqnarray}A^{1}(X,D)=\mathbb{H}^{2}(X,\mathbb{Z}(2)_{(X,D)}^{{\mathcal{D}}^{\ast }})\simeq H^{1}(X,(1+{\mathcal{I}}_{D})^{\times }),\end{eqnarray}$$
$$\begin{eqnarray}A^{1}(X,D)=\mathbb{H}^{2}(X,\mathbb{Z}(2)_{(X,D)}^{{\mathcal{D}}^{\ast }})\simeq H^{1}(X,(1+{\mathcal{I}}_{D})^{\times }),\end{eqnarray}$$
where
![]() ${\mathcal{I}}_{D}$
is the ideal sheaf of
${\mathcal{I}}_{D}$
is the ideal sheaf of
![]() $D\subset X$
. It follows from [Reference Suslin and VoevodskySV96, Lemma 2.1] that
$D\subset X$
. It follows from [Reference Suslin and VoevodskySV96, Lemma 2.1] that
 $H^{1}(X,(1+{\mathcal{I}}_{D})^{\times })\simeq \operatorname{Pic}(X,D)$
and the proposition follows. We can thus assume that
$H^{1}(X,(1+{\mathcal{I}}_{D})^{\times })\simeq \operatorname{Pic}(X,D)$
and the proposition follows. We can thus assume that
![]() $d\geqslant 2$
.
$d\geqslant 2$
.
We can assume that
![]() $X$
is connected. Since the singular cohomology satisfies the Mayer–Vietoris property with respect to the square (8.1), we are left to show that
$X$
is connected. Since the singular cohomology satisfies the Mayer–Vietoris property with respect to the square (8.1), we are left to show that
 $$\begin{eqnarray}\mathbb{H}^{2d-1}(S_{X},\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{{<}d})\xrightarrow[{}]{i_{+}^{\ast }}\mathbb{H}^{2d-1}(X,\unicode[STIX]{x1D6FA}_{(X,D)}^{{<}d})\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{H}^{2d-1}(S_{X},\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{{<}d})\xrightarrow[{}]{i_{+}^{\ast }}\mathbb{H}^{2d-1}(X,\unicode[STIX]{x1D6FA}_{(X,D)}^{{<}d})\end{eqnarray}$$
is bijective. Here,
 $\unicode[STIX]{x1D6FA}_{(X,D)}^{{<}d}=\text{Cone}(\unicode[STIX]{x1D6FA}_{X}^{{<}d}\rightarrow \unicode[STIX]{x1D6FA}_{D}^{{<}d})[-1]$
and the morphism between the cohomology groups is induced by the restriction along
$\unicode[STIX]{x1D6FA}_{(X,D)}^{{<}d}=\text{Cone}(\unicode[STIX]{x1D6FA}_{X}^{{<}d}\rightarrow \unicode[STIX]{x1D6FA}_{D}^{{<}d})[-1]$
and the morphism between the cohomology groups is induced by the restriction along
 $i_{+}:X{\hookrightarrow}S_{X}$
.
$i_{+}:X{\hookrightarrow}S_{X}$
.
Using GAGA, it is equivalent to prove the bijectivity for the cohomology of the associated Zariski sheaves of differential forms. It is easy to check from (2.6) that
![]() $i_{\ast }^{\ast }$
induces an isomorphism
$i_{\ast }^{\ast }$
induces an isomorphism
 ${\mathcal{I}}_{X_{-}}\xrightarrow[{}]{\simeq }{\mathcal{I}}_{D}$
, where
${\mathcal{I}}_{X_{-}}\xrightarrow[{}]{\simeq }{\mathcal{I}}_{D}$
, where
![]() ${\mathcal{I}}_{D}$
is the ideal sheaf for
${\mathcal{I}}_{D}$
is the ideal sheaf for
 $D\subset X_{+}$
. Furthermore,
$D\subset X_{+}$
. Furthermore,
 $(S_{X}\setminus D)=(X_{-}\setminus D)\amalg (X_{+}\setminus D)$
. This information can be used to get a commutative diagram of exact sequences.
$(S_{X}\setminus D)=(X_{-}\setminus D)\amalg (X_{+}\setminus D)$
. This information can be used to get a commutative diagram of exact sequences.

We therefore have to prove that the map of Zariski cohomology groups
 $$\begin{eqnarray}\mathbb{H}^{2d-2}(S_{X},\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{[1,d-1]})\xrightarrow[{}]{i_{+}^{\ast }}\mathbb{H}^{2d-2}(X,\unicode[STIX]{x1D6FA}_{(X,D)}^{[1,d-1]})\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{H}^{2d-2}(S_{X},\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{[1,d-1]})\xrightarrow[{}]{i_{+}^{\ast }}\mathbb{H}^{2d-2}(X,\unicode[STIX]{x1D6FA}_{(X,D)}^{[1,d-1]})\end{eqnarray}$$
is bijective.
We start by proving surjectivity. Letting
![]() ${\mathcal{F}}_{1}[-1]$
and
${\mathcal{F}}_{1}[-1]$
and
![]() ${\mathcal{F}}_{2}[-1]$
denote the kernel and the cokernel of the left vertical arrow in (8.8), respectively, we have an exact sequence
${\mathcal{F}}_{2}[-1]$
denote the kernel and the cokernel of the left vertical arrow in (8.8), respectively, we have an exact sequence
 $$\begin{eqnarray}0\rightarrow {\mathcal{F}}_{1}\rightarrow \unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{[1,d-1]}\xrightarrow[{}]{i_{+}^{\ast }}\unicode[STIX]{x1D6FA}_{(X,D)}^{[1,d-1]}\rightarrow {\mathcal{F}}_{2}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{F}}_{1}\rightarrow \unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{[1,d-1]}\xrightarrow[{}]{i_{+}^{\ast }}\unicode[STIX]{x1D6FA}_{(X,D)}^{[1,d-1]}\rightarrow {\mathcal{F}}_{2}\rightarrow 0.\end{eqnarray}$$
Setting
 ${\mathcal{G}}=\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{[1,d-1]}/{\mathcal{F}}_{1}$
, we obtain a diagram of exact sequences.
${\mathcal{G}}=\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{[1,d-1]}/{\mathcal{F}}_{1}$
, we obtain a diagram of exact sequences.

Since
![]() $d\geqslant 2$
and
$d\geqslant 2$
and
![]() ${\mathcal{F}}_{i}$
are complexes of coherent sheaves supported on
${\mathcal{F}}_{i}$
are complexes of coherent sheaves supported on
![]() $D$
, a standard spectral sequence argument shows that
$D$
, a standard spectral sequence argument shows that
 $\mathbb{H}^{2d-2+j}({\mathcal{F}}_{i})=0$
for
$\mathbb{H}^{2d-2+j}({\mathcal{F}}_{i})=0$
for
![]() $i=1,2$
and
$i=1,2$
and
![]() $j\geqslant 0$
. Analyzing the spectral sequence computing the cohomology group
$j\geqslant 0$
. Analyzing the spectral sequence computing the cohomology group
 $H^{2d-3}({\mathcal{F}}_{2})$
, we see that thanks to the same dimension argument used above, the only surviving term is given by
$H^{2d-3}({\mathcal{F}}_{2})$
, we see that thanks to the same dimension argument used above, the only surviving term is given by
 $H^{d-1}(\unicode[STIX]{x1D6FA}_{(X,D)}^{d-1}/\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{d-1})$
. We thus get an exact sequence
$H^{d-1}(\unicode[STIX]{x1D6FA}_{(X,D)}^{d-1}/\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{d-1})$
. We thus get an exact sequence
 $$\begin{eqnarray}0\rightarrow \frac{H^{d-1}(\unicode[STIX]{x1D6FA}_{(X,D)}^{d-1}/\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{d-1})}{\mathbb{H}^{2d-3}(X,\unicode[STIX]{x1D6FA}_{(X,D)}^{[1,d-1]})}\rightarrow \mathbb{H}^{2d-2}(S_{X},\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{[1,d-1]})\xrightarrow[{}]{i_{+}^{\ast }}\mathbb{H}^{2d-2}(X,\unicode[STIX]{x1D6FA}_{(X,D)}^{[1,d-1]})\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \frac{H^{d-1}(\unicode[STIX]{x1D6FA}_{(X,D)}^{d-1}/\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{d-1})}{\mathbb{H}^{2d-3}(X,\unicode[STIX]{x1D6FA}_{(X,D)}^{[1,d-1]})}\rightarrow \mathbb{H}^{2d-2}(S_{X},\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{[1,d-1]})\xrightarrow[{}]{i_{+}^{\ast }}\mathbb{H}^{2d-2}(X,\unicode[STIX]{x1D6FA}_{(X,D)}^{[1,d-1]})\rightarrow 0\end{eqnarray}$$
and this proves the surjectivity of
![]() $i_{+}^{\ast }$
.
$i_{+}^{\ast }$
.
We now prove injectivity. Write
![]() $D_{\text{sing}}$
for
$D_{\text{sing}}$
for
![]() $|D|_{\text{sing}}$
. Let
$|D|_{\text{sing}}$
. Let
 $U=X\setminus D_{\text{sing}}{\hookrightarrow}X$
and write
$U=X\setminus D_{\text{sing}}{\hookrightarrow}X$
and write
![]() $D_{U}$
for the restriction of
$D_{U}$
for the restriction of
![]() $D$
to
$D$
to
![]() $U$
. We note that
$U$
. We note that
 $(D_{U})_{\text{red}}$
is a smooth (possibly non-connected) divisor on
$(D_{U})_{\text{red}}$
is a smooth (possibly non-connected) divisor on
![]() $U$
. We claim that the restriction to
$U$
. We claim that the restriction to
![]() $U$
of the sheaf
$U$
of the sheaf
 ${\mathcal{F}}_{3}=\unicode[STIX]{x1D6FA}_{(X,D)}^{d-1}/\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{d-1}$
is zero. Note that since
${\mathcal{F}}_{3}=\unicode[STIX]{x1D6FA}_{(X,D)}^{d-1}/\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{d-1}$
is zero. Note that since
![]() ${\mathcal{F}}_{3}$
is anyway supported on
${\mathcal{F}}_{3}$
is anyway supported on
![]() $D$
, our claim actually implies that
$D$
, our claim actually implies that
![]() ${\mathcal{F}}_{3}$
is supported on
${\mathcal{F}}_{3}$
is supported on
 $Y=D_{\text{sing}}$
. Since
$Y=D_{\text{sing}}$
. Since
 $\dim (Y)\leqslant d-2$
, this will give the desired vanishing of the cohomology group
$\dim (Y)\leqslant d-2$
, this will give the desired vanishing of the cohomology group
 $H^{d-1}(\unicode[STIX]{x1D6FA}_{(X,D)}^{d-1}/\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{d-1})$
. Since the first term of the sequence (8.11) is a quotient of
$H^{d-1}(\unicode[STIX]{x1D6FA}_{(X,D)}^{d-1}/\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{d-1})$
. Since the first term of the sequence (8.11) is a quotient of
 $H^{d-1}(\unicode[STIX]{x1D6FA}_{(X,D)}^{d-1}/\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{d-1})$
, this will complete the proof of the proposition.
$H^{d-1}(\unicode[STIX]{x1D6FA}_{(X,D)}^{d-1}/\unicode[STIX]{x1D6FA}_{(S_{X},X_{-})}^{d-1})$
, this will complete the proof of the proposition.
We now prove the claim. Since all the components of
 $(D_{U})_{\text{red}}$
are regular and disjoint, we can assume that at a point
$(D_{U})_{\text{red}}$
are regular and disjoint, we can assume that at a point
![]() $y$
of
$y$
of
![]() $U$
, a local equation for
$U$
, a local equation for
![]() $D_{U}$
is given by
$D_{U}$
is given by
![]() $x^{n}$
, where
$x^{n}$
, where
 $(x,x_{1},\ldots ,x_{d-1})$
is a regular system of parameters in
$(x,x_{1},\ldots ,x_{d-1})$
is a regular system of parameters in
 $A={\mathcal{O}}_{X,y}$
. Write
$A={\mathcal{O}}_{X,y}$
. Write
 $A^{\prime }=A/(x^{n})$
,
$A^{\prime }=A/(x^{n})$
,
 $B=A/(x)$
and let
$B=A/(x)$
and let
![]() $R$
be the double construction applied to the pair
$R$
be the double construction applied to the pair
 $(A,(x^{n}))$
. Write
$(A,(x^{n}))$
. Write
 $\unicode[STIX]{x1D6FA}_{(R,A_{-})}^{d-1}$
for the kernel of the second projection
$\unicode[STIX]{x1D6FA}_{(R,A_{-})}^{d-1}$
for the kernel of the second projection
 $i_{-}^{\ast }:\unicode[STIX]{x1D6FA}_{R/\mathbb{C}}^{d-1}{\twoheadrightarrow}\unicode[STIX]{x1D6FA}_{A/\mathbb{C}}^{d-1}$
and write
$i_{-}^{\ast }:\unicode[STIX]{x1D6FA}_{R/\mathbb{C}}^{d-1}{\twoheadrightarrow}\unicode[STIX]{x1D6FA}_{A/\mathbb{C}}^{d-1}$
and write
![]() $\unicode[STIX]{x1D6FA}_{(A,A^{\prime })}^{d-1}$
for the kernel of the restriction map
$\unicode[STIX]{x1D6FA}_{(A,A^{\prime })}^{d-1}$
for the kernel of the restriction map
 $j^{\ast }:\unicode[STIX]{x1D6FA}_{A/\mathbb{C}}^{d-1}{\twoheadrightarrow}\unicode[STIX]{x1D6FA}_{A^{\prime }/\mathbb{C}}^{d-1}$
. The claim is equivalent to showing that the induced map
$j^{\ast }:\unicode[STIX]{x1D6FA}_{A/\mathbb{C}}^{d-1}{\twoheadrightarrow}\unicode[STIX]{x1D6FA}_{A^{\prime }/\mathbb{C}}^{d-1}$
. The claim is equivalent to showing that the induced map
 $$\begin{eqnarray}i_{+}^{\ast }:\unicode[STIX]{x1D6FA}_{(R,A_{-})}^{d-1}\rightarrow \unicode[STIX]{x1D6FA}_{(A,A^{\prime })}^{d-1}\end{eqnarray}$$
$$\begin{eqnarray}i_{+}^{\ast }:\unicode[STIX]{x1D6FA}_{(R,A_{-})}^{d-1}\rightarrow \unicode[STIX]{x1D6FA}_{(A,A^{\prime })}^{d-1}\end{eqnarray}$$
is surjective.
Since
![]() $A$
is a regular local ring of dimension
$A$
is a regular local ring of dimension
![]() $d$
,
$d$
,
![]() $B$
is a regular local ring of dimension
$B$
is a regular local ring of dimension
![]() $d-1$
and the infinitesimal lifting property (see [Reference HartshorneHar10, Proposition 4.4]) gives a splitting of the projection
$d-1$
and the infinitesimal lifting property (see [Reference HartshorneHar10, Proposition 4.4]) gives a splitting of the projection
 $A^{\prime }\rightarrow B$
. Since the relative embedding dimension of
$A^{\prime }\rightarrow B$
. Since the relative embedding dimension of
![]() $A^{\prime }$
in
$A^{\prime }$
in
![]() $A$
is one, this gives an isomorphism
$A$
is one, this gives an isomorphism
 $A^{\prime }\simeq B[x]/(x^{n})$
. We can then compute the following modules:
$A^{\prime }\simeq B[x]/(x^{n})$
. We can then compute the following modules:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}_{A^{\prime }/\mathbb{C}}^{1} & = & \displaystyle (\unicode[STIX]{x1D6FA}_{B/\mathbb{C}}^{1}\otimes _{B}A^{\prime })\oplus \biggl(\bigoplus _{j=0}^{n-2}Bx^{j}\,dx\biggr)\quad \text{as }B\text{-module};\nonumber\\ \displaystyle \unicode[STIX]{x1D6FA}_{A^{\prime }/\mathbb{C}}^{d-1} & = & \displaystyle (\unicode[STIX]{x1D6FA}_{B/\mathbb{C}}^{d-2}\otimes _{B}A/(x^{n-1})\,dx)\oplus (\unicode[STIX]{x1D6FA}_{B/\mathbb{C}}^{d-1}\otimes _{B}A^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \bigoplus _{i=1}^{d-1}A/(x^{n-1})\,dx\wedge dx_{1}\wedge \cdots \wedge \overset{\vee }{dx_{i}}\wedge \cdots \wedge dx_{d-1}\oplus A^{\prime }\,dx_{1}\wedge \cdots \wedge dx_{d-1};\nonumber\\ \displaystyle \unicode[STIX]{x1D6FA}_{A/\mathbb{C}}^{d-1} & = & \displaystyle \bigoplus _{i=1}^{d-1}(A\,dx\wedge dx_{1}\wedge \cdots \wedge \overset{\vee }{dx_{i}}\wedge \cdots \wedge dx_{d-1})\oplus A\,dx_{1}\wedge \cdots \wedge dx_{d-1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}_{A^{\prime }/\mathbb{C}}^{1} & = & \displaystyle (\unicode[STIX]{x1D6FA}_{B/\mathbb{C}}^{1}\otimes _{B}A^{\prime })\oplus \biggl(\bigoplus _{j=0}^{n-2}Bx^{j}\,dx\biggr)\quad \text{as }B\text{-module};\nonumber\\ \displaystyle \unicode[STIX]{x1D6FA}_{A^{\prime }/\mathbb{C}}^{d-1} & = & \displaystyle (\unicode[STIX]{x1D6FA}_{B/\mathbb{C}}^{d-2}\otimes _{B}A/(x^{n-1})\,dx)\oplus (\unicode[STIX]{x1D6FA}_{B/\mathbb{C}}^{d-1}\otimes _{B}A^{\prime })\nonumber\\ \displaystyle & = & \displaystyle \bigoplus _{i=1}^{d-1}A/(x^{n-1})\,dx\wedge dx_{1}\wedge \cdots \wedge \overset{\vee }{dx_{i}}\wedge \cdots \wedge dx_{d-1}\oplus A^{\prime }\,dx_{1}\wedge \cdots \wedge dx_{d-1};\nonumber\\ \displaystyle \unicode[STIX]{x1D6FA}_{A/\mathbb{C}}^{d-1} & = & \displaystyle \bigoplus _{i=1}^{d-1}(A\,dx\wedge dx_{1}\wedge \cdots \wedge \overset{\vee }{dx_{i}}\wedge \cdots \wedge dx_{d-1})\oplus A\,dx_{1}\wedge \cdots \wedge dx_{d-1}.\nonumber\end{eqnarray}$$
One can easily check from the above expressions that
![]() $\unicode[STIX]{x1D6FA}_{(A,A^{\prime })}^{d-1}$
is generated by the forms
$\unicode[STIX]{x1D6FA}_{(A,A^{\prime })}^{d-1}$
is generated by the forms
 $x^{n}\,dx_{1}\wedge \cdots \wedge dx_{d-1}$
and
$x^{n}\,dx_{1}\wedge \cdots \wedge dx_{d-1}$
and
 $(x^{n-1}\,dx\wedge dx_{1}\wedge \cdots \wedge \overset{\vee }{dx_{i}}\wedge \cdots \wedge dx_{d-1})_{i=1}^{d-1}$
as
$(x^{n-1}\,dx\wedge dx_{1}\wedge \cdots \wedge \overset{\vee }{dx_{i}}\wedge \cdots \wedge dx_{d-1})_{i=1}^{d-1}$
as
![]() $A$
-module.
$A$
-module.
We now consider the following diagram.

We can lift (up to multiplication by elements in
![]() $\mathbb{C}^{\times }$
) the generators
$\mathbb{C}^{\times }$
) the generators
 $x^{n}\,dx_{1}\wedge \cdots \wedge dx_{d-1}$
and
$x^{n}\,dx_{1}\wedge \cdots \wedge dx_{d-1}$
and
 $(x^{n-1}\,dx\wedge dx_{1}\wedge \cdots \wedge \overset{\vee }{dx_{i}}\wedge \cdots \wedge dx_{d-1})_{i=1}^{d-1}$
of
$(x^{n-1}\,dx\wedge dx_{1}\wedge \cdots \wedge \overset{\vee }{dx_{i}}\wedge \cdots \wedge dx_{d-1})_{i=1}^{d-1}$
of
![]() $\unicode[STIX]{x1D6FA}_{(A,A^{\prime })}^{d-1}$
via the projection
$\unicode[STIX]{x1D6FA}_{(A,A^{\prime })}^{d-1}$
via the projection
![]() $i_{+}^{\ast }$
to elements
$i_{+}^{\ast }$
to elements
 $$\begin{eqnarray}\displaystyle & & \displaystyle (x^{n},0)\,d(x_{1},x_{1})\wedge \cdots \wedge d(x_{d-1},x_{d-1}),\nonumber\\ \displaystyle & & \displaystyle (d(x^{n},0)\wedge d(x_{1},x_{1})\wedge \cdots \wedge \overset{\vee }{d(x_{i},x_{i})}\wedge \cdots \wedge d(x_{d-1},x_{d-1}))_{i=1}^{d-1}\quad \text{in }\unicode[STIX]{x1D6FA}_{R/\mathbb{C}}^{d-1}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (x^{n},0)\,d(x_{1},x_{1})\wedge \cdots \wedge d(x_{d-1},x_{d-1}),\nonumber\\ \displaystyle & & \displaystyle (d(x^{n},0)\wedge d(x_{1},x_{1})\wedge \cdots \wedge \overset{\vee }{d(x_{i},x_{i})}\wedge \cdots \wedge d(x_{d-1},x_{d-1}))_{i=1}^{d-1}\quad \text{in }\unicode[STIX]{x1D6FA}_{R/\mathbb{C}}^{d-1}\nonumber\end{eqnarray}$$
and we immediately see that they go to zero via the second projection
![]() $i_{-}^{\ast }$
, so that they lift to elements in
$i_{-}^{\ast }$
, so that they lift to elements in
 $\unicode[STIX]{x1D6FA}_{(R,A_{-})}^{d-1}$
, proving that (8.12) is surjective and therefore completing the proof of the proposition.◻
$\unicode[STIX]{x1D6FA}_{(R,A_{-})}^{d-1}$
, proving that (8.12) is surjective and therefore completing the proof of the proposition.◻
As a consequence of Proposition 8.1, (8.4) and (8.5), it follows that
 $A^{d}(X|D)$
is an extension of the abelian variety
$A^{d}(X|D)$
is an extension of the abelian variety
![]() $A^{d}(X)$
by the linear group
$A^{d}(X)$
by the linear group
 $G=\mathbb{H}^{2d-1}(D,\mathbb{Z}(d)_{D}^{{\mathcal{D}}^{\ast }})/\mathbb{H}^{2d-1}(X,\mathbb{Z}(d)_{X}^{{\mathcal{D}}})$
.
$G=\mathbb{H}^{2d-1}(D,\mathbb{Z}(d)_{D}^{{\mathcal{D}}^{\ast }})/\mathbb{H}^{2d-1}(X,\mathbb{Z}(d)_{X}^{{\mathcal{D}}})$
.
Remark 8.2. If
![]() $X$
is a surface, then one checks that
$X$
is a surface, then one checks that
 $\mathbb{Z}(2)_{(X,D)}^{{\mathcal{D}}^{\ast }}$
is quasi-isomorphic to the complex
$\mathbb{Z}(2)_{(X,D)}^{{\mathcal{D}}^{\ast }}$
is quasi-isomorphic to the complex
 $j_{!}(\mathbb{Z})\rightarrow {\mathcal{I}}_{D}\rightarrow \unicode[STIX]{x1D6FA}_{(X,D)}^{1}$
(see [Reference LevineLev92, § 4]), where
$j_{!}(\mathbb{Z})\rightarrow {\mathcal{I}}_{D}\rightarrow \unicode[STIX]{x1D6FA}_{(X,D)}^{1}$
(see [Reference LevineLev92, § 4]), where
 $j:X\setminus D{\hookrightarrow}X$
is the open inclusion. When
$j:X\setminus D{\hookrightarrow}X$
is the open inclusion. When
![]() $D_{\text{red}}$
is a strict normal crossing divisor, the complex
$D_{\text{red}}$
is a strict normal crossing divisor, the complex
 $j_{!}(\mathbb{Z})\rightarrow {\mathcal{I}}_{D}\rightarrow \unicode[STIX]{x1D6FA}_{(X,D)}^{1}$
is used in [Reference Binda and SaitoBS16] to construct a universal regular quotient of
$j_{!}(\mathbb{Z})\rightarrow {\mathcal{I}}_{D}\rightarrow \unicode[STIX]{x1D6FA}_{(X,D)}^{1}$
is used in [Reference Binda and SaitoBS16] to construct a universal regular quotient of
 $\text{CH}_{0}(X|D)_{\deg 0}$
. One consequence of Proposition 8.1 is that it provides a cohomological proof that the Albanese variety with modulus of § 8.2.1 coincides with the one constructed in [Reference Binda and SaitoBS16] when
$\text{CH}_{0}(X|D)_{\deg 0}$
. One consequence of Proposition 8.1 is that it provides a cohomological proof that the Albanese variety with modulus of § 8.2.1 coincides with the one constructed in [Reference Binda and SaitoBS16] when
![]() $X$
is a surface and
$X$
is a surface and
![]() $D_{\text{red}}$
is strict normal crossing. The universality Theorem 10.3 will tell us, more generally, that the two constructions agree in higher dimension as well, whenever
$D_{\text{red}}$
is strict normal crossing. The universality Theorem 10.3 will tell us, more generally, that the two constructions agree in higher dimension as well, whenever
![]() $D_{\text{red}}$
is strict normal crossing divisor.
$D_{\text{red}}$
is strict normal crossing divisor.
9 An interlude on regular homomorphisms
Let
![]() $k$
be an algebraically closed field and let
$k$
be an algebraically closed field and let
![]() $Y$
be a projective reduced scheme over
$Y$
be a projective reduced scheme over
![]() $k$
. Let
$k$
. Let
 $\text{CH}_{0}^{\text{LW}}(Y)=\text{CH}_{0}^{\text{LW}}(Y,Y_{\text{sing}})$
and
$\text{CH}_{0}^{\text{LW}}(Y)=\text{CH}_{0}^{\text{LW}}(Y,Y_{\text{sing}})$
and
 $\text{CH}_{0}(Y)=\text{CH}_{0}(Y,Y_{\text{sing}})$
be the groups of zero-cycles associated to
$\text{CH}_{0}(Y)=\text{CH}_{0}(Y,Y_{\text{sing}})$
be the groups of zero-cycles associated to
![]() $Y$
. Let
$Y$
. Let
![]() $U$
be a dense open subscheme of
$U$
be a dense open subscheme of
![]() $Y_{\text{reg}}$
and choose a base point
$Y_{\text{reg}}$
and choose a base point
![]() $x_{i}$
in every irreducible component
$x_{i}$
in every irreducible component
![]() $U_{i}$
of
$U_{i}$
of
![]() $U$
. The following definition is taken from [Reference Esnault, Srinivas and ViehwegESV99].
$U$
. The following definition is taken from [Reference Esnault, Srinivas and ViehwegESV99].
Definition 9.1. Let
![]() $G$
be smooth commutative algebraic group over
$G$
be smooth commutative algebraic group over
![]() $k$
. We say that a group homomorphism
$k$
. We say that a group homomorphism
 $\unicode[STIX]{x1D70C}^{\prime }:\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}\rightarrow G$
of abstract groups is a regular homomorphism if the map
$\unicode[STIX]{x1D70C}^{\prime }:\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}\rightarrow G$
of abstract groups is a regular homomorphism if the map
 $\unicode[STIX]{x1D70B}:U\rightarrow G$
with
$\unicode[STIX]{x1D70B}:U\rightarrow G$
with
 $\unicode[STIX]{x1D70B}_{|U_{i}}(x)=\unicode[STIX]{x1D70C}^{\prime }([x]-[x_{i}])$
is a morphism of schemes (i.e., there exists a morphism of schemes whose restriction to closed points coincides with
$\unicode[STIX]{x1D70B}_{|U_{i}}(x)=\unicode[STIX]{x1D70C}^{\prime }([x]-[x_{i}])$
is a morphism of schemes (i.e., there exists a morphism of schemes whose restriction to closed points coincides with
![]() $\unicode[STIX]{x1D70B}$
).
$\unicode[STIX]{x1D70B}$
).
The same definition allows us to talk about regular homomorphisms from the Chow group
 $\text{CH}_{0}(Y)_{\deg 0}$
instead.
$\text{CH}_{0}(Y)_{\deg 0}$
instead.
Remark 9.2. In [Reference Esnault, Srinivas and ViehwegESV99, Definition 1.14], there are other equivalent definitions of regular map from the Levine–Weibel Chow group of 0-cycles on a singular projective variety to a smooth commutative algebraic group. We will not need this explicitly, but we recall one of them for the reader who wishes to remove a reference to the base points.
Let
![]() $U$
be an open dense in
$U$
be an open dense in
![]() $Y_{\text{reg}}$
. Let
$Y_{\text{reg}}$
. Let
 $U_{1},\ldots ,U_{s}$
be the irreducible components of
$U_{1},\ldots ,U_{s}$
be the irreducible components of
![]() $U$
. Consider the map
$U$
. Consider the map
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}^{(-)}:\unicode[STIX]{x1D6F1}_{U}=\mathop{\bigcup }_{i=1}^{s}U_{i}\times U_{i}\rightarrow \text{CH}_{0}^{\text{LW}}(Y)_{ deg0}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}^{(-)}:\unicode[STIX]{x1D6F1}_{U}=\mathop{\bigcup }_{i=1}^{s}U_{i}\times U_{i}\rightarrow \text{CH}_{0}^{\text{LW}}(Y)_{ deg0}\end{eqnarray}$$
defined by
 $\unicode[STIX]{x1D6FE}^{(-)}(u,u^{\prime })=[u]-[u^{\prime }]$
. We then have the following.
$\unicode[STIX]{x1D6FE}^{(-)}(u,u^{\prime })=[u]-[u^{\prime }]$
. We then have the following.
Proposition 9.3 (Corollary 1.13, [Reference Esnault, Srinivas and ViehwegESV99]).
Let
![]() $G$
be a smooth commutative algebraic group. Let
$G$
be a smooth commutative algebraic group. Let
 $\unicode[STIX]{x1D70C}^{\prime }:\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}\rightarrow G$
be a group homomorphism. Then the following conditions are equivalent.
$\unicode[STIX]{x1D70C}^{\prime }:\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}\rightarrow G$
be a group homomorphism. Then the following conditions are equivalent.
-
(i) The composition
 $\unicode[STIX]{x1D70C}^{\prime }\circ \unicode[STIX]{x1D6FE}^{(-)}:\unicode[STIX]{x1D6F1}_{Y_{\text{reg}}}\rightarrow G$
is a morphism of scheme.
$\unicode[STIX]{x1D70C}^{\prime }\circ \unicode[STIX]{x1D6FE}^{(-)}:\unicode[STIX]{x1D6F1}_{Y_{\text{reg}}}\rightarrow G$
is a morphism of scheme. -
(ii) The morphism
 $\unicode[STIX]{x1D70C}^{\prime }$
is regular in the sense of Definition 9.1.
$\unicode[STIX]{x1D70C}^{\prime }$
is regular in the sense of Definition 9.1.
As above, the expression ‘the map
![]() $\unicode[STIX]{x1D719}$
is a morphism of schemes’, stands for ‘there exists a morphisms of schemes whose restriction to closed points coincides with
$\unicode[STIX]{x1D719}$
is a morphism of schemes’, stands for ‘there exists a morphisms of schemes whose restriction to closed points coincides with
![]() $\unicode[STIX]{x1D719}$
’.
$\unicode[STIX]{x1D719}$
’.
9.1 The case of the double
Let
![]() $X$
be now a smooth connected projective
$X$
be now a smooth connected projective
![]() $k$
-variety, equipped with an effective Cartier divisor
$k$
-variety, equipped with an effective Cartier divisor
![]() $D$
and let
$D$
and let
![]() $X_{+}$
and
$X_{+}$
and
![]() $X_{-}$
denote as above the irreducible components of the double
$X_{-}$
denote as above the irreducible components of the double
![]() $S_{X}$
of
$S_{X}$
of
![]() $X$
along
$X$
along
![]() $D$
. Given any dense open subset
$D$
. Given any dense open subset
 $V\subset (S_{X})_{\text{reg}}$
, we denote by
$V\subset (S_{X})_{\text{reg}}$
, we denote by
![]() $V_{+}$
and
$V_{+}$
and
![]() $V_{-}$
the intersection of
$V_{-}$
the intersection of
![]() $V$
with
$V$
with
![]() $X_{+}^{o}$
and
$X_{+}^{o}$
and
![]() $X_{-}^{o}$
respectively. We adapt the definition of regular homomorphism recalled above to the particular geometry of the double
$X_{-}^{o}$
respectively. We adapt the definition of regular homomorphism recalled above to the particular geometry of the double
![]() $S_{X}$
.
$S_{X}$
.
Definition 9.4. Let
![]() $G$
be a smooth commutative algebraic group over
$G$
be a smooth commutative algebraic group over
![]() $k$
. A homomorphism
$k$
. A homomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\prime }:\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow G\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\prime }:\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow G\end{eqnarray}$$
is called a regular homomorphism if given base points
![]() $x_{0,\pm }$
on each irreducible components
$x_{0,\pm }$
on each irreducible components
![]() $V_{\pm }$
of some open dense subscheme
$V_{\pm }$
of some open dense subscheme
![]() $V$
of
$V$
of
![]() $(S_{X})_{\text{reg}}$
, the composition of
$(S_{X})_{\text{reg}}$
, the composition of
![]() $\unicode[STIX]{x1D70C}^{\prime }$
with the map
$\unicode[STIX]{x1D70C}^{\prime }$
with the map
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{x_{0,\pm }}^{V}:V\rightarrow \text{CH}_{0}(S_{X})_{\deg 0},\quad x\mapsto [x]-[x_{0,\unicode[STIX]{x1D703}(x)}],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{x_{0,\pm }}^{V}:V\rightarrow \text{CH}_{0}(S_{X})_{\deg 0},\quad x\mapsto [x]-[x_{0,\unicode[STIX]{x1D703}(x)}],\end{eqnarray}$$
where
 $\unicode[STIX]{x1D703}(x)=\pm$
according to
$\unicode[STIX]{x1D703}(x)=\pm$
according to
![]() $x\in V_{\pm }$
, is a morphism of schemes. In a similar fashion, one can define the notion of regular homomorphism using the Levine–Weibel Chow group of
$x\in V_{\pm }$
, is a morphism of schemes. In a similar fashion, one can define the notion of regular homomorphism using the Levine–Weibel Chow group of
![]() $0$
-cycles on the double
$0$
-cycles on the double
![]() $S_{X}$
.
$S_{X}$
.
It follows from [Reference Esnault, Srinivas and ViehwegESV99, Lemma 1.4] that the image of a regular homomorphism is a connected algebraic closed subgroup of
![]() $G$
. The initial object (whose underlying map is necessarily surjective) in the category of regular maps
$G$
. The initial object (whose underlying map is necessarily surjective) in the category of regular maps
 $\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow G$
is called the universal regular quotient of
$\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow G$
is called the universal regular quotient of
 $\text{CH}_{0}(S_{X})_{\deg 0}$
. It was shown in [Reference Esnault, Srinivas and ViehwegESV99] that the universal regular quotient of
$\text{CH}_{0}(S_{X})_{\deg 0}$
. It was shown in [Reference Esnault, Srinivas and ViehwegESV99] that the universal regular quotient of
 $\text{CH}^{\text{LW}}(Y)_{\deg 0}$
always exists for any projective variety
$\text{CH}^{\text{LW}}(Y)_{\deg 0}$
always exists for any projective variety
![]() $Y$
over
$Y$
over
![]() $k$
. We state this theorem below for
$k$
. We state this theorem below for
![]() $S_{X}$
.
$S_{X}$
.
Theorem 9.5 [Reference Esnault, Srinivas and ViehwegESV99, Theorem 1].
There exists a smooth connected algebraic group
 $\text{Alb}(S_{X})$
, together with a regular surjective homomorphism
$\text{Alb}(S_{X})$
, together with a regular surjective homomorphism
 $\unicode[STIX]{x1D70C}_{S_{X}}:\text{CH}_{0}^{\text{LW}}(S_{X})_{\deg 0}\rightarrow \text{Alb}(S_{X})$
such that
$\unicode[STIX]{x1D70C}_{S_{X}}:\text{CH}_{0}^{\text{LW}}(S_{X})_{\deg 0}\rightarrow \text{Alb}(S_{X})$
such that
![]() $\unicode[STIX]{x1D70C}_{S_{X}}$
is universal among regular homomorphisms from
$\unicode[STIX]{x1D70C}_{S_{X}}$
is universal among regular homomorphisms from
 $\text{CH}_{0}^{\text{LW}}(S_{X})_{\deg 0}$
to smooth commutative algebraic groups. When
$\text{CH}_{0}^{\text{LW}}(S_{X})_{\deg 0}$
to smooth commutative algebraic groups. When
![]() $k=\mathbb{C}$
, then
$k=\mathbb{C}$
, then
 $\text{Alb}(S_{X})$
coincides with the Albanese variety
$\text{Alb}(S_{X})$
coincides with the Albanese variety
 $A^{d}(S_{X})$
introduced in (8.3).
$A^{d}(S_{X})$
introduced in (8.3).
9.2 The universal semi-abelian quotient of
 $\text{CH}_{0}(Y)_{\deg 0}$
$\text{CH}_{0}(Y)_{\deg 0}$
Let
![]() $Y$
be a reduced projective scheme of dimension
$Y$
be a reduced projective scheme of dimension
![]() $d\geqslant 1$
over an algebraically closed field
$d\geqslant 1$
over an algebraically closed field
![]() $k$
. Let us assume the characteristic of
$k$
. Let us assume the characteristic of
![]() $k$
to be positive in this subsection. In this case, do not know if the canonical map
$k$
to be positive in this subsection. In this case, do not know if the canonical map
 $\text{CH}_{0}^{\text{LW}}(Y)\rightarrow \text{CH}_{0}(Y)$
is an isomorphism. A weaker question is if the Albanese map
$\text{CH}_{0}^{\text{LW}}(Y)\rightarrow \text{CH}_{0}(Y)$
is an isomorphism. A weaker question is if the Albanese map
 $\unicode[STIX]{x1D70C}_{Y}:\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}\rightarrow \text{Alb}(Y)$
factors through
$\unicode[STIX]{x1D70C}_{Y}:\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}\rightarrow \text{Alb}(Y)$
factors through
 $\text{CH}_{0}(Y)_{\deg 0}$
. We expect this to be true, but we do not yet know how to verify this either. The reason for this is that, one does not know any description of the Albanese variety in positive characteristic except its existence. We however show in this section that the semi-abelian Albanese variety of
$\text{CH}_{0}(Y)_{\deg 0}$
. We expect this to be true, but we do not yet know how to verify this either. The reason for this is that, one does not know any description of the Albanese variety in positive characteristic except its existence. We however show in this section that the semi-abelian Albanese variety of
![]() $Y$
indeed has this property. We shall use this to prove a comparison result for the two Chow groups in positive characteristic.
$Y$
indeed has this property. We shall use this to prove a comparison result for the two Chow groups in positive characteristic.
The following description of the semi-abelian Albanese variety of
![]() $Y$
is recalled from [Reference MallickMal09, § 2]. Let
$Y$
is recalled from [Reference MallickMal09, § 2]. Let
 $\unicode[STIX]{x1D70B}:Y^{N}\rightarrow Y$
denote the normalization map. Let
$\unicode[STIX]{x1D70B}:Y^{N}\rightarrow Y$
denote the normalization map. Let
 $\text{Cl}(Y^{N})$
and
$\text{Cl}(Y^{N})$
and
 $\operatorname{Pic}_{W}(Y^{N})$
denote the class group and the Weil Picard group of
$\operatorname{Pic}_{W}(Y^{N})$
denote the class group and the Weil Picard group of
![]() $Y^{N}$
. Recall (see e.g. [Reference WeilWei54]) that
$Y^{N}$
. Recall (see e.g. [Reference WeilWei54]) that
 $\operatorname{Pic}_{W}(Y^{N})$
is the subgroup of
$\operatorname{Pic}_{W}(Y^{N})$
is the subgroup of
 $\text{Cl}(Y^{N})$
consisting of Weil divisors which are algebraically equivalent to zero in the sense of [Reference FultonFul98, ch. 19]. Let
$\text{Cl}(Y^{N})$
consisting of Weil divisors which are algebraically equivalent to zero in the sense of [Reference FultonFul98, ch. 19]. Let
![]() $\text{Div}(Y)$
denote the free abelian group of Weil divisors on
$\text{Div}(Y)$
denote the free abelian group of Weil divisors on
![]() $Y$
. Let
$Y$
. Let
![]() $\unicode[STIX]{x1D6EC}_{1}(Y)$
denote the subgroup of
$\unicode[STIX]{x1D6EC}_{1}(Y)$
denote the subgroup of
 $\text{Div}(Y^{N})$
generated by the Weil divisors which are supported on
$\text{Div}(Y^{N})$
generated by the Weil divisors which are supported on
 $\unicode[STIX]{x1D70B}^{-1}(Y_{\text{sing}})$
. This gives us a map
$\unicode[STIX]{x1D70B}^{-1}(Y_{\text{sing}})$
. This gives us a map
 $\unicode[STIX]{x1D704}_{Y}:\unicode[STIX]{x1D6EC}_{1}(Y)\rightarrow \text{Cl}(Y^{N})/\text{Pic}_{W}(Y^{N})$
.
$\unicode[STIX]{x1D704}_{Y}:\unicode[STIX]{x1D6EC}_{1}(Y)\rightarrow \text{Cl}(Y^{N})/\text{Pic}_{W}(Y^{N})$
.
Let
![]() $\unicode[STIX]{x1D6EC}(Y)$
denote the kernel of the canonical map
$\unicode[STIX]{x1D6EC}(Y)$
denote the kernel of the canonical map
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{1}(Y)\xrightarrow[{}]{(\unicode[STIX]{x1D704}_{Y},\unicode[STIX]{x1D70B}_{\ast })}\frac{\text{Cl}(Y^{N})}{\operatorname{Pic}_{W}(Y^{N})}\oplus \text{Div}(Y).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{1}(Y)\xrightarrow[{}]{(\unicode[STIX]{x1D704}_{Y},\unicode[STIX]{x1D70B}_{\ast })}\frac{\text{Cl}(Y^{N})}{\operatorname{Pic}_{W}(Y^{N})}\oplus \text{Div}(Y).\end{eqnarray}$$
The semi-abelian Albanese variety of
![]() $Y$
is the Cartier dual of the 1-motive
$Y$
is the Cartier dual of the 1-motive
 $$\begin{eqnarray}[\unicode[STIX]{x1D6EC}(Y)\rightarrow \operatorname{Pic}_{W}(Y^{N})]\end{eqnarray}$$
$$\begin{eqnarray}[\unicode[STIX]{x1D6EC}(Y)\rightarrow \operatorname{Pic}_{W}(Y^{N})]\end{eqnarray}$$
and is denoted by
![]() $J^{d}(Y)$
. It follows from [Reference MallickMal09, § 4] that
$J^{d}(Y)$
. It follows from [Reference MallickMal09, § 4] that
![]() $J^{d}(Y)$
is the universal semi-abelian quotient of the Esnault–Srinivas–Viehweg Albanese variety
$J^{d}(Y)$
is the universal semi-abelian quotient of the Esnault–Srinivas–Viehweg Albanese variety
![]() $\text{Alb}(Y)$
. Let
$\text{Alb}(Y)$
. Let
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{Y}^{\text{semi}}:\text{CH}_{0}^{\text{LW}}(Y)_{ deg0}{\twoheadrightarrow}J^{d}(Y)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{Y}^{\text{semi}}:\text{CH}_{0}^{\text{LW}}(Y)_{ deg0}{\twoheadrightarrow}J^{d}(Y)\end{eqnarray}$$
denote the universal regular homomorphism.
Lemma 9.6. Let
 $f:Z\rightarrow Y$
be a smooth projective morphism of relative dimension
$f:Z\rightarrow Y$
be a smooth projective morphism of relative dimension
![]() $r$
. Then there is a push-forward map
$r$
. Then there is a push-forward map
 $f_{\ast }^{\text{semi}}:J^{d+r}(Z)\rightarrow J^{d}(Y)$
and a commutative diagram.
$f_{\ast }^{\text{semi}}:J^{d+r}(Z)\rightarrow J^{d}(Y)$
and a commutative diagram.

Proof. Since
![]() $f$
is smooth and projective, it follows that
$f$
is smooth and projective, it follows that
 $f^{N}:Z^{N}\rightarrow Y^{N}$
is also smooth and projective. It is clear that the flat pull-back
$f^{N}:Z^{N}\rightarrow Y^{N}$
is also smooth and projective. It is clear that the flat pull-back
![]() $f^{N,\ast }$
takes integral Weil divisors to integral Weil divisors. It is also clear that this map preserves Weil divisors which are algebraically equivalent to zero. Since
$f^{N,\ast }$
takes integral Weil divisors to integral Weil divisors. It is also clear that this map preserves Weil divisors which are algebraically equivalent to zero. Since
 $Z_{\text{sing}}=f^{-1}(Y_{\text{sing}})$
, we see that
$Z_{\text{sing}}=f^{-1}(Y_{\text{sing}})$
, we see that
 $f^{N,\ast }(\unicode[STIX]{x1D6EC}_{1}(Y))\subset \unicode[STIX]{x1D6EC}_{1}(Z)$
. Furthermore, it follows from [Reference FultonFul98, Proposition 1.7] that
$f^{N,\ast }(\unicode[STIX]{x1D6EC}_{1}(Y))\subset \unicode[STIX]{x1D6EC}_{1}(Z)$
. Furthermore, it follows from [Reference FultonFul98, Proposition 1.7] that
 $f^{N,\ast }(\text{Ker}(\unicode[STIX]{x1D6EC}_{1}(Y))\rightarrow \text{Div}(Y))\subset \text{Ker}(\unicode[STIX]{x1D6EC}_{1}(Z)\rightarrow \text{Div}(Z))$
. We conclude that
$f^{N,\ast }(\text{Ker}(\unicode[STIX]{x1D6EC}_{1}(Y))\rightarrow \text{Div}(Y))\subset \text{Ker}(\unicode[STIX]{x1D6EC}_{1}(Z)\rightarrow \text{Div}(Z))$
. We conclude that
![]() $f^{\ast }$
induces a morphism of 1-motives
$f^{\ast }$
induces a morphism of 1-motives
 $f^{\ast }:[\unicode[STIX]{x1D6EC}(Y)\rightarrow \operatorname{Pic}_{W}(Y^{N})]\rightarrow [\unicode[STIX]{x1D6EC}(Z)\rightarrow \operatorname{Pic}_{W}(Z^{N})]$
and hence a map
$f^{\ast }:[\unicode[STIX]{x1D6EC}(Y)\rightarrow \operatorname{Pic}_{W}(Y^{N})]\rightarrow [\unicode[STIX]{x1D6EC}(Z)\rightarrow \operatorname{Pic}_{W}(Z^{N})]$
and hence a map
 $f_{\ast }:J^{d+r}(Z)\rightarrow J^{d}(Y)$
.
$f_{\ast }:J^{d+r}(Z)\rightarrow J^{d}(Y)$
.
To show the commutative diagram (9.2), we need to observe that
![]() $J^{d}(Y)$
is a quotient of the Cartier dual
$J^{d}(Y)$
is a quotient of the Cartier dual
 $J_{\text{Serre}}^{d}(Y)$
of the 1-motive
$J_{\text{Serre}}^{d}(Y)$
of the 1-motive
 $[\unicode[STIX]{x1D6EC}_{1}(Y)\rightarrow \operatorname{Pic}_{W}(Y^{N})]$
and this dual semi-abelian variety is the universal object in the category of morphisms from
$[\unicode[STIX]{x1D6EC}_{1}(Y)\rightarrow \operatorname{Pic}_{W}(Y^{N})]$
and this dual semi-abelian variety is the universal object in the category of morphisms from
![]() $Y_{\text{reg}}$
to semi-abelian varieties (see [Reference SerreSer60]). Since
$Y_{\text{reg}}$
to semi-abelian varieties (see [Reference SerreSer60]). Since
 $Z_{\text{reg}}=f^{-1}(Y_{\text{reg}})$
, it follows from this universality of
$Z_{\text{reg}}=f^{-1}(Y_{\text{reg}})$
, it follows from this universality of
 $J_{\text{Serre}}^{d}(Y)$
that there is a commutative diagram as in (9.2) if we replace
$J_{\text{Serre}}^{d}(Y)$
that there is a commutative diagram as in (9.2) if we replace
![]() $J^{d}(Y)$
by
$J^{d}(Y)$
by
 $J_{\text{Serre}}^{d}(Y)$
. The commutative diagram
$J_{\text{Serre}}^{d}(Y)$
. The commutative diagram

now finishes the proof. ◻
Proposition 9.7. The semi-abelian variety
![]() $J^{d}(Y)$
is the universal regular semi-abelian variety quotient of
$J^{d}(Y)$
is the universal regular semi-abelian variety quotient of
 $\text{CH}_{0}(Y)_{\deg 0}$
.
$\text{CH}_{0}(Y)_{\deg 0}$
.
Proof. Let
![]() $S$
denote the singular locus of
$S$
denote the singular locus of
![]() $Y$
. It is enough to show that
$Y$
. It is enough to show that
 $\unicode[STIX]{x1D70C}_{Y}^{\text{semi}}:\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}{\twoheadrightarrow}J^{d}(Y)$
factors through the canonical map
$\unicode[STIX]{x1D70C}_{Y}^{\text{semi}}:\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}{\twoheadrightarrow}J^{d}(Y)$
factors through the canonical map
 $\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}{\twoheadrightarrow}\text{CH}_{0}(Y)_{\deg 0}$
. Let then
$\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}{\twoheadrightarrow}\text{CH}_{0}(Y)_{\deg 0}$
. Let then
 $\unicode[STIX]{x1D708}:C\rightarrow Y$
be a finite l.c.i. map from a good curve
$\unicode[STIX]{x1D708}:C\rightarrow Y$
be a finite l.c.i. map from a good curve
![]() $C$
relative to
$C$
relative to
![]() $S\subset Y$
and let
$S\subset Y$
and let
 $f\in {\mathcal{O}}_{C,E}^{\times }$
for
$f\in {\mathcal{O}}_{C,E}^{\times }$
for
 $E=C_{\text{sing}}\cup \unicode[STIX]{x1D708}^{-1}(S)$
.
$E=C_{\text{sing}}\cup \unicode[STIX]{x1D708}^{-1}(S)$
.
As in Lemma 5.2, we factor
![]() $\unicode[STIX]{x1D708}$
as composition
$\unicode[STIX]{x1D708}$
as composition
 $\unicode[STIX]{x1D708}=\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D707}$
, where
$\unicode[STIX]{x1D708}=\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D707}$
, where
 $\unicode[STIX]{x1D707}:C{\hookrightarrow}\mathbb{P}_{Y}^{N}$
is a regular embedding and
$\unicode[STIX]{x1D707}:C{\hookrightarrow}\mathbb{P}_{Y}^{N}$
is a regular embedding and
 $\unicode[STIX]{x1D70B}:\mathbb{P}_{Y}^{N}\rightarrow Y$
is the projection. By Lemma 9.6, we have the commutative diagram
$\unicode[STIX]{x1D70B}:\mathbb{P}_{Y}^{N}\rightarrow Y$
is the projection. By Lemma 9.6, we have the commutative diagram

where
![]() $\tilde{\unicode[STIX]{x1D70C}}^{\text{semi}}$
denotes on both vertical sides of the diagram the composition of the universal map
$\tilde{\unicode[STIX]{x1D70C}}^{\text{semi}}$
denotes on both vertical sides of the diagram the composition of the universal map
![]() $\unicode[STIX]{x1D70C}^{\text{semi}}$
with the canonical map
$\unicode[STIX]{x1D70C}^{\text{semi}}$
with the canonical map
 ${\mathcal{Z}}_{0}(-)_{\deg 0}\rightarrow \text{CH}_{0}^{\text{LW}}(-)_{\deg 0}$
. Since
${\mathcal{Z}}_{0}(-)_{\deg 0}\rightarrow \text{CH}_{0}^{\text{LW}}(-)_{\deg 0}$
. Since
 $\tilde{\unicode[STIX]{x1D70C}}_{\mathbb{P}_{Y}^{N}}^{\text{semi}}(\unicode[STIX]{x1D707}_{\ast }((\text{div})_{C}(f)))=0$
in
$\tilde{\unicode[STIX]{x1D70C}}_{\mathbb{P}_{Y}^{N}}^{\text{semi}}(\unicode[STIX]{x1D707}_{\ast }((\text{div})_{C}(f)))=0$
in
 $J^{d+N}(\mathbb{P}_{Y}^{N})$
, the result follows.◻
$J^{d+N}(\mathbb{P}_{Y}^{N})$
, the result follows.◻
Using Proposition 9.7 and Theorem 11.1, we obtain the following comparison between the torsion parts of the Levine–Weibel Chow group and our modified definition.
Theorem 9.8. Let
![]() $Y$
be an equidimensional reduced projective scheme of dimension
$Y$
be an equidimensional reduced projective scheme of dimension
![]() $d\geqslant 1$
over an algebraically closed field
$d\geqslant 1$
over an algebraically closed field
![]() $k$
of exponential characteristic
$k$
of exponential characteristic
![]() $p$
. Then the canonical map
$p$
. Then the canonical map
 $\text{CH}_{0}^{\text{LW}}(Y)\{l\}\xrightarrow[{}]{\simeq }\text{CH}_{0}(Y)\{l\}$
between the
$\text{CH}_{0}^{\text{LW}}(Y)\{l\}\xrightarrow[{}]{\simeq }\text{CH}_{0}(Y)\{l\}$
between the
![]() $l$
-primary torsion subgroups, is an isomorphism for every prime
$l$
-primary torsion subgroups, is an isomorphism for every prime
![]() $l\neq p$
.
$l\neq p$
.
Proof. Let
![]() $L$
denote the kernel of the canonical surjective map
$L$
denote the kernel of the canonical surjective map
 $\text{CH}_{0}^{\text{LW}}(Y){\twoheadrightarrow}\text{CH}_{0}(Y)$
. We first show that
$\text{CH}_{0}^{\text{LW}}(Y){\twoheadrightarrow}\text{CH}_{0}(Y)$
. We first show that
![]() $L$
is a
$L$
is a
![]() $p$
-primary group of bounded exponent. It follows from Proposition 9.7 that the semi-Albanese map
$p$
-primary group of bounded exponent. It follows from Proposition 9.7 that the semi-Albanese map
![]() $\unicode[STIX]{x1D70C}_{Y}^{\text{semi}}$
from
$\unicode[STIX]{x1D70C}_{Y}^{\text{semi}}$
from
 $\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}$
to
$\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}$
to
![]() $J^{d}(Y)$
factors through
$J^{d}(Y)$
factors through
 $\text{CH}_{0}(Y)_{\deg 0}$
. Since
$\text{CH}_{0}(Y)_{\deg 0}$
. Since
![]() $\unicode[STIX]{x1D70C}_{Y}^{\text{semi}}$
is an isomorphism on
$\unicode[STIX]{x1D70C}_{Y}^{\text{semi}}$
is an isomorphism on
![]() $n$
-torsion subgroups for
$n$
-torsion subgroups for
![]() $n$
prime to
$n$
prime to
![]() $p$
by Theorem 11.1, we immediately deduce that
$p$
by Theorem 11.1, we immediately deduce that
![]() $L$
(which is the same as
$L$
(which is the same as
 $\text{Ker}(\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}\rightarrow \text{CH}_{0}(Y)_{\deg 0})$
) is a
$\text{Ker}(\text{CH}_{0}^{\text{LW}}(Y)_{\deg 0}\rightarrow \text{CH}_{0}(Y)_{\deg 0})$
) is a
![]() $p$
-torsion group. We now show that
$p$
-torsion group. We now show that
![]() $L$
has a bounded exponent.
$L$
has a bounded exponent.
We first note from Lemma 3.13 that there is a factorization
 $$\begin{eqnarray}\text{CH}_{0}^{\text{LW}}(Y)\xrightarrow[{}]{\text{can}}\text{CH}_{0}(Y)\xrightarrow[{}]{\text{cyc}_{Y}}K_{0}(Y)\end{eqnarray}$$
$$\begin{eqnarray}\text{CH}_{0}^{\text{LW}}(Y)\xrightarrow[{}]{\text{can}}\text{CH}_{0}(Y)\xrightarrow[{}]{\text{cyc}_{Y}}K_{0}(Y)\end{eqnarray}$$
of the cycle class map
![]() $\text{cyc}_{Y}^{\text{LW}}$
from the Levine–Weibel Chow group to
$\text{cyc}_{Y}^{\text{LW}}$
from the Levine–Weibel Chow group to
![]() $K_{0}(Y)$
. On the other hand, it follows from [Reference LevineLev85b, Corollary 5.4] (see also [Reference LevineLev87, Corollary 2.7]) that the kernel of the map
$K_{0}(Y)$
. On the other hand, it follows from [Reference LevineLev85b, Corollary 5.4] (see also [Reference LevineLev87, Corollary 2.7]) that the kernel of the map
![]() $\text{cyc}_{Y}^{\text{LW}}$
is a group of exponent
$\text{cyc}_{Y}^{\text{LW}}$
is a group of exponent
 $N_{d}:=(d-1)!$
. We conclude that
$N_{d}:=(d-1)!$
. We conclude that
 $N_{d}\cdot L=0$
.
$N_{d}\cdot L=0$
.
We write
 $N_{d}=p^{a}q$
, where
$N_{d}=p^{a}q$
, where
![]() $a\geqslant 0$
and
$a\geqslant 0$
and
![]() $p\nmid q$
. We fix a cycle
$p\nmid q$
. We fix a cycle
![]() $\unicode[STIX]{x1D6FC}\in L$
. Since
$\unicode[STIX]{x1D6FC}\in L$
. Since
![]() $L$
is a
$L$
is a
![]() $p$
-primary group, we can write
$p$
-primary group, we can write
 $p^{n}\unicode[STIX]{x1D6FC}=0$
for some
$p^{n}\unicode[STIX]{x1D6FC}=0$
for some
![]() $n\gg a$
. We then have an identity
$n\gg a$
. We then have an identity
 $xq+yp^{n-a}=1$
for some
$xq+yp^{n-a}=1$
for some
 $x,y\in \mathbb{Z}$
. This yields
$x,y\in \mathbb{Z}$
. This yields
 $$\begin{eqnarray}p^{a}\unicode[STIX]{x1D6FC}=(xq+yp^{n-a})p^{a}\unicode[STIX]{x1D6FC}=(xqp^{a}+yp^{n})\unicode[STIX]{x1D6FC}=xN_{d}\unicode[STIX]{x1D6FC}+yp^{n}\unicode[STIX]{x1D6FC}=0.\end{eqnarray}$$
$$\begin{eqnarray}p^{a}\unicode[STIX]{x1D6FC}=(xq+yp^{n-a})p^{a}\unicode[STIX]{x1D6FC}=(xqp^{a}+yp^{n})\unicode[STIX]{x1D6FC}=xN_{d}\unicode[STIX]{x1D6FC}+yp^{n}\unicode[STIX]{x1D6FC}=0.\end{eqnarray}$$
Since
![]() $a\in \mathbb{Z}$
depends only on
$a\in \mathbb{Z}$
depends only on
![]() $N_{d}$
and not on
$N_{d}$
and not on
![]() $\unicode[STIX]{x1D6FC}$
, we get
$\unicode[STIX]{x1D6FC}$
, we get
 $p^{a}\cdot L=0$
.
$p^{a}\cdot L=0$
.
It is easy to see, using the Five Lemma, that for every prime
![]() $l\neq p$
, there is an exact sequence
$l\neq p$
, there is an exact sequence
 $$\begin{eqnarray}0\rightarrow L\{l\}\rightarrow \text{CH}_{0}^{\text{LW}}(Y)\{l\}\rightarrow \text{CH}_{0}(Y)\{l\}\rightarrow L\otimes _{\mathbb{Z}}\mathbb{Q}_{l}/\mathbb{Z}_{l}.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow L\{l\}\rightarrow \text{CH}_{0}^{\text{LW}}(Y)\{l\}\rightarrow \text{CH}_{0}(Y)\{l\}\rightarrow L\otimes _{\mathbb{Z}}\mathbb{Q}_{l}/\mathbb{Z}_{l}.\end{eqnarray}$$
Since
![]() $L$
is a
$L$
is a
![]() $p$
-primary group of bounded exponent and
$p$
-primary group of bounded exponent and
![]() $\mathbb{Q}_{l}/\mathbb{Z}_{l}$
is
$\mathbb{Q}_{l}/\mathbb{Z}_{l}$
is
![]() $p$
-divisible, we must have
$p$
-divisible, we must have
 $L\{l\}=0=L\otimes _{\mathbb{Z}}\mathbb{Q}_{l}/\mathbb{Z}_{l}$
. In particular,
$L\{l\}=0=L\otimes _{\mathbb{Z}}\mathbb{Q}_{l}/\mathbb{Z}_{l}$
. In particular,
 $\text{CH}_{0}^{\text{LW}}(Y)\{l\}\xrightarrow[{}]{\simeq }\text{CH}_{0}(Y)\{l\}$
.◻
$\text{CH}_{0}^{\text{LW}}(Y)\{l\}\xrightarrow[{}]{\simeq }\text{CH}_{0}(Y)\{l\}$
.◻
Corollary 9.9. Let
![]() $k$
be an algebraically closed field of exponential characteristic
$k$
be an algebraically closed field of exponential characteristic
![]() $p$
. Let
$p$
. Let
![]() $Y$
be an equidimensional reduced projective scheme of dimension
$Y$
be an equidimensional reduced projective scheme of dimension
![]() $d\leqslant p$
. Then the canonical map
$d\leqslant p$
. Then the canonical map
 $\text{CH}_{0}^{\text{LW}}(Y)\rightarrow \text{CH}_{0}(Y)$
is an isomorphism.
$\text{CH}_{0}^{\text{LW}}(Y)\rightarrow \text{CH}_{0}(Y)$
is an isomorphism.
9.3 Regular homomorphism from Chow group with modulus
We now turn to the definition of a regular morphism for the Chow group of
![]() $0$
-cycles with modulus. Let
$0$
-cycles with modulus. Let
![]() $(X,D)$
be as in 9.1. We write
$(X,D)$
be as in 9.1. We write
![]() $X^{o}$
for the open complement of
$X^{o}$
for the open complement of
![]() $D$
in
$D$
in
![]() $X$
.
$X$
.
Definition 9.10. We fix a closed point
 $x_{0}\in X^{o}$
. For
$x_{0}\in X^{o}$
. For
 $U\subset X^{o}$
open with
$U\subset X^{o}$
open with
![]() $x_{0}\in U$
, we define the map of sets
$x_{0}\in U$
, we define the map of sets
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{x_{0}}^{U}:U\rightarrow \text{CH}_{0}(X|D)_{\deg 0},\quad x\mapsto [x]-[x_{0}],\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{x_{0}}^{U}:U\rightarrow \text{CH}_{0}(X|D)_{\deg 0},\quad x\mapsto [x]-[x_{0}],\end{eqnarray}$$
where
![]() $[x]$
and
$[x]$
and
![]() $[x_{0}]$
denote the classes of
$[x_{0}]$
denote the classes of
![]() $x$
and
$x$
and
![]() $x_{0}$
respectively in
$x_{0}$
respectively in
 $\text{CH}_{0}(X|D)$
. For a commutative algebraic group
$\text{CH}_{0}(X|D)$
. For a commutative algebraic group
![]() $G$
over
$G$
over
![]() $k$
, we say that a homomorphism of abelian groups
$k$
, we say that a homomorphism of abelian groups
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow G\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow G\end{eqnarray}$$
is regular if there exists an open subset
![]() $U$
of
$U$
of
![]() $X^{o}$
and a closed point
$X^{o}$
and a closed point
![]() $x_{0}\in U$
such that
$x_{0}\in U$
such that
 $\unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D70B}_{x_{0}}^{U}:U\rightarrow G$
is a morphism of algebraic varieties.
$\unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D70B}_{x_{0}}^{U}:U\rightarrow G$
is a morphism of algebraic varieties.
10 The Abel–Jacobi map with modulus and its universality
Let
![]() $X$
be a smooth projective scheme of dimension
$X$
be a smooth projective scheme of dimension
![]() $d\geqslant 1$
over
$d\geqslant 1$
over
![]() $\mathbb{C}$
and let
$\mathbb{C}$
and let
![]() $D\subset X$
be an effective Cartier divisor. In this section, we show that
$D\subset X$
be an effective Cartier divisor. In this section, we show that
 $A^{d}(X|D)$
constructed in § 8.2.1 has a natural structure of a connected commutative algebraic group and it is the universal regular quotient of
$A^{d}(X|D)$
constructed in § 8.2.1 has a natural structure of a connected commutative algebraic group and it is the universal regular quotient of
 $\text{CH}_{0}(X|D)_{\text{deg}\,0}$
via an Abel–Jacobi map. Since we are working over
$\text{CH}_{0}(X|D)_{\text{deg}\,0}$
via an Abel–Jacobi map. Since we are working over
![]() $\mathbb{C}$
, we keep identifying
$\mathbb{C}$
, we keep identifying
 $\text{CH}_{0}^{\text{LW}}(Z)$
with
$\text{CH}_{0}^{\text{LW}}(Z)$
with
 $\text{CH}_{0}(Z)$
in this section (using Theorem 3.17) for any projective scheme
$\text{CH}_{0}(Z)$
in this section (using Theorem 3.17) for any projective scheme
![]() $Z$
.
$Z$
.
10.1 The Abel–Jacobi map
Let
![]() $(X,D)$
be as above. We write again
$(X,D)$
be as above. We write again
![]() $X^{o}$
for the open complement of
$X^{o}$
for the open complement of
![]() $D$
in
$D$
in
![]() $X$
and
$X$
and
![]() $S_{X}$
for the double construction applied to the pair
$S_{X}$
for the double construction applied to the pair
![]() $(X,D)$
. Recall from [Reference Esnault and ViehwegEV98] (see also [Reference Esnault, Srinivas and ViehwegESV99, Lemma 2.1]) that given
$(X,D)$
. Recall from [Reference Esnault and ViehwegEV98] (see also [Reference Esnault, Srinivas and ViehwegESV99, Lemma 2.1]) that given
 $x\in (S_{X})_{\text{reg}}=X^{o}\amalg X^{o}$
, there is a unique element
$x\in (S_{X})_{\text{reg}}=X^{o}\amalg X^{o}$
, there is a unique element
 $[x]\in \mathbb{H}_{\{x\}}^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}^{{\mathcal{D}}^{\ast }})$
mapping to the topological cycle class of
$[x]\in \mathbb{H}_{\{x\}}^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}^{{\mathcal{D}}^{\ast }})$
mapping to the topological cycle class of
![]() $x$
in
$x$
in
 $H_{\{x\}}^{2d}(S_{X},\mathbb{Z}(d))$
as well as to the de Rham cycle class of
$H_{\{x\}}^{2d}(S_{X},\mathbb{Z}(d))$
as well as to the de Rham cycle class of
![]() $x$
in
$x$
in
 $\mathbb{H}_{\{x\}}^{2d}(S_{X},\unicode[STIX]{x1D6FA}_{S_{X}}^{{\geqslant}d})$
. Using the canonical forget support map
$\mathbb{H}_{\{x\}}^{2d}(S_{X},\unicode[STIX]{x1D6FA}_{S_{X}}^{{\geqslant}d})$
. Using the canonical forget support map
 $\mathbb{H}_{\{x\}}^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}^{{\mathcal{D}}^{\ast }})\rightarrow \mathbb{H}^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}^{{\mathcal{D}}^{\ast }})$
and extending linearly, this gives rise to a well-defined map
$\mathbb{H}_{\{x\}}^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}^{{\mathcal{D}}^{\ast }})\rightarrow \mathbb{H}^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}^{{\mathcal{D}}^{\ast }})$
and extending linearly, this gives rise to a well-defined map
 $$\begin{eqnarray}\text{cyc}_{S_{X}}^{{\mathcal{D}}}:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow \mathbb{H}^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}^{{\mathcal{D}}^{\ast }})\end{eqnarray}$$
$$\begin{eqnarray}\text{cyc}_{S_{X}}^{{\mathcal{D}}}:{\mathcal{Z}}_{0}(S_{X},D)\rightarrow \mathbb{H}^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}^{{\mathcal{D}}^{\ast }})\end{eqnarray}$$
that composed with
 $\mathbb{H}^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}^{{\mathcal{D}}^{\ast }})\rightarrow H^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}})=\mathbb{Z}\oplus \mathbb{Z}$
coincides with the degree map. The same construction on
$\mathbb{H}^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}}^{{\mathcal{D}}^{\ast }})\rightarrow H^{2d}(S_{X},\mathbb{Z}(d)_{S_{X}})=\mathbb{Z}\oplus \mathbb{Z}$
coincides with the degree map. The same construction on
![]() $X$
gives rise to the diagram
$X$
gives rise to the diagram

whose commutativity is easily checked. We also note that
![]() $\text{cyc}^{{\mathcal{D}}}$
commutes with the map
$\text{cyc}^{{\mathcal{D}}}$
commutes with the map
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}^{\ast }:{\mathcal{Z}}_{0}(X,D)\rightarrow {\mathcal{Z}}_{0}(S_{X},D).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}^{\ast }:{\mathcal{Z}}_{0}(X,D)\rightarrow {\mathcal{Z}}_{0}(S_{X},D).\end{eqnarray}$$
By [Reference Esnault, Srinivas and ViehwegESV99, Lemma 2.6], the cycle class map
![]() $\operatorname{cyc}_{S_{X}}^{{\mathcal{D}}}$
factors through the Chow group
$\operatorname{cyc}_{S_{X}}^{{\mathcal{D}}}$
factors through the Chow group
 $\text{CH}_{0}(S_{X})$
and therefore determines a homomorphism
$\text{CH}_{0}(S_{X})$
and therefore determines a homomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{S_{X}}:\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow A^{d}(S_{X}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{S_{X}}:\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow A^{d}(S_{X}),\end{eqnarray}$$
where
 $\text{CH}_{0}(S_{X})_{\deg 0}$
denotes the kernel of the degree map
$\text{CH}_{0}(S_{X})_{\deg 0}$
denotes the kernel of the degree map
 $\deg :\text{CH}_{0}(S_{X}){\twoheadrightarrow}\mathbb{Z}\oplus \mathbb{Z}$
, that is the generalized Abel–Jacobi map of [Reference Esnault, Srinivas and ViehwegESV99]. Since the cycle class map to Deligne cohomology anyway factors through the usual Chow group of
$\deg :\text{CH}_{0}(S_{X}){\twoheadrightarrow}\mathbb{Z}\oplus \mathbb{Z}$
, that is the generalized Abel–Jacobi map of [Reference Esnault, Srinivas and ViehwegESV99]. Since the cycle class map to Deligne cohomology anyway factors through the usual Chow group of
![]() $0$
-cycles for smooth projective varieties (see [Reference Esnault and ViehwegEV98]), we have then the following commutative diagram, with split exact rows
$0$
-cycles for smooth projective varieties (see [Reference Esnault and ViehwegEV98]), we have then the following commutative diagram, with split exact rows

where
 $\unicode[STIX]{x1D70C}_{X}:\text{CH}_{0}(X)_{\deg 0}\rightarrow A^{d}(X)$
is the usual Abel–Jacobi map and
$\unicode[STIX]{x1D70C}_{X}:\text{CH}_{0}(X)_{\deg 0}\rightarrow A^{d}(X)$
is the usual Abel–Jacobi map and
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)\end{eqnarray}$$
is the induced map on the kernels. Note that thanks to the existence of the splitting
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
of
$\unicode[STIX]{x1D6E5}^{\ast }$
of
![]() $i_{-}^{\ast }$
and its compatibility with the degree maps, the exactness of the first row follows immediately from our main Theorem 7.1. We shall call
$i_{-}^{\ast }$
and its compatibility with the degree maps, the exactness of the first row follows immediately from our main Theorem 7.1. We shall call
![]() $\unicode[STIX]{x1D70C}_{X|D}$
the Abel–Jacobi map with modulus.
$\unicode[STIX]{x1D70C}_{X|D}$
the Abel–Jacobi map with modulus.
10.2 Regularity of
 $\unicode[STIX]{x1D70C}_{X|D}$
$\unicode[STIX]{x1D70C}_{X|D}$
We now fix base points
 $x_{0,\pm }=x_{0}$
on each irreducible components of
$x_{0,\pm }=x_{0}$
on each irreducible components of
![]() $(S_{X})_{\text{reg}}$
and consider the diagram
$(S_{X})_{\text{reg}}$
and consider the diagram

where
 $\unicode[STIX]{x1D713}|_{X_{-}}=\text{Id}_{X}$
and
$\unicode[STIX]{x1D713}|_{X_{-}}=\text{Id}_{X}$
and
 $\unicode[STIX]{x1D713}|_{X_{+}}=x_{0}$
so that the left square commutes.
$\unicode[STIX]{x1D713}|_{X_{+}}=x_{0}$
so that the left square commutes.
The map
![]() $\unicode[STIX]{x1D713}$
is a morphism of schemes, and the composite map on the bottom is a regular morphism. It follows that the composite map
$\unicode[STIX]{x1D713}$
is a morphism of schemes, and the composite map on the bottom is a regular morphism. It follows that the composite map
 $$\begin{eqnarray}X_{+}^{o}\amalg X_{-}^{o}\rightarrow \text{CH}_{0}(S_{X})_{\deg 0}\rightarrow \text{CH}_{0}(X)_{\deg 0}\rightarrow A^{d}(X)\end{eqnarray}$$
$$\begin{eqnarray}X_{+}^{o}\amalg X_{-}^{o}\rightarrow \text{CH}_{0}(S_{X})_{\deg 0}\rightarrow \text{CH}_{0}(X)_{\deg 0}\rightarrow A^{d}(X)\end{eqnarray}$$
is a morphism of schemes. It follows from the universal property of
 $A^{d}(S_{X})$
that there is a unique regular homomorphism of algebraic groups
$A^{d}(S_{X})$
that there is a unique regular homomorphism of algebraic groups
 $\widetilde{i_{-}^{\ast }}:A^{d}(S_{X})\rightarrow A^{d}(X)$
such that the right square commutes.
$\widetilde{i_{-}^{\ast }}:A^{d}(S_{X})\rightarrow A^{d}(X)$
such that the right square commutes.
On the other hand, the right square in (10.2) also commutes. Since
 $\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow A^{d}(S_{X})$
is surjective, it follows that
$\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow A^{d}(S_{X})$
is surjective, it follows that
![]() $\widetilde{i_{-}^{\ast }}=i_{-}^{\ast }$
. We conclude that the map
$\widetilde{i_{-}^{\ast }}=i_{-}^{\ast }$
. We conclude that the map
![]() $i_{-}^{\ast }$
on the bottom row of (10.2) is a regular homomorphism of connected commutative algebraic groups. Since
$i_{-}^{\ast }$
on the bottom row of (10.2) is a regular homomorphism of connected commutative algebraic groups. Since
 $A^{d}(X|D)$
is the inverse image of the identity element under this homomorphism, it follows that
$A^{d}(X|D)$
is the inverse image of the identity element under this homomorphism, it follows that
 $A^{d}(X|D)$
is a commutative algebraic group. We have thus shown that
$A^{d}(X|D)$
is a commutative algebraic group. We have thus shown that
 $A^{d}(S_{X})$
is an extension of the abelian variety
$A^{d}(S_{X})$
is an extension of the abelian variety
![]() $A^{d}(X)$
by the connected commutative algebraic group
$A^{d}(X)$
by the connected commutative algebraic group
 $A^{d}(X|D)$
.
$A^{d}(X|D)$
.
Lemma 10.1. The group homomorphism
 $\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
is regular and surjective, making
$\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
is regular and surjective, making
 $A^{d}(X|D)$
a regular quotient of
$A^{d}(X|D)$
a regular quotient of
 $\text{CH}_{0}(X|D)_{\deg 0}$
.
$\text{CH}_{0}(X|D)_{\deg 0}$
.
Proof. The surjectivity of the generalized Abel–Jacobi map
![]() $\unicode[STIX]{x1D70C}_{X|D}$
is a consequence of the definition. Indeed,
$\unicode[STIX]{x1D70C}_{X|D}$
is a consequence of the definition. Indeed,
![]() $\unicode[STIX]{x1D70C}_{S_{X}}$
is surjective by Theorem 9.5 while
$\unicode[STIX]{x1D70C}_{S_{X}}$
is surjective by Theorem 9.5 while
![]() $\unicode[STIX]{x1D70C}_{X}$
is classically known to be surjective. The surjectivity of
$\unicode[STIX]{x1D70C}_{X}$
is classically known to be surjective. The surjectivity of
![]() $\unicode[STIX]{x1D70C}_{X|D}$
follows then from the existence of the splitting
$\unicode[STIX]{x1D70C}_{X|D}$
follows then from the existence of the splitting
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)_{\deg 0}\rightarrow \text{CH}_{0}(S_{X})_{\deg 0}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)_{\deg 0}\rightarrow \text{CH}_{0}(S_{X})_{\deg 0}\end{eqnarray}$$
that makes the induced map
 $\text{Ker}(\unicode[STIX]{x1D70C}_{S_{X}})\rightarrow \text{Ker}(\unicode[STIX]{x1D70C}_{X})$
surjective (see (10.2)).
$\text{Ker}(\unicode[STIX]{x1D70C}_{S_{X}})\rightarrow \text{Ker}(\unicode[STIX]{x1D70C}_{X})$
surjective (see (10.2)).
For the regularity, let
![]() $V$
be an open dense subset of
$V$
be an open dense subset of
![]() $(S_{X})_{\text{reg}}$
such that
$(S_{X})_{\text{reg}}$
such that
 $\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D70B}_{x_{0}}^{V}$
is regular. By Theorem 9.5, such
$\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D70B}_{x_{0}}^{V}$
is regular. By Theorem 9.5, such
![]() $V$
exists. Up to shrinking
$V$
exists. Up to shrinking
![]() $V$
further, we can assume that
$V$
further, we can assume that
![]() $V$
is of the form
$V$
is of the form
![]() $U\amalg U$
, for
$U\amalg U$
, for
 $U\subset X^{o}$
open (dense) subset of
$U\subset X^{o}$
open (dense) subset of
![]() $X$
disjoint from
$X$
disjoint from
![]() $D$
. Let
$D$
. Let
![]() $i_{U,+}$
denote the inclusion
$i_{U,+}$
denote the inclusion
 $U\rightarrow U\amalg U$
of the first component. Then we clearly have
$U\rightarrow U\amalg U$
of the first component. Then we clearly have
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{S_{X}}\circ p_{+,\ast }\circ \unicode[STIX]{x1D70B}_{x_{0}}^{U}=\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}\circ i_{U,+}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{S_{X}}\circ p_{+,\ast }\circ \unicode[STIX]{x1D70B}_{x_{0}}^{U}=\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}\circ i_{U,+}\end{eqnarray}$$
so that the composition
 $U\rightarrow \text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D){\hookrightarrow}A^{d}(S_{X})$
is a morphism of schemes. Since
$U\rightarrow \text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D){\hookrightarrow}A^{d}(S_{X})$
is a morphism of schemes. Since
 $A^{d}(X|D){\hookrightarrow}A^{d}(S_{X})$
is a closed immersion, we obtain the claim.◻
$A^{d}(X|D){\hookrightarrow}A^{d}(S_{X})$
is a closed immersion, we obtain the claim.◻
10.3 Universality of
 $\unicode[STIX]{x1D70C}_{X|D}$
$\unicode[STIX]{x1D70C}_{X|D}$
Our next goal is to prove that the Abel–Jacobi map with modulus
 $\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
makes
$\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
makes
 $A^{d}(X|D)$
the universal regular quotient of
$A^{d}(X|D)$
the universal regular quotient of
 $\text{CH}_{0}(X|D)_{\deg 0}$
.
$\text{CH}_{0}(X|D)_{\deg 0}$
.
Lemma 10.2. The homomorphism
 $\unicode[STIX]{x1D6E5}^{\ast }:A^{d}(X)\rightarrow A^{d}(S_{X})$
of (10.2) is a morphism of schemes.
$\unicode[STIX]{x1D6E5}^{\ast }:A^{d}(X)\rightarrow A^{d}(S_{X})$
of (10.2) is a morphism of schemes.
Proof. We have seen in the proof of Lemma 10.1 that there is a dense open subset
 $U\subset X^{o}$
and a closed point
$U\subset X^{o}$
and a closed point
 $x_{0}=x_{0,\pm }\in U$
such that the composition
$x_{0}=x_{0,\pm }\in U$
such that the composition
 $U\amalg U\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}}\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow A^{d}(S_{X})$
is a morphism of schemes. Let
$U\amalg U\xrightarrow[{}]{\unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}}\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow A^{d}(S_{X})$
is a morphism of schemes. Let
 $i_{U,\pm }:U{\hookrightarrow}U\amalg U$
denote the inclusions into the first and the second component, respectively. Again from the proof of Lemma 10.1, we have that the maps
$i_{U,\pm }:U{\hookrightarrow}U\amalg U$
denote the inclusions into the first and the second component, respectively. Again from the proof of Lemma 10.1, we have that the maps
 $\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}\circ i_{U,\pm }$
are both morphisms of schemes. In particular, the composition
$\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}\circ i_{U,\pm }$
are both morphisms of schemes. In particular, the composition
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{U}:U\xrightarrow[{}]{\unicode[STIX]{x1D713}}A^{d}(S_{X})\times A^{d}(S_{X})\xrightarrow[{}]{+}A^{d}(S_{X})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{U}:U\xrightarrow[{}]{\unicode[STIX]{x1D713}}A^{d}(S_{X})\times A^{d}(S_{X})\xrightarrow[{}]{+}A^{d}(S_{X})\end{eqnarray}$$
is also a morphism of schemes, where
 $\unicode[STIX]{x1D713}=(\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}\circ i_{U,+},\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}\circ i_{U,-})$
and the second arrow in (10.4) is the addition.
$\unicode[STIX]{x1D713}=(\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}\circ i_{U,+},\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}\circ i_{U,-})$
and the second arrow in (10.4) is the addition.
We now consider a diagram

where the first arrow on the bottom is
 $(\unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}\circ i_{U,+})+(\unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}\circ i_{U,-})$
. It is clear from the definition of
$(\unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}\circ i_{U,+})+(\unicode[STIX]{x1D70B}_{x_{0},\pm }^{U\amalg U}\circ i_{U,-})$
. It is clear from the definition of
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
in the middle that the left square of (10.5) commutes. The composite map on the bottom is same as
$\unicode[STIX]{x1D6E5}^{\ast }$
in the middle that the left square of (10.5) commutes. The composite map on the bottom is same as
![]() $\unicode[STIX]{x1D703}_{U}$
, which we just showed above to be a morphism of schemes. We conclude that the map
$\unicode[STIX]{x1D703}_{U}$
, which we just showed above to be a morphism of schemes. We conclude that the map
 $\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D6E5}^{\ast }$
is a regular homomorphism. It follows from the universality of
$\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D6E5}^{\ast }$
is a regular homomorphism. It follows from the universality of
![]() $A^{d}(X)$
that there is a unique morphism of algebraic groups
$A^{d}(X)$
that there is a unique morphism of algebraic groups
 $\widetilde{\unicode[STIX]{x1D6E5}^{\ast }}:A^{d}(X)\rightarrow A^{d}(S_{X})$
such that the right square of (10.5) commutes.
$\widetilde{\unicode[STIX]{x1D6E5}^{\ast }}:A^{d}(X)\rightarrow A^{d}(S_{X})$
such that the right square of (10.5) commutes.
On the other hand, we have seen in (10.2) that right square also commutes if we replace
![]() $\widetilde{\unicode[STIX]{x1D6E5}^{\ast }}$
by
$\widetilde{\unicode[STIX]{x1D6E5}^{\ast }}$
by
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
. Since
$\unicode[STIX]{x1D6E5}^{\ast }$
. Since
![]() $\unicode[STIX]{x1D70C}_{X}$
is surjective, we must have
$\unicode[STIX]{x1D70C}_{X}$
is surjective, we must have
 $\widetilde{\unicode[STIX]{x1D6E5}^{\ast }}=\unicode[STIX]{x1D6E5}^{\ast }$
. In particular,
$\widetilde{\unicode[STIX]{x1D6E5}^{\ast }}=\unicode[STIX]{x1D6E5}^{\ast }$
. In particular,
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
is morphism of schemes.◻
$\unicode[STIX]{x1D6E5}^{\ast }$
is morphism of schemes.◻
To prove the universality of
 $A^{d}(X|D)$
, we begin with the following construction. Consider the homomorphism
$A^{d}(X|D)$
, we begin with the following construction. Consider the homomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}^{\ast }:A^{d}(S_{X})\rightarrow A^{d}(S_{X}),\quad \unicode[STIX]{x1D70F}^{\ast }=\text{Id}_{S_{X}}-\unicode[STIX]{x1D6E5}^{\ast }\circ i_{-}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}^{\ast }:A^{d}(S_{X})\rightarrow A^{d}(S_{X}),\quad \unicode[STIX]{x1D70F}^{\ast }=\text{Id}_{S_{X}}-\unicode[STIX]{x1D6E5}^{\ast }\circ i_{-}^{\ast }.\end{eqnarray}$$
Note that
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
is a morphism of schemes by Lemma 10.2 and we have shown in § 10.2 that
$\unicode[STIX]{x1D6E5}^{\ast }$
is a morphism of schemes by Lemma 10.2 and we have shown in § 10.2 that
![]() $i_{-}^{\ast }$
is also a morphism of schemes. We conclude that
$i_{-}^{\ast }$
is also a morphism of schemes. We conclude that
![]() $\unicode[STIX]{x1D70F}^{\ast }$
is morphism of algebraic groups.
$\unicode[STIX]{x1D70F}^{\ast }$
is morphism of algebraic groups.
Note that
![]() $\unicode[STIX]{x1D70F}^{\ast }$
uniquely factors through
$\unicode[STIX]{x1D70F}^{\ast }$
uniquely factors through
 $A^{d}(X|D)$
, since
$A^{d}(X|D)$
, since
 $i_{-}^{\ast }\circ \unicode[STIX]{x1D70F}^{\ast }=0$
and we have already identified
$i_{-}^{\ast }\circ \unicode[STIX]{x1D70F}^{\ast }=0$
and we have already identified
 $A^{d}(X|D)$
with the fiber over the identity element of
$A^{d}(X|D)$
with the fiber over the identity element of
![]() $A^{d}(X)$
via
$A^{d}(X)$
via
![]() $i_{-}^{\ast }$
. The map
$i_{-}^{\ast }$
. The map
![]() $\unicode[STIX]{x1D70F}^{\ast }$
gives then an explicit isomorphism of algebraic groups
$\unicode[STIX]{x1D70F}^{\ast }$
gives then an explicit isomorphism of algebraic groups
 $$\begin{eqnarray}(\unicode[STIX]{x1D70F}^{\ast },i_{-}^{\ast }):A^{d}(S_{X})\xrightarrow[{}]{\simeq }A^{d}(X|D)\times A^{d}(X).\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70F}^{\ast },i_{-}^{\ast }):A^{d}(S_{X})\xrightarrow[{}]{\simeq }A^{d}(X|D)\times A^{d}(X).\end{eqnarray}$$
Moreover, since
 $i_{\ast }^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}_{A^{d}(X)}$
, we get an extension of commutative algebraic groups
$i_{\ast }^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}_{A^{d}(X)}$
, we get an extension of commutative algebraic groups
 $$\begin{eqnarray}0\rightarrow A^{d}(X)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}^{\ast }}A^{d}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70F}^{\ast }}A^{d}(X|D)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow A^{d}(X)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}^{\ast }}A^{d}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70F}^{\ast }}A^{d}(X|D)\rightarrow 0.\end{eqnarray}$$
We now claim that the diagram

commutes. To see this, we can write, using Theorem 7.1, any element
 $\unicode[STIX]{x1D6FC}\in \text{CH}_{0}(S_{X})_{\deg 0}$
as
$\unicode[STIX]{x1D6FC}\in \text{CH}_{0}(S_{X})_{\deg 0}$
as
 $\unicode[STIX]{x1D6FC}=~p_{+,\ast }(\unicode[STIX]{x1D6FC}_{1})+\unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FC}_{2})$
. Since
$\unicode[STIX]{x1D6FC}=~p_{+,\ast }(\unicode[STIX]{x1D6FC}_{1})+\unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FC}_{2})$
. Since
 $\unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=0$
, by definitions, we get
$\unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=0$
, by definitions, we get
 $\unicode[STIX]{x1D70C}_{X|D}\circ \unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D70C}_{X|D}(\unicode[STIX]{x1D6FC}_{1})$
by (10.2).
$\unicode[STIX]{x1D70C}_{X|D}\circ \unicode[STIX]{x1D70F}_{X}^{\ast }(\unicode[STIX]{x1D6FC})=\unicode[STIX]{x1D70C}_{X|D}(\unicode[STIX]{x1D6FC}_{1})$
by (10.2).
On the other hand,
 $\unicode[STIX]{x1D70F}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=0$
and
$\unicode[STIX]{x1D70F}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=0$
and
 $\unicode[STIX]{x1D70F}^{\ast }\circ p_{+,\ast }=\text{Id}_{A^{d}(X|D)}$
so that
$\unicode[STIX]{x1D70F}^{\ast }\circ p_{+,\ast }=\text{Id}_{A^{d}(X|D)}$
so that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}^{\ast }\circ \unicode[STIX]{x1D70C}_{S_{X}}(\unicode[STIX]{x1D6FC}) & = & \displaystyle \unicode[STIX]{x1D70F}^{\ast }\circ \unicode[STIX]{x1D70C}_{S_{X}}\circ p_{+,\ast }(\unicode[STIX]{x1D6FC}_{1})+\unicode[STIX]{x1D70F}^{\ast }\circ \unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FC}_{2})\nonumber\\ \displaystyle & ~=^{\dagger } & \displaystyle \unicode[STIX]{x1D70F}^{\ast }\circ p_{+,\ast }\circ \unicode[STIX]{x1D70C}_{X|D}(\unicode[STIX]{x1D6FC}_{1})+\unicode[STIX]{x1D70F}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }\circ \unicode[STIX]{x1D70C}_{X}(\unicode[STIX]{x1D6FC}_{2})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70C}_{X|D}(\unicode[STIX]{x1D6FC}_{1}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70F}^{\ast }\circ \unicode[STIX]{x1D70C}_{S_{X}}(\unicode[STIX]{x1D6FC}) & = & \displaystyle \unicode[STIX]{x1D70F}^{\ast }\circ \unicode[STIX]{x1D70C}_{S_{X}}\circ p_{+,\ast }(\unicode[STIX]{x1D6FC}_{1})+\unicode[STIX]{x1D70F}^{\ast }\circ \unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FC}_{2})\nonumber\\ \displaystyle & ~=^{\dagger } & \displaystyle \unicode[STIX]{x1D70F}^{\ast }\circ p_{+,\ast }\circ \unicode[STIX]{x1D70C}_{X|D}(\unicode[STIX]{x1D6FC}_{1})+\unicode[STIX]{x1D70F}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }\circ \unicode[STIX]{x1D70C}_{X}(\unicode[STIX]{x1D6FC}_{2})\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70C}_{X|D}(\unicode[STIX]{x1D6FC}_{1}),\nonumber\end{eqnarray}$$
where
![]() $=^{\dagger }$
follows from (10.2). This proves the commutativity of (10.8).
$=^{\dagger }$
follows from (10.2). This proves the commutativity of (10.8).
Theorem 10.3. The Abel–Jacobi map
 $\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
makes
$\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
makes
 $A^{d}(X|D)$
the universal regular quotient of
$A^{d}(X|D)$
the universal regular quotient of
 $\text{CH}_{0}(X|D)_{\deg 0}$
.
$\text{CH}_{0}(X|D)_{\deg 0}$
.
Proof. We only need to prove the universality. Let
![]() $G$
be a commutative algebraic group and let
$G$
be a commutative algebraic group and let
 $\unicode[STIX]{x1D713}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow G$
be a regular homomorphism. Let
$\unicode[STIX]{x1D713}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow G$
be a regular homomorphism. Let
 $U\subset X^{o}$
be an open dense subset so that the composite
$U\subset X^{o}$
be an open dense subset so that the composite
![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70B}_{x_{0}}^{U}$
is a morphism of schemes, for
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70B}_{x_{0}}^{U}$
is a morphism of schemes, for
![]() $x_{0}\in U$
a base point. Let
$x_{0}\in U$
a base point. Let
 $V=U\amalg U$
. We claim that
$V=U\amalg U$
. We claim that
 $\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{V}$
is a morphism of schemes, where
$\unicode[STIX]{x1D6FF}=\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{V}$
is a morphism of schemes, where
 $\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow \text{CH}_{0}(X|D)_{\deg 0}$
is splitting the map
$\unicode[STIX]{x1D70F}_{X}^{\ast }:\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow \text{CH}_{0}(X|D)_{\deg 0}$
is splitting the map
![]() $p_{+,\ast }$
of Theorem 7.1. Indeed, it is actually enough to show that the restriction of
$p_{+,\ast }$
of Theorem 7.1. Indeed, it is actually enough to show that the restriction of
![]() $\unicode[STIX]{x1D6FF}$
to the two components
$\unicode[STIX]{x1D6FF}$
to the two components
![]() $U_{\pm }$
of
$U_{\pm }$
of
![]() $V$
is a morphism of schemes. But we have, for
$V$
is a morphism of schemes. But we have, for
![]() $x\in U_{+}$
,
$x\in U_{+}$
,
 $$\begin{eqnarray}\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{V}(x)=\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70F}_{X}^{\ast }([x]_{+}-[x_{0,+}])=\unicode[STIX]{x1D713}([x]-[x_{0}])=\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70B}_{x_{0}}^{U}(x),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{V}(x)=\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70F}_{X}^{\ast }([x]_{+}-[x_{0,+}])=\unicode[STIX]{x1D713}([x]-[x_{0}])=\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70B}_{x_{0}}^{U}(x),\end{eqnarray}$$
where
![]() $[x]_{+}$
denotes the class in
$[x]_{+}$
denotes the class in
 $\text{CH}_{0}(S_{X})$
of the closed point
$\text{CH}_{0}(S_{X})$
of the closed point
![]() $x$
in the component
$x$
in the component
![]() $X_{+}$
of
$X_{+}$
of
![]() $S_{X}$
. Since
$S_{X}$
. Since
![]() $\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70B}_{x_{0}}^{U}$
is by assumption a morphism of schemes, this proves the claim for the restriction to
$\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70B}_{x_{0}}^{U}$
is by assumption a morphism of schemes, this proves the claim for the restriction to
![]() $U_{+}$
. Similarly for
$U_{+}$
. Similarly for
![]() $x\in U_{-}$
, we have
$x\in U_{-}$
, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{V}(x)=\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70F}_{X}^{\ast }([x]_{-}-[x_{0,-}])=\unicode[STIX]{x1D713}(-[x]+[x_{0}])=-\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70B}_{x_{0}}^{U}(x)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D70B}_{x_{0},\pm }^{V}(x)=\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70F}_{X}^{\ast }([x]_{-}-[x_{0,-}])=\unicode[STIX]{x1D713}(-[x]+[x_{0}])=-\unicode[STIX]{x1D713}\circ \unicode[STIX]{x1D70B}_{x_{0}}^{U}(x)\end{eqnarray}$$
that is also a morphism of schemes, since
![]() $G$
is an algebraic group.
$G$
is an algebraic group.
By the claim and Theorem 9.5, there is then a unique morphism of algebraic groups
 $\tilde{\unicode[STIX]{x1D713}}:A^{d}(S_{X})\rightarrow G$
such that there is a commutative square.
$\tilde{\unicode[STIX]{x1D713}}:A^{d}(S_{X})\rightarrow G$
such that there is a commutative square.

We now claim that the composition
 $$\begin{eqnarray}A^{d}(X)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}^{\ast }}A^{d}(S_{X})\xrightarrow[{}]{\tilde{\unicode[STIX]{x1D713}}}G\end{eqnarray}$$
$$\begin{eqnarray}A^{d}(X)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}^{\ast }}A^{d}(S_{X})\xrightarrow[{}]{\tilde{\unicode[STIX]{x1D713}}}G\end{eqnarray}$$
is equal to the constant map
 $A^{d}(X)\rightarrow 0$
. Indeed, since the left square of the diagram
$A^{d}(X)\rightarrow 0$
. Indeed, since the left square of the diagram

also commutes by (10.2) and since
![]() $\unicode[STIX]{x1D70C}_{X}$
is surjective, it is enough to show that
$\unicode[STIX]{x1D70C}_{X}$
is surjective, it is enough to show that
 $\tilde{\unicode[STIX]{x1D713}}\circ \unicode[STIX]{x1D6E5}^{\ast }\circ \unicode[STIX]{x1D70C}_{X}=0$
.
$\tilde{\unicode[STIX]{x1D713}}\circ \unicode[STIX]{x1D6E5}^{\ast }\circ \unicode[STIX]{x1D70C}_{X}=0$
.
But
 $\tilde{\unicode[STIX]{x1D713}}\circ \unicode[STIX]{x1D6E5}^{\ast }\circ \unicode[STIX]{x1D70C}_{X}=\tilde{\unicode[STIX]{x1D713}}\circ \unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D6E5}^{\ast }=\unicode[STIX]{x1D713}\circ (\unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D6E5}_{X}^{\ast })=0$
since
$\tilde{\unicode[STIX]{x1D713}}\circ \unicode[STIX]{x1D6E5}^{\ast }\circ \unicode[STIX]{x1D70C}_{X}=\tilde{\unicode[STIX]{x1D713}}\circ \unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D6E5}^{\ast }=\unicode[STIX]{x1D713}\circ (\unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D6E5}_{X}^{\ast })=0$
since
 $\unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D6E5}_{X}^{\ast }=0$
. This proves the claim. Using this fact, the exact sequence (10.7) and the commutative diagram (10.8), it follows immediately that there exists a unique morphism of algebraic groups
$\unicode[STIX]{x1D70F}_{X}^{\ast }\circ \unicode[STIX]{x1D6E5}_{X}^{\ast }=0$
. This proves the claim. Using this fact, the exact sequence (10.7) and the commutative diagram (10.8), it follows immediately that there exists a unique morphism of algebraic groups
 $\unicode[STIX]{x1D713}_{G}:A^{d}(X|D)\rightarrow G$
such that
$\unicode[STIX]{x1D713}_{G}:A^{d}(X|D)\rightarrow G$
such that
 $\unicode[STIX]{x1D713}_{G}\circ \unicode[STIX]{x1D70C}_{X|D}=\unicode[STIX]{x1D713}$
. This finishes the proof.◻
$\unicode[STIX]{x1D713}_{G}\circ \unicode[STIX]{x1D70C}_{X|D}=\unicode[STIX]{x1D713}$
. This finishes the proof.◻
10.4 Roitman’s theorem for 0-cycles with modulus
The first application of our approach to study algebraic cycles with modulus was already given in Theorem 14.1. As second application, we now prove the following Roitman torsion theorem for 0-cycles with modulus on smooth projective schemes over
![]() $\mathbb{C}$
. This will be generalized to positive characteristic in the next section.
$\mathbb{C}$
. This will be generalized to positive characteristic in the next section.
Theorem 10.4. Let
![]() $X$
be a smooth projective variety of dimension
$X$
be a smooth projective variety of dimension
![]() $d\geqslant 1$
over
$d\geqslant 1$
over
![]() $\mathbb{C}$
and let
$\mathbb{C}$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then the Abel–Jacobi map
$D\subset X$
be an effective Cartier divisor. Then the Abel–Jacobi map
 $\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
induces an isomorphism on the torsion subgroups.
$\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
induces an isomorphism on the torsion subgroups.
Proof. We have the following commutative diagram with split exact rows.

Since the maps
![]() $i_{-}^{\ast }$
on the top and the bottom rows are split by
$i_{-}^{\ast }$
on the top and the bottom rows are split by
![]() $\unicode[STIX]{x1D6E5}^{\ast }$
, the two sequences remain exact even after passing to the torsion subgroups. The statement then follows from the theorem of Roitman [Reference RojtmanRoi80] for
$\unicode[STIX]{x1D6E5}^{\ast }$
, the two sequences remain exact even after passing to the torsion subgroups. The statement then follows from the theorem of Roitman [Reference RojtmanRoi80] for
![]() $\unicode[STIX]{x1D70C}_{X}$
and the theorem of Biswas–Srinivas [Reference Biswas and SrinivasBS99] for
$\unicode[STIX]{x1D70C}_{X}$
and the theorem of Biswas–Srinivas [Reference Biswas and SrinivasBS99] for
![]() $\unicode[STIX]{x1D70C}_{S_{X}}$
.◻
$\unicode[STIX]{x1D70C}_{S_{X}}$
.◻
10.5 Bloch’s conjecture for 0-cycles with modulus
Let
![]() $X$
be a reduced projective surface over
$X$
be a reduced projective surface over
![]() $\mathbb{C}$
. Recall that the Chow group of 0-cycles
$\mathbb{C}$
. Recall that the Chow group of 0-cycles
 $\text{CH}_{0}(X)$
is said to be finite dimensional if the Abel–Jacobi map
$\text{CH}_{0}(X)$
is said to be finite dimensional if the Abel–Jacobi map
 $\unicode[STIX]{x1D70C}_{X}:\text{CH}_{0}(X)_{\deg 0}\rightarrow A^{2}(X)$
is an isomorphism. Recall that the famous Bloch conjecture about 0-cycles on surfaces says the following.
$\unicode[STIX]{x1D70C}_{X}:\text{CH}_{0}(X)_{\deg 0}\rightarrow A^{2}(X)$
is an isomorphism. Recall that the famous Bloch conjecture about 0-cycles on surfaces says the following.
Conjecture 10.5 (Bloch).
Let
![]() $X$
be a smooth projective surface over
$X$
be a smooth projective surface over
![]() $\mathbb{C}$
such that
$\mathbb{C}$
such that
 $H^{2}(X,{\mathcal{O}}_{X})=0$
. Then
$H^{2}(X,{\mathcal{O}}_{X})=0$
. Then
 $\text{CH}_{0}(X)$
is finite dimensional.
$\text{CH}_{0}(X)$
is finite dimensional.
This conjecture is known to be true for surfaces of Kodaira dimension less than two [Reference Bloch, Kas and LiebermanBKL76] and is open in general. It has been shown by Voisin [Reference VoisinVoi04] that a generalized version of this conjecture in higher dimensions is very closely related to the Hodge conjecture.
Let
![]() $X$
be a smooth projective surface over
$X$
be a smooth projective surface over
![]() $\mathbb{C}$
and let
$\mathbb{C}$
and let
![]() $D\subset X$
be an effective Cartier divisor. Let
$D\subset X$
be an effective Cartier divisor. Let
![]() ${\mathcal{I}}_{D}$
denote the subsheaf of ideals in
${\mathcal{I}}_{D}$
denote the subsheaf of ideals in
![]() ${\mathcal{O}}_{X}$
defining
${\mathcal{O}}_{X}$
defining
![]() $D$
. We shall say that
$D$
. We shall say that
 $\text{CH}_{0}(X|D)$
is finite dimensional if the map
$\text{CH}_{0}(X|D)$
is finite dimensional if the map
 $\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
is an isomorphism. We can now state the following analogue of the Bloch conjecture for 0-cycles with modulus.
$\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
is an isomorphism. We can now state the following analogue of the Bloch conjecture for 0-cycles with modulus.
Conjecture 10.6. Let
![]() $X$
be a smooth projective surface over
$X$
be a smooth projective surface over
![]() $\mathbb{C}$
. Let
$\mathbb{C}$
. Let
![]() $D\subset X$
be an effective Cartier divisor such that
$D\subset X$
be an effective Cartier divisor such that
 $H^{2}(X,{\mathcal{I}}_{D})=0$
. Then
$H^{2}(X,{\mathcal{I}}_{D})=0$
. Then
 $\text{CH}_{0}(X|D)$
is finite dimensional.
$\text{CH}_{0}(X|D)$
is finite dimensional.
Remark 10.7. As explained in [Reference Binda and SaitoBS16, 2.1.2], the Chow groups with modulus can be used to define a notion of Chow groups with compact support for the complement
 $X^{o}=X\setminus |D|$
. In this perspective, we can view Conjecture 10.6 as an analogue of Bloch’s conjecture for the open surface
$X^{o}=X\setminus |D|$
. In this perspective, we can view Conjecture 10.6 as an analogue of Bloch’s conjecture for the open surface
![]() $X^{o}$
.
$X^{o}$
.
As an application of Theorem 7.1, we can show the following.
Theorem 10.8. Let
![]() $X$
be a smooth projective surface over
$X$
be a smooth projective surface over
![]() $\mathbb{C}$
. Let
$\mathbb{C}$
. Let
![]() $D\subset X$
be an effective Cartier divisor such that
$D\subset X$
be an effective Cartier divisor such that
 $H^{2}(X,{\mathcal{I}}_{D})=0$
. Assume that Conjecture 10.5 holds for
$H^{2}(X,{\mathcal{I}}_{D})=0$
. Assume that Conjecture 10.5 holds for
![]() $X$
. Then
$X$
. Then
 $\text{CH}_{0}(X|D)$
is finite dimensional.
$\text{CH}_{0}(X|D)$
is finite dimensional.
Proof. We first observe that
 $\unicode[STIX]{x1D70B}:\overline{S_{X}}:=X\amalg X\rightarrow S_{X}$
is the normalization map and hence the Bloch conjecture for
$\unicode[STIX]{x1D70B}:\overline{S_{X}}:=X\amalg X\rightarrow S_{X}$
is the normalization map and hence the Bloch conjecture for
![]() $X$
is same as that for
$X$
is same as that for
![]() $\overline{S_{X}}$
. Since
$\overline{S_{X}}$
. Since
 $H^{2}(X,{\mathcal{I}}_{D}){\twoheadrightarrow}H^{2}(X,{\mathcal{O}}_{X})$
, it follows that
$H^{2}(X,{\mathcal{I}}_{D}){\twoheadrightarrow}H^{2}(X,{\mathcal{O}}_{X})$
, it follows that
 $H^{2}(X,{\mathcal{O}}_{X})=0$
. In particular,
$H^{2}(X,{\mathcal{O}}_{X})=0$
. In particular,
 $\text{CH}_{0}(X)$
and
$\text{CH}_{0}(X)$
and
 $\text{CH}_{0}(\overline{S_{X}})$
are finite dimensional.
$\text{CH}_{0}(\overline{S_{X}})$
are finite dimensional.
Since the map
 ${\mathcal{I}}_{X_{-}}\rightarrow {\mathcal{I}}_{D}$
is an isomorphism (see (8.8)), there is an exact sequence
${\mathcal{I}}_{X_{-}}\rightarrow {\mathcal{I}}_{D}$
is an isomorphism (see (8.8)), there is an exact sequence
 $$\begin{eqnarray}H^{2}(X,{\mathcal{I}}_{D})\rightarrow H^{2}(S_{X},{\mathcal{O}}_{S_{X}})\rightarrow H^{2}(X,{\mathcal{O}}_{X})\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(X,{\mathcal{I}}_{D})\rightarrow H^{2}(S_{X},{\mathcal{O}}_{S_{X}})\rightarrow H^{2}(X,{\mathcal{O}}_{X})\rightarrow 0.\end{eqnarray}$$
We conclude that
 $H^{2}(S_{X},{\mathcal{O}}_{S_{X}})=0$
. We now apply [Reference KrishnaKri09, Theorem 1.3] to conclude that
$H^{2}(S_{X},{\mathcal{O}}_{S_{X}})=0$
. We now apply [Reference KrishnaKri09, Theorem 1.3] to conclude that
 $\text{CH}_{0}(S_{X})$
is finite dimensional. We remark here that the statement of this cited result assumes validity of Conjecture 10.5 for all smooth surfaces, but its proof (see [Reference KrishnaKri09, § 7]) only uses the fact that the normalization of the surface (which is already smooth in our case) is finite dimensional. We now use (10.9) to conclude that
$\text{CH}_{0}(S_{X})$
is finite dimensional. We remark here that the statement of this cited result assumes validity of Conjecture 10.5 for all smooth surfaces, but its proof (see [Reference KrishnaKri09, § 7]) only uses the fact that the normalization of the surface (which is already smooth in our case) is finite dimensional. We now use (10.9) to conclude that
 $\text{CH}_{0}(X|D)$
is finite dimensional.◻
$\text{CH}_{0}(X|D)$
is finite dimensional.◻
A combination of Theorem 10.8 and [Reference Bloch, Kas and LiebermanBKL76] yields the following.
Corollary 10.9. Let
![]() $X$
be a smooth projective surface over
$X$
be a smooth projective surface over
![]() $\mathbb{C}$
of Kodaira dimension less than two. Let
$\mathbb{C}$
of Kodaira dimension less than two. Let
![]() $D\subset X$
be an effective Cartier divisor such that
$D\subset X$
be an effective Cartier divisor such that
 $H^{2}(X,{\mathcal{I}}_{D})=0$
. Then
$H^{2}(X,{\mathcal{I}}_{D})=0$
. Then
 $\text{CH}_{0}(X|D)$
is finite dimensional.
$\text{CH}_{0}(X|D)$
is finite dimensional.
Infinite-dimensionality of
 $\text{CH}_{0}(X|D)$
: the following result provides examples of smooth projective surfaces
$\text{CH}_{0}(X|D)$
: the following result provides examples of smooth projective surfaces
![]() $X$
with an effective Cartier divisor
$X$
with an effective Cartier divisor
![]() $D\subset X$
such that
$D\subset X$
such that
 $\text{CH}_{0}(X)$
is finite dimensional but
$\text{CH}_{0}(X)$
is finite dimensional but
 $\text{CH}_{0}(X|D)$
is not. In particular, it provides a partial converse to Theorem 10.8.
$\text{CH}_{0}(X|D)$
is not. In particular, it provides a partial converse to Theorem 10.8.
Theorem 10.10. Let
![]() $X$
be a smooth projective surface over
$X$
be a smooth projective surface over
![]() $\mathbb{C}$
. Let
$\mathbb{C}$
. Let
![]() $D\subset X$
be an effective Cartier divisor such that
$D\subset X$
be an effective Cartier divisor such that
 $H^{2}(X,{\mathcal{I}}_{D})\neq 0$
. Assume that
$H^{2}(X,{\mathcal{I}}_{D})\neq 0$
. Assume that
![]() $X$
is regular with
$X$
is regular with
 $p_{g}(X)=0$
and that the Bloch conjecture is true for
$p_{g}(X)=0$
and that the Bloch conjecture is true for
![]() $X$
. Then
$X$
. Then
 $\text{CH}_{0}(X|D)$
is not finite dimensional.
$\text{CH}_{0}(X|D)$
is not finite dimensional.
Proof. The exact sequence
 $$\begin{eqnarray}H^{1}(X,{\mathcal{O}}_{X})\rightarrow H^{2}(X,{\mathcal{I}}_{D})\rightarrow H^{2}(S_{X},{\mathcal{O}}_{S_{X}})\rightarrow H^{2}(X,{\mathcal{O}}_{X})\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}H^{1}(X,{\mathcal{O}}_{X})\rightarrow H^{2}(X,{\mathcal{I}}_{D})\rightarrow H^{2}(S_{X},{\mathcal{O}}_{S_{X}})\rightarrow H^{2}(X,{\mathcal{O}}_{X})\rightarrow 0\end{eqnarray}$$
and our assumption together imply that
 $H^{2}(S_{X},{\mathcal{O}}_{S_{X}})\neq 0$
. We claim that the map
$H^{2}(S_{X},{\mathcal{O}}_{S_{X}})\neq 0$
. We claim that the map
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{S_{X}}:\text{CH}_{0}(S_{X})_{\text{deg}\,0}\rightarrow A^{2}(S_{X})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{S_{X}}:\text{CH}_{0}(S_{X})_{\text{deg}\,0}\rightarrow A^{2}(S_{X})\end{eqnarray}$$
is not injective. Suppose on the contrary, that
![]() $\unicode[STIX]{x1D70C}_{S_{X}}$
is injective. But then it must be an isomorphism. It follows then from [Reference Esnault, Srinivas and ViehwegESV99, Theorem 7.2] (see its proof on p. 657) that there are finitely many reduced Cartier curves
$\unicode[STIX]{x1D70C}_{S_{X}}$
is injective. But then it must be an isomorphism. It follows then from [Reference Esnault, Srinivas and ViehwegESV99, Theorem 7.2] (see its proof on p. 657) that there are finitely many reduced Cartier curves
 $\{C_{1},\ldots ,C_{r}\}$
on
$\{C_{1},\ldots ,C_{r}\}$
on
![]() $X$
such that the map
$X$
such that the map
 $\bigoplus _{i=1}^{r}\text{CH}_{0}(C_{i})_{\text{deg}\,0}\rightarrow \text{CH}_{0}(S_{X})_{\text{deg}\,0}$
is surjective. However, as
$\bigoplus _{i=1}^{r}\text{CH}_{0}(C_{i})_{\text{deg}\,0}\rightarrow \text{CH}_{0}(S_{X})_{\text{deg}\,0}$
is surjective. However, as
 $H^{2}(S_{X},{\mathcal{O}}_{S_{X}})\neq 0$
, [Reference SrinivasSri00, Theorem 5.2] tells us that this is not possible. This proves the claim. Our assumption says that the map
$H^{2}(S_{X},{\mathcal{O}}_{S_{X}})\neq 0$
, [Reference SrinivasSri00, Theorem 5.2] tells us that this is not possible. This proves the claim. Our assumption says that the map
![]() $\unicode[STIX]{x1D70C}_{X}$
in (10.9) is an isomorphism. It follows that
$\unicode[STIX]{x1D70C}_{X}$
in (10.9) is an isomorphism. It follows that
 $\text{Ker}(\unicode[STIX]{x1D70C}_{X|D})\neq 0$
.◻
$\text{Ker}(\unicode[STIX]{x1D70C}_{X|D})\neq 0$
.◻
If we let
 $D\subset \mathbb{P}_{\mathbb{C}}^{2}$
be a smooth hypersurface of degree 3, we have
$D\subset \mathbb{P}_{\mathbb{C}}^{2}$
be a smooth hypersurface of degree 3, we have
 $$\begin{eqnarray}H^{2}(\mathbb{P}_{\mathbb{ C}}^{2},{\mathcal{I}}_{D})\simeq H^{2}(\mathbb{P}_{\mathbb{ C}}^{2},{\mathcal{O}}_{\mathbb{ P}_{\mathbb{C}}^{2}}(-D))\simeq H^{2}(\mathbb{P}_{\mathbb{ C}}^{2},{\mathcal{O}}_{\mathbb{ P}_{\mathbb{C}}^{2}}(-3))\simeq \mathbb{C}.\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(\mathbb{P}_{\mathbb{ C}}^{2},{\mathcal{I}}_{D})\simeq H^{2}(\mathbb{P}_{\mathbb{ C}}^{2},{\mathcal{O}}_{\mathbb{ P}_{\mathbb{C}}^{2}}(-D))\simeq H^{2}(\mathbb{P}_{\mathbb{ C}}^{2},{\mathcal{O}}_{\mathbb{ P}_{\mathbb{C}}^{2}}(-3))\simeq \mathbb{C}.\end{eqnarray}$$
All conditions of Theorem 10.10 are clearly satisfied and we get an example of a (smooth) pair
![]() $(X,D)$
such that
$(X,D)$
such that
 $\text{CH}_{0}(X)_{\text{deg}\,0}=0$
but
$\text{CH}_{0}(X)_{\text{deg}\,0}=0$
but
 $\text{CH}_{0}(X|D)$
is infinite dimensional.
$\text{CH}_{0}(X|D)$
is infinite dimensional.
11 Albanese with modulus in arbitrary characteristic
In this section, we generalize the results of § 10 for 0-cycles with modulus on smooth projective varieties over an arbitrary algebraically closed field. Most of the arguments are straightforward copies of those in § 10. So we keep the discussion brief. We fix an algebraically closed field
![]() $k$
of exponential characteristic
$k$
of exponential characteristic
![]() $p\geqslant 1$
.
$p\geqslant 1$
.
Let again
![]() $Y$
be a projective reduced
$Y$
be a projective reduced
![]() $k$
-variety of dimension
$k$
-variety of dimension
![]() $d$
and write
$d$
and write
![]() $\text{Alb}(Y)$
for the Esnault–Srinivas–Viehweg Albanese variety. While there is an explicit description of
$\text{Alb}(Y)$
for the Esnault–Srinivas–Viehweg Albanese variety. While there is an explicit description of
 $\text{Alb}(Y)=A^{d}(Y)$
over
$\text{Alb}(Y)=A^{d}(Y)$
over
![]() $\mathbb{C}$
(as recalled in 8.2) using Hodge theory, in positive characteristic, [Reference Esnault, Srinivas and ViehwegESV99] gives only an existence statement and little is known on the properties of
$\mathbb{C}$
(as recalled in 8.2) using Hodge theory, in positive characteristic, [Reference Esnault, Srinivas and ViehwegESV99] gives only an existence statement and little is known on the properties of
![]() $\text{Alb}(Y)$
(some pathological properties of
$\text{Alb}(Y)$
(some pathological properties of
![]() $\text{Alb}(Y)$
for specific singular varieties are studied in [Reference Esnault, Srinivas and ViehwegESV99, § 3]).
$\text{Alb}(Y)$
for specific singular varieties are studied in [Reference Esnault, Srinivas and ViehwegESV99, § 3]).
In [Reference MallickMal09], Mallick proves the following Roitman-style theorem.
Theorem 11.1 [Reference MallickMal09, Theorem 16].
For any reduced projective variety
![]() $Y$
of dimension
$Y$
of dimension
![]() $d$
over
$d$
over
![]() $k$
and for
$k$
and for
![]() $n$
coprime with the characteristic of
$n$
coprime with the characteristic of
![]() $k$
, the map
$k$
, the map
![]() $\unicode[STIX]{x1D70C}_{Y}$
induces an isomorphism on
$\unicode[STIX]{x1D70C}_{Y}$
induces an isomorphism on
![]() $n$
-torsion subgroups
$n$
-torsion subgroups
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{Y}:_{n}\text{CH}_{0}^{\text{LW}}(Y)_{ deg0}\xrightarrow[{}]{\simeq }\text{}_{n}\text{Alb}(Y)=\text{}_{n}J^{d}(Y).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{Y}:_{n}\text{CH}_{0}^{\text{LW}}(Y)_{ deg0}\xrightarrow[{}]{\simeq }\text{}_{n}\text{Alb}(Y)=\text{}_{n}J^{d}(Y).\end{eqnarray}$$
For the rest of this section, the Albanese variety
![]() $\text{Alb}(Y)$
will be denoted by
$\text{Alb}(Y)$
will be denoted by
![]() $A^{d}(Y)$
to keep consistency with the notations of the previous sections.
$A^{d}(Y)$
to keep consistency with the notations of the previous sections.
11.1 Albanese with modulus and its universality in any characteristic
Let
![]() $X$
be a smooth projective scheme of dimension
$X$
be a smooth projective scheme of dimension
![]() $d\geqslant 1$
over
$d\geqslant 1$
over
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Write as usual
$D\subset X$
be an effective Cartier divisor. Write as usual
![]() $S_{X}$
for the double construction applied to the pair
$S_{X}$
for the double construction applied to the pair
![]() $(X,D)$
. Using Theorem 7.3, we shall again identify the two Chow groups
$(X,D)$
. Using Theorem 7.3, we shall again identify the two Chow groups
 $\text{CH}_{0}^{\text{LW}}(S_{X})$
and
$\text{CH}_{0}^{\text{LW}}(S_{X})$
and
 $\text{CH}_{0}(S_{X})$
throughout this section.
$\text{CH}_{0}(S_{X})$
throughout this section.
Let
![]() $U$
be an open dense subset contained in
$U$
be an open dense subset contained in
 $X^{o}=X\setminus D$
,
$X^{o}=X\setminus D$
,
![]() $x_{0}\in U$
a closed point and
$x_{0}\in U$
a closed point and
 $V=U\amalg U\subset (S_{X})_{\text{reg}}$
such that the compositions
$V=U\amalg U\subset (S_{X})_{\text{reg}}$
such that the compositions
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{x_{0},\pm }^{V}:V\rightarrow \text{CH}_{0}(S_{X})_{\deg 0}\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{S_{X}}}A^{d}(S_{X}),\quad \unicode[STIX]{x1D70B}_{x_{0}}^{U}:U\rightarrow \text{CH}_{0}(X)_{\deg 0}\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{X}}A^{d}(X)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{x_{0},\pm }^{V}:V\rightarrow \text{CH}_{0}(S_{X})_{\deg 0}\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{S_{X}}}A^{d}(S_{X}),\quad \unicode[STIX]{x1D70B}_{x_{0}}^{U}:U\rightarrow \text{CH}_{0}(X)_{\deg 0}\xrightarrow[{}]{\unicode[STIX]{x1D70C}_{X}}A^{d}(X)\end{eqnarray}$$
are morphisms of schemes (see Definition 9.10 for the notation
![]() $\unicode[STIX]{x1D70B}_{x_{0},\pm }^{V}$
and
$\unicode[STIX]{x1D70B}_{x_{0},\pm }^{V}$
and
![]() $\unicode[STIX]{x1D70B}_{x_{0}}^{U}$
).
$\unicode[STIX]{x1D70B}_{x_{0}}^{U}$
).
Theorem 7.1 gives the familiar split short exact sequence on the group of zero cycles
 $$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)_{\deg 0}\xrightarrow[{}]{p_{+,\ast }}\text{CH}_{0}(S_{X})_{\deg 0}\xrightarrow[{}]{\unicode[STIX]{x1D704}_{-}^{\ast }}\text{CH}_{0}(X)_{\deg 0}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)_{\deg 0}\xrightarrow[{}]{p_{+,\ast }}\text{CH}_{0}(S_{X})_{\deg 0}\xrightarrow[{}]{\unicode[STIX]{x1D704}_{-}^{\ast }}\text{CH}_{0}(X)_{\deg 0}\rightarrow 0\end{eqnarray}$$
and there is a homomorphism
 $\unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)_{\deg 0}\rightarrow \text{CH}_{0}(S_{X})_{\deg 0}$
such that
$\unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)_{\deg 0}\rightarrow \text{CH}_{0}(S_{X})_{\deg 0}$
such that
 $i_{-}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}$
.
$i_{-}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}$
.
It follows from the discussion in § 10.2 and the proof of Lemma 10.2 that the homomorphisms
 $\unicode[STIX]{x1D70C}_{X}\circ i_{-}^{\ast }:\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow A^{d}(X)$
and
$\unicode[STIX]{x1D70C}_{X}\circ i_{-}^{\ast }:\text{CH}_{0}(S_{X})_{\deg 0}\rightarrow A^{d}(X)$
and
 $\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)_{\deg 0}\rightarrow A^{d}(S_{X})$
are both regular. It follows from the universality of
$\unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D6E5}^{\ast }:\text{CH}_{0}(X)_{\deg 0}\rightarrow A^{d}(S_{X})$
are both regular. It follows from the universality of
![]() $A^{d}(X)$
and
$A^{d}(X)$
and
 $A^{d}(S_{X})$
that there are unique homomorphisms of algebraic groups
$A^{d}(S_{X})$
that there are unique homomorphisms of algebraic groups
 $i_{-}^{\ast }:A^{d}(S_{X})\rightarrow A^{d}(X)$
and
$i_{-}^{\ast }:A^{d}(S_{X})\rightarrow A^{d}(X)$
and
 $\unicode[STIX]{x1D6E5}^{\ast }:A^{d}(X)\rightarrow A^{d}(S_{X})$
such that the diagram
$\unicode[STIX]{x1D6E5}^{\ast }:A^{d}(X)\rightarrow A^{d}(S_{X})$
such that the diagram

is commutative.
It also follows from this commutative diagram that
 $i_{-}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }:A^{d}(X)\rightarrow A^{d}(X)$
is the identity. Indeed, any
$i_{-}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }:A^{d}(X)\rightarrow A^{d}(X)$
is the identity. Indeed, any
 $\unicode[STIX]{x1D6FC}\in A^{d}(X)$
can be written as
$\unicode[STIX]{x1D6FC}\in A^{d}(X)$
can be written as
 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70C}_{X}(\unicode[STIX]{x1D6FD})$
and then
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70C}_{X}(\unicode[STIX]{x1D6FD})$
and then
 $$\begin{eqnarray}i_{-}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }\circ \unicode[STIX]{x1D70C}_{X}(\unicode[STIX]{x1D6FD})=i_{-}^{\ast }\circ \unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D70C}_{X}\circ i_{-}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D70C}_{X}(\unicode[STIX]{x1D6FD}).\end{eqnarray}$$
$$\begin{eqnarray}i_{-}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }\circ \unicode[STIX]{x1D70C}_{X}(\unicode[STIX]{x1D6FD})=i_{-}^{\ast }\circ \unicode[STIX]{x1D70C}_{S_{X}}\circ \unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D70C}_{X}\circ i_{-}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }(\unicode[STIX]{x1D6FD})=\unicode[STIX]{x1D70C}_{X}(\unicode[STIX]{x1D6FD}).\end{eqnarray}$$
Definition 11.2. We define
 $A^{d}(X|D)$
to be the closed algebraic subgroup of
$A^{d}(X|D)$
to be the closed algebraic subgroup of
 $A^{d}(S_{X})$
given by the inverse image of the identity element of
$A^{d}(S_{X})$
given by the inverse image of the identity element of
![]() $A^{d}(X)$
via
$A^{d}(X)$
via
![]() $\unicode[STIX]{x1D704}_{-}^{\ast }$
. As before, we denote the inclusion
$\unicode[STIX]{x1D704}_{-}^{\ast }$
. As before, we denote the inclusion
 $A^{d}(X|D){\hookrightarrow}A^{d}(S_{X})$
by
$A^{d}(X|D){\hookrightarrow}A^{d}(S_{X})$
by
![]() $p_{+,\ast }$
. It follows from (11.2) that there is a unique surjective homomorphism
$p_{+,\ast }$
. It follows from (11.2) that there is a unique surjective homomorphism
 $\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}{\twoheadrightarrow}A^{d}(X|D)$
such that
$\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}{\twoheadrightarrow}A^{d}(X|D)$
such that
 $\unicode[STIX]{x1D70C}_{S_{X}}\circ p_{+,\ast }=p_{+,\ast }\circ \unicode[STIX]{x1D70C}_{X|D}$
.
$\unicode[STIX]{x1D70C}_{S_{X}}\circ p_{+,\ast }=p_{+,\ast }\circ \unicode[STIX]{x1D70C}_{X|D}$
.
The reader can now check easily that using (11.2) and (11.3), the proofs of Lemma 10.1 and Theorem 10.3 go through mutatis mutandis to give the following generalization of the latter.
Theorem 11.3. The group homomorphism
 $\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
is regular and surjective and makes
$\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
is regular and surjective and makes
 $A^{d}(X|D)$
the universal regular quotient of
$A^{d}(X|D)$
the universal regular quotient of
 $\text{CH}_{0}(X|D)_{\deg 0}$
.
$\text{CH}_{0}(X|D)_{\deg 0}$
.
Remark 11.4. Since
![]() $X$
is smooth and projective, the Albanese variety
$X$
is smooth and projective, the Albanese variety
![]() $A^{d}(X)$
is an abelian variety over
$A^{d}(X)$
is an abelian variety over
![]() $k$
. By [Reference Esnault, Srinivas and ViehwegESV99], the generalized Albanese
$k$
. By [Reference Esnault, Srinivas and ViehwegESV99], the generalized Albanese
 $A^{d}(S_{X})$
is a smooth commutative algebraic group of general type, i.e., an extension of an abelian variety by a linear algebraic group. An immediate consequence of the definition and of Theorem 11.3 is that the linear part of
$A^{d}(S_{X})$
is a smooth commutative algebraic group of general type, i.e., an extension of an abelian variety by a linear algebraic group. An immediate consequence of the definition and of Theorem 11.3 is that the linear part of
 $A^{d}(S_{X})$
coincides with the linear part of the Albanese with modulus
$A^{d}(S_{X})$
coincides with the linear part of the Albanese with modulus
 $A^{d}(X|D)$
.
$A^{d}(X|D)$
.
11.2 Roitman theorem in arbitrary characteristic
Using Theorem 11.1, we can now generalize Theorem 10.4 over any algebraically closed field as follows. We keep the notations and the assumptions of 11.1.
Theorem 11.5. Let
![]() $X$
be a smooth projective variety of dimension
$X$
be a smooth projective variety of dimension
![]() $d\geqslant 1$
over an algebraically closed field
$d\geqslant 1$
over an algebraically closed field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Let
$D\subset X$
be an effective Cartier divisor. Let
![]() $n$
be an integer prime to the exponential characteristic of
$n$
be an integer prime to the exponential characteristic of
![]() $k$
. Then the Albanese map
$k$
. Then the Albanese map
 $\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
induces an isomorphism on
$\unicode[STIX]{x1D70C}_{X|D}:\text{CH}_{0}(X|D)_{\deg 0}\rightarrow A^{d}(X|D)$
induces an isomorphism on
![]() $n$
-torsion subgroups
$n$
-torsion subgroups
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{X|D}:\text{}_{n}\text{CH}_{0}(X|D)_{\deg 0}\xrightarrow[{}]{\simeq }\text{}_{n}A^{d}(X|D).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{X|D}:\text{}_{n}\text{CH}_{0}(X|D)_{\deg 0}\xrightarrow[{}]{\simeq }\text{}_{n}A^{d}(X|D).\end{eqnarray}$$
Proof. We consider the following commutative diagram.

It follows from (11.2) that the top and the bottom rows are compatibly split exact. The original Roitman’s theorem [Reference RojtmanRoi80] says that the vertical arrow on the left is an isomorphism. It follows from Theorems 7.3 and 11.1 that the middle vertical arrow is an isomorphism. The theorem follows. ◻
Remark 11.6. We note that the linear part of
 $A^{d}(X|D)$
(that coincides with the linear part of
$A^{d}(X|D)$
(that coincides with the linear part of
 $A^{d}(S_{X})$
) depends heavily on the geometry of
$A^{d}(S_{X})$
) depends heavily on the geometry of
![]() $D$
and will have, in general, both a unipotent and a torus part. For example, if
$D$
and will have, in general, both a unipotent and a torus part. For example, if
![]() $D$
is a smooth divisor inside a smooth surface, the presence of a
$D$
is a smooth divisor inside a smooth surface, the presence of a
![]() $\mathbb{G}_{m}$
part in
$\mathbb{G}_{m}$
part in
 $A^{d}(X|D)$
depends on the class of
$A^{d}(X|D)$
depends on the class of
![]() $D$
in the Neron–Severi group of
$D$
in the Neron–Severi group of
![]() $X$
.
$X$
.
12 Cycle class map to relative
 $K$
-theory
$K$
-theory
As we mentioned in § 1, one of the motivations for studying cycles with modulus is to find a cohomology theory which can describe relative
![]() $K$
-theory of divisors in a scheme in terms of algebraic cycles. If the higher Chow groups with modulus are indeed the right objects which serve this purpose, there must be a cycle class map from the Chow groups with modulus to relative
$K$
-theory of divisors in a scheme in terms of algebraic cycles. If the higher Chow groups with modulus are indeed the right objects which serve this purpose, there must be a cycle class map from the Chow groups with modulus to relative
![]() $K$
-groups. Moreover, this map must describe the Chow group as a part of relative
$K$
-groups. Moreover, this map must describe the Chow group as a part of relative
![]() $K$
-groups in most of the cases. Our goal in this section is to use our double construction to answer these questions for the 0-cycles with modulus. We first consider the case of line bundles in this setting.
$K$
-groups in most of the cases. Our goal in this section is to use our double construction to answer these questions for the 0-cycles with modulus. We first consider the case of line bundles in this setting.
12.1 Vector bundles on the double and relative Picard groups
Let
![]() $k$
be any field and let
$k$
be any field and let
![]() $X$
be a smooth quasi-projective scheme over
$X$
be a smooth quasi-projective scheme over
![]() $k$
with an effective Cartier divisor
$k$
with an effective Cartier divisor
![]() $D$
. Let
$D$
. Let
![]() $X^{o}$
be the open complement
$X^{o}$
be the open complement
![]() $X\setminus D$
. We denote as above by
$X\setminus D$
. We denote as above by
![]() $S_{X}$
the double
$S_{X}$
the double
 $S(X,D)$
.
$S(X,D)$
.
12.1.1 Vector bundles on the double
Let
 ${\mathcal{P}}_{S}={\mathcal{P}}_{S(X,D)}$
denote the category of locally free sheaves of finite rank on
${\mathcal{P}}_{S}={\mathcal{P}}_{S(X,D)}$
denote the category of locally free sheaves of finite rank on
![]() $S_{X}$
. Since
$S_{X}$
. Since
![]() $X$
is quasi-projective,
$X$
is quasi-projective,
![]() $S_{X}$
is quasi-projective as well and therefore it admits an ample family of line bundles. Thus we can replace Thomason spectrum
$S_{X}$
is quasi-projective as well and therefore it admits an ample family of line bundles. Thus we can replace Thomason spectrum
![]() $K(S_{X})$
built out of perfect complexes on
$K(S_{X})$
built out of perfect complexes on
![]() $S_{X}$
with
$S_{X}$
with
 $\unicode[STIX]{x1D6FA}BQ{\mathcal{P}}_{S}$
, at least for computing the groups
$\unicode[STIX]{x1D6FA}BQ{\mathcal{P}}_{S}$
, at least for computing the groups
 $K_{p}(S_{X})$
for
$K_{p}(S_{X})$
for
![]() $p\geqslant 0$
, and similarly for
$p\geqslant 0$
, and similarly for
![]() $X$
and
$X$
and
![]() $D$
. By construction, the category
$D$
. By construction, the category
![]() ${\mathcal{P}}_{S}$
is equivalent to the category of triples
${\mathcal{P}}_{S}$
is equivalent to the category of triples
 $(E,E^{\prime },\unicode[STIX]{x1D719})$
, where
$(E,E^{\prime },\unicode[STIX]{x1D719})$
, where
![]() $E$
and
$E$
and
![]() $E^{\prime }$
are locally free sheaves on
$E^{\prime }$
are locally free sheaves on
![]() $X$
and
$X$
and
 $\unicode[STIX]{x1D719}:\unicode[STIX]{x1D704}_{D}^{\ast }E\rightarrow \unicode[STIX]{x1D704}_{D}^{\ast }E^{\prime }$
is a fixed isomorphism on the restriction to
$\unicode[STIX]{x1D719}:\unicode[STIX]{x1D704}_{D}^{\ast }E\rightarrow \unicode[STIX]{x1D704}_{D}^{\ast }E^{\prime }$
is a fixed isomorphism on the restriction to
![]() $D$
(see [Reference LevineLev94], but also [Reference MilnorMil71, Theorem 2.1]). This description gives us the following.
$D$
(see [Reference LevineLev94], but also [Reference MilnorMil71, Theorem 2.1]). This description gives us the following.
Lemma 12.1. The composite map of spectra
 $$\begin{eqnarray}K(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{1}^{\ast },\unicode[STIX]{x1D704}_{2}^{\ast }}K(X)\amalg K(X)\xrightarrow[{}]{f}K(D)\end{eqnarray}$$
$$\begin{eqnarray}K(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{1}^{\ast },\unicode[STIX]{x1D704}_{2}^{\ast }}K(X)\amalg K(X)\xrightarrow[{}]{f}K(D)\end{eqnarray}$$
is homotopy trivial, where
 $$\begin{eqnarray}f=\unicode[STIX]{x1D704}_{D}^{\ast }\oplus -\unicode[STIX]{x1D704}_{D}^{\ast }:K(X)\amalg K(X)\xrightarrow[{}]{(\text{id},-\text{id})}K(X)\amalg K(X)\xrightarrow[{}]{\unicode[STIX]{x1D704}_{D}^{\ast }+\unicode[STIX]{x1D704}_{D}^{\ast }}K(D).\end{eqnarray}$$
$$\begin{eqnarray}f=\unicode[STIX]{x1D704}_{D}^{\ast }\oplus -\unicode[STIX]{x1D704}_{D}^{\ast }:K(X)\amalg K(X)\xrightarrow[{}]{(\text{id},-\text{id})}K(X)\amalg K(X)\xrightarrow[{}]{\unicode[STIX]{x1D704}_{D}^{\ast }+\unicode[STIX]{x1D704}_{D}^{\ast }}K(D).\end{eqnarray}$$
Notice that the maps in the definition of
![]() $f$
make sense because they are defined in the homotopy category of spectra which is an additive category.
$f$
make sense because they are defined in the homotopy category of spectra which is an additive category.
12.1.2 Relative Picard group
We denote by
 $\operatorname{Pic}(X,D)$
the group of isomorphism classes of pairs
$\operatorname{Pic}(X,D)$
the group of isomorphism classes of pairs
![]() $({\mathcal{L}},\unicode[STIX]{x1D70E})$
consisting of a line bundle
$({\mathcal{L}},\unicode[STIX]{x1D70E})$
consisting of a line bundle
![]() ${\mathcal{L}}$
on
${\mathcal{L}}$
on
![]() $X$
together with a fixed trivialization
$X$
together with a fixed trivialization
 $\unicode[STIX]{x1D70E}:{\mathcal{L}}_{|D}\xrightarrow[{}]{\simeq }{\mathcal{O}}_{D}$
along
$\unicode[STIX]{x1D70E}:{\mathcal{L}}_{|D}\xrightarrow[{}]{\simeq }{\mathcal{O}}_{D}$
along
![]() $D$
, under tensor product operation. It is called the relative Picard group of the pair
$D$
, under tensor product operation. It is called the relative Picard group of the pair
![]() $(X,D)$
. Write
$(X,D)$
. Write
![]() $G$
for the group of isomorphism classes of triples
$G$
for the group of isomorphism classes of triples
 $\{({\mathcal{L}}_{+},{\mathcal{L}}_{-},\unicode[STIX]{x1D719})\}$
for
$\{({\mathcal{L}}_{+},{\mathcal{L}}_{-},\unicode[STIX]{x1D719})\}$
for
![]() ${\mathcal{L}}_{\pm }$
line bundles on
${\mathcal{L}}_{\pm }$
line bundles on
![]() $X$
with a given isomorphism
$X$
with a given isomorphism
 $\unicode[STIX]{x1D719}:{\mathcal{L}}_{+}|_{D}\xrightarrow[{}]{\simeq }{\mathcal{L}}_{-}|_{D}$
along
$\unicode[STIX]{x1D719}:{\mathcal{L}}_{+}|_{D}\xrightarrow[{}]{\simeq }{\mathcal{L}}_{-}|_{D}$
along
![]() $D$
. The above description of the category of vector bundles on
$D$
. The above description of the category of vector bundles on
![]() $S_{X}$
gives in particular two maps, one inverse to the other,
$S_{X}$
gives in particular two maps, one inverse to the other,
 $$\begin{eqnarray}\unicode[STIX]{x1D703}:\operatorname{Pic}(S_{X})\rightarrow G,\quad \unicode[STIX]{x1D702}:G\rightarrow \operatorname{Pic}(S_{X})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}:\operatorname{Pic}(S_{X})\rightarrow G,\quad \unicode[STIX]{x1D702}:G\rightarrow \operatorname{Pic}(S_{X})\end{eqnarray}$$
defined by
 $$\begin{eqnarray}\unicode[STIX]{x1D703}({\mathcal{L}})=({\mathcal{L}}_{+}=\unicode[STIX]{x1D704}_{+}^{\ast }({\mathcal{L}}),{\mathcal{L}}_{-}=\unicode[STIX]{x1D704}_{-}^{\ast }({\mathcal{L}}),\unicode[STIX]{x1D719}:\unicode[STIX]{x1D704}_{D}^{\ast }\unicode[STIX]{x1D704}_{+}^{\ast }{\mathcal{L}}\simeq \unicode[STIX]{x1D704}_{D}^{\ast }\unicode[STIX]{x1D704}_{-}^{\ast }{\mathcal{L}}),\quad \unicode[STIX]{x1D702}(({\mathcal{L}}_{+},{\mathcal{L}}_{-},\unicode[STIX]{x1D719}))={\mathcal{L}}_{+}\times _{\unicode[STIX]{x1D719}}{\mathcal{L}}_{-}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}({\mathcal{L}})=({\mathcal{L}}_{+}=\unicode[STIX]{x1D704}_{+}^{\ast }({\mathcal{L}}),{\mathcal{L}}_{-}=\unicode[STIX]{x1D704}_{-}^{\ast }({\mathcal{L}}),\unicode[STIX]{x1D719}:\unicode[STIX]{x1D704}_{D}^{\ast }\unicode[STIX]{x1D704}_{+}^{\ast }{\mathcal{L}}\simeq \unicode[STIX]{x1D704}_{D}^{\ast }\unicode[STIX]{x1D704}_{-}^{\ast }{\mathcal{L}}),\quad \unicode[STIX]{x1D702}(({\mathcal{L}}_{+},{\mathcal{L}}_{-},\unicode[STIX]{x1D719}))={\mathcal{L}}_{+}\times _{\unicode[STIX]{x1D719}}{\mathcal{L}}_{-}\end{eqnarray}$$
where
 ${\mathcal{L}}_{+}\times _{\unicode[STIX]{x1D719}}{\mathcal{L}}_{-}$
is the gluing of
${\mathcal{L}}_{+}\times _{\unicode[STIX]{x1D719}}{\mathcal{L}}_{-}$
is the gluing of
![]() ${\mathcal{L}}_{+}$
and
${\mathcal{L}}_{+}$
and
![]() ${\mathcal{L}}_{-}$
along
${\mathcal{L}}_{-}$
along
![]() $\unicode[STIX]{x1D719}$
.
$\unicode[STIX]{x1D719}$
.
We will then identify the group
 $\operatorname{Pic}(S_{X})$
with
$\operatorname{Pic}(S_{X})$
with
![]() $G$
. In this way we can easily define maps
$G$
. In this way we can easily define maps
 $$\begin{eqnarray}p_{\pm ,\ast }:\operatorname{Pic}(X,D)\rightrightarrows \operatorname{Pic}(S_{X}),\quad \unicode[STIX]{x1D70F}_{X}^{\ast }:\operatorname{Pic}(S_{X})\rightarrow \operatorname{Pic}(X,D)\end{eqnarray}$$
$$\begin{eqnarray}p_{\pm ,\ast }:\operatorname{Pic}(X,D)\rightrightarrows \operatorname{Pic}(S_{X}),\quad \unicode[STIX]{x1D70F}_{X}^{\ast }:\operatorname{Pic}(S_{X})\rightarrow \operatorname{Pic}(X,D)\end{eqnarray}$$
using formally the same definitions that we gave for
![]() $0$
-cycles in § 5. Explicitly, we have
$0$
-cycles in § 5. Explicitly, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }(({\mathcal{L}}_{+},{\mathcal{L}}_{-},\unicode[STIX]{x1D719}))=({\mathcal{L}}_{+}\otimes {\mathcal{L}}_{-}^{-1},\unicode[STIX]{x1D719}\otimes \text{id}_{\unicode[STIX]{x1D704}_{D}^{\ast }{\mathcal{L}}_{-}^{-1}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{X}^{\ast }(({\mathcal{L}}_{+},{\mathcal{L}}_{-},\unicode[STIX]{x1D719}))=({\mathcal{L}}_{+}\otimes {\mathcal{L}}_{-}^{-1},\unicode[STIX]{x1D719}\otimes \text{id}_{\unicode[STIX]{x1D704}_{D}^{\ast }{\mathcal{L}}_{-}^{-1}})\end{eqnarray}$$
for
 $\unicode[STIX]{x1D719}\otimes \text{id}_{\unicode[STIX]{x1D704}_{D}^{\ast }{\mathcal{L}}_{-}^{-1}}:\unicode[STIX]{x1D704}_{D}^{\ast }({\mathcal{L}}_{+}\otimes {\mathcal{L}}_{-}^{-1})=\unicode[STIX]{x1D704}_{D}^{\ast }{\mathcal{L}}_{+}\otimes _{{\mathcal{O}}_{D}}\unicode[STIX]{x1D704}_{D}^{\ast }{\mathcal{L}}_{-}^{-1}\xrightarrow[{}]{\unicode[STIX]{x1D719}\otimes 1}\unicode[STIX]{x1D704}_{D}^{\ast }({\mathcal{L}}_{-})\otimes \unicode[STIX]{x1D704}_{D}^{\ast }({\mathcal{L}}_{-})^{-1}\xrightarrow[{}]{\text{can}}{\mathcal{O}}_{D},$
and
$\unicode[STIX]{x1D719}\otimes \text{id}_{\unicode[STIX]{x1D704}_{D}^{\ast }{\mathcal{L}}_{-}^{-1}}:\unicode[STIX]{x1D704}_{D}^{\ast }({\mathcal{L}}_{+}\otimes {\mathcal{L}}_{-}^{-1})=\unicode[STIX]{x1D704}_{D}^{\ast }{\mathcal{L}}_{+}\otimes _{{\mathcal{O}}_{D}}\unicode[STIX]{x1D704}_{D}^{\ast }{\mathcal{L}}_{-}^{-1}\xrightarrow[{}]{\unicode[STIX]{x1D719}\otimes 1}\unicode[STIX]{x1D704}_{D}^{\ast }({\mathcal{L}}_{-})\otimes \unicode[STIX]{x1D704}_{D}^{\ast }({\mathcal{L}}_{-})^{-1}\xrightarrow[{}]{\text{can}}{\mathcal{O}}_{D},$
and
 $p_{+,\ast }({\mathcal{L}},\unicode[STIX]{x1D70E})={\mathcal{L}}\times _{\unicode[STIX]{x1D70E}}{\mathcal{O}}_{X}=({\mathcal{L}},{\mathcal{O}}_{X},\unicode[STIX]{x1D70E})$
(and similarly for
$p_{+,\ast }({\mathcal{L}},\unicode[STIX]{x1D70E})={\mathcal{L}}\times _{\unicode[STIX]{x1D70E}}{\mathcal{O}}_{X}=({\mathcal{L}},{\mathcal{O}}_{X},\unicode[STIX]{x1D70E})$
(and similarly for
![]() $p_{-,\ast }$
).
$p_{-,\ast }$
).
It is immediate to check that
![]() $p_{\pm ,\ast }$
are injective, splitting
$p_{\pm ,\ast }$
are injective, splitting
![]() $\unicode[STIX]{x1D70F}_{X}^{\ast }$
. Moreover, we have maps
$\unicode[STIX]{x1D70F}_{X}^{\ast }$
. Moreover, we have maps
 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{\pm }^{\ast }:\operatorname{Pic}(S_{X})\rightrightarrows \operatorname{Pic}(X),\quad \unicode[STIX]{x1D6E5}_{X}^{\ast }:\operatorname{Pic}(X)\rightarrow \operatorname{Pic}(S_{X})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{\pm }^{\ast }:\operatorname{Pic}(S_{X})\rightrightarrows \operatorname{Pic}(X),\quad \unicode[STIX]{x1D6E5}_{X}^{\ast }:\operatorname{Pic}(X)\rightarrow \operatorname{Pic}(S_{X})\end{eqnarray}$$
given on isomorphism classes by
 $\unicode[STIX]{x1D704}_{+}^{\ast }(({\mathcal{L}}_{+},{\mathcal{L}}_{-},\unicode[STIX]{x1D719}))={\mathcal{L}}_{+},$
$\unicode[STIX]{x1D704}_{+}^{\ast }(({\mathcal{L}}_{+},{\mathcal{L}}_{-},\unicode[STIX]{x1D719}))={\mathcal{L}}_{+},$
 $\unicode[STIX]{x1D704}_{-}^{\ast }(({\mathcal{L}}_{+},{\mathcal{L}}_{-},\unicode[STIX]{x1D719}))={\mathcal{L}}_{-}$
and
$\unicode[STIX]{x1D704}_{-}^{\ast }(({\mathcal{L}}_{+},{\mathcal{L}}_{-},\unicode[STIX]{x1D719}))={\mathcal{L}}_{-}$
and
 $\unicode[STIX]{x1D6E5}_{X}^{\ast }({\mathcal{L}})=({\mathcal{L}},{\mathcal{L}},\text{id})$
. And one clearly has that the composition
$\unicode[STIX]{x1D6E5}_{X}^{\ast }({\mathcal{L}})=({\mathcal{L}},{\mathcal{L}},\text{id})$
. And one clearly has that the composition
 $\unicode[STIX]{x1D704}_{\pm }^{\ast }\circ \unicode[STIX]{x1D6E5}_{X}^{\ast }$
is the identity.
$\unicode[STIX]{x1D704}_{\pm }^{\ast }\circ \unicode[STIX]{x1D6E5}_{X}^{\ast }$
is the identity.
We summarize the result in the following proposition, which is the analogue of Theorem 7.1 for line bundles and is used in § 8.
Proposition 12.2. Let
![]() $X$
be a smooth quasi-projective scheme over
$X$
be a smooth quasi-projective scheme over
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then there are maps
$D\subset X$
be an effective Cartier divisor. Then there are maps
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}^{\ast }:\operatorname{Pic}(X)\rightarrow \operatorname{Pic}(S_{X})\quad \text{and}\quad \unicode[STIX]{x1D704}_{\pm }^{\ast }:\operatorname{Pic}(S_{X})\rightarrow \operatorname{Pic}(X), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70F}_{X}^{\ast }:\operatorname{Pic}(X)\rightarrow \operatorname{Pic}(X,D)\quad \text{and}\quad p_{\pm ,\ast }:\operatorname{Pic}(X,D)\rightarrow \operatorname{Pic}(S_{X}) & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6E5}^{\ast }:\operatorname{Pic}(X)\rightarrow \operatorname{Pic}(S_{X})\quad \text{and}\quad \unicode[STIX]{x1D704}_{\pm }^{\ast }:\operatorname{Pic}(S_{X})\rightarrow \operatorname{Pic}(X), & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70F}_{X}^{\ast }:\operatorname{Pic}(X)\rightarrow \operatorname{Pic}(X,D)\quad \text{and}\quad p_{\pm ,\ast }:\operatorname{Pic}(X,D)\rightarrow \operatorname{Pic}(S_{X}) & \displaystyle \nonumber\end{eqnarray}$$
such that
 $\unicode[STIX]{x1D704}_{\pm }^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}$
on
$\unicode[STIX]{x1D704}_{\pm }^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}$
on
![]() $\operatorname{Pic}(X)$
and
$\operatorname{Pic}(X)$
and
 $\unicode[STIX]{x1D70F}_{X}^{\ast }\circ p_{\pm ,\ast }=\pm \text{Id}$
on
$\unicode[STIX]{x1D70F}_{X}^{\ast }\circ p_{\pm ,\ast }=\pm \text{Id}$
on
 $\operatorname{Pic}(X,D)$
. Moreover, the sequences
$\operatorname{Pic}(X,D)$
. Moreover, the sequences
 $$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow \operatorname{Pic}(X,D)\xrightarrow[{}]{p_{+,\ast }}\operatorname{Pic}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{-}^{\ast }}\operatorname{Pic}(X)\rightarrow 0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle 0\rightarrow \operatorname{Pic}(X)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}^{\ast }}\operatorname{Pic}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70F}_{X}^{\ast }}\operatorname{Pic}(X,D)\rightarrow 0 & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow \operatorname{Pic}(X,D)\xrightarrow[{}]{p_{+,\ast }}\operatorname{Pic}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{-}^{\ast }}\operatorname{Pic}(X)\rightarrow 0, & \displaystyle \nonumber\\ \displaystyle & \displaystyle 0\rightarrow \operatorname{Pic}(X)\xrightarrow[{}]{\unicode[STIX]{x1D6E5}^{\ast }}\operatorname{Pic}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D70F}_{X}^{\ast }}\operatorname{Pic}(X,D)\rightarrow 0 & \displaystyle \nonumber\end{eqnarray}$$
are split exact.
12.2 Cycle class map for 0-cycles with modulus
The goal of this subsection is the proof of Theorem 1.5. In order to do define the cycle class map from the Chow group with modulus to relative
![]() $K$
-group and prove its injectivity, we need to have an analogue of Theorem 7.1 for the relative
$K$
-group and prove its injectivity, we need to have an analogue of Theorem 7.1 for the relative
![]() $K$
-theory. Our strategy for proving this is to first construct a variant of relative
$K$
-theory. Our strategy for proving this is to first construct a variant of relative
![]() $K$
-theory, which we call the
$K$
-theory, which we call the
![]() $K$
-theory with modulus, for which Theorem 7.1 is immediate. We then show that this
$K$
-theory with modulus, for which Theorem 7.1 is immediate. We then show that this
![]() $K$
-theory with modulus coincides with the known relative
$K$
-theory with modulus coincides with the known relative
![]() $K$
-theory in as many cases as possible.
$K$
-theory in as many cases as possible.
Recall that for any map of schemes
 $f:X\rightarrow Y$
, the relative
$f:X\rightarrow Y$
, the relative
![]() $K$
-theory of the pair
$K$
-theory of the pair
![]() $(X,Y)$
is the spectrum defined as the homotopy fiber of the map
$(X,Y)$
is the spectrum defined as the homotopy fiber of the map
 $f^{\ast }:K(Y)\rightarrow K(X)$
. Let
$f^{\ast }:K(Y)\rightarrow K(X)$
. Let
![]() $X$
be a smooth quasi-projective scheme over
$X$
be a smooth quasi-projective scheme over
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Let
$D\subset X$
be an effective Cartier divisor. Let
 $K(X|D)$
denote the homotopy fiber of the restriction map
$K(X|D)$
denote the homotopy fiber of the restriction map
 $i_{-}^{\ast }:K(S_{X})\rightarrow K(X)$
. It is clear that
$i_{-}^{\ast }:K(S_{X})\rightarrow K(X)$
. It is clear that
 $K(X|D)$
is another notation for the relative
$K(X|D)$
is another notation for the relative
![]() $K$
-theory
$K$
-theory
 $K(S_{X},X_{-})$
. We call
$K(S_{X},X_{-})$
. We call
 $K(X|D)$
the
$K(X|D)$
the
![]() $K$
-theory with modulus. We have
$K$
-theory with modulus. We have
 $i_{-}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}_{K(X)}$
and a commutative diagram of homotopy fiber sequences.
$i_{-}^{\ast }\circ \unicode[STIX]{x1D6E5}^{\ast }=\text{Id}_{K(X)}$
and a commutative diagram of homotopy fiber sequences.

We have the following analogue of Proposition 8.1 for affine schemes.
Proposition 12.3 [Reference MilnorMil71, Theorem 6.2, Lemma 4.1].
Let
 $X=\operatorname{Spec}(A)$
be an affine scheme and let
$X=\operatorname{Spec}(A)$
be an affine scheme and let
![]() $I$
be the ideal defining
$I$
be the ideal defining
![]() $D\subset X$
. Then the map
$D\subset X$
. Then the map
![]() $\unicode[STIX]{x1D719}$
defines isomorphisms
$\unicode[STIX]{x1D719}$
defines isomorphisms
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{i}:K_{i}(X|D)\xrightarrow[{}]{{\sim}}K_{i}(X,D)\quad \text{for }i=0,1.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{i}:K_{i}(X|D)\xrightarrow[{}]{{\sim}}K_{i}(X,D)\quad \text{for }i=0,1.\end{eqnarray}$$
We do not know if Proposition 12.3 is true for non-affine schemes. But we can show that this is indeed the case for curves and surfaces when
![]() $i=0$
. The case of curves follows directly from Proposition 12.2. We shall prove this for surfaces in Proposition 13.2.
$i=0$
. The case of curves follows directly from Proposition 12.2. We shall prove this for surfaces in Proposition 13.2.
We can now prove the main result of this section.
Theorem 12.4. Let
![]() $X$
be a smooth quasi-projective scheme of dimension
$X$
be a smooth quasi-projective scheme of dimension
![]() $d\geqslant 1$
over a perfect field
$d\geqslant 1$
over a perfect field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then, there is a cycle class map
$D\subset X$
be an effective Cartier divisor. Then, there is a cycle class map
 $$\begin{eqnarray}\text{cyc}_{X|D}:\text{CH}_{0}(X|D)\rightarrow K_{0}(X,D).\end{eqnarray}$$
$$\begin{eqnarray}\text{cyc}_{X|D}:\text{CH}_{0}(X|D)\rightarrow K_{0}(X,D).\end{eqnarray}$$
This map is injective if
![]() $k$
is algebraically closed and
$k$
is algebraically closed and
![]() $X$
is affine.
$X$
is affine.
Proof. We have a commutative diagram of short exact sequences.

The maps
![]() $\text{cyc}_{X}$
and
$\text{cyc}_{X}$
and
![]() $\text{cyc}_{S_{X}}$
are the cycle class maps of Lemma 3.13 (where
$\text{cyc}_{S_{X}}$
are the cycle class maps of Lemma 3.13 (where
 $Y=(S_{X})_{\text{sing}}$
for
$Y=(S_{X})_{\text{sing}}$
for
![]() $\text{cyc}_{S_{X}}$
and
$\text{cyc}_{S_{X}}$
and
![]() $Y=\emptyset$
for
$Y=\emptyset$
for
![]() $\text{cyc}_{X}$
. See also [Reference Levine and WeibelLW85, § 2]). The above diagram uniquely defines a cycle class map map
$\text{cyc}_{X}$
. See also [Reference Levine and WeibelLW85, § 2]). The above diagram uniquely defines a cycle class map map
 $\widetilde{\text{cyc}}_{X|D}:\text{CH}_{0}(X|D)\rightarrow K_{0}(X|D)$
such that
$\widetilde{\text{cyc}}_{X|D}:\text{CH}_{0}(X|D)\rightarrow K_{0}(X|D)$
such that
 $p_{+,\ast }\circ \widetilde{\text{cyc}}_{X|D}=\text{cyc}_{S_{X}}\circ p_{+,\ast }$
. We set
$p_{+,\ast }\circ \widetilde{\text{cyc}}_{X|D}=\text{cyc}_{S_{X}}\circ p_{+,\ast }$
. We set
 $\text{cyc}_{X|D}=\unicode[STIX]{x1D719}_{0}\circ \widetilde{\text{cyc}}_{X|D}$
.
$\text{cyc}_{X|D}=\unicode[STIX]{x1D719}_{0}\circ \widetilde{\text{cyc}}_{X|D}$
.
If
![]() $k$
is algebraically closed and
$k$
is algebraically closed and
![]() $X$
is affine, the map
$X$
is affine, the map
![]() $\text{cyc}_{S_{X}}$
is injective by [Reference KrishnaKri15b, Corollary 7.3]. It follows that
$\text{cyc}_{S_{X}}$
is injective by [Reference KrishnaKri15b, Corollary 7.3]. It follows that
![]() $\widetilde{\text{cyc}}_{X|D}$
is injective. We finish proof of the injectivity of
$\widetilde{\text{cyc}}_{X|D}$
is injective. We finish proof of the injectivity of
![]() $\text{cyc}_{X|D}$
using Proposition 12.3.◻
$\text{cyc}_{X|D}$
using Proposition 12.3.◻
Remark 12.5. There are (at least) two general constructions of a cycle class map
 $$\begin{eqnarray}\text{cyc}_{X|D}^{d+n,n}:\text{CH}^{d+n}(X|D,n)\rightarrow K_{n}(X,D)\end{eqnarray}$$
$$\begin{eqnarray}\text{cyc}_{X|D}^{d+n,n}:\text{CH}^{d+n}(X|D,n)\rightarrow K_{n}(X,D)\end{eqnarray}$$
from higher Chow groups with modulus in the sense of [Reference Binda and SaitoBS16] to higher relative
![]() $K$
-groups (here
$K$
-groups (here
 $d=\dim X$
). See [Reference BindaBin16, I.4] for one of them. We will study the properties of this map in a different work.
$d=\dim X$
). See [Reference BindaBin16, I.4] for one of them. We will study the properties of this map in a different work.
13 The case of surfaces
In this section, we shall apply Theorem 7.1 to establish the relation between cycles with modulus and relative
![]() $K$
-theory for surfaces. In particular, we prove a modulus version of Bloch’s formula. Before we do this, we need to prove a generalization of Proposition 12.3 for non-affine surfaces.
$K$
-theory for surfaces. In particular, we prove a modulus version of Bloch’s formula. Before we do this, we need to prove a generalization of Proposition 12.3 for non-affine surfaces.
Lemma 13.1. Let
![]() $X$
be a reduced quasi-projective surface over any field
$X$
be a reduced quasi-projective surface over any field
![]() $k$
containing at least three elements. Let
$k$
containing at least three elements. Let
 $F^{2}K_{0}(X)$
be the subgroup of
$F^{2}K_{0}(X)$
be the subgroup of
![]() $K_{0}(X)$
generated by the cycle classes of regular points of
$K_{0}(X)$
generated by the cycle classes of regular points of
![]() $X$
. Then, there is a canonical isomorphism
$X$
. Then, there is a canonical isomorphism
 $H^{2}(X,{\mathcal{K}}_{2,X})\xrightarrow[{}]{\simeq }F^{2}K_{0}(X)$
.
$H^{2}(X,{\mathcal{K}}_{2,X})\xrightarrow[{}]{\simeq }F^{2}K_{0}(X)$
.
Proof. By the Thomason–Trobaugh spectral sequence for
![]() $K$
-theory, we get an exact sequence
$K$
-theory, we get an exact sequence
 $$\begin{eqnarray}K_{1}(X)\rightarrow H^{0}(X,{\mathcal{K}}_{1,X})\xrightarrow[{}]{\unicode[STIX]{x2202}}H^{2}(X,{\mathcal{K}}_{2,X})\rightarrow K_{0}(X).\end{eqnarray}$$
$$\begin{eqnarray}K_{1}(X)\rightarrow H^{0}(X,{\mathcal{K}}_{1,X})\xrightarrow[{}]{\unicode[STIX]{x2202}}H^{2}(X,{\mathcal{K}}_{2,X})\rightarrow K_{0}(X).\end{eqnarray}$$
On the other hand, it is well known that the map
 $K_{1}(X)\rightarrow H^{0}(X,{\mathcal{K}}_{1,X})$
is surjective (see, for example, [Reference KrishnaKri15a, § 2]). It follows that
$K_{1}(X)\rightarrow H^{0}(X,{\mathcal{K}}_{1,X})$
is surjective (see, for example, [Reference KrishnaKri15a, § 2]). It follows that
 $H^{2}(X,{\mathcal{K}}_{2}){\hookrightarrow}K_{0}(X)$
.
$H^{2}(X,{\mathcal{K}}_{2}){\hookrightarrow}K_{0}(X)$
.
We are only left to show that
 $H^{2}(X,{\mathcal{K}}_{2,X}){\twoheadrightarrow}F^{2}K_{0}(X)$
. But this follows by the results of Levine [Reference LevineLev85a], because he shows that there is a surjective map
$H^{2}(X,{\mathcal{K}}_{2,X}){\twoheadrightarrow}F^{2}K_{0}(X)$
. But this follows by the results of Levine [Reference LevineLev85a], because he shows that there is a surjective map
 ${\mathcal{Z}}_{0}(X,X_{\text{sing}})=\amalg _{x\in X_{\text{reg}}}\mathbb{Z}{\twoheadrightarrow}H^{2}(X,{\mathcal{K}}_{2,X})$
such that the composite
${\mathcal{Z}}_{0}(X,X_{\text{sing}})=\amalg _{x\in X_{\text{reg}}}\mathbb{Z}{\twoheadrightarrow}H^{2}(X,{\mathcal{K}}_{2,X})$
such that the composite
 ${\mathcal{Z}}_{0}(X,X_{\text{sing}})\rightarrow H^{2}(X,{\mathcal{K}}_{2,X})\rightarrow K_{0}(X)$
is the cycle class map. We only need to remark here that at the outset of [Reference LevineLev85a], Levine assumes the ground field to be infinite. But the surjectivity of the map
${\mathcal{Z}}_{0}(X,X_{\text{sing}})\rightarrow H^{2}(X,{\mathcal{K}}_{2,X})\rightarrow K_{0}(X)$
is the cycle class map. We only need to remark here that at the outset of [Reference LevineLev85a], Levine assumes the ground field to be infinite. But the surjectivity of the map
 ${\mathcal{Z}}_{0}(X,X_{\text{sing}}){\twoheadrightarrow}H^{2}(X,{\mathcal{K}}_{2,X})$
does not require this assumption. The assumption on the cardinality of
${\mathcal{Z}}_{0}(X,X_{\text{sing}}){\twoheadrightarrow}H^{2}(X,{\mathcal{K}}_{2,X})$
does not require this assumption. The assumption on the cardinality of
![]() $k$
is required to use Matsumoto’s presentation of Quillen
$k$
is required to use Matsumoto’s presentation of Quillen
![]() $K_{2}$
of a field.◻
$K_{2}$
of a field.◻
Proposition 13.2. Let
![]() $X$
be a smooth quasi-projective surface over a field
$X$
be a smooth quasi-projective surface over a field
![]() $k$
containing at least three elements. Let
$k$
containing at least three elements. Let
![]() $D\subset X$
be an effective Cartier divisor. Then the canonical map
$D\subset X$
be an effective Cartier divisor. Then the canonical map
 $\unicode[STIX]{x1D719}_{0}:K_{0}(X|D)\rightarrow K_{0}(X,D)$
is an isomorphism.
$\unicode[STIX]{x1D719}_{0}:K_{0}(X|D)\rightarrow K_{0}(X,D)$
is an isomorphism.
Proof. We have convergent spectral sequences
 $$\begin{eqnarray}H^{p}(S_{X},{\mathcal{K}}_{q,X|D})\Rightarrow \unicode[STIX]{x1D70B}_{-p-q}K(S_{X},X_{-})=\unicode[STIX]{x1D70B}_{-p-q}K(X|D),\end{eqnarray}$$
$$\begin{eqnarray}H^{p}(S_{X},{\mathcal{K}}_{q,X|D})\Rightarrow \unicode[STIX]{x1D70B}_{-p-q}K(S_{X},X_{-})=\unicode[STIX]{x1D70B}_{-p-q}K(X|D),\end{eqnarray}$$
 $$\begin{eqnarray}H^{p}(X,{\mathcal{K}}_{q,(X,D)})\Rightarrow \unicode[STIX]{x1D70B}_{-p-q}K(X,D)\end{eqnarray}$$
$$\begin{eqnarray}H^{p}(X,{\mathcal{K}}_{q,(X,D)})\Rightarrow \unicode[STIX]{x1D70B}_{-p-q}K(X,D)\end{eqnarray}$$
induced by the Thomason–Trobaugh spectral sequence for the
![]() $K$
-theory of
$K$
-theory of
![]() $S_{X}$
,
$S_{X}$
,
![]() $X$
and
$X$
and
![]() $D$
. Here,
$D$
. Here,
![]() ${\mathcal{K}}_{q,X|D}$
is the Zariski sheaf associated to
${\mathcal{K}}_{q,X|D}$
is the Zariski sheaf associated to
 $U\mapsto K_{q}(U|D\cap U)$
and
$U\mapsto K_{q}(U|D\cap U)$
and
 ${\mathcal{K}}_{q,(X,D)}$
denotes the Zariski sheaf associated to
${\mathcal{K}}_{q,(X,D)}$
denotes the Zariski sheaf associated to
 $U\mapsto K_{q}(U,U\cap D)$
. We denote by
$U\mapsto K_{q}(U,U\cap D)$
. We denote by
 $F^{i}K_{0}(X,D)$
the filtration on
$F^{i}K_{0}(X,D)$
the filtration on
 $K_{0}(X,D)$
induced by (13.1).
$K_{0}(X,D)$
induced by (13.1).
Since
 ${\mathcal{K}}_{0,X|D}=\text{Ker}({\mathcal{K}}_{0,S_{X}}=\mathbb{Z}\rightarrow {\mathcal{K}}_{0,X}=\mathbb{Z})=0$
, we have
${\mathcal{K}}_{0,X|D}=\text{Ker}({\mathcal{K}}_{0,S_{X}}=\mathbb{Z}\rightarrow {\mathcal{K}}_{0,X}=\mathbb{Z})=0$
, we have
 $$\begin{eqnarray}0\rightarrow F^{1}K_{0}(X|D)\rightarrow K_{0}(X|D)\rightarrow H^{0}(S_{X},{\mathcal{K}}_{0,X|D})=0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow F^{1}K_{0}(X|D)\rightarrow K_{0}(X|D)\rightarrow H^{0}(S_{X},{\mathcal{K}}_{0,X|D})=0\end{eqnarray}$$
and therefore
 $F^{1}K_{0}(X|D)\xrightarrow[{}]{\simeq }K_{0}(X|D)$
. Next, we have the exact sequence
$F^{1}K_{0}(X|D)\xrightarrow[{}]{\simeq }K_{0}(X|D)$
. Next, we have the exact sequence
 $$\begin{eqnarray}0\rightarrow F^{2}K_{0}(X|D)\rightarrow F^{1}K_{0}(X|D)=K_{0}(X|D)\rightarrow H^{1}(S_{X},{\mathcal{K}}_{1,X|D})\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow F^{2}K_{0}(X|D)\rightarrow F^{1}K_{0}(X|D)=K_{0}(X|D)\rightarrow H^{1}(S_{X},{\mathcal{K}}_{1,X|D})\rightarrow 0\end{eqnarray}$$
and a canonical map
 $H^{2}(S_{X},{\mathcal{K}}_{2,X|D})\rightarrow F^{2}K_{0}(X|D)$
. Since
$H^{2}(S_{X},{\mathcal{K}}_{2,X|D})\rightarrow F^{2}K_{0}(X|D)$
. Since
![]() $X$
is a smooth surface, the corresponding map
$X$
is a smooth surface, the corresponding map
 $H^{2}(X,{\mathcal{K}}_{2,X})\rightarrow F^{2}K_{0}(X)$
is an isomorphism and the same holds for the map
$H^{2}(X,{\mathcal{K}}_{2,X})\rightarrow F^{2}K_{0}(X)$
is an isomorphism and the same holds for the map
 $H^{2}(S_{X},{\mathcal{K}}_{2,S_{X}})\rightarrow F^{2}K_{0}(S_{X})$
by Lemma 13.1. By construction, the sequence of sheaves
$H^{2}(S_{X},{\mathcal{K}}_{2,S_{X}})\rightarrow F^{2}K_{0}(S_{X})$
by Lemma 13.1. By construction, the sequence of sheaves
 $$\begin{eqnarray}0\rightarrow {\mathcal{K}}_{i,X|D}\rightarrow {\mathcal{K}}_{i,S_{X}}\rightarrow {\mathcal{K}}_{i,X}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{K}}_{i,X|D}\rightarrow {\mathcal{K}}_{i,S_{X}}\rightarrow {\mathcal{K}}_{i,X}\rightarrow 0\end{eqnarray}$$
is split exact and the space
 $K(X|D)$
is a retract of
$K(X|D)$
is a retract of
![]() $K(S_{X})$
, so that by taking cohomology and comparing with the
$K(S_{X})$
, so that by taking cohomology and comparing with the
![]() $F^{2}$
-piece of the filtration on the
$F^{2}$
-piece of the filtration on the
![]() $\unicode[STIX]{x1D70B}_{0}$
groups, we obtain that
$\unicode[STIX]{x1D70B}_{0}$
groups, we obtain that
 $H^{2}(S_{X},{\mathcal{K}}_{2,X|D})\rightarrow F^{2}K_{0}(X|D)$
is indeed an isomorphism. In particular, we have a short exact sequence
$H^{2}(S_{X},{\mathcal{K}}_{2,X|D})\rightarrow F^{2}K_{0}(X|D)$
is indeed an isomorphism. In particular, we have a short exact sequence
 $$\begin{eqnarray}0\rightarrow H^{2}(S_{X},{\mathcal{K}}_{2,X|D})\rightarrow K_{0}(X|D)\rightarrow H^{1}(S_{X},{\mathcal{K}}_{1,X|D})\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H^{2}(S_{X},{\mathcal{K}}_{2,X|D})\rightarrow K_{0}(X|D)\rightarrow H^{1}(S_{X},{\mathcal{K}}_{1,X|D})\rightarrow 0.\end{eqnarray}$$
Consider now the second spectral sequence (13.2). Since
 ${\mathcal{K}}_{0,(X,D)}=0$
as well, we have another exact sequence
${\mathcal{K}}_{0,(X,D)}=0$
as well, we have another exact sequence
 $$\begin{eqnarray}0\rightarrow H^{2}(X,{\mathcal{K}}_{2,(X,D)})\rightarrow K_{0}(X,D)\rightarrow H^{1}(X,{\mathcal{K}}_{1,(X,D)})\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H^{2}(X,{\mathcal{K}}_{2,(X,D)})\rightarrow K_{0}(X,D)\rightarrow H^{1}(X,{\mathcal{K}}_{1,(X,D)})\rightarrow 0\end{eqnarray}$$
where the first map is injective by [Reference KrishnaKri15a, Lemma 2.1]. The natural map
 $\unicode[STIX]{x1D719}:K(X|D)\rightarrow K(X,D)$
induces then a commutative diagram, with exact rows.
$\unicode[STIX]{x1D719}:K(X|D)\rightarrow K(X,D)$
induces then a commutative diagram, with exact rows.

As
 $H^{1}(S_{X},{\mathcal{K}}_{1})\simeq \operatorname{Pic}(S_{X})$
and
$H^{1}(S_{X},{\mathcal{K}}_{1})\simeq \operatorname{Pic}(S_{X})$
and
 $H^{1}(X,{\mathcal{K}}_{1})\simeq \operatorname{Pic}(X)$
, applying cohomology to (13.3) with
$H^{1}(X,{\mathcal{K}}_{1})\simeq \operatorname{Pic}(X)$
, applying cohomology to (13.3) with
![]() $i=1$
gives
$i=1$
gives
 $$\begin{eqnarray}0\rightarrow H^{1}(S_{X},{\mathcal{K}}_{1,X|D})\rightarrow \operatorname{Pic}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{-}^{\ast }}\operatorname{Pic}(X)\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H^{1}(S_{X},{\mathcal{K}}_{1,X|D})\rightarrow \operatorname{Pic}(S_{X})\xrightarrow[{}]{\unicode[STIX]{x1D704}_{-}^{\ast }}\operatorname{Pic}(X)\rightarrow 0\end{eqnarray}$$
and by Proposition 12.2, we have an identification
 $H^{1}(S_{X},{\mathcal{K}}_{1,X|D})=\operatorname{Pic}(X,D)$
. Similarly, we have
$H^{1}(S_{X},{\mathcal{K}}_{1,X|D})=\operatorname{Pic}(X,D)$
. Similarly, we have
 $H^{1}(X,{\mathcal{K}}_{1,(X,D)})=\operatorname{Pic}(X,D)$
by [Reference Suslin and VoevodskySV96, Lemma 2.1] and hence the right vertical map is an isomorphism. To finish the proof of the proposition, we are now left with proving the following lemma.◻
$H^{1}(X,{\mathcal{K}}_{1,(X,D)})=\operatorname{Pic}(X,D)$
by [Reference Suslin and VoevodskySV96, Lemma 2.1] and hence the right vertical map is an isomorphism. To finish the proof of the proposition, we are now left with proving the following lemma.◻
Lemma 13.3. The map
 $H^{2}(S_{X},{\mathcal{K}}_{2,X|D})\rightarrow H^{2}(X,{\mathcal{K}}_{2,(X,D)})$
is an isomorphism.
$H^{2}(S_{X},{\mathcal{K}}_{2,X|D})\rightarrow H^{2}(X,{\mathcal{K}}_{2,(X,D)})$
is an isomorphism.
Proof. Given an open subset
 $W\subset D$
, let
$W\subset D$
, let
 $U=S_{X}\setminus (D\setminus W)$
be the open subset of
$U=S_{X}\setminus (D\setminus W)$
be the open subset of
![]() $S_{X}$
. Let
$S_{X}$
. Let
 ${\mathcal{K}}_{i,(S_{X},X_{-},D)}$
be the sheaf on
${\mathcal{K}}_{i,(S_{X},X_{-},D)}$
be the sheaf on
![]() $D$
associated to the presheaf
$D$
associated to the presheaf
 $W\mapsto K_{i}(U,X_{+}\cap U,X_{-}\cap U)=\text{hofib}(K(U,X_{-}\cap U)\xrightarrow[{}]{i_{+}^{\ast }}K(X_{+}\cap U,D\cap U))$
(see [Reference Pedrini and WeibelPW94, Proposition A.5]). There is an exact sequence of
$W\mapsto K_{i}(U,X_{+}\cap U,X_{-}\cap U)=\text{hofib}(K(U,X_{-}\cap U)\xrightarrow[{}]{i_{+}^{\ast }}K(X_{+}\cap U,D\cap U))$
(see [Reference Pedrini and WeibelPW94, Proposition A.5]). There is an exact sequence of
![]() $K$
-theory sheaves
$K$
-theory sheaves
 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{\ast }({\mathcal{K}}_{2,(S_{X},X_{-},D)})\rightarrow {\mathcal{K}}_{2,(S_{X},X_{-})}\rightarrow {\mathcal{K}}_{2,(X_{+},D)}\rightarrow \unicode[STIX]{x1D704}_{\ast }({\mathcal{K}}_{1,(S_{X},X_{-},D)}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{\ast }({\mathcal{K}}_{2,(S_{X},X_{-},D)})\rightarrow {\mathcal{K}}_{2,(S_{X},X_{-})}\rightarrow {\mathcal{K}}_{2,(X_{+},D)}\rightarrow \unicode[STIX]{x1D704}_{\ast }({\mathcal{K}}_{1,(S_{X},X_{-},D)}),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D704}:D{\hookrightarrow}S_{X}$
is the inclusion. We have
$\unicode[STIX]{x1D704}:D{\hookrightarrow}S_{X}$
is the inclusion. We have
 ${\mathcal{K}}_{1,(S_{X},X_{-},D)}={\mathcal{I}}_{D}/{\mathcal{I}}_{D}^{2}\otimes _{D}\unicode[STIX]{x1D6FA}_{D/X}^{1}$
by [Reference Geller and WeibelGW83, Theorem 1.1] and the latter term is zero. Since
${\mathcal{K}}_{1,(S_{X},X_{-},D)}={\mathcal{I}}_{D}/{\mathcal{I}}_{D}^{2}\otimes _{D}\unicode[STIX]{x1D6FA}_{D/X}^{1}$
by [Reference Geller and WeibelGW83, Theorem 1.1] and the latter term is zero. Since
 ${\mathcal{K}}_{2,(S_{X},X_{-})}={\mathcal{K}}_{2,X|D}$
by definition, we get then an exact sequence
${\mathcal{K}}_{2,(S_{X},X_{-})}={\mathcal{K}}_{2,X|D}$
by definition, we get then an exact sequence
 $$\begin{eqnarray}\unicode[STIX]{x1D704}_{\ast }({\mathcal{K}}_{2,(S_{X},X_{-},D)})\rightarrow {\mathcal{K}}_{2,X|D}\rightarrow {\mathcal{K}}_{2,(X_{+},D)}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}_{\ast }({\mathcal{K}}_{2,(S_{X},X_{-},D)})\rightarrow {\mathcal{K}}_{2,X|D}\rightarrow {\mathcal{K}}_{2,(X_{+},D)}\rightarrow 0.\end{eqnarray}$$
Since
 $H^{2}(S_{X},\unicode[STIX]{x1D704}_{\ast })({\mathcal{K}}_{2,(S_{X},X_{-},D)})=H^{2}(D,{\mathcal{K}}_{2,(S_{X},X_{-},D)})=0$
, the lemma follows.◻
$H^{2}(S_{X},\unicode[STIX]{x1D704}_{\ast })({\mathcal{K}}_{2,(S_{X},X_{-},D)})=H^{2}(D,{\mathcal{K}}_{2,(S_{X},X_{-},D)})=0$
, the lemma follows.◻
We now prove our main result on cycles with modulus on surfaces.
Theorem 13.4. Let
![]() $X$
be a smooth quasi-projective surface over an algebraically closed field
$X$
be a smooth quasi-projective surface over an algebraically closed field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then the following hold.
$D\subset X$
be an effective Cartier divisor. Then the following hold.
-
(1) The cycle class map
 $\text{cyc}_{X|D}:\text{CH}_{0}(X|D)\rightarrow K_{0}(X,D)$
induces a short exact sequence and the image of
$\text{cyc}_{X|D}:\text{CH}_{0}(X|D)\rightarrow K_{0}(X,D)$
induces a short exact sequence and the image of $$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\rightarrow K_{0}(X,D)\rightarrow \operatorname{Pic}(X,D)\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\rightarrow K_{0}(X,D)\rightarrow \operatorname{Pic}(X,D)\rightarrow 0\end{eqnarray}$$
 $\text{CH}_{0}(X|D)$
agrees with
$\text{CH}_{0}(X|D)$
agrees with
 $F^{2}K_{0}(X|D)$
.
$F^{2}K_{0}(X|D)$
.
-
(2) There are isomorphisms
 $$\begin{eqnarray}\text{CH}_{0}(X|D)\xrightarrow[{}]{\simeq }H_{\text{zar}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M})\xrightarrow[{}]{\simeq }H_{\text{nis}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M}).\end{eqnarray}$$
$$\begin{eqnarray}\text{CH}_{0}(X|D)\xrightarrow[{}]{\simeq }H_{\text{zar}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M})\xrightarrow[{}]{\simeq }H_{\text{nis}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M}).\end{eqnarray}$$
Proof. The injectivity of the cycle class map follows exactly like Theorem 12.4 by using Proposition 13.2 instead of Proposition 12.3. Next, (13.4) and Proposition 13.2 show that the exactness of (1) is equivalent to showing that
 $\text{CH}_{0}(X|D)\simeq F^{2}K_{0}(X|D)$
. But this follows again by observing that
$\text{CH}_{0}(X|D)\simeq F^{2}K_{0}(X|D)$
. But this follows again by observing that
![]() $\text{cyc}_{S_{X}}$
and
$\text{cyc}_{S_{X}}$
and
![]() $\text{cyc}_{X}$
become isomorphisms (using [Reference LevineLev85a, Main Theorem]) if we replace the middle row of (12.3) by
$\text{cyc}_{X}$
become isomorphisms (using [Reference LevineLev85a, Main Theorem]) if we replace the middle row of (12.3) by
 $F^{2}K_{0}(-)$
which keeps the row exact.
$F^{2}K_{0}(-)$
which keeps the row exact.
To prove (2), recall that
 ${\mathcal{K}}_{2,(X,D)}^{M}$
is, by definition, the kernel of the map of Milnor
${\mathcal{K}}_{2,(X,D)}^{M}$
is, by definition, the kernel of the map of Milnor
![]() $K$
-theory sheaves
$K$
-theory sheaves
 ${\mathcal{K}}_{2,X}^{M}{\twoheadrightarrow}{\mathcal{K}}_{2,D}^{M}$
. If we let
${\mathcal{K}}_{2,X}^{M}{\twoheadrightarrow}{\mathcal{K}}_{2,D}^{M}$
. If we let
 ${\mathcal{K}}_{2,X|D}^{M}=\text{Ker}(\unicode[STIX]{x1D6E5}_{\ast }({\mathcal{K}}_{2,S_{X}}^{M})\rightarrow {\mathcal{K}}_{2,X}^{M})$
, then the top square of (12.3) has factorization as follows.
${\mathcal{K}}_{2,X|D}^{M}=\text{Ker}(\unicode[STIX]{x1D6E5}_{\ast }({\mathcal{K}}_{2,S_{X}}^{M})\rightarrow {\mathcal{K}}_{2,X}^{M})$
, then the top square of (12.3) has factorization as follows.

The commutative square

now shows that there is a factorization
 $\text{CH}_{0}(X|D)\rightarrow H^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M})\rightarrow K_{0}(X,D)$
of the map
$\text{CH}_{0}(X|D)\rightarrow H^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M})\rightarrow K_{0}(X,D)$
of the map
![]() $\text{cyc}_{X|D}$
. It follows from (1) that the first map is injective. On the other hand, it follows from [Reference KrishnaKri15a, Theorem 1.2] that this map is surjective. We conclude that the map
$\text{cyc}_{X|D}$
. It follows from (1) that the first map is injective. On the other hand, it follows from [Reference KrishnaKri15a, Theorem 1.2] that this map is surjective. We conclude that the map
 $\text{CH}_{0}(X|D)\rightarrow H_{\text{zar}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M})$
is an isomorphism. Furthermore, [Reference KrishnaKri15a, Lemma 2.1] implies that
$\text{CH}_{0}(X|D)\rightarrow H_{\text{zar}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M})$
is an isomorphism. Furthermore, [Reference KrishnaKri15a, Lemma 2.1] implies that
 $$\begin{eqnarray}H_{\text{zar}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M})\xrightarrow[{}]{\simeq }H_{\text{nis}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M})\end{eqnarray}$$
$$\begin{eqnarray}H_{\text{zar}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M})\xrightarrow[{}]{\simeq }H_{\text{nis}}^{2}(X,{\mathcal{K}}_{2,(X,D)}^{M})\end{eqnarray}$$
as required. ◻
14 0-cycles with modulus on affine schemes
In Theorem 12.4, we gave our first application of Theorem 7.1 to 0-cycles with modulus on affine schemes. In this section, we deduce more applications of Theorem 7.1 for such schemes.
14.1 Affine Roitman torsion for 0-cycles with modulus
For affine schemes, our second application is the following Roitman torsion theorem for 0-cycles with modulus.
Theorem 14.1. Let
![]() $X$
be a smooth affine scheme of dimension
$X$
be a smooth affine scheme of dimension
![]() $d\geqslant 2$
over an algebraically closed field
$d\geqslant 2$
over an algebraically closed field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then
$D\subset X$
be an effective Cartier divisor. Then
 $\text{CH}_{0}(X|D)$
is torsion-free.
$\text{CH}_{0}(X|D)$
is torsion-free.
Proof. The proof is immediate from Theorem 7.1 and [Reference KrishnaKri15b, Theorem 1.1], using the comparison given by Theorem 7.3 (or Theorem 3.17). ◻
Remark 14.2. An independent proof of the vanishing of the prime-to-
![]() $p$
torsion part of
$p$
torsion part of
 $\text{CH}_{0}(X|D)$
for affine varieties (where
$\text{CH}_{0}(X|D)$
for affine varieties (where
![]() $p$
denotes the exponential characteristic of
$p$
denotes the exponential characteristic of
![]() $k$
) can be found in [Reference BindaBin18]. The argument in [Reference BindaBin18] does not rely on our decomposition Theorem 7.1, but follows instead closely the approach of Levine in [Reference LevineLev87].
$k$
) can be found in [Reference BindaBin18]. The argument in [Reference BindaBin18] does not rely on our decomposition Theorem 7.1, but follows instead closely the approach of Levine in [Reference LevineLev87].
14.2 Vanishing theorems
As another application of Theorem 7.1, we get the following vanishing theorems.
Corollary 14.3. Let
![]() $X$
be a smooth affine scheme of dimension
$X$
be a smooth affine scheme of dimension
![]() $d\geqslant 2$
over
$d\geqslant 2$
over
![]() $\overline{\mathbb{F}_{p}}$
and let
$\overline{\mathbb{F}_{p}}$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then
$D\subset X$
be an effective Cartier divisor. Then
 $\text{CH}_{0}(X|D)=0$
.
$\text{CH}_{0}(X|D)=0$
.
Proof. Using Theorems 3.17 and 7.1, it is enough to know that
 $\text{CH}_{0}(S_{X})=0$
. But this follows from [Reference Krishna and SrinivasKS07, Theorem 6.4.1].◻
$\text{CH}_{0}(S_{X})=0$
. But this follows from [Reference Krishna and SrinivasKS07, Theorem 6.4.1].◻
The same argument, using [Reference Krishna and SrinivasKS07, Theorem 6.4.2], shows the following.
Corollary 14.4. Let
 $X=\operatorname{Spec}(A)$
be a smooth affine algebra of dimension
$X=\operatorname{Spec}(A)$
be a smooth affine algebra of dimension
![]() $d\geqslant 2$
over
$d\geqslant 2$
over
![]() $\overline{\mathbb{Q}}$
. Assume that
$\overline{\mathbb{Q}}$
. Assume that
 $A=\bigoplus _{n\geqslant 0}A_{n}$
is a graded algebra with
$A=\bigoplus _{n\geqslant 0}A_{n}$
is a graded algebra with
 $A_{0}=\overline{\mathbb{Q}}$
. Assume moreover that
$A_{0}=\overline{\mathbb{Q}}$
. Assume moreover that
![]() $D\subset X$
is a divisor on
$D\subset X$
is a divisor on
![]() $X$
defined by a homogeneous element of
$X$
defined by a homogeneous element of
![]() $A$
. Then
$A$
. Then
 $\text{CH}_{0}(X|D)=0$
.
$\text{CH}_{0}(X|D)=0$
.
14.3 Decomposition of
 $K_{0}(X,D)$
$K_{0}(X,D)$
Let
![]() $X$
be a smooth quasi-projective scheme over a field
$X$
be a smooth quasi-projective scheme over a field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Let
$D\subset X$
be an effective Cartier divisor. Let
 ${\mathcal{Z}}^{1}(X|D)$
denote the free abelian group on integral closed subschemes
${\mathcal{Z}}^{1}(X|D)$
denote the free abelian group on integral closed subschemes
![]() $Z\subset X$
of codimension one such that
$Z\subset X$
of codimension one such that
 $D\cap Z=\emptyset$
. Let
$D\cap Z=\emptyset$
. Let
 ${\mathcal{R}}^{1}(X|D)=\mathop{\varinjlim }\nolimits_{U}\text{Ker}({\mathcal{O}}^{\times }(U)\rightarrow {\mathcal{O}}^{\times }(D))$
, where
${\mathcal{R}}^{1}(X|D)=\mathop{\varinjlim }\nolimits_{U}\text{Ker}({\mathcal{O}}^{\times }(U)\rightarrow {\mathcal{O}}^{\times }(D))$
, where
![]() $U$
ranges over open subsets of
$U$
ranges over open subsets of
![]() $X$
containing
$X$
containing
![]() $D$
. Note that if
$D$
. Note that if
![]() $D$
has an affine open neighborhood in
$D$
has an affine open neighborhood in
![]() $X$
then this limit is same as the limit taken over
$X$
then this limit is same as the limit taken over
![]() $X\setminus Z$
, where
$X\setminus Z$
, where
![]() $Z\subset X$
is a divisor disjoint from
$Z\subset X$
is a divisor disjoint from
![]() $D$
and is principal in an affine neighborhood of
$D$
and is principal in an affine neighborhood of
![]() $D$
.
$D$
.
Recall from [Reference Binda and SaitoBS16, § 3] that the Chow group of codimension one cycles with modulus
 $\text{CH}^{1}(X|D)$
is the cokernel of the map
$\text{CH}^{1}(X|D)$
is the cokernel of the map
 ${\mathcal{R}}^{1}(X|D)\xrightarrow[{}]{\operatorname{div}}{\mathcal{Z}}^{1}(X|D)$
. We often write
${\mathcal{R}}^{1}(X|D)\xrightarrow[{}]{\operatorname{div}}{\mathcal{Z}}^{1}(X|D)$
. We often write
 $\text{CH}^{1}(X|D)$
as
$\text{CH}^{1}(X|D)$
as
 $\text{CH}_{d-1}(X|D)$
if
$\text{CH}_{d-1}(X|D)$
if
 $\dim (X)=d$
. If
$\dim (X)=d$
. If
![]() $X$
is a smooth affine surface, we can refine Theorem 13.4 to completely describe
$X$
is a smooth affine surface, we can refine Theorem 13.4 to completely describe
 $K_{0}(X,D)$
in terms of the Chow groups with modulus. In order to do this, we need the following elementary result from commutative algebra. For any commutative noetherian ring
$K_{0}(X,D)$
in terms of the Chow groups with modulus. In order to do this, we need the following elementary result from commutative algebra. For any commutative noetherian ring
![]() $A$
and
$A$
and
![]() $a\in A$
, let
$a\in A$
, let
![]() $M_{a}$
denote the localization
$M_{a}$
denote the localization
![]() $M[a^{-1}]$
if
$M[a^{-1}]$
if
![]() $M$
is an
$M$
is an
![]() $A$
-module.
$A$
-module.
Lemma 14.5. Let
![]() $A$
be a commutative noetherian ring and let
$A$
be a commutative noetherian ring and let
![]() $I\subset A$
be an ideal. Let
$I\subset A$
be an ideal. Let
![]() $P$
be a projective
$P$
be a projective
![]() $A$
-module of rank one and let
$A$
-module of rank one and let
 $\unicode[STIX]{x1D719}:P/IP\xrightarrow[{}]{\simeq }A/I$
be a given
$\unicode[STIX]{x1D719}:P/IP\xrightarrow[{}]{\simeq }A/I$
be a given
![]() $A/I$
-linear isomorphism. Then we can find an element
$A/I$
-linear isomorphism. Then we can find an element
![]() $a\in A$
such that
$a\in A$
such that
![]() $a\equiv 1$
mod
$a\equiv 1$
mod
![]() $I$
and an isomorphism
$I$
and an isomorphism
 $\widetilde{\unicode[STIX]{x1D719}}:P_{a}\xrightarrow[{}]{\simeq }A_{a}$
and a commutative diagram.
$\widetilde{\unicode[STIX]{x1D719}}:P_{a}\xrightarrow[{}]{\simeq }A_{a}$
and a commutative diagram.

Proof. As
![]() $P$
is projective, we do have an
$P$
is projective, we do have an
![]() $A$
-linear map
$A$
-linear map
 $\widetilde{\unicode[STIX]{x1D719}}:P\rightarrow A$
and a commutative diagram.
$\widetilde{\unicode[STIX]{x1D719}}:P\rightarrow A$
and a commutative diagram.

Letting
 $M=\text{Coker}(\widetilde{\unicode[STIX]{x1D719}})$
, our assumption says that
$M=\text{Coker}(\widetilde{\unicode[STIX]{x1D719}})$
, our assumption says that
 $IM=M$
. But this implies by the Nakayama lemma that there exists
$IM=M$
. But this implies by the Nakayama lemma that there exists
![]() $a\in A$
such that
$a\in A$
such that
![]() $a\equiv 1$
mod
$a\equiv 1$
mod
![]() $I$
and
$I$
and
![]() $M_{a}=0$
. It follows that
$M_{a}=0$
. It follows that
 $\widetilde{\unicode[STIX]{x1D719}}:P_{a}\rightarrow A_{a}$
is surjective and hence an isomorphism.◻
$\widetilde{\unicode[STIX]{x1D719}}:P_{a}\rightarrow A_{a}$
is surjective and hence an isomorphism.◻
Theorem 14.6. Let
![]() $X$
be a smooth affine surface over an algebraically closed field
$X$
be a smooth affine surface over an algebraically closed field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then, there is a short exact sequence
$D\subset X$
be an effective Cartier divisor. Then, there is a short exact sequence
 $$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\rightarrow K_{0}(X,D)\rightarrow \text{CH}_{1}(X|D)\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \text{CH}_{0}(X|D)\rightarrow K_{0}(X,D)\rightarrow \text{CH}_{1}(X|D)\rightarrow 0.\end{eqnarray}$$
Proof. In view of Theorem 13.4, we only need to show that
 $\text{CH}_{1}(X|D)\simeq \operatorname{Pic}(X,D)$
. Since
$\text{CH}_{1}(X|D)\simeq \operatorname{Pic}(X,D)$
. Since
 $H^{1}(X,{\mathcal{K}}_{1,(X,D)})\simeq \operatorname{Pic}(X,D)$
as we have seen above, we need to show that
$H^{1}(X,{\mathcal{K}}_{1,(X,D)})\simeq \operatorname{Pic}(X,D)$
as we have seen above, we need to show that
 $$\begin{eqnarray}\text{CH}_{1}(X|D)=\text{CH}^{1}(X|D)\simeq H^{1}(X,{\mathcal{K}}_{1,(X,D)}).\end{eqnarray}$$
$$\begin{eqnarray}\text{CH}_{1}(X|D)=\text{CH}^{1}(X|D)\simeq H^{1}(X,{\mathcal{K}}_{1,(X,D)}).\end{eqnarray}$$
For a closed subset
![]() $Z\subset X$
of dimension one with
$Z\subset X$
of dimension one with
 $Z\cap D=\emptyset$
, there is an exact sequence
$Z\cap D=\emptyset$
, there is an exact sequence
 $$\begin{eqnarray}H^{0}(X\setminus Z,{\mathcal{K}}_{1,(X\setminus Z,D)})\rightarrow H_{Z}^{1}(X,{\mathcal{K}}_{1,(X,D)})\rightarrow H^{1}(X,{\mathcal{K}}_{1,(X,D)})\rightarrow H^{1}(X\setminus Z,{\mathcal{K}}_{1,(X\setminus Z,D)}).\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(X\setminus Z,{\mathcal{K}}_{1,(X\setminus Z,D)})\rightarrow H_{Z}^{1}(X,{\mathcal{K}}_{1,(X,D)})\rightarrow H^{1}(X,{\mathcal{K}}_{1,(X,D)})\rightarrow H^{1}(X\setminus Z,{\mathcal{K}}_{1,(X\setminus Z,D)}).\end{eqnarray}$$
The excision theorem says that
 $H_{Z}^{1}(X,{\mathcal{K}}_{1,(X,D)})=H_{Z}^{1}(X\setminus D,{\mathcal{K}}_{1,(X,D)})=H_{Z}^{1}(X\setminus D,{\mathcal{K}}_{1,X\setminus D})$
and it follows easily from the Gersten resolution of
$H_{Z}^{1}(X,{\mathcal{K}}_{1,(X,D)})=H_{Z}^{1}(X\setminus D,{\mathcal{K}}_{1,(X,D)})=H_{Z}^{1}(X\setminus D,{\mathcal{K}}_{1,X\setminus D})$
and it follows easily from the Gersten resolution of
![]() ${\mathcal{K}}_{1,X\setminus D}$
and the Thomason–Trobaugh spectral sequence
${\mathcal{K}}_{1,X\setminus D}$
and the Thomason–Trobaugh spectral sequence
 $H_{Z}^{p}(X\setminus D,{\mathcal{K}}_{q,X\setminus D})\Rightarrow K_{q-p}(Z)$
that
$H_{Z}^{p}(X\setminus D,{\mathcal{K}}_{q,X\setminus D})\Rightarrow K_{q-p}(Z)$
that
 $H_{Z}^{1}(X,{\mathcal{K}}_{1,X\setminus D})$
is the free abelian group on the irreducible components of
$H_{Z}^{1}(X,{\mathcal{K}}_{1,X\setminus D})$
is the free abelian group on the irreducible components of
![]() $Z$
. Using the isomorphism
$Z$
. Using the isomorphism
 $H^{1}(X\setminus Z,{\mathcal{K}}_{1,(X\setminus Z,D)})\simeq \operatorname{Pic}(X\setminus Z,D)$
, Lemma 14.5 tells us precisely that
$H^{1}(X\setminus Z,{\mathcal{K}}_{1,(X\setminus Z,D)})\simeq \operatorname{Pic}(X\setminus Z,D)$
, Lemma 14.5 tells us precisely that
 $\mathop{\varinjlim }\nolimits_{Z}H^{1}(X\setminus Z,{\mathcal{K}}_{1,(X\setminus Z,D)})=0$
.
$\mathop{\varinjlim }\nolimits_{Z}H^{1}(X\setminus Z,{\mathcal{K}}_{1,(X\setminus Z,D)})=0$
.
Taking the colimit (14.2) over all closed subschemes
![]() $Z$
as above, we thus get an exact sequence
$Z$
as above, we thus get an exact sequence
 $$\begin{eqnarray}{\mathcal{R}}^{1}(X|D)\rightarrow {\mathcal{Z}}^{1}(X|D)\rightarrow H^{1}(X,{\mathcal{K}}_{1,(X,D)})\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{R}}^{1}(X|D)\rightarrow {\mathcal{Z}}^{1}(X|D)\rightarrow H^{1}(X,{\mathcal{K}}_{1,(X,D)})\rightarrow 0.\end{eqnarray}$$
It follows by a direct comparison of this exact sequence with the similar sequence for
![]() ${\mathcal{K}}_{1,X}$
that the arrow on the left is just the divisor map. We conclude that there is a canonical isomorphism
${\mathcal{K}}_{1,X}$
that the arrow on the left is just the divisor map. We conclude that there is a canonical isomorphism
 $\text{CH}^{1}(X|D)\xrightarrow[{}]{\simeq }H^{1}(X,{\mathcal{K}}_{1,(X,D)})$
.◻
$\text{CH}^{1}(X|D)\xrightarrow[{}]{\simeq }H^{1}(X,{\mathcal{K}}_{1,(X,D)})$
.◻
14.4 Nil-invariance of 0-cycles with modulus
As another application of Theorem 7.1, we can prove the following result showing that the Chow group of 0-cycles with modulus on a smooth affine surface depends only on the support of the underlying Cartier divisor.
Theorem 14.7. Let
![]() $X$
be a smooth affine surface over a perfect field
$X$
be a smooth affine surface over a perfect field
![]() $k$
and let
$k$
and let
![]() $D\subset X$
be an effective Cartier divisor. Then the canonical map
$D\subset X$
be an effective Cartier divisor. Then the canonical map
 $$\begin{eqnarray}\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(X|D_{\text{red}})\end{eqnarray}$$
$$\begin{eqnarray}\text{CH}_{0}(X|D)\rightarrow \text{CH}_{0}(X|D_{\text{red}})\end{eqnarray}$$
is an isomorphism.
Proof. Using Theorem 13.4, it suffices to show that
 $F^{2}K_{0}(X|D)\rightarrow F^{2}K_{0}(X|D_{\text{red}})$
is an isomorphism.
$F^{2}K_{0}(X|D)\rightarrow F^{2}K_{0}(X|D_{\text{red}})$
is an isomorphism.
Write
 $X=\operatorname{Spec}(A)$
,
$X=\operatorname{Spec}(A)$
,
 $D^{\prime }=D_{\text{red}}=\operatorname{Spec}(A/I)$
. Write
$D^{\prime }=D_{\text{red}}=\operatorname{Spec}(A/I)$
. Write
 $S_{n}=S(X,nD^{\prime })=\operatorname{Spec}(R_{n})$
for the double construction applied to the pair
$S_{n}=S(X,nD^{\prime })=\operatorname{Spec}(R_{n})$
for the double construction applied to the pair
![]() $(A,I^{n})$
. Then we have a chain of inclusions of rings
$(A,I^{n})$
. Then we have a chain of inclusions of rings
 $$\begin{eqnarray}\cdots \subset R_{n+1}\subset R_{n}\subset \cdots \subset R_{1}\subset R_{0}=A\times A,\end{eqnarray}$$
$$\begin{eqnarray}\cdots \subset R_{n+1}\subset R_{n}\subset \cdots \subset R_{1}\subset R_{0}=A\times A,\end{eqnarray}$$
where
 $R_{n}=\{(a,b)\in R_{0}\mid a-b\in I^{n}\}$
. This gives a corresponding sequence of maps of schemes
$R_{n}=\{(a,b)\in R_{0}\mid a-b\in I^{n}\}$
. This gives a corresponding sequence of maps of schemes
 $$\begin{eqnarray}S_{0}=X\amalg X\rightarrow S_{1}\rightarrow S_{2}\rightarrow \cdots S_{n}\rightarrow \cdots \xrightarrow[{}]{\unicode[STIX]{x1D6E5}}X.\end{eqnarray}$$
$$\begin{eqnarray}S_{0}=X\amalg X\rightarrow S_{1}\rightarrow S_{2}\rightarrow \cdots S_{n}\rightarrow \cdots \xrightarrow[{}]{\unicode[STIX]{x1D6E5}}X.\end{eqnarray}$$
By [Reference Barbieri-Viale, Pedrini and WeibelBPW96, Theorem 3.3] and the fact that
 $SK_{1}(B)=SK_{1}(B_{\text{red}})$
for any commutative ring
$SK_{1}(B)=SK_{1}(B_{\text{red}})$
for any commutative ring
![]() $B$
(see [Reference BassBas68, ch. IX, Propositions 1.3, 1.9]), we have for every
$B$
(see [Reference BassBas68, ch. IX, Propositions 1.3, 1.9]), we have for every
![]() $n\geqslant 1$
an exact sequence
$n\geqslant 1$
an exact sequence

(Apply [Reference Barbieri-Viale, Pedrini and WeibelBPW96, Theorem 3.3] to
 $X=S_{n}$
,
$X=S_{n}$
,
![]() $\tilde{X}=S_{0}$
and
$\tilde{X}=S_{0}$
and
 $Y=D_{n}=\operatorname{Spec}(A/I^{n})$
. Note that
$Y=D_{n}=\operatorname{Spec}(A/I^{n})$
. Note that
 $F^{2}K_{0}(S_{n})=SK_{0}(S_{n})$
and
$F^{2}K_{0}(S_{n})=SK_{0}(S_{n})$
and
 $F^{2}K_{0}(S_{0})=SK_{0}(S_{0})$
in the notations of [Reference Barbieri-Viale, Pedrini and WeibelBPW96].) The natural maps
$F^{2}K_{0}(S_{0})=SK_{0}(S_{0})$
in the notations of [Reference Barbieri-Viale, Pedrini and WeibelBPW96].) The natural maps
 $\unicode[STIX]{x1D70C}_{n}:K_{0}(S_{n})\rightarrow K_{0}(S_{1})$
give then a commutative diagram with exact rows (for
$\unicode[STIX]{x1D70C}_{n}:K_{0}(S_{n})\rightarrow K_{0}(S_{1})$
give then a commutative diagram with exact rows (for
![]() $n\geqslant 1$
).
$n\geqslant 1$
).

It follows that
 $F^{2}K_{0}(S_{n})\simeq F^{2}K_{0}(S_{1})$
. Combining this with Proposition 12.3 and the commutative diagram of exact sequences
$F^{2}K_{0}(S_{n})\simeq F^{2}K_{0}(S_{1})$
. Combining this with Proposition 12.3 and the commutative diagram of exact sequences

we get
 $F^{2}K_{0}(X,nD^{\prime })\xrightarrow[{}]{\simeq }F^{2}K_{0}(X,D^{\prime })$
for every
$F^{2}K_{0}(X,nD^{\prime })\xrightarrow[{}]{\simeq }F^{2}K_{0}(X,D^{\prime })$
for every
![]() $n\geqslant 1$
. Finally, we have inclusions
$n\geqslant 1$
. Finally, we have inclusions
 $D^{\prime }\subset D\subset nD^{\prime }$
for
$D^{\prime }\subset D\subset nD^{\prime }$
for
![]() $n\gg 1$
and hence a sequence of maps
$n\gg 1$
and hence a sequence of maps
 $F^{2}K_{0}(X,nD^{\prime })\rightarrow F^{2}K_{0}(X,D)\rightarrow F^{2}K_{0}(X,D^{\prime })$
. It is easy to see using the isomorphism
$F^{2}K_{0}(X,nD^{\prime })\rightarrow F^{2}K_{0}(X,D)\rightarrow F^{2}K_{0}(X,D^{\prime })$
. It is easy to see using the isomorphism
 $\text{CH}_{0}(X|nD^{\prime })\simeq F^{2}K_{0}(X,nD^{\prime })$
that two maps in this sequence are surjective. Since the composite map is injective, the theorem follows.◻
$\text{CH}_{0}(X|nD^{\prime })\simeq F^{2}K_{0}(X,nD^{\prime })$
that two maps in this sequence are surjective. Since the composite map is injective, the theorem follows.◻
Acknowledgements
The first-named author wishes to heartily thank Marc Levine for constant support and encouragement. He is also very grateful to Shuji Saito for many friendly and inspiring conversations on these topics. Finally, he would like to thank the Tata Institute of Fundamental Research for its hospitality during three visits in September 2014, September 2015 and November 2016 where part of this paper was written. The second-named author would like to thank Marc Levine for the invitation and support to visit the Universität Duisburg-Essen at Essen in the spring of 2015, where a significant part of this work was carried out. The authors would like to thank Marc Levine for going through an earlier version of this manuscript, providing valuable suggestions and for his help in fixing a gap in a previous version of the paper. The authors would also like to thank Hélène Esnault, Moritz Kerz and Takao Yamazaki for their interest in this work and for being generous with their advice on improving the results. Finally, the authors would like to warmly thank Shuji Saito for pointing out an important incongruence in a previous version of this manuscript and for providing much advice on it. We thank the referee(s) for helpful suggestions and a careful reading.