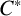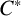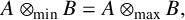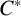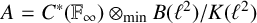1 Introduction
Generally speaking, a
![]() $C^{*}$
-algebra A is said to detect a certain property
$C^{*}$
-algebra A is said to detect a certain property
![]() $\mathcal {P}$
(or is a
$\mathcal {P}$
(or is a
![]() $\mathcal {P}$
detector) if, for any
$\mathcal {P}$
detector) if, for any
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $B,$
we have
$B,$
we have
![]() $A\otimes _{\mathrm{min}} B = A\otimes _{\mathrm{max}} B$
if and only if B has property
$A\otimes _{\mathrm{min}} B = A\otimes _{\mathrm{max}} B$
if and only if B has property
![]() $\mathcal {P}.$
Examples illustrating this notion go back to Kirchberg’s seminal paper [Reference Kirchberg6], where he proved that
$\mathcal {P}.$
Examples illustrating this notion go back to Kirchberg’s seminal paper [Reference Kirchberg6], where he proved that
![]() $C^{*}(\mathbb {F}_{\infty })$
detects Lance’s weak expectation property (WEP) and that
$C^{*}(\mathbb {F}_{\infty })$
detects Lance’s weak expectation property (WEP) and that
![]() $B(H)$
detects the local lifting property (LLP). Recently, more examples of WEP detectors were found in [Reference Courtney2].
$B(H)$
detects the local lifting property (LLP). Recently, more examples of WEP detectors were found in [Reference Courtney2].
The existence of a
![]() $C^{*}$
-algebra which detects nuclearity remained an open problem for a long time. When an answer emerged, it was circulated as folklore among several experts, but it has never appeared in the literature. It stated that the
$C^{*}$
-algebra which detects nuclearity remained an open problem for a long time. When an answer emerged, it was circulated as folklore among several experts, but it has never appeared in the literature. It stated that the
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $A = C^{*}(\mathbb {F}_{\infty })\otimes _{\mathrm{min}} B(\ell ^{2})/K(\ell ^{2})$
is a nuclearity detector. More recently, Kavruk (Corollary 2.3 in [Reference Kavruk4]) constructed an example of a unital, separable
$A = C^{*}(\mathbb {F}_{\infty })\otimes _{\mathrm{min}} B(\ell ^{2})/K(\ell ^{2})$
is a nuclearity detector. More recently, Kavruk (Corollary 2.3 in [Reference Kavruk4]) constructed an example of a unital, separable
![]() $C^{*}$
-algebra which detects nuclearity. Kavruk’s example comes from operator systems via a universal construction. Namely, the universal
$C^{*}$
-algebra which detects nuclearity. Kavruk’s example comes from operator systems via a universal construction. Namely, the universal
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $C^{*}_{u}(\mathcal {W}_{32})$
of the operator system
$C^{*}_{u}(\mathcal {W}_{32})$
of the operator system
 $$ \begin{align*} \mathcal{W}_{32} = \left\{ \left[ \begin{array}{cccccc} a & b & 0 & 0 & 0 & 0 \\ b & a & 0 & 0 & 0 & 0\\ 0 & 0 & a & c & 0 & 0 \\ 0 & 0 & c & a & 0 & 0 \\ 0 & 0 & 0 & 0 & a & d \\ 0 & 0 & 0 & 0 & d & a \end{array} \right] : a,b,c,d \in \mathbb{C} \right\} \subset M_{6}(\mathbb{C}) \end{align*} $$
$$ \begin{align*} \mathcal{W}_{32} = \left\{ \left[ \begin{array}{cccccc} a & b & 0 & 0 & 0 & 0 \\ b & a & 0 & 0 & 0 & 0\\ 0 & 0 & a & c & 0 & 0 \\ 0 & 0 & c & a & 0 & 0 \\ 0 & 0 & 0 & 0 & a & d \\ 0 & 0 & 0 & 0 & d & a \end{array} \right] : a,b,c,d \in \mathbb{C} \right\} \subset M_{6}(\mathbb{C}) \end{align*} $$
is shown to detect nuclearity. As explained in [Reference Kirchberg and Wassermann8], universal algebras of this kind are very difficult to describe. While several additional nonself-adjoint detectors were presented in [Reference Harris and Kim3], the fact remains that, so far,
![]() $C^{*}(\mathbb {F}_{\infty })\otimes _{\mathrm{min}} B(\ell ^{2})/K(\ell ^{2})$
remains the only concrete example of a nuclearity detecting
$C^{*}(\mathbb {F}_{\infty })\otimes _{\mathrm{min}} B(\ell ^{2})/K(\ell ^{2})$
remains the only concrete example of a nuclearity detecting
![]() $C^{*}$
-algebra. The goal of this note is to present a detailed account of this fact. To make it easier for the reader, we include several background and auxiliary results required for the proof.
$C^{*}$
-algebra. The goal of this note is to present a detailed account of this fact. To make it easier for the reader, we include several background and auxiliary results required for the proof.
While Kavruk’s universal construction represents a separable nuclearity detector, finding a concrete example of such an algebra remains, for the moment, an open problem. Another open problem is whether or not the Calkin algebra alone detects nuclearity. Equivalently (see Section 4), must an exact
![]() $C^{*}$
-algebra with the LLP be necessarily nuclear?
$C^{*}$
-algebra with the LLP be necessarily nuclear?
2 Background and basics
We begin by recalling the definitions of the minimal and maximal
![]() $C^{*}$
-cross-norms and refer the reader to [Reference Paulsen10, Reference Pisier11] for more details. Throughout the paper, we will denote an arbitrary Hilbert space by H and by
$C^{*}$
-cross-norms and refer the reader to [Reference Paulsen10, Reference Pisier11] for more details. Throughout the paper, we will denote an arbitrary Hilbert space by H and by
![]() $\ell ^{2}$
a separable Hilbert space. The notion of complete positivity is shortened to c.p., while u.c.p. stands for a unital, completely positive map. Let
$\ell ^{2}$
a separable Hilbert space. The notion of complete positivity is shortened to c.p., while u.c.p. stands for a unital, completely positive map. Let
![]() $A_{1}$
and
$A_{1}$
and
![]() $A_{2}$
be unital
$A_{2}$
be unital
![]() $C^{*}$
-algebras. A
$C^{*}$
-algebras. A
![]() $C^{*}$
-cross-norm on the algebraic tensor product
$C^{*}$
-cross-norm on the algebraic tensor product
![]() $A_{1} \otimes A_{2}$
is a
$A_{1} \otimes A_{2}$
is a
![]() $C^{*}$
-norm
$C^{*}$
-norm
![]() $\gamma $
satisfying the additional condition
$\gamma $
satisfying the additional condition
![]() $||a\otimes b||_{\gamma } = ||a||\cdot ||b||.$
If
$||a\otimes b||_{\gamma } = ||a||\cdot ||b||.$
If
![]() $\pi _{1} : A_{1} \rightarrow B(H_{1} )$
and
$\pi _{1} : A_{1} \rightarrow B(H_{1} )$
and
![]() $\pi _ 2 : A_{2}\rightarrow B(H_{2} )$
are unital
$\pi _ 2 : A_{2}\rightarrow B(H_{2} )$
are unital
![]() $*\mbox {-homomorphisms}$
, we get a unital,
$*\mbox {-homomorphisms}$
, we get a unital,
![]() $*$
-preserving homomorphism
$*$
-preserving homomorphism
![]() $\pi _ 1 \otimes \pi _{2} : A_{1} \otimes A_{2}\rightarrow B(H_{1}\otimes H_{2} )$
by letting
$\pi _ 1 \otimes \pi _{2} : A_{1} \otimes A_{2}\rightarrow B(H_{1}\otimes H_{2} )$
by letting
![]() $\pi _ 1 \otimes \pi _{2} (a \otimes b) = \pi _{1} (a) \otimes \pi _{2} (b). $
Thus, if for
$\pi _ 1 \otimes \pi _{2} (a \otimes b) = \pi _{1} (a) \otimes \pi _{2} (b). $
Thus, if for
![]() $x\in A_{1}\otimes A_{2}$
, we set
$x\in A_{1}\otimes A_{2}$
, we set
![]() $||x||_{\mathrm{min}} = \sup \{ \pi _ 1 \otimes \pi _2 (x) : \pi _ i : A _i \rightarrow B(H_ i ) ~ \mbox {unital }{*}\mbox{-homomorphism}, i = 1, 2\},$
then we obtain a
$||x||_{\mathrm{min}} = \sup \{ \pi _ 1 \otimes \pi _2 (x) : \pi _ i : A _i \rightarrow B(H_ i ) ~ \mbox {unital }{*}\mbox{-homomorphism}, i = 1, 2\},$
then we obtain a
![]() $C^{*}$
-cross-norm on
$C^{*}$
-cross-norm on
![]() $A_{1}\otimes A_{2}.$
The completion of
$A_{1}\otimes A_{2}.$
The completion of
![]() $A_ 1 \otimes A_ 2$
in this norm is denoted by
$A_ 1 \otimes A_ 2$
in this norm is denoted by
![]() $A_{1}\otimes _{\mathrm{min}} A_{2} $
and is called the minimal (or the spatial) tensor norm. It is the smallest possible
$A_{1}\otimes _{\mathrm{min}} A_{2} $
and is called the minimal (or the spatial) tensor norm. It is the smallest possible
![]() $C^{*}$
-cross-norm on the algebraic tensor product
$C^{*}$
-cross-norm on the algebraic tensor product
![]() $A_{1}\otimes A_{2}.$
It is not difficult to see that the minimal tensor norm is given by
$A_{1}\otimes A_{2}.$
It is not difficult to see that the minimal tensor norm is given by
![]() $||\sum _{i=1}^{n} a_{i}\otimes b_{i} ||_{\mathrm{min}} = || \sum _{i=1}^{n} \pi _{1}(a_{i})\otimes \pi _{2}(b_{i}) ||$
in
$||\sum _{i=1}^{n} a_{i}\otimes b_{i} ||_{\mathrm{min}} = || \sum _{i=1}^{n} \pi _{1}(a_{i})\otimes \pi _{2}(b_{i}) ||$
in
![]() $B(H)\otimes B(K)\subset B(H\otimes K),$
where
$B(H)\otimes B(K)\subset B(H\otimes K),$
where
![]() $\pi _{1}:A\rightarrow B(H)$
and
$\pi _{1}:A\rightarrow B(H)$
and
![]() $\pi _{2}:B\rightarrow B(K)$
are arbitrary faithful
$\pi _{2}:B\rightarrow B(K)$
are arbitrary faithful
![]() $*$
-representations.
$*$
-representations.
Let now
![]() $ \pi _ 1 : A \rightarrow B(H)$
and
$ \pi _ 1 : A \rightarrow B(H)$
and
![]() $\pi _{2} : B \rightarrow B(H)$
be unital
$\pi _{2} : B \rightarrow B(H)$
be unital
![]() $*$
-homomorphisms such that
$*$
-homomorphisms such that
![]() $\pi _{1} (a)\pi _{2} (b) = \pi _ 2 (b)\pi _ 1 (a) $
for all
$\pi _{1} (a)\pi _{2} (b) = \pi _ 2 (b)\pi _ 1 (a) $
for all
![]() $a\in A_{1}$
and
$a\in A_{1}$
and
![]() $b\in A_{2}.$
Define a unital
$b\in A_{2}.$
Define a unital
![]() $*\mbox{-homomorphism } \pi : A \otimes B \rightarrow B(H)$
by
$*\mbox{-homomorphism } \pi : A \otimes B \rightarrow B(H)$
by
![]() $\pi (x) = \sum _{i=1}^{n} \pi _{1}(a_{i})\pi _{2}(b_{i}),$
where
$\pi (x) = \sum _{i=1}^{n} \pi _{1}(a_{i})\pi _{2}(b_{i}),$
where
![]() $x = \sum ^{n}_{ i=1} a_{i}\otimes b_ i. $
Conversely, if we have a unital
$x = \sum ^{n}_{ i=1} a_{i}\otimes b_ i. $
Conversely, if we have a unital
![]() $*$
-homomorphism
$*$
-homomorphism
![]() $\pi : A \otimes B \rightarrow B(H)$
and we define
$\pi : A \otimes B \rightarrow B(H)$
and we define
![]() $\pi _{1} (a) = \pi (a \otimes I), ~ \pi _{2} (b) = \pi (I\otimes b),$
we obtain a pair of unital
$\pi _{1} (a) = \pi (a \otimes I), ~ \pi _{2} (b) = \pi (I\otimes b),$
we obtain a pair of unital
![]() $*$
-homomorphisms of A and
$*$
-homomorphisms of A and
![]() $B,$
respectively, with commuting ranges such that
$B,$
respectively, with commuting ranges such that
![]() $\pi (a \otimes b) = \pi _ 1 (a)\pi _ 2 (b).$
We define
$\pi (a \otimes b) = \pi _ 1 (a)\pi _ 2 (b).$
We define
![]() $||x||_{ \max } = \sup \{ || \pi (x)|| : \pi : A \otimes B \rightarrow B(H) ~ \mbox { unital }*\mbox{-homomorphisms}\}.$
The completion of
$||x||_{ \max } = \sup \{ || \pi (x)|| : \pi : A \otimes B \rightarrow B(H) ~ \mbox { unital }*\mbox{-homomorphisms}\}.$
The completion of
![]() $A \otimes B$
in this norm, denoted by
$A \otimes B$
in this norm, denoted by
![]() $A\otimes _{\mathrm{max}} B, $
is called the maximal tensor norm, and is the largest possible
$A\otimes _{\mathrm{max}} B, $
is called the maximal tensor norm, and is the largest possible
![]() $C^{*}$
-cross-norm on the algebraic tensor product
$C^{*}$
-cross-norm on the algebraic tensor product
![]() $A\otimes B.$
$A\otimes B.$
In the nonunital case, both min and max tensor products are taken to be the respective subalgebras of
![]() $A^{+}\otimes _{\mathrm{min}} B^{+}$
and
$A^{+}\otimes _{\mathrm{min}} B^{+}$
and
![]() $A^{+}\otimes _{\mathrm{max}} B^{+},$
where
$A^{+}\otimes _{\mathrm{max}} B^{+},$
where
![]() $A^{+}$
and
$A^{+}$
and
![]() $B^{+}$
are the unitisations of A and
$B^{+}$
are the unitisations of A and
![]() $B.$
A
$B.$
A
![]() $C^{*}$
-algebra is called nuclear if
$C^{*}$
-algebra is called nuclear if
![]() $A\otimes _{\mathrm{min}}B = A\otimes _{\mathrm{max}} B$
for every
$A\otimes _{\mathrm{min}}B = A\otimes _{\mathrm{max}} B$
for every
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $B.$
It is well known that abelian
$B.$
It is well known that abelian
![]() $C^{*}$
-algebras,
$C^{*}$
-algebras,
![]() $M_{n}(\mathbb {C}),$
and the algebra of compact operators
$M_{n}(\mathbb {C}),$
and the algebra of compact operators
![]() $K(H)$
are nuclear. We recall that a
$K(H)$
are nuclear. We recall that a
![]() $C^{*}$
-algebra A is exact if the sequence
$C^{*}$
-algebra A is exact if the sequence
is exact for every
![]() $C^{*}$
-algebra B and every closed, two-sided ideal
$C^{*}$
-algebra B and every closed, two-sided ideal
![]() $J\subset B.$
$J\subset B.$
Two important and well-known results that we will use repeatedly are collected in the next proposition. We refer the reader to [Reference Pisier11], where the first is a particular case of Corollary 4.18 and the second is Proposition 7.15.
Proposition 2.1.
-
(a) If
 $\varphi :A\rightarrow B$
is a u.c.p. map, then
$\varphi :A\rightarrow B$
is a u.c.p. map, then
 $\varphi $
extends to a u.c.p. map
$\varphi $
extends to a u.c.p. map
 $\varphi \otimes \mathrm {id}:A\otimes _{\mathrm{max}} C\rightarrow B\otimes _{\mathrm{max}} C$
.
$\varphi \otimes \mathrm {id}:A\otimes _{\mathrm{max}} C\rightarrow B\otimes _{\mathrm{max}} C$
. -
(b) The short exact sequence
 $0\rightarrow A/J \rightarrow J \rightarrow A \rightarrow 0 $
extends to the short exact sequence
$0\rightarrow A/J \rightarrow J \rightarrow A \rightarrow 0 $
extends to the short exact sequence
 $0\rightarrow A/J\otimes _{\mathrm{max}}B \rightarrow J\otimes _{\mathrm{max}} B\rightarrow A\otimes _{\mathrm{max}} B \rightarrow 0$
.
$0\rightarrow A/J\otimes _{\mathrm{max}}B \rightarrow J\otimes _{\mathrm{max}} B\rightarrow A\otimes _{\mathrm{max}} B \rightarrow 0$
.
It can be proved without difficulty that if
![]() $A_{i}\subset B_{i}, ~ i=1,2,$
then
$A_{i}\subset B_{i}, ~ i=1,2,$
then
![]() $A_{1}\otimes _{\mathrm{min}} A_{2} \subset B_{1}\otimes _{\mathrm{min}} B_{2},$
but this is no longer the case for the max norm. Specifically, if
$A_{1}\otimes _{\mathrm{min}} A_{2} \subset B_{1}\otimes _{\mathrm{min}} B_{2},$
but this is no longer the case for the max norm. Specifically, if
![]() $A\subset B,$
then it is possible that the inclusion
$A\subset B,$
then it is possible that the inclusion
![]() $A\otimes C\subset B\otimes _{\mathrm{max}} C$
does not induce the max norm on
$A\otimes C\subset B\otimes _{\mathrm{max}} C$
does not induce the max norm on
![]() $A\otimes C.$
If it does, we write
$A\otimes C.$
If it does, we write
![]() $A\otimes _{\mathrm{max}} C\subset B\otimes _{\mathrm{max}} C.$
$A\otimes _{\mathrm{max}} C\subset B\otimes _{\mathrm{max}} C.$
In [Reference Lance9], Lance observed that
![]() $A\otimes _{\mathrm{max}} C\subset A^{**}\otimes _{\mathrm{max}} C$
for all
$A\otimes _{\mathrm{max}} C\subset A^{**}\otimes _{\mathrm{max}} C$
for all
![]() $C^{*}$
-algebras A and
$C^{*}$
-algebras A and
![]() $C,$
and introduced the following property: given a unital inclusion
$C,$
and introduced the following property: given a unital inclusion
![]() $A\subset B,$
we say that A is weakly c.p. complemented in B if there exists a u.c.p. map
$A\subset B,$
we say that A is weakly c.p. complemented in B if there exists a u.c.p. map
![]() $\psi :B\rightarrow A^{**}$
such that
$\psi :B\rightarrow A^{**}$
such that
![]() $\psi (a) = a$
for all
$\psi (a) = a$
for all
![]() $a\in A.$
If the above map
$a\in A.$
If the above map
![]() $\psi $
takes values in
$\psi $
takes values in
![]() $A,$
then A is said to be c.p. complemented in
$A,$
then A is said to be c.p. complemented in
![]() $B.$
It is easy to see that if
$B.$
It is easy to see that if
![]() $A\subset B\subset C$
and A is (weakly) c.p. complemented in
$A\subset B\subset C$
and A is (weakly) c.p. complemented in
![]() $C,$
then A will be (weakly) c.p. complemented in B as well.
$C,$
then A will be (weakly) c.p. complemented in B as well.
Lance proved in [Reference Lance9] that if A is weakly c.p. complemented in
![]() $B,$
then
$B,$
then
![]() $A\otimes _{\mathrm{max}} C \subset B\otimes _{\mathrm{max}} C$
for any
$A\otimes _{\mathrm{max}} C \subset B\otimes _{\mathrm{max}} C$
for any
![]() $C.$
The particular case when A is c.p. complemented in B will be used subsequently, so we present it as Lemma 3.1 for the benefit of the reader. A
$C.$
The particular case when A is c.p. complemented in B will be used subsequently, so we present it as Lemma 3.1 for the benefit of the reader. A
![]() $C^{*}$
-algebra A has the WEP if, for some faithful representation on a Hilbert space
$C^{*}$
-algebra A has the WEP if, for some faithful representation on a Hilbert space
![]() $H,$
A is weakly c.p. complemented in
$H,$
A is weakly c.p. complemented in
![]() $B(H).$
It can be seen [Reference Lance9] that this definition does not depend on the particular representation of
$B(H).$
It can be seen [Reference Lance9] that this definition does not depend on the particular representation of
![]() $A.$
$A.$
A u.c.p. map
![]() $\varphi :A\rightarrow B/J$
is said to be u.c.p. liftable if there exists a u.c.p. map
$\varphi :A\rightarrow B/J$
is said to be u.c.p. liftable if there exists a u.c.p. map
![]() $\psi :E\rightarrow B$
such that
$\psi :E\rightarrow B$
such that
![]() $\varphi |_{E}= q\circ \psi ,$
where q is the quotient map. The map
$\varphi |_{E}= q\circ \psi ,$
where q is the quotient map. The map
![]() $\varphi :A\rightarrow B/J$
is locally u.c.p. liftable if, for every finite dimensional operator system
$\varphi :A\rightarrow B/J$
is locally u.c.p. liftable if, for every finite dimensional operator system
![]() $E\subset A,$
there exists a u.c.p. map
$E\subset A,$
there exists a u.c.p. map
![]() $\psi :E\rightarrow B$
such that
$\psi :E\rightarrow B$
such that
![]() $\varphi |_{E}= q\circ \psi .$
A
$\varphi |_{E}= q\circ \psi .$
A
![]() $C^{*}$
-algebra has the lifting property (LP) (respectively the LLP) if every u.c.p. map from A to
$C^{*}$
-algebra has the lifting property (LP) (respectively the LLP) if every u.c.p. map from A to
![]() $B/J$
is u.c.p. liftable (respectively locally u.c.p. liftable) to
$B/J$
is u.c.p. liftable (respectively locally u.c.p. liftable) to
![]() $B.$
$B.$
In [Reference Choi and Effros1], Choi and Effros proved that separable nuclear
![]() $C^{*}$
-algebras have the LP, while Kirchberg [Reference Kirchberg7] proved the same for the nonnuclear
$C^{*}$
-algebras have the LP, while Kirchberg [Reference Kirchberg7] proved the same for the nonnuclear
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $C^{*}(\mathbb {F}_{\infty }),$
the full
$C^{*}(\mathbb {F}_{\infty }),$
the full
![]() $C^{*}$
-algebra of the free group on countably many generators.
$C^{*}$
-algebra of the free group on countably many generators.
The next proposition contains several fundamental results based on Kirchberg’s work [Reference Kirchberg6].
Proposition 2.2.
-
(i) A
 $C^{*}$
-algebra A has the WEP if and only if
$C^{*}$
-algebra A has the WEP if and only if
 $A \otimes _{\mathrm{max}} C^{*}(F_{\infty }) = A\otimes _{\mathrm{min}} C^{*}(F_{\infty }).$
$A \otimes _{\mathrm{max}} C^{*}(F_{\infty }) = A\otimes _{\mathrm{min}} C^{*}(F_{\infty }).$
-
(ii) A
 $C^{*}$
-algebra A has the LLP if and only if
$C^{*}$
-algebra A has the LLP if and only if
 $A \otimes _{\mathrm{max}} B(H) = A\otimes _{\mathrm{min}} B(H).$
$A \otimes _{\mathrm{max}} B(H) = A\otimes _{\mathrm{min}} B(H).$
-
(iii)
 $A\otimes _{\mathrm{max}} B = A\otimes _{\mathrm{min}} B$
if A has the LLP and B has the WEP.
$A\otimes _{\mathrm{max}} B = A\otimes _{\mathrm{min}} B$
if A has the LLP and B has the WEP. -
(iv) If
 $A\otimes _{\mathrm{max}} B = A\otimes _{\mathrm{min}} B$
for every separable
$A\otimes _{\mathrm{max}} B = A\otimes _{\mathrm{min}} B$
for every separable
 $C^{*}$
-algebra B with the WEP, then A has the LLP.
$C^{*}$
-algebra B with the WEP, then A has the LLP.
Proof. Statements (i), (ii) and (iii) constitute Proposition 1.1 in [Reference Kirchberg6]. To prove statement (iv), suppose that
![]() $A \otimes _{\mathrm{max}} B(H) \neq A\otimes _{\mathrm{min}} B(H)$
and choose operators
$A \otimes _{\mathrm{max}} B(H) \neq A\otimes _{\mathrm{min}} B(H)$
and choose operators
![]() $a_{i} \in A, b_{i}\in B(H), ~ i=1,\ldots ,n,$
such that
$a_{i} \in A, b_{i}\in B(H), ~ i=1,\ldots ,n,$
such that
 $$ \begin{align*}\bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{min}} B(H)} < \bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{max}} B(H)}.\end{align*} $$
$$ \begin{align*}\bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{min}} B(H)} < \bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{max}} B(H)}.\end{align*} $$
By Lemma 2.4 in [Reference Kirchberg6], there exists a separable
![]() $C^{*}$
-subalgebra
$C^{*}$
-subalgebra
![]() $B\subset B(H)$
with the WEP such that
$B\subset B(H)$
with the WEP such that
![]() $b_{i}\in B, ~ i=1,\ldots ,n.$
Then B is weakly c.p. complemented in
$b_{i}\in B, ~ i=1,\ldots ,n.$
Then B is weakly c.p. complemented in
![]() $B(H)$
and
$B(H)$
and
 $$ \begin{align*}\bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{max}} B} {=} \bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{max}} B(H)}> \bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{min}} B(H)} {=} \bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{min}} B}, \end{align*} $$
$$ \begin{align*}\bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{max}} B} {=} \bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{max}} B(H)}> \bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{min}} B(H)} {=} \bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{min}} B}, \end{align*} $$
a contradiction.
3 Preliminary results
In this section, we collect several facts that will be used subsequently in proving the main results.
Lemma 3.1. Let
![]() $A\subset B$
be an inclusion of
$A\subset B$
be an inclusion of
![]() $C^{*}$
-algebras and suppose that there exists a u.c.p. map
$C^{*}$
-algebras and suppose that there exists a u.c.p. map
![]() $\theta :B\rightarrow A$
such that
$\theta :B\rightarrow A$
such that
![]() $\theta (a) = a$
for all
$\theta (a) = a$
for all
![]() $a\in A.$
Then
$a\in A.$
Then
![]() $A\otimes _{\mathrm{max}} C \subset B\otimes _{\mathrm{max}} C$
for every
$A\otimes _{\mathrm{max}} C \subset B\otimes _{\mathrm{max}} C$
for every
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $C.$
$C.$
Proof. By Proposition 2.1(b), the inclusion
![]() $\iota :A\rightarrow B$
extends to a u.c.p. map
$\iota :A\rightarrow B$
extends to a u.c.p. map
![]() $\iota \otimes \mathrm {id}:A\otimes _{\mathrm{max}} C\rightarrow B\otimes _{\mathrm{max}} C$
. Therefore, for all
$\iota \otimes \mathrm {id}:A\otimes _{\mathrm{max}} C\rightarrow B\otimes _{\mathrm{max}} C$
. Therefore, for all
![]() $a_{1},\ldots ,a_{n} \in A$
and
$a_{1},\ldots ,a_{n} \in A$
and
![]() $c_{1},\ldots ,c_{n} \in C$
,
$c_{1},\ldots ,c_{n} \in C$
,
 $$ \begin{align*} \bigg\|\sum_{i=1}^{n} a_{i} \otimes c_{i}\bigg\|_{B\otimes_{\mathrm{max}} C} = \bigg\|\sum_{i=1}^{n} \iota(a_{i}) \otimes c_{i}\bigg\|_{B\otimes_{\mathrm{max}} C} & = \bigg\|(\iota\otimes \mathrm{id})\bigg(\sum_{i=1}^{n} a_{i} \otimes c_{i}\bigg) \bigg\|_{B\otimes_{\mathrm{max}} C} \\ & \leq \bigg\|\sum_{i=1}^{n} a_{i}\otimes c_{i}\bigg\|_{A\otimes_{\mathrm{max}}C}. \end{align*} $$
$$ \begin{align*} \bigg\|\sum_{i=1}^{n} a_{i} \otimes c_{i}\bigg\|_{B\otimes_{\mathrm{max}} C} = \bigg\|\sum_{i=1}^{n} \iota(a_{i}) \otimes c_{i}\bigg\|_{B\otimes_{\mathrm{max}} C} & = \bigg\|(\iota\otimes \mathrm{id})\bigg(\sum_{i=1}^{n} a_{i} \otimes c_{i}\bigg) \bigg\|_{B\otimes_{\mathrm{max}} C} \\ & \leq \bigg\|\sum_{i=1}^{n} a_{i}\otimes c_{i}\bigg\|_{A\otimes_{\mathrm{max}}C}. \end{align*} $$
Similarly,
![]() $\theta $
extends to a u.c.p. map
$\theta $
extends to a u.c.p. map
![]() $\theta \otimes \mathrm {id}:B\otimes _{\mathrm{max}}C \rightarrow A\otimes _{\mathrm{max}} C,$
so
$\theta \otimes \mathrm {id}:B\otimes _{\mathrm{max}}C \rightarrow A\otimes _{\mathrm{max}} C,$
so
 $$ \begin{align*} \bigg\|\sum_{i=1}^{n} a_{i}\otimes c_{i}\bigg\|_{A\otimes_{\mathrm{max}}C} = \bigg\| \sum_{i=1}^{n} \theta(a_{i})\otimes c_{i}\bigg\|_{A\otimes_{\mathrm{max}}C} & = \bigg\|(\theta\otimes \mathrm{id})\bigg(\sum_{i=1}^{n} a_{i} \otimes c_{i}\bigg) \bigg\|_{A\otimes_{\mathrm{max}} C} \\ & \leq \bigg\|\sum_{i=1}^{n} a_{i}\otimes c_{i}\bigg\|_{B\otimes_{\mathrm{max}}C}. \\[-3.7pc] \end{align*} $$
$$ \begin{align*} \bigg\|\sum_{i=1}^{n} a_{i}\otimes c_{i}\bigg\|_{A\otimes_{\mathrm{max}}C} = \bigg\| \sum_{i=1}^{n} \theta(a_{i})\otimes c_{i}\bigg\|_{A\otimes_{\mathrm{max}}C} & = \bigg\|(\theta\otimes \mathrm{id})\bigg(\sum_{i=1}^{n} a_{i} \otimes c_{i}\bigg) \bigg\|_{A\otimes_{\mathrm{max}} C} \\ & \leq \bigg\|\sum_{i=1}^{n} a_{i}\otimes c_{i}\bigg\|_{B\otimes_{\mathrm{max}}C}. \\[-3.7pc] \end{align*} $$
Corollary 3.2.
-
(a) For any unital
 $C^{*}$
-algebras
$C^{*}$
-algebras
 $A, B$
and C, we have
$A, B$
and C, we have  $$ \begin{align*}A\otimes_{\mathrm{max}} C \subset (A\otimes_{\mathrm{min}} B)\otimes_{\mathrm{max}} C \quad\mbox{and}\quad A\otimes_{\mathrm{max}} C \subset (B\otimes_{\mathrm{min}} A)\otimes_{\mathrm{max}} C.\end{align*} $$
$$ \begin{align*}A\otimes_{\mathrm{max}} C \subset (A\otimes_{\mathrm{min}} B)\otimes_{\mathrm{max}} C \quad\mbox{and}\quad A\otimes_{\mathrm{max}} C \subset (B\otimes_{\mathrm{min}} A)\otimes_{\mathrm{max}} C.\end{align*} $$
-
(b) For any unital
 $C^{*}$
-algebras
$C^{*}$
-algebras
 $A_{1}, A_{2},\ldots , A_{n}$
and B and for
$A_{1}, A_{2},\ldots , A_{n}$
and B and for
 $1\leq i\leq n$
, we have
$1\leq i\leq n$
, we have
 $A_{i}\otimes _{\mathrm{max}} B \subset (A_{1}\otimes _{\mathrm{min}}A_{2}\otimes _{\mathrm{min}}\cdots \otimes _{\mathrm{min}} A_{n})\otimes _{\mathrm{max}} B.$
$A_{i}\otimes _{\mathrm{max}} B \subset (A_{1}\otimes _{\mathrm{min}}A_{2}\otimes _{\mathrm{min}}\cdots \otimes _{\mathrm{min}} A_{n})\otimes _{\mathrm{max}} B.$
Proof. (a) We apply Lemma 3.1 for B replaced by
![]() $A\otimes _{\mathrm{min}} B$
(respectively
$A\otimes _{\mathrm{min}} B$
(respectively
![]() $B\otimes _{\mathrm{min}} A$
) and identify A with the subalgebra
$B\otimes _{\mathrm{min}} A$
) and identify A with the subalgebra
![]() $A\otimes I$
(respectively
$A\otimes I$
(respectively
![]() $I\otimes A$
) of
$I\otimes A$
) of
![]() $ A\otimes _{\mathrm{min}} B.$
As far as
$ A\otimes _{\mathrm{min}} B.$
As far as
![]() $\theta $
is concerned, choose an arbitrary state
$\theta $
is concerned, choose an arbitrary state
![]() $\varphi $
on B and define
$\varphi $
on B and define
![]() $\theta :A\otimes _{\mathrm{min}} B\rightarrow A$
by
$\theta :A\otimes _{\mathrm{min}} B\rightarrow A$
by
 $$ \begin{align*}\theta\bigg(\sum_{i=1}^{n} a_{i}\otimes b_{i} \bigg) = \sum_{i=1}^{n} \varphi(b_{i}) a_{i}. \end{align*} $$
$$ \begin{align*}\theta\bigg(\sum_{i=1}^{n} a_{i}\otimes b_{i} \bigg) = \sum_{i=1}^{n} \varphi(b_{i}) a_{i}. \end{align*} $$
Respectively, define
![]() $\theta :B\otimes _{\mathrm{min}} A\rightarrow A$
by
$\theta :B\otimes _{\mathrm{min}} A\rightarrow A$
by
 $$ \begin{align*}\theta\bigg(\sum_{i=1}^{n} b_{i}\otimes a_{i} \bigg) = \sum_{i=1}^{n} \varphi(b_{i}) a_{i}. \end{align*} $$
$$ \begin{align*}\theta\bigg(\sum_{i=1}^{n} b_{i}\otimes a_{i} \bigg) = \sum_{i=1}^{n} \varphi(b_{i}) a_{i}. \end{align*} $$
(b) We use induction. The case
![]() $n=2$
is part (a). Suppose now that the property is true for n and consider
$n=2$
is part (a). Suppose now that the property is true for n and consider
![]() $n+1$
algebras
$n+1$
algebras
![]() $A_{1}, \ldots , A_{n+1}.$
For
$A_{1}, \ldots , A_{n+1}.$
For
![]() $i=1$
,
$i=1$
,
by part (a), while for
![]() $2\leq i \leq n+1$
,
$2\leq i \leq n+1$
,
by the inductive hypothesis and
by part (a). The conclusion follows.
4 Tensor products with the Calkin algebra
In this section, we prove that a
![]() $C^{*}$
-algebra whose max and min tensor products with the Calkin algebra are equal must be exact and have the LLP. This result, which represents the core technical ingredient needed in the proof of the main result, has also been folklore for a while. It first appeared in print recently as Corollary 10.10 in [Reference Pisier11]. The proof we present here is different and shorter than the one in [Reference Pisier11].
$C^{*}$
-algebra whose max and min tensor products with the Calkin algebra are equal must be exact and have the LLP. This result, which represents the core technical ingredient needed in the proof of the main result, has also been folklore for a while. It first appeared in print recently as Corollary 10.10 in [Reference Pisier11]. The proof we present here is different and shorter than the one in [Reference Pisier11].
Proposition 4.1. A
![]() $C^{*}$
-algebra A satisfies
$C^{*}$
-algebra A satisfies
![]() $A\otimes _{\mathrm{min}} B(\ell ^{2})/K(\ell ^{2}) = A\otimes _{\mathrm{max}} B(\ell ^{2})/K(\ell ^{2}) $
if and only if A has the LLP and is exact.
$A\otimes _{\mathrm{min}} B(\ell ^{2})/K(\ell ^{2}) = A\otimes _{\mathrm{max}} B(\ell ^{2})/K(\ell ^{2}) $
if and only if A has the LLP and is exact.
Proof.
![]() $\Leftarrow $
The sequence
$\Leftarrow $
The sequence
is exact and, since A is exact, so is the sequence
Since A has the LLP,
![]() $A\otimes _{\mathrm{min}} B(\ell ^{2}) = A\otimes _{\mathrm{max}} B(\ell ^{2}).$
This, together with the fact that
$A\otimes _{\mathrm{min}} B(\ell ^{2}) = A\otimes _{\mathrm{max}} B(\ell ^{2}).$
This, together with the fact that
![]() $A\otimes _{\mathrm{min}} K(\ell ^{2}) = A\otimes _{\mathrm{max}} K(\ell ^{2})$
(since
$A\otimes _{\mathrm{min}} K(\ell ^{2}) = A\otimes _{\mathrm{max}} K(\ell ^{2})$
(since
![]() $K(\ell ^{2})$
is nuclear), leads to the conclusion.
$K(\ell ^{2})$
is nuclear), leads to the conclusion.
![]() $\Rightarrow $
First we prove that A has the LLP. To get a contradiction, suppose, by using Proposition 2.2(iv), that there exists a separable WEP
$\Rightarrow $
First we prove that A has the LLP. To get a contradiction, suppose, by using Proposition 2.2(iv), that there exists a separable WEP
![]() $C^{*}$
-algebra B with the property
$C^{*}$
-algebra B with the property
![]() $A\otimes _{\mathrm{min}} B \neq A\otimes _{\mathrm{max}} B.$
As a consequence, there exist operators
$A\otimes _{\mathrm{min}} B \neq A\otimes _{\mathrm{max}} B.$
As a consequence, there exist operators
![]() $a_{i}\in A, b_{i}\in B, i=1,\ldots ,n,$
and
$a_{i}\in A, b_{i}\in B, i=1,\ldots ,n,$
and
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
 $$ \begin{align*}\bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{max}}B} =1 \quad\mbox{and}\quad \bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{min}}B} < 1-\varepsilon. \end{align*} $$
$$ \begin{align*}\bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{max}}B} =1 \quad\mbox{and}\quad \bigg\|\sum_{i=1}^{n} a_{i} \otimes b_{i}\bigg\|_{A\otimes_{\mathrm{min}}B} < 1-\varepsilon. \end{align*} $$
We may assume without loss of generality that B is faithfully represented on a separable Hilbert space, viewed as
![]() $\ell ^{2},$
in such a way that
$\ell ^{2},$
in such a way that
![]() $B \cap K(\ell ^{2}) = \{0\}.$
Then the quotient map
$B \cap K(\ell ^{2}) = \{0\}.$
Then the quotient map
![]() $\pi : B(\ell ^{2}) \rightarrow B(\ell ^{2})/K(\ell ^{2})$
induces a
$\pi : B(\ell ^{2}) \rightarrow B(\ell ^{2})/K(\ell ^{2})$
induces a
![]() $*$
-isomorphism between B and
$*$
-isomorphism between B and
![]() $\pi (B) \subset B(\ell ^{2})/K(\ell ^{2}).$
If we view the Calkin algebra represented faithfully on some (nonseparable) Hilbert space
$\pi (B) \subset B(\ell ^{2})/K(\ell ^{2}).$
If we view the Calkin algebra represented faithfully on some (nonseparable) Hilbert space
![]() $H,$
then
$H,$
then
Since
![]() $\pi (B)$
has the WEP, it is weakly c.p. complemented in
$\pi (B)$
has the WEP, it is weakly c.p. complemented in
![]() $B(H);$
therefore, also weakly c.p. complemented in
$B(H);$
therefore, also weakly c.p. complemented in
![]() $B(\ell ^{2})/K(\ell ^{2}),$
as remarked in Section 2. In particular,
$B(\ell ^{2})/K(\ell ^{2}),$
as remarked in Section 2. In particular,
![]() $ A\otimes _{\mathrm{max}} \pi (B) \subset A \otimes _{\mathrm{max}} B(\ell ^{2})/K(\ell ^{2}).$
It follows that
$ A\otimes _{\mathrm{max}} \pi (B) \subset A \otimes _{\mathrm{max}} B(\ell ^{2})/K(\ell ^{2}).$
It follows that
 $$ \begin{align*} \bigg\|\sum_{i=1}^{n} a_{i}\otimes b_{i} \bigg\|_{A\otimes_{\mathrm{max}} B} = \bigg\|\sum_{i=1}^{n} a_{i}\otimes \pi(b_{i}) \bigg\| _{A\otimes_{\mathrm{max}} \pi(B)} = \bigg\|\sum_{i=1}^{n} a_{i}\otimes \pi(b_{i}) \bigg\| _{A\otimes_{\mathrm{max}} B(\ell^{2})/K(\ell^{2})}. \end{align*} $$
$$ \begin{align*} \bigg\|\sum_{i=1}^{n} a_{i}\otimes b_{i} \bigg\|_{A\otimes_{\mathrm{max}} B} = \bigg\|\sum_{i=1}^{n} a_{i}\otimes \pi(b_{i}) \bigg\| _{A\otimes_{\mathrm{max}} \pi(B)} = \bigg\|\sum_{i=1}^{n} a_{i}\otimes \pi(b_{i}) \bigg\| _{A\otimes_{\mathrm{max}} B(\ell^{2})/K(\ell^{2})}. \end{align*} $$
However, by using the hypothesis, we obtain
 $$ \begin{align*} \bigg\| \sum_{i=1}^{n} a_{i}\otimes \pi(b_{i}) \bigg\| _{A\otimes_{\mathrm{max}} B(\ell^{2})/K(\ell^{2})} & = \bigg\|\sum_{i=1}^{n} a_{i}\otimes \pi(b_{i}) \bigg\| _{A\otimes_{\mathrm{min}} B(\ell^{2})/K(\ell^{2})} \\ = \bigg\|\sum_{i=1}^{n} a_{i}\otimes \pi(b_{i}) \bigg\| _{A\otimes_{\mathrm{min}} \pi(B)} & = \bigg\|\sum_{i=1}^{n} a_{i}\otimes b_{i} \bigg\| _{A\otimes_{\mathrm{min}} B} < 1 - \varepsilon. \end{align*} $$
$$ \begin{align*} \bigg\| \sum_{i=1}^{n} a_{i}\otimes \pi(b_{i}) \bigg\| _{A\otimes_{\mathrm{max}} B(\ell^{2})/K(\ell^{2})} & = \bigg\|\sum_{i=1}^{n} a_{i}\otimes \pi(b_{i}) \bigg\| _{A\otimes_{\mathrm{min}} B(\ell^{2})/K(\ell^{2})} \\ = \bigg\|\sum_{i=1}^{n} a_{i}\otimes \pi(b_{i}) \bigg\| _{A\otimes_{\mathrm{min}} \pi(B)} & = \bigg\|\sum_{i=1}^{n} a_{i}\otimes b_{i} \bigg\| _{A\otimes_{\mathrm{min}} B} < 1 - \varepsilon. \end{align*} $$
It follows that
![]() ${ ||\sum _{i=1}^{n} a_{i}\otimes b_{i} ||_{A\otimes _{\mathrm{max}} B} < 1 - \varepsilon ,}$
which contradicts the assumption that
${ ||\sum _{i=1}^{n} a_{i}\otimes b_{i} ||_{A\otimes _{\mathrm{max}} B} < 1 - \varepsilon ,}$
which contradicts the assumption that
![]() ${ ||\sum _{i=1}^{n} a_{i}\otimes b_{i} ||_{A\otimes _{\mathrm{max}} B} = 1.}$
We conclude that A has the LLP.
${ ||\sum _{i=1}^{n} a_{i}\otimes b_{i} ||_{A\otimes _{\mathrm{max}} B} = 1.}$
We conclude that A has the LLP.
To prove exactness, we will show that in the short exact sequence
we can replace ‘max’ by ‘min’. Since A has the LLP, it follows that
![]() $A\otimes _{\mathrm{max}} B(\ell ^{2}) = A\otimes _{\mathrm{min}} B(\ell ^{2}).$
By hypothesis, we also have
$A\otimes _{\mathrm{max}} B(\ell ^{2}) = A\otimes _{\mathrm{min}} B(\ell ^{2}).$
By hypothesis, we also have
![]() $A\otimes _{\mathrm{max}} B(\ell ^{2})/K(\ell ^{2}) = A\otimes _{\mathrm{min}} B(\ell ^{2})/K(\ell ^{2}) $
which, together with
$A\otimes _{\mathrm{max}} B(\ell ^{2})/K(\ell ^{2}) = A\otimes _{\mathrm{min}} B(\ell ^{2})/K(\ell ^{2}) $
which, together with
![]() $A\otimes _{\mathrm{max}} K(\ell ^{2}) = A\otimes _{\mathrm{min}} K(\ell ^{2}),$
leads to
$A\otimes _{\mathrm{max}} K(\ell ^{2}) = A\otimes _{\mathrm{min}} K(\ell ^{2}),$
leads to
This implies that A is exact by Theorem 1.1 in [Reference Kirchberg5].
5 Detecting nuclearity
This section is devoted to the main results.
Definition 5.1.
-
(i) A unital
 $C^{*}$
-algebra A is said to detect nuclearity if, whenever a
$C^{*}$
-algebra A is said to detect nuclearity if, whenever a
 $C^{*}$
-algebra B satisfies
$C^{*}$
-algebra B satisfies
 $A\otimes _{\mathrm{min}} B = A\otimes _{\mathrm{max}} B,$
it follows that B is nuclear.
$A\otimes _{\mathrm{min}} B = A\otimes _{\mathrm{max}} B,$
it follows that B is nuclear. -
(ii) A set
 $\mathbb {S} = \{ A_{1}, A_{2},\ldots ,A_{n}\}$
of unital
$\mathbb {S} = \{ A_{1}, A_{2},\ldots ,A_{n}\}$
of unital
 $C^{*}$
-algebras is said to detect nuclearity if, whenever a
$C^{*}$
-algebras is said to detect nuclearity if, whenever a
 $C^{*}$
-algebra B satisfies
$C^{*}$
-algebra B satisfies
 $A_{i}\otimes _{\mathrm{min}} B = A_{i}\otimes _{\mathrm{max}} B$
for all
$A_{i}\otimes _{\mathrm{min}} B = A_{i}\otimes _{\mathrm{max}} B$
for all
 $i=1,\ldots ,n,$
it follows that B is nuclear.
$i=1,\ldots ,n,$
it follows that B is nuclear.
Remark 5.2. Without loss of generality, we can assume that B is also unital. Otherwise, if
![]() $B^{+}$
denotes the unitisation of
$B^{+}$
denotes the unitisation of
![]() $B,$
$B,$
![]() $A\otimes _{\mathrm{min}} B = A\otimes _{\mathrm{max}} B$
implies
$A\otimes _{\mathrm{min}} B = A\otimes _{\mathrm{max}} B$
implies
![]() $A\otimes _{\mathrm{min}} B^{+} = A\otimes _{\mathrm{max}} B^{+}$
by Lemma 5.4 in [Reference Harris and Kim3]. If A detects nuclearity among unital
$A\otimes _{\mathrm{min}} B^{+} = A\otimes _{\mathrm{max}} B^{+}$
by Lemma 5.4 in [Reference Harris and Kim3]. If A detects nuclearity among unital
![]() $C^{*}$
-algebras, then
$C^{*}$
-algebras, then
![]() $B^{+}$
is nuclear; therefore, B is nuclear as an ideal of
$B^{+}$
is nuclear; therefore, B is nuclear as an ideal of
![]() $B^{+}.$
$B^{+}.$
The connection between the two notions in the above definition is given in the next proposition.
Proposition 5.3. If the set
![]() $\mathbb {S} = \{ A_{1}, A_{2},\ldots ,A_{n}\}$
of unital
$\mathbb {S} = \{ A_{1}, A_{2},\ldots ,A_{n}\}$
of unital
![]() $C^{*}$
-algebras detects nuclearity, then so does
$C^{*}$
-algebras detects nuclearity, then so does
![]() $A_{1}\otimes _{\mathrm{min}} A_{2}\otimes _{\mathrm{min}} \cdots \otimes _{\mathrm{min}} A_{n}.$
$A_{1}\otimes _{\mathrm{min}} A_{2}\otimes _{\mathrm{min}} \cdots \otimes _{\mathrm{min}} A_{n}.$
Proof. Suppose that B satisfies
By Corollary 3.2(b),
 $$ \begin{align*} A_{i}\otimes_{\mathrm{max}} B &\subset (A_{1}\otimes_{\mathrm{min}} A_{2}\otimes_{\mathrm{min}} \cdots \otimes_{\mathrm{min}} A_{n})\otimes_{\mathrm{max}} B\\ & = (A_{1}\otimes_{\mathrm{min}} A_{2}\otimes_{\mathrm{min}} \cdots \otimes_{\mathrm{min}} A_{n})\otimes_{\mathrm{min}} B; \end{align*} $$
$$ \begin{align*} A_{i}\otimes_{\mathrm{max}} B &\subset (A_{1}\otimes_{\mathrm{min}} A_{2}\otimes_{\mathrm{min}} \cdots \otimes_{\mathrm{min}} A_{n})\otimes_{\mathrm{max}} B\\ & = (A_{1}\otimes_{\mathrm{min}} A_{2}\otimes_{\mathrm{min}} \cdots \otimes_{\mathrm{min}} A_{n})\otimes_{\mathrm{min}} B; \end{align*} $$
therefore,
![]() $A_{i}\otimes _{\mathrm{min}} B = A_{i}\otimes _{\mathrm{max}} B$
for
$A_{i}\otimes _{\mathrm{min}} B = A_{i}\otimes _{\mathrm{max}} B$
for
![]() $1\leq i \leq n.$
Since
$1\leq i \leq n.$
Since
![]() $\mathbb {S}$
detects nuclearity, the conclusion follows.
$\mathbb {S}$
detects nuclearity, the conclusion follows.
We arrive at the main result of this section.
Proposition 5.4. The
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $ C^{*}(\mathbb {F}_{\infty })\otimes _{\mathrm{min}} B(\ell ^{2})/K(\ell ^{2})$
detects nuclearity.
$ C^{*}(\mathbb {F}_{\infty })\otimes _{\mathrm{min}} B(\ell ^{2})/K(\ell ^{2})$
detects nuclearity.
Proof. By Proposition 5.3, it suffices to show that the set
![]() $\mathbb {S} = \{ C^{*}(\mathbb {F}_{\infty }), B(\ell ^{2})/K(\ell ^{2}) \}$
detects nuclearity. Let B be a
$\mathbb {S} = \{ C^{*}(\mathbb {F}_{\infty }), B(\ell ^{2})/K(\ell ^{2}) \}$
detects nuclearity. Let B be a
![]() $C^{*}$
-algebra satisfying
$C^{*}$
-algebra satisfying
![]() $A\otimes _{\mathrm{min}} B = A\otimes _{\mathrm{max}} B$
for all
$A\otimes _{\mathrm{min}} B = A\otimes _{\mathrm{max}} B$
for all
![]() $A\in \mathbb {S}.$
From
$A\in \mathbb {S}.$
From
![]() $B(\ell ^{2})/K(\ell ^{2})\otimes _{\mathrm{min}} B = B(\ell ^{2})/K(\ell ^{2}) \otimes _{\mathrm{max}} B$
, we see that B is exact and has the LLP by Proposition 4.1. However,
$B(\ell ^{2})/K(\ell ^{2})\otimes _{\mathrm{min}} B = B(\ell ^{2})/K(\ell ^{2}) \otimes _{\mathrm{max}} B$
, we see that B is exact and has the LLP by Proposition 4.1. However,
![]() $ C^{*}(\mathbb {F}_{\infty })\otimes _{\mathrm{min}} B = C^{*}(\mathbb {F}_{\infty })\otimes _{\mathrm{max}} B$
implies that B has the WEP (Proposition 2.2(i)). Since B is both WEP and exact, it must be nuclear (see for example [Reference Pop12, 4.2] or [Reference Pisier11, 10.9]).
$ C^{*}(\mathbb {F}_{\infty })\otimes _{\mathrm{min}} B = C^{*}(\mathbb {F}_{\infty })\otimes _{\mathrm{max}} B$
implies that B has the WEP (Proposition 2.2(i)). Since B is both WEP and exact, it must be nuclear (see for example [Reference Pop12, 4.2] or [Reference Pisier11, 10.9]).
Remark 5.5. In the category of QWEP
![]() $C^{*}$
-algebras (quotients of
$C^{*}$
-algebras (quotients of
![]() $C^{*}$
-algebras with the WEP), the Calkin algebra detects nuclearity. This is a consequence of the fact that exactness and LLP plus QWEP imply nuclearity. Indeed, a
$C^{*}$
-algebras with the WEP), the Calkin algebra detects nuclearity. This is a consequence of the fact that exactness and LLP plus QWEP imply nuclearity. Indeed, a
![]() $C^{*}$
-algebra with QWEP and LLP must have the WEP (Corollary 2.6(ii) in [Reference Kirchberg6]), and WEP plus exactness imply nuclearity as seen in the previous paragraph.
$C^{*}$
-algebra with QWEP and LLP must have the WEP (Corollary 2.6(ii) in [Reference Kirchberg6]), and WEP plus exactness imply nuclearity as seen in the previous paragraph.
6 Other tensor product characterisations of nuclearity
In the same circle of ideas as nuclearity detection, we mention the issue of characterising nuclearity by the equality of the min and max norms on certain tensor products.
To illustrate this idea, we recall that a
![]() $C^{*}$
-algebra is nuclear if and only if any Hilbert space representation generates an injective von Neumann algebra. Equivalently, A is nuclear if and only if
$C^{*}$
-algebra is nuclear if and only if any Hilbert space representation generates an injective von Neumann algebra. Equivalently, A is nuclear if and only if
![]() $A^{**}$
is injective [Reference Pisier11, 8.16]. Since, for von Neumann algebras, injectivity and the WEP are equivalent [Reference Pisier11, 9.26], we obtain the following characterisation of nuclearity [Reference Pisier11, 9.27].
$A^{**}$
is injective [Reference Pisier11, 8.16]. Since, for von Neumann algebras, injectivity and the WEP are equivalent [Reference Pisier11, 9.26], we obtain the following characterisation of nuclearity [Reference Pisier11, 9.27].
Proposition 6.1. A
![]() $C^{*}$
-algebra A is nuclear if and only if
$C^{*}$
-algebra A is nuclear if and only if
Recall that, given a
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $A,$
the opposite
$A,$
the opposite
![]() $C^{*}$
-algebra, denoted by
$C^{*}$
-algebra, denoted by
![]() $A^{\mathrm{op}},$
is the same algebra with the same involution but with reversed product, so that the product of a and b in
$A^{\mathrm{op}},$
is the same algebra with the same involution but with reversed product, so that the product of a and b in
![]() $A^{\mathrm{op}}$
is defined as
$A^{\mathrm{op}}$
is defined as
![]() $ba.$
We conclude with one more characterisation of nuclearity.
$ba.$
We conclude with one more characterisation of nuclearity.
Proposition 6.2. A
![]() $C^{*}$
-algebra A is nuclear if and only if
$C^{*}$
-algebra A is nuclear if and only if
Proof. We use Corollary 3.2(a) to get
![]() $A\otimes _{\mathrm{min}} (B(\ell ^{2})/K(\ell ^{2})) = A\otimes _{\mathrm{max}} (B(\ell ^{2})/K(\ell ^{2})) $
and
$A\otimes _{\mathrm{min}} (B(\ell ^{2})/K(\ell ^{2})) = A\otimes _{\mathrm{max}} (B(\ell ^{2})/K(\ell ^{2})) $
and
![]() $A\otimes _{\mathrm{min}} A^{\mathrm{op}} = A\otimes _{\mathrm{max}} A^{\mathrm{op}}.$
The former implies that A is exact, by Proposition 4.1, while the latter shows that A has the WEP, as a consequence of Theorem 23.43 in [Reference Pisier11]. As previously seen, exactness and WEP imply nuclearity.
$A\otimes _{\mathrm{min}} A^{\mathrm{op}} = A\otimes _{\mathrm{max}} A^{\mathrm{op}}.$
The former implies that A is exact, by Proposition 4.1, while the latter shows that A has the WEP, as a consequence of Theorem 23.43 in [Reference Pisier11]. As previously seen, exactness and WEP imply nuclearity.