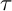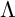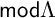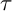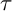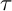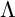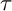1 Introduction
In the study of module categories of rings and algebras, certain classes of subcategories play a prominent role. Torsion pairs are pairs
![]() $({\mathcal T}, {\mathcal F})$
of subcategories, where the torsion classes
$({\mathcal T}, {\mathcal F})$
of subcategories, where the torsion classes
![]() ${\mathcal T}$
are characterized by being closed under extensions and factors, and
${\mathcal T}$
are characterized by being closed under extensions and factors, and
![]() ${\mathcal F} = {\mathcal T}^{\perp } \colon =\{X \mid \operatorname {{\mathrm {Hom}}}({\mathcal T},X) = 0\}$
. Together with their triangulated siblings, the t-structures, such pairs are closely connected to classical tilting theory, for example, via the Brenner–Butler theorem (see [Reference Brenner and Butler8]) and HRS-tilting (see [Reference Happel, Reiten and Smalø15]). More recently, inspired by links to cluster combinatorics, Adachi, Iyama, and Reiten defined support
${\mathcal F} = {\mathcal T}^{\perp } \colon =\{X \mid \operatorname {{\mathrm {Hom}}}({\mathcal T},X) = 0\}$
. Together with their triangulated siblings, the t-structures, such pairs are closely connected to classical tilting theory, for example, via the Brenner–Butler theorem (see [Reference Brenner and Butler8]) and HRS-tilting (see [Reference Happel, Reiten and Smalø15]). More recently, inspired by links to cluster combinatorics, Adachi, Iyama, and Reiten defined support
![]() $\tau $
-tilting modules in [Reference Adachi, Iyama and Reiten1]. They showed that functorially finite torsion classes are exactly those of the form
$\tau $
-tilting modules in [Reference Adachi, Iyama and Reiten1]. They showed that functorially finite torsion classes are exactly those of the form
![]() $\mathsf {Gen} M$
(i.e., all modules which are generated by sums of copies of M), where M is a support
$\mathsf {Gen} M$
(i.e., all modules which are generated by sums of copies of M), where M is a support
![]() $\tau $
-tilting module. This strengthens a classical result of Auslander and Smalø [Reference Auslander and Smalø4].
$\tau $
-tilting module. This strengthens a classical result of Auslander and Smalø [Reference Auslander and Smalø4].
Wide subcategories are exact abelian subcategories. They were first considered by Hovey [Reference Hovey16] in the setting of commutative Noetherian rings. The importance of such subcategories in dealing with categories
![]() $\mathsf {mod} \Lambda $
of finitely generated modules over finite-dimensional algebras has been highlighted by work of Ingalls–Thomas [Reference Ingalls and Thomas20] and Marks–Šťovíček [Reference Marks and Šťovíček23]. In particular, [Reference Marks and Šťovíček23] shows that there is a natural injective map from the set of wide subcategories to the set of torsion classes of
$\mathsf {mod} \Lambda $
of finitely generated modules over finite-dimensional algebras has been highlighted by work of Ingalls–Thomas [Reference Ingalls and Thomas20] and Marks–Šťovíček [Reference Marks and Šťovíček23]. In particular, [Reference Marks and Šťovíček23] shows that there is a natural injective map from the set of wide subcategories to the set of torsion classes of
![]() $\mathsf {mod} \Lambda $
, and also that there is an injective map from functorially finite torsion classes to functorially finite wide subcategories. The wide subcategories in the image of this map are called left finite wide subcategories, and there is also a dual notion of right finite wide subcategories. For
$\mathsf {mod} \Lambda $
, and also that there is an injective map from functorially finite torsion classes to functorially finite wide subcategories. The wide subcategories in the image of this map are called left finite wide subcategories, and there is also a dual notion of right finite wide subcategories. For
![]() $\tau $
-tilting finite algebras, all wide subcategories and torsion classes are functorially finite, and the above maps are actually bijections between finite sets.
$\tau $
-tilting finite algebras, all wide subcategories and torsion classes are functorially finite, and the above maps are actually bijections between finite sets.
Functorially finite wide subcategories are known to be exactly those which are equivalent to module categories, and are hence of special interest. Examples of such are the left-finite and right-finite wide subcategories, and also the Serre subcategories. The latter are subcategories of
![]() $\mathsf {mod} \Lambda $
which are equivalent to
$\mathsf {mod} \Lambda $
which are equivalent to
![]() $\mathsf {mod} (\Lambda /I)$
for I generated by an idempotent in
$\mathsf {mod} (\Lambda /I)$
for I generated by an idempotent in
![]() $\Lambda $
. Another important source of functorially finite wide categories is the
$\Lambda $
. Another important source of functorially finite wide categories is the
![]() $\tau $
-perpendicular categories, first considered by Jasso [Reference Jasso22]. These are categories given by
$\tau $
-perpendicular categories, first considered by Jasso [Reference Jasso22]. These are categories given by
![]() $M^{\perp } \cap {^{\perp }(\tau M)} \cap P^{\perp }$
, where
$M^{\perp } \cap {^{\perp }(\tau M)} \cap P^{\perp }$
, where
![]() $(M,P)$
is a pair of modules with
$(M,P)$
is a pair of modules with
![]() $\operatorname {{\mathrm {Hom}}}(M, \tau M) = 0$
and P a projective module satisfying
$\operatorname {{\mathrm {Hom}}}(M, \tau M) = 0$
and P a projective module satisfying
![]() $\operatorname {{\mathrm {Hom}}}(P,M) = 0$
. These generalize both Serre subcategories and, moreover, classical Geigle–Lenzing perpendicular categories (see [Reference Geigle and Lenzing13]), which have been much studied in the hereditary setting. There is also a dual concept of
$\operatorname {{\mathrm {Hom}}}(P,M) = 0$
. These generalize both Serre subcategories and, moreover, classical Geigle–Lenzing perpendicular categories (see [Reference Geigle and Lenzing13]), which have been much studied in the hereditary setting. There is also a dual concept of
![]() $\tau ^{-1}$
-perpendicular categories (see Definition 3.4).
$\tau ^{-1}$
-perpendicular categories (see Definition 3.4).
Our first main result gives a characterization of
![]() $\tau $
-perpendicular categories, showing how the different classes mentioned above are related.
$\tau $
-perpendicular categories, showing how the different classes mentioned above are related.
Theorem 1.1 (Theorem 4.5).
Let
![]() $\Lambda $
be a finite-dimensional algebra, and let
$\Lambda $
be a finite-dimensional algebra, and let
![]() ${\mathcal W}\subseteq \mathsf {mod}\Lambda $
be a wide subcategory. Then the following are equivalent.
${\mathcal W}\subseteq \mathsf {mod}\Lambda $
be a wide subcategory. Then the following are equivalent.
-
1.
 ${\mathcal W}$
is a
${\mathcal W}$
is a
 $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
 $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
. -
2.
 ${\mathcal W}$
is a
${\mathcal W}$
is a
 $\tau ^{-1}$
-perpendicular subcategory of
$\tau ^{-1}$
-perpendicular subcategory of
 $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
. -
3.
 ${\mathcal W}$
is a Serre subcategory of a left-finite wide subcategory.
${\mathcal W}$
is a Serre subcategory of a left-finite wide subcategory. -
4.
 ${\mathcal W}$
is a Serre subcategory of a right-finite wide subcategory.
${\mathcal W}$
is a Serre subcategory of a right-finite wide subcategory. -
5. There exists a functorially finite torsion class
 ${\mathcal T}\subseteq \mathsf {mod}\Lambda $
and a functorially finite torsion-free class
${\mathcal T}\subseteq \mathsf {mod}\Lambda $
and a functorially finite torsion-free class
 ${\mathcal F}\subseteq \mathsf {mod}\Lambda $
with
${\mathcal F}\subseteq \mathsf {mod}\Lambda $
with
 ${\mathcal T}^{\perp } \subseteq {\mathcal F}$
such that
${\mathcal T}^{\perp } \subseteq {\mathcal F}$
such that
 ${\mathcal W} = {\mathcal T}\cap {\mathcal F}$
.
${\mathcal W} = {\mathcal T}\cap {\mathcal F}$
.
We note that Serre subcategories of wide subcategories also occur in Asai and Pfeifer’s classification of so-called “wide intervals” of torsion classes (see [Reference Asai and Pfeifer3]). We discuss the relationship between Theorem 1.1, the results of Asai and Pfeifer, and the “brick labeling” of the lattice of torsion classes in Remark 4.6.
It is a consequence of Theorem 1.1 that the left-finite wide subcategories, right-finite wide subcategories, and Serre subcategories are examples of
![]() $\tau $
-perpendicular subcategories. In particular, this leads to the following consequence.
$\tau $
-perpendicular subcategories. In particular, this leads to the following consequence.
Corollary 1.2 (Corollary 6.7).
Let
![]() $\Lambda $
be a finite-dimensional algebra. Let
$\Lambda $
be a finite-dimensional algebra. Let
![]() $\mathcal V\subseteq {\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a chain of subcategories such that
$\mathcal V\subseteq {\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a chain of subcategories such that
![]() $\mathcal V$
is a
$\mathcal V$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() ${\mathcal W}$
and
${\mathcal W}$
and
![]() ${\mathcal W}$
is a
${\mathcal W}$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
. Then
$\mathsf {mod}\Lambda $
. Then
![]() $\mathcal V$
is a
$\mathcal V$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
.
Considering the finite poset
![]() $\mathcal {S}$
of all wide subcategories of a
$\mathcal {S}$
of all wide subcategories of a
![]() $\tau $
-tilting finite algebra
$\tau $
-tilting finite algebra
![]() $\Lambda $
, it was shown in [Reference Buan and Marsh9] that there is a natural definition of a category
$\Lambda $
, it was shown in [Reference Buan and Marsh9] that there is a natural definition of a category
![]() $\mathfrak {W}(\Lambda )$
, with the elements in
$\mathfrak {W}(\Lambda )$
, with the elements in
![]() $\mathcal {S}$
as objects and maps parameterized by support
$\mathcal {S}$
as objects and maps parameterized by support
![]() $\tau $
-rigid objects. Following [Reference Hanson and Igusa14], we call
$\tau $
-rigid objects. Following [Reference Hanson and Igusa14], we call
![]() $\mathfrak {W}(\Lambda )$
the
$\mathfrak {W}(\Lambda )$
the
![]() $\tau $
-cluster morphism category of
$\tau $
-cluster morphism category of
![]() $\Lambda $
. The concept of (signed)
$\Lambda $
. The concept of (signed)
![]() $\tau $
-exceptional sequences (see [Reference Buan and Marsh10]) is closely related, as such sequences can be interpreted as compositions of irreducible maps in
$\tau $
-exceptional sequences (see [Reference Buan and Marsh10]) is closely related, as such sequences can be interpreted as compositions of irreducible maps in
![]() $\mathfrak {W}(\Lambda )$
. This extended earlier work of Igusa–Todorov [Reference Igusa and Todorov18], who dealt with the hereditary case. The study of
$\mathfrak {W}(\Lambda )$
. This extended earlier work of Igusa–Todorov [Reference Igusa and Todorov18], who dealt with the hereditary case. The study of
![]() $\mathfrak {W}(\Lambda )$
was motivated by the link to the study of picture groups (see [Reference Igusa, Todorov and Weyman19]) in the hereditary case, which was extended to the general (
$\mathfrak {W}(\Lambda )$
was motivated by the link to the study of picture groups (see [Reference Igusa, Todorov and Weyman19]) in the hereditary case, which was extended to the general (
![]() $\tau $
-tilting finite) case in [Reference Hanson and Igusa14].
$\tau $
-tilting finite) case in [Reference Hanson and Igusa14].
As an application of Theorem 1.1, we show that one obtains a natural generalization of the above for all finite-dimensional algebras by restricting to
![]() $\tau $
-perpendicular subcategories. More precisely, we define a category
$\tau $
-perpendicular subcategories. More precisely, we define a category
![]() $\mathfrak {W}(\Lambda )$
whose objects are the
$\mathfrak {W}(\Lambda )$
whose objects are the
![]() $\tau $
-perpendicular subcategories of
$\tau $
-perpendicular subcategories of
![]() $\mathsf {mod}\Lambda $
and whose morphisms with source
$\mathsf {mod}\Lambda $
and whose morphisms with source
![]() ${\mathcal W}$
are parameterized by the support
${\mathcal W}$
are parameterized by the support
![]() $\tau $
-rigid objects of
$\tau $
-rigid objects of
![]() ${\mathcal W}$
. The following is then our second main result.
${\mathcal W}$
. The following is then our second main result.
Theorem 1.3 (Theorem 6.13).
Let
![]() $\Lambda $
be a finite-dimensional algebra. Then the
$\Lambda $
be a finite-dimensional algebra. Then the
![]() $\tau $
-cluster morphism category
$\tau $
-cluster morphism category
![]() $\mathfrak {W}(\Lambda )$
is a well-defined category.
$\mathfrak {W}(\Lambda )$
is a well-defined category.
The proof we give of Theorem 1.3 also gives a significant simplification of the proof in the
![]() $\tau $
-tilting finite case, given in [Reference Buan and Marsh9].
$\tau $
-tilting finite case, given in [Reference Buan and Marsh9].
The article is organized as follows: We first recall results and definitions concerning torsion pairs and
![]() $\tau $
-tilting theory in §2. Then, we consider various classes of functorially finite wide subcategories in §3 and proceed by proving the first main theorem in §4. We review a reduction formula for support
$\tau $
-tilting theory in §2. Then, we consider various classes of functorially finite wide subcategories in §3 and proceed by proving the first main theorem in §4. We review a reduction formula for support
![]() $\tau $
-rigid objects in §5, which is used to prove the second main theorem in §6. We conclude by working out a concrete example of a
$\tau $
-rigid objects in §5, which is used to prove the second main theorem in §6. We conclude by working out a concrete example of a
![]() $\tau $
-cluster morphism category in the final section.
$\tau $
-cluster morphism category in the final section.
2 Torsion pairs and
 $\tau $
-tilting theory
$\tau $
-tilting theory
In this section, we recall necessary background on torsion pairs and
![]() $\tau $
-tilting theory. Throughout this article,
$\tau $
-tilting theory. Throughout this article,
![]() $\Lambda $
shall always denote a finite-dimensional basic algebra over a field K, and
$\Lambda $
shall always denote a finite-dimensional basic algebra over a field K, and
![]() $\mathsf {mod} \Lambda $
denotes the category of finitely generated left
$\mathsf {mod} \Lambda $
denotes the category of finitely generated left
![]() $\Lambda $
-modules. Furthermore, the Auslander–Reiten (AR) translate in
$\Lambda $
-modules. Furthermore, the Auslander–Reiten (AR) translate in
![]() $\mathsf {mod} \Lambda $
is denoted by
$\mathsf {mod} \Lambda $
is denoted by
![]() $\tau $
.
$\tau $
.
The study of
![]() $\tau $
-tilting theory has become instrumental in the study of finitely generated
$\tau $
-tilting theory has become instrumental in the study of finitely generated
![]() $\Lambda $
-modules since its inception in [Reference Adachi, Iyama and Reiten1]. We follow the notation of [Reference Buan and Marsh9], and denote
$\Lambda $
-modules since its inception in [Reference Adachi, Iyama and Reiten1]. We follow the notation of [Reference Buan and Marsh9], and denote
![]() $\mathcal C(\mathsf {mod}\Lambda ):= \mathsf {mod}\Lambda \sqcup \mathsf {mod}\Lambda [1] \subseteq \mathcal {D}^b(\mathsf {mod}\Lambda )$
, where
$\mathcal C(\mathsf {mod}\Lambda ):= \mathsf {mod}\Lambda \sqcup \mathsf {mod}\Lambda [1] \subseteq \mathcal {D}^b(\mathsf {mod}\Lambda )$
, where
![]() $\mathcal {D}^b(\mathsf {mod}\Lambda )$
denotes the bounded derived category of
$\mathcal {D}^b(\mathsf {mod}\Lambda )$
denotes the bounded derived category of
![]() $\Lambda $
. An (usually assumed basic) object
$\Lambda $
. An (usually assumed basic) object
![]() $U = M\sqcup P[1]\in \mathcal C(\mathsf {mod}\Lambda )$
is called a support
$U = M\sqcup P[1]\in \mathcal C(\mathsf {mod}\Lambda )$
is called a support
![]() $\tau $
-rigid pair if:
$\tau $
-rigid pair if:
-
1.
 $M \in \mathsf {mod}\Lambda $
satisfies
$M \in \mathsf {mod}\Lambda $
satisfies
 $\operatorname {{\mathrm {Hom}}}(M,\tau M) = 0$
.
$\operatorname {{\mathrm {Hom}}}(M,\tau M) = 0$
. -
2.
 $P \in \mathsf {mod}\Lambda $
is projective and satisfies
$P \in \mathsf {mod}\Lambda $
is projective and satisfies
 $\operatorname {{\mathrm {Hom}}}(P,M) = 0$
.
$\operatorname {{\mathrm {Hom}}}(P,M) = 0$
.
If U is basic, we denote by
![]() $\mathsf {rk}(U)$
the number of indecomposable direct summands of U (up to isomorphism). If
$\mathsf {rk}(U)$
the number of indecomposable direct summands of U (up to isomorphism). If
![]() $\mathsf {rk}(U) = \mathsf {rk}(\Lambda )$
, then U is called support
$\mathsf {rk}(U) = \mathsf {rk}(\Lambda )$
, then U is called support
![]() $\tau $
-tilting. When
$\tau $
-tilting. When
![]() $P = 0$
, the module
$P = 0$
, the module
![]() $U = M$
can be referred to as a
$U = M$
can be referred to as a
![]() $\tau $
-rigid (or
$\tau $
-rigid (or
![]() $\tau $
-tilting if it is sincere and
$\tau $
-tilting if it is sincere and
![]() $\mathsf {rk}(U) = \mathsf {rk}(\Lambda )$
) module.
$\mathsf {rk}(U) = \mathsf {rk}(\Lambda )$
) module.
By a subcategory of
![]() $\mathsf {mod}\Lambda $
, we shall always mean a full subcategory which is closed under isomorphisms. Given such a subcategory
$\mathsf {mod}\Lambda $
, we shall always mean a full subcategory which is closed under isomorphisms. Given such a subcategory
![]() $\mathcal {A}\subseteq \mathsf {mod}\Lambda $
, we denote by
$\mathcal {A}\subseteq \mathsf {mod}\Lambda $
, we denote by
![]() $\mathcal P(\mathcal {A})$
the category of modules which are ext-projective in
$\mathcal P(\mathcal {A})$
the category of modules which are ext-projective in
![]() $\mathcal {A}$
. That is,
$\mathcal {A}$
. That is,
![]() $Q \in \mathcal P(\mathcal {A})$
if and only if
$Q \in \mathcal P(\mathcal {A})$
if and only if
![]() $\operatorname {{\mathrm {Ext}}}^1(Q,X) = 0$
for all
$\operatorname {{\mathrm {Ext}}}^1(Q,X) = 0$
for all
![]() $X \in \mathcal {A}$
.
$X \in \mathcal {A}$
.
Moreover, given a subcategory
![]() $\mathcal {A}\subseteq \mathsf {mod}\Lambda $
, we denote by
$\mathcal {A}\subseteq \mathsf {mod}\Lambda $
, we denote by
![]() $\mathsf {Gen}(\mathcal {A})$
(resp.
$\mathsf {Gen}(\mathcal {A})$
(resp.
![]() $\mathsf {Cogen}(\mathcal {A})$
) the subcategory of
$\mathsf {Cogen}(\mathcal {A})$
) the subcategory of
![]() $\mathsf {mod}\Lambda $
consisting of objects which are factors (resp. subobjects) of direct sums of objects in
$\mathsf {mod}\Lambda $
consisting of objects which are factors (resp. subobjects) of direct sums of objects in
![]() $\mathcal {A}$
. We likewise denote by
$\mathcal {A}$
. We likewise denote by
![]() $\mathsf {Filt}(\mathcal {A})$
the subcategory of modules which admit finite filtrations whose subsequent subfactors all lie in
$\mathsf {Filt}(\mathcal {A})$
the subcategory of modules which admit finite filtrations whose subsequent subfactors all lie in
![]() $\mathcal {A}$
. Given a module
$\mathcal {A}$
. Given a module
![]() $X \in \mathsf {mod}\Lambda $
, we define
$X \in \mathsf {mod}\Lambda $
, we define
![]() $\mathsf {Gen} X:= \mathsf {Gen}(\mathsf {add} X)$
, and so forth, where
$\mathsf {Gen} X:= \mathsf {Gen}(\mathsf {add} X)$
, and so forth, where
![]() $\mathsf {add} X$
is the subcategory of direct summands of finite direct sums of X.
$\mathsf {add} X$
is the subcategory of direct summands of finite direct sums of X.
For any subcategory
![]() $\mathcal {A}\subseteq \mathsf {mod}\Lambda $
, we associate two additional subcategories:
$\mathcal {A}\subseteq \mathsf {mod}\Lambda $
, we associate two additional subcategories:

Given a module
![]() $X \in \mathsf {mod}\Lambda $
, we likewise have
$X \in \mathsf {mod}\Lambda $
, we likewise have
![]() $X^{\perp } = (\mathsf {add} X)^{\perp }$
and
$X^{\perp } = (\mathsf {add} X)^{\perp }$
and
.
Finally, we recall that a subcategory
![]() $\mathcal {A} \subseteq \mathsf {mod}\Lambda $
is called functorially finite if for all
$\mathcal {A} \subseteq \mathsf {mod}\Lambda $
is called functorially finite if for all
![]() $X \in \mathsf {mod}\Lambda $
:
$X \in \mathsf {mod}\Lambda $
:
-
1. There exists
 $A_X \in \mathcal {A}$
and
$A_X \in \mathcal {A}$
and
 $a_X:A_X\rightarrow X$
such that every morphism with source in
$a_X:A_X\rightarrow X$
such that every morphism with source in
 $\mathcal {A}$
and target X factors through
$\mathcal {A}$
and target X factors through
 $a_X$
. The morphism
$a_X$
. The morphism
 $a_X$
is called a right
$a_X$
is called a right
 $\mathcal {A}$
-approximation.
$\mathcal {A}$
-approximation. -
2. There exists
 $A^X \in \mathcal {A}$
and
$A^X \in \mathcal {A}$
and
 $a^X:X\rightarrow A^X$
such that every morphism with source X and target in
$a^X:X\rightarrow A^X$
such that every morphism with source X and target in
 $\mathcal {A}$
and target X factors through
$\mathcal {A}$
and target X factors through
 $a^X$
. The morphism
$a^X$
. The morphism
 $a^X$
is called a left
$a^X$
is called a left
 $\mathcal {A}$
-approximation.
$\mathcal {A}$
-approximation.
We are now ready to discuss torsion pairs. A torsion pair is a pair
![]() $({\mathcal T},{\mathcal F})$
of subcategories of
$({\mathcal T},{\mathcal F})$
of subcategories of
![]() $\mathsf {mod}\Lambda $
such that
$\mathsf {mod}\Lambda $
such that
![]() ${\mathcal T}^{\perp } = {\mathcal F}$
and
${\mathcal T}^{\perp } = {\mathcal F}$
and
![]() . In this case, we call
. In this case, we call
![]() ${\mathcal T}$
a torsion class and
${\mathcal T}$
a torsion class and
![]() ${\mathcal F}$
a torsion-free class. It is well known that a pair
${\mathcal F}$
a torsion-free class. It is well known that a pair
![]() $({\mathcal T},{\mathcal T}^{\perp })$
(resp.
$({\mathcal T},{\mathcal T}^{\perp })$
(resp.
![]() ) is a torsion pair if and only if
) is a torsion pair if and only if
![]() ${\mathcal T}$
is closed under extensions and quotients (resp.
${\mathcal T}$
is closed under extensions and quotients (resp.
![]() ${\mathcal F}$
is closed under extensions and subobjects). Moreover, given a torsion pair
${\mathcal F}$
is closed under extensions and subobjects). Moreover, given a torsion pair
![]() $({\mathcal T},{\mathcal F})$
, we have that
$({\mathcal T},{\mathcal F})$
, we have that
![]() ${\mathcal T}$
is functorially finite if and only if
${\mathcal T}$
is functorially finite if and only if
![]() ${\mathcal F}$
is functorially finite (see [Reference Smalø25]).
${\mathcal F}$
is functorially finite (see [Reference Smalø25]).
If
![]() $({\mathcal T},{\mathcal F})$
is a torsion pair, then every
$({\mathcal T},{\mathcal F})$
is a torsion pair, then every
![]() $M \in \mathsf {mod}\Lambda $
admits a unique exact sequence of the form
$M \in \mathsf {mod}\Lambda $
admits a unique exact sequence of the form
with
![]() $t_{\mathcal T}(M) \in {\mathcal T}$
and
$t_{\mathcal T}(M) \in {\mathcal T}$
and
![]() $f_{\mathcal F}(M) \in {\mathcal F}$
. In particular, the map
$f_{\mathcal F}(M) \in {\mathcal F}$
. In particular, the map
![]() $\iota $
is a minimal right
$\iota $
is a minimal right
![]() ${\mathcal T}$
-approximation and the map q is a minimal left
${\mathcal T}$
-approximation and the map q is a minimal left
![]() ${\mathcal F}$
-approximation. We note that the operations
${\mathcal F}$
-approximation. We note that the operations
![]() $t_{\mathcal T}(-)$
and
$t_{\mathcal T}(-)$
and
![]() $f_{{\mathcal F}}(-)$
are both functorial.
$f_{{\mathcal F}}(-)$
are both functorial.
We will need the following observation for our discussion of Example 4.9.
Lemma 2.1. Let
![]() ${\mathcal T}$
be a functorially finite torsion class, and let
${\mathcal T}$
be a functorially finite torsion class, and let
![]() ${\mathcal F}$
be a functorially finite torsion-free class. Then
${\mathcal F}$
be a functorially finite torsion-free class. Then
![]() ${\mathcal T}\cap {\mathcal F}$
is functorially finite.
${\mathcal T}\cap {\mathcal F}$
is functorially finite.
Proof. We will show only that left
![]() $({\mathcal T} \cap {\mathcal F})$
-approximations exist, as the argument for right approximations is analogous. Let
$({\mathcal T} \cap {\mathcal F})$
-approximations exist, as the argument for right approximations is analogous. Let
![]() $X \in \mathsf {mod}\Lambda $
. Let
$X \in \mathsf {mod}\Lambda $
. Let
![]() $t^X: X\rightarrow T^X$
be a left
$t^X: X\rightarrow T^X$
be a left
![]() ${\mathcal T}$
-approximation of
${\mathcal T}$
-approximation of
![]() $X,$
and let
$X,$
and let
![]() $f^X: T^X \rightarrow f_{\mathcal F}(T^X)$
be the left
$f^X: T^X \rightarrow f_{\mathcal F}(T^X)$
be the left
![]() ${\mathcal F}$
-approximation of
${\mathcal F}$
-approximation of
![]() $T^X$
coming from Equation (1). We note that
$T^X$
coming from Equation (1). We note that
![]() $f^X$
is surjective, and so
$f^X$
is surjective, and so
![]() $f_{\mathcal F}(T^X) \in {\mathcal T}\cap {\mathcal F}$
. It is then straightforward to show that
$f_{\mathcal F}(T^X) \in {\mathcal T}\cap {\mathcal F}$
. It is then straightforward to show that
![]() $f^X \circ t^X$
is a left
$f^X \circ t^X$
is a left
![]() $({\mathcal T}\cap {\mathcal F})$
-approximation of X.
$({\mathcal T}\cap {\mathcal F})$
-approximation of X.
We now turn our attention to the well-established relationship between torsion pairs and support
![]() $\tau $
-rigid objects.
$\tau $
-rigid objects.
Torsion pairs are closely related to support
![]() $\tau $
-rigid objects, as the following shows.
$\tau $
-rigid objects, as the following shows.
Theorem 2.2 [Reference Adachi, Iyama and Reiten1, Sect. 2.2 and 2.3].
Let
![]() $\Lambda $
be a finite-dimensional algebra. Then:
$\Lambda $
be a finite-dimensional algebra. Then:
-
1. If
 $U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
is support
$U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
is support
 $\tau $
-rigid, then both
$\tau $
-rigid, then both
 $\mathsf {Gen} M$
and
$\mathsf {Gen} M$
and
 are functorially finite torsion classes in
are functorially finite torsion classes in
 $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
. -
2. If
 $U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
is support
$U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
is support
 $\tau $
-tilting, then
$\tau $
-tilting, then
 . Moreover, this association gives a bijection between support
. Moreover, this association gives a bijection between support
 $\tau $
-tilting objects in
$\tau $
-tilting objects in
 $\mathcal C(\mathsf {mod}\Lambda )$
and functorially finite torsion classes of
$\mathcal C(\mathsf {mod}\Lambda )$
and functorially finite torsion classes of
 $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
. -
3. Let
 ${\mathcal T} \subseteq \mathsf {mod}\Lambda $
be a functorially finite torsion class, let
${\mathcal T} \subseteq \mathsf {mod}\Lambda $
be a functorially finite torsion class, let
 $M \in \mathsf {mod}\Lambda $
be basic such that
$M \in \mathsf {mod}\Lambda $
be basic such that
 $\mathsf {add} M = \mathcal P({\mathcal T})$
, and let
$\mathsf {add} M = \mathcal P({\mathcal T})$
, and let
 $P \in \mathcal P(\mathsf {mod}\Lambda )$
be the maximal basic projective module which satisfies
$P \in \mathcal P(\mathsf {mod}\Lambda )$
be the maximal basic projective module which satisfies
 $\operatorname {{\mathrm {Hom}}}(P,M) = 0$
. Then
$\operatorname {{\mathrm {Hom}}}(P,M) = 0$
. Then
 $M\sqcup P[1]$
is support
$M\sqcup P[1]$
is support
 $\tau $
-tilting and satisfies
$\tau $
-tilting and satisfies
 .
.
Before continuing, we recall the following characterization of Auslander and Smalø, which will be useful in several of our proofs.
Proposition 2.3 [Reference Auslander and Smalø4, Prop. 5.8].
Let
![]() $M, N \in \mathsf {mod}\Lambda $
. Then
$M, N \in \mathsf {mod}\Lambda $
. Then
![]() $\operatorname {{\mathrm {Hom}}}(N,\tau M) = 0$
if and only if
$\operatorname {{\mathrm {Hom}}}(N,\tau M) = 0$
if and only if
![]() $\operatorname {{\mathrm {Ext}}}^1(M,\mathsf {Gen} N) = 0$
.
$\operatorname {{\mathrm {Ext}}}^1(M,\mathsf {Gen} N) = 0$
.
It is implicit in Theorem 2.2 that any basic support
![]() $\tau $
-rigid object is the direct summand of at least one support
$\tau $
-rigid object is the direct summand of at least one support
![]() $\tau $
-tilting object. In particular, we have the following.
$\tau $
-tilting object. In particular, we have the following.
Theorem 2.4 [Reference Adachi, Iyama and Reiten1, Sec. 2.2].
Let
![]() $U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
be a basic support
$U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
be a basic support
![]() $\tau $
-rigid object. Then:
$\tau $
-rigid object. Then:
-
1. There exists a unique module
 $B_U \in \mathsf {mod}\Lambda $
such that
$B_U \in \mathsf {mod}\Lambda $
such that
 $B_U\sqcup U$
is support
$B_U\sqcup U$
is support
 $\tau $
-tilting and
$\tau $
-tilting and
 . In particular, this means
. In particular, this means 
-
2. There exists a unique object
 $C_U = N\sqcup Q[1] \in \mathcal C(\mathsf {mod}\Lambda )$
such that
$C_U = N\sqcup Q[1] \in \mathcal C(\mathsf {mod}\Lambda )$
such that
 $C_U\sqcup U$
is support
$C_U\sqcup U$
is support
 $\tau $
-tilting and
$\tau $
-tilting and
 $\mathsf {add}(N\sqcup M) = \mathcal P(\mathsf {Gen} M)$
. In particular, this means
$\mathsf {add}(N\sqcup M) = \mathcal P(\mathsf {Gen} M)$
. In particular, this means 
The module
![]() $B_U$
in Theorem 2.4 is called the Bongartz complement of U. Following, for example, [Reference Buan and Marsh10] and [Reference Demonet, Iyama, Reading, Reiten and Thomas11], we refer to
$B_U$
in Theorem 2.4 is called the Bongartz complement of U. Following, for example, [Reference Buan and Marsh10] and [Reference Demonet, Iyama, Reading, Reiten and Thomas11], we refer to
![]() $C_U$
in Theorem 2.4 as the co-Bongartz complement of U.
$C_U$
in Theorem 2.4 as the co-Bongartz complement of U.
Remark 2.5.
-
1. In [Reference Adachi, Iyama and Reiten1], the Bongartz complement is only explicitly defined when
 $P = 0$
(so
$P = 0$
(so
 $U = M$
is a
$U = M$
is a
 $\tau $
-rigid module). Nevertheless, the more general definition is often given the same attribution (see, e.g., [Reference Demonet, Iyama, Reading, Reiten and Thomas11, Sec. 4]).
$\tau $
-rigid module). Nevertheless, the more general definition is often given the same attribution (see, e.g., [Reference Demonet, Iyama, Reading, Reiten and Thomas11, Sec. 4]). -
2. If
 $P = 0$
, then
$P = 0$
, then
 $B_U\sqcup M$
is a sincere module. In general, we can instead see
$B_U\sqcup M$
is a sincere module. In general, we can instead see
 $B_U\sqcup M$
as a sincere object in the Serre subcategory
$B_U\sqcup M$
as a sincere object in the Serre subcategory
 $P^{\perp }$
. In this case, it is straightforward to show that M is
$P^{\perp }$
. In this case, it is straightforward to show that M is
 $\tau $
-rigid in
$\tau $
-rigid in
 $P^{\perp }$
and that the Bongartz complement of M in
$P^{\perp }$
and that the Bongartz complement of M in
 $P^{\perp }$
is precisely
$P^{\perp }$
is precisely
 $B_U$
(see [Reference Buan and Marsh9, Lem. 3.8]).
$B_U$
(see [Reference Buan and Marsh9, Lem. 3.8]).
We next recall two results which give us a “canonical decomposition” of a support
![]() $\tau $
-tilting pair. The first can be seen as a combination of [Reference Ingalls and Thomas20, Lem. 2.8] and [Reference Marks and Šťovíček23, Lem. 3.7]. We recall that a module X in a subcategory
$\tau $
-tilting pair. The first can be seen as a combination of [Reference Ingalls and Thomas20, Lem. 2.8] and [Reference Marks and Šťovíček23, Lem. 3.7]. We recall that a module X in a subcategory
![]() $\mathcal {A}\subseteq \mathsf {mod}\Lambda $
is called split projective (in
$\mathcal {A}\subseteq \mathsf {mod}\Lambda $
is called split projective (in
![]() $\mathcal {A}$
) if every epimorphism in
$\mathcal {A}$
) if every epimorphism in
![]() $\mathcal {A}$
with target X is split.
$\mathcal {A}$
with target X is split.
Lemma 2.6. Let
![]() ${\mathcal T} \subseteq \mathsf {mod}\Lambda $
be a functorially finite torsion class, and let
${\mathcal T} \subseteq \mathsf {mod}\Lambda $
be a functorially finite torsion class, and let
![]() $M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
be the support
$M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
be the support
![]() $\tau $
-tilting pair which satisfies
$\tau $
-tilting pair which satisfies
![]() $\mathcal P({\mathcal T}) = \mathsf {add} M$
. Then:
$\mathcal P({\mathcal T}) = \mathsf {add} M$
. Then:
-
1. There is a decomposition
 $M = M_s \sqcup M_{ns}$
such that
$M = M_s \sqcup M_{ns}$
such that
 $M_s$
is split projective in
$M_s$
is split projective in
 ${\mathcal T}$
and no direct summand of
${\mathcal T}$
and no direct summand of
 $M_{ns}$
is split projective in
$M_{ns}$
is split projective in
 ${\mathcal T}$
. In particular,
${\mathcal T}$
. In particular,
 ${\mathcal T} = \mathsf {Gen} M_s$
.
${\mathcal T} = \mathsf {Gen} M_s$
. -
2. Let
be an exact sequence such that g is a minimal left $$ \begin{align*}\Lambda \xrightarrow{g}T_0\rightarrow T_1\rightarrow 0\end{align*} $$
$$ \begin{align*}\Lambda \xrightarrow{g}T_0\rightarrow T_1\rightarrow 0\end{align*} $$
 ${\mathcal T}$
-approximation. Then
${\mathcal T}$
-approximation. Then
 $\mathsf {add} T_0 = \mathsf {add} M_s$
and
$\mathsf {add} T_0 = \mathsf {add} M_s$
and
 $\mathsf {add} T_1 = \mathsf {add} M_{ns}$
.
$\mathsf {add} T_1 = \mathsf {add} M_{ns}$
.
The second result relates the direct summands
![]() $M_s$
and
$M_s$
and
![]() $M_{ns}$
to Bongartz and co-Bongartz complements.
$M_{ns}$
to Bongartz and co-Bongartz complements.
Proposition 2.7. Consider the setup in Lemma 2.6. Then
![]() $M_s$
is the Bongartz complement of
$M_s$
is the Bongartz complement of
![]() $M_{ns}\sqcup P[1]$
and
$M_{ns}\sqcup P[1]$
and
![]() $M_{ns}\sqcup P[1]$
is the co-Bongartz complement of
$M_{ns}\sqcup P[1]$
is the co-Bongartz complement of
![]() $M_s$
. In particular, we have
$M_s$
. In particular, we have
Proof. It is shown in [Reference Demonet, Iyama, Reading, Reiten and Thomas11, Lem. 4.5] that
![]() $M_s$
is the Bongartz complement of
$M_s$
is the Bongartz complement of
![]() $M_{ns}\sqcup P[1]$
. Moreover, it is clear from Lemma 2.6 that
$M_{ns}\sqcup P[1]$
. Moreover, it is clear from Lemma 2.6 that
![]() $\mathsf {Gen} M_s = \mathsf {Gen} M$
. The result thus follows from Theorem 2.4.
$\mathsf {Gen} M_s = \mathsf {Gen} M$
. The result thus follows from Theorem 2.4.
We conclude this section with a brief description of the dual theory of
![]() $\tau ^{-1}$
-tilting. In order to state this in our context, given an indecomposable stalk complex
$\tau ^{-1}$
-tilting. In order to state this in our context, given an indecomposable stalk complex
![]() $M[m] \in \mathcal {D}^b(\mathsf {mod}\Lambda )$
with
$M[m] \in \mathcal {D}^b(\mathsf {mod}\Lambda )$
with
![]() $M \in \mathsf {mod}\Lambda $
, we denote
$M \in \mathsf {mod}\Lambda $
, we denote
 $$ \begin{align*}\overline{\tau}(M[m]) := \begin{cases} \tau M[m], & M \notin \mathcal P(\mathsf{mod}\Lambda),\\ \nu M[m-1], & M \in \mathcal P(\mathsf{mod}\Lambda),\end{cases}\end{align*} $$
$$ \begin{align*}\overline{\tau}(M[m]) := \begin{cases} \tau M[m], & M \notin \mathcal P(\mathsf{mod}\Lambda),\\ \nu M[m-1], & M \in \mathcal P(\mathsf{mod}\Lambda),\end{cases}\end{align*} $$
where
![]() $\nu $
denotes the Nakayama functor. We then say a (usually assumed basic) object
$\nu $
denotes the Nakayama functor. We then say a (usually assumed basic) object
![]() $U = I[-1]\sqcup M \in \mathcal C(\mathsf {mod}\Lambda )[-1]$
is support
$U = I[-1]\sqcup M \in \mathcal C(\mathsf {mod}\Lambda )[-1]$
is support
![]() $\tau ^{-1}$
-rigid if:
$\tau ^{-1}$
-rigid if:
-
1.
 $M \in \mathsf {mod}\Lambda $
and
$M \in \mathsf {mod}\Lambda $
and
 $\operatorname {{\mathrm {Hom}}}(\tau ^{-1} M, M) = 0$
.
$\operatorname {{\mathrm {Hom}}}(\tau ^{-1} M, M) = 0$
. -
2.
 $I \in \mathsf {mod}\Lambda $
is injective and
$I \in \mathsf {mod}\Lambda $
is injective and
 $\operatorname {{\mathrm {Hom}}}(M,I) = 0$
.
$\operatorname {{\mathrm {Hom}}}(M,I) = 0$
.
We likewise say U is
![]() $\tau ^{-1}$
-tilting if U is basic and
$\tau ^{-1}$
-tilting if U is basic and
![]() $\mathsf {rk}(U) = \mathsf {rk}(\Lambda )$
. It is shown in [Reference Adachi, Iyama and Reiten1, Sec. 2.2] that
$\mathsf {rk}(U) = \mathsf {rk}(\Lambda )$
. It is shown in [Reference Adachi, Iyama and Reiten1, Sec. 2.2] that
![]() $U \in \mathcal C(\mathsf {mod}\Lambda )[-1]$
is support
$U \in \mathcal C(\mathsf {mod}\Lambda )[-1]$
is support
![]() $\tau ^{-1}$
-rigid (resp. support
$\tau ^{-1}$
-rigid (resp. support
![]() $\tau ^{-1}$
-tilting) if and only if there exists some support
$\tau ^{-1}$
-tilting) if and only if there exists some support
![]() $\tau $
-rigid (resp. support
$\tau $
-rigid (resp. support
![]() $\tau $
-tilting)
$\tau $
-tilting)
![]() $V \in \mathcal C(\mathsf {mod}\Lambda )$
such that
$V \in \mathcal C(\mathsf {mod}\Lambda )$
such that
![]() $U = \overline {\tau }V$
.
$U = \overline {\tau }V$
.
3 Wide subcategories
In this section, we recall the definition and basic properties of wide subcategories and discuss important classes of examples of functorially finite wide subcategories:
![]() $\tau $
-perpendicular subcategories, left-/right-finite wide subcategories, and Serre subcategories.
$\tau $
-perpendicular subcategories, left-/right-finite wide subcategories, and Serre subcategories.
Recall that wide subcategories are exactly embedded abelian subcategories, and that a subcategory
![]() ${\mathcal W}\subseteq \mathsf {mod}\Lambda $
is wide if and only if it is closed under extensions, kernels, and cokernels. It is well known that a wide subcategory
${\mathcal W}\subseteq \mathsf {mod}\Lambda $
is wide if and only if it is closed under extensions, kernels, and cokernels. It is well known that a wide subcategory
![]() ${\mathcal W}\subseteq \mathsf {mod}\Lambda $
is functorially finite if and only if it is equivalent to
${\mathcal W}\subseteq \mathsf {mod}\Lambda $
is functorially finite if and only if it is equivalent to
![]() $\mathsf {mod}\Lambda _{\mathcal W}$
for some basic finite-dimensional algebra
$\mathsf {mod}\Lambda _{\mathcal W}$
for some basic finite-dimensional algebra
![]() $\Lambda _{\mathcal W}. $
(This is made explicit in [Reference Enomoto12, Prop. 4.12].) Given such a wide subcategory, we denote by
$\Lambda _{\mathcal W}. $
(This is made explicit in [Reference Enomoto12, Prop. 4.12].) Given such a wide subcategory, we denote by
![]() $\mathsf {rk}({\mathcal W})$
the number of simple objects in
$\mathsf {rk}({\mathcal W})$
the number of simple objects in
![]() ${\mathcal W}$
(or equivalently simple modules in
${\mathcal W}$
(or equivalently simple modules in
![]() $\mathsf {mod}\Lambda _{\mathcal W}$
) up to isomorphism. We note that if
$\mathsf {mod}\Lambda _{\mathcal W}$
) up to isomorphism. We note that if
![]() $P \in {\mathcal W}$
is basic and
$P \in {\mathcal W}$
is basic and
![]() $\mathcal P({\mathcal W}) = \mathsf {add}(P)$
, then
$\mathcal P({\mathcal W}) = \mathsf {add}(P)$
, then
![]() $\mathsf {rk}({\mathcal W}) = \mathsf {rk}(P)$
. In particular,
$\mathsf {rk}({\mathcal W}) = \mathsf {rk}(P)$
. In particular,
![]() $\mathsf {rk}(\Lambda ) = \mathsf {rk}(\mathsf {mod}\Lambda )$
.
$\mathsf {rk}(\Lambda ) = \mathsf {rk}(\mathsf {mod}\Lambda )$
.
As wide subcategories are abelian categories in their own right, they have their own wide subcategories, torsion classes, and torsion-free classes. We will be concerned with such subcategories in the sequel, and so the following well-known and easily proved fact is useful.
Proposition 3.1. Let
![]() ${\mathcal W}\subseteq \mathsf {mod}\Lambda $
be a wide subcategory.
${\mathcal W}\subseteq \mathsf {mod}\Lambda $
be a wide subcategory.
-
1. Suppose that
 ${\mathcal W}$
is functorially finite, and let
${\mathcal W}$
is functorially finite, and let
 $\mathcal {A}\subseteq {\mathcal W}$
be a functorially finite subcategory of
$\mathcal {A}\subseteq {\mathcal W}$
be a functorially finite subcategory of
 ${\mathcal W}$
. Then
${\mathcal W}$
. Then
 $\mathcal {A}$
is a functorially finite subcategory of
$\mathcal {A}$
is a functorially finite subcategory of
 $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
. -
2. Let
 $\mathcal {V}$
be a wide subcategory of
$\mathcal {V}$
be a wide subcategory of
 ${\mathcal W}$
. Then
${\mathcal W}$
. Then
 $\mathcal {V}$
is a wide subcategory of
$\mathcal {V}$
is a wide subcategory of
 $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
.
We are now ready to define our main categories of interest.
Definition 3.2. A full subcategory
![]() ${\mathcal W} \subseteq \mathsf {mod}\Lambda $
is called a
${\mathcal W} \subseteq \mathsf {mod}\Lambda $
is called a
![]() $\tau $
-perpendicular subcategory if there exists a support
$\tau $
-perpendicular subcategory if there exists a support
![]() $\tau $
-rigid object
$\tau $
-rigid object
![]() $U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
such that
$U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
such that
![]() ${\mathcal W} = \mathcal J(U)$
, where
${\mathcal W} = \mathcal J(U)$
, where
Such categories were first considered by Jasso [Reference Jasso22], who proved that they are equivalent to module categories, and hence, they are functorially finite. Actually, Jasso explicitly dealt with the case
![]() $P=0$
, but his proofs and statements can be easily modified. This is mentioned explicitly in [Reference Demonet, Iyama, Reading, Reiten and Thomas11], where it is also shown that such categories are in fact wide. Summarizing, we have the following.
$P=0$
, but his proofs and statements can be easily modified. This is mentioned explicitly in [Reference Demonet, Iyama, Reading, Reiten and Thomas11], where it is also shown that such categories are in fact wide. Summarizing, we have the following.
Theorem 3.3 [Reference Demonet, Iyama, Reading, Reiten and Thomas11, Th. 4.12 and 4.16], [Reference Jasso22, Th. 3.8].
Let
![]() $U = M\sqcup P[1]\in \mathcal C(\mathsf {mod}\Lambda )$
be support
$U = M\sqcup P[1]\in \mathcal C(\mathsf {mod}\Lambda )$
be support
![]() $\tau $
-rigid. Then
$\tau $
-rigid. Then
![]() $\mathcal J(U)$
is a functorially finite wide subcategory of
$\mathcal J(U)$
is a functorially finite wide subcategory of
![]() $\mathsf {mod}\Lambda $
. Moreover, if
$\mathsf {mod}\Lambda $
. Moreover, if
![]() $M\sqcup P[1]$
is basic, then
$M\sqcup P[1]$
is basic, then
![]() $\mathsf {rk}(\mathcal J(U)) + \mathsf {rk}(M) + \mathsf {rk}(P) = \mathsf {rk}(\Lambda )$
.
$\mathsf {rk}(\mathcal J(U)) + \mathsf {rk}(M) + \mathsf {rk}(P) = \mathsf {rk}(\Lambda )$
.
By identifying a
![]() $\tau $
-perpendicular subcategory
$\tau $
-perpendicular subcategory
![]() ${\mathcal W} = \mathcal J(U)$
with a module category, one can consider the
${\mathcal W} = \mathcal J(U)$
with a module category, one can consider the
![]() $\tau $
-tilting theory of
$\tau $
-tilting theory of
![]() ${\mathcal W}$
. That is, we consider the category
${\mathcal W}$
. That is, we consider the category
![]() $\mathcal C({\mathcal W}) := {\mathcal W}\sqcup {\mathcal W}[1] \subseteq \mathcal C(\mathsf {mod}\Lambda )$
. We then say an object
$\mathcal C({\mathcal W}) := {\mathcal W}\sqcup {\mathcal W}[1] \subseteq \mathcal C(\mathsf {mod}\Lambda )$
. We then say an object
![]() $N\sqcup Q[1] \in \mathcal C({\mathcal W})$
is support
$N\sqcup Q[1] \in \mathcal C({\mathcal W})$
is support
![]() $\tau $
-rigid in
$\tau $
-rigid in
![]() ${\mathcal W}$
if:
${\mathcal W}$
if:
-
1.
 $N \in {\mathcal W}$
satisfies
$N \in {\mathcal W}$
satisfies
 $\operatorname {{\mathrm {Hom}}}(N,\tau _{\mathcal W} N) = 0$
, where
$\operatorname {{\mathrm {Hom}}}(N,\tau _{\mathcal W} N) = 0$
, where
 $\tau _W$
denotes the AR translate in
$\tau _W$
denotes the AR translate in
 ${\mathcal W}$
.
${\mathcal W}$
. -
2.
 $Q \in {\mathcal W}$
is projective in
$Q \in {\mathcal W}$
is projective in
 ${\mathcal W}$
and satisfies
${\mathcal W}$
and satisfies
 $\operatorname {{\mathrm {Hom}}}(Q,N) = 0$
.
$\operatorname {{\mathrm {Hom}}}(Q,N) = 0$
.
We emphasize that, in general, objects which are projective in
![]() ${\mathcal W}$
may not be projective in
${\mathcal W}$
may not be projective in
![]() $\mathsf {mod}\Lambda $
. Likewise, we may have that
$\mathsf {mod}\Lambda $
. Likewise, we may have that
![]() $\tau _{\mathcal W} N \not \cong \tau N$
, so in general, we can have modules which are not
$\tau _{\mathcal W} N \not \cong \tau N$
, so in general, we can have modules which are not
![]() $\tau $
-rigid in
$\tau $
-rigid in
![]() $\mathsf {mod} \Lambda $
, but still are
$\mathsf {mod} \Lambda $
, but still are
![]() $\tau $
-rigid in
$\tau $
-rigid in
![]() ${\mathcal W}$
. However, it is a direct consequence of Proposition 2.3 and the fact that
${\mathcal W}$
. However, it is a direct consequence of Proposition 2.3 and the fact that
![]() ${\mathcal W}$
is an exactly embedded subcategory that
${\mathcal W}$
is an exactly embedded subcategory that
![]() $\tau $
-rigid (or projective) objects in
$\tau $
-rigid (or projective) objects in
![]() $\mathsf {mod} \Lambda $
remain
$\mathsf {mod} \Lambda $
remain
![]() $\tau $
-rigid (or projective) in
$\tau $
-rigid (or projective) in
![]() ${\mathcal W}$
.
${\mathcal W}$
.
Note also that since
![]() ${\mathcal W}$
is an exact subcategory of
${\mathcal W}$
is an exact subcategory of
![]() $\mathsf {mod} \Lambda $
, the category
$\mathsf {mod} \Lambda $
, the category
![]() $\mathcal C({\mathcal W})$
can be considered as sitting either inside
$\mathcal C({\mathcal W})$
can be considered as sitting either inside
![]() $\mathcal C(\mathsf {mod}\Lambda ) \subseteq \mathcal {D}^b(\mathsf {mod}\Lambda )$
(as we have defined it) or inside of
$\mathcal C(\mathsf {mod}\Lambda ) \subseteq \mathcal {D}^b(\mathsf {mod}\Lambda )$
(as we have defined it) or inside of
![]() $\mathcal {D}^b({\mathcal W})$
. Indeed, for
$\mathcal {D}^b({\mathcal W})$
. Indeed, for
![]() $X, Y \in {\mathcal W}$
, we have a canonical isomorphism
$X, Y \in {\mathcal W}$
, we have a canonical isomorphism
Continuing in this way, if
![]() $V = N\sqcup Q[1]$
is
$V = N\sqcup Q[1]$
is
![]() $\tau $
-rigid in
$\tau $
-rigid in
![]() ${\mathcal W}$
, we denote
${\mathcal W}$
, we denote
We also have the following dual concept.
Definition 3.4. A subcategory
![]() ${\mathcal W} \subseteq \mathsf {mod}\Lambda $
is called a
${\mathcal W} \subseteq \mathsf {mod}\Lambda $
is called a
![]() $\tau ^{-1}$
-perpendicular subcategory if there exists a support
$\tau ^{-1}$
-perpendicular subcategory if there exists a support
![]() $\tau ^{-1}$
-rigid object
$\tau ^{-1}$
-rigid object
![]() $U = I[-1]\sqcup M \in \mathcal C(\mathsf {mod}\Lambda )[-1]$
such that
$U = I[-1]\sqcup M \in \mathcal C(\mathsf {mod}\Lambda )[-1]$
such that
We show as part of Theorem 1.1 that
![]() $\tau ^{-1}$
-perpendicular subcategories and
$\tau ^{-1}$
-perpendicular subcategories and
![]() $\tau $
-perpendic- ular subcategories coincide. Moreover, it will be a consequence of Theorem 1.1 that not all functorially finite wide subcategories are
$\tau $
-perpendic- ular subcategories coincide. Moreover, it will be a consequence of Theorem 1.1 that not all functorially finite wide subcategories are
![]() $\tau $
-perpendicular subcategories (see Example 4.9).
$\tau $
-perpendicular subcategories (see Example 4.9).
We proceed to discuss another central class of functorially finite wide subcategories. These arise from applying the so-called Ingalls–Thomas bijections [Reference Ingalls and Thomas20, Reference Marks and Šťovíček23] to functorially finite torsion classes and torsion-free classes. We recall these constructions now.
Definition 3.5.
-
1. Let
 ${\mathcal T}\subseteq \mathsf {mod}\Lambda $
be a torsion class. The left-wide subcategory of
${\mathcal T}\subseteq \mathsf {mod}\Lambda $
be a torsion class. The left-wide subcategory of
 $\mathsf {mod}\Lambda $
corresponding to
$\mathsf {mod}\Lambda $
corresponding to
 ${\mathcal T}$
is
${\mathcal T}$
is  $$ \begin{align*} {\mathcal W}_L({\mathcal T}) := \{X \in {\mathcal T} \mid (Y\in{\mathcal T},f:Y\rightarrow X)\implies \ker f \in {\mathcal T}\}. \end{align*} $$
$$ \begin{align*} {\mathcal W}_L({\mathcal T}) := \{X \in {\mathcal T} \mid (Y\in{\mathcal T},f:Y\rightarrow X)\implies \ker f \in {\mathcal T}\}. \end{align*} $$
-
2. Let
 ${\mathcal F}\subseteq \mathsf {mod}\Lambda $
be a torsion-free class. The right-wide subcategory of
${\mathcal F}\subseteq \mathsf {mod}\Lambda $
be a torsion-free class. The right-wide subcategory of
 $\mathsf {mod}\Lambda $
corresponding to
$\mathsf {mod}\Lambda $
corresponding to
 ${\mathcal F}$
is
${\mathcal F}$
is  $$ \begin{align*}{\mathcal W}_R({\mathcal F}) := \{X \in {\mathcal F} \mid (Y\in{\mathcal F},f:X\rightarrow Y)\implies \operatorname{{\mathrm{coker}}} f \in {\mathcal F}\}.\end{align*} $$
$$ \begin{align*}{\mathcal W}_R({\mathcal F}) := \{X \in {\mathcal F} \mid (Y\in{\mathcal F},f:X\rightarrow Y)\implies \operatorname{{\mathrm{coker}}} f \in {\mathcal F}\}.\end{align*} $$
One of the key results of [Reference Ingalls and Thomas20] (hereditary case) and [Reference Marks and Šťovíček23] (general case) is that for any wide subcategory
![]() ${\mathcal W}$
, one has
${\mathcal W}$
, one has
They also show that
![]() $\mathsf {Filt}\mathsf {Gen}(W_L({\mathcal T})) = {\mathcal T}$
(resp.
$\mathsf {Filt}\mathsf {Gen}(W_L({\mathcal T})) = {\mathcal T}$
(resp.
![]() $\mathsf {Filt}\mathsf {Cogen}{\mathcal W}_R({\mathcal F}) ={\mathcal F}$
), when
$\mathsf {Filt}\mathsf {Cogen}{\mathcal W}_R({\mathcal F}) ={\mathcal F}$
), when
![]() ${\mathcal T}$
(resp.
${\mathcal T}$
(resp.
![]() ${\mathcal F}$
) is functorially finite. Following Asai [Reference Asai2], a wide subcategory
${\mathcal F}$
) is functorially finite. Following Asai [Reference Asai2], a wide subcategory
![]() ${\mathcal W} \subseteq \mathsf {mod}\Lambda $
is called left finite (resp. right finite) if it is of the form
${\mathcal W} \subseteq \mathsf {mod}\Lambda $
is called left finite (resp. right finite) if it is of the form
![]() ${\mathcal W}_L({\mathcal T})$
(resp.
${\mathcal W}_L({\mathcal T})$
(resp.
![]() ${\mathcal W}_R({\mathcal F})$
) for some functorially finite torsion class
${\mathcal W}_R({\mathcal F})$
) for some functorially finite torsion class
![]() ${\mathcal T}$
(resp. torsion-free class
${\mathcal T}$
(resp. torsion-free class
![]() ${\mathcal F}$
). It is straightforward that if
${\mathcal F}$
). It is straightforward that if
![]() ${\mathcal W}$
is either left finite or right finite, then it is functorially finite. The converse, however, does not hold in general (see [Reference Asai2, Exam. 3.13] or Example 4.9).
${\mathcal W}$
is either left finite or right finite, then it is functorially finite. The converse, however, does not hold in general (see [Reference Asai2, Exam. 3.13] or Example 4.9).
We conclude this section by discussing a well understood class of functorially finite wide subcategories, namely, the Serre subcategories. A subcategory
![]() $\mathcal {S}$
is Serre if for any short exact sequence
$\mathcal {S}$
is Serre if for any short exact sequence
in
![]() $\mathsf {mod}\Lambda $
, we have
$\mathsf {mod}\Lambda $
, we have
![]() $Y \in \mathcal {S}$
if and only if
$Y \in \mathcal {S}$
if and only if
![]() $X,Z \in \mathcal {S}$
. That is,
$X,Z \in \mathcal {S}$
. That is,
![]() $\mathcal {S}$
is closed under extensions, quotients, and subobjects.
$\mathcal {S}$
is closed under extensions, quotients, and subobjects.
Serre subcategories are indeed examples of wide subcategories. In fact, they are also both torsion classes and torsion-free classes, as the following shows.
Proposition 3.6. Let
![]() $\mathcal {S} \subseteq \mathsf {mod}\Lambda $
be a subcategory. Then the following are equivalent:
$\mathcal {S} \subseteq \mathsf {mod}\Lambda $
be a subcategory. Then the following are equivalent:
-
1.
 $\mathcal {S}$
is a Serre subcategory.
$\mathcal {S}$
is a Serre subcategory. -
2.
 $\mathcal {S}$
is any two of a torsion class, a torsion-free class, and a wide subcategory.
$\mathcal {S}$
is any two of a torsion class, a torsion-free class, and a wide subcategory. -
3.
 $\mathcal {S}$
is a torsion class, a torsion-free class, and a wide subcategory.
$\mathcal {S}$
is a torsion class, a torsion-free class, and a wide subcategory. -
4.
 $\mathcal {S} = P^{\perp }$
for some projective
$\mathcal {S} = P^{\perp }$
for some projective
 $P \in \mathcal P(\mathsf {mod}\Lambda )$
.
$P \in \mathcal P(\mathsf {mod}\Lambda )$
. -
5.
 $\mathcal {S}$
is a wide subcategory and every object which is simple in
$\mathcal {S}$
is a wide subcategory and every object which is simple in
 $\mathcal {S}$
is simple in
$\mathcal {S}$
is simple in
 $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
.
Proof. The equivalence of (1), (4), and (5) is contained in [Reference Geigle and Lenzing13, Prop. 5.3], and the equivalence of (1)–(3) follows straightforwardly from the definitions.
As useful consequences, we obtain the following corollaries.
Corollary 3.7. There is a bijection between isomorphism classes of basic projective modules in
![]() $\mathcal P(\mathsf {mod}\Lambda )$
and Serre subcategories of
$\mathcal P(\mathsf {mod}\Lambda )$
and Serre subcategories of
![]() $\mathsf {mod}\Lambda $
given by
$\mathsf {mod}\Lambda $
given by
![]() $P\mapsto P^{\perp }$
.
$P\mapsto P^{\perp }$
.
Corollary 3.8. Let
![]() $\mathcal {S}\subseteq \mathsf {mod}\Lambda $
be a Serre subcategory. Then
$\mathcal {S}\subseteq \mathsf {mod}\Lambda $
be a Serre subcategory. Then
![]() $\mathcal {S}$
is both a left-finite wide subcategory and a right-finite wide subcategory.
$\mathcal {S}$
is both a left-finite wide subcategory and a right-finite wide subcategory.
4 Characterizing
 $\tau $
-perpendicular subcategories
$\tau $
-perpendicular subcategories
In this section, we give the proof of Theorem 1.1, restated as Theorem 4.5. This characterizes
![]() $\tau $
-perpendicular subcategories as precisely the Serre subcategories of left-finite and right-finite wide subcategories of
$\tau $
-perpendicular subcategories as precisely the Serre subcategories of left-finite and right-finite wide subcategories of
![]() $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
.
The following technical result will be useful for the proof.
Proposition 4.1 [Reference Barnard, Todorov and Zhu6, Prop. 5.2.1].
Let
![]() $({\mathcal T},{\mathcal F})$
be a torsion pair in
$({\mathcal T},{\mathcal F})$
be a torsion pair in
![]() $\mathsf {mod}\Lambda ,$
and let
$\mathsf {mod}\Lambda ,$
and let
![]() $X \in {\mathcal W}_R({\mathcal F})$
. Then X is simple in
$X \in {\mathcal W}_R({\mathcal F})$
. Then X is simple in
![]() ${\mathcal W}_R({\mathcal F})$
if and only if the following hold:
${\mathcal W}_R({\mathcal F})$
if and only if the following hold:
-
1. Every proper factor of X lies in
 ${\mathcal T}$
.
${\mathcal T}$
. -
2. If
 $0\rightarrow X \rightarrow Y\rightarrow Z\rightarrow 0$
is a nonsplit exact sequence and
$0\rightarrow X \rightarrow Y\rightarrow Z\rightarrow 0$
is a nonsplit exact sequence and
 $Z \in {\mathcal T}$
, then
$Z \in {\mathcal T}$
, then
 $Y \in {\mathcal T}$
.
$Y \in {\mathcal T}$
. -
3.
 $X \in {\mathcal F}$
.
$X \in {\mathcal F}$
.
Remark 4.2.
-
1. Our statement of Proposition 4.1 is actually the dual of [Reference Barnard, Todorov and Zhu6, Prop. 5.2.1].
-
2. The simple objects of
 ${\mathcal W}_R({\mathcal F})$
are given an alternative characterization in terms of 2-term simple-minded collections in [Reference Asai2]. The characterization in [Reference Barnard, Todorov and Zhu6], on the other hand, shows that the simple objects of
${\mathcal W}_R({\mathcal F})$
are given an alternative characterization in terms of 2-term simple-minded collections in [Reference Asai2]. The characterization in [Reference Barnard, Todorov and Zhu6], on the other hand, shows that the simple objects of
 ${\mathcal W}_R({\mathcal F})$
are precisely the “minimal extending modules” for the torsion class
${\mathcal W}_R({\mathcal F})$
are precisely the “minimal extending modules” for the torsion class
 ${\mathcal T}$
, introduced in [Reference Barnard, Carroll and Zhu5].
${\mathcal T}$
, introduced in [Reference Barnard, Carroll and Zhu5].
We now start building toward our proof of Theorem 1.1 with the following lemmas.
Lemma 4.3. Let
![]() $({\mathcal T},{\mathcal F})$
be a functorially finite torsion pair, and let
$({\mathcal T},{\mathcal F})$
be a functorially finite torsion pair, and let
![]() $M\sqcup P[1]$
be the support
$M\sqcup P[1]$
be the support
![]() $\tau $
-tilting object in
$\tau $
-tilting object in
![]() $\mathcal C(\mathsf {mod}\Lambda )$
for which
$\mathcal C(\mathsf {mod}\Lambda )$
for which
![]() $\mathsf {add}(M) = \mathcal P({\mathcal T})$
. Write
$\mathsf {add}(M) = \mathcal P({\mathcal T})$
. Write
![]() $M \cong M_s\sqcup M_{ns}$
as in Lemma 2.6. Then:
$M \cong M_s\sqcup M_{ns}$
as in Lemma 2.6. Then:
-
1.
 ${\mathcal W}_L({\mathcal T}) = \mathcal J(M_{ns}\sqcup P[1])$
.
${\mathcal W}_L({\mathcal T}) = \mathcal J(M_{ns}\sqcup P[1])$
. -
2.
 ${\mathcal W}_R({\mathcal F}) = \mathcal J(M_s)$
.
${\mathcal W}_R({\mathcal F}) = \mathcal J(M_s)$
.
In particular, any wide subcategory of
![]() $\mathsf {mod}\Lambda $
which is either left finite or right finite is also a
$\mathsf {mod}\Lambda $
which is either left finite or right finite is also a
![]() $\tau $
-perpendicular subcategory.
$\tau $
-perpendicular subcategory.
We note that (1) also appears as [Reference Yurikusa26, Eq. 1.2].
Proof. (1) It is shown in [Reference Marks and Šťovíček23, Lem. 3.8] that
![]() . Moreover, by Proposition 2.7, we have that
. Moreover, by Proposition 2.7, we have that
![]() . This proves the result.
. This proves the result.
(2) First, let X be a simple object of
![]() ${\mathcal W}_R({\mathcal F})$
. (Note that X is not necessarily simple in
${\mathcal W}_R({\mathcal F})$
. (Note that X is not necessarily simple in
![]() $\mathsf {mod}\Lambda $
.) We will show that
$\mathsf {mod}\Lambda $
.) We will show that
![]() $X \in \mathcal J(M_s)$
. Since
$X \in \mathcal J(M_s)$
. Since
![]() $\mathcal J(M_s)$
is closed under extensions, this will imply that
$\mathcal J(M_s)$
is closed under extensions, this will imply that
![]() ${\mathcal W}_R({\mathcal F}) \subseteq \mathcal J(M_s)$
.
${\mathcal W}_R({\mathcal F}) \subseteq \mathcal J(M_s)$
.
We first note that
![]() ${\mathcal W}_R({\mathcal F}) \subseteq {\mathcal F} = M_s^{\perp }$
, so we need only show that
${\mathcal W}_R({\mathcal F}) \subseteq {\mathcal F} = M_s^{\perp }$
, so we need only show that
![]() $\operatorname {{\mathrm {Hom}}}(X,\tau M_s) = 0$
. Suppose to the contrary that
$\operatorname {{\mathrm {Hom}}}(X,\tau M_s) = 0$
. Suppose to the contrary that
![]() $\operatorname {{\mathrm {Hom}}}(X,\tau M_s) \neq 0$
. By Proposition 2.3, this means there exists
$\operatorname {{\mathrm {Hom}}}(X,\tau M_s) \neq 0$
. By Proposition 2.3, this means there exists
![]() $X' \in \mathsf {Gen} X$
and a nonsplit exact sequence of the form
$X' \in \mathsf {Gen} X$
and a nonsplit exact sequence of the form
By Proposition 4.1, we note that
![]() $X'$
cannot be a proper quotient of X. Indeed, if this were the case, we would have
$X'$
cannot be a proper quotient of X. Indeed, if this were the case, we would have
![]() , a contradiction. Therefore, we can assume that
, a contradiction. Therefore, we can assume that
![]() $X' = X$
. Applying Proposition 4.1 again, this implies that
$X' = X$
. Applying Proposition 4.1 again, this implies that
![]() $E \in {\mathcal T}$
. Since
$E \in {\mathcal T}$
. Since
![]() $M_s$
is split projective in
$M_s$
is split projective in
![]() ${\mathcal T}$
, this is a contradiction.
${\mathcal T}$
, this is a contradiction.
Now, let
![]() $Y \in \mathcal J(M_s)$
. It is clear that
$Y \in \mathcal J(M_s)$
. It is clear that
![]() $Y \in {\mathcal F} = M_s^{\perp }$
. Thus, let
$Y \in {\mathcal F} = M_s^{\perp }$
. Thus, let
![]() $Z \in {\mathcal F} = M_s^{\perp }$
and
$Z \in {\mathcal F} = M_s^{\perp }$
and
![]() $g:Y\rightarrow Z$
. We then have an exact sequence
$g:Y\rightarrow Z$
. We then have an exact sequence
where the last term is zero by Proposition 2.3 and the fact that
![]() $\operatorname {{\mathrm {image}}} g$
is a quotient of Y. We conclude that
$\operatorname {{\mathrm {image}}} g$
is a quotient of Y. We conclude that
![]() $\operatorname {{\mathrm {coker}}} g \in {\mathcal F}$
, and therefore,
$\operatorname {{\mathrm {coker}}} g \in {\mathcal F}$
, and therefore,
![]() $Y \in {\mathcal W}_R({\mathcal F})$
. This completes the proof.
$Y \in {\mathcal W}_R({\mathcal F})$
. This completes the proof.
Lemma 4.4. Let
![]() $\mathcal V \subseteq {\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a chain of subcategories such that
$\mathcal V \subseteq {\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a chain of subcategories such that
![]() $\mathcal V$
is a Serre subcategory of
$\mathcal V$
is a Serre subcategory of
![]() ${\mathcal W}$
and
${\mathcal W}$
and
![]() ${\mathcal W}$
is a
${\mathcal W}$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
. Then
$\mathsf {mod}\Lambda $
. Then
![]() $\mathcal V$
is a
$\mathcal V$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
.
Proof. Let
![]() $U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
be support
$U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
be support
![]() $\tau $
-rigid, and let
$\tau $
-rigid, and let
![]() $\mathcal {S}$
be a Serre subcategory of
$\mathcal {S}$
be a Serre subcategory of
![]() $\mathcal J(U)$
. By Proposition 3.6, there exists
$\mathcal J(U)$
. By Proposition 3.6, there exists
![]() $Q \in \mathcal P(\mathcal J(U))$
so that
$Q \in \mathcal P(\mathcal J(U))$
so that
![]() $\mathcal {S} = Q^{\perp } \cap \mathcal J(U)$
. It follows from [Reference Jasso22, Prop. 3.14] and Theorem 2.2 that
$\mathcal {S} = Q^{\perp } \cap \mathcal J(U)$
. It follows from [Reference Jasso22, Prop. 3.14] and Theorem 2.2 that
![]() $Q = f_{M^{\perp }}(B)$
for some direct summand B of the Bongartz complement
$Q = f_{M^{\perp }}(B)$
for some direct summand B of the Bongartz complement
![]() $B_U$
of U. We then have an exact sequence
$B_U$
of U. We then have an exact sequence
and since
![]() $t_{\mathsf {Gen} M}(B)$
is in
$t_{\mathsf {Gen} M}(B)$
is in
![]() $\mathsf {Gen} M$
, we have
$\mathsf {Gen} M$
, we have
![]() $\operatorname {{\mathrm {Hom}}}(t_{\mathsf {Gen} M}(B), \mathcal J(U)) = 0$
. Hence, we have
$\operatorname {{\mathrm {Hom}}}(t_{\mathsf {Gen} M}(B), \mathcal J(U)) = 0$
. Hence, we have
![]() $\mathcal {S} = Q^{\perp } \cap \mathcal J(U) = B^{\perp } \cap \mathcal J(U) = \mathcal J(B\sqcup U)$
, and so
$\mathcal {S} = Q^{\perp } \cap \mathcal J(U) = B^{\perp } \cap \mathcal J(U) = \mathcal J(B\sqcup U)$
, and so
![]() $\mathcal {S}$
is a
$\mathcal {S}$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
.
We are now ready to prove our first main result.
Theorem 4.5 (Theorem 1.1).
Let
![]() $\Lambda $
be a finite-dimensional algebra, and let
$\Lambda $
be a finite-dimensional algebra, and let
![]() ${\mathcal W}\subseteq \mathsf {mod}\Lambda $
be a wide subcategory. Then the following are equivalent.
${\mathcal W}\subseteq \mathsf {mod}\Lambda $
be a wide subcategory. Then the following are equivalent.
-
1.
 ${\mathcal W}$
is a
${\mathcal W}$
is a
 $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
 $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
. -
2.
 ${\mathcal W}$
is a
${\mathcal W}$
is a
 $\tau ^{-1}$
-perpendicular subcategory of
$\tau ^{-1}$
-perpendicular subcategory of
 $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
. -
3.
 ${\mathcal W}$
is a Serre subcategory of a left-finite wide subcategory.
${\mathcal W}$
is a Serre subcategory of a left-finite wide subcategory. -
4.
 ${\mathcal W}$
is a Serre subcategory of a right-finite wide subcategory.
${\mathcal W}$
is a Serre subcategory of a right-finite wide subcategory. -
5. There exists a functorially finite torsion class
 ${\mathcal T}\subseteq \mathsf {mod}\Lambda $
and a functorially finite torsion-free class
${\mathcal T}\subseteq \mathsf {mod}\Lambda $
and a functorially finite torsion-free class
 ${\mathcal F}\subseteq \mathsf {mod}\Lambda $
with
${\mathcal F}\subseteq \mathsf {mod}\Lambda $
with
 ${\mathcal T}^{\perp } \subseteq {\mathcal F}$
such that
${\mathcal T}^{\perp } \subseteq {\mathcal F}$
such that
 ${\mathcal W} = {\mathcal T}\cap {\mathcal F}$
.
${\mathcal W} = {\mathcal T}\cap {\mathcal F}$
.
Proof.
![]() $(1\iff 2):$
Recall that if
$(1\iff 2):$
Recall that if
![]() $U \in \mathcal C(\mathsf {mod}\Lambda )$
is support
$U \in \mathcal C(\mathsf {mod}\Lambda )$
is support
![]() $\tau $
-rigid, then
$\tau $
-rigid, then
![]() $\overline {\tau }U \in \mathcal C(\mathsf {mod}\Lambda )[-1]$
is support
$\overline {\tau }U \in \mathcal C(\mathsf {mod}\Lambda )[-1]$
is support
![]() $\tau ^{-1}$
-rigid, and moreover, that every support
$\tau ^{-1}$
-rigid, and moreover, that every support
![]() $\tau ^{-1}$
-rigid object in
$\tau ^{-1}$
-rigid object in
![]() $\mathcal C(\mathsf {mod}\Lambda )[-1]$
occurs in this way. Thus, suppose
$\mathcal C(\mathsf {mod}\Lambda )[-1]$
occurs in this way. Thus, suppose
![]() $U = M\sqcup P[1]$
is support
$U = M\sqcup P[1]$
is support
![]() $\tau $
-rigid and write
$\tau $
-rigid and write
![]() $M \cong M_p\sqcup M_{np}$
, where
$M \cong M_p\sqcup M_{np}$
, where
![]() $M_p \in \mathcal P(\mathsf {mod}\Lambda )$
and
$M_p \in \mathcal P(\mathsf {mod}\Lambda )$
and
![]() $M_{np}$
has no projective direct summand. We note that
$M_{np}$
has no projective direct summand. We note that
and
. Moreover, we have
![]() $\overline {\tau }(U) = (\nu M_p)[-1]\sqcup \tau M_{np} \sqcup \nu P$
, where
$\overline {\tau }(U) = (\nu M_p)[-1]\sqcup \tau M_{np} \sqcup \nu P$
, where
![]() $\tau M_{np}$
has no injective direct summand. This means
$\tau M_{np}$
has no injective direct summand. This means

This proves the result.
![]() $(1\implies 5)$
: This follows from Theorem 2.2 and the definition of
$(1\implies 5)$
: This follows from Theorem 2.2 and the definition of
![]() $\mathcal J(U)$
.
$\mathcal J(U)$
.
![]() $(5\implies 3)$
: Write
$(5\implies 3)$
: Write
![]() ${\mathcal W} = {\mathcal T}\cap {\mathcal F}$
with
${\mathcal W} = {\mathcal T}\cap {\mathcal F}$
with
![]() ${\mathcal T}$
a functorially finite torsion class and
${\mathcal T}$
a functorially finite torsion class and
![]() ${\mathcal F}$
a functorially finite torsion-free class. We will first show that
${\mathcal F}$
a functorially finite torsion-free class. We will first show that
![]() ${\mathcal W}\subseteq {\mathcal W}_L({\mathcal T})$
using an argument similar to [Reference Marks and Šťovíček23, Lem. 3.8]. Let
${\mathcal W}\subseteq {\mathcal W}_L({\mathcal T})$
using an argument similar to [Reference Marks and Šťovíček23, Lem. 3.8]. Let
![]() $X \in {\mathcal W},$
and let
$X \in {\mathcal W},$
and let
![]() $g:Y\rightarrow X$
be a morphism in
$g:Y\rightarrow X$
be a morphism in
![]() ${\mathcal T}$
. Note that
${\mathcal T}$
. Note that
![]() $\operatorname {{\mathrm {image}}} g \in {\mathcal W}$
since it is a subobject of X and a quotient of Y. Now, consider the canonical exact sequence with respect to the torsion pair
$\operatorname {{\mathrm {image}}} g \in {\mathcal W}$
since it is a subobject of X and a quotient of Y. Now, consider the canonical exact sequence with respect to the torsion pair
:
By assumption, we have
![]() $f_{\mathcal F}(Y) \in {\mathcal T}\cap {\mathcal F} = {\mathcal W}$
and
$f_{\mathcal F}(Y) \in {\mathcal T}\cap {\mathcal F} = {\mathcal W}$
and
. In particular, we have that
, and so
![]() $\operatorname {{\mathrm {image}}} g$
is a quotient of
$\operatorname {{\mathrm {image}}} g$
is a quotient of
![]() $f_{\mathcal F}(Y)$
. That is, we obtain the following diagram with rows and columns exact.
$f_{\mathcal F}(Y)$
. That is, we obtain the following diagram with rows and columns exact.

Now,
since
![]() ${\mathcal W}$
is closed under kernels. Therefore,
${\mathcal W}$
is closed under kernels. Therefore,
![]() $\ker g \in {\mathcal T}$
since
$\ker g \in {\mathcal T}$
since
![]() ${\mathcal T}$
is closed under extensions. We conclude that
${\mathcal T}$
is closed under extensions. We conclude that
![]() $X \in {\mathcal W}_L({\mathcal T})$
.
$X \in {\mathcal W}_L({\mathcal T})$
.
We will now show that
![]() ${\mathcal W}$
is a Serre subcategory of
${\mathcal W}$
is a Serre subcategory of
![]() ${\mathcal W}_L({\mathcal T})$
. Let
${\mathcal W}_L({\mathcal T})$
. Let
be a short exact sequence in
![]() ${\mathcal W}_L({\mathcal T})$
. It is clear that if
${\mathcal W}_L({\mathcal T})$
. It is clear that if
![]() $X,Z \in {\mathcal W},$
then
$X,Z \in {\mathcal W},$
then
![]() $Y \in {\mathcal W}$
. Thus, suppose
$Y \in {\mathcal W}$
. Thus, suppose
![]() $Y \in {\mathcal W} = {\mathcal T}\cap {\mathcal F}$
. It follows that
$Y \in {\mathcal W} = {\mathcal T}\cap {\mathcal F}$
. It follows that
![]() $X \in {\mathcal W}$
since it is in
$X \in {\mathcal W}$
since it is in
![]() ${\mathcal W}_L({\mathcal T}) \subseteq {\mathcal T}$
and
${\mathcal W}_L({\mathcal T}) \subseteq {\mathcal T}$
and
![]() ${\mathcal F}$
is closed under subobjects. Since
${\mathcal F}$
is closed under subobjects. Since
![]() ${\mathcal W}$
is closed under cokernels, it follows that
${\mathcal W}$
is closed under cokernels, it follows that
![]() $Z \in {\mathcal W}$
as well.
$Z \in {\mathcal W}$
as well.
![]() $(5\implies 4)$
: The proof is dual to that of
$(5\implies 4)$
: The proof is dual to that of
![]() $(5\implies 3)$
, but we include the details here for convenience. We will first show that
$(5\implies 3)$
, but we include the details here for convenience. We will first show that
![]() ${\mathcal W} \subseteq {\mathcal W}_R({\mathcal F})$
. Let
${\mathcal W} \subseteq {\mathcal W}_R({\mathcal F})$
. Let
![]() $X \in {\mathcal W}$
, and let
$X \in {\mathcal W}$
, and let
![]() $g:X\rightarrow Y$
be a morphism in
$g:X\rightarrow Y$
be a morphism in
![]() ${\mathcal F}$
. We note that
${\mathcal F}$
. We note that
![]() $\operatorname {{\mathrm {image}}} g \in {\mathcal W}$
since it is a quotient of X and a subobject of Y. Now consider the canonical exact sequence with respect to the torsion pair
$\operatorname {{\mathrm {image}}} g \in {\mathcal W}$
since it is a quotient of X and a subobject of Y. Now consider the canonical exact sequence with respect to the torsion pair
![]() $({\mathcal T},{\mathcal T}^{\perp })$
:
$({\mathcal T},{\mathcal T}^{\perp })$
:
By assumption, we have
![]() $t_{\mathcal T}(Y) \in {\mathcal T}\cap {\mathcal F} = {\mathcal W}$
and
$t_{\mathcal T}(Y) \in {\mathcal T}\cap {\mathcal F} = {\mathcal W}$
and
![]() $f_{({\mathcal T}^{\perp })}(Y) \in {\mathcal T}^{\perp } \subseteq {\mathcal F}$
. In particular, we have
$f_{({\mathcal T}^{\perp })}(Y) \in {\mathcal T}^{\perp } \subseteq {\mathcal F}$
. In particular, we have
![]() $\operatorname {{\mathrm {image}}} g \subseteq t_{\mathcal T}(T)$
. Therefore, we have an exact sequence
$\operatorname {{\mathrm {image}}} g \subseteq t_{\mathcal T}(T)$
. Therefore, we have an exact sequence
Since
![]() ${\mathcal W}$
is wide, we have
${\mathcal W}$
is wide, we have
![]() $t_{\mathcal T}(Y)/\operatorname {{\mathrm {image}}} g \in {\mathcal W}\subseteq {\mathcal F}$
. Since
$t_{\mathcal T}(Y)/\operatorname {{\mathrm {image}}} g \in {\mathcal W}\subseteq {\mathcal F}$
. Since
![]() ${\mathcal F}$
is closed under extensions, this implies that
${\mathcal F}$
is closed under extensions, this implies that
![]() $\operatorname {{\mathrm {coker}}} g \in {\mathcal F}$
. We conclude that
$\operatorname {{\mathrm {coker}}} g \in {\mathcal F}$
. We conclude that
![]() $X \in {\mathcal W}_R({\mathcal F})$
.
$X \in {\mathcal W}_R({\mathcal F})$
.
We will now show that
![]() ${\mathcal W}$
is a Serre subcategory of
${\mathcal W}$
is a Serre subcategory of
![]() ${\mathcal W}_R({\mathcal F})$
. Let
${\mathcal W}_R({\mathcal F})$
. Let
be a short exact sequence in
![]() ${\mathcal W}_R({\mathcal F})$
. It is clear that if
${\mathcal W}_R({\mathcal F})$
. It is clear that if
![]() $X,Z \in {\mathcal W}$
then
$X,Z \in {\mathcal W}$
then
![]() $Y \in {\mathcal W}$
. Thus suppose
$Y \in {\mathcal W}$
. Thus suppose
![]() $Y \in {\mathcal W} = {\mathcal T}\cap {\mathcal F}$
. It follows that
$Y \in {\mathcal W} = {\mathcal T}\cap {\mathcal F}$
. It follows that
![]() $Z \in {\mathcal W}$
since it is in
$Z \in {\mathcal W}$
since it is in
![]() ${\mathcal W}_R({\mathcal F}) \subseteq {\mathcal F}$
and
${\mathcal W}_R({\mathcal F}) \subseteq {\mathcal F}$
and
![]() ${\mathcal T}$
is closed under subobjects. Since
${\mathcal T}$
is closed under subobjects. Since
![]() ${\mathcal W}$
is closed under kernels, it follows that
${\mathcal W}$
is closed under kernels, it follows that
![]() $X \in {\mathcal W}$
as well.
$X \in {\mathcal W}$
as well.
![]() $(3\implies 1)$
: Let
$(3\implies 1)$
: Let
![]() ${\mathcal W}\subseteq {\mathcal W}_L({\mathcal T})$
be a Serre subcategory of a left-finite wide subcategory of
${\mathcal W}\subseteq {\mathcal W}_L({\mathcal T})$
be a Serre subcategory of a left-finite wide subcategory of
![]() $\mathsf {mod}\Lambda $
. By Lemma 4.3, we have that
$\mathsf {mod}\Lambda $
. By Lemma 4.3, we have that
![]() ${\mathcal W}_L({\mathcal T})$
is
${\mathcal W}_L({\mathcal T})$
is
![]() $\tau $
-perpendicular in
$\tau $
-perpendicular in
![]() $\mathsf {mod}\Lambda $
. It then follows from Lemma 4.4 that
$\mathsf {mod}\Lambda $
. It then follows from Lemma 4.4 that
![]() ${\mathcal W}$
is
${\mathcal W}$
is
![]() $\tau $
-perpendicular in
$\tau $
-perpendicular in
![]() $\mathsf {mod}\Lambda $
as well.
$\mathsf {mod}\Lambda $
as well.
![]() $(4\implies 1)$
: The proof is analogous to that of
$(4\implies 1)$
: The proof is analogous to that of
![]() $(3\implies 1)$
.
$(3\implies 1)$
.
Remark 4.6. We note that the equivalences between (3), (4), and (5) in Theorem 4.5 can also be deduced from [Reference Asai and Pfeifer3, Cor. 6.8] in Asai and Pfeifer’s work on “wide intervals” in the lattice of torsion classes. (They deduce this corollary after working with wide subcategories and torsion classes which are not necessarily functorially finite.) This yields a characterization of
![]() $\tau $
-perpendicular subcategories using the “brick labeling” of the lattice of torsion classes, defined in [Reference Asai2] for functorially finite torsion classes and in [Reference Barnard, Carroll and Zhu5], [Reference Demonet, Iyama, Reading, Reiten and Thomas11] for all torsion classes. Namely, let
$\tau $
-perpendicular subcategories using the “brick labeling” of the lattice of torsion classes, defined in [Reference Asai2] for functorially finite torsion classes and in [Reference Barnard, Carroll and Zhu5], [Reference Demonet, Iyama, Reading, Reiten and Thomas11] for all torsion classes. Namely, let
![]() $\mathcal {T}$
be a functorially finite torsion class, and choose a set of cover relations of the form
$\mathcal {T}$
be a functorially finite torsion class, and choose a set of cover relations of the form
![]() $\mathcal {U}_i \subsetneq \mathcal {T}$
. Then
$\mathcal {U}_i \subsetneq \mathcal {T}$
. Then
![]() $\left [ \bigcap _i \mathcal {U}_i,\mathcal {T}\right ]$
is a “wide interval” by [Reference Asai and Pfeifer3, Th. 5.2]. By definition, this means that the intersection
$\left [ \bigcap _i \mathcal {U}_i,\mathcal {T}\right ]$
is a “wide interval” by [Reference Asai and Pfeifer3, Th. 5.2]. By definition, this means that the intersection
![]() $\mathcal {W} := \left (\bigcap _i \mathcal {U}_i\right )^{\perp } \cap \mathcal {T}$
is a wide subcategory. Now, the torsion class
$\mathcal {W} := \left (\bigcap _i \mathcal {U}_i\right )^{\perp } \cap \mathcal {T}$
is a wide subcategory. Now, the torsion class
![]() $\bigcap _i \mathcal {U}_i$
is functorially finite by [Reference Jasso22, Th. 3.14] (see also [Reference Asai and Pfeifer3, Cor. 6.8]), and so the intersection
$\bigcap _i \mathcal {U}_i$
is functorially finite by [Reference Jasso22, Th. 3.14] (see also [Reference Asai and Pfeifer3, Cor. 6.8]), and so the intersection
![]() $\mathcal {W}$
is a
$\mathcal {W}$
is a
![]() $\tau $
-perpendicular subcategory by Theorem 4.5. Moreover, the simple objects of
$\tau $
-perpendicular subcategory by Theorem 4.5. Moreover, the simple objects of
![]() $\mathcal {W}$
are precisely the “brick labels” of the chosen cover relations by [Reference Asai and Pfeifer3, Th. 4.2(3)]. Finally, all
$\mathcal {W}$
are precisely the “brick labels” of the chosen cover relations by [Reference Asai and Pfeifer3, Th. 4.2(3)]. Finally, all
![]() $\tau $
-perpendicular subcategories will be of this form, again by [Reference Asai and Pfeifer3, Cor. 6.8] and Theorem 4.5.
$\tau $
-perpendicular subcategories will be of this form, again by [Reference Asai and Pfeifer3, Cor. 6.8] and Theorem 4.5.
Remark 4.7. Due to the equivalence between
![]() $\tau $
-perpendicular and
$\tau $
-perpendicular and
![]() $\tau ^{-1}$
-perpendicular subcategories of
$\tau ^{-1}$
-perpendicular subcategories of
![]() $\mathsf {mod}\Lambda $
, we will dispense with discussing the support
$\mathsf {mod}\Lambda $
, we will dispense with discussing the support
![]() $\tau ^{-1}$
-rigid case for the remainder of this article. We nevertheless remark that the majority of our results can be restated for
$\tau ^{-1}$
-rigid case for the remainder of this article. We nevertheless remark that the majority of our results can be restated for
![]() $\tau ^{-1}$
-perpendicular subcategories by applying Theorem 4.5.
$\tau ^{-1}$
-perpendicular subcategories by applying Theorem 4.5.
We conclude this section by tabulating several consequences of Theorem 4.5 and the preceding lemmas.
Corollary 4.8. Let
![]() ${\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a functorially finite wide subcategory with
${\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a functorially finite wide subcategory with
![]() $\mathsf {rk}({\mathcal W}) + 1 = \mathsf {rk}(\Lambda )$
. Then the following are equivalent.
$\mathsf {rk}({\mathcal W}) + 1 = \mathsf {rk}(\Lambda )$
. Then the following are equivalent.
-
1.
 ${\mathcal W}$
is a left-finite wide subcategory.
${\mathcal W}$
is a left-finite wide subcategory. -
2.
 ${\mathcal W}$
is a right-finite wide subcategory.
${\mathcal W}$
is a right-finite wide subcategory. -
3.
 ${\mathcal W}$
is a
${\mathcal W}$
is a
 $\tau $
-perpendicular subcategory.
$\tau $
-perpendicular subcategory.
Proof. The implications
![]() $(1\implies 3)$
and
$(1\implies 3)$
and
![]() $(2\implies 3)$
are contained in Lemma 4.3. Thus, assume (3). By Theorem 4.5, there exists a left-finite wide subcategory
$(2\implies 3)$
are contained in Lemma 4.3. Thus, assume (3). By Theorem 4.5, there exists a left-finite wide subcategory
![]() $\mathcal V \subseteq \mathsf {mod}\Lambda $
such that
$\mathcal V \subseteq \mathsf {mod}\Lambda $
such that
![]() ${\mathcal W}$
is a Serre subcategory of
${\mathcal W}$
is a Serre subcategory of
![]() $\mathcal V$
. Lemma 4.3 and Theorem 3.3 then imply that
$\mathcal V$
. Lemma 4.3 and Theorem 3.3 then imply that
Now, if
![]() $\mathsf {rk}({\mathcal W}) = \mathsf {rk}(\mathcal V)$
, then
$\mathsf {rk}({\mathcal W}) = \mathsf {rk}(\mathcal V)$
, then
![]() ${\mathcal W} = \mathcal V$
as a consequence of the same lemma and theorem. In particular,
${\mathcal W} = \mathcal V$
as a consequence of the same lemma and theorem. In particular,
![]() ${\mathcal W}$
is a left-finite wide subcategory of
${\mathcal W}$
is a left-finite wide subcategory of
![]() $\mathsf {mod}\Lambda $
in this case. Otherwise,
$\mathsf {mod}\Lambda $
in this case. Otherwise,
![]() $\mathcal V = \mathsf {mod}\Lambda $
by the same argument, and so
$\mathcal V = \mathsf {mod}\Lambda $
by the same argument, and so
![]() ${\mathcal W}$
is a left-finite wide subcategory of
${\mathcal W}$
is a left-finite wide subcategory of
![]() $\mathsf {mod}\Lambda $
by Corollary 3.8. We conclude that (3) implies (1). The proof that (3) implies (2) is identical.
$\mathsf {mod}\Lambda $
by Corollary 3.8. We conclude that (3) implies (1). The proof that (3) implies (2) is identical.
In [Reference Asai2, Exam. 3.13], Asai gives an example of a functorially finite wide subcategory which is right finite but not left finite. (It is, however, a Serre subcategory of a left-finite wide subcategory, consistent with Theorem 4.5.) By modifying Asai’s example, we obtain an example of a functorially finite wide subcategory which is not a
![]() $\tau $
-perpendicular subcategory.
$\tau $
-perpendicular subcategory.
Example 4.9. Consider the quiver

and let
![]() $\Lambda = KQ/(\beta _2\alpha _1,\beta _1\alpha _2)$
. Consider the
$\Lambda = KQ/(\beta _2\alpha _1,\beta _1\alpha _2)$
. Consider the
![]() $\Lambda $
-modules
$\Lambda $
-modules
We will demonstrate that
![]() ${\mathcal W}:= \mathsf {Filt}(X_1,X_2)$
is a functorially finite wide subcategory of
${\mathcal W}:= \mathsf {Filt}(X_1,X_2)$
is a functorially finite wide subcategory of
![]() $\mathsf {mod}\Lambda $
which is not a
$\mathsf {mod}\Lambda $
which is not a
![]() $\tau $
-perpendicular subcategory.
$\tau $
-perpendicular subcategory.
We first note that
![]() $\operatorname {{\mathrm {Hom}}}(X_1,X_2) = 0 = \operatorname {{\mathrm {Hom}}}(X_2,X_1)$
and that
$\operatorname {{\mathrm {Hom}}}(X_1,X_2) = 0 = \operatorname {{\mathrm {Hom}}}(X_2,X_1)$
and that
![]() $\operatorname {{\mathrm {End}}}(X_1) \cong K \cong \operatorname {{\mathrm {End}}}(X_2)$
. Moreover, it is straightforward to show that
$\operatorname {{\mathrm {End}}}(X_1) \cong K \cong \operatorname {{\mathrm {End}}}(X_2)$
. Moreover, it is straightforward to show that
In particular,
![]() $\operatorname {{\mathrm {Hom}}}(X_1,\tau X_2) = 0 = \operatorname {{\mathrm {Hom}}}(X_2,\tau X_1)$
and every morphism
$\operatorname {{\mathrm {Hom}}}(X_1,\tau X_2) = 0 = \operatorname {{\mathrm {Hom}}}(X_2,\tau X_1)$
and every morphism
![]() $X_1\rightarrow \tau X_1$
(or
$X_1\rightarrow \tau X_1$
(or
![]() $X_2\rightarrow \tau X_2$
) factors through the injective
$X_2\rightarrow \tau X_2$
) factors through the injective
![]() $I(2)$
. By the AR formulas, we conclude that
$I(2)$
. By the AR formulas, we conclude that
![]() $\operatorname {{\mathrm {Ext}}}^1(X_i,X_j)$
for any
$\operatorname {{\mathrm {Ext}}}^1(X_i,X_j)$
for any
![]() $i,j \in \{1,2\}$
. This means
$i,j \in \{1,2\}$
. This means
![]() ${\mathcal W}$
is a wide subcategory equivalent to the module category of a semisimple algebra, so in particular,
${\mathcal W}$
is a wide subcategory equivalent to the module category of a semisimple algebra, so in particular,
![]() ${\mathcal W}$
is functorially finite.
${\mathcal W}$
is functorially finite.
We will now show that
![]() ${\mathcal W}$
is not a
${\mathcal W}$
is not a
![]() $\tau $
-perpendicular subcategory. By Corollary 4.8, the fact that
$\tau $
-perpendicular subcategory. By Corollary 4.8, the fact that
![]() $\mathsf {rk}({\mathcal W}) = \mathsf {rk}(\Lambda )-1$
means we need only show that
$\mathsf {rk}({\mathcal W}) = \mathsf {rk}(\Lambda )-1$
means we need only show that
![]() ${\mathcal W}$
is not left finite. To see this, we note that the Serre subcategory
${\mathcal W}$
is not left finite. To see this, we note that the Serre subcategory
![]() $P(3)^{\perp }$
is equivalent to the module category of the Kronecker path algebra. Thus, we can consider the Ingalls–Thomas bijection (Definition 3.5)
$P(3)^{\perp }$
is equivalent to the module category of the Kronecker path algebra. Thus, we can consider the Ingalls–Thomas bijection (Definition 3.5)
![]() ${\mathcal W}_L^{P(3)^{\perp }}$
in the category
${\mathcal W}_L^{P(3)^{\perp }}$
in the category
![]() $P(3)^{\perp }$
. Then the wide subcategory
$P(3)^{\perp }$
. Then the wide subcategory
![]() $\mathcal V = {\mathcal W}_L^{P(3)^{\perp }}(\mathsf {Filt}\mathsf {Gen}({\mathcal W})\cap P(3)^{\perp }) = {\mathcal W}_L^{P(3)^{\perp }}(\mathsf {Filt}\mathsf {Gen}(\tau X_1,\tau X_2))$
is the additive closure of a pair of homogeneous tubes having
$\mathcal V = {\mathcal W}_L^{P(3)^{\perp }}(\mathsf {Filt}\mathsf {Gen}({\mathcal W})\cap P(3)^{\perp }) = {\mathcal W}_L^{P(3)^{\perp }}(\mathsf {Filt}\mathsf {Gen}(\tau X_1,\tau X_2))$
is the additive closure of a pair of homogeneous tubes having
![]() $\tau X_1$
and
$\tau X_1$
and
![]() $\tau X_2$
at their mouths. It is then a well-known fact that right
$\tau X_2$
at their mouths. It is then a well-known fact that right
![]() $\mathcal V$
-approximations will in general not exist, and hence,
$\mathcal V$
-approximations will in general not exist, and hence,
![]() $\mathcal V$
is not functorially finite (in either
$\mathcal V$
is not functorially finite (in either
![]() $P(3)^{\perp }$
or in
$P(3)^{\perp }$
or in
![]() $\mathsf {mod}\Lambda $
). In particular, this means
$\mathsf {mod}\Lambda $
). In particular, this means
![]() $\mathcal V$
is not a left-finite wide subcategory of
$\mathcal V$
is not a left-finite wide subcategory of
![]() $P(3)^{\perp }$
, and so
$P(3)^{\perp }$
, and so
![]() $\mathsf {Filt}\mathsf {Gen}({\mathcal W})\cap P(3)^{\perp }$
is not functorially finite. Since
$\mathsf {Filt}\mathsf {Gen}({\mathcal W})\cap P(3)^{\perp }$
is not functorially finite. Since
![]() $P(3)^{\perp }$
is a functorially finite torsion-free class of
$P(3)^{\perp }$
is a functorially finite torsion-free class of
![]() $\mathsf {mod}\Lambda $
(see Proposition 3.6 and Corollary 3.8), Lemma 2.1 then implies that the torsion class
$\mathsf {mod}\Lambda $
(see Proposition 3.6 and Corollary 3.8), Lemma 2.1 then implies that the torsion class
![]() $\mathsf {Filt}\mathsf {Gen}({\mathcal W})$
is not functorially finite; that is, that
$\mathsf {Filt}\mathsf {Gen}({\mathcal W})$
is not functorially finite; that is, that
![]() ${\mathcal W}$
is not left finite. (Note that, as a consequence of Corollary 4.8,
${\mathcal W}$
is not left finite. (Note that, as a consequence of Corollary 4.8,
![]() ${\mathcal W}$
is not right finite either. This can also be seen directly using duality.)
${\mathcal W}$
is not right finite either. This can also be seen directly using duality.)
Remark 4.10. Summarizing, we have the following inclusions of classes of subcategories of
![]() $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
.

Moreover, each of these inclusions can be proper. Indeed, (2) can be proper by Example 4.9 and (3) and (4) can be proper by [Reference Asai2, Exam. 3.13] and its dual. It is clear that if
![]() $\Lambda $
is not
$\Lambda $
is not
![]() $\tau $
-tilting finite, then (1) will in general be proper. Likewise, (5) and (6) will be proper unless
$\tau $
-tilting finite, then (1) will in general be proper. Likewise, (5) and (6) will be proper unless
![]() $\Lambda $
is semisimple or local. We note that all six of these classes coincide when
$\Lambda $
is semisimple or local. We note that all six of these classes coincide when
![]() $\Lambda $
is semisimple or local, and that all but the Serre subcategories coincide when
$\Lambda $
is semisimple or local, and that all but the Serre subcategories coincide when
![]() $\Lambda $
is
$\Lambda $
is
![]() $\tau $
-tilting finite. Moreover, if
$\tau $
-tilting finite. Moreover, if
![]() $\Lambda $
is hereditary, then (2)–(4) are all equalities by [Reference Ingalls and Thomas20, Cor. 2.17].
$\Lambda $
is hereditary, then (2)–(4) are all equalities by [Reference Ingalls and Thomas20, Cor. 2.17].
5 Reduction of support
 $\tau $
-rigid objects
$\tau $
-rigid objects
The proof of our second main theorem will rely on a reduction formula, which allows us to compare
![]() $\tau $
-rigid objects in
$\tau $
-rigid objects in
![]() $\mathcal C(\mathsf {mod}\Lambda )$
with those in
$\mathcal C(\mathsf {mod}\Lambda )$
with those in
![]() $\mathcal C({\mathcal W})$
, with
$\mathcal C({\mathcal W})$
, with
![]() ${\mathcal W}\subseteq \mathsf {mod}\Lambda $
a
${\mathcal W}\subseteq \mathsf {mod}\Lambda $
a
![]() $\tau $
-perpendicular subcategory. Theorem 5.1 extends Jasso’s reduction of
$\tau $
-perpendicular subcategory. Theorem 5.1 extends Jasso’s reduction of
![]() $\tau $
-rigid modules (see [Reference Jasso22, Cor. 3.18]) to account for shifted projectives in the reduction. Note that there is an analogous, and related, formulation in terms of torsion classes (see [Reference Demonet, Iyama, Reading, Reiten and Thomas11, Th. 4.12] and [Reference Jasso22, Th. 3.12 and 3.13]). For the statements in this section, we recall the notation for the canonical exact sequence of a module with respect to a torsion pair from Equation (1) in Section 2.
$\tau $
-rigid modules (see [Reference Jasso22, Cor. 3.18]) to account for shifted projectives in the reduction. Note that there is an analogous, and related, formulation in terms of torsion classes (see [Reference Demonet, Iyama, Reading, Reiten and Thomas11, Th. 4.12] and [Reference Jasso22, Th. 3.12 and 3.13]). For the statements in this section, we recall the notation for the canonical exact sequence of a module with respect to a torsion pair from Equation (1) in Section 2.
Theorem 5.1. Let
![]() ${\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a functorially finite wide subcategory.
${\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a functorially finite wide subcategory.
-
1. [Reference Buan and Marsh10, Prop. 5.6] Let
 $M \in {\mathcal W}$
be basic and
$M \in {\mathcal W}$
be basic and
 $\tau $
-rigid in
$\tau $
-rigid in
 ${\mathcal W}$
. Then there is a bijection
${\mathcal W}$
. Then there is a bijection  $$ \begin{align*} \{V \in \mathcal C({\mathcal W}) \mid M\sqcup V \text{ is basic and } \tau\text{-rigid in }\mathcal C({\mathcal W})\} \end{align*} $$
$$ \begin{align*} \{V \in \mathcal C({\mathcal W}) \mid M\sqcup V \text{ is basic and } \tau\text{-rigid in }\mathcal C({\mathcal W})\} \end{align*} $$
 $$ \begin{align*}\downarrow\mathcal E_M^{\mathcal W}\end{align*} $$
summarized as follows:
$$ \begin{align*}\downarrow\mathcal E_M^{\mathcal W}\end{align*} $$
summarized as follows: $$ \begin{align*} \{V' \in \mathcal C(\mathcal J_{\mathcal W}(M)) \mid V' \text{ is basic and } \tau\text{-rigid in } {\mathcal C}({\mathcal J}_{{\mathcal W}}(M))\} \end{align*} $$
$$ \begin{align*} \{V' \in \mathcal C(\mathcal J_{\mathcal W}(M)) \mid V' \text{ is basic and } \tau\text{-rigid in } {\mathcal C}({\mathcal J}_{{\mathcal W}}(M))\} \end{align*} $$
-
(a) If
 $N \in {\mathcal W}$
is indecomposable,
$N \in {\mathcal W}$
is indecomposable,
 $M\sqcup N$
is
$M\sqcup N$
is
 $\tau $
-rigid in
$\tau $
-rigid in
 $\mathcal C({\mathcal W})$
, and
$\mathcal C({\mathcal W})$
, and
 $N \notin \mathsf {Gen} M$
, then
$N \notin \mathsf {Gen} M$
, then
 $\mathcal E^{\mathcal W}_M(N) = f_{(M^{\perp })}(N)$
.
$\mathcal E^{\mathcal W}_M(N) = f_{(M^{\perp })}(N)$
. -
(b) If
 $N \in {\mathcal W}$
is indecomposable,
$N \in {\mathcal W}$
is indecomposable,
 $M\sqcup N$
is
$M\sqcup N$
is
 $\tau $
-rigid in
$\tau $
-rigid in
 $\mathcal C({\mathcal W})$
, and
$\mathcal C({\mathcal W})$
, and
 $N \in \mathsf {Gen} M$
, then there exists an indecomposable direct summand B of the Bongartz complement of M (in
$N \in \mathsf {Gen} M$
, then there exists an indecomposable direct summand B of the Bongartz complement of M (in
 ${\mathcal W}$
) such that
${\mathcal W}$
) such that
 $\mathcal E^{\mathcal W}_M(N) = f_{(M^{\perp })}(B)[1]$
.
$\mathcal E^{\mathcal W}_M(N) = f_{(M^{\perp })}(B)[1]$
. -
(c) If
 $Q \in \mathcal P({\mathcal W})$
and
$Q \in \mathcal P({\mathcal W})$
and
 $M\sqcup Q[1]$
is support
$M\sqcup Q[1]$
is support
 $\tau $
-rigid in
$\tau $
-rigid in
 $\mathcal C({\mathcal W})$
, then there exists a direct summand B of the Bongartz complement of M (in
$\mathcal C({\mathcal W})$
, then there exists a direct summand B of the Bongartz complement of M (in
 ${\mathcal W}$
) such that
${\mathcal W}$
) such that
 $\mathcal E_M^{\mathcal W}(Q[1]) = f_{(M^{\perp })}(B)[1]$
.
$\mathcal E_M^{\mathcal W}(Q[1]) = f_{(M^{\perp })}(B)[1]$
.
The bijection then extends additively.
-
-
2. [Reference Buan and Marsh10, Prop. 5.10a] Let
 $P \in \mathcal P({\mathcal W})$
be projective in
$P \in \mathcal P({\mathcal W})$
be projective in
 ${\mathcal W}$
. Then there is a bijection
${\mathcal W}$
. Then there is a bijection  $$ \begin{align*} \{V \in \mathcal C({\mathcal W}) \mid V\sqcup P[1] \text{ is basic and } \tau\text{-rigid in }\mathcal C({\mathcal W})\} \end{align*} $$
$$ \begin{align*} \{V \in \mathcal C({\mathcal W}) \mid V\sqcup P[1] \text{ is basic and } \tau\text{-rigid in }\mathcal C({\mathcal W})\} \end{align*} $$
 $$ \begin{align*} \downarrow\mathcal E_{P[1]}^{\mathcal W} \end{align*} $$
given by
$$ \begin{align*} \downarrow\mathcal E_{P[1]}^{\mathcal W} \end{align*} $$
given by $$ \begin{align*} \{V' \in \mathcal C(\mathcal J_{\mathcal W}(P[1])) \mid V' \text{ is basic and } \tau\text{-rigid in }\mathcal C(\mathcal J_{\mathcal W}(P[1]))\} \end{align*} $$
$$ \begin{align*} \{V' \in \mathcal C(\mathcal J_{\mathcal W}(P[1])) \mid V' \text{ is basic and } \tau\text{-rigid in }\mathcal C(\mathcal J_{\mathcal W}(P[1]))\} \end{align*} $$
 $$ \begin{align*}\mathcal E_{P[1]}^{\mathcal W}(N\sqcup Q[1]) = N\sqcup f_{(P^{\perp})}(Q)[1].\end{align*} $$
$$ \begin{align*}\mathcal E_{P[1]}^{\mathcal W}(N\sqcup Q[1]) = N\sqcup f_{(P^{\perp})}(Q)[1].\end{align*} $$
-
3. [Reference Buan and Marsh9, Th. 3.6] Let
 $U = M\sqcup P[1] \in \mathcal C({\mathcal W})$
be basic and support
$U = M\sqcup P[1] \in \mathcal C({\mathcal W})$
be basic and support
 $\tau $
-rigid in
$\tau $
-rigid in
 $\mathcal C({\mathcal W})$
and define Then
$\mathcal C({\mathcal W})$
and define Then $$ \begin{align*}\mathcal E_{U}^{\mathcal W}:= \mathcal E_{\mathcal E_M^{\mathcal W}(P[1])}^{\mathcal J_{\mathcal W}(M)}\circ \mathcal E_M^{\mathcal W}.\end{align*} $$
$$ \begin{align*}\mathcal E_{U}^{\mathcal W}:= \mathcal E_{\mathcal E_M^{\mathcal W}(P[1])}^{\mathcal J_{\mathcal W}(M)}\circ \mathcal E_M^{\mathcal W}.\end{align*} $$
 $\mathcal E^{\mathcal W}_{M\sqcup P[1]}$
is a bijection
$\mathcal E^{\mathcal W}_{M\sqcup P[1]}$
is a bijection  $$ \begin{align*} \{V \in \mathcal C({\mathcal W}) \mid U\sqcup V \text{ is basic and support } \tau\text{-rigid in } \mathcal C({\mathcal W})\} \end{align*} $$
$$ \begin{align*} \{V \in \mathcal C({\mathcal W}) \mid U\sqcup V \text{ is basic and support } \tau\text{-rigid in } \mathcal C({\mathcal W})\} \end{align*} $$
 $$ \begin{align*}\downarrow\mathcal E_U^{\mathcal W}\end{align*} $$
$$ \begin{align*}\downarrow\mathcal E_U^{\mathcal W}\end{align*} $$
 $$ \begin{align*} \{V' \in \mathcal C(\mathcal J_{\mathcal W}(U)) \mid V' \text{ is basic and support } \tau\text{-rigid in } {\mathcal C}(\mathcal J_{\mathcal W}(U))\}. \end{align*} $$
$$ \begin{align*} \{V' \in \mathcal C(\mathcal J_{\mathcal W}(U)) \mid V' \text{ is basic and support } \tau\text{-rigid in } {\mathcal C}(\mathcal J_{\mathcal W}(U))\}. \end{align*} $$
Remark 5.2. Since
![]() $\mathcal E_U^{\mathcal W}$
is defined additively, it follows immediately from Theorem 3.3 that
$\mathcal E_U^{\mathcal W}$
is defined additively, it follows immediately from Theorem 3.3 that
![]() $U \sqcup V$
is support
$U \sqcup V$
is support
![]() $\tau $
-tilting in
$\tau $
-tilting in
![]() $\mathcal C({\mathcal W})$
if and only if
$\mathcal C({\mathcal W})$
if and only if
![]() $\mathcal E_U^{\mathcal W}(V)$
is support
$\mathcal E_U^{\mathcal W}(V)$
is support
![]() $\tau $
-tilting in
$\tau $
-tilting in
![]() $\mathcal J_{\mathcal W}(U)$
.
$\mathcal J_{\mathcal W}(U)$
.
In case
![]() ${\mathcal W} = \mathsf {mod}\Lambda $
, we will sometimes denote
${\mathcal W} = \mathsf {mod}\Lambda $
, we will sometimes denote
![]() $\mathcal E_U:= \mathcal E_U^{\mathsf {mod}\Lambda }$
. In Theorem 6.12, we will show that these “
$\mathcal E_U:= \mathcal E_U^{\mathsf {mod}\Lambda }$
. In Theorem 6.12, we will show that these “
![]() $\mathcal E$
-maps” satisfy an associativity property as follows: If
$\mathcal E$
-maps” satisfy an associativity property as follows: If
![]() ${\mathcal W} \subseteq \mathsf {mod}\Lambda $
is a
${\mathcal W} \subseteq \mathsf {mod}\Lambda $
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
and
$\mathsf {mod}\Lambda $
and
![]() $U\sqcup V$
is basic and support
$U\sqcup V$
is basic and support
![]() $\tau $
-rigid in
$\tau $
-rigid in
![]() $\mathcal C({\mathcal W})$
, then
$\mathcal C({\mathcal W})$
, then
![]() $\mathcal E_{U\sqcup V}^{\mathcal W} = \mathcal E^{\mathcal J_{\mathcal W}(U)}_{\mathcal E^{\mathcal W}_U(V)}\circ \mathcal E^W_U$
. This result is established in [Reference Buan and Marsh9, Th. 5.9] in the case that
$\mathcal E_{U\sqcup V}^{\mathcal W} = \mathcal E^{\mathcal J_{\mathcal W}(U)}_{\mathcal E^{\mathcal W}_U(V)}\circ \mathcal E^W_U$
. This result is established in [Reference Buan and Marsh9, Th. 5.9] in the case that
![]() $\Lambda $
is
$\Lambda $
is
![]() $\tau $
-tilting finite.
$\tau $
-tilting finite.
For the remainder of this section, we recall some technical results about these bijections and their relationship with Bongartz complements. In essence, these lemmas are well-known (see, e.g., [Reference Buan and Marsh10, Lem. 4.13]), but we give proofs here for completeness.
Lemma 5.3. Let
![]() $U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
be support
$U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
be support
![]() $\tau $
-rigid, and let
$\tau $
-rigid, and let
![]() $B_U$
be the Bongartz complement of U. Then no direct summand of
$B_U$
be the Bongartz complement of U. Then no direct summand of
![]() $B_U$
lies in
$B_U$
lies in
![]() $\mathsf {Gen} M$
.
$\mathsf {Gen} M$
.
Proof. Let B be an indecomposable direct summand of
![]() $B_U$
. By Theorem 2.4, we have
$B_U$
. By Theorem 2.4, we have
Moreover, by [Reference Buan and Marsh9, Lem. 3.8],
![]() $B\sqcup M$
is
$B\sqcup M$
is
![]() $\tau $
-rigid in the Serre subcategory
$\tau $
-rigid in the Serre subcategory
![]() $P^{\perp }$
and satisfies
$P^{\perp }$
and satisfies
Since
![]() $\mathsf {Gen}(B\sqcup M)\subseteq P^{\perp }$
, it then follows by applying [Reference Adachi, Iyama and Reiten1, Prop. 2.22] in the category
$\mathsf {Gen}(B\sqcup M)\subseteq P^{\perp }$
, it then follows by applying [Reference Adachi, Iyama and Reiten1, Prop. 2.22] in the category
![]() $P^{\perp }$
that
$P^{\perp }$
that
![]() $B \notin \mathsf {Gen} M$
.
$B \notin \mathsf {Gen} M$
.
Lemma 5.4. Let
![]() $U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
be support
$U = M\sqcup P[1] \in \mathcal C(\mathsf {mod}\Lambda )$
be support
![]() $\tau $
-rigid and basic. Let
$\tau $
-rigid and basic. Let
![]() $B_U$
and
$B_U$
and
![]() $C_U$
be the Bongartz complement and co-Bongartz complement of U, respectively. Then:
$C_U$
be the Bongartz complement and co-Bongartz complement of U, respectively. Then:
-
1. For
 $B \in \mathsf {add}(B_U)$
, we have
$B \in \mathsf {add}(B_U)$
, we have
 $\mathcal J(B\sqcup U) = B^{\perp } \cap \mathcal J(U) = (\mathcal E_U(B))^{\perp } \cap \mathcal J(U).$
$\mathcal J(B\sqcup U) = B^{\perp } \cap \mathcal J(U) = (\mathcal E_U(B))^{\perp } \cap \mathcal J(U).$
-
2.
 $\mathcal P(\mathcal J(U)) = \mathsf {add}(\mathcal E_{U}(B_U)).$
$\mathcal P(\mathcal J(U)) = \mathsf {add}(\mathcal E_{U}(B_U)).$
-
3.
 $\mathcal P(\mathcal J(U)) = \mathsf {add}(\mathcal E_U(C_U)[-1])$
.
$\mathcal P(\mathcal J(U)) = \mathsf {add}(\mathcal E_U(C_U)[-1])$
.
Proof. (1) We leave out the proof, since it is identical to the proof of Lemma 4.4, using Theorem 5.1(1)(a) and Lemma 5.3.
(2) By Proposition 3.1, we note that
![]() $\mathsf {rk}(B_U) = \mathsf {rk}(\mathcal E_U(B_U)) = \mathsf {rk}(\mathcal J(U))$
. Thus, it suffices to show that
$\mathsf {rk}(B_U) = \mathsf {rk}(\mathcal E_U(B_U)) = \mathsf {rk}(\mathcal J(U))$
. Thus, it suffices to show that
![]() $\mathsf {Gen}(\mathcal E_U(B_U))\cap \mathcal J(U) = \mathcal J(U)$
. Now, let
$\mathsf {Gen}(\mathcal E_U(B_U))\cap \mathcal J(U) = \mathcal J(U)$
. Now, let
![]() $X \in \mathcal J(U)$
, so in particular,
$X \in \mathcal J(U)$
, so in particular,
![]() . By Theorem 2.4, we have that
. By Theorem 2.4, we have that
![]() . Since
. Since
![]() $\operatorname {{\mathrm {Hom}}}(M,X) = 0$
, this means there exists
$\operatorname {{\mathrm {Hom}}}(M,X) = 0$
, this means there exists
![]() $B \in \mathsf {add} B_U$
and an epimorphism
$B \in \mathsf {add} B_U$
and an epimorphism
![]() $g:B\rightarrow X$
. Again using the fact that
$g:B\rightarrow X$
. Again using the fact that
![]() $\operatorname {{\mathrm {Hom}}}(M,X) = 0$
, we obtain an epimorphism
$\operatorname {{\mathrm {Hom}}}(M,X) = 0$
, we obtain an epimorphism
![]() $g': f_{(M^{\perp })}(B) \rightarrow X$
. By Theorem 5.1, we conclude that
$g': f_{(M^{\perp })}(B) \rightarrow X$
. By Theorem 5.1, we conclude that
![]() $f_{(M^{\perp })}(B) \in \mathsf {add}(\mathcal E_U(B))$
and, therefore,
$f_{(M^{\perp })}(B) \in \mathsf {add}(\mathcal E_U(B))$
and, therefore,
![]() $X \in \mathsf {Gen}(\mathcal E_U(B)) \cap \mathcal J(U)$
as claimed.
$X \in \mathsf {Gen}(\mathcal E_U(B)) \cap \mathcal J(U)$
as claimed.
(3) By Theorem 5.1, we have that
![]() $\mathcal E_U(C_U)$
is support
$\mathcal E_U(C_U)$
is support
![]() $\tau $
-tilting in
$\tau $
-tilting in
![]() $\mathcal C(\mathcal J(U))$
and is contained in
$\mathcal C(\mathcal J(U))$
and is contained in
![]() $\mathcal J(U)[1]$
. This means
$\mathcal J(U)[1]$
. This means
![]() $\mathcal E_U(C_U)$
must be the direct sum of the shifts of the indecomposable projectives in
$\mathcal E_U(C_U)$
must be the direct sum of the shifts of the indecomposable projectives in
![]() $\mathcal P(\mathcal J(U))$
.
$\mathcal P(\mathcal J(U))$
.
6
 $\tau $
-cluster morphism categories
$\tau $
-cluster morphism categories
In this section, we apply our previous results to extend the definition of the
![]() $\tau $
-cluster morphism category to arbitrary finite-dimensional algebras. This is a small category whose objects correspond to the
$\tau $
-cluster morphism category to arbitrary finite-dimensional algebras. This is a small category whose objects correspond to the
![]() $\tau $
-perpendicular subcategories of
$\tau $
-perpendicular subcategories of
![]() $\mathsf {mod}\Lambda $
and whose morphisms are indexed by support
$\mathsf {mod}\Lambda $
and whose morphisms are indexed by support
![]() $\tau $
-rigid pairs in these subcategories (see Definition 6.1). This category was defined by Igusa and Todorov for hereditary algebras in [Reference Igusa and Todorov18] under the name “cluster morphism category.” A combinatorial interpretation in Dynkin type A using noncrossing partitions and binary forests was also given by Igusa in [Reference Igusa17]. The definition was extended to
$\tau $
-rigid pairs in these subcategories (see Definition 6.1). This category was defined by Igusa and Todorov for hereditary algebras in [Reference Igusa and Todorov18] under the name “cluster morphism category.” A combinatorial interpretation in Dynkin type A using noncrossing partitions and binary forests was also given by Igusa in [Reference Igusa17]. The definition was extended to
![]() $\tau $
-tilting finite algebras by Marsh and the first author in [Reference Buan and Marsh9] under the name “a category of wide subcategories” and given the name “
$\tau $
-tilting finite algebras by Marsh and the first author in [Reference Buan and Marsh9] under the name “a category of wide subcategories” and given the name “
![]() $\tau $
-cluster morphism category” in [Reference Hanson and Igusa14]. We state our extension of this definition to arbitrary finite-dimensional algebras now.
$\tau $
-cluster morphism category” in [Reference Hanson and Igusa14]. We state our extension of this definition to arbitrary finite-dimensional algebras now.
Definition 6.1. Let
![]() $\Lambda $
be a finite-dimensional algebra. We define the
$\Lambda $
be a finite-dimensional algebra. We define the
![]() $\tau $
-cluster morphism category of
$\tau $
-cluster morphism category of
![]() $\Lambda $
, denoted
$\Lambda $
, denoted
![]() $\mathfrak {W}(\Lambda )$
, as follows:
$\mathfrak {W}(\Lambda )$
, as follows:
-
1. The objects of
 $\mathfrak {W}(\Lambda )$
are the
$\mathfrak {W}(\Lambda )$
are the
 $\tau $
-perpendicular subcategories of
$\tau $
-perpendicular subcategories of
 $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
. -
2. For
 ${\mathcal W}\subseteq \mathsf {mod}\Lambda $
a
${\mathcal W}\subseteq \mathsf {mod}\Lambda $
a
 $\tau $
-perpendicular subcategory and
$\tau $
-perpendicular subcategory and
 $U \in \mathcal C({\mathcal W})$
support
$U \in \mathcal C({\mathcal W})$
support
 $\tau $
-rigid and basic, define a formal symbol
$\tau $
-rigid and basic, define a formal symbol
 $g_U^{\mathcal W}$
.
$g_U^{\mathcal W}$
. -
3. Given
 ${\mathcal W}_1,{\mathcal W}_2$
two
${\mathcal W}_1,{\mathcal W}_2$
two
 $\tau $
-perpendicular subcategories of
$\tau $
-perpendicular subcategories of
 $\mathsf {mod}\Lambda $
, we define In particular:
$\mathsf {mod}\Lambda $
, we define In particular: $$ \begin{align*}\operatorname{{\mathrm{Hom}}}_{\mathfrak{W}(\Lambda)}({\mathcal W}_1, {\mathcal W}_2) = \left\{g_U^{{\mathcal W}_1} \middle\vert \begin{array}{l}U \text{ is a basic support } \tau\text{-rigid object in } \mathcal C({\mathcal W}_1) \\ \text{and }{\mathcal W}_2 = \mathcal J_{{\mathcal W}_1}(U)\end{array}\!\!\!\!\right\}.\end{align*} $$
$$ \begin{align*}\operatorname{{\mathrm{Hom}}}_{\mathfrak{W}(\Lambda)}({\mathcal W}_1, {\mathcal W}_2) = \left\{g_U^{{\mathcal W}_1} \middle\vert \begin{array}{l}U \text{ is a basic support } \tau\text{-rigid object in } \mathcal C({\mathcal W}_1) \\ \text{and }{\mathcal W}_2 = \mathcal J_{{\mathcal W}_1}(U)\end{array}\!\!\!\!\right\}.\end{align*} $$
-
(a) If
 ${\mathcal W}_1 \not \supseteq {\mathcal W}_2$
, then
${\mathcal W}_1 \not \supseteq {\mathcal W}_2$
, then
 $\operatorname {{\mathrm {Hom}}}_{\mathfrak {W}(\Lambda )}({\mathcal W}_1, {\mathcal W}_2) = \emptyset $
.
$\operatorname {{\mathrm {Hom}}}_{\mathfrak {W}(\Lambda )}({\mathcal W}_1, {\mathcal W}_2) = \emptyset $
. -
(b)
 $\operatorname {{\mathrm {Hom}}}_{\mathfrak {W}(\Lambda )}({\mathcal W}_1, {\mathcal W}_1) = g_0^{{\mathcal W}_1}.$
$\operatorname {{\mathrm {Hom}}}_{\mathfrak {W}(\Lambda )}({\mathcal W}_1, {\mathcal W}_1) = g_0^{{\mathcal W}_1}.$
-
-
4. Given
 $g_U^{{\mathcal W}_1}:{\mathcal W}_1 \rightarrow {\mathcal W}_2$
and
$g_U^{{\mathcal W}_1}:{\mathcal W}_1 \rightarrow {\mathcal W}_2$
and
 $g_V^{{\mathcal W}_2}:{\mathcal W}_2\rightarrow {\mathcal W}_3$
in
$g_V^{{\mathcal W}_2}:{\mathcal W}_2\rightarrow {\mathcal W}_3$
in
 $\mathfrak {W}(\Lambda )$
, denote
$\mathfrak {W}(\Lambda )$
, denote
 $\widetilde {V}:= \left (\mathcal E_U^{{\mathcal W}_1}\right )^{-1}(V)$
. We define
$\widetilde {V}:= \left (\mathcal E_U^{{\mathcal W}_1}\right )^{-1}(V)$
. We define  $$ \begin{align*}g_V^{{\mathcal W}_2} \circ g_U^{{\mathcal W}_1} = g_{U\sqcup \widetilde{V}}^{{\mathcal W}_1}.\end{align*} $$
$$ \begin{align*}g_V^{{\mathcal W}_2} \circ g_U^{{\mathcal W}_1} = g_{U\sqcup \widetilde{V}}^{{\mathcal W}_1}.\end{align*} $$
Remark 6.2. For
![]() $\tau $
-tilting finite algebras, it is well-known (see [Reference Marks and Šťovíček23]) that all wide subcategories are both left and right finite, so in particular, they are
$\tau $
-tilting finite algebras, it is well-known (see [Reference Marks and Šťovíček23]) that all wide subcategories are both left and right finite, so in particular, they are
![]() $\tau $
-perpendicular. The above definition therefore specializes to the definition in [Reference Buan and Marsh9].
$\tau $
-perpendicular. The above definition therefore specializes to the definition in [Reference Buan and Marsh9].
Remark 6.3. An independent generalization of the
![]() $\tau $
-cluster morphism category to arbitrary finite-dimensional algebras is given in the concurrent work of Børve [Reference Børve7]. The construction given there replaces
$\tau $
-cluster morphism category to arbitrary finite-dimensional algebras is given in the concurrent work of Børve [Reference Børve7]. The construction given there replaces
![]() $\tau $
-perpendicular subcategories with certain thick subcategories of the bounded derived category
$\tau $
-perpendicular subcategories with certain thick subcategories of the bounded derived category
![]() $\mathcal {D}^b(\mathsf {mod}\Lambda )$
and replaces support
$\mathcal {D}^b(\mathsf {mod}\Lambda )$
and replaces support
![]() $\tau $
-rigid objects with 2-term presilting objects. The composition law can then be described in terms of the (pre)silting reduction of Iyama–Yang [Reference Iyama and Yang21]. It is shown explicitly in [Reference Børve7] that our generalization and Børve’s yield categories which are equivalent.
$\tau $
-rigid objects with 2-term presilting objects. The composition law can then be described in terms of the (pre)silting reduction of Iyama–Yang [Reference Iyama and Yang21]. It is shown explicitly in [Reference Børve7] that our generalization and Børve’s yield categories which are equivalent.
The main goal of this section is to prove that the
![]() $\tau $
-cluster morphism category is indeed a well-defined category (Theorem 1.3, restated as Theorem 6.13). As with [Reference Buan and Marsh9, Reference Igusa17, Reference Igusa and Todorov18], the main technicality is in showing that the composition law is well-defined and associative. In the present article, this will be a consequence of the following generalization of [Reference Buan and Marsh9, Th. 4.3].
$\tau $
-cluster morphism category is indeed a well-defined category (Theorem 1.3, restated as Theorem 6.13). As with [Reference Buan and Marsh9, Reference Igusa17, Reference Igusa and Todorov18], the main technicality is in showing that the composition law is well-defined and associative. In the present article, this will be a consequence of the following generalization of [Reference Buan and Marsh9, Th. 4.3].
Theorem 6.4. Let
![]() ${\mathcal W}\subseteq \mathsf {mod}\Lambda $
be a
${\mathcal W}\subseteq \mathsf {mod}\Lambda $
be a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
. Let
$\mathsf {mod}\Lambda $
. Let
![]() $U\sqcup V$
be basic and support
$U\sqcup V$
be basic and support
![]() $\tau $
-rigid in
$\tau $
-rigid in
![]() $\mathcal C({\mathcal W})$
. Then
$\mathcal C({\mathcal W})$
. Then
Our proof of Theorem 6.4 is largely contained in the two technical lemmas which follow.
Lemma 6.5. Let
![]() $U \in \mathcal C(\mathsf {mod}\Lambda )$
and
$U \in \mathcal C(\mathsf {mod}\Lambda )$
and
![]() $N\in \mathsf {mod}\Lambda $
such that
$N\in \mathsf {mod}\Lambda $
such that
![]() $U\sqcup N$
is support
$U\sqcup N$
is support
![]() $\tau $
-rigid and basic. Write
$\tau $
-rigid and basic. Write
![]() $U = M \sqcup P[1]$
, and let
$U = M \sqcup P[1]$
, and let
![]() $\overline {N}$
be the direct sum of the indecomposable direct summands of N which do not lie in
$\overline {N}$
be the direct sum of the indecomposable direct summands of N which do not lie in
![]() $\mathsf {Gen} M$
. Then the following coincide:
$\mathsf {Gen} M$
. Then the following coincide:
-
1.
 $(\mathsf {Gen} N)\cap \mathcal J(U).$
$(\mathsf {Gen} N)\cap \mathcal J(U).$
-
2.
 $(\mathsf {Gen}(M\sqcup N))\cap \mathcal J(U).$
$(\mathsf {Gen}(M\sqcup N))\cap \mathcal J(U).$
-
3.
 $f_{(M^{\perp })}(\mathsf {Gen}(M\sqcup N)).$
$f_{(M^{\perp })}(\mathsf {Gen}(M\sqcup N)).$
-
4.
 $(\mathsf {Gen}(f_{(M^{\perp })}(N))) \cap \mathcal J(U).$
$(\mathsf {Gen}(f_{(M^{\perp })}(N))) \cap \mathcal J(U).$
-
5.
 $(\mathsf {Gen}(\mathcal E_U(\overline {N})))\cap \mathcal J(U).$
$(\mathsf {Gen}(\mathcal E_U(\overline {N})))\cap \mathcal J(U).$
Proof. The equality
![]() $(1) = (2)$
follows immediately from the fact that
$(1) = (2)$
follows immediately from the fact that
![]() $\mathcal J(U) \subseteq M^{\perp }$
.
$\mathcal J(U) \subseteq M^{\perp }$
.
We next show that
![]() $(2) = (3)$
. Note that by definition
$(2) = (3)$
. Note that by definition
Moreover, we have that
![]() since
since
![]() $U\sqcup N$
is support
$U\sqcup N$
is support
![]() $\tau $
-rigid. Now, if
$\tau $
-rigid. Now, if
![]() $X \in (\mathsf {Gen}(M\sqcup N))\cap \mathcal J(U)$
, then in particular,
$X \in (\mathsf {Gen}(M\sqcup N))\cap \mathcal J(U)$
, then in particular,
![]() $X \in M^{\perp }$
and so
$X \in M^{\perp }$
and so
![]() $f_{(M^{\perp })}(X) = X$
. We conclude that
$f_{(M^{\perp })}(X) = X$
. We conclude that
![]() $(2) = (3)$
.
$(2) = (3)$
.
We now show that
![]() $(3) = (4)$
. It is shown in [Reference Buan and Marsh9, Lem. 5.5] that
$(3) = (4)$
. It is shown in [Reference Buan and Marsh9, Lem. 5.5] that
Moreover, since
![]() $N \in P^{\perp }$
and
$N \in P^{\perp }$
and
![]() $f_{(M^{\perp })}(N) \in \mathsf {Gen} N$
, we have that
$f_{(M^{\perp })}(N) \in \mathsf {Gen} N$
, we have that
![]() $\mathsf {Gen}(f_{(M^{\perp })}(N)) \subseteq P^{\perp }$
. It follows that
$\mathsf {Gen}(f_{(M^{\perp })}(N)) \subseteq P^{\perp }$
. It follows that
![]() $(3) = (4)$
.
$(3) = (4)$
.
It remains to show that
![]() $(4) = (5)$
. This follows from the definition of
$(4) = (5)$
. This follows from the definition of
![]() $\mathcal E_U$
(see Theorem 5.1) and the fact that
$\mathcal E_U$
(see Theorem 5.1) and the fact that
![]() $f_{(M^{\perp })}(N) = f_{(M^{\perp })}(\overline {N})$
.
$f_{(M^{\perp })}(N) = f_{(M^{\perp })}(\overline {N})$
.
Lemma 6.6. Let
![]() $U \sqcup V \in \mathcal C(\mathsf {mod}\Lambda )$
be support
$U \sqcup V \in \mathcal C(\mathsf {mod}\Lambda )$
be support
![]() $\tau $
-rigid and basic. Let B be the Bongartz complement of
$\tau $
-rigid and basic. Let B be the Bongartz complement of
![]() $U\sqcup V$
(in
$U\sqcup V$
(in
![]() $\mathsf {mod}\Lambda $
). Write
$\mathsf {mod}\Lambda $
). Write
![]() $U = M\sqcup P[1], V = N\sqcup Q[1]$
, and
$U = M\sqcup P[1], V = N\sqcup Q[1]$
, and
![]() $\mathcal E_U(V) = L\sqcup R[1]$
. Then the following coincide:
$\mathcal E_U(V) = L\sqcup R[1]$
. Then the following coincide:
-
1.

-
2.

-
3.
 $\mathsf {Gen}(B\sqcup N \sqcup M)\cap \mathcal J(U).$
$\mathsf {Gen}(B\sqcup N \sqcup M)\cap \mathcal J(U).$
-
4.
 $\mathsf {Gen}(\mathcal E_U(B)\sqcup L)\cap \mathcal J(U).$
$\mathsf {Gen}(\mathcal E_U(B)\sqcup L)\cap \mathcal J(U).$
-
5.

Proof. The equality
![]() $(1) = (2)$
follows immediately from the fact that
$(1) = (2)$
follows immediately from the fact that
![]() . Likewise, the equality
. Likewise, the equality
![]() $(2) = (3)$
follows immediately from the definition of the Bongartz complement (Theorem 2.4).
$(2) = (3)$
follows immediately from the definition of the Bongartz complement (Theorem 2.4).
We next show that
![]() $(3) = (4)$
. By Theorem 5.1 and Lemma 5.3, we note that
$(3) = (4)$
. By Theorem 5.1 and Lemma 5.3, we note that
![]() $\mathcal E_U(B) \in \mathsf {mod}\Lambda $
. Moreover, Theorem 5.1 also implies (see Remark 5.2) that
$\mathcal E_U(B) \in \mathsf {mod}\Lambda $
. Moreover, Theorem 5.1 also implies (see Remark 5.2) that
![]() $\mathcal E_U(B) \sqcup L \sqcup R[1] = \mathcal E_U(B \sqcup V)$
is support
$\mathcal E_U(B) \sqcup L \sqcup R[1] = \mathcal E_U(B \sqcup V)$
is support
![]() $\tau $
-tilting in
$\tau $
-tilting in
![]() $\mathcal C(\mathcal J(U))$
. This means
$\mathcal C(\mathcal J(U))$
. This means
![]() $(3) = (4)$
is a special case of equation
$(3) = (4)$
is a special case of equation
![]() $(2) = (5)$
in Lemma 6.5.
$(2) = (5)$
in Lemma 6.5.
We proceed to show that
![]() $(4) \subseteq (5)$
. First, note that since R is projective in
$(4) \subseteq (5)$
. First, note that since R is projective in
![]() $\mathcal J(U)$
, we have that
$\mathcal J(U)$
, we have that
![]() is closed under factors in
is closed under factors in
![]() $\mathcal J(U)$
, and hence, it suffices to show that
$\mathcal J(U)$
, and hence, it suffices to show that
![]() . This follows from the fact that
. This follows from the fact that
![]() $\mathcal E_U(B) \sqcup L \sqcup R[1]$
is support
$\mathcal E_U(B) \sqcup L \sqcup R[1]$
is support
![]() $\tau $
-tilting in
$\tau $
-tilting in
![]() $\mathcal C(\mathcal J(U))$
.
$\mathcal C(\mathcal J(U))$
.
We will conclude by showing that
![]() $(5) \subseteq (2)$
. Let
$(5) \subseteq (2)$
. Let
![]() $B'$
be the Bongartz complement of
$B'$
be the Bongartz complement of
![]() $\mathcal E_U(V)$
in
$\mathcal E_U(V)$
in
![]() $\mathcal J(U)$
. Since
$\mathcal J(U)$
. Since
![]() $B'$
is a module, Theorem 5.1 implies that
$B'$
is a module, Theorem 5.1 implies that
![]() $\overline {B}:= \mathcal E_U^{-1}(B') \in \mathsf {mod}\Lambda $
and that
$\overline {B}:= \mathcal E_U^{-1}(B') \in \mathsf {mod}\Lambda $
and that
![]() $\overline {B}\sqcup U \sqcup V$
is support
$\overline {B}\sqcup U \sqcup V$
is support
![]() $\tau $
-tilting. We claim that
$\tau $
-tilting. We claim that

The first equality follows from Theorem 2.4, and the second from the equality
![]() $(2)= (5)$
in Lemma 6.5. The inclusion follows from the fact that
$(2)= (5)$
in Lemma 6.5. The inclusion follows from the fact that
![]() $\overline {B}\sqcup U \sqcup V$
is support
$\overline {B}\sqcup U \sqcup V$
is support
![]() $\tau $
-tilting, using that
$\tau $
-tilting, using that
![]() $(2)$
is closed under factors in
$(2)$
is closed under factors in
![]() $\mathcal J(U)$
.
$\mathcal J(U)$
.
We now proceed with our proof of Theorem 6.4.
Proof of Theorem 6.4
Since
![]() ${\mathcal W}$
is equivalent to the module category of a basic finite-dimensional algebra, it suffices to consider the case where
${\mathcal W}$
is equivalent to the module category of a basic finite-dimensional algebra, it suffices to consider the case where
![]() ${\mathcal W} = \mathsf {mod}\Lambda $
. Write
${\mathcal W} = \mathsf {mod}\Lambda $
. Write
![]() $U = M\sqcup P[1]$
,
$U = M\sqcup P[1]$
,
![]() $V = N\sqcup Q[1]$
, and
$V = N\sqcup Q[1]$
, and
![]() $\mathcal E_U(V) = L\sqcup R[1]$
. For readability, denote
$\mathcal E_U(V) = L\sqcup R[1]$
. For readability, denote
![]() ${\mathcal T}_0 = \mathsf {Gen}(N\sqcup M)$
and
${\mathcal T}_0 = \mathsf {Gen}(N\sqcup M)$
and
. Noting that
![]() $\mathcal J(U\sqcup V) \subseteq \mathcal J(U)$
, Lemmas 6.5 and 6.6 then imply that
$\mathcal J(U\sqcup V) \subseteq \mathcal J(U)$
, Lemmas 6.5 and 6.6 then imply that

Before, we proceed with proving the second main theorem, we note that Theorem 6.4 has some interesting consequences.
Corollary 6.7 (Corollary 1.2).
Let
![]() $\Lambda $
be a finite-dimensional algebra. Let
$\Lambda $
be a finite-dimensional algebra. Let
![]() $\mathcal V\subseteq {\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a chain of subcategories such that
$\mathcal V\subseteq {\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a chain of subcategories such that
![]() $\mathcal V$
is a
$\mathcal V$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() ${\mathcal W}$
and
${\mathcal W}$
and
![]() ${\mathcal W}$
is a
${\mathcal W}$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
. Then
$\mathsf {mod}\Lambda $
. Then
![]() $\mathcal V$
is a
$\mathcal V$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
.
Proof. Let
![]() $U \in \mathcal C(\mathsf {mod}\Lambda )$
and
$U \in \mathcal C(\mathsf {mod}\Lambda )$
and
![]() $V \in \mathcal C({\mathcal W})$
such that
$V \in \mathcal C({\mathcal W})$
such that
![]() ${\mathcal W} = \mathcal J(U)$
and
${\mathcal W} = \mathcal J(U)$
and
![]() $\mathcal V = \mathcal J_{\mathcal W}(V)$
. By Theorems 5.1 and 6.4, it follows that
$\mathcal V = \mathcal J_{\mathcal W}(V)$
. By Theorems 5.1 and 6.4, it follows that
![]() $U \sqcup \left (\mathcal E_U^{-1}(V)\right ) \in \mathcal C(\mathsf {mod}\Lambda )$
is support
$U \sqcup \left (\mathcal E_U^{-1}(V)\right ) \in \mathcal C(\mathsf {mod}\Lambda )$
is support
![]() $\tau $
-rigid and satisfies
$\tau $
-rigid and satisfies
We conclude that
![]() $\mathcal V$
is a
$\mathcal V$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
.
$\mathsf {mod}\Lambda $
.
In many cases, the converse of Corollary 1.2 holds as well. For example, in the
![]() $\tau $
-tilting finite case, all wide subcategories are
$\tau $
-tilting finite case, all wide subcategories are
![]() $\tau $
-perpendicular and in the hereditary case,
$\tau $
-perpendicular and in the hereditary case,
![]() $\tau $
-perpendicular subcategories and left-finite wide subcategories coincide. Each of these implies that if
$\tau $
-perpendicular subcategories and left-finite wide subcategories coincide. Each of these implies that if
![]() $\mathcal V$
and
$\mathcal V$
and
![]() ${\mathcal W}$
are
${\mathcal W}$
are
![]() $\tau $
-perpendicular subcategories of
$\tau $
-perpendicular subcategories of
![]() $\mathsf {mod}\Lambda $
with
$\mathsf {mod}\Lambda $
with
![]() $\mathcal V \subseteq {\mathcal W}$
, then
$\mathcal V \subseteq {\mathcal W}$
, then
![]() $\mathcal V$
is a
$\mathcal V$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() ${\mathcal W}$
. We expect that this is the case in general; that is, we propose the following conjecture.
${\mathcal W}$
. We expect that this is the case in general; that is, we propose the following conjecture.
Conjecture 6.8. Let
![]() $\Lambda $
be a finite-dimensional algebra. Let
$\Lambda $
be a finite-dimensional algebra. Let
![]() ${\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a
${\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
, and let
$\mathsf {mod}\Lambda $
, and let
![]() $\mathcal V \subseteq {\mathcal W}$
be a wide subcategory of
$\mathcal V \subseteq {\mathcal W}$
be a wide subcategory of
![]() ${\mathcal W}$
. Then
${\mathcal W}$
. Then
![]() $\mathcal V$
is a
$\mathcal V$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
if and only if
$\mathsf {mod}\Lambda $
if and only if
![]() $\mathcal V$
is a
$\mathcal V$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() ${\mathcal W}$
.
${\mathcal W}$
.
As another consequence of Theorem 6.4, we have the following.
Corollary 6.9. Let
![]() $\Lambda $
be a finite-dimensional algebra, and let
$\Lambda $
be a finite-dimensional algebra, and let
![]() ${\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a subcategory. Then
${\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a subcategory. Then
![]() ${\mathcal W}$
is a
${\mathcal W}$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
if and only if there exists a subcategory
$\mathsf {mod}\Lambda $
if and only if there exists a subcategory
![]() $\mathcal V$
with
$\mathcal V$
with
![]() ${\mathcal W}\subseteq \mathcal V\subseteq \mathsf {mod}\Lambda $
such that
${\mathcal W}\subseteq \mathcal V\subseteq \mathsf {mod}\Lambda $
such that
![]() $\mathcal V$
is a left-finite wide subcategory of
$\mathcal V$
is a left-finite wide subcategory of
![]() $\mathsf {mod}\Lambda $
and
$\mathsf {mod}\Lambda $
and
![]() ${\mathcal W}$
is a left-finite wide subcategory of
${\mathcal W}$
is a left-finite wide subcategory of
![]() $\mathcal V$
. Moreover, the statement is true if one or both instances of “left” are replaced with “right.”
$\mathcal V$
. Moreover, the statement is true if one or both instances of “left” are replaced with “right.”
Proof. First, suppose
![]() ${\mathcal W} = \mathcal J(U)$
is a
${\mathcal W} = \mathcal J(U)$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
. By Theorem 4.5, there exists
$\mathsf {mod}\Lambda $
. By Theorem 4.5, there exists
![]() ${\mathcal W} \subseteq \mathcal V \subseteq \mathsf {mod}\Lambda $
such that
${\mathcal W} \subseteq \mathcal V \subseteq \mathsf {mod}\Lambda $
such that
![]() $\mathcal V$
is a left-finite wide subcategory of
$\mathcal V$
is a left-finite wide subcategory of
![]() $\mathsf {mod}\Lambda $
and
$\mathsf {mod}\Lambda $
and
![]() ${\mathcal W}$
is a Serre subcategory of
${\mathcal W}$
is a Serre subcategory of
![]() $\mathcal V$
. By Corollary 3.8, it follows that
$\mathcal V$
. By Corollary 3.8, it follows that
![]() ${\mathcal W}$
is a left-finite wide subcategory of
${\mathcal W}$
is a left-finite wide subcategory of
![]() $\mathcal V$
as well.
$\mathcal V$
as well.
Now, suppose that there exists
![]() ${\mathcal W} \subseteq \mathcal V \subseteq \mathsf {mod}\Lambda $
such that
${\mathcal W} \subseteq \mathcal V \subseteq \mathsf {mod}\Lambda $
such that
![]() ${\mathcal W}$
is a left-finite wide subcategory of
${\mathcal W}$
is a left-finite wide subcategory of
![]() $\mathcal V$
and
$\mathcal V$
and
![]() $\mathcal V$
is a left-finite wide subcategory of
$\mathcal V$
is a left-finite wide subcategory of
![]() $\mathsf {mod}\Lambda $
. Then
$\mathsf {mod}\Lambda $
. Then
![]() ${\mathcal W}$
is a
${\mathcal W}$
is a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda $
as an immediate consequence of Lemma 4.3 and Corollary 6.7.
$\mathsf {mod}\Lambda $
as an immediate consequence of Lemma 4.3 and Corollary 6.7.
The proofs where one or both instances of “left” are replaced with “right” are identical.
We now proceed with the proof of the main theorem. In [Reference Buan and Marsh9], which deals with the
![]() $\tau $
-tilting finite case, one establishes associativity of the composition operation, by proving that
$\tau $
-tilting finite case, one establishes associativity of the composition operation, by proving that
for any basic support
![]() $\tau $
-rigid
$\tau $
-rigid
![]() $U\sqcup V \in \mathcal C(\mathsf {mod}\Lambda )$
. This is shown to be a consequence of the fact that
$U\sqcup V \in \mathcal C(\mathsf {mod}\Lambda )$
. This is shown to be a consequence of the fact that
However, the proof that (5) implies (4) given in [Reference Buan and Marsh9, Sec. 5–9] does not use that
![]() $\Lambda $
is
$\Lambda $
is
![]() $\tau $
-tilting finite. We have shown in Theorem 6.4 that Equation (5) holds for
$\tau $
-tilting finite. We have shown in Theorem 6.4 that Equation (5) holds for
![]() $\tau $
-perpendicular subcategories in the general case, and hence, we obtain (4) for free. Note that in the
$\tau $
-perpendicular subcategories in the general case, and hence, we obtain (4) for free. Note that in the
![]() $\tau $
-tilting finite case, in fact, all wide subcategories are
$\tau $
-tilting finite case, in fact, all wide subcategories are
![]() $\tau $
-perpendicular.
$\tau $
-perpendicular.
We will here provide an alternative and much more efficient proof of why (5) implies (4) in the general case, which only builds on two short lemmas in [Reference Buan and Marsh9], namely, Lemmas 5.5 (via Lemma 6.5 in the present article) and 6.2. This is completed in Theorem 6.12, but we first prepare with an additional technical lemma.
Lemma 6.10. Let
![]() $U\sqcup V \in \mathcal C(\mathsf {mod}\Lambda )$
and
$U\sqcup V \in \mathcal C(\mathsf {mod}\Lambda )$
and
![]() $L \in \mathsf {mod}\Lambda $
such that
$L \in \mathsf {mod}\Lambda $
such that
![]() $U\sqcup V \sqcup L$
is support
$U\sqcup V \sqcup L$
is support
![]() $\tau $
-rigid and basic. Let
$\tau $
-rigid and basic. Let
![]() $\overline {N}$
be the direct sum of the indecomposable direct summands of N which do not lie in
$\overline {N}$
be the direct sum of the indecomposable direct summands of N which do not lie in
![]() $\mathsf {Gen} M$
. Let
$\mathsf {Gen} M$
. Let
![]() $L'$
be an indecomposable direct summand of L. Then the following are equivalent.
$L'$
be an indecomposable direct summand of L. Then the following are equivalent.
-
1.
 $\mathcal E_{U\sqcup V}(L')$
is a module.
$\mathcal E_{U\sqcup V}(L')$
is a module. -
2.
 $L' \notin \mathsf {Gen}(M\sqcup N).$
$L' \notin \mathsf {Gen}(M\sqcup N).$
-
3.
 $L' \notin \mathsf {Gen} M$
and
$L' \notin \mathsf {Gen} M$
and
 $f_{(M^{\perp })}(L') \notin (\mathsf {Gen}(f_{(M^{\perp })}(\overline {N})))\cap \mathcal J(U).$
$f_{(M^{\perp })}(L') \notin (\mathsf {Gen}(f_{(M^{\perp })}(\overline {N})))\cap \mathcal J(U).$
-
4.
 $\mathcal E_U(L')$
is a module and
$\mathcal E_U(L')$
is a module and
 $\mathcal E_U(L') \notin (\mathsf {Gen}(\mathcal E_U(\overline {N})))\cap \mathcal J(U).$
$\mathcal E_U(L') \notin (\mathsf {Gen}(\mathcal E_U(\overline {N})))\cap \mathcal J(U).$
-
5.
 $\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_{U}(L')$
is a module.
$\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_{U}(L')$
is a module.
Moreover, if (1)–(5) hold, then
![]() $\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_{U}(L') = \mathcal E_{U\sqcup V}(L')$
.
$\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_{U}(L') = \mathcal E_{U\sqcup V}(L')$
.
Proof. The equivalences
![]() $(1\iff 2)$
,
$(1\iff 2)$
,
![]() $(3\iff 4)$
, and
$(3\iff 4)$
, and
![]() $(4\iff 5)$
all follow from the definitions of the “
$(4\iff 5)$
all follow from the definitions of the “
![]() $\mathcal E$
-maps” given in Theorem 5.1.
$\mathcal E$
-maps” given in Theorem 5.1.
For the equivalence
![]() $(2\iff 3)$
, we note that
$(2\iff 3)$
, we note that
![]() $L' \notin \mathsf {Gen}(M\sqcup N)$
if and only if
$L' \notin \mathsf {Gen}(M\sqcup N)$
if and only if
by Lemma 6.5. This, together with the fact that if
![]() $L' \notin \mathsf {Gen}(M\sqcup N),$
then
$L' \notin \mathsf {Gen}(M\sqcup N),$
then
![]() $L' \notin \mathsf {Gen} M$
, proves the equivalence of (2) and (3).
$L' \notin \mathsf {Gen} M$
, proves the equivalence of (2) and (3).
Now suppose that (1)–(5) hold. For readability, denote
![]() $L":= f_{(M^{\perp })}(L')$
and denote
$L":= f_{(M^{\perp })}(L')$
and denote
![]() ${\mathcal T} := f_{(M^{\perp })}(\mathsf {Gen}(M\sqcup N))$
. Recall from Lemma 6.5 that
${\mathcal T} := f_{(M^{\perp })}(\mathsf {Gen}(M\sqcup N))$
. Recall from Lemma 6.5 that
![]() ${\mathcal T} = (\mathsf {Gen}(f_{(M^{\perp })}(N))) \cap \mathcal J(U)$
. In particular, we have
${\mathcal T} = (\mathsf {Gen}(f_{(M^{\perp })}(N))) \cap \mathcal J(U)$
. In particular, we have
![]() ${\mathcal T} \subseteq \mathcal J(U)\subseteq \mathcal J(M)$
. Now, denote by
${\mathcal T} \subseteq \mathcal J(U)\subseteq \mathcal J(M)$
. Now, denote by
the canonical exact sequence with respect to the torsion pair
![]() $({\mathcal T},{\mathcal T}^{\perp } \cap \mathcal J(U))$
in
$({\mathcal T},{\mathcal T}^{\perp } \cap \mathcal J(U))$
in
![]() $\mathcal J(U)$
. Likewise, denote by
$\mathcal J(U)$
. Likewise, denote by
the canonical exact sequence with respect to the torsion pair
![]() $({\mathcal T},{\mathcal T}^{\perp } \cap \mathcal J(M))$
in
$({\mathcal T},{\mathcal T}^{\perp } \cap \mathcal J(M))$
in
![]() $\mathcal J(M)$
. Since both sequences start with
$\mathcal J(M)$
. Since both sequences start with
![]() $t_{\mathcal T}(L")$
, we see that
$t_{\mathcal T}(L")$
, we see that
![]() $f_{({\mathcal T}^{\perp }\cap \mathcal J(U))}(L") = f_{({\mathcal T}^{\perp }\cap \mathcal J(M))}(L")$
.
$f_{({\mathcal T}^{\perp }\cap \mathcal J(U))}(L") = f_{({\mathcal T}^{\perp }\cap \mathcal J(M))}(L")$
.
We now observe that
![]() $\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_{U}(L') = f_{({\mathcal T}^{\perp }\cap \mathcal J(U))}(L")$
and
$\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_{U}(L') = f_{({\mathcal T}^{\perp }\cap \mathcal J(U))}(L")$
and
![]() $\mathcal E_{(U\sqcup V)} = f_{((M\sqcup N)^{\perp })}(L')$
by construction. Finally, it is shown in [Reference Buan and Marsh9, Lem. 6.2] that
$\mathcal E_{(U\sqcup V)} = f_{((M\sqcup N)^{\perp })}(L')$
by construction. Finally, it is shown in [Reference Buan and Marsh9, Lem. 6.2] that
![]() $f_{({\mathcal T}^{\perp }\cap \mathcal J(M))}(L") = f_{((M\sqcup N)^{\perp })}(L')$
. We conclude that
$f_{({\mathcal T}^{\perp }\cap \mathcal J(M))}(L") = f_{((M\sqcup N)^{\perp })}(L')$
. We conclude that
![]() $\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_{U}(L') = \mathcal E_{U\sqcup V}(L')$
as desired.
$\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_{U}(L') = \mathcal E_{U\sqcup V}(L')$
as desired.
Remark 6.11. Since the bijections
![]() $\mathcal E_U$
and
$\mathcal E_U$
and
![]() $\mathcal E^{\mathcal W}_U$
are additive, the assumption that
$\mathcal E^{\mathcal W}_U$
are additive, the assumption that
![]() $L'$
is indecomposable in Lemma 6.6 can be replaced with the assumption that no direct summand of
$L'$
is indecomposable in Lemma 6.6 can be replaced with the assumption that no direct summand of
![]() $L'$
lies in
$L'$
lies in
![]() $\mathsf {Gen}(M\sqcup N)$
.
$\mathsf {Gen}(M\sqcup N)$
.
We are now prepared to verify Equation (4).
Theorem 6.12. Let
![]() ${\mathcal W}\subseteq \mathsf {mod}\Lambda $
be a
${\mathcal W}\subseteq \mathsf {mod}\Lambda $
be a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() $\mathsf {mod}\Lambda ,$
and let
$\mathsf {mod}\Lambda ,$
and let
![]() $U\sqcup V \in \mathcal C({\mathcal W})$
be support
$U\sqcup V \in \mathcal C({\mathcal W})$
be support
![]() $\tau $
-rigid and basic. Then
$\tau $
-rigid and basic. Then
Proof. Since
![]() ${\mathcal W}$
is equivalent to the module category of a basic finite-dimensional algebra, it suffices to consider the case where
${\mathcal W}$
is equivalent to the module category of a basic finite-dimensional algebra, it suffices to consider the case where
![]() ${\mathcal W} = \mathsf {mod}\Lambda $
.
${\mathcal W} = \mathsf {mod}\Lambda $
.
Let
![]() $W \in \mathcal C(\mathsf {mod}\Lambda )$
such that
$W \in \mathcal C(\mathsf {mod}\Lambda )$
such that
![]() $U\sqcup V\sqcup W$
is support
$U\sqcup V\sqcup W$
is support
![]() $\tau $
-rigid and basic. Write
$\tau $
-rigid and basic. Write
![]() $U = M\sqcup P[1]$
and
$U = M\sqcup P[1]$
and
![]() $V = N\sqcup Q[1]$
. Let
$V = N\sqcup Q[1]$
. Let
![]() $\overline {L}$
be the direct sum of the indecomposable direct summands of W which are modules and do not lie in
$\overline {L}$
be the direct sum of the indecomposable direct summands of W which are modules and do not lie in
![]() $\mathsf {Gen}(M\sqcup N)$
, and let
$\mathsf {Gen}(M\sqcup N)$
, and let
![]() $W' \in \mathcal C(\mathsf {mod}\Lambda )$
such that
$W' \in \mathcal C(\mathsf {mod}\Lambda )$
such that
![]() $\overline {L}\sqcup W' = W$
. Let
$\overline {L}\sqcup W' = W$
. Let
![]() $B \in \mathsf {mod}\Lambda $
be the Bongartz complement of
$B \in \mathsf {mod}\Lambda $
be the Bongartz complement of
![]() $U\sqcup V\sqcup W$
. We recall from Lemma 5.3 that no direct summand of B lies in
$U\sqcup V\sqcup W$
. We recall from Lemma 5.3 that no direct summand of B lies in
![]() $\mathsf {Gen}(M\sqcup N)$
. Therefore, by Lemma 6.10 and Remark 6.11, we have that
$\mathsf {Gen}(M\sqcup N)$
. Therefore, by Lemma 6.10 and Remark 6.11, we have that
![]() $\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_U(B\sqcup \overline {L}) = \mathcal E_{U\sqcup V}(B\sqcup \overline {L})$
. Moreover, this equation also holds if
$\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_U(B\sqcup \overline {L}) = \mathcal E_{U\sqcup V}(B\sqcup \overline {L})$
. Moreover, this equation also holds if
![]() $B\sqcup \overline {L}$
is replaced with any of its (not necessarily indecomposable) direct summands.
$B\sqcup \overline {L}$
is replaced with any of its (not necessarily indecomposable) direct summands.
For readability, denote
![]() $B' := \mathcal E_{U\sqcup V}(B)$
and
$B' := \mathcal E_{U\sqcup V}(B)$
and
![]() $L' := \mathcal E_{U\sqcup V}(\overline {L})$
. Now, recall from Theorem 6.4 that
$L' := \mathcal E_{U\sqcup V}(\overline {L})$
. Now, recall from Theorem 6.4 that
![]() $\mathcal J(U\sqcup V) = \mathcal J_{\mathcal J(U)}(\mathcal E_U(V))$
. Theorem 2.4 and Lemma 6.6 then imply that (i) both
$\mathcal J(U\sqcup V) = \mathcal J_{\mathcal J(U)}(\mathcal E_U(V))$
. Theorem 2.4 and Lemma 6.6 then imply that (i) both
![]() $\mathcal E_{U\sqcup V}(W')$
and
$\mathcal E_{U\sqcup V}(W')$
and
![]() $\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_U(W')$
lie in
$\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_U(W')$
lie in
![]() $\mathcal J(U\sqcup V)[1]$
, and (ii) both
$\mathcal J(U\sqcup V)[1]$
, and (ii) both
![]() $B'\sqcup L' \sqcup \mathcal E_{U\sqcup V}(W')$
and
$B'\sqcup L' \sqcup \mathcal E_{U\sqcup V}(W')$
and
![]() $B'\sqcup L'\sqcup \mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_U(W')$
are support
$B'\sqcup L'\sqcup \mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_U(W')$
are support
![]() $\tau $
-tilting in
$\tau $
-tilting in
![]() $\mathcal C(\mathcal J(U\sqcup V))$
. This implies that
$\mathcal C(\mathcal J(U\sqcup V))$
. This implies that
![]() $\mathcal E_U(W') = \mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_U(W')$
, as both coincide with the co-Bongartz complement of
$\mathcal E_U(W') = \mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)} \circ \mathcal E_U(W')$
, as both coincide with the co-Bongartz complement of
![]() $B'\sqcup L'$
in
$B'\sqcup L'$
in
![]() $\mathcal J(U\sqcup V)$
.
$\mathcal J(U\sqcup V)$
.
Now, recall that
![]() $W = \overline {L}\sqcup W'$
. Since all of the bijections
$W = \overline {L}\sqcup W'$
. Since all of the bijections
![]() $\mathcal E_U$
,
$\mathcal E_U$
,
![]() $\mathcal E_{U\sqcup V}$
, and
$\mathcal E_{U\sqcup V}$
, and
![]() $\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)}$
are additive, the previous two paragraphs imply that
$\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)}$
are additive, the previous two paragraphs imply that
![]() $\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)}\circ \mathcal E_U(W) = \mathcal E_{U\sqcup V}(W)$
. This completes the proof.
$\mathcal E_{\mathcal E_U(V)}^{\mathcal J(U)}\circ \mathcal E_U(W) = \mathcal E_{U\sqcup V}(W)$
. This completes the proof.
We are now ready to complete the proof that the
![]() $\tau $
-cluster morphism category is indeed a category. This essentially follows from Theorem 6.12 identically as in [Reference Buan and Marsh9, Cor. 1.8], [Reference Igusa17, Sec. 1], and [Reference Igusa and Todorov18, Cor. 1.10].
$\tau $
-cluster morphism category is indeed a category. This essentially follows from Theorem 6.12 identically as in [Reference Buan and Marsh9, Cor. 1.8], [Reference Igusa17, Sec. 1], and [Reference Igusa and Todorov18, Cor. 1.10].
Theorem 6.13 (Theorem 1.3).
Let
![]() $\Lambda $
be a finite-dimensional algebra. Then
$\Lambda $
be a finite-dimensional algebra. Then
![]() $\mathfrak {W}(\Lambda )$
is a well-defined category.
$\mathfrak {W}(\Lambda )$
is a well-defined category.
Proof. It is straightforward to show that for any
![]() $\tau $
-perpendicular subcategory
$\tau $
-perpendicular subcategory
![]() ${\mathcal W} \subseteq \mathsf {mod}\Lambda $
, the morphism
${\mathcal W} \subseteq \mathsf {mod}\Lambda $
, the morphism
![]() $g_0^{\mathcal W}$
is the identity of
$g_0^{\mathcal W}$
is the identity of
![]() ${\mathcal W}$
. Thus, we need only show that the composition law is associative. Consider
${\mathcal W}$
. Thus, we need only show that the composition law is associative. Consider
a sequence of three composable morphisms in
![]() $\mathfrak {W}$
. Then, by Theorem 6.12 and the additivity of the “
$\mathfrak {W}$
. Then, by Theorem 6.12 and the additivity of the “
![]() $\mathcal E$
-maps,” we have
$\mathcal E$
-maps,” we have
 $$ \begin{align*} \left(g_W^{{\mathcal W}_3}\circ g_{V}^{{\mathcal W}_2}\right)\circ g_U^{{\mathcal W}_1} &= g_{V\sqcup \left(\mathcal E_V^{{\mathcal W}_2}\right)^{-1}(W)}^{{\mathcal W}_2}\circ g_U^{{\mathcal W}_1}\\ &= g_{U\sqcup \left(\mathcal E_U^{{\mathcal W}_1}\right)^{-1}(V) \sqcup \left(\mathcal E_V^{{\mathcal W}_2}\circ \mathcal E_U^{{\mathcal W}_1}\right)^{-1}(W)}^{{\mathcal W}_1}\\ &= g_W^{{\mathcal W}_3} \circ g_{U\sqcup \left(\mathcal E_W^{{\mathcal W}_1}\right)^{-1}(V)}^{{\mathcal W}_1}\\ &= g_W^{{\mathcal W}_3}\circ\left( g_{V}^{{\mathcal W}_2}\circ g_W^{{\mathcal W}_1}\right).\\[-37pt] \end{align*} $$
$$ \begin{align*} \left(g_W^{{\mathcal W}_3}\circ g_{V}^{{\mathcal W}_2}\right)\circ g_U^{{\mathcal W}_1} &= g_{V\sqcup \left(\mathcal E_V^{{\mathcal W}_2}\right)^{-1}(W)}^{{\mathcal W}_2}\circ g_U^{{\mathcal W}_1}\\ &= g_{U\sqcup \left(\mathcal E_U^{{\mathcal W}_1}\right)^{-1}(V) \sqcup \left(\mathcal E_V^{{\mathcal W}_2}\circ \mathcal E_U^{{\mathcal W}_1}\right)^{-1}(W)}^{{\mathcal W}_1}\\ &= g_W^{{\mathcal W}_3} \circ g_{U\sqcup \left(\mathcal E_W^{{\mathcal W}_1}\right)^{-1}(V)}^{{\mathcal W}_1}\\ &= g_W^{{\mathcal W}_3}\circ\left( g_{V}^{{\mathcal W}_2}\circ g_W^{{\mathcal W}_1}\right).\\[-37pt] \end{align*} $$
For
![]() ${\mathcal W}\subseteq \mathsf {mod}\Lambda $
a
${\mathcal W}\subseteq \mathsf {mod}\Lambda $
a
![]() $\tau $
-perpendicular subcategory, we can likewise define the
$\tau $
-perpendicular subcategory, we can likewise define the
![]() $\tau $
-cluster morphism category
$\tau $
-cluster morphism category
![]() $\mathfrak {W}({\mathcal W})$
in the usual way; that is, by identifying
$\mathfrak {W}({\mathcal W})$
in the usual way; that is, by identifying
![]() ${\mathcal W}$
with some module category. We then obtain the following.
${\mathcal W}$
with some module category. We then obtain the following.
Proposition 6.14. Let
![]() ${\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a
${\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a
![]() $\tau $
-perpendicular subcategory. Then
$\tau $
-perpendicular subcategory. Then
![]() $\mathfrak {W}({\mathcal W})$
is equivalent to the full subcategory of
$\mathfrak {W}({\mathcal W})$
is equivalent to the full subcategory of
![]() $\mathfrak {W}(\Lambda )$
whose objects are the
$\mathfrak {W}(\Lambda )$
whose objects are the
![]() $\tau $
-perpendicular subcategories of
$\tau $
-perpendicular subcategories of
![]() ${\mathcal W}$
.
${\mathcal W}$
.
Proof. This is a straightforward consequence of Corollary 6.7.
We conclude this section by generalizing the results of [Reference Buan and Marsh9, Sec. 10].
Proposition 6.15.
-
1. Let M be an indecomposable non-projective
 $\tau $
-rigid module, and let
$\tau $
-rigid module, and let
 $B_M$
be the Bongartz complement of M. Then
$B_M$
be the Bongartz complement of M. Then
 $M \in \mathsf {Gen} B_M$
and
$M \in \mathsf {Gen} B_M$
and
 $\mathcal J(M) = {\mathcal W}_L(\mathsf {Gen} B_M)$
.
$\mathcal J(M) = {\mathcal W}_L(\mathsf {Gen} B_M)$
. -
2. Let M and N be indecomposable
 $\tau $
-rigid modules. Then
$\tau $
-rigid modules. Then
 $\mathcal J(M) = \mathcal J(N)$
if and only if
$\mathcal J(M) = \mathcal J(N)$
if and only if
 $M \cong N$
.
$M \cong N$
.
Proof. (1) As in the proof of [Reference Buan and Marsh9, Lem. 10.6], we have that the indecomposable direct summands of B are split projective in
![]() . If in addition, M is split projective in
. If in addition, M is split projective in
![]() , then
, then
![]() $\mathsf {Gen}(B \sqcup M) = \mathsf {mod}\Lambda $
by Theorem 2.4 and Proposition 2.7. Since
$\mathsf {Gen}(B \sqcup M) = \mathsf {mod}\Lambda $
by Theorem 2.4 and Proposition 2.7. Since
![]() $B\sqcup M$
is
$B\sqcup M$
is
![]() $\tau $
-tilting, this implies that
$\tau $
-tilting, this implies that
![]() $B\sqcup M = \Lambda $
and M is projective, a contradiction. We conclude that M is not split projective in
$B\sqcup M = \Lambda $
and M is projective, a contradiction. We conclude that M is not split projective in
![]() , and so the result is a special case of Lemma 4.3.
, and so the result is a special case of Lemma 4.3.
(2) Suppose that
![]() $\mathcal J(M) = \mathcal J(N)$
. We first consider the case where neither M nor N is projective. Let
$\mathcal J(M) = \mathcal J(N)$
. We first consider the case where neither M nor N is projective. Let
![]() $B_M$
be the Bongartz complement of M and
$B_M$
be the Bongartz complement of M and
![]() $B_N$
the Bongartz complement of N. Then by (1), we have
$B_N$
the Bongartz complement of N. Then by (1), we have
![]() ${\mathcal W}_L(\mathsf {Gen} B_M) = \mathcal J(M) = \mathcal J(N) = {\mathcal W}_L(\mathsf {Gen} B_N)$
. This then implies that
${\mathcal W}_L(\mathsf {Gen} B_M) = \mathcal J(M) = \mathcal J(N) = {\mathcal W}_L(\mathsf {Gen} B_N)$
. This then implies that
![]() $\mathsf {Gen} B_M = \mathsf {Gen} B_N$
. It follows that
$\mathsf {Gen} B_M = \mathsf {Gen} B_N$
. It follows that
![]() $M \cong N$
is the unique indecomposable ext-projective in this torsion class which is not split-projective.
$M \cong N$
is the unique indecomposable ext-projective in this torsion class which is not split-projective.
Now, suppose that M is projective. Since M is indecomposable, we note that
![]() $\mathsf {top}(M)$
is simple. Moreover, given an arbitrary simple
$\mathsf {top}(M)$
is simple. Moreover, given an arbitrary simple
![]() $S \in \mathsf {mod}\Lambda $
, we have that
$S \in \mathsf {mod}\Lambda $
, we have that
![]() $S \in \mathcal J(M)$
if and only if
$S \in \mathcal J(M)$
if and only if
![]() $S \ncong \mathsf {top}(M)$
. In particular, if
$S \ncong \mathsf {top}(M)$
. In particular, if
![]() $S \ncong \mathsf {top}(M)$
, then
$S \ncong \mathsf {top}(M)$
, then
![]() $\operatorname {{\mathrm {Hom}}}(N,S) = 0 = \operatorname {{\mathrm {Hom}}}(S,\tau N)$
. We conclude that
$\operatorname {{\mathrm {Hom}}}(N,S) = 0 = \operatorname {{\mathrm {Hom}}}(S,\tau N)$
. We conclude that
![]() $\mathsf {top}(M) \cong \mathsf {top}(N)$
and that
$\mathsf {top}(M) \cong \mathsf {top}(N)$
and that
![]() $\mathsf {soc}(\tau N) = 0$
. In particular, this means
$\mathsf {soc}(\tau N) = 0$
. In particular, this means
![]() $M \cong N$
.
$M \cong N$
.
Theorem 6.16. Let
![]() $\Lambda $
be a finite-dimensional algebra, and let
$\Lambda $
be a finite-dimensional algebra, and let
![]() ${\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a
${\mathcal W} \subseteq \mathsf {mod}\Lambda $
be a
![]() $\tau $
-perpendicular subcategory. Let
$\tau $
-perpendicular subcategory. Let
![]() $\mathcal V \subseteq {\mathcal W}$
be a
$\mathcal V \subseteq {\mathcal W}$
be a
![]() $\tau $
-perpendicular subcategory of
$\tau $
-perpendicular subcategory of
![]() ${\mathcal W}$
such that
${\mathcal W}$
such that
![]() $\mathsf {rk}({\mathcal W}) = \mathsf {rk}(\mathcal V) + 1$
. Then exactly one of the following occurs:
$\mathsf {rk}({\mathcal W}) = \mathsf {rk}(\mathcal V) + 1$
. Then exactly one of the following occurs:
-
1. There is exactly one morphism in
 $\mathfrak {W}(\Lambda )$
from
$\mathfrak {W}(\Lambda )$
from
 ${\mathcal W}$
to
${\mathcal W}$
to
 $\mathcal V$
and
$\mathcal V$
and
 $\mathcal V = \mathcal J_{\mathcal W}(M)$
for some indecomposable module M which is
$\mathcal V = \mathcal J_{\mathcal W}(M)$
for some indecomposable module M which is
 $\tau $
-rigid, but not projective, in
$\tau $
-rigid, but not projective, in
 ${\mathcal W}$
.
${\mathcal W}$
. -
2. There are exactly two morphisms in
 $\mathfrak {W}(\Lambda )$
from
$\mathfrak {W}(\Lambda )$
from
 ${\mathcal W}$
to
${\mathcal W}$
to
 $\mathcal V$
and
$\mathcal V$
and
 $\mathcal V = \mathcal J_{\mathcal W}(P) = \mathcal J_{\mathcal W}(P[1])$
for some indecomposable module P which is projective in
$\mathcal V = \mathcal J_{\mathcal W}(P) = \mathcal J_{\mathcal W}(P[1])$
for some indecomposable module P which is projective in
 ${\mathcal W}$
.
${\mathcal W}$
.
Proof. By Proposition 6.14, we can assume that
![]() ${\mathcal W} = \mathsf {mod}\Lambda $
. Theorem 3.3 then implies that there exists an indecomposable support
${\mathcal W} = \mathsf {mod}\Lambda $
. Theorem 3.3 then implies that there exists an indecomposable support
![]() $\tau $
-rigid
$\tau $
-rigid
![]() $U \in \mathcal C(\mathsf {mod}\Lambda )$
such that
$U \in \mathcal C(\mathsf {mod}\Lambda )$
such that
![]() $\mathcal J(U) = \mathcal V$
. The result then follows from Proposition 6.15 and the fact that
$\mathcal J(U) = \mathcal V$
. The result then follows from Proposition 6.15 and the fact that
![]() $\mathcal J(P) = \mathcal J(P[1])$
for any projective module P.
$\mathcal J(P) = \mathcal J(P[1])$
for any projective module P.
Remark 6.17. In [Reference Buan and Marsh9, Sec. 10], the results generalized here are stated as relationships between the lattice of wide subcategories and the
![]() $\tau $
-cluster morphism category. (The partial order on the lattice of wide subcategories is given by containment, and the meet of two wide subcategories is their intersection.) In the
$\tau $
-cluster morphism category. (The partial order on the lattice of wide subcategories is given by containment, and the meet of two wide subcategories is their intersection.) In the
![]() $\tau $
-tilting infinite case, however, the set of
$\tau $
-tilting infinite case, however, the set of
![]() $\tau $
-perpendicular subcategories may not be closed under intersections and may not form a lattice. See, for example, [Reference Ringel24, Exam. 3.2.2 and 3.2.3], which show that path algebras of type
$\tau $
-perpendicular subcategories may not be closed under intersections and may not form a lattice. See, for example, [Reference Ringel24, Exam. 3.2.2 and 3.2.3], which show that path algebras of type
![]() $\widetilde {A}_{2,1}$
and
$\widetilde {A}_{2,1}$
and
![]() $\widetilde {A}_{2,2}$
, respectively, exhibit such behavior.Footnote
1
The authors thank Haruhisa Enomoto for sharing these examples with them.
$\widetilde {A}_{2,2}$
, respectively, exhibit such behavior.Footnote
1
The authors thank Haruhisa Enomoto for sharing these examples with them.
7 An example
In this section, we consider a pair of examples. As examples in the
![]() $\tau $
-tilting finite case can be found in [Reference Buan and Marsh9, Sec. 12], our examples are both
$\tau $
-tilting finite case can be found in [Reference Buan and Marsh9, Sec. 12], our examples are both
![]() $\tau $
-tilting infinite. This means the corresponding
$\tau $
-tilting infinite. This means the corresponding
![]() $\tau $
-cluster morphism categories are infinite as well.
$\tau $
-cluster morphism categories are infinite as well.
We first consider the Kronecker path algebra
![]() $\Lambda _1 = K(1\rightrightarrows 2).$
For
$\Lambda _1 = K(1\rightrightarrows 2).$
For
![]() $i \in \mathbb {N}$
, we denote by
$i \in \mathbb {N}$
, we denote by
![]() $M_{(i,i+1)}$
and
$M_{(i,i+1)}$
and
![]() $M_{(i+1,i)}$
the unique (up to isomorphism) indecomposable
$M_{(i+1,i)}$
the unique (up to isomorphism) indecomposable
![]() $\Lambda _1$
-modules with dimension vectors
$\Lambda _1$
-modules with dimension vectors
![]() $(i,i+1)$
and
$(i,i+1)$
and
![]() $(i+1,i)$
. We note that
$(i+1,i)$
. We note that
![]() $P(1) = M_{(1,2)}$
,
$P(1) = M_{(1,2)}$
,
![]() $S(1) = M_{(1,0)}$
, and
$S(1) = M_{(1,0)}$
, and
![]() $P(2) = S(2) = M_{(0,1)}$
.
$P(2) = S(2) = M_{(0,1)}$
.
Figure 1 is an illustration of the category
![]() $\mathfrak {W}(\Lambda _1)$
. The vertices are the
$\mathfrak {W}(\Lambda _1)$
. The vertices are the
![]() $\tau $
-perpendicular subcategories of
$\tau $
-perpendicular subcategories of
![]() $\mathsf {mod}\Lambda $
(which in this case are precisely the functorially finite wide subcategories). An irreducible morphism
$\mathsf {mod}\Lambda $
(which in this case are precisely the functorially finite wide subcategories). An irreducible morphism
![]() $g_U^{\mathcal W}:{\mathcal W}\rightarrow \mathcal V$
(so that U is indecomposable and support
$g_U^{\mathcal W}:{\mathcal W}\rightarrow \mathcal V$
(so that U is indecomposable and support
![]() $\tau $
-rigid in
$\tau $
-rigid in
![]() $\mathcal C({\mathcal W})$
and
$\mathcal C({\mathcal W})$
and
![]() $\mathcal J_{\mathcal W}(U) = \mathcal V)$
is shown as an arrow
$\mathcal J_{\mathcal W}(U) = \mathcal V)$
is shown as an arrow
![]() ${\mathcal W}\rightarrow \mathcal V$
labeled by U. The wide subcategories
${\mathcal W}\rightarrow \mathcal V$
labeled by U. The wide subcategories
![]() $\mathsf {add}\{M_{(i,i+1)}\}$
generated by the preprojective modules all appear above the horizontal dashed line, with i increasing as one moves counter clockwise. Likewise, the wide subcategories
$\mathsf {add}\{M_{(i,i+1)}\}$
generated by the preprojective modules all appear above the horizontal dashed line, with i increasing as one moves counter clockwise. Likewise, the wide subcategories
![]() $\mathsf {add}\{M_{(i+1,i)}\}$
generated by the preinjective modules all appear below the horizontal dashed line, with i increasing as one moves clockwise. The category is drawn so that every square commutes, and wide subcategories which appear more than once in the figure should be identified.
$\mathsf {add}\{M_{(i+1,i)}\}$
generated by the preinjective modules all appear below the horizontal dashed line, with i increasing as one moves clockwise. The category is drawn so that every square commutes, and wide subcategories which appear more than once in the figure should be identified.

Figure 1 The category
![]() $\mathfrak {W}(\Lambda _1)$
for
$\mathfrak {W}(\Lambda _1)$
for
![]() $\Lambda _1 = K(1\rightrightarrows 2)$
.
$\Lambda _1 = K(1\rightrightarrows 2)$
.
For our second example, we consider quiver
![]() $Q = 1\rightrightarrows 2 \rightarrow 3$
and the algebra
$Q = 1\rightrightarrows 2 \rightarrow 3$
and the algebra
![]() $\Lambda _2 = KQ/\mathrm {rad}^2 KQ$
. Again for
$\Lambda _2 = KQ/\mathrm {rad}^2 KQ$
. Again for
![]() $i \in \mathbb {N}$
, we denote by
$i \in \mathbb {N}$
, we denote by
![]() $M_{(i,i+1,0)}$
and
$M_{(i,i+1,0)}$
and
![]() $M_{(i+1,i,0)}$
the unique (up to isomorphism)
$M_{(i+1,i,0)}$
the unique (up to isomorphism)
![]() $\Lambda _2$
-modules with dimension vectors
$\Lambda _2$
-modules with dimension vectors
![]() $(i,i+1,0)$
and
$(i,i+1,0)$
and
![]() $(i+1,i,0)$
. The irreducible morphisms in
$(i+1,i,0)$
. The irreducible morphisms in
![]() $\mathfrak {W}(\Lambda _2)$
with source
$\mathfrak {W}(\Lambda _2)$
with source
![]() $\mathsf {mod}\Lambda _2$
are shown in Figure 2. Similarly to before, a morphism
$\mathsf {mod}\Lambda _2$
are shown in Figure 2. Similarly to before, a morphism
![]() $g_U^{\mathsf {mod}\Lambda _2}: \mathsf {mod}\Lambda _2 \rightarrow {\mathcal W}$
is labeled by U. Moreover, every module of the form
$g_U^{\mathsf {mod}\Lambda _2}: \mathsf {mod}\Lambda _2 \rightarrow {\mathcal W}$
is labeled by U. Moreover, every module of the form
![]() $M_{(i,i+1,0)}$
or
$M_{(i,i+1,0)}$
or
![]() $M_{(i+1,i,0)}$
corresponds to some morphism with source
$M_{(i+1,i,0)}$
corresponds to some morphism with source
![]() $\mathsf {mod}\Lambda _2$
.
$\mathsf {mod}\Lambda _2$
.

Figure 2 The irreducible morphisms in
![]() $\mathfrak {W}(\Lambda _2)$
with source
$\mathfrak {W}(\Lambda _2)$
with source
![]() $\mathsf {mod}\Lambda _2$
. Here,
$\mathsf {mod}\Lambda _2$
. Here,
![]() $\Lambda _2 = K(1\rightrightarrows 2\rightarrow 3)/\mathrm {rad^2}$
.
$\Lambda _2 = K(1\rightrightarrows 2\rightarrow 3)/\mathrm {rad^2}$
.
To complete the picture, we can utilize Proposition 6.14. The Serre subcategory
![]() $P(3)^{\perp }$
is equivalent to
$P(3)^{\perp }$
is equivalent to
![]() $\mathsf {mod}\Lambda _1$
, so there is a copy of
$\mathsf {mod}\Lambda _1$
, so there is a copy of
![]() $\mathfrak {W}(\Lambda _1)$
sitting inside of
$\mathfrak {W}(\Lambda _1)$
sitting inside of
![]() $\mathfrak {W}(\Lambda _2)$
which has
$\mathfrak {W}(\Lambda _2)$
which has
![]() $P(3)^{\perp }$
identified with
$P(3)^{\perp }$
identified with
![]() $\mathsf {mod}\Lambda _1$
. The Serre subcategory
$\mathsf {mod}\Lambda _1$
. The Serre subcategory
![]() $P(1)^{\perp } = \mathsf {add}\{P(2),S(2),P(3)\}$
is equivalent to the module category of the path algebra of type
$P(1)^{\perp } = \mathsf {add}\{P(2),S(2),P(3)\}$
is equivalent to the module category of the path algebra of type
![]() $A_2$
. Thus,
$A_2$
. Thus,
![]() $\mathfrak {W}(\Lambda _2)$
contains five irreducible morphisms which have source
$\mathfrak {W}(\Lambda _2)$
contains five irreducible morphisms which have source
![]() $\mathsf {add}\{P(2),S(2),P(3)\}$
and five morphisms
$\mathsf {add}\{P(2),S(2),P(3)\}$
and five morphisms
![]() $\mathsf {add}\{P(2),S(2),P(3)\} \rightarrow 0$
. The remaining subcategories shown are semisimple, so each is the source of four irreducible morphisms and four morphisms with target 0 in
$\mathsf {add}\{P(2),S(2),P(3)\} \rightarrow 0$
. The remaining subcategories shown are semisimple, so each is the source of four irreducible morphisms and four morphisms with target 0 in
![]() $\mathfrak {W}(\Lambda _2)$
.
$\mathfrak {W}(\Lambda _2)$
.
Acknowledgments
The authors wish to thank Erlend D. Børve and Håvard U. Terland for many insightful conversations. They also wish to thank Haruhisa Enomoto for pointing out a mistake in the first version of this manuscript, and for sharing with them the examples from [Reference Ringel24] discussed in Remark 6.17. Finally, they thank an anonymous referee for useful suggestions.