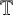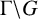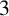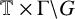1 Introduction
Let
![]() $(X, T)$
be a topological dynamic system, where X is a compact metric space and
$(X, T)$
be a topological dynamic system, where X is a compact metric space and
![]() $T: X\to X$
a continuous map. The Möbius function
$T: X\to X$
a continuous map. The Möbius function
![]() $\mu : \mathbb {N} \rightarrow \{-1, 0, 1\}$
is defined by
$\mu : \mathbb {N} \rightarrow \{-1, 0, 1\}$
is defined by
![]() $\mu (1)=1$
,
$\mu (1)=1$
,
![]() $\mu (n) =(-1)^k$
when n is the product of k distinct primes and
$\mu (n) =(-1)^k$
when n is the product of k distinct primes and
![]() $\mu (n) = 0$
otherwise. The Sarnak conjecture [Reference Sarnak12, Reference Sarnak13] (also called the Möbius disjointness conjecture) is the following statement.
$\mu (n) = 0$
otherwise. The Sarnak conjecture [Reference Sarnak12, Reference Sarnak13] (also called the Möbius disjointness conjecture) is the following statement.
Conjecture 1.1. Let
![]() $(X, T)$
be a topological dynamical system with zero topological entropy. Then
$(X, T)$
be a topological dynamical system with zero topological entropy. Then
 $$ \begin{align*} \lim_{N\to\infty}\frac{1}{N}\sum_{n=1}^{N}f(T^nx)\mu(n)=0 \quad\mbox{for all }f\in C(X) \mbox{ and all } x\in X. \end{align*} $$
$$ \begin{align*} \lim_{N\to\infty}\frac{1}{N}\sum_{n=1}^{N}f(T^nx)\mu(n)=0 \quad\mbox{for all }f\in C(X) \mbox{ and all } x\in X. \end{align*} $$
In recent years, there have been many results supporting the Möbius disjointness conjecture (see the comprehensive survey [Reference Ferenczi, Kułaga-Przymus, Lemańczyk, Ferenczi, Kułaga-Przymus and Lemańczyk2]). Here we discuss only the historical developments that are more relevant to this paper.
We consider the skew product
![]() $(\mathbb {T}^2, T)$
, where
$(\mathbb {T}^2, T)$
, where
![]() $\mathbb {T}^2=(\mathbb {R}/\mathbb {Z})^2$
, T is the transformation
$\mathbb {T}^2=(\mathbb {R}/\mathbb {Z})^2$
, T is the transformation
![]() $T: (x,y) \mapsto (x+\alpha ,y+h(x))$
and
$T: (x,y) \mapsto (x+\alpha ,y+h(x))$
and
![]() $h \colon \mathbb {T} \rightarrow \mathbb {T}$
is a continuous function. Since T is distal and distal systems have zero topological entropy [Reference Parry, Auslander and Gottschalk11], T should satisfy the Möbius disjointness conjecture. In fact, skew products are building blocks of distal flows according to Furstenberg’s structure theorem of minimal distal flows [Reference Furstenberg3].
$h \colon \mathbb {T} \rightarrow \mathbb {T}$
is a continuous function. Since T is distal and distal systems have zero topological entropy [Reference Parry, Auslander and Gottschalk11], T should satisfy the Möbius disjointness conjecture. In fact, skew products are building blocks of distal flows according to Furstenberg’s structure theorem of minimal distal flows [Reference Furstenberg3].
The skew product was first considered by Liu and Sarnak [Reference Liu and Sarnak10]. They proved Conjecture 1.1 for h analytic and
![]() $\lvert \widehat {h}(m)\rvert \gg e^{-\tau \lvert m\rvert }$
for some
$\lvert \widehat {h}(m)\rvert \gg e^{-\tau \lvert m\rvert }$
for some
![]() $\tau>0$
, where
$\tau>0$
, where
![]() $\widehat {h}(m)$
is the mth Fourier coefficient of h. After that, Wang [Reference Wang16] removed the additional condition and hence obtained the Möbius disjointness conjecture for all analytic skew products on
$\widehat {h}(m)$
is the mth Fourier coefficient of h. After that, Wang [Reference Wang16] removed the additional condition and hence obtained the Möbius disjointness conjecture for all analytic skew products on
![]() $(\mathbb {T}^2,T)$
. Huang et al. [Reference Huang, Wang and Ye7] improved the result, assuming that h is
$(\mathbb {T}^2,T)$
. Huang et al. [Reference Huang, Wang and Ye7] improved the result, assuming that h is
![]() $C^\infty $
-smooth. Recently, Kanigowski et al. [Reference Kanigowski, Lemańczyk and Radziwiłł8] proved it when h is
$C^\infty $
-smooth. Recently, Kanigowski et al. [Reference Kanigowski, Lemańczyk and Radziwiłł8] proved it when h is
![]() $C^{2+\varepsilon}$
-smoothand
$C^{2+\varepsilon}$
-smoothand
![]() $\widehat {h}(0)=0$
, and de Faveri [Reference de Faveri1] proved it just assuming that h is
$\widehat {h}(0)=0$
, and de Faveri [Reference de Faveri1] proved it just assuming that h is
![]() $C^{1+\varepsilon }$
-smooth. Kułaga-Przymus and Lemańczyk [Reference Kułaga-Przymus and Lemańczyk9] proved that, if h is
$C^{1+\varepsilon }$
-smooth. Kułaga-Przymus and Lemańczyk [Reference Kułaga-Przymus and Lemańczyk9] proved that, if h is
![]() $C^{1+\varepsilon }$
-smooth and
$C^{1+\varepsilon }$
-smooth and
![]() $\alpha $
is topological generic, then the Möbius disjointness conjecture is true. In 2020, Wang and Yao [Reference Wang and Yao15] proved strong orthogonality between the Möbius function and the skew products when h is
$\alpha $
is topological generic, then the Möbius disjointness conjecture is true. In 2020, Wang and Yao [Reference Wang and Yao15] proved strong orthogonality between the Möbius function and the skew products when h is
![]() $C^{3+\varepsilon }$
-smooth and
$C^{3+\varepsilon }$
-smooth and
![]() $\alpha $
is measure-theoretically generic. A nilsystem is also a distal flow and the Möbius disjointness conjecture for nilsystems was proved by Green and Tao [Reference Green and Tao5].
$\alpha $
is measure-theoretically generic. A nilsystem is also a distal flow and the Möbius disjointness conjecture for nilsystems was proved by Green and Tao [Reference Green and Tao5].
Recently, Huang et al. [Reference Huang, Liu and Wang6] considered the Möbius disjointness conjecture for skew products on
![]() $\mathbb {T} \times {\Gamma \backslash G}$
, where G is a
$\mathbb {T} \times {\Gamma \backslash G}$
, where G is a
![]() $3$
-dimensional Heisenberg group with the cocompact discrete subgroup
$3$
-dimensional Heisenberg group with the cocompact discrete subgroup
![]() $\Gamma $
, namely
$\Gamma $
, namely
 $$ \begin{align*} G= \begin{pmatrix} 1 & {\mathbb{R}} & {\mathbb{R}} \\ 0 & 1 & {\mathbb{R}} \\ 0 & 0 & 1 \end{pmatrix} , \quad \Gamma= \begin{pmatrix} 1 & {\mathbb{Z}} & {\mathbb{Z}} \\ 0 & 1 & {\mathbb{Z}} \\ 0 & 0 & 1 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} G= \begin{pmatrix} 1 & {\mathbb{R}} & {\mathbb{R}} \\ 0 & 1 & {\mathbb{R}} \\ 0 & 0 & 1 \end{pmatrix} , \quad \Gamma= \begin{pmatrix} 1 & {\mathbb{Z}} & {\mathbb{Z}} \\ 0 & 1 & {\mathbb{Z}} \\ 0 & 0 & 1 \end{pmatrix}. \end{align*} $$
Then
![]() ${\Gamma \backslash G}$
is the
${\Gamma \backslash G}$
is the
![]() $3$
-dimensional Heisenberg nilmanifold. Their main result is as follows.
$3$
-dimensional Heisenberg nilmanifold. Their main result is as follows.
Theorem 1.2 (Huang et al., [Reference Huang, Liu and Wang6]).
Let
![]() $\mathbb {T}$
be the unit circle and
$\mathbb {T}$
be the unit circle and
![]() ${\Gamma \backslash G}$
the
${\Gamma \backslash G}$
the
![]() $3$
-dimensional Heisenberg nilmanifold. Let
$3$
-dimensional Heisenberg nilmanifold. Let
![]() $\alpha \in [0,1)$
and let
$\alpha \in [0,1)$
and let
![]() $\varphi , \psi $
be
$\varphi , \psi $
be
![]() $C^{\infty }$
-smooth periodic functions from
$C^{\infty }$
-smooth periodic functions from
![]() $\mathbb {R}$
to
$\mathbb {R}$
to
![]() $\mathbb {R}$
with period
$\mathbb {R}$
with period
![]() $1$
such that
$1$
such that
 $$ \begin{align*} \int_{0}^{1} \varphi(t) \,{d}t = 0. \end{align*} $$
$$ \begin{align*} \int_{0}^{1} \varphi(t) \,{d}t = 0. \end{align*} $$
Let the skew product T on
![]() ${\mathbb {T} \times \Gamma \backslash G}$
be given by
${\mathbb {T} \times \Gamma \backslash G}$
be given by
 $$ \begin{align} T: (t,\Gamma g) \mapsto \left( t+\alpha, \Gamma g \begin{pmatrix} 1 & {\varphi(t)} & {\psi(t)} \\ 0 & 1 & {\varphi(t)} \\ 0 & 0 & 1 \end{pmatrix} \right). \end{align} $$
$$ \begin{align} T: (t,\Gamma g) \mapsto \left( t+\alpha, \Gamma g \begin{pmatrix} 1 & {\varphi(t)} & {\psi(t)} \\ 0 & 1 & {\varphi(t)} \\ 0 & 0 & 1 \end{pmatrix} \right). \end{align} $$
Then, for any
![]() $(t_0,\Gamma g_0) \in {\mathbb {T} \times \Gamma \backslash G}$
and any
$(t_0,\Gamma g_0) \in {\mathbb {T} \times \Gamma \backslash G}$
and any
![]() $f \in C({\mathbb {T} \times \Gamma \backslash G})$
,
$f \in C({\mathbb {T} \times \Gamma \backslash G})$
,
 $$ \begin{align*} \lim_{N \rightarrow \infty} \frac{1}{N}\sum_{n=1}^N \mu(n)f(T^n(t_0,\Gamma g_0))=0. \end{align*} $$
$$ \begin{align*} \lim_{N \rightarrow \infty} \frac{1}{N}\sum_{n=1}^N \mu(n)f(T^n(t_0,\Gamma g_0))=0. \end{align*} $$
Remark 1.3. In [Reference Huang, Liu and Wang6], it is also proved that the skew product (1.1) on
![]() $\mathbb {T}\times {\Gamma \backslash G}$
is a distal flow.
$\mathbb {T}\times {\Gamma \backslash G}$
is a distal flow.
As mentioned by Huang et al. [Reference Huang, Liu and Wang6], we can combine the ideas from [Reference de Faveri1, Reference Huang, Liu and Wang6, Reference Kanigowski, Lemańczyk and Radziwiłł8] to give the following new theorem, which improves the result in Theorem 1.2.
Theorem 1.4. Let
![]() $\mathbb {T}$
be the unit circle and
$\mathbb {T}$
be the unit circle and
![]() ${\Gamma \backslash G}$
the
${\Gamma \backslash G}$
the
![]() $3$
-dimensional Heisenberg nilmanifold. Let
$3$
-dimensional Heisenberg nilmanifold. Let
![]() $\alpha \in [0,1)$
. Let
$\alpha \in [0,1)$
. Let
![]() $\phi :\mathbb {T}\rightarrow \mathbb {R}$
be a
$\phi :\mathbb {T}\rightarrow \mathbb {R}$
be a
![]() $C^{2+\varepsilon }$
-smooth function and let
$C^{2+\varepsilon }$
-smooth function and let
![]() $\psi : \mathbb {T} \rightarrow \mathbb {R}$
be a
$\psi : \mathbb {T} \rightarrow \mathbb {R}$
be a
![]() $C^{1+\varepsilon }$
-smooth function. Moreover, assume that
$C^{1+\varepsilon }$
-smooth function. Moreover, assume that
![]() $\hat {\psi }(0) = \hat {\phi }(0)=0$
. Let the skew product T on
$\hat {\psi }(0) = \hat {\phi }(0)=0$
. Let the skew product T on
![]() ${\mathbb {T} \times \Gamma \backslash G}$
be given by
${\mathbb {T} \times \Gamma \backslash G}$
be given by
 $$ \begin{align} T: (t,\Gamma g) \mapsto \left( t+\alpha, \Gamma g \begin{pmatrix} 1 & {\phi(t)} & {\psi(t)} \\ 0 & 1 & {\phi(t)} \\ 0 & 0 & 1 \end{pmatrix} \right). \end{align} $$
$$ \begin{align} T: (t,\Gamma g) \mapsto \left( t+\alpha, \Gamma g \begin{pmatrix} 1 & {\phi(t)} & {\psi(t)} \\ 0 & 1 & {\phi(t)} \\ 0 & 0 & 1 \end{pmatrix} \right). \end{align} $$
Then, for any
![]() $(t_0,\Gamma g_0) \in {\mathbb {T} \times \Gamma \backslash G}$
and any
$(t_0,\Gamma g_0) \in {\mathbb {T} \times \Gamma \backslash G}$
and any
![]() $f \in C({\mathbb {T} \times \Gamma \backslash G})$
,
$f \in C({\mathbb {T} \times \Gamma \backslash G})$
,
 $$ \begin{align*} \lim_{N \rightarrow \infty} \frac{1}{N}\sum_{n=1}^N \mu(n)f(T^n(t_0,\Gamma g_0))=0. \end{align*} $$
$$ \begin{align*} \lim_{N \rightarrow \infty} \frac{1}{N}\sum_{n=1}^N \mu(n)f(T^n(t_0,\Gamma g_0))=0. \end{align*} $$
Remark 1.5. From the definition of T in (1.2), we can easily compute
 $$ \begin{align*} T^n:(t,\Gamma g)\mapsto\left( t+n\alpha, \Gamma g \begin{pmatrix} 1 & {\Phi(n,t)} & {\Psi(n,t)+\frac{1}{2}\Phi^2(n,t)-\frac{1}{2}H(n,t)} \\ 0 & 1 & {\Phi(n,t)} \\ 0 & 0 & 1 \end{pmatrix} \right), \end{align*} $$
$$ \begin{align*} T^n:(t,\Gamma g)\mapsto\left( t+n\alpha, \Gamma g \begin{pmatrix} 1 & {\Phi(n,t)} & {\Psi(n,t)+\frac{1}{2}\Phi^2(n,t)-\frac{1}{2}H(n,t)} \\ 0 & 1 & {\Phi(n,t)} \\ 0 & 0 & 1 \end{pmatrix} \right), \end{align*} $$
where
![]() $\Phi (n,t)=\sum _{l=0}^{n-1}\phi (l\alpha +t)$
,
$\Phi (n,t)=\sum _{l=0}^{n-1}\phi (l\alpha +t)$
,
![]() $\Psi (n,t)=\sum _{l=0}^{n-1}\psi (l\alpha +t)$
and
$\Psi (n,t)=\sum _{l=0}^{n-1}\psi (l\alpha +t)$
and
![]() $H(n,t)=\sum _{l=0}^{n-1}\phi ^2(l\alpha +t)$
.
$H(n,t)=\sum _{l=0}^{n-1}\phi ^2(l\alpha +t)$
.
Notation. For a topological dynamical system, let
![]() $M(X,T)$
be the set of T-invariant Borel probability measures on X. We write
$M(X,T)$
be the set of T-invariant Borel probability measures on X. We write
![]() $e(x)$
for
$e(x)$
for
![]() $e^{2\pi i x}$
and
$e^{2\pi i x}$
and
![]() $\lVert x\rVert = \min _{n \in \mathbb {Z}} \lvert x-n\rvert $
for the distance between x and the nearest integer. For positive A, the notation
$\lVert x\rVert = \min _{n \in \mathbb {Z}} \lvert x-n\rvert $
for the distance between x and the nearest integer. For positive A, the notation
![]() $B=O(A)$
or
$B=O(A)$
or
![]() $B \ll A$
means that there exists a positive constant c such that
$B \ll A$
means that there exists a positive constant c such that
![]() $\lvert B\rvert \leq cA$
. If the constant c depends on a parameter b, we write
$\lvert B\rvert \leq cA$
. If the constant c depends on a parameter b, we write
![]() $B=O_{b}(A)$
or
$B=O_{b}(A)$
or
![]() $B \ll _{b} A$
. The notation
$B \ll _{b} A$
. The notation
![]() $A \asymp B$
means that
$A \asymp B$
means that
![]() $A \ll B$
and
$A \ll B$
and
![]() $B \ll A$
. For a topological space X, we use
$B \ll A$
. For a topological space X, we use
![]() $C(X)$
to denote the set of all continuous complex-valued functions on X.
$C(X)$
to denote the set of all continuous complex-valued functions on X.
2 Theorem 1.4 for rational
 $\alpha $
$\alpha $
Let G be the
![]() $3$
-dimensional Heisenberg group, with the cocompact discrete subgroup
$3$
-dimensional Heisenberg group, with the cocompact discrete subgroup
![]() $\Gamma $
, and
$\Gamma $
, and
![]() ${\Gamma \backslash G}$
the
${\Gamma \backslash G}$
the
![]() $3$
-dimensional Heisenberg nilmanifold. We follow the papers of Huang et al. [Reference Huang, Liu and Wang6, Section 2] and Tolimieri [Reference Tolimieri14] for the following lemmas.
$3$
-dimensional Heisenberg nilmanifold. We follow the papers of Huang et al. [Reference Huang, Liu and Wang6, Section 2] and Tolimieri [Reference Tolimieri14] for the following lemmas.
For
![]() $0 \leq j \leq m-1$
,
$0 \leq j \leq m-1$
,
![]() $j,m\in \mathbb {Z}$
, we define the functions
$j,m\in \mathbb {Z}$
, we define the functions
![]() $\phi _{mj}$
and
$\phi _{mj}$
and
![]() $\phi _{mj}^{*}$
on G by
$\phi _{mj}^{*}$
on G by
 $$ \begin{align*} \phi_{mj} \begin{pmatrix} 1 & {y} & {z} \\ 0 & 1 & {x} \\ 0 & 0 & 1 \end{pmatrix} =e(mz+jx) \sum_{k \in \mathbb{Z}}e^{-\pi(y+k+{j}/{m})^2}e(mkx), \end{align*} $$
$$ \begin{align*} \phi_{mj} \begin{pmatrix} 1 & {y} & {z} \\ 0 & 1 & {x} \\ 0 & 0 & 1 \end{pmatrix} =e(mz+jx) \sum_{k \in \mathbb{Z}}e^{-\pi(y+k+{j}/{m})^2}e(mkx), \end{align*} $$
and
 $$ \begin{align*} \phi_{mj}^* \begin{pmatrix} 1 & {y} & {z} \\ 0 & 1 & {x} \\ 0 & 0 & 1 \end{pmatrix} = ie(mz+jx) \sum_{k \in \mathbb{Z}} e^{-\pi(y+k+{j}/{m}+{1}/{2})^2}e\bigg(\frac{1}{2}\bigg( y+k+\frac{j}{m}\bigg) +mkx\bigg). \end{align*} $$
$$ \begin{align*} \phi_{mj}^* \begin{pmatrix} 1 & {y} & {z} \\ 0 & 1 & {x} \\ 0 & 0 & 1 \end{pmatrix} = ie(mz+jx) \sum_{k \in \mathbb{Z}} e^{-\pi(y+k+{j}/{m}+{1}/{2})^2}e\bigg(\frac{1}{2}\bigg( y+k+\frac{j}{m}\bigg) +mkx\bigg). \end{align*} $$
We can check that
![]() $\phi _{mj}$
and
$\phi _{mj}$
and
![]() $\phi _{mj} ^*$
are
$\phi _{mj} ^*$
are
![]() $\Gamma $
-invariant, that is,
$\Gamma $
-invariant, that is,
for any
![]() $g \in G$
and for any
$g \in G$
and for any
![]() $\gamma \in \Gamma .$
Thus,
$\gamma \in \Gamma .$
Thus,
![]() $\phi _{mj}$
and
$\phi _{mj}$
and
![]() $\phi _{mj}^*$
can be regarded as functions on the nilmanifold
$\phi _{mj}^*$
can be regarded as functions on the nilmanifold
![]() ${\Gamma \backslash G}$
.
${\Gamma \backslash G}$
.
Lemma 2.1 [Reference Huang, Liu and Wang6, Proposition 2.3].
Let
![]() $\mathcal {A}$
be the subset of
$\mathcal {A}$
be the subset of
![]() $f \in C({\mathbb {T} \times \Gamma \backslash G})$
such that
$f \in C({\mathbb {T} \times \Gamma \backslash G})$
such that
 $$ \begin{align*} f: \left( t,\Gamma \begin{pmatrix} 1 & {y} & {z} \\ 0 & 1 & {x} \\ 0 & 0 & 1 \end{pmatrix} \right) \mapsto e(\xi_1 t + \xi_2 x + \xi_3 y) \phi\left( \Gamma \begin{pmatrix} 1 & {y} & {z} \\ 0 & 1 & {x} \\ 0 & 0 & 1 \end{pmatrix} \right), \end{align*} $$
$$ \begin{align*} f: \left( t,\Gamma \begin{pmatrix} 1 & {y} & {z} \\ 0 & 1 & {x} \\ 0 & 0 & 1 \end{pmatrix} \right) \mapsto e(\xi_1 t + \xi_2 x + \xi_3 y) \phi\left( \Gamma \begin{pmatrix} 1 & {y} & {z} \\ 0 & 1 & {x} \\ 0 & 0 & 1 \end{pmatrix} \right), \end{align*} $$
where
![]() $\xi _1,\xi _2,\xi _3 \in \mathbb {Z}$
and
$\xi _1,\xi _2,\xi _3 \in \mathbb {Z}$
and
![]() $\phi = \phi _{mj}, \overline {\phi }_{mj}, \phi _{mj}^{*}$
or
$\phi = \phi _{mj}, \overline {\phi }_{mj}, \phi _{mj}^{*}$
or
![]() $\overline {\phi }^{*}_{mj}$
for some
$\overline {\phi }^{*}_{mj}$
for some
![]() $0 \leq j \leq m-1$
. Here,
$0 \leq j \leq m-1$
. Here,
![]() $\overline {\phi }_{mj}$
and
$\overline {\phi }_{mj}$
and
![]() $\overline {\phi }^{*}_{mj}$
stand for the complex conjugates of
$\overline {\phi }^{*}_{mj}$
stand for the complex conjugates of
![]() $\phi _{mj}$
and
$\phi _{mj}$
and
![]() $\phi _{mj}^{*}$
, respectively. Let
$\phi _{mj}^{*}$
, respectively. Let
![]() $\mathcal {B}$
be the subset of
$\mathcal {B}$
be the subset of
![]() $f \in C({\mathbb {T} \times \Gamma \backslash G})$
satisfying
$f \in C({\mathbb {T} \times \Gamma \backslash G})$
satisfying
![]() $f: (t,\Gamma g) \mapsto f_1(t)f_2(\Gamma g)$
with
$f: (t,\Gamma g) \mapsto f_1(t)f_2(\Gamma g)$
with
![]() $ f_1\in C(\mathbb {T})$
and
$ f_1\in C(\mathbb {T})$
and
![]() $f_2 \in C_0({\Gamma \backslash G})$
. Then the
$f_2 \in C_0({\Gamma \backslash G})$
. Then the
![]() $\mathbb {C}$
-linear subspace spanned by
$\mathbb {C}$
-linear subspace spanned by
![]() $\mathcal {A} \cup \mathcal {B}$
is dense in
$\mathcal {A} \cup \mathcal {B}$
is dense in
![]() $C({\mathbb {T} \times \Gamma \backslash G})$
.
$C({\mathbb {T} \times \Gamma \backslash G})$
.
To prove Theorem 1.4 for rational
![]() $\alpha $
, we need to consider two cases:
$\alpha $
, we need to consider two cases:
![]() $f\in \mathcal {A}$
and
$f\in \mathcal {A}$
and
![]() $f\in \mathcal {B}$
. We use the argument given by Huang et al. [Reference Huang, Liu and Wang6, Section 3].
$f\in \mathcal {B}$
. We use the argument given by Huang et al. [Reference Huang, Liu and Wang6, Section 3].
Lemma 2.2 [Reference de Faveri1, Theorem 1].
Let
![]() $\alpha \in \mathbb {R}$
and let
$\alpha \in \mathbb {R}$
and let
![]() $h \colon \mathbb {T} \rightarrow \mathbb {T}$
be
$h \colon \mathbb {T} \rightarrow \mathbb {T}$
be
![]() $C^{1+\varepsilon }$
-smooth. Define the skew product
$C^{1+\varepsilon }$
-smooth. Define the skew product
![]() $T \colon \mathbb {T}^2 \rightarrow \mathbb {T}^2$
by
$T \colon \mathbb {T}^2 \rightarrow \mathbb {T}^2$
by
Then the Möbius disjointness conjecture holds for this
![]() $(\mathbb {T}^2,T)$
.
$(\mathbb {T}^2,T)$
.
Corollary 2.3. Let
![]() $\alpha \in \mathbb {R}$
and let
$\alpha \in \mathbb {R}$
and let
![]() $h_1,h_2 \colon \mathbb {T} \rightarrow \mathbb {T}$
be
$h_1,h_2 \colon \mathbb {T} \rightarrow \mathbb {T}$
be
![]() $C^{1+\varepsilon }$
-smooth functions. Let
$C^{1+\varepsilon }$
-smooth functions. Let
![]() $T \colon \mathbb {T}^3 \rightarrow \mathbb {T}^3$
be given by
$T \colon \mathbb {T}^3 \rightarrow \mathbb {T}^3$
be given by
Then the Möbius disjointness conjecture holds for
![]() $(\mathbb {T}^3,T)$
.
$(\mathbb {T}^3,T)$
.
Proof. The proof is similar to the proof of [Reference Huang, Liu and Wang6, Corollary 3.2]; at the last step, we use Lemma 2.2.
Lemma 2.4. Let
![]() $\mathcal {B} \subset C({\mathbb {T} \times \Gamma \backslash G})$
be as in Lemma 2.1. Let T be as in Theorem 1.4 and let
$\mathcal {B} \subset C({\mathbb {T} \times \Gamma \backslash G})$
be as in Lemma 2.1. Let T be as in Theorem 1.4 and let
![]() $f \in \mathcal {B}$
. Then, for any
$f \in \mathcal {B}$
. Then, for any
![]() $(t_0,\Gamma g_0) \in {\mathbb {T} \times \Gamma \backslash G}$
,
$(t_0,\Gamma g_0) \in {\mathbb {T} \times \Gamma \backslash G}$
,
 $$ \begin{align*} \lim_{N \rightarrow \infty} \frac{1}{N}\sum_{n=1}^N \mu(n)f(T^n(t_0,\Gamma g_0))=0. \end{align*} $$
$$ \begin{align*} \lim_{N \rightarrow \infty} \frac{1}{N}\sum_{n=1}^N \mu(n)f(T^n(t_0,\Gamma g_0))=0. \end{align*} $$
Proof. The proof is similar to the proof of [Reference Huang, Liu and Wang6, Corollary 3.2] but using Corollary 2.3.
Lemma 2.5 [Reference Huang, Liu and Wang6, Proposition 3.5].
Let
![]() $({\mathbb {T} \times \Gamma \backslash G},T)$
be as in Theorem 1.4 and assume
$({\mathbb {T} \times \Gamma \backslash G},T)$
be as in Theorem 1.4 and assume
![]() ${\alpha \in \mathbb {Q} \cap [0,1)}$
. Let
${\alpha \in \mathbb {Q} \cap [0,1)}$
. Let
![]() $\mathcal {A}$
be as in Proposition 2.1. Then, for any
$\mathcal {A}$
be as in Proposition 2.1. Then, for any
![]() $(t_0,\Gamma g_0) \in {\mathbb {T} \times \Gamma \backslash G}$
, any
$(t_0,\Gamma g_0) \in {\mathbb {T} \times \Gamma \backslash G}$
, any
![]() $f\in \mathcal {A}$
and any
$f\in \mathcal {A}$
and any
![]() $A>0$
,
$A>0$
,
 $$ \begin{align*} \sum_{n \leq N} \mu(n)f(T^n(t_0,\Gamma g_0)) \ll_A \frac{N}{\log^A N}, \end{align*} $$
$$ \begin{align*} \sum_{n \leq N} \mu(n)f(T^n(t_0,\Gamma g_0)) \ll_A \frac{N}{\log^A N}, \end{align*} $$
where the implied constant depends on A and
![]() $\alpha $
only.
$\alpha $
only.
Proposition 2.6. Theorem 1.4 holds for rational
![]() $\alpha $
.
$\alpha $
.
3 Theorem 1.4 for irrational
 $\alpha $
$\alpha $
Before proving Theorem 1.4 for irrational
![]() $\alpha $
, we choose a proper metric on
$\alpha $
, we choose a proper metric on
![]() ${\mathbb {T} \times \Gamma \backslash G}$
. This can be found in [Reference Green and Tao4, Sections 2 and 5] and [Reference Huang, Liu and Wang6, Section 5]. Let the closed connected subgroups
${\mathbb {T} \times \Gamma \backslash G}$
. This can be found in [Reference Green and Tao4, Sections 2 and 5] and [Reference Huang, Liu and Wang6, Section 5]. Let the closed connected subgroups
![]() $G= G_1 \supseteq G_2 \supseteq G_3= \{\mathrm {id}_G\}$
be the lower central series filtration
$G= G_1 \supseteq G_2 \supseteq G_3= \{\mathrm {id}_G\}$
be the lower central series filtration
![]() $G_{\bullet }$
on G. Let
$G_{\bullet }$
on G. Let
 $$ \begin{align*} X_1= \begin{pmatrix} 1 & {0} & {0} \\ 0 & 1 & {1} \\ 0 & 0 & 1 \end{pmatrix} , \quad X_2= \begin{pmatrix} 1 & {1} & {0} \\ 0 & 1 & {0} \\ 0 & 0 & 1 \end{pmatrix} , \quad X_3 = \begin{pmatrix} 1 & {0} & {1} \\ 0 & 1 & {0} \\ 0 & 0 & 1 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} X_1= \begin{pmatrix} 1 & {0} & {0} \\ 0 & 1 & {1} \\ 0 & 0 & 1 \end{pmatrix} , \quad X_2= \begin{pmatrix} 1 & {1} & {0} \\ 0 & 1 & {0} \\ 0 & 0 & 1 \end{pmatrix} , \quad X_3 = \begin{pmatrix} 1 & {0} & {1} \\ 0 & 1 & {0} \\ 0 & 0 & 1 \end{pmatrix}. \end{align*} $$
Then
![]() $\mathcal {X}=\{X_1,X_2,X_3\}$
is a Mal’cev basis adapted to
$\mathcal {X}=\{X_1,X_2,X_3\}$
is a Mal’cev basis adapted to
![]() $G_{\bullet }$
. The corresponding Mal’cev coordinate map
$G_{\bullet }$
. The corresponding Mal’cev coordinate map
![]() $\kappa : G \rightarrow \mathbb {R}^3$
is given by
$\kappa : G \rightarrow \mathbb {R}^3$
is given by
 $$ \begin{align} \kappa \begin{pmatrix} 1 & {y} & {z} \\ 0 & 1 & {x} \\ 0 & 0 & 1 \end{pmatrix} = (x,y,z-xy). \end{align} $$
$$ \begin{align} \kappa \begin{pmatrix} 1 & {y} & {z} \\ 0 & 1 & {x} \\ 0 & 0 & 1 \end{pmatrix} = (x,y,z-xy). \end{align} $$
The metric
![]() $d_G:G\times G\rightarrow \mathbb {R}_{\geq 0}$
on G is defined to be the largest metric such that
$d_G:G\times G\rightarrow \mathbb {R}_{\geq 0}$
on G is defined to be the largest metric such that
![]() $d_G(g_1,g_2) \leq \lvert \kappa (g_1 ^{-1} g_2)\rvert $
, where
$d_G(g_1,g_2) \leq \lvert \kappa (g_1 ^{-1} g_2)\rvert $
, where
![]() $\lvert \cdot \rvert $
is the
$\lvert \cdot \rvert $
is the
![]() $l^{\infty }$
-norm on
$l^{\infty }$
-norm on
![]() $\mathbb {R}^3$
. This metric can be more explicitly expressed as
$\mathbb {R}^3$
. This metric can be more explicitly expressed as
 $$ \begin{align*} d_G(g_1,g_2)=\inf\bigg\{\sum_{i=0}^{n-1}\min(\lvert\kappa(h_{i-1}^{-1}h_i)\rvert, \lvert\kappa(h_i ^{-1}h_{i-1})\rvert) \colon h_0,\ldots,h_n \in G; h_0=g_1, h_n = g_2 \bigg\}, \end{align*} $$
$$ \begin{align*} d_G(g_1,g_2)=\inf\bigg\{\sum_{i=0}^{n-1}\min(\lvert\kappa(h_{i-1}^{-1}h_i)\rvert, \lvert\kappa(h_i ^{-1}h_{i-1})\rvert) \colon h_0,\ldots,h_n \in G; h_0=g_1, h_n = g_2 \bigg\}, \end{align*} $$
from which we can see that
![]() $d_G$
is left-invariant. By (3.1),
$d_G$
is left-invariant. By (3.1),
 $$ \begin{align*} \left|\kappa \begin{pmatrix} 1 & {y} & {z} \\ 0 & 1 & {x} \\ 0 & 0 & 1 \end{pmatrix} \right| \leq \lvert x\rvert + \lvert y\rvert + \lvert z\rvert \end{align*} $$
$$ \begin{align*} \left|\kappa \begin{pmatrix} 1 & {y} & {z} \\ 0 & 1 & {x} \\ 0 & 0 & 1 \end{pmatrix} \right| \leq \lvert x\rvert + \lvert y\rvert + \lvert z\rvert \end{align*} $$
provided that
![]() $x,y \in [0,1)$
. The above metric on G descends to a metric on
$x,y \in [0,1)$
. The above metric on G descends to a metric on
![]() ${\Gamma \backslash G}$
given by
${\Gamma \backslash G}$
given by
It can be proved that
![]() $d_{{\Gamma \backslash G}}$
is indeed a metric on
$d_{{\Gamma \backslash G}}$
is indeed a metric on
![]() ${\Gamma \backslash G}$
. Since
${\Gamma \backslash G}$
. Since
![]() $d_{G}$
is left-invariant, we also have
$d_{G}$
is left-invariant, we also have
Finally, we take
![]() $d_{\mathbb {T}}$
to be the canonical Euclidean metric on
$d_{\mathbb {T}}$
to be the canonical Euclidean metric on
![]() $\mathbb {T}$
, and
$\mathbb {T}$
, and
![]() $d=d_{{\mathbb {T} \times \Gamma \backslash G}}$
the
$d=d_{{\mathbb {T} \times \Gamma \backslash G}}$
the
![]() $l^{2}$
-product metric of
$l^{2}$
-product metric of
![]() $d_{\mathbb {T}}$
and
$d_{\mathbb {T}}$
and
![]() $d_{{\Gamma \backslash G}}$
given by
$d_{{\Gamma \backslash G}}$
given by
To prove Theorem 1.4 for irrational
![]() $\alpha $
, we use the recent new ideas of Kanigowski et al. [Reference Kanigowski, Lemańczyk and Radziwiłł8, Theorem 1] and de Faveri [Reference de Faveri1] to give the following lemmas.
$\alpha $
, we use the recent new ideas of Kanigowski et al. [Reference Kanigowski, Lemańczyk and Radziwiłł8, Theorem 1] and de Faveri [Reference de Faveri1] to give the following lemmas.
Lemma 3.1. Let
![]() $0<\varepsilon < {1}/{100}$
and
$0<\varepsilon < {1}/{100}$
and
![]() $\alpha $
be an irrational number. Let
$\alpha $
be an irrational number. Let
![]() $\phi :\mathbb {T}\rightarrow \mathbb {R}$
be a
$\phi :\mathbb {T}\rightarrow \mathbb {R}$
be a
![]() $C^{2+\varepsilon }$
-smooth function and let
$C^{2+\varepsilon }$
-smooth function and let
![]() $\psi : \mathbb {T} \rightarrow \mathbb {R}$
be a
$\psi : \mathbb {T} \rightarrow \mathbb {R}$
be a
![]() $C^{1+\varepsilon }$
-smooth function. Assume that
$C^{1+\varepsilon }$
-smooth function. Assume that
![]() $\hat {\psi }(0) = \hat {\phi }(0)=0$
. Then there exists an unbounded sequence
$\hat {\psi }(0) = \hat {\phi }(0)=0$
. Then there exists an unbounded sequence
![]() $\{r_n\}_{n\geq 1}$
of
$\{r_n\}_{n\geq 1}$
of
![]() $\mathbb {N}$
such that
$\mathbb {N}$
such that
 $$ \begin{align*} \int_{\mathbb{T}\times {\Gamma \backslash G}}\,d(T^{r_n}(t,\Gamma g),(t,\Gamma g))^2\,d\nu(t,\Gamma g)\ll r_n^{-\varepsilon/100} \end{align*} $$
$$ \begin{align*} \int_{\mathbb{T}\times {\Gamma \backslash G}}\,d(T^{r_n}(t,\Gamma g),(t,\Gamma g))^2\,d\nu(t,\Gamma g)\ll r_n^{-\varepsilon/100} \end{align*} $$
for any
![]() $\nu \in M(\mathbb {T}\times {\Gamma \backslash G}, T)$
.
$\nu \in M(\mathbb {T}\times {\Gamma \backslash G}, T)$
.
Lemma 3.2 [Reference Kanigowski, Lemańczyk and Radziwiłł8].
Let
![]() $(X,T)$
be a topological dynamical system and assume that for every
$(X,T)$
be a topological dynamical system and assume that for every
![]() $\nu \in M(X,T)$
,
$\nu \in M(X,T)$
,
![]() $(X,\mathcal {B},\nu ,T)$
satisfies the PR rigidity condition: there exists a linearly dense set
$(X,\mathcal {B},\nu ,T)$
satisfies the PR rigidity condition: there exists a linearly dense set
![]() $\mathcal {F} \subset C(X)$
such that for each
$\mathcal {F} \subset C(X)$
such that for each
![]() $f \in \mathcal {F}$
, we can find
$f \in \mathcal {F}$
, we can find
![]() $\delta> 0$
and a sequence
$\delta> 0$
and a sequence
![]() $\{q_n\}_{n\geq 1}$
satisfying
$\{q_n\}_{n\geq 1}$
satisfying
 $$ \begin{align*} \sum\limits_{j=-q_n^\delta}^{q_n^\delta}\lVert f\circ T^{jq_n}-f\rVert^2_{L^2(\nu)}\rightarrow 0. \end{align*} $$
$$ \begin{align*} \sum\limits_{j=-q_n^\delta}^{q_n^\delta}\lVert f\circ T^{jq_n}-f\rVert^2_{L^2(\nu)}\rightarrow 0. \end{align*} $$
Then,
![]() $(X,T)$
is Möbius disjoint, that is,
$(X,T)$
is Möbius disjoint, that is,
 $$ \begin{align*} \lim_{N \rightarrow \infty}\frac{1}{N}\sum_{n=1}^{N}\mu(n)f(T^nx)=0. \end{align*} $$
$$ \begin{align*} \lim_{N \rightarrow \infty}\frac{1}{N}\sum_{n=1}^{N}\mu(n)f(T^nx)=0. \end{align*} $$
Proof of Theorem 1.4 assuming Lemma 3.1.
The case that
![]() $\alpha $
is rational has been proved in Proposition 2.6. So we assume that
$\alpha $
is rational has been proved in Proposition 2.6. So we assume that
![]() $\alpha $
is irrational. Let
$\alpha $
is irrational. Let
![]() $\{r_n\}_{n\geq 1}$
be the sequence from Lemma 3.1. For any
$\{r_n\}_{n\geq 1}$
be the sequence from Lemma 3.1. For any
![]() $\nu \in M(\mathbb {T}\times {\Gamma \backslash G}, T)$
,
$\nu \in M(\mathbb {T}\times {\Gamma \backslash G}, T)$
,
 $$ \begin{align} \Vert f \circ T^{k r_n} - f \Vert_{L^2(\nu)}^2 \leq \lvert k\rvert \sum_{j = 1}^{\lvert k\rvert} \Vert f \circ T^{j r_n} - f \circ T^{(j-1) r_n} \Vert_{L^2(\nu)}^2 = k^2 \cdot \Vert f \circ T^{r_n} - f \Vert_{L^2(\nu)}^2. \end{align} $$
$$ \begin{align} \Vert f \circ T^{k r_n} - f \Vert_{L^2(\nu)}^2 \leq \lvert k\rvert \sum_{j = 1}^{\lvert k\rvert} \Vert f \circ T^{j r_n} - f \circ T^{(j-1) r_n} \Vert_{L^2(\nu)}^2 = k^2 \cdot \Vert f \circ T^{r_n} - f \Vert_{L^2(\nu)}^2. \end{align} $$
Here we use the triangle inequality and the T-invariance of
![]() $\nu $
. If f is also Lipschitz continuous, then, by Lemma 3.1,
$\nu $
. If f is also Lipschitz continuous, then, by Lemma 3.1,
 $$ \begin{align} \Vert f \circ T^{r_n} - f \Vert_{L^2(\nu)}^2 \ll_f \int_{\mathbb{T} \times {\Gamma \backslash G}}\, d(T^{r_n}(t,\Gamma g), (t,\Gamma g))^2\,d\nu(t,\Gamma g) \ll r_n^{-\varepsilon/100}. \end{align} $$
$$ \begin{align} \Vert f \circ T^{r_n} - f \Vert_{L^2(\nu)}^2 \ll_f \int_{\mathbb{T} \times {\Gamma \backslash G}}\, d(T^{r_n}(t,\Gamma g), (t,\Gamma g))^2\,d\nu(t,\Gamma g) \ll r_n^{-\varepsilon/100}. \end{align} $$
 $$ \begin{align*} \lim_{n\to \infty} \sum_{\lvert k\rvert \leq r_n^{\varepsilon/400}} \Vert f \circ T^{k r_n} - f\Vert_{L^2(\nu)}^2 = 0 \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty} \sum_{\lvert k\rvert \leq r_n^{\varepsilon/400}} \Vert f \circ T^{k r_n} - f\Vert_{L^2(\nu)}^2 = 0 \end{align*} $$
for every
![]() $\nu \in M(\mathbb {T}\times {\Gamma \backslash G}, T)$
, which satisfies the condition of Lemma 3.2 and Theorem 1.4 is proved.
$\nu \in M(\mathbb {T}\times {\Gamma \backslash G}, T)$
, which satisfies the condition of Lemma 3.2 and Theorem 1.4 is proved.
4 Proof of Lemma 3.1
In this section, we prove Lemma 3.1 and hence finish the proof of our main result. We assume that
![]() $\alpha $
is irrational. Let
$\alpha $
is irrational. Let
 $$ \begin{align*} \alpha=[0;a_1,a_2, \ldots , a_k, \ldots ]=\frac{1}{a_1+\dfrac{1}{a_2+\dfrac{1}{a_3+\cdots}}} \end{align*} $$
$$ \begin{align*} \alpha=[0;a_1,a_2, \ldots , a_k, \ldots ]=\frac{1}{a_1+\dfrac{1}{a_2+\dfrac{1}{a_3+\cdots}}} \end{align*} $$
be the continued fraction expansion of
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $p_k/q_k=[0;a_1,a_2, \ldots ,a_k]$
be the kth convergent of
$p_k/q_k=[0;a_1,a_2, \ldots ,a_k]$
be the kth convergent of
![]() $\alpha $
. Then we have the following well-known properties of
$\alpha $
. Then we have the following well-known properties of
![]() $p_k/q_k$
.
$p_k/q_k$
.
Lemma 4.1. Let
![]() $\alpha \in [0,1)$
be an irrational number and
$\alpha \in [0,1)$
be an irrational number and
![]() $p_k/q_k$
the kth convergent of
$p_k/q_k$
the kth convergent of
![]() $\alpha $
. Then:
$\alpha $
. Then:
-
(i)
 $p_0=0, p_1=1$
and
$p_0=0, p_1=1$
and
 $p_{k+2}=a_{k+2} p_{k+1}+ p_{k}$
for any
$p_{k+2}=a_{k+2} p_{k+1}+ p_{k}$
for any
 $k \geq 0$
;
$k \geq 0$
;
 $q_0=1, q_1=a_1$
and
$q_0=1, q_1=a_1$
and
 $q_{k+2}=a_{k+2} q_{k+1}+ q_{k}$
for all
$q_{k+2}=a_{k+2} q_{k+1}+ q_{k}$
for all
 $k \geq 0$
;
$k \geq 0$
; -
(ii)
 ${1}/{(q_k+q_{k+1})} < \lVert q_k \alpha \rVert < {1}/{q_{k+1}}$
for any
${1}/{(q_k+q_{k+1})} < \lVert q_k \alpha \rVert < {1}/{q_{k+1}}$
for any
 $k\geq 1$
;
$k\geq 1$
; -
(iii) if
 $0<q<q_{k+1}$
, then
$0<q<q_{k+1}$
, then
 $\lVert q_k\alpha \rVert \leq \lVert q\alpha \rVert $
.
$\lVert q_k\alpha \rVert \leq \lVert q\alpha \rVert $
.
We also need the following two lemmas.
Lemma 4.2. For
![]() $\alpha \in \mathbb {R}\setminus \mathbb {Q}$
and
$\alpha \in \mathbb {R}\setminus \mathbb {Q}$
and
![]() $k \geq 2$
,
$k \geq 2$
,
 $$ \begin{align*} \sum_{0 < \lvert q\rvert < q_k} \frac{1}{\Vert q \alpha \Vert^{2}} \asymp q_k^2 \quad \mbox{and} \quad \sum_{0 < \lvert q\rvert < q_k} \frac{1}{\Vert q \alpha \Vert} \asymp q_k \log q_k. \end{align*} $$
$$ \begin{align*} \sum_{0 < \lvert q\rvert < q_k} \frac{1}{\Vert q \alpha \Vert^{2}} \asymp q_k^2 \quad \mbox{and} \quad \sum_{0 < \lvert q\rvert < q_k} \frac{1}{\Vert q \alpha \Vert} \asymp q_k \log q_k. \end{align*} $$
Proof. The first part is from [Reference de Faveri1, Lemma 2] and we can similarly get the second.
Lemma 4.3. For
![]() $\alpha \in \mathbb {R}\setminus \mathbb {Q}$
,
$\alpha \in \mathbb {R}\setminus \mathbb {Q}$
,
![]() $k \geq 1$
and
$k \geq 1$
and
![]() $1 \leq c \leq q_k$
,
$1 \leq c \leq q_k$
,
 $$ \begin{align*} \sum_{q_k \leq \lvert q\rvert < q_{k+1}} \frac{1}{q^2} \min\bigg\{\frac{1}{\Vert q \alpha \Vert^{2}}, c^2\bigg\} \ll \frac{c}{q_k} \quad \mbox{and} \quad \sum_{q_k \leq \lvert q\rvert < q_{k+1}} \frac{1}{q^{2+\varepsilon}} \min\bigg\{\frac{1}{\Vert q \alpha \Vert}, c\bigg\} \ll \frac{c}{q_k ^{1+\varepsilon}}. \end{align*} $$
$$ \begin{align*} \sum_{q_k \leq \lvert q\rvert < q_{k+1}} \frac{1}{q^2} \min\bigg\{\frac{1}{\Vert q \alpha \Vert^{2}}, c^2\bigg\} \ll \frac{c}{q_k} \quad \mbox{and} \quad \sum_{q_k \leq \lvert q\rvert < q_{k+1}} \frac{1}{q^{2+\varepsilon}} \min\bigg\{\frac{1}{\Vert q \alpha \Vert}, c\bigg\} \ll \frac{c}{q_k ^{1+\varepsilon}}. \end{align*} $$
Proof. The first part is from [Reference de Faveri1, Lemma 3] and we can similarly get the second.
Now we are ready to give the proof of Lemma 3.1.
Proof of Lemma 3.1.
Let
![]() $\Phi (n,t)=\sum _{l=0}^{n-1}\phi (l\alpha +t)$
,
$\Phi (n,t)=\sum _{l=0}^{n-1}\phi (l\alpha +t)$
,
![]() $\Psi (n,t)=\sum _{l=0}^{n-1}\psi (l\alpha +t)$
and
$\Psi (n,t)=\sum _{l=0}^{n-1}\psi (l\alpha +t)$
and
![]() $H(n,t)=\sum _{l=0}^{n-1}\phi ^2(l\alpha +t)$
, then
$H(n,t)=\sum _{l=0}^{n-1}\phi ^2(l\alpha +t)$
, then
 $$ \begin{align*} T^n(t,\Gamma g)=\left( t+n\alpha, \Gamma g \begin{pmatrix} 1 & {\Phi(n,t)} & {\Psi(n,t)+\frac{1}{2} \Phi^2(n,t)-\frac{1}{2}H(n,t)} \\ 0 & 1 & {\Phi(n,t)} \\ 0 & 0 & 1 \end{pmatrix} \right). \end{align*} $$
$$ \begin{align*} T^n(t,\Gamma g)=\left( t+n\alpha, \Gamma g \begin{pmatrix} 1 & {\Phi(n,t)} & {\Psi(n,t)+\frac{1}{2} \Phi^2(n,t)-\frac{1}{2}H(n,t)} \\ 0 & 1 & {\Phi(n,t)} \\ 0 & 0 & 1 \end{pmatrix} \right). \end{align*} $$
We consider
 $$ \begin{align*} &d((t, \Gamma g),T^n(t, \Gamma g))^2 \\ &\quad =\lVert n\alpha\rVert^2+d_{{\Gamma \backslash G}}^2\left( \Gamma g, \Gamma g \begin{pmatrix} 1 & {\Phi(n,t)} & {\Psi(n,t)+\frac{1}{2}\Phi^2(n,t)-\frac{1}{2}H(n,t)} \\ 0 & 1 & {\Phi(n,t)} \\ 0 & 0 & 1 \end{pmatrix} \right)\\ &\quad \leq \lVert n\alpha\rVert^2+d_{G}^2\left( g, g \begin{pmatrix} 1 & {\Phi(n,t)} & {\Psi(n,t)+\frac{1}{2}\Phi^2(n,t)-\frac{1}{2}H(n,t)} \\ 0 & 1 & {\Phi(n,t)} \\ 0 & 0 & 1 \end{pmatrix}\right)\\ &\quad \leq \lVert n\alpha\rVert^2 + \left|\kappa \begin{pmatrix} 1 & {\Phi(n,t)} & {\Psi(n,t)+\frac{1}{2}\Phi^2(n,t)-\frac{1}{2}H(n,t)} \\ 0 & 1 & {\Phi(n,t)} \\ 0 & 0 & 1 \end{pmatrix} \right|{}^2\\ &\quad \ll \lVert n\alpha\rVert^2 + \lvert \Phi(n,t)\rvert^2 + \lvert \Psi(n,t)\rvert^2+ \lvert \Phi(n,t)\rvert^4 + \lvert H(n,t)\rvert^2. \end{align*} $$
$$ \begin{align*} &d((t, \Gamma g),T^n(t, \Gamma g))^2 \\ &\quad =\lVert n\alpha\rVert^2+d_{{\Gamma \backslash G}}^2\left( \Gamma g, \Gamma g \begin{pmatrix} 1 & {\Phi(n,t)} & {\Psi(n,t)+\frac{1}{2}\Phi^2(n,t)-\frac{1}{2}H(n,t)} \\ 0 & 1 & {\Phi(n,t)} \\ 0 & 0 & 1 \end{pmatrix} \right)\\ &\quad \leq \lVert n\alpha\rVert^2+d_{G}^2\left( g, g \begin{pmatrix} 1 & {\Phi(n,t)} & {\Psi(n,t)+\frac{1}{2}\Phi^2(n,t)-\frac{1}{2}H(n,t)} \\ 0 & 1 & {\Phi(n,t)} \\ 0 & 0 & 1 \end{pmatrix}\right)\\ &\quad \leq \lVert n\alpha\rVert^2 + \left|\kappa \begin{pmatrix} 1 & {\Phi(n,t)} & {\Psi(n,t)+\frac{1}{2}\Phi^2(n,t)-\frac{1}{2}H(n,t)} \\ 0 & 1 & {\Phi(n,t)} \\ 0 & 0 & 1 \end{pmatrix} \right|{}^2\\ &\quad \ll \lVert n\alpha\rVert^2 + \lvert \Phi(n,t)\rvert^2 + \lvert \Psi(n,t)\rvert^2+ \lvert \Phi(n,t)\rvert^4 + \lvert H(n,t)\rvert^2. \end{align*} $$
Therefore,
 $$ \begin{align*} \begin{aligned} &\int_{\mathbb{T}\times {\Gamma \backslash G}} d(T^{n}(t,\Gamma g),(t,\Gamma g))^2\,d\nu(t,\Gamma g)\\ &\quad \ll \lVert n\alpha\rVert^2+\int_{\mathbb{T} \times {\Gamma \backslash G}}(\lvert \Phi(n,t)\rvert^2 + \lvert \Psi(n,t)\rvert^2 + \lvert\Phi(n,t)\rvert^4 + \lvert H(n,t)\rvert^2)\,d\nu(t,\Gamma g). \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} &\int_{\mathbb{T}\times {\Gamma \backslash G}} d(T^{n}(t,\Gamma g),(t,\Gamma g))^2\,d\nu(t,\Gamma g)\\ &\quad \ll \lVert n\alpha\rVert^2+\int_{\mathbb{T} \times {\Gamma \backslash G}}(\lvert \Phi(n,t)\rvert^2 + \lvert \Psi(n,t)\rvert^2 + \lvert\Phi(n,t)\rvert^4 + \lvert H(n,t)\rvert^2)\,d\nu(t,\Gamma g). \end{aligned} \end{align*} $$
So we should choose a sequence
![]() $\{r_n\}_{n\geq 1}$
of
$\{r_n\}_{n\geq 1}$
of
![]() $\mathbb {N}$
such that
$\mathbb {N}$
such that
![]() $\lVert r_n\alpha \rVert ^2$
,
$\lVert r_n\alpha \rVert ^2$
,
![]() $\int _{\mathbb {T} \times {\Gamma \backslash G}}\lvert \Phi (r_n,t)\rvert ^2\,d\nu (t,\Gamma g)$
,
$\int _{\mathbb {T} \times {\Gamma \backslash G}}\lvert \Phi (r_n,t)\rvert ^2\,d\nu (t,\Gamma g)$
,
![]() $\int _{\mathbb {T} \times {\Gamma \backslash G}}\lvert \Psi (r_n,t)\rvert ^2\,d\nu (t,\Gamma g)$
,
$\int _{\mathbb {T} \times {\Gamma \backslash G}}\lvert \Psi (r_n,t)\rvert ^2\,d\nu (t,\Gamma g)$
,
![]() $\int _{\mathbb {T} \times {\Gamma \backslash G}}\lvert \Phi (r_n,t)\rvert ^4\,d\nu (t,\Gamma g)$
and
$\int _{\mathbb {T} \times {\Gamma \backslash G}}\lvert \Phi (r_n,t)\rvert ^4\,d\nu (t,\Gamma g)$
and
![]() $\int _{\mathbb {T} \times {\Gamma \backslash G}}\lvert H(r_n,t)\rvert ^2\,d\nu (t,\Gamma g)$
are bounded. The following argument is similar to [Reference de Faveri1, Reference Kanigowski, Lemańczyk and Radziwiłł8].
$\int _{\mathbb {T} \times {\Gamma \backslash G}}\lvert H(r_n,t)\rvert ^2\,d\nu (t,\Gamma g)$
are bounded. The following argument is similar to [Reference de Faveri1, Reference Kanigowski, Lemańczyk and Radziwiłł8].
First, we consider
![]() $\int _{\mathbb {T} \times {\Gamma \backslash G}}\lvert \Phi (n,t)\rvert ^2\,d\nu (t,\Gamma g)$
. This integral is only dependent on the first coordinate t. With the projection map
$\int _{\mathbb {T} \times {\Gamma \backslash G}}\lvert \Phi (n,t)\rvert ^2\,d\nu (t,\Gamma g)$
. This integral is only dependent on the first coordinate t. With the projection map
![]() $\pi (t,\Gamma g)=t$
, we can rewrite the integral as
$\pi (t,\Gamma g)=t$
, we can rewrite the integral as
 $$ \begin{align} \int_{\mathbb{T} \times {\Gamma \backslash G}}\lvert\Phi(n,\pi(t,\Gamma g))\rvert^2\,d\nu(t,\Gamma g)=\int_{\mathbb{T}}\lvert\Phi(n,t)\rvert^2\,d(\pi_*\nu)(t), \end{align} $$
$$ \begin{align} \int_{\mathbb{T} \times {\Gamma \backslash G}}\lvert\Phi(n,\pi(t,\Gamma g))\rvert^2\,d\nu(t,\Gamma g)=\int_{\mathbb{T}}\lvert\Phi(n,t)\rvert^2\,d(\pi_*\nu)(t), \end{align} $$
where the Borel probability measure
![]() $\pi _*\nu $
is the Lebesgue measure on
$\pi _*\nu $
is the Lebesgue measure on
![]() $\mathbb {T}$
since
$\mathbb {T}$
since
![]() $\alpha $
is irrational. Since
$\alpha $
is irrational. Since
![]() $\phi (t)=\sum _{m\neq 0}\widehat {\phi }(m)e(mt)$
, we have
$\phi (t)=\sum _{m\neq 0}\widehat {\phi }(m)e(mt)$
, we have
 $$ \begin{align*} \Phi(n,t)=\sum\limits_{l=0}^{n-1}\phi(l\alpha+t)=\sum\limits_{l=0}^{n-1}\sum\limits_{m\neq 0}\widehat{\phi}(m)e(m(l\alpha+t))=\sum\limits_{m\neq 0}\widehat{\phi}(m)e(mt)\frac{1-e(mn\alpha)}{1-e(m\alpha)}. \end{align*} $$
$$ \begin{align*} \Phi(n,t)=\sum\limits_{l=0}^{n-1}\phi(l\alpha+t)=\sum\limits_{l=0}^{n-1}\sum\limits_{m\neq 0}\widehat{\phi}(m)e(m(l\alpha+t))=\sum\limits_{m\neq 0}\widehat{\phi}(m)e(mt)\frac{1-e(mn\alpha)}{1-e(m\alpha)}. \end{align*} $$
By substituting this into (4.1), we get
 $$ \begin{align} \int_{\mathbb{T}} \lvert\Phi(n,t)\rvert^2\, dt = \int_{\mathbb{T}}\bigg|\sum\limits_{m\neq 0}\widehat{\phi}(m)e(mt)\frac{1-e(mn\alpha)}{1-e(m\alpha)}\bigg|^2\,dt = \sum\limits_{m\neq 0}\lvert\widehat{\phi}(m)\rvert^2\bigg|\frac{1-e(mn\alpha)}{1-e(m\alpha)}\bigg|^2. \end{align} $$
$$ \begin{align} \int_{\mathbb{T}} \lvert\Phi(n,t)\rvert^2\, dt = \int_{\mathbb{T}}\bigg|\sum\limits_{m\neq 0}\widehat{\phi}(m)e(mt)\frac{1-e(mn\alpha)}{1-e(m\alpha)}\bigg|^2\,dt = \sum\limits_{m\neq 0}\lvert\widehat{\phi}(m)\rvert^2\bigg|\frac{1-e(mn\alpha)}{1-e(m\alpha)}\bigg|^2. \end{align} $$
Now we can choose the desired sequence
![]() $\{r_n\}_{n\geq 1}$
of
$\{r_n\}_{n\geq 1}$
of
![]() $\mathbb {N}$
.Temporarily choose
$\mathbb {N}$
.Temporarily choose
![]() $r_n=q_n$
, where
$r_n=q_n$
, where
![]() $q_n$
is defined in Lemma 4.1. Then we break the sum in (4.2) into two sums according to
$q_n$
is defined in Lemma 4.1. Then we break the sum in (4.2) into two sums according to
![]() $0<\lvert m\rvert <q_n$
and
$0<\lvert m\rvert <q_n$
and
![]() $\lvert m\rvert \geq q_n$
.
$\lvert m\rvert \geq q_n$
.
For the second sum, we use the fact that
![]() $\widehat {\phi }(m)\ll m^{-1-\varepsilon }(m\neq 0)$
. (We only need
$\widehat {\phi }(m)\ll m^{-1-\varepsilon }(m\neq 0)$
. (We only need
![]() $\phi $
to be
$\phi $
to be
![]() $C^{1+\varepsilon }$
-smooth here, but the stronger assumption that
$C^{1+\varepsilon }$
-smooth here, but the stronger assumption that
![]() $\phi $
is
$\phi $
is
![]() $C^{2+\varepsilon }$
-smooth is needed later.) We also have
$C^{2+\varepsilon }$
-smooth is needed later.) We also have
![]() $\lvert 1-e(m\alpha )\rvert \asymp \lVert m\alpha \rVert $
,
$\lvert 1-e(m\alpha )\rvert \asymp \lVert m\alpha \rVert $
,
![]() $\lvert 1-e(mn\alpha )\rvert \leq 2$
and the trivial bound
$\lvert 1-e(mn\alpha )\rvert \leq 2$
and the trivial bound
![]() $\lvert {(1-e(mn\alpha ))}/{(1-e(m\alpha ))}\rvert \leq n$
. Then
$\lvert {(1-e(mn\alpha ))}/{(1-e(m\alpha ))}\rvert \leq n$
. Then
 $$ \begin{align} \sum_{\lvert m\rvert \geq q_n} \lvert\widehat{\phi}(m)\rvert^2 \bigg| \frac{1 - e(m r_n \alpha)}{1 - e(m \alpha)} \bigg|^2 &\ll \sum_{\lvert m\rvert \geq q_n} \frac{1}{\lvert m\rvert^{2+2\varepsilon}} \min\bigg\{\frac{1}{\Vert m \alpha \Vert^{2}}, r_n^2\bigg\} \nonumber\\ &< q_n^{-2\varepsilon} \sum_{k=n}^\infty \sum_{q_k \leq \lvert m\rvert < q_{k+1}} \frac{1}{m^{2}} \min\bigg\{\frac{1} {\Vert m \alpha \Vert^{2}}, q_n^2\bigg\} \nonumber\\ &\ll q_n^{-2\varepsilon }\sum_{k = n}^\infty \frac{q_n}{q_k} \ll r_n^{-2\varepsilon} \quad \mbox{(by Lemma 4.3)}. \end{align} $$
$$ \begin{align} \sum_{\lvert m\rvert \geq q_n} \lvert\widehat{\phi}(m)\rvert^2 \bigg| \frac{1 - e(m r_n \alpha)}{1 - e(m \alpha)} \bigg|^2 &\ll \sum_{\lvert m\rvert \geq q_n} \frac{1}{\lvert m\rvert^{2+2\varepsilon}} \min\bigg\{\frac{1}{\Vert m \alpha \Vert^{2}}, r_n^2\bigg\} \nonumber\\ &< q_n^{-2\varepsilon} \sum_{k=n}^\infty \sum_{q_k \leq \lvert m\rvert < q_{k+1}} \frac{1}{m^{2}} \min\bigg\{\frac{1} {\Vert m \alpha \Vert^{2}}, q_n^2\bigg\} \nonumber\\ &\ll q_n^{-2\varepsilon }\sum_{k = n}^\infty \frac{q_n}{q_k} \ll r_n^{-2\varepsilon} \quad \mbox{(by Lemma 4.3)}. \end{align} $$
For the first sum, we use the fact that
![]() $\lvert 1-e(m\alpha )\rvert \asymp \lVert m\alpha \rVert $
and
$\lvert 1-e(m\alpha )\rvert \asymp \lVert m\alpha \rVert $
and
![]() $\lvert 1-e(mr_n\alpha )\rvert \asymp \lVert mq_n\alpha \rVert \leq m^2 \lVert q_n\alpha \rVert ^2<m^2q_{n+1}^{-2}$
. Then
$\lvert 1-e(mr_n\alpha )\rvert \asymp \lVert mq_n\alpha \rVert \leq m^2 \lVert q_n\alpha \rVert ^2<m^2q_{n+1}^{-2}$
. Then
 $$ \begin{align} \sum_{0<\lvert m\rvert < q_n} \lvert \widehat{\phi}(m)\rvert^2 \bigg| \frac{1 - e(m r_n \alpha)}{1 - e(m \alpha)} \bigg|^2 &\ll \frac{1}{q_{n+1}^{2}} \sum_{0 < \lvert m\rvert <q_n} \frac{1}{\lvert m\rvert^{2\varepsilon}} \frac{1}{\Vert m \alpha \Vert^{2}}. \end{align} $$
$$ \begin{align} \sum_{0<\lvert m\rvert < q_n} \lvert \widehat{\phi}(m)\rvert^2 \bigg| \frac{1 - e(m r_n \alpha)}{1 - e(m \alpha)} \bigg|^2 &\ll \frac{1}{q_{n+1}^{2}} \sum_{0 < \lvert m\rvert <q_n} \frac{1}{\lvert m\rvert^{2\varepsilon}} \frac{1}{\Vert m \alpha \Vert^{2}}. \end{align} $$
For this sum, we consider the following two cases:
Case A. There is a subsequence
![]() $\{q_{b_n}\}_{n \geq 1}$
of
$\{q_{b_n}\}_{n \geq 1}$
of
![]() $\{q_n\}_{n \geq 1}$
such that
$\{q_n\}_{n \geq 1}$
such that
![]() $q_{b_n + 1} \geq q_{b_n}^2$
for all
$q_{b_n + 1} \geq q_{b_n}^2$
for all
![]() $n \geq 1$
.
$n \geq 1$
.
In this case, we replace
![]() $\{r_n\}_{n \geq 1}$
by
$\{r_n\}_{n \geq 1}$
by
![]() $\{q_{b_n}\}_{n\geq 1}$
and notice that the estimate (4.3) still holds for this new
$\{q_{b_n}\}_{n\geq 1}$
and notice that the estimate (4.3) still holds for this new
![]() $\{r_n\}_{n \geq 1}$
. By Lemma 4.2,
$\{r_n\}_{n \geq 1}$
. By Lemma 4.2,
 $$ \begin{align*} \frac{1}{q_{b_n+1}^{2}} \sum_{0 < \lvert m\rvert <q_{b_n}} \frac{1}{\lvert m\rvert^{2\varepsilon}} \frac{1}{\Vert m \alpha \Vert^{2}} \leq \frac{1}{q_{b_n}^{4}} \sum_{0 < \lvert m\rvert <q_{b_n}} \frac{1}{\Vert m \alpha \Vert^{2}}\ll q_{b_n}^{-2} \leq r_{n}^{-2}. \end{align*} $$
$$ \begin{align*} \frac{1}{q_{b_n+1}^{2}} \sum_{0 < \lvert m\rvert <q_{b_n}} \frac{1}{\lvert m\rvert^{2\varepsilon}} \frac{1}{\Vert m \alpha \Vert^{2}} \leq \frac{1}{q_{b_n}^{4}} \sum_{0 < \lvert m\rvert <q_{b_n}} \frac{1}{\Vert m \alpha \Vert^{2}}\ll q_{b_n}^{-2} \leq r_{n}^{-2}. \end{align*} $$
Case B. For all sufficiently large n, we have
![]() $q_{n+1} < q_n^2$
.
$q_{n+1} < q_n^2$
.
In this case, for any
![]() $0<k<n$
, Lemma 4.2 gives
$0<k<n$
, Lemma 4.2 gives
 $$ \begin{align} \sum_{0 < \lvert m\rvert <q_n} \frac{1}{\lvert m\rvert^{2\varepsilon}} \frac{1}{\Vert m \alpha \Vert^{2}}&=\sum_{0 < \lvert m\rvert <q_k} \frac{1}{\lvert m\rvert^{2\varepsilon}} \frac{1}{\Vert m \alpha \Vert^{2}}+\sum_{q_k \leq \lvert m\rvert <q_n} \frac{1}{\lvert m\rvert^{2\varepsilon}} \frac{1}{\Vert m \alpha \Vert^{2}} \nonumber \\ &<\sum_{0 < \lvert m\rvert <q_k} \frac{1}{\Vert m \alpha \Vert^{2}}+q_k^{-2\varepsilon}\sum_{q_k \leq \lvert m\rvert <q_n} \frac{1}{\Vert m \alpha \Vert^{2}}\nonumber\\ &\ll q_k^2+q_k^{-2\varepsilon}q_n^2. \end{align} $$
$$ \begin{align} \sum_{0 < \lvert m\rvert <q_n} \frac{1}{\lvert m\rvert^{2\varepsilon}} \frac{1}{\Vert m \alpha \Vert^{2}}&=\sum_{0 < \lvert m\rvert <q_k} \frac{1}{\lvert m\rvert^{2\varepsilon}} \frac{1}{\Vert m \alpha \Vert^{2}}+\sum_{q_k \leq \lvert m\rvert <q_n} \frac{1}{\lvert m\rvert^{2\varepsilon}} \frac{1}{\Vert m \alpha \Vert^{2}} \nonumber \\ &<\sum_{0 < \lvert m\rvert <q_k} \frac{1}{\Vert m \alpha \Vert^{2}}+q_k^{-2\varepsilon}\sum_{q_k \leq \lvert m\rvert <q_n} \frac{1}{\Vert m \alpha \Vert^{2}}\nonumber\\ &\ll q_k^2+q_k^{-2\varepsilon}q_n^2. \end{align} $$
We choose k with
![]() $0<k<n$
such that
$0<k<n$
such that
![]() $q_k\in [q_n^{1/4}, q_n^{1/2}]$
, which is possible since for all sufficiently large n, we have
$q_k\in [q_n^{1/4}, q_n^{1/2}]$
, which is possible since for all sufficiently large n, we have
![]() $q_{n+1} < q_n^2$
. Then (4.4) and (4.5) give
$q_{n+1} < q_n^2$
. Then (4.4) and (4.5) give
 $$ \begin{align*} \frac{1}{q_{n+1}^{2}} \sum_{0 < \lvert m\rvert <q_n} \frac{1}{\lvert m\rvert^{2\varepsilon}} \frac{1}{\Vert m \alpha \Vert^{2}} \ll \frac{1}{q_{n+1}^{2}}(q_k^2+q_k^{-2\varepsilon}q_n^2) \leq \frac{1}{q_{n+1}^{2}}(q_n+q_n^{2-\varepsilon/2}) \ll q_n^{-\varepsilon/2}\leq r_n^{-\varepsilon / 2}. \end{align*} $$
$$ \begin{align*} \frac{1}{q_{n+1}^{2}} \sum_{0 < \lvert m\rvert <q_n} \frac{1}{\lvert m\rvert^{2\varepsilon}} \frac{1}{\Vert m \alpha \Vert^{2}} \ll \frac{1}{q_{n+1}^{2}}(q_k^2+q_k^{-2\varepsilon}q_n^2) \leq \frac{1}{q_{n+1}^{2}}(q_n+q_n^{2-\varepsilon/2}) \ll q_n^{-\varepsilon/2}\leq r_n^{-\varepsilon / 2}. \end{align*} $$
This proves that
![]() $\int _{\mathbb {T} \times {\Gamma \backslash G}}\lvert \Phi (r_n,t)\rvert ^2\,d\nu (t,\Gamma g)\ll r_n^{-\lambda }$
for some
$\int _{\mathbb {T} \times {\Gamma \backslash G}}\lvert \Phi (r_n,t)\rvert ^2\,d\nu (t,\Gamma g)\ll r_n^{-\lambda }$
for some
![]() $\lambda> \varepsilon /100$
. By the same argument, we see that with this choice of
$\lambda> \varepsilon /100$
. By the same argument, we see that with this choice of
![]() $\{r_n\}_{n \geq 1}$
, the same estimate also holds for the integrals of
$\{r_n\}_{n \geq 1}$
, the same estimate also holds for the integrals of
![]() $\lvert \Psi (r_n,t)\rvert ^2$
.
$\lvert \Psi (r_n,t)\rvert ^2$
.
For the first term
![]() $\lVert n\alpha \rVert $
, we have
$\lVert n\alpha \rVert $
, we have
where
![]() $b_n$
is the sequence of indices with
$b_n$
is the sequence of indices with
![]() $q_{b_n + 1} \geq q_{b_n}^2$
in Case A and
$q_{b_n + 1} \geq q_{b_n}^2$
in Case A and
![]() $b_n = n$
in Case B.
$b_n = n$
in Case B.
The estimates for integrals of
![]() $\lvert H(r_n,t)\rvert ^2$
and
$\lvert H(r_n,t)\rvert ^2$
and
![]() $\lvert \Phi (r_n,t)\rvert ^4$
are similar, so we only state the differences in the proof.
$\lvert \Phi (r_n,t)\rvert ^4$
are similar, so we only state the differences in the proof.
For the integral of
![]() $\lvert H(r_n,t)\rvert ^2$
, we need to slightly modify the choice of
$\lvert H(r_n,t)\rvert ^2$
, we need to slightly modify the choice of
![]() $r_n$
since now the zeroth Fourier coefficient of
$r_n$
since now the zeroth Fourier coefficient of
![]() $\eta (t) := \varphi ^2(t)$
does not vanish in general. Therefore, we should consider the extra term
$\eta (t) := \varphi ^2(t)$
does not vanish in general. Therefore, we should consider the extra term
![]() $\Vert r_n \hat {\eta }(0)\Vert $
. To overcome this difficulty, we follow the idea of de Faveri [Reference de Faveri1]. By Dirichlet’s approximation theorem, for any
$\Vert r_n \hat {\eta }(0)\Vert $
. To overcome this difficulty, we follow the idea of de Faveri [Reference de Faveri1]. By Dirichlet’s approximation theorem, for any
![]() $n \geq 1$
, we can find some
$n \geq 1$
, we can find some
![]() $s_n \leq q_n ^{\delta }$
such that
$s_n \leq q_n ^{\delta }$
such that
![]() $\Vert s_n q_n \hat {\eta }(0)\Vert < q_n ^{-\delta }$
where
$\Vert s_n q_n \hat {\eta }(0)\Vert < q_n ^{-\delta }$
where
![]() $0<\delta <\varepsilon /10$
. Then we can slightly modify the definition of
$0<\delta <\varepsilon /10$
. Then we can slightly modify the definition of
![]() $r_n$
by setting
$r_n$
by setting
![]() $r_n = s_n q_n$
. Since
$r_n = s_n q_n$
. Since
![]() $s_n$
is quite small compared with
$s_n$
is quite small compared with
![]() $q_n$
, the above argument for this new choice of
$q_n$
, the above argument for this new choice of
![]() $r_n$
is still valid.
$r_n$
is still valid.
For the integral of
![]() $\lvert \Phi (r_n,t)\rvert ^4$
, we cannot use the Parseval identity, so we estimate it pointwise. At this point, we need the stronger smoothness for
$\lvert \Phi (r_n,t)\rvert ^4$
, we cannot use the Parseval identity, so we estimate it pointwise. At this point, we need the stronger smoothness for
![]() $\phi $
to obtain the desired upper bound for the Fourier coefficients. We consider the same two cases.
$\phi $
to obtain the desired upper bound for the Fourier coefficients. We consider the same two cases.
Case A. In this case, we have
![]() $q_{n+1} < q_n ^2$
for all sufficiently large n and
$q_{n+1} < q_n ^2$
for all sufficiently large n and
![]() $r_n = s_n q_n$
. Since
$r_n = s_n q_n$
. Since
![]() $\phi $
is
$\phi $
is
![]() $C^{2+\varepsilon }$
-smooth, we have
$C^{2+\varepsilon }$
-smooth, we have
![]() $\hat {\phi }(m) \ll \lvert m\rvert ^{-2-\varepsilon }$
for
$\hat {\phi }(m) \ll \lvert m\rvert ^{-2-\varepsilon }$
for
![]() $m \neq 0$
. Thus,
$m \neq 0$
. Thus,
 $$ \begin{align*} \Phi(r_n,t) = \sum_{m \neq 0} \lvert\hat{\phi}(m)\rvert \bigg| \frac{1-e(mr_n \alpha)}{1-e(m \alpha)}\bigg| \ll \bigg( \sum_{0 < \lvert m\rvert < q_n} + \sum_{ \lvert m\rvert \geq q_n} \bigg) \frac{1}{\lvert m\rvert^{2+\varepsilon}} \min \bigg\{ r_n , \frac{1}{\Vert m \alpha \Vert}\bigg\}. \end{align*} $$
$$ \begin{align*} \Phi(r_n,t) = \sum_{m \neq 0} \lvert\hat{\phi}(m)\rvert \bigg| \frac{1-e(mr_n \alpha)}{1-e(m \alpha)}\bigg| \ll \bigg( \sum_{0 < \lvert m\rvert < q_n} + \sum_{ \lvert m\rvert \geq q_n} \bigg) \frac{1}{\lvert m\rvert^{2+\varepsilon}} \min \bigg\{ r_n , \frac{1}{\Vert m \alpha \Vert}\bigg\}. \end{align*} $$
For
![]() $\lvert m\rvert \geq q_n$
, by Lemma 4.3,
$\lvert m\rvert \geq q_n$
, by Lemma 4.3,
 $$ \begin{align*} \sum_{\lvert m\rvert \geq q_n} \frac{1}{\lvert m\rvert^{2+\varepsilon}} \min \bigg\{ r_n , \frac{1}{\Vert m \alpha \Vert}\bigg\} &= \sum_{k=n}^{\infty} \frac{r_n}{q_k ^{1+\varepsilon}} \leq \sum_{k=n}^{\infty} \frac{q_n ^{1+\delta}}{q_k ^{1+\varepsilon}} \\ &\leq q_n ^{\delta - \varepsilon} \sum_{k=n}^{\infty} \frac{q_n}{q_k} \leq r_n ^{-(1-\gamma)(\varepsilon -\delta)} \leq r_n ^{-\lambda}. \end{align*} $$
$$ \begin{align*} \sum_{\lvert m\rvert \geq q_n} \frac{1}{\lvert m\rvert^{2+\varepsilon}} \min \bigg\{ r_n , \frac{1}{\Vert m \alpha \Vert}\bigg\} &= \sum_{k=n}^{\infty} \frac{r_n}{q_k ^{1+\varepsilon}} \leq \sum_{k=n}^{\infty} \frac{q_n ^{1+\delta}}{q_k ^{1+\varepsilon}} \\ &\leq q_n ^{\delta - \varepsilon} \sum_{k=n}^{\infty} \frac{q_n}{q_k} \leq r_n ^{-(1-\gamma)(\varepsilon -\delta)} \leq r_n ^{-\lambda}. \end{align*} $$
For
![]() $\lvert m\rvert < q_n$
,
$\lvert m\rvert < q_n$
,
 $$ \begin{align*} \sum_{0 < \lvert m\rvert < q_n} \lvert\phi(m)\rvert \bigg|\frac{1-e(mr_n \alpha)}{1-e(m \alpha)}\bigg| &\ll \sum_{0 < \lvert m\rvert < q_n} \frac{1}{\lvert m\rvert^{2+\varepsilon}} \frac{s_n \lvert m\rvert\, \Vert q_n \alpha\Vert}{\Vert m \alpha \Vert} \\ &\ll \frac{q_n ^{\delta}}{ q_{n+1}} \sum_{0<\lvert m\rvert <q_n} \frac{1}{\lvert m\rvert^{1+\varepsilon}} \frac{1}{\Vert m\alpha \Vert}. \end{align*} $$
$$ \begin{align*} \sum_{0 < \lvert m\rvert < q_n} \lvert\phi(m)\rvert \bigg|\frac{1-e(mr_n \alpha)}{1-e(m \alpha)}\bigg| &\ll \sum_{0 < \lvert m\rvert < q_n} \frac{1}{\lvert m\rvert^{2+\varepsilon}} \frac{s_n \lvert m\rvert\, \Vert q_n \alpha\Vert}{\Vert m \alpha \Vert} \\ &\ll \frac{q_n ^{\delta}}{ q_{n+1}} \sum_{0<\lvert m\rvert <q_n} \frac{1}{\lvert m\rvert^{1+\varepsilon}} \frac{1}{\Vert m\alpha \Vert}. \end{align*} $$
Now since
![]() $q_{n+1} < q_n ^2$
, there exists some
$q_{n+1} < q_n ^2$
, there exists some
![]() $q_k \in [q_n ^{1/4}, q_n ^{1/2} ]$
. So
$q_k \in [q_n ^{1/4}, q_n ^{1/2} ]$
. So
 $$ \begin{align*} \frac{q_n ^{\delta}}{ q_{n+1}} \sum_{0<\lvert m\rvert<q_n} \frac{1}{\lvert m\rvert^{1+\varepsilon}} \frac{1}{\Vert m\alpha \Vert} &= \frac{q_n ^{\delta}}{ q_{n+1}} \bigg( \sum_{0< \lvert m\rvert < 5q_k}+\sum_{q_k \leq \lvert m\rvert < q_n} \bigg) \frac{1}{\lvert m\rvert^{1+\varepsilon}} \frac{1}{\Vert m \alpha \Vert} \\ &\ll \frac{q_n ^{\delta}}{q_n} (q_k \log q_k + q_{k} ^{-1-\varepsilon} q_n \log q_n) \quad \mbox{(by Lemma 4.2)} \\ &\ll q_n ^{\delta - 1/4 - \varepsilon/4+1/100} \ll r_n ^{-\lambda/4} \end{align*} $$
$$ \begin{align*} \frac{q_n ^{\delta}}{ q_{n+1}} \sum_{0<\lvert m\rvert<q_n} \frac{1}{\lvert m\rvert^{1+\varepsilon}} \frac{1}{\Vert m\alpha \Vert} &= \frac{q_n ^{\delta}}{ q_{n+1}} \bigg( \sum_{0< \lvert m\rvert < 5q_k}+\sum_{q_k \leq \lvert m\rvert < q_n} \bigg) \frac{1}{\lvert m\rvert^{1+\varepsilon}} \frac{1}{\Vert m \alpha \Vert} \\ &\ll \frac{q_n ^{\delta}}{q_n} (q_k \log q_k + q_{k} ^{-1-\varepsilon} q_n \log q_n) \quad \mbox{(by Lemma 4.2)} \\ &\ll q_n ^{\delta - 1/4 - \varepsilon/4+1/100} \ll r_n ^{-\lambda/4} \end{align*} $$
provided that
![]() $\lambda $
is sufficiently small.
$\lambda $
is sufficiently small.
Case B. In this case, there is a subsequene
![]() $\{q_{b_n}\}$
of
$\{q_{b_n}\}$
of
![]() $\{q_n\}$
such that
$\{q_n\}$
such that
![]() $q_{b_n+1} \geq q_{b_n} ^2$
and we choose
$q_{b_n+1} \geq q_{b_n} ^2$
and we choose
![]() $r_n = s_{b_n}q_{b_n}$
. Then, by the same argument as in Case A,
$r_n = s_{b_n}q_{b_n}$
. Then, by the same argument as in Case A,
 $$ \begin{align*} \sum_{\lvert m\rvert\geq q_{b_n}} \lvert \phi(m)\rvert^2 \bigg|\frac{1-e(mr_n \alpha)}{1-e(m \alpha)}\bigg|^2 \ll q_{b_n} ^{\delta-\varepsilon} \ll r_n^{-\lambda} \end{align*} $$
$$ \begin{align*} \sum_{\lvert m\rvert\geq q_{b_n}} \lvert \phi(m)\rvert^2 \bigg|\frac{1-e(mr_n \alpha)}{1-e(m \alpha)}\bigg|^2 \ll q_{b_n} ^{\delta-\varepsilon} \ll r_n^{-\lambda} \end{align*} $$
if
![]() $\lambda $
is sufficiently small.
$\lambda $
is sufficiently small.
Finally, for
![]() $0<\lvert m\rvert < q_{b_n}$
,
$0<\lvert m\rvert < q_{b_n}$
,
 $$ \begin{align*} \sum_{0 < \lvert m\rvert < q_{b_n}} \lvert \phi(m)\rvert \bigg|\frac{1-e(mr_n \alpha)}{1-e(m \alpha)}\bigg| &\ll \sum_{0 < \lvert m\rvert < q_{b_n}} \frac{1}{\lvert m\rvert^{2+\varepsilon}} \frac{s_{b_n} \lvert m\rvert\, \Vert q_{b_n} \alpha\Vert}{\Vert m \alpha \Vert} \\ &\ll \frac{q_{b_n} ^{\delta}}{ q_{b_n+1}} \sum_{0<\lvert m\rvert <q_{b_n}} \frac{1}{\lvert m\rvert^{1+\varepsilon}} \frac{1}{\Vert m\alpha \Vert} \\ &\ll \frac{q_{b_n} ^{\delta}}{q_{b_n} ^2} q_{b_n} \log q_{b_n} \ll r_n ^{-\lambda} \quad \mbox{(by Lemma 4.2)} \end{align*} $$
$$ \begin{align*} \sum_{0 < \lvert m\rvert < q_{b_n}} \lvert \phi(m)\rvert \bigg|\frac{1-e(mr_n \alpha)}{1-e(m \alpha)}\bigg| &\ll \sum_{0 < \lvert m\rvert < q_{b_n}} \frac{1}{\lvert m\rvert^{2+\varepsilon}} \frac{s_{b_n} \lvert m\rvert\, \Vert q_{b_n} \alpha\Vert}{\Vert m \alpha \Vert} \\ &\ll \frac{q_{b_n} ^{\delta}}{ q_{b_n+1}} \sum_{0<\lvert m\rvert <q_{b_n}} \frac{1}{\lvert m\rvert^{1+\varepsilon}} \frac{1}{\Vert m\alpha \Vert} \\ &\ll \frac{q_{b_n} ^{\delta}}{q_{b_n} ^2} q_{b_n} \log q_{b_n} \ll r_n ^{-\lambda} \quad \mbox{(by Lemma 4.2)} \end{align*} $$
provided that
![]() $\lambda $
is sufficiently small. This proves Lemma 3.1.
$\lambda $
is sufficiently small. This proves Lemma 3.1.
Acknowledgement
We are grateful to the anonymous referees for the helpful corrections and suggestions.