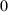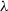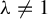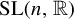1 Introduction and main results
An essentially free, ergodic, non-singular action
![]() $G \curvearrowright (X,\mu )$
of a countable group G on a standard probability space is said to be orbit equivalence (OE) superrigid if the group G and its action on
$G \curvearrowright (X,\mu )$
of a countable group G on a standard probability space is said to be orbit equivalence (OE) superrigid if the group G and its action on
![]() $(X,\mu )$
can be entirely retrieved from the orbit equivalence relation
$(X,\mu )$
can be entirely retrieved from the orbit equivalence relation
![]() $\mathcal {R}(G \curvearrowright X) = \{(x,g \cdot x) \mid x \in X, g \in G\}$
. Especially in the case where
$\mathcal {R}(G \curvearrowright X) = \{(x,g \cdot x) \mid x \in X, g \in G\}$
. Especially in the case where
![]() $\mu $
is a G-invariant probability measure, several OE-superrigidity theorems were proven in the context of Popa’s deformation/rigidity theory; see, for example, [Reference Drimbe, Ioana and PetersonDIP19, Reference IoanaIoa08, Reference PopaPop05, Reference Platonov and RapinchukPop06].
$\mu $
is a G-invariant probability measure, several OE-superrigidity theorems were proven in the context of Popa’s deformation/rigidity theory; see, for example, [Reference Drimbe, Ioana and PetersonDIP19, Reference IoanaIoa08, Reference PopaPop05, Reference Platonov and RapinchukPop06].
Beyond the probability measure-preserving setting, OE-superrigidity results are more scarce; see, for example, [Reference Drimbe and VaesDV21, Reference IoanaIoa14, Reference Popa and VaesPV08]. In all these cases, the group action
![]() $G \curvearrowright (X,\mu )$
has one of the following Krieger types: II
$G \curvearrowright (X,\mu )$
has one of the following Krieger types: II
![]() $_1$
, II
$_1$
, II
![]() $_\infty $
or III
$_\infty $
or III
![]() $_1$
(see §2 for definitions). There is a conceptual reason why it is harder to prove OE superrigidity for actions of type III
$_1$
(see §2 for definitions). There is a conceptual reason why it is harder to prove OE superrigidity for actions of type III
![]() $_\unicode{x3bb} $
,
$_\unicode{x3bb} $
,
![]() $\unicode{x3bb} \in [0,1)$
. One typically proves OE superrigidity for
$\unicode{x3bb} \in [0,1)$
. One typically proves OE superrigidity for
![]() $G \curvearrowright (X,\mu )$
by showing that every measurable
$G \curvearrowright (X,\mu )$
by showing that every measurable
![]() $1$
-cocycle
$1$
-cocycle
![]() $\omega : G \times X \to \Lambda $
with values in an arbitrary countable group
$\omega : G \times X \to \Lambda $
with values in an arbitrary countable group
![]() $\Lambda $
is cohomologous to a group homomorphism
$\Lambda $
is cohomologous to a group homomorphism
![]() $\delta : G \to \Lambda $
. When the measure
$\delta : G \to \Lambda $
. When the measure
![]() $\mu $
is not G-invariant, the logarithm of the Radon–Nikodym derivative
$\mu $
is not G-invariant, the logarithm of the Radon–Nikodym derivative
![]() $d(g^{-1}\cdot \mu )/d\mu $
provides a
$d(g^{-1}\cdot \mu )/d\mu $
provides a
![]() $1$
-cocycle
$1$
-cocycle
![]() $\omega : G \times X \to \mathbb {R}$
. In type III
$\omega : G \times X \to \mathbb {R}$
. In type III
![]() $_\unicode{x3bb} $
with
$_\unicode{x3bb} $
with
![]() $\unicode{x3bb} \in [0,1)$
, this
$\unicode{x3bb} \in [0,1)$
, this
![]() $1$
-cocycle is ‘essentially’ similar to a
$1$
-cocycle is ‘essentially’ similar to a
![]() $1$
-cocycle with values in a countable group. Therefore, cocycle superrigidity tends to fail.
$1$
-cocycle with values in a countable group. Therefore, cocycle superrigidity tends to fail.
In this paper, we obtain the first OE-superrigidity results in type III
![]() $_\unicode{x3bb} $
when
$_\unicode{x3bb} $
when
![]() $\unicode{x3bb} \neq 1$
. In Theorem C, we prove OE superrigidity for the affine action of dense subgroups
$\unicode{x3bb} \neq 1$
. In Theorem C, we prove OE superrigidity for the affine action of dense subgroups
![]() $G < \operatorname {SL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
on
$G < \operatorname {SL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
on
![]() $X = \mathbb {R}^n$
. These actions can be of type III
$X = \mathbb {R}^n$
. These actions can be of type III
![]() $_\unicode{x3bb} $
for any
$_\unicode{x3bb} $
for any
![]() $\unicode{x3bb} \in (0,1]$
. In this result, OE superrigidity holds in its strongest possible form: for every essentially free, ergodic, non-singular action
$\unicode{x3bb} \in (0,1]$
. In this result, OE superrigidity holds in its strongest possible form: for every essentially free, ergodic, non-singular action
![]() $\Lambda \curvearrowright (Z,\zeta )$
that is stably orbit equivalent to
$\Lambda \curvearrowright (Z,\zeta )$
that is stably orbit equivalent to
![]() $G \curvearrowright (X,\mu )$
, there exists an injective group homomorphism
$G \curvearrowright (X,\mu )$
, there exists an injective group homomorphism
![]() $\delta : G \to \Lambda $
such that
$\delta : G \to \Lambda $
such that
![]() $\Lambda \curvearrowright (Z,\zeta )$
is isomorphic to the induction of
$\Lambda \curvearrowright (Z,\zeta )$
is isomorphic to the induction of
![]() $G \curvearrowright (X,\mu )$
along
$G \curvearrowright (X,\mu )$
along
![]() $\delta $
.
$\delta $
.
In Theorem C, we also prove that this strongest form of OE superrigidity can basically never hold for actions of type III
![]() $_0$
. In type III
$_0$
. In type III
![]() $_0$
, it is necessary to further reduce the other action
$_0$
, it is necessary to further reduce the other action
![]() $\Lambda \curvearrowright (Z,\zeta )$
: after writing
$\Lambda \curvearrowright (Z,\zeta )$
: after writing
![]() $\Lambda \curvearrowright Z$
as an induction of
$\Lambda \curvearrowright Z$
as an induction of
![]() $\Lambda _0 \curvearrowright Z_0$
, we need to take a quotient
$\Lambda _0 \curvearrowright Z_0$
, we need to take a quotient
![]() $\Lambda _0 / \Sigma \curvearrowright Z_0 / \Sigma $
by a normal subgroup
$\Lambda _0 / \Sigma \curvearrowright Z_0 / \Sigma $
by a normal subgroup
![]() $\Sigma $
whose action on
$\Sigma $
whose action on
![]() $Z_0$
admits a fundamental domain, before arriving at an action that is conjugate with
$Z_0$
admits a fundamental domain, before arriving at an action that is conjugate with
![]() $G \curvearrowright (X,\mu )$
.
$G \curvearrowright (X,\mu )$
.
This leads to a second, slightly weaker version of OE superrigidity that we denote, without too much inspiration, as OE superrigidity (v2). In Theorem A and Corollary B, we then prove that natural skew product actions of dense subgroups of
![]() $\operatorname {SL}(n,\mathbb {R})$
are OE superrigid (v2), of type III
$\operatorname {SL}(n,\mathbb {R})$
are OE superrigid (v2), of type III
![]() $_0$
, with any prescribed associated flow.
$_0$
, with any prescribed associated flow.
Before stating our main results, we make this terminology more precise. Note that the concepts of (stable) orbit equivalence, induced actions, conjugate actions, etc., are recalled in §2.
Beyond the probability measure-preserving setting, one cannot distinguish between orbit equivalence and stable orbit equivalence. Therefore, induced actions will appear in any OE-superrigidity statement. We thus formally define the following property for a free, ergodic, non-singular action
![]() $G \curvearrowright (X,\mu )$
.
$G \curvearrowright (X,\mu )$
.
-
• OE superrigidity (v1) of
 $G \curvearrowright (X,\mu )$
: any free, ergodic, non-singular action that is stably orbit equivalent to
$G \curvearrowright (X,\mu )$
: any free, ergodic, non-singular action that is stably orbit equivalent to
 $G \curvearrowright (X,\mu )$
is conjugate to an induction of
$G \curvearrowright (X,\mu )$
is conjugate to an induction of
 $G \curvearrowright (X,\mu )$
.
$G \curvearrowright (X,\mu )$
.
As we prove in Theorem C, this (v1) of OE superrigidity can basically never hold for actions of type III
![]() $_0$
, but does hold for several actions of type III
$_0$
, but does hold for several actions of type III
![]() $_\unicode{x3bb} $
with
$_\unicode{x3bb} $
with
![]() $\unicode{x3bb} \in (0,1]$
. For actions of type III
$\unicode{x3bb} \in (0,1]$
. For actions of type III
![]() $_0$
, unavoidably the following extra freedom is needed, accommodating the canonical stable orbit equivalences that come with induction and with quotients by normal subgroups whose action admits a fundamental domain.
$_0$
, unavoidably the following extra freedom is needed, accommodating the canonical stable orbit equivalences that come with induction and with quotients by normal subgroups whose action admits a fundamental domain.
-
• OE superrigidity (v2) of
 $G \curvearrowright (X,\mu )$
: if a free, ergodic, non-singular action
$G \curvearrowright (X,\mu )$
: if a free, ergodic, non-singular action
 $\Lambda \curvearrowright (Z,\zeta )$
is stably orbit equivalent to
$\Lambda \curvearrowright (Z,\zeta )$
is stably orbit equivalent to
 $G \curvearrowright (X,\mu )$
, there exist subgroups
$G \curvearrowright (X,\mu )$
, there exist subgroups
 $\Sigma < \Lambda _0 < \Lambda $
and a non-negligible
$\Sigma < \Lambda _0 < \Lambda $
and a non-negligible
 $Z_0 \subset Z$
such that
$Z_0 \subset Z$
such that
 $\Lambda \curvearrowright Z$
is induced from
$\Lambda \curvearrowright Z$
is induced from
 $\Lambda _0 \curvearrowright Z_0$
,
$\Lambda _0 \curvearrowright Z_0$
,
 $\Sigma \lhd \Lambda _0$
is normal, the action
$\Sigma \lhd \Lambda _0$
is normal, the action
 $\Sigma \curvearrowright Z_0$
admits a fundamental domain and
$\Sigma \curvearrowright Z_0$
admits a fundamental domain and
 $G \curvearrowright (X,\mu )$
is conjugate with
$G \curvearrowright (X,\mu )$
is conjugate with
 $\Lambda _0/\Sigma \curvearrowright Z_0/\Sigma $
.
$\Lambda _0/\Sigma \curvearrowright Z_0/\Sigma $
.
To obtain technically less involved statements, one may restrict to simple actions: in Definition 4.1, we say that a free, ergodic, non-singular action
![]() $G \curvearrowright (X,\mu )$
is simple if the action is not induced and if G has no non-trivial normal subgroups whose action on
$G \curvearrowright (X,\mu )$
is simple if the action is not induced and if G has no non-trivial normal subgroups whose action on
![]() $(X,\mu )$
admits a fundamental domain. Then both versions of OE superrigidity for a simple action
$(X,\mu )$
admits a fundamental domain. Then both versions of OE superrigidity for a simple action
![]() $G \curvearrowright (X,\mu )$
immediately imply that any stably orbit equivalent simple action must be conjugate to
$G \curvearrowright (X,\mu )$
immediately imply that any stably orbit equivalent simple action must be conjugate to
![]() $G \curvearrowright X$
, bringing us back to a statement that looks similar to the probability measure-preserving setting.
$G \curvearrowright X$
, bringing us back to a statement that looks similar to the probability measure-preserving setting.
We use the following skew product construction to obtain OE-superrigid actions of type III
![]() $_0$
. Given any non-singular ergodic action
$_0$
. Given any non-singular ergodic action
![]() $G \curvearrowright (X,\mu )$
of type III
$G \curvearrowright (X,\mu )$
of type III
![]() $_1$
, with logarithm of the Radon–Nikodym cocycle denoted by
$_1$
, with logarithm of the Radon–Nikodym cocycle denoted by
![]() $\omega : G \times X \to \mathbb {R}$
, and given any ergodic flow
$\omega : G \times X \to \mathbb {R}$
, and given any ergodic flow
![]() $\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
, we consider
$\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
, we consider
We prove in Proposition 3.4 that this action is ergodic and that its associated flow is given by the adjoint flow
![]() $\widehat {\alpha }$
, a new concept that we introduce in Definition 3.2. Since the adjoint operation is involutive, meaning that the adjoint of
$\widehat {\alpha }$
, a new concept that we introduce in Definition 3.2. Since the adjoint operation is involutive, meaning that the adjoint of
![]() $\widehat {\alpha }$
is isomorphic to
$\widehat {\alpha }$
is isomorphic to
![]() $\alpha $
, the skew product construction (1.1) provides a streamlined way of defining group actions with a prescribed associated flow.
$\alpha $
, the skew product construction (1.1) provides a streamlined way of defining group actions with a prescribed associated flow.
The main result of this paper is the following OE-superrigidity theorem for actions of type III
![]() $_0$
.
$_0$
.
Theorem A. Let
![]() $G \curvearrowright (X,\mu )$
be a free, ergodic, non-singular action of type III
$G \curvearrowright (X,\mu )$
be a free, ergodic, non-singular action of type III
![]() $_1$
. Assume that G is finitely generated and has trivial center. Assume that the Maharam extension of
$_1$
. Assume that G is finitely generated and has trivial center. Assume that the Maharam extension of
![]() $G \curvearrowright (X,\mu )$
is simple and cocycle superrigid with countable targets. Denote by
$G \curvearrowright (X,\mu )$
is simple and cocycle superrigid with countable targets. Denote by
![]() $\omega : G \times X \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle.
$\omega : G \times X \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle.
For any ergodic flow
![]() $\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
, the action
$\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
, the action
![]() $G \curvearrowright (X \times Y,\mu \times \eta )$
defined in (1.1) is OE superrigid (v2) and has associated flow
$G \curvearrowright (X \times Y,\mu \times \eta )$
defined in (1.1) is OE superrigid (v2) and has associated flow
![]() $\widehat {\alpha }$
.
$\widehat {\alpha }$
.
We provide a more precise version of Theorem A as Corollary 5.6 below. In this more precise version, the possible group actions
![]() $\Lambda _0 \curvearrowright Z_0$
with normal subgroup
$\Lambda _0 \curvearrowright Z_0$
with normal subgroup
![]() $\Sigma \lhd \Lambda _0$
that appear in the definition of OE superrigidity (v2) are explicitly described.
$\Sigma \lhd \Lambda _0$
that appear in the definition of OE superrigidity (v2) are explicitly described.
As we explain in Example 5.7 and Theorem 5.8, there are many concrete type III
![]() $_1$
actions
$_1$
actions
![]() $G \curvearrowright (X,\mu )$
satisfying the assumptions of Theorem A. In particular, we obtain the following result.
$G \curvearrowright (X,\mu )$
satisfying the assumptions of Theorem A. In particular, we obtain the following result.
Recall that given a commutative ring
![]() $\mathcal {A}$
and an integer
$\mathcal {A}$
and an integer
![]() $n \geq 2$
, the group
$n \geq 2$
, the group
![]() $E(n,\mathcal {A})$
is the subgroup of
$E(n,\mathcal {A})$
is the subgroup of
![]() $\operatorname {SL}(n,\mathcal {A})$
generated by the elementary matrices having
$\operatorname {SL}(n,\mathcal {A})$
generated by the elementary matrices having
![]() $1$
s on the diagonal and an element of
$1$
s on the diagonal and an element of
![]() $\mathcal {A}$
as an off-diagonal entry. For several rings, including
$\mathcal {A}$
as an off-diagonal entry. For several rings, including
![]() $\mathbb {Z}[\mathcal {S}^{-1}]$
where
$\mathbb {Z}[\mathcal {S}^{-1}]$
where
![]() $\mathcal {S}$
is a finite set of prime numbers and the ring of integers
$\mathcal {S}$
is a finite set of prime numbers and the ring of integers
![]() $\mathcal {O}_K$
of an algebraic number field, we have that
$\mathcal {O}_K$
of an algebraic number field, we have that
![]() $E(n,\mathcal {A}) = \operatorname {SL}(n,\mathcal {A})$
(see Example 6.8 for references and more examples).
$E(n,\mathcal {A}) = \operatorname {SL}(n,\mathcal {A})$
(see Example 6.8 for references and more examples).
Corollary B. Let
![]() $n \geq 3$
be an odd integer and let
$n \geq 3$
be an odd integer and let
![]() $\mathcal {A} \subset \mathbb {R}$
be a subring containing an algebraic number that does not belong to
$\mathcal {A} \subset \mathbb {R}$
be a subring containing an algebraic number that does not belong to
![]() $\mathbb {Z}$
. Assume that
$\mathbb {Z}$
. Assume that
![]() $\mathcal {A}$
is finitely generated as a ring. For every ergodic flow
$\mathcal {A}$
is finitely generated as a ring. For every ergodic flow
![]() $\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
, consider the action
$\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
, consider the action
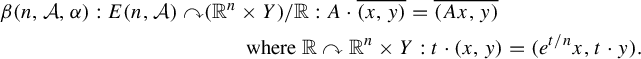 $$ \begin{align*} \beta(n,\mathcal{A},\alpha) : E(n,\mathcal{A}) \curvearrowright &(\mathbb{R}^n \times Y)/\mathbb{R} : A \cdot \overline{(x,y)} = \overline{(A x,y)} \\ &\qquad\text{where }\mathbb{R} \curvearrowright \mathbb{R}^n \times Y : t \cdot (x,y) = (e^{t/n} x,t \cdot y).\quad\quad \end{align*} $$
$$ \begin{align*} \beta(n,\mathcal{A},\alpha) : E(n,\mathcal{A}) \curvearrowright &(\mathbb{R}^n \times Y)/\mathbb{R} : A \cdot \overline{(x,y)} = \overline{(A x,y)} \\ &\qquad\text{where }\mathbb{R} \curvearrowright \mathbb{R}^n \times Y : t \cdot (x,y) = (e^{t/n} x,t \cdot y).\quad\quad \end{align*} $$
-
(1) The actions
 $\beta (n,\mathcal {A},\alpha )$
are essentially free, ergodic, simple and OE superrigid (v2), with associated flow
$\beta (n,\mathcal {A},\alpha )$
are essentially free, ergodic, simple and OE superrigid (v2), with associated flow
 $\widehat {\alpha }$
.
$\widehat {\alpha }$
. -
(2) The actions
 $\beta (n,\mathcal {A},\alpha )$
and
$\beta (n,\mathcal {A},\alpha )$
and
 $\beta (n',\mathcal {A}',\alpha ')$
are stably orbit equivalent if and only if
$\beta (n',\mathcal {A}',\alpha ')$
are stably orbit equivalent if and only if
 $n = n'$
,
$n = n'$
,
 $\mathcal {A} = \mathcal {A}'$
and
$\mathcal {A} = \mathcal {A}'$
and
 $\alpha $
is isomorphic to
$\alpha $
is isomorphic to
 $\alpha '$
.
$\alpha '$
.
We prove Corollary B as Corollary 6.7 below, in which we also describe the outer automorphism group
![]() $\operatorname {Out}(\mathcal {R}(n,\mathcal {A},\alpha ))$
of the orbit equivalence relations
$\operatorname {Out}(\mathcal {R}(n,\mathcal {A},\alpha ))$
of the orbit equivalence relations
![]() $\mathcal {R}(n,\mathcal {A},\alpha )$
of the actions
$\mathcal {R}(n,\mathcal {A},\alpha )$
of the actions
![]() $\beta (n,\mathcal {A},\alpha )$
appearing in Corollary B. In Remark 6.9, we also show that the family of group actions
$\beta (n,\mathcal {A},\alpha )$
appearing in Corollary B. In Remark 6.9, we also show that the family of group actions
![]() $\beta (n,\mathcal {A},\alpha )$
in Corollary B is large and complex in a descriptive set-theoretic sense of the word.
$\beta (n,\mathcal {A},\alpha )$
in Corollary B is large and complex in a descriptive set-theoretic sense of the word.
As mentioned above, OE superrigidity (v1) is impossible for actions of type III
![]() $_0$
, but does happen for actions of type III
$_0$
, but does happen for actions of type III
![]() $_\unicode{x3bb} $
when
$_\unicode{x3bb} $
when
![]() $\unicode{x3bb} \in (0,1]$
. The precise result goes as follows and provides the first examples of OE superrigidity (v1) for actions of type III
$\unicode{x3bb} \in (0,1]$
. The precise result goes as follows and provides the first examples of OE superrigidity (v1) for actions of type III
![]() $_\unicode{x3bb} $
with
$_\unicode{x3bb} $
with
![]() $\unicode{x3bb} \in (0,1)$
. Examples of type III
$\unicode{x3bb} \in (0,1)$
. Examples of type III
![]() $_1$
were given before; see, for example, [Reference Popa and VaesPV08, Theorem 5.8] and [Reference Drimbe and VaesDV21, Proposition 3.3], as well as Corollary 4.7 below.
$_1$
were given before; see, for example, [Reference Popa and VaesPV08, Theorem 5.8] and [Reference Drimbe and VaesDV21, Proposition 3.3], as well as Corollary 4.7 below.
Theorem C
-
(1) Let
 $n \geq 3$
be an integer, p a prime number and
$n \geq 3$
be an integer, p a prime number and
 $0 < \unicode{x3bb} < 1$
. Consider the ring
$0 < \unicode{x3bb} < 1$
. Consider the ring
 $\mathcal {A} = \mathbb {Z}[\unicode{x3bb} ,\unicode{x3bb} ^{-1},p^{-1}]$
. Define the subgroup
$\mathcal {A} = \mathbb {Z}[\unicode{x3bb} ,\unicode{x3bb} ^{-1},p^{-1}]$
. Define the subgroup
 $\Gamma < \operatorname {GL}(n,\mathcal {A})$
of matrices A with
$\Gamma < \operatorname {GL}(n,\mathcal {A})$
of matrices A with
 $\det A \in \unicode{x3bb} ^{\mathbb {Z}}$
. Then the action of
$\det A \in \unicode{x3bb} ^{\mathbb {Z}}$
. Then the action of
 $\Gamma \ltimes \mathcal {A}^n$
on
$\Gamma \ltimes \mathcal {A}^n$
on
 $\mathbb {R}^n$
by
$\mathbb {R}^n$
by
 $(A,a) \cdot x = A(a+x)$
is essentially free, ergodic, simple, of type III
$(A,a) \cdot x = A(a+x)$
is essentially free, ergodic, simple, of type III
 $_\unicode{x3bb} $
. It is OE superrigid (v1).
$_\unicode{x3bb} $
. It is OE superrigid (v1). -
(2) Let
 $G \curvearrowright (X,\mu )$
be any essentially free, ergodic, simple, type III
$G \curvearrowright (X,\mu )$
be any essentially free, ergodic, simple, type III
 $_0$
action. Then
$_0$
action. Then
 $G \curvearrowright (X,\mu )$
is not OE superrigid (v1).
$G \curvearrowright (X,\mu )$
is not OE superrigid (v1).
We prove Theorem C at the end of §4.
For every free, ergodic, non-singular action
![]() $G \curvearrowright (X,\mu )$
of a countable group G, the crossed product
$G \curvearrowright (X,\mu )$
of a countable group G, the crossed product
![]() $M = L^\infty (X) \rtimes G$
is a factor. A group action
$M = L^\infty (X) \rtimes G$
is a factor. A group action
![]() $G \curvearrowright (X,\mu )$
is called W
$G \curvearrowright (X,\mu )$
is called W
![]() $^*$
-superrigid if
$^*$
-superrigid if
![]() $G \curvearrowright (X,\mu )$
can be entirely recovered from this group measure space construction
$G \curvearrowright (X,\mu )$
can be entirely recovered from this group measure space construction
![]() $L^\infty (X) \rtimes G$
. This is a strictly stronger property than OE superrigidity, and both properties coincide if one can prove that M has a unique (group measure space) Cartan subalgebra; see, for example, [Reference Popa and VaesPV09]. When dealing with actions that are not measure-preserving, and especially with actions of type III
$L^\infty (X) \rtimes G$
. This is a strictly stronger property than OE superrigidity, and both properties coincide if one can prove that M has a unique (group measure space) Cartan subalgebra; see, for example, [Reference Popa and VaesPV09]. When dealing with actions that are not measure-preserving, and especially with actions of type III
![]() $_0$
, the same nuances as with OE superrigidity appear and we get the natural definitions of W
$_0$
, the same nuances as with OE superrigidity appear and we get the natural definitions of W
![]() $^*$
-superrigidity (v1) and (v2).
$^*$
-superrigidity (v1) and (v2).
For none of the concrete actions in Corollary B and Theorem C is it known whether the crossed product has a unique (group measure space) Cartan subalgebra, up to unitary conjugacy. Nevertheless, repeating the construction of [Reference VaesVae13, Proposition D], we obtain ad hoc examples of group actions that are W
![]() $^*$
-superrigid (v2), of type III
$^*$
-superrigid (v2), of type III
![]() $_0$
, with a prescribed associated flow. We explain this in Remark 6.10.
$_0$
, with a prescribed associated flow. We explain this in Remark 6.10.
2 Preliminaries
Recall that an action of a countable group G on a standard probability space
![]() $(X,\mu )$
is called non-singular if it preserves Borel sets of measure zero. We write
$(X,\mu )$
is called non-singular if it preserves Borel sets of measure zero. We write
![]() $(g \cdot \mu )(\mathcal {U}) = \mu (g^{-1} \cdot \mathcal {U})$
and consider the Radon–Nikodym derivatives
$(g \cdot \mu )(\mathcal {U}) = \mu (g^{-1} \cdot \mathcal {U})$
and consider the Radon–Nikodym derivatives
![]() $d(g \cdot \mu ) / d\mu $
, which are well defined almost everywhere. Given a non-singular action
$d(g \cdot \mu ) / d\mu $
, which are well defined almost everywhere. Given a non-singular action
![]() $G \curvearrowright (X,\mu )$
of a countable group G on a standard probability space
$G \curvearrowright (X,\mu )$
of a countable group G on a standard probability space
![]() $(X,\mu )$
, we consider the associated Maharam extension
$(X,\mu )$
, we consider the associated Maharam extension
where
![]() $\omega (g,x) = \log (d(g^{-1} \cdot \mu )/d\mu )(x)$
is the logarithm of the Radon–Nikodym
$\omega (g,x) = \log (d(g^{-1} \cdot \mu )/d\mu )(x)$
is the logarithm of the Radon–Nikodym
![]() $1$
-cocycle. We may and always will assume that
$1$
-cocycle. We may and always will assume that
![]() $\omega $
is a strict
$\omega $
is a strict
![]() $1$
-cocycle, meaning that the cocycle identity holds everywhere. We equip
$1$
-cocycle, meaning that the cocycle identity holds everywhere. We equip
![]() $X \times \mathbb {R}$
with the G-invariant
$X \times \mathbb {R}$
with the G-invariant
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $d\mu (x) \times e^{-s}\,ds$
. One considers the measure-scaling action
$d\mu (x) \times e^{-s}\,ds$
. One considers the measure-scaling action
which commutes with the Maharam extension
![]() $G \curvearrowright X \times \mathbb {R}$
. Denote by
$G \curvearrowright X \times \mathbb {R}$
. Denote by
![]() $(Y,\eta )$
the space of ergodic components of
$(Y,\eta )$
the space of ergodic components of
![]() $G \curvearrowright X \times \mathbb {R}$
, together with the non-singular factor map
$G \curvearrowright X \times \mathbb {R}$
, together with the non-singular factor map
![]() $\pi : X \times \mathbb {R} \to Y$
. Since the actions of G and
$\pi : X \times \mathbb {R} \to Y$
. Since the actions of G and
![]() $\mathbb {R}$
on
$\mathbb {R}$
on
![]() $X \times \mathbb {R}$
commute, there is an essentially unique non-singular action
$X \times \mathbb {R}$
commute, there is an essentially unique non-singular action
![]() $\mathbb {R} \curvearrowright (Y,\eta )$
such that for all
$\mathbb {R} \curvearrowright (Y,\eta )$
such that for all
![]() $t \in \mathbb {R}$
, we have that
$t \in \mathbb {R}$
, we have that
![]() $\pi (t \cdot (x,s)) = t \cdot \pi (x,s)$
for almost every (a.e.)
$\pi (t \cdot (x,s)) = t \cdot \pi (x,s)$
for almost every (a.e.)
![]() $(x,s) \in X \times \mathbb {R}$
. The action
$(x,s) \in X \times \mathbb {R}$
. The action
![]() $\mathbb {R} \curvearrowright (Y,\eta )$
is Krieger’s associated flow of the action
$\mathbb {R} \curvearrowright (Y,\eta )$
is Krieger’s associated flow of the action
![]() $G \curvearrowright (X,\mu )$
.
$G \curvearrowright (X,\mu )$
.
By [Reference ZimmerZim84, Proposition B.5], after discarding from
![]() $(X,\mu )$
a G-invariant Borel null set, we may assume that the factor map
$(X,\mu )$
a G-invariant Borel null set, we may assume that the factor map
![]() $\pi : X \times \mathbb {R} \to Y$
is strictly G-invariant and
$\pi : X \times \mathbb {R} \to Y$
is strictly G-invariant and
![]() $\mathbb {R}$
-equivariant, that is,
$\mathbb {R}$
-equivariant, that is,
![]() $\pi (g \cdot (x,s)) = \pi (x,s)$
and
$\pi (g \cdot (x,s)) = \pi (x,s)$
and
![]() $\pi (x,s+t) = t \cdot \pi (x,s)$
for all
$\pi (x,s+t) = t \cdot \pi (x,s)$
for all
![]() $g \in G$
,
$g \in G$
,
![]() $t {\kern-1.2pt}\in{\kern-1.2pt} \mathbb {R}$
and
$t {\kern-1.2pt}\in{\kern-1.2pt} \mathbb {R}$
and
![]() $(x,s) {\kern-1.2pt}\in{\kern-1.2pt} X {\kern-1.2pt}\times{\kern-1.2pt} \mathbb {R}$
. Writing
$(x,s) {\kern-1.2pt}\in{\kern-1.2pt} X {\kern-1.2pt}\times{\kern-1.2pt} \mathbb {R}$
. Writing
![]() $\psi (x) {\kern-1pt}={\kern-1pt} \pi (x,0)$
, we have found a Borel map
$\psi (x) {\kern-1pt}={\kern-1pt} \pi (x,0)$
, we have found a Borel map
![]() $\psi : X {\kern-1.2pt}\to{\kern-1.2pt} Y$
satisfying
$\psi : X {\kern-1.2pt}\to{\kern-1.2pt} Y$
satisfying
for all
![]() $x \in X$
,
$x \in X$
,
![]() $s \in \mathbb {R}$
,
$s \in \mathbb {R}$
,
![]() $g \in G$
.
$g \in G$
.
Let
![]() $G \curvearrowright (X,\mu )$
be an essentially free, ergodic, non-singular action of a countable group G on a non-atomic standard probability space
$G \curvearrowright (X,\mu )$
be an essentially free, ergodic, non-singular action of a countable group G on a non-atomic standard probability space
![]() $(X,\mu )$
. Recall that the type of this action is defined as follows: if there exists a G-invariant probability measure
$(X,\mu )$
. Recall that the type of this action is defined as follows: if there exists a G-invariant probability measure
![]() $\nu \sim \mu $
, the action is of type II
$\nu \sim \mu $
, the action is of type II
![]() $_1$
; if there exists a G-invariant infinite measure
$_1$
; if there exists a G-invariant infinite measure
![]() $\nu \sim \mu $
, the action is of type II
$\nu \sim \mu $
, the action is of type II
![]() $_\infty $
; in all other cases, the action is of type III. Also recall that
$_\infty $
; in all other cases, the action is of type III. Also recall that
![]() $G \curvearrowright (X,\mu )$
is of type II
$G \curvearrowright (X,\mu )$
is of type II
![]() $_1$
or II
$_1$
or II
![]() $_\infty $
if and only if the associated flow is isomorphic to the translation action
$_\infty $
if and only if the associated flow is isomorphic to the translation action
![]() $\mathbb {R} \curvearrowright \mathbb {R}$
. When the associated flow is not the translation action, there are three possibilities: if Y is reduced to one point, the action is said to be of type III
$\mathbb {R} \curvearrowright \mathbb {R}$
. When the associated flow is not the translation action, there are three possibilities: if Y is reduced to one point, the action is said to be of type III
![]() $_1$
; if the associated flow is isomorphic to the periodic flow
$_1$
; if the associated flow is isomorphic to the periodic flow
![]() $\mathbb {R} \curvearrowright \mathbb {R} / \mathbb {Z} \log \unicode{x3bb} $
with
$\mathbb {R} \curvearrowright \mathbb {R} / \mathbb {Z} \log \unicode{x3bb} $
with
![]() $0 < \unicode{x3bb} < 1$
, the action is said to be of type III
$0 < \unicode{x3bb} < 1$
, the action is said to be of type III
![]() $_\unicode{x3bb} $
; finally, when the associated flow is properly ergodic, the action is said to be of type III
$_\unicode{x3bb} $
; finally, when the associated flow is properly ergodic, the action is said to be of type III
![]() $_0$
.
$_0$
.
Two non-singular actions
![]() $G \curvearrowright (X,\mu )$
and
$G \curvearrowright (X,\mu )$
and
![]() $\Lambda \curvearrowright (Z,\zeta )$
are said to be conjugate if there exist an isomorphism of groups
$\Lambda \curvearrowright (Z,\zeta )$
are said to be conjugate if there exist an isomorphism of groups
![]() $\delta : G \to \Lambda $
and a non-singular isomorphism
$\delta : G \to \Lambda $
and a non-singular isomorphism
![]() $\Delta : (X,\mu ) \to (Z,\zeta )$
such that
$\Delta : (X,\mu ) \to (Z,\zeta )$
such that
![]() $\Delta (g \cdot x) = \delta (g) \cdot \Delta (x)$
for all
$\Delta (g \cdot x) = \delta (g) \cdot \Delta (x)$
for all
![]() $g \in G$
and a.e.
$g \in G$
and a.e.
![]() $x \in X$
. Two non-singular actions
$x \in X$
. Two non-singular actions
![]() $G \curvearrowright (X,\mu )$
and
$G \curvearrowright (X,\mu )$
and
![]() $G \curvearrowright (Z,\zeta )$
of the same group G are said to be isomorphic if there exists a non-singular isomorphism
$G \curvearrowright (Z,\zeta )$
of the same group G are said to be isomorphic if there exists a non-singular isomorphism
![]() $\Delta : (X,\mu ) \to (Z,\zeta )$
such that
$\Delta : (X,\mu ) \to (Z,\zeta )$
such that
![]() $\Delta (g \cdot x) = g \cdot \Delta (x)$
for all
$\Delta (g \cdot x) = g \cdot \Delta (x)$
for all
![]() $g \in G$
and a.e.
$g \in G$
and a.e.
![]() $x \in X$
.
$x \in X$
.
Two essentially free, ergodic, non-singular actions
![]() $G \curvearrowright (X,\mu )$
and
$G \curvearrowright (X,\mu )$
and
![]() $\Lambda \curvearrowright (Z,\zeta )$
are called stably orbit equivalent if there exist non-negligible Borel sets
$\Lambda \curvearrowright (Z,\zeta )$
are called stably orbit equivalent if there exist non-negligible Borel sets
![]() $\mathcal {U} \subset X$
,
$\mathcal {U} \subset X$
,
![]() $\mathcal {V} \subset Z$
and a non-singular isomorphism
$\mathcal {V} \subset Z$
and a non-singular isomorphism
![]() $\Delta : \mathcal {U} \to \mathcal {V}$
such that
$\Delta : \mathcal {U} \to \mathcal {V}$
such that
![]() $\Delta (\mathcal {U} \cap G \cdot x) = \mathcal {V} \cap \Lambda \cdot \Delta (x)$
for a.e.
$\Delta (\mathcal {U} \cap G \cdot x) = \mathcal {V} \cap \Lambda \cdot \Delta (x)$
for a.e.
![]() $x \in \mathcal {U}$
. The actions are called orbit equivalent if we may choose
$x \in \mathcal {U}$
. The actions are called orbit equivalent if we may choose
![]() $\mathcal {U} = X$
and
$\mathcal {U} = X$
and
![]() $\mathcal {V} = Z$
. When the actions are both of type II
$\mathcal {V} = Z$
. When the actions are both of type II
![]() $_\infty $
or type III, stable orbit equivalence is the same as orbit equivalence. Recall that the associated flow is invariant under stable orbit equivalence.
$_\infty $
or type III, stable orbit equivalence is the same as orbit equivalence. Recall that the associated flow is invariant under stable orbit equivalence.
We say that a non-singular action
![]() $G \curvearrowright (X,\mu )$
is induced if there exist a proper subgroup
$G \curvearrowright (X,\mu )$
is induced if there exist a proper subgroup
![]() $G_0 < G$
and a
$G_0 < G$
and a
![]() $G_0$
-invariant Borel set
$G_0$
-invariant Borel set
![]() $X_0 \subset X$
such that the sets
$X_0 \subset X$
such that the sets
![]() $(g \cdot X_0)_{g \in G/G_0}$
are disjoint and
$(g \cdot X_0)_{g \in G/G_0}$
are disjoint and
![]() $\mu (X \setminus G \cdot X_0) = 0$
. We then say that
$\mu (X \setminus G \cdot X_0) = 0$
. We then say that
![]() $G \curvearrowright X$
is induced from
$G \curvearrowright X$
is induced from
![]() $G_0 \curvearrowright X_0$
. Given any non-singular action
$G_0 \curvearrowright X_0$
. Given any non-singular action
![]() $G_0 \curvearrowright (X_0,\mu _0)$
and a larger countable group G containing
$G_0 \curvearrowright (X_0,\mu _0)$
and a larger countable group G containing
![]() $G_0$
, there is, up to isomorphism, a unique non-singular action
$G_0$
, there is, up to isomorphism, a unique non-singular action
![]() $G \curvearrowright X$
that is induced from
$G \curvearrowright X$
that is induced from
![]() $G_0 \curvearrowright X_0$
. Note that by construction, if
$G_0 \curvearrowright X_0$
. Note that by construction, if
![]() $G \curvearrowright X$
is induced from
$G \curvearrowright X$
is induced from
![]() $G_0 \curvearrowright X_0$
, then
$G_0 \curvearrowright X_0$
, then
![]() $G \curvearrowright X$
and
$G \curvearrowright X$
and
![]() $G_0 \curvearrowright X_0$
are stably orbit equivalent. For later reference, we record the following lemma.
$G_0 \curvearrowright X_0$
are stably orbit equivalent. For later reference, we record the following lemma.
Lemma 2.1. An ergodic non-singular action
![]() $G \curvearrowright (X,\mu )$
is not induced if and only if for every action
$G \curvearrowright (X,\mu )$
is not induced if and only if for every action
![]() $G \curvearrowright I$
of G on a countable set I, every G-equivariant Borel map
$G \curvearrowright I$
of G on a countable set I, every G-equivariant Borel map
![]() $X \to I$
is constant almost everywhere.
$X \to I$
is constant almost everywhere.
Proof. If
![]() $G \curvearrowright (X,\mu )$
is not induced,
$G \curvearrowright (X,\mu )$
is not induced,
![]() $G \curvearrowright I$
and
$G \curvearrowright I$
and
![]() $\varphi : X \to I$
is G-equivariant, we can take
$\varphi : X \to I$
is G-equivariant, we can take
![]() $i_0 \in I$
such that
$i_0 \in I$
such that
![]() $X_0 = \{x \in X \mid \varphi (x) = i_0\}$
is non-negligible. Defining
$X_0 = \{x \in X \mid \varphi (x) = i_0\}$
is non-negligible. Defining
![]() $G_0 = \{g \in G \mid g \cdot i_0 = i_0\}$
, it follows that
$G_0 = \{g \in G \mid g \cdot i_0 = i_0\}$
, it follows that
![]() $X_0$
is
$X_0$
is
![]() $G_0$
-invariant and that
$G_0$
-invariant and that
![]() $(g \cdot X_0)_{g \in G/G_0}$
is a partition of X, up to measure zero. Since
$(g \cdot X_0)_{g \in G/G_0}$
is a partition of X, up to measure zero. Since
![]() $G \curvearrowright X$
is not induced, it follows that
$G \curvearrowright X$
is not induced, it follows that
![]() $G_0 = G$
and that
$G_0 = G$
and that
![]() $X_0 = X$
, up to measure zero. This means that
$X_0 = X$
, up to measure zero. This means that
![]() $\varphi $
is essentially constant.
$\varphi $
is essentially constant.
If
![]() $G \curvearrowright X$
is induced from
$G \curvearrowright X$
is induced from
![]() $G_0 \curvearrowright X_0$
, the map
$G_0 \curvearrowright X_0$
, the map
![]() $x \mapsto gG_0$
for
$x \mapsto gG_0$
for
![]() $x \in g \cdot X_0$
is a G-equivariant map
$x \in g \cdot X_0$
is a G-equivariant map
![]() $X \to G/G_0$
that is not essentially constant.
$X \to G/G_0$
that is not essentially constant.
An essentially free, non-singular action
![]() $\Sigma \curvearrowright (X,\mu )$
is said to admit a fundamental domain if there exists a Borel set
$\Sigma \curvearrowright (X,\mu )$
is said to admit a fundamental domain if there exists a Borel set
![]() $\mathcal {U} \subset X$
such that all
$\mathcal {U} \subset X$
such that all
![]() $g \cdot \mathcal {U}$
,
$g \cdot \mathcal {U}$
,
![]() $g \in \Sigma $
, are disjoint and
$g \in \Sigma $
, are disjoint and
![]() $\mu (X \setminus \Sigma \cdot \mathcal {U}) = 0$
. In that case, the quotient
$\mu (X \setminus \Sigma \cdot \mathcal {U}) = 0$
. In that case, the quotient
![]() $X/\Sigma $
is a well-defined standard measure space and identified with
$X/\Sigma $
is a well-defined standard measure space and identified with
![]() $(\mathcal {U},\mu )$
.
$(\mathcal {U},\mu )$
.
3 Adjoint flows and type III
 $_0$
actions with prescribed associated flow
$_0$
actions with prescribed associated flow
We say that a flow
![]() $\mathbb {R} \curvearrowright (Z,\zeta )$
scales the
$\mathbb {R} \curvearrowright (Z,\zeta )$
scales the
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $\zeta $
if
$\zeta $
if
![]() $t \cdot \zeta = e^t \, \zeta $
for all
$t \cdot \zeta = e^t \, \zeta $
for all
![]() $t \in \mathbb {R}$
.
$t \in \mathbb {R}$
.
Proposition 3.1. Let
![]() $\mathbb {R} \curvearrowright (Y,\eta )$
be an ergodic flow. Up to isomorphism, there is a unique non-singular ergodic action
$\mathbb {R} \curvearrowright (Y,\eta )$
be an ergodic flow. Up to isomorphism, there is a unique non-singular ergodic action
![]() $\mathbb {R}^2 \curvearrowright (Z,\zeta )$
of
$\mathbb {R}^2 \curvearrowright (Z,\zeta )$
of
![]() $\mathbb {R}^2$
on a standard,
$\mathbb {R}^2$
on a standard,
![]() $\sigma $
-finite measure space
$\sigma $
-finite measure space
![]() $(Z,\zeta )$
such that the actions of both
$(Z,\zeta )$
such that the actions of both
![]() $\mathbb {R} \times \{0\}$
and
$\mathbb {R} \times \{0\}$
and
![]() $\{0\} \times \mathbb {R}$
scale the measure
$\{0\} \times \mathbb {R}$
scale the measure
![]() $\zeta $
and such that
$\zeta $
and such that
![]() $\mathbb {R} \curvearrowright Z/(\{0\} \times \mathbb {R})$
is isomorphic to
$\mathbb {R} \curvearrowright Z/(\{0\} \times \mathbb {R})$
is isomorphic to
![]() $\mathbb {R} \curvearrowright Y$
.
$\mathbb {R} \curvearrowright Y$
.
Proof. Denote by
![]() $\omega : \mathbb {R} \times Y \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle. Define the measure
$\omega : \mathbb {R} \times Y \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle. Define the measure
![]() $\gamma $
on
$\gamma $
on
![]() $\mathbb {R}$
by
$\mathbb {R}$
by
![]() $d\gamma (t) = e^{-t} \, dt$
. Define
$d\gamma (t) = e^{-t} \, dt$
. Define
![]() $(Z,\zeta ) = (Y \times \mathbb {R},\eta \times \gamma )$
and define the action
$(Z,\zeta ) = (Y \times \mathbb {R},\eta \times \gamma )$
and define the action
Both the actions by
![]() $(t,0)$
and by
$(t,0)$
and by
![]() $(0,r)$
scale the measure
$(0,r)$
scale the measure
![]() $\zeta $
. By construction,
$\zeta $
. By construction,
![]() $Z/(\{0\} \times \mathbb {R}) = Y$
.
$Z/(\{0\} \times \mathbb {R}) = Y$
.
Now assume that
![]() $\mathbb {R}^2 \curvearrowright (Z',\zeta ')$
is a non-singular ergodic action such that the actions of both
$\mathbb {R}^2 \curvearrowright (Z',\zeta ')$
is a non-singular ergodic action such that the actions of both
![]() $\mathbb {R} \times \{0\}$
and
$\mathbb {R} \times \{0\}$
and
![]() $\{0\} \times \mathbb {R}$
scale the measure
$\{0\} \times \mathbb {R}$
scale the measure
![]() $\zeta '$
and such that
$\zeta '$
and such that
![]() $\mathbb {R} \curvearrowright Z'/(\{0\} \times \mathbb {R})$
is isomorphic to
$\mathbb {R} \curvearrowright Z'/(\{0\} \times \mathbb {R})$
is isomorphic to
![]() $\mathbb {R} \curvearrowright Y$
. We prove that
$\mathbb {R} \curvearrowright Y$
. We prove that
![]() $\mathbb {R}^2 \curvearrowright (Z',\zeta ')$
is isomorphic to
$\mathbb {R}^2 \curvearrowright (Z',\zeta ')$
is isomorphic to
![]() $\mathbb {R}^2 \curvearrowright (Z,\zeta )$
.
$\mathbb {R}^2 \curvearrowright (Z,\zeta )$
.
Since the action of
![]() $\{0\} \times \mathbb {R}$
scales the measure
$\{0\} \times \mathbb {R}$
scales the measure
![]() $\zeta '$
and
$\zeta '$
and
![]() $\mathbb {R} \curvearrowright Z'/(\{0\} \times \mathbb {R})$
is isomorphic to
$\mathbb {R} \curvearrowright Z'/(\{0\} \times \mathbb {R})$
is isomorphic to
![]() $\mathbb {R} \curvearrowright Y$
, we find a
$\mathbb {R} \curvearrowright Y$
, we find a
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $\mu ' \sim \mu $
on Y and a measure-preserving isomorphism
$\mu ' \sim \mu $
on Y and a measure-preserving isomorphism
![]() $\Delta : (Y \times \mathbb {R},\mu ' \times \gamma ) \to (Z',\zeta ')$
such that for all
$\Delta : (Y \times \mathbb {R},\mu ' \times \gamma ) \to (Z',\zeta ')$
such that for all
![]() $(t,r) \in \mathbb {R}^2$
,
$(t,r) \in \mathbb {R}^2$
,
where
![]() $\zeta : \mathbb {R} \times Y \to \mathbb {R}$
is a
$\zeta : \mathbb {R} \times Y \to \mathbb {R}$
is a
![]() $1$
-cocycle. Precomposing
$1$
-cocycle. Precomposing
![]() $\Delta $
with the measure-preserving map
$\Delta $
with the measure-preserving map
and replacing
![]() $\zeta $
by a cohomologous
$\zeta $
by a cohomologous
![]() $1$
-cocycle, we may assume that
$1$
-cocycle, we may assume that
![]() $\mu ' = \mu $
. Expressing that the action of
$\mu ' = \mu $
. Expressing that the action of
![]() $\mathbb {R} \times \{0\}$
scales the measure
$\mathbb {R} \times \{0\}$
scales the measure
![]() $\mu \times \gamma $
gives us that
$\mu \times \gamma $
gives us that
![]() $\zeta (t,y) = \omega (t,y) + t$
. So we have found the required isomorphism.
$\zeta (t,y) = \omega (t,y) + t$
. So we have found the required isomorphism.
Given the uniqueness of
![]() $\mathbb {R}^2 \curvearrowright (Z,\zeta )$
in Proposition 3.1, we get the following well-defined notion of an adjoint flow and we automatically have that this adjoint is an involutive operation: the adjoint of
$\mathbb {R}^2 \curvearrowright (Z,\zeta )$
in Proposition 3.1, we get the following well-defined notion of an adjoint flow and we automatically have that this adjoint is an involutive operation: the adjoint of
![]() $\widehat {\alpha }$
is isomorphic to
$\widehat {\alpha }$
is isomorphic to
![]() $\alpha $
.
$\alpha $
.
Definition 3.2. Given an ergodic flow
![]() $\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
, the adjoint flow
$\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
, the adjoint flow
![]() $\mathbb {R} \curvearrowright ^{\widehat {\alpha }} (\widehat {Y},\widehat {\eta })$
is defined as the ergodic flow
$\mathbb {R} \curvearrowright ^{\widehat {\alpha }} (\widehat {Y},\widehat {\eta })$
is defined as the ergodic flow
![]() $\mathbb {R} \curvearrowright Z/(\mathbb {R} \times \{0\})$
, where
$\mathbb {R} \curvearrowright Z/(\mathbb {R} \times \{0\})$
, where
![]() $\mathbb {R}^2 \curvearrowright Z$
is the unique action given by Proposition 3.1.
$\mathbb {R}^2 \curvearrowright Z$
is the unique action given by Proposition 3.1.
Note that we can also define the adjoint flow
![]() $\widehat {\alpha }$
more concretely. Denoting by
$\widehat {\alpha }$
more concretely. Denoting by
![]() $\omega : \mathbb {R} \times Y \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle of an ergodic flow
$\omega : \mathbb {R} \times Y \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle of an ergodic flow
![]() $\mathbb {R} \curvearrowright ^\alpha Y$
, we consider the quotient
$\mathbb {R} \curvearrowright ^\alpha Y$
, we consider the quotient
![]() $(Y \times \mathbb {R})/\mathbb {R}$
, where
$(Y \times \mathbb {R})/\mathbb {R}$
, where
![]() $\mathbb {R}$
is acting by
$\mathbb {R}$
is acting by
![]() $t \cdot (y,s) = (t \cdot y, t + \omega (t,y) + s)$
. On this quotient, we let
$t \cdot (y,s) = (t \cdot y, t + \omega (t,y) + s)$
. On this quotient, we let
![]() $\mathbb {R}$
act by translation in the second variable. This is the adjoint flow
$\mathbb {R}$
act by translation in the second variable. This is the adjoint flow
![]() $\widehat {\alpha }$
.
$\widehat {\alpha }$
.
From this concrete description, it immediately follows that
![]() $\alpha \cong \widehat {\alpha }$
whenever the flow
$\alpha \cong \widehat {\alpha }$
whenever the flow
![]() $\alpha $
admits a finite or
$\alpha $
admits a finite or
![]() $\sigma $
-finite equivalent
$\sigma $
-finite equivalent
![]() $\mathbb {R}$
-invariant measure. In general,
$\mathbb {R}$
-invariant measure. In general,
![]() $\alpha $
need not be isomorphic to
$\alpha $
need not be isomorphic to
![]() $\widehat {\alpha }$
, as the following example shows.
$\widehat {\alpha }$
, as the following example shows.
Example 3.3. Let
![]() $\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
be the ergodic flow given as the induction of an ergodic, type III
$\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
be the ergodic flow given as the induction of an ergodic, type III
![]() $_1$
action
$_1$
action
![]() $\mathbb {Z} \curvearrowright ^{\alpha _0} (Y_0,\eta _0)$
. We prove that the adjoint flow
$\mathbb {Z} \curvearrowright ^{\alpha _0} (Y_0,\eta _0)$
. We prove that the adjoint flow
![]() $\widehat {\alpha }$
is not isomorphic to
$\widehat {\alpha }$
is not isomorphic to
![]() $\alpha $
.
$\alpha $
.
Recall that the induced flow
![]() $\alpha $
is defined as follows. Consider the action
$\alpha $
is defined as follows. Consider the action
![]() $\mathbb {R} \times \mathbb {Z} \curvearrowright \mathbb {R} \times Y_0 : (t,n) \cdot (s,y) = (t-n+s,n \cdot y)$
. Then
$\mathbb {R} \times \mathbb {Z} \curvearrowright \mathbb {R} \times Y_0 : (t,n) \cdot (s,y) = (t-n+s,n \cdot y)$
. Then
![]() $\alpha $
is defined as the action of
$\alpha $
is defined as the action of
![]() $\mathbb {R}$
on
$\mathbb {R}$
on
![]() $(\mathbb {R} \times Y_0)/(\{0\} \times \mathbb {Z})$
. To determine the adjoint flow
$(\mathbb {R} \times Y_0)/(\{0\} \times \mathbb {Z})$
. To determine the adjoint flow
![]() $\widehat {\alpha }$
, denote by
$\widehat {\alpha }$
, denote by
![]() $\omega : \mathbb {Z} \times Y_0 \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle for
$\omega : \mathbb {Z} \times Y_0 \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle for
![]() $\alpha _0$
. Denote by
$\alpha _0$
. Denote by
![]() $\unicode{x3bb} $
the Lebesgue measure on
$\unicode{x3bb} $
the Lebesgue measure on
![]() $\mathbb {R}$
and define the measure
$\mathbb {R}$
and define the measure
![]() $\gamma $
such that
$\gamma $
such that
![]() $(d\gamma /d\unicode{x3bb} )(t) = e^{-t}$
. Then consider the action
$(d\gamma /d\unicode{x3bb} )(t) = e^{-t}$
. Then consider the action
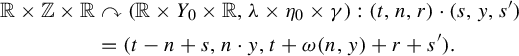 $$ \begin{align*}\mathbb{R} \times \mathbb{Z} \times \mathbb{R} &\curvearrowright (\mathbb{R} \times Y_0 \times \mathbb{R},\unicode{x3bb} \times \eta_0 \times \gamma) : (t,n,r) \cdot (s,y,s')\\ &= (t - n + s, n \cdot y, t+\omega(n,y) + r + s').\end{align*} $$
$$ \begin{align*}\mathbb{R} \times \mathbb{Z} \times \mathbb{R} &\curvearrowright (\mathbb{R} \times Y_0 \times \mathbb{R},\unicode{x3bb} \times \eta_0 \times \gamma) : (t,n,r) \cdot (s,y,s')\\ &= (t - n + s, n \cdot y, t+\omega(n,y) + r + s').\end{align*} $$
The action of
![]() $\{0\} \times \mathbb {Z} \times \{0\}$
is measure-preserving. The actions of
$\{0\} \times \mathbb {Z} \times \{0\}$
is measure-preserving. The actions of
![]() $\mathbb {R} \times \{(0,0)\}$
and
$\mathbb {R} \times \{(0,0)\}$
and
![]() $\{(0,0)\} \times \mathbb {R}$
are measure-scaling. By construction,
$\{(0,0)\} \times \mathbb {R}$
are measure-scaling. By construction,
![]() $\alpha $
is given by
$\alpha $
is given by
![]() $\mathbb {R} \curvearrowright (\mathbb {R} \times Y_0 \times \mathbb {R})/(\{0\} \times \mathbb {Z} \times \mathbb {R})$
. We conclude that the adjoint flow
$\mathbb {R} \curvearrowright (\mathbb {R} \times Y_0 \times \mathbb {R})/(\{0\} \times \mathbb {Z} \times \mathbb {R})$
. We conclude that the adjoint flow
![]() $\widehat {\alpha }$
is given by
$\widehat {\alpha }$
is given by
![]() $\mathbb {R} \curvearrowright (\mathbb {R} \times Y_0 \times \mathbb {R})/(\mathbb {R} \times \mathbb {Z} \times \{0\})$
.
$\mathbb {R} \curvearrowright (\mathbb {R} \times Y_0 \times \mathbb {R})/(\mathbb {R} \times \mathbb {Z} \times \{0\})$
.
By construction, the flow
![]() $\alpha $
comes with an
$\alpha $
comes with an
![]() $\mathbb {R}$
-equivariant map
$\mathbb {R}$
-equivariant map
![]() $Y \to \mathbb {R}/\mathbb {Z}$
. We prove that such an
$Y \to \mathbb {R}/\mathbb {Z}$
. We prove that such an
![]() $\mathbb {R}$
-equivariant map does not exist for the adjoint flow
$\mathbb {R}$
-equivariant map does not exist for the adjoint flow
![]() $\widehat {\alpha }$
. Assuming the contrary, we find a map
$\widehat {\alpha }$
. Assuming the contrary, we find a map
![]() $\theta : \mathbb {R} \times Y_0 \times \mathbb {R} \to \mathbb {R}/\mathbb {Z}$
that is invariant for the action of
$\theta : \mathbb {R} \times Y_0 \times \mathbb {R} \to \mathbb {R}/\mathbb {Z}$
that is invariant for the action of
![]() $\mathbb {R} \times \mathbb {Z} \times \{0\}$
and that is equivariant for the action of
$\mathbb {R} \times \mathbb {Z} \times \{0\}$
and that is equivariant for the action of
![]() $\{(0,0)\} \times \mathbb {R}$
. By the invariance under
$\{(0,0)\} \times \mathbb {R}$
. By the invariance under
![]() $\mathbb {R} \times \{(0,0)\}$
and the equivariance under
$\mathbb {R} \times \{(0,0)\}$
and the equivariance under
![]() $\{(0,0)\} \times \mathbb {R}$
, the map
$\{(0,0)\} \times \mathbb {R}$
, the map
![]() $\theta $
must be of the form
$\theta $
must be of the form
![]() $\theta (s,y,s') = -s + s' + \varphi (y)$
where
$\theta (s,y,s') = -s + s' + \varphi (y)$
where
![]() $\varphi : Y_0 \to \mathbb {R}/\mathbb {Z}$
. The invariance under
$\varphi : Y_0 \to \mathbb {R}/\mathbb {Z}$
. The invariance under
![]() $\{0\} \times \mathbb {Z} \times \{0\}$
then says that
$\{0\} \times \mathbb {Z} \times \{0\}$
then says that
This means that the map
![]() $Y_0 \times \mathbb {R} \to \mathbb {R}/\mathbb {Z} : (y,s) \mapsto s + \varphi (y)$
is invariant under the action
$Y_0 \times \mathbb {R} \to \mathbb {R}/\mathbb {Z} : (y,s) \mapsto s + \varphi (y)$
is invariant under the action
![]() $\mathbb {Z} \curvearrowright Y_0 \times \mathbb {R} : n \cdot (y,s) = (n\cdot y, \omega (n,y) + s)$
. This action is ergodic because
$\mathbb {Z} \curvearrowright Y_0 \times \mathbb {R} : n \cdot (y,s) = (n\cdot y, \omega (n,y) + s)$
. This action is ergodic because
![]() $\mathbb {Z} \curvearrowright Y_0$
is assumed to be of type III
$\mathbb {Z} \curvearrowright Y_0$
is assumed to be of type III
![]() $_1$
. So the map
$_1$
. So the map
![]() $(y,s) \mapsto s + \varphi (y)$
is essentially constant, which is absurd. So we have proven that
$(y,s) \mapsto s + \varphi (y)$
is essentially constant, which is absurd. So we have proven that
![]() $\widehat {\alpha }$
is not isomorphic to
$\widehat {\alpha }$
is not isomorphic to
![]() $\alpha $
.
$\alpha $
.
Proposition 3.4. Let
![]() $G \curvearrowright (X,\mu )$
be a non-singular ergodic action of type III
$G \curvearrowright (X,\mu )$
be a non-singular ergodic action of type III
![]() $_1$
, with logarithm of the Radon–Nikodym cocycle
$_1$
, with logarithm of the Radon–Nikodym cocycle
![]() $\omega : G \times X \to \mathbb {R}$
. Let
$\omega : G \times X \to \mathbb {R}$
. Let
![]() $\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
be any ergodic flow. Then the action
$\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
be any ergodic flow. Then the action
is ergodic and has associated flow
![]() $\widehat {\alpha }$
.
$\widehat {\alpha }$
.
Proof. Let
![]() $\mathbb {R}^2 \curvearrowright (Z,\zeta )$
be the unique action given by Proposition 3.1, associated with the ergodic flow
$\mathbb {R}^2 \curvearrowright (Z,\zeta )$
be the unique action given by Proposition 3.1, associated with the ergodic flow
![]() $\mathbb {R} \curvearrowright (Y,\eta )$
. Consider the action
$\mathbb {R} \curvearrowright (Y,\eta )$
. Consider the action
The action of
![]() $\{e\} \times \mathbb {R}$
scales the measure, while the action of
$\{e\} \times \mathbb {R}$
scales the measure, while the action of
![]() $G \times \{0\}$
is measure-preserving. By definition, the action of G on
$G \times \{0\}$
is measure-preserving. By definition, the action of G on
![]() $(X \times Z)/(\{e\} \times \mathbb {R})$
is isomorphic to
$(X \times Z)/(\{e\} \times \mathbb {R})$
is isomorphic to
![]() $G \curvearrowright X \times Y$
. It thus follows that the action in (3.2) is the Maharam extension of
$G \curvearrowright X \times Y$
. It thus follows that the action in (3.2) is the Maharam extension of
![]() $G \curvearrowright X \times Y$
together with its measure-scaling action of
$G \curvearrowright X \times Y$
together with its measure-scaling action of
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
By the uniqueness of
![]() $\mathbb {R}^2 \curvearrowright (Z,\zeta )$
, we may as well identify
$\mathbb {R}^2 \curvearrowright (Z,\zeta )$
, we may as well identify
![]() $(Z,\zeta ) = (\mathbb {R} \times \widehat {Y}, \gamma \times \widehat {\eta })$
with
$(Z,\zeta ) = (\mathbb {R} \times \widehat {Y}, \gamma \times \widehat {\eta })$
with
where
![]() $\widehat {\beta } : \mathbb {R} \times \widehat {Y} \to \mathbb {R}$
is the logarithm of the Radon–Nikodym cocycle for the adjoint flow
$\widehat {\beta } : \mathbb {R} \times \widehat {Y} \to \mathbb {R}$
is the logarithm of the Radon–Nikodym cocycle for the adjoint flow
![]() $\mathbb {R} \curvearrowright ^{\widehat {\alpha }} \widehat {Y}$
. Then the action in (3.2) becomes
$\mathbb {R} \curvearrowright ^{\widehat {\alpha }} \widehat {Y}$
. Then the action in (3.2) becomes
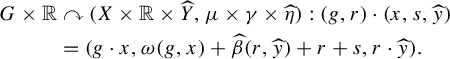 $$ \begin{align*}G \times \mathbb{R} &\curvearrowright (X \times \mathbb{R} \times \widehat{Y}, \mu \times \gamma \times \widehat{\eta}) : (g,r) \cdot (x,s,\widehat{y})\\ &= (g \cdot x, \omega(g,x) + \widehat{\beta}(r,\widehat{y}) + r + s, r \cdot \widehat{y}).\end{align*} $$
$$ \begin{align*}G \times \mathbb{R} &\curvearrowright (X \times \mathbb{R} \times \widehat{Y}, \mu \times \gamma \times \widehat{\eta}) : (g,r) \cdot (x,s,\widehat{y})\\ &= (g \cdot x, \omega(g,x) + \widehat{\beta}(r,\widehat{y}) + r + s, r \cdot \widehat{y}).\end{align*} $$
Since
![]() $G \curvearrowright (X,\mu )$
is ergodic and of type III
$G \curvearrowright (X,\mu )$
is ergodic and of type III
![]() $_1$
, the Maharam extension
$_1$
, the Maharam extension
![]() $G \curvearrowright X \times \mathbb {R}$
is ergodic. It follows that the G-invariant functions on
$G \curvearrowright X \times \mathbb {R}$
is ergodic. It follows that the G-invariant functions on
![]() $X \times \mathbb {R} \times \widehat {Y}$
are the functions that only depend on the
$X \times \mathbb {R} \times \widehat {Y}$
are the functions that only depend on the
![]() $\widehat {Y}$
-variable. Since
$\widehat {Y}$
-variable. Since
![]() $\mathbb {R} \curvearrowright \widehat {Y}$
is ergodic, we conclude that the action in (3.2) is ergodic. We have proven that the action in (3.1) is ergodic and that its associated flow is identified with
$\mathbb {R} \curvearrowright \widehat {Y}$
is ergodic, we conclude that the action in (3.2) is ergodic. We have proven that the action in (3.1) is ergodic and that its associated flow is identified with
![]() $\widehat {\alpha } : \mathbb {R} \curvearrowright \widehat {Y}$
.
$\widehat {\alpha } : \mathbb {R} \curvearrowright \widehat {Y}$
.
4 Versions of OE superrigidity in the type III setting
Definition 4.1. We say that a free, ergodic, non-singular action
![]() $G \curvearrowright (X,\mu )$
of a countable group G is simple if the action is not induced and if there are no non-trivial normal subgroups
$G \curvearrowright (X,\mu )$
of a countable group G is simple if the action is not induced and if there are no non-trivial normal subgroups
![]() $\Sigma \lhd G$
for which
$\Sigma \lhd G$
for which
![]() $\Sigma \curvearrowright (X,\mu )$
admits a fundamental domain.
$\Sigma \curvearrowright (X,\mu )$
admits a fundamental domain.
The motivation for this ad hoc notion of simplicity is the following. When
![]() $G \curvearrowright (X,\mu )$
is induced from
$G \curvearrowright (X,\mu )$
is induced from
![]() $G_0 \curvearrowright X_0$
, we have a canonical stable orbit equivalence between
$G_0 \curvearrowright X_0$
, we have a canonical stable orbit equivalence between
![]() $G \curvearrowright X$
and
$G \curvearrowright X$
and
![]() $G_0 \curvearrowright X_0$
. When
$G_0 \curvearrowright X_0$
. When
![]() $\Sigma \lhd G$
is a normal subgroup such that
$\Sigma \lhd G$
is a normal subgroup such that
![]() $\Sigma \curvearrowright (X,\mu )$
admits a fundamental domain, we have a canonical stable orbit equivalence between
$\Sigma \curvearrowright (X,\mu )$
admits a fundamental domain, we have a canonical stable orbit equivalence between
![]() $G \curvearrowright X$
and
$G \curvearrowright X$
and
![]() $G/\Sigma \curvearrowright X/\Sigma $
. So when
$G/\Sigma \curvearrowright X/\Sigma $
. So when
![]() $G \curvearrowright (X,\mu )$
is not simple, there always is a certain absence of OE superrigidity and describing all stably orbit equivalent actions is necessarily cumbersome. For this reason, we mainly restrict ourselves to simple actions in this paper.
$G \curvearrowright (X,\mu )$
is not simple, there always is a certain absence of OE superrigidity and describing all stably orbit equivalent actions is necessarily cumbersome. For this reason, we mainly restrict ourselves to simple actions in this paper.
Recall that a non-singular action
![]() $G \curvearrowright (X,\mu )$
of a countable group G on a standard probability space
$G \curvearrowright (X,\mu )$
of a countable group G on a standard probability space
![]() $(X,\mu )$
is called cocycle superrigid with countable target groups if every
$(X,\mu )$
is called cocycle superrigid with countable target groups if every
![]() $1$
-cocycle
$1$
-cocycle
![]() $\Omega : G \times X \to \Lambda $
with values in a countable group
$\Omega : G \times X \to \Lambda $
with values in a countable group
![]() $\Lambda $
is cohomologous to a group homomorphism
$\Lambda $
is cohomologous to a group homomorphism
![]() $\delta : G \to \Lambda $
, viewed as a
$\delta : G \to \Lambda $
, viewed as a
![]() $1$
-cocycle that is independent of the X-variable.
$1$
-cocycle that is independent of the X-variable.
Recall from the introduction the two versions (v1) and (v2) of OE superrigidity. For simple actions, version (v1) of OE superrigidity turns out to be equivalent to cocycle superrigidity with countable targets.
Proposition 4.2. Let
![]() $G \curvearrowright (X,\mu )$
be any free, ergodic, non-singular, simple action. Then
$G \curvearrowright (X,\mu )$
be any free, ergodic, non-singular, simple action. Then
![]() $G \curvearrowright (X,\mu )$
satisfies OE superrigidity (v1) if and only if
$G \curvearrowright (X,\mu )$
satisfies OE superrigidity (v1) if and only if
![]() $G \curvearrowright (X,\mu )$
is cocycle superrigid with countable targets.
$G \curvearrowright (X,\mu )$
is cocycle superrigid with countable targets.
Proof. The implication from cocycle superrigidity to OE superrigidity was first proven, in a probability measure-preserving setting, in [Reference ZimmerZim84, Proposition 4.2.11]. The version that we need is literally proven in [Reference Drimbe and VaesDV21, Lemma 2.4].
Conversely, assume that
![]() $\Omega : G \times X \to \Lambda $
is a
$\Omega : G \times X \to \Lambda $
is a
![]() $1$
-cocycle with values in a countable group
$1$
-cocycle with values in a countable group
![]() $\Lambda $
. Consider the free, non-singular, ergodic action
$\Lambda $
. Consider the free, non-singular, ergodic action
By construction, this action is stably orbit equivalent to
![]() $G \curvearrowright X$
. Assume that this action is conjugate to an induction of
$G \curvearrowright X$
. Assume that this action is conjugate to an induction of
![]() $G \curvearrowright X$
. We have to prove that
$G \curvearrowright X$
. We have to prove that
![]() $\Omega $
is cohomologous to a group homomorphism.
$\Omega $
is cohomologous to a group homomorphism.
Take an injective group homomorphism
![]() $\delta : G \to G \times \Lambda : \delta (g) = (\delta _1(g),\delta _2(g))$
and a measure space isomorphism
$\delta : G \to G \times \Lambda : \delta (g) = (\delta _1(g),\delta _2(g))$
and a measure space isomorphism
![]() $\Delta : X \to Z \subset X \times \Lambda $
such that
$\Delta : X \to Z \subset X \times \Lambda $
such that
![]() $G \times \Lambda \curvearrowright X \times \Lambda $
is induced from
$G \times \Lambda \curvearrowright X \times \Lambda $
is induced from
![]() $\delta (G) \curvearrowright Z$
and
$\delta (G) \curvearrowright Z$
and
![]() $\Delta $
is a conjugacy with respect to
$\Delta $
is a conjugacy with respect to
![]() $\delta $
.
$\delta $
.
Since the action of
![]() $\Lambda $
on
$\Lambda $
on
![]() $X \times \Lambda $
admits a fundamental domain, the same is true for the action
$X \times \Lambda $
admits a fundamental domain, the same is true for the action
![]() $\operatorname {Ker} \delta _1 \curvearrowright X$
. Since
$\operatorname {Ker} \delta _1 \curvearrowright X$
. Since
![]() $G \curvearrowright X$
is simple, we find that
$G \curvearrowright X$
is simple, we find that
![]() $\delta _1$
is faithful. Since
$\delta _1$
is faithful. Since
![]() $\delta (G) \subset \delta _1(G) \times \Lambda $
and since
$\delta (G) \subset \delta _1(G) \times \Lambda $
and since
![]() $G \times \Lambda \curvearrowright X \times \Lambda $
is induced from
$G \times \Lambda \curvearrowright X \times \Lambda $
is induced from
![]() $\delta (G) \curvearrowright Z$
, we find a fortiori that
$\delta (G) \curvearrowright Z$
, we find a fortiori that
![]() $G \times \Lambda \curvearrowright X \times \Lambda $
is induced from
$G \times \Lambda \curvearrowright X \times \Lambda $
is induced from
![]() $\delta _1(G) \times \Lambda \curvearrowright Z_1$
with
$\delta _1(G) \times \Lambda \curvearrowright Z_1$
with
![]() $Z_0 \subset Z_1$
. Since
$Z_0 \subset Z_1$
. Since
![]() $Z_1$
is
$Z_1$
is
![]() $\Lambda $
-invariant, we find that
$\Lambda $
-invariant, we find that
![]() $Z_1 = X_0 \times \Lambda $
and conclude that
$Z_1 = X_0 \times \Lambda $
and conclude that
![]() $G \curvearrowright X$
is induced from
$G \curvearrowright X$
is induced from
![]() $\delta _1(G) \curvearrowright X_0$
. Since
$\delta _1(G) \curvearrowright X_0$
. Since
![]() $G \curvearrowright X$
is simple, we conclude that
$G \curvearrowright X$
is simple, we conclude that
![]() $\delta _1(G) = G$
. So
$\delta _1(G) = G$
. So
![]() $\delta _1$
is an automorphism of the group G.
$\delta _1$
is an automorphism of the group G.
Define the group homomorphism
![]() $\gamma : G \to \Lambda : \gamma = \delta _2 \circ \delta _1^{-1}$
. We have
$\gamma : G \to \Lambda : \gamma = \delta _2 \circ \delta _1^{-1}$
. We have
![]() $\delta (g) = (\delta _1(g),\gamma (\delta _1(g)))$
and the map
$\delta (g) = (\delta _1(g),\gamma (\delta _1(g)))$
and the map
is a bijection satisfying
![]() $\psi ((g,a) \cdot i) = \gamma (g) \psi (i) a^{-1}$
for all
$\psi ((g,a) \cdot i) = \gamma (g) \psi (i) a^{-1}$
for all
![]() $(g,a) \in G \times \Lambda $
and
$(g,a) \in G \times \Lambda $
and
![]() $i \in (G \times \Lambda )/\delta (G)$
.
$i \in (G \times \Lambda )/\delta (G)$
.
Since
![]() $G \times \Lambda \curvearrowright X \times \Lambda $
is induced from
$G \times \Lambda \curvearrowright X \times \Lambda $
is induced from
![]() $\delta (G) \curvearrowright Z$
, we find a
$\delta (G) \curvearrowright Z$
, we find a
![]() $(G \times \Lambda )$
-equivariant map from
$(G \times \Lambda )$
-equivariant map from
![]() $X \times \Lambda $
to
$X \times \Lambda $
to
![]() $(G \times \Lambda ) / \delta (G)$
. We denote by
$(G \times \Lambda ) / \delta (G)$
. We denote by
![]() $\theta $
its composition with
$\theta $
its composition with
![]() $\psi $
. By
$\psi $
. By
![]() $\Lambda $
-equivariance, we get that
$\Lambda $
-equivariance, we get that
![]() $\theta (x,a) = \theta _0(x) a$
, where
$\theta (x,a) = \theta _0(x) a$
, where
![]() $\theta _0 : X \to \Lambda $
is a Borel map. Expressing the G-equivariance gives us that
$\theta _0 : X \to \Lambda $
is a Borel map. Expressing the G-equivariance gives us that
so that
![]() $\Omega $
is cohomologous to a group homomorphism.
$\Omega $
is cohomologous to a group homomorphism.
As an essential ingredient to prove the first part of Theorem C, as well as to prove Corollary B, we need to establish cocycle superrigidity for linear and for affine actions on
![]() $\mathbb {R}^n$
. We first recall the notion of essential cocycle superrigidity introduced in [Reference Drimbe and VaesDV21, Definition B]. We only formulate the version for connected Lie groups, which is the one that we need in this paper.
$\mathbb {R}^n$
. We first recall the notion of essential cocycle superrigidity introduced in [Reference Drimbe and VaesDV21, Definition B]. We only formulate the version for connected Lie groups, which is the one that we need in this paper.
Definition 4.3. [Reference Drimbe and VaesDV21, Definition B]
A countable dense subgroup
![]() $\Gamma < G$
of a connected Lie group G, with universal cover
$\Gamma < G$
of a connected Lie group G, with universal cover
![]() $\pi : \widetilde {G} \to G$
and
$\pi : \widetilde {G} \to G$
and
![]() $\widetilde {\Gamma } = \pi ^{-1}(\Gamma )$
, is said to be essentially cocycle superrigid with countable targets if for every
$\widetilde {\Gamma } = \pi ^{-1}(\Gamma )$
, is said to be essentially cocycle superrigid with countable targets if for every
![]() $1$
-cocycle
$1$
-cocycle
![]() $\omega : \Gamma \times G \to \Lambda $
of the translation action
$\omega : \Gamma \times G \to \Lambda $
of the translation action
![]() $\Gamma \curvearrowright G$
with values in a countable group
$\Gamma \curvearrowright G$
with values in a countable group
![]() $\Lambda $
, the lifted
$\Lambda $
, the lifted
![]() $1$
-cocycle
$1$
-cocycle
![]() $\widetilde {\omega } : \widetilde {\Gamma } \times \widetilde {G} \to \Lambda : \widetilde {\omega } = \omega \circ (\pi \times \pi )$
is cohomologous to a group homomorphism
$\widetilde {\omega } : \widetilde {\Gamma } \times \widetilde {G} \to \Lambda : \widetilde {\omega } = \omega \circ (\pi \times \pi )$
is cohomologous to a group homomorphism
![]() $\delta : \widetilde {\Gamma } \to \Lambda $
.
$\delta : \widetilde {\Gamma } \to \Lambda $
.
In [Reference Drimbe and VaesDV21, Propositions 4.1 and 4.2], it was proven that for every integer
![]() $n \geq 3$
, non-empty set of prime numbers
$n \geq 3$
, non-empty set of prime numbers
![]() $\mathcal {S}$
and real algebraic number field
$\mathcal {S}$
and real algebraic number field
![]() $\mathbb {Q} \varsubsetneq K \subset \mathbb {R}$
with ring of integers
$\mathbb {Q} \varsubsetneq K \subset \mathbb {R}$
with ring of integers
![]() $\mathcal {O}_K$
, the dense subgroups
$\mathcal {O}_K$
, the dense subgroups
![]() $\operatorname {SL}(n,\mathbb {Z}[\mathcal {S}^{-1}])$
and
$\operatorname {SL}(n,\mathbb {Z}[\mathcal {S}^{-1}])$
and
![]() $\operatorname {SL}(n,\mathcal {O}_K)$
of
$\operatorname {SL}(n,\mathcal {O}_K)$
of
![]() $\operatorname {SL}(n,\mathbb {R})$
are essentially cocycle superrigid with countable targets. We prove the same result for a much larger family of dense subgroups of
$\operatorname {SL}(n,\mathbb {R})$
are essentially cocycle superrigid with countable targets. We prove the same result for a much larger family of dense subgroups of
![]() $\operatorname {SL}(n,\mathbb {R})$
and also for their corresponding subgroups of
$\operatorname {SL}(n,\mathbb {R})$
and also for their corresponding subgroups of
![]() $\operatorname {SL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
.
$\operatorname {SL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
.
For every integer
![]() $n \geq 2$
and commutative ring
$n \geq 2$
and commutative ring
![]() $\mathcal {A}$
, we denote by
$\mathcal {A}$
, we denote by
![]() $\operatorname {SL}(n,\mathcal {A})$
and
$\operatorname {SL}(n,\mathcal {A})$
and
![]() $\operatorname {GL}(n,\mathcal {A})$
the groups of
$\operatorname {GL}(n,\mathcal {A})$
the groups of
![]() $n \times n$
matrices with entries in
$n \times n$
matrices with entries in
![]() $\mathcal {A}$
and determinant
$\mathcal {A}$
and determinant
![]() $1$
, belonging to
$1$
, belonging to
![]() $\mathcal {A}^*$
. Whenever
$\mathcal {A}^*$
. Whenever
![]() $1 \leq i,j \leq n$
with
$1 \leq i,j \leq n$
with
![]() $i \neq j$
and
$i \neq j$
and
![]() $a \in \mathcal {A}$
, we denote by
$a \in \mathcal {A}$
, we denote by
![]() $e_{ij}(a) \in \operatorname {SL}(n,\mathcal {A})$
the elementary matrix with
$e_{ij}(a) \in \operatorname {SL}(n,\mathcal {A})$
the elementary matrix with
![]() $1$
s on the diagonal, a in position
$1$
s on the diagonal, a in position
![]() $ij$
and
$ij$
and
![]() $0$
s elsewhere. We denote by
$0$
s elsewhere. We denote by
![]() $E(n,\mathcal {A}) \subset \operatorname {SL}(n,\mathcal {A})$
the subgroup generated by the elementary matrices. By Suslin’s theorem (see [Reference Hahn and O’MearaHOM89, Theorem 1.2.13]), for all
$E(n,\mathcal {A}) \subset \operatorname {SL}(n,\mathcal {A})$
the subgroup generated by the elementary matrices. By Suslin’s theorem (see [Reference Hahn and O’MearaHOM89, Theorem 1.2.13]), for all
![]() $n \geq 3$
,
$n \geq 3$
,
![]() $E(n,\mathcal {A})$
is a normal subgroup of
$E(n,\mathcal {A})$
is a normal subgroup of
![]() $\operatorname {GL}(n,\mathcal {A})$
. For several rings
$\operatorname {GL}(n,\mathcal {A})$
. For several rings
![]() $\mathcal {A}$
, it is known that
$\mathcal {A}$
, it is known that
![]() $E(n,\mathcal {A}) = \operatorname {SL}(n,\mathcal {A})$
(see Example 6.8 for references).
$E(n,\mathcal {A}) = \operatorname {SL}(n,\mathcal {A})$
(see Example 6.8 for references).
Theorem 4.4. Let
![]() $\mathcal {A} \subset \mathbb {R}$
be any countable subring containing an algebraic number that does not belong to
$\mathcal {A} \subset \mathbb {R}$
be any countable subring containing an algebraic number that does not belong to
![]() $\mathbb {Z}$
. Let
$\mathbb {Z}$
. Let
![]() $n \geq 3$
and let
$n \geq 3$
and let
![]() $E(n,\mathcal {A}) < \Gamma < \operatorname {SL}(n,\mathcal {A})$
be any intermediate subgroup.
$E(n,\mathcal {A}) < \Gamma < \operatorname {SL}(n,\mathcal {A})$
be any intermediate subgroup.
-
(1) The dense subgroup
 $\Gamma < \operatorname {SL}(n,\mathbb {R})$
is essentially cocycle superrigid with countable targets.
$\Gamma < \operatorname {SL}(n,\mathbb {R})$
is essentially cocycle superrigid with countable targets. -
(2) The dense subgroup
 $\Gamma \ltimes \mathcal {A}^n < \operatorname {SL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
is essentially cocycle superrigid with countable targets.
$\Gamma \ltimes \mathcal {A}^n < \operatorname {SL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
is essentially cocycle superrigid with countable targets.
Before proving Theorem 4.4, we need two elementary lemmas, which are essentially contained in [Reference IoanaIoa14, Lemma 5.1].
Lemma 4.5. Let G be a connected locally compact second countable group and let
![]() $\Gamma < G$
be a countable dense subgroup. Then the translation action
$\Gamma < G$
be a countable dense subgroup. Then the translation action
![]() $\Gamma \curvearrowright G$
is ergodic and not induced.
$\Gamma \curvearrowright G$
is ergodic and not induced.
Proof. Let
![]() $\Gamma _0 < \Gamma $
be a subgroup and
$\Gamma _0 < \Gamma $
be a subgroup and
![]() $\pi : G \to \Gamma /\Gamma _0$
a Borel map such that
$\pi : G \to \Gamma /\Gamma _0$
a Borel map such that
![]() $\pi (g h) = g \pi (h)$
for all
$\pi (g h) = g \pi (h)$
for all
![]() $g \in \Gamma $
and a.e.
$g \in \Gamma $
and a.e.
![]() $h \in G$
. We have to prove that
$h \in G$
. We have to prove that
![]() $\pi $
is essentially constant. Since
$\pi $
is essentially constant. Since
![]() $\Gamma /\Gamma _0$
is countable, the set
$\Gamma /\Gamma _0$
is countable, the set
![]() $\mathcal {U} = \{(h,k) \in G \times G \mid \pi (h) = \pi (k)\}$
is non-negligible.
$\mathcal {U} = \{(h,k) \in G \times G \mid \pi (h) = \pi (k)\}$
is non-negligible.
Since
![]() $\pi (g h) = g \pi (h)$
when
$\pi (g h) = g \pi (h)$
when
![]() $g \in \Gamma $
, the set
$g \in \Gamma $
, the set
![]() $\mathcal {U}$
is essentially invariant under the diagonal translation action
$\mathcal {U}$
is essentially invariant under the diagonal translation action
![]() $\Gamma \curvearrowright G \times G$
. By continuity,
$\Gamma \curvearrowright G \times G$
. By continuity,
![]() $\mathcal {U}$
is essentially invariant under the diagonal translation action of G. We thus find a non-negligible Borel set
$\mathcal {U}$
is essentially invariant under the diagonal translation action of G. We thus find a non-negligible Borel set
![]() $\mathcal {V} \subset G$
such that, up to measure zero,
$\mathcal {V} \subset G$
such that, up to measure zero,
![]() $\mathcal {U} = \{(h,h k) \mid h \in G, k \in \mathcal {V}\}$
.
$\mathcal {U} = \{(h,h k) \mid h \in G, k \in \mathcal {V}\}$
.
Define
![]() $G_0 = \{k \in G \mid \pi (h) = \pi (hk) \;\text {for a.e. }h \in G\}$
. Since
$G_0 = \{k \in G \mid \pi (h) = \pi (hk) \;\text {for a.e. }h \in G\}$
. Since
![]() $\mathcal {V}$
is non-negligible,
$\mathcal {V}$
is non-negligible,
![]() $G_0$
is also non-negligible. By definition,
$G_0$
is also non-negligible. By definition,
![]() $G_0$
is a subgroup of G. So
$G_0$
is a subgroup of G. So
![]() $G_0$
must be an open subgroup of G. Since G is connected, we conclude that
$G_0$
must be an open subgroup of G. Since G is connected, we conclude that
![]() $G_0 = G$
. This means that
$G_0 = G$
. This means that
![]() $\pi $
is essentially constant.
$\pi $
is essentially constant.
The following lemma is also essentially contained in [Reference IoanaIoa14, Lemma 5.1] and allows us to extend cocycle superrigidity from a subgroup
![]() $\Gamma _0 < \Gamma $
to its normalizer
$\Gamma _0 < \Gamma $
to its normalizer
![]() $\mathcal {N}_\Gamma (\Gamma _0)$
. Such a result goes back to [Reference PopaPop05, Proposition 3.6].
$\mathcal {N}_\Gamma (\Gamma _0)$
. Such a result goes back to [Reference PopaPop05, Proposition 3.6].
Lemma 4.6. Let
![]() $\Gamma \curvearrowright (X,\mu )$
be a free, ergodic, non-singular action and let
$\Gamma \curvearrowright (X,\mu )$
be a free, ergodic, non-singular action and let
![]() $\Omega : \Gamma \times X \to \Lambda $
be a
$\Omega : \Gamma \times X \to \Lambda $
be a
![]() $1$
-cocycle with values in a countable group
$1$
-cocycle with values in a countable group
![]() $\Lambda $
. Let
$\Lambda $
. Let
![]() $\Gamma _0 < \Gamma $
be a subgroup and let
$\Gamma _0 < \Gamma $
be a subgroup and let
![]() $(X_y,\mu _y)_{y \in (Y,\eta )}$
be the ergodic decomposition of the action
$(X_y,\mu _y)_{y \in (Y,\eta )}$
be the ergodic decomposition of the action
![]() $\Gamma _0 \curvearrowright (X,\mu )$
, with corresponding factor map
$\Gamma _0 \curvearrowright (X,\mu )$
, with corresponding factor map
![]() $\pi : (X,\mu ) \to (Y,\eta )$
. Assume that for
$\pi : (X,\mu ) \to (Y,\eta )$
. Assume that for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $y \in Y$
, the action
$y \in Y$
, the action
![]() $\Gamma _0 \curvearrowright (X_y,\mu _y)$
is not induced.
$\Gamma _0 \curvearrowright (X_y,\mu _y)$
is not induced.
If for every
![]() $h \in \Gamma _0$
, the function
$h \in \Gamma _0$
, the function
![]() $x \mapsto \Omega (h,x)$
factors through
$x \mapsto \Omega (h,x)$
factors through
![]() $\pi $
, then
$\pi $
, then
![]() $x \mapsto \Omega (g,x)$
factors through
$x \mapsto \Omega (g,x)$
factors through
![]() $\pi $
for every
$\pi $
for every
![]() $g \in \mathcal {N}_\Gamma (\Gamma _0)$
.
$g \in \mathcal {N}_\Gamma (\Gamma _0)$
.
Proof. Fix
![]() $g \in \mathcal {N}_\Gamma (\Gamma _0)$
and denote by
$g \in \mathcal {N}_\Gamma (\Gamma _0)$
and denote by
![]() $\alpha : \Gamma _0 \to \Gamma _0$
the automorphism
$\alpha : \Gamma _0 \to \Gamma _0$
the automorphism
![]() $\alpha (h) = g h g^{-1}$
. Since for every
$\alpha (h) = g h g^{-1}$
. Since for every
![]() $h \in \Gamma _0$
, the function
$h \in \Gamma _0$
, the function
![]() $x \mapsto \Omega (h,x)$
factors through
$x \mapsto \Omega (h,x)$
factors through
![]() $\pi $
, we find a measurable family
$\pi $
, we find a measurable family
![]() $(\delta _y)_{y \in Y}$
of group homomorphisms
$(\delta _y)_{y \in Y}$
of group homomorphisms
![]() $\delta _y : \Gamma _0 \to \Lambda $
such that
$\delta _y : \Gamma _0 \to \Lambda $
such that
![]() $\Omega (h,x) = \delta _{\pi (x)}(h)$
for all
$\Omega (h,x) = \delta _{\pi (x)}(h)$
for all
![]() $h \in \Gamma _0$
and a.e.
$h \in \Gamma _0$
and a.e.
![]() $x \in X$
. Applying the
$x \in X$
. Applying the
![]() $1$
-cocycle relation to
$1$
-cocycle relation to
![]() $g h = \alpha (h) g$
gives us that
$g h = \alpha (h) g$
gives us that
![]() $\Omega (g,h \cdot x) \, \delta _{\pi (x)}(h) = \delta _{\pi (g \cdot x)}(\alpha (h)) \, \Omega (g,x)$
for a.e.
$\Omega (g,h \cdot x) \, \delta _{\pi (x)}(h) = \delta _{\pi (g \cdot x)}(\alpha (h)) \, \Omega (g,x)$
for a.e.
![]() $x \in X$
.
$x \in X$
.
For every
![]() $g \in \mathcal {N}_\Gamma (\Gamma _0)$
, the map
$g \in \mathcal {N}_\Gamma (\Gamma _0)$
, the map
![]() $x \mapsto \pi (g \cdot x)$
is
$x \mapsto \pi (g \cdot x)$
is
![]() $\Gamma _0$
-invariant. We can thus define the non-singular action
$\Gamma _0$
-invariant. We can thus define the non-singular action
![]() $\mathcal {N}_\Gamma (\Gamma _0) \curvearrowright (Y,\eta )$
such that
$\mathcal {N}_\Gamma (\Gamma _0) \curvearrowright (Y,\eta )$
such that
![]() $\pi (g \cdot x) = g \cdot \pi (x)$
for all
$\pi (g \cdot x) = g \cdot \pi (x)$
for all
![]() $g \in \mathcal {N}_\Gamma (\Gamma _0)$
and a.e.
$g \in \mathcal {N}_\Gamma (\Gamma _0)$
and a.e.
![]() $x \in X$
. We conclude that for a.e.
$x \in X$
. We conclude that for a.e.
![]() $y \in Y$
, we have
$y \in Y$
, we have
The action
![]() $\Gamma _0 \curvearrowright (X_y,\mu _y)$
is ergodic and not induced. Also (4.1) is saying that the map
$\Gamma _0 \curvearrowright (X_y,\mu _y)$
is ergodic and not induced. Also (4.1) is saying that the map
![]() $X_y \to \Lambda : x \mapsto \Omega (g,x)$
is
$X_y \to \Lambda : x \mapsto \Omega (g,x)$
is
![]() $\Gamma _0$
-equivariant, where
$\Gamma _0$
-equivariant, where
![]() $\Gamma _0$
is acting on
$\Gamma _0$
is acting on
![]() $\Lambda $
by
$\Lambda $
by
![]() $h \cdot \unicode{x3bb} = \delta _{g \cdot y}(\alpha (h)) \, \unicode{x3bb} \, \delta _y(h)^{-1}$
. By Lemma 2.1, the map
$h \cdot \unicode{x3bb} = \delta _{g \cdot y}(\alpha (h)) \, \unicode{x3bb} \, \delta _y(h)^{-1}$
. By Lemma 2.1, the map
![]() $x \mapsto \Omega (g,x)$
is essentially constant on
$x \mapsto \Omega (g,x)$
is essentially constant on
![]() $(X_y,\mu _y)$
. Since this holds for a.e.
$(X_y,\mu _y)$
. Since this holds for a.e.
![]() $y \in Y$
, we have proven that
$y \in Y$
, we have proven that
![]() $x \mapsto \Omega (g,x)$
factors through
$x \mapsto \Omega (g,x)$
factors through
![]() $\pi $
.
$\pi $
.
Note that Lemma 4.5 also implies the following result, which we will use in combination with Lemma 4.6: if G is a locally compact second countable group and
![]() $\Gamma < G$
is a countable subgroup whose closure
$\Gamma < G$
is a countable subgroup whose closure
![]() $H = \overline {\Gamma }$
is connected, then the map
$H = \overline {\Gamma }$
is connected, then the map
![]() $\pi : G \to H \backslash G : \pi (g) = H g$
realizes the ergodic decomposition of the translation action
$\pi : G \to H \backslash G : \pi (g) = H g$
realizes the ergodic decomposition of the translation action
![]() $\Gamma \curvearrowright G$
and, for every
$\Gamma \curvearrowright G$
and, for every
![]() $H g \in H \backslash G$
, the action of
$H g \in H \backslash G$
, the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\pi ^{-1}(Hg)$
is isomorphic to the translation action
$\pi ^{-1}(Hg)$
is isomorphic to the translation action
![]() $\Gamma \curvearrowright H$
and thus not induced by Lemma 4.5.
$\Gamma \curvearrowright H$
and thus not induced by Lemma 4.5.
Proof of Theorem 4.4
By our assumption, the ring
![]() $\mathcal {A}$
contains a rational number
$\mathcal {A}$
contains a rational number
![]() $q \in \mathbb {Q} \setminus \mathbb {Z}$
or an irrational algebraic number
$q \in \mathbb {Q} \setminus \mathbb {Z}$
or an irrational algebraic number
![]() $\alpha $
. In the first case, by taking a multiple of q, we find a prime p and a positive integer
$\alpha $
. In the first case, by taking a multiple of q, we find a prime p and a positive integer
![]() $N \in \mathbb {N} \setminus \{0\}$
with
$N \in \mathbb {N} \setminus \{0\}$
with
![]() $p \nmid N$
such that
$p \nmid N$
such that
![]() $N p^{-1} \in \mathcal {A}$
. Since
$N p^{-1} \in \mathcal {A}$
. Since
![]() $p \nmid N$
, we can take integers
$p \nmid N$
, we can take integers
![]() $a,b \in \mathbb {Z}$
such that
$a,b \in \mathbb {Z}$
such that
![]() $aN + bp = 1$
, so that
$aN + bp = 1$
, so that
![]() $p^{-1} = a Np^{-1} + b$
. We conclude that
$p^{-1} = a Np^{-1} + b$
. We conclude that
![]() $p^{-1} \in \mathcal {A}$
and denote
$p^{-1} \in \mathcal {A}$
and denote
![]() $\mathcal {A}_0 = \mathbb {Z}[p^{-1}]$
. In the second case, we define the algebraic number field
$\mathcal {A}_0 = \mathbb {Z}[p^{-1}]$
. In the second case, we define the algebraic number field
![]() $K = \mathbb {Q}(\alpha )$
. Let
$K = \mathbb {Q}(\alpha )$
. Let
![]() $d \geq 2$
be the degree of the minimal polynomial of
$d \geq 2$
be the degree of the minimal polynomial of
![]() $\alpha $
. The ring
$\alpha $
. The ring
![]() $\mathcal {O}_K$
of integers of K is a finitely generated
$\mathcal {O}_K$
of integers of K is a finitely generated
![]() $\mathbb {Z}$
-module that is contained in K, which has
$\mathbb {Z}$
-module that is contained in K, which has
![]() $\{1,\alpha ,\ldots ,\alpha ^{d-1}\}$
as a
$\{1,\alpha ,\ldots ,\alpha ^{d-1}\}$
as a
![]() $\mathbb {Q}$
-vector space basis. We can thus take a positive integer
$\mathbb {Q}$
-vector space basis. We can thus take a positive integer
![]() $N \in \mathbb {N} \setminus \{0\}$
such that
$N \in \mathbb {N} \setminus \{0\}$
such that
![]() $N \mathcal {O}_K \subset \mathbb {Z}[\alpha ] \subset \mathcal {A}$
. We denote
$N \mathcal {O}_K \subset \mathbb {Z}[\alpha ] \subset \mathcal {A}$
. We denote
![]() $\mathcal {A}_0 = \mathbb {Z} + N \mathcal {O}_K$
.
$\mathcal {A}_0 = \mathbb {Z} + N \mathcal {O}_K$
.
We start by proving that
![]() $E(n,\mathcal {A}_0) < \operatorname {SL}(n,\mathbb {R})$
is essentially cocycle superrigid with countable targets. When
$E(n,\mathcal {A}_0) < \operatorname {SL}(n,\mathbb {R})$
is essentially cocycle superrigid with countable targets. When
![]() $\mathcal {A}_0 = \mathbb {Z}[p^{-1}]$
, we know by [Reference Hahn and O’MearaHOM89, Theorem 4.3.9] that
$\mathcal {A}_0 = \mathbb {Z}[p^{-1}]$
, we know by [Reference Hahn and O’MearaHOM89, Theorem 4.3.9] that
![]() $E(n,\mathcal {A}_0) = \operatorname {SL}(n,\mathcal {A}_0)$
and we know from [Reference Drimbe and VaesDV21, Proposition 4.1] that
$E(n,\mathcal {A}_0) = \operatorname {SL}(n,\mathcal {A}_0)$
and we know from [Reference Drimbe and VaesDV21, Proposition 4.1] that
![]() $\operatorname {SL}(n,\mathcal {A}_0) < \operatorname {SL}(n,\mathbb {R})$
is essentially cocycle superrigid with countable targets.
$\operatorname {SL}(n,\mathcal {A}_0) < \operatorname {SL}(n,\mathbb {R})$
is essentially cocycle superrigid with countable targets.
Next consider the case where
![]() $\mathcal {A}_0 = \mathbb {Z} + N \mathcal {O}_K$
. The ring
$\mathcal {A}_0 = \mathbb {Z} + N \mathcal {O}_K$
. The ring
![]() $\mathcal {A}_1 = \mathcal {O}_K / (N \mathcal {O}_K)$
is finite and the kernel of the canonical homomorphism
$\mathcal {A}_1 = \mathcal {O}_K / (N \mathcal {O}_K)$
is finite and the kernel of the canonical homomorphism
![]() $\operatorname {SL}(n,\mathcal {O}_K) \to \operatorname {SL}(n,\mathcal {A}_1)$
is contained in
$\operatorname {SL}(n,\mathcal {O}_K) \to \operatorname {SL}(n,\mathcal {A}_1)$
is contained in
![]() $\operatorname {SL}(n,\mathcal {A}_0)$
. Thus,
$\operatorname {SL}(n,\mathcal {A}_0)$
. Thus,
![]() $\operatorname {SL}(n,\mathcal {A}_0) < \operatorname {SL}(n,\mathcal {O}_K)$
has finite index. Using the real and complex embeddings of K, the group
$\operatorname {SL}(n,\mathcal {A}_0) < \operatorname {SL}(n,\mathcal {O}_K)$
has finite index. Using the real and complex embeddings of K, the group
![]() $\operatorname {SL}(n,\mathcal {O}_K)$
is an irreducible lattice in a product of copies of
$\operatorname {SL}(n,\mathcal {O}_K)$
is an irreducible lattice in a product of copies of
![]() $\operatorname {SL}(n,\mathbb {R})$
and
$\operatorname {SL}(n,\mathbb {R})$
and
![]() $\operatorname {SL}(n,\mathbb {C})$
; see, for example, [Reference Platonov and RapinchukPR94, Theorems 5.7 and 7.12]. The groups
$\operatorname {SL}(n,\mathbb {C})$
; see, for example, [Reference Platonov and RapinchukPR94, Theorems 5.7 and 7.12]. The groups
![]() $\operatorname {SL}(n,\mathbb {R})$
and
$\operatorname {SL}(n,\mathbb {R})$
and
![]() $\operatorname {SL}(n,\mathbb {C})$
both have property (T); see, for example, [Reference Bekka, de la Harpe and ValetteBHV08, Theorem 1.4.15]. Then the finite-index subgroup
$\operatorname {SL}(n,\mathbb {C})$
both have property (T); see, for example, [Reference Bekka, de la Harpe and ValetteBHV08, Theorem 1.4.15]. Then the finite-index subgroup
![]() $\operatorname {SL}(n,\mathcal {A}_0)$
of
$\operatorname {SL}(n,\mathcal {A}_0)$
of
![]() $\operatorname {SL}(n,\mathcal {O}_K)$
is also such an irreducible lattice. In particular,
$\operatorname {SL}(n,\mathcal {O}_K)$
is also such an irreducible lattice. In particular,
![]() $\operatorname {SL}(n,\mathcal {A}_0)$
satisfies Margulis’s normal subgroup theorem. Since
$\operatorname {SL}(n,\mathcal {A}_0)$
satisfies Margulis’s normal subgroup theorem. Since
![]() $E(n,\mathcal {A}_0)$
is an infinite normal subgroup of
$E(n,\mathcal {A}_0)$
is an infinite normal subgroup of
![]() $\operatorname {SL}(n,\mathcal {A}_0)$
, we conclude that
$\operatorname {SL}(n,\mathcal {A}_0)$
, we conclude that
![]() $E(n,\mathcal {A}_0) < \operatorname {SL}(n,\mathcal {A}_0)$
has finite index. So
$E(n,\mathcal {A}_0) < \operatorname {SL}(n,\mathcal {A}_0)$
has finite index. So
![]() $E(n,\mathcal {A}_0)$
is also an irreducible lattice in a product of copies of
$E(n,\mathcal {A}_0)$
is also an irreducible lattice in a product of copies of
![]() $\operatorname {SL}(n,\mathbb {R})$
and
$\operatorname {SL}(n,\mathbb {R})$
and
![]() $\operatorname {SL}(n,\mathbb {C})$
. By part 2 of [Reference Drimbe and VaesDV21, Theorem C] (and this is essentially [Reference IoanaIoa14, Theorem B]), we get that
$\operatorname {SL}(n,\mathbb {C})$
. By part 2 of [Reference Drimbe and VaesDV21, Theorem C] (and this is essentially [Reference IoanaIoa14, Theorem B]), we get that
![]() $E(n,\mathcal {A}_0) < \operatorname {SL}(n,\mathbb {R})$
is essentially cocycle superrigid with countable targets.
$E(n,\mathcal {A}_0) < \operatorname {SL}(n,\mathbb {R})$
is essentially cocycle superrigid with countable targets.
We also need the following observation: given a countable dense subgroup
![]() $\Gamma $
of a connected Lie group G with universal cover
$\Gamma $
of a connected Lie group G with universal cover
![]() $\pi : \widetilde {G} \to G$
, the subgroup
$\pi : \widetilde {G} \to G$
, the subgroup
![]() $\Gamma < G$
is essentially cocycle superrigid with countable targets if and only if the translation action of the dense subgroup
$\Gamma < G$
is essentially cocycle superrigid with countable targets if and only if the translation action of the dense subgroup
![]() $\widetilde {\Gamma } = \pi ^{-1}(\Gamma )$
on
$\widetilde {\Gamma } = \pi ^{-1}(\Gamma )$
on
![]() $\widetilde {G}$
is cocycle superrigid with countable targets. One implication is obvious. So assume that
$\widetilde {G}$
is cocycle superrigid with countable targets. One implication is obvious. So assume that
![]() $\Gamma < G$
is essentially cocycle superrigid with countable targets and that
$\Gamma < G$
is essentially cocycle superrigid with countable targets and that
![]() $\omega : \widetilde {\Gamma } \times \widetilde {G} \to \Lambda $
is a
$\omega : \widetilde {\Gamma } \times \widetilde {G} \to \Lambda $
is a
![]() $1$
-cocycle with values in a countable group
$1$
-cocycle with values in a countable group
![]() $\Lambda $
. Since the action of
$\Lambda $
. Since the action of
![]() $\operatorname {Ker} \pi $
on
$\operatorname {Ker} \pi $
on
![]() $\widetilde {G}$
admits a fundamental domain,
$\widetilde {G}$
admits a fundamental domain,
![]() $\omega $
is cohomologous with a
$\omega $
is cohomologous with a
![]() $1$
-cocycle
$1$
-cocycle
![]() $\omega _1$
satisfying
$\omega _1$
satisfying
![]() $\omega _1(g,x) = e$
for all
$\omega _1(g,x) = e$
for all
![]() $g \in \operatorname {Ker} \pi $
and a.e.
$g \in \operatorname {Ker} \pi $
and a.e.
![]() $x \in \widetilde {G}$
. This means that
$x \in \widetilde {G}$
. This means that
![]() $\omega _1(g,x) = \omega _2(\pi (g),\pi (x))$
for all
$\omega _1(g,x) = \omega _2(\pi (g),\pi (x))$
for all
![]() $g \in \widetilde {\Gamma }$
and a.e.
$g \in \widetilde {\Gamma }$
and a.e.
![]() $x \in \widetilde {G}$
, where
$x \in \widetilde {G}$
, where
![]() $\omega _2 : \Gamma \times G \to \Lambda $
is a
$\omega _2 : \Gamma \times G \to \Lambda $
is a
![]() $1$
-cocycle. By our assumption,
$1$
-cocycle. By our assumption,
![]() $\omega _1$
, and hence also
$\omega _1$
, and hence also
![]() $\omega $
, is cohomologous with a group homomorphism from
$\omega $
, is cohomologous with a group homomorphism from
![]() $\widetilde {\Gamma }$
to
$\widetilde {\Gamma }$
to
![]() $\Lambda $
.
$\Lambda $
.
We then prove statement (1). Take
![]() $E(n,\mathcal {A}) < \Gamma < \operatorname {SL}(n,\mathcal {A})$
. We write
$E(n,\mathcal {A}) < \Gamma < \operatorname {SL}(n,\mathcal {A})$
. We write
![]() $G = \operatorname {SL}(n,\mathbb {R})$
and denote by
$G = \operatorname {SL}(n,\mathbb {R})$
and denote by
![]() $\pi : \widetilde {G} \to G$
its universal cover. Since
$\pi : \widetilde {G} \to G$
its universal cover. Since
![]() $n \geq 3$
,
$n \geq 3$
,
![]() $\operatorname {Ker} \pi $
is a central subgroup of order
$\operatorname {Ker} \pi $
is a central subgroup of order
![]() $2$
in
$2$
in
![]() $\widetilde {G}$
. Define
$\widetilde {G}$
. Define
![]() $\widetilde {\Gamma } = \pi ^{-1}(\Gamma )$
. Let
$\widetilde {\Gamma } = \pi ^{-1}(\Gamma )$
. Let
![]() $\omega : \Gamma \times G \to \Lambda $
be a
$\omega : \Gamma \times G \to \Lambda $
be a
![]() $1$
-cocycle, with lift
$1$
-cocycle, with lift
![]() $\widetilde {\omega } : \widetilde {\Gamma } \times \widetilde {G} \to \Lambda $
. We have to prove that
$\widetilde {\omega } : \widetilde {\Gamma } \times \widetilde {G} \to \Lambda $
. We have to prove that
![]() $\widetilde {\omega }$
is cohomologous to a group homomorphism.
$\widetilde {\omega }$
is cohomologous to a group homomorphism.
Since we have proven that
![]() $E(n,\mathcal {A}_0) < G$
is essentially cocycle superrigid, it follows from the observation above that
$E(n,\mathcal {A}_0) < G$
is essentially cocycle superrigid, it follows from the observation above that
![]() $\widetilde {\omega }$
is cohomologous with a
$\widetilde {\omega }$
is cohomologous with a
![]() $1$
-cocycle
$1$
-cocycle
![]() $\gamma : \widetilde {\Gamma } \times \widetilde {G} \to \Lambda $
that has the property that
$\gamma : \widetilde {\Gamma } \times \widetilde {G} \to \Lambda $
that has the property that
![]() $x \mapsto \gamma (g,x)$
is essentially constant for every
$x \mapsto \gamma (g,x)$
is essentially constant for every
![]() $g \in \pi ^{-1}(E(n,\mathcal {A}_0))$
.
$g \in \pi ^{-1}(E(n,\mathcal {A}_0))$
.
Write
![]() $[n] = \{1,\ldots ,n\}$
. For every
$[n] = \{1,\ldots ,n\}$
. For every
![]() $k \in [n]$
and for every subring
$k \in [n]$
and for every subring
![]() $\mathcal {B} \subset \mathbb {R}$
, we define the following subgroups of
$\mathcal {B} \subset \mathbb {R}$
, we define the following subgroups of
![]() $E(n,\mathcal {B})$
: the group
$E(n,\mathcal {B})$
: the group
![]() $C_k(\mathcal {B}) \cong \mathcal {B}^{n-1}$
generated by
$C_k(\mathcal {B}) \cong \mathcal {B}^{n-1}$
generated by
![]() $\{e_{ik}(b) \mid i \in [n] \setminus \{k\}, b \in \mathcal {B}\}$
; the group
$\{e_{ik}(b) \mid i \in [n] \setminus \{k\}, b \in \mathcal {B}\}$
; the group
![]() $R_k(\mathcal {B}) \cong \mathcal {B}^{n-1}$
generated by
$R_k(\mathcal {B}) \cong \mathcal {B}^{n-1}$
generated by
![]() $\{e_{kj}(b) \mid j \in [n] \setminus \{k\}, b \in \mathcal {B}\}$
; and the group
$\{e_{kj}(b) \mid j \in [n] \setminus \{k\}, b \in \mathcal {B}\}$
; and the group
![]() $H_k(\mathcal {B}) \cong E(n-1,\mathcal {B})$
generated by
$H_k(\mathcal {B}) \cong E(n-1,\mathcal {B})$
generated by
![]() $\{e_{ij}(b) \mid i,j \in [n] \setminus \{k\}, i \neq j, b \in \mathcal {B}\}$
. Note that
$\{e_{ij}(b) \mid i,j \in [n] \setminus \{k\}, i \neq j, b \in \mathcal {B}\}$
. Note that
![]() $H_k(\mathcal {B})$
normalizes both
$H_k(\mathcal {B})$
normalizes both
![]() $C_k(\mathcal {B})$
and
$C_k(\mathcal {B})$
and
![]() $R_k(\mathcal {B})$
. If
$R_k(\mathcal {B})$
. If
![]() $\mathcal {B} \subset \mathbb {R}$
is dense,
$\mathcal {B} \subset \mathbb {R}$
is dense,
![]() $H_k(\mathcal {B})$
,
$H_k(\mathcal {B})$
,
![]() $C_k(\mathcal {B})$
and
$C_k(\mathcal {B})$
and
![]() $R_k(\mathcal {B})$
are also dense in
$R_k(\mathcal {B})$
are also dense in
![]() $H_k(\mathbb {R})$
,
$H_k(\mathbb {R})$
,
![]() $C_k(\mathbb {R})$
and
$C_k(\mathbb {R})$
and
![]() $R_k(\mathbb {R})$
respectively, and the latter are closed subgroups of G.
$R_k(\mathbb {R})$
respectively, and the latter are closed subgroups of G.
Since
![]() $\mathbb {R}$
is simply connected, there is for all
$\mathbb {R}$
is simply connected, there is for all
![]() $i \neq j$
a unique continuous group homomorphism
$i \neq j$
a unique continuous group homomorphism
![]() $\widetilde {e}_{ij} : \mathbb {R} \to \widetilde {G}$
such that
$\widetilde {e}_{ij} : \mathbb {R} \to \widetilde {G}$
such that
![]() $\pi (\widetilde {e}_{ij}(t)) = e_{ij}(t)$
for all
$\pi (\widetilde {e}_{ij}(t)) = e_{ij}(t)$
for all
![]() $t \in \mathbb {R}$
. When
$t \in \mathbb {R}$
. When
![]() $i,j \in [n] \setminus \{k\}$
and
$i,j \in [n] \setminus \{k\}$
and
![]() $s,t \in \mathbb {R}$
, the image
$s,t \in \mathbb {R}$
, the image
![]() $\pi ([\widetilde {e}_{ik}(t),\widetilde {e}_{jk}(s)])$
of the commutator equals the identity element. Thus,
$\pi ([\widetilde {e}_{ik}(t),\widetilde {e}_{jk}(s)])$
of the commutator equals the identity element. Thus,
![]() $[\widetilde {e}_{ik}(t),\widetilde {e}_{jk}(s)] \in \operatorname {Ker} \pi $
for all
$[\widetilde {e}_{ik}(t),\widetilde {e}_{jk}(s)] \in \operatorname {Ker} \pi $
for all
![]() $s,t \in \mathbb {R}$
. By connectedness of
$s,t \in \mathbb {R}$
. By connectedness of
![]() $\mathbb {R}^2$
, we find that
$\mathbb {R}^2$
, we find that
![]() $\widetilde {e}_{ik}(t)$
commutes with
$\widetilde {e}_{ik}(t)$
commutes with
![]() $\widetilde {e}_{jk}(s)$
. There thus is a unique continuous group homomorphism
$\widetilde {e}_{jk}(s)$
. There thus is a unique continuous group homomorphism
![]() $C_k(\mathbb {R}) \to \widetilde {G} : e_{ik}(t) \mapsto \widetilde {e}_{ik}(t)$
.
$C_k(\mathbb {R}) \to \widetilde {G} : e_{ik}(t) \mapsto \widetilde {e}_{ik}(t)$
.
For every
![]() $k \in [n]$
and subring
$k \in [n]$
and subring
![]() $\mathcal {B} \subset \mathbb {R}$
, we denote by
$\mathcal {B} \subset \mathbb {R}$
, we denote by
![]() $\widetilde {C}_k(\mathcal {B})$
the subgroup of
$\widetilde {C}_k(\mathcal {B})$
the subgroup of
![]() $\widetilde {G}$
generated by
$\widetilde {G}$
generated by
![]() $\{\widetilde {e}_{ik}(b) \mid i \in [n] \setminus \{k\}, b \in \mathcal {B}\}$
. Note that
$\{\widetilde {e}_{ik}(b) \mid i \in [n] \setminus \{k\}, b \in \mathcal {B}\}$
. Note that
![]() $\widetilde {C}_k(\mathbb {R})$
is a connected closed subgroup of
$\widetilde {C}_k(\mathbb {R})$
is a connected closed subgroup of
![]() $\widetilde {G}$
and that
$\widetilde {G}$
and that
![]() $\pi : \widetilde {C}_k(\mathbb {R}) \to C_k(\mathbb {R})$
is an isomorphism. We also have that
$\pi : \widetilde {C}_k(\mathbb {R}) \to C_k(\mathbb {R})$
is an isomorphism. We also have that
![]() $\widetilde {C}_k(\mathbb {R})$
is the connected component of the identity in
$\widetilde {C}_k(\mathbb {R})$
is the connected component of the identity in
![]() $\pi ^{-1}(C_k(\mathbb {R}))$
and that
$\pi ^{-1}(C_k(\mathbb {R}))$
and that
![]() $\widetilde {C}_k(\mathcal {B}) = \widetilde {C}_k(\mathbb {R}) \cap \pi ^{-1}(C_k(\mathcal {B}))$
.
$\widetilde {C}_k(\mathcal {B}) = \widetilde {C}_k(\mathbb {R}) \cap \pi ^{-1}(C_k(\mathcal {B}))$
.
Define
![]() $c_k : \widetilde {G} \to \widetilde {C}_k(\mathbb {R}) \backslash \widetilde {G} : c_k(x) = \widetilde {C}_k(\mathbb {R}) x$
. Since
$c_k : \widetilde {G} \to \widetilde {C}_k(\mathbb {R}) \backslash \widetilde {G} : c_k(x) = \widetilde {C}_k(\mathbb {R}) x$
. Since
![]() $\widetilde {C}_k(\mathcal {A})$
commutes with
$\widetilde {C}_k(\mathcal {A})$
commutes with
![]() $\widetilde {C}_k(\mathcal {A}_0)$
and since
$\widetilde {C}_k(\mathcal {A}_0)$
and since
![]() $\widetilde {C}_k(\mathcal {A}_0)$
is dense in
$\widetilde {C}_k(\mathcal {A}_0)$
is dense in
![]() $\widetilde {C}_k(\mathbb {R})$
, it follows from Lemmas 4.5 and 4.6 that for every
$\widetilde {C}_k(\mathbb {R})$
, it follows from Lemmas 4.5 and 4.6 that for every
![]() $g \in \widetilde {C}_k(\mathcal {A})$
, the map
$g \in \widetilde {C}_k(\mathcal {A})$
, the map
![]() $x \mapsto \gamma (g,x)$
factors through
$x \mapsto \gamma (g,x)$
factors through
![]() $c_k$
.
$c_k$
.
Take
![]() $g \in \pi ^{-1}(H_k(\mathcal {A}) C_k(\mathcal {A}))$
. Since g normalizes
$g \in \pi ^{-1}(H_k(\mathcal {A}) C_k(\mathcal {A}))$
. Since g normalizes
![]() $\pi ^{-1}(C_k(\mathbb {R}))$
, the element g also normalizes its connected component of the identity
$\pi ^{-1}(C_k(\mathbb {R}))$
, the element g also normalizes its connected component of the identity
![]() $\widetilde {C}_k(\mathbb {R})$
. Since g normalizes
$\widetilde {C}_k(\mathbb {R})$
. Since g normalizes
![]() $\pi ^{-1}(C_k(\mathcal {A}))$
as well, it follows that g normalizes
$\pi ^{-1}(C_k(\mathcal {A}))$
as well, it follows that g normalizes
![]() $\widetilde {C}_k(\mathcal {A})$
. Another application of Lemmas 4.5 and 4.6 then says that the map
$\widetilde {C}_k(\mathcal {A})$
. Another application of Lemmas 4.5 and 4.6 then says that the map
![]() $x \mapsto \gamma (g,x)$
factors through
$x \mapsto \gamma (g,x)$
factors through
![]() $c_k$
.
$c_k$
.
Fix
![]() $i \neq j$
and fix
$i \neq j$
and fix
![]() $g \in \pi ^{-1}(e_{ij}(\mathcal {A}))$
. In the following paragraphs, we prove that
$g \in \pi ^{-1}(e_{ij}(\mathcal {A}))$
. In the following paragraphs, we prove that
![]() $x \mapsto \gamma (g,x)$
is essentially constant.
$x \mapsto \gamma (g,x)$
is essentially constant.
We have proven that the map
![]() $x \mapsto \gamma (g,x)$
factors through
$x \mapsto \gamma (g,x)$
factors through
![]() $c_k$
for all
$c_k$
for all
![]() $k \neq i$
. This means that for all
$k \neq i$
. This means that for all
![]() $b \neq i$
,
$b \neq i$
,
![]() $a \neq b$
and
$a \neq b$
and
![]() $t \in \mathbb {R}$
, we have
$t \in \mathbb {R}$
, we have
![]() $\gamma (g,\widetilde {e}_{ab}(t)x) = \gamma (g,x)$
for a.e.
$\gamma (g,\widetilde {e}_{ab}(t)x) = \gamma (g,x)$
for a.e.
![]() $x \in \widetilde {G}$
. Since we can reason analogously using the subgroups
$x \in \widetilde {G}$
. Since we can reason analogously using the subgroups
![]() $R_k$
, we also get for all
$R_k$
, we also get for all
![]() $a \neq j$
,
$a \neq j$
,
![]() $b \neq a$
and
$b \neq a$
and
![]() $t \in \mathbb {R}$
that
$t \in \mathbb {R}$
that
![]() $\gamma (g,\widetilde {e}_{ab}(t)x) = \gamma (g,x)$
for a.e.
$\gamma (g,\widetilde {e}_{ab}(t)x) = \gamma (g,x)$
for a.e.
![]() $x \in \widetilde {G}$
.
$x \in \widetilde {G}$
.
Define
![]() $\widetilde {T} = \{h \in \widetilde {G} \mid \gamma (g,hx) = \gamma (g,x) \;\;\text {for a.e. }x \in \widetilde {G}\;\}$
. Then
$\widetilde {T} = \{h \in \widetilde {G} \mid \gamma (g,hx) = \gamma (g,x) \;\;\text {for a.e. }x \in \widetilde {G}\;\}$
. Then
![]() $\widetilde {T}$
is a closed subgroup of
$\widetilde {T}$
is a closed subgroup of
![]() $\widetilde {G}$
. Define
$\widetilde {G}$
. Define
![]() $T = \pi (\widetilde {T})$
. By the previous paragraph,
$T = \pi (\widetilde {T})$
. By the previous paragraph,
![]() $e_{ab}(\mathbb {R}) \subset T$
when
$e_{ab}(\mathbb {R}) \subset T$
when
![]() $a \neq b$
,
$a \neq b$
,
![]() $a \neq j$
or
$a \neq j$
or
![]() $b \neq i$
. When
$b \neq i$
. When
![]() $a = j$
and
$a = j$
and
![]() $b =i$
, we choose
$b =i$
, we choose
![]() $c \in [n] \setminus \{i,j\}$
and note that for all
$c \in [n] \setminus \{i,j\}$
and note that for all
![]() $t \in \mathbb {R}$
,
$t \in \mathbb {R}$
,
so that again
![]() $e_{ab}(\mathbb {R}) \subset T$
. It follows that
$e_{ab}(\mathbb {R}) \subset T$
. It follows that
![]() $T = G$
. The closed subgroup
$T = G$
. The closed subgroup
![]() $\widetilde {T} \subset \widetilde {G}$
thus has index at most
$\widetilde {T} \subset \widetilde {G}$
thus has index at most
![]() $2$
, so that
$2$
, so that
![]() $\widetilde {T} \subset \widetilde {G}$
is open. Since
$\widetilde {T} \subset \widetilde {G}$
is open. Since
![]() $\widetilde {G}$
is connected, it follows that
$\widetilde {G}$
is connected, it follows that
![]() $\widetilde {T} = \widetilde {G}$
. This means that
$\widetilde {T} = \widetilde {G}$
. This means that
![]() $x \mapsto \gamma (g,x)$
is essentially constant.
$x \mapsto \gamma (g,x)$
is essentially constant.
We have thus proven that
![]() $x \mapsto \gamma (g,x)$
is essentially constant for every
$x \mapsto \gamma (g,x)$
is essentially constant for every
![]() $g \in \pi ^{-1}(E(n,\mathcal {A}))$
. Since
$g \in \pi ^{-1}(E(n,\mathcal {A}))$
. Since
![]() $\pi ^{-1}(E(n,\mathcal {A}))$
is a normal subgroup of
$\pi ^{-1}(E(n,\mathcal {A}))$
is a normal subgroup of
![]() $\widetilde {\Gamma }$
, a final application of Lemmas 4.5 and 4.6 implies that
$\widetilde {\Gamma }$
, a final application of Lemmas 4.5 and 4.6 implies that
![]() $x \mapsto \gamma (g,x)$
is essentially constant for every
$x \mapsto \gamma (g,x)$
is essentially constant for every
![]() $g \in \widetilde {\Gamma }$
. This concludes the proof of statement (1).
$g \in \widetilde {\Gamma }$
. This concludes the proof of statement (1).
To prove statement (2), we still write
![]() $G = \operatorname {SL}(n,\mathbb {R})$
with universal cover
$G = \operatorname {SL}(n,\mathbb {R})$
with universal cover
![]() $\pi : \widetilde {G} \to G$
. Note that
$\pi : \widetilde {G} \to G$
. Note that
![]() $\widetilde {G} \ltimes \mathbb {R}^n$
is the universal cover of
$\widetilde {G} \ltimes \mathbb {R}^n$
is the universal cover of
![]() $G \ltimes \mathbb {R}^n$
. Let
$G \ltimes \mathbb {R}^n$
. Let
![]() $\omega : (\Gamma \ltimes \mathcal {A}^n) \times (G \ltimes \mathbb {R}^n) \to \Lambda $
be a
$\omega : (\Gamma \ltimes \mathcal {A}^n) \times (G \ltimes \mathbb {R}^n) \to \Lambda $
be a
![]() $1$
-cocycle, with lift
$1$
-cocycle, with lift
![]() $\widetilde {\omega } : (\widetilde {\Gamma } \ltimes \mathcal {A}^n) \times (\widetilde {G} \ltimes \mathbb {R}^n) \to \Lambda $
.
$\widetilde {\omega } : (\widetilde {\Gamma } \ltimes \mathcal {A}^n) \times (\widetilde {G} \ltimes \mathbb {R}^n) \to \Lambda $
.
By the same argument as at the beginning of this proof,
![]() $E(n,\mathcal {A}_0) \ltimes \mathcal {A}_0^n$
is an irreducible lattice in a product of copies of
$E(n,\mathcal {A}_0) \ltimes \mathcal {A}_0^n$
is an irreducible lattice in a product of copies of
![]() $\operatorname {SL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
and
$\operatorname {SL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
and
![]() $\operatorname {SL}(n,\mathbb {C}) \ltimes \mathbb {C}^n$
. By [Reference Bekka, de la Harpe and ValetteBHV08, Corollary 1.4.16], these groups have property (T). By part 2 of [Reference Drimbe and VaesDV21, Theorem C], it follows that the dense subgroup
$\operatorname {SL}(n,\mathbb {C}) \ltimes \mathbb {C}^n$
. By [Reference Bekka, de la Harpe and ValetteBHV08, Corollary 1.4.16], these groups have property (T). By part 2 of [Reference Drimbe and VaesDV21, Theorem C], it follows that the dense subgroup
![]() $E(n,\mathcal {A}_0) \ltimes \mathcal {A}_0^n$
of
$E(n,\mathcal {A}_0) \ltimes \mathcal {A}_0^n$
of
![]() $\operatorname {SL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
is essentially cocycle superrigid with countable targets.
$\operatorname {SL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
is essentially cocycle superrigid with countable targets.
By the observation at the beginning of the proof, we thus find that
![]() $\widetilde {\omega }$
is cohomologous with a
$\widetilde {\omega }$
is cohomologous with a
![]() $1$
-cocycle
$1$
-cocycle
![]() $\gamma $
such that
$\gamma $
such that
![]() $x \mapsto \gamma (g,x)$
is essentially constant for every
$x \mapsto \gamma (g,x)$
is essentially constant for every
![]() $g \in \pi ^{-1}(E(n,\mathcal {A}_0)) \ltimes \mathcal {A}_0^n$
. Denote by
$g \in \pi ^{-1}(E(n,\mathcal {A}_0)) \ltimes \mathcal {A}_0^n$
. Denote by
![]() $\theta : \widetilde {G} \ltimes \mathbb {R}^n \to \widetilde {G}$
the natural quotient map. Since
$\theta : \widetilde {G} \ltimes \mathbb {R}^n \to \widetilde {G}$
the natural quotient map. Since
![]() $\mathcal {A}_0^n$
is dense in
$\mathcal {A}_0^n$
is dense in
![]() $\mathbb {R}^n$
and since
$\mathbb {R}^n$
and since
![]() $\mathcal {A}^n$
commutes with
$\mathcal {A}^n$
commutes with
![]() $\mathcal {A}_0^n$
, it follows from Lemmas 4.5 and 4.6 that
$\mathcal {A}_0^n$
, it follows from Lemmas 4.5 and 4.6 that
![]() $x \mapsto \gamma (a,x)$
factors through
$x \mapsto \gamma (a,x)$
factors through
![]() $\theta $
for all
$\theta $
for all
![]() $a \in \mathcal {A}^n$
. Since
$a \in \mathcal {A}^n$
. Since
![]() $\mathcal {A}^n$
is a normal subgroup of
$\mathcal {A}^n$
is a normal subgroup of
![]() $\widetilde {\Gamma } \ltimes \mathcal {A}^n$
, another application of Lemmas 4.5 and 4.6 implies that
$\widetilde {\Gamma } \ltimes \mathcal {A}^n$
, another application of Lemmas 4.5 and 4.6 implies that
![]() $x \mapsto \gamma (g,x)$
factors through
$x \mapsto \gamma (g,x)$
factors through
![]() $\theta $
for all
$\theta $
for all
![]() $g \in \widetilde {\Gamma } \ltimes \mathcal {A}^n$
.
$g \in \widetilde {\Gamma } \ltimes \mathcal {A}^n$
.
We thus find a Borel map
![]() $\gamma _1 : (\widetilde {\Gamma } \ltimes \mathcal {A}^n) \times \widetilde {G} \to \Lambda $
such that for all
$\gamma _1 : (\widetilde {\Gamma } \ltimes \mathcal {A}^n) \times \widetilde {G} \to \Lambda $
such that for all
![]() $g \in \widetilde {\Gamma } \ltimes \mathcal {A}^n$
and a.e.
$g \in \widetilde {\Gamma } \ltimes \mathcal {A}^n$
and a.e.
![]() $x \in \widetilde {G} \ltimes \mathbb {R}^n$
, we have
$x \in \widetilde {G} \ltimes \mathbb {R}^n$
, we have
![]() $\gamma (g,x) = \gamma _1(g,\theta (x))$
. From now on, we denote by g the elements of
$\gamma (g,x) = \gamma _1(g,\theta (x))$
. From now on, we denote by g the elements of
![]() $\widetilde {\Gamma }$
and we denote by a the elements of
$\widetilde {\Gamma }$
and we denote by a the elements of
![]() $\mathcal {A}^n$
. The restriction of
$\mathcal {A}^n$
. The restriction of
![]() $\gamma _1$
to
$\gamma _1$
to
![]() $\widetilde {\Gamma } \times \widetilde {G}$
is a
$\widetilde {\Gamma } \times \widetilde {G}$
is a
![]() $1$
-cocycle for the translation action
$1$
-cocycle for the translation action
![]() $\widetilde {\Gamma } \curvearrowright \widetilde {G}$
. Above, we have proven that this action is cocycle superrigid with countable target groups. Choose a Borel map
$\widetilde {\Gamma } \curvearrowright \widetilde {G}$
. Above, we have proven that this action is cocycle superrigid with countable target groups. Choose a Borel map
![]() $\varphi : \widetilde {G} \to \Lambda $
and a group homomorphism
$\varphi : \widetilde {G} \to \Lambda $
and a group homomorphism
![]() $\delta : \widetilde {\Gamma } \to \Lambda $
such that
$\delta : \widetilde {\Gamma } \to \Lambda $
such that
![]() $\gamma _1(g,y) = \varphi (gy)^{-1} \, \delta (g) \, \varphi (y)$
for all
$\gamma _1(g,y) = \varphi (gy)^{-1} \, \delta (g) \, \varphi (y)$
for all
![]() $g \in \widetilde {\Gamma }$
and a.e.
$g \in \widetilde {\Gamma }$
and a.e.
![]() $y \in \widetilde {G}$
. Replacing
$y \in \widetilde {G}$
. Replacing
![]() $\gamma $
with the cohomologous
$\gamma $
with the cohomologous
![]() $1$
-cocycle
$1$
-cocycle
![]() $(g,x) \mapsto \varphi (\theta (gx)) \, \gamma (g,x) \, \varphi (\theta (x))^{-1}$
, we may thus assume that
$(g,x) \mapsto \varphi (\theta (gx)) \, \gamma (g,x) \, \varphi (\theta (x))^{-1}$
, we may thus assume that
![]() $\gamma _1(g,y) = \delta (g)$
for all
$\gamma _1(g,y) = \delta (g)$
for all
![]() $g \in \widetilde {\Gamma }$
and a.e.
$g \in \widetilde {\Gamma }$
and a.e.
![]() $y \in \widetilde {G}$
. We denote
$y \in \widetilde {G}$
. We denote
![]() $\delta _y(a) = \gamma _1(a,y)$
and note that
$\delta _y(a) = \gamma _1(a,y)$
and note that
![]() $\delta _y : \mathcal {A}^n \to \Lambda $
is a measurable family of group homomorphisms. To conclude the proof of the theorem, we have to show that for all
$\delta _y : \mathcal {A}^n \to \Lambda $
is a measurable family of group homomorphisms. To conclude the proof of the theorem, we have to show that for all
![]() $a \in \mathcal {A}^n$
, the map
$a \in \mathcal {A}^n$
, the map
![]() $y \mapsto \delta _y(a)$
is essentially constant.
$y \mapsto \delta _y(a)$
is essentially constant.
When
![]() $g \in \widetilde {\Gamma }$
, we have that
$g \in \widetilde {\Gamma }$
, we have that
![]() $\pi (g) \in \operatorname {SL}(n,\mathcal {A}^n)$
so that
$\pi (g) \in \operatorname {SL}(n,\mathcal {A}^n)$
so that
![]() $\pi (g)(a) \in \mathcal {A}^n$
. The group law in
$\pi (g)(a) \in \mathcal {A}^n$
. The group law in
![]() $\widetilde {\Gamma } \ltimes \mathcal {A}^n$
can then be expressed by
$\widetilde {\Gamma } \ltimes \mathcal {A}^n$
can then be expressed by
![]() $g \, a = \pi (g)(a) \, g$
for all
$g \, a = \pi (g)(a) \, g$
for all
![]() $g \in \widetilde {\Gamma }$
,
$g \in \widetilde {\Gamma }$
,
![]() $a \in \mathcal {A}^n$
. Applying the
$a \in \mathcal {A}^n$
. Applying the
![]() $1$
-cocycle relation for
$1$
-cocycle relation for
![]() $\gamma $
, we conclude that
$\gamma $
, we conclude that
Fix
![]() $i \in [n]$
. Using the notation introduced above, denote by
$i \in [n]$
. Using the notation introduced above, denote by
![]() $L_i(\mathcal {A})$
the subgroup of
$L_i(\mathcal {A})$
the subgroup of
![]() $\Gamma $
generated by
$\Gamma $
generated by
![]() $H_i(\mathcal {A})$
and
$H_i(\mathcal {A})$
and
![]() $R_i(\mathcal {A})$
. Similarly define
$R_i(\mathcal {A})$
. Similarly define
![]() $L_i(\mathbb {R})$
. Then
$L_i(\mathbb {R})$
. Then
![]() $L_i(\mathcal {A})$
is dense in
$L_i(\mathcal {A})$
is dense in
![]() $L_i(\mathbb {R})$
and
$L_i(\mathbb {R})$
and
![]() $L_i(\mathbb {R})$
consists of the matrices
$L_i(\mathbb {R})$
consists of the matrices
![]() $A \in \operatorname {SL}(n,\mathbb {R})$
satisfying
$A \in \operatorname {SL}(n,\mathbb {R})$
satisfying
![]() $A(e_i) = e_i$
, where
$A(e_i) = e_i$
, where
![]() $e_i$
is the ith standard basis vector. Since the inclusion
$e_i$
is the ith standard basis vector. Since the inclusion
![]() $\operatorname {SL}(n-1,\mathbb {R}) \cong H_i(\mathbb {R}) < \operatorname {SL}(n,\mathbb {R})$
induces a surjective homomorphism between the fundamental groups, we get that
$\operatorname {SL}(n-1,\mathbb {R}) \cong H_i(\mathbb {R}) < \operatorname {SL}(n,\mathbb {R})$
induces a surjective homomorphism between the fundamental groups, we get that
![]() $\pi ^{-1}(L_i(\mathbb {R}))$
is a connected subgroup of
$\pi ^{-1}(L_i(\mathbb {R}))$
is a connected subgroup of
![]() $\widetilde {G}$
.
$\widetilde {G}$
.
For every
![]() $a \in \mathcal {A}$
, denote
$a \in \mathcal {A}$
, denote
![]() $e_i(a) = a e_i \in \mathcal {A}^n$
. It follows from (4.2) that for all
$e_i(a) = a e_i \in \mathcal {A}^n$
. It follows from (4.2) that for all
![]() $g \in \pi ^{-1}(L_i(\mathcal {A}))$
, we have
$g \in \pi ^{-1}(L_i(\mathcal {A}))$
, we have
![]() $\delta _{gy}(e_i(a)) = \delta (g) \, \delta _y(e_i(a)) \, \delta (g)^{-1}$
. By Lemma 4.5, for every fixed
$\delta _{gy}(e_i(a)) = \delta (g) \, \delta _y(e_i(a)) \, \delta (g)^{-1}$
. By Lemma 4.5, for every fixed
![]() $i \in [n]$
and
$i \in [n]$
and
![]() $a \in \mathcal {A}$
, the map
$a \in \mathcal {A}$
, the map
![]() $y \mapsto \delta _y(e_i(a))$
is invariant under left translation by the connected group
$y \mapsto \delta _y(e_i(a))$
is invariant under left translation by the connected group
![]() $\pi ^{-1}(L_i(\mathbb {R}))$
, and thus of the form
$\pi ^{-1}(L_i(\mathbb {R}))$
, and thus of the form
![]() $y \mapsto \zeta (\pi (y)^{-1}(e_i))$
for some Borel map
$y \mapsto \zeta (\pi (y)^{-1}(e_i))$
for some Borel map
![]() $\zeta : \mathbb {R}^n \to \Lambda $
. This means that we find measurable families
$\zeta : \mathbb {R}^n \to \Lambda $
. This means that we find measurable families
![]() $(\rho _{i,z})_{z \in \mathbb {R}^n}$
of group homomorphisms
$(\rho _{i,z})_{z \in \mathbb {R}^n}$
of group homomorphisms
![]() $\rho _{i,z} : \mathcal {A} \to \Lambda $
such that
$\rho _{i,z} : \mathcal {A} \to \Lambda $
such that
![]() $\delta _y(e_i(a)) = \rho _{i,\pi (y)^{-1}(e_i)}(a)$
for all
$\delta _y(e_i(a)) = \rho _{i,\pi (y)^{-1}(e_i)}(a)$
for all
![]() $i \in [n]$
,
$i \in [n]$
,
![]() $a \in \mathcal {A}$
and a.e.
$a \in \mathcal {A}$
and a.e.
![]() $y \in \widetilde {G}$
.
$y \in \widetilde {G}$
.
Take
![]() $i \neq j$
. We now apply (4.2) for
$i \neq j$
. We now apply (4.2) for
![]() $g \in \widetilde {\Gamma }$
with
$g \in \widetilde {\Gamma }$
with
![]() $\pi (g) = e_{ij}(-1)$
and
$\pi (g) = e_{ij}(-1)$
and
![]() $e_j(a) \in \mathcal {A}^n$
. We conclude that
$e_j(a) \in \mathcal {A}^n$
. We conclude that
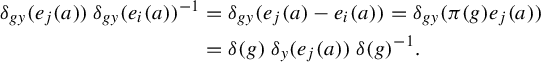 $$ \begin{align*}\delta_{gy}(e_j(a)) \, \delta_{gy}(e_i(a))^{-1} &= \delta_{gy}(e_j(a) - e_i(a)) = \delta_{gy}(\pi(g)e_j(a))\\ &= \delta(g) \, \delta_y(e_j(a)) \, \delta(g)^{-1}.\end{align*} $$
$$ \begin{align*}\delta_{gy}(e_j(a)) \, \delta_{gy}(e_i(a))^{-1} &= \delta_{gy}(e_j(a) - e_i(a)) = \delta_{gy}(\pi(g)e_j(a))\\ &= \delta(g) \, \delta_y(e_j(a)) \, \delta(g)^{-1}.\end{align*} $$
Since
![]() $\pi (g)^{-1}(e_i) = e_i$
and
$\pi (g)^{-1}(e_i) = e_i$
and
![]() $\pi (g)^{-1}(e_j) = e_i + e_j$
, we find that
$\pi (g)^{-1}(e_j) = e_i + e_j$
, we find that
for all
![]() $a \in \mathcal {A}$
and a.e.
$a \in \mathcal {A}$
and a.e.
![]() $y \in \widetilde {G}$
. Since
$y \in \widetilde {G}$
. Since
![]() $n \geq 3$
, the map
$n \geq 3$
, the map
![]() $\widetilde {G} \to \mathbb {R}^n \times \mathbb {R}^n : y \mapsto (\pi (y)^{-1}(e_i), \pi (y)^{-1}(e_j))$
is a non-singular factor map. We thus conclude that
$\widetilde {G} \to \mathbb {R}^n \times \mathbb {R}^n : y \mapsto (\pi (y)^{-1}(e_i), \pi (y)^{-1}(e_j))$
is a non-singular factor map. We thus conclude that
Denote by
![]() $\mathcal {P}$
the Polish group of Borel maps from
$\mathcal {P}$
the Polish group of Borel maps from
![]() $\mathbb {R}^n$
to
$\mathbb {R}^n$
to
![]() $\Lambda $
, where two such maps are identified if they are equal almost everywhere, where the topology is given by convergence in measure and where the group law is defined pointwise. For every
$\Lambda $
, where two such maps are identified if they are equal almost everywhere, where the topology is given by convergence in measure and where the group law is defined pointwise. For every
![]() $v \in \mathbb {R}^n$
and
$v \in \mathbb {R}^n$
and
![]() $F \in \mathcal {P}$
, define
$F \in \mathcal {P}$
, define
![]() $F_v \in \mathcal {P}$
by
$F_v \in \mathcal {P}$
by
![]() $F_v(u) = F(u+v)$
. Then the map
$F_v(u) = F(u+v)$
. Then the map
![]() $\mathbb {R}^n \to \mathcal {P} : v \mapsto F_v$
is continuous. Fix
$\mathbb {R}^n \to \mathcal {P} : v \mapsto F_v$
is continuous. Fix
![]() $a \in \mathcal {A}$
and define
$a \in \mathcal {A}$
and define
![]() $F,G \in \mathcal {P}$
by
$F,G \in \mathcal {P}$
by
![]() $F(u) = \rho _{j,u}(a)$
and
$F(u) = \rho _{j,u}(a)$
and
![]() $G(u) = \rho _{i,u}(a)^{-1}$
. Then the map
$G(u) = \rho _{i,u}(a)^{-1}$
. Then the map
![]() $\mathbb {R}^n \to \mathcal {P} : v \mapsto F_v \, G$
is continuous. By (4.3), this map takes values in the discrete subgroup
$\mathbb {R}^n \to \mathcal {P} : v \mapsto F_v \, G$
is continuous. By (4.3), this map takes values in the discrete subgroup
![]() $\Lambda < \mathcal {P}$
of constant functions. Since
$\Lambda < \mathcal {P}$
of constant functions. Since
![]() $\mathbb {R}^n$
is connected, it follows that
$\mathbb {R}^n$
is connected, it follows that
![]() $v \mapsto F_v$
is essentially constant. That means that we find group homomorphisms
$v \mapsto F_v$
is essentially constant. That means that we find group homomorphisms
![]() $\rho _j : \mathcal {A} \to \Lambda $
such that
$\rho _j : \mathcal {A} \to \Lambda $
such that
![]() $\rho _{j,u}(a) = \rho _j(a)$
for a.e.
$\rho _{j,u}(a) = \rho _j(a)$
for a.e.
![]() $y \in \mathbb {R}^n$
.
$y \in \mathbb {R}^n$
.
We conclude that for all
![]() $j \in [n]$
and every
$j \in [n]$
and every
![]() $a \in \mathcal {A}$
, the map
$a \in \mathcal {A}$
, the map
![]() $y \mapsto \delta _y(e_j(a))$
is essentially constant. So
$y \mapsto \delta _y(e_j(a))$
is essentially constant. So
![]() $y \mapsto \delta _y(a)$
is also essentially constant for every
$y \mapsto \delta _y(a)$
is also essentially constant for every
![]() $a \in \mathcal {A}^n$
. This concludes the proof of the theorem.
$a \in \mathcal {A}^n$
. This concludes the proof of the theorem.
The first part of Theorem C can now be immediately deduced from Theorem 4.4. We state and prove the following more general version.
Corollary 4.7. Let
![]() $\mathcal {A} \subset \mathbb {R}$
be any countable subring containing an algebraic number that does not belong to
$\mathcal {A} \subset \mathbb {R}$
be any countable subring containing an algebraic number that does not belong to
![]() $\mathbb {Z}$
. Let
$\mathbb {Z}$
. Let
![]() $\mathcal {F} \subset \mathcal {A}^*$
be a subgroup and
$\mathcal {F} \subset \mathcal {A}^*$
be a subgroup and
![]() $n \geq 3$
an integer. Define
$n \geq 3$
an integer. Define
![]() $\Gamma < \operatorname {GL}(n,\mathcal {A})$
as the group of matrices with
$\Gamma < \operatorname {GL}(n,\mathcal {A})$
as the group of matrices with
![]() $\det A \in \mathcal {F}$
. Consider the action of
$\det A \in \mathcal {F}$
. Consider the action of
![]() $G = \Gamma \ltimes \mathcal {A}^n$
on
$G = \Gamma \ltimes \mathcal {A}^n$
on
![]() $X=\mathbb {R}^n$
by
$X=\mathbb {R}^n$
by
![]() $(A,a) \cdot x = A(a+x)$
.
$(A,a) \cdot x = A(a+x)$
.
The action
![]() $G \curvearrowright X$
is essentially free, ergodic, non-singular, simple and cocycle superrigid with countable targets. So the action is also OE superrigid (v1).
$G \curvearrowright X$
is essentially free, ergodic, non-singular, simple and cocycle superrigid with countable targets. So the action is also OE superrigid (v1).
Denote by T the closure of
![]() $\{ |a| \mid a \in \mathcal {F} \}$
in
$\{ |a| \mid a \in \mathcal {F} \}$
in
![]() $\mathbb {R}^*_+$
. If
$\mathbb {R}^*_+$
. If
![]() $T = \mathbb {R}^*_+$
, the action is of type III
$T = \mathbb {R}^*_+$
, the action is of type III
![]() $_1$
. If
$_1$
. If
![]() $T = \unicode{x3bb} ^{\mathbb {Z}}$
, the action is of type III
$T = \unicode{x3bb} ^{\mathbb {Z}}$
, the action is of type III
![]() $_\unicode{x3bb} $
. If
$_\unicode{x3bb} $
. If
![]() $T = \{1\}$
, the action is of type II
$T = \{1\}$
, the action is of type II
![]() $_\infty $
.
$_\infty $
.
Proof. Since
![]() $\mathcal {A}^n$
is dense in
$\mathcal {A}^n$
is dense in
![]() $\mathbb {R}^n$
, by Lemma 4.5, the action
$\mathbb {R}^n$
, by Lemma 4.5, the action
![]() $\mathcal {A}^n \curvearrowright \mathbb {R}^n$
is ergodic and not induced. A fortiori,
$\mathcal {A}^n \curvearrowright \mathbb {R}^n$
is ergodic and not induced. A fortiori,
![]() $G \curvearrowright \mathbb {R}^n$
is ergodic and not induced. Assume that
$G \curvearrowright \mathbb {R}^n$
is ergodic and not induced. Assume that
![]() $\Sigma \lhd G$
is a normal subgroup whose action on
$\Sigma \lhd G$
is a normal subgroup whose action on
![]() $\mathbb {R}^n$
admits a fundamental domain. Write
$\mathbb {R}^n$
admits a fundamental domain. Write
![]() $\Sigma _0 = \Sigma \cap \mathcal {A}^n$
. Let
$\Sigma _0 = \Sigma \cap \mathcal {A}^n$
. Let
![]() $(A,a) \in \Sigma $
. If
$(A,a) \in \Sigma $
. If
![]() $A \neq 1$
, then for all
$A \neq 1$
, then for all
![]() $b \in \mathcal {A}^n$
,
$b \in \mathcal {A}^n$
,
so that
![]() $\Sigma _0 \neq \{0\}$
. Since
$\Sigma _0 \neq \{0\}$
. Since
![]() $\Sigma _0$
is globally invariant under
$\Sigma _0$
is globally invariant under
![]() $\operatorname {SL}(n,\mathcal {A})$
, the closure of
$\operatorname {SL}(n,\mathcal {A})$
, the closure of
![]() $\Sigma _0$
in
$\Sigma _0$
in
![]() $\mathbb {R}^n$
is a non-trivial closed subgroup of
$\mathbb {R}^n$
is a non-trivial closed subgroup of
![]() $\mathbb {R}^n$
that is globally invariant under
$\mathbb {R}^n$
that is globally invariant under
![]() $\operatorname {SL}(n,\mathbb {R})$
. So
$\operatorname {SL}(n,\mathbb {R})$
. So
![]() $\Sigma _0$
is dense in
$\Sigma _0$
is dense in
![]() $\mathbb {R}^n$
. It follows that
$\mathbb {R}^n$
. It follows that
![]() $\Sigma _0 \curvearrowright \mathbb {R}^n$
is ergodic, contradicting the assumption that
$\Sigma _0 \curvearrowright \mathbb {R}^n$
is ergodic, contradicting the assumption that
![]() $\Sigma _0 \curvearrowright \mathbb {R}^n$
admits a fundamental domain. So
$\Sigma _0 \curvearrowright \mathbb {R}^n$
admits a fundamental domain. So
![]() $A = 1$
, and we have proven that
$A = 1$
, and we have proven that
![]() $\Sigma \subset \mathcal {A}^n$
. If
$\Sigma \subset \mathcal {A}^n$
. If
![]() $\Sigma \neq \{0\}$
, we again find that
$\Sigma \neq \{0\}$
, we again find that
![]() $\Sigma $
is dense in
$\Sigma $
is dense in
![]() $\mathbb {R}^n$
. So
$\mathbb {R}^n$
. So
![]() $\Sigma $
is trivial, and we have proven that
$\Sigma $
is trivial, and we have proven that
![]() $G \curvearrowright \mathbb {R}^n$
is a simple action.
$G \curvearrowright \mathbb {R}^n$
is a simple action.
Write
![]() $G_0 = \operatorname {SL}(n,\mathcal {A}) \ltimes \mathcal {A}^n$
. By Theorem 4.4, the dense subgroup
$G_0 = \operatorname {SL}(n,\mathcal {A}) \ltimes \mathcal {A}^n$
. By Theorem 4.4, the dense subgroup
![]() $G_0$
of
$G_0$
of
![]() $\operatorname {SL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
is essentially cocycle superrigid with countable targets. By [Reference Drimbe and VaesDV21, Proposition 3.3], the action
$\operatorname {SL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
is essentially cocycle superrigid with countable targets. By [Reference Drimbe and VaesDV21, Proposition 3.3], the action
![]() $G_0 \curvearrowright \mathbb {R}^n$
is cocycle superrigid with countable targets. As mentioned above, this action is ergodic and not induced. Since
$G_0 \curvearrowright \mathbb {R}^n$
is cocycle superrigid with countable targets. As mentioned above, this action is ergodic and not induced. Since
![]() $G_0$
is a normal subgroup of G, it follows from Lemma 4.6 that
$G_0$
is a normal subgroup of G, it follows from Lemma 4.6 that
![]() $G \curvearrowright \mathbb {R}^n$
is also cocycle superrigid with countable targets. By Proposition 4.2, the action is also OE superrigid (v1).
$G \curvearrowright \mathbb {R}^n$
is also cocycle superrigid with countable targets. By Proposition 4.2, the action is also OE superrigid (v1).
The Maharam extension of
![]() $G \curvearrowright \mathbb {R}^n$
can be identified with the action
$G \curvearrowright \mathbb {R}^n$
can be identified with the action
![]() $G \curvearrowright \mathbb {R}^n \times \mathbb {R}$
given by
$G \curvearrowright \mathbb {R}^n \times \mathbb {R}$
given by
Since the translation action
![]() $\mathcal {A}^n \curvearrowright \mathbb {R}^n$
is ergodic, it follows that the G-invariant functions on
$\mathcal {A}^n \curvearrowright \mathbb {R}^n$
is ergodic, it follows that the G-invariant functions on
![]() $\mathbb {R}^n \times \mathbb {R}$
are precisely the functions on
$\mathbb {R}^n \times \mathbb {R}$
are precisely the functions on
![]() $\mathbb {R}$
that are invariant under translation by all
$\mathbb {R}$
that are invariant under translation by all
![]() $\log |\det A|$
,
$\log |\det A|$
,
![]() $A \in \operatorname {GL}(n,\mathcal {A})$
,
$A \in \operatorname {GL}(n,\mathcal {A})$
,
![]() $\det A \in \mathcal {F}$
. So these are the functions on
$\det A \in \mathcal {F}$
. So these are the functions on
![]() $\mathbb {R}$
that are invariant under translation by
$\mathbb {R}$
that are invariant under translation by
![]() $\{\log |a| \mid a \in \mathcal {F}\}$
, so that the type of
$\{\log |a| \mid a \in \mathcal {F}\}$
, so that the type of
![]() $G \curvearrowright \mathbb {R}^n$
is as described in the corollary.
$G \curvearrowright \mathbb {R}^n$
is as described in the corollary.
Proposition 4.8. Let
![]() $G \curvearrowright (X,\mu )$
be a free, ergodic, non-singular action of type III
$G \curvearrowright (X,\mu )$
be a free, ergodic, non-singular action of type III
![]() $_0$
. If
$_0$
. If
![]() $G \curvearrowright X$
is not induced, then
$G \curvearrowright X$
is not induced, then
![]() $G \curvearrowright X$
is not cocycle superrigid with countable targets. If
$G \curvearrowright X$
is not cocycle superrigid with countable targets. If
![]() $G \curvearrowright X$
is simple, then
$G \curvearrowright X$
is simple, then
![]() $G \curvearrowright (X,\mu )$
is not OE superrigid (v1).
$G \curvearrowright (X,\mu )$
is not OE superrigid (v1).
Proof. Let
![]() $G \curvearrowright (X,\mu )$
be a free, ergodic, non-singular action of type III
$G \curvearrowright (X,\mu )$
be a free, ergodic, non-singular action of type III
![]() $_0$
. Assume that every
$_0$
. Assume that every
![]() $1$
-cocycle
$1$
-cocycle
![]() $\Omega : G \times X \to \mathbb {Z}$
is cohomologous to a group homomorphism. We prove that
$\Omega : G \times X \to \mathbb {Z}$
is cohomologous to a group homomorphism. We prove that
![]() $G \curvearrowright X$
must be an induced action. By Proposition 4.2, this suffices to prove the proposition.
$G \curvearrowright X$
must be an induced action. By Proposition 4.2, this suffices to prove the proposition.
Combining [Reference SchmidtSch79, Theorem 2.7 and Remark 2.9] and [Reference Jones and SchmidtJS85, Theorem 2.1], we find a free, ergodic, probability measure-preserving action
![]() $\mathbb {Z} \curvearrowright (Y,\eta )$
and a Borel map
$\mathbb {Z} \curvearrowright (Y,\eta )$
and a Borel map
![]() $\pi : X \to Y$
such that
$\pi : X \to Y$
such that
![]() $\pi _*(\mu ) \sim \eta $
and
$\pi _*(\mu ) \sim \eta $
and
![]() $\pi (G \cdot x) \subset \mathbb {Z} \cdot \pi (x)$
for a.e.
$\pi (G \cdot x) \subset \mathbb {Z} \cdot \pi (x)$
for a.e.
![]() $x \in X$
. Since all free, ergodic, probability measure-preserving actions of
$x \in X$
. Since all free, ergodic, probability measure-preserving actions of
![]() $\mathbb {Z}$
are orbit equivalent, we may assume that the action
$\mathbb {Z}$
are orbit equivalent, we may assume that the action
![]() $\mathbb {Z} \curvearrowright (Y,\eta )$
is the profinite
$\mathbb {Z} \curvearrowright (Y,\eta )$
is the profinite
![]() $\mathbb {Z} \curvearrowright \mathbb {Z}_2$
, viewed as the inverse limit of
$\mathbb {Z} \curvearrowright \mathbb {Z}_2$
, viewed as the inverse limit of
![]() $\mathbb {Z} \curvearrowright \mathbb {Z} / 2^k \mathbb {Z}$
,
$\mathbb {Z} \curvearrowright \mathbb {Z} / 2^k \mathbb {Z}$
,
![]() $k \in \mathbb {N}$
.
$k \in \mathbb {N}$
.
Define the
![]() $1$
-cocycle
$1$
-cocycle
![]() $\Omega : G \times X \to \mathbb {Z}$
such that
$\Omega : G \times X \to \mathbb {Z}$
such that
![]() $\pi (g \cdot x) = \Omega (g,x) \cdot \pi (x)$
for all
$\pi (g \cdot x) = \Omega (g,x) \cdot \pi (x)$
for all
![]() $g \in G$
and a.e.
$g \in G$
and a.e.
![]() $x \in X$
. By our assumption, we find a Borel map
$x \in X$
. By our assumption, we find a Borel map
![]() $\varphi : X \to \mathbb {Z}$
and a group homomorphism
$\varphi : X \to \mathbb {Z}$
and a group homomorphism
![]() $\delta : G \to \mathbb {Z}$
such that
$\delta : G \to \mathbb {Z}$
such that
![]() $\Omega (g,x) = -\varphi (g \cdot x) + \delta (g) + \varphi (x)$
for all
$\Omega (g,x) = -\varphi (g \cdot x) + \delta (g) + \varphi (x)$
for all
![]() $g \in G$
and a.e.
$g \in G$
and a.e.
![]() $x \in X$
. Define the Borel map
$x \in X$
. Define the Borel map
![]() $\pi _1 : X \to Y : \pi _1(x) = \varphi (x) \cdot \pi (x)$
. By construction,
$\pi _1 : X \to Y : \pi _1(x) = \varphi (x) \cdot \pi (x)$
. By construction,
![]() $\pi _1(g \cdot x) = \delta (g) \cdot \pi _1(x)$
.
$\pi _1(g \cdot x) = \delta (g) \cdot \pi _1(x)$
.
Note that
![]() $\pi _1$
is not essentially constant, since otherwise
$\pi _1$
is not essentially constant, since otherwise
![]() $\pi (x)$
takes values in a countable set for a.e.
$\pi (x)$
takes values in a countable set for a.e.
![]() $x \in X$
, contradicting
$x \in X$
, contradicting
![]() $\pi _*(\mu ) \sim \eta $
. We can then choose
$\pi _*(\mu ) \sim \eta $
. We can then choose
![]() $k \in \mathbb {N}$
large enough such that, denoting by
$k \in \mathbb {N}$
large enough such that, denoting by
![]() $\psi : \mathbb {Z}_2 \to \mathbb {Z} / 2^k \mathbb {Z}$
the canonical quotient map,
$\psi : \mathbb {Z}_2 \to \mathbb {Z} / 2^k \mathbb {Z}$
the canonical quotient map,
![]() $\theta = \psi \circ \pi $
is not essentially constant. Since
$\theta = \psi \circ \pi $
is not essentially constant. Since
![]() $\theta (g \cdot x) = \delta (g) + \theta (x)$
for all
$\theta (g \cdot x) = \delta (g) + \theta (x)$
for all
![]() $g \in G$
and a.e.
$g \in G$
and a.e.
![]() $x \in X$
, it follows that the action
$x \in X$
, it follows that the action
![]() $G \curvearrowright (X,\mu )$
is induced in a non-trivial way.
$G \curvearrowright (X,\mu )$
is induced in a non-trivial way.
5 Cocycle and OE superrigidity for actions of type III
 $_0$
$_0$
Let
![]() $G \curvearrowright (X,\mu )$
be a non-singular action, with logarithm of the Radon–Nikodym
$G \curvearrowright (X,\mu )$
be a non-singular action, with logarithm of the Radon–Nikodym
![]() $1$
-cocycle
$1$
-cocycle
![]() $\omega : G \times X \to \mathbb {R}$
. Consider the Maharam extension
$\omega : G \times X \to \mathbb {R}$
. Consider the Maharam extension
![]() $G \curvearrowright X \times \mathbb {R}$
, together with the commuting measure-scaling action
$G \curvearrowright X \times \mathbb {R}$
, together with the commuting measure-scaling action
![]() $\mathbb {R} \curvearrowright X \times \mathbb {R}$
(see (2.1) and (2.2)). Denote by
$\mathbb {R} \curvearrowright X \times \mathbb {R}$
(see (2.1) and (2.2)). Denote by
![]() $\mathbb {R} \curvearrowright (Y,\eta )$
the associated flow. As explained at the start of §2, we have a strictly G-invariant and
$\mathbb {R} \curvearrowright (Y,\eta )$
the associated flow. As explained at the start of §2, we have a strictly G-invariant and
![]() $\mathbb {R}$
-equivariant Borel map
$\mathbb {R}$
-equivariant Borel map
![]() $\pi : X \times \mathbb {R} \to Y$
and we define
$\pi : X \times \mathbb {R} \to Y$
and we define
![]() $\psi : X \to Y$
by (2.3).
$\psi : X \to Y$
by (2.3).
Given a subgroup
![]() $\Lambda _0 < \Lambda $
, we denote by
$\Lambda _0 < \Lambda $
, we denote by
![]() $C_\Lambda (\Lambda _0) = \{g \in \Lambda \mid gh = hg \;\text {for all }h \in \Lambda _0\}$
the centralizer of
$C_\Lambda (\Lambda _0) = \{g \in \Lambda \mid gh = hg \;\text {for all }h \in \Lambda _0\}$
the centralizer of
![]() $\Lambda _0$
inside
$\Lambda _0$
inside
![]() $\Lambda $
.
$\Lambda $
.
Theorem 5.1. Let
![]() $G \curvearrowright (X,\mu )$
be a non-singular action of a countable group G on a standard probability space
$G \curvearrowright (X,\mu )$
be a non-singular action of a countable group G on a standard probability space
![]() $(X,\mu )$
. Let
$(X,\mu )$
. Let
![]() $\omega : G \times X \to \mathbb {R}$
be the logarithm of the Radon–Nikodym cocycle and let
$\omega : G \times X \to \mathbb {R}$
be the logarithm of the Radon–Nikodym cocycle and let
![]() $G \curvearrowright (\widetilde {X},\widetilde {\mu })$
be the Maharam extension, with ergodic decomposition
$G \curvearrowright (\widetilde {X},\widetilde {\mu })$
be the Maharam extension, with ergodic decomposition
![]() $(\widetilde {X}_y,\widetilde {\mu }_y)_{y \in Y}$
, associated flow
$(\widetilde {X}_y,\widetilde {\mu }_y)_{y \in Y}$
, associated flow
![]() $\mathbb {R} \curvearrowright (Y,\eta )$
and Borel map
$\mathbb {R} \curvearrowright (Y,\eta )$
and Borel map
![]() $\psi : X \to Y$
as in (2.3).
$\psi : X \to Y$
as in (2.3).
Let
![]() $\Lambda $
be a countable group. Assume that G is finitely generated and that for
$\Lambda $
be a countable group. Assume that G is finitely generated and that for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $y \in Y$
, the ergodic action
$y \in Y$
, the ergodic action
![]() $G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
is not induced and cocycle superrigid with target
$G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
is not induced and cocycle superrigid with target
![]() $\Lambda $
. Then for any
$\Lambda $
. Then for any
![]() $1$
-cocycle
$1$
-cocycle
![]() $\Omega : G \times X \to \Lambda $
, there exist a group homomorphism
$\Omega : G \times X \to \Lambda $
, there exist a group homomorphism
![]() $\delta : G \to \Lambda $
and a strict
$\delta : G \to \Lambda $
and a strict
![]() $1$
-cocycle
$1$
-cocycle
![]() $\gamma : \mathbb {R} \times Y \to C_\Lambda (\delta (G))$
such that
$\gamma : \mathbb {R} \times Y \to C_\Lambda (\delta (G))$
such that
![]() $\Omega $
is cohomologous with the
$\Omega $
is cohomologous with the
![]() $1$
-cocycle
$1$
-cocycle
Proof. Define the
![]() $1$
-cocycle
$1$
-cocycle
![]() $\widetilde {\Omega } : (G \times \mathbb {R}) \times \widetilde {X} \to \Lambda : \widetilde {\Omega }((g,t),(x,s)) = \Omega (g,x)$
. First restrict
$\widetilde {\Omega } : (G \times \mathbb {R}) \times \widetilde {X} \to \Lambda : \widetilde {\Omega }((g,t),(x,s)) = \Omega (g,x)$
. First restrict
![]() $\widetilde {\Omega }$
to a
$\widetilde {\Omega }$
to a
![]() $1$
-cocycle for the action
$1$
-cocycle for the action
![]() $G \curvearrowright \widetilde {X}$
with ergodic decomposition given by
$G \curvearrowright \widetilde {X}$
with ergodic decomposition given by
![]() $\pi : \widetilde {X} \to Y$
. As explained in detail in [Reference Fisher, Morris and WhyteFMW04], we may consider
$\pi : \widetilde {X} \to Y$
. As explained in detail in [Reference Fisher, Morris and WhyteFMW04], we may consider
![]() $\widetilde {\Omega }$
as a measurable family
$\widetilde {\Omega }$
as a measurable family
![]() $(\widetilde {\Omega }_y)_{y \in Y}$
of
$(\widetilde {\Omega }_y)_{y \in Y}$
of
![]() $1$
-cocycles for the measurable family of actions
$1$
-cocycles for the measurable family of actions
![]() $G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
. By assumption,
$G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
. By assumption,
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $\widetilde {\Omega }_y$
is cohomologous to a group homomorphism
$\widetilde {\Omega }_y$
is cohomologous to a group homomorphism
![]() $\delta _y : G \to \Lambda $
.
$\delta _y : G \to \Lambda $
.
By [Reference Fisher, Morris and WhyteFMW04, Corollary 3.11], we find a Borel family of group homomorphisms
![]() $\delta _y : G \to \Lambda $
, indexed by
$\delta _y : G \to \Lambda $
, indexed by
![]() $y \in Y$
, and a Borel map
$y \in Y$
, and a Borel map
![]() $\varphi : \widetilde {X} \to \Lambda $
such that for all
$\varphi : \widetilde {X} \to \Lambda $
such that for all
![]() $g \in G$
, we have that
$g \in G$
, we have that
Define the
![]() $1$
-cocycle
$1$
-cocycle
![]() $\Psi : (G \times \mathbb {R}) \times \widetilde {X} \to \Lambda $
by
$\Psi : (G \times \mathbb {R}) \times \widetilde {X} \to \Lambda $
by
By construction,
![]() $\Psi \sim \widetilde {\Omega }$
as
$\Psi \sim \widetilde {\Omega }$
as
![]() $1$
-cocycles for
$1$
-cocycles for
![]() $G \times \mathbb {R} \curvearrowright \widetilde {X}$
and for all
$G \times \mathbb {R} \curvearrowright \widetilde {X}$
and for all
![]() $g \in G$
,
$g \in G$
,
![]() $\Psi ((g,0),(x,s)) = \delta _{\pi (x,s)}(g)$
for
$\Psi ((g,0),(x,s)) = \delta _{\pi (x,s)}(g)$
for
![]() $\widetilde {\mu }$
-a.e.
$\widetilde {\mu }$
-a.e.
![]() $(x,s) \in \widetilde {X}$
. Define
$(x,s) \in \widetilde {X}$
. Define
![]() $\zeta _t(x,s) = \Psi ((e,t),(x,s))$
. From the
$\zeta _t(x,s) = \Psi ((e,t),(x,s))$
. From the
![]() $1$
-cocycle relation for
$1$
-cocycle relation for
![]() $\Psi $
applied to
$\Psi $
applied to
![]() $(g,0)(e,t) = (g,t) = (e,t)(g,0)$
, it follows that for all
$(g,0)(e,t) = (g,t) = (e,t)(g,0)$
, it follows that for all
![]() $t \in \mathbb {R}$
,
$t \in \mathbb {R}$
,
![]() $g \in G$
, we have
$g \in G$
, we have
Fix
![]() $t \in \mathbb {R}$
. Then (5.1) is saying that for
$t \in \mathbb {R}$
. Then (5.1) is saying that for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $y \in Y$
,
$y \in Y$
,
![]() $\zeta _t$
is a G-equivariant Borel map from
$\zeta _t$
is a G-equivariant Borel map from
![]() $(\widetilde {X}_y,\widetilde {\mu }_y)$
to the countable set
$(\widetilde {X}_y,\widetilde {\mu }_y)$
to the countable set
![]() $\Lambda $
on which G is acting by
$\Lambda $
on which G is acting by
![]() $g \cdot \unicode{x3bb} = \delta _{t \cdot y}(g) \unicode{x3bb} \delta _y(g)^{-1}$
. Since we assumed that for
$g \cdot \unicode{x3bb} = \delta _{t \cdot y}(g) \unicode{x3bb} \delta _y(g)^{-1}$
. Since we assumed that for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $y \in Y$
, the action
$y \in Y$
, the action
![]() $G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
is not induced, it follows that for
$G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
is not induced, it follows that for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $y \in Y$
, the map
$y \in Y$
, the map
![]() $\zeta _t$
is
$\zeta _t$
is
![]() $\widetilde {\mu }_y$
-almost everywhere constant on
$\widetilde {\mu }_y$
-almost everywhere constant on
![]() $\widetilde {X}_y$
.
$\widetilde {X}_y$
.
We thus find a Borel map
![]() $\gamma _0 : \mathbb {R} \times Y \to \Lambda $
such that for all
$\gamma _0 : \mathbb {R} \times Y \to \Lambda $
such that for all
![]() $t \in \mathbb {R}$
, we have that
$t \in \mathbb {R}$
, we have that
![]() $\zeta _t(x,s) = \gamma _0(t,\pi (x,s))$
for
$\zeta _t(x,s) = \gamma _0(t,\pi (x,s))$
for
![]() $\widetilde {\mu }$
-a.e.
$\widetilde {\mu }$
-a.e.
![]() $(x,s) \in \widetilde {X}$
. Since
$(x,s) \in \widetilde {X}$
. Since
![]() $\widetilde {\Omega }((e,t),(x,s)) = e$
, we have
$\widetilde {\Omega }((e,t),(x,s)) = e$
, we have
![]() $\zeta _t(x,s) = \varphi (x,t+s) \, \varphi (x,s)^{-1}$
for
$\zeta _t(x,s) = \varphi (x,t+s) \, \varphi (x,s)^{-1}$
for
![]() $\widetilde {\mu }$
-a.e.
$\widetilde {\mu }$
-a.e.
![]() $(x,s) \in \widetilde {X}$
. Therefore, for every
$(x,s) \in \widetilde {X}$
. Therefore, for every
![]() $t \in \mathbb {R}$
,
$t \in \mathbb {R}$
,
So
![]() $\gamma _0 : \mathbb {R} \times Y \to \Lambda $
is a
$\gamma _0 : \mathbb {R} \times Y \to \Lambda $
is a
![]() $1$
-cocycle. Then (5.1) is saying that for all
$1$
-cocycle. Then (5.1) is saying that for all
![]() $t \in \mathbb {R}$
,
$t \in \mathbb {R}$
,
![]() $g \in G$
, we have
$g \in G$
, we have
Since G is finitely generated, the set of group homomorphisms from G to
![]() $\Lambda $
is countable. We thus find a group homomorphism
$\Lambda $
is countable. We thus find a group homomorphism
![]() $\delta : G \to \Lambda $
such that
$\delta : G \to \Lambda $
such that
![]() $\delta _y = \delta $
for all y in a non-negligible Borel subset
$\delta _y = \delta $
for all y in a non-negligible Borel subset
![]() $\mathcal {U} \subset Y$
. Combining (5.3) with the ergodicity of
$\mathcal {U} \subset Y$
. Combining (5.3) with the ergodicity of
![]() $\mathbb {R} \curvearrowright (Y,\eta )$
, it follows that
$\mathbb {R} \curvearrowright (Y,\eta )$
, it follows that
![]() $\delta _y$
is conjugate to
$\delta _y$
is conjugate to
![]() $\delta $
for
$\delta $
for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $y \in Y$
. We then find a Borel map
$y \in Y$
. We then find a Borel map
![]() $\rho : Y \to \Lambda $
so that
$\rho : Y \to \Lambda $
so that
![]() $\delta _y(g) = \rho (y)^{-1} \, \delta (g) \, \rho (y)$
for
$\delta _y(g) = \rho (y)^{-1} \, \delta (g) \, \rho (y)$
for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $y \in Y$
and all
$y \in Y$
and all
![]() $g \in G$
. Replacing
$g \in G$
. Replacing
![]() $\varphi (x,s)$
by
$\varphi (x,s)$
by
![]() $\rho (\pi (x,s)) \varphi (x,s)$
, we may assume that
$\rho (\pi (x,s)) \varphi (x,s)$
, we may assume that
![]() $\delta _y = \delta $
for
$\delta _y = \delta $
for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $y \in Y$
.
$y \in Y$
.
The
![]() $1$
-cocycle
$1$
-cocycle
![]() $\Psi : (G \times \mathbb {R}) \times \widetilde {X} \to \Lambda $
thus has the property that for all
$\Psi : (G \times \mathbb {R}) \times \widetilde {X} \to \Lambda $
thus has the property that for all
![]() $g \in G$
and
$g \in G$
and
![]() $t \in \mathbb {R}$
,
$t \in \mathbb {R}$
,
for
![]() $\widetilde {\mu }$
-a.e.
$\widetilde {\mu }$
-a.e.
![]() $(x,s) \in \widetilde {X}$
. The cocycle identity for
$(x,s) \in \widetilde {X}$
. The cocycle identity for
![]() $\Psi $
then forces
$\Psi $
then forces
![]() $\gamma _0$
to take values almost everywhere in the centralizer
$\gamma _0$
to take values almost everywhere in the centralizer
![]() $C_\Lambda (\delta (G))$
.
$C_\Lambda (\delta (G))$
.
Choose a strict
![]() $1$
-cocycle
$1$
-cocycle
![]() $\gamma : \mathbb {R} \times Y \to C_\Lambda (\delta (G))$
such that for every
$\gamma : \mathbb {R} \times Y \to C_\Lambda (\delta (G))$
such that for every
![]() $t \in \mathbb {R}$
, we have that
$t \in \mathbb {R}$
, we have that
![]() $\gamma (t,y) = \gamma _0(t,y)$
for
$\gamma (t,y) = \gamma _0(t,y)$
for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $y \in Y$
. Define the Borel map
$y \in Y$
. Define the Borel map
![]() $\theta : \widetilde {X} \to C_\Lambda (\delta (G)) : \theta (x,s) = \gamma (s,\psi (x))$
. Consider the cohomologous
$\theta : \widetilde {X} \to C_\Lambda (\delta (G)) : \theta (x,s) = \gamma (s,\psi (x))$
. Consider the cohomologous
![]() $1$
-cocycle
$1$
-cocycle
![]() $\Psi _1 \sim \Psi $
defined by
$\Psi _1 \sim \Psi $
defined by
Since
![]() $\gamma $
is a strict
$\gamma $
is a strict
![]() $1$
-cocycle, we find for every
$1$
-cocycle, we find for every
![]() $t \in \mathbb {R}$
and
$t \in \mathbb {R}$
and
![]() $g \in G$
that
$g \in G$
that
![]() $\Psi _1((e,t),(x,s)) = e$
and
$\Psi _1((e,t),(x,s)) = e$
and
![]() $\Psi _1((g,0),(x,s)) = \delta (g) \, \gamma (-\omega (g,x),\psi (x))$
for
$\Psi _1((g,0),(x,s)) = \delta (g) \, \gamma (-\omega (g,x),\psi (x))$
for
![]() $\widetilde {\mu }$
-a.e.
$\widetilde {\mu }$
-a.e.
![]() $(x,s) \in \widetilde {X}$
. So, defining the
$(x,s) \in \widetilde {X}$
. So, defining the
![]() $1$
-cocycle
$1$
-cocycle
we have proven that the
![]() $1$
-cocycles
$1$
-cocycles
![]() $\Omega $
and
$\Omega $
and
![]() $\Psi _0$
are cohomologous when viewed as
$\Psi _0$
are cohomologous when viewed as
![]() $1$
-cocycles for
$1$
-cocycles for
![]() $G \times \mathbb {R} \curvearrowright \widetilde {X}$
. The
$G \times \mathbb {R} \curvearrowright \widetilde {X}$
. The
![]() $\mathbb {R}$
-invariance of both
$\mathbb {R}$
-invariance of both
![]() $1$
-cocycles forces the Borel function implementing the cohomology
$1$
-cocycles forces the Borel function implementing the cohomology
![]() $\Omega \sim \Psi _0$
to be essentially
$\Omega \sim \Psi _0$
to be essentially
![]() $\mathbb {R}$
-invariant as well. We have thus proven that
$\mathbb {R}$
-invariant as well. We have thus proven that
![]() $\Omega \sim \Psi _0$
.
$\Omega \sim \Psi _0$
.
Remark 5.2. The conclusion of Theorem 5.1 can also be formulated in the following way. Consider the Maharam extension, together with its measure-scaling action,
![]() $G \times \mathbb {R} \curvearrowright \widetilde {X} = X \times \mathbb {R}$
. The conclusion of Theorem 5.1 says that the
$G \times \mathbb {R} \curvearrowright \widetilde {X} = X \times \mathbb {R}$
. The conclusion of Theorem 5.1 says that the
![]() $1$
-cocycles for
$1$
-cocycles for
![]() $G \times \mathbb {R} \curvearrowright X \times \mathbb {R}$
given by
$G \times \mathbb {R} \curvearrowright X \times \mathbb {R}$
given by
and which are both trivial on
![]() $\mathbb {R}$
, are cohomologous. But using the map
$\mathbb {R}$
, are cohomologous. But using the map
![]() $(x,t) \mapsto \gamma (t,\psi (x))$
, this second
$(x,t) \mapsto \gamma (t,\psi (x))$
, this second
![]() $1$
-cocycle is also cohomologous to
$1$
-cocycle is also cohomologous to
![]() $((g,r),(x,t)) \mapsto \delta (g) \gamma (r,\pi (x,t))$
, where
$((g,r),(x,t)) \mapsto \delta (g) \gamma (r,\pi (x,t))$
, where
![]() $\pi : X \times \mathbb {R} \to Y$
is the ergodic decomposition of
$\pi : X \times \mathbb {R} \to Y$
is the ergodic decomposition of
![]() $G \curvearrowright X \times \mathbb {R}$
.
$G \curvearrowright X \times \mathbb {R}$
.
Theorem 5.1 applies in particular to the type III actions of the form (1.1). This then leads to the following cocycle superrigidity result.
Theorem 5.3. Let
![]() $G \curvearrowright (X,\mu )$
be a free, ergodic, non-singular action of type III
$G \curvearrowright (X,\mu )$
be a free, ergodic, non-singular action of type III
![]() $_1$
. Denote by
$_1$
. Denote by
![]() $\omega : G \times X \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle. Let
$\omega : G \times X \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle. Let
![]() $\mathbb {R} \curvearrowright (Y,\eta )$
be an ergodic flow and consider
$\mathbb {R} \curvearrowright (Y,\eta )$
be an ergodic flow and consider
as in (1.1).
If G is finitely generated and if the Maharam extension of
![]() $G \curvearrowright (X,\mu )$
is not induced and cocycle superrigid with countable targets, then every
$G \curvearrowright (X,\mu )$
is not induced and cocycle superrigid with countable targets, then every
![]() $1$
-cocycle
$1$
-cocycle
![]() $\Omega : G \times X \times Y \to \Lambda $
for the action (5.4) with values in a countable group
$\Omega : G \times X \times Y \to \Lambda $
for the action (5.4) with values in a countable group
![]() $\Lambda $
is cohomologous with a
$\Lambda $
is cohomologous with a
![]() $1$
-cocycle of the form
$1$
-cocycle of the form
where
![]() $\delta : G \to \Lambda $
is a group homomorphism and
$\delta : G \to \Lambda $
is a group homomorphism and
![]() $\gamma : \mathbb {R} \times Y \to C_\Lambda (\delta (G))$
is a
$\gamma : \mathbb {R} \times Y \to C_\Lambda (\delta (G))$
is a
![]() $1$
-cocycle.
$1$
-cocycle.
Proof. As in the proof of Proposition 3.4, we take the unique action
![]() $\mathbb {R}^2 \curvearrowright (Z,\zeta )$
given by Proposition 3.1, associated with the ergodic flow
$\mathbb {R}^2 \curvearrowright (Z,\zeta )$
given by Proposition 3.1, associated with the ergodic flow
![]() $\mathbb {R} \curvearrowright (Y,\eta )$
. Identify
$\mathbb {R} \curvearrowright (Y,\eta )$
. Identify
![]() $Y = Z / (\{0\} \times \mathbb {R})$
and denote by
$Y = Z / (\{0\} \times \mathbb {R})$
and denote by
![]() $\pi _1 : Z \to Y$
the corresponding factor map. Also write
$\pi _1 : Z \to Y$
the corresponding factor map. Also write
![]() $\widehat {Y} = Z/(\mathbb {R} \times \{0\})$
and denote by
$\widehat {Y} = Z/(\mathbb {R} \times \{0\})$
and denote by
![]() $\pi _2 : Z \to \widehat {Y}$
the corresponding factor map. The Maharam extension of
$\pi _2 : Z \to \widehat {Y}$
the corresponding factor map. The Maharam extension of
![]() $G \curvearrowright X \times Y$
together with its measure-scaling action of
$G \curvearrowright X \times Y$
together with its measure-scaling action of
![]() $\mathbb {R}$
is then given by
$\mathbb {R}$
is then given by
The map
![]() $(x,z) \mapsto \pi _2(z)$
identifies the associated flow of the action
$(x,z) \mapsto \pi _2(z)$
identifies the associated flow of the action
![]() $G \curvearrowright X \times Y$
with
$G \curvearrowright X \times Y$
with
![]() $\mathbb {R} \curvearrowright \widehat {Y}$
. Identifying
$\mathbb {R} \curvearrowright \widehat {Y}$
. Identifying
![]() $Z = \mathbb {R} \times \widehat {Y}$
, the ergodic decomposition of
$Z = \mathbb {R} \times \widehat {Y}$
, the ergodic decomposition of
![]() $G \curvearrowright X \times Z$
is almost everywhere given by the Maharam extension
$G \curvearrowright X \times Z$
is almost everywhere given by the Maharam extension
![]() $G \curvearrowright X \times \mathbb {R}$
of the initial type III
$G \curvearrowright X \times \mathbb {R}$
of the initial type III
![]() $_1$
action
$_1$
action
![]() $G \curvearrowright X$
. So
$G \curvearrowright X$
. So
![]() $G \curvearrowright X \times Y$
satisfies the assumptions of Theorem 5.1.
$G \curvearrowright X \times Y$
satisfies the assumptions of Theorem 5.1.
Let
![]() $\Lambda $
be a countable group and
$\Lambda $
be a countable group and
![]() $\Omega : G \times X \times Y \to \Lambda $
a
$\Omega : G \times X \times Y \to \Lambda $
a
![]() $1$
-cocycle. Define the
$1$
-cocycle. Define the
![]() $1$
-cocycle
$1$
-cocycle
It follows from Theorem 5.1 and Remark 5.2 that
![]() $\widetilde {\Omega }$
is cohomologous with
$\widetilde {\Omega }$
is cohomologous with
![]() $\Omega _1$
, where
$\Omega _1$
, where
with
![]() $\delta : G \to \Lambda $
a group homomorphism and
$\delta : G \to \Lambda $
a group homomorphism and
![]() $\gamma _1 : \mathbb {R} \times \widehat {Y} \to C_\Lambda (\delta (G))$
a
$\gamma _1 : \mathbb {R} \times \widehat {Y} \to C_\Lambda (\delta (G))$
a
![]() $1$
-cocycle. Define the
$1$
-cocycle. Define the
![]() $1$
-cocycle
$1$
-cocycle
Since the action of
![]() $\{0\} \times \mathbb {R}$
on Z is measure-scaling,
$\{0\} \times \mathbb {R}$
on Z is measure-scaling,
![]() $\widetilde {\gamma }_1$
is cohomologous to a
$\widetilde {\gamma }_1$
is cohomologous to a
![]() $1$
-cocycle
$1$
-cocycle
![]() $\gamma _2$
of the form
$\gamma _2$
of the form
![]() $\gamma _2((r,t),z) = \gamma (r,\pi _1(z))$
, where
$\gamma _2((r,t),z) = \gamma (r,\pi _1(z))$
, where
![]() $\gamma : \mathbb {R} \times Y \to C_\Lambda (\delta (G))$
is a
$\gamma : \mathbb {R} \times Y \to C_\Lambda (\delta (G))$
is a
![]() $1$
-cocycle. Choose a Borel map
$1$
-cocycle. Choose a Borel map
![]() $\varphi : Z \to C_\Lambda (\delta (G))$
implementing this cohomology, so that for all
$\varphi : Z \to C_\Lambda (\delta (G))$
implementing this cohomology, so that for all
![]() $(r,t) \in \mathbb {R}^2$
, we have
$(r,t) \in \mathbb {R}^2$
, we have
Define the
![]() $1$
-cocycle
$1$
-cocycle
![]() $\Omega _2 : (G \times \mathbb {R}) \times (X \times Z) \to \Lambda $
by
$\Omega _2 : (G \times \mathbb {R}) \times (X \times Z) \to \Lambda $
by
By construction,
![]() $\widetilde {\Omega } \sim \Omega _2$
and
$\widetilde {\Omega } \sim \Omega _2$
and
Since both
![]() $\widetilde {\Omega }$
and
$\widetilde {\Omega }$
and
![]() $\Omega _2$
are trivial on
$\Omega _2$
are trivial on
![]() $\{0\} \times \mathbb {R}$
, this means that
$\{0\} \times \mathbb {R}$
, this means that
![]() $\Omega $
is cohomologous with the
$\Omega $
is cohomologous with the
![]() $1$
-cocycle
$1$
-cocycle
Remark 5.4. When
![]() $G \curvearrowright (X,\mu )$
is a free, ergodic, non-singular action of type III, with Maharam extension
$G \curvearrowright (X,\mu )$
is a free, ergodic, non-singular action of type III, with Maharam extension
![]() $G \curvearrowright (\widetilde {X},\widetilde {\mu })$
whose ergodic decomposition is denoted by
$G \curvearrowright (\widetilde {X},\widetilde {\mu })$
whose ergodic decomposition is denoted by
![]() $(\widetilde {X}_y,\widetilde {\mu }_y)_{y \in Y}$
, it follows from [Reference TakesakiTak03, Theorem XII.1.1] that for a.e.
$(\widetilde {X}_y,\widetilde {\mu }_y)_{y \in Y}$
, it follows from [Reference TakesakiTak03, Theorem XII.1.1] that for a.e.
![]() $y \in Y$
, the action
$y \in Y$
, the action
![]() $G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
is of type II
$G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
is of type II
![]() $_\infty $
. To give examples where Theorem 5.1 applies, we thus need cocycle superrigidity for concrete actions of type II
$_\infty $
. To give examples where Theorem 5.1 applies, we thus need cocycle superrigidity for concrete actions of type II
![]() $_\infty $
. For the specific actions appearing in Theorem 5.3, by construction, the actions
$_\infty $
. For the specific actions appearing in Theorem 5.3, by construction, the actions
![]() $G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
are almost everywhere the same.
$G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
are almost everywhere the same.
Both Theorems 5.1 and 5.3 immediately lead to OE-superrigidity results. We start with the following result.
Corollary 5.5. Let G be a finitely generated group with trivial center and let
![]() $G \curvearrowright (X,\mu )$
be an essentially free, non-singular, ergodic action. Let
$G \curvearrowright (X,\mu )$
be an essentially free, non-singular, ergodic action. Let
![]() $\omega : G \times X \to \mathbb {R}$
be the logarithm of the Radon–Nikodym cocycle and let
$\omega : G \times X \to \mathbb {R}$
be the logarithm of the Radon–Nikodym cocycle and let
![]() $G \curvearrowright (\widetilde {X},\widetilde {\mu })$
be the Maharam extension, with associated flow
$G \curvearrowright (\widetilde {X},\widetilde {\mu })$
be the Maharam extension, with associated flow
![]() $\mathbb {R} \curvearrowright (Y,\eta )$
and Borel map
$\mathbb {R} \curvearrowright (Y,\eta )$
and Borel map
![]() $\psi : X \to Y$
as in (2.3). Assume that for
$\psi : X \to Y$
as in (2.3). Assume that for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $y \in Y$
, the action
$y \in Y$
, the action
![]() $G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
is simple and cocycle superrigid with countable target groups.
$G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
is simple and cocycle superrigid with countable target groups.
Then
![]() $G \curvearrowright (X,\mu )$
satisfies the OE-superrigidity property (v2) defined in the introduction.
$G \curvearrowright (X,\mu )$
satisfies the OE-superrigidity property (v2) defined in the introduction.
More precisely, any free non-singular ergodic action that is stably orbit equivalent to
![]() $G \curvearrowright (X,\mu )$
is conjugate to an induction of an action of the form
$G \curvearrowright (X,\mu )$
is conjugate to an induction of an action of the form
where
![]() $\Lambda $
is a countable group and
$\Lambda $
is a countable group and
![]() $\gamma : \mathbb {R} \times Y \to \Lambda $
is a strict
$\gamma : \mathbb {R} \times Y \to \Lambda $
is a strict
![]() $1$
-cocycle.
$1$
-cocycle.
Proof. Let
![]() $\Gamma \curvearrowright (Z,\zeta )$
be a free, ergodic, non-singular action and let
$\Gamma \curvearrowright (Z,\zeta )$
be a free, ergodic, non-singular action and let
![]() $\Delta : \mathcal {U} \subset X \to Z$
be a stable orbit equivalence between
$\Delta : \mathcal {U} \subset X \to Z$
be a stable orbit equivalence between
![]() $G \curvearrowright X$
and
$G \curvearrowright X$
and
![]() $\Gamma \curvearrowright Z$
. By ergodicity of
$\Gamma \curvearrowright Z$
. By ergodicity of
![]() $G \curvearrowright (X,\mu )$
, we can choose a Borel map
$G \curvearrowright (X,\mu )$
, we can choose a Borel map
![]() $\theta : X \to G$
such that
$\theta : X \to G$
such that
![]() $\theta (x) = e$
for all
$\theta (x) = e$
for all
![]() $x \in \mathcal {U}$
and
$x \in \mathcal {U}$
and
![]() $\theta (x) \cdot x \in \mathcal {U}$
for a.e.
$\theta (x) \cdot x \in \mathcal {U}$
for a.e.
![]() $x \in X$
. Define
$x \in X$
. Define
![]() $\Delta _0 : X \to Z : \Delta _0(x) = \Delta (\theta (x) \cdot x)$
. We then define the Zimmer
$\Delta _0 : X \to Z : \Delta _0(x) = \Delta (\theta (x) \cdot x)$
. We then define the Zimmer
![]() $1$
-cocycle
$1$
-cocycle
![]() $\Omega : G \times X \to \Gamma $
such that
$\Omega : G \times X \to \Gamma $
such that
![]() $\Delta _0(g \cdot x) = \Omega (g,x) \cdot \Delta _0(x)$
for all
$\Delta _0(g \cdot x) = \Omega (g,x) \cdot \Delta _0(x)$
for all
![]() $g \in G$
and a.e.
$g \in G$
and a.e.
![]() $x \in X$
.
$x \in X$
.
To translate the cocycle superrigidity Theorem 5.1 to an OE-superrigidity theorem, we use the connection with measure equivalence as developed in [Reference FurmanFur98, §3] (see also [Reference Drimbe and VaesDV21, Lemma 2.2] for a result that exactly suits our purposes). Define the action
which commutes with the right translation action by
![]() $\Gamma $
in the second variable. By the results cited above, the action
$\Gamma $
in the second variable. By the results cited above, the action
![]() $G \curvearrowright X \times \Gamma $
admits a fundamental domain and there is a natural isomorphism of
$G \curvearrowright X \times \Gamma $
admits a fundamental domain and there is a natural isomorphism of
![]() $\Gamma $
-actions
$\Gamma $
-actions
![]() $\alpha : G \backslash (X \times \Gamma ) \to Z$
with the property that
$\alpha : G \backslash (X \times \Gamma ) \to Z$
with the property that
![]() $\Delta (x) \in \Gamma \cdot \alpha (x,e)$
for a.e.
$\Delta (x) \in \Gamma \cdot \alpha (x,e)$
for a.e.
![]() $x \in \mathcal {U}$
.
$x \in \mathcal {U}$
.
By Theorem 5.1, we find a group homomorphism
![]() $\delta : G \to \Gamma $
and a
$\delta : G \to \Gamma $
and a
![]() $1$
-cocycle
$1$
-cocycle
![]() $\gamma : \mathbb {R} \times Y \to C_\Gamma (\delta (G))$
such that
$\gamma : \mathbb {R} \times Y \to C_\Gamma (\delta (G))$
such that
![]() $\Omega $
is cohomologous with the
$\Omega $
is cohomologous with the
![]() $1$
-cocycle
$1$
-cocycle
Let
![]() $\varphi : X \to \Gamma $
be a Borel map such that
$\varphi : X \to \Gamma $
be a Borel map such that
![]() $\Omega _1(g,x) = \varphi (g \cdot x) \, \Omega (g,x) \, \varphi (x)^{-1}$
. The map
$\Omega _1(g,x) = \varphi (g \cdot x) \, \Omega (g,x) \, \varphi (x)^{-1}$
. The map
![]() $(x,b) \mapsto (x,\varphi (x)b)$
implements an isomorphism between the action
$(x,b) \mapsto (x,\varphi (x)b)$
implements an isomorphism between the action
![]() $G \curvearrowright X \times \Gamma $
in (5.6) and the action
$G \curvearrowright X \times \Gamma $
in (5.6) and the action
Moreover, the action and the isomorphism commute with the
![]() $\Gamma $
-action. We thus still find an isomorphism of
$\Gamma $
-action. We thus still find an isomorphism of
![]() $\Gamma $
-actions
$\Gamma $
-actions
![]() $\alpha _1 : G \backslash (X \times \Gamma ) \to Z$
with the property that
$\alpha _1 : G \backslash (X \times \Gamma ) \to Z$
with the property that
![]() $\Delta (x) \in \Gamma \cdot \alpha _1(x,e)$
for a.e.
$\Delta (x) \in \Gamma \cdot \alpha _1(x,e)$
for a.e.
![]() $x \in \mathcal {U}$
.
$x \in \mathcal {U}$
.
The
![]() $1$
-cocycle
$1$
-cocycle
![]() $\widetilde {\Omega }_1 : G \times \widetilde {X} : \widetilde {\Omega }_1(g,(x,s)) = \Omega _1(g,x)$
for the Maharam extension
$\widetilde {\Omega }_1 : G \times \widetilde {X} : \widetilde {\Omega }_1(g,(x,s)) = \Omega _1(g,x)$
for the Maharam extension
![]() $G \curvearrowright \widetilde {X}$
is, by construction, cohomologous with the
$G \curvearrowright \widetilde {X}$
is, by construction, cohomologous with the
![]() $1$
-cocycle
$1$
-cocycle
![]() $(g,(x,s)) \mapsto \delta (g)$
. Since the action
$(g,(x,s)) \mapsto \delta (g)$
. Since the action
![]() $G \curvearrowright X \times \Gamma $
admits a fundamental domain, a fortiori, the same holds for the action
$G \curvearrowright X \times \Gamma $
admits a fundamental domain, a fortiori, the same holds for the action
![]() $G \curvearrowright \widetilde {X} \times \Gamma : g \cdot (x,s,b) = (g \cdot (x,s), \delta (g)b)$
, and thus for the action
$G \curvearrowright \widetilde {X} \times \Gamma : g \cdot (x,s,b) = (g \cdot (x,s), \delta (g)b)$
, and thus for the action
![]() $\operatorname {Ker} \delta \curvearrowright \widetilde {X}$
. Since we assumed that a.e. action
$\operatorname {Ker} \delta \curvearrowright \widetilde {X}$
. Since we assumed that a.e. action
![]() $G \curvearrowright \widetilde {X}_y$
is simple, the normal subgroup
$G \curvearrowright \widetilde {X}_y$
is simple, the normal subgroup
![]() $\operatorname {Ker} \delta $
must be trivial. So
$\operatorname {Ker} \delta $
must be trivial. So
![]() $\delta : G \to \Gamma $
is faithful. Define
$\delta : G \to \Gamma $
is faithful. Define
![]() $\Lambda = C_\Gamma (\delta (G))$
. Since G has trivial center,
$\Lambda = C_\Gamma (\delta (G))$
. Since G has trivial center,
![]() $\delta (G) \cap \Lambda = \{e\}$
. We have thus found a subgroup
$\delta (G) \cap \Lambda = \{e\}$
. We have thus found a subgroup
![]() $\delta (G) \times \Lambda < \Gamma $
.
$\delta (G) \times \Lambda < \Gamma $
.
Since
![]() $\Omega _1$
takes values in
$\Omega _1$
takes values in
![]() $\delta (G) \times \Lambda $
, the action
$\delta (G) \times \Lambda $
, the action
![]() $\Gamma \curvearrowright G \backslash (X \times \Gamma )$
is induced from
$\Gamma \curvearrowright G \backslash (X \times \Gamma )$
is induced from
![]() $\delta (G) \times \Lambda \curvearrowright G \backslash (X \times \delta (G) \times \Lambda )$
. Under the natural identification
$\delta (G) \times \Lambda \curvearrowright G \backslash (X \times \delta (G) \times \Lambda )$
. Under the natural identification
![]() $G \backslash (X \times \delta (G) \times \Lambda ) = X \times \Lambda $
and the isomorphism
$G \backslash (X \times \delta (G) \times \Lambda ) = X \times \Lambda $
and the isomorphism
![]() $\delta \times \mathord {\mathrm {id}} : G \times \Lambda \to \delta (G) \times \Lambda $
, this last action is precisely the action given by (5.5).
$\delta \times \mathord {\mathrm {id}} : G \times \Lambda \to \delta (G) \times \Lambda $
, this last action is precisely the action given by (5.5).
In exactly the same way as Theorem 5.3 is deduced from Theorem 5.1, we can deduce the following result from Corollary 5.5. We thus omit the proof. Note that Theorem A is contained in the following corollary.
Corollary 5.6. Let
![]() $G \curvearrowright (X,\mu )$
be a free, ergodic, non-singular action of type III
$G \curvearrowright (X,\mu )$
be a free, ergodic, non-singular action of type III
![]() $_1$
. Assume that G is finitely generated and has trivial center. Assume that the Maharam extension of
$_1$
. Assume that G is finitely generated and has trivial center. Assume that the Maharam extension of
![]() $G \curvearrowright (X,\mu )$
is simple and cocycle superrigid with countable targets. Denote by
$G \curvearrowright (X,\mu )$
is simple and cocycle superrigid with countable targets. Denote by
![]() $\omega : G \times X \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle. Let
$\omega : G \times X \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle. Let
![]() $\mathbb {R} \curvearrowright (Y,\eta )$
be an ergodic flow and consider
$\mathbb {R} \curvearrowright (Y,\eta )$
be an ergodic flow and consider
as in (1.1).
Then
![]() $G \curvearrowright (X \times Y,\mu \times \eta )$
satisfies the OE-superrigidity property (v2) defined in the introduction.
$G \curvearrowright (X \times Y,\mu \times \eta )$
satisfies the OE-superrigidity property (v2) defined in the introduction.
More precisely, any free non-singular ergodic action that is stably orbit equivalent to the action (5.8) is conjugate to an induction of an action of the form
where
![]() $\Lambda $
is a countable group and
$\Lambda $
is a countable group and
![]() $\gamma : \mathbb {R} \times Y \to \Lambda $
is a
$\gamma : \mathbb {R} \times Y \to \Lambda $
is a
![]() $1$
-cocycle.
$1$
-cocycle.
There are several concrete group actions that satisfy the assumptions of Corollary 5.6. We start with the following example of [Reference Popa and VaesPV08].
Example 5.7. Whenever
![]() $n \geq 5$
is an odd integer and
$n \geq 5$
is an odd integer and
![]() $G < \operatorname {SL}(n,\mathbb {R})$
is a lattice, the action
$G < \operatorname {SL}(n,\mathbb {R})$
is a lattice, the action
![]() $G \curvearrowright \mathbb {R}^n/\mathbb {R}^*_+$
satisfies the hypotheses of Corollary 5.6. Indeed, by [Reference Popa and VaesPV08, Theorem 1.3], the Maharam extension
$G \curvearrowright \mathbb {R}^n/\mathbb {R}^*_+$
satisfies the hypotheses of Corollary 5.6. Indeed, by [Reference Popa and VaesPV08, Theorem 1.3], the Maharam extension
![]() $G \curvearrowright \mathbb {R}^n$
is cocycle superrigid. Moreover, these groups G have property (T), so that they are finitely generated. Since n is odd, G has trivial center. By [Reference Popa and VaesPV08, Lemmas 5.6 and 6.1], the action
$G \curvearrowright \mathbb {R}^n$
is cocycle superrigid. Moreover, these groups G have property (T), so that they are finitely generated. Since n is odd, G has trivial center. By [Reference Popa and VaesPV08, Lemmas 5.6 and 6.1], the action
![]() $G \curvearrowright \mathbb {R}^n$
is doubly ergodic and not induced. By Margulis’s normal subgroup theorem, a normal subgroup of G is either trivial (because n is odd) or of finite index, and thus acting ergodically on
$G \curvearrowright \mathbb {R}^n$
is doubly ergodic and not induced. By Margulis’s normal subgroup theorem, a normal subgroup of G is either trivial (because n is odd) or of finite index, and thus acting ergodically on
![]() $\mathbb {R}^n$
. So the action
$\mathbb {R}^n$
. So the action
![]() $G \curvearrowright \mathbb {R}^n$
is simple.
$G \curvearrowright \mathbb {R}^n$
is simple.
In the following theorem, we prove that all the assumptions of Corollary 5.6 are satisfied for the action
![]() $G \curvearrowright \mathbb {R}^n / \mathbb {R}^*_+$
when G ranges over a broad family of dense subgroups
$G \curvearrowright \mathbb {R}^n / \mathbb {R}^*_+$
when G ranges over a broad family of dense subgroups
![]() $\operatorname {SL}(n,\mathbb {R})$
and
$\operatorname {SL}(n,\mathbb {R})$
and
![]() $n \geq 3$
is an odd integer. This then leads to the proof of point (1) in Corollary B (see Corollary 6.7 below).
$n \geq 3$
is an odd integer. This then leads to the proof of point (1) in Corollary B (see Corollary 6.7 below).
Theorem 5.8. Let
![]() $\mathcal {A} \subset \mathbb {R}$
be any countable subring containing an algebraic number that does not belong to
$\mathcal {A} \subset \mathbb {R}$
be any countable subring containing an algebraic number that does not belong to
![]() $\mathbb {Z}$
. Let
$\mathbb {Z}$
. Let
![]() $n \geq 3$
be an integer and
$n \geq 3$
be an integer and
![]() $E(n,\mathcal {A}) < G < \operatorname {SL}(n,\mathcal {A})$
. Then the linear action
$E(n,\mathcal {A}) < G < \operatorname {SL}(n,\mathcal {A})$
. Then the linear action
![]() $G \curvearrowright \mathbb {R}^n$
is essentially free, ergodic, non-singular, not induced and cocycle superrigid with countable targets. If n is odd, then G has trivial center and the action is simple. If
$G \curvearrowright \mathbb {R}^n$
is essentially free, ergodic, non-singular, not induced and cocycle superrigid with countable targets. If n is odd, then G has trivial center and the action is simple. If
![]() $\mathcal {A}$
is finitely generated as a ring, then
$\mathcal {A}$
is finitely generated as a ring, then
![]() $E(n,\mathcal {A})$
is a finitely generated group.
$E(n,\mathcal {A})$
is a finitely generated group.
Proof. Since
![]() $G < \operatorname {SL}(n,\mathbb {R})$
is dense, it follows from Lemma 4.5 that the action
$G < \operatorname {SL}(n,\mathbb {R})$
is dense, it follows from Lemma 4.5 that the action
![]() $G \curvearrowright \mathbb {R}^n$
is ergodic and not induced. By density of
$G \curvearrowright \mathbb {R}^n$
is ergodic and not induced. By density of
![]() $G < \operatorname {SL}(n,\mathbb {R})$
, the center of G belongs to the center of
$G < \operatorname {SL}(n,\mathbb {R})$
, the center of G belongs to the center of
![]() $\operatorname {SL}(n,\mathbb {R})$
, which is trivial if n is odd. If n is odd and
$\operatorname {SL}(n,\mathbb {R})$
, which is trivial if n is odd. If n is odd and
![]() $\Sigma \lhd G$
is a normal subgroup whose action on
$\Sigma \lhd G$
is a normal subgroup whose action on
![]() $\mathbb {R}^n$
admits a fundamental domain, then the closure
$\mathbb {R}^n$
admits a fundamental domain, then the closure
![]() $\overline {\Sigma }$
of
$\overline {\Sigma }$
of
![]() $\Sigma $
in
$\Sigma $
in
![]() $\operatorname {SL}(n,\mathbb {R})$
is, by density of G, a normal subgroup of
$\operatorname {SL}(n,\mathbb {R})$
is, by density of G, a normal subgroup of
![]() $\operatorname {SL}(n,\mathbb {R})$
. Since n is odd, it follows that either
$\operatorname {SL}(n,\mathbb {R})$
. Since n is odd, it follows that either
![]() $\overline {\Sigma } = \{1\}$
or
$\overline {\Sigma } = \{1\}$
or
![]() $\overline {\Sigma } = \operatorname {SL}(n,\mathbb {R})$
. In the second case,
$\overline {\Sigma } = \operatorname {SL}(n,\mathbb {R})$
. In the second case,
![]() $\Sigma $
is a dense subgroup of
$\Sigma $
is a dense subgroup of
![]() $\operatorname {SL}(n,\mathbb {R})$
, so that
$\operatorname {SL}(n,\mathbb {R})$
, so that
![]() $\Sigma \curvearrowright \mathbb {R}^n$
is ergodic. It thus follows that
$\Sigma \curvearrowright \mathbb {R}^n$
is ergodic. It thus follows that
![]() $\Sigma = \{1\}$
.
$\Sigma = \{1\}$
.
By Theorem 4.4,
![]() $G < \operatorname {SL}(n,\mathbb {R})$
is essentially cocycle superrigid with countable targets. By [Reference Drimbe and VaesDV21, Proposition 3.3], the action
$G < \operatorname {SL}(n,\mathbb {R})$
is essentially cocycle superrigid with countable targets. By [Reference Drimbe and VaesDV21, Proposition 3.3], the action
![]() $G \curvearrowright \mathbb {R}^n$
is cocycle superrigid with countable targets.
$G \curvearrowright \mathbb {R}^n$
is cocycle superrigid with countable targets.
By [Reference Hahn and O’MearaHOM89, Proposition 4.3.11], the group
![]() $E(n,\mathcal {A})$
is finitely generated when
$E(n,\mathcal {A})$
is finitely generated when
![]() $n \geq 3$
and
$n \geq 3$
and
![]() $\mathcal {A}$
is finitely generated as a ring.
$\mathcal {A}$
is finitely generated as a ring.
6 Conjugacy and classification results
In Corollary 5.5, we proved that free, non-singular, ergodic actions
![]() $G \curvearrowright (X,\mu )$
with a sufficiently rigid Maharam extension
$G \curvearrowright (X,\mu )$
with a sufficiently rigid Maharam extension
![]() $G \curvearrowright (\widetilde {X},\widetilde {\mu })$
satisfy the OE-superrigidity property (v2) and we described all stably orbit equivalent actions. We now prove the following complete classification up to conjugacy of this class of stably orbit equivalent actions.
$G \curvearrowright (\widetilde {X},\widetilde {\mu })$
satisfy the OE-superrigidity property (v2) and we described all stably orbit equivalent actions. We now prove the following complete classification up to conjugacy of this class of stably orbit equivalent actions.
For the formulation of the following proposition, note that every conjugacy of actions (and actually every stable orbit equivalence) gives rise to a canonical associated isomorphism between the associated flows.
Proposition 6.1. Let
![]() $G \curvearrowright (X,\mu )$
be an essentially free, non-singular, ergodic action. Make the same assumptions as in Corollary 5.5. Whenever
$G \curvearrowright (X,\mu )$
be an essentially free, non-singular, ergodic action. Make the same assumptions as in Corollary 5.5. Whenever
![]() $\gamma : \mathbb {R} \times Y \to \Lambda $
is a strict
$\gamma : \mathbb {R} \times Y \to \Lambda $
is a strict
![]() $1$
-cocycle with values in a countable group
$1$
-cocycle with values in a countable group
![]() $\Lambda $
and whenever
$\Lambda $
and whenever
![]() $\sigma : G \times \Lambda \to \Gamma $
is a faithful group homomorphism to a countable group
$\sigma : G \times \Lambda \to \Gamma $
is a faithful group homomorphism to a countable group
![]() $\Gamma $
, we denote by
$\Gamma $
, we denote by
![]() $\beta (\gamma ,\sigma )$
the
$\beta (\gamma ,\sigma )$
the
![]() $\Gamma $
-action defined as the induction of the action
$\Gamma $
-action defined as the induction of the action
along the embedding
![]() $\sigma : G \times \Lambda \to \Gamma $
.
$\sigma : G \times \Lambda \to \Gamma $
.
-
(1) An essentially free, non-singular, ergodic action is stably orbit equivalent to
 $G \curvearrowright (X,\mu )$
if and only if it is conjugate to
$G \curvearrowright (X,\mu )$
if and only if it is conjugate to
 $\beta (\gamma ,\sigma )$
for some
$\beta (\gamma ,\sigma )$
for some
 $\gamma ,\sigma $
as above.
$\gamma ,\sigma $
as above. -
(2) The actions
 $\beta (\gamma ,\sigma )$
and
$\beta (\gamma ,\sigma )$
and
 $\beta (\gamma ',\sigma ')$
are conjugate if and only if there exist subgroups
$\beta (\gamma ',\sigma ')$
are conjugate if and only if there exist subgroups
 $\Lambda _0 < \Lambda $
,
$\Lambda _0 < \Lambda $
,
 $\Lambda ^{\prime }_0 < \Lambda '$
, an automorphism
$\Lambda ^{\prime }_0 < \Lambda '$
, an automorphism
 $\delta \in \operatorname {Aut}(G)$
, group isomorphisms
$\delta \in \operatorname {Aut}(G)$
, group isomorphisms
 $\rho : \Lambda _0 \to \Lambda ^{\prime }_0$
and
$\rho : \Lambda _0 \to \Lambda ^{\prime }_0$
and
 $\alpha : \Gamma \to \Gamma '$
, and a
$\alpha : \Gamma \to \Gamma '$
, and a
 $\delta $
-conjugacy
$\delta $
-conjugacy
 $\Delta : X \to X'$
with associated isomorphism
$\Delta : X \to X'$
with associated isomorphism
 $\Delta _0 : Y \to Y'$
of flows such that:
$\Delta _0 : Y \to Y'$
of flows such that:-
•
 $\gamma ,\gamma '$
are cohomologous to strict
$\gamma ,\gamma '$
are cohomologous to strict
 $1$
-cocycles
$1$
-cocycles
 $\gamma _0,\gamma ^{\prime }_0$
that take values in
$\gamma _0,\gamma ^{\prime }_0$
that take values in
 $\Lambda _0,\Lambda ^{\prime }_0$
;
$\Lambda _0,\Lambda ^{\prime }_0$
; -
•
 $\alpha (\sigma (g,a)) = \sigma '(\delta (g),\rho (a))$
for all
$\alpha (\sigma (g,a)) = \sigma '(\delta (g),\rho (a))$
for all
 $g \in G$
and
$g \in G$
and
 $a \in \Lambda _0$
;
$a \in \Lambda _0$
; -
• the
 $1$
-cocycles
$1$
-cocycles
 $\rho \circ \gamma _0$
and
$\rho \circ \gamma _0$
and
 $\gamma ^{\prime }_0 \circ (\mathord {\mathrm { id}} \times \Delta _0)$
are cohomologous as
$\gamma ^{\prime }_0 \circ (\mathord {\mathrm { id}} \times \Delta _0)$
are cohomologous as
 $1$
-cocycles
$1$
-cocycles
 $\mathbb {R} \times Y \to \Lambda _0'$
.
$\mathbb {R} \times Y \to \Lambda _0'$
.
-
Point (1) of Proposition 6.1 is just a repetition of Corollary 5.5. We deduce point (2) of Proposition 6.1 from the following two results. First, in Proposition 6.2, we describe when and how an action of the form
![]() $\beta (\gamma )$
in (6.1) is induced. Second, in Proposition 6.3, we prove when two actions of the form
$\beta (\gamma )$
in (6.1) is induced. Second, in Proposition 6.3, we prove when two actions of the form
![]() $\beta (\gamma )$
are conjugate.
$\beta (\gamma )$
are conjugate.
For our main family of group actions
![]() $G \curvearrowright X \times Y$
defined in (1.1), it then remains to analyze when two such actions are conjugate. Under the appropriate assumption, we prove in Proposition 6.4 that this happens if and only if the G-actions
$G \curvearrowright X \times Y$
defined in (1.1), it then remains to analyze when two such actions are conjugate. Under the appropriate assumption, we prove in Proposition 6.4 that this happens if and only if the G-actions
![]() $G \curvearrowright X$
are conjugate and the flows
$G \curvearrowright X$
are conjugate and the flows
![]() $\mathbb {R} \curvearrowright Y$
are isomorphic. In particular, we find the outer automorphism groups of these type III
$\mathbb {R} \curvearrowright Y$
are isomorphic. In particular, we find the outer automorphism groups of these type III
![]() $_0$
orbit equivalence relations.
$_0$
orbit equivalence relations.
Before proving Proposition 6.1, we clarify the following subtle point. When
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma '$
are strict
$\gamma '$
are strict
![]() $1$
-cocycles that are cohomologous, expressed by the almost everywhere equality
$1$
-cocycles that are cohomologous, expressed by the almost everywhere equality
![]() $\gamma '(t,y) = \varphi (t \cdot y) \, \gamma (t,y) \, \varphi (y)^{-1}$
, there is a natural isomorphism
$\gamma '(t,y) = \varphi (t \cdot y) \, \gamma (t,y) \, \varphi (y)^{-1}$
, there is a natural isomorphism
![]() $\Delta _{\gamma ',\gamma }$
between the actions
$\Delta _{\gamma ',\gamma }$
between the actions
![]() $\beta (\gamma )$
and
$\beta (\gamma )$
and
![]() $\beta (\gamma ')$
. This follows immediately by observing that the Maharam extension of
$\beta (\gamma ')$
. This follows immediately by observing that the Maharam extension of
![]() $\beta (\gamma )$
, together with its commuting
$\beta (\gamma )$
, together with its commuting
![]() $\mathbb {R}$
-action, is isomorphic to
$\mathbb {R}$
-action, is isomorphic to
Moreover, the map
is
![]() $\mathbb {R}$
-invariant and
$\mathbb {R}$
-invariant and
![]() $(G \times \Lambda )$
-equivariant.
$(G \times \Lambda )$
-equivariant.
Then the map
![]() $(x,s,b) \mapsto (x,s,\varphi (\pi (x,s))b)$
is a well-defined isomorphism between the Maharam extensions. Taking the quotient by the action of
$(x,s,b) \mapsto (x,s,\varphi (\pi (x,s))b)$
is a well-defined isomorphism between the Maharam extensions. Taking the quotient by the action of
![]() $\mathbb {R}$
, we find
$\mathbb {R}$
, we find
![]() $\Delta _{\gamma ',\gamma }$
.
$\Delta _{\gamma ',\gamma }$
.
Proposition 6.2. Let
![]() $G \curvearrowright (X,\mu )$
be an essentially free, non-singular, ergodic action with Maharam extension
$G \curvearrowright (X,\mu )$
be an essentially free, non-singular, ergodic action with Maharam extension
![]() $G \curvearrowright (\widetilde {X},\widetilde {\mu })$
and associated flow
$G \curvearrowright (\widetilde {X},\widetilde {\mu })$
and associated flow
![]() $\mathbb {R} \curvearrowright (Y,\eta )$
. Assume that for
$\mathbb {R} \curvearrowright (Y,\eta )$
. Assume that for
![]() $\eta $
-a.e.
$\eta $
-a.e.
![]() $y \in Y$
, the action
$y \in Y$
, the action
![]() $G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
is not induced. Let
$G \curvearrowright (\widetilde {X}_y,\widetilde {\mu }_y)$
is not induced. Let
![]() $\gamma : \mathbb {R} \times Y \to \Lambda $
be a strict
$\gamma : \mathbb {R} \times Y \to \Lambda $
be a strict
![]() $1$
-cocycle with values in a countable group
$1$
-cocycle with values in a countable group
![]() $\Lambda $
.
$\Lambda $
.
The action
![]() $\beta (\gamma )$
in (6.1) is induced from a subgroup
$\beta (\gamma )$
in (6.1) is induced from a subgroup
![]() $\Gamma < G \times \Lambda $
acting on
$\Gamma < G \times \Lambda $
acting on
![]() $Z \subset X \times \Lambda $
if and only if
$Z \subset X \times \Lambda $
if and only if
![]() $\Gamma = G \times \Lambda _0$
for a subgroup
$\Gamma = G \times \Lambda _0$
for a subgroup
![]() $\Lambda _0 < \Lambda $
,
$\Lambda _0 < \Lambda $
,
![]() $\gamma $
is cohomologous with a strict
$\gamma $
is cohomologous with a strict
![]() $1$
-cocycle
$1$
-cocycle
![]() $\gamma _0$
taking values in
$\gamma _0$
taking values in
![]() $\Lambda _0$
and
$\Lambda _0$
and
![]() $\Delta _{\gamma _0,\gamma }(Z) = X \times \Lambda _0$
.
$\Delta _{\gamma _0,\gamma }(Z) = X \times \Lambda _0$
.
Proof. If
![]() $\gamma $
takes values in
$\gamma $
takes values in
![]() $\Lambda _0$
, we have by construction that
$\Lambda _0$
, we have by construction that
![]() $\beta (\gamma )$
is induced from
$\beta (\gamma )$
is induced from
![]() $G \times \Lambda _0$
acting on
$G \times \Lambda _0$
acting on
![]() $X \times \Lambda _0$
. So we only prove the converse and assume that
$X \times \Lambda _0$
. So we only prove the converse and assume that
![]() $\beta (\gamma )$
is induced from
$\beta (\gamma )$
is induced from
![]() $\Gamma \curvearrowright Z$
. Write
$\Gamma \curvearrowright Z$
. Write
![]() $I = (G \times \Lambda )/\Gamma $
. Consider the Maharam extension of
$I = (G \times \Lambda )/\Gamma $
. Consider the Maharam extension of
![]() $\beta (\gamma )$
given by (6.2). Since
$\beta (\gamma )$
given by (6.2). Since
![]() $\beta (\gamma )$
is induced from
$\beta (\gamma )$
is induced from
![]() $\Gamma \curvearrowright Z$
, we find a Borel map
$\Gamma \curvearrowright Z$
, we find a Borel map
![]() $\theta : X \times \mathbb {R} \times \Lambda \to I$
that is
$\theta : X \times \mathbb {R} \times \Lambda \to I$
that is
![]() $\mathbb {R}$
-invariant and
$\mathbb {R}$
-invariant and
![]() $(G \times \Lambda )$
-equivariant.
$(G \times \Lambda )$
-equivariant.
Since for a.e.
![]() $y \in Y$
, we have that
$y \in Y$
, we have that
![]() $G \curvearrowright \widetilde {X}_y$
is not induced, the G-equivariance of
$G \curvearrowright \widetilde {X}_y$
is not induced, the G-equivariance of
![]() $\theta $
implies that
$\theta $
implies that
![]() $\theta (x,s,b) = \theta _1(\pi (x,s),b)$
, where
$\theta (x,s,b) = \theta _1(\pi (x,s),b)$
, where
![]() $\theta _1 : Y \times \Lambda \to I$
. In particular,
$\theta _1 : Y \times \Lambda \to I$
. In particular,
![]() $\theta $
is a G-invariant map. It follows that
$\theta $
is a G-invariant map. It follows that
![]() $G \times \{e\} \subset \Gamma $
, so that
$G \times \{e\} \subset \Gamma $
, so that
![]() $\Gamma = G \times \Lambda _0$
for some subgroup
$\Gamma = G \times \Lambda _0$
for some subgroup
![]() $\Lambda _0 < \Lambda $
. From now on, we identify
$\Lambda _0 < \Lambda $
. From now on, we identify
![]() $I = \Lambda / \Lambda _0$
, on which G acts trivially.
$I = \Lambda / \Lambda _0$
, on which G acts trivially.
The
![]() $\Lambda $
-equivariance of
$\Lambda $
-equivariance of
![]() $\theta $
implies that
$\theta $
implies that
![]() $\theta _1$
is also
$\theta _1$
is also
![]() $\Lambda $
-equivariant and thus of the form
$\Lambda $
-equivariant and thus of the form
![]() $\theta _1(y,b) = b^{-1} \theta _2(y) \Lambda _0$
for some Borel map
$\theta _1(y,b) = b^{-1} \theta _2(y) \Lambda _0$
for some Borel map
![]() $\theta _2 : Y \to \Lambda $
. Expressing the
$\theta _2 : Y \to \Lambda $
. Expressing the
![]() $\mathbb {R}$
-invariance of
$\mathbb {R}$
-invariance of
![]() $\theta $
and thus the invariance of
$\theta $
and thus the invariance of
![]() $\theta _1$
under the action
$\theta _1$
under the action
![]() $t \cdot (y,s) = (t \cdot y, \gamma (t,y) s)$
, we find that
$t \cdot (y,s) = (t \cdot y, \gamma (t,y) s)$
, we find that
This means precisely that the cohomologous
![]() $1$
-cocycle
$1$
-cocycle
![]() $\gamma _0(t,y) = \theta _2(t \cdot y)^{-1} \gamma (t,y) \theta _2(y)$
takes values in
$\gamma _0(t,y) = \theta _2(t \cdot y)^{-1} \gamma (t,y) \theta _2(y)$
takes values in
![]() $\Lambda _0$
. Using the notation introduced before the proposition, this also means that
$\Lambda _0$
. Using the notation introduced before the proposition, this also means that
![]() $\Delta _{\gamma _0,\gamma }(Z) = X \times \Lambda _0$
.
$\Delta _{\gamma _0,\gamma }(Z) = X \times \Lambda _0$
.
Proposition 6.3. For
![]() $i \in \{1,2\}$
, let
$i \in \{1,2\}$
, let
![]() $G_i \curvearrowright (X_i,\mu _i)$
be essentially free, non-singular, ergodic actions with Maharam extension
$G_i \curvearrowright (X_i,\mu _i)$
be essentially free, non-singular, ergodic actions with Maharam extension
![]() $G_i \curvearrowright (\widetilde {X}_i,\widetilde {\mu }_i)$
and associated flow
$G_i \curvearrowright (\widetilde {X}_i,\widetilde {\mu }_i)$
and associated flow
![]() $\mathbb {R} \curvearrowright (Y_i,\eta _i)$
. Assume that for
$\mathbb {R} \curvearrowright (Y_i,\eta _i)$
. Assume that for
![]() $\eta _i$
-a.e.
$\eta _i$
-a.e.
![]() $y \in Y_i$
, the action
$y \in Y_i$
, the action
![]() $G_i \curvearrowright (\widetilde {X}_{i,y},\widetilde {\mu }_{i,y})$
is simple. Assume that the groups
$G_i \curvearrowright (\widetilde {X}_{i,y},\widetilde {\mu }_{i,y})$
is simple. Assume that the groups
![]() $G_i$
have trivial center. Let
$G_i$
have trivial center. Let
![]() $\gamma _i : \mathbb {R} \times Y_i \to \Lambda _i$
be strict
$\gamma _i : \mathbb {R} \times Y_i \to \Lambda _i$
be strict
![]() $1$
-cocycles.
$1$
-cocycles.
The actions
![]() $\beta (\gamma _i)$
given by (6.1) are conjugate if and only if there exist group isomorphisms
$\beta (\gamma _i)$
given by (6.1) are conjugate if and only if there exist group isomorphisms
![]() $\delta : G_1 \to G_2$
,
$\delta : G_1 \to G_2$
,
![]() $\rho : \Lambda _1 \to \Lambda _2$
and a
$\rho : \Lambda _1 \to \Lambda _2$
and a
![]() $\delta $
-conjugacy
$\delta $
-conjugacy
![]() $\Delta : X_1 \to X_2$
such that, denoting by
$\Delta : X_1 \to X_2$
such that, denoting by
![]() $\Delta _0 : Y_1 \to Y_2$
the associated isomorphism of flows, the
$\Delta _0 : Y_1 \to Y_2$
the associated isomorphism of flows, the
![]() $1$
-cocycles
$1$
-cocycles
![]() $\gamma _2 \circ (\mathord {\mathrm {id}} \times \Delta _0)$
and
$\gamma _2 \circ (\mathord {\mathrm {id}} \times \Delta _0)$
and
![]() $\rho \circ \gamma _1$
are cohomologous.
$\rho \circ \gamma _1$
are cohomologous.
Proof. We start by proving the following claim. Under the assumptions of Proposition 6.2, if the group G has trivial center and if
![]() $\Sigma \lhd G \times \Lambda $
is a normal subgroup whose action on
$\Sigma \lhd G \times \Lambda $
is a normal subgroup whose action on
![]() $X \times \Lambda $
admits a fundamental domain, then
$X \times \Lambda $
admits a fundamental domain, then
![]() $\Sigma \subset \{e\} \times \Lambda $
.
$\Sigma \subset \{e\} \times \Lambda $
.
Since
![]() $\Sigma \curvearrowright X \times \Lambda $
admits a fundamental domain, a fortiori, the same holds for the action of
$\Sigma \curvearrowright X \times \Lambda $
admits a fundamental domain, a fortiori, the same holds for the action of
![]() $\Sigma $
on
$\Sigma $
on
![]() $X \times \mathbb {R} \times \Lambda $
given in (6.2). Since
$X \times \mathbb {R} \times \Lambda $
given in (6.2). Since
![]() $G \curvearrowright \widetilde {X}_y$
is simple for a.e.
$G \curvearrowright \widetilde {X}_y$
is simple for a.e.
![]() $y \in Y$
, there is no non-trivial normal subgroup of G whose action on
$y \in Y$
, there is no non-trivial normal subgroup of G whose action on
![]() $X \times \mathbb {R} \times \Lambda $
admits a fundamental domain. Hence,
$X \times \mathbb {R} \times \Lambda $
admits a fundamental domain. Hence,
![]() $\Sigma \cap (G \times \{e\}) = \{(e,e)\}$
. Now let
$\Sigma \cap (G \times \{e\}) = \{(e,e)\}$
. Now let
![]() $(g,a) \in \Sigma $
be an arbitrary element. We have to prove that
$(g,a) \in \Sigma $
be an arbitrary element. We have to prove that
![]() $g = e$
. By normality of
$g = e$
. By normality of
![]() $\Sigma $
, also
$\Sigma $
, also
![]() $(h g h^{-1},a) = (h,e) (g,a) (h,e)^{-1} \in \Sigma $
. Since
$(h g h^{-1},a) = (h,e) (g,a) (h,e)^{-1} \in \Sigma $
. Since
![]() $(g,a) \in \Sigma $
, also
$(g,a) \in \Sigma $
, also
![]() $(hgh^{-1}g^{-1},e) \in \Sigma $
. Since we have proven that
$(hgh^{-1}g^{-1},e) \in \Sigma $
. Since we have proven that
![]() $\Sigma $
intersects
$\Sigma $
intersects
![]() $G \times \{e\}$
trivially, it follows that
$G \times \{e\}$
trivially, it follows that
![]() $hgh^{-1}g^{-1}=e$
for all
$hgh^{-1}g^{-1}=e$
for all
![]() $h \in G$
. This means that g belongs to the center of G, which is assumed to be trivial. This proves the claim.
$h \in G$
. This means that g belongs to the center of G, which is assumed to be trivial. This proves the claim.
Now assume that
![]() $\Delta _1 : X_1 \times \Lambda _1 \to X_2 \times \Lambda _2$
is a conjugacy with respect to the group isomorphism
$\Delta _1 : X_1 \times \Lambda _1 \to X_2 \times \Lambda _2$
is a conjugacy with respect to the group isomorphism
![]() $\delta _1 = G_1 \times \Lambda _1 \to G_2 \times \Lambda _2$
. Since the action of
$\delta _1 = G_1 \times \Lambda _1 \to G_2 \times \Lambda _2$
. Since the action of
![]() $\{e\} \times \Lambda _i$
on
$\{e\} \times \Lambda _i$
on
![]() $X_i \times \Lambda _i$
has
$X_i \times \Lambda _i$
has
![]() $X_i \times \{e\}$
as a fundamental domain, the claim above implies that
$X_i \times \{e\}$
as a fundamental domain, the claim above implies that
![]() $\delta _1(\{e\} \times \Lambda _1) = \{e\} \times \Lambda _2$
. We define the group isomorphism
$\delta _1(\{e\} \times \Lambda _1) = \{e\} \times \Lambda _2$
. We define the group isomorphism
![]() $\rho : \Lambda _1 \to \Lambda _2$
such that
$\rho : \Lambda _1 \to \Lambda _2$
such that
![]() $\delta _1(e,a) = (e,\rho (a))$
for all
$\delta _1(e,a) = (e,\rho (a))$
for all
![]() $a \in \Lambda _1$
.
$a \in \Lambda _1$
.
For every
![]() $i \in \{1,2\}$
, we consider the Maharam extension
$i \in \{1,2\}$
, we consider the Maharam extension
![]() $G_i \times \Lambda _i \times \mathbb {R} \curvearrowright X_i \times \mathbb {R} \times \Lambda _i$
given by (6.2), together with the factor map
$G_i \times \Lambda _i \times \mathbb {R} \curvearrowright X_i \times \mathbb {R} \times \Lambda _i$
given by (6.2), together with the factor map
![]() $\Phi _i : X_i \times \mathbb {R} \times \Lambda _i \to X_i \times \Lambda _i$
defined by (6.3). Therefore,
$\Phi _i : X_i \times \mathbb {R} \times \Lambda _i \to X_i \times \Lambda _i$
defined by (6.3). Therefore,
![]() $\Delta _1$
canonically lifts to a non-singular isomorphism
$\Delta _1$
canonically lifts to a non-singular isomorphism
![]() $\Delta _2 : X_1 \times \mathbb {R} \times \Lambda _1 \to X_2 \times \mathbb {R} \times \Lambda _2$
that is
$\Delta _2 : X_1 \times \mathbb {R} \times \Lambda _1 \to X_2 \times \mathbb {R} \times \Lambda _2$
that is
![]() $\mathbb {R}$
-equivariant and a
$\mathbb {R}$
-equivariant and a
![]() $\delta _1$
-conjugacy. Since
$\delta _1$
-conjugacy. Since
![]() $\Delta _2$
is a
$\Delta _2$
is a
![]() $\rho $
-conjugacy for the actions of
$\rho $
-conjugacy for the actions of
![]() $\Lambda _i$
, the map
$\Lambda _i$
, the map
![]() $\Delta _2$
must be of the form
$\Delta _2$
must be of the form
![]() $\Delta _2(x,s,b) = (\Delta _3(x,s),\zeta (x,s) \rho (b))$
.
$\Delta _2(x,s,b) = (\Delta _3(x,s),\zeta (x,s) \rho (b))$
.
Since
![]() $\delta _1(e,a) = (e,\rho (a))$
where
$\delta _1(e,a) = (e,\rho (a))$
where
![]() $\rho : \Lambda _1 \to \Lambda _2$
is an isomorphism, the isomorphism
$\rho : \Lambda _1 \to \Lambda _2$
is an isomorphism, the isomorphism
![]() $\delta _1$
must be of the form
$\delta _1$
must be of the form
![]() $\delta _1(g,a) = (\delta (g),\alpha (g)\rho (a))$
, where
$\delta _1(g,a) = (\delta (g),\alpha (g)\rho (a))$
, where
![]() $\delta : G_1 \to G_2$
is an isomorphism and
$\delta : G_1 \to G_2$
is an isomorphism and
![]() $\alpha : G_1 \to \Lambda _2$
is a group homomorphism. Expressing that
$\alpha : G_1 \to \Lambda _2$
is a group homomorphism. Expressing that
![]() $\Delta _2((g,e) \cdot (x,s,e)) = (\delta (g),\alpha (g)) \cdot \Delta _2(x,s,e)$
, we find that
$\Delta _2((g,e) \cdot (x,s,e)) = (\delta (g),\alpha (g)) \cdot \Delta _2(x,s,e)$
, we find that
![]() $\zeta (g \cdot (x,s))^{-1} = \alpha (g) \zeta (x,s)^{-1}$
. By our assumptions, for a.e.
$\zeta (g \cdot (x,s))^{-1} = \alpha (g) \zeta (x,s)^{-1}$
. By our assumptions, for a.e.
![]() $y \in Y_1$
, the action
$y \in Y_1$
, the action
![]() $G_1 \curvearrowright \widetilde {X}_{1,y}$
is not induced. Therefore,
$G_1 \curvearrowright \widetilde {X}_{1,y}$
is not induced. Therefore,
![]() $\alpha (g) = e$
for all
$\alpha (g) = e$
for all
![]() $g \in G_1$
and
$g \in G_1$
and
![]() $\zeta (x,s) = \zeta _1(\pi _1(x,s))$
where
$\zeta (x,s) = \zeta _1(\pi _1(x,s))$
where
![]() $\zeta _1 : Y_1 \to \Lambda _2$
.
$\zeta _1 : Y_1 \to \Lambda _2$
.
By construction,
![]() $\Delta _3 : X_1 \times \mathbb {R} \to X_2 \times \mathbb {R}$
is
$\Delta _3 : X_1 \times \mathbb {R} \to X_2 \times \mathbb {R}$
is
![]() $\mathbb {R}$
-equivariant and a
$\mathbb {R}$
-equivariant and a
![]() $\delta $
-conjugacy. After replacing
$\delta $
-conjugacy. After replacing
![]() $\mu _2$
by an equivalent probability measure, we find that
$\mu _2$
by an equivalent probability measure, we find that
![]() $\Delta _3(x,s) = (\Delta (x),s)$
, where
$\Delta _3(x,s) = (\Delta (x),s)$
, where
![]() $\Delta : X_1 \to X_2$
is a measure-preserving
$\Delta : X_1 \to X_2$
is a measure-preserving
![]() $\delta $
-conjugacy, so that
$\delta $
-conjugacy, so that
![]() $\omega _2(\delta (g),\Delta (x)) = \omega _1(g,x)$
. The
$\omega _2(\delta (g),\Delta (x)) = \omega _1(g,x)$
. The
![]() $\delta $
-conjugacy
$\delta $
-conjugacy
![]() $\Delta : X_1 \to X_2$
induces an isomorphism
$\Delta : X_1 \to X_2$
induces an isomorphism
![]() $\Delta _0 : Y_1 \to Y_2$
of associated flows. By construction,
$\Delta _0 : Y_1 \to Y_2$
of associated flows. By construction,
![]() $\Delta _0 \circ \pi _1 = \pi _2 \circ \Delta _3$
.
$\Delta _0 \circ \pi _1 = \pi _2 \circ \Delta _3$
.
Since
![]() $\Delta _2$
is
$\Delta _2$
is
![]() $\mathbb {R}$
-equivariant, we also find that
$\mathbb {R}$
-equivariant, we also find that
This means precisely that the
![]() $1$
-cocycles
$1$
-cocycles
![]() $\gamma _2 \circ (\mathord {\mathrm {id}} \times \Delta _0)$
and
$\gamma _2 \circ (\mathord {\mathrm {id}} \times \Delta _0)$
and
![]() $\rho \circ \gamma _1$
are cohomologous.
$\rho \circ \gamma _1$
are cohomologous.
Proposition 6.1 is now an immediate consequence of Corollary 5.5 and Propositions 6.2 and 6.3. For completeness, we include a detailed argument.
Proof of Proposition 6.1
Point (1) was already proven in Corollary 5.5. To prove point (2), we start with the easy implication. If we are given all the data mentioned in point (2), we replace
![]() $\mu '$
by the equivalent measure
$\mu '$
by the equivalent measure
![]() $\Delta _*(\mu )$
, so that
$\Delta _*(\mu )$
, so that
![]() $\omega '(\delta (g),\Delta (x)) = \omega (g,x)$
. We replace
$\omega '(\delta (g),\Delta (x)) = \omega (g,x)$
. We replace
![]() $\gamma ,\gamma '$
by the cohomologous
$\gamma ,\gamma '$
by the cohomologous
![]() $1$
-cocycles
$1$
-cocycles
![]() $\gamma _0,\gamma _0'$
. Further replacing
$\gamma _0,\gamma _0'$
. Further replacing
![]() $\gamma ^{\prime }_0$
by a cohomologous,
$\gamma ^{\prime }_0$
by a cohomologous,
![]() $\Lambda ^{\prime }_0$
-valued
$\Lambda ^{\prime }_0$
-valued
![]() $1$
-cocycle, we may assume that
$1$
-cocycle, we may assume that
![]() $\rho \circ \gamma _0 = \gamma ^{\prime }_0 \circ (\mathord {\mathrm {id}} \times \Delta _0)$
. By construction,
$\rho \circ \gamma _0 = \gamma ^{\prime }_0 \circ (\mathord {\mathrm {id}} \times \Delta _0)$
. By construction,
![]() $\Delta \times \rho $
defines a
$\Delta \times \rho $
defines a
![]() $(\delta \times \rho )$
-conjugacy of the actions
$(\delta \times \rho )$
-conjugacy of the actions
![]() $\beta (\gamma _0)$
and
$\beta (\gamma _0)$
and
![]() $\beta (\gamma ^{\prime }_0)$
.
$\beta (\gamma ^{\prime }_0)$
.
Denote by
![]() $\sigma _0, \sigma ^{\prime }_0$
the restriction of
$\sigma _0, \sigma ^{\prime }_0$
the restriction of
![]() $\sigma ,\sigma '$
to
$\sigma ,\sigma '$
to
![]() $G \times \Lambda _0$
,
$G \times \Lambda _0$
,
![]() $G \times \Lambda ^{\prime }_0$
. Since
$G \times \Lambda ^{\prime }_0$
. Since
![]() $\alpha \circ \sigma _0 = \sigma ^{\prime }_0 \circ (\delta \times \rho )$
, it follows from the previous paragraph that the actions
$\alpha \circ \sigma _0 = \sigma ^{\prime }_0 \circ (\delta \times \rho )$
, it follows from the previous paragraph that the actions
![]() $\beta (\gamma _0,\sigma _0)$
and
$\beta (\gamma _0,\sigma _0)$
and
![]() $\beta (\gamma ^{\prime }_0,\sigma ^{\prime }_0)$
are
$\beta (\gamma ^{\prime }_0,\sigma ^{\prime }_0)$
are
![]() $\alpha $
-conjugate. By construction, the first action is isomorphic to
$\alpha $
-conjugate. By construction, the first action is isomorphic to
![]() $\beta (\gamma ,\sigma )$
and the second action is isomorphic to
$\beta (\gamma ,\sigma )$
and the second action is isomorphic to
![]() $\beta (\gamma ',\sigma ')$
. We have thus proven that
$\beta (\gamma ',\sigma ')$
. We have thus proven that
![]() $\beta (\gamma ,\sigma )$
and
$\beta (\gamma ,\sigma )$
and
![]() $\beta (\gamma ',\sigma ')$
are conjugate.
$\beta (\gamma ',\sigma ')$
are conjugate.
Conversely, assume that there is an
![]() $\alpha $
-conjugacy between
$\alpha $
-conjugacy between
![]() $\beta (\gamma ,\sigma )$
and
$\beta (\gamma ,\sigma )$
and
![]() $\beta (\gamma ',\sigma ')$
. When an ergodic group action
$\beta (\gamma ',\sigma ')$
. When an ergodic group action
![]() $\Gamma \curvearrowright Z$
is induced from both
$\Gamma \curvearrowright Z$
is induced from both
![]() $\Gamma _0 \curvearrowright Z_0$
and
$\Gamma _0 \curvearrowright Z_0$
and
![]() $\Gamma _1 \curvearrowright Z_1$
, there exists a
$\Gamma _1 \curvearrowright Z_1$
, there exists a
![]() $g \in \Gamma $
such that
$g \in \Gamma $
such that
![]() $\Gamma \curvearrowright Z$
is induced from the action of
$\Gamma \curvearrowright Z$
is induced from the action of
![]() $\Gamma _0 \cap g \Gamma _1 g^{-1}$
on
$\Gamma _0 \cap g \Gamma _1 g^{-1}$
on
![]() $Z_0 \cap g \cdot Z_1$
. After composing
$Z_0 \cap g \cdot Z_1$
. After composing
![]() $\alpha $
with an inner automorphism and using Proposition 6.2, we find subgroups
$\alpha $
with an inner automorphism and using Proposition 6.2, we find subgroups
![]() $\Lambda _0 < \Lambda $
and
$\Lambda _0 < \Lambda $
and
![]() $\Lambda ^{\prime }_0 < \Lambda '$
such that
$\Lambda ^{\prime }_0 < \Lambda '$
such that
![]() $\alpha (\sigma (G \times \Lambda _0)) = \sigma '(G \times \Lambda ^{\prime }_0)$
and such that
$\alpha (\sigma (G \times \Lambda _0)) = \sigma '(G \times \Lambda ^{\prime }_0)$
and such that
![]() $\gamma ,\gamma '$
are cohomologous with
$\gamma ,\gamma '$
are cohomologous with
![]() $\gamma _0,\gamma ^{\prime }_0$
taking values in
$\gamma _0,\gamma ^{\prime }_0$
taking values in
![]() $\Lambda _0,\Lambda ^{\prime }_0$
. We also find the group isomorphism
$\Lambda _0,\Lambda ^{\prime }_0$
. We also find the group isomorphism
![]() $\delta _1 : G \times \Lambda _0 \to G \times \Lambda ^{\prime }_0$
, with
$\delta _1 : G \times \Lambda _0 \to G \times \Lambda ^{\prime }_0$
, with
![]() $\alpha \circ \sigma = \sigma ' \circ \delta _1$
, such that the actions
$\alpha \circ \sigma = \sigma ' \circ \delta _1$
, such that the actions
![]() $\beta (\gamma _0)$
and
$\beta (\gamma _0)$
and
![]() $\beta (\gamma ^{\prime }_0)$
are
$\beta (\gamma ^{\prime }_0)$
are
![]() $\delta _1$
-conjugate. The conclusion then follows from Proposition 6.3.
$\delta _1$
-conjugate. The conclusion then follows from Proposition 6.3.
We finally turn to our main family of group actions, given by (1.1). For
![]() $i \in \{1,2\}$
, let
$i \in \{1,2\}$
, let
![]() $G_i \curvearrowright (X_i,\mu _i)$
be non-singular actions and denote by
$G_i \curvearrowright (X_i,\mu _i)$
be non-singular actions and denote by
![]() $\omega _i : G_i \times X_i \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle. Let
$\omega _i : G_i \times X_i \to \mathbb {R}$
the logarithm of the Radon–Nikodym cocycle. Let
![]() $\mathbb {R} \curvearrowright (Y_i,\eta _i)$
be non-singular flows. Consider the actions
$\mathbb {R} \curvearrowright (Y_i,\eta _i)$
be non-singular flows. Consider the actions
If
![]() $\Delta _1 : X_1 \to X_2$
is a conjugacy between the actions
$\Delta _1 : X_1 \to X_2$
is a conjugacy between the actions
![]() $G_1 \curvearrowright X_1$
and
$G_1 \curvearrowright X_1$
and
![]() $G_2 \curvearrowright X_2$
and if
$G_2 \curvearrowright X_2$
and if
![]() $\Delta _2 : Y_1 \to Y_2$
is an isomorphism of the flows, writing
$\Delta _2 : Y_1 \to Y_2$
is an isomorphism of the flows, writing
![]() $\rho (x) = \log (d((\Delta _1)_* \mu _1)/d\mu _2)$
, the map
$\rho (x) = \log (d((\Delta _1)_* \mu _1)/d\mu _2)$
, the map
is a conjugacy between
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
.
$\sigma _2$
.
We now prove in Proposition 6.4 that under the appropriate assumption, the converse also holds. In Lemma 6.6, we explain that this assumption indeed holds for actions of the form
![]() $G \curvearrowright \mathbb {R}^n/\mathbb {R}^*_+$
when
$G \curvearrowright \mathbb {R}^n/\mathbb {R}^*_+$
when
![]() $G < \operatorname {SL}(n,\mathbb {R})$
is a countable dense subgroup. This then leads to a proof of Corollary B.
$G < \operatorname {SL}(n,\mathbb {R})$
is a countable dense subgroup. This then leads to a proof of Corollary B.
Proposition 6.4. For
![]() $i \in \{1,2\}$
, let
$i \in \{1,2\}$
, let
![]() $G_i \curvearrowright (X_i,\mu _i)$
be essentially free, ergodic, non-singular actions of type III
$G_i \curvearrowright (X_i,\mu _i)$
be essentially free, ergodic, non-singular actions of type III
![]() $_1$
. Assume that the Maharam extensions
$_1$
. Assume that the Maharam extensions
![]() $G_i \curvearrowright (\widetilde {X}_i,\widetilde {\mu }_i)$
admit a unique measure-scaling action commuting with the
$G_i \curvearrowright (\widetilde {X}_i,\widetilde {\mu }_i)$
admit a unique measure-scaling action commuting with the
![]() $G_i$
-action. Let
$G_i$
-action. Let
![]() $\mathbb {R} \curvearrowright (Y_i,\eta _i)$
be ergodic flows.
$\mathbb {R} \curvearrowright (Y_i,\eta _i)$
be ergodic flows.
Every conjugacy between the actions
![]() $\sigma _i$
in (6.4) is of the form (6.5) for a conjugacy
$\sigma _i$
in (6.4) is of the form (6.5) for a conjugacy
![]() $\Delta _1$
between
$\Delta _1$
between
![]() $G_1 \curvearrowright X_1$
and
$G_1 \curvearrowright X_1$
and
![]() $G_2 \curvearrowright X_2$
and an isomorphism of flows
$G_2 \curvearrowright X_2$
and an isomorphism of flows
![]() $\Delta _2 : Y_1 \to Y_2$
.
$\Delta _2 : Y_1 \to Y_2$
.
Proof. Denote by
![]() $\mathbb {R}^2 \curvearrowright (Z_i,\zeta _i)$
the unique actions associated with the flows
$\mathbb {R}^2 \curvearrowright (Z_i,\zeta _i)$
the unique actions associated with the flows
![]() ${\mathbb {R} \curvearrowright (Y_i,\eta _i)}$
given by Proposition 3.1, together with the factor maps
${\mathbb {R} \curvearrowright (Y_i,\eta _i)}$
given by Proposition 3.1, together with the factor maps
![]() $\pi _i : Z_i \to Y_i$
satisfying
$\pi _i : Z_i \to Y_i$
satisfying
![]() $\pi _i((t,r) \cdot z) = t \cdot \pi _i(z)$
. We realize the Maharam extension of
$\pi _i((t,r) \cdot z) = t \cdot \pi _i(z)$
. We realize the Maharam extension of
![]() $\sigma _i$
together with its measure-scaling action as
$\sigma _i$
together with its measure-scaling action as
We have the canonical factor map
![]() $\Psi _i : X_i \times Z_i \to X_i \times Y_i : \Psi _i(x,z) = (x,\pi _i(z))$
satisfying
$\Psi _i : X_i \times Z_i \to X_i \times Y_i : \Psi _i(x,z) = (x,\pi _i(z))$
satisfying
![]() $\Psi _i((g,r) \cdot (x,z)) = g \cdot \Psi _i(x,z)$
.
$\Psi _i((g,r) \cdot (x,z)) = g \cdot \Psi _i(x,z)$
.
Assume that
![]() $\delta : G_1 \to G_2$
is a group isomorphism and
$\delta : G_1 \to G_2$
is a group isomorphism and
![]() $\Delta : X_1 \times Y_1 \to X_2 \times Y_2$
is a
$\Delta : X_1 \times Y_1 \to X_2 \times Y_2$
is a
![]() $\delta $
-conjugacy between
$\delta $
-conjugacy between
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
. Denote by
$\sigma _2$
. Denote by
![]() $\widetilde {\Delta } : X_1 \times Z_1 \to X_2 \times Z_2$
the canonical measure-preserving lift, which is a
$\widetilde {\Delta } : X_1 \times Z_1 \to X_2 \times Z_2$
the canonical measure-preserving lift, which is a
![]() $(\delta \times \mathord {\mathrm {id}})$
-conjugacy for the actions
$(\delta \times \mathord {\mathrm {id}})$
-conjugacy for the actions
![]() $\widetilde {\sigma }_i$
in (6.6) and which satisfies
$\widetilde {\sigma }_i$
in (6.6) and which satisfies
![]() $\Psi _2 \circ \widetilde {\Delta } = \Delta \circ \Psi _1$
.
$\Psi _2 \circ \widetilde {\Delta } = \Delta \circ \Psi _1$
.
Define the action
![]() $\gamma : \mathbb {R} \curvearrowright X_i \times Z_i : \gamma _t(x,z) = (x,(t,0) \cdot z)$
. Note that
$\gamma : \mathbb {R} \curvearrowright X_i \times Z_i : \gamma _t(x,z) = (x,(t,0) \cdot z)$
. Note that
![]() $\gamma $
commutes with
$\gamma $
commutes with
![]() $\widetilde {\sigma }_i$
. We claim that
$\widetilde {\sigma }_i$
. We claim that
![]() $\widetilde {\Delta }$
is automatically
$\widetilde {\Delta }$
is automatically
![]() $\gamma $
-equivariant.
$\gamma $
-equivariant.
To prove this claim, we temporarily identify
![]() $Z_i = \mathbb {R} \times \widehat {Y}_i$
with the action
$Z_i = \mathbb {R} \times \widehat {Y}_i$
with the action
![]() $\mathbb {R}^2 \curvearrowright Z_i$
given by
$\mathbb {R}^2 \curvearrowright Z_i$
given by
![]() $(t,r) \cdot (s,\widehat {y}) = (t+r+\widehat {\beta }(r,\widehat {y})+s,r \cdot \widehat {y})$
. Under this identification,
$(t,r) \cdot (s,\widehat {y}) = (t+r+\widehat {\beta }(r,\widehat {y})+s,r \cdot \widehat {y})$
. Under this identification,
![]() $\widetilde {\Delta } : X_1 \times \mathbb {R} \times \widehat {Y}_1 \to X_2 \times \mathbb {R} \times \widehat {Y}_2$
is a
$\widetilde {\Delta } : X_1 \times \mathbb {R} \times \widehat {Y}_1 \to X_2 \times \mathbb {R} \times \widehat {Y}_2$
is a
![]() $\delta $
-conjugacy for the actions
$\delta $
-conjugacy for the actions
Since
![]() $G_i \curvearrowright X_i$
is of type III
$G_i \curvearrowright X_i$
is of type III
![]() $_1$
, the Maharam extension
$_1$
, the Maharam extension
![]() $G_i \curvearrowright X_i \times \mathbb {R}$
is ergodic. Therefore,
$G_i \curvearrowright X_i \times \mathbb {R}$
is ergodic. Therefore,
![]() $\widetilde {\Delta }$
must be of the form
$\widetilde {\Delta }$
must be of the form
![]() $\widetilde {\Delta }(x,s,\widehat {y}\kern0.5pt) = (\theta _{\kern0.5pt\widehat {y}}(x,s),\Phi (\widehat {y}\kern0.5pt))$
, where
$\widetilde {\Delta }(x,s,\widehat {y}\kern0.5pt) = (\theta _{\kern0.5pt\widehat {y}}(x,s),\Phi (\widehat {y}\kern0.5pt))$
, where
![]() $\Phi : \widehat {Y}_1 \to \widehat {Y}_2$
is a non-singular isomorphism and, for a.e.
$\Phi : \widehat {Y}_1 \to \widehat {Y}_2$
is a non-singular isomorphism and, for a.e.
![]() $\widehat {y} \in \widehat {Y}_1$
, the map
$\widehat {y} \in \widehat {Y}_1$
, the map
![]() $\theta _{\kern0.5pt\widehat {y}} : X_1 \times \mathbb {R} \to X_2 \times \mathbb {R}$
is a
$\theta _{\kern0.5pt\widehat {y}} : X_1 \times \mathbb {R} \to X_2 \times \mathbb {R}$
is a
![]() $\delta $
-conjugacy of the Maharam extensions
$\delta $
-conjugacy of the Maharam extensions
![]() $G_i \curvearrowright X_i \times \mathbb {R}$
. Since
$G_i \curvearrowright X_i \times \mathbb {R}$
. Since
![]() $\widetilde {\Delta }$
is measure-preserving, a.e.
$\widetilde {\Delta }$
is measure-preserving, a.e.
![]() $\theta _{\widehat {y}}$
is measure-scaling. We assumed that these Maharam extensions admit a unique commuting measure-scaling action. It follows that
$\theta _{\widehat {y}}$
is measure-scaling. We assumed that these Maharam extensions admit a unique commuting measure-scaling action. It follows that
![]() $\theta _{\widehat {y}}$
is equivariant with respect to translation in the second variable. This means that
$\theta _{\widehat {y}}$
is equivariant with respect to translation in the second variable. This means that
![]() $\widetilde {\Delta }$
is equivariant with respect to translation in the second variable. Thus, the claim is proven.
$\widetilde {\Delta }$
is equivariant with respect to translation in the second variable. Thus, the claim is proven.
We thus consider the actions
![]() $G_i \times \mathbb {R}^2 \curvearrowright X_i \times Z_i : (g,t,r) \cdot (x,z) = (g \cdot x, (\omega (g,x)+t,r) \cdot z)$
and we have proven that
$G_i \times \mathbb {R}^2 \curvearrowright X_i \times Z_i : (g,t,r) \cdot (x,z) = (g \cdot x, (\omega (g,x)+t,r) \cdot z)$
and we have proven that
![]() $\widetilde {\Delta }$
is a
$\widetilde {\Delta }$
is a
![]() $(\delta \times \mathord {\mathrm {id}})$
-conjugacy between these actions. Since the action of
$(\delta \times \mathord {\mathrm {id}})$
-conjugacy between these actions. Since the action of
![]() $\mathbb {R}^2$
on
$\mathbb {R}^2$
on
![]() $Z_i$
is ergodic, this forces
$Z_i$
is ergodic, this forces
![]() $\widetilde {\Delta }$
to be of the form
$\widetilde {\Delta }$
to be of the form
![]() $\widetilde {\Delta }(x,z) = (\Delta _1(x),\Phi _x(z))$
, where
$\widetilde {\Delta }(x,z) = (\Delta _1(x),\Phi _x(z))$
, where
![]() $\Delta _1 : X_1 \to X_2$
is a
$\Delta _1 : X_1 \to X_2$
is a
![]() $\delta $
-conjugacy and, for a.e.
$\delta $
-conjugacy and, for a.e.
![]() $x \in X_1$
,
$x \in X_1$
,
![]() $\Phi _x : Z_1 \to Z_2$
is an isomorphism between the actions
$\Phi _x : Z_1 \to Z_2$
is an isomorphism between the actions
![]() $\mathbb {R}^2 \curvearrowright Z_i$
.
$\mathbb {R}^2 \curvearrowright Z_i$
.
Define
![]() $\rho (x) = \log (d((\Delta _1)_* \mu _1)/d\mu _2)$
and denote
$\rho (x) = \log (d((\Delta _1)_* \mu _1)/d\mu _2)$
and denote
![]() $\Phi ^{\prime }_x(z) = (\rho (\Delta _1(x)),0) \cdot \Phi _x(z)$
. We still have that
$\Phi ^{\prime }_x(z) = (\rho (\Delta _1(x)),0) \cdot \Phi _x(z)$
. We still have that
![]() $\Phi ^{\prime }_x$
is an isomorphism between the actions
$\Phi ^{\prime }_x$
is an isomorphism between the actions
![]() $\mathbb {R}^2 \curvearrowright Z_i$
. With respect to the measures
$\mathbb {R}^2 \curvearrowright Z_i$
. With respect to the measures
![]() $\mu _i \times \zeta _i$
on
$\mu _i \times \zeta _i$
on
![]() $X_i \times Z_i$
, the isomorphism
$X_i \times Z_i$
, the isomorphism
![]() $\widetilde {\Delta }$
is measure-preserving. It then follows that a.e.
$\widetilde {\Delta }$
is measure-preserving. It then follows that a.e.
![]() $\Phi ^{\prime }_x$
is measure-preserving with respect to the measures
$\Phi ^{\prime }_x$
is measure-preserving with respect to the measures
![]() $\zeta _i$
on
$\zeta _i$
on
![]() $Z_i$
.
$Z_i$
.
Expressing that
![]() $\widetilde {\Delta }$
is a
$\widetilde {\Delta }$
is a
![]() $\delta $
-conjugacy for the actions of
$\delta $
-conjugacy for the actions of
![]() $G_i$
and using that
$G_i$
and using that
![]() $\Phi _x$
is an isomorphism between the actions of
$\Phi _x$
is an isomorphism between the actions of
![]() $\mathbb {R}^2$
, we find that
$\mathbb {R}^2$
, we find that
![]() $(\omega _1(g,x),0) \cdot \Phi _{g \cdot x}(z) = (\omega _2(\delta (g),\Delta _1(x)),0) \cdot \Phi _x(z)$
. Since
$(\omega _1(g,x),0) \cdot \Phi _{g \cdot x}(z) = (\omega _2(\delta (g),\Delta _1(x)),0) \cdot \Phi _x(z)$
. Since
![]() $\omega _i$
are the logarithms of the Radon–Nikodym cocycles for
$\omega _i$
are the logarithms of the Radon–Nikodym cocycles for
![]() $G_i \curvearrowright (X_i,\mu _i)$
and since
$G_i \curvearrowright (X_i,\mu _i)$
and since
![]() $\Delta _1$
is a
$\Delta _1$
is a
![]() $\delta $
-conjugacy, we have by definition of
$\delta $
-conjugacy, we have by definition of
![]() $\rho $
that
$\rho $
that
![]() $\omega _2(\delta (g),\Delta _1(x)) = \rho (\Delta _1(x)) - \rho (\Delta _1(g \cdot x)) + \omega _1(g,x)$
. We conclude that
$\omega _2(\delta (g),\Delta _1(x)) = \rho (\Delta _1(x)) - \rho (\Delta _1(g \cdot x)) + \omega _1(g,x)$
. We conclude that
![]() $\Phi ^{\prime }_{g \cdot x}(z) = \Phi ^{\prime }_x(z)$
. Since the action
$\Phi ^{\prime }_{g \cdot x}(z) = \Phi ^{\prime }_x(z)$
. Since the action
![]() $G_1 \curvearrowright X_1$
is ergodic, we find a measure-preserving isomorphism
$G_1 \curvearrowright X_1$
is ergodic, we find a measure-preserving isomorphism
![]() $\Phi : Z_1 \to Z_2$
between the actions
$\Phi : Z_1 \to Z_2$
between the actions
![]() $\mathbb {R}^2 \curvearrowright Z_i$
such that
$\mathbb {R}^2 \curvearrowright Z_i$
such that
![]() $\Phi ^{\prime }_x = \Phi $
for a.e.
$\Phi ^{\prime }_x = \Phi $
for a.e.
![]() $x \in X_1$
.
$x \in X_1$
.
For such an isomorphism
![]() $\Phi $
, there is a unique isomorphism
$\Phi $
, there is a unique isomorphism
![]() $\Delta _2 : Y_1 \to Y_2$
for the actions
$\Delta _2 : Y_1 \to Y_2$
for the actions
![]() $\mathbb {R} \curvearrowright Y_i$
such that
$\mathbb {R} \curvearrowright Y_i$
such that
![]() $\pi _2 \circ \Phi = \Delta _2 \circ \pi _1$
. Define the
$\pi _2 \circ \Phi = \Delta _2 \circ \pi _1$
. Define the
![]() $\delta $
-conjugacy
$\delta $
-conjugacy
![]() $\Delta _0 : X_1 \times Y_1 \to X_2 \times Y_2$
by (6.5), that is,
$\Delta _0 : X_1 \times Y_1 \to X_2 \times Y_2$
by (6.5), that is,
![]() $\Delta _0(x,y) = (\Delta _1(x),-\rho (\Delta _1(x)) \cdot \Delta _2(y))$
. By construction,
$\Delta _0(x,y) = (\Delta _1(x),-\rho (\Delta _1(x)) \cdot \Delta _2(y))$
. By construction,
![]() $\Psi _2 \circ \widetilde {\Delta } = \Delta _0 \circ \Psi _1$
. It follows that
$\Psi _2 \circ \widetilde {\Delta } = \Delta _0 \circ \Psi _1$
. It follows that
![]() $\Delta = \Delta _0$
.
$\Delta = \Delta _0$
.
Recall that a unitary representation
![]() $\pi : \mathcal {G} \to \mathcal {U}(H)$
of a locally compact group
$\pi : \mathcal {G} \to \mathcal {U}(H)$
of a locally compact group
![]() $\mathcal {G}$
is said to be a
$\mathcal {G}$
is said to be a
![]() $C_0$
-representation if for every
$C_0$
-representation if for every
![]() $\varepsilon> 0$
and
$\varepsilon> 0$
and
![]() $\xi ,\eta \in H$
, there exists a compact subset
$\xi ,\eta \in H$
, there exists a compact subset
![]() $K \subset \mathcal {G}$
such that
$K \subset \mathcal {G}$
such that
![]() $|\langle \pi (g)\xi ,\eta \rangle | < \varepsilon $
for all
$|\langle \pi (g)\xi ,\eta \rangle | < \varepsilon $
for all
![]() $g \in \mathcal {G} \setminus K$
.
$g \in \mathcal {G} \setminus K$
.
Lemma 6.5. Let
![]() $n \geq 1$
be an integer. Write
$n \geq 1$
be an integer. Write
![]() $\mathcal {G} = \operatorname {GL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
. Then the unitary representation
$\mathcal {G} = \operatorname {GL}(n,\mathbb {R}) \ltimes \mathbb {R}^n$
. Then the unitary representation
![]() $\pi : \mathcal {G} \to \mathcal {U}(L^2(\mathbb {R}^n)) : (\pi (A,a)\xi )(x) = |\det A|^{-1/2} \xi (A^{-1}(x) -a)$
is a
$\pi : \mathcal {G} \to \mathcal {U}(L^2(\mathbb {R}^n)) : (\pi (A,a)\xi )(x) = |\det A|^{-1/2} \xi (A^{-1}(x) -a)$
is a
![]() $C_0$
-representation.
$C_0$
-representation.
In particular, the action
![]() $\mathcal {G} \curvearrowright \mathbb {R}^n : (A,a) \cdot x = A(a+x)$
induces a homeomorphism of
$\mathcal {G} \curvearrowright \mathbb {R}^n : (A,a) \cdot x = A(a+x)$
induces a homeomorphism of
![]() $\mathcal {G}$
onto a closed subgroup of the Polish group of non-singular automorphisms of
$\mathcal {G}$
onto a closed subgroup of the Polish group of non-singular automorphisms of
![]() $\mathbb {R}^n$
with the Lebesgue measure.
$\mathbb {R}^n$
with the Lebesgue measure.
Proof. Assume the contrary. We then find
![]() $\xi ,\eta \in L^2(\mathbb {R}^n)$
,
$\xi ,\eta \in L^2(\mathbb {R}^n)$
,
![]() $\varepsilon> 0$
and a sequence
$\varepsilon> 0$
and a sequence
![]() $(A_k,a_k) \in \mathcal {G}$
that tends to infinity in
$(A_k,a_k) \in \mathcal {G}$
that tends to infinity in
![]() $\mathcal {G}$
such that
$\mathcal {G}$
such that
![]() $|\langle \pi (A_k,a_k) \xi , \eta \rangle |> \varepsilon $
for all k.
$|\langle \pi (A_k,a_k) \xi , \eta \rangle |> \varepsilon $
for all k.
We view
![]() $\operatorname {GL}(n,\mathbb {R})$
as a subgroup of
$\operatorname {GL}(n,\mathbb {R})$
as a subgroup of
![]() $\mathcal {G}$
and we denote by
$\mathcal {G}$
and we denote by
![]() $D_n < \operatorname {GL}(n,\mathbb {R})$
the subgroup of diagonal matrices with positive real numbers on the diagonal. Since
$D_n < \operatorname {GL}(n,\mathbb {R})$
the subgroup of diagonal matrices with positive real numbers on the diagonal. Since
![]() $\operatorname {GL}(n,\mathbb {R}) = O(n,\mathbb {R}) D_n O(n,\mathbb {R})$
, we can write
$\operatorname {GL}(n,\mathbb {R}) = O(n,\mathbb {R}) D_n O(n,\mathbb {R})$
, we can write
![]() $(A_k,a_k) = g_k (d_k,b_k) h_k$
with
$(A_k,a_k) = g_k (d_k,b_k) h_k$
with
![]() $g_k,h_k \in O(n,\mathbb {R})$
,
$g_k,h_k \in O(n,\mathbb {R})$
,
![]() $d_k \in D_n$
and
$d_k \in D_n$
and
![]() $b_k \in \mathbb {R}^n$
. After passing to a subsequence, we may assume that
$b_k \in \mathbb {R}^n$
. After passing to a subsequence, we may assume that
![]() $g_k$
and
$g_k$
and
![]() $h_k$
converge to g and h, respectively. Replacing
$h_k$
converge to g and h, respectively. Replacing
![]() $\xi $
by
$\xi $
by
![]() $\pi (h) \xi $
and replacing
$\pi (h) \xi $
and replacing
![]() $\eta $
by
$\eta $
by
![]() $\pi (g)^* \eta $
, we may then further assume that
$\pi (g)^* \eta $
, we may then further assume that
![]() $|\langle \pi (d_k,b_k) \xi , \eta \rangle |> \varepsilon $
for all k.
$|\langle \pi (d_k,b_k) \xi , \eta \rangle |> \varepsilon $
for all k.
To reach a contradiction, it thus suffices to prove that the representation
![]() $\theta : \mathbb {R}^*_+ \ltimes \mathbb {R} \to \mathcal {U}(L^2(\mathbb {R})) : (\theta (d,b)\xi )(x) = d^{-1/2} \xi (d^{-1} x - b)$
is a
$\theta : \mathbb {R}^*_+ \ltimes \mathbb {R} \to \mathcal {U}(L^2(\mathbb {R})) : (\theta (d,b)\xi )(x) = d^{-1/2} \xi (d^{-1} x - b)$
is a
![]() $C_0$
-representation. Denote by
$C_0$
-representation. Denote by
![]() $\unicode{x3bb} $
the Lebesgue measure on
$\unicode{x3bb} $
the Lebesgue measure on
![]() $\mathbb {R}$
. When
$\mathbb {R}$
. When
![]() $N \in \mathbb {R}_+$
and
$N \in \mathbb {R}_+$
and
![]() $\mathcal {U},\mathcal {V} \subset [-N,N]$
are Borel sets with indicator functions
$\mathcal {U},\mathcal {V} \subset [-N,N]$
are Borel sets with indicator functions
![]() $1_{\mathcal {U}}, 1_{\mathcal {V}} \in L^2(\mathbb {R})$
, we have
$1_{\mathcal {U}}, 1_{\mathcal {V}} \in L^2(\mathbb {R})$
, we have
![]() $\theta (d,b) 1_{\mathcal {U}} = d^{-1/2} 1_{d(\mathcal {U}+b)}$
, so that
$\theta (d,b) 1_{\mathcal {U}} = d^{-1/2} 1_{d(\mathcal {U}+b)}$
, so that
![]() $\langle \theta (d,b) 1_{\mathcal {U}}, 1_{\mathcal {V}} \rangle = d^{-1/2} \, \unicode{x3bb} (d(\mathcal {U} + b) \cap \mathcal {V})$
. We conclude that
$\langle \theta (d,b) 1_{\mathcal {U}}, 1_{\mathcal {V}} \rangle = d^{-1/2} \, \unicode{x3bb} (d(\mathcal {U} + b) \cap \mathcal {V})$
. We conclude that
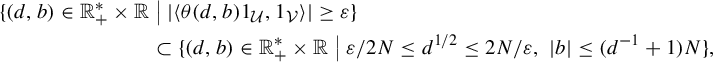 $$\begin{align*} \{ (d,b) \in \mathbb{R}^*_+ &\times \mathbb{R} \bigm| |\langle \theta(d,b) 1_{\mathcal{U}}, 1_{\mathcal{V}} \rangle| \geq \varepsilon \} \\& \qquad \subset \{ (d,b) \in \mathbb{R}^*_+ \times \mathbb{R} \bigm| \varepsilon/2N \leq d^{1/2} \leq 2N/\varepsilon, \; |b| \leq (d^{-1} + 1) N \}, \end{align*}$$
$$\begin{align*} \{ (d,b) \in \mathbb{R}^*_+ &\times \mathbb{R} \bigm| |\langle \theta(d,b) 1_{\mathcal{U}}, 1_{\mathcal{V}} \rangle| \geq \varepsilon \} \\& \qquad \subset \{ (d,b) \in \mathbb{R}^*_+ \times \mathbb{R} \bigm| \varepsilon/2N \leq d^{1/2} \leq 2N/\varepsilon, \; |b| \leq (d^{-1} + 1) N \}, \end{align*}$$
which is compact.
Lemma 6.6. For
![]() $i = 1,2$
and integers
$i = 1,2$
and integers
![]() $n_i \geq 2$
, let
$n_i \geq 2$
, let
![]() $G_i < \operatorname {SL}(n_i,\mathbb {R})$
be dense subgroups and consider the actions
$G_i < \operatorname {SL}(n_i,\mathbb {R})$
be dense subgroups and consider the actions
![]() $G_i \curvearrowright \mathbb {R}^{n_i}$
.
$G_i \curvearrowright \mathbb {R}^{n_i}$
.
If
![]() $\Delta : \mathbb {R}^{n_1} \to \mathbb {R}^{n_2}$
is a
$\Delta : \mathbb {R}^{n_1} \to \mathbb {R}^{n_2}$
is a
![]() $\delta $
-conjugacy between these actions, we have
$\delta $
-conjugacy between these actions, we have
![]() $n_1 = n_2$
and there is a unique
$n_1 = n_2$
and there is a unique
![]() $A \in \operatorname {GL}(n_1,\mathbb {R})$
such that
$A \in \operatorname {GL}(n_1,\mathbb {R})$
such that
![]() $\Delta (x) = A(x)$
for a.e.
$\Delta (x) = A(x)$
for a.e.
![]() $x \in \mathbb {R}^{n_1}$
and
$x \in \mathbb {R}^{n_1}$
and
![]() $\delta (g) = AgA^{-1}$
for all
$\delta (g) = AgA^{-1}$
for all
![]() $g \in G_1$
.
$g \in G_1$
.
In particular, if
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $G < \operatorname {SL}(n,\mathbb {R})$
is a dense subgroup, then the action
$G < \operatorname {SL}(n,\mathbb {R})$
is a dense subgroup, then the action
![]() $\mathbb {R} \curvearrowright \mathbb {R}^n : t \cdot x = e^{-t/n} x$
is the unique measure-scaling action that commutes with
$\mathbb {R} \curvearrowright \mathbb {R}^n : t \cdot x = e^{-t/n} x$
is the unique measure-scaling action that commutes with
![]() $G \curvearrowright \mathbb {R}^n$
.
$G \curvearrowright \mathbb {R}^n$
.
Proof. Denote by
![]() $\operatorname {Aut}(\mathbb {R}^{n_i})$
the Polish group of non-singular automorphisms of
$\operatorname {Aut}(\mathbb {R}^{n_i})$
the Polish group of non-singular automorphisms of
![]() $\mathbb {R}^{n_i}$
. By Lemma 6.5, we may view
$\mathbb {R}^{n_i}$
. By Lemma 6.5, we may view
![]() $\operatorname {SL}(n_i,\mathbb {R})$
as a closed subgroup of
$\operatorname {SL}(n_i,\mathbb {R})$
as a closed subgroup of
![]() $\operatorname {Aut}(\mathbb {R}^{n_i})$
. By our assumption,
$\operatorname {Aut}(\mathbb {R}^{n_i})$
. By our assumption,
![]() $\Delta G_1 \Delta ^{-1} = G_2$
. Taking the closure in
$\Delta G_1 \Delta ^{-1} = G_2$
. Taking the closure in
![]() $\operatorname {Aut}(\mathbb {R}^{n_i})$
, we find that
$\operatorname {Aut}(\mathbb {R}^{n_i})$
, we find that
![]() ${\Delta \operatorname {SL}(n_1,\mathbb {R}) \Delta ^{-1} = \operatorname {SL}(n_2,\mathbb {R})}$
. This means in particular that
${\Delta \operatorname {SL}(n_1,\mathbb {R}) \Delta ^{-1} = \operatorname {SL}(n_2,\mathbb {R})}$
. This means in particular that
![]() $\delta $
extends to a group isomorphism and homeomorphism
$\delta $
extends to a group isomorphism and homeomorphism
![]() $\delta : \operatorname {SL}(n_1,\mathbb {R}) \to \operatorname {SL}(n_2,\mathbb {R})$
. It follows that
$\delta : \operatorname {SL}(n_1,\mathbb {R}) \to \operatorname {SL}(n_2,\mathbb {R})$
. It follows that
![]() $n_1 = n_2$
and we write
$n_1 = n_2$
and we write
![]() $n = n_1 = n_2$
.
$n = n_1 = n_2$
.
Write
![]() $\mathcal {G} = \operatorname {SL}(n,\mathbb {R})$
and denote by
$\mathcal {G} = \operatorname {SL}(n,\mathbb {R})$
and denote by
![]() $\mathcal {H} < \mathcal {G}$
the closed subgroup fixing the first basis vector
$\mathcal {H} < \mathcal {G}$
the closed subgroup fixing the first basis vector
![]() $e_1$
. We view
$e_1$
. We view
![]() $\Delta $
as a
$\Delta $
as a
![]() $\delta $
-conjugacy for the transitive action
$\delta $
-conjugacy for the transitive action
![]() $\mathcal {G} \curvearrowright \mathcal {G}/\mathcal {H}$
. This means that
$\mathcal {G} \curvearrowright \mathcal {G}/\mathcal {H}$
. This means that
![]() $\delta (\mathcal {H}) = g_0 \mathcal {H} g_0^{-1}$
for some
$\delta (\mathcal {H}) = g_0 \mathcal {H} g_0^{-1}$
for some
![]() $g_0 \in \mathcal {G}$
and
$g_0 \in \mathcal {G}$
and
![]() $\Delta (g\mathcal {H}) = \delta (g)g_0\mathcal {H}$
for a.e.
$\Delta (g\mathcal {H}) = \delta (g)g_0\mathcal {H}$
for a.e.
![]() $g \in \mathcal {G}$
. Since
$g \in \mathcal {G}$
. Since
![]() $\delta $
is an automorphism of
$\delta $
is an automorphism of
![]() $\operatorname {SL}(n,\mathbb {R})$
, we find
$\operatorname {SL}(n,\mathbb {R})$
, we find
![]() $B \in \operatorname {GL}(n,\mathbb {R})$
such that either
$B \in \operatorname {GL}(n,\mathbb {R})$
such that either
![]() $\delta (g) = B g B^{-1}$
for all
$\delta (g) = B g B^{-1}$
for all
![]() $g \in \mathcal {G}$
, or
$g \in \mathcal {G}$
, or
![]() $\delta (g) = B (g^{-1})^T B^{-1}$
for all
$\delta (g) = B (g^{-1})^T B^{-1}$
for all
![]() $g \in \mathcal {G}$
. In the second case,
$g \in \mathcal {G}$
. In the second case,
![]() $\delta (\mathcal {H})$
and
$\delta (\mathcal {H})$
and
![]() $\mathcal {H}$
are not conjugate. So we are in the first case. We get that
$\mathcal {H}$
are not conjugate. So we are in the first case. We get that
![]() $g_0 = B C$
where
$g_0 = B C$
where
![]() $C \in \operatorname {GL}(n,\mathbb {R})$
normalizes
$C \in \operatorname {GL}(n,\mathbb {R})$
normalizes
![]() $\mathcal {H}$
. That means that
$\mathcal {H}$
. That means that
![]() $C e_1 = a e_1$
for some
$C e_1 = a e_1$
for some
![]() $a \in \mathbb {R}^*$
. Translating the formula
$a \in \mathbb {R}^*$
. Translating the formula
![]() $\Delta (g\mathcal {H}) = \delta (g)g_0\mathcal {H}$
to
$\Delta (g\mathcal {H}) = \delta (g)g_0\mathcal {H}$
to
![]() $\mathbb {R}^n$
, we have proven that
$\mathbb {R}^n$
, we have proven that
![]() $\Delta (x) = a B(x)$
for a.e.
$\Delta (x) = a B(x)$
for a.e.
![]() $x \in \mathbb {R}^n$
. Writing
$x \in \mathbb {R}^n$
. Writing
![]() $A = a B$
, the first part of the lemma is proven.
$A = a B$
, the first part of the lemma is proven.
In particular, if
![]() $G < \operatorname {SL}(n,\mathbb {R})$
is a dense subgroup, then the only non-singular automorphisms of
$G < \operatorname {SL}(n,\mathbb {R})$
is a dense subgroup, then the only non-singular automorphisms of
![]() $\mathbb {R}^n$
that commute with
$\mathbb {R}^n$
that commute with
![]() $G \curvearrowright \mathbb {R}^n$
are given by
$G \curvearrowright \mathbb {R}^n$
are given by
![]() $x \mapsto a x$
for some
$x \mapsto a x$
for some
![]() $a \in \mathbb {R}^*$
. This transformation scales the measure by
$a \in \mathbb {R}^*$
. This transformation scales the measure by
![]() $|a|^n$
. The only measure-scaling action
$|a|^n$
. The only measure-scaling action
![]() $\mathbb {R} \curvearrowright \mathbb {R}^n$
commuting with
$\mathbb {R} \curvearrowright \mathbb {R}^n$
commuting with
![]() $G \curvearrowright \mathbb {R}^n$
is thus given by
$G \curvearrowright \mathbb {R}^n$
is thus given by
![]() $t \cdot x = e^{-t/n} x$
.
$t \cdot x = e^{-t/n} x$
.
We have now gathered enough material to prove Corollary B. We also add the computation of the outer automorphism group of these type III
![]() $_0$
orbit equivalence relations. For every ergodic flow
$_0$
orbit equivalence relations. For every ergodic flow
![]() $\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
, we denote by
$\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
, we denote by
![]() $\operatorname {Aut}_{\mathbb {R}}(\alpha )$
the Polish group of all non-singular automorphisms of
$\operatorname {Aut}_{\mathbb {R}}(\alpha )$
the Polish group of all non-singular automorphisms of
![]() $(Y,\eta )$
that commute with the flow
$(Y,\eta )$
that commute with the flow
![]() $\alpha $
. Note that
$\alpha $
. Note that
![]() $\mathbb {R} \subset \operatorname {Aut}_{\mathbb {R}}(\alpha )$
by definition.
$\mathbb {R} \subset \operatorname {Aut}_{\mathbb {R}}(\alpha )$
by definition.
Corollary 6.7. Corollary B holds.
Moreover, writing
![]() $K = \{a/b \mid a,b \in \mathcal {A}, b \neq 0\}$
, the outer automorphism group
$K = \{a/b \mid a,b \in \mathcal {A}, b \neq 0\}$
, the outer automorphism group
![]() $\operatorname {Out}(\mathcal {R}(n,\mathcal {A},\alpha ))$
of the orbit equivalence relation
$\operatorname {Out}(\mathcal {R}(n,\mathcal {A},\alpha ))$
of the orbit equivalence relation
![]() $\mathcal {R}(n,\mathcal {A},\alpha )$
of the action
$\mathcal {R}(n,\mathcal {A},\alpha )$
of the action
![]() $\beta (n,\mathcal {A},\alpha )$
is given by
$\beta (n,\mathcal {A},\alpha )$
is given by
In particular, when
![]() $\mathcal {A} = \mathbb {Z}[\mathcal {S}^{-1}]$
for some finite non-empty set of prime numbers
$\mathcal {A} = \mathbb {Z}[\mathcal {S}^{-1}]$
for some finite non-empty set of prime numbers
![]() $\mathcal {S}$
, we have
$\mathcal {S}$
, we have
![]() $E(n,\mathcal {A}) = \operatorname {SL}(n,\mathbb {Z}[\mathcal {S}^{-1}])$
and
$E(n,\mathcal {A}) = \operatorname {SL}(n,\mathbb {Z}[\mathcal {S}^{-1}])$
and
When
![]() $\mathcal {A} = \mathcal {O}_K$
, where
$\mathcal {A} = \mathcal {O}_K$
, where
![]() $K \subset \mathbb {R}$
is an algebraic number field with
$K \subset \mathbb {R}$
is an algebraic number field with
![]() $[K:\mathbb {Q}] \geq 2$
, we denote by
$[K:\mathbb {Q}] \geq 2$
, we denote by
![]() $\operatorname {Cl}(K)$
its ideal class group and consider the subgroup
$\operatorname {Cl}(K)$
its ideal class group and consider the subgroup
![]() $\operatorname {Cl}_n(K) = \{J \in \operatorname {Cl}(K) \mid J^n = 1\}$
. Then
$\operatorname {Cl}_n(K) = \{J \in \operatorname {Cl}(K) \mid J^n = 1\}$
. Then
![]() $E(n,\mathcal {A}) = \operatorname {SL}(n,\mathcal {O}_K)$
and
$E(n,\mathcal {A}) = \operatorname {SL}(n,\mathcal {O}_K)$
and
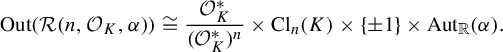 $$ \begin{align} \operatorname{Out}(\mathcal{R}(n,\mathcal{O}_K,\alpha)) \cong \frac{\mathcal{O}_K^*}{(\mathcal{O}_K^*)^n} \times \operatorname{Cl}_n(K) \times \{\pm 1\} \times \operatorname{Aut}_{\mathbb{R}}(\alpha). \end{align} $$
$$ \begin{align} \operatorname{Out}(\mathcal{R}(n,\mathcal{O}_K,\alpha)) \cong \frac{\mathcal{O}_K^*}{(\mathcal{O}_K^*)^n} \times \operatorname{Cl}_n(K) \times \{\pm 1\} \times \operatorname{Aut}_{\mathbb{R}}(\alpha). \end{align} $$
Proof. By Theorem 5.8, under the hypotheses of Corollary B, the actions
![]() $E(n,\mathcal {A}) \curvearrowright \mathbb {R}^n / \mathbb {R}^*_+$
satisfy all the assumptions of Corollary 5.6. So by Corollary 5.6, the actions
$E(n,\mathcal {A}) \curvearrowright \mathbb {R}^n / \mathbb {R}^*_+$
satisfy all the assumptions of Corollary 5.6. So by Corollary 5.6, the actions
![]() $\beta (n,\mathcal {A},\alpha )$
are essentially free, ergodic, simple and OE superrigid (v2), with associated flow
$\beta (n,\mathcal {A},\alpha )$
are essentially free, ergodic, simple and OE superrigid (v2), with associated flow
![]() $\widehat {\alpha }$
.
$\widehat {\alpha }$
.
In particular, if
![]() $\beta (n,\mathcal {A},\alpha )$
and
$\beta (n,\mathcal {A},\alpha )$
and
![]() $\beta (n',\mathcal {A}',\alpha ')$
are stably orbit equivalent, the actions must be conjugate. By Proposition 6.4 and Lemma 6.6, the flows
$\beta (n',\mathcal {A}',\alpha ')$
are stably orbit equivalent, the actions must be conjugate. By Proposition 6.4 and Lemma 6.6, the flows
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
are isomorphic and the actions
$\alpha '$
are isomorphic and the actions
![]() $E(n,\mathcal {A}) \curvearrowright \mathbb {R}^n/\mathbb {R}^*_+$
and
$E(n,\mathcal {A}) \curvearrowright \mathbb {R}^n/\mathbb {R}^*_+$
and
![]() $E(n',\mathcal {A}') \curvearrowright \mathbb {R}^{n'}/\mathbb {R}^*_+$
are conjugate. Then their Maharam extensions
$E(n',\mathcal {A}') \curvearrowright \mathbb {R}^{n'}/\mathbb {R}^*_+$
are conjugate. Then their Maharam extensions
![]() $E(n,\mathcal {A}) \curvearrowright \mathbb {R}^n$
and
$E(n,\mathcal {A}) \curvearrowright \mathbb {R}^n$
and
![]() $E(n',\mathcal {A}') \curvearrowright \mathbb {R}^{n'}$
are also conjugate. By Lemma 6.6,
$E(n',\mathcal {A}') \curvearrowright \mathbb {R}^{n'}$
are also conjugate. By Lemma 6.6,
![]() $n=n'$
and there is an
$n=n'$
and there is an
![]() $A \in \operatorname {GL}(n,\mathbb {R})$
such that
$A \in \operatorname {GL}(n,\mathbb {R})$
such that
![]() $A E(n,\mathcal {A}) A^{-1} = E(n,\mathcal {A}')$
.
$A E(n,\mathcal {A}) A^{-1} = E(n,\mathcal {A}')$
.
For every subring
![]() $\mathcal {A}_1 \subset \mathbb {R}$
, we denote by
$\mathcal {A}_1 \subset \mathbb {R}$
, we denote by
![]() $M(n,\mathcal {A}_1)$
the ring of
$M(n,\mathcal {A}_1)$
the ring of
![]() $n \times n$
matrices with entries in
$n \times n$
matrices with entries in
![]() $\mathcal {A}_1$
. We claim that the subring
$\mathcal {A}_1$
. We claim that the subring
![]() $N(n,\mathcal {A}_1) \subset M(n,\mathcal {A}_1)$
generated by
$N(n,\mathcal {A}_1) \subset M(n,\mathcal {A}_1)$
generated by
![]() $E(n,\mathcal {A}_1)$
is equal to
$E(n,\mathcal {A}_1)$
is equal to
![]() $M(n,\mathcal {A}_1)$
. For all
$M(n,\mathcal {A}_1)$
. For all
![]() $i,j \in \{1,\ldots ,n\}$
and
$i,j \in \{1,\ldots ,n\}$
and
![]() $a \in \mathcal {A}_1$
, we denote by
$a \in \mathcal {A}_1$
, we denote by
![]() $E_{ij}(a)$
the matrix that has the entry a in position
$E_{ij}(a)$
the matrix that has the entry a in position
![]() $ij$
and
$ij$
and
![]() $0$
s elsewhere. When
$0$
s elsewhere. When
![]() $i \neq j$
and
$i \neq j$
and
![]() $a \in \mathcal {A}_1$
, we have that
$a \in \mathcal {A}_1$
, we have that
![]() $1 + E_{ij}(a) \in E(n,\mathcal {A}_1)$
and
$1 + E_{ij}(a) \in E(n,\mathcal {A}_1)$
and
![]() $1 \in E(n,\mathcal {A}_1)$
. Thus,
$1 \in E(n,\mathcal {A}_1)$
. Thus,
![]() $E_{ij}(a) \in N(n,\mathcal {A}_1)$
. Since
$E_{ij}(a) \in N(n,\mathcal {A}_1)$
. Since
![]() $\operatorname {SL}(n,\mathbb {Z}) = E(n,\mathbb {Z}) \subset E(n,\mathcal {A}_1)$
, given
$\operatorname {SL}(n,\mathbb {Z}) = E(n,\mathbb {Z}) \subset E(n,\mathcal {A}_1)$
, given
![]() $i \neq j$
, the matrix
$i \neq j$
, the matrix
![]() $\sigma _{ij}$
with entry
$\sigma _{ij}$
with entry
![]() $1$
in position
$1$
in position
![]() $ij$
, entry
$ij$
, entry
![]() $-1$
in position
$-1$
in position
![]() $ji$
, and
$ji$
, and
![]() $0$
s elsewhere belongs to
$0$
s elsewhere belongs to
![]() $E(n,\mathcal {A}_1)$
. Thus, also
$E(n,\mathcal {A}_1)$
. Thus, also
![]() $E_{ii}(a) = \sigma _{ij} E_{ji}(a) \in N(n,\mathcal {A}_1)$
. This proves the claim.
$E_{ii}(a) = \sigma _{ij} E_{ji}(a) \in N(n,\mathcal {A}_1)$
. This proves the claim.
Since
![]() $A E(n,\mathcal {A}) A^{-1} = E(n,\mathcal {A}')$
, the claim above implies that
$A E(n,\mathcal {A}) A^{-1} = E(n,\mathcal {A}')$
, the claim above implies that
![]() $A M(n,\mathcal {A}) A^{-1} = M(n,\mathcal {A}')$
. So for every
$A M(n,\mathcal {A}) A^{-1} = M(n,\mathcal {A}')$
. So for every
![]() $i \in \{1,\ldots ,n\}$
and
$i \in \{1,\ldots ,n\}$
and
![]() $a \in \mathcal {A}$
, we have that
$a \in \mathcal {A}$
, we have that
![]() $A E_{ii}(a) A^{-1} \in M(n,\mathcal {A}')$
. Taking the
$A E_{ii}(a) A^{-1} \in M(n,\mathcal {A}')$
. Taking the
![]() $jj$
-entry, it follows that
$jj$
-entry, it follows that
![]() $A_{ji} (A^{-1})_{ij} a \in \mathcal {A}'$
. Summing over i, it follows that
$A_{ji} (A^{-1})_{ij} a \in \mathcal {A}'$
. Summing over i, it follows that
![]() $a \in \mathcal {A}'$
. So
$a \in \mathcal {A}'$
. So
![]() $\mathcal {A} \subset \mathcal {A}'$
. By symmetry, also the converse inclusion holds, so that
$\mathcal {A} \subset \mathcal {A}'$
. By symmetry, also the converse inclusion holds, so that
![]() $\mathcal {A} = \mathcal {A}'$
.
$\mathcal {A} = \mathcal {A}'$
.
The arguments above apply in particular to the self orbit equivalences of
![]() $\beta (n,\mathcal {A},\alpha )$
and give us that
$\beta (n,\mathcal {A},\alpha )$
and give us that
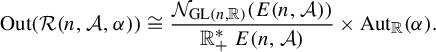 $$ \begin{align*} \operatorname{Out}(\mathcal{R}(n,\mathcal{A},\alpha)) \cong \frac{\mathcal{N}_{\operatorname{GL}(n,\mathbb{R})}(E(n,\mathcal{A}))}{\mathbb{R}^*_+ \, E(n,\mathcal{A})} \times \operatorname{Aut}_{\mathbb{R}}(\alpha). \end{align*} $$
$$ \begin{align*} \operatorname{Out}(\mathcal{R}(n,\mathcal{A},\alpha)) \cong \frac{\mathcal{N}_{\operatorname{GL}(n,\mathbb{R})}(E(n,\mathcal{A}))}{\mathbb{R}^*_+ \, E(n,\mathcal{A})} \times \operatorname{Aut}_{\mathbb{R}}(\alpha). \end{align*} $$
Write
![]() $\mathcal {G}_+ = \{A \in \operatorname {GL}(n,\mathbb {R}) \mid \det A> 0\}$
. Since n is odd, we have that
$\mathcal {G}_+ = \{A \in \operatorname {GL}(n,\mathbb {R}) \mid \det A> 0\}$
. Since n is odd, we have that
![]() $\operatorname {GL}(n,\mathbb {R}) = \{\pm 1\} \times \mathcal {G}_+$
. It follows that
$\operatorname {GL}(n,\mathbb {R}) = \{\pm 1\} \times \mathcal {G}_+$
. It follows that
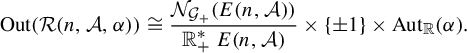 $$ \begin{align} \operatorname{Out}(\mathcal{R}(n,\mathcal{A},\alpha)) \cong \frac{\mathcal{N}_{\mathcal{G}_+}(E(n,\mathcal{A}))}{\mathbb{R}^*_+ \, E(n,\mathcal{A})} \times \{\pm 1\} \times \operatorname{Aut}_{\mathbb{R}}(\alpha). \end{align} $$
$$ \begin{align} \operatorname{Out}(\mathcal{R}(n,\mathcal{A},\alpha)) \cong \frac{\mathcal{N}_{\mathcal{G}_+}(E(n,\mathcal{A}))}{\mathbb{R}^*_+ \, E(n,\mathcal{A})} \times \{\pm 1\} \times \operatorname{Aut}_{\mathbb{R}}(\alpha). \end{align} $$
We have also proven above that every
![]() $A \in \mathcal {N}_{\operatorname {GL}(n,\mathbb {R})}(E(n,\mathcal {A}))$
satisfies
$A \in \mathcal {N}_{\operatorname {GL}(n,\mathbb {R})}(E(n,\mathcal {A}))$
satisfies
![]() $A M(n,\mathcal {A}) A^{-1} = M(n,\mathcal {A})$
, meaning that
$A M(n,\mathcal {A}) A^{-1} = M(n,\mathcal {A})$
, meaning that
![]() $A_{ij} (A^{-1})_{kl} \in \mathcal {A}$
for all
$A_{ij} (A^{-1})_{kl} \in \mathcal {A}$
for all
![]() $i,j,k,l$
. Denoting by
$i,j,k,l$
. Denoting by
![]() $K = \{a/b \mid a,b \in \mathcal {A}, b \neq 0\}$
the field of fractions of
$K = \{a/b \mid a,b \in \mathcal {A}, b \neq 0\}$
the field of fractions of
![]() $\mathcal {A}$
, it follows in particular that A must be a multiple of a matrix with entries in K. It follows that
$\mathcal {A}$
, it follows in particular that A must be a multiple of a matrix with entries in K. It follows that
 $$ \begin{align} \frac{\mathcal{N}_{\mathcal{G}_+}(E(n,\mathcal{A}))}{\mathbb{R}^*_+ \, E(n,\mathcal{A})} = \frac{\mathcal{N}_{\mathcal{G}_+ \cap \operatorname{GL}(n,K)}(E(n,\mathcal{A}))}{(\mathbb{R}^*_+ \cap K) \, E(n,\mathcal{A})} = \frac{\mathcal{N}_{\operatorname{GL}(n,K)}(E(n,\mathcal{A}))}{K^* \, E(n,\mathcal{A})}. \end{align} $$
$$ \begin{align} \frac{\mathcal{N}_{\mathcal{G}_+}(E(n,\mathcal{A}))}{\mathbb{R}^*_+ \, E(n,\mathcal{A})} = \frac{\mathcal{N}_{\mathcal{G}_+ \cap \operatorname{GL}(n,K)}(E(n,\mathcal{A}))}{(\mathbb{R}^*_+ \cap K) \, E(n,\mathcal{A})} = \frac{\mathcal{N}_{\operatorname{GL}(n,K)}(E(n,\mathcal{A}))}{K^* \, E(n,\mathcal{A})}. \end{align} $$
Combining this with (6.11), we have proven (6.8).
By [Reference O’MearaOM65, Theorem B], a matrix
![]() $A \in \operatorname {GL}(n,K)$
normalizes
$A \in \operatorname {GL}(n,K)$
normalizes
![]() $E(n,\mathcal {A})$
if and only if
$E(n,\mathcal {A})$
if and only if
![]() $A(\mathcal {A}^n) = \mathfrak {a} \mathcal {A}^n$
for an invertible fractional ideal
$A(\mathcal {A}^n) = \mathfrak {a} \mathcal {A}^n$
for an invertible fractional ideal
![]() $\mathfrak {a} \subset K$
.
$\mathfrak {a} \subset K$
.
When
![]() $\mathcal {A} = \mathbb {Z}[\mathcal {S}^{-1}]$
, every fractional ideal of
$\mathcal {A} = \mathbb {Z}[\mathcal {S}^{-1}]$
, every fractional ideal of
![]() $\mathcal {A}$
is principal, so that
$\mathcal {A}$
is principal, so that
![]() $\mathcal {N}_{\operatorname {GL}(n,K)} (E(n,\mathcal {A})) = K^* \operatorname {GL}(n,\mathcal {A})$
. By [Reference Hahn and O’MearaHOM89, Theorem 4.3.9], we also have that
$\mathcal {N}_{\operatorname {GL}(n,K)} (E(n,\mathcal {A})) = K^* \operatorname {GL}(n,\mathcal {A})$
. By [Reference Hahn and O’MearaHOM89, Theorem 4.3.9], we also have that
![]() $E(n,\mathcal {A}) = \operatorname {SL}(n,\mathcal {A})$
. So the natural map
$E(n,\mathcal {A}) = \operatorname {SL}(n,\mathcal {A})$
. So the natural map
is surjective and has kernel
![]() $\{A \in \operatorname {GL}(n,\mathcal {A}) \mid \det A \in (\mathcal {A}^*)^n\}$
. The group of units of
$\{A \in \operatorname {GL}(n,\mathcal {A}) \mid \det A \in (\mathcal {A}^*)^n\}$
. The group of units of
![]() $\mathcal {A} = \mathbb {Z}[\mathcal {S}^{-1}]$
is the free abelian group generated by
$\mathcal {A} = \mathbb {Z}[\mathcal {S}^{-1}]$
is the free abelian group generated by
![]() $p \in \mathcal {S}$
, so that combining (6.11) en (6.12), we have proven (6.9).
$p \in \mathcal {S}$
, so that combining (6.11) en (6.12), we have proven (6.9).
When K is an algebraic number field with
![]() $[K:\mathbb {Q}] \geq 2$
and
$[K:\mathbb {Q}] \geq 2$
and
![]() $\mathcal {A} = \mathcal {O}_K$
, again by [Reference Hahn and O’MearaHOM89, Theorem 4.3.9], we have that
$\mathcal {A} = \mathcal {O}_K$
, again by [Reference Hahn and O’MearaHOM89, Theorem 4.3.9], we have that
![]() $E(n,\mathcal {A}) = \operatorname {SL}(n,\mathcal {A})$
. Denote by
$E(n,\mathcal {A}) = \operatorname {SL}(n,\mathcal {A})$
. Denote by
![]() $I(K)$
the group of fractional ideals in K. As mentioned in [Reference O’MearaOM65, Example 6.5], the following two statements hold. If
$I(K)$
the group of fractional ideals in K. As mentioned in [Reference O’MearaOM65, Example 6.5], the following two statements hold. If
![]() $A \in \operatorname {GL}(n,K)$
,
$A \in \operatorname {GL}(n,K)$
,
![]() $\mathfrak {a} \in I(K)$
and
$\mathfrak {a} \in I(K)$
and
![]() $A(\mathcal {A}^n) = \mathfrak {a} \mathcal {A}^n$
, we have
$A(\mathcal {A}^n) = \mathfrak {a} \mathcal {A}^n$
, we have
![]() $\mathfrak {a}^n = \det (A) \, \mathcal {A}$
. Conversely, if
$\mathfrak {a}^n = \det (A) \, \mathcal {A}$
. Conversely, if
![]() $\mathfrak {a} \in I(K)$
,
$\mathfrak {a} \in I(K)$
,
![]() $\alpha \in K^*$
and
$\alpha \in K^*$
and
![]() $\mathfrak {a}^n = \alpha \, \mathcal {A}$
, there exists an
$\mathfrak {a}^n = \alpha \, \mathcal {A}$
, there exists an
![]() $A \in \operatorname {GL}(n,K)$
such that
$A \in \operatorname {GL}(n,K)$
such that
![]() $A(\mathcal {A}^n) = \mathfrak {a} \mathcal {A}^n$
and
$A(\mathcal {A}^n) = \mathfrak {a} \mathcal {A}^n$
and
![]() $\det A = \alpha $
. For completeness, we provide a more detailed argument. The first implication is contained in [Reference O’MearaOM73, 81:7]. For the second implication, take
$\det A = \alpha $
. For completeness, we provide a more detailed argument. The first implication is contained in [Reference O’MearaOM73, 81:7]. For the second implication, take
![]() $\mathfrak {a} \in I(K)$
and
$\mathfrak {a} \in I(K)$
and
![]() $\alpha \in K^*$
with
$\alpha \in K^*$
with
![]() $\mathfrak {a}^n = \alpha \, \mathcal {A}$
. Denote by
$\mathfrak {a}^n = \alpha \, \mathcal {A}$
. Denote by
![]() $e_1,\ldots ,e_n$
the standard basis of
$e_1,\ldots ,e_n$
the standard basis of
![]() $K^n$
. By [Reference O’MearaOM73, 81:5], we find
$K^n$
. By [Reference O’MearaOM73, 81:5], we find
![]() $\mathfrak {b} \in I(K)$
and
$\mathfrak {b} \in I(K)$
and
![]() $B \in \operatorname {GL}(n,K)$
such that
$B \in \operatorname {GL}(n,K)$
such that
![]() $\mathfrak {a} \mathcal {A}^n = B(\mathfrak {b} e_1 + \mathcal {A} e_2 + \cdots + \mathcal {A} e_n)$
. By our assumption and [Reference O’MearaOM73, 81:7], we have
$\mathfrak {a} \mathcal {A}^n = B(\mathfrak {b} e_1 + \mathcal {A} e_2 + \cdots + \mathcal {A} e_n)$
. By our assumption and [Reference O’MearaOM73, 81:7], we have
![]() $\alpha \, \mathcal {A} = \mathfrak {a}^n = \det (B) \, \mathfrak {b}$
. Denote by
$\alpha \, \mathcal {A} = \mathfrak {a}^n = \det (B) \, \mathfrak {b}$
. Denote by
![]() $D \in GL(n,K)$
the diagonal matrix with
$D \in GL(n,K)$
the diagonal matrix with
![]() $D_{11} = \alpha \det (B)^{-1}$
and
$D_{11} = \alpha \det (B)^{-1}$
and
![]() $D_{ii} = 1$
for
$D_{ii} = 1$
for
![]() $i \neq 1$
. Since
$i \neq 1$
. Since
![]() $\mathfrak {b} = D_{11} \, \mathcal {A}$
, writing
$\mathfrak {b} = D_{11} \, \mathcal {A}$
, writing
![]() $A = BD$
, we conclude that
$A = BD$
, we conclude that
![]() $A(\mathcal {A}^n) = \mathfrak {a} \mathcal {A}^n$
. By construction,
$A(\mathcal {A}^n) = \mathfrak {a} \mathcal {A}^n$
. By construction,
![]() $\det (A) = \alpha $
.
$\det (A) = \alpha $
.
Define the subgroup
![]() $X_n(K)$
of the abelian group
$X_n(K)$
of the abelian group
![]() $I(K) \times K^*$
by
$I(K) \times K^*$
by
![]() $X_n(K) = \{(\mathfrak {a},\alpha ) \in I(K) \times K^* \mid \mathfrak {a}^n = \alpha \mathcal {A}\}$
. Define the subgroup
$X_n(K) = \{(\mathfrak {a},\alpha ) \in I(K) \times K^* \mid \mathfrak {a}^n = \alpha \mathcal {A}\}$
. Define the subgroup
![]() $Y_n(K) \subset X_n(K)$
by
$Y_n(K) \subset X_n(K)$
by
![]() $Y_n(K) = \{(\beta \mathcal {A}, \beta ^n) \mid \beta \in K^*\}$
. Define
$Y_n(K) = \{(\beta \mathcal {A}, \beta ^n) \mid \beta \in K^*\}$
. Define
![]() $V_n(K) = X_n(K) / Y_n(K)$
. To conclude the proof of the corollary, we prove the following two statements:
$V_n(K) = X_n(K) / Y_n(K)$
. To conclude the proof of the corollary, we prove the following two statements:
 $$ \begin{align*}V_n(K) \cong \frac{\mathcal{A}^*}{(\mathcal{A}^*)^n} \times \operatorname{Cl}_n(K) \quad \text{and}\quad V_n(K) \cong \frac{\mathcal{N}_{\operatorname{GL}(n,K)}(\operatorname{SL}(n,\mathcal{A}))}{K^* \operatorname{SL}(n,\mathcal{A})}.\end{align*} $$
$$ \begin{align*}V_n(K) \cong \frac{\mathcal{A}^*}{(\mathcal{A}^*)^n} \times \operatorname{Cl}_n(K) \quad \text{and}\quad V_n(K) \cong \frac{\mathcal{N}_{\operatorname{GL}(n,K)}(\operatorname{SL}(n,\mathcal{A}))}{K^* \operatorname{SL}(n,\mathcal{A})}.\end{align*} $$
The projection on the first coordinate gives a surjective group homomorphism
![]() $V_n(K) \to \operatorname {Cl}_n(K)$
with kernel
$V_n(K) \to \operatorname {Cl}_n(K)$
with kernel
![]() $\mathcal {A}^* / (\mathcal {A}^*)^n$
. We prove that this homomorphism is split. Since
$\mathcal {A}^* / (\mathcal {A}^*)^n$
. We prove that this homomorphism is split. Since
![]() $\operatorname {Cl}_n(K)$
is a finite abelian group in which the order of every element divides n, it suffices to prove that every element of order
$\operatorname {Cl}_n(K)$
is a finite abelian group in which the order of every element divides n, it suffices to prove that every element of order
![]() $k \mid n$
in
$k \mid n$
in
![]() $\operatorname {Cl}_n(K)$
can be lifted to an element of order k in
$\operatorname {Cl}_n(K)$
can be lifted to an element of order k in
![]() $V_n(K)$
. When
$V_n(K)$
. When
![]() $\mathfrak {a} \in I(K)$
and
$\mathfrak {a} \in I(K)$
and
![]() $\mathfrak {a}^k = \beta \mathcal {A}$
with
$\mathfrak {a}^k = \beta \mathcal {A}$
with
![]() $\beta \in K^*$
, write
$\beta \in K^*$
, write
![]() $n = k m$
and note that
$n = k m$
and note that
![]() $(\mathfrak {a},\beta ^m)$
defines such a lift of order k. So
$(\mathfrak {a},\beta ^m)$
defines such a lift of order k. So
![]() $V_n(K) \cong \mathcal {A}^* / (\mathcal {A}^*)^n \times \operatorname {Cl}_n(K)$
.
$V_n(K) \cong \mathcal {A}^* / (\mathcal {A}^*)^n \times \operatorname {Cl}_n(K)$
.
For every
![]() $(\mathfrak {a},\alpha ) \in X_n(K)$
, by the discussion above, we can choose
$(\mathfrak {a},\alpha ) \in X_n(K)$
, by the discussion above, we can choose
![]() $A \in \operatorname {GL}(n,K)$
such that
$A \in \operatorname {GL}(n,K)$
such that
![]() $A(\mathcal {A}^n) = \mathfrak {a} \mathcal {A}^n$
and
$A(\mathcal {A}^n) = \mathfrak {a} \mathcal {A}^n$
and
![]() $\det A = \alpha $
. This matrix A is uniquely determined up to right multiplication by a matrix in
$\det A = \alpha $
. This matrix A is uniquely determined up to right multiplication by a matrix in
![]() $\operatorname {SL}(n,\mathcal {A})$
. This realizes a surjective group homomorphism
$\operatorname {SL}(n,\mathcal {A})$
. This realizes a surjective group homomorphism
and the kernel of this homomorphism is by construction equal to
![]() $Y_n(K)$
. This concludes the proof of the corollary.
$Y_n(K)$
. This concludes the proof of the corollary.
Example 6.8. Let
![]() $\mathcal {A} = \mathbb {Z}[\mathcal {S}^{-1}]$
where
$\mathcal {A} = \mathbb {Z}[\mathcal {S}^{-1}]$
where
![]() $\mathcal {S}$
is a finite non-empty set of prime numbers, or let
$\mathcal {S}$
is a finite non-empty set of prime numbers, or let
![]() $\mathcal {A} = \mathcal {O}_K$
be the ring of integers of an algebraic number field
$\mathcal {A} = \mathcal {O}_K$
be the ring of integers of an algebraic number field
![]() $K \subset \mathbb {R}$
with
$K \subset \mathbb {R}$
with
![]() $[K:\mathbb {Q}] \geq 2$
. As mentioned above, we have
$[K:\mathbb {Q}] \geq 2$
. As mentioned above, we have
![]() $E(n,\mathcal {A}) = \operatorname {SL}(n,\mathcal {A})$
for all
$E(n,\mathcal {A}) = \operatorname {SL}(n,\mathcal {A})$
for all
![]() $n \geq 3$
, and a proof can, for instance, be found in [Reference Hahn and O’MearaHOM89, Theorem 4.3.9].
$n \geq 3$
, and a proof can, for instance, be found in [Reference Hahn and O’MearaHOM89, Theorem 4.3.9].
By [Reference SuslinSus77, Corollaries 6.6 and 7.10], for the same rings
![]() $\mathcal {A}$
as in the previous paragraph and for all integers
$\mathcal {A}$
as in the previous paragraph and for all integers
![]() $0 \leq k \leq s$
, we also have that
$0 \leq k \leq s$
, we also have that
![]() $E(n,\mathcal {A}_1) = \operatorname {SL}(n,\mathcal {A}_1)$
when
$E(n,\mathcal {A}_1) = \operatorname {SL}(n,\mathcal {A}_1)$
when
![]() $\mathcal {A}_1$
is the ring of (Laurent) polynomials over
$\mathcal {A}_1$
is the ring of (Laurent) polynomials over
![]() $\mathcal {A}$
, defined by
$\mathcal {A}$
, defined by
![]() $\mathcal {A}_1 = \mathcal {A}[X_1,\ldots ,X_k,X_{k+1}^{\pm 1},\ldots ,X_s^{\pm 1}]$
, and
$\mathcal {A}_1 = \mathcal {A}[X_1,\ldots ,X_k,X_{k+1}^{\pm 1},\ldots ,X_s^{\pm 1}]$
, and
![]() $n \geq 3$
. Therefore, whenever
$n \geq 3$
. Therefore, whenever
![]() $\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _s \in \mathbb {R}$
are algebraically independent transcendental numbers, we find that the rings
$\unicode{x3bb} _1,\ldots ,\unicode{x3bb} _s \in \mathbb {R}$
are algebraically independent transcendental numbers, we find that the rings
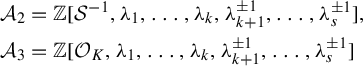 $$ \begin{align*}\mathcal{A}_2 &= \mathbb{Z}[\mathcal{S}^{-1},\unicode{x3bb}_1,\ldots,\unicode{x3bb}_k,\unicode{x3bb}_{k+1}^{\pm 1},\ldots,\unicode{x3bb}_s^{\pm 1}] , \\ \mathcal{A}_3 &= \mathbb{Z}[\mathcal{O}_K,\unicode{x3bb}_1,\ldots,\unicode{x3bb}_k,\unicode{x3bb}_{k+1}^{\pm 1},\ldots,\unicode{x3bb}_s^{\pm 1}]\end{align*} $$
$$ \begin{align*}\mathcal{A}_2 &= \mathbb{Z}[\mathcal{S}^{-1},\unicode{x3bb}_1,\ldots,\unicode{x3bb}_k,\unicode{x3bb}_{k+1}^{\pm 1},\ldots,\unicode{x3bb}_s^{\pm 1}] , \\ \mathcal{A}_3 &= \mathbb{Z}[\mathcal{O}_K,\unicode{x3bb}_1,\ldots,\unicode{x3bb}_k,\unicode{x3bb}_{k+1}^{\pm 1},\ldots,\unicode{x3bb}_s^{\pm 1}]\end{align*} $$
also satisfy
![]() $E(n,\mathcal {A}_i) = \operatorname {SL}(n,\mathcal {A}_i)$
for all
$E(n,\mathcal {A}_i) = \operatorname {SL}(n,\mathcal {A}_i)$
for all
![]() $n \geq 3$
and
$n \geq 3$
and
![]() $i \in \{2,3\}$
. The associated group actions
$i \in \{2,3\}$
. The associated group actions
![]() $\beta (n,\mathcal {A}_i,\alpha )$
are OE superrigid (v2). Moreover, the outer automorphism groups
$\beta (n,\mathcal {A}_i,\alpha )$
are OE superrigid (v2). Moreover, the outer automorphism groups
![]() $\operatorname {Out}(\beta (n,\mathcal {A}_i,\alpha ))$
are still given by formulas similar to (6.9) and (6.10):
$\operatorname {Out}(\beta (n,\mathcal {A}_i,\alpha ))$
are still given by formulas similar to (6.9) and (6.10):
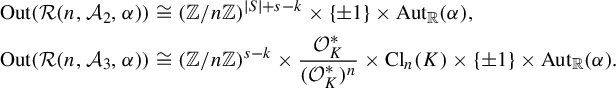 $$ \begin{align*}\begin{split} & \operatorname{Out}(\mathcal{R}(n,\mathcal{A}_2,\alpha)) \cong (\mathbb{Z}/n\mathbb{Z})^{|S|+s-k} \times \{\pm 1\} \times \operatorname{Aut}_{\mathbb{R}}(\alpha),\\ & \operatorname{Out}(\mathcal{R}(n,\mathcal{A}_3,\alpha)) \cong (\mathbb{Z}/n\mathbb{Z})^{s-k} \times \frac{\mathcal{O}_K^*}{(\mathcal{O}_K^*)^n} \times \operatorname{Cl}_n(K) \times \{\pm 1\} \times \operatorname{Aut}_{\mathbb{R}}(\alpha). \end{split}\end{align*} $$
$$ \begin{align*}\begin{split} & \operatorname{Out}(\mathcal{R}(n,\mathcal{A}_2,\alpha)) \cong (\mathbb{Z}/n\mathbb{Z})^{|S|+s-k} \times \{\pm 1\} \times \operatorname{Aut}_{\mathbb{R}}(\alpha),\\ & \operatorname{Out}(\mathcal{R}(n,\mathcal{A}_3,\alpha)) \cong (\mathbb{Z}/n\mathbb{Z})^{s-k} \times \frac{\mathcal{O}_K^*}{(\mathcal{O}_K^*)^n} \times \operatorname{Cl}_n(K) \times \{\pm 1\} \times \operatorname{Aut}_{\mathbb{R}}(\alpha). \end{split}\end{align*} $$
The reason for this is that by [Reference Anderson and AndersonAA81, Corollary 5.6], the invertible fractional ideals in the (Laurent) polynomial rings
![]() $\mathcal {A}_1$
above are all the product of a principal ideal and a fractional ideal in
$\mathcal {A}_1$
above are all the product of a principal ideal and a fractional ideal in
![]() $\mathcal {A}$
. The only difference compared to (6.9) and (6.10) thus comes from the group of units in
$\mathcal {A}$
. The only difference compared to (6.9) and (6.10) thus comes from the group of units in
![]() $\mathcal {A}_i$
.
$\mathcal {A}_i$
.
Remark 6.9. We remark that Corollary B provides a family of OE superrigid actions, with a prescribed associated flow, that is large and complex in a descriptive set-theoretic sense of the word. Fix a prime number p. For every finite subset
![]() $\mathcal {F} \in \mathbb {R}$
, we consider the ring
$\mathcal {F} \in \mathbb {R}$
, we consider the ring
![]() $\mathbb {Z}[p^{-1},\mathcal {F}]$
, which satisfies the assumptions of Corollary B, so that the actions
$\mathbb {Z}[p^{-1},\mathcal {F}]$
, which satisfies the assumptions of Corollary B, so that the actions
![]() $\beta (n,\mathbb {Z}[p^{-1},\mathcal {F}],\alpha )$
are OE superrigid (v2).
$\beta (n,\mathbb {Z}[p^{-1},\mathcal {F}],\alpha )$
are OE superrigid (v2).
By Corollary B, to decide when two such actions are stably orbit equivalent, we have to decide if
![]() $\mathbb {Z}[p^{-1},\mathcal {F}] = \mathbb {Z}[p^{-1},\mathcal {F}']$
. This defines a complicated equivalence relation
$\mathbb {Z}[p^{-1},\mathcal {F}] = \mathbb {Z}[p^{-1},\mathcal {F}']$
. This defines a complicated equivalence relation
![]() $\mathcal {R}$
on the Borel space of finite subsets of
$\mathcal {R}$
on the Borel space of finite subsets of
![]() $\mathbb {R}$
. When
$\mathbb {R}$
. When
![]() $\unicode{x3bb} ,\unicode{x3bb} ' \in \mathbb {R}$
are transcendental, we get that
$\unicode{x3bb} ,\unicode{x3bb} ' \in \mathbb {R}$
are transcendental, we get that
![]() $\mathbb {Z}[p^{-1},\unicode{x3bb} ] = \mathbb {Z}[p^{-1},\unicode{x3bb} ']$
if and only if there exist
$\mathbb {Z}[p^{-1},\unicode{x3bb} ] = \mathbb {Z}[p^{-1},\unicode{x3bb} ']$
if and only if there exist
![]() $a \in \mathbb {Z}[p^{-1}]^*$
and
$a \in \mathbb {Z}[p^{-1}]^*$
and
![]() $b \in \mathbb {Z}[p^{-1}]$
with
$b \in \mathbb {Z}[p^{-1}]$
with
![]() $\unicode{x3bb} = a \unicode{x3bb} ' + b$
. So at least the equivalence relation
$\unicode{x3bb} = a \unicode{x3bb} ' + b$
. So at least the equivalence relation
![]() $\mathcal {R}$
is not smooth.
$\mathcal {R}$
is not smooth.
Remark 6.10. As mentioned in the introduction, we can combine the construction of [Reference VaesVae13, Proposition D] with Corollary 5.6 to give ad hoc examples of non-singular actions
![]() $G \curvearrowright (X,\mu )$
that are W
$G \curvearrowright (X,\mu )$
that are W
![]() $^*$
-superrigid (v2) and that have any prescribed associated flow.
$^*$
-superrigid (v2) and that have any prescribed associated flow.
As in [Reference VaesVae13, Proposition D], denote by
![]() $\Sigma < \operatorname {SL}(5,\mathbb {Z})$
the subgroup of matrices A satisfying
$\Sigma < \operatorname {SL}(5,\mathbb {Z})$
the subgroup of matrices A satisfying
![]() $A(e_i) = e_i$
for
$A(e_i) = e_i$
for
![]() $i=1,2$
. Define G as the amalgamated free product
$i=1,2$
. Define G as the amalgamated free product
![]() $G = \operatorname {SL}(5,\mathbb {Z}) \ast _\Sigma (\Sigma \times \mathbb {Z})$
, with canonical homomorphism
$G = \operatorname {SL}(5,\mathbb {Z}) \ast _\Sigma (\Sigma \times \mathbb {Z})$
, with canonical homomorphism
![]() $\pi : G \to \operatorname {SL}(5,\mathbb {Z})$
. Consider the probability measure-preserving Bernoulli action
$\pi : G \to \operatorname {SL}(5,\mathbb {Z})$
. Consider the probability measure-preserving Bernoulli action
![]() $G \curvearrowright ([0,1],\unicode{x3bb} )^G$
. Given any ergodic flow
$G \curvearrowright ([0,1],\unicode{x3bb} )^G$
. Given any ergodic flow
![]() $\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
, consider the action
$\mathbb {R} \curvearrowright ^\alpha (Y,\eta )$
, consider the action
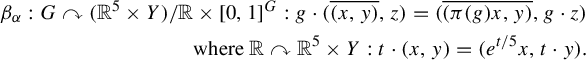 $$\begin{align*} \beta_\alpha : G \curvearrowright (\mathbb{R}^5 \times Y)/\mathbb{R} \times [0,1]^G : g \cdot (\overline{(x,y)},z) = (\overline{(\pi(g)x,y)},g \cdot z)\\ \text{where }\mathbb{R} \curvearrowright \mathbb{R}^5 \times Y : t \cdot (x,y) = (e^{t/5}x, t \cdot y). \end{align*}$$
$$\begin{align*} \beta_\alpha : G \curvearrowright (\mathbb{R}^5 \times Y)/\mathbb{R} \times [0,1]^G : g \cdot (\overline{(x,y)},z) = (\overline{(\pi(g)x,y)},g \cdot z)\\ \text{where }\mathbb{R} \curvearrowright \mathbb{R}^5 \times Y : t \cdot (x,y) = (e^{t/5}x, t \cdot y). \end{align*}$$
Then
![]() $\beta _\alpha $
is essentially free, non-singular, ergodic, simple and W
$\beta _\alpha $
is essentially free, non-singular, ergodic, simple and W
![]() $^*$
-superrigid (v2), with associated flow
$^*$
-superrigid (v2), with associated flow
![]() $\widehat {\alpha }$
.
$\widehat {\alpha }$
.
To prove this result, one uses [Reference VaesVae13, Theorem 8.1 and Proposition D] to show that the crossed product factor associated with
![]() $\beta _\alpha $
has a unique Cartan subalgebra, up to unitary conjugacy. It then suffices to prove that
$\beta _\alpha $
has a unique Cartan subalgebra, up to unitary conjugacy. It then suffices to prove that
![]() $\beta _\alpha $
is OE superrigid (v2). Since G is finitely generated and has trivial center, by Corollary 5.6, it suffices to prove that the action
$\beta _\alpha $
is OE superrigid (v2). Since G is finitely generated and has trivial center, by Corollary 5.6, it suffices to prove that the action
![]() $G \curvearrowright \mathbb {R}^5 \times [0,1]^G : g \cdot (x,z) = (\pi (g) x, g \cdot z)$
is simple and cocycle superrigid with countable targets. Simplicity is easy to check and cocycle superrigidity was proven in [Reference VaesVae13, Proposition D].
$G \curvearrowright \mathbb {R}^5 \times [0,1]^G : g \cdot (x,z) = (\pi (g) x, g \cdot z)$
is simple and cocycle superrigid with countable targets. Simplicity is easy to check and cocycle superrigidity was proven in [Reference VaesVae13, Proposition D].
Acknowledgements
S.V. is supported by FWO research project G090420N of the Research Foundation Flanders and by long-term structural funding—Methusalem grant of the Flemish government. B.V. holds PhD grant 1139721N fundamental research of the Research Foundation—Flanders.