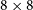1. Introduction
Our understanding of the early Universe has advanced significantly in the past two decades. The study of the Cosmic Microwave Background radiation (CMB) (Planck Collaboration et al. Reference Collaboration2020), for instance, has provided crucial insights into the initial density structure of the Universe, shedding light on the early stages of the Universe after recombination. Despite these significant advances, our knowledge of the later phases of the early Universe, such as the Dark Ages, Cosmic Dawn, and the Epoch of Reionisation, remains relatively limited. The Epoch of Reionisation is particularly interesting as it is the period when the radiation from the first luminous sources re-ionised the Universe. By studying the period of reionisation, we can understand how the first stars and galaxies were formed, the nature of the first luminous sources and the process of galaxy formation (Furlanetto et al. Reference Furlanetto, Oh and Briggs2006; Morales & Wyithe Reference Morales and Wyithe2010; Mesinger Reference Mesinger2016). Despite the early attempts to constrain the period of reionisation
$(5.4 <\sim z <\sim 10)$
(Furlanetto et al. Reference Furlanetto, Oh and Briggs2006; Morales & Wyithe Reference Morales and Wyithe2010; Mesinger Reference Mesinger2016), the unanswered questions regarding reionisation still prevail. There are many ways to probe the early Universe, but the most promising method is to study the 21 cm cosmological signal of neutral hydrogen (Pritchard & Loeb Reference Pritchard and Loeb2012).
Figure 1. The sky response of the MWA telescope for EoR0 field shown in the upper panel (Minus2 pointing: Altitude
$76.3^\circ$
, Azimuth
$90^\circ$
) and EoR2 field shown in the lower panel (zenith pointing: Altitude
$90^\circ$
, Azimuth
$0^\circ$
) at 183 MHz. The black contours on the map represent the primary beam response of the MWA telescope. The blue dots represent the compact radio catalogued sources.
Figure 2. The Phase II MWA array compact configuration with the CRAM. The two hexagonal arrays are shown in black markings, the original MWA Phase I tiles shown in green markings. The new CRAM is located within the southern hexagonal compact array configuration is shown in red.
Despite the combined efforts made by the 21 cm community, the cosmological signal from the early Universe is yet to be detected. The primary reason for the non-detection is because the 21 cm signal evolving through the redshifted space is an exceptionally weak signal. Therefore, the 21 cm experiments require high sensitivity to detect the signal successfully. Beyond achieving the necessary sensitivity, 21 cm experiments face the serious problem of foreground contaminations. The low-frequency radio sky is dominated by the galactic and extragalactic foregrounds of magnitude three to four greater than the cosmological signal (Oh & Mack Reference Oh and Mack2003; Santos et al. Reference Santos, Cooray and Knox2005). The Galactic foregrounds comprising of diffused synchrotron radiation and free-free emission from the Milky Way dominate at angular scales greater than a degree (Bernardi et al. Reference Bernardi2009; Lian et al. Reference Lian, Xu, Zhu and Hu2020) and the extragalactic foregrounds of radio emission from Active Galactic Nuclei and star-forming galaxies dominate at smaller angular scales (Di Matteo et al. Reference Di Matteo, Perna, Abel and Rees2002, Reference Di Matteo, Ciardi and Miniati2004). Besides, these foregrounds also exhibit polarization properties contaminating the cosmological signal, thus making the extraction and analysis challenging (Jelić et al. Reference Jelić2010; Moore et al. Reference Moore, Aguirre, Parsons, Jacobs and Pober2013; Jelić et al. Reference Jelić2014; Spinelli et al. Reference Spinelli, Bernardi and Santos2018; Byrne et al. Reference Byrne2022). For a successful detection of the cosmological signal, these foregrounds must be removed from the EoR datasets. Over the years, several foreground mitigation methods have been developed (Chapman et al. Reference Chapman2015; Liu & Shaw Reference Liu and Shaw2020) relying on the spectral smoothness of the foregrounds, which allows for their separation from the cosmological signal characterized to have spectral fluctuations (Morales & Hewitt Reference Morales and Hewitt2004; Morales et al. Reference Morales, Hazelton, Sullivan and Beardsley2012). However, due to the intrinsic chromatic nature of the instruments, the foregrounds can cause leakage and contaminate the cosmological signal. Therefore, for a successful detection, it is important to understand the complex properties of the foregrounds in detail in the context of 21 cm cosmology. In addition to the problems caused by the dominant astrophysical foregrounds, the 21 cm experiments face additional complications from systematic effects, such as ionospheric activities (Zheng et al. Reference Zheng, Tegmark and Dillon2017) and radio frequency interference (RFI) (Offringa et al. Reference Offringa, van de Gronde and Roerdink2012).
The challenges of detection are further compounded by the size of the observation region in the sky, as seen by the instrument. Although the 21 cm experiments can be of instruments with a large FoV, it implies that the instrument has a large sample space of foregrounds that must be removed from the dataset for successfully detecting the cosmological signal. In this work, we focus on the Murchison Widefield Array radio telescope (MWA, Tingay et al. Reference Tingay2013), an interferometer-based approach aimed at measuring the differential brightness temperature fluctuations of the 21 cm signal. Fig. 1 shows how the MWA telescope observes the sky in the field of EoR0 (RA = 0 h, DEC =
$-27^{\circ}$
) and EoR2 (RA =
$10.3$
h, DEC =
$-10^{\circ}$
). In both these fields, the MWA telescope observes numerous point sources in its primary beam along with the Galactic plane in the sidelobes. To detect the signal successfully, it is important to remove these sources from the dataset. Trott et al. (Reference Trott2020) demonstrated the importance of better models of the Galactic plane to improve the analysis in the EoR2 field.
The systematic effects caused by the large observing regions can further complicate the challenges faced by the 21 cm experiments (Trott et al. Reference Trott, Wayth and Tingay2012; Pober et al. Reference Pober2016). Therefore, foregrounds and problems caused by foregrounds need serious consideration to detect the 21 cm signal successfully. For example, Cook et al. (Reference Cook, Trott and Line2022) investigates the impact of extended radio sources such as Centaurus A and Galactic supernova remnants on the 21 cm experiments.
Figure 3. The CRAM as installed at the centre of the southern hexagon array of the MWA Phase II configuration, looking west. In the lower centre of the image is the second-stage beamformer, first-stage beamformers are visible on the left and right of the image.
In response to the challenges and complications, we installed a new zenith-pointing instrument, the Central Redundant Array Mega-tile (CRAM) and integrated it into the existing MWA array configuration. The primary motivation for installing the new instrument is to reduce the impact of foregrounds on the EoR datasets by changing the size of the tile array. The CRAM is twice the size of a regular MWA tile in each dimension (which consists of
$4 \times 4$
dipoles), and therefore, it has half the FoV at each frequency under consideration. Even though the FoV of the new instrument is smaller than the existing MWA, it is still capable of measuring the characteristic size scales of the cosmological signal (Turner Reference Turner2015). The reduction in the FoV is equivalent to an increase in the antenna directivity and a narrower primary main lobe with multiple sidelobes of reduced response. With the CRAM, the foregrounds present near the field centre will be restricted in accordance with the primary beamshape and the contamination from the foreground sources far from the pointing centre will be reduced because of the reduced response of the sidelobes of the large array.
The primary objective of this paper is to introduce the CRAM to the scientific community. This paper (defined as Paper I hereafter) focuses on describing the instrumental details of the CRAM and reports its on-sky performance. This paper is accompanied by Paper II, where the CRAM will be used in the context of EoR science to show the improvement obtained in the power spectrum when compared with the regular MWA tile. Section 2 of this paper describes the new instrument located at the centre of the southern hexagonal compact configuration of Phase II MWA. Further, Section 2.1 details the system architecture of the instrument consisting of the first-stage and second-stage CRAM beamformers. Prior to the development of CRAM for EoR science, it is necessary to understand and model the response of the instrument. Therefore, Section 3 is dedicated to understanding the primary beam response of the instrument in comparison with the existing MWA tile response. Section 4 describes the details of the data acquired by the instrument and further in Section 5 discusses how the data obtained is used to estimate gain and receiver temperature parameters for the instrument. Finally in Section 7 we conclude the work done in this paper.
Figure 4. The physical layout of the CRAM system. Each of the
$4 \times 4$
sections of the array is connected to a first-stage beamformer (BF1, BF2, BF3, BF4). The signals from all four first-stage beamformers are combined and sent to the second-stage beamformer shown as BF5. Both polarisations are processed, but only one is shown for clarity.
2. Instrument description
To enhance the scope of EoR science, the MWA community upgraded the MWA to Phase II configuration by including two additional sets of arrays to the existing configuration of Tingay et al. (Reference Tingay2013). The upgraded array configuration includes an additional 128 tiles, where 72 tiles are arranged in two standard hexagonal compact array configurations and the remaining 56 extended baseline tiles are located beyond the existing array (Wayth et al. Reference Wayth2018). The compact configuration is well-suited for EoR science as the regular configuration is internally redundant and co-redundant, thus allowing the benefits of redundant calibration (Dillon & Parsons Reference Dillon and Parsons2016). Additionally, the compact array configuration provides targeted sensitivity for EoR power spectrum measurements (Parsons et al. Reference Parsons, Pober, McQuinn, Jacobs and Aguirre2012).
Figure 5. Electrical schematic representation of the CTB for a single polarisation (X). The system is identical for the second polarisation.
The CRAM was commissioned and installed at Inyarrimanha Ilgari Bundara, CSIRO’s Murchison Radio-astronomy Observatory (MRO), in the Murchison region of Western Australia in 2019. In the Phase II MWA, the geometry of the compact configuration leaves a spatial gap at the centre of each hexagonal array. We exploit this physical gap accounting for a minimal cost by including the new and larger tile, the CRAM, within the southern hexagon as depicted in Fig. 2. Fig. 3 shows the position of the CRAM installed at the site within the southern hexagonal array. The CRAM’s position within the regular compact array configuration produces redundant and non-redundant baselines and thus can be used to exploit the benefits of redundant calibration.
The CRAM is a specially built
$8 \times 8$
tile with modified MWA dipoles as implemented in the Engineering Development Array (EDA, Wayth et al. Reference Wayth2017). The EDA dipole antennas feature a modified low-noise amplifier (LNA) to extend the lower frequency limit for observations from 80 MHz to 50 MHz. The CRAM is larger than the size of a regular MWA tile, so the normal MWA beamformers cannot be used for it. Instead, the CRAM uses a custom-built zenith-pointing two-stage beamformer, which adds the signals collected by the CRAM dipole antennas and transmits the summed signals to the receiver via optical fibre links.
2.1 System architecture
The complete architecture of CRAM consists of a two-stage beamformer defined as the CRAM beamformer (CTB), the data capture system, signal-processing components and other antenna hardware as shown in Fig. 4. The CTB was designed by the work described in Bhatia (Reference Bhatia2018). The CTB is responsible for distributing power to the 64 LNAs within the dipoles and combining the radio frequency signals from the dipoles. As shown in Fig. 5, the RF signals collected by a single polarisation of the sixteen antennas are the input to each first-stage (Stage A) beamformer. The output from each first-stage beamformer is connected to the second-stage beamformer via a phase-matched fourteen-metre co-axial cable (LMR-100) and is combined by a four-way combiner inside the second-stage (Stage B) beamformer. The final combined signal (64 RF signals for each polarisation) after amplification is converted to the optical domain via an ASTRON RF-over-fibre driver (Model 350) for transmission through a fibre link to the receiver hut.
The receiver hut, informally known as the T-hut, is an RF-shielded equipment container present on site and provides
$+48$
V power from the in-house designed power supply unit (PSU) for the ASTRON RF-over-fibre (RFoF) drivers and the LNAs inside the first-stage beamformer and internal to the dipole antennas. A receiver module within the T-hut converts the optical signals back to electrical and passes them through an anti-aliasing low-pass filter prior to digitisation.
2.1.1 First-stage beamformer
The first-stage beamformers are arranged in a configuration similar to the MWA, where each is connected to sixteen dual-polarised dipole antennas. The internal architecture of the first-stage beamformer is shown in Fig. 6. A power cable supplying
$+48$
V from the receiver hut distributes power to each of the four first-stage beamformers via a terminal barrier at the backside of the beamformer chassis. This input power is passed through a
$+48$
V distribution unit designed in-house to provide
$+48$
V output to each of the four power supply units (LM2576). These in-house designed PSUs down-convert the power to
$+5$
V and provide input power to the two LNAs inside the beamformer and the LNAs inside the dipole antennas. The RF signals collected from the sixteen dipole antennas are passed through a Croatia Microwave LNA4ALL bias-tee (CM-T) to the MiniCircuits sixteen-way combiner (ZC16PD-222-S+). The combined signal is amplified by the MiniCircuits LNA (ZX60-P105LN+) and fed out as the output of the first-stage beamformer.
Figure 6. The internal architecture of the first-stage beamformer connected to the sixteen dipoles from the southeast section of the CRAM. The first-stage beamformer houses a power combiner, DC-DC converter and additional power supply units to power the boards.
Figure 7. The internal architecture of the second-stage beamformer connected to each of the four first-stage beamformers. The second-stage beamformer houses a power combiner, LNAs, Beamformer Interface PCB unit along with RFoF drivers and additional power supply units to power the board.
Figure 8. The CRAM receiver unit placed inside the T-hut along with the MWA clock system.
2.1.2 Second-stage beamformer
The RF signal for each polarisation from the four first-stage beamformers is combined inside the second-stage beamformer. The assembly of the second-stage beamformer is shown in Fig. 7. The power cable from the receiver hut is used to deliver power to the second-stage beamformer. This power cable contains an electromagnetic shield enclosure to prevent any coupling of electromagnetic emissions into the RF signal, with terminal barriers to pass power in and out of the enclosure.
The LNAs inside the second-stage beamformer amplify the combined RF signal for each polarisation and are converted to the optical domain via an ASTRON RFoF driver. A Beamformer Interface (BFIF) PCB unit was developed, based on a modified MWA Phase II RFoF module, to interface the ASTRON Model 350 RFoF drivers using a USB connection, with the dual polarisation RF output on co-axial cables with SMA connectors. The BFIF unit also integrates a DC-DC down-converter (LM2576; PSU) to power the LNAs and RFoF modules. The final combined and amplified signals are then transmitted to the receiver for further processing and storage.
2.1.3 Receiver-side system design
The CRAM receiver present inside the T-hut is shown in Fig. 8. In addition to the RFoF receiver and data acquisition system, the T-hut contains connections to the MWA monitor/control and networks and a client system for the MWA telescope clock. The MWA clock is reticulated via a White Rabbit system and provides a 1PPS signal and 10 MHz frequency reference. This, in turn, drives a Valon frequency synthesiser to generate the 655.36 Msamp/sec signal required for the digitiser.
The digital system comprises a Signatec PX1500-2 data acquisition card and Nvidia GTX 1050 Ti GPU installed within a server present inside the T-hut. Captured data is time-tagged and passed through a GPU-based polyphase filterbank that mimics the MWA’s receivers (Prabu et al. Reference Prabu2015), and is reformatted to match the new MWAX coarse channel data format (see Morrison et al. Reference Morrison2023, for details of the MWA’s new signal processing architecture). CRAM data are sent via a high-speed network link directly connected to the MWA’s CISCO 9k data switch.
In addition to channelised raw data, the data capture system generates 2 s time-averaged total power spectra, which are used for system characterisation as described below.
Figure 9. The primary beam response of the MWA with
$4 \times 4$
array configuration in comparison with the primary beam response of the CRAM with
$8 \times 8$
array configuration at 150 MHz.
3. Modelling the primary beam response
In developing the CRAM for EoR science aimed at the work in Paper II, it is important to understand the response of the instrument in great detail. Therefore, we begin with modelling the primary beam response of the CRAM. Building from the array factor response of the antenna dipoles in a two-dimensional geometry of
$8 \times 8$
configuration and the field response of a single element at the reference, the analytical primary beam is simulated for the CRAM for a given frequency. The overall field of the antenna array configuration is obtained by multiplying the array factor with the dipole beam pattern.
Fig. 9a shows the primary beam response of the regular MWA tile at the standard MWA frequency of 150 MHz and Fig. 9b shows the primary beam response of the CRAM at the same frequency. As expected, the beam response of the larger array CRAM has a smaller FoV when compared with the beam response of the MWA; specifically, the solid angle is reduced by a factor of four. The CRAM, composed of a similar grid structure as MWA has an integer multiple of the MWA dipoles; therefore, the beam nulls align at each frequency. Additionally, in comparison with the regular MWA tile, the CRAM has a larger number of sidelobes with a smaller magnitude, consistent with a larger physical aperture.
Figure 10. 1D cross-section of the power response calculated for MWA-MWA (shown in black marking) and CRAM-MWA baselines (shown in red marking) at 150 MHz. The nulls of both patterns align as the number of dipoles present is an integral multiple of each other. The CRAM-MWA power pattern has reduced response when compared to the MWA-MWA baseline pattern.
In the context of interferometry, where cross-correlated beams are necessary to compute the visibility measurements, we compute the cross-tile power patterns using the primary beam response of MWA and CRAM. The two-dimensional power patterns for MWA-MWA and CRAM-MWA baselines are sliced to obtain the one-dimensional power response as shown in Fig. 10. The cross-tile CRAM-MWA baseline has a reduced response when compared to the response of the regular MWA-MWA baselines. The reduced response is directly related to the larger size of the CRAM that corresponds to a smaller FoV. As a result, the CRAM will have reduced responses from sources near the horizon which with MWA baselines, will have a higher response. Additionally, we note that the CRAM-MWA baselines have negative responses within the primary beam of the MWA-MWA baseline, in the first sidelobe of the CRAM beam. This is important for comparison as the CRAM-MWA baselines will have different responses to the same source at those negative positions of the beam compared to the MWA-MWA baselines. Paper II, accompanied with this work, further explores these differences and understands how they impact EoR science using power spectrum estimations.
Figure 11. The time versus frequency waterfall plot obtained for a 24 hrs observation on June 9, 2023. The third axis of the plot is the uncalibrated power measured by the instrument from the X-polarisation channel. The plot shows the Galactic centre transiting around 12 hrs UTC. The spikes at
$\sim$
137 MHz are from ORBCOMM satellites, the spikes at 110–150 MHz are from various aircrafts, and the bright lines at 250 MHz are from military satellites. The ripples present are because of the cable reflections between dipoles and beamformers.
4. Observations
In 2019, during the EoR0 field observation run, the CRAM witnessed its first light with drift-scan observations. The CRAM successfully collected data over 14 different days. The data were recorded continuously and split into 10 minute long FITS format files for the ease of processing. Each file contains the total power from X and Y polarisation, and the X-Y cross-power accumulated over two seconds.
Following an idle period during the COVID-19 era, the CRAM resumed operations in 2023 after maintenance. Fig. 11 shows the waterfall plot of the total power obtained for one day of observation. The bright lines at 250 MHz are from military satellites, the spikes at
$\sim$
137 MHz are from ORBCOMM satellites, and the spikes at 110–150 MHz are from various aircrafts. The ripples present are because of the cable reflections between dipoles and beamformers.
Fig. 12 shows the uncalibrated measured power extracted at a frequency of 150 MHz from the waterfall plot across the local sidereal time (LST) for several days of observation. The plot shows the resultant power measured by the instrument as the sky transits through the primary beam of CRAM. As the CRAM has a small FoV, the Galactic plane transiting through is seen as a sharp peak at around 18 hrs LST. The Galactic centre falls off quickly, and the beginning and end of the graph are aligned. This plot is promising as it suggests that without any normalisation, all of the data are aligned with each other, implying that the CRAM has stable gain.
Figure 12. The uncalibrated measured power extracted from X-polarisation channel at 150 MHz frequency, across different days of observation.
5. Gain and Receiver temperature calculation
The phased array antennas during installation can introduce perturbations in amplitude, phase, element position, and antenna patterns. Therefore, calibration must account for the perturbations to improve the system’s performance. The conventional method of calibration is to switch between hot and cold loads connected to the amplifier (Pauliny-Toth & Shakeshaft Reference Pauliny-Toth and Shakeshaft1962). However, such a calibration in active antennas is difficult as there is no standard impedance between the antenna and amplifiers. Instead, in low-frequency arrays, calibration is performed using sky brightness models (Rogers et al. Reference Rogers, Pratap, Kratzenberg and Diaz2004).
The frequency-dependent system temperature of the instrument,
$T_{sys}(\nu,\mathrm{LST})$
, is the sum of the antenna temperature,
$T_{ant}(\nu,\mathrm{LST})$
, and receiver temperature,
$T_{rec}(\nu)$
. Among the two, the antenna temperature is dominated by the sky temperature and is a function of frequency and LST; therefore, it changes with time due to the rotation of the Earth. The antenna temperature, defined as the beam-weighted average sky temperature, is given by
\begin{equation} T_{ant}(\nu, \mathrm{LST}) = \frac{\int_{4\pi}^{}B(\nu, \unicode{x03B8}, \unicode{x03D5})T_{sky}(\nu, \unicode{x03B8}, \unicode{x03D5}, \mathrm{LST})d\Omega}{\int_{4\pi}^{}B(\nu, \unicode{x03B8}, \unicode{x03D5})d\Omega}, \end{equation}
where
$B(\nu, \unicode{x03B8}, \unicode{x03D5})$
is the beam pattern of the instrument for zenith angle
$\unicode{x03B8}$
and azimuthal angle
$\unicode{x03D5}$
, and
$T_{sky}(\nu, \unicode{x03B8}, \unicode{x03D5}, \mathrm{LST}$
) is the brightness temperature of the sky at a frequency (
$\nu$
). The beam model is the antenna power pattern calculated using the analytical function defined for a dipole with a given polarisation, as described in Section 3. Based on the calculations of beam-weighted antenna temperature and total system temperature measured with the instrument (Rogers et al. Reference Rogers, Pratap, Kratzenberg and Diaz2004), the receiver temperature is calculated using
\begin{equation} P{(\nu)} = g(\nu)\big( T_{ant}(\nu, \mathrm{LST}) + T_{rec}(\nu) \big), \end{equation}
where
$P{(\nu)}$
is the uncalibrated measured power output from the antenna and
$g(\nu)$
is the system gain. The system gain and receiver temperature are obtained by fitting a first-order polynomial to the modelled antenna temperature and measured power. The slope of the straight line corresponds to the gain, and the ratio of the y-intercept to the gain will provide the receiver temperature of the antenna.
Figure 13. Mollview projection of the sky at 150 MHz in equatorial coordinates at 0 hrs LST.
Figure 14. Mollview projection of the primary beam of CRAM at 150 MHz after rotating by the longitude of LST in degrees and latitude of
$-26.70^\circ$
in Celestial coordinates.
Figure 15. The total power measured by the CRAM instrument at 150 MHz across LST is shown in black, and the modelled beam-weighted average sky temperature is shown in red curve at 150 MHz. Both of the power measurement corresponds to the X-polarisation channel.
Figure 16. The total power measured by the instrument at 210 MHz is shown in black curve. The beam-weighted average sky temperature includes the Sun. The presence of the Sun transiting through the sidelobes of the instrument results in a peak at
$\sim$
13 hrs in both data and the model. Both of the power measurement corresponds to the X-polarisation channel.
The typical approach in estimating the antenna temperature is using the all-sky Haslam map at 408 MHz (Haslam et al. Reference Haslam, Salter, Stoffel and Wilson1982), where the map is scaled with a spectral index of
$-2.55$
for lower frequencies. In the simulations performed for this work, along with the Haslam map, we use the Global Sky Model GSM2008 (de Oliveira-Costa et al. Reference de Oliveira-Costa2008) and GSM2016 (Zheng et al. Reference Zheng, Tegmark and Dillon2017) to simulate the sky model at a given LST in the frequency range of 80–320 MHz. Fig. 13 shows the mollview projection of the sky map at a frequency of 150 MHz at 0 hrs LST obtained from the PyGDSM Python package of Global Sky Model GSM2008. The analytical beam model obtained for the east-west (XX) polarisation dipole at a given frequency is rotated such that the centre of the beam is at the LST of observation and the declination matching the latitude of the observatory (
$-26.70^{\circ}$
). The resultant beam model of the CRAM at 150 MHz is shown in Fig. 14. In Fig. 15, the black curve shows the total power measured by the CRAM instrument at a frequency of 150 MHz and the curve in red shows the model power computed using Equation (1). It is evident from the plot that there is an excellent correlation between the data and model power. Fig. 16 shows a similar plot at 210 MHz, where the Sun is included in the model simulations and the detailed description is provided in Appendix A. The peak present at
$\sim$
13 hrs in both the model and data is because of the Sun transiting through the sidelobes of the CRAM.
Figure 17. The gain and receiver temperature measurements for the data obtained on June 9, 2023. The plot in black corresponds to the measurements obtained from the X-polarisation channel and the plot in red corresponds to the measurements obtained from the Y-polarisation channel. In the given horizontal panel, the plot on the left shows the gain variations in the frequency range of 80–320 MHz and the gain has point directivity at the centre frequency. The right-hand side plot shows the corresponding receiver temperature for the instrument that decreases with the frequency until 240 MHz, beyond which the RFI from military satellites are dominant in the measurements.
For a given day of observation, the gain and receiver temperature are calculated for the frequency range of 80–320 MHz using Equation (2) and are shown in Fig. 17. The rise in the lower band is consistent with the MWA system and is due to the dipoles becoming very electrically short at lower frequencies. The results demonstrate that the receiver temperature reduces with increasing frequency until 240 MHz, beyond which the RFI is dominant in the measurements. The simulations report a receiver temperature of
$\sim$
70 K at 150 MHz, an expected measurement at the given frequency (Sutinjo et al. Reference Sutinjo, Ung and Juswardy2018; Ung et al. Reference Ung, Sokolowski, Sutinjo and Davidson2020) (see Figures 14, 16 in Sutinjo et al. Reference Sutinjo, Ung and Juswardy2018 and Figure 8, 9 in Ung et al. Reference Ung, Sokolowski, Sutinjo and Davidson2020). The simulations are repeated with the Global Sky Model GSM2016 and the Haslam map. We also use the 159 MHz sky map (Kriele et al. Reference Kriele, Wayth, Bentum, Juswardy and Trott2022) for the simulations. As previously discussed, the procedure to include these sky models in the simulations remains the same. The receiver temperature measurements calculated using the three different sky models correspond to a systematic error of
$\pm 5$
K.
6. Key outcomes
The primary goal of this work is to introduce the new CRAM, a zenith-pointing instrument to the scientific community. This paper, Paper I, describes the details of the CRAM system installed at the Inyarrimanha Ilgari Bundara, CSIRO Murchison Radio-astronomy Observatory in Western Australia. In this paper, we have:
-
Confirmed that the CRAM has a smaller field of view when compared to the regular MWA tile;
-
Demonstrated using simulations, that the power patterns obtained using the CRAM-MWA baseline have reduced response when compared with the response obtained using the MWA-MWA baselines;
-
Demonstrated that the measured total power shows excellent agreement with the model and was repeatable over many days;
-
Used the measurements and models to derive the system temperature over the frequency range 80–320 MHz.
In this work, we note that a simple analytical beam model has been used in this work rather than a full EM simulation, as is often used for MWA science (Sokolowski et al. Reference Sokolowski2017). Given the excellent agreement between the simulated sky power and measured power, a more sophisticated model was not deemed necessary. Nevertheless, we expect to develop a full EM model of the CRAM for future work. In consideration of the factors and measurements above, we have characterised the CRAM system performance and report it is ready for scientific observations. This paper is accompanied by Paper II (submitted, Selvaraj et al. Reference Selvaraj, Trott and Wayth2023), where the CRAM will be used in the context of EoR science to show the improvement obtained in the power spectrum when compared with the regular MWA tiles using simulated data. The instrument is yet to be integrated with the existing MWA tiles to obtain correlated visibility measurements. The real data thus acquired from the instrument will be incorporated for EoR analysis in the future work planned with this instrument.
7. Conclusion
In this work, we introduce the Central Redundant Array Mega-tile, or ‘CRAM’, to the scientific community. It is a zenith-pointing larger tile configuration with
$8 \times 8$
dipoles installed within the southern hexagonal array of the Phase II MWA configuration. The primary goal of this instrument is to aid EoR science in detecting the 21 cm signal. This work has demonstrated that the new instrument has a reduced beam response compared to the regular MWA beam response. The power pattern results are compelling towards using the CRAM-MWA baseline as it indicates that the CRAM-MWA baselines can view the sky under observation differently from the usual MWA-MWA baseline. These differences are of great importance for EoR science. With this work, we present the characteristics of the new instrument and report that the CRAM intended for EoR science is functional and collecting data. This paper also reports the data collected with the instrument, system temperature, and gain calculations.
Data availability
Data used in this work will be made available upon suitable requests.
Acknowledgement
This research was partly supported by the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), through project number CE170100013. CMT was supported by an ARC Future Fellowship under grant FT180100321. The International Centre for Radio Astronomy Research (ICRAR) is a joint venture between Curtin University and The University of Western Australia, funded by the Western Australian State government. This scientific work uses data obtained from Inyarrimanha Ilgari Bundara, CSIRO’s Murchison Radio-astronomy Observatory. We acknowledge the Wajarri Yamaji People as the Traditional Owners and native title holders of the Observatory site. The establishment of CSIRO’s Murchison Radio-astronomy Observatory is an initiative of the Australian Government, with support from the Government of Western Australia and the Science and Industry Endowment Fund. Support for the operation of the MWA is provided by the Australian Government (NCRIS) under a contract to Curtin University administered by Astronomy Australia Limited. This work was supported by resources provided by the Pawsey Supercomputing Research Centre with funding from the Australian Government and the Government of Western Australia. We thank Mr Andrew McPhail, Mr David Kenney, Jishnu N. Thekkeppattu and the Operations team at Curtin Institute of Radio Astronomy (CIRA) for the support provided during on-site installation and maintenance activity. We also acknowledge the staff at Boolardy station and CSIRO for facilitating our travel and stay at the Observatory.
Appendix A. Adding the Sun to simulations
The data from the 2019 and 2023 observation run is used to estimate the receiver temperature and gain calculations. As the observations are conducted for 24 hrs, the Sun must be included in the simulations while calculating the receiver temperature and gain parameters. The Sun is a wideband radio transmitter that emits radio signals at all wavelengths and times. The quiet emission from the Sun produced by free-free emission in the atmosphere establishes the minimum radiation level possible. This component of the solar radio emission is constant in time and is the strongest source in the sky at meter wavelengths (Benz Reference Benz2009). The quiet solar radio flux density has three distinctive regions and can be approximated by
Figure A1. The spectrum of quiet solar flux density versus frequency.
\begin{align}F_{\odot} &= 1.94\times10^{-4}f^{1.992}, 30 - 350\,\mathrm{MHz}, \end{align}
\begin{align}F_{\odot} &= 8.45\times10^{-1}f^{0.5617}, 350 - 6\,000\,\mathrm{MHz},\end{align}
\begin{align}F_{\odot} &= 2.79\times10^{-5}f^{1.748}, 6\,000- 400\,00\,\mathrm{MHz},\end{align}
where
$F_{\odot}$
is the solar flux density in Jansky (Jy). For frequencies in the range of 30 MHz and 40 GHz, we use Equation (A1) to calculate the corresponding solar flux density and the resultant solar flux density is shown in Fig. A1. In the simulations, for a given frequency, the corresponding solar flux density is calculated using the corresponding equation and added to the simulations, where the Sun is considered a compact source. However, the units of the sky used in the simulations are in Kelvin, while the units of the solar flux density is in Jy. Therefore, Rayleigh-Jeans law is used to convert the units from Jy to Kelvin and is given by
\begin{align} T&= \frac{\lambda^2 S_{\nu}}{2k_{B}\unicode{x03B8}_{s}^{2}}, \end{align}
where
$S_{\nu}$
is the solar flux density in Jy,
$\lambda$
is the wavelength,
$k_{B}$
is the Boltzmann’s constant and
$\unicode{x03B8}_{s}$
is the size of the source in steradians.
The position of the Sun is calculated using astropy module in Python, based on the time of observation and is defined as the right ascension (RA) and declination (DEC) in degrees. After converting to the corresponding pixel location, the intensity value of the Sun in Kelvin is added to the sky model to be included in the simulations.
Open access
