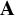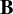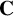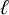1 Introduction
The local-global conjectures are currently some of the most interesting and challenging problems in the representation theory of finite groups. Among others, these include the McKay Conjecture [Reference McKay44], the Alperin–McKay Conjecture [Reference Alperin1] and Alperin’s Weight Conjecture [Reference Alperin2] all of which can be deduced by a deeper statement known as Dade’s Conjecture [Reference Dade21], [Reference Dade22], [Reference Dade23]. The latter also implies the celebrated Brauer’s Height Zero Conjecture introduced in [Reference Brauer4] and whose proof has recently been completed in [Reference Malle, Navarro, Schaffer Fry and Tiep39] and [Reference Ruhstorfer60] while relying on a combined effort of many other authors.
In this paper, we are particularly interested in Dade’s Conjecture which, for every prime number
![]() $\ell $
, suggests a precise formula for counting the number of irreducible characters of a finite group, with a given
$\ell $
, suggests a precise formula for counting the number of irreducible characters of a finite group, with a given
![]() $\ell $
-defect and belonging to a given Brauer
$\ell $
-defect and belonging to a given Brauer
![]() $\ell $
-block, in terms of the
$\ell $
-block, in terms of the
![]() $\ell $
-local structure of the group itself. This conjecture has been further extended in [Reference Späth64] where the Character Triple Conjecture was formulated by introducing a compatibility with N-block isomorphisms of character triples, hereinafter denoted by
$\ell $
-local structure of the group itself. This conjecture has been further extended in [Reference Späth64] where the Character Triple Conjecture was formulated by introducing a compatibility with N-block isomorphisms of character triples, hereinafter denoted by ![]() , as defined in [Reference Späth64, Definition 3.6]. This notion plays a fundamental role in many aspects of group representation theory and, as we will see later, gives us a way to control the representation theory of local subgroups. Furthermore, it was exploited to reduce Dade’s Conjecture to finite quasi-simple groups as explained in [Reference Späth64, Theorem 1.3].
, as defined in [Reference Späth64, Definition 3.6]. This notion plays a fundamental role in many aspects of group representation theory and, as we will see later, gives us a way to control the representation theory of local subgroups. Furthermore, it was exploited to reduce Dade’s Conjecture to finite quasi-simple groups as explained in [Reference Späth64, Theorem 1.3].
Our aim is to adapt and prove the two conjectures described in the previous paragraph to the case of unipotent characters of finite reductive groups. The approach considered here is inspired by ideas introduced by the author in [Reference Rossi57] and provides further evidence for the conjectures formulated in that paper [Reference Rossi57, Conjecture C and Conjecture D]. The latter have been shown to imply Dade’s Conjecture and the Character Triple Conjecture, respectively, for all finite reductive groups in nondefining characteristic (see [Reference Rossi56, Theorem E and Theorem F]). In particular, thanks to the results obtained in [Reference Rossi56] (see also [Reference Rossi58]), the
![]() $\ell $
-local structures considered above are replaced by more suitable e-local structures arising from the geometry of the underlying algebraic group that are compatible with the framework of Deligne–Lusztig theory. Therefore, our results also suggest the existence of an e-local-global principle for the representation theory of finite reductive groups.
$\ell $
-local structures considered above are replaced by more suitable e-local structures arising from the geometry of the underlying algebraic group that are compatible with the framework of Deligne–Lusztig theory. Therefore, our results also suggest the existence of an e-local-global principle for the representation theory of finite reductive groups.
More precisely, let
![]() ${\mathbf {G}}$
be a connected reductive group defined over an algebraically closed field
${\mathbf {G}}$
be a connected reductive group defined over an algebraically closed field
![]() $\mathbb {F}$
of positive characteristic p and let
$\mathbb {F}$
of positive characteristic p and let
![]() $F:{\mathbf {G}}\to {\mathbf {G}}$
be a Frobenius endomorphism endowing
$F:{\mathbf {G}}\to {\mathbf {G}}$
be a Frobenius endomorphism endowing
![]() ${\mathbf {G}}$
, as a variety, with an
${\mathbf {G}}$
, as a variety, with an
![]() $\mathbb {F}_q$
-structure for some power q of p. We denote by
$\mathbb {F}_q$
-structure for some power q of p. We denote by
![]() ${\mathbf {G}}^F$
the finite reductive group consisting of the
${\mathbf {G}}^F$
the finite reductive group consisting of the
![]() $\mathbb {F}_q$
-rational points on
$\mathbb {F}_q$
-rational points on
![]() ${\mathbf {G}}$
. Furthermore, we fix an odd prime
${\mathbf {G}}$
. Furthermore, we fix an odd prime
![]() $\ell $
different from p and denote by e the multiplicative order of q modulo
$\ell $
different from p and denote by e the multiplicative order of q modulo
![]() $\ell $
. We let
$\ell $
. We let
![]() ${\mathcal {L}}_e({\mathbf {G}},F)$
denote the set of e-chains of
${\mathcal {L}}_e({\mathbf {G}},F)$
denote the set of e-chains of
![]() $({\mathbf {G}},F)$
of the form
$({\mathbf {G}},F)$
of the form
![]() $\sigma =\{{\mathbf {G}}={\mathbf {L}}_0>{\mathbf {L}}_1>\dots >{\mathbf {L}}_n\}$
, where each
$\sigma =\{{\mathbf {G}}={\mathbf {L}}_0>{\mathbf {L}}_1>\dots >{\mathbf {L}}_n\}$
, where each
![]() ${\mathbf {L}}_i$
is an e-split Levi subgroup of
${\mathbf {L}}_i$
is an e-split Levi subgroup of
![]() $({\mathbf {G}},F)$
. The final term of the e-chain
$({\mathbf {G}},F)$
. The final term of the e-chain
![]() $\sigma $
is denoted by
$\sigma $
is denoted by
![]() ${\mathbf {L}}(\sigma )={\mathbf {L}}_n$
, while
${\mathbf {L}}(\sigma )={\mathbf {L}}_n$
, while
![]() $|\sigma |:=n$
is the length of
$|\sigma |:=n$
is the length of
![]() $\sigma $
. Observe that the latter induces a partition of the set
$\sigma $
. Observe that the latter induces a partition of the set
![]() ${\mathcal {L}}_e({\mathbf {G}},F)$
into the sets
${\mathcal {L}}_e({\mathbf {G}},F)$
into the sets
![]() ${\mathcal {L}}_e({\mathbf {G}},F)_\pm $
consisting of those e-chains
${\mathcal {L}}_e({\mathbf {G}},F)_\pm $
consisting of those e-chains
![]() $\sigma $
that satisfy
$\sigma $
that satisfy
![]() $(-1)^{|\sigma |}=\pm 1$
. Furthermore, notice that
$(-1)^{|\sigma |}=\pm 1$
. Furthermore, notice that
![]() ${\mathbf {G}}^F$
acts by conjugation on the set
${\mathbf {G}}^F$
acts by conjugation on the set
![]() ${\mathcal {L}}_e({\mathbf {G}},F)$
and indicate by
${\mathcal {L}}_e({\mathbf {G}},F)$
and indicate by
![]() ${\mathbf {G}}_\sigma ^F$
the stabiliser of the e-chain
${\mathbf {G}}_\sigma ^F$
the stabiliser of the e-chain
![]() $\sigma $
. It follows directly from the definition that this action preserves the length of e-chains and, in particular, it restricts to an action of
$\sigma $
. It follows directly from the definition that this action preserves the length of e-chains and, in particular, it restricts to an action of
![]() ${\mathbf {G}}^F$
on the set
${\mathbf {G}}^F$
on the set
![]() ${\mathcal {L}}_e({\mathbf {G}},F)_{>0}$
of e-chains of positive length.
${\mathcal {L}}_e({\mathbf {G}},F)_{>0}$
of e-chains of positive length.
Now, to each nonnegative integer d and Brauer
![]() $\ell $
-block B of the finite group
$\ell $
-block B of the finite group
![]() ${\mathbf {G}}^F$
, we associate a set
${\mathbf {G}}^F$
, we associate a set
![]() ${\mathcal {L}}_{\mathrm{u}}^d(B)_\pm $
consisting of quadruples
${\mathcal {L}}_{\mathrm{u}}^d(B)_\pm $
consisting of quadruples
![]() $(\sigma ,{\mathbf {M}},\mu ,\vartheta )$
where
$(\sigma ,{\mathbf {M}},\mu ,\vartheta )$
where
![]() $\sigma $
is an e-chain belonging to
$\sigma $
is an e-chain belonging to
![]() ${\mathcal {L}}_e({\mathbf {G}},F)_\pm $
,
${\mathcal {L}}_e({\mathbf {G}},F)_\pm $
,
![]() $({\mathbf {M}},\mu )$
is a unipotent e-cuspidal pair of
$({\mathbf {M}},\mu )$
is a unipotent e-cuspidal pair of
![]() $({\mathbf {L}}(\sigma ),F)$
such that
$({\mathbf {L}}(\sigma ),F)$
such that
![]() ${\mathbf {M}}$
does not coincide with
${\mathbf {M}}$
does not coincide with
![]() ${\mathbf {G}}$
, and
${\mathbf {G}}$
, and
![]() $\vartheta $
is an irreducible character of the e-chain stabiliser
$\vartheta $
is an irreducible character of the e-chain stabiliser
![]() ${\mathbf {G}}_\sigma ^F$
belonging to the character set
${\mathbf {G}}_\sigma ^F$
belonging to the character set
![]() $\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
defined by the choice of d, B,
$\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
defined by the choice of d, B,
![]() $\sigma $
and
$\sigma $
and
![]() $({\mathbf {M}},\mu )$
as described in Definition 5.5. Once again, the group
$({\mathbf {M}},\mu )$
as described in Definition 5.5. Once again, the group
![]() ${\mathbf {G}}^F$
acts by conjugation on
${\mathbf {G}}^F$
acts by conjugation on
![]() ${\mathcal {L}}_{\mathrm{u}}^d(B)_\pm $
and we indicate the corresponding set of
${\mathcal {L}}_{\mathrm{u}}^d(B)_\pm $
and we indicate the corresponding set of
![]() ${\mathbf {G}}^F$
-orbits by
${\mathbf {G}}^F$
-orbits by
![]() ${\mathcal {L}}^d_{\mathrm{u}}(B)_\pm /{\mathbf {G}}^F$
. Moreover, for every such orbit
${\mathcal {L}}^d_{\mathrm{u}}(B)_\pm /{\mathbf {G}}^F$
. Moreover, for every such orbit
![]() $\omega $
, we denote by
$\omega $
, we denote by
![]() $\omega ^\bullet $
the corresponding
$\omega ^\bullet $
the corresponding
![]() ${\mathbf {G}}^F$
-orbit of pairs
${\mathbf {G}}^F$
-orbit of pairs
![]() $(\sigma ,\vartheta )$
such that
$(\sigma ,\vartheta )$
such that
![]() $(\sigma ,{\mathbf {M}},\mu ,\vartheta )\in \omega $
for some unipotent e-cuspidal pair
$(\sigma ,{\mathbf {M}},\mu ,\vartheta )\in \omega $
for some unipotent e-cuspidal pair
![]() $({\mathbf {M}},\mu )$
.
$({\mathbf {M}},\mu )$
.
With the above notation, we are now able to state our first main result. In order to avoid unnecessary technical complications, in the next theorem we assume that the prime
![]() $\ell $
does not divide
$\ell $
does not divide
![]() $|{\mathbf {Z}}({\mathbf {G}})^F:{\mathbf {Z}}^\circ ({\mathbf {G}})^F|$
keeping in mind, however, that this assumption can be removed as explained Theorem 5.10 (see also Remark 5.8).
$|{\mathbf {Z}}({\mathbf {G}})^F:{\mathbf {Z}}^\circ ({\mathbf {G}})^F|$
keeping in mind, however, that this assumption can be removed as explained Theorem 5.10 (see also Remark 5.8).
Theorem A. Suppose that
![]() ${\mathbf {G}}$
is a simply connected group whose irreducible components are of type
${\mathbf {G}}$
is a simply connected group whose irreducible components are of type
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
and consider an odd prime
$\mathbf {C}$
and consider an odd prime
![]() $\ell $
not dividing
$\ell $
not dividing
![]() $|{\mathbf {Z}}({\mathbf {G}})^F:{\mathbf {Z}}^\circ ({\mathbf {G}})^F|$
. For every Brauer
$|{\mathbf {Z}}({\mathbf {G}})^F:{\mathbf {Z}}^\circ ({\mathbf {G}})^F|$
. For every Brauer
![]() $\ell $
-block B of
$\ell $
-block B of
![]() ${\mathbf {G}}^F$
and every nonnegative integer d, there exists an
${\mathbf {G}}^F$
and every nonnegative integer d, there exists an
![]() $\mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)_B$
-equivariant bijection
$\mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)_B$
-equivariant bijection
such that
for every
![]() $\omega \in {\mathcal {L}}^d_{\mathrm{u}}(B)_+/{\mathbf {G}}^F$
,
$\omega \in {\mathcal {L}}^d_{\mathrm{u}}(B)_+/{\mathbf {G}}^F$
,
![]() $(\sigma ,\vartheta )\in \omega ^\bullet $
,
$(\sigma ,\vartheta )\in \omega ^\bullet $
,
![]() $(\rho ,\chi )\in \Lambda (\omega )^\bullet $
and where
$(\rho ,\chi )\in \Lambda (\omega )^\bullet $
and where
![]() $X:={\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
and
$X:={\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
and
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
is the group of automorphisms described in Section 3.1.
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
is the group of automorphisms described in Section 3.1.
The above statement describes a local-global phenomenon analogous to that introduced by Späth’s Character Triple Conjecture but in the framework of Deligne–Lusztig theory for the unipotent characters of finite reductive groups. Theorem A also offers further evidence for the validity of [Reference Rossi57, Conjecture D], in fact the set
![]() ${\mathcal {L}}_{\mathrm{u}}^d(B)_\pm $
introduced above is a subset of the set of quadruples
${\mathcal {L}}_{\mathrm{u}}^d(B)_\pm $
introduced above is a subset of the set of quadruples
![]() ${\mathcal {L}}^d(B)_\pm $
considered in [Reference Rossi57, Conjecture D]. Furthermore, notice that the Brauer
${\mathcal {L}}^d(B)_\pm $
considered in [Reference Rossi57, Conjecture D]. Furthermore, notice that the Brauer
![]() $\ell $
-block B in Theorem A is not required to be unipotent. In fact, the character set
$\ell $
-block B in Theorem A is not required to be unipotent. In fact, the character set
![]() $\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
might be nonempty even in the case where B is not unipotent (see Remark 5.6).
$\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
might be nonempty even in the case where B is not unipotent (see Remark 5.6).
Next, we obtain a formula for counting the number of unipotent characters of
![]() $\ell $
-defect d in the Brauer
$\ell $
-defect d in the Brauer
![]() $\ell $
-block B in terms of local invariants associated to e-local structures. For each e-chain
$\ell $
-block B in terms of local invariants associated to e-local structures. For each e-chain
![]() $\sigma $
of
$\sigma $
of
![]() $({\mathbf {G}},F)$
with positive length, we define
$({\mathbf {G}},F)$
with positive length, we define
![]() ${\mathbf {k}}^d_{\mathrm{u}}(B_{\sigma })$
to be the number of characters belonging to one of the character sets
${\mathbf {k}}^d_{\mathrm{u}}(B_{\sigma })$
to be the number of characters belonging to one of the character sets
![]() $\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
for some unipotent e-cuspidal pair
$\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
for some unipotent e-cuspidal pair
![]() $({\mathbf {M}},\mu )$
of
$({\mathbf {M}},\mu )$
of
![]() $({\mathbf {L}}(\sigma ),F)$
up to
$({\mathbf {L}}(\sigma ),F)$
up to
![]() ${\mathbf {G}}^F_\sigma $
-conjugation (see also (5.8)). Furthermore, let
${\mathbf {G}}^F_\sigma $
-conjugation (see also (5.8)). Furthermore, let
![]() ${\mathbf {k}}^d_{\mathrm{ u}}(B)$
and
${\mathbf {k}}^d_{\mathrm{ u}}(B)$
and
![]() ${\mathbf {k}}_{\mathrm{c, u}}^d(B)$
be the number of irreducible characters with
${\mathbf {k}}_{\mathrm{c, u}}^d(B)$
be the number of irreducible characters with
![]() $\ell $
-defect d and belonging to the Brauer
$\ell $
-defect d and belonging to the Brauer
![]() $\ell $
-block B that are unipotent and unipotent e-cuspidal, respectively. Then, by using the bijection given by Theorem A we can determine the difference
$\ell $
-block B that are unipotent and unipotent e-cuspidal, respectively. Then, by using the bijection given by Theorem A we can determine the difference
![]() ${\mathbf {k}}^d_{\mathrm{u}}(B)-{\mathbf {k}}^d_{\mathrm{c, u}}(B)$
in terms of an alternating sum involving the terms
${\mathbf {k}}^d_{\mathrm{u}}(B)-{\mathbf {k}}^d_{\mathrm{c, u}}(B)$
in terms of an alternating sum involving the terms
![]() ${\mathbf {k}}^d_{\mathrm{u}}(B_\sigma )$
arising from the e-local structure
${\mathbf {k}}^d_{\mathrm{u}}(B_\sigma )$
arising from the e-local structure
![]() ${\mathbf {G}}_\sigma ^F$
.
${\mathbf {G}}_\sigma ^F$
.
Theorem B. Suppose that
![]() ${\mathbf {G}}$
is a simple, simply connected group of type
${\mathbf {G}}$
is a simple, simply connected group of type
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
and consider an odd prime
$\mathbf {C}$
and consider an odd prime
![]() $\ell $
. For every Brauer
$\ell $
. For every Brauer
![]() $\ell $
-block B of
$\ell $
-block B of
![]() ${\mathbf {G}}^F$
and every nonnegative integer d, we have the equality
${\mathbf {G}}^F$
and every nonnegative integer d, we have the equality
where
![]() $\sigma $
runs over a set of representatives for the action of
$\sigma $
runs over a set of representatives for the action of
![]() ${\mathbf {G}}^F$
on
${\mathbf {G}}^F$
on
![]() ${\mathcal {L}}_e({\mathbf {G}},F)_{>0}$
.
${\mathcal {L}}_e({\mathbf {G}},F)_{>0}$
.
We point out that the restriction on the prime
![]() $\ell $
made for simplification in Theorem A only concerns the condition on isomorphisms of character triples and hence does not affect Theorem B. In Theorem 5.11, we also give a (perhaps less explicit) version of Theorem B for nonsimple algebraic groups. As before, this result provides an adaptation of Dade’s Conjecture to the framework of Deligne–Lusztig theory for the unipotent characters of finite reductive groups and gives new evidence in favour of [Reference Rossi57, Conjecture C]. The necessity for the introduction of the corrective term
$\ell $
made for simplification in Theorem A only concerns the condition on isomorphisms of character triples and hence does not affect Theorem B. In Theorem 5.11, we also give a (perhaps less explicit) version of Theorem B for nonsimple algebraic groups. As before, this result provides an adaptation of Dade’s Conjecture to the framework of Deligne–Lusztig theory for the unipotent characters of finite reductive groups and gives new evidence in favour of [Reference Rossi57, Conjecture C]. The necessity for the introduction of the corrective term
![]() ${\mathbf {k}}^d_{\mathrm{c,u}}(B)$
in the equality of Theorem B can be understood as an analogue to the exclusion of the case of blocks with central defect in the statement of Dade’s Conjecture or, depending on the formulation under consideration, of the case where
${\mathbf {k}}^d_{\mathrm{c,u}}(B)$
in the equality of Theorem B can be understood as an analogue to the exclusion of the case of blocks with central defect in the statement of Dade’s Conjecture or, depending on the formulation under consideration, of the case where
![]() $d=0$
. We refer the reader to the more detailed discussion given in the paragraph following Definition 5.2.
$d=0$
. We refer the reader to the more detailed discussion given in the paragraph following Definition 5.2.
The result obtained in Theorem B is related to a principle introduced and advocated by Broué, Fong and Srinivasan according to which the theories developed by Brauer and Lusztig should agree when considering finite reductive groups. Following these ideas, Broué suggested a statement, known to the public as the AMIDRUNK Conjecture, which embodies the work of Alperin, McKay, Isaacs, Dade, Robinson, Uno, Navarro and Knörr (see, for instance, [Reference Broué6]). This statement also hints at the presence of derived equivalences of block algebras in the spirit of Broué’s Abelian Defect Group Conjecture from [Reference Broué5]. More recently, Broué posed a question of a similar nature that further considers the generic nature of unipotent characters (see the end of [Reference Broué7]). Our Theorem B provides evidence for the validity of these remarkable conjectures.
It is particularly interesting to notice that, to the author’s knowledge, Theorem B cannot be obtained directly using techniques available at the present time but only as a consequence of the existence of
![]() ${\mathbf {G}}^F$
-block isomorphisms of character triples as those considered in Theorem A. In fact, while Deligne–Lusztig theory allows us to control the representation theory of finite reductive groups, it is not sufficient to control the representation theory of e-chain stabilisers
${\mathbf {G}}^F$
-block isomorphisms of character triples as those considered in Theorem A. In fact, while Deligne–Lusztig theory allows us to control the representation theory of finite reductive groups, it is not sufficient to control the representation theory of e-chain stabilisers
![]() ${\mathbf {G}}^F_\sigma $
. However, observe that the stabiliser
${\mathbf {G}}^F_\sigma $
. However, observe that the stabiliser
![]() ${\mathbf {G}}_\sigma ^F$
contains the finite reductive group
${\mathbf {G}}_\sigma ^F$
contains the finite reductive group
![]() ${\mathbf {L}}(\sigma )^F$
as a normal subgroup. Therefore, we can first use Deligne–Lusztig theory to study the characters of
${\mathbf {L}}(\sigma )^F$
as a normal subgroup. Therefore, we can first use Deligne–Lusztig theory to study the characters of
![]() ${\mathbf {L}}(\sigma )^F$
and then apply Clifford theory via
${\mathbf {L}}(\sigma )^F$
and then apply Clifford theory via
![]() ${\mathbf {G}}^F$
-block isomorphisms of character triples to control the characters of
${\mathbf {G}}^F$
-block isomorphisms of character triples to control the characters of
![]() ${\mathbf {G}}^F_\sigma $
(see Proposition 4.5 and Proposition 5.7 for further details).
${\mathbf {G}}^F_\sigma $
(see Proposition 4.5 and Proposition 5.7 for further details).
In order to achieve the latter step, we need to make Deligne–Lusztig theory and, more precisely, e-Harish-Chandra theory for unipotent characters compatible with
![]() ${\mathbf {G}}^F$
-block isomorphisms of character triples. This ideas was first suggested by the author in [Reference Rossi57, Parametrisation B] and further studied in [Reference Rossi54]. Our next result, which is a key ingredient in the proofs of Theorem A and Theorem B, establishes this conjectured parametrisation in the unipotent case under the assumption specified above. This can also be seen as an extension of the parametrisation introduced by Broué, Malle and Michel in [Reference Broué, Malle and Michel9, Theorem 3.2 (2)] to the language of
${\mathbf {G}}^F$
-block isomorphisms of character triples. This ideas was first suggested by the author in [Reference Rossi57, Parametrisation B] and further studied in [Reference Rossi54]. Our next result, which is a key ingredient in the proofs of Theorem A and Theorem B, establishes this conjectured parametrisation in the unipotent case under the assumption specified above. This can also be seen as an extension of the parametrisation introduced by Broué, Malle and Michel in [Reference Broué, Malle and Michel9, Theorem 3.2 (2)] to the language of
![]() ${\mathbf {G}}^F$
-block isomorphisms of character triples.
${\mathbf {G}}^F$
-block isomorphisms of character triples.
Theorem C. Suppose that
![]() ${\mathbf {G}}$
is a simple, simply connected group of type
${\mathbf {G}}$
is a simple, simply connected group of type
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
and consider an odd prime
$\mathbf {C}$
and consider an odd prime
![]() $\ell $
. For every unipotent e-cuspidal pair
$\ell $
. For every unipotent e-cuspidal pair
![]() $({\mathbf {L}},\lambda )$
of the group
$({\mathbf {L}},\lambda )$
of the group
![]() $({\mathbf {G}},F)$
, there exists an
$({\mathbf {G}},F)$
, there exists an
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-equivariant bijection
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-equivariant bijection
that preserves the
![]() $\ell $
-defect of characters and such that
$\ell $
-defect of characters and such that
for every
![]() $\chi \in {\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
and where
$\chi \in {\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
and where
![]() $X:={\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
.
$X:={\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
.
The proof of Theorem C, and therefore of Theorem A and Theorem B, partially relies on certain conditions on the extendibility of characters of e-split Levi subgroups that were first introduced to settle the inductive conditions for the McKay Conjecture and the Alperin–McKay Conjecture and then further studied in the context of Parametrisation B of [Reference Rossi57] (see the exact statement given in [Reference Rossi54, Definition 5.2]). These conditions were obtain, under certain assumptions, for groups of type
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() $\mathbf {C}$
in the papers [Reference Brough11], [Reference Brough and Späth13] and [Reference Brough and Ruhstorfer12], respectively. Nonetheless, a version of these results is expected to hold in general and hence we believe that the above theorems, obtained here for types
$\mathbf {C}$
in the papers [Reference Brough11], [Reference Brough and Späth13] and [Reference Brough and Ruhstorfer12], respectively. Nonetheless, a version of these results is expected to hold in general and hence we believe that the above theorems, obtained here for types
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() $\mathbf {C}$
with respect to an odd prime
$\mathbf {C}$
with respect to an odd prime
![]() $\ell $
, will extend to the general case as well and with respect to any good prime.
$\ell $
, will extend to the general case as well and with respect to any good prime.
1.1 Structure of the paper
The paper is organised as follows. In Section 2, we introduce the necessary notation and recall the main definitions and results used throughout the paper. Furthermore, in Section 2.4 we introduce the notion of pseudo-unipotent character (see Definition 2.2) and prove a result on the regularity of blocks covering those containing such characters. Next, in Section 3, we start working towards a proof of Theorem C. First, in Section 3.1, we consider certain equivariance properties that can be established in the presence of extendibility conditions for characters of e-split Levi subgroups. Here, we also present a candidate for the bijection
![]() $\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}$
required by Theorem C. Next, in Section 3.2, we construct the required
$\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}$
required by Theorem C. Next, in Section 3.2, we construct the required
![]() ${\mathbf {G}}^F$
-block isomorphisms of character triples. Using these results, we can then prove Theorem C in Section 3.3. The following step is to extend the parametrisation of unipotent e-Harish-Chandra series in the group
${\mathbf {G}}^F$
-block isomorphisms of character triples. Using these results, we can then prove Theorem C in Section 3.3. The following step is to extend the parametrisation of unipotent e-Harish-Chandra series in the group
![]() ${\mathbf {G}}$
, as given by Theorem C, to a parametrisation of pseudo-unipotent e-Harish-Chandra series in F-stable Levi subgroups
${\mathbf {G}}$
, as given by Theorem C, to a parametrisation of pseudo-unipotent e-Harish-Chandra series in F-stable Levi subgroups
![]() ${\mathbf {K}}$
of
${\mathbf {K}}$
of
![]() $({\mathbf {G}},F)$
. This is done in Theorem 4.4. Once this is established, in Section 4.2, we exploit the theory of
$({\mathbf {G}},F)$
. This is done in Theorem 4.4. Once this is established, in Section 4.2, we exploit the theory of
![]() ${\mathbf {G}}^F$
-block isomorphisms to obtain bijections above e-Harish-Chandra series that are required to control the representation theory of the e-chain stabilisers
${\mathbf {G}}^F$
-block isomorphisms to obtain bijections above e-Harish-Chandra series that are required to control the representation theory of the e-chain stabilisers
![]() ${\mathbf {G}}_\sigma ^F$
. A more detailed analysis of the characters of
${\mathbf {G}}_\sigma ^F$
. A more detailed analysis of the characters of
![]() ${\mathbf {G}}_\sigma ^F$
is carried out in Section 5.1. In particular, we obtain a parametrisation of the character sets
${\mathbf {G}}_\sigma ^F$
is carried out in Section 5.1. In particular, we obtain a parametrisation of the character sets
![]() $\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
in Proposition 5.7. Finally, in Section 5.2 and Section 5.3, we apply these results to prove Theorem A and Theorem B, respectively.
$\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
in Proposition 5.7. Finally, in Section 5.2 and Section 5.3, we apply these results to prove Theorem A and Theorem B, respectively.
2 Notation and background material
2.1 Characters and blocks of finite groups
We recall some standard notation from representation theory of finite groups as can be found in [Reference Isaacs32] and [Reference Navarro46], for instance. Let
![]() $\mathrm{Irr}(G)$
be the set of ordinary irreducible characters. If
$\mathrm{Irr}(G)$
be the set of ordinary irreducible characters. If
![]() $N\unlhd G$
and
$N\unlhd G$
and
![]() $\vartheta \in \mathrm{Irr}(N)$
, then we denote by
$\vartheta \in \mathrm{Irr}(N)$
, then we denote by
![]() $\mathrm{Irr}(G\mid \vartheta )$
the set of irreducible characters of G that lie above
$\mathrm{Irr}(G\mid \vartheta )$
the set of irreducible characters of G that lie above
![]() $\vartheta $
. More generally, if
$\vartheta $
. More generally, if
![]() $\mathcal {S}$
is a subset of irreducible characters of N, then we denote by
$\mathcal {S}$
is a subset of irreducible characters of N, then we denote by
![]() $\mathrm{Irr}(G\mid \mathcal {S})$
the union of the sets
$\mathrm{Irr}(G\mid \mathcal {S})$
the union of the sets
![]() $\mathrm{Irr}(G\mid \vartheta )$
for
$\mathrm{Irr}(G\mid \vartheta )$
for
![]() $\vartheta \in \mathcal {S}$
, that is, the set of irreducible characters of G that lie above some character in the set
$\vartheta \in \mathcal {S}$
, that is, the set of irreducible characters of G that lie above some character in the set
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Next, we denote by
![]() $G_\vartheta $
the stabiliser of the irreducible character
$G_\vartheta $
the stabiliser of the irreducible character
![]() $\vartheta \in \mathrm{Irr}(N)$
under the conjugacy action of G and say that
$\vartheta \in \mathrm{Irr}(N)$
under the conjugacy action of G and say that
![]() $\vartheta $
is G-invariant if
$\vartheta $
is G-invariant if
![]() $G=G_\vartheta $
. In this case, we say that
$G=G_\vartheta $
. In this case, we say that
![]() $(G,N,\vartheta )$
is a character triple. These objects provide important information in the study of Clifford theory and play a crucial role in many aspects of the local-global conjectures. Of paramount importance is the introduction of certain binary relations on the set of character triples. We refer the reader to [Reference Navarro47, Chapter 5 and 10] and [Reference Späth65] for a more detailed introduction to these ideas and for the necessary background on projective representations. The binary relation considered here was introduced in [Reference Späth64, Definition 3.6] and is known as N-block isomorphism of character triples, denoted by
$(G,N,\vartheta )$
is a character triple. These objects provide important information in the study of Clifford theory and play a crucial role in many aspects of the local-global conjectures. Of paramount importance is the introduction of certain binary relations on the set of character triples. We refer the reader to [Reference Navarro47, Chapter 5 and 10] and [Reference Späth65] for a more detailed introduction to these ideas and for the necessary background on projective representations. The binary relation considered here was introduced in [Reference Späth64, Definition 3.6] and is known as N-block isomorphism of character triples, denoted by ![]() . This equivalence relation has further been studied in [Reference Rossi52].
. This equivalence relation has further been studied in [Reference Rossi52].
In order to construct N-block isomorphisms of character triples, it is often useful to prove certain results on the extendibility of characters. Here, we introduce the notion of maximal extendibility (see [Reference Malle and Späth40, Definition 3.5]) that will be considered in the following sections. Let
![]() $N\unlhd G$
be finite groups, and consider
$N\unlhd G$
be finite groups, and consider
![]() $\mathcal {S}$
a subset of irreducible characters of N. Then, we say that maximal extendibility holds for the set
$\mathcal {S}$
a subset of irreducible characters of N. Then, we say that maximal extendibility holds for the set
![]() $\mathcal {S}$
with respect to the inclusion
$\mathcal {S}$
with respect to the inclusion
![]() $N\unlhd G$
if every character
$N\unlhd G$
if every character
![]() $\vartheta \in \mathcal {S}$
extends to its stabiliser
$\vartheta \in \mathcal {S}$
extends to its stabiliser
![]() $G_\vartheta $
. More precisely, we can specify an extension map
$G_\vartheta $
. More precisely, we can specify an extension map
that sends each character
![]() $\vartheta \in \mathcal {S}$
to an extension
$\vartheta \in \mathcal {S}$
to an extension
![]() $\Lambda (\vartheta )$
of
$\Lambda (\vartheta )$
of
![]() $\vartheta $
to the stabiliser
$\vartheta $
to the stabiliser
![]() $G_\vartheta $
.
$G_\vartheta $
.
Next, we consider modular representation theory with respect to a fixed prime number
![]() $\ell $
. For
$\ell $
. For
![]() $\chi \in \mathrm{Irr}(G)$
, there exist unique nonnegative integers
$\chi \in \mathrm{Irr}(G)$
, there exist unique nonnegative integers
![]() $d(\chi )$
, called the
$d(\chi )$
, called the
![]() $\ell $
-defect of
$\ell $
-defect of
![]() $\chi $
, such that
$\chi $
, such that
![]() $\ell ^{d(\chi )}=|G|_\ell /\chi (1)_\ell $
and where for an integer n we denote by
$\ell ^{d(\chi )}=|G|_\ell /\chi (1)_\ell $
and where for an integer n we denote by
![]() $n_\ell $
the largest power of
$n_\ell $
the largest power of
![]() $\ell $
that divides n. For any
$\ell $
that divides n. For any
![]() $d\geq 0$
, let
$d\geq 0$
, let
![]() $\mathrm{Irr}^d(G)$
be the set of irreducible characters
$\mathrm{Irr}^d(G)$
be the set of irreducible characters
![]() $\chi $
of G that satisfy
$\chi $
of G that satisfy
![]() $d(\chi )=d$
and denote by
$d(\chi )=d$
and denote by
![]() ${\mathbf {k}}^d(G)$
its cardinality. Associated to the prime
${\mathbf {k}}^d(G)$
its cardinality. Associated to the prime
![]() $\ell $
, we also have the set of Brauer
$\ell $
, we also have the set of Brauer
![]() $\ell $
-blocks of G. Each block is uniquely determined by the central functions
$\ell $
-blocks of G. Each block is uniquely determined by the central functions
![]() $\lambda _B$
(see [Reference Navarro46, p. 49]). For every
$\lambda _B$
(see [Reference Navarro46, p. 49]). For every
![]() $\chi \in \mathrm{Irr}(G)$
, we denote by
$\chi \in \mathrm{Irr}(G)$
, we denote by
![]() $\mathrm{bl}(\chi )$
the unique block that satisfies
$\mathrm{bl}(\chi )$
the unique block that satisfies
![]() $\chi \in \mathrm{Irr}(\mathrm{ bl}(\chi ))$
. Furthermore, if
$\chi \in \mathrm{Irr}(\mathrm{ bl}(\chi ))$
. Furthermore, if
![]() $H\leq G$
and b is a block of H, then
$H\leq G$
and b is a block of H, then
![]() $b^G$
denotes the block of G obtained via Brauer’s induction (when it is defined). If B is a block of G and
$b^G$
denotes the block of G obtained via Brauer’s induction (when it is defined). If B is a block of G and
![]() $d\geq 0$
, then let
$d\geq 0$
, then let
![]() $\mathrm{Irr}^d(B)$
be the set of irreducible characters belonging to the block B and having defect d. The cardinality of
$\mathrm{Irr}^d(B)$
be the set of irreducible characters belonging to the block B and having defect d. The cardinality of
![]() $\mathrm{Irr}^d(B)$
is denoted by
$\mathrm{Irr}^d(B)$
is denoted by
![]() ${\mathbf {k}}^d(B)$
.
${\mathbf {k}}^d(B)$
.
We conclude this introductory section with an analogue of [Reference Isaacs32, Problem 5.3] for blocks that will be used in the sequel.
Lemma 2.1. Let
![]() $H\leq G$
be finite groups and consider blocks b of H and B of G. If
$H\leq G$
be finite groups and consider blocks b of H and B of G. If
![]() $\zeta $
is a linear character of G, then:
$\zeta $
is a linear character of G, then:
-
(i) there are blocks
 $b\cdot \zeta _H$
of H and
$b\cdot \zeta _H$
of H and
 $B\cdot \zeta $
of G satisfying
$B\cdot \zeta $
of G satisfying  $$\begin{align*}\mathrm{Irr}(b\cdot\zeta_H)=\{\psi\zeta_H\mid \psi\in\mathrm{Irr}(b)\}\qquad\text{and}\qquad\mathrm{Irr}(B\cdot\zeta)=\{\chi\zeta\mid \chi\in\mathrm{Irr}(B)\};\end{align*}$$
$$\begin{align*}\mathrm{Irr}(b\cdot\zeta_H)=\{\psi\zeta_H\mid \psi\in\mathrm{Irr}(b)\}\qquad\text{and}\qquad\mathrm{Irr}(B\cdot\zeta)=\{\chi\zeta\mid \chi\in\mathrm{Irr}(B)\};\end{align*}$$
-
(ii) If
 $b^G=B$
, then
$b^G=B$
, then
 $(b\cdot \zeta _H)^G=B\cdot \zeta $
.
$(b\cdot \zeta _H)^G=B\cdot \zeta $
.
Proof. The first point is [Reference Rizo51, Lemma 2.1]. Denote by
![]() $\mathcal {R}$
the ring of algebraic integers in
$\mathcal {R}$
the ring of algebraic integers in
![]() $\mathbb {C}$
and by
$\mathbb {C}$
and by
![]() $\overline {\mathcal {R}}$
its quotient modulo a fixed maximal ideal
$\overline {\mathcal {R}}$
its quotient modulo a fixed maximal ideal
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathcal {R}$
containing
$\mathcal {R}$
containing
![]() $\ell \mathcal {R}$
. Let
$\ell \mathcal {R}$
. Let
![]() $g\in G$
and denote by
$g\in G$
and denote by
![]() ${\mathfrak {Cl}}_G(g)$
the G-conjugacy class of g and by
${\mathfrak {Cl}}_G(g)$
the G-conjugacy class of g and by
![]() ${\mathfrak {Cl}}_G(g)^+$
the corresponding conjugacy class sum in the group algebra over
${\mathfrak {Cl}}_G(g)^+$
the corresponding conjugacy class sum in the group algebra over
![]() $\overline {\mathcal {R}}$
. Since the intersection
$\overline {\mathcal {R}}$
. Since the intersection
![]() ${\mathfrak {Cl}}_G(g)\cap H$
is a union of H-conjugacy classes, we can find
${\mathfrak {Cl}}_G(g)\cap H$
is a union of H-conjugacy classes, we can find
![]() $h_1,\dots ,h_n\in {\mathfrak {Cl}}_G(g)\cap H$
such that
$h_1,\dots ,h_n\in {\mathfrak {Cl}}_G(g)\cap H$
such that
 $$\begin{align*}{\mathfrak{Cl}}_G(g)\cap H=\coprod\limits_{i=1}^n{\mathfrak{Cl}}_H(h_i)\end{align*}$$
$$\begin{align*}{\mathfrak{Cl}}_G(g)\cap H=\coprod\limits_{i=1}^n{\mathfrak{Cl}}_H(h_i)\end{align*}$$
and where n is zero if
![]() ${\mathfrak {Cl}}_G(g)\cap H$
is empty. In particular, observe that
${\mathfrak {Cl}}_G(g)\cap H$
is empty. In particular, observe that
![]() $\zeta (h_i)=\zeta (g)$
since
$\zeta (h_i)=\zeta (g)$
since
![]() $\zeta $
is a class function of G. Notice also that
$\zeta $
is a class function of G. Notice also that
![]() $\zeta $
is a group homomorphism. Now, using the notation of [Reference Navarro46, p.87] and recalling for a block B its central character is denoted by
$\zeta $
is a group homomorphism. Now, using the notation of [Reference Navarro46, p.87] and recalling for a block B its central character is denoted by
![]() $\lambda _B$
, we obtain
$\lambda _B$
, we obtain
 $$ \begin{align*} \lambda_{B\cdot\zeta}\left({\mathfrak{Cl}}_G(g)^+\right)&=\lambda_B\left({\mathfrak{Cl}}_G(g)^+\right)\overline{\zeta(g)} \\ &=\lambda_b^G\left({\mathfrak{Cl}}_G(g)^+\right)\overline{\zeta(g)} \\ &=\sum\limits_{i=1}^n\lambda_b\left({\mathfrak{Cl}}_H(h_i)^+\right)\overline{\zeta(g)} \\ &=\sum\limits_{i=1}^n\lambda_b\left({\mathfrak{Cl}}_H(h_i)^+\right)\overline{\zeta_H(h_i)} \\ &=\sum\limits_{i=1}^n\lambda_{b\cdot\zeta_H}\left({\mathfrak{Cl}}_H(h_i)^+\right)=\lambda_{b\cdot\zeta_H}^G\left({\mathfrak{Cl}}_G(g)^+\right), \end{align*} $$
$$ \begin{align*} \lambda_{B\cdot\zeta}\left({\mathfrak{Cl}}_G(g)^+\right)&=\lambda_B\left({\mathfrak{Cl}}_G(g)^+\right)\overline{\zeta(g)} \\ &=\lambda_b^G\left({\mathfrak{Cl}}_G(g)^+\right)\overline{\zeta(g)} \\ &=\sum\limits_{i=1}^n\lambda_b\left({\mathfrak{Cl}}_H(h_i)^+\right)\overline{\zeta(g)} \\ &=\sum\limits_{i=1}^n\lambda_b\left({\mathfrak{Cl}}_H(h_i)^+\right)\overline{\zeta_H(h_i)} \\ &=\sum\limits_{i=1}^n\lambda_{b\cdot\zeta_H}\left({\mathfrak{Cl}}_H(h_i)^+\right)=\lambda_{b\cdot\zeta_H}^G\left({\mathfrak{Cl}}_G(g)^+\right), \end{align*} $$
where for every algebraic integer
![]() $\alpha \in \mathcal {R}$
we denote by
$\alpha \in \mathcal {R}$
we denote by
![]() $\overline {\alpha }$
its reduction modulo
$\overline {\alpha }$
its reduction modulo
![]() $\mathcal {M}$
. This shows that
$\mathcal {M}$
. This shows that
![]() $B\cdot \zeta =(b\cdot \zeta _H)^G$
and we are done.
$B\cdot \zeta =(b\cdot \zeta _H)^G$
and we are done.
2.2 Finite reductive groups and unipotent characters
Let
![]() ${\mathbf {G}}$
be a connected reductive group defined over an algebraic closure of a field of positive characteristic p different from
${\mathbf {G}}$
be a connected reductive group defined over an algebraic closure of a field of positive characteristic p different from
![]() $\ell $
, and consider a Frobenius endomorphism
$\ell $
, and consider a Frobenius endomorphism
![]() $F:{\mathbf {G}}\to {\mathbf {G}}$
associated with an
$F:{\mathbf {G}}\to {\mathbf {G}}$
associated with an
![]() $\mathbb {F}_q$
-structure for a power q of p. The set of
$\mathbb {F}_q$
-structure for a power q of p. The set of
![]() $\mathbb {F}_q$
-rational points on the variety
$\mathbb {F}_q$
-rational points on the variety
![]() ${\mathbf {G}}$
is denoted by
${\mathbf {G}}$
is denoted by
![]() ${\mathbf {G}}^F$
and is called a finite reductive group. By abuse of notation, we also refer to the pair
${\mathbf {G}}^F$
and is called a finite reductive group. By abuse of notation, we also refer to the pair
![]() $({\mathbf {G}},F)$
as a finite reductive group. In this paper, we say that the algebraic group
$({\mathbf {G}},F)$
as a finite reductive group. In this paper, we say that the algebraic group
![]() ${\mathbf {G}}$
is simply connected, if its derived subgroup
${\mathbf {G}}$
is simply connected, if its derived subgroup
![]() $[{\mathbf {G}},{\mathbf {G}}]$
is simply connected.
$[{\mathbf {G}},{\mathbf {G}}]$
is simply connected.
Let
![]() ${\mathbf {L}}$
be a Levi subgroup of a parabolic subgroup
${\mathbf {L}}$
be a Levi subgroup of a parabolic subgroup
![]() ${\mathbf {P}}$
of
${\mathbf {P}}$
of
![]() ${\mathbf {G}}$
, and assume that
${\mathbf {G}}$
, and assume that
![]() ${\mathbf {L}}$
(but not necessarily
${\mathbf {L}}$
(but not necessarily
![]() ${\mathbf {P}}$
) is F-stable. Using
${\mathbf {P}}$
) is F-stable. Using
![]() $\ell $
-adic cohomology, Deligne–Lusztig [Reference Deligne and Lusztig24] and Lusztig [Reference Lusztig37] defined a
$\ell $
-adic cohomology, Deligne–Lusztig [Reference Deligne and Lusztig24] and Lusztig [Reference Lusztig37] defined a
![]() $\mathbb {Z}$
-linear map
$\mathbb {Z}$
-linear map
with adjoint
The exact definition can be found in [Reference Cabanes and Enguehard17, Section 8.3]. These maps are known to be independent of the choice of the parabolic subgroup
![]() ${\mathbf {P}}$
in almost all cases (see [Reference Bonnafé and Michel3] and [Reference Taylor66]) and, in particular, in those considered in this paper. Therefore, we will always omit
${\mathbf {P}}$
in almost all cases (see [Reference Bonnafé and Michel3] and [Reference Taylor66]) and, in particular, in those considered in this paper. Therefore, we will always omit
![]() ${\mathbf {P}}$
and denote
${\mathbf {P}}$
and denote
![]() ${\mathbf {R}}_{{\mathbf {L}}\leq {\mathbf {P}}}^{\mathbf {G}}$
simply by
${\mathbf {R}}_{{\mathbf {L}}\leq {\mathbf {P}}}^{\mathbf {G}}$
simply by
![]() ${\mathbf {R}}_{\mathbf {L}}^{\mathbf {G}}$
. Next, using Deligne–Lusztig induction we define the unipotent characters of
${\mathbf {R}}_{\mathbf {L}}^{\mathbf {G}}$
. Next, using Deligne–Lusztig induction we define the unipotent characters of
![]() ${\mathbf {G}}^F$
. These are the irreducible characters
${\mathbf {G}}^F$
. These are the irreducible characters
![]() $\chi $
of
$\chi $
of
![]() ${\mathbf {G}}^F$
that appear as an irreducible constituent of the virtual character
${\mathbf {G}}^F$
that appear as an irreducible constituent of the virtual character
![]() ${\mathbf {R}}_{{\mathbf {T}}}^{{\mathbf {G}}}(1_{\mathbf {T}})$
for some F-stable maximal torus
${\mathbf {R}}_{{\mathbf {T}}}^{{\mathbf {G}}}(1_{\mathbf {T}})$
for some F-stable maximal torus
![]() ${\mathbf {T}}$
of
${\mathbf {T}}$
of
![]() ${\mathbf {G}}$
. The set of unipotent characters of
${\mathbf {G}}$
. The set of unipotent characters of
![]() ${\mathbf {G}}^F$
is denoted by
${\mathbf {G}}^F$
is denoted by
![]() $\mathrm{Uch}({\mathbf {G}}^F)$
and its cardinality by
$\mathrm{Uch}({\mathbf {G}}^F)$
and its cardinality by
![]() ${\mathbf {k}}_{\mathrm{u}}({\mathbf {G}}^F)$
. Similarly, if B is a block of
${\mathbf {k}}_{\mathrm{u}}({\mathbf {G}}^F)$
. Similarly, if B is a block of
![]() ${\mathbf {G}}^F$
and d a nonnegative integer, then
${\mathbf {G}}^F$
and d a nonnegative integer, then
![]() ${\mathbf {k}}_{\mathrm{u}}^d(B)$
denotes the cardinality of the intersection
${\mathbf {k}}_{\mathrm{u}}^d(B)$
denotes the cardinality of the intersection
![]() $\mathrm{Uch}({\mathbf {G}}^F)\cap \mathrm{Irr}^d(B)$
.
$\mathrm{Uch}({\mathbf {G}}^F)\cap \mathrm{Irr}^d(B)$
.
2.3 e-Harish-Chandra theory for unipotent characters
Denote by e the multiplicative order of q modulo
![]() $\ell $
, if
$\ell $
, if
![]() $\ell $
is odd, or modulo
$\ell $
is odd, or modulo
![]() $4$
, if
$4$
, if
![]() $\ell =2$
. In this section, we collect the main results of e-Harish-Chandra theory for unipotent characters. This was first introduced by Fong and Srinivasan [Reference Fong and Srinivasan28] for classical groups and then further developed by Broué, Malle and Michel [Reference Broué, Malle and Michel9] for unipotent characters. The compatibility of this theory with Brauer
$\ell =2$
. In this section, we collect the main results of e-Harish-Chandra theory for unipotent characters. This was first introduced by Fong and Srinivasan [Reference Fong and Srinivasan28] for classical groups and then further developed by Broué, Malle and Michel [Reference Broué, Malle and Michel9] for unipotent characters. The compatibility of this theory with Brauer
![]() $\ell $
-blocks was first described by Fong and Srinivasan for classical groups [Reference Fong and Srinivasan27], [Reference Fong and Srinivasan29] and then completed by Broué, Malle and Michel for large primes [Reference Broué, Malle and Michel9], by Cabanes and Enguehard for all good primes [Reference Cabanes and Enguehard15] and by Enguehard for the remaining bad primes [Reference Enguehard26]. These results also provide a description of the characters belonging to unipotent blocks (see [Reference Cabanes and Enguehard15, Theorem (iii)]). Another description of these characters was provided by the author in [Reference Rossi57] under certain restrictions on the prime
$\ell $
-blocks was first described by Fong and Srinivasan for classical groups [Reference Fong and Srinivasan27], [Reference Fong and Srinivasan29] and then completed by Broué, Malle and Michel for large primes [Reference Broué, Malle and Michel9], by Cabanes and Enguehard for all good primes [Reference Cabanes and Enguehard15] and by Enguehard for the remaining bad primes [Reference Enguehard26]. These results also provide a description of the characters belonging to unipotent blocks (see [Reference Cabanes and Enguehard15, Theorem (iii)]). Another description of these characters was provided by the author in [Reference Rossi57] under certain restrictions on the prime
![]() $\ell $
(see also [Reference Rossi57, Remark 4.14] for a comparison between the two descriptions). We refer the reader to the monographs [Reference Cabanes and Enguehard17] and [Reference Geck and Malle30] for a more complete account of e-Harish-Chandra theory and to the papers [Reference Cabanes and Enguehard16] and [Reference Kessar and Malle34] for results on nonunipotent blocks.
$\ell $
(see also [Reference Rossi57, Remark 4.14] for a comparison between the two descriptions). We refer the reader to the monographs [Reference Cabanes and Enguehard17] and [Reference Geck and Malle30] for a more complete account of e-Harish-Chandra theory and to the papers [Reference Cabanes and Enguehard16] and [Reference Kessar and Malle34] for results on nonunipotent blocks.
The theory of
![]() $\Phi _e$
-subgroups that constitutes the foundation of e-Harish-Chandra theory was introduced in [Reference Broué and Malle8]. Following their terminology, we say that an F-stable torus
$\Phi _e$
-subgroups that constitutes the foundation of e-Harish-Chandra theory was introduced in [Reference Broué and Malle8]. Following their terminology, we say that an F-stable torus
![]() ${\mathbf {S}}$
of
${\mathbf {S}}$
of
![]() ${\mathbf {G}}$
is a
${\mathbf {G}}$
is a
![]() $\Phi _e$
-torus if its order polynomial
$\Phi _e$
-torus if its order polynomial
![]() $P_{({\mathbf {S}},F)}$
is a power of the e-th cyclotomic polynomial, that is, if
$P_{({\mathbf {S}},F)}$
is a power of the e-th cyclotomic polynomial, that is, if
![]() $P_{({\mathbf {S}},F)}=\Phi _e^{n}$
for some integer n and where
$P_{({\mathbf {S}},F)}=\Phi _e^{n}$
for some integer n and where
![]() $\Phi _e$
denotes the e-th cyclotomic polynomial (see [Reference Cabanes and Enguehard17, Definition 13.3]). Then, we say that a Levi subgroup
$\Phi _e$
denotes the e-th cyclotomic polynomial (see [Reference Cabanes and Enguehard17, Definition 13.3]). Then, we say that a Levi subgroup
![]() ${\mathbf {L}}$
of
${\mathbf {L}}$
of
![]() ${\mathbf {G}}$
is an e-split Levi subgroup if there exists a
${\mathbf {G}}$
is an e-split Levi subgroup if there exists a
![]() $\Phi _e$
-torus
$\Phi _e$
-torus
![]() ${\mathbf {S}}$
such that
${\mathbf {S}}$
such that
![]() ${\mathbf {L}}={\mathbf {C}}_{\mathbf {G}}({\mathbf {S}})$
. More precisely, we say that
${\mathbf {L}}={\mathbf {C}}_{\mathbf {G}}({\mathbf {S}})$
. More precisely, we say that
![]() ${\mathbf {L}}$
is an e-split Levi subgroup of
${\mathbf {L}}$
is an e-split Levi subgroup of
![]() $({\mathbf {G}},F)$
to emphasise the role of the Frobenius endomorphism F. Observe that, for any F-stable torus
$({\mathbf {G}},F)$
to emphasise the role of the Frobenius endomorphism F. Observe that, for any F-stable torus
![]() ${\mathbf {T}}$
, there exists a unique maximal
${\mathbf {T}}$
, there exists a unique maximal
![]() $\Phi _e$
-torus of
$\Phi _e$
-torus of
![]() ${\mathbf {T}}$
denoted by
${\mathbf {T}}$
denoted by
![]() ${\mathbf {T}}_{\Phi _e}$
(see [Reference Cabanes and Enguehard17, Proposition 13.5]). Then, it can be shown that an F-stable Levi subgroup
${\mathbf {T}}_{\Phi _e}$
(see [Reference Cabanes and Enguehard17, Proposition 13.5]). Then, it can be shown that an F-stable Levi subgroup
![]() ${\mathbf {L}}$
of
${\mathbf {L}}$
of
![]() ${\mathbf {G}}$
is e-split if and only if
${\mathbf {G}}$
is e-split if and only if
![]() ${\mathbf {L}}={\mathbf {C}}_{\mathbf {G}}({\mathbf {Z}}^\circ ({\mathbf {L}})_{\Phi _e})$
(see, for instance, [Reference Geck and Malle30, Proposition 3.5.5]).
${\mathbf {L}}={\mathbf {C}}_{\mathbf {G}}({\mathbf {Z}}^\circ ({\mathbf {L}})_{\Phi _e})$
(see, for instance, [Reference Geck and Malle30, Proposition 3.5.5]).
Next, recall that
![]() $({\mathbf {L}},\lambda )$
is an e-cuspidal pair of
$({\mathbf {L}},\lambda )$
is an e-cuspidal pair of
![]() $({\mathbf {G}},F)$
if
$({\mathbf {G}},F)$
if
![]() ${\mathbf {L}}$
is an e-split Levi subgroup of
${\mathbf {L}}$
is an e-split Levi subgroup of
![]() $({\mathbf {G}},F)$
and
$({\mathbf {G}},F)$
and
![]() $\lambda \in \mathrm{Irr}({\mathbf {L}}^F)$
satisfies
$\lambda \in \mathrm{Irr}({\mathbf {L}}^F)$
satisfies
![]() $^*{\mathbf {R}}_{{\mathbf {M}}}^{\mathbf {L}}(\lambda )=0$
for every e-split Levi subgroup
$^*{\mathbf {R}}_{{\mathbf {M}}}^{\mathbf {L}}(\lambda )=0$
for every e-split Levi subgroup
![]() ${\mathbf {M}}<{\mathbf {L}}$
. A character
${\mathbf {M}}<{\mathbf {L}}$
. A character
![]() $\lambda $
with the property above is said to be an e-cuspidal character of
$\lambda $
with the property above is said to be an e-cuspidal character of
![]() ${\mathbf {L}}^F$
. If in addition the character
${\mathbf {L}}^F$
. If in addition the character
![]() $\lambda $
is unipotent, then we say that
$\lambda $
is unipotent, then we say that
![]() $({\mathbf {L}},\lambda )$
is a unipotent e-cuspidal pair and that
$({\mathbf {L}},\lambda )$
is a unipotent e-cuspidal pair and that
![]() $\lambda $
is a unipotent e-cuspidal character. We denote by
$\lambda $
is a unipotent e-cuspidal character. We denote by
![]() ${\mathcal {C} \mathcal {P}_{\mathrm{u}}}({\mathbf {G}},F)$
the set of unipotent e-cuspidal pairs of
${\mathcal {C} \mathcal {P}_{\mathrm{u}}}({\mathbf {G}},F)$
the set of unipotent e-cuspidal pairs of
![]() $({\mathbf {G}},F)$
and by
$({\mathbf {G}},F)$
and by
![]() ${\mathbf {k}}_{\mathrm{c,u}}({\mathbf {G}}^F)$
the number of unipotent e-cuspidal characters of
${\mathbf {k}}_{\mathrm{c,u}}({\mathbf {G}}^F)$
the number of unipotent e-cuspidal characters of
![]() ${\mathbf {G}}^F$
. Moreover, we define the e-Harish-Chandra series associated to the e-cuspidal pair
${\mathbf {G}}^F$
. Moreover, we define the e-Harish-Chandra series associated to the e-cuspidal pair
![]() $({\mathbf {L}},\lambda )$
to be the set of irreducible constituents of the virtual character
$({\mathbf {L}},\lambda )$
to be the set of irreducible constituents of the virtual character
![]() ${\mathbf {R}}_{\mathbf {L}}^{\mathbf {G}}(\lambda )$
, denoted by
${\mathbf {R}}_{\mathbf {L}}^{\mathbf {G}}(\lambda )$
, denoted by
![]() ${\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
. As before, when
${\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
. As before, when
![]() $\lambda $
is unipotent we say that
$\lambda $
is unipotent we say that
![]() ${\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
is a unipotent e-Harish-Chandra series.
${\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
is a unipotent e-Harish-Chandra series.
Unipotent characters were parametrised by Broué, Malle and Michel [Reference Broué, Malle and Michel9, Theorem 3.2] by using e-Harish-Chandra theory. Their description can be divided into two parts. First, each unipotent character lies in a unique e-Harish-Chandra series, that is,
 $$\begin{align*}\mathrm{Uch}\left({\mathbf{G}}^F\right)=\coprod\limits_{({\mathbf{L}},\lambda)}{\mathcal{E}}\left({\mathbf{G}}^F,({\mathbf{L}},\lambda)\right)\end{align*}$$
$$\begin{align*}\mathrm{Uch}\left({\mathbf{G}}^F\right)=\coprod\limits_{({\mathbf{L}},\lambda)}{\mathcal{E}}\left({\mathbf{G}}^F,({\mathbf{L}},\lambda)\right)\end{align*}$$
where
![]() $({\mathbf {L}},\lambda )$
runs over a set of representatives for the action of
$({\mathbf {L}},\lambda )$
runs over a set of representatives for the action of
![]() ${\mathbf {G}}^F$
on the set of unipotent e-cuspidal pairs of
${\mathbf {G}}^F$
on the set of unipotent e-cuspidal pairs of
![]() $({\mathbf {G}},F)$
as explained in [Reference Broué, Malle and Michel9, Theorem 3.2 (1)]. This is a well-known fact and will be used throughout the paper without further reference. As a consequence of the partition above, it now remains to parametrise the unipotent e-Harish-Chandra series. If
$({\mathbf {G}},F)$
as explained in [Reference Broué, Malle and Michel9, Theorem 3.2 (1)]. This is a well-known fact and will be used throughout the paper without further reference. As a consequence of the partition above, it now remains to parametrise the unipotent e-Harish-Chandra series. If
![]() $({\mathbf {L}},\lambda )$
is a unipotent e-cuspidal pair, we denote by
$({\mathbf {L}},\lambda )$
is a unipotent e-cuspidal pair, we denote by
![]() $W_{\mathbf {G}}({\mathbf {L}},\lambda )^F:={\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F_\lambda /{\mathbf {L}}^F$
the corresponding relative Weyl group. Then, [Reference Broué, Malle and Michel9, Theorem 3.2 (2)] parametrises the characters in an e-Harish-Chandra series in terms of the characters in the relative Weyl group by showing the existence of a bijection
$W_{\mathbf {G}}({\mathbf {L}},\lambda )^F:={\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F_\lambda /{\mathbf {L}}^F$
the corresponding relative Weyl group. Then, [Reference Broué, Malle and Michel9, Theorem 3.2 (2)] parametrises the characters in an e-Harish-Chandra series in terms of the characters in the relative Weyl group by showing the existence of a bijection
In Section 3, we reformulate (2.2) in order to obtain Theorem C.
Unipotent e-Harish-Chandra series are also used to parametrise the so-called unipotent blocks, that is, those blocks that contain unipotent characters. This was proved in [Reference Cabanes and Enguehard15] (see also [Reference Broué, Malle and Michel9] for the case of large primes). More precisely, if
![]() $\ell $
is odd and good for
$\ell $
is odd and good for
![]() ${\mathbf {G}}$
, with
${\mathbf {G}}$
, with
![]() $\ell \neq 3$
if
$\ell \neq 3$
if
![]() ${^3\mathbf {{D}}_4}$
is an irreducible rational component of
${^3\mathbf {{D}}_4}$
is an irreducible rational component of
![]() $({\mathbf {G}},F)$
, then for every
$({\mathbf {G}},F)$
, then for every
![]() $\ell $
-block B of
$\ell $
-block B of
![]() ${\mathbf {G}}^F$
there exists a unipotent e-cuspidal pair
${\mathbf {G}}^F$
there exists a unipotent e-cuspidal pair
![]() $({\mathbf {L}},\lambda )$
, with
$({\mathbf {L}},\lambda )$
, with
![]() $({\mathbf {L}},\lambda )$
unique up to
$({\mathbf {L}},\lambda )$
unique up to
![]() ${\mathbf {G}}^F$
-conjugation such that all the irreducible constituents of
${\mathbf {G}}^F$
-conjugation such that all the irreducible constituents of
![]() ${\mathbf {R}}_{\mathbf {L}}^{\mathbf {G}}(\lambda )$
belongs to the block B. In this case, we write
${\mathbf {R}}_{\mathbf {L}}^{\mathbf {G}}(\lambda )$
belongs to the block B. In this case, we write
![]() $B=b_{{\mathbf {G}}^F}({\mathbf {L}},\lambda )$
and we also have
$B=b_{{\mathbf {G}}^F}({\mathbf {L}},\lambda )$
and we also have
Moreover, [Reference Cabanes and Enguehard15, Proposition 3.3 (ii) and Proposition 4.2] imply that
![]() $\mathrm{bl}(\lambda )^{{\mathbf {G}}^F}=B$
.
$\mathrm{bl}(\lambda )^{{\mathbf {G}}^F}=B$
.
2.4 Pseudo-unipotent characters
We denote by
![]() $({\mathbf {G}}^*,F^*)$
a group in duality with
$({\mathbf {G}}^*,F^*)$
a group in duality with
![]() $({\mathbf {G}},F)$
with respect to a choice of an F-stable maximal torus
$({\mathbf {G}},F)$
with respect to a choice of an F-stable maximal torus
![]() ${\mathbf {T}}$
of
${\mathbf {T}}$
of
![]() ${\mathbf {G}}$
and an
${\mathbf {G}}$
and an
![]() $F^*$
-stable maximal torus
$F^*$
-stable maximal torus
![]() ${\mathbf {T}}^*$
of
${\mathbf {T}}^*$
of
![]() ${\mathbf {G}}^*$
. If
${\mathbf {G}}^*$
. If
![]() $\tau :{\mathbf {G}}_{\mathrm{sc}}\to [{\mathbf {G}},{\mathbf {G}}]$
is a simply connected covering (see [Reference Geck and Malle30, Remark 1.5.13]), then there exists an isomorphisms between the abelian groups
$\tau :{\mathbf {G}}_{\mathrm{sc}}\to [{\mathbf {G}},{\mathbf {G}}]$
is a simply connected covering (see [Reference Geck and Malle30, Remark 1.5.13]), then there exists an isomorphisms between the abelian groups
 $$ \begin{align*} {\mathbf{Z}}\left({\mathbf{G}}^*\right)^{F^*}&\to\mathrm{Irr}\ \left({\mathbf{G}}^F/\tau({\mathbf{G}}_{\mathrm{sc}})^F\right) \\ z &\mapsto \hat{z}_{{\mathbf{G}}} \end{align*} $$
$$ \begin{align*} {\mathbf{Z}}\left({\mathbf{G}}^*\right)^{F^*}&\to\mathrm{Irr}\ \left({\mathbf{G}}^F/\tau({\mathbf{G}}_{\mathrm{sc}})^F\right) \\ z &\mapsto \hat{z}_{{\mathbf{G}}} \end{align*} $$
according to [Reference Cabanes and Enguehard17, (8.19)]. Notice that, if
![]() ${\mathbf {L}}$
is an F-stable Levi subgroup of
${\mathbf {L}}$
is an F-stable Levi subgroup of
![]() ${\mathbf {G}}$
, then its dual
${\mathbf {G}}$
, then its dual
![]() ${\mathbf {L}}^*$
is an
${\mathbf {L}}^*$
is an
![]() $F^*$
-stable Levi subgroup of
$F^*$
-stable Levi subgroup of
![]() ${\mathbf {G}}^*$
and we have
${\mathbf {G}}^*$
and we have
![]() ${\mathbf {Z}}({\mathbf {G}}^*)^{F^*}\leq {\mathbf {Z}}({\mathbf {L}}^*)^{F^*}$
. In particular, every element
${\mathbf {Z}}({\mathbf {G}}^*)^{F^*}\leq {\mathbf {Z}}({\mathbf {L}}^*)^{F^*}$
. In particular, every element
![]() $z\in {\mathbf {Z}}({\mathbf {G}}^*)^{F^*}$
defines a linear characters of
$z\in {\mathbf {Z}}({\mathbf {G}}^*)^{F^*}$
defines a linear characters of
![]() $\hat {z}_{{\mathbf {L}}}$
and restriction of characters yields the equality
$\hat {z}_{{\mathbf {L}}}$
and restriction of characters yields the equality
In the next definition, we consider characters that are obtained by multiplying these linear characters with unipotent characters.
Definition 2.2. Let
![]() $({\mathbf {K}},F)$
be a finite reductive group, and consider a Levi subgroup of
$({\mathbf {K}},F)$
be a finite reductive group, and consider a Levi subgroup of
![]() ${\mathbf {L}}\leq {\mathbf {K}}$
and an irreducible character
${\mathbf {L}}\leq {\mathbf {K}}$
and an irreducible character
![]() $\theta \in \mathrm{Irr}({\mathbf {L}}^F)$
. We say that
$\theta \in \mathrm{Irr}({\mathbf {L}}^F)$
. We say that
![]() $\theta $
is
$\theta $
is
![]() $({\mathbf {K}},F)$
-pseudo-unipotent if there exists an element
$({\mathbf {K}},F)$
-pseudo-unipotent if there exists an element
![]() $z\in {\mathbf {Z}}({\mathbf {K}}^*)^{F^*}$
such that
$z\in {\mathbf {Z}}({\mathbf {K}}^*)^{F^*}$
such that
![]() $\theta \hat {z}_{{\mathbf {L}}}$
is unipotent. Moreover, for every unipotent character
$\theta \hat {z}_{{\mathbf {L}}}$
is unipotent. Moreover, for every unipotent character
![]() $\lambda \in \mathrm{ Uch}({\mathbf {L}}^F)$
, we denote by
$\lambda \in \mathrm{ Uch}({\mathbf {L}}^F)$
, we denote by
![]() $\mathrm{ps}_{\mathbf {K}}(\lambda )$
the set of
$\mathrm{ps}_{\mathbf {K}}(\lambda )$
the set of
![]() $({\mathbf {K}},F)$
-pseudo-unipotent characters of
$({\mathbf {K}},F)$
-pseudo-unipotent characters of
![]() ${\mathbf {L}}^F$
of the form
${\mathbf {L}}^F$
of the form
![]() $\lambda \hat {z}_{{\mathbf {L}}}$
for some
$\lambda \hat {z}_{{\mathbf {L}}}$
for some
![]() $z\in {\mathbf {Z}}({\mathbf {K}}^*)^{F^*}$
. Moreover, we denote by
$z\in {\mathbf {Z}}({\mathbf {K}}^*)^{F^*}$
. Moreover, we denote by
![]() $\mathrm{ps}_{{\mathbf {K}}}({\mathbf {L}}^F)$
the set of all
$\mathrm{ps}_{{\mathbf {K}}}({\mathbf {L}}^F)$
the set of all
![]() $({\mathbf {K}},F)$
-pseudo unipotent characters of
$({\mathbf {K}},F)$
-pseudo unipotent characters of
![]() ${\mathbf {L}}^F$
. When the group
${\mathbf {L}}^F$
. When the group
![]() ${\mathbf {K}}$
coincides with
${\mathbf {K}}$
coincides with
![]() ${\mathbf {L}}$
, we denote the set of characters
${\mathbf {L}}$
, we denote the set of characters
![]() $\mathrm{ps}_{\mathbf {L}}({\mathbf {L}}^F)$
simply by
$\mathrm{ps}_{\mathbf {L}}({\mathbf {L}}^F)$
simply by
![]() $\mathrm{ps}({\mathbf {L}}^F)$
.
$\mathrm{ps}({\mathbf {L}}^F)$
.
In accordance with the terminology introduced above, we say that an e-Harish-Chandra series of
![]() $({\mathbf {K}},F)$
is pseudo-unipotent if it is of the form
$({\mathbf {K}},F)$
is pseudo-unipotent if it is of the form
![]() ${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\nu ))$
for some
${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\nu ))$
for some
![]() $\nu \in \mathrm{ps}_{\mathbf {K}}(\lambda )$
and where
$\nu \in \mathrm{ps}_{\mathbf {K}}(\lambda )$
and where
![]() $({\mathbf {L}},\lambda )$
is a unipotent e-cuspidal pair of
$({\mathbf {L}},\lambda )$
is a unipotent e-cuspidal pair of
![]() $({\mathbf {K}},F)$
. In this case, we also say that
$({\mathbf {K}},F)$
. In this case, we also say that
![]() $({\mathbf {L}},\nu )$
is a pseudo-unipotent e-cuspidal pair. We define the union of all the series associated to characters in
$({\mathbf {L}},\nu )$
is a pseudo-unipotent e-cuspidal pair. We define the union of all the series associated to characters in
![]() $\mathrm{ps}_{\mathbf {K}}(\lambda )$
by
$\mathrm{ps}_{\mathbf {K}}(\lambda )$
by
![]() ${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\mathrm{ps}_{\mathbf {K}}(\lambda )))$
. Since
${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\mathrm{ps}_{\mathbf {K}}(\lambda )))$
. Since
for every
![]() $z\in {\mathbf {Z}}({\mathbf {K}}^*)^{F^*}$
by [Reference Cabanes and Enguehard17, (8.20)], we deduce that the elements of the pseudo-unipotent e-Harish-Chandra series
$z\in {\mathbf {Z}}({\mathbf {K}}^*)^{F^*}$
by [Reference Cabanes and Enguehard17, (8.20)], we deduce that the elements of the pseudo-unipotent e-Harish-Chandra series
![]() ${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\lambda \hat {z}))$
are exactly the irreducible characters of the form
${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\lambda \hat {z}))$
are exactly the irreducible characters of the form
![]() $\varphi \hat {z}_{{\mathbf {K}}}$
for some unipotent character
$\varphi \hat {z}_{{\mathbf {K}}}$
for some unipotent character
![]() $\varphi \in {\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\lambda ))$
. Moreover, we point out that
$\varphi \in {\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\lambda ))$
. Moreover, we point out that
![]() $\lambda $
is the unique unipotent character in the set
$\lambda $
is the unique unipotent character in the set
![]() $\mathrm{ps}_{\mathbf {K}}(\lambda )$
according to [Reference Cabanes and Enguehard17, Proposition 8.26]. Similarly, the unipotent characters in the set
$\mathrm{ps}_{\mathbf {K}}(\lambda )$
according to [Reference Cabanes and Enguehard17, Proposition 8.26]. Similarly, the unipotent characters in the set
![]() ${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\mathrm{ps}_{\mathbf {K}}(\lambda )))$
are those in the series
${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\mathrm{ps}_{\mathbf {K}}(\lambda )))$
are those in the series
![]() ${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\lambda ))$
.
${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\lambda ))$
.
Our next lemma shows that blocks covering pseudo-unipotent characters are regular as defined in [Reference Navarro46, p.210].
Lemma 2.3. Let
![]() ${\mathbf {L}}$
be an F-stable Levi subgroup of
${\mathbf {L}}$
be an F-stable Levi subgroup of
![]() ${\mathbf {G}}$
, and suppose that
${\mathbf {G}}$
, and suppose that
![]() $\ell $
is odd and good for
$\ell $
is odd and good for
![]() ${\mathbf {G}}$
. Furthermore, suppose that
${\mathbf {G}}$
. Furthermore, suppose that
![]() $\ell \neq 3$
if
$\ell \neq 3$
if
![]() $({\mathbf {G}},F)$
has an irreducible rational component of type
$({\mathbf {G}},F)$
has an irreducible rational component of type
![]() ${{}^3{\mathbf {D}}}_4$
. For every
${{}^3{\mathbf {D}}}_4$
. For every
![]() ${\mathbf {L}}^F\leq H\leq {\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
and every character
${\mathbf {L}}^F\leq H\leq {\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
and every character
![]() $\vartheta \in \mathrm{Irr}(H)$
lying above some pseudo-unipotent character in
$\vartheta \in \mathrm{Irr}(H)$
lying above some pseudo-unipotent character in
![]() $\mathrm{ ps}({\mathbf {L}}^F)$
, the block
$\mathrm{ ps}({\mathbf {L}}^F)$
, the block
![]() $\mathrm{bl}(\vartheta )$
is
$\mathrm{bl}(\vartheta )$
is
![]() ${\mathbf {L}}^F$
-regular. In particular, the Brauer induced block
${\mathbf {L}}^F$
-regular. In particular, the Brauer induced block
![]() $\mathrm{bl}(\vartheta )^H$
is defined and is the unique block of H covering
$\mathrm{bl}(\vartheta )^H$
is defined and is the unique block of H covering
![]() $\mathrm{ bl}(\vartheta )$
.
$\mathrm{ bl}(\vartheta )$
.
Proof. Let
![]() $\varphi \in \mathrm{Uch}({\mathbf {L}}^F)$
and
$\varphi \in \mathrm{Uch}({\mathbf {L}}^F)$
and
![]() $z\in {\mathbf {Z}}({\mathbf {L}}^*)^{F^*}$
such that
$z\in {\mathbf {Z}}({\mathbf {L}}^*)^{F^*}$
such that
![]() $\varphi \hat {z}_{{\mathbf {L}}}$
lies below the character
$\varphi \hat {z}_{{\mathbf {L}}}$
lies below the character
![]() $\vartheta $
and choose a unipotent e-cuspidal pair
$\vartheta $
and choose a unipotent e-cuspidal pair
![]() $({\mathbf {M}},\mu )$
of
$({\mathbf {M}},\mu )$
of
![]() ${\mathbf {L}}$
such that
${\mathbf {L}}$
such that
![]() $\varphi \in {\mathcal {E}}({\mathbf {L}}^F,({\mathbf {M}},\mu ))$
. In particular,
$\varphi \in {\mathcal {E}}({\mathbf {L}}^F,({\mathbf {M}},\mu ))$
. In particular,
![]() $\mathrm{bl}(\varphi )=b_{{\mathbf {L}}^F}({\mathbf {M}},\mu )$
according to [Reference Cabanes and Enguehard15]. If
$\mathrm{bl}(\varphi )=b_{{\mathbf {L}}^F}({\mathbf {M}},\mu )$
according to [Reference Cabanes and Enguehard15]. If
![]() $Q:={\mathbf {Z}}({\mathbf {M}})_\ell ^F$
, then
$Q:={\mathbf {Z}}({\mathbf {M}})_\ell ^F$
, then
![]() ${\mathbf {M}}^F={\mathbf {C}}_{{\mathbf {G}}^F}(Q)$
according to [Reference Cabanes and Enguehard15, Proposition 3.3 (ii)]. Moreover, observe that [Reference Cabanes and Enguehard15, Proposition 4.2] implies that
${\mathbf {M}}^F={\mathbf {C}}_{{\mathbf {G}}^F}(Q)$
according to [Reference Cabanes and Enguehard15, Proposition 3.3 (ii)]. Moreover, observe that [Reference Cabanes and Enguehard15, Proposition 4.2] implies that
![]() $\mathrm{bl}(\varphi )=b_{{\mathbf {L}}^F}({\mathbf {M}},\mu )=\mathrm{bl}(\mu )^{{\mathbf {L}}^F}$
while [Reference Rizo51, Lemma 2.1] implies that
$\mathrm{bl}(\varphi )=b_{{\mathbf {L}}^F}({\mathbf {M}},\mu )=\mathrm{bl}(\mu )^{{\mathbf {L}}^F}$
while [Reference Rizo51, Lemma 2.1] implies that
![]() $\mathrm{bl}(\varphi )$
and
$\mathrm{bl}(\varphi )$
and
![]() $\mathrm{bl}(\varphi \hat {z}_{\mathbf {L}})$
have the same defect groups. Now, applying [Reference Navarro46, Lemma 4.13 and Theorem 9.26], we can find defect groups
$\mathrm{bl}(\varphi \hat {z}_{\mathbf {L}})$
have the same defect groups. Now, applying [Reference Navarro46, Lemma 4.13 and Theorem 9.26], we can find defect groups
![]() $D_\vartheta $
,
$D_\vartheta $
,
![]() $D_\varphi $
and
$D_\varphi $
and
![]() $D_\mu $
of
$D_\mu $
of
![]() $\mathrm{bl}(\vartheta )$
,
$\mathrm{bl}(\vartheta )$
,
![]() $\mathrm{bl}(\varphi )$
and
$\mathrm{bl}(\varphi )$
and
![]() $\mathrm{bl}(\mu )$
respectively with the property that
$\mathrm{bl}(\mu )$
respectively with the property that
![]() $D_\mu \leq D_\varphi \leq D_\vartheta $
. Since
$D_\mu \leq D_\varphi \leq D_\vartheta $
. Since
![]() $Q\leq {\mathbf {O}}_\ell ({\mathbf {M}}^F)\leq D_\mu $
by [Reference Navarro46, Theorem 4.8], we deduce that
$Q\leq {\mathbf {O}}_\ell ({\mathbf {M}}^F)\leq D_\mu $
by [Reference Navarro46, Theorem 4.8], we deduce that
![]() $Q\leq D_\vartheta $
and hence
$Q\leq D_\vartheta $
and hence
![]() ${\mathbf {C}}_H(D_\vartheta )\leq {\mathbf {C}}_H(Q)={\mathbf {M}}^F\leq {\mathbf {L}}^F$
. By [Reference Navarro46, Lemma 9.20], we conclude that the block
${\mathbf {C}}_H(D_\vartheta )\leq {\mathbf {C}}_H(Q)={\mathbf {M}}^F\leq {\mathbf {L}}^F$
. By [Reference Navarro46, Lemma 9.20], we conclude that the block
![]() $\mathrm{bl}(\vartheta )$
is
$\mathrm{bl}(\vartheta )$
is
![]() ${\mathbf {L}}^F$
-regular. The second part of the lemma now follows from [Reference Navarro46, Theorem 9.19].
${\mathbf {L}}^F$
-regular. The second part of the lemma now follows from [Reference Navarro46, Theorem 9.19].
3 Compatibility with isomorphisms of character triples
The aim of this section is to show how the bijection (2.2) can be made compatible with isomorphisms of character triples and with the action of automorphisms. This property was first suggested by the author in [Reference Rossi57, Parametrisation B] and further studied in [Reference Rossi54]. Our Theorem C gives a solution of this conjectured result for unipotent e-Harish-Chandra series and groups of type
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
and
$\mathbf {B}$
and
![]() $\mathbf {C}$
. Before proceeding further, we show how the parametrisation (2.2) can be reformulated in a more convenient form. For this, let
$\mathbf {C}$
. Before proceeding further, we show how the parametrisation (2.2) can be reformulated in a more convenient form. For this, let
![]() $({\mathbf {L}},\lambda )$
be a unipotent e-cuspidal pair of
$({\mathbf {L}},\lambda )$
be a unipotent e-cuspidal pair of
![]() $({\mathbf {G}},F)$
and assume that
$({\mathbf {G}},F)$
and assume that
![]() $\widehat {\lambda }$
is an extension of
$\widehat {\lambda }$
is an extension of
![]() $\lambda $
to the stabiliser
$\lambda $
to the stabiliser
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F_\lambda $
. Then, by applying Gallagher’s theorem [Reference Isaacs32, Corollary 6.17] and the Clifford correspondence [Reference Isaacs32, Theorem 6.11] we obtain a bijection
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F_\lambda $
. Then, by applying Gallagher’s theorem [Reference Isaacs32, Corollary 6.17] and the Clifford correspondence [Reference Isaacs32, Theorem 6.11] we obtain a bijection
 $$ \begin{align*} \mathrm{Irr}\ \left(W_{\mathbf{G}}({\mathbf{L}},\lambda)^F\right)&\to\mathrm{Irr}\ \left({\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F\enspace\middle|\enspace\lambda\right) \\ \eta&\mapsto \left(\widehat{\lambda}\eta\right)^{{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F}, \end{align*} $$
$$ \begin{align*} \mathrm{Irr}\ \left(W_{\mathbf{G}}({\mathbf{L}},\lambda)^F\right)&\to\mathrm{Irr}\ \left({\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F\enspace\middle|\enspace\lambda\right) \\ \eta&\mapsto \left(\widehat{\lambda}\eta\right)^{{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F}, \end{align*} $$
and therefore, (2.2) holds if and only if there exists a bijection
This new reformulation will allow us to introduce the aforementioned compatibility with isomorphisms of character triple isomorphisms.
3.1 Equivariance and maximal extendibility
In this section, we consider some equivariance properties for the parametrisation (3.1) which are related to maximal extendibility (see (2.1)) of unipotent characters.
As in the previous sections, consider a connected reductive group
![]() ${\mathbf {G}}$
with a Frobenius endomorphism
${\mathbf {G}}$
with a Frobenius endomorphism
![]() $F:{\mathbf {G}}\to {\mathbf {G}}$
defining an
$F:{\mathbf {G}}\to {\mathbf {G}}$
defining an
![]() $\mathbb {F}_q$
-structure on
$\mathbb {F}_q$
-structure on
![]() ${\mathbf {G}}$
. We denote by
${\mathbf {G}}$
. We denote by
![]() $\mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
the set of those automorphisms of
$\mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
the set of those automorphisms of
![]() ${\mathbf {G}}^F$
obtained by restricting some bijective morphism of algebraic groups
${\mathbf {G}}^F$
obtained by restricting some bijective morphism of algebraic groups
![]() $\sigma :{\mathbf {G}}\to {\mathbf {G}}$
that commutes with F to the set of
$\sigma :{\mathbf {G}}\to {\mathbf {G}}$
that commutes with F to the set of
![]() $\mathbb {F}_q$
-rational points
$\mathbb {F}_q$
-rational points
![]() ${\mathbf {G}}^F$
. Notice that the restriction of such a morphism
${\mathbf {G}}^F$
. Notice that the restriction of such a morphism
![]() $\sigma $
to
$\sigma $
to
![]() ${\mathbf {G}}^F$
, which by abuse of notation we denote again by
${\mathbf {G}}^F$
, which by abuse of notation we denote again by
![]() $\sigma $
, is an automorphism of the finite group
$\sigma $
, is an automorphism of the finite group
![]() ${\mathbf {G}}^F$
. We refer the reader to [Reference Cabanes and Späth18, Section 2.4] for further details. In particular, observe that any morphism
${\mathbf {G}}^F$
. We refer the reader to [Reference Cabanes and Späth18, Section 2.4] for further details. In particular, observe that any morphism
![]() $\sigma $
with the properties above is determined by its restriction to
$\sigma $
with the properties above is determined by its restriction to
![]() ${\mathbf {G}}^F$
up to a power of F (this follows from [Reference Gorenstein, Lyons and Solomon31, Lemma 2.5.7]) and hence it follows that
${\mathbf {G}}^F$
up to a power of F (this follows from [Reference Gorenstein, Lyons and Solomon31, Lemma 2.5.7]) and hence it follows that
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
acts on the set of F-stable closed connected subgroups of
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
acts on the set of F-stable closed connected subgroups of
![]() ${\mathbf {G}}$
. Then, given an F-stable closed connected subgroup
${\mathbf {G}}$
. Then, given an F-stable closed connected subgroup
![]() ${\mathbf {H}}$
of
${\mathbf {H}}$
of
![]() ${\mathbf {G}}$
, we can define the set
${\mathbf {G}}$
, we can define the set
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{\mathbf {H}}$
consisting of those automorphisms
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{\mathbf {H}}$
consisting of those automorphisms
![]() $\sigma $
as above that stabilise the algebraic group
$\sigma $
as above that stabilise the algebraic group
![]() ${\mathbf {H}}$
.
${\mathbf {H}}$
.
Now, let
![]() $\ell $
be a prime number not dividing q and denote by e the order of q modulo
$\ell $
be a prime number not dividing q and denote by e the order of q modulo
![]() $\ell $
or q modulo
$\ell $
or q modulo
![]() $4$
if
$4$
if
![]() $\ell =2$
. In order to control the action of automorphisms on unipotent e-Harish-Chandra series, we exploit a result of Cabanes and Späth. More precisely, in [Reference Cabanes and Späth18, Theorem 3.4] it was shown that the parametrisation given by Broué, Malle and Michel in [Reference Broué, Malle and Michel9, Theorem 3.2 (2)] commutes with the action of those automorphisms in the set
$\ell =2$
. In order to control the action of automorphisms on unipotent e-Harish-Chandra series, we exploit a result of Cabanes and Späth. More precisely, in [Reference Cabanes and Späth18, Theorem 3.4] it was shown that the parametrisation given by Broué, Malle and Michel in [Reference Broué, Malle and Michel9, Theorem 3.2 (2)] commutes with the action of those automorphisms in the set
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
. Notice that the statement of [Reference Cabanes and Späth18, Theorem 3.4] only considers unipotent e-cuspidal pairs
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
. Notice that the statement of [Reference Cabanes and Späth18, Theorem 3.4] only considers unipotent e-cuspidal pairs
![]() $({\mathbf {L}},\lambda )$
, where
$({\mathbf {L}},\lambda )$
, where
![]() ${\mathbf {L}}$
is a minimal e-split Levi subgroup (which is enough for the purpose of dealing with the McKay Conjecture). However, their proof works for the general case as well.
${\mathbf {L}}$
is a minimal e-split Levi subgroup (which is enough for the purpose of dealing with the McKay Conjecture). However, their proof works for the general case as well.
Proposition 3.1. For every unipotent e-cuspidal pair
![]() $({\mathbf {L}},\lambda )$
of the group
$({\mathbf {L}},\lambda )$
of the group
![]() $({\mathbf {G}},F)$
, there exists an
$({\mathbf {G}},F)$
, there exists an
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-equivariant bijection
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-equivariant bijection
such that
for every
![]() $\eta \in \mathrm{Irr}(W_{\mathbf {G}}({\mathbf {L}},\lambda )^F)$
.
$\eta \in \mathrm{Irr}(W_{\mathbf {G}}({\mathbf {L}},\lambda )^F)$
.
Proof. This follows from the proof of [Reference Cabanes and Späth18, Theorem 3.4]. See also [Reference Rossi54, Theorem 3.4].
As explained at the beginning of this section, if
![]() $\lambda $
extends to the stabiliser
$\lambda $
extends to the stabiliser
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F_\lambda $
, then we can use the bijection (2.2) to obtain (3.1). A similar argument can be used to include the equivariance property described above and obtain an equivariant version of (3.1). Observe that, by the discussion on automorphisms above, it follows that the group
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F_\lambda $
, then we can use the bijection (2.2) to obtain (3.1). A similar argument can be used to include the equivariance property described above and obtain an equivariant version of (3.1). Observe that, by the discussion on automorphisms above, it follows that the group
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
acts on the set of e-cuspidal pairs
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
acts on the set of e-cuspidal pairs
![]() $({\mathbf {L}},\lambda )$
, and therefore, we can define the stabiliser
$({\mathbf {L}},\lambda )$
, and therefore, we can define the stabiliser
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
. Furthermore, recall that we denote by
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
. Furthermore, recall that we denote by
![]() $d(\chi )$
the
$d(\chi )$
the
![]() $\ell $
-defect of an irreducible character
$\ell $
-defect of an irreducible character
![]() $\chi $
.
$\chi $
.
Corollary 3.2. Let
![]() $({\mathbf {L}},\lambda )$
be a unipotent e-cuspidal pair of
$({\mathbf {L}},\lambda )$
be a unipotent e-cuspidal pair of
![]() $({\mathbf {G}},F)$
, and suppose that
$({\mathbf {G}},F)$
, and suppose that
![]() $\lambda $
has an extension
$\lambda $
has an extension
![]() $\lambda ^\diamond \in \mathrm{Irr}({\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F)$
. Then there exists a bijection
$\lambda ^\diamond \in \mathrm{Irr}({\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F)$
. Then there exists a bijection
such that
for every
![]() $\chi \in {\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
. Furthermore, the bijection
$\chi \in {\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
. Furthermore, the bijection
![]() $\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}$
is
$\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}$
is
![]() $\mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-equivariant whenever the extension
$\mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-equivariant whenever the extension
![]() $\lambda ^\diamond $
is
$\lambda ^\diamond $
is
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-invariant.
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-invariant.
Proof. Consider the bijection
![]() $I^{{\mathbf {G}}}_{({\mathbf {L}},\lambda )}$
given by Proposition 3.1, and define the map
$I^{{\mathbf {G}}}_{({\mathbf {L}},\lambda )}$
given by Proposition 3.1, and define the map
 $$ \begin{align*} \Omega_{({\mathbf{L}},\lambda)}^{\mathbf{G}}:{\mathcal{E}}\left({\mathbf{G}}^F,({\mathbf{L}},\lambda)\right)&\to\mathrm{Irr}\ \left({\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F\enspace\middle|\enspace \lambda\right) \\ I_{({\mathbf{L}},\lambda)}^{\mathbf{G}}(\eta)&\mapsto\left(\lambda^\diamond\eta\right)^{{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F} \end{align*} $$
$$ \begin{align*} \Omega_{({\mathbf{L}},\lambda)}^{\mathbf{G}}:{\mathcal{E}}\left({\mathbf{G}}^F,({\mathbf{L}},\lambda)\right)&\to\mathrm{Irr}\ \left({\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F\enspace\middle|\enspace \lambda\right) \\ I_{({\mathbf{L}},\lambda)}^{\mathbf{G}}(\eta)&\mapsto\left(\lambda^\diamond\eta\right)^{{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F} \end{align*} $$
for every
![]() $\eta \in \mathrm{Irr}(W_{\mathbf {G}}({\mathbf {L}},\lambda )^F)$
and where
$\eta \in \mathrm{Irr}(W_{\mathbf {G}}({\mathbf {L}},\lambda )^F)$
and where
![]() $\lambda ^\diamond $
is the extension of
$\lambda ^\diamond $
is the extension of
![]() $\lambda $
to
$\lambda $
to
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F$
given in the statement. This is a well defined bijection by the Clifford correspondence [Reference Isaacs32, Theorem 6.11] and Gallagher’s theorem [Reference Isaacs32, Corollary 6.17]. Moreover, for every
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F$
given in the statement. This is a well defined bijection by the Clifford correspondence [Reference Isaacs32, Theorem 6.11] and Gallagher’s theorem [Reference Isaacs32, Corollary 6.17]. Moreover, for every
![]() $\alpha \in \mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
such that
$\alpha \in \mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
such that
![]() $({\mathbf {L}},\lambda )^\alpha =({\mathbf {L}},\lambda )$
and every
$({\mathbf {L}},\lambda )^\alpha =({\mathbf {L}},\lambda )$
and every
![]() $\eta \in \mathrm{Irr}(W_{\mathbf {G}}({\mathbf {L}},\lambda )^F)$
we have
$\eta \in \mathrm{Irr}(W_{\mathbf {G}}({\mathbf {L}},\lambda )^F)$
we have
 $$ \begin{align*} \left(\left(\lambda^\diamond\eta\right)^{{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F}\right)^\alpha&=\left(\left(\lambda^\diamond\eta\right)^\alpha\right)^{{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F} \\ &=\left(\lambda^\diamond\eta^\alpha\right)^{{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F} \end{align*} $$
$$ \begin{align*} \left(\left(\lambda^\diamond\eta\right)^{{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F}\right)^\alpha&=\left(\left(\lambda^\diamond\eta\right)^\alpha\right)^{{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F} \\ &=\left(\lambda^\diamond\eta^\alpha\right)^{{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F} \end{align*} $$
whenever
![]() $\alpha $
stabilises
$\alpha $
stabilises
![]() $\lambda ^\diamond $
. On the other hand,
$\lambda ^\diamond $
. On the other hand,
by Proposition 3.1 and hence we conclude that
![]() $\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}$
is
$\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}$
is
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-equivariant provided that
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-equivariant provided that
![]() $\lambda ^\diamond $
is
$\lambda ^\diamond $
is
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-invariant. Furthermore, if we consider
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-invariant. Furthermore, if we consider
![]() $\eta \in \mathrm{Irr}(W_{\mathbf {G}}({\mathbf {L}},\lambda )^F)$
and define the characters
$\eta \in \mathrm{Irr}(W_{\mathbf {G}}({\mathbf {L}},\lambda )^F)$
and define the characters
![]() $\chi :=I_{({\mathbf {L}},\lambda )}^{\mathbf {G}}(\eta )$
and
$\chi :=I_{({\mathbf {L}},\lambda )}^{\mathbf {G}}(\eta )$
and
![]() $\psi :=(\lambda ^\diamond \eta )^{{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F}$
, then the degree formula from Proposition 3.1 implies that
$\psi :=(\lambda ^\diamond \eta )^{{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F}$
, then the degree formula from Proposition 3.1 implies that
 $$ \begin{align*} \ell^{d(\chi)}=\dfrac{\left|\hspace{1pt}{\mathbf{G}}^F\hspace{1pt}\right|{}_\ell}{\chi(1)_\ell}=\dfrac{\left|\hspace{1pt}{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}},\lambda)^F\hspace{1pt}\right|{}_\ell}{\lambda(1)_\ell\cdot\eta(1)_\ell}=\dfrac{\left|\hspace{1pt}{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F\hspace{1pt}\right|{}_\ell}{\psi(1)_\ell}=\ell^{d(\psi)} \end{align*} $$
$$ \begin{align*} \ell^{d(\chi)}=\dfrac{\left|\hspace{1pt}{\mathbf{G}}^F\hspace{1pt}\right|{}_\ell}{\chi(1)_\ell}=\dfrac{\left|\hspace{1pt}{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}},\lambda)^F\hspace{1pt}\right|{}_\ell}{\lambda(1)_\ell\cdot\eta(1)_\ell}=\dfrac{\left|\hspace{1pt}{\mathbf{N}}_{\mathbf{G}}({\mathbf{L}})^F\hspace{1pt}\right|{}_\ell}{\psi(1)_\ell}=\ell^{d(\psi)} \end{align*} $$
and hence we deduce that
![]() $d(\chi )=d(\psi )$
as required.
$d(\chi )=d(\psi )$
as required.
Next, we consider a regular embedding
![]() ${\mathbf {G}}\leq \widetilde {{\mathbf {G}}}$
as defined in [Reference Cabanes and Enguehard17, (15.1)]. Then,
${\mathbf {G}}\leq \widetilde {{\mathbf {G}}}$
as defined in [Reference Cabanes and Enguehard17, (15.1)]. Then,
![]() $\widetilde {{\mathbf {G}}}$
is a connected reductive group with connected centre and whose derived subgroup coincides with that of
$\widetilde {{\mathbf {G}}}$
is a connected reductive group with connected centre and whose derived subgroup coincides with that of
![]() ${\mathbf {G}}$
, that is,
${\mathbf {G}}$
, that is,
![]() $[\widetilde {{\mathbf {G}}},\widetilde {{\mathbf {G}}}]=[{\mathbf {G}},{\mathbf {G}}]$
. In particular, observe that
$[\widetilde {{\mathbf {G}}},\widetilde {{\mathbf {G}}}]=[{\mathbf {G}},{\mathbf {G}}]$
. In particular, observe that
![]() $\widetilde {{\mathbf {G}}}={\mathbf {Z}}(\widetilde {{\mathbf {G}}}){\mathbf {G}}$
, that
$\widetilde {{\mathbf {G}}}={\mathbf {Z}}(\widetilde {{\mathbf {G}}}){\mathbf {G}}$
, that
![]() ${\mathbf {G}}$
is normal in
${\mathbf {G}}$
is normal in
![]() $\widetilde {{\mathbf {G}}}$
and that the quotient
$\widetilde {{\mathbf {G}}}$
and that the quotient
![]() $\widetilde {{\mathbf {G}}}/{\mathbf {G}}$
is an abelian group. For every Levi subgroup
$\widetilde {{\mathbf {G}}}/{\mathbf {G}}$
is an abelian group. For every Levi subgroup
![]() ${\mathbf {L}}$
of
${\mathbf {L}}$
of
![]() ${\mathbf {G}}$
, and recalling that Levi subgroups are exactly the centralisers of tori, we deduce that
${\mathbf {G}}$
, and recalling that Levi subgroups are exactly the centralisers of tori, we deduce that
![]() $\widetilde {{\mathbf {L}}}:={\mathbf {Z}}(\widetilde {{\mathbf {G}}}){\mathbf {L}}$
is a Levi subgroup of
$\widetilde {{\mathbf {L}}}:={\mathbf {Z}}(\widetilde {{\mathbf {G}}}){\mathbf {L}}$
is a Levi subgroup of
![]() $\widetilde {{\mathbf {G}}}$
and that
$\widetilde {{\mathbf {G}}}$
and that
![]() ${\mathbf {L}}\leq \widetilde {{\mathbf {L}}}$
is again a regular embedding. Notice also that
${\mathbf {L}}\leq \widetilde {{\mathbf {L}}}$
is again a regular embedding. Notice also that
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})={\mathbf {N}}_{\widetilde {{\mathbf {G}}}}(\widetilde {{\mathbf {L}}})$
. These observations will be used throughout this paper without further reference.
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})={\mathbf {N}}_{\widetilde {{\mathbf {G}}}}(\widetilde {{\mathbf {L}}})$
. These observations will be used throughout this paper without further reference.
We also recall that, according to [Reference Digne and Michel25, Proposition 13.20], restriction of characters yields a bijection between the unipotent characters of
![]() $\widetilde {{\mathbf {G}}}^F$
and those of
$\widetilde {{\mathbf {G}}}^F$
and those of
![]() ${\mathbf {G}}^F$
. In particular, every unipotent character of
${\mathbf {G}}^F$
. In particular, every unipotent character of
![]() ${\mathbf {G}}^F$
is
${\mathbf {G}}^F$
is
![]() $\widetilde {{\mathbf {G}}}^F$
-invariant. Using this observation, we can compare the relative Weyl groups in
$\widetilde {{\mathbf {G}}}^F$
-invariant. Using this observation, we can compare the relative Weyl groups in
![]() $\widetilde {{\mathbf {G}}}^F$
with those in
$\widetilde {{\mathbf {G}}}^F$
with those in
![]() ${\mathbf {G}}^F$
.
${\mathbf {G}}^F$
.
Lemma 3.3. Let
![]() $({\mathbf {L}},\lambda )$
be a unipotent e-cuspidal pair of
$({\mathbf {L}},\lambda )$
be a unipotent e-cuspidal pair of
![]() $({\mathbf {G}},F)$
, set
$({\mathbf {G}},F)$
, set
![]() $\widetilde {{\mathbf {L}}}={\mathbf {L}}{\mathbf {Z}}(\widetilde {{\mathbf {G}}})$
and denote by
$\widetilde {{\mathbf {L}}}={\mathbf {L}}{\mathbf {Z}}(\widetilde {{\mathbf {G}}})$
and denote by
![]() $\widetilde {\lambda }$
the unipotent extension of
$\widetilde {\lambda }$
the unipotent extension of
![]() $\lambda $
to
$\lambda $
to
![]() $\widetilde {{\mathbf {L}}}^F$
. Then,
$\widetilde {{\mathbf {L}}}^F$
. Then,
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_\lambda ={\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_{\widetilde {\lambda }}$
, and we have an isomorphism
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_\lambda ={\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_{\widetilde {\lambda }}$
, and we have an isomorphism
![]() $W_{\widetilde {{\mathbf {G}}}}(\widetilde {{\mathbf {L}}},\widetilde {\lambda })^F\simeq W_{\mathbf {G}}({\mathbf {L}},\lambda )^F$
.
$W_{\widetilde {{\mathbf {G}}}}(\widetilde {{\mathbf {L}}},\widetilde {\lambda })^F\simeq W_{\mathbf {G}}({\mathbf {L}},\lambda )^F$
.
Proof. Since
![]() $\widetilde {\lambda }$
extends
$\widetilde {\lambda }$
extends
![]() $\lambda $
, it is clear that the stabiliser
$\lambda $
, it is clear that the stabiliser
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_{\widetilde {\lambda }}$
is contained in
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_{\widetilde {\lambda }}$
is contained in
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_\lambda $
. On the other hand, let
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_\lambda $
. On the other hand, let
![]() $x\in {\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_\lambda $
and observe that
$x\in {\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_\lambda $
and observe that
![]() $\widetilde {\lambda }^x$
is a unipotent character of
$\widetilde {\lambda }^x$
is a unipotent character of
![]() $\widetilde {{\mathbf {L}}}^F$
that restricts to
$\widetilde {{\mathbf {L}}}^F$
that restricts to
![]() $\lambda ^x=\lambda $
. Then, [Reference Digne and Michel25, Proposition 13.20] implies that
$\lambda ^x=\lambda $
. Then, [Reference Digne and Michel25, Proposition 13.20] implies that
![]() $\widetilde {\lambda }^x=\widetilde {\lambda }$
, and therefore,
$\widetilde {\lambda }^x=\widetilde {\lambda }$
, and therefore,
![]() $x\in {\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_{\widetilde {\lambda }}$
. From this, we also conclude that
$x\in {\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_{\widetilde {\lambda }}$
. From this, we also conclude that
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_{\widetilde {\lambda }}=\widetilde {{\mathbf {L}}}^F{\mathbf {N}}_{{\mathbf {G}}}({\mathbf {L}})^F_\lambda $
and therefore that
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_{\widetilde {\lambda }}=\widetilde {{\mathbf {L}}}^F{\mathbf {N}}_{{\mathbf {G}}}({\mathbf {L}})^F_\lambda $
and therefore that
![]() $W_{\widetilde {{\mathbf {G}}}}(\widetilde {{\mathbf {L}}},\widetilde {\lambda })^F\simeq W_{\mathbf {G}}({\mathbf {L}},\lambda )^F$
recalling that
$W_{\widetilde {{\mathbf {G}}}}(\widetilde {{\mathbf {L}}},\widetilde {\lambda })^F\simeq W_{\mathbf {G}}({\mathbf {L}},\lambda )^F$
recalling that
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})={\mathbf {N}}_{\widetilde {{\mathbf {G}}}}(\widetilde {{\mathbf {L}}})$
.
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})={\mathbf {N}}_{\widetilde {{\mathbf {G}}}}(\widetilde {{\mathbf {L}}})$
.
As a consequence of the lemma above, we show that when
![]() $\lambda $
extends to its stabiliser
$\lambda $
extends to its stabiliser
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F_\lambda $
, then every irreducible character of
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F_\lambda $
, then every irreducible character of
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})$
that lies above
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})$
that lies above
![]() $\lambda $
is
$\lambda $
is
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
-invariant and extends to
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
-invariant and extends to
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F={\mathbf {N}}_{\widetilde {{\mathbf {G}}}}(\widetilde {{\mathbf {L}}})^F$
.
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F={\mathbf {N}}_{\widetilde {{\mathbf {G}}}}(\widetilde {{\mathbf {L}}})^F$
.
Corollary 3.4. Let
![]() $({\mathbf {L}},\lambda )$
be a unipotent e-cuspidal pair of
$({\mathbf {L}},\lambda )$
be a unipotent e-cuspidal pair of
![]() $({\mathbf {G}},F)$
, and suppose that
$({\mathbf {G}},F)$
, and suppose that
![]() $\lambda $
has an extension
$\lambda $
has an extension
![]() $\lambda ^\diamond \in \mathrm{Irr}({\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F)$
. Then every character of
$\lambda ^\diamond \in \mathrm{Irr}({\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F)$
. Then every character of
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
lying above
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
lying above
![]() $\lambda $
extends to
$\lambda $
extends to
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
.
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
.
Proof. Let
![]() $\widetilde {\lambda }$
be the unipotent extension of
$\widetilde {\lambda }$
be the unipotent extension of
![]() $\lambda $
to
$\lambda $
to
![]() $\widetilde {{\mathbf {L}}}^F$
, and recall that
$\widetilde {{\mathbf {L}}}^F$
, and recall that
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_\lambda ={\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_{\widetilde {\lambda }}$
according to Lemma 3.3. Then, applying [Reference Späth62, Lemma 4.1 (a)] we deduce that there exists an extension
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_\lambda ={\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_{\widetilde {\lambda }}$
according to Lemma 3.3. Then, applying [Reference Späth62, Lemma 4.1 (a)] we deduce that there exists an extension
![]() $\widetilde {\lambda }^\diamond $
of
$\widetilde {\lambda }^\diamond $
of
![]() $\lambda ^\diamond $
to
$\lambda ^\diamond $
to
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_\lambda $
that also extends
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_\lambda $
that also extends
![]() $\widetilde {\lambda }$
. Consider now an irreducible character
$\widetilde {\lambda }$
. Consider now an irreducible character
![]() $\psi $
of
$\psi $
of
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
lying above
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
lying above
![]() $\lambda $
. By Gallagher’s theorem [Reference Isaacs32, Corollary 6.17] and the Clifford correspondence [Reference Isaacs32, Theorem 6.11], it follows that there exists an irreducible character
$\lambda $
. By Gallagher’s theorem [Reference Isaacs32, Corollary 6.17] and the Clifford correspondence [Reference Isaacs32, Theorem 6.11], it follows that there exists an irreducible character
![]() $\eta $
of the relative Weyl group
$\eta $
of the relative Weyl group
![]() $W_{\mathbf {G}}({\mathbf {L}},\lambda )^F$
such that
$W_{\mathbf {G}}({\mathbf {L}},\lambda )^F$
such that
![]() $\psi $
is induced from the irreducible character
$\psi $
is induced from the irreducible character
![]() $\psi _0:=\eta \lambda ^\diamond $
of
$\psi _0:=\eta \lambda ^\diamond $
of
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F$
. Moreover, by using Lemma 3.3, we have
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F$
. Moreover, by using Lemma 3.3, we have
![]() $W_{\widetilde {{\mathbf {G}}}}(\widetilde {{\mathbf {L}}},\widetilde {\lambda })^F\simeq W_{\mathbf {G}}({\mathbf {L}},\lambda )^F$
. Then,
$W_{\widetilde {{\mathbf {G}}}}(\widetilde {{\mathbf {L}}},\widetilde {\lambda })^F\simeq W_{\mathbf {G}}({\mathbf {L}},\lambda )^F$
. Then,
![]() $\eta $
, viewed as a character of
$\eta $
, viewed as a character of
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F_\lambda $
, admits an extension, say
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F_\lambda $
, admits an extension, say
![]() $\widetilde {\eta }$
, to
$\widetilde {\eta }$
, to
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_\lambda $
. Now, define
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_\lambda $
. Now, define
![]() $\widetilde {\psi }_0:=\widetilde {\eta }\widetilde {\lambda }^\diamond $
and observe that
$\widetilde {\psi }_0:=\widetilde {\eta }\widetilde {\lambda }^\diamond $
and observe that
![]() $\widetilde {\psi }_0$
lies above
$\widetilde {\psi }_0$
lies above
![]() $\widetilde {\lambda }$
. By the Clifford correspondence, it follows that the character
$\widetilde {\lambda }$
. By the Clifford correspondence, it follows that the character
![]() $\widetilde {\psi }$
of
$\widetilde {\psi }$
of
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
induced from
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
induced from
![]() $\widetilde {\psi }_0$
is irreducible and therefore, applying [Reference Isaacs32, Problem 5.2], we conclude that
$\widetilde {\psi }_0$
is irreducible and therefore, applying [Reference Isaacs32, Problem 5.2], we conclude that
![]() $\widetilde {\psi }$
extends
$\widetilde {\psi }$
extends
![]() $\psi $
. The proof is now complete.
$\psi $
. The proof is now complete.
We can now construct a parametrisation of unipotent e-Harish-Chandra series in the group
![]() $\widetilde {{\mathbf {G}}}^F$
which agrees with the bijection
$\widetilde {{\mathbf {G}}}^F$
which agrees with the bijection
![]() $\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}$
from Corollary 3.2 via restriction of characters.
$\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}$
from Corollary 3.2 via restriction of characters.
Proposition 3.5. Let
![]() $({\mathbf {L}},\lambda )$
be a unipotent e-cuspidal pair of
$({\mathbf {L}},\lambda )$
be a unipotent e-cuspidal pair of
![]() $({\mathbf {G}},F)$
, and suppose that
$({\mathbf {G}},F)$
, and suppose that
![]() $\lambda $
has an extension
$\lambda $
has an extension
![]() $\lambda ^\diamond \in \mathrm{Irr}({\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F)$
. If
$\lambda ^\diamond \in \mathrm{Irr}({\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F)$
. If
![]() $\widetilde {\lambda }$
is the unipotent extension of
$\widetilde {\lambda }$
is the unipotent extension of
![]() $\lambda $
to
$\lambda $
to
![]() $\widetilde {{\mathbf {L}}}^F$
, then there exists a bijection
$\widetilde {{\mathbf {L}}}^F$
, then there exists a bijection
![]() $\widetilde {\Omega }_{(\widetilde {{\mathbf {L}}},\widetilde {\lambda })}^{\widetilde {{\mathbf {G}}}}$
making the following diagram commute
$\widetilde {\Omega }_{(\widetilde {{\mathbf {L}}},\widetilde {\lambda })}^{\widetilde {{\mathbf {G}}}}$
making the following diagram commute

and where
![]() $\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}$
is the bijection given by Corollary 3.2.
$\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}$
is the bijection given by Corollary 3.2.
Proof. First, observe that
![]() $\lambda $
has a unique unipotent extension
$\lambda $
has a unique unipotent extension
![]() $\widetilde {\lambda }$
to
$\widetilde {\lambda }$
to
![]() $\widetilde {{\mathbf {L}}}^F$
according to [Reference Digne and Michel25, Proposition 13.20]. Moreover, restriction from
$\widetilde {{\mathbf {L}}}^F$
according to [Reference Digne and Michel25, Proposition 13.20]. Moreover, restriction from
![]() $\widetilde {{\mathbf {G}}}^F$
to
$\widetilde {{\mathbf {G}}}^F$
to
![]() ${\mathbf {G}}^F$
induces a bijection from the set
${\mathbf {G}}^F$
induces a bijection from the set
![]() ${\mathcal {E}}(\widetilde {{\mathbf {G}}}^F,(\widetilde {{\mathbf {L}}},\widetilde {\lambda }))$
to
${\mathcal {E}}(\widetilde {{\mathbf {G}}}^F,(\widetilde {{\mathbf {L}}},\widetilde {\lambda }))$
to
![]() ${\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
according to [Reference Cabanes and Enguehard15, Proposition 3.1]. Consider a character
${\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
according to [Reference Cabanes and Enguehard15, Proposition 3.1]. Consider a character
![]() $\psi \in \mathrm{Irr}({\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F)$
lying above
$\psi \in \mathrm{Irr}({\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F)$
lying above
![]() $\lambda $
and observe that
$\lambda $
and observe that
![]() $\psi $
admits an extension
$\psi $
admits an extension
![]() $\widetilde {\psi }_0\in \mathrm{Irr}({\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F)$
by Corollary 3.4. Let
$\widetilde {\psi }_0\in \mathrm{Irr}({\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F)$
by Corollary 3.4. Let
![]() $\widetilde {\lambda }_0$
be an irreducible constituent of the restriction
$\widetilde {\lambda }_0$
be an irreducible constituent of the restriction
![]() $\widetilde {\psi }_{0,\widetilde {{\mathbf {L}}}^F}$
, and notice that
$\widetilde {\psi }_{0,\widetilde {{\mathbf {L}}}^F}$
, and notice that
![]() $\widetilde {\lambda _0}$
is an extension of
$\widetilde {\lambda _0}$
is an extension of
![]() $\lambda $
since
$\lambda $
since
![]() $\widetilde {{\mathbf {L}}}^F/{\mathbf {L}}^F$
is abelian. Now, Gallagher’s theorem [Reference Isaacs32, Corollary 6.17] implies that there exists a linear character
$\widetilde {{\mathbf {L}}}^F/{\mathbf {L}}^F$
is abelian. Now, Gallagher’s theorem [Reference Isaacs32, Corollary 6.17] implies that there exists a linear character
![]() $\nu \in \mathrm{ Irr}(\widetilde {{\mathbf {L}}}^F/{\mathbf {L}}^F)$
such that
$\nu \in \mathrm{ Irr}(\widetilde {{\mathbf {L}}}^F/{\mathbf {L}}^F)$
such that
![]() $\widetilde {\lambda }_0\nu =\widetilde {\lambda }$
. Since
$\widetilde {\lambda }_0\nu =\widetilde {\lambda }$
. Since
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F/{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F\simeq \widetilde {{\mathbf {L}}}^F/{\mathbf {L}}^F$
, we can identify
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F/{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F\simeq \widetilde {{\mathbf {L}}}^F/{\mathbf {L}}^F$
, we can identify
![]() $\nu $
with a character of
$\nu $
with a character of
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
. Then, it follows that the character
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
. Then, it follows that the character
![]() $\widetilde {\psi }:=\widetilde {\psi }_0\nu $
is an extension of
$\widetilde {\psi }:=\widetilde {\psi }_0\nu $
is an extension of
![]() $\psi $
to
$\psi $
to
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
lying above
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
lying above
![]() $\widetilde {\lambda }$
. Then the assignment
$\widetilde {\lambda }$
. Then the assignment
![]() $\psi \mapsto \widetilde {\psi }$
defines a bijection between
$\psi \mapsto \widetilde {\psi }$
defines a bijection between
![]() $\mathrm{ Irr}({\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F\mid \lambda )$
and
$\mathrm{ Irr}({\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F\mid \lambda )$
and
![]() $\mathrm{Irr}({\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F\mid \widetilde {\lambda })$
whose inverse is given by restriction of characters. We can now define
$\mathrm{Irr}({\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F\mid \widetilde {\lambda })$
whose inverse is given by restriction of characters. We can now define
for every
![]() $\widetilde {\chi }\in {\mathcal {E}}(\widetilde {{\mathbf {G}}}^F,(\widetilde {{\mathbf {L}}},\widetilde {\lambda }))$
and
$\widetilde {\chi }\in {\mathcal {E}}(\widetilde {{\mathbf {G}}}^F,(\widetilde {{\mathbf {L}}},\widetilde {\lambda }))$
and
![]() $\widetilde {\psi }\in \mathrm{Irr}({\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F\mid \widetilde {\lambda })$
whenever
$\widetilde {\psi }\in \mathrm{Irr}({\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F\mid \widetilde {\lambda })$
whenever
![]() $\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}(\widetilde {\chi }_{{\mathbf {G}}^F})=\widetilde {\psi }_{{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F}$
.
$\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}(\widetilde {\chi }_{{\mathbf {G}}^F})=\widetilde {\psi }_{{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F}$
.
3.2 Construction of
 ${\mathbf {G}}^F$
-block isomorphisms of character triples
${\mathbf {G}}^F$
-block isomorphisms of character triples
For the rest of this section, we assume that
![]() ${\mathbf {G}}$
is simple, simply connected and of type
${\mathbf {G}}$
is simple, simply connected and of type
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
.
$\mathbf {C}$
.
We now give a more explicit construction of the group of automorphisms
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
. Fix a maximally split torus
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
. Fix a maximally split torus
![]() ${\mathbf {T}}_0$
contained in an F-stable Borel subgroup
${\mathbf {T}}_0$
contained in an F-stable Borel subgroup
![]() ${\mathbf {B}}_0$
of
${\mathbf {B}}_0$
of
![]() ${\mathbf {G}}$
. This choice corresponds to a set of graph automorphisms
${\mathbf {G}}$
. This choice corresponds to a set of graph automorphisms
![]() $\gamma :{\mathbf {G}}\to {\mathbf {G}}$
and a field endomorphism
$\gamma :{\mathbf {G}}\to {\mathbf {G}}$
and a field endomorphism
![]() $F_0:{\mathbf {G}}\to {\mathbf {G}}$
. More precisely, if we consider the set of simple roots
$F_0:{\mathbf {G}}\to {\mathbf {G}}$
. More precisely, if we consider the set of simple roots
![]() $\Delta \subseteq \Phi ({\mathbf {G}},{\mathbf {T}}_0)$
corresponding to the choice
$\Delta \subseteq \Phi ({\mathbf {G}},{\mathbf {T}}_0)$
corresponding to the choice
![]() ${\mathbf {T}}_0\subseteq {\mathbf {B}}_0$
, then we have an automorphism
${\mathbf {T}}_0\subseteq {\mathbf {B}}_0$
, then we have an automorphism
![]() $\gamma :{\mathbf {G}}\to {\mathbf {G}}$
given by
$\gamma :{\mathbf {G}}\to {\mathbf {G}}$
given by
![]() $\gamma (x_\alpha (t)):=x_{\gamma (\alpha )}(t)$
for every
$\gamma (x_\alpha (t)):=x_{\gamma (\alpha )}(t)$
for every
![]() $t\in \mathbb {G}_{\mathrm{a}}$
and
$t\in \mathbb {G}_{\mathrm{a}}$
and
![]() $\alpha \in \pm \Delta $
and where
$\alpha \in \pm \Delta $
and where
![]() $\gamma $
is a symmetry of the Dynkin diagram of
$\gamma $
is a symmetry of the Dynkin diagram of
![]() $\Delta $
, while
$\Delta $
, while
![]() $F_0(x_\alpha (t)):=x_{\alpha }(t^p)$
for every
$F_0(x_\alpha (t)):=x_{\alpha }(t^p)$
for every
![]() $t\in \mathbb {G}_{\mathrm{a}}$
and
$t\in \mathbb {G}_{\mathrm{a}}$
and
![]() $\alpha \in \Phi ({\mathbf {G}},{\mathbf {T}}_0)$
. Here, we denote by
$\alpha \in \Phi ({\mathbf {G}},{\mathbf {T}}_0)$
. Here, we denote by
![]() $x_\alpha :\mathbb {G}_{\mathrm{a}}\to {\mathbf {G}}$
the homomorphism corresponding to
$x_\alpha :\mathbb {G}_{\mathrm{a}}\to {\mathbf {G}}$
the homomorphism corresponding to
![]() $\alpha \in \Phi ({\mathbf {G}},{\mathbf {T}}_0)$
. We define the subgroup
$\alpha \in \Phi ({\mathbf {G}},{\mathbf {T}}_0)$
. We define the subgroup
![]() $\mathcal {A}$
of
$\mathcal {A}$
of
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
generated by the graph and field automorphisms described above.
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
generated by the graph and field automorphisms described above.
In addition, we choose our regular embedding
![]() ${\mathbf {G}}\leq \widetilde {{\mathbf {G}}}$
to be defined in such a way that the graph and field automorphisms extend to
${\mathbf {G}}\leq \widetilde {{\mathbf {G}}}$
to be defined in such a way that the graph and field automorphisms extend to
![]() $\widetilde {{\mathbf {G}}}$
(see, for instance, [Reference Malle and Späth40, Section 2B]). In particular, the group
$\widetilde {{\mathbf {G}}}$
(see, for instance, [Reference Malle and Späth40, Section 2B]). In particular, the group
![]() $\mathcal {A}$
acts via automorphisms on
$\mathcal {A}$
acts via automorphisms on
![]() $\widetilde {{\mathbf {G}}}^F$
and we can form the external semidirect product
$\widetilde {{\mathbf {G}}}^F$
and we can form the external semidirect product
![]() $\widetilde {{\mathbf {G}}}^F\rtimes \mathcal {A}$
which acts on
$\widetilde {{\mathbf {G}}}^F\rtimes \mathcal {A}$
which acts on
![]() ${\mathbf {G}}^F$
. It turns out that
${\mathbf {G}}^F$
. It turns out that
![]() $\widetilde {{\mathbf {G}}}^F\rtimes \mathcal {A}$
and
$\widetilde {{\mathbf {G}}}^F\rtimes \mathcal {A}$
and
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
induce the same set of automorphisms on the finite group
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
induce the same set of automorphisms on the finite group
![]() ${\mathbf {G}}^F$
(see, for instance, [Reference Gorenstein, Lyons and Solomon31, Section 2.5]).
${\mathbf {G}}^F$
(see, for instance, [Reference Gorenstein, Lyons and Solomon31, Section 2.5]).
Throughout this section, we consider a fixed unipotent e-cuspidal pair
![]() $({\mathbf {L}},\lambda )$
of
$({\mathbf {L}},\lambda )$
of
![]() $({\mathbf {G}},F)$
and a unipotent extension
$({\mathbf {G}},F)$
and a unipotent extension
![]() $\widetilde {\lambda }$
of
$\widetilde {\lambda }$
of
![]() $\lambda $
to
$\lambda $
to
![]() $\widetilde {{\mathbf {L}}}^F$
(whose existence is ensured by [Reference Digne and Michel25, Proposition 13.20]) where, as always, we define
$\widetilde {{\mathbf {L}}}^F$
(whose existence is ensured by [Reference Digne and Michel25, Proposition 13.20]) where, as always, we define
![]() $\widetilde {{\mathbf {L}}}:={\mathbf {L}}{\mathbf {Z}}(\widetilde {{\mathbf {G}}})$
. In the next lemma, we show that the hypothesis of Corollary 3.2 is satisfied under our assumptions.
$\widetilde {{\mathbf {L}}}:={\mathbf {L}}{\mathbf {Z}}(\widetilde {{\mathbf {G}}})$
. In the next lemma, we show that the hypothesis of Corollary 3.2 is satisfied under our assumptions.
Lemma 3.6. There exists an extension
![]() $\lambda ^\diamond $
of
$\lambda ^\diamond $
of
![]() $\lambda $
to
$\lambda $
to
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F$
that is
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F$
that is
![]() $(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}$
-invariant.
$(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}$
-invariant.
Proof. Using [Reference Brough and Späth13, Theorem 4.3 (i)], [Reference Brough11, Theorem 1.2 (a)] and the results of [Reference Brough and Ruhstorfer12], we obtain an extension
![]() $\lambda ^\diamond $
of
$\lambda ^\diamond $
of
![]() $\lambda $
to the stabiliser
$\lambda $
to the stabiliser
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F$
which is
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})_\lambda ^F$
which is
![]() $({\mathbf {G}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}$
-invariant. Since
$({\mathbf {G}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}$
-invariant. Since
![]() $(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}=\widetilde {{\mathbf {L}}}^F({\mathbf {G}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}$
, it suffices to show that
$(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}=\widetilde {{\mathbf {L}}}^F({\mathbf {G}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}$
, it suffices to show that
![]() $\lambda ^\diamond $
is
$\lambda ^\diamond $
is
![]() $\widetilde {{\mathbf {L}}}^F$
-invariant. However, the latter assertion follows immediately from the fact that
$\widetilde {{\mathbf {L}}}^F$
-invariant. However, the latter assertion follows immediately from the fact that
![]() $\lambda ^\diamond $
extends to
$\lambda ^\diamond $
extends to
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_{\lambda }$
according to Lemma 3.3 and [Reference Späth62, Lemma 4.1 (a)].
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F_{\lambda }$
according to Lemma 3.3 and [Reference Späth62, Lemma 4.1 (a)].
As an immediate consequence of the lemma above, we deduce that every character of
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
lying above
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
lying above
![]() $\lambda $
extends to
$\lambda $
extends to
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
. This can be considered as a local analogue of [Reference Digne and Michel25, Proposition 13.20].
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
. This can be considered as a local analogue of [Reference Digne and Michel25, Proposition 13.20].
Lemma 3.7. Every irreducible character of
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
lying above
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
lying above
![]() $\lambda $
extends to
$\lambda $
extends to
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
.
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
.
We point out that, under our assumptions, every irreducible character of
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
lying above
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
lying above
![]() $\lambda $
extends to its stabiliser in
$\lambda $
extends to its stabiliser in
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
because the quotient
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
because the quotient
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F/{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
is cyclic according to [Reference Geck and Malle30, Proposition 1.7.5]. However, in the lemma above we are also showing, using independent methods, that each such character is
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F/{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
is cyclic according to [Reference Geck and Malle30, Proposition 1.7.5]. However, in the lemma above we are also showing, using independent methods, that each such character is
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
-invariant.
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
-invariant.
Using Lemma 3.6, we can define bijections
![]() $\Omega :=\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}$
and
$\Omega :=\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}$
and
![]() $\widetilde {\Omega }_{(\widetilde {{\mathbf {L}}},\widetilde {\lambda })}^{\widetilde {{\mathbf {G}}}}$
as described in Corollary 3.2 and Proposition 3.5 respectively. In what follows, we consider the sets of characters
$\widetilde {\Omega }_{(\widetilde {{\mathbf {L}}},\widetilde {\lambda })}^{\widetilde {{\mathbf {G}}}}$
as described in Corollary 3.2 and Proposition 3.5 respectively. In what follows, we consider the sets of characters
![]() $\mathcal {G}:={\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
,
$\mathcal {G}:={\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
,
![]() $\mathcal {L}:=\mathrm{Irr}({\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F\mid \lambda )$
,
$\mathcal {L}:=\mathrm{Irr}({\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F\mid \lambda )$
,
![]() $\widetilde {\mathcal {G}}:={\mathcal {E}}(\widetilde {{\mathbf {G}}}^F,(\widetilde {{\mathbf {L}}},\widetilde {\lambda }))$
and
$\widetilde {\mathcal {G}}:={\mathcal {E}}(\widetilde {{\mathbf {G}}}^F,(\widetilde {{\mathbf {L}}},\widetilde {\lambda }))$
and
![]() $\widetilde {\mathcal {L}}:=\mathrm{Irr}({\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F\mid \widetilde {\lambda })$
. Our next aim is to show that the parametrisation
$\widetilde {\mathcal {L}}:=\mathrm{Irr}({\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F\mid \widetilde {\lambda })$
. Our next aim is to show that the parametrisation
![]() $\Omega $
is compatible with
$\Omega $
is compatible with
![]() ${\mathbf {G}}^F$
-block isomorphisms of character triples. We start by checking the group theoretic properties required for the existence of such isomorphisms (see [Reference Späth64, Remark 3.7 (i)]).
${\mathbf {G}}^F$
-block isomorphisms of character triples. We start by checking the group theoretic properties required for the existence of such isomorphisms (see [Reference Späth64, Remark 3.7 (i)]).
Lemma 3.8. For every
![]() $\chi \in \mathcal {G}$
and
$\chi \in \mathcal {G}$
and
![]() $\psi :=\Omega (\chi )\in \mathcal {L}$
, we have
$\psi :=\Omega (\chi )\in \mathcal {L}$
, we have
![]() $(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{{\mathbf {L}},\chi }=(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{{\mathbf {L}},\psi }$
and
$(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{{\mathbf {L}},\chi }=(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{{\mathbf {L}},\psi }$
and
![]() $\widetilde {{\mathbf {G}}}^F\mathcal {A}_\chi ={\mathbf {G}}^F(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{{\mathbf {L}},\psi }$
.
$\widetilde {{\mathbf {G}}}^F\mathcal {A}_\chi ={\mathbf {G}}^F(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{{\mathbf {L}},\psi }$
.
Proof. We argue as in the proof of [Reference Rossi57, Lemma 4.2]. To start, we observe that because the map
![]() $\Omega $
is
$\Omega $
is
![]() $(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}$
-equivariant it follows that
$(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}$
-equivariant it follows that
![]() $(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\chi }=(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\psi }$
. Set
$(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\chi }=(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\psi }$
. Set
![]() $U:=(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{{\mathbf {L}}}$
, and consider the stabilisers
$U:=(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{{\mathbf {L}}}$
, and consider the stabilisers
![]() $U_\chi $
and
$U_\chi $
and
![]() $U_\psi $
. First, consider
$U_\psi $
. First, consider
![]() $x\in U_\chi $
and observe that according to [Reference Broué, Malle and Michel9, Theorem 3.2 (1)] there exists
$x\in U_\chi $
and observe that according to [Reference Broué, Malle and Michel9, Theorem 3.2 (1)] there exists
![]() $y\in {\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
such that
$y\in {\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
such that
![]() $({\mathbf {L}},\lambda )^{xy}=({\mathbf {L}},\lambda )$
. In particular,
$({\mathbf {L}},\lambda )^{xy}=({\mathbf {L}},\lambda )$
. In particular,
![]() $xy\in (\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\chi }=(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\psi }$
and hence
$xy\in (\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\chi }=(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\psi }$
and hence
![]() $x\in U_\psi $
since
$x\in U_\psi $
since
![]() $\psi ^y=\psi $
. This shows that
$\psi ^y=\psi $
. This shows that
![]() $U_\chi \leq U_\psi $
. On the other hand, suppose that
$U_\chi \leq U_\psi $
. On the other hand, suppose that
![]() $x\in U_\psi )$
. By Clifford’s theorem, there exists
$x\in U_\psi )$
. By Clifford’s theorem, there exists
![]() $y\in {\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
such that
$y\in {\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
such that
![]() $\lambda ^{xy}=\lambda $
and so
$\lambda ^{xy}=\lambda $
and so
![]() $xy\in (\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\psi }=(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\chi }$
. Since
$xy\in (\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\psi }=(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\chi }$
. Since
![]() $\chi ^y=\chi $
, we deduce that
$\chi ^y=\chi $
, we deduce that
![]() $x\in U_\chi $
and hence
$x\in U_\chi $
and hence
![]() $U_\chi =U_\psi $
. To conclude, it is enough to show that
$U_\chi =U_\psi $
. To conclude, it is enough to show that
![]() $\widetilde {{\mathbf {G}}}^F\mathcal {A}_\chi ={\mathbf {G}}^F U_\chi $
. First, notice that
$\widetilde {{\mathbf {G}}}^F\mathcal {A}_\chi ={\mathbf {G}}^F U_\chi $
. First, notice that
![]() ${\mathbf {G}}^F U_\chi \leq \widetilde {{\mathbf {G}}}^F\mathcal {A}_\chi $
since
${\mathbf {G}}^F U_\chi \leq \widetilde {{\mathbf {G}}}^F\mathcal {A}_\chi $
since
![]() $\chi $
is
$\chi $
is
![]() $\widetilde {{\mathbf {G}}}^F$
-invariant. On the other hand, for
$\widetilde {{\mathbf {G}}}^F$
-invariant. On the other hand, for
![]() $x\in \widetilde {{\mathbf {G}}}^F\mathcal {A}_\chi $
we know that
$x\in \widetilde {{\mathbf {G}}}^F\mathcal {A}_\chi $
we know that
![]() $({\mathbf {L}},\lambda )^{x}$
is
$({\mathbf {L}},\lambda )^{x}$
is
![]() ${\mathbf {G}}^F$
-conjugate to
${\mathbf {G}}^F$
-conjugate to
![]() $({\mathbf {L}},\lambda )$
thanks to [Reference Broué, Malle and Michel9, Theorem 3.2 (1)]. Therefore, we obtain
$({\mathbf {L}},\lambda )$
thanks to [Reference Broué, Malle and Michel9, Theorem 3.2 (1)]. Therefore, we obtain
![]() $x\in {\mathbf {G}}^F U_\chi $
, and as explained above this concludes the proof.
$x\in {\mathbf {G}}^F U_\chi $
, and as explained above this concludes the proof.
We now apply Lemma 3.8 to show that the map
![]() $\widetilde {\Omega }$
satisfies some useful equivariance properties. Before doing so, we need to introduce some notation. For this purpose, consider a pair
$\widetilde {\Omega }$
satisfies some useful equivariance properties. Before doing so, we need to introduce some notation. For this purpose, consider a pair
![]() $({\mathbf {G}}^*,F^*)$
dual to
$({\mathbf {G}}^*,F^*)$
dual to
![]() $({\mathbf {G}},F)$
and a pair
$({\mathbf {G}},F)$
and a pair
![]() $(\widetilde {{\mathbf {G}}}^*,F^*)$
dual to
$(\widetilde {{\mathbf {G}}}^*,F^*)$
dual to
![]() $(\widetilde {{\mathbf {G}}},F)$
. Let
$(\widetilde {{\mathbf {G}}},F)$
. Let
![]() $i^*:\widetilde {{\mathbf {G}}}^*\to {\mathbf {G}}^*$
be the surjection induced by duality from the inclusion
$i^*:\widetilde {{\mathbf {G}}}^*\to {\mathbf {G}}^*$
be the surjection induced by duality from the inclusion
![]() ${\mathbf {G}}\leq \widetilde {{\mathbf {G}}}$
, and observe that
${\mathbf {G}}\leq \widetilde {{\mathbf {G}}}$
, and observe that
![]() $\mathrm{Ker}(i^*)={\mathbf {Z}}(\widetilde {{\mathbf {G}}}^*)$
since
$\mathrm{Ker}(i^*)={\mathbf {Z}}(\widetilde {{\mathbf {G}}}^*)$
since
![]() ${\mathbf {G}}$
is simply connected (see [Reference Cabanes and Enguehard17, Section 15.1]). As shown in [Reference Cabanes and Enguehard17, (15.2)], there exists an isomorphism
${\mathbf {G}}$
is simply connected (see [Reference Cabanes and Enguehard17, Section 15.1]). As shown in [Reference Cabanes and Enguehard17, (15.2)], there exists an isomorphism
 $$ \begin{align} \mathrm{Ker}(i^*)^F&\to \mathrm{Irr}\ \left(\widetilde{{\mathbf{G}}}^F/{\mathbf{G}}^F\right) \\ z&\mapsto \widehat{z}_{\widetilde{{\mathbf{G}}}}\nonumber. \end{align} $$
$$ \begin{align} \mathrm{Ker}(i^*)^F&\to \mathrm{Irr}\ \left(\widetilde{{\mathbf{G}}}^F/{\mathbf{G}}^F\right) \\ z&\mapsto \widehat{z}_{\widetilde{{\mathbf{G}}}}\nonumber. \end{align} $$
Furthermore, if
![]() ${\mathbf {L}}$
is an F-stable Levi subgroup of
${\mathbf {L}}$
is an F-stable Levi subgroup of
![]() ${\mathbf {G}}$
and
${\mathbf {G}}$
and
![]() $z\in \mathrm{Ker}(i^*)$
, then we define
$z\in \mathrm{Ker}(i^*)$
, then we define
![]() $\widehat {z}_{\widetilde {{\mathbf {L}}}}$
to be the restriction of
$\widehat {z}_{\widetilde {{\mathbf {L}}}}$
to be the restriction of
![]() $\widehat {z}_{\widetilde {{\mathbf {G}}}}$
to
$\widehat {z}_{\widetilde {{\mathbf {G}}}}$
to
![]() $\widetilde {{\mathbf {L}}}^F$
and
$\widetilde {{\mathbf {L}}}^F$
and
![]() $\widehat {z}_{{\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})}$
to be the restriction of
$\widehat {z}_{{\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})}$
to be the restriction of
![]() $\widehat {z}_{\widetilde {{\mathbf {G}}}}$
to
$\widehat {z}_{\widetilde {{\mathbf {G}}}}$
to
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
. We set
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
. We set
![]() $\mathcal {K}:=\mathrm{Ker}(i^*)$
and obtain an action of the group
$\mathcal {K}:=\mathrm{Ker}(i^*)$
and obtain an action of the group
![]() $\mathcal {K}$
on the characters of
$\mathcal {K}$
on the characters of
![]() $\widetilde {{\mathbf {G}}}^F$
,
$\widetilde {{\mathbf {G}}}^F$
,
![]() $\widetilde {{\mathbf {L}}}^F$
and
$\widetilde {{\mathbf {L}}}^F$
and
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
as defined in [Reference Rossi54, Definition 2.1]. Moreover, we consider the external semidirect product
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
as defined in [Reference Rossi54, Definition 2.1]. Moreover, we consider the external semidirect product
![]() $(\widetilde {{\mathbf {G}}}^F\mathcal {A})\ltimes \mathcal {K}$
given by defining
$(\widetilde {{\mathbf {G}}}^F\mathcal {A})\ltimes \mathcal {K}$
given by defining
![]() $z^x$
as the unique element of
$z^x$
as the unique element of
![]() $\mathcal {K}$
corresponding to the character
$\mathcal {K}$
corresponding to the character
![]() $(\widehat {z}_{\widetilde {{\mathbf {G}}}})^x$
of the quotient
$(\widehat {z}_{\widetilde {{\mathbf {G}}}})^x$
of the quotient
![]() $\widetilde {{\mathbf {G}}}^F/{\mathbf {G}}^F$
via the isomorphism specified in (3.2), whenever
$\widetilde {{\mathbf {G}}}^F/{\mathbf {G}}^F$
via the isomorphism specified in (3.2), whenever
![]() $x\in \widetilde {{\mathbf {G}}}^F\mathcal {A}$
and
$x\in \widetilde {{\mathbf {G}}}^F\mathcal {A}$
and
![]() $z\in \mathcal {K}$
. Then, for every F-stable Levi subgroup
$z\in \mathcal {K}$
. Then, for every F-stable Levi subgroup
![]() ${\mathbf {L}}$
of
${\mathbf {L}}$
of
![]() ${\mathbf {G}}$
, we obtain an action of
${\mathbf {G}}$
, we obtain an action of
![]() $(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{\mathbf {L}}\ltimes \mathcal {K}$
on the irreducible characters of
$(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{\mathbf {L}}\ltimes \mathcal {K}$
on the irreducible characters of
![]() $\widetilde {{\mathbf {L}}}^F$
and
$\widetilde {{\mathbf {L}}}^F$
and
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
. We denote by
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
. We denote by
![]() $((\widetilde {{\mathbf {G}}}^F\mathcal {A})_{\mathbf {L}}\ltimes \mathcal {K})_{\widetilde {\lambda }}$
the stabiliser of
$((\widetilde {{\mathbf {G}}}^F\mathcal {A})_{\mathbf {L}}\ltimes \mathcal {K})_{\widetilde {\lambda }}$
the stabiliser of
![]() $\widetilde {\lambda }\in \mathrm{Irr}(\widetilde {{\mathbf {L}}}^F)$
. In particular, it follows that
$\widetilde {\lambda }\in \mathrm{Irr}(\widetilde {{\mathbf {L}}}^F)$
. In particular, it follows that
![]() $((\widetilde {{\mathbf {G}}}^F\mathcal {A})_{\mathbf {L}}\ltimes \mathcal {K})_{\widetilde {\lambda }}$
acts on the sets of characters
$((\widetilde {{\mathbf {G}}}^F\mathcal {A})_{\mathbf {L}}\ltimes \mathcal {K})_{\widetilde {\lambda }}$
acts on the sets of characters
![]() $\widetilde {\mathcal {G}}$
and
$\widetilde {\mathcal {G}}$
and
![]() $\widetilde {\mathcal {L}}$
. Next, we show that the bijection
$\widetilde {\mathcal {L}}$
. Next, we show that the bijection
![]() $\widetilde {\Omega }$
is compatible with this action.
$\widetilde {\Omega }$
is compatible with this action.
Lemma 3.9. The bijection
![]() $\widetilde {\Omega }$
is
$\widetilde {\Omega }$
is
![]() $({\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}\rtimes \mathcal {K})_{\widetilde {\lambda }}$
-equivariant.
$({\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}\rtimes \mathcal {K})_{\widetilde {\lambda }}$
-equivariant.
Proof. Let
![]() $\widetilde {\chi }\in \widetilde {\mathcal {G}}$
and
$\widetilde {\chi }\in \widetilde {\mathcal {G}}$
and
![]() $\widetilde {\psi }\in \widetilde {\mathcal {L}}$
. By the definition of
$\widetilde {\psi }\in \widetilde {\mathcal {L}}$
. By the definition of
![]() $\widetilde {\Omega }$
, we have
$\widetilde {\Omega }$
, we have
![]() $\widetilde {\Omega }(\widetilde {\chi })=\widetilde {\psi }$
if and only if
$\widetilde {\Omega }(\widetilde {\chi })=\widetilde {\psi }$
if and only if
![]() $\Omega (\chi )=\psi $
, where
$\Omega (\chi )=\psi $
, where
![]() $\chi :=\widetilde {\chi }_{{\mathbf {G}}^F}$
and
$\chi :=\widetilde {\chi }_{{\mathbf {G}}^F}$
and
![]() $\psi :=\widetilde {\psi }_{{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F}$
. Now, if we consider
$\psi :=\widetilde {\psi }_{{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F}$
. Now, if we consider
![]() $g\in {\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
,
$g\in {\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
,
![]() $x\in (\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}$
and
$x\in (\widetilde {{\mathbf {G}}}^F\mathcal {A})_{({\mathbf {L}},\lambda )}$
and
![]() $z\in \mathcal {K}$
such that
$z\in \mathcal {K}$
such that
![]() $(gx,z)$
stabilises
$(gx,z)$
stabilises
![]() ${\widetilde {\lambda }}$
, then we obtain
${\widetilde {\lambda }}$
, then we obtain
if and only if
However, since the restriction of
![]() $\widetilde {\chi }^{(gx,z)}$
to
$\widetilde {\chi }^{(gx,z)}$
to
![]() ${\mathbf {G}}^F$
coincides with
${\mathbf {G}}^F$
coincides with
![]() $\chi ^x$
and the restriction of
$\chi ^x$
and the restriction of
![]() $\widetilde {\psi }^{(gx,z)}$
to
$\widetilde {\psi }^{(gx,z)}$
to
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
coincides with
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
coincides with
![]() $\psi ^x$
, we deduce that the equality in (3.3) holds by the equivariance properties of
$\psi ^x$
, we deduce that the equality in (3.3) holds by the equivariance properties of
![]() $\Omega $
as described in Corollary 3.2.
$\Omega $
as described in Corollary 3.2.
One of the main ingredients for the construction of the projective representations needed to obtain
![]() ${\mathbf {G}}^F$
-block isomorphisms of character triples is given by the following two lemmas on maximal extendibility.
${\mathbf {G}}^F$
-block isomorphisms of character triples is given by the following two lemmas on maximal extendibility.
Lemma 3.10. Maximal extendibility holds for
![]() $\mathcal {G}$
with respect to
$\mathcal {G}$
with respect to
![]() ${\mathbf {G}}^F\unlhd {\mathbf {G}}^F\mathcal {A}$
, that is, every character
${\mathbf {G}}^F\unlhd {\mathbf {G}}^F\mathcal {A}$
, that is, every character
![]() $\chi \in \mathcal {G}$
extends to
$\chi \in \mathcal {G}$
extends to
![]() ${\mathbf {G}}^F\mathcal {A}_\chi $
.
${\mathbf {G}}^F\mathcal {A}_\chi $
.
Proof. If
![]() ${\mathbf {G}}$
is of type
${\mathbf {G}}$
is of type
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
, then the result follows from [Reference Isaacs32, Corollary 11.22] since
$\mathbf {C}$
, then the result follows from [Reference Isaacs32, Corollary 11.22] since
![]() $\mathcal {A}$
is cyclic. Then, we can assume that
$\mathcal {A}$
is cyclic. Then, we can assume that
![]() ${\mathbf {G}}$
is of type
${\mathbf {G}}$
is of type
![]() $\mathbf {A}$
in which case the result follows from [Reference Cabanes and Späth19, Theorem 4.1] (see also [Reference Malle38, Theorem 2.4]).
$\mathbf {A}$
in which case the result follows from [Reference Cabanes and Späth19, Theorem 4.1] (see also [Reference Malle38, Theorem 2.4]).
The local version of the lemma above is a consequence of the results obtained in [Reference Brough and Späth13].
Lemma 3.11. Maximal extendibility holds for
![]() $\mathcal {L}$
with respect to
$\mathcal {L}$
with respect to
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F\unlhd ({\mathbf {G}}^F\mathcal {A})_{\mathbf {L}}$
, that is, every character
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F\unlhd ({\mathbf {G}}^F\mathcal {A})_{\mathbf {L}}$
, that is, every character
![]() $\psi \in \mathcal {L}$
extends to
$\psi \in \mathcal {L}$
extends to
![]() $({\mathbf {G}}^F\mathcal {A})_{{\mathbf {L}},\psi }$
.
$({\mathbf {G}}^F\mathcal {A})_{{\mathbf {L}},\psi }$
.
Proof. As in the proof of Lemma 3.10, it is enough to prove the result in the case where
![]() ${\mathbf {G}}$
is of type
${\mathbf {G}}$
is of type
![]() $\mathbf {A}$
. In fact, if
$\mathbf {A}$
. In fact, if
![]() ${\mathbf {G}}$
is of type
${\mathbf {G}}$
is of type
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
, then the quotient
$\mathbf {C}$
, then the quotient
![]() $({\mathbf {G}}^F\mathcal {A})_{({\mathbf {L}},\psi )}/{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
is cyclic because it is a subquotient of
$({\mathbf {G}}^F\mathcal {A})_{({\mathbf {L}},\psi )}/{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
is cyclic because it is a subquotient of
![]() $\mathcal {A}$
. Now, if
$\mathcal {A}$
. Now, if
![]() ${\mathbf {G}}$
is of type
${\mathbf {G}}$
is of type
![]() $\mathbf {A}$
the result follows from [Reference Brough and Späth13, Theorem 1.2].
$\mathbf {A}$
the result follows from [Reference Brough and Späth13, Theorem 1.2].
Finally, we can start constructing isomorphisms of character triples for the bijection
![]() $\Omega $
. As a first step, we obtain a weaker isomorphism, known as
$\Omega $
. As a first step, we obtain a weaker isomorphism, known as
![]() ${\mathbf {G}}^F$
-central isomorphism of character triples and denoted by
${\mathbf {G}}^F$
-central isomorphism of character triples and denoted by ![]() , whose requirements are given by [Reference Späth64, Remark 3.7 (i)-(iii)] and replacing the condition on defect groups by imposing that
, whose requirements are given by [Reference Späth64, Remark 3.7 (i)-(iii)] and replacing the condition on defect groups by imposing that
![]() ${\mathbf {C}}_G(N)\leq H_1\cap H_2$
with the notations used there. We refer the reader to [Reference Rossi53, Definition 3.3.4] for a precise definition.
${\mathbf {C}}_G(N)\leq H_1\cap H_2$
with the notations used there. We refer the reader to [Reference Rossi53, Definition 3.3.4] for a precise definition.
Proposition 3.12. For every
![]() $\chi \in \mathcal {G}$
and
$\chi \in \mathcal {G}$
and
![]() $\psi :=\Omega (\chi )\in \mathcal {L}$
, we have
$\psi :=\Omega (\chi )\in \mathcal {L}$
, we have
Proof. First, notice that
![]() $(\widetilde {{\mathbf {G}}}^F\mathcal {A})_\chi =\widetilde {{\mathbf {G}}}^F\mathcal {A}_\chi $
since
$(\widetilde {{\mathbf {G}}}^F\mathcal {A})_\chi =\widetilde {{\mathbf {G}}}^F\mathcal {A}_\chi $
since
![]() $\chi $
is
$\chi $
is
![]() $\widetilde {{\mathbf {G}}}^F$
-invariant. We start by constructing projective representations associated with
$\widetilde {{\mathbf {G}}}^F$
-invariant. We start by constructing projective representations associated with
![]() $\chi $
and
$\chi $
and
![]() $\psi $
. According to Proposition 3.5, we can find a unipotent extension
$\psi $
. According to Proposition 3.5, we can find a unipotent extension
![]() $\widetilde {\chi }\in \widetilde {\mathcal {G}}$
of
$\widetilde {\chi }\in \widetilde {\mathcal {G}}$
of
![]() $\chi $
to
$\chi $
to
![]() $\widetilde {{\mathbf {G}}}^F$
. Furthermore, by Lemma 3.10, there exists an extension
$\widetilde {{\mathbf {G}}}^F$
. Furthermore, by Lemma 3.10, there exists an extension
![]() $\chi '$
of
$\chi '$
of
![]() $\chi $
to
$\chi $
to
![]() ${\mathbf {G}}^F\mathcal {A}_\chi $
. Let
${\mathbf {G}}^F\mathcal {A}_\chi $
. Let
![]() $\widetilde {\mathcal {D}}_{\mathrm{glo}}$
be a representation of
$\widetilde {\mathcal {D}}_{\mathrm{glo}}$
be a representation of
![]() $\widetilde {{\mathbf {G}}}^F$
affording
$\widetilde {{\mathbf {G}}}^F$
affording
![]() $\widetilde {\chi }$
and
$\widetilde {\chi }$
and
![]() $\mathcal {D}^{\prime }_{\mathrm{glo}}$
a representation of
$\mathcal {D}^{\prime }_{\mathrm{glo}}$
a representation of
![]() ${\mathbf {G}}^F\mathcal {A}_\chi $
affording
${\mathbf {G}}^F\mathcal {A}_\chi $
affording
![]() $\chi '$
. Now, [Reference Späth63, Lemma 2.11] implies that
$\chi '$
. Now, [Reference Späth63, Lemma 2.11] implies that
defined by
![]() ${\mathcal {P}}_{\mathrm{glo}}(x_1x_2):=\widetilde {\mathcal {D}}_{\mathrm{glo}}(x_1)\mathcal {D}^{\prime }_{\mathrm{glo}}(x_2)$
for every
${\mathcal {P}}_{\mathrm{glo}}(x_1x_2):=\widetilde {\mathcal {D}}_{\mathrm{glo}}(x_1)\mathcal {D}^{\prime }_{\mathrm{glo}}(x_2)$
for every
![]() $x_1\in \widetilde {{\mathbf {G}}}^F$
and
$x_1\in \widetilde {{\mathbf {G}}}^F$
and
![]() $x_2\in {\mathbf {G}}^F\mathcal {A}_\chi $
is a projective representation associated with
$x_2\in {\mathbf {G}}^F\mathcal {A}_\chi $
is a projective representation associated with
![]() $\chi $
. Next, observe that
$\chi $
. Next, observe that
![]() $\widetilde {\psi }:=\widetilde {\Omega }(\widetilde {\chi })\in \widetilde {\mathcal {L}}$
is an extension of
$\widetilde {\psi }:=\widetilde {\Omega }(\widetilde {\chi })\in \widetilde {\mathcal {L}}$
is an extension of
![]() $\psi $
to
$\psi $
to
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
, and consider an extension
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
, and consider an extension
![]() $\psi '$
of
$\psi '$
of
![]() $\psi $
to
$\psi $
to
![]() $({\mathbf {G}}^F\mathcal {A})_{{\mathbf {L}},\psi }$
given by Lemma 3.11. Let
$({\mathbf {G}}^F\mathcal {A})_{{\mathbf {L}},\psi }$
given by Lemma 3.11. Let
![]() $\widetilde {\mathcal {D}}_{\mathrm{loc}}$
be a representation of
$\widetilde {\mathcal {D}}_{\mathrm{loc}}$
be a representation of
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
affording
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
affording
![]() $\widetilde {\psi }$
and
$\widetilde {\psi }$
and
![]() $\mathcal {D}^{\prime }_{\mathrm{loc}}$
a representation of
$\mathcal {D}^{\prime }_{\mathrm{loc}}$
a representation of
![]() $({\mathbf {G}}^F\mathcal {A})_{{\mathbf {L}},\psi }$
affording
$({\mathbf {G}}^F\mathcal {A})_{{\mathbf {L}},\psi }$
affording
![]() $\psi '$
. Once again, [Reference Späth63, Lemma 2.11] shows that the map
$\psi '$
. Once again, [Reference Späth63, Lemma 2.11] shows that the map
given by
![]() ${\mathcal {P}}_{\mathrm{loc}}(x_1x_2):=\widetilde {\mathcal {D}}_{\mathrm{loc}}(x_1)\mathcal {D}^{\prime }_{\mathrm{loc}}(x_2)$
for every
${\mathcal {P}}_{\mathrm{loc}}(x_1x_2):=\widetilde {\mathcal {D}}_{\mathrm{loc}}(x_1)\mathcal {D}^{\prime }_{\mathrm{loc}}(x_2)$
for every
![]() $x_1\in {\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
and
$x_1\in {\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
and
![]() $x_2\in ({\mathbf {G}}^F\mathcal {A})_{{\mathbf {L}},\psi }$
is a projective representation associated with
$x_2\in ({\mathbf {G}}^F\mathcal {A})_{{\mathbf {L}},\psi }$
is a projective representation associated with
![]() $\psi $
. We denote by
$\psi $
. We denote by
![]() $\alpha _{\mathrm{glo}}$
and
$\alpha _{\mathrm{glo}}$
and
![]() $\alpha _{\mathrm{loc}}$
the factor set of
$\alpha _{\mathrm{loc}}$
the factor set of
![]() ${\mathcal {P}}_{\mathrm{glo}}$
and
${\mathcal {P}}_{\mathrm{glo}}$
and
![]() ${\mathcal {P}}_{\mathrm{loc}}$
, respectively. As explained in the proof of [Reference Rossi54, Theorem 4.3], in order to prove that
${\mathcal {P}}_{\mathrm{loc}}$
, respectively. As explained in the proof of [Reference Rossi54, Theorem 4.3], in order to prove that
![]() $\alpha _{\mathrm{glo}}$
coincides with
$\alpha _{\mathrm{glo}}$
coincides with
![]() $\alpha _{\mathrm{loc}}$
via the isomorphism
$\alpha _{\mathrm{loc}}$
via the isomorphism
![]() $\widetilde {{\mathbf {G}}}^F\mathcal {A}_\chi /{\mathbf {G}}^F\simeq (\widetilde {{\mathbf {G}}}^F\mathcal {A})_{{\mathbf {L}},\psi }/{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
, it suffices to show that
$\widetilde {{\mathbf {G}}}^F\mathcal {A}_\chi /{\mathbf {G}}^F\simeq (\widetilde {{\mathbf {G}}}^F\mathcal {A})_{{\mathbf {L}},\psi }/{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
, it suffices to show that
for every
![]() $x\in ({\mathbf {G}}^F\mathcal {A})_{{\mathbf {L}},\chi }$
and where
$x\in ({\mathbf {G}}^F\mathcal {A})_{{\mathbf {L}},\chi }$
and where
![]() $\mu _x^{\mathrm{glo}}\in \mathrm{Irr}(\widetilde {{\mathbf {G}}}^F/{\mathbf {G}}^F)$
and
$\mu _x^{\mathrm{glo}}\in \mathrm{Irr}(\widetilde {{\mathbf {G}}}^F/{\mathbf {G}}^F)$
and
![]() $\mu _x^{\mathrm{loc}}\in \mathrm{ Irr}({\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F/{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F)$
are determined by Gallagher’s theorem (see [Reference Isaacs32, Corollary 6.17]) via the equalities
$\mu _x^{\mathrm{loc}}\in \mathrm{ Irr}({\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F/{\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F)$
are determined by Gallagher’s theorem (see [Reference Isaacs32, Corollary 6.17]) via the equalities
![]() $\widetilde {\chi }=\mu _x^{\mathrm{glo}}\widetilde {\chi }^x$
and
$\widetilde {\chi }=\mu _x^{\mathrm{glo}}\widetilde {\chi }^x$
and
![]() $\widetilde {\psi }=\mu _x^{\mathrm{loc}}\widetilde {\psi }^x$
respectively. Because
$\widetilde {\psi }=\mu _x^{\mathrm{loc}}\widetilde {\psi }^x$
respectively. Because
![]() $({\mathbf {G}}^F\mathcal {A})_{{\mathbf {L}},\chi }={\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F({\mathbf {G}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\chi }$
, we may assume that x stabilises
$({\mathbf {G}}^F\mathcal {A})_{{\mathbf {L}},\chi }={\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F({\mathbf {G}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\chi }$
, we may assume that x stabilises
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $z\in \mathcal {K}$
such that
$z\in \mathcal {K}$
such that
![]() $\mu _x^{\mathrm{glo}}=\hat {z}_{\widetilde {{\mathbf {G}}}}$
, and observe that
$\mu _x^{\mathrm{glo}}=\hat {z}_{\widetilde {{\mathbf {G}}}}$
, and observe that
![]() $(x,z)$
is an element of
$(x,z)$
is an element of
![]() $({\mathbf {G}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\chi }\rtimes \mathcal {K}$
that stabilises
$({\mathbf {G}}^F\mathcal {A})_{({\mathbf {L}},\lambda ),\chi }\rtimes \mathcal {K}$
that stabilises
![]() $\widetilde {\chi }$
. Then, applying [Reference Broué, Malle and Michel9, Theorem 3.2 (1)], we deduce that
$\widetilde {\chi }$
. Then, applying [Reference Broué, Malle and Michel9, Theorem 3.2 (1)], we deduce that
![]() $\widetilde {\lambda }$
and
$\widetilde {\lambda }$
and
![]() $\widetilde {\lambda }^{(x,z)}$
are
$\widetilde {\lambda }^{(x,z)}$
are
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
-conjugate and we may choose
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
-conjugate and we may choose
![]() $g\in {\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
such that
$g\in {\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
such that
![]() $\widetilde {\lambda }=(\widetilde {\lambda }^{(x,z)})^g=\widetilde {\lambda }^{(xg,z)}$
. In other words,
$\widetilde {\lambda }=(\widetilde {\lambda }^{(x,z)})^g=\widetilde {\lambda }^{(xg,z)}$
. In other words,
and thus Lemma 3.9 implies that the equality
![]() $\widetilde {\chi }=\widetilde {\chi }^{(xg,z)}$
holds if and only if
$\widetilde {\chi }=\widetilde {\chi }^{(xg,z)}$
holds if and only if
![]() $\widetilde {\psi }=\widetilde {\psi }^{(xg,z)}$
. From this, we immediately deduce the equality required in (3.4).
$\widetilde {\psi }=\widetilde {\psi }^{(xg,z)}$
. From this, we immediately deduce the equality required in (3.4).
Next, denote by
![]() $\zeta _{\mathrm{glo}}$
and
$\zeta _{\mathrm{glo}}$
and
![]() $\zeta _{\mathrm{loc }}$
the scalar functions associated to
$\zeta _{\mathrm{loc }}$
the scalar functions associated to
![]() ${\mathcal {P}}_{\mathrm{glo}}$
and
${\mathcal {P}}_{\mathrm{glo}}$
and
![]() ${\mathcal {P}}_{\mathrm{loc}}$
, respectively. To conclude the proof, it remains to show that the central functions
${\mathcal {P}}_{\mathrm{loc}}$
, respectively. To conclude the proof, it remains to show that the central functions
![]() $\zeta _{\mathrm{glo}}$
and
$\zeta _{\mathrm{glo}}$
and
![]() $\zeta _{\mathrm{loc}}$
coincide on
$\zeta _{\mathrm{loc}}$
coincide on
![]() ${\mathbf {C}}_{(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{\chi }}({\mathbf {G}}^F)={\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)$
. As in the proof of [Reference Rossi54, Theorem 4.3], it is enough to show that the restrictions of
${\mathbf {C}}_{(\widetilde {{\mathbf {G}}}^F\mathcal {A})_{\chi }}({\mathbf {G}}^F)={\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)$
. As in the proof of [Reference Rossi54, Theorem 4.3], it is enough to show that the restrictions of
![]() $\widetilde {\chi }$
and
$\widetilde {\chi }$
and
![]() $\widetilde {\psi }$
to
$\widetilde {\psi }$
to
![]() ${\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)$
are multiples of a common irreducible constituent. This follows from the fact that unipotent characters contain the center in their kernel. In fact, on one hand,
${\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)$
are multiples of a common irreducible constituent. This follows from the fact that unipotent characters contain the center in their kernel. In fact, on one hand,
![]() $1_{{\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)}$
is the unique irreducible constituent of
$1_{{\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)}$
is the unique irreducible constituent of
![]() $\widetilde {\chi }_{{\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)}$
because
$\widetilde {\chi }_{{\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)}$
because
![]() $\widetilde {\chi }$
is unipotent. On the other hand,
$\widetilde {\chi }$
is unipotent. On the other hand,
![]() $\widetilde {\psi }$
lies above
$\widetilde {\psi }$
lies above
![]() $\widetilde {\lambda }$
and, since
$\widetilde {\lambda }$
and, since
![]() ${\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)\leq {\mathbf {Z}}(\widetilde {{\mathbf {L}}}^F)$
and
${\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)\leq {\mathbf {Z}}(\widetilde {{\mathbf {L}}}^F)$
and
![]() $\widetilde {\lambda }$
is unipotent, we deduce that
$\widetilde {\lambda }$
is unipotent, we deduce that
![]() $1_{{\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)}$
is the unique irreducible constituent of
$1_{{\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)}$
is the unique irreducible constituent of
![]() $\widetilde {\psi }_{{\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)}$
. This completes the proof.
$\widetilde {\psi }_{{\mathbf {Z}}(\widetilde {{\mathbf {G}}}^F)}$
. This completes the proof.
We conclude this section by verifying the remaining condition [Reference Späth64, Remark 3.7 (iv)] and obtain the required
![]() ${\mathbf {G}}^F$
-block isomorphisms of character triples for the map
${\mathbf {G}}^F$
-block isomorphisms of character triples for the map
![]() $\Omega $
.
$\Omega $
.
Proposition 3.13. If the prime
![]() $\ell $
is odd, then we have
$\ell $
is odd, then we have
for every
![]() $\chi \in \mathcal {G}$
and where
$\chi \in \mathcal {G}$
and where
![]() $\psi :=\Omega (\chi )$
.
$\psi :=\Omega (\chi )$
.
Proof. By Proposition 3.12, it is enough to check the block theoretic requirement given by [Reference Späth64, Remark 3.7 (ii) and (iv)]. First, observe that under our assumption [Reference Cabanes and Enguehard15, Proposition 3.3 (ii)] shows that
![]() ${{\mathbf {L}}^F={\mathbf {C}}_{{\mathbf {G}}^F}(E)}$
where
${{\mathbf {L}}^F={\mathbf {C}}_{{\mathbf {G}}^F}(E)}$
where
![]() $E:={\mathbf {Z}}({\mathbf {L}})^F_\ell $
. In particular,
$E:={\mathbf {Z}}({\mathbf {L}})^F_\ell $
. In particular,
![]() ${\mathbf {N}}_J({\mathbf {L}})={\mathbf {N}}_J(E)$
for every
${\mathbf {N}}_J({\mathbf {L}})={\mathbf {N}}_J(E)$
for every
![]() ${\mathbf {G}}^F\leq J\leq \widetilde {{\mathbf {G}}}^F$
. Furthermore, for every block
${\mathbf {G}}^F\leq J\leq \widetilde {{\mathbf {G}}}^F$
. Furthermore, for every block
![]() $C_0$
of
$C_0$
of
![]() ${\mathbf {N}}_J({\mathbf {L}})$
and every defect group D of
${\mathbf {N}}_J({\mathbf {L}})$
and every defect group D of
![]() $C_0$
, we have
$C_0$
, we have
![]() $E\leq {\mathbf {O}}_\ell ({\mathbf {N}}_J({\mathbf {L}}))\leq D$
and hence
$E\leq {\mathbf {O}}_\ell ({\mathbf {N}}_J({\mathbf {L}}))\leq D$
and hence
![]() ${\mathbf {C}}_{\widetilde {{\mathbf {G}}}^F}(D)\leq {\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
. Now, [Reference Koshitani and Späth36, Theorem B] implies that for every block C of
${\mathbf {C}}_{\widetilde {{\mathbf {G}}}^F}(D)\leq {\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
. Now, [Reference Koshitani and Späth36, Theorem B] implies that for every block C of
![]() ${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
covering
${\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F$
covering
![]() $C_0$
, the induced blocks
$C_0$
, the induced blocks
![]() $B:=C^{\widetilde {{\mathbf {G}}}^F}$
and
$B:=C^{\widetilde {{\mathbf {G}}}^F}$
and
![]() $B_0:=C_0^J$
are well defined and B covers
$B_0:=C_0^J$
are well defined and B covers
![]() $B_0$
.
$B_0$
.
Let
![]() $\widetilde {\chi }\in \widetilde {\mathcal {G}}$
be an extension of
$\widetilde {\chi }\in \widetilde {\mathcal {G}}$
be an extension of
![]() $\chi $
, and set
$\chi $
, and set
![]() $\widetilde {\psi }:=\widetilde {\Omega }(\widetilde {\chi })$
. By Lemma 2.3, the block of
$\widetilde {\psi }:=\widetilde {\Omega }(\widetilde {\chi })$
. By Lemma 2.3, the block of
![]() $\widetilde {C}$
of
$\widetilde {C}$
of
![]() $\widetilde {\psi }$
coincides with the induced block
$\widetilde {\psi }$
coincides with the induced block
![]() $\mathrm{bl}(\widetilde {\lambda })^{{\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F}$
. Furthermore, by [Reference Cabanes and Enguehard15, Proposition 4.2] we know that the block
$\mathrm{bl}(\widetilde {\lambda })^{{\mathbf {N}}_{\widetilde {{\mathbf {G}}}}({\mathbf {L}})^F}$
. Furthermore, by [Reference Cabanes and Enguehard15, Proposition 4.2] we know that the block
![]() $\widetilde {B}$
of
$\widetilde {B}$
of
![]() $\widetilde {\chi }$
coincides with
$\widetilde {\chi }$
coincides with
![]() $b_{\widetilde {{\mathbf {G}}}^F}(\widetilde {{\mathbf {L}}},\widetilde {\lambda })=\mathrm{bl}(\widetilde {\lambda })^{\widetilde {{\mathbf {G}}}^F}$
. Then, by the transitivity of block induction we get
$b_{\widetilde {{\mathbf {G}}}^F}(\widetilde {{\mathbf {L}}},\widetilde {\lambda })=\mathrm{bl}(\widetilde {\lambda })^{\widetilde {{\mathbf {G}}}^F}$
. Then, by the transitivity of block induction we get
![]() $\widetilde {B}=\widetilde {C}^{\widetilde {{\mathbf {G}}}^F}$
. Consider now
$\widetilde {B}=\widetilde {C}^{\widetilde {{\mathbf {G}}}^F}$
. Consider now
![]() ${\mathbf {G}}^F\leq J\leq \widetilde {{\mathbf {G}}}^F$
as in the previous paragraph and notice that
${\mathbf {G}}^F\leq J\leq \widetilde {{\mathbf {G}}}^F$
as in the previous paragraph and notice that
![]() $\mathrm{ bl}(\widetilde {\chi }_J)$
is the unique block of J covered by
$\mathrm{ bl}(\widetilde {\chi }_J)$
is the unique block of J covered by
![]() $\widetilde {B}$
. Now, since
$\widetilde {B}$
. Now, since
![]() $\mathrm{bl}(\widetilde {\psi }_{{\mathbf {N}}_J({\mathbf {L}})})$
is covered by
$\mathrm{bl}(\widetilde {\psi }_{{\mathbf {N}}_J({\mathbf {L}})})$
is covered by
![]() $\widetilde {C}$
, we deduce that
$\widetilde {C}$
, we deduce that
![]() $\mathrm{ bl}(\widetilde {\psi }_{{\mathbf {N}}_J({\mathbf {L}})})^J$
is covered by
$\mathrm{ bl}(\widetilde {\psi }_{{\mathbf {N}}_J({\mathbf {L}})})^J$
is covered by
![]() $\widetilde {B}$
and therefore
$\widetilde {B}$
and therefore
As explained in the proof of [Reference Rossi54, Theorem 4.8], we can now use (3.5) together with Proposition 3.12 to conclude the proof via an application of [Reference Späth64, Theorem 4.1 (i)].
3.3 Proof of Theorem C
Proof of Theorem C.
The hypothesis of Corollary 3.2 is satisfied under our restrictions on
![]() ${\mathbf {G}}$
according to Lemma 3.6, and therefore, we obtain an
${\mathbf {G}}$
according to Lemma 3.6, and therefore, we obtain an
![]() $\mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-equivariant bijection
$\mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{({\mathbf {L}},\lambda )}$
-equivariant bijection
that, furthermore, preserves the
![]() $\ell $
-defect of characters. Next, observe that the groups
$\ell $
-defect of characters. Next, observe that the groups
![]() $\widetilde {{\mathbf {G}}}^F\mathcal {A}$
and
$\widetilde {{\mathbf {G}}}^F\mathcal {A}$
and
![]() $X:={\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
induce the same automorphisms on
$X:={\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
induce the same automorphisms on
![]() ${\mathbf {G}}^F$
according to the description given in [Reference Gorenstein, Lyons and Solomon31, Section 2.5]. Then, by applying [Reference Späth64, Theorem 5.3] and Proposition 3.13, we conclude that
${\mathbf {G}}^F$
according to the description given in [Reference Gorenstein, Lyons and Solomon31, Section 2.5]. Then, by applying [Reference Späth64, Theorem 5.3] and Proposition 3.13, we conclude that
for every
![]() $\chi \in {\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
and where
$\chi \in {\mathcal {E}}({\mathbf {G}}^F,({\mathbf {L}},\lambda ))$
and where
![]() $\psi :=\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}(\chi )$
and the proof is now complete.
$\psi :=\Omega _{({\mathbf {L}},\lambda )}^{\mathbf {G}}(\chi )$
and the proof is now complete.
4 Consequences of Theorem C
In this section, we collect some consequences of Theorem C. First, we extend the parametrisation obtained in Theorem C from unipotent e-Harish-Chandra series of the simple group
![]() ${\mathbf {G}}$
to pseudo-unipotent (see Definition 2.2) e-Harish-Chandra series of the Levi subgroups of
${\mathbf {G}}$
to pseudo-unipotent (see Definition 2.2) e-Harish-Chandra series of the Levi subgroups of
![]() ${\mathbf {G}}$
. More precisely, for every F-stable Levi subgroup
${\mathbf {G}}$
. More precisely, for every F-stable Levi subgroup
![]() ${\mathbf {K}}$
of
${\mathbf {K}}$
of
![]() ${\mathbf {G}}$
, we construct a parametrisation of the e-Harish-Chandra series associated to e-cuspidal pairs of the form
${\mathbf {G}}$
, we construct a parametrisation of the e-Harish-Chandra series associated to e-cuspidal pairs of the form
![]() $({\mathbf {L}},\lambda )$
for some
$({\mathbf {L}},\lambda )$
for some
![]() $({\mathbf {K}},F)$
-pseudo-unipotent character
$({\mathbf {K}},F)$
-pseudo-unipotent character
![]() $\lambda \in \mathrm{ps}_{\mathbf {K}}({\mathbf {L}}^F)$
. In a second step, we construct character bijections above this parametrisation by exploiting results on isomorphisms of character triples (see Corollary 4.6). This will allow us to control the characters of e-chain stabilisers lying above pseudo-unipotent characters (see Proposition 5.7).
$\lambda \in \mathrm{ps}_{\mathbf {K}}({\mathbf {L}}^F)$
. In a second step, we construct character bijections above this parametrisation by exploiting results on isomorphisms of character triples (see Corollary 4.6). This will allow us to control the characters of e-chain stabilisers lying above pseudo-unipotent characters (see Proposition 5.7).
4.1 Parametrisation of pseudo-unipotent characters of Levi subgroups
In this section, we assume that
![]() ${\mathbf {G}}$
is a simply connected reductive group whose irreducible components are of type
${\mathbf {G}}$
is a simply connected reductive group whose irreducible components are of type
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
. Recall that, by abuse of terminology, we say that
$\mathbf {C}$
. Recall that, by abuse of terminology, we say that
![]() ${\mathbf {G}}$
is simply connected if so is its derived subgroup
${\mathbf {G}}$
is simply connected if so is its derived subgroup
![]() $[{\mathbf {G}},{\mathbf {G}}]$
(a semisimple group). Furthermore, we assume that the prime
$[{\mathbf {G}},{\mathbf {G}}]$
(a semisimple group). Furthermore, we assume that the prime
![]() $\ell $
is odd.
$\ell $
is odd.
Let
![]() ${\mathbf {K}}$
be an F-stable Levi subgroup of
${\mathbf {K}}$
be an F-stable Levi subgroup of
![]() ${\mathbf {G}}$
, and set
${\mathbf {G}}$
, and set
![]() ${\mathbf {K}}_0:=[{\mathbf {K}},{\mathbf {K}}]$
. Observe that since the group
${\mathbf {K}}_0:=[{\mathbf {K}},{\mathbf {K}}]$
. Observe that since the group
![]() ${\mathbf {G}}$
is simply connected, the subgroup
${\mathbf {G}}$
is simply connected, the subgroup
![]() ${\mathbf {K}}_0$
is also simply connected according to [Reference Malle and Testerman41, Proposition 12.14]. In addition, under our assumption on the type of
${\mathbf {K}}_0$
is also simply connected according to [Reference Malle and Testerman41, Proposition 12.14]. In addition, under our assumption on the type of
![]() ${\mathbf {G}}$
, we deduce that the simple components of
${\mathbf {G}}$
, we deduce that the simple components of
![]() ${\mathbf {K}}_0$
can only be of some of the types
${\mathbf {K}}_0$
can only be of some of the types
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
.
$\mathbf {C}$
.
Proposition 4.1. For every unipotent e-cuspidal pair
![]() $({\mathbf {L}}_0,\lambda _0)$
of
$({\mathbf {L}}_0,\lambda _0)$
of
![]() $({\mathbf {K}}_0,F)$
, there exists a defect preserving
$({\mathbf {K}}_0,F)$
, there exists a defect preserving
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {K}}_0^F)_{({\mathbf {L}}_0,\lambda _0)}$
-equivariant bijection
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {K}}_0^F)_{({\mathbf {L}}_0,\lambda _0)}$
-equivariant bijection
such that
for every
![]() $\vartheta \in {\mathcal {E}}({\mathbf {K}}_0^F,({\mathbf {L}}_0,\lambda _0))$
and where
$\vartheta \in {\mathcal {E}}({\mathbf {K}}_0^F,({\mathbf {L}}_0,\lambda _0))$
and where
![]() $Y:={\mathbf {K}}_0^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {K}}_0^F)$
.
$Y:={\mathbf {K}}_0^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {K}}_0^F)$
.
Proof. Notice that
![]() ${\mathbf {K}}_0$
is the direct product of simple algebraic groups
${\mathbf {K}}_0$
is the direct product of simple algebraic groups
![]() ${\mathbf {K}}_1,\dots , {\mathbf {K}}_n$
and that the action of F permutes the simple components
${\mathbf {K}}_1,\dots , {\mathbf {K}}_n$
and that the action of F permutes the simple components
![]() ${\mathbf {K}}_i$
. Denote the direct product of the simple components in each F-orbit by
${\mathbf {K}}_i$
. Denote the direct product of the simple components in each F-orbit by
![]() ${\mathbf {H}}_j$
for
${\mathbf {H}}_j$
for
![]() $j=1,\dots , t$
. The
$j=1,\dots , t$
. The
![]() $({\mathbf {H}}_j,F)$
are the irreducible rational components of
$({\mathbf {H}}_j,F)$
are the irreducible rational components of
![]() $({\mathbf {K}}_0,F)$
, and we have
$({\mathbf {K}}_0,F)$
, and we have
![]() ${\mathbf {K}}_0^F={\mathbf {H}}_1^F\times \cdots \times {\mathbf {H}}_t^F$
. Similarly, if we define the intersections
${\mathbf {K}}_0^F={\mathbf {H}}_1^F\times \cdots \times {\mathbf {H}}_t^F$
. Similarly, if we define the intersections
![]() ${\mathbf {M}}_j:={\mathbf {L}}_0\cap {\mathbf {H}}_j$
, then we have a decomposition
${\mathbf {M}}_j:={\mathbf {L}}_0\cap {\mathbf {H}}_j$
, then we have a decomposition
![]() ${\mathbf {L}}_0^F={\mathbf {M}}_1^F\times \cdots \times {\mathbf {M}}_t^F$
. In particular, we can write
${\mathbf {L}}_0^F={\mathbf {M}}_1^F\times \cdots \times {\mathbf {M}}_t^F$
. In particular, we can write
![]() $\lambda _0=\mu _1\times \cdots \times \mu _t$
with
$\lambda _0=\mu _1\times \cdots \times \mu _t$
with
![]() $\mu _j\in \mathrm{Irr}({\mathbf {M}}_j^F)$
. In this case, notice that
$\mu _j\in \mathrm{Irr}({\mathbf {M}}_j^F)$
. In this case, notice that
![]() $({\mathbf {M}}_j,\mu _j)$
is a unipotent e-cuspidal pair of
$({\mathbf {M}}_j,\mu _j)$
is a unipotent e-cuspidal pair of
![]() $({\mathbf {H}}_j,F)$
. Next, suppose that
$({\mathbf {H}}_j,F)$
. Next, suppose that
![]() ${\mathbf {H}}_j={\mathbf {H}}_{j,1}\times \dots \times {\mathbf {H}}_{j,m_j}$
, and observe that
${\mathbf {H}}_j={\mathbf {H}}_{j,1}\times \dots \times {\mathbf {H}}_{j,m_j}$
, and observe that
![]() ${\mathbf {H}}_j^F\simeq {\mathbf {H}}_{j,1}^{F^{m_j}}$
. By the discussion at the beginning of this section, we know that
${\mathbf {H}}_j^F\simeq {\mathbf {H}}_{j,1}^{F^{m_j}}$
. By the discussion at the beginning of this section, we know that
![]() ${\mathbf {H}}_{j,1}$
is a simple, simply connected group of type
${\mathbf {H}}_{j,1}$
is a simple, simply connected group of type
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
and hence it satisfies the assumptions of Theorem C. Then, via the isomorphism
$\mathbf {C}$
and hence it satisfies the assumptions of Theorem C. Then, via the isomorphism
![]() ${\mathbf {H}}_j^F\simeq {\mathbf {H}}_{j,1}^{F^{m_j}}$
, we obtain an
${\mathbf {H}}_j^F\simeq {\mathbf {H}}_{j,1}^{F^{m_j}}$
, we obtain an
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {H}}_j^F)_{({\mathbf {M}}_j,\mu _j)}$
-equivariant bijection
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {H}}_j^F)_{({\mathbf {M}}_j,\mu _j)}$
-equivariant bijection
that preserves the defect of characters and such that
for every
![]() $\vartheta \in {\mathcal {E}}({\mathbf {H}}_j^F,({\mathbf {M}}_j,\mu _j))$
and where
$\vartheta \in {\mathcal {E}}({\mathbf {H}}_j^F,({\mathbf {M}}_j,\mu _j))$
and where
![]() $Y_j:={\mathbf {H}}_j^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {H}}_j^F)$
. Since the characters in the sets
$Y_j:={\mathbf {H}}_j^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {H}}_j^F)$
. Since the characters in the sets
![]() ${\mathcal {E}}({\mathbf {K}}_0^F,({\mathbf {L}}_0,\lambda _0))$
and
${\mathcal {E}}({\mathbf {K}}_0^F,({\mathbf {L}}_0,\lambda _0))$
and
![]() $\mathrm{Irr}({\mathbf {N}}_{{\mathbf {K}}_0}({\mathbf {L}}_0)^F\mid \lambda _0)$
are products of characters belonging to the sets
$\mathrm{Irr}({\mathbf {N}}_{{\mathbf {K}}_0}({\mathbf {L}}_0)^F\mid \lambda _0)$
are products of characters belonging to the sets
![]() ${\mathcal {E}}({\mathbf {H}}_j^F,({\mathbf {M}}_j,\mu _j))$
and
${\mathcal {E}}({\mathbf {H}}_j^F,({\mathbf {M}}_j,\mu _j))$
and
![]() $\mathrm{Irr}({\mathbf {N}}_{{\mathbf {H}}_j}({\mathbf {M}}_j)^F\mid \mu _j)$
, respectively, we obtain a bijection
$\mathrm{Irr}({\mathbf {N}}_{{\mathbf {H}}_j}({\mathbf {M}}_j)^F\mid \mu _j)$
, respectively, we obtain a bijection
by setting
for every
![]() $\vartheta _j\in {\mathcal {E}}({\mathbf {H}}_j^F,({\mathbf {M}}_j,\mu _j))$
. Finally, arguing as in the proof of [Reference Rossi57, Proposition 6.5], we deduce that the bijection
$\vartheta _j\in {\mathcal {E}}({\mathbf {H}}_j^F,({\mathbf {M}}_j,\mu _j))$
. Finally, arguing as in the proof of [Reference Rossi57, Proposition 6.5], we deduce that the bijection
![]() $\Omega ^{{\mathbf {K}}_0}_{({\mathbf {L}}_0,\lambda _0)}$
preserves the defect of characters, is
$\Omega ^{{\mathbf {K}}_0}_{({\mathbf {L}}_0,\lambda _0)}$
preserves the defect of characters, is
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {K}}_0^F)_{({\mathbf {L}}_0,\lambda _0)}$
-equivariant, and, using (4.1), it induces the
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {K}}_0^F)_{({\mathbf {L}}_0,\lambda _0)}$
-equivariant, and, using (4.1), it induces the
![]() ${\mathbf {K}}_0^F$
-block isomorphisms of character triples required in the statement.
${\mathbf {K}}_0^F$
-block isomorphisms of character triples required in the statement.
In our next result, we replace the automorphism group
![]() $Y:={\mathbf {K}}_0^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {K}}_0^F)$
with the group of automorphisms of
$Y:={\mathbf {K}}_0^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {K}}_0^F)$
with the group of automorphisms of
![]() ${\mathbf {G}}^F$
stabilising
${\mathbf {G}}^F$
stabilising
![]() ${\mathbf {K}}$
, that is,
${\mathbf {K}}$
, that is,
![]() $X:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{\mathbf {K}}$
. To do so, we apply the so-called Butterfly Theorem [Reference Späth64, Theorem 5.3] which basically states that, for any finite group G, the notion of G-block isomorphism of character triples only depends on the automorphisms induced on G.
$X:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{\mathbf {K}}$
. To do so, we apply the so-called Butterfly Theorem [Reference Späth64, Theorem 5.3] which basically states that, for any finite group G, the notion of G-block isomorphism of character triples only depends on the automorphisms induced on G.
Corollary 4.2. If
![]() $({\mathbf {L}}_0,\lambda _0)$
is a unipotent e-cuspidal pair of
$({\mathbf {L}}_0,\lambda _0)$
is a unipotent e-cuspidal pair of
![]() $({\mathbf {K}}_0,F)$
, then the map
$({\mathbf {K}}_0,F)$
, then the map
![]() $\Omega _{({\mathbf {L}}_0,\lambda _0)}^{{\mathbf {K}}_0}$
given by Proposition 4.1 is
$\Omega _{({\mathbf {L}}_0,\lambda _0)}^{{\mathbf {K}}_0}$
given by Proposition 4.1 is
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{{\mathbf {K}},({\mathbf {L}}_0,\lambda _0)}$
-equivariant and satisfies
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{{\mathbf {K}},({\mathbf {L}}_0,\lambda _0)}$
-equivariant and satisfies
for every
![]() $\vartheta \in {\mathcal {E}}({\mathbf {K}}_0^F,({\mathbf {L}}_0,\lambda _0))$
and where
$\vartheta \in {\mathcal {E}}({\mathbf {K}}_0^F,({\mathbf {L}}_0,\lambda _0))$
and where
![]() $X:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{\mathbf {K}}$
.
$X:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{\mathbf {K}}$
.
Proof. First, observe that
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{\mathbf {K}}$
is contained in
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{\mathbf {K}}$
is contained in
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {K}}_0^F)$
because
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {K}}_0^F)$
because
![]() ${\mathbf {K}}_0$
is an F-stable characteristic subgroup of
${\mathbf {K}}_0$
is an F-stable characteristic subgroup of
![]() ${\mathbf {K}}$
. In particular, we deduce that the map
${\mathbf {K}}$
. In particular, we deduce that the map
![]() $\Omega _{({\mathbf {L}}_0,\lambda _0)}^{{\mathbf {K}}_0}$
is equivariant with respect to the action of
$\Omega _{({\mathbf {L}}_0,\lambda _0)}^{{\mathbf {K}}_0}$
is equivariant with respect to the action of
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{{\mathbf {K}},({\mathbf {L}}_0,\lambda _0)}$
. Next, to obtain (4.2), we apply [Reference Späth64, Lemma 3.8 and Theorem 5.3] to the isomorphism of character triples given by Proposition 4.1 as explained in the proof of [Reference Rossi57, Corollary 6.8].
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{{\mathbf {K}},({\mathbf {L}}_0,\lambda _0)}$
. Next, to obtain (4.2), we apply [Reference Späth64, Lemma 3.8 and Theorem 5.3] to the isomorphism of character triples given by Proposition 4.1 as explained in the proof of [Reference Rossi57, Corollary 6.8].
The notion of isomorphism of character triples, introduced by Isaacs, plays a fundamental role in representation theory of finite groups and in the study of the local-global conjectures. One of the most important consequences of the existence of isomorphisms of character triples is the possibility to lift character bijections. For instance, the main result of [Reference Navarro and Späth48] shows how to apply this technique to construct bijections above characters of height zero in the context of the Alperin–McKay Conjecture [Reference Navarro and Späth48, Theorem B]. The main consequence of this result, which follows from an argument introduced by Murai [Reference Murai45], is a reduction theorem for the celebrated Brauer’s Height Zero Conjecture [Reference Navarro and Späth48, Theorem A]. This strategy ultimately lead to the solution of Brauer’s conjecture (see [Reference Malle, Navarro, Schaffer Fry and Tiep39] and [Reference Ruhstorfer60]). For other applications of isomorphisms of character triples, see [Reference Martínez and Rossi42, Proposition 1.1], [Reference Martínez, Rizo and Rossi43], [Reference Navarro, Späth and Vallejo49], [Reference Rossi52], [Reference Rossi55], [Reference Rossi59], [Reference Ruhstorfer61] and [Reference Turull68].
In our next result, we exploit this idea in order to lift the bijections given by Proposition 4.1 to the Levi subgroup
![]() ${\mathbf {K}}$
. Consequently, we extend the parametrisation of unipotent e-Harish-Chandra series given by Theorem C for the simple group
${\mathbf {K}}$
. Consequently, we extend the parametrisation of unipotent e-Harish-Chandra series given by Theorem C for the simple group
![]() ${\mathbf {G}}$
to a parametrisation of e-Harish-Chandra series associated to
${\mathbf {G}}$
to a parametrisation of e-Harish-Chandra series associated to
![]() $({\mathbf {K}},F)$
-pseudo-unipotent characters for every F-stable Levi subgroup
$({\mathbf {K}},F)$
-pseudo-unipotent characters for every F-stable Levi subgroup
![]() ${\mathbf {K}}$
of
${\mathbf {K}}$
of
![]() ${\mathbf {G}}$
. First, we need a preliminary lemma.
${\mathbf {G}}$
. First, we need a preliminary lemma.
Lemma 4.3. Let
![]() $({\mathbf {L}},\lambda )$
be a unipotent e-cuspidal pair of
$({\mathbf {L}},\lambda )$
be a unipotent e-cuspidal pair of
![]() $({\mathbf {K}},F)$
, and define the normaliser
$({\mathbf {K}},F)$
, and define the normaliser
![]() $X:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{\mathbf {K}}$
. If
$X:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{\mathbf {K}}$
. If
![]() ${\mathbf {K}}^F\leq H\leq {\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
and Q is an
${\mathbf {K}}^F\leq H\leq {\mathbf {N}}_{\mathbf {G}}({\mathbf {L}})^F$
and Q is an
![]() $\ell $
-radical subgroup of
$\ell $
-radical subgroup of
![]() ${\mathbf {N}}_H({\mathbf {L}})$
, then
${\mathbf {N}}_H({\mathbf {L}})$
, then
![]() ${\mathbf {C}}_X(Q)\leq {\mathbf {N}}_X({\mathbf {L}})$
.
${\mathbf {C}}_X(Q)\leq {\mathbf {N}}_X({\mathbf {L}})$
.
Proof. Let
![]() $E:={\mathbf {Z}}({\mathbf {L}})_\ell ^F$
, and observe that
$E:={\mathbf {Z}}({\mathbf {L}})_\ell ^F$
, and observe that
![]() ${\mathbf {L}}={\mathbf {C}}_{{\mathbf {G}}}^\circ (E)$
according to [Reference Cabanes and Enguehard15, Proposition 3.3 (ii)]. Now, since
${\mathbf {L}}={\mathbf {C}}_{{\mathbf {G}}}^\circ (E)$
according to [Reference Cabanes and Enguehard15, Proposition 3.3 (ii)]. Now, since
![]() ${\mathbf {O}}_\ell ({\mathbf {N}}_H({\mathbf {L}}))$
is the smallest
${\mathbf {O}}_\ell ({\mathbf {N}}_H({\mathbf {L}}))$
is the smallest
![]() $\ell $
-radical subgroup of
$\ell $
-radical subgroup of
![]() ${\mathbf {N}}_H({\mathbf {L}})$
[Reference Dade21, Proposition 1.4], we deduce that
${\mathbf {N}}_H({\mathbf {L}})$
[Reference Dade21, Proposition 1.4], we deduce that
![]() $E\leq {\mathbf {O}}_\ell ({\mathbf {N}}_H({\mathbf {L}}))\leq Q$
, and it follows that
$E\leq {\mathbf {O}}_\ell ({\mathbf {N}}_H({\mathbf {L}}))\leq Q$
, and it follows that
![]() ${\mathbf {C}}_X(Q)\leq {\mathbf {C}}_X(E)\leq {\mathbf {N}}_X({\mathbf {L}})$
as wanted.
${\mathbf {C}}_X(Q)\leq {\mathbf {C}}_X(E)\leq {\mathbf {N}}_X({\mathbf {L}})$
as wanted.
Theorem 4.4. Suppose that
![]() ${\mathbf {G}}$
is a simply connected group whose irreducible components are of type
${\mathbf {G}}$
is a simply connected group whose irreducible components are of type
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
, and assume that
$\mathbf {C}$
, and assume that
![]() $\ell $
is odd. For every F-stable Levi subgroup
$\ell $
is odd. For every F-stable Levi subgroup
![]() ${\mathbf {K}}\leq {\mathbf {G}}$
and every unipotent e-cuspidal pair
${\mathbf {K}}\leq {\mathbf {G}}$
and every unipotent e-cuspidal pair
![]() $({\mathbf {L}},\lambda )$
of
$({\mathbf {L}},\lambda )$
of
![]() $({\mathbf {K}},F)$
, there exists a defect preserving
$({\mathbf {K}},F)$
, there exists a defect preserving
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{{\mathbf {K}},({\mathbf {L}},\lambda )}$
-equivariant bijection
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{{\mathbf {K}},({\mathbf {L}},\lambda )}$
-equivariant bijection
such that
for every
![]() $\chi \in {\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\mathrm{ps}_{\mathbf {K}}(\lambda )))$
and where
$\chi \in {\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\mathrm{ps}_{\mathbf {K}}(\lambda )))$
and where
![]() $X:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{\mathbf {K}}$
.
$X:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{\mathbf {K}}$
.
Proof. Recall that
![]() ${\mathbf {K}}_0=[{\mathbf {K}},{\mathbf {K}}]$
, and define
${\mathbf {K}}_0=[{\mathbf {K}},{\mathbf {K}}]$
, and define
![]() ${\mathbf {L}}_0:={\mathbf {L}}\cap {\mathbf {K}}_0$
and
${\mathbf {L}}_0:={\mathbf {L}}\cap {\mathbf {K}}_0$
and
![]() $\lambda _0$
the restriction of
$\lambda _0$
the restriction of
![]() $\lambda $
to
$\lambda $
to
![]() ${\mathbf {L}}_0^F$
. Observe that
${\mathbf {L}}_0^F$
. Observe that
![]() $({\mathbf {L}}_0,\lambda _0)$
is a unipotent e-cuspidal pair of
$({\mathbf {L}}_0,\lambda _0)$
is a unipotent e-cuspidal pair of
![]() $({\mathbf {K}}_0,F)$
. Let
$({\mathbf {K}}_0,F)$
. Let
![]() $z\in {\mathbf {Z}}({\mathbf {K}}^*)^{F^*}$
, and consider a character
$z\in {\mathbf {Z}}({\mathbf {K}}^*)^{F^*}$
, and consider a character
![]() $\chi $
belonging to
$\chi $
belonging to
![]() ${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\lambda \hat {z}_{\mathbf {L}}))$
. Since the restriction of
${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\lambda \hat {z}_{\mathbf {L}}))$
. Since the restriction of
![]() $\lambda \hat {z}_{\mathbf {L}}$
to
$\lambda \hat {z}_{\mathbf {L}}$
to
![]() ${\mathbf {L}}_0^F$
coincides with
${\mathbf {L}}_0^F$
coincides with
![]() $\lambda _0$
, [Reference Geck and Malle30, Corollary 3.3.25] implies that
$\lambda _0$
, [Reference Geck and Malle30, Corollary 3.3.25] implies that
![]() $\chi $
lies above some character in
$\chi $
lies above some character in
![]() ${\mathcal {E}}({\mathbf {K}}^F_0({\mathbf {L}}_0,\lambda _0))$
. On the other hand, assume that
${\mathcal {E}}({\mathbf {K}}^F_0({\mathbf {L}}_0,\lambda _0))$
. On the other hand, assume that
![]() $\chi \in \mathrm{Irr}({\mathbf {K}}^F)$
lies above
$\chi \in \mathrm{Irr}({\mathbf {K}}^F)$
lies above
![]() $\chi _0\in {\mathcal {E}}({\mathbf {K}}^F_0,({\mathbf {L}}_0,\lambda _0))$
. By [Reference Cabanes and Enguehard15, Proposition 3.1], the character
$\chi _0\in {\mathcal {E}}({\mathbf {K}}^F_0,({\mathbf {L}}_0,\lambda _0))$
. By [Reference Cabanes and Enguehard15, Proposition 3.1], the character
![]() $\chi _0$
has an extension
$\chi _0$
has an extension
![]() $\chi '\in {\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\lambda ))$
and hence, using Gallagher’s theorem [Reference Isaacs32, Corollary 6.17] and [Reference Cabanes and Enguehard17, (8.19)], we can find
$\chi '\in {\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\lambda ))$
and hence, using Gallagher’s theorem [Reference Isaacs32, Corollary 6.17] and [Reference Cabanes and Enguehard17, (8.19)], we can find
![]() $z\in {\mathbf {Z}}({\mathbf {K}}^*)^{F^*}$
such that
$z\in {\mathbf {Z}}({\mathbf {K}}^*)^{F^*}$
such that
![]() $\chi =\chi '\hat {z}_{\mathbf {K}}$
. Since
$\chi =\chi '\hat {z}_{\mathbf {K}}$
. Since
![]() $\chi '\hat {z}_{\mathbf {K}}$
is a character of
$\chi '\hat {z}_{\mathbf {K}}$
is a character of
![]() ${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\lambda \hat {z}_{\mathbf {L}}))$
according to [Reference Cabanes and Enguehard17, (8.20)], we conclude that
${\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\lambda \hat {z}_{\mathbf {L}}))$
according to [Reference Cabanes and Enguehard17, (8.20)], we conclude that
Next, suppose that
![]() $\psi \in \mathrm{Irr}({\mathbf {N}}_{\mathbf {K}}({\mathbf {L}})^F\mid \lambda \hat {z}_{\mathbf {L}})$
. In this case,
$\psi \in \mathrm{Irr}({\mathbf {N}}_{\mathbf {K}}({\mathbf {L}})^F\mid \lambda \hat {z}_{\mathbf {L}})$
. In this case,
![]() $\psi $
lies above the restriction of
$\psi $
lies above the restriction of
![]() $\lambda \hat {z}_{\mathbf {L}}$
to
$\lambda \hat {z}_{\mathbf {L}}$
to
![]() ${\mathbf {L}}_0^F$
which coincides with
${\mathbf {L}}_0^F$
which coincides with
![]() $\lambda _0$
. In particular, there exists some
$\lambda _0$
. In particular, there exists some
![]() $\varphi \in \mathrm{Irr}({\mathbf {N}}_{{\mathbf {K}}_0}({\mathbf {L}}_0)^F\mid \lambda _0)$
such that
$\varphi \in \mathrm{Irr}({\mathbf {N}}_{{\mathbf {K}}_0}({\mathbf {L}}_0)^F\mid \lambda _0)$
such that
![]() $\psi $
lies above
$\psi $
lies above
![]() $\varphi $
. On the other, if
$\varphi $
. On the other, if
![]() $\chi $
lies above such a character
$\chi $
lies above such a character
![]() $\varphi \in \mathrm{Irr}({\mathbf {N}}_{{\mathbf {K}}_0}({\mathbf {L}}_0)^F\mid \lambda _0)$
, then it lies above
$\varphi \in \mathrm{Irr}({\mathbf {N}}_{{\mathbf {K}}_0}({\mathbf {L}}_0)^F\mid \lambda _0)$
, then it lies above
![]() $\lambda _0$
, and therefore, we can find
$\lambda _0$
, and therefore, we can find
![]() $z\in {\mathbf {Z}}({\mathbf {K}}^*)^{F^*}$
such that
$z\in {\mathbf {Z}}({\mathbf {K}}^*)^{F^*}$
such that
![]() $\psi \in \mathrm{Irr}({\mathbf {N}}_{\mathbf {K}}({\mathbf {L}})^F\mid \lambda \hat {z}_{\mathbf {L}})$
. This shows that
$\psi \in \mathrm{Irr}({\mathbf {N}}_{\mathbf {K}}({\mathbf {L}})^F\mid \lambda \hat {z}_{\mathbf {L}})$
. This shows that
Finally, consider the map
![]() $\Omega _{({\mathbf {L}}_0,\lambda _0)}^{{\mathbf {K}}_0}$
given by Proposition 4.1. Then, the result follows from (4.3) and (4.4) by applying [Reference Rossi57, Proposition 6.1 and Remark 6.2] as explained in the proof of [Reference Rossi57, Corollary 6.10] and using the
$\Omega _{({\mathbf {L}}_0,\lambda _0)}^{{\mathbf {K}}_0}$
given by Proposition 4.1. Then, the result follows from (4.3) and (4.4) by applying [Reference Rossi57, Proposition 6.1 and Remark 6.2] as explained in the proof of [Reference Rossi57, Corollary 6.10] and using the
![]() ${\mathbf {K}}^F$
-block isomorphisms of character triples obtained in Corollary 4.2. Here, we consider
${\mathbf {K}}^F$
-block isomorphisms of character triples obtained in Corollary 4.2. Here, we consider
![]() $A:={\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
,
$A:={\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
,
![]() $A_0:={\mathbf {N}}_A({\mathbf {L}})$
,
$A_0:={\mathbf {N}}_A({\mathbf {L}})$
,
![]() $K:={\mathbf {K}}_0^F$
,
$K:={\mathbf {K}}_0^F$
,
![]() $K_0={\mathbf {N}}_{{\mathbf {K}}_0}({\mathbf {L}})^F={\mathbf {N}}_{{\mathbf {K}}_0}({\mathbf {L}}_0)^F$
,
$K_0={\mathbf {N}}_{{\mathbf {K}}_0}({\mathbf {L}})^F={\mathbf {N}}_{{\mathbf {K}}_0}({\mathbf {L}}_0)^F$
,
![]() $G:={\mathbf {G}}^F$
,
$G:={\mathbf {G}}^F$
,
![]() $X:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{\mathbf {K}}$
,
$X:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{\mathbf {K}}$
,
![]() $\mathcal {S}:={\mathcal {E}}({\mathbf {K}}_0^F,({\mathbf {L}}_0,\lambda _0))$
,
$\mathcal {S}:={\mathcal {E}}({\mathbf {K}}_0^F,({\mathbf {L}}_0,\lambda _0))$
,
![]() $\mathcal {S}_0:=\mathrm{Irr}({\mathbf {N}}_{{\mathbf {K}}_0}({\mathbf {L}}_0)^F\mid \lambda _0)$
,
$\mathcal {S}_0:=\mathrm{Irr}({\mathbf {N}}_{{\mathbf {K}}_0}({\mathbf {L}}_0)^F\mid \lambda _0)$
,
![]() $V:=({\mathbf {G}}^F\rtimes \mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{{\mathbf {K}},\mathcal {S}}$
and
$V:=({\mathbf {G}}^F\rtimes \mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{{\mathbf {K}},\mathcal {S}}$
and
![]() $U:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{{\mathbf {K}},{\mathbf {L}},\lambda _0}$
. Observe that the condition on defect groups required by [Reference Rossi57, Proposition 6.1] is satisfied by Lemma 4.3.
$U:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{{\mathbf {K}},{\mathbf {L}},\lambda _0}$
. Observe that the condition on defect groups required by [Reference Rossi57, Proposition 6.1] is satisfied by Lemma 4.3.
4.2 Above e-Harish-Chandra series
We now further extend Theorem C by lifting the character bijections from Theorem 4.4 with respect to normal inclusions.
Proposition 4.5. Consider the setup of Theorem 4.4, and let
![]() ${\mathbf {K}}^F\leq H\leq {\mathbf {N}}_{\mathbf {G}}({\mathbf {K}})^F$
. Then, there exists a defect preserving
${\mathbf {K}}^F\leq H\leq {\mathbf {N}}_{\mathbf {G}}({\mathbf {K}})^F$
. Then, there exists a defect preserving
![]() $\mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{H,{\mathbf {K}},({\mathbf {L}},\lambda )}$
-equivariant bijection
$\mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{H,{\mathbf {K}},({\mathbf {L}},\lambda )}$
-equivariant bijection
such that
for every
![]() $\chi \in \mathrm{Irr}(H\mid {\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\mathrm{ps}_{\mathbf {K}}(\lambda ))))$
and where
$\chi \in \mathrm{Irr}(H\mid {\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\mathrm{ps}_{\mathbf {K}}(\lambda ))))$
and where
![]() $X:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{\mathbf {K}}$
.
$X:=({\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F))_{\mathbf {K}}$
.
Proof. We apply [Reference Rossi57, Proposition 6.1] to the bijection given by Theorem 4.4. We consider the choices
![]() $A:={\mathbf {G}}^F\rtimes \mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
,
$A:={\mathbf {G}}^F\rtimes \mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
,
![]() $G:={\mathbf {G}}^F$
,
$G:={\mathbf {G}}^F$
,
![]() $K:={\mathbf {K}}^F$
,
$K:={\mathbf {K}}^F$
,
![]() $A_0:={\mathbf {N}}_A({\mathbf {L}})$
,
$A_0:={\mathbf {N}}_A({\mathbf {L}})$
,
![]() $X:={\mathbf {N}}_A({\mathbf {K}})$
,
$X:={\mathbf {N}}_A({\mathbf {K}})$
,
![]() $\mathcal {S}:={\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\mathrm{ ps}_{\mathbf {K}}(\lambda )))$
,
$\mathcal {S}:={\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\mathrm{ ps}_{\mathbf {K}}(\lambda )))$
,
![]() $\mathcal {S}_0:=\mathrm{Irr}({\mathbf {N}}_{\mathbf {K}}({\mathbf {L}})^F\mid \mathrm{ps}_{\mathbf {K}}(\lambda ))$
,
$\mathcal {S}_0:=\mathrm{Irr}({\mathbf {N}}_{\mathbf {K}}({\mathbf {L}})^F\mid \mathrm{ps}_{\mathbf {K}}(\lambda ))$
,
![]() $U:=X_{0,\lambda }$
,
$U:=X_{0,\lambda }$
,
![]() $V:=X_{\mathcal {S}}$
and
$V:=X_{\mathcal {S}}$
and
![]() $J:=H$
. Notice that the conditions (i)-(iii) of [Reference Rossi57, Proposition 6.1] are satisfied by [Reference Broué, Malle and Michel9, Theorem 3.2 (1)]. Furthermore, the requirements about defect groups are satisfied by Lemma 4.3. Therefore, as explained in [Reference Rossi57, Proposition 6.11], we obtain the claimed result by applying [Reference Rossi57, Proposition 6.1 and Remark 6.2].
$J:=H$
. Notice that the conditions (i)-(iii) of [Reference Rossi57, Proposition 6.1] are satisfied by [Reference Broué, Malle and Michel9, Theorem 3.2 (1)]. Furthermore, the requirements about defect groups are satisfied by Lemma 4.3. Therefore, as explained in [Reference Rossi57, Proposition 6.11], we obtain the claimed result by applying [Reference Rossi57, Proposition 6.1 and Remark 6.2].
Before proceeding further, we point out an interesting analogy with another important character correspondence. The Glauberman correspondence plays a fundamental role in the study of the local-global counting conjectures and lies at the heart of most reduction theorems. In its most basic form, it states that for every finite
![]() $\ell $
-group L acting on a finite
$\ell $
-group L acting on a finite
![]() $\ell '$
-group K, there exists a bijection
$\ell '$
-group K, there exists a bijection
between the set of L-invariant characters of K and the characters of the normaliser
![]() ${\mathbf {N}}_K(L)$
(see, for instance, [Reference Navarro47, Section 2.3]). A deep result due to Dade [Reference Dade20], and recently reproved by Turull [Reference Turull67], shows that, if K and L are subgroups of a finite group G and
${\mathbf {N}}_K(L)$
(see, for instance, [Reference Navarro47, Section 2.3]). A deep result due to Dade [Reference Dade20], and recently reproved by Turull [Reference Turull67], shows that, if K and L are subgroups of a finite group G and
![]() $KL\leq H\leq K{\mathbf {N}}_G(L)$
, then the Glauberman correspondence
$KL\leq H\leq K{\mathbf {N}}_G(L)$
, then the Glauberman correspondence
![]() $f_L$
can be lifted to a character correspondence for H, that is, there exists a bijection
$f_L$
can be lifted to a character correspondence for H, that is, there exists a bijection
for every
![]() $\chi \in \mathrm{Irr}_L(K)$
. On the other hand, the parametrisation of unipotent e-Harish-Chandra series obtained by Broué, Malle and Michel [Reference Broué, Malle and Michel9, Theorem 3.2] lies at the centre of the proofs of the local-global counting conjectures for finite reductive groups. It is interesting to note that our methods yield a character bijection above e-Harish-Chandra series which is analogous to (4.5) in the context of the Glauberman correspondence. This is an immediate consequence of Proposition 4.5.
$\chi \in \mathrm{Irr}_L(K)$
. On the other hand, the parametrisation of unipotent e-Harish-Chandra series obtained by Broué, Malle and Michel [Reference Broué, Malle and Michel9, Theorem 3.2] lies at the centre of the proofs of the local-global counting conjectures for finite reductive groups. It is interesting to note that our methods yield a character bijection above e-Harish-Chandra series which is analogous to (4.5) in the context of the Glauberman correspondence. This is an immediate consequence of Proposition 4.5.
Corollary 4.6. Consider the setup of Theorem 4.4, and let
![]() ${\mathbf {K}}^F\leq H\leq {\mathbf {N}}_{\mathbf {G}}({\mathbf {K}})^F$
. Then, there exists a bijection
${\mathbf {K}}^F\leq H\leq {\mathbf {N}}_{\mathbf {G}}({\mathbf {K}})^F$
. Then, there exists a bijection
for every
![]() $\chi \in {\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\mathrm{ps}_{\mathbf {K}}(\lambda )))$
.
$\chi \in {\mathcal {E}}({\mathbf {K}}^F,({\mathbf {L}},\mathrm{ps}_{\mathbf {K}}(\lambda )))$
.
Proof. This follows immediately from the proof of Proposition 4.5 by following the construction made in [Reference Rossi57, Proposition 6.1].
5 Towards Theorem A and Theorem B
Finally, we apply the results obtained in the previous sections to prove Theorem A which is our main result. Then, we obtain Theorem B as a corollary by applying the e-Harish-Chandra theory for unipotent characters developed by Broué, Malle and Michel [Reference Broué, Malle and Michel9] and by Cabanes and Enguehard [Reference Cabanes and Enguehard15]. Before doing so, we introduce the relevant notation and prove some preliminary results.
5.1 Preliminaries on e-chains
Our first aim is to define e-local structures for finite reductive groups that play a role analogous to that of
![]() $\ell $
-chains in the context of Dade’s Conjecture and the Character Triple Conjecture. The connection between the set of e-chains and that of
$\ell $
-chains in the context of Dade’s Conjecture and the Character Triple Conjecture. The connection between the set of e-chains and that of
![]() $\ell $
-chains has already been studied in [Reference Rossi57, Section 7.2]. These results provide a way to obtain Dade’s Conjecture and the Character Triple Conjecture as a consequence of [Reference Rossi57, Conjecture C and Conjecture D]. The possibility to use different types of chains is crucial in the study of Dade’s Conjecture and has been introduced by Knörr and Robinson [Reference Knörr and Robinson35]. Their results were insipred by previous studies conducted by many authors including Brown [Reference Brown14] and Quillen [Reference Quillen50] who analysed the homotopy theory of associated simplicial complexes. As in the previous section, we assume that
$\ell $
-chains has already been studied in [Reference Rossi57, Section 7.2]. These results provide a way to obtain Dade’s Conjecture and the Character Triple Conjecture as a consequence of [Reference Rossi57, Conjecture C and Conjecture D]. The possibility to use different types of chains is crucial in the study of Dade’s Conjecture and has been introduced by Knörr and Robinson [Reference Knörr and Robinson35]. Their results were insipred by previous studies conducted by many authors including Brown [Reference Brown14] and Quillen [Reference Quillen50] who analysed the homotopy theory of associated simplicial complexes. As in the previous section, we assume that
![]() ${\mathbf {G}}$
is a simply connected reductive group whose irreducible components are of type
${\mathbf {G}}$
is a simply connected reductive group whose irreducible components are of type
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
and that
$\mathbf {C}$
and that
![]() $\ell $
is an odd prime.
$\ell $
is an odd prime.
Definition 5.1. We denote by
![]() ${\mathcal {L}}_e({\mathbf {G}},F)$
the set of e
-chains of the finite reductive group
${\mathcal {L}}_e({\mathbf {G}},F)$
the set of e
-chains of the finite reductive group
![]() $({\mathbf {G}},F)$
, that is, chains of the form
$({\mathbf {G}},F)$
, that is, chains of the form
where n is a nonnegative integer and each
![]() ${\mathbf {L}}_i$
is an e-split Levi subgroup of
${\mathbf {L}}_i$
is an e-split Levi subgroup of
![]() $({\mathbf {G}},F)$
. We denote by
$({\mathbf {G}},F)$
. We denote by
![]() $|\sigma |:=n$
the length of the e-chain
$|\sigma |:=n$
the length of the e-chain
![]() $\sigma $
and by
$\sigma $
and by
![]() ${\mathbf {L}}(\sigma )$
its last term. Furthermore, we define
${\mathbf {L}}(\sigma )$
its last term. Furthermore, we define
![]() ${\mathcal {L}}_e({\mathbf {G}},F)_{>0}$
to be the set of e-chains having length strictly larger than
${\mathcal {L}}_e({\mathbf {G}},F)_{>0}$
to be the set of e-chains having length strictly larger than
![]() $0$
.
$0$
.
Observe that the notion of length defined above induces a partition of the set
![]() ${\mathcal {L}}_e({\mathbf {G}},F)$
into e-chains of even and odd length. More precisely, we denote by
${\mathcal {L}}_e({\mathbf {G}},F)$
into e-chains of even and odd length. More precisely, we denote by
![]() ${\mathcal {L}}_e({\mathbf {G}},F)_\pm $
the subset of those e-chains
${\mathcal {L}}_e({\mathbf {G}},F)_\pm $
the subset of those e-chains
![]() $\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
that satisfy
$\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
that satisfy
![]() $(-1)^{|\sigma |}=\pm 1$
.
$(-1)^{|\sigma |}=\pm 1$
.
In what follows, given an e-chain
![]() $\sigma $
and an e-split Levi subgroup
$\sigma $
and an e-split Levi subgroup
![]() ${\mathbf {M}}$
of
${\mathbf {M}}$
of
![]() $({\mathbf {L}}(\sigma ),F)$
, we denote by
$({\mathbf {L}}(\sigma ),F)$
, we denote by
![]() $\sigma +{\mathbf {M}}$
the e-chain obtained by adding
$\sigma +{\mathbf {M}}$
the e-chain obtained by adding
![]() ${\mathbf {M}}$
at the end of
${\mathbf {M}}$
at the end of
![]() $\sigma $
. We also allow the possibility that
$\sigma $
. We also allow the possibility that
![]() ${\mathbf {M}}={\mathbf {L}}(\sigma )$
, in which case we define
${\mathbf {M}}={\mathbf {L}}(\sigma )$
, in which case we define
![]() $\sigma +{\mathbf {L}}(\sigma ):=\sigma $
. Vice versa, we denote by
$\sigma +{\mathbf {L}}(\sigma ):=\sigma $
. Vice versa, we denote by
![]() $\sigma -{\mathbf {L}}(\sigma )$
the e-chain obtained by removing the last term
$\sigma -{\mathbf {L}}(\sigma )$
the e-chain obtained by removing the last term
![]() ${\mathbf {L}}(\sigma )$
from
${\mathbf {L}}(\sigma )$
from
![]() $\sigma $
. Here, we use the convention that
$\sigma $
. Here, we use the convention that
![]() $\sigma _0-{\mathbf {L}}(\sigma _0)=\sigma _0=\sigma _0+{\mathbf {G}}$
where
$\sigma _0-{\mathbf {L}}(\sigma _0)=\sigma _0=\sigma _0+{\mathbf {G}}$
where
![]() $\sigma _0=\{{\mathbf {G}}\}$
is the trivial e-chain.
$\sigma _0=\{{\mathbf {G}}\}$
is the trivial e-chain.
Next, consider the action of
![]() ${\mathbf {G}}^F$
on the set of e-chains
${\mathbf {G}}^F$
on the set of e-chains
![]() ${\mathcal {L}}_e({\mathbf {G}},F)$
induced by conjugation: for every
${\mathcal {L}}_e({\mathbf {G}},F)$
induced by conjugation: for every
![]() $g\in {\mathbf {G}}^F$
and
$g\in {\mathbf {G}}^F$
and
![]() $\sigma =\{{\mathbf {L}}_i\}_i$
, we define
$\sigma =\{{\mathbf {L}}_i\}_i$
, we define
It follows from this definition that the stabiliser
![]() ${\mathbf {G}}^F_\sigma $
coincides with the intersection of the normalisers
${\mathbf {G}}^F_\sigma $
coincides with the intersection of the normalisers
![]() ${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}}_i)^F$
for
${\mathbf {N}}_{\mathbf {G}}({\mathbf {L}}_i)^F$
for
![]() $i=1,\dots , n$
. Similarly, we can define an action of
$i=1,\dots , n$
. Similarly, we can define an action of
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
on
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
on
![]() ${\mathcal {L}}_e({\mathbf {G}},F)$
and give an analogous description of the chain stabilisers
${\mathcal {L}}_e({\mathbf {G}},F)$
and give an analogous description of the chain stabilisers
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_\sigma $
. In particular, notice that the last term of the chain satisfies
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_\sigma $
. In particular, notice that the last term of the chain satisfies
![]() ${\mathbf {L}}(\sigma )^F\unlhd {\mathbf {G}}_\sigma ^F$
. Using this observation, we can use the results of Section 4.2 to control the characters of
${\mathbf {L}}(\sigma )^F\unlhd {\mathbf {G}}_\sigma ^F$
. Using this observation, we can use the results of Section 4.2 to control the characters of
![]() ${\mathbf {G}}^F_\sigma $
that lie above pseudo-unipotent series of
${\mathbf {G}}^F_\sigma $
that lie above pseudo-unipotent series of
![]() ${\mathbf {L}}(\sigma )$
.
${\mathbf {L}}(\sigma )$
.
Definition 5.2. For every e-chain
![]() $\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
, we denote by
$\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
, we denote by
![]() ${\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
the set of unipotent e-cuspidal pairs
${\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
the set of unipotent e-cuspidal pairs
![]() $({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{u}}}({\mathbf {L}}(\sigma ),F)$
that satisfy
$({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{u}}}({\mathbf {L}}(\sigma ),F)$
that satisfy
![]() ${\mathbf {M}}<{\mathbf {G}}$
. Furthermore, for any such pair
${\mathbf {M}}<{\mathbf {G}}$
. Furthermore, for any such pair
![]() $({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
, we define the character set
$({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
, we define the character set
 $$\begin{align*}\mathrm{Irr}_{\mathrm{ps}}({\mathbf{G}}^F_\sigma,({\mathbf{M}},\mu)):=\begin{cases} \mathrm{Irr}\ \left({\mathbf{G}}_\sigma^F\enspace\middle|\enspace{\mathcal{E}}\left({\mathbf{L}}(\sigma)^F,\left({\mathbf{M}},\mathrm{ps}_{{\mathbf{L}}(\sigma)}(\mu)\right)\right)\right)& {\mathbf{L}}(\sigma)>{\mathbf{M}} \\ \mathrm{Irr}\ \left({\mathbf{G}}_\sigma^F\enspace\middle|\enspace{\mathcal{E}}\left({\mathbf{L}}(\sigma)^F,\left({\mathbf{M}},\mathrm{ps}_{{\mathbf{L}}(\sigma-{\mathbf{L}}(\sigma))}(\mu)\right)\right)\right)& {\mathbf{L}}(\sigma)={\mathbf{M}}. \end{cases}\end{align*}$$
$$\begin{align*}\mathrm{Irr}_{\mathrm{ps}}({\mathbf{G}}^F_\sigma,({\mathbf{M}},\mu)):=\begin{cases} \mathrm{Irr}\ \left({\mathbf{G}}_\sigma^F\enspace\middle|\enspace{\mathcal{E}}\left({\mathbf{L}}(\sigma)^F,\left({\mathbf{M}},\mathrm{ps}_{{\mathbf{L}}(\sigma)}(\mu)\right)\right)\right)& {\mathbf{L}}(\sigma)>{\mathbf{M}} \\ \mathrm{Irr}\ \left({\mathbf{G}}_\sigma^F\enspace\middle|\enspace{\mathcal{E}}\left({\mathbf{L}}(\sigma)^F,\left({\mathbf{M}},\mathrm{ps}_{{\mathbf{L}}(\sigma-{\mathbf{L}}(\sigma))}(\mu)\right)\right)\right)& {\mathbf{L}}(\sigma)={\mathbf{M}}. \end{cases}\end{align*}$$
The need to distinguish the cases in the above definition will become apparent in the proofs of Proposition 5.7 and Theorem 5.10 below. Observe that in the definition above, we are excluding the degenerate case where
![]() ${\mathbf {G}}={\mathbf {L}}(\sigma )={\mathbf {M}}$
. To understand the reason why we are excluding this case, we can consider an analogy with Dade’s Conjecture. For every finite group G, recall that
${\mathbf {G}}={\mathbf {L}}(\sigma )={\mathbf {M}}$
. To understand the reason why we are excluding this case, we can consider an analogy with Dade’s Conjecture. For every finite group G, recall that
![]() ${\mathbf {k}}(G)$
denotes the number of its irreducible characters and that, for any nonnegative integer d, the symbol
${\mathbf {k}}(G)$
denotes the number of its irreducible characters and that, for any nonnegative integer d, the symbol
![]() ${\mathbf {k}}^d(G)$
denotes the number of those irreducible characters of
${\mathbf {k}}^d(G)$
denotes the number of those irreducible characters of
![]() $\ell $
-defect d. The local-global counting conjectures provide a way to determine the global invariants
$\ell $
-defect d. The local-global counting conjectures provide a way to determine the global invariants
![]() ${\mathbf {k}}^d(G)$
in terms of
${\mathbf {k}}^d(G)$
in terms of
![]() $\ell $
-local structures. This idea was made precise by Isaacs and Navarro [Reference Isaacs and Navarro33]. According to their definitions, the block-free version of Dade’s Conjecture can be stated by saying that the functions
$\ell $
-local structures. This idea was made precise by Isaacs and Navarro [Reference Isaacs and Navarro33]. According to their definitions, the block-free version of Dade’s Conjecture can be stated by saying that the functions
![]() ${\mathbf {k}}^d$
are chain local for every
${\mathbf {k}}^d$
are chain local for every
![]() $d>0$
. Consequently, and because a sum of chain local functions is chain local, we deduce that the difference
$d>0$
. Consequently, and because a sum of chain local functions is chain local, we deduce that the difference
![]() ${\mathbf {k}}-{\mathbf {k}}^0=\sum _{d>0}{\mathbf {k}}^d$
is (conjecturally) a chain local function. On the other hand, using the fact that groups admitting a character of
${\mathbf {k}}-{\mathbf {k}}^0=\sum _{d>0}{\mathbf {k}}^d$
is (conjecturally) a chain local function. On the other hand, using the fact that groups admitting a character of
![]() $\ell $
-defect zero have trivial
$\ell $
-defect zero have trivial
![]() $\ell $
-core, it is easy to see that
$\ell $
-core, it is easy to see that
![]() ${\mathbf {k}}^0$
is not chain local. The exclusion of the case
${\mathbf {k}}^0$
is not chain local. The exclusion of the case
![]() ${\mathbf {G}}={\mathbf {L}}(\sigma )={\mathbf {M}}$
can be explained by interpreting these observations in the context of unipotent characters. Recall that
${\mathbf {G}}={\mathbf {L}}(\sigma )={\mathbf {M}}$
can be explained by interpreting these observations in the context of unipotent characters. Recall that
![]() ${\mathbf {k}}_{\mathrm{u}}({\mathbf {G}}^F)$
and
${\mathbf {k}}_{\mathrm{u}}({\mathbf {G}}^F)$
and
![]() ${\mathbf {k}}_{\mathrm{ c,u}}({\mathbf {G}}^F)$
denote the number of unipotent characters of
${\mathbf {k}}_{\mathrm{ c,u}}({\mathbf {G}}^F)$
denote the number of unipotent characters of
![]() ${\mathbf {G}}^F$
and unipotent e-cuspidal characters of
${\mathbf {G}}^F$
and unipotent e-cuspidal characters of
![]() ${\mathbf {G}}^F$
respectively. If
${\mathbf {G}}^F$
respectively. If
![]() $\ell $
does not divide the order of
$\ell $
does not divide the order of
![]() ${\mathbf {Z}}({\mathbf {G}}^F)$
, then [Reference Cabanes and Enguehard15] implies that the unipotent e-cuspidal characters of
${\mathbf {Z}}({\mathbf {G}}^F)$
, then [Reference Cabanes and Enguehard15] implies that the unipotent e-cuspidal characters of
![]() ${\mathbf {G}}^F$
have
${\mathbf {G}}^F$
have
![]() $\ell $
-defect zero. Therefore, as in the case of Dade’s Conjecture, the global invariant we want to determine e-locally is the difference
$\ell $
-defect zero. Therefore, as in the case of Dade’s Conjecture, the global invariant we want to determine e-locally is the difference
![]() ${\mathbf {k}}_{\mathrm{u}}({\mathbf {G}}^F)-{\mathbf {k}}_{\mathrm{c,u}}({\mathbf {G}}^F)$
. Finally, notice that
${\mathbf {k}}_{\mathrm{u}}({\mathbf {G}}^F)-{\mathbf {k}}_{\mathrm{c,u}}({\mathbf {G}}^F)$
. Finally, notice that
![]() ${\mathbf {k}}_{\mathrm{c,u}}({\mathbf {G}}^F)$
is exactly the number of unipotent e-cuspidal pairs
${\mathbf {k}}_{\mathrm{c,u}}({\mathbf {G}}^F)$
is exactly the number of unipotent e-cuspidal pairs
![]() $({\mathbf {M}},\mu )$
of
$({\mathbf {M}},\mu )$
of
![]() ${\mathbf {L}}(\sigma )$
satisfying
${\mathbf {L}}(\sigma )$
satisfying
![]() ${\mathbf {G}}={\mathbf {L}}(\sigma )={\mathbf {M}}$
.
${\mathbf {G}}={\mathbf {L}}(\sigma )={\mathbf {M}}$
.
In the following lemma, we show that if the set
![]() $\mathrm{Irr}_{\mathrm{ps}}({\mathbf {G}}_\sigma ^F,({\mathbf {M}},\mu ))$
is nonempty then
$\mathrm{Irr}_{\mathrm{ps}}({\mathbf {G}}_\sigma ^F,({\mathbf {M}},\mu ))$
is nonempty then
![]() $({\mathbf {M}},\mu )$
is uniquely defined up to
$({\mathbf {M}},\mu )$
is uniquely defined up to
![]() ${\mathbf {G}}_\sigma ^F$
-conjugation.
${\mathbf {G}}_\sigma ^F$
-conjugation.
Lemma 5.3. Let
![]() $\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
and consider two unipotent e-cuspidal pairs
$\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
and consider two unipotent e-cuspidal pairs
![]() $({\mathbf {M}},\mu )$
and
$({\mathbf {M}},\mu )$
and
![]() $({\mathbf {K}},\kappa )$
in
$({\mathbf {K}},\kappa )$
in
![]() ${\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
. If the sets
${\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
. If the sets
![]() $\mathrm{Irr}_{\mathrm{ps}}({\mathbf {G}}_\sigma ^F,({\mathbf {M}},\mu ))$
and
$\mathrm{Irr}_{\mathrm{ps}}({\mathbf {G}}_\sigma ^F,({\mathbf {M}},\mu ))$
and
![]() $\mathrm{Irr}_{\mathrm{ps}}({\mathbf {G}}_\sigma ^F,({\mathbf {K}},\kappa ))$
have nontrivial intersection, then
$\mathrm{Irr}_{\mathrm{ps}}({\mathbf {G}}_\sigma ^F,({\mathbf {K}},\kappa ))$
have nontrivial intersection, then
![]() $({\mathbf {M}},\mu )$
and
$({\mathbf {M}},\mu )$
and
![]() $({\mathbf {K}},\kappa )$
are
$({\mathbf {K}},\kappa )$
are
![]() ${\mathbf {G}}^F_\sigma $
-conjugate.
${\mathbf {G}}^F_\sigma $
-conjugate.
Proof. Suppose that
![]() $\vartheta $
is a character belonging to both character sets
$\vartheta $
is a character belonging to both character sets
![]() $\mathrm{Irr}_{\mathrm{ps}}({\mathbf {G}}_\sigma ^F,({\mathbf {M}},\mu ))$
and
$\mathrm{Irr}_{\mathrm{ps}}({\mathbf {G}}_\sigma ^F,({\mathbf {M}},\mu ))$
and
![]() $\mathrm{Irr}_{\mathrm{ps}}({\mathbf {G}}_\sigma ^F,({\mathbf {K}},\kappa ))$
. If we set
$\mathrm{Irr}_{\mathrm{ps}}({\mathbf {G}}_\sigma ^F,({\mathbf {K}},\kappa ))$
. If we set
![]() ${\mathbf {L}}:={\mathbf {L}}(\sigma )$
, then we can find elements
${\mathbf {L}}:={\mathbf {L}}(\sigma )$
, then we can find elements
![]() $s,t\in {\mathbf {Z}}({\mathbf {L}}^*)^{F^*}$
and irreducible characters
$s,t\in {\mathbf {Z}}({\mathbf {L}}^*)^{F^*}$
and irreducible characters
![]() $\varphi \in {\mathcal {E}}({\mathbf {L}}^F,({\mathbf {M}},\mu ))$
and
$\varphi \in {\mathcal {E}}({\mathbf {L}}^F,({\mathbf {M}},\mu ))$
and
![]() $\psi \in {\mathcal {E}}({\mathbf {L}}^F,({\mathbf {K}},\kappa ))$
such that
$\psi \in {\mathcal {E}}({\mathbf {L}}^F,({\mathbf {K}},\kappa ))$
such that
![]() $\vartheta $
lies above
$\vartheta $
lies above
![]() $\varphi \hat {s}_{\mathbf {L}}$
and
$\varphi \hat {s}_{\mathbf {L}}$
and
![]() $\psi \hat {t}_{\mathbf {L}}$
. By Clifford’s theorem, we deduce that
$\psi \hat {t}_{\mathbf {L}}$
. By Clifford’s theorem, we deduce that
![]() $\varphi \hat {s}_{\mathbf {L}}=(\psi \hat {t}_{\mathbf {L}})^g$
for some
$\varphi \hat {s}_{\mathbf {L}}=(\psi \hat {t}_{\mathbf {L}})^g$
for some
![]() $g\in {\mathbf {G}}_\sigma ^F$
. Furthermore, since
$g\in {\mathbf {G}}_\sigma ^F$
. Furthermore, since
![]() $\hat {s}$
is a linear character, we obtain that
$\hat {s}$
is a linear character, we obtain that
![]() $\varphi =\psi ^g(\hat {t}_{\mathbf {L}})^g(\hat {s}_{\mathbf {L}})^{-1}$
. Since both
$\varphi =\psi ^g(\hat {t}_{\mathbf {L}})^g(\hat {s}_{\mathbf {L}})^{-1}$
. Since both
![]() $\varphi $
and
$\varphi $
and
![]() $\psi ^g$
are unipotent characters of
$\psi ^g$
are unipotent characters of
![]() ${\mathbf {L}}^F$
, using [Reference Cabanes and Enguehard17, Proposition 8.26] we deduce that
${\mathbf {L}}^F$
, using [Reference Cabanes and Enguehard17, Proposition 8.26] we deduce that
![]() $(\hat {t}_{\mathbf {L}})^g(\hat {s}_{\mathbf {L}})^{-1}=1_{\mathbf {L}}$
, and therefore,
$(\hat {t}_{\mathbf {L}})^g(\hat {s}_{\mathbf {L}})^{-1}=1_{\mathbf {L}}$
, and therefore,
![]() $\varphi =\psi ^g$
. But then, [Reference Broué, Malle and Michel9, Theorem 3.2(1)] shows that
$\varphi =\psi ^g$
. But then, [Reference Broué, Malle and Michel9, Theorem 3.2(1)] shows that
![]() $({\mathbf {M}},\mu )$
and
$({\mathbf {M}},\mu )$
and
![]() $({\mathbf {K}},\kappa )^g$
are
$({\mathbf {K}},\kappa )^g$
are
![]() ${\mathbf {L}}^F$
-conjugate and the result follows.
${\mathbf {L}}^F$
-conjugate and the result follows.
Next, we describe the block theory associated to characters in the sets introduced in Definition 5.2.
Lemma 5.4. Let
![]() $\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
, and consider a unipotent e-cuspidal pair
$\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
, and consider a unipotent e-cuspidal pair
![]() $({\mathbf {M}},\mu )$
belonging to
$({\mathbf {M}},\mu )$
belonging to
![]() ${\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
and a character
${\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
and a character
![]() $\vartheta \in \mathrm{Irr}_{\mathrm{ps}}({\mathbf {G}}_\sigma ^F,({\mathbf {M}},\mu ))$
. Recall that
$\vartheta \in \mathrm{Irr}_{\mathrm{ps}}({\mathbf {G}}_\sigma ^F,({\mathbf {M}},\mu ))$
. Recall that
![]() $\ell $
is odd. Then:
$\ell $
is odd. Then:
-
(i) the block
 $\mathrm{bl}(\vartheta )$
is
$\mathrm{bl}(\vartheta )$
is
 ${\mathbf {L}}(\sigma )^F$
-regular;
${\mathbf {L}}(\sigma )^F$
-regular; -
(ii) if
 $\vartheta $
lies above a given
$\vartheta $
lies above a given
 $\varphi \hat {z}_{{\mathbf {L}}(\sigma )}\in {\mathcal {E}}({\mathbf {L}}(\sigma )^F,({\mathbf {M}},\mu \hat {z}_{\mathbf {M}}))$
for some
$\varphi \hat {z}_{{\mathbf {L}}(\sigma )}\in {\mathcal {E}}({\mathbf {L}}(\sigma )^F,({\mathbf {M}},\mu \hat {z}_{\mathbf {M}}))$
for some
 $z\in {\mathbf {Z}}({\mathbf {L}}(\sigma )^*)^{F^*}$
, then we have
$z\in {\mathbf {Z}}({\mathbf {L}}(\sigma )^*)^{F^*}$
, then we have  $$\begin{align*}\mathrm{bl}(\varphi\hat{z}_{{\mathbf{L}}(\sigma)})=\mathrm{bl}(\mu\hat{z}_{\mathbf{M}})^{{\mathbf{L}}(\sigma)^F}\hspace{15pt}\text{ and }\hspace{15pt}\mathrm{bl}(\vartheta)=\mathrm{ bl}(\varphi\hat{z}_{{\mathbf{L}}(\sigma)})^{{\mathbf{G}}_\sigma^F}=\mathrm{bl}(\mu\hat{z}_{\mathbf{M}})^{{\mathbf{G}}_\sigma^F}\end{align*}$$
$$\begin{align*}\mathrm{bl}(\varphi\hat{z}_{{\mathbf{L}}(\sigma)})=\mathrm{bl}(\mu\hat{z}_{\mathbf{M}})^{{\mathbf{L}}(\sigma)^F}\hspace{15pt}\text{ and }\hspace{15pt}\mathrm{bl}(\vartheta)=\mathrm{ bl}(\varphi\hat{z}_{{\mathbf{L}}(\sigma)})^{{\mathbf{G}}_\sigma^F}=\mathrm{bl}(\mu\hat{z}_{\mathbf{M}})^{{\mathbf{G}}_\sigma^F}\end{align*}$$
-
(iii) the induced block
 $\mathrm{bl}(\vartheta )^{{\mathbf {G}}^F}$
is defined.
$\mathrm{bl}(\vartheta )^{{\mathbf {G}}^F}$
is defined.
Proof. The first point follows from Lemma 2.3 by choosing
![]() ${\mathbf {L}}={\mathbf {L}}(\sigma )$
and
${\mathbf {L}}={\mathbf {L}}(\sigma )$
and
![]() $H={\mathbf {G}}_\sigma ^F$
. Furthermore, in the second case of Definition 5.2 observe that
$H={\mathbf {G}}_\sigma ^F$
. Furthermore, in the second case of Definition 5.2 observe that
![]() ${\mathbf {L}}(\sigma )\leq {\mathbf {L}}(\sigma -{\mathbf {L}}(\sigma ))$
from which it follows that
${\mathbf {L}}(\sigma )\leq {\mathbf {L}}(\sigma -{\mathbf {L}}(\sigma ))$
from which it follows that
![]() ${\mathbf {Z}}({\mathbf {L}}(\sigma -{\mathbf {L}}(\sigma ))^*)\leq {\mathbf {Z}}({\mathbf {L}}(\sigma )^*)$
. Therefore, we can always find
${\mathbf {Z}}({\mathbf {L}}(\sigma -{\mathbf {L}}(\sigma ))^*)\leq {\mathbf {Z}}({\mathbf {L}}(\sigma )^*)$
. Therefore, we can always find
![]() $\varphi $
and z as in the statement of (ii). Since
$\varphi $
and z as in the statement of (ii). Since
![]() $\varphi $
is an irreducible constituent of the virtual character
$\varphi $
is an irreducible constituent of the virtual character
![]() ${\mathbf {R}}_{\mathbf {M}}^{{\mathbf {L}}(\sigma )}(\mu )$
, it follows from [Reference Cabanes and Enguehard15, Proposition 4.2] (whose assumptions are satisfied by [Reference Cabanes and Enguehard15, Proposition 3.3 (ii)]) that
${\mathbf {R}}_{\mathbf {M}}^{{\mathbf {L}}(\sigma )}(\mu )$
, it follows from [Reference Cabanes and Enguehard15, Proposition 4.2] (whose assumptions are satisfied by [Reference Cabanes and Enguehard15, Proposition 3.3 (ii)]) that
![]() $\mathrm{bl}(\varphi )=b_{{\mathbf {L}}(\sigma )^F}({\mathbf {M}},\mu )=\mathrm{bl}(\mu )^{{\mathbf {L}}(\sigma )^F}$
. Then, since
$\mathrm{bl}(\varphi )=b_{{\mathbf {L}}(\sigma )^F}({\mathbf {M}},\mu )=\mathrm{bl}(\mu )^{{\mathbf {L}}(\sigma )^F}$
. Then, since
![]() $\hat {z}_{\mathbf {M}}$
is the restriction of the linear character
$\hat {z}_{\mathbf {M}}$
is the restriction of the linear character
![]() $\hat {z}_{{\mathbf {L}}(\sigma )}$
to
$\hat {z}_{{\mathbf {L}}(\sigma )}$
to
![]() ${\mathbf {M}}^F$
, we deduce from Lemma 2.1 that
${\mathbf {M}}^F$
, we deduce from Lemma 2.1 that
Now, [Reference Navarro46, Theorem 9.19] implies that
and the second point follows by the transitivity of block induction. Finally, set
![]() $Q:={\mathbf {Z}}({\mathbf {M}})^F_\ell $
and observe that
$Q:={\mathbf {Z}}({\mathbf {M}})^F_\ell $
and observe that
![]() $Q{\mathbf {C}}_{{\mathbf {G}}^F}(Q)={\mathbf {M}}^F\leq {\mathbf {N}}_{{\mathbf {G}}^F}(Q)$
by [Reference Cabanes and Enguehard15, Proposition 3.3(ii)]. Then, [Reference Navarro46, Theorem 4.14] implies that
$Q{\mathbf {C}}_{{\mathbf {G}}^F}(Q)={\mathbf {M}}^F\leq {\mathbf {N}}_{{\mathbf {G}}^F}(Q)$
by [Reference Cabanes and Enguehard15, Proposition 3.3(ii)]. Then, [Reference Navarro46, Theorem 4.14] implies that
![]() $\mathrm{bl}(\mu \hat {z}_{\mathbf {M}})^{{\mathbf {G}}^F}$
is defined and so is
$\mathrm{bl}(\mu \hat {z}_{\mathbf {M}})^{{\mathbf {G}}^F}$
is defined and so is
![]() $\mathrm{bl}(\vartheta )^{{\mathbf {G}}^F}$
by (ii) and transitivity of block induction. This concludes the proof.
$\mathrm{bl}(\vartheta )^{{\mathbf {G}}^F}$
by (ii) and transitivity of block induction. This concludes the proof.
Using the lemma above, we can now define the following character set. This yields the e-local object through which we can determine the number of (pseudo-)unipotent characters in a given block B of
![]() ${\mathbf {G}}^F$
and with a given defect
${\mathbf {G}}^F$
and with a given defect
![]() $d\geq 0$
(see Section 5.3).
$d\geq 0$
(see Section 5.3).
Definition 5.5. Let B be a block of
![]() ${\mathbf {G}}^F$
and d a nonnegative integer. For every e-chain
${\mathbf {G}}^F$
and d a nonnegative integer. For every e-chain
![]() $\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
and unipotent e-cuspidal pair
$\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
and unipotent e-cuspidal pair
![]() $({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{ u}}}(\sigma )$
, we define the character set
$({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{ u}}}(\sigma )$
, we define the character set
where
![]() $\mathrm{bl}(\vartheta )^{{\mathbf {G}}^F}$
is defined according to Lemma 5.4 (iii). Furthermore, we denote the cardinality of this set by
$\mathrm{bl}(\vartheta )^{{\mathbf {G}}^F}$
is defined according to Lemma 5.4 (iii). Furthermore, we denote the cardinality of this set by
In the following remark, we explain that the character sets defined above might be nonempty even if B is not a unipotent block.
Remark 5.6. Let
![]() $\sigma $
be an e-chain of
$\sigma $
be an e-chain of
![]() $({\mathbf {G}},F)$
, and suppose that
$({\mathbf {G}},F)$
, and suppose that
![]() $({\mathbf {M}},\mu )$
is a unipotent e-cuspidal pair such that
$({\mathbf {M}},\mu )$
is a unipotent e-cuspidal pair such that
![]() ${\mathbf {M}}<{\mathbf {L}}(\sigma )$
. If
${\mathbf {M}}<{\mathbf {L}}(\sigma )$
. If
![]() $\ell $
is odd and good for
$\ell $
is odd and good for
![]() ${\mathbf {G}}$
, then [Reference Cabanes and Enguehard15, Proposition 3.3 (ii)] implies that
${\mathbf {G}}$
, then [Reference Cabanes and Enguehard15, Proposition 3.3 (ii)] implies that
![]() ${\mathbf {M}}^F={\mathbf {C}}_{{\mathbf {G}}^F}(Q)$
for
${\mathbf {M}}^F={\mathbf {C}}_{{\mathbf {G}}^F}(Q)$
for
![]() $Q:={\mathbf {Z}}({\mathbf {M}})_\ell ^F$
. Next, assume that
$Q:={\mathbf {Z}}({\mathbf {M}})_\ell ^F$
. Next, assume that
![]() ${\mathbf {Z}}({\mathbf {L}}(\sigma )^*)^{F^*}$
is not an
${\mathbf {Z}}({\mathbf {L}}(\sigma )^*)^{F^*}$
is not an
![]() $\ell $
-group and fix an
$\ell $
-group and fix an
![]() $\ell '$
-element
$\ell '$
-element
![]() $z\in {\mathbf {Z}}({\mathbf {L}}(\sigma )^*)^{F^*}$
. We choose an irreducible character
$z\in {\mathbf {Z}}({\mathbf {L}}(\sigma )^*)^{F^*}$
. We choose an irreducible character
![]() $\vartheta $
of
$\vartheta $
of
![]() ${\mathbf {G}}_\sigma ^F$
lying above some character of
${\mathbf {G}}_\sigma ^F$
lying above some character of
![]() ${\mathcal {E}}({\mathbf {L}}(\sigma )^F,({\mathbf {M}},\mu \hat {z}_{\mathbf {M}}))$
and define
${\mathcal {E}}({\mathbf {L}}(\sigma )^F,({\mathbf {M}},\mu \hat {z}_{\mathbf {M}}))$
and define
![]() $d:=d(\vartheta )$
and
$d:=d(\vartheta )$
and
![]() $B=\mathrm{bl}(\vartheta )^{{\mathbf {G}}^F}$
. By the above choices, we know that
$B=\mathrm{bl}(\vartheta )^{{\mathbf {G}}^F}$
. By the above choices, we know that
![]() $({\mathbf {M}},\mu \hat {z}_{\mathbf {M}})$
is an e-cuspidal pair of
$({\mathbf {M}},\mu \hat {z}_{\mathbf {M}})$
is an e-cuspidal pair of
![]() $({\mathbf {G}},F)$
, where the character
$({\mathbf {G}},F)$
, where the character
![]() $\mu \widehat {z}_{\mathbf {M}}$
lies in the Lusztig series
$\mu \widehat {z}_{\mathbf {M}}$
lies in the Lusztig series
![]() ${\mathcal {E}}({\mathbf {M}}^F,[z])$
with z of order prime to
${\mathcal {E}}({\mathbf {M}}^F,[z])$
with z of order prime to
![]() $\ell $
. Since
$\ell $
. Since
![]() $\mathrm{bl}(\mu \hat {z}_{\mathbf {M}})^{{\mathbf {G}}^F}=B$
according to Lemma 5.4, we conclude that the irreducible constituents of
$\mathrm{bl}(\mu \hat {z}_{\mathbf {M}})^{{\mathbf {G}}^F}=B$
according to Lemma 5.4, we conclude that the irreducible constituents of
![]() ${\mathbf {R}}_{\mathbf {M}}^{\mathbf {G}}(\mu \hat {z}_{\mathbf {M}})$
belong to the block B as a consequence of [Reference Cabanes and Enguehard16, Theorem] (to use this result, we further assume that
${\mathbf {R}}_{\mathbf {M}}^{\mathbf {G}}(\mu \hat {z}_{\mathbf {M}})$
belong to the block B as a consequence of [Reference Cabanes and Enguehard16, Theorem] (to use this result, we further assume that
![]() $\ell \geq 5$
with
$\ell \geq 5$
with
![]() $\ell \geq 7$
if
$\ell \geq 7$
if
![]() ${\mathbf {G}}$
has a component of type
${\mathbf {G}}$
has a component of type
![]() $\mathbf {{E}}_8$
). Then, applying [Reference Broué and Michel10] it follows that the block B is not unipotent. On the other hand, the character
$\mathbf {{E}}_8$
). Then, applying [Reference Broué and Michel10] it follows that the block B is not unipotent. On the other hand, the character
![]() $\vartheta $
belongs to the set
$\vartheta $
belongs to the set
![]() $\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
.
$\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
.
We now show that Proposition 4.5 can be used to parametrise the character sets from Definition 5.5.
Proposition 5.7. Suppose that
![]() ${\mathbf {G}}$
is a simply connected group whose irreducible components are of type
${\mathbf {G}}$
is a simply connected group whose irreducible components are of type
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
, and assume that
$\mathbf {C}$
, and assume that
![]() $\ell $
is odd. Let B be a block of
$\ell $
is odd. Let B be a block of
![]() ${\mathbf {G}}^F$
and d a nonnegative integer. If
${\mathbf {G}}^F$
and d a nonnegative integer. If
![]() $\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
and
$\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
and
![]() $({\mathbf {M}},\mu )$
is a unipotent e-cuspidal pair in
$({\mathbf {M}},\mu )$
is a unipotent e-cuspidal pair in
![]() ${\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
, then there exists an
${\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
, then there exists an
![]() $\mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{B,\sigma ,({\mathbf {M}},\mu )}$
-equivariant bijection
$\mathrm{ Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{B,\sigma ,({\mathbf {M}},\mu )}$
-equivariant bijection
such that
for every
![]() $\vartheta \in \mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
and where
$\vartheta \in \mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
and where
![]() $X:={\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
.
$X:={\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
.
Proof. First, observe that if
![]() ${\mathbf {M}}$
coincides with the last term
${\mathbf {M}}$
coincides with the last term
![]() ${\mathbf {L}}(\sigma )$
of the chain
${\mathbf {L}}(\sigma )$
of the chain
![]() $\sigma $
, then we have
$\sigma $
, then we have
![]() $\sigma +{\mathbf {M}}=\sigma $
which implies
$\sigma +{\mathbf {M}}=\sigma $
which implies
![]() $\mathrm{Irr}_{\mathrm{ ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))=\mathrm{Irr}_{\mathrm{ps}}^d(B_{\sigma +{\mathbf {M}}},({\mathbf {M}},\mu ))$
. In this case, the result holds by defining
$\mathrm{Irr}_{\mathrm{ ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))=\mathrm{Irr}_{\mathrm{ps}}^d(B_{\sigma +{\mathbf {M}}},({\mathbf {M}},\mu ))$
. In this case, the result holds by defining
![]() $\Omega _{\sigma ,({\mathbf {M}},\mu )}^{B,d}$
as the identity. Therefore, we can assume that
$\Omega _{\sigma ,({\mathbf {M}},\mu )}^{B,d}$
as the identity. Therefore, we can assume that
![]() ${\mathbf {M}}<{\mathbf {L}}(\sigma )$
and define
${\mathbf {M}}<{\mathbf {L}}(\sigma )$
and define
![]() $\rho :=\sigma +{\mathbf {M}}$
. Now, according to the first case in Definition 5.2 we have
$\rho :=\sigma +{\mathbf {M}}$
. Now, according to the first case in Definition 5.2 we have
On the other hand, noticing that
![]() ${\mathbf {M}}$
coincides with the last term
${\mathbf {M}}$
coincides with the last term
![]() ${\mathbf {L}}(\rho )$
of the chain
${\mathbf {L}}(\rho )$
of the chain
![]() $\rho $
and that
$\rho $
and that
![]() $\rho -{\mathbf {L}}(\rho )=\sigma $
, we obtain the equality
$\rho -{\mathbf {L}}(\rho )=\sigma $
, we obtain the equality
![]() ${\mathcal {E}}({\mathbf {L}}(\rho )^F,({\mathbf {M}},\mathrm{ps}_{{\mathbf {L}}(\rho -{\mathbf {L}}(\rho ))}(\mu )))=\mathrm{ps}_{{\mathbf {L}}(\sigma )}(\mu )$
. Then, observing that
${\mathcal {E}}({\mathbf {L}}(\rho )^F,({\mathbf {M}},\mathrm{ps}_{{\mathbf {L}}(\rho -{\mathbf {L}}(\rho ))}(\mu )))=\mathrm{ps}_{{\mathbf {L}}(\sigma )}(\mu )$
. Then, observing that
![]() ${\mathbf {G}}_\rho ^F={\mathbf {N}}_{{\mathbf {G}}_\sigma ^F}({\mathbf {M}})$
, we can apply the second case of Definition 5.2 to obtain the equality
${\mathbf {G}}_\rho ^F={\mathbf {N}}_{{\mathbf {G}}_\sigma ^F}({\mathbf {M}})$
, we can apply the second case of Definition 5.2 to obtain the equality
Next, we apply Proposition 4.5 by choosing the groups in that statement to be
![]() $H={\mathbf {G}}_\sigma ^F$
,
$H={\mathbf {G}}_\sigma ^F$
,
![]() ${\mathbf {K}}={\mathbf {L}}(\sigma )$
and
${\mathbf {K}}={\mathbf {L}}(\sigma )$
and
![]() $({\mathbf {L}},\lambda )=({\mathbf {M}},\mu )$
. By (5.1) and (5.2), there exists an
$({\mathbf {L}},\lambda )=({\mathbf {M}},\mu )$
. By (5.1) and (5.2), there exists an
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{\sigma ,({\mathbf {M}},\mu )}$
-equivariant bijection
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_{\sigma ,({\mathbf {M}},\mu )}$
-equivariant bijection
Moreover, using the H-block isomorphisms given by Proposition 4.5 together with [Reference Späth64, Lemma 3.8 (b)], we deduce that
for every
![]() $\vartheta \in \mathrm{Irr}_{\mathrm{ps}}^d({\mathbf {G}}_\sigma ^F,({\mathbf {M}},\mu ))$
. To conclude, observe first that
$\vartheta \in \mathrm{Irr}_{\mathrm{ps}}^d({\mathbf {G}}_\sigma ^F,({\mathbf {M}},\mu ))$
. To conclude, observe first that
![]() $\Omega ^{{\mathbf {L}}(\sigma ),{\mathbf {G}}_\sigma ^F}_{({\mathbf {M}},\mu )}$
sends characters of defect d to characters of defect d. Moreover, by the transitivity of block induction and using (5.4), we deduce that
$\Omega ^{{\mathbf {L}}(\sigma ),{\mathbf {G}}_\sigma ^F}_{({\mathbf {M}},\mu )}$
sends characters of defect d to characters of defect d. Moreover, by the transitivity of block induction and using (5.4), we deduce that
This shows that the bijection from (5.3) sends characters in the set
![]() $\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
to characters in the set
$\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
to characters in the set
![]() $\mathrm{ Irr}_{\mathrm{ps}}^d(B_{\sigma +{\mathbf {M}}},({\mathbf {M}},\mu ))$
, and therefore, it restricts to a bijection, denoted by
$\mathrm{ Irr}_{\mathrm{ps}}^d(B_{\sigma +{\mathbf {M}}},({\mathbf {M}},\mu ))$
, and therefore, it restricts to a bijection, denoted by
![]() $\Omega ^{B,d}_{\sigma ,({\mathbf {M}},\mu )}$
, satisfying the properties required in the statement. This completes the proof.
$\Omega ^{B,d}_{\sigma ,({\mathbf {M}},\mu )}$
, satisfying the properties required in the statement. This completes the proof.
We conclude this section with a remark on the isomorphisms of character triples obtained in Proposition 5.7.
Remark 5.8. If in addition
![]() $\ell $
is good for
$\ell $
is good for
![]() ${\mathbf {G}}$
and does not divide
${\mathbf {G}}$
and does not divide
![]() $|{\mathbf {Z}}({\mathbf {G}})^F:{\mathbf {Z}}^\circ ({\mathbf {G}})^F|$
, then every e-split Levi subgroup
$|{\mathbf {Z}}({\mathbf {G}})^F:{\mathbf {Z}}^\circ ({\mathbf {G}})^F|$
, then every e-split Levi subgroup
![]() ${\mathbf {L}}$
of
${\mathbf {L}}$
of
![]() ${\mathbf {G}}$
satisfies
${\mathbf {G}}$
satisfies
![]() ${\mathbf {L}}={\mathbf {C}}_{\mathbf {G}}^\circ ({\mathbf {Z}}({\mathbf {L}})^F_\ell )$
according to [Reference Cabanes and Enguehard17, Proposition 13.19]. This fact can be used to show that the
${\mathbf {L}}={\mathbf {C}}_{\mathbf {G}}^\circ ({\mathbf {Z}}({\mathbf {L}})^F_\ell )$
according to [Reference Cabanes and Enguehard17, Proposition 13.19]. This fact can be used to show that the
![]() ${\mathbf {G}}^F_\sigma $
-block isomorphisms of character triples given by Proposition 5.7 can be extended to
${\mathbf {G}}^F_\sigma $
-block isomorphisms of character triples given by Proposition 5.7 can be extended to
![]() ${\mathbf {G}}^F$
-block isomorphisms of character triples. First, we claim that
${\mathbf {G}}^F$
-block isomorphisms of character triples. First, we claim that
for every irreducible character
![]() $\vartheta $
of
$\vartheta $
of
![]() ${\mathbf {G}}^F_\sigma $
and every
${\mathbf {G}}^F_\sigma $
and every
![]() $\ell $
-radical subgroup D of
$\ell $
-radical subgroup D of
![]() ${\mathbf {G}}_{\sigma +{\mathbf {M}}}^F$
. Define
${\mathbf {G}}_{\sigma +{\mathbf {M}}}^F$
. Define
![]() $Q_i:={\mathbf {Z}}^\circ ({\mathbf {L}}_i)_\ell ^F$
for every e-split Levi subgroup
$Q_i:={\mathbf {Z}}^\circ ({\mathbf {L}}_i)_\ell ^F$
for every e-split Levi subgroup
![]() ${\mathbf {L}}_i$
appearing in the chain
${\mathbf {L}}_i$
appearing in the chain
![]() $\sigma $
. Then, using the fact that D is
$\sigma $
. Then, using the fact that D is
![]() $\ell $
-radical, we obtain the inclusions
$\ell $
-radical, we obtain the inclusions
![]() $Q_i\leq {\mathbf {O}}_\ell ({\mathbf {G}}_\sigma ^F)\leq D$
. Therefore, every element
$Q_i\leq {\mathbf {O}}_\ell ({\mathbf {G}}_\sigma ^F)\leq D$
. Therefore, every element
![]() $x\in {\mathbf {G}}^FX_{\sigma ,\vartheta }$
that centralises D centralises also each
$x\in {\mathbf {G}}^FX_{\sigma ,\vartheta }$
that centralises D centralises also each
![]() $Q_i$
and hence normalises each
$Q_i$
and hence normalises each
![]() ${\mathbf {L}}_i$
. It follows that
${\mathbf {L}}_i$
. It follows that
as required by (5.5). We can now apply [Reference Rossi52, Lemma 2.11] to the
![]() ${\mathbf {G}}^F_\sigma $
-block isomorphisms given by Proposition 5.7 to show that
${\mathbf {G}}^F_\sigma $
-block isomorphisms given by Proposition 5.7 to show that
for every
![]() $\vartheta \in \mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
.
$\vartheta \in \mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
.
5.2 Proof of Theorem A
We are finally ready to prove our main theorem which provides a bijection for unipotent characters in the spirit of the Character Triple Conjecture [Reference Späth64, Conjecture 6.3]. In this section, we prove a slightly stronger result that provides further information on the type of e-chains and isomorphisms of character triples. In the following definition we introduce the analogue of the set
![]() ${\mathcal {C}}^d(B)_\pm $
considered in the Character Triple Conjecture as defined in [Reference Späth64, p. 1097].
${\mathcal {C}}^d(B)_\pm $
considered in the Character Triple Conjecture as defined in [Reference Späth64, p. 1097].
Definition 5.9. Let B be a block of
![]() ${\mathbf {G}}^F$
and consider a nonnegative integer d. We define the set
${\mathbf {G}}^F$
and consider a nonnegative integer d. We define the set
The conjugacy action of
![]() ${\mathbf {G}}^F$
induces an action of
${\mathbf {G}}^F$
induces an action of
![]() ${\mathbf {G}}^F$
on
${\mathbf {G}}^F$
on
![]() ${\mathcal {L}}^d_{\mathrm{u}}(B)_\pm $
which is defined by setting
${\mathcal {L}}^d_{\mathrm{u}}(B)_\pm $
which is defined by setting
![]() $(\sigma ,{\mathbf {M}},\mu ,\vartheta )^g:=\left (\sigma ^g,{\mathbf {M}}^g,\mu ^g,\vartheta ^g\right )$
for every element
$(\sigma ,{\mathbf {M}},\mu ,\vartheta )^g:=\left (\sigma ^g,{\mathbf {M}}^g,\mu ^g,\vartheta ^g\right )$
for every element
![]() $g\in {\mathbf {G}}^F$
and
$g\in {\mathbf {G}}^F$
and
![]() $(\sigma ,{\mathbf {M}},\mu ,\vartheta )\in {\mathcal {L}}^d_{\mathrm{u}}(B)_\pm $
. We denote by
$(\sigma ,{\mathbf {M}},\mu ,\vartheta )\in {\mathcal {L}}^d_{\mathrm{u}}(B)_\pm $
. We denote by
![]() ${\mathcal {L}}^d_{\mathrm{u}}(B)_\pm /{\mathbf {G}}^F$
the corresponding set of
${\mathcal {L}}^d_{\mathrm{u}}(B)_\pm /{\mathbf {G}}^F$
the corresponding set of
![]() ${\mathbf {G}}^F$
-orbits of tuples. Moreover, for every such orbit
${\mathbf {G}}^F$
-orbits of tuples. Moreover, for every such orbit
![]() $\omega $
, we denote by
$\omega $
, we denote by
![]() $\omega ^\bullet $
the corresponding
$\omega ^\bullet $
the corresponding
![]() ${\mathbf {G}}^F$
-orbit of pairs
${\mathbf {G}}^F$
-orbit of pairs
![]() $(\sigma ,\vartheta )$
such that
$(\sigma ,\vartheta )$
such that
![]() $(\sigma ,{\mathbf {M}},\mu ,\vartheta )\in \omega $
for some
$(\sigma ,{\mathbf {M}},\mu ,\vartheta )\in \omega $
for some
![]() $({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
. In other words, if we indicate by
$({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
. In other words, if we indicate by
![]() $\overline {(\sigma ,{\mathbf {M}},\mu ,\vartheta )}$
the
$\overline {(\sigma ,{\mathbf {M}},\mu ,\vartheta )}$
the
![]() ${\mathbf {G}}^F$
-orbit of
${\mathbf {G}}^F$
-orbit of
![]() $(\sigma ,{\mathbf {M}},\mu ,\vartheta )$
, then
$(\sigma ,{\mathbf {M}},\mu ,\vartheta )$
, then
![]() $\overline {(\sigma ,{\mathbf {M}},\mu ,\vartheta )}^\bullet $
is the
$\overline {(\sigma ,{\mathbf {M}},\mu ,\vartheta )}^\bullet $
is the
![]() ${\mathbf {G}}^F$
-orbit of the pairs
${\mathbf {G}}^F$
-orbit of the pairs
![]() $(\sigma ^g,\vartheta ^g)$
.
$(\sigma ^g,\vartheta ^g)$
.
Similarly, if
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_B$
denotes the set of those automorphisms
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_B$
denotes the set of those automorphisms
![]() $\alpha \in \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
that stabilise B, then we can define
$\alpha \in \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
that stabilise B, then we can define
![]() $(\sigma ,{\mathbf {M}},\mu ,\vartheta )^\alpha :=\left (\sigma ^\alpha ,{\mathbf {M}}^\alpha ,\mu ^\alpha ,\vartheta ^\alpha \right )$
for every
$(\sigma ,{\mathbf {M}},\mu ,\vartheta )^\alpha :=\left (\sigma ^\alpha ,{\mathbf {M}}^\alpha ,\mu ^\alpha ,\vartheta ^\alpha \right )$
for every
![]() $\alpha \in \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_B$
and
$\alpha \in \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_B$
and
![]() $(\sigma ,{\mathbf {M}},\mu ,\vartheta )\in {\mathcal {L}}_{\mathrm{u}}^d(B)$
. In this way, we obtain an action of the group
$(\sigma ,{\mathbf {M}},\mu ,\vartheta )\in {\mathcal {L}}_{\mathrm{u}}^d(B)$
. In this way, we obtain an action of the group
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_B$
on the set
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_B$
on the set
![]() ${\mathcal {L}}_{\mathrm{u}}^d(B)_\pm $
and on the corresponding set of orbits
${\mathcal {L}}_{\mathrm{u}}^d(B)_\pm $
and on the corresponding set of orbits
![]() ${\mathcal {L}}_{\mathrm{u}}^d(B)_\pm /{\mathbf {G}}^F$
.
${\mathcal {L}}_{\mathrm{u}}^d(B)_\pm /{\mathbf {G}}^F$
.
Theorem 5.10. Suppose that
![]() ${\mathbf {G}}$
is a simply connected group whose irreducible components are of type
${\mathbf {G}}$
is a simply connected group whose irreducible components are of type
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
, and assume that
$\mathbf {C}$
, and assume that
![]() $\ell $
is odd. For every block B of
$\ell $
is odd. For every block B of
![]() ${\mathbf {G}}^F$
and every nonnegative integer d, there exists an
${\mathbf {G}}^F$
and every nonnegative integer d, there exists an
![]() $\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_B$
-equivariant bijection
$\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)_B$
-equivariant bijection
Moreover, for every
![]() $\omega \in {\mathcal {L}}^d_{\mathrm{u}}(B)_+/{\mathbf {G}}^F$
, any
$\omega \in {\mathcal {L}}^d_{\mathrm{u}}(B)_+/{\mathbf {G}}^F$
, any
![]() $(\sigma ,\vartheta )\in \omega ^\bullet $
and any
$(\sigma ,\vartheta )\in \omega ^\bullet $
and any
![]() $(\rho ,\chi )\in \Lambda (\omega )^\bullet $
, we have
$(\rho ,\chi )\in \Lambda (\omega )^\bullet $
, we have
and
with
![]() $J={\mathbf {G}}^F_\sigma $
, if
$J={\mathbf {G}}^F_\sigma $
, if
![]() $|\sigma |=|\rho |-1$
, or
$|\sigma |=|\rho |-1$
, or
![]() $J={\mathbf {G}}_\rho ^F$
, if
$J={\mathbf {G}}_\rho ^F$
, if
![]() $|\sigma |=|\rho |+1$
, and where
$|\sigma |=|\rho |+1$
, and where
![]() $X:={\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
.
$X:={\mathbf {G}}^F\rtimes \mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
.
Proof. Define
![]() $A:=\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
, and observe that
$A:=\mathrm{Aut}_{\mathbb {F}}({\mathbf {G}}^F)$
, and observe that
![]() $X={\mathbf {G}}^F\rtimes A$
. In a first step, we construct an equivariant bijection between triples of the form
$X={\mathbf {G}}^F\rtimes A$
. In a first step, we construct an equivariant bijection between triples of the form
![]() $(\sigma ,{\mathbf {M}},\mu )$
. More precisely, let
$(\sigma ,{\mathbf {M}},\mu )$
. More precisely, let
![]() $\mathcal {S}$
denote the set of such triples
$\mathcal {S}$
denote the set of such triples
![]() $(\sigma ,{\mathbf {M}},\mu )$
with
$(\sigma ,{\mathbf {M}},\mu )$
with
![]() $\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
and
$\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
and
![]() $({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
. We define a map
$({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
. We define a map
by setting
 $$\begin{align*}\Delta\left((\sigma,{\mathbf{M}},\mu)\right):=\begin{cases} \left(\sigma+{\mathbf{M}},{\mathbf{M}},\mu\right),& {\mathbf{L}}(\sigma)>{\mathbf{M}} \\ \left(\sigma-{\mathbf{M}},{\mathbf{M}},\mu\right),& {\mathbf{L}}(\sigma)={\mathbf{M}}. \end{cases}\end{align*}$$
$$\begin{align*}\Delta\left((\sigma,{\mathbf{M}},\mu)\right):=\begin{cases} \left(\sigma+{\mathbf{M}},{\mathbf{M}},\mu\right),& {\mathbf{L}}(\sigma)>{\mathbf{M}} \\ \left(\sigma-{\mathbf{M}},{\mathbf{M}},\mu\right),& {\mathbf{L}}(\sigma)={\mathbf{M}}. \end{cases}\end{align*}$$
Notice that, from the definition above it follows that the map
![]() $\Delta $
is A-equivariant and satisfies
$\Delta $
is A-equivariant and satisfies
![]() $\Delta ^2=\mathrm{Id}$
. Therefore, observing that
$\Delta ^2=\mathrm{Id}$
. Therefore, observing that
![]() $|\sigma \pm {\mathbf {M}}|=|\sigma |\pm 1$
, we conclude that
$|\sigma \pm {\mathbf {M}}|=|\sigma |\pm 1$
, we conclude that
![]() $\Delta $
restricts to an A-equivariant bijection
$\Delta $
restricts to an A-equivariant bijection
where
![]() $\mathcal {S}_\pm $
denotes the set of those triples
$\mathcal {S}_\pm $
denotes the set of those triples
![]() $(\sigma ,{\mathbf {M}},\mu )$
of
$(\sigma ,{\mathbf {M}},\mu )$
of
![]() $\mathcal {S}$
that satisfy
$\mathcal {S}$
that satisfy
![]() $\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)_\pm $
. Furthermore, notice once again that if
$\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)_\pm $
. Furthermore, notice once again that if
![]() $\Delta ((\sigma ,{\mathbf {M}},\mu ))=(\rho ,{\mathbf {K}},\kappa )$
, then
$\Delta ((\sigma ,{\mathbf {M}},\mu ))=(\rho ,{\mathbf {K}},\kappa )$
, then
Now, fix an
![]() $A_B$
-transversal
$A_B$
-transversal
![]() $\mathcal {T}_+$
in
$\mathcal {T}_+$
in
![]() $\mathcal {S}_+$
and observe that the image of
$\mathcal {S}_+$
and observe that the image of
![]() $\mathcal {T}_+$
under the map
$\mathcal {T}_+$
under the map
![]() $\Delta $
, denoted by
$\Delta $
, denoted by
![]() $\mathcal {T}_-$
, is an
$\mathcal {T}_-$
, is an
![]() $A_B$
-transversal in
$A_B$
-transversal in
![]() $\mathcal {S}_-$
because of the equivariance property of
$\mathcal {S}_-$
because of the equivariance property of
![]() $\Delta $
. Consider
$\Delta $
. Consider
![]() $(\sigma ,{\mathbf {M}},\mu )\in \mathcal {T}_+$
, and write
$(\sigma ,{\mathbf {M}},\mu )\in \mathcal {T}_+$
, and write
![]() $\Delta ((\sigma ,{\mathbf {M}},\mu ))=(\rho ,{\mathbf {M}},\mu )$
. In what follows, we may assume without loss of generality that
$\Delta ((\sigma ,{\mathbf {M}},\mu ))=(\rho ,{\mathbf {M}},\mu )$
. In what follows, we may assume without loss of generality that
![]() ${\mathbf {L}}(\sigma )>{\mathbf {M}}$
and that
${\mathbf {L}}(\sigma )>{\mathbf {M}}$
and that
![]() $\rho =\sigma +{\mathbf {M}}$
, otherwise we repeat the arguments verbatim by replacing
$\rho =\sigma +{\mathbf {M}}$
, otherwise we repeat the arguments verbatim by replacing
![]() $(\sigma ,{\mathbf {M}},\mu )$
with
$(\sigma ,{\mathbf {M}},\mu )$
with
![]() $(\rho ,{\mathbf {M}},\mu )$
. By Proposition 5.7, we obtain an
$(\rho ,{\mathbf {M}},\mu )$
. By Proposition 5.7, we obtain an
![]() $A_{B,\sigma ,({\mathbf {M}},\mu )}$
-equivariant bijection
$A_{B,\sigma ,({\mathbf {M}},\mu )}$
-equivariant bijection
such that
for every
![]() $\vartheta \in \mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
and where
$\vartheta \in \mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
and where
![]() $\chi $
is the image of
$\chi $
is the image of
![]() $\vartheta $
. Consequently, if
$\vartheta $
. Consequently, if
![]() $\mathcal {U}_{+}^{(\sigma ,{\mathbf {M}},\mu )}$
is an
$\mathcal {U}_{+}^{(\sigma ,{\mathbf {M}},\mu )}$
is an
![]() $A_{B,(\sigma ,{\mathbf {M}},\mu )}$
-transversal in the character set
$A_{B,(\sigma ,{\mathbf {M}},\mu )}$
-transversal in the character set
![]() $\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
, then its image, denoted by
$\mathrm{Irr}_{\mathrm{ps}}^d(B_\sigma ,({\mathbf {M}},\mu ))$
, then its image, denoted by
![]() $\mathcal {U}_{-}^{(\rho ,{\mathbf {M}},\mu )}$
, under the bijection above is an
$\mathcal {U}_{-}^{(\rho ,{\mathbf {M}},\mu )}$
, under the bijection above is an
![]() $A_{B,(\rho ,{\mathbf {M}},\mu )}$
-transversal in the set
$A_{B,(\rho ,{\mathbf {M}},\mu )}$
-transversal in the set
![]() $\mathrm{Irr}_{\mathrm{ps}}^d(B_\rho ,({\mathbf {M}},\mu ))$
because
$\mathrm{Irr}_{\mathrm{ps}}^d(B_\rho ,({\mathbf {M}},\mu ))$
because
![]() $A_{B,(\sigma ,{\mathbf {M}},\mu )}=A_{B,(\rho ,{\mathbf {M}},\mu )}$
.
$A_{B,(\sigma ,{\mathbf {M}},\mu )}=A_{B,(\rho ,{\mathbf {M}},\mu )}$
.
Now, by the discussion in the previous paragraph and using Lemma 5.3, we conclude that the sets of
![]() ${\mathbf {G}}^F$
-orbits
${\mathbf {G}}^F$
-orbits
and
are
![]() $A_B$
-transversals in the sets
$A_B$
-transversals in the sets
![]() ${\mathcal {L}}^d_{\mathrm{u}}(B)_+/{\mathbf {G}}^F$
and
${\mathcal {L}}^d_{\mathrm{u}}(B)_+/{\mathbf {G}}^F$
and
![]() ${\mathcal {L}}^d_{\mathrm{u}}(B)_-/{\mathbf {G}}^F$
respectively. Finally, we can define the bijection
${\mathcal {L}}^d_{\mathrm{u}}(B)_-/{\mathbf {G}}^F$
respectively. Finally, we can define the bijection
![]() $\Lambda $
by setting
$\Lambda $
by setting
for every
![]() $x\in A_B$
and every
$x\in A_B$
and every
![]() $(\sigma ,{\mathbf {M}},\mu ,\vartheta )\in \mathcal {L}_+$
and
$(\sigma ,{\mathbf {M}},\mu ,\vartheta )\in \mathcal {L}_+$
and
![]() $(\rho ,{\mathbf {M}},\mu ,\chi )\in \mathcal {L}_-$
satisfying the equality
$(\rho ,{\mathbf {M}},\mu ,\chi )\in \mathcal {L}_-$
satisfying the equality
![]() $\Delta (\sigma ,{\mathbf {M}},\mu )=(\rho ,{\mathbf {M}},\mu )$
and such that
$\Delta (\sigma ,{\mathbf {M}},\mu )=(\rho ,{\mathbf {M}},\mu )$
and such that
 $$\begin{align*}\chi=\begin{cases}\Omega^{B,d}_{\sigma,({\mathbf{M}},\mu)}(\vartheta),& \rho=\sigma+{\mathbf{M}} \\ \left(\Omega^{B,d}_{\rho,({\mathbf{M}},\mu)}\right)^{-1}(\vartheta),& \rho=\sigma-{\mathbf{M}}. \end{cases}\end{align*}$$
$$\begin{align*}\chi=\begin{cases}\Omega^{B,d}_{\sigma,({\mathbf{M}},\mu)}(\vartheta),& \rho=\sigma+{\mathbf{M}} \\ \left(\Omega^{B,d}_{\rho,({\mathbf{M}},\mu)}\right)^{-1}(\vartheta),& \rho=\sigma-{\mathbf{M}}. \end{cases}\end{align*}$$
Using (5.6) and (5.7) together with the definition of
![]() $\Lambda $
, we conclude that the properties required in the statement are satisfied and the proof is now complete.
$\Lambda $
, we conclude that the properties required in the statement are satisfied and the proof is now complete.
Now, as a consequence of Theorem 5.10 and Remark 5.8, we can finally prove Theorem A.
Proof of Theorem A.
We assume now that
![]() $\ell $
does not divide
$\ell $
does not divide
![]() $|{\mathbf {Z}}({\mathbf {G}})^F:{\mathbf {Z}}^\circ ({\mathbf {G}})^F|$
. Consider the bijection
$|{\mathbf {Z}}({\mathbf {G}})^F:{\mathbf {Z}}^\circ ({\mathbf {G}})^F|$
. Consider the bijection
![]() $\Lambda $
from Theorem 5.10, and choose
$\Lambda $
from Theorem 5.10, and choose
![]() $\omega \in {\mathcal {L}}^d_{\mathrm{ u}}(B)_+/{\mathbf {G}}^F$
,
$\omega \in {\mathcal {L}}^d_{\mathrm{ u}}(B)_+/{\mathbf {G}}^F$
,
![]() $(\sigma ,\vartheta )\in \omega ^\bullet $
and
$(\sigma ,\vartheta )\in \omega ^\bullet $
and
![]() $(\rho ,\chi )\in \Lambda (\omega )^\bullet $
. Then, we have
$(\rho ,\chi )\in \Lambda (\omega )^\bullet $
. Then, we have
with
![]() $J={\mathbf {G}}^F_\sigma $
, if
$J={\mathbf {G}}^F_\sigma $
, if
![]() $|\sigma |=|\rho |-1$
, or
$|\sigma |=|\rho |-1$
, or
![]() $J={\mathbf {G}}_\rho ^F$
, if
$J={\mathbf {G}}_\rho ^F$
, if
![]() $|\sigma |=|\rho |+1$
. In both cases, applying Remark 5.8, we deduce that
$|\sigma |=|\rho |+1$
. In both cases, applying Remark 5.8, we deduce that
as required by Theorem A.
5.3 Proof of Theorem B
Our final goal is to obtain a counting argument for unipotent characters as a consequence of Theorem 5.10. Recall that Dade’s Conjecture provides a way to determine the number of characters in a given
![]() $\ell $
-block B and with a given defect d in terms of
$\ell $
-block B and with a given defect d in terms of
![]() $\ell $
-local structures. Theorem B provides an adaptation of this idea to the unipotent characters of finite reductive groups by means of e-local structures compatible with e-Harish-Chandra theory (see Definition 5.5). For every
$\ell $
-local structures. Theorem B provides an adaptation of this idea to the unipotent characters of finite reductive groups by means of e-local structures compatible with e-Harish-Chandra theory (see Definition 5.5). For every
![]() $\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
, we define
$\sigma \in {\mathcal {L}}_e({\mathbf {G}},F)$
, we define
 $$ \begin{align} {\mathbf{k}}^d_{\mathrm{u}}(B_\sigma):=\sum\limits_{({\mathbf{M}},\mu)}{\mathbf{k}}_{\mathrm{ps}}^d(B_\sigma,({\mathbf{M}},\mu)), \end{align} $$
$$ \begin{align} {\mathbf{k}}^d_{\mathrm{u}}(B_\sigma):=\sum\limits_{({\mathbf{M}},\mu)}{\mathbf{k}}_{\mathrm{ps}}^d(B_\sigma,({\mathbf{M}},\mu)), \end{align} $$
where
![]() $({\mathbf {M}},\mu )$
runs over a set of representatives for the action of
$({\mathbf {M}},\mu )$
runs over a set of representatives for the action of
![]() ${\mathbf {G}}^F_\sigma $
on
${\mathbf {G}}^F_\sigma $
on
![]() ${\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
. First, we show a direct consequence of Theorem 5.10.
${\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
. First, we show a direct consequence of Theorem 5.10.
Theorem 5.11. Suppose that
![]() ${\mathbf {G}}$
is a simply connected group whose irreducible components are of type
${\mathbf {G}}$
is a simply connected group whose irreducible components are of type
![]() $\mathbf {A}$
,
$\mathbf {A}$
,
![]() $\mathbf {B}$
or
$\mathbf {B}$
or
![]() $\mathbf {C}$
, and assume that
$\mathbf {C}$
, and assume that
![]() $\ell $
is odd. For every block B of
$\ell $
is odd. For every block B of
![]() ${\mathbf {G}}^F$
and every nonnegative integer d, we have
${\mathbf {G}}^F$
and every nonnegative integer d, we have
where
![]() $\sigma $
runs over a set of representatives for the action of
$\sigma $
runs over a set of representatives for the action of
![]() ${\mathbf {G}}^F$
on
${\mathbf {G}}^F$
on
![]() ${\mathcal {L}}_e({\mathbf {G}},F)$
.
${\mathcal {L}}_e({\mathbf {G}},F)$
.
Proof. We determine the cardinality of the sets of
![]() ${\mathbf {G}}^F$
-orbits
${\mathbf {G}}^F$
-orbits
![]() ${\mathcal {L}}_{\mathrm{u}}^d(B)_\pm /{\mathbf {G}}^F$
. By applying Lemma 5.3, we obtain
${\mathcal {L}}_{\mathrm{u}}^d(B)_\pm /{\mathbf {G}}^F$
. By applying Lemma 5.3, we obtain
 $$ \begin{align} \left|{\mathcal{L}}_{\mathrm{u}}^d(B)_\pm/{\mathbf{G}}^F\right|=\sum\limits_{\sigma, ({\mathbf{M}},\mu)}{\mathbf{k}}^d_{\mathrm{ps}}(B_\sigma,({\mathbf{M}},\mu))=\sum\limits_{\sigma}{\mathbf{k}}^d_{\mathrm{u}}(B_\sigma), \end{align} $$
$$ \begin{align} \left|{\mathcal{L}}_{\mathrm{u}}^d(B)_\pm/{\mathbf{G}}^F\right|=\sum\limits_{\sigma, ({\mathbf{M}},\mu)}{\mathbf{k}}^d_{\mathrm{ps}}(B_\sigma,({\mathbf{M}},\mu))=\sum\limits_{\sigma}{\mathbf{k}}^d_{\mathrm{u}}(B_\sigma), \end{align} $$
where
![]() $\sigma $
runs over a set of representatives for the action of
$\sigma $
runs over a set of representatives for the action of
![]() ${\mathbf {G}}^F$
on
${\mathbf {G}}^F$
on
![]() ${\mathcal {L}}_e({\mathbf {G}},F)_\pm $
and
${\mathcal {L}}_e({\mathbf {G}},F)_\pm $
and
![]() $({\mathbf {M}},\mu )$
runs over a set of representatives for the action of
$({\mathbf {M}},\mu )$
runs over a set of representatives for the action of
![]() ${\mathbf {G}}^F_\sigma $
on
${\mathbf {G}}^F_\sigma $
on
![]() ${\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
. Since the sets
${\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma )$
. Since the sets
![]() ${\mathcal {L}}_{\mathrm{u}}^d(B)_+/{\mathbf {G}}^F$
and
${\mathcal {L}}_{\mathrm{u}}^d(B)_+/{\mathbf {G}}^F$
and
![]() ${\mathcal {L}}_{\mathrm{u}}^d(B)_-/{\mathbf {G}}^F$
have the same cardinality by Theorem 5.10, the equality in (5.9) implies that
${\mathcal {L}}_{\mathrm{u}}^d(B)_-/{\mathbf {G}}^F$
have the same cardinality by Theorem 5.10, the equality in (5.9) implies that
where now
![]() $\sigma $
runs over a set of representatives for the action of
$\sigma $
runs over a set of representatives for the action of
![]() ${\mathbf {G}}^F$
on
${\mathbf {G}}^F$
on
![]() ${\mathcal {L}}_e({\mathbf {G}},F)$
as claimed in the statement.
${\mathcal {L}}_e({\mathbf {G}},F)$
as claimed in the statement.
Before proving Theorem B, recall that
![]() ${\mathbf {k}}^d_{\mathrm{u}}(B)$
and
${\mathbf {k}}^d_{\mathrm{u}}(B)$
and
![]() ${\mathbf {k}}^d_{\mathrm{c, u}}(B)$
denote the number of irreducible characters belonging to the block B and with defect d that are unipotent and unipotent e-cuspidal, respectively.
${\mathbf {k}}^d_{\mathrm{c, u}}(B)$
denote the number of irreducible characters belonging to the block B and with defect d that are unipotent and unipotent e-cuspidal, respectively.
Proof of Theorem B.
Let
![]() ${\mathcal {L}}_\pm $
be a fixed set of representatives for the action of
${\mathcal {L}}_\pm $
be a fixed set of representatives for the action of
![]() ${\mathbf {G}}^F$
on
${\mathbf {G}}^F$
on
![]() ${\mathcal {L}}_e({\mathbf {G}},F)_\pm $
. We want isolate the contribution given by the trivial chain
${\mathcal {L}}_e({\mathbf {G}},F)_\pm $
. We want isolate the contribution given by the trivial chain
![]() $\sigma _0:=\{{\mathbf {G}}\}\in {\mathcal {L}}_e({\mathbf {G}},F)_+$
to the sum in (5.9). Since
$\sigma _0:=\{{\mathbf {G}}\}\in {\mathcal {L}}_e({\mathbf {G}},F)_+$
to the sum in (5.9). Since
![]() ${\mathbf {G}}$
is simple and simply connected, we deduce that
${\mathbf {G}}$
is simple and simply connected, we deduce that
![]() ${\mathbf {Z}}({\mathbf {G}}^*)^{F^*}$
is trivial and hence, recalling that
${\mathbf {Z}}({\mathbf {G}}^*)^{F^*}$
is trivial and hence, recalling that
![]() ${\mathbf {L}}(\sigma _0)={\mathbf {G}}$
, we obtain
${\mathbf {L}}(\sigma _0)={\mathbf {G}}$
, we obtain
![]() $\mathrm{ps}_{{\mathbf {L}}(\sigma )}(\mu )=\{\mu \}$
for every
$\mathrm{ps}_{{\mathbf {L}}(\sigma )}(\mu )=\{\mu \}$
for every
![]() $({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma _0)$
. Consequently, using Definition 5.2 and Definition 5.5, we deduce that
$({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma _0)$
. Consequently, using Definition 5.2 and Definition 5.5, we deduce that
 $$ \begin{align} {\mathbf{k}}_{\mathrm{u}}^d(B_{\sigma_0})&=\sum\limits_{({\mathbf{M}},\mu)}{\mathbf{k}}_{\mathrm{ps}}^d(B_{\sigma_0},({\mathbf{M}},\mu)) \\ &=\sum\limits_{({\mathbf{M}},\mu)}\left|\mathrm{Irr}^d(B)\cap {\mathcal{E}}({\mathbf{G}}^F,({\mathbf{M}},\mu))\right|\nonumber \\ &={\mathbf{k}}_{\mathrm{u}}^d(B)-{\mathbf{k}}_{\mathrm{c,u}}^d(B)\nonumber, \end{align} $$
$$ \begin{align} {\mathbf{k}}_{\mathrm{u}}^d(B_{\sigma_0})&=\sum\limits_{({\mathbf{M}},\mu)}{\mathbf{k}}_{\mathrm{ps}}^d(B_{\sigma_0},({\mathbf{M}},\mu)) \\ &=\sum\limits_{({\mathbf{M}},\mu)}\left|\mathrm{Irr}^d(B)\cap {\mathcal{E}}({\mathbf{G}}^F,({\mathbf{M}},\mu))\right|\nonumber \\ &={\mathbf{k}}_{\mathrm{u}}^d(B)-{\mathbf{k}}_{\mathrm{c,u}}^d(B)\nonumber, \end{align} $$
where the last equality follows from [Reference Broué, Malle and Michel9, Theorem 3.2 (1)] since each
![]() $({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma _0)$
satisfies
$({\mathbf {M}},\mu )\in {\mathcal {C} \mathcal {P}_{\mathrm{u}}}(\sigma _0)$
satisfies
![]() ${\mathbf {M}}<{\mathbf {G}}={\mathbf {L}}(\sigma _0)$
. Next, Theorem 5.10 implies that
${\mathbf {M}}<{\mathbf {G}}={\mathbf {L}}(\sigma _0)$
. Next, Theorem 5.10 implies that
![]() ${\mathcal {L}}_{\mathrm{u}}^d(B)_+/{\mathbf {G}}^F$
and
${\mathcal {L}}_{\mathrm{u}}^d(B)_+/{\mathbf {G}}^F$
and
![]() ${\mathcal {L}}_{\mathrm{u}}^d(B)_-/{\mathbf {G}}^F$
have the same cardinality, and therefore, we conclude from (5.9) and (5.10) that
${\mathcal {L}}_{\mathrm{u}}^d(B)_-/{\mathbf {G}}^F$
have the same cardinality, and therefore, we conclude from (5.9) and (5.10) that
 $$ \begin{align} {\mathbf{k}}^d_{\mathrm{u}}(B)-{\mathbf{k}}_{\mathrm{c,u}}^d(B)+\sum\limits_{\substack{\sigma\in{\mathcal{L}}_+\\\sigma\neq \sigma_0}}{\mathbf{k}}^d_{\mathrm{u}}(B_\sigma)=\sum\limits_{\sigma\in{\mathcal{L}}_+}{\mathbf{k}}^d_{\mathrm{ u}}(B_\sigma)=\sum\limits_{\sigma\in{\mathcal{L}}_-}{\mathbf{k}}^d_{\mathrm{u}}(B_\sigma). \end{align} $$
$$ \begin{align} {\mathbf{k}}^d_{\mathrm{u}}(B)-{\mathbf{k}}_{\mathrm{c,u}}^d(B)+\sum\limits_{\substack{\sigma\in{\mathcal{L}}_+\\\sigma\neq \sigma_0}}{\mathbf{k}}^d_{\mathrm{u}}(B_\sigma)=\sum\limits_{\sigma\in{\mathcal{L}}_+}{\mathbf{k}}^d_{\mathrm{ u}}(B_\sigma)=\sum\limits_{\sigma\in{\mathcal{L}}_-}{\mathbf{k}}^d_{\mathrm{u}}(B_\sigma). \end{align} $$
Finally, noticing that
![]() $(-1)^{|\sigma |+1}=\mp 1$
for every
$(-1)^{|\sigma |+1}=\mp 1$
for every
![]() $\sigma \in {\mathcal {L}}_\pm $
, we can rewrite (5.11) as
$\sigma \in {\mathcal {L}}_\pm $
, we can rewrite (5.11) as
 $$\begin{align*}{\mathbf{k}}^d_{\mathrm{u}}(B)-{\mathbf{k}}_{\mathrm{c,u}}^d(B)=\sum\limits_{\substack{\sigma\in{\mathcal{L}}_-\cup{\mathcal{L}}_+\\ \sigma\neq \sigma_0}}(-1)^{|\sigma|+1}{\mathbf{k}}^d_{\mathrm{u}}(B_\sigma)\end{align*}$$
$$\begin{align*}{\mathbf{k}}^d_{\mathrm{u}}(B)-{\mathbf{k}}_{\mathrm{c,u}}^d(B)=\sum\limits_{\substack{\sigma\in{\mathcal{L}}_-\cup{\mathcal{L}}_+\\ \sigma\neq \sigma_0}}(-1)^{|\sigma|+1}{\mathbf{k}}^d_{\mathrm{u}}(B_\sigma)\end{align*}$$
which is exactly the equality in the statement of Theorem B.
Acknowledgements
This paper was initiated during a research visit of the author at the Universitá degli Studi di Firenze. The author would like to thank Silvio Dolfi and all the members of the algebra group in the Department of Mathematics for their hospitality and, in particular, Carolina Vallejo for some comments concerning the local-global principle. Moreover, the author would like to thank Lucas Ruhstorfer for a helpful conversation on the paper [Reference Brough and Ruhstorfer12], Marc Cabanes for an insightful discussion on the historical development of some of the questions addressed in this work, Gunter Malle for several comments and suggestions on an earlier version that significantly improved the exposition of this paper and, finally, the anonymous referee for the valuable comments provided.
Competing interests
The author has no competing interests to declare.
Financial support
This work is supported by the grant EP/T
![]() $004592/1$
of the EPSRC and by the Walter Benjamin Programme of the DFG - Project number 525464727.
$004592/1$
of the EPSRC and by the Walter Benjamin Programme of the DFG - Project number 525464727.