1 INTRODUCTION
Sky-subtraction is one of the key links with vital importance in the data processing of the multi-object fibre spectroscopy. The precision will be affected by the mixed astigmatism in the telescope, the contamination of adjacent fibres, the transmission efficiency of the optical fibres, the accuracy of the wavelength calibration, etc. Except for reducing the influence of the aforementioned pretreatment processing by ramping up their degree of precision, it is particularly important to study the high precision methods for sky-substraction to improve the accuracy of the sky-subtraction fundamentally. Therefore, the focus of this paper lies in researching the sky-subtraction methods that are exist and being used on the famous multi-object fibre spectroscopic telescopes and proposing a new sky-subtraction method with higher precision.
Relatively well-known sky-subtraction methods are listed as follows. The traditional sky-subtraction method is beam-switching method (Barden et al. Reference Barden, Elston, Armandroff, Pryor and Gray1993). The object fibres and the corresponding sampling sky fibres are observed in pairs, sacrificing half of the object fibres or half of the observing time. To solve the problem, the nod-shuffle method is proposed (Glazebrook & Bland-Hawthorn Reference Glazebrook and Bland-Hawthorn2001). The object spectra and the corresponding sky spectra are obtained almost simultaneously and the accuracy of sky-subtraction under the condition of faint light is improved. The nod-shuffle method is used on pipeline of the Wide Field Spectrograph (WiFeS) (Childress et al. Reference Childress, Vogt, Nielsen and Sharp2014) in Australia. The sky background simulation methods are proposed to improve the efficiency of the optical observation, such as the B-spline curve fitting method (Kelson Reference Kelson2003). The B-spline curve fitting method has the ability of modelling the sky background flexibly. However, by B-spline curve fitting, all the sky fibres need to be arranged based on the wavelength and be combined into a complete sky fibre. In this procedure, all the sky fibres are thought to be the same. When the sky area is large, neglecting the differences amongst the sky fibres will bring superior error. Besides, due to the time consuming of the curve fitting modelling process, the method has low efficiency on processing the large-scale spectral data. The B-spline curve fitting method was used on SDSS on early stage (Gunn et al. Reference Gunn2006), and it is being used on Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST) (Luo et al. Reference Luo2015), the optical integral-field units (IFUs) of the Gemini GMOS-N spectrograph (Bolton & Burles Reference Bolton and Burles2007). The principal component analysis (PCA) is the common sky-subtraction method of the current frontier multi-object fibre spectroscopic data processing system, which was first put forward by Kurtz & Mink (Reference Kurtz and Mink2000). Then comes some improved and variant methods (Mink & Kurtz Reference Mink, Kurtz, Harnden, Primini and Payne2001; Wild & Hewett Reference Wild and Hewett2005; Sharp & Parkinson Reference Sharp and Parkinson2010). The PCA method is being used on the APOGEE pipeline of SDSS (Nidever et al. Reference Nidever2015), the WiggleZ Dark Energy survey (Drinkwater et al. Reference Drinkwater2010), and the Galaxy And Mass Assembly (GAMA) of AAOmega (Liske et al. Reference Liske2015).
Non-negative Matrix Factorisation (NMF) originates from PCA. The components in the vase vectors obtained from PCA have positive values and negative values, which is contradictory to the objective reality in many applications. NMF ensures the results to be non-negative, with the advantages of simple implementation and fast decomposition, it has been successfully applied in many fields of data analysis, especially for machine learning. NMF can automatically discover the hidden patterns or trends in the data. It is an effective tool to deal with large scale data processing and analysis. In view of the non-negativity of spectral energy, NMF method can be used to do sky-subtraction. A non-negative matrix factorisation with sparsity (NMF+S) method is proposed in this paper to achieve high-precision sky-subtraction.
The LAMOST is designed with both large aperture (effective aperture of 3.6–4.9 m) and wide field of view (FOV) (5°) (Cui et al. Reference Cui2012). It is equipped with 4 000 optical fibres and has 16 spectrographs with 32 CCDs. In each spectrograph, there are 250 fibres, 10 of them are sky fibres and the others are used for observing the targets, i.e the object fibres. The experiments are carried on simulated data from the LAMOST software system (Cui et al. Reference Cui2012; Zhang Reference Zhang2007), which are designed based on the parameters and characters of LAMOST, and real data provided by the LAMOST astronomical observatory (Luo et al. Reference Luo2015). Because of the similar mechanism of multi-object fibre spectroscopic telescopes, the method proposed can also be applied to other telescopes and has referential significance for other surveys.
2 THE NMF+S SKY-SUBTRACTION METHOD
2.1. Proposing a new NMF+S method
NMF is a method by which a m × n matrix X, is approximated by the product of m × r matrix W and r × n matrix H, enforcing the constraint that all matrices are non-negative,
To find an approximate factorisation of equation (1), a cost function can be constructed using some measure of distance between W and H (Lee & Seung Reference Lee and Seung2001). Considering the feature of skylight, to effectively correspond to a Poission process, the generalised Kullback–Leibler (KL) divergence is chosen here:
Sparse NMF is an extension of NMF, an additional sparsity constraint is added to the cost function (Schmidt & Olsson Reference Schmidt and Olsson2006):
Considering the characteristic of the skylight, the flux of the sky fibres on each position in wavelength orientation has consistency, so an additional two-norm constraint is enforced on the matrix W.
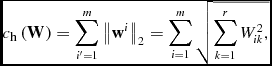 $$\begin{equation}
{c_{\text{h}}}\left( {{\bf W}} \right) = \sum \limits_{i^{\prime } = 1}^m {{{\left\Vert {{{{\bf w}}^i}} \right\Vert }_2}} = \sum \limits_{i = 1}^m {\sqrt{\sum \limits_{k = 1}^r {W_{ik}^2}, } }
\end{equation}$$
$$\begin{equation}
{c_{\text{h}}}\left( {{\bf W}} \right) = \sum \limits_{i^{\prime } = 1}^m {{{\left\Vert {{{{\bf w}}^i}} \right\Vert }_2}} = \sum \limits_{i = 1}^m {\sqrt{\sum \limits_{k = 1}^r {W_{ik}^2}, } }
\end{equation}$$
where w i is a row vector of W. ‖w i ‖2 stands for the norm of vector w i .
Thus, the cost function is defined as
where α is a penalty term that enforces the sparsity and controls the trade-off between sparsity and accuracy of the approximation. β is the penalty term of the consistency constraint.
The multiplicative update rules are used to minimise equation (5) (Le Roux, Weninger, & Hershey Reference Le Roux, Weninger and Hershey2015). The gradients of the cost function are calculated to gain the update criterions of H and W.
 $$\begin{equation}
\begin{array}{*{20}{l}}\frac{{\partial c\left( {{{\bf W}},{{\bf H}}} \right)}}{{\partial {W_{ik}}}}\\
{ = \frac{\partial }{{\partial {W_{ik}}}}\left( {\sum \limits _{ij} {\left( {{X_{ij}}\log \frac{{{X_{ij}}}}{{\left( {{W_{ik}} \cdot {H_{kj}}} \right)}} - {X_{ij}} + {W_{ik}} \cdot {H_{kj}}} \right)} } \right.}\\
\quad{\left. { + \alpha \sum \limits _{k,j} {{H_{kj}}} + \beta \sum \limits _{i = 1}^m {\sqrt{\sum \limits _{k = 1}^r {W_{ik}^2} } } } \right)}\\
{ = - \sum \limits _j {{X_{ij}} \cdot \frac{1}{{{W_{ik}} \cdot {H_{kj}}}}} \cdot {H_{kj}} + \sum \limits _j {{H_{kj}}} {\rm { + }}\beta \cdot \frac{1}{{\sqrt{\sum \limits _{k = 1}^r {W_{ik}^2} } }} \cdot {W_{ik}}} \end{array}
\end{equation}$$
$$\begin{equation}
\begin{array}{*{20}{l}}\frac{{\partial c\left( {{{\bf W}},{{\bf H}}} \right)}}{{\partial {W_{ik}}}}\\
{ = \frac{\partial }{{\partial {W_{ik}}}}\left( {\sum \limits _{ij} {\left( {{X_{ij}}\log \frac{{{X_{ij}}}}{{\left( {{W_{ik}} \cdot {H_{kj}}} \right)}} - {X_{ij}} + {W_{ik}} \cdot {H_{kj}}} \right)} } \right.}\\
\quad{\left. { + \alpha \sum \limits _{k,j} {{H_{kj}}} + \beta \sum \limits _{i = 1}^m {\sqrt{\sum \limits _{k = 1}^r {W_{ik}^2} } } } \right)}\\
{ = - \sum \limits _j {{X_{ij}} \cdot \frac{1}{{{W_{ik}} \cdot {H_{kj}}}}} \cdot {H_{kj}} + \sum \limits _j {{H_{kj}}} {\rm { + }}\beta \cdot \frac{1}{{\sqrt{\sum \limits _{k = 1}^r {W_{ik}^2} } }} \cdot {W_{ik}}} \end{array}
\end{equation}$$
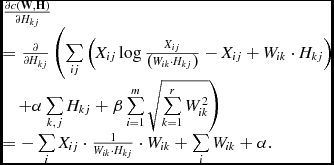 $$\begin{equation}
\begin{array}{*{20}{l}}\frac{{\partial c\left( {{{\bf W}},{{\bf H}}} \right)}}{{\partial {H_{kj}}}}\\
{ = \frac{\partial }{{\partial {H_{kj}}}}\left( {\sum \limits _{ij} {\left( {{X_{ij}}\log \frac{{{X_{ij}}}}{{\left( {{W_{ik}} \cdot {H_{kj}}} \right)}} - {X_{ij}} + {W_{ik}} \cdot {H_{kj}}} \right)} } \right.}\\
\quad{\left. { + \alpha \sum \limits _{k,j} {{H_{kj}}} + \beta \sum \limits _{i = 1}^m {\sqrt{\sum \limits _{k = 1}^r {W_{ik}^2} } } } \right)}\\
{ = - \sum \limits _i {{X_{ij}} \cdot \frac{1}{{{W_{ik}} \cdot {H_{kj}}}}} \cdot {W_{ik}} + \sum \limits _i {{W_{ik}}} + \alpha }. \end{array}
\end{equation}$$
$$\begin{equation}
\begin{array}{*{20}{l}}\frac{{\partial c\left( {{{\bf W}},{{\bf H}}} \right)}}{{\partial {H_{kj}}}}\\
{ = \frac{\partial }{{\partial {H_{kj}}}}\left( {\sum \limits _{ij} {\left( {{X_{ij}}\log \frac{{{X_{ij}}}}{{\left( {{W_{ik}} \cdot {H_{kj}}} \right)}} - {X_{ij}} + {W_{ik}} \cdot {H_{kj}}} \right)} } \right.}\\
\quad{\left. { + \alpha \sum \limits _{k,j} {{H_{kj}}} + \beta \sum \limits _{i = 1}^m {\sqrt{\sum \limits _{k = 1}^r {W_{ik}^2} } } } \right)}\\
{ = - \sum \limits _i {{X_{ij}} \cdot \frac{1}{{{W_{ik}} \cdot {H_{kj}}}}} \cdot {W_{ik}} + \sum \limits _i {{W_{ik}}} + \alpha }. \end{array}
\end{equation}$$
Extending equations (6) and (7) to vector derivation, we have
 $$\begin{eqnarray*}
\begin{array}{l}{\bf D} = \beta \cdot diag\left( {{\bf d}} \right)\\
{{\bf d}} = {\left( {\frac{1}{{{{\left\Vert {{{{\bf w}}^1}} \right\Vert }_2}}}, \ldots ,\frac{1}{{{{\left\Vert {{{{\bf w}}^i}} \right\Vert }_2}}}, \ldots ,\frac{1}{{{{\left\Vert {{{{\bf w}}^m}} \right\Vert }_2}}}} \right)^T}, \end{array}
\end{eqnarray*}$$
$$\begin{eqnarray*}
\begin{array}{l}{\bf D} = \beta \cdot diag\left( {{\bf d}} \right)\\
{{\bf d}} = {\left( {\frac{1}{{{{\left\Vert {{{{\bf w}}^1}} \right\Vert }_2}}}, \ldots ,\frac{1}{{{{\left\Vert {{{{\bf w}}^i}} \right\Vert }_2}}}, \ldots ,\frac{1}{{{{\left\Vert {{{{\bf w}}^m}} \right\Vert }_2}}}} \right)^T}, \end{array}
\end{eqnarray*}$$
where diag(d) indicates a square diagonal matrix with the elements of vector d on the main diagonal. 1 stands for a m × n matrix with all elements equal to 1.
Then, the complete algorithm for the proposed NMF+S is given by the following rules:
-
(1) Initialise H and W randomly.
-
(2) Normalise the basis vectors according to
 ${{\bf W}} \leftarrow {{\bf \bar{W}}}$
, where
${{\bf W}} \leftarrow {{\bf \bar{W}}}$
, where
 ${{{\bf \bar{W}}}}$
is the columnwise normalised basis matrix.
${{{\bf \bar{W}}}}$
is the columnwise normalised basis matrix. -
(3) Calculate the reconstruction according to
(10) $$\begin{equation}
{{\bf \hat{X}}}{\rm {\; =\; }}{{\bf \bar{W}H}}.
\end{equation}$$
$$\begin{equation}
{{\bf \hat{X}}}{\rm {\; =\; }}{{\bf \bar{W}H}}.
\end{equation}$$
-
(4) Update the activities according to
(11) $$\begin{equation}
{{\bf H}} \leftarrow {{\bf H}} \bullet \frac{{{{{{\bf \bar{W}}}}^{{\bf T}}} \cdot \left( {\frac{{{\bf X}}}{{{{\bf \bar{W}H}}}}} \right)}}{{{{{{\bf \bar{W}}}}^{{\bf T}}} \cdot {{\bf 1}} + \alpha }}.
\end{equation}$$
$$\begin{equation}
{{\bf H}} \leftarrow {{\bf H}} \bullet \frac{{{{{{\bf \bar{W}}}}^{{\bf T}}} \cdot \left( {\frac{{{\bf X}}}{{{{\bf \bar{W}H}}}}} \right)}}{{{{{{\bf \bar{W}}}}^{{\bf T}}} \cdot {{\bf 1}} + \alpha }}.
\end{equation}$$
The operator • indicates pointwise multiplication and
 ${\frac{{{\bf X}}}{{{{\bf \bar{W}H}}}}}$
indicates pointwise division.
${\frac{{{\bf X}}}{{{{\bf \bar{W}H}}}}}$
indicates pointwise division. -
(5) Calculate the reconstruction with the new activities according to
(12) $$\begin{equation}
{{\bf \hat{X}}}{\rm { = }}{{\bf \bar{W}H}}.
\end{equation}$$
$$\begin{equation}
{{\bf \hat{X}}}{\rm { = }}{{\bf \bar{W}H}}.
\end{equation}$$
-
(6) Update the basis vectors according to
(13) $$\begin{equation}
{{\bf W}} \leftarrow {{\bf W}} \bullet \frac{{\left( {\frac{{{\bf X}}}{{{{\bf \bar{W}H}}}}} \right) \cdot {{{\bf H}}^{{\bf T}}}}}{{{{\bf 1}} \cdot {{{\bf H}}^{{\bf T}}} + {{\bf D}} \cdot {{\bf \bar{W}}}}}.
\end{equation}$$
$$\begin{equation}
{{\bf W}} \leftarrow {{\bf W}} \bullet \frac{{\left( {\frac{{{\bf X}}}{{{{\bf \bar{W}H}}}}} \right) \cdot {{{\bf H}}^{{\bf T}}}}}{{{{\bf 1}} \cdot {{{\bf H}}^{{\bf T}}} + {{\bf D}} \cdot {{\bf \bar{W}}}}}.
\end{equation}$$
-
(7) Normalise the basis vectors according to
 ${{\bf W}} \leftarrow {{\bf \bar{W}}}$
.
${{\bf W}} \leftarrow {{\bf \bar{W}}}$
. -
(8) Return to (3) until convergence.
2.2. Sky-subtraction using the proposed NMF+S method
In reducing the skylight, fibre efficiency corrections for the sky fibres and the object fibres are done first. Due to the different dispersion curves of each fibre, the wavelengths of each fibre are interpolated to a uniform wavelength coordinate.
The sky spectrum is composed of sky emission lines
![]() ${{\bf \tilde{S}}}$
and continuous spectrum
${{\bf \tilde{S}}}$
and continuous spectrum
![]() ${{\bf \bar{S}}}$
. To separate them, median filtering is done on each sky spectrum. As the deviation of the continuous spectrum in each sky fibre is small, the mean value of the continuous spectrum of all the sky fibres is taken as the continuous spectrum flux. Subtracting the continuous spectrum flux from each sky spectrum, the flux of the sky emission lines
${{\bf \bar{S}}}$
. To separate them, median filtering is done on each sky spectrum. As the deviation of the continuous spectrum in each sky fibre is small, the mean value of the continuous spectrum of all the sky fibres is taken as the continuous spectrum flux. Subtracting the continuous spectrum flux from each sky spectrum, the flux of the sky emission lines
![]() ${{\bf \tilde{S}}}$
is obtained to do the NMF training. Do the median filtering in the same way on the object spectra O, the flux of the sky emission lines
${{\bf \tilde{S}}}$
is obtained to do the NMF training. Do the median filtering in the same way on the object spectra O, the flux of the sky emission lines
![]() ${{\bf \tilde{O}}}$
of the object spectra is obtained to do the NMF testing.
${{\bf \tilde{O}}}$
of the object spectra is obtained to do the NMF testing.
In order to improve the operational speed of NMF, formulate a criteria to select the pixels containing components of skylights, such as calculating the variance or mean value of the flux on each wavelength position of each fibre. As the sky emission lines are considered to be positive, the non-negativeness of the flux is also included in the criteria. Mark the locations of these points on the sky emission lines
![]() ${{\bf \tilde{S}}}$
. The selected pixels of sky fibres form a sky sample matrix
${{\bf \tilde{S}}}$
. The selected pixels of sky fibres form a sky sample matrix
![]() ${{{\bf X}}_{\tilde{S}}}$
for NMF training. Select the pixels in the same marked locations in the wavelength orientation on the object spectra, forming the object sampling matrix
${{{\bf X}}_{\tilde{S}}}$
for NMF training. Select the pixels in the same marked locations in the wavelength orientation on the object spectra, forming the object sampling matrix
![]() ${{{\bf X}}_{\tilde{O}}}$
for NMF testing.
${{{\bf X}}_{\tilde{O}}}$
for NMF testing.
For the 10 sky fibres on LAMOST, the selected sample matrix
![]() ${{{\bf X}}_{\tilde{S}}}$
can be formulated as
${{{\bf X}}_{\tilde{S}}}$
can be formulated as
Utilising the NMF+S method in Section 2.1 for training, W is obtained. Then, take it as the base vectors, keeping fixed, to do testing with the selected sample matrix of the object fibres, by the NMF+S method in Section 2.1.
Through the NMF+S method, the sky emission lines on the selected positions
![]() ${{{\bf \tilde{S}}}_{\text{select}}}$
are rebuilt by
${{{\bf \tilde{S}}}_{\text{select}}}$
are rebuilt by
Replacing the flux of
![]() ${{{\bf \tilde{S}}}_{\text{select}}}$
in
${{{\bf \tilde{S}}}_{\text{select}}}$
in
![]() ${{\bf \tilde{S}}}$
on the selected positions and remaining the flux of other positions unchanged,
${{\bf \tilde{S}}}$
on the selected positions and remaining the flux of other positions unchanged,
![]() ${{\bf \tilde{S}}}$
is refreshed as
${{\bf \tilde{S}}}$
is refreshed as
![]() ${{{\bf \tilde{S}}}^\prime }$
. Adding the continuous spectral part of the sky
${{{\bf \tilde{S}}}^\prime }$
. Adding the continuous spectral part of the sky
![]() ${{\bf \bar{S}}}$
, the sky is reconstructed. The flux of the object spectra after sky-subtraction can be expressed as
${{\bf \bar{S}}}$
, the sky is reconstructed. The flux of the object spectra after sky-subtraction can be expressed as
3 EXPERIMENTS AND DISCUSSION
3.1. Simulated data on LAMOST
The experiments in this part are simulated data from LAMOST software system (Cui et al. Reference Cui2012). The data is designed strictly in accordance with the characteristics of LAMOST. The 250 fibres, 10 of which are sky fibres, are exactly simulated as the real data on LAMOST. Each of the fibres has 4 096 pixels in the wavelength orientation. The detailed simulation mechanisms and the relevant parameters can be found in a dissertation (Zhang Reference Zhang2007).
Taking all the errors of the instruments and the influences of noises into account, the simulated object spectra can be expressed as
 $$\begin{equation}
\begin{array}{l}O\left( {i,\lambda } \right) = \left\lbrace {\left[ {{O_{\text{r}}}\left( {i,\lambda } \right) \times {d_{\text{sky}}}\left( \lambda \right) + \rm sk{y_r}\left( \lambda \right)} \right] \times {d_{\text{tel}}}\left( \lambda \right)} \right.\\
\quad\left. { \times {d_{\text{fib}}}\left( {i,\lambda } \right) \times {d_{\text{spm}}}\left( {i,\lambda } \right) + \text{scatter}\left( {i,\lambda } \right)} \right\rbrace \times {d_{\text{CCD}}}\left( {i,\lambda } \right)\\
\quad + {c_{\text{h}}}\left( {i,\lambda } \right) + \text{Bias} \end{array}
\end{equation}$$
$$\begin{equation}
\begin{array}{l}O\left( {i,\lambda } \right) = \left\lbrace {\left[ {{O_{\text{r}}}\left( {i,\lambda } \right) \times {d_{\text{sky}}}\left( \lambda \right) + \rm sk{y_r}\left( \lambda \right)} \right] \times {d_{\text{tel}}}\left( \lambda \right)} \right.\\
\quad\left. { \times {d_{\text{fib}}}\left( {i,\lambda } \right) \times {d_{\text{spm}}}\left( {i,\lambda } \right) + \text{scatter}\left( {i,\lambda } \right)} \right\rbrace \times {d_{\text{CCD}}}\left( {i,\lambda } \right)\\
\quad + {c_{\text{h}}}\left( {i,\lambda } \right) + \text{Bias} \end{array}
\end{equation}$$
where,
![]() ${O_{\text{r}}}$
is the flux of the object outside the atmosphere.
${O_{\text{r}}}$
is the flux of the object outside the atmosphere.
![]() ${d_{\text{sky}}}$
is the atmospheric extinction function. skyr is the flux of the sky.
${d_{\text{sky}}}$
is the atmospheric extinction function. skyr is the flux of the sky.
![]() ${d_{\text{tel}}}$
is the flux response function of the optical telescope system.
${d_{\text{tel}}}$
is the flux response function of the optical telescope system.
![]() ${d_{\text{fib}}}$
is the optical fibre transmissivity.
${d_{\text{fib}}}$
is the optical fibre transmissivity.
![]() ${d_{\text{spm}}}$
is the flux response function of the spectrograph, i.e. the influence of spectrometer dispersion on flux, containing the distortion and the vignetting of the spectra.
${d_{\text{spm}}}$
is the flux response function of the spectrograph, i.e. the influence of spectrometer dispersion on flux, containing the distortion and the vignetting of the spectra.
![]() $\text{scatter}$
is the flux of the stray light, containing the uniform stray light and the contamination from adjacent fibres.
$\text{scatter}$
is the flux of the stray light, containing the uniform stray light and the contamination from adjacent fibres.
![]() ${d_{\text{CCD}}}$
is the response function of CCDs.
${d_{\text{CCD}}}$
is the response function of CCDs.
![]() ${c_{\text{h}}}$
is the flux of the cosmic ray.
${c_{\text{h}}}$
is the flux of the cosmic ray.
![]() $\text{Bias}$
is the background flux of the CCDs.
$\text{Bias}$
is the background flux of the CCDs.
The sky can be expressed as
More details of the simulation refer to Zhang (Reference Zhang2007).
The sky spectrum contains emission lines and continuous spectrum. The emission lines are simulated by the existing empirical data. The continuous spectrum is derived from the empirical formula. Since the sky emission lines assume highly localised distributions in the red channel, and the flux of them is generally higher than the blue channel, the experiments are carried on the red channel as the condition described above is more difficult for sky-subtraction. The sky-subtraction is carried out after the bias subtraction, flat field correction, centroid tracing, spectrum extraction, and wavelength calibration (Luo et al. Reference Luo2015).
The two B-spline curve fitting methods in Zhu & Ye (Reference Zhu and Ye2012) (The 2-D B-spline method has been proposed in it. The 1-D B-spline method in it is being used on LAMOST (Luo et al. Reference Luo2015)) and the PCA method (Sharp & Parkinson Reference Sharp and Parkinson2010) being used on the APOGEE pipeline of SDSS (Nidever et al. Reference Nidever2015) are contrast methods to demonstrate the effectiveness and superiority of the proposed NMF+S sky-subtraction method.
In the experiments, considering the width of the sky emission lines, a median filter with window length 111 is done on the flux of the sky to calculate the continuous spectrum of skylight
![]() ${{\bf \bar{S}}}$
. The criterion to select the sample pixels in the NMF+S method is selecting the pixels whose flux is bigger than 10% of the max flux. By debugging the parameters, we found that the parameters chosen in the training and testing of the proposed NMF method are the same. The parameters in the proposed method are chosen as α = 1.5, β = 6. The number of basis vectors is 15, which is a little bigger than the number of sky fibres, i.e. 10, to retain some redundancy.
${{\bf \bar{S}}}$
. The criterion to select the sample pixels in the NMF+S method is selecting the pixels whose flux is bigger than 10% of the max flux. By debugging the parameters, we found that the parameters chosen in the training and testing of the proposed NMF method are the same. The parameters in the proposed method are chosen as α = 1.5, β = 6. The number of basis vectors is 15, which is a little bigger than the number of sky fibres, i.e. 10, to retain some redundancy.
The sky-subtraction result on fibre 130 by the proposed method is shown in Figure 1.

Figure 1. Sky-subtraction results on fibre 130 in the red channel by the proposed NMF+S method, from top to bottom: The original object spectrum, the reconstructed sky spectrum, the object spectrum after sky-subtraction.
The experimental results on contrast methods are shown in Figures 2 and 3.

Figure 2. Comparison results of the reconstructed sky spectrum on fibre 130 in the red channel. (a) B-spline method in LAMOST reduction. (b) 2-D B-spline method in Zhu & Ye (Reference Zhu and Ye2012). (c) PCA method (d) NMF+S method.

Figure 3. Comparison results of the object spectrum after sky-subtraction on fibre 130 in the red channel. (a) B-spline method in LAMOST reduction. (b) 2-D B-spline method in Zhu & Ye (Reference Zhu and Ye2012). (c) PCA method (d) NMF+S method.
The experimental result figures show that the PCA method and the NMF+S method are more accurate than the B-spline methods, based on the facts that the object spectrum after sky-subtraction is more smooth with less burrs, illustrating that the sky emission lines are subtracted more completely. Since the difference between the PCA method and the NMF+S method is not obvious, and moreover, to validate the performance of the proposed algorithm, a target of variance is defined to measure the accuracy of the methods objectively and mathematically. The variance of the object spectrum after sky-subtraction is defined as
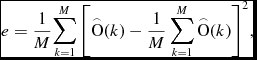 $$\begin{equation}
{{e}} = \frac{1}{M}{\sum \limits _{k = 1}^M {\left[ {{\rm {\mathord {\buildrel{\lower3pt\hbox{$\scriptscriptstyle \frown $}} \over O} }}(k) - \frac{1}{M}\sum \limits _{k = 1}^M {{\rm {\mathord {\buildrel{\lower3pt\hbox{$\scriptscriptstyle \frown $}} \over O} }}(k)} } \right]} ^2},
\end{equation}$$
$$\begin{equation}
{{e}} = \frac{1}{M}{\sum \limits _{k = 1}^M {\left[ {{\rm {\mathord {\buildrel{\lower3pt\hbox{$\scriptscriptstyle \frown $}} \over O} }}(k) - \frac{1}{M}\sum \limits _{k = 1}^M {{\rm {\mathord {\buildrel{\lower3pt\hbox{$\scriptscriptstyle \frown $}} \over O} }}(k)} } \right]} ^2},
\end{equation}$$
where
![]() ${\rm {\mathord {\buildrel{\lower3pt\hbox{$\scriptscriptstyle \frown $}} \over O} }}(k)$
stands for the flux of the object spectrum after sky-subtraction, M is the number of pixels on the wavelength of the full object spectrum. The smaller the value of e is, the less the sky emission lines residuals of the object spectrum are, i.e. the more complete the sky-subtraction is.
${\rm {\mathord {\buildrel{\lower3pt\hbox{$\scriptscriptstyle \frown $}} \over O} }}(k)$
stands for the flux of the object spectrum after sky-subtraction, M is the number of pixels on the wavelength of the full object spectrum. The smaller the value of e is, the less the sky emission lines residuals of the object spectrum are, i.e. the more complete the sky-subtraction is.
Ten object fibre spectra are selected randomly and the variances of them after sky-subtraction are shown in Table 1.
Table 1. The variances e of the object spectra after sky-subtraction by contrast methods.
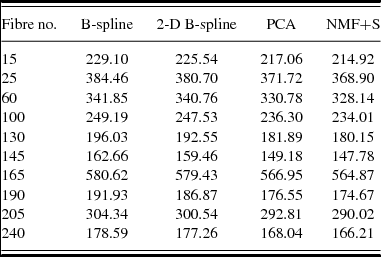
The statistical data in the Table 1 shows that the proposed NMF+S method on sky reduction has the minimum variance, indicating that it is the most thorough sky-subtraction method to some extent. Furthermore, as the NMF methods have many variant, with appropriate improvements, the algorithm proposed has great room for improvement.
3.2. Real data on LAMOST
To verify the accuracy and practicability of the proposed algorithm, we repeat the experiments on LAMOST real data. The data are provided by LAMOST astronomical observatory (Luo et al. Reference Luo2015). In view of the performances of the methods in section 3.1, the PCA method (Sharp & Parkinson Reference Sharp and Parkinson2010) is taken as the contrast method.
As there are cosmic rays in real data, to avoid the influence of them in sky background modelling, the cosmic rays in the sky should be eliminated when choosing the sky sample matrix
![]() ${{{\bf X}}_{\tilde{S}}}$
. The criterions to select the sample pixels in the NMF+S method and the PCA method are both based on the flux and the variance of the spectra. For the NMF+S method, the non-negativeness of the sample pixels is also considered as an additional criterion. The numbers of the sample pixels in both the NMF+S method and the PCA method are about the same. The parameters in the proposed method are chosen as α = 0.1, β = 3. Other parameters used are the same as section 3.1.
${{{\bf X}}_{\tilde{S}}}$
. The criterions to select the sample pixels in the NMF+S method and the PCA method are both based on the flux and the variance of the spectra. For the NMF+S method, the non-negativeness of the sample pixels is also considered as an additional criterion. The numbers of the sample pixels in both the NMF+S method and the PCA method are about the same. The parameters in the proposed method are chosen as α = 0.1, β = 3. Other parameters used are the same as section 3.1.
The sky-subtraction result on fibre 130 by the proposed method is shown in Figure 4.

Figure 4. Sky-subtraction results on fibre 40 in the red channel by the proposed NMF+S method, from top to bottom: The original object spectrum, the reconstructed sky spectrum, the object spectrum after sky-subtraction. To make it seem more clear, the original object spectrum is moved up to 30 000, the reconstructed sky spectrum is moved up to 10 000.
The experimental results on contrast method are shown in Figures 5 and 6.

Figure 5. Comparison results of the reconstructed sky spectrum on fibre 40 in the red channel. top: PCA method; bottom: NMF+S method.

Figure 6. Comparison results of the object spectrum after sky-subtraction on fibre 40 in the red channel. top: PCA method; bottom: NMF+S method.
The high flux emission lines of in Figures 5 and 6 are the cosmic rays in the object spectrum fibre 40. The cosmic rays in the object spectra will be removed in the subsequent processing steps.
Ten object fibre spectra are selected randomly and the variances of them after sky-subtraction are shown in Table 2. The cosmic rays in the object spectra is included when calculating the variances.
Table 2. The variances e of the object spectra after sky-subtraction by contrast methods.
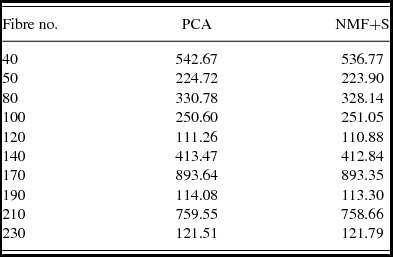
The results of the experiments on real data show that in most instances, the accuracy of the NMF+S method is higher than the PCA method. As the real data is more unstable, the performance of the proposed method is close to but better than the PCA method.
4 CONCLUSION
A novel sky-subtraction method based on an improved NMF+S method has been proposed in this paper. The method has been designed for sky-subtraction step of the surveys on multi-object fibre spectroscopy. Taking the characteristics of the skylights into account, the proposed NMF+S method has a sparseness constraint term and a homogeneity constraint term. By experiments on LAMOST data, the proposed method has higher accuracy and flexibility, contrasted to the universal sky-subtraction methods, such as the B-spline curve fitting methods and the PCA method. Since the mechanisms of the multi-object fibre spectroscopic telescopes are similar, the proposed NMF+S method has research value for sky-subtraction in the surveys on all multi-object fibre spectroscopic telescopes.
ACKNOWLEDGEMENTS
The authors acknowledge support from the National Natural Science Foundation of China (NSFC 11078016).











