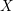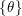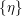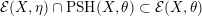1 Introduction and main results
Since the fundamental work of Aubin [Reference AubinAub78] and Yau [Reference YauYau78], the complex Monge–Ampère operator has found many important applications in differential geometry. In this vast area of research, pluripotential theory plays a crucial role, initiated by the seminal work of Bedford and Taylor [Reference Bedford and TaylorBT76, Reference Bedford and TaylorBT82, Reference Bedford and TaylorBT87] and Kołodziej [Reference KołodziejKoł98], to only mention a few.
Guedj and Zeriahi extended Bedford–Taylor theory to compact Kähler manifolds
![]() $(X,\unicode[STIX]{x1D714})$
[Reference Guedj and ZeriahiGZ05, Reference Guedj and ZeriahiGZ07]. Their idea was to extend the definition of the complex Monge–Ampère operator to much larger sets of potentials, not only bounded ones. As a result, an adequate variational theory could be devised for global equations of complex Monge–Ampère type [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11] that has found many striking applications in Kähler geometry.
$(X,\unicode[STIX]{x1D714})$
[Reference Guedj and ZeriahiGZ05, Reference Guedj and ZeriahiGZ07]. Their idea was to extend the definition of the complex Monge–Ampère operator to much larger sets of potentials, not only bounded ones. As a result, an adequate variational theory could be devised for global equations of complex Monge–Ampère type [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11] that has found many striking applications in Kähler geometry.
Additionally, the methods of [Reference Guedj and ZeriahiGZ07] have proven to be very robust, as they also apply in case of big cohomology classes that are non-Kähler, as explored in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10]. Given a closed smooth
![]() $(1,1)$
-form
$(1,1)$
-form
![]() $\unicode[STIX]{x1D703}$
on
$\unicode[STIX]{x1D703}$
on
![]() $X$
, we say that the class
$X$
, we say that the class
![]() $\{\unicode[STIX]{x1D703}\}$
is big, if there exists a quasi-plurisubharmonic function
$\{\unicode[STIX]{x1D703}\}$
is big, if there exists a quasi-plurisubharmonic function
![]() $u$
on
$u$
on
![]() $X$
such that
$X$
such that
 $\unicode[STIX]{x1D703}+dd^{c}u\geqslant \unicode[STIX]{x1D700}\unicode[STIX]{x1D714}$
for some
$\unicode[STIX]{x1D703}+dd^{c}u\geqslant \unicode[STIX]{x1D700}\unicode[STIX]{x1D714}$
for some
![]() $\unicode[STIX]{x1D700}>0$
. Non-Kähler big classes arise naturally in constructions of algebraic geometry. Given a one point blowup of an arbitrary Kähler manifold, the simplest such example is given by the sum of the exceptional divisor class and a ‘sufficiently small’ Kähler class.
$\unicode[STIX]{x1D700}>0$
. Non-Kähler big classes arise naturally in constructions of algebraic geometry. Given a one point blowup of an arbitrary Kähler manifold, the simplest such example is given by the sum of the exceptional divisor class and a ‘sufficiently small’ Kähler class.
When varying Kähler classes, one often has to study degenerate classes as well, and there has been a lot of work in trying to characterize the degenerate classes that admit special Kähler metrics [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11, Reference DarvasDar16, Reference Spotti, Sun and YaoSSY16]. Recently, the solution to the complex Monge–Ampère equation in a big class has been used to show that on a projective manifold the cone of pseudoeffective classes is dual to the movable cone, solving an important open problem in complex algebraic geometry [Reference Witt Nyström and BoucksomWB16].
In most of the above-mentioned works that study degenerate metrics, finite energy pluripotential theory plays an important role. Partly motivated by this, and partly by a survey of open questions [Reference Dinew, Guedj and ZeriahiDGZ16], we will investigate further the finite energy pluripotential theory of big cohomology classes. For a big class
![]() $\{\unicode[STIX]{x1D703}\}$
, the class of full mass currents
$\{\unicode[STIX]{x1D703}\}$
, the class of full mass currents
![]() ${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
is of central interest, as in many ways it is the analog of the classical Sobolev spaces, given the role it plays in the variational study of complex Monge–Ampère equations (for the precise definition, see § 2.1). Our first main result clarifies the local/global singular behavior of potentials in
${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
is of central interest, as in many ways it is the analog of the classical Sobolev spaces, given the role it plays in the variational study of complex Monge–Ampère equations (for the precise definition, see § 2.1). Our first main result clarifies the local/global singular behavior of potentials in
![]() ${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
in various settings of geometric interest.
${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
in various settings of geometric interest.
Theorem 1.1. Let
![]() $(X,\unicode[STIX]{x1D714})$
be a Kähler manifold. Assume that
$(X,\unicode[STIX]{x1D714})$
be a Kähler manifold. Assume that
![]() $\unicode[STIX]{x1D703}$
is a smooth closed
$\unicode[STIX]{x1D703}$
is a smooth closed
![]() $(1,1)$
-form such that
$(1,1)$
-form such that
![]() $\{\unicode[STIX]{x1D703}\}$
is big. Let
$\{\unicode[STIX]{x1D703}\}$
is big. Let
![]() $V_{\unicode[STIX]{x1D703}}$
be the envelope of
$V_{\unicode[STIX]{x1D703}}$
be the envelope of
![]() $\unicode[STIX]{x1D703}$
. Then we have the following.
$\unicode[STIX]{x1D703}$
. Then we have the following.
-
(i) For any
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
we have where
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
we have where $$\begin{eqnarray}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)=\unicode[STIX]{x1D708}(V_{\unicode[STIX]{x1D703}},x)\quad \text{and}\quad {\mathcal{I}}(t\unicode[STIX]{x1D711},x)={\mathcal{I}}(tV_{\unicode[STIX]{x1D703}},x),\quad \forall x\in X,t>0,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)=\unicode[STIX]{x1D708}(V_{\unicode[STIX]{x1D703}},x)\quad \text{and}\quad {\mathcal{I}}(t\unicode[STIX]{x1D711},x)={\mathcal{I}}(tV_{\unicode[STIX]{x1D703}},x),\quad \forall x\in X,t>0,\end{eqnarray}$$
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)$
is the Lelong number of
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)$
is the Lelong number of
 $\unicode[STIX]{x1D711}$
at
$\unicode[STIX]{x1D711}$
at
 $x$
, and
$x$
, and
 ${\mathcal{I}}(t\unicode[STIX]{x1D711},x)$
is the germ of the multiplier ideal sheaf of
${\mathcal{I}}(t\unicode[STIX]{x1D711},x)$
is the germ of the multiplier ideal sheaf of
 $t\unicode[STIX]{x1D711}$
at
$t\unicode[STIX]{x1D711}$
at
 $x$
.
$x$
.
-
(ii) If
 $\{\unicode[STIX]{x1D702}\}$
is a big and nef class, then In particular, when
$\{\unicode[STIX]{x1D702}\}$
is a big and nef class, then In particular, when $$\begin{eqnarray}{\mathcal{E}}(X,\unicode[STIX]{x1D702})\cap \operatorname{PSH}(X,\unicode[STIX]{x1D703})\subset {\mathcal{E}}(X,\unicode[STIX]{x1D703}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}(X,\unicode[STIX]{x1D702})\cap \operatorname{PSH}(X,\unicode[STIX]{x1D703})\subset {\mathcal{E}}(X,\unicode[STIX]{x1D703}).\end{eqnarray}$$
 $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D714}$
, this last inclusion gives that
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D714}$
, this last inclusion gives that
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)=0$
for any
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)=0$
for any
 $x\in X$
,
$x\in X$
,
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D702})$
.
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D702})$
.
In the above statement
![]() $V_{\unicode[STIX]{x1D703}}$
is the ‘least singular’ element of
$V_{\unicode[STIX]{x1D703}}$
is the ‘least singular’ element of
 $\operatorname{PSH}(X,\unicode[STIX]{x1D703})$
defined as
$\operatorname{PSH}(X,\unicode[STIX]{x1D703})$
defined as
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D703}}:=\{\unicode[STIX]{x1D711}\quad \unicode[STIX]{x1D703}\text{-}\text{psh},\unicode[STIX]{x1D711}\leqslant 0~\text{on}~X\}.\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D703}}:=\{\unicode[STIX]{x1D711}\quad \unicode[STIX]{x1D703}\text{-}\text{psh},\unicode[STIX]{x1D711}\leqslant 0~\text{on}~X\}.\end{eqnarray}$$
For a precise definition of all other concepts in the above result we refer to § 2.1. The statement of part (ii) cannot hold in case
![]() $\{\unicode[STIX]{x1D702}\}$
is merely big. Indeed, if
$\{\unicode[STIX]{x1D702}\}$
is merely big. Indeed, if
![]() $\{\unicode[STIX]{x1D702}\}$
is big but not nef, the envelope
$\{\unicode[STIX]{x1D702}\}$
is big but not nef, the envelope
![]() $V_{\unicode[STIX]{x1D702}}$
may have a positive Lelong number at some point
$V_{\unicode[STIX]{x1D702}}$
may have a positive Lelong number at some point
![]() $x\in X$
, hence its complex Monge–Ampère measure cannot have full mass with respect to a Kähler form
$x\in X$
, hence its complex Monge–Ampère measure cannot have full mass with respect to a Kähler form
![]() $\unicode[STIX]{x1D714}\geqslant \unicode[STIX]{x1D702}$
, as shown in [Reference Guedj and ZeriahiGZ07, Corollary 1.8]. Let us also emphasize that the very last statement of Theorem 1.1 also follows from the statement of part (i) together with the fact that, when
$\unicode[STIX]{x1D714}\geqslant \unicode[STIX]{x1D702}$
, as shown in [Reference Guedj and ZeriahiGZ07, Corollary 1.8]. Let us also emphasize that the very last statement of Theorem 1.1 also follows from the statement of part (i) together with the fact that, when
![]() $\{\unicode[STIX]{x1D703}\}$
is big and nef, the Lelong numbers of
$\{\unicode[STIX]{x1D703}\}$
is big and nef, the Lelong numbers of
![]() $V_{\unicode[STIX]{x1D703}}$
are zero thanks to [Reference BoucksomBou04, Propositions 3.2 and 3.6].
$V_{\unicode[STIX]{x1D703}}$
are zero thanks to [Reference BoucksomBou04, Propositions 3.2 and 3.6].
In the particular case when
![]() $\{\unicode[STIX]{x1D703}\}$
is semi-positive and big, Theorem 1.1 answers affirmatively an open question in [Reference Dinew, Guedj and ZeriahiDGZ16, Question 36], saying that potentials in
$\{\unicode[STIX]{x1D703}\}$
is semi-positive and big, Theorem 1.1 answers affirmatively an open question in [Reference Dinew, Guedj and ZeriahiDGZ16, Question 36], saying that potentials in
![]() ${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
have zero Lelong numbers. A very specific instance of this was verified in [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11, Theorem 1.1], using techniques from algebraic geometry.
${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
have zero Lelong numbers. A very specific instance of this was verified in [Reference Berman, Boucksom, Eyssidieux, Guedj and ZeriahiBBEGZ11, Theorem 1.1], using techniques from algebraic geometry.
Our arguments use the envelope construction originally due to Ross and Witt Nyström [Reference Ross and Witt NyströmRW14] that we recall now. For an upper semicontinuous function
![]() $f$
on
$f$
on
![]() $X$
, we let
$X$
, we let
![]() $P_{\unicode[STIX]{x1D703}}(f)$
be the largest
$P_{\unicode[STIX]{x1D703}}(f)$
be the largest
![]() $\unicode[STIX]{x1D703}$
-plurisubharmonic (
$\unicode[STIX]{x1D703}$
-plurisubharmonic (
![]() $\unicode[STIX]{x1D703}$
-psh) function lying below
$\unicode[STIX]{x1D703}$
-psh) function lying below
![]() $f$
, i.e.
$f$
, i.e.
 $P_{\unicode[STIX]{x1D703}}(f)=\sup \{u\mid \unicode[STIX]{x1D703}\text{-}\text{psh}\;u\leqslant f\}$
. Given
$P_{\unicode[STIX]{x1D703}}(f)=\sup \{u\mid \unicode[STIX]{x1D703}\text{-}\text{psh}\;u\leqslant f\}$
. Given
![]() $\unicode[STIX]{x1D713},\unicode[STIX]{x1D711}$
, two
$\unicode[STIX]{x1D713},\unicode[STIX]{x1D711}$
, two
![]() $\unicode[STIX]{x1D703}$
-psh functions, we define
$\unicode[STIX]{x1D703}$
-psh functions, we define
 $$\begin{eqnarray}P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711}):=\Bigl\{\lim _{C\rightarrow +\infty }P_{\unicode[STIX]{x1D703}}(\min (\unicode[STIX]{x1D713}+C,\unicode[STIX]{x1D711}))\Bigr\}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711}):=\Bigl\{\lim _{C\rightarrow +\infty }P_{\unicode[STIX]{x1D703}}(\min (\unicode[STIX]{x1D713}+C,\unicode[STIX]{x1D711}))\Bigr\}^{\ast }.\end{eqnarray}$$
In § 2, we prove that whenever
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
belong to
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
belong to
![]() ${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
then
${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
then
 $P_{\unicode[STIX]{x1D703}}(\min (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}))$
also belongs to
$P_{\unicode[STIX]{x1D703}}(\min (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}))$
also belongs to
![]() ${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. Coincidentally, with the help of this result we can settle a conjecture in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Remark 2.16], regarding the convexity of finite energy classes associated to a big cohomology class (Corollary 2.12).
${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. Coincidentally, with the help of this result we can settle a conjecture in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Remark 2.16], regarding the convexity of finite energy classes associated to a big cohomology class (Corollary 2.12).
To familiarize the reader with the flavor of our arguments, we sketch the proof of the statement involving Lelong numbers in Theorem 1.1(i). If
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
it follows from an approximation and balayage argument [Reference Bedford and TaylorBT82] that the non-pluripolar Monge–Ampère measure of
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
it follows from an approximation and balayage argument [Reference Bedford and TaylorBT82] that the non-pluripolar Monge–Ampère measure of
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(0)$
vanishes on
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(0)$
vanishes on
 $\{P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D703}})<V_{\unicode[STIX]{x1D703}}\}$
(see Proposition 2.14 cf. [Reference Ross and Witt NyströmRW14, Theorem 4.1]). It thus follows from the domination principle that
$\{P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D703}})<V_{\unicode[STIX]{x1D703}}\}$
(see Proposition 2.14 cf. [Reference Ross and Witt NyströmRW14, Theorem 4.1]). It thus follows from the domination principle that
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D703}})=V_{\unicode[STIX]{x1D703}}$
. A local argument involving the pluricomplex Green function now implies that the Lelong numbers of
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D703}})=V_{\unicode[STIX]{x1D703}}$
. A local argument involving the pluricomplex Green function now implies that the Lelong numbers of
![]() $\unicode[STIX]{x1D711}$
are the same as those of
$\unicode[STIX]{x1D711}$
are the same as those of
![]() $V_{\unicode[STIX]{x1D703}}$
(see (21)).
$V_{\unicode[STIX]{x1D703}}$
(see (21)).
In the case when
![]() $\unicode[STIX]{x1D703}$
is Kähler a surprising characterization of the class
$\unicode[STIX]{x1D703}$
is Kähler a surprising characterization of the class
![]() ${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
in terms of the envelope construction of (1) was obtained in [Reference DarvasDar17a, Theorem 4], [Reference DarvasDar17b, Theorem 3]. Our next result, which is a vital ingredient in our proof of Theorem 1.1(ii), shows that this characterization holds in the context of big classes as well.
${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
in terms of the envelope construction of (1) was obtained in [Reference DarvasDar17a, Theorem 4], [Reference DarvasDar17b, Theorem 3]. Our next result, which is a vital ingredient in our proof of Theorem 1.1(ii), shows that this characterization holds in the context of big classes as well.
Theorem 1.2. Let
![]() $\{\unicode[STIX]{x1D703}\}$
be a big cohomology class and fix
$\{\unicode[STIX]{x1D703}\}$
be a big cohomology class and fix
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. Then a function
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. Then a function
 $\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
belongs to
$\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
belongs to
![]() ${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
if and only if
${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
if and only if
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711})=\unicode[STIX]{x1D711}$
.
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711})=\unicode[STIX]{x1D711}$
.
The implication ‘
 $\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})\Longrightarrow P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711})=\unicode[STIX]{x1D711}$
’ follows essentially from the domination principle, by the arguments of [Reference DarvasDar17b, Reference Ross and Witt NyströmRW14]. In order to prove the other implication, we introduce the seemingly unrelated notion of weak geodesics in big cohomology classes, mimicking Berndtsson’s construction in the Kähler case [Reference BerndtssonBer15, § 2.2], and we prove that the Monge–Ampère energy
$\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})\Longrightarrow P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711})=\unicode[STIX]{x1D711}$
’ follows essentially from the domination principle, by the arguments of [Reference DarvasDar17b, Reference Ross and Witt NyströmRW14]. In order to prove the other implication, we introduce the seemingly unrelated notion of weak geodesics in big cohomology classes, mimicking Berndtsson’s construction in the Kähler case [Reference BerndtssonBer15, § 2.2], and we prove that the Monge–Ampère energy
![]() $\text{I}$
(sometimes called Aubin–Yau or Aubin–Mabuchi energy) is convex/linear along weak subgeodesics/geodesics (Theorems 3.8 and 3.12). Compared to the Kähler case, this is a very subtle issue and it serves as the key technical ingredient in the proof of Theorem 1.2.
$\text{I}$
(sometimes called Aubin–Yau or Aubin–Mabuchi energy) is convex/linear along weak subgeodesics/geodesics (Theorems 3.8 and 3.12). Compared to the Kähler case, this is a very subtle issue and it serves as the key technical ingredient in the proof of Theorem 1.2.
When varying big classes, an important question is to understand how the class of full mass currents changes. Theorem 1.1(ii) already establishes a result in this direction in the particular case of big and nef classes. Paralleling this, as a consequence of Theorem 1.2, we can characterize the pairs of big classes that have ‘additive’ full mass currents, greatly generalizing [Reference Di NezzaDiN15, Theorem B] in the process.
Theorem 1.3. Let
 $\{\unicode[STIX]{x1D703}_{1}\},\{\unicode[STIX]{x1D703}_{2}\}$
be big classes on
$\{\unicode[STIX]{x1D703}_{1}\},\{\unicode[STIX]{x1D703}_{2}\}$
be big classes on
![]() $X$
. The following are equivalent:
$X$
. The following are equivalent:
-
(i)
 $V_{\unicode[STIX]{x1D703}_{1}}+V_{\unicode[STIX]{x1D703}_{2}}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})$
;
$V_{\unicode[STIX]{x1D703}_{1}}+V_{\unicode[STIX]{x1D703}_{2}}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})$
; -
(ii) for any
 $u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{1}),v\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{2})$
we have
$u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{1}),v\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{2})$
we have  $$\begin{eqnarray}u+v\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})\Longleftrightarrow u\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}),v\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{2}).\end{eqnarray}$$
$$\begin{eqnarray}u+v\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})\Longleftrightarrow u\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}),v\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{2}).\end{eqnarray}$$
As it turns out, when
 $\{\unicode[STIX]{x1D703}_{1}\},\{\unicode[STIX]{x1D703}_{2}\}$
are big and nef, condition (i) in the above theorem is automatically satisfied (Corollary 4.2). This result also helps to partially confirm [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Conjecture 1.23] concerning log concavity of the non-pluripolar complex Monge–Ampère measure in the case of full mass currents of big and nef classes (see Corollary 5.3).
$\{\unicode[STIX]{x1D703}_{1}\},\{\unicode[STIX]{x1D703}_{2}\}$
are big and nef, condition (i) in the above theorem is automatically satisfied (Corollary 4.2). This result also helps to partially confirm [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Conjecture 1.23] concerning log concavity of the non-pluripolar complex Monge–Ampère measure in the case of full mass currents of big and nef classes (see Corollary 5.3).
Organization of the paper. Section 2 mostly reviews background material on the pluripotential theory of big cohomology classes and we establish some preliminary results. In § 3 we develop the theory of weak geodesics in big cohomology classes following Berndtsson’s ideas, and then we prove Theorems 1.2 and 1.3. Theorem 1.1 will be proved in § 4 while some other applications will be discussed in § 5.
2 Pluripotential theory in big cohomology classes
2.1 Non-pluripolar Monge–Ampère measures
We recall basic facts concerning pluripotential theory of big cohomology classes. We borrow notation and terminology from [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10], and we also refer to this work for further details.
Let
![]() $(X,\unicode[STIX]{x1D714})$
be a compact Kähler manifold of dimension
$(X,\unicode[STIX]{x1D714})$
be a compact Kähler manifold of dimension
![]() $n$
. We fix
$n$
. We fix
![]() $\unicode[STIX]{x1D703}$
a smooth closed
$\unicode[STIX]{x1D703}$
a smooth closed
![]() $(1,1)$
-form on
$(1,1)$
-form on
![]() $X$
such that
$X$
such that
![]() $\{\unicode[STIX]{x1D703}\}$
is big, i.e., there exists
$\{\unicode[STIX]{x1D703}\}$
is big, i.e., there exists
 $\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
such that
$\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
such that
 $\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D713}\geqslant \unicode[STIX]{x1D700}\unicode[STIX]{x1D714}$
for some small constant
$\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D713}\geqslant \unicode[STIX]{x1D700}\unicode[STIX]{x1D714}$
for some small constant
![]() $\unicode[STIX]{x1D700}>0$
. Here,
$\unicode[STIX]{x1D700}>0$
. Here,
![]() $d$
and
$d$
and
![]() $d^{c}$
are real differential operators defined as
$d^{c}$
are real differential operators defined as
 $d:=\unicode[STIX]{x2202}+\bar{\unicode[STIX]{x2202}}$
,
$d:=\unicode[STIX]{x2202}+\bar{\unicode[STIX]{x2202}}$
,
 $d^{c}:=(i/2\unicode[STIX]{x1D70B})(\bar{\unicode[STIX]{x2202}}-\unicode[STIX]{x2202})$
. A function
$d^{c}:=(i/2\unicode[STIX]{x1D70B})(\bar{\unicode[STIX]{x2202}}-\unicode[STIX]{x2202})$
. A function
 $\unicode[STIX]{x1D711}:X\rightarrow \mathbb{R}\cup \{-\infty \}$
is called quasi-plurisubharmonic if it is locally written as the sum of a plurisubharmonic function and a smooth function.
$\unicode[STIX]{x1D711}:X\rightarrow \mathbb{R}\cup \{-\infty \}$
is called quasi-plurisubharmonic if it is locally written as the sum of a plurisubharmonic function and a smooth function.
![]() $\unicode[STIX]{x1D711}$
is called
$\unicode[STIX]{x1D711}$
is called
![]() $\unicode[STIX]{x1D703}$
-psh if it is quasi-psh such that
$\unicode[STIX]{x1D703}$
-psh if it is quasi-psh such that
 $\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D711}\geqslant 0$
in the sense of currents. We let
$\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D711}\geqslant 0$
in the sense of currents. We let
 $\operatorname{PSH}(X,\unicode[STIX]{x1D703})$
denote the set of
$\operatorname{PSH}(X,\unicode[STIX]{x1D703})$
denote the set of
![]() $\unicode[STIX]{x1D703}$
-psh functions which are not identically
$\unicode[STIX]{x1D703}$
-psh functions which are not identically
![]() $-\infty$
(equivalently, it consists of
$-\infty$
(equivalently, it consists of
![]() $\unicode[STIX]{x1D703}$
-psh functions which are integrable on
$\unicode[STIX]{x1D703}$
-psh functions which are integrable on
![]() $X$
).
$X$
).
A
![]() $\unicode[STIX]{x1D703}$
-psh function
$\unicode[STIX]{x1D703}$
-psh function
![]() $\unicode[STIX]{x1D711}$
is said to have analytic singularities if there exists
$\unicode[STIX]{x1D711}$
is said to have analytic singularities if there exists
![]() $c>0$
such that locally on
$c>0$
such that locally on
![]() $X$
,
$X$
,
 $$\begin{eqnarray}\unicode[STIX]{x1D711}=\frac{c}{2}\log \mathop{\sum }_{j=1}^{N}|f_{j}|^{2}+u,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}=\frac{c}{2}\log \mathop{\sum }_{j=1}^{N}|f_{j}|^{2}+u,\end{eqnarray}$$
where
![]() $u$
is smooth and
$u$
is smooth and
 $f_{1},\ldots ,f_{N}$
are local holomorphic functions. The ample locus
$f_{1},\ldots ,f_{N}$
are local holomorphic functions. The ample locus
 $\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
of
$\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
of
![]() $\{\unicode[STIX]{x1D703}\}$
is the set of points
$\{\unicode[STIX]{x1D703}\}$
is the set of points
![]() $x\in X$
such that there exists a Kähler current
$x\in X$
such that there exists a Kähler current
 $T\in \{\unicode[STIX]{x1D703}\}$
(satisfying
$T\in \{\unicode[STIX]{x1D703}\}$
(satisfying
![]() $T\geqslant \unicode[STIX]{x1D700}\unicode[STIX]{x1D714}$
for some
$T\geqslant \unicode[STIX]{x1D700}\unicode[STIX]{x1D714}$
for some
![]() $\unicode[STIX]{x1D700}>0$
) with analytic singularities and smooth in a neighborhood of
$\unicode[STIX]{x1D700}>0$
) with analytic singularities and smooth in a neighborhood of
![]() $x$
. The ample locus
$x$
. The ample locus
 $\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
is a Zariski open subset, and it is non-empty [Reference BoucksomBou04].
$\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
is a Zariski open subset, and it is non-empty [Reference BoucksomBou04].
Let
![]() $x\in X$
. Fixing a holomorphic chart
$x\in X$
. Fixing a holomorphic chart
 $x\in U\subset X$
, the Lelong number
$x\in U\subset X$
, the Lelong number
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)$
of
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)$
of
 $\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is defined as follows:
$\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is defined as follows:
 $$\begin{eqnarray}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)=\sup \{\unicode[STIX]{x1D6FE}\geqslant 0\mid \unicode[STIX]{x1D711}(z)\leqslant \unicode[STIX]{x1D6FE}\log \Vert z-x\Vert +O(1)~\text{on}~U\}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)=\sup \{\unicode[STIX]{x1D6FE}\geqslant 0\mid \unicode[STIX]{x1D711}(z)\leqslant \unicode[STIX]{x1D6FE}\log \Vert z-x\Vert +O(1)~\text{on}~U\}.\end{eqnarray}$$
One can also associate to
![]() $\unicode[STIX]{x1D711}$
a collection of multiplier ideal sheafs
$\unicode[STIX]{x1D711}$
a collection of multiplier ideal sheafs
![]() ${\mathcal{I}}(t\unicode[STIX]{x1D711})$
,
${\mathcal{I}}(t\unicode[STIX]{x1D711})$
,
![]() $t\geqslant 0,$
whose germs are defined by
$t\geqslant 0,$
whose germs are defined by
 $$\begin{eqnarray}{\mathcal{I}}(t\unicode[STIX]{x1D711},x)=\biggl\{f\in {\mathcal{O}}_{x}\biggm\vert\int _{V}|f|e^{-t\unicode[STIX]{x1D711}}\unicode[STIX]{x1D714}^{n}<\infty ~\text{for some open set}~x\in V\subset X\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{I}}(t\unicode[STIX]{x1D711},x)=\biggl\{f\in {\mathcal{O}}_{x}\biggm\vert\int _{V}|f|e^{-t\unicode[STIX]{x1D711}}\unicode[STIX]{x1D714}^{n}<\infty ~\text{for some open set}~x\in V\subset X\biggr\}.\end{eqnarray}$$
If
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $\unicode[STIX]{x1D711}^{\prime }$
are two
$\unicode[STIX]{x1D711}^{\prime }$
are two
![]() $\unicode[STIX]{x1D703}$
-psh functions on
$\unicode[STIX]{x1D703}$
-psh functions on
![]() $X$
, then
$X$
, then
![]() $\unicode[STIX]{x1D711}^{\prime }$
is said to be less singular than
$\unicode[STIX]{x1D711}^{\prime }$
is said to be less singular than
![]() $\unicode[STIX]{x1D711}$
if they satisfy
$\unicode[STIX]{x1D711}$
if they satisfy
 $\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D711}^{\prime }+C$
for some
$\unicode[STIX]{x1D711}\leqslant \unicode[STIX]{x1D711}^{\prime }+C$
for some
![]() $C\in \mathbb{R}$
. A
$C\in \mathbb{R}$
. A
![]() $\unicode[STIX]{x1D703}$
-psh function
$\unicode[STIX]{x1D703}$
-psh function
![]() $\unicode[STIX]{x1D711}$
is said to have minimal singularities if it is less singular than any other
$\unicode[STIX]{x1D711}$
is said to have minimal singularities if it is less singular than any other
![]() $\unicode[STIX]{x1D703}$
-psh function. Such
$\unicode[STIX]{x1D703}$
-psh function. Such
![]() $\unicode[STIX]{x1D703}$
-psh functions with minimal singularities always exist, one can consider for example
$\unicode[STIX]{x1D703}$
-psh functions with minimal singularities always exist, one can consider for example
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D703}}:=\sup \{\unicode[STIX]{x1D711}~\unicode[STIX]{x1D703}\text{-}\text{psh},\unicode[STIX]{x1D711}\leqslant 0~\text{on}~X\}.\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D703}}:=\sup \{\unicode[STIX]{x1D711}~\unicode[STIX]{x1D703}\text{-}\text{psh},\unicode[STIX]{x1D711}\leqslant 0~\text{on}~X\}.\end{eqnarray}$$
Trivially, a
![]() $\unicode[STIX]{x1D703}$
-psh function with minimal singularities has locally bounded potential in
$\unicode[STIX]{x1D703}$
-psh function with minimal singularities has locally bounded potential in
 $\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
. It follows from Demailly’s approximation theorem that
$\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
. It follows from Demailly’s approximation theorem that
![]() $V_{\unicode[STIX]{x1D703}}$
is continuous in the ample locus
$V_{\unicode[STIX]{x1D703}}$
is continuous in the ample locus
 $\operatorname{Amp}(\unicode[STIX]{x1D703})$
.
$\operatorname{Amp}(\unicode[STIX]{x1D703})$
.
More generally, if
![]() $f$
is a function on
$f$
is a function on
![]() $X$
, we define the Monge–Ampère envelope of
$X$
, we define the Monge–Ampère envelope of
![]() $f$
in the class
$f$
in the class
 $\operatorname{PSH}(X,\unicode[STIX]{x1D703})$
by
$\operatorname{PSH}(X,\unicode[STIX]{x1D703})$
by
 $$\begin{eqnarray}P_{\unicode[STIX]{x1D703}}(f):=(\sup \{u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})\mid u\leqslant f\})^{\ast },\end{eqnarray}$$
$$\begin{eqnarray}P_{\unicode[STIX]{x1D703}}(f):=(\sup \{u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})\mid u\leqslant f\})^{\ast },\end{eqnarray}$$
with the convention that
 $\sup \emptyset =-\infty$
. Observe that
$\sup \emptyset =-\infty$
. Observe that
![]() $P_{\unicode[STIX]{x1D703}}(f)$
is a
$P_{\unicode[STIX]{x1D703}}(f)$
is a
![]() $\unicode[STIX]{x1D703}$
-psh function on
$\unicode[STIX]{x1D703}$
-psh function on
![]() $X$
if and only if there exists some
$X$
if and only if there exists some
 $u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
lying below
$u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
lying below
![]() $f$
. Note also that
$f$
. Note also that
 $V_{\unicode[STIX]{x1D703}}=P_{\unicode[STIX]{x1D703}}(0)$
.
$V_{\unicode[STIX]{x1D703}}=P_{\unicode[STIX]{x1D703}}(0)$
.
Given
 $T_{1}:=\unicode[STIX]{x1D703}_{1}+dd^{c}\unicode[STIX]{x1D711}_{1},\ldots ,T_{p}:=\unicode[STIX]{x1D703}_{p}+dd^{c}\unicode[STIX]{x1D711}_{p}$
positive
$T_{1}:=\unicode[STIX]{x1D703}_{1}+dd^{c}\unicode[STIX]{x1D711}_{1},\ldots ,T_{p}:=\unicode[STIX]{x1D703}_{p}+dd^{c}\unicode[STIX]{x1D711}_{p}$
positive
![]() $(1,1)$
-currents, where
$(1,1)$
-currents, where
![]() $\unicode[STIX]{x1D703}_{j}$
are closed smooth
$\unicode[STIX]{x1D703}_{j}$
are closed smooth
![]() $(1,1)$
-forms, following the construction of Bedford and Taylor [Reference Bedford and TaylorBT87] in the local setting, it has been shown in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10] that the sequence of currents
$(1,1)$
-forms, following the construction of Bedford and Taylor [Reference Bedford and TaylorBT87] in the local setting, it has been shown in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10] that the sequence of currents
 $$\begin{eqnarray}\mathbf{1}_{\mathop{\bigcap }_{j}\{\unicode[STIX]{x1D711}_{j}>V_{\unicode[STIX]{x1D703}_{j}}-k\}}(\unicode[STIX]{x1D703}_{1}+dd^{c}\max (\unicode[STIX]{x1D711}_{1},V_{\unicode[STIX]{x1D703}_{1}}-k))\wedge \cdots \wedge (\unicode[STIX]{x1D703}_{p}+dd^{c}\max (\unicode[STIX]{x1D711}_{p},V_{\unicode[STIX]{x1D703}_{p}}-k))\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{1}_{\mathop{\bigcap }_{j}\{\unicode[STIX]{x1D711}_{j}>V_{\unicode[STIX]{x1D703}_{j}}-k\}}(\unicode[STIX]{x1D703}_{1}+dd^{c}\max (\unicode[STIX]{x1D711}_{1},V_{\unicode[STIX]{x1D703}_{1}}-k))\wedge \cdots \wedge (\unicode[STIX]{x1D703}_{p}+dd^{c}\max (\unicode[STIX]{x1D711}_{p},V_{\unicode[STIX]{x1D703}_{p}}-k))\end{eqnarray}$$
is non-decreasing in
![]() $k$
and converges weakly to the so called non-pluripolar product
$k$
and converges weakly to the so called non-pluripolar product
 $$\begin{eqnarray}\langle T_{1}\wedge \cdots \wedge T_{p}\rangle =\langle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{1}}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\langle T_{1}\wedge \cdots \wedge T_{p}\rangle =\langle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{1}}\rangle .\end{eqnarray}$$
The resulting positive
![]() $(p,p)$
-current does not charge pluripolar sets and it is closed. The particular case when
$(p,p)$
-current does not charge pluripolar sets and it is closed. The particular case when
 $T_{1}=\cdots =T_{p}$
will be important for us in the sequel. For a
$T_{1}=\cdots =T_{p}$
will be important for us in the sequel. For a
![]() $\unicode[STIX]{x1D703}$
-psh function
$\unicode[STIX]{x1D703}$
-psh function
![]() $\unicode[STIX]{x1D711}$
, the non-pluripolar complex Monge–Ampère measure of
$\unicode[STIX]{x1D711}$
, the non-pluripolar complex Monge–Ampère measure of
![]() $\unicode[STIX]{x1D711}$
is
$\unicode[STIX]{x1D711}$
is
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}:=\langle (\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D711})^{n}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}:=\langle (\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D711})^{n}\rangle .\end{eqnarray}$$
The volume of a big class
![]() $\{\unicode[STIX]{x1D703}\}$
is defined by
$\{\unicode[STIX]{x1D703}\}$
is defined by
 $$\begin{eqnarray}\operatorname{Vol}(\{\unicode[STIX]{x1D703}\}):=\int _{X}\unicode[STIX]{x1D703}_{V_{\unicode[STIX]{x1D703}}}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Vol}(\{\unicode[STIX]{x1D703}\}):=\int _{X}\unicode[STIX]{x1D703}_{V_{\unicode[STIX]{x1D703}}}^{n}.\end{eqnarray}$$
Alternatively, by [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem 1.16], in the above expression one can replace
![]() $V_{\unicode[STIX]{x1D703}}$
with any
$V_{\unicode[STIX]{x1D703}}$
with any
![]() $\unicode[STIX]{x1D703}$
-psh function with minimal singularities. A
$\unicode[STIX]{x1D703}$
-psh function with minimal singularities. A
![]() $\unicode[STIX]{x1D703}$
-psh function
$\unicode[STIX]{x1D703}$
-psh function
![]() $\unicode[STIX]{x1D711}$
is said to have full Monge–Ampère mass if
$\unicode[STIX]{x1D711}$
is said to have full Monge–Ampère mass if
 $$\begin{eqnarray}\int _{X}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}=\operatorname{Vol}(\{\unicode[STIX]{x1D703}\}),\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}=\operatorname{Vol}(\{\unicode[STIX]{x1D703}\}),\end{eqnarray}$$
and we then write
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. Let us stress that since the non-pluripolar product does not charge pluripolar sets, for a general
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. Let us stress that since the non-pluripolar product does not charge pluripolar sets, for a general
![]() $\unicode[STIX]{x1D703}$
-psh function
$\unicode[STIX]{x1D703}$
-psh function
![]() $\unicode[STIX]{x1D711}$
we only have
$\unicode[STIX]{x1D711}$
we only have
 $\operatorname{Vol}(\{\unicode[STIX]{x1D703}\})\geqslant \int _{X}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}$
.
$\operatorname{Vol}(\{\unicode[STIX]{x1D703}\})\geqslant \int _{X}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}$
.
By a weight function, we mean a smooth increasing function
 $\unicode[STIX]{x1D712}:\mathbb{R}\rightarrow \mathbb{R}$
such that
$\unicode[STIX]{x1D712}:\mathbb{R}\rightarrow \mathbb{R}$
such that
 $\unicode[STIX]{x1D712}(0)=0$
and
$\unicode[STIX]{x1D712}(0)=0$
and
 $\unicode[STIX]{x1D712}(-\infty )=-\infty$
. We say that
$\unicode[STIX]{x1D712}(-\infty )=-\infty$
. We say that
 $\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
has finite
$\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
has finite
![]() $\unicode[STIX]{x1D712}$
-energy if
$\unicode[STIX]{x1D712}$
-energy if
 $$\begin{eqnarray}E_{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D711}):=\int _{X}(-\unicode[STIX]{x1D712})(\unicode[STIX]{x1D711}-V_{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}<+\infty .\end{eqnarray}$$
$$\begin{eqnarray}E_{\unicode[STIX]{x1D712}}(\unicode[STIX]{x1D711}):=\int _{X}(-\unicode[STIX]{x1D712})(\unicode[STIX]{x1D711}-V_{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}<+\infty .\end{eqnarray}$$
We denote by
 ${\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
the set of full mass
${\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
the set of full mass
![]() $\unicode[STIX]{x1D703}$
-psh potentials having finite
$\unicode[STIX]{x1D703}$
-psh potentials having finite
![]() $\unicode[STIX]{x1D712}$
-energy. If
$\unicode[STIX]{x1D712}$
-energy. If
![]() ${\mathcal{W}}^{-}$
denotes the set of weights
${\mathcal{W}}^{-}$
denotes the set of weights
![]() $\unicode[STIX]{x1D712}$
that are convex on
$\unicode[STIX]{x1D712}$
that are convex on
![]() $\mathbb{R}^{-}$
, then by [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.11] we have
$\mathbb{R}^{-}$
, then by [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.11] we have
 $$\begin{eqnarray}{\mathcal{E}}(X,\unicode[STIX]{x1D703}):=\mathop{\bigcup }_{\unicode[STIX]{x1D712}\in {\mathcal{W}}^{-}}{\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703}).\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{E}}(X,\unicode[STIX]{x1D703}):=\mathop{\bigcup }_{\unicode[STIX]{x1D712}\in {\mathcal{W}}^{-}}{\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703}).\end{eqnarray}$$
In the special case when
![]() $\unicode[STIX]{x1D712}=\text{Id}$
we simply denote the space
$\unicode[STIX]{x1D712}=\text{Id}$
we simply denote the space
 ${\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
by
${\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
by
 ${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
. When
${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
. When
 $\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
has minimal singularities, the Monge–Ampère energy (in the class
$\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
has minimal singularities, the Monge–Ampère energy (in the class
![]() $\{\unicode[STIX]{x1D703}\}$
) is defined by the formula
$\{\unicode[STIX]{x1D703}\}$
) is defined by the formula
 $$\begin{eqnarray}\text{I}(\unicode[STIX]{x1D711}):=\frac{1}{(n+1)\operatorname{Vol}(\unicode[STIX]{x1D703})}\mathop{\sum }_{k=0}^{n}\int _{X}(\unicode[STIX]{x1D711}-V_{\unicode[STIX]{x1D703}})\langle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{k}\wedge \unicode[STIX]{x1D703}_{V_{\unicode[STIX]{x1D703}}}^{n-k}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\text{I}(\unicode[STIX]{x1D711}):=\frac{1}{(n+1)\operatorname{Vol}(\unicode[STIX]{x1D703})}\mathop{\sum }_{k=0}^{n}\int _{X}(\unicode[STIX]{x1D711}-V_{\unicode[STIX]{x1D703}})\langle \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{k}\wedge \unicode[STIX]{x1D703}_{V_{\unicode[STIX]{x1D703}}}^{n-k}\rangle .\end{eqnarray}$$
For general
 $\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
, using the monotonicity property of
$\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
, using the monotonicity property of
![]() $\text{I}$
, we have the following definition
$\text{I}$
, we have the following definition
 $$\begin{eqnarray}\text{I}(\unicode[STIX]{x1D711}):=\lim _{k\rightarrow \infty }\text{I}(\max (\unicode[STIX]{x1D711},V_{\unicode[STIX]{x1D703}}-k)).\end{eqnarray}$$
$$\begin{eqnarray}\text{I}(\unicode[STIX]{x1D711}):=\lim _{k\rightarrow \infty }\text{I}(\max (\unicode[STIX]{x1D711},V_{\unicode[STIX]{x1D703}}-k)).\end{eqnarray}$$
Though the above limit exists, it is possible that
 $\text{I}(\unicode[STIX]{x1D711})=-\infty$
. It was proved in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10] that
$\text{I}(\unicode[STIX]{x1D711})=-\infty$
. It was proved in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10] that
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
if and only if
$\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
if and only if
![]() $\text{I}(\unicode[STIX]{x1D711})$
is finite. Moreover,
$\text{I}(\unicode[STIX]{x1D711})$
is finite. Moreover,
![]() $\text{I}$
is continuous under monotone and uniform convergence [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.10, Theorem 2.17].
$\text{I}$
is continuous under monotone and uniform convergence [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.10, Theorem 2.17].
2.2 Degenerate complex Monge–Ampère equation
We summarize recent results on the resolution of degenerate complex Monge–Ampère equations in big cohomology classes. The main sources are [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10] and [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13]. Let
![]() $\unicode[STIX]{x1D707}$
be a non-pluripolar measure on
$\unicode[STIX]{x1D707}$
be a non-pluripolar measure on
![]() $X$
, i.e. a positive Borel measure that puts no mass on pluripolar sets. We want to solve the complex Monge–Amère equation
$X$
, i.e. a positive Borel measure that puts no mass on pluripolar sets. We want to solve the complex Monge–Amère equation
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}=e^{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D711}}\unicode[STIX]{x1D707},\quad \unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}=e^{\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D711}}\unicode[STIX]{x1D707},\quad \unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D714}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FD}>0$
is a constant. As the treatment is the same for all
$\unicode[STIX]{x1D6FD}>0$
is a constant. As the treatment is the same for all
![]() $\unicode[STIX]{x1D6FD}$
, we assume that
$\unicode[STIX]{x1D6FD}$
, we assume that
![]() $\unicode[STIX]{x1D6FD}=1$
. If
$\unicode[STIX]{x1D6FD}=1$
. If
![]() $\unicode[STIX]{x1D707}$
is a smooth volume form (or it has bounded density with respect to
$\unicode[STIX]{x1D707}$
is a smooth volume form (or it has bounded density with respect to
![]() $\unicode[STIX]{x1D714}^{n}$
), then one can use a fixed point argument [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, § 6.1] to solve the equation. For the general case we use the variational method of [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13] to show existence of a solution
$\unicode[STIX]{x1D714}^{n}$
), then one can use a fixed point argument [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, § 6.1] to solve the equation. For the general case we use the variational method of [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13] to show existence of a solution
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
. The proof that we give below is extracted from [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13], except for the argument of Theorem 2.2, which is inspired from [Reference Lu and NguyenLN15]. The main point is to make it clear that the result is independent of [Reference Berman and DemaillyBD12].
$\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
. The proof that we give below is extracted from [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13], except for the argument of Theorem 2.2, which is inspired from [Reference Lu and NguyenLN15]. The main point is to make it clear that the result is independent of [Reference Berman and DemaillyBD12].
2.2.1 The variational method
Let
![]() $\unicode[STIX]{x1D707}$
be a non-pluripolar positive measure on
$\unicode[STIX]{x1D707}$
be a non-pluripolar positive measure on
![]() $X$
. For convenience we normalize
$X$
. For convenience we normalize
![]() $\unicode[STIX]{x1D703}$
so that its volume is 1.
$\unicode[STIX]{x1D703}$
so that its volume is 1.
Consider the following functional
 $$\begin{eqnarray}F(\unicode[STIX]{x1D711}):=\text{I}(\unicode[STIX]{x1D711})-L_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}),\quad \unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D714}),\end{eqnarray}$$
$$\begin{eqnarray}F(\unicode[STIX]{x1D711}):=\text{I}(\unicode[STIX]{x1D711})-L_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}),\quad \unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D714}),\end{eqnarray}$$
where
 $L_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}):=\int _{X}e^{\unicode[STIX]{x1D711}}\,d\unicode[STIX]{x1D707}$
. It follows from [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10] that
$L_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}):=\int _{X}e^{\unicode[STIX]{x1D711}}\,d\unicode[STIX]{x1D707}$
. It follows from [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10] that
![]() $\text{I}$
is upper semicontinuous with respect to
$\text{I}$
is upper semicontinuous with respect to
![]() $L^{1}$
-convergence. Assume that
$L^{1}$
-convergence. Assume that
![]() $\unicode[STIX]{x1D711}_{j}$
is a sequence of
$\unicode[STIX]{x1D711}_{j}$
is a sequence of
![]() $\unicode[STIX]{x1D703}$
-psh functions converging in
$\unicode[STIX]{x1D703}$
-psh functions converging in
 $L^{1}(X,\unicode[STIX]{x1D714}^{n})$
to
$L^{1}(X,\unicode[STIX]{x1D714}^{n})$
to
 $\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
. Then by Hartogs’ lemma
$\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
. Then by Hartogs’ lemma
 $\sup _{X}\unicode[STIX]{x1D711}_{j}$
is uniformly bounded, hence the sequence
$\sup _{X}\unicode[STIX]{x1D711}_{j}$
is uniformly bounded, hence the sequence
![]() $e^{\unicode[STIX]{x1D711}_{j}}$
stays in
$e^{\unicode[STIX]{x1D711}_{j}}$
stays in
 $\operatorname{PSH}(X,A\unicode[STIX]{x1D714})$
for some positive constant
$\operatorname{PSH}(X,A\unicode[STIX]{x1D714})$
for some positive constant
![]() $A$
and
$A$
and
![]() $e^{\unicode[STIX]{x1D711}_{j}}$
converges to
$e^{\unicode[STIX]{x1D711}_{j}}$
converges to
![]() $e^{\unicode[STIX]{x1D711}}$
in
$e^{\unicode[STIX]{x1D711}}$
in
 $L^{1}(X,\unicode[STIX]{x1D714}^{n})$
. Since
$L^{1}(X,\unicode[STIX]{x1D714}^{n})$
. Since
![]() $\unicode[STIX]{x1D707}$
is non-pluripolar it thus follows from an argument due to Cegrell [Reference CegrellCe98, Lemma 5.2] (see [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Theorem 3.10] or [Reference Guedj and ZeriahiGZ17, Lemma 11.5] for a proof in the compact case) that
$\unicode[STIX]{x1D707}$
is non-pluripolar it thus follows from an argument due to Cegrell [Reference CegrellCe98, Lemma 5.2] (see [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Theorem 3.10] or [Reference Guedj and ZeriahiGZ17, Lemma 11.5] for a proof in the compact case) that
 $L_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{j})\rightarrow L_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711})$
. This means
$L_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711}_{j})\rightarrow L_{\unicode[STIX]{x1D707}}(\unicode[STIX]{x1D711})$
. This means
![]() $L_{\unicode[STIX]{x1D707}}$
is continuous with respect to the
$L_{\unicode[STIX]{x1D707}}$
is continuous with respect to the
![]() $L^{1}$
-topology, hence
$L^{1}$
-topology, hence
![]() $F$
is upper semicontinuous on
$F$
is upper semicontinuous on
 ${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
.
${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
.
Proposition 2.1. There exists
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
such that
$\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
such that
 $F(\unicode[STIX]{x1D711})=\sup _{\unicode[STIX]{x1D713}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})}F(\unicode[STIX]{x1D713})$
.
$F(\unicode[STIX]{x1D711})=\sup _{\unicode[STIX]{x1D713}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})}F(\unicode[STIX]{x1D713})$
.
Proof. Let
![]() $(\unicode[STIX]{x1D711}_{j})$
be a sequence in
$(\unicode[STIX]{x1D711}_{j})$
be a sequence in
 ${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
such that
${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
such that
 $\lim _{j}F(\unicode[STIX]{x1D711}_{j})=\sup _{{\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})}F>-\infty$
. We claim that
$\lim _{j}F(\unicode[STIX]{x1D711}_{j})=\sup _{{\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})}F>-\infty$
. We claim that
 $\sup _{X}\unicode[STIX]{x1D711}_{j}$
is uniformly bounded from above. Indeed, assume that it were not the case. Then by relabeling the sequence we can assume that
$\sup _{X}\unicode[STIX]{x1D711}_{j}$
is uniformly bounded from above. Indeed, assume that it were not the case. Then by relabeling the sequence we can assume that
 $\sup _{X}\unicode[STIX]{x1D711}_{j}$
increases to
$\sup _{X}\unicode[STIX]{x1D711}_{j}$
increases to
![]() $+\infty$
. By compactness property [Reference Guedj and ZeriahiGZ05, Proposition 2.7] it follows that the sequence
$+\infty$
. By compactness property [Reference Guedj and ZeriahiGZ05, Proposition 2.7] it follows that the sequence
 $\unicode[STIX]{x1D713}_{j}:=\unicode[STIX]{x1D711}_{j}-\sup _{X}\unicode[STIX]{x1D711}_{j}$
converges in
$\unicode[STIX]{x1D713}_{j}:=\unicode[STIX]{x1D711}_{j}-\sup _{X}\unicode[STIX]{x1D711}_{j}$
converges in
 $L^{1}(X,\unicode[STIX]{x1D714}^{n})$
to some
$L^{1}(X,\unicode[STIX]{x1D714}^{n})$
to some
 $\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
such that
$\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
such that
 $\sup _{X}\unicode[STIX]{x1D713}=0$
. In particular
$\sup _{X}\unicode[STIX]{x1D713}=0$
. In particular
 $\int _{X}e^{\unicode[STIX]{x1D713}}\,d\unicode[STIX]{x1D707}>0$
. It thus follows that
$\int _{X}e^{\unicode[STIX]{x1D713}}\,d\unicode[STIX]{x1D707}>0$
. It thus follows that
 $$\begin{eqnarray}\int _{X}e^{\unicode[STIX]{x1D711}_{j}}\,d\unicode[STIX]{x1D707}=e^{\sup _{X}\unicode[STIX]{x1D711}_{j}}\int _{X}e^{\unicode[STIX]{x1D713}_{j}}\,d\unicode[STIX]{x1D707}\geqslant ce^{\sup _{X}\unicode[STIX]{x1D711}_{j}}\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}e^{\unicode[STIX]{x1D711}_{j}}\,d\unicode[STIX]{x1D707}=e^{\sup _{X}\unicode[STIX]{x1D711}_{j}}\int _{X}e^{\unicode[STIX]{x1D713}_{j}}\,d\unicode[STIX]{x1D707}\geqslant ce^{\sup _{X}\unicode[STIX]{x1D711}_{j}}\end{eqnarray}$$
for some positive constant
![]() $c$
. Since
$c$
. Since
 $\text{I}(\unicode[STIX]{x1D711}_{j})\leqslant \sup _{X}\unicode[STIX]{x1D711}_{j}$
, the above inequality gives that
$\text{I}(\unicode[STIX]{x1D711}_{j})\leqslant \sup _{X}\unicode[STIX]{x1D711}_{j}$
, the above inequality gives that
![]() $F(\unicode[STIX]{x1D711}_{j})$
converges to
$F(\unicode[STIX]{x1D711}_{j})$
converges to
![]() $-\infty$
, a contradiction. Thus
$-\infty$
, a contradiction. Thus
 $\sup _{X}\unicode[STIX]{x1D711}_{j}$
is bounded from above as claimed. Since
$\sup _{X}\unicode[STIX]{x1D711}_{j}$
is bounded from above as claimed. Since
 $F(\unicode[STIX]{x1D711}_{j})\leqslant \text{I}(\unicode[STIX]{x1D711}_{j})\leqslant \sup _{X}\unicode[STIX]{x1D711}_{j}$
it follows that
$F(\unicode[STIX]{x1D711}_{j})\leqslant \text{I}(\unicode[STIX]{x1D711}_{j})\leqslant \sup _{X}\unicode[STIX]{x1D711}_{j}$
it follows that
![]() $\text{I}(\unicode[STIX]{x1D711}_{j})$
and hence
$\text{I}(\unicode[STIX]{x1D711}_{j})$
and hence
 $\sup _{X}\unicode[STIX]{x1D711}_{j}$
is also bounded from below. It follows again from [Reference Guedj and ZeriahiGZ05, Proposition 2.7] that a subsequence of
$\sup _{X}\unicode[STIX]{x1D711}_{j}$
is also bounded from below. It follows again from [Reference Guedj and ZeriahiGZ05, Proposition 2.7] that a subsequence of
![]() $\unicode[STIX]{x1D711}_{j}$
(still denoted by
$\unicode[STIX]{x1D711}_{j}$
(still denoted by
![]() $\unicode[STIX]{x1D711}_{j}$
) converges in
$\unicode[STIX]{x1D711}_{j}$
) converges in
 $L^{1}(X,\unicode[STIX]{x1D714}^{n})$
to some
$L^{1}(X,\unicode[STIX]{x1D714}^{n})$
to some
 $\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
. Since
$\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
. Since
![]() $\text{I}$
is upper semicontinuous it follows that
$\text{I}$
is upper semicontinuous it follows that
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
. Moreover, by continuity of
$\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
. Moreover, by continuity of
![]() $L_{\unicode[STIX]{x1D707}}$
it follows that
$L_{\unicode[STIX]{x1D707}}$
it follows that
 $F(\unicode[STIX]{x1D711})\geqslant \sup _{{\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})}F$
completing the proof.◻
$F(\unicode[STIX]{x1D711})\geqslant \sup _{{\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})}F$
completing the proof.◻
Next we prove that the maximizer obtained above is actually the solution to the complex Monge–Ampère equation (3). The proof relies on a differentiability property of the Monge–Ampère energy functional.
Theorem 2.2. Fix
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
and let
$\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
and let
![]() $\unicode[STIX]{x1D712}$
be a continuous real valued function
$\unicode[STIX]{x1D712}$
be a continuous real valued function
![]() $X$
. Set
$X$
. Set
 $\unicode[STIX]{x1D711}_{t}=P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}+t\unicode[STIX]{x1D712})$
,
$\unicode[STIX]{x1D711}_{t}=P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}+t\unicode[STIX]{x1D712})$
,
![]() $t\in \mathbb{R}$
. Then
$t\in \mathbb{R}$
. Then
 $t\mapsto I(\unicode[STIX]{x1D711}_{t})$
is differentiable and its derivative is given by
$t\mapsto I(\unicode[STIX]{x1D711}_{t})$
is differentiable and its derivative is given by
 $$\begin{eqnarray}\frac{d}{dt}\text{I}(\unicode[STIX]{x1D711}_{t})=\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n},\quad \forall t\in \mathbb{R}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{d}{dt}\text{I}(\unicode[STIX]{x1D711}_{t})=\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n},\quad \forall t\in \mathbb{R}.\end{eqnarray}$$
Note that
 $\unicode[STIX]{x1D711}_{t}\geqslant \unicode[STIX]{x1D711}-|t|\sup _{X}|\unicode[STIX]{x1D712}|$
, hence
$\unicode[STIX]{x1D711}_{t}\geqslant \unicode[STIX]{x1D711}-|t|\sup _{X}|\unicode[STIX]{x1D712}|$
, hence
 $\unicode[STIX]{x1D711}_{t}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
for all
$\unicode[STIX]{x1D711}_{t}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
for all
![]() $t\in \mathbb{R}$
. This result was first proved in [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Lemma 4.2] using [Reference Berman and BoucksomBB10]. A simplification of the original argument has been given in [Reference Lu and NguyenLN15], and we follow this approach here.
$t\in \mathbb{R}$
. This result was first proved in [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Lemma 4.2] using [Reference Berman and BoucksomBB10]. A simplification of the original argument has been given in [Reference Lu and NguyenLN15], and we follow this approach here.
Proof. Let
![]() $u$
be a continuous function on
$u$
be a continuous function on
![]() $X$
and set
$X$
and set
 $u_{t}:=P_{\unicode[STIX]{x1D703}}(u+t\unicode[STIX]{x1D712})$
,
$u_{t}:=P_{\unicode[STIX]{x1D703}}(u+t\unicode[STIX]{x1D712})$
,
![]() $t\in \mathbb{R}$
. Then for each
$t\in \mathbb{R}$
. Then for each
![]() $t\in \mathbb{R}$
,
$t\in \mathbb{R}$
,
![]() $u_{t}$
is a
$u_{t}$
is a
![]() $\unicode[STIX]{x1D703}$
-psh function with minimal singularities. We claim that
$\unicode[STIX]{x1D703}$
-psh function with minimal singularities. We claim that
 $$\begin{eqnarray}\frac{d}{dt}\text{I}(u_{t})=\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{u_{t}}^{n},\quad \forall t\in \mathbb{R}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{d}{dt}\text{I}(u_{t})=\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{u_{t}}^{n},\quad \forall t\in \mathbb{R}.\end{eqnarray}$$
It suffices to prove the claim for
![]() $t=0$
. We only prove the equality for the right-derivative since the same argument can be applied to deal with the left-derivative. We fix
$t=0$
. We only prove the equality for the right-derivative since the same argument can be applied to deal with the left-derivative. We fix
![]() $t>0$
. It follows from the concavity of
$t>0$
. It follows from the concavity of
![]() $\text{I}$
[Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10] that
$\text{I}$
[Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10] that
 $$\begin{eqnarray}\int _{X}(u_{t}-u_{0})\unicode[STIX]{x1D703}_{u_{t}}^{n}\leqslant \text{I}(u_{t})-\text{I}(u_{0})\leqslant \int _{X}(u_{t}-u_{0})\unicode[STIX]{x1D703}_{u_{0}}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}(u_{t}-u_{0})\unicode[STIX]{x1D703}_{u_{t}}^{n}\leqslant \text{I}(u_{t})-\text{I}(u_{0})\leqslant \int _{X}(u_{t}-u_{0})\unicode[STIX]{x1D703}_{u_{0}}^{n}.\end{eqnarray}$$
On the other hand, since
![]() $u+t\unicode[STIX]{x1D712}$
is continuous on
$u+t\unicode[STIX]{x1D712}$
is continuous on
![]() $X$
, it follows from a balayage argument (see [Reference Bedford and TaylorBT82]) that
$X$
, it follows from a balayage argument (see [Reference Bedford and TaylorBT82]) that
![]() $\unicode[STIX]{x1D703}_{u_{t}}^{n}$
is supported on the contact set
$\unicode[STIX]{x1D703}_{u_{t}}^{n}$
is supported on the contact set
 $\{u_{t}=u+t\unicode[STIX]{x1D712}\}$
. It thus follows that
$\{u_{t}=u+t\unicode[STIX]{x1D712}\}$
. It thus follows that
 $$\begin{eqnarray}\int _{X}(u_{t}-u_{0})\unicode[STIX]{x1D703}_{u_{t}}^{n}=\int _{X}(u+t\unicode[STIX]{x1D712}-u_{0})\unicode[STIX]{x1D703}_{u_{t}}^{n}\geqslant t\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{u_{t}}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}(u_{t}-u_{0})\unicode[STIX]{x1D703}_{u_{t}}^{n}=\int _{X}(u+t\unicode[STIX]{x1D712}-u_{0})\unicode[STIX]{x1D703}_{u_{t}}^{n}\geqslant t\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{u_{t}}^{n}.\end{eqnarray}$$
By a similar argument we also get
 $$\begin{eqnarray}\int _{X}(u_{t}-u_{0})\unicode[STIX]{x1D703}_{u_{0}}^{n}=\int _{X}(u_{t}-u)\unicode[STIX]{x1D703}_{u_{0}}^{n}\leqslant t\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{u_{0}}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}(u_{t}-u_{0})\unicode[STIX]{x1D703}_{u_{0}}^{n}=\int _{X}(u_{t}-u)\unicode[STIX]{x1D703}_{u_{0}}^{n}\leqslant t\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{u_{0}}^{n}.\end{eqnarray}$$
We note that
![]() $u_{t}$
converges uniformly to
$u_{t}$
converges uniformly to
![]() $u_{0}$
as
$u_{0}$
as
![]() $t\rightarrow 0^{+}$
, hence by [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10] we have that
$t\rightarrow 0^{+}$
, hence by [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10] we have that
![]() $\unicode[STIX]{x1D703}_{u_{t}}^{n}$
converges weakly to
$\unicode[STIX]{x1D703}_{u_{t}}^{n}$
converges weakly to
![]() $\unicode[STIX]{x1D703}_{u_{0}}^{n}$
. Since
$\unicode[STIX]{x1D703}_{u_{0}}^{n}$
. Since
![]() $\unicode[STIX]{x1D712}$
is continuous, we can divide all of the above estimates with
$\unicode[STIX]{x1D712}$
is continuous, we can divide all of the above estimates with
![]() $t>0$
, and let
$t>0$
, and let
![]() $t\rightarrow 0$
to finish the proof of the claim.
$t\rightarrow 0$
to finish the proof of the claim.
Now, we come back to the proof of the theorem. We approximate
![]() $\unicode[STIX]{x1D711}$
from above by a sequence
$\unicode[STIX]{x1D711}$
from above by a sequence
![]() $\unicode[STIX]{x1D711}_{j}$
of continuous functions on
$\unicode[STIX]{x1D711}_{j}$
of continuous functions on
![]() $X$
. For each
$X$
. For each
![]() $j$
, we set
$j$
, we set
 $\unicode[STIX]{x1D711}_{t,j}:=P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}_{j}+t\unicode[STIX]{x1D712})$
and note that
$\unicode[STIX]{x1D711}_{t,j}:=P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}_{j}+t\unicode[STIX]{x1D712})$
and note that
![]() $\unicode[STIX]{x1D711}_{t,j}$
decreases pointwise to
$\unicode[STIX]{x1D711}_{t,j}$
decreases pointwise to
![]() $\unicode[STIX]{x1D711}_{t}$
as
$\unicode[STIX]{x1D711}_{t}$
as
 $j\rightarrow +\infty$
. Since
$j\rightarrow +\infty$
. Since
![]() $\unicode[STIX]{x1D712}$
is continuous on
$\unicode[STIX]{x1D712}$
is continuous on
![]() $X$
and
$X$
and
![]() $\unicode[STIX]{x1D711}_{t,j}$
converges uniformly to
$\unicode[STIX]{x1D711}_{t,j}$
converges uniformly to
![]() $\unicode[STIX]{x1D711}_{s,j}$
as
$\unicode[STIX]{x1D711}_{s,j}$
as
![]() $t\rightarrow s$
it follows from continuity of the complex Monge–Ampère operator together with our claim that the function
$t\rightarrow s$
it follows from continuity of the complex Monge–Ampère operator together with our claim that the function
 $t\mapsto \text{I}(\unicode[STIX]{x1D711}_{t,j})$
is of class
$t\mapsto \text{I}(\unicode[STIX]{x1D711}_{t,j})$
is of class
![]() ${\mathcal{C}}^{1}$
on
${\mathcal{C}}^{1}$
on
![]() $\mathbb{R}$
. We thus have that
$\mathbb{R}$
. We thus have that
 $$\begin{eqnarray}\text{I}(\unicode[STIX]{x1D711}_{t,j})-\text{I}(\unicode[STIX]{x1D711}_{0,j})=\int _{0}^{t}\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{s,j}}^{n}\,ds.\end{eqnarray}$$
$$\begin{eqnarray}\text{I}(\unicode[STIX]{x1D711}_{t,j})-\text{I}(\unicode[STIX]{x1D711}_{0,j})=\int _{0}^{t}\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{s,j}}^{n}\,ds.\end{eqnarray}$$
Letting
 $j\rightarrow +\infty$
, and using the dominated convergence theorem we obtain
$j\rightarrow +\infty$
, and using the dominated convergence theorem we obtain
 $$\begin{eqnarray}\text{I}(\unicode[STIX]{x1D711}_{t})-\text{I}(\unicode[STIX]{x1D711}_{0})=\int _{0}^{t}\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{s}}^{n}\,ds.\end{eqnarray}$$
$$\begin{eqnarray}\text{I}(\unicode[STIX]{x1D711}_{t})-\text{I}(\unicode[STIX]{x1D711}_{0})=\int _{0}^{t}\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{s}}^{n}\,ds.\end{eqnarray}$$
By continuity of the Monge–Ampère operator the function
 $s\mapsto \int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{s}}^{n}$
is continuous on
$s\mapsto \int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{s}}^{n}$
is continuous on
![]() $\mathbb{R}$
. Therefore, from the above equality we see that
$\mathbb{R}$
. Therefore, from the above equality we see that
 $t\mapsto \text{I}(\unicode[STIX]{x1D711}_{t})$
is differentiable and its derivative is exactly as in the statement of the theorem.◻
$t\mapsto \text{I}(\unicode[STIX]{x1D711}_{t})$
is differentiable and its derivative is exactly as in the statement of the theorem.◻
We are now ready to solve (3).
Theorem 2.3. Let
![]() $\unicode[STIX]{x1D707}$
be a non-pluripolar positive measure on
$\unicode[STIX]{x1D707}$
be a non-pluripolar positive measure on
![]() $X$
. Then there exists a unique
$X$
. Then there exists a unique
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
solving (3). Moreover, if
$\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
solving (3). Moreover, if
 $\unicode[STIX]{x1D707}=f\unicode[STIX]{x1D714}^{n}$
for some bounded non-negative function
$\unicode[STIX]{x1D707}=f\unicode[STIX]{x1D714}^{n}$
for some bounded non-negative function
![]() $f$
, then
$f$
, then
![]() $\unicode[STIX]{x1D711}$
has minimal singularities.
$\unicode[STIX]{x1D711}$
has minimal singularities.
Proof. As before we can assume that
![]() $\unicode[STIX]{x1D6FD}=1$
. It follows from Proposition 2.1 that there exists
$\unicode[STIX]{x1D6FD}=1$
. It follows from Proposition 2.1 that there exists
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
such that
$\unicode[STIX]{x1D711}\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
such that
 $F(\unicode[STIX]{x1D711})=\sup _{{\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})}F$
. Fix a continuous function
$F(\unicode[STIX]{x1D711})=\sup _{{\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})}F$
. Fix a continuous function
![]() $\unicode[STIX]{x1D712}$
and set
$\unicode[STIX]{x1D712}$
and set
 $$\begin{eqnarray}g(t):=I(\unicode[STIX]{x1D711}_{t})-\int _{X}e^{\unicode[STIX]{x1D711}+t\unicode[STIX]{x1D712}}\,d\unicode[STIX]{x1D707},\quad t\in \mathbb{R},\end{eqnarray}$$
$$\begin{eqnarray}g(t):=I(\unicode[STIX]{x1D711}_{t})-\int _{X}e^{\unicode[STIX]{x1D711}+t\unicode[STIX]{x1D712}}\,d\unicode[STIX]{x1D707},\quad t\in \mathbb{R},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D711}_{t}:=P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}+t\unicode[STIX]{x1D712})\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
. Since
$\unicode[STIX]{x1D711}_{t}:=P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}+t\unicode[STIX]{x1D712})\in {\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
. Since
 $\unicode[STIX]{x1D711}_{t}\leqslant \unicode[STIX]{x1D711}+t\unicode[STIX]{x1D712}$
and since
$\unicode[STIX]{x1D711}_{t}\leqslant \unicode[STIX]{x1D711}+t\unicode[STIX]{x1D712}$
and since
![]() $\unicode[STIX]{x1D711}$
maximizes
$\unicode[STIX]{x1D711}$
maximizes
![]() $F$
on
$F$
on
 ${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
we have
${\mathcal{E}}^{1}(X,\unicode[STIX]{x1D703})$
we have
 $$\begin{eqnarray}g(0)=F(\unicode[STIX]{x1D711})\geqslant F(\unicode[STIX]{x1D711}_{t})\geqslant g(t),\quad \forall t\in \mathbb{R}.\end{eqnarray}$$
$$\begin{eqnarray}g(0)=F(\unicode[STIX]{x1D711})\geqslant F(\unicode[STIX]{x1D711}_{t})\geqslant g(t),\quad \forall t\in \mathbb{R}.\end{eqnarray}$$
Thus
![]() $g$
attains its maximum at 0. It follows from Theorem 2.2 and the dominated convergence theorem that
$g$
attains its maximum at 0. It follows from Theorem 2.2 and the dominated convergence theorem that
![]() $g$
is differentiable at 0, hence
$g$
is differentiable at 0, hence
 $g^{\prime }(0)=0$
which means
$g^{\prime }(0)=0$
which means
 $$\begin{eqnarray}\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}=\int _{X}\unicode[STIX]{x1D712}e^{\unicode[STIX]{x1D711}}\,d\unicode[STIX]{x1D707}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}\unicode[STIX]{x1D712}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}=\int _{X}\unicode[STIX]{x1D712}e^{\unicode[STIX]{x1D711}}\,d\unicode[STIX]{x1D707}.\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D712}$
was chosen arbitrarily it follows that (3) is satisfied in the weak sense of measure.
$\unicode[STIX]{x1D712}$
was chosen arbitrarily it follows that (3) is satisfied in the weak sense of measure.
The uniqueness follows from Lemma 2.5 below. Finally, if
![]() $\unicode[STIX]{x1D707}$
has bounded density, then the right-hand side in (3) has bounded density (because
$\unicode[STIX]{x1D707}$
has bounded density, then the right-hand side in (3) has bounded density (because
![]() $\unicode[STIX]{x1D711}$
is bounded from above), hence it follows from [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Thereom 4.1] that
$\unicode[STIX]{x1D711}$
is bounded from above), hence it follows from [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Thereom 4.1] that
![]() $\unicode[STIX]{x1D711}$
has minimal singularities.◻
$\unicode[STIX]{x1D711}$
has minimal singularities.◻
2.2.2 The domination principle
The following domination principle was proved in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Corollary 2.5] for two
![]() $\unicode[STIX]{x1D703}$
-psh functions
$\unicode[STIX]{x1D703}$
-psh functions
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
with
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
with
![]() $\unicode[STIX]{x1D711}$
having minimal singularities. The argument of Dinew [Reference Bloom and LevenbergBL12] gives a generalization of this result to the case when
$\unicode[STIX]{x1D711}$
having minimal singularities. The argument of Dinew [Reference Bloom and LevenbergBL12] gives a generalization of this result to the case when
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
does not necessarily have minimal singularities.
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
does not necessarily have minimal singularities.
Proposition 2.4. Let
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
be
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
be
![]() $\unicode[STIX]{x1D703}$
-psh functions such that
$\unicode[STIX]{x1D703}$
-psh functions such that
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. If
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. If
![]() $\unicode[STIX]{x1D713}\leqslant \unicode[STIX]{x1D711}$
almost everywhere with respect to
$\unicode[STIX]{x1D713}\leqslant \unicode[STIX]{x1D711}$
almost everywhere with respect to
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}$
, then
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}$
, then
![]() $\unicode[STIX]{x1D713}\leqslant \unicode[STIX]{x1D711}$
everywhere.
$\unicode[STIX]{x1D713}\leqslant \unicode[STIX]{x1D711}$
everywhere.
Proof. Fix
![]() $t>0$
. As
$t>0$
. As
 $\{\unicode[STIX]{x1D711}>\unicode[STIX]{x1D713}-t\}$
is plurifine open, it follows from locality of the non-pluripolar product with respect to the plurifine topology [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 1.4] that
$\{\unicode[STIX]{x1D711}>\unicode[STIX]{x1D713}-t\}$
is plurifine open, it follows from locality of the non-pluripolar product with respect to the plurifine topology [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 1.4] that
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}-t)}^{n}\geqslant \mathbf{1}_{\{\unicode[STIX]{x1D711}>\unicode[STIX]{x1D713}-t\}}\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}-t)}^{n}=\mathbf{1}_{\{\unicode[STIX]{x1D711}>\unicode[STIX]{x1D713}-t\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}-t)}^{n}\geqslant \mathbf{1}_{\{\unicode[STIX]{x1D711}>\unicode[STIX]{x1D713}-t\}}\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}-t)}^{n}=\mathbf{1}_{\{\unicode[STIX]{x1D711}>\unicode[STIX]{x1D713}-t\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n},\end{eqnarray}$$
where in the last identity we used the assumption that
 $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}(\{\unicode[STIX]{x1D711}<\unicode[STIX]{x1D713}\})=0$
. As
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}(\{\unicode[STIX]{x1D711}<\unicode[STIX]{x1D713}\})=0$
. As
 $\max (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}-t)$
also has full mass, the above inequality becomes equality. This together with the uniqueness theorem, proved in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem A] which is an adaptation of the original proof in the Kähler case due to Dinew [Reference DinewDin09], gives that
$\max (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}-t)$
also has full mass, the above inequality becomes equality. This together with the uniqueness theorem, proved in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem A] which is an adaptation of the original proof in the Kähler case due to Dinew [Reference DinewDin09], gives that
 $\max (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}-t)=\unicode[STIX]{x1D711}+C$
, for some constant
$\max (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}-t)=\unicode[STIX]{x1D711}+C$
, for some constant
![]() $C$
which can be easily seen to be zero. Letting
$C$
which can be easily seen to be zero. Letting
![]() $t\rightarrow 0^{+}$
we obtain the desired result.◻
$t\rightarrow 0^{+}$
we obtain the desired result.◻
Lemma 2.5. Fix
![]() $\unicode[STIX]{x1D6FD}>0$
and
$\unicode[STIX]{x1D6FD}>0$
and
![]() $\unicode[STIX]{x1D707}$
a non-pluripolar positive measure on
$\unicode[STIX]{x1D707}$
a non-pluripolar positive measure on
![]() $X$
. Assume that
$X$
. Assume that
 $v\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
and
$v\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
and
 $u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
satisfy
$u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
satisfy
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{u}^{n}\geqslant e^{\unicode[STIX]{x1D6FD}u}e^{-\unicode[STIX]{x1D719}}\unicode[STIX]{x1D707};\quad \unicode[STIX]{x1D703}_{v}^{n}\leqslant e^{\unicode[STIX]{x1D6FD}v}e^{-\unicode[STIX]{x1D719}}\unicode[STIX]{x1D707},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{u}^{n}\geqslant e^{\unicode[STIX]{x1D6FD}u}e^{-\unicode[STIX]{x1D719}}\unicode[STIX]{x1D707};\quad \unicode[STIX]{x1D703}_{v}^{n}\leqslant e^{\unicode[STIX]{x1D6FD}v}e^{-\unicode[STIX]{x1D719}}\unicode[STIX]{x1D707},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D719}$
is some Borel measurable function on
$\unicode[STIX]{x1D719}$
is some Borel measurable function on
![]() $X$
. Then
$X$
. Then
![]() $u\leqslant v$
on
$u\leqslant v$
on
![]() $X$
.
$X$
.
Proof. It follows from the comparison principle (see [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Corollary 2.3]) that
 $$\begin{eqnarray}\int _{\{v<u\}}e^{\unicode[STIX]{x1D6FD}u-\unicode[STIX]{x1D719}}\,d\unicode[STIX]{x1D707}\leqslant \int _{\{v<u\}}\unicode[STIX]{x1D703}_{u}^{n}\leqslant \int _{\{v<u\}}\unicode[STIX]{x1D703}_{v}^{n}\leqslant \int _{\{v<u\}}e^{\unicode[STIX]{x1D6FD}v-\unicode[STIX]{x1D719}}\,d\unicode[STIX]{x1D707}\leqslant \int _{\{v<u\}}e^{\unicode[STIX]{x1D6FD}u-\unicode[STIX]{x1D719}}\,d\unicode[STIX]{x1D707}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\{v<u\}}e^{\unicode[STIX]{x1D6FD}u-\unicode[STIX]{x1D719}}\,d\unicode[STIX]{x1D707}\leqslant \int _{\{v<u\}}\unicode[STIX]{x1D703}_{u}^{n}\leqslant \int _{\{v<u\}}\unicode[STIX]{x1D703}_{v}^{n}\leqslant \int _{\{v<u\}}e^{\unicode[STIX]{x1D6FD}v-\unicode[STIX]{x1D719}}\,d\unicode[STIX]{x1D707}\leqslant \int _{\{v<u\}}e^{\unicode[STIX]{x1D6FD}u-\unicode[STIX]{x1D719}}\,d\unicode[STIX]{x1D707}.\end{eqnarray}$$
Thus, the inequalities above become equalities and we have in particular that
 $$\begin{eqnarray}\int _{\{v<u\}}(e^{\unicode[STIX]{x1D6FD}u}-e^{\unicode[STIX]{x1D6FD}v})e^{-\unicode[STIX]{x1D719}}\,d\unicode[STIX]{x1D707}=0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\{v<u\}}(e^{\unicode[STIX]{x1D6FD}u}-e^{\unicode[STIX]{x1D6FD}v})e^{-\unicode[STIX]{x1D719}}\,d\unicode[STIX]{x1D707}=0.\end{eqnarray}$$
Since
![]() $\unicode[STIX]{x1D719}$
is bounded from above on
$\unicode[STIX]{x1D719}$
is bounded from above on
![]() $X$
it follows that
$X$
it follows that
 $\int _{\{v<u\}}(e^{\unicode[STIX]{x1D6FD}u}-e^{\unicode[STIX]{x1D6FD}v})\,d\unicode[STIX]{x1D707}=0$
. We then deduce that
$\int _{\{v<u\}}(e^{\unicode[STIX]{x1D6FD}u}-e^{\unicode[STIX]{x1D6FD}v})\,d\unicode[STIX]{x1D707}=0$
. We then deduce that
 $\unicode[STIX]{x1D707}(\{-\infty <v<u\})=0$
. Since
$\unicode[STIX]{x1D707}(\{-\infty <v<u\})=0$
. Since
![]() $\unicode[STIX]{x1D707}$
is non-pluripolar it follows that
$\unicode[STIX]{x1D707}$
is non-pluripolar it follows that
 $\unicode[STIX]{x1D707}(\{v<u\})=0$
. Consequently
$\unicode[STIX]{x1D707}(\{v<u\})=0$
. Consequently
 $\unicode[STIX]{x1D703}_{v}^{n}(\{v<u\})=0$
, and the domination principle (Proposition 2.4) gives that
$\unicode[STIX]{x1D703}_{v}^{n}(\{v<u\})=0$
, and the domination principle (Proposition 2.4) gives that
![]() $u\leqslant v$
on
$u\leqslant v$
on
![]() $X$
.◻
$X$
.◻
2.3 Regularity of quasi-psh envelopes
By a deep result of Berman and Demailly [Reference Berman and DemaillyBD12], the envelope
![]() $V_{\unicode[STIX]{x1D703}}$
has locally bounded Laplacian in the ample locus
$V_{\unicode[STIX]{x1D703}}$
has locally bounded Laplacian in the ample locus
 $\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
and its complex Monge–Ampère measure satisfies
$\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
and its complex Monge–Ampère measure satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{V_{\unicode[STIX]{x1D703}}}^{n}=\mathbf{1}_{\{V_{\unicode[STIX]{x1D703}}=0\}}\unicode[STIX]{x1D703}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{V_{\unicode[STIX]{x1D703}}}^{n}=\mathbf{1}_{\{V_{\unicode[STIX]{x1D703}}=0\}}\unicode[STIX]{x1D703}^{n}.\end{eqnarray}$$
In the case when
![]() $\{\unicode[STIX]{x1D703}\}$
is integral, this result has been obtained by Berman [Reference BermanBer09] using different methods. In [Reference BermanBer13], Berman introduced a new approximation scheme of the envelope by solving a suitably chosen family of complex Monge–Ampère equations. In the case when the class
$\{\unicode[STIX]{x1D703}\}$
is integral, this result has been obtained by Berman [Reference BermanBer09] using different methods. In [Reference BermanBer13], Berman introduced a new approximation scheme of the envelope by solving a suitably chosen family of complex Monge–Ampère equations. In the case when the class
![]() $\{\unicode[STIX]{x1D703}\}$
is big and nef, using this method, he gave a proof of the regularity of
$\{\unicode[STIX]{x1D703}\}$
is big and nef, using this method, he gave a proof of the regularity of
![]() $V_{\unicode[STIX]{x1D703}}$
using partial differential equations. Given the almost
$V_{\unicode[STIX]{x1D703}}$
using partial differential equations. Given the almost
![]() ${\mathcal{C}}^{1,1}$
-regularity of
${\mathcal{C}}^{1,1}$
-regularity of
![]() $V_{\unicode[STIX]{x1D703}}$
it is classical to obtain (4). In the general case of a big class Berman’s method gives the following weaker version of (4).
$V_{\unicode[STIX]{x1D703}}$
it is classical to obtain (4). In the general case of a big class Berman’s method gives the following weaker version of (4).
Theorem 2.6. Suppose
![]() $(X,\unicode[STIX]{x1D714})$
is Kähler. Let
$(X,\unicode[STIX]{x1D714})$
is Kähler. Let
![]() $\unicode[STIX]{x1D703}$
be a smooth
$\unicode[STIX]{x1D703}$
be a smooth
![]() $(1,1)$
-form such that
$(1,1)$
-form such that
![]() $\{\unicode[STIX]{x1D703}\}$
is big. Then the envelope
$\{\unicode[STIX]{x1D703}\}$
is big. Then the envelope
![]() $V_{\unicode[STIX]{x1D703}}$
satisfies
$V_{\unicode[STIX]{x1D703}}$
satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{V_{\unicode[STIX]{x1D703}}}^{n}\leqslant \mathbf{1}_{\{V_{\unicode[STIX]{x1D703}}=0\}}\unicode[STIX]{x1D703}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{V_{\unicode[STIX]{x1D703}}}^{n}\leqslant \mathbf{1}_{\{V_{\unicode[STIX]{x1D703}}=0\}}\unicode[STIX]{x1D703}^{n}.\end{eqnarray}$$
We will use Theorem 2.6 in the construction of the rooftop envelope of two functions in
![]() ${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
(see Theorem 2.10). In the case when
${\mathcal{E}}(X,\unicode[STIX]{x1D703})$
(see Theorem 2.10). In the case when
![]() $\{\unicode[STIX]{x1D703}\}$
is Kähler a detailed study of this envelope has been done in [Reference Darvas and RubinsteinDR16, Reference DarvasDar17a] which has found many interesting applications in Kähler geometry.
$\{\unicode[STIX]{x1D703}\}$
is Kähler a detailed study of this envelope has been done in [Reference Darvas and RubinsteinDR16, Reference DarvasDar17a] which has found many interesting applications in Kähler geometry.
For a proof of Theorem 2.6 we refer to [Reference BermanBer13] (see the paragraph ‘on the proof’ at [Reference BermanBer13, p. 6 and Lemma 2.12 in version 3]). An alternative proof using viscosity theory was recently given in [Reference Guedj, Lu and ZeriahiGLZ17, Proposition 5.2].
2.4 Comparison of capacities
Given a big class
![]() $\{\unicode[STIX]{x1D703}\}$
, recall that the
$\{\unicode[STIX]{x1D703}\}$
, recall that the
![]() $\unicode[STIX]{x1D703}$
-capacity of a set
$\unicode[STIX]{x1D703}$
-capacity of a set
![]() $E\subset X$
is defined as follows (see [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, § 4.1] for further details):
$E\subset X$
is defined as follows (see [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, § 4.1] for further details):
 $$\begin{eqnarray}\operatorname{Cap}_{\unicode[STIX]{x1D703}}(E):=\sup \biggl\{\int _{E}\unicode[STIX]{x1D703}_{u}^{n}\mid u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})~V_{\unicode[STIX]{x1D703}}-1\leqslant u\leqslant V_{\unicode[STIX]{x1D703}}\biggr\}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cap}_{\unicode[STIX]{x1D703}}(E):=\sup \biggl\{\int _{E}\unicode[STIX]{x1D703}_{u}^{n}\mid u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})~V_{\unicode[STIX]{x1D703}}-1\leqslant u\leqslant V_{\unicode[STIX]{x1D703}}\biggr\}.\end{eqnarray}$$
The global extremal
![]() $\unicode[STIX]{x1D703}$
-psh function of
$\unicode[STIX]{x1D703}$
-psh function of
![]() $E$
is defined as the upper semicontinuous (usc) regularization of
$E$
is defined as the upper semicontinuous (usc) regularization of
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D703},E}:=\sup \{u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})\mid u\leqslant 0~\text{on}~E\}.\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D703},E}:=\sup \{u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})\mid u\leqslant 0~\text{on}~E\}.\end{eqnarray}$$
By the definition of
![]() $V_{\unicode[STIX]{x1D703},E}$
it follows that
$V_{\unicode[STIX]{x1D703},E}$
it follows that
 $V_{\unicode[STIX]{x1D703},E}^{\ast }=V_{\unicode[STIX]{x1D703},F}^{\ast }$
if
$V_{\unicode[STIX]{x1D703},E}^{\ast }=V_{\unicode[STIX]{x1D703},F}^{\ast }$
if
 $E=F\cup P$
for some pluripolar set
$E=F\cup P$
for some pluripolar set
![]() $P$
. To see this it suffices to observe that any pluripolar set is contained in the
$P$
. To see this it suffices to observe that any pluripolar set is contained in the
![]() $-\infty$
locus of some
$-\infty$
locus of some
 $\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
. The latter standard fact can be quickly explained as follows. If
$\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
. The latter standard fact can be quickly explained as follows. If
![]() $E$
is pluripolar, then by [Reference Guedj and ZeriahiGZ05, Theorem 7.2] there exists
$E$
is pluripolar, then by [Reference Guedj and ZeriahiGZ05, Theorem 7.2] there exists
 $u\in \operatorname{PSH}(X,\unicode[STIX]{x1D714})$
such that
$u\in \operatorname{PSH}(X,\unicode[STIX]{x1D714})$
such that
 $u(x)=-\infty$
for all
$u(x)=-\infty$
for all
![]() $x\in E$
. As
$x\in E$
. As
![]() $\{\unicode[STIX]{x1D703}\}$
is big, there exists
$\{\unicode[STIX]{x1D703}\}$
is big, there exists
 $\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
such that
$\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
such that
 $\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D713}\geqslant \unicode[STIX]{x1D700}\unicode[STIX]{x1D714}$
for some small constant
$\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D713}\geqslant \unicode[STIX]{x1D700}\unicode[STIX]{x1D714}$
for some small constant
![]() $\unicode[STIX]{x1D700}>0$
. It is clear that the function
$\unicode[STIX]{x1D700}>0$
. It is clear that the function
 $\unicode[STIX]{x1D711}:=\unicode[STIX]{x1D713}+\unicode[STIX]{x1D700}u$
belongs to
$\unicode[STIX]{x1D711}:=\unicode[STIX]{x1D713}+\unicode[STIX]{x1D700}u$
belongs to
 $\operatorname{PSH}(X,\unicode[STIX]{x1D703})$
and takes value
$\operatorname{PSH}(X,\unicode[STIX]{x1D703})$
and takes value
![]() $-\infty$
on
$-\infty$
on
![]() $E$
as we claimed.
$E$
as we claimed.
Denote by
 $T_{\unicode[STIX]{x1D703}}(E):=\exp (-M_{\unicode[STIX]{x1D703},E}):=\exp (-\sup _{X}V_{\unicode[STIX]{x1D703},E}^{\star })$
the Alexander–Taylor capacity of
$T_{\unicode[STIX]{x1D703}}(E):=\exp (-M_{\unicode[STIX]{x1D703},E}):=\exp (-\sup _{X}V_{\unicode[STIX]{x1D703},E}^{\star })$
the Alexander–Taylor capacity of
![]() $E$
. We recall the following useful relation between the
$E$
. We recall the following useful relation between the
![]() $\unicode[STIX]{x1D703}$
-capacity and the Alexander–Taylor capacity (see [Reference Di NezzaDiN15, Proposition 5.4] and [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Lemma 4.2]).
$\unicode[STIX]{x1D703}$
-capacity and the Alexander–Taylor capacity (see [Reference Di NezzaDiN15, Proposition 5.4] and [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Lemma 4.2]).
Proposition 2.7. There exists
![]() $A>0$
such that for all Borel subsets
$A>0$
such that for all Borel subsets
![]() $E\subset X$
,
$E\subset X$
,
 $$\begin{eqnarray}\exp \biggl[-\frac{A}{\operatorname{Cap}_{\unicode[STIX]{x1D703}}(E)}\biggr]\leqslant T_{\unicode[STIX]{x1D703}}(E)\leqslant e\cdot \exp \biggl[-\biggl(\frac{\operatorname{Vol}(\{\unicode[STIX]{x1D703}\})}{\operatorname{Cap}_{\unicode[STIX]{x1D703}}(E)}\biggr)^{1/n}\biggr].\end{eqnarray}$$
$$\begin{eqnarray}\exp \biggl[-\frac{A}{\operatorname{Cap}_{\unicode[STIX]{x1D703}}(E)}\biggr]\leqslant T_{\unicode[STIX]{x1D703}}(E)\leqslant e\cdot \exp \biggl[-\biggl(\frac{\operatorname{Vol}(\{\unicode[STIX]{x1D703}\})}{\operatorname{Cap}_{\unicode[STIX]{x1D703}}(E)}\biggr)^{1/n}\biggr].\end{eqnarray}$$
The second inequality was proved in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10] while the first one was proved in [Reference Di NezzaDiN15, Proposition 5.4] using the main result of [Reference Berman and DemaillyBD12]. But, what was actually used in the proof of [Reference Di NezzaDiN15, Proposition 5.4] is the inequality in Theorem 2.6. Thus Proposition 2.7 is independent of [Reference Berman and DemaillyBD12].
Using Proposition 2.7 and a sharp analysis in the ample locus we get the following comparison between two
![]() $\unicode[STIX]{x1D703}$
-capacities. Let us emphasize that this result significantly extends [Reference Di NezzaDiN15, Theorem 5.6] where an extra assumption is required (see [Reference Di NezzaDiN15, Definition 4.2]).
$\unicode[STIX]{x1D703}$
-capacities. Let us emphasize that this result significantly extends [Reference Di NezzaDiN15, Theorem 5.6] where an extra assumption is required (see [Reference Di NezzaDiN15, Definition 4.2]).
Theorem 2.8. Suppose
![]() $\{\unicode[STIX]{x1D703}_{1}\}$
and
$\{\unicode[STIX]{x1D703}_{1}\}$
and
![]() $\{\unicode[STIX]{x1D703}_{2}\}$
are big. Then there exists
$\{\unicode[STIX]{x1D703}_{2}\}$
are big. Then there exists
 $C=C(\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2})>0$
such that
$C=C(\unicode[STIX]{x1D703}_{1},\unicode[STIX]{x1D703}_{2})>0$
such that
 $$\begin{eqnarray}C^{-1}\operatorname{Cap}_{\unicode[STIX]{x1D703}_{1}}^{n}(E)\leqslant \operatorname{Cap}_{\unicode[STIX]{x1D703}_{2}}(E)\leqslant C\operatorname{Cap}_{\unicode[STIX]{x1D703}_{1}}^{1/n}(E),\end{eqnarray}$$
$$\begin{eqnarray}C^{-1}\operatorname{Cap}_{\unicode[STIX]{x1D703}_{1}}^{n}(E)\leqslant \operatorname{Cap}_{\unicode[STIX]{x1D703}_{2}}(E)\leqslant C\operatorname{Cap}_{\unicode[STIX]{x1D703}_{1}}^{1/n}(E),\end{eqnarray}$$
for all Borel subsets
![]() $E\subset X$
.
$E\subset X$
.
Proof. Since
![]() $\{\unicode[STIX]{x1D703}_{2}\}$
is big we can find
$\{\unicode[STIX]{x1D703}_{2}\}$
is big we can find
 $\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{2})$
that is smooth in
$\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{2})$
that is smooth in
 $\operatorname{Amp}(\{\unicode[STIX]{x1D703}_{2}\})$
,
$\operatorname{Amp}(\{\unicode[STIX]{x1D703}_{2}\})$
,
![]() $\unicode[STIX]{x1D713}$
has analytic singularities such that
$\unicode[STIX]{x1D713}$
has analytic singularities such that
 $\unicode[STIX]{x1D703}_{2}+dd^{c}\unicode[STIX]{x1D713}\geqslant \unicode[STIX]{x1D700}\unicode[STIX]{x1D714}\geqslant \unicode[STIX]{x1D700}\unicode[STIX]{x1D703}_{1}$
for some
$\unicode[STIX]{x1D703}_{2}+dd^{c}\unicode[STIX]{x1D713}\geqslant \unicode[STIX]{x1D700}\unicode[STIX]{x1D714}\geqslant \unicode[STIX]{x1D700}\unicode[STIX]{x1D703}_{1}$
for some
![]() $\unicode[STIX]{x1D700}>0$
[Reference BoucksomBou04]. Normalize
$\unicode[STIX]{x1D700}>0$
[Reference BoucksomBou04]. Normalize
![]() $\unicode[STIX]{x1D713}$
by
$\unicode[STIX]{x1D713}$
by
 $\sup _{X}\unicode[STIX]{x1D713}=0$
and denote by
$\sup _{X}\unicode[STIX]{x1D713}=0$
and denote by
 $U=\{\unicode[STIX]{x1D713}>-1\}$
which is a non-empty open subset of
$U=\{\unicode[STIX]{x1D713}>-1\}$
which is a non-empty open subset of
![]() $X$
, hence
$X$
, hence
 $M_{\unicode[STIX]{x1D703}_{1},U}=\sup _{X}V_{\unicode[STIX]{x1D703}_{1},U}<+\infty$
. Now, the function
$M_{\unicode[STIX]{x1D703}_{1},U}=\sup _{X}V_{\unicode[STIX]{x1D703}_{1},U}<+\infty$
. Now, the function
 $u=\unicode[STIX]{x1D713}+\unicode[STIX]{x1D700}V_{\unicode[STIX]{x1D703}_{1},E}^{\ast }$
is
$u=\unicode[STIX]{x1D713}+\unicode[STIX]{x1D700}V_{\unicode[STIX]{x1D703}_{1},E}^{\ast }$
is
![]() $\unicode[STIX]{x1D703}_{2}$
-psh and satisfies
$\unicode[STIX]{x1D703}_{2}$
-psh and satisfies
![]() $u\leqslant 0$
on
$u\leqslant 0$
on
![]() $E$
(modulo a pluripolar set). Thus by definition we have
$E$
(modulo a pluripolar set). Thus by definition we have
 $u\leqslant V_{\unicode[STIX]{x1D703}_{2},E}^{\ast }$
. It follows that
$u\leqslant V_{\unicode[STIX]{x1D703}_{2},E}^{\ast }$
. It follows that
 $$\begin{eqnarray}M_{\unicode[STIX]{x1D703}_{2},E}\geqslant \sup _{U}u\geqslant \unicode[STIX]{x1D700}\sup _{U}V_{\unicode[STIX]{x1D703}_{1},E}^{\ast }-1.\end{eqnarray}$$
$$\begin{eqnarray}M_{\unicode[STIX]{x1D703}_{2},E}\geqslant \sup _{U}u\geqslant \unicode[STIX]{x1D700}\sup _{U}V_{\unicode[STIX]{x1D703}_{1},E}^{\ast }-1.\end{eqnarray}$$
On the other hand
 $V_{\unicode[STIX]{x1D703}_{1},E}^{\ast }-\sup _{U}V_{\unicode[STIX]{x1D703}_{1},E}^{\ast }$
is
$V_{\unicode[STIX]{x1D703}_{1},E}^{\ast }-\sup _{U}V_{\unicode[STIX]{x1D703}_{1},E}^{\ast }$
is
![]() $\unicode[STIX]{x1D703}_{1}$
-psh and takes non-positive values on
$\unicode[STIX]{x1D703}_{1}$
-psh and takes non-positive values on
![]() $U$
, hence
$U$
, hence
 $V_{\unicode[STIX]{x1D703}_{1},E}^{\ast }-\sup _{U}V_{\unicode[STIX]{x1D703}_{1},E}^{\ast }\leqslant V_{\unicode[STIX]{x1D703}_{1},U}$
. This together with the above inequality yields
$V_{\unicode[STIX]{x1D703}_{1},E}^{\ast }-\sup _{U}V_{\unicode[STIX]{x1D703}_{1},E}^{\ast }\leqslant V_{\unicode[STIX]{x1D703}_{1},U}$
. This together with the above inequality yields
 $$\begin{eqnarray}M_{\unicode[STIX]{x1D703}_{2},E}\geqslant \unicode[STIX]{x1D700}(M_{\unicode[STIX]{x1D703}_{1},E}-M_{\unicode[STIX]{x1D703}_{1},U})-1,\end{eqnarray}$$
$$\begin{eqnarray}M_{\unicode[STIX]{x1D703}_{2},E}\geqslant \unicode[STIX]{x1D700}(M_{\unicode[STIX]{x1D703}_{1},E}-M_{\unicode[STIX]{x1D703}_{1},U})-1,\end{eqnarray}$$
giving that, for some
![]() $C>0$
fixed we have
$C>0$
fixed we have
 $T_{\unicode[STIX]{x1D703}_{2}}(E)\leqslant CT_{\unicode[STIX]{x1D703}_{1}}(E)^{\unicode[STIX]{x1D700}}$
. An elementary calculation using the double estimate of Proposition 2.7 finishes the proof.◻
$T_{\unicode[STIX]{x1D703}_{2}}(E)\leqslant CT_{\unicode[STIX]{x1D703}_{1}}(E)^{\unicode[STIX]{x1D700}}$
. An elementary calculation using the double estimate of Proposition 2.7 finishes the proof.◻
From this comparison of capacities and standard arguments in pluripotential theory we immediately get the following convergence result.
Corollary 2.9. Assume that
![]() $\{\unicode[STIX]{x1D703}\}$
is big and
$\{\unicode[STIX]{x1D703}\}$
is big and
 $\{\unicode[STIX]{x1D711}_{j}^{i}\}_{j},i=1,\ldots ,n$
are sequences of
$\{\unicode[STIX]{x1D711}_{j}^{i}\}_{j},i=1,\ldots ,n$
are sequences of
![]() $\unicode[STIX]{x1D703}$
-psh functions with minimal singularities that converge decreasingly (or uniformly) to
$\unicode[STIX]{x1D703}$
-psh functions with minimal singularities that converge decreasingly (or uniformly) to
 $\unicode[STIX]{x1D711}^{i},i=1,\ldots ,n$
(also with minimal singularities). If
$\unicode[STIX]{x1D711}^{i},i=1,\ldots ,n$
(also with minimal singularities). If
![]() $f_{j}$
is a sequence of uniformly bounded quasi-continuous functions converging monotonically to
$f_{j}$
is a sequence of uniformly bounded quasi-continuous functions converging monotonically to
![]() $f$
(also quasi-continuous), then
$f$
(also quasi-continuous), then
 $$\begin{eqnarray}\int _{X}f_{j}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\rightarrow \int _{X}f\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}f_{j}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\rightarrow \int _{X}f\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}}.\end{eqnarray}$$
Proof. Let
![]() $\unicode[STIX]{x1D714}$
be a Kähler form on
$\unicode[STIX]{x1D714}$
be a Kähler form on
![]() $X$
. By the definition of quasi-continuity, for any
$X$
. By the definition of quasi-continuity, for any
![]() $\unicode[STIX]{x1D700}>0$
one can find an open set
$\unicode[STIX]{x1D700}>0$
one can find an open set
![]() $U\subset X$
such that all
$U\subset X$
such that all
![]() $f_{j}$
are continuous in
$f_{j}$
are continuous in
![]() $X\setminus U$
and
$X\setminus U$
and
 $\text{Cap}_{\unicode[STIX]{x1D714}}(U)\leqslant \unicode[STIX]{x1D700}$
. Using Theorem 2.8, a standard argument now gives that
$\text{Cap}_{\unicode[STIX]{x1D714}}(U)\leqslant \unicode[STIX]{x1D700}$
. Using Theorem 2.8, a standard argument now gives that
 $$\begin{eqnarray}\int _{U}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\leqslant C\unicode[STIX]{x1D700}^{1/n},\quad \int _{U}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}}\leqslant C\unicode[STIX]{x1D700}^{1/n}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{U}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\leqslant C\unicode[STIX]{x1D700}^{1/n},\quad \int _{U}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}}\leqslant C\unicode[STIX]{x1D700}^{1/n}.\end{eqnarray}$$
Now we can use Tietze’s theorem to extend each
 $f_{j}|_{X\setminus U},f|_{X\setminus U}$
to a continuous functions
$f_{j}|_{X\setminus U},f|_{X\setminus U}$
to a continuous functions
![]() $\tilde{f}_{j},\tilde{f}$
on
$\tilde{f}_{j},\tilde{f}$
on
![]() $X$
whose
$X$
whose
![]() $L^{\infty }$
norm is controlled. It follows from [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem 2.17] that for
$L^{\infty }$
norm is controlled. It follows from [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem 2.17] that for
![]() $j_{0}$
fixed we have
$j_{0}$
fixed we have
 $$\begin{eqnarray}\int _{X}\tilde{f}_{j_{0}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\rightarrow \int _{X}\tilde{f}_{j_{0}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}},\quad \int _{X}\tilde{f}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\rightarrow \int _{X}\tilde{f}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}\tilde{f}_{j_{0}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\rightarrow \int _{X}\tilde{f}_{j_{0}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}},\quad \int _{X}\tilde{f}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\rightarrow \int _{X}\tilde{f}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}}.\end{eqnarray}$$
Using (5) and the uniform boundedness of
 $f_{j},\tilde{f}_{j},f,\tilde{f}$
, we can subsequently write that
$f_{j},\tilde{f}_{j},f,\tilde{f}$
, we can subsequently write that
 $$\begin{eqnarray}\int _{X}f_{j_{0}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\rightarrow \int _{X}f_{j_{0}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}},\quad \int _{X}f\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\rightarrow \int _{X}f\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}f_{j_{0}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\rightarrow \int _{X}f_{j_{0}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}},\quad \int _{X}f\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\rightarrow \int _{X}f\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}}.\end{eqnarray}$$
Finally, using the above and the monotonicity of
![]() $f_{j}$
we can write that
$f_{j}$
we can write that
 $$\begin{eqnarray}\lim _{j_{0}\rightarrow \infty }\int _{X}f_{j_{0}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}}\geqslant \lim _{j\rightarrow \infty }\int _{X}f_{j}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\geqslant \int _{X}f\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}}.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{j_{0}\rightarrow \infty }\int _{X}f_{j_{0}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}}\geqslant \lim _{j\rightarrow \infty }\int _{X}f_{j}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}^{n}}\geqslant \int _{X}f\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{1}}\wedge \cdots \wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}^{n}}.\end{eqnarray}$$
After invoking the dominated convergence theorem, the proof is finished. ◻
2.5 The operator
 $P(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
$P(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
Consider
![]() $X$
a compact Kähler manifold and
$X$
a compact Kähler manifold and
![]() $\{\unicode[STIX]{x1D703}\}$
a big cohomology class. Given a usc function
$\{\unicode[STIX]{x1D703}\}$
a big cohomology class. Given a usc function
![]() $f$
on
$f$
on
![]() $X$
, it is natural to ask whether there exists
$X$
, it is natural to ask whether there exists
 $u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
lying below
$u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
lying below
![]() $f$
. We will pay particular attention to the case when
$f$
. We will pay particular attention to the case when
 $f=\min (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
, where
$f=\min (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})$
, where
 $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
, in which case more can be said. Indeed, when
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
, in which case more can be said. Indeed, when
![]() $\{\unicode[STIX]{x1D703}\}$
is Kähler and
$\{\unicode[STIX]{x1D703}\}$
is Kähler and
 $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, it was shown in [Reference DarvasDar17a] that
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, it was shown in [Reference DarvasDar17a] that
 $P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. The analogue of this result holds in the big case as well.
$P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. The analogue of this result holds in the big case as well.
Theorem 2.10. Let
 $\unicode[STIX]{x1D712}\in {\mathcal{W}}^{-}$
, i.e.,
$\unicode[STIX]{x1D712}\in {\mathcal{W}}^{-}$
, i.e.,
![]() $\unicode[STIX]{x1D712}$
is convex increasing with
$\unicode[STIX]{x1D712}$
is convex increasing with
 $\unicode[STIX]{x1D712}(0)=0$
and
$\unicode[STIX]{x1D712}(0)=0$
and
 $\unicode[STIX]{x1D712}(-\infty )=-\infty$
. If
$\unicode[STIX]{x1D712}(-\infty )=-\infty$
. If
 $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
, then
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
, then
 $P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}):=P_{\unicode[STIX]{x1D703}}(\min (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}))\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
. In particular, if
$P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}):=P_{\unicode[STIX]{x1D703}}(\min (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}))\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
. In particular, if
 $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, then
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, then
 $P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, thus
$P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, thus
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711})\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
.
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711})\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
.
Proof. Without loss of generality we can assume that
 $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\leqslant 0$
. Let
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}\leqslant 0$
. Let
 $\unicode[STIX]{x1D711}_{j}:=\max (\unicode[STIX]{x1D711},V_{\unicode[STIX]{x1D703}}-j)$
,
$\unicode[STIX]{x1D711}_{j}:=\max (\unicode[STIX]{x1D711},V_{\unicode[STIX]{x1D703}}-j)$
,
 $\unicode[STIX]{x1D713}_{j}:=\max (\unicode[STIX]{x1D713},V_{\unicode[STIX]{x1D703}}-j)$
be the canonical approximants. For each
$\unicode[STIX]{x1D713}_{j}:=\max (\unicode[STIX]{x1D713},V_{\unicode[STIX]{x1D703}}-j)$
be the canonical approximants. For each
![]() $j>0$
, it follows from Lemma 2.11 below that there exists a unique
$j>0$
, it follows from Lemma 2.11 below that there exists a unique
 $u_{j}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities such that
$u_{j}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities such that
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{u_{j}}^{n}=e^{u_{j}-\unicode[STIX]{x1D711}_{j}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}}^{n}+e^{u_{j}-\unicode[STIX]{x1D713}_{j}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{j}}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{u_{j}}^{n}=e^{u_{j}-\unicode[STIX]{x1D711}_{j}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}}^{n}+e^{u_{j}-\unicode[STIX]{x1D713}_{j}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{j}}^{n}.\end{eqnarray}$$
Additionally, it follows from Lemma 2.5 (see also the proof of the uniqueness part in Lemma 2.11) that
 $u_{j}\leqslant \min (\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{j})$
. Consequently
$u_{j}\leqslant \min (\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{j})$
. Consequently
 $u_{j}\leqslant P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{j})$
.
$u_{j}\leqslant P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{j})$
.
Next we claim that
 $$\begin{eqnarray}\inf _{j}\int _{X}\unicode[STIX]{x1D712}(u_{j}-V_{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D703}_{u_{j}}^{n}>-\infty .\end{eqnarray}$$
$$\begin{eqnarray}\inf _{j}\int _{X}\unicode[STIX]{x1D712}(u_{j}-V_{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D703}_{u_{j}}^{n}>-\infty .\end{eqnarray}$$
To prove the claim, in view of (6) it suffices to prove that
 $$\begin{eqnarray}\inf _{j}\int _{X}\unicode[STIX]{x1D712}(u_{j}-V_{\unicode[STIX]{x1D703}})e^{u_{j}-\unicode[STIX]{x1D711}_{j}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}}^{n}>-\infty .\end{eqnarray}$$
$$\begin{eqnarray}\inf _{j}\int _{X}\unicode[STIX]{x1D712}(u_{j}-V_{\unicode[STIX]{x1D703}})e^{u_{j}-\unicode[STIX]{x1D711}_{j}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}}^{n}>-\infty .\end{eqnarray}$$
By convexity of
![]() $\unicode[STIX]{x1D712}$
it follows that
$\unicode[STIX]{x1D712}$
it follows that
 $\unicode[STIX]{x1D712}(t+s)\geqslant \unicode[STIX]{x1D712}(t)+\unicode[STIX]{x1D712}(s)$
, and also
$\unicode[STIX]{x1D712}(t+s)\geqslant \unicode[STIX]{x1D712}(t)+\unicode[STIX]{x1D712}(s)$
, and also
 $\unicode[STIX]{x1D712}(t)e^{t}\geqslant -C,$
for all
$\unicode[STIX]{x1D712}(t)e^{t}\geqslant -C,$
for all
![]() $t,s\leqslant 0$
for some
$t,s\leqslant 0$
for some
![]() $C>0$
. Thus to prove (7) it suffices to check that
$C>0$
. Thus to prove (7) it suffices to check that
 $$\begin{eqnarray}\inf _{j}\int _{X}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}_{j}-V_{\unicode[STIX]{x1D703}})e^{u_{j}-\unicode[STIX]{x1D711}_{j}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}}^{n}>-\infty .\end{eqnarray}$$
$$\begin{eqnarray}\inf _{j}\int _{X}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D711}_{j}-V_{\unicode[STIX]{x1D703}})e^{u_{j}-\unicode[STIX]{x1D711}_{j}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}}^{n}>-\infty .\end{eqnarray}$$
But this holds since
 $u_{j}\leqslant \unicode[STIX]{x1D711}_{j}$
and
$u_{j}\leqslant \unicode[STIX]{x1D711}_{j}$
and
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
. Thus the claim is proved.
$\unicode[STIX]{x1D711}\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
. Thus the claim is proved.
Since
 $\unicode[STIX]{x1D712}(-\infty )=-\infty$
, the claim implies that
$\unicode[STIX]{x1D712}(-\infty )=-\infty$
, the claim implies that
 $\sup _{X}u_{j}$
is uniformly bounded. It thus follows from [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.19] that some subsequence of
$\sup _{X}u_{j}$
is uniformly bounded. It thus follows from [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.19] that some subsequence of
![]() $u_{j}$
converges in
$u_{j}$
converges in
 $L^{1}(X,\unicode[STIX]{x1D714}^{n})$
to some
$L^{1}(X,\unicode[STIX]{x1D714}^{n})$
to some
 $u\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
. Since
$u\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
. Since
 $u_{j}\leqslant P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{j})$
it follows that
$u_{j}\leqslant P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}_{j},\unicode[STIX]{x1D713}_{j})$
it follows that
 $u\leqslant P_{\unicode[STIX]{x1D703}}(\min (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}))$
. Now, it follows from [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.14] that
$u\leqslant P_{\unicode[STIX]{x1D703}}(\min (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}))$
. Now, it follows from [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.14] that
 $P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
and so is
$P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
and so is
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711})$
.◻
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711})$
.◻
Lemma 2.11. Assume that
 $u,v\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities. Then there exists a unique
$u,v\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities. Then there exists a unique
 $\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities such that
$\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities such that
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}=e^{\unicode[STIX]{x1D711}-u}\unicode[STIX]{x1D703}_{u}^{n}+e^{\unicode[STIX]{x1D711}-v}\unicode[STIX]{x1D703}_{v}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}=e^{\unicode[STIX]{x1D711}-u}\unicode[STIX]{x1D703}_{u}^{n}+e^{\unicode[STIX]{x1D711}-v}\unicode[STIX]{x1D703}_{v}^{n}.\end{eqnarray}$$
Proof. The uniqueness follows from the Lemma 2.5. Indeed, assume that
 $\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
is another solution, i.e.
$\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
is another solution, i.e.
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}^{n}=e^{\unicode[STIX]{x1D713}-u}\unicode[STIX]{x1D703}_{u}^{n}+e^{\unicode[STIX]{x1D713}-v}\unicode[STIX]{x1D703}_{v}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}^{n}=e^{\unicode[STIX]{x1D713}-u}\unicode[STIX]{x1D703}_{u}^{n}+e^{\unicode[STIX]{x1D713}-v}\unicode[STIX]{x1D703}_{v}^{n}.\end{eqnarray}$$
Set
 $\unicode[STIX]{x1D707}=e^{u}\unicode[STIX]{x1D703}_{v}^{n}+e^{v}\unicode[STIX]{x1D703}_{u}^{n}$
and
$\unicode[STIX]{x1D707}=e^{u}\unicode[STIX]{x1D703}_{v}^{n}+e^{v}\unicode[STIX]{x1D703}_{u}^{n}$
and
 $\unicode[STIX]{x1D719}:=u+v$
. Then we can write
$\unicode[STIX]{x1D719}:=u+v$
. Then we can write
 $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}=e^{\unicode[STIX]{x1D711}-\unicode[STIX]{x1D719}}\unicode[STIX]{x1D707}$
and
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}=e^{\unicode[STIX]{x1D711}-\unicode[STIX]{x1D719}}\unicode[STIX]{x1D707}$
and
 $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}^{n}=e^{\unicode[STIX]{x1D713}-\unicode[STIX]{x1D719}}\unicode[STIX]{x1D707}$
. It thus follows from Lemma 2.5 that
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}^{n}=e^{\unicode[STIX]{x1D713}-\unicode[STIX]{x1D719}}\unicode[STIX]{x1D707}$
. It thus follows from Lemma 2.5 that
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D713}$
.
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D713}$
.
To prove the existence we approximate
![]() $u$
by
$u$
by
 $u_{j}:=\max (u,-j)$
and note that these are bounded functions. Observe that, for each
$u_{j}:=\max (u,-j)$
and note that these are bounded functions. Observe that, for each
![]() $j$
,
$j$
,
 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{j}:=e^{-u_{j}}\unicode[STIX]{x1D703}_{u}^{n}+e^{-v_{j}}\unicode[STIX]{x1D703}_{v}^{n}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{j}:=e^{-u_{j}}\unicode[STIX]{x1D703}_{u}^{n}+e^{-v_{j}}\unicode[STIX]{x1D703}_{v}^{n}\end{eqnarray}$$
is a non-pluripolar positive measure on
![]() $X$
. For each
$X$
. For each
![]() $j>0$
it follows from Theorem 2.3 that there exists
$j>0$
it follows from Theorem 2.3 that there exists
 $\unicode[STIX]{x1D711}_{j}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities such that
$\unicode[STIX]{x1D711}_{j}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities such that
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}}^{n}=e^{\unicode[STIX]{x1D711}_{j}}\unicode[STIX]{x1D707}_{j}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}}^{n}=e^{\unicode[STIX]{x1D711}_{j}}\unicode[STIX]{x1D707}_{j}.\end{eqnarray}$$
Let
![]() $C>0$
be a constant such that
$C>0$
be a constant such that
 $\sup _{X}|u-v|\leqslant 2C$
. This is possible because
$\sup _{X}|u-v|\leqslant 2C$
. This is possible because
![]() $u$
and
$u$
and
![]() $v$
have minimal singularities. The function
$v$
have minimal singularities. The function
 $\unicode[STIX]{x1D719}:=(u+v)/2-C-n\log 2$
is
$\unicode[STIX]{x1D719}:=(u+v)/2-C-n\log 2$
is
![]() $\unicode[STIX]{x1D703}$
-psh with minimal singularities and it satisfies
$\unicode[STIX]{x1D703}$
-psh with minimal singularities and it satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D719}}^{n}\geqslant e^{\unicode[STIX]{x1D719}}\unicode[STIX]{x1D707}_{j}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D719}}^{n}\geqslant e^{\unicode[STIX]{x1D719}}\unicode[STIX]{x1D707}_{j}.\end{eqnarray}$$
It thus follows from Lemma 2.5 that
![]() $\unicode[STIX]{x1D711}_{j}\geqslant \unicode[STIX]{x1D719}$
for all
$\unicode[STIX]{x1D711}_{j}\geqslant \unicode[STIX]{x1D719}$
for all
![]() $j$
. It also follows from Lemma 2.5 that
$j$
. It also follows from Lemma 2.5 that
![]() $\unicode[STIX]{x1D711}_{j}$
is decreasing in
$\unicode[STIX]{x1D711}_{j}$
is decreasing in
![]() $j$
, the pointwise limit
$j$
, the pointwise limit
 $\unicode[STIX]{x1D711}:=\lim _{j\rightarrow +\infty }\unicode[STIX]{x1D711}_{j}$
has minimal singularities. By continuity of the Monge–Ampère operator (see [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10]) it follows that
$\unicode[STIX]{x1D711}:=\lim _{j\rightarrow +\infty }\unicode[STIX]{x1D711}_{j}$
has minimal singularities. By continuity of the Monge–Ampère operator (see [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10]) it follows that
![]() $\unicode[STIX]{x1D711}$
is the solution we are looking for.◻
$\unicode[STIX]{x1D711}$
is the solution we are looking for.◻
As a simple consequence of the above result, we can settle the conjecture of [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Remark 2.16] about the convexity of the classes
 ${\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
. A similar result in the Kähler case was obtained in [Reference DarvasDar17a].
${\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
. A similar result in the Kähler case was obtained in [Reference DarvasDar17a].
Corollary 2.12. Suppose
 $\unicode[STIX]{x1D712}\in {\mathcal{W}}^{-}$
. Then
$\unicode[STIX]{x1D712}\in {\mathcal{W}}^{-}$
. Then
 ${\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
is convex.
${\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
is convex.
Proof. Given
 $u_{0},u_{1}\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
it follows that
$u_{0},u_{1}\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
it follows that
 $P_{\unicode[STIX]{x1D703}}(u_{0},u_{1})\leqslant tu_{0}+(1-t)u_{1}$
,
$P_{\unicode[STIX]{x1D703}}(u_{0},u_{1})\leqslant tu_{0}+(1-t)u_{1}$
,
 $t\in [0,1]$
. By the above result
$t\in [0,1]$
. By the above result
 $P_{\unicode[STIX]{x1D703}}(u_{0},u_{1})\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
. Now [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.14] implies that
$P_{\unicode[STIX]{x1D703}}(u_{0},u_{1})\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
. Now [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.14] implies that
 $tu_{0}+(1-t)u_{1}\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
.◻
$tu_{0}+(1-t)u_{1}\in {\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703})$
.◻
If
![]() $f$
is smooth, it follows from a balayage argument that
$f$
is smooth, it follows from a balayage argument that
![]() $\unicode[STIX]{x1D703}_{P_{\unicode[STIX]{x1D703}}(f)}^{n}$
is concentrated on the contact set
$\unicode[STIX]{x1D703}_{P_{\unicode[STIX]{x1D703}}(f)}^{n}$
is concentrated on the contact set
 $\{P_{\unicode[STIX]{x1D703}}(f)=f\}$
. Using the capacity theory developed in the previous subsection, the result also holds for more general functions
$\{P_{\unicode[STIX]{x1D703}}(f)=f\}$
. Using the capacity theory developed in the previous subsection, the result also holds for more general functions
![]() $f$
.
$f$
.
Proposition 2.13. Assume that
![]() $\{\unicode[STIX]{x1D703}\}$
is big,
$\{\unicode[STIX]{x1D703}\}$
is big,
 $P_{\unicode[STIX]{x1D703}}(f)\neq -\infty$
and
$P_{\unicode[STIX]{x1D703}}(f)\neq -\infty$
and
![]() $f$
is quasi-continuous and usc on
$f$
is quasi-continuous and usc on
![]() $X$
. Then
$X$
. Then
![]() $\unicode[STIX]{x1D703}_{P_{\unicode[STIX]{x1D703}}(f)}^{n}$
does not charge
$\unicode[STIX]{x1D703}_{P_{\unicode[STIX]{x1D703}}(f)}^{n}$
does not charge
 $\{P_{\unicode[STIX]{x1D703}}(f)<f\}$
.
$\{P_{\unicode[STIX]{x1D703}}(f)<f\}$
.
Proof. Without loss of generality we can assume that
![]() $f\leqslant 0$
. If
$f\leqslant 0$
. If
![]() $f$
is smooth, then the result follows from a balayage argument (or directly from Theorem 2.6). To treat the general case, we approximate
$f$
is smooth, then the result follows from a balayage argument (or directly from Theorem 2.6). To treat the general case, we approximate
![]() $f$
from above (by semicontinuity) by a sequence of smooth functions
$f$
from above (by semicontinuity) by a sequence of smooth functions
![]() $(f_{j})$
. We can also assume that
$(f_{j})$
. We can also assume that
![]() $f_{j}\leqslant 0$
. Set
$f_{j}\leqslant 0$
. Set
 $\unicode[STIX]{x1D711}_{j}:=P_{\unicode[STIX]{x1D703}}(f_{j})$
,
$\unicode[STIX]{x1D711}_{j}:=P_{\unicode[STIX]{x1D703}}(f_{j})$
,
 $\unicode[STIX]{x1D711}:=P_{\unicode[STIX]{x1D703}}(f)$
and note that
$\unicode[STIX]{x1D711}:=P_{\unicode[STIX]{x1D703}}(f)$
and note that
 $\unicode[STIX]{x1D711}_{j}{\searrow}\unicode[STIX]{x1D711}$
. For each
$\unicode[STIX]{x1D711}_{j}{\searrow}\unicode[STIX]{x1D711}$
. For each
![]() $j\in \mathbb{N}$
the measure
$j\in \mathbb{N}$
the measure
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}}^{n}$
vanishes in the set
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}}^{n}$
vanishes in the set
 $\{\unicode[STIX]{x1D711}_{j}<f_{j}\}$
. Now, we want to pass to the limit as
$\{\unicode[STIX]{x1D711}_{j}<f_{j}\}$
. Now, we want to pass to the limit as
 $j\rightarrow +\infty$
. We first fix
$j\rightarrow +\infty$
. We first fix
 $k,l\in \mathbb{N}$
and set
$k,l\in \mathbb{N}$
and set
 $$\begin{eqnarray}U_{k,l}=\{\unicode[STIX]{x1D711}_{k}<f\}\cap \{\unicode[STIX]{x1D711}>V_{\unicode[STIX]{x1D703}}-l\}.\end{eqnarray}$$
$$\begin{eqnarray}U_{k,l}=\{\unicode[STIX]{x1D711}_{k}<f\}\cap \{\unicode[STIX]{x1D711}>V_{\unicode[STIX]{x1D703}}-l\}.\end{eqnarray}$$
For any
![]() $j>k$
, note that on
$j>k$
, note that on
![]() $U_{k,l}$
we have
$U_{k,l}$
we have
 $\unicode[STIX]{x1D711}_{j}\geqslant \unicode[STIX]{x1D711}>V_{\unicode[STIX]{x1D703}}-l$
and
$\unicode[STIX]{x1D711}_{j}\geqslant \unicode[STIX]{x1D711}>V_{\unicode[STIX]{x1D703}}-l$
and
 $\{\unicode[STIX]{x1D711}_{k}<f\}\subset \{\unicode[STIX]{x1D711}_{j}<f_{j}\}$
. It thus follows from definition of the non-pluripolar product (see [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10]) that for any
$\{\unicode[STIX]{x1D711}_{k}<f\}\subset \{\unicode[STIX]{x1D711}_{j}<f_{j}\}$
. It thus follows from definition of the non-pluripolar product (see [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10]) that for any
![]() $j>k$
, the measure
$j>k$
, the measure
 $\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711}_{j},V_{\unicode[STIX]{x1D703}}-l)}^{n}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}}^{n}$
vanishes on
$\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711}_{j},V_{\unicode[STIX]{x1D703}}-l)}^{n}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{j}}^{n}$
vanishes on
![]() $U_{k,l}$
. By assumption
$U_{k,l}$
. By assumption
![]() $f$
is quasi-continuous, hence
$f$
is quasi-continuous, hence
![]() $U_{k,l}$
is quasi open. More precisely, for any fixed
$U_{k,l}$
is quasi open. More precisely, for any fixed
![]() $\unicode[STIX]{x1D700}>0$
there exists an open set
$\unicode[STIX]{x1D700}>0$
there exists an open set
![]() $V_{\unicode[STIX]{x1D700}}$
such that the set
$V_{\unicode[STIX]{x1D700}}$
such that the set
 $G_{\unicode[STIX]{x1D700}}:=(V_{\unicode[STIX]{x1D700}}\setminus U_{k,l}\cup U_{k,l}\setminus V_{\unicode[STIX]{x1D700}})$
satisfies
$G_{\unicode[STIX]{x1D700}}:=(V_{\unicode[STIX]{x1D700}}\setminus U_{k,l}\cup U_{k,l}\setminus V_{\unicode[STIX]{x1D700}})$
satisfies
 $\operatorname{Cap}_{\unicode[STIX]{x1D714}}(G_{\unicode[STIX]{x1D700}})\leqslant \unicode[STIX]{x1D700}$
. Observe that for fixed
$\operatorname{Cap}_{\unicode[STIX]{x1D714}}(G_{\unicode[STIX]{x1D700}})\leqslant \unicode[STIX]{x1D700}$
. Observe that for fixed
![]() $l$
all the functions
$l$
all the functions
 $\max (\unicode[STIX]{x1D711}_{j},V_{\unicode[STIX]{x1D703}}-l)$
are sandwiched between
$\max (\unicode[STIX]{x1D711}_{j},V_{\unicode[STIX]{x1D703}}-l)$
are sandwiched between
![]() $V_{\unicode[STIX]{x1D703}}-l$
and
$V_{\unicode[STIX]{x1D703}}-l$
and
![]() $V_{\unicode[STIX]{x1D703}}$
. It then follows that
$V_{\unicode[STIX]{x1D703}}$
. It then follows that
 $$\begin{eqnarray}\sup _{j\in \mathbb{N}}\int _{G_{\unicode[STIX]{x1D700}}}\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711}_{j},V_{\unicode[STIX]{x1D703}}-l)}^{n}\leqslant A\operatorname{Cap}_{\unicode[STIX]{x1D703}}(G_{\unicode[STIX]{x1D700}})\leqslant A^{\prime }\operatorname{Cap}_{\unicode[STIX]{x1D714}}^{1/n}(G_{\unicode[STIX]{x1D700}})\leqslant A^{\prime }\unicode[STIX]{x1D700}^{1/n},\end{eqnarray}$$
$$\begin{eqnarray}\sup _{j\in \mathbb{N}}\int _{G_{\unicode[STIX]{x1D700}}}\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711}_{j},V_{\unicode[STIX]{x1D703}}-l)}^{n}\leqslant A\operatorname{Cap}_{\unicode[STIX]{x1D703}}(G_{\unicode[STIX]{x1D700}})\leqslant A^{\prime }\operatorname{Cap}_{\unicode[STIX]{x1D714}}^{1/n}(G_{\unicode[STIX]{x1D700}})\leqslant A^{\prime }\unicode[STIX]{x1D700}^{1/n},\end{eqnarray}$$
where the last inequality follows from the comparison of capacities in Theorem 2.8. Consequently,
 $\sup _{j\in \mathbb{N}}\int _{V_{\unicode[STIX]{x1D700}}}\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711}_{j},V_{\unicode[STIX]{x1D703}}-l)}^{n}\leqslant A^{\prime }\unicode[STIX]{x1D700}^{1/n}$
, and the continuity of the Monge–Ampère operator allows to take the limit, and we ultimately obtain
$\sup _{j\in \mathbb{N}}\int _{V_{\unicode[STIX]{x1D700}}}\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711}_{j},V_{\unicode[STIX]{x1D703}}-l)}^{n}\leqslant A^{\prime }\unicode[STIX]{x1D700}^{1/n}$
, and the continuity of the Monge–Ampère operator allows to take the limit, and we ultimately obtain
 $$\begin{eqnarray}\int _{U_{k,l}}\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711},V_{\unicode[STIX]{x1D703}}-l)}^{n}\leqslant C\unicode[STIX]{x1D700}^{1/n},\end{eqnarray}$$
$$\begin{eqnarray}\int _{U_{k,l}}\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711},V_{\unicode[STIX]{x1D703}}-l)}^{n}\leqslant C\unicode[STIX]{x1D700}^{1/n},\end{eqnarray}$$
for some positive constant
![]() $C$
independent of
$C$
independent of
![]() $\unicode[STIX]{x1D700}$
(but dependent on
$\unicode[STIX]{x1D700}$
(but dependent on
![]() $l$
). Now letting
$l$
). Now letting
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
we see that
$\unicode[STIX]{x1D700}\rightarrow 0$
we see that
 $\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711},V_{\unicode[STIX]{x1D703}}-l)}^{n}$
vanishes in
$\unicode[STIX]{x1D703}_{\max (\unicode[STIX]{x1D711},V_{\unicode[STIX]{x1D703}}-l)}^{n}$
vanishes in
![]() $U_{k,l}$
. Letting
$U_{k,l}$
. Letting
 $l\rightarrow +\infty$
, and using the definition of the non-pluripolar product, we see that
$l\rightarrow +\infty$
, and using the definition of the non-pluripolar product, we see that
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}$
vanishes in
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}}^{n}$
vanishes in
 $\{\unicode[STIX]{x1D711}_{k}<f\}$
. Now, letting
$\{\unicode[STIX]{x1D711}_{k}<f\}$
. Now, letting
 $k\rightarrow +\infty$
we obtain the result.◻
$k\rightarrow +\infty$
we obtain the result.◻
With the previous result in hands, we can prove that the non-pluripolar Monge–Ampère measure of
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(\unicode[STIX]{x1D713})$
is supported on the contact set
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(\unicode[STIX]{x1D713})$
is supported on the contact set
 $\{P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(\unicode[STIX]{x1D713})=\unicode[STIX]{x1D713}\}$
. The latter was already proved in [Reference Ross and Witt NyströmRW14, Lemma 4.9] when
$\{P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(\unicode[STIX]{x1D713})=\unicode[STIX]{x1D713}\}$
. The latter was already proved in [Reference Ross and Witt NyströmRW14, Lemma 4.9] when
![]() $\{\unicode[STIX]{x1D703}\}$
is a Kähler class and
$\{\unicode[STIX]{x1D703}\}$
is a Kähler class and
![]() $\unicode[STIX]{x1D713}$
is continuous.
$\unicode[STIX]{x1D713}$
is continuous.
Proposition 2.14. Let
![]() $\{\unicode[STIX]{x1D703}\}$
be a big class. Assume that
$\{\unicode[STIX]{x1D703}\}$
be a big class. Assume that
 $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713},P(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
. Then
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713},P(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
. Then
 $\unicode[STIX]{x1D703}_{P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(\unicode[STIX]{x1D713})}^{n}$
does not charge
$\unicode[STIX]{x1D703}_{P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(\unicode[STIX]{x1D713})}^{n}$
does not charge
 $\{P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(\unicode[STIX]{x1D713})<\unicode[STIX]{x1D713}\}$
.
$\{P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(\unicode[STIX]{x1D713})<\unicode[STIX]{x1D713}\}$
.
Proof. For each
![]() $t>0$
, since
$t>0$
, since
 $\min (\unicode[STIX]{x1D711}+t,\unicode[STIX]{x1D713})$
is usc and quasi-continuous, it follows from Proposition 2.13 that
$\min (\unicode[STIX]{x1D711}+t,\unicode[STIX]{x1D713})$
is usc and quasi-continuous, it follows from Proposition 2.13 that
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}$
vanishes on
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}$
vanishes on
 $\{\unicode[STIX]{x1D713}_{t}<\min (\unicode[STIX]{x1D711}+t,\unicode[STIX]{x1D713})\}$
, where
$\{\unicode[STIX]{x1D713}_{t}<\min (\unicode[STIX]{x1D711}+t,\unicode[STIX]{x1D713})\}$
, where
 $\unicode[STIX]{x1D713}_{t}:=P_{\unicode[STIX]{x1D703}}(\min (\unicode[STIX]{x1D711}+t,\unicode[STIX]{x1D713}))$
. Because
$\unicode[STIX]{x1D713}_{t}:=P_{\unicode[STIX]{x1D703}}(\min (\unicode[STIX]{x1D711}+t,\unicode[STIX]{x1D713}))$
. Because
 $\{\unicode[STIX]{x1D713}_{t}<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+t\}\subset \{\unicode[STIX]{x1D713}_{t}<\min (\unicode[STIX]{x1D711}+t,\unicode[STIX]{x1D713})\}$
it thus follows that
$\{\unicode[STIX]{x1D713}_{t}<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+t\}\subset \{\unicode[STIX]{x1D713}_{t}<\min (\unicode[STIX]{x1D711}+t,\unicode[STIX]{x1D713})\}$
it thus follows that
 $$\begin{eqnarray}\int _{\{\unicode[STIX]{x1D713}_{t}<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+t\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}=0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\{\unicode[STIX]{x1D713}_{t}<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+t\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}=0.\end{eqnarray}$$
Fix
 $s>0,j>0$
and set
$s>0,j>0$
and set
 $v:=P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(\unicode[STIX]{x1D713})=(\lim _{t\rightarrow +\infty }\unicode[STIX]{x1D713}_{t})^{\ast }$
,
$v:=P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(\unicode[STIX]{x1D713})=(\lim _{t\rightarrow +\infty }\unicode[STIX]{x1D713}_{t})^{\ast }$
,
 $\unicode[STIX]{x1D713}_{t,j}:=\max (\unicode[STIX]{x1D713}_{t},V_{\unicode[STIX]{x1D703}}-j)$
,
$\unicode[STIX]{x1D713}_{t,j}:=\max (\unicode[STIX]{x1D713}_{t},V_{\unicode[STIX]{x1D703}}-j)$
,
 $v_{j}:=\,\max (v,V_{\unicode[STIX]{x1D703}}-j)$
. It is clear that
$v_{j}:=\,\max (v,V_{\unicode[STIX]{x1D703}}-j)$
. It is clear that
 $\unicode[STIX]{x1D713}_{t,j}{\nearrow}v_{j}$
almost everywhere as
$\unicode[STIX]{x1D713}_{t,j}{\nearrow}v_{j}$
almost everywhere as
![]() $t{\nearrow}\infty$
. By the plurifine property of the non-pluripolar Monge–Ampère measure it follows that
$t{\nearrow}\infty$
. By the plurifine property of the non-pluripolar Monge–Ampère measure it follows that
 $$\begin{eqnarray}\int _{\{V_{\unicode[STIX]{x1D703}}-j<\unicode[STIX]{x1D713}_{t}<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+t\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t,j}}^{n}=0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\{V_{\unicode[STIX]{x1D703}}-j<\unicode[STIX]{x1D713}_{t}<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+t\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t,j}}^{n}=0.\end{eqnarray}$$
For
![]() $t>s$
, we have
$t>s$
, we have
 $\unicode[STIX]{x1D713}_{s}\leqslant \unicode[STIX]{x1D713}_{t}\leqslant v\leqslant \unicode[STIX]{x1D713}$
. Consequently,
$\unicode[STIX]{x1D713}_{s}\leqslant \unicode[STIX]{x1D713}_{t}\leqslant v\leqslant \unicode[STIX]{x1D713}$
. Consequently,
 $\{V_{\unicode[STIX]{x1D703}}-j<\unicode[STIX]{x1D713}_{s}\leqslant v<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+s\}\subset \{V_{\unicode[STIX]{x1D703}}-j<\unicode[STIX]{x1D713}_{t}<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+t\}$
and we have
$\{V_{\unicode[STIX]{x1D703}}-j<\unicode[STIX]{x1D713}_{s}\leqslant v<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+s\}\subset \{V_{\unicode[STIX]{x1D703}}-j<\unicode[STIX]{x1D713}_{t}<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+t\}$
and we have
 $$\begin{eqnarray}\int _{\{V_{\unicode[STIX]{x1D703}}-j<\unicode[STIX]{x1D713}_{s}\leqslant v<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+s\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t,j}}^{n}=0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\{V_{\unicode[STIX]{x1D703}}-j<\unicode[STIX]{x1D713}_{s}\leqslant v<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+s\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t,j}}^{n}=0.\end{eqnarray}$$
Now, using the same trick as in the proof of Proposition 2.13 we let
 $t\rightarrow +\infty$
and arrive at
$t\rightarrow +\infty$
and arrive at
 $$\begin{eqnarray}\int _{\{V_{\unicode[STIX]{x1D703}}-j<\unicode[STIX]{x1D713}_{s}\leqslant v<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+s\}}\unicode[STIX]{x1D703}_{v_{j}}^{n}=0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\{V_{\unicode[STIX]{x1D703}}-j<\unicode[STIX]{x1D713}_{s}\leqslant v<\unicode[STIX]{x1D713}<\unicode[STIX]{x1D711}+s\}}\unicode[STIX]{x1D703}_{v_{j}}^{n}=0.\end{eqnarray}$$
Letting
 $s\rightarrow +\infty$
, then
$s\rightarrow +\infty$
, then
 $j\rightarrow +\infty$
, and noting that
$j\rightarrow +\infty$
, and noting that
![]() $\unicode[STIX]{x1D703}_{v}^{n}$
is a non-pluripolar measure, we can conclude that
$\unicode[STIX]{x1D703}_{v}^{n}$
is a non-pluripolar measure, we can conclude that
![]() $\unicode[STIX]{x1D703}_{v}^{n}$
vanishes on
$\unicode[STIX]{x1D703}_{v}^{n}$
vanishes on
 $\{v<\unicode[STIX]{x1D713}\}$
. This concludes the proof.◻
$\{v<\unicode[STIX]{x1D713}\}$
. This concludes the proof.◻
Theorem 2.15. Assume that
 $\unicode[STIX]{x1D713},\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. Then
$\unicode[STIX]{x1D713},\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. Then
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(\unicode[STIX]{x1D713})=\unicode[STIX]{x1D713}$
.
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(\unicode[STIX]{x1D713})=\unicode[STIX]{x1D713}$
.
3 Weak geodesics in big cohomology classes
3.1 Berndtsson’s construction
We introduce a notion of weak geodesics in big cohomology classes mimicking Berndtsson’s construction in [Reference BerndtssonBer15, § 2.2]. Fix
![]() $\unicode[STIX]{x1D703}$
a smooth closed
$\unicode[STIX]{x1D703}$
a smooth closed
![]() $(1,1)$
-form such that
$(1,1)$
-form such that
![]() $\{\unicode[STIX]{x1D703}\}$
is big and also fix
$\{\unicode[STIX]{x1D703}\}$
is big and also fix
 $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities. A subgeodesic of
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities. A subgeodesic of
![]() $\unicode[STIX]{x1D711}_{0}$
,
$\unicode[STIX]{x1D711}_{0}$
,
![]() $\unicode[STIX]{x1D711}_{1}$
is a curve
$\unicode[STIX]{x1D711}_{1}$
is a curve
 $[0,1]\ni t\mapsto u_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
such that:
$[0,1]\ni t\mapsto u_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
such that:
-
(i) for each
 $t\in [0,1]$
, the function
$t\in [0,1]$
, the function
 $u_{t}$
has minimal singularities;
$u_{t}$
has minimal singularities; -
(ii)
 $u_{0,1}=\lim _{t\rightarrow 0,1}u_{t}\leqslant \unicode[STIX]{x1D711}_{0,1}$
pointwise;
$u_{0,1}=\lim _{t\rightarrow 0,1}u_{t}\leqslant \unicode[STIX]{x1D711}_{0,1}$
pointwise; -
(iii) the complexification
 $X\times D\ni (x,z)\mapsto U(x,z):=u_{\log |z|}(x)$
is
$X\times D\ni (x,z)\mapsto U(x,z):=u_{\log |z|}(x)$
is
 $\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}$
-psh on
$\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}$
-psh on
 $X\times D$
, where
$X\times D$
, where
 $D:=\{z\in \mathbb{C}\mid 1<|z|<e\}$
is the annulus in
$D:=\{z\in \mathbb{C}\mid 1<|z|<e\}$
is the annulus in
 $\mathbb{C}$
and
$\mathbb{C}$
and
 $\unicode[STIX]{x1D70B}:X\times D\rightarrow X$
is the trivial projection.
$\unicode[STIX]{x1D70B}:X\times D\rightarrow X$
is the trivial projection.
Let us mention that a curve
 $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\in t\rightarrow u_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is a (general) subgeodesic if it satisfies only the appropriate version of (iii) above. In this case
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD})\in t\rightarrow u_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is a (general) subgeodesic if it satisfies only the appropriate version of (iii) above. In this case
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
may even take
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
may even take
![]() $\pm \infty$
as a value. We will not make a difference between the curve
$\pm \infty$
as a value. We will not make a difference between the curve
![]() $t\rightarrow u_{t}$
and its complexification
$t\rightarrow u_{t}$
and its complexification
![]() $U$
.
$U$
.
The weak geodesic
 $[0,1]\ni t\rightarrow \unicode[STIX]{x1D711}_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities joining
$[0,1]\ni t\rightarrow \unicode[STIX]{x1D711}_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities joining
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
is defined as the envelope of all subgeodesics, i.e.,
$\unicode[STIX]{x1D711}_{1}$
is defined as the envelope of all subgeodesics, i.e.,
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{l}(x):=\sup \{u_{l}(x),\text{where}~t\rightarrow u_{t}~\text{is a subgeodesic of}~\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\},\quad l\in [0,1],x\in X.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{l}(x):=\sup \{u_{l}(x),\text{where}~t\rightarrow u_{t}~\text{is a subgeodesic of}~\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\},\quad l\in [0,1],x\in X.\end{eqnarray}$$
Lemma 3.1. Let
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
be the weak geodesic joining
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
be the weak geodesic joining
 $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities, constructed as above. Then there exists
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities, constructed as above. Then there exists
 $C=C(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})>0$
such that
$C=C(\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})>0$
such that
 $$\begin{eqnarray}|\unicode[STIX]{x1D711}_{t}-\unicode[STIX]{x1D711}_{t^{\prime }}|\leqslant C|t-t^{\prime }|,\quad t,t^{\prime }\in [0,1].\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D711}_{t}-\unicode[STIX]{x1D711}_{t^{\prime }}|\leqslant C|t-t^{\prime }|,\quad t,t^{\prime }\in [0,1].\end{eqnarray}$$
Additionally, for the complexification
 $\unicode[STIX]{x1D6F7}(x,z):=\unicode[STIX]{x1D711}_{\log |z|}(x)$
we have
$\unicode[STIX]{x1D6F7}(x,z):=\unicode[STIX]{x1D711}_{\log |z|}(x)$
we have
 $$\begin{eqnarray}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}=0\quad \text{on}~\text{Amp}(\{\unicode[STIX]{x1D703}\})\times D,\end{eqnarray}$$
$$\begin{eqnarray}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}=0\quad \text{on}~\text{Amp}(\{\unicode[STIX]{x1D703}\})\times D,\end{eqnarray}$$
where equality is understood in the weak sense of measures.
Proof. The proof is essentially the same as in [Reference BerndtssonBer15, § 2.2], so we only point out the ideas. Consider the following (barrier) subgeodesic of
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
:
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
:
 $$\begin{eqnarray}u_{t}(x):=\max (\unicode[STIX]{x1D711}_{0}-Ct,\unicode[STIX]{x1D711}_{1}+C(t-1)),\end{eqnarray}$$
$$\begin{eqnarray}u_{t}(x):=\max (\unicode[STIX]{x1D711}_{0}-Ct,\unicode[STIX]{x1D711}_{1}+C(t-1)),\end{eqnarray}$$
where
![]() $C$
is a positive constant such that
$C$
is a positive constant such that
 $\unicode[STIX]{x1D711}_{1}-C\leqslant \unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}+C$
. It is clear that
$\unicode[STIX]{x1D711}_{1}-C\leqslant \unicode[STIX]{x1D711}_{0}\leqslant \unicode[STIX]{x1D711}_{1}+C$
. It is clear that
 $[0,1]\ni t\rightarrow u_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is a subgeodesic of
$[0,1]\ni t\rightarrow u_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is a subgeodesic of
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
, and by
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
, and by
![]() $t$
-convexity of
$t$
-convexity of
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
we can write
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
we can write
 $u_{t}\leqslant \unicode[STIX]{x1D711}_{t}\leqslant (1-t)\unicode[STIX]{x1D711}_{0}+t\unicode[STIX]{x1D711}_{1}$
, hence the conclusion about Lipschitz continuity of
$u_{t}\leqslant \unicode[STIX]{x1D711}_{t}\leqslant (1-t)\unicode[STIX]{x1D711}_{0}+t\unicode[STIX]{x1D711}_{1}$
, hence the conclusion about Lipschitz continuity of
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
follows.
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
follows.
The proof of (10) follows from a standard balayage argument and we refer the interested reader to [Reference BerndtssonBer15, § 2.2], to see how the ideas from there generalize to our setting. ◻
Next we prove a version of the comparison principle.
Proposition 3.2. Assume that
 $u,v\in \operatorname{PSH}(X\times D,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703})$
satisfies
$u,v\in \operatorname{PSH}(X\times D,\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703})$
satisfies
 $V_{\unicode[STIX]{x1D703}}-C\leqslant u_{s},v_{s},s\in D$
for some
$V_{\unicode[STIX]{x1D703}}-C\leqslant u_{s},v_{s},s\in D$
for some
![]() $C>0$
. If
$C>0$
. If
 $\liminf _{(x,z)\rightarrow X\times \unicode[STIX]{x2202}D}(u-v)\geqslant 0$
, then
$\liminf _{(x,z)\rightarrow X\times \unicode[STIX]{x2202}D}(u-v)\geqslant 0$
, then
 $$\begin{eqnarray}\int _{\{u<v\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}v)^{n+1}\leqslant \int _{\{u<v\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\{u<v\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}v)^{n+1}\leqslant \int _{\{u<v\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}.\end{eqnarray}$$
Proof. Fix
![]() $\unicode[STIX]{x1D700}>0$
,
$\unicode[STIX]{x1D700}>0$
,
![]() $\unicode[STIX]{x1D6FF}>0$
. As
$\unicode[STIX]{x1D6FF}>0$
. As
![]() $\unicode[STIX]{x1D703}$
is big we can find
$\unicode[STIX]{x1D703}$
is big we can find
 $\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
,
$\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
,
 $\sup _{X}\unicode[STIX]{x1D713}=0$
, with analytic singularities such that
$\sup _{X}\unicode[STIX]{x1D713}=0$
, with analytic singularities such that
 $X\setminus \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})=\{\unicode[STIX]{x1D713}=-\infty \}$
and
$X\setminus \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})=\{\unicode[STIX]{x1D713}=-\infty \}$
and
 $\unicode[STIX]{x1D713}\leqslant u_{s},v_{s},~s\in D$
, such that
$\unicode[STIX]{x1D713}\leqslant u_{s},v_{s},~s\in D$
, such that
 $\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D713}$
dominates a Kähler form. Consider
$\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D713}$
dominates a Kähler form. Consider
 $$\begin{eqnarray}u_{\unicode[STIX]{x1D700}}:=\max (u,v_{\unicode[STIX]{x1D700}}),\quad v_{\unicode[STIX]{x1D700}}:=(1-\unicode[STIX]{x1D6FF})v+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D713}-\unicode[STIX]{x1D700},\end{eqnarray}$$
$$\begin{eqnarray}u_{\unicode[STIX]{x1D700}}:=\max (u,v_{\unicode[STIX]{x1D700}}),\quad v_{\unicode[STIX]{x1D700}}:=(1-\unicode[STIX]{x1D6FF})v+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D713}-\unicode[STIX]{x1D700},\end{eqnarray}$$
for some constant
![]() $\unicode[STIX]{x1D706}>1$
. If
$\unicode[STIX]{x1D706}>1$
. If
![]() $\unicode[STIX]{x1D706}-1$
is small enough we have
$\unicode[STIX]{x1D706}-1$
is small enough we have
 $$\begin{eqnarray}\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D706}\unicode[STIX]{x1D713}=\unicode[STIX]{x1D706}(\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D713})+(1-\unicode[STIX]{x1D706})\unicode[STIX]{x1D703}\geqslant \unicode[STIX]{x1D706}\unicode[STIX]{x1D714}+(1-\unicode[STIX]{x1D706})\unicode[STIX]{x1D703}\geqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D706}\unicode[STIX]{x1D713}=\unicode[STIX]{x1D706}(\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D713})+(1-\unicode[STIX]{x1D706})\unicode[STIX]{x1D703}\geqslant \unicode[STIX]{x1D706}\unicode[STIX]{x1D714}+(1-\unicode[STIX]{x1D706})\unicode[STIX]{x1D703}\geqslant 0,\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D714}$
is a Kähler form on
$\unicode[STIX]{x1D714}$
is a Kähler form on
![]() $X$
. Thus
$X$
. Thus
![]() $v_{\unicode[STIX]{x1D700}}$
is
$v_{\unicode[STIX]{x1D700}}$
is
![]() $\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}$
-psh on
$\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}$
-psh on
![]() $X\times D$
. Observe that for some open relatively compact
$X\times D$
. Observe that for some open relatively compact
 $\unicode[STIX]{x1D6FA}^{\prime }\Subset \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
(
$\unicode[STIX]{x1D6FA}^{\prime }\Subset \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
(
![]() $\unicode[STIX]{x1D6FA}^{\prime }$
depends on
$\unicode[STIX]{x1D6FA}^{\prime }$
depends on
![]() $\unicode[STIX]{x1D706}$
),
$\unicode[STIX]{x1D706}$
),
![]() $K\Subset D$
, we have
$K\Subset D$
, we have
![]() $u_{\unicode[STIX]{x1D700}}\equiv u$
in a neighborhood containing
$u_{\unicode[STIX]{x1D700}}\equiv u$
in a neighborhood containing
 $(X\setminus \unicode[STIX]{x1D6FA}^{\prime })\times (D\setminus K)$
. It follows that
$(X\setminus \unicode[STIX]{x1D6FA}^{\prime })\times (D\setminus K)$
. It follows that
 $\int _{Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}=\int _{Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u_{\unicode[STIX]{x1D700}})^{n+1}$
, where
$\int _{Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}=\int _{Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u_{\unicode[STIX]{x1D700}})^{n+1}$
, where
 $Y:=\unicode[STIX]{x1D6FA}^{\prime }\times K$
. Indeed, for any test function
$Y:=\unicode[STIX]{x1D6FA}^{\prime }\times K$
. Indeed, for any test function
 $0\leqslant \unicode[STIX]{x1D712}\in {\mathcal{C}}^{\infty }(Y)$
which is identically
$0\leqslant \unicode[STIX]{x1D712}\in {\mathcal{C}}^{\infty }(Y)$
which is identically
![]() $1$
in an open neighborhood
$1$
in an open neighborhood
![]() $U$
inside
$U$
inside
![]() $Y$
such that
$Y$
such that
 $\{u<u_{\unicode[STIX]{x1D700}}\}\subset U$
we have
$\{u<u_{\unicode[STIX]{x1D700}}\}\subset U$
we have
 $$\begin{eqnarray}\int _{Y}\unicode[STIX]{x1D712}[(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}-(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u_{\unicode[STIX]{x1D700}})^{n+1}]=\int _{Y}(u-u_{\unicode[STIX]{x1D700}})dd^{c}\unicode[STIX]{x1D712}\wedge T=0,\end{eqnarray}$$
$$\begin{eqnarray}\int _{Y}\unicode[STIX]{x1D712}[(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}-(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u_{\unicode[STIX]{x1D700}})^{n+1}]=\int _{Y}(u-u_{\unicode[STIX]{x1D700}})dd^{c}\unicode[STIX]{x1D712}\wedge T=0,\end{eqnarray}$$
where
![]() $T$
is a positive
$T$
is a positive
![]() $(n,n)$
-current.
$(n,n)$
-current.
Recall that for locally bounded
![]() $\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}$
-psh functions
$\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}$
-psh functions
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
, the maximum principle for the complex Monge–Ampère operator yields
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
, the maximum principle for the complex Monge–Ampère operator yields
 $$\begin{eqnarray}\mathbf{1}_{\{\unicode[STIX]{x1D711}<\unicode[STIX]{x1D713}\}}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}\max (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}))^{n+1}=\mathbf{1}_{\{\unicode[STIX]{x1D711}<\unicode[STIX]{x1D713}\}}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D713})^{n+1}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{1}_{\{\unicode[STIX]{x1D711}<\unicode[STIX]{x1D713}\}}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}\max (\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}))^{n+1}=\mathbf{1}_{\{\unicode[STIX]{x1D711}<\unicode[STIX]{x1D713}\}}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D713})^{n+1}.\end{eqnarray}$$
Using the above facts we can write
 $$\begin{eqnarray}\displaystyle \int _{\{u<v_{\unicode[STIX]{x1D700}}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}v_{\unicode[STIX]{x1D700}})^{n+1} & = & \displaystyle \int _{\{u<v_{\unicode[STIX]{x1D700}}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u_{\unicode[STIX]{x1D700}})^{n+1}\nonumber\\ \displaystyle & = & \displaystyle \int _{Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u_{\unicode[STIX]{x1D700}})^{n+1}-\int _{\{u\geqslant v_{\unicode[STIX]{x1D700}}\}\cap Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u_{\unicode[STIX]{x1D700}})^{n+1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \int _{Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}-\int _{\{u>v_{\unicode[STIX]{x1D700}}\}\cap Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u_{\unicode[STIX]{x1D700}})^{n+1}\nonumber\\ \displaystyle & = & \displaystyle \int _{Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}-\int _{\{u>v_{\unicode[STIX]{x1D700}}\}\cap Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \int _{\{u<(1-\unicode[STIX]{x1D6FF})v+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D713}-\unicode[STIX]{x1D700}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \int _{\{u<v_{\unicode[STIX]{x1D700}}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}v_{\unicode[STIX]{x1D700}})^{n+1} & = & \displaystyle \int _{\{u<v_{\unicode[STIX]{x1D700}}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u_{\unicode[STIX]{x1D700}})^{n+1}\nonumber\\ \displaystyle & = & \displaystyle \int _{Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u_{\unicode[STIX]{x1D700}})^{n+1}-\int _{\{u\geqslant v_{\unicode[STIX]{x1D700}}\}\cap Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u_{\unicode[STIX]{x1D700}})^{n+1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \int _{Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}-\int _{\{u>v_{\unicode[STIX]{x1D700}}\}\cap Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u_{\unicode[STIX]{x1D700}})^{n+1}\nonumber\\ \displaystyle & = & \displaystyle \int _{Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}-\int _{\{u>v_{\unicode[STIX]{x1D700}}\}\cap Y}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \int _{\{u<(1-\unicode[STIX]{x1D6FF})v+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}\unicode[STIX]{x1D713}-\unicode[STIX]{x1D700}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}u)^{n+1}.\nonumber\end{eqnarray}$$
The left-hand side in the above estimate can be further estimated in the following way:
 $$\begin{eqnarray}\int _{\{u<v_{\unicode[STIX]{x1D700}}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}v_{\unicode[STIX]{x1D700}})^{n+1}\geqslant (1-\unicode[STIX]{x1D6FF})^{n}\int _{\{u<v_{\unicode[STIX]{x1D700}}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}v)^{n+1}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\{u<v_{\unicode[STIX]{x1D700}}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}v_{\unicode[STIX]{x1D700}})^{n+1}\geqslant (1-\unicode[STIX]{x1D6FF})^{n}\int _{\{u<v_{\unicode[STIX]{x1D700}}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}v)^{n+1}.\end{eqnarray}$$
Letting
 $\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D700}\rightarrow 0$
, the proof is finished.◻
$\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D700}\rightarrow 0$
, the proof is finished.◻
Proposition 3.3. Let
 $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities and
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities and
 $[0,1]\ni t\rightarrow u_{t}$
be a subgeodesic of
$[0,1]\ni t\rightarrow u_{t}$
be a subgeodesic of
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
with minimal singularities satisfying (9) and
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
with minimal singularities satisfying (9) and
 $u_{0,1}=\unicode[STIX]{x1D711}_{0,1}$
. If the complexification satisfies
$u_{0,1}=\unicode[STIX]{x1D711}_{0,1}$
. If the complexification satisfies
 $(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}U)^{n+1}=0$
on
$(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}U)^{n+1}=0$
on
 $\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D$
, then
$\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D$
, then
![]() $t\rightarrow u_{t}$
is the weak geodesic connecting
$t\rightarrow u_{t}$
is the weak geodesic connecting
![]() $\unicode[STIX]{x1D711}_{0}$
to
$\unicode[STIX]{x1D711}_{0}$
to
![]() $\unicode[STIX]{x1D711}_{1}$
.
$\unicode[STIX]{x1D711}_{1}$
.
Proof. Let
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
be the weak geodesic connecting
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
be the weak geodesic connecting
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
. It suffices to show that
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
. It suffices to show that
![]() $\unicode[STIX]{x1D6F7}\leqslant U$
. Fix
$\unicode[STIX]{x1D6F7}\leqslant U$
. Fix
![]() $\unicode[STIX]{x1D70C}$
a smooth function in
$\unicode[STIX]{x1D70C}$
a smooth function in
![]() $D$
such that
$D$
such that
![]() $\unicode[STIX]{x1D70C}=0$
on the boundary and
$\unicode[STIX]{x1D70C}=0$
on the boundary and
 $dd^{c}\unicode[STIX]{x1D70C}=\sqrt{-1}\,dz\wedge d\bar{z}$
. Fix also
$dd^{c}\unicode[STIX]{x1D70C}=\sqrt{-1}\,dz\wedge d\bar{z}$
. Fix also
 $\unicode[STIX]{x1D70F}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities such that
$\unicode[STIX]{x1D70F}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
with minimal singularities such that
 $(\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D70F})^{n}=c\unicode[STIX]{x1D714}^{n}$
, for some positive normalization constant
$(\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D70F})^{n}=c\unicode[STIX]{x1D714}^{n}$
, for some positive normalization constant
![]() $c$
and some fixed Kähler form
$c$
and some fixed Kähler form
![]() $\unicode[STIX]{x1D714}$
on
$\unicode[STIX]{x1D714}$
on
![]() $X$
. Observe that such a potential exists thanks to [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem 4.1]. We normalize
$X$
. Observe that such a potential exists thanks to [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem 4.1]. We normalize
![]() $\unicode[STIX]{x1D70F}$
so that
$\unicode[STIX]{x1D70F}$
so that
 $\unicode[STIX]{x1D70F}\leqslant \min (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
. Applying the comparison principle (Proposition 3.2) for
$\unicode[STIX]{x1D70F}\leqslant \min (\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1})$
. Applying the comparison principle (Proposition 3.2) for
 $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}:=(1-\unicode[STIX]{x1D700})\unicode[STIX]{x1D6F7}+\unicode[STIX]{x1D700}(\unicode[STIX]{x1D70C}+\unicode[STIX]{x1D70F})$
and
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}:=(1-\unicode[STIX]{x1D700})\unicode[STIX]{x1D6F7}+\unicode[STIX]{x1D700}(\unicode[STIX]{x1D70C}+\unicode[STIX]{x1D70F})$
and
![]() $U$
we get
$U$
we get
 $$\begin{eqnarray}\int _{\{U<\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}})^{n+1}\leqslant \int _{\{U<\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}U)^{n+1}=0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\{U<\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}})^{n+1}\leqslant \int _{\{U<\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}\}\cap \operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D}(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}U)^{n+1}=0.\end{eqnarray}$$
By expanding
 $(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}})^{n+1}\geqslant \unicode[STIX]{x1D700}^{n}(\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D70F})^{n}\wedge dd^{c}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D700}^{n}c\unicode[STIX]{x1D714}^{n}\wedge dd^{c}\unicode[STIX]{x1D70C}>0$
, the inequality above gives that
$(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}})^{n+1}\geqslant \unicode[STIX]{x1D700}^{n}(\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D70F})^{n}\wedge dd^{c}\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D700}^{n}c\unicode[STIX]{x1D714}^{n}\wedge dd^{c}\unicode[STIX]{x1D70C}>0$
, the inequality above gives that
![]() $U\geqslant \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}$
almost everywhere, hence everywhere in
$U\geqslant \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}$
almost everywhere, hence everywhere in
![]() $X\times D$
. Letting
$X\times D$
. Letting
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
we get the desired result.◻
$\unicode[STIX]{x1D700}\rightarrow 0$
we get the desired result.◻
In the Kähler case, geodesics joining smooth potentials are
![]() $C^{1,\bar{1}}$
-smooth and the Monge–Ampère energy is linear along these geodesics. When
$C^{1,\bar{1}}$
-smooth and the Monge–Ampère energy is linear along these geodesics. When
![]() $\unicode[STIX]{x1D703}$
is also nef, by adapting the proof of Chen [Reference ChenChe00] (see [Reference BoucksomBou12]), we expect that a similar regularity result still holds in the ample locus of
$\unicode[STIX]{x1D703}$
is also nef, by adapting the proof of Chen [Reference ChenChe00] (see [Reference BoucksomBou12]), we expect that a similar regularity result still holds in the ample locus of
![]() $\{\unicode[STIX]{x1D703}\}$
.
$\{\unicode[STIX]{x1D703}\}$
.
Recall that for potentials with minimal singularities the Monge–Ampère energy is defined by the following expression:
 $$\begin{eqnarray}\text{I}(u):=\frac{1}{(n+1)\operatorname{Vol}(\unicode[STIX]{x1D703})}\mathop{\sum }_{j=0}^{n}\int _{X}(u-V_{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D703}_{u}^{j}\wedge \unicode[STIX]{x1D703}_{V_{\unicode[STIX]{x1D703}}}^{n-j}.\end{eqnarray}$$
$$\begin{eqnarray}\text{I}(u):=\frac{1}{(n+1)\operatorname{Vol}(\unicode[STIX]{x1D703})}\mathop{\sum }_{j=0}^{n}\int _{X}(u-V_{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D703}_{u}^{j}\wedge \unicode[STIX]{x1D703}_{V_{\unicode[STIX]{x1D703}}}^{n-j}.\end{eqnarray}$$
We proceed now to show that, as perhaps expected, the Monge–Ampère energy is linear/convex along geodesics/subgeodesics with minimal singularities. However to argue this, we will need to use a careful mollification argument for subgeodesics in the time variable that will be detailed in the next subsection.
3.2 Approximation of subgeodesics
Unless specified otherwise, assume for this subsection that
 $(0,1)\ni t\rightarrow \unicode[STIX]{x1D711}_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is a subgeodesic with minimal singularities such that
$(0,1)\ni t\rightarrow \unicode[STIX]{x1D711}_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is a subgeodesic with minimal singularities such that
 $|\unicode[STIX]{x1D711}_{t}-\unicode[STIX]{x1D711}_{t^{\prime }}|\leqslant C|t-t^{\prime }|$
, for some positive constant
$|\unicode[STIX]{x1D711}_{t}-\unicode[STIX]{x1D711}_{t^{\prime }}|\leqslant C|t-t^{\prime }|$
, for some positive constant
![]() $C$
. Consider a smoothing kernel
$C$
. Consider a smoothing kernel
 $\unicode[STIX]{x1D712}:\mathbb{R}\rightarrow [0,1]$
supported in
$\unicode[STIX]{x1D712}:\mathbb{R}\rightarrow [0,1]$
supported in
![]() $[-1,1]$
with
$[-1,1]$
with
 $\int _{\mathbb{R}}\unicode[STIX]{x1D712}(t)\,dt=1$
and
$\int _{\mathbb{R}}\unicode[STIX]{x1D712}(t)\,dt=1$
and
 $\unicode[STIX]{x1D712}(t)=\unicode[STIX]{x1D712}(-t)$
. We then set
$\unicode[STIX]{x1D712}(t)=\unicode[STIX]{x1D712}(-t)$
. We then set
 $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(t):=(1/\unicode[STIX]{x1D700})\unicode[STIX]{x1D712}(t/\unicode[STIX]{x1D700})$
, so that the support of
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(t):=(1/\unicode[STIX]{x1D700})\unicode[STIX]{x1D712}(t/\unicode[STIX]{x1D700})$
, so that the support of
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}$
is
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}$
is
![]() $[-\unicode[STIX]{x1D700},\unicode[STIX]{x1D700}]$
and
$[-\unicode[STIX]{x1D700},\unicode[STIX]{x1D700}]$
and
 $\int _{\mathbb{R}}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(t)\,dt=1$
. For each
$\int _{\mathbb{R}}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(t)\,dt=1$
. For each
![]() $\unicode[STIX]{x1D700}>0$
we consider
$\unicode[STIX]{x1D700}>0$
we consider
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}(x):=\int _{0}^{1}\unicode[STIX]{x1D711}_{s}(x)\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(t-s)\,ds,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}(x):=\int _{0}^{1}\unicode[STIX]{x1D711}_{s}(x)\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(t-s)\,ds,\end{eqnarray}$$
which is well defined for
 $t\in (\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700})$
.
$t\in (\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700})$
.
Lemma 3.4. For each
![]() $\unicode[STIX]{x1D700}>0$
,
$\unicode[STIX]{x1D700}>0$
,
 $(\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700})\ni t\rightarrow \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is a
$(\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700})\ni t\rightarrow \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is a
![]() $t$
-Lipschitz subgeodesic with minimal singularities.
$t$
-Lipschitz subgeodesic with minimal singularities.
Proof. The fact that
 $t\rightarrow \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}$
is a subgeodesic is trivial. Because
$t\rightarrow \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}$
is a subgeodesic is trivial. Because
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
is
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
is
![]() $t$
-Lipschitz, it follows that
$t$
-Lipschitz, it follows that
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}$
has minimal singularities for all
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}$
has minimal singularities for all
 $t\in [\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700}]$
. Working directly with (11) we obtain
$t\in [\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700}]$
. Working directly with (11) we obtain
 $|\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}-\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t^{\prime }}|\leqslant C|t-t^{\prime }|$
.◻
$|\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}-\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t^{\prime }}|\leqslant C|t-t^{\prime }|$
.◻
The next observation is simple but will be crucial for our approximation procedure.
Lemma 3.5. There exists
 $A_{\unicode[STIX]{x1D700}},B_{\unicode[STIX]{x1D700}}>0$
(that may blow up as
$A_{\unicode[STIX]{x1D700}},B_{\unicode[STIX]{x1D700}}>0$
(that may blow up as
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
) such that
$\unicode[STIX]{x1D700}\rightarrow 0$
) such that
![]() $\dot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}/A_{\unicode[STIX]{x1D700}}$
,
$\dot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}/A_{\unicode[STIX]{x1D700}}$
,
![]() $\ddot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}/B_{\unicode[STIX]{x1D700}}$
can be written as a difference of
$\ddot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}/B_{\unicode[STIX]{x1D700}}$
can be written as a difference of
![]() $\unicode[STIX]{x1D703}$
-psh functions with minimal singularities
$\unicode[STIX]{x1D703}$
-psh functions with minimal singularities
 $t\in (\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700})$
.
$t\in (\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700})$
.
Proof. Write
 $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}^{\prime }(t)=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{+}(t)-\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{-}(t)$
, where
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}^{\prime }(t)=\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{+}(t)-\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{-}(t)$
, where
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{+},\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{-}$
are the positive and negative parts of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{+},\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{-}$
are the positive and negative parts of
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}^{\prime }(t)$
. They are clearly bounded (but the bound blows up as
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}^{\prime }(t)$
. They are clearly bounded (but the bound blows up as
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
). Now, let
$\unicode[STIX]{x1D700}\rightarrow 0$
). Now, let
 $$\begin{eqnarray}u_{\unicode[STIX]{x1D700},t}^{\pm }(x):=\int _{0}^{1}\unicode[STIX]{x1D711}_{s}(x)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{\pm }(t-s)\,ds.\end{eqnarray}$$
$$\begin{eqnarray}u_{\unicode[STIX]{x1D700},t}^{\pm }(x):=\int _{0}^{1}\unicode[STIX]{x1D711}_{s}(x)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{\pm }(t-s)\,ds.\end{eqnarray}$$
It follows that
 $$\begin{eqnarray}dd^{c}u_{\unicode[STIX]{x1D700},t}^{\pm }=\int _{0}^{1}(dd^{c}\unicode[STIX]{x1D711}_{s})\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{\pm }(t-s)\,ds\geqslant -A_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D703},\end{eqnarray}$$
$$\begin{eqnarray}dd^{c}u_{\unicode[STIX]{x1D700},t}^{\pm }=\int _{0}^{1}(dd^{c}\unicode[STIX]{x1D711}_{s})\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{\pm }(t-s)\,ds\geqslant -A_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D703},\end{eqnarray}$$
where
 $A_{\unicode[STIX]{x1D700}}=\int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{+}=\int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{-}$
. Observe indeed that
$A_{\unicode[STIX]{x1D700}}=\int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{+}=\int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{-}$
. Observe indeed that
 $\int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{+}-\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{-}=\int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}^{\prime }=0$
. To see that
$\int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{+}-\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{-}=\int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}^{\prime }=0$
. To see that
![]() $u_{\unicode[STIX]{x1D700},t}^{\pm }/A_{\unicode[STIX]{x1D700}}$
has minimal singularities we note that
$u_{\unicode[STIX]{x1D700},t}^{\pm }/A_{\unicode[STIX]{x1D700}}$
has minimal singularities we note that
 $|\unicode[STIX]{x1D711}_{t}-\unicode[STIX]{x1D711}_{t^{\prime }}|\leqslant C|t-t^{\prime }|$
, hence
$|\unicode[STIX]{x1D711}_{t}-\unicode[STIX]{x1D711}_{t^{\prime }}|\leqslant C|t-t^{\prime }|$
, hence
 $$\begin{eqnarray}u_{\unicode[STIX]{x1D700},t}^{\pm }(x):=\int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{t-s}(x)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{\pm }(s)\,ds\leqslant \int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{t^{\prime }-s}(x)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{\pm }(s)\,ds+CA_{\unicode[STIX]{x1D700}}|t-t^{\prime }|.\end{eqnarray}$$
$$\begin{eqnarray}u_{\unicode[STIX]{x1D700},t}^{\pm }(x):=\int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{t-s}(x)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{\pm }(s)\,ds\leqslant \int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D711}_{t^{\prime }-s}(x)\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{\pm }(s)\,ds+CA_{\unicode[STIX]{x1D700}}|t-t^{\prime }|.\end{eqnarray}$$
For
![]() $\ddot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}$
, a similar argument works with the choice
$\ddot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}$
, a similar argument works with the choice
 $B_{\unicode[STIX]{x1D700}}:=\int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\max (\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}^{\prime \prime }(t),0)\,dt$
.◻
$B_{\unicode[STIX]{x1D700}}:=\int _{-\unicode[STIX]{x1D700}}^{\unicode[STIX]{x1D700}}\max (\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}^{\prime \prime }(t),0)\,dt$
.◻
Lemma 3.6. The Monge–Ampère energy is twice differentiable along
 $t\rightarrow \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}$
and the derivatives are given by
$t\rightarrow \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}$
and the derivatives are given by
 $$\begin{eqnarray}\frac{d}{dt}\text{I}(\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t})=\int _{X}\dot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}}^{n},\quad \frac{d^{2}}{dt^{2}}\text{I}(\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t})=\int _{X}\ddot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}}^{n}-n\int _{X}\,d\dot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}\wedge d^{c}\dot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}\wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n-1}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{d}{dt}\text{I}(\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t})=\int _{X}\dot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}}^{n},\quad \frac{d^{2}}{dt^{2}}\text{I}(\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t})=\int _{X}\ddot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}}^{n}-n\int _{X}\,d\dot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}\wedge d^{c}\dot{\unicode[STIX]{x1D711}}_{\unicode[STIX]{x1D700},t}\wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n-1}.\end{eqnarray}$$
Proof. For notational convenience we remove the subscript
![]() $\unicode[STIX]{x1D700}$
. By basic properties of the
$\unicode[STIX]{x1D700}$
. By basic properties of the
![]() $\text{I}$
functional (see [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Reference Berman and BoucksomBB10]) we have, for
$\text{I}$
functional (see [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Reference Berman and BoucksomBB10]) we have, for
 $t\in (\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700}),s>0$
,
$t\in (\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700}),s>0$
,
 $$\begin{eqnarray}\int _{X}(\unicode[STIX]{x1D711}_{t+s}-\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t+s}}^{n}\leqslant \text{I}(\unicode[STIX]{x1D711}_{t+s})-\text{I}(\unicode[STIX]{x1D711}_{t})\leqslant \int _{X}(\unicode[STIX]{x1D711}_{t+s}-\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}(\unicode[STIX]{x1D711}_{t+s}-\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t+s}}^{n}\leqslant \text{I}(\unicode[STIX]{x1D711}_{t+s})-\text{I}(\unicode[STIX]{x1D711}_{t})\leqslant \int _{X}(\unicode[STIX]{x1D711}_{t+s}-\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}.\end{eqnarray}$$
Dividing by
![]() $s>0$
the right-hand side then converges (as
$s>0$
the right-hand side then converges (as
![]() $s\rightarrow 0$
) to
$s\rightarrow 0$
) to
 $\int _{X}\dot{\unicode[STIX]{x1D711}}_{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}$
. The left-hand side can be estimated by
$\int _{X}\dot{\unicode[STIX]{x1D711}}_{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}$
. The left-hand side can be estimated by
 $$\begin{eqnarray}\frac{1}{s}\int _{X}(\unicode[STIX]{x1D711}_{t+s}-\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t+s}}^{n}\geqslant \int _{X}\dot{\unicode[STIX]{x1D711}}_{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t+s}}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{s}\int _{X}(\unicode[STIX]{x1D711}_{t+s}-\unicode[STIX]{x1D711}_{t})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t+s}}^{n}\geqslant \int _{X}\dot{\unicode[STIX]{x1D711}}_{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t+s}}^{n}.\end{eqnarray}$$
As
![]() $\dot{\unicode[STIX]{x1D711}}_{t}$
is bounded and quasi-continuous (with respect to the Monge–Ampère capacity
$\dot{\unicode[STIX]{x1D711}}_{t}$
is bounded and quasi-continuous (with respect to the Monge–Ampère capacity
![]() $\operatorname{Cap}_{\unicode[STIX]{x1D714}}$
), Corollary 2.9 allows to pass to the limit as
$\operatorname{Cap}_{\unicode[STIX]{x1D714}}$
), Corollary 2.9 allows to pass to the limit as
![]() $s\rightarrow 0$
and the differentiability of
$s\rightarrow 0$
and the differentiability of
![]() $\text{I}(\unicode[STIX]{x1D711}_{t})$
follows.
$\text{I}(\unicode[STIX]{x1D711}_{t})$
follows.
To prove the formula for the second derivative we fix
 $t\in (\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700})$
and
$t\in (\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700})$
and
![]() $s>0$
small enough and prove that
$s>0$
small enough and prove that
 $$\begin{eqnarray}\lim _{s\rightarrow 0^{+}}d(s):=\lim _{s\rightarrow 0^{+}}\frac{1}{s}\biggl(\int _{X}\dot{\unicode[STIX]{x1D711}}_{t+s}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t+s}}^{n}-\dot{\unicode[STIX]{x1D711}}_{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}\biggr)\end{eqnarray}$$
$$\begin{eqnarray}\lim _{s\rightarrow 0^{+}}d(s):=\lim _{s\rightarrow 0^{+}}\frac{1}{s}\biggl(\int _{X}\dot{\unicode[STIX]{x1D711}}_{t+s}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t+s}}^{n}-\dot{\unicode[STIX]{x1D711}}_{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}\biggr)\end{eqnarray}$$
equals to the right-hand side of (12). The same formula for the left limit will then follow automatically, as we can always ‘reverse’ the time direction of a subgeodesic. Setting
 $T_{s}:=\sum _{j=1}^{n-1}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{j}\wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t+s}}^{n-1-j}$
, we can write
$T_{s}:=\sum _{j=1}^{n-1}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{j}\wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t+s}}^{n-1-j}$
, we can write
 $$\begin{eqnarray}d(s)=\frac{1}{s}\biggl(\int _{X}\dot{\unicode[STIX]{x1D711}}_{t+s}dd^{c}(\unicode[STIX]{x1D711}_{t+s}-\unicode[STIX]{x1D711}_{t})\wedge T_{s}+\int _{X}(\dot{\unicode[STIX]{x1D711}}_{t+s}-\dot{\unicode[STIX]{x1D711}}_{t})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}d(s)=\frac{1}{s}\biggl(\int _{X}\dot{\unicode[STIX]{x1D711}}_{t+s}dd^{c}(\unicode[STIX]{x1D711}_{t+s}-\unicode[STIX]{x1D711}_{t})\wedge T_{s}+\int _{X}(\dot{\unicode[STIX]{x1D711}}_{t+s}-\dot{\unicode[STIX]{x1D711}}_{t})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}\biggr).\end{eqnarray}$$
Thanks to [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem 1.14] we can integrate by parts in the first term and obtain
 $$\begin{eqnarray}d(s)=\frac{1}{s}\biggl(\int _{X}(\unicode[STIX]{x1D711}_{t+s}-\unicode[STIX]{x1D711}_{t})dd^{c}\dot{\unicode[STIX]{x1D711}}_{t+s}\wedge T_{s}+\int _{X}(\dot{\unicode[STIX]{x1D711}}_{t+s}-\dot{\unicode[STIX]{x1D711}}_{t})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}\biggr).\end{eqnarray}$$
$$\begin{eqnarray}d(s)=\frac{1}{s}\biggl(\int _{X}(\unicode[STIX]{x1D711}_{t+s}-\unicode[STIX]{x1D711}_{t})dd^{c}\dot{\unicode[STIX]{x1D711}}_{t+s}\wedge T_{s}+\int _{X}(\dot{\unicode[STIX]{x1D711}}_{t+s}-\dot{\unicode[STIX]{x1D711}}_{t})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}\biggr).\end{eqnarray}$$
As
![]() $s\rightarrow 0$
,
$s\rightarrow 0$
,
 $(\unicode[STIX]{x1D711}_{t+s}-\unicode[STIX]{x1D711}_{t})/s$
decreases to
$(\unicode[STIX]{x1D711}_{t+s}-\unicode[STIX]{x1D711}_{t})/s$
decreases to
![]() $\dot{\unicode[STIX]{x1D711}}_{t}$
, all of them being quasi-continuous and uniformly bounded. On the other hand, by Lemma 3.5 we can write
$\dot{\unicode[STIX]{x1D711}}_{t}$
, all of them being quasi-continuous and uniformly bounded. On the other hand, by Lemma 3.5 we can write
 $\dot{\unicode[STIX]{x1D711}}_{t+s}/A_{\unicode[STIX]{x1D700}}=u_{t+s}^{+}-u_{t+s}^{-}$
, where
$\dot{\unicode[STIX]{x1D711}}_{t+s}/A_{\unicode[STIX]{x1D700}}=u_{t+s}^{+}-u_{t+s}^{-}$
, where
![]() $u_{t+s}^{\pm }$
are
$u_{t+s}^{\pm }$
are
![]() $\unicode[STIX]{x1D703}$
-psh functions with minimal singularities that converge uniformly to
$\unicode[STIX]{x1D703}$
-psh functions with minimal singularities that converge uniformly to
![]() $u_{t}^{\pm }$
as
$u_{t}^{\pm }$
as
![]() $s\rightarrow 0$
. By using Corollary 2.9, the first term in the right-hand side of (13) converges to
$s\rightarrow 0$
. By using Corollary 2.9, the first term in the right-hand side of (13) converges to
 $n\int _{X}\dot{\unicode[STIX]{x1D711}}_{t}dd^{c}\dot{\unicode[STIX]{x1D711}}_{t}\wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n-1}$
. Moreover, using dominated convergence for the second term we obtain
$n\int _{X}\dot{\unicode[STIX]{x1D711}}_{t}dd^{c}\dot{\unicode[STIX]{x1D711}}_{t}\wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n-1}$
. Moreover, using dominated convergence for the second term we obtain
 $$\begin{eqnarray}\lim _{s\rightarrow 0^{+}}\frac{1}{s}\int _{X}(\dot{\unicode[STIX]{x1D711}}_{t+s}-\dot{\unicode[STIX]{x1D711}}_{t})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}=\int _{X}\ddot{\unicode[STIX]{x1D711}}_{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}.\end{eqnarray}$$
$$\begin{eqnarray}\lim _{s\rightarrow 0^{+}}\frac{1}{s}\int _{X}(\dot{\unicode[STIX]{x1D711}}_{t+s}-\dot{\unicode[STIX]{x1D711}}_{t})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}=\int _{X}\ddot{\unicode[STIX]{x1D711}}_{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}.\end{eqnarray}$$
Observe in fact that
![]() $\ddot{\unicode[STIX]{x1D711}}_{t}$
is uniformly bounded from above as it can be written as the difference of two quasi-plurisubharmonic functions. Finally, an integration by parts gives
$\ddot{\unicode[STIX]{x1D711}}_{t}$
is uniformly bounded from above as it can be written as the difference of two quasi-plurisubharmonic functions. Finally, an integration by parts gives
 $$\begin{eqnarray}\lim _{s\rightarrow 0^{+}}d(s)=-n\int _{X}\,d\dot{\unicode[STIX]{x1D711}}_{t}\wedge d^{c}\dot{\unicode[STIX]{x1D711}}_{t}\wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n-1}+\int _{X}\ddot{\unicode[STIX]{x1D711}}_{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}.\Box\end{eqnarray}$$
$$\begin{eqnarray}\lim _{s\rightarrow 0^{+}}d(s)=-n\int _{X}\,d\dot{\unicode[STIX]{x1D711}}_{t}\wedge d^{c}\dot{\unicode[STIX]{x1D711}}_{t}\wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n-1}+\int _{X}\ddot{\unicode[STIX]{x1D711}}_{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}.\Box\end{eqnarray}$$
Corollary 3.7. The Monge–Ampère energy is convex along
 $t\rightarrow \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}$
.
$t\rightarrow \unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}$
.
Proof. We again drop the
![]() $\unicode[STIX]{x1D700}$
subscript and fix
$\unicode[STIX]{x1D700}$
subscript and fix
 $t\in (\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700})$
for the duration of the proof. In view of Lemma 3.6 it is enough to prove that
$t\in (\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700})$
for the duration of the proof. In view of Lemma 3.6 it is enough to prove that
 $$\begin{eqnarray}-n\,d\dot{\unicode[STIX]{x1D711}}_{t}\wedge d^{c}\dot{\unicode[STIX]{x1D711}}_{t}\wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n-1}+\ddot{\unicode[STIX]{x1D711}}_{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}\geqslant 0\end{eqnarray}$$
$$\begin{eqnarray}-n\,d\dot{\unicode[STIX]{x1D711}}_{t}\wedge d^{c}\dot{\unicode[STIX]{x1D711}}_{t}\wedge \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n-1}+\ddot{\unicode[STIX]{x1D711}}_{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D711}_{t}}^{n}\geqslant 0\end{eqnarray}$$
in the weak sense of measures in
 $\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
. This property is local, hence we can work in relatively compact open subset
$\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
. This property is local, hence we can work in relatively compact open subset
![]() $K$
of
$K$
of
 $\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
, and approximate
$\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})$
, and approximate
![]() $\unicode[STIX]{x1D711}_{t}(x)$
using a convolution in the space variable
$\unicode[STIX]{x1D711}_{t}(x)$
using a convolution in the space variable
![]() $x$
. As we show now, since
$x$
. As we show now, since
![]() $\dot{\unicode[STIX]{x1D711}}_{t}$
,
$\dot{\unicode[STIX]{x1D711}}_{t}$
,
![]() $\ddot{\unicode[STIX]{x1D711}}_{t}$
are bounded in
$\ddot{\unicode[STIX]{x1D711}}_{t}$
are bounded in
![]() $K$
and can be written as the difference of two quasi-psh functions with minimal singularities, the convergence of the appropriate approximating measures to the left-hand side in (14) follows from standard pluripotential theory. Indeed, fix a coordinate ball
$K$
and can be written as the difference of two quasi-psh functions with minimal singularities, the convergence of the appropriate approximating measures to the left-hand side in (14) follows from standard pluripotential theory. Indeed, fix a coordinate ball
![]() $B\subset K$
. We will show that (14) holds in
$B\subset K$
. We will show that (14) holds in
![]() $B$
in the weak sense of measures.
$B$
in the weak sense of measures.
We can assume existence of a smooth local potential
 $\unicode[STIX]{x1D70F}\in C^{\infty }(B)$
such that
$\unicode[STIX]{x1D70F}\in C^{\infty }(B)$
such that
 $\unicode[STIX]{x1D703}=dd^{c}\unicode[STIX]{x1D70F}$
. Let
$\unicode[STIX]{x1D703}=dd^{c}\unicode[STIX]{x1D70F}$
. Let
![]() $\tilde{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D6FF}}(x)$
be a smoothing kernel in
$\tilde{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D6FF}}(x)$
be a smoothing kernel in
![]() $\mathbb{C}^{n}$
and consider
$\mathbb{C}^{n}$
and consider
 $$\begin{eqnarray}\tilde{\unicode[STIX]{x1D711}}_{t}^{\unicode[STIX]{x1D6FF}}(x):=\int _{B}(\unicode[STIX]{x1D70F}(x-\unicode[STIX]{x1D701})+\unicode[STIX]{x1D711}_{t}(x-\unicode[STIX]{x1D701}))\tilde{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D701})\,dV(\unicode[STIX]{x1D701})-\unicode[STIX]{x1D70F}(x).\end{eqnarray}$$
$$\begin{eqnarray}\tilde{\unicode[STIX]{x1D711}}_{t}^{\unicode[STIX]{x1D6FF}}(x):=\int _{B}(\unicode[STIX]{x1D70F}(x-\unicode[STIX]{x1D701})+\unicode[STIX]{x1D711}_{t}(x-\unicode[STIX]{x1D701}))\tilde{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D701})\,dV(\unicode[STIX]{x1D701})-\unicode[STIX]{x1D70F}(x).\end{eqnarray}$$
Since the complexification of
![]() $\tilde{\unicode[STIX]{x1D711}}_{t}^{\unicode[STIX]{x1D6FF}}$
is smooth and
$\tilde{\unicode[STIX]{x1D711}}_{t}^{\unicode[STIX]{x1D6FF}}$
is smooth and
![]() $\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}$
-psh in
$\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703}$
-psh in
 $B_{\unicode[STIX]{x1D6FF}}\times D_{\unicode[STIX]{x1D700}}$
, it follows that (14) holds for
$B_{\unicode[STIX]{x1D6FF}}\times D_{\unicode[STIX]{x1D700}}$
, it follows that (14) holds for
![]() $\tilde{\unicode[STIX]{x1D711}}_{t}^{\unicode[STIX]{x1D6FF}}$
and
$\tilde{\unicode[STIX]{x1D711}}_{t}^{\unicode[STIX]{x1D6FF}}$
and
 $\tilde{\unicode[STIX]{x1D711}}_{t}^{\unicode[STIX]{x1D6FF}}{\searrow}\unicode[STIX]{x1D711}_{t}$
.
$\tilde{\unicode[STIX]{x1D711}}_{t}^{\unicode[STIX]{x1D6FF}}{\searrow}\unicode[STIX]{x1D711}_{t}$
.
By Lemma 3.5 we can write
 $\dot{\unicode[STIX]{x1D711}}_{t}:=u_{+}-u_{-}$
, where
$\dot{\unicode[STIX]{x1D711}}_{t}:=u_{+}-u_{-}$
, where
![]() $u_{+},u_{-}$
are bounded quasi psh functions on
$u_{+},u_{-}$
are bounded quasi psh functions on
![]() $B_{\unicode[STIX]{x1D6FF}}$
. Then the corresponding smooth quasi psh functions
$B_{\unicode[STIX]{x1D6FF}}$
. Then the corresponding smooth quasi psh functions
![]() $v_{\pm }^{\unicode[STIX]{x1D6FF}}$
, defined by
$v_{\pm }^{\unicode[STIX]{x1D6FF}}$
, defined by
 $$\begin{eqnarray}v_{\pm }^{\unicode[STIX]{x1D6FF}}(x):=\int _{0}^{1}\int _{B}(\unicode[STIX]{x1D70F}(x-\unicode[STIX]{x1D701})+\unicode[STIX]{x1D711}_{s}(x-\unicode[STIX]{x1D701}))\tilde{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D701})\,\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{\pm }(t-s)\,ds\,dV(\unicode[STIX]{x1D701}),\end{eqnarray}$$
$$\begin{eqnarray}v_{\pm }^{\unicode[STIX]{x1D6FF}}(x):=\int _{0}^{1}\int _{B}(\unicode[STIX]{x1D70F}(x-\unicode[STIX]{x1D701})+\unicode[STIX]{x1D711}_{s}(x-\unicode[STIX]{x1D701}))\tilde{\unicode[STIX]{x1D70C}}_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D701})\,\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D700}}^{\pm }(t-s)\,ds\,dV(\unicode[STIX]{x1D701}),\end{eqnarray}$$
converge decreasingly to
![]() $u_{\pm }$
and we have
$u_{\pm }$
and we have
 $\dot{\tilde{\unicode[STIX]{x1D711}}}_{t}^{\unicode[STIX]{x1D6FF}}=v_{+}^{\unicode[STIX]{x1D6FF}}-v_{-}^{\unicode[STIX]{x1D6FF}}$
. A similar thing is true for the second derivatives
$\dot{\tilde{\unicode[STIX]{x1D711}}}_{t}^{\unicode[STIX]{x1D6FF}}=v_{+}^{\unicode[STIX]{x1D6FF}}-v_{-}^{\unicode[STIX]{x1D6FF}}$
. A similar thing is true for the second derivatives
![]() $\ddot{\unicode[STIX]{x1D711}}_{t},\ddot{\tilde{\unicode[STIX]{x1D711}}}_{t}^{\unicode[STIX]{x1D6FF}}$
as well. As all the functions involved are quasi psh and bounded on
$\ddot{\unicode[STIX]{x1D711}}_{t},\ddot{\tilde{\unicode[STIX]{x1D711}}}_{t}^{\unicode[STIX]{x1D6FF}}$
as well. As all the functions involved are quasi psh and bounded on
![]() $B_{\unicode[STIX]{x1D6FF}}$
, by Bedford–Taylor theory, positivity in (14) is preserved as we take the limit
$B_{\unicode[STIX]{x1D6FF}}$
, by Bedford–Taylor theory, positivity in (14) is preserved as we take the limit
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
, and (14) holds restricted to
$\unicode[STIX]{x1D6FF}\rightarrow 0$
, and (14) holds restricted to
![]() $B_{\unicode[STIX]{x1D6FF}}$
, finishing the proof.◻
$B_{\unicode[STIX]{x1D6FF}}$
, finishing the proof.◻
Theorem 3.8. Assume that
![]() $\{\unicode[STIX]{x1D703}\}$
is big and
$\{\unicode[STIX]{x1D703}\}$
is big and
 $(0,1)\ni t\rightarrow \unicode[STIX]{x1D711}_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is a subgeodesic with minimal singularities. Then the Monge–Ampère energy
$(0,1)\ni t\rightarrow \unicode[STIX]{x1D711}_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is a subgeodesic with minimal singularities. Then the Monge–Ampère energy
![]() $\text{I}$
is convex along
$\text{I}$
is convex along
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
.
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
.
Proof. Fix
![]() $\unicode[STIX]{x1D700}>0$
for the moment. As it suffices to show convexity of
$\unicode[STIX]{x1D700}>0$
for the moment. As it suffices to show convexity of
 $t\rightarrow \text{I}(\unicode[STIX]{x1D711}_{t})$
on
$t\rightarrow \text{I}(\unicode[STIX]{x1D711}_{t})$
on
 $(\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700})$
, and
$(\unicode[STIX]{x1D700},1-\unicode[STIX]{x1D700})$
, and
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
has minimal singularity potentials, without loss of generality we can assume that
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
has minimal singularity potentials, without loss of generality we can assume that
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
is Lipschitz in
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
is Lipschitz in
![]() $t$
and let
$t$
and let
![]() $C>0$
be such that
$C>0$
be such that
 $|\unicode[STIX]{x1D711}_{t}-\unicode[STIX]{x1D711}_{t^{\prime }}|\leqslant C|t-t^{\prime }|$
. Let
$|\unicode[STIX]{x1D711}_{t}-\unicode[STIX]{x1D711}_{t^{\prime }}|\leqslant C|t-t^{\prime }|$
. Let
![]() $\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}$
be the subgeodesics approximating
$\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t}$
be the subgeodesics approximating
![]() $t\rightarrow \unicode[STIX]{x1D711}_{t}$
constructed above. Since
$t\rightarrow \unicode[STIX]{x1D711}_{t}$
constructed above. Since
 $\text{I}(\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t})\rightarrow \text{I}(\unicode[STIX]{x1D711}_{t})$
as
$\text{I}(\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t})\rightarrow \text{I}(\unicode[STIX]{x1D711}_{t})$
as
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
[Reference Berman and BoucksomBB10, Proposition 4.3], it suffices to prove the convexity of
$\unicode[STIX]{x1D700}\rightarrow 0$
[Reference Berman and BoucksomBB10, Proposition 4.3], it suffices to prove the convexity of
 $t\rightarrow \text{I}(\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t})$
. But this follows from Corollary 3.7.◻
$t\rightarrow \text{I}(\unicode[STIX]{x1D711}_{\unicode[STIX]{x1D700},t})$
. But this follows from Corollary 3.7.◻
3.3 Linearity of the Monge–Ampère energy along geodesics
The regularization technique in § 3.2 can also be used to prove linearity of Monge–Ampère energy along geodesics in big classes. Although this result is not essentially used in this paper (in the proof of the important direction in Lemma 3.15 one only needs Theorem 3.8), we think it will be useful in the future.
Assume
![]() $\unicode[STIX]{x1D703}$
is a smooth closed
$\unicode[STIX]{x1D703}$
is a smooth closed
![]() $(1,1)$
-form whose cohomology class is big. Fix
$(1,1)$
-form whose cohomology class is big. Fix
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
two
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
two
![]() $\unicode[STIX]{x1D703}$
-psh functions on
$\unicode[STIX]{x1D703}$
-psh functions on
![]() $X$
with minimal singularities. The complex plane
$X$
with minimal singularities. The complex plane
![]() $\mathbb{C}$
is now viewed as a piece of
$\mathbb{C}$
is now viewed as a piece of
![]() $\mathbb{C}\mathbb{P}^{1}$
(so that
$\mathbb{C}\mathbb{P}^{1}$
(so that
 $\mathbb{C}\mathbb{P}^{1}=\mathbb{C}\cup H_{\infty }$
) equipped with the Fubini–Study metric
$\mathbb{C}\mathbb{P}^{1}=\mathbb{C}\cup H_{\infty }$
) equipped with the Fubini–Study metric
![]() $\unicode[STIX]{x1D714}_{FS}$
. Accordingly, the product
$\unicode[STIX]{x1D714}_{FS}$
. Accordingly, the product
 $M:=X\times \mathbb{C}\mathbb{P}^{1}$
is equipped with a smooth
$M:=X\times \mathbb{C}\mathbb{P}^{1}$
is equipped with a smooth
![]() $(1,1)$
-form
$(1,1)$
-form
 $\unicode[STIX]{x1D6E9}:=\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}+\unicode[STIX]{x1D70B}_{2}^{\ast }\unicode[STIX]{x1D714}_{FS}$
. We use the following change of coordinates between
$\unicode[STIX]{x1D6E9}:=\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}+\unicode[STIX]{x1D70B}_{2}^{\ast }\unicode[STIX]{x1D714}_{FS}$
. We use the following change of coordinates between
![]() $\mathbb{C}\mathbb{P}^{1}$
and
$\mathbb{C}\mathbb{P}^{1}$
and
![]() $\mathbb{C}$
:
$\mathbb{C}$
:
 $$\begin{eqnarray}\mathbb{C}\mathbb{P}^{1}\setminus H_{\infty }\ni [z_{1}:z_{2}]\mapsto \frac{z_{1}}{z_{2}}\in \mathbb{C},\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{C}\mathbb{P}^{1}\setminus H_{\infty }\ni [z_{1}:z_{2}]\mapsto \frac{z_{1}}{z_{2}}\in \mathbb{C},\end{eqnarray}$$
where
 $H_{\infty }:=\{z_{2}=0\}$
.
$H_{\infty }:=\{z_{2}=0\}$
.
Lemma 3.9. One has
 $V_{\unicode[STIX]{x1D6E9}}(x,z):=V_{\unicode[STIX]{x1D703}}(x)$
for all
$V_{\unicode[STIX]{x1D6E9}}(x,z):=V_{\unicode[STIX]{x1D703}}(x)$
for all
 $z\in \mathbb{C}\mathbb{P}^{1}$
.
$z\in \mathbb{C}\mathbb{P}^{1}$
.
Proof. By definition
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D6E9}}(x,z):=\sup \{U(x,z)\unicode[STIX]{x1D6E9}\text{-}\text{psh}:U\leqslant 0~\text{on}~M\}.\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D6E9}}(x,z):=\sup \{U(x,z)\unicode[STIX]{x1D6E9}\text{-}\text{psh}:U\leqslant 0~\text{on}~M\}.\end{eqnarray}$$
Clearly
 $V_{\unicode[STIX]{x1D6E9}}(x,z)\geqslant V_{\unicode[STIX]{x1D703}}(x)$
since
$V_{\unicode[STIX]{x1D6E9}}(x,z)\geqslant V_{\unicode[STIX]{x1D703}}(x)$
since
![]() $V_{\unicode[STIX]{x1D703}}(x)$
is a candidate in the envelope. Moreover, we observe that for each
$V_{\unicode[STIX]{x1D703}}(x)$
is a candidate in the envelope. Moreover, we observe that for each
 $z\in \mathbb{C}\mathbb{P}^{1}$
,
$z\in \mathbb{C}\mathbb{P}^{1}$
,
 $V_{\unicode[STIX]{x1D6E9}}(x,z)$
is a
$V_{\unicode[STIX]{x1D6E9}}(x,z)$
is a
![]() $\unicode[STIX]{x1D703}$
-psh function and
$\unicode[STIX]{x1D703}$
-psh function and
 $V_{\unicode[STIX]{x1D6E9}}(x,z)\leqslant 0$
on
$V_{\unicode[STIX]{x1D6E9}}(x,z)\leqslant 0$
on
![]() $X$
, thus
$X$
, thus
 $V_{\unicode[STIX]{x1D6E9}}(x,z)\leqslant V_{\unicode[STIX]{x1D703}}(x)$
. Hence the conclusion.◻
$V_{\unicode[STIX]{x1D6E9}}(x,z)\leqslant V_{\unicode[STIX]{x1D703}}(x)$
. Hence the conclusion.◻
Lemma 3.10. Let
 $F\in {\mathcal{C}}^{\infty }(M,\mathbb{R})$
be a smooth function on
$F\in {\mathcal{C}}^{\infty }(M,\mathbb{R})$
be a smooth function on
![]() $M$
which is
$M$
which is
![]() $S^{1}$
-invariant when restricted to
$S^{1}$
-invariant when restricted to
![]() $X\times \mathbb{C}$
. Denote by
$X\times \mathbb{C}$
. Denote by
 $\unicode[STIX]{x1D6F7}:=P_{\unicode[STIX]{x1D6E9}}(F)$
the Monge–Ampère envelope on
$\unicode[STIX]{x1D6F7}:=P_{\unicode[STIX]{x1D6E9}}(F)$
the Monge–Ampère envelope on
![]() $M$
of
$M$
of
![]() $F$
with respect to
$F$
with respect to
![]() $\unicode[STIX]{x1D6E9}$
. Then the function
$\unicode[STIX]{x1D6E9}$
. Then the function
 $\mathbb{C}\mathbb{P}^{1}\ni z\mapsto G(z):=\text{I}(\unicode[STIX]{x1D6F7}(\cdot ,z))$
satisfies
$\mathbb{C}\mathbb{P}^{1}\ni z\mapsto G(z):=\text{I}(\unicode[STIX]{x1D6F7}(\cdot ,z))$
satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{FS}+dd_{z}^{c}G=(\unicode[STIX]{x1D70B}_{2})_{\star }(\unicode[STIX]{x1D6E9}+dd_{x,z}^{c}\unicode[STIX]{x1D6F7})^{n+1},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{FS}+dd_{z}^{c}G=(\unicode[STIX]{x1D70B}_{2})_{\star }(\unicode[STIX]{x1D6E9}+dd_{x,z}^{c}\unicode[STIX]{x1D6F7})^{n+1},\end{eqnarray}$$
in the sense of currents.
Proof. As
![]() $H_{\infty }$
is pluripolar in
$H_{\infty }$
is pluripolar in
![]() $\mathbb{C}\mathbb{P}^{1}$
it suffices to prove (15) in
$\mathbb{C}\mathbb{P}^{1}$
it suffices to prove (15) in
![]() $\mathbb{C}$
. As
$\mathbb{C}$
. As
![]() $F$
is
$F$
is
![]() $S^{1}$
-invariant it follows that
$S^{1}$
-invariant it follows that
![]() $\unicode[STIX]{x1D6F7}(x,z)$
is also
$\unicode[STIX]{x1D6F7}(x,z)$
is also
![]() $S^{1}$
-invariant in
$S^{1}$
-invariant in
![]() $z$
. Using convolution as in § 3.2 we denote by
$z$
. Using convolution as in § 3.2 we denote by
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}$
the approximants, i.e.
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}$
the approximants, i.e.
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(x,z):=\int _{\mathbb{C}}\unicode[STIX]{x1D6F7}(x,\unicode[STIX]{x1D701})\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(|z-\unicode[STIX]{x1D701}|^{2})\,dV(\unicode[STIX]{x1D701}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(x,z):=\int _{\mathbb{C}}\unicode[STIX]{x1D6F7}(x,\unicode[STIX]{x1D701})\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(|z-\unicode[STIX]{x1D701}|^{2})\,dV(\unicode[STIX]{x1D701}),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}$
is a family of smoothing kernels. For each
$\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}$
is a family of smoothing kernels. For each
![]() $\unicode[STIX]{x1D700}>0$
,
$\unicode[STIX]{x1D700}>0$
,
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}$
is
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}$
is
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D700}}$
-psh on
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D700}}$
-psh on
![]() $M$
where
$M$
where
 $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D700}}:=\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D70B}_{2}^{\ast }\unicode[STIX]{x1D714}_{FS}$
, with
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D700}}:=\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}+\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D70B}_{2}^{\ast }\unicode[STIX]{x1D714}_{FS}$
, with
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}>1$
decreasing to 1. Indeed,
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}>1$
decreasing to 1. Indeed,
 $$\begin{eqnarray}dd_{x,z}^{c}\unicode[STIX]{x1D6F7}\star \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}=dd^{c}\unicode[STIX]{x1D6F7}\star \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}\geqslant (-\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}_{FS})\star \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}\geqslant -\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}_{FS}\star \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}.\end{eqnarray}$$
$$\begin{eqnarray}dd_{x,z}^{c}\unicode[STIX]{x1D6F7}\star \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}=dd^{c}\unicode[STIX]{x1D6F7}\star \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}\geqslant (-\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}_{FS})\star \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}\geqslant -\unicode[STIX]{x1D703}-\unicode[STIX]{x1D714}_{FS}\star \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}.\end{eqnarray}$$
Moreover, since
![]() $\unicode[STIX]{x1D714}_{FS}$
is smooth on
$\unicode[STIX]{x1D714}_{FS}$
is smooth on
![]() $\mathbb{C}\mathbb{P}^{1}$
, we have
$\mathbb{C}\mathbb{P}^{1}$
, we have
 $$\begin{eqnarray}|\unicode[STIX]{x1D714}_{FS}-\unicode[STIX]{x1D714}_{FS}\star \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}|\leqslant \int _{\mathbb{C}}|\unicode[STIX]{x1D714}_{FS}(z)-\unicode[STIX]{x1D714}_{FS}(z-\unicode[STIX]{x1D701})|\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(|\unicode[STIX]{x1D701}|^{2})\,dV(\unicode[STIX]{x1D701})\leqslant C\int _{\mathbb{ C}}|\unicode[STIX]{x1D701}|\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(|z^{\prime }|^{2})\,dV(z^{\prime })\leqslant C\unicode[STIX]{x1D700}.\end{eqnarray}$$
$$\begin{eqnarray}|\unicode[STIX]{x1D714}_{FS}-\unicode[STIX]{x1D714}_{FS}\star \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}|\leqslant \int _{\mathbb{C}}|\unicode[STIX]{x1D714}_{FS}(z)-\unicode[STIX]{x1D714}_{FS}(z-\unicode[STIX]{x1D701})|\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(|\unicode[STIX]{x1D701}|^{2})\,dV(\unicode[STIX]{x1D701})\leqslant C\int _{\mathbb{ C}}|\unicode[STIX]{x1D701}|\,\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(|z^{\prime }|^{2})\,dV(z^{\prime })\leqslant C\unicode[STIX]{x1D700}.\end{eqnarray}$$
This means that we can find
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}$
decreasing to 1 such that
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}$
decreasing to 1 such that
 $\unicode[STIX]{x1D714}_{FS}\star \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}\leqslant \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}_{FS}$
. It can be shown in the same way as in § 3.2 that
$\unicode[STIX]{x1D714}_{FS}\star \unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}\leqslant \unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}_{FS}$
. It can be shown in the same way as in § 3.2 that
 $G_{\unicode[STIX]{x1D700}}(z):=\text{I}(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(\cdot ,z))$
is smooth and its complex Hessian is given by
$G_{\unicode[STIX]{x1D700}}(z):=\text{I}(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(\cdot ,z))$
is smooth and its complex Hessian is given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}_{FS}+dd_{z}^{c}G_{\unicode[STIX]{x1D700}}(z)=(\unicode[STIX]{x1D70B}_{2})_{\star }(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D700}}+dd_{x,z}^{c}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}})^{n+1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}_{FS}+dd_{z}^{c}G_{\unicode[STIX]{x1D700}}(z)=(\unicode[STIX]{x1D70B}_{2})_{\star }(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D700}}+dd_{x,z}^{c}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}})^{n+1}.\end{eqnarray}$$
To prove this we first explain how to compute all the second-order partial derivatives of
![]() $G_{\unicode[STIX]{x1D700}}$
. Fix
$G_{\unicode[STIX]{x1D700}}$
. Fix
 $\unicode[STIX]{x1D709}\in \mathbb{C}=\mathbb{R}^{2}$
a unit vector and denote by
$\unicode[STIX]{x1D709}\in \mathbb{C}=\mathbb{R}^{2}$
a unit vector and denote by
 $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}f(z):=\lim _{h\rightarrow 0^{+}}(f(z+h\unicode[STIX]{x1D709})-f(z))/h$
the derivative of
$\unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}f(z):=\lim _{h\rightarrow 0^{+}}(f(z+h\unicode[STIX]{x1D709})-f(z))/h$
the derivative of
![]() $f$
in the direction
$f$
in the direction
![]() $\unicode[STIX]{x1D709}$
. Note that
$\unicode[STIX]{x1D709}$
. Note that
 $$\begin{eqnarray}\frac{1}{h}[\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(|z+h\unicode[STIX]{x1D709}|^{2})-\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(|z|^{2})]\rightarrow \unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(|z|^{2}))\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{h}[\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(|z+h\unicode[STIX]{x1D709}|^{2})-\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(|z|^{2})]\rightarrow \unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D712}_{\unicode[STIX]{x1D700}}(|z|^{2}))\end{eqnarray}$$
as
![]() $h\rightarrow 0$
uniformly in
$h\rightarrow 0$
uniformly in
![]() $z$
. It follows that
$z$
. It follows that
 $$\begin{eqnarray}\frac{1}{h}[\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(x,z+h\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(x,z)]\rightarrow \unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(z)\end{eqnarray}$$
$$\begin{eqnarray}\frac{1}{h}[\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(x,z+h\unicode[STIX]{x1D709})-\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(x,z)]\rightarrow \unicode[STIX]{x2202}_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(z)\end{eqnarray}$$
as
![]() $h\rightarrow 0$
uniformly in
$h\rightarrow 0$
uniformly in
![]() $x,z$
. By the same arguments as in § 3.2 the first and second partial derivatives of
$x,z$
. By the same arguments as in § 3.2 the first and second partial derivatives of
 $z\mapsto \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(x,z)$
can be written as
$z\mapsto \unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(x,z)$
can be written as
 $C_{\unicode[STIX]{x1D700}}(u^{+}-u^{-})$
where
$C_{\unicode[STIX]{x1D700}}(u^{+}-u^{-})$
where
![]() $u^{\pm }$
are
$u^{\pm }$
are
![]() $\unicode[STIX]{x1D703}$
-psh functions with minimal singularities. They are thus uniformly bounded by a constant
$\unicode[STIX]{x1D703}$
-psh functions with minimal singularities. They are thus uniformly bounded by a constant
![]() $C_{\unicode[STIX]{x1D700}}^{\prime }$
(which blows up as
$C_{\unicode[STIX]{x1D700}}^{\prime }$
(which blows up as
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
). Thus the same arguments as in § 3.2 show that
$\unicode[STIX]{x1D700}\rightarrow 0$
). Thus the same arguments as in § 3.2 show that
 $z\mapsto G_{\unicode[STIX]{x1D700}}(z)$
is twice differentiable (even smooth). Set
$z\mapsto G_{\unicode[STIX]{x1D700}}(z)$
is twice differentiable (even smooth). Set
 $g_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}\log (1+|z|^{2})$
, where
$g_{\unicode[STIX]{x1D700}}=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}\log (1+|z|^{2})$
, where
 $g=\log (1+|z|^{2})$
is the potential of
$g=\log (1+|z|^{2})$
is the potential of
![]() $\unicode[STIX]{x1D714}_{FS}$
in
$\unicode[STIX]{x1D714}_{FS}$
in
![]() $\mathbb{C}$
. The second derivative
$\mathbb{C}$
. The second derivative
![]() $\unicode[STIX]{x2202}_{z}\unicode[STIX]{x2202}_{\bar{z}}$
of
$\unicode[STIX]{x2202}_{z}\unicode[STIX]{x2202}_{\bar{z}}$
of
![]() $G_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}}$
is given by
$G_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}}$
is given by
 $$\begin{eqnarray}\unicode[STIX]{x2202}_{z}\unicode[STIX]{x2202}_{\bar{z}}(G_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}})=\int _{X}\unicode[STIX]{x2202}_{z}\unicode[STIX]{x2202}_{\bar{z}}(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}})(\unicode[STIX]{x1D703}+dd_{x}^{c}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}})^{n}-n\,d_{x}\unicode[STIX]{x2202}_{z}(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}})\wedge d_{x}^{c}\unicode[STIX]{x2202}_{\bar{z}}(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}})\wedge (\unicode[STIX]{x1D703}+dd_{x}^{c}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}})^{n-1}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x2202}_{z}\unicode[STIX]{x2202}_{\bar{z}}(G_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}})=\int _{X}\unicode[STIX]{x2202}_{z}\unicode[STIX]{x2202}_{\bar{z}}(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}})(\unicode[STIX]{x1D703}+dd_{x}^{c}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}})^{n}-n\,d_{x}\unicode[STIX]{x2202}_{z}(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}})\wedge d_{x}^{c}\unicode[STIX]{x2202}_{\bar{z}}(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}})\wedge (\unicode[STIX]{x1D703}+dd_{x}^{c}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}})^{n-1}.\end{eqnarray}$$
Let
![]() $H(z)$
denote the integrand in the right-hand side which is a positive measure on
$H(z)$
denote the integrand in the right-hand side which is a positive measure on
![]() $X$
. Indeed, since it is a local property we can argue locally and use an approximation technique as in the proof of Corollary 3.7. Moreover, we infer that
$X$
. Indeed, since it is a local property we can argue locally and use an approximation technique as in the proof of Corollary 3.7. Moreover, we infer that
 $(\sqrt{-1}/\unicode[STIX]{x1D70B})H(z)\,dz\wedge d\bar{z}$
is the Monge–Ampère measure of
$(\sqrt{-1}/\unicode[STIX]{x1D70B})H(z)\,dz\wedge d\bar{z}$
is the Monge–Ampère measure of
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}}$
with respect to the form
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}}$
with respect to the form
![]() $\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}$
, i.e.
$\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}$
, i.e.
 $(\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}+dd^{c}(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}}))^{n+1}$
. This together with
$(\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}+dd^{c}(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}+g_{\unicode[STIX]{x1D700}}))^{n+1}$
. This together with
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}_{FS}+dd_{z}^{c}G_{\unicode[STIX]{x1D700}}(z)=dd_{z}^{c}(g_{\unicode[STIX]{x1D700}}+G_{\unicode[STIX]{x1D700}})=dd_{z}^{c}\text{I}(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(\cdot ,z)+g_{\unicode[STIX]{x1D700}}(z))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D700}}\unicode[STIX]{x1D714}_{FS}+dd_{z}^{c}G_{\unicode[STIX]{x1D700}}(z)=dd_{z}^{c}(g_{\unicode[STIX]{x1D700}}+G_{\unicode[STIX]{x1D700}})=dd_{z}^{c}\text{I}(\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}(\cdot ,z)+g_{\unicode[STIX]{x1D700}}(z))\end{eqnarray}$$
justify the formula (16).
Fix
 $\unicode[STIX]{x1D712}:\mathbb{C}\rightarrow \mathbb{R}$
a smooth function with compact support in
$\unicode[STIX]{x1D712}:\mathbb{C}\rightarrow \mathbb{R}$
a smooth function with compact support in
![]() $\mathbb{C}$
. We want to prove that
$\mathbb{C}$
. We want to prove that
 $$\begin{eqnarray}\int _{\mathbb{C}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D714}_{FS}+dd^{c}G)=\int _{M}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6E9}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\mathbb{C}}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D714}_{FS}+dd^{c}G)=\int _{M}\unicode[STIX]{x1D712}(\unicode[STIX]{x1D6E9}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}.\end{eqnarray}$$
The above formula is true for the approximants
![]() $G_{\unicode[STIX]{x1D700}}$
and
$G_{\unicode[STIX]{x1D700}}$
and
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D700}}$
as we discussed above. Now we explain how we can insure the convergence when we take the limit in (16) as
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D700}}$
as we discussed above. Now we explain how we can insure the convergence when we take the limit in (16) as
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
. To deal with the left-hand side we prove that
$\unicode[STIX]{x1D700}\rightarrow 0$
. To deal with the left-hand side we prove that
![]() $G_{\unicode[STIX]{x1D700}}$
converge pointwise to
$G_{\unicode[STIX]{x1D700}}$
converge pointwise to
![]() $G$
. For fixed
$G$
. For fixed
![]() $z\in \mathbb{C}$
we can find constants
$z\in \mathbb{C}$
we can find constants
![]() $c_{\unicode[STIX]{x1D700}}$
converging to
$c_{\unicode[STIX]{x1D700}}$
converging to
![]() $0$
such that
$0$
such that
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}+c_{\unicode[STIX]{x1D700}}$
decreases to
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}}+c_{\unicode[STIX]{x1D700}}$
decreases to
![]() $\unicode[STIX]{x1D6F7}$
. Then
$\unicode[STIX]{x1D6F7}$
. Then
![]() $G_{\unicode[STIX]{x1D700}}(z)$
converges to
$G_{\unicode[STIX]{x1D700}}(z)$
converges to
![]() $G(z)$
by basic properties of the
$G(z)$
by basic properties of the
![]() $\text{I}$
functional [Reference Berman and BoucksomBB10, Proposition 4.3]. As
$\text{I}$
functional [Reference Berman and BoucksomBB10, Proposition 4.3]. As
![]() $G_{\unicode[STIX]{x1D700}}$
is uniformly bounded independent of
$G_{\unicode[STIX]{x1D700}}$
is uniformly bounded independent of
![]() $\unicode[STIX]{x1D700}$
, the convergence of the current
$\unicode[STIX]{x1D700}$
, the convergence of the current
![]() $dd^{c}G_{\unicode[STIX]{x1D700}}$
follows. Now we treat the convergence of the right-hand side of (16). Fix a Kähler form
$dd^{c}G_{\unicode[STIX]{x1D700}}$
follows. Now we treat the convergence of the right-hand side of (16). Fix a Kähler form
![]() $\unicode[STIX]{x1D714}_{M}$
on
$\unicode[STIX]{x1D714}_{M}$
on
![]() $M$
and
$M$
and
![]() $\unicode[STIX]{x1D6FF}>0$
. Let
$\unicode[STIX]{x1D6FF}>0$
. Let
![]() $U$
be an open neighborhood of the pluripolar set
$U$
be an open neighborhood of the pluripolar set
 $E=(X\setminus \operatorname{Amp}(\{\unicode[STIX]{x1D703}\}))\times H_{\infty }$
such that
$E=(X\setminus \operatorname{Amp}(\{\unicode[STIX]{x1D703}\}))\times H_{\infty }$
such that
 $\operatorname{Cap}_{\unicode[STIX]{x1D714}_{M}}(U)<\unicode[STIX]{x1D6FF}$
. Note that Theorem 2.8 gives that
$\operatorname{Cap}_{\unicode[STIX]{x1D714}_{M}}(U)<\unicode[STIX]{x1D6FF}$
. Note that Theorem 2.8 gives that
 $$\begin{eqnarray}\operatorname{Cap}_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D700}}}(U)\leqslant C\operatorname{Cap}_{\unicode[STIX]{x1D714}_{M}}(U)^{1/n}=O(\unicode[STIX]{x1D6FF}^{1/n}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Cap}_{\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D700}}}(U)\leqslant C\operatorname{Cap}_{\unicode[STIX]{x1D714}_{M}}(U)^{1/n}=O(\unicode[STIX]{x1D6FF}^{1/n}),\end{eqnarray}$$
where
![]() $C$
is independent of
$C$
is independent of
![]() $\unicode[STIX]{x1D700}$
. And, by Bedford–Taylor theory [Reference Bedford and TaylorBT82] the Monge–Ampère measure
$\unicode[STIX]{x1D700}$
. And, by Bedford–Taylor theory [Reference Bedford and TaylorBT82] the Monge–Ampère measure
 $(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}})^{n+1}$
converges to
$(\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D700}}+dd^{c}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D700}})^{n+1}$
converges to
 $(\unicode[STIX]{x1D6E9}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}$
in
$(\unicode[STIX]{x1D6E9}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}$
in
![]() $M\setminus U$
. Letting
$M\setminus U$
. Letting
![]() $\unicode[STIX]{x1D700}\rightarrow 0$
and then
$\unicode[STIX]{x1D700}\rightarrow 0$
and then
![]() $\unicode[STIX]{x1D6FF}\rightarrow 0$
we arrive at the conclusion.◻
$\unicode[STIX]{x1D6FF}\rightarrow 0$
we arrive at the conclusion.◻
We move forward to proving the linearity of the
![]() $\text{I}$
functional. Consider
$\text{I}$
functional. Consider
![]() $(M,\unicode[STIX]{x1D6E9})$
as above and let
$(M,\unicode[STIX]{x1D6E9})$
as above and let
 $\unicode[STIX]{x1D70C}:D\rightarrow \mathbb{R}$
be a smooth potential of
$\unicode[STIX]{x1D70C}:D\rightarrow \mathbb{R}$
be a smooth potential of
![]() $\unicode[STIX]{x1D714}_{FS}$
in
$\unicode[STIX]{x1D714}_{FS}$
in
 $D\subset \mathbb{C}\mathbb{P}^{1}$
with zero boundary values.
$D\subset \mathbb{C}\mathbb{P}^{1}$
with zero boundary values.
Lemma 3.11. Assume that
![]() $F$
is a smooth function on
$F$
is a smooth function on
![]() $M$
which is
$M$
which is
![]() $S^{1}$
-invariant in
$S^{1}$
-invariant in
![]() $X\times \mathbb{C}$
in the variable
$X\times \mathbb{C}$
in the variable
![]() $z$
. Let
$z$
. Let
![]() $\unicode[STIX]{x1D711}_{t}$
be the geodesic connecting
$\unicode[STIX]{x1D711}_{t}$
be the geodesic connecting
 $\unicode[STIX]{x1D711}_{0}=P_{\unicode[STIX]{x1D703}}(F(\cdot ,1))$
to
$\unicode[STIX]{x1D711}_{0}=P_{\unicode[STIX]{x1D703}}(F(\cdot ,1))$
to
 $\unicode[STIX]{x1D711}_{1}=P_{\unicode[STIX]{x1D703}}(F(\cdot ,e))$
. Let
$\unicode[STIX]{x1D711}_{1}=P_{\unicode[STIX]{x1D703}}(F(\cdot ,e))$
. Let
![]() $\unicode[STIX]{x1D6F7}$
be the envelope on
$\unicode[STIX]{x1D6F7}$
be the envelope on
![]() $M$
of
$M$
of
![]() $F$
with respect to
$F$
with respect to
![]() $\unicode[STIX]{x1D6E9}$
. If
$\unicode[STIX]{x1D6E9}$
. If
 $F(x,z)+\unicode[STIX]{x1D70C}(z)>\unicode[STIX]{x1D711}_{\log |z|}(x)$
in
$F(x,z)+\unicode[STIX]{x1D70C}(z)>\unicode[STIX]{x1D711}_{\log |z|}(x)$
in
![]() $X\times D$
, then
$X\times D$
, then
 $z\mapsto \text{I}(\unicode[STIX]{x1D6F7}(\cdot ,z)+\unicode[STIX]{x1D70C}(z))$
is harmonic in
$z\mapsto \text{I}(\unicode[STIX]{x1D6F7}(\cdot ,z)+\unicode[STIX]{x1D70C}(z))$
is harmonic in
![]() $D$
.
$D$
.
Proof. When restricted to
![]() $X\times D$
, we have
$X\times D$
, we have
![]() $\unicode[STIX]{x1D6F7}+\unicode[STIX]{x1D70C}$
is
$\unicode[STIX]{x1D6F7}+\unicode[STIX]{x1D70C}$
is
![]() $\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}$
-psh and has boundary values
$\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}$
-psh and has boundary values
![]() $\unicode[STIX]{x1D711}_{0,1}$
, thus by definition,
$\unicode[STIX]{x1D711}_{0,1}$
, thus by definition,
 $\unicode[STIX]{x1D6F7}\leqslant \unicode[STIX]{x1D711}_{t}-\unicode[STIX]{x1D70C}<F$
. It follows from [Reference Bedford and TaylorBT82] that
$\unicode[STIX]{x1D6F7}\leqslant \unicode[STIX]{x1D711}_{t}-\unicode[STIX]{x1D70C}<F$
. It follows from [Reference Bedford and TaylorBT82] that
 $(\unicode[STIX]{x1D6E9}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}=0$
in
$(\unicode[STIX]{x1D6E9}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}=0$
in
![]() $X\times D$
, which in turn implies that
$X\times D$
, which in turn implies that
 $\text{I}(\unicode[STIX]{x1D6F7}(\cdot ,z)+\unicode[STIX]{x1D70C}(z))$
is harmonic in
$\text{I}(\unicode[STIX]{x1D6F7}(\cdot ,z)+\unicode[STIX]{x1D70C}(z))$
is harmonic in
![]() $D$
thanks to Lemma 3.10.◻
$D$
thanks to Lemma 3.10.◻
Theorem 3.12. The
![]() $\text{I}$
energy is linear along weak geodesics with minimal singularities.
$\text{I}$
energy is linear along weak geodesics with minimal singularities.
Proof. Fix
![]() $f_{0},f_{1}$
two smooth functions in
$f_{0},f_{1}$
two smooth functions in
![]() $X$
and denote by
$X$
and denote by
 $\unicode[STIX]{x1D711}_{i}=P_{\unicode[STIX]{x1D703}}(f_{i}),i=0,1$
the envelopes of
$\unicode[STIX]{x1D711}_{i}=P_{\unicode[STIX]{x1D703}}(f_{i}),i=0,1$
the envelopes of
![]() $f_{0},f_{1}$
respectively. Let
$f_{0},f_{1}$
respectively. Let
![]() $\unicode[STIX]{x1D711}_{t}$
be the geodesic connecting
$\unicode[STIX]{x1D711}_{t}$
be the geodesic connecting
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
. Observe also that by approximating any two given potentials with minimal singularities with a sequence of smooth functions, it suffices to prove linearity of
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
. Observe also that by approximating any two given potentials with minimal singularities with a sequence of smooth functions, it suffices to prove linearity of
![]() $\text{I}$
along
$\text{I}$
along
![]() $\unicode[STIX]{x1D711}_{t}$
.
$\unicode[STIX]{x1D711}_{t}$
.
Let
![]() $F$
be a function on
$F$
be a function on
![]() $M$
which is
$M$
which is
![]() $S^{1}$
-invariant in
$S^{1}$
-invariant in
![]() $X\times \mathbb{C}$
in the variable
$X\times \mathbb{C}$
in the variable
![]() $z$
and such that
$z$
and such that
 $F=f_{0,1}$
on
$F=f_{0,1}$
on
 $X\times \unicode[STIX]{x2202}D$
and
$X\times \unicode[STIX]{x2202}D$
and
![]() $+\infty$
elsewhere. Consider a sequence
$+\infty$
elsewhere. Consider a sequence
![]() $(F_{j})_{j}$
of smooth functions
$(F_{j})_{j}$
of smooth functions
![]() $F_{j}\uparrow F$
, which are also
$F_{j}\uparrow F$
, which are also
![]() $S^{1}$
-invariant in
$S^{1}$
-invariant in
![]() $X\times \mathbb{C}$
in the variable
$X\times \mathbb{C}$
in the variable
![]() $z$
and such that
$z$
and such that
 $F_{j}+\unicode[STIX]{x1D70C}>\unicode[STIX]{x1D711}_{\log |z|}(x)$
in
$F_{j}+\unicode[STIX]{x1D70C}>\unicode[STIX]{x1D711}_{\log |z|}(x)$
in
![]() $X\times D$
. Let
$X\times D$
. Let
![]() $\unicode[STIX]{x1D6F7}_{j}$
be the envelope on
$\unicode[STIX]{x1D6F7}_{j}$
be the envelope on
![]() $M$
of
$M$
of
![]() $F_{j}$
with respect to
$F_{j}$
with respect to
![]() $\unicode[STIX]{x1D6E9}$
. Then
$\unicode[STIX]{x1D6E9}$
. Then
 $(\unicode[STIX]{x1D6E9}+dd^{c}\unicode[STIX]{x1D6F7}_{j})^{n+1}$
is supported on
$(\unicode[STIX]{x1D6E9}+dd^{c}\unicode[STIX]{x1D6F7}_{j})^{n+1}$
is supported on
 $\{\unicode[STIX]{x1D6F7}_{j}=F_{j}\}$
. As
$\{\unicode[STIX]{x1D6F7}_{j}=F_{j}\}$
. As
 $X\times \unicode[STIX]{x2202}D$
is non-pluripolar in
$X\times \unicode[STIX]{x2202}D$
is non-pluripolar in
![]() $M$
it follows that
$M$
it follows that
![]() $\unicode[STIX]{x1D6F7}_{j}$
is uniformly bounded from above. Thus
$\unicode[STIX]{x1D6F7}_{j}$
is uniformly bounded from above. Thus
![]() $\unicode[STIX]{x1D6F7}_{j}$
converges increasingly (almost everywhere) to
$\unicode[STIX]{x1D6F7}_{j}$
converges increasingly (almost everywhere) to
![]() $\unicode[STIX]{x1D6F7}$
a
$\unicode[STIX]{x1D6F7}$
a
![]() $\unicode[STIX]{x1D6E9}$
-psh function with minimal singularities. We claim that
$\unicode[STIX]{x1D6E9}$
-psh function with minimal singularities. We claim that
 $$\begin{eqnarray}\int _{\{\unicode[STIX]{x1D6F7}<P_{\unicode[STIX]{x1D6E9}}(F)\}}(\unicode[STIX]{x1D6E9}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}=0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\{\unicode[STIX]{x1D6F7}<P_{\unicode[STIX]{x1D6E9}}(F)\}}(\unicode[STIX]{x1D6E9}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}=0.\end{eqnarray}$$
To see this we observe that the Monge–Ampère measure of
![]() $\unicode[STIX]{x1D6F7}$
is concentrated on
$\unicode[STIX]{x1D6F7}$
is concentrated on
 $X\times \unicode[STIX]{x2202}D$
and that
$X\times \unicode[STIX]{x2202}D$
and that
 $\{\unicode[STIX]{x1D6F7}<P_{\unicode[STIX]{x1D6E9}}(F)\}\subset X\times (\mathbb{C}\mathbb{P}^{1}\setminus \unicode[STIX]{x2202}D)$
since
$\{\unicode[STIX]{x1D6F7}<P_{\unicode[STIX]{x1D6E9}}(F)\}\subset X\times (\mathbb{C}\mathbb{P}^{1}\setminus \unicode[STIX]{x2202}D)$
since
 $\unicode[STIX]{x1D6F7}=P_{\unicode[STIX]{x1D6E9}}(F)=\unicode[STIX]{x1D711}_{0,1}$
on
$\unicode[STIX]{x1D6F7}=P_{\unicode[STIX]{x1D6E9}}(F)=\unicode[STIX]{x1D711}_{0,1}$
on
 $X\times \unicode[STIX]{x2202}D$
. Indeed, on any open relatively compact subset
$X\times \unicode[STIX]{x2202}D$
. Indeed, on any open relatively compact subset
![]() $K$
of
$K$
of
 $X\times (\mathbb{C}\mathbb{P}^{1}\setminus \unicode[STIX]{x2202}D)$
one has that
$X\times (\mathbb{C}\mathbb{P}^{1}\setminus \unicode[STIX]{x2202}D)$
one has that
 $\unicode[STIX]{x1D6F7}_{j}<F_{j}$
for
$\unicode[STIX]{x1D6F7}_{j}<F_{j}$
for
![]() $j$
large enough (since
$j$
large enough (since
![]() $F_{j}$
increases to
$F_{j}$
increases to
![]() $+\infty$
uniformly in
$+\infty$
uniformly in
![]() $K$
and
$K$
and
![]() $\unicode[STIX]{x1D6F7}_{j}$
is uniformly bounded from above). By the continuity property of the complex Monge–Ampère operator we get that
$\unicode[STIX]{x1D6F7}_{j}$
is uniformly bounded from above). By the continuity property of the complex Monge–Ampère operator we get that
 $(\unicode[STIX]{x1D6E9}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}(K)=0$
. It follows from (17) and the domination principle [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Corollary 2.5] that
$(\unicode[STIX]{x1D6E9}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}(K)=0$
. It follows from (17) and the domination principle [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Corollary 2.5] that
 $\unicode[STIX]{x1D6F7}=P_{\unicode[STIX]{x1D6E9}}(F)$
.
$\unicode[STIX]{x1D6F7}=P_{\unicode[STIX]{x1D6E9}}(F)$
.
Now, we claim that
 $\unicode[STIX]{x1D6F7}+\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D711}_{\log |z|}$
in
$\unicode[STIX]{x1D6F7}+\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D711}_{\log |z|}$
in
![]() $X\times D$
. Indeed, consider
$X\times D$
. Indeed, consider
 $$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}U_{0}(x,z):=\unicode[STIX]{x1D711}_{0}(x)+A(\log (|z|^{2}+3)-\log (|z|^{2}+1)-\log 2);\quad \\ U_{1}(x,z):=\unicode[STIX]{x1D711}_{1}(x)+A(\log |z|^{2}-\log (|z|^{2}+1)+\log (e^{2}+1)-2).\quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}l@{}}U_{0}(x,z):=\unicode[STIX]{x1D711}_{0}(x)+A(\log (|z|^{2}+3)-\log (|z|^{2}+1)-\log 2);\quad \\ U_{1}(x,z):=\unicode[STIX]{x1D711}_{1}(x)+A(\log |z|^{2}-\log (|z|^{2}+1)+\log (e^{2}+1)-2).\quad \end{array}\right.\end{eqnarray}$$
For
![]() $A>0$
big enough
$A>0$
big enough
 $U:=\max (U_{0},U_{1})=\unicode[STIX]{x1D711}_{0,1}$
on
$U:=\max (U_{0},U_{1})=\unicode[STIX]{x1D711}_{0,1}$
on
![]() $\unicode[STIX]{x2202}D$
and it is
$\unicode[STIX]{x2202}D$
and it is
![]() $\unicode[STIX]{x1D6E9}_{A}$
-psh, where
$\unicode[STIX]{x1D6E9}_{A}$
-psh, where
 $\unicode[STIX]{x1D703}_{A}:=\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}+A\unicode[STIX]{x1D70B}_{2}^{\ast }\unicode[STIX]{x1D714}_{FS}$
. So we can apply our previous analysis with this
$\unicode[STIX]{x1D703}_{A}:=\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}+A\unicode[STIX]{x1D70B}_{2}^{\ast }\unicode[STIX]{x1D714}_{FS}$
. So we can apply our previous analysis with this
![]() $(1,1)$
-form
$(1,1)$
-form
![]() $\unicode[STIX]{x1D6E9}_{A}$
instead of
$\unicode[STIX]{x1D6E9}_{A}$
instead of
![]() $\unicode[STIX]{x1D6E9}$
. By definition of envelope we have
$\unicode[STIX]{x1D6E9}$
. By definition of envelope we have
![]() $\unicode[STIX]{x1D6F7}\geqslant U$
and in particular
$\unicode[STIX]{x1D6F7}\geqslant U$
and in particular
 $\unicode[STIX]{x1D6F7}\geqslant \unicode[STIX]{x1D711}_{0,1}$
on
$\unicode[STIX]{x1D6F7}\geqslant \unicode[STIX]{x1D711}_{0,1}$
on
 $X\times \unicode[STIX]{x2202}D$
. Moreover, for each
$X\times \unicode[STIX]{x2202}D$
. Moreover, for each
![]() $z\in \unicode[STIX]{x2202}D$
,
$z\in \unicode[STIX]{x2202}D$
,
![]() $\unicode[STIX]{x1D6F7}(\cdot ,z)$
is
$\unicode[STIX]{x1D6F7}(\cdot ,z)$
is
![]() $\unicode[STIX]{x1D703}$
-psh and dominated by
$\unicode[STIX]{x1D703}$
-psh and dominated by
 $F=f_{0,1}$
. It then follows that
$F=f_{0,1}$
. It then follows that
 $\unicode[STIX]{x1D6F7}\leqslant \unicode[STIX]{x1D711}_{0,1}$
on
$\unicode[STIX]{x1D6F7}\leqslant \unicode[STIX]{x1D711}_{0,1}$
on
 $X\times \unicode[STIX]{x2202}D$
, giving the equality on the boundary. Furthermore, it follows from the proof of Lemma 3.11 and the continuity of the Monge–Ampère operator that the Monge–Ampère measure
$X\times \unicode[STIX]{x2202}D$
, giving the equality on the boundary. Furthermore, it follows from the proof of Lemma 3.11 and the continuity of the Monge–Ampère operator that the Monge–Ampère measure
 $(\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D70C}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}$
vanishes in
$(\unicode[STIX]{x1D70B}_{1}^{\ast }\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D70C}+dd^{c}\unicode[STIX]{x1D6F7})^{n+1}$
vanishes in
![]() $X\times D$
. Proposition 3.3 thus insures that
$X\times D$
. Proposition 3.3 thus insures that
![]() $\unicode[STIX]{x1D6F7}+\unicode[STIX]{x1D70C}$
is the unique weak geodesic with minimal singularities joining
$\unicode[STIX]{x1D6F7}+\unicode[STIX]{x1D70C}$
is the unique weak geodesic with minimal singularities joining
![]() $\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
. Hence the claim.
$\unicode[STIX]{x1D711}_{0},\unicode[STIX]{x1D711}_{1}$
. Hence the claim.
Now, thanks to Lemma 3.11 and [Reference Berman and BoucksomBB10, Proposition 4.3], we know that
 $\text{I}(\unicode[STIX]{x1D6F7}(\cdot ,z)+\unicode[STIX]{x1D70C}(z))=\text{I}(\unicode[STIX]{x1D711}_{\log |z|})$
is harmonic in
$\text{I}(\unicode[STIX]{x1D6F7}(\cdot ,z)+\unicode[STIX]{x1D70C}(z))=\text{I}(\unicode[STIX]{x1D711}_{\log |z|})$
is harmonic in
![]() $D$
(and
$D$
(and
![]() $S^{1}$
-invariant!). Hence,
$S^{1}$
-invariant!). Hence,
![]() $\text{I}$
is linear along
$\text{I}$
is linear along
![]() $\unicode[STIX]{x1D711}_{t}$
, with
$\unicode[STIX]{x1D711}_{t}$
, with
 $t=\log |z|$
. This is what we wanted.◻
$t=\log |z|$
. This is what we wanted.◻
3.4 Geodesic rays and the proof of Theorem 1.2
Given
![]() $\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D713}$
two
$\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D713}$
two
![]() $\unicode[STIX]{x1D703}$
-psh functions such that
$\unicode[STIX]{x1D703}$
-psh functions such that
![]() $\unicode[STIX]{x1D711}$
has minimal singularities, we define the weak geodesic ray attached to
$\unicode[STIX]{x1D711}$
has minimal singularities, we define the weak geodesic ray attached to
![]() $\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
in the following way (see [Reference DarvasDar17b] for the Kähler case). For fixed
$\unicode[STIX]{x1D711},\unicode[STIX]{x1D713}$
in the following way (see [Reference DarvasDar17b] for the Kähler case). For fixed
![]() $l>0$
, we denote by
$l>0$
, we denote by
 $[0,l]\ni t\rightarrow u_{t}^{l}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
the weak geodesic segment joining
$[0,l]\ni t\rightarrow u_{t}^{l}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
the weak geodesic segment joining
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
 $\max (\unicode[STIX]{x1D711}-l,\unicode[STIX]{x1D713})$
. The same argument as in [Reference DarvasDar17b, Lemma 4.2] shows that
$\max (\unicode[STIX]{x1D711}-l,\unicode[STIX]{x1D713})$
. The same argument as in [Reference DarvasDar17b, Lemma 4.2] shows that
![]() $u^{l}$
forms an increasing family of weak geodesics and we can then define the limit subgeodesic ray:
$u^{l}$
forms an increasing family of weak geodesics and we can then define the limit subgeodesic ray:
 $$\begin{eqnarray}v(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})_{t}:=\Bigl(\lim _{l\rightarrow +\infty }u_{t}^{l}\Bigr)^{\ast },\quad t\in [0,+\infty ).\end{eqnarray}$$
$$\begin{eqnarray}v(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})_{t}:=\Bigl(\lim _{l\rightarrow +\infty }u_{t}^{l}\Bigr)^{\ast },\quad t\in [0,+\infty ).\end{eqnarray}$$
Lemma 3.13. Assume that
![]() $\unicode[STIX]{x1D703}$
is big. The subgeodesic ray
$\unicode[STIX]{x1D703}$
is big. The subgeodesic ray
 $[0,\infty )\ni t\rightarrow v(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is a weak geodesic ray.
$[0,\infty )\ni t\rightarrow v(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is a weak geodesic ray.
Proof. As all complexifications
 $U^{l}\in \operatorname{PSH}(X\times D_{l},\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703})$
satisfy the appropriate complex Monge–Ampère equation on the domains
$U^{l}\in \operatorname{PSH}(X\times D_{l},\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D703})$
satisfy the appropriate complex Monge–Ampère equation on the domains
 $\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D_{l}$
and are locally bounded there, it follows from continuity property of the complex Monge–Ampère operator that the complexification of
$\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D_{l}$
and are locally bounded there, it follows from continuity property of the complex Monge–Ampère operator that the complexification of
 $t\rightarrow v(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})_{t}$
satisfies the homogeneous Monge–Ampère equation on
$t\rightarrow v(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})_{t}$
satisfies the homogeneous Monge–Ampère equation on
 $\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D_{\infty }$
as well. Since all the curves
$\operatorname{Amp}(\{\unicode[STIX]{x1D703}\})\times D_{\infty }$
as well. Since all the curves
![]() $t\rightarrow u_{t}^{l}$
are uniformly
$t\rightarrow u_{t}^{l}$
are uniformly
![]() $t$
-Lipschitz continuous, so is their limit
$t$
-Lipschitz continuous, so is their limit
 $t\rightarrow v(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})_{t}$
, hence Proposition 3.3 gives that
$t\rightarrow v(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})_{t}$
, hence Proposition 3.3 gives that
 $t\rightarrow v(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})_{t}$
must be a weak geodesic ray, i.e., for any closed interval
$t\rightarrow v(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})_{t}$
must be a weak geodesic ray, i.e., for any closed interval
 $I\subset [0,\infty )$
, the restriction
$I\subset [0,\infty )$
, the restriction
 $I\ni t\rightarrow v(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is the weak geodesic joining the potentials corresponding to the endpoints of
$I\ni t\rightarrow v(\unicode[STIX]{x1D711},\unicode[STIX]{x1D713})_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
is the weak geodesic joining the potentials corresponding to the endpoints of
![]() $I$
.◻
$I$
.◻
Now we introduce an invariant of
![]() $\unicode[STIX]{x1D713}$
. It is clear that
$\unicode[STIX]{x1D713}$
. It is clear that
 $[0,\infty )\ni t\rightarrow \max (\unicode[STIX]{x1D711}-t,\unicode[STIX]{x1D713})$
is a subgeodesic ray with minimal singularities. Thus
$[0,\infty )\ni t\rightarrow \max (\unicode[STIX]{x1D711}-t,\unicode[STIX]{x1D713})$
is a subgeodesic ray with minimal singularities. Thus
 $t\rightarrow \text{I}(\max (\unicode[STIX]{x1D711}-t,\unicode[STIX]{x1D713}))$
is convex by Theorem 3.8 and decreasing by [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.8]. This implies that the following limit is well defined:
$t\rightarrow \text{I}(\max (\unicode[STIX]{x1D711}-t,\unicode[STIX]{x1D713}))$
is convex by Theorem 3.8 and decreasing by [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 2.8]. This implies that the following limit is well defined:
 $$\begin{eqnarray}c_{\unicode[STIX]{x1D713}}:=\lim _{t\rightarrow \infty }\frac{\text{I}(\max (\unicode[STIX]{x1D711}-t,\unicode[STIX]{x1D713}))-\text{I}(\unicode[STIX]{x1D711})}{t}\leqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}c_{\unicode[STIX]{x1D713}}:=\lim _{t\rightarrow \infty }\frac{\text{I}(\max (\unicode[STIX]{x1D711}-t,\unicode[STIX]{x1D713}))-\text{I}(\unicode[STIX]{x1D711})}{t}\leqslant 0.\end{eqnarray}$$
Recall the cocycle formula of [Reference Berman and BoucksomBB10, Corollary 3.2]:
 $$\begin{eqnarray}\text{I}(u)-\text{I}(v)=\frac{1}{\operatorname{Vol}(\unicode[STIX]{x1D703})(n+1)}\mathop{\sum }_{j=0}^{n}\int _{X}(u-v)\unicode[STIX]{x1D703}_{u}^{j}\wedge \unicode[STIX]{x1D703}_{v}^{n-j},\end{eqnarray}$$
$$\begin{eqnarray}\text{I}(u)-\text{I}(v)=\frac{1}{\operatorname{Vol}(\unicode[STIX]{x1D703})(n+1)}\mathop{\sum }_{j=0}^{n}\int _{X}(u-v)\unicode[STIX]{x1D703}_{u}^{j}\wedge \unicode[STIX]{x1D703}_{v}^{n-j},\end{eqnarray}$$
where
 $u,v\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
have minimal singularities. From this formula it follows that
$u,v\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
have minimal singularities. From this formula it follows that
![]() $c_{\unicode[STIX]{x1D713}}$
is independent of the choice of potential with minimal singularities
$c_{\unicode[STIX]{x1D713}}$
is independent of the choice of potential with minimal singularities
![]() $\unicode[STIX]{x1D711}$
satisfying
$\unicode[STIX]{x1D711}$
satisfying
![]() $\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D713}$
. Finally, the following result gives an attractive characterization of potentials
$\unicode[STIX]{x1D711}\geqslant \unicode[STIX]{x1D713}$
. Finally, the following result gives an attractive characterization of potentials
![]() $\unicode[STIX]{x1D713}$
for which
$\unicode[STIX]{x1D713}$
for which
![]() $c_{\unicode[STIX]{x1D713}}=0$
.
$c_{\unicode[STIX]{x1D713}}=0$
.
Proposition 3.14. Given
 $\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
, we have
$\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
, we have
![]() $c_{\unicode[STIX]{x1D713}}=0$
if and only if
$c_{\unicode[STIX]{x1D713}}=0$
if and only if
 $\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
.
$\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
.
Proof. The proof is an adaptation of the arguments of [Reference DarvasDar17b, Theorem 2.5] to our more general setting. As
![]() $c_{\unicode[STIX]{x1D713}}$
only depends on
$c_{\unicode[STIX]{x1D713}}$
only depends on
![]() $\unicode[STIX]{x1D713}$
it is enough to work with the special subgeodesic ray
$\unicode[STIX]{x1D713}$
it is enough to work with the special subgeodesic ray
 $t\rightarrow \unicode[STIX]{x1D713}_{t}:=\max (V_{\unicode[STIX]{x1D703}}-t,\unicode[STIX]{x1D713})$
. The cocycle formula (19) implies that
$t\rightarrow \unicode[STIX]{x1D713}_{t}:=\max (V_{\unicode[STIX]{x1D703}}-t,\unicode[STIX]{x1D713})$
. The cocycle formula (19) implies that
 $c_{\unicode[STIX]{x1D713}}=c_{\unicode[STIX]{x1D713}+c}$
, thus we can assume that
$c_{\unicode[STIX]{x1D713}}=c_{\unicode[STIX]{x1D713}+c}$
, thus we can assume that
 $\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}\leqslant 0$
. By [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Proposition 2.8]
$\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}\leqslant 0$
. By [Reference Berman, Boucksom, Guedj and ZeriahiBBGZ13, Proposition 2.8]
 $$\begin{eqnarray}\int _{X}(\unicode[STIX]{x1D713}_{t}-V_{\unicode[STIX]{x1D703}})\,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}\leqslant \text{I}(\unicode[STIX]{x1D713}_{t})\leqslant (n+1)^{-1}\int _{X}(\unicode[STIX]{x1D713}_{t}-V_{\unicode[STIX]{x1D703}})\,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}(\unicode[STIX]{x1D713}_{t}-V_{\unicode[STIX]{x1D703}})\,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}\leqslant \text{I}(\unicode[STIX]{x1D713}_{t})\leqslant (n+1)^{-1}\int _{X}(\unicode[STIX]{x1D713}_{t}-V_{\unicode[STIX]{x1D703}})\,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}\end{eqnarray}$$
so our claim is equivalent to showing that
 $$\begin{eqnarray}\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})\Longleftrightarrow t^{-1}\int _{X}(\unicode[STIX]{x1D713}_{t}-V_{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})\Longleftrightarrow t^{-1}\int _{X}(\unicode[STIX]{x1D713}_{t}-V_{\unicode[STIX]{x1D703}})\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}\rightarrow 0.\end{eqnarray}$$
Fix
 $s\in (0,1)$
. Note that on
$s\in (0,1)$
. Note that on
 $\{\unicode[STIX]{x1D713}>V_{\unicode[STIX]{x1D703}}-t\}$
, the two measures
$\{\unicode[STIX]{x1D713}>V_{\unicode[STIX]{x1D703}}-t\}$
, the two measures
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}$
and
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}$
and
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}^{n}$
coincide. Additionally, using that
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}^{n}$
coincide. Additionally, using that
 $X=\{\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}-t\}\cup \{V_{\unicode[STIX]{x1D703}}-t<\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}-st\}\cup \{V_{\unicode[STIX]{x1D703}}-st<\unicode[STIX]{x1D713}\}$
we can estimate the right-hand side above as follows:
$X=\{\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}-t\}\cup \{V_{\unicode[STIX]{x1D703}}-t<\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}-st\}\cup \{V_{\unicode[STIX]{x1D703}}-st<\unicode[STIX]{x1D713}\}$
we can estimate the right-hand side above as follows:
 $$\begin{eqnarray}0\geqslant \int _{X}\frac{\unicode[STIX]{x1D713}_{t}-V_{\unicode[STIX]{x1D703}}}{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}\geqslant -\int _{\{\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}-t\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}-\int _{\{\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}-ts\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}^{n}-s\operatorname{Vol}(\unicode[STIX]{x1D703}).\end{eqnarray}$$
$$\begin{eqnarray}0\geqslant \int _{X}\frac{\unicode[STIX]{x1D713}_{t}-V_{\unicode[STIX]{x1D703}}}{t}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}\geqslant -\int _{\{\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}-t\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}-\int _{\{\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}-ts\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}}^{n}-s\operatorname{Vol}(\unicode[STIX]{x1D703}).\end{eqnarray}$$
By [Reference Guedj and ZeriahiGZ07, Lemma 1.2],
 $\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
if and only if
$\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
if and only if
 $\int _{\{\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}-t\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}\rightarrow 0$
as
$\int _{\{\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}-t\}}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D713}_{t}}^{n}\rightarrow 0$
as
 $t\rightarrow +\infty$
. Hence, the above estimates give the conclusion.◻
$t\rightarrow +\infty$
. Hence, the above estimates give the conclusion.◻
Lemma 3.15. Suppose
 $\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
satisfies
$\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
satisfies
![]() $\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}$
. Let
$\unicode[STIX]{x1D713}\leqslant V_{\unicode[STIX]{x1D703}}$
. Let
 $t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})$
be the geodesic ray constructed in (18). Then
$t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})$
be the geodesic ray constructed in (18). Then
 $$\begin{eqnarray}\text{I}(v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t})=tc_{\unicode[STIX]{x1D713}}.\end{eqnarray}$$
$$\begin{eqnarray}\text{I}(v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t})=tc_{\unicode[STIX]{x1D713}}.\end{eqnarray}$$
In particular,
 $t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
is constant if and only if
$t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
is constant if and only if
 $\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
.
$\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
.
Proof. We go back to the construction of
 $t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
in (18). By Theorem 3.12, for each
$t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
in (18). By Theorem 3.12, for each
![]() $l$
fixed, the function
$l$
fixed, the function
 $t\rightarrow \text{I}(u_{t}^{l})$
is linear, and hence we can write
$t\rightarrow \text{I}(u_{t}^{l})$
is linear, and hence we can write
 $$\begin{eqnarray}\text{I}(u_{t}^{l})=\text{I}(V_{\unicode[STIX]{x1D703}})+\frac{t}{l}(\text{I}(\max (\unicode[STIX]{x1D713},V_{\unicode[STIX]{x1D703}}-l))-\text{I}(V_{\unicode[STIX]{x1D703}}))=\frac{t}{l}(\text{I}(\max (\unicode[STIX]{x1D713},V_{\unicode[STIX]{x1D703}}-l))-\text{I}(V_{\unicode[STIX]{x1D703}})).\end{eqnarray}$$
$$\begin{eqnarray}\text{I}(u_{t}^{l})=\text{I}(V_{\unicode[STIX]{x1D703}})+\frac{t}{l}(\text{I}(\max (\unicode[STIX]{x1D713},V_{\unicode[STIX]{x1D703}}-l))-\text{I}(V_{\unicode[STIX]{x1D703}}))=\frac{t}{l}(\text{I}(\max (\unicode[STIX]{x1D713},V_{\unicode[STIX]{x1D703}}-l))-\text{I}(V_{\unicode[STIX]{x1D703}})).\end{eqnarray}$$
Letting
 $l\rightarrow +\infty$
, by [Reference Berman and BoucksomBB10, Proposition 3.3] we obtain (20). If
$l\rightarrow +\infty$
, by [Reference Berman and BoucksomBB10, Proposition 3.3] we obtain (20). If
 $t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
is constant equal to
$t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
is constant equal to
![]() $V_{\unicode[STIX]{x1D703}}$
, it follows that
$V_{\unicode[STIX]{x1D703}}$
, it follows that
![]() $c_{\unicode[STIX]{x1D713}}=0$
, thus by Proposition 3.14 we get
$c_{\unicode[STIX]{x1D713}}=0$
, thus by Proposition 3.14 we get
 $\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. Conversely, if
$\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
. Conversely, if
 $\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, then Proposition 3.14 yields that
$\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, then Proposition 3.14 yields that
![]() $c_{\unicode[STIX]{x1D713}}=0$
, hence
$c_{\unicode[STIX]{x1D713}}=0$
, hence
![]() $\text{I}$
is constant along
$\text{I}$
is constant along
 $v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})$
, and thus
$v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})$
, and thus
 $v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})$
is constant.◻
$v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})$
is constant.◻
Remark 3.16. To show that if
 $t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
is constant then
$t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
is constant then
 $\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, we only need to prove the estimate
$\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, we only need to prove the estimate
 $\text{I}(v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t})\leqslant tc_{\unicode[STIX]{x1D713}}$
. This last inequality is a simple consequence of the convexity of the Monge–Ampère energy (Theorem 3.8) and the construction of the ray
$\text{I}(v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t})\leqslant tc_{\unicode[STIX]{x1D713}}$
. This last inequality is a simple consequence of the convexity of the Monge–Ampère energy (Theorem 3.8) and the construction of the ray
 $t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
(18).
$t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
(18).
Lemma 3.17. Given a weak geodesic ray
 $[0,+\infty )\ni t\rightarrow \unicode[STIX]{x1D719}_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
, its Legendre transform
$[0,+\infty )\ni t\rightarrow \unicode[STIX]{x1D719}_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
, its Legendre transform
 $\mathbb{R}\ni \unicode[STIX]{x1D70F}\rightarrow \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }=\inf _{t\in [0,+\infty )}(\unicode[STIX]{x1D719}_{t}-t\unicode[STIX]{x1D70F})$
satisfies
$\mathbb{R}\ni \unicode[STIX]{x1D70F}\rightarrow \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }=\inf _{t\in [0,+\infty )}(\unicode[STIX]{x1D719}_{t}-t\unicode[STIX]{x1D70F})$
satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }=P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }+C,\unicode[STIX]{x1D719}_{0}),\quad \unicode[STIX]{x1D70F}\in \mathbb{R},C>0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }=P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }+C,\unicode[STIX]{x1D719}_{0}),\quad \unicode[STIX]{x1D70F}\in \mathbb{R},C>0.\end{eqnarray}$$
In particular,
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }]}(\unicode[STIX]{x1D719}_{0})=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }$
.
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }]}(\unicode[STIX]{x1D719}_{0})=\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }$
.
Proof. One can repeat the argument in [Reference DarvasDar17b, Theorem 5.3]. Fix
![]() $\unicode[STIX]{x1D70F}\in \mathbb{R}$
. The fact that
$\unicode[STIX]{x1D70F}\in \mathbb{R}$
. The fact that
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }$
is
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }$
is
![]() $\unicode[STIX]{x1D703}$
-psh follows from Kiselman’s minimum principle [Reference KiselmanKis78]. Suppose that
$\unicode[STIX]{x1D703}$
-psh follows from Kiselman’s minimum principle [Reference KiselmanKis78]. Suppose that
 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }\neq -\infty$
and fix
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }\neq -\infty$
and fix
![]() $C>0$
. Since
$C>0$
. Since
 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }\leqslant \unicode[STIX]{x1D719}_{0}$
, it results that
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }\leqslant \unicode[STIX]{x1D719}_{0}$
, it results that
 $P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }+C,\unicode[STIX]{x1D719}_{0})\geqslant \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }$
. Hence we only have to argue that
$P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }+C,\unicode[STIX]{x1D719}_{0})\geqslant \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }$
. Hence we only have to argue that
 $$\begin{eqnarray}P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }+C,\unicode[STIX]{x1D719}_{0})\leqslant \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }+C,\unicode[STIX]{x1D719}_{0})\leqslant \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }.\end{eqnarray}$$
Let
 $[0,1]\ni t\rightarrow g_{t}^{l},h_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
,
$[0,1]\ni t\rightarrow g_{t}^{l},h_{t}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
,
![]() $l\geqslant 0$
, be the weak geodesic segments defined by the formulas
$l\geqslant 0$
, be the weak geodesic segments defined by the formulas
 $$\begin{eqnarray}\displaystyle & g_{t}^{l}=\unicode[STIX]{x1D719}_{tl}-tl\unicode[STIX]{x1D70F}, & \displaystyle \nonumber\\ \displaystyle & h_{t}=P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }+C,\unicode[STIX]{x1D719}_{0})-Ct. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & g_{t}^{l}=\unicode[STIX]{x1D719}_{tl}-tl\unicode[STIX]{x1D70F}, & \displaystyle \nonumber\\ \displaystyle & h_{t}=P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }+C,\unicode[STIX]{x1D719}_{0})-Ct. & \displaystyle \nonumber\end{eqnarray}$$
Then we have
 $h_{0}\leqslant \unicode[STIX]{x1D719}_{0}=\lim _{t\rightarrow 0}g_{t}^{l}=g_{0}^{l}$
and
$h_{0}\leqslant \unicode[STIX]{x1D719}_{0}=\lim _{t\rightarrow 0}g_{t}^{l}=g_{0}^{l}$
and
 $h_{1}\leqslant \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }\leqslant g_{1}^{l}$
for any
$h_{1}\leqslant \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }\leqslant g_{1}^{l}$
for any
![]() $l\geqslant 0$
. Hence, by definition of weak geodesics (8) we have
$l\geqslant 0$
. Hence, by definition of weak geodesics (8) we have
 $$\begin{eqnarray}h_{t}\leqslant g_{t}^{l},\quad t\in [0,1],l\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}h_{t}\leqslant g_{t}^{l},\quad t\in [0,1],l\geqslant 0.\end{eqnarray}$$
Taking the infimum in the above estimate over
 $l\in [0,+\infty )$
and then taking the supremum over
$l\in [0,+\infty )$
and then taking the supremum over
 $t\in [0,1]$
, we obtain
$t\in [0,1]$
, we obtain
 $$\begin{eqnarray}P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }+C,\unicode[STIX]{x1D719}_{0})\leqslant \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }+C,\unicode[STIX]{x1D719}_{0})\leqslant \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D70F}}^{\ast }.\end{eqnarray}$$
Letting
 $C\rightarrow +\infty$
we obtain the last statement of the proposition.◻
$C\rightarrow +\infty$
we obtain the last statement of the proposition.◻
Proof of Theorem 1.2
Theorem 1.2 is a consequence of the following result.
Theorem 3.18. Let
![]() $\unicode[STIX]{x1D703}$
be a smooth closed
$\unicode[STIX]{x1D703}$
be a smooth closed
![]() $(1,1)$
-form whose cohomology class is big. For any
$(1,1)$
-form whose cohomology class is big. For any
 $\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
, the following are equivalent:
$\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
, the following are equivalent:
-
(i)
 $\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
;
$\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
; -
(ii)
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711})\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
for all
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711})\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
for all
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
;
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
; -
(iii)
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711})=\unicode[STIX]{x1D711}$
for all
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(\unicode[STIX]{x1D711})=\unicode[STIX]{x1D711}$
for all
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
;
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
; -
(iv)
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(V_{\unicode[STIX]{x1D703}})\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
;
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(V_{\unicode[STIX]{x1D703}})\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
; -
(v)
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(V_{\unicode[STIX]{x1D703}})=V_{\unicode[STIX]{x1D703}}$
.
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(V_{\unicode[STIX]{x1D703}})=V_{\unicode[STIX]{x1D703}}$
.
Proof. We can assume without loss of generality that
![]() $\unicode[STIX]{x1D713}\leqslant 0$
. The implication
$\unicode[STIX]{x1D713}\leqslant 0$
. The implication
 $(\text{i})\Longrightarrow (\text{iii})$
follows from Theorem 2.15 while the implications
$(\text{i})\Longrightarrow (\text{iii})$
follows from Theorem 2.15 while the implications
 $(\text{iii})\Longrightarrow (\text{ii})\Longrightarrow (\text{iv})$
and
$(\text{iii})\Longrightarrow (\text{ii})\Longrightarrow (\text{iv})$
and
 $\text{(iii)}\Longrightarrow (\text{v})$
are trivial. The implication
$\text{(iii)}\Longrightarrow (\text{v})$
are trivial. The implication
 $(\text{iv})\Longrightarrow (\text{v})$
simply follows from Proposition 2.14 and the domination principle (Proposition 2.4).
$(\text{iv})\Longrightarrow (\text{v})$
simply follows from Proposition 2.14 and the domination principle (Proposition 2.4).
We now prove that
 $(\text{v})\Longrightarrow (\text{i})$
. Suppose that
$(\text{v})\Longrightarrow (\text{i})$
. Suppose that
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(V_{\unicode[STIX]{x1D703}})=V_{\unicode[STIX]{x1D703}}$
. From the construction of the ray
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(V_{\unicode[STIX]{x1D703}})=V_{\unicode[STIX]{x1D703}}$
. From the construction of the ray
 $t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
in (18) it automatically follows that
$t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
in (18) it automatically follows that
 $v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}\geqslant \unicode[STIX]{x1D713}$
. This trivially gives
$v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}\geqslant \unicode[STIX]{x1D713}$
. This trivially gives
 $v_{0}^{\ast }=\inf _{t\in [0,\infty )}v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}\geqslant \unicode[STIX]{x1D713}$
. By definition of envelope we have
$v_{0}^{\ast }=\inf _{t\in [0,\infty )}v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}\geqslant \unicode[STIX]{x1D713}$
. By definition of envelope we have
 $V_{\unicode[STIX]{x1D703}}\geqslant P_{[\unicode[STIX]{x1D703},v_{0}^{\ast }]}(V_{\unicode[STIX]{x1D703}})\geqslant P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(V_{\unicode[STIX]{x1D703}})=V_{\unicode[STIX]{x1D703}}$
. Combining this with Lemma 3.17 we obtain that
$V_{\unicode[STIX]{x1D703}}\geqslant P_{[\unicode[STIX]{x1D703},v_{0}^{\ast }]}(V_{\unicode[STIX]{x1D703}})\geqslant P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D713}]}(V_{\unicode[STIX]{x1D703}})=V_{\unicode[STIX]{x1D703}}$
. Combining this with Lemma 3.17 we obtain that
 $v_{0}^{\ast }=P_{[\unicode[STIX]{x1D703},v_{0}^{\ast }]}(V_{\unicode[STIX]{x1D703}})=V_{\unicode[STIX]{x1D703}}$
. As the ray
$v_{0}^{\ast }=P_{[\unicode[STIX]{x1D703},v_{0}^{\ast }]}(V_{\unicode[STIX]{x1D703}})=V_{\unicode[STIX]{x1D703}}$
. As the ray
 $t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
is decreasing in
$t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
is decreasing in
![]() $t$
, this automatically gives that
$t$
, this automatically gives that
 $V_{\unicode[STIX]{x1D703}}=v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{0}\geqslant v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}\geqslant v_{0}^{\ast }=V_{\unicode[STIX]{x1D703}}$
, hence
$V_{\unicode[STIX]{x1D703}}=v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{0}\geqslant v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}\geqslant v_{0}^{\ast }=V_{\unicode[STIX]{x1D703}}$
, hence
 $t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
is constant. Invoking Lemma 3.15 we obtain that
$t\rightarrow v(V_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D713})_{t}$
is constant. Invoking Lemma 3.15 we obtain that
 $\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
.◻
$\unicode[STIX]{x1D713}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
.◻
Theorem 1.3 follows directly from Theorem 1.2.
Theorem 3.19. Let
 $\{\unicode[STIX]{x1D703}_{1}\},\{\unicode[STIX]{x1D703}_{2}\}$
be big classes. The following are equivalent:
$\{\unicode[STIX]{x1D703}_{1}\},\{\unicode[STIX]{x1D703}_{2}\}$
be big classes. The following are equivalent:
-
(i)
 $V_{\unicode[STIX]{x1D703}_{1}}+V_{\unicode[STIX]{x1D703}_{2}}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})$
;
$V_{\unicode[STIX]{x1D703}_{1}}+V_{\unicode[STIX]{x1D703}_{2}}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})$
; -
(ii) for any
 $u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{1}),v\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{2})$
we have
$u\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{1}),v\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{2})$
we have  $$\begin{eqnarray}u+v\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})\Longleftrightarrow u\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}),v\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{2}).\end{eqnarray}$$
$$\begin{eqnarray}u+v\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})\Longleftrightarrow u\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}),v\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{2}).\end{eqnarray}$$
Proof. Since
 $V_{\unicode[STIX]{x1D703}_{j}}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{j}),j=1,2$
, the implication
$V_{\unicode[STIX]{x1D703}_{j}}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{j}),j=1,2$
, the implication
 $(\text{ii})\Longrightarrow (\text{i})$
is trivial. Assume (i) holds. The implication
$(\text{ii})\Longrightarrow (\text{i})$
is trivial. Assume (i) holds. The implication
![]() $(\Longrightarrow )$
in (ii) follows from [Reference Di NezzaDiN15, Theorem B]. Assume that
$(\Longrightarrow )$
in (ii) follows from [Reference Di NezzaDiN15, Theorem B]. Assume that
 $\unicode[STIX]{x1D711}_{j}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{j}),j=1,2$
. We want to show that
$\unicode[STIX]{x1D711}_{j}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{j}),j=1,2$
. We want to show that
 $\unicode[STIX]{x1D711}:=\unicode[STIX]{x1D711}_{1}+\unicode[STIX]{x1D711}_{2}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})$
. By assumption that (i) holds we get that
$\unicode[STIX]{x1D711}:=\unicode[STIX]{x1D711}_{1}+\unicode[STIX]{x1D711}_{2}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})$
. By assumption that (i) holds we get that
 $V_{\unicode[STIX]{x1D703}_{1}}+V_{\unicode[STIX]{x1D703}_{2}}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})$
. Hence, by definition of envelopes we can write
$V_{\unicode[STIX]{x1D703}_{1}}+V_{\unicode[STIX]{x1D703}_{2}}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})$
. Hence, by definition of envelopes we can write
 $$\begin{eqnarray}P_{[\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D703}_{1}}+V_{\unicode[STIX]{x1D703}_{2}})\geqslant P_{[\unicode[STIX]{x1D703}_{1},u]}(V_{\unicode[STIX]{x1D703}_{1}})+P_{[\unicode[STIX]{x1D703}_{2},v]}(V_{\unicode[STIX]{x1D703}_{2}})=V_{\unicode[STIX]{x1D703}_{1}}+V_{\unicode[STIX]{x1D703}_{2}}.\end{eqnarray}$$
$$\begin{eqnarray}P_{[\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D703}_{1}}+V_{\unicode[STIX]{x1D703}_{2}})\geqslant P_{[\unicode[STIX]{x1D703}_{1},u]}(V_{\unicode[STIX]{x1D703}_{1}})+P_{[\unicode[STIX]{x1D703}_{2},v]}(V_{\unicode[STIX]{x1D703}_{2}})=V_{\unicode[STIX]{x1D703}_{1}}+V_{\unicode[STIX]{x1D703}_{2}}.\end{eqnarray}$$
Ultimately, it follows from Theorem 1.2 that
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})$
.◻
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})$
.◻
4 Proof of Theorem 1.1
In this section we give the proof of Theorem 1.1 and discuss some immediate consequences.
Proof of Theorem 1.1.
We first argue the equality of Lelong numbers in part (i) of Theorem 1.1. If
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, then, as follows from Theorem 2.15,
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, then, as follows from Theorem 2.15,
 $P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D703}})=V_{\unicode[STIX]{x1D703}}$
. For any fixed
$P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D703}})=V_{\unicode[STIX]{x1D703}}$
. For any fixed
![]() $x\in X$
one trivially has
$x\in X$
one trivially has
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)\geqslant \unicode[STIX]{x1D708}(V_{\unicode[STIX]{x1D703}},x)$
. Assume, for the sake of seeking a contradiction, that
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)\geqslant \unicode[STIX]{x1D708}(V_{\unicode[STIX]{x1D703}},x)$
. Assume, for the sake of seeking a contradiction, that
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)>\unicode[STIX]{x1D708}(V_{\unicode[STIX]{x1D703}},x)$
. Fix a holomorphic coordinate around
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)>\unicode[STIX]{x1D708}(V_{\unicode[STIX]{x1D703}},x)$
. Fix a holomorphic coordinate around
![]() $x$
so that we identify
$x$
so that we identify
![]() $x$
with
$x$
with
 $0\in \mathbb{B}\subset \mathbb{C}^{n}$
where
$0\in \mathbb{B}\subset \mathbb{C}^{n}$
where
![]() $B$
is the unit ball in
$B$
is the unit ball in
![]() $\mathbb{C}^{n}$
. By definition of the Lelong numbers (2) we have
$\mathbb{C}^{n}$
. By definition of the Lelong numbers (2) we have
 $$\begin{eqnarray}\unicode[STIX]{x1D711}(z)\leqslant \unicode[STIX]{x1D6FE}\log \Vert z\Vert +O(1),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}(z)\leqslant \unicode[STIX]{x1D6FE}\log \Vert z\Vert +O(1),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)>0$
. Let
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D708}(\unicode[STIX]{x1D711},x)>0$
. Let
![]() $g$
be a smooth local potential for
$g$
be a smooth local potential for
![]() $\unicode[STIX]{x1D703}$
in
$\unicode[STIX]{x1D703}$
in
![]() $\mathbb{B}$
and observe that if
$\mathbb{B}$
and observe that if
 $\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
then
$\unicode[STIX]{x1D713}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
then
![]() $g+\unicode[STIX]{x1D713}$
is psh in
$g+\unicode[STIX]{x1D713}$
is psh in
![]() $\mathbb{B}$
. Furthermore, without loss of generality we can assume that
$\mathbb{B}$
. Furthermore, without loss of generality we can assume that
 $g+\unicode[STIX]{x1D711},g+V_{\unicode[STIX]{x1D703}}\leqslant 0$
in
$g+\unicode[STIX]{x1D711},g+V_{\unicode[STIX]{x1D703}}\leqslant 0$
in
![]() $\mathbb{B}$
. By the definition of the envelope we have the inequality
$\mathbb{B}$
. By the definition of the envelope we have the inequality
 $$\begin{eqnarray}V_{\unicode[STIX]{x1D703}}+g=P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D703}})+g\leqslant \sup \{v\in \operatorname{PSH}(\mathbb{B})\mid v\leqslant 0,v\leqslant \unicode[STIX]{x1D6FE}\log \Vert z\Vert +O(1)\},\end{eqnarray}$$
$$\begin{eqnarray}V_{\unicode[STIX]{x1D703}}+g=P_{[\unicode[STIX]{x1D703},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D703}})+g\leqslant \sup \{v\in \operatorname{PSH}(\mathbb{B})\mid v\leqslant 0,v\leqslant \unicode[STIX]{x1D6FE}\log \Vert z\Vert +O(1)\},\end{eqnarray}$$
in
![]() $\mathbb{B}$
. The right-hand side is the pluricomplex Green function
$\mathbb{B}$
. The right-hand side is the pluricomplex Green function
 $G_{\mathbb{B}}(z,0)$
of
$G_{\mathbb{B}}(z,0)$
of
![]() $\mathbb{B}$
with a logarithmic pole at 0 of order
$\mathbb{B}$
with a logarithmic pole at 0 of order
![]() $\unicode[STIX]{x1D6FE}$
. By [Reference KlimekKli91, Proposition 6.1] we have that
$\unicode[STIX]{x1D6FE}$
. By [Reference KlimekKli91, Proposition 6.1] we have that
 $$\begin{eqnarray}G_{\mathbb{B}}(z,0)=\unicode[STIX]{x1D6FE}\log \Vert z\Vert +O(1).\end{eqnarray}$$
$$\begin{eqnarray}G_{\mathbb{B}}(z,0)=\unicode[STIX]{x1D6FE}\log \Vert z\Vert +O(1).\end{eqnarray}$$
But this contradicts with the assumption that
 $\unicode[STIX]{x1D708}(V_{\unicode[STIX]{x1D703}},x)<\unicode[STIX]{x1D6FE}$
.
$\unicode[STIX]{x1D708}(V_{\unicode[STIX]{x1D703}},x)<\unicode[STIX]{x1D6FE}$
.
Now we argue the equality of multiplier ideal sheafs in part (i). This will be an application of Theorem 1.2 and the resolution of the strong openness conjecture of Guan and Zhou [Reference Guan and ZhouGZ15], in the specific form provided by Lempert [Reference LempertLem14]. Indeed, from Theorem 1.2 it follows that
 $$\begin{eqnarray}P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}+c,V_{\unicode[STIX]{x1D703}})(x){\nearrow}V_{\unicode[STIX]{x1D703}}(x)\quad \text{as}~c\rightarrow \infty ,\text{ for a.e. }x\in X.\end{eqnarray}$$
$$\begin{eqnarray}P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}+c,V_{\unicode[STIX]{x1D703}})(x){\nearrow}V_{\unicode[STIX]{x1D703}}(x)\quad \text{as}~c\rightarrow \infty ,\text{ for a.e. }x\in X.\end{eqnarray}$$
As
 $\unicode[STIX]{x1D711}\leqslant V_{\unicode[STIX]{x1D703}}+c^{\prime }$
for some
$\unicode[STIX]{x1D711}\leqslant V_{\unicode[STIX]{x1D703}}+c^{\prime }$
for some
![]() $c^{\prime }\in \mathbb{R}$
, we note that
$c^{\prime }\in \mathbb{R}$
, we note that
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
 $P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}+c,V_{\unicode[STIX]{x1D703}})$
have the same singularity type for any
$P_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}+c,V_{\unicode[STIX]{x1D703}})$
have the same singularity type for any
![]() $c\in \mathbb{R}$
, ultimately giving
$c\in \mathbb{R}$
, ultimately giving
 ${\mathcal{I}}(tP_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}+c,V_{\unicode[STIX]{x1D703}}),x)={\mathcal{I}}(t\unicode[STIX]{x1D711},x)$
,
${\mathcal{I}}(tP_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}+c,V_{\unicode[STIX]{x1D703}}),x)={\mathcal{I}}(t\unicode[STIX]{x1D711},x)$
,
![]() $x\in X$
,
$x\in X$
,
![]() $t\geqslant 0$
.
$t\geqslant 0$
.
Finally, (22) and [Reference LempertLem14, Theorem 1.1] imply that
 ${\mathcal{I}}(tP_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}+c,V_{\unicode[STIX]{x1D703}}),x)={\mathcal{I}}(tV_{\unicode[STIX]{x1D703}},x)$
for large enough
${\mathcal{I}}(tP_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x1D711}+c,V_{\unicode[STIX]{x1D703}}),x)={\mathcal{I}}(tV_{\unicode[STIX]{x1D703}},x)$
for large enough
![]() $c$
, proving that
$c$
, proving that
 ${\mathcal{I}}(t\unicode[STIX]{x1D711},x)={\mathcal{I}}(tV_{\unicode[STIX]{x1D703}},x)$
.
${\mathcal{I}}(t\unicode[STIX]{x1D711},x)={\mathcal{I}}(tV_{\unicode[STIX]{x1D703}},x)$
.
Now we turn to part (ii). Fix
![]() $\unicode[STIX]{x1D714}$
a Kähler form on
$\unicode[STIX]{x1D714}$
a Kähler form on
![]() $X$
. We can suppose that
$X$
. We can suppose that
 $\unicode[STIX]{x1D703},\unicode[STIX]{x1D702}\leqslant \tilde{\unicode[STIX]{x1D714}}:=\unicode[STIX]{x1D702}+\unicode[STIX]{x1D714}$
and
$\unicode[STIX]{x1D703},\unicode[STIX]{x1D702}\leqslant \tilde{\unicode[STIX]{x1D714}}:=\unicode[STIX]{x1D702}+\unicode[STIX]{x1D714}$
and
![]() $\tilde{\unicode[STIX]{x1D714}}$
is Kähler. Assume that
$\tilde{\unicode[STIX]{x1D714}}$
is Kähler. Assume that
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D702})\cap \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
. By Theorem 1.2 we get that
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D702})\cap \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
. By Theorem 1.2 we get that
 $P_{[\unicode[STIX]{x1D702},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D702}})=V_{\unicode[STIX]{x1D702}}$
. This implies
$P_{[\unicode[STIX]{x1D702},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D702}})=V_{\unicode[STIX]{x1D702}}$
. This implies
 $P_{[\tilde{\unicode[STIX]{x1D714}},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D702}})=V_{\unicode[STIX]{x1D702}}$
since
$P_{[\tilde{\unicode[STIX]{x1D714}},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D702}})=V_{\unicode[STIX]{x1D702}}$
since
 $P_{[\unicode[STIX]{x1D702},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D702}})\leqslant P_{[\tilde{\unicode[STIX]{x1D714}},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D702}})\leqslant V_{\unicode[STIX]{x1D702}}$
.
$P_{[\unicode[STIX]{x1D702},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D702}})\leqslant P_{[\tilde{\unicode[STIX]{x1D714}},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D702}})\leqslant V_{\unicode[STIX]{x1D702}}$
.
Furthermore, we claim that
 $V_{\unicode[STIX]{x1D702}}\in {\mathcal{E}}(X,\tilde{\unicode[STIX]{x1D714}})$
, i.e.,
$V_{\unicode[STIX]{x1D702}}\in {\mathcal{E}}(X,\tilde{\unicode[STIX]{x1D714}})$
, i.e.,
 $\int _{X}\tilde{\unicode[STIX]{x1D714}}_{V_{\unicode[STIX]{x1D702}}}^{n}=\operatorname{Vol}(\tilde{\unicode[STIX]{x1D714}})$
. Indeed, as
$\int _{X}\tilde{\unicode[STIX]{x1D714}}_{V_{\unicode[STIX]{x1D702}}}^{n}=\operatorname{Vol}(\tilde{\unicode[STIX]{x1D714}})$
. Indeed, as
![]() $\unicode[STIX]{x1D703}$
is nef, expanding the sum of Kähler classes
$\unicode[STIX]{x1D703}$
is nef, expanding the sum of Kähler classes
 $(\unicode[STIX]{x1D702}+(1+\unicode[STIX]{x1D700})\unicode[STIX]{x1D714})^{n}$
gives
$(\unicode[STIX]{x1D702}+(1+\unicode[STIX]{x1D700})\unicode[STIX]{x1D714})^{n}$
gives
 $$\begin{eqnarray}\operatorname{Vol}(\{\unicode[STIX]{x1D702}+(1+\unicode[STIX]{x1D700})\unicode[STIX]{x1D714}\})^{n}=\mathop{\sum }_{k=0}^{n}\binom{n}{k}\{\unicode[STIX]{x1D702}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}\}^{k}\cdot \{\unicode[STIX]{x1D714}\}^{n-k}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Vol}(\{\unicode[STIX]{x1D702}+(1+\unicode[STIX]{x1D700})\unicode[STIX]{x1D714}\})^{n}=\mathop{\sum }_{k=0}^{n}\binom{n}{k}\{\unicode[STIX]{x1D702}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D714}\}^{k}\cdot \{\unicode[STIX]{x1D714}\}^{n-k}.\end{eqnarray}$$
It follows from the comments after [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Definition 1.17] and [Reference Boucksom, Favre and JonssonBFJ09, Proposition 2.9] that the left-hand side converges to
![]() $\operatorname{Vol}(\tilde{\unicode[STIX]{x1D714}})$
while the right-hand side converges to
$\operatorname{Vol}(\tilde{\unicode[STIX]{x1D714}})$
while the right-hand side converges to
 $\sum _{k=0}^{n}\binom{n}{k}\{\unicode[STIX]{x1D702}\}^{k}\cdot \{\unicode[STIX]{x1D714}\}^{n-k}$
, ultimately giving
$\sum _{k=0}^{n}\binom{n}{k}\{\unicode[STIX]{x1D702}\}^{k}\cdot \{\unicode[STIX]{x1D714}\}^{n-k}$
, ultimately giving
 $$\begin{eqnarray}\operatorname{Vol}(\{\tilde{\unicode[STIX]{x1D714}}\})=\operatorname{Vol}(\{\unicode[STIX]{x1D702}+\unicode[STIX]{x1D714}\})=\mathop{\sum }_{k=0}^{n}\binom{n}{k}\{\unicode[STIX]{x1D702}\}^{k}\cdot \{\unicode[STIX]{x1D714}\}^{n-k}.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Vol}(\{\tilde{\unicode[STIX]{x1D714}}\})=\operatorname{Vol}(\{\unicode[STIX]{x1D702}+\unicode[STIX]{x1D714}\})=\mathop{\sum }_{k=0}^{n}\binom{n}{k}\{\unicode[STIX]{x1D702}\}^{k}\cdot \{\unicode[STIX]{x1D714}\}^{n-k}.\end{eqnarray}$$
On the other hand, by multilinearity of the non-pluripolar product we get
 $$\begin{eqnarray}\int _{X}\tilde{\unicode[STIX]{x1D714}}_{V_{\unicode[STIX]{x1D702}}}^{n}=\int _{X}(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D714}+dd^{c}V_{\unicode[STIX]{x1D702}})^{n}=\mathop{\sum }_{k=0}^{n}\binom{n}{k}\int _{X}(\unicode[STIX]{x1D702}+dd^{c}V_{\unicode[STIX]{x1D702}})^{k}\wedge \unicode[STIX]{x1D714}^{n-k},\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}\tilde{\unicode[STIX]{x1D714}}_{V_{\unicode[STIX]{x1D702}}}^{n}=\int _{X}(\unicode[STIX]{x1D702}+\unicode[STIX]{x1D714}+dd^{c}V_{\unicode[STIX]{x1D702}})^{n}=\mathop{\sum }_{k=0}^{n}\binom{n}{k}\int _{X}(\unicode[STIX]{x1D702}+dd^{c}V_{\unicode[STIX]{x1D702}})^{k}\wedge \unicode[STIX]{x1D714}^{n-k},\end{eqnarray}$$
and moreover
 $\{(\unicode[STIX]{x1D702}+dd^{c}V_{\unicode[STIX]{x1D702}})^{k}\}=\{\unicode[STIX]{x1D702}\}^{k}$
for each
$\{(\unicode[STIX]{x1D702}+dd^{c}V_{\unicode[STIX]{x1D702}})^{k}\}=\{\unicode[STIX]{x1D702}\}^{k}$
for each
 $0\leqslant k\leqslant n-1$
thanks to [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Definition 1.17], proving the claim.
$0\leqslant k\leqslant n-1$
thanks to [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Definition 1.17], proving the claim.
Given that
 $P_{[\tilde{\unicode[STIX]{x1D714}},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D702}})=V_{\unicode[STIX]{x1D702}}$
and
$P_{[\tilde{\unicode[STIX]{x1D714}},\unicode[STIX]{x1D711}]}(V_{\unicode[STIX]{x1D702}})=V_{\unicode[STIX]{x1D702}}$
and
 $V_{\unicode[STIX]{x1D702}}\in {\mathcal{E}}(X,\tilde{\unicode[STIX]{x1D714}}),$
we can use [Reference DarvasDar17a, Theorem 4] to conclude that
$V_{\unicode[STIX]{x1D702}}\in {\mathcal{E}}(X,\tilde{\unicode[STIX]{x1D714}}),$
we can use [Reference DarvasDar17a, Theorem 4] to conclude that
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\tilde{\unicode[STIX]{x1D714}})$
. Because
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\tilde{\unicode[STIX]{x1D714}})$
. Because
![]() $\unicode[STIX]{x1D703}\leqslant \tilde{\unicode[STIX]{x1D714}}$
and
$\unicode[STIX]{x1D703}\leqslant \tilde{\unicode[STIX]{x1D714}}$
and
 $\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
, we get
$\unicode[STIX]{x1D711}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703})$
, we get
 $\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, as follows from [Reference Di NezzaDiN15, Theorem B].◻
$\unicode[STIX]{x1D711}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
, as follows from [Reference Di NezzaDiN15, Theorem B].◻
Remark 4.1. Observe that Theorem 1.1(ii) is in general false for classes
![]() $\{\unicode[STIX]{x1D702}\}$
that are big but not nef. Indeed, if
$\{\unicode[STIX]{x1D702}\}$
that are big but not nef. Indeed, if
![]() $\{\unicode[STIX]{x1D702}\}$
is only big, it may happen that
$\{\unicode[STIX]{x1D702}\}$
is only big, it may happen that
![]() $V_{\unicode[STIX]{x1D702}}$
has a non-zero Lelong number at some point, and then [Reference Guedj and ZeriahiGZ07, Corollary 2.18] would give us that
$V_{\unicode[STIX]{x1D702}}$
has a non-zero Lelong number at some point, and then [Reference Guedj and ZeriahiGZ07, Corollary 2.18] would give us that
![]() $V_{\unicode[STIX]{x1D702}}$
does not have full mass with respect to any Kähler class
$V_{\unicode[STIX]{x1D702}}$
does not have full mass with respect to any Kähler class
![]() $\{\unicode[STIX]{x1D703}\}$
satisfying
$\{\unicode[STIX]{x1D703}\}$
satisfying
![]() $\unicode[STIX]{x1D702}\leqslant \unicode[STIX]{x1D703}$
, contradicting
$\unicode[STIX]{x1D702}\leqslant \unicode[STIX]{x1D703}$
, contradicting
 ${\mathcal{E}}(X,\unicode[STIX]{x1D702})\cap \operatorname{PSH}(X,\unicode[STIX]{x1D703})\subset {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
.
${\mathcal{E}}(X,\unicode[STIX]{x1D702})\cap \operatorname{PSH}(X,\unicode[STIX]{x1D703})\subset {\mathcal{E}}(X,\unicode[STIX]{x1D703})$
.
As a direct consequence we obtain the following additivity property of the set of full mass currents of big and nef cohomology classes, effectively proving that condition (i) in Theorem 1.3 is automatically satisfied.
Corollary 4.2. Let
 $\{\unicode[STIX]{x1D703}_{1}\},\{\unicode[STIX]{x1D703}_{2}\}$
be big and nef classes. Then for any
$\{\unicode[STIX]{x1D703}_{1}\},\{\unicode[STIX]{x1D703}_{2}\}$
be big and nef classes. Then for any
 $\unicode[STIX]{x1D711}_{1}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{1})$
and
$\unicode[STIX]{x1D711}_{1}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{1})$
and
 $\unicode[STIX]{x1D711}_{2}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{2})$
we have
$\unicode[STIX]{x1D711}_{2}\in \operatorname{PSH}(X,\unicode[STIX]{x1D703}_{2})$
we have
 $$\begin{eqnarray}\unicode[STIX]{x1D711}_{1}+\unicode[STIX]{x1D711}_{2}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})\Longleftrightarrow \unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}),\unicode[STIX]{x1D711}_{2}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{2}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{1}+\unicode[STIX]{x1D711}_{2}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})\Longleftrightarrow \unicode[STIX]{x1D711}_{1}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}),\unicode[STIX]{x1D711}_{2}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{2}).\end{eqnarray}$$
Proof. Fix a Kähler form
![]() $\unicode[STIX]{x1D714}$
such that
$\unicode[STIX]{x1D714}$
such that
 $\unicode[STIX]{x1D703}_{j}\leqslant \unicode[STIX]{x1D714},j=1,2$
. It follows from part (ii) of Theorem 1.1 that
$\unicode[STIX]{x1D703}_{j}\leqslant \unicode[STIX]{x1D714},j=1,2$
. It follows from part (ii) of Theorem 1.1 that
 $\unicode[STIX]{x1D711}_{j}\in {\mathcal{E}}(X,\unicode[STIX]{x1D714}),\forall j=1,2$
. By the convexity of
$\unicode[STIX]{x1D711}_{j}\in {\mathcal{E}}(X,\unicode[STIX]{x1D714}),\forall j=1,2$
. By the convexity of
 ${\mathcal{E}}(X,\unicode[STIX]{x1D714})$
proved in [Reference Guedj and ZeriahiGZ07, Proposition 1.6] it follows that
${\mathcal{E}}(X,\unicode[STIX]{x1D714})$
proved in [Reference Guedj and ZeriahiGZ07, Proposition 1.6] it follows that
 $\unicode[STIX]{x1D711}_{1}+\unicode[STIX]{x1D711}_{2}$
belongs to
$\unicode[STIX]{x1D711}_{1}+\unicode[STIX]{x1D711}_{2}$
belongs to
 ${\mathcal{E}}(X,2\unicode[STIX]{x1D714})$
. Now, [Reference Di NezzaDiN15, Theorem B] gives that
${\mathcal{E}}(X,2\unicode[STIX]{x1D714})$
. Now, [Reference Di NezzaDiN15, Theorem B] gives that
 $\unicode[STIX]{x1D711}_{1}+\unicode[STIX]{x1D711}_{2}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})$
, and hence the result follows.◻
$\unicode[STIX]{x1D711}_{1}+\unicode[STIX]{x1D711}_{2}\in {\mathcal{E}}(X,\unicode[STIX]{x1D703}_{1}+\unicode[STIX]{x1D703}_{2})$
, and hence the result follows.◻
5 Further applications
5.1 Invariance of finite energy classes
The following result says that finite energy classes are invariant under bimeromorphic maps as soon as the volume is preserved. The result was recently obtained in [Reference Di Nezza, Floris and TrapaniDFT17]. As an application of Theorem 1.1 we give a slightly different proof of the ‘baby case’, i.e. when
![]() $f$
is a blow-up along a smooth center.
$f$
is a blow-up along a smooth center.
Proposition 5.1. Let
 $\unicode[STIX]{x1D70B}:X\rightarrow Y$
be a blow up with smooth center
$\unicode[STIX]{x1D70B}:X\rightarrow Y$
be a blow up with smooth center
![]() ${\mathcal{Z}}$
between Kähler manifolds and
${\mathcal{Z}}$
between Kähler manifolds and
![]() $E$
be the exceptional divisor. Let
$E$
be the exceptional divisor. Let
 $\unicode[STIX]{x1D6FC}\in H^{1,1}(X,\mathbb{R})$
be a big class. Then the following conditions are equivalent:
$\unicode[STIX]{x1D6FC}\in H^{1,1}(X,\mathbb{R})$
be a big class. Then the following conditions are equivalent:
-
(i)
 $\operatorname{Vol}(\unicode[STIX]{x1D6FC})=\operatorname{Vol}(\unicode[STIX]{x1D70B}_{\star }\unicode[STIX]{x1D6FC})$
;
$\operatorname{Vol}(\unicode[STIX]{x1D6FC})=\operatorname{Vol}(\unicode[STIX]{x1D70B}_{\star }\unicode[STIX]{x1D6FC})$
; -
(ii) given a positive
 $(1,1)$
-current
$(1,1)$
-current
 $T$
in
$T$
in
 $\unicode[STIX]{x1D70B}_{\star }\unicode[STIX]{x1D6FC}$
, then
$\unicode[STIX]{x1D70B}_{\star }\unicode[STIX]{x1D6FC}$
, then
 $S=\unicode[STIX]{x1D70B}^{\star }T+\unicode[STIX]{x1D6FE}[E]$
, where
$S=\unicode[STIX]{x1D70B}^{\star }T+\unicode[STIX]{x1D6FE}[E]$
, where
 $\unicode[STIX]{x1D6FE}$
is a cohomological factor, is a positive
$\unicode[STIX]{x1D6FE}$
is a cohomological factor, is a positive
 $(1,1)$
-current on
$(1,1)$
-current on
 $X$
;
$X$
; -
(iii)
 $\unicode[STIX]{x1D70B}_{\star }({\mathcal{E}}(X,\unicode[STIX]{x1D703}))={\mathcal{E}}(Y,f_{\star }\unicode[STIX]{x1D703})$
;
$\unicode[STIX]{x1D70B}_{\star }({\mathcal{E}}(X,\unicode[STIX]{x1D703}))={\mathcal{E}}(Y,f_{\star }\unicode[STIX]{x1D703})$
; -
(iv)
 $\unicode[STIX]{x1D70B}_{\star }({\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703}))={\mathcal{E}}_{\unicode[STIX]{x1D712}}(Y,f_{\star }\unicode[STIX]{x1D703})$
for any weight
$\unicode[STIX]{x1D70B}_{\star }({\mathcal{E}}_{\unicode[STIX]{x1D712}}(X,\unicode[STIX]{x1D703}))={\mathcal{E}}_{\unicode[STIX]{x1D712}}(Y,f_{\star }\unicode[STIX]{x1D703})$
for any weight
 $\unicode[STIX]{x1D712}$
.
$\unicode[STIX]{x1D712}$
.
Proof. Recall that, given a smooth representative
![]() $\unicode[STIX]{x1D703}$
of the class
$\unicode[STIX]{x1D703}$
of the class
![]() $\unicode[STIX]{x1D6FC}$
, it follows from
$\unicode[STIX]{x1D6FC}$
, it follows from
![]() $\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma that any positive
$\unicode[STIX]{x2202}\bar{\unicode[STIX]{x2202}}$
-lemma that any positive
![]() $(1,1)$
-current can be written as
$(1,1)$
-current can be written as
 $T=\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D711}$
where the global potential
$T=\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D711}$
where the global potential
![]() $\unicode[STIX]{x1D711}$
is a
$\unicode[STIX]{x1D711}$
is a
![]() $\unicode[STIX]{x1D703}$
-psh function, i.e.
$\unicode[STIX]{x1D703}$
-psh function, i.e.
 $\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D711}\geqslant 0$
. The implications
$\unicode[STIX]{x1D703}+dd^{c}\unicode[STIX]{x1D711}\geqslant 0$
. The implications
 $(\text{iii})\Rightarrow (\text{i})$
and
$(\text{iii})\Rightarrow (\text{i})$
and
 $(\text{iv})\Rightarrow (\text{i})$
are trivial while the fact that (ii) implies (i), (iii) and (iv) are [Reference Di NezzaDiN15, Proposition 3.3]. We want to prove
$(\text{iv})\Rightarrow (\text{i})$
are trivial while the fact that (ii) implies (i), (iii) and (iv) are [Reference Di NezzaDiN15, Proposition 3.3]. We want to prove
 $(\text{i})\Rightarrow (\text{ii})$
. it suffices to show that for any positive
$(\text{i})\Rightarrow (\text{ii})$
. it suffices to show that for any positive
![]() $(1,1)$
-current
$(1,1)$
-current
![]() $T$
we have
$T$
we have
 $\unicode[STIX]{x1D6FE}\geqslant -\unicode[STIX]{x1D708}(T,{\mathcal{Z}})$
. Let
$\unicode[STIX]{x1D6FE}\geqslant -\unicode[STIX]{x1D708}(T,{\mathcal{Z}})$
. Let
![]() $S_{\min }$
be a positive current with minimal singularities in
$S_{\min }$
be a positive current with minimal singularities in
![]() $\unicode[STIX]{x1D6FC}$
, then it writes as
$\unicode[STIX]{x1D6FC}$
, then it writes as
 $$\begin{eqnarray}S_{\min }=\unicode[STIX]{x1D70B}^{\star }T_{Y}+\unicode[STIX]{x1D6FE}[E],\end{eqnarray}$$
$$\begin{eqnarray}S_{\min }=\unicode[STIX]{x1D70B}^{\star }T_{Y}+\unicode[STIX]{x1D6FE}[E],\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6FE}\geqslant -\unicode[STIX]{x1D708}(T_{Y},{\mathcal{Z}})$
. It easy to check that
$\unicode[STIX]{x1D6FE}\geqslant -\unicode[STIX]{x1D708}(T_{Y},{\mathcal{Z}})$
. It easy to check that
 $T_{Y}\in {\mathcal{E}}(Y,\unicode[STIX]{x1D70B}_{\star }\unicode[STIX]{x1D6FC})$
. Indeed,
$T_{Y}\in {\mathcal{E}}(Y,\unicode[STIX]{x1D70B}_{\star }\unicode[STIX]{x1D6FC})$
. Indeed,
 $$\begin{eqnarray}\operatorname{Vol}(\unicode[STIX]{x1D70B}_{\star }\unicode[STIX]{x1D6FC})=\operatorname{Vol}(\unicode[STIX]{x1D6FC})=\int _{X}\langle S_{\min }^{n}\rangle =\int _{Y}\langle T_{Y}^{n}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Vol}(\unicode[STIX]{x1D70B}_{\star }\unicode[STIX]{x1D6FC})=\operatorname{Vol}(\unicode[STIX]{x1D6FC})=\int _{X}\langle S_{\min }^{n}\rangle =\int _{Y}\langle T_{Y}^{n}\rangle .\end{eqnarray}$$
Thus, it follows from Theorem 1.1 that
 $\unicode[STIX]{x1D708}(T_{Y},y)=\unicode[STIX]{x1D708}(T_{\min },y)$
for any
$\unicode[STIX]{x1D708}(T_{Y},y)=\unicode[STIX]{x1D708}(T_{\min },y)$
for any
![]() $y\in Y$
and for any
$y\in Y$
and for any
![]() $T_{\min }$
current with minimal singularities on
$T_{\min }$
current with minimal singularities on
![]() $Y$
. Hence
$Y$
. Hence
 $\unicode[STIX]{x1D708}(T_{\min },{\mathcal{Z}})+\unicode[STIX]{x1D6FE}\geqslant 0$
. Furthermore any positive current
$\unicode[STIX]{x1D708}(T_{\min },{\mathcal{Z}})+\unicode[STIX]{x1D6FE}\geqslant 0$
. Furthermore any positive current
 $T\in \unicode[STIX]{x1D70B}_{\star }\unicode[STIX]{x1D6FC}$
is such that
$T\in \unicode[STIX]{x1D70B}_{\star }\unicode[STIX]{x1D6FC}$
is such that
 $\unicode[STIX]{x1D708}(T_{\min },{\mathcal{Z}})\leqslant \unicode[STIX]{x1D708}(T,{\mathcal{Z}})$
, and thus
$\unicode[STIX]{x1D708}(T_{\min },{\mathcal{Z}})\leqslant \unicode[STIX]{x1D708}(T,{\mathcal{Z}})$
, and thus
 $\unicode[STIX]{x1D708}(T,{\mathcal{Z}})+\unicode[STIX]{x1D6FE}\geqslant 0$
.◻
$\unicode[STIX]{x1D708}(T,{\mathcal{Z}})+\unicode[STIX]{x1D6FE}\geqslant 0$
.◻
5.2 Log concavity of non-pluripolar product
It was conjectured in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Conjecture 1.23] that
 $$\begin{eqnarray}\int _{X}\langle T_{1}\wedge \cdots \wedge T_{n}\rangle \geqslant \biggl(\int _{X}\langle T_{1}^{n}\rangle \biggr)^{1/n}\cdots \biggl(\int _{X}\langle T_{n}^{n}\rangle \biggr)^{1/n},\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}\langle T_{1}\wedge \cdots \wedge T_{n}\rangle \geqslant \biggl(\int _{X}\langle T_{1}^{n}\rangle \biggr)^{1/n}\cdots \biggl(\int _{X}\langle T_{n}^{n}\rangle \biggr)^{1/n},\end{eqnarray}$$
for all positive currents
 $T_{1},\ldots ,T_{n}$
. The result holds for currents with analytic singularities as mentioned in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10]. In this subsection we confirm this conjecture in the case of full mass currents in big and nef classes.
$T_{1},\ldots ,T_{n}$
. The result holds for currents with analytic singularities as mentioned in [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10]. In this subsection we confirm this conjecture in the case of full mass currents in big and nef classes.
With the help of Corollary 4.2, we can make obvious adjustments in the proof of [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Corollary 2.15] to get the following result.
Proposition 5.2. Let
![]() $\unicode[STIX]{x1D6FC}_{i}$
,
$\unicode[STIX]{x1D6FC}_{i}$
,
 $i=1,\ldots ,n$
be big and nef cohomology classes and let
$i=1,\ldots ,n$
be big and nef cohomology classes and let
 $T_{i}\in {\mathcal{E}}(X,\unicode[STIX]{x1D6FC}_{i})$
. Then we have
$T_{i}\in {\mathcal{E}}(X,\unicode[STIX]{x1D6FC}_{i})$
. Then we have
 $$\begin{eqnarray}\int _{X}\langle T_{1}\wedge \cdots \wedge T_{n}\rangle =\int _{X}\langle T_{1,\min }\wedge \cdots \wedge T_{n,\text{min}}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\int _{X}\langle T_{1}\wedge \cdots \wedge T_{n}\rangle =\int _{X}\langle T_{1,\min }\wedge \cdots \wedge T_{n,\text{min}}\rangle .\end{eqnarray}$$
Using this we can prove the log concavity of full mass currents in the big and nef case.
Corollary 5.3. If
 $T_{j},j=1,\ldots ,n$
, are full mass currents in big and nef cohomology classes, then (23) holds.
$T_{j},j=1,\ldots ,n$
, are full mass currents in big and nef cohomology classes, then (23) holds.
Proof. Let
![]() $\unicode[STIX]{x1D707}$
denote the non-pluripolar measure
$\unicode[STIX]{x1D707}$
denote the non-pluripolar measure
 $\unicode[STIX]{x1D707}:=\langle T_{1}\wedge \cdots \wedge T_{n}\rangle$
and let
$\unicode[STIX]{x1D707}:=\langle T_{1}\wedge \cdots \wedge T_{n}\rangle$
and let
![]() $\unicode[STIX]{x1D706}_{j}$
,
$\unicode[STIX]{x1D706}_{j}$
,
 $j=1,\ldots ,n$
be positive constants such that
$j=1,\ldots ,n$
be positive constants such that
 $$\begin{eqnarray}\unicode[STIX]{x1D706}_{j}\unicode[STIX]{x1D707}(X)=\int _{X}\langle T_{j}^{n}\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D706}_{j}\unicode[STIX]{x1D707}(X)=\int _{X}\langle T_{j}^{n}\rangle .\end{eqnarray}$$
For each
![]() $j$
, using [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem A] there exists a positive full mass current
$j$
, using [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Theorem A] there exists a positive full mass current
 $S_{j}\in \{T_{j}\}$
such that
$S_{j}\in \{T_{j}\}$
such that
 $$\begin{eqnarray}\langle S_{j}^{n}\rangle =\unicode[STIX]{x1D706}_{j}\unicode[STIX]{x1D707}.\end{eqnarray}$$
$$\begin{eqnarray}\langle S_{j}^{n}\rangle =\unicode[STIX]{x1D706}_{j}\unicode[STIX]{x1D707}.\end{eqnarray}$$
By [Reference Boucksom, Eyssidieux, Guedj and ZeriahiBEGZ10, Proposition 1.11] we have that
 $$\begin{eqnarray}\langle S_{1}\wedge \cdots \wedge S_{n}\rangle \geqslant (\unicode[STIX]{x1D706}_{1}\cdots \unicode[STIX]{x1D706}_{n})^{1/n}\unicode[STIX]{x1D707}.\end{eqnarray}$$
$$\begin{eqnarray}\langle S_{1}\wedge \cdots \wedge S_{n}\rangle \geqslant (\unicode[STIX]{x1D706}_{1}\cdots \unicode[STIX]{x1D706}_{n})^{1/n}\unicode[STIX]{x1D707}.\end{eqnarray}$$
Proposition 5.2 gives that
 $\int _{X}\langle S_{1}\wedge \cdots \wedge S_{n}\rangle =\int _{X}\langle T_{1}\wedge \cdots \wedge T_{n}\rangle$
. Hence after integrating the above inequality, due to (24), the result follows.◻
$\int _{X}\langle S_{1}\wedge \cdots \wedge S_{n}\rangle =\int _{X}\langle T_{1}\wedge \cdots \wedge T_{n}\rangle$
. Hence after integrating the above inequality, due to (24), the result follows.◻
Acknowledgements
The first named author has been partially supported by BSF grant 2012236 and NSF grant DMS-1610202. The second named author is supported by a Marie Sklodowska Curie individual fellowship 660940-KRF-CY (MSCA-IF). The last named author has been supported by the SNS project ‘Pluripotential theory in differential geometry’.
The last named author would like to thank D. Angella and S. Calamai for organizing a PhD course at the University of Florence, which inspired part of this work. At the time this paper was written, the first and second named authors were in residence at the Mathematical Sciences Research Institute in Berkeley, California, attending the ‘Differential Geometry’ thematic semester, and were supported by the NSF grant DMS-1440140.
We thank V. Tosatti for reading an initial version of this article, generously sharing some of his ideas, and pointing out the connection with multiplier ideal sheaves that we ultimately integrated into Theorem 1.1. We would like to thank V. Guedj and the anonymous referees for their suggestions that improved the presentation of the paper.