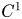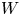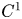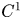1. Introduction
Consider a functional
defined on mappings $u:\Omega \subset {\mathbb {R}}^n\to {\mathbb {R}}^m$![]() , where $\Omega$
, where $\Omega$![]() is an open set and $Du(x)$
is an open set and $Du(x)$![]() denotes the total derivative of $u$
denotes the total derivative of $u$![]() at $x$
at $x$![]() . Here, $\mathcal {W}[u]$
. Here, $\mathcal {W}[u]$![]() could, for example, be the energy of an elastic deformation of a hyperelastic material, in which case $n=m$
could, for example, be the energy of an elastic deformation of a hyperelastic material, in which case $n=m$![]() , but there are other examples from physics in which $n\neq m$
, but there are other examples from physics in which $n\neq m$![]() . In this paper, we will however exclusively consider the case $n=m$
. In this paper, we will however exclusively consider the case $n=m$![]() . If $u\in C^1(\Omega,{\mathbb {R}}^m)\cap C^0(\overline {\Omega },{\mathbb {R}}^m)$
. If $u\in C^1(\Omega,{\mathbb {R}}^m)\cap C^0(\overline {\Omega },{\mathbb {R}}^m)$![]() is a critical point of (1.1), then by considering outer variations $u_\varepsilon =u+\varepsilon \phi$
is a critical point of (1.1), then by considering outer variations $u_\varepsilon =u+\varepsilon \phi$![]() for $\phi \in C^\infty _0(\Omega,{\mathbb {R}}^m)$
for $\phi \in C^\infty _0(\Omega,{\mathbb {R}}^m)$![]() , one can show that $u$
, one can show that $u$![]() solves the Euler–Lagrange equations in weak form
solves the Euler–Lagrange equations in weak form
for all $\phi \in C^\infty _0(\Omega,{\mathbb {R}}^m)$![]() , and if in addition $u\in C^2$
, and if in addition $u\in C^2$![]() , the $u$
, the $u$![]() also solves the Euler–Lagrange equations
also solves the Euler–Lagrange equations
in the classical sense in $\Omega$![]() . Of course when considering weak solutions, we can also consider much less regular functions $u$
. Of course when considering weak solutions, we can also consider much less regular functions $u$![]() , so that $u$
, so that $u$![]() is only Lipschitz continuous or $u$
is only Lipschitz continuous or $u$![]() is a Sobolev mapping, for example.
is a Sobolev mapping, for example.
The outer variations are however not the only type of variations we may consider. Instead, we could consider the inner-variations instead. These are generated by a one-parameter family of diffeomorphisms $\phi _\varepsilon \in C^\infty (\overline {\Omega },{\mathbb {R}}^n)$![]() which in turn is generated by a smooth compactly supported vector field $\lambda$
which in turn is generated by a smooth compactly supported vector field $\lambda$![]() so that
so that
The energy–momentum equations, also called Noether's equations, are then given by considering the variations $u_\varepsilon =u(\phi _\varepsilon )$![]() and setting
and setting
The weak form of energy–momentum equations is given by
for all $\lambda \in C^\infty _0(\Omega, {\mathbb {R}}^n)$![]() . For a derivation see [Reference Giaquinta and Hildebrandt13, p. 147–150]. By defining the energy–momentum tensor
. For a derivation see [Reference Giaquinta and Hildebrandt13, p. 147–150]. By defining the energy–momentum tensor
we see that $T(x)$![]() is divergence free in the sense of distributions. In the case of a $C^2$
is divergence free in the sense of distributions. In the case of a $C^2$![]() -solution, there is a relation between the Euler–Lagrange equations and the energy–momentum equation given by the identity
-solution, there is a relation between the Euler–Lagrange equations and the energy–momentum equation given by the identity
Thus, if $u$![]() is a $C^2$
is a $C^2$![]() -solution to the Euler–Lagrange equations, it is also a solution to the energy–momentum equations. Conversely, if $u$
-solution to the Euler–Lagrange equations, it is also a solution to the energy–momentum equations. Conversely, if $u$![]() is a $C^2$
is a $C^2$![]() -solution of the energy–momentum equations and $Du(x)^\ast$
-solution of the energy–momentum equations and $Du(x)^\ast$![]() is everywhere injective, then $u$
is everywhere injective, then $u$![]() is also a solution to the Euler–Lagrange equations.
is also a solution to the Euler–Lagrange equations.
In general however, and in particular in the case of vector-valued mappings $u$![]() , solutions of either (1.3) or (1.6) are generically not $C^2$
, solutions of either (1.3) or (1.6) are generically not $C^2$![]() , and the weak form of the equations should be considered as independent conditions. In particular, there are weak solutions of the Euler–Lagrange equations associated to outer variations that are not weak solutions of (1.6) and vice versa, see for example [Reference Jost20]. Moreover, any strong local minimizer of (1.2) satisfy both the weak Euler–Lagrange and the weak energy–momentum equations (provided $W$
, and the weak form of the equations should be considered as independent conditions. In particular, there are weak solutions of the Euler–Lagrange equations associated to outer variations that are not weak solutions of (1.6) and vice versa, see for example [Reference Jost20]. Moreover, any strong local minimizer of (1.2) satisfy both the weak Euler–Lagrange and the weak energy–momentum equations (provided $W$![]() satisfies some suitable structural conditions, see [Reference Ball5, Thm. 2.4]). For the definitions of weak and strong local minimizer, we refer the reader to [Reference Giaquinta and Hildebrandt13, Ch. 4] and [Reference Taheri32]).
satisfies some suitable structural conditions, see [Reference Ball5, Thm. 2.4]). For the definitions of weak and strong local minimizer, we refer the reader to [Reference Giaquinta and Hildebrandt13, Ch. 4] and [Reference Taheri32]).
Another conspicuous difference between the Euler–Lagrange and energy– momentum equations regards the formal determinedness of the equations. If $u:\Omega \subset {\mathbb {R}}^n\to {\mathbb {R}}^m$![]() , then the Euler–Lagrange equations are always formally determined, whereas for the energy–momentum equations, they are overdetermined if $n>m$
, then the Euler–Lagrange equations are always formally determined, whereas for the energy–momentum equations, they are overdetermined if $n>m$![]() , determined if $n=m$
, determined if $n=m$![]() and underdetermined if $n< m$
and underdetermined if $n< m$![]() . Moreover, in non-linear elasticity and geometric function theory for instance, we only want to minimize (1.1) among mappings that are also homeomorphisms. In this case, we want to have
. Moreover, in non-linear elasticity and geometric function theory for instance, we only want to minimize (1.1) among mappings that are also homeomorphisms. In this case, we want to have
in $\Omega$![]() . This pointwise constraint is a priori incompatible with the outer variations as they may violate the constraint. Therefore, it is unknown if the Euler–Lagrange equations hold or not even for minimizers. The inner variations however are compatible with the constraint (1.7), and for many natural material models in elasticity, one can show that the weak energy–momentum equations are satisfied (see [Reference Ball4]).
. This pointwise constraint is a priori incompatible with the outer variations as they may violate the constraint. Therefore, it is unknown if the Euler–Lagrange equations hold or not even for minimizers. The inner variations however are compatible with the constraint (1.7), and for many natural material models in elasticity, one can show that the weak energy–momentum equations are satisfied (see [Reference Ball4]).
These facts raise the natural question of what can be said about solutions of (1.4), for example, under Dirichlet boundary conditions. Could these equations serve as a substitute for the Euler–Lagrange equations? This leads us to the main results of this paper.
Theorem 1.1 Generic ill-posedness of the energy–momentum equations
Assume that $W\in C^\infty (GL({\mathbb {R}}^n),{\mathbb {R}})$![]() . Furthermore, assume that $W(RX)=X$
. Furthermore, assume that $W(RX)=X$![]() for all $X\in \mathcal {L}({\mathbb {R}}^n)$
for all $X\in \mathcal {L}({\mathbb {R}}^n)$![]() and $R\in O({\mathbb {R}}^n)$
and $R\in O({\mathbb {R}}^n)$![]() . Then for every $\phi \in W^{1,\infty }(\Omega, {\mathbb {R}}^n)$
. Then for every $\phi \in W^{1,\infty }(\Omega, {\mathbb {R}}^n)$![]() such that $D\phi (x)\in int co O({\mathbb {R}}^n)$
such that $D\phi (x)\in int co O({\mathbb {R}}^n)$![]() for almost every $x\in \Omega$
for almost every $x\in \Omega$![]() the Dirichlet problem
the Dirichlet problem
has infinitely many solutions $u$![]() which can be taken to be nowhere $C^1$
which can be taken to be nowhere $C^1$![]() .
.
This theorem shows that in order to hope for any type of partial regularity or uniqueness for solutions of the energy–momentum equations, the assumption $\det (Du(x))>0$![]() a.e. or a smallness assumption on $\vert Du(x)\vert$
a.e. or a smallness assumption on $\vert Du(x)\vert$![]() is essential. We can also ask if any solution (1.8) which is not $C^1$
is essential. We can also ask if any solution (1.8) which is not $C^1$![]() can be a solution of the Euler–Lagrange equations? The next theorem shows that this cannot be the case under natural assumptions on the Lagrangian $W$
can be a solution of the Euler–Lagrange equations? The next theorem shows that this cannot be the case under natural assumptions on the Lagrangian $W$![]() .
.
Theorem 1.2 Assume that $W\in C^1(\mathcal {L}({\mathbb {R}}^n))$![]() is frame-indifferent $($
is frame-indifferent $($![]() see definition 2.1 below$)$
see definition 2.1 below$)$![]() and strictly rank-one convex. Then any weak solution $u\in W^{1,\infty }$
and strictly rank-one convex. Then any weak solution $u\in W^{1,\infty }$![]() which is not $C^1$
which is not $C^1$![]() to the differential inclusion $Du(x)\in \text {O}({\mathbb {R}}^n)$
to the differential inclusion $Du(x)\in \text {O}({\mathbb {R}}^n)$![]() a.e. is not a weak solution of the Euler–Lagrange equations
a.e. is not a weak solution of the Euler–Lagrange equations
1.1 Previously known results
The perhaps easiest non-smooth solution of the energy–momentum equation is the map $u:B_1(0)=\{x\in {\mathbb {R}}^3: \vert x\vert \leq 1\}\to S^2$![]() given by
given by
This map belongs to $W^{1,2}(B_1(0),S^2)$![]() and is in fact (see [Reference Lin23]) an absolute minimizer for the Dirichlet energy with its own boundary values in the space $W^{1,2}(B_1(0),S^2)$
and is in fact (see [Reference Lin23]) an absolute minimizer for the Dirichlet energy with its own boundary values in the space $W^{1,2}(B_1(0),S^2)$![]() , a so-called harmonic map to the unit sphere. As such, it is also a weak solution of both the Euler–Lagrange equations and the energy–momentum equations. Due to the pointwise constraint $\vert u(x)\vert ^2=1$
, a so-called harmonic map to the unit sphere. As such, it is also a weak solution of both the Euler–Lagrange equations and the energy–momentum equations. Due to the pointwise constraint $\vert u(x)\vert ^2=1$![]() , the Euler–Lagrange equations take the form
, the Euler–Lagrange equations take the form
However, the inner variations are fully compatible with pointwise constraints on the target, and are therefore the same as without the constraint. This is a general fact which can be used to construct various irregular solutions of the energy–momentum equations. Furthermore, since
it follows that for all $x\neq 0$![]() , $Du(x)$
, $Du(x)$![]() is nowhere injective and $\det (Du(x))=0$
is nowhere injective and $\det (Du(x))=0$![]() a.e. Building on this example, and using a construction due to Ball and Murat in [Reference Ball and Murat6], in [Reference Sivaloganathan and Spector28] Sivaloganathan and Spector considered a class of frame-indifferent (with respect to $SO({\mathbb {R}}^n)$
a.e. Building on this example, and using a construction due to Ball and Murat in [Reference Ball and Murat6], in [Reference Sivaloganathan and Spector28] Sivaloganathan and Spector considered a class of frame-indifferent (with respect to $SO({\mathbb {R}}^n)$![]() ) and isotropic $W$
) and isotropic $W$![]() satisfying conditions that allow for cavitation solutions. They then construct a weak solution $u\in W^{1,p}({\mathbb {R}}^n)$
satisfying conditions that allow for cavitation solutions. They then construct a weak solution $u\in W^{1,p}({\mathbb {R}}^n)$![]() , $1\leq p< n$
, $1\leq p< n$![]() , of the energy–momentum equations such that $u$
, of the energy–momentum equations such that $u$![]() has infinitely many discontinuities and yet is injective almost everywhere. They furthermore give an example of a $C^1$
has infinitely many discontinuities and yet is injective almost everywhere. They furthermore give an example of a $C^1$![]() -solution of the energy–momentum equation which is not $C^2$
-solution of the energy–momentum equation which is not $C^2$![]() . Finally, in [Reference Tione33, § 7] Tione used convex integration theory to construct irregular solutions of the energy–momentum equations of a specific functional. His method is however different from the present paper and gives weaker results.
. Finally, in [Reference Tione33, § 7] Tione used convex integration theory to construct irregular solutions of the energy–momentum equations of a specific functional. His method is however different from the present paper and gives weaker results.
In the positive direction and only restricted to dimension 2, in [Reference Bauman, Owen and Phillips7] Bauman, Owen and Philips consider an energy density $W$![]() of the form
of the form
where $F$![]() is a quasi-convex function and $H$
is a quasi-convex function and $H$![]() is a non-negative convex function. They show that any $C^{1,\alpha }$
is a non-negative convex function. They show that any $C^{1,\alpha }$![]() solution of the energy–momentum equation in dimension 2 is in fact $C^{2,\alpha }$
solution of the energy–momentum equation in dimension 2 is in fact $C^{2,\alpha }$![]() and $\det (Du(x))>0$
and $\det (Du(x))>0$![]() for all $x$
for all $x$![]() in the domain.
in the domain.
On the other hand also in dimension 2, Iwaniec, Kovalev and Oninnen prove in [Reference Iwaniec, Kovalev and Onninen15] that for a large class of $W$![]() , any solution $u\in W^{1,2}(\Omega,{\mathbb {R}}^n)$
, any solution $u\in W^{1,2}(\Omega,{\mathbb {R}}^n)$![]() of the energy–momentum equations which in addition satisfies $\det (Du(x))>0$
of the energy–momentum equations which in addition satisfies $\det (Du(x))>0$![]() a.e. is in fact Lipschitz. See also [Reference Martin and Yao24, Thm. 1.4 and Thm. 1.6] for cases when solutions of the energy–momentum equations are in fact also homeomorphisms and unique. These regularity results for the energy–momentum equation are the strongest ones known to the author.
a.e. is in fact Lipschitz. See also [Reference Martin and Yao24, Thm. 1.4 and Thm. 1.6] for cases when solutions of the energy–momentum equations are in fact also homeomorphisms and unique. These regularity results for the energy–momentum equation are the strongest ones known to the author.
1.2 Notation
Let $\mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m)$![]() denote the space of linear maps from ${\mathbb {R}}^n$
denote the space of linear maps from ${\mathbb {R}}^n$![]() to ${\mathbb {R}}^m$
to ${\mathbb {R}}^m$![]() . When $n=m$
. When $n=m$![]() , we write $\mathcal {L}({\mathbb {R}}^n)$
, we write $\mathcal {L}({\mathbb {R}}^n)$![]() instead of $\mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^n)$
instead of $\mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^n)$![]() . For $X,Y\in \mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m)$
. For $X,Y\in \mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m)$![]() , we let $\vert X\vert =\sqrt {\text {tr}(X^\ast X)}$
, we let $\vert X\vert =\sqrt {\text {tr}(X^\ast X)}$![]() denote the Hilbert–Schmidt norm, $\Vert X\Vert$
denote the Hilbert–Schmidt norm, $\Vert X\Vert$![]() the operator norm and $\langle X,Y\rangle ={\rm tr} (X^\ast Y)$
the operator norm and $\langle X,Y\rangle ={\rm tr} (X^\ast Y)$![]() the euclidean inner product. Furthermore, let
the euclidean inner product. Furthermore, let

If $X\in \mathcal {L}({\mathbb {R}}^n)$![]() , we let $\text {cof}\,(X)$
, we let $\text {cof}\,(X)$![]() denote the cofactor matrix of $X$
denote the cofactor matrix of $X$![]() and $\text {adj}\,(X)=\text {cof}\,(X)^\ast$
and $\text {adj}\,(X)=\text {cof}\,(X)^\ast$![]() denote the adjugate matrix of $X$
denote the adjugate matrix of $X$![]() .
.
If $K\subset {\mathbb {R}}^n$![]() is a subset, then $co K$
is a subset, then $co K$![]() denotes its convex hull, $Rco K$
denotes its convex hull, $Rco K$![]() denotes its rank-convex hull and $int K$
denotes its rank-convex hull and $int K$![]() denotes the interior of $K$
denotes the interior of $K$![]() .
.
2. Energy–momentum equations, symmetry and frame indifference
Definition 2.1 Frame indifference
Let $W\in C^2(\mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m))$![]() and consider the functional
and consider the functional
for an open set $\Omega \subset {\mathbb {R}}^n$![]() . We say that the functional is frame-indifferent if $W(RX)=W(X)$
. We say that the functional is frame-indifferent if $W(RX)=W(X)$![]() for all $R\in O({\mathbb {R}}^m)$
for all $R\in O({\mathbb {R}}^m)$![]() , where $O({\mathbb {R}}^m)$
, where $O({\mathbb {R}}^m)$![]() denotes the orthogonal group of ${\mathbb {R}}^m$
denotes the orthogonal group of ${\mathbb {R}}^m$![]() .
.
Remark 2.2 The reader should observe that the condition of frame indifference does not impose any material symmetry restrictions. Indeed, frame indifference is just a manifestation of the fact that the energy should not change if an observer either rotates or reflects the coordinate system, i.e. if the mapping $u$![]() is changed to $Ru$
is changed to $Ru$![]() for some $R\in O({\mathbb {R}}^n)$
for some $R\in O({\mathbb {R}}^n)$![]() . Sometimes, some authors only require invariance under the special orthogonal group $SO({\mathbb {R}}^n)$
. Sometimes, some authors only require invariance under the special orthogonal group $SO({\mathbb {R}}^n)$![]() rather than the full orthogonal group. However, it is natural to require invariance also under change of orientation of the coordinate system, at least for variational problems coming from classical physics.
rather than the full orthogonal group. However, it is natural to require invariance also under change of orientation of the coordinate system, at least for variational problems coming from classical physics.
Definition 2.3 The energy–momentum mapping $T: \mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m)\to \mathcal {L}({\mathbb {R}}^n)$![]() associated to a Lagrangian $W\in C^\infty (\mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m),{\mathbb {R}})$
associated to a Lagrangian $W\in C^\infty (\mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m),{\mathbb {R}})$![]() is defined according to
is defined according to
where $I_{{\mathbb {R}}^n}$![]() is the identity mapping on ${\mathbb {R}}^n$
is the identity mapping on ${\mathbb {R}}^n$![]() .
.
When no confusion can arise, we write $I$![]() instead of $I_{{\mathbb {R}}^n}$
instead of $I_{{\mathbb {R}}^n}$![]() .
.
Proposition 2.4 Energy–momentum mappings for frame-indifferent Lagrangians
Let $W\in C^\infty (\mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^n),{\mathbb {R}})$![]() be a frame-indifferent Lagrangian, i.e. $W(RX)=W(X)$
be a frame-indifferent Lagrangian, i.e. $W(RX)=W(X)$![]() for every $R\in O({\mathbb {R}}^n)$
for every $R\in O({\mathbb {R}}^n)$![]() . Then the energy–momentum mapping
. Then the energy–momentum mapping
is $O({\mathbb {R}}^n)$![]() -invariant, i.e. $T(RX)=T(X)$
-invariant, i.e. $T(RX)=T(X)$![]() for every $R\in O({\mathbb {R}}^n)$
for every $R\in O({\mathbb {R}}^n)$![]() .
.
Proof. Let $X=RS$![]() be the left polar factorization of $X$
be the left polar factorization of $X$![]() , where $S=\sqrt {X^\ast X}$
, where $S=\sqrt {X^\ast X}$![]() and $R\in O({\mathbb {R}}^n)$
and $R\in O({\mathbb {R}}^n)$![]() . Thus, $W(X)=W(RS)=W(S)$
. Thus, $W(X)=W(RS)=W(S)$![]() . Thus, there exists a function $\widetilde {W}(X^\ast X)=W(X)$
. Thus, there exists a function $\widetilde {W}(X^\ast X)=W(X)$![]() ($\widetilde {W}(X^\ast X):=W(\sqrt {X^\ast X})$
($\widetilde {W}(X^\ast X):=W(\sqrt {X^\ast X})$![]() ). Then
). Then

Furthermore, using the cyclic invariance of the trace, we find

Thus,
This shows that $T(RX)=T(X)$![]() for all $R\in O({\mathbb {R}}^n)$
for all $R\in O({\mathbb {R}}^n)$![]() .
.
Remark 2.5 By [Reference Ball3, lemma 6.3, p. 723] $\widetilde {W}$![]() is $C^\infty$
is $C^\infty$![]() if $W$
if $W$![]() is $C^\infty$
is $C^\infty$![]() on the set $\{X\in \mathcal {L}({\mathbb {R}}^n): \det (X)\neq 0\}$
on the set $\{X\in \mathcal {L}({\mathbb {R}}^n): \det (X)\neq 0\}$![]() . Therefore, in the proof of proposition, we have implicitly assumed that $\det (X)\neq 0$
. Therefore, in the proof of proposition, we have implicitly assumed that $\det (X)\neq 0$![]() . The relation $T(RX)=T(X)$
. The relation $T(RX)=T(X)$![]() for all $X$
for all $X$![]() is then deduced by continuity of $T$
is then deduced by continuity of $T$![]() and the fact that $\{X\in \mathcal {L}({\mathbb {R}}^n): \det (X)\neq 0\}$
and the fact that $\{X\in \mathcal {L}({\mathbb {R}}^n): \det (X)\neq 0\}$![]() is open and dense in $\mathcal {L}({\mathbb {R}}^n)$
is open and dense in $\mathcal {L}({\mathbb {R}}^n)$![]() .
.
Remark 2.6 Note that $T(X)$![]() need not be a symmetric tensor. Furthermore, note that the structure field $DW(X)=X(D\widetilde {W}(X^\ast X)+D\widetilde {W}(X^\ast X)^\ast )$
need not be a symmetric tensor. Furthermore, note that the structure field $DW(X)=X(D\widetilde {W}(X^\ast X)+D\widetilde {W}(X^\ast X)^\ast )$![]() is not $O({\mathbb {R}}^n)$
is not $O({\mathbb {R}}^n)$![]() -invariant but $O({\mathbb {R}}^n)$
-invariant but $O({\mathbb {R}}^n)$![]() -equivariant, i.e. $DW(RX)=RDW(X)$
-equivariant, i.e. $DW(RX)=RDW(X)$![]() for all $R\in O({\mathbb {R}}^n)$
for all $R\in O({\mathbb {R}}^n)$![]() . Also note that in the case when $W$
. Also note that in the case when $W$![]() is strictly convex, the map $DW:\mathcal {L}({\mathbb {R}}^n)\to \mathcal {L}({\mathbb {R}}^n)$
is strictly convex, the map $DW:\mathcal {L}({\mathbb {R}}^n)\to \mathcal {L}({\mathbb {R}}^n)$![]() is strictly monotone and hence invertible. This is not the case for $T$
is strictly monotone and hence invertible. This is not the case for $T$![]() .
.
Definition 2.7 Reduced energy–momentum tensor
Let $W$![]() be a smooth frame-indifferent Lagrangian and let $\widetilde {W}(X^\ast X)=W(X)$
be a smooth frame-indifferent Lagrangian and let $\widetilde {W}(X^\ast X)=W(X)$![]() for all $X\in \mathcal {L}({\mathbb {R}}^n)$
for all $X\in \mathcal {L}({\mathbb {R}}^n)$![]() . The reduced energy–momentum tensor $\mathcal {T}$
. The reduced energy–momentum tensor $\mathcal {T}$![]() is defined according to
is defined according to
Note that since $X^\ast X$![]() is a symmetric non-negative linear map, we think of the reduced energy–momentum tensor as defined only on the cone $\text {Sym}_+(n)\subset \mathcal {L}({\mathbb {R}}^n)$
is a symmetric non-negative linear map, we think of the reduced energy–momentum tensor as defined only on the cone $\text {Sym}_+(n)\subset \mathcal {L}({\mathbb {R}}^n)$![]() of positive semidefinite linear maps.
of positive semidefinite linear maps.
Proposition 2.8 Symmetric energy–momentum tensors
Let $W\in C^2(\mathcal {L}({\mathbb {R}}^n),{\mathbb {R}})$![]() satisfy $W(XR)=W(X)$
satisfy $W(XR)=W(X)$![]() for all $R\in SO({\mathbb {R}}^n)$
for all $R\in SO({\mathbb {R}}^n)$![]() . Then $T(X)$
. Then $T(X)$![]() is symmetric, i.e $T(X)^\ast =T(X)$
is symmetric, i.e $T(X)^\ast =T(X)$![]() .
.
Proof. By the right polar factorization $X=SR$![]() where $S=\sqrt {XX^\ast }$
where $S=\sqrt {XX^\ast }$![]() , there exists $\widetilde {W}$
, there exists $\widetilde {W}$![]() such that $\widetilde {W}(XX^\ast )=W(X)$
such that $\widetilde {W}(XX^\ast )=W(X)$![]() for all $X$
for all $X$![]() . Computing the gradient of $W$
. Computing the gradient of $W$![]() using a similar computation as in the proof of proposition (2.5) shows that
using a similar computation as in the proof of proposition (2.5) shows that
Thus, in this case, the energy–momentum tensor becomes
which is symmetric.
Remark 2.9 Note that the case of symmetric energy–momentum tensor has been studied in the framework of compensated integrability due to D. Serre in [Reference Serre27] in the case of hyperbolic evolution equations.
3. Differential inclusions and generic ill-posedness
3.1 Differential inclusions in the orthogonal group
In this section, we will consider some background material concerning differential inclusions into the orthogonal group. Consider the relaxation of the orthogonal group $O({\mathbb {R}}^n)$![]() , i.e. its convex hull given by
, i.e. its convex hull given by
Theorem 3.1 Let $\Omega \subset {\mathbb {R}}^n$![]() be a Lipschitz domain and let $\phi \in W^{1,\infty }(\Omega,{\mathbb {R}}^n)$
be a Lipschitz domain and let $\phi \in W^{1,\infty }(\Omega,{\mathbb {R}}^n)$![]() be a Lipschitz map such that $D\phi (x)\in int co O({\mathbb {R}}^n)$
be a Lipschitz map such that $D\phi (x)\in int co O({\mathbb {R}}^n)$![]() for a.e. $x\in \Omega$
for a.e. $x\in \Omega$![]() . Then the differential inclusion
. Then the differential inclusion
for $u\in W^{1,\infty }(\Omega,{\mathbb {R}}^n)$![]() possesses infinitely many solutions that are nowhere $C^1$
possesses infinitely many solutions that are nowhere $C^1$![]() .
.
The key to this result is that $O({\mathbb {R}}^n)$![]() possesses many rank-one connections, i.e. there exit matrices $X,Y\in O({\mathbb {R}}^n)$
possesses many rank-one connections, i.e. there exit matrices $X,Y\in O({\mathbb {R}}^n)$![]() such that
such that
for some $u,v\in {\mathbb {R}}^n$![]() .
.
A proof of theorem 3.1 can be found in [Reference Székelyhidi30, § 5.1].
Solutions of differential inclusions need not necessarily be very irregular.
Definition 3.2 Let $u\in C^{0,1}(\Omega,{\mathbb {R}}^m)$![]() be a Lipschitz map. Let
be a Lipschitz map. Let
denote the singular set of $u$![]() .
.
In [Reference Dacorogna, Marcellini and Paolini10], the authors consider solutions of (3.1) with affine boundary values generated by origami maps. These maps are piecewise $C^1$![]() and the Hausdorff measure $\mathscr {H}^{n-1}(\Sigma (u))$
and the Hausdorff measure $\mathscr {H}^{n-1}(\Sigma (u))$![]() is locally finite in the interior of the domain. However, to satisfy the boundary conditions, $\Sigma (u)$
is locally finite in the interior of the domain. However, to satisfy the boundary conditions, $\Sigma (u)$![]() will become fractal-like as we approach the boundary and $\mathscr {H}^{n-1}(\Sigma (u))=+\infty$
will become fractal-like as we approach the boundary and $\mathscr {H}^{n-1}(\Sigma (u))=+\infty$![]() in the whole domain. Similar types of solutions are also considered in [Reference Iwaniec, Verchota and Vogel19] and also for the energy–momentum equations for the Dirichlet energy in [Reference Iwaniec and Onninen18, § 3.6]. In both cases $Du(x)\in K$
in the whole domain. Similar types of solutions are also considered in [Reference Iwaniec, Verchota and Vogel19] and also for the energy–momentum equations for the Dirichlet energy in [Reference Iwaniec and Onninen18, § 3.6]. In both cases $Du(x)\in K$![]() , where $K$
, where $K$![]() is a finite subset of $O({\mathbb {R}}^n)$
is a finite subset of $O({\mathbb {R}}^n)$![]() .
.
3.2 Generic ill-posedness
As we have seen in proposition 2.5, the mapping $T: \mathcal {L}({\mathbb {R}}^n)\to \mathcal {L}({\mathbb {R}}^n)$![]() is not invertible for a frame-indifferent Lagrangian $W$
is not invertible for a frame-indifferent Lagrangian $W$![]() . In particular, the level sets of
. In particular, the level sets of
for some fixed $Y\in T(\mathcal {L}({\mathbb {R}}^n))$![]() are $O({\mathbb {R}}^n)$
are $O({\mathbb {R}}^n)$![]() -invariant.
-invariant.
Lemma 3.3 Any solution $Du(x)\in O({\mathbb {R}}^n)A$![]() for some $A\in \mathcal {L}({\mathbb {R}}^n)$
for some $A\in \mathcal {L}({\mathbb {R}}^n)$![]() is a solution of the energy–momentum equations.
is a solution of the energy–momentum equations.
Proof. If $Du(x)\in O({\mathbb {R}}^n)A$![]() a.e., then
a.e., then
is constant a.e. and hence a weak solution of $\text {div}\,T(Du(x))=0$![]() .
.
This leads to differential inclusions of the form
for some fixed $Y$![]() such that $T^{-1}(Y)\neq \varnothing$
such that $T^{-1}(Y)\neq \varnothing$![]() .
.
There are similar results for the lack of partial regularity for the Euler–Lagrange equations for elliptic systems. In [Reference Müller and S̆verák26, theorem 4.1], the authors show that there exists a smooth strongly quasiconvex function $W:\mathcal {L}({\mathbb {R}}^2)\to {\mathbb {R}}$![]() such that there exists a Lipschitz continuous solution of $\text {div}DW(Du(x))=0$
such that there exists a Lipschitz continuous solution of $\text {div}DW(Du(x))=0$![]() that is nowhere $C^1$
that is nowhere $C^1$![]() . This is done by rewriting the Euler–Lagrange equation as a differential inclusion and using methods from convex integration theory. The result was extended in [Reference Székelyhidi31] to apply also to smooth strongly polyconvex functions. Moreover, the solutions in [Reference Székelyhidi31] are also weak local minimizers. This also applies to the example in [Reference Müller and S̆verák26] by the work of [Reference Kristensen and Taheri22]. It is however important to note that weak local minimizers $u_0\in W^{1,\infty }$
. This is done by rewriting the Euler–Lagrange equation as a differential inclusion and using methods from convex integration theory. The result was extended in [Reference Székelyhidi31] to apply also to smooth strongly polyconvex functions. Moreover, the solutions in [Reference Székelyhidi31] are also weak local minimizers. This also applies to the example in [Reference Müller and S̆verák26] by the work of [Reference Kristensen and Taheri22]. It is however important to note that weak local minimizers $u_0\in W^{1,\infty }$![]() need not be weak solutions of the energy–momentum equations. Indeed, let $\Omega \subset {\mathbb {R}}^n$
need not be weak solutions of the energy–momentum equations. Indeed, let $\Omega \subset {\mathbb {R}}^n$![]() be a domain and let $\lambda \in C^\infty _0(\Omega,{\mathbb {R}}^n)$
be a domain and let $\lambda \in C^\infty _0(\Omega,{\mathbb {R}}^n)$![]() . Let $u_0\in W^{1,\infty }(\Omega,{\mathbb {R}}^n)$
. Let $u_0\in W^{1,\infty }(\Omega,{\mathbb {R}}^n)$![]() and let $u_\varepsilon (x)=u_0(x+\varepsilon \lambda (x))$
and let $u_\varepsilon (x)=u_0(x+\varepsilon \lambda (x))$![]() be an inner variation. Then
be an inner variation. Then

Since $Du_0$![]() is not continuous, it may happen that $\vert Du_0(x)-Du_0(x+\varepsilon \lambda (x))\vert \geq 1+\varepsilon \Vert \vert Du\vert \Vert _{L^\infty (\Omega )}\Vert \vert D\lambda \vert \Vert _{L^\infty (\Omega )}$
is not continuous, it may happen that $\vert Du_0(x)-Du_0(x+\varepsilon \lambda (x))\vert \geq 1+\varepsilon \Vert \vert Du\vert \Vert _{L^\infty (\Omega )}\Vert \vert D\lambda \vert \Vert _{L^\infty (\Omega )}$![]() for every $\varepsilon >0$
for every $\varepsilon >0$![]() and thus that $\Vert u_0-u_\varepsilon \Vert _{W^{1,\infty }(\Omega )}>1$
and thus that $\Vert u_0-u_\varepsilon \Vert _{W^{1,\infty }(\Omega )}>1$![]() for all $\varepsilon >0$
for all $\varepsilon >0$![]() . Thus, inner variations need not be close in $W^{1,\infty }(\Omega )$
. Thus, inner variations need not be close in $W^{1,\infty }(\Omega )$![]() -norm. Therefore, $u_0$
-norm. Therefore, $u_0$![]() being a weak local minimizer need not imply that $u_0$
being a weak local minimizer need not imply that $u_0$![]() solves the energy–momentum equations.
solves the energy–momentum equations.
It is therefore a natural question if the differential inclusions giving solutions to the energy–momentum equations are also weak solutions of the Euler–Lagrange equations? For this purpose, we first consider a special class of solutions given by laminations, the reason being that any solution in, for example, [Reference Dacorogna, Marcellini and Paolini10, Reference Iwaniec, Verchota and Vogel19] is locally a lamination outside a small closed set. Given a first-order partial differential operator $\mathscr {A}$![]() with constant coefficients and its associated symbol $\mathbb {A}(\xi )$
with constant coefficients and its associated symbol $\mathbb {A}(\xi )$![]() with $\xi \in \mathbb {S}^{n-1}$
with $\xi \in \mathbb {S}^{n-1}$![]() , consider functions of the form
, consider functions of the form
where $h:{\mathbb {R}}\to \{0,1\}$![]() is measurable and $\lambda -\mu \in \text {ker}\,\mathbb {A}(\xi )$
is measurable and $\lambda -\mu \in \text {ker}\,\mathbb {A}(\xi )$![]() . These are solutions to two-state rigidity problem
. These are solutions to two-state rigidity problem
In the case when $\mu,\lambda \in O({\mathbb {R}}^n)$![]() are rank-one connected, then the laminate solution (3.3) gives a solution to the differential inclusion $Du(x)\in O({\mathbb {R}}^n)$
are rank-one connected, then the laminate solution (3.3) gives a solution to the differential inclusion $Du(x)\in O({\mathbb {R}}^n)$![]() a.e. with $\mathcal {A}=\text {curl}$
a.e. with $\mathcal {A}=\text {curl}$![]() , where $\text {curl}$
, where $\text {curl}$![]() denotes the matrix curl operator. In this case, the boundary values for non-trivial measurable functions $h$
denotes the matrix curl operator. In this case, the boundary values for non-trivial measurable functions $h$![]() are, however, not smooth. Furthermore, we want the rank-one connected laminate to be such that $v(x)=DW(D(x))$
are, however, not smooth. Furthermore, we want the rank-one connected laminate to be such that $v(x)=DW(D(x))$![]() is two-state laminate solution for $\mathscr {A}=\text {div}$
is two-state laminate solution for $\mathscr {A}=\text {div}$![]() , where $\text {div}$
, where $\text {div}$![]() is the matrix divergence. By [Reference Kristensen and Raita21, p. 8], $\mathbb {A}(\xi )X=X\xi$
is the matrix divergence. By [Reference Kristensen and Raita21, p. 8], $\mathbb {A}(\xi )X=X\xi$![]() for an $n\times n$
for an $n\times n$![]() -matrix $X$
-matrix $X$![]() and hence we must have that $(DW(\mu )-DW(\lambda ))\xi =0$
and hence we must have that $(DW(\mu )-DW(\lambda ))\xi =0$![]() as well. This leads us to the following proposition.
as well. This leads us to the following proposition.
Proposition 3.4 Let $W$![]() satisfy the assumptions in theorem 1.1. Let $A,B\in O({\mathbb {R}}^n)$
satisfy the assumptions in theorem 1.1. Let $A,B\in O({\mathbb {R}}^n)$![]() be rank-one connected and consider the laminate
be rank-one connected and consider the laminate
for some measurable $h:{\mathbb {R}}\to \{0,1\}$![]() and such that $B-A=a\otimes \xi$
and such that $B-A=a\otimes \xi$![]() for some $a\in {\mathbb {R}}^n$
for some $a\in {\mathbb {R}}^n$![]() and $\xi \in \mathbb {S}^{n-1}$
and $\xi \in \mathbb {S}^{n-1}$![]() . Then the laminate is a distributional solution to the Euler–Lagrange equation
. Then the laminate is a distributional solution to the Euler–Lagrange equation
if and only if $\langle \xi, T(I)\xi \rangle =-W(I)$![]() or equivalently if and only if $\langle \xi, DW(I)\xi \rangle =0$
or equivalently if and only if $\langle \xi, DW(I)\xi \rangle =0$![]() .
.
Proof. Let $\lambda =DW(A)$![]() and $\mu =DW(B)$
and $\mu =DW(B)$![]() . Then for the matrix field $M(x)=DW(Du(x))$
. Then for the matrix field $M(x)=DW(Du(x))$![]() to be divergence free in the sense of distributions, we must have $(DW(B)-DW(A))n=0$
to be divergence free in the sense of distributions, we must have $(DW(B)-DW(A))n=0$![]() . Since $O({\mathbb {R}}^n)$
. Since $O({\mathbb {R}}^n)$![]() acts transitively on itself, there exists a $U\in O({\mathbb {R}}^n)$
acts transitively on itself, there exists a $U\in O({\mathbb {R}}^n)$![]() such that
such that
On the other hand, we have
which implies
Using that $DW$![]() is $O({\mathbb {R}}^n)$
is $O({\mathbb {R}}^n)$![]() -equivariant by remark 2.5, we find that
-equivariant by remark 2.5, we find that

Thus, $\langle \xi, T(A)\xi \rangle +W(A)=0$![]() . Since $A\in O({\mathbb {R}}^n)$
. Since $A\in O({\mathbb {R}}^n)$![]() and $T$
and $T$![]() and $W$
and $W$![]() are $O({\mathbb {R}}^n)$
are $O({\mathbb {R}}^n)$![]() -invariant $\langle \xi, T(A)\xi \rangle +W(A)=\langle \xi, T(I)\xi \rangle +W(I)=0$
-invariant $\langle \xi, T(A)\xi \rangle +W(A)=\langle \xi, T(I)\xi \rangle +W(I)=0$![]() .
.
Remark 3.5 If $W$![]() is the energy density of a hyperelastic material, it is physically reasonable that scalings $x\mapsto tx$
is the energy density of a hyperelastic material, it is physically reasonable that scalings $x\mapsto tx$![]() for $t>0$
for $t>0$![]() cost energy. Consequently, the function
cost energy. Consequently, the function
should have a minimum at $t=1$![]() . Since
. Since
we find that the condition $j'(1)=0$![]() implies that $0={\rm tr} (DW(I))={\rm tr} (T(I)+W(I)I)={\rm tr} (T(I))+nW(I)$
implies that $0={\rm tr} (DW(I))={\rm tr} (T(I)+W(I)I)={\rm tr} (T(I))+nW(I)$![]() . Since we have for an ON-basis $\{e_j\}_{j=1}^n$
. Since we have for an ON-basis $\{e_j\}_{j=1}^n$![]()

we see that the condition $j'(1)=0$![]() can be seen as an averaged condition of the previous proposition 3.4.
can be seen as an averaged condition of the previous proposition 3.4.
It is easy to produce frame-indifferent smooth functions $W$![]() which satisfy $DW(I)=0$
which satisfy $DW(I)=0$![]() , $W(X)=(\vert X\vert ^2-4)^2$
, $W(X)=(\vert X\vert ^2-4)^2$![]() for example will do. However, $W$
for example will do. However, $W$![]() is not rank-one convex and therefore not polyconvex either. In example 4.5, we give a less trivial example coming from geometric function theory and in particular the study of mappings of finite distortion. This functional is not globally polyconvex but polyconvex when restricted to $GL_+({\mathbb {R}}^n)$
is not rank-one convex and therefore not polyconvex either. In example 4.5, we give a less trivial example coming from geometric function theory and in particular the study of mappings of finite distortion. This functional is not globally polyconvex but polyconvex when restricted to $GL_+({\mathbb {R}}^n)$![]() .
.
Proposition 3.6 Assume that $W\in C^1(\mathcal {L}({\mathbb {R}}^n))$![]() is frame-indifferent and strictly rank-one convex. Let $u$
is frame-indifferent and strictly rank-one convex. Let $u$![]() be a laminate solution to the differential inclusion $Du(x)\in \text {O}({\mathbb {R}}^n)$
be a laminate solution to the differential inclusion $Du(x)\in \text {O}({\mathbb {R}}^n)$![]() as in proposition 3.4. Then $u$
as in proposition 3.4. Then $u$![]() is not a weak solution to the Euler–Lagrange equations.
is not a weak solution to the Euler–Lagrange equations.
Proof. By a previous remark, it is sufficient to consider solutions with $Du(x)\in \{I,R\}$![]() and $R\in O({\mathbb {R}}^n)$
and $R\in O({\mathbb {R}}^n)$![]() rank-one connected to $I$
rank-one connected to $I$![]() . Let $R-I=a\otimes \xi$
. Let $R-I=a\otimes \xi$![]() for some $\xi \in S^{n-1}$
for some $\xi \in S^{n-1}$![]() and some $a\in {\mathbb {R}}^n$
and some $a\in {\mathbb {R}}^n$![]() . Furthermore, since $R^\ast R=I$
. Furthermore, since $R^\ast R=I$![]() , we get the equation
, we get the equation
which implies that $a=-2\xi$![]() .
.
For $u$![]() to solve the Euler–Lagrange equations, we must use the $\text {O}({\mathbb {R}}^n)$
to solve the Euler–Lagrange equations, we must use the $\text {O}({\mathbb {R}}^n)$![]() -equivariance of $DW$
-equivariance of $DW$![]()
and so $\langle \xi,DW(I)\xi \rangle =0$![]() . Now consider the function
. Now consider the function
By frame indifference, $\phi (0)=\phi (1)$![]() and
and
By assumption, $\phi (t)$![]() is strictly convex. Hence, $\phi '(0)\neq 0$
is strictly convex. Hence, $\phi '(0)\neq 0$![]() and $\phi '(1)\neq 0$
and $\phi '(1)\neq 0$![]() . On the other hand
. On the other hand
contradicting the strict convexity of $\phi$![]() .
.
Proof of theorem 1.2 We note that by the frame indifference of $W$![]() (remark 2.6) $DW(I)^\ast =DW(I)$
(remark 2.6) $DW(I)^\ast =DW(I)$![]() . Furthermore, since any rank-one connected matrix $R\in \text {O}({\mathbb {R}}^n)$
. Furthermore, since any rank-one connected matrix $R\in \text {O}({\mathbb {R}}^n)$![]() to $I$
to $I$![]() is of the form $I-2\xi \otimes \xi$
is of the form $I-2\xi \otimes \xi$![]() for some $\xi \in S^{n-1}$
for some $\xi \in S^{n-1}$![]() , we have for $\phi _\xi (t)=W(I-2t\xi \otimes \xi )$
, we have for $\phi _\xi (t)=W(I-2t\xi \otimes \xi )$![]()
and the strict rank-one convexity assumption implies that $\phi _\xi '(0)=\phi '_\xi (1)\neq 0$![]() for all $\xi \in S^{n-1}$
for all $\xi \in S^{n-1}$![]() we find that the quadratic form $Q(\xi )=\langle DW(I), \xi \otimes \xi \rangle =\langle \xi,DW(I)\xi \rangle \neq 0$
we find that the quadratic form $Q(\xi )=\langle DW(I), \xi \otimes \xi \rangle =\langle \xi,DW(I)\xi \rangle \neq 0$![]() for all $\xi \in S^{n-1}$
for all $\xi \in S^{n-1}$![]() . Thus, either $Q(\xi )>0$
. Thus, either $Q(\xi )>0$![]() or $Q(\xi )<0$
or $Q(\xi )<0$![]() . We may assume the former case. Hence, $DW(I)$
. We may assume the former case. Hence, $DW(I)$![]() is positive definite. Set $A=DW(I)$
is positive definite. Set $A=DW(I)$![]() and define the linear map $L\in \mathcal {L}(\mathcal {L}({\mathbb {R}}^n))$
and define the linear map $L\in \mathcal {L}(\mathcal {L}({\mathbb {R}}^n))$![]() by
by
Then $L$![]() is symmetric and positive definite. Indeed,
is symmetric and positive definite. Indeed,
Furthermore, using that $A$![]() is diagonalizable with diagonal matrix $D$
is diagonalizable with diagonal matrix $D$![]() and eigenvalues $0<\lambda _1\leq \lambda _2\leq...\leq \lambda _n$
and eigenvalues $0<\lambda _1\leq \lambda _2\leq...\leq \lambda _n$![]() such that $A=RDR^\ast$
such that $A=RDR^\ast$![]() and setting $Y=XR$
and setting $Y=XR$![]() , we find
, we find

Now assume that $u$![]() is a solution of the differential inclusion $Du(x)\in O({\mathbb {R}}^n)$
is a solution of the differential inclusion $Du(x)\in O({\mathbb {R}}^n)$![]() that is not $C^1$
that is not $C^1$![]() and that in addition $u$
and that in addition $u$![]() is a weak solution of the Euler–Lagrange equations on some domain $\Omega \subset {\mathbb {R}}^n$
is a weak solution of the Euler–Lagrange equations on some domain $\Omega \subset {\mathbb {R}}^n$![]() . Then for any $\varphi \in C^\infty _0(\Omega, {\mathbb {R}}^n)$
. Then for any $\varphi \in C^\infty _0(\Omega, {\mathbb {R}}^n)$![]() and using the $\text {O}({\mathbb {R}}^n)$
and using the $\text {O}({\mathbb {R}}^n)$![]() -equivariance of $W$
-equivariance of $W$![]() , we find
, we find

Thus, $u$![]() is a weak solution of the very strongly elliptic constant coefficient equation (in the sense of [Reference Giaquinta and Martinazzi14, definition 3.36 (3.16), p.53])
is a weak solution of the very strongly elliptic constant coefficient equation (in the sense of [Reference Giaquinta and Martinazzi14, definition 3.36 (3.16), p.53])
However, by elliptic regularity theory ([Reference Giaquinta and Martinazzi14, theorem 4.11]) $u\in C^\infty$![]() , a contradiction.
, a contradiction.
Remark 3.7 Note that the assumption that $W$![]() is $C^1$
is $C^1$![]() and strictly rank-one convex implies that $DW(I)$
and strictly rank-one convex implies that $DW(I)$![]() is positive definite and is incompatible with ${\rm tr} (DW(I))=0$
is positive definite and is incompatible with ${\rm tr} (DW(I))=0$![]() , which is a natural condition in non-linear elasticity. See the discussion in remark 3.5.
, which is a natural condition in non-linear elasticity. See the discussion in remark 3.5.
Remark 3.8 There has been other attempts in [Reference De Lellis, De Philippis, Kirchheim and Tione11] to construct stationary points of strictly polyconvex functionals by extending the methods in [Reference Müller and S̆verák26]. The main result of [Reference De Lellis, De Philippis, Kirchheim and Tione11] is that the methods do not extend to this case, giving further indication that stationary points may in fact possess some form of partial regularity.
4. Invertibility of the reduced energy–momentum mapping and double well inclusion
So far we have considered solutions $u\in W^{1,\infty }$![]() to the differential inclusion $Du(x)\in O({\mathbb {R}}^n)$
to the differential inclusion $Du(x)\in O({\mathbb {R}}^n)$![]() a.e. All these solutions have in common that the essential range of $\det (Du(\Omega ))$
a.e. All these solutions have in common that the essential range of $\det (Du(\Omega ))$![]() lies in $\{-1,1\}$
lies in $\{-1,1\}$![]() . One can ask, in particular with respect to the results in [Reference Müller and S̆verák25], whether it is possible to find other types of differential inclusions which are also solutions of the energy–momentum equations and such that $\det (Du(x))>0$
. One can ask, in particular with respect to the results in [Reference Müller and S̆verák25], whether it is possible to find other types of differential inclusions which are also solutions of the energy–momentum equations and such that $\det (Du(x))>0$![]() . Moreover, one can ask if the Lipschitz regularity result in [Reference Iwaniec, Kovalev and Onninen15] can be improved to a partial regularity result, i.e if one can show that the singular set $\Sigma _u$
. Moreover, one can ask if the Lipschitz regularity result in [Reference Iwaniec, Kovalev and Onninen15] can be improved to a partial regularity result, i.e if one can show that the singular set $\Sigma _u$![]() of definition 3.2 is a closed set with $\mathscr {H}^{n-1}(\Sigma _u)=0$
of definition 3.2 is a closed set with $\mathscr {H}^{n-1}(\Sigma _u)=0$![]() . We now formulate an obstruction to such a result.
. We now formulate an obstruction to such a result.
Indeed, if we assume that the reduced energy–momentum tensor $\mathcal {T}:\text {Sym}_+(n)\to \mathcal {L}({\mathbb {R}}^n)$![]() is not injective, then we could find two solutions $A,B\in \text {Sym}_+(n)$
is not injective, then we could find two solutions $A,B\in \text {Sym}_+(n)$![]() such that
such that
with $\det (A)>0$![]() and $\det (B)>0$
and $\det (B)>0$![]() . In particular, we would have
. In particular, we would have
and solutions of the differential inclusion $Du(x)=SO(n)A\cup SO(n)B$![]() for a.e. $x\in \Omega$
for a.e. $x\in \Omega$![]() would also be solutions of the energy–momentum equations. This differential inclusion is studied in [Reference Dacorogna9, Reference Müller and S̆verák25] in the case when $n=2$
would also be solutions of the energy–momentum equations. This differential inclusion is studied in [Reference Dacorogna9, Reference Müller and S̆verák25] in the case when $n=2$![]() . The following theorem holds.
. The following theorem holds.
Theorem 4.1 [Reference Müller and S̆verák25, corollary 1.4 ], [Reference Dacorogna9, theorem 10.28]
Let $A,B\in \mathcal {L}({\mathbb {R}}^2)$![]() be diagonal matrices whose diagonal entries are $a_1,a_2$
be diagonal matrices whose diagonal entries are $a_1,a_2$![]() and $b_1,b_2$
and $b_1,b_2$![]() respectively. Assume that $0< b_1< a_1\leq a_2< b_2$
respectively. Assume that $0< b_1< a_1\leq a_2< b_2$![]() and $\det (A)\leq \det (B)$
and $\det (A)\leq \det (B)$![]() . Let $T\in int Rco (SO_+({\mathbb {R}}^2)A\cup SO_+({\mathbb {R}}^2)B)$
. Let $T\in int Rco (SO_+({\mathbb {R}}^2)A\cup SO_+({\mathbb {R}}^2)B)$![]() . Let $\phi (x)=Tx+c$
. Let $\phi (x)=Tx+c$![]() , with $c\in {\mathbb {R}}^n$
, with $c\in {\mathbb {R}}^n$![]() . Then the differential inclusion
. Then the differential inclusion
has infinitely many solutions.
Remark 4.2 In theorem 4.1, the assumption that $A$![]() and $B$
and $B$![]() are diagonal matrices is not essential, as one can always reduce to this case. Also note the importance that $A\neq \alpha I$
are diagonal matrices is not essential, as one can always reduce to this case. Also note the importance that $A\neq \alpha I$![]() and $B\neq \beta I$
and $B\neq \beta I$![]() for some constants $\alpha >0,\beta >0$
for some constants $\alpha >0,\beta >0$![]() , since (4.1) in this case implies that $u$
, since (4.1) in this case implies that $u$![]() is a conformal map and by Liouville's theorem [Reference Iwaniec, Martin and Onninen16, theorem 5.1.1] any conformal map $u\in W^{1,n}$
is a conformal map and by Liouville's theorem [Reference Iwaniec, Martin and Onninen16, theorem 5.1.1] any conformal map $u\in W^{1,n}$![]() is a Möbius transformation of ${\mathbb {R}}^n\cup \{\infty \}$
is a Möbius transformation of ${\mathbb {R}}^n\cup \{\infty \}$![]() .
.
Remark 4.3 Note that solutions of (4.1) need in no way be locally injective. In particular, since both $I$![]() and $-I$
and $-I$![]() belong to $\text {SO}_+({\mathbb {R}}^2)$
belong to $\text {SO}_+({\mathbb {R}}^2)$![]() and $0=\frac {1}{2}I-\frac {1}{2}I\in \text {co}(\text {SO}_+({\mathbb {R}}^2))$
and $0=\frac {1}{2}I-\frac {1}{2}I\in \text {co}(\text {SO}_+({\mathbb {R}}^2))$![]() , the inverse function theorem for Lipschitz mappings due to Clarke [Reference Clarke8] does not apply.
, the inverse function theorem for Lipschitz mappings due to Clarke [Reference Clarke8] does not apply.
If a convex, polyconvex or quasiconvex $W$![]() whose reduced energy–momentum tensor is not an injective map, and such that there exist diagonal matrices $A,B\in \text {Sym}_+({\mathbb {R}}^n)$
whose reduced energy–momentum tensor is not an injective map, and such that there exist diagonal matrices $A,B\in \text {Sym}_+({\mathbb {R}}^n)$![]() that satisfy the assumption of theorem 4.1, then theorem 4.1 would show (at least in dimension two) that there are energy–momentum tensors for which well-posedness of the Dirichlet problem for the energy–momentum equations fails, even with the additional constraint $\det (Du(x))>0$
that satisfy the assumption of theorem 4.1, then theorem 4.1 would show (at least in dimension two) that there are energy–momentum tensors for which well-posedness of the Dirichlet problem for the energy–momentum equations fails, even with the additional constraint $\det (Du(x))>0$![]() for a.e. $x$
for a.e. $x$![]() and furthermore no partial $C^1$
and furthermore no partial $C^1$![]() -regularity holds. In all the examples, we study there are cases when the reduced energy–momentum tensor fails to be injective. The solutions to $\mathcal {T}^{-1}(Z)$
-regularity holds. In all the examples, we study there are cases when the reduced energy–momentum tensor fails to be injective. The solutions to $\mathcal {T}^{-1}(Z)$![]() however fail to satisfy the conditions of theorem 4.1.
however fail to satisfy the conditions of theorem 4.1.
Open Problem. Does there exists a smooth strictly convex, polyconvex or quasiconvex $W\in C^\infty (\mathcal {L}({\mathbb {R}}^2),{\mathbb {R}})$![]() for which its reduced energy–momentum tensor fails to be an injective map and for which there exists matrices $A$
for which its reduced energy–momentum tensor fails to be an injective map and for which there exists matrices $A$![]() and $B$
and $B$![]() that satisfy the assumptions of theorem 4.1 and such that $\mathcal {T}(A)=\mathcal {T}(B)$
that satisfy the assumptions of theorem 4.1 and such that $\mathcal {T}(A)=\mathcal {T}(B)$![]() ?
?
4.1 Invertibility of the reduced energy–momentum tensor in a number of interesting cases
In this section, we will consider a number of important functionals that occur in non-linear elasticity and geometric functions theory. We will show that in all these cases, the reduced energy–momentum mapping $\mathcal {T}$![]() is typically not injective, yet the conditions of theorem 4.1 are not satisfied. In addition, they all have the feature that their Lagrangian $W$
is typically not injective, yet the conditions of theorem 4.1 are not satisfied. In addition, they all have the feature that their Lagrangian $W$![]() in addition to being frame-indifferent is also isotropic, i.e.
in addition to being frame-indifferent is also isotropic, i.e.
for all $R\in O({\mathbb {R}}^n)$![]() and all $X\in \mathcal {L}({\mathbb {R}}^n)$
and all $X\in \mathcal {L}({\mathbb {R}}^n)$![]() . We begin with the Dirichlet $p$
. We begin with the Dirichlet $p$![]() -energy.
-energy.
Example 4.4 Let $1< p<+\infty$![]() and let for $u\in W^{1,p}(\Omega,{\mathbb {R}}^n)$
and let for $u\in W^{1,p}(\Omega,{\mathbb {R}}^n)$![]()
Since $W(X)=\vert X\vert ^p$![]() we find that $DW(X)=p\vert X\vert ^{p-2}X$
we find that $DW(X)=p\vert X\vert ^{p-2}X$![]() and the energy–momentum mapping becomes
and the energy–momentum mapping becomes
The reduced energy–momentum mapping becomes with $Y=X^\ast X$![]()
Note that
which is different from $0$![]() if and only if $p\neq n$
if and only if $p\neq n$![]() . Let $Z\in \mathcal {T}(\text {Sym}_+(n))$
. Let $Z\in \mathcal {T}(\text {Sym}_+(n))$![]() . Consider the equation for $p\neq n$
. Consider the equation for $p\neq n$![]()
Taking traces of both sides gives us
Thus,

Since $Y$![]() is positive semi-definite, it has a unique positive semi-definite square root $\sqrt {Y}$
is positive semi-definite, it has a unique positive semi-definite square root $\sqrt {Y}$![]() . In particular, all solutions of $T(X)=Z$
. In particular, all solutions of $T(X)=Z$![]() are given by
are given by

and the situation (4.1) cannot occur. Furthermore, by theorem 1.2 and in view of Uhlenbeck's regularity result [Reference Uhlenbeck34], weak solutions $u\in W^{1,p}(\Omega,{\mathbb {R}}^n)$![]() of the Euler–Lagrange equations of the Dirichlet $p$
of the Euler–Lagrange equations of the Dirichlet $p$![]() -energy are always $C^{1,\alpha }$
-energy are always $C^{1,\alpha }$![]() for some $0<\alpha <1$
for some $0<\alpha <1$![]() . Hence, the weak solutions of the energy–momentum equations which are not $C^{1,\alpha }$
. Hence, the weak solutions of the energy–momentum equations which are not $C^{1,\alpha }$![]() are not weak solutions of the Euler–Lagrange equations. In the conformally invariant case $p=n$
are not weak solutions of the Euler–Lagrange equations. In the conformally invariant case $p=n$![]() , the formula (4.2) does not hold and in fact we now show that $\mathcal {T}(Y)$
, the formula (4.2) does not hold and in fact we now show that $\mathcal {T}(Y)$![]() is not injective. It follows from the equation $\mathcal {T}(Y)=Z$
is not injective. It follows from the equation $\mathcal {T}(Y)=Z$![]() that $[Y,Z]=0$
that $[Y,Z]=0$![]() , so if $Z$
, so if $Z$![]() is diagonalizable so is $Y$
is diagonalizable so is $Y$![]() . Thus, we restrict to considering only diagonal matrices $Y$
. Thus, we restrict to considering only diagonal matrices $Y$![]() and only consider the case $n=2$
and only consider the case $n=2$![]() . We find that if
. We find that if
where $c\geq 0$![]() we find the system of equations
we find the system of equations
Hence, if $\alpha =t$![]() , $\beta =t-c$
, $\beta =t-c$![]() and $t\geq c$
and $t\geq c$![]() parametrizes the solutions. Thus, $\mathcal {T}$
parametrizes the solutions. Thus, $\mathcal {T}$![]() is not an injective map. On the other hand, we can find no two $t_1,t_2$
is not an injective map. On the other hand, we can find no two $t_1,t_2$![]() such that the condition of theorem 4.1 is satisfied.
such that the condition of theorem 4.1 is satisfied.
Example 4.5 $q$ -mean distortion
-mean distortion
Let $u:\Omega \subset {\mathbb {R}}^n \to {\mathbb {R}}^n$![]() be a map in $W^{1,n}(\Omega,{\mathbb {R}}^n)$
be a map in $W^{1,n}(\Omega,{\mathbb {R}}^n)$![]() and consider the $q$
and consider the $q$![]() -mean distortion functional
-mean distortion functional
where $q\geq 1$![]() . $W$
. $W$![]() is a priori only well-defined when $\det (X)>0$
is a priori only well-defined when $\det (X)>0$![]() , however we can extend $W$
, however we can extend $W$![]() to $\widetilde {W}\in C^\infty (\text {GL}_+({\mathbb {R}}^n)\cup \text {GL}_-({\mathbb {R}}^n))$
to $\widetilde {W}\in C^\infty (\text {GL}_+({\mathbb {R}}^n)\cup \text {GL}_-({\mathbb {R}}^n))$![]() as a frame-indifferent function by defining
as a frame-indifferent function by defining
This extension is however not polyconvex due to the blow up when $\det (X)=0$![]() (except in the case $X=tI$
(except in the case $X=tI$![]() and $t\to 0$
and $t\to 0$![]() ). The only polyconvex extension is to define $\mathbb {K}(x,u)^q=+\infty$
). The only polyconvex extension is to define $\mathbb {K}(x,u)^q=+\infty$![]() whenever $\det (X)\leq 0$
whenever $\det (X)\leq 0$![]() . For more on this functional, we refer the reader to [Reference Iwaniec, Martin and Onninen17] and references there in. We will however use $\widetilde {W}$
. For more on this functional, we refer the reader to [Reference Iwaniec, Martin and Onninen17] and references there in. We will however use $\widetilde {W}$![]() and by abuse of notation also write $W$
and by abuse of notation also write $W$![]() for its frame-indifferent extension. Set $W(X)=(f(X)g(X))^q$
for its frame-indifferent extension. Set $W(X)=(f(X)g(X))^q$![]() where $f(X)=\vert X\vert ^n$
where $f(X)=\vert X\vert ^n$![]() and $g(X)=\vert \det (X)\vert ^{-1}$
and $g(X)=\vert \det (X)\vert ^{-1}$![]() . Then
. Then
By (A.1)

Thus,
and

Thus,

and $\langle T(I)\xi,\xi \rangle =-W(I)$![]() .
.
Hence, $T$![]() does satisfy the assumptions of proposition 3.4 and there are stationary points of the functional which are nowhere $C^1$
does satisfy the assumptions of proposition 3.4 and there are stationary points of the functional which are nowhere $C^1$![]() . Indeed, as an explicit example, take $n=2$
. Indeed, as an explicit example, take $n=2$![]() and $q=1$
and $q=1$![]() and let
and let
Then $I-R=2e_2\otimes e_2$![]() and so $R$
and so $R$![]() is rank-one connected to $I$
is rank-one connected to $I$![]() . Furthermore,
. Furthermore,
and
and
Thus, $u$![]() is also a solution to the Euler–Lagrange equations. The reduced energy–momentum tensor becomes
is also a solution to the Euler–Lagrange equations. The reduced energy–momentum tensor becomes

provided $\det (Y)\neq 0$![]() and ${\rm tr} (Y)\neq 0$
and ${\rm tr} (Y)\neq 0$![]() . We now specialize to the case when $n=2$
. We now specialize to the case when $n=2$![]() and $q=1$
and $q=1$![]() . Then
. Then

Assume that $Z\in \text {im}(\mathcal {T})$![]() and that furthermore $Y$
and that furthermore $Y$![]() is a diagonal matrix. Then we recall that $Y-{\rm tr} (Y)I=-\text{adj} (Y)$
is a diagonal matrix. Then we recall that $Y-{\rm tr} (Y)I=-\text{adj} (Y)$![]() . This gives us the equation
. This gives us the equation
or upon multiplying by $Y$![]() ,
,
Set $t=\sqrt {\det (Y)}$![]() . This gives the one-parameter family of solutions
. This gives the one-parameter family of solutions
for $t>0$![]() given a solution $Y_0$
given a solution $Y_0$![]() such that $\mathcal {T}(Y_0)=Z$
such that $\mathcal {T}(Y_0)=Z$![]() . For example, if $Y_0=I$
. For example, if $Y_0=I$![]() , then $Z=-2I$
, then $Z=-2I$![]() , and $Y(t)=tI$
, and $Y(t)=tI$![]() . Again one may verify that no two solutions of (4.4) satisfy the assumptions of theorem 4.1.
. Again one may verify that no two solutions of (4.4) satisfy the assumptions of theorem 4.1.
Example 4.6 Let $W:\mathcal {L}({\mathbb {R}}^n)\to {\mathbb {R}}$![]() be given by
be given by
This is an example from [Reference Iwaniec, Martin and Onninen17] and comes from geometric function theory and non-linear elasticity. $W$![]() is polyconvex when restricted to $\text {GL}_+({\mathbb {R}}^n)$
is polyconvex when restricted to $\text {GL}_+({\mathbb {R}}^n)$![]() but not on the entire $\mathcal {L}({\mathbb {R}}^n)$
but not on the entire $\mathcal {L}({\mathbb {R}}^n)$![]() . Using (A.2), we find that
. Using (A.2), we find that


Thus,
The reduced energy–momentum tensor becomes
We now assume that $p=n=2$![]() . By the Cayley–Hamilton theorem, we have
. By the Cayley–Hamilton theorem, we have
This gives

Let $Y=\alpha I$![]() , $\alpha >0$
, $\alpha >0$![]() . Then
. Then

Thus, $\mathcal {T}$![]() is not injective, but there exists no two $\alpha _1\neq \alpha _2$
is not injective, but there exists no two $\alpha _1\neq \alpha _2$![]() so that $\alpha _1I$
so that $\alpha _1I$![]() and $\alpha _2I$
and $\alpha _2I$![]() satisfy the assumptions of theorem 4.1.
satisfy the assumptions of theorem 4.1.
Example 4.7 Ball class
Let $\Omega \subset {\mathbb {R}}^n$![]() be a Lipschitz domain and define the class of mappings
be a Lipschitz domain and define the class of mappings
where $p\geq n-1$![]() and $q\geq p/(p-1)$
and $q\geq p/(p-1)$![]() . This is studied in [Reference Ball1, Reference Ball2, Reference Šverák29], see also [Reference Fusco and Hutchinson12] for a similar class of polyconvex functionals. The associated energy to this function class is
. This is studied in [Reference Ball1, Reference Ball2, Reference Šverák29], see also [Reference Fusco and Hutchinson12] for a similar class of polyconvex functionals. The associated energy to this function class is
and
which is a frame-indifferent strictly polyconvex function. Using that $W(X)= \vert {\rm tr} (X^\ast X)\vert ^{p/2}+ \vert {\rm tr} (\text{adj} (X)^\ast X)\vert ^{q/2}$![]() and lemma A.11, we have
and lemma A.11, we have

and thus,

Thus, $T$![]() does not satisfy the assumptions of proposition 3.4.
does not satisfy the assumptions of proposition 3.4.
The reduced energy–momentum tensor becomes
We now specialize to dimension $n=2$![]() and choose $p=q=2$
and choose $p=q=2$![]() . We get
. We get
If $Y$![]() is a diagonal matrix, then ${\rm tr} (\text{adj} (Y))={\rm tr} (Y)$
is a diagonal matrix, then ${\rm tr} (\text{adj} (Y))={\rm tr} (Y)$![]() and we get
and we get
We now consider the equation $\mathcal {T}(Y)=Z$![]() for some positive definite diagonal matrix $Z$
for some positive definite diagonal matrix $Z$![]() , which implies that $Y=Z/4$
, which implies that $Y=Z/4$![]() . Thus, we have a unique solution and the assumptions of theorem 4.1 are not satisfied.
. Thus, we have a unique solution and the assumptions of theorem 4.1 are not satisfied.
Appendix A. Notions of convexity
We here recall the notions of polyconvexity and quasiconvexity.
Definition A.1 Rank-one convexity
A locally bounded Borel measurable function $W:\mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m)\to {\mathbb {R}}$![]() is called rank-one convex if for every $A,B\in \mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m)$
is called rank-one convex if for every $A,B\in \mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m)$![]() such that $\text {rank}(B)\leq 1$
such that $\text {rank}(B)\leq 1$![]() the function $\varphi :{\mathbb {R}}\to {\mathbb {R}}\cup \{\infty \}$
the function $\varphi :{\mathbb {R}}\to {\mathbb {R}}\cup \{\infty \}$![]() given by
given by
is convex. If in addition for all such $A$![]() and $B$
and $B$![]() the function $\varphi$
the function $\varphi$![]() is strictly convex, we say that $W$
is strictly convex, we say that $W$![]() is strictly rank-one convex. If $W\in C^2(\mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m))$
is strictly rank-one convex. If $W\in C^2(\mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m))$![]() , then the rank-one convexity is equivalent to the ellipticity condition (also called Legendre–Hadamard condition)
, then the rank-one convexity is equivalent to the ellipticity condition (also called Legendre–Hadamard condition)
for every $X\in \mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m)$![]() and every $u\in {\mathbb {R}}^n$
and every $u\in {\mathbb {R}}^n$![]() and $v\in {\mathbb {R}}^m$
and $v\in {\mathbb {R}}^m$![]() .
.
Definition A.2 Quasiconvex
A locally bounded Borel measurable function $W:\mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m)\to {\mathbb {R}}$![]() is called quasiconvex if
is called quasiconvex if
for every $A\in \mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m)$![]() and every $\phi \in W^{1,\infty }_0(B_1(0),{\mathbb {R}}^m)$
and every $\phi \in W^{1,\infty }_0(B_1(0),{\mathbb {R}}^m)$![]()
Definition A.3 Exterior extension of linear map
Let $T\in \mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m)$![]() . The exterior extension $\Lambda T$
. The exterior extension $\Lambda T$![]() is the unique extension of $T$
is the unique extension of $T$![]() to an exterior algebra homomorphism $\Lambda T: \Lambda {\mathbb {R}}^n \to \Lambda {\mathbb {R}}^m$
to an exterior algebra homomorphism $\Lambda T: \Lambda {\mathbb {R}}^n \to \Lambda {\mathbb {R}}^m$![]() such that
such that
(i) $\Lambda T(1)=1$
 .
.(ii) $\Lambda T(v_1\wedge v_2\wedge \ldots \wedge v_k)=T(v_1)\wedge T(v_2)\wedge \ldots \wedge T(v_k)$
 for any vector $v_1,v_2,\ldots, v_k\in {\mathbb {R}}^n$
for any vector $v_1,v_2,\ldots, v_k\in {\mathbb {R}}^n$ .
.(iii) $\Lambda T(\alpha w_1+\beta w_2)=\alpha \Lambda T(w_1)+\beta \Lambda T(w_2)$
 for any $\alpha,\beta \in {\mathbb {R}}$
for any $\alpha,\beta \in {\mathbb {R}}$ and any $w_1,w_2\in \Lambda {\mathbb {R}}^n$
and any $w_1,w_2\in \Lambda {\mathbb {R}}^n$ .
.
We furthermore let $\Lambda ^kT=\Lambda T\vert _{\Lambda ^k {\mathbb {R}}^n}$![]() .
.
Note that in particular $\Lambda ^0T(\alpha )=\alpha$![]() for all $\alpha \in {\mathbb {R}}$
for all $\alpha \in {\mathbb {R}}$![]() and $\Lambda ^nT(w)=\det (T)w$
and $\Lambda ^nT(w)=\det (T)w$![]() for $w\in \Lambda ^n{\mathbb {R}}^n$
for $w\in \Lambda ^n{\mathbb {R}}^n$![]() . Furthermore, if $\text {rank}(T)=k$
. Furthermore, if $\text {rank}(T)=k$![]() , then $\Lambda ^lT=0$
, then $\Lambda ^lT=0$![]() for $l>k$
for $l>k$![]() .
.
Definition A.4 Grade preserving linear map
A linear map $T\in \mathcal {L}(\Lambda {\mathbb {R}}^n,\Lambda {\mathbb {R}}^m)$![]() is called grade preserving if $T(\Lambda ^k{\mathbb {R}}^n)\subset \Lambda ^k{\mathbb {R}}^m$
is called grade preserving if $T(\Lambda ^k{\mathbb {R}}^n)\subset \Lambda ^k{\mathbb {R}}^m$![]() for every $k=0,1,2,\ldots,n$
for every $k=0,1,2,\ldots,n$![]() . The space of grade preserving linear maps will be denoted by $\widehat {\mathcal {L}}(\Lambda {\mathbb {R}}^n,\Lambda {\mathbb {R}}^m)$
. The space of grade preserving linear maps will be denoted by $\widehat {\mathcal {L}}(\Lambda {\mathbb {R}}^n,\Lambda {\mathbb {R}}^m)$![]() .
.
Note that $\text {dim}(\widehat {\mathcal {L}}(\Lambda {\mathbb {R}}^n,\Lambda {\mathbb {R}}^m))=\sum _{k=0}^{\text {min}\{n,m\}}\binom {m}{k}\binom {n}{k}$![]() . In particular, in the case when $m=n$
. In particular, in the case when $m=n$![]() , then $\text {dim}(\widehat {\mathcal {L}}(\Lambda {\mathbb {R}}^n,\Lambda {\mathbb {R}}^n))=\binom {2n}{n}$
, then $\text {dim}(\widehat {\mathcal {L}}(\Lambda {\mathbb {R}}^n,\Lambda {\mathbb {R}}^n))=\binom {2n}{n}$![]() .
.
Definition A.5 Polyconvex
A locally bounded Borel measurable function $W:\mathcal {L}({\mathbb {R}}^n,{\mathbb {R}}^m)\to {\mathbb {R}}$![]() is called polyconvex if there exists a convex function $\sigma : \widehat {\mathcal {L}}(\Lambda {\mathbb {R}}^n,\Lambda {\mathbb {R}}^m)\to {\mathbb {R}}$
is called polyconvex if there exists a convex function $\sigma : \widehat {\mathcal {L}}(\Lambda {\mathbb {R}}^n,\Lambda {\mathbb {R}}^m)\to {\mathbb {R}}$![]() such that
such that
We say that $W$![]() is strictly polyconvex if $\sigma$
is strictly polyconvex if $\sigma$![]() is strictly polyconvex.
is strictly polyconvex.
In coordinates, polyconvexity means that $W$![]() can be written as a convex function of $X$
can be written as a convex function of $X$![]() and all its minors. Also we typically let $\sigma$
and all its minors. Also we typically let $\sigma$![]() be independent of $\Lambda ^0T=\text {id}\vert _{{\mathbb {R}}}$
be independent of $\Lambda ^0T=\text {id}\vert _{{\mathbb {R}}}$![]() so that $W(X)=\sigma (T,\Lambda ^2T,\Lambda ^3T,\ldots,\Lambda ^n T )$
so that $W(X)=\sigma (T,\Lambda ^2T,\Lambda ^3T,\ldots,\Lambda ^n T )$![]() .
.
Appendix A.1 Matrix computations
For the convenience of the reader, we here state a number of useful results regarding functions of matrices.
Lemma A.6 Let $W(X)=\det (X)$![]() . Then
. Then
Proof. For $X,H\in \mathcal {L}({\mathbb {R}}^n)$![]() we have the expansion
we have the expansion
Thus, if $W(X)=\det (X)$![]() , then
, then

Lemma A.7 Let $W(X)=\vert X^{-1}\vert ^2={\rm tr} ((X^{-1})^\ast X^{-1})$![]() . Then for $\det (X)\neq 0$
. Then for $\det (X)\neq 0$![]()
More generally, for $W_p(X)=\vert X^{-1}\vert ^p$![]() and $\det (X)\neq 0$
and $\det (X)\neq 0$![]()
Proof. For $X,H\in \mathcal {L}({\mathbb {R}}^n)$![]() we have the expansion
we have the expansion
Thus,

and

Lemma A.8 Let $n=2$![]() and assume that
and assume that
for some smooth function $\sigma :{\mathbb {R}}^2\to {\mathbb {R}}$![]() such that $W$
such that $W$![]() is smooth. Then, with $Y=X^\ast X$
is smooth. Then, with $Y=X^\ast X$![]()
Proof. Since

we have

and

Lemma A.9
Proof. If $\det (X)\neq 0$![]() then
then

Lemma A.10 If $W(X)={\rm tr} (\text{adj} (X)^\ast \text{adj} (X))$![]() and if $\det (X)\neq 0$
and if $\det (X)\neq 0$![]() then
then
and
Proof. Using lemma A.9 and the identities $\text{adj} (XY)=\text{adj} (Y)\text{adj} (X)$![]() and $\text{adj} (X)^\ast =\text{adj} (X^\ast )$
and $\text{adj} (X)^\ast =\text{adj} (X^\ast )$![]()

Thus,

Hence,
and

Combining the previous lemmata we find$:$![]()
Lemma A.11 Let $\Phi _i:\{x\in {\mathbb {R}}: x>0\}\to {\mathbb {R}}$![]() be $C^1$
be $C^1$![]() for $i=1,2,3$
for $i=1,2,3$![]() and let $W_1(X)=\Phi _1( {\rm tr} (X^\ast X))$
and let $W_1(X)=\Phi _1( {\rm tr} (X^\ast X))$![]() , $W_2(X)=\Phi _2( {\rm tr} (\text{adj} (X^\ast ) \text{adj} (X)))$
, $W_2(X)=\Phi _2( {\rm tr} (\text{adj} (X^\ast ) \text{adj} (X)))$![]() and $W_3(X)=\Phi _3( \det (X^\ast X))$
and $W_3(X)=\Phi _3( \det (X^\ast X))$![]() for $X\in \mathcal {L}({\mathbb {R}}^n)$
for $X\in \mathcal {L}({\mathbb {R}}^n)$![]() . Then
. Then

and

Acknowledgements
Erik Duse was supported by the Knut and Alice Wallenberg Foundation grant KAW 2015.0270. The author thanks Daniel Faraco for providing references and explaining results regarding differential inclusions into the orthogonal group. Finally, the author thanks Pekka Pankka for interesting discussions on the energy–momentum equations.