2.1. Base state

A steady-state, fully developed pressure-driven bilayer flow has base-state velocities

(2.6a)$$\begin{gather} \bar{v}_x^{(1)}= \frac{y [y-1 - H (\mu_r-1) (H - y)]}{(H-1) H}, \end{gather}$$

(2.6b)$$\begin{gather}\bar{v}_x^{(2)}= \frac{(y-1) [y-H (\mu_r-1) (H -1 - y)]}{(H-1) H\mu_r}. \end{gather}$$

Similarly, the base-state temperature gradients are

(2.6c)$$\begin{gather} \frac{\partial \bar{T}^{(1)}}{\partial y}=1; \quad \frac{\partial \bar{T}^{(2)}}{\partial y} = \frac{1}{\kappa_r}, \end{gather}$$

(2.6d)$$\begin{gather}\beta_1 = \frac{\kappa_2 (T^*_2 - T^*_1)}{[(1-H)\kappa_1+ H \kappa_2] R}. \end{gather}$$

The subsequent linear stability analysis is performed with respect to this base state.

2.2. Linearised perturbation equations

For the linear stability analysis, dynamical quantities such as velocities, temperatures and pressures are decomposed into the base-state and perturbed state, as ${\mathcal {F}}(\boldsymbol {x},t)=\bar {\mathcal {F}}(y)+{\mathcal {F}}'(\boldsymbol {x},t)$. Here, ${\mathcal {F}}(\boldsymbol {x},t)$ is any dynamic quantity and a prime signifies the small perturbation quantity. In the linearised governing equations, the normal modes of the following form are then substituted:

(2.7)\begin{equation} {\mathcal{F}}'(\boldsymbol{x},t)=\tilde{\mathcal{F}}(y) \exp({{\rm i} (k x + m z - \omega t)}). \end{equation}

Here $k$ and $m$ are the wavenumbers and $\tilde {\mathcal {F}}(y)$ is the eigenfunction of ${\mathcal {F}}'(\boldsymbol {x},t)$. The other parameter, $\omega =\omega _r+ {\rm i} \omega _i$, is the complex frequency, which characterises the temporal phase speed and growth of the disturbances. For the temporal stability analysis, the wavenumbers are treated as real numbers, while for the spatio-temporal analysis, the wavenumbers are complex numbers. The flow is considered temporally unstable if at least one eigenvalue satisfies the condition $\omega _i>0$. As described in § 6.2, the flow is absolutely unstable if the imaginary part of the complex frequency at the cusp point ($\omega _{i0}$) satisfies the condition $\omega _{i0}>0$, otherwise, convectively unstable. After the substitution of the normal modes, the linearised governing equations become

(2.8a)$$\begin{gather} {\rm i} k \tilde v^{(i)}_x + D \tilde v^{(i)}_y=0, \end{gather}$$

(2.8b)$$\begin{gather}Re [ -{\rm i} \omega \tilde v^{(i)}_x + {\rm i} k \bar v^{(i)}_x \tilde v^{(i)}_x + \tilde v^{(i)}_y D \bar v^{(i)}_x] ={-}{\rm i} k \tilde p^{(i)} + \mu^{(i)} (D^{2}-k^{2}-m^2) \tilde v^{(i)}_x, \end{gather}$$

(2.8c)$$\begin{gather}Re [ -{\rm i} \omega \tilde v^{(i)}_y + {\rm i} k \bar v^{(i)}_x \tilde v^{(i)}_y ] ={-}D \tilde p^{(i)} + \mu^{(i)} (D^{2}-k^{2}-m^2) \tilde v^{(i)}_y, \end{gather}$$

(2.8d)$$\begin{gather}Re [ -{\rm i} \omega \tilde v^{(i)}_z + {\rm i} k \bar v^{(i)}_x \tilde v^{(i)}_z ] ={-}{\rm i}m \tilde p^{(i)} + \mu^{(i)} (D^{2}-k^{2}-m^2) \tilde v^{(i)}_z, \end{gather}$$

(2.8e)$$\begin{gather}Re\, Pr [ -{\rm i} \omega \tilde T^{(i)} + {\rm i} k \bar v^{(i)}_x \tilde T^{(i)} + D \bar T^{(i)} \tilde v^{(i)}_y] = \kappa^{(i)} (D^{2}-k^{2}-m^2) \tilde T^{(i)}, \end{gather}$$

where $D={\rm d}/{{\rm d} y}$.

The above equations are to be solved using the following boundary conditions. At $y=0$ and $y=1$, the assumption of no-slip, impermeability and imposed temperature gradient along the plates gives

(2.9a)$$\begin{gather} \tilde v^{(1)}_x =0; \quad \tilde v^{(1)}_y =0; \quad \tilde v^{(1)}_z =0; \quad \tilde T^{(1)} =0, \quad \text{at} \ y=0, \end{gather}$$

(2.9b)$$\begin{gather}\tilde v^{(2)}_x =0; \quad \tilde v^{(2)}_y =0; \quad \tilde v^{(2)}_z =0; \quad \tilde T^{(2)} =0, \quad \text{at} \ y=1. \end{gather}$$

At $y=H$, oscillations of the fluid–fluid interface will be induced due to the perturbations. Thus, the infinitesimal displacement of the interface will play a role. These boundary conditions, after substitution of the normal modes, become

(2.9c)\begin{gather} {\rm i} (k\bar v^{(1)}_x -\omega) \tilde \xi = \tilde v^{(1)}_y , \end{gather}

(2.9d)\begin{gather} \tilde v^{(1)}_x + D \bar v^{(1)}_x \tilde \xi = \tilde v^{(2)}_x + D \bar v^{(2)}_x \tilde \xi, \end{gather}

(2.9e)\begin{gather} \tilde v^{(1)}_y = \tilde v^{(2)}_y, \end{gather}

(2.9f)\begin{gather} \tilde v^{(1)}_z = \tilde v^{(2)}_z, \end{gather}

(2.9g)$$\begin{gather} D \tilde v^{(1)}_x + {\rm i}k \tilde v^{(1)}_y + [ D^2 \bar v^{(1)}_x - \mu_r D^2 \bar v^{(2)}_x ] \tilde \xi \nonumber\\ =\mu_r ( D \tilde v^{(2)}_x + {\rm i}k \tilde v^{(2)}_y) - {\rm i} k Ma (\tilde T^{(1)} + D \bar T^{(1)} \tilde\xi), \end{gather}$$

(2.9h)\begin{gather} D \tilde v^{(1)}_z + {\rm i}m \tilde v^{(1)}_y = \mu_r (D \tilde v^{(2)}_z + {\rm i}m \tilde v^{(2)}_y) - {\rm i} m Ma (\tilde T^{(1)} + D \bar T^{(1)} \tilde \xi), \end{gather}

(2.9i)\begin{gather} -\tilde p^{(1)} + 2 D v^{(1)}_y ={-}\tilde p^{(2)} + 2 \mu_r D v^{(2)}_y - Ca^{{-}1} (k^2+m^2) \tilde \xi, \end{gather}

(2.9j)\begin{gather} \tilde T^{(1)} + D \bar T^{(1)} \tilde \xi = \tilde T^{(2)} + D \bar T^{(2)} \tilde \xi, \end{gather}

(2.9k)\begin{gather} D\tilde T^{(1)} = \kappa_r D \tilde T^{(2)}, \end{gather}

where all quantities are evaluated at $y=H$.

4.1. Streamwise mode ($m=0$)

For $m=0$ and $\tilde v_z =0$, the momentum perturbation equations in (2.8) can be reduced to two-dimensional Orr–Sommerfeld equations

(4.1) \begin{equation} {\rm i} Re (k \bar v_x^{(i)} - \omega ) ( D^2 - k^2 ) \tilde v_y^{(i)} = \mu^{(i)} ( D^2 - k^2 )^2 \tilde v_y^{(i)} - {\rm i}k Re D^2 \bar v_x^{(i)}\tilde v_y^{(i)}, \end{equation}

whereas the energy equation in (2.8) is modified by substituting $m=0$. Next, the velocity and temperature fields and the complex frequency $\omega$ are expanded as the series in terms of a small wavenumber $k$, as

(4.2a)$$\begin{gather} \tilde v_y^{(i)}= v_{y0}^{(i)} + k v_{y1}^{(i)} + k^2 v_{y2}^{(i)} +\cdots, \end{gather}$$

(4.2b)$$\begin{gather}\omega=k c_0 + k^2 c_1 + k^3 c_2 +\cdots, \end{gather}$$

(4.2c)$$\begin{gather}\tilde T^{(i)}= \frac{1}{k} T_{0}^{(i)} + T_{1}^{(i)} + k T_{2}^{(i)} +\cdots. \end{gather}$$

The above expansions are then substituted into the Orr–Sommerfeld equation (4.1), the energy equation (2.8e) and the boundary conditions (2.9). Similar expansion in powers of $k$ for $\tilde v_x^{(i)}$ can be obtained from the continuity equations and, for $\tilde p^{(i)}$, can be obtained from the $x$-momentum equation.

At $O(1)$, the governing equations read

(4.3a,b)\begin{equation} D^4 v_{y0}^{(i)} = 0; \quad D^2 T_{0}^{(i)} = 0. \end{equation}

Using the expansions (4.2), the $O(1)$ eigenvalue is

(4.4)\begin{equation} c_0 ={-}\frac{[(H^2-2H) (\mu_r-1)-1] [1 + H^2 (\mu_r-1)]}{1 + H (\mu_r -1) [4 - 6 H + 4 H^2 - H^3 + H^3 \mu_r] }. \end{equation}

The $O(1)$ eigenvalue, $c_0$, is a real quantity, thus, these are purely travelling disturbances. For $H=0.5$, the above expression reduces to equation (46) of Yih (Reference Yih1967), thereby validating the procedure. The above expression is independent of the capillary number $Ca$ in agreement with Yih (Reference Yih1967). Furthermore, $c_0$ for both the flows is independent of $\kappa _r$, representing the thermal conductivity stratification, and $Ma$, reflecting the thermal stresses. This implies that the thermocapillarity and thermal properties do not affect the phase speed of the disturbances, while they might affect at $O(k)$ or higher. Thus, we proceed with higher-order correction, i.e. $O(k)$.

At $O(k)$, the governing equations are

(4.5a)$$\begin{gather} \mu^{(i)} D^4 v_{y1}^{(i)} + {\rm i} Re (c_0 - \bar v_{x}^{(i)}) D^2 v_{y0}^{(i)} - Re D^2 \bar v_{x}^{(i)} v_{y0}^{(i)}= 0, \end{gather}$$

(4.5b)$$\begin{gather}\kappa^{(i)} D^2 T_{1}^{(i)} + {\rm i} Re\,Pr ( c_0 - \bar v_{x}^{(i)}) T_{0}^{(i)} - Re\,Pr D \bar T^{(i)} v_{y0}^{(i)} = 0. \end{gather}$$

Solving (4.5) in the same way as for $O(1)$ above, yields

(4.6)\begin{equation} c_1={\rm i} \, [ f_1 (H,\mu_r, \kappa_r) \, Ma + f_2 (H,\mu_r) \, Re], \end{equation}

where

(4.7a)$$\begin{gather} f_1=\frac{g_1}{g_2}; \quad f_2 = \frac{g_3}{g_4}, \end{gather}$$

(4.7b)$$\begin{gather}g_1 = (H-1)^2 H^2 (2 H - H^2 + \mu_r H^2 - 1), \end{gather}$$

(4.7c) $$\begin{gather}g_2 = [1 + (\kappa_r-1) H] \, [2 + 2 H (\mu_r-1) (4 - 6 H + 4 H^2 - H^3 + \mu_r H^3)],\\ g_3 ={-}(2 H \,{-}\, H^2 + \mu_r H^2-1) \{1 \,{-}\, \mu_r + 5 H^{14} (\mu_r\,{-}\,1)^7 (1 + \mu_r) + 2 H ({-}4 + 3 \mu_r + \mu_r^2)\nonumber\\ -2 H^{13} (\mu_r-1)^6 ({-}32 + 19 \mu_r + 3 \mu_r^2) + H^{12} (\mu_r-1)^5 (377 - 694 \mu_r + 177 \mu_r^2) \nonumber\\ +H^2 (13 + 4 \mu_r + 15 \mu_r^2 - 32 \mu_r^3) + 8 H^3 (13 - 34 \mu_r + 16 \mu_r^2 + 5 \mu_r^3) \nonumber\\ -8 H^{11} (\mu_r-1)^4 ({-}169 + 472 \mu_r - 258 \mu_r^2 + 29 \mu_r^3) \nonumber\\ -2 H^5 (\mu_r-1)^2 ({-}1144 + 1441 \mu_r - 1107 \mu_r^2 + 112 \mu_r^3) \nonumber\\ +2 H^9 (\mu_r-1)^3 ({-}2860 + 8635 \mu_r - 4718 \mu_r^2 + 223 \mu_r^3) \nonumber\\ +H^8 (\mu_r-1)^3 (7293 - 17490 \mu_r + 5341 \mu_r^2 + 472 \mu_r^3) \nonumber\\ +H^6 (\mu_r-1)^2 ({-}4719 + 9240 \mu_r - 6473 \mu_r^2 + 776 \mu_r^3)\nonumber\\ +H^4 ({-}715 + 1925 \mu_r - 2061 \mu_r^2 + 1259 \mu_r^3 - 408 \mu_r^4) \nonumber\\ -16 H^7 (\mu_r-1)^2 ({-}429 + 1155 \mu_r - 873 \mu_r^2 + 112 \mu_r^3 + 14 \mu_r^4) \nonumber\\ +H^{10} (\mu_r-1)^3 (3289 - 11517 \mu_r + 9743 \mu_r^2 - 2115 \mu_r^3 + 88 \mu_r^4)\}, \end{gather}$$

(4.7d) $$\begin{gather}g_4 = 420 (1 + H (4 - 6 H + 4 H^2 - H^3 + \mu_r H^4) (\mu_r-1))^3 \mu_r^2. \end{gather}$$

Using (4.4) and (4.6), the eigenvalue $\omega$ up to $O(k)$ correction is

(4.8)\begin{equation} \omega=k c_0(H,\mu_r)+{\rm i} \, k^2 \, [ f_1 (H,\mu_r, \kappa_r) \, Ma + f_2 (H,\mu_r) \, Re ]. \end{equation}

The function $f_1 (H,\mu _r, \kappa _r)$ represents the combined effect of the thermocapillarity and viscosity stratification along the interface while the function $f_2 (H,\mu _r)$ represents the inertial stresses alone. The function $f_2 (H,\mu _r)$ is similar to the coefficient of $Re$ in the analysis of Yih (Reference Yih1967), thus representing the shear-flow instability due to the viscosity stratification in the absence of an imposed temperature gradient. The first function $f_1 (H,\mu _r, \kappa _r)$ is dependent on both the viscosity and thermal conductivity stratification and represents an additional term due to the imposed temperature gradient. Clearly, the mechanism responsible for the instability stems from shearing action ($Re$ term) along the interface, which results in the ‘shear-flow mode’ and thermocapillary stresses ($Ma$ term) along the interface, which leads to the ‘thermocapillary mode’. Additionally, from (4.8), the long-wave instability is independent of $Pr$, which is present only in the energy equation as a coefficient of the convection term. Thus, although the momentum convection terms affect the long-wave instability (through the $Re$ term), the energy convection does not affect the long-wave instability. The effect of the energy appears only through the Marangoni terms implying the vital role played by the thermocapillary stresses (through the $Ma$ term) in determining the stability of the flow.

From (4.8), the instability can exist ($\omega _i >0$) for an arbitrary $Re$ and $Ma>0$ if $f_1 >0$ and $f_2 >0$. When $f_1>0$ and $f_2<0$, then a minimum value of $Ma>0$ will be necessary to set in the instability. If $f_1<0$ and $f_2>0$ then the flow is unconditionally unstable for $Ma<0$, implying the necessity of a negative temperature gradient across fluid 1. For $f_1<0$ and $f_2<0$, a minimum value of $Ma<0$ is necessary to make flow unstable. Thus, the rest of the analysis aims to evaluate the required critical value and sign of the critical Marangoni number $Ma_c$ to stabilise/destabilise the flow. Equating the imaginary part of (4.8) to zero, we obtain the expression for the critical Marangoni number

(4.9)\begin{equation} Ma_c ={-}\frac{f_2 (H,\mu_r)}{f_1 (H,\mu_r, \kappa_r)} Re, \end{equation}

implying $Re$ merely enters as a multiplier; thus, in the present study we have presented and discussed the results for the temporal instability for a fixed $Re=0.1$.

The comparison of the growth rate ($\omega _i$) of the unstable streamwise mode predicted by the numerical approach and the asymptotic approach (4.6) is presented in figure 4. On expected lines, the asymptotic and numerical approaches are in excellent agreement for $k<0.5$. From the $O(k)$ expression for the eigenvalue, the shear-flow instability is independent of $Ca$. To accommodate this in the numerical approach, $Ca=\infty$ has been used.

Figure 4. Comparison between the asymptotic and numerical approaches in the prediction of the growth rate $\omega _i$ with wavenumber $k$ at $Re=0.1, H=0.3, \mu _r=0.3, \kappa _r=3, Ca=\infty$ and $Pr=7$ for the return flow. The excellent agreement between the asymptotic and numerical approaches for $k<0.5$ validates the numerical methodology utilised here. For $\omega _i >0$, the flow is unstable.

The orthonormalised velocity and temperature perturbations for the streamwise mode are shown in figure 5. The eigenfunctions vanish at the boundaries of the channel, i.e. $y=0$ and $y=1$ due to the impermeability condition and the absence of the temperature perturbations at the wall given by boundary conditions (2.9a) and (2.9b). Also, both the eigenfunctions achieve maximum at the interface, implying that the instability is driven by the shear and thermocapillary stresses at the interface.

Figure 5. The variation of the orthonormalised velocity and temperature eigenfunctions (for fluid 1) in the $x$–$y$ plane at $Re=10, Pr=7, \mu _r=0.5, H=0.4, \kappa _r=1, Ma=-10, Ca=0.001$ and $k=0.1$ for the streamwise mode $\omega = 0.111936 + 0.000924 \, {\rm i}$. The eigenfunctions exhibit maximum variation near $y=0.4$, i.e. the interface, indicating the destabilisation introduced by the shearing and thermocapillary stresses along the interface. The plotted eigenfunctions are the modulus or absolute value of the respective eigenfunctions.

The critical parameter curves (corresponding to $\omega _i=0$) in $Ma_c - H$ parametric space as a function of $\mu _r$ and $\kappa _r$ are shown in figure 6. From (4.7a), (4.7b) and (4.7d), the factor $(2 H - H^2 + \mu _r H^2 - 1)$ is common in the numerator for both $f_1 (H,\mu _r, \kappa _r)$ and $f_2 (H,\mu _r)$ with $g_3$ having a negative sign preceding the factor, thus, both functions have a common root $H=({\sqrt {\mu _r}-1})/({\mu _r-1})$. The remaining factors of $g_1$, namely, $(H-1)^2$, $H^2$ and $g_2$ do not affect the sign of $f_1$ for $\mu _r <1$. Similarly, the remaining factors of $g_3$ and $g_4$ do not affect the sign of $f_2$. Thus, for a given value of $H$ and $\mu _r$, both functions will possess an opposite sign and their signs will switch at the root $H=({\sqrt {\mu _r}-1})/({\mu _r-1})$. This is precisely the case depicted in figure 6 with the location of the vertical line parallel to the $Ma_c$ axis indicating the root. For example, for $\mu _r =0.1$, the root is $H=0.76$ with $f_1>0$ and $f_2<0$ for $H<0.76$ and $f_1<0$ and $f_2>0$ for $H>0.76$ separated by a vertical line at $H=0.76$ in figure 6(a). Thus, for $Ma>0$, for $H<0.76$, the thermocapillarity stabilises while the shear force has a destabilising influence. The opposite is the case for $f_1<0$ and $f_2>0$ for $H>0.76$. Also, the root $H=({\sqrt {\mu _r}-1})/({\mu _r-1})$ is independent of $\kappa _r$, thus, variation in $\kappa _r$ does not affect the location of the vertical line shown in figure 6.

Figure 6. Variation in the critical Marangoni number $Ma_c$ with the relative position of the interface $H$ at ${Re=0.1}$. The capillary number $Ca$ and Prandtl number $Pr$ do not affect the critical parameters for the long-wave instability, as seen in (4.8). (a) For $H<0.76$, $f_1<0$ and $f_2>0$; thus, the thermocapillarity has a stabilising effect (if $\beta _1>0$) while the shearing force has a destabilising effect. As a result, the flow is unstable for $Ma< Ma_c$. However, for $H>0.76$, $f_1>0$ and $f_2<0$, which leads to the swapping of the stable and unstable regimes. (b) For $H<0.24$, $f_1<0$ and $f_2<0$; thus, both thermocapillarity and the shearing force have a stabilising effect (if $\beta _1>0$). However, if $\beta _1 <0$ then the flow becomes unstable for $Ma<0$. For $H>0.24$, the shearing force has a destabilising effect, while thermocapillarity with $\beta _1$ has a stabilising effect. (c) A decreasing $\kappa _2$ or an increasing $\kappa _1$ shifts the neutral stability boundary to a lower $Ma$. (d) Illustrates the opposite scenario of panel (c). Results are shown for (a) $\kappa _r=1$ and $\mu _r=0.1$, (b) $\kappa _r=1$ and $\mu _r=10$, (c) $\kappa _r=0.1$ and $\mu _r=0.1$, (d) $\kappa _r=10$ and $\mu _r=0.1$.

For $\mu _r>1$, as shown in figure 6(b), a negative temperature gradient is necessary to stabilise or destabilise the flow. In this case, functions $f_1$ and $f_2$ have $H=0.24$ as the common root. For $H<0.24$, both $f_1$ and $f_2$ are negative, thus, both the thermocapillary and inertial terms have a stabilising influence due to which a negative temperature gradient is necessary to set in the instability. While for $H>0.24$, both $f_1$ and $f_2$ are positive, thus, both the thermocapillary and inertial terms have a destabilising influence. A negative temperature gradient then becomes necessary to stabilise the flow. The physical mechanism of the stabilisation or destabilisation due to the viscosity stratification, i.e. impact of variation in the parameter $\mu _r$ is explained in § 5.

The effect of the thermal conductivity stratification on the stable and unstable zones in $Ma_c-H$ parametric space is shown in figure 6(c,d). Figure 6(c) shows that if fluid 2 has a lower thermal conductivity than fluid 1, i.e. $\kappa _r<1$, then compared with the only viscosity stratification shown in figure 6(a), the critical parameter curves shift to a lower $Ma_c$ while the opposite occurs for $\kappa _r>1$. The physical picture of the impact of variation in the parameter $\kappa _r$ on the thermocapillary mode is discussed in § 5.

The analysis of Wei (Reference Wei2006), which considered a two-layer plane Couette flow subjected to a temperature gradient, assumed one of the fluid layers in the thin-film limit implied $H \to 0$ or $H\to 1$. He concluded that the shear-flow mode could be stabilised for an arbitrary $H$ by the thermocapillary mode. However, from figure 6, for $\mu _r<1$, the thermocapillarity is unable to stabilise the flow as $H\to 0$ while, for $\mu _r>1$, again thermocapillarity is incapable of stabilising the flow as $H\to 1$. This implies that the analysis of Wei (Reference Wei2006) has limited applicability to a two-layer pressure-driven flow subjected to a temperature gradient. Furthermore, Wei (Reference Wei2006) predicted two neutral states when the interface tension is weak, but there is no such region found in the present analysis highlighting the difference between the two-layer planar Couette and pressure-driven flows or a possible failure of the thin-film assumption of Wei (Reference Wei2006).

4.2. Spanwise mode ($k=0$)

For $k=0$ and $\tilde v_x = 0$, the momentum perturbation equations in (2.8) reduce to

(4.10) \begin{equation} -{\rm i} \omega \, Re ( D^2 - m^2) \tilde v_y^{(i)} = \mu^{(i)} ( D^2 - m^2)^2 \tilde v_y^{(i)}, \end{equation}

and the energy equations in (2.8) are modified by substituting $k=0$ and $\tilde v_x = 0$. Similar to the case of the streamwise perturbations, the velocity and temperature fields and the complex frequency $\omega$ are expanded as the series in terms of spanwise wavenumber $m$,

(4.11)$$\begin{gather} \tilde v_y^{(i)}= v_{y0}^{(i)} + m v_{y1}^{(i)} + m^2 v_{y2}^{(i)} +\cdots, \end{gather}$$

(4.12)$$\begin{gather}\omega=m c_0 + m^2 c_1 + m^3 c_2 +\cdots, \end{gather}$$

(4.13)$$\begin{gather}\tilde T^{(i)}= \frac{1}{m} T_{0}^{(i)} + T_{1}^{(i)} + m T_{2}^{(i)} +\cdots. \end{gather}$$

The above expansions are then substituted in (4.10), the energy equation (2.8e) for $k=0$ and the boundary conditions (2.9). The expansions in powers of $m$ for $\tilde v_x^{(i)}$ and $\tilde p^{(i)}$ are obtained from the continuity equations and the $z$-momentum equations, respectively.

At $O(1)$, the governing equations read

(4.14a,b)\begin{equation} D^4 v_{y0}^{(i)} = 0; \quad D^2 T_{0}^{(i)} = 0. \end{equation}

At $O(1)$, the eigenvalue is

(4.15)\begin{equation} c_0 = 0. \end{equation}

This shows that the spanwise mode is stationary. At $O(m)$, the governing equations are

(4.16a)$$\begin{gather} \mu^{(i)} D^4 v_{y1}^{(i)} + {\rm i} Re c_0 D^2 v_{y0}^{(i)} = 0, \end{gather}$$

(4.16b)$$\begin{gather}D^2 T_{1}^{(i)} + {\rm i} Re\,Pr c_0 T_{0}^{(i)} - Re\,Pr \frac{\partial \bar T^{(i)}}{ \partial y} v_{y0}^{(i)} = 0. \end{gather}$$

Solving (4.16) in the same way as for $O(1)$ above, yields

(4.17)\begin{equation} c_1={\rm i} \, f_1(H,\mu_r, \kappa_r) \, Ma, \end{equation}

where $f_1$ is a function defined in (4.7a). Using (4.15) and (4.17), the eigenvalue $\omega$ up to $O(m)$ correction is

(4.18)\begin{equation} \omega={\rm i} \, m^2 \, f_1(H,\mu_r, \kappa_r) \, Ma. \end{equation}

A comparison of the above expression for $\omega$ with the expression for the complex frequency for the streamwise mode (4.8) shows the absence of the shear-flow term (i.e. $Re$ term) for the spanwise mode. The shear-flow term is absent since the base-state flow is only in the streamwise direction, while there is no base-state velocity present in the spanwise direction. This is also the reason that the $O(1)$ eigenvalue vanishes, thereby implying a stationary mode.

From (4.18), the spanwise mode is unstable if the product $f_1 Ma > 0$. From figure 7(a), for a given $\mu _r$, there exists a range of $H$ for which $f_1>0$. For such a range, the spanwise perturbations become unstable for a positive temperature gradient, i.e. $Ma>0$. While for $f_1<0$, a negative temperature gradient, i.e. $Ma<0$, is essential for destabilising the spanwise mode. For example, from the curve for $\mu _r=0.1$, $f_1<0$ for $H<0.76$ and $f_1>0$ for $H>0.76$; thus, to destabilise the spanwise perturbations, $Ma<0$ for $H<0.76$ and $Ma>0$ for $H>0.76$ will be necessary.

Figure 7. Variation of the function $f_1$ with the relative position of the liquid–liquid interface $H$. (a) An increasing $\mu _r$ increases the range of $H$ for which $f_1>0$. (b) A decreasing $\kappa _r$ increases maximum $|f_1|$ values. The spanwise mode is unstable for the $H$ range that satisfies the condition $f_1 > 0$. Results are shown for (a) $\kappa _r=1$, (b) $\mu _r=0.1$.

The dominant mode of instability, i.e. the mode with the higher growth rate between the streamwise and spanwise modes, and its range can be decided as follows. When $f_2<0$, then from (4.8), the streamwise mode will have to overcome the stabilising effect of the inertial term to destabilise the flow, which is not the case with the spanwise mode since the inertial term is absent (see (4.18)). Thus, the spanwise mode will dominate the stability of the flow in the parametric regime for which $f_2<0$. The opposite is true when the inertial term has a destabilising effect, i.e. $f_2>0$. In this case, the streamwise mode will have a higher growth rate than the spanwise mode, thereby becoming the dominant mode.

4.3. Oblique modes

The above discussion was limited to only the extremes, i.e. streamwise and spanwise instability modes. However, the streamwise and spanwise instability modes turn out to be the dominant modes of instability as follows. A comparison of (4.8) and (4.18) shows that the difference between the two modes is due to the term $f_2(H,\mu _r) Re$. Thus, if $f_2<0$ then the spanwise mode will possess a higher growth rate than the streamwise mode, and the opposite will be true for $f_2>0$. Any oblique mode with $k \neq 0$ and $m\neq 0$ will have both $Ma$ and $Re$ terms. The function $f_1$ will remain the same for all oblique modes since it remains the same for the extremes, i.e. streamwise and spanwise modes. However, the $Re$ term will diminish as one goes from a streamwise to spanwise mode. Thus, if $f_2<0$, all oblique and streamwise modes will have a growth rate lower than the spanwise mode, while for $f_2>0$, the streamwise mode will possess a higher growth rate than oblique and spanwise modes. Thus, the analysis presented here successfully captures the dominant modes of instability, viz., streamwise and spanwise modes. The case with $f_2>0$ is illustrated in figure 8.

Figure 8. The growth rate variation due to variations in $k$ and $m$ in the $\omega _r - \omega _i$ plane at $Re=10, H=0.3, \mu _r=0.1, \kappa _r=3, Ma=-10, Ca=0.01$ and $Pr=7$. The figure demonstrates that any oblique mode will have a growth rate between the streamwise and spanwise modes. In the illustrated case, $f_2>0$, thus, the streamwise mode exhibits a higher growth rate than the oblique and spanwise modes.

5.1. Purely thermocapillary mode ($Re=0$)

In the following section we discuss the role of shear and Marangoni stresses exerted on the liquid–liquid interface in causing the predicted instabilities. The physical mechanism behind the Marangoni instability in a liquid layer with a free surface subjected to a negative vertical temperature gradient is well understood (Smith & Davis Reference Smith and Davis1983a,Reference Smith and Davisb; Patne et al. Reference Patne, Agnon and Oron2021).

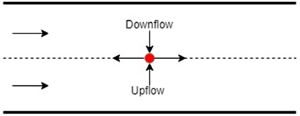
Consider a ‘hot spot’ generated randomly due to the temperature fluctuations at the interface as schematically shown in figure 9. The surface tension at the hot spot decreases correspondingly, which sets fluid flows away from the hot spot along the interface as shown by arrows pointing away from the hot spot in figure 9. To maintain the local mass conservation, upward and downward flows develop in fluids 1 and 2, respectively. Simultaneously, the hot spot loses thermal energy due to thermal diffusion to the surrounding fluid. These upward and downward flows are also opposed by viscous forces. Thus, the fate of the hot spot, i.e. growth or decay, is determined by the combined effects of the generated flows and the viscosity and thermal diffusivity of the fluids.

Figure 9. A schematic of the hot spot (red opaque circle) evolution at the interface. The temperature at the interface $T=T_i$ differs from the wall temperatures due to the imposed temperature gradient. The thermocapillarity generates flow away from the hot spot along the interface. To fill in the so-formed mass deficiency, an upflow in fluid 1 and a downflow in fluid 2 emerge. The combination of these flows leads to the stabilising or destabilising effects of the thermocapillary stresses discussed in § 4.

For the positive temperature gradient across fluid 1, i.e. $\beta _1>0$, the fluid layer adjacent to the interface on the fluid 1 side is at a lower temperature than the interface. The opposite is the case with fluid 2. Thus, the upflow will try to cool down the hot spot while the downflow will try to heat it up. The cooling action of the upflow and the heating action of the downflow will be reinforced/opposed by the viscous forces and thermal diffusion of energy. For example, the cooling action of the upflow reinforces the thermal energy loss due to the thermal diffusion from the hot spot. Thus, for the instability to exist, the downflow must overcome the cooling action of the upflow, viscous forces and the thermal diffusion of the thermal energy that is a function of the parameters $H,\mu _r$ and $\kappa _r$.

5.2. Purely shear-flow mode ($Ma=0$)

The mechanism for the shear-flow instability arising due to viscosity stratification was explained by Yih (Reference Yih1967), Hinch (Reference Hinch1984), Smith (Reference Smith1990) and Charru & Hinch (Reference Charru and Hinch2000). For the long-wave instability, the explanation suggested by Charru & Hinch (Reference Charru and Hinch2000) was that, due to the viscosity stratification, perturbations in the longitudinal velocity component develop, which then lead to the emergence of pressure perturbations. It must be noted that, from (4.8), the shear-flow component of the long-wave instability, i.e. the term containing the Reynolds number $Re$, remains unaffected by the presence of the Marangoni stresses. Thus, the destabilisation mechanism proposed by Charru & Hinch (Reference Charru and Hinch2000) for the long-wave instability is also applicable here.

5.3. Combined thermocapillary and shear-flow mode

The thermal and velocity perturbations are related by the tangential stress balance conditions (2.9g) and (2.9h) at the interface and through the base-state–perturbed-state terms in the linearised energy equation (2.8e). Thus, when a thermocapillary mode of instability becomes unstable by the mechanism discussed in § 5.1, then the thermal perturbations start to grow, which then leads to the growth of the velocity perturbations through the relations (2.9g), (2.9h) and (2.8e). Similarly, when the shear-flow mode becomes unstable by the mechanism discussed in § 5.2, longitudinal velocity perturbations start to develop. This growth in the velocity perturbations then leads to the growth of the thermal perturbations through the relations (2.9g), (2.9h) and (2.8e). Depending on the stable/unstable nature of both modes, the superposition between the thermocapillary and shear-flow modes can be classified into the following two types.

6.1. Temporal stability analysis ($k_i=0$)

To obtain the dispersion relation, we linearise (6.13) and substitute $h(x,t)=H+\delta {\rm e}^{{\rm i}(kx-\omega t)}$ where $\delta \ll 1$ in the resulting linearised equation to obtain the dispersion relation

(6.14)\begin{equation} \omega = k f_0(H,\mu_r) q + {\rm i} \, k^2 [f_1(H,\mu_r,\kappa_r) Ma + f_2(H,\mu_r) Re]+{\rm i} \, k^4 \frac{ f_3(H,\mu_r)}{Ca}, \end{equation}

where $f_1$ and $f_2$ are defined in (4.7a) and

(6.15)$$\begin{gather} f_0= \frac{6 \mu_r (H-1) H [(H^2-2H) (\mu_r-1)-1] [1 + H^2 (\mu_r-1)] }{[1+H(\mu_r-1) (4 - 6 H + 4 H^2 - H^3 + H^3 \mu_r)]^2}, \end{gather}$$

(6.16)$$\begin{gather}f_3=\frac{(H-1)^3 H^3 [1 + H (\mu_r-1)]}{3+3H(\mu_r-1) (4 - 6 H + 4 H^2 - H^3 + H^3 \mu_r)}, \end{gather}$$

where the function $f_3<0$ for arbitrary $\mu _r$ and $H$. For (4.8) and (6.14) to give the same eigenvalue requires $q=c_0/f_0$, thereby obtaining $q$. The dispersion relation for the spanwise mode can be simply obtained from (6.14) by substituting $q=0$, $k=m$ and $Re=0$,

(6.17)\begin{equation} \omega = {\rm i} \, m^2 f_1(H,\mu_r,\kappa_r)+{\rm i} \, m^4 \frac{ f_3(H,\mu_r)}{Ca}. \end{equation}

Figure 10 shows the efficacy of the long-wave approach in predicting the dispersion curves compared with the numerical approach for $k<0.2$. For $k>0.2$, the dispersion curves predicted by both approaches start to differ such that the long-wave approach predicts a higher growth rate. This indicates that the higher-order terms missed due to the truncation of the solution to $O(\epsilon )$ terms lead to an additional stabilisation. It must be noted that one can extend the above model beyond $O(\epsilon )$ terms by following the procedure outlined by Ruyer-Quil & Manneville (Reference Ruyer-Quil and Manneville1998), which could further improve the agreement between the numerical and long-wave approaches. Despite the quantitative differences in the growth rate predicted by the long-wave approach however, it does succeed in capturing the qualitative characteristics of the dispersion curve for an arbitrary wavenumber such as stabilisation due to the interface tension. Additionally, the evolution equation approach yields an equation that can be utilised to study the spatio-temporal and weakly nonlinear evolution of the flow as discussed below. Due to this, the evolution equation approach is more useful than the asymptotic approach but the latter offers a simpler mathematical treatment compared with the former.

Figure 10. Comparison between the growth rate predicted by the numerical and long-wave approaches for the streamwise mode at $Re=10, H=0.4, \mu _r=0.1, \kappa _r=1, Ca=0.1$ and $Pr=7$. The excellent agreement between both approaches for $k<0.2$ validates the long-wave analysis. For $k>0.2$, the dispersion curve predicted by the long-wave analysis predicts a higher growth rate compared with the numerically obtained dispersion curve. The spanwise mode also shows a similar trend.

6.2. Spatio-temporal stability analysis ($k_i \neq 0$)

The GLSA in § 4 and long-wave stability studied in § 6.1 carry out the temporal stability analysis since the frequency of the disturbances, $\omega$, is considered to be a complex number while the wavenumbers, $k$ and $m$, are assumed to be real numbers (Drazin & Reid Reference Drazin and Reid1981). The temporal stability analysis is used to determine the evolution of the disturbances with time. Similarly, spatial stability analysis studies the evolution of disturbances in space. For the spatial stability analysis, $\omega$ is taken as a real number and $k$ as a complex number (Drazin Reference Drazin2002). The spatio-temporal stability analysis predicts the evolution of the disturbances in both space and time. In this case, both $\omega$ and $k$ are treated as complex numbers (Huerre & Monkewitz Reference Huerre and Monkewitz1990; Schmid & Henningson Reference Schmid and Henningson2001) and instability is classified as either an absolute or convective instability.

The existence of absolute instability implies the growth of disturbances in both upstream and downstream directions, while the presence of convective instability signifies that the disturbances develop only in the downstream direction from the source of the disturbances (Briggs Reference Briggs1964). Thus, in a convectively unstable flow, at any fixed position in space the unstable disturbances will decay if provided sufficient time (Huerre & Monkewitz Reference Huerre and Monkewitz1990), resulting in mixing only in the downstream direction, while in an absolutely unstable flow, the disturbances will induce mixing both upstream and downstream. This can be illustrated by considering the response of a given base velocity profile to an impulse excitation at asymptotically long times (Huerre & Monkewitz Reference Huerre and Monkewitz1990), where the obtained response is used to determine whether the flow is absolutely or convectively unstable. This section is aimed at understanding the effect of thermocapillarity and shear flow in introducing absolute instability. It must be noted that, for a system with a sustained inlet noise, the convectively unstable flow can also lead to enhancement in mixing.

To understand the absolute and convective instabilities, assume a dispersion relation of the form $\omega ={\mathcal {G}}(k)$, where ${\mathcal {G}}(k)$ is a continuous and differentiable function of $k$. For the absolute instability to exist, the group velocity of the disturbances must vanish for at least one value of $k$, so that ${\partial \omega }/{\partial k}=0$ (Huerre & Monkewitz Reference Huerre and Monkewitz1990; Schmid & Henningson Reference Schmid and Henningson2001). However, the determined saddle point must also obey the causality principle for the existence of the absolute instability (Huerre & Monkewitz Reference Huerre and Monkewitz1990). To obtain the sufficient condition, the equation ${\partial \omega }/{\partial k}=0$ is solved for $k$, which gives the saddle points of the dispersion relation. If the saddle point is of first order in the $k$ plane (denoted by $k_0$) and $\omega _0$ is the value of $\omega$ at the saddle point $k_0$, then a local Taylor expansion about this point gives $(\omega -\omega _{0})\sim (k-k_{0})^{2}$. This shows that the mapping from the $k$ plane to the $\omega$ plane is characterised by angle doubling (i.e. phase doubling) provided that the saddle point is of the first order. Here, the $k$ and $\omega$ planes refer to the $k_r - k_i$ and $\omega _r - \omega _i$ planes, respectively. If for at least one saddle point $\omega _{0i}>0$ then the flow is absolutely unstable else convectively unstable (Huerre & Monkewitz Reference Huerre and Monkewitz1990).

Following the procedure outlined above, we differentiate the dispersion relation (6.14) once with respect to $k$ and solving the resulting equation for $k$ yields three roots. Among the three roots, one is purely imaginary, thus, a spurious saddle point. The other two roots have an equal absolute value of $k_r$ and $k_i$ but $k_r$ are of opposite signs. Thus, there is a mirror cusp point for $k_r<0$ with the same growth rate but having a negative frequency $\omega _r<0$. Here, we restrict ourselves to $k_r>0$, thus, the cusp point under consideration has $\omega _r>0$. It must be noted that both the cusp points have the same critical parameters. To illustrate, consider the saddle point and cusp point for $H=0.4,\mu _r=0.1,\kappa _r=1,Re=10,Ca=0.01$ and $Ma=-10$. The above analysis yields three roots,

(6.18)$$\begin{gather} k_{01}=0.533172 {\rm i} \quad \text{corresponds to}\ \omega_{01}=0.562612{\rm i}, \end{gather}$$

(6.19)$$\begin{gather}k_{02}=0.71133 - 0.266586 {\rm i} \quad \text{corresponds to} \ \omega_{02}= 1.05618 - 0.163357 {\rm i}, \end{gather}$$

(6.20)$$\begin{gather}k_{03}={-}0.71133 - 0.266586 {\rm i} \quad \text{corresponds to}\ \omega_{03}={-}1.05618 - 0.163357 {\rm i}, \end{gather}$$

of which the first root (or saddle point) gives a spurious mode since the corresponding temporally unstable mode does not exist. The second root gives the correct cusp point while the third root gives the mirror cusp point. Furthermore, $\omega _{i0}<0$, thus, a convectively unstable flow. The saddle point for arbitrary parameters is

(6.21)\begin{equation} k_0=\frac{l_1+l_2}{l_3}, \end{equation}

where

(6.22)$$\begin{gather} l_1=2 {\rm i} Ca f_3 3^{1/6} (3 {\rm i} + \sqrt{3}) (f_1 Ma + f_2 Re), \end{gather}$$

(6.23)$$\begin{gather}l_2=3^{1/3} ({\rm i} + \sqrt{3}) \left[9 Ca f_3^2 \omega_0 + \sqrt{3} \sqrt{-Ca^2 f_3^3 [8 Ca (f_1 Ma + f_2 Re)^3 - 27 f_3 \omega_0^2]}\right]^{2/3}, \end{gather}$$

(6.24)$$\begin{gather}l_3 = 12 f_3 \left[9 Ca f_3^2 \omega_0 + \sqrt{3} \sqrt{Ca^2 f_3^3 [{-}8 Ca (f_1 Ma + f_2 Re)^3 + 27 \omega_0^2]}\right]^{1/3}, \end{gather}$$

where $q=\omega _0/f_0$ has been used. The corresponding cusp point can be readily obtained by substituting $k=k_0$ in the dispersion relation (6.14). To understand the role of thermocapillarity and shear flow in causing absolute instability individually and combined, the spatio-temporal analysis results have been divided into three cases.

6.2.1. Purely shear-flow mode ($Ma=0$)

This case corresponds to the case studied by Sahu & Matar (Reference Sahu and Matar2011). The saddle point (6.24) can be readily obtained by substituting $Ma=0$. For realistic dispersion relations, finding the saddle point in the $k$ plane and a cusp point in the $\omega$ plane according to Briggs (Reference Briggs1964) method becomes a cumbersome mathematical and numerical task. A simpler alternative is the method of Kupfer, Bers & Ram (Reference Kupfer, Bers and Ram1987), in which for the prediction of an absolute instability, only the formation of the cusp point in the $\omega$ plane is necessary. If the formed cusp point corresponds to $\omega _{i0}>0$ and is genuine, then the flow is absolutely unstable. Given the relative ease of the Kupfer et al. (Reference Kupfer, Bers and Ram1987) method, it will be employed in the present study, to determine whether the flow is absolutely or convectively unstable.

Briefly, the Kupfer et al. (Reference Kupfer, Bers and Ram1987) method is as follows. First, a temporal stability curve is obtained in the $\omega$ plane by fixing $k_i=0$ and varying $k_r$ in the dispersion relation. Next, a negative value of $k_i$ is fixed and $k_r$ is varied, to obtain a curve in the $\omega$ plane. This step is repeated until a cusp point forms in the $\omega$ plane. A straight line is then drawn parallel to the $\omega _i$ axis from the cusp point extending to $\omega _i \rightarrow \infty$, which will intersect the temporal stability curve at least once. If the number of intersections with the temporal stability curve is an odd number then the formed cusp point is genuine; if the count is even then it is an evanescent cusp point. The existence of a genuine cusp point implies the presence of absolute instability, while that of an evanescent mode signifies a spurious cusp point (Yeo, Khoo & Zhao Reference Yeo, Khoo and Zhao1999, Reference Yeo, Khoo and Zhao2001; Patne & Shankar Reference Patne and Shankar2017; Patne & Ramon Reference Patne and Ramon2020).

Figure 11 illustrates the genuine cusp points in the $\omega$ plane exhibiting absolute and convectively unstable flows. Figure 11 also shows that as the Reynolds number is increased, the flow can become absolutely unstable, thus, there is a critical value of the Reynolds number, $Re_a$, beyond which the flow is absolutely unstable. The saddle point (6.24) and dispersion relation (6.14) are utilised to find out $Re_a$ at which $\omega _{i0} = 0$ for varying $H$. The result is plotted in figure 12. For $H<0.4$, $Re_a$ rapidly increases with increasing $H$ but plateaus in $0.4< H<0.5$ and once again starts steeply increasing for $H>0.6$. The flow is temporally unstable for $H<0.76$, otherwise stable such that, for $H<0.76$, as long as $Re \neq 0$ the flow is temporally unstable, but figure 12 shows that there is a finite $Re$ required to set in absolute instability. Consequently, for $Re< Re_a$, the temporally unstable disturbances will only grow with respect to time but will decay at any fixed position. However, for $Re>Re_a$, the disturbances will start growing both upstream and downstream which will lead to the enhancement of the mixing and may lead to the development of the global mode of instability (Huerre & Monkewitz Reference Huerre and Monkewitz1990). A similar curve can also be obtained for $\mu _r=10$, not shown here for brevity. By symmetry, for such a system, the shear-flow mode will be temporally unstable for $H>0.24$ which will exhibit an absolutely unstable region for $H>0.24$ and stable region for $H<0.24$ with $Re_a \to \infty$ as $H \to 0.24$.

Figure 11. The existence of the (a) absolutely unstable flow at $Re=45$ and (b) convectively unstable flow at $Re=25$ due to the shear-flow mode of instability. The other parameters are $H=0.4,\mu _r=0.1,Ca=0.01$ and $Ma=0$. To determine the genuine character of the formed cusp point, a straight line is drawn from the cusp point and the number of times its intersections with the curve for $k_i=0$ are counted. In both cases, such a line intersects the $k_i=0$ curve once, thus, an odd number of times. Thus, both the cusp points are genuine. In panel (a), $\omega _{i0}>0$, thus, an absolutely unstable flow, while in panel (b), $\omega _{i0}<0$ implying a convectively unstable flow. (a) Absolutely unstable, (b) convectively unstable.

Figure 12. The variation of the critical Reynolds number for the onset of the absolute instability $Re_a$ with $H$ at $\mu _r=0.1, \kappa _r=1, Ma=0$ and $Ca=0.01$. The figure shows the absolutely and convectively unstable regions due to the shear-flow instability. For $H>0.76$, the shear-flow mode is temporally stable.

6.2.2. Purely thermocapillary mode ($Re=0$)

In this case, $Re=0$ is substituted in the dispersion relation (6.14) and the saddle point (6.24). First, consider the case with $q=0$, i.e. the base state is a stationary two-layer system. In such a case, the thermocapillary mode of instability is a stationary mode that is inherently absolutely unstable provided that the flow is temporally unstable. Thus, the system due to pure thermocapillarity in the absence of the base-state flow becomes simultaneously temporally and absolutely unstable. Furthermore, for $q=0$, dispersion relations for the streamwise mode (6.14) and spanwise mode (6.17) become identical, thus, both modes become unstable at the same critical parameters.

Next, consider the case with $q> 0$ but $Re=0$ implying a creeping or stokes flow where the inertial terms in the governing equations are negligible compared with the viscous terms. In this case, the imaginary parts of the complex frequency for streamwise and spanwise modes are identical (see (6.14) and (6.17)), thus, both modes will become temporally unstable at the same critical parameters. However, the streamwise mode has a non-zero base-state flow and is thus a travelling mode while the spanwise mode is stationary. The base-state flow may lead to the existence of the convectively unstable flow due to the streamwise mode, as illustrated in figure 13(b). It must be noted that the streamwise mode does become absolutely unstable albeit at a higher $|Ma|$, as shown in figure 13(a). The spanwise mode, however, becomes absolutely and temporally unstable at identical $|Ma|$ since there is no shear flow in the spanwise direction, thereby making the flow absolutely unstable even in the presence of the shear flow. This also implies that the spanwise mode will dominate the absolute instability region for $Re=0$.

Figure 13. The existence of an (a) absolutely unstable flow at $Ma=-30$ and (b) convectively unstable flow at $Ma=-20$ due to the streamwise thermocapillary mode. The other parameters are $H=0.4,\mu _r=0.1,Ca=0.01,\kappa _r=1$ and $Re=0$. The figure illustrates that the streamwise mode may become convectively or absolutely unstable due to the shear flow. (a) Absolutely unstable, (b) convectively unstable.

6.2.3. Combined shear-flow and thermocapillary mode

This case corresponds to the problem under consideration where we have both active shear-flow and thermocapillary modes of instability with the relevant dispersion relations (6.14) and (6.17) and saddle point (6.24). For the parametric range where the shear flow destabilises and thermocapillarity stabilises, from (6.17) the spanwise mode is stable while from (6.17) the streamwise mode is unstable, thus, only the latter can give rise to the absolute instability. However, for the streamwise mode to introduce absolute instability, it must overcome the thermocapillarity stabilisation.

For the parametric range where the thermocapillarity destabilises, the spanwise mode will lead to absolute and temporal instability at an identical $|Ma|$. Thus, for the streamwise mode to cause an absolute instability with a higher $\omega _{i0}$ at a lower $|Ma|$, the shear-flow mode must be absolutely unstable, i.e. $Re>Re_a$. A high $Re$ implies the requirement of a higher velocity and from figure 12, $Re_a \sim O(1-10^3)$ which puts a restriction on the ability of the streamwise mode to introduce the absolute instability at a higher $\omega _{i0}$. From table 1, if both thermocapillarity and shear flow have a destabilising effect and $Re>Re_a$ ($Re< Re_a$) then the streamwise (spanwise) mode will dominate the absolute instability region. If thermocapillarity has a destabilising (stabilising) effect and shear flow has a stabilising (destabilising) effect then the spanwise (streamwise) mode will dominate the absolute instability region.

Table 1. The table shows the parametric regime in which the streamwise and spanwise modes will dominate the absolutely unstable region. The conclusions can be inferred using the dispersion relations (6.14) and (6.17) for the streamwise and spanwise modes, respectively, and figure 12.

6.3. Weakly nonlinear analysis

Unlike linear stability analysis, to study the weakly nonlinear stability analysis, we must retain the full nonlinear equation. However, working on weakly nonlinear analysis using such an equation even with MATHEMATICA software becomes a cumbersome exercise; thus, the subsequent analysis is restricted to the creeping-flow limit, i.e. $Re \rightarrow 0$. Thus, the aim of this section reduces to determine the effect of the shear flow on the weakly nonlinear evolution of the thermocapillary instability through the volumetric flow rate $q$. It must be noted that a two-layer plane Poiseuille flow with a purely long-wave shear-flow instability generally undergoes a supercritical bifurcation but may undergo a subcritical bifurcation for $H \sim 0.5$ (Hooper & Grimshaw Reference Hooper and Grimshaw1985; Barthelet, Charru & Fabre Reference Barthelet, Charru and Fabre1995).

Following Cheng, Chen & Lai (Reference Cheng, Chen and Lai2001) and Patne et al. (Reference Patne, Agnon and Oron2021), we introduce slow time scales $T_1=\xi t, T_2=\xi ^2 t$, where $\xi \ll 1$ is a small parameter related to the deviation of the Marangoni number $Ma$ from its critical value $Ma_{c}$,

(6.25)\begin{equation} \xi^2 = \frac{Ma-Ma_{c}}{Ma_{c}}. \end{equation}

Next, we expand $Ma$ and $h(x,t)$ into series of $\xi$,

(6.26a)$$\begin{gather} Ma=Ma_{c} (1 + \xi^2), \end{gather}$$

(6.26b)$$\begin{gather}h(x,t) = \xi h_1 (x,t,T_1,T_2) + \xi^2 h_2 (x,t,T_1,T_2)+ \xi^3 h_3 (x,t,T_1,T_2)+\cdots, \end{gather}$$

where $Ma_{c}$ is the critical value of the Marangoni number obtained by solving dispersion relation (6.17) for $\omega _i=0$ with $k=k_c=2 {\rm \pi}/L$ being the cutoff wavenumber and $L$ the length of the periodic domain,

(6.27)\begin{equation} f_1(H,\mu_r,\kappa_r) Ma_c + \frac{f_3(H,\mu_r)}{21} k_c^2 =0. \end{equation}

Next, $k_c=2 {\rm \pi}/L$ and $Ma_{c}$ obtained in the previous step are substituted into the generalized equation (6.8a). The problem is then solved order by order in $\xi$ in terms of $h_i$.

At $O(\delta )$, the linear stability equation is obtained with the solution of the form $h_1 (x,t,T_1,T_2)= A(T_1,T_2) \exp {({\rm i} k_c x - \omega _r t)} + {\rm c.c.}$, where $A(T_1,T_2)$ is the unknown complex amplitude of the perturbation and ${\rm c.c.}$ denotes complex conjugate. It must be noted that the spanwise mode is stationary (see (6.17)), thus, for the spanwise mode, $\omega _r=0$ in the solution while, for the streamwise mode, $\omega _r$ will be the real part of the dispersion relation (6.14). At $O(\xi ^2)$, the solvability condition yields a linear differential equation in terms of the temporal growth rate of the amplitude $A(T_1,T_2)$ in the slow time scale $T_1$. Additionally, the solution of the differential equation at $O(\xi ^2)$ is similar to $h_1$, such that $h_2 (x,t,T_1,T_2)= B(T_1,T_2) \exp {( 2({\rm i} k_c x - \omega t) )} + {\rm c.c.}$ with the complex amplitude $B(T_1,T_2)$ proportional to $A(T_1,T_2)^2$.

At $O(\xi ^3)$, the Landau equation governing the weakly nonlinear temporal evolution of the amplitude function $A \equiv A(T_1,T_2)$ in slow time $T_2$ is obtained,

(6.28)\begin{equation} \partial_{T_2} A=\lambda_1 A + \lambda_2 |A|^2 A, \end{equation}

where the parameter $\lambda _1$ is concerned about the linear growth of the perturbations and will be proportional to $Ma-Ma_c$. For the spanwise mode at $\kappa _r=1$,

(6.29)$$\begin{gather} \lambda_1 ={-}\frac{2}{\xi^2} Ca H^3 k_c^4 (Ma-Ma_c) (1 - H)^3 [1 + H (\mu_r - 1)] \nonumber\\ [1+H (\mu_r - 1) (4 - 6 H + 4 H^2 + H^3 (\mu_r - 1))]. \end{gather}$$

At the onset of instability, $\lambda _1$ vanishes. The other parameter $\lambda _2$ is associated with the weakly nonlinear temporal evolution of the perturbations near the critical point. For the spanwise mode at $\kappa _r=1$,

(6.30)\begin{align} \left. \begin{aligned} & \lambda_2 = Ca (H-1) H k_c^4 \, \frac{\alpha}{\beta},\\ & \alpha = (H-1)^{10} (75 -414 H + 67 H^2)\\ & \quad-2 \mu_r H (H-1)^7 (299 - 1424 H + 2455 H^2 - 1163 H^3 + 201 H^4) \\ & \quad+ H^2 \mu_r^2 (H-1)^5 ({-}1086 + 6394 H - 14433 H^2 + 13839 H^3 - 4415 H^4 + 1005 H^5)\\ & \quad-2 H^3 \mu_r^3 (H-1)^3 (292 - 2727 H + 8735 H^2 - 12686 H^3 + 8018 H^4 - 2010 H^5 + 670 H^6)\\ & \quad+ H^5 \mu_r^4 (H-1)^2 ({-}1304 + 6410 H - 10644 H^2 + 6229 H^3 - 610 H^4 + 1005 H^5)\\ & \quad-2 H^7 \mu_r^5 (H-1) (368 - 801 H + 172 H^2 + 359 H^3 + 201 H^4)\\ & \quad+H^{10} \mu_r^6 ({-}272 + 280 H + 67 H^2),\\ & \beta = 5 [1 + H (\mu_r - 1)] [1 -2 H + H^2 - H^2 \mu_r]^2. \end{aligned} \right\} \end{align}

Similar expressions for $\lambda _1$ and $\lambda _2$ could also be derived for the streamwise mode. However, those will be more complicated owing to non-zero $\omega _r$ and $q$, thus, will not be given here.

For a stationary liquid layer on a heated substrate and other surfaces exposed to an inert gas, $\lambda _2>0$ (Patne et al. Reference Patne, Agnon and Oron2021) and $\lambda _2$ is a real number, thus, the layer undergoes a subcritical pitchfork bifurcation and perturbations will grow beyond the critical parameters. The present analysis for the explored parameter range shows that for a stationary two-layer system, in the absence of the shear flow (i.e. $q=0$), subjected to a wall-normal temperature gradient both streamwise and spanwise modes exhibit a subcritical pitchfork bifurcation. For example, at $\mu _r=2, H=0.8,\kappa _r=1$ and $Ca=0.001$, $\lambda _2 = 0.00114$. However, in the presence of the shear flow (i.e. $q>0$), $\lambda _2$ becomes a complex number, thus, the system will undergo a Hopf bifurcation. The real part of $\lambda _2$, i.e. $\lambda _{2r}$, may become negative for $q>0$, thereby showing the existence of a supercritical Hopf bifurcation. It must be noted that $q$ is not an independent quantity but a function of $\mu _r$ and $H$, viz.,

(6.31)\begin{equation} q = \frac{1+H(\mu_r-1)[4 - 6 H + 4 H^2 + H^3 (\mu_r-1)]}{6 H \mu_r (H-1)} \end{equation}

obtained by integrating the base-state velocity profiles (2.6b) over the flow domain. To illustrate the impact of the shear flow, consider the same case at $\mu _r=2, H=0.8,\kappa _r=1$ and $Ca=0.001$ but with $q=1.4675$, then $\lambda _2 = -5.7177 + 2.4066\textrm {i}$ with $\lambda _{2r}<0$ and $\lambda _{2i} \neq 0$, thus, the flow undergoes a supercritical Hopf bifurcation.

The physical consequence of the transition from a subcritical to supercritical bifurcation could be explained as follows. A stationary liquid layer on a heated substrate and other free surface ruptures or forms dry spots due to thermocapillary instability as follows (Oron et al. Reference Oron, Davis and Bankoff1997; Oron Reference Oron2000). At $Ma=Ma_c$, the layer becomes linearly unstable via the process explained in § 5, thereby leading to unstable thermal perturbations. For $Ma>Ma_c$, the layer undergoes subcritical bifurcation, thus, from (6.28) the amplitude of the unstable thermal perturbations will start increasing which leads to increasing peaks and troughs in the perturbation wave. The trough eventually becomes sufficiently deep to result in the dry spot formation or rupture. As in the present case, if a shear flow is introduced then the symmetry is broken and there will be a net movement of the fluid from left to right assuming a decreasing pressure gradient. In this case, when a trough forms, the net movement of the liquid will fill that trough while decreasing the height of the peak simultaneously. This leads to the absence of the film rupture. Thus, the shear flow could hamper the film rupture and lead to a supercritical bifurcation.