1. Introduction
Due to their small sizes, swimming microorganisms such as bacteria and spermatozoa live in a low-Reynolds-number world, where viscous forces dominate inertial forces. They use a variety of strategies to overcome the challenge of generating self-propulsion at low Reynolds number (Purcell Reference Purcell1977). Extensive studies have elucidated the hydrodynamics of these biological propulsion mechanisms and shed light on their profound roles in various biological processes (Fauci & Dillon Reference Fauci and Dillon2006; Lauga & Powers Reference Lauga and Powers2009). In recent decades, there are also growing interests in developing synthetic active particles that can self-propel like living microorganisms for biomedical and microfluidic applications, including self-assembly (Schwarz-Linek et al. Reference Schwarz-Linek, Valeriani, Cacciuto, Cates, Marenduzzo, Morozov and Poon2012; Wensink et al. Reference Wensink, Kantsler, Goldstein and Dunkel2014), drug delivery (Gao & Wang Reference Gao and Wang2014) and motion-based microsensing (Kagan et al. Reference Kagan, Calvo-Marzal, Balasubramanian, Sattayasamitsathit, Manesh, Flechsig and Wang2009). Some synthetic active particle designs are inspired by biological systems, such as artificial helical propellers (Ghosh & Fischer Reference Ghosh and Fischer2009; Zhang et al. Reference Zhang, Abbott, Dong, Peyer, Kratochvil, Zhang, Bergeles and Nelson2009), which mimic the helical structure of bacterial flagella (Lauga Reference Lauga2016). Other novel designs exploit different physical or physico-chemical mechanisms to achieve self-propulsion (Schweitzer & Farmer Reference Schweitzer and Farmer2003; Bechinger et al. Reference Bechinger, Di Leonardo, Löwen, Reichhardt, Volpe and Volpe2016; Patteson, Gopinath & Arratia Reference Patteson, Gopinath and Arratia2016; Moran & Posner Reference Moran and Posner2017).
In particular, a major class of synthetic active particles converts chemical energy into motility by asymmetric chemical reactions on the particle surface. A variety of novel synthetic active colloids has been developed (Buttinoni et al. Reference Buttinoni, Volpe, Kümmel, Volpe and Bechinger2012; Patiño et al. Reference Patiño, Arqué, Mestre, Palacios and Sánchez2018; Zhou et al. Reference Zhou, Zhang, Tang and Wang2018). For instance, microspheres half-coated in platinum, also known as Janus particles, can self-propel via catalytic decomposition of hydrogen peroxide on the platinum-coated surface (Howse et al. Reference Howse, Jones, Ryan, Gough, Vafabakhsh and Golestanian2007; Sánchez, Soler & Katuri Reference Sánchez, Soler and Katuri2015). While the exact mechanism underlying the resulting motion is still under debate (Brown & Poon Reference Brown and Poon2014; Ebbens et al. Reference Ebbens, Gregory, Dunderdale, Howse, Ibrahim, Liverpool and Golestanian2014; Eloul et al. Reference Eloul, Poon, Farago and Frenkel2020), it has been hypothesized that the motion is diffusiophoretic as a result of the gradients of molecular oxygen produced by the catalytic decomposition on the half-coated surface (Golestanian, Liverpool & Ajdari Reference Golestanian, Liverpool and Ajdari2005, Reference Golestanian, Liverpool and Ajdari2007; Moran & Posner Reference Moran and Posner2017). Since the solute concentration gradient is self-generated, the motion of these active particles is also referred to as self-diffusiophoresis. To model the self-diffusiophoretic motion, a common approach is to separate the fluid domain into outer (the bulk fluid) and inner (the interaction layer) regions, where the short-range solute–particle interaction is assumed to be confined in the interaction layer (Anderson Reference Anderson1989; Jülicher & Prost Reference Jülicher and Prost2009). When the interaction layer is thin relative to particle size, the phoretic effects can be represented by a distribution of effective slip velocities at the particle surface, analogous to the squirmer model (Lighthill Reference Lighthill1952; Blake Reference Blake1971; Pedley Reference Pedley2016) proposed for swimming ciliates such as Paramecium and Volvox. While the slip velocity in the squirmer model is determined by the beating motion of short cilia covering the cell, the slip velocity of a self-diffusiophoretic particle is proportional to the solute concentration gradient and phoretic mobility calculated from the interaction potential in the interaction layer (Anderson Reference Anderson1989; Jülicher & Prost Reference Jülicher and Prost2009). As a remark, recent studies have indicated that the standard self-diffusiophoretic framework described may become ineffective when the reactive species are charged (Brown et al. Reference Brown, Poon, Holm and De Graaf2017; De Corato et al. Reference De Corato, Arqué, Patiño, Arroyo, Sánchez and Pagonabarraga2020; Asmolov, Nizkaya & Vinogradova Reference Asmolov, Nizkaya and Vinogradova2022).
Extensive studies have elucidated various interesting features of self-diffusiophoretic motion in a Newtonian fluid (Moran & Posner Reference Moran and Posner2017). However, most biological fluids such as blood and mucus display non-Newtonian (complex) rheological behaviours, including viscoelasticity and shear-thinning viscosity (Hwang, Litt & Forsman Reference Hwang, Litt and Forsman1969; Baskurt & Meiselman Reference Baskurt and Meiselman2003). Since these synthetic active particles will invariably encounter biological fluids in their biomedical applications, a fundamental question is how different non-Newtonian rheological behaviours impact the propulsion of these active particles (Patteson et al. Reference Patteson, Gopinath and Arratia2016). While many previous theoretical and experimental studies focused on swimming in viscoelastic fluids (Sznitman & Arratia Reference Sznitman and Arratia2014; De Corato, Greco & Maffettone Reference De Corato, Greco and Maffettone2015; Elfring & Lauga Reference Elfring and Lauga2015; Bechinger et al. Reference Bechinger, Di Leonardo, Löwen, Reichhardt, Volpe and Volpe2016; Natale et al. Reference Natale, Datt, Hatzikiriakos and Elfring2017; Saad & Natale Reference Saad and Natale2019; Zöttl & Yeomans Reference Zöttl and Yeomans2019; Li, Lauga & Ardekani Reference Li, Lauga and Ardekani2021; Spagnolie & Underhill Reference Spagnolie and Underhill2023), recent studies have begun to address the effect of shear-thinning viscosity (Montenegro-Johnson, Smith & Loghin Reference Montenegro-Johnson, Smith and Loghin2013; Vélez-Cordero & Lauga Reference Vélez-Cordero and Lauga2013; Gagnon, Keim & Arratia Reference Gagnon, Keim and Arratia2014; Li & Ardekani Reference Li and Ardekani2015; Park et al. Reference Park, Kim, Shin and Weitz2016; Gómez et al. Reference Gómez, Godínez, Lauga and Zenit2017). A shear-thinning fluid loses its viscosity with applied shear due to changes in its microstructure. Such a non-Newtonian behaviour was found to impact the propulsion of various low-Reynolds-number swimmers in qualitatively different manners (Datt et al. Reference Datt, Zhu, Elfring and Pak2015, Reference Datt, Natale, Hatzikiriakos and Elfring2017; Demir et al. Reference Demir, Lordi, Ding and Pak2020; Qu & Breuer Reference Qu and Breuer2020; Qin et al. Reference Qin, Peng, Chen, Nganguia, Zhu and Pak2021; van Gogh et al. Reference van Gogh, Demir, Palaniappan and Pak2022). In particular, Datt et al. (Reference Datt, Zhu, Elfring and Pak2015) considered a general spherical squirmer model in a shear-thinning fluid, and demonstrated how shear-thinning rheology can both enhance and hinder its propulsion, depending on specific details of the slip velocity. Interestingly, in a later study (Datt et al. Reference Datt, Natale, Hatzikiriakos and Elfring2017), spherical self-diffusiophoretic particles were found to always swim slower in a shear-thinning fluid than in a Newtonian fluid for any level of active surface coverage. This also prompts the question of to what extent the conclusion of hindered swimming continues to hold for non-spherical self-diffusiophoretic particles.
Swimmers with non-spherical shapes are commonly found in both nature and engineered systems. For instance, ciliates such as Paramecium and Tetrahymena have approximately prolate spheroidal body shapes. Keller & Wu (Reference Keller and Wu1977) considered a spheroidal squirmer model, which was extended by later studies to probe the effect of geometrical shape upon ciliary locomotion (Ishimoto & Gaffney Reference Ishimoto and Gaffney2013; Theers et al. Reference Theers, Westphal, Gompper and Winkler2016; Poehnl, Popescu & Uspal Reference Poehnl, Popescu and Uspal2020). Furthermore, synthetic active particles of non-spherical shapes, including prolate spheroids and general slender bodies, were also fabricated and studied experimentally and theoretically (Champion & Mitragotri Reference Champion and Mitragotri2006; Champion, Katare & Mitragotri Reference Champion, Katare and Mitragotri2007; Glotzer & Solomon Reference Glotzer and Solomon2007; Shemi & Solomon Reference Shemi and Solomon2018; Yariv Reference Yariv2019; Poehnl et al. Reference Poehnl, Popescu and Uspal2020; Poehnl & Uspal Reference Poehnl and Uspal2021; Katsamba et al. Reference Katsamba, Butler, Koens and Montenegro-Johnson2022; Zhu & Zhu Reference Zhu and Zhu2023). In particular, Poehnl et al. (Reference Poehnl, Popescu and Uspal2020) analysed the self-diffusiophoretic motion of spheroidal particles in a Newtonian fluid. However, much less is known about these spheroidal active particles in non-Newtonian fluids. A recent study has suggested that shear-thinning rheology can indeed enhance the propulsion of a squirming spheroid (van Gogh et al. Reference van Gogh, Demir, Palaniappan and Pak2022). However, it remains unclear whether or not a spheroidal self-diffusiophoretic particle can swim faster in a shear-thinning fluid than in a Newtonian fluid, which was shown to be impossible for the spherical case (Datt et al. Reference Datt, Natale, Hatzikiriakos and Elfring2017). In this work, we fill in this knowledge gap by analysing the self-diffusiophoretic motion of a spheroidal particle in a shear-thinning fluid. We use asymptotic analysis and numerical simulations to reveal how shear-thinning viscosity impacts the propulsion speed of a prolate spheroidal self-diffusiophoretic particle with different eccentricities and levels of active surface coverage. Our results have uncovered some propulsion behaviours not observed in the spherical case, and we present symmetry considerations to help elucidate the emergence of these new features as a combined effect of particle anisotropy and nonlinear fluid rheology.
2. Problem formulation
2.1. Geometrical set-up
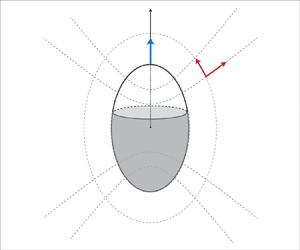
We examine a prolate spheroidal particle characterized by a major axis 
$a$, and a minor axis 
$b$, as illustrated in figure 1. The prolate spheroidal coordinates 
$(\tau, \zeta, \phi )$, where 
$\tau \in [1,\infty )$, 
$\zeta \in [-1,1]$ and 
$\phi \in [0, 2{\rm \pi} )$, are employed in this work. The prolate spheroidal coordinates can be related to the cylindrical coordinates 
$(r, z, \phi )$ as
\begin{equation} r =c_f\,\sqrt{\tau^2-1}\,\sqrt{1-\zeta^2} ,\quad z = c_f \tau\zeta, \end{equation}
where 
$r^2=x^2+y^2$, and 
$c_f = \sqrt {a^2-b^2}$. The surface of the spheroidal particle is given by
\begin{equation} \frac{z^2}{a^2}+\frac{r^2}{b^2} = 1, \end{equation}
which translates to 
$r = b\sqrt {1-\zeta ^2}$ and 
$z = a\zeta$. Comparing with (2.1a,b), the spheroidal particle surface can be simply represented by
\begin{equation} \tau =\tau_0 = 1/e, \end{equation}
where 
$e = c_f/a$ is the eccentricity. The basis vectors in the prolate spheroidal coordinates, represented as 
$(\boldsymbol {e}_\tau,\boldsymbol {e}_\zeta,\boldsymbol {e}_\phi )$, are related to the basis vectors in cylindrical coordinates, denoted 
$(\boldsymbol {e}_r,\boldsymbol {e}_z,\boldsymbol {e}_\phi )$, in the following manner:
\begin{equation} \boldsymbol{e}_\tau = \frac{c_f\tau}{h_\zeta}\,\boldsymbol{e}_r+\frac{c_f\zeta}{h_\tau}\,\boldsymbol{e}_z, \quad \boldsymbol{e}_\zeta =-\frac{c_f \zeta}{h_\tau}\,\boldsymbol{e}_r+\frac{c_f \tau}{h_\zeta}\,\boldsymbol{e}_z. \end{equation}The metric coefficients for the prolate spheroidal coordinates are given by
\begin{equation} h_\tau = \frac{c_f\,\sqrt{\tau^2-\zeta^2}}{\sqrt{\tau^2-1}},\quad h_\zeta = \frac{ c_f\, \sqrt{\tau^2-\zeta^2}} {\sqrt{1-\zeta^2}} ,\quad h_{\phi} = c_f\, \sqrt{\tau^2-1}\,\sqrt{1-\zeta^2}. \end{equation}
On the surface of the prolate spheroidal particle, the unit normal vector pointing outwards is given by 
$\boldsymbol {n} = \boldsymbol {e}_\tau$, and the unit tangent vector pointing upwards is given by 
$\boldsymbol {t} = \boldsymbol {e}_\zeta$, as illustrated in figure 1.
Figure 1. Geometric configuration of a spheroidal Janus particle. The model is presented in prolate spheroidal coordinates 
$(\tau,\zeta,\phi )$. The coordinate grid is indicated by dashed lines, and the basis vectors are denoted 
$\boldsymbol {e}_\tau$ and 
$\boldsymbol {e}_\zeta$. The active cap of the particle, depicted in grey, spans from 
$\zeta = -1$ to 
$\zeta _0$. The rest of the surface is inert.
2.2. Governing equations and boundary conditions
We treat the problem within the continuum framework of self-diffusiophoretic propulsion (Golestanian et al. Reference Golestanian, Liverpool and Ajdari2007; Michelin & Lauga Reference Michelin and Lauga2014), where the particle interacts with a solute species of local concentration 
$C$. Here, we consider an axisymmetric Janus spheroidal particle with chemically active and inert compartments, with the polar position 
$\zeta _0$ specifying the active surface coverage as illustrated in figure 1. On the active portion of the particle surface (
$\tau = \tau _0$, 
$\zeta \leq \zeta _0$), we assume that the solute is emitted/absorbed with a fixed flux characterized by the activity 
$A$:
\begin{equation} D\boldsymbol{n}\boldsymbol{\cdot}\boldsymbol{\nabla} C =-A, \end{equation}
where 
$D$ is the diffusivity, 
$A>0$ corresponds to solute emission, and 
$A<0$ corresponds to the solute absorption. The activity becomes zero (
$A=0$) on the inert portion of the particle surface (
$\tau = \tau _0$, 
$\zeta >\zeta _0$). Under the assumption of a thin interaction layer (Golestanian et al. Reference Golestanian, Liverpool and Ajdari2005, Reference Golestanian, Liverpool and Ajdari2007; Michelin & Lauga Reference Michelin and Lauga2014; Datt et al. Reference Datt, Natale, Hatzikiriakos and Elfring2017), the effective slip velocity at the surface of the particle,
\begin{equation} \boldsymbol{u}_s = M (\boldsymbol{I}-\boldsymbol{n}\boldsymbol{n})\boldsymbol{\cdot}\boldsymbol{\nabla} C, \end{equation}
is proportional to the tangential concentration gradients and the phoretic mobility 
$M$ determined by the interaction potential profile (Anderson Reference Anderson1989; Michelin & Lauga Reference Michelin and Lauga2014). In general, when the interactions are attractive, 
$M<0$ and the slip velocity is opposite to the concentration gradients; when the interactions are repulsive, 
$M>0$ and the slip velocity is along the concentration gradients. In this work, we present results for the case where 
$M>0$ and 
$A>0$ without loss of generality. By symmetry and linearity, a flipping of the sign of 
$M$ or 
$A$ only inverts the direction of swimming velocity in the results presented below.
In the bulk fluid, the solute concentration is governed by an advection–diffusion equation
\begin{equation} \frac{\partial C}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla}C = D\,\nabla^2 C, \end{equation}
where 
$\boldsymbol {u}$ is the velocity of the flow, and the solute concentration in the far field is denoted by 
$C_\infty$. In the inertialess regime, the flow generated by the phoretic slip velocity is governed by the momentum and continuity equations, respectively, as
\begin{equation} \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{\sigma} = \boldsymbol{0},\quad \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{u} = 0, \end{equation}
where 
$\boldsymbol {\sigma } = -p \boldsymbol {I} + \boldsymbol {T}$, 
$p$ is the pressure, 
$\boldsymbol {I}$ is the identity tensor, and 
$\boldsymbol {T}$ is the deviatoric stress tensor. The boundary condition for the velocity field on the particle surface in the laboratory frame is given by
\begin{equation} \boldsymbol{u}(\tau = \tau_0) = \boldsymbol{u}_s(\zeta)+\boldsymbol{U}, \end{equation}
where 
$\boldsymbol {u}_s$ is the phoretic slip velocity given by (2.7), and 
$\boldsymbol {U} = U \boldsymbol {e}_z$ is the unknown propulsion velocity, which occurs in the 
$z$-direction by axisymmetry. The flow decays to zero in the far field, 
$\boldsymbol {u}(\tau \to \infty ) = \boldsymbol {0}$. The system of equations is closed by enforcing the force-free condition on the particle,
\begin{equation} \int_S \boldsymbol{n}\boldsymbol{\cdot} \boldsymbol{\sigma}\, {\rm d}S= \boldsymbol{0}, \end{equation}
where 
$S$ denotes the particle surface.
2.3. Shear-thinning rheology
To probe the effect of shear-thinning rheology on the self-diffusiophoretic motion, we consider here the Carreau constitutive model (Bird, Armstrong & Hassager Reference Bird, Armstrong and Hassager1987), which has been shown to be effective in capturing the shear-thinning viscosity of different biological fluids (Vélez-Cordero & Lauga Reference Vélez-Cordero and Lauga2013). In the Carreau model, the deviatoric stress is given by
\begin{equation} \boldsymbol{T} =[
\mu_\infty+(\mu_0-\mu_\infty)(1+\tfrac{1}{2}\lambda^2\dot{\boldsymbol{\gamma}}
: \dot{\boldsymbol{\gamma}}
)^{({n-1})/{2}}]\dot{\boldsymbol{\gamma}}, \end{equation}
where 
$\mu _0$ and 
$\mu _\infty$ represent, respectively, the viscosities when the shear rate is zero and infinite, 
$1/\lambda$ characterizes the critical shear rate at which the non-Newtonian behaviour becomes significant, and 
$\dot {\boldsymbol {\gamma }} = \boldsymbol {\nabla } \boldsymbol {u}+ \left ( \boldsymbol {\nabla } \boldsymbol {u} \right )^{\rm T}$ is the strain rate tensor. For low and high shear rates (relative to the critical shear rate), the fluid tends to behave as a Newtonian fluid with viscosity, respectively, 
$\mu _0$ and 
$\mu _\infty$. In the intermediate regime, the fluid displays a power fluid behaviour, with the index 
$n < 1$ characterizing the degree of shear-thinning.
2.4. Non-dimensionalization
We non-dimensionalize the problem by scaling lengths with 
$a$, velocities with 
$MA/D$, stresses with 
$\mu _0 MA/Da$, and the solute concentration with 
$Aa/D$. Hereafter, we consider only dimensionless quantities and use the same symbols as their dimensional counterparts for convenience.
We denote the solute concentration relative to the far-field solute concentration as 
$c=C-C_\infty$, which satisfies the dimensionless advection–diffusion equation,
\begin{equation} Pe \left(\frac{\partial c}{\partial t}+\boldsymbol{u}\boldsymbol{\cdot}\boldsymbol{\nabla}c\right)= \nabla^2 c. \end{equation}
Here, the Péclet number 
$Pe = MAa/D^2$ characterizes the relative importance of advective to diffusive transport of the solute. We assume that the diffusivity is high enough and neglect the alteration in solute distribution caused by the flow from phoretic effects, and that the solute concentration becomes harmonic,
\begin{equation} \nabla^2 c= 0. \end{equation}
The dimensionless boundary condition on the active portion of the particle surface (
$\tau = \tau _0$, 
$\zeta \leq \zeta _0$) is given by
\begin{equation} \boldsymbol{n}\boldsymbol{\cdot}\boldsymbol{\nabla} c =-1, \end{equation}
whereas that on the inert portion (
$\tau = \tau _0$, 
$\zeta >\zeta _0$) is simply
\begin{equation} \boldsymbol{n}\boldsymbol{\cdot}\boldsymbol{\nabla} c = 0. \end{equation}The relative solute concentration decays to zero at infinity:
\begin{equation} c(\tau \rightarrow \infty) = 0. \end{equation}Given that the solute concentration is decoupled, the governing equations for the fluid align with those presented in (2.9a,b). The Carreau constitutive equation is rendered dimensionless as
\begin{equation} \boldsymbol{T}
=\dot{\boldsymbol{\gamma}}+ (1-\beta)[-1
+(1+\tfrac{1}{2}{\textit{Cu}}^2\dot{\boldsymbol{\gamma}}
: \dot{\boldsymbol{\gamma}}
)^{({n-1})/{2}}]\dot{\boldsymbol{\gamma}},
\end{equation}
where 
$\beta = \mu _\infty /\mu _0$ is the viscosity ratio, and 
${\textit {Cu}}= \lambda MA/aD$ is the Carreau number, which compares the characteristic shear rate 
$MA/aD$ to the critical shear rate 
$1/\lambda$.
In the laboratory frame, the dimensionless boundary condition for the velocity field on the particle surface is given by 
$\boldsymbol {u}(\tau = \tau _0) = \boldsymbol {u}_s + U \boldsymbol {e}_z$, where the slip velocity in dimensionless form reads
\begin{equation} \boldsymbol{u}_s = (\boldsymbol{I}-\boldsymbol{n}\boldsymbol{n})\boldsymbol{\cdot}\boldsymbol{\nabla}c, \end{equation}
and the flow decays to zero in the far field, 
$\boldsymbol {u}(\tau \to \infty ) = \boldsymbol {0}$. In the following calculations, we determine the unknown propulsion speed 
$U$ of the spheroidal self-diffusiophoretic particle in a shear-thinning fluid.
3. Asymptotic analysis and numerical simulations
3.1. Asymptotic analysis
The solute concentration can be obtained by solving the Laplace equation (2.14) with boundary conditions (2.15)–(2.17) in the prolate spheroidal coordinates. An analytical solution in form of a series is given by (Popescu et al. Reference Popescu, Dietrich, Tasinkevych and Ralston2010)
\begin{equation} c(\tau,\zeta) = \sum_{n=0}^\infty \rho_n\,Q_n(\tau)\,P_n(\zeta), \end{equation}
where 
$P_n(\zeta )$ and 
$Q_n(\tau )$ are, respectively, the Legendre functions of the first and second kinds. As 
$\tau \geq \tau _0>1$, the Legendre functions of the second kind vanish when 
${\tau \to \infty}$, satisfying the far-field boundary condition for the relative concentration, (2.17). By substituting the solution (3.1) into the boundary conditions at the particle surface, (2.15)–(2.16), and employing the orthogonality of the Legendre functions, the coefficients 
$\rho _n$ in the series solution are determined as
\begin{equation} \rho_n(\tau_0,\zeta_0) =-\frac{2n+1}{2}\,\frac{1}{Q'_n(\tau_0)\,\tau_0\,\sqrt{\tau_0^2-1}}\int_{-1}^{\zeta_0} \sqrt{\tau_0^2-\zeta^2}\,P_n(\zeta) \,\text{d}\zeta. \end{equation}
By employing the solution (3.1) in (2.19), the resulting phoretic slip velocity at the particle surface, 
$\boldsymbol {u}_s(\zeta ) = u_s \boldsymbol {e}_\zeta$, is given by
\begin{equation} u_s(\zeta) = \tau_0\sum_{n=0}^\infty B_n\,\frac{P^1_n(\zeta)}{\sqrt{\tau_0^2-\zeta^2}}, \end{equation}where the phoretic modes are given by
\begin{equation} B_n =-\rho_n(\tau_0,\zeta_0)\,Q_n(\tau_0), \end{equation}
and 
$P_n^1$ is the associated Legendre function with order 1.
We perform an asymptotic analysis in the weakly non-Newtonian regime where the deviation of the viscosity ratio from unity, 
$\epsilon = 1-\beta$, is small. We expand the physical quantities in powers of 
$\epsilon$ as
\begin{align} \{\boldsymbol{u}, \dot{\boldsymbol{\gamma}}, \boldsymbol{\sigma}, p, \boldsymbol{T},U\} = \{\boldsymbol{u}_0, \dot{\boldsymbol{\gamma}}_0,\boldsymbol{\sigma}_0, p_0, \boldsymbol{T}_0,U_0\} +\epsilon \{\boldsymbol{u}_1, \dot{\boldsymbol{\gamma}}_1,\boldsymbol{\sigma}_1, p_1, \boldsymbol{T}_1,U_1\}+O(\epsilon^2). \end{align}
The zeroth-order problem corresponds to the Newtonian problem, where 
$\boldsymbol {\sigma }_0 =-p_0\boldsymbol {I}+ \dot {\boldsymbol {\gamma }}_0$ and 
$\dot {\boldsymbol {\gamma }}_0 = \boldsymbol {\nabla }\boldsymbol {u}_0+(\boldsymbol {\nabla }\boldsymbol {u}_0)^{\rm T}$. For boundary conditions, we have 
$\boldsymbol {u}_0(\tau = \tau _0) =U_0\boldsymbol {e}_z+ u_s \boldsymbol {e}_\zeta$ on the particle surface, and 
$\boldsymbol {u}_0(\tau \to \infty ) = \boldsymbol {0}$ in the far field, where 
$u_s$ is given in (3.3). The flow field 
$\boldsymbol {u}_0$ and propulsion speed 
$U_0$ of this zeroth-order Newtonian problem were obtained in previous works (Leshansky et al. Reference Leshansky, Kenneth, Gat and Avron2007; Popescu et al. Reference Popescu, Dietrich, Tasinkevych and Ralston2010; Lauga & Michelin Reference Lauga and Michelin2016; Poehnl et al. Reference Poehnl, Popescu and Uspal2020), which we summarize in Appendix A.
We consider the first-order non-Newtonian correction to the Newtonian problem. To the order of 
$\epsilon$, the flow satisfies
$$\begin{gather} \boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{\sigma}_1 = \boldsymbol{0}, \end{gather}$$
$$\begin{gather}\boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{u}_1 = 0, \end{gather}$$
where 
$\boldsymbol {\sigma }_1 = -p_1 \boldsymbol {I}+\boldsymbol {T}_1$, and the stress tensor is 
$\boldsymbol {T}_1 = \dot {\boldsymbol {\gamma }}_1 + \boldsymbol{\mathsf{A}}$, with
\begin{equation}
\boldsymbol{\mathsf{A}} = [-1
+(1+\tfrac{1}{2}{\textit{Cu}}^2\dot{\boldsymbol{\gamma}}_0
: \dot{\boldsymbol{\gamma}}_0
)^{({n-1})/{2}}]\dot{\boldsymbol{\gamma}}_0.
\end{equation}
For boundary conditions, we have the first correction to the Newtonian propulsion velocity, 
$\boldsymbol {u}_1(\tau = \tau _0) =\boldsymbol {U}_1 = U_1\boldsymbol {e}_z$, on the particle surface, and 
$\boldsymbol {u}_1(\tau \to \infty ) = \boldsymbol {0}$ in the far field. To obtain the propulsion speed 
$U_1$, we bypass detailed calculations of the flow via a reciprocal theorem approach (Lauga Reference Lauga2014). By considering an auxiliary Stokes flow due to a prolate spheroid of the same geometry translating at a velocity 
$\hat {\boldsymbol {U}}$, where the velocity 
$\hat {\boldsymbol {u}}$ and stress 
$\hat {\boldsymbol {\sigma }}$ fields satisfy 
$\boldsymbol {\nabla }\boldsymbol {\cdot }\hat {\boldsymbol {\sigma }} = \boldsymbol {0}$ and 
$\boldsymbol {\nabla }\boldsymbol {\cdot }\hat {\boldsymbol {u}}=0$, one can form the relation
\begin{equation} \hat{\boldsymbol{u}}\boldsymbol{\cdot}(\boldsymbol{\nabla}\boldsymbol{\cdot}\boldsymbol{\sigma}_1) = \boldsymbol{u}_1\boldsymbol{\cdot}(\boldsymbol{\nabla}\boldsymbol{\cdot}\hat{\boldsymbol{\sigma}}) = 0. \end{equation}
By integrating the relation over the fluid volume 
$V$ exterior to the particle surface 
$S$ and applying the divergence theorem, one can obtain
\begin{equation} \int_S{\boldsymbol{n}\boldsymbol{\cdot}\hat{{\boldsymbol{\sigma}}}\boldsymbol{\cdot}{\boldsymbol{u}}_1} \,\text{d}S - \int_S{\boldsymbol{n}\boldsymbol{\cdot}{\boldsymbol{\sigma}}_1 \boldsymbol{\cdot}{\hat{\boldsymbol{u}}}} \, \text{d}S=\int_V{\boldsymbol{\sigma}_1:\boldsymbol{\nabla}\hat{\boldsymbol{u}}}\, \text{d}V-\int_V{\hat{\boldsymbol{\sigma}}:\boldsymbol{\nabla}\boldsymbol{u}_1} \,\text{d}V. \end{equation}
We note that due to the force-free condition at 
$O(\epsilon )$, 
$\int _S{\boldsymbol {n}\boldsymbol {\cdot }{\boldsymbol {\sigma }}_1 } \,\text {d}S = \boldsymbol {0}$, the second integral on the left-hand side of (3.10) is given by 
$\int _S{\boldsymbol {n}\boldsymbol {\cdot }{\boldsymbol {\sigma }}_1 \boldsymbol {\cdot }{\hat {\boldsymbol {u}}}} \, \text {d}S = (\int _S{\boldsymbol {n}\boldsymbol {\cdot }{\boldsymbol {\sigma }}_1 } \,\text {d}S)\boldsymbol {\cdot } \hat {\boldsymbol {U}} = 0$. Upon substituting the constitutive equations for 
$\hat {\boldsymbol {\sigma }}$ and 
$\boldsymbol {\sigma }_1$, and applying the boundary condition 
$\boldsymbol {u}_1 = \boldsymbol {U}_1$ on 
$S$, (3.10) simplifies to
\begin{equation} \hat{\boldsymbol{F}} \boldsymbol{\cdot} \boldsymbol{U}_1 =\int_V{\boldsymbol{\mathsf{A}}:\boldsymbol{\nabla}\hat{\boldsymbol{u}}}\,\text{d}V, \end{equation}
where 
$\hat {\boldsymbol {F}} = \int _S \boldsymbol {n}\boldsymbol {\cdot }\hat {\boldsymbol {\sigma }} \,\text {d}S =-8{\rm \pi} \tau _0^{-1}[(\tau _0^2+1)\coth ^{-1}\tau _0-\tau _0]^{-1}\boldsymbol {e}_z$ is the drag on the translating prolate spheroid in the auxiliary problem. Therefore, the first-order correction to the phoretic speed is given in terms of a volume integral in prolate spheroidal coordinates as
\begin{equation} U_1 =-\frac{(\tau_0^2+1)\coth^{-1}\tau_0-\tau_0}{4 \tau_0^2}\int_{\tau_0}^\infty \int_{-1}^1 (\boldsymbol{\mathsf{A}}:\boldsymbol{\nabla}\hat{\boldsymbol{u}})(\tau^2-\zeta^2) \,\text{d}\zeta \,\text{d}\tau, \end{equation}which can be evaluated with quadrature.
3.2. Numerical simulation
To extend the results beyond the weakly non-Newtonian regime considered in the asymptotic analysis in § 3.1, we develop numerical simulations based on the finite element method using the partial differential equation (PDE) module of the commercial package COMSOL to perform fully coupled simulations of the momentum and continuity equations (2.9a,b) with the Carreau–Yasuda constitutive equation (2.18), and the solute transport equation (2.14). We use an axisymmetric computational domain with dimensionless radius 
$500$ to simulate the self-propulsion of the Janus particle in an unbounded fluid. A sufficiently large domain size is important to guarantee accuracy due to the slow spatial decay of flows at low Reynolds numbers. The Janus particle is modelled as a half-spheroid whose major axis coincides with the axis of symmetry. The simulations are performed in a reference frame that is co-moving with the particle, and the far-field velocity is equal to the negative swimming velocity determined by the force-free condition (2.11). The computational domain is discretized by approximately 100 000–127 000 triangular elements, and the mesh is locally refined near the particle to properly resolve the spatial variation of the viscosity. Taylor–Hood and quadratic Lagrange elements are adopted to discretize the flow field (
$\boldsymbol {u}, p$) and the concentration field 
$c$, respectively. It is important to note that, theoretically, there exists a discontinuous alteration in surface activity between the active and inert compartments of the Janus particle. However, when modelled numerically, this abrupt transition can cause significant numerical errors, particularly at lower 
${\textit {Cu}}$ values. To alleviate the numerical errors, we introduce a minor smoothing transition, dependent on the mesh size, to the surface activity in the vicinity of the discontinuity.
In addition to comparing with the asymptotic results in this work, we have validated our numerical implementation against previous results for a spherical Janus particle in a shear-thinning fluid (Datt et al. Reference Datt, Natale, Hatzikiriakos and Elfring2017) and a spheroidal Janus particle in a Newtonian fluid (Popescu et al. Reference Popescu, Dietrich, Tasinkevych and Ralston2010); see Appendix B for more details.
4. Results and discussion
4.1. Effect of particle eccentricity on self-diffusiophoresis in a shear-thinning fluid
In a Newtonian fluid, the dependence of the self-diffusiophoretic propulsion speed on the particle geometry and catalyst coverage was examined in detail by previous works (Popescu et al. Reference Popescu, Dietrich, Tasinkevych and Ralston2010; Poehnl et al. Reference Poehnl, Popescu and Uspal2020). Here, we investigate how shear-thinning rheology impacts the propulsion speeds (
$U$) relative to their corresponding Newtonian values (
$U_0$). The special case of a spherical Janus particle was examined by Datt et al. (Reference Datt, Natale, Hatzikiriakos and Elfring2017), and it was shown to always swim slower in a shear-thinning fluid than in a Newtonian fluid across a wide range of 
${\textit {Cu}}$. In figure 2(a), we reproduce these results by setting the eccentricity to zero (
$e=0$, black solid line and black circles): the spherical Janus particle displays reduced propulsion speed (
$U/U_0 < 1$) as 
${\textit {Cu}}$ increases from zero, reaching a local minimum when 
${\textit {Cu}}$ is around 
${O}(1)$, before approaching the Newtonian value again when 
${\textit {Cu}}$ becomes exceedingly large. We employ the spherical case as a benchmark to probe the effect of particle geometry by varying the eccentricity from 
$e=0$ to 
$e=0.99$. From spherical to moderately spheroidal particles (e.g. 
$e=0.6$), the increased eccentricity does not affect the qualitative features of the speed dependence on 
${\textit {Cu}}$.
Figure 2. (a) Swimming speed of a spheroidal Janus particle 
$U$ in a shear-thinning fluid relative to its corresponding Newtonian value 
$U_0$ as a function of the Carreau number for different values of eccentricity 
$e$ when the shear-thinning effect is weak (
$\beta = 0.9$). The asymptotic results in the small 
$\epsilon = 1-\beta$ limit (lines) agree well with numerical simulations (symbols). For large eccentricities (e.g. 
$e = 0.9$ and 0.99), the Janus particle can swim faster in a shear-thinning fluid than in a Newtonian fluid. (b) Numerical results for a strong shear-thinning effect (
$\beta = 0.1$); the qualitative behaviours remain the same, the speed variations are substantially larger. In both (a,b), the active coverage of the particle is 
$\zeta _0 = 0$, and the shear-thinning power law index is 
$n = 0.25$.
However, for more slender spheroidal particles (e.g. 
$e=0.99$), our results reveal that a self-diffusiophoretic particle can also swim faster in a shear-thinning fluid than in a Newtonian fluid (blue dotted lines and blue upward triangles), which was shown to be impossible for a spherical particle (black solid line and black circles) (Datt et al. Reference Datt, Natale, Hatzikiriakos and Elfring2017). These new behaviours are predicted by both the asymptotic results from the reciprocal theorem (lines) and results from numerical simulations (symbols) in the weakly shear-thinning regime (
$\beta =0.9$), which display excellent agreement, as shown in figure 2(a). We verify that these new features continue to exist beyond the weakly non-Newtonian regime by considering a small viscosity ratio (
$\beta =0.1$) in figure 2(b), where we observe the same qualitative behaviours but with greater magnitudes of speed enhancement and reduction at different 
${\textit {Cu}}$.
4.2. Effect of active surface coverage on self-diffusiophoresis in a shear-thinning fluid
We focus in § 4.1 on Janus particles with half active surface coverage (
$\zeta _0 = 0$), which was shown to maximize the self-diffusiophoretic propulsion speed of spherical and spheroidal particles in a Newtonian fluid. Here, we examine whether or not this feature remains the same when the fluid displays shear-thinning rheology. In figure 3(a), we display the propulsion speed relative to its Newtonian value as a function of particle eccentricity and active surface coverage, which varies between 
$\zeta _0=-1$ (no active surface coverage) and 
$\zeta _0=1$ (full active surface coverage). It is observed that, regardless of the active surface coverage, the regime of enhanced propulsion (
$U/U_0>1$, indicated by the dashed line in figure 3a) occurs only when the particle eccentricity goes beyond a threshold value of approximately 0.7. In addition, the enhanced propulsion occurs for a wider range of active surface coverage with increased particle eccentricity. For instance, among all the values of active surface coverage examined in figure 3(a), while enhanced propulsion is observed in only approximately 
$15\,\%$ of the cases when 
$e=0.8$, the percentage increases to more than 60 % when 
$e=0.99$. Another interesting feature is the asymmetry in the occurrence of enhanced propulsion with respect to the active surface coverage: the regime is not symmetrically distributed around 
$\zeta _0$, but instead skewed towards the positive direction of 
$\zeta$. This observation also suggests that the specific case of half active coverage (
${\zeta _0=0}$), which was shown to maximize self-diffusiophoretic propulsion in previous works (Popescu et al. Reference Popescu, Dietrich, Tasinkevych and Ralston2010; Datt et al. Reference Datt, Natale, Hatzikiriakos and Elfring2017; Poehnl et al. Reference Poehnl, Popescu and Uspal2020), may no longer be optimal for spheroidal particles in shear-thinning fluids.
Figure 3. (a) Swimming speed of a spheroidal Janus particle in a shear-thinning fluid with different values of eccentricity 
$e$ and active coverage 
$\zeta _0$. The dashed line indicates the particles for which the swimming speed is enhanced by the shear-thinning effect. (b) Relative swimming efficiency of a spheroidal Janus particle with different values of eccentricity and active coverage. For all data points, 
${\textit {Cu}} = 20\,000$, 
$\beta = 0.1$ and 
$n = 0.25$.
In addition to propulsion speed, efficiency is another relevant performance measure of the swimming motion. Recent studies have investigated how the geometrical shapes of active particles influence their efficiency of swimming in a Newtonian fluid (Daddi-Moussa-Ider et al. Reference Daddi-Moussa-Ider, Nasouri, Vilfan and Golestanian2021; Guo et al. Reference Guo, Zhu, Liu, Bonnet and Veerapaneni2021). Here, we adopt the widely used definition of swimming efficiency introduced by Lighthill (Reference Lighthill1975) for low-Reynolds-number swimmers, 
$\eta = \boldsymbol {F} \boldsymbol {\cdot } \boldsymbol {U}/P$, to characterize the efficiency of swimming in a shear-thinning fluid. Lighthill's efficiency compares the power dissipation of the swimmer, 
$P = \int_S \boldsymbol {n} \boldsymbol {\cdot } \boldsymbol {\sigma } \boldsymbol {\cdot } \boldsymbol {u} \,{\rm d}S$, with the power required to move a particle with identical shape at the same swimming velocity 
$\boldsymbol {U}$ against the drag force 
$\boldsymbol {F}$. Our results show that while speed enhancement occurs only in a specific domain of eccentricity and active surface coverage (figure 3a), the swimming efficiency in a shear-thinning fluid is consistently enhanced, 
$\eta /\eta _0>1$, relative to the corresponding swimming efficiency in a Newtonian fluid (
$\eta _0$) in the entire domain shown in figure 3(b). Taken together, these results reveal that self-diffusiophoretic propulsion can be enhanced both speed-wise and efficiency-wise in a shear-thinning fluid relative to the corresponding case in a Newtonian fluid.
Next, we further examine the asymmetry observed in the enhanced propulsion speed with respect to the active surface coverage shown in figure 3(a). We display in figure 4(a) the absolute propulsion speed of spherical and spheroidal particles as functions of active surface coverage at different values of 
${\textit {Cu}}$. In figure 4(a), we observe that the propulsion speed of a spherical particle is symmetric about the half surface coverage (
$\zeta _0$), which maximizes the speed in both Newtonian (
${\textit {Cu}}=0$) and shear-thinning (
${\textit {Cu}}>0$) fluids. In contrast, for a spheroidal particle with 
$e=0.99$ shown in figure 4(b), while the aforementioned features still hold in the Newtonian limit (
${\textit {Cu}}=0$, blue downward triangles), when the fluid is shear-thinning (e.g. 
${\textit {Cu}}=500$, red upward triangles), the variation of the propulsion becomes asymmetric about 
$\zeta _0=0$, which no longer maximizes the self-diffusiophoretic propulsion speed. Instead, the maximum propulsion speed occurs at a positive active surface coverage (
$\zeta _0>0$) as shown in figure 4(b), depending on parameters measuring the shear-thinning effect, including 
$\beta$ and 
${\textit {Cu}}$. The emergence of this novel feature requires the combined presence of both non-Newtonian rheology and non-spherical geometry, which we attempt to better understand via symmetry arguments presented in the next subsection.
Figure 4. Swimming speeds of (a) spherical (
$e=0$) and (b) spheroidal (
$e=0.99$) Janus particles as functions of 
$\zeta _0$, with 
$\beta = 0.1$. Three fluids are considered: 
${\textit {Cu}} = 0$ (blue downward-pointing triangle, Newtonian fluid), 
${\textit {Cu}}=500$ (red upward-pointing triangle) and 
${\textit {Cu}}=20\,000$ (black circle).
4.3. Symmetry considerations
To examine the feature of symmetry breaking across the full range of 
${\textit {Cu}}$, we compare the swimming speed of two complementarily coated particles with 
$\zeta _0 = \pm 0.5$ for the spherical (
$e = 0$, figure 5a) and spheroidal (
$e = 0.99$, figure 5b) cases. For spherical particles, figure 5(a) shows that the swimming speed of a particle with 
$\zeta _0 = -0.5$ (blue triangles) is identical to that with 
$\zeta _0 = 0.5$ (black circles) over the entire range of 
${\textit {Cu}}$, despite the latter having a significantly larger active surface coverage. On the contrary, figure 5(b) demonstrates that the swimming speeds of two complementarily coated spheroidal particles (
$\zeta _0 = \pm 0.5$) approach the same value only when 
${\textit {Cu}}$ is exceedingly small or large, where the fluid medium becomes effectively Newtonian. At intermediate values of 
${\textit {Cu}}$, the spheroidal particle with 
$\zeta _0 = -0.5$ (blue triangles) generally exhibits a considerably different swimming speed compared with its complementarily coated counterpart (
$\zeta _0 = 0.5$, black circles) as shown in figure 5(b).
Figure 5. Swimming speeds of (a) a pair of complementarily coated spherical 
$(e=0)$ and (b) spheroidal 
$(e=0.99)$ particles in a shear-thinning fluid with active coverage 
$\zeta _0 = \pm 0.5$. The complementarily coated spherical swimmers are propelled with the same speed, while spheroidal swimmers break this symmetry. In both (a,b), 
$\beta = 0.1$ and 
$n = 0.25$.
One may understand the above feature as a combined result of symmetry breaking and nonlinear rheology, as illustrated in figure 6. We denote the phoretic slip velocity on the surface of a particle with an active coverage 
$\zeta _0$ as 
$u_s(\zeta ;\zeta _0)$, and the corresponding propulsion speed as 
$U(\zeta _0)$. We note that in the zero-
$Pe$ limit considered here, the linearity of the Laplace equation allows superposition in the solute concentration problem. Now, considering a fully coated particle, the phoretic slip velocity can be decomposed into two complementary cases, 
$u_s(\zeta ;1) = u_s(\zeta ;-\zeta _0)-u_s(-\zeta ;\zeta _0)$, as shown in figure 6 for spherical and spheroidal particles. For a fully coated spherical particle, the slip velocity is zero everywhere on the particle surface due to isotropy, 
$u_s(\zeta ;1)=0$. This property leads to the result 
$u_s(\zeta ;-\zeta _0) = u_s(-\zeta ;\zeta _0)$, which means that the boundary conditions on two complementarily coated spherical particles become identical upon a reflection about 
$z=0$. This result is illustrated in figure 7(a) for the slip velocity of two complementarily coated spherical particles, which consequently, upon a reflection about 
$z=0$, generate the same flow field as shown in figure 7(c). The identical propulsion speed of these complementarily coated particles, 
$U(\zeta _0)=U(-\zeta _0)$, is therefore a direct result of isotropy for spherical self-diffusiophoretic particles, regardless of whether the fluid is Newtonian or non-Newtonian.
Figure 6. Schematics illustrating the symmetry considerations for a pair of complementarily coated particles. The phoretic slip velocity on the surface of a particle with an active coverage 
$\zeta _0$ is denoted as 
$u_s(\zeta ; \zeta _0)$, and the corresponding propulsion speed as 
$U (\zeta _0)$. The slip velocity on a fully-coated spherical particle is zero everywhere due to the isotropy. Consequently, the flow induced by the particles with active region 
$\pm \zeta _0$ always shows symmetry, which leads to identical speeds. As the slip velocity on a fully-coated anisotropic particle is not zero, the flow and the slip velocity do not have the reflection symmetry, and the particle speeds are not the same in general. However, if the flow is Newtonian, then the speeds are the same due to the linearity.
Figure 7. The slip velocity and the flow field around the particles with active region 
$\zeta _0 = \pm 0.5$, in a shear-thinning fluid with 
${\textit {Cu}} = 1$, 
$\beta = 0.1$ and 
$n = 0.25$. (a,c) The slip velocity and the flow field around the spherical swimmers have an upside-down symmetry, which does not appear in (b,d), those around the spheroidal swimmers (
$e = 0.99$).
When particle eccentricity is introduced, the anisotropy implies that the slip velocity of a fully coated spheroidal particle does not vanish everywhere on the surface of the particle, 
$u_s(\zeta ; 1) \neq 0$. As illustrated in figure 7(b), the boundary conditions on two complementarily coated spheroidal particles therefore no longer have the reflection symmetry about 
$z=0$, 
$u_s(\zeta ;-\zeta _0) \neq u_s(-\zeta ;\zeta _0)$, leading to generally distinct flows surrounding the spheroidal particles, as shown in figure 7(d). Consequently, unlike spherical particles, one may expect two complementarily coated spheroidal particles to have distinct propulsion speeds in general. This conclusion is largely true, as shown in figure 5(b), except for the special case when the fluid is Newtonian. For a Newtonian fluid, the linearity of the governing equations allows the superposition of the solutions associated with the pair of particles with complementary coatings to form the solution of a particle with full coating (figure 6a), leading to the result 
$U(1) = U(\zeta _0)-U(-\zeta _0)$. Since 
$U(1) = 0$ for a fully coated particle, we obtain the conclusion 
$U(\zeta _0) = U(-\zeta _0)$ for a Newtonian fluid, which holds for both spherical and spheroidal particles, despite the absence of reflection symmetry in their slip velocities. When the fluid is non-Newtonian, the superposition described above no longer holds, allowing the propulsion speeds of two complementarily coated spheroidal particles to be different.
To summarize, isotropy in spherical geometry alone guarantees that two complementarily coated particles propel with identical speeds, regardless of whether the fluid is Newtonian or not. In parallel, in a Newtonian fluid, the linearity of the problem alone guarantees the same, regardless of whether the particle is spherical or not. Hence to propel two complementarily coated particles with different speeds, both isotropy and linearity need to be broken. The emergence of different speeds for a pair of complementarily coated spheroidal particles in a shear-thinning fluid reported here therefore serves as a specific example illustrating this general feature.
5. Concluding remarks
Shear-thinning viscosity is a non-Newtonian behaviour that active particles often encounter in biological fluids. The investigation into how this ubiquitous non-Newtonian rheology impacts the propulsion speed of active particles has garnered considerable recent interest. In particular, previous studies have demonstrated how shear-thinning rheology slows down spherical active particles (Datt et al. Reference Datt, Zhu, Elfring and Pak2015, Reference Datt, Natale, Hatzikiriakos and Elfring2017). A more recent investigation (van Gogh et al. Reference van Gogh, Demir, Palaniappan and Pak2022) has suggested that by tuning the geometrical shape of a squirmer, it is possible for a spheroidal squirmer to swim faster in a shear-thinning fluid than in a Newtonian fluid. In this work, we have extended the analysis by van Gogh et al. (Reference van Gogh, Demir, Palaniappan and Pak2022) on the spheroidal squirmer model to self-diffusiophoretic particles, a major physico-chemical propulsion mechanism of synthetic active particles. Unlike the squirmer model, where the velocity distribution on the particle surface is prescribed, the effective slip velocity of a self-diffusiophoretic particle is determined by the solute concentration gradient and the phoretic mobility. Using asymptotic analysis to probe the weakly non-Newtonian behaviour, we have demonstrated that shear-thinning viscosity can indeed enhance self-diffusiophoretic propulsion of spheroidal particles with a large particle eccentricity in a specific regime of Carreau number. This result is in stark contrast with spherical self-diffusiophoretic particles, which always swim more slowly in a shear-thinning fluid (Datt et al. Reference Datt, Natale, Hatzikiriakos and Elfring2017). We have also used numerical simulations to verify that the new features uncovered by the asymptotic analysis continue to hold beyond the weakly non-Newtonian regime.
We have also systematically characterized the dependence of the self-diffusiophoretic propulsion speed on the particle's active surface coverage in a shear-thinning fluid. Previous studies showed that a pair of complementarily coated spherical or spheroidal particles always propel at the same speed in a Newtonian fluid. When the fluid becomes shear-thinning, the same propulsion speed still occurs when the complementarily coated particles are spherical in shape. However, we have found distinct propulsion speeds for two complementarily coated spheroidal particles in a shear-thinning fluid. We have also presented symmetry arguments to better understand how this new feature emerges as a combined effect of anisotropy associated with the spheroidal geometry and nonlinearity associated with the non-Newtonian rheology. Such symmetry breaking might hint at using anisotropic active particles as a tool for probing microrheology of complex fluids.
We remark on several limitations of the current work, and discuss potential directions for further investigations. First, we have neglected the effect of solute advection by considering the zero 
$Pe$ limit. It remains unclear how the flow modifications due to shear-thinning rheology influence solute advection and thereby the phoretic propulsion. In particular, the symmetry considerations presented in § 4.3, which require the linearity of the Laplace equation, would no longer hold for finite 
$Pe$. It would therefore be interesting to probe how the nonlinearity associated with solute advection affects the symmetry breaking observed for the propulsion of complementarily coated particles. Second, we have followed previous work (Datt et al. Reference Datt, Natale, Hatzikiriakos and Elfring2017) to focus on the non-Newtonian effect in the bulk fluid in this work, neglecting the influence of fluid rheology on the surface slip of a self-diffusiophoretic particle, which was shown to modify the propulsion speed of a spherical Janus particle in intriguing manners (Choudhary, Renganathan & Pushpavanam Reference Choudhary, Renganathan and Pushpavanam2020). In particular, in a weakly shear-thinning fluid, the effect due to the modified slip velocity could dominate the retardation due to the bulk non-Newtonian stress, leading to the speed enhancement of a Janus spherical particle. An investigation is currently underway to extend the analysis beyond the weakly non-Newtonian regime and examine the effect of particle geometry in this more complex physical scenario, where the non-Newtonian effects on both slip and mobility of self-diffusiophoretic particles are taken into account. We also call for future efforts in developing a comprehensive physical understanding of the findings reported in this work. Finally, we focus on the effect of shear-thinning viscosity here, while complex biological fluids also display other non-Newtonian fluid behaviours, including viscoelasticity. Future work accounting for the viscoelastic stress and its combined effects with shear-thinning rheology will shed light on how the geometric shape of self-diffusiophoretic particles should be tuned to maximize their propulsion in biological fluids.
Funding
We acknowledge support from the National Science Foundation under grant nos 1931292 and 2323046 (to O.S.P.), the National Natural Science Foundation of China under grant no. 12372258 (to Y.M.), and the Fundamental Research Funds for the Central Universities, Peking University (to Y.M.). L.Z. acknowledges partial support from the Singapore Ministry of Education Academic Research Fund Tier 2 (MOE-T2EP50122-0015). The computation of the work was performed on resources of the National Supercomputing Centre, Singapore (https://www.nscc.sg).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Solution to the zeroth-order (Newtonian) problem
Here we summarize the solution to the zeroth-order problem, which corresponds to the self-diffusiophoretic motion of a spheroidal particle in a Newtonian fluid considered in previous works (Leshansky et al. Reference Leshansky, Kenneth, Gat and Avron2007; Popescu et al. Reference Popescu, Dietrich, Tasinkevych and Ralston2010; Lauga & Michelin Reference Lauga and Michelin2016; Poehnl et al. Reference Poehnl, Popescu and Uspal2020). In particular, we follow the approach by Poehnl et al. (Reference Poehnl, Popescu and Uspal2020) here to determine the unknown velocity field 
$\boldsymbol {u}_0$ and propulsion velocity 
$\boldsymbol {U}_0$.
The unknown propulsion velocity 
$\boldsymbol {U}_0$ can be obtained using the Lorentz reciprocal theorem (Stone & Samuel Reference Stone and Samuel1996; Popescu et al. Reference Popescu, Dietrich, Tasinkevych and Ralston2010; Poehnl et al. Reference Poehnl, Popescu and Uspal2020), by considering an auxiliary Stokes flow problem 
$(\hat {\boldsymbol {u}}, \hat {\boldsymbol {\sigma }})$ of a translating prolate spheroidal particle of the same geometry along its major axis. Via the reciprocal theorem (Popescu et al. Reference Popescu, Dietrich, Tasinkevych and Ralston2010; Poehnl et al. Reference Poehnl, Popescu and Uspal2020), an integral relation is obtained as
\begin{equation} \hat{\boldsymbol{F}}\boldsymbol{\cdot}\boldsymbol{U}_0=-\int_S \boldsymbol{u}_s\boldsymbol{\cdot}(\boldsymbol{n}\boldsymbol{\cdot}\hat{\boldsymbol{\sigma}})\,{\rm d}S, \end{equation}
which relates the force on the translating particle in the auxiliary problem 
$\hat {\boldsymbol {F}}$ to the unknown propulsion velocity 
$\boldsymbol {U}_0$ via a surface integral involving the surface velocity 
$\boldsymbol {u}_s$. By using the known solution to the auxiliary problem (Happel & Brenner Reference Happel and Brenner2012) and simplifying the surface integral in the prolate spheroidal coordinates, the propulsion velocity 
$\boldsymbol {U}_0 = U_0 \boldsymbol {e}_z$ is obtained in terms of the integral (Popescu et al. Reference Popescu, Dietrich, Tasinkevych and Ralston2010; Poehnl et al. Reference Poehnl, Popescu and Uspal2020):
\begin{equation} U_0 =- \frac{\tau_0}{2}\int_{-1}^1 u_s\,\frac{\sqrt{1-\zeta^2}}{\sqrt{\tau_0^2-\zeta^2}}\,{\rm d}\zeta. \end{equation}
Upon substituting the slip velocity given by (3.3), one obtains the final expression of the propulsion speed for 
$N$ phoretic modes as (Poehnl et al. Reference Poehnl, Popescu and Uspal2020)
\begin{equation} U_0 = \frac{\tau_0^2}{2} \sum_{n=1, \ \text{odd $n$}}^{N} B_n \int_{-1}^1 \frac{P_1^1(\zeta)\,P_n^1(\zeta)}{\tau_0^2 - \zeta^2} \,{\rm d}\zeta .\end{equation} To determine the velocity field, we consider a streamfunction 
$\psi _0$ for the axisymmetric flow in the co-moving frame
\begin{equation} \boldsymbol{u}_0-\boldsymbol{U}_0 = \frac{1}{h_\zeta h_\phi}\,\frac{\partial\psi_0}{\partial\zeta}\,\boldsymbol{e}_\tau- \frac{1}{h_\tau h_\phi}\,\frac{\partial\psi_0}{\partial\tau}\,\boldsymbol{e}_\zeta, \end{equation}
where the far field corresponds to a uniform flow given by 
$-\boldsymbol {U}_0$. A general solution of the streamfunction can be expanded in terms of products of the Gegenbauer functions in the prolate spheroidal coordinates. For a bounded solution satisfying the far-field and force-free condition, the streamfunction takes the form (Poehnl et al. Reference Poehnl, Popescu and Uspal2020)
\begin{equation} \psi_0(\tau,\zeta)= \sum_{n=2}^\infty g_n(\tau)\,G_n(\zeta), \end{equation}
with 
$g_2(\tau ) = C_4\,H_4(\tau )+D_2\,H_2(\tau )-2c^2U_0\,G_2(\tau )$, 
$g_3(\tau ) = C_3+C_5\,H_5(\tau )+D_3\,H_3(\tau )$ and 
$g_n(\tau ) = C_{n+2}\,H_{n+2}(\tau )+C_n\,H_{n-2}(\tau )+D_n\,H_n(\tau )$ for 
$n\geq 4$, where 
$G_n$ and 
$H_n$ are the Gegenbauer polynomials of the first and second kinds, respectively. The coefficients 
$C_n$ and 
$D_n$ are determined by the tangential slip velocity and the zero normal velocity on the particle surface. If we consider a slip velocity (3.3) expansion of only 
$N$ modes and apply the boundary conditions to the streamfunction expansion (A5) with only 
$N$ terms ranging from 
$n = 2$ to 
$n = N+1$, then the following system of equations is obtained:
$$\begin{gather} g_n(\tau_0) = 0, \quad \text{for} \ 2\leq n \leq N+1, \end{gather}$$
$$\begin{gather}\left.\frac{\partial g_n}{\partial \tau} \right|_{\tau = \tau_0} = \tau_0 c^2 n(n-1)B_{n-1}, \quad \text{for} \ 2\leq n \leq N+1. \end{gather}$$
These equations can be separated into a system with coefficients that have only even indices, and a system with coefficients that have only only odd indices, as all the indices of 
$C_n$ and 
$D_n$ in 
$g_n$ are always the same parity (Poehnl et al. Reference Poehnl, Popescu and Uspal2020). The odd system of equations always has one more unknown than equation; a solvable system of equations is obtained by setting
\begin{equation} C_{N+3-m} = 0, \quad \text{where} \ m= \begin{cases} 1, & \text{when $N$ is odd}, \\ 0, & \text{when $N$ is even}, \end{cases} \end{equation}
for 
$N \geq 2$. Upon obtaining the phoretic modes 
$B_n$ using (3.2) and (3.4), and using the result given by (A3), the system (A6)–(A7) is solved for the coefficients 
$C_n$ and 
$D_n$ for the zeroth-order velocity field. Interested readers are referred to previous works for further details (Popescu et al. Reference Popescu, Dietrich, Tasinkevych and Ralston2010; Poehnl et al. Reference Poehnl, Popescu and Uspal2020).
Appendix B. Validation of numerical simulations
In this appendix, we include results on the validation of our numerical approach against previously reported findings. First, we follow the numerical implementation described in § 3.2 to simulate the self-propulsion of a spherical Janus particle in a shear-thinning fluid, and compare the numerical results with the asymptotic solution obtained by Datt et al. (Reference Datt, Natale, Hatzikiriakos and Elfring2017) in the weakly nonlinear limit (
$\beta =0.99$). As shown in figure 8(a), the results display satisfactory agreement for a wide range of 
${\textit {Cu}}$ for different active surface coverage 
$\zeta _0$. Second, we assess the capability of our numerical approach for handling non-spherical geometries by simulating the self-propulsion of spheroidal Janus particles with different eccentricities in a Newtonian fluid, and compare the numerical results with the solution obtained by Popescu et al. (Reference Popescu, Dietrich, Tasinkevych and Ralston2010). As shown in figure 8(b), the results again agree satisfactorily, validating our numerical implementation.
Figure 8. Validation of the numerical approach against previously reported results. (a) Comparison of the numerical results (symbols) on the swimming velocity of a spherical Janus particle as a function of 
$Cu$ for different values of active surface coverage 
$\zeta _0$ with the asymptotic solution (lines) of the scaled first-order swimming velocity (
$U_1/U_0$) obtained by Datt et al. (Reference Datt, Natale, Hatzikiriakos and Elfring2017) in a weakly shear-thinning fluid (
$\beta =0.99$). (b) Comparison of the numerical results (symbols) on the swimming velocity 
$U$ of a spheroidal Janus particle as a function of 
$\zeta _0$ for different eccentricities 
$e$ with the solution (lines) obtained by Popescu et al. (Reference Popescu, Dietrich, Tasinkevych and Ralston2010) in a Newtonian fluid. Note that the Janus particles simulated here are coated on the bottom to maintain consistency, and correspondingly, we set 
$A=-1$ and 
$M=1$ in both plots.
